Active Control of Highly Autocorrelated Machinery Noise in Multivariate Nonminimum Phase Systems

Abstract

In this paper, a novel multivariate active noise control scheme, designed to attenuate disturbances with high autocorrelation characteristics and preserve background signals, is proposed. The algorithm belongs to the class of feedback controllers and, unlike the popular feedforward FX-LMS approach, does not require availability of a reference signal. The proposed approach draws its inspiration from the iterative learning control and repetitive mode control methods, and employs a modified inverse model learning law. The classical inverse model learning law is well known to offer fast convergence and high steady-state performance, provided that the secondary path is minimum phase and well known. The proposed modified inverse model learning law employs a spectral factorization trick, which allows one to use the method with nonminimum phase plants of arbitrary order. Moreover, our scheme includes a controller bandwidth limiting mechanism that can be used to tune the disturbance rejection bandwidth and to improve the closed-loop robustness to errors in the model of the secondary path. The algorithm’s behavior and performance are verified with computer simulations that demonstrate suppression of electrical transformer noise and include realistic models of the secondary path. The results show high-level selective attenuation and fast convergence.

1 Introduction

One of the significant problems related to modern civilization growth is the increasing acoustic noise level and the resulting impact on the quality of life. Conventional means of reducing noise, which involves barriers, mufflers or dampers, often require heavy materials and are not particularly effective at low frequencies. Active noise control (ANC) technology [9], which works best where the conventional approach fails, is a promising alternative solution. An ANC system employs digital signal processing to generate an antinoise that destructively interferes with the unwanted (so-called primary) noise, creating a limited volume of reduced noise levels around a point of interest [1, 4, 5, 7].

There exist many approaches to active noise control that draw inspiration from adaptive filtering or control theory, among others [11]. In the first group, the filtered-x least mean square (FX-LMS) [18] algorithm is the most prominent. The FX-LMS controller is a feedforward scheme that requires one to provide a reference signal which carries information about the disturbance ahead of time. The controller employs a modified variant of the least mean squares (LMS) adaptive filter to transform the reference signal into the antinoise. Modifications of the FX-LMS controller include the filtered-U least mean squares (FU-LMS) method, designed to cope with the parasitic feedback in the control loop [11], or its version employing the lattice form [10], among others. The second group of methods mostly relies on pure feedback, i.e., they do not require any reference signals. These methods can differ considerably in their underlying methodologies assumptions, e.g., regarding the knowledge [6, 13] or the lack of it about the controlled plant [20, 23], disturbance frequency [2, 21], its spectral structure [19] or the structure of the controller [27]. Note that, in contrast to the feedforward approach, which is capable of canceling any class of noise, feedback methods are effective only against narrowband (periodic) noise. A variety of algorithms was also developed to address nonlinearities present in ANC systems—see, e.g., [29] or a survey paper [15] for an overview. A related, and recently very popular, class of nonlinear control algorithms involves artificial networks [25, 28]. In this paper, however, we will focus on the linear case.

Despite multitude of adopted approaches, relatively little attention was devoted to the application of the so-called iterative learning control (ILC) or repetitive mode control in ANC applications so far. Iterative learning control was originally developed for industrial robotic applications and it is particularly useful in improving the control of repetitive tasks performed by robots, such as the movement of a robotic arm between two points. ILC control, due to the ease of implementation and simplicity of integration with standard feedback control algorithms, found applications in numerous domains, such as computer numerical control (CNC) tools, process controls and autonomous vehicles, to name just a few [3]. The repetitive mode control is closely related to ILC but is better suited for real-time applications involving high sampling rates due to its recursive, rather than block-based, nature [24].

There is a wide class of periodic noises that allows potential use of the above two methodologies in ANC. Examples include electrical machinery noise or the sound produced during functional magnetic resonance imaging (fMRI), among others [9]. In these applications, an algorithm with very good selective noise suppression properties can improve the convenience and safety of electrical and mechanical machinery staff or improve the comfort of patients during the fMRI examination.

In our recent paper [12], we proposed a novel method of active noise control inspired by ILC and repetitive mode control. This work expands our previous results in two important directions. First, we generalize the method to the multiple-input multiple-output (MIMO) case, which broadens the range of potential applications considerably. Second, the proposed control law includes an optional noncausal low-pass filter. The low-pass filter is an important feature that allows one to modify the control loop bandwidth. The primary reason to limit the control loop bandwidth is that it increases its robustness to modeling uncertainty. In active noise control systems, modeling uncertainty typically grows with frequency due to decreasing wavelength—at short wavelengths, even small changes in geometry might lead to considerable changes in phase response of the secondary path. Such changes might cause the active noise controller to actually increase noise level at high frequencies or, in the worst case, they might cause destabilization of the closed loop. By taking advantage of the low-pass filter present in the proposed control, one can reduce the loop bandwidth to a level that avoids these undesirable effects. Importantly, our design employs a noncausal filter, because it exhibits several advantages over its causal counterpart, such as lower group delay and larger stability margins.

The paper is organized as follows. Section 2 presents the problem formulation. Section 3 introduces and develops the proposed control approach and extends the method to also include the case of a noncausal low-pass filter. Section 4 present results of computer simulations and comparison to the FxLMS algorithm. Finally, Sect. 5 concludes the paper.

2 Problem Statement

Consider the problem of feedback cancelation of a periodic disturbance $\varvec{d}(t)$ (bold symbols denote vectors or matrices) acting at the output of a $M\times M$ multivariate system

$$\begin{aligned} \varvec{y}(t)=\varvec{S}(z^{-1})\varvec{u}(t) + \varvec{d}(t)\;, \end{aligned}$$

(1)

where $t=0,1,2,\dots$ denotes discrete, dimensionless time, $\varvec{y}(t)$ is the M-element vector of system output, ${\textbf {u}}(t)$ is the M-element input (control) signal vector, $z^{-1}$ denotes the backward-shift operator, $z^{-1}\varvec{u}(t)=\varvec{u}(t-1)$, and $\varvec{S}(z^{-1})$ is a $M\times M$ multiple-input multiple-output (MIMO) transfer function matrix of the plant (i.e., the secondary path).

$$\begin{aligned} \varvec{S}(z^{-1}) = \begin{bmatrix} S_{11}(z^{-1}) &{} \dots &{} S_{1M}(z^{-1})\\ \vdots &{} \ddots &{} \vdots \\ S_{M1}(z^{-1}) &{} \dots &{} S_{MM}(z^{-1}) \end{bmatrix} \end{aligned}$$

(2)

Because we consider mainly acoustic signals, we can assume that the disturbance $\varvec{d}(t)$ is zero mean

$$\begin{aligned} \sum _{t=0}^{T-1} \varvec{d}(t) = \varvec{0}\;. \end{aligned}$$

We also assume that the disturbance period denoted T is known and equal to an integer number of sampling periods

$$\begin{aligned} \varvec{d}(t)=\varvec{d}(t-T)\;. \end{aligned}$$

(3)

In practice, the above assumption allows one to cancel semi-periodic disturbances, i.e., disturbances that satisfy the above equality approximately.

The only constraints imposed on the secondary path $\varvec{S}(z^{-1})$ are that it is stable and that it does not have zeros at the frequencies $\omega _k=2\pi k/T$, $k=1,2,\dots$

$$\begin{aligned} \det ( \varvec{S}(e^{-j\omega _k}) ) \ne 0\;. \end{aligned}$$

3 Proposed Solution

3.1 Preliminary Solution

The proposed control technique is inspired by results from the iterative learning control [3] and repetitive mode control [24], and was originally developed for the single-input single-output (SISO) case in [12]. Its nontrivial extension to the MIMO case is described below.

Iterative learning controllers work in two phases that are executed repeatedly. During each iteration, a response of the controlled plant is stored in memory. In the short time between iterations, the controller uses the stored plant response to design the control for the next iteration. The designed control is then applied to the plant, and its response is stored to be used in the next cycle.

Let $j=0,1,\dots$ denote the iteration index and $n=0,1,\dots ,T-1$ denote a local time, i.e., a time variable that is internal to an iteration. The ILC control law has the form

$$\begin{aligned} \varvec{u}_{j}(n)=Q(z^{-1})\left[ \varvec{u}_{j-1}(n) - \varvec{L}(z^{-1})\varvec{y}_{j-1}(n)\right] \;, \end{aligned}$$

(4)

where $\varvec{u}_{j-1}(n)$ and $\varvec{y}_{j-1}(n)$ denote the stored input and output from the iteration preceding jth one, $\varvec{L}(z^{-1})$ is a so-called learning law and $Q(z^{-1})$ is an optional low-pass filter whose role is to limit the controller’s bandwidth and improve robustness of the closed loop.

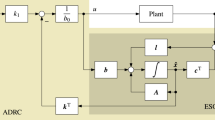
An interesting feature of (4) is that the learning law $\varvec{L}(z^{-1})$ can be a noncausal transfer function, because the controller operates on stored signals. On the other hand, the block-mode operation of (4) is undesirable in active noise control, particularly for high sampling rates, because a substantial amount of computations has to be performed in the very short time between two consecutive blocks. A natural recursive counterpart of (4), which can work on a sample-by-sample basis, is a repetitive mode controller (Fig. 1),

$$\begin{aligned} \varvec{u}(t)=Q(z^{-1})\left[ \varvec{u}(t-T) - \varvec{L}(z^{-1})\varvec{y}(t-T)\right] \;. \end{aligned}$$

(5)

Fig. 1

General repetitive control scheme of a linear time-invariant and causal SISO system

Consider the following variant of the above control law

$$\begin{aligned} \varvec{u}(t)=Q(z^{-1})\left[ \varvec{u}(t-T) - \alpha {\hat{\varvec{S}}}^{-1}(z^{-1})\varvec{y}(t-T)\right] \;, \end{aligned}$$

(6)

where $0< \alpha < 1$ is a gain, ${{\hat{\varvec{S}}}}(z^{-1})$ denotes a finite impulse response (FIR) estimate of the transfer function of the secondary path

$$\begin{aligned} {\hat{\varvec{S}}}(z^{-1})&= \begin{bmatrix} {\hat{S}}_{11}(z^{-1}) &{} \dots &{} {\hat{S}}_{1M}(z^{-1})\\ \vdots &{} \ddots &{} \vdots \\ {\hat{S}}_{M1}(z^{-1}) &{} \dots &{} {\hat{S}}_{MM}(z^{-1}) \end{bmatrix} \nonumber \\ \hat{S}_{ij}(z^{-1})&=\sum _{k=0}^{K-1} s_{ij,k} z^{-k}\quad i,j=1,\dots ,M \end{aligned}$$

(7)

and $s_{ij,k}$, $i,j=1,\dots ,M$, $k=0,1,\dots ,K$ is the impulse response in the path from jth input to ith output.

If the true secondary path is a minimum phase transfer function and its estimate is accurate, ${{\hat{\varvec{S}}}}(z^{-1}) \simeq \varvec{S}(z^{-1})$, the controller (6) offers rapid convergence, which can be as quick as one period (for $Q(z^{-1})=1$ and $\alpha =1$). To see this, it is sufficient to substitute (6) into (1). After straightforward manipulations, one obtains that

$$\begin{aligned} \varvec{y}(t) = (1-z^{-T})\varvec{d}(t)\;, \end{aligned}$$

which, given (3), means that $\varvec{y}(t)=0$ after one period.

Unfortunately, if ${\hat{\varvec{S}}}(z^{-1})$ has zeros outside the unit circle its inverse ${\hat{\varvec{S}}}^{-1}(z^{-1})$ will be an unstable transfer function and the closed-loop system will become internally unstable [26].

To understand the source of instability better, one can rewrite the inverse of ${\hat{\varvec{S}}}(z^{-1})$ in the following form

$$\begin{aligned} {\hat{\varvec{S}}}^{-1}(z^{-1}) = \frac{1}{S_d(z^{-1})} \varvec{C}^\mathrm {T}(z^{-1}), \end{aligned}$$

(8)

where

$$\begin{aligned} S_d(z^{-1})=\det ( \varvec{S}( z^{-1}) )\;, \end{aligned}$$

$\varvec{C}(z^{-1})$ is the cofactor matrix of ${\hat{\varvec{S}}}(z^{-1})$, formed by all its cofactors

$$\begin{aligned} \varvec{C}(z^{-1})=\begin{bmatrix} C_{11}(z^{-1}) &{} \cdots &{} C_{1M}(z^{-1}) \\ \vdots &{} \ddots &{} \vdots \\ C_{M1}(z^{-1}) &{} \cdots &{} C_{MM}(z^{-1}) \end{bmatrix} \;, \end{aligned}$$

(9)

and $\varvec{C}^\mathrm {T}(z^{-1})$ is its transpose which can be interpreted as a decoupling mechanism.

Since the computation of all cofactors and $S_d(z^{-1})$ involves only multiplications and additions, we obtain that: 1. All cofactors and $S_d(z^{-1})$ are FIR filters [c.f. (7)]. 2. The only source of potential internal instability of the closed loop lies in the inverse of $S_d(z^{-1})$.

In the next subsection, we will develop a control law that avoids this pitfall by exploiting the fact that $\varvec{L}(z^{-1})$ can be a noncausal transfer function not only for an ILC controller, but also in the case of the repetitive mode control law (6).

3.2 Semi-Noncausal Plant Inversion

It is well known that one can construct a stable inverse of a nonminimum phase transfer function $S_d(z^{-1})$ if the inverse is allowed to be noncausal. Consider the following decomposition of $S_d(z^{-1})$

$$\begin{aligned} {S_d}(z^{-1})={S}_{\min }(z^{-1}) {S}_{\max }(z^{-1})\;, \end{aligned}$$

where ${S}_{\min }(z^{-1})$ has all roots inside the unit circle on the complex plane, and ${S}_{\max }(z^{-1})$ has all roots outside it. Assuming that ${S}_{\max }(z^{-1})$ has the following form

$$\begin{aligned} {S}_{\max }(z^{-1}) = a_0 + a_1 z^{-1} + \dots + a_{M-1} z^{-M+1} + a_M z^{-M}\; \end{aligned}$$

and introducing

$$\begin{aligned} {S}_{\max }^*(z) = a_0 z^M + a_1 z^{M-1} + \dots + a_{M-1} z^{1} + a_M \;, \end{aligned}$$

i.e., its reciprocal polynomial in the variable z which, unlike $z^{-1}$, represents the forward-shift operation $z\varvec{u}(t)=\varvec{u}(t+1)$, one may present ${S}_{\max }(z^{-1})$ as

$$\begin{aligned} {S}_{\max }(z^{-1}) = z^{-M} {S}_{\max }^*(z)\;. \end{aligned}$$

Consequently, one can express the inverse of ${S_d}(z^{-1})$ as a cascade of a stable causal filter $1/{S}_{\min }(z^{-1})$ and a stable anticausal filter $z^M/{S}_{\max }^*(z)$

$$\begin{aligned} \frac{1}{{S_d}(z^{-1})}=\frac{1}{{S}_{\min }(z^{-1})} \frac{z^M}{{S}_{\max }^*(z)}\;. \end{aligned}$$

(10)

An efficient and numerically robust way of computing $S_d^{-1}(z^{-1})$ involves the spectral factorization technique. Denote by $F(z^{-1})$ the spectral factor of ${S_d}(z^{-1})$, i.e., a minimum phase transfer function that satisfies

$$\begin{aligned} {S_d}(z^{-1}){S_d}(z) = F(z^{-1})F(z)\;. \end{aligned}$$

(11)

Note that $F(z^{-1})$ can be computed without explicitly solving for roots of $\hat{S}_d(z^{-1})$ using, e.g., the recursive technique presented in [16, 17].

It is straightforward to verify that

$$\begin{aligned} F(z^{-1}) = {S}_{\min }(z^{-1}) {S}_{\max }^*(z^{-1})\;. \end{aligned}$$

This fact allows one to rewrite $S_d^{-1}(z^{-1})$ in the following form

$$\begin{aligned} S_d^{-1}(z^{-1})&=\frac{ S_{\min }(z) S_{\max }(z)}{ S_{\min }(z^{-1}) S_{\max }^*(z^{-1}) S_{\min }(z) S_{\max }^*(z)} \nonumber \\&= \frac{1}{F(z^{-1})} \frac{S_d(z)}{F(z)}\;, \end{aligned}$$

(12)

which can be interpreted as a cascade of a stable causal filter $1/F(z^{-1})$ and a stable anticausal all-pass filter $S_d(z)/F(z)$. Note that computation of (12) does not require one to compute roots of $S_d(z^{-1})$.

Substituting (12) into (6) and performing minor manipulations result in

$$\begin{aligned} \varvec{u}(t)=Q(z^{-1})\Big [&\varvec{u}(t-T) - \alpha \varvec{C}^\mathrm {T}(z^{-1}) \frac{S_d(z)}{F(z)}\frac{1}{F(z^{-1})} \varvec{y}(t-T)\Big ]\;. \end{aligned}$$

(13)

To reach a causal controller, we will perform several additional steps. Let

$$\begin{aligned} {\bar{\varvec{y}}}(t)=\frac{1}{F(z^{-1})} \varvec{y}(t)\;. \end{aligned}$$

We approximate the filter $S_d(z)/F(z)$ with a FIR filter

$$\begin{aligned} \frac{S_d(z)}{F(z)} \simeq \sum _{r=0}^R h_r z^{r}\;, \end{aligned}$$

which leads to

$$\begin{aligned} \frac{S_d(z)}{F(z)}\frac{1}{F(z^{-1})} \varvec{y}(t-T) \simeq \sum _{r=0}^R h_r {\bar{\varvec{y}}}(t-T+r)\;. \end{aligned}$$

Observe that if $R>T$ the sum above will require future samples of ${\bar{\varvec{y}}}(t)$. Due to the fact that the disturbance is assumed periodic, one may approximate such samples of ${\bar{\varvec{y}}}(t)$ with their values from the previous period, ${\bar{\varvec{y}}}(t+k) \approx {\bar{\varvec{y}}}(t-T+k)$. This idea can be implemented by “wrapping” the impulse response $h_r$, $r=0,1,\dots ,R$, to one period

$$\begin{aligned} \frac{S_d(z)}{F(z)} {\bar{\varvec{y}}}(t-T) \simeq \sum _{r=0}^{T-1} {\bar{h}}_r {\bar{\varvec{y}}}(t-T+r)\;, \end{aligned}$$

(14)

where

$$\begin{aligned} {\bar{h}}_r = \sum _{n=0}^{\lceil R/T \rceil } h_{r+nT}\;. \end{aligned}$$

(15)

Summarizing the above discussion, the proposed feedback control law has the form

$$\begin{aligned} {\bar{\varvec{y}}}(t)&=\frac{1}{F(z^{-1})} \varvec{y}(t) \nonumber \\ \bar{{\bar{\varvec{y}}}}(t)&= \sum _{r=0}^{T-1} {\bar{h}}_r {\bar{\varvec{y}}}(t-T+r) \nonumber \\ \varvec{u}(t)&=Q(z^{-1})\left[ \varvec{u}(t-T) - \alpha \varvec{C}^\mathrm {T}(z^{-1}) \bar{{\bar{\varvec{y}}}}(t)\right] \;. \end{aligned}$$

(16)

3.3 Low-pass Filter $Q(z^{-1})$

So far we have almost neglected the presence of the low-pass filter $Q(z^{-1})$ in the proposed control law. This filter can be very useful because it allows one to influence the bandwidth of the controller, i.e., the range of frequencies where the controller attempts to cancel $\varvec{d}(t)$. There are several good reasons for $Q(z^{-1})$ to be a zero phase transfer function. First, going back to (6) one can obtain that, under general $\alpha$ and $Q(z^{-1})$,

$$\begin{aligned} \varvec{y}(t)=\frac{1-Q(z^{-1})z^{-T}}{1-Q(z^{-1}) z^{-T} + \alpha z^{-T}}\varvec{d}(t)\;. \end{aligned}$$

(17)

Note that a frequency $\omega _k=2\pi k/T$, $k=1,2,\dots$ is canceled only if $1-Q(e^{-j\omega _k})e^{-j\omega _kT} = 1-Q(e^{-j\omega _k}) = 0$, i.e., when $Q(e^{-j\omega _k})\approx 1$. This condition is difficult to satisfy with good accuracy using a causal low-pass filter, because its phase response drops with growing frequency. Second, the decreasing phase response of $Q(z^{-1})$ reduces the phase margin of the closed loop, which can result in instability. Suppose, on the other hand, that $Q(z^{-1})$ is a zero phase noncausal filter. Decompose $Q(z^{-1})$ as

$$\begin{aligned} Q(z^{-1})=Q^{-}(z^{-1}) Q^{+}(z)\;, \end{aligned}$$

(18)

where $Q^{-}(z^{-1})$ is the causal part and $Q^{+}(z)$ is the anticausal part. Recall (13) and let

$$\begin{aligned} {\bar{\varvec{y}}}(t)&= \frac{Q^{-}(z^{-1})}{F(z^{-1})} \varvec{y}(t)\\ {\bar{\varvec{u}}}(t)&= Q^{-}(z^{-1}) \varvec{u}(t)\;. \end{aligned}$$

Then one can rewrite (13) as

$$\begin{aligned} \varvec{u}(t)=Q^{+}(z){\bar{\varvec{u}}}(t-T)- \alpha \varvec{C}^\mathrm {T}(z^{-1}) \frac{Q^{+}(z) S_d(z)}{F(z)} {\bar{\varvec{y}}}(t-T). \end{aligned}$$

Similar to the previous section, we approximate the noncausal transfer functions with FIR filters

$$\begin{aligned} \frac{Q^{+}(z) S_d(z)}{F(z)}&\simeq \sum _{r=0}^R h_r z^{r} \\ Q^{+}(z)&\simeq \sum _{r=0}^R g_r z^{r}\;, \end{aligned}$$

and, using the fact that the signals in the closed loop are close to periodic, “wrap them”

$$\begin{aligned} \frac{Q^{+}(z) S_d(z)}{F(z)} {\bar{\varvec{y}}}(t-T)&\simeq \sum _{r=0}^{T-1} {\bar{h}}_r {\bar{\varvec{y}}}(t-T+r) \nonumber \\ Q^{+}(z) {\bar{\varvec{u}}}(t-T)&\simeq \sum _{r=0}^{T-1} {\bar{g}}_r {\bar{\varvec{u}}}(t-T+r)\;. \end{aligned}$$

(19)

This results in the following control law

$$\begin{aligned} {\bar{\varvec{y}}}(t)&=\frac{Q^{-}(z^{-1})}{F(z^{-1})} \varvec{y}(t) \end{aligned}$$

(20)

$$\begin{aligned} \bar{{\bar{\varvec{y}}}}(t)&= \sum _{r=0}^{T-1} {\bar{h}}_r {\bar{\varvec{y}}}(t-T+r) \end{aligned}$$

(21)

$$\begin{aligned} \bar{{\bar{\varvec{u}}}}(t)&= \sum _{r=0}^{T-1} {\bar{g}}_r {\bar{\varvec{u}}}(t-T+r) \end{aligned}$$

(22)

$$\begin{aligned} \varvec{u}(t)&=\bar{{\bar{\varvec{u}}}}(t) - \alpha \varvec{C}^\mathrm {T}(z^{-1}) \bar{{\bar{\varvec{y}}}}(t) \end{aligned}$$

(23)

$$\begin{aligned} {\bar{\varvec{u}}}(t)&= Q^{-}(z^{-1}) \varvec{u}(t) \; \end{aligned}$$

(24)

presented in block diagram form in Fig. 2a, b.

3.4 Computational Complexity

In this subsection, computational complexity of the proposed algorithm will be discussed. We will focus only on the part of the algorithm running in real time, as initialization requires a spectral factorization algorithm for which it is difficult to define computational complexity clearly.

The algorithm’s complexity depends on several factors, such as the system dimension M (equal number of inputs and outputs will be assumed in this subsection), the lag T corresponding to the disturbance period, the length of the filter $Q(z^{-1})$, denoted $N_Q$, or $N_{\mathbf {C}}$, the total number of tap weights in the matrix $\varvec{C}(z^{-1})$ from (9), among others.

Note that there exist multiple options for implementing individual equations that make the proposed algorithm. For example, Eq. (20) can be implemented as an IIR filter or converted to an FIR filter and folded into one period as proposed in (14). Similar approach can be applied to (21) and (22) as well. Generally, we assume the FIR implementation, in which case the upper limit on the number of computations depends on T.

Furthermore, recall that (9) and (23) that results from it can be interpreted as a decoupling mechanism for which various realizations exist [8, 14]. We will assume a very straightforward implementation, however, in order to simplify the analysis.

The upper bounds on the computational complexity of all the considered equations are shown in Table 1.

Table 1 Breakdown of the proposed controller’s computational complexity

Fig. 2

Block diagram of the proposed algorithm

4 Results of Computer Simulations

We verified the behavior of the proposed approach with computer simulations of a two-input two-output system. This case is particularly important to active noise control. Practical examples include, among others, active headrest systems [22] or anti-snore systems [5]. For this class of systems

$$\begin{aligned} \varvec{C}^{\mathsf {T}}(z^{-1}) = \begin{bmatrix} {\hat{S}}_{22}(z^{-1}) &{} -{\hat{S}}_{12}(z^{-1})\\ -{\hat{S}}_{21}(z^{-1}) &{} {\hat{S}}_{11}(z^{-1}) \end{bmatrix} \end{aligned}$$

and

$$\begin{aligned} S_{d}(z^{-1}) = {\hat{S}}_{11}(z^{-1}) {\hat{S}}_{22}(z^{-1}) - {\hat{S}}_{12}(z^{-1}) {\hat{S}}_{21}(z^{-1})\;. \end{aligned}$$

Our simulations were conducted using a realistic model of an acoustic plant obtained in a system identification experiment. The impulse responses of the identified 256-tap FIR filters are shown in Fig. 3. We also employed a real-world acoustic signal generated by an electric transformer. The transformer noise is caused by a phenomenon called magnetostriction, which causes a piece of magnetic steel sheet to extend and contract twice during the full cycle of magnetization. Therefore, the fundamental frequency of the transformer noise is twice the supply power frequency, i.e., 100 Hz or 120 Hz, depending on location. In our simulation, the fundamental frequency of the transformer noise is 100 Hz and the harmonics reach 1200 Hz. Finally, our simulation also included useful acoustic signal, in the form of speech, which should preferably remain unaltered by the operation of the ANC system.

Strictly speaking, the adopted disturbance signal is not periodic. It does exhibit a high autocorrelation value at T that corresponds to the delay of 0.01 s, however, so it can be regarded as nearly periodic. The proposed method is sensitive to a mismatch between the assumed and true peak autocorrelation lag T, because this parameter is extensively used in all the equations to wrap filter impulse responses and restore causality. For the method to work correctly, the parameter T needs to be known during the design phase, and it is assumed constant. This assumption is valid for a class of analyzed machinery noise signals, and it is not a limitation in practice.

It is difficult to define an autocorrelation coefficient range for which the proposed method can be applied with the largest benefit, because it depends on the signal properties strongly. Generally, the higher the autocorrelation coefficient is, the better the attenuation can be achieved. When autocorrelation decreases, more aggressive tuning needs to be applied. Because of fast convergence properties, the new method can be useful even for small autocorrelation values.

To tune the controller gain $\alpha$, we performed multiple simulations with different $\alpha$ settings and evaluated the noise reduction in the mean-squared closed-loop output, averaged over the period between the first and the third second. Simulations were performed for 100 $\alpha$-gain point equally distributed between values 0.01 and 1. The same secondary path model and test signal (transformer noise) were used for tuning as for later simulations. For detailed settings description, please refer to Sec. 4.1.1. The resultant plots are shown in Fig. 4 (Note that, because our simulation includes speech and the proposed algorithm works selectively at design frequencies, the suppression levels presented in the plot might seem low.) The attenuation is quickly increasing with gain and reaches a plateau around the point $\alpha =0.3$. Each value in a range (0.3; 0.8) should be appropriate, but we used $\alpha = 0.7$ to balance speed and robustness. Figure 5 compares the magnitude spectra with ANC system off and on, computed from 100 seconds of the transformer noise using the Welch periodogram with segments made of 16384 samples, 50% segment overlap, and with the Hamming window applied. It is apparent that the main harmonics of the transformer noise were effectively suppressed, and that the background speech signal was mostly unaffected—see Fig. 6 for the time-domain comparison of the initial one second of the original and the suppressed signals.

To demonstrate the use of the low-pass filter $Q(z^{-1})$, we designed a 65-tap linear phase low-pass filter using standard techniques. Its frequency response is shown in Fig. 7. This design serves as $Q^{-}(z^{-1})$ in (18). The filter $Q^{+}(z)$ is obtained by replacing $z^{-1}$ with z, $Q^{+}(z)=Q^{-}(z)$, which corresponds to reversing the impulse response of $Q^{-}(z^{-1})$ and results in the same amplitude and reverse phase response curves. That is, the filter $Q(z^{-1})=Q^{-}(z^{-1})Q^{+}(z)$ is a zero phase filter with the 3dB bandwidth equal to 400 Hz which, according to (17), should limit the action of the controller to below 400 Hz.

Fig. 3

Impulse responses of the simulated two-input two-output plant

Fig. 4

Dependency of the steady-state noise attenuation level on the learning gain $\alpha$ for two output channels

Fig. 5

Comparison of magnitude spectra of real-world transformer noise without ANC system (top plot) and with ANC system (bottom plot) for $\alpha =0.3$

Fig. 6

Comparison of time-domain transformer noise and speech signal with ANC system off (top plot) and on (bottom plot)

Fig. 7

Amplitude and phase responses of the filter $Q^{-}(z^{-1})$ used in the simulation experiment

Figure 8 compares the attenuation versus frequency curves obtained in both channels for the controller that does not include low-pass filtering (i.e., $Q(z^{-1})=1$) and the modified design. Figure 8c, d shows that the inclusion of the low-pass filter limited the range of frequencies where the controller is effective to below 400 Hz, as expected. The in-bandwidth attenuation decreased somewhat, which can be attributed to the ripple present in the amplitude response of $Q(z^{-1})$. Since a ripple in $Q(z^{-1})$ as small as $\pm 0.5$ dB [i.e., $\pm 0.25$ dB in $Q^{-}(z^{-1})$] limits the achievable attenuation to approx. 25 dB [c.f. (17)], the controller is particularly sensitive to this issue. On the other hand, the behavior of amplitude response of $Q(z^{-1})$ outside its 3 dB bandwidth was not found to be an important factor in the efficiency of the controller. For example, Fig. 8e and 8f shows the attenuation of the controller that employed an equiripple filter $Q^{-}(z^{-1})$ with $\pm 0.2$ ripple in the 0–700 Hz band and 20 dB attenuation outside it.

Fig. 8

Attenuation versus frequency with ANC turned on

4.1 Comparison to Multidimensional FxLMS

The proposed method was compared to a multidimensional FxLMS algorithm described in Ref.  [22]. It should be emphasized that such a benchmark is demanding because the results strongly depend on the experiment construction and algorithm tuning. Differences in algorithms’ structures further complicate the creation of an appropriate test procedure. The authors tried to fairly compare the two methods, but the experiments were constructed in such a way as to underline the key differences between FxLMS and the proposed algorithm. The comparison was conducted in two parts. Section 4.1.2 shows the behavior of both algorithms when trying to suppress a simple signal composed of sinusoids. Section 4.1.3 describes suppression of a real-world recording of a transformer noise with a speech signal added.

4.1.1 Comparison Conditions and Settings

A band-limiting filter with a cutoff frequency of 4 kHz was added to the proposed method to present the band limitation feature of the new algorithm. High cutoff frequency was chosen not to decrease the attenuated range too much as this could significantly impact the comparison results.

The secondary path model used in both algorithms was modified to include small model uncertainties present in real-world applications. This effect was obtained by adding a zero-mean Gaussian noise with a standard deviation of $5\cdot 10^{-4}$ to the FIR filter representing the secondary path model from Fig. 3. It should be noted that model uncertainties can cause closed-loop instability because the proposed method is not immune to wrong phase estimation in the secondary path. This problem reveals itself with increased intensity in the MIMO case and will be addressed in future publications.

Fig. 9

Dependency of the steady-state noise attenuation level for two output channels on the FxLMS learning gain $\mu$

To make the comparison fair, the FxLMS algorithm could benefit from the information about the suppressed frequency. Reference signal fed to the algorithms was an artificially generated pulse wave with a frequency equal to the frequency of the main harmonic and a duty of 6.25%. The FxLMS algorithm was tuned by performing a series of simulations and optimizing the noise attenuation level averaged over the period between the second and third seconds. Results of simulations are presented in Fig. 9. A similar method was applied to the proposed method. The tuning results and other important configuration parameters of the algorithm are summarized in Table 2.

The algorithms setting was the same for both experiments described below.

Table 2 Tuning parameters of compared algorithms and resultant attenuation of strongest harmonic

4.1.2 Simple Sinusoidal Signal Attenuation Comparison

The first signal tested consists of a simple combination of two sinusoids. The first sinusoid (the main component) had a fundamental frequency of 100 Hz, and it was the frequency that ideally should be attenuated to zero. The second sine wave of $\approx$ 302 Hz was added to simulate the desired signal part, which should not be removed by the algorithm. Its presence should also not affect the quality of attenuation of the main signal component. The amplitude of the 2nd sine wave was 20 dB lower than the amplitude of the main one.

Fig. 10

Attenuation comparison of proposed method and multidimensional FxLMS algorithm for simple sinusoidal signal (one out of two channels presented)

Figure 10 clearly shows the essential differences between both algorithms and the difference in attenuation quality obtained for the simplified signal. We can see that the proposed algorithm has much better attenuation of the main signal component and that the additional sine wave has no effect on the attenuation quality. The desired signal is virtually unaffected by the algorithm and will be heard at the output practically unchanged. This is not due to the addition of the bandwidth limiting filter but due to the very design of the algorithm, which focuses only on a given signal part.

In the case of the FxLMS algorithm, the additional component is canceled to some degree and the residue contains multiple harmonics that were not originally present in the primary disturbance signal.

4.1.3 Transformer Noise Attenuation Comparison

The second presented example compares the two methods when attempting to suppress noise created during electric transformer operation. All simulation settings and scripts used to generate plots described in Sect. 4.1.2 stayed unaltered.

In Figure 11, one can see a comparison of the frequency characteristics of the original noise and the suppressed signals obtained from the algorithms. The simulation was performed on a MIMO model, but only one channel was presented to save space. The results for channel two were very similar to the first channel.

From the comparison, we can see a clear advantage of the proposed solution over the FxLMS algorithm. The total attenuation of the new algorithm was higher although the FxLMS algorithm achieved slightly better attenuation for the strongest harmonic. FxLMS performance in total was poorer because of a weaker reduction of the subsequent signal components. It should be noted, however, that both methods performed exceptionally well in attenuating the transformer signal. In the listening, the original noise is almost inaudible in both cases.

Fig. 11

Attenuation comparison of proposed method and multidimensional FxLMS algorithm for transformer noise signal (one out of two channels presented

5 Conclusions

MIMO active noise control systems are often complex and difficult to analyze, which makes it difficult to extend SISO active noise control algorithm to the MIMO case. The often-used assumption of weak interactions can simplify the design greatly, but does not necessarily lead to optimal performance.

We described a generic multivariate solution of the problem of selectively suppressing disturbance signals with high autocorrelation. The proposed control algorithm was inspired by the ILC controllers, but employs an efficient recursive form, which is particularly important when high sampling rates are used. Thanks to a nontrivial spectral factorization trick, the scheme can be applied with nonminimum phase secondary paths.