1 Introduction

It is well known that biomedical signals can provide useful information for diagnosis of many diseases [7, 14, 17]. However, many biomedical signals acquired from physical sensors are inevitably contaminated by noise interference that imposes uncertainty to signals [4, 22]. As signal quality is reduced, diagnostic performance may be degraded. Hence, suppressing noise while enhancing the important features of signals plays a very important role in many biomedical signal processing applications such as medical diagnosis and estimation of index of well-being based on biomedical signals [7, 14, 17, 27].

AWGN is a common interference noise during the process of data acquisition, and many works have been done to suppress AWGN. To suppress noise, different types of methods have been proposed. For structure-based methods, structural features of biomedical signals are employed for suppressing noise. A strategy dependent on finding locations of the QRS complexes of electrocardiograph (ECG) signal and estimating pulse wave translation time (PWTT) of photoplethysmography (PPG) signal is employed to suppress noise [19, 27]. In addition, one-dimension non-local mean filter based on patch features of ECG signal is also employed for suppressing noise [23]. As these features-based methods exploit specific features of special signals such as the QRS complexes of ECG signal and PWTT of PPG signal, these methods are only useful for specific applications.

In order to generalize these denoising strategies to different biomedical signals, general properties of AWGN are exploited. For an example, linear methods such as low-pass filtering method are employed. This method is widely used because filters can be easily designed and implemented. However, these methods assume that the statistic of noise is stationary. Nevertheless, the statistic of noise contaminating the biomedical signals is non-stationary. To address this issue, wavelet thresholding method [2] is employed for performing denoising. However, this method requires to predefine kernels. Since there may be mismatch between the bandwidths of signals and those of predefined kernels, this approach may lead to poor denoising results.

EMD decomposes signals into several oscillatory components called IMFs. Since IMFs depend only on the signal itself but they do not depend on any predefined function [5, 20], EMD is an adaptive decomposition method. Moreover, as IMFs are sequentially extracted from the fine temporal scales to the coarse temporal scales of signal, EMD is a time–frequency decomposition method. Because of these properties, EMD [8] is used for suppressing noise in many biomedical signal processing applications. More precisely, statistical properties of IMFs of signals contaminated by AWGN have been studied [3, 24]. It is found that high-frequency IMFs are usually considered as noise components and low-frequency IMFs are usually considered as information components. As a result, IMFs can be partitioned into two groups based on a certain criterion. They are the group of information components and the group of noise components. The group of information components can be used to construct denoised signal. On the other hand, the group of noise components can be discarded. Consequently, conventional EMD-based denoising methods are proposed based on determination of the IMF index via a certain criterion. Here, IMFs with their indices higher than determinate index are regarded as information components and IMFs with their indices lower than or equal to determinate index are regarded as noise components. The common criteria for determining the IMF index include correlation-dependent-based thresholding criterion [21], CMSE-based criterion [1], probability density function-based L2 norm criterion (PDF-L2) [12] and relative percentage error-based criterion [10]. Nevertheless, noise components still contain a certain amount of useful information even though they have low correlations with original signal. In this case, some important information will be lost if these IMFs are completely discarded.

To address the above issue, a hierarchical multiresolution analysis-based EMD denoising strategy [11, 26] is proposed. Here, noise components in the first level of decomposition are further decomposed by EMD. In particular, IMFs in the first level of decomposition are classified into either the information group of IMFs or the noise group of IMFs. Then, EMD is applied to each IMF in the first level of decomposition in the noise group to obtain IMFs in the second level of decomposition. IMFs in the second level of decomposition are classified into either the information group of IMFs or the noise group of IMFs again. Here, IMFs in the second level of decomposition in the noise group are discarded and denoised signal is obtained by summing up IMFs in both the first level of decomposition and the second level of decomposition in the information groups. Since useful information in noise components in the first level of decomposition can be retained by further level decomposition without using any predefined kernel, better denoising performance can be achieved. However, discarded components in the second level of decomposition still contain a certain amount of useful information even though two levels of decomposition have been performed.

In order to further improve denoising performance, thresholding strategy, permutating strategy and averaging strategy are exploited. Here, the working principle of permutating and averaging the noise is as follow. Since AWGN is an independent identically distributed processes, permutating AWGN is still an independent identically distributed process. By the central limiting theorem [6], variance of averaged noise is small than that of individual noise. Therefore, this paper proposes to combine hierarchical multiresolution analysis-based EMD, thresholding strategy and averaging strategy together for performing denoising. This is novelty and major contribution of this paper. In particular, this paper permutates the first IMF in the second level of decomposition, regenerates noisy signal, re-applies hierarchical multiresolution analysis-based EMD to regenerated noisy signal, applies thresholding to noisy IMFs, generates denoised signal and averages these denoised signals for performing denoising. To the best of our knowledge, no such work has been done based on IMFs in the second level of decomposition. There are two challenges for combining hierarchical multiresolution analysis-based EMD, thresholding strategy and averaging strategy together. The first challenge is to determine the threshold applied to IMFs in the second level of decomposition. Since existing thresholding strategy only considered IMFs in the first level of decomposition [13, 25], while hierarchical multiresolution analysis-based EMD denoising method requires to determine the appropriate thresholds applied to IMFs in the second level of decomposition, the thresholds applied to IMFs in the second level of decomposition are unknown. In order to address this issue, our proposed method determines the appropriate thresholds applied to IMFs in the second level of decomposition based on thresholds applied to IMFs in the first level of decomposition by employing DFA [18]. The second challenge is on the development of a strategy for generating different realizations of the noisy signal for performing averaging operation. In order to generate different realizations of noisy signal for performing averaging operation, the first IMF in the second level of decomposition is used for performing permutation. Compared with other IMFs in the first level of decomposition, the first IMF in the first level of decomposition is suitable for being used for performing permutation. However, the first IMF in the first level of decomposition still contains signal information. Since it is assumed that noise is with the zero mean, while signal component is usually not with the zero mean, it may have negative effect when permutation and averaging operations are performed. To address this issue, the first IMF in the second level of decomposition is employed for performing permutation and averaging instead.

The organization of this paper is as follows. The hierarchical multiresolution analysis-based EMD denoising is reviewed in Sect. 2. Section 3 presents our proposed denoising strategy. The numerical results are presented in Sect. 4. Finally, a conclusion is drawn in Sect. 5.

2 Hierarchical Multiresolution Analysis-Based EMD Denoising

A signal component is said to be an IMF if it satisfies the following two conditions. (1) The difference between its total number of extrema and its total number of zero crossing points is either equal to zero or equal to one. (2) Its local mean is equal to zero.

Each IMF can be obtained by performing the shifting process. The procedures are as follows:

  • Step (a) Find maxima and minima of input signal. Then, perform interpolation on these maxima and minima to obtain upper envelop and lower envelop of the signal, respectively.

  • Step (b) Compute mean envelop of signal by averaging its upper envelop and its lower envelop.

  • Step (c) Subtract mean envelop from input signal. If obtained sequence satisfies the conditions of IMF, then obtained sequence is taken as an IMF. Next, repeat Step a) by replacing input signal with obtained sequence. Otherwise, repeat Step c) by replacing mean envelop with obtained sequence.

It is worth noting that input signal can be expressed as the sum of IMFs. Let \(x[n]\), \(c_{i} [n]\) and \(r_{M} [n]\) be input signal, the ith IMF and the residue, respectively. Let M be the total number of IMFs. Then, we have:

$$ x[n] = \sum\limits_{i = 0}^{M - 1} {c_{i} [n]} + r_{M} [n]. $$
(1)

The basic working principal of EMD-based denoising method is to find IMF index and to classify IMFs into either the noise group of IMFs or the information group of IMFs according to the found IMF index. Let \(y[n]\) be denoised signal and \(q\) be the found IMF index. Here, it is required to find the value of \(q\) and to develop a grouping strategy. For oversampled signal, energy of signal is usually localized in low-frequency band. Hence, high frequency part of noisy signal always has a lower signal-to-noise ratio compared to its low frequency part. On the other hand, frequency bands of IMFs decrease as the order of IMFs increases. Therefore, IMFs with high order are usually classified into the information group of IMFs while those with low orders are usually classified into the noise group of IMFs. Let \(y[n]\) be denoised signal based on the first level of decomposition. Then, we have:

$$ y[n] = \sum\limits_{i = q}^{M - 1} {c_{i} [n]} + r_{M} [n]. $$
(2)

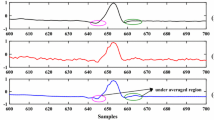
For an example, about 90% of energy of ECG signals is localized in the frequency band between 0.25 and 35 Hz. Since sampling frequency of ECG signals in MIT BIH Arrhythmia database [16] is 360 Hz, most of energy of ECG signals is localized in low-frequency band. Figure 1 shows frequency spectrum of ECG signal (blue line), noisy ECG signal (red line) and the first IMF decomposed from noisy ECG signal (orange line). It can be seen from Fig. 1 that energy of ECG without contaminated by the noise is basically localized in low-frequency band. On the other hand, ECG signal contaminated by noise contains more energy in the high frequency band compared to cleaned ECG signal. Therefore, high frequency part of noisy ECG signal is more likely to belong to noise.

Fig. 1
figure 1

The frequency spectrum of ECG signal, noisy ECG signal and the first IMF

Full size image

To determine the value of \(q\), it is worth noting that IMFs classified into the noise group of the IMFs should have AWGN characteristics. Let \(a[n]\) be AWGN. Let N be the length of the ith IMF. Denote mean(·) as mean operator. Let \(\rho_{i}\) be the correlation coefficient between the ith IMF in the first level of decomposition and AWGN. It is defined as follows:

$$ \rho _{i} = \tfrac{{\sum\limits_{{n = 0}}^{{N - 1}} {\left( {c_{i} \left[ n \right] - mean\left( {c_{i} \left[ n \right]} \right)} \right)\left( {a\left[ n \right] - mean\left( {a\left[ n \right]} \right)} \right)} }}{{\sqrt {\sum\limits_{{n = 0}}^{{N - 1}} {\left( {c_{i} \left[ n \right] - mean\left( {c_{i} \left[ n \right]} \right)} \right)^{2} } } \sqrt {\sum\limits_{{n = 0}}^{{N - 1}} {\left( {a\left[ n \right] - mean\left( {a\left[ n \right]} \right)} \right)^{2} } } }}. $$
(3)

Here, it can be seen that the greater the absolute value of correlation coefficient between IMF in the first level of decomposition and AWGN refers to the closer IMF in the first level of decomposition to the AWGN. Hence, the correlation coefficient is used as the metric for evaluating the closeness between IMF and AWGN. Figure 2 shows the correlation coefficients between IMFs in the first level of decomposition and AWGN at different IMF orders. It can be seen from Fig. 2 that the first IMF in the first level of decomposition is the most correlated with AGWN compared to other IMFs in the first level of decomposition. Hence, the first IMF in the first level of the decomposition is employed to estimate the local noise. Besides, it can also be seen from Fig. 1 that the first IMF in the first level of decomposition contains large portion of energy of noisy signal in high frequency band. As most of energy of clean signal is localized in 4low frequency band, the first IMF in the first level of decomposition should be classified into the noise group of the IMFs from this viewpoint. Therefore, we set \(q=1\) for this case.

Fig. 2
figure 2

The plot of the correlation coefficient between IMFs in the first level of the decomposition and AWGN against IMF order. a The ECG. b The PPG

Full size image

It is discussed in Sect. 1 that IMFs in the noise group of IMFs in the first level of the decomposition obtained by performing EMD also contain a certain amount of useful information for reconstructing clean signal [26]. Hence, IMFs in the noise group of IMFs in the first level of the decomposition should be further decomposed by EMD. Nevertheless, IMFs are obtained only when the iterative sifting process converges. Therefore, the same IMFs will be obtained if EMD is directly applied to these IMFs. This implies that no further iterated sifting process can be performed on IMFs and no further level of decomposition can be obtained.

To address this issue, zero padding technique in the frequency domain is proposed. First, an IMF is represented in the discrete cosine transform (DCT) domain via multiplying vector of signal in the time domain to DCT matrix. Then, a number of zeros are inserted to this vector in the DCT domain. Next, this zero padded vector is represented in the time domain via multiplying this zero padded vector in the DCT domain to the inverse DCT (IDCT) matrix. Now, IMFs in the next level of the decomposition can be obtained via performing EMD on this extended length signal. Let \(c_{i}^{0} [n]\) be the ith IMF in the first level of decomposition and \(c_{j,i}^{1} [n]\) be the ith IMF in the second level of decomposition decomposed from \(c_{j}^{0} [n]\). Let \(M_{0}^{0}\) be the total number of IMFs in the first level of decomposition and \(M_{j}^{1}\) be the total number of the IMFs in the second level of decomposition decomposed from \(c_{j}^{0} [n]\). Let \(r_{{_{{M_{0}^{0} }} }}^{0} [n]\) be the residue in the first level of decomposition and \(r_{{_{{M_{j}^{1} }} }}^{1} [n]\) be the residue in the second level of decomposition decomposed from \(c_{j}^{0} [n]\). Let \(q\) be the IMF index for classifying IMFs into the noise group of IMFs or the information group of IMFs in the first level of decomposition and \(k_{j}\) be the IMF index for classifying IMFs into the noise group of IMFs or the information group of IMFs in the second level of decomposition decomposed from \(c_{j}^{0} [n]\). Let \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{y} \left[ n \right]\) be denoised signal based on the two-level decomposition. Then, we have [1]:

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{y} [n] = \tilde{z}[n] + \sum\limits_{i = q}^{{M_{0}^{0} - 1}} {c_{i}^{0} [n]} + r_{{_{{M_{0}^{0} }} }}^{0} [n], $$
(4)

where

$$ \tilde{z}[n] = \sum\limits_{{\eta = k_{0} }}^{{M_{0}^{1} - 1}} {c_{0,\eta }^{1} [n]} + r_{{_{{M_{0}^{1} }} }}^{1} [n] + \cdots + \sum\limits_{{\eta = k_{q - 1} }}^{{M_{q - 1}^{1} - 1}} {c_{q - 1,\eta }^{1} [n]} + r_{{_{{M_{q - 1}^{1} }} }}^{1} [n]. $$
(5)

Since IMFs with very narrow bandwidths can be obtained by repeating the above procedures using more than one-level decomposition, a better denoising performance can be achieved.

3 Our Proposed Denoising Strategy

3.1 Permutation Strategy

Since AWGN is an independent identically distributed process, a new noise realization obtained by permutating segments of AWGN is still an independent identically distributed process. Figure 3 shows the average of 20 permutated AWGNs. It can be seen from Fig. 3 that power of averaged noise is significantly reduced. This demonstrates that averaging operation can effectively suppress noise. However, it is required to generate different realizations of noisy signal.

Fig. 3
figure 3

The original AWGN and the average of 20 permutated AWGNs

Full size image

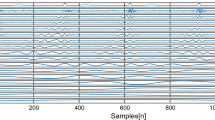
It is worth noting that the first IMF in the first level of decomposition may contain some useful information even though it is the noisiest IMF. Figure 4a shows an ECG signal contaminated by AWGN. Figure 4b shows its first IMF in the first level of decomposition. It can be seen from Fig. 4b that the first IMF in the first level of decomposition contains some useful information about the QRS complex. Hence, the first IMF in the first level of decomposition is required to be further decomposed via hierarchical multiresolution analysis-based EMD [26]. Figure 4c shows IMFs in the second level of decomposition decomposed from the first IMF in the first level of decomposition. It can be seen from Fig. 4c that the residual information about the QRS complex is suppressed in the first IMF in the second level of decomposition. Hence, the first IMF in the second level of decomposition is used for performing permutation.

Fig. 4
figure 4

An example demonstrating the superiority of applying hierarchical multiresolution analysis-based EMD for performing permutation. a An ECG signal contaminated by AWGN. b The first IMF in the first level of decomposition. c The IMFs in the second level of decomposition decomposed by applying EMD to the first IMF in the first level of decomposition

Full size image

The first IMF in the second level of decomposition is non-overlappingly segmented into various pieces, and these segments are permutated for generating different realizations of noisy signal. Let k be the total number of these segments and \(p-1\) be the total number of the generated realizations of noisy signal. For these k segments, there are \(k!\) permutations. It is assumed that \(k!\ge p-1\). Now, \(p-1\) permutations are randomly selected from these \(k!\) permutations. Each permutated IMF and the rest of IMFs in both the first level of decomposition and the second level of decomposition are summed together to produce a new realization of noisy signal. The procedures for performing permutation are summarized below:

  1. (a)

    Performing EMD on noisy signal to obtain IMFs in the first level of decomposition.

  2. (b)

    Performing further level decomposition on the first IMF in the first level of decomposition and IMFs in the second level of decomposition are obtained.

  3. (c)

    The first IMF in the second level of the decomposition is non-overlappingly segmented into k pieces, and these segments are permutated.

  4. (d)

    From these k! permutations, \(p-1\) permutations are randomly selected.

  5. (e)

    Each permutated IMF and the rest of the IMFs in both the first level of the decomposition and the second level of the decomposition are summed together to generate a new realization of the noisy signal.

3.2 Thresholding Strategy

The thresholding is applied to both original signal and each realization of regenerated noisy signal discussed in Sect. 3.1. Here, IMFs in the first level of decomposition are classified into the information group of IMFs or the noise group of IMFs by CMSE. Then, useful information in IMFs in the noise group in the first level of decomposition is extracted out by performing further level decomposition without any predefined kernels. In particular, EMD is applied to IMFs in the noise group in the first level of decomposition to obtain IMFs in the second level of decomposition. After that, IMFs in the second level of decomposition are classified into the information group of IMFs or the noise group of IMFs by DFA approach. Here, DFA is employed because DFA is a useful tool for finding scaling exponent [6]. In general, the larger the value of the scaling exponent refers to the smoother of the signal. Hence, the correlation between signal with large value of the scaling exponent and noise is low. As a result, more parts of signal with large value of the scaling exponent should be retained. On the contrary, the smaller the value of the scaling exponent refers to the more oscillations in the signal. Hence, the correlation between signal with small value of the scaling exponent and the noise is high. As a result, less parts of signal with small value of the scaling exponent should be retained. However, the discarded components in the second level of decomposition still contain some useful information. In order to further extract out this useful information, thresholding strategy is applied to IMFs in the noise group in the second level of decomposition. The block diagram for performing thresholding strategy is shown in Fig. 5.

Fig. 5
figure 5

The block diagram for performing thresholding strategy on hierarchical multiresolution analysis based EMD denoising

Full size image

In this paper, interval thresholding [25] is employed. This is because it can preserve the continuity of signal within interval. For applying conventional interval thresholding, let \(\tilde{c}_{j,i}^{1} [n]\) be the ith IMF in the second level of decomposition decomposed from the jth IMF in the first level of decomposition based on a realization of noisy signal generated using method discussed in Sect. 3.1. Let sp and sp+1 be two consecutive zero crossing points in \(\tilde{c}_{j,i}^{1} [n]\) and sp be interval containing these two consecutive zero crossing points. That is, sp = [sp sp+1]. Let e be time instant in sp such that \(\left| {\tilde{c}_{j,i}^{1} [e]} \right| \ge \left| {\tilde{c}_{j,i}^{1} [n]} \right|\) ∀n ∈ sp. Let \(T_{j,i}^{^{\prime}}\) be a threshold value defined based on sp. Let \(\overline{c}_{j,i}^{1} [n]\) be the value processed by interval thresholding. Then, interval thresholding can be expressed as:

$$ \overline{c}_{j,i}^{1} [n] = \left\{ {\begin{array}{*{20}l} {\tilde{c}_{j,i}^{1} [n]} \hfill & {\left| {\tilde{c}_{j,i}^{1} [e]} \right| > T_{j,i}^{^{\prime}} } \hfill \\ 0 \hfill & {\left| {\tilde{c}_{j,i}^{1} [e]} \right| \le T_{j,i}^{^{\prime}} } \hfill \\ \end{array} } \right. $$
(6)

∀n ∈ sp for hard thresholding and

$$ \overline{c}_{j,i}^{1} [n] = \left\{ {\begin{array}{*{20}l} {{\text{sgn}} \left( {\tilde{c}_{j,i}^{1} [n]} \right)\left( {\left| {\tilde{c}_{j,i}^{1} [n]} \right| - T_{j,i}^{^{\prime}} } \right)} \hfill & {\left| {\tilde{c}_{j,i}^{1} [e]} \right| > T_{j,i}^{^{\prime}} } \hfill \\ 0 \hfill & {\left| {\tilde{c}_{j,i}^{1} [e]} \right| \le T_{j,i}^{^{\prime}} } \hfill \\ \end{array} } \right. $$
(7)

∀n ∈ sp for soft thresholding. To determine the value of \(T_{j,i}^{^{\prime}}\), first consider an AWGN model. Let Ej be energy of the jth IMF of the AWGN in the first level of decomposition. Let β and μ be parameters for estimating Ej. Let Tj be threshold for the jth. IMF of AWGN in the first level of decomposition. Then, Tj is set to [13]

$$ T_{j} = \sqrt {E_{j} \times 2\ln N} \;{\text{for}}\;j = 1,2,3, \ldots , $$
(8)

where

$$ E_{j} = \frac{{E_{1} }}{\beta }\mu^{ - j} {\text{for}}\;j = {2},{3},{4}, \ldots . $$
(9)

Here, β and μ are set to 0.719 and 2.01, respectively [14]. Traditionally, the first IMF of noisy signal in the first level of decomposition is regarded as the noise. Hence, E1 for AWGN is the same as energy of the first IMF of noisy signal in the first level of decomposition [8]. As a result, T1 for AWGN is also the same as threshold for the first IMF of noisy signal in the first level of decomposition. However, all IMFs of AWGN in the first level of the decomposition are IMFs in the noise group. Nevertheless, only some IMFs of noisy signal in the first level of decomposition are the IMFs in the noise group. From here, it can be seen that this AWGN-based model may not be appropriate for biomedical signals.

To address this issue, EMD is applied to IMFs in the first level of decomposition to obtain IMFs in the noise group in the second level of decomposition. Let \(h_{j,i}\) be the scaling exponent of the ith IMF in the second level of decomposition decomposed from the jth IMF in the first level of decomposition. Let \(h_{j}^{^{\prime}}\) be the scaling exponent of the jth IMF in the first level of decomposition. Since the scaling exponent of IMFs in the noise group in the second level of decomposition should be smaller than that of corresponding IMF in the noise group in the first level of decomposition, \(T_{j,i}^{^{\prime}}\) should be reformulated based on both \(h_{j,i}\) and \(h_{j}^{^{\prime}}\). In particular, \(T_{j,i}^{^{\prime}}\) is set to the product of \(T_{j}\) and the ratio of \(\frac{{h_{j,i} }}{{h_{j}^{^{\prime}} }}\). Let \(\hat{y}\left[ n \right]\) be denoised signal after performing thresholding. Then, we have:

$$ T_{j,i}^{^{\prime}} = \frac{{h_{j,i} }}{{h_{i}^{^{\prime}} }}T_{i} . $$
(10)

As a result, we have:

$$ \hat{y}[n] = z^{\prime}[n] + \sum\limits_{i = q}^{{M_{0} - 1}} {c_{i}^{0} [n]} + r_{{_{{M_{0} }} }}^{0} [n], $$
(11)

where

$$\begin{aligned} z^{\prime}[n]& = \sum\limits_{\eta = 0}^{{k_{0} - 1}} {\overline{c}_{0,\eta }^{1} [n]} + \sum\limits_{{\eta = k_{0} }}^{{M_{0}^{1} - 1}} {c_{0,\eta }^{1} [n]} + r_{{_{{M_{0} }} }}^{1} [n] + \cdots + \sum\limits_{\eta = 0}^{{k_{q - 1} - 1}} {\overline{c}_{q - 1,\eta }^{1} [n]} \\ &\quad + \sum\limits_{{\eta = k_{q - 1} }}^{{M_{q - 1}^{1} - 1}} {c_{q - 1,\eta }^{1} [n]} + r_{{_{{M_{q - 1} }} }}^{1} [n].\end{aligned} $$
(12)

The detail procedures for performing thresholding strategy are summarized below:

  1. (a)

    Let \(x_{0} [n] = x[n]\) and \({x}_{i}[n]\) for \(1\le i\le p-1\) be noisy signal generated based on method discussed in Sect. 3.1.

  2. (b)

    Apply conventional EMD to \({x}_{i}[n]\) for \(0\le i\le p-1\) to obtain IMFs in the first level of decomposition.

  3. (c)

    Apply CMSE method to obtain IMF index for classifying IMFs in the first level of decomposition into the noise group of IMFs or the information group of IMFs.

  4. (d)

    Apply EMD to IMFs in the noise group in the first level of decomposition to obtain IMFs in the second level of decomposition.

  5. (e)

    Apply DFA method to obtain IMF indices for classifying IMFs in the second level of decomposition into the noise group of the IMFs or the information group of IMFs. It is worth noting that each IMF in the second level of decomposition has its corresponding IMF in the first level of decomposition.

  6. (f)

    Apply thresholding strategy to IMFs in the noise group in the second level of decomposition.

3.3 Averaging Strategy

Let \(\hat{y}_{i} [n]\) for \(0\le i\le p-1\) be denoised signal processed on \({x}_{i}[n]\) for \(0\le i\le p-1\) based on method discussed in Sect. 3.2. Here, the average of \(\hat{y}_{i} [n]\) is computed. That is:

$$ y^{\prime}[n] = \frac{{\hat{y}_{0} [n] + \hat{y}_{1} [n] + \cdots + \hat{y}_{p - 1} [n]}}{p}. $$
(13)

4 Numerical Results

To test the effectiveness of our proposed strategy, the numerical simulations are conducted on some practical biomedical signals that are downloaded from both the MIT-BIH database on the arrhythmia [16] and the database on the multi-parameter intelligent monitoring in the intensive care unit (MIMIC) [15]. The MIT-BIH arrhythmia database contains 23 recordings that are chosen randomly from a set of 4000 recordings on 24 h ambulatory ECG signals. The sampling frequency is 360 Hz. On the other hand, the MIMIC database is a large and a single-center database that comprises of PPG signals. The sampling frequency is 125 Hz. The lengths of both EEG signals and PPG signals are 2048. The difference between the processed SNR and the input SNR is employed for evaluating the performance of our proposed denoising algorithm. Here, the input SNR refers to the ratio of signal power to noise power before performing denoising, while the processed SNR refers to the ratio of signal power to noise power after performing denoising. It is also called the output SNR. In addition, our proposed strategy is evaluated under both soft thresholding strategy and hard thresholding strategy.

4.1 Simulation 1

Figure 6 shows relationships between the processed SNRs and the total number of realizations of denoised signals using various signals at various input SNRs via our proposed method. Here, the legends show the input SNRs of signals. When the total number of the realization of denoised signals is equal to one, no averaging operation has been performed. It can be seen from Fig. 6 that the processed SNRs increase and then eventually reach convergence as the total number of realizations of denoised signals increases. In general, the total number of realizations of denoised signals required for reaching the convergence is less than 25 and the exact values are dependent on the input SNRs and the types of signals. From Fig. 6, it can be seen that the converged processed SNRs are 0.8–2.5 dB higher than the processed SNRs obtained using only one realization of denoised signals. This implies that averaging operation in general can improve denoising performance. Besides, it is found that the differences between the input SNRs and the processed SNRs obtained at the converged total numbers of the realizations of the denoised signals are ranged between 5 and 9 dB. This demonstrates the effectiveness of our proposed method.

Fig. 6
figure 6

The relationships between the processed SNRs and the total numbers of realizations of denoised signals using various signals at various input SNRs via our proposed method. a The ECG processed by hard thresholding method. b The ECG processed by soft thresholding method. c The PPG processed by hard thresholding method. d The PPG processed by soft thresholding method

Full size image

4.2 Simulation 2

Figure 7 shows the relationships between the processed SNRs and the total number of realizations of denoised signals using various signals at various input SNRs via our proposed method obtained using only \(c_{0}^{0} \left[ n \right]\) or obtained only using \(c_{0}^{1} \left[ n \right]\) with both hard thresholding strategy and soft thresholding strategy. It can be seen from Fig. 7 that the converged processed SNRs obtained only using \(c_{0}^{1} \left[ n \right]\) are higher than those obtained only using \(c_{0}^{0} \left[ n \right]\). This implies that denoising based on two-level decomposition outperforms denoising based on one-level decomposition. Besides, it is worth noting that no averaging operation has been performed when the total number of the realization of the denoised signals is equal to one. It can be seen from Fig. 7 that the converged processed SNRs obtained only using \(c_{0}^{1} \left[ n \right]\) are also higher than the processed SNRs obtained using only one realization of denoised signals. On the other hand, this is not the general true for the converged processed SNRs obtained only using \(c_{0}^{0} \left[ n \right]\). There are some converged processed SNRs obtained only using \(c_{0}^{0} \left[ n \right]\) being lower than the processed SNRs obtained using only one realization of denoised signals. For examples, for ECG signal with the input SNR being equal to 15 dB under both hard thresholding strategy and soft thresholding strategy as well as for ECG signal with the input SNR being equal to 10 dB under soft thresholding strategy, the converged processed SNRs are lower than the processed SNRs obtained using only one realization of denoised signals. In these cases, averaging operation introduces negative effects on denoising performances.

Fig. 7
figure 7figure 7

The relationships between the processed SNRs and the total numbers of realizations of denoised signals using various signals at various input SNRs via our proposed method using only \(c_{0}^{0} \left[ n \right]\) or only using \(c_{0}^{1} \left[ n \right]\) with both hard thresholding strategy and soft thresholding strategy. a The ECG with the input SNR being equal to 10 dB under soft thresholding strategy. b The ECG with the input SNR being equal to 15 dB under soft thresholding strategy. c The ECG with the input SNR being equal to 10 dB under hard thresholding strategy. d The ECG with the input SNR being equal to 15 dB under hard thresholding strategy. e The PPG with the input SNR being equal to 10 dB under soft thresholding strategy. f The PPG with the input SNR being equal to 15 dB under soft thresholding strategy. g The PPG with the input SNR being equal to 10 dB under hard thresholding strategy. h The PPG with the input SNR being equal to 15 dB under hard thresholding strategy

Full size image

4.3 Simulation 3

To show the qualitative performance of our proposed method, the numerical simulations are conducted on various biomedical signals with the lengths of signals being equal to 2048. Figure 8 shows denoised signals obtained via our proposed method based on soft thresholding strategy with averaging 20 realizations of denoised signals, with averaging 10 realizations of denoised signals as well as without performing averaging operation using various biomedical signals. Similarly, Fig. 9 shows denoised signals obtained via our proposed method based on hard thresholding strategy with averaging 20 realizations of denoised signals, with averaging 10 realizations of denoised signals as well as without performing averaging operation. On the other hand, to show the quantitative performance of our proposed method, Table 1 shows the processed SNRs of various biomedical signals at various input SNRs obtained via our proposed method based on soft thresholding strategy with averaging 20 realizations of denoised signals, with averaging 10 realizations of denoised signals as well as without performing averaging operation. Likewise, Table 2 shows the processed SNRs of various biomedical signals at various input SNRs obtained via our proposed method based on hard thresholding strategy with averaging 20 realizations of denoised signals, with averaging 10 realizations of denoised signals as well as without performing averaging operation. It can be seen from Tables 1 and 2 that our proposed method based on both soft thresholding strategy and hard thresholding strategy with averaging 20 denoised signals outperforms than that with averaging other numbers of denoised signals. In addition, our proposed method based on both soft thresholding strategy and hard thresholding strategy with averaging 10 denoised signals also outperforms than that without performing the averaging operation. From here, it can be concluded that the averaging strategy can significantly improve the denoising performance. This is because the averaging strategy can significantly suppress the noise power.

Fig. 8
figure 8figure 8

The denoising performances obtained via our proposed method based on the soft thresholding strategy. a The noisy ECG. b The denoised ECG obtained via our proposed method without performing the averaging operation. c The denoised ECG obtained via our proposed method with averaging 10 realizations of the denoised signals. d The denoised ECG obtained via our proposed method with averaging 20 realizations of the denoising signals. e The noisy PPG. f The denoised PPG obtained via our proposed method without performing the averaging operation. g The denoised PPG obtained via our proposed method with averaging 10 realizations of the denoised signals. h The denoised PPG obtained via our proposed method with averaging 20 realizations of the denoised signals

Full size image
Fig. 9
figure 9figure 9

The denoising performances obtained via our proposed method based on hard thresholding strategy. a The noisy ECG. b The denoised ECG obtained via our proposed method without performing averaging operation. c The denoised ECG obtained via our proposed method with averaging 10 realizations of denoised signals. d The denoised ECG obtained via our proposed method with averaging 20 realizations of denoising signals. e The noisy PPG. f The denoised PPG obtained via our proposed method without performing averaging operation. g The denoised PPG obtained via our proposed method with averaging 10 realizations of denoised signals. h The denoised PPG obtained via our proposed method with averaging 20 realizations of denoised signals

Full size image
Table 1 The comparisons on the processed SNRs of various biomedical signals at various input SNRs among various soft thresholding methods
Full size table
Table 2 The comparisons on the processed SNRs of various biomedical signals at various input SNRs among various hard thresholding methods
Full size table

4.4 Simulation 4

The processed SNRs obtained by our proposed method via soft thresholding strategy with averaging 20 denoised signals, with averaging 10 denoised signals as well as without performing averaging operation, are compared to six other different methods including wavelet-based soft thresholding denoising method, EMD-based interval soft thresholding denoising method [25], EMD-based direct soft thresholding denoising method [13], singular spectrum analysis (SSA)-based denoising method [9], CMSE-based denoising method [1] and denoising method discussed in [26]. Here, all the comparisons are based on the same databases. Table 1 shows the comparison results. It is found that our proposed method via soft thresholding strategy without performing averaging operation achieves better results compared to EMD-based interval soft thresholding denoising method [25], EMD-based direct soft thresholding denoising method [13], CMSE-based denoising method [1], wavelet-based soft thresholding denoising method and denoising method discussed in [26]. This is because our proposed method via soft thresholding strategy without performing averaging operation can extract the more detail information from the noisy IMFs in both the first level of decomposition and the second level of decomposition. However, SSA-based denoising method [9] achieves better results compared to our proposed method via the soft thresholding strategy without performing the averaging operation. This is because the correlation between the noise and the signal can be effectively explored in SSA-based denoising method. On the other hand, wavelet-based soft thresholding denoising method achieves the worst performance. This is because wavelet-based soft thresholding denoising method requires to predefine basis functions for performing denoising in which it is difficult to find the optimal basis function for a given biomedical signal.

In addition, our proposed method via hard thresholding strategy with averaging 20 denoised signals, with averaging 10 denoised signals as well as without performing averaging operation, is compared to wavelet-based hard thresholding denoising method, EMD-based interval hard thresholding denoising method [25] and EMD-based direct hard thresholding denoising method [13]. Table 2 shows the comparison results. Likewise, wavelet-based hard thresholding denoising method achieves the worst results for the majority cases for the similar reason. Also, our proposed method via hard thresholding strategy with all averaging strategies yields the best results compared to the other methods for the similar reason.

4.5 Discussions

In this subsection, the simulation results are discussed. About the relationships between the processed SNRs and the total number of realizations of denoised signals using various signals at various input SNRs via our proposed method, it has been shown that the processed SNRs increase initially and then eventually reach the convergence as the total number of realizations of denoised signals increase. It is worth noting that AWGN is an independent and identically distributed process and it is assumed to be with the zero mean. Hence, the average of different realizations of AWGN is still an independent and identically distributed process with its variance being smaller than that of the individual one. As a result, energy of noise component in noisy signal is reduced. Therefore, the processed SNRs increase initially. However, the processed SNRs converge. Overall, our proposed method with performing averaging operation outperforms that without performing averaging operation.

Compare the processed SNRs obtained via our proposed method to that obtained via other methods, the processed SNRs obtained via our proposed method without performing averaging operation using various signals at various input SNRs are higher than those obtained via conventional EMD-based thresholding methods. This is because our proposed method can extract more detail information from noisy IMFs in both the first level of decomposition and the second level of decomposition, while conventional EMD-based thresholding methods extract information only from noisy IMFs in the first level of decomposition. Overall, our proposed method does not only achieve the best quantitative denoising performance, but it also achieves the best qualitative denoising performance.

5 Conclusion

This paper proposes hierarchical multiresolution analysis-based EMD method for performing denoising on noisy biomedical signals. Since AWGN is an independent identically distributed process, permutating the segments of AWGN is also an independent identically distributed process. By permutating noisy IMF, more than one realization of noisy signal can be generated. On the other hand, as discarded IMF in the second level of decomposition may also contain some useful information, thresholding strategy is applied to this noisy permutated IMF. Finally, these filtered signals are averaged together to obtain final denoised signal.

Since one of the advantages of the proposed method is that the total number of level decomposition in hierarchical multiresolution analysis is flexible, and the appropriate level of decomposition in hierarchical multiresolution analysis will be investigated in future.