On Weighted Least Squares Estimators of Parameters of a Chirp Model

Abstract

The least squares method seems to be a natural choice in estimating the parameters of a chirp model. But the least squares estimators are very sensitive to the outliers. Even in presence of very few outliers, the performance of the least squares estimators becomes quite unsatisfactory. Due to this reason, the least absolute deviation method has been proposed in the literature. But implementing the least absolute deviation method is quite challenging particularly for the multicomponent chirp model. In this paper, we propose to use the weighted least squares estimators, which seem to be more robust in presence of a few outliers. First, we consider the weighted least squares estimators of the unknown parameters of a single component chirp signal model. It is assumed that the weight function is a finite degree polynomial and the errors are independent and identically distributed random variables with mean zero and finite variance. It is observed that the weighted least squares estimators are strongly consistent and they have the same convergence rate as the least squares estimators. The weighted least squares estimators can be obtained by solving a two dimensional optimization problem. In case of the multicomponent chirp signal, we provide a sequential weighted least squares estimators and provide the consistency and asymptotic normality properties of these sequential weighted least squares estimators. To compute the sequential weighted least squares estimators one needs to solve only one two dimensional optimization problem at each stage. Extensive simulations have been performed to see the performances of the proposed estimators. Two data sets have been analyzed for illustrative purposes.

Appendices

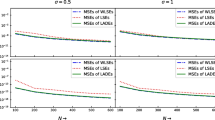
Appendix A

We need the following lemmas to prove Theorem 1.

Lemma 1

If $\{X(t)\}$s are i.i.d. random variables with mean 0 and variance $\sigma ^2$, and w(s) are same as in Theorem 1, and $0< \alpha , \beta < \pi$, then as $N \rightarrow \infty$,

$$\begin{aligned} \sup _{\alpha ,\beta } \left\| {\frac{1}{N}} \sum _{t=1}^N X(t) w \left( \frac{t}{N} \right) \cos (\alpha t) \cos (\beta t^2) \right\| {\mathop {\rightarrow }\limits ^{a.s.}} 0. \end{aligned}$$

Proof of Lemma 1

Consider the following random variable

$$\begin{aligned} Z(t) = \left\{ \begin{array}{ccc} X(t) &{} \hbox {if} &{} |X(t)| \le t^{\frac{3}{4}} \\ 0 &{} o.w. &{} \end{array} \right. \end{aligned}$$

Then

$$\begin{aligned} \sum _{t=1}^{\infty } P[X(t) \ne Z(t)]= & {} \sum _{t=1}^{\infty } P[|X(t)|> t^{\frac{3}{4}}] = \sum _{t=1}^{\infty } \sum _{2^{t-1} \le s< 2^t} P[|X(t)|> s^{\frac{3}{4}}] \\\le & {} \sum _{t=1}^{\infty } \sum _{2^{t-1} \le s< 2^t} P \left[ |X(1)|> 2^{(t-1)\frac{3}{4}} \right] \\\le & {} \sum _{t=1}^{\infty } 2^t P \left[ |X(1)| > 2^{(t-1)\frac{3}{4}} \right] \\\le & {} \sum _{t=1}^{\infty } 2^t \frac{E|X(1)|^2}{2^{(t-1)\frac{3}{2}}} \le C \sum _{t=1}^{\infty } 2^{-\frac{t}{2}} < \infty . \end{aligned}$$

Therefore, $\{X(t)\}$ and $\{Z(t)\}$ are equivalent sequences. So

$$\begin{aligned}&\sup _{\alpha ,\beta } \left\| \frac{1}{N} \sum _{t=1}^N X(t) w \left( \frac{t}{N} \right) \cos (\alpha t) \cos (\beta t^2) \right\| {\mathop {\rightarrow }\limits ^{a.s.}} 0 \Leftrightarrow \\&\sup _{\alpha , \beta } \left\| \frac{1}{N} \sum _{t=1}^N Z(t) w \left( \frac{t}{N} \right) \cos (\alpha t) \cos (\beta t^2) \right\| {\mathop {\rightarrow }\limits ^{a.s.}} 0. \end{aligned}$$

Let $U(t) = Z(t) - E(Z(t))$. Therefore,

$$\begin{aligned} \sup _{\alpha , \beta } \left\| \frac{1}{N} \sum _{t=1}^N E(Z(t)) w \left( \frac{t}{N} \right) \cos (\alpha t) \cos (\beta t^2) \right\|\le & {} \frac{K}{N} \sum _{t=1}^N |E(Z(t))| \\= & {} \frac{K}{N} \sum _{t=1}^N \left\| \int _{|x| < t^{\frac{3}{4}}} x \hbox {d}F(x) \right\| \rightarrow 0, \end{aligned}$$

where $\sup _{0 \le s \le 1} w(s) \le K$, same as defined in Section 3 and F(x) is the distribution of X(1). Therefore, it is enough to prove that

$$\begin{aligned} \sup _{\alpha , \beta } \left\| \frac{1}{N} \sum _{t=1}^N U(t) w \left( \frac{t}{N} \right) \cos (\alpha t) \cos (\beta t^2) \right\| {\mathop {\rightarrow }\limits ^{a.s.}} 0. \end{aligned}$$

For any fixed $\alpha , \beta$ and $\epsilon > 0$, and $0 \le h \le \frac{1}{4KN^{\frac{3}{4}}}$, we have

$$\begin{aligned}&P \left[ \left\| \frac{1}{N} \sum _{t=1}^N U(t) w \left( \frac{t}{N} \right) \cos (\alpha t) \cos (\beta t^2) \right\| \ge \epsilon \right] \\&\quad \le 2 e^{-h N \epsilon } \prod _{t=1}^N E(e^{h U(t) w \left( \frac{t}{N} \right) \cos (\alpha t) \cos (\beta t^2)}) \\&\quad \le 2 e^{-hN\epsilon } \prod _{t=1}^N(1+h^2\sigma ^2) \le 2^{-h N \epsilon + N h^2 \sigma ^2}. \end{aligned}$$

The first inequality follows from Markov inequality. From the definition of Z(t), $V(U(t)) = V(Z(t)) \le V(X(t)) = \sigma ^2$. Since $\Vert h U(t) w \left( \frac{t}{N} \right) \cos (\alpha t) \cos (\beta t^2)\Vert \le \frac{1}{2}$, and for $|x| \le \frac{1}{2}$, $e^x \le 1 + x + x^2$, the second inequality holds true.

Choose $\displaystyle h = \frac{1}{4 K N^{\frac{3}{4}}}$, therefore for large N,

$$\begin{aligned} \left[ \left\| \frac{1}{N} \sum _{t=1}^N U(t) w \left( \frac{t}{N} \right) \cos (\alpha t) \cos (\beta t^2) \right\| \ge \epsilon \right] \le 2 e^{-\frac{N^{\frac{1}{4}} \epsilon }{4} + \frac{\sigma ^2}{16 N^{\frac{1}{2}}}} \le 4 e^{-\frac{N^{\frac{1}{4}} \epsilon }{4}}. \end{aligned}$$

Let $J = N^6$, and choose J points $(\alpha _1, \beta _1), \ldots , (\alpha _J, \beta _J)$, such that for any point $(\alpha , \beta )$ in $[0,\pi ] \times [0,\pi ]$, we have a point $(\alpha _k, \beta _k)$ satisfying

$$\begin{aligned} \Vert \alpha _k-\alpha \Vert \le \frac{\pi }{N^3} \ \ \ \hbox {and} \ \ \ \Vert \beta _k-\beta \Vert \le \frac{\pi }{N^3}. \end{aligned}$$

Now by Taylor series expansion can be used to estimate

$$\begin{aligned} \Vert \cos (\beta t^2) - \cos (\beta _k t^2)\Vert \le t^2\Vert \beta -\beta _k\Vert \ \ \ \text {and} \ \ \ \Vert \cos (\alpha t) - \cos (\alpha _k t)\Vert \le \Vert t\Vert \Vert \alpha -\alpha _k\Vert \end{aligned}$$

therefore,

$$\begin{aligned}&\left\| \frac{1}{N} \sum _{t=1}^N U(t) w \left( \frac{t}{N} \right) \left\{ \cos (\alpha t)\cos (\beta t^2) - \cos (\alpha _k t) \cos (\beta _k t^2) \right\} \right\| \\&\quad \le \left\| \frac{1}{N} \sum _{t=1}^N U(t) w \left( \frac{t}{N} \right) \cos (\alpha t) \left\{ \cos (\beta t^2) - \cos (\beta _k t^2) \right\} \right\| \\&\qquad + \left\| \frac{1}{N} \sum _{t=1}^N U(t) w \left( \frac{t}{N} \right) \cos (\beta _k t^2)\left\{ \cos (\alpha t) - \cos (\alpha _k t) \right\} \right\| \\&\quad \le C \left[ \frac{1}{N} \sum _{t=1}^N t^{\frac{3}{4}} t^2 \frac{\pi }{N^3} + \frac{1}{N} \sum _{t=1}^N t^{\frac{3}{4}} t \frac{\pi }{N^3} \right] \le C \left[ \frac{\pi }{N^{\frac{1}{4}}} + \frac{\pi }{N^{\frac{5}{4}}} \right] \rightarrow 0. \end{aligned}$$

Therefore, for large N

$$\begin{aligned}&P \left[ \sup _{a,b} \left\| \frac{1}{N} \sum _{t=1}^N U(t) w \left( \frac{t}{N} \right) \cos (\alpha t) \cos (\beta t^2) \right\| \ge 2 \epsilon \right] \\&\quad \le P \left[ \max _{k \le N^6} \left\| \frac{1}{N} \sum _{t=1}^N U(t) w \left( \frac{t}{N} \right) \cos (\alpha _k t) \cos (\beta _k t^2) \right\| \ge 2 \epsilon \right] \le 4 N^6 e^{-\frac{N^{\frac{1}{4}} \epsilon }{4}}. \end{aligned}$$

Since $\displaystyle \sum \nolimits _{N=1}^{\infty } N^6 e^{-\frac{N^{\frac{1}{4}} \epsilon }{4}} < \infty$, by using Borel-Cantelli lemma the result follows. $\square$

Lemma 2

Let us denote

$$\begin{aligned} S_c = \{\theta : \theta = (A,B,\alpha ,\beta )^{\top }, \Vert \theta -\theta ^0\Vert \ge 4c\}. \end{aligned}$$

If there exists a $c > 0$,

$$\begin{aligned} \underline{\lim } \inf _{\theta \in S_c} \frac{1}{N} [Q(\theta ) - Q(\theta ^0)] > 0 \ \ \ \ a.s. \end{aligned}$$

(21)

then $\widehat{\theta }$ is a strongly consistent estimator of $\theta ^0$.

Proof of Lemma 2

It follows by simple argument by contradiction, exactly similar to a lemma by Wu [15]. $\square$

Proof of Theorem 1

Consider

$$\begin{aligned} \frac{1}{N} [Q(\theta ) - Q(\theta ^0)]= & {} \frac{1}{N} \left[ \sum _{t=1}^N w \left( \frac{t}{N} \right) (y(t) - \mu (t;\theta ))^2 - \sum _{t=1}^N w \left( \frac{t}{N} \right) X^2(t) \right] \\= & {} \frac{1}{N} \left[ \sum _{t=1}^N w \left( \frac{t}{N} \right) (\mu (t;\theta ^0) - \mu (t;\theta ))^2 \right] \\&\quad + \frac{2}{N} \left[ \sum _{t=1}^N w \left( \frac{t}{N} \right) X(t)(\mu (t;\theta ^0) - \mu (t;\theta )) \right] \\&= f_1(\theta ) + f_2(\theta ). \end{aligned}$$

Here

$$\begin{aligned}&f_1(\theta ) = \frac{1}{N} \sum _{t=1}^N w \Bigl (\frac{t}{N} \Bigr )\Bigl (\mu (t;\theta ^0) - \mu (t;\theta ) \Bigr )^2\\&f_2(\theta ) = \frac{2}{N} \sum _{t=1}^N w \left( \frac{t}{N} \right) X(t) \Bigl (\mu (t;\theta ^0) - \mu (t;\theta ) \Bigr ). \end{aligned}$$

Consider

$$\begin{aligned}&S_{c,1} = \{\theta : \theta = (A,B,\alpha ,\beta )^{\top }, \Vert A-A^0\Vert \ge c\} \\&S_{c,2} = \{\theta : \theta = (A,B,\alpha ,\beta )^{\top }, \Vert B-B^0\Vert \ge c\} \\&S_{c,3} = \{\theta : \theta = (A,B,\alpha ,\beta )^{\top }, \Vert \alpha -\alpha ^0\Vert \ge c\} \\&S_{c,4} = \{\theta : \theta = (A,B,\alpha ,\beta )^{\top }, \Vert \beta -\beta ^0\Vert \ge c\}. \end{aligned}$$

Then $S_c \subset S_{c,1} \cup S_{c,2} \cup S_{c,3} \cup S_{c,4} = S$. Therefore,

$$\begin{aligned} \underline{\lim } \inf _{\theta \in S_c} f_1(\theta ) \ge \underline{\lim } \inf _{\theta \in S} f_1(\theta ) = \underline{\lim } \inf _{\theta \in \cup _j S_{c,j}} f_1(\theta ). \end{aligned}$$

Now

$$\begin{aligned} \underline{\lim } \inf _{\theta \in S_{c,1}} f_1(\theta )= & {} \underline{\lim } \inf _{\Vert A-A^0\Vert \ge c} (A-A^0)^2 \frac{1}{N} \sum _{t=1}^N w \left( \frac{t}{N} \right) \cos ^2(\alpha ^0 t+ \beta ^0 t^2) \\\ge & {} \gamma \ \ \underline{\lim } \inf _{\Vert A-A^0\Vert \ge c} (A-A^0)^2 \frac{1}{N} \sum _{t=1}^N \cos ^2(\alpha ^0 t+ \beta ^0 t^2) > 0. \\& (\hbox {using Result 1}). \end{aligned}$$

Similarly, it can be shown for $S_{c,2}, S_{c,3}$ and $S_{c,4}$ also. Therefore,

$$\begin{aligned} \underline{\lim } \inf _{\theta \in S_c} f_1(\theta ) > 0. \end{aligned}$$

Since from Lemma 1, it follows that

$$\begin{aligned} \lim \sup _{\theta } \Vert f_2(\theta )\Vert = 0, \end{aligned}$$

hence, we have

$$\begin{aligned} \underline{\lim } \inf _{\theta \in S_c} \frac{1}{N} [Q(\theta ) - Q(\theta ^0)] > 0 \ \ \ \ a.s. \end{aligned}$$

Using Lemma 2, the result follows. $\square$

Appendix B

In this Appendix we provide the Proof of Statement 1 based on Conjecture A.

Since

$$\begin{aligned} Q(\theta ) = \sum _{t=1}^N w \left( \frac{t}{N} \right) \left( y(t) - \mu (t; \theta ) \right) ^2, \end{aligned}$$

therefore,

$$\begin{aligned} Q'(\theta ^0)= & {} \left[ \begin{array}{c} \frac{\partial Q(\theta )}{\partial A} \\ \frac{\partial Q(\theta )}{\partial B} \\ \frac{\partial Q(\theta )}{\partial \alpha } \\ \frac{\partial Q(\theta )}{\partial \beta } \end{array} \right] _{\theta = \theta ^0} \\= & {} -2 \left[ \begin{array}{c} \sum _{t=1}^N w \left( \frac{t}{N} \right) X(t) \cos (\alpha ^0 t + \beta ^0 t^2) \\ \sum _{t=1}^N w \left( \frac{t}{N} \right) X(t) \sin (\alpha ^0 t + \beta ^0 t^2) \\ \sum _{t=1}^N t w \left( \frac{t}{N} \right) X(t) (B^0 \cos (\alpha ^0 t + \beta ^0 t^2) - A^0 \sin (\alpha ^0 t + \beta ^0 t^2)) \\ \sum _{t=1}^N t^2 w \left( \frac{t}{N} \right) X(t) (B^0 \cos (\alpha ^0 t + \beta ^0 t^2) - A^0 \sin (\alpha ^0 t + \beta ^0 t^2)) \end{array} \right] \\ Q^{''}(\theta ^0)= & {} \left[ \begin{array}{cccc} \frac{\partial ^2 Q(\theta )}{\partial A^2} &{} \frac{\partial ^2 Q(\theta )}{\partial A \partial B} &{} \frac{\partial ^2 Q(\theta )}{\partial A \partial \alpha } &{} \frac{\partial ^2 Q(\theta )}{\partial A \partial \beta } \\ \frac{\partial ^2 Q(\theta )}{\partial B \partial A} &{} \frac{\partial ^2 Q(\theta )}{\partial B^2} &{} \frac{\partial ^2 Q(\theta )}{\partial B \partial \alpha } &{} \frac{\partial ^2 Q(\theta )}{\partial B \partial \beta } \\ \frac{\partial ^2 Q(\theta )}{\partial \alpha \partial A} &{} \frac{\partial ^2 Q(\theta )}{\partial \alpha \partial B} &{} \frac{\partial ^2 Q(\theta )}{\partial \alpha ^2} &{} \frac{\partial ^2 Q(\theta )}{\partial \alpha \partial \beta } \\ \frac{\partial ^2 Q(\theta )}{\partial \beta \partial A} &{} \frac{\partial ^2 Q(\theta )}{\partial \beta \partial B} &{} \frac{\partial ^2 Q(\theta )}{\partial \beta \partial \alpha } &{} \frac{\partial ^2 Q(\theta )}{\partial \beta ^2} \end{array} \right] _{\theta = \theta ^0}. \end{aligned}$$

The elements of $Q^{''}(\theta ^0)$ are given at the end of this appendix. Let us denote

$$\begin{aligned} {{\varvec{D}}} = \hbox {diag}(N^{-1/2},N^{-1/2},N^{-3/2},N^{-5/2}). \end{aligned}$$

(22)

Then using Result 1, it follows that

$$\begin{aligned} {{\varvec{D}}} Q'(\theta ^0) {\mathop {\rightarrow }\limits ^{d}} N_4({{\varvec{0}}}, 2 \sigma ^2 \ {\varvec{\Sigma }}), \end{aligned}$$

where ${\varvec{\Sigma }}$ is same as defined in (9). Now expanding $Q'(\widehat{\theta })$ around $\theta ^0$ using Taylor series we obtain

$$\begin{aligned} Q'(\widehat{\theta }) = Q'(\theta ^0) + Q''(\bar{\theta })(\widehat{\theta }-\theta ^0), \end{aligned}$$

where $\bar{\theta }$ lies on the line joining $\widehat{\theta }$ and $\theta ^0$. Since $Q'(\widehat{\theta }) = {{\varvec{0}}}$, therefore

$$\begin{aligned} {{\varvec{D}}} Q'(\theta ^0) = - {{\varvec{D}}} Q''(\bar{\theta }){{\varvec{D}}}{{\varvec{D}}}^{-1}(\widehat{\theta }-\theta ^0). \end{aligned}$$

Since $\widehat{\theta } {\mathop {\rightarrow }\limits ^{a.s}} \theta ^0$, then using explicit expressions of the elements of $Q''(\theta ^0)$, and repeated use of Result 1, we obtain

$$\begin{aligned} \lim _{N \rightarrow \infty } {{\varvec{D}}} Q^{''}(\bar{\theta }) {{\varvec{D}}} = \lim _{N \rightarrow \infty } {{\varvec{D}}} Q^{''}(\theta ^0) {{\varvec{D}}} = {{\varvec{G}}}, \end{aligned}$$

where ${{\varvec{G}}}$ is same as in (10). Hence the results follow. $\square$

In the following we provide the second order derivatives of $Q(\theta )$ with respect to elements of $\theta$ at $\theta ^0$.

$$\begin{aligned} \frac{\partial ^2 Q(\theta ^0)}{\partial A^2}= & {} 2 \sum _{t=1}^N w \left( \frac{t}{N} \right) \left\{ \cos ^2(\alpha ^0 t + \beta ^0 t^2) \right\} , \\ \frac{\partial ^2 Q(\theta ^0)}{\partial B^2}= & {} 2 \sum _{t=1}^N w \left( \frac{t}{N} \right) \left\{ \sin ^2(\alpha ^0 t + \beta ^0 t^2) \right\} , \\ \frac{\partial ^2 Q(\theta ^0)}{\partial A \partial B}= & {} 2 \sum _{t=1}^N w \left( \frac{t}{N} \right) \left\{ \cos (\alpha ^0 t + \beta ^0 t^2) \sin (\alpha ^0 t + \beta ^0 t^2) \right\} , \\ \frac{\partial ^2 Q(\theta ^0)}{\partial \alpha ^2}= & {} 2 \sum _{t=1}^N w \left( \frac{t}{N} \right) \left\{ (B^0 t\cos (\alpha ^0 t + \beta ^0 t^2) - A^0 t \sin (\alpha ^0 t + \beta ^0 t^2))^2 \right\} \\&- 2 \sum _{t=1}^N t^2 w \left( \frac{t}{N} \right) X(t) \left\{ A^0 \sin (\alpha ^0 t + \beta ^0 t^2) + B^0 \cos (\alpha ^0 t + \beta ^0 t^2)\right\} , \\ \frac{\partial ^2 Q(\theta ^0)}{\partial \beta ^2}= & {} 2 \sum _{t=1}^N w \left( \frac{t}{N} \right) \left\{ (B^0 t^2 \cos (\alpha ^0 t + \beta ^0 t^2) - A^0 t^2 \sin (\alpha ^0 t + \beta ^0 t^2))^2 \right\} \\&- 2 \sum _{t=1}^N t^4 w \left( \frac{t}{N} \right) X(t) \left\{ A^0 \sin (\alpha ^0 t + \beta ^0 t^2) + B^0 \cos (\alpha ^0 t + \beta ^0 t^2)\right\} , \\ \frac{\partial ^2 Q(\theta ^0)}{\partial A \partial \alpha }= & {} 2 \sum _{t=1}^N w \left( \frac{t}{N} \right) (B^0 t\cos (\alpha ^0 t + \beta ^0 t^2) - A^0 t \sin (\alpha ^0 t + \beta ^0 t^2))\cos (\alpha ^0 t + \beta ^0 t^2) \\&+ 2 \sum _{t=1}^N t w \left( \frac{t}{N} \right) X(t) \sin (\alpha ^0 t + \beta ^0 t^2), \\ \frac{\partial ^2 Q(\theta ^0)}{\partial A \partial \beta }= & {} 2 \sum _{t=1}^N w \left( \frac{t}{N} \right) (B^0 t^2 \cos (\alpha ^0 t + \beta ^0 t^2) - A^0 t^2 \sin (\alpha ^0 t + \beta ^0 t^2))\cos (\alpha ^0 t + \beta ^0 t^2) \\&+ 2 \sum _{t=1}^N t^2 w \left( \frac{t}{N} \right) X(t) \sin (\alpha ^0 t + \beta ^0 t^2), \\ \frac{\partial ^2 Q(\theta ^0)}{\partial B \partial \alpha }= & {} 2 \sum _{t=1}^N w \left( \frac{t}{N} \right) (B^0 t\cos (\alpha ^0 t + \beta ^0 t^2) - A^0 t \sin (\alpha ^0 t + \beta ^0 t^2))\sin (\alpha ^0 t + \beta ^0 t^2) \\&- 2 \sum _{t=1}^N t w \left( \frac{t}{N} \right) X(t) \cos (\alpha ^0 t + \beta ^0 t^2),\\ \frac{\partial ^2 Q(\theta ^0)}{\partial B \partial \beta }= & {} 2 \sum _{t=1}^N w \left( \frac{t}{N} \right) (B^0 t^2 \cos (\alpha ^0 t + \beta ^0 t^2) - A^0 t^2 \sin (\alpha ^0 t + \beta ^0 t^2))\sin (\alpha ^0 t + \beta ^0 t^2) \\&- 2 \sum _{t=1}^N t^2 w \left( \frac{t}{N} \right) X(t) \cos (\alpha ^0 t + \beta ^0 t^2), \\ \frac{\partial ^2 Q(\theta ^0)}{\partial \alpha \partial \beta }= & {} 2 \sum _{t=1}^N t^3 w \left( \frac{t}{N} \right) (B^0 \cos (\alpha ^0 t + \beta ^0 t^2) - A^0 \sin (\alpha ^0 t + \beta ^0 t^2))^2 \\&- 2 \sum _{t=1}^N t^3 w \left( \frac{t}{N} \right) X(t) (A^0 \sin (\alpha ^0 t + \beta ^0 t^2) + B^0 \cos (\alpha ^0 t + \beta ^0 t^2)). \end{aligned}$$

Appendix C

We need the following lemma to prove Theorem 3.

Lemma 3

Let us denote

$$\begin{aligned} S_{1c} = \{\theta : \theta = (A,B,\alpha ,\beta )^{\top }, \Vert \theta -\theta _1^0\Vert \ge 4c\}. \end{aligned}$$

If there exists a $c > 0$,

$$\begin{aligned} \underline{\lim } \inf _{\theta \in S_{1c}} \frac{1}{N} [Q_1(\theta ) - Q_1(\theta _1^0)] > 0 \ \ \ \ a.s. \end{aligned}$$

(23)

then $\widetilde{\theta }_1$ that minimises $Q_1(\theta )$, is a strongly consistent estimator of $\theta ^0_1$.

Proof

It follows by contradiction using simple arguments. $\square$

Proof of Theorem 5

Consider

$$\begin{aligned}&\frac{1}{N} [Q_1(\theta ) - Q_1(\theta ^0)] \\&\quad = \frac{1}{N} \left[ \sum _{t=1}^N w \left( \frac{t}{N} \right) (y(t) - \mu (t;\theta ))^2 - \sum _{t=1}^N w \left( \frac{t}{N} \right) \left( X(t) + \sum _{k=2}^p \mu (t;\theta _k^0) \right) ^2 \right] \\&\quad = f_{11}(\theta ) + f_{21}(\theta ) \end{aligned}$$

where

$$\begin{aligned} f_{11}(\theta )= & {} \frac{1}{N} \left[ \sum _{t=1}^N w \left( \frac{t}{N} \right) (\mu (t;\theta _1^0) - \mu (t;\theta ))^2 \right] \\&+ \frac{2}{N} \left[ \sum _{t=1}^N w \left( \frac{t}{N} \right) (\mu (t;\theta _1^0) - \mu (t;\theta )) \sum _{k=2}^p \mu (t;\theta _k^0) \right] \\ f_{21}(\theta )= & {} \frac{2}{N} \left[ \sum _{t=1}^N w \left( \frac{t}{N} \right) X(t)(\mu (t;\theta _1^0) - \mu (t;\theta )) \right] . \end{aligned}$$

Using Lemma 1, it follows that

$$\begin{aligned} \sup _{\theta \in S_{1c}}\Vert f_{21}(\theta )\Vert {\mathop {\rightarrow }\limits ^{a.s.}} 0, \end{aligned}$$

and using lengthy but straight forward calculations and splitting the set $S_{1c}$ as in Theorem 1, it follows that

$$\begin{aligned} \underline{\lim } \inf _{\theta \in S_{1c}} f_{11}(\theta ) > 0 \ \ \ \ a.s. \end{aligned}$$

Hence,

$$\begin{aligned} \underline{\lim } \inf _{\theta \in S_{1c}} \frac{1}{N} [Q_1(\theta ) - Q_1(\theta _1^0)] > 0 \ \ \ \ a.s. \end{aligned}$$

and the result follows. $\square$

Appendix D

In this Appendix we provide the proof of Statement 3 based on Conjecture A.

Let us denote $Q'_1(\theta )$ as the $4 \times 1$ derivative vector and $Q_1^{''}(\theta )$ as the $4 \times 4$ second derivative matrix of $Q_1(\theta )$. Therefore, using multivariate Taylor series expansion of $Q_1'(\widetilde{\theta }_1)$ around $\theta _1^0$, we can get

$$\begin{aligned} Q_1'(\widetilde{\theta }_1) - Q_1'(\theta _1^0) = Q_1^{''}(\bar{\theta }_1) (\widetilde{\theta }_1 - \theta _1^0), \end{aligned}$$

(24)

where $\bar{\theta }_1$ is a point on the line joining $\widetilde{\theta }_1$ and $\theta _1^0$. Now following exactly the same procedure as Theorem 2, we can obtain

$$\begin{aligned} {{\varvec{D}}} Q_1'(\theta _1^0) {\mathop {\rightarrow }\limits ^{d}} N_4({{\varvec{0}}}, 2 \sigma ^2 {\varvec{\Sigma }}_1) \end{aligned}$$

and

$$\begin{aligned} \lim _{N \rightarrow \infty } {{\varvec{D}}} Q^{''}(\bar{\theta }_1) {{\varvec{D}}} = \lim _{N \rightarrow \infty } {{\varvec{D}}} Q^{''}(\theta _1^0) {{\varvec{D}}} = {{\varvec{G}}}_1, \end{aligned}$$

hence the result follows. $\square$

To prove Theorem 4, we need the following Lemma.

Lemma 6

$N(\widetilde{\alpha }_1 - \alpha _1^0) {\mathop {\rightarrow }\limits ^{a.s}} 0$ and $N^2(\widetilde{\beta }_1 - \beta _1^0) {\mathop {\rightarrow }\limits ^{a.s}} 0$.

Proof of Lemma 6

Let us denote the $4 \times 4$ diagonal matrix ${{\varvec{D}}}_1 = \hbox {diag} (1, 1, N^{-1}, N^{-2})$. Since $Q_1'(\widetilde{\theta }_1) = {{\varvec{0}}}$, therefore, from (24), we can write

$$\begin{aligned} - \frac{1}{N} {{\varvec{D}}}_1 Q_1'(\theta _1^0) = \left[ \frac{1}{N} {{\varvec{D}}}_1 Q_1^{''}(\bar{\theta }_1){{\varvec{D}}}_1 \right] {{\varvec{D}}}_1^{-1}(\widetilde{\theta }_1 - \theta _1^0). \end{aligned}$$

Using Lemma 1, it can be shown that $\displaystyle \frac{1}{N} {{\varvec{D}}}_1 Q_1'(\theta _1^0) {\mathop {\rightarrow }\limits ^{a.s}} {{\varvec{0}}}$ and

$$\begin{aligned} \lim _{N \rightarrow \infty } \frac{1}{N} {{\varvec{D}}}_1 Q_1^{''}(\bar{\theta }_1){{\varvec{D}}}_1 = \lim _{N \rightarrow \infty } {{\varvec{D}}} Q_1^{''}(\bar{\theta }_1){{\varvec{D}}} = {{\varvec{G}}}_1. \end{aligned}$$

Since ${{\varvec{G}}}_1$ is a positive definite matrix, the result follows. $\square$

Now to prove Theorem 7, note that using Lemma 6, we obtain

$$\begin{aligned}&\widetilde{A}_1 {\mathop {=}\limits ^{a.s.}} A_1^0 + o(1), \ \ \ \ \widetilde{B}_1 {\mathop {=}\limits ^{a.s.}} B_1^0 + o(1), \\&\widetilde{\alpha }_1 {\mathop {=}\limits ^{a.s.}} \alpha _1^0 + o\left( \frac{1}{N} \right) , \ \ \ \ \widetilde{\beta }_1 {\mathop {=}\limits ^{a.s.}} \beta _1^0 + o\left( \frac{1}{N^2} \right) . \end{aligned}$$

Here a random variable $U = o(1)$ means $U {\mathop {\rightarrow }\limits ^{a.s.}} 0$, $U = o\left( \frac{1}{N} \right)$ means $NU {\mathop {\rightarrow }\limits ^{a.s.}} 0$ and $U = o\left( \frac{1}{N^2} \right)$ means $N^2U {\mathop {\rightarrow }\limits ^{a.s.}} 0$. Therefore

$$\begin{aligned} \mu (t; \widetilde{\theta }_1) {\mathop {=}\limits ^{a.s}} \mu (t; \theta ^0_1) + o(1). \end{aligned}$$

Hence, the result follows. $\square$

Proof of Theorem 5

Note that it is enough to prove the following. If X(t) is same as defined before and $\widehat{A}$, $\widehat{B}$, $\widehat{\alpha }$ and $\widehat{\beta }$ minimize

$$\begin{aligned} \frac{1}{N} \sum _{t=1}^N w \left( \frac{t}{N} \right) (X(t) - \mu (t; \theta ))^2, \end{aligned}$$

then $\widehat{A} {\mathop {\rightarrow }\limits ^{a.s}} 0$ and $\widehat{B} {\mathop {\rightarrow }\limits ^{a.s}} 0$.

To prove the above statement, we denote $\widehat{A}$, $\widehat{B}$, $\widehat{\alpha }$ and $\widehat{\beta }$ by $\widehat{A}_N$, $\widehat{B}_N$, $\widehat{\alpha }_N$ and $\widehat{\beta }_N$, respectively, to emphasis that they depend on N. Suppose $\widehat{A}_N$ does not converge to zero a.s., and the same for $\widehat{B}_N$. Since $\widehat{A}_N$, $\widehat{B}_N$, $\widehat{\alpha }_N$ and $\widehat{\beta }_N$ are all bounded, therefore, there exists a subsequence $\{N_k\}$ of $\{N\}$ such that $\widehat{A}_{N_k} {\mathop {\rightarrow }\limits ^{a.s}} \bar{A} > 0$, $\widehat{B}_{N_k} {\mathop {\rightarrow }\limits ^{a.s}} \bar{B} > 0$, $\widehat{\alpha }_{N_k} {\mathop {\rightarrow }\limits ^{a.s}} \bar{\alpha }$ and $\widehat{\beta }_{N_k} {\mathop {\rightarrow }\limits ^{a.s}} \bar{\beta }$. Therefore, if $\widehat{\theta }_{N_k} = (\widehat{A}_{N_k},\widehat{B}_{N_k},\widehat{\alpha }_{N_k},\widehat{\beta }_{N_k})^{\top }$, then

$$\begin{aligned} \lim _{N_k \rightarrow \infty } \frac{1}{N_k} \sum _{t=1}^{N_k} w \left( \frac{t}{N_k} \right) (X(t) - \mu (t; \widehat{\theta }_{N_k}))^2 {\mathop {\rightarrow }\limits ^{a.s.}} \sigma ^2 c_1 + \frac{1}{2} (\bar{A}^2+\bar{B}^2). \end{aligned}$$

Consider a point $\theta ' = (\frac{1}{2} \bar{A},\frac{1}{2} \bar{B},\bar{\alpha },\bar{\beta })^{\top }$, then

$$\begin{aligned}&\lim _{N_k \rightarrow \infty } \frac{1}{N_k} \sum _{t=1}^{N_k} w \left( \frac{t}{N_k} \right) (X(t) - \mu (t; \theta _{N_k}))^2 \le \\&\ \ \ \lim _{N_k \rightarrow \infty } \frac{1}{N_k} \sum _{t=1}^{N_k} w \left( \frac{t}{N_k} \right) (X(t) - \mu (t; \theta '))^2 {\mathop {\rightarrow }\limits ^{a.s.}} \sigma ^2 c_1 + \frac{1}{4} (\bar{A}^2+\bar{B}^2), \end{aligned}$$

which is a contradiction. Hence the result follows. $\square$

Appendix E

We will show

$$\begin{aligned} \lim _{N \rightarrow \infty } \frac{1}{N} \sum _{t=1}^N w \left( \frac{t}{N} \right) \cos ^2 (\theta _1 t + \theta _2 t^2) = \frac{1}{2} \int _0^1 w(t) \hbox {d}t. \end{aligned}$$

For $\epsilon > 0$, there exists a polynomial $p_{\epsilon }(x)$, such that $\displaystyle \Vert w(x) - p_{\epsilon }(x)\Vert \le \epsilon$, for all $x \in [0,1]$. Hence,

$$\begin{aligned} \int _0^1 w(x) \hbox {d}x - \epsilon \le \int _0^1 p_{\epsilon }(x) \hbox {d}x \le \int _0^1 w(x) \hbox {d}x + \epsilon . \end{aligned}$$

Further

$$\begin{aligned}&\frac{1}{N} \sum _{t=1}^N p_{\epsilon } \left( \frac{t}{N} \right) \cos ^2(\theta _1 t + \theta _2 t^2) - \frac{\epsilon }{N} \sum _{t=1}^N \cos ^2(\theta _1 t + \theta _2 t^2) \\&\quad \le \frac{1}{N} \sum _{t=1}^N w \left( \frac{t}{N} \right) \cos ^2(\theta _1 t + \theta _2 t^2) \\&\quad \le \frac{1}{N} \sum _{t=1}^N p_{\epsilon } \left( \frac{t}{N} \right) \cos ^2(\theta _1 t + \theta _2 t^2) + \frac{\epsilon }{N} \sum _{t=1}^N \cos ^2(\theta _1 t + \theta _2 t^2). \end{aligned}$$

Suppose

$$\begin{aligned} p_{\epsilon }(x) = a_0 + a_1 x + \cdots + a_k x^k \ \Rightarrow \ \int _0^1 p_{\epsilon }(x) \hbox {d}x = a_0 + \frac{a_1}{2} + \cdots + \frac{a_k}{k+1}. \end{aligned}$$

Now due to Result 1,

$$\begin{aligned}&\frac{1}{N} \sum _{t=1}^N p_{\epsilon } \left( \frac{t}{N} \right) \cos ^2(\theta _1 t + \theta _2 t^2)\\&= \frac{1}{N} \sum _{t=1}^N \left\{ a_0 + \frac{a_1t}{N} + \cdots + \frac{a_k t^k}{N^k} \right\} \cos ^2(\theta _1 t + \theta _2 t^2) \\&\longrightarrow \frac{1}{2} \left[ a_0 + \frac{a_1}{2} + \cdots + \frac{a_k}{k+1} \right] = \frac{1}{2} \int _0^1 p_{\epsilon }(x) \hbox {d}x. \end{aligned}$$

Therefore,

$$\begin{aligned}&\lim _{N \rightarrow \infty } \frac{1}{N} \sum _{t=1}^N p_{\epsilon } \left( \frac{t}{N} \right) \cos ^2(\theta _1 t + \theta _2 t^2) - \frac{\epsilon }{2}\\&\le \lim _{N \rightarrow \infty } \frac{1}{N} \sum _{t=1}^N w \left( \frac{t}{N} \right) \cos ^2(\theta _1 t + \theta _2 t^2) \le \\&\lim _{N \rightarrow \infty } \frac{1}{N} \sum _{t=1}^N p_{\epsilon } \left( \frac{t}{N} \right) \cos ^2(\theta _1 t + \theta _2 t^2) + \frac{\epsilon }{2}. \end{aligned}$$

Hence

$$\begin{aligned} \frac{1}{2} \int _0^1 w(t) \hbox {d}t - 2 \epsilon \le \lim _{N \rightarrow \infty } \frac{1}{N} \sum _{t=1}^N w \left( \frac{t}{N} \right) \cos ^2(\theta _1 t + \theta _2 t^2) \le \frac{1}{2} \int _0^1 w(t) \hbox {d}t + 2 \epsilon . \end{aligned}$$

Since $\epsilon$ is arbitrary, the result follows. Exactly, the same proof will go through for

$$\begin{aligned} \lim _{N \rightarrow \infty } \frac{1}{N} \sum _{t=1}^N w \left( \frac{t}{N} \right) \sin ^2 (\theta _1 t + \theta _2 t^2) = \frac{1}{2} \int _0^1 w(t) \hbox {d}t. \end{aligned}$$

$\square$