High-Radix Formats for Enhancing Floating-Point FPGA Implementations

Abstract

This article proposes a family of high-radix floating-point representation to efficiently deal with floating-point addition in FPGA devices with no native floating-point support. Since variable shifter implementation (required in any FP adder) has a very high cost in FPGA, high-radix formats considerably reduce the number of possible shifts, decreasing the execution time and area highly. Although the high-radix format produces also a significant penalty in the implementation of multipliers, the experimental results show that the adder improvement overweights the multiplication penalty for most of the practical and common cases (digital filters, matrix multiplications, etc.). We also provide the designer with guidelines on selecting a suitable radix as a function of the ratio between the number of additions and multiplications of the targeted algorithm. For applications with similar numbers of additions and multiplications, the high-radix version may be up to 26% faster and even having a wider dynamic range and using higher number of significant bits. Furthermore, thanks to the proposed efficient converters between the standard IEEE-754 format and our internal high-radix format, the cost of the input/output conversions in FPGA accelerators is negligible.

1 Introduction

In recent years we are witnessing an enormous acceleration in the inclusion of FPGAs in the basic architecture of computational systems. These systems range from large servers for cloud computing to low-power embedded systems for IoT or signal processing. In those heterogeneous architectures, generally, the FPGA is used as an accelerator to implement the most demanding task of the system. Although fixed-point arithmetic has been used traditionally in FPGA, in this model, the utilization of floating-point arithmetic is preferred for many applications such as advanced signal processing [6, 7, 15], industrial [16, 17, 20], wireless communication [8, 21], and other advanced applications [11,12,13,14, 18, 19, 22]. Although the fixed-point number operation has the advantages of fast computation and easy implementation, floating-point (FP) arithmetic offers a larger dynamic range and higher numeric stability.

Most FPGA implementations that use FP arithmetic follow the IEEE-754 standard [10] or a very similar data format. That is even more true when the FPGA device or the system also includes embedded processors, which always fulfilled the standard. In fact, the newest FPGAs from Intel include hardened floating-point operators compliant with the IEEE-754 standard. However, the IEEE-754 standard was defined concerning general-purpose processors, which are implemented using ASIC technologies. Thus, some requirements of this standard may not match the typical characteristics of FPGA devices. A more efficient implementation of FP arithmetic for FPGAs could be achieved if the architecture was defined taking into account the resources available in FPGA devices [2, 4, 9]

For instance, FP addition involves two variable shifters and a leading zero detector (for alignment and normalization), which are very slow when they are implemented in FPGAs. If the maximum number of digits to be shifted is reduced, the penalty due to this operation also decreases. Some implementation results of a radix 4 and 16 for addition and multiplication for FPGA-specific devices were presented in [2], in which negligible gain for codes with a balanced number of additions and multiplications (about 1% speedup) was obtained. This is a serious handicap since the most frequent operations in typical applications involve massive multiplications and additions/subtractions.

This paper shows that using higher radices allows achieving very significant speedup and area reduction for the adder implementation. These improvements are so significant that they overweight the multiplier penalty when the number of additions and multiplications is balanced. This paper is an extension of our work on radix 64 FP, presented in [23], where we obtained a net gain of 23% of speed for circuits where the number of multipliers equals the number of adders. This paper extends the radix 64 adder, multiplier, and converter design proposed in [23] to any radix. We also studied how the number of significant bits of the mantissa and the dynamic range increase with the radix. Besides that, it offers guidelines for selecting a suitable radix as a function of the additions/multiplications ratio and the optimization goal. The designer can assess whether a high-radix representation is required, and if so, select a suitable radix as a function of improving either the area or the delay.

The rest of this paper is structured as follows: Sect. 2 presents the proposed high-radix format as a function of the radix, how it affects the number of significant bits and the dynamic range, and how to perform conversions between this format and the standard IEEE-754; Sect. 3 proposes the algorithm and architecture to perform high-radix FP addition; Sect. 4 summarizes the modifications require in the multipliers architecture; Sect. 5 presents the implementations results and comparison; and finally Sect. 6 summarizes the conclusion of this work.

2 The Proposed High-Radix Floating-Point Format

As we state in introduction, nowadays, the most likely scenario for an FPGA implementation using FP arithmetic is an architecture that includes processors and accelerators implemented in the reconfigurable logic of the FPGA. Hence, it is very likely that the input and output data were provided in IEEE-754 FP representation. Without any loss of generality, let us consider this input and output values are under the IEEE-754 single-precision FP format.

The representation of an IEEE-754 FP number x is

$$\begin{aligned} x = (-1)^{S_x} M_x \cdot 2^{E_x} \end{aligned}$$

(1)

where $S_x \in \{0,1\}$ is the sign, $M_x$ is the magnitude of the significand (24 significant bits for single precision, also called mantissa), and $E_x$ is the exponent (8 bits, bias 127). The significand is a radix 2 normalized number with one integer bit $M_x = 1.F$ (F is the fraction).

We propose using a radix $2^r$ (with r being an integer and $r>1)$ for the base of the representation of a FP number instead of radix 2.

Let us define the representation of a FP number x as follows:

$$\begin{aligned} x = (-1)^{S'_x}M'_x \cdot (2^r)^{E'_x} \end{aligned}$$

(2)

where $S'_x$ is the sign bit, $M'_x$ is the magnitude of the significand, $2^r$ is the base or radix, and $E'_x$ is the new exponent.

For the base $2^r$, the value of r corresponds to an integer number such that $1< r \le 24$ (the case r=1 is the standard radix 2 representation), and it also means that each digit has r bits. The significand $M'_x$ is a radix $2^r$ normalized number such that $1 \le M'_x < 2^r$. Due to this normalization, $M'_x$ is composed of one integer digit and $\left\lceil \frac{24}{r} \right\rceil$ fractional ones, where each digit is composed of r-bits. Let us denote the number of fractional digits as f

$$\begin{aligned} f= \left\lceil \frac{24}{r} \right\rceil \end{aligned}$$

(3)

and the number of fractional bits as w such that

$$\begin{aligned} w= r\left\lceil \frac{24}{r} \right\rceil \end{aligned}$$

(4)

Thus,

$$\begin{aligned} M'_x = D_0.D_1D_2 \cdot \cdot \cdot D_f \end{aligned}$$

(5)

where $D_0$ through $D_f$ are digits of r bits ($D_i$ represents the digit of relative weight $(2^r)^{-i}$). Basically, this means that the integer part of the significand is the MSD ($D_0$), whereas the fractional part is composed of the remaining digits ($D1\cdot \cdot \cdot Df$). Figure 1 shows the different fields and parameters of the significand for the proposed generic radix $2^r$ format.

Fig. 1

Normalized significand in radix $2^r$

The $1+ f$ digits used and the proposed normalization $(D0.D1\cdot \cdot \cdot Df)$ ensure that the minimum number of significant bits is $1 + w > 24$, which corresponds to an integer part equal to one ($1 \le M'_x <2^{r}$) and w fractional bits (see Fig. 1). In fact, the number of significant bits ranges from $1 + w$ to $r+w$, depending on the magnitude of the integer part of $M'_x$, that is, the leading zeros of the digit $D_0$ (see Fig. 1). Thus, the proposed format always has several significant bits greater than that of IEEE 754 (24 bits).

2.1 Exponent Width

Assuming the same characteristic as the standard format for the exponent of the new format $E'_x$, the largest nonzero and positive normalized representable number is $[ 2^r-2^{-w} ] (2^r)^{E'_{x_{\max }}}$, where $[2^r-2^{-w}]$ corresponds to the maximum significand (all bits set to 1 for all digits Di) and $E'_{x_{\max }}$ is the maximum positive value of the exponent. This value has to be greater than or equal to that of the single-precision IEEE standard, that is $(2-2^{-23})2^{127}$. Thus,

$$\begin{aligned}{}[ 2^r-2^{-w} ] (2^r)^{E'_{x_{\max }}} \ge 2^{128}-2^{104} \end{aligned}$$

(6)

Reducing this expression we have

$$\begin{aligned} 2^{rE'_{x_{\max }}+r} - 2^{rE'_{x_{\max }}-w } \ge 2^{128}-2^{104} \end{aligned}$$

(7)

Thus, since $2^{rE'_{x_{\max }}+r} > 2^{rE'_{x_{\max }}-w }$ we have

$$\begin{aligned} 2^{rE'_{x_{\max }}+r} > 2^{128}-2^{104} \end{aligned}$$

(8)

From this expression we deduce that the value of the new exponent that ensures expression (6) has to be

$$\begin{aligned} E'_{x_{\max }} > \frac{\log _2(2^{128}-2^{104})}{r} -1 \end{aligned}$$

(9)

On the other hand, the smallest nonzero and positive normalized representable number is $(2^r)^{E'_{x_{\min }}}$, where $E'_{x_{\min }}$ is the smallest exponent (in this case, the smallest significand is 1). This number has to be less than or equal to the smallest nonzero and positive number of IEEE: $2^{rE'_{x_{\min }}} \le 2^{-128}$. This expression is fulfilled if the exponent reaches the value $E'_{x_{\max }} \le -\frac{128}{r}$. In conclusion, to cover the dynamic range, we need an exponent $E'_x$ ranging $-\frac{128}{r}$ through $\frac{\log _2(2^{128}-2^{104})}{r} -1$. Thus, the width of the exponent $\hbox {width}(E'_x)$ has to accomplish:

$$\begin{aligned} \hbox {width}(E'_x) \ge \log _2 \left( \frac{\log _2(2^{128}-2^{104})}{r} -1 + \frac{128}{r}\right) \end{aligned}$$

(10)

Taking into account that $\log _2(2^{128}-2^{104}) > 128-2^{-23}$, we have

$$\begin{aligned} \hbox {width}(E'_x) \ge \log _2 \left( \frac{256}{r} - 1 -\frac{2^{-23}}{r}\right) \end{aligned}$$

(11)

Taking into account that the minimum value of r is r=2:

$$\begin{aligned} \hbox {width}(E'_x) \ge \log _2\left( \frac{256}{r} - 1 - 2^{-24}\right) \end{aligned}$$

(12)

The width of $E'_x$ has to be an integer, thus

$$\begin{aligned} \hbox {width}(E'_x) = \left\lceil \log _2(\frac{256}{r} - 1 - 2^{-24}) \right\rceil \end{aligned}$$

(13)

On the other hand, since r is an integer and $1<r\le 24$ , we have checked all the possible values of r and verified

$$\begin{aligned} \left\lceil \log _2(\frac{256}{r} - 1 - 2^{-24}) \right\rceil = \left\lceil \log _2(\frac{256}{r} ) \right\rceil \end{aligned}$$

(14)

As a consequence, we conclude that the number of bits of the exponent to cover the dynamic range of IEEE is

$$\begin{aligned} \hbox {width}(E'_x) = \left\lceil \log _2\frac{256}{r} \right\rceil = \left\lceil 8-\log _2r \right\rceil \end{aligned}$$

(15)

2.2 Dynamic Range

Once we know the number of bits of the new exponent $E'_x$, we can derive the dynamic range of the new representation. The dynamic range is

$$\begin{aligned} \left[ (2^r)^{E'_{x_{\min }}}, (2^r-2^{-w}) (2^r)^{E'_{x_{\max }}}\right] \end{aligned}$$

(16)

Taking into account that the number of bits of the exponent is given by $\left\lceil 8-\log _2r \right\rceil$ (see expression (15)), the smallest value for the exponent is $E'_{x_{\min }}=-2^{\left\lceil 8-\log _2r \right\rceil -1}$. On the other hand, the largest value of the exponent is $E'_{x_{\max }}= 2^{\left\lceil 8-\log _2r \right\rceil -1}-1$. Substituting these values in expression (16) and operating we conclude that the dynamic range for radix r is:

$$\begin{aligned} \left[ 2^{-r(2^{\left\lceil 8-\log _2r \right\rceil -1})}, \left( 2-2^{-w-r+1}\right) 2^{r( 2^{\left\lceil 8-\log _2r \right\rceil -1})-1} \right] \end{aligned}$$

(17)

Table 1 shows the different parameters for some radices. These radices correspond to the actual implemented architectures of Sect. 5. All parameters of Table 1 are derived from expressions (3), (4), (15) and (17). The first row shows the parameters for the radix 2 IEEE 754 single precision. From Table 1 can see that for all the radices, the number of significant bits (column Signif. bits) is greater than 24, and the dynamic range is also greater than that of radix 2 IEEE.

Table 1 Parameters for different radices for single precision

To make the text more readable, from this point on we illustrate the different general expressions with a specific example of radix 64 (r=6), which corresponds to the work of [23]. For example, for radix 64 the significand $M'_x$ ranges $1 \le M'_x < 64$ . The parameter $f=4$ (by application of Eq. (3) for $r=6$) and thus $M'_x$ is composed of five 6-bit digits with one integer digit and four fractional ones ($M'_x = D_0.D_1D_2D_3D_4$) (see Eq. (5)). The width of the exponent $E'_x$ is 6 and the parameter $w=24$, which ensures a dynamic range of $[1\cdot 2^{-192},(64-2^{-24})\cdot 2^{186}]$ (see Eq. (17)), which is wider than that of the IEEE-754. The number of significant bits ranges from 25 to 30 bits.

2.3 Format Conversion and Architectures

This subsection analyzes the conversion of a normalized single- precision IEEE-754 number (Eq. (1)) to/from the new format indicated by Eq. (2) and their associated architectures. Three parameters have to be obtained $(S'_x,M'_x,E'_x)$ from those of the IEEE-754 representation of a number $(S_x,M_x,E_x)$. The sign is trivial ($S'_x = S_x$). The exponent is obtained as

$$\begin{aligned} E'_x = \left\lfloor \frac{E_x-127}{r} \right\rfloor + 2^{r-1} \end{aligned}$$

(18)

To obtain the new mantissa $M'_x$ from $M_x$ we need to align it. The new mantissa requires the following operation:

$$\begin{aligned} M'_x = M_x 2^{(E_x-127) \ mod*\ r } \end{aligned}$$

(19)

where mod* is an operator such as

$$\begin{aligned} A \ mod*\ B = \left\{ \begin{array}{cl} A \ mod\ B &{} \hbox {if} \ A \ge 0 \\ -(|A| \ mod\ B)+B &{} \hbox {if} \ A < 0 \end{array} \right. \end{aligned}$$

(20)

Table 2 Parameters for different radices for the adder, converters and multiplier

Figure 2 shows a possible architecture to convert a single-precision IEEE-745 FP number to the proposed format for a generic radix $2^r$. It has two modules, namely a look-up table and a binary right shifter. Since our final device is an FPGA, we design conversion functions (18) and (19) utilizing a small look-up table instead of implementing the corresponding logic circuits, as shown in the module Look-up table of Fig. 2. The input to this module is the exponent of the IEEE-754 number $E_x$ (8 bits, 256 inputs), and the outputs of this module are the new exponent $E'_x$ ($\lceil 8-\log _2r \rceil$-bits width) and the number of bits to be right-shifted for the mantissa (the exponent of equation (19), $\lceil \log _2r \rceil$-bits width). A binary variable shifter module is required for this operation. The size of the look-up table for different radices is shown in row T1 of Table 2. For radix 64 (r = 6), the size of the look-up table is $8\times 9$ bits (9 bits = 6 for the new exponent plus 3 for the binary shifter).

Fig. 2

Format conversion (direct)

On the other hand, Fig. 3 shows the architecture to convert a number from our internal format to the IEEE-754 format, for a general radix $2^r$. It is a more complex circuit that has six modules, namely a Look-up table (dealing with the exponent), a leading one detector (determining the number of zeros of the MSD), a right shifter (shifting $r-1-k$ bits), a rounding module and two adder modules (for the final new exponent and significand). Next, we describe the functionality of each module and their interrelationships in detail.

The sign has a direct conversion. To obtain the significand, the module leading one detector in Fig. 3 is in charge of obtaining the number of leading zeros of the MSD (we call this number k). For the same reason as in the direct conversion, the implementation of this module is conducted using a look-up table of size $(2^r\times r-1)$. A right shift of $r-1-k$ bits is required for the significand of $r+w$ bits, which results in a number with 24 bits. This operation is done by the shifter module called $2^{r-1-k}$ in Fig. 3.

Rounding is required since there may be some shifted out bits in the LSD. The module Rounding is in charge of obtaining the value 1 or 0 to be added to the shifted significand. This rounding requires analyzing the LSD as well as the value $r-1-k$ (given by the leading one detector module). The exponent is obtained by

$$\begin{aligned} E_x = r (E'_x-2^{r-1}) + 127 + (r-1-k) \end{aligned}$$

(21)

We can use a small $\lceil 8-\log _2r \rceil$-input bits look-up table ($2^{\lceil 8-\log _2r \rceil } \times 8$ bits), which gives the value $r (E'_x-2^{r-1}) + 127$, as shown in Fig. 3. The size of the look-up table module for different radices is shown in row T2 of Table 2. For radix 64 ($r=6$), the size of the required tables is $6\times 8$ (for the exponent conversion) and $64\times 5$ (for the leading zero detector).

Finally, if there is an overflow due to rounding, the significand would be of the form “10.000...”. In this case, the exponent is increased by connecting the overflow signal of the right-side adder (Ovf) with the carry input of the left-side adder (Cin) as shown in Fig. 3).

Fig. 3

Format conversion (inverse)

3 Addition with the New Format

Let x and y be two FP numbers in radix r according to the format of expression (2). The addition (subtraction) under the new format is similar to the addition of two standard IEEE FP numbers and consists of six steps. First, the exponents are subtracted. If the difference of exponents is greater than f, the sticky bit of the second operand is set for rounding operation. If it is less than f, the addition is conducted in the next step by aligning the significand, and the sticky bit of the shifted out digits is required for further operations. If the exponent difference is zero, the significands are aligned, and then the sticky bit is only required in case of an overflow.

To align the significands (second step) have to shift right $d=|E'_x-E'_y|$ positions (digits) the significand of the operand with the smallest exponent and select the largest exponent as the exponent of the result. Note that $|E'_x-E'_y| = \{0,1,\ldots ,\lceil 24/r \rceil \}$ ($\{0,1,2,3,4\}$ for radix 64) is a reduced set of shifts compared to the standard case ($\{0,1,\ldots ,23\}$) (the higher radix, the shorter set of shifts). The sticky bit of the shifted out digit has to be calculated. In the third step, the significands are added (subtracted). $1 + f$ digits are involved in each operation. The next step is normalization. Due to the characteristics of the proposed format, a non-normalized result is only possible under the overflow of the significand (addition, one-digit right-shift) or if the integer part of the result is zero (subtraction, a left-shift up to f digits).

The fifth step is rounding (rounding to nearest, to even when tie) and the sixth is normalization.

Let us decompose the final significand of the result of an operation $M'$ as a function of the number of bits of the fractional part of the normalized significand (w):

$$\begin{aligned} M'=M'^{(w)} + M'^{(d)}2^{-w} \end{aligned}$$

(22)

where $M'^{(w)}$ is composed of the integer part of $M'$ plus the w most significant fractional bits, and $0 \le M'^{(d)} < 1$. Namely, $M'^{(w)}$ has the precision of the significand in our FP system and $M'^{(d)}$ represents the rest of the bits. Let G denote the bit with weight $2^{-w}$ (that is, the LSB of the LSD, see Fig. 1). We define the rounding to nearest of the significand $r(M')$ as follows:

$$\begin{aligned} r(M')= \left\{ \begin{array}{ll} M'^{(w)} + G\cdot 2^{-w} &{} \hbox {if} \ M'^{(d)} \ne 0 \\ M'^{(w)} &{} \hbox {if} \ M'^{(d)} = 0 \end{array} \right. \end{aligned}$$

(23)

In comparison with the corresponding IEEE-754 round to nearest, the final rounded value of our approach always has a precision greater than that of IEEE-754 since the IEEE-754 standard defines a significand of 23 fractional bits, whereas we have w fractional bits, and $w \ge 24$ (see Fig. 1 and Table 1). To prove this, note that

$$\begin{aligned} w=r\lceil 24/r \rceil \rightarrow \left\{ \begin{array}{ll} = 24 &{} \mathrm{when~~} (24~mod~r) = 0 \\ > 24 &{} \mathrm{when~~} (24~mod~r) \ne 0 \end{array} \right. \end{aligned}$$

(24)

In other words, the round to nearest mode (not tie) is quite similar to that of the standard, but uses at least 24 fractional bits (worst case) instead of 23. In the following, we consider the worst case of having $w=24$ in the different analyses.

In case of a tie, the IEEE standard proposes the tie-to-even solution. In our case, since in the worst case we have at least 25 significant bits (one significant bit in the integer digit plus 24 bits in the fractional digits) instead of 24 fixed significant bits, the middle value $M'^{(d)}=0$ can be covered by the G bit. Let us address the subtraction operation. Since our format has $1+f$ digits ($r+w$ bits), in most cases, the result of a subtraction has more than 24 significant bits and rounding can be conducted using the G bit, as proposed in Eq. (23).

Nevertheless, some extreme cases require some extra guard bits. Having analyzed all these cases, we deduce that two extra bits are required for rounding: a guard bit and the sticky bit (see [23] for details). Thus, the path for the actual implementation of the addition/subtraction operation requires two extra fractional bits, up to 26. Nevertheless, for the cases in which the number of fractional bits w is 25 ($w=25$), only one extra fractional bit is required (the sticky bit), whereas the cases with $w \ge 26$ do not need any extra guard bits, although the LSB of the LSD can be replaced by the sticky bit. In other words, if the number of fractional bits w of the selected format is greater than 24, the extra bits in the LSD can be used as guard bits and the sticky bit. In any case, rounding is conducted based on the final result by applying Eq. (23). In [23], the proposed rounding is compared with that of the IEEE, proving that the proposed rounding uses more significant bits and has a greater precision since our format has a precision of between 25 and $r+w$ bits (due to normalization) and the single-precision IEEE has 24 bits.

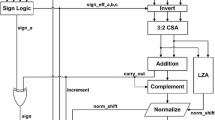
3.1 Architecture

In this section, we explain in detail Fig. 4 which shows the proposed architecture for radix $2^r$. Our design is based on that of the standard radix 2 single-path architecture [5] which is intended to minimize the critical path. We select this architecture among many others since it is accepted as a standard for floating-point addition by most authors. Nevertheless, the techniques presented here can be applied to any design. To be precise, the key to improving our architecture for FPGA-based designs is the use of high radix since it simplifies the variable shifters, and this element is found in all floating-point designs.

Fig. 4

Architecture for addition/subtraction for radix $2^r$

We extend the radix 2 architecture of [5] to a generic radix $2^r$, which is not straightforward due to some aligning issues (use digits instead of bits). The minimization of the critical path is achieved by the simultaneous operation of the comparison of the significands (module compare in Fig. 4) and the variable shifter (module $(2^r)^{-d}$).

Figure 4 is made up of three functional blocks, and each block has several modules. Now we explain in detail every functional block and its modules.

Block 1 of Fig. 4 is devoted to the significand alignment and addition, and it has eight modules: a module for subtracting the exponents (generating the signal d difference of exponents); a module for comparison of the significands (which control the final inverter modules of this block); a Swap module (which leaves the provisional largest operand in the left output); a high-radix variable shift module ($(2^r)^{-d}$ that carries out a right shift of d digits); a Sticky1 module (generating the rounding bit R and the sticky bit T); two conditional bit inverter modules (ensuring the largest operand on the left side); and, finally, an adder/subtractor (adding/subtracting the significands aligned suitably). Next, we explain the functioning of these modules in detail.

The objective of the different modules above the general adder/subtractor of block 1 of Fig. 4 (module +/-) is to place the largest operand on the left input and the smallest one on the right input of the adder/subtractor (and consequently, the result is always a positive (or zero) number). In order to do that, the exponents of the operands are subtracted to find out which operand is the largest (from the difference of the exponents d). The sign of d is used to place the significand of the largest operand in the left output of the module Swap. Nevertheless, if the difference of exponent is 0 (that is $d=0$), then the significands have to be compared to determine the largest one. This operation is carried out by the module Compare of block 1. The output of this module controls the operation of the inverters. The inversion is needed to correct a possible wrong placing at the inputs of the adder/subtractor (for $d=0$ and effective subtraction operation only). If this happens, we change the sign of the operands at the input of the adder/subtractor and then the result is always a positive value (or zero), see [5].

In block 1 of Fig. 4, the difference of exponents (d) is used to shift the significand of the smallest operand (high-radix variable shifter module $(2^{r})^{-d}$, for radix $2^r$). The module Sticky1 is in charge of obtaining the two extra guard bits required in a subtraction (the rounding bit R and the sticky bit T). As stated before, the two extra bits can be integrated in the extra bits of the LSD (those beyond the precision of 24 fractional bits) if that is possible. If it is not the case, they have to be explicitly appended to the data path (for example, for radix 128 ($r=7$ bits per digit, $w=28$ fractional bits, see expressions (3) and (4)), the LSD has 4 extra bits, two out of them can be used as R and T bits). Thus, the adder/subtractor has inputs of $r+w+2$ bits if the number of fractional bits $w=24$ (for instance, $r+w+2=32$ bits for radix 64), $r+w+1$ if $w=25$ or $r+w$ if $w\ge 26$ (see Sect. 3 and Table 1). The word length of the adder/subtractor for several radices is shown in the column WL of Table 2.

Block 2 of Fig. 4 is devoted to the overflow and rounding, and it has five modules. The module $(2^{r})^{-1}$ in block 2 is a fixed one-digit right shifter that is used in case of overflow, and the MUX module selects the suitable value (depending on whether there is an overflow or not). The module Sticky2 generates the bits R and T (similar to block 1). The module Rounding Calculus produces the bit for rounding (depending on G, R, and T bits). Finally, the adder of block 2 performs the addition operation for rounding. Next, we explain the functioning of these modules in detail.

If an overflow is produced in the adder/subtractor of block 1, a right shift of one digit is required in the case of overflow (only for the addition operation, module called $(2^{r})^{-1}$ in block 2 of Fig. 4). The extra bits required (due to the shift out of the LSD) are obtained by the module Sticky2 of the block 2 and generates the bits R and T. In the case of subtraction, the bits R and T do not need to be re-computed. The module Sticky2 controls the final value of R and T depending on the operation.

The Rounding Calculus module of block 2 performs the computation of a 0 or 1 according to Eq. (23). In this equation, the value of $M'{(d)}$ corresponds to the bits R and T (a logic OR). The adder carries out the final rounding.

Block 3 of Fig. 4 is devoted to normalization. It has five modules, namely the module Digit Leading Zero Detector (for counting the number of leading zeros ldz of the output of the adder), a high-radix left shifter module $(2^{r})^{+ldz}$ (shifting ldz digits), a multiplexor module MUX (selecting the suitable value), a module for updating the exponent, and a final register $M'z$. Next, we explain the functioning of these modules in detail.

If an overflow is produced after rounding (in the adder of block 2), the result is a leading 1 followed by all zeros ( that is $10\cdot \cdot \cdot 0.000\cdot \cdot \cdot 000$). This situation requires updating the exponent (module Update Exp. of block 3 of Fig. 4) and also the value 1.0 as the final significand of the operation (this is why one of the inputs of the multiplexor module is 1.0 in block 3, and the overflow signal ovf2 controls the MUX module).

If the involved operation is an effective subtraction, it is possible to have several leading zero digits. The module Digit Leading Zero Detector of block 3 is in charge of counting the number of zero digits, and then the corresponding digit left shift is performed by the module $(2^{r})^{+lzd}$ (ldz is the number of digits to be shifted). If all digits of the result are zero, it is a special value that must be handled separately (the corresponding hardware is not shown in the figure for clarity).

Finally, the exponent $E'$ must be updated ($E'$ is the maximum of the initial exponents). The module entitled Update Exp. of block 3 is in charge of adding 1 if an overflow is produced or subtracting the value lzd in case of having a left shift.

4 Multiplication

FP multiplication does not involve shift operations. The improvement in addition (due to the improvement in the shift operation) does not speedup multiplication; in fact it slows it down, as shown in [2]. This degradation is because the longer the word length, the larger the multiplier and, as a consequence, the longer the execution time.

Since most applications use both multiplications and additions, we must consider multiplication for numbers under our high-radix FP format. In our case, the significand has $r+w$ bits instead of 24.

Let $x'$ and $y'$ be the operands of two FP numbers using our format, which are represented by $(S'_x,E'_x,M'_x)$ and $(S'_y,E'_y,M'_y)$, respectively. The result $z'= x' \times y'$ is represented by $(S'_z,E'_z,M'_z)$. The resulting sign is $S'_z= s'_x \oplus s'_y$, the exponent is $E'_z= E'_x + E'_y$, and the new significand is $M'z = M'_x \times M'_y$, where a $(r+w)\times (r+w)$ unsigned multiplier is required ($1+f$ digits for each operand, for instance, 5 digits for radix 64).

Let us address normalization. The result of the multiplication has $2(f+1)$ digits (for example, 10 digits for radix 64), and we have to select the $1+f$ most significant nonzero digits (5 digits for radix 64). Let us call the $2(f+1)$ digits of the result $D_0,D_1,...,D_{2f+1}$ ($D_0$ is the most significant). Since $M'_x$ and $M'_y$ are both greater than or equal to one (that is, the MSD of both operands is greater than or equal to one), the normalized significand of the result is

$$\begin{aligned} M'_z= \left\{ \begin{array}{ll} (D_0.D_1\cdot \cdot \cdot D_{f}) &{} if \ D_0 \ne 0 \\ (D_1.D_2\cdot \cdot \cdot D_{f+1}) &{} if \ D_0 = 0 \end{array} \right. \end{aligned}$$

(25)

If $D_0 = 0$ the exponent has to be updated $E'_z= E'_z - 1$.

Regarding the rounding, the same solution as the addition operation is used since the normalized result has at least 25 significant bits (see Eq. (23)). In this case, the value of $M'^{(d)}$ (the sticky bit) has to be computed from either $D_{f+1}$ through $D_{2f+1}$ or $D_{f+2}$ through $D_{2f+1}$ (see Eq. 25).

5 Implementation Results and Comparison

Before starting the evaluation of our proposal, we must remind the reader that the goal of this work is to improve the implementation of FP architectures in FPGA devices with no native support for IEEE 754 single-precision FP (like the Xilinx ones). Therefore, we will not compare our approach with hardened floating-point operators like the one in Arria 10 FPGA family [1]. In what follows, we study and compare the different radix alternatives, providing a helpful guideline to the designers to select the suitable radix for their applications in Xilinx-like FPGA devices.

The proposed adder, multiplier, and conversion circuits have been implemented in VHDL for different radices. Tables 1 and 2 show the different parameters used for these implementations. For comparison purpose, the corresponding modules generated by the open-source library FloPoCo [3] and the ones corresponding to the Xilinx IP library LogiCORE FP operators v6.0 [24] have been used as representative of the radix 2 FP format. For a fair comparison with FloPoCo’s modules, special cases are handled in our architectures in the same way as in the FloPoCo one. Similarly, for the sake of simplicity, all the designs are compared using the fully combinational version.

All these modules were simulated using ModelSim SE 6.3f and were synthesized using Xilinx ISE 13.4, targeting a Virtex-6 device (xc6vlx240t-1). The results corresponding to the Xilinx IP library are directly extracted from the data sheet [24] for the same FPGA family. Table 3 shows a summary of the implementation results for all FP adders and multipliers. To facilitate the comparison, we also have a row for the combined area of an adder and a multiplier and, similarly, for the delay. Let us analyze the behavior of the adder, the multiplier, and the adder+multiplier together for actual implementations (shown in Table 3) and use Tables 1 and 2 as a theoretical reference.

Table 3 Implementation results for a Virtex-6 device (xc6vlx240t-1)

Regarding the two implementations of the typical radix-2 adder, the Xilinx IP requires significantly more area than the FloPoCo one. That is because the former is optimized to reduce latency and also due to the simplify handling of the special values performed by FloPoCo FP implementation. Compared to any of them, the high-radix ones reduce the number of resources required. In the FPGA implementation of the FP adder, the variable shift is the most complex and slowest circuit (module $(2^r)^{-d}$ in Fig. 4). The reduction in the complexity of the shifter is achieved by increasing the radix. In contrast, the higher the radix, the wider the data path, and as a consequence, the other elements of the architecture involve more hardware and delay (mainly the comparator and the fixed adders, see Fig. 4).

Let us analyze this situation from a quantitative point of view. The higher the radix, the lower the number of shifts. The number of shifts is given by the number of fractional digits (parameter f in Table 1), which decreases as the radix increases. For radix 2, 16, 64, 256, 4096, and $2^{24}$, the number of shifts is $f= 23, 6, 4, 3, 2, 1$, respectively (see Table 1). On the other hand, the bit width of the data path increases as the radix increases, in such a way that for radix 2, 16, 64, 256, 4096, and $2^{24}$, the word length is WL=27, 30, 32, 34, 38, and 50, respectively (see Fig. 4 and column WL (word length) in Table 2). As a consequence, we can see in Table 3 that the area of the adder decreases from radix 2, 16, 64, and 256 (f=23, 6, 4, 3, and WL=27, 30, 32, 34, respectively), whereas it increases for the very high radix, 4096 and $2^{24}$ (f=2, 1, and WL=38, 50, respectively). This behavior can be explained considering that the reduction factor of the shifter is greater than the increase factor of the other elements of the architecture for a radix less than or equal to 256; the situation is reversed for higher radices (4096 and $2^{24}$).

Regarding latency of the radix 2 adders, as expected, the Xilinx adder has significantly less latency than the FloPoCo one. On the other hand, there is a striking speedup for radix 16 and 64 (72% and 68%, respectively, compared to FloPoCo adder, and 38% and 35%, respectively, compared to the Xilinx one). However, the speedup is more moderate as the radix increases (down to 27% and 10%, respectively, for radix $2^{24}$). The fundamental reason for this behavior is the same as that for the area: the compensation between the time reduction factor of the shifter and the time increase factor of the remaining elements of the architecture.

In summary, for applications that only use additions, the best latency is obtained for radix 16 (72% speedup, and 5% less area, compared to the FloPoCo one; and 38% speedup and 34% less area, compared to the Xilinx one). Similarly, the best area is achieved for radix 256 (52% speedup, and 35% less area, compared to the FloPoCo one; and 21% speedup, and 55% less area, compared to the Xilinx one).

The implementation of the FP multiplier does not require the utilization of variable shifters. Hence, there is no advantage of using high-radix implementation. On the contrary, the greater the radix, the greater the word length, and, as a consequence, the larger the area and the longer the delay for the multiplier. This theoretical behavior is corroborated by the experimental result, as shown in Table 3. Therefore, in a hypothetical application with only multiplications, the use of a high radix is not advisable and the most efficient implementation would be the standard radix 2.

However, if our application has a mixture of multiplications and additions (which corresponds to the most widespread and realistic applications), there is an improvement/degradation in both latency and area depending on the relative proportion of additions versus multiplications in our algorithm. Having more additions means less latency and area, whereas having more multiplications means more latency and area. For applications involving multiplications and additions, the slowdown of the multiplication is satisfactorily compensated by the high speedup of the addition. Thus, the key parameter is the choice of the radix for our architecture. A trade-off solution has to be found since the faster the adder, the slower the multiplier.

Fig. 5

Speedup compared to [3] as a function of % additions/multiplications and radix

Figure 5 presents the speedup compared to [3] as a function of the percentage of additions/multiplications in the code and also as a function of the selected radix. This figure shows that the speedup decreases as the radix increases, and for any selected radix, the speedup decreases as the percentage of multiplications of the code increases. For radix 16 and 64, the delay is very similar, and they are drawn as a single line in Fig. 5 (also see Table 3). This figure shows that, for any radix, if the dominant operation in the targeted algorithm is addition, a huge speedup is achieved (i.e., for summations), whereas if the dominant operation is multiplication, a negative speedup occurs (i.e., for products).

Let us focus our attention on the case of having balanced codes (codes with a similar number of multiplications and additions) since this covers many practical cases, for instance, in control and DSP systems (i.e., digital filters, matrix product, etc.). To help us in the analysis of this important case, we show the total area and delay for one addition plus one multiplication in the third row of Table 3. The third row shows that the best options are radix 256 for the area and radix 16 for the delay. Let us focus on the central area of Fig. 5 (50% add and 50% mult). We can see that the behavior of radix 16 and 64 is similar, and the best results are obtained compared to radix 256 and above. In conclusion, for balanced codes, two good trade-off solutions are radix 16 and 64 (radix 16 is slightly faster than radix 64 (+1.7%) with a little more area (+9%)). However, it depends on the specific constraints, and each case needs a careful study, and this evaluation may help to perform it.

In case it is required, the cost of format conversion is not high for several reasons. First, converters only use about a third of the area utilized by an adder, and their delay is less than half of that of the adder or multiplier. Second, and more importantly, taking into account that in the model considered here, the FPGA is used as an accelerator, conversions are only required when data move in or out of the FPGA. The number of internal operations has to be much greater than data movement to have a really useful accelerator. Therefore, the number of FP operations will be much higher than the number of conversions and then the cost of conversions, negligible.

Fig. 6

Example of an application: a simple pipeline for matrix product

Let us illustrate the advantages of the proposed approach by using the widespread matrix multiplication as an example. Figure 6 provides a basic pipeline architecture to perform this operation. The first and the last modules of this figure represent the conversion stage to/from IEEE, and they are only used if data come from the general processor. For a given radix, the multiplier and adder proposed in our implementation have a very similar delay (see Table 3). This is a great advantage that facilitates the design of simple pipeline architectures (like that proposed in Fig. 6), where the stages are well-balanced. Nevertheless, the corresponding counterpart radix 2 units are not well-balanced (see Table 3). Figure 6 also shows the throughput, speedup and the slowest stage (which determines the critical path) for different radices. The clock cycle is dictated by the slowest stage (critical path). The mean throughput of our pipelined implementations is about 72.1 MHz, whereas the counterpart radix 2 pipeline implementation is 47.1 MHz, which improves throughput by about 53%.

Regarding previous work in high-radix FP, in [2] a radix 4 and radix 16 adder and multiplier are proposed for FPGA devices, and radix 16 offered the best results. A detailed comparison between the radix 64 design and the radix 16 architecture of [2] was presented in [23]. Here, we extend this comparison with the new radices. Table 4 shows the speedup achievable for the common operation, summation, and matrix multiplication. The behavior of the design of [2] is also shown in Fig. 5.

Regarding addition, the improvement of [2], (+7%), is very modest compared with any of our high-radix implementations (+35% to +72%; see Fig. 5). Nevertheless, regarding multiplication, deterioration ($-6$%) is less than that of any of our architectures ($-24$% to $-57$%; see Fig. 5). For balanced codes (see central area of Fig. 5), the net gain for [2] is practically negligible (+1%), whereas there is a net gain for our designs of radix 16 (+26%), 64 (+23%), and 256 (+16%). For radix 4096 and above, these implementations are ineffective. We have to notice also that the higher the radix, the higher the number of significant bits of the mantissa and the wider the dynamic range, as can be seen in Table 1.

Table 4 Speedup for summation and matrix multiplication

Summarizing, among the studies designs, the fastest architecture for algorithms in which addition is dominant is radix 16 and the best area is obtained for radix 256. For algorithms in which multiplication is dominant, regular radix 2 is the best option, but for balanced codes (predominant in many algorithms), the best speed is obtained with radix 16, the best area with radix 256, and a good trade-off solution is obtained with radix 64.

6 Conclusion

This paper analyzes the design of efficient FP adders for high-radix FP formats and their impact on the implementation of FP arithmetic in FPGAs with no native FP support. For applications with data obtained from an IEEE-754 FP source, the proposed converters to/from any radix allow working at high speeds inside the FPGA and return the output numbers in IEEE-754 format if required, while increasing the number of significant bits used and dynamic range compared to the IEEE-754 standard. The implementation results show that the significant savings in area and delay obtained when implementing high-radix FP adders on FPGAs may significantly overweight the associate penalty of implementing high-radix FP multipliers. For algorithms that involve both additions and multiplications, our proposal allows selecting the best suitable radix of the FP arithmetic representation as a function of the ratio between the number of additions and multiplications of the targeted algorithm. This guide allows the designer to choose between maximum speed, area, or a trade-off solution depending on the need of the designer’s specific application. In many operations, the number of additions equals the number of multiplications, such as dot product, matrix by matrix multiplications, convolutions, and others. In many others, the addition is the dominant operation, such as matrix and vector addition, or average calculation. These operations are massively used in signal processing applications, machine learning, deep learning, computer graphics, wireless communications, etc. In all these applications, this approach can help engineers design more efficient architectures in FPGA-based designs while maintaining and even increasing the operations’ precision.