1 Introduction

Over the last decade the annual global Internet protocol (IP) traffic has been rising at an enormous rate and is going to increase further. Overall IP traffic will grow at a compound annual growth rate of \(22 \%\) from 2015 to 2020 [10], resulting in a tripling of the overall traffic in 5.5 years. The increasing demand for high data rates requires optical network capacity to advance. Flexible transmitters based on DACs are highly desirable, since they can vary the modulation bandwidth and the modulation format of the transmitted signal adaptively. Furthermore, an improved transmission performance can be achieved by using pre-distortion, which mitigates the impact of transmission channel impairments, such as the chromatic dispersion of the fiber. By analyzing the capacity bottlenecks in fiber-optic links, it leaps to the eye that the bandwidth of the photonic components, e.g., modulators and photo diodes, is greater than that of their electrical counterparts, e.g., DACs and analog-to-digital converters (ADCs). Thus, in order to achieve a transmission capacity increase, the bandwidth limitations of the electronic components, especially the DACs need to be addressed. However, technological constraints limit the achievable bandwidth of a single DAC and therefore, the concept of parallelization or interleaving has been introduced into the DAC design, whereby three concepts have been identified to be viable:

  1. 1.

    time interleaving DAC (TI-DAC) [14, 16],

  2. 2.

    multiplexing DAC (MUX-DAC) [13, 40, 41] and

  3. 3.

    (FI) DAC (FI-DAC) [8, 23, 34, 36].

The first two concepts are realized in the time domain. The first one makes use of a power combiner (TI-DAC), and the second one uses a high-speed analog multiplexer (MUX) (MUX-DAC), respectively, in order to aggregate signals of multiple DACs to a higher rate. With the TI-DAC concept, sample rates of up to 100 GS/s have been realized by combining the output signals of multiple DACs [14, 16]. The increased sample rate can either be used to generate signals containing higher frequencies or to cancel images beyond the first Nyquist zone [2, 11, 22, 32, 39]. A good overview on TI-DAC concepts can be found in [3]. The previously mentioned references are focused on zero-order-hold (ZOH)-DACs; however, other pulse shaping approaches are viable as well, such as partial-order-hold (POH), which has been demonstrated for a TI-DAC in [18]. Anyhow, by using the TI-DAC concept the sample rate could be increased, though the bandwidth is still limited by the DACs’ low-pass characteristic as well as the sinc roll-off.

In order to overcome the bandwidth limitation of the TI-DAC concept, two different nonlinear concepts have been introduced, namely MUX-DAC and FI-DAC. For the MUX-DAC concept a high-speed analog MUX is utilized, switching between the output signals of multiple DACs. Recently, an 80 GBd signal with 40 GHz bandwidth was generated by multiplexing two DAC signals [28, 41]. The same authors showed the generation of a 300 Gb/s discrete multi-tone (DMT) signal in [40]. The MUX-DAC concept relies on the availability of analog high-speed MUXs, which are not commercially available so far. The concept enhances both the sample rate and the bandwidth [41].

The other concept leading to a bandwidth increase is based on a concept originally introduced for ADCs called digital bandwidth interleaving (DBI) [24, 31]. This scheme was proposed for DACs in [23], whereby multiple spectral bands are generated by analog processing and then combined in order to achieve both a higher overall sample rate and bandwidth as shown in Fig. 1. Contrary to the concept for oscilloscopes, the spectral splitting of the signal into sub-signals is performed digitally and the combining of the spectral sub-bands is performed in the analog domain. Note that the concept is rather based on a bandwidth aggregation than on a bandwidth interleaving. Recently, multiple publications [8, 9, 34,35,36] originated on this topic, in which two different approaches are pursued. The authors experimentally verified the concept with two frequency bands, firstly with DACs in the MHz range [34] and later with high-speed DACs in the GHz range [36]. The frequency bands were combined with a diplexer, to generate both a 40 GHz 80 GBd 2- and 4-level pulse amplitude modulation (PAM) signal in order to show the first open eye diagrams without post-processing [36].

Fig. 1
figure 1

Block diagram of the FI-DAC concept with multiple DACs, low-pass filters, mixers and a frequency multiplexer for filtering and combining the frequency bands

Full size image

In [8, 9], the concept was demonstrated with the same triplexer, which is used for DBI LeCroys’ oscilloscopes. Three sub-bands are generated, achieving a total bandwidth of 100 GHz at a sample rate of 240 GS/s, though with a high signal-to-noise ratio (SNR) penalty.

Next to the FI-DAC concept, which is the focus of this paper, a similar concept with independent frequency bands and an in-phase and quadrature (I/Q) mixer was shown in [20, 21], whereby up to 178 Gb/s was transmitted over a short-range optical link.

With a FI-DAC an ultra-broadband waveform can be generated. The concept has been demonstrated so far with two and three DACs, respectively, though it is possible to scale it to N DACs. In order to design an FI-DAC, certain conditions need to be fulfilled, e.g., a continuous waveform without any spectral gaps is desired. Therefore, multiple parameters need to be determined and defined, i.e., DAC sample rate, mixer frequencies, analog frequency responses, number of samples, etc. However, these parameters are interdependent and hence need to be chosen in a joint manner. For a FI-DAC consisting of few DACs, the complexity is overseeable in order to obtain a feasible parameter set. Nonetheless, scaling the FI-DAC concept to more DACs requires a profound mathematical framework.

In this paper, an analytical formulation for the FI-DAC concept as well as an algebraic solution for the mathematical problem of distributing the data samples among the DACs is provided. Furthermore, a mathematical optimization program is introduced, in order to balance multiple parameters, which simplifies considerably the design of an FI-DAC for large numbers of DACs. Examples for the parameter balancing are provided for a FI-DAC consisting of three DACs as well as numerical simulation results with this FI-DAC, which focus on the preprocessing’s effect on the frequency responses. Experimental results for a FI-DAC consisting of two DACs with a custom-designed diplexer are used as a first verification of the concept.

The paper is organized as follows. First, the FI-DAC concept is explained in detail in Sect. 2. Then, the mathematical is introduced in Sect. 3, consisting of definitions, the problem of distributing the data samples among the DACs, the necessary mixer frequencies, and the achievable symbol rates. In Sects. 4 and 5, algorithms to balancing the FI-DAC’s parameters as well as examples are presented. Subsequently, both simulation and experimental results, presented in Sects. 6 and 7, respectively, validate the concept. An outlook on implementation issues completes this paper.

2 Frequency Interleaving for DACs

FI uses multiple DACs in parallel to perform the digital-to-analog (D/A) conversion for a digital signal, whereby each DAC performs the D/A conversion for a spectral fraction of the digital signal. In Fig. 1, a conceptual block diagram of an FI-DAC is shown. The digital signal is split by means of digital signal processing (DSP) into sub-signals, which correspond to different spectral fractions of the digital signal, which are called sub-spectra in the following. The sub-spectra are then converted back to their native frequency locations by means of mixers. For the upconversion, different mixer types can be used, i.e., radio frequency (RF) mixers and I/Q mixers, whereby for the RF mixer, either the lower side band (LSB) or the upper side band (USB) is utilized. Finally, the sub-spectra are filtered and combined, in order to generate the analog representation of the digital signal, which has a total bandwidth greater than the bandwidth of the incorporated DACs. Note that filtering and combining can be achieved, e.g., with a single device, i.e., a frequency multiplexer (diplexer, triplexer, quadruplexer, etc.), as shown in the figure or by using filters and a power combiner separately.

Fig. 2
figure 2

Digital and analog signal processing steps for an FI-DAC: The digital signal (a, b) is split into sub-signals (c), which are D/A converted by multiple DACs (d). The sub-signals are upconverted, filtered (e) and combined (f) to generate the analog representation (g, h) of a

Full size image

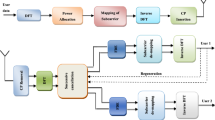
In Fig. 2, both the digital and analog signal processing for the FI concept is shown for an exemplary FI-DAC with five DACs. The upper part of Fig. 2a–c deals with the DSP, where the input spectrum is de-interleaved and partitioned into sub-spectra, which are then fed to the DACs. The lower part of Fig. 2d–h illustrates the analog processing, where the DAC output signals are upconverted, filtered and combined, i.e., frequency interleaved in the analog domain.

For the digital frequency de-interleaving, the digital signal in Fig. 2a is passed through a Fourier transform and the resulting spectrum is shown schematically in Fig. 2b. Next, the spectrum is partitioned into sub-spectra as visualized in Fig. 2c and the corresponding sub-signals are fed to the DACs. The partitioning of the spectrum is usually done in accordance with the specifications of the analog components, i.e., both the DACs sample rate and bandwidth, the filters bandwidth, the mixers bandwidth, etc., which is explained in detail in Sects. 3.2–4.

After partitioning, the frequency domain samples of each sub-spectrum are selected and placed into the baseband, whereby digital downconversion and filtering are achieved implicitly. Prior to D/A conversion, oversampling is applied to the sub-spectra for both low and high frequencies, denoted with lighter colors in Fig. 2d, whereby the former is also known as digital upconversion.

In general, the oversampling is needed in order to realize guard bands to suppress DAC aliases and redundant RF mixers’ side band as well as the local oscillator (LO) feed through with analog filters. For the depicted case as a frequency domain implementation, oversampling for both low and high frequencies is achieved by inserting additional samples, i.e., zeros, in the frequency domain representation of the sub-signals. Note that the individual signals are further pre-equalized in order to mitigate mismatches between the different analog paths [8, 36]. The signals are passed through an inverse Fourier transform in order to feed the time domain sub-signals to the DACs.

After D/A conversion the sub-signals are low-pass-filtered, upconverted to their native frequency positions and further band-pass-filtered as shown in Fig. 2e. The band-pass filters suppress harmonics of the mixers as well as one of the unused RF mixer side bands (\(\hbox {II}^{*}\) and \(\hbox {III}^{*}\)). The LO frequencies depend on the oversampling used for the sub-signals as shown in Sect. 3.3. Note that if the lower side band (LSB) of an RF mixer is used (II), the signal must be generated in reversed frequency position, which is denoted by the superscript *. This operation could be performed as shown in [34]. If an I/Q mixer is used (IV and V), a broader sub-spectrum can be generated, since both spectral side bands are used. The sub-signals IV’ and V’ are the real and the imaginary part of the two-sided spectrum given by [IV, V]. In Fig. 2f the sub-spectra are finally combined to form a single continuous spectrum and thus the analog representation shown in Fig. 2g, h of the digital signal in Fig. 2a. The resulting frequency response of the combined DAC is composed of the frequency responses of the individual analog paths. Due to the necessary preprocessing mentioned in the previous paragraph, the combined frequency response can be both digitally defined and adapted to the users needs. The preprocessing could generate sub-signals, which are non-overlapping, but if stitched together, they form a continuous waveform without any spectral gaps.

Note that single side band (SSB) mixers can be employed as well, which correspond to using RF-LSB mixers and RF-USB mixers, respectively, without the need for filtering the unwanted sideband.

3 Mathematical Framework

As has been pointed out in Sect. 1, the design of a FI-DAC requires that an analog waveform without any spectral gaps is generated that is a correct representation of the digital input signal. Therefore, multiple interdependent parameters need to be determined and defined, i.e., DAC sample rate, mixer frequencies, analog frequency responses, number of samples, etc.

The operation of the FI-DAC requires the distribution of the data samples of the digital input signal among the DACs, such that each DAC converts a sub-spectrum of the input signal. Two scenarios for the data block length of the system need to be considered: infinite and finite. The former is present in real-time systems with a continuously operating time domain signal processing. The latter is present in both real-time systems with a block-based frequency domain signal processing [30] and in “offline” systems, where a repetitive data signal is used, e.g., in an arbitrary waveform generator (AWG). This paper focuses on the latter system type with a finite data block length, where a fixed number of data samples are D/A converted. The mathematical problem consists in splitting the data samples among the DACs, such that each DAC converts a partition of the data samples.

In this section, a profound mathematical framework for the FI-DAC concept is introduced. Starting with some definitions, the distribution of data samples among the DACs with respect to guard bands is addressed in Sect. 3.2. These guard bands, realized by oversampling, are necessary to suppress DAC aliases and unwanted mixing products with analog filters. This is an extension of our findings in [35]. In turn, the guard bands define the local oscillator frequencies for different mixer types, which is shown in Sect. 3.3. Furthermore, the combined bandwidth and symbol rate, respectively, is dependent on the size of the guard bands and hence is subject to limitations regarding the number of data samples, as discussed in Sect. 3.4.

Table 1 Variables for the FI-DAC
Full size table

3.1 Definitions

In order to develop a mathematical framework, some definitions need to be given. The variables are summarized in Table 1. Since FI is a frequency domain approach, we refer to frequency domain samples. Note that the number of frequency domain samples is naturally equal to the number of samples of the corresponding time domain signal.

The FI-DAC consists of N DACs, and the set of DACs is given by \(\varLambda = \{1,\ldots ,N\}\), where the individual DAC is denoted by index n. The data samples of the digital signal \(K_{D,\text {tot}}\) need to be distributed among the DACs, such the nth DAC converts \(K_{D,n}\) data samples individually. Eventually, all data samples need to be D/A converted in order to generate a correct analog representation of the digital signal. Thus, we have the total number of data samples given by

$$\begin{aligned} K_{D,\text {tot}} = \sum _{n\in \varLambda }{K_{D,n}}. \end{aligned}$$
(1)

Besides converting the data samples \(K_{D,n}\), additional samples for oversampling \(K_{O,n}\) are inserted in the frequency domain representation of the digital signal. These samples are needed to realize guard bands to move image frequency components away from the desired frequency components as shown in Fig. 2d, e. In general, the oversampling ratio \(p_n\) for DAC n is given by

$$\begin{aligned} p_{n} = \frac{K_{S,n}}{K_{D,n}} = \frac{K_{D,n} + K_{O,n}}{K_{D,n}} = 1 + \frac{K_{O,n}}{K_{D,n}}, \end{aligned}$$
(2)

where \(K_{S,n}\) is the number of total samples for the nth DAC, consisting of \(K_{D,n}\) data samples and \(K_{O,n}\) additional samples for oversampling.

Fig. 3
figure 3

Preprocessed digital data spectrum consists of additional samples for oversampling at low frequencies \(K_{OL,n}\) and at high frequencies \(K_{OH,n}\) and data samples \(K_{D,n}\)

Full size image

As shown in Fig. 3, the number of additional samples for oversampling \(K_{O,n}\) consists of \(K_{OL,n}\) samples at low frequencies and \(K_{OH,n}\) at high frequencies, i.e.,

$$\begin{aligned} K_{O,n} = K_{OL,n} + K_{OH,n}. \end{aligned}$$
(3)

These additional samples are used as guard bands in order to filter DAC hold spectra and mixer side bands with analog filters. The number of samples for the nth DAC is thus given by

$$\begin{aligned} K_{S,n} = K_{D,n} + K_{OL,n} + K_{OH,n}. \end{aligned}$$
(4)

Therefore, two individual oversampling ratios can be specified for oversampling at both low frequencies \(p_{L,n}\) and high frequencies \(p_{H,n}\):

$$\begin{aligned} p_{L,n}&= \frac{K_{D,n}+K_{OL,n}+K_{OH,n}}{K_{D,n}+K_{OH,n}} = 1+\frac{K_{OL,n}}{K_{D,n}+K_{OH,n}} \end{aligned}$$
(5)
$$\begin{aligned} p_{H,n}&= \frac{K_{D,n}+K_{OL,n}+K_{OH,n}}{K_{D,n}+K_{OL,n}} = 1+\frac{K_{OH,n}}{K_{D,n}+K_{OL,n}}. \end{aligned}$$
(6)

For each sub-DAC, the minimum and the maximum generated frequencies of each sub-signal are given, based on the oversampling ratios, by

$$\begin{aligned} f_{\text {min},n}&= \frac{f_{s,n}}{2}\left( 1-\frac{1}{p_{L,n}}\right) ,~ \text {and} \end{aligned}$$
(7)
$$\begin{aligned} f_{\text {max},n}&= \frac{f_{s,n}}{2}\frac{1}{p_{H,n}}, \end{aligned}$$
(8)

where \(f_{s,n}\) denotes the sampling rate \(f_s\) of DAC n. The frequencies are highlighted in Fig. 3 next to the number of samples.

Thus, the total symbol rate \(f_\text {sym,tot}\) generated by the FI-DAC is given by twice the sum of the sub-spectra bandwidth:

$$\begin{aligned} f_\text {sym,tot} = 2\cdot \sum \limits _{n\in \varLambda } \left( f_{\text {max},n}-f_{\text {min},n}\right) , \end{aligned}$$
(9)

The sample rate of the combined DAC is given by

$$\begin{aligned} f_{s,\text {tot}} = \sum \limits _{n\in \varLambda } f_{s,n}, \end{aligned}$$
(10)

and for a real-world application, where \(f_{s,n} = f_s~\forall n\in \varLambda \), we have

$$\begin{aligned} f_{s,\text {tot}} = N\cdot f_{s}. \end{aligned}$$
(11)

Thus, the theoretical maximum \(f_\text {sym,tot}\) is achieved, if the DACs are operated without oversampling yielding

$$\begin{aligned} f_\text {sym,tot}\Big |_{p_n=1~\forall n\in \varLambda } = f_{s,\text {tot}}. \end{aligned}$$
(12)

However, by not using oversampling cross talk between the sub-signals occurs, but could be mitigated by means of digital signal processing as shown in [34].

3.2 Distribution of Data Samples

In order to distribute the data samples among the DACs, the number of data samples for each DAC \(K_{D,n}\) needs to be calculated. As mentioned in the introduction of Sec. 3, the mathematical problem consists in splitting the data samples \(K_{D,\text {tot}}\) among the N DACs and taking into account the guard bands, specified by the oversampling ratios \(p_{L,n}\) and \(p_{H,n}\). For this derivation it is assumed that the oversampling ratios for both low frequencies \(p_{L,n}\) and high frequencies \(p_{H,n}\) are given for all DACs \(n\in \varLambda \) and that the number of data samples \(K_{D,\text {tot}}\) is known.

For our derivation we further assume that the DACs are running at identical sampling rates and that all DACs receive their input signals from memories of equal size:

$$\begin{aligned} f_{s,n}= & {} f_s \quad \forall ~ n \in \varLambda \end{aligned}$$
(13)
$$\begin{aligned} K_{S,n}= & {} K_S \quad \forall ~ n \in \varLambda \end{aligned}$$
(14)

In order to simplify the mathematical problem, the solution is obtained in two steps. Firstly, a joint oversampling ratio \(p_n\) based on \(p_{L,n}\) and \(p_{H,n}\) is calculated for each DAC. Secondly, the distribution of the data samples among the DAC is obtained by solving a linear equation system.

3.2.1 Problem Solution Part I: Calculating a Joint Oversampling Ratio for Each DAC

As described before, \(p_{L,n}\) and \(p_{H,n}\) are given for each DAC and a joint oversampling ratio \(p_n(p_{L,n},p_{H,n})\) for DAC n needs to be determined. In (2), \(p_n(K_{D,n},\,K_{OL,n}, K_{OH,n})\) is given, but depends on samples rather than on oversampling ratios. Therefore, \(K_{OL,n}\) and \(K_{OH,n}\) based on \(p_{L,n}\) and \(p_{H,n}\) are obtained by solving the linear equation system given by (5) and (6) for \(K_{OL,n}\) and \(K_{OH,n}\).

The solution is trivially given by

$$\begin{aligned} K_{OL,n}&= \frac{p_{H,n}(1-p_{L,n})}{p_{L,n}p_{H,n}-p_{L,n}-p_{H,n}}K_{D,n}, \end{aligned}$$
(15)
$$\begin{aligned} K_{OH,n}&= \frac{p_{L,n} (1-p_{H,n})}{p_{L,n}p_{H,n} -p_{L,n}-p_{H,n}}K_{D,n}. \end{aligned}$$
(16)

In order to calculate \(p_n(p_{L,n},p_{H,n})\), (15) and (16) are inserted into (2):

$$\begin{aligned} p_{n}&= 1+\frac{K_{OL,n}+K_{OH,n}}{K_{D,n}} = \frac{p_{L,n}p_{H,n}}{p_{L,n}+p_{H,n}-p_{H,n}p_{L,n}}. \end{aligned}$$
(17)

Now, there is a joint oversampling ratio \(p_n(p_{L,n},p_{H,n})\) for each DAC n based on \(p_{L,n}\) and \(p_{H,n}\). The dependence on \(K_{D,n}\), which is still unknown at this point, could be canceled out.

3.2.2 Problem Solution Part II: Calculate the Number of Data Samples for Each DAC

In order to distribute the data samples \(K_{D,\text {tot}}\) among the N DACs according to the oversampling ratios \(p_n\) obtained in the previous section, a linear equation system needs to be solved:

$$\begin{aligned} \sum \limits _{n\in \varLambda } K_{D,n}&= K_{D,\text {tot}} \end{aligned}$$
(18)
$$\begin{aligned} p_k K_{D,k}&= p_l K_{D,l}\quad \forall ~k,l\in \varLambda \wedge k\ne l. \end{aligned}$$
(19)

Equation (18) results from the fact that the digital signal needs to be completely reconstructed in the analog domain, such that all data samples are D/A converted, as given in (1). Equation (19) results from the fact that each DAC uses a memory of equal size as stated in (14) in combination with (2), meaning that the number of samples loaded into each DAC is equal.

The linear equation system given by (18) and (19) needs to be solved for \(K_{D,n}~\forall n \in \varLambda \). The solution is given by

$$\begin{aligned} K_{D,n} = \frac{\prod \nolimits _{l\in \varLambda _n}p_l}{\sum \nolimits _{k\in \varLambda }\prod \nolimits _{i\in \varLambda _k}p_i} K_{D,\text {tot}} \quad \forall n \in \varLambda , \end{aligned}$$
(20)

where \(\varLambda _k = \varLambda \backslash \{k\},~k\in \varLambda \). The complete derivation can be found in Appendix.

With (20) the number of data samples for each DAC can be calculated. By using (15) and (16), the number of additional samples for oversampling, \(K_{OL,n}\) and \(K_{OH,n}\), can be calculated as well. The resulting symbol rate \(f_\text {sym,tot}\) can be obtained according to (9). Thus, all values needed to generate the sub-signals for each DAC are given.

However, the system parameters are naturally linked by the equations introduced in Sect. 3.1 and are, thus, interdependent. In order to generate the sub-signals, integer values are required for \(K_{D,n}\), \(K_{OL,n}\) and \(K_{OH,n}\), which is not given by default in (20) as shown in [35]. Therefore, certain limitations arise on both the necessary LO frequencies and the feasible symbol rates, which are highlighted in the following section.

3.3 Local Oscillator Frequencies

As shown in Fig. 2 the LOs frequencies depend on the mixers used as well as on the oversampling values \(p_{L,n}\) and \(p_{H,n}\), defined for each DAC. In principle different types of mixers could be utilized, i.e., RF mixers using either the LSB or the USB, as well as I/Q mixers being able to generate a broader sub-band. In the following, formulas for the calculation of the LO frequency for frequency band n are provided for different mixer types.

If RF mixers are used, where the USB is used and the LSB is suppressed, the frequencies of the LOs are determined by:

$$\begin{aligned} f_{\mathrm{LO},\mathrm{USB},n}&= {\left\{ \begin{array}{ll} 0,&{}\quad n=1 \\ \sum \limits _{i=2}^n f_{\text {max},i-1}-f_{\text {min},i},&{}\quad n>1. \end{array}\right. } \end{aligned}$$
(21)

If RF mixers are utilized, where the LSB is used and the USB is suppressed, the frequencies of the LOs are given by:

$$\begin{aligned} f_{\mathrm{LO},\mathrm{LSB},n}&= {\left\{ \begin{array}{ll} 0,&{}\quad n=1 \\ \sum \limits _{i=1}^n f_{\text {max},i}-f_{\text {min},i-1}, &{}\quad n>1, \end{array}\right. } \end{aligned}$$
(22)

whereby \(f_{\text {min},1} = f_{\text {min},0} = 0\) for this case.

If I/Q mixers are used the frequencies of the LOs are given by

$$\begin{aligned} f_{\mathrm{LO},\mathrm{IQ},n}&= {\left\{ \begin{array}{ll} 0,&{}~ n=1 \\ \sum \limits _{i=1}^{n-(n\mod 2)} f_{\text {max},i},&{}~n>1. \end{array}\right. } \end{aligned}$$
(23)

If SSB mixers are used, these formulas can be used as well: \(f_{\mathrm{LO,LSB},n}\) can be used for SSB-LSB and \(f_{\mathrm{LO,USB},n}\) can be used for SSB-USB.

3.4 Achievable Symbol Rates

As has been noted before, due to the discrete number of samples in combination with the fact that all parameters are interdependent, there are certain limitations on the feasible symbol rates, which is explained in this section.

If a single DAC is used with oversampling, the ability to generate a certain symbol rate depends on the number of data samples, the sample rate of the DAC and the oversampling ratio. Eventually, there needs to be an integer number of samples for the signal to be generated. If an FI-DAC is used, this condition is preserved. However, the ability to generate the desired symbol rate \(f_\text {sym,tot}\) now depends on the number of data samples, the total sample rate \(f_{s,tot}\) and the oversampling ratios for all DACs. The condition for an FI-DAC is given by

$$\begin{aligned} K_{S,\text {tot}}~\in ~\mathbb {N}. \end{aligned}$$
(24)

with the total number of samples given by

$$\begin{aligned} K_{S,\text {tot}} = \sum \limits _{n\in \varLambda }K_{S,n} = \frac{f_{s,\text {tot}}}{f_\text {sym,tot}} \cdot K_{D,\text {tot}}. \end{aligned}$$
(25)

Note that this condition is independent on the distribution of the additional samples for oversampling among the DACs. Next to this condition, the total number of samples need to be distributable among the DACs, yielding a second condition:

$$\begin{aligned} \frac{K_{S,\text {tot}}}{N}~\in ~\mathbb {N}. \end{aligned}$$
(26)

The total symbol rate \(f_\text {sym,tot}\) is then given according to

$$\begin{aligned} f_\text {sym,tot} = \left. \frac{K_{D,\text {tot}}}{K_{S, \text {tot}}}f_{s, \text {tot}}~\right| _{\frac{K_{S,\text {tot}}}{N}\in \mathbb {N}}, \end{aligned}$$
(27)

which is equivalent to the formula for the single DAC for \(N=1\) [29].

Two examples are provided in Fig. 4, whereby Fig. 4a covers the standard case of a single DAC and Fig. 4b covers the case of a FI-DAC consisting of multiple DACs.

In Fig. 4a, the feasible integer symbol rates \(f_\text {sym,tot}\) in the GBd regime are shown for the case of a single DAC as a function of integer sample rates \(f_s\) in the GS/s regime, respectively. Two different number of data samples \(K_{D,\text {tot}}\) are plotted: \(2^{10}-1=1\,023\) and \(2^{10}=1\,024\), corresponding to a pseudo-random binary sequence (PRBS) and a two’s complement sequence. Naturally, the higher the sample rate is, the higher the symbol rate will be, as shown by the general triangular shape of the plot. However, not every integer GBd symbol rate could be addressed, since there are gaps in the plot. Moreover, though the number of data samples only differs by one, it is obvious that there are rarely common symbol rates for \(K_{D,\text {tot}} = 1\,023\) and \(K_{D,\text {tot}} = 1\,024\).

Fig. 4
figure 4

Feasible integer GBd symbol rates for different integer GS/s sample rates for: a a single DAC for two different number of data samples; b an FI-DAC converting \(2^{10}-1\) data samples consisting of different number of DACs

Full size image

As an example, the vertical dots for a sample rate of 80 GS/s are analyzed. It is observed that the symbol rates \(\{80,\,66,\,62,\,60,\,55,\,48,\,44,\,40\,\ldots \}\) GBd and \(\{80,\,40\,\ldots \}\) GBd could be addressed for \(K_{D,\text {tot}}=1\,023\) and \(K_{D,\text {tot}}=1\,024\) data samples, respectively. Hence, not every integer symbol rate could be addressed and moreover, the two number of data samples only share 80 and 40 GBd as common symbol rates. Another noteworthy feature of the plot is the prominent diagonals , e.g., the diagonal from the bottom left corner to the upper right corner (100 GS/s, 100 GBd) corresponds to a total oversampling ratio of one sample per symbol and the diagonal from the bottom left corner to the middle of the vertical axis on the right (100 GS/s, 50 GBd) corresponds to a total oversampling ratio of two samples per symbol. For these two diagonals, both number of data samples can always be addressed due to the integer oversampling ratios.

In Fig. 4b, the feasible integer symbol rates for an FI-DAC are shown for the case of \(K_{D,\text {tot}}=2^{10}-1\) data samples with the number of DACs N being varied between one and three. By increasing the number of DACs, the total sample rate \(f_{s,\text {tot}}\) increases, and thus, the number of addressable symbol rates rises as well. The symbol rates that can be addressed with N DACs could be addressed with \(N+1\) DACs as well, which can be seen in the figure by the points plotted for \(N\in \{2,3\}\) being on top of the points plotted for \(N=1\). As for the case of a single DAC, not all integer GBd symbol rates could be addressed.

As an example, the vertical dots for a sample rate of again 80 GS/s per DAC are analyzed in detail. It can be observed that the symbol rates \(\{240,\,220,\,186,\,176,\,165\}\) GBd can be addressed solely with three DACs as shown by the red dots in the plot. The following lower symbol rates, i.e., \(\{155,\,132,\,124,\,\ldots \}\) GBd could be addressed with a FI-DAC consisting of either two or three DACs as shown by the red dots framed by the yellow squares. Symbol rates \(\le \,80\) GBd can be addressed by one, two or three DACs as shown by the red dots framed by the yellow squares and encircled in blue. The dots \(\le \,80\) GBd correspond to the dots shown in Fig. 4a for \(K_{D,\text {tot}}=2^{10}-1\). However, note that an odd number of DACs puts an additional constraint on the number of feasible symbol rates, if an even number of data samples is given.

As has been discussed in this section, the number of data samples and the chosen DAC sample rate put constraints on the achievable symbol rates with a FI-DAC. This need to be taken thoroughly into account when designing a FI-DAC.

4 Parameter Balancing

As seen in the previous sections, all system parameters are interdependent, i.e., the number of data samples, the sample rate of the DACs, the achievable symbol rate, the oversampling ratios and the LO frequencies. Furthermore, there are integer constraints on the number of samples for each DAC. Hence, in order to balance these various parameters for a proper system concept regarding the requirements and the limitations of the analog components, a mathematical optimization technique is introduced.

The objective of mathematical optimization consists of minimizing or maximizing a cost function with respect to a set of constraints, which are summarized in a mathematical optimization program [5, 6]. In this particular case, a mixed-integer nonlinear optimization program (MINLP) is used, since the variables, for which the mathematical program needs to be solved, consist of integer as well as real numbers [4, 25].

We present two optimization programs balancing the system’s parameters: firstly, a simple optimization program in Sec. 4.1, which represents the problem already solved in Sect. 3.2 with additional integer constraints and which is referred to as standard ABI optimization program. Secondly, an extended optimization program in Sect. 4.2, which contains additional parameters and equations.

The algebraic solutions obtained in Sect. 3.2 could be used for the formulation of the optimization program as well. However, the problem is sufficiently described with the original equations and the computer-based solver implicitly solves the interdependencies.

4.1 Standard FI-DAC Optimization Program

The optimization program, which we refer as standard FI-DAC optimization program, is a MINLP corresponding to the “simple” problem presented and solved in Sect. 3.2. Next to the equations used before, the findings of Sec. 3.3 and 3.4 are taken into account by adding (10), (25) and (27) as constraints to the optimization program. Next, we add integer constraints. The objective of the optimization function is to maximize the total symbol rate \(f_\text {sym,tot}\). Parameters for the optimization program are the sample rate \(f_s\), the number of data samples \(K_{D,\text {tot}}\) and the number of DACs N. We further assume lower and upper limits for the oversampling ratios \(p_{L,n}\) and \(p_{H,n}\). We demand the number of samples \(K_{D,n}\), \(K_{OL,n}\), \(K_{OH,n}\), \(K_{O,n}\), \(K_{S,n}\), as well as the symbol rate, to be integer-valued.

The optimization program is given as:

$$\begin{aligned} \begin{array}{llll} \text {max} &{} \quad \quad f_\text {sym,tot} &{} &{} \\ \text {s.t.} &{} \quad \quad (1)\,--\,(9), \,(10),\, (25),\, (27) &{} &{} \\ &{} \quad \quad p_{L,n} &{}\quad \quad \ge ~p_{L,n}^{\min }&{} \quad \quad (28)\\ &{} \quad \quad p_{L,n} &{}\quad \quad \le ~p_{L,n}^{\max }&{} \quad \quad (29)\\ &{} \quad \quad p_{H,n} &{}\quad \quad \ge ~p_{H,n}^{\min }&{} \quad \quad (30)\\ &{} \quad \quad p_{H,n} &{}\quad \quad \le ~p_{H,n}^{\max }&{} \quad \quad (31)\\ &{} \quad \quad K_{D,n},\,K_{OL,n},\,K_{OH,n},~\ldots &{} &{} \\ &{} \quad \quad K_{O,n},\,K_{S,n},\,K_{S,\text {tot}} &{}\quad \quad \in ~\mathbb {N}~\forall \, n \in \varLambda &{} \\ &{} \quad \quad f_\text {sym,tot} &{}\quad \quad \in ~\mathbb {R} &{} \\ &{} \quad \quad p_{L,n},\,p_{H,n} &{}\quad \quad \in ~\mathbb {R}~\forall \, n \in \varLambda 7 &{} \\ \end{array} \end{aligned}$$

The output of the optimization program will be an optimal solution set containing the values for the variables \(f_\text {sym,tot}\), \(K_{D,n}\), \(K_{OL,n}\), \(K_{OH,n}\), \(K_{O,n}\), \(K_{S,n}\), \(p_{L,n}\) and \(p_{H,n}\).

4.2 Extended FI-DAC Optimization Program

The standard optimization program introduced previously needs to be extended in order to cover additional parameters, which need to be balanced with respect to the other parameters.

For the system it is interesting to have integer ratios between the LO frequencies \(f_{\text {LO},M_n,n}\) introduced in Sect. 3.3 and the DAC clock \(f_\text {DAC}\) in order to efficiently generate the frequencies by dividers and multipliers, respectively. This is represented in the optimization program by the additional Eqs. (21)–(23) and (36). The type of mixer for each DAC is given by the ordered set \(\varGamma =\{M_1,\ldots ,M_N\}\) with \(M_n\in \{\{\},~\text {LSB},~\text {USB},~\text {IQ}\}\) and \(M_1 = \{\}\) in order to generate a baseband signal.

Furthermore, there is commonly an integer ratio between the DAC clock \(f_\text {DAC}\) and the sample rate \(f_s\), which is represented by (37), whereby \(x_\text {DAC}\) is a parameter.

Moreover, it is desirable to generate a certain symbol rate, instead of just maximizing it. Therefore, the constraint (38) is added which puts an upper bound on the symbol rate, and thus, the optimizer tries to find a solution closest to this target symbol rate \(f_\text {sym,tot,target}\).

The extended optimization program is given as:

$$\begin{aligned} \begin{array}{lllll} \max &{} \quad \quad f_\text {sym,tot} &{} &{} \\ \text {s.t.} &{} \quad \quad (1)\text {--}(9), \,(10),\, (25),\, (27),\, (21)\,\text {-}\, (23) &{} &{} \\ &{}\quad \quad p_{L,n} &{}\quad \quad \ge ~ p_{L,n}^{\min } &{}\quad \quad (32)\\ &{}\quad \quad p_{L,n} &{}\quad \quad \le ~ p_{L,n}^{\max } &{}\quad \quad (33)\\ &{}\quad \quad p_{H,n} &{}\quad \quad \ge ~ p_{H,n}^{\min } &{}\quad \quad (34)\\ &{}\quad \quad p_{H,n} &{}\quad \quad \le ~ p_{H,n}^{\max } &{}\quad \quad (35)\\ &{}\quad \quad f_{\text {LO},M_n,n} &{}\quad \quad =~x_{\text {LO},M_n,n}f_\text {DAC} &{}\quad \quad (36) \\ &{}\quad \quad f_s &{}\quad \quad = ~ x_\text {DAC}f_\text {DAC} &{}\quad \quad (37)\\ &{}\quad \quad f_\text {sym,tot} &{}\quad \quad \le ~ f_\text {sym,tot,target} &{}\quad \quad (38)\\ &{}\quad \quad K_{D,n},\,K_{OL,n},\,K_{OH,n},\,K_{O,n},~\ldots &{} &{} \\ &{}\quad \quad K_{S,n},\,x_{\text {LO},M_n,n},\,K_{S,\text {tot}} &{}\quad \quad \in ~ \mathbb {N}~\forall \, n \in \varLambda &{} \\ &{}\quad \quad f_\text {sym,tot} &{}\quad \quad \in ~\mathbb {N} &{} \\ &{}\quad \quad p_{L,n},\,p_{H,n},\,f_{\text {LO},M_n,n} &{}\quad \quad \in ~\mathbb {R}~\forall \, n \in \varLambda &{} \\ \end{array} \end{aligned}$$

5 Parameter Balancing Examples

In this section, examples are provided to demonstrate the usefulness of mathematical nonlinear optimization in order to balance the various system parameters. In order to formulate and solve the optimization program, the MINLP is implemented in ZIMPL [19] and solved with the SCIP solver [1] from Konrad Zuse Center Berlin.

As an example, we use a system consisting of \(N=3\) DACs, each running at a sample rate of \(f_s = 80\) GS/s in order to show the challenges of the FI-DAC concept. A configuration as shown in Fig. 2 for the sub-signals I, II and III is used, meaning that the first sub-signal is a baseband signal and that both the second and the third sub-signals are upconverted. The lower sideband of sub-signal II and the upper sideband of sub-signal III are used. The triplexer used to combine the sub-signals is assumed to have cutoff frequencies at 34.5 and 66.5 GHz as in [8]. The number of data samples is chosen to be \(K_{D,\text {tot}} = 1\,023\) as in the example in Sect. 3.4.

In the following, the parameter balancing is investigated with both the standard FI-DAC optimization program and the extended FI-DAC optimization program.

Fig. 5
figure 5

Solutions of the FI optimization program showing the digital input spectrum as a function of samples (left) and the analog output spectrum as a function of frequency (right) for an exemplary FI-DAC consisting of three DACs, each running at \(f_s=80\) GS/s and jointly converting \(K_{D,\text {tot}}=1\,023\) data samples. The equation numbers of the applied constraints are displayed to the right as well as the total symbol rate \(f_\text {sym,tot}\). a, b Standard FI optimization program without constraints; c, d standard FI optimization program with oversampling ratio constraints; e, f extended FI optimization program with oversampling ratio constraints and integer symbol rate constraint; g, h extended FI optimization program with oversampling ratio constraints, integer symbol rate constraint and integer ratio constraint between DAC clock and LO frequencies

Full size image

5.1 Standard FI-DAC Optimization Program

For the standard FI-DAC optimization program two scenarios are investigated. First, there are no constraints put on the oversampling ratios in (28)–(31); thus, the generated symbol rate is maximized. The result of the optimization is shown in Fig. 5a, b. Figure 5a shows the distribution of the samples among the three DACs, whereby each DAC is loaded with \(K_S=341\) samples. Since \(K_{D,\text {tot}} = 1\,023\) is divisible by \(N=3\), all DACs are used to their full extent. The corresponding analog signal is shown in Fig. 5b, whereby a total symbol rate of \(f_\text {sym,tot} = 240\) GBd is generated. The bandwidth of each sub-spectrum is 40 GHz. The LOs are located both at 80 GHz.

Second, lower and upper bounds for the oversampling ratios \(p_{L,n}\) and \(p_{H,n}\) are introduced in order to account for the triplexer’s cutoff frequencies at 34.5 and 66.5 GHz, respectively. In order to match the first sub-signal to this filter a lower bound for the oversampling ratio is introduced, i.e., \(p_{H,1}^\text {min}=40/34.5\). In order to filter the DAC aliases of both upper bands, the oversampling ratio bound is chosen to be \(p_{H,n}^\text {min}=40/37~\forall \,n\,\in \,\{2,3\}\), thereby assuming that a spectral gap of \(2\times 3\) GHz to be sufficient. Furthermore, in order to suppress redundant mixer side bands, a spectral gap of equal width is assumed to be needed, resulting in an oversampling ratio of \(p_{L,n}^\text {min}=40/(40-3)\forall n \in \{2,3\}\). In order to match the second sub-signal to the triplexer’s characteristic, the value of \(p_{H,2}^\text {min}\) is further increased to 40 / 35. The DACs are now used with oversampling, and the result is visualized in Fig. 5c, d. The bandwidths match the characteristic of the triplexer, whereby the bandwidth of the sub-spectra, given by 34.43, 31.88 and 33.74 GHz, respectively, add up to a total bandwidth of 100.05 GHz, corresponding to a symbol rate of 200.10 GBd. The corresponding LO frequencies are given by 69.34 and 63.08 GHz.

For the communication system design it is generally desirable to have an integer symbol rate. Hence, in order to generate an overall integer symbol rate the standard FI-DAC optimization program is insufficient and thus, in the next section the extended FI-DAC optimization program is used.

5.2 Extended FI-DAC Optimization Program

Based on the scenario presented in the previous section, we introduce an additional integer constraint for the symbol rate \(f_\text {sym,tot}\) by setting \(f_\text {sym,tot}\) to be in \(\mathbb {N}\). As shown in Fig. 4 the amount of feasible integer GBd symbol rates is limited and they are given by: \(240,220,186,176,165,155,132,\ldots \). The result of the optimization is shown in Fig. 5e, f. The symbol rate is reduced to \(f_\text {sym,tot} = 186\) GBd. Therefore, especially the third frequency band was shrunk down to 26.73 GHz. The LO frequencies are 69.36 and 63.18 GHz.

For the DAC system design it is further desirable to have an integer ratio between the DAC clock and the LO frequencies in order to build a clock distribution network with a small amount of frequency dividers and multipliers, respectively. Thus, the constraints (36) and (37) are added. Hereby, it is assumed that the DAC clock is given by \(f_\text {DAC} = f_s/32 = 2.5\) GHz as in [8, 36]. However, with the constraints formulated earlier, the problem becomes infeasible. Thus, some of the previous constraints are mildly relaxed in order to obtain a feasible solution. The results of the optimization are shown in Fig. 5g, h. The symbol rate is still 186 GBd, but the LO frequencies are now set at integer ratios of the DAC clock at 70 and 60 GHz. The distribution of the data samples among the DACs resembles the distribution in the previous scenario.

In the examples provided above, the upcoming challenges when designing an FI-DAC became visible, including the fact that not every symbol rate could be addressed as well as the interdepencies between the systems’ parameters. In terms of implementation, the last configuration would be chosen, since the required LOs are easier to both generate and control during operation. Note that next to the presented solutions, other optimal solutions with a different distribution of both data samples and additional samples for oversampling are viable as well. They could be obtained by tweaking existing constraints or by adding additional constraints. These additional constraints could be used in order to include further aspects of the system design, which have not been covered yet, e.g., equal oversampling ratios \(p_{H,1} = p_{H,2}\) or else. If scaling the FI-DAC concept to an arbitrary number of DACs, the presented optimization programs will be very helpful in order to manage the system’s complexity.

6 Simulation Results

A simulation is conducted in order to demonstrate both the correction of magnitude and phase of the frequency bands and the necessity for oversampling. The simulation setup is visualized in Fig. 6, which shows a FI-DAC consisting of three DACs, two RF mixers and a triplexer for combining the sub-signals. The parameters for the digital splitting are chosen as in example (e) in Sect. 5. For the data signal, a PAM-4 modulation is chosen and the length is set to ten times the block size of given by \(K_{D,\text {tot}}\) in order to provide a sufficient data signal length. All components are assumed ideal, except for the DACs’ low-pass characteristic, the anti-aliasing filter following the DACs, as well as the triplexer characteristic. The frequency responses of these filters are approximated by using Butterworth and Bessel filters according to the measured frequency responses of the system presented in [8].

The resulting frequency responses of the individual signals paths of the FI-DAC are shown in Fig. 7a–f, and the LO frequencies are included for better comprehensibility, though they are ideally suppressed for the simulation. In Fig. 7a, b, both the magnitude and phase of the uncompensated frequency responses are shown. There are drops of the frequency responses, and moreover, cross talk between the frequency bands can be observed. By using oversampling in combination with Nyquist pulse shaping, the cross talk components are moved away from the signal bands and can be suppressed by the analog filters as shown in Fig. 7c, d. The frequency responses are further corrected by means of zero-forcing frequency domain pre-equalizers as shown in Fig. 7e, f, which correct for both magnitude and phase mismatches.

Fig. 6
figure 6

Simulation setup consisting of three DACs, two mixers and a triplexer

Full size image

In Fig. 7g, the output spectrum of the PAM-4 signal with Nyquist pulse shaping is plotted and in Fig. 7h, the corresponding clearly open 186 GBd 4-level PAM eye diagram is visualized.

The simulation results indicate that the concept is practical and that the pre-equalization of the individual sub-signals enables a combined signal with an open eye diagram. In the next section, the pre-equalization will be tested with a real-world setup.

Fig. 7
figure 7

Magnitude and phase of the frequency responses of the exemplary FI-DAC with local oscillator frequencies: a, b uncompensated FI-DAC; c, d FI-DAC with Nyquist pulse shaping; e, f FI-DAC with Nyquist pulse shaping and zero-forcing equalizer; g output spectrum; h eye diagram

Full size image

7 Experimental Results

In order to validate the concept of the FI-DAC, an experiment with two DACs is set up, each having a 3 dB bandwidth of 19 GHz and running at a sample rate of 90 GS/s. The combined output signal will have a sample rate of 180 GS/s and 40 GHz bandwidth. This is an improved version of the experimental results previously presented in [36] and an extended version of these improved results in [37].

7.1 Setup

The experimental setup is visualized in Fig. 8a. The digital signal is processed in an offline DSP unit. First, the digital signal is pulse-shaped with a raised cosine filter with a roll-off-factor of 0.0313 and then split into two sub-signals. Then, the sub-signals are individually pre-equalized with a zero-forcing (ZF) frequency domain equalizer (FDE), which mitigates amplitude and phase mismatches between the two asymmetrical analog paths.

In order to ensure a stable phase relationship between the DAC clock and the LO, the externally generated LO frequency is split into two, whereby one copy is divided by 16 in order to generate the 2.8125 GHz clock signal for the DACs. The other copy is amplified in order to drive the passive mixer.

The two 8-bit DACs are running at a sample rate of 90 GS/s and generate the analog representations of the two sub-signals. The first and the second sub-signals contain frequencies from DC to 22.5 and 5 to 22.5 GHz, respectively. Both sub-signals are amplified with variable gain amplifiers in order to match their spectral power. Both sub-signals are further low-pass-filtered in order to suppress DAC hold spectra, whereby the LPF for the first sub-signal is included in the diplexer. The second sub-signal is upconverted with a passive RF mixer to a frequency of 45 GHz in order to utilize the lower side band. Both signals are combined in the diplexer, which has a crossover frequency of 22.5 GHz. A LPF follows the diplexer in order to suppress both the fed-through LO and the upper side band of the second sub-signal. The combined signal is digitized with a real-time oscilloscope with 160 GS/s sample rate and 63 GHz analog bandwidth.

7.2 Results

In Fig. 8b, the magnitude and phase of the uncompensated frequency responses are shown, which are obtained with a least squares (LS) \(2\times 1\) multiple-input multiple-output (MIMO) channel estimation in the time domain. There is a 20 dB drop of the frequency response of the first path and a 10 dB drop of the frequency response of the second DAC to the crossover frequency of 22.5 GHz. The phase is fairly linear in the frequency ranges, where considerable magnitude components are present. By applying pre-distortion, the effects of the analog components can be mitigated and the clearly open 80 GBd PAM-4 eye diagram as well as the corresponding spectrum are visualized in Fig. 8c. The bit error rate is \(2.19\times 10^{-4}\). A flat spectrum can be observed with a still present strong LO at 45 GHz, which could not be suppressed sufficiently with the LPF with 43 GHz cutoff frequency. Note that the LO frequency was digitally removed prior to plotting the eye diagram.

In Fig. 8d, the centered impulse response of the corrected combined system is shown. There are only little distortions visible; however, in the frequency domain representation shown in Fig. 8e, residual distortions of both magnitude and phase are visible. The magnitude is fairly flat for the first sub-signal, but has distortions of ± 1 dB for the second sub-signal. The phase is linear for the first sub-signal, corresponding to a linear time shift. For the second sub-signal there are phase discontinuities visible. These distortions can be possibly attributed to the reduced phase stability between the LO frequency and the DAC clock, due to the on-chip phase-locked loop (PLL) of the DAC.

As for the simulation, the experimental results show that the pre-equalization of both sub-signals enables an open eye diagram for the combined signal. However, there are still residual distortions, which could not be mitigated. In the following paragraph the observations and challenges obtained in the experiments are summarized.

Fig. 8
figure 8

Experimental setup and results for an FI-DAC consisting of two DACs: a experimental setup; b uncompensated individual frequency responses; c eye diagram and output spectrum; d compensated combined impulse response; e compensated combined frequency response

Full size image

7.3 Observations and Challenges

FI-DAC is a concept to enhance the bandwidth of a DAC beyond the current technological limits. Hence, for an implementation, the designer will start with a given high-speed DAC and will then choose mixers and filters suitable for the FI-DAC system. Note that the commercial availability of high-speed components is limited and thus, trade-offs might be taken into account. The signal processing is then adapted to the specifications of the analog components in order to mitigate the analog impairments by both pre-equalization and oversampling. In this section, a short introduction on the impairments of the utilized analog components is given as well as ways to mitigate them.

High-speed DACs usually operate in ZOH mode; thus, they generate sinc-shaped frequency images, which need to be suppressed, since they appear as cross talk for the neighboring frequency bands. Digital oversampling in combination with an analog low-pass filter (LPF) can be used as described in Sect. 2 and shown in Sects. 6 and 7. Furthermore, each DAC’s output signal appears to be random in the time domain, since the signal information is distributed among several sub-signals; hence, the sub-signals have a characteristic similar to orthogonal frequency division multiplexing (OFDM) signals, i.e., high peak-to-average power ratio (PAPR). Eventually, DACs with a high resolution are needed in order to generate the individual sub-signals with sufficient accuracy.

High-speed passive broadband mixers usually suffer from a frequency-dependent conversion loss, spurious products due to inter-modulation, a strong LO feed through, LO harmonics, as well as spurious products located around the LO harmonics [8, 12, 26, 27]. The influence of the frequency-dependent conversion loss as well as spurious products due to inter-modulation could be partly mitigated by linear and nonlinear digital preprocessing. The other effects generate frequency components outside of the upconverted band; thus, they could be suppressed by using oversampling in combination with analog filters. Analog filters used in the frequency multiplexer can be designed with roll-offs of 4–11 dB/GHz [8, 36].

Note that the LOs for the mixers and the clock for the DACs need to be phase-locked in order to ensure the correct generation of the combined signal with the sub-signals being in phase.

In principle, the concept is scalable to N DACs. For each additional frequency band, a DAC, an LPF, an LO, a mixer, a band-pass filter and an additional port in the combiner are needed. Mixers are available for different frequency bands, even for hundreds of GHz [17, 38]. However, the complexity and size of the combiner will finally limit the number of DACs that can be interleaved. The parasitic effects in the combiner rise with increasing number of frequency bands, which in turn decreases the analog bandwidth. Furthermore, the phase noise requirements are rising for higher frequencies; hence, the required precision for both clock generation and distribution rises accordingly, whereby the highest LO frequency will have the topmost phase noise requirements. Note that if all clock and LO frequencies are derived from a common frequency in a frequency divider-based clock tree, phase stability between the frequency bands would not be a limiting factor, since DAC clocks and LO frequencies have a statistically dependent phase noise. More information can be found in [8, 34, 36].

8 Conclusion

In this paper, we presented an analytical framework for the FI-DAC concept and provided an initial verification of the concept by means of simulations and experiments. Our analysis highlights the inherent interdependencies between multiple system parameters. A closed algebraic expression for the distribution of the data samples among the DACs was presented, taking into account different oversampling ratios in order to realize guard bands suppressing DAC aliases and unused mixer side bands. Furthermore, the limitations on generating a specific symbol rate were presented and visualized with examples. In order to balance the interdependent system parameters, a mathematical optimization approach was introduced in the form of two MINLPs. Examples for finding feasible FI-DAC configurations with respect to numerous constraints for the system design were provided as well as simulation results showing the effects of guard bands and pre-equalization. Experimental results validated the FI-DAC concept with two DACs generating a combined 80 GBd PAM-4 signal at 180 GS/s.

The concept has a high application potential in the optical domain as well, in order to generate ultra-broadband waveforms spanning multiple THz [15, 33]. The mathematical framework provided in this paper will be a valuable basis for scaling the concept to systems with a large number of wavelengths.