1 Introduction

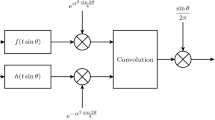
The Wiener filter [15] is a well-known tool in signal processing and communications [9]. It presents a classical approach to determining the optimum filter by providing the minimum mean-squared error estimate of a desired process \(d\left( t \right) \), from a noisy random input signal \(x\left( t \right) \), as illustrated in Fig. 1.

In Fig. 1, \(x\left( t \right) \) and \(d\left( t \right) \) are assumed to be jointly wide-sense stationary random processes with known autocorrelations, \({R_x}(\tau ) = E\left\{ {x(t + \tau ){x^ * }(t)} \right\} \) and \({R_d}(\tau ) = E\left\{ {d(t + \tau ){d^ * }(t)} \right\} \), and a known cross-correlation, \({R_{dx}}(\tau ) = E\left\{ {d(t + \tau ){x^ * }(t)} \right\} \) , in which \(E\left\{ \bullet \right\} \) denotes the mathematical expectation and the asterisk indicates the complex conjugation operation. The output of the filter is \(\hat{d}(t)\), which denotes the estimate of \(d\left( t \right) \) and is given by

$$\begin{aligned} \hat{d}(t)=\int _{-\infty }^{\infty }x\left( t-\tau \right) w\left( \tau \right) \hbox {d}\tau \end{aligned}$$
(1)

The estimated error is

$$\begin{aligned} e(t)=d(t)-\hat{d}(t) \end{aligned}$$
(2)

The mean-squared error is

$$\begin{aligned} E\left\{ {{{\left| {e(t)} \right| }^2}} \right\}= & {} E\left\{ {\left( {\hbox {d}(t) - \int _{-\infty }^\infty {x(t - \tau )w(\tau )\hbox {d}\tau } } \right) \left( {{d^{*}}(t) - \int _{-\infty }^\infty {{x^{*} }(t - \theta ){w^{*} }(\theta )\hbox {d}\theta } } \right) } \right\} \nonumber \\= & {} {R_d}(0) - \int _{-\infty }^{\infty } {R_{dx}^{*} (\tau )w(\tau )\hbox {d}\tau } - \int _{-\infty }^\infty {{R_{dx}}(\theta ){w^ * }(\theta )\hbox {d}\theta }\nonumber \\&+ \int _{-\infty }^{\infty } {\int _{-\infty }^\infty {{R_x}(\theta - \tau )w(\tau ){w^ * }(\theta )\hbox {d}\tau \hbox {d}\theta } } \end{aligned}$$
(3)
Fig. 1
figure 1

Diagram of the Wiener filter

Full size image

The optimum filter, denoted by \({w_\mathrm{opt}}(t)\), is determined by minimizing \(E\left\{ {{{\left| {e(t)} \right| }^2}} \right\} \).

In the classical principle of the Wiener filter design, there is only one causality restriction on the filter to be considered. However, in practice, to meet the needs of different applications, the filter may be subject to more broad constraints. For example, in signal prediction problems and adaptive control applications, the filter is generally required to be a time-limited system to realize finite-step prediction or finite-order control [10]. In past years, numerous researchers have studied the design of the Wiener filter with finite support in the time domain [4, 6, 14]. Other common restrictions on the Wiener filter are in the frequency domain. For example, the Wiener filter may be required to be band-limited, band-pass, or low-pass or to satisfy other bandwidth limitations to guarantee that the frequency support of the filter can match the bandwidth of the desired signal and to avoid situations in which the filter works in noise-only periods [7, 8, 12]. For instance, in a speech enhancement system, to reduce the effects of environmental noise, the Wiener filter usually operates in the audible frequency range. Much research has been reported on constrained Wiener filters in binaural hearing aids and speech enhancement [1, 2, 4, 5, 12]. In addition to time-domain and frequency-domain constraints, linear constraints, which require the Wiener filter to satisfy a set of linear equations, are also widely applied in many fields, including adaptive beamforming [13], spectral analysis, and function interpolation [11]. Moreover, in filter design, when the power spectrum of the input is close to zero at some frequency points, the corresponding frequency response of the filter at these frequency points will become unbounded. A filter with a boundless frequency response is undesirable because it will be sensitive to noise and data errors. In this situation, the finite-energy constraint is imposed to smooth the peak value of the frequency response of the filter. The performance of the Wiener filter with the finite-energy constraint is better than that of the unconstrained Wiener filter [3]. In addition to the common constraints described above, studies on wider classes of constraints for the Wiener filter can be found in the literature [7, 8], including the output-spectrum constraint, the estimated signal-power constraint, the filter-energy constraint, and the filter-stability constraint. Moreover, the closed-form solutions to these constrained design problems have been derived.

The work presented in this paper makes three contributions. First, this is the first work to incorporate the different constraint conditions into a single integration equation. Moreover, since the functions in the integral can be chosen according to different application needs, single integration allows more flexibility and applicability in processing various restrictions on the Wiener filter. Second, we develop a closed formula to represent the optimal solution of the Wiener filter under the constrained integration equation. Because the closed formula has one additional term compared to the Wiener–Hopf equation, the formula is called the extended Wiener–Hopf equation in this paper. Third, we develop a uniform analytical method along with an iterative algorithm to solve the extended Wiener–Hopf equation. Finally, some simulation examples are given to further illustrate the solution steps of our algorithm.

2 Constraint Condition

Assume that w(t) is subject to the following constraint:

$$\begin{aligned} \int _{\mathrm{{-}}\infty }^\infty {\left( {w(t) - g(t)} \right) {\lambda ^ * }(t)} \hbox {d}t = \beta \end{aligned}$$
(4)

where g(t), \(\lambda (t)\), and \(\beta \) may be fully known or some of their characteristics may be known.

In particular, Eq. (4) is a more general expression of the following three constraints.

2.1 Time-Domain Constraints

In this case, w(t) is equal to a given function g(t) within the time subset T, i.e.,

$$\begin{aligned} w(t)=g(t),t\in T \end{aligned}$$
(5)

More specifically, if \(g(t)=0\) and \(T=\left( -\infty ,0\right) \), then w(t) is obviously required to be causal; if \(g(t)=0\) and \(T=\left( -\infty ,0\right) \cup [t_{0},\infty )\), where \(t_{0}>0\), then w(t) is a causal time-limited system.

For this case, if we take \(\lambda (t)=0,t\notin T\) and \(\beta =0\), then Eq. (5) can be described by Eq. (4).

2.2 Frequency-Domain Constraints

Here, W(f) is limited by

$$\begin{aligned} W(f)=G(f),f\in \Omega \end{aligned}$$
(6)

where W(f) is the Fourier transformation of the filter w(t), G(f) is a known frequency-domain function, and \(\Omega \) indicates a subset of the frequency domain. If \(G(f)=0\) and \(\Omega =\left( -\infty ,-\sigma \right) \cup \left( \sigma ,\infty \right) \), in which \(\sigma \) is a positive number, w(t) must be a low-pass filter. If \(G(f)=0\) and \(\Omega =\left( -\infty ,0\right) \), then w(t) is required to be an analytic function. If \(G(f)=0\) and \(\Omega =\left( -\infty ,-\sigma _{2}\right) \cup \left( -\sigma _{1},\sigma _{1}\right) \cup \left( \sigma _{2},\infty \right) \), where \(\sigma _{2}>\sigma _{1}>0\), then w(t) must be a band-pass system.

For this state, we take \(\Lambda (f)=0\), \(f\notin \Omega \), and \(\beta =0\). Thus:

$$\begin{aligned} \int _{-\infty }^{\infty }\left( W(f)-G(f)\right) \Lambda ^{*}(f){\hbox {d}}f=\beta \end{aligned}$$
(7)

According to Parseval’s theorem [9], Eq. (7) can be regarded as the expression of Eq. (4) in the frequency domain.

2.3 Orthogonal Constraints

In this case, w(t) is assumed to be orthogonal to the signal space H, i.e.,

$$\begin{aligned} \int _{-\infty }^{\infty }w(t)\lambda ^{*}(t){\hbox {d}}t=0,\quad \forall \lambda (t)\in H \end{aligned}$$
(8)

Equation (8) is a special case of Eq. (4), in which \(g(t)=0\) and \(\beta =0\). In practice, the orthogonal space of the filter w(t) is usually viewed as noisy space or undesirable signal space, which needs to be depressed by introducing the constraint defined in Eq. (8).

According to these three particular cases, we can construct the Wiener filter with more general constraints to meet the requirements of different practical applications because there are many possibilities for g(t) or \(\lambda (t)\).

3 Principle

To consider the constraints of Eq. (4), we first multiply the two sides of Eq. (4) by a Lagrange factor \(\mu \). As a result, we have \({\mu ^ * }(\int _{\mathrm{{ - }}\infty }^\infty {\left( {w(t) - g(t)} \right) }\) \({\lambda ^ * }(t){\hbox {d}}t - \beta ) = 0\). Then, we add it and its conjugate to Eq. (3) as follows:

$$\begin{aligned} L\left( w,\mu \right)= & {} E\left\{ \left| e(t)\right| ^{2}\right\} +\mu ^{*}\left( \int _{-\infty }^{\infty }\Bigl (g(t)-w(t)\Bigr )\lambda ^{*}(t)\hbox {d}t-\beta \right) \nonumber \\&\quad +\,\mu \left( \int _{-\infty }^{\infty }\Bigl (g(t)-w(t)\Bigr )^{*}\lambda (t)\hbox {d}t-\beta ^{*}\right) \nonumber \\= & {} R_{d}\left( 0\right) -\int _{-\infty }^{\infty }R_{dx}^{*}\left( \tau \right) w\left( \tau \right) \hbox {d}\tau \nonumber -\int _{-\infty }^{\infty }R_{dx}\left( \theta \right) w^{*}\left( \theta \right) \hbox {d}\theta \\&\quad +\,\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }R_{x}\left( \theta -\tau \right) w^{*}\left( \theta \right) w\left( \tau \right) \hbox {d}\tau \hbox {d}\theta \nonumber \\&\quad +\,\int _{-\infty }^{\infty }\Bigl (w(t)-g(t)\Bigr )\mu ^{*}\lambda ^{*}(t)\hbox {d}t-\mu ^{*}\beta \nonumber \\&\quad +\,\int _{-\infty }^{\infty }\Bigl (w(t)-g(t)\Bigr )^{*}\mu \lambda (t)\hbox {d}t-\mu \beta ^{*} \end{aligned}$$
(9)

Let \(S_{x}(f)\), \(S_{d}(f)\), \(S_{dx}(f)\), W(f), G(f), and \(\Lambda (f)\) denote the Fourier transformations of \(R_{x}(t)\), \(R_{d}(t)\), \(R_{dx}(t)\), w(t), g(t), and \(\lambda (t)\), respectively. Note that the Fourier transformation of \(\int _{-\infty }^{\infty }R_{x}\left( \theta -\tau \right) w\left( \tau \right) \hbox {d}\tau \) is \(S_{x}(f)W(f)\), where \(S_{x}(f)\) is nonnegative. We assume \(S_{x}(f)>0\). Therefore, according to Parseval’s equation, we have

$$\begin{aligned}&L(w,\mu ) = \int _{\mathrm{{ - }}\infty }^\infty {\left( {{S_d}(f) - S_{dx}^ * (f)W(f) - {S_{dx}}(f){W^ * }(f) + {S_x}(f){{\left| {W(f)} \right| }^2}} \right) \hbox {d}f} \nonumber \\&\qquad +\, \int _{ - \infty }^\infty {\left( {W(f) - G(f)} \right) } {\mu ^ * }{\Lambda ^ * }(f)\hbox {d}f + \int _{ - \infty }^\infty {\left( {{W^ * }(f) - {G^ * }(f)} \right) } \mu \Lambda (f)\hbox {d}f - {\mu ^ * }\beta - \mu {\beta ^ * }\nonumber \\&\quad = \int _{ - \infty }^\infty {{S_d}(f)\hbox {d}f }+\,\int _{ - \infty }^\infty \left( {S_x}(f){{\left| {W(f)} \right| }^2} - \frac{{{{\left( {{S_{dx}}(f) - \mu \Lambda (f)} \right) }^ * }}}{{\sqrt{{S_x}(f)} }}\sqrt{{S_x}(f)} W(f)\right. \nonumber \\&\quad \quad \left. - \frac{{\left( {{S_{dx}}(f) - \mu \Lambda (f)} \right) }}{{\sqrt{{S_x}(f)} }}\sqrt{{S_x}(f)} {W^ * }(f) \right) \hbox {d}f \nonumber \\&\quad \quad +\, \int _{ - \infty }^\infty \left( \frac{{{{\left| {\left( {{S_{dx}}(f) - \mu \Lambda (f)} \right) } \right| }^\mathrm{{2}}}}}{{{S_x}(f)}} -\, \frac{{{{\left| {\left( {{S_{dx}}(f) - \mu \Lambda (f)} \right) } \right| }^\mathrm{{2}}}}}{{{S_x}(f)}} \right) \hbox {d}f \nonumber \\&\quad \quad -\, \int _{ - \infty }^\infty {\left( {G(f){\mu ^ * }{\Lambda ^ * }(f) + {G^ * }(f)\mu \Lambda (f)} \right) \hbox {d}f} - {\mu ^ * }\beta - \mu {\beta ^ * }\nonumber \\&\quad = \int _{ - \infty }^\infty {{S_d}(f)\hbox {d}f + } \int _{ - \infty }^\infty {\left( {{S_x}(f){{\left| {W(f) - \frac{{\left( {{S_{dx}}(f) - \mu \Lambda (f)} \right) }}{{{S_x}(f)}}} \right| }^\mathrm{{2}}} - \frac{{{{\left| {\left( {{S_{dx}}(f) - \mu \Lambda (f)} \right) } \right| }^\mathrm{{2}}}}}{{{S_x}(f)}}} \right) \hbox {d}f}\nonumber \\&\quad \quad -\, \int _{ - \infty }^\infty {\left( {G(f){\mu ^ * }{\Lambda ^ * }(f) + {G^ * }(f)\mu \Lambda (f)} \right) \hbox {d}f} - {\mu ^ * }\beta - \mu {\beta ^ * } \end{aligned}$$
(10)

Consequently, if W(f) is taken to be equal to \(\frac{S_{dx}(f)-\mu \Lambda (f)}{S_{x}(f)}\), then \(L\left( w,\mu \right) \) achieves the minimum of \(E\left\{ \left| e(t)\right| ^{2}\right\} \), denoted by \(L_{min}\left( w_\mathrm{opt},\mu \right) \), and we have

$$\begin{aligned} {L_{\min }}({w_\mathrm{opt}},\mu )= & {} \int _{ - \infty }^\infty {\left( {{S_x}(f) - \frac{{{{\left| {\left( {{S_{dx}}(f) - \mu \Lambda (f)} \right) } \right| }^\mathrm{{2}}}}}{{{S_x}(f)}}} \right) \hbox {d}f}\nonumber \\&-\, \int _{ - \infty }^\infty {\left( {G(f){\mu ^{*}}{\Lambda ^{*}}(f) + {G^{*}}(f)\mu \Lambda (f)} \right) \hbox {d}f} - {\mu ^{*} }\beta - \mu {\beta ^{*}}\nonumber \\ \end{aligned}$$
(11)

and

$$\begin{aligned} W_\mathrm{opt}(f)=\frac{S_{dx}(f)-\mu \Lambda (f)}{S_{x}(f)} \end{aligned}$$
(12)

or, equivalently,

$$\begin{aligned} S_{x}(f)W_\mathrm{opt}(f)=S_{dx}(f)-\mu \Lambda (f) \end{aligned}$$
(13)

Correspondingly, by the inverse Fourier transform, in the time domain, Eq. (13) can be converted into a convolution integral of the following form,

$$\begin{aligned} \int _{-\infty }^{\infty }R_{x}\left( \tau -\theta \right) w_\mathrm{opt}\left( \theta \right) \mathrm{d}\theta =R_{dx}\left( \tau \right) -\mu \lambda \left( \tau \right) \end{aligned}$$
(14)

Equation (14) has one more term, \(-\mu \lambda \left( \tau \right) \), than the Wiener–Hopf equation [9], i.e., \(\int _{-\infty }^{\infty }R_{x}\left( \tau -\theta \right) w_\mathrm{opt}\left( \theta \right) \hbox {d}\theta =R_{dx}\left( \tau \right) \), which is easily derived from the unconstrained Wiener filter design problem [9] or from Eq. (9) or (10) by ignoring the integral of the constraint. Since \(\mu \lambda \left( \tau \right) \) is the function of the constraint on the design result and since \(\mu \lambda \left( \tau \right) =0\) if and only if there is no constraint on the Wiener filter, Eq. (14) can be called the extended Wiener–Hopf equation. Finally, we take our familiar causal constraint as an example to further illustrate the role of \(\mu \lambda \left( \tau \right) \) in the extended Wiener–Hopf equation. As stated in the discussion in Eq. (5), requiring the filter to be causal is equivalent to requiring that \(w(t)=g(t)=0\) for \(t\in \left( -\infty ,0\right) \) and \(\lambda (t)=0\) for \(t\in [0,\infty )\) in Eq. (4). Consequently, in the corresponding extended Wiener–Hopf equation under the causal constraint, \(\mu \lambda \left( \tau \right) \) is an anti-causal function whose purpose is to offset the non-causal component of the Wiener–Hopf equation and to guarantee that the optimal filter is a causal system.

In addition, we develop the other computational formulas of the minimum mean-squared error of the Wiener filter under the integral constraint. From Eqs. (3), (12), (13), and (9), we can obtain

$$\begin{aligned} L(w,\mu )= & {} \int _{\mathrm{{ - }}\infty }^\infty {\left( {{S_d}(f) - S_{dx}^ * (f){W_\mathrm{opt}}(f) - {S_{dx}}(f)W_\mathrm{opt}^ * (f) + {S_x}(f){{\left| {{W_\mathrm{opt}}(f)} \right| }^2}} \right) \hbox {d}f}\nonumber \\= & {} \int _{ - \infty }^\infty {{S_d}(f)\hbox {d}f - } \int _{ - \infty }^\infty {{S_x}(f){{\left| {{W_\mathrm{opt}}(f)} \right| }^\mathrm{{2}}}\hbox {d}f} \nonumber \\&-\, \int _{ - \infty }^\infty {\left( {G(f){\mu ^ * }{\Lambda ^ * }(f) + {G^ * }(f)\mu \Lambda (f)} \right) \hbox {d}f} - {\mu ^ * }\beta - \mu {\beta ^ * }\nonumber \\= & {} \int _{ - \infty }^\infty {{S_d}(f)\hbox {d}f - } \int _{ - \infty }^\infty {\left( {{S_{dx}}(f) - \mu \Lambda (f)} \right) W_\mathrm{opt}^ * (f)\hbox {d}f} \nonumber \\&-\, \int _{ - \infty }^\infty {\left( {G(f){\mu ^ * }{\Lambda ^ * }(f) + {G^ * }(f)\mu \Lambda (f)} \right) \hbox {d}f} - {\mu ^ * }\beta - \mu {\beta ^ * }\nonumber \\= & {} \int _{ - \infty }^\infty {{S_d}(f)\hbox {d}f - } \int _{ - \infty }^\infty {{S_{dx}}(f)W_\mathrm{opt}^ * (f)\hbox {d}f} - \int _{ - \infty }^\infty {G(f){\mu ^ * }{\Lambda ^ * }(f)\hbox {d}f} - {\mu ^ * }\beta \nonumber \\ \end{aligned}$$
(15)

The first equality is immediately derived from the Fourier transformation of Eq. (3), after w(t) is replaced by \(w_\mathrm{opt}(t)\). The second equality is obtained by replacing \(S_{dx}(f)-\mu \Lambda (f)\) with \(S_{x}(f)W_\mathrm{opt}(f)\) in Eq. (11), since \(S_{x}(f)W_\mathrm{opt}(f)=S_{dx}(f)-\mu \Lambda (f)\). The third equality is obtained by replacing \(S_{x}(f)\left| W_\mathrm{opt}(f)\right| ^{2}\) with \(S_{dx}(f)W_\mathrm{opt}^{*}(f)-\mu \Lambda (f)W_\mathrm{opt}^{*}(f)\) in the second equality. The last equality is a simplification of the third equality since \(\mu \left( \int _{-\infty }^{\infty }\left( W_\mathrm{opt}(f)-G(f)\right) ^{*}\Lambda (f)\hbox {d}f-\beta ^{*}\right) =0\).

4 Algorithms

In this section, we discuss how \(W_\mathrm{opt}(f)\) can be obtained from Eq. (12). First, we give the solution of Eq. (12) for the constraint condition in which the filter is required to have finite frequency support. Then, we develop an analytical approach and an iterative technique to obtain \(W_\mathrm{opt}(f)\) from Eq. (13).

In practice, the filter may be required to be low-pass, band-pass, high-pass, or band-limited. These restrictions can be summarized as the finite frequency-support constraint, which is explained as follows:

If the filter is required to satisfy

$$\begin{aligned} W(f)=0,f\notin \Omega \end{aligned}$$
(16)

where \(\Omega \) denotes a non-empty subset of the frequency domain, then the filter has finite frequency support. In this case, \(\Lambda (f)\) should be chosen such that

$$\begin{aligned} \Lambda (f)=0\text {,}f\in \Omega \end{aligned}$$
(17)

Then ,we have the corresponding constrained integral \(\int _{-\infty }^{\infty }W(f)\Lambda ^{*}(f)\hbox {d}f=0\).

Let

$$\begin{aligned} \varGamma (f)={\left\{ \begin{array}{ll} 1, &{}\quad f\in \Omega \\ 0, &{} \quad f\notin \Omega \end{array}\right. } \end{aligned}$$
(18)

From Eqs. (17) and (18), we have \(W(f)\varGamma (f)=W(f)\) and \(\Lambda (f)\varGamma (f)=0\). Then, we multiply both sides of Eq. (12) by \(\varGamma (f)\). As a result, we obtain the solution of the Wiener filter with finite frequency support:

$$\begin{aligned} W_\mathrm{opt}(f)&= W_\mathrm{opt}(f)\varGamma (f)=\frac{S_{dx}(f)-\mu \Lambda (f)}{S_{x}(f)}\varGamma (f)\nonumber \\&= \frac{S_{dx}(f)}{S_{x}(f)}\varGamma (f)={\left\{ \begin{array}{ll} \frac{S_{dx}(f)}{S_{x}(f)}, &{}\quad f\in \Omega \\ 0, &{}\quad f\notin \Omega \end{array}\right. } \end{aligned}$$
(19)

Next, we introduce the analytical approach. By inserting \(\frac{S_{dx}(f)-\mu \varLambda (f)}{S_{x}(f)}\) into the frequency form of Eq. (4), we have \(\int _{-\infty }^{\infty }\left( \frac{S_{dx}(f)-\mu \Lambda (f)}{S_{x}(f)}-G(f)\right) \Lambda ^{*}(f)\hbox {d}f=\beta \). Then, solving this integration equation, we obtain the Lagrange factor \(\mu \) as

$$\begin{aligned} \mu =\left( \int _{-\infty }^{\infty }\left( \frac{S_{dx}(f)}{S_{x} (f)}-G(f)\right) \Lambda ^{*}(f) \hbox {d}f-\beta \right) \bigg /\int _{-\infty }^{\infty }\frac{\left| \Lambda (f)\right| ^{2}}{S_{x}(f)}\hbox {d}f \end{aligned}$$
(20)

As a result, \(W_\mathrm{opt}(f)\) can be analytically calculated from Eqs. (20) and (12) if the analytical form of \(\Lambda (f)\) is known. However, this approach is invalid when \(\Lambda (f)\) is unknown or when only its characteristics are known without any information about its form.

Now, we introduce an iterative technique, which is valid regardless of whether the analytical form of \(\Lambda (f)\) is known. The iterative formulas are given in the frequency domain by Eq. (21):

$$\begin{aligned}&W'_{i+1}(f)=W_{i}(f)+\eta \left( S_{dx}(f)-S_{x}(f)W_{i}(f)\right) \end{aligned}$$
(21a)
$$\begin{aligned}&\int _{-\infty }^{\infty }\left( W_{i+1}^{'}(f)-G(f)\right) \Lambda ^{*}(f)\hbox {d}f=\beta _{i+1}\end{aligned}$$
(21b)
$$\begin{aligned}&\rho _{i+1}=\left( \beta _{i+1}-\beta \right) \bigg /\int _{-\infty }^{\infty }\left| \Lambda (f)\right| ^{2}\hbox {d}f\end{aligned}$$
(21c)
$$\begin{aligned}&W_{i+1}(f)=W'_{i+1}(f)-\rho _{i}\Lambda (f)\end{aligned}$$
(21d)
$$\begin{aligned}&d\left( W_{i+1},W_{i}\right) =\int _{-\infty }^{\infty }\left| W_{i+1}(f)-W_{i}(f)\right| ^{2}\hbox {d}f \end{aligned}$$
(21e)

where \(\eta \) is the convergence factor and the subscript \(\left( i\right) \) denotes the iteration number. \(W'_{i+1}(f)\) represents the result of iteration (i+1), and \(W_{i+1}(f)\) is the largest constrained component of \(W'_{i+1}(f)\), which will be defined in the next paragraph. Because \(W'_{i+1}(f)\) generally does not meet the constraint defined in Eq. (4), for the sake of the restriction condition in the next iterative operation and fast convergence, we need to extract the largest constrained component of \(W'_{i+1}(f)\) to satisfy Eq. (4) . The iterative procedure can be summarized as follows:

  1. (1)

    Set the convergence factor \(0<\eta <\frac{2}{\max S_{x}(f)}\) and a positive number \(\varepsilon \), which is the iteration termination threshold. Then, arbitrarily choose an initial value \(W_{0}(f)\) and insert it into Eq. (21a) to obtain \(W'_{1}(f)\).

  2. (2)

    Using Eq. (21b) through Eq. (21d), or by immediately applying the constraint condition, extract the largest constrained component of \(W'_{1}(f)\), denoted by \(W_{1}(f)\).

  3. (3)

    Insert \(W_{1}(f)\) and \(W_{0}(f)\) into (21e) to obtain \(d\left( W_{1},W_{0}\right) \). If \(d\left( W_{1},W_{0}\right) <\varepsilon \), the iteration cycle is terminated and \(W_{1}(f)\) is taken as \(W_\mathrm{opt}(f)\); otherwise, \(W_{1}(f)\) is carried into Eq. (21a) to another iteration cycle.

Before discussing the convergence, we define the largest constrained component.

Definition 1

The largest constrained component of \(W'_{i}(f)\), denoted by \(W_{i}(f)\), along with its residual \(\Delta W_{i}(f)\), is defined as follows:

  1. (a)

    \(W'_{i}(f)=W_{i}(f)+\Delta W_{i}(f)\), \(i>0\)

  2. (b)

    \(W_{i}(f)\) meets the constraint defined in Eq. (4)

  3. (c)

    The sum of \(W_{1}(f)\) and any component of \(\Delta W_{i}(f)\) does not satisfy Eq. (4).

To show that the largest constrained component is well defined, one immediate task is to show the existence and uniqueness of \(W_{i}(f)\). First, we analyze the existence of \(W_{i}(f)\) as follows:

If \(W_{i}^{'}(f)\) naturally satisfies Eq. (4), then \(W_{i}(f)\) is simply the largest constrained component; in this case, \(W_{i}(f)=W'_{i}(f)\). If \(W'_{i}(f)\) does not satisfy Eq. (4), i.e.,

$$\begin{aligned} \int _{-\infty }^{\infty }\left( W'_{i}(f)-G(f)\right) \Lambda ^{*}(f)\hbox {d}f=\beta _{i}\ne \beta \end{aligned}$$
(22)

Then let \(\Delta W_{i}(f)=\rho _{i}\Lambda (f)\), in which \(\rho _{i}=\frac{\left( \beta _{i}-\beta \right) }{\int _{-\infty }^{\infty }\left| \Lambda (f)\right| ^{2}\hbox {d}f}\). We will show that \(W'_{i}(f)-\Delta W_{i}(f)\) satisfies the above definition and thus is the largest constrained component. We insert \(W'_{i}(f)-\Delta W_{i}(f)\) into the frequency-domain form of Eq. (4). By applying Eq. (22), we obtain

$$\begin{aligned}&\int _{-\infty }^{\infty }\left( W'_{i}(f)-\Delta W_{i}(f)-G(f)\right) \Lambda ^{*}(f)\hbox {d}f\\&\quad = \int _{-\infty }^{\infty }\left( W'_{i}(f)-G(f)\right) \Lambda ^{*}(f)\hbox {d}f-\int _{-\infty }^{\infty }\Delta W_{i}(f)\Lambda ^{*}(f)\hbox {d}f\\&\quad = \beta _{i}-\int _{-\infty }^{\infty }\rho _{i}\Lambda (f)\Lambda ^{*}(f)\hbox {d}f=\beta _{i}-\left( \beta _{i}-\beta \right) \\&\quad = \beta \end{aligned}$$

Therefore, \(W'_{i}(f)-\Delta W_{i}(f)\) satisfies item (b) of the above definition. We call this term a constrained component of \(W'_{i}(f)\), and \(\Delta W_{i}(f)\) is the corresponding residual. Let us assume that there is a nonzero component of \(\Delta W_{i}(f)\), denoted \(\partial W_{i}(f)\), such that \(W'_{i}(f)-\Delta W_{i}(f)+\partial W_{i}(f)\) also satisfies Eq. (4). We insert \(W'_{i}(f)-\Delta W_{i}(f)+\partial W_{i}(f)\) into Eq. (4) and can easily obtain \(\int _{-\infty }^{\infty }\partial W_{i}(f)\Lambda ^{*}(f)\hbox {d}f=0\). Since \(\Delta W_{i}(f)=\rho _{i}\Lambda (f)\), \(\Delta W_{i}(f)\) is orthogonal to its own component \(\partial W_{i}(f)\). However, this orthogonality is possible only if \(\partial W_{i}(f)\) is equal to zero. As a consequence, \(W'_{i}(f)-\Delta W_{i}(f)\) satisfies item (c) of the above definition and is thus the largest constrained component of \(W'_{i}(f)\). This completes the proof of existence.

We can rewrite the calculation formula for the largest component of \(W'_{i}(f)\), i.e., \(W_{i}(f)\), as follows:

$$\begin{aligned} W_{i}(f)=W'_{i}(f)-\Delta W_{i}(f) \end{aligned}$$
(23)

where \(\Delta W_{i}(f)=\rho _{i}\Lambda (f)\), \(\rho _{i}=\left( \beta _{i}-\beta \right) /\int _{-\infty }^{\infty }\left| \Lambda (f)\right| ^{2}\hbox {d}f\). In other words, using the result of the ith iteration of \(W_{i}^{'}(f)\) and Eqs. (22) and (23), we can easily obtain \(W_{i}(f)\). Then, the next iteration will be implemented.

Finally, it should be mentioned that because \(\Delta W_{i}(f)\) is dependent on \(\Lambda (f)\), when \(\Lambda (f)\) is known, \(W_{i}(f)\) can be immediately derived from Eq. (23). If only some characteristics of W(f) or \(\Lambda (f)\) are known, we can make use of these characteristics to extract \(W_{i}(f)\) from \(W'_{i}(f)\). In these cases, \(W_{i}(f)\) is sometimes easily extracted; in Sect. 5, we will present a simulation example for further illustration.

Now we discuss the uniqueness. Let us assume that the largest constrained component of \(W'_{i}(f)\) is not unique, namely both \(W_{i,0}(f)\) and \(W_{i,1}(f)\) satisfy the above definition, along with their residuals \(\Delta W_{i,0}(f)\) and \(\Delta W_{i,1}(f)\), respectively. It is easy to show that \(W_{i,0}(f)-W_{i,1}(f)\) is orthogonal to \(\Lambda (f)\) since they both satisfy Eq. (4). Because \(W_{i,0}(f)+\Delta W_{i,0}(f)=W_{i,1}(f)+\Delta W_{i,1}(f)=W'(f)\), \(\Delta W_{i,1}(f)-\Delta W_{i,0}(f)\) is also orthogonal to \(\Lambda (f)\). Let \(\partial \Lambda (f)\) denote \(\Delta W_{i,1}(f)-\Delta W_{i,0}(f)\). Without loss of generality, let \(W_{i,0}(f)=W'_{i}(f)-\rho _{i}\Lambda (f)\). Then \(\Delta W_{i,0}(f)=\rho _{i}\Lambda (f)\) and \(\Delta W_{i,1}(f)=\rho _{i}\Lambda (f)+\partial \Lambda (f)\). Because \(\partial \Lambda (f)\) is orthogonal to \(\Lambda (f)\), \(\partial \Lambda (f)\) can be regarded as a component of \(\Delta W_{i,1}(f)\). For the orthogonality between \(\Lambda (f)\) and \(\partial \Lambda (f)\), \(W_{i,1}(f)+\partial \Lambda (f)\) satisfies Eq. (4), which means that \(W_{i,1}(f)\) cannot be the largest component if \(\partial \Lambda (f)\ne 0\), which contradicts the conjecture. Therefore, \(\partial \Lambda (f)\) is equal to zero. As a result, \(\Delta W_{i,1}(f)=\Delta W_{i,0}(f)\) and \(W_{i,0}(f)=W_{i,1}(f)\). This completes the proof of the uniqueness.

Now we prove that \(W_{i}(f)\xrightarrow {i\rightarrow \infty }W_\mathrm{opt}(f)\) in the sense of the \(l_{2}\) norm when \(0<\eta <\frac{2}{\max S_{x}(f)}\).

i.e., if:

$$\begin{aligned} \Bigl |1-\eta S_{x}(f)\Bigr |<1 \end{aligned}$$
(24)

then

$$\begin{aligned} \underset{i\rightarrow \infty }{\lim }\int _{-\infty }^{\infty }\left| W_{i}(f)-W_\mathrm{opt}(f)\right| ^{2}\hbox {d}f=0 \end{aligned}$$
(25)

Proof

According to the definition, \(W_{i+1}(f)\) is the largest constrained component of \(W'_{i+1}(f)\) and satisfies the restriction condition. Thus, we have

$$\begin{aligned} \int _{-\infty }^{\infty }\left( W_{i+1}(f)-G(f)\right) \Lambda ^{*}(f)\hbox {d}f=\beta \end{aligned}$$
(26)

Note that

$$\begin{aligned} \int _{-\infty }^{\infty }\left( W_\mathrm{opt}(f)-G(f)\right) \Lambda ^{*}(f)\hbox {d}f=\beta \end{aligned}$$
(27)

Hence, by subtracting Eq. (26) from (27), we obtain

$$\begin{aligned} \int _{-\infty }^{\infty }\left( W_\mathrm{opt}(f)-W_{i+1}(f)\right) \Lambda ^{*}(f)\hbox {d}f=0 \end{aligned}$$
(28)

In other words, \(W_\mathrm{opt}(f)-W_{i+1}(f)\) and \(\Lambda (f)\) are mutually orthogonal. Since \(\Delta W_{i+1}(f)=\rho _{i+1}\Lambda (f)\), \(W_\mathrm{opt}-W_{i+1}(f)\)is also orthogonal to \(\Delta W_{i+1}(f)\).

After finishing the orthogonality analysis, we will prove Eq. (25) in the following discussion.

By subtracting \(W_\mathrm{opt}(f)\) from both sides of Eq. (21) and substituting \(S_{x}(f)W_\mathrm{opt}(f)+\mu \Lambda (f)\) for \(S_{dx}(f)\) in Eq. (21), we have

$$\begin{aligned} W'_{i+1}(f)-W_\mathrm{opt}(f)=\left( 1-\eta S_{x}(f)\right) \left( W_{i}(f)-W_\mathrm{opt}(f)\right) +\eta \mu \Lambda (f) \end{aligned}$$
(29)

By replacing \(W'_{i+1}(f)\) with \(W_{i+1}(f)+\rho _{i+1}\Lambda (f)\) in Eq. (29), we obtain

$$\begin{aligned} \left( 1-\eta S_{dx}(f)\right) \left( W_{i}(f)-W_\mathrm{opt}(f)\right) =W_{i+1}(f)-W_\mathrm{opt}(f)+\left( \rho _{i+1}-\eta \mu \right) \Lambda (f) \end{aligned}$$

Since \(W_{i+1}(f)-W_\mathrm{opt}(f)\) and \(\Lambda (f)\) are mutually orthogonal, we have

$$\begin{aligned}&\int _{-\infty }^{\infty }\Bigl |\Bigl (1-\eta S_{dx}(f)\Bigr )\Bigl (W_{i}(f)-W_\mathrm{opt}(f)\Bigr )\Bigr |^{2}\hbox {d}f\\&\quad = \int _{-\infty }^{\infty }\Bigl |\Bigl (W_{i+1}(f)-W_\mathrm{opt}(f)\Bigr )+\left( \rho _{i+1}-\eta \mu \right) \Lambda (f)\Bigr |^{2}\hbox {d}f\\&\quad = \int _{-\infty }^{\infty }\Bigl |W_{i+1}(f)-W_\mathrm{opt}(f)\Bigr |^{2}\hbox {d}f+\left| \rho _{i+1}-\eta \mu \right| ^{2}\int _{-\infty }^{\infty }\Bigl |\Lambda (f)\Bigr |^{2}\hbox {d}f\\&\quad \ge \int _{-\infty }^{\infty }\Bigl |W_{i+1}(f)-W_\mathrm{opt}(f)\Bigr |^{2}\hbox {d}f \end{aligned}$$

Then, if Eq. (24) is satisfied, i.e., \(\left| 1-\eta S_{x}(f)\right| <1\), we obtain

$$\begin{aligned} \int _{-\infty }^{\infty }\Bigl |W_{i}(f)-W_\mathrm{opt}(f)\Bigr |^{2}\hbox {d}f> & {} \int _{-\infty }^{\infty }\Bigl |\left( 1-\eta S_{dx}(f)\right) \left( W_{i}(f)-W_\mathrm{opt}(f)\right) \Bigr |^{2}\hbox {d}f\nonumber \\\ge & {} \int _{-\infty }^{\infty }\Bigl |W_{i+1}(f)-W_\mathrm{opt}(f)\Bigr |^{2}\hbox {d}f \end{aligned}$$
(30)

As a result, \(W_{i+1}(f)\) converges to \(W_\mathrm{opt}(f)\) in the \(l_{2}\) norm. Expanding Eq. (24), we have

$$\begin{aligned} 0<\eta <\frac{2}{\max S_{x}(f)} \end{aligned}$$
(31)

This completes the proof of convergence for the iterative algorithm.

When \(W_{i+1}(f)\) converges to \(W_\mathrm{opt}(f)\), \(W_{i+1}(f)-W_{i}(f)\) will converge to zero in the same norm. Hence, we can take \(d\left( W_{i+1},W_{i}\right) <\varepsilon \) as the criterion to terminate the iterative procedure. In addition, we define the approximation error of \(W_\mathrm{opt}(f)\) by \(W_{i+1}(f)\) as

$$\begin{aligned} \delta \left( W_\mathrm{opt}(f),W_{i+1}(f)\right) =\frac{d\left( W_\mathrm{opt}(f),W_{i+1}(f)\right) }{d\left( W_\mathrm{opt}(f),0\right) }\times 100\% \end{aligned}$$
(32)

It is clear that \(\delta \left( W_\mathrm{opt}(f),W_{i+1}(f)\right) \) is positively correlated with \(\varepsilon \). Therefore, to obtain a high approximation degree, \(\varepsilon \) should be as small as possible, but this increases the number of iterations that must be computed.

Finally, it should be mentioned that although the iterative technique is developed in the frequency domain, it may be possible to implement this technique in the time domain by making use of the Fourier transformation.

5 Examples

In this section, three simulation examples are presented to illustrate the applicability of our methods. In all three examples, we take the same noisy random input x(t) and the same desired output d(t), but impose different restrictions. We assume that \(R_{x}\left( \tau \right) =e^{-0.01\left| \tau \right| }+0.01^{2}\delta \left( \tau \right) \), \(R_{dx}\left( \tau \right) =R_{d}\left( \tau \right) =e^{-0.01\left| \tau \right| }\), \(S_{x}(f)=\frac{0.02}{0.01^{2}+\left( 2\pi f\right) ^{2}}+0.01^{2}\), and \(S_{dx}(f)=S_{d}(f)=\frac{0.02}{0.01^{2}+\left( 2\pi f\right) ^{2}}\).

Case 1

The Wiener filter is required to be a low-pass system with a 40-Hz bandwidth, i.e.,

$$\begin{aligned} W(f)=0,f\notin \left( -20,20\right) \end{aligned}$$
(33)

Obviously, this is a finite frequency-support constraint. From Eqs. (16), (18), and (19), we obtain

$$\begin{aligned} W_\mathrm{opt}(f)={\left\{ \begin{array}{ll} \frac{S_{dx}(f)}{S_{x}(f)}=\frac{0.02}{0.02+0.01^{4}+\left( 0.02\pi f\right) ^{2}}, &{}\quad f\in \left( -20,20\right) \\ 0, &{}\quad f\notin \left( -20,20\right) \end{array}\right. } \end{aligned}$$

The wave form of \(W_\mathrm{opt}(f)\) is shown in Fig. 2.

Fig. 2
figure 2

The wave form of \({W_\mathrm{opt}}(f)\) with a low-pass constraint

Full size image

Case 2

The Wiener filter is required to satisfy the following integration equation:

$$\begin{aligned} \int _{-200}^{200}W(f)\hbox {d}f=2 \end{aligned}$$
(34)

It is straightforward to show that this integral is equivalent to Eq. (4) when \(G(f)=0\) and

$$\begin{aligned} \Lambda (f)={\left\{ \begin{array}{ll} 1, &{}\quad f\in \left( -200,200\right) \\ 0, &{}\quad f\notin \left( -200,200\right) \end{array}\right. } \end{aligned}$$
(35)

The computational procedure of the analytical method is very simple. First, using Eq. (20), we obtain \(\mu =1.36\times 10^{-5}\). Then, from Eq. (12), we obtain

$$\begin{aligned} W_\mathrm{opt}(f)= & {} \frac{S_{dx}(f)-\mu \Lambda (f)}{S_{x}(f)}=\frac{0.02-1.36\times 10^{-5}\times \left( 0.01^{2}+\left( 2\pi f\right) ^{2}\right) \Lambda (f)}{0.02+0.01^{4}+\left( 0.02\pi f\right) ^{2}}\\\approx & {} \frac{0.02-0.536\times 10^{-3}f^{2}\Lambda (f)}{0.02+0.01^{4}+\left( 0.02\pi f\right) ^{2}} \end{aligned}$$

The wave form of \(W_\mathrm{opt}(f)\) is shown in Fig. 3.

Fig. 3
figure 3

The wave form of \({W_\mathrm{opt}}(f)\) from the analytical method for case 2

Full size image

Next, we use the iterative algorithm to solve this problem again. The initial parameters of this iteration is chosen as \(W_{0}(f)=\frac{S_{dx}(f)}{S_{x}(f)}=\frac{0.02}{0.02+0.01^{4}+\left( 0.02\pi f\right) ^{2}}\), \(\varepsilon =10^{-6}\), and \(\eta =0.0099<\frac{2}{\max S_{x}(f)}\approx 0.01\). In the above iterative algorithm, after 171 iterations, the criterion to end the iterative procedure is satisfied. As a result, we obtain \(W_{171}(f)\) as shown in Fig. 4.

From Eq. (32), we obtain the approximation error, \(\delta \left( W_\mathrm{opt}(f),W_{i+1}(f)\right) =1.37\%\). We can further decrease \(\delta \left( W_\mathrm{opt}(f),W_{i+1}(f)\right) \) by reducing \(\varepsilon \), but the computation time will increase. In this instance, if we take \(\varepsilon =10^{-13}\) and hold the other initial parameters constant, then, after 162,834 iterations, the iterative procedure is terminated, and we obtain \(\delta \left( W_\mathrm{opt}(f),W_{162834}(f)\right) =0.33\%\).

Case 3

The Wiener filter is required to satisfy the following constraint condition:

$$\begin{aligned} w(t)={\left\{ \begin{array}{ll} g(t), &{} \quad t\notin [0,500\text {)}\\ unknown, &{} \quad t\in [0,500\text {)} \end{array}\right. } \end{aligned}$$
(36)

where

$$\begin{aligned} g(t)={\left\{ \begin{array}{ll} 0.03\hbox {e}^{-10t}\sin \left( 40\pi t\right) , &{} t\in [500,1000)\\ 0, &{} t\notin [500,1000) \end{array}\right. } \end{aligned}$$
(37)

For this restriction, we take

$$\begin{aligned} \lambda (t)={\left\{ \begin{array}{ll} unknown, &{} t\notin [0,500)\\ 0, &{} t\in [0,500) \end{array}\right. } \end{aligned}$$
(38)

Then we can convert the restriction condition to the integration equation

$$\begin{aligned} \int _{-\infty }^{\infty }\left( w(t)-g(t)\right) \lambda ^{*}(t)\hbox {d}t=0 \end{aligned}$$

Because \(\lambda (t)\) is unknown, we can use only the iterative algorithm.

Fig. 4
figure 4

The wave form of \({W_{171}}(f)\) from the iterative method for case 2

Full size image
Fig. 5
figure 5

The wave form of \({w_{4}}(t)\) from the iterative algorithm for case 3

Full size image

We implement the iterative procedure in the time domain. We set \(w_{0}(t)=IFT\left\{ \frac{S_{dx}(f)}{S_{x}(f)}\right\} \), \(\varepsilon =10^{-25}\), and \(\eta =0.0099\), where \(IFT\left\{ \bullet \right\} \) denotes the inverse Fourier transform. In this instance, we cannot use Eq. (23) to extract the largest component of \(w'_{i}(t)\), because \(\lambda (t)\) is unknown. However, according to the constraint given in Eq. (36), we can immediately obtain

$$\begin{aligned} w_{i}(t)={\left\{ \begin{array}{ll} g(t) &{} ,t\notin [0,500)\\ w'_{i}(t) &{} ,t\in [0,500) \end{array}\right. } \end{aligned}$$

For this instance, in the fourth iteration, the criterion for terminating the iterative procedure is satisfied. We obtain \(w_{4}(t)\) as shown in Fig. 5.

6 Conclusions

This paper presents a general theoretical method for designing Wiener filters with additional constraint conditions. By introducing an integral expression to represent the constraints, we derive and analytically solve the formula for a more constrained Wiener filter. Compared to the classical design method, our new approach not only incorporates broader constraints but also relaxes the requirement of rational power spectra. The classical method of designing Wiener filters is appropriate only for cases of causality, and the causal solution is obtained only if the input self-power spectrum and the cross-power spectrum of the input and the output are both rational functions. Finally, this paper demonstrates several practical applications of our techniques using simulations.