Design of Reverse Converters for a New Flexible RNS Five-Moduli Set $\{ 2^k, 2^n-1, 2^n+1, 2^{n+1}-1, 2^{n-1}-1 \}$ (n Even)

Abstract

This paper presents the design methods of residue-to-binary (reverse) converters for the new flexible balanced five-moduli set $\{ 2^k, 2^n-1, 2^n+1,$ $2^{n+1}-1, 2^{n-1}-1 \}$ for the pairs of positive integers ${n \ge 4}$ (even) and any ${k>0}$, which can provide the exact required dynamic range of the residue number system. This modulus set is the generalisation of the five-moduli set $\{ 2^n, 2^n-1, 2^n+1, 2^{n+1}-1, 2^{n-1}-1 \}$ (n even) with only a single parameter, n. The reverse converter for the new modulus set is the first ever proposed. Synthesis results obtained for the 65 nm technology for all dynamic ranges from 19 to 88 bits have shown that the state-of-the-art converters available for the five-modulus sets with a single parameter n ${\{ 2^n, 2^n-1, 2^n+1, 2^{n+1}-1, 2^{n-1}-1 \}}$ (n even) and ${\{ 2^n-1, 2^n, 2^n+1, 2^{n+1}+1, 2^{n-1}+1 \} }$ (n odd) not only introduce from 28 to 40% larger delay but also still consume more area and power than the converters proposed here.

1 Introduction

There has been growing demand for digital signal processing (DSP) to be performed at greater real-time bandwidths, with higher precision and lower complexity. Several DSP computations like digital filtering and various transforms can be formulated as a sum of products (vector inner products) [15]. Such arithmetic expressions have particularly efficient implementations using a residue number system (RNS) [1], an unweighted arithmetic system in which calculations are performed in parallel, independent channels. Because most digital systems operate on data using a positional representation, using the RNS representation requires conversions of numbers back and forth to RNS, performed respectively by reverse and forward converters. While forward conversion is basically an extraction of residue from a positional number using residue generators, the reverse conversion requires application of special methods like the Chinese remainder theorem (CRT) and the mixed radix conversion (MRC) [1], as well as the new CRT [31].

To guarantee that the advantages of datapaths implemented in an RNS offset the extra cost of converters, it is desirable that the moduli $m_i$ selected to form an RNS have efficient implementations of basic modulo arithmetic operations. Three low-cost classes of moduli (in their order of appearance) are an even modulus $m_i = 2^\mathrm{b}$, an odd modulus $m_i = 2^\mathrm{b} -1$, and $m_i = 2^\mathrm{b} +1$, for which hardware implementations of the basic arithmetic circuits can be found: two-operand adders [8, 11,12,13, 17, 35], multi-operand modular adders (MOMAs) and residue generators (used to build forward converters) [21, 23], multipliers [16, 34, 35], multiplier-accumulators (MACs) and complete residue datapaths [9, 14, 24, 25].

Because the performance of the reverse converter is usually the major bottleneck of RNS-based systems, several special moduli sets with not only particularly efficient implementations of the datapaths but also highly regular structures of reverse converters have been proposed. Here, we are interested in low-cost moduli sets which also enjoy well-balanced performance of all residue datapath channels (i.e. the area/time characteristics of all channels are as close as possible). The best-known three-moduli sets are: $\{2^n-1, 2^n, 2^n+1\}$ – for which reverse converters have been proposed, for example in [10, 22, 32] – and its generalisation $\{2^n-1, 2^k, 2^n+1\}$ with flexible even modulus $2^k$, for which the reverse converter for $n \le k \le 2n$ was proposed in [7]. The four-moduli sets include those with a single parameter n: $\{ 2^n - 1, 2^{n}, 2^{n-1} - 1, 2^{n-1} +1 \}$ (n odd) [28], $\{ 2^n - 1, 2^n, 2^n + 1, 2^{n+1}-1 \}$ (n even) [2, 3, 5, 28, 30], $\{ 2^n, 2^n-1, 2^n+1, 2^{n-1}-1 \}$ (n even) [5], $\{ 2^n -1, 2^n, 2^n + 1, 2^{n+1}+1 \}$ (n odd) [2, 29], and $\{ 2^n+1, 2^n-1, 2^n, 2^{n-1}+1 \}$ (n odd) [20], as well as some of their recently proposed generalisations with a flexible even modulus $2^k$: $\{ 2^k, 2^n-1, 2^n+1, 2^{n+1}-1 \}$ (n even and arbitrary k such that $n \le k \le 2n$) [6], $\{ 2^{n-1} -1, 2^{n+1} - 1, 2^k, 2^n - 1 \}$ (n even and $k > 2$) [33] and $\{ 2^k, 2^n - 1, 2^n +1, 2^{n+1} -1, 2^{n\pm 1} -1 \}$ [19] (n even and $k > 2$). Further reduction of the widths of residue channels for a given dynamic range allow for two special five-moduli sets composed only of low-cost moduli: $\{ 2^n-1, 2^n, 2^n+1, 2^{n+1}-1, 2^{n-1}-1 \}$ (n even) [4] and $\{ 2^n-1, 2^n, 2^n+1, 2^{n+1}+1, 2^{n-1}+1 \}$ (n odd) [18]. The dynamic ranges of these two RNSs make it possible to represent all integers up to $5n-1$ bits (n even) and 5n bits (n odd), respectively. Either moduli set offers a resolution of 10 bits only: the dynamic ranges for $n=4, 6, 8, \ldots$ are 19, 29, 39, $\ldots$ bits for the former, and those for $n=5, 7, 9, \ldots$ are 25, 35, 45, $\ldots$ bits for the latter. These two moduli sets are complementary in the sense that altogether they allow periodically for a 4- or 6-bit resolution of the dynamic range. The major limitation of these two moduli sets is that, should a dynamic range other than those listed above be needed, a designer must use a moduli set whose dynamic range is larger than actually needed, with the closest sufficiently large n. If the dynamic range of 20 bits is needed, the moduli set of [18] for $n=5$, i.e. $\{ 31, 32, 33, 65, 17 \}$, is the best choice currently available, although its 25-bit dynamic range is unnecessarily large and results in too-large residue datapaths. Finally, note that the dynamic range of the moduli set of [4] for $n=4$ (i.e. $\{ 15, 16, 17, 31, 7 \}$) is too small by only 1 bit and that replacing the even modulus $2^4=16$ with $2^5=32$ would suffice. To date, no reverse converter for any five-moduli set composed of low-cost moduli including a flexible even modulus $2^k$ has been proposed.

In this paper, we introduce a new balanced RNS composed of five moduli $\{2^k, 2^n-1, 2^n+1, 2^{n+1}-1, 2^{n-1}-1 \}$ (for n even), which can be seen both as the generalisation of the five-moduli set $\{2^n, 2^n-1, 2^n+1, 2^{n+1}-1, 2^{n-1}-1 \}$ with a single parameter n of [4] (also for n even) and as an extension of the four-moduli flexible set $\{2^k, 2^n-1, 2^n+1, 2^{n+1}-1 \}$ (proposed by us in [19]) by including the fifth modulus $2^{n-1}-1$. For this new five-moduli set, we will propose the design method of reverse converters, which will be built on the basis of the reverse converters for the four-moduli flexible set $\{2^k, 2^n-1, 2^n+1, 2^{n+1}-1 \}$ from [19]. The architecture proposed is essentially based on using the general concept of the two-channel MRC converter that combines the result of the four-moduli converter with the remaining fifth modulus. However, its actual hardware structure does not rely on a direct MRC implementation because several modifications leading to significant delay reduction with no area penalty are introduced.

This paper is organised as follows. In Sect. 2, some useful properties of residue arithmetic are presented. In Sect. 3, the general method for designing two optimised versions of the reverse converters for the new five-moduli set is detailed. In Sects. 4 and 5, the complexity evaluation of the reverse converters proposed here and their existing counterparts is presented: it includes both the gate-level evaluations of delay and area and more accurate evaluations of the delay, area and power consumption of all circuits, synthesised in 65 nm technology. Section 6 presents some conclusions and suggestions for future research.

2 RNS Background

In this section, we will present the basic concepts of RNS, the properties of arithmetic mod $2^n-1$ and closed formulas for some multiplicative inverses, all of which will be used directly in the reverse conversion methods proposed here.

2.1 Basic Concepts

An RNS is defined by the set of $r \ge 2$ mutually prime positive integers $\{ m_1, \ldots , m_r \}$ called moduli, whose product $M = \prod _{i=1}^r m_i$ determines the dynamic range and, as in two’s complement positional system, the RNS arithmetic is exact as long as the final result is bounded within its dynamic range. Throughout this paper we assume that the equivalent bit range of the RNS is $a = \lfloor \log _2 M \rfloor$. Any number $X \in {\mathbb {Z}}_M = \{ 0, 1 ,\ldots , M - 1 \}$ has a unique RNS representation $X \leftrightarrow \{ x_1, \ldots , x_r \}$, where $x_i = X\,\bmod \,m_i$, $1 \le i \le r$, is the result of the integer division of X by $m_i$, written $x_i = |X|_{m_i}$ and $0 \le |X|_{m_i} \le m_i-1$. Arithmetic in an RNS is defined by pair-wise modular operations, and because for any arithmetic operation $\circ \in \{ +, -, \times \}$, it follows that if $0 \le Z < M$, then $Z = |X \circ Y|_M$ is isomorphic to $Z=\{ z_1, \ldots , z_r \}$, where $z_i = | x_i \circ y_i|_{m_i}$, $1 \le i \le r$. RNS arithmetic is thus performed within r channels whose word width is bounded by $a_i = \lceil \log _2 m_i \rceil$, which is significantly smaller than a bits of its 2’s complement positional integer counterpart.

Throughout this paper we will need explicitly the reverse conversion for two moduli only, to do which the MRC is more practical, which is defined for the two-moduli set $\{ m_1, m_2 \}$ and two respective residues $\{x_1,x_2 \}$ as

(1)

2.2 Properties of Arithmetic Modulo $2^n-1$ [19]

Let n, s and d be arbitrary positive integers and z and y be positive integers such that $0 \le z \le 2^n-1$ and $0 \le y \le 2^{sn}-1$. The binary representations of z and y are respectively $(z_{n-1}\ldots z_0)$ and $(y_{sn-1}\ldots y_0)$. If y is more than an $(s-1)n$-bit and less than an sn-bit number, then it is preceded by leading zeros and then partitioned into sn-bit wide slices $B_i$ beginning with the least significant bits (LSBs), i.e. $y = (B_{n-1} \Vert \cdots \Vert B_1 \Vert B_0)$, where $B_0 = (y_{n-1} \ldots y_{0})$, $B_1 = (y_{2n-1} \ldots y_{n})$, etc. (the symbol $\Vert$ denotes the concatenation of binary vectors). Some residue mod $2^n-1$ operations are executed as follows:

• The sign change of z modulo $2^n-1$ (additive inverse of z) is obtained by bit-by-bit complementing, i.e. $| -z|_{2^n-1}=| {\bar{z}}|_{2^n-1}= | ( {\bar{z}}_{n-1}\ldots {\bar{z}}_{0}) |_{2^n-1}$.

• The multiplication of z by $2^d$ mod $2^n-1$ (d is an integer) is obtained by the left cyclic shift of z by $e=|d|_n$ positions (equivalent to the right cyclic shift of z by $n-e$ positions), i.e. $|2^dz|_{2^n-1} = | (z_{n-e-1} \ldots z_0 z_{n-1}\ldots z_{n-e}) |_{2^n-1}$. We assume that this operation comes at no additional hardware cost.

• The residue generation of y mod $2^n-1$ is computed as

  $$\begin{aligned} |y|_{2^n-1} = \left| \sum _{i=0}^{s-1} 2^{in} B_i \right| _{2^n-1} = \left| \sum _{i=0}^{s-1} B_i \right| _{2^n-1}. \end{aligned}$$

  (2)

2.3 Multiplicative Inverses

A multiplicative inverse of g mod m ($0<g<m$) is such an integer h ($0<h<m$) that $|hg|_m=1$, written $h=| 1/g |_m$ or $h=| g^{-1} |_m$. A multiplicative inverse exists provided that g and m are co-prime. In the reverse conversion methods proposed here, for positive integers even $n \ge 4$ and an arbitrary k, the following multiplicative inverses will be used:

$$\begin{aligned}&\left| \frac{1}{2^k} \right| _{2^{n}-1} = \left| \frac{1}{2^e} \right| _{2^{n}-1} = \left| {2^{n-e}} \right| _{2^{n}-1} , \nonumber \\&\quad \hbox {where}\,e=|k|_n\quad \hbox {and}\quad 0 \le e \le n-1 , \end{aligned}$$

(3)

$$\begin{aligned}&\left| \frac{1}{\left( 2^{n+1}-1\right) \left( 2^{2n}-1\right) } \right| _{2^{n-1}-1} \nonumber \\&\quad = \left| \frac{1}{\left( 2^{2}-1\right) \left( 2^{2}-1\right) } \right| _{2^{n-1}-1} = \left| \frac{1}{9} \right| _{2^{n-1}-1} \nonumber \\&\quad = \left\{ \begin{array}{ll} 2^{n-2} &{}\quad {\mathrm{if }}\, n = 4\\ 7\sum \nolimits _{i=0}^{(n-6)/6} 2^{6i} &{}\quad {\mathrm{if }}\, n = 6, 12, 18, \ldots \\ 1 + 7\sum \nolimits _{i=0}^{(n-8)/6} 2^{6i+4} &{}\quad {\mathrm{if }}\, n = 8, 14, 20, \ldots \\ 2^{n-2} + 7\sum \nolimits _{i=0}^{(n-10)/6} 2^{6i+2} &{}\quad {\mathrm{if }}\, n = 10, 16, 22, \ldots \end{array} \right. \end{aligned}$$

(4)

Equation (3) holds because $| 1/2^k |_{2^{n}-1} = | 1 \cdot 2^{-k}|_{2^{n}-1} = | 2^n \cdot 2^{-k}|_{2^{n}-1} = | {2^{n-k}}|_{2^{n}-1}$. As for Eq. (4), first notice that $| 1/[(2^{n+1}-1)(2^{2n}-1)] |_{2^{n-1}-1} = | 1/9 |_{2^{n-1}-1}$ because $|2^{n+1}|_{2^{n-1}-1} = |2^2 \cdot 2^{n-1}|_{2^{n-1}-1} =4$ and $|2^{2n}|_{2^{n-1}-1} = |(2 \cdot 2^{n-1})^2|_{2^{n-1}-1} =4$. Then the proof of correctness of the four expressions of Eq. (4) is given below by showing that the multiplication mod $2^{n-1} -1$ of each of them by its multiplicative inverse equal to 9 results in a product equal to 1.

For $n=4$, we have $|9\cdot 2^2|_7=1$.

For $n=6,12\ldots$, we have

$$\begin{aligned}&\left| 9\cdot 7\sum _{i=0}^{(n-6)/6} 2^{6i} \right| _{2^{n-1}-1} = \left| \left( 2^6-1\right) \sum _{i=0}^{(n-6)/6} 2^{6i} \right| _{2^{n-1}-1}\\&\quad = \left| \sum _{i=1}^{n/6} 2^{6i} - \sum _{i=0}^{(n-6)/6} 2^{6i} \right| _{2^{n-1}-1} \quad =\left| 2^n - 2^0 \right| _{2^{n-1}-1} =2 - 1 =1. \end{aligned}$$

For $n=8,14\ldots$, we have

$$\begin{aligned}&\left| 9\cdot \left( 1 + 7\sum _{i=0}^{(n-8)/6} 2^{6i+4} \right) \right| _{2^{n-1}-1}\\&\quad = \left| \left( 2^3+1\right) \cdot \left( 1 + \left( 2^3-1\right) \sum _{i=0}^{(n-8)/6} 2^{6i+4} \right) \right| _{2^{n-1}-1}\\&\quad = \left| 9 + \left( 2^6-1\right) \sum _{i=0}^{(n-8)/6} 2^{6i+4} \right| _{2^{n-1}-1}\\&\quad = \left| 9 + 2^4\left( \sum _{i=1}^{(n-2)/6} 2^{6i} - \sum _{i=0}^{(n-8)/6} 2^{6i} \right) \right| _{2^{n-1}-1}\\&\quad = \left| 2^3+1 + 2^4\left( 2^{n-2} - 1 \right) \right| _{2^{n-1}-1}\\&\quad = \left| 2^3+1 + 2^3 \cdot 2^{n-1}-2^4 \right| _{2^{n-1}-1} =1. \end{aligned}$$

For $n=10,16\ldots$, we have

$$\begin{aligned}&\left| 9\cdot \left( 2^{n-2} + 7\sum _{i=0}^{(n-10)/6} 2^{6i+2} \right) \right| _{2^{n-1}-1}\\&\quad = \left| (2^3+1)\cdot \left( 2^{n-2} + 2^2\left( 2^3-1\right) \sum _{i=0}^{(n-10)/6} 2^{6i} \right) \right| _{2^{n-1}-1}\\&\quad = \left| 9\cdot 2^{n-2} + 2^2\left( 2^6-1\right) \sum _{i=0}^{(n-10)/6} 2^{6i} \right| _{2^{n-1}-1}\\&\quad = \left| 9\cdot 2^{n-2} + 2^2\left( \sum _{i=1}^{(n-4)/6} 2^{6i} - \sum _{i=0}^{(n-10)/6} 2^{6i} \right) \right| _{2^{n-1}-1}\\&\quad = \left| 9\cdot 2^{n-2} + 2^2\left( 2^{n-4}-1 \right) \right| _{2^{n-1}-1}\nonumber \\&\quad = \left| 10 \cdot 2^{n-2}-4 \right| _{2^{n-1}-1} = \left| 5 \cdot 2^{n-1}-4 \right| _{2^{n-1}-1} = 1. \end{aligned}$$

3 Design of Reverse Converters

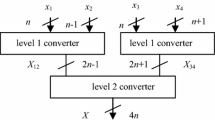
In this section, we will present the method for designing reverse converters for the new RNS defined by the following ordered set of five moduli: $\{ m_1, m_2, m_3, m_4, m_5 \} = \{ 2^k, 2^n-1, 2^n+1, 2^{n+1}-1, 2^{n-1}-1 \}$, n even. An input to the converter is an integer X represented in the RNS by the ordered set of five residues $\{ x_1, x_2, x_3, x_4, x_5 \}$. Basically, the conversion can be reduced to executing two steps:

• 1. We assume that the subset of four residues $\{ x_1, x_2, x_3, x_4 \}$ defines $0 \le X_4 < m_1m_2m_3m_4$, which can be computed using the converter for the four-moduli set $\{ 2^k, 2^n-1, 2^n+1, 2^{n+1}-1 \}$ of [19]. Thus, we obtain a new representation of $X=\{ X_4, x_5 \}$ in a two-moduli RNS $\{ m_1m_2m_3 m_4, m_5 \}$.

• 2. To obtain X, we apply MRC to the two-moduli set $\{ m_1m_2m_3 m_4, m_5 \}$ as $X = \{ X_4, m_5 \}$. (The design approach based on the MRC applied to two moduli obtained like the preceding moduli has already been used to build some other converters, e.g. [4, 26, 27].)

Although a direct simple implementation of the converter is possible, it is inefficient, and hence it will not be presented here. Instead, we will propose a more sophisticated implementation which maximally reduces delay and area. In particular, we will not use directly the value of $X_4$, which could be generated by the four-moduli converter of [19], but only the intermediate variables $X_h$ and $R_4$, which appear in the latter converter.

We propose two versions of the converter which differ in the decomposition of the calculations, whose block diagrams are shown in Fig. 1. The first version benefits of sophisticated transformations leading to multi-operand addition mod $2^{n-1}-1$, whereas the next faster version is obtained by also taking into account the possibility of shifting out of the critical path some non-critical components of addition.

Fig. 1

Block diagram of new converter: a general schema, b calculation of $L_5$ and V for version 1 and c calculation of $L_5$ and V for version 2

We will use the following two variables, which represent some intermediate results in the converter of [19] [given there by Eqs. (11) and (29), respectively]

$$\begin{aligned} X_h= \left| \left( m_3 x_2 \left| \frac{1}{m_3}\right| _{m_2} + m_2 x_3 \left| \frac{1}{m_2}\right| _{m_3} -x_1\right) \left| \frac{1}{m_1}\right| _{m_2m_3}\right| _{ m_2m_3 } \end{aligned}$$

(5)

and

$$\begin{aligned} R_4 = \left| \frac{1}{m_1m_2m_3} \underbrace{\left| \underbrace{x_4-(x_1}_{L'_4=\left| x_4-x_1 \right| _{m_4}} \overbrace{ \phantom {( x_1} + m_1X_h ) }^{X_1} \right| _{m_4} }_{L_4=\left| L'_4-m_1X_h\right| _{m_4}}\right| _{m_4} \end{aligned}$$

(6)

[here, we rewrite from [19] R of (29) as $R_4$ and $X_1=x_1+m_1X_h$ of (10)]. (Note: The preceding equation also defines the new variables $L_4$ and $L^{\prime }_4$, which will facilitate hardware complexity evaluation in Table 1.)

Table 1 Hardware complexity comparison

The implementation details of the four-moduli converter (including detailed bit-level manipulations and multiplication by multiplicative inverse) may be found in [19] or, alternatively, [2] (but only for the special case of $k=n$, with other notation and a more complex design). Then the final result generated by the four-moduli converter is written as

$$\begin{aligned} X_4= & {} x_1 + m_1 X_h + m_1m_2m_3 R_4. \end{aligned}$$

(7)

We adapt the MRC equation (1) to the special case of the two-moduli set $\{ m_1m_2m_3 m_4, m_5\}$ with residues $\{ X_4, x_5 \}$ using two additional variables $L_5 = |x_5-X_4|_{m_5}$ and $R_5 = | L_5/(m_1m_2m_3m_4) |_{m_5}$ in the following form:

$$\begin{aligned} X=X_4 + m_1m_2m_3 m_4 \underbrace{\left| \frac{1}{m_1m_2m_3 m_4} \underbrace{\left| x_5 - X_4 \right| _{m_5}}_{L_5} \right| _{m_5}}_{R_5}. \end{aligned}$$

(8)

Obviously, the multiplicative inverse $|1/m_1m_2m_3 m_4|_{m_5}$ exists because the assumption that all moduli $m_i$ are pairwise relatively prime implies that $m_1m_2m_3 m_4$ and $m_5$ are also relatively prime. By substituting $X_4$ according to Eq. (7) and introducing

$$\begin{aligned} V = X_h+m_2m_3R_4 + m_2m_3m_4R_5 \end{aligned}$$

(9)

we obtain

$$\begin{aligned} X= & {} X_4 + m_1m_2m_3m_4 R_5 \nonumber \\= & {} x_1 + m_1 X_h + m_1m_2m_3 R_4 + m_1m_2m_3m_4 R_5 \nonumber \\= & {} x_1 + m_1 \underbrace{\left( X_h + m_2m_3 R_4 + m_2m_3m_4 R_5 \right) }_V \nonumber \\= & {} x_1 + m_1 V = x_1 + 2^k V = ( x_1 \Vert V ). \end{aligned}$$

(10)

Because $R_4$ and $X_h$ are provided by the four-moduli converter, we only need to calculate $L_5$ and $R_5$. Depending on the actual implementation of Eq. (10), two different versions will be designed.

3.1 Version 1

The expression for $L_5$ of (8) can be rewritten as follows:

$$\begin{aligned} L_5= & {} \left| x_5 - X_4 \right| _{m_5} = \left| x_5 - \left( x_1+m_1X_h+m_1m_2m_3R_4 \right) \right| _{m_5} \nonumber \\= & {} \left| x_5 - \left( x_1+ 2^k X_h+ 2^k \left( 2^{2n}-1 \right) R_4 \right) \right| _{2^{n-1}-1} \nonumber \\= & {} \left| x_5 - x_1 + 2^k \left( - X_h + (1-4) R_4 \right) \right| _{2^{n-1}-1} . \end{aligned}$$

(11)

First, we simplify the term $( - X_h + (1-4) R_4)$. Because both the 2n-bit variable $X_h$ and the $(n+1)$-bit variable $R_4$ are involved in the calculations mod $2^{n-1}-1$ [i.e. on $(n-1)$-bit vectors], we will present them in the following forms, which are adapted for further transformations: $(\underbrace{0 \ldots 0}_{n-3} \Vert X_h)$ and $(\underbrace{0 \ldots 0}_{n-3} \Vert R_4)$ are the $3(n - 1)$- and $2(n - 1)$-bit vectors respectively. Consequently, $|-X_h|_{2^{n-1}-1} = |( \underbrace{1\ldots 1}_{n-3} \Vert {\bar{X}}_h )|_{2^{n-1}-1}$ and $|-4R_4|_{2^{n-1}-1} = |(\underbrace{ 1\ldots 1 }_{ n-5 } \Vert {\bar{R}}_4 \Vert 11)|_{2^{n-1}-1}$ [since $|-R_4|_{2^{n-1}-1} = |(\underbrace{ 1\ldots 1 }_{ n-3 } \Vert {\bar{R}}_4 ) |_{2^{n-1}-1}$]. We also observe that two least significant 1s from a first term and $(n-3)$ most significant 1s from a second term in the addition $| (\underbrace{ 1\ldots 1 }_{ n-5 } \Vert {\bar{R}}_4 \Vert 11)$ $+ (\underbrace{1\ldots 1}_{n-3} \Vert {\bar{X}}_h) |_{2^{n-1}-1}$ form an $(n-1)$-bit long string of 1s which is equal to 0 mod $2^{n-1}-1$. Thus, by rewriting the term $( - X_h + (1-4) R_4)$, collapsing that $(n-1)$-bit string of 1s and concatenating $(\underbrace{1\ldots 1}_{ n-5 }\Vert {\bar{R}}_4\Vert 00)$ with $R_4$ as $(\underbrace{1\ldots 1}_{ n-5 }\Vert {\bar{R}}_4\Vert R_4)$ we obtain

$$\begin{aligned}&\left| -X_h -4R_4 + R_4 \right| _{2^{n-1}-1}\nonumber \\&\quad = \left| \left( \underbrace{1\ldots 1}_{n-3} \Vert {\bar{X}}_h\right) + \left( \underbrace{ 1\ldots 1 }_{ n-5 } \Vert {\bar{R}}_4 \Vert 11\right) + R_4 \right| _{2^{n-1}-1}\nonumber \\&\quad = \left| \left( \underbrace{0\ldots 0}_{n-3} \Vert {\bar{X}}_h\right) + \left( \underbrace{ 1\ldots 1 }_{ n-5 } \Vert {\bar{R}}_4 \Vert R_4\right) \right| _{2^{n-1}-1}. \end{aligned}$$

(12)

We will benefit from the properties that multiplication by $2^k$ modulo $2^{n-1}-1$ is the left cyclic shift by k bits over $n-1$ bits and that $|-x_1|_{2^{n-1}-1} = | (\underbrace{1\ldots 1}_{ |-k|_{n-1} } \Vert {\bar{x}}_1 )|_{2^{n-1}-1}$. Now, $L_5$ is calculated using the $( \lceil k/(n-1) \rceil + 7 )$-operand carry-save adder (CSA) tree mod $2^{n-1}-1$, producing the carry-save pair $(L_{5,\mathrm{c}}, L_{5,\mathrm{s}})$ as

$$\begin{aligned} L_5= & {} \left| \begin{array}{l} x_5 + \left( \underbrace{1\ldots 1}_{ |-k|_{n-1} } \Vert {\bar{x}}_1\right) + 2^k\left( \underbrace{0\ldots 0}_{ n-3 } \Vert {\bar{X}}_h\right) \\ +2^k\left( \underbrace{1\ldots 1}_{ n-5 } \Vert {\bar{R}}_4 \Vert R_4\right) \end{array}\right| _{2^{n-1}-1} \end{aligned}$$

(13)

$$\begin{aligned}&\mathop {=}\limits ^{{\tiny {\text{ CSA }}}}&\left| L_{5,\mathrm{c}} + L_{5,\mathrm{s}}\right| _{2^{n-1}-1}. \end{aligned}$$

(14)

For a special case where $n<5$ ($n=4$), we add $(n-1)$ 1s to pad the vector $( \underbrace{1\ldots 1}_{ n-5 } \Vert {\bar{R}}_4 \Vert R_4 )$ to a multiple of $n-1$ bits, i.e.

$$\begin{aligned} L_5= & {} \left| \begin{array}{l} x_5 + \left( \underbrace{1\ldots 1}_{ |-k|_3 } \Vert {\bar{x}}_1\right) + 2^k\left( 0 \Vert {\bar{X}}_h\right) +2^k\left( 11 \Vert {\bar{R}}_4 \Vert R_4\right) \end{array}\right| _7 \mathop {=}\limits ^{{\tiny {\text{ CSA }}}} \left| L_{5,\mathrm{c}} + L_{5,\mathrm{s}}\right| _7.\nonumber \\ \end{aligned}$$

(15)

All the preceding operations involving the vectors $X_h$, $R_4$ and $x_1$ are collectively shown in the left-hand part of Fig. 1b as a single block called Bit-level manipulations.

According to (8), $R_5$ is calculated as the multiplication of $L_5$ by a constant as $R_5 =|L_5/(m_1m_2m_3m_4)|_{m_5}$. Similarly to [19], this can be done using a constant multiplier block which takes a pair of inputs $(L_{5,\mathrm{c}},L_{5,\mathrm{s}})$, multiplies it by $| 1/(9\cdot 2^k)|_{2^{n-1}-1}$ and returns the output $(R_{5,\mathrm{c}},R_{5,\mathrm{s}})$, which, again, denotes the temporary value of R in the form of a pair of carry-save vectors to be added by the two-operand adder mod $2^{n-1}-1$. All this is formally written

$$\begin{aligned} R_5= & {} \left| L_5 \frac{1}{ 2^k\left( 2^{n+1}-1\right) \left( 2^{2n}-1\right) } \right| _{2^{n-1}-1} \end{aligned}$$

(16a)

$$\begin{aligned}= & {} \left| \frac{1}{9\cdot 2^k} \left( L_{5,\mathrm{c}} + L_{5,\mathrm{s}} \right) \right| _{2^{n-1}-1} \end{aligned}$$

(16b)

$$\begin{aligned}&\mathop {=}\limits ^{{\tiny {\text{ CM }}}}&\left| R_{5,\mathrm{c}} + R_{5,\mathrm{s}} \right| _{2^{n-1}-1}, \end{aligned}$$

(16c)

where $\mathop {=}\limits ^{{\tiny {\text{ CM }}}}$ denotes the multiplication in a constant multiplier.

Next, we rewrite the 4n-bit vector V from (10) to get

$$\begin{aligned} V= & {} X_h + m_2m_3R_4 + m_2m_3m_4R_5 \nonumber \\= & {} X_h + \left( 2^{2n}-1 \right) R_4 + \left( 2^{2n}-1 \right) \left( 2^{n+1}-1 \right) R_5. \end{aligned}$$

(17)

By observing that, due to the width of the final value of V, $X_h+(2^{2n}-1)R_4$ is 4n bits wide and $X_h$ is a 2n-bit vector, and we can replace (i) the addition with concatenation, i.e. $2^{2n}R_4+X_h = R_4\Vert X_h$, and (ii) the subtraction with two’s complement 4n-bit addition, i.e. $-R_4=(\underbrace{1\ldots 1}_{3n-1}\Vert {\bar{R}}_4)+1$, which leads to

$$\begin{aligned}&X_h + \left( 2^{2n}-1 \right) R_4 \nonumber \\&\quad = X_h + 2^{2n} R_4 - R_4 = 2^{2n} R_4 + X_h + \left( \underbrace{1\ldots 1}_{3n-1}{\bar{R}}_4\right) + 1 \nonumber \\&\quad = \underbrace{2^{2n} R_4+X_h}_{(R_4\Vert X_h)} + {\bar{R}}_4 + \left( \underbrace{1\ldots 1}_{3n-1}\Vert \underbrace{0\ldots 0}_{n}\Vert 1\right) + 1 \nonumber \\&\quad = (R_4\Vert X_h) + {\bar{R}}_4 + 2^{4n}-2^{n+1} + 1 . \end{aligned}$$

(18)

To enable further bit-level manipulations in the remaining part of Eq. (17), i.e. $(2^{2n}-1)(2^{n+1}-1)R_5$, we note that $2^{n-1}R_5+R_5 = R_5\Vert R_5$ and $-2^{n+1}(R_5\Vert R_5) =$ $2^{n+1}({\bar{R}}_5\Vert {\bar{R}}_5) + 2^{4n}-2^{3n-1}+2^{n+1}$, which leads to

$$\begin{aligned}&\left( 2^{2n}-1 \right) \left( 2^{n+1}-1 \right) R_5 \nonumber \\&\quad = 2^{3n+1} R_5 -2^{n+1} \left( 2^{n-1} R_5 + R_5 \right) + R_5 \nonumber \\&\quad = 2^{3n+1} R_5 -2^{n+1} ( R_5 \Vert R_5 ) + R_5 \nonumber \\&\quad = 2^{3n+1} R_5 + 2^{n+1}\left( {\bar{R}}_5 \Vert {\bar{R}}_5 \right) + 2^{4n} - 2^{3n-1} + 2^{n+1} + R_5 \nonumber \\&\quad = \left( R_5\Vert 00\Vert {\bar{R}}_5\Vert {\bar{R}}_5 \Vert 00\Vert R_5 \right) + 2^{4n}- 2^{3n-1} + 2^{n+1}. \end{aligned}$$

(19)

By substituting in Eq. (17) all the terms detailed by Eqs. (18) and (19), we get

$$\begin{aligned} V= & {} \left( R_4\Vert X_h \right) + {\bar{R}}_4 + 2^{4n}-2^{n+1} + 1 \nonumber \\&+ \left( R_5 \Vert 00\Vert {\bar{R}}_5 \Vert {\bar{R}}_5 \Vert 00 \Vert R_5 \right) + 2^{4n}- 2^{3n-1} + 2^{n+1} \end{aligned}$$

(20a)

$$\begin{aligned}= & {} \left( R_4\Vert X_h \right) +{\bar{R}}_4 + \left( R_5 \Vert 00\Vert {\bar{R}}_5 \Vert {\bar{R}}_5 \Vert 00\Vert R_5 \right) + \underbrace{2^{4n+1} - 2^{3n-1} + 1}_{C_1^{\prime }}. \end{aligned}$$

(20b)

All three input variable components of the summation in Eq. (20a) (i.e. $R_4$, $X_h$ and $R_5$) are prepared earlier separately by the bit-level manipulations block shown in the right part of Fig. 1b. Then V can be computed according to Eq. (20b) using the four-operand 4n-bit adder, whose inputs are three variables and the accumulated constant term $C_1^{\prime }$. Notice, however, that the addition in (20) is 4n bits wide, whereas $C_1^{\prime }$ is a $(4n+1)$-bit number. Therefore, the most significant bit of $C_1^{\prime }$ can be discarded, which is equivalent to replacing $C_1^{\prime } = 2^{4n} + (2^{4n}-2^{3n-1}+1)$ with $C_1=2^{4n}-2^{3n-1}+1$, so that Eq. (20b) can be written

$$\begin{aligned} V= & {} \left( R_4\Vert X_h \right) + {\bar{R}}_4 + \left( R_5 \Vert 00\Vert {\bar{R}}_5 \Vert {\bar{R}}_5 \Vert 00\Vert R_5 \right) + \underbrace{2^{4n} - 2^{3n-1} + 1}_{C_1} . \end{aligned}$$

(21)

Now, according to Eq. (10), the final result X is obtained by concatenating V with $x_1$.

3.2 Version 2

Version 2 can be obtained from Eq. (10) by first observing that

$$\begin{aligned} \left| -X_4 \right| _{2^{n-1}-1}= & {} \left| \begin{array}{l} \left( \underbrace{1\ldots 1}_{ |-k|_{n-1} } \Vert {\bar{x}}_1\right) + 2^k\left( \underbrace{0\ldots 0}_{ n-3 } \Vert {\bar{X}}_h\right) \\ + 2^k \left( 1\ldots 1 \Vert {\bar{R}}_4 \Vert R_4\right) \end{array}\right| _{2^{n-1}-1}. \end{aligned}$$

(22)

By letting $L^{\prime }_5 = | x_5 + ( \underbrace{1\ldots 1}_{ |-k|_{n-1} } \Vert {\bar{x}}_1) + 2^k( \underbrace{0\ldots 0}_{ n-3 } \Vert {\bar{X}}_h ) |_{2^{n-1}-1}$ we obtain

$$\begin{aligned} L_5 = \left| L^{\prime }_5 + 2^k\left( \underbrace{1\ldots 1}_{ n-5 } \Vert {\bar{R}}_4 \Vert R_4\right) \right| _{2^{n-1}-1}, \end{aligned}$$

(23)

where, similarly to Eq. (13), the operations involving the vectors $X_h$, $R_4$ and $x_1$ are collectively shown in the left part of Fig. 1c as two separate bit-level manipulations blocks.

The calculation of V in Eq. (20) is the four-operand addition ($R_4$, $X_h$, $R_5$ and the constant), which could be implemented using two CSAs and one carry-propagate adder (CPA). However, of these four operands, only $R_5$ is on the critical path. We thus propose to precalculate the sum of non-critical components as one variable $V^{\prime }$ by a three-operand adder and then add the critical component to $V^{\prime }$. Let

$$\begin{aligned} V^{\prime } = \left( R_4\Vert X_h \right) + {\bar{R}}_4 + 2^{4n}- 2^{3n-1} + 1. \end{aligned}$$

(24)

Now Eq. (20) can be rewritten

$$\begin{aligned} V= & {} \underbrace{\left( R_4\Vert X_h\right) + {\bar{R}}_4 + 2^{4n} - 2^{3n-1} + 1 }_{V^{\prime }} + \left( R_5 \Vert 00 \Vert {\bar{R}}_5 \Vert {\bar{R}}_5 \Vert 00 \Vert R_5 \right) \nonumber \\= & {} V^{\prime } + \left( R_5 \Vert 00 \Vert {\bar{R}}_5 \Vert {\bar{R}}_5 \Vert 00 \Vert R_5 \right) , \end{aligned}$$

(25)

which can be implemented using one 4n-bit two-operand CPA. All operands that occur in the summations in Eqs. (24) and (25) are prepared by two independent bit-level manipulations blocks, shown in the right part of Fig. 1c.

3.3 Example

Consider the five-moduli set with $n=4$ and $k=5$, i.e. $\{ m_1, m_2, m_3, m_4 , m_5\} = \{ 32, 15, 17, 31, 7 \}$, and a sample set of five residues $\{ x_1, x_2, x_3, x_4, x_5 \} = \{ 1, 2, 3, 4, 5 \}$. We will show how Version 1 of our converter calculates X, which corresponds to $\{ x_1, x_2, x_3, x_4, x_5 \}$. First, to obtain $X_4$, which corresponds to $\{ x_1, x_2, x_3, x_4 \}$, we calculate $X_h$ and $R_4$ from Eqs. (5) and (6) respectively (to avoid ambiguities, the binary numbers are marked by the subscript ‘b’):

$$\begin{aligned} X_h= & {} \left| \frac{ 17\left| \frac{2}{17}\right| _{15} + 15\left| \frac{3}{15}\right| _{17} -1 }{32} \right| _{15\cdot 17} = 203 = 11001011_\mathrm{b},\\ R_4= & {} \left| \frac{4 - (1 + 32\cdot 203 )}{32\cdot 15\cdot 17} \right| _{31} = 29 = 11101_\mathrm{b}. \end{aligned}$$

Now $X_4$ is calculated according to (7) as

$$\begin{aligned} X_4 = 1 + 32\cdot 203 + 32\cdot 15\cdot 17\cdot 29 = 243137. \end{aligned}$$

Next, $X_h$, $R_4$, $m_5=7$ and $x_5=5$ are used to calculate $L_5$ from Eq. (15):

Once $L_5$ is available in the form of the carry-save pair, $R_5$ can be calculated. For $n=4$ and $k=5$, the multiplicative inverse given by Eq. (4) is $| 1/9 |_{2^{4-1}-1} = | 1/9 |_{7} = 2^{2} =4$ and $| \frac{1}{9\cdot 2^5} |_7 =|4/32|_7=1$. From (16b) we then have

Now V can be calculated from Eq. (20) as

$$\begin{aligned} V= & {} \left| \begin{array}{l} (11101 \Vert 11001011)_\mathrm{b} + \left( \overline{ 11101 }\right) _\mathrm{b} \\ \quad + 2^{16} - 2^{11} + 1 \\ \quad + \left( 011 \Vert 00 \Vert \overline{ 011 } \Vert \overline{ 011 } \Vert 00 \Vert 011\right) _b \end{array} \right| _{2^{16}} \\= & {} \left| \begin{array}{l} \underbrace{11101\ 11001011_\mathrm{b}}_{ 7627 } + \underbrace{ 00010_\mathrm{b}}_{ 2 } \\ \quad +\underbrace{ 011\ 00\ 100\ 100\ 00\ 011_b}_{ 49446 } + \underbrace{2^{16} - 2^{11} + 1}_{ 63489 } \end{array} \right| _{2^{16}} \\= & {} 55028. \end{aligned}$$

Finally, we obtain $X= 1 + 32\cdot 55028 = 1760897$. One can easily verify that $| 1760897 |_{ \{ 32,15,17,31,7 \} } = \{1,2,3,4,5\}$.

4 Gate-Level Complexity Evaluation

In this section, we will evaluate and compare the gate-level complexity of our converters and their closest counterparts: $\{ 2^n, 2^n-1, 2^n+1, 2^{n+1}-1, 2^{n-1}-1 \}$ (n even), proposed in [4] (special case of our moduli set with $k=n$), and $\{ 2^n-1, 2^n, 2^n+1, 2^{n+1}+1, 2^{n-1}+1 \}$ (n odd), proposed in [18]. The gate-level complexity evaluations of hardware and delay appear in Tables 1, 2 and 3. Big-omega ($\varOmega$) notation is used for the lower bound of the area complexity of multiplication by the multiplicative inverse [19].

We consider reverse converters as datapaths whose basic components are mainly adders in the forms of CSAs and CPAs rather than complex combinational circuits composed of primitive gates. The gate-level complexity of CSA is O(n) and its delay is O(1), and the complexity of CPAs in most evaluations is given as O(n), while the actual synthesis results are then provided with the use of parallel-prefix adders (PPAs) [17] exhibiting $O(n\log n)$ gate complexity and $O(\log n)$ delay. Bit-level manipulations are mainly shifts and inversions, with only a very small fraction of them involving other logic operations. Thus, we first provide an analysis of higher-level representations like CSAs and CPAs, whereas detailed complexity characteristics expressed in terms of primitive gates will be presented subsequently in Table 3.

Table 2 Delay estimations of various converters

Table 1 details all adders used in our converters and their counterparts of [4] and [18]. As for the number of CPAs, Version 1 of our converter allows us to spare one CPA mod $2^{n+1}-1$, one CPA mod $2^{n-1}-1$ and one 4n-bit ordinary CPA, whereas Version 2 of our converter requires the same number of CPAs as its counterpart of [4] (or CPAs mod $2^{n\pm 1}+1$ as its counterpart of [18]). The comparison of the number of CSAs is slightly more complicated because (i) this number depends on k and (ii) different circuitry is used to carry out the multiplication by multiplicative inverses in the calculations of $R_4$ and $R_5$. While comparing Versions 1 and 2 of our converters, we notice that the number of CSAs in Version 2 in the calculation of $L_4$ and $L_5$ is constant because the main part of the calculations is performed for $L^{\prime }_4$ and $L^{\prime }_5$ respectively. As we compare Version 1 of our converter with the converters from [4, 18] for the special case of $k=n$, we notice that the number of CSAs in the calculation of $L_4$ is the same as in [4, 18], whereas we use one more CSA in the calculation of $L_5$ (recall, however, that we have already spared two CPAs). Our implementation of the multiplication by multiplicative inverses in the calculations of $R_4$ and $R_5$ is less complex than in [4, 18], because the latter use a traditional single CSA tree structure in which the number of CSAs grows linearly with n, while we use the constant multiplier block of [19] with the logarithmically growing number of CSAs.

Table 2 compares the delays of our converters and their counterparts from [4, 18], where $d_{\mathrm{CSA}}(a)$ denotes the delay of an a-operand CSA, $d_{\mathrm{CPAm}}(a)$ [$d_{\mathrm{CPAp}}(a)$] denotes the delay of an a-bit [$(a+1)$-bit] adder mod $2^{a}-1$ ($2^{a}+1)$, whereas $d_{\mathrm{ADD}}(a)$ is the delay of an ordinary a-bit CPA. As k has little impact on the delay, we consider the special case of $k=n$. The critical path leads from any of the inputs $x_1$, $x_2$ and $x_3$ through $X_h$, $L_4$/$R_4$, $L_5$/$R_5$ and V to the output X (see Fig. 1a, Eqs. (5) and (6) and the description of the four-moduli converter in [19]). The delay of constant multiplication blocks can be expressed as $O(\log _{\sqrt{2}}a)$, which is very close to the delay of equivalent CSA trees given by $d_{\mathrm{CSA}}(a) \approx O(\log _{1.5}a)$ [19]. The constant multiplication block of [19] allows for a carry-save representation of its input, which is not the case in [4, 18], where the multiplication by multiplicative inverse must be implemented as a regular CSA tree requiring a preceding CPA. Because the delay of the constant multiplication block is comparable to the delay of the regular CSA tree, our designs gain a considerable speed advantage since they spare two CPAs from the critical path.

Finally, to facilitate any initial complexity estimation for chosen parameters n and k, gate-level details of the basic blocks of the proposed converters as well as their overall gate-level complexity characteristics can be found in Table 3. Similarly to previous estimations, for example in [2], the delay and complexity of CPAs is carried out for ripple-carry adders.

Table 3 Gate-level hardware complexity estimations of new converters

5 Experimental Evaluation and Comparison

All the considered converters were synthesised using Cadence RC Compiler v.8.1 over the commercial CMOS065LP low-power library from ST Microelectronics, with the results shown in Figs. 2, 3 and 4. All descriptions were coded using parametrised structural Verilog, following identical coding guidelines, with the same datapath components (CSAs, CPAs and MOMAs) and input and output registers. The MOMAs mod $2^a -1$ (mod $2^a +1$) were implemented according to [21] using the a-bit CSA with end-around-carry (EAC) (inverted EAC) followed by the a-bit parallel-prefix CPAs from [17, 35]).

While the selection of even or odd n imposed on the converters from [4, 18], respectively, allows one to cover partially complementary dynamic ranges, each with a resolution of 10 bits, our converter makes it possible to cover precisely any required dynamic range $\hbox {DR}$ with a few alternative combinations of n and k such that $\hbox {DR}=4n+k-1$, $n \ge 4$ even, and $k>0$. To consider the datapaths as being well balanced, the width of the even channel $2^k$ should be no smaller than that of the odd channels, yielding in – for a given n – the recommended values of k such that $n \le k \le n+9$ cover the entire set of consecutive dynamic ranges with one pair of n and k for every dynamic range. Consequently, we have synthesised our converters for the selection of n and k covering all consecutive dynamic ranges from 19 to 88 bits, whereas the converters from [4, 18] were synthesised for the dynamic ranges corresponding to even $n\in \{4, \ldots , 16 \}$ and odd $n \in \{ 7, \ldots , 17\}$, respectively.

Fig. 2

Minimum delay as a function of dynamic range

Fig. 3

Power at minimum delay

Fig. 4

Area at minimum delay

The delay of all components like CSA trees, CPAs implemented as parallel-prefix adders and constant multipliers, is $O(\log n)$ and grows mainly with n, with only a minor contribution of k (Table 2), and is revealed as discrete logarithmic growth in Fig. 2. A slightly inconsistent minor growth between steps on the stair-like curve result from the heuristics used by the synthesiser, with Version 1 slightly smoother than for Version 2, as a result of a higher and faster-growing number of CSA stages on its critical path. Differences in delays between both versions of our converter and their counterparts – average 10% of Version 1 over Version 2 and 20% over the converters from [4, 18] – result from the number of CPAs on the critical path being smaller by two (from using the carry-save input to the constant multiplier – both $L_4$ and $L_5$ have carry-save forms), and the number of CSAs on the critical path involving calculation of $L_4$ and $L_5$ is smaller and invariable (thanks to the precalculation of non-critical components as $L^{\prime }_4$ and $L^{\prime }_5$).

Figure 3 shows the power consumption of all converters, which is obtained from synthesis tool estimation depending on the set of library gates used in the synthesised circuit, the operating frequency (which is the target delay in our case) and the architecture of the circuit. The curves for both our converters are stair-like with steps at changes of n, exactly at the same points as on the delay curves of Fig. 2, and Version 1 generally consumes more power, which is particularly evident for $DR\in \{ 49, \ldots , 58, 69, \ldots , 88 \}$ bits. Version 2 of our converter not only is significantly faster but also consumes less power, which is particularly interesting because the area of Version 2 is larger than that of Version 1 (note, however, that extra adders are located outside of the critical path). We find power advantage of Version 2 of our converter as a result of a greater dispersion of data across signal paths and less strain on the critical path, which in turn results in gates being selected by the synthesis tools which are smaller and consume less power. Either version of our converter consumes less power than their counterparts from [4, 18], except two isolated cases of $\hbox {DR}=19$ and 49 bits for [4].

Figure 4 shows the sums of areas occupied by logic cells and interconnections. The faster Version 2 occupies a larger area than Version 1 as a result of the need for the extra hardware (CPAs) required to precalculate $L^{\prime }_4$ and $L^{\prime }_5$ along with accompanying CSAs and larger cells selected by the synthesis tools for faster designs. Our designs are smaller than those of [4, 18]; this is a direct outcome of using two fewer CPAs (especially on the critical path) and significantly smaller blocks used to perform multiplications by multiplicative inverses [viz. $\varOmega (\log \frac{n}{3})$ vs. $O(\frac{n}{3})$]; the area growth due to the smaller delay is offset by gains resulting from architectural advantages. For either version of our converters, the growth of the area depends mainly on n, which is seen on a highly regular stair-like curve of Fig. 4: every increase in n by two is accompanied by a noticeable growth of the area. Linear growth of the area along with k occurs only for smaller dynamic ranges from 19 to 58 (corresponding to n from 4 to 7).

6 Conclusion

In this paper, a new RNS composed of five flexible balanced moduli $\{ 2^k, 2^n-1, 2^n+1, 2^{n+1}-1, 2^{n-1}-1 \}$ for the pairs of positive integers $n \ge 4$ (even) and any $k>0$ was introduced; it can provide the required dynamic range with one-bit resolution. From the set of basic functions, two versions of a reverse (residue-to-binary) converter with varying performance characteristics were designed for this new RNS. The converters for the new RNS as well as those for two other known five-moduli sets also composed of low-cost balanced moduli but with a single parameter n only, were synthesised using industrial tools, and the experimental results obtained suggest that our converters have 28–40% smaller delay while still consuming less area and power. The widths of all residue datapaths in our moduli equalled about one-fifth the width of their two’s complement counterpart, and their delay can be balanced thanks to the possibility of adapting the size of the even modulus $2^k$. Thanks to the use of low-cost moduli, forward converters and channels may be implemented in a regular and efficient way, which makes them well suited not only for traditional DSP systems but also for cryptographic applications. Some dynamic ranges are require k to be significantly larger than n, such that they may negatively impact the balance of the even residue datapath channel. Thus, some other new flexible five-moduli sets which are better adapted to cover new dynamic ranges may be the subject of further research.