1 Introduction

In many digital signal processing applications, such as synchronization in digital modems [14, 37], incommensurate sampling rate conversion [8, 15, 20, 29], and speech coding [9, 26], there is a necessity for delaying signals. This problem can be readily solved when a signal needs to be delayed by an integer multiple of a sampling period. In such a situation, signal samples are merely stored in a register for several sampling periods. However, in many cases, like in the modeling of musical instruments sounds [28, 33] and time delay estimation (TDE) [11, 27], a required delay is a fraction of a sampling period and fractional delay (FD) filters [1, 17, 23, 24] must be utilized. Moreover, in many of these applications a variable fractional delay (VFD) [1, 7, 13, 16, 17] is required. This involves continuous changes of filter impulse response, often for each processed sample, which creates a need for simple and efficient design algorithms.

The ideal FD filter has infinite impulse response, which is described by only one parameter—the total delay [24]. In order to implement an FD filter in real time, its impulse response is usually approximated with causal finite impulse response (FIR), which leads to inevitable approximation errors [12]. From all FIR FD filters, the most efficient are optimal FD filters, which offer the best performance for the given filter length and approximation band. One of the most commonly utilized types of optimal FD filters are filters which are optimal in the least squares (LS) sense, filters optimal in the Chebyshev sense (also called minimax filters), and maximally flat (MF) filters [1, 10, 24]. Among the above mentioned types of optimal FD filters, MF filters are the easiest to design but leave the designer with no control over the approximation band and even though there are some workarounds for this problem, like truncation of MF filter impulse response [36], the obtained solution is not optimal. In contrast, there are LS and minimax filters which have more complex design formulas but satisfy specific quality requirements including requirements on the approximation band. Nevertheless, these filters are very hard to design in real time because of complicated design algorithms, which makes them unsuitable for most VFD applications.

Alternatively, a very simple filter design method is the commonly known window method [12, 25]. The design procedure consists only of the ideal impulse response multiplication by a window function. The simplicity of the window method makes it ideal for VFD filter design but the selection of window satisfying given specifications is usually difficult. This is why a filter design using the window method requires an iterative approach which still often produces results significantly worse than optimal.

In this paper we demonstrate that nearly optimal FD filters can be designed using a slightly modified window method. In the approach investigated in this paper, called the extracted window method (Fig. 1), instead of searching for the best window formula, a window is extracted from the optimal filter with some arbitrarily selected fixed FD (called the reference delay, \(d_\mathrm{ref})\) [3, 6, 17]. An additional advantage of the presented method is that a single symmetric window can be used to design a VFD filter [4, 6, 17, 30]. However, the gain of the designed filter must be corrected with different values for each desired FD [3, 5, 6, 17, 30]. The gain correction factor can be sampled and stored in a look-up table (LUT) or approximated with a low order polynomial. During runtime (the implementation stage in Fig. 1), the design of the filter with any FD \(d\) is simple and consists only of the ideal filter impulse response \(h_\mathrm{id}\)[\(n\)] (which is a sampled sinc function) multiplication by the reference window \(w_\mathrm{ref}\)[\(n\)] (like in the traditional window method) and additional filter gain correction \(\alpha (d)\). On this basis we have proposed the universal VFD filter structure based on the Farrow structure [7, 13, 34]. The proposed structure can be easily switched to a different VFD filter type and length simply by changing the reference window and the coefficients of polynomial approximating gain correction curve.

Fig. 1
figure 1

General diagram of the extracted window method; graphs demonstrate typical shapes of the ideal and optimal FD filter impulse responses, extracted windows as well as gain correction curves

Full size image

The presented research is based on the concept of an extracted window proposed in [17], where even length nearly optimal minimax FD filters are designed using a window extracted from a symmetric FD filter with the FD \(d_\mathrm{ref} =\) 0.5. We have extended this concept to filters of any length (even and odd) and applied it not only to minimax FD filters but also to LS and MF ones using even part of the window extracted for an arbitrary FD. The same symmetric reference window can be directly obtained using the formulas proposed in this paper. In such case, it is already properly scaled for FD filter design for the given reference delay. We have also improved the method of calculation of gain correction factor, which must be applied to designed filters. The approach proposed in [17] is based on comparing the in-band gain of optimal and designed filters for several delays, which means that several optimal filters need to be designed. We have proposed a formula for direct calculation of gain correction factor for all required delays based only on a single reference window, without the need for optimal filters design. All the improvements were possible thanks to the new approach to analysis of the windows extracted from optimal filters based on their division into even and odd parts.

The paper is organized as follows. In Sect. 2 the FD filter is introduced and optimal FD filters design is shortly described. Section 3 is dedicated to the extracted window concept and the general outline of the proposed extracted window method. Next in Sect. 4 properties of windows extracted from optimal filters are investigated. In this section we have demonstrated that using a single window extracted from the optimal FD filter for any arbitrary FD (which is generally asymmetric) we can reconstruct the extracted window for all FDs. In Sect. 5 a symmetric even part of the extracted window is proposed for the VFD filter design and in Sect. 6 a formula for the gain correction factor required to obtain nearly optimal filters is derived. Section 7 is dedicated to a procedure for direct design of a symmetric window, which is an alternative for window extraction from optimal FD filters. In Sect. 8 the structure for the implementation of the VFD filter based on the proposed window method is presented and performance of resulting filters is compared with optimal FD filters. Finally, the paper is summarized in Sect. 9.

2 FD Filter

The ideal FD filter [17, 24] with a total delay \(\tau _\mathrm{d}\) is characterized by the following frequency response

$$\begin{aligned} H_\mathrm{id} (f)=\left| {H_\mathrm{id} (f)} \right| \exp ( {j\Phi _\mathrm{id} (f)})=\exp (-j2\pi f\tau _\mathrm{d} ),\quad \vert f\vert <1/2, \end{aligned}$$
(1)

where \(f\) is the normalized frequency. The magnitude response \(\vert H_\mathrm{id}(f)\vert \) of the ideal FD filter is constant and equal to 1, while the phase response \(\Phi _\mathrm{id}(f)\) is linear, which results in constant group delay equal to the assumed total filter delay \(\tau _\mathrm{d}\).

The impulse response corresponding to the frequency response (1) is a sampled sinc function [24]

$$\begin{aligned} h_\mathrm{id} [n]=\hbox { sinc}(n-\tau _\mathrm{d} ),\quad n=0,\pm 1,\ldots , \end{aligned}$$
(2)

where \(n\) is the discrete-time index.

The total delay \(\tau _\mathrm{d}\) of any FD filter can be split into an integer delay \( D =\) round (\(\tau _\mathrm{d})\) and a FD \(d\in [-1/2, 1/2)\)

$$\begin{aligned} \tau _\mathrm{d} =D+d. \end{aligned}$$
(3)

One should notice that for a non-integer total delay, the impulse response (2) is infinite as well as non-causal and a filter with such an impulse response cannot be implemented. This leads us to the problem of the ideal frequency response \(H_\mathrm{id}\) (1) approximation using a causal filter with a FIR \(h_{N}\)[\(n\)]. Since approximation errors are inevitable, they must be taken into account during design. The most general measure of approximation errors is the complex approximation error

$$\begin{aligned} E(f)=H_N (f)-H_\mathrm{id} (f), \end{aligned}$$
(4)

where

$$\begin{aligned} H_N (f)=\sum \limits _{n=0}^{N-1} {h_N [n]\exp (-j2\pi fn)} ,\quad \vert f\vert {}\le 1/2 \end{aligned}$$
(5)

represents the frequency response of the FIR filter approximating the ideal FD filter frequency response \(H_\mathrm{id}\) (1).

In practice, instead of the complex approximation error (4), scalar parameters are used, which allow for simpler evaluation of filter performance. Examples are peak error (PE)

$$\begin{aligned} \mathrm{PE}(f_\mathrm{a} )=\mathop {\max }\limits _{f\in [-f_\mathrm{a} ,f_\mathrm{a} ]} \left| {E(f)} \right| \end{aligned}$$
(6)

and squared error (SE)

$$\begin{aligned} \hbox {SE}(f_\mathrm{a} )=\int \limits _{-f_\mathrm{a} }^{f_\mathrm{a} } {\left| {E(f)} \right| ^2\mathrm{d}f} \end{aligned}$$
(7)

evaluated in the desired approximation band limited by its upper frequency \(f_\mathrm{a}\).

Depending on which design method we use, particular requirements for PE or SE and an approximation band width may be satisfied by FIR filters with different impulse response lengths. As mentioned earlier, there exist methods for optimal or nearly optimal FD filter design [1, 10, 19, 24]. Filters designed using these methods demonstrate minimal approximation errors for the given impulse response length. When we use such design methods we can readily find filters which satisfy our quality requirements with minimal length. In the case of optimal LS and minimax filters (minimizing SE (7) and PE (6), respectively), error is minimized only in the approximation band [–\(f_\mathrm{a}\), \(f_\mathrm{a}\)]. Disregarding error function outside this band, results in better performance in the approximation band.

A different approach characterizes MF filter design, for which the complex approximation error (4) [10, 16, 24] and its \(N\)–1 derivatives satisfy the following conditions

$$\begin{aligned} \left. {\frac{\mathrm{d}^nE(f)}{\mathrm{d}f^n}} \right| _{f=0} =0,\quad n=0,1,\ldots ,N-1 \end{aligned}$$
(8)

which guarantees maximal flatness of its frequency response.

The impulse response h of the MF filter can be calculated by solving a set of linear equations [24] which can be written in the matrix form

$$\begin{aligned} \mathbf {Ph} = \mathbf {p} \end{aligned}$$
(9a)

and further transformed into the following formula

$$\begin{aligned} \mathbf {h}=\left[ {{\begin{array}{llll} {h[0],} &{} {h[1],} &{} {\ldots ,} &{} {h[N-1]} \\ \end{array} }} \right] ^\mathrm{T}={\mathbf {P}}^{-1}{\mathbf {p}}, \end{aligned}$$
(9b)

where \(^\mathrm{T}\) represents matrix transposition. The P matrix is a square Vandermonde matrix with elements [24]

$$\begin{aligned} P_{k+1,n+1} =n^k;\quad k,n=0,1,\ldots ,N-1 \end{aligned}$$
(10a)

and P \(^{-1}\) is the inverse of the matrix P. The column vector p is composed of the following elements

$$\begin{aligned} p_{k+1,1} =\tau _\mathrm{d}^k. \end{aligned}$$
(10b)

The design of the optimal LS FD filter, for which SE (7) is minimized, can be performed analogically to MF filters using matrix equations (9a) and (9b) [24] with elements of matrix P and vector p expressed as

$$\begin{aligned} P_{k+1,n+1} =2f_\mathrm{a} \hbox { sinc}( {2f_\mathrm{a} (k-n)})\end{aligned}$$
(11a)
$$\begin{aligned} p_{k+1,1} =2f_\mathrm{a} \hbox { sinc}( {2f_\mathrm{a} (k-\tau _\mathrm{d} )}). \end{aligned}$$
(11b)

Similarly, the design of FD filters optimal in the Chebyshev sense minimizing PE (6) [1, 19, 24] can be formulated using the same matrix formulas (9a) and (9b). In this case, however, we need to use matrix P and vector p with sizes increased by one

$$\begin{aligned} P_{k+1,n+1} =\cos (2\pi f_k (n-\tau _N ))-\sin (2\pi f_k (n-\tau _N ))\quad \mathrm{and}\quad P_{k+1,N+1} =(-1)^k \end{aligned}$$
(12a)
$$\begin{aligned} p_{k+1,1} =\cos (2\pi f_k (\tau _\mathrm{d} -\tau _N ))-\sin (2\pi f_k (\tau _\mathrm{d} -\tau _N )), \end{aligned}$$
(12b)

where \(\tau _{N} = (N-1)/2\) is the bulk delay and \(k =\) 0, 1,\(\ldots \), \(N\). The impulse response vector (9b) also includes an additional element \(\delta \)

$$\begin{aligned} {\hat{\mathbf{h}}}=\left[ {{\begin{array}{llll} {h[0],} &{} {h[1],} &{} {\ldots ,} &{} {h[N-1],\delta }\\ \end{array} }} \right] ^\mathrm{T} \end{aligned}$$
(13)

representing the value of PE (6) calculated for the set of \(N~\)+ 1 frequency points \(f_{k}\in [-f_\mathrm{a}, f_\mathrm{a}]\), called extremal points, where \(f_{k}<f_{k+1}, f_{0} =- f_\mathrm{a}\) and \(f_{N-1}=f_\mathrm{a}\). In the case of the Chebyshev criterion, proper location of extremal points has to be determined in order to obtain the optimal solution, which can be achieved using the iterative complex Remez algorithm [1, 22]. In each iteration of this algorithm, the solution of matrix equations (9a) and (9b) is calculated and on this basis a location of extremal points \(f_{k}\) is corrected.

3 Extracted Window Method

The optimal methods are the best choice if the best filter performance is required but this goal is achieved at the expense of high computational costs of filter coefficients calculations. On the other hand, the window method in which the ideal impulse response \(h_\mathrm{id}\)[\(n\)] (2) is simply multiplied by a window \(w_{N}\)[\(n\)]

$$\begin{aligned} h_N [n]=w_N [n]h_\mathrm{id} [n] \end{aligned}$$
(14)

is simple and numerically efficient. This approach is, however, limited by the difficulty of window selection which leads to rather poor performance of the designed filter. Taking into consideration advantages and disadvantages of these design methods the following question can be posed: “Is it possible to design FD filters close to the optimal solution using the window method?”

A simple example of the optimal FD filter which can be designed using the window method is full band LS filter (\(f_\mathrm{a} =\) 0.5). In this case the matrix P in equations (12) simplifies to a unit matrix, and thus, we obtain the following formula

$$\begin{aligned} \mathbf {h}=\mathbf {p}=\left[ {{\begin{array}{llll} {\hbox {sinc}( {0-\tau _\mathrm{d} })} &{} {\hbox {sinc}( {1-\tau _\mathrm{d} })} &{} \cdots &{} {\hbox {sinc}( {N-1-\tau _\mathrm{d} })} \\ \end{array} }} \right] ^\mathrm{T}. \end{aligned}$$
(15)

As we can see, the impulse response of full band LS FD filter (15) is a truncated impulse response of the ideal FD filter (2). This means that this type of FD filter can be designed using the rectangular window

$$\begin{aligned} w_N [n]=1,\quad n=0,1,\ldots ,N-1. \end{aligned}$$
(16)

Since the full band optimization leads to poor performance filters, a more practical example is the MF FD filter. It has been proven that its impulse response can be calculated by multiplying the ideal impulse response (2) by the scaled binomial window \(w_{b}\)[\(n\)] [10, 21, 23, 35]

$$\begin{aligned} h_\mathrm{MF} [n]=\alpha (\tau _\mathrm{d} )w_\mathrm{b} [n]h_\mathrm{id} [n], \end{aligned}$$
(17)

where

$$\begin{aligned} w_\mathrm{b} [n]=\left( {{\begin{array}{c} {N-1} \\ n \\ \end{array}}}\right) ,\quad n=0,1,\ldots ,N-1 \end{aligned}$$
(18)

and the window scaling factor dependent on the desired delay

$$\begin{aligned} \alpha (\tau _\mathrm{d} )=(-1)^{N+1}\frac{\pi N}{\sin (\pi \tau _\mathrm{d} )}\left( {\begin{array}{l} \tau _\mathrm{d} \\ N \\ \end{array}}\right) . \end{aligned}$$
(19)

The Newton symbol \({\small \left( {\begin{array}{l} a \\ b \\ \end{array}}\right) }\) in formulas (18) and (19) represents the binomial coefficient, which for negative and non-integer values of \(a\) or \(b\) can be computed using gamma function \(\Gamma () \) [10].

The formula (17) shows that the MF filter can be designed using the well-known window method, though additional gain correction dependent on the desired delay is necessary.

Simplicity of the design process is a huge advantage of MF FD filters but width of their approximation band depends only on their length. On the other hand, LS and minimax filters allow for minimization of SE (7) and PE (6) in the specified approximation band for the given filter length. Unfortunately, there are no formulas for windows that can be used in bandlimited LS and in minimax FD filters design. However, design equation of the window method (14) can be reversed and a window \(w_\mathrm{opt}\)[\(n\)] can be extracted from the optimal FD filter for a given reference delay \(d_\mathrm{ref}\) [17]

$$\begin{aligned} w_\mathrm{opt} [n]=h_\mathrm{opt} [n]/h_\mathrm{id} [n] \end{aligned}$$
(20)

on condition that \(h_\mathrm{id}\)[\(n\)] \(\ne \) 0, which is satisfied for \(d_\mathrm{ref}\) \(\ne \) 0.

Based on the formula (20) we propose a procedure for design and implementation of high quality VFD filter with the use of the extracted window method, presented in Fig. 1. The design procedure is split into two stages. All the most time consuming computations are performed at the preparations stage. At this stage a single optimal filter with impulse response \(h_{\mathrm{opt},d_\mathrm{ref} } [n]\) is designed and samples of the ideal filter impulse response \(h_{\mathrm{id},d_\mathrm{ref} } [n]\) (2) are computed for the same arbitrary reference delay \(d_\mathrm{ref}\) (Sect. 2). Based on computed impulse responses a symmetric reference window \(w_\mathrm{ref}\)[\(n\)] is extracted using formula (20). Additionally, like in the case of MF filters, we need a gain correction factor \(\alpha (d)\). Computation of this factor is too complex for real-time application requiring frequent delay changes but it can be calculated beforehand for all desired delays based on the reference window obtained previously. Next, computed factor values can be approximated with a polynomial of the order \(p\)

$$\begin{aligned} \alpha _p (d)=\sum \limits _{k=0}^p {a_k d^k} \end{aligned}$$
(21)

or simply stored in a LUT for further use at the next stage.

At the runtime, which is marked as the implementation stage in Fig. 1, for each required delay \(d\) we need to calculate a truncated impulse response of the ideal filter \(h_{\mathrm{id},d}\)[\(n\)] (2) and compute the gain correction factor \(\alpha (d)\) using the polynomial coefficients or take it from the LUT table. In the next step \(h_{\mathrm{id},d}\)[\(n\)] is multiplied by the reference window \(w_\mathrm{ref}\)[\(n\)] (like in traditional window method) and filter gain is corrected.

4 Properties of Extracted Windows

The first problem which needs to be resolved in the proposed VFD filter design method (Fig. 1) is proper selection of the reference window. To check if we can assume that nearly optimal LS and minimax filters can be designed using window method (14) like MF filters, we have investigated properties of windows extracted from optimal filters using formula (20) for different fractional delays.

An impulse response of the FD filter and, thus an extracted window \(w_\mathrm{opt}\)[\(n\)] (20), are in general asymmetric, so in order to verify properties of the extracted window we split it into even

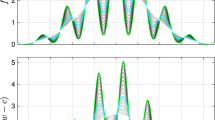
$$\begin{aligned} w_\mathrm{e} [n]={(w_\mathrm{opt} [n]+w_\mathrm{opt} [N-1-n])}/2 \end{aligned}$$
(22a)

and odd part

$$\begin{aligned} w_\mathrm{o} [n]={(w_\mathrm{opt} [n]-w_\mathrm{opt} [N-1-n])} /2. \end{aligned}$$
(22b)

As we can see in Fig. 2a, the even part of the extracted window seems to be independent of the filter delay regardless of the optimal filter type. Additionally, the odd part of the extracted window is significantly smaller but non-zero, which indicates asymmetry of the window (Fig. 2b). Analysis of windows presented in Fig. 2 reveals no noticeable changes in the shape of both even and odd part of the extracted window. Therefore, we propose to assume that only scale of even and odd part of the extracted window changes with filter delay (Fig. 3). This assumption means that a single asymmetric window, a reference window, extracted from the optimal filter with the FD \(d_\mathrm{ref}\) with proper scaling of its even and odd part can be used to reconstruct a window \(w_{\mathrm{rec},d}\)[\(n\)] which can be used to design the optimal filter with different FD \(d\) \(\ne \) \(d_\mathrm{ref}\)

$$\begin{aligned} w_{\mathrm{opt},d} [n]\cong w_{\mathrm{rec},d} [n]=\alpha (d)w_{\mathrm{e,ref}} [n]+\beta (d)w_{\mathrm{o,ref}} [n]. \end{aligned}$$
(23)
Fig. 2
figure 2

Even (a) and odd (b) parts of windows extracted from filters of length N \(=\) 9 with \(f_\mathrm{a}\,=\,0.35\) optimal in the Chebyshev sense for different FDs d; dashed lines show values for d \(=\) 0 and \(n=(N-1)/2\)

Full size image
Fig. 3
figure 3

Curves of \(\alpha (d)\) (a) and \(\beta (d)\) (b) factors computed for windows extracted from FD filters from Fig. 2 and reference window selected at FD \(d_\mathrm{ref}=-0.5\); values of these factors reflect changes in scale of even (a) and odd (b) parts of windows extracted from optimal filters with different fractional delays d

Full size image

Factors \(\alpha (d)\) and \(\beta (d)\) used in Eq. (23) can be computed using the following formulas

$$\begin{aligned}&\displaystyle \alpha (d)\cong \frac{1}{f_\mathrm{a} }\int \limits _0^{f_\mathrm{a} } {{\left| {H_\mathrm{e} (f)} \right| } / {\left| {H_{\mathrm{e,ref}} (f)} \right| \mathrm{d}f}}&\end{aligned}$$
(24a)
$$\begin{aligned}&\displaystyle \beta (d)\cong \frac{\mathrm{sgn}(d_\mathrm{ref} )\mathrm{sgn}(d)}{f_\mathrm{a} }\int \limits _0^{f_\mathrm{a} } {{\left| {H_\mathrm{o} (f)} \right| } / {\left| {H_{\mathrm{o,ref}} (f)} \right| \mathrm{d}f}{\begin{array}{l} \quad {d_\mathrm{ref} \ne \pm 0.5 \quad \hbox {for even}\; N} \\ \quad {d_\mathrm{ref} \ne 0 \quad \hbox { for odd }N,}\\ \end{array} }}&\nonumber \\ \end{aligned}$$
(24b)

where \(H_\mathrm{e}(f)\) is the frequency response of the FD filter with FD d designed using the even part of window \(w_{\mathrm{opt},d}\)[n], while \(H_\mathrm{e,ref}(f)\) is the frequency response of the FD filter designed using the even part of the reference window \(w_\mathrm{ref}\)[n]. Impulse responses of these filters are described by the following formulas

$$\begin{aligned} h_\mathrm{e} [n]=h_{\mathrm{id},d} [n]w_{\mathrm{e},d} [n]\; \hbox {and}\; h_{\mathrm{e,ref}} [n]=h_{\mathrm{id},d} [n]w_{\mathrm{e,ref}} [n]. \end{aligned}$$
(25)

By analogy, \(H_\mathrm{o}(f)\) and \(H_\mathrm{o,ref}(f)\) are frequency responses of the FD filters designed using the odd parts of the windows \(w_{\mathrm{opt},d}\)[\(n\)] and \(w_\mathrm{ref}\)[n]. Impulse responses of these filters are described by the following equations:

$$\begin{aligned} h_\mathrm{o} [n]=h_{\mathrm{id},d} [n]w_{\mathrm{o},d} [n]\;\hbox {and}\;h_{\mathrm{o,ref}} [n]=h_{\mathrm{id},d} [n]w_{\mathrm{o,ref}} [n]. \end{aligned}$$
(26)

Typical curves of \(\alpha \) and \(\beta \) factors are presented in Fig. 3. As we can see, the scale \(\alpha (d)\) of the even part of the extracted window varies slightly (Fig. 3a), while the odd part is approximately proportional to the FD (Fig. 3b).

Due to the fact that FD filter impulse response satisfies the property

$$\begin{aligned} h_{d}[n] = h_{-d}[N-1-n] \end{aligned}$$
(27)

filter approximation errors as well as gain correction factors are symmetric with respect to FDs. For example, it can be noticed that \(\alpha (d)\) and \(\beta (d)\) curves satisfy the following properties

$$\begin{aligned} \alpha (d)=\alpha (-d)\;\mathrm{and }\;\beta (d)=-\beta (-d). \end{aligned}$$
(28)

Therefore, results for negative FDs \(d\) are not presented in the next part of this paper.

With the assumption that changes in the shape of parts of the extracted window are negligible, windows extracted from optimal FD filters at different delays can be reconstructed using a window extracted for one particular delay value (23). Performed experiments confirmed that a good reconstruction is achieved for both parts of extracted windows [31]. In particular, for windows extracted from LS filters, there is no noticeable variation in the shape of even and odd parts of the window. Therefore, a perfect reconstruction of the extracted window for all FDs can be achieved. On the other hand, in the case of minimax filters, some minor changes in the shape of the extracted window can be observed, which result in small reconstruction errors. That is why, as we will demonstrate in the next part of the paper, for minimax filters, VFD filter design using the extracted window method is characterized with slightly lower performance in comparison to the LS case.

5 Symmetric Reference Window

In the previous section we have demonstrated that asymmetric window required for the optimal filter design for any FD can be reconstructed based on a single extracted window. In this section we propose to use as a reference window, only the even part of the window extracted from the optimal filter with particular reference delay \(d_\mathrm{ref}\)

$$\begin{aligned} w_\mathrm{ref} [n]=w_\mathrm{e} [n]={(w_\mathrm{opt} [n]+w_\mathrm{opt} [N-1-n])} /2 \end{aligned}$$
(29)

with single gain correction factor \(\alpha \) (dependent on the desired delay d), to achieve similar result with simpler procedure presented in Fig. 1. It is worth noting that we can use reference windows obtained from filters with any delay. However, due to FD filter impulse response properties as well as numerical limitations, it is advisable not to use \(d_\mathrm{ref}\)  \(\cong \) 0.

With the symmetric reference window (29) extracted at \(d_\mathrm{ref}\) (Fig. 1), the proposed design procedure for reconstructing impulse response \(h_{\mathrm{opt},d}\)[\(n\)] of optimal FD filter with any FD \(d \) can be described by the following formula

$$\begin{aligned} h_{\mathrm{opt},d} [n]\cong h_{\mathrm{rec},d} [n]=h_{\mathrm{id},d} [n]w_{\mathrm{rec},d} [n]=h_{\mathrm{id},d} [n]\alpha (d)w_\mathrm{ref} [n]. \end{aligned}$$
(30)

The key problem in the above design formula is the calculation of proper gain correction factor \(\alpha (d)\). The simplest solution is to compute \(\alpha (d)\) values using formula (24a) and assume that \(\beta (d)\) in formula (23) is equal to zero, which means that we ignore the odd part of the extracted window. Design effects for this assumption are presented in Figs. 4 and 5.

Fig. 4
figure 4

Magnitudes of complex approximation errors for minimax FD filters of length N \(=\) 17 with d \(=\) 0.48 (a) and their equivalents with discarded odd part of extracted windows (b); filter gain correction is not applied

Full size image
Fig. 5
figure 5

PE versus N (a) and \(f_\mathrm{a}\) (b) for minimax FD filters with different FDs (black lines) and their equivalents with discarded odd part of extracted windows and without filter gain correction (gray lines); \(f_\mathrm{a} =\) 0.4 (a); N \(=\) 27 (b)

Full size image

Performed research indicates that for high performance FD filters, with PE (6) or SE (7) below \(-70\) dB (Figs. 4, 5), the odd part of the extracted window although small is still vital. In such case discarding the odd part of the extracted window results in significant degradation of designed filter performance. As a result, this approach is not adequate for high quality VFD filters. For such filters, additional optimization of gain correction factor has to be performed.

6 Gain Correction

As indicated in the previous section, simply ignoring the odd part of the window extracted from the optimal filter is not an option for high performance VFD filter design. Such filters require further optimization of the gain correction factor \(\alpha \). Our research has confirmed that for fixed filter length \(N\), approximation band \(f_\mathrm{a}\), and FD \(d\), there is only one optimum value of the gain correction factor \(\alpha \) (\(\alpha _\mathrm{opt})\) that minimizes the desired error (PE for a window extracted from a minimax filter or SE for a window extracted from an LS filter) (Fig. 6).

Fig. 6
figure 6

PE (a) and SE (b) versus gain correction factor \(\alpha \) for FD filters with different FDs d designed using the extracted window method—thick black lines; reference windows extracted at \(d_\mathrm{ref}=0.5\) from optimal filters with N \(=\) 11 and \(f_\mathrm{a}\)  \(=\) 0.35 (a) as well as N \(=\) 62 and \(f_\mathrm{a}\)  \(=\) 0.45 (b); dotted lines represent optimum \(\alpha \) with corresponding error levels and dashed lines mark \(\alpha \) computed using formula (24a)

Full size image

For each desired FD we can start from \(\alpha (d)\) computed using formula (24a) (Fig. 6) and optimize this correction factor for the best performance of the designed filter (PE or SE). The optimum gain correction factor \(\alpha _\mathrm{opt}\) can be easily found using any algorithm minimizing the value of PE (6) or SE (7) computed based on the following complex approximation error

$$\begin{aligned} E(f)=\alpha (d)H_{\mathrm{ref},d} (f)-H_{\mathrm{id},d} (f), \end{aligned}$$
(31)

where \(H_{\mathrm{ref},d}(f)\) is the frequency response of the filter designed using reference window (29) without gain correction (\(\alpha =\) 1) for the given FD \(d\) and \(H_{\mathrm{id},d}(f)\) is the frequency response of the ideal filter (1) with the same FD d. A simple recursive algorithm which can be used for \(\alpha (d)\) optimization is described in [30]. The use of optimized \(\alpha (d)\) factors in the design formula (30) compensates for the lack of the odd part of the extracted window and results in nearly optimal VFD filter performance.

The phenomenon behind the proposed design method lies in the distribution of the introduced errors over normalized frequency f. Let us consider the optimal filter with FD d. Its impulse response can be expressed in the following form

$$\begin{aligned} h_{\mathrm{opt},d} [n]=w_{\mathrm{e},d} [n]h_{\mathrm{id},d} [n]+w_{\mathrm{o},d} [n]h_{\mathrm{id},d} [n]. \end{aligned}$$
(32)

On the other hand, the formula for the impulse response of the filter designed using the even part of the window extracted for the FD \(d\) is as follows

$$\begin{aligned} h_d [n]=\alpha _\mathrm{opt} (d)w_{\mathrm{e},d} [n]h_{\mathrm{id},d} [n]. \end{aligned}$$
(33)

For nearly optimal filter designed using (33), the error

$$\begin{aligned} \Delta e[n]=h_d [n]-h_{\mathrm{opt},d} [n]=\Delta h_\mathrm{e} [n]-\Delta h_\mathrm{o} [n] \end{aligned}$$
(34)

must be close to zero. In formula (34) \(\Delta h_e [n]\) is the impulse response correction related to the even part of the reference window

$$\begin{aligned} \Delta h_\mathrm{e} [n]=(\alpha _\mathrm{opt} (d)-1)w_{\mathrm{e},d} [n]h_{\mathrm{id},d} [n] \end{aligned}$$
(35a)

which compensates for the lack of the part of the impulse response related to the odd part of the reference window

$$\begin{aligned} \Delta h_\mathrm{o} [n]=w_{\mathrm{o},d} [n]h_{\mathrm{id},d} [n]. \end{aligned}$$
(35b)

However, because of different symmetries of \(w_{\mathrm{e},d}\)[\(n\)] and \(w_{\mathrm{o},d}\)[\(n\)]

$$\begin{aligned} (\alpha _\mathrm{opt} (d)-1)w_{\mathrm{e},d} [n]\ne w_{\mathrm{o},d} [n] \end{aligned}$$
(36)

and thus generally \(\Delta e\)[\(n\)] \(\ne \) 0.

The results presented in Fig. 7 confirm that \(\Delta h_\mathrm{e} [n]\) and \(\Delta h_\mathrm{o} [n]\) have similar magnitude responses in the approximation band (up to \(f_\mathrm{a})\) and the error (34) is about 50–60 dB smaller than the approximation error \(E_\mathrm{opt}(f)\) (4) of the optimal solution. Since most of the energy of the error \(\Delta e\)[\(n\)] (34) is located outside of the approximation band (above \(f_\mathrm{a})\) (Fig. 7), it is best to limit minimization of this error to the approximation band (up to \(f_\mathrm{a})\). Additionally, in Fig. 7 we can see that the magnitude response of \(\Delta h_\mathrm{o} [n]\) stays at the similar level for different filters, only slightly decreasing for high performance FD filters (Fig. 7b). As a result, for the low performance optimal filter, \(\Delta h_\mathrm{o} [n]\) is much smaller than the approximation error of the filter (Fig. 7a) and for such filters the odd part of the extracted window can be simply discarded without noticeable loss of performance. On the other hand, for high performance filters (Fig. 7b), the magnitude response of \(\Delta h_\mathrm{o} [n]\) is higher than the approximation error of the filter and the gain correction factor in (35a) needs to be adjusted. Since we need to compensate for the lack of the odd part of the extracted window, we should select \(\alpha _\mathrm{opt} (d)\) such that frequency responses of \(\Delta h_\mathrm{e} [n]\) and \(\Delta h_\mathrm{o} [n]\) are approximately the same for \(f\in [0,f_\mathrm{a} )\).

Fig. 7
figure 7

Illustration of compensation of discarded odd part of the reference window with adjusted gain of its even part for FD filters of length N \(=\) 20 with d \(=\) 0.3, \(f_\mathrm{a} =\) 0.43 (a) and \(f_\mathrm{a} =\) 0.34 (b); plots represent magnitudes responses of the following errors: approximation error of the optimal solution \(e_\mathrm{opt}[n] = h_\mathrm{opt}[n]-h_\mathrm{id}\)[n] (solid line), \(\Delta h_\mathrm{e}\)[n] (solid line with x-marks), \(\Delta h_\mathrm{o}\)[n] (dash-dot line) and \(\Delta \) e[n] (dashed line)

Full size image

Using these observations the iterative procedure of \(\alpha _\mathrm{opt}(d)\) search (Fig. 6) can be replaced with nearly optimal gain correction factor computation. For convenience, in our derivation we use a modified approximation error with removed phase rotation resulting from non-zero delay

$$\begin{aligned} E_\mathrm{m} (f)=E(f)H_\mathrm{id}^*(f)=H_\mathrm{ref,d} (f)H_\mathrm{id}^*(f)-1, \end{aligned}$$
(37)

where \(E(f)\) is the complex approximation error (4), \(H_\mathrm{id}(f)\) is the frequency response of the ideal FD filter (1), * is the complex conjugation symbol, and \(H_{\mathrm{ref},d}(f)\) is the frequency response of the filter with impulse response designed using formula (30) without gain correction (\(\alpha =\) 1) for the given FD \(d\).

The modified error \(E_{m}(f)\) of the filter designed using the extracted window with incorrect gain differs from the modified error \(E_\mathrm{opt,m}(f)\) of the optimal filter only by a real constant value [5]

$$\begin{aligned} E_\mathrm{opt,m} (f)\cong E_\mathrm{m} (f)+(1-1/\alpha _\mathrm{opt} )\,\hbox {for}\,f\in \left[ {0,f_\mathrm{a} } \right] . \end{aligned}$$
(38)

Taking only the real part of the above formula and assuming that the real part of the error \(E_\mathrm{opt,m}(f)\) is equal to zero we can find a formula for approximate value of optimum gain correction factor \(\alpha _\mathrm{opt}\)

$$\begin{aligned} \alpha _\mathrm{opt} (d)\cong 1 /{\left( {1+\frac{1}{f_\mathrm{a} }\int \limits _0^{f_\mathrm{a} } {\mathrm{Re}\left\{ {E_\mathrm{m} (f)} \right\} \mathrm{d}f} }\right) }. \end{aligned}$$
(39)

Using this formula a nearly optimal gain correction factor can be computed in a single step based on the average value of the real part of the modified error (37) of the filter designed with the extracted window for \(\alpha =\) 1. Formula (39) can be further transformed into more practical form

$$\begin{aligned} \begin{array}{l} \alpha _\mathrm{opt} (d)\cong 1 \Bigg /{\left( {\sum \limits _{n=0}^{N-1} {h_{\mathrm{ref},d} [n]} \hbox { sinc}(2f_\mathrm{a} (n-\tau _\mathrm{d} ))}\right) }\\ \quad \quad \quad =1 \Bigg /{\left( {\sum \limits _{n=0}^{N-1} {\hbox { sinc}(2f_\mathrm{a} (n-\tau _\mathrm{d} ))w_\mathrm{ref} [n]h_{\mathrm{id},d} [n]} }\right) }, \\ \end{array} \end{aligned}$$
(40)

where \(h_{\mathrm{ref},d}\)[n] is the impulse response of the filter designed using formula (30) without gain correction (\(\alpha =\) 1) for the given FD d.

It is interesting that although in this paper we discuss only the use of symmetric reference windows, high quality VFD filters can be designed with both symmetric and asymmetric reference windows [31]. According to our research [31], using asymmetric reference window, optimal results are achieved for the selected reference delay and nearly optimal results for other delays. On the other hand, a symmetric reference window offers comparable performance and additionally a half of the reference window coefficients is the same and the gain correction factor is a symmetric function of filter delay which can result in lower utilization of DSP resources. For that reason in this paper only symmetric reference windows are considered.

Figure 8 presents the difference between PE/SE errors of filters designed using the extracted window approach and their optimal equivalents. Regardless of the used optimality criteria, filters designed using symmetric reference windows are virtually identical with the optimal filters. The difference is only about 0.01 dB for the Chebyshev optimality criterion (Fig. 8a) and even smaller for the LS optimality criterion (Fig. 8b). Performed research indicates that the difference decreases with impulse response length and increases with width of filter approximation band.

Fig. 8
figure 8

Difference in errors between VFD filters and their optimal equivalents for (a) filters of length N \(=\) 9 with different approximation bands (reference windows extracted from minimax filters) and (b) filters with \(f_\mathrm{a} =\) 0.45 and different lengths (reference windows extracted from LS filters); for all cases \(d_\mathrm{ref}~\)=\(~0.25\)

Full size image

An interesting difference between minimax and LS cases can be noticed, though. As mentioned in Sect. 4, for LS filters shape of the even part of the extracted window is independent of the delay. This means that selection of the reference delay \(d_\mathrm{ref}\) at which window is extracted does not matter and the best solution is always achieved for the FD d \(=\) 0 for odd length filters and d \(= \pm \)0.5 for even length filters (Fig. 8b). On the other hand, the shape of the even part of the window extracted from minimax filter changes slightly with delay and the performance of the designed filter is the nearest to the optimal solution at the delay close to the reference delay \(d_\mathrm{ref}\) (Fig. 8a).

7 Direct Design of Symmetric Reference Window

Although in the extracted window method (Fig. 1) the impulse response of the optimal filter is used, we are not really interested in it. We just need a window extracted from such a filter. Therefore, we propose to convert the optimal filter design equation (9a) into the formula

$$\begin{aligned} {{\hat{\mathbf{P}}\mathbf{w}}}=\mathbf {p}, \end{aligned}$$
(41)

where

$$\begin{aligned} \mathbf {w}=\left[ {{\begin{array}{llll} {w_\mathrm{opt} [0],} &{} {w_\mathrm{opt} [1],} &{} {\ldots ,} &{} {w_\mathrm{opt} [N-1]} \\ \end{array} }} \right] ^T={\hat{\mathbf{P}}}^{-1}\mathbf {p} \end{aligned}$$
(42)

which allows for direct design of the window w extracted from optimal filter [4]. Now, let us assume that optimal filter impulse response h (9b) could be calculated by ideal filter impulse response h \(_\mathrm{id}\) multiplication by the window w (42)

$$\begin{aligned} \mathbf {h}=\mathbf {h}_{\mathbf {id}} \mathrm{\mathbf{w}}, \end{aligned}$$
(43)

where

$$\begin{aligned} \mathrm{\mathbf{h}}_\mathrm{id} =\left[ {{\begin{array}{*{20}c} {h_\mathrm{id} [0]} &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad 0 \\ 0 &{}\quad {h_\mathrm{id} [1]} &{}\quad 0 &{}\quad \cdots &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad &{}\quad &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad &{}\quad \ddots &{}\quad \vdots \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \cdots &{}\quad {h_\mathrm{id} [N-1]} \\ \end{array} }} \right] . \end{aligned}$$
(44)

The ideal impulse response factor h \(_\mathrm{id}\) can be removed from vector h in (9a) and incorporated into matrix P forming matrix \({\hat{\mathbf{P}}}\)

$$\begin{aligned} \mathrm{\mathbf{Ph}}=\mathrm{\mathbf{Ph}}_{\mathbf {id}} \mathbf {w}= {\hat{\mathbf{P}}}\mathrm{\mathbf{w}}=\mathbf {p} \end{aligned}$$
(45)

with elements given by the following formula

$$\begin{aligned} \hat{P}_{k+1,n+1} =h_\mathrm{id} [n]P_{k+1,n+1} ;\forall k\;\mathrm{and}\;n= 0,1,\ldots ,N-1. \end{aligned}$$
(46)

As already discussed in Sect. 3, MF FD filters can be designed using window method with symmetric binomial window (18) and gain correction factor dependent on the desired delay (19). For LS and minimax FD filters extracted windows are not symmetric (Fig. 2) with small but vital odd parts (Figs. 4, 5). However, as we have demonstrated, with optimum gain correction (40) nearly optimal results can be achieved. For that reason we propose to assume symmetry of the reference window. With this assumption instead of computing \(N\) samples of the extracted window we need to calculate only L \(=\) \(\lceil \) N/2\(\rceil \) (\(\lceil \rceil \) symbol represents rounding up function) samples of vector v

$$\begin{aligned} \mathbf {v}=\left\{ {{\begin{array}{llll} {\left[ {{\begin{array}{llll} {w_\mathrm{ref} [0],} &{} {w_\mathrm{ref} [1],} &{} {\ldots ,} &{} {w_\mathrm{ref} [L-1]} \\ \end{array} }} \right] ^\mathrm{T}} &{} {\hbox {for odd }N} \\ {\left[ {{\begin{array}{llll} {w_\mathrm{ref} [0],} &{} {w_\mathrm{ref} [1],} &{} {\ldots ,} &{} {w_\mathrm{ref} [L-1]/2}\\ \end{array} }} \right] ^\mathrm{T}} &{} {\hbox {for even }N} \\ \end{array} }} \right. \end{aligned}$$
(47)

The values of the vector v can be computed using the formula

$$\begin{aligned} {\mathbf {v}}={\hat{\mathbf{P}}}_\mathrm{e}^{-1} {\mathbf {p}}_\mathrm{e}, \end{aligned}$$
(48)

where elements of matrix \({\hat{\mathbf{P}}}_\mathrm{\mathbf{e}} \) are given by the following equation

$$\begin{aligned} \hat{P}_{\mathrm{e}\;m+1,n+1} =\hat{P}_{k(m)+1,n+1} +\hat{P}_{k(m)+1,N-n};\quad n= 0,1,\ldots ,L-1 \end{aligned}$$
(49)

with additional elements for minimax filters

$$\begin{aligned} \hat{P}_{\mathrm{e}\;m+1,L+1} =(-1)^{k(m)}. \end{aligned}$$
(50)

In order to use formula (48) we also need the vector p \(_{\mathrm{e}}\) which consists of the selected rows of the p vector (10b), (11b), (12b)

$$\begin{aligned} p_{\mathrm{e}\;m+1,1} =p_{k(m)+1,1}. \end{aligned}$$
(51)

The indices m and k(m) used in formulas (49)–(51) can be defined as follows

$$\begin{aligned} m=\left\{ {\begin{array}{l} 0,1,\ldots ,L-1\hbox { for MF and LS filters} \\ 0,1,\ldots ,L\hbox { for minimax filters} \\ \end{array}} \right. \end{aligned}$$
(52)
$$\begin{aligned} k(m)=\left\{ {\begin{array}{l} 2m\hbox { for MF filters} \\ m\hbox { for LS and minimax filters} \\ \end{array}} \right. \end{aligned}$$
(53)

The proposed design formula (48) is the equivalent of a symmetric reference window extraction. In the case of MF filters it leads to obtaining binomial window (18) scaled by the proper gain correction factor (19). With such a window we can design the optimal MF filter. Analogically, for LS and minimax FD filters formula (48) gives us appropriately scaled (by gain correction factor (40)) symmetric reference windows (29), which can be used for a nearly optimal filter design [6, 30, 31].

The symmetric reference window design method presented in this section reduces the size of design equations set by half. As a result, in the case of LS FD filter design this approach offers better resistance to numerical errors, which strongly affect high performance filters. In Fig. 9a we can see that with direct design of the optimal LS filter, the performance of the designed filter is degraded. It is worth noting that VFD filter performance can be improved by use of the window method with even part of the window extracted from optimal filter designed for \(d_\mathrm{ref} =\) 0.5. Further improvement comes from the use of directly designed symmetric window for each \(d\) value with best results when a single symmetric window designed for \(d_\mathrm{ref} =\) 0.5 is used along with proper gain correction. These facts are summarized in Fig. 9b. As can be observed, direct optimal filter design offers FD filters with error not smaller than \(-\)130 dB, while using the extracted window method with directly designed symmetric window we can obtain filters with error about \(-\)150 dB.

Fig. 9
figure 9

SE versus FD d for VFD filter of length N \(=\) 22 with \(f_\mathrm{a} =\) 0.3 (a) designed using: (1) optimal method, (2) window method with gain correction using window extracted from optimal LS filter with \(d_\mathrm{ref} =\) 0.5, (3) window method using directly designed symmetric window separately for each d, (4) window method with gain correction using directly designed symmetric window for \(d_\mathrm{ref} =\) 0.5 and gain correction; (b) SE versus filter length for d \(=\) 0.25 and different \(f_\mathrm{a}\) for (1) optimal LS filter and (2) FD filter obtained using window method with gain correction for directly designed symmetric window for \(d_\mathrm{ref} =0.5\)

Full size image

Unfortunately, for minimax filters we cannot take full advantage of the smaller size of the design formulas due to the necessity of iterative search for extremal points. Our experiments indicated that it is possible to apply the complex Remez algorithm to design filters using the proposed reference window design method. Nonetheless, the convergence of the algorithm in such case is significantly slower and the initial set of extremal points has to be more precisely determined.

8 VFD Filter Implementation

There are two problems with VFD filter implementation based on the proposed extracted window method which have not been discussed yet. These are computation of the gain correction factor and the ideal impulse response (2) during runtime for each new fractional delay.

The problem with the optimum gain correction factor is that it depends on the desired filter delay and must be updated for each new delay. Formula (40) looks quite simple but it might be computationally too demanding for real time application, therefore, in most cases another approach must be applied. The two main approaches in such case are a LUT and a polynomial approximation.

In the first of these options, several values of \(\alpha _\mathrm{opt}\) computed for a given set of delays are stored in a LUT and selected based on the desired filter delay. As we can see in Fig. 10, the performance of designed filters is practically optimal at delays for which \(\alpha _\mathrm{opt}\) factors are stored. Conversely, for high performance filters (Fig. 10a, \(f_\mathrm{a} = 0.29\)) a single \(\alpha _\mathrm{opt}\) value can be used only in extremely narrow delay range, thus, in such case this approach requires a large LUT. This fact is also clearly visible in Fig. 10b, especially for higher filter lengths. Consequently, using a LUT of \(\alpha _\mathrm{opt}\) can be sensible in some applications, however, in most cases it is better to use a polynomial approximation of gain correction factor (40).

Fig. 10
figure 10

PE versus d for minimax FD filters with N \(=\) 11 and their equivalents designed using single reference window and LUT of optimum gain correction factors (a); maximum PE for d \(\in [0, 0.5]\) versus N for minimax VFD filters with \(f_\mathrm{a} =\) 0.4 and their equivalents designed using LUT of different sizes (b)

Full size image

In order to thoroughly investigate the possibility of gain correction factor polynomial approximation, a number of \(\alpha _\mathrm{opt}(d)\) curves for different windows, filter lengths, and approximation bands has been analyzed (Fig. 11). For all examined cases \(\alpha _\mathrm{opt}\) is a continuous even function of FD \(d\) and can be easily approximated by a low order polynomial [6, 17, 30]. Coefficients of such a polynomial can be stored in signal processor memory and used to calculate \(\alpha _\mathrm{opt}\) factor at runtime with low numerical costs. This makes high quality VFD filter design using the extracted window method suitable for most applications.

Fig. 11
figure 11

Optimum gain correction factor \(\alpha _\mathrm{opt}\) versus FD d for minimax VFD filters with \(f_\mathrm{a}\)  \(=\) 0.35 and different lengths (a) as well as for LS VFD filters with N \(=\) 15 and different approximation bands (b); \(d_\mathrm{ref} =\) 0.2 (a) and \(d_\mathrm{ref} =\) 0.3 (b)

Full size image

The influence of polynomial approximation of the gain correction factor on VFD filter performance is demonstrated in Fig. 12. As we see in Fig. 12a, for high performance short filters a higher polynomial order is required, however, there is no need for orders larger than 4 even if required PE or SE is about \(-\)100 dB. It is interesting that for longer filters or with wider approximation band (Fig. 12b) lower polynomial order is sufficient, with order p \(=\) 2 giving excellent results for the filters of the length \(N =30\). It is also worth noting that the approximation error of all VFD filters is significantly smaller for FDs close to zero (Fig. 12a) and thus the degradation of filter performance for these delays is less important in filter implementation than for fractional delays close to 0.5.

Fig. 12
figure 12

SE(d) for filters of length N \(=\) 11 for polynomial approximation of \(\alpha (\textit{d})\) curve (a) and maximum SE for d \(\in [0, 0.5]\) versus filter length N for different \(f_\mathrm{a}\) and orders p of polynomial approximating \(\alpha (\textit{d})\) (b); dots in (a) indicate the set of delays used to compute coefficients of polynomial approximating \(\alpha (\textit{d})\) curve; \(d_\mathrm{ref} = 0.5\)

Full size image

The second problem with VFD filter implementation using the presented approach is the computation of the ideal impulse response (2). Each time we need to update the impulse response of the VFD filter, a new set of samples of a non-linear sinc function must be obtained. The problem can be dealt with a Farrow structure [2, 7, 11, 13, 18, 27, 32, 34, 38], in which each sample of the ideal impulse response (2) is computed using a polynomial

$$\begin{aligned} h_\mathrm{id} [n]=\sum \limits _{m=0}^q {c_m [n]d^m} \end{aligned}$$
(54)

This leads to the following formula describing the ideal FD filter

$$\begin{aligned} y[n]=\sum \limits _{k=0}^{N-1} {h_\mathrm{id} [k]x[n-k]} =\sum \limits _{m=0}^q {y_m [n]d^m}, \end{aligned}$$
(55)

where

$$\begin{aligned} y_m [n]=\sum \limits _{k=0}^{N-1} {c_m [k]x[n-k]}. \end{aligned}$$
(56)

Formulas (55) and (56) lead to the structure presented in Fig. 13a, where each row of coefficients implements separate filter with impulse response \(c_{m}\)[n] (56) with all the filters sharing the same input buffer. In order to use this structure along with the extracted window method only two things have to be changed (Fig. 13b). Firstly, the input buffer needs to be replaced with a pseudo input buffer which stores input samples multiplied by samples of the reference window at the output. Secondly, gain correction must be introduced, which in Fig. 13b is performed at the output based on a polynomial approximation. Increase of the structure order by one allows for implementation of FD filters with performance improved by 20 dB. For example, filters with approximation error about \(-\)100 dB require a structure of the order q \(=\) 7 [6, 7].

Fig. 13
figure 13

Farrow structure of the order q \(=\) 2 implementing VFD filter (a) and its modification based on the extracted window method and polynomial approximation of gain correction factor (21) (b)

Full size image

The structure in Fig. 13b is similar to the concept proposed in [34], where Farrow structure subfilters are designed as \(m\)th order differentiators using the window method. The difference is that we use the extracted window and incorporate windowing into the input buffer. Also the gain correction placed at the output of the proposed structure is necessary in case of high performance FD filter implementation. For comparison of both concepts ([34] and ours) see the demonstrations presented in Online Resource 1 and the demonstration code provided in Online Resource 2.

It is worth noting that coefficients \(c_{m}\)[n] in the proposed structure (Fig. 13b) are independent of the implemented filter type or the width of its approximation band. Additionally, the increase in filter length can be simply achieved by attaching new branches at the beginning (left side) and the end (right side) of the structure prepared for a shorter filter. This means that we only need to design a structure for the longest filter which we want to implement and simply switch the segments of the structure on or off, which corresponds to adding or discarding samples of impulse response without the need for a change in the coefficients set (demonstration of this concept can be found in Online Resource 1 and 2). We must remember, however, that we actually need two structures (sets of coefficients) as the polynomials used in Farrow structure approximate different sections of sinc function for even and odd filter lengths.

As we can see in Fig. 8, filters designed using the proposed window method are virtually optimal. Therefore, we can say that structures from Fig. 13 are equivalent. Moreover, the order required for direct implementation of optimal VFD filter using the Farrow structure (Fig. 13a) is practically the same as that required for the proposed structure (Fig. 13b) [2, 7], which needs only a few additional numerical operations. This small overhead in numerical costs allows for a change of filter type and/or length by simple replacement of an extracted window and coefficients of polynomial approximating gain correction factor for this window, which is the advantage of the proposed structure.

Since the extracted window method is well suited for runtime VFD filter implementation its performance in fixed-point arithmetic is also important. Performed research [6] demonstrates that for the extracted window method filter performance loss indicated by increase of PE/SE is similar to that of the optimal filter with coefficients quantized directly. Also magnitude responses of the overall filters of sampling rate conversion algorithm based on FD filters [8, 10] implemented using the extracted window approach [6] were investigated. The obtained results indicate that in fixed-point arithmetic, overall performance is comparable to direct use of the optimal filters but is characterized with different error distributions. These facts prove that the proposed design method leads to nearly optimal results and can be exceedingly useful in VFD filter design and implementation.

9 Conclusions

In the paper we have demonstrated that nearly optimal minimax and LS filters can be designed using symmetric window method with practically negligible errors of the order of 0.01 dB (comparing to the optimal case) or smaller. Such high performance can be obtained due to the fact that most energy of the error introduced by using symmetric reference window concentrates in the off-care band of the filter. The investigations were inspired by the extracted window method [17] with windows extracted from filters obtained using optimal design methods. In this approach only a single window is required to design the entire family of FD filters differing only in FD. In the original paper [17] the approach was proposed for the design of even length minimax FD filters with symmetric window extracted from symmetric impulse response of the filter with FD equal to 0.5. We have extended the concept to both even and odd FD filters optimal in the minimax, LS, and MF sense with even part of window extracted for an arbitrary FD used as the reference window. Additionally, we have proposed the method for direct design of the symmetric reference window, which for LS FD filters offers more numerically robust design than the direct optimal FD filter design. Comparing to [17], we have also improved the method of calculating gain correction factor, which can be now directly computed without the need for design of optimal filters.

The proposed approach includes two design stages: preparation and implementation. At the first stage an asymmetric window is extracted from optimal FD filter but only its even part is further used as the reference window. Instead of using the window extraction procedure, the symmetric reference window can also be directly designed using formulas presented in the paper. In order to compensate for the lack of the extracted window odd part, the investigated method requires additional gain correction dependent on the desired delay. Therefore, several gain correction factor values for different delays have to be computed based on the selected reference window. Later these values can be stored in a LUT or used to approximate the gain correction curve with a polynomial. Notwithstanding, the use of LUT should be rather considered in the case of low performance filters as with decreasing approximation error the required size of LUT increases rapidly. Therefore, polynomial approximation is a better option for high performance filters. A polynomial of order not greater than four was sufficient in every analyzed case with second order polynomial being adequate for longer filters.

At the implementation stage (at runtime), VFD filter coefficients update for any arbitrary delay simplifies to multiplication of the ideal filter impulse response (sampled sinc function) by the reference window computed before just like in traditional window method. However, additional filter gain correction dependent on the desired delay has to be applied using values stored in memory (LUT) or calculated using the approximating polynomial. The only problem is the computation of the truncated ideal impulse response, which can be solved using the Farrow structure. Since the design overhead related to the proposed Farrow structure approach does not consume many signal processor resources, the proposed method can be easily implemented in real time. The structure can be used to implement MF or minimax and LS filters for different approximation bands and lengths. This versatile structure can be useful especially in multimedia applications, particularly in sampling rate conversion. Different sampling rates and quality requirements result in different specifications of VFD filter used in the processing, which with prepared beforehand set of extracted windows and associated gain correction curves can be satisfied with single structure at low numerical costs.