1 Introduction

Due to the remarkable mechanical properties of cellular structures, engineered and architectured materials have become a highly researched topic in a variety of engineering fields, ranging from aeronautics to biomechanics [1,2,3]. Taking inspiration from nature, these cellular structures have unconventional properties in terms of energy absorption and stiffness, while being lightweight, making them impact-resistant and resilient. A well-known example is the mantis shrimp’s multiregional structure with mineralized fiber layers that provide remarkable impact resistance and energy absorbance capabilities [4,5,6]. Recently, the advancements in additive manufacturing techniques have made it possible to easily produce and optimize them for engineering purposes. Indeed, the latest developments in topology design have resulted in the production of sandwich panels that are lightweight and have internal structures based on trusses. These structures are highly compressible, making them capable of absorbing extreme dynamic loads caused by impacts and shock waves [7,8,9,10].

Homogenization techniques represent a powerful tool to model cellular structures, architected materials and metamaterials, see, e.g., [11,12,13,14,15]. A detailed analysis of honeycomb structures is given in [16], deriving closed-form expressions for the homogenized properties of lattice structures based on relative density. Similarly, in [17], a two-scale computational homogenization method is proposed to determine the effective elastic parameters of regular cell materials, whereas various literature homogenization schemes are compared in [18], discussing their assumptions and limitations. The behavior of architected materials with nonlinear constitutive law is addressed in [19], using a numerical homogenization approach to derive macroscopic stress–strain relationships. On the other hand, a direct 1D technique can be employed to represent the macroscopic behavior of beam-like structures embedded in 3D space [20,21,22,23,24,25,26,27,28], in a wide range of mechanical problems and phenomena.

Moreover, wave propagation in lattice materials is characterized by peculiar features like size effects, wave dispersivity, or energy focusing that may also manifest in static regimes if the size of the structure and the unit cell size differ by a small scale separation [29]. In this scenario, a generalized continuum model is required to capture these effects, as done in previous studies [29,30,31,32] in accordance with [33].

Besides, topology optimization is a key process in the definition of architected solids with an effective material distribution. In this framework, optimization problems are commonly solved using the penalization method (Solid Isotropic Material with Penalization, SIMP) to achieve the best distribution of a fixed amount of material that maximizes stiffness [34,35,36]. The method considers the volume factor as the control variable (0 in void domains and 1 in solid domains) and relates the resulting stress tensor to the volume factor and the actual material Young’s modulus. The goal of the procedure can be to minimize deformability and weight [37] or to minimize stress [38]. In some cases, the study may also include nonlinear elastic materials [39]. To identify the ideal geometry and topology of composite materials, a level set approach is used. This approach considers multi-phase elastic materials. When the original elastic material is changed into a periodic lattice of unit cells, the problem becomes more complex. If the algorithms are extended to three dimensions and the orientation of the unit cells is considered, the mathematical complexity of the algorithms increases significantly [40,41,42]. These latter aspects go actually beyond the scope of the proposed work, where the considered optimization actually consists in a smooth variation of the cells inner wall thickness. This allows to derive different mass, and therefore stiffness, distribution within the volume of the optimized solid giving raise to tailored graded mechanical properties.

The vulnerability of periodic lattices to buckling phenomena, owing to their remarkable slenderness, makes the failure mechanisms of great interest. Several studies have examined the failure mechanisms of honeycomb structures [43,44,45], discussing the elasto-plastic behavior of materials and the potential buckling modes under different loading conditions. To assess in-plane biaxial buckling of elastic hexagonal honeycombs, an approach for homogenization of finite deformation based on the virtual work principle is proposed in [46]. Other studies explore the impact of joint constraint circumstances on local buckling of periodic lattice composites [47], investigate if changing the cell cross-section can alter and fine-tune the actual shape of the buckling mode [48] and use group theory methods to explore the buckling and crushing mechanics of cellular honeycomb materials [49]. In [50], the impact of imperfections, including absent bars, dislocated nodes and undulating cell walls, on periodic lattice structures with very small cells was also investigated.

In this work, the design framework first proposed in [51] is adopted to develop architected solids with an optimized distribution of the unit cell density. This activity is conducted on a different case study (in terms of unit cell, aspect ratio, number of cells, geometry, loads) in order also to validate the procedure previously proposed.Taking inspiration from [51], different unit cell geometries are adopted, namely circular and square, and are here considered and a systematic comparison of the different optimized solids is conducted with respect to the hexagonal architected solid. A Bloch–Floquet homogenization technique [29, 30, 52] is adopted to derive an equivalent model for the three different unit cells, and discussion on the relative density validity range is reported. It is also assumed that the scale separation ratio is large enough to allow the use of a conventional continuum model (Cauchy). Differently from [51], the topological optimization procedure is conducted by adopting two different objective function, thus leading to different optimization strategies. In both cases, the optimization procedure actually consists in a smooth variation of the cells inner wall thickness, maintaining fixed the number of cells and their orientation. The performance of the optimization strategies is analyzed through finite-element analyses on equivalent and refined models, i.e., built-up with Cauchy 2D elements, and it is compared in terms of the architected solids static and buckling behaviors.

The paper is organized as follows. In Sect. 2, the design strategy to achieve an optimized architected composite is presented. In Sect. 3, the homogenization procedure is carried out and the properties of the continuum with graded density are derived. In Sect. 4, the topological optimization is performed and the optimal layout are presented. In Sect. 5, the structural analyses of the optimized graded architected solid are conducted and its responses are compared to discuss the performance of the different type of unit cells. Finally, in Sect. 6 some conclusions are drawn.

2 Design process

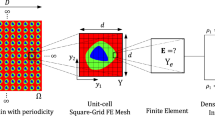
The design process of an architected composite with tailored mechanical process is here described. The framework is schematically represented in Fig. 1 and is retrieved from [51]. A structural problem has first to be addressed in terms of geometry, loads, constraints together with specific design requirements. In this case, a 2D periodic microstructured solid with constant equivalent density and three different types of local architecture is considered and is represented in Fig. 2 with: (a) hexagonal, (b) circular and (c) square unit cell, respectively.

Fig. 1
figure 1

Schematic representation of the design process

Full size image

Note that the type of cell determines the equivalent mechanical properties of a homogenized model that are derived via a Bloch–Floquet homogenization approach (see next section for details). An optimization process, consisting in a smooth variation of the inner cells wall thickness, maintaining fixed the number of cells and their orientation, is then carried out on the homogenized model in order to find the optimal density configuration: Contrarily to conventional approaches, here intermediate densities are allowed to ensure a smooth variation of the cell walls. Note that the procedure introduced in [51] can be applied to different objective functions and restraints, therefore here the performance of two distinct optimization approaches is discussed. From the density map, a de-homogenization is performed in order to retrieve the final layout of the optimized microstructured solid and numerical (or even experimental) tests need to be carried out for performance analysis of the designed solids, i.e., to verify if the obtained solution matches the design requirements. If not, the procedure needs to be iterated.

The proposed design framework is investigated in the following numerical analyses by focusing on a specific case study. The considered structural problem is schematically represented in Fig. 2. It represents a set of beam-like lattice structures with three different unit cells, that as illustrated in Fig. 2: (a) hexagonal unit cell; (b) circular unit cell; and (c) square unit cell. The dimensions of the structure are: \(h=60\) mm, \(\ell =150\) mm, \(d=15\) mm (out of plane thickness).

Fig. 2
figure 2

Schematic of the case study. It consists of a periodic microstructure with constant density but different unit cells: a hexagonal; b circular; c square

Full size image

In particular, the hexagonal lattice is chosen to have a unit cell size \(a=6.9282\) mm and an overall number of cells equal to 220; the resulting overall height and length are \(h=60\) mm and \(\ell =152.42\) mm. On the other hand, the circular and square lattices have a unit cell size \(a=6\) mm and an overall number of cells equal to 250; the resulting overall height and length are \(h=60\) mm and \(\ell =150\) mm. The difference in the layouts is due to the fact that the circles and square unit cell are exactly inscribed in a square of size a, whereas this is not possible for the hexagonal unit cell. The bulk material is PLA with a Young’s modulus \(E_\textrm{b} = 3\) GPa, a Poisson’s ratio \(\nu _\textrm{b} = 0.3\) and a density of \(\rho _\textrm{b} = 1100\) kg/m, while the external force is \(F=2.5\) kN, the same in all the cases.

3 Resume of the homogenization procedure

In this section, the up-scaling method employed in this study to extract the homogenized properties of various lattices is outlined. The primary objective is to establish a comprehensive mapping of the homogenized elastic properties corresponding to specific mass densities for all geometries. This mapping facilitates an in-depth understanding of the overall mechanical behavior of the structures, as well as the related numerical analyses, enabling the utilization of topological homogenization algorithms not directly on the refined model of architectured solid, but, more efficiently, on its homogenized equivalent twin.

To calculate the properties of the homogenized lattice, considering the periodicity of the meso-structure, an approach based on Bloch–Floquet analysis is adopted (for more in-depth information, refer to [52]). This approach aligns with the methodology used in [51]. In the general scenario, the elastodynamics equation for a periodic continuum is expressed as follows:

$$\begin{aligned} \text {div} \left[ {\mathbb {C}}_\textrm{b}({\textbf{r}}):\left( {\textbf{u}}({\textbf{r}},t)\otimes {\underline{\nabla }}\right) \right] =\rho _\textrm{b} \chi ({\textbf{r}}) \ddot{{\textbf{u}}}({\textbf{r}},t) \end{aligned}$$
(1)

where \(\text {div}\) is the divergence operator, \({\underline{\nabla }}\) is the gradient operator,  :  denotes a double contraction, \(\otimes \) denotes the tensor product, t is the time, and the over dot denotes time differentiation, \({\textbf{r}}\) is the position vector, \({\textbf{u}}({\textbf{r}},t)\) is the displacement, \(\rho _\textrm{b}\) is the mass density of the bulk material, \(\chi ({\textbf{r}})\) is a binary function that identifies the presence of the material, and \(\mathbb {C}_\textrm{b}({\textbf{r}})\) is the fourth-order elasticity tensor of the bulk material, which are quantities periodic in space.

This periodic heterogeneous material will be identified introducing an effective homogenized model, which will be associated with a couple of effective constitutive quantities \(\rho _\textrm{eff}\) and \(\mathbb {C}_\textrm{eff}\). The elastodynamic equations for the equivalent continuum read:

$$\begin{aligned} \text {div} \left[ {\mathbb {C}}_\textrm{eff}:{\textbf{v}}({\textbf{r}},t)\otimes {\underline{\nabla }}\right] =\rho _\textrm{eff} \ddot{{\textbf{v}}}({\textbf{r}},t) \end{aligned}$$
(2)

where \({\textbf{v}}\) verifies \(<{\textbf{u}}>={\textbf{v}}\), \(<.>\) denotes the spatial average operator over the unit cell, and \({\textbf{u}}\) is the displacement field solution to the heterogeneous problem stated in Eq. 1. This relationship between meso- and macro- displacements also ensures that Hill–Mandel conditions are verified [53].

In the present work, the equivalent elasticity tensor \({\mathbb {C}}_\textrm{eff}\) will be estimated using a Bloch–Floquet homogenization procedure, as already done in [51]. From a numerical point of view, the strategy is based on the computation of the first two eigenfrequencies \(\omega _{1,2}\) of the unit cell, by considering a particular boundary value problem corresponding to a periodically modulated plane wave, with wavevector \({\textbf{k}}\), traveling inside the material. This is achieved by imposing Bloch–Floquet boundary conditions [52] on the boundaries of the unit cell. When the wavelength \(\lambda =2\pi /\Vert {\textbf{k}}\Vert \) is large with respect to the size of the unit cell, the phase velocities (computed from the eigenfrequencies of the numerical problem as \(v_{1,2}=\omega _{1,2}/\Vert {\textbf{k}}\Vert \)) can be used to retrieve \({\mathbb {C}}_\textrm{eff}\). If more than two coefficients need to be identified, i.e., for an isotropic medium, more direction of propagation can be considered by acting on the wavevector \({\textbf{k}}\). In this work, given that the composite is obtained by extruding a 2D pattern, we consider plane strain assumptions and a 2D elastodynamic problem will be solved. The structure of \({\mathbb {C}}_\textrm{eff}\) for each type of unit cell will be given in the next sections.

3.1 Definition of the unit cell geometries

Three different unit cells geometries, illustrated in Fig. 3, are introduced, namely: a hexagonal cell, a square cell with a circular hole and a square cell with a square hole. By examining these diverse configurations, our aim is to explore the influence of geometry of the cells and of the holes on the mechanical properties and behavior of the resulting composites.

The characteristic size of the unit cells, denoted as a, is kept fixed. The size of the holes is instead varied by changing the thickness t of unit cell walls, through a non-dimensional parameter \(\alpha =t/a\), having the physical meaning of an inverse of a slenderness and representing the filling degree of the holes.

Fig. 3
figure 3

Unit cell characteristics: a hexagonal; b circular; and c square

Full size image

Once the geometry of the cells is defined, the material relative density \(\rho \), which is proportional to the volume fraction of the material of each cell, needs to be evaluated. It is worth to note that the relative density represents the ratio between the density of the architected solids \(\rho _\textrm{eff}\) and the bulk material \(\rho _\textrm{b}\), so that \(\rho =\rho _\textrm{eff}/\rho _\textrm{b}\). It turns out that \(\rho =\rho (\alpha )\), i.e., that the relative density depends on the filling degree. Accordingly, once the function \(\rho (\alpha )\) is determined for the three architectures, as reported in Table 1, it can be plotted as shown in Fig. 4. It can be seen that for all the laws \(\rho =1\) when the \(\alpha =1\) (full solid). On the other hand, hexagons and squares share the same function which starts from zero, while the circles are characterized by a nonzero initial value. This is due to the fact that when the internal diameter (void region) equals the cell size a, the wall thickness is zero but a full region always remains in corners (see Fig. 3b): The remaining non-empty region is \(1-\pi /4\) as depicted in Fig. 4.

Table 1 Relative density in function of the geometric parameter \(\alpha \)
Full size table
Fig. 4
figure 4

Relative density variation with \(\alpha \)

Full size image

3.2 Computation of the homogenized elastic constants

To obtain the homogenized elastic properties, the dynamic homogenization procedure previously described is here detailed. As mentioned before, the wave velocities for long wavelengths along specified propagation directions need to be computed by solving the elastodynamic equations of a plane strain two-dimensional problem. In the present case, a wavenumber \(k=1\) rad/m is taken, which corresponds to a wavelength 6.28 m.

Let us start with the hexagonal lattice case, for which the homogeneous continuum is known to be isotropic for large wavelengths. In this case, the effective elastic tensor has the following form, in Voigt notation with respect to the base \({\mathcal {B}}=({\textbf{e}}_1,{\textbf{e}}_2)\):

$$\begin{aligned} {\mathbb {C}}_\textrm{eff}= \begin{pmatrix} c_{11} &{} c_{11}-2 c_{44} &{}0 \\ c_{11}-2 c_{44} &{} c_{11} &{}0 \\ 0 &{} 0 &{} c_{44} \\ \end{pmatrix}_{{\mathcal {B}}} \end{aligned}$$
(3)

Then, it is needed to determine two independent constitutive parameters, namely \(c_{11}\) and \(c_{44}\). This can be easily achieved by considering the relationship between the phase velocities \(v_\textrm{T}\) and \(v_\textrm{L}\) of transverse (subscript T) and longitudinal (subscript L) waves, respectively, propagating inside the material. Specifically, the relationship is as follows:

$$\begin{aligned} c_{11} = \rho _\textrm{h} v_\textrm{L}^2, \quad c_{44} = \rho _\textrm{h} v_\textrm{T}^2 \end{aligned}$$

These quantities can be easily related to engineering constants such as Young’s modulus and Poisson ratio. Since structures with different geometries will be compared in this work, and in order to avoid ambiguity between 2D and 3D notations, the components of the elastic tensor are used.

In the case of circular and square lattices, the homogeneous continuum will have a tetragonal symmetry, and the elastic tensor has the following form:

$$\begin{aligned} {\mathbb {C}}_\textrm{eff}= \begin{pmatrix} c_{11} &{} c_{12} &{}0 \\ c_{12} &{} c_{11} &{}0 \\ 0 &{} 0 &{} c_{44} \\ \end{pmatrix}_{{\mathcal {B}}} \end{aligned}$$
(4)
Fig. 5
figure 5

Effective non-dimensional constitutive coefficient for the considered cells as a function of the relative density \(\rho \)

Full size image

Consequently, three independent constants, \(c_{11}\), \(c_{12}\) and \(c_{44}\), need to be computed. To achieve this, at least three phase velocities should be utilized for computing the elasticity tensor. Hence, two different directions of propagation will be considered (0 and \(\pi /4\) rad), as depicted in Fig. 3. In this scenario, the stiffness constants are given by:

$$\begin{aligned} c_{11} = \rho _\textrm{c,s} \left( v_\textrm{L}^{0}\right) ^2, \quad c_{44} = \rho _\textrm{c,s} \left( v_\textrm{T}^{0}\right) ^2, \quad c_{12} = 2 \rho _\textrm{c,s} \left( v_\textrm{L}^{\pi /4}\right) ^2 -c_{11}-2c_{44} \end{aligned}$$

where \(v_{\textrm{L}_{0}}\), \(v_{\textrm{T}_{0}}\) and \(v_\textrm{L}^{\pi /4}\) are the phase velocities of the transverse and longitudinal waves, propagating at 0 rad and \(\pi /4\) rad.

The results of the homogenization are presented in Fig. 5, where the constitutive coefficients \(c_{11}\), \(c_{12}\) and \(c_{44}\), normalized with respect to the properties of the bulk material (superscript b in the labels), are plotted against \(\rho \). As expected, all the curves reaches the value one when \(\rho =1\), which corresponds to full cells. At a first glance, it can be remarked that for the \(c_{11}\) coefficients, which correspond to a constrained compressibility modulus, the results are quite different for a low density ratio, where the square geometry exhibits a stiffer behavior, and they almost superimposed when \(\rho \) increases. For the \(c_{44}\) coefficients, which is a shear modulus, hexagonal and square geometries have a stiffer behavior than the circle ones. The difference is more pronounced for the \(c_{12}\), which is due to the different symmetries in the constitutive law, namely isotropic for the hexagonal geometry and tetragonal for the others.

3.3 Validation of homogenization

The homogenization technique is numerically validated for the structural problem of Fig. 2. The displacement is evaluated in the midspan section for different values of the relative density, namely \(\rho \in (0.3,0.8)\). The response is illustrated in Fig. 6, where the dots denote the solution obtained with the fine model, while the continuous line represents the solution of the homogenized model.

Fig. 6
figure 6

Validation of the homogenization approach. Midspan displacement with \(\rho \in (0.3,0.8)\): a hexagonal cell; b circular cell; and c square cell

Full size image

4 Topological optimization

The optimization problem is stated according to two different design criteria. The first approach is to minimize the overall density with a corresponding constraint on the maximum allowable deformation. This can be stated as follows

$$\begin{aligned} \left\{ \begin{aligned}&\min \int \limits _{\Omega }\rho _\textrm{p} \textrm{d}S\\&\int \limits _{\Omega }\frac{1}{2}\sigma \varepsilon \textrm{d}S\le W_\textrm{ref}\\&\rho _\textrm{down}<\rho _\textrm{p}\le \rho _\textrm{up} \end{aligned}\right. \end{aligned}$$
(5)

where the first is the objective function that has to be minimized, i.e., the density, while the second represents the constraint on the deformation in terms of elastic energy. The third is the constraint on the actual minimum and maximum relative densities, namely \(\rho _\textrm{down}\) and \(\rho _\textrm{up}\), respectively, that can be achieved in the fabrication process or induced by other design constraints (such as premature local buckling, see, e.g., [51]). This approach is here referred to as optimization strategy I.

As mentioned before, the design procedure described in [51] can be employed also with different objective functions and constraints, depending on specific design requirements. From an engineering perspective, it may be requested to minimize the structural mass by accepting greater deformation (strategy I); on the other hand, it may be useful to minimize the deformation with a prescribed material quantity. Therefore, here, a second optimization process is carried out by reversing the point of view of strategy I: The deformability of the system has to be minimized with a constraint on the maximum allowable average density (also known as the compliance minimization problem [54]). This gives rise to the second optimization strategy, here referred to as optimization strategy II, that is formalized as follows.

$$\begin{aligned} \left\{ \begin{aligned}&\min \int \limits _{\Omega }\frac{1}{2}\sigma \varepsilon \textrm{d}S\\&\int \limits _{\Omega }\rho _\textrm{p} \textrm{d}S\le \rho _{\max }\\&\rho _\textrm{down}<\rho _\textrm{p}\le \rho _\textrm{up} \end{aligned}\right. \end{aligned}$$
(6)

The results in terms of de-homogenized geometry are represented in Fig. 7 for the hexagonal microarchitected solid, in Fig. 8 for the square cell one and in Fig. 9 for the circle cell one. The resulting layouts are very similar from a qualitative point of view: They give rise to pseudo-arch structures, meaning that the region with thicker cells appears in the correspondence of an ideal arch-like structure. However, it can be noted that all the layouts derived via the optimization strategy I, i.e., Eq. (5), are characterized by a bottom layer that is much more evident than that obtained via the strategy II, i.e., Eq. (6). It is thus remarked that solution obtained via Eq. (5) gives an architected solid with an embedded pseudo-closed arch, while those obtained via Eq. (6) furnish an embedded pseudo-open arch, the latter being significantly more deformable with respect to the former.

Fig. 7
figure 7

De-homogenized layout with the hexagonal cell according to: a optimization strategy I; b optimization strategy II

Full size image
Fig. 8
figure 8

De-homogenized layout with the square cell according to: a optimization strategy I; b optimization strategy II

Full size image
Fig. 9
figure 9

De-homogenized layout with the circular cell according to: a optimization strategy I; b optimization strategy II

Full size image

5 Post-process

The optimal de-homogenized solids obtained in the previous section are here extensively analyzed to verify on one hand if the homogenized model well captures the fine de-homogenized model behavior, on the other hand if the optimized layout fulfills the primary design criteria. To this end, fine models of the optimized layouts are solved via FEM analysis in the Comsol Multiphysics software, by adopting quadratic serendipity elements with a geometry dependent mesh (i.e., the maximum size of the elements is equal to half of the wall cell thickness).

At the end of the optimization process, the midspan displacement of each homogenized model is evaluated. This is then compared with the value obtained in the optimized de-homogenized fine model to analyze the accuracy of the homogenization procedure in the optimization design approach. The obtained values are reported in Table 2 for the optimization strategy I, since the results for the strategy II are qualitatively close.

Table 2 Midspan displacement in mm of the optimized homogenized model compared to those of the optimized de-homogenized fine model, according to the first optimization strategy
Full size table

5.1 Comparison of the different approaches

The slight differences observed in the previous section between the different layouts are here analyzed from the mechanical point of view. The response of the optimized layouts is evaluated under the design load, and the vertical displacement is illustrated as a contour map in Fig. 10 for the hexagonal microstructure, in Fig. 11 for the circular one and in Fig. 12 for the squared one.

Fig. 10
figure 10

Contour plot of the vertical displacement in mm of the optimized solid with hexagonal unit cell: a optimization strategy I; b optimization strategy II

Full size image

As expected, the closed-arch-type layouts derived via the optimization strategy I are less deformable then the open-arch-type layouts of the optimization strategy II.

Fig. 11
figure 11

Contour plot of the vertical displacement in mm of the optimized solid with circular unit cell: a optimization strategy I; b optimization strategy II

Full size image

What is more evident, from Fig. 12, is the cusp exhibited by the bottom layer of the square layout of strategy II: The extreme slenderness of the cells in that region associated with the non-optimal orientation of the cells with respect to the load direction causes a localization of the deformation close to the midspan section.

Fig. 12
figure 12

Contour plot of the vertical displacement in mm of the optimized solid with square unit cell: a optimization strategy I; b optimization strategy II

Full size image

Quantitatively, the results are reported in Fig. 13. The midspan displacement is evaluated at different load values, \(F\in (0,10)\) kN; the solution derived with hexagonal microstructure is represented in dark blue, that with the circular one in light blue and that with the squared one in cyan, respectively. As expected, the hexagons deliver the stiffer solution, and the circles give rise to a behavior that is close to the hexagons, whereas the squares are the most deformable. Moreover, as observed in the previous results, strategy II confirms that it delivers more deformable layouts, independently on the choice of the geometry of the unit cell.

Fig. 13
figure 13

Midspan vertical displacement with \(F\in (0,10)\) kN: a optimization strategy 1; b optimization strategy 2. The solution derived with hexagonal cells is represented in dark blue, that with circular cells in light blue and that with square cells in cyan, respectively

Full size image

5.2 Buckling analysis of the optimized structure

In this section, the critical buckling load is evaluated for the not optimized solid and for those optimized according to strategy I and II, by considering as pre-stress condition the same dead load considered in the previous analyses. The results are reported in Table 3 in terms of critical load increment (in kN) and in Figs. 14, 15, 16 in terms of critical mode shapes.

Table 3 Critical buckling loads in kN for the not optimized solid and for those optimized according to strategy I and II
Full size table
Fig. 14
figure 14

Critical buckling modes for the hexagonal unit cell: a not optimized; b optimization strategy I; and c optimization strategy II

Full size image
Fig. 15
figure 15

Critical buckling modes for the circle unit cell: a not optimized; b optimization strategy I; and c optimization strategy II

Full size image
Fig. 16
figure 16

Critical buckling modes for the square unit cell: a not optimized; b optimization strategy I; and c optimization strategy II

Full size image

6 Concluding remarks

A robust and reliable procedure to design architected solids has been here investigated. The present framework, previously introduced by the authors in [51], has been here adopted to obtain density and stiffness space-varying microstructured solids, by extending the procedure of [51] to different unit cells and different optimization approaches. The obtained results are considered as a validation of the design framework and as its extension to a more general context. The main achievements are summarized below.

  • The adopted homogenization approach allows to account for different types of unit cells, leading to isotropic as well as tetragonal equivalent continua.

  • The mechanical behavior of the homogenized solid is in a very good agreement with the corresponding fine model for a large range of relative densities. (Some minor differences are observed for considerably small equivalent densities.)

  • The adopted optimization strategies furnish architected solids with a slightly different inherent layout: The one based on the mass minimization (strategy I) delivers a microstructured solid with a closed-arch-type layout, while that based on the deformability minimization (strategy II) leads to an open-arch-type layout.

  • Closed-arch-type layouts reveal a better static performance compared to the open-arch-type layouts, leading to a stiffer response with the same relative density.

  • The buckling load multiplier is higher in the closed-arch type, with significant improvement with respect to the non-optimized solid.

  • As a general remark, the hexagonal unit cell (due to its isotropic behavior) has a better performance with respect to the circular cells. The square unit cells reveal to be the worst.

As future developments of this work, experimental campaigns will be conducted to validate the procedure. Different types of prototypes will be fabricated via additive manufacturing, and their mechanical behavior will be tested under different loading conditions. The aim is then to compare the response of the optimized solids to that of the conventional lattice structures, also detecting their behavior at the microscale. The experimental investigation may be then also extended to the inelastic regimes up to failure.