Transverse compression of a thin elastic disc

Abstract

The mathematical formulations for transverse compression of a thin elastic disc are considered, including various boundary conditions along the faces of the disc. The mixed boundary conditions corresponding to the loading by normal stresses in absence of sliding are studied in detail. These conditions support an explicit solution in a Fourier series for the boundary layers localised near the edge of the disc and also do not assume making use of the Saint-Venant principle underlying the traditional asymptotic theory for thin elastic structures. As an example, an axisymmetric problem is studied. Along with the leading order solution for a plane boundary layer, a two-term outer expansion is derived. The latter is expressed through the derivatives of the prescribed stresses. Generalisations of the developed approach are addressed.

1 Introduction

Analytical treatment of a thin elastic disc subject to transverse compression along its faces is important for various industrial applications, including manufacturing of gaskets and dampers, characterisation of soft materials, and microfabrication of nanostructures. The engineering considerations on the subject, see [5, 6, 17, 19, 20, 22, 23] and references therein, often rely on kinematic assumptions regarding displacement and stress variation across the thickness. A few papers also exploit separation of variables, e.g. see [3, 21]. All cited publications do not consider the boundary layers along the edges of the disc, adapting ad hoc boundary conditions on the solutions for the disc interior.

The mathematical formulations governing transverse compression of a thin disc may vary depending on the type of surface loading. In particular, compression may be specified by prescribing either normal displacements or normal stresses. There is also a room for modelling of tangential sliding, including the assumption of no sliding. The asymptotic theory for thin elastic structures [1, 7,8,9, 14, 16, 24] seems to be the most appropriate framework for tackling all possible scenarios.

For the so-called classical boundary conditions along faces, i.e. boundary conditions expressed in terms of stresses, the term corresponding to transverse compression appears in the right hand side of 2D differential equations of motion [7, 9, 14]. In this case, the boundary conditions at structure edges follow from the asymptotic generalisation of the canonical Saint-Venant principle [7, 10,11,12,13], ensuring decay of boundary layers. It is worth noting that numerous engineering plate theories usually do not consider the effect of transverse compression and also do not implement rational mathematical arguments for establishing effective boundary conditions.

The non-classical boundary conditions along faces, i.e. the boundary conditions involving constrains on displacements, apart from those for a sliding contact [4] do not require solving differential equations for interior domains [1, 2, 8]. In this case, the outer solution can be readily expressed through the derivatives of given data, e.g. normal displacements. Transverse compression by a uniform normal displacement field is usually studied in the majority of the publications on the subject, see references above. At the same time, the Saint-Venant principle is not applicable for the transverse compression problems involving non-classical boundary conditions along faces. For the latter, the decay of the boundary layers localised near edges is guaranteed a priori.

In this paper, transverse compression is modelled via mixed boundary conditions along both faces. The focus is on the axisymmetric deformation of a thin elastic disc compressed by normal stresses assuming zero tangential displacements along the faces. The thickness of the disc is small compared to its radius. For definiteness, the disc contour is assumed to be traction-free. In contrast with a number of papers in this area, we assume that compression is due to a given stress but not a displacement. The main benefit of the chosen mixed boundary conditions is that they support a simple solution for the boundary layer expressed through a Fourier series.

As usual, the asymptotic solution of the formulated problem is split into outer and inner (boundary layer) components, [1, 7]. The asymptotic behaviour of the outer one is radically different from that in a similar transverse compression problem within the traditional thin plate theory, when the tangential stresses but not the displacements are equal to zero along disc faces [9, 14]. The two-term asymptotic expansion of the outer solution is derived from the canonical elasticity relations for displacements and stresses. For comparison, the leading-order solution is also presented in terms of the Love potential in Appendix. The obtained explicit formulae express all sought for quantities through the derivatives of arbitrary normal stresses prescribed along faces. In this case, however, a discrepancy arises in the homogeneous boundary conditions originally imposed on the edge of the disc.

To eliminate the discrepancy, we construct a plane boundary layer, localised near the edge, e.g. see [1, 7]. At leading order, it is given by the plane strain equations. The adapted mixed boundary conditions along faces both ensure an exponential decay of the boundary layer at the scale of the thickness and, as it has been already mentioned, lead to an explicit trigonometric solution, similar to that in [15]. This analytical solution is compared with a FEM one, in order to validate a numerical framework for further developments. The point is that only mixed boundary conditions do not assume a numerical treatment supporting the separation of variables.

2 Statement of the problem

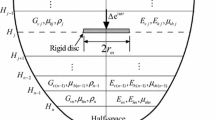
Consider a thin disc of the uniform thickness 2h, with the radius R, compressed by normal stresses p along its faces, see Fig. 1. The disc is assumed to be isotropic and linearly elastic. Let a cylindrical coordinate system with the origin at the mid-plane of the disc be defined such that z axis is perpendicular to the mid-plane, while the polar radius r is parallel to it. We also assume that the edge $r=R$ is traction-free and there is no sliding along the faces $z=\pm h$.

Fig. 1

A thin elastic disc under transverse compression

In what follows, we restrict ourselves to analysis of an axisymmetric problem, when the equilibrium equations are written as

$$\begin{aligned} \begin{aligned}&\dfrac{{{\partial }\sigma _{r}}}{{\partial {r}}}+\dfrac{{{\partial }\tau _{rz}}}{{\partial {z}}}+\dfrac{\sigma _{r}-\sigma _{\varphi }}{r}=0,\\&\dfrac{{{\partial }\sigma _{z}}}{{\partial {z}}}+\dfrac{{{\partial }\tau _{rz}}}{{\partial {r}}}+\dfrac{\tau _{rz}}{r}=0, \end{aligned} \end{aligned}$$

(1)

where $\sigma _{r}$, $\sigma _{\varphi }$, $\sigma _{z}$ and $\tau _{rz}$ are the components of the Cauchy stress tensor. Here and below, see [18] for more detail.

The constitutive relations for a linear isotropic elastic solid are given by

$$\begin{aligned} \begin{aligned} \sigma _{r}&=(\lambda +2\mu )\dfrac{{{\partial }u}}{{\partial {r}}}+\lambda \Big (\dfrac{u}{r}+\dfrac{{{\partial }w}}{{\partial {z}}}\Big ),\\ \sigma _{\varphi }&=(\lambda +2\mu )\dfrac{u}{r}+\lambda \Big (\dfrac{{{\partial }u}}{{\partial {r}}}+\dfrac{{{\partial }w}}{{\partial {z}}}\Big ),\\ \sigma _{z}&=(\lambda +2\mu )\dfrac{{{\partial }w}}{{\partial {z}}}+\lambda \Big (\dfrac{u}{r}+\dfrac{{{\partial }u}}{{\partial {r}}}\Big ),\\ \tau _{rz}&=\mu \Big (\dfrac{{{\partial }u}}{{\partial {z}}}+\dfrac{{{\partial }w}}{{\partial {r}}}\Big ), \end{aligned} \end{aligned}$$

(2)

where u and w are the components of the displacement vector; $\lambda$ and $\mu$ are the Lamé’s constants.

The boundary conditions at the disc faces $z=\pm h$ are taken in the form

$$\begin{aligned} \sigma _{z}=-p, \,\,\,\,\,\, u=0, \end{aligned}$$

(3)

where $p=p(r)$ denotes a prescribed normal stress. These mixed boundary conditions are not a feature of the canonical plate and shell theories, e.g. see [1, 7, 8] operating with Neumann type boundary conditions expressed in terms of stresses only.

Besides, we impose traction free boundary conditions at the edge $r=R$, which can be written as

$$\begin{aligned} \sigma _{r}=0, \,\,\,\,\,\, \tau _{rz}=0. \end{aligned}$$

(4)

It is obvious that the adapted boundary conditions support the solution for which u, $\sigma _{r}$, $\sigma _{\varphi }$ and $\sigma _{z}$ are even functions of the transverse variable z, while w and $\tau _{rz}$ are odd ones.

The goal of the paper is to develop an asymptotic procedure oriented to a thin disc specifying a small geometric parameter given by $\varepsilon =h /R\ll 1$. In this case, we implement the traditional scheme, e.g. see [1, 7], separating the sought for solution into outer and inner (boundary layer) components.

3 Outer solution

Consider first the interior domain of the disc, outside a narrow vicinity of its edge. To this end, we scale original variables as

$$\begin{aligned} \xi =\dfrac{r}{R}, \,\,\,\,\,\, \eta =\dfrac{z}{h} \end{aligned}$$

(5)

and define dimensionless quantities

$$\begin{aligned} \begin{aligned}&u^{*}=\dfrac{u}{h},\,\,\,\,w^{*}=\dfrac{w}{R},\,\,\,\,\sigma ^{*}_{r}=\dfrac{\varepsilon }{\mu }\sigma _{r},\,\,\,\,\sigma ^{*}_{\varphi }=\dfrac{\varepsilon }{\mu }\sigma _{\varphi }, \\&\sigma ^{*}_{z}=\dfrac{\varepsilon }{\mu }\sigma _{z},\,\,\,\,\tau ^{*}_{rz}=\dfrac{1}{\mu }\tau _{rz} \,\,\,\text {and}\,\,\, p^{*}=\dfrac{\varepsilon }{\mu }p, \end{aligned} \end{aligned}$$

(6)

where all quantities with the asterisk are of the same asymptotic order.

The equilibrium equations and constitutive relations in a non-dimensional form may now be rewritten as

$$\begin{aligned} \begin{aligned}&\dfrac{{{\partial }\sigma _{r}^{*}}}{{\partial {\xi }}}+\dfrac{{{\partial }\tau _{rz}^{*}}}{{\partial {\eta }}}+\dfrac{\sigma _{r}^{*}-\sigma _{\varphi }^{*}}{\xi }=0,\\&\dfrac{{{\partial }\sigma _{z}^{*}}}{{\partial {\eta }}}+\varepsilon ^{2}\Big (\dfrac{{{\partial }\tau _{rz}^{*}}}{{\partial {\xi }}}+\dfrac{\tau _{rz}^{*}}{\xi }\Big )=0,\\&\sigma ^{*}_{r}=\alpha \dfrac{{{\partial }w^{*}}}{{\partial {\eta }}}+\varepsilon ^{2}\Big ((\alpha +2)\dfrac{{{\partial }u^{*}}}{{\partial {\xi }}}+\alpha \dfrac{u^{*}}{\xi }\Big ),\\&\sigma ^{*}_{\varphi }=\alpha \dfrac{{{\partial }w^{*}}}{{\partial {\eta }}}+\varepsilon ^{2}\Big ((\alpha +2) \dfrac{u^{*}}{\xi }+\alpha \dfrac{{{\partial }u^{*}}}{{\partial {\xi }}}\Big ),\\&\sigma ^{*}_{z}=(\alpha +2)\dfrac{{{\partial }w^{*}}}{{\partial {\eta }}}+\alpha \varepsilon ^{2}\Big (\dfrac{{{\partial }u^{*}}}{{\partial {\xi }}}+ \dfrac{u^{*}}{\xi }\Big ),\\&\tau _{rz}^{*}=\dfrac{{{\partial }u^{*}}}{{\partial {\eta }}}+\dfrac{{{\partial }w^{*}}}{{\partial {\xi }}}, \end{aligned} \end{aligned}$$

(7)

where $\alpha =\dfrac{\lambda }{\mu }$.

The boundary conditions become

$$\begin{aligned} \sigma _{z}^{*}=-p^{*}, \,\,\,\,\,\, u^{*}=0 \,\,\,\,\, \text {at}\,\,\, \eta =\pm 1 \end{aligned}$$

(8)

and

$$\begin{aligned} \sigma _{r}^{*}=0, \,\,\,\,\,\, \tau _{rz}^{*}=0 \,\,\,\,\,\,\, \text {at}\,\,\,\, \xi = 1. \end{aligned}$$

(9)

Next, we expand the displacements and stresses in the asymptotic series in terms of the small parameter $\varepsilon$ as

$$\begin{aligned} \left( \begin{array}{c} u^{*} \\ w^{*} \\ \sigma _{r}^{*}\\ \sigma _{\varphi }^{*}\\ \sigma _{z}^{*}\\ \tau _{rz}^{*}\\ \end{array} \right) =\left( \begin{array}{c} u^{(0)} \\ w^{(0)} \\ \sigma _{r}^{(0)}\\ \sigma _{\varphi }^{(0)}\\ \sigma _{z}^{(0)}\\ \tau _{rz}^{(0)}\\ \end{array} \right) +\varepsilon ^{2}\left( \begin{array}{c} u^{(1)} \\ w^{(1)} \\ \sigma _{r}^{(1)}\\ \sigma _{\varphi }^{(1)}\\ \sigma _{z}^{(1)}\\ \tau _{rz}^{(1)}\\ \end{array} \right) +.... \end{aligned}$$

(10)

Substituting these expansions into Eq. (7), and the boundary conditions (8) along the faces, we obtain at leading order

$$\begin{aligned} \begin{aligned}&\dfrac{{{\partial }\sigma _{r}^{(0)}}}{{\partial {\xi }}}+\dfrac{{{\partial }\tau _{rz}^{(0)}}}{{\partial {\eta }}}+\dfrac{\sigma _{r}^{(0)}-\sigma _{\varphi }^{(0)}}{\xi }=0,\\&\dfrac{{{\partial }\sigma _{z}^{(0)}}}{{\partial {\eta }}}=0,\\&\sigma ^{(0)}_{r}=\alpha \dfrac{{{\partial }w^{(0)}}}{{\partial {\eta }}},\\&\sigma ^{(0)}_{\varphi }=\alpha \dfrac{{{\partial }w^{(0)}}}{{\partial {\eta }}},\\&\sigma ^{(0)}_{z}=(\alpha +2)\dfrac{{{\partial }w^{(0)}}}{{\partial {\eta }}},\\&\tau _{rz}^{(0)}=\dfrac{{{\partial }u^{(0)}}}{{\partial {\eta }}}+\dfrac{{{\partial }w^{(0)}}}{{\partial {\xi }}}, \end{aligned} \end{aligned}$$

(11)

with

$$\begin{aligned} \sigma _{z}^{(0)}=-p^{*}(\xi ), \,\,\,\,\,\, u^{(0)}=0 \,\,\,\,\, \text {at}\,\,\, \eta =\pm 1. \end{aligned}$$

(12)

Integrating Eqs. (11) and (12) in $\eta$, we have

$$\begin{aligned} \begin{aligned}&u^{(0)}=\dfrac{\alpha +1}{2(\alpha +2)}\dfrac{{{\partial }p^{*}}(\xi )}{{\partial {\xi }}}(\eta ^{2}-1),\\&w^{(0)}=-\dfrac{\eta }{\alpha +2}p^{*}(\xi ),\\&\sigma _{r}^{(0)}=\sigma _{\varphi }^{(0)}=-\dfrac{\alpha }{\alpha +2}p^{*}(\xi ),\\&\sigma _{z}^{(0)}=-p^{*}(\xi ),\\&\tau _{rz}^{(0)}=\dfrac{\alpha }{\alpha +2}\dfrac{{{\partial }p^{*}}(\xi )}{{\partial {\xi }}}\eta . \end{aligned} \end{aligned}$$

(13)

At next order, the equations and boundary conditions are given by

$$\begin{aligned} \begin{aligned}&\dfrac{{{\partial }\tau _{rz}^{(0)}}}{{\partial {\xi }}}+\dfrac{\tau _{rz}^{(0)}}{\xi }+\dfrac{{{\partial }\sigma _{z}^{(1)}}}{{\partial {\eta }}}=0,\\&\sigma ^{(1)}_{r}=(\alpha +2)\dfrac{{{\partial }u^{(0)}}}{{\partial {\xi }}}+\alpha \dfrac{u^{(0)}}{\xi }+\alpha \dfrac{{{\partial }w^{(1)}}}{{\partial {\eta }}},\\&\sigma ^{(1)}_{\varphi }=\alpha \dfrac{{{\partial }u^{(0)}}}{{\partial {\xi }}}+(\alpha +2)\dfrac{u^{(0)}}{\xi }+\alpha \dfrac{{{\partial }w^{(1)}}}{{\partial {\eta }}},\\&\sigma ^{(1)}_{z}=(\alpha +2)\dfrac{{{\partial }w^{(1)}}}{{\partial {\eta }}}+\alpha \Big (\dfrac{{{\partial }u^{(0)}}}{{\partial {\xi }}}+\dfrac{u^{(0)}}{\xi }\Big ),\\&\tau _{rz}^{(1)}=\dfrac{{{\partial }u^{(1)}}}{{\partial {\eta }}}+\dfrac{{{\partial }w^{(1)}}}{{\partial {\xi }}}, \end{aligned} \end{aligned}$$

(14)

with

$$\begin{aligned} \sigma _{z}^{(1)}=0, \,\,\,\,\,\, u^{(1)}=0 \,\,\,\,\, \text {at}\,\,\, \eta =\pm 1. \end{aligned}$$

(15)

As a result,

$$\begin{aligned} \begin{aligned}&u^{(1)}=\dfrac{(\alpha +1)}{2(\alpha +2)}\Big (\dfrac{{{\partial ^{3}}p^{*}(\xi )}}{{\partial {\xi ^{3}}}}+\dfrac{1}{\xi }\dfrac{{{\partial ^{2}}p^{*}(\xi )}}{{\partial {\xi ^{2}}}}-\dfrac{1}{\xi ^{2}}\dfrac{{{\partial }p^{*}(\xi )}}{{\partial {\xi }}}\Big )\Big (\eta ^{2}-\dfrac{\eta ^{4}}{6}-\dfrac{5}{6}\Big ),\\&w^{(1)}=\dfrac{\alpha }{2(\alpha +2)}\Big (\dfrac{{{\partial ^{2}}p^{*}(\xi )}}{{\partial {\xi ^{2}}}}+\dfrac{1}{\xi }\dfrac{{{\partial }p^{*}(\xi )}}{{\partial {\xi }}}\Big )\Big (\eta -\dfrac{\eta ^{3}}{3}\Big ),\\&\sigma ^{(1)}_{r}=-\dfrac{1}{2(\alpha +2)}\Big ((3\alpha +2)\dfrac{{{\partial ^{2}}p^{*}(\xi )}}{{\partial {\xi ^{2}}}}+\dfrac{\alpha }{\xi }\dfrac{{{\partial }p^{*}(\xi )}}{{\partial {\xi }}}\Big )\Big (1-\eta ^{2}\Big ),\\&\sigma ^{(1)}_{\varphi }=-\dfrac{1}{2(\alpha +2)}\Big (\alpha \dfrac{{{\partial ^{2}}p^{*}(\xi )}}{{\partial {\xi ^{2}}}}+\dfrac{(3\alpha +2)}{\xi }\dfrac{{{\partial }p^{*}(\xi )}}{{\partial {\xi }}}\Big )\Big (1-\eta ^{2}\Big ),\\&\sigma ^{(1)}_{z}=\dfrac{\alpha }{2(\alpha +2)}\Big (\dfrac{{{\partial ^{2}}p^{*}(\xi )}}{{\partial {\xi ^{2}}}}+\dfrac{1}{\xi }\dfrac{{{\partial }p^{*}(\xi )}}{{\partial {\xi }}}\Big )\Big (1-\eta ^{2}\Big ),\\&\tau ^{(1)}_{rz}=\dfrac{(3\alpha +2)}{2(\alpha +2)}\Big (\dfrac{{{\partial ^{3}}p^{*}(\xi )}}{{\partial {\xi ^{3}}}}+\dfrac{1}{\xi }\dfrac{{{\partial ^{2}}p^{*}(\xi )}}{{\partial {\xi ^{2}}}}-\dfrac{1}{\xi ^{2}}\dfrac{{{\partial }p^{*}(\xi )}}{{\partial {\xi }}}\Big )\Big (\eta -\dfrac{\eta ^{3}}{3}\Big ).\\ \end{aligned} \end{aligned}$$

(16)

Now, keeping two terms in the outer expansion (10), together with the formulae (5) and (6), the displacements and stresses may be written in a dimensional form as

$$\begin{aligned} \begin{aligned} u(r,z)&=-\dfrac{(\alpha +1)}{2\mu (\alpha +2)}\left[ \dfrac{{{\partial }p(r)}}{{\partial {r}}}(h^{2}-z^{2})+\left( \dfrac{{{\partial ^{3}}p(r)}}{{\partial {r^{3}}}}+\dfrac{1}{r}\dfrac{{{\partial ^{2}}p(r)}}{{\partial {r^{2}}}}\right. \right. \\&\quad \left. \left. -\dfrac{1}{r^{2}}\dfrac{{{\partial }p(r)}}{{\partial {r}}}\right) \left( \dfrac{5}{6}h^{4}-h^{2}z^{2}+\dfrac{1}{6}z^{4}\right) \right] ,\\&w(r,z)=\dfrac{z}{\mu (\alpha +2)}\left[ -p(r)+\dfrac{\alpha }{2}\left( \dfrac{{{\partial ^{2}}p(r)}}{{\partial {r^{2}}}}+\dfrac{1}{r}\dfrac{{{\partial }p(r)}}{{\partial {r}}}\right) \left( h^{2}-\dfrac{1}{3}z^{2}\right) \right] ,\\ \sigma _{r}(r,z)&=-\dfrac{\alpha }{\alpha +2}\left[ p(r)+\dfrac{1}{2}\left( \dfrac{(3\alpha +2)}{\alpha }\dfrac{{{\partial ^{2}}p(r)}}{{\partial {r^{2}}}}+\dfrac{1}{r}\dfrac{{{\partial }p(r)}}{{\partial {r}}}\right) \left( h^{2}-z^{2}\right) \right] ,\\ \sigma _{\varphi }(r,z)&=-\dfrac{\alpha }{\alpha +2}\left[ p(r)+\dfrac{1}{2}\left( \dfrac{{{\partial ^{2}}p(r)}}{{\partial {r^{2}}}}+\dfrac{(3\alpha +2)}{\alpha }\dfrac{1}{r}\dfrac{{{\partial }p(r)}}{{\partial {r}}}\right) \left( h^{2}-z^{2}\right) \right] ,\\ \sigma _{z}(r,z)&=-p(r)+\dfrac{\alpha }{2(\alpha +2)}\left( \dfrac{{{\partial ^{2}}p(r)}}{{\partial {r^{2}}}}+\dfrac{1}{r}\dfrac{{{\partial }p(r)}}{{\partial {r}}}\right) \left( h^{2}-z^{2}\right) ,\\ \tau _{rz}(r,z)&=\dfrac{\alpha }{\alpha +2}z\left[ \dfrac{{{\partial }p(r)}}{{\partial {r}}}+\dfrac{3\alpha +2}{\alpha }\left( \dfrac{{{\partial ^{3}}p(r)}}{{\partial {r^{3}}}}+\dfrac{1}{r}\dfrac{{{\partial ^{2}}p(r)}}{{\partial {r^{2}}}}\right. \right. \\&\left. \left. \quad -\dfrac{1}{r^{2}}\dfrac{{{\partial }p(r)}}{{\partial {r}}}\right) \left( h^{2}-\dfrac{1}{3}z^{2}\right) \right] .\\ \end{aligned} \end{aligned}$$

(17)

These expressions are different to the predictions of the theory for thin elastic plates, e.g. see [1, 9, 14], since the adapted asymptotic behaviour (6) is not the same as that for prescribed stresses characteristic of this theory. In particular, the displacement u in the last formulae demonstrates a parabolic variation in the transverse variable z, but not a uniform one as for a plate loaded by given stresses. It is worth mentioning that a parabolic variation in this displacement is a popular kinematic hypothesis within many engineering formulations for compression problems, e.g. see references in [21]. At the same time, the refined expressions (17) can only be deduced using the asymptotic methodology.

Finally, we remark that for uniform loading $p(r)=const$ the aforementioned formula (17) reduces to the exact solution of the problem, for which we have

$$\begin{aligned} \begin{aligned} w&=-\dfrac{z}{\alpha +2}\dfrac{p}{\mu },\\ \sigma _{z}&=-p,\\ \sigma _{r}&=\sigma _{\varphi }=-\dfrac{\alpha }{\alpha +2}p,\\ u&=\tau _{rz}=0.\\ \end{aligned} \end{aligned}$$

(18)

4 Discrepancy at a traction-free edge and boundary layer

The two-term asymptotic expansions (17) derived in the previous section do not satisfy the homogeneous boundary conditions (4) at the free edge $r=R$. The associated discrepancies are

$$\begin{aligned} \begin{aligned} \begin{aligned} \sigma _{r}(R,z)&=-\dfrac{\alpha }{\alpha +2}\left[ p(R)+\dfrac{1}{2}\left( \dfrac{(3\alpha +2)}{\alpha }\dfrac{{{\partial ^{2}}p(r)}}{{\partial {r^{2}}}}\right| _{r=R}\right. \\\\ {}&\quad \left. \left. \left. +\dfrac{1}{R}\dfrac{{{\partial }p(r)}}{{\partial {r}}}\right| _{r=R}\right) \left( h^{2}-z^{2}\right) \right] ,\\\\ \tau _{rz}(R,z)&=\dfrac{\alpha }{\alpha +2}z\left[ \dfrac{{{\partial }p(r)}}{{\partial {r}}}\right| _{r=R}+\dfrac{3\alpha +2}{\alpha }\left( \dfrac{{{\partial ^{3}}p(r)}}{{\partial {r^{3}}}}\right| _{r=R}\\\\ {}&\quad \left. \left. \left. +\dfrac{1}{R}\dfrac{{{\partial ^{2}}p(r)}}{{\partial {r^{2}}}}\right| _{r=R}-\left. \dfrac{1}{R^{2}}\dfrac{{{\partial }p(r)}}{{\partial {r}}}\right| _{r=R}\right) \left( h^{2}-\dfrac{1}{3}z^{2}\right) \right] .\\\\ \end{aligned} \end{aligned} \end{aligned}$$

(19)

To eliminate the latter, we take into consideration the so-called plane boundary layer, e.g. see [1, 7], localised in a small $O(\varepsilon )$ vicinity of the edge. Let us demonstrate that this boundary layer is governed by the equations in plane elasticity over a semi-infinite strip of thickness 2h, see Fig. 2. Changing variables in the original relations (1) and (2) by

$$\begin{aligned} \gamma =\dfrac{R-r}{h}, \,\,\,\,\,\, \xi =\dfrac{z}{h}, \end{aligned}$$

(20)

Fig. 2

Plane boundary layer

we obtain

$$\begin{aligned} \begin{aligned}&-\dfrac{{{\partial }\sigma _{r}}}{{\partial {\gamma }}}+\dfrac{{{\partial }\tau _{rz}}}{{\partial {\xi }}}+\dfrac{\varepsilon }{1-\varepsilon \gamma }\Big (\sigma _{r}-\sigma _{\varphi }\Big )=0,\\&-\dfrac{{{\partial }\tau _{rz}}}{{\partial {\gamma }}}+\dfrac{{{\partial }\sigma _{z}}}{{\partial {\xi }}}+\dfrac{\varepsilon }{1-\varepsilon \gamma }\tau _{rz}=0 \end{aligned} \end{aligned}$$

(21)

and

$$\begin{aligned} \begin{aligned} \dfrac{h}{\mu }\sigma _{r}&=-(\alpha +2)\dfrac{{{\partial }u}}{{\partial {\gamma }}}+\alpha \left( \dfrac{{{\partial }w}}{{\partial {\xi }}}+\dfrac{\varepsilon }{1-\varepsilon \gamma }u\right) ,\\ \dfrac{h}{\mu }\sigma _{\varphi }&=\dfrac{\varepsilon }{1-\varepsilon \gamma }(\alpha +2)u+\alpha \left( \dfrac{{{\partial }w}}{{\partial {\xi }}}-\dfrac{{{\partial }u}}{{\partial {\gamma }}}\right) ,\\ \dfrac{h}{\mu }\sigma _{z}&=(\alpha +2)\dfrac{{{\partial }w}}{{\partial {\xi }}}+\alpha \left( \dfrac{\varepsilon }{1-\varepsilon \gamma }u-\dfrac{{{\partial }u}}{{\partial {\gamma }}}\right) ,\\ \dfrac{h}{\mu }\tau _{rz}&=\left( \dfrac{{{\partial }u}}{{\partial {\xi }}}-\dfrac{{{\partial }w}}{{\partial {\gamma }}}\right) . \end{aligned} \end{aligned}$$

(22)

Neglecting in the last formulae $O(\varepsilon )$ terms, we arrive at the equations in plane elasticity in the dimensional variables $x=h\gamma$ and z. They can be written as

$$\begin{aligned} \begin{aligned}&\dfrac{{{\partial }\sigma _{xx}}}{{\partial {x}}}+\dfrac{{{\partial }\tau _{xz}}}{{\partial {z}}}=0,\\&\dfrac{{{\partial }\tau _{xz}}}{{\partial {x}}}+\dfrac{{{\partial }\sigma _{zz}}}{{\partial {z}}}=0 \end{aligned} \end{aligned}$$

(23)

and

$$\begin{aligned} \begin{aligned} \dfrac{1}{\mu }\sigma _{xx}&=(\alpha +2)\dfrac{{{\partial }u}}{{\partial {x}}}+\alpha \dfrac{{{\partial }w}}{{\partial {z}}},\\ \dfrac{1}{\mu }\sigma _{zz}&=(\alpha +2)\dfrac{{{\partial }w}}{{\partial {z}}}+\alpha \dfrac{{{\partial }u}}{{\partial {x}}},\\ \dfrac{1}{\mu }\tau _{xz}&=\Big (\dfrac{{{\partial }u}}{{\partial {z}}}+\dfrac{{{\partial }w}}{{\partial {x}}}\Big ). \end{aligned} \end{aligned}$$

(24)

The stress $\sigma _{\varphi }$ transforms to the normal stress orthogonal to (x, z) plane. The latter is not of great interest for plane elasticity and may be omitted.

Equations (23) and (24) are related to their counterparts (21) and (22) by the substitutions

$$\begin{aligned} u\rightarrow -u, \,\,\,\, w\rightarrow w,\,\,\,\, \sigma _{r}\rightarrow \sigma _{xx},\,\,\,\, \sigma _{z}\rightarrow \sigma _{zz},\,\,\,\, \tau _{rz}\rightarrow -\tau _{xz}. \end{aligned}$$

(25)

We have to subject the studied plane strain equations to inhomogeneous boundary conditions at the edge $x=0$, in order to eliminate the discrepancies given by (19). At leading order, we get, due to the asymptotic setup (6),

$$\begin{aligned} \sigma _{xx}=q,\,\,\,\,\,\,\,\, \tau _{xz}=0, \end{aligned}$$

(26)

where $q=\dfrac{\lambda }{\lambda +2\mu }p(R)$.

We also impose mixed homogeneous boundary conditions at the disc faces $z=\pm h$. They are

$$\begin{aligned} \sigma _{zz}=0,\,\,\,\,\,\,\,\, u=0. \end{aligned}$$

(27)

5 Calculation of boundary layer

Consider the boundary value problem (23), (24), (26) and (27). First, expanding the function $q=const$ in a Fourier series, we rewrite the boundary conditions (26) as

$$\begin{aligned} \sigma _{xx}=\dfrac{4q}{\pi }\sum _{n=1}^\infty \dfrac{(-1)^{n-1}}{(2n-1)}\cos (k_{n}z),\,\,\,\,\,\,\,\, \tau _{xz}=0, \end{aligned}$$

(28)

where $k_{n}=\dfrac{(2n-1)\pi }{h},\,\,\,\, n=1,2,3,...$

Next, we introduce the Airy stress function $\varphi (x,z)$, e.g. see [18] in Eqs. (23) and (24), having

$$\begin{aligned} \sigma _{xx}= & {} \dfrac{{{\partial ^{2}}\varphi }}{{\partial {z^{2}}}},\,\,\,\,\, \sigma _{zz}=\dfrac{{{\partial ^{2}}\varphi }}{{\partial {x^{2}}}},\,\,\,\,\,\\ \tau _{xz}= & {} -\dfrac{{{\partial ^{2}}\varphi }}{{\partial {x}}{\partial {z}}}\,\,\,\,\, \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \dfrac{{{\partial }u}}{{\partial {x}}}&=\dfrac{1-\nu ^{2}}{E}\Big (\dfrac{{{\partial ^{2}}\varphi }}{{\partial {z^{2}}}}-\dfrac{\nu }{1-\nu }\dfrac{{{\partial ^{2}}\varphi }}{{\partial {x^{2}}}}\Big ),\\\\ \dfrac{{{\partial }w}}{{\partial {z}}}&=\dfrac{1-\nu ^{2}}{E}\Big (\dfrac{{{\partial ^{2}}\varphi }}{{\partial {x^{2}}}}-\dfrac{\nu }{1-\nu }\dfrac{{{\partial ^{2}}\varphi }}{{\partial {z^{2}}}}\Big ) \end{aligned} \end{aligned}$$

(29)

with $E=\dfrac{\mu (3\lambda +2\mu )}{\lambda +\mu }$ and $\nu =\dfrac{\lambda }{2(\lambda +\mu )}$ denoting Young’s modulus and Poisson’s ratio, respectively.

The Airy function satisfies the bi-harmonic equation. Thus,

$$\begin{aligned} \Delta ^{2}\varphi =0, \end{aligned}$$

(30)

where

$$\begin{aligned}\Delta ^{2}=\dfrac{{{\partial ^{4}}}}{{\partial {x^{4}}}}+2\dfrac{{{\partial ^{4}}}}{{\partial {x^{2}}}{\partial {z^{2}}}}+\dfrac{{{\partial ^{4}}}}{{\partial {z^{4}}}}. \end{aligned}$$

The boundary conditions (26) and (27) then become

$$\begin{aligned} \dfrac{{{\partial ^{2}}\varphi }}{{\partial {z^{2}}}}\Big |_{x=0}=q,\,\,\,\,\,\,\,\, \dfrac{{{\partial ^{2}}\varphi }}{{\partial {x}}{\partial {z}}}\Big |_{x=0}=0,\,\,\,\,\,\,\,\,\dfrac{{{\partial ^{2}}\varphi }}{{\partial {z^{2}}}}\Big |_{z=\pm h}=0,\,\,\,\,\,\,\,\,\dfrac{{{\partial ^{2}}\varphi }}{{\partial {x^{2}}}}\Big |_{z=\pm h}=0. \end{aligned}$$

(31)

Let us now expand the sought for function $\varphi$ as

$$\begin{aligned} \varphi (x,z)=\sum _{n=1}^\infty \varphi _{n}(x,z) \end{aligned}$$

(32)

with

$$\begin{aligned} \varphi _{n}(x,z)=f_{n}(x)\cos (k_{n}z), \end{aligned}$$

(33)

satisfying both boundary conditions along the faces $z=\pm h$ in (31). In this case, the ordinary differential equation for the functions $f_{n}$ takes the form

$$\begin{aligned} f^{(IV)}_{n}(x)-2k^{2}_{n}f^{''}_{n}(x)+k^{4}_{n}f_{n}(x)=0. \end{aligned}$$

(34)

The decaying solution of this equation can be written as

$$\begin{aligned} f_{n}(x)=C_{n}e^{-k_{n}x}+D_{n}xe^{-k_{n}x}, \end{aligned}$$

(35)

where $C_{n}$ and $D_{n}$ are unknown constants.

Then, substituting (32) into the homogeneous boundary condition at the edge $x=0$ in (31), we obtain

$$\begin{aligned} D_{n}=C_{n}k_{n}. \end{aligned}$$

(36)

As a result, we have from the inhomogeneous boundary condition in (31)

$$\begin{aligned} C_{n}=\dfrac{(-1)^{n}4qh^{2}}{(2n-1)^{3}\pi ^{3}}. \end{aligned}$$

(37)

Finally, we derive from (29) and the related intermediate formulae

$$\begin{aligned} \begin{aligned}&u(x,z)=2\dfrac{1-\nu ^{2}}{E}\sum ^{\infty }_{n=1}C_{n}k_{n}\left( 1+\dfrac{1}{2(1-\nu )}k_{n}x\right) e^{-k_{n}x}\cos (k_{n}z),\\&w(x,z)=-\dfrac{1+\nu }{E}(1-2\nu )\sum ^{\infty }_{n=1}C_{n}k_{n}\left( 1-\dfrac{1}{1-2\nu }k_{n}x\right) e^{-k_{n}x}\sin (k_{n}z),\\&\sigma _{xx}(x,z)=-\sum ^{\infty }_{n=1}C_{n}k^{2}_{n}(1+k_{n}x)e^{-k_{n}x}\cos (k_{n}z),\\&\sigma _{zz}(x,z)=-\sum ^{\infty }_{n=1}C_{n}k^{2}_{n}(1-k_{n}x)e^{-k_{n}x}\cos (k_{n}z),\\&\tau _{xz}(x,z)=-\sum ^{\infty }_{n=1}C_{n}k^{3}_{n}x e^{-k_{n}x}\sin (k_{n}z). \end{aligned} \end{aligned}$$

(38)

6 Numerical results

Below we compare the analytical results for the boundary layer obtained in the previous section with FEM calculations. The chosen values of the problem parameters are presented in Table 1. The stresses and displacements calculated by the formulae (38) are compared with those obtained using FEA free software LISA 8.0 (http://lisafea.com/).

Table 1 Problem parameters

Fig. 3

Displacement variation along x-coordinate (a) and (c) and along z-coordinate (b) and (d)

Fig. 4

Stress variation along x-coordinate (a), (c) and (e) and along z-coordinate (b), (d) and (f)

Figures 3 and 4 show the variation in displacements and stresses along x-coordinate for $z=5,4.5,3,0\,\, [mm]$, as well as their variation along z-coordinate for $x=0,1,10,20 \,\,[\text {mm}]$. The solid line in all figures corresponds to the analytical solution, while FEM predictions are plotted with dots.

The numerical data presented in these figures demonstrate an excellent agreement between analytical and FEM results with virtually the only exception of the stresses $\sigma _{xx}$ and $\tau _{xz}$ entering the boundary conditions at the edge $x=0$. The latter is a consequence of the expected effect of FEM modelling.

7 Concluding remarks

A full asymptotic solution of the axisymmetric problem for transverse compression of a thin elastic disc is obtained. The adapted mixed boundary conditions along disc faces support an explicit inner solution corresponding to a plane boundary layer. The exponential decay of the latter is a priori guaranteed, in contrast with the setup, involving the classical Neumann type boundary conditions [7, 8] that assumes the implementation of the Saint-Venant principle. The two-term outer solution derived from the 2D equations for displacements and stresses is valid for arbitrary loading. It is expressed through the derivatives of the prescribed normal stresses. For comparison, the leading-order outer solution is also deduced using the Love potential.

The developed methodology is not restricted to the considered problem. It can be easily extending to a disc of a general shape with a variety of non-classical boundary conditions along its faces. In this case, however, an anti-plane boundary layer may also arise along with a plane one [1, 7]. In addition, simple solutions for the boundary layers, like that for mixed boundary conditions studied in this paper, are usually not achievable, motivating FEM calculations. Among other natural extensions of the proposed asymptotic scheme, we mention analysis of a transversely inhomogeneous disc, including a functionally graded one. The latter topic seems to be of interest for various technologies.

APPENDIX

The bi-harmonic equation for the Love potential $\psi (r,z)$ can be written as, e.g. see [18]

$$\begin{aligned} \Delta ^{2}\psi =0 \end{aligned}$$

(A1)

with

$$\begin{aligned} \Delta =\dfrac{{{\partial ^{2}}}}{{\partial {r^{2}}}}+\dfrac{1}{r}\dfrac{{{\partial }}}{{\partial {r}}}+\dfrac{{{\partial ^{2}}}}{{\partial {z^{2}}}}. \end{aligned}$$

(A2)

The quantities in the boundary conditions (3) along disc faces are expressed through this potential as

$$\begin{aligned} \begin{aligned}&u=-\dfrac{1}{2\mu }\dfrac{{{\partial ^{2}{\psi }}}}{{\partial {r}}{\partial {z}}},\\&\sigma _{z}=\dfrac{{{\partial }}}{{\partial {z}}}\left( \dfrac{3\alpha +4}{2(\alpha +1)}\Delta -\dfrac{{{\partial ^{2}}}}{{\partial {z^{2}}}}\right) \psi .\\ \end{aligned} \end{aligned}$$

(A3)

Let us rewrite the formulae (A1) and boundary conditions (3) in the dimensionless variables (5), having

$$\begin{aligned} \Delta _{*}^{2}\psi _{*}=0, \end{aligned}$$

(A4)

where $\psi _{*}=\dfrac{\varepsilon }{\mu h^{3}}\psi$ and

$$\begin{aligned} \Delta _{*}=h^{2}\Delta =\dfrac{{{\partial ^{2}}}}{{\partial {\eta ^{2}}}}+\varepsilon ^{2}\left( \dfrac{{{\partial ^{2}}}}{{\partial {\xi ^{2}}}}+\dfrac{1}{\xi }\dfrac{{{\partial }}}{{\partial {\xi }}}\right) , \end{aligned}$$

(A5)

subject to

$$\begin{aligned} \dfrac{{{\partial ^{2}{\psi _{*}}}}}{{\partial {\xi }}{\partial {\eta }}}=0,\,\,\,\,\dfrac{{{\partial }}}{{\partial {\eta }}}\left( \dfrac{3\alpha +4}{2(\alpha +1)}\Delta _{*}-\dfrac{{{\partial ^{2}}}}{{\partial {\eta ^{2}}}}\right) \psi _{*}=-p_{*} \end{aligned}$$

(A6)

at $\eta =\pm 1$.

At leading order $\Big (\psi _{*}=\psi _{0}+O(\varepsilon ^{2})\Big )$, we have

$$\begin{aligned} \dfrac{{{\partial ^{4}{\psi _{0}}}}}{{\partial {\xi ^{4}}}}=0 \end{aligned}$$

(A7)

and

$$\begin{aligned} \dfrac{{{\partial ^{2}{\psi _{0}}}}}{{\partial {\xi }}{\partial {\eta }}}=0,\,\,\,\,\dfrac{\alpha +2}{2(\alpha +1)}\dfrac{{{\partial ^{3}{\psi _{0}}}}}{{\partial {\eta ^{3}}}}=-p_{*}. \end{aligned}$$

(A8)

The solution of this problem is given by

$$\begin{aligned} \psi _{0}=A(\xi )\eta +B(\xi )\eta ^{3} \end{aligned}$$

(A9)

with

$$\begin{aligned} \dfrac{dA}{d\xi }=\dfrac{\alpha +1}{\alpha +2}\dfrac{{{\partial ^{2}{p_{*}}}}}{{\partial {\xi }}},\,\,\,\,\,\, B=-\dfrac{p_{*}}{3}\dfrac{\alpha +1}{\alpha +2}. \end{aligned}$$

(A10)

Substituting the last formula into (A3), we arrive at the same relations as in (13). Other stress and displacement components in (13) can be also expressed through the potential $\psi$.