On a mathematical model for cancer invasion with repellent pH-taxis and nonlocal intraspecific interaction

Abstract

Starting from a mesoscopic description of cell migration and intraspecific interactions, we obtain by upscaling an effective reaction–diffusion–taxis equation for the cell population density involving spatial nonlocalities in the source term and biasing its motility and growth behavior according to environmental acidity. We prove global existence, uniqueness, and boundedness of a nonnegative solution to a simplified version of the coupled system describing cell and acidity dynamics. A 1D study of pattern formation is performed. Numerical simulations illustrate the qualitative behavior of solutions.

1 Introduction

Migration, proliferation, and differentiation of cells are influenced by biochemical and biophysical characteristics of their surroundings, which they perceive by way of transmembrane units like ion channels, receptors, etc. Increasing experimental evidence suggests that cells are able to sense such cues not only where they are, but also at larger distances, up to several cell diameters around their current position [24, 30, 47]. This led to mathematical models accounting for various types of nonlocalities; most of them addressing cell-cell and/or cell-matrix adhesions; we refer to the review article [9] and references therein. The settings typically involve reaction, diffusion and drift terms, whereby the latter contain an integral operator to characterize the so-called adhesion velocity over the interaction range. In [18] was performed a rigorous passage from a cell-matrix adhesion model to a reaction–diffusion–haptotaxis equation when the sensing radius is becoming infinitesimally small, thus recovering the local PDE formulation from that featuring the mentioned nonlocality. The remote sensing of signals by cells affects, however, not only motility, but also proliferation, growth, and phenotypic switch, either directly—by occupancy of transmembrane units on cellular extensions like cytonemes and filopodia and subsequently initiated signaling pathways, or in an indirect manner—as effects of altered migratory and aggregation behavior. Models involving reaction–diffusion equations with nonlocal source terms have been proposed in various contexts, including biological and ecological ones, see, e.g., [28, 54] and references therein for rather generic settings, [4, 5, 46] for chemotaxis systems, and [41, 49, 50] for equations dedicated to tumor growth. We refer to [9, 28, 54] for some reviews of model classes addressing this type of nonlocality.

As far as growth and migration of cell populations are concerned, the reaction–diffusion models with nonlocal source terms

$$\begin{aligned} u_t=\nabla \cdot (D\nabla u)+F(u) \end{aligned}$$

(1.1)

typically feature $F(u)=\mu J*u(1-u)$ to describe nonlocal stimulation of growth (see, e.g., [50, 54]), or $F(u)=\mu u^\alpha (1-J*u^\beta )$, which characterizes competition between (bunches of) cells for available resources in their surroundings, attempting, e.g., to prevent overcrowding. In the context of (tumor) cell migration such models have been handled, e.g., in [49], where intra- and interspecific nonlocal interactions led to an ODE-PDE system for the interplay between cancer cells performing linear diffusion and haptotaxis with the extracellular matrix being (nonlocally) degraded by the cells and remodeled with the mentioned growth limitation. We also refer to [9, 35] for short reviews of models with source terms of this type and therewith associated mathematical challenges.

In this note, we propose and analyze a model for tumor cell migration involving myopic diffusion, repellent pH-taxis, and a nonlocal source term of the competition type mentioned above. The cross-diffusion system is obtained upon starting from the mesoscopic description of cell migration via a kinetic transport equation for the space-time distribution function of cells sharing some velocity regime. An appropriate upscaling relying on diffusion dominance then leads to the effective macroscopic equation for the cancer cell density, with precisely specified diffusion and drift coefficients. The remaining of this paper is structured as follows: Sect. 2 contains the model deduction with the mentioned upscaling. Section 3 is dedicated to the mathematical analysis of the obtained nonlocal macroscopic system, in terms of global existence, uniqueness, and boundedness of a solution to a simplified version of the problem. In Sect. 4 we study the asymptotic behavior. Section 5 offers a 1D study of pattern formation for the equations handled in Sect. 3, but only involving constant motility coefficients. In Sect. 6, we provide numerical simulations to illustrate the qualitative behavior of solutions to the investigated nonlocal problem. Section 7 contains a discussion of the results.

2 Modeling

In this section, we start from a mesoscopic description of cell migration and intrapopulation interactions and deduce (in a non-rigorous way) effective equations on the macroscopic scale of cell population dynamics. The deduction closely follows that in [35], however, extends it, by accounting here for the repellent effects of acidity eventually leading on the population scale to chemorepellent pH-taxis.

Tumor migration and spread are typically assessed on the macroscopic scale of the cancer cell population via biomedical imaging. The involved processes are, however, highly complex and originate at the lower levels of cell aggregates sharing—beside time-space dynamics—one or several further traits (e.g., velocity, phenotypic state or other so called ’activity variables’), down to microscopic events on individual cells. This multiscale character of cell migration can be captured (at least partially) by models within the kinetic theory of active particles (KTAP) framework formulated by Bellomo et al. (see, e.g., [1, 3] and references therein). Starting from kinetic transport equations (KTEs), a large variety of (spatially) local and nonlocal models have been proposed and various kinds of upscaling and moment closure methods have been performed in order to deduce their macroscopic limits which enable a mathematically more efficient handling, see, e.g., [7, 8, 10,11,12,13,14, 17, 20,21,22, 26, 31, 32, 37, 59]. The obtained macroscopic equations carry in the coefficients of their motility and source terms some of the traits from the mesoscale on which KTEs were formulated. Those coefficients are no longer ’guessed’ as in the case of stating reaction–diffusion–taxis directly on the population level and the diffusion is often of the ’myopic’ type, involving a drift correction. We will perform here a diffusion-dominated upscaling of mesoscale dynamics.

We will use the following notations:

• $p=p(t,x,v)$: distribution function of cells having at time t and position $x\in \mathbb {R}^n$ the velocity $v\in V$;

• $V=[s_1,s_2]\times \mathbb {S}^{n-1}$: velocity space. Thereby, $s_1,s_2$ denote the minimum, respectively, the maximum speed of a cell, $\theta \in \mathbb {S}^{n-1}$ represents the cell direction;

• $u(t,x)=\int \limits _Vp(t,x,v)\ \textrm{d}v$: macroscopic cell density;

• h(t, x): concentration of protons. This is a macroscopic quantity throughout this note.

The kinetic transport equation (KTE)

$$\begin{aligned} p_t+v\cdot \nabla _xp=\mathcal {L}[h]p+\tilde{\mu }\mathcal {I}[p,p] \end{aligned}$$

(2.1)

characterizes the mesoscopic dynamics of the considered cell population. This is the framework set in [43], which assumes that changes in p are due to velocity jumps accompanied by reorientations dictated by a turning kernel contained in the operator $\mathcal {L}[h]$.

The first term on the right hand side of (2.1) represents the so-called turning operator. The second term describes growth/decay of cells due to intraspecific proliferative/competitive interactions, while $\tilde{\mu }>0$ is the constant interaction rate.¹ With a small constant $\epsilon >0$ relating to the cell size and to the distance at which cells can sense signals in their proximity, we will assume that $\tilde{\mu }=\epsilon ^2\mu$. This means that cells have a much higher preference to motility (in particular, to changing direction) than to interaction and crowding.

We assume that the turning operator is of the form

$$\begin{aligned} \mathcal {L}[h](p)=\int \limits _V\Big (T[h](v,v')p(t,x,v')-T[h](v',v)p(t,x,v)\Big )\ \textrm{d}v', \end{aligned}$$

(2.2)

with the turning rate $T[h](v,v')\ge 0$ chosen such that the reorientation is a Poisson process with rate

$$\begin{aligned} \lambda [h]=\int \limits _VT[h](v,v')\textrm{d}v, \end{aligned}$$

hence such that $T[h]/\lambda [h]$ is a kernel giving the probability density for a change of the velocity regime of a cell from $v'$ to v. In particular, this means that $\mathcal {L}[h]$ is preserving mass. The reorientation of cells depends on the acidity of their environment (expressed by the concentration h of protons).

In the following, we assume that the turning rate has an asymptotic expansion of the form

$$\begin{aligned} T[h]=T_0[h]+\epsilon T_1[h]+O(\epsilon ^2), \end{aligned}$$

(2.3)

thus the turning operator admits itself an expansion

$$\begin{aligned} \mathcal {L}[h](p):=L_0[h](p)+\epsilon L_1[h](p)+O(\epsilon ^2), \end{aligned}$$

(2.4)

where $L_0[h]$ and $L_1[h]$ are linear operators,

$$\begin{aligned} L_i[h](p)(t,x,v)&=\int \limits _V[T_i[h](v,v')p(t,x,v')-T_i[h](v',v)p(t,x,v)]\ \textrm{d}v',\qquad i=0,1. \end{aligned}$$

(2.5)

For $\mathcal {I}$, we consider as in [35] the form

$$\begin{aligned} \mathcal {I}[p,p](t,x,v)=\frac{p^\alpha (t,x,v)}{\int \limits _VM^\alpha (x,v)\ \textrm{d}v}-\frac{1}{\int \limits _VM^{\alpha +\beta }(x,v)}p^\alpha (t,x,v)\int \limits _\Omega J(x,x') p^\beta (t,x',v)\ \textrm{d}x', \end{aligned}$$

(2.6)

where $\alpha ,\beta >0$ are constants, $J(x,x')$ is a function weighting the interactions between (bunches of) cells sharing the same velocity regime within a bounded domain $\Omega \subset \mathbb {R}^n$. We assume that J depends on the distance between interacting (clusters of) cells and take $J(x,x')=J(x-x')$, also requiring J to satisfy

$$\begin{aligned}&\int \limits _VJ(x)\ \textrm{d}x=1 \end{aligned}$$

(2.7)

$$\begin{aligned}&\inf \limits _{B_{\text {diam}(\Omega )}(0)}J\ge \eta \quad \text {for some }\eta >0. \end{aligned}$$

(2.8)

We also assume that there exists a bounded velocity distribution $M(x,v)>0$ such that:

• 1. $\int \limits _VM(x,v)\ \textrm{d}v=1$, i.e., M is a kernel w.r.t. v.

• 2. $\int \limits _VvM(x,v)\ \textrm{d}v=0$, i.e., the flow produced by the equilibrium distribution M(v) vanishes.

• 3. The rate $T_0[h](v,v')$ satisfies the detailed balance equation

  $$\begin{aligned} T_0[h](v,v')M(v')=T_0[h](v',v)M(v). \end{aligned}$$

• 4. The turning rate $T_0[h](v,v')$ is bounded and there exists $\sigma >0$ such that

  $$\begin{aligned} T_0[h](v,v')\ge \sigma M(x,v),\quad \text {for all }(v,v')\in V\times V,\ x\in \mathbb {R}^n,\ t>0. \end{aligned}$$

The following lemma summarizing the properties of the operator $-L_0$ can be easily verified (see, e.g., [2, 7]).

Lemma 2.1

Let $L_0[h]$ be the operator defined in (2.5). Then, $-L_0[h]$ has the following properties:

• (i) $-L_0[h]$ is positive definite w.r.t. the scalar product and the associated norm in the weighted space $L^2(V,\frac{\textrm{d}v}{M(x,v)})$, and self-adjoint: for all $p,\zeta \in L^2(V,\frac{\textrm{d}v}{M(x,v)})$ it holds that

  $$\begin{aligned} \int \limits _VL_0[h](p)(v)\frac{\zeta (v)}{M(v)}\ \textrm{d}v=\int \limits _VL_0[h](\zeta )(v)\frac{p(v)}{M(v)}\ \textrm{d}v. \end{aligned}$$

• (ii) For $\phi \in L^2(V,\frac{\textrm{d}v}{M(x,v)})$, the equation $L_0[h](\zeta ) =\phi$ has a unique solution $\zeta \in L^2(V,\frac{\textrm{d}v}{M(x,v)})$ satisfying²$\bar{\zeta }=0$ iff $\bar{\phi }=0$.

• (iii) $\text {Ker }L_0[h]=\text {span }(M(v))$.

• (iv) The equation $L_0[h]( \psi ) =vM(v)$ has a unique solution $\psi (v)=:L_0[h]^{-1}(vM(v))$ (this is actually a pseudoinverse).

Example 2.2

Consider $T_0[h](v,v'):=\lambda _0[h]M(v)$, with $\lambda [h]\ge \lambda _0[h]>0$ for any h. This obviously satisfies the properties 3. and 4. in our above assumption. With this choice,

$$\begin{aligned} L_0[h](p)=\lambda _0[h](M(v)u-p) \end{aligned}$$

(2.9)

and it is straightforward to see that this operator satisfies the properties in Lemma 2.1 and the function $\psi$ in (iv) becomes $\psi (v)=-vM(v)/\lambda _0[h]$ if $\psi \in (\text {span }(M(v)))^\perp$.³

Equation (2.1) is supplemented with the macroscopic PDE for proton concentration:

$$\begin{aligned} h_t=D_H\Delta h+g(u,h), \end{aligned}$$

(2.10)

where $D_H>0$ is the diffusion constant and g(u, h) represents production by tumor cells and uptake (e.g., by blood capillaries—not explicitly modeled in this note) or decay.

We also consider initial conditions for p and h:

$$\begin{aligned} p(0,x,v)=p_0(x,v),\qquad h(0,x)=h_0(x), \quad x\in \Omega \subseteq \mathbb {R}^n,\ v\in V. \end{aligned}$$

(2.11)

Together with these, Eqs. (2.1), (2.10) form a meso–macro-system describing the dynamics of the (mesoscopic) cell distribution in response to acidity in the extracellular space.

We perform a parabolic scaling to obtain the diffusion limit of the KTE (2.1). This means that we rescale the time and space variables as follows:

$$\begin{aligned} \hat{t}=\epsilon ^2t,\quad \hat{x}=\epsilon x. \end{aligned}$$

Subsequently we will drop the ’ $\hat{}$ ’ symbol and the $\epsilon$-dependency of the solution $p^\epsilon$ to the resulting KTE, in order not to complicate the writing. Then, (2.1) becomes

$$\begin{aligned} \epsilon p_t+v\cdot \nabla _xp=\frac{1}{\epsilon }\mathcal {L}[h]p+\mu \epsilon \mathcal {I}[p,p]. \end{aligned}$$

(2.12)

Now consider the decomposition (Chapman–Enskog expansion)

$$\begin{aligned} p(t,x,v)=F(u)(t,x,v)+\epsilon p^\perp (t,x,v), \end{aligned}$$

(2.13)

with $\int \limits _Vp^\perp (t,x,v)\ \textrm{d}v=0$, thus $p^\perp \in (\text {span }(M(v)))^\perp$, and $F(u)\in \text {span }(M(v))$ such that $\int \limits _VF(u)\ \textrm{d}v=u$. A natural choice is $F(u)(t,x,v):=M(x,v)u(t,x)$, which we will subsequently adopt.

Then, observe that

$$\begin{aligned} \mathcal {I}[p,p]=\mathcal {I}[M(v)u+\epsilon p^\perp ,M(v)u+\epsilon p^\perp ]=\mathcal {I}[M(v)u,M(v)u]+O(\epsilon ) \end{aligned}$$

and (2.12) becomes

$$\begin{aligned} \partial _t(M(v)u)+\epsilon \partial _tp^\perp +\frac{1}{\epsilon }v\cdot \nabla _x(M(v)u)+v\cdot \nabla _xp^\perp =\frac{1}{\epsilon }L_0[h](p^\perp )&+\frac{1}{\epsilon }L_1[h](M(v)u)+ L_1[h](p^\perp )\nonumber \\ {}&+\mu \mathcal {I}[M(v)u,M(v)u]+O(\epsilon ). \end{aligned}$$

(2.14)

Let $P:L^2(V,\frac{\textrm{d}v}{M(v)})\rightarrow \text {Ker }L_0[h]$ be the projection operator. Then,

$$\begin{aligned} P(\phi )=M(v)\bar{\phi },\qquad \phi \in L^2(V,\frac{\textrm{d}v}{M(v)}). \end{aligned}$$

It is easy to verify that the following lemma holds (see, e.g., [2]).

Lemma 2.3

The projection operator P has the following properties:

• (i) $(I-P)(M(v)u)=P(p^\perp )=0$.

• (ii) $(I-P)(v\cdot \nabla _x(M(v)u))=v\cdot \nabla _x(M(v)u)$.

• (iii) $(I-P)(L_0[h](M(v)u))=L_0[h](M(v)u)$ and $(I-P)(L_1[h](M(v)u))=L_1[h](M(v)u)$.

• (iv) $(I-P)(L_1[h](p^\perp ))=L_1[h](p^\perp )$.

If we now apply $I-P$ to (2.14), we get

$$\begin{aligned} \epsilon \partial _tp^\perp +\frac{1}{\epsilon }v\cdot \nabla _x(Mu)+(I-P)(v\cdot \nabla _xp^\perp )=\frac{1}{\epsilon }L_0[h](p^\perp )&+\frac{1}{\epsilon }L_1[h](Mu)+L_1[h](p^\perp ) \nonumber \\&+\mu \mathcal {I}[Mu,Mu]+O(\epsilon ). \end{aligned}$$

(2.15)

Integrating (2.14) w.r.t. v gives (at leading order) the macroscopic PDE⁴

$$\begin{aligned} u_t+\int \limits _Vv\cdot \nabla _xp^\perp \ \textrm{d}v=\mu \int \limits _V\mathcal {I}[Mu,Mu]\ \textrm{d}v. \end{aligned}$$

(2.16)

On the other hand, from (2.15) we obtain (again at leading order)

$$\begin{aligned} L_0[h](p^\perp )=v\cdot \nabla _x(Mu)-L_1[h](Mu). \end{aligned}$$

(2.17)

Since $\int \limits _VL_1[h](Mu)\ \textrm{d}v=0$, we see that the integral w.r.t. v of the right hand side in (2.17) vanishes, so we can pseudo-invert $L_0[h]$ to obtain

$$\begin{aligned} p^\perp =L_0[h]^{-1}\Big (v\cdot \nabla _x(Mu)- L_1[h](Mu) \Big ). \end{aligned}$$

(2.18)

Plugging this into (2.16) gives

$$\begin{aligned} u_t+\int \limits _Vv\cdot \nabla _x\Big (L_0[h]^{-1}(v\cdot \nabla _x(Mu))- L_0[h]^{-1}(L_1[h](Mu)) \Big ) =\mu \int \limits _V\mathcal {I}[Mu,Mu]\ \textrm{d}v. \end{aligned}$$

(2.19)

For the right hand side in (2.19), we have

$$\begin{aligned} \mu \int \limits _V\mathcal {I}[Mu,Mu]\ \textrm{d}v=\mu u^\alpha (1-J*u^\beta ). \end{aligned}$$

For the first transport term on the left hand side, we compute

$$\begin{aligned} \int \limits _Vv\cdot \nabla _x \Big (L_0[h]^{-1}(v\cdot \nabla _x(Mu))\Big )\ \textrm{d}v&=\nabla _x\cdot \Big (\frac{1}{\lambda _0[h]}\nabla _x \cdot \Big (\int \limits _Vv\otimes vM(v)\ \textrm{d}v\ u\Big )\Big )\\&=-\nabla _x\cdot \Big (\frac{1}{\lambda _0[h]}\nabla _x \cdot (\mathbb D\ u )\Big ), \end{aligned}$$

where we applied the observations made at the end of example 2.2 and denoted by

$$\begin{aligned} \mathbb D(x):=\int \limits _Vv\otimes vM(x,v)\ \textrm{d}v \end{aligned}$$

the diffusion tensor of tumor cells.

For the second transport term on the left hand side of (2.19), we have

$$\begin{aligned} -\int \limits _Vv\cdot \nabla _x\Big (L_0[h]^{-1}(L_1[h](M(v)u))\Big )\ \textrm{d}v&=- \nabla _x\cdot \int \limits _Vv L_0[h]^{-1}(L_1[h](M(v)u))\ \textrm{d}v\\&=-\nabla _x\cdot \int \limits _VvM(v) \frac{1}{M(v)}L_0[h]^{-1}(L_1[h](M(v)u))\ \textrm{d}v\\&=-\nabla _x\cdot \int \limits _VL_0[h](\psi (v))\frac{1}{M(v)}L_0[h]^{-1}(L_1[h](M(v)u))\ \textrm{d}v\\&=- \nabla _x\cdot \Big (\int \limits _V\frac{\psi (v)}{M(v)}L_1[h](M(v))\ \textrm{d}v\ u\Big )\\&= \nabla _x\cdot \Big (u\Gamma [h]\Big ), \end{aligned}$$

where we used the fact that $L_0$ is self-adjoint, $\psi (v)=-vM(v)$ is its pseudo-inverse, and the notation

$$\begin{aligned} \Gamma [h](x):=\frac{1}{\lambda _0[h]}\int \limits _VvL_1[h](M(x,v))\ \textrm{d}v. \end{aligned}$$

With the above calculations (2.19) becomes

$$\begin{aligned} u_t -\nabla _x\cdot \Big (\frac{1}{\lambda _0[h]}\nabla _x \cdot (\mathbb D\ u )\Big ) +\nabla _x\cdot \Big (u\Gamma [h]\Big )=\mu u^\alpha (1-J*u^\beta ). \end{aligned}$$

(2.20)

To specify $\Gamma [h]$ we consider⁵$T_1[h](v,v'):=-a(h)v\cdot \nabla h+b(h)v'\cdot \nabla h$ with $a,b\ge 0$. Then we compute

$$\begin{aligned} \int \limits _V vL_1[h](M(x,v))\ \textrm{d}v=-a(h)\frac{s_2^{n+2}-s_1^{n+2}}{n(n+2)}|\mathbb {S}^{n-1}|\ \mathbb I \nabla h-\frac{b(h)}{|V|}\mathbb D\nabla h, \end{aligned}$$

recalling that $V=[s_1,s_2]\times \mathbb {S}^{n-1}$, thus $|V|=\frac{s_2^n-s_1^n}{n}|\mathbb {S}^{n-1}|$. With the notation $\mathbb T(x):=a(h)\frac{s_2^{n+2}-s_1^{n+2}}{n(n+2)} |\mathbb {S}^{n-1}|\ \mathbb I+\frac{b(h)}{|V|}\mathbb D$ we obtain

$$\begin{aligned} \Gamma [h](x)=-\frac{1}{\lambda _0[h]}\mathbb T(x)\nabla h, \end{aligned}$$

which leads to the macroscopic PDE

$$\begin{aligned} u_t=\nabla _x\cdot \Big (\frac{1}{\lambda _0[h]}\nabla _x \cdot (\mathbb D(x) u )\Big )+\nabla _x\cdot \Big (\frac{u}{\lambda _0[h]}\mathbb T(x)\nabla h \Big )+\mu u^\alpha (1-J*u^\beta ). \end{aligned}$$

(2.21)

The particular choice $\lambda _0[h]:=1$, $a(h):=0$, $b(h):=|V|$ leads to the first equation in (3.1).

The first term on the right hand side of (2.21) represents (myopic) diffusion, the second one characterizes repellent chemotaxis, away from increasing gradients of proton concentration,⁶ while the last is a source term accounting for tumor cell growth enhanced or limited by intraspecific interactions.

The above deduction of a macroscopic reaction–diffusion–taxis is merely formal; the nonlinear source term prevents applying the proof of the rigorous derivation from [7]. The following section will be dedicated to proving global existence and boundedness of nonnegative solutions to the coupled PDE system for u and h obtained on the macrolevel by considering the above much simplified forms of the coefficient functions $\lambda _0,a, b$. The previous calculations were made for $x\in \mathbb {R}^n$; however, we can restrict to a bounded domain $\Omega \subset \mathbb {R}^n$ upon proceeding as in [14, 17, 45] and assuming no flux of cells or protons through the boundary.

3 Mathematical analysis

Let $\Omega \subset \mathbb {R}^n$ be a bounded domain with smooth enough boundary and outer unit normal $\nu$. We consider the model

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t = \nabla \nabla :(\mathbb {D}(x)u) + \nabla \cdot (\mathbb {D}(x)u\nabla h) + \mu (h) u^{\alpha }(1- J *u^{\beta }), &{} x\in \Omega , \, t> 0,\\ h_t = D_H \Delta h + g(u,h), &{} x \in \Omega , \, t> 0,\\ (\mathbb {D}(x)\nabla u + \nabla \cdot \mathbb {D}(x)u + \mathbb {D}(x) u \nabla h) \cdot \nu = \nabla h \cdot \nu = 0, &{} x \in \partial \Omega , \, t>0,\\ u(x,0) = u_0(x), \, h(x,0) = h_0(x), &{} x \in \Omega , \end{array}\right. } \end{aligned}$$

(3.1)

where u denotes the cell density and h the acid concentration. Here, the convolution over $\Omega$ is as usually given by

$$\begin{aligned} J *u^{\beta }(x,t) = \int \limits _{\Omega } J(x-y) u^{\beta }(y,t) \, \text {d}y. \end{aligned}$$

For our diffusion tensor $\mathbb {D}= \left( d_{ij}\right) _{i,j=1,...,n}$, we assume that $d_{ij}\in C^{1}(\bar{\Omega })$. Moreover, $\mathbb {D}$ satisfies the uniform parabolicity and boundedness condition, i.e., there are $B_1,\, B_2 >0$ such that for all $\xi \in \mathbb {R}^n$ and $x \in \bar{\Omega }$ it holds that

$$\begin{aligned} B_1 |\xi |^2 \le \sum _{i, j =1}^n d_{ij}(x) \xi _j \xi _i \le B_2 |\xi |^2. \end{aligned}$$

(3.2)

Additionally, we assume that for $x \in \partial \Omega$ and $\xi \in \mathbb {R}^n$ with $\xi \cdot \nu = 0$ on $\partial \Omega$ and $|\xi | \ne 0$ it holds that

$$\begin{aligned} 4 \sum _{i,j=1}^n d_{ij}\xi _i \xi _k \sum _{k,l = 1}^n d_{kl} \nu _k \nu _l - \left( \sum _{i,j=1}^n d_{ij}(\xi _i \nu _j + \xi _j \nu _i)\right) ^2 >0. \end{aligned}$$

(3.3)

Condition (3.3) is, for example, satisfied if $\mathbb {D}$ is a multiple of the identity.

The exponents $\alpha , \beta \ge 1$ satisfy (as in [35])

$$\begin{aligned} \alpha < {\left\{ \begin{array}{ll} 1+ \beta , &{}\quad n= 1,2,\\ 1+ \frac{2\beta }{n}, &{}\quad n >2.\end{array}\right. } \end{aligned}$$

(3.4)

On the remaining functions and parameters, we make the subsequent assumptions:

• $u_0 \in C(\bar{\Omega })$ and $u_0 \ge 0$,

• $h_0 \in W^{1,\infty }(\Omega )$ and $0 \le h_0 \le H$, $h_0 \not \equiv H$, where H is a positive constant,

• $\mu$ is Lipschitz-continuous with constant $L_{\mu }$, satisfying $0 \le \mu$ and $\mu (h) \ge \delta >0$ for $h \le H$,

• $g \in C^1(\mathbb {R}_0^+ \times \mathbb {R}_0^+)$ with $\nabla g \in (L^{\infty }(\mathbb {R}_0^+ \times \mathbb {R}_0^+))^2$, $0 \le g(u,0) \le G$ and $g(u, H) \le 0$ for $u \in \mathbb {R}_0^+$,

• $J \in L^p(B_{\text {diam}(\Omega )}(0))$ for some $p \in (1, \infty )$, $0 < \eta \le J$,

• $D_H > 0$.

By convention the term $C_i > 0$ denotes a positive constant for all $i \in \mathbb {N}$ (or, respectively, a positive function of its arguments).

3.1 Local existence in an approximate problem

The Stone–Weierstraß theorem implies that there is a sequence of diffusion tensors $(\mathbb {D}_l)_{l \in \mathbb {N}}$ with $\mathbb {D}_l = \left( d_{lij}\right) _{i,j=1,...,n}$ s.t. $d_{lij} \in C^{2+\vartheta }(\bar{\Omega })$ for $\vartheta \in (0,1)$ and $\mathbb {D}_l \rightarrow \mathbb {D}$ in $C^1(\bar{\Omega })^{n\times n}$ for $l\rightarrow \infty$. Moreover, $\mathbb {D}_l$ satisfies (3.3) and the uniform parabolicity condition for all $l \in \mathbb {N}$, i.e., there are $0< D_1< B_1< B_2 < D_2$ such that for all $\xi \in \mathbb {R}^n$, $x \in \bar{\Omega }$ and $l \in \mathbb {N}$ it holds that

$$\begin{aligned} D_1 |\xi |^2 \le \sum _{i, j =1}^n d_{lij}(x) \xi _j \xi _i \le D_2 |\xi |^2. \end{aligned}$$

(3.5)

For $l \in \mathbb {N}$ we consider the approximate problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _tu_l = \nabla \nabla :(\mathbb {D}_l(x)u_l) + \nabla \cdot (\mathbb {D}_l(x)u_l\nabla h_l) + \mu (h_l) u^{\alpha }_l (1- J *u^{\beta }_l), &{} x\in \Omega , \, t> 0,\\ \partial _th_l = D_H \Delta h_l + g(u_l,h_l), &{} x \in \Omega , \, t> 0,\\ (\mathbb {D}_l(x)\nabla u_l + \nabla \cdot \mathbb {D}_l(x)u_l + \mathbb {D}_l (x) u_l \nabla h_l) \cdot \nu = \nabla h_l \cdot \nu = 0, &{} x \in \partial \Omega , \, t>0,\\ u_l(x,0) = u_0(x), \, h(x,0) = h_0(x), &{} x \in \Omega . \end{array}\right. } \end{aligned}$$

(3.6)

Lemma 3.1

For all $l \in \mathbb {N}$ there are $T_{max}>0$ and a weak solution $(u_l,h_l)$ of (3.6) such that for all $T \in (0,T_{max})$ it holds that $u_l \in C(\bar{\Omega }\times [0,T])) \cap L^2(0,T;H^1(\Omega ))$ and⁷$h_l \in C(\bar{\Omega }\times [0,T]) \cap L^{\infty }(0,T;W^{1,{\infty }}(\Omega )) \cap W^{2,1}_{2}(\Omega \times (0,T))$ and (u, h) satisfies for a.e. $t \in (0,T)$ and all $\eta \in W^{1,1}_2(\Omega \times (0,T))$ that

$$\begin{aligned}&\int \limits _{\Omega } u_l(x,t) \eta (x,t) \,\textrm{d}x - \int \limits _0^t \int \limits _{\Omega } u_l \eta _t \,\textrm{d}x\,\textrm{d}s + \int \limits _0^t \int \limits _{\Omega } \left( \nabla \cdot \mathbb {D}_l u_l + \mathbb {D}_l \nabla u_l + \mathbb {D}_l u_l\nabla h_l\right) \cdot \nabla \eta \,\textrm{d}x\,\textrm{d}s \nonumber \\&\quad = \int \limits _0^t \int \limits _{\Omega } \mu (h_l)u^{\alpha }_l (1- J *u^{\beta }_l)\eta \,\textrm{d}x\,\textrm{d}s + \int \limits _{\Omega } u_0(x) \eta (x,0) \, \textrm{d}x, \end{aligned}$$

(3.7)

$$\begin{aligned}&u_l(0) = u_0 \text { in } L^2(\Omega ) \end{aligned}$$

(3.8)

and

$$\begin{aligned} \partial _th_l&= D_H \Delta h_l + g(u_l,h_l) \quad&\text { a.e. in } \Omega \times (0,T_{max}) \end{aligned}$$

(3.9)

$$\begin{aligned} \nabla h_l \cdot \nu&= 0&\text { a.e. in } \partial \Omega \times (0,T_{max}), \end{aligned}$$

(3.10)

$$\begin{aligned} h_l(0)&= h_0&\text { in } H^1(\Omega ). \end{aligned}$$

(3.11)

It holds either $T_{max}= \infty$ or $T_{max}< \infty$ and

$$\begin{aligned} \lim \limits _{t \nearrow T_{max}} \left( \Vert u_l(\cdot ,t)\Vert _{L^{\infty }(\Omega )} + \Vert h_l(\cdot , t)\Vert _{W^{1,{\infty }}(\Omega )} \right) = \infty . \end{aligned}$$

(3.12)

Proof

Fix $l \in \mathbb {N}$. Due to the Stone–Weierstrass theorem there is a sequence $(u_{0k})_{k \in \mathbb {N}} \subset C^{0,1}(\bar{\Omega })$, $u_{0k} \ge 0$ with limit $u_0$ in $C(\bar{\Omega })$. We set $M:= \sup _{k \in \mathbb {N}} \Vert u_{0k}\Vert _{L^{\infty }(\Omega )} < \infty$. For $h<0$ and $\bar{u}\ge 0$ extend the coefficients by

$$\begin{aligned} g(\bar{u},h):= 2 g(\bar{u},0) - g(\bar{u},-h) \text { and } \mu (h):= \mu (-h). \end{aligned}$$

We show the existence of a solution $(u_{lk},h_{lk})$ of (3.6) with initial value $u_{0k}$ instead of $u_0$ in the sense of (3.7) and (3.9) for $k \in \mathbb {N}$ by showing the existence of a fixed point of the operator F introduced below similarly to [51]. Namely, we define for some small enough $T>0$ the set

$$\begin{aligned} S:= \{ \bar{u}\in L^{\infty }(\Omega \times (0,T))\, : \, 0 \le \bar{u}\le M+1 \text{ a.e. } \text{ in } \Omega \times (0,T)\}. \end{aligned}$$

For $\bar{u}\in S$ we consider the IBVPs

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t u_{lk} = \nabla \nabla :(\mathbb {D}(x)u_{lk}) + \nabla \cdot (\mathbb {D}(x)u_{lk} \nabla h_{lk}) + \mu (h_{lk}) \bar{u}^{\alpha -1} (1- J *\bar{u}^\beta )u_{lk}, &{} x\in \Omega , \, t \in (0,T),\\ (\mathbb {D}(x)\nabla u_{lk} + \nabla \cdot \mathbb {D}(x)u_{lk}+\mathbb {D}(x) u_{lk} \nabla h_{lk}) \cdot \nu = 0, &{} x \in \partial \Omega , \, t \in (0,T),\\ u_{lk}(x,0) = u_{0k}(x), &{} x \in \Omega , \end{array}\right. } \end{aligned}$$

(3.13)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _th_{lk} = D_H \Delta h_{lk} + g(\bar{u},h_{lk}), &{} x \in \Omega , \, t \in (0,T),\\ \nabla h_{lk} \cdot \nu = 0, &{} x \in \partial \Omega , \, t\in (0,T),\\ h_{lk}(x,0) = h_0(x), &{} x \in \Omega . \end{array}\right. } \end{aligned}$$

(3.14)

Here, T can be chosen independent of $\bar{u}$ and k. Through a fixed point argument similar to [27], we conclude that there is a unique function $h_{lk} \in L^{\infty }(0,T;W^{1,\infty }(\Omega ))$ that satisfies

$$\begin{aligned} h_{lk} = e^{tD_H \Delta }h_0 + \int \limits _0^t e^{(t-s)D_H \Delta } g(\bar{u},h_{lk}) \, \text {d}s. \end{aligned}$$

(3.15)

Moreover, $h_{lk}$ is the unique weak solution of (3.14) in the sense that for a.e. $t \in (0,T)$ and all $\eta \in W^{1,1}_2(\Omega \times (0,T))$ it holds that

$$\begin{aligned}&\int \limits _{\Omega } h_{lk}(x,t) \eta (x,t) \,\textrm{d}x - \int \limits _0^t \int \limits _{\Omega } h_{lk} \eta _t \,\textrm{d}x\,\textrm{d}s + D_H \int \limits _0^t \int \limits _{\Omega } \nabla h_{lk} \cdot \nabla \eta \,\textrm{d}x\,\textrm{d}s\\&\quad = \int \limits _0^t \int \limits _{\Omega } g(\bar{u},h_{lk}) \eta \,\textrm{d}x\,\textrm{d}s + \int \limits _{\Omega } h_0(x) \eta (x,0) \, \textrm{d}x. \end{aligned}$$

As in Lemma 3.3 and due to Theorem IV.9.1 (and the remark at the end of that section) in [33], it follows that

(3.16)

and

(3.17)

Hence, $h_{lk}$ solves (3.14) in the sense of (3.9). Moreover, the continuity of $h_{lk}$ follows from Theorem 4 in [16] due to $W^{2,1}_2(\Omega \times (0,T)) \subset C(0,T;L^2(\Omega ))$ and the embedding of $W^{1,\infty }(\Omega )$ into some Hölder space on $\Omega$. Now, Theorems III.5.1 and 7.1 in [33] (that also hold for our no-flux boundary condition), Theorem 4 in [16], and Gronwall’s inequality imply that there is a unique $u_{lk}$ in the space $S \cap C^{\kappa ,\frac{\kappa }{2}}(\bar{\Omega }\times [0,T])$, such that it solves (3.13) in the sense of (3.7) (with $u_{0k}$ instead of $u_0$) and satisfies

(3.18)

for some $\kappa \in (0,1)$. Note that , and are independent from $\bar{u}$ and k. Hence, the operator

$$\begin{aligned} F:S \mapsto S, \quad \bar{u}\mapsto u_{lk}, \end{aligned}$$

where $u_{lk}$ solves (3.13) for $\bar{u}$ in the sense of (3.7), is well-defined. Moreover, as $C^{\kappa ,\frac{\kappa }{2}}(\bar{\Omega }\times [0,T])\hookrightarrow \hookrightarrow C(\bar{\Omega }\times [0,T])$ due to the Arzelà–Ascoli theorem, F maps bounded sets on precompact ones. To apply the Leray–Schauder theorem it remains to show that F is closed and, consequently, a compact operator. Let

$$\begin{aligned} \bar{u}_m&\underset{m \rightarrow \infty }{\rightarrow }\ \bar{u}\text { in } L^{\infty }(\Omega \times (0,T)) \end{aligned}$$

(3.19)

$$\begin{aligned} u_{lkm}:= F(\bar{u}_m)&\underset{m \rightarrow \infty }{\rightarrow }\ u_{lk} \text { in } L^{\infty }(\Omega \times (0,T)). \end{aligned}$$

(3.20)

We want to show that $F(\bar{u}) = u_{lk}$.

Let $h_{lkm}$ be the solution of (3.14) that corresponds to $\bar{u}_m$ for $m \in \mathbb {N}$. Due to (3.17), we conclude from the Lions–Aubin lemma and the Banach–Alaoglu theorem that there are $h_{lk} \in W^{2,1}_2(\Omega \times (0,T))$ and subsequences

$$\begin{aligned} h_{lkm_{o}}&\underset{o \rightarrow \infty }{\rightharpoonup }\ h_{lk} \text { in } L^2(0,T;H^2(\Omega )), \nonumber \\ h_{lkm_{o}}&\underset{o \rightarrow \infty }{\rightarrow }\ h_{lk} \text { in } L^2(0,T;H^1(\Omega )) \text { and a.e. in } \Omega \times (0,T),\nonumber \\ \partial _t h_{lkm_{o}}&\underset{o \rightarrow \infty }{\rightharpoonup }\ \partial _t h_{lk} \text { in } L^2( \Omega \times (0,T)). \end{aligned}$$

(3.21)

Therefore, due to (3.21) and the Lipschitz-continuity of g for a.e. $t \in (0,T)$ and all $\eta \in W_2^{1,1}(\Omega \times (0,T))$ it holds that $h_{lk}$ is a solution of (3.14) in the sense of (3.9).

From (3.7) we conclude as in [33] that for a.e. $t\in (0,T)$ and all $\eta \in W_2^{1,1}(\Omega \times (0,T))$ it holds that

$$\begin{aligned}&\frac{1}{2} \Vert u_{lkm}(\cdot ,t)\Vert _{L^2(\Omega )}^2 + \int \limits _0^t \int \limits _{\Omega } \left( \nabla \cdot \mathbb {D}_l u_{lkm} + \mathbb {D}_l \nabla u_{lkm} + \mathbb {D}_l u_{lkm} \nabla h_{lkm}\right) \cdot \nabla u_{lkm} \, \text {d}x\, \text {d}s \nonumber \\&\quad = \int \limits _0^t\int \limits _{\Omega } \mu (h_{lkm})\bar{u}_m^{\alpha -1}(1-J*\bar{u}_m^{\beta })u_{lkm}^2 \, \text {d}x \, \text {d}s + \frac{1}{2}\Vert u_{0k}\Vert _{L^2(\Omega )}^2. \end{aligned}$$

(3.22)

Using Hölder’s and Young’s inequalities and (3.16), we estimate

(3.23)

Inserting this into (3.22) and using (3.16), Young’s inequality, the continuity of $h_{lk}$ and the Lipschitz-continuity of $\mu$, we conclude that for a.e. $t \in (0,T)$ it holds

From Gronwall’s inequality, we obtain a constant such that for all $m \in \mathbb {N}$.⁸ Hence, the Banach–Alaoglu theorem implies that (by switching to a subsequence, if necessary)

$$\begin{aligned} \nabla u_{lkm_{o}} \underset{{o} \rightarrow \infty }{\rightharpoonup } \nabla u_{lk} \text { in } L^2(\Omega \times (0,T)). \end{aligned}$$

(3.24)

Then, (3.19)–(3.21), (3.24) and the dominated convergence theorem imply that $u_{lk}$ is a solution of (3.13) in the sense of (3.7), and therefore $F(\bar{u}) = u_{lk}$ and F is a compact operator. Consequently, by a Leray–Schauder argument we obtain the existence of a fixed point $u_{lk}$ of F, that satisfies for a.e. $t \in (0,T)$ and all $\eta \in W_2^{1,1}(\Omega )$ the weak formulation (3.7) for $u_{0}$ replaced by $u_{0k}$.

Now, (3.18) and the compact embedding of $C^{\kappa ,\frac{\kappa }{2}}(\bar{\Omega }\times [0,T])$ in $C(\bar{\Omega }\times [0,T])$ imply that there is a convergent subsequence of $(u_{lk})_k$ such that

$$\begin{aligned} u_{lk_o} \underset{o \rightarrow \infty }{\rightarrow }\ u_{l} \text { in } C(\bar{\Omega }\times [0,T]). \end{aligned}$$

Then, with the same arguments as before we obtain the desired weak solution $(u_{l},h_{l})$ of (3.6).

Finally, for such pair property (3.12) follows from a standard extensibility argument. $\square$

Theorem 3.2

There is $T_{max}\in (0, \infty ]$ and a unique solution $(u_l,h_l)$ of (3.6) with $0 \le u_{l}$ and $0 \le h_{l} {<} H$,

$$\begin{aligned} u_{l},h_{l} \in C(\bar{\Omega }\times [0, T_{max})) \cap C^{2,1}( \bar{\Omega }\times (0, T_{max})). \end{aligned}$$

(3.25)

Proof

1. Regularity: Let ${l \in \mathbb {N}},$ $0< T_1<T_{max}$ and consider the weak solution $(u_l,h_l)$ from Lemma 3.1. Again from Theorem 4 in [16] it follows that $u_l, h_l \in C^{\lambda , \frac{\lambda }{2}}(\bar{\Omega }\times (0,T_1])$ for some $\lambda \in (0,1)$. Combining this with the Lipschitz continuity of g, Theorem III.12.2 in [33] implies $h_l \in C^{2+\lambda , 1+\frac{\lambda }{2}}(\Omega \times (0,T_1))$.

Further, we know from Lemma 3.1 that $h_l \in W_2^{2,1}(\Omega \times (0,T)) \cap C(\bar{\Omega }\times [0,T_1])$ and hence, for a.e. $T_0 \in (0,T_1)$ it holds that $h_l(\cdot ,T_0) \in H^2(\Omega ) \cap L^{\infty }(\Omega )$ and $\nabla h_l(\cdot , T_0) \cdot \nu = 0$ a.e. on $\partial \Omega$.

If $h_l(\cdot , T_0) \in W_r^2(\Omega ) \cap L^{\infty }(\Omega )$ for some $r \in (1,\infty )$, from the Gagliardo–Nirenberg inequality (see, e.g., Corollary 5.1 in [6]) it follows that $h_l(\cdot ,T_0) \in W_{r+1}^{2-\frac{1}{r+1}}(\Omega )$. Then, Theorem IV.9.1 in [33] implies that $h_l \in W_{r+1}^{2,1}(\Omega \times (T_0,T_1))$. We start with $r=2$ and apply this procedure iteratively until $h_{l} \in W_{r^*}^{2,1}(\Omega \times (T_0,T_1))$ for some $r^* > n+2$. Then, $W_{r^*}^{2,1}(\Omega \times (T_0,T_1)) \hookrightarrow C^{1+\lambda ^*,\frac{1+ \lambda ^*}{2}}(\bar{\Omega }\times [T_0,T_1])$ for some $\lambda ^* \in (0,1)$. Consequently, $h_{l} \in C^{2,1}(\Omega \times (0,T_1))$ with $\nabla h \in C(\bar{\Omega }\times (0,T_1])$ is a classical solution of the heat equation in (3.6). Finally, Theorem 5.18 in [36] implies that $h_{l} \in C^{2,1}(\bar{\Omega }\times (0, T_{max}))$. This follows analogously for $u_{l}$, thereby using Theorem 2.1 from [15] instead of Theorem IV.9.1 in [33].

The boundedness and nonnegativity of $h_l$ ($0 \le h_l < H$) follow from the comparison principle of the semilinear heat equation with Neumann boundary condition and our assumptions on g.

2. Uniqueness: With an ansatz similar to [4] we want to show the uniqueness of the solution. Assume that there are two solutions $(u_{l,1},h_{l,1}), \, (u_{l,2}, h_{l,2})$ of (3.6) satisfying (3.25). The functions $h_{l,1}$ and $h_{l,2}$ satisfy

$$\begin{aligned} \partial _t (h_{l,1} -h_{l,2}) = D_H \Delta (h_{l,1} - h_{l,2}) + g(u_{l,1},h_{l,1}) -g(u_{l,2},h_{l,2}) \end{aligned}$$

in $\Omega \times (0,T_1)$. We multiply this equation with $h_{l,1} -h_{l,2}$ and integrate over $\Omega$. Then, using the boundary condition, the Lipschitz continuity of g, and Young’s and Gronwall’s inequalities, we conclude

(3.26)

Moreover, we can rewrite

$$\begin{aligned} \partial _t(u_{l,1}-u_{l,2}) =&\nabla \nabla :(\mathbb {D}_{l}(u_{l,1}-u_{l,2})) + \nabla \cdot (\mathbb {D}_{l}(u_{l,1}-u_{l,2})\nabla h_1) + \nabla \cdot (\mathbb {D}_{l} u_{l,2}\nabla (h_{l,1}-h_{l,2})) \\&+ (\mu (h_{l,1})-\mu (h_{l,2}))u^{\alpha }_1(1-J*u^{\beta }_1) + \mu (h_{l,2}) (u^{\alpha }_1-u^{\alpha }_2)(1-J*u^{\beta }_1) + \mu (h_{l,2}) u^{\alpha }_2J*(u^{\beta }_2-u^{\beta }_1). \end{aligned}$$

Again, we multiply this equation with $u_{l,1} - u_{l,2}$ and integrate over $\Omega$ for $t \in (0,T_1)$. Then, using the boundary condition together with Young’s, Hölder’s, and the Gagliardo–Nirenberg inequalities (also compare (3.23)), the mean value theorem, and the boundedness of $u_{l,1}$ and $u_{l,2}$ on $\Omega \times (0,T_1)$ by some , it follows that

Integrating over (0, t) for $t \in (0,T_1)$ and using (3.26) we conclude that for a.e. $t \in (0,T_1)$ it holds that

Consequently, Gronwall’s inequality implies $u_1 \equiv u_2$ a.e. on $\Omega \times (0,T_1).$ $\square$

3.2 Global existence and boundedness of u in the approximate problem

Lemma 3.3

It holds that

Proof

With Lemma 1.3 from [55] and (3.15), we estimate for $t \in (0,T_{max})$ that

holds for $q \in (1,\infty )$, where $\lambda _1$ is the first eigenvalue of $-\Delta$ on $\Omega$ with Neumann boundary condition. Using the properties of g and the boundedness of h, we obtain that for $t \in (T_0,T_{max})$ it holds that

Consequently,

$\square$

We will show the global boundedness of u as in the proof of Theorem 1.1 in [35].

Lemma 3.4

It holds that $u_l \in L^{\infty }(0,T_{max};L^q(\Omega ))$ for $q \in [1, \infty )$.

Proof

Let $q \ge \max \{1, \beta + \alpha -1 \}$. Due to (3.25) the terms in the estimates below are well-defined for a.e. $t \in (0,T_{max})$. Multiplying the first equation of (3.6) by $q u_l^{q-1}$, integrating over $\Omega$ and using partial integration, we obtain

$$\begin{aligned} \frac{d}{dt}\int \limits _{\Omega } u_l^q \, \text {d}x =&q\int \limits _{\Omega } \nabla \cdot \left( \mathbb {D}_l \nabla u_l + \nabla \cdot \mathbb {D}_l u_l^{q-1} + \mathbb {D}_l u_l \nabla h_l \right) u_l^{q-1} + \mu (h_l) u^{q-1+\alpha }_l (1- J *u^{\beta }_l) \,\text{ d }x \nonumber \\ =&- q(q-1) \int \limits _{\Omega } u_l^{q-2} (\mathbb {D}_l \nabla u_l) \cdot \nabla u_l + u_l^{q-1} \nabla \cdot \mathbb {D}_l \cdot \nabla u_l +u_l^{q-1} (\mathbb {D}_l \nabla h_l) \cdot \nabla u_l \text{ d }x \nonumber \\ {}&+ q\int \limits _{\Omega } \mu (h_l) u^{q-1+\alpha }_l (1- J *u^{\beta }_l) \, \text {d}x. \end{aligned}$$

(3.27)

Using the uniform parabolicity of $\mathbb {D}$, we estimate

$$\begin{aligned} q(q-1) \int \limits _{\Omega } u_l^{q-2} (\mathbb {D}_l \nabla u_l) \cdot \nabla u_l \, \text {d}x = \frac{4(q-1)}{q} \sum _{i,j = 1}^n \int \limits _{\Omega } d_{_lij} \left( u_l^{\frac{q}{2}}\right) _{x_i}\left( u_l^{\frac{q}{2}}\right) _{x_j} \, \text {d}x \ge \frac{4(q-1)}{q}{D_1} \int \limits _{\Omega } |\nabla u_l^{\frac{q}{2}}|^2 \, \text {d}x. \end{aligned}$$

Further, due to Young’s inequality we obtain the estimate

$$\begin{aligned}&q(q-1) \left| \int \limits _{\Omega } u^{q-1} (\nabla \cdot \mathbb {D})\cdot \nabla u + u^{q-1}(\mathbb {D}\nabla h) \cdot \nabla u \, \text{ d }x \right| \\ {}&\quad \le \frac{2(q-1)}{q }D_1 \int \limits _{\Omega } |\nabla u^{\frac{q}{2}}|^2 \, \text{ d }x + \frac{(q-1)}{D_1}\left( \Vert \nabla \cdot \mathbb {D}\Vert _{\infty }^2 + \Vert \mathbb {D}\Vert _{\infty }^2 \Vert \nabla h\Vert _{\infty }^2 \right) \int \limits _{\Omega } u^q \, \text{ d }x. \end{aligned}$$

Inserting these estimates into (3.27) and using our assumptions on $\mu$ and J, the boundedness of h, and

$$\begin{aligned} \int \limits _{\Omega } u_l^q \, \text {d}x \le \int \limits _{\Omega } u_l^{q + \alpha -1} \, \text {d}x + |\Omega |, \end{aligned}$$

(3.28)

it follows that

(3.29)

where

Adding on both sides of (3.29) and using Young’s inequality one more time, we obtain

(3.30)

Similarly to Step 1 in the proof of Theorem 1.1 in [35] it follows that

where

with

Here, $C_S >0$ denotes the Sobolev embedding constant from page 8 in [35], $C_P>0$ the constant from the Poincaré inequality, and

$$\begin{aligned} s {\left\{ \begin{array}{ll} =\infty , &{} n=1\\ \in (\frac{2(q+\alpha -1+\beta )}{q-\alpha +1+\beta },\infty ), &{}n=2\\ =\frac{2n}{n-2}, &{} n>2. \end{array}\right. } \end{aligned}$$

(3.31)

Hence, for $t \in (0,T_{max})$ we conclude that

(3.32)

Hence, for $t \in (0,T_{max})$ and $q \ge \max \{\beta +\alpha -1,1\}$ we obtain from (3.32) the upper bound

(3.33)

$\square$

Remark 3.5

As in [35] we cannot directly conclude from Lemma 3.4 that $u_{l}$ is bounded on $\Omega \times (0,T_{max})$ as

Theorem 3.6

For all $l\in \mathbb {N}$ there is a unique bounded and nonnegative solution $(u_l,h_l)$ of (3.6) consisting of nonnegative functions

$$\begin{aligned} u_l,h_l \in C(\bar{\Omega }\times [0, \infty )) \cap C^{2,1}( \bar{\Omega }\times (0, \infty )) \end{aligned}$$

and $h_l < H$. Thereby, there is some that does not depend on l s.t. .

Moreover, if $\Omega$ is convex for some ’small’ enough choice of parameters specified in (3.38) and (3.39) below, then for any $K>1$

(3.34)

where

for some function G to be adequately chosen and we set s from (3.31) equal to $\infty$ for $n=2$.

Proof

Let $l\in \mathbb {N}$. We proceed with a Moser iteration as in Step 2 in Theorem 1.1. in [35].

Set $q_k:= 2^k + a$ with $a:= \frac{2(s-1)(\alpha -1)}{s-2}$ for $k \in \mathbb {N}$ and s as in (3.31). Analogously to [35] we obtain for $t \in (0,T_{max})$ the estimate

(3.35)

where

As $\mathbb {D}_l$ tends to $\mathbb {D}$ in $C^1(\bar{\Omega })^{n\times n}$, there is s.t. for all $l \in \mathbb {N}$. We can further estimate that

for

For $k\in \mathbb {N}$ and $t\in (0,T_{max})$ we set

$$\begin{aligned} y_k(t) := \Vert u_l(\cdot ,t)\Vert _{L^{q_k}}^{q_k}. \end{aligned}$$

Inserting this into (3.35) we obtain

Moreover, we estimate that

with

(3.36)

Hence, from Lemma 2.1 in [35] it follows that for $m \ge 1$ and $t \in (0,T_{max})$ it holds that

Consequently, for $t \in (0, T_{max})$ and $m \ge 1$ it holds that

(3.37)

Due to (3.33) and

there is s.t. for all $l \in \mathbb {N}$.

Consequently, $u_l$ is bounded on $\bar{\Omega }\times [0,T_{max})$. Combining this with the boundedness of $h_l$, Lemma 3.3 and (3.12) in Theorem 3.2, $T_{max}= \infty$ follows.

If $\Omega$ is convex we proceed as in Step 3 of [35]. First, we fix some m and choose our parameters sufficiently ’small’ such that it holds that

(3.38)

and

(3.39)

This depends on our choice of $\mathbb {D}$, $\mu$, g, $\Vert \nabla h_0\Vert _{L^{ \infty }}$, and $D_H$. Consequently, we conclude as in [35] that for any $K>1$ we find ’small’ enough parameters (satisfying (3.38) and (3.39) for some large m) such that (3.34) holds, where due to Theorems 2.1 and 3.1 from [38] we have

for

$$\begin{aligned} G(s,n):= \frac{\pi ^{\frac{s}{n}}\Gamma (\frac{s-2}{2s}n)}{n\Gamma (\frac{s-1}{s}n)}\left( \frac{\Gamma (n)}{\Gamma (\frac{n}{2})}\right) ^{\frac{s-2}{s}} \end{aligned}$$

and we set s from (3.31) equal to $\infty$ for $n=2$. $\square$

3.3 Global existence and boundedness in the original problem

Theorem 3.7

There is a unique bounded and nonnegative weak solution (u, h) of (3.1) s.t. for a.e. $T >0$ it holds that $u \in C(0,T;L^2(\Omega )) \cap L^2(0,T;H^1(\Omega ))$ with $\partial _t u \in L^2(0,T;(H^1(\Omega ))^*)$ and $h \in C(0,T; H^1(\Omega )) \cap W^{2,1}_{2}(\Omega \times (0,T))$ and u satisfies (3.7) and (3.8) (with T instead of t) for all $\eta \in W^{1,1}_2(\Omega \times (0,T))$ and h satisfies (3.9) - (3.11) a.e. in $\Omega \times (0,\infty )$.

Moreover, it holds that $h \le H$ and $\nabla h \in L^{\infty }(\Omega \times (0,\infty ))$. If $\Omega$ is convex then u satisfies (3.34) for the parameter choice from Theorem 3.6.

Proof

Let $\varphi \in H^1(\Omega )$. Obviously, for a.e. $T>0$ and each $l \in \mathbb {N}$ the function $u_l$ satisfies

$$\begin{aligned} \int \limits _{\Omega } \partial _tu_{l} \varphi \, \text {d}x&= - \int \limits _{\Omega } ( \mathbb {D}_l \nabla u_l + \nabla \cdot \mathbb {D}_l u_l + \mathbb {D}_l u_l\nabla h_l) \cdot \nabla \varphi \, \text {d}x + \int \limits _{\Omega } \mu (h_l) u_l^{\alpha } (1-J*u_l^\beta ) \, \text {d}x, \end{aligned}$$

(3.40)

as it is a classical solution. Due to Theorem IV.9.1 (and the remark at the end of that chapter) in [33], $h_l$ satisfies

(3.41)

where is independent from l due to the properties of g and $h_l {<} H$ for all $l\in \mathbb {N}$.

Setting $\varphi =u_l$ in (3.40) and using Hölder’s and Young’s inequalities, the facts that , and the uniform boundedness of $u_l$ from Lemma 3.6, we can estimate that

Consequently, from Gronwall’s inequality follows

Similarly it follows that

Putting this together with the uniform boundedness of $u_l$ and (3.41), the Lions–Aubin and Banach–Alaoglu theorems imply that there are $u \in C(0,T;L^2(\Omega )) \cap L^2(0,T;H^1(\Omega ))$ with $\partial _t u \in L^2(0,T;(H^1(\Omega ))^*)$ and $h \in C(0,T; H^1(\Omega )) \cap W^{2,1}_{2}(\Omega \times (0,T))$ s.t. (after switching to a subsequence if necessary)

$$\begin{aligned} u_l&\underset{l \rightarrow \infty }{\rightarrow }\ u&\text { in } L^2(\Omega \times (0,T)) \text { and pointwise a.e.}, \nonumber \\ u_l&\underset{l \rightarrow \infty }{\rightharpoonup }\ u&\text { in } L^2(0,T;H^1(\Omega )), \nonumber \\ (u_l)_t&\underset{l \rightarrow \infty }{\rightharpoonup }\ u_t&\text { in } L^2(0,T;(H^1(\Omega ))^*),\nonumber \\ h_l&\underset{l \rightarrow \infty }{\rightarrow }\ h&\text { in } L^2(0,T;H^1(\Omega )) \text { and pointwise a.e.},\nonumber \\ h_l&\underset{l \rightarrow \infty }{\rightharpoonup }\ h&\text { in } L^2(0,T;H^2(\Omega )),\nonumber \\ (h_l)_t&\underset{l \rightarrow \infty }{\rightharpoonup }\ h_t&\text { in } L^2(\Omega \times (0,T)). \end{aligned}$$

(3.42)

From this, the dominated convergence theorem, the uniform boundedness of $u_l$, $h_l$ and $\nabla h_l$ from Lemma 3.3 and the Lipschitz-continuity of $\mu$ and g, it follows that (u, h) solves (3.1) in the required sense.

The a.e. boundedness and nonnegativity of u and h follow from the pointwise convergence and the uniform boundedness and nonnegativity of $u_l$ and $h_l$. Uniqueness follows similarly to Theorem 3.2.

4 Long time behavior

We consider the long time behavior of our solution under the additional assumptions that we make from now on:

• the domain $\Omega$ is convex,

• the parameters satisfy (3.38) and (3.39),

• $u_0 \not \equiv 0$,

• we extend J by 0 to $\mathbb {R}^n{\setminus } B_{\text {diam}(\Omega )}(0)$ and assume $\Vert J\Vert _{L^1(\mathbb {R}^n)} = 1$,

• there are $h^* \in [0,H]$ and constants $C_H>0$ and $C_U \ge 0$ s.t.

  $$\begin{aligned} g(u,h)(h-h^*) \le - C_H (h-h^*)^2 + C_U u^{\alpha -1} (u^{\beta }-1)^2 \end{aligned}$$

  (4.1)

  for $0\le h\le H$ and $0 < u \le U$, where U is some upper bound on u (that exists and is independent from l, due to Theorem 3.6),

• the parameters

  

  where for all $l \in \mathbb {N}$ (see proof of Theorem 3.6), satisfy $C_A^2>4C_B$, $C_A<0$, $C_B \in (0,1)$ and

  $$\begin{aligned} C_B < -\frac{C_A}{2} + \sqrt{\frac{C_A^2}{4}-C_B} . \end{aligned}$$

Moreover, let

$$\begin{aligned} M := \left\{ \mathbb {D} \in \left( C^{2+\vartheta }(\bar{\Omega })\right) ^{n\times n}: \, (\nabla \cdot \mathbb {D} ) \cdot \nu = 0 \text { on } \partial \Omega , \, \nabla \cdot (\nabla \cdot \mathbb {D}) = 0 \text { on } \Omega \right\} . \end{aligned}$$

We assume that $\mathbb {D}$ is in the closure of M in the $(C^1(\bar{\Omega }))^{n \times n}$-norm and that the sequence $(\mathbb {D}_l)_{l\in \mathbb {N}}$ from above is the sequence in M that approaches $\mathbb {D}$.

Remark 4.1

The inequality (4.1) implies that such $h^*$ is unique and $g(1,h^*) = 0$ holds.

We proceed by combining the methods from [35] and [31].

Lemma 4.2

For all $l \in \mathbb {N}$ it holds that

$$\begin{aligned} \lim _{t\rightarrow \infty } \Vert u_l( \cdot , t)^{\frac{\alpha -1}{2}}(u_l^{\beta }(\cdot , t) - 1) \Vert _{L^2(\Omega )} = \lim _{t\rightarrow \infty } \Vert h_l( \cdot , t) -h^* \Vert _{L^2(\Omega )} = 0. \end{aligned}$$

(4.2)

Proof

Let $l \in \mathbb {N}$. We conclude from the strong maximum principle and the assumption $u_0 \not \equiv 0$ that $u_l>0$ holds in $\Omega \times (0,\infty )$.

As in [35] we define $a(s):= \frac{s}{\beta } -\frac{1}{\beta } \ln (s) - \frac{1}{\beta }$ with $a(s) \ge 0$ for $s \in (0,\infty )$. By multiplying the equation for $u_l$ in (3.6) by $u_l^{\beta - 1} - u_l^{-1}$, integrating over $\Omega$ and using partial integration and our additional assumptions on $\mathbb {D}_l$, we obtain

$$\begin{aligned}&\frac{d}{dt} \mathop \int \limits _{\Omega }a(u_l^{\beta }) \, \text {d}x\\&\quad = \mathop \int \limits _{\Omega }\nabla \cdot \left( \mathbb {D}_l \nabla u_l + \nabla \cdot \mathbb {D}_lu_l +\mathbb {D}_l u_l \nabla h_l \right) \left( u_l^{\beta -1} - u_l^{-1}\right) \, \text {d}x + \mathop \int \limits _{\Omega }\mu (h_l)u^{\alpha }_l (1- J *u^{\beta }_l)(u_l^{\beta -1} - u_l^{-1}) \, \text {d}x\\&\quad = - \mathop \int \limits _{\Omega }\left( \mathbb {D}_l \nabla u_l + \nabla \cdot \mathbb {D}_l u_l +\mathbb {D}_l u_l \nabla h_l \right) \left( (\beta -1)u^{\beta }_l + 1\right) \cdot \frac{\nabla u_l}{u_l^2} \, \text {d}x + \mathop \int \limits _{\Omega }\mu (h_l)u^{\alpha }_l (1- J *u^{\beta }_l)(u_l^{\beta -1} - u_l^{-1}) \, \text {d}x, \end{aligned}$$

where using again partial integration

$$\begin{aligned}&\mathop \int \limits _{\Omega }\nabla \cdot \mathbb {D}_l u_l ((\beta -1)u^{\beta }_l + 1)\cdot \frac{\nabla u_l}{u_l^2} \, \text {d}x \\&\quad = \mathop \int \limits _{\Omega }\nabla \cdot \mathbb {D}_l ((\beta -1)u_l^{\beta -1} + u_l^{-1}) \cdot \nabla u_l \, \text {d}x\\&\quad = \mathop \int \limits _{\Omega }\nabla \cdot \mathbb {D}_l \cdot \nabla \left( \frac{\beta - 1}{\beta }u^{\beta }_l +\ln (u_l) \right) \, \text {d}x\\&\quad = - \mathop \int \limits _{\Omega }\nabla \cdot (\nabla \cdot \mathbb {D}_l) \left( \frac{\beta -1}{\beta } u^{\beta }_l + \ln (u_l)\right) \, \text {d}x + \int \limits _{\partial \Omega } \left( \frac{\beta -1}{\beta }u^{\beta }_l +\ln (u_l)\right) (\nabla \cdot \mathbb {D}_l) \cdot \nu \text {d}\sigma = 0. \end{aligned}$$

Hence, we can estimate using the positivity of $u_l$ that

$$\begin{aligned}&\frac{d}{dt} \mathop \int \limits _{\Omega }a(u^{\beta }_l) \, \text {d}x + \mathop \int \limits _{\Omega }\left( \frac{\nabla u_l}{u_l}\right) ^T \mathbb {D}_l \frac{\nabla u_l}{u_l} \,\text {d}x \nonumber \\&\quad \le \mathop \int \limits _{\Omega }\left( (\beta -1)u^{\beta }_l + 1\right) \left| \left( \nabla h_l\right) ^T \mathbb {D}_l \frac{\nabla u_l}{u_l} \right| \, \text {d}x \nonumber \\&\qquad + \mathop \int \limits _{\Omega }\mu (h_l) u^{\alpha -1}_l \left( 1-J*u^{\beta }_l\right) \left( u^{\beta }_l-1\right) \, \text {d}x. \end{aligned}$$

(4.3)

Then, we extend $u_l$ by 0 to $\mathbb {R}^n \setminus \Omega$ and proceed similarly to the proof of Proposition 3.1 in [35] to obtain using Hölder’s inequality that

$$\begin{aligned}&\mathop \int \limits _{\Omega }\mu (h_l(x))u^{\alpha -1}_l(x)(1-J*u^{\beta }_l(x)) (u^{\beta }_l(x) -1) \, \text {d}x \nonumber \\&\quad \le \mathop \int \limits _{\Omega }\mu (h_l(x)) u_l^{\alpha -1}(x) \left( \,\,\int \limits _{\mathbb {R}^n} J(y) \, \text {d}y - \mathop \int \limits _{\Omega }J(x-y) u^{\beta }_l(y) \, \text {d}y \right) \left( u^{\beta }_l(x) -1 \right) \, \text {d}x \nonumber \\&\quad \le \mathop \int \limits _{\Omega }\mu (h_l(x)) u_l^{\alpha -1}(x) \left( \,\,\mathop \int \limits _{\Omega }J(x-y) (1- u^{\beta }_l(y)) \, \text {d}y \right) \left( u^{\beta }_l(x) -1\right) \, \text {d}x \nonumber \\&\quad \le -\mathop \int \limits _{\Omega }\mu (h_l(x)) u_l^{\alpha -1}(x) \mathop \int \limits _{\Omega }J(x-y) (u^{\beta }_l(x) - 1)^2 \, \text {d}y \, \text {d}x \nonumber \\&\qquad + \mathop \int \limits _{\Omega }\mu (h_l(x)) u_l^{\alpha -1}(x) \mathop \int \limits _{\Omega }J(x-y) (u^{\beta }_l(x) - u^{\beta }_l(y))(u^{\beta }_l(x)-1) \, \text {d}y \, \text {d}x \nonumber \\&\quad \le -(1-\varepsilon )\mathop \int \limits _{\Omega }\mathop \int \limits _{\Omega }\mu (h_l(x)) u_l^{\alpha -1}(x) J(x-y) (u^{\beta }_l(x) - 1)^2 \, \text {d}y \, \text {d}x \nonumber \\&\qquad + \frac{1}{4\varepsilon } \left( L_{\mu } H + \mu (0)\right) \mathop \int \limits _{\Omega }\mathop \int \limits _{\Omega }u_l^{\alpha -1}(x) J(x-y) (u^{\beta }_l(x) - u^{\beta }_l(y))^2 \, \text {d}y \, \text {d}x \end{aligned}$$

(4.4)

for

$$\begin{aligned} \varepsilon \in \left\{ \max \left\{ - \frac{C_A}{2} - \sqrt{\frac{C_A^2}{4} - C_B} ;C_B \right\} ,\min \left\{ - \frac{C_A}{2} + \sqrt{\frac{C_A^2}{4} - C_B} ;1 \right\} \right\} , \end{aligned}$$

where the interval on the right hand side is nonempty due to our assumptions on $C_A$ and $C_B$.

Moreover, due to the convexity of $\Omega$ and using the uniform boundedness of $(u_l)_l$ by U we can estimate

$$\begin{aligned} \mathop \int \limits _{\Omega }\mathop \int \limits _{\Omega }u_l^{\alpha -1}(x) J(x-y) (u^{\beta }_l(x) - u^{\beta }_l(y))^2 \, \text {d}y \, \text {d}x \le \left( |\text {diam}(\Omega )|\beta \right) ^2 {U^{2\beta +\alpha -1}} \mathop \int \limits _{\Omega }\frac{|\nabla u_l|^2}{u_l^2} \, \text {d}x. \end{aligned}$$

Now, inserting this in (4.4), using our assumptions on J and $\mu$, and the uniform boundedness of $(u_l)_l$, we conclude

$$\begin{aligned}&\mathop \int \limits _{\Omega }\mu (h_l(x))u^{\alpha -1}_l(x)(1-J*u^{\beta }_l(x)) (u^{\beta }_l(x) -1) \, \text {d}x \\&\quad \le \frac{1}{\varepsilon } D_1 C_B \mathop \int \limits _{\Omega }\frac{|\nabla u_l|^2}{u_l^2} \, \text {d}x - (1-\varepsilon )\delta \eta |\Omega | \mathop \int \limits _{\Omega }u^{\alpha -1}_l(u^{\beta }_l - 1)^2 \, \text {d}x \end{aligned}$$

Inserting this into (4.3), it follows that

(4.5)

Multiplying the equation for $h_l$ by $h_l - h^*$ and using (4.1), we obtain

$$\begin{aligned} \frac{1}{2} \frac{d}{dt} \mathop \int \limits _{\Omega }(h_l - h^*)^2 \, \text {d}x + D_H \mathop \int \limits _{\Omega }|\nabla h_l|^2 \, \text {d}x \le -C_H \mathop \int \limits _{\Omega }(h-h^*)^2 \, \text {d}x + C_U \mathop \int \limits _{\Omega }u^{\alpha -1}_l(u^{\beta }_l - 1)^2 \, \text {d}x. \end{aligned}$$

Further, we multiply this by and add it to (4.5) to obtain

(4.6)

(4.7)

Due to our assumptions on $C_A, C_B$ and our choice of $\varepsilon$ it holds that . Now, Gronwall’s inequality implies (4.2). $\square$

Now we can conclude uniform convergence:

Theorem 4.3

For all $l \in \mathbb {N}$ it holds that

$$\begin{aligned} \lim _{t\rightarrow \infty } \Vert u_l( \cdot , t) - c \Vert _{L^{\infty }(\Omega )} = \lim _{t\rightarrow \infty } \Vert h_l( \cdot , t) -h^* \Vert _{L^{\infty }(\Omega )} = 0, \end{aligned}$$

(4.8)

where $c \in \{0,1\}$ for $\alpha >1$ and $c=1$ for $\alpha =1$.

Proof

As in Lemma 3.10 in [52] we can conclude from Lemma 4.2 that

$$\begin{aligned} \lim _{t\rightarrow \infty } \Vert u_l(t, \cdot )^{\frac{\alpha -1}{2}}(u_l^{\beta }(t,\cdot ) - 1) \Vert _{L^{\infty }(\Omega )} = \lim _{t\rightarrow \infty } \Vert h_l(t, \cdot ) -h^* \Vert _{L^{\infty }(\Omega )} = 0. \end{aligned}$$

Combining this with the uniform continuity of $u_l$ for all $l \in \mathbb {N}$ we get the convergence stated in (4.8). $\square$

Now we can conclude pointwise convergence of u and h:

Theorem 4.4

For a.e. $x \in \Omega$ it holds that $\lim _{t\rightarrow \infty } u(x,t) = c$ and $\lim _{t\rightarrow \infty } h(x,t) = h^*$, where $c \in \{0,1\}$ for $\alpha >1$ and $c=1$ for $\alpha =1$.

Proof

For h and in the case $\alpha =1$ convergence follows directly from Theorem 4.3. We consider the case $\alpha >1$. From (3.42) we know that (after switching to a subsequence if necessary) $u_l$ converges to u pointwise a.e. in $\Omega \times (0,\infty )$. Hence, for all (x, t) the sequence $(u_l(x,t))_l$ is Cauchy and we can conclude that for large enough l the sequence $u_l(t)$ converges to the same $c \in \{0,1\}$. Hence, for a.e. (x, t) and large enough l it holds that

$$\begin{aligned} |u(x,t) - c| \le |u(x,t) - u_l(x,t)| + |u_l(x,t) -c| \rightarrow 0 \end{aligned}$$

for $t\rightarrow \infty$ and $l\rightarrow \infty$ due to (3.42) and Theorem 4.3.

5 Pattern formation: a 1D study

We want to investigate pattern formation in our model (see [39]). For this aim we adapt some of the assumptions on our functions and parameters:

• $J \in L^1(\mathbb {R})$, $J(x) = J(-x)$ for $x \in \mathbb {R}$ and $\int \limits _{\mathbb {R}} J(x) \, \textrm{d}x=1$ and $J \circledast u (x):= \int \limits _{\mathbb {R}} J(x-y)u(y) \, dy$, whereas we drop the condition that $0<\eta <J$;

• $d \in \mathbb {R}$ constant;

• there is exactly one $h^* >0$ with $g(1,h^*)= 0$, moreover, for this $h^*$ it holds that $\mu (h^*) >0$, $\partial _u g(1,h^*) \ge 0$ and $\partial _h g(1,h^*)<0$. This means that when the cancer cells are at their carrying capacity (corresponding to an acidity level $h^*$), the production of protons is increasing with the cell mass and decreasing with enhancing proton concentration. Indeed, crowded tumor cells are highly hypoxic, and a too acidic environment leads to quiescence or necrosis, thus reducing proton expression. Moreover, we assume that $\mu '(h^*)<0$, thus the growth rate is decreasing with the proton concentration in the neighborhood of the critical value $h^*$.

• w.l.o.g. we consider $\Omega = [-a,a]$ for $a \in \mathbb {R}$.

Hence, we consider the model

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t = du_{xx} + d(uh_x)_x + \mu (h) u^{\alpha }(1- J \circledast u^{\beta }), &{} x\in \Omega , \, t> 0,\\ h_t = D_H h_{xx} + g(u,h), &{} x \in \Omega , \, t> 0,\\ u_x = h_x = 0, &{} x \in \partial \Omega , \, t>0,\\ u(x,0) = u_0(x), \, h(x,0) = h_0(x), &{} x \in \Omega . \end{array}\right. } \end{aligned}$$

(5.1)

5.1 Stability in the local model without diffusion and taxis

We start by establishing the equilibria of the non-spatial local model that corresponds to (5.1), i.e.,

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t u &{}= \mu (h) u^{\alpha }(1- u^{\beta }), \\ \partial _t h &{}= g(u,h). \end{array}\right. } \end{aligned}$$

(5.2)

The biologically more interesting one is given by $(u^*,h^*) = (1,h^*)$, where $h^*$ is the unique solution of $g(1,h) = 0$. The corresponding characteristic equation of the Jacobian in $(1,h^*)$ is given by

$$\begin{aligned} \lambda ^2 + (\beta \mu (h^*)-\partial _hg(1,h^*))\lambda - \beta \mu (h^*) \partial _h g(1,h^*) = 0. \end{aligned}$$

The corresponding eigenvalues are

$$\begin{aligned} \lambda _{1} = -\beta \mu (h^*) \text { and } \lambda _2 = \partial _h g(1,h^*) \end{aligned}$$

and both have negative real parts due to the assumption $\partial _h g (1,h^*) < 0$. Hence, the steady state $(1,h^*)$ is stable in this case.

5.2 Stability in the local model with diffusion and taxis

We continue by adding again the diffusion and taxis term to the local model (5.2). Adapting the ansatz from [44] we consider perturbations of $(1,h^*)$ of the form $u = 1 + \varepsilon \bar{u}(k)$ and $h = h^* + \varepsilon \bar{h}(k)$, where $\bar{u}(k) = \tilde{u} e^{\lambda (k)t}\cos (kx)$ and $\bar{h}(k) = \tilde{h} e^{\lambda (k)t}\cos (kx)$ for $\tilde{u}, \tilde{h} \in \mathbb {R}$ and wavenumber $k \in \mathbb {N}$ and $|\varepsilon | \ll 1$. Here, $\lambda (k)$ denotes some eigenvalue of the corresponding characteristic equation. As in [42] we use the fact that $\frac{e^{ikx}+e^{-ikx}}{2} = \cos (kx)$ to ensure that our perturbations are real.

Inserting these u and h into our model and linearizing about the steady state $(1,h^*)$, we obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} \lambda (k)\bar{u} &{}= -k^2d\bar{u} - dk^2\bar{h} - \beta \mu (h^*) \bar{u},\\ \lambda (k)\bar{h} &{}= -D_Hk^2 \bar{h} + \partial _u g(1,h^*) \bar{u} + \partial _h g(1,h^*)\bar{h}. \end{array}\right. } \end{aligned}$$

(5.3)

The corresponding eigenvalues are given by

$$\begin{aligned} \lambda _{1,2}(k) = \frac{\text {tr}(J_{u,h}(k)) \pm \sqrt{\text {tr}(J_{u,h}(k))^2 -4 \det (J_{u,h}(k))}}{2}, \end{aligned}$$

where we denote by $J_{u,h}$ the Jacobian of the right hand side in system (5.3) at $(1,h*)$ and its determinant and trace are, respectively, given by

$$\begin{aligned} \text {tr}(J_{u,h}(k))=&-(d+D_H)k^2-\beta \mu (h^*) + \partial _h g(1,h^*) <0,\\ \det (J_{u,h}(k))=&dD_H k^4 + (d (\partial _u g(1,h^*) - \partial _h g(1,h^*)) + \beta \mu (h^*)D_H)k^2 \\&-\beta \mu (h^*)\partial _hg(1,h^*)>0. \end{aligned}$$

Hence, the equilibrium $(1,h^*)$ is stable. The local model does not lead to any Turing type patterns.

5.3 Stability in the nonlocal model

We consider u and h as in the previous section and linearize the convolution term about $(1,h^*)$ similarly to [44]. Hence, inserting u in the convolution term and using the symmetry of J, we compute that

$$\begin{aligned} J*u^{\beta }\approx 1+ \varepsilon \beta \bar{u} (2\pi )^{\frac{1}{2}}\hat{J}(k). \end{aligned}$$

Here, $\hat{J}$ denotes the Fourier transform of J. Hence, linearizing system (5.1), we obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} \lambda (k)\bar{u} &{}= -dk^2\bar{u} - dk^2\bar{h} - \beta \mu (h^*)(2\pi )^{\frac{1}{2}}\hat{J}(k) \bar{u},\\ \lambda (k)\bar{h} &{}= -D_Hk^2 \bar{h} + \partial _u g(1,h^*) \bar{u} + \partial _h g(1,h^*)\bar{h}. \end{array}\right. } \end{aligned}$$

(5.4)

The corresponding eigenvalues are as above given by

$$\begin{aligned} \lambda _{1,2}(k) = \frac{\text {tr}(J_{u,h}(k)) \pm \sqrt{\text {tr}(J_{u,h}(k))^2 -4 \det (J_{u,h}(k))}}{2}, \end{aligned}$$

where we denote by $J_{u,h}$ the Jacobian of the right hand side in (5.4) at $(1,h^*)$ and its trace and determinant are given by

$$\begin{aligned} \text {tr}(J_{u,h})(k)=&-(d+D_H)k^2-\beta \mu (h^*)(2\pi )^{\frac{1}{2}}\hat{J}(k) + \partial _h g(1,h^*),\\ \det (J_{u,h})(k)=&dD_H k^4 + (d (\partial _u g(1,h^*) - \partial _h g(1,h^*)) + \beta \mu (h^*)(2\pi )^{\frac{1}{2}}\hat{J}(k)D_H)k^2\\&-\beta \mu (h^*)(2\pi )^{\frac{1}{2}}\hat{J}(k)\partial _hg(1,h^*). \end{aligned}$$

The sign of the real part of the eigenvalues is ambiguous here and depends especially on the sign of $\hat{J}(k)$, which depends on k. As above, we have stability here if

$$\begin{aligned} \text {tr}{J_{u,h}(k)}<0 \text { and } \det {J_{u,h}(k)} >0 \end{aligned}$$

(5.5)

for all $k = \frac{\pi }{a} z$, where $z \in \mathbb {Z}$. We make this restriction due to our boundary condition $u_x = h_x =0$.

Now, we are looking for a critical $k_c$ (that is not necessarily of the form $\frac{\pi }{a} z$) depending on our choice of parameters, where we distinguish as in [42] the occurrence of Turing instabilities in the case $\text {Im}(\lambda (k_c)) = 0$ for some arbitrary critical $k_c$, Hopf instabilities in the case $\text {Im}(\lambda (0)) \ne 0$, and wave instabilities in the case $\text {Im}(\lambda (k_c))\ne 0$ for some critical $k_c\ne 0$. If $\hat{J}$ is symmetric it suffices to consider only positive $k_c$.

A Turing bifurcation can occur if we find $k_c$ such that

$$\begin{aligned} \det (J_{u,h})(k_c)= 0 \text { and } \text {tr}(J_{u,h})(k_c)<0. \end{aligned}$$

Now, rewriting these conditions we conclude that the equality

$$\begin{aligned} \hat{J}(k_c)= - d\frac{k_c^2}{\beta (2\pi )^{\frac{1}{2}}\mu (h^*)} \left( 1 + \frac{\partial _u g(1,h^*)}{D_Hk_c^2-\partial _hg(1,h^*)}\right) \end{aligned}$$

(5.6)

and the inequality

$$\begin{aligned} \frac{\partial _h g(1,h^*)-(d+D_H)k_c^2}{\beta \mu (h^*) (2\pi )^{\frac{1}{2}}} < \hat{J}(k_c) \end{aligned}$$

(5.7)

have to hold for one or several critical $k_c$ in a set $K_c$, whereas (5.5) holds for all $k \notin K_c$ that are of the form $\frac{\pi }{n}z$. Such $k_c$ exist depending on the choice of parameters, on the functions $\mu$ and g, and especially on the sign of the Fourier transform of J. Moreover, due to our assumptions the terms on the right-hand side of (5.6) and on the left-hand side of (5.7) are negative and tend to $- \infty$ for $k\rightarrow \pm \infty$. On the other hand, a Hopf or a wave instability can occur if we find $k_c$ such that

$$\begin{aligned} \text {tr}(J_{u,h})(k_c) = 0 \text { and } \det {J_{u,h}}(k_c) >0, \end{aligned}$$

whereas (5.5) holds for all k that do not satisfy this and are of the form $\frac{\pi }{n}z$. Hence, a Hopf instability occurs if

$$\begin{aligned} \frac{\partial _hg(1,h^*)}{\mu { (h^*)} \beta (2\pi )^{\frac{1}{2}}} = \hat{J}(0) \text { and } \hat{J}(0) >0, \end{aligned}$$

whereas (5.5) holds for all $k \ne 0$. On the other hand, a wave instability occurs if

$$\begin{aligned} \frac{\partial _h g(1,h^*) - (d+D_H)k_c^2}{\mu (h^*)\beta (2\pi )^{\frac{1}{2}}} = \hat{J}(k_c) \end{aligned}$$

and

$$\begin{aligned} -d\frac{k_c^2}{\beta (2\pi )^{\frac{1}{2}}\mu (h^*)} \left( 1 + \frac{\partial _u g(1,h^*)}{D_Hk_c^2-\partial _hg(1,h^*)}\right) < \hat{J}(k_c) \end{aligned}$$

holds for one or several $k_c \ne 0$, whereas (5.5) holds for all other k that are of the form $\frac{\pi }{n}z$ and do not satisfy the above equality and inequality

From the above considerations, we conclude that the occurrence of a Turing, Hopf or wave instability depends on the concrete choice of J, as we need to find suitable k of the form $\frac{\pi }{a} z$. If the Fourier transform $\hat{J}$ is nonnegative, no Turing patterns occur.

Remark 5.1

If there is a steady state of the form $(0,h^{**})$ for some $h^{**}>0$ and $\partial _h g(0,h^{**}) \le 0$, then this equilibrium is stable in the case with diffusion, taxis and nonlocal term. If, on the other hand, $\partial _h g(0,h^{**})>0$, this steady state is unstable already in the case without diffusion and taxis. This case is, however, unrealistic for the biological problem investigated here. Indeed, the proton expression by hypoxic cells is much reduced and there must be at least some very weak acid buffering, lest all cells (and surrounding tissue) become apoptotic.

Likewise, the steady state $(1,h^*)$ is unstable already in the case without diffusion and taxis if $\partial _h g(1,h^*) >0$. This situation may occur at least in a transient manner, e.g., when the cells can still extrude protons while their environment is quite acidic and if the cells are at their carrying capacity and the proton buffering is relatively low. That can lead, e.g., to a choice of the form $g(u,h)=u+uh-\gamma h^2$ with $\gamma \le 4/5$.

6 Numerical simulations

In this section, we perform numerical simulations of system (5.1), in order to illustrate the solution behavior. The equations are discretized by using the algorithm in [40]; the motility terms were discretized with finite differences (centered for the diffusion, upwind for the drift). The initial conditions are as in [35]:

$$\begin{aligned} u_0(x)=\left\{ \begin{array}{cc} e^{-(x-x_l)^2},&{}\text {for }x_l<x\le 0\\ e^{-x_l^2}(1-\frac{x}{x_r}),&{}\text {for }0<x\le x_r\\ \end{array}\right. ,\qquad \text {with }x_l=-5,\ x_r=5. \end{aligned}$$

Unless otherwise stated we take $g(u,h)=u(1-h)$, $\mu (h)=\mu /(1+h)$, with $\mu >0$ a constant and $d=1$.

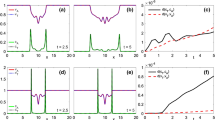
In a first test we took $\beta =1$, $\mu =1$, along with the logistic kernel $J(x)=1/(2+e^x+e^{-x})$ (see, e.g., [34]) and the uniform kernel $J(x;\rho )=\frac{1}{2\rho }\mathbb {1}_{[-\rho ,\rho ]}$. The first two columns of Fig. 1 show simulation results for $\alpha =2$, which is the ’limit value’ in (3.4). The solution ceased (in finite time) to exist for sufficiently large $\alpha$ in each of these situations ($\alpha \sim 6.25$ and $\alpha \sim 8.2$, respectively), u exhibiting strong aggregation near the initial bulk of cells, cf. last two columns in Fig. 1. This behavior was also observed for increasing values of $\mu$, with the difference of singularities already occurring for smaller $\alpha$ values.

Fig. 1

Simulation results for (5.1) with $\beta =\mu =1$. First two columns: $\alpha =2$, 3rd column: $\alpha =6.2$, last column: $\alpha =8.15$. Uniform kernel used with $\rho =1$

Increasing the values of $\mu$ and $\beta$ leads to patterns, the shape of which depends decisively on the interaction kernel J and also on the values of $\alpha$ and d. Figure 2 shows 1D space-time patterns of the cell density u for $\beta =20$, $\mu =100$, and several combinations of $\alpha$ and J. The results for the proton concentration h are not shown, as there are only small quantitative differences between the respective cases. Figure 2 suggests that, irrespective of the chosen kernel,⁹ higher cooperative intraspecific interactions (larger $\alpha$ values) or slower diffusion delay the invasion of cells in the whole region, leading instead to enhanced proliferation. On the long run the cells tend to fill the whole space and remain at their carrying capacity. This behavior endorses the results in Sect. 4 and is particularly well visible for the logistic kernel, which satisfies all conditions in the proofs of the theoretical results of Sects. 3 and 4; the process is much slower when a uniform kernel is used; however, it has eventually the same outcome. The last row in Fig. 2 exhibits the situation of a cell diffusion which is much slower than that of protons. The effect is a delayed filling of the space with cells (and produced protons) and a later formation of the patterns observed in the upper rows. The asymptotic behavior is similar, only it takes longer for the solution to reach the respective states.

Fig. 2

Simulation results for (5.1) with $\beta =20$ and $\mu =100$. Upper row: $\alpha =2$, lower row: $\alpha =10$. First column J logistic, other columns J uniform: 2nd column: $\rho =1$, 3rd column: $\rho =0.6$, 4th column: $\rho =0.05$. Upper rows: $d=D_H=1$, last row: $d\ll D_H$

To assess the effect of nonlocality, we performed simulations with the source term in the u-equation of (5.1) replaced by $\mu (h)u^\alpha (1-u^\beta )$. The results are shown in Fig. 3. The first two columns illustrate the case with the same source term for proton concentration as above, namely $g(u,h)=u(1-h)$, for which no patterns seem to develop (we tried several combinations of parameters, including those used for the patterns in Fig. 2). In fact, decreasing the value of $\rho$ in the uniform kernel $J(x;\rho )$ eventually leads to the local version of the system. The plots in the leftmost column were produced with $d=D_H$, while those in the middle column used $d\ll D_H$. The behavior of u and h is the same, with the difference of the second case inferring a slower spread of cells and protons. The last column in Fig. 2 already shows the tendency of disappearing patterns when approaching the local case. The last column of Fig. 3 shows the case where the source term in the h-equation is replaced by $g(u,h)=u+uh-\gamma h^2$, as proposed in Remark 5.1.¹⁰

No patterns for u were observed for the local model, which, together with the simulations performed for intermediary values of $\rho$, suggests that the patterns are driven by the nonlocality of cell-cell interactions, more precisely by intraspecific competition. The simulations also confirm the long time behavior of the system, even in the local case.

Fig. 3

Simulation results for (5.1) with local source term $\mu (h)u^\alpha (1-u^\beta )$ replacing the one in the equation for u. Left and middle column: $g(u,h)=u(1-h)$ with $d=D_H$ and $d\ll D_H$, respectively. Right column: $g(u,h)=u+uh-\gamma h^2$, $d=D_H$

7 Discussion

In this note, we investigated a model describing pH-tactic behavior of cells with nonlocal source terms. As such, this work is extending the one in [35], which studied the Fisher-KPP equation with nonlocal intraspecific competition with various powers of the solution. In contrast to [35] we handled here a problem in a bounded domain, and the population dynamics was coupled to that of the proton concentration, which also led to a taxis term. The proof of our results concerning global well-posedness and long time behavior relied, however, to a substantial extent on the methods in [35]. We also dealt here with space-dependent tensor coefficients in the motility terms, which involve myopic rather than Fickian diffusion. The dissipative effect of the repellent pH-taxis contributed to reducing some of the difficulties in the analysis - as long as the required conditions on the functions involved in the system are satisfied.

Among the relatively few existing models with nonlocal source terms, the one in [49] is closely related; however, it features several differences: the cells perform attractive haptotaxis toward gradients of extracellular matrix (ECM), the nonlocal source terms are contained in both equations, do not involve any powers, and the Fickian diffusion of cells has a constant coefficient. Our model requires less regularity for the interaction kernel and the motility coefficients involve a tensor and are more general. On the other hand, the nonexploding solution behavior is favorized in our case by repellent chemotaxis. We also provided an informal model deduction and an assessment of the long time solution behavior. The analysis done in [41] for a model with standard motility and with nonlocal source terms as in [49], but with one or two species performing chemotaxis toward the same attractant imposes certain requirements on the forcing term of the latter, mainly in order to obtain the asymptotic behavior of the cell-related solution components. Our condition (4.1) imposed for similar purposes on the source term of the tactic signal looks rather differently. The attraction–repulsion chemotaxis models considered in [46] have closer similarities with our setting, as far as the nonlocal intraspecific interactions are concerned. Major differences occur through our system only featuring two equations, in the source terms of the chemical cues, and in the motility terms: the latter involve in our case the space-dependent tensor $\mathbb D(x)$ and myopic diffusion, while the nonlocal reaction term in the proton dynamics is more general. We also prove an explicit long time behavior of both solution components and provide a short analysis of space-time patterns (in 1D), along with numerical simulations.

Our preliminary analysis in Sect. 5 and the simulation results in Sect. 6 suggest that patterns occur only in the nonlocal model, are not of Turing type, and seem to be driven by the nonlocal source terms and influenced by the chosen kernel and the combination of parameters in the nonlocal term. This is in line with the pattern behavior observed in [35] and with other works concerning reaction–diffusion problems with nonlocal intra- and/or interspecific competition, cf., e.g., [23, 25, 44, 48, 53, 58]. Those works involved more or less similar source terms and no taxis, however the repellent pH-taxis contained in our model does not seem to have a relevant influence on the patterns.

Open problems relate to a thorough study of patterns depending on the interplay between the parameters $\alpha$, $\beta$, $\mu$ and the influence of the kernel J. Moreover, the well-posedness, asymptotic and blow-up behavior, along with patterning, are largely unknown in the case of a degenerating motility tensor—the less so in combination with myopic diffusion and/or other types of taxis. Indeed, these can lead in the local case to very complex issues even in 1D, as shown, e.g., in [56, 57].