Skip to main content
SpringerLink
Log in

Dynamics of a reaction–diffusion epidemic model with general incidence and protection awareness for multi-transmission pathways

  • Published:
Zeitschrift für angewandte Mathematik und Physik Aims and scope Submit manuscript

Abstract

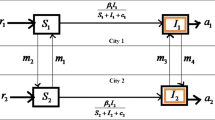
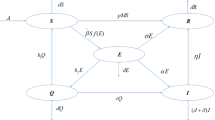
We develop, in this paper, a reaction–diffusion epidemic model with the general incidence rate and personal protection awareness, where, the direct transmission and indirect transmission are also introduced to describe the complexity of the spread of infectious diseases. The existence, uniqueness and boundedness of global solution are obtained first. And then, the basic reproduction number \({\mathcal {R}}_{0}\) is derived to go as the threshold value for predicting the persistence and extinction of disease. To be more specific, model admits a globally asymptotically stable disease-free steady state if \({\mathcal {R}}_{0}<1\), while the disease is persistent for \({\mathcal {R}}_{0}>1\). Further, for \({\mathcal {R}}_{0}=1\), the global asymptotic stability of the disease-free steady state is demonstrated when all diffusion coefficients are constants. In addition, the global asymptotical stability of the endemic equilibrium of this model with spatially homogeneous is derived if the corresponding basic reproduction is great than 1. Particularly, we also discuss the existence of traveling wave solution and the minimum wave speed \(c^{*}\) of the spatial homology model. Numerical simulations are presented to validate the main results and provide some recommendations for the control of multi-transmission diseases.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Tien, J.H., Earn, D.J.D.: Multiple transmission pathways and disease dynamics in a waterborne pathogen model. Bull. Math. Biol. 72, 1506–1533 (2010)

    MathSciNet  Google Scholar 

  2. Eisenberg, M.C., Robertson, S.L., Tien, J.H.: Identifiability and estimation of multiple transmission pathways in cholera and waterborne disease. J. Theor. Biol. 324, 84–102 (2013)

    MathSciNet  Google Scholar 

  3. Masud, M.A., Islam, M.H., Kim, B.N.: Understanding the role of environmental transmission on COVID-19 herd immunity and invasion potential. Bull. Math. Biol. 84, 116 (2022)

    MathSciNet  Google Scholar 

  4. Song, C.W., Xu, R., Song, N., et al.: Global dynamics and optimal control of a cholera transmission model with vaccination strategy and multiple pathways. Math. Biosci. Eng. 17, 4210–4224 (2020)

    MathSciNet  Google Scholar 

  5. Memarbashi, R., Mahmoudi, S.M.: A dynamic model for the COVID-19 with direct and indirect transmission pathways. Math. Biosci. Eng. 44, 5873–5887 (2021)

    MathSciNet  Google Scholar 

  6. Li, M.T., Jin, Z., Sun, G.Q., et al.: Modeling direct and indirect disease transmission using multi-group model. J. Math. Anal. Appl. 446, 1292–1309 (2017)

    MathSciNet  Google Scholar 

  7. Yuan, X.Y., He, D.H., Wang, J.L., et al.: A zika endemic model for the contribution of multiple transmission routes. Bull. Math. Biol. 83, 111 (2021)

    MathSciNet  Google Scholar 

  8. Yuan, Y.R., Yuan, N.L.: Optimal control and cost-effectiveness analysis for a COVID-19 model with individual protection awareness. Phys. A 603, 127804 (2022)

    MathSciNet  Google Scholar 

  9. Gondim, J.A.M.: Preventing epidemics by wearing masks: an application to COVID-19. Chaos Solitons Fract. 143, 110599 (2021)

    MathSciNet  Google Scholar 

  10. Kobe, J., Pritchard, N., Short, Z., et al.: A game-theoretic model of Cholera with optimal personal protection strategies. Bull. Math. Biol. 80, 2580–2599 (2018)

    MathSciNet  Google Scholar 

  11. Chen, F.H.: On the transmission of HIV with self-protective behavior and preferred mixing. Math. Biosci. 199, 141–159 (2006)

    MathSciNet  Google Scholar 

  12. Zheng, T.T., Nie, L.F.: Modelling the transmission dynamics of two-strain Dengue in the presence awareness and vector control. J. Theor. Biol. 443, 82–91 (2018)

    MathSciNet  Google Scholar 

  13. Hu, L., Nie, L.F.: Dynamic modeling and analysis of COVID-19 in different transmission process and control strategies. Math. Methods Appl. Sci. 44, 1409–1422 (2021)

    MathSciNet  Google Scholar 

  14. Kassa, S.M., Ouhinou, A.: The impact of self-protective measures in the optimal interventions for controlling infectious diseases of human population. J. Math. Biol. 70, 213–236 (2015)

    MathSciNet  Google Scholar 

  15. Mezouaghi, A., Djillali, S., Zeb, A., et al.: Global proprieties of a delayed epidemic model with partial susceptible protection. Math. Biosci. Eng. 19, 209–224 (2022)

    MathSciNet  Google Scholar 

  16. Martcheva, M.: An Introduction to Mathematical Epidemiology. Springer, New York (2015)

    Google Scholar 

  17. Zhao, X.Q.: Dynamical Systems in Population Biology, 2nd edn. Springer, Cham (2017)

    Google Scholar 

  18. Cantrell, R.S., Cosner, C.: Spatial Ecology via Reaction–Diffusion Equations. Wiley, Hoboken (2003)

    Google Scholar 

  19. Allen, L.J.S., Bolker, B.M., Lou, Y., et al.: Asymptotic profiles of the steady states for an SIS epidemic reaction–diffusion model. Discrete Contin. Dyn. Syst. 21, 1–20 (2008)

    MathSciNet  Google Scholar 

  20. Magal, P., Webb, G.F., Wu, Y.X.: On the basic reproduction number of reaction–diffusion epidemic models. SIAM J. Appl. Math. 79, 284–304 (2019)

    MathSciNet  Google Scholar 

  21. Yang, Y., Zou, L., Zhou, J.L., et al.: Dynamics of a waterborne pathogen model with spatial heterogeneity and general incidence rate. Nonlinear Anal. RWA 53, 103065 (2020)

    MathSciNet  Google Scholar 

  22. Tu, Y.B., Meng, X.Z., Gao, S.J., et al.: Dynamics and strategies evaluations of a novel reaction–diffusion COVID-19 model with direct and aerosol transmission. J. Frankl. Inst. 359, 10058–10097 (2022)

    MathSciNet  Google Scholar 

  23. Cai, Y.L., Kang, Y., Malay, M., et al.: Complex dynamics of a host-parasite model with both horizontal and vertical transmissions in a spatial heterogeneous environment. Nonlinear Anal. RWA 40, 444–465 (2018)

    MathSciNet  Google Scholar 

  24. Zhou, J.L., Yang, Y., Zhang, T.H.: Global dynamics of a reaction–diffusion waterborne pathogen model with general incidence rate. J. Math. Anal. Appl. 466, 835–859 (2018)

    MathSciNet  Google Scholar 

  25. Zhang, X.Y., Zhang, Y.X.: Spatial dynamics of a reaction–diffusion cholera model with spatial heterogeneity. Discrete Contin. Dyn. Syst. Ser. B 23, 2625–2640 (2018)

    MathSciNet  Google Scholar 

  26. Anderson, R.M., May, R.M.: Population biology of infectious diseases: part I. Nature 280, 361–367 (1979)

    Google Scholar 

  27. Kumar, A.: Nilam: stability of a time delayed SIR epidemic model along with nonlinear incidence rate and Holling type-II treatment rate. Int. J. Comput. Methods 15, 1850055 (2018)

    MathSciNet  Google Scholar 

  28. Dubey, B., Dubey, P., Dubey, U.S.: Dynamics of an SIR model with nonlinear incidence and treatment rate. Appl. Appl. Math. 10, 718–737 (2015)

    MathSciNet  Google Scholar 

  29. Upadhyay, R.K., et al.: Dynamics of an SEIR epidemic model with nonlinear incidence and treatment rates. Nonlinear Dyn. 96, 2351–2368 (2019)

    Google Scholar 

  30. Lou, Y.J., Zhao, X.Q.: A reaction-diffusion malaria model with incubation period in the vector population. J. Math. Biol. 62, 543–568 (2011)

    MathSciNet  Google Scholar 

  31. Smith, H.L.: Monotone Dynamical Systems: An Introduction to the Theory of Competitive and Cooperative Systems. American Mathematical Society, Providence (1995)

    Google Scholar 

  32. Martin, R.H., Smith, H.L.: Abstract functional differential equations and reaction–diffusion systems. Trans. Am. Math. Soc. 321, 1–44 (1990)

    MathSciNet  Google Scholar 

  33. Guo, Z.M., Wang, F.B., Zou, X.F.: Threshold dynamics of an infective disease model with a fixed latent period and non-local infections. J. Math. Biol. 65, 1387–1410 (2012)

    MathSciNet  Google Scholar 

  34. Groeger, J.: Divergence theorems and the supersphere. J. Geom. Phys. 77, 13–29 (2014)

    MathSciNet  Google Scholar 

  35. Guenther, R.B., Lee, J.W.: Partial Differential Equations of Mathematical Physics and Integral Equations. Dover Publications, New York (1996)

    Google Scholar 

  36. Wang, M.: Nonlinear Elliptic Equations. Science Press, Beijing (2010)

    Google Scholar 

  37. Wu, J.H.: Theory and Applications of Partial Functional Differential Equations. Springer, New York (1996)

    Google Scholar 

  38. Hale, J.K.: Asymptotic Behavior of Dissipative Systems. American Mathematical Society, Providence (1988)

    Google Scholar 

  39. Wang, M.X.: Nonlinear Second Order Parabolic Equations. CRC Press, Boca Raton (2021)

    Google Scholar 

  40. Wang, W.D., Zhao, X.Q.: Basic reproduction numbers for reaction–diffusion epidemic models. SIAM J. Appl. Dyn. Syst. 11, 1652–1673 (2012)

    MathSciNet  Google Scholar 

  41. Wang, J.L., Wang, J.: Analysis of a reaction–diffusion cholera model with distinct dispersal rates in the human population. J. Dyn. Differ. Equ. 33, 549–575 (2021)

    MathSciNet  Google Scholar 

  42. Smith, H.L., Zhao, X.Q.: Robust persistence for semidynamical systems. Nonlinear Anal. 47, 6169–6179 (2001)

    MathSciNet  Google Scholar 

  43. Magal, P., Zhao, X.Q.: Global attractors and steady states for uniformly persistent dynamical systems. SIAM J. Math. Anal. 37, 251–275 (2005)

    MathSciNet  Google Scholar 

  44. Cui, R.H., Lam, K.Y., Lou, Y.: Dynamics and asymptotic profiles of steady states of an eqiaemic model in adective environments. J. Differ. Equ. 263, 2343–2373 (2017)

    Google Scholar 

  45. Yang, Y., Zhang, T.H., Zhou, J.L.: Global stability of a degenerate reaction–diffusion host–pathogen model in critical case. Appl. Math. Lett. 140, 108572 (2023)

    MathSciNet  Google Scholar 

  46. Hess, P.: Periodic-Parabolic Boundary Value Problems and Positivity. Longman Scientific and Technical, New York (1991)

    Google Scholar 

  47. Webb, G.F.: Theory of Nonlinear Age-Dependent Population Dynamics. Marcel Dekker, New York (1985)

    Google Scholar 

  48. Jury, E., Mansour, M.: Positivity and nonnegativity conditions of a quartic equation and related problems. IEEE Trans. Autom. Control 26, 444–451 (1981)

    MathSciNet  Google Scholar 

  49. Zhang, T.: Minimal wave speed for a class of non-cooperative reaction–diffusion systems of three equations. J. Differ. Equ. 262, 4724–4770 (2017)

    MathSciNet  Google Scholar 

  50. Lupica, A., Gumel, A.B., Palumbo, A.: The computation of reproduction numbers for the environment–host–environment cholera transmission dynamics. J. Biol. Syst. 28, 183–231 (2020)

    MathSciNet  Google Scholar 

  51. Wang, X.Y., Gao, D.Z., Wang, J.: Influence of human behavior on cholera dynamics. Math. Biosci. 267, 41–52 (2015)

    MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Mathematics and System Sciences, Xinjiang University, Urumqi, 830017, People’s Republic of China

    Jingyun Shen, Shengfu Wang & Linfei Nie

Authors
  1. Jingyun Shen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shengfu Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Linfei Nie
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

JS and LN wrote the main manuscript text and JS and SW prepared Figs. 1, 2, 3, 4, 5 and 6. All authors reviewed the manuscript.

Corresponding author

Correspondence to Linfei Nie.

Ethics declarations

Conflict of interest

The authors declare no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This research is partially supported by the Natural Science Foundation of Xinjiang Uygur Autonomous Region (Grant Nos. 2022TSYCCX0015 and 2021D01E12), the National Natural Science Foundation of China (Grant Nos. 12361103, 11961066).

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shen, J., Wang, S. & Nie, L. Dynamics of a reaction–diffusion epidemic model with general incidence and protection awareness for multi-transmission pathways. Z. Angew. Math. Phys. 74, 248 (2023). https://doi.org/10.1007/s00033-023-02144-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00033-023-02144-0

Keywords

Mathematics Subject Classification

Search

Navigation