Abstract
Electrophoresis facilitated cancer treatment has demonstrated experimental efficacy in enhancing drug delivery within vascularised tumours. However, the lack of realistic mathematical models with direct measurements in the context of electrochemotherapy poses a challenge. We investigate the impact of an applied electric potential on the flow of Darcian-type fluid occurring in two distinct phases: the tumour and healthy regions. We employ the asymptotic homogenisation technique, assuming that the macroscale of the tumour domain is larger than the microscale characterised by vessel heterogeneities. We retain information about the microstructure by encoding information in the homogenised coefficients. We take into account both vascularisation and the microscale variations of the leading order and fine scale electric potential. The resulting effective differential problem reads as a Darcy-type system of PDEs, where the flow is driven by an effective source. The novel model can be used to predict the effect of an applied electric field on cancerous biological tissues, paving a new way of improving current electrochemotherapy protocols.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Real-world physical systems such as fluid transport in biological tissues have multiscale nature, exhibiting different chemical and physical behaviour on different levels. Upon zooming in a hierarchical system, one can see a variety of distinct arrangements, where the peculiarity in mechanical behaviour should be taken into account to realistically model the overall behaviour. Undisputedly, in the context of vascularised tumours the hierarchical structure must be taken into consideration.
Tumour tissue exhibits different properties than healthy tissue. Both the conductivity and permittivity of tumours are greater than normal tissue, and this difference is larger at low frequencies. This difference in the dielectric properties is due to the fact that cancer cells have a more hyperpolarised mitochondrial membrane potential and higher ROS (reactive oxygen species) levels than normal cells, and this is highly related to malignancy [10, 25]. Tumours sprout new vessels to obtain more nutrients and accelerate their growth in a process called angiogenesis [4]. Since tumour vessels are much leakier and tortuous than in the healthy tissue, it will result in an impaired blood supply and lead to hypoxia, where the low oxygen levels can disrupt the cell cycle, alter responses to chemotherapy and enhance metastasis. On average, tumour vasculature is more permeable than normal tissue vasculature, although the microvascular permeability is nonuniform in tumours. On the microscopic scale, the permeability changes along the same microvessel or among a few microvessels. In addition, the microvascular density is low at the centre of the tumour and high at the periphery. This kind of distribution pattern of the vessels breaks down the tumour into two subdomains that receive substantially different blood supply and thus different exposure to chemotherapeutic drugs. On the macroscopic scale, a tumour may simultaneously contain some regions with high vascular permeability and others that are impermeable. These heterogeneities in the microvessel distribution and blood flow limit the ability to reach aggressive cells within the tumour. The aggressive cancer cells have replicative immortality, i.e. they are capable of repopulating the tumour microenvironment, even after the death of non-resistant cells [4, 18]. In essence, the main reasons for vascular obstacles in transportation of drugs are uneven blood vessel distribution within the tumour, spatial and temporal heterogeneity in blood flow and heterogeneous microvascular permeability.
The primary difficulty in any intravenous cancer treatment is delivering drugs to the tumour in a sufficient amount and thus reducing the risk of metastasis. Intravenous therapies can be made more effective by enhancing the fluid flow in the vascular system, and one way of accomplishing this is via electrophoresis. Electrophoresis refers to the well-documented phenomenon of charged molecule movement driven by external electric field [18].
Electrochemotherapy is particularly useful when the tumours are unresponsive to the most common modes of treatments, such as surgery, chemotherapy and radiotherapy. It combines the delivery of chemotherapeutic drugs and electric pulses and is very effective for solid tumours, as whenever the drug is present in the tumour (surrounding the tumour cells, but not being able to penetrate the cell through its membrane), inducing a sufficiently high transmembrane voltage enhances drug transportation by increasing the permeability of plasma membrane, allowing adequate amount of drug to enter the cell, increasing drug cytotoxicity [9, 30].
Applied electric field treatment has experimentally shown (both in vivo and in vitro) to improve drug delivery in a variety of tumour tissues [24]. However, as highlighted in [12, 26], there are lack of realistic mathematical models with direct measurements. So far the existing models focused on the electric field distribution within the tumour [16, 29], optimisation of parameters such as electrode shapes, sizes and arrangements [7, 39], but there has been lack of focus on the mathematical modelling of the tumour’s response to the electric field treatment. Therefore, a quantitative model with direct measurements would greatly improve current electrochemotherapy protocols.
From a mathematical standpoint, it is challenging to resolve multiscale systems at reduced computational costs, since as imaging techniques have become more advanced with highly detailed data, it is practically impossible to fully undertake the microscale material with its geometric complexity (e.g. including every single capillary in the model). On the other hand, measurements of in vivo and in vitro experiments generally give averaged data on a macroscale, where the difference between the constituents cannot be easily identified. However, we do not want the crucial role of the microstructure to be lost. Hence, we use the asymptotic homogenisation technique (see, e.g. [11, 32], and [5] among many others) to derive a novel homogenised multiscale model of fluid transport in tumour tissues subjected to the action of an electric potential by generalising the work [37]. The results provide us with a computationally feasible macroscopic framework while also taking the microscale variations into account by embedding them in the components of the model, hence incorporating as much information as possible about the microstructure. We express the body force by a gradient of a scalar potential assuming it exhibits spatial variations on two well-separated length scales and we set the divergence of the fluid velocity equal to a source instead of zero, accounting for the microvascular vessel pressure and tissue hydraulic permeability. The major novelty of our homogenised multiscale model lies in the macroscale divergence which appears as an effective source, and in the effective body force driving the macroscale fluid flow, as they both contain several additional contributions. The new model can be used to predict the effect of an applied electric field on cancerous biological tissues, paving a new way of improving current electrochemotherapy protocols.
In Sect. 2, we introduce the Darcy equation for a heterogeneous porous domain consisting of healthy and tumour regions, assuming spatial heterogeneity of body forces and hydraulic conductivities. In Sect. 3, we decouple spatial variations by means of asymptotic homogenisation. The homogenised macroscale problem obtained in Sect. 5 incorporates our main result, and we further derive the leading order macroscale velocity profile in Sect. 5.1. In Sect. 6, we discuss our theoretical findings, and in Sect. 7, we provide results for a simple geometry, concerning the relative interstitial fluid pressure and fluid velocity in the presence of different magnitudes of electric field and varying proportions of tumour and healthy tissue in the domain, accounting for invasiveness. In Sect. 8, we describe some possible applications and explore future directions for the study.
2 Darcian fluid flow for inhomogeneous body forces
We use Darcy’s law to describe the fluid flow in a biological setting, where we consider the domain to be a porous medium consisting of healthy and tumour tissue. Let us consider a heterogeneous porous medium identified with an open and bounded domain \(\Omega \subset {\mathbb {R}}^{n}, n=2,3\) made of N non-intersecting inclusions such that
where \(\alpha \in \{0,1,2, \ldots , N\}\) and \( \beta \in \{1,2, \ldots , N\}.\) Assume that each phase is characterised by a symmetric and positive definite hydraulic conductivity tensor \({\textsf{K}}_{\alpha }({\textbf{x}}), {\textbf{x}} \in \Omega _{\alpha }\),
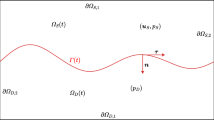
where \({\textbf{a}}\) is a constant vector, see Fig. 1.
Heterogeneous porous domain and vessel structure in 2D, showing the tumour domain with N inclusions, each one consisting of a fluid and solid phase. Each inclusion is characterised by a different vessel structure and the scale geometries for each phase will be encoded in \({\textsf{K}}_{\alpha }({\textbf{x}}),\) where each inclusion \(\alpha \) will have a different hydraulic conductivity
The flow of an incompressible Newtonian fluid slowly transuding through the porous domain is described by Darcy’s law, i.e. the fluid flow in each \(\Omega _{\alpha }\) is given by the linear relation of fluid discharge to the gradient of the pressure via the hydraulic conductivity tensor and externally applied volume load such that
where \({\textbf{u}}_{\alpha }({\textbf{x}})\) is the fluid velocity, \({\textsf{K}}_{\alpha }({\textbf{x}})\) is the hydraulic conductivity tensor, \(p_{\alpha }({\textbf{x}})\) is the interstitial fluid pressure, and \({\textbf{f}}_{\alpha }({\textbf{x}})\) is the body force. Note that as our starting point in formulating our model is Darcy’s law, we will consider the pore structure with the solid and fluid phase to be already smoothed out. In fact, relationship (3) can be obtained by performing upscaling of the Stokes’ problem at the pore scale by means of standard homogenisation techniques, including asymptotic homogenisation (see, e.g. [20, 34]), as well as mixture theory, see for example the comprehensive review [38]. As such, the volume load \({\textbf{f}}_{\alpha }\) represents the average of a pore scale force affecting the fluid flow at the scale characterising the distance between two adjacent tumorous heterogeneities. We define \({\textbf{f}}_{\alpha }({\textbf{x}})\) to be a product of a function of position \(c({\textbf{x}})\) and the gradient of electric potential \(\varvec{\phi }_{\alpha }({\textbf{x}}),\) so that
The function \(c({\textbf{x}})\) is normally related with the charge density and the number of ions depending on the specific scenario at hand, see, e.g. [8]. Moreover, let the divergence of the fluid velocity equal to a source \(S_{\alpha }({\textbf{x}}):\)
where \(S_{0}\) and \( S_{\textrm{I}}\) represent the driving sources of healthy and tumour tissue states, \(L_{p_{0}}, L_{p_{\textrm{I}}}\) represent the membrane permeability of healthy and tumour vessels, and \(p_{v_{0}}, p_{v_{\textrm{I}}}\) account for the microvascular vessel pressure (MVP) in healthy and tumour vessels, respectively.
We will also have two interface conditions for every \(\beta =1,2,\ldots , N\) the continuity of pressure and the continuity of fluid flux across interface can be expressed as
where \({\textbf{n}}_{\beta }\) is the outward vector normal to the interface \(\Gamma _{\beta }:=\partial \Omega _{0} \cap \partial \Omega _{\beta }.\)
In particular, by exploiting (3) and (4) we can rewrite (7) as follows:
3 The asymptotic homogenisation technique
The chief motivation for exploiting the asymptotic homogenisation technique is to acquire an effective differential problem describing the macroscale behaviour of a physical system driven by the system of PDEs (5)–(8). However, we do not wish to resolve the full details of the microscale, as the multidimensional porous structure is overly complex and is practically impossible to solve with numerical techniques.
The most crucial assumption for asymptotic homogenisation is the sharp length scale separation. We assume that the macroscale (also known as coarse/global scale) is much larger than the microscale (fine/local scale).
Assumption 1
Length scale separation Assume that there exist two well-separated spatial scales, the macroscale denoted by L, and the microscale denoted by d such that their ratio is:
For our model, the multiscale nature of the problem is due to geometrical reasons, as we will assume that the global size of the domain L, is much larger than the distance between adjacent inclusions d, see Fig.2. On the fine scale, individual heterogeneities are identifiable in the medium. We will also decouple these spatial scales to make the problem multiscale, for which the following assumption will be used.
Assumption 2
Spatial variations decoupling We assume that every unknown field is a function of two formally independent spatial variables, \({\textbf{x}}\), referred to as the macroscale variable and
referred to as the microscale variable. As a consequence of Assumption 2, the differential operator will undergo the following transformation according to the chain rule, i.e.
where \(\nabla _{{\textbf{x}}}\) and \(\nabla _{{\textbf{y}}}\) represent the gradients with respect to the macroscale and microscale variables, \({\textbf{x}}\) and \({\textbf{y}}.\)
In addition, since we are interested in determining the macroscale behaviour of the problem, the following assumption is needed.
Assumption 3
Power series expansion We assume that the multiscale unknowns in (3)–(4) can be formally represented by a regular expansion in power series of \(\epsilon ,\) namely
Remark 1
For the sake of simplicity, and in order to reduce computational complexity, we assume \({\textbf{y}}\)-periodicity of the fields and material properties involved in (3)–(4), as done in [37]. As such, all the fields \( {\textbf{u}}_{\alpha }({{\textbf{x}}}, {\textbf{y}} ), p_{\alpha }({{\textbf{x}}}, {\textbf{y}}),\) and \( \varvec{\phi }_{\alpha }({{\textbf{x}}}, {\textbf{y}}),\) as well as the hydraulic conductivity tensors \({\textsf{K}}_{\alpha }({{\textbf{x}}}, {\textbf{y}})\) are assumed \({\textbf{y}}\)-periodic. We also suppose macroscopic uniformity, that is, we assume that the periodic cell does not exhibit any parametric dependence with respect to the macroscale \({\textbf{x}}\) and hence
For possible generalisations concerning non-macroscopic uniform media in homogenisation, the reader can, for example, refer to [13, 19, 33, 35].
Remark 2
We consider \(\Omega \) to be our periodic cell, and we will focus on one inclusion only in \(\Omega ,\) i.e. \(\alpha =0,1\) and \(\beta =1,\) such that
where \(\Omega _0\) is the host matrix phase and \(\Omega _I\) represents the inclusion cell portion. We will also use the index \(\textrm{I}\) instead of 1 and we set
where \(\Gamma \) and \({\textbf{n}}\) denote, respectively, the interface between the matrix and the inclusion and the unit outward vector normal to the interface \(\Gamma \).
4 The homogenised problem
First and foremost, for the sake of clarity, we substitute (3) equipped with (4) into (5), resulting in the following equation
We start the asymptotic homogenisation process by exploiting Assumptions 1–3 to Equations (5), (6) (8). Next, we gather equations (18), (8), and (6) and start our model formulation by enforcing Assumption 2, i.e. applying the chain rule according to the spatial scale decoupling as per Assumption 1. We also substitute the power series representations (12)–(14) into the equations we gathered.
After some rearranging and multiplying both sides by a suitable power of \(\epsilon \) (which in our case is \(\epsilon ^2\)), we obtain the following homogenised multiscale system of PDEs
In the forthcoming sections, we will equate the same powers of \(\epsilon \) in ascending order until we obtain a closed macroscale differential problem for the leading order pressure.
4.1 Differential conditions for \(\epsilon ^0\)
Equating (19)–(22) to the powers of \(\epsilon ^0\) and taking Remark 2 into account with denoting the healthy tissue region by \(\Omega _0\) and the tumour tissue region by \(\Omega _{\textrm{I}}\) yields the following equations
The problem (23)–(26) reads as a diffusion-type periodic cell problem for the leading order pressure supplemented by the interface condition. This problem is driven by both the microscale divergences of the leading order pressure and leading electric potential along with the microscale variations of the hydraulic conductivity tensor.
Now we propose the following change of variables for the leading order pressure
Upon substituting (27) and (28) into (23)–(26), we have
From Equations (29), (30), assuming that the electric potential is continuous across the interface \(\Gamma \), we can deduce that \(\tilde{p}\) only depends on the macroscale and in particular
4.2 Differential conditions for \(\epsilon ^1\)
Equating to the powers of \(\epsilon ^1\) in (19–22) results in
Now, by taking into account (27), (28) from the coarse scale cell problem, along with (33), and substituting these in the system (34)–(37), we can simplify the fine scale cell problem as follows:
Again we have a diffusion-type periodic cell problem, but now for the first-order pressure. The problem (38)–(41) is directed by the macroscale and fine scale variations of the leading order pressure and electric potential, as well as by both the macroscale and fine scale divergences of the hydraulic conductivity tensor.
We write the following ansätze for the first-order pressures
where \(t({\textbf{x}})\) is a \({\textbf{y}}\)-constant function. Equations (42) and (43) provide solutions to the fine scale problem (38–41) up to a \({\textbf{y}}\)-constant function, given that necessary conditions are set for \({\textbf{g}}_{0}({\textbf{x}}, {\textbf{y}}),\) \({\textbf{g}}_{\textrm{I}}({\textbf{x}}, {\textbf{y}}),\) \(\varvec{\gamma }_0 ({\textbf{x}}, {\textbf{y}}),\) \(\varvec{\gamma }_{\textrm{I}}({\textbf{x}}, {\textbf{y}})\) and \(\tilde{g}_{0}({\textbf{x}}, {\textbf{y}}),\) \(\tilde{g}_{\textrm{I}}({\textbf{x}}, {\textbf{y}}).\)
The auxiliary vectors \({\textbf{g}}_{0}({\textbf{x}}, {\textbf{y}})\) and \({\textbf{g}}_{\textrm{I}}({\textbf{x}}, {\textbf{y}})\) solve the following cell problem equipped with the interface condition
The auxiliary vectors \(\varvec{\gamma }_{0}({\textbf{x}}, {\textbf{y}})\) and \(\varvec{\gamma }_{\textrm{I}}({\textbf{x}}, {\textbf{y}})\) solve the following cell problem equipped with the interface condition
The auxiliary scalar functions \(\tilde{g}_{0}({\textbf{x}}, {\textbf{y}})\) and \(\tilde{g}_{\textrm{I}}({\textbf{x}}, {\textbf{y}}) \) are chosen so that they solve the system below
Additionally, we note that the vectors \({\textbf{g}}_{0}({\textbf{x}}, {\textbf{y}}),\) \({\textbf{g}}_{\textrm{I}}({\textbf{x}}, {\textbf{y}}),\) \( \varvec{\gamma }_0 ({\textbf{x}}, {\textbf{y}}),\) \(\varvec{\gamma }_{\textrm{I}} ({\textbf{x}}, {\textbf{y}})\) and functions \(\tilde{g}_{0}({\textbf{x}}, {\textbf{y}}),\) \(\tilde{g}_{\textrm{I}}({\textbf{x}}, {\textbf{y}}) \) are \({\textbf{y}}\)-periodic, and we can ensure their uniqueness by fixing their integral average over \(\Omega .\)
Remark 3
Solvability condition of the cell problem Since the differential problem (38)–(41) exhibits additional contributions, we will show that there exist proper compatibility conditions between the driving forces in the cell portions and interface conditions. We take Equations (3) and (4) with power series expansions (12)–(14) to obtain the leading order velocities \({\textbf{u}}_0^{(0)}({\textbf{x}}, {\textbf{y}})\) and \( {\textbf{u}}_{\textrm{I}}^{(0)}({\textbf{x}}, {\textbf{y}})\) given by
Now we substitute ansätze (27) and (28) from the coarse scale cell problem which yields
Using the gradient rule in (58) and (59), we obtain
Now considering the fine scale cell problem with ansätze (42) and (43), we have
Next, we rewrite equations (38)–(40) in terms of (57)–(63), by taking the divergence of the leading order macroscale velocity profiles:
Summing up the integral over respective cell portions of (64) and (65) and applying the divergence theorem with respect to the microscale variable \({\textbf{y}}\) results in
In the above, \({\textbf{n}}_{\partial \Omega _0}\) and \( {\textbf{n}}_{\partial \Omega _{\textrm{I}}}\) represent the outward unit normal vectors to the boundary of \(\Omega _0\) and \(\Omega _{\textrm{I}},\) respectively. Moreover, since the following holds on \(\Gamma :\)
therefore we have:
Furthermore, as a result of equation (70) the first term in (71) will vanish, so we have
where the right hand side of (72) also reduces to zero due to \({\textbf{y}}\)-periodicity on cell periodic boundaries.
5 Differential conditions for \(\epsilon ^2\) and the resulting Darcy’s type macroscale model
Lastly, by equating the same powers of \(\epsilon ^2\) in (19)–(22) and accounting for ansätze (27) and (28), we obtain
Additionally, we consider ansätze (42) and (43) from the fine scale cell problem, and perform an integral average of Eqs. (73) and (74) over their respective cell portions \(\Omega _{0}\) and \(\Omega _{\textrm{I}},\) by applying the following cell average operator
where \({|\Omega |}\) is the volume of the periodic cell. We then obtain after some rearranging
Now we sum up Eqs. (78)–(79) and apply the divergence theorem with respect to the microscale variable \({\textbf{y}}\) as follows:
Note that the contributions over the periodic boundaries \(\partial \Omega _0 \backslash {\Gamma }\) and \( \partial \Omega _{\textrm{I}} \backslash {\Gamma }\) will cancel out due to local periodicity and the remaining one will reduce to zero when we take the interface condition (75) into account.
Equation (80) can be further rearranged into a macroscale Darcy’s type problem for the leading order macroscale pressure \(p^{(0)}\) such that
where
In the above, \(\hat{{\textsf{K}}}({\textbf{x}})\) represents the effective hydraulic conductivity tensor, \(\hat{L}_p\) accounts for the effective membrane permeability, and \(\varphi ({\textbf{x}})\) is the effective source. By means of (81), we have obtained a Darcy’s type problem which is to be solved on the macroscale only, which was precisely our goal. The fine scale variations are embedded in the components of the effective source and \(\hat{{\textsf{K}}}({\textbf{x}}),\) which can be computed by solving the diffusion-type fine scale cell problem given by (44)–(47). More detailed discussion of the meaning of the above formulae can be found in Sect. 6.
5.1 Macroscale velocity profile
Ultimately, we obtain an effective governing equation for the macroscale velocity profile, relating the leading order velocity field to the leading order pressure and to the leading order and fine scale electric potential. We take Equations (62) and (63) and apply the average operator (77). Additionally, we sum them up to obtain the leading order macroscale Darcy’s law:
We can further rewrite Eq. (85) for the macroscale leading order velocity field given by \({\textbf{u}}_M({\textbf{x}})\) such that
where
In Eq. (86), \(\hat{{\textsf{K}}}({\textbf{x}})\) is the effective hydraulic conductivity tensor that has been introduced previously in (81), and \(\tilde{{\textbf{f}}}({\textbf{x}})\) represents the effective body force.
Finally, we observe that by considering the definitions of the average macroscale velocity and body force given by (88), as well as Eq. (85) and given the resulting differential problem as per (81), then the macroscale divergence of the average macroscale velocity \({\textbf{u}}_M\) is given by:
The above equation represents the expected macroscale mass balance for a system comprising two intrinsically incompressible fluid phases supplemented by blood supplies due to their respective vascularisations.
6 Discussion of the theoretical results
In this section, we give a physical interpretation for the components of the homogenised model and we discuss how our model differs from what can be previously found in the literature. In Sect. 5, we have derived a Darcy’s type problem given by (81). The model differs from Penta et al. [37], as it contains additional contributions, which we will highlight prospectively. The main novelties are:
-
(A)
We have expressed the body force as the gradient of a scalar potential assuming it exhibits spatial variations on two well-separated length scales, i.e. the microscale variations of the electric potential were taken into account.
-
(B)
As opposed to Penta et al. [37], we take into account the blood supply in both the healthy and tumour compartments. This is done via a source which depends on the difference between the vessels and interstitial pressures.
The major novelty of our homogenised multiscale model lies in the macroscale divergence which appears as an effective source (84), and in the effective body force (88) driving the macroscale fluid flow, as they both contain several further terms emerging from (A) and (B).
As a consequence of (A), both the effective body source and effective body force contain extra terms. Specifically, in contrast to Penta et al. [37], we got an additional periodic cell problem on the coarse scale given by (29)–(32), which reads as a well-defined differential problem solely driven by the fine scale divergence of the leading order electric potential. Furthermore, on the fine scale, the right hand sides of Equations (52)–(54) are all new contributions arising from A. Besides, the cell problem (52)–(55) also reads as a well-defined differential problem and it is driven by both the macroscale and fine scale divergence of the leading order electric potential and leading order pressure, as well as the fine scale divergence of the first-order electric potential. Now we will give a brief summary of the physical interpretation of the components of the effective source \(\varphi ({\textbf{x}}),\) which drives the macroscale Darcy’s type problem.
-
(I)
The expressions below are related to the microscale variations of the fine scale electric potential:
$$\begin{aligned}{} & {} -\nabla _{\textbf{x}}\cdot \left( \left\langle \textsf{K}_{0}(\textbf{x}, \textbf{y}) \nabla _{\textbf{y}} \varvec{\phi }_{0}^{(1)}(\textbf{x}, \textbf{y})\right\rangle _{\Omega _{0}}c(\textbf{x})\right) , \quad -\nabla _{\textbf{x}}\cdot \left( \left\langle \textsf{K}_{\textrm{I}}(\textbf{x}, \textbf{y}) \nabla _{\textbf{y}} \varvec{\phi }_{\textrm{I}}^{(1)}(\textbf{x}, \textbf{y})\right\rangle _{\Omega _{\textrm{I}}}c(\textbf{x})\right) .\\{} & {} -\nabla _{{\textbf{x}}}\cdot \left\langle {\textsf{K}}_0({\textbf{x}}, {\textbf{y}})\nabla _{{\textbf{y}}}\tilde{g}_0({\textbf{x}}, {\textbf{y}})\right\rangle _{\Omega _0}, \quad -\nabla _{{\textbf{x}}}\cdot \left\langle {\textsf{K}}_{\textrm{I}}({\textbf{x}}, {\textbf{y}})\nabla _{{\textbf{y}}}\tilde{g}_{\textrm{I}}({\textbf{x}}, {\textbf{y}})\right\rangle _{\Omega _{\textrm{I}}}. \end{aligned}$$ -
(II)
The following terms are related to the microscale variations of the leading order electric potential:
$$\begin{aligned} -\nabla _{\textbf{x}}\cdot \left( \left\langle \textsf{K}_0(\textbf{x}, \textbf{y})\nabla _{\textbf{y}}\varvec{\gamma }_0(\textbf{x}, \textbf{y})\right\rangle _{\Omega _0}\nabla _{\textbf{x}}c(\textbf{x})\right) , \quad -\nabla _{\textbf{x}}\cdot \left( \left\langle \textsf{K}_{\textrm{I}}(\textbf{x}, \textbf{y})\nabla _{\textbf{y}}\varvec{\gamma }_{\textrm{I}}(\textbf{x}, \textbf{y})\right\rangle _{\Omega _{\textrm{I}}}\nabla _{\textbf{x}}c(\textbf{x})\right) . \end{aligned}$$ -
(III)
The terms beneath are related to macroscale variations of leading order electric potential:
$$\begin{aligned}{} & {} -\nabla _{\textbf{x}}\cdot \left( \left\langle \textsf{K}_0(\textbf{x}, \textbf{y})\nabla _{\textbf{x}}\varvec{\phi }_{0}^{(0)}(\textbf{x},\textbf{y})\right\rangle _{\Omega _0}c(\textbf{x})\right) , \quad -\nabla _{\textbf{x}}\cdot \left( \left\langle \textsf{K}_{\textrm{I}}(\textbf{x}, \textbf{y})\nabla _{\textbf{x}}\varvec{\phi }_{\textrm{I}}^{(0)}(\textbf{x},\textbf{y})\right\rangle _{\Omega _{\textrm{I}}} c(\textbf{x})\right) ,\\{} & {} -\nabla _{{\textbf{x}}}\cdot \left\langle {\textsf{K}}_0({\textbf{x}},{\textbf{y}})\nabla _{{\textbf{y}}}{\textbf{g}}_0({\textbf{x}}, {\textbf{y}})\nabla _{{\textbf{x}}}\left( c({\textbf{x}})\varvec{\phi }_0^{(0)}({\textbf{x}}, {\textbf{y}})\right) \right\rangle _{\Omega _0}, \quad -\nabla _{{\textbf{x}}}\cdot \left\langle {\textsf{K}}_{\textrm{I}}({\textbf{x}},{\textbf{y}})\nabla _{{\textbf{y}}}{\textbf{g}}_{\textrm{I}}({\textbf{x}}, {\textbf{y}})\nabla _{{\textbf{x}}}\left( c({\textbf{x}})\varvec{\phi }_{\textrm{I}}^{(0)}({\textbf{x}}, {\textbf{y}})\right) \right\rangle _{\Omega _{\textrm{I}}}. \end{aligned}$$ -
(IV)
Finally, the terms below are associated with the microvascular vessel pressures in both compartments, related to the blood supply due to the vascularisations arising merely from (B).
$$\begin{aligned} -\left\langle L_{p_{0}}p_{v_0}\right\rangle _{\Omega _{0}}, \quad - \left\langle L_{p_{\textrm{I}}}p_{v_{\textrm{I}}}\right\rangle _{\Omega _{\textrm{I}}}. \end{aligned}$$
This last contribution is indeed related to the course scale mass balance (89).
7 The solution of the model for a simple test case
In this section, we will streamline our derived model by making some simplifying assumptions that will allow us to find analytical solutions to the homogenised Eq. (81). For that purpose, we will first assume that the electric potential only depends on the macroscale and in particular that the resulting electric field \({\textbf{E}}=-\nabla \phi \) is constant. We also assume that the hydraulic conductivity is constant so that equation (82) reduces to \(\hat{{\textsf{K}}}=K {\textsf{I}}\), where \({\textsf{I}}\) is the identity tensor and K is a constant. By taking these simplifications into account, the effective source (84) simply reduces to
where \(\varphi \) has become a negative constant as well. Moreover, the homogenised macroscale model (81) can then be rewritten as
After some rearranging and dividing by \(\hat{L}_p\), we obtain
Now we let
then, since \(\dfrac{\varphi }{\hat{L}_p}\) is constant, our simplified model (92) becomes a Sturm–Liouville problem expressed as follows:
Now we will focus on a simple geometry by adapting [36] and transforming (94) into spherical coordinates assuming radial symmetry. This will be necessary, as providing solutions for the full model is beyond the scope of this paper. We require the fluid flux at the centre to be zero, hence we may write
We also require the boundary condition of the fluid flux at the exterior to be \(\bar{p}|_{r=R}=0\). Noting that the Laplacian transform assuming radial symmetry is given by
the problem (94) can be written in terms of the radius r such that
Now let
Substituting (98) into (97) and multiplying by r and \(\omega ^2\) yields
The characteristic equation of (99) is given by \(\lambda ^2-\omega ^2=0, \) where \(\lambda =\pm \omega .\) The solution in general would be \(\xi (r)=A e^{\omega r}+Be^{-\omega r},\) but this will not work because if we divide by r, \(\dfrac{e^{\omega r}}{r} \rightarrow \infty \) and \(\dfrac{e^{-\omega r}}{r} \rightarrow \infty \) as \(r\rightarrow 0.\) Therefore, we rather choose a linear combination of the above, i.e. the solution is given by
Next, divide by r to obtain
Now, \(\cosh {(\omega r)}=1 \) if \(r=0\) and so the second term on the right hand side of (101)
Hence we set \(B=0,\) and then (101) becomes
By the condition (95), we set
Recall that by (98), \(\omega =\sqrt{\frac{\hat{L}_p}{K}}.\) Therefore, we have
Substituting (104) into (103) yields
We now introduce the following relationships
so that the relative interstitial fluid pressure, which we denote by \(\hat{p}(\hat{r})\), reads
We now need to obtain an expression for the relative interstitial fluid velocity in spherical coordinates. By starting from equation (86), in the current simplified setting the radial component of the macroscale interstitial fluid velocity can be expressed as follows:
where \(E_r\) is the radial component of the electric field. Substituting the derivative of (105) into (108) gives
Accounting for relationships (106), the radial component of the relative interstitial fluid velocity is given by
where \(\hat{E}_r=\dfrac{c\hat{L_p}R}{\varphi }E_r\) is the relative radial component of the electric field.
7.1 Parameter setting
In this section, we present the appropriate parameters that will be used in modelling concerning the relative interstitial fluid pressure (IFP) and relative interstitial fluid velocity (IFV). We also discuss the motive behind setting the coefficients.
Membrane permeability Firstly, we note that when we take the average of \(L_{p_0}\) and \(L_{p_{\textrm{I}}}\) over the periodic cell \(\Omega ,\) we get
where we will denote the proportion of normal tissue and tumour tissue by \(V_0=\frac{|\Omega _0|}{|\Omega |}\) and \(V_{\textrm{I}}=\frac{|\Omega _{\textrm{I}}|}{|\Omega |},\) respectively. Accounting for (111) and (112), we can express the effective membrane permeability as follows:
In the next section, we will investigate how varying the proportion of \(V_0\) and \(V_{\textrm{I}}\) affects the relative interstitial fluid pressure.
Hydraulic conductivity In the previous section, we have reduced our effective hydraulic conductivity tensor to be a constant K. The tissue hydraulic conductivity vastly depends on the blood supply within the tissue (e.g. the lung and muscle is highly conductive, whereas cartilage and bone have quite low conductivity), hence we will use a representative value for K. Furthermore, we will assume that the hydraulic conductivity will not differ significantly for healthy and tumour tissue, since the tumour originates from the host cells in which it resides, and thus we will set the same constant for healthy and tumour regions [21].
A summary of the parameters that will be used for simulations can be found in Table 1.
7.2 Modelling of relative IFP and IFV
We will start this section by examining how the relative IFP varies for different proportions of tumour regions. Then we will further investigate the relative IFV for sample cases of tumour invasion in the presence of an applied electric field that we will vary.
We now plot the relative IFP by means of Eq. (107). We have set the proportions of tumour tissue in the domain to be 5, 20, 30, 50, 60, 70, 80, 95%. Recall that by (113), \(V_0\) represents the proportion of healthy tissue and \(V_1=1-V_0\) represents the proportion of tumour tissue. Figure 3 shows that the higher percentage of tumour tissue, the greater the increase in relative IFP as in [21]. Also, we can observe an increase in the pressure for a larger tumour radius. The overall elevated IFP profile of tumour regions, and the fact that it is the highest at the centre of the tumour and decreases towards the periphery is coherent with the angiogenic properties of cancer progression and the fact that tumours have a necrotic core.
Next, we used Eq. (110) for the relative IFV and set the MVPs to take the maximum values from Table 1, i.e. we set \(p_{v_0}=25\, \mathrm{[mm Hg]}, p_{v_{\textrm{I}}}=34\, \mathrm{[mm Hg]}.\) At first, we investigated the relative IFV for different percentages of tumour invasion without the presence of an applied electric field.
Figure 4 exhibits a substantial increase in IFV as the invasion progresses. Moreover, the increase is more significant at the tumour periphery and lower at the centre, which could indeed foster tumour growth on the outside and lead to metastasis.
Subsequently, we have chosen to explore the effect of an applied electric field in the cases of 5, 20, 50 and 95% cancer invasion, considering tumour radii 0.5 and 1.25 cm. We set the density constant to be \(c=0.05,\) and set the electric field to take the values 0, 150, 250, 350, 450, 550, 650, 750, 1000 in [V/cm].
Firstly, we have fixed \(V_0=0.95\) to account for 5% tumour tissue in the domain shown at the top left panels in Figs. 5 and 6. Note that there is an increase in fluid velocity towards the periphery for the case when \({\textbf{E}}=\textbf{0}\), since our driving force is given by vascular pressures. We can see that even when the tumour percentage is low, there is a dramatic boost in convection as a consequence of the applied electric field, see Figs. 5 and 6.
We can see that the rising electric field increases the overall velocity profile. Additionally, for larger tumour radii, greater number of vascularisations occur at the periphery (proliferating zone), resulting in a further augmentation of the IFV profile. In the context of anticancer therapies, it is beneficial to increase blood convection in the tumour centre, as it enhances drug transport inside the tumour and thus, reducing metastasis. When considering higher proportions of tumour tissue in the domain, the increase in convection is significantly more pronounced at the periphery than at the centre. Although electrophoresis does enhance the velocity at the centre of the tumour, its impact on the velocity profile at the periphery is notably more substantial. This can actually contribute to tumour growth, as the blood flow increases outside the tumour, it can obtain more nutrients to advance its growth, while the drugs cannot enter the inside of the tumour in a sufficient amount. Thus, tuning the electric field properly is imperative in order to find a balance between the IFV boost at the centre and periphery.
8 Conclusions and further perspectives
We derived a new mathematical model which describes the behaviour of vascularised, heterogeneous porous materials subjected to the influence of a volume load which is assumed to be proportional to the gradient of a given potential.
The chief motivation for this work is the development of a model which can predict the effect of externally applied electric field on fluids flowing in vascularised porous media such as tumour tissues in the context of electrophoresis. Electrophoresis on tumour tissues has a broad range of applicability, from screening multi-target anticancer drug combinations to initiating immunogenic cell death with nanopulse stimulation, see, e.g. [6, 30, 42, 45].
Our resulting model is of Darcy’s type, and represents a significant extension of the work [37] in that (a) the results reflect the interplay between microscale and microscale variations of the components of the potential as mediated by the microstructure through additional microscale problems in comparison with Penta et al. [37], and (b) the final balance equation for the leading order pressure incorporates the role of the vascularisation of the porous phases, cf. also mass balance (89).
As the influence of the body force is being modelled by taking into account a representation of the body force in terms of the gradient of a scalar potential, this model enhances the practical applicability of the mathematical framework developed in [37] when specialised to the application of electric fields to porous media. This is because the electric potential can usually be controlled in experimental setups.
The current work is open to a variety of improvements and extensions. While the theoretical framework takes into account possible discrepancies between the tumour and healthy tissues hydraulic conductivities, as well as macroscale and microscale inhomogeneties of the electric potential, numerical simulations of appropriate periodic cell problems (or semi-analytical approaches in case of simplified geometries, see, e.g. [40]) will be required to accurately capture those contributions.
We also considered that the underlying pore structure for each of the considered phases can be described by the simple Darcy’s law (supplmented by appropriate inhonogenous body forces and mass supply in each phase), whereas a more accurate representation of the pore structures for tumour modelling application could be provided by considering a Darcy–Brinkman approach, as suggested in [8] and recently developed in the context of asympotic homogenisation for the lymph node in [17].
Furthermore, we consider a multiscale representation of the electric potential, which means that contributions arising from the solution of a multiscale system of PDEs in terms of the electric potential could be readily incorporated in our framework as long as the electric potential is considered independent from the fluid flow. This could include time variations of the electric potential and in fact, nanosecond pulsed electric fields stimulate the production of ROS; hence, the model could be used to develop more effective pro-oxidative therapies, see, e.g. [29] and [31]. Discrepancies in the electric properties between the different phases would instead require an extension of the modelling approach itself, see, e.g. [15] in the context of electrosensitive elastic composites. In addition, further development of this modelling framework should also take into account the crucial role of mechanical deformations, see, e.g. [14].
The model could also be extended to account for the microvessels’ geometry (i.e. tortuosity), as done in [1, 2, 27, 33, 36] in order to enhance our understanding of the vascular response to electroporation-based treatments and its implications on drug delivery and distribution within tumour tissues.
Electrophoresis has the advantage of being a fast and efficient strategy for studying different drug interactions in the tumour microenvironment, while also triggering an adaptive immune response capable of eradicating metastasis. As highlighted in [12], current electrochemotherapy protocols are based on experimental measurements, and there is a lack of realistic mathematical models for the prediction of extravasation and delivery of large therapeutic molecules to target tissues by virtue of applied electric field. There is a substantial demand for the development of mathematical models for electrophoresis-facilitated molecular transport with direct measurements. Our mathematical model, once validated against experimental data, could be used to improve current electrochemotherapy protocols by providing predictions on the optimal application of the electric fields depending on patient-specific tumour microenvironments.
Availability of data and materials
Not applicable.
References
Al Sariri, T., Penta, R.: Multi-scale modelling of nanoparticle delivery and heat transport in vascularised tumours. Math. Med. Biol.: J. IMA 39(4), 332–367 (2022)
Al Sariri, T., Simitev, R.D., Penta, R.: Optimal heat transport induced by magnetic nanoparticle delivery in vascularised tumours. J. Theor. Biol. 561, 111372 (2023)
Andrade, D.L., et al.: Electrochemotherapy treatment safety under parallel needle deflection. Sci. Rep. 12(1), 2766 (2022)
Baghban, R., et al.: Tumor microenvironment complexity and therapeutic implications at a glance. Cell Commun. Signal 18, 1–19 (2020)
Bakhvalov, N.S., Panasenko, G.: Homogenisation: Averaging Processes in Periodic Media: Mathematical Problems in the Mechanics of Composite Materials, vol. 36. Springer (2012)
Beebe, S.J., et al.: Nanosecond pulsed electric field (nsPEF) effects on cells and tissues: apoptosis induction and tumor growth inhibition. IEEE Trans. Plasma Sci. 30(1), 286–292 (2002)
Berkenbrock, J.A., Machado, R.G. and Suzuki, D.O.H.: Electrochemotherapy effectiveness loss due to electric field indentation between needle electrodes: a numerical study. J. Healthc. Eng. 2018 (2018)
Bhattacharyya, S., De, S., Gopmandal, P.P.: Electrophoresis of a colloidal particle embedded in electrolyte saturated porous media. Chem. Eng. Sci. 118, 184–191 (2014)
Bommakanti, S., et al.: A simulation analysis of large multi-electrode needle arrays for efficient electrochemotherapy of cancer tissues. In: 2011 Annual Report Conference on Electrical Insulation and Dielectric Phenomena, pp. 187–190. IEEE (2011)
Chenna, S., et al.: Mechanisms and mathematical modeling of ROS production by the mitochondrial electron transport chain. Am. J. Physiol.-Cell Physiol. 323(1), C69–C83 (2022)
Cioranescu, D., Donato, P.: An Introduction to Homogenization, Oxford Lecture Series in Mathematics and its Applications, vol. 17 (1999)
Corovic, S., et al.: Modeling of microvascular permeability changes after electroporation. PLoS One 10(3), e0121370 (2015)
Dalwadi, M.P., Griffiths, I.M., Bruna, M.: Understanding how porosity gradients can make a better filter using homogenization theory. Proc. R. Soc. A: Math., Phys. Eng. Sci. 471(2182), 20150464 (2015)
Dehghani, H., et al.: The role of microscale solid matrix compressibility on the mechanical behaviour of poroelastic materials. Eur. J. Mech.-A/Solids 83, 103996 (2020)
Di Stefano, S., et al.: Effective balance equations for electrostrictive composites. Z. Angew. Math. Phys. 71, 1–36 (2020)
Geboers, B., et al.: High-voltage electrical pulses in oncology: irreversible electroporation, electrochemotherapy, gene electrotransfer, electrofusion, and electroimmunotherapy. Radiology 295(2), 254–272 (2020)
Girelli, A., et al.: Effective governing equations for dual porosity Darcy-Brinkman systems subjected to inhomogeneous body forces and their application to the lymph node. Proc. R. Soc. A 479(2276), 20230137 (2023)
Henshaw, J.W., Yuan, F.: Field distribution and DNA transport in solid tumors during electric field-mediated gene delivery. J. Pharm. Sci. 97(2), 691–711 (2008)
Holmes, M.: Introduction to Perturbation Method. Springer (1995)
Hornung, U.: Homogenization and Porous Media. Springer, New York (1997)
Jain, R.K., Tong, R.T., Munn, L.L.: Effect of vascular normalization by antiangiogenic therapy on interstitial hypertension, peritumor edema, and lymphatic metastasis: insights from a mathematical model. Cancer Res. 67(6), 2729–2735 (2007)
Kotnik, T., et al.: Membrane electroporation and electropermeabilization: mechanisms and models. Ann. Rev. Biophys. 48, 63–91 (2019)
Kurban, L.A.S., et al.: Pathological nature of renal tumors-does size matter? Urol. Ann. 9(4), 330 (2017)
Larkin, J.O., et al.: Electrochemotherapy: aspects of preclinical development and early clinical experience. Ann. Surg. 245(3), 469 (2007)
Liou, G.-Y., Storz, P.: Reactive oxygen species in cancer. Free Rad. Res. 44(5), 479–496 (2010)
Maryam, M., Jennifer, A.P.: Fundamental mathematical model shows that applied electrical field enhances chemotherapy delivery to tumors. Math. Biosci. 272, 1–5 (2016)
Mascheroni, P., Penta, R.: The role of the microvascular network structure on diffusion and consumption of anticancer drugs. Int. J. Numer. Methods Biomed. Eng. 33(10), e2857 (2017)
Mondal, N., Chakravarty, K., Dalal, D.C.: A mathematical model of drug dynamics in an electroporated tissue. Math. Biosci. Eng. 18(6), 8641–8660 (2021)
Novickij, V., et al.: Electrochemotherapy using doxorubicin and nanosecond electric field pulses: a pilot in vivo study. Molecules 25(20), 4601 (2020)
Nuccitelli, R.: Application of pulsed electric fields to cancer therapy. Bioelectricity 1(1), 30–34 (2019)
Pakhomova, O.N., et al.: Oxidative effects of nanosecond pulsed electric field exposure in cells and cell-free media. Arch. Biochem. Biophys. 527(1), 55–64 (2012)
Papanicolau, G., Bensoussan, A., Lions, J. L.: Asymptotic Analysis for Periodic Structures. Elsevier (1978)
Penta, R., Ambrosi, D., Quarteroni, A.: Multiscale homogenization for fluid and drug transport in vascularized malignant tissues. Math. Models Methods Appl. Sci. 25(01), 79–108 (2015)
Penta, R., Gerisch, A.: An Introduction to Asymptotic Homogenization. In: Lecture Notes in Computational Science and Engineering, pp. 1–26. Springer (2017)
Penta, R., Ambrosi, D., Shipley, R.: Effective governing equations for poroelastic growing media. Q. J. Mech. Appl. Math. 67(1), 69–91 (2014)
Penta, R., Ambrosi, D.: The role of the microvascular tortuosity in tumor transport phenomena. J. Theor. Biol. 364, 80–97 (2015)
Penta, R., et al.: Effective governing equations for heterogenous porous media subject to inhomogeneous body forces. Math. Eng. 3(4), 1–17 (2021)
Rajagopal, K.R.: On a hierarchy of approximate models for flows of incompressible fluids through porous solids. Math. Models Methods Appl. Sci. 17(2), 215–252 (2007)
Raji, S.: Influence of electrodes on electric field distribution for effective electrochemotherapy. J. Cancer Prevent. Curr. Res. 4(1) (2016)
Ramírez-Torres, A., et al.: The role of malignant tissue on the thermal distribution of cancerous breast. J. Theor. Biol. 426, 152–161 (2017)
Serša, I., et al.: Electric current density imaging of mice tumors. Magnet. Resonan. Med. 37(3), 404–409 (1997)
Taffetani, M., et al.: Biomechanical modelling in nanomedicine: multiscale approaches and future challenges. Arch. Appl. Mech. 84(9–11), 1627–1645 (2014)
Urbañska, K., et al.: Glioblastoma multiforme—an overview. Contemp. Oncol./Współczesna Onkol. 18(5), 307–312 (2014)
Wu, G., et al.: Importance of tumor size at diagnosis as a prognostic factor for hepatocellular carcinoma survival: a population-based study. Cancer Manag. Res. 4401–4410 (2018)
Ruijun, W., et al.: Rapid screening of multi-target antitumor drugs by nonimmobilized tumor cells/tissues capillary electrophoresis. Analyt. Chim. Acta 1045, 152–161 (2019)
Acknowledgements
ART and RP conducted the research by following the inspiring principles of the Italian Association for Higher Mathematics (Indam), GNFM group.
Funding
ZBF is supported by EPSRC scholarship EP/W523823/1. RP is partially funded by EPSRC Grants EP/S030875/1 and EP/T017899/1.
Author information
Authors and Affiliations
Contributions
ZBF was involved in writing—original draft, writing—review & editing, conceptualisation, formal analysis, software, visualisation. ART contributed to writing—review & editing, conceptualisation, software, methodology, supervision. RP contributed to writing—review & editing, writing—original draft, conceptualisation, software, methodology, supervision, project administration. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no competing interests as defined by Springer, or other interests that might be perceived to influence the results and/or discussion reported in this paper.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fülöp, Z.B., Ramírez-Torres, A. & Penta, R. Multiscale modelling of fluid transport in vascular tumours subjected to electrophoresis anticancer therapies. Z. Angew. Math. Phys. 75, 9 (2024). https://doi.org/10.1007/s00033-023-02141-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00033-023-02141-3