Kinematics of shock waves in a radiating ideal gas containing dust particles

Abstract

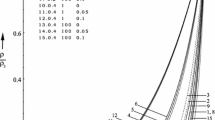
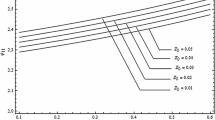
Shock waves propagating through an ideal radiating gas containing solid dust particles of arbitrary strength are studied in this work. To analyze shock front kinematics, an infinite set of transport equations determining shock strength and induced discontinuities is obtained. A truncation approach of the infinite system of transport equations yields an efficient shock propagation system of finite ordinary differential equations. The analysis appropriately reflects the nonlinear steepening effects of the flow behind shock fronts due to the dynamic interaction between shock fronts and the flow behind them. The effects due to dust parameters and radiation on shock propagation are discussed with the help of a graphical representation. The decay laws for weak shocks in a non-radiating gas are precisely recovered by the second-order truncation approximation. The characteristic rule and the first- and second-order approximations are compared for shock waves of arbitrary strength.

Appendix

Coefficients present in Eq. (3.13) are as follows:

$$\begin{aligned} {h_{11}}= & {} \frac{{\Gamma {p_1}\chi }}{{\left( {1 - \theta {\rho _1}} \right) }} - \mu ,\quad {h_{12}} = \frac{{\frac{{\Gamma {p_1}}}{{{\rho _1}\left( {1 - \theta {\rho _1}} \right) }} - {\mu ^2}}}{{{h_{11}}}},\quad {h_{13}} = \frac{{\frac{{\Gamma {p_1}}}{{\left( {1 - \theta {\rho _1}} \right) }}\left( {{\chi ^2} - \frac{{{\hat{\chi }} }}{{\rho _1^2}}} \right) + {\omega _{11}}}}{{{h_{11}}}},\\ {\omega _{11}}= & {} - \frac{{\Gamma \mu \chi }}{{{{\left( {1 - \theta {\rho _1}} \right) }^2}}}\left\{ {{p_1}\theta {\hat{\chi }} + \left( {1 - \theta {\rho _1}} \right) + \frac{{{{\left( {1 - \theta {\rho _1}} \right) }^2}}}{\Gamma }} \right\} ,\\ {h_{14}}= & {} \frac{{\frac{{\Gamma {p_1}}}{{\left( {1 - \theta {\rho _1}} \right) }}\left( {\frac{{d\chi }}{{dt}} + 2\chi \phi - \frac{{{\hat{\phi }} }}{{\rho _1^2}} - \mu w\phi } \right) + {\omega _{12}}}}{{{h_{11}}}},\\ {\omega _{12}}= & {} - \mu \phi - \frac{{\Gamma \mu \phi }}{{\left( {1 - \theta {\rho _1}} \right) }} - \frac{{\Gamma \mu w{u_1}}}{{\left( {1 - \theta {\rho _1}} \right) }} + {\omega _{13}},\\ {\omega _{13}}= & {} - \frac{{\Gamma {p_1}\mu \theta }}{{{{\left( {1 - \theta {\rho _1}} \right) }^2}}}\left( {{\hat{\chi }} \phi + {\hat{\chi }} w{u_1} + \chi {\hat{\phi }} } \right) + {\omega _{14}},\\ {\omega _{14}}= & {} - \frac{{\left( {\Gamma - 1} \right) \mu {\hat{\chi }} }}{{\left( {1 - \theta {\rho _1}} \right) }}\left\{ {\frac{{\theta {Q_1}}}{{\left( {1 - \theta {\rho _1}} \right) }} + {{\left( {{Q_\rho }} \right) }_1}} \right\} ,\\ {h_{15}}= & {} \frac{{\frac{{\Gamma {p_1}}}{{\left( {1 - \theta {\rho _1}} \right) }}\left\{ {\frac{{d\phi }}{{dt}} + {\phi ^2} - \mu w\phi - \mu {u_1}w' - \frac{{\theta \mu }}{{\left( {1 - \theta {\rho _1}} \right) }}{\hat{\phi }} \left( {\phi + w{u_1}} \right) } \right\} + {\omega _{15}}}}{{{h_{11}}}},\\ {\omega _{15}}= & {} - \frac{{\left( {\Gamma - 1} \right) \mu {\hat{\phi }} }}{{\left( {1 - \theta {\rho _1}} \right) }}\left\{ {\frac{{\theta {Q_1}}}{{\left( {1 - \theta {\rho _1}} \right) }} + {{\left( {{Q_\rho }} \right) }_1}} \right\} . \end{aligned}$$