1 Introduction

1.1 Previous work

The first researcher to study planing in an analytic manner was Sretensky [27] and Sretensky [28]. He laid out the foundation for planing of two-dimensional profiles in deep water. In his work, he assumed that the water is inviscid and that the free-surface kinematic and dynamic conditions are to be linearized.

These are reasonable assumptions considering that most practical applications of efficient planing require the trim angle to be small, implying that the presence of viscosity does not affect the generation of the pressure distribution and that the only effect of viscosity is to create the frictional resistance, which can be accounted for through the selection of a suitable formula.

Further early and similar work was performed by Sedov [24], Sedov [25, Chap. VII], Maruo [19], Maruo [20], Maruo [21], Maruo [22] and Squire [26].

Nonlinear planing, in which the full two free-surface conditions are employed was considered by Green [13], Green [14] and Green [15].

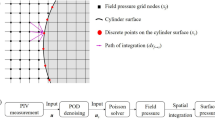
In all cases, the planing surface is represented by an unknown pressure distribution, which is to be found as part of the solution. Doctors [7] developed a simple and effective approach in which the pressure is composed of overlapping triangular elements, as depicted in Fig. 1a.

The purpose of the current work is to gain insight into the intellectually interesting physics behind planing phenomena. The engineering application of this research is to naval architecture design practice, in which the designer wishes to develop efficient planing vessels.

Fig. 1
figure 1

Definition of the problem

Full size image

1.2 Current work

We shall here build upon the previous work of Doctors [7] and, in the first instance, extend the collocation method he used to the Galerkin method, in which the kinematic condition is applied in an average sense over the longitudinal extent of the field element—rather than just at its center.

We shall also consider the performance of various curved profiles and apply the methodology to practical planing surfaces in which the wetted length is unknown and is to be found as part of the numerical solution. Figure 1a presents the nomenclature used in this work. There are \(N-1\) elements with a length 2a, as indicated, and the wetted planing length \(l=2aN\) is predefined in a straightforward application of the theory. The trailing-edge elevation \(h_T\) is unknown and is part of the solution.

Figure 1b illustrates the elementary profiles of the planing surfaces under consideration. In order of complexity, these are: flat (linear), parabolic, cubic, sinusoidal and angular. The first three profiles are defined by the general power formula

$$\begin{aligned} z/l= & {} (x/l)^n \ \text { for } \ {n=1,2 \text { and } 3} \,, \end{aligned}$$
(1)

while the sinusoidal profile is defined as

$$\begin{aligned} z/l= & {} x/l - \sin (\pi x/l)/\pi \,, \end{aligned}$$
(2)

and the angular formula is

$$\begin{aligned} z/l= & {} \left\{ \begin{array}{ll}0 &{} \text {for}\ {x/l \le 1/2} \\ 2x/l -1 &{} \text {for} \ {x/l > 1/2}\end{array}\right. \,. \end{aligned}$$
(3)

Later in this study we will combine the elementary profiles with the intention of creating more efficient practical profiles—those with a higher lift-to-drag ratio.

It has been pointed out in the literature that the pressure distribution contains a square-root singularity at the leading edge, which implies the creation of a spray jet that is directed forward. This phenomenon corresponds to the leading-edge suction in thin-airfoil theory. In the case of planing, we must consequently not normally apply the kinematic condition at the leading edge; this results in an error e at the leading edge.

2 Theory

2.1 Potential flow

We employ the classic inviscid-fluid approach and assume linearized kinematic and dynamic conditions at the free surface, as well as the kinematic condition on the bottom at \(z=-\infty \). The velocity potential for a two-dimensional pressure patch traveling with a speed U was given by Doctors [8, p 341, Eqs. 9.2 and 9.3]. A detailed explanation of the solution was published by Lamb [17, Articles 243 and 244, pp 400–406].

The desired wave elevation is obtained through the use of the dynamic condition and was published by Doctors [8, Eq. 9.4]:

(4)

where k is the circular wave number, \(p(x)=\rho g\delta (x)\) is the local surface pressure, \(\rho \) is the water density, g is the acceleration due to gravity, \(\delta \) is the local pressure “head” and \(k_0\) is the fundamental circular wave number given by the formula

$$\begin{aligned} k_0= & {} g/U^2 \,. \end{aligned}$$
(5)

The two-dimensional Kochin functions are

$$\begin{aligned} \mathcal {P}(k) + \textrm{i}\mathcal {Q}(k)= & {} \int \limits \delta (x) \exp (\textrm{i}kx) \, \textrm{d}x \,. \end{aligned}$$
(6)

2.2 Collocation response function

The Kochin functions \(\mathcal {P}\) and \(\mathcal {Q}\) for a triangular element possessing fore-and-aft symmetry with nominal length \(\textrm{d}x=2a\) was given by Doctors [8, Eq. 9.5] as

$$\begin{aligned} \mathcal {P}= & {} \frac{2\delta _0}{ak^2} \cdot \sin ^2(ka) \,, \\ \mathcal {Q}= & {} 0 \,, \nonumber \end{aligned}$$
(7)

in which \(\delta _0\) is the nominal (peak) pressure of the element.

The integration in Eq. 4 can be performed analytically using the two auxiliary functions for the cosine and the sine integrals, defined by Abramowitz and Stegun [1, Sect. 5.2, pp. 231–233]:

$$\begin{aligned} f(z)= & {} \int \limits _0^\infty \frac{\sin (t)}{z + t} \, \textrm{d}t \,, \end{aligned}$$
(8)
$$\begin{aligned} g(z)= & {} \int \limits _0^\infty \frac{\cos (t)}{z + t} \, \textrm{d}t \,. \end{aligned}$$
(9)

We also require the two integration formulas:

$$\begin{aligned} \int \limits _0^\infty \,\textrm{sgn}(z) f(|z|) \, \textrm{d}z= & {} g(|z|) + \ln (|z|) \,, \end{aligned}$$
(10)
$$\begin{aligned} \int \limits _0^\infty g(|z|) \, \textrm{d}z= & {} \,\textrm{sgn}(z)\bigl [\frac{\pi }{2} - f(|z|)\bigr ] \,. \end{aligned}$$
(11)

These two auxiliary functions can be computed to double-precision accuracy using the method of [23, Pages 148 and 149]. Care should be used when using other sources of information on these special functions, where slightly different notation and/or definitions are sometimes evident.

After some algebra utilizing these special functions, the k integration in Eq. 4 leads to the required result:

$$\begin{aligned} \zeta _i/\delta _j= & {} \sum _{k=-1}^{1} w_i C_{i,j+k} \,, \end{aligned}$$
(12)

with the three weights

$$\begin{aligned}{}[w]= & {} [-1, 2, -1] \,, \end{aligned}$$
(13)

in which the corner function C is given by

$$\begin{aligned} C_{ij}= & {} \frac{1}{2ak_0} \Bigl \{\frac{1}{\pi }[ g(|\lambda _{ij}|) + \ln (|\lambda _{ij}|)] + H(-\lambda _{ij})[2\sin (\lambda _{ij}) - \lambda _{ij}] \Bigr \} \,, \end{aligned}$$
(14)

where H is the Heaviside step function and the dimensionless distance from the center of the source element with index j to the field point with index i is

$$\begin{aligned} \lambda _{ij}= & {} k_0(x_i - x_j) \,. \end{aligned}$$
(15)

2.3 Galerkin response function

In this approach, we average the response at the field point by a weighted integration over the field panel, with the weighting function given by the triangular function. This process involves two more integrations. Care must be taken with these integrations, because the special functions involve the absolute values of their arguments. The final result is

$$\begin{aligned} \zeta _i/\delta _j= & {} \sum _{k=-2}^{2} w_i C_{i,j+k} \,, \end{aligned}$$
(16)

with the five weights

$$\begin{aligned}{}[w]= & {} [1, -4, 6, -4, 1] \,, \end{aligned}$$
(17)

in which the corner function C is now given by

$$\begin{aligned} C_{ij}= & {} \frac{1}{(2ak_0)^3} \left\{ \frac{1}{\pi }[ g(|\lambda _{ij}|) + \ln (|\lambda _{ij}|) - \frac{1}{2}\lambda _{ij}^2\ln (|\lambda _{ij}|) + \frac{3}{4}\lambda _{ij}^2 + \frac{\pi }{2}|\lambda _{ij}|]\right. \nonumber \\{} & {} \left. + H(-\lambda _{ij})[2\sin (\lambda _{ij}) + \frac{1}{6}\lambda _{ij}^3] \right\} \,. \end{aligned}$$
(18)

The two parts of Fig. 2 compare the collocation and the Galerkin response functions in the far field and the near field respectively, for three different values of the parameter \(ak_0\). The second subfigure particularly demonstrates that there is little difference between the two methods of calculation—except very close to the source panel. As implied by the methodology, the Galerkin result represents a weighted average over the field panel.

Fig. 2
figure 2

Response functions

Full size image

2.4 Assembly of pressure elements

The solution of the planing problem is effected by applying the kinematic condition at each of the points indicated in Fig. 1a. The condition requires that the sum of the free-surface responses from the pressure elements equates to the local elevation. That is,

$$\begin{aligned} \sum _{j=1}^{N-1} \delta _j K_{ij}= & {} h_T + z_i \text { for }{i = 0 \text { to } N - 1} \,, \end{aligned}$$
(19)
$$\begin{aligned} K_{ij}= & {} \zeta _i/\delta _j \,. \end{aligned}$$
(20)

2.5 Convergence

The four parts of Fig. 3 present some examples of the convergence of the numerical predictions for a flat plate with respect to the number of pressure panels N.

Fig. 3
figure 3

Convergence behavior for flat plate

Full size image

Figure 3a is a plot of the pressure distribution along the plate at a wetted-length Froude number \(F=U/\sqrt{gl}\) of 1, for five values of the number of panels, using the collocation method. The pressure is rendered dimensionless using the wetted plate length l and the lift L on the plate. This graph shows that 40 or 80 panels suffice to obtain good convergence.

Figure 3b is the corresponding graph using the Galerkin method. It is somewhat disappointing to observe the poor and oscillatory behavior of the curve of pressure for small values of the number of panels. However, the process does converge properly as the number of panels increases.

The lift L is made dimensionless with respect to the at-rest lift (buoyancy) \(L_0\) in Fig. 3c and is plotted as a function of the number of panels. Despite the apparent misbehavior of the pressure distribution exhibited by the Galerkin method in Fig. 3b, the lift convergences faster using the more sophisticated Galerkin method. A similar statement can be made about the dimensionless center of pressure \(\overline{x}/l\) in Fig. 3d.

3 Sample results

3.1 Power profiles

Planing surfaces with a flat, parabolic and cubic profile are considered in Fig. 4. The dimensionless lift for all three algebraic profiles is presented in Fig. 4a. The use of the traditional lift coefficient \(C_L=L/\frac{1}{2}\rho U^2l\) is eschewed here because it inconveniently approaches infinity as the speed approaches zero. The veracity of the calculations is demonstrated by comparing the predictions of the collocation and the Galerkin methods. The dimensionless lift equals unity at zero speed.

Fig. 4
figure 4

Comparison of elementary profiles

Full size image

Figure 4b shows the dimensionless center of pressure. As a check on the curves, for the flat plate at-rest, the value is 1/3, while the high-speed limit is 3/4. The former is the correct result for a floating triangular centerplane profile. The latter is the established result for the center of pressure for a two-dimensional flat airfoil. The trailing-edge elevation (made dimensionless against the at-rest value) is plotted in Fig. 4c.

The ratio of the wave resistance to the pressure resistance is given in Fig. 4d. To this end, we remind the reader that the pressure resistance (drag in an inviscid fluid) is given by the formula

$$\begin{aligned} R_P= & {} {} \sum _{i=1}^{N-1} p_i s_i \Delta x \,, \end{aligned}$$
(21)

while the wave resistance was given by Lamb [17, Article 249, Pages 415 and 416]:

$$\begin{aligned} R_W= & {} \frac{1}{4}\rho g (A_C^2 + A_S^2) \,, \end{aligned}$$
(22)
$$\begin{aligned} A_C= & {} - \frac{4\sin ^2(k_0a)}{k_0a} \sum _{i=1}^{N-1} \delta _i \sin (k_0x_i) \,, \end{aligned}$$
(23)
$$\begin{aligned} A_S= & {} - \frac{4\sin ^2(k_0a)}{k_0a} \sum _{i=1}^{N-1} \delta _i \cos (k_0x_i) \end{aligned}$$
(24)

and so the spray resistance is simply

$$\begin{aligned} R_S= & {} {} R_P - R_W \,. \end{aligned}$$
(25)

In these equations, \(s_i\) is the slope of the planing surface at the ith field point, while \(A_C\) and \(A_S\) are the inphase and quadrature components of the downstream wave amplitude.

3.2 Splash-free profiles

Figure 4d shows that the spray resistance becomes increasingly dominant, as the speed of the planing surface increases. The linear theory cannot be used directly to compute the spray resistance, because the physics relates to the spray jet that is thrown forward at the leading edge, where the elevation of the free surface is double-valued in the real nonlinear situation. However, the spray resistance can be deduced by means of the simple subtraction in Eq. 25.

It is for this reason that the kinematic condition is not applied at \(i=N\) at the leading edge as shown in Fig. 1a, where the error e in not matching the water elevation at the plate is indicated. This error can be obtained from Eq. 19 as

$$\begin{aligned} e= & {} \sum _{j=1}^{N-1} \delta _j K_{Nj} - h_T - z_N \,. \end{aligned}$$
(26)

We can create a splash-free profile by means of a linear combination of two elementary profiles through the use of the simple formula:

$$\begin{aligned} e= & {} \alpha e_1 + \beta e_2 \nonumber \\= & {} 0 \,. \end{aligned}$$
(27)

Hydrodynamic planing surfaces behave similarly to aerodynamic wings, and particularly so at high Froude numbers. Efficient wings are shock free, meaning that the incoming air flow meets the leading edge of the wing at the same angle as that of the profile, so that there is no flow separation. For the planing surface, this is usually referred to as the splash-free condition.

An example of this idea is considered in Fig. 5 for a combination of a flat and a parabolic profile. Table 1 should be consulted for the abbreviations used in the annotations in this figure and throughout the remainder of this paper.

Table 1 Annotation used in figures
Full size table

The convergence of the pressure distribution with respect to the number of panels, for the collocation and the Galerkin methods, is presented in the first two parts of Fig. 5. The rate of convergence appears to be better than that in Fig. 3a, because the difference in the curves for \(N=40\) and \(N=80\) is now almost indistinguishable for the collocation method in Fig. 5a. However, once again, the pressure obtained from the Galerkin method in Fig. 5b exhibits minor problems at the ends of the curved plate.

Fig. 5
figure 5

Convergence behavior for splash-free profiles

Full size image

The previously mentioned choice of, say, 80 panels provides a prediction for integrated results such as lift and center of pressure converged to better than one percent, which is generally sufficient for engineering design purposes. These results are plotted in Fig. 5c and d.

The splash-free concept is explored further in Fig. 6. The pressure distribution is presented for six values of the Froude number in Fig. 6a. There is insignificant difference between the cases of \(F=3\) and \(F=\infty \). The latter case corresponds to two-dimensional airfoil theory, for which there is a simple analytic solution. The curve is simply one half of an ellipse.

Fig. 6
figure 6

Behavior of splash-free profiles

Full size image

The pressure possesses increasingly fore-and-aft symmetry as the speed increases. This point is reinforced by examining the behavior of the center of pressure in Fig. 6b, which indeed approaches 1/2 for large values of the Froude number.

The corresponding result for the lift is seen in Fig. 6c. At high speeds, the curves for the three elementary secondary profiles in Eq. 27—parabolic, sinusoidal and angular—are separated by a constant difference in the logarithmic plot. In reality, this corresponds to a fixed ratio.

Finally, the ratio \(\beta /\alpha \) of the two factors in Eq. 27 is plotted against the Froude number in Fig. 6d. Because of the way the elementary profiles are defined in Eqs. 1–3, this ratio equals \(-1/2\) at zero speed and it approaches \(-1\) at infinite speed.

4 Practical applications

4.1 Free flat profiles

In a practical case of planing, the weight and the center of gravity are predefined and the boat consequently adjusts itself with respect to the wetted length and the trim so that it is in equilibrium. In the results presented so far, the wetted length l is defined, so that the predictions are not directly in a usable form. In the simplest example of an equilibrium calculation, we shall fix the trim angle \(\alpha \) equal to the at-rest value \(\alpha _0\); thus equilibrium with respect to weight or lift only is considered.

We clarify that, in the case of a flat profile, \(\alpha \) represents both the first profile coefficient and the trim angle.

In principle, it is necessary to iterate the wetted length until the desired equilibrium with regard to lift is achieved. One can circumvent this difficulty by simply performing a single planing calculation and then relating the results to the relevant zero-speed condition. Thus the at-rest lift \(L_0\) is given in terms of the at-rest wetted length \(l_0\) and the at-rest trim angle \(\alpha _0\) by the formulas

$$\begin{aligned} \alpha= & {} \alpha _0 \,, \nonumber \\ L= & {} L_0 \end{aligned}$$
(28)
$$\begin{aligned}= & {} \frac{1}{2}\rho g l_0^2 \alpha _0 \,, \end{aligned}$$
(29)

so we obtain

$$\begin{aligned} l_0= & {} \sqrt{2L/\rho g \alpha _0} \,. \end{aligned}$$
(30)

Figure 7a shows the predictions for the wetted length, trailing-edge elevation and wave resistance. The abscissa is the Froude number \(F_0\) based on the at-rest wetted length. The data are made dimensionless as indicated. The curves are the result of the current theory, while the symbols represent data extracted from Squire [26, Table 5].

Fig. 7
figure 7

Free flat profiles

Full size image

The more practical case of equilibrium requires ensuring that the moments of the weight and the hydrodynamic force balance each other, in addition to the forces. To this end, we note that the center of pressure of the flat plate at rest \(\overline{x}_0\) is located at 1/3 the at-rest length. We also utilize Eq. 29 and make use of the calculation of the dynamic lift L based on an assumed trim angle \(\alpha _0\), which must be scaled according to the required at-rest lift (the at-rest buoyancy):

$$\begin{aligned} l_0= & {} 3\overline{x}\,, \end{aligned}$$
(31)
$$\begin{aligned} \alpha= & {} \rho g l_0^2 \alpha _0^2/2L \,. \end{aligned}$$
(32)

The remaining five parts of Fig. 7 are devoted to the flat plate which is in equilibrium for both lift and moment (the practical case). Thus Fig. 7b shows the predicted wetted length, trailing-edge elevation and the trim angle as a function of the at-rest-wetted-length Froude number \(F_0\). Also shown are dotted lines which are the high-Froude number approximations taken from Squire [26]. The high-Froude number approximations are quite acceptable for \(F_0>0.7\).

An example of the resistance components for an at-rest wetted length \(l_0\) of 10 m is presented in Fig. 7c. The predictions have been plotted as a function of the two-dimensional volumetric Froude number \(F_\nabla =U/\sqrt{g\nabla ^{1/2}}\), where \(\nabla \) is the displacement volume per unit width. This is the two-dimensional equivalent of the traditional volumetric Froude number. This choice of Froude number was made to enable the proper comparison of planing surfaces of differing length but supporting the same load.

To make this theoretical exercise useful, we have assumed a typical value of the water kinematic viscosity, as annotated on the plot. The ITTC (1957) formula, as described by Clements [5, Page 374] and by Lewis [18, Sects. 3.5, pp. 7–15], has been used here to estimate the frictional drag \(R_\textrm{F}\). Additionally, to further make the prediction realistic, a correlation allowance \(C_A={4\!\times \!10^{-4}}\) has been used. This leads to the correlation resistance \(R_A\) which accounts for a basic roughness in the hull. Further information on these matters can be found in Doctors [8, Sect. 3.3]. Figure 7c vividly demonstrates that viscosity is the source of the lion’s share of the total resistance at the higher speeds.

Different at-rest wetted lengths are the subject of Fig. 7d. As in all matters of engineering optimization, the best choice depends on the design requirements. The curves show that greater vessel lengths reduce the total resistance \(R_\textrm{T}\) at low speeds, while the opposite is true at high speeds.

The wetted length is plotted in Fig. 7e and the trim angle is plotted in Fig. 7f.

The humps in the curves plotted in Fig. 7d–f shift to higher volumetric Froude numbers as the at-rest wetted length \(l_0\) is increased. This is very evident in the case of Fig. 7e and f, where viscosity does not play a rôle. Because we are studying simple flat shapes, which are self-similar, it can be shown that any volumetric Froude number \(F_\nabla \) of interest is precisely proportional to the square root of the at-rest wetted length \(l_0\).

4.2 Free flat-plus-parabolic profiles

The equilibrium calculation for a flat-plus-parabolic profile of the form

$$\begin{aligned} z/l_0= & {} \alpha _0 (x/l_0) + \beta _0 (x/l_0)^2 \,, \end{aligned}$$
(33)

where \(\alpha _0\) and \(\beta _0\) are the coefficients of the linear (flat) and parabolic contributions in the at-rest condition, is more challenging. To gain an understanding of Eq. 33, we first note that the longitudinal and the vertical coordinates x and z have been divided by \(l_0\). Thus, if \(\beta _0=0\) this represents the simple flat shape. If \(\beta _0\) is negative, the plate is curved downward, similar to the traditional aircraft wing. This is known to be an efficient choice.

The challenge in utilizing Eq. 33 is due to the wetted length l varying with the speed and hence the proportion of the two at-speed corresponding coefficients \(\alpha \) and \(\beta \) is unknown. Nevertheless, the approach described in the previous section can be generalized as follows. We first equate the at-rest lift \(L_0\) and the at-rest moment \(M_0\) to the dynamic values:

$$\begin{aligned} L_0= & {} \alpha \widehat{L}_1 + \beta \widehat{L}_2 \,, \end{aligned}$$
(34)
$$\begin{aligned} M_0= & {} \alpha \widehat{M}_1 + \beta \widehat{M}_2 \,, \end{aligned}$$
(35)

in which the \(\widehat{~}\) symbol indicates the value of the relevant lift or moment for a unit value of the corresponding coefficient. In the current problem, these two equations can be expanded as

$$\begin{aligned} \frac{1}{2}\rho gl_0^2\alpha _0 + \frac{2}{3}\rho gl_0^2\beta _0= & {} \alpha \widehat{L}_1 + \beta _0 r^2 \widehat{L}_2 \,, \end{aligned}$$
(36)
$$\begin{aligned} \frac{1}{6}\rho gl_0^3\alpha _0 + \frac{1}{4}\rho gl_0^3\beta _0= & {} \alpha \widehat{M}_1 + \beta _0 r^2 \widehat{M}_2 \,, \end{aligned}$$
(37)
$$\begin{aligned} r= & {} l/l_0 \,, \end{aligned}$$
(38)

in which we have introduced r the ratio of the dynamic to the at-rest wetted lengths. This factor is required to modify the contribution from the parabolic term; it accounts for the fact that, with speed, the parabolic contributions to the lift and the moment increase with the square of the changing wetted length. The two equations of equilibrium can be combined, by eliminating \(\alpha \) between them. This process produces a single equation in the one variable r:

$$\begin{aligned} \widehat{M}_1\Big [\rho g(l^2/r^2) \big (\frac{1}{2}\alpha _0 + \frac{2}{3}\beta _0\big ) - \widehat{L}_2\beta _0 r^2\Big ] \quad{} & {} \nonumber \\ {} - \widehat{L}_1\Big [\rho g(l^3/r^3)\big (\frac{1}{6}\alpha _0 + \frac{1}{4}\beta _0\big ) - \widehat{M}_2\beta _0 r^2\Big ]&= ~0&\,. \end{aligned}$$
(39)

The solution of Eq. 39 is achieved rapidly, firstly through a simple search with respect to the wetted-length ratio, by stepping the values of r from 0 to 4 in increments of 0.1. Once the required interval is determined, the efficient Newton–Raphson method may be employed, as described by de Vahl Davis [6, Sect. 2.8].

Examples of the equilibrium of a flat-plus-parabolic planing surface are provided in Fig. 8. In the first subfigure, the specific resistance \(R_\textrm{T}/\textrm{W}\) is plotted as a function of the two-dimensional volumetric Froude number \(F_\nabla \). Values of the ratio \(\beta _0/\alpha _0\) range from 0 (flat) to \(-0.6\) (substantial downward curvature). As indicated in Eq. 33, this is the ratio of the parabolic to the linear term describing the shape of the plate in the at-rest condition. As an example, \(\beta _0/\alpha _0 = -1\) defines a surface with strong downward curvature in which the elevation of the leading edge equals that of the trailing edge.

Fig. 8
figure 8

Free flat-plus-parabolic profiles

Full size image

For small negative values of the parabolic coefficient (0 to \(-0.457\)) in Fig. 8a, increasing the negativity (downward curvature) reduces the drag at high speed. There is an opposite effect at low speeds. For larger negative values of the curvature (\(-0.457\) to \(-0.6\)), there is a separate group of results. That is, there is a discontinuity in behavior for \(\beta _0/\alpha _0\) equal to \(-0.457\). Further investigation of this surprising result revealed that there can be either one or two solutions for r in Eq. 39. The index \(i_r\) for this solution is annotated on the plot. Thus it was decided manually to choose the first (lower-value) solution for the first group of curves. On the other hand, the second (higher-value) solution was chosen for the second group of curves. This important point will be examined further in Fig. 9.

Fig. 9
figure 9

Incorrect free flat-plus-parabolic profiles

Full size image

The corresponding wetted-length ratio is plotted in Fig. 8b, where the division of the results into two distinct groups is also clear. Similarly, the trailing-edge elevation is plotted in Fig. 8c. Lastly, the change in trim angle from the at-rest condition is shown in Fig. 8d. An unexpected result is that, for the case of \(\beta _0/\alpha _0=-0.457\), the two solutions for the change in trim angle merge perfectly within plotting accuracy when \(F_\nabla >3\).

The matter of the possibility of two solutions to the flat-plus-parabolic planing problem is the subject of Fig. 9. The four parts of this figure correspond to the four parts of Fig. 8. However, in the current graphs a deliberate choice of the wrong solution for the wetted length (where there were two possibilities) has been made.

Comparison of Figs. 9a and Fig. 8a confirms the strong differences. The source of the bizarre problem is clear from the curves of wetted length in Fig. 9b. The curves do not approach unity in a smooth manner at zero speed. This plot confirms the suspicion that the additional solution of the equilibrium given by Eq. 39 is a mathematical artifice and should be rejected.

For the sake of completion we also provide results for the trailing-edge elevation in Fig. 9c, while the increase in trim angle relative to the at-rest condition is shown in Fig. 9d.

5 Improved profiles

5.1 Splash-free profiles

With the desire to optimize the planing profile, we will first consider splash-free forms, as already discussed earlier. Ideally, a splash-free form could be implemented in practice by installing an adjustable bottom in the vessel. That is, the concept would require altering the shape according to the speed, as exemplified by Fig. 10d.

This concept is clearly difficult to implement and so a simplified version would be to shape the bottom to be optimal for one particular speed. This simplified approach is analogous to the dynaplane, which is described in some detail in Doctors [9, pp. 485–488, Sect. 11.5.4]. In essence, the hull of the vessel resembles a typical high-speed planing vessel fitted with a step. The wetted surface just ahead of the step possesses a downwardly concave profile and so bears a strong resemblance to the current proposed concept.

The location of the center of gravity is a challenge so that a typical dynaplane vessel is fitted with a stabilizer at the stern. This stabilizer could be a hydrofoil or a secondary planing surface.

Therefore the results presented in Fig. 10 are based on the abovementioned splash-free analysis. However, the calculations require adjusting the lift in order to support the weight. This process requires scaling \(\alpha \) and \(\beta \) accordingly. The frictional resistance has been included in order to make the predictions useful.

Fig. 10
figure 10

Splash-free flat-plus-parabolic profiles

Full size image

Figure 10a shows the specific total resistance for five different wetted lengths. We remind the reader that in this somewhat hypothetical exercise, the dynamic wetted length equals the at-rest wetted length. The curves show that the best wetted length depends on the required operating speed, with lesser lengths being better at the higher speeds.

The first profile coefficient \(\alpha \) is plotted in Fig. 10b. This coefficient at first increases but then approaches zero at high speeds. The second coefficient \(\beta \) in Fig. 10c behaves in a similar manner (but negatively, of course). Finally, the ratio between the two coefficients is shown in Fig. 10d. This plot is reminiscent of Fig. 6d.

5.2 Optimal profiles

The optimal flat-plus-parabolic profile can be found by writing the profile, the lift, the moment and the resistance as

$$\begin{aligned} z/l= & {} \alpha (x/l) + \beta (x/l)^2 \,,\\ L= & {} \int \limits (\alpha \widehat{p}_1 + \beta \widehat{p}_2) \, \textrm{d}x \nonumber \end{aligned}$$
(40)
$$\begin{aligned}= & {} \alpha \widehat{L}_1 + \beta \widehat{L}_2 \,, \end{aligned}$$
(41)
$$\begin{aligned} M= & {} \int \limits (\alpha \widehat{p}_1 + \beta \widehat{p}_2) x \, \textrm{d}x \nonumber \\= & {} \alpha \widehat{M}_1 + \beta \widehat{M}_2 \,, \end{aligned}$$
(42)
$$\begin{aligned} R= & {} \int \limits (\alpha \widehat{p}_1 + \beta \widehat{p}_2) [\alpha + 2\beta (x/l)] \, \textrm{d}x \nonumber \\= & {} \alpha ^2\widehat{L}_1 + 2\alpha \beta \widehat{M}'_1 + \alpha \beta \widehat{L}_2 + 2\beta ^2\widehat{M}'_2 \,. \end{aligned}$$
(43)

The \(\widehat{~}\) symbol indicates the value of the relevant pressure for a unit value of the corresponding coefficient. The prime \(\prime \) is used to indicate that the moment has been divided by l so that it has the same dimensions as the lift.

We seek a minimum resistance subject to a specified lift, so we substitute \(\beta \) from Eq. 41 into Eq. 43, from which the following quadratic equation for the resistance is obtained:

$$\begin{aligned} R= & {} a_0 + a_1\alpha + a_2\alpha ^2 \,, \end{aligned}$$
(44)
$$\begin{aligned} a_0= & {} 2L^2\widehat{M}'_2/\widehat{L}_2^2 \,, \end{aligned}$$
(45)
$$\begin{aligned} a_1= & {} L(1 + 2\widehat{M}'_1/\widehat{L}_2 - 4\widehat{L}_1\widehat{M}'_2/\widehat{L}_2^2) \,, \end{aligned}$$
(46)
$$\begin{aligned} a_2= & {} 2(\widehat{L}_1^2\widehat{M}'_2/\widehat{L}_2^2 - \widehat{L}_1\widehat{M}'_1/\widehat{L}_2) \,. \end{aligned}$$
(47)

The minimum of Eq. 44 occurs when

$$\begin{aligned} \alpha= & {} - a_1/2a_2 \,. \end{aligned}$$
(48)

A partial check on the correctness of this algebra is provided by noting that Eq. 48 indicates that \(\alpha \propto L\) and, as a consequence, we can also state that \(\beta \propto L\).

A further point is that the frictional resistance component has been ignored in the optimization process. This would add a constant to the value of \(a_0\) in Eq. 44 and would therefore not affect the final result for the optimal coefficients in Eq. 48.

We now proceed to Fig. 11 in which the four subfigures correspond to those in Fig. 10. Referring first to Fig. 11a, the optimal resistance approaches zero at low speed, while the splash-free resistance does not. In the latter case, the resistance at zero speed is not zero because of the hydrostatic resistance. The calculation of the hydrostatic resistance has assumed that the transom is fully dry. At high speeds, the optimal resistance is the same as the splash-free resistance.

Fig. 11
figure 11

Optimal Flat-Plus-Parabolic Profiles

Full size image

Similarly, \(\alpha \) in Fig. 11b differs from that in Fig. 10b at low speeds but not at high speeds. The same statement can be made when comparing \(\beta \) in Fig. 11c with that in Fig. 10c. The ratio of the two coefficients \(\beta /\alpha \) in (d) of the two figures consequently also differ from each other.

To further clarify these points, the final set of results in Fig. 12 compare the splash-free and the optimal results on the same plots.

Figure 12a shows the specific total resistance for the two plate lengths, namely \(l=5\) m and \(l=20\) m. At low speeds, the optimal resistance is certainly less than the splash-free value. In the high-speed range there is no difference between the two methods of analysis.

The first profile coefficient \(\alpha \) is plotted in Fig. 12b. At zero speed the splash-free condition is substantially different from the optimal condition and so there is a substantial difference there between the two values of \(\alpha \). At higher speeds this coefficient is the same for the splash-free condition and the optimal condition, because the two methods of analysis are equivalent then.

Fig. 12
figure 12

Splash-Free and Optimal Flat-Plus-Parabolic Profiles

Full size image

5.3 Ventilation of transom

The computational results presented so far are based on the assumption that the transom is fully ventilated. In reality, this is not true at low forward speeds. There is a growing literature on this subject, which has been summarized by Doctors [8, Chap. 4]. A workable idealization of the water flow past a partly ventilated stern is depicted in Fig. 13a.

The water immediately behind the transom is assumed to be essentially stagnant. Furthermore the drawdown of the water is considered to be caused by a simple suction process. So the elevation \(\zeta _t\) of the water (negative in value) is given by the following formula:

$$\begin{aligned} \rho g\zeta _t= & {} C_p \frac{1}{2}\rho U^2 \,, \end{aligned}$$
(49)

where \(C_p\) is a suitably chosen (negative) pressure coefficient, as suggested in Doctors [8, Table 4.1]. We then assume that the water pressure on the face of the transom increases linearly with the local depth below the water surface. This gives the transom force as

$$\begin{aligned} F_t= & {} \frac{1}{2}\rho g (T_t + \zeta _t)^2 \,, \end{aligned}$$
(50)

in which \(T_t\) is the transom draft at rest. Thus an improved theory requires the subtraction of \(F_t\) from the pressure drag acting on the planing surface.

Some sample results for the total resistance are presented in Fig. 13b, for three of the cases already plotted in Fig. 7d. These new sophisticated calculations demonstrate the more acceptable prediction of the resistance, which now increases smoothly from a value of zero when the vessel is at rest. A value of \(C_p=-0.25\) has been employed here.

The critical Froude number at which the transom is fully ventilated can be deduced, for the simple case of a flat planing surface, by first expressing the displacement volume as follows:

$$\begin{aligned} \nabla= & {} \frac{1}{2}\zeta _t^2/\alpha _0 \,, \nonumber \\= & {} \frac{1}{2}\left( C_p\cdot U^2/2g\right) ^2/\alpha _0 \,, \end{aligned}$$
(51)

in which we have equated the water-level drop \(-\zeta _t\) with the transom draft \(T_t\) at rest. These equations can be manipulated to give the critical volumetric Froude number and the critical static-length Froude number:

$$\begin{aligned} F_\nabla= & {} \root 4 \of {16\nabla /C_p^2l_0^2} \,, \end{aligned}$$
(52)
$$\begin{aligned} F_0= & {} \sqrt{-4\nabla /C_pl_0^2} \,. \end{aligned}$$
(53)

The three critical two-dimensional-volumetric Froude numbers in Fig. 13b are predicted to be 1.504, 1.271 and 1.064; these numbers correlate with the relevant curves. For additional clarification, we have also shown the predictions of total resistance, in which the transom ventilation has been ignored.

6 Concluding comments

6.1 Current work

Fig. 13
figure 13

Ventilation of Transom

Full size image

  • The Galerkin method has been shown to be not much more effective than the simpler collocation method. This is particularly true of the predicted pressure distribution, which suffers from undesired oscillations unless a large number of panels is used. It is thought that the oscillations result from the singular behavior of planing at the ends of the surface.

  • We have shown that the theory can be applied to practical problems of planing without iteration where, in principle, there would be a need to do so. This is because the linear theory has the desirable property of being scalable. This allows us to obtain a single planing solution and then to reverse-engineer the results to the original at-rest vessel.

  • Optimal planing profiles show promise of modifying flat surfaces in terms of reducing the drag. These possess the characteristic of a downward curvature as in the dynaplane concept. This geometric feature is directly related to the corresponding aerodynamic problem.

  • At high speeds the optimal planing profile coincides with the splash-free form. At low speeds, the optimal profile is much better than the splash-free form.

  • The optimization form depends on the contribution of the frictional resistance. Were the friction to be ignored, the optimal planing form would be an infinity long plate set at a vanishingly small trim angle.

  • The first person to study optimal forms was Froude [12, Page 44] who considered the frictional and pressure components of resistance of a flat surface, using experiments in order to obtain the relevant lift and drag forces. His conclusion was that the optimal angle was \(3.312^\circ \) giving a total resistance-to-weight ratio of 0.1156. A study of Fig. 8a shows an optimal value of 0.09556 in the high-speed range. This is only marginally better and is applicable at one speed only. The somewhat unrealistic example of Fig. 11a indicates a best result of 0.08569 in the high-speed range. This example requires an adjustable planing surface. So even with a carefully constructed parabolic surface, the improvement over a simple flat surface is still not remarkable.

  • Inclusion of the back pressure of the stagnant water on the surface of the transom stern, when it is partly ventilated, is shown to reduce the resistance at low speeds. However, at high speeds—those of relevance to this work—the transom is fully ventilated. So this refinement to the theory is generally irrelevant.

6.2 Future work

It would be instructive to investigate further the matter of double solutions for the free flat-plus-parabolic surfaces in Fig. 8. This could be achieved either through towing-tank experiments or through the use of computational fluid dynamics.

It is planned to extend this work to three-dimensional planing surfaces. Some recent papers on this subject were written by Kohansal and Ghassemi [16], Ayob et al. [2], Blount [3], Brizzolara et al. [4], Doctors [10], Doctors [11] and Wang, Zhu et al. [29].