Mathematical insights into the influence of interventions on sexually transmitted diseases

Abstract

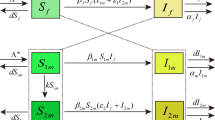
We establish a mathematical model to analyze what factors cause the epidemics of sexually transmitted diseases (STDs) and how to eliminate or mitigate them. According to the level of prevention awareness, we divide the susceptible population into two groups of individuals, whose behavior, population size, and recruitment rate are affected by the interventions. First, the threshold, $R_0$, of STDs model is obtained. If $R_0 < 1$, the disease-free equilibrium is globally asymptotically stable. We also obtain the conditions for switching the equilibrium state of the model among disease-free equilibrium, endemic equilibrium, and limit cycle. Second, the threshold and transcritical bifurcation show that interventions for high-risk sexual behaviors of high-risk susceptible individuals can eliminate STDs. Additionally, sex education, influenced by the size of infected individuals and by interventions, can effectively cut down the size of STDs. Third, extending the survival time of the infected individual may prolong the time to end STDs unless they reject high-risk sexual behavior. Fourth, we analyze the existence, stability, and direction of Hopf bifurcation, which may explain the periodic oscillation in the size of infected population.

Appendices

Appendix A: Proof of Theorem 3.3

Jacobian matrix $J\left( {{E_{1}}} \right)$ is

$$\begin{aligned} {J_{{a_{ij}}}}\left( {{E_1}} \right) = {\left( {\begin{array}{*{20}{c}} {\frac{{ - \beta {{\bar{I}}_1} - \beta \eta {{\bar{I}}_1}^2}}{{{{\left[ {1 + \eta \left( {{{\bar{S}}_1} + {{\bar{I}}_1}} \right) } \right] }^2}}} - \tau {{\bar{I}}_1} - d}&{}{\frac{{ - \beta {{\bar{S}}_1} - \beta \eta \bar{S}_1^2}}{{{{\left[ {1 + \eta \left( {{{\bar{S}}_1} + {{\bar{I}}_1}} \right) } \right] }^2}}} - \tau {{\bar{S}}_1}}&{}{ - \Lambda }\\ {\frac{{\beta {{\bar{I}}_1} + \beta \eta \bar{I}_1^2}}{{{{\left[ {1 + \eta \left( {{{\bar{S}}_1} + {{\bar{I}}_1}} \right) } \right] }^2}}}}&{}{ - \frac{{\beta \eta {{\bar{S}}_1}{{\bar{I}}_1}}}{{{{\left[ {1 + \eta \left( {{{\bar{S}}_1} + {{\bar{I}}_1}} \right) } \right] }^2}}}}&{}0\\ 0&{}{\frac{{rm\rho }}{{{K_2}}}{{\bar{x}}_1}\left( {1 - \frac{{{{\bar{x}}_1}}}{{{K_1}}}} \right) }&{}0 \end{array}} \right) _{3 \times 3}}. \end{aligned}$$

For equilibrium ${E_1}$, when ${{\bar{x}}_1} \ne {K_1}$ and ${{\bar{x}}_1} \ne 0$, its characteristic equation is

$$\begin{aligned} \lambda _{10}^3 - {T_{10}}\lambda _{10}^2 + {H_{10}}{\lambda _{10}} + {D_{10}} = 0, \end{aligned}$$

(5.1)

where ${T_{10}} = {a_{11\left( {{E_1}} \right) }} + {a_{22\left( {{E_1}} \right) }} < 0$, ${H_{10}} = {a_{11\left( {{E_1}} \right) }}{a_{22\left( {{E_1}} \right) }} - {a_{12\left( {{E_1}} \right) }}{a_{21\left( {{E_1}} \right) }}>0$, and ${D_{10}} = {a_{21\left( {{E_1}} \right) }}{a_{32\left( {{E_1}} \right) }}\Lambda$.

According to Routh–Hurwitz criterion [42], if ${{\bar{x}}_1} > {K_1}$, ${E_1}$ is a saddle; if ${{\bar{x}}_1} < {K_1}$ and ${T_{10}}{H_{10}} + {D_{10}} < 0$, ${E_1}$ is a locally stable node; if ${{\bar{x}}_1} < {K_1}$ and ${T_{10}}{H_{10}} + {D_{10}} > 0$, Eq. (5.1) has two positive roots and a negative root; then, ${E_1}$ is a saddle.

When ${{\bar{x}}_1} = {K_1}$ or ${{\bar{x}}_1} = 0$, the characteristic equation can be represented as follows

$$\begin{aligned} \lambda _{10}^2 - {T_{10}}{\lambda _{10}} + {H_{10}} = 0, \end{aligned}$$

(5.2)

then matrix $J\left( {{E_1}} \right)$ has one zero eigenvalue and two negative eigenvalues, ${ \lambda _1 }$, ${ \lambda _2}$, with corresponding eigenvectors ${T_{12}} = \left( {{V_{111}},{V_{112}},{V_{113}}} \right)$, where

$$\begin{aligned} {V_{111}} = \left( {\begin{array}{*{20}{c}} 1\\ {\frac{{{a_{21\left( {{E_1}} \right) }}}}{{{\lambda _1} - {a_{22\left( {{E_1}} \right) }}}}}\\ 0 \end{array}} \right) , {V_{112}} = \left( {\begin{array}{*{20}{c}} 1\\ {\frac{{{a_{21\left( {{E_1}} \right) }}}}{{{\lambda _2} - {a_{22\left( {{E_1}} \right) }}}}}\\ 0 \end{array}} \right) , {V_{113}} = \left( {\begin{array}{*{20}{c}} 1\\ { - \frac{{{a_{21\left( {{E_1}} \right) }}}}{{{a_{22\left( {{E_1}} \right) }}}}}\\ {\frac{{{a_{11\left( {{E_1}} \right) }}}}{\Lambda } - \frac{{{a_{12\left( {{E_1}} \right) }}{a_{21\left( {{E_1}} \right) }}}}{{\Lambda {a_{22\left( {{E_1}} \right) }}}}} \end{array}} \right) . \end{aligned}$$

We make the following transformations

$$\begin{aligned} \bar{S} = S - {\bar{S}_1},\ \bar{I} = I - {\bar{I}_1},\ \bar{X} = x - {\bar{x}_1}, \end{aligned}$$

and

$$\begin{aligned} \left( {\begin{array}{*{20}{c}} {\bar{Y}}\\ {\bar{Z}}\\ {\bar{X}} \end{array}} \right) = {T_{12}}\left( {\begin{array}{*{20}{c}} {\tilde{S}}\\ {\tilde{I}}\\ {\tilde{X}} \end{array}} \right) , \end{aligned}$$

then the system can be described as follows

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {\mathop {\tilde{S}}\limits ^. = {\lambda _1}\tilde{S} + \sum \limits _{i,j,k \in \mathrm{{N}}}^{i + j + k = 2} {{a_{ijk}}} {{\tilde{S}}^i}{{\tilde{I}}^j}{{\tilde{X}}^k} + o\left( {{{\left| {\tilde{S},\tilde{I},\tilde{X}} \right| }^3}} \right) ,}\\ {\mathop {\tilde{I}}\limits ^. = {\lambda _2}\tilde{I} + \sum \limits _{i,j,k \in \mathrm{{N}}}^{i + j + k = 2} {{b_{ijk}}} {{\tilde{S}}^i}{{\tilde{I}}^j}{{\tilde{X}}^k} + o\left( {{{\left| {\tilde{S},\tilde{I},\tilde{X}} \right| }^3}} \right) ,}\\ {\mathop {\tilde{X}}\limits ^. = \sum \limits _{i,j,k \in \mathrm{{N}}}^{i + j + k = 2} {{c_{ijk}}} {{\tilde{S}}^i}{{\tilde{I}}^j}{{\tilde{X}}^k} + o\left( {{{\left| {\tilde{S},\tilde{I},\tilde{X}} \right| }^3}} \right) .} \end{array}} \right. \end{aligned}$$

When ${{\bar{x}}_1} = {K_1}$, we have

$$\begin{aligned} {{{ c}_{002}} = \frac{{{a_{21\left( {{E_1}} \right) }}}}{{{a_{22\left( {{E_1}} \right) }}}}\left( {\frac{{{a_{11\left( {{E_1}} \right) }}}}{\Lambda } - \frac{{{a_{12\left( {{E_1}} \right) }}{a_{21\left( {{E_1}} \right) }}}}{{\Lambda {a_{22\left( {{E_1}} \right) }}}}} \right) \frac{{\Lambda {a_{22\left( {{E_1}} \right) }}}}{{{a_{11\left( {{E_1}} \right) }}{a_{22\left( {{E_1}} \right) }} - {\Lambda ^2}{a_{12\left( {{E_1}} \right) }}{a_{21\left( {{E_1}} \right) }}}}\frac{{mr\rho }}{{{K_2}}} \ne 0;} \end{aligned}$$

when ${{\bar{x}}_1} = 0$, we have

$$\begin{aligned} {{{ c}_{002}} = - \frac{{{a_{21\left( {{E_1}} \right) }}}}{{{a_{22\left( {{E_1}} \right) }}}}\left( {\frac{{{a_{11\left( {{E_1}} \right) }}}}{\Lambda } - \frac{{{a_{12\left( {{E_1}} \right) }}{a_{21\left( {{E_1}} \right) }}}}{{\Lambda {a_{22\left( {{E_1}} \right) }}}}} \right) \frac{{\Lambda {a_{22\left( {{E_1}} \right) }}}}{{{a_{11\left( {{E_1}} \right) }}{a_{22\left( {{E_1}} \right) }} - {\Lambda ^2}{a_{12\left( {{E_1}} \right) }}{a_{21\left( {{E_1}} \right) }}}}\frac{{mr\rho }}{{{K_2}}} \ne 0.} \end{aligned}$$

Hence, ${E_{1}}$ is a saddle node of codimension 1 [27]. The proof is complete. $\square$

Appendix B: Proof of Theorem 3.4

When ${{\bar{I}}_i} < \frac{{{K_2}}}{m}$ or ${{\bar{I}}_i} > \frac{{{K_2}}}{m}$, the results can be easily verified. When ${{\bar{I}}_i} = \frac{{{K_2}}}{m}$, we have

$$\begin{aligned} {J_{{a_{m,n}}}}\left( {{E_i}} \right) = {\left( {\begin{array}{*{20}{c}} {\frac{{ - \beta {I_i} - \beta \eta I_i^2}}{{{{\left[ {1 + \eta \left( {{S_i} + {I_i}} \right) } \right] }^2}}} - \tau {I_i} - d}&{}{\frac{{ - \beta {S_i} - \beta \eta S_i^2}}{{{{\left[ {1 + \eta \left( {{S_i} + {I_i}} \right) } \right] }^2}}} - \tau {S_i}}&{}{ - \Lambda }\\ {\frac{{\beta {I_i} + \beta \eta I_i^2}}{{{{\left[ {1 + \eta \left( {{S_i} + {I_i}} \right) } \right] }^2}}}}&{}{ - \frac{{\beta \eta {S_i}{I_i}}}{{{{\left[ {\eta \left( {{I_i} + {S_i}} \right) + 1} \right] }^2}}}}&{}0\\ 0&{}0&{}0 \end{array}} \right) _{3 \times 3}}. \end{aligned}$$

The characteristic equation is as follows

$$\begin{aligned} \lambda _{i}^2 - {T_{i}}{\lambda _{i}} + {H_{i}} = 0, \end{aligned}$$

(5.3)

where ${T_{i}} = {a_{11\left( {{E_i}} \right) }} + {a_{22\left( {{E_i}} \right) }} < 0$, ${H_{i}} = {a_{11\left( {{E_i}} \right) }}{a_{22\left( {{E_i}} \right) }} - {a_{12\left( {{E_i}} \right) }}{a_{21\left( {{E_i}} \right) }}>0$, then matrix $J\left( {{E_i}} \right)$ has one zero eigenvalue and two negative eigenvalues, ${{\bar{\lambda }}_i}$, ${{\tilde{\lambda }}_i}$, with corresponding eigenvectors ${T_{i}} = \left( {{V_{i1}},{V_{i2}},{V_{i3}}} \right)$, where

$$\begin{aligned} {V_{i1}} = \left( {\begin{array}{*{20}{c}} 1\\ {\frac{{{a_{21\left( {{E_i}} \right) }}}}{{{{\bar{\lambda }}_i} - {a_{22\left( {{E_i}} \right) }}}}}\\ 0 \end{array}} \right) , {V_{i2}} = \left( {\begin{array}{*{20}{c}} 1\\ {\frac{{{a_{21\left( {{E_i}} \right) }}}}{{{{\tilde{\lambda }}_i} - {a_{22\left( {{E_i}} \right) }}}}}\\ 0 \end{array}} \right) , {V_{i3}} = \left( {\begin{array}{*{20}{c}} 1\\ { - \frac{{{a_{21\left( {{E_i}} \right) }}}}{{{a_{22\left( {{E_i}} \right) }}}}}\\ {\frac{{{a_{11\left( {{E_i}} \right) }}}}{\Lambda } - \frac{{{a_{12\left( {{E_i}} \right) }}{a_{21\left( {{E_i}} \right) }}}}{{\Lambda {a_{22\left( {{E_i}} \right) }}}}} \end{array}} \right) . \end{aligned}$$

We make the following transformations successively

$$\begin{aligned} {{\bar{Y}_i}} = S - {S_i},\ {{\bar{Z}}_i} = I - {I_i},\ {{\bar{X}}_i} = x - {x_i}, \end{aligned}$$

and

$$\begin{aligned} \left( {\begin{array}{*{20}{c}} {{{\bar{Y}}_i}}\\ {{{\bar{Z}}_i}}\\ {{{\bar{X}}_i}} \end{array}} \right) = {T_{i}}\left( {\begin{array}{*{20}{c}} {{{\hat{Y}}_i}}\\ {{{\hat{Z}}_i}}\\ {{{\hat{X}}_i}} \end{array}} \right) , \end{aligned}$$

then system (3.1) can be rewritten as canonical form

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{\hat{Y_i}}}} = {{\bar{\lambda }}_i}{{\hat{Y}}_i} + \sum \limits _{l,j,k \in \textrm{N}}^{l + j + k = 2} {{{\tilde{a}}_{ljk}}} \hat{Y}_i^l\hat{Z}_i^j\hat{X}_i^k + o\left( {{{\left| {{{\hat{Y}}_i},{{\hat{Z}}_i},{{\hat{X}}_i}} \right| }^3}} \right) ,\\ {{\dot{\hat{Z_i}}}} = {{\tilde{\lambda }}_i}{{\hat{Z}}_i} + \sum \limits _{l,j,k \in \textrm{N}}^{l + j + k = 2} {{{\tilde{b}}_{ljk}}} \hat{Y}_i^l\hat{Z}_i^j\hat{X}_i^k + o\left( {{{\left| {{{\hat{Y}}_i},{{\hat{Z}}_i},{{\hat{X}}_i}} \right| }^3}} \right) ,\\ {{\dot{\hat{X_i}}}} = \sum \limits _{l,j,k \in \textrm{N}}^{l + j + k = 2} {{{\tilde{c}}_{ljk}}} \hat{Y}_i^l\hat{Z}_i^j\hat{X}_i^k + o\left( {{{\left| {{{\hat{Y}}_i},{{\hat{Z}}_i},{{\hat{X}}_i}} \right| }^3}} \right) . \end{array} \right. \end{aligned}$$

when $i = 2$, we have

$$\begin{aligned} {{\tilde{c}_{002}} = \frac{{{a_{21\left( {{E_i}} \right) }}}}{{{a_{22\left( {{E_i}} \right) }}}}\left( {\frac{{{a_{11\left( {{E_i}} \right) }}}}{\Lambda } - \frac{{{a_{12\left( {{E_i}} \right) }}{a_{21\left( {{E_i}} \right) }}}}{{\Lambda {a_{22\left( {{E_i}} \right) }}}}} \right) \frac{{\Lambda {a_{22\left( {{E_i}} \right) }}}}{{{a_{11\left( {{E_i}} \right) }}{a_{22\left( {{E_i}} \right) }} - {\Lambda ^2}{a_{12\left( {{E_i}} \right) }}{a_{21\left( {{E_i}} \right) }}}}\frac{{mr\rho }}{{{K_2}}} \ne 0;} \end{aligned}$$

When $i = 3$, we have

$$\begin{aligned} {{\tilde{c}_{002}} = - \frac{{{a_{21\left( {{E_i}} \right) }}}}{{{a_{22\left( {{E_i}} \right) }}}}\left( {\frac{{{a_{11\left( {{E_i}} \right) }}}}{\Lambda } - \frac{{{a_{12\left( {{E_i}} \right) }}{a_{21\left( {{E_i}} \right) }}}}{{\Lambda {a_{22\left( {{E_i}} \right) }}}}} \right) \frac{{\Lambda {a_{22\left( {{E_i}} \right) }}}}{{{a_{11\left( {{E_i}} \right) }}{a_{22\left( {{E_i}} \right) }} - {\Lambda ^2}{a_{12\left( {{E_i}} \right) }}{a_{21\left( {{E_i}} \right) }}}}\frac{{mr\rho }}{{{K_2}}} \ne 0.} \end{aligned}$$

Hence, ${E_{i}}$ is a saddle node of codimension 1. The proof is complete. $\square$