1 Introduction

The static behaviour of a thin cylindrical shell exhibits remarkable features arising from virtually negligible shear and circumferential extension of its mid-surface. This is especially important for sufficiently long shells, for which the simplest membrane model fails, and some of the moments (stress couples) have to be retained in the equilibrium equations. The associated semi-membrane (semi-momentless) formulation was initially developed in Ref. [1] using an ad hoc engineering approach. Later, it was asymptotically justified within the framework of 2D classical shell theory, see [2]. The semi-membrane theory for cylindrical shells is also mentioned in more recent books, e.g. see [3, 4].

The aforementioned geometric constraints also support the family of lowest cut-off frequencies, e.g. see [5, 6] with their values tending to zero at the thin shell limit. In this case, the near-cut-off behaviour is very peculiar also because of the presence of two small parameters. The first of them is the ratio of the shell thickness and its mid-surface radius, while the second one is given by the ratio of the latter and a typical wavelength. The associated shortened equations of motion are derived in Ref. [6] using a straightforward asymptotic procedure in the framework of the Sanders–Koiter version of 2D shell theory. Earlier, similar ad hoc equations were established in [7], see also [8, 9], inspired by modelling of elongated carbon nanotubes, e.g. see [10, 11]. The results in Ref. [6] were extended to an anisotropic cylindrical shell in Ref. [12], see also [13] dealing with a functionally graded material.

Previously, near-cut-off asymptotic analysis of elastic shells was focussed on the high-frequency domain with the cut-off frequencies corresponding to thickness resonances, e.g. see books [14, 15] and journal publications [16, 17]. We also mention related publications studying high-frequency trapped modes, e.g. see [18, 19]. In contrast to the current context, the effect of the ratio of the radius and wavelength is not that sophisticated for high-frequency near-cut-off behaviour.

Asymptotic validation of the considerations in [6] starting from the 3D set-up seems to be of an obvious interest. The point is that the general asymptotic scaling underlying dynamic behaviour of a shell of arbitrary shape, see [14] and references therein, degenerates for a thin cylinder due to specific constraints on a part of mid-surface deformations. As might be expected, the related cancellation of leading-order terms is especially pronounced near the smallest cut-off frequencies. In the latter case, higher-order terms retained in [6] within the 2D framework may hypothetically be negligible in comparison with the truncation in the equations of motion in 3D elasticity. This motivates the derivation of the low-frequency equations for a cylindrical shell from the original 3D formulation.

Below, we start from the scaling generalising that in [6] to the 3D case, since, as it was already mentioned, the previous considerations for an arbitrary shell cannot be adapted. The developed asymptotic procedure appears to be very technical. For the sake of simplicity, we study only the scenario, in which the ratios of the thickness to the radius and the radius to a typical wavelength are of the same order. Nevertheless, the derivation of a leading-order shortened equation necessitates operating with four-term expansions of 3D equations.

It is surprising, in a sense, that most of the coefficients in the established low-frequency equation are identical to their counterpart in [6]. The exception is the essential correction to the leading-order estimation for the cut-off frequency, which, however, coincides with that obtained in [20, 21] from the related plane strain problem. At the same time, the leading-order expressions for the mid-surface circumferential extension and the tangential shear stress resultants are different from those in [6], whereas the tangential normal stress resultants and mid-plane shear deformation are the same.

The paper is organised as follows. The statement of the problem in terms of 3D elasticity is presented in Sect. 2. A single circumferential mode is studied. The asymptotic scaling is determined in Sect. 3. Special arrangements are made to incorporate the generation of the deformations corresponding to mid-surface shear and circumferential extension. The leading-order estimation for the lowest cut-off frequency is obtained in Sect. 4. Section 5 completes the derivation of the sought-for equation of motion. Section 6 is concerned with comparisons of the established results with previous developments, including the coefficients in the above-mentioned equation, as well as the asymptotic formulae for stress resultants and mid-surface deformations.

2 Statement of the problem

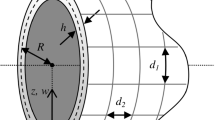
Consider free harmonic vibrations of a thin elastic cylindrical shell of thickness 2h with the mid-surface radius R for which \( \eta = h/R \) is a small geometrical parameter, i.e. \( h \ll R \), see Fig. 1. Take the traditional three orthogonal coordinates along the mid-surface \( \alpha _i\), \( i=1,2,3\), in the form

$$\begin{aligned} \alpha _{1}= \dfrac{R^2}{h} \xi , \qquad \alpha _{2}=R\theta ,\qquad \alpha _{3}=h\zeta , \end{aligned}$$
(1)

where \( \xi \) is the longitudinal coordinate (\( -\infty< \xi < \infty \)), \( \theta \) is the circumferential coordinate (\( 0 \le \theta < 2 \pi \)), and \( \zeta \) is the transverse coordinate (\( -1 \le \zeta \le 1 \)). Also, define the dimensionless frequency by

$$\begin{aligned} \Omega = \dfrac{ \omega R}{\eta } \sqrt{\dfrac{2(1+\nu ) \rho }{E}}, \end{aligned}$$
(2)

where \( \omega \) is the original frequency, \( \rho \) is the mass density, E is the Young’s modulus and \( \nu \) is the Poisson’s ratio; in what follows, the factor \( e^{i \omega t} \), where t is time, is omitted.

Fig. 1
figure 1

A thin elastic shell

Full size image

The first formula (1) defines a typical wavelength L of order \( R^2/h \) which is much greater not only than the shell thickness (\( h/L \sim \eta ^2 \ll 1 \) ) but also than the shell radius ( \( R/L \sim \eta \ll 1 \)). Assuming, in addition, \( \Omega \sim 1 \) we restrict ourselves to the lowest vibration modes investigated in [6] within the framework of 2D shell theory.

Let us present the 3D displacement and stress components \( v_i (\xi , \theta , \zeta ) \) and \( \sigma _{ij}(\xi , \theta , \zeta )\) (\(i,j=1,2,3\)) as

$$\begin{aligned} v_{1}=u_1 \cos {n \theta } ,\quad v_{2}= u_2 \sin {n \theta } ,\quad v_{3}= u_3 \cos {n \theta }, \end{aligned}$$
(3)

and

$$\begin{aligned}&\sigma _{11}= s_{11}\cos {n \theta } ,\quad \sigma _{22}= s_{22}\cos {n \theta }, \quad \sigma _{21}= s_{21}\sin {n \theta }, \nonumber \\&\sigma _{31}= s_{31}\cos {n \theta }, \quad \sigma _{32}= s_{32}\sin {n \theta },\quad \sigma _{33}= s_{33}\cos {n \theta }, \end{aligned}$$
(4)

where \( u_i(\xi ,\zeta ) \), \( \sigma _{ij}(\xi ,\zeta ) \) denote unknown Fourier coefficients and n is the circumferential wavenumber.

Then, equations of motion in 3D elasticity, see, e.g. [14], become

$$\begin{aligned}&\eta ^2 \dfrac{\partial s_{1i}}{\partial \xi }+ (-1)^{i-1}\frac{n \eta }{1 + \eta \zeta } s_{2i} + \dfrac{\partial s_{3i}}{\partial \zeta }+\frac{2^{i-1} \eta }{1 + \eta \zeta } s_{3i} + \eta ^3 \dfrac{E}{2(1+\nu )R } \Omega ^2 u_{i}=0,\quad i=1,2 \end{aligned}$$
(5)

and

$$\begin{aligned}&\eta ^2 \dfrac{\partial s_{31}}{\partial \xi }+\frac{n \eta }{1 + \eta \zeta } s_{32} + \dfrac{\partial s_{33}}{\partial \zeta } - \frac{\eta }{1+ \eta \zeta } s_{22} + \frac{\eta }{1+ \eta \zeta } s_{33} + \eta ^3 \dfrac{E}{2(1+\nu )R } \Omega ^2 u_3 =0, \end{aligned}$$
(6)

together with

$$\begin{aligned}&s_{11}=\frac{E}{(1-\nu ^2)R}\left( \dfrac{\nu e}{1 + \eta \zeta } + \eta \dfrac{\partial u_1}{\partial \xi } \right) +\frac{\nu }{1-\nu } s_{33}, \end{aligned}$$
(7)
$$\begin{aligned}&s_{22}=\frac{E}{(1-\nu ^2)R}\left( \frac{e}{1 + \eta \zeta } + \eta \nu \dfrac{\partial u_1}{\partial \xi } \right) +\frac{\nu }{1-\nu } s_{33}, \end{aligned}$$
(8)
$$\begin{aligned}&s_{21}=\frac{E}{2(1+\nu )R} \dfrac{\eta }{1 + \eta \zeta } \left( s + \eta \zeta \dfrac{\partial u_2}{\partial \xi } \right) , \end{aligned}$$
(9)
$$\begin{aligned}&\dfrac{E}{h} \dfrac{\partial u_3}{\partial \zeta }=s_{33}-\nu \left( s_{11} + s_{22}\right) , \end{aligned}$$
(10)
$$\begin{aligned}&s_{31}=\frac{E}{2(1+\nu ) h}\left( \dfrac{\partial u_1}{\partial \zeta } + \eta ^2 \dfrac{\partial u_3}{\partial \xi } \right) , \end{aligned}$$
(11)
$$\begin{aligned}&s_{32}=\frac{E}{2(1+\nu ) R }\left( \frac{1}{\eta } \dfrac{\partial u_2}{\partial \zeta } - \dfrac{1}{1 + \eta \zeta } \left( u_2 + n u_3 \right) \right) , \end{aligned}$$
(12)

where

$$\begin{aligned} e= n u_2 + u_3, \qquad s= \dfrac{\partial u_2}{\partial \xi } - \dfrac{n}{\eta } u_1. \end{aligned}$$
(13)

We also impose homogeneous boundary conditions at traction free faces, i.e.

$$\begin{aligned} s_{3k}=0, \qquad \zeta = \pm 1 \qquad k=1,2,3. \end{aligned}$$
(14)

The aim of the paper is to reduce the equations above to a 1D form over the long-wave, low-frequency domain defined in this section.

3 Scaling of stresses and displacements

Let us introduce the dimensionless displacement and stress components in the form

$$\begin{aligned} u_1 = \eta R u_1^*,\qquad u_2=R u_2^*,\qquad u_3 = R u_3^* \end{aligned}$$
(15)

and

$$\begin{aligned}&s_{11} = E\eta s_{11}^*,{} & {} s_{12} = E \eta ^2 s_{12}^*,{} & {} s_{22} = E \eta s_{22}^*,\nonumber \\&s_{31}=E\eta ^3 s_{31}^*,{} & {} s_{32}= E \eta ^2 s_{32}^*,{} & {} s_{33}= E \eta ^2 s_{33}^*. \end{aligned}$$
(16)

In addition, we set

$$\begin{aligned} e= \eta R e_*, \qquad s = \eta R s_* \end{aligned}$$
(17)

reflecting the specific behaviour of a cylindrical shell related to its asymptotically small circumferential extension and tangential shear, see [2] for greater detail.

In the formulae above, all starred quantities are assumed to be of order unity. The adapted scaling is motivated by the asymptotic consideration in [6] within the framework of Sanders–Koiter version of 2D classical shell theory.

Inserting the scaled stress and displacement components given by formulae (15) and (16) into Eqs. (5)–(12), we obtain

$$\begin{aligned}&\dfrac{\partial s_{11}^*}{\partial \xi }+\frac{n}{1+\eta \zeta } s_{21}^*+\dfrac{\partial s_{31}^*}{\partial \zeta }+\frac{\eta }{1+\eta \zeta }s_{31}^*+\frac{\eta }{2(1+\nu )}\Omega ^2 u_1^*=0, \end{aligned}$$
(18)
$$\begin{aligned}&\eta ^2 \dfrac{\partial s_{21}^*}{\partial \xi }-\frac{n}{1+\eta \zeta } s_{22}^*+\dfrac{\partial s_{32}^*}{\partial \zeta }+\frac{2\eta }{1+\eta \zeta } s_{32}^*+\frac{\eta }{2(1+\nu )}\Omega ^2 u_2^*=0, \end{aligned}$$
(19)
$$\begin{aligned}&\eta ^3 \dfrac{\partial s_{31}^*}{\partial \xi }+\frac{\eta n}{1+\eta \zeta } s_{32}^*+\dfrac{\partial s_{33}^*}{\partial \zeta }-\frac{1}{1+\eta \zeta } s_{22}^*+\frac{\eta }{1+\eta \zeta } s_{33}^* +\frac{\eta }{2(1+\nu )}\Omega ^2 u_3^*=0, \end{aligned}$$
(20)

with

$$\begin{aligned}&s_{11}^* = \frac{1}{1-\nu ^2}\left( \frac{\nu e_*}{1 + \eta \zeta } + \eta \dfrac{\partial u_1^*}{\partial \xi } \right) +\eta \frac{\nu }{1-\nu } s_{33}^*, \end{aligned}$$
(21)
$$\begin{aligned}&s_{22}^* = \frac{1}{1-\nu ^2}\left( \frac{e_* }{1 + \eta \zeta } + \eta \nu \dfrac{\partial u_1^*}{\partial \xi } \right) +\eta \frac{\nu }{1-\nu } s_{33}^*, \end{aligned}$$
(22)
$$\begin{aligned}&\dfrac{\partial u_3^*}{\partial \zeta }=\eta ^3 s_{33}^*-\nu \eta ^2 \left( s_{11}^* + s_{22}^*\right) , \end{aligned}$$
(23)
$$\begin{aligned}&\dfrac{\partial u_1^*}{\partial \zeta } = -\eta \dfrac{\partial u_3^*}{\partial \xi }+ 2 \eta ^3 (1+\nu ) s_{31}^*, \end{aligned}$$
(24)
$$\begin{aligned}&\dfrac{\partial u_2^*}{\partial \zeta }=\frac{\eta }{1+\eta \zeta } \left( n u_3^* + u_2^* \right) +2\eta ^3 (1+\nu ) s_{32}^*, \end{aligned}$$
(25)
$$\begin{aligned}&s_{21}^* = \frac{1}{2(1+\nu )} \dfrac{1}{1+\eta \zeta } \left( s_* + \zeta \dfrac{\partial u_2^*}{\partial \xi } \right) . \end{aligned}$$
(26)

We also have from (13)

$$\begin{aligned} n u_2^{*}+ u_3^{*}=\eta e_{*}, \qquad \dfrac{\partial u_2^*}{\partial \xi }- n u_1^* =\eta s_*. \end{aligned}$$
(27)

In addition, boundary conditions (14) take the form

$$\begin{aligned} s_{3k}^*=0,\qquad \zeta =\pm 1, \quad k=1,2,3. \end{aligned}$$
(28)

Now, we expand all the starred stress and displacement components, as well as the deformations in (27), in asymptotic series as

$$\begin{aligned} f^*=f^{(0)}+\eta f^{(1)}+\eta ^2 f^{(2)}+\cdots , \end{aligned}$$
(29)

taking into account that \( (1 + \eta \zeta )^{-1} = 1 - \eta \zeta + \eta ^2 \zeta ^2 + \cdots \). In this case, we also have for the dimensionless frequency

$$\begin{aligned} \Omega ^2 = \Omega _0^2 + \eta \Omega _1^2 + \eta ^2 \Omega _2^2 + \cdots \end{aligned}$$
(30)

corresponding to a near-cut-off expansion around the frequency value \( \Omega \approx \Omega _0 \), earlier adapted within the 2D set-up in [21] and many others.

4 Cut-off frequency

First, at leading order, integrating Eqs. (24), (25) and (23) with respect to thickness variable \(\zeta \), we obtain, respectively,

$$\begin{aligned} u_1^{(0)}(\xi , \zeta ) = U^{(0)}(\xi ),\quad u_2^{(0)}(\xi , \zeta ) =V^{(0)}(\xi ),\quad \text {and } u_3^{(0)}(\xi , \zeta ) = W^{(0)}(\xi ), \end{aligned}$$
(31)

where \(U^{(0)}\), \(V^{(0)}\) and \(W^{(0)}\) are unknown 1D functions. On account of (27), the latter are related to each other by

$$\begin{aligned} W^{(0)}=-n V^{(0)} \quad \text { and } \quad U^{(0)} = \dfrac{1}{n} \dfrac{\partial V^{(0)}}{\partial \xi } \end{aligned}$$
(32)

from which we also deduce that

$$\begin{aligned} U^{(0)} = -\dfrac{1}{n^2} \dfrac{\partial W^{(0)}}{\partial \xi }. \end{aligned}$$
(33)

Next, integrating Eq. (19) across the thickness, we have

$$\begin{aligned} s_{32}^{(0)}=-n \int \limits _{\zeta }^{1} s_{22}^{(0)}(s)\,{\text {d}}s. \end{aligned}$$
(34)

Thus, as it follows from the boundary condition (28) at \( \zeta = -1 \), we have

$$\begin{aligned} \int \limits _{-1}^{1} s_{22}^{(0)}(s)\,{\text {d}}s=0, \end{aligned}$$
(35)

demonstrating that normal circumferential stress resultant disappears at leading order. As a result, the associated stress couple appears to be more significant. This observation nicely illustrates the basic idea of the semi-membrane shell theory, see [2]

We also have from (20)

$$\begin{aligned} s_{33}^{(0)}=-\int \limits _{\zeta }^{1} s_{22}^{(0)}(s)\,{\text {d}}s. \end{aligned}$$
(36)

The relations above do not allow calculating the leading-order term \( \Omega _0^2 \) in the asymptotic series (30). This necessitates proceeding to the next order approximation.

We now integrate Eqs. (24), (25) and (23) with respect to \( \zeta \) at first order, yielding, respectively

$$\begin{aligned} u_1^{(1)}&=n\zeta \dfrac{\partial V^{(0)}}{\partial \xi }+U^{(1)}, \qquad u_2^{(1)}= \left( 1-n^2\right) \zeta V^{(0)} + V^{(1)} \quad \text {and} \quad u_3^{(1)} =W^{(1)}. \end{aligned}$$
(37)

In this case, the relations (27) give

$$\begin{aligned} e^{(0)}&= n \left( 1-n^2\right) \zeta V^{(0)} + n V^{(1)} + W^{(1)}, \end{aligned}$$
(38)

and

$$\begin{aligned} s^{(0)}&= \left( 1-2n^2\right) \zeta \dfrac{\partial V^{(0)}}{\partial \xi } - n U^{(1)} + \dfrac{\partial V^{(1)}}{\partial \xi }. \end{aligned}$$
(39)

Then, we integrate (22) through the thickness, using (38) along with (35), we first obtain

$$\begin{aligned} W^{(1)}=-n V^{(1)}, \end{aligned}$$
(40)

and, hence

$$\begin{aligned} s_{22}^{(0)} = \frac{n\left( 1-n^2\right) }{1-\nu ^2}\zeta V^{(0)}. \end{aligned}$$
(41)

Similarly,

$$\begin{aligned} s_{11}^{(0)}=\frac{\nu n\left( 1-n^2\right) }{1-\nu ^2}\zeta V^{(0)}. \end{aligned}$$
(42)

Equations (34) and (36), due to (41), become

$$\begin{aligned} s_{32}^{(0)}&=-\frac{n^2\left( 1-n^2\right) }{2\left( 1-\nu ^2\right) }\left( 1-\zeta ^2\right) V^{(0)}, \end{aligned}$$
(43)

and

$$\begin{aligned} s_{33}^{(0)}&=-\frac{n\left( 1-n^2\right) }{2\left( 1-\nu ^2\right) }\left( 1-\zeta ^2\right) V^{(0)}. \end{aligned}$$
(44)

Now, insert (26) with (27)\(_2\) in (18). The solvability of the latter, taking into account homogeneous boundary conditions (28), yields

$$\begin{aligned} U^{(1)}= \dfrac{1}{n} \dfrac{\partial V^{(1)}}{\partial \xi } \end{aligned}$$
(45)

and, consequently

$$\begin{aligned} s_{21}^{(0)}= \frac{1-n^2}{1+\nu } \zeta \dfrac{\partial V^{(0)}}{\partial \xi }. \end{aligned}$$
(46)

Integrating, again, (18) with respect to \(\zeta \), and satisfying (28), we finally get

$$\begin{aligned} s_{31}^{(0)}=\frac{n\left( 1-n^2\right) }{2\left( 1-\nu ^2\right) }\left( 1-\zeta ^2\right) \dfrac{\partial V^{(0)}}{\partial \xi }. \end{aligned}$$
(47)

In the same manner, we derive from (19) and (20) together with (28), respectively,

$$\begin{aligned}&s_{32}^{(1)}=- n\int \limits _{\zeta }^{1} s_{22}^{(1)}(s)\,{\text {d}}s + \dfrac{\zeta -1}{2(1+\nu )} \left( \frac{2 n^2\left( 1-n^2\right) }{3(1-\nu )}\left( 1-2\zeta - 2\zeta ^{2}\right) -\Omega _{0}^{2} \right) V^{(0)}, \end{aligned}$$
(48)

and

$$\begin{aligned}&s_{33}^{(1)} = -\int \limits _{\zeta }^{1} s_{22}^{(1)}(s)\,{\text {d}}s + \frac{n(1-\zeta )}{2(1+\nu )} \left( \frac{1-n^2}{3(1-\nu )}\left( 3\zeta (1+\zeta )-n^2\left( 2- \zeta - \zeta ^{2}\right) \right) -\Omega _{0}^{2} \right) V^{(0)}. \end{aligned}$$
(49)

As a result, the solvabilities of (19) and (20) with (28) are given by

$$\begin{aligned} \int \limits _{-1}^{1} s_{22}^{(1)}(s)\, {\text {d}}s = - \frac{1}{n(1+\nu )} \left( \frac{2n^2\left( 1-n^2\right) }{3(1-\nu )} -\Omega _{0}^{2} \right) V^{(0)}, \end{aligned}$$
(50)

and

$$\begin{aligned} \int \limits _{-1}^{1} s_{22}^{(1)}(s)\,{\text {d}}s = - \frac{n}{1+\nu } \left( \frac{2n^2\left( 1-n^2\right) }{3(1-\nu )} +\Omega _{0}^{2} \right) V^{(0)}. \end{aligned}$$
(51)

On comparing the latter, we arrive at

$$\begin{aligned} \Omega _{0}^{2}=\frac{2}{3(1-\nu )}\frac{n^2\left( 1-n^2\right) ^2}{1+n^2}. \end{aligned}$$
(52)

At a given n, this is the expression of the lowest cut-off frequency within the classical 2D shell theory, e.g. see [5] and [6] along with the related plane strain set-up in Fig.2. For \( n=0\) and \( n=1 \), we have \( \Omega _0^2= 0\). In this case, the assumptions underlying the asymptotic consideration above are violated. These two modes correspond to the so-called bar (or beam)-type vibration of a cylindrical shell and assume a special treatment.

Fig. 2
figure 2

Cross section of the shell

Full size image

Although we determined the frequency, we do not yet have the sought-for equation of motion. Therefore, we should proceed to higher orders.

5 Near-cut-off equation of motion

At second order, we have from (24), (25) and (23), respectively,

$$\begin{aligned} u_1^{(2)} = n \zeta \dfrac{\partial V^{(1)}}{\partial \xi }+U^{(2)}, \quad u_2^{(2)} = (1-n^2) \zeta V^{(1)} +V^{(2)}, \quad \text {and} \quad u_3^{(2)} = - \frac{ \nu n\left( 1-n^2\right) }{2(1-\nu )}\zeta ^2V^{(0)}+W^{(2)} \end{aligned}$$
(53)

We also get from (27)

$$\begin{aligned} e^{(1)}&= - \dfrac{\nu n\left( 1-n^2\right) }{2(1-\nu )} \zeta ^2 V^{(0)}+ n(1-n^2) \zeta V^{(1)} + n V^{(2)} + W^{(2)}, \end{aligned}$$
(54)

and

$$\begin{aligned} s^{(1)}&= (1-2n^2) \zeta \frac{\partial V^{(1)}}{\partial \xi } - n U^{(2)} +\frac{\partial V^{(2)}}{\partial \xi }. \end{aligned}$$
(55)

Now, integrating (22) with respect to \(\zeta \) over the interval \( -1 \le \zeta \le 1 \) and considering (38), (44), (51) and (54), we obtain

$$\begin{aligned} W^{(2)}+n V^{(2)} = \frac{n(1-n^2)}{6(1-\nu )\left( 1+n^2\right) } \left( 2 + \nu -n^2 (2 - 5 \nu )\right) V^{(0)}-\frac{\nu }{n}\dfrac{\partial ^2 V^{(0)}}{\partial \xi ^2}. \end{aligned}$$
(56)

Then, inserting (56) back into (22), we derive

$$\begin{aligned} s_{22}^{(1)} = \frac{n\left( 1-n^2\right) }{3\left( 1-\nu ^2\right) } \left( \dfrac{1-n^2-3\left( 1+n^2\right) \zeta ^2}{1+n^2} V^{(0)} + 3 \zeta V^{(1)} \right) . \end{aligned}$$
(57)

Similarly, (21) becomes

$$\begin{aligned} \begin{aligned} s_{11}^{(1)} = \frac{1}{n}\dfrac{\partial ^2 V^{(0)}}{\partial \xi ^2} - \dfrac{n (1 - n^2)\left( 1 + 5n^2 + 3(1+n^2)\zeta ^2 \right) }{6\left( 1-\nu ^2\right) \left( 1+n^2\right) }V^{(0)} + \frac{\nu n\left( 1-n^2\right) }{1-\nu ^2}\zeta V^{(1)} . \end{aligned} \end{aligned}$$
(58)

Hence, we obtain from (48) and (49), respectively,

$$\begin{aligned} s_{32}^{(1)}=&\frac{n^2\left( 1-n^2\right) }{1-\nu ^2} \zeta \left( 1-\zeta ^2\right) V^{(0)} -\frac{n^2\left( 1-n^2\right) }{2\left( 1-\nu ^2\right) }(1-\zeta ^2) V^{(1)} , \end{aligned}$$
(59)

and

$$\begin{aligned} s_{33}^{(1)} = \frac{n\left( 1-n^2\right) \left( 5+n^2\right) }{6(1-\nu ^2)}\zeta \left( 1-\zeta ^2\right) V^{(0)} -\frac{n\left( 1-n^2\right) }{2\left( 1-\nu ^2\right) }\left( 1-\zeta ^2\right) V^{(1)}. \end{aligned}$$
(60)

This time, the solvability condition for (18), expressed through formulae above, takes the form

$$\begin{aligned} \frac{1}{1+\nu }\left( n U^{(2)} - \dfrac{\partial V^{(2)}}{\partial \xi } \right) =\frac{2}{n^2}\dfrac{\partial ^{3} V^{(0)}}{\partial \xi ^3}+\frac{1-4n^2+3n^4}{3(1-\nu )\left( 1+n^2\right) }\dfrac{\partial V^{(0)}}{\partial \xi }, \end{aligned}$$
(61)

whereas (26) results in

$$\begin{aligned} \begin{aligned} s_{21}^{(1)}=- \frac{1}{n^2}\dfrac{\partial ^3 V^{(0)}}{\partial \xi ^3}-\frac{\left( 1-4n^2+3n^4\right) (1+\nu )+3\left( 1-n^4\right) (1-\nu )\zeta ^{2}}{6\left( 1-\nu ^2\right) \left( 1+n^2\right) }\dfrac{\partial V^{(0)}}{\partial \xi } + \frac{\left( 1-n^2\right) }{1+\nu } \zeta \dfrac{\partial V^{(1)}}{\partial \xi }. \end{aligned} \end{aligned}$$
(62)

Next, integrating (19) and (20) across the thickness and satisfying boundary conditions (28) at \( \zeta = 1 \) we obtain, respectively,

$$\begin{aligned} s_{32}^{(2)} =&-n \int \limits _{\zeta }^{1} s_{22}^{(2)}(s)\,{\text {d}}s + \frac{\left( 1-n^{2}\right) \left( 1-\zeta ^{2}\right) }{2(1+\nu )}\dfrac{\partial ^2 V^{(0)}}{\partial \xi ^2} \nonumber \\&+ \dfrac{1-\zeta }{2(1+\nu )} \left( \left( \frac{n\left( 1-n^2\right) \left( 7-3n^2+2n^4-15\left( 1+n^2\right) \zeta ^2 \right) }{6(1-\nu )\left( 1+n^2\right) } (1+\zeta ) + \Omega _{1}^{2} \right) V^{(0)} \right. \nonumber \\&\left. + \dfrac{4n^2\left( 1-n^2\right) \left( \zeta + \zeta ^2 -n^2\left( 1- \zeta - \zeta ^2\right) \right) }{3(1-\nu )\left( 1+n^2\right) } V^{(1)} \right) \end{aligned}$$
(63)

and

$$\begin{aligned} s_{33}^{(2)} =&- \int \limits _{\zeta }^{1} s_{22}^{(2)}(s)\,{\text {d}}s \nonumber \\&+ \dfrac{n (1-\zeta )}{2(1+\nu )} \left( \dfrac{\left( 1-n^2\right) \left( n^2\left( 1+5n^2\right) -5\left( 2 + 3n^2 + n^4\right) \zeta ^2\right) }{6(1-\nu )\left( 1+n^2\right) } (1 + \zeta ) - \Omega _{1}^{2}\right) V^{(0)}. \nonumber \\&- \dfrac{n\left( 1-n^2\right) \left( 4n^2-\left( 3 + 8n^2 + n^4\right) \zeta + \left( 3 + 4 n^2 + n^4\right) \zeta ^3 \right) }{6\left( 1-\nu ^2\right) \left( 1+n^2\right) } V^{(1)} \end{aligned}$$
(64)

The last two equations taken at \( \zeta = -1 \), due to boundary conditions (28), reduce to

$$\begin{aligned} \begin{aligned} \int \limits _{-1}^{1} s_{22}^{(2)}(s)\,{\text {d}}s = \frac{1}{n(1+\nu )} \Omega _{1}^{2}V^{(0)} - \frac{4 n ^3 \left( 1-n^2\right) }{3 \left( 1-\nu ^2\right) \left( 1+n^2\right) }V^{(1)}, \end{aligned} \end{aligned}$$
(65)

and

$$\begin{aligned} \begin{aligned} \int \limits _{-1}^{1} s_{22}^{(2)}(s)\,{\text {d}}s =&- \frac{n}{1+\nu }\Omega _{1}^{2}V^{(0)} - \frac{4 n ^3 \left( 1-n^2\right) }{3 \left( 1-\nu ^2\right) \left( 1+n^2\right) }V^{(1)}. \end{aligned} \end{aligned}$$
(66)

Therefore,

$$\begin{aligned} \Omega _{1}^{2}=0, \end{aligned}$$

i.e. there is no first-order correction to the lowest cut-off frequency which is in agreement with [6, 21].

Thus, we need to proceed to the next asymptotic order. First, integrating Eqs. (24), (25) and (23) with respect to \(\zeta \), we obtain

$$\begin{aligned} u_1^{(3)}= & {} \dfrac{n\left( 1-n^2\right) }{6(1-\nu )} \left( 6\zeta - (2-\nu )\zeta ^3 \right) \frac{\partial V^{(0)}}{\partial \xi }-\zeta \frac{\partial W^{(2)}}{\partial \xi }, \end{aligned}$$
(67)
$$\begin{aligned} u_2^{(3)}= & {} - \dfrac{n\left( 1-n^2\right) }{6(1-\nu )} \left( 6\zeta - (2-\nu )\zeta ^3 \right) V^{(0)} + \zeta V^{(2)}+V^{(3)}\nonumber \\{} & {} + n \zeta W^{(2)}, \end{aligned}$$
(68)

and

$$\begin{aligned} \begin{aligned} u_3^{(3)} =&-\frac{\nu }{n} \zeta \frac{\partial ^2 V^{(0)}}{\partial \xi ^2} - \frac{n\left( 1-n^2\right) }{6(1-\nu )\left( 1+n^2\right) } \left( 3-\nu + n^2(3-5\nu ) -(1+\nu )\left( 1+n^2\right) \zeta ^2 \right) \zeta V^{(0)} \\&- \frac{\nu n(1-n^2)}{2(1-\nu )} \zeta ^2 V^{(1)} +W^{(3)}. \end{aligned} \end{aligned}$$
(69)

Also,

$$\begin{aligned} e^{(2)} =&- \dfrac{2 \nu }{n} \zeta \dfrac{\partial ^2 V^{(0)}}{\partial \xi ^2} \nonumber \\&- \dfrac{n\left( 1-n^2\right) \left( 1-2\nu - (1+\nu ) \zeta ^2 + n^2(11-10 \nu -3 \zeta ^2) + n^4 \left( 6- (2-\nu ) \zeta ^2\right) \right) }{6(1-\nu )\left( 1+n^2\right) } \zeta V^{(0)} \nonumber \\&- \dfrac{\nu n \left( 1-n^2\right) }{2(1-\nu )} \zeta ^2 V^{(1)} -\left( 1-n^2\right) \zeta W^{(2)} + n V^{(3)} + W^{(3)}, \end{aligned}$$
(70)

and

$$\begin{aligned} s^{(2)} =&- \dfrac{\nu }{n^2} \zeta \dfrac{\partial ^3 V^{(0)}}{\partial \xi ^3}\nonumber \\&+ \dfrac{(1-n^2) \left( 2+\nu -n^2(14-5\nu -2(2-\nu ) \zeta ^2) + 2n^4 (6-(2-\nu )\zeta ^2) \right) }{6(1-\nu )(1+n^2)} \zeta \dfrac{\partial V^{(0)}}{\partial \xi } \nonumber \\&+ \dfrac{2n^2-1}{n} \zeta \dfrac{\partial W^{(2)}}{\partial \xi } + \dfrac{\partial V^{(3)}}{ \partial \xi }. \end{aligned}$$
(71)

Then, integrating (22) and incorporating (66), we have

$$\begin{aligned} \begin{aligned} W^{(3)} + n V^{(3)}&= -\frac{\nu }{n}\dfrac{\partial ^2 V^{(1)}}{\partial \xi ^2} + \dfrac{n(1-n^2) \left( 2+\nu -n^2(2-5\nu ) \right) }{6(1-\nu )\left( 1+n^2\right) } V^{(1)}. \end{aligned} \end{aligned}$$
(72)

Next, inserting the latter back into (22), we arrive at

$$\begin{aligned} \begin{aligned} s_{22}^{(2)}&= -\frac{\nu \left( 1-n^2\right) }{n\left( 1-\nu ^2\right) } \zeta \dfrac{\partial ^2 V^{(0)}}{\partial \xi ^2} + \frac{n \left( 1 - n^2 \right) }{6 \left( 1-\nu ^2\right) (1+\nu ) \left( n^2+1\right) } \\&\times \zeta \left( 3-6 \nu - 7 (1- \nu ) \zeta ^2 + n^2 \left( 9 - 11 \nu - 9 (1-\nu ) \zeta ^2 \right) + n^4 \left( 6-\nu +2 (\nu -1) \zeta ^2 \right) \right) V^{(0)}\\&-\frac{1-n^2}{1-\nu ^2} \left( \frac{n\left( 1-3 \zeta ^2 - n^2\left( 1+3\zeta ^2\right) \right) }{3(1+n^2)} V^{(1)} + \zeta W^{(2)} \right) . \end{aligned} \end{aligned}$$
(73)

Now, substituting (73) into (63) and (64), we get

$$\begin{aligned} s_{32}^{(2)}&= \frac{\left( 1-n^{2}\right) }{2\left( 1-\nu ^2\right) } \left( 1-\zeta ^2\right) \dfrac{\partial ^2 V^{(0)}}{\partial \xi ^2} \nonumber \\&\quad + \dfrac{n^2\left( 1-n^2\right) }{24(1-\nu )\left( 1-\nu ^2\right) \left( 1+n^2\right) } \left( 3-19\nu +76(1-\nu ) \zeta ^2 + 2n^4 \left( 7- 2 \nu + (1-\nu ) \zeta ^2 \right) \right) \left( 1-\zeta ^2\right) V^{(0)}\nonumber \\&\quad + \frac{n\left( 1-n^2\right) }{2\left( 1-\nu ^2\right) }(1-\zeta ) \left( 2 n \zeta V^{(1)} + (1+\zeta ) W^{(2)} \right) , \end{aligned}$$
(74)

and

$$\begin{aligned} s_{33}^{(2)}&= \frac{\left( 1-n^2\right) \nu \left( 1-\zeta ^{2}\right) }{2n\left( 1-\nu ^2\right) }\dfrac{\partial ^2 V^{(0)}}{\partial \xi ^2} -\dfrac{n\left( 1-n^2\right) }{24(1-\nu )\left( 1-\nu ^2\right) } \nonumber \\&\times \left( 1 + 5 \nu -n^2(11-5\nu ) -10 n^4(2-\nu ) + 3(1-\nu )\left( 4n^4 + 3n^2 + 9\right) \zeta ^2 \right) \left( 1-\zeta ^2\right) V^{(0)}\nonumber \\&+\dfrac{1-n^2}{6\left( 1-\nu ^2\right) }\left( 1-\zeta ^2\right) \left( n\left( 5+n^2\right) \zeta V^{(1)} + 3 W^{(2)} \right) . \end{aligned}$$
(75)

At this order, the solvability of (19) together with the boundary conditions (28) is given by

$$\begin{aligned} \int \limits _{-1}^{1} s_{22}^{(3)}(s)\,{\text {d}}s&= -\frac{2}{n^3}\dfrac{\partial ^4 V^{(0)}}{\partial \xi ^4}+\frac{2\left( 1-n^2\right) \left( 1-\nu +n^2(3+\nu )\right) }{3n\left( 1-\nu ^2\right) (1+n^2)}\dfrac{\partial ^2 V^{(0)}}{\partial \xi ^2} \nonumber \\&\quad - \frac{1}{n(1+\nu )} \left( \frac{n^2\left( 1-n^2\right) \left( (39\nu -24) +n^2 (32 - 22 \nu ) -n^4(44-19\nu ) \right) }{45(1-\nu )^2\left( 1+n^2\right) } - \Omega _{2}^{2} \right) V^{(0)} \nonumber \\&\quad + \frac{2\left( 1-n^2\right) }{3\left( 1-\nu ^2\right) } \left( \frac{n\left( 1-n^2\right) }{1+n^2} V^{(2)} + W^{(2)} \right) \end{aligned}$$
(76)

Similarly, for (20) and (28) we have

$$\begin{aligned} \int \limits _{-1}^{1} s_{22}^{(3)}(s)\,{\text {d}}s = \,&2\dfrac{\partial ^2 V^{(0)}}{\partial \xi ^2} \nonumber \\&+\frac{n}{1+\nu } \left( \frac{2n^4\left( 1-n^2\right) \left( 7-17\nu -6n^2(1-\nu )+n^4 (17-7\nu ) \right) }{45(1-\nu )^2\left( 1+n^2\right) } - \Omega _{2}^{2} \right) V^{(0)}\nonumber \\&+ \dfrac{4n^2\left( 1-n^2\right) }{3\left( 1-\nu ^2\right) \left( 1+n^2\right) }W^{(2)} \end{aligned}$$
(77)

Comparison of the last two formulae leads to

$$\begin{aligned} \Omega _{2}^{2}V^{(0)} =&\dfrac{2(1+\nu )}{n^2\left( 1+n^2\right) } \dfrac{\partial ^4 V^{(0)}}{\partial \xi ^4} - \dfrac{2\left( 1-n^2\right) ^2 \left( 2n^2 +1 - \nu \right) }{3(1-\nu )\left( 1+n^2\right) ^2} \dfrac{\partial ^2 V^{(0)}}{\partial \xi ^2} \nonumber \\&-\dfrac{n^2\left( 1-n^2\right) \left( 24-39 \nu -n^2(22-17 \nu ) + 2n^4 (17-7\nu ) \right) }{45(1-\nu )^2\left( 1+n^2\right) ^2} V^{(0)} \nonumber \\&-\dfrac{2n\left( 1-n^2\right) ^2}{3(1-\nu )\left( 1+n^2\right) ^2} \left( n V^{(2)} + W^{(2)} \right) . \end{aligned}$$
(78)

Finally, on using the relations (30), (32) and (56) in the last equation, we arrive at

$$\begin{aligned}&\dfrac{2 \eta ^2 (1+\nu )}{n^2\left( 1+n^2\right) } \dfrac{\partial ^4 W^{(0)}}{\partial \xi ^4} - \dfrac{2\eta ^2 \left( 1-n^2\right) ^2 (2n^2 +1 -2 \nu )}{3(1-\nu )\left( 1+n^2\right) ^2} \dfrac{\partial ^2 W^{(0)}}{\partial \xi ^2} \nonumber \\&+ \dfrac{2n^2 \left( 1-n^2\right) ^2}{3(1-\nu )\left( 1+n^2\right) } \left( 1- \eta ^2 \dfrac{ 17(1-\nu ) - n^2(9+\nu ) + 11n^4(1 - \nu ) + n^6(17 - 7\nu )}{15(1-\nu )\left( 1+n^2\right) ^2} \right) W^{(0)} \nonumber \\&- \Omega ^2 W^{(0)} = 0. \end{aligned}$$
(79)

6 Discussion

Introducing \( W = R W^{(0)} \) and setting \( \omega ^2 W = - \partial ^2 W/ \partial t^2 \), the last equation in the previous section may be rewritten in the original variables as

$$\begin{aligned} \gamma R^2 \dfrac{\partial ^4 W}{\partial \alpha _1^4}&- 4 \delta \dfrac{h^2}{ R^2} \dfrac{\partial ^2 W}{\partial \alpha _1^2} + \dfrac{1-\nu }{2} \dfrac{h^2}{R^4} \left( \Omega _0^2 + \dfrac{h^2}{R^2} \Omega _2^2 \right) W + \dfrac{\rho \left( 1-\nu ^2\right) }{E} \dfrac{\partial ^2 W}{\partial t^2} = 0. \end{aligned}$$
(80)

where

$$\begin{aligned} \gamma = \dfrac{1-\nu ^2}{n^2\left( 1+n^2\right) }, \qquad \delta = \dfrac{\left( 1-n^2\right) ^2 \left( 2n^2 + 1 -2 \nu \right) }{12\left( 1+n^2\right) ^2}, \end{aligned}$$
(81)

with

$$\begin{aligned} \Omega _2^2 = - \dfrac{2n^2\left( 1-n^2\right) ^2 \left( 17(1-\nu )-n^2(9+\nu ) + 11n^4(1-\nu )+n^6(17-7\nu ) \right) }{45(1-\nu )^2 \left( 1+n^2\right) ^3} \end{aligned}$$
(82)

and \( \Omega _0^2 \) is given by (52). The graph of the coefficients given by (52), (81) and (82) versus Poisson’s ratio \( \nu \) is displayed in Figs. 3 and 4 for \( n=2, 3, 4 \).

Fig. 3
figure 3

Coefficients \( \gamma \) and \( \delta \) given by (81) versus the Poisson’s ratio \( \nu \) for \(n= 2, 3, 4 \)

Full size image
Fig. 4
figure 4

Nondimensional frequencies \( \Omega _0^2 \) and \( \Omega _2^2 \) given, respectively, by (52) and (82) versus the Poisson’s ratio \( \nu \) for \(n=2, 3, 4\)

Full size image

The solutions of Eq. (80) can be substituted into the formulae in the previous two sections in order to derive the expressions for stress and strain components. As an example, we present the asymptotic estimations for the quantities e and s, see (13), at the mid-surface \( \zeta = 0\). We stress once more that these quantities are key ones for a cylindrical shell. Starting from formulae (56) and (61), along with other intermediate relations, we readily deduce, at leading order,

$$\begin{aligned} e&= \, \dfrac{\nu R^2}{n^2} \dfrac{\partial ^2 W}{\partial \alpha _1^2} - \dfrac{\left( 1-n^2\right) \left( 2 + \nu -n^2(2-5\nu )\right) }{6(1-\nu )\left( 1+n^2\right) } \dfrac{h^2}{R^2} W \end{aligned}$$
(83)

and

$$\begin{aligned} s&=\, \dfrac{2(1+\nu )}{n} \dfrac{R^2}{h} \left( \dfrac{R^2}{n^2} \dfrac{\partial ^3 W}{\partial \alpha _1^3} +\dfrac{\left( 1-n^2\right) \left( 1-3n^2\right) }{6(1-\nu )\left( 1+n^2\right) } \dfrac{h^2}{R^2} \dfrac{\partial W}{\partial \alpha _1} \right) \end{aligned}$$
(84)

We also present the expressions for the tangential stress resultants in terms of W. These become

$$\begin{aligned} F_i = \int \limits _{-h}^{h} \left( 1 + \frac{\alpha _3}{R_j} \right) s_{ii} \, {\text {d}}\alpha _3, \quad \text {and} \quad Q_{ij} = \int \limits _{-h}^{h} \left( 1 + \frac{\alpha _3}{R_j} \right) s_{ij} \, {\text {d}}\alpha _3, \end{aligned}$$
(85)

where \( i \ne j = 1,2 \). Let us set, according to (29)

$$\begin{aligned} s_{kl} = \dfrac{E h}{R} \left( s_{kl}^{(0)} + \dfrac{h}{R} s_{kl}^{(1)} + \cdots \right) , \quad k,l = 1,2. \end{aligned}$$
(86)

First, insert the latter into the first formula in (85) taking into consideration (41), (42) and (57), (58), together with (32), we obtain at leading order

$$\begin{aligned} F_1&= - \dfrac{2 E h}{R} \left( \dfrac{R^2}{n^2} \dfrac{\partial ^2 W}{\partial \alpha _1^2} - \dfrac{2 \nu n^2\left( 1-n^2\right) }{3\left( 1-\nu ^2\right) \left( 1+n^2\right) } \dfrac{h^2}{R^2} W \right) , \end{aligned}$$
(87)

and

$$\begin{aligned} F_2&= \dfrac{4 E h^3}{3\left( 1-\nu ^2\right) R^3} \dfrac{n^2 (1-n^2)}{1+n^2} W. \end{aligned}$$
(88)

Similarly, substituting equations (46) and (62) into the second equation in (85), we arrive at the following leading-order expressions:

$$\begin{aligned} Q_{12}&= \dfrac{2 E h}{3\left( 1-\nu ^2\right) } \left( \dfrac{3\left( 1-\nu ^2\right) R^2}{n^3} \dfrac{\partial ^3 W }{\partial \alpha _1^3} + \dfrac{\left( 1-n^2\right) \left( \nu - n^2(2+\nu )\right) }{n\left( 1+n^2\right) } \dfrac{h^2}{R^2} \dfrac{\partial W}{\partial \alpha _1} \right) , \end{aligned}$$
(89)

and

$$\begin{aligned} Q_{21}&= \dfrac{2 E h}{3\left( 1-\nu ^2\right) } \left( \dfrac{3\left( 1-\nu ^2\right) R^2}{n^3} \dfrac{\partial ^3 W }{\partial \alpha _1^3} + \dfrac{\left( 1-n^2\right) \left( 1 - n^2(1+2\nu )\right) }{n\left( 1+n^2\right) } \dfrac{h^2}{R^2} \dfrac{\partial W }{\partial \alpha _1} \right) . \end{aligned}$$
(90)

Let us compare now the formulae above in this section with the predictions of the 2D Sanders–Koiter theory in [6]. First of all, we note that all coefficients in the equation of motion (80), apart from the correction to the cut-off frequency \( \Omega _2^2 \) given by (82), which is denoted in [6] by \( \Omega _1^2\), see formula (3.6) there, are identical to those arising from the Sanders–Koiter theory. At the same time, the value \( \Omega _2^2 \) in (82) is the same as in the plane strain problem studied in [21] and also [20].

For the quantities e and s, we proceed with the refined formulae (5.1) and (5.2) derived in [6] for mid-surface displacements. In terms of the notation of the current paper, they can be written as

$$\begin{aligned} u_2 + \dfrac{1}{n} u_3&= \, \dfrac{\nu R^2}{n^3} \dfrac{\partial ^2 u_3}{\partial \alpha _1^2} + \dfrac{2n(1-n^2)}{3(1+n^2)} \dfrac{h^2}{R^2} u_3, \end{aligned}$$
(91)

and

$$\begin{aligned} u_1 + \dfrac{R}{n^2} \dfrac{\partial u_3}{\partial \alpha _1}&= \, \dfrac{R}{(1-\nu ) n^2} \left( \dfrac{\left( \nu (1+\nu )-2 \right) R^2}{n^2} \dfrac{\partial ^3 u_3}{\partial \alpha _1^3} \right. \nonumber \\ {}&\left. -\dfrac{(1-n^2)(1+\nu -n^2(5 + \nu ))}{3(1+n^2)} \dfrac{h^2}{R^2} \dfrac{\partial u_3}{\partial \alpha _1} \right) . \end{aligned}$$
(92)

These relations are similar but not identical to formulae (56) and (61). First, insert (91) into (13) to have

$$\begin{aligned} e&=\, \dfrac{\nu R^2}{n^2} \dfrac{\partial ^2 W}{\partial \alpha _1^2} + \dfrac{2n^2\left( 1-n^2\right) }{3\left( 1+n^2\right) } \dfrac{h^2}{R^2} W, \end{aligned}$$
(93)

where only the term with the second-order derivative coincides with its counterpart in (84). However, the last term in the right-hand side of this formula is identical to that in [21]. Next, using (91) and (92) in (13) we arrive at formula (84).

Now, substitute (91) and (92) into the traditional expressions for tangential stress resultants in 2D shell theory, e.g. see [2, 5], given by

$$\begin{aligned} F_1&=\, \dfrac{2 E h}{1-\nu ^2} \left( \dfrac{\partial u_1}{\partial \alpha _1} + \dfrac{\nu e}{R} \right) , \end{aligned}$$
(94)
$$\begin{aligned} F_2&= \, \dfrac{2 E h}{1-\nu ^2} \left( \dfrac{e}{R} + \nu \dfrac{\partial u_1}{\partial \alpha _1} \right) , \end{aligned}$$
(95)

and

$$\begin{aligned} Q_{12}&=\, \dfrac{E h^2}{(1+\nu )R^2} \left( s + \dfrac{2}{3}h \left( \dfrac{\partial u_2}{\partial \alpha _1} + n \dfrac{\partial u_3}{\partial \alpha _1} \right) \right) , \end{aligned}$$
(96)
$$\begin{aligned} Q_{21}&= \, \dfrac{E h^2}{(1+\nu )R^2} s, \end{aligned}$$
(97)

where e and s are given by (93) and (84), respectively. As a result, the formulae for \( F_i \) are identical to (87) and (88) in spite of the deviation between the expressions for mid-plane circumferential extension e given by (83) and (93). At the same time, the last two formulae for the tangential shear stress resultants \( Q_{ij} \) coincide with (89) and (90) only with respect to the coefficients at the highest-order derivatives taking the form

$$\begin{aligned} Q_{12}&= \dfrac{2 E h}{n} \left( \dfrac{R^2}{n^2} \dfrac{\partial ^3 W}{\partial \alpha _1^3} - \dfrac{\left( 1-n^2\right) \left( 1-3\nu + n^2(5+\nu )\right) }{6\left( 1-\nu ^2\right) \left( 1+n^2\right) } \dfrac{h^2}{R^2} \dfrac{\partial W}{\partial \alpha _1} \right) \end{aligned}$$
(98)

and

$$\begin{aligned} Q_{21}&= \dfrac{2 E h}{n} \left( \dfrac{R^2}{n^2} \dfrac{\partial ^3 W}{\partial \alpha _1^3} + \dfrac{\left( 1-n^2\right) \left( 1-3n^2\right) }{6(1-\nu )\left( 1+n^2\right) } \dfrac{h^2}{R^2} \dfrac{\partial W}{\partial \alpha _1} \right) . \end{aligned}$$
(99)

It is worth noting that the deviation between two above-mentioned sets of formulae occurs despite the same expression for the tangential shear s given by (84). This happens due to the presence of the \( \zeta ^2 \) term in (62), see also (85) and (86). Thus, the coincidence of the tangential shear deformations along the mid-surface does not guarantee asymptotic correct expressions for the tangential shear stress resultants calculated from the classical 2D shell theory.

7 Concluding Remarks

Apart from \( \Omega _2^2 \) given (82), all other coefficients in the fourth-order equation (80) coincide with their counterparts in the Sanders–Koiter shell theory, see [6]. At the same time, for the cancellation of the leading-order terms in the formulae for the mid-surface circumferential extension, the refined expression obtained in [6] is not identical to that derived in this paper; cf. (83) and (93). Similarly, the relations for the tangential shear stress resultants are also different; cf. (89)–(90) and (98)–(99). The last observation implies, in particular, that the boundary conditions at the free edge of an elongated cylindrical shell generally cannot be treated within the existing 2D shell theory.

The derivations in the paper are based on the assumption that the ratio of the shell thickness to its radius is of the same order as that of the radius to a typical wavelength. It might be expected, see also the dispersion analysis in [6], that the established asymptotic formulation is also valid over a broader parameter range. In the latter case, the terms with fourth and second derivatives in equation (80) may not be of the same asymptotic order. Moreover, for this scenario, in which the term with a second derivative dominates, the number of boundary conditions is less than that usually adapted for a cylindrical shell. In fact, analysis of a near-cut-off behaviour starting from approximate models may often involve a revisit of the original problems, e.g. the related 3D dynamic problem in elasticity within the current context.

The circumferential modes with \( n=0 \) and \( n=1 \) are not considered in the paper. They correspond to vibrations of a bar with zero cut-off frequencies. In particular, the mode with \( n=1 \) is concerned with bending of a thin-walled beam, e.g. see [2] for greater detail. The higher-order modes (\( n \gg 1\)) also are not explicitly mentioned. The related generalisation is not expected to be particularly sophisticated, e.g. see [5].