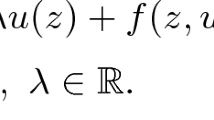Ground-state nodal solutions for superlinear perturbations of the Robin eigenvalue problem

Abstract

We consider a perturbed version of the Robin eigenvalue problem for the p-Laplacian. The perturbation is $(p - 1)$-superlinear. Using the Nehari manifold method, we show that for all parameters $\lambda < {\hat{\lambda }}_1$ (= the principal eigenvalue of the differential operator), there exists a ground-state nodal solution of the problem.

1 Introduction

Suppose that $\Omega \subseteq {\mathbb {R}}^N$ is a bounded domain with a $C^2$-boundary $\partial \Omega$. In this paper, we study the following nonlinear parametric Robin problem:

In this problem, $\Delta _p$ denotes the p-Laplace differential operator defined by

$$\begin{aligned} \Delta _p u=\mathrm{div\,}(|Du|^{p-2}Du)=|Du|^{p-4}[|Du|^2\Delta u+(p-2)\sum _{i,j=1}^N u_{x_i}u_{x_j} u_{x_ix_j} ] \hbox { for all } u \in W^{1,p}(\Omega ). \end{aligned}$$

On the set $[Du=0]$ of critical points, this operator is degenerate for $p>2$ and is singular if $1<p<2$. The analysis developed in this paper includes the borderline case $p=N$. In this situation, the Dirichlet energy $\int \limits _\Omega |Du|^N\mathrm{d}x$ is conformally invariant. The borderline case is important in the theory of quasi-conformal mappings.

Problem ($P_\lambda$) contains the perturbation $u \mapsto \xi (z)|u|^{p - 2} u$ with the potential function $\xi \in L^\infty (\Omega )$, $\xi (z) \geqslant 0$ for a.a. $z \in \Omega$. In the reaction (right-hand side of problem ($P_\lambda$)), we have the combined effects of a parametric term $u \mapsto \lambda |u|^{p-2} u$ and of a Carathéodory perturbation f(z, x). (That is, for all $x \in {\mathbb {R}}$ the mapping $z \mapsto f(z,x)$ is measurable and for a.a. $z \in \Omega$ the function $x \mapsto f(z,x)$ is continuous.) We assume that f(z, x) exhibits $(p -1)$-superlinear growth as $x \rightarrow \pm \infty$.

We can view problem ($P_\lambda$) as a superlinear perturbation of the Robin eigenvalue problem for the operator $u \mapsto - \Delta _p u + \xi (z) |u|^{p-2} u$. In the boundary condition, $\frac{\partial u}{\partial n_p}$ denotes the conormal derivative of u corresponding to the p-Laplace differential operator. This directional derivative is interpreted using the nonlinear Green’s identity (see Papageorgiou et al. [13, p. 35]), and if $u \in C^1({\overline{\Omega }})$, then

$$\begin{aligned} \frac{\partial u}{\partial n_p} = |D u|^{p-2} \frac{\partial u}{\partial n}, \end{aligned}$$

with $n(\cdot )$ being the outward unit normal on $\partial \Omega$. The boundary coefficient $\beta \in C^{0,\alpha }(\partial \Omega )$ with $0< \alpha < 1$ satisfies $\beta (z) \geqslant 0$ for all $z \in \partial \Omega$.

The nonlinear Robin boundary condition in problem ($P_\lambda$) is motivated by certain nonlinear patterns in which the flux across the boundary is not linearly proportional to the density function. A typical example is Boltzmann’s fourth power law in heat transfer problems, where

$$\begin{aligned} \begin{aligned} \frac{\partial u}{\partial n}+\sigma (u^4-h_0^4)=0\quad (\sigma >0), \end{aligned} \end{aligned}$$

where $h_0$ is the surrounding temperature; see Özisik [10]. Another example is based on the Michaelis–Menten hypothesis in some biochemical reaction problems where the substrate concentration satisfies the boundary condition

$$\begin{aligned} \frac{\partial u}{\partial n}+\frac{u}{1+au}=0\quad (a>0), \end{aligned}$$

see Ross [15].

We are looking for ground-state (that is, least energy) nodal (sign-changing) solutions of problem ($P_\lambda$). Using the Nehari manifold method, we show that if $\lambda < {\hat{\lambda }}_1$ (here ${\hat{\lambda }}_1$ is the principal eigenvalue of the differential operator $u \mapsto - \Delta _p u + \xi (z) |u|^{p-2}u$ with Robin boundary condition), then problem ($P_\lambda$) has a ground-state nodal solution. We prove this result by relaxing the usual Nehari monotonicity hypothesis which is the following:

• (N) “For a.e. $z \in \Omega$, the quotient function $x \mapsto \frac{f(z,x)}{|x|^{p -1}}$ is strictly increasing on $\mathring{{\mathbb {R}}}_- \cup \mathring{{\mathbb {R}}}_+$ with $\mathring{{\mathbb {R}}}_- =(-\infty , 0)$ and $\mathring{{\mathbb {R}}}_+ =(0,+\infty )$.”

This condition was used by Szulkin and Weth [16] to have uniqueness of the projection on the Nehari manifold. Instead, in the present paper, we assume that the quotient is simply increasing.

In the past, the problem of the existence of ground-state solutions for such parametric problems was investigated only in the context of semilinear Dirichlet problems driven by the Laplace differential operator. We mention the work of Szulkin and Weth [16], who produce a ground-state solution using the stronger monotonicity condition (N), but they do not show that their ground-state solution is nodal. Later, Tang [17] obtained a ground-state solution using the relaxed monotonicity condition, but the ground-state solution need not be nodal. Ground-state nodal solutions under the relaxed monotonicity hypothesis were obtained recently by Lin and Tang [7]. All the aforementioned works deal with semilinear equations (that is, $p=2$), and the boundary condition is Dirichlet. Ground-state nodal solutions under the strong Nehari monotonicity condition (see hypothesis (N) above) were obtained by Liu and Dai [8] (Dirichlet problems) and Gasiński and Papageorgiou [4] (problems with a nonlinear boundary condition). In both these works, the reaction is nonparametric and has a different structure. We also mention the work of Papageorgiou, Rădulescu and Repovš [12], who studied problem ($P_\lambda$) when $p=2$ (semilinear equation) looking for positive solutions and proved a bifurcation-type result with critical parameter being ${\hat{\lambda }}_1$. Finally, we point out that eigenvalue problems with nonlinear Robin boundary condition naturally arise in the study of reaction–diffusion equation where a distributed absorption competes with a boundary source; see Lacey et al. [5] for details.

Our main result in this paper is the following theorem. Hypotheses ${H}_0$ and ${H}_1$ on the data of the problem can be found in Sect. 2.

Theorem 1

If hypotheses ${H_0},$ ${H_1}$ are fulfilled and $\lambda < {\hat{\lambda }}_1,$ then the following properties hold true.

• (a) Problem ($P_\lambda$) has a ground-state nodal solution $u_* \in C^1({\overline{\Omega }});$

• (b) If, in addition, $e(z,x) > 0$ for a.a. $z \in \Omega ,$ all $x \ne 0,$ then $u_*$ has two nodal domains; here, $e(z,x)=f(z,x)x-pF(Z,x)$

2 Mathematical preliminaries and hypotheses

The main space in the analysis of problem ($P_\lambda$) is the Sobolev space $W^{1,p}(\Omega )$. By $\Vert \cdot \Vert$, we denote the norm of $W^{1,p}(\Omega )$ defined by

$$\begin{aligned} \Vert u\Vert = \left( \Vert u\Vert _p^p + \Vert Du\Vert _p^p\right) ^{1/p} \hbox { for all } u \in W^{1,p}(\Omega ). \end{aligned}$$

Also, we will use the boundary Lebesgue spaces $L^p(\partial \Omega )$. On $\partial \Omega$, we consider the $(N-1)$-dimensional Hausdorff (surface) measure $\sigma (\cdot )$. Using this measure, we can define in the usual way the “boundary” Lebesgue spaces $L^q(\partial \Omega )$, $1 \leqslant q \leqslant + \infty$. From the theory of Sobolev spaces, we know that there exists a unique continuous linear operator ${\hat{\gamma }}_0 : W^{1,p}(\Omega )\mapsto L^p(\partial \Omega )$, known as the “trace operator,” such that

$$\begin{aligned} {\hat{\gamma }}_0(u) = u|_{\partial \Omega } \hbox { for all } u \in W^{1,p}(\Omega )\cap C({\overline{\Omega }}). \end{aligned}$$

So, the trace operator extends the notion of boundary values to all Sobolev functions. We know that this operator is compact into $L^r(\partial \Omega )$ for $r < \frac{(N-1)p}{N-p}$ if $p<N$ and into $L^r(\partial \Omega )$ for $1 \leqslant r < + \infty$ if $N \leqslant p$. The trace operator is not surjective, and we have

$$\begin{aligned} \mathrm{im\,}{\hat{\gamma }}_0=W^{\frac{1}{p'},p}(\partial \Omega )\ \left( \frac{1}{p} + \frac{1}{p'} = 1\right) ,\ \mathrm{ker\,} {\hat{\gamma }}_0 = W_0^{1,p}(\Omega ). \end{aligned}$$

We introduce our hypotheses on the potential function $\xi (\cdot )$ and on the boundary coefficient $\beta (\cdot )$.

$H_0$: $\xi \in L^\infty (\Omega )$, $\xi (z) \geqslant 0$ for a.a. $z \in \Omega$, $\beta \in C^{0,\alpha }(\partial \Omega )$ with $0< \alpha < 1$, $\beta (z) \geqslant 0$ for all $z \in \partial \Omega$ and $\xi \not \equiv 0$ or $\beta \not \equiv 0$.

Remark 1

We see that these hypotheses incorporate also the Neumann problem $(\beta \equiv 0).$

In what follows, by $\gamma _p : W^{1,p}(\Omega )\mapsto {\mathbb {R}}$ we denote the $C^1$-functional defined by

$$\begin{aligned} \gamma _p(u) = \Vert D u\Vert _p^p + \int \limits _\Omega \xi (z) |u|^p \mathrm{d}z + \int \limits _{\partial \Omega } \beta (z) |u|^p \mathrm{d}\sigma \end{aligned}$$

for all $u \in W^{1,p}(\Omega )$.

Using Lemma 4.11 of Mugnai and Papageorgiou [9] and Proposition 2.4 of Gasiński and Papageorgiou [3], we have

$$\begin{aligned} c_0 \Vert u\Vert ^p \leqslant \gamma _p(u) \hbox { for some } c_0 > 0, \hbox { all } u \in W^{1,p}(\Omega ). \end{aligned}$$

(1)

Another way to see this is via a simple contradiction argument. So, suppose that we could find $\{u_n\}_{n\in {\mathbb {N}}}\subseteq W^{1,p}(\Omega )$ such that for all $n\in {\mathbb {N}}$

$$\begin{aligned} \Vert Du_n\Vert ^p_p+\int \limits _\Omega \xi (z)|u_n|^p\mathrm{d}z+\int \limits _{\partial \Omega }\beta (z)|u_n|^p\mathrm{d}\sigma <\frac{1}{n}\,\Vert u_n\Vert ^p. \end{aligned}$$

By homogeneity, we may assume that $\Vert u_n\Vert =1$ for all $n\in {\mathbb {N}}$. So, we may assume that

$$\begin{aligned} u_n\xrightarrow w u\ \hbox {in}\ W^{1,p}(\Omega ) \ \hbox {and}\ u_n\rightarrow u\ \hbox {in } L^p(\Omega )\hbox { and in }L^p(\partial \Omega ). \end{aligned}$$

Then, in the limit as $n\rightarrow \infty$ and since the norm in a Banach space is weakly lowers semicontinuous, we obtain

$$\begin{aligned} \begin{array}{ll} &{}\displaystyle \Vert Du\Vert ^p_p+\int \limits _\Omega \xi (z)|u|^p\mathrm{d}z+\int \limits _{\partial \Omega }\beta (z)|u|^p\mathrm{d}\sigma \leqslant 0,\\ \Rightarrow &{} Du(z)=0\ \hbox {a.e. in }\Omega ,\hbox { hence }u\equiv c\in {\mathbb {R}}.\end{array} \end{aligned}$$

We have

$$\begin{aligned} \begin{array}{ll} &{}\displaystyle c\left( \int \limits _\Omega \xi (z)\mathrm{d}z+\int \limits _{\partial \Omega }\beta (z)\mathrm{d}\sigma \right) \leqslant 0,\\ \Rightarrow &{} c=0\ (\hbox {see hypothesis }{H}_0). \end{array} \end{aligned}$$

But then we have

$$\begin{aligned} u_n\rightarrow 0\ \hbox {in}\ W^{1,p}(\Omega ), \end{aligned}$$

a contradiction to the fact that $\Vert u_n\Vert =1$ for all $n\in {\mathbb {N}}$.

We consider the nonlinear eigenvalue problem

$$\begin{aligned} \left\{ \begin{array}{lll} -\Delta _p u + \xi (z) |u|^{p - 2} u = {\hat{\lambda }} |u|^{p - 2} u\hbox { in }\Omega , \\ \frac{\partial u}{\partial n_p} + \beta (z) |u|^{p - 2} u = 0 \hbox { on } \partial \Omega . \end{array} \right\} \end{aligned}$$

(2)

We say that ${\hat{\lambda }} \in {\mathbb {R}}$ is an eigenvalue of the operator $u \mapsto - \Delta _p u + \xi (z) |u|^{p- 2} u$ with Robin boundary condition, if problem (2) admits a nontrivial solution ${\hat{u}} \in W^{1,p}(\Omega )$, known as an eigenfunction corresponding to the eigenvalue ${\hat{\lambda }}$.

By using the Lagrange multiplier rule, we see that problem (2) has a smallest eigenvalue ${\hat{\lambda }}_1$, which is characterized variationally by

$$\begin{aligned} {\hat{\lambda }}_1 = \inf \left\{ \frac{\gamma _p(u)}{\Vert u\Vert _p^p} : u \in W^{1,p}(\Omega ),\ u \ne 0\right\} . \end{aligned}$$

(3)

On account of (1), we see that ${\hat{\lambda }}_1 > 0$. Also, this eigenvalue is isolated in the spectrum and simple. The infimum in (3) is realized on the corresponding one dimensional eigenspace and so the eigenfunctions corresponding to ${\hat{\lambda }}_1 > 0$ have fixed sign. By ${\hat{u}}_1$, we denote the positive, $L^p$-normalized (that is, $\Vert {\hat{u}}_1\Vert _p = 1$) eigenfunction corresponding to ${\hat{\lambda }}_1$. The nonlinear regularity theory (see Lieberman [6]) and the nonlinear maximum principle (see Pucci and Serrin [14]) imply that ${\hat{u}}_1 \in \mathrm{int\,} C_+ = \left\{ u \in C^1({\overline{\Omega }}) : u(z) > 0 \hbox { for all } z \in {\overline{\Omega }}\right\}$ (the interior of positive (order) cone $C_+ = \left\{ u \in C^1({\overline{\Omega }}) : u(z) \geqslant 0 \hbox { for all } z \in {\overline{\Omega }}\right\}$ of $C^1({\overline{\Omega }})$). The Ljusternik–Schnirelmann minimax scheme implies the existence of a whole strictly increasing sequence $\left\{ {\hat{\lambda }}_k\right\} _{k \in {\mathbb {N}}}$ of eigenvalues of problem (2) such that ${\hat{\lambda }}_k \rightarrow + \infty$, known as “variational eigenvalues.” We do not know if they exhaust the spectrum of the operator. We know that if ${\hat{\lambda }} \ne {\hat{\lambda }}_1$ is a nonprincipal eigenvalue, then the corresponding eigenfunctions ${\hat{u}} \in C^1({\overline{\Omega }})$ (regularity theory) are nodal functions. Details can be found in Fragnelli et al. [2].

Let $A_p : W^{1,p}(\Omega )\mapsto W^{1,p}(\Omega )^*$ be the nonlinear map defined by

$$\begin{aligned} \langle A_p(u),h\rangle = \int \limits _\Omega |Du|^{p-2}(Du,Dh)_{{\mathbb {R}}^N} \mathrm{d}z \hbox { for all } u,\ h \in W^{1,p}(\Omega ). \end{aligned}$$

It is well known that this map is bounded (maps bounded sets to bounded sets), continuous, monotone (thus maximal monotone too) and of type $(S)_+$, that is

$$\begin{aligned} ``&\hbox {if } u_n \xrightarrow w u \hbox { in } W^{1,p}(\Omega )\hbox { and } \limsup _{n \rightarrow \infty } \langle A_p(u_n),u_n-u\rangle \leqslant 0,\\&\hbox {then } u_n \rightarrow u \hbox { in } W^{1,p}(\Omega ).'' \end{aligned}$$

We have

$$\begin{aligned} \langle \gamma _p'(u),h \rangle = \langle A_p(u),h\rangle + \int \limits _\Omega \xi (z) |u|^{p-2}uh \mathrm{d}z + \int \limits _{\partial \Omega } \beta (z) |u|^{p-2}uh \mathrm{d}\sigma \end{aligned}$$

for all u, $h \in W^{1,p}(\Omega )$.

Now, we introduce our hypotheses on the perturbation f(z, x). Recall that

$$\begin{aligned} p^*={\left\{ \begin{array}{ll} \ \frac{Np}{N-p} &{} \hbox { if } p < N\\ \ + \infty &{}\hbox { if } N \leqslant p \end{array}\right. } \ (\hbox {the critical Sobolev exponent for } p). \end{aligned}$$

${H_1}$: $f : \Omega \times {\mathbb {R}}\mapsto {\mathbb {R}}$ is a Carathéodory function such that $f(z,0) = 0$ for a.a. $z \in \Omega$ and

• (i) $| f(z,x) | \leqslant a(z) \left( 1+|x|^{r-1}\right)$ for a.a. $z \in \Omega$, all $x \in {\mathbb {R}}$, with $a \in L^\infty (\Omega )$ and $p<r<p^*$;

• (ii) if $F(z,x)=\int \limits _0^x f(z,s) \mathrm{d}s$, then $\lim _{x \rightarrow \pm \infty }\frac{F(z,x)}{|x|^p} = +\infty$ uniformly for a.a. $z \in \Omega$;

• (iii) $\lim _{x \rightarrow 0} \frac{f(z,x)}{|x|^{p-2}x} = 0$ uniformly for a.a. $z \in \Omega$;

• (v) for a.a. $z \in \Omega$, the quotient function $x \mapsto \frac{f(z,x)}{|x|^{p-1}}$ is increasing on $\mathring{{\mathbb {R}}}_- \cup \mathring{{\mathbb {R}}}_+$.

Remark 2

If $f(z,\cdot )$ is $(p-1)$-superlinear as $x \rightarrow \pm \infty ,$ then hypothesis ${H_1}$(ii) is satisfied. Note that we use the relaxed Nehari monotonicity condition (see hypothesis ${H_1}$(iv)).

We will prove our existence theorem first using the strong Nehari monotonicity condition (see (N)), and then via approximations of the perturbation, we will establish the result for the general case. For this reason, we introduce the following set of hypotheses:

${H_1'}$: $f : \Omega \times {\mathbb {R}}\mapsto {\mathbb {R}}$ is a Carathéodory function such that $f(z,0) = 0$ for a.a. $z \in \Omega$, hypotheses ${H_1'}$(i), (ii), (iii) are the same as the corresponding hypotheses in ${H_1}$ and

• (iv) hypothesis (N) holds.

If $u \in W^{1,p}(\Omega )$, then we define $u^\pm = \max \left\{ \pm u,0\right\}$ and we have

$$\begin{aligned} u^\pm \in W^{1,p}(\Omega ),\ u = u^+ - u^-,\ |u| = u^+ + u^-. \end{aligned}$$

We denote by $|\cdot |_N$ the Lebesgue measure on ${\mathbb {R}}^N$.

Let $\varphi _\lambda : W^{1,p}(\Omega )\mapsto {\mathbb {R}}$ be the energy (Euler) functional defined by

$$\begin{aligned} \varphi _\lambda (u) = \frac{1}{p} \gamma _p(u) - \frac{\lambda }{p} \Vert u\Vert _p^p - \int \limits _\Omega F(z,u) \mathrm{d}z \hbox { for all } u \in W^{1,p}(\Omega ). \end{aligned}$$

Evidently, $\varphi _\lambda \in C^1(W^{1,p}(\Omega ))$. We introduce the following two sets:

$$\begin{aligned} {N} =&\left\{ u \in W^{1,p}(\Omega ): \langle \varphi _\lambda '(u),u\rangle = 0, \ u \ne 0\right\} ,\\ {N_0} =&\left\{ u \in W^{1,p}(\Omega ): \langle \varphi _\lambda '(u),u^+ \rangle = \langle \varphi _\lambda '(u),u^- \rangle =0,\ u^\pm \ne 0 \right\} . \end{aligned}$$

We see that ${N_0} \subseteq {N}$. The set N is known as the “Nehari manifold” for the functional $\varphi _\lambda (\cdot )$. Note that every nontrivial solution of problem ($P_\lambda$) belongs to the Nehari manifold. Since we look for nodal solutions, we introduce the Nehari submanifold ${N_0}$. Hypotheses ${H_0}$, ${H_1'}$ imply that $\emptyset \ne {N_0} \subseteq {N}$ (see also Proposition 5 and Papageorgiou et al. [11]).

3 Ground-state nodal solutions

We define

$$\begin{aligned} {\hat{m}}_\lambda ^0 = \inf _{N_0} \varphi _\lambda . \end{aligned}$$

We look for an element of ${N_0}$ which realizes the infimum ${\hat{m}}_\lambda ^0$ and which is a critical point of $\varphi _\lambda$. Such a function will be a ground-state nodal solution of problem ($P_\lambda$).

Proposition 2

If hypotheses ${H_0},$ ${H_1}$ hold,  then for all $\tau ,$ $t \geqslant 0$ and all $u \in W^{1,p}(\Omega )$ we have

$$\begin{aligned} \varphi _\lambda (u) \geqslant \varphi _\lambda (\tau u^+ - t u^-) + \frac{1-\tau ^p}{p}\langle \varphi _\lambda '(u),u^+ \rangle - \frac{1-t^p}{p}\langle \varphi _\lambda '(u),u^- \rangle . \end{aligned}$$

Proof

We have

$$\begin{aligned}&\varphi _\lambda (u) - \varphi _\lambda (\tau u^+ - tu^-)\nonumber \\&\quad = \frac{1}{p} \gamma _p(u) - \frac{\lambda }{p} \Vert u\Vert _p^p - \int \limits _\Omega F(z,u) \mathrm {d}z\nonumber \\&\qquad - \frac{1}{p} \gamma _p(\tau u^+ - tu^-) + \frac{\lambda }{p} \Vert \tau u^+ - tu^-\Vert _p^p + \int \limits _\Omega F(z,\tau u^+ - tu^-) \mathrm {d}z\nonumber \\&\quad = \frac{1}{p} \left( \gamma _p(u) - \gamma _p(\tau u^+ - tu^-)\right) - \frac{\lambda }{p} \left( \Vert u\Vert _p^p - \Vert \tau u^+ - tu^-\Vert _p^p\right) \nonumber \\&\qquad - \int \limits _\Omega \left( F(z,u) - F(z,\tau u^+ - tu^-)\right) \mathrm {d}z. \end{aligned}$$

(4)

Using the fact that $\left\{ u^+> 0\right\} \cap \left\{ u^- > 0\right\} = \emptyset$, we have

$$\begin{aligned}&\frac{1}{p} \left( \gamma _p(u) - \gamma _p(\tau u^+ - tu^-)\right) \nonumber \\&\quad = \frac{1}{p} \left( \gamma _p(u^+) - \tau ^p \gamma _p(u^+) + \gamma _p(u^-) - t^p\gamma _p(u^-)\right) \nonumber \\&\quad = \frac{1 - \tau ^p}{p} \gamma _p(u^+) + \frac{1 - t^p}{p} \gamma _p(u^-). \end{aligned}$$

(5)

Similarly, we have

$$\begin{aligned}&\frac{\lambda }{p} \left( \Vert u\Vert _p^p - \Vert \tau u^+ - t u^-\Vert _p^p\right) \nonumber \\&\quad = \frac{\lambda }{p}\left( \Vert u^+\Vert _p^p - \tau ^p \Vert u^+\Vert _p^p + \Vert u^-\Vert _p^p - t^p \Vert u^-\Vert _p^p\right) \nonumber \\&\quad = \frac{\lambda (1 - \tau ^p)}{p} \Vert u^+\Vert _p^p + \frac{\lambda (1 - t^p)}{p} \Vert u^-\Vert _p^p. \end{aligned}$$

(6)

Finally, we have

$$\begin{aligned}&\int \limits _\Omega \left( F(z,u) - F(z, \tau u^+ - t u^-)\right) \mathrm{d}z\nonumber \\&\quad = \int \limits _\Omega \left( F(z,u^+) + F(z,-u^-) - F(z,\tau u^+) - F(z, -t u^-)\right) \mathrm{d}z. \end{aligned}$$

(7)

Let $x \ne 0$ and $\mu \geqslant 0$. Then,

$$\begin{aligned}&\frac{1- \mu ^p}{p} f(z,x) x + F(z,\mu x) - F(z,x)\nonumber \\&\quad = \int \limits ^1_\mu f(z,x) x s^{p-1} \mathrm{d}s - \int \limits ^1_\mu \frac{\mathrm{d}}{\mathrm{d}s} F(z,s x) \mathrm{d}s \nonumber \\&\quad = \int \limits ^1_\mu f(z,x) x s^{p-1} \mathrm{d}s - \int \limits ^1_\mu f(z,sx) x \mathrm{d}s\ (\hbox {using the chain rule})\nonumber \\&\quad = \int \limits ^1_\mu \left( \frac{f(z,x)}{|x|^{p-1}} - \frac{f(z,s x)}{(s |x|)^{p-1}}\right) s^{p-1} x |x|^{p-1} \mathrm{d}s\nonumber \\&\quad \geqslant 0\ (\hbox {see hypothesis } H_1\mathrm{(iv)}). \end{aligned}$$

(8)

Returning to (7) and using (8), we obtain

$$\begin{aligned}&\int \limits _\Omega \left( F(z,u) - F(z, \tau u^+ - t u^-)\right) \mathrm{d}z\nonumber \\&\quad \geqslant - \frac{1-\tau ^p}{p} \int \limits _\Omega f(z,u^+) u^+ \mathrm{d}z + \frac{1- t^p}{p} \int \limits _\Omega f(z,-u^-)(-u^-) \mathrm{d}z. \end{aligned}$$

(9)

Finally, we use (5), (6) and (9) in (4) and obtain

$$\begin{aligned} \varphi _\lambda (u) - \varphi _\lambda (\tau u^+ - t u^-) \geqslant \frac{1-\tau ^p}{p} \langle \varphi _\lambda '(u),u^+\rangle - \frac{1-t^p}{p} \langle \varphi _\lambda '(u),u^-\rangle . \end{aligned}$$

This proof is now complete. $\square$

From this proposition, we infer at once the following two useful corollaries.

Corollary 3

If hypotheses ${H_0},$ ${H_1}$ hold and $u \in {N_0},$ then $\varphi _\lambda (u) = \max _{\tau ,t \geqslant 0} \varphi _\lambda (\tau u^+ - t u^-).$

Corollary 4

If hypotheses ${H_0},$ ${H_1}$ hold and $u \in {N},$ then $\varphi _\lambda (u) = \max _{\tau \geqslant 0} \varphi _\lambda (\tau u).$

Evidently, Corollary 3 implies $\emptyset \ne {N_0} \subseteq {N}$.

Next, we relate nodal elements of $W^{1,p}(\Omega )$ with the Nehari submanifold ${N_0}$. In particular, we infer that ${N_0} \ne \emptyset$.

Proposition 5

If hypotheses ${H_0},$ ${H_1'}$ hold, $\lambda < {\hat{\lambda }}_1$ and $u \in W^{1,p}(\Omega )$ with $u^\pm \ne 0,$ then we can find a unique pair $(\tau _u,t_u) \in \mathring{{\mathbb {R}}}_+ \times \mathring{{\mathbb {R}}}_+$ such that $\tau _u u^+ - t_u u^- \in {N_0}.$

Proof

Let $u \in W^{1,p}(\Omega )$ with $u^\pm \ne 0$ (nodal function) and consider the corresponding fibering function

$$\begin{aligned} \theta _\lambda (t) = \varphi _\lambda (t u^+) \hbox { for all } t > 0. \end{aligned}$$

Using the chain rule, we see that for all $t > 0$ the following equivalence holds:

$$\begin{aligned} \theta _\lambda '(t) = 0 \Longleftrightarrow \gamma _p(u^+) - \lambda \Vert u^+\Vert _p^p = \int \limits _\Omega \frac{f(z,t u^+) u^+}{t^{p - 1}} \mathrm{d}z. \end{aligned}$$

(10)

On account of hypothesis $H_1'\mathrm{(iv)}=(N)$, the integral in the right-hand side of (10) is strictly increasing in $t > 0$.

Hypotheses $H_1'\mathrm{(iv)},$ (iii) imply that given $\varepsilon > 0$, we can find $c_1 = c_1(\varepsilon ) > 0$ such that

$$\begin{aligned} F(z,x) \leqslant \frac{\varepsilon }{p} |x|^p + c_1 |x|^r \hbox { for a.a. } z \in \Omega , \hbox { all } x \in {\mathbb {R}}. \end{aligned}$$

(11)

Then, we have

$$\begin{aligned} \theta _\lambda (t) = \varphi _\lambda (t u^+)&\geqslant \frac{t^p}{p} \gamma _p(u^+) - \frac{\lambda + \varepsilon }{p} t^p \Vert u^+\Vert _p^p - c_1 t^r \Vert u^+\Vert _r^r \ (\hbox {see }(11))\\&\geqslant \frac{t^p}{p} \left( {\hat{\lambda }}_1 - (\lambda + \varepsilon )\right) \Vert u^+\Vert _p^p - c_1 t^r \Vert u^+\Vert _r^r \ (\hbox {see } (3)). \end{aligned}$$

Choosing $\varepsilon \in (0, {\hat{\lambda }}_1 - \lambda )$ (recall that $\lambda < {\hat{\lambda }}_1$), we obtain

$$\begin{aligned}&\theta _\lambda (t) \geqslant c_2 t^p - c_3 t^r \hbox { for some } c_2,\ c_3> 0,\\&\quad \Rightarrow \theta _\lambda (t)> 0 \hbox { for all } t > 0\hbox { small } (\hbox {since } p < r). \end{aligned}$$

On the other hypotheses $H_1'\mathrm{(i)}$, (ii) imply that given $\eta > 0$, we can find $c_4 = c_4(\eta ) > 0$ such that

$$\begin{aligned} F(z,x) \geqslant \eta |x|^p - c_4 \hbox { for a.a. } z \in \Omega , \hbox { all } x \in {\mathbb {R}}. \end{aligned}$$

(12)

Then, we have

$$\begin{aligned} \theta _\lambda (t) = \varphi _\lambda (t u ^+) \leqslant \frac{t^p}{p} \gamma _p(u^+) - \frac{\lambda t^p}{p}\Vert u^+\Vert _p^p - \frac{\eta t^p}{p} \Vert u^+\Vert _p^p + c_5 \end{aligned}$$

for some $c_5 > 0$ (see (12)).

Recall that $\eta > 0$ is arbitrary. So, choosing $\eta > 0$ large we have

$$\begin{aligned}&\theta _\lambda (t) \leqslant c_5 - c_6 t^p \hbox { for some } c_6> 0, \hbox { all } t> 0,\\&\quad \Rightarrow \theta _\lambda (t) < 0 \hbox { for all } t > 0 \hbox { big}. \end{aligned}$$

We conclude that there exists unique $\tau _u > 0$ (see (10)) such that

$$\begin{aligned} \max _{t > 0} \theta _\lambda (t) = \theta _\lambda (\tau _u) = \varphi _\lambda (\tau _u u^+). \end{aligned}$$

In a similar fashion, working this time with the fibering function

$$\begin{aligned} \kappa _\lambda (t) = \varphi _\lambda (t(-u^-)), \end{aligned}$$

we produce a unique $t_u > 0$ such that

$$\begin{aligned} \max _{t > 0} \kappa _\lambda (t) = \kappa _\lambda (t_u) = \varphi _\lambda (t_u(-u^-)). \end{aligned}$$

We conclude that

$$\begin{aligned} \tau _u u^+ - t_u u^- \in {N_0}. \end{aligned}$$

This ends the proof of the proposition. $\square$

Using the previous proposition, we can have a minimax characterization of ${\hat{m}}_\lambda ^0 = \inf _{N_0} \varphi _\lambda$. Let $W_n = \left\{ u \in W^{1,p}(\Omega ): u^\pm \ne 0\right\}$ (the nodal elements of the Sobolev space $W^{1,p}(\Omega )$).

Proposition 6

If hypotheses ${H_0}, {H_1'}$ hold and $\lambda < {\hat{\lambda }}_1,$ then ${\hat{m}}_\lambda ^0 = \inf _{u \in W_n} \max _{\tau , t \geqslant 0} \varphi _\lambda (\tau u^+ - t u^-).$

Proof

Let $\xi _\lambda = \inf _{u \in W_n} \max _{\tau , t \geqslant 0} \varphi _\lambda (\tau u^+ - t u^-) < + \infty$ (since ${N_0} \subseteq W_n$). We have

$$\begin{aligned} \xi _\lambda&\leqslant \inf _{u \in N_0} \max _{\tau , t \geqslant 0} \varphi _\lambda (\tau u^+ - t u^-)\ (\hbox {since } {N_0 \subseteq W_n})\nonumber \\&= \inf _{u \in N_0} \varphi _\lambda \ (\hbox {see Corollary~} 3)\nonumber \\&= {\hat{m}}_\lambda ^0. \end{aligned}$$

(13)

On the other hand, we have

$$\begin{aligned}&\max _{\tau , t \geqslant 0} \varphi _\lambda (\tau u^+ - t u^-) \nonumber \\&\quad \geqslant \varphi _\lambda (\tau _u u^+ - t_u u^-)\nonumber \\&\quad \geqslant \inf _{N_0} \varphi _\lambda \ (\text{ see } \text{ Proposition } 5)\nonumber \\&\quad = {\hat{m}}_\lambda ^0,\nonumber \\&\quad \Rightarrow \xi _\lambda \geqslant {\hat{m}}_\lambda ^0. \end{aligned}$$

(14)

From (13) and (14), we conclude that $\xi _\lambda = {\hat{m}}_\lambda ^0.$ $\square$

Next, we show that ${\hat{m}}_\lambda ^0$ is realized on ${N_0}$.

Proposition 7

If hypotheses ${H_0},$ ${H_1'}$ hold and $\lambda < {\hat{\lambda }}_1,$ then there exists ${\hat{u}} \in {N_0}$ such that $\varphi _\lambda ({\hat{u}}) = {\hat{m}}_\lambda ^0 > 0.$

Proof

Let $\left\{ u_n\right\} _{n \in {\mathbb {N}}} \subseteq {N_0}$ be a minimizing sequence. We show that this sequence is bounded in $W^{1,p}(\Omega )$. Arguing by contradiction, suppose that up to a subsequence, we have $\Vert u_n\Vert \rightarrow + \infty$. Let $v_n = \frac{u_n}{\Vert u_n\Vert }$, $n \in {\mathbb {N}}$. We have that $\Vert v_n\Vert = 1$ for all $n \in {\mathbb {N}}$ and so we may assume that

$$\begin{aligned} v_n \xrightarrow w v \hbox { in } W^{1,p}(\Omega )\hbox { and } v_n \rightarrow v \hbox { in } L^r(\Omega )\hbox { and } L^p(\partial \Omega ). \end{aligned}$$

(15)

Suppose that $v = 0$. Using (11), we see that for every $\rho > 0$ we have

$$\begin{aligned}&\int \limits _\Omega F(z,\rho v_n) \mathrm{d}z \leqslant \varepsilon \rho ^p \Vert v_n\Vert _p^p + c_1 \rho ^r \Vert v_n\Vert _r^r,\nonumber \\&\quad \Rightarrow \limsup _{n \rightarrow \infty } \int \limits _\Omega F(z,\rho v_n) \mathrm{d}z \leqslant 0 \ (\hbox {see} (15)\hbox { and recall that } v = 0). \end{aligned}$$

(16)

With $\varepsilon _n \rightarrow 0^+$ and $t_n = \frac{\rho }{\Vert v_n\Vert }$ ($n \in {\mathbb {N}}$), we have

$$\begin{aligned} {\hat{m}}_\lambda ^0 + \varepsilon _n&= \varphi _\lambda (u_n)\\&\geqslant \varphi _\lambda (t_n u_n) \ (\text{ see } \text{ Corollary } 4)\\&= \frac{\rho ^p}{p} \left( \gamma _p(v_n) - \lambda \Vert v_n\Vert _p^p\right) - \int \limits _\Omega F(z,\rho v_n) \mathrm {d}z\\&\geqslant c_7 \rho ^p \Vert v_n\Vert _p^p - \int \limits _\Omega F(z, \rho v_n) \mathrm {d}z\\&\text{ for } \text{ some } c_7 > 0, \text{ all } n \in {\mathbb {N}}\ (\text{ see } (3) \text{ and } \text{ recall } \text{ that } \lambda < {\hat{\lambda }}_1),\\&\quad \Rightarrow {\hat{m}}_\lambda ^0\geqslant c_7 \rho ^p \ (\text{ see } (16)). \end{aligned}$$

But $\rho > 0$ is arbitrary. Let $\rho \rightarrow + \infty$ to reach a contradiction. Therefore, $v \ne 0$.

Let $\Omega _* = \left\{ z \in \Omega : v(z) \ne 0\right\}$. We have $|\Omega _*|_N > 0$ and

$$\begin{aligned} |u_n(z)| \rightarrow + \infty \hbox { as } n \rightarrow \infty \hbox { for a.a. } z \in \Omega _*. \end{aligned}$$

Hypotheses $H_1'\mathrm{(i)},$ (ii) imply that there exists $c_8 > 0$ such that

$$\begin{aligned} F(z,x) \geqslant - c_8 \hbox { for a.a } z \in \Omega , \hbox { all } x \in {\mathbb {R}}. \end{aligned}$$

(17)

We have

$$\begin{aligned} \frac{{\hat{m}}_\lambda ^0 + \varepsilon _n}{\Vert u_n\Vert ^p}&= \frac{\varphi _\lambda (u_n)}{\Vert u_n\Vert ^p}\\&= \frac{1}{p} \gamma _p(v_n) - \frac{\lambda }{p} \Vert v_n\Vert _p^p - \int \limits _\Omega \frac{F(z,u_n)}{\Vert u_n\Vert ^p} \mathrm{d}z\\&\leqslant \frac{1}{p} \gamma _p(v_n) - \int \limits _\Omega \frac{F(z,u_n)}{\Vert u_n\Vert ^p} \mathrm{d}z\\&\leqslant c_9 - \int \limits _\Omega \frac{F(z,u_n)}{\Vert u_n\Vert ^p} \mathrm{d}z \hbox { for some } c_9 > 0, \hbox { all } n \in {\mathbb {N}},\\&\quad \Rightarrow 0 \leqslant c_9 - \liminf _{n \rightarrow \infty } \int \limits _\Omega \frac{F(z,u_n)}{\Vert u_n\Vert ^p} \mathrm{d}z\\&= c_9 - \liminf _{n \rightarrow \infty } \left( \int \limits _{\Omega _*} \frac{F(z,u_n)}{\Vert u_n\Vert ^p} \mathrm{d}z + \int \limits _{\Omega {\setminus } \Omega _*} \frac{F(z,u_n)}{\Vert u_n\Vert ^p} \mathrm{d}z\right) \\&\leqslant c_9 - \liminf _{n \rightarrow \infty } \int \limits _{\Omega _*} \frac{F(z,u_n)}{\Vert u_n\Vert ^p} \mathrm{d}z \ (\hbox {see }(16))\\&\leqslant c_9 - \int \limits _{\Omega _*} \liminf _{n \rightarrow \infty } \frac{F(z,u_n)}{|u_n|^p} |v_n|^p \mathrm{d}z \ (\hbox {by Fatou's lemma, see} (17))\\&= - \infty \ (\hbox {see hypothesis } H_1\mathrm{(ii)}), \end{aligned}$$

a contradiction. So, the minimizing sequence $\left\{ u_n\right\} _{n \in {\mathbb {N}}} \subseteq {N_0}$ is bounded in $W^{1,p}(\Omega )$. We may assume that

$$\begin{aligned} \left\{ \begin{array}{lll} u_n \xrightarrow w {\hat{u}} \hbox { in } W^{1,p}(\Omega ),\ u_n \rightarrow {\hat{u}} \hbox { in } L^p(\Omega )\hbox { and } L^r(\partial \Omega ), \\ u_n ^+ \xrightarrow w y_+ \hbox { and } u_n^- \xrightarrow w y_- \hbox { in } W^{1,p}(\Omega ),\ y_+,\ y_- \geqslant 0. \end{array} \right\} \end{aligned}$$

(18)

From (18), it follows that

$$\begin{aligned}&u_n = u_n^+ - u_n^- \xrightarrow w {\hat{u}} = y_+ + y_- \hbox { in } W^{1,p}(\Omega ),\nonumber \\&\quad \Rightarrow {\hat{u}}^+ = y_+ \hbox { and } {\hat{u}}^- = y_-. \end{aligned}$$

(19)

Since $u_n \in {N_0}$ ($n \in {\mathbb {N}}$), we have

$$\begin{aligned} 0 = \langle \varphi _\lambda '(u_n),u_n^+\rangle = \gamma _p(u_n^+) - \lambda \Vert u_n^+\Vert _p^p - \int \limits _\Omega f(z,u_n^+)u_n^+ \mathrm{d}z. \end{aligned}$$

From (18), (19) and the sequential weak lower semicontinuity of $\gamma _p(\cdot )$, we have

$$\begin{aligned}&\gamma _p({\hat{u}}^+) - \lambda \Vert {\hat{u}}^+\Vert _p^p - \int \limits _\Omega f(z,{\hat{u}}^+) {\hat{u}}^+ \mathrm{d}z \leqslant 0,\nonumber \\&\quad \Rightarrow \langle \varphi _\lambda '({\hat{u}}), {\hat{u}}^+ \rangle \leqslant 0. \end{aligned}$$

(20)

Similarly, we show that

$$\begin{aligned} \langle \varphi _\lambda '({\hat{u}}), -{\hat{u}}^- \rangle \leqslant 0. \end{aligned}$$

(21)

We have

$$\begin{aligned} {\hat{m}}_\lambda ^0&= \lim _{n \rightarrow \infty } \left( \varphi _\lambda (u_n)\right) - \frac{1}{p} \langle \varphi _\lambda '(u_n), u_n \rangle \ (\hbox {since } u_n \in {N_0} \subseteq {\mathbb {N}}) \nonumber \\&= \lim _{n \rightarrow \infty } \int \limits _\Omega \left( \frac{1}{p} f(z,u_n) u_n - F(z,u_n)\right) \mathrm{d}z \nonumber \\&= \int \limits _\Omega \left( \frac{1}{p} f(z,{\hat{u}}) {\hat{u}} - F(z,{\hat{u}})\right) \mathrm{d}z \ (\hbox {see} (18))\nonumber \\&= \varphi _\lambda ({\hat{u}}) - \frac{1}{p} \langle \varphi _\lambda '({\hat{u}}),{\hat{u}} \rangle \nonumber \\&\geqslant \varphi _\lambda (\tau _{{\hat{u}}} {\hat{u}}^+ - t_{{\hat{u}}} {\hat{u}}^-) + \frac{1 - \tau _{{\hat{u}}}^p}{p} \langle \varphi _\lambda '({\hat{u}}),{\hat{u}}^+ \rangle - \frac{1- t_{{\hat{u}}}^p}{p} \langle \varphi _\lambda '({\hat{u}}),{\hat{u}}^- \rangle \nonumber \\&\quad - \frac{1}{p} \langle \varphi _\lambda '({\hat{u}}),{\hat{u}} \rangle \ (\hbox {see Proposition}~2)\nonumber \\&\geqslant {\hat{m}}_\lambda ^0 - \frac{\tau _{{\hat{u}}}^p}{p} \langle \varphi _\lambda '({\hat{u}}),{\hat{u}}^+ \rangle + \frac{t_{{\hat{u}}}^p}{p} \langle \varphi _\lambda '({\hat{u}}),{\hat{u}}^-\rangle \ (\hbox {see Proposition~}5),\nonumber \\&\quad \Rightarrow \langle \varphi _\lambda '({\hat{u}}),{\hat{u}}^+ \rangle = \langle \varphi _\lambda '({\hat{u}}),{\hat{u}}^- \rangle = 0 \ (\hbox {see} (20), \ (21)). \end{aligned}$$

(22)

On account of hypotheses $H_1'\mathrm{(i)}$, (iii), given $\varepsilon > 0$, we can find $c_{10} = c_{10}(\varepsilon ) > 0$ such that

$$\begin{aligned} f(z,x) x \leqslant \varepsilon |x|^p + c_{10} |x|^r \hbox { for a.a. } z \in \Omega , \hbox { all } x \in {\mathbb {R}}. \end{aligned}$$

(23)

Since $u_n \in {N_0}$ ($n \in {\mathbb {N}}$), we have

$$\begin{aligned}&\gamma _p(u_n^+) - \lambda \Vert u_n^+\Vert _p^p = \int \limits _\Omega f(z,u_n^+) u_n^+ \mathrm{d}z,\nonumber \\&\quad \Rightarrow c_{11} \Vert u_n^+\Vert ^p \leqslant c_{12} \left( \varepsilon \Vert u_n^+\Vert ^p + \Vert u_n^+\Vert ^r\right) \nonumber \\&\qquad \hbox {for some } c_{11},\ c_{12} > 0, \hbox { all } n \in {\mathbb {N}}\ (\hbox {see }(23)) \hbox { and recall that } \lambda < {\hat{\lambda }}_1). \end{aligned}$$

(24)

Choose $\varepsilon \in \left( 0,\frac{c_{11}}{c_{12}}\right)$. Then,

$$\begin{aligned} c_{13} \leqslant \Vert u_n^+\Vert \hbox { for some } c_{13} > 0, \hbox { all } n \in {\mathbb {N}}\ (\hbox {since } p < r). \end{aligned}$$

(25)

Then, from (23), (24) and (25), we have

$$\begin{aligned}&c_{14} \leqslant \Vert u_n^+\Vert _r^r \hbox { for some } c_{14} > 0, \hbox { all } n \in {\mathbb {N}},\\&\quad \Rightarrow c_{14} \leqslant \Vert {\hat{u}}^+\Vert _r^r \ (\hbox {see }(18) \hbox { and recall that } y_+ = {\hat{u}}^+),\\&\quad \Rightarrow {\hat{u}}^+ \ne 0. \end{aligned}$$

In a similar fashion, we show that ${\hat{u}}^- \ne 0$. Then, from (22), it follows that

$$\begin{aligned} {\hat{u}} \in {N_0} \hbox { and } {\hat{m}}_\lambda ^0 = \varphi _\lambda ({\hat{u}}). \end{aligned}$$

(26)

It remains to show that ${\hat{m}}_\lambda ^0 > 0$. We have

$$\begin{aligned} {\hat{m}}_\lambda ^0 = \varphi _\lambda ({\hat{u}})&= \varphi _\lambda ({\hat{u}}) - \frac{1}{p} \varphi _\lambda '({\hat{u}}),{\hat{u}}\rangle \ (\hbox {since } {\hat{u}} \in {N_0} \subseteq {N}, \hbox { see } (26))\nonumber \\&= \int \limits _\Omega \left( \frac{1}{p} f(z,{\hat{u}}) {\hat{u}} - F(z,{\hat{u}})\right) \mathrm{d}z \end{aligned}$$

(27)

We define $e(z,x) = f(z,x) x - p F(z,x)$.

Claim: For a.a. $z \in \Omega$, $e(z,\cdot )$ is strictly increasing on ${\mathbb {R}}_+ = [0,+ \infty )$ and strictly decreasing on ${\mathbb {R}}_- = (- \infty , 0]$.

First, we show the claim under the extra condition that for a.a. $z \in \Omega$, $f(z,\cdot )$ is differentiable. Then, for $x > 0$, we have

$$\begin{aligned} 0&< \frac{d}{dx} \left( \frac{f(z,x)}{x^{p-1}}\right) \ (\hbox {see hypothesis } H_1'\mathrm{(iv)} = (N))\\&=\frac{f_x'(z,x) x^{p-1} - (p-1) x^{p-2} f(z,x)}{x^{2(p-1)}}\\&= \frac{e_x'(z,x)}{x^p},\\&\Rightarrow \ \ 0 < e_x'(z,x). \end{aligned}$$

In a similar fashion, we show that

$$\begin{aligned} e_x'(z,x)< 0 \hbox { for a.a. } z \in \Omega , \hbox { all } x < 0. \end{aligned}$$

Therefore, the claim is true if $f(z.\cdot )$ is differentiable.

Next, we drop the differentiability hypothesis on $f(z,\cdot )$. To this end, we consider a mollifier $\theta \in C_c^\infty ({\mathbb {R}})$ such that

$$\begin{aligned} 0 \leqslant \theta \leqslant 1, \ \mathrm{supp\,} \theta \subseteq [0,1],\ \int \limits ^{+\infty }_{-\infty } \theta (s) \mathrm{d}s =1. \end{aligned}$$

We set $\theta _\varepsilon (t) = \frac{1}{\varepsilon } \theta \left( \frac{t}{\varepsilon }\right)$. Then, $\theta _\varepsilon \in C_c^\infty ({\mathbb {R}})$, $\mathrm{supp \,} \theta _\varepsilon \subseteq [0,\varepsilon ]$, $\int \limits ^{+\infty }_{-\infty } \theta _\varepsilon (s) \mathrm{d}s =1$. We define

$$\begin{aligned} f_\varepsilon (z,x) = \int \limits ^{+\infty }_{-\infty } \theta _\varepsilon (x-s) f(z,s) \mathrm{d}s = \int \limits ^\varepsilon _0 \theta _\varepsilon (\tau ) f(z,x - \tau ) \mathrm{d}\tau . \end{aligned}$$

From Evans and Gariepy [1, pp. 122–123], we know that for a.a. $z \in \Omega$

$$\begin{aligned}&f_\varepsilon (z,\cdot ) \in C_c^\infty ({\mathbb {R}}),\\&f_\varepsilon (z,x) \rightarrow f(z,x) \hbox { as } \varepsilon \rightarrow 0^+ \hbox { uniformly on compacta.} \end{aligned}$$

For $x> u > 0$, we have

$$\begin{aligned}&\frac{f_\varepsilon (z,x)}{x^{p-1}} - \frac{f_\varepsilon (z,u)}{u^{p-1}}\\&\quad \geqslant \int \limits ^\varepsilon _0 \theta _\varepsilon (\tau ) \frac{f(z,u-\tau )}{(u-\tau )^{p-1}} \left( \left( \frac{x-\tau }{x}\right) ^{p-1} - \left( \frac{u-\tau }{u}\right) ^{p-1}\right) \mathrm{d}\tau \\&\qquad (\hbox {see hypothesis } H_1'\mathrm{(iv)} = (N))\\&\quad \geqslant {\hat{c}}_0(x,u) > 0 \hbox { for all } \varepsilon \in \left( 0, \frac{1}{2}u\right) . \end{aligned}$$

Since $f_\varepsilon (z,\cdot )$ is differentiable, from the first part of the proof of the claim we have that

$$\begin{aligned} 0 < {\hat{c}}(x,u) \leqslant e_\varepsilon (z,x) - e_\varepsilon (z,u) \hbox { for all } \varepsilon \in \left( 0,\frac{1}{2} u\right) , \end{aligned}$$

where $e_\varepsilon (z,x) = f_\varepsilon (z,x)x - p F_\varepsilon (z,x)$, $F_\varepsilon (z,x) = \int \limits ^x_0 f_\varepsilon (z,s) \mathrm{d}s$. Passing to the limit as $\varepsilon \rightarrow 0^+$, we obtain

$$\begin{aligned} e(z,u)< e(z,x) \hbox { for a.a. } z \in \Omega , \hbox { all } 0< u < x. \end{aligned}$$

Similarly we show that

$$\begin{aligned} e(z,x)< e(z,v) \hbox { for a.a. } z \in \Omega , \hbox { all } v< x < 0. \end{aligned}$$

This proves the claim.

Returning to (27) and recalling that $e(z,0) = 0$ for a.a. $z \in \Omega$ we infer that

$$\begin{aligned} {\hat{m}}_\lambda ^0 > 0. \end{aligned}$$

Therefore, finally we have

$$\begin{aligned} {\hat{u}} \in {N_0}, \ 0 < {\hat{m}}_\lambda ^0 = \varphi _\lambda ({\hat{u}}). \end{aligned}$$

This proof is now complete. $\square$

Remark 3

We indicate an alternative way show that ${\hat{m}}_\lambda ^0 > 0.$ Using a contradiction argument as in the proof Proposition 7, we can show that $\varphi _\lambda |_{N}$ is coercive. Since $\varphi _\lambda$ is sequentially weakly lower semicontinuous,  invoking the Weierstrass–Tonelli theorem,  we can find ${\hat{u}}_0 \in {N}$ such that $\varphi _\lambda ({\hat{u}}_0) = \inf _{N} \varphi _\lambda = {\hat{m}}_\lambda .$ Since N is a natural constraint for $\varphi _\lambda$ (see [13]), we have that ${\hat{u}}_0 \in K_{\varphi _\lambda } \subseteq C^1({\overline{\Omega }})$ (nonlinear regularity theory). From Corollary 4,  we know that $\varphi _\lambda ({\hat{u}}_0) = \max _{\tau \geqslant 0} \varphi _\lambda (\tau {\hat{u}}_0)$ and on account of hypothesis $H_1'\mathrm{(iii)}$ and since $\lambda < {\hat{\lambda }}_1,$ for $\tau \in (0,1)$ small we have $\varphi _\lambda (\tau {\hat{u}}_0) > 0,$ hence $0 < {\hat{m}}_\lambda = \varphi _\lambda ({\hat{u}}_0).$ But clearly ${\hat{m}}_\lambda \leqslant {\hat{m}}_\lambda ^0$ (since ${N_0 \subseteq N}).$

Next, following the arguments of Willem [18, p. 74] and of Szulkin and Weth [16, p. 612], we show that the Nehari submanifold ${N_0}$ is a natural constraint (see [13, p. 425]).

Proposition 8

If hypotheses ${H_0}, {H_1'}$ hold,  $\lambda < {\hat{\lambda }}_1$ and ${\hat{u}} \in {N_0}$ is as in Proposition 7, then ${\hat{u}} \in K_{\varphi _\lambda } = \left\{ u \in W^{1,p}(\Omega ): \varphi _\lambda '(u) = 0\right\}$ (the critical set of $\varphi _\lambda ).$

Proof

Since ${\hat{u}} \in {N_0}$, we have

$$\begin{aligned} \langle \varphi _\lambda '({\hat{u}}^+),{\hat{u}}^+ \rangle = 0 = \langle \varphi _\lambda '(-{\hat{u}}^-),-{\hat{u}}^- \rangle . \end{aligned}$$

(28)

For $\tau ,$ $t \in \mathring{{\mathbb {R}}} {\setminus } \{1\}$, we have

$$\begin{aligned} \varphi _\lambda (\tau {\hat{u}}^+ - t {\hat{u}}^-)&= \varphi _\lambda (\tau {\hat{u}}^+) + \varphi _\lambda (t(-{\hat{u}}^-))\nonumber \\&< \varphi _\lambda ({\hat{u}}^+) + \varphi (-{\hat{u}}^-)\nonumber \\&(\hbox {see Corollary~} 3 \hbox { and Proposition~}5)\nonumber \\&= \varphi _\lambda ({\hat{u}}) = {\hat{m}}_\lambda ^0. \end{aligned}$$

(29)

Arguing by contradiction, suppose that $\varphi _\lambda '({\hat{u}}) \ne 0$. Then, we can find $\delta > 0$ and $\eta > 0$ such that

$$\begin{aligned} \Vert u - {\hat{u}}\Vert \leqslant 3 \delta \Longrightarrow \Vert \varphi _\lambda '(u)\Vert _* \geqslant \eta >0. \end{aligned}$$

Consider the parallelogram $D=\left( \frac{1}{2},\frac{3}{2}\right) ^2$ and the function $\mu (\tau ,t) = \tau u^+ - t u^-$, $\tau$, $t \geqslant 0$. From (29), we see that

$$\begin{aligned} \ell = \max _{(\tau ,t) \in \partial D} \varphi _\lambda (\mu (\tau ,t)) < {\hat{m}}_\lambda ^0. \end{aligned}$$

Using Lemma 2.3 of Willem [18, p. 38], with $\varepsilon = \min \left\{ \frac{{\hat{m}}_\lambda ^0 - \ell }{4}, \frac{\eta \delta }{8}\right\}$, $S = {\overline{B}}_\delta ({\hat{u}})= \left\{ u \in W^{1,p}(\Omega ): \Vert u - {\hat{u}} \Vert { \leqslant } \delta \right\}$, we can find a deformation ${\hat{h}}(t,u)$ such that

$$\begin{aligned}&{\hat{h}}(1,u) = u \hbox { if } u \in \varphi _\lambda ^{-1} \left( [{\hat{m}}_\lambda ^0 - 2 \varepsilon , {\hat{m}}_\lambda ^0 + 2 \varepsilon ]\right) ,\\&\quad {\hat{h}}\left( 1,\varphi _\lambda ^{{\hat{m}}_\lambda ^0 + \varepsilon } \cap {\overline{B}}_\delta ({\hat{u}})\right) \subseteq \varphi _\lambda ^{{\hat{m}}_\lambda ^0 - \varepsilon }\\&\quad \left( \hbox {for every } c \in {\mathbb {R}},\ \varphi _\lambda ^c = \left\{ u \in W^{1,p}(\Omega ): \varphi _\lambda (u) \leqslant c\right\} \right) ,\\&\quad \varphi _\lambda (h(1,u)) \leqslant \varphi _\lambda (u) \hbox { for all } u \in W^{1,p}(\Omega ). \end{aligned}$$

From these properties of the deformation, we infer that

$$\begin{aligned} \max _{(\tau ,t) \in D} \varphi _\lambda \left( {\hat{h}}(1,\mu (\tau ,t)\right) < {\hat{m}}_\lambda ^0. \end{aligned}$$

(30)

Let $\beta (\tau ,t) = {\hat{h}}(1,\mu (\tau ,t))$ and set

$$\begin{aligned}&k_0(\tau ,t) = \left( \langle \varphi _\lambda '(\tau {\hat{u}}),{\hat{u}}^+\rangle , \langle \varphi _\lambda '(t u), -{\hat{u}}^-\rangle \right) ,\\&k_1(\tau ,t) = \left( \frac{1}{\tau } \langle \varphi _\lambda '(\beta (\tau ,t)), \beta ^+(\tau ,t)\rangle , \frac{1}{t} \langle \varphi _\lambda '(\beta (\tau ,t)), - \beta ^-(\tau ,t) \rangle \right) \hbox { for all } (\tau ,t) \in D. \end{aligned}$$

By ${\hat{d}}_B$, we denote the Brouwer degree. From the proof Proposition 5, we see that

$$\begin{aligned} {\hat{d}}_B(k_0,D,0) = 1. \end{aligned}$$

(31)

Note that $\mu |_{\partial D} = \beta |_{\partial D}$ (see (30)), the definition of $\ell$ and the choice of $\varepsilon > 0$). So, from the properties of the Brouwer degree (see [13, p. 178]), we have

$$\begin{aligned}&{\hat{d}}_B(k_0,D,0) = {\hat{d}}_B(k_1,D,0),\\&\quad \Rightarrow {\hat{d}}_B(k_1,D,0) = 1 \ (\hbox {see }(31)),\\&\quad \Rightarrow {\hat{h}}(t,\mu (D)) \cap {N_0} \ne \emptyset , \end{aligned}$$

which contradicts (30).

Therefore, we conclude that ${\hat{u}} \in K_{\varphi _\lambda }$. $\square$

So, under the stronger monotonicity hypothesis $(N) = H_1'\mathrm{(iv)}$, we have proved the existence of a ground-state nodal solution for problem ($P_\lambda$), when $\lambda < {\hat{\lambda }}_1$.

Next, we replace the strong monotonicity condition by the relaxed one $H_1'\mathrm{(iv)}$. To be able to treat this more general situation, let $\theta > 0$ and consider the following perturbation of f(z, x):

$$\begin{aligned} f_\theta (z,x) = f(z,x) + \theta r |x|^{r-2}x. \end{aligned}$$

Then, $f_\theta (z,x)$ is a Carathéodory function which satisfies hypothesis ${H_1'}$. We set $F_\theta (z,x) = \int \limits ^x_0 f_\theta (z,s) \mathrm{d}s$ and consider the $C^1$-functional $\varphi _\lambda ^\theta : W^{1,p}(\Omega )\mapsto {\mathbb {R}}$ defined by

$$\begin{aligned} \varphi _\lambda ^\theta (u) = \frac{1}{p} \gamma _p(u) - \frac{\lambda }{p} \Vert u\Vert _p^p- \int \limits _\Omega F_\theta (z,u) \mathrm{d}z \end{aligned}$$

for all $u \in W^{1,p}(\Omega )$.

We see that

$$\begin{aligned} \varphi _\lambda ^\theta (u) = \varphi _\lambda (u) - \theta \Vert u\Vert _r^r \hbox { for all } u \in W^{1,p}(\Omega ). \end{aligned}$$

For this functional, we introduce the Nehari manifold

$$\begin{aligned} {N}^\theta = \left\{ u \in W^{1,p}(\Omega ): \langle (\varphi _\lambda ^\theta )'(u),u\rangle = 0,\ u \ne 0\right\} \end{aligned}$$

and the Nehari submanifold

$$\begin{aligned} {N}_0^\theta = \left\{ u \in W^{1,p}(\Omega ): \langle (\varphi _\lambda ^\theta )'(u),u^+\rangle = \langle (\varphi _\lambda ^\theta )'(u),u^-\rangle = 0,\ u^\pm \ne 0\right\} . \end{aligned}$$

Proposition 9

If hypotheses ${H_0}, {H_1}$ hold and $\lambda < {\hat{\lambda }}_1,$ then we can find $\nu _0 > 0$ such that

$$\begin{aligned} \varphi _\lambda ^\theta (u) \geqslant \nu _0 > 0 \hbox { for all } u \in {N}^\theta , \hbox { for all } \theta \in (0,1]. \end{aligned}$$

Proof

Let $u \in {N}^\theta$. We have

$$\begin{aligned} \varphi _\lambda ^\theta (u)&= \max _{t \geqslant 0} \varphi _\lambda ^\theta (t u) \ (\hbox {see Corollary~} 4)\\&=\max _{t \geqslant 0} \left( \frac{t^p}{p} \left( \gamma _p(u) - \lambda \Vert u\Vert _p^p\right) - \int \limits _\Omega F(z,tu) \mathrm{d}z - \theta t^r \Vert u\Vert _r^r\right) \\&\geqslant \max _{t \geqslant 0} \left( c_{15} t^p - c_{16} t^r\right) \\&\quad \hbox {for some } c_{15},\ c_{16} > 0 \ (\hbox {see }(11)\hbox { and let } \varepsilon \in (0,{\hat{\lambda }}_1 - \lambda )). \end{aligned}$$

Since $r > p$, for $t \in (0,1)$ small we have

$$\begin{aligned} \varphi _\lambda ^\theta (u) \geqslant \nu _0 > 0 \hbox { for all } u \in {N}^\theta , \ \theta \in (0,1]. \end{aligned}$$

The proof of the proposition is now complete. $\square$

Now, we are ready to state and prove the main result of this paper, Theorem 1, which establishes the existence of a ground-state nodal solution under the relaxed monotonicity condition $H_1\mathrm{(iv)}$.

3.1 Proof of Theorem 1

(a) Let ${\overline{u}} \in {N}_0$. We have

$$\begin{aligned} \varphi _\lambda ({\overline{u}})&\geqslant \varphi _\lambda ^\theta ({\overline{u}})\nonumber \\&\geqslant \varphi _\lambda ^\theta (\tau _{{\overline{u}}} {\overline{u}}^+ - t_{{\overline{u}}} {\overline{u}}^-) \ (\hbox {see Proposition}~5)\nonumber \\&\geqslant {\hat{m}}_\lambda ^\theta \ ({\hat{m}}_\lambda ^\theta = \inf _{{N}_0^\theta } \varphi _\lambda ^\theta )\nonumber \\&> 0 \ (\hbox {see Proposition~}7). \end{aligned}$$

(32)

Now let $\theta _n \rightarrow 0^+$. Using Propositions 7, 8, 9 and (32), we see that we can $u_n= u_{\theta _n} \in {N}^{\theta _n}$ ($n \in {\mathbb {N}}$) such that

$$\begin{aligned} \left\{ \begin{array}{lll} \varphi _\lambda ^{\theta _n}(u_n) = {\hat{m}}_\lambda ^{\theta _n} \rightarrow m_* > 0, \\ (\varphi _\lambda ^{\theta _n})'(u_n) = 0 \hbox { for all } n \in {\mathbb {N}}. \end{array} \right\} \end{aligned}$$

(33)

Claim: The sequence $\left\{ u_n\right\} _{n \in {\mathbb {N}}} \subseteq W^{1,p}(\Omega )$ is bounded.

We argue indirectly. So, suppose that the claim is not true. Then, for at least a subsequence, we have

$$\begin{aligned} \Vert u_n\Vert \rightarrow +\infty . \end{aligned}$$

Let $v_n = \frac{u_n}{\Vert u_n\Vert }$, $n \in {\mathbb {N}}$. Then, $\Vert v_n\Vert = 1$ for all $n \in {\mathbb {N}}$ and so we may assume that

$$\begin{aligned} v_n \xrightarrow w v \text{ in } W^{1,p}(\Omega ) \text{ and } v_n \rightarrow L^r(\Omega ) \text{ and } \text{ in } L^p(\partial \Omega ). \end{aligned}$$

(34)

Suppose that $v =0$. Let $k > 1$. From (33), we have

$$\begin{aligned} {\hat{m}}_\lambda ^{\theta _n} = \varphi _\lambda ^{\theta _n}(u_n)&\geqslant \varphi _\lambda \left( \frac{k}{\Vert u_n\Vert } u_n\right) \\&\quad (\hbox {see Corollary~} 4\hbox { and recall that } {N}_0^{\theta _n} \subseteq {N}^{\theta _n})\\&\geqslant \varphi _\lambda ^{\theta _n}(k v_n)\\&\geqslant \frac{k^p}{p} \left( \gamma _p(v_n) -\lambda \Vert v_n\Vert _p^p\right) - \int \limits _\Omega F(z,k v_n) \mathrm{d}z - \theta _n k^r \Vert v_n\Vert _r^r\\&\geqslant \frac{k^p}{p} c_{17} - \int \limits _\Omega F(z, k v_n) \mathrm{d}z - \theta _n k^r \Vert v_n\Vert _r^r\\&\quad \hbox {for some } c_{17} > 0, \hbox { all } n \in {\mathbb {N}}\ (\hbox {since } \lambda < {\hat{\lambda }}_1,\ \Vert v_n\Vert =1). \end{aligned}$$

We pass to the limit as $n \rightarrow \infty$. Since $v = 0$, from (34) we obtain

$$\begin{aligned} m_* \geqslant \frac{k^p}{p} c_{17} > 0. \end{aligned}$$

But $k > 1$ is arbitrary. So, let $k \rightarrow +\infty$ to have a contradiction.

Next, we assume that $v \ne 0$. We set ${\hat{\Omega }} = \left\{ z \in \Omega : v(z) \ne 0\right\}$. Then, $|{\hat{\Omega }}|_N > 0$ and we have $|u_n(z)| \rightarrow + \infty$ for a.a. $z \in {\hat{\Omega }}$. We have

$$\begin{aligned} 0 < \frac{{\hat{m}}_\lambda ^{\theta _n}}{\Vert u_n\Vert ^p}&= \frac{\varphi _\lambda ^{\theta _n}(u_n)}{\Vert u_n\Vert ^p}\nonumber \\&\leqslant \frac{1}{p} \gamma _p(v_n) - \int \limits _\Omega \frac{F(z,u_n)}{\Vert u_n\Vert ^p} \mathrm{d}z \nonumber \\&\leqslant c_{18} - \int \limits _\Omega \frac{F(z,u_n)}{\Vert u_n\Vert ^p} \mathrm{d}z\nonumber \\&\quad \hbox {for some } c_{18} > 0, \hbox { all } n \in {\mathbb {N}}\ (\hbox {see }(34)). \end{aligned}$$

(35)

Since $|{\hat{\Omega }}|_N > 0$ and $|u_n(z)| \rightarrow + \infty$ for a.a. $z \in {\hat{\Omega }}$, using hypothesis $H_1\mathrm{(ii)}$ and reasoning as in the proof Proposition 7, we show that

$$\begin{aligned} \int \limits _\Omega \frac{F(z,u_n)}{\Vert u_n\Vert ^p} \mathrm{d}z \rightarrow + \infty . \end{aligned}$$

So, if in (35) we pass to the limit as $n \rightarrow \infty$, we have a contradiction. This proves the claim.

On account of the claim, we can say that

$$\begin{aligned} u_n \xrightarrow w u_* \hbox { in } W^{1,p}(\Omega )\hbox { and } u_n \rightarrow u_* \hbox { in } L^r(\Omega )\hbox { and in } L^p(\partial \Omega ). \end{aligned}$$

(36)

From (33), we have

$$\begin{aligned} \langle \gamma _p'(u_n),h\rangle = \lambda \int \limits _\Omega |u_n|^{p-2} u_n h \mathrm{d}z + \int \limits _\Omega f(z,u_n) h \mathrm{d}z + \theta _n r \int \limits _\Omega |u_n|^{r-2} u_n h \mathrm{d}z \end{aligned}$$

(37)

for all $h \in W^{1,p}(\Omega )$, all $n \in {\mathbb {N}}$.

In (37) we use the test function $h = u_n - u_* \in W^{1,p}(\Omega )$. Passing to the limit as $n \rightarrow \infty$ and using (36), we obtain

$$\begin{aligned}&\lim _{n \rightarrow \infty } \langle A_p(u_n), u_n - u_* \rangle = 0,\nonumber \\&\quad \Rightarrow u_n \rightarrow u_* \hbox { in } W^{1,p}(\Omega ),\nonumber \\&\quad \Rightarrow u_n^+ \rightarrow u_*^+ \hbox { and } u_n^- \rightarrow u_*^- \hbox { in } W^{1,p}(\Omega ). \end{aligned}$$

(38)

Since $u_n^\pm \in {N}^{\theta _n}$ ($n \in {\mathbb {N}}$), using Proposition 9 and (38), we have

$$\begin{aligned}&\varphi _\lambda (u_*^\pm ) = \lim _{n \rightarrow \infty } \varphi _\lambda ^{\theta _n}(u_n^\pm ) \geqslant \nu _0 > 0= \varphi _\lambda (0)\\&\quad \Rightarrow u_*^\pm \ne 0 \hbox { and so } u_* \in {N}_0. \end{aligned}$$

Then, we have

$$\begin{aligned} m_* = \varphi _\lambda (u_*) \geqslant {\hat{m}}_\lambda ^0. \end{aligned}$$

We will show that in fact equality holds. Given $\varepsilon > 0$ let $y_\varepsilon \in {N}_0$ such that

$$\begin{aligned} \varphi _\lambda (y_\varepsilon ) \leqslant {\hat{m}}_\lambda ^0 + \varepsilon . \end{aligned}$$

For $\tau$, $t > 0$ we have

$$\begin{aligned}&\varphi _\lambda ^{\theta _n} (\tau y_\varepsilon ^+ - t y_\varepsilon ^-)\\&\quad = \frac{\tau ^p}{p} \left( \gamma _p(y_\varepsilon ^+) - \lambda \Vert y_\varepsilon ^+\Vert _p^p\right) - \int \limits _\Omega F(z, \tau y_\varepsilon ^+) \mathrm{d}z - \theta _n \Vert y_\varepsilon ^+\Vert _r^r\\&\qquad + \frac{t^p}{p} \left( \gamma _p (y_\varepsilon ^-) - \lambda \Vert y_\varepsilon ^-\Vert _p^p\right) - \int \limits _\Omega F(z, - t y_\varepsilon ^-) \mathrm{d}z - \theta _n \Vert y_\varepsilon ^-\Vert _r^r. \end{aligned}$$

On account of hypothesis $H_1\mathrm{(ii)}$, we see that we can find $M > 1$ such that

$$\begin{aligned} \varphi _\lambda ^{\theta _n} \left( \tau y_\varepsilon ^+ - t y_\varepsilon ^-\right) < 0 \hbox { for all } \tau ,\ t \geqslant M, \hbox { all } n \in {\mathbb {N}}. \end{aligned}$$

(39)

From Proposition 5, we know that there exist $\tau _n$, $t_n > 0$ ($n \in {\mathbb {N}}$) unique such that

$$\begin{aligned} \tau _n y_\varepsilon ^+ - t_n y_\varepsilon ^- \in {N}_0^{\theta _n} \hbox { for all } n \in {\mathbb {N}}. \end{aligned}$$

(40)

Since ${\hat{m}}_\lambda ^{\theta _n} > 0$ (see Proposition 7) and $\varphi _\lambda ^{\theta _n}\left( \tau _n y_\varepsilon ^+ - t_n y_\varepsilon ^- \right) \geqslant {\hat{m}}_\lambda ^{\theta _n} > 0$ (see (40)). Hence, from (39) we infer that $\tau _n$, $t_n < M$ for all $n \in {\mathbb {N}}$. We have

$$\begin{aligned} {\hat{m}}_\lambda ^0 + \varepsilon&\geqslant \varphi _\lambda (y_\varepsilon )\\&= \varphi _\lambda ^{\theta _n}(y_\varepsilon ) + \theta _n\Vert y_\varepsilon \Vert _r^r\\&\geqslant \varphi _\lambda ^{\theta _n} \left( \tau _n y_\varepsilon ^+ - t_n y_\varepsilon ^-\right) + \frac{1 -\tau _n^p}{p} \langle (\varphi _\lambda ^{\theta _n})'(y_\varepsilon ), y_\varepsilon ^+ \rangle \\&\quad + \frac{1 -t_n^p}{p} \langle (\varphi _\lambda ^{\theta _n})'(y_\varepsilon ), - y_\varepsilon ^- \rangle \ (\hbox {see Proposition~}2)\\&\geqslant {\hat{m}}_\lambda ^{\theta _n} - \frac{1 +M^p}{p} \left| \langle (\varphi _\lambda ^{\theta _n})'(y_\varepsilon ), y_\varepsilon ^+ \rangle \right| \\&\quad - \frac{1 +M^p}{p} \left| \langle (\varphi _\lambda ^{\theta _n})'(y_\varepsilon ), - y_\varepsilon ^- \rangle \right| \\&= {\hat{m}}_\lambda ^{\theta _n} - \frac{1 + M^p}{p} \theta _n r \Vert y_\varepsilon ^+\Vert _r^r - \frac{1 + M^p}{p} \theta _n r \Vert y_\varepsilon ^-\Vert _r^r\\&\hbox {for all } n \in {\mathbb {N}}\ (\hbox {since } y_\varepsilon \in {N}_0). \end{aligned}$$

We pass to the limit as $n \rightarrow \infty$ and obtain

$$\begin{aligned} {\hat{m}}_\lambda ^0 + \varepsilon \geqslant m_*. \end{aligned}$$

Since $\varepsilon > 0$ is arbitrary, we let $\varepsilon \downarrow 0$ and obtain

$$\begin{aligned}&{\hat{m}}_\lambda ^0 \geqslant m_*,\\&\quad \Rightarrow m_* = {\hat{m}}_\lambda ^0,\\&\quad \Rightarrow u_* \in {N}_0,\ \varphi _\lambda (u_*) = {\hat{m}}_\lambda ^0,\ u_* \in K_{\varphi _\lambda }\ (\hbox {see Proposition~}8). \end{aligned}$$

The regularity theory of Lieberman [6] implies that $u_* \in C^1({\overline{\Omega }})$.

(b) With the additional assumption that $e(z,x) > 0$ for a.a. $z \in \Omega$, all $x \ne 0$, we will show that $u_*$ has two nodal domains.

We argue by contradiction. So, suppose that

$$\begin{aligned} u_* = {\hat{u}}_1 + {\hat{u}}_2 + {\hat{u}}_3 \end{aligned}$$

and $\Omega _1 = \left\{ {\hat{u}}_1 > 0\right\}$, $\Omega _2 = \left\{ {\hat{u}}_2 < 0\right\}$ are connected open subsets of $\Omega$, $\Omega _1 \cap \Omega _2 = \emptyset$ and

$$\begin{aligned} {\hat{u}}_1 \big |_{\Omega {\setminus } (\Omega _1 \cup \Omega _2)} = {\hat{u}}_2 \big |_{\Omega {\setminus } (\Omega _1 \cup \Omega _2)} = {\hat{u}}_3 \big |_{\Omega _1 \cup \Omega _2}. \end{aligned}$$

(41)

Let $y = {\hat{u}}_1 + {\hat{u}}_2$. Then, $y^+ = {\hat{u}}_1$, $y^- = - {\hat{u}}_2$. We have

$$\begin{aligned} \varphi _\lambda '(u_*) = 0 \hbox { and } \langle \varphi _\lambda '(u_*), {\hat{u}}_1 \rangle = \langle \varphi _\lambda '(u_*), {\hat{u}}_2 \rangle = 0. \end{aligned}$$

(42)

Then,

$$\begin{aligned} {\hat{m}}_\lambda ^0&= \varphi _\lambda (u_*)\\&= \varphi _\lambda (u_*) - \frac{1}{p} \langle \varphi _\lambda '(u_*), u_* \rangle \ (\hbox {since } u_* \in {N}_0 \subseteq {N})\\&= \varphi _\lambda (y) + \varphi _\lambda ({\hat{u}}_3) - \frac{1}{p} \langle \varphi _\lambda '({\hat{u}}_3), {\hat{u}}_3 \rangle \ (\hbox {see }(41), (42))\\&\geqslant \varphi _\lambda \left( \tau {\hat{u}}_1 + t {\hat{u}}_2\right) + \varphi _\lambda ({\hat{u}}_3) - \frac{1}{p} \langle \varphi _\lambda '({\hat{u}}_3),{\hat{u}}_3 \rangle \ (\hbox {see Corollary~}3)\\&\geqslant {\hat{m}}_\lambda ^0 + \int \limits _\Omega \frac{1}{p} e(z,{\hat{u}}_3) \mathrm{d}z\\&> {\hat{m}}_\lambda ^0 \hbox { if } {\hat{u}}_3 \ne 0, \end{aligned}$$

which is a contradiction. Hence, ${\hat{u}}_3 = 0$ and we conclude that $u_*$ has two nodal domains.

The proof of Theorem 1 is now complete. $\square$