Hydroelastic analysis of very large rectangular plate floating on shallow water

Abstract

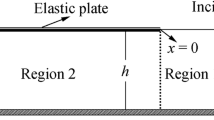
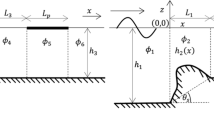
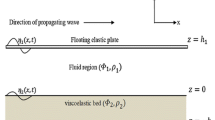
In the present study, the interaction of surface gravity waves with a very large rectangular floating flexible plate is analyzed in shallow water depth. The horizontal dimensions of the floating structure are much larger than the wavelength of the incident wave. The associated boundary value problem (BVP) is solved by considering the draft of the plate is negligible, and the bottom surface of the plate is floating on the still water level (SWL). The solution technique is based on the parabolic approximation in which the solutions in the open water regions are matched appropriately with the solution in the plate covered region. The effect of the compressive force on the plate deflection is analyzed in a detailed manner. Further, the occurrences of the blocking phenomena above the critical value of the compressive force are illustrated.

Appendices

Appendix A

In Fig. 1 if no edge is present at $y=0$, then the plate vibration is uniform in y and Eq. (6) is modified as

$$\begin{aligned} \displaystyle {\mathcal {D}}\frac{d^6\phi }{dx^6}+{\mathcal {Q}} \frac{d^4\phi }{dx^4}+\rho g\frac{d^2\phi }{dx^2}+\rho g k_0^2\phi =0. \end{aligned}$$

(A.1)

Assuming

$$\begin{aligned} {\mathcal {D}}={\mathcal {O}}(k_0^{-4}),\;\;{\mathcal {Q}} ={\mathcal {O}}(k_0^{-2}),\;\; \text{ and }\;\;\frac{d}{dx} ={\mathcal {O}}(k_0), \end{aligned}$$

(A.2)

every terms in Eq. (A.1) is of order ${\mathcal {O}}(k_0^{2})$ (see Stoker [7] for details). It is to be noted that if $D>>{\mathcal {O}}(k_0^{-4})$ i.e., if the plate is more stiffer than usual, no transverse vibrations occur. For a flexible plate, a solution of Eq. (A.1) is of the form

$$\begin{aligned} \phi =\sum _{j=1}^{6} A_{j}e^{\kappa _{j}x}, \end{aligned}$$

(A.3)

where $\kappa _j$ satisfy the following relation

$$\begin{aligned} {\mathcal {D}} \kappa _{j}^6+{\mathcal {Q}} \kappa _{j}^4 +\rho g \kappa _{j}^2+\rho g k_{0}^2=0. \end{aligned}$$

(A.4)

The six roots of Eq. (A.4) are as follows

$$\begin{aligned} \kappa _{1,4}=\mp \mathrm{i}k_a,\;\;\kappa _{2,5}=\mp l, \;\;\kappa _{3,6}=\mp l^{*},\;\;\; |\text{ arg }(l)|<\frac{\pi }{2} \end{aligned}$$

(A.5)

where $l^{*}$ represents the complex conjugate of l, and also

$$\begin{aligned} k_a=|(u+v)|^{\frac{1}{2}},\;\;l=\left[ -\frac{1}{2}(u+v)+\mathrm{i} \frac{\sqrt{3}}{2}(u-v)\right] ^{\frac{1}{2}}, \end{aligned}$$

where

$$\begin{aligned} u=\left[ -\frac{q}{2}+\sqrt{\left( \frac{q^2}{4} +\frac{p^3}{27}\right) }\right] ^{\frac{1}{3}}, \;\;v=\left[ -\frac{q}{2}-\sqrt{\left( \frac{q^2}{4} +\frac{p^3}{27}\right) }\right] ^{\frac{1}{3}}, \end{aligned}$$

with

$$\begin{aligned} p=b-\frac{a^2}{3},\;\; q=\frac{2a^3-9ab+27c}{27}, \;\; a=\frac{{\mathcal {Q}}}{{\mathcal {D}}}, \;\;b=\frac{\rho g}{{\mathcal {D}}}, \;\;c=\frac{\rho g k_0^2}{{\mathcal {D}}}, \end{aligned}$$

It is easy to show that $l={\mathcal {O}}(k_0)$. This guarantee that the assumptions in Eq. (A.2) are accurate.

Appendix B

The unknown coefficients in Eq.(A.3) are calculated as following. The values of $A_5, A_6$ are zeros due to the boundedness of $\phi$ as $x\rightarrow +\infty$, and as no waves are coming from $x=+\infty$, the value of $A_4=0.$ The remaining unknown coefficients $A_1, A_2, A_3$ are obtained using the edge conditions (8.1) and (8.2), i.e., the zero shear force and bending moment along the edge $x=0, y<0$. Substituting the expression for $\phi$ as in Eq.(A.3) for $j=1,2,3$ into Eqs. (8.1)-(8.2) and using the condition for continuity of mass and energy flux at $x=0$ with the wave solution in $R_1$, we obtained the following system of equations as

$$\begin{aligned} AX=B \end{aligned}$$

(B.1)

where

$$\begin{aligned}&A=\left( \begin{array}{cccc} D \kappa _1^5+Q \kappa _1^3 &{} D \kappa _2^5+Q \kappa _2^3 &{} D \kappa _3^5+Q \kappa _3^3 &{}0\\ \kappa _1^{4} &{} \kappa _2^{4} &{} \kappa _3^{4} &{}0\\ 1 &{} 1 &{} 1 &{}-1\\ \kappa _1 &{} \kappa _2 &{} \kappa _{3} &{}-\mathrm{i}k_0 \end{array}\right) ,\;\; X=\left( \begin{array}{c} A_1 \\ A_2 \\ A_3 \\ R \end{array}\right) \\&B=\left( \begin{array}{c} 0 \\ 0 \\ 1 \\ -\mathrm{i}k_0 \end{array}\right) \end{aligned}$$

Solve the linear system of equations Eq.(B.2) to determine the unknown values $A_1, A_2, A_3, R$.

Appendix C. Parabolic approximation

Under the assumption of linear shallow water wave theory, i.e., $k_0h<<1$ where $k_0$ and h are the incident wavenumber and the water depth, respectively, the governing equation for the velocity potential is the Helmholtz equation in two-dimensional (see [7, 39]),

$$\begin{aligned} \displaystyle \frac{\partial ^2 \phi }{\partial x^2} +\frac{\partial ^2 \phi }{\partial y^2}+k_0^2\phi =0. \end{aligned}$$

(C.1)

Assuming the floating plate is elongated in the x-direction, it is reasonable to consider the velocity potential of the form

$$\begin{aligned} \displaystyle \phi (x,y)=\psi (x,y)e^{-\mathrm{i}k_0x}. \end{aligned}$$

(C.2)

Substituting Eq. (C.2) into Eq. (C.1), it results

$$\begin{aligned} \displaystyle -2\mathrm{i}k_0\frac{\partial \psi }{\partial x} +\frac{\partial ^2 \psi }{\partial x^2} +\frac{\partial ^2 \psi }{\partial y^2}=0, \end{aligned}$$

(C.3)

Further, it is assumed that the variation of $\psi (x,y)$ in x-direction is smaller than the variation in y-direction. Therefore, the term ${\partial ^2 \psi }/{\partial x^2}$ can be ignored. Finally, the parabolic approximation is given by

$$\begin{aligned} \displaystyle -2\mathrm{i}k_0\frac{\partial \psi }{\partial x} +\frac{\partial ^2 \psi }{\partial y^2}=0. \end{aligned}$$

(C.4)

Clearly, when $x={\mathcal {O}}(1)$ and $y={\mathcal {O}}(k_0^{-1/2})$, the terms involving in (D.4) have equal order of magnitude with relative error ${\mathcal {O}}(k_0^{-1})$. Therefore, the parabolic approximation is valid for the water region $x={\mathcal {O}}(1)$ and $y={\mathcal {O}}(k_0^{-1/2})$. To solve Eq. (C.4), appropriate initial data and far-field condition are required.