On a Solution of the Multidimensional Truncated Matrix-Valued Moment Problem

Abstract

We will consider the multidimensional truncated $p \times p$ Hermitian matrix-valued moment problem. We will prove a characterisation of truncated $p \times p$ Hermitian matrix-valued multisequence with a minimal positive semidefinite matrix-valued representing measure via the existence of a flat extension, i.e., a rank preserving extension of a multivariate Hankel matrix (built from the given truncated matrix-valued multisequence). Moreover, the support of the representing measure can be computed via the intersecting zeros of the determinants of matrix-valued polynomials which describe the flat extension. We will also use a matricial generalisation of Tchakaloff’s theorem due to the first author together with the above result to prove a characterisation of truncated matrix-valued multisequences which have a representing measure. When $p = 1$, our result recovers the celebrated flat extension theorem of Curto and Fialkow. The bivariate quadratic matrix-valued problem and the bivariate cubic matrix-valued problem are explored in detail.

1 Introduction

In this paper, we will investigate the multidimensional truncated matrix-valued moment problem. Given a truncated multisequence $S = (S_{\gamma })_{{\mathop {\gamma \in {\mathbb {N}}_0^d}\limits ^{0 \le |\gamma | \le m}} }$, where $S_{\gamma } \in {\mathcal {H}}_p$ (i.e., $S_{\gamma }$ is a $p \times p$ Hermitian matrix), we wish to find necessary and sufficient conditions on S for the existence of a $p \times p$ positive matrix-valued measure T on ${\mathbb {R}}^d$, with convergent moments, such that

$$\begin{aligned} S_{\gamma } = \int _{{\mathbb {R}}^d} x^{\gamma } dT(x):= \int \cdots \int _{{\mathbb {R}}^d} \prod _{j=1}^d x_j^{\gamma _j} dT(x_1, \ldots , x_d) \end{aligned}$$

(1.1)

for all $\gamma = (\gamma _1, \ldots , \gamma _d) \in {\mathbb {N}}_0^d$ such that $0 \le |\gamma | \le m$. We would also like to find a positive matrix-valued measure $T = \sum _{a=1}^{\kappa } Q_a \delta _{w^{(a)}}$ on ${\mathbb {R}}^d$ such that (1.1) holds and and

$$\begin{aligned} \sum _{a=1}^{\kappa } \mathrm{rank}\, Q_a\text { is as small as possible}, \end{aligned}$$

(1.2)

i.e., T is a finitely atomic measure of the form $T = \sum _{a=1}^{\kappa } \delta _{w^{(a)}} Q_a$ with $\sum _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a = {{\,\mathrm{rank}\,}}M(n)$ (confer Remark 3.4). If (1.1) holds, then T is called a representing measure for S. If (1.1) and (1.2) are in force, then T is called a minimal representing measure for S.

Before proceeding any further, we will first introduce frequently used notation. Commonly used sets are ${\mathbb {N}}_0, {\mathbb {R}}, {\mathbb {C}}$ denoting the sets of nonnegative integers, real numbers and complex numbers respectively. Given a nonempty set E,  we let

$$\begin{aligned} E^d=\{(x_1,\dots , x_d):x_j \in E \;\; \text{ for } \; j=1, \dots , d\}. \end{aligned}$$

Next, we let ${\mathbb {C}}^{p \times p}$ denote the set of $p\times p$ matrices with entries in ${\mathbb {C}}$ and ${\mathcal {H}}_p\subseteq {\mathbb {C}}^{p \times p}$ denote the set of $p\times p$ Hermitian matrices with entries in ${\mathbb {C}}.$ Given $x= (x_1,\dots , x_d) \in {\mathbb {R}}^d$ and $\lambda = (\lambda _1, \dots , \lambda _d)\in {\mathbb {N}}_0^d,$ we define

$$\begin{aligned} x^\lambda = \prod \limits _{j=1}^{d} x_j^{ \lambda _j}\quad \text {and}\quad |\lambda |= \lambda _1+\dots +\lambda _d \end{aligned}$$

and

$$\begin{aligned} \Gamma _{m, d}:= \{\gamma \in {\mathbb {N}}_0^d: 0\le \vert \gamma \vert \le m \}. \end{aligned}$$

Throughout the entirety of this paper we will assume that the given ${\mathcal {H}}_p$-valued truncated multisequence $S = (S_{\gamma })_{\gamma \in \Gamma _{2n,d}}$ satisfies

$$\begin{aligned} S_{0_d} = I_p. \end{aligned}$$

(1.3)

Let us justify this assumption. If $S_{0_d} \succ 0$ (i.e., $S_{0_d}$ is positive definite), then we can simply replace S by ${\widetilde{S}} = ({\widetilde{S}}_{\gamma } )_{\gamma \in \Gamma _{2n,d}}$, where ${\widetilde{S}}_{\gamma } = S_{0_d}^{-1/2} \, S_{\gamma } \, S_{0_d}^{-1/2}$. If $S_{0_d} \succeq 0$ (i.e., $S_{0_d}$ is positive semidefinite) and not invertible, then Lemma 5.50 and Smuljan’s lemma (see Lemma 2.1) readily show that we must necessarily have that ${{\,\mathrm{Ran}\,}}S_{\gamma } \subseteq {{\,\mathrm{Ran}\,}}S_{0_d}$ and hence $\mathrm{Ker}S_{0_d} \subseteq \mathrm{Ker}S_{\gamma }$ for all $\gamma \in \Gamma _{2n,d}$. Consequently, we can find a unitary matrix $U \in {\mathbb {C}}^{p \times p}$ such that

$$\begin{aligned} U^* S_{\gamma } U = \begin{pmatrix} {\widetilde{S}}_{\gamma } &{}\quad 0 \\ 0 &{}\quad 0 \end{pmatrix} \end{aligned}$$

and we may replace S by ${\widetilde{S}} = ({\widetilde{S}}_{\gamma })_{\gamma \in \Gamma _{2n,d}}$, where ${\widetilde{S}}_{\gamma } \in {\mathbb {C}}^{{\tilde{p}} \times {\tilde{p}}}$ with ${\tilde{p}} = {{\,\mathrm{rank}\,}}S_{0_d}$, and normalise as above.

Main Contributions

• (C1) We will characterise positive infinite d-Hankel matrices based on a ${\mathcal {H}}_p$-valued multisequence via an integral representation. Indeed, we will see that $S^{(\infty )} = (S_{\gamma })_{\gamma \in {\mathbb {N}}_0^d}$ gives rise to a positive infinite d-Hankel matrix $M(\infty )$ with finite rank if and only if there exists a finitely atomic positive ${\mathcal {H}}_p$-valued measure T on ${\mathbb {R}}^d$ such that

  $$\begin{aligned} S_{\gamma } = \int _{{\mathbb {R}}^d} x^{\gamma } \, dT(x) \quad \quad \mathrm{for} \quad \gamma \in {\mathbb {N}}_0^d. \end{aligned}$$

  In this case, the support of the positive ${\mathcal {H}}_p$-valued measure T agrees with ${\mathcal {V}}({\mathcal {I}})$, where ${\mathcal {V}}({\mathcal {I}})$ is the variety of a right ideal of matrix-valued polynomials based on the kernel of $M(\infty )$ (see Definition 5.20) and the cardinality of the support of T is exactly ${{\,\mathrm{rank}\,}}M(\infty )$ (see Theorem 5.65).

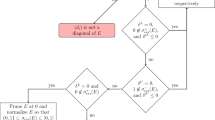
• (C2) Let $S = (S_{\gamma })_{\gamma \in \Gamma _{2n,d}}$ be a given truncated ${\mathcal {H}}_p$-valued multisequence. We will see that S has a minimal representing measure $T = \sum _{a=1}^{\kappa } Q_a \delta _{w^{(a)}}$ if and only if the corresponding d-Hankel matrix M(n) based on S (see Definition 3.2) has a flat extension $M(n+1)$, i.e., a positive rank preserving extension. In this case, the support of T agrees with ${\mathcal {V}}(M(n+1))$, where ${\mathcal {V}}(M(n+1))$ is the variety of the d-Hankel matrix $M(n+1)$ (see Definition 3.5) and $\sum _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a = \sum _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}M(n)$.

• (C3) Let S be as in (C2). S has a representing measure if and only if the corresponding d-Hankel matrix M(n) has an eventual extension $M(n+k)$ which admits a flat extension.

• (C4) Let $S = (S_{00}, S_{10}, S_{01}, S_{20}, S_{11}, S_{02})$ be a given ${\mathcal {H}}_p$-valued truncated bisequence. We will see that necessary and sufficient conditions for S to have a minimal representing measure consist of M(1) being positive semidefinite and a system of matrix equations having a solution. We will also see that if M(1) is positive definite and obeys an extra condition (which is automatically satisfied if $p=1$), then S has a minimal representing measure. However, if M(1) is singular and $p \ge 2$, then S need not have a minimal representing measure.

Background and Motivation

The moment problem on ${\mathbb {R}}^d$ is a well-known problem in classical analysis and has been studied by mathematicians and engineers since the late 19th century, beginning with Stieltjes [77], Hamburger [42, 43], Hausdorff [44] and Riesz [67]. The full moment problem on ${\mathbb {R}}$ has a concrete solution discovered by Hamburger [42, 43] which can be communicated solely in terms of the positivity of Hankel matrices built from the given sequence. It is natural to wonder about a multidimensional analogue of the full moment problem on ${\mathbb {R}},$ that is, the full moment problem on ${\mathbb {R}}^d,$ where the given sequence is a multisequence indexed by d-tuples of nonnegative integers. It is well known that a natural analogue of Hamburger’s theorem fails (see, e.g., Schmüdgen [72]), i.e., there exist multisequences such that the corresponding multivariable Hankel matrices are positive semidefinite yet the multisequences do not have a representing measure. It turns out that the Hamburger moment problem on ${\mathbb {R}}^d$ is a special case of the full K-moment problem on ${\mathbb {R}}^d$ (where we wish to find a positive measure which is supported on a given closed set $K\subseteq {\mathbb {R}}^d$). We refer the reader to Riesz [67] (solution on ${\mathbb {R}}$), Haviland [45, 46] (generalisation for $d>1$) and Schmüdgen [70] (when K is a compact semialgebraic set). For a solution to the truncated K-moment problem on ${\mathbb {R}}^d$ based on commutativity conditions of certain matrices see the first author [52], where an application to the subnormal completion problem is considered. Moment problems on ${\mathbb {R}}^d$ intertwine many different areas of mathematics such as matrix and operator theory, probability theory, optimisation theory, and the theory of orthogonal polynomials. Various applications for moment problems on ${\mathbb {R}}^d$ can be found in control theory, polynomial optimisation and mathematical finance (see, e.g., Lasserre [59] and Laurent [60]). For approaches to the multidimensional moment problem which utilise techniques from real algebra see Marshall [61] and Prestel and Delzell [66]. For a treatment of the abstract multidimensional moment problem see Berg, Christensen and Ressel [7] and Sasvári [68], which, in addition, treats indefinite analogues of multidimensional moment problems.

The truncated moment problem on ${\mathbb {R}},$ that is, where one is given a truncated sequence $(s_j)_{j=0}^m$ with $s_j\in {\mathbb {R}}$ for $j=0, \dots , m,$ has a concrete solution which can be communicated in terms of positivity of a Hankel matrix and checking a range inclusion. Moreover, a minimal representing measure can be constructed from the zeros of the polynomial describing a rank-preserving positive extension. We refer the reader to the classical works of Akhiezer [1], Akhiezer and Krein [2], Krein and Nudel’man [58], Shohat and Tamarkin [73] and the fairly recent work of Curto and Fialkow [15]. An area of active interest concerns the truncated moment problem on ${\mathbb {N}}_0$ where one seeks a measure whose support is contained in a given closed subset $K\subseteq {\mathbb {N}}_0$ (see, e.g., Infusino, Kuna, Lebowitz and Speer [49]).

Curto and Fialkow in a series of papers studied scalar truncated moment problems on ${\mathbb {R}}^d$ and ${\mathbb {C}}^d$ (which is equivalent to the truncated moment problem on ${\mathbb {R}}^{2d}$). We refer the reader to [16,17,18,19,20,21,22] where concrete conditions for a solution to various moment problems are investigated. For connections between bivariate moment matrices and flat extensions see Fialkow and Nie [37, 38], Fialkow [35] and Curto and Yoo [25]. For the bivariate cubic moment problem we refer the reader to Curto, Lee and Yoon [24], the first author [50], and Curto and Yoo [26].

We next wish to mention alternative approaches to the flat extension theorem for the truncated moment problem on ${\mathbb {R}}^d$. The core variety approach to the truncated moment problem began with the study of Fialkow [36]. Subsequently, Blekherman and Fialkow in [8] strengthened the core variety approach to feature a necessary and sufficient condition for a solution. For additional results related to the core variety approach see Schmüdgen [72] and di Dio and Schmüdgen [30]. Recently, in [23], Curto, Ghasemi, Infusino and Kuhlmann investigated the theory of positive extensions of linear functionals showing the existence of an integral representation for the linear functional.

We now wish to bring the matrix-valued and operator-valued moment problem into focus. The matrix-valued moment problem on ${\mathbb {R}}$ was initially investigated by Krein [56, 57]. See [65] for a thorough review on Krein’s work on moment problems. Andô in [4] was the first to study the truncated moment problem in the operator-valued case. Narcowich studied the matrix-valued and operator-valued Stieltjes moment problem in [64]. Kovalishina studied the nondegenerate case in [54, 55]. Bolotnikov considered the degenerate truncated matrix-valued Hamburger and Stieltjes moment problems in terms of a linear fractional transformation, see [10,11,12]. Dym [31] considered the truncated matrix-valued Hamburger moment problem associating it with parametrised solutions of a matrix interpolation problem. Alpay and Loubaton in [3] treated the partial trigonometric moment problem on an interval in the matrix case, where Toeplitz matrices built from the moments are associated to orthogonal polynomials. For connections between matrix-valued orthogonal polynomials and CMV matrices we refer the reader to Dym and the first author [32].

Simonov studied the strong matrix-valued Hamburger moment problem in [74, 75]. The truncated matrix-valued moment problem on a finite closed interval was studied by Choque Rivero, Dyukarev, Fritzsche and Kirstein [13, 14]. Using Potapov’s method of Fundamental Matrix Inequalities they characterised the solutions by nonnegative Hermitian block Hankel matrices and they investigated further the case of an odd number of prescribed moments. Dyukarev, Fritzsche, Kirstein, Mädler and Thiele [34] studied the truncated matrix-valued Hamburger moment problem with an algebraic approach based on matrix-valued polynomials built from a nonnegative Hermitian block Hankel matrix. Dyukarev, Fritzsche, Kirstein and Mädler [33] studied the truncated matrix-valued Stieltjes moment problem via a similar approach.

Bakonyi and Woerdeman in [5] studied the univariate truncated matrix-valued Hamburger moment problem and the odd case of the bivariate truncated matrix-valued moment problem. The first author and Woerdeman in [53] investigated the odd case of the truncated matrix-valued K-moment problem on ${\mathbb {R}}^d,$ ${\mathbb {C}}^d$ and ${\mathbb {T}}^d,$ where they discovered easily checked commutativity conditions for the existence of a minimal representing measure.

Applications of matrix-valued moment problems and related topics have been studied extensively in recent years. Geronimo [39] studied scattering theory and matrix orthogonal polynomials with the construction of a matrix-valued distribution function built from matrix-valued moments. Dette and Studden in [27] investigated matrix orthogonal polynomials and matrix-valued measures associated with certain matricial moments from a numerical analysis point of view. In [28], Dette and Studden considered optimal design problems in linear models as a statistical application of the problem of maximising matrix-valued Hankel determinants built from matricial moments. Moreover, Dette and Tomecki in [29] studied the distribution of random Hankel block matrices and random Hankel determinant processes with respect to certain matricial moments.

In [63], Mourrain and Schmüdgen studied extensions and representations for Hermitian functionals $L: {\mathscr {A}}\rightarrow {\mathbb {C}},$ where ${\mathscr {A}}$ is a unital $*$-algebra. Let ${\mathscr {C}}$ be a $*$-invariant subspace of a unital $*$-algebra ${\mathscr {A}}$ and ${\mathscr {C}}^2:=\mathrm {span}\{a b:a, b\in {\mathscr {C}} \}.$ Suppose ${\mathscr {B}}\subseteq {\mathscr {C}}$ is a $*$-invariant subspace of ${\mathscr {A}}$ such that $1\in {\mathscr {B}}.$ Mourrain and Schmüdgen say that a Hermitian linear functional $L: {\mathscr {C}}^2\rightarrow {\mathbb {C}}$ has a flat extension with respect to ${\mathscr {B}}$ if

$$\begin{aligned} {\mathscr {C}}={\mathscr {B}}+K_{L}({\mathscr {C}}), \end{aligned}$$

where $K_{L}({\mathscr {C}}):=\{a\in {\mathscr {C}}: L(b^*a)=0 \}$. In [63], Mourrain and Schmüdgen showed that every positive flat linear functional $L: {\mathscr {C}}\rightarrow {\mathbb {C}}$ has a unique extension ${\tilde{L}}: {\mathscr {A}}\rightarrow {\mathbb {C}}.$ Mourrain and Schmüdgen also showed that if ${\mathscr {A}}={\mathbb {C}}^{d\times d}[x_1,\dots , x_d]$ (see Definition 2.12), ${\mathscr {B}}={\mathbb {C}}^{d\times d}_n[x_1,\dots , x_d]$ (see Definition 2.13), ${\mathscr {C}}={\mathbb {C}}^{d\times d}_{n+1}[x_1,\dots , x_d]$ and $L: {\mathscr {C}}^2\rightarrow {\mathbb {C}}$ is a positive linear functional which has a flat extension with respect to ${\mathscr {B}},$ then

$$\begin{aligned} L\big ((p_{jk})_{j,k=1}^{d}\big )=\sum _{j,k=1}^{d}\sum _{i=1}^{r} p_{jk}(t_i)u_{ki}{\bar{u}}_{ji} \quad \quad \mathrm{for} \quad (p_{jk}) \in {\mathbb {C}}^{d \times d}[x_1, \ldots , x_d]\qquad \quad \end{aligned}$$

(1.4)

for some choice of $t_1,\dots , t_r\in {\mathbb {R}}^d$ and $u_1,\dots , u_r \in {\mathbb {C}}^d$ with $u_i={{\,\mathrm{col}\,}}(u_{ki})_{k=1}^{d}$ for $i=1,\dots ,r,$ and in particular,

$$\begin{aligned} L(x^\gamma I_d)=\sum _{j=1}^{d}\sum _{i=1}^{r} t_i^\gamma |{u}_{ji}|^2 \quad \quad \mathrm{for} \quad 0\le |\gamma |\le 2n+2. \end{aligned}$$

(1.5)

Structure

The paper is organised as follows. In Sects. 2, 3 and 4, we will formulate a number of definitions and basic results for future use. In Sect. 5.1, we will define infinite d-Hankel matrices and prove a number of results on the right ideal of matrix polynomials beloning to the kernel of a d-Hankel matrix. In Sect. 5.2 we will show that every ${\mathcal {H}}_p$-valued multisequence which gives rise to a positive infinite d-Hankel matrix with finite rank has a representing measure. In Sect. 5.3, we will prove a number of necessary conditions for a ${\mathcal {H}}_p$-valued multisequence to have a representing measure. In Sect. 5.4, we will precisely formulate and proof (C1). In Sect. 5.5, we will formulate a lemma which states that once a d-Hankel matrix has a flat extension, one can construct a sequence of flat extensions of all orders giving rise to positive infinite d-Hankel matrix with finite rank. In Sect. 6, we will prove our flat extension theorem, i.e., (C2). In Sect. 7, we will prove an abstract characterisation of truncated ${\mathcal {H}}_p$-valued multisequences with a representing measure, i.e., (C3). In Sect. 8.1, we will provide necessary and sufficient conditions for the bivariate quadratic matrix-valued moment problem to have a minimal solution. In Sect. 8.2, we will analyse the bivariate quadratic matrix-valued moment problem when the 2-Hankel matrix M(1) is block diagonal. In Sect. 8.3, we will consider some singular cases of the bivariate quadratic matrix-valued moment problem. In Sect. 8.4, we will see that the bivariate quadratic matrix-valued moment problem has a minimal solution whenever the corresponding 2-Hankel matrix M(1) is positive definite and satisfies a certain condition which automatically holds if $p=1$, i.e., the first part of (C4). In Sect. 8.5 we will go through a number of examples for the bivariate quadratic matrix-valued moment problem. In particular, we will see that $S_{00} = I_p$ and $M(1) \succeq 0$ is not enough to guarantee that a minimal solution exists. Finally, in Sect. 9, we will consider a particular case of the bivariate cubic matrix-valued moment problem.

For the convenience of the reader we have compiled a list of commonly used notation that appears throughout the paper.

Notation

${\mathbb {R}}^{m \times n}$ and ${\mathbb {C}}^{m \times n }$ denote the vector spaces of real and complex matrices of size $m \times n$, respectively. We will let ${\mathcal {H}}_p$ denote the real vector space of $p \times p$ Hermitian matrices in ${\mathbb {C}}^{p \times p}$.

The $p \times p$ identity matrix will be denoted by $I_p$ or I (when no confusion can possibly arise) and the $p \times p$ matrix of zeros will be denoted by $0_{p \times p}$ or 0 (when no confusion can possible arise).

${\mathbb {C}}^p$ denotes the p-dimensional complex vector space equipped with the standard inner product $\langle \xi , \eta \rangle = \eta ^*\xi ,$ where $\xi , \eta \in {\mathbb {C}}^p.$ The standard basis vectors in ${\mathbb {C}}^p$ will be denoted by $\mathrm{e}_1, \ldots \mathrm{e}_p$.

$A^*$ and $A^T$ denote the conjugate transpose and transpose, respectively, of a matrix $A \in {\mathbb {C}}^{n \times n}$. If $A \in {\mathbb {C}}^{n \times n}$ is invertible, then we will let $A^{-*}:= (A^{-1})^* = (A^*)^{-1}$.

Let $M \in {\mathbb {C}}^{m \times n}$. Then ${\mathcal {C}}_{M}$ and $\mathrm{ker}(M)$ denote the column space and null space, respectively.

$\sigma (A)$ denotes the spectrum of a matrix $A \in {\mathbb {C}}^{n \times n}$.

We will write $A \succeq 0$ (resp. $A \succ 0$) if A is positive semidefinite (resp. positive definite).

${{\,\mathrm{col}\,}}(C_{\lambda })_{\lambda \in \Lambda }$ and ${{\,\mathrm{row}\,}}(C_{\lambda })_{\lambda \in \Lambda }$ denote the column and row vectors with entries $(C_{\lambda })_{\lambda \in \Lambda }$, respectively.

${\mathbb {N}}_0^d$, ${\mathbb {R}}^d$ and ${\mathbb {C}}^d$ denote the set of d-tuples of nonnegative integers, real numbers and complex numbers, respectively.

$|\gamma |:= \displaystyle \sum _{j=1}^d \gamma _j$ for $\gamma = (\gamma _1, \ldots , \gamma _d) \in {\mathbb {N}}_0^d$.

$x^{\gamma }:= \displaystyle \prod _{j=1}^d x_j^{\gamma _j}$ for $x = (x_1, \ldots ,x_d) \in {\mathbb {R}}^d$ and $\gamma = (\gamma _1, \ldots , \gamma _d) \in {\mathbb {N}}_0^d$.

$\varepsilon _j \in {\mathbb {N}}_0^d$ denotes a d-tuple of zeros with 1 in the j-th entry.

$\Gamma (m, d):= \{ \gamma \in {\mathbb {N}}_0^d: 0 \le |\gamma | \le m \}$.

$\prec _{\mathrm {grlex}}$ denotes the graded lexicographic order

${\mathbb {C}}^{p \times p}[x_1, \ldots , x_d]$ denotes the ring of matrix polynomials in d indeterminate variables $x_1, \ldots , x_d$ with coefficients in ${\mathbb {C}}^{p \times p}$.

${\mathbb {C}}^{p \times p}_n[x_1, \ldots , x_d]$ denotes the subset of ${\mathbb {C}}^{p \times p}[x_1, \ldots , x_d]$ of matrix polynomials of total degree at most n, i.e., matrix polynomials of the form

$$\begin{aligned} P(x) = \sum _{\lambda \in \Gamma _{n,d}} x^{\lambda } \, P_{\lambda }. \end{aligned}$$

${\mathcal {V}}(M(n))$ will denote the variety of the d-Hankel matrix M(n) (see Definition 3.5).

${\mathscr {B}}({\mathbb {R}}^d)$ will denote the sigma algebra of Borel sets on ${\mathbb {R}}^d$.

${{\,\mathrm{card}\,}}\Omega$ denotes the cardinality of the set $\Omega \subseteq {\mathbb {R}}^d$.

2 Preliminaries

In this section we shall provide preliminary definitions and results for future use.

We will begin with a useful characterisation for positive extensions given by Smuljan [76] via the following result.

Lemma 2.1

([76]) Let $A\in {\mathbb {C}}^{n\times n}, A \succeq 0, B\in {\mathbb {C}}^{n\times m}, C\in {\mathbb {C}}^{m\times m}$ and let

$$\begin{aligned} {\tilde{A}}:=\begin{pmatrix} A &{}\quad B \\ B^* &{}\quad C \\ \end{pmatrix}. \end{aligned}$$

Then the following statements hold:

• (i) ${\tilde{A}}$ is positive semidefinite if and only if $B=AW$ for some $W\in {\mathbb {C}}^{n\times m}$ and $C\succeq W^*AW.$

• (ii) ${\tilde{A}}$ is positive semidefinite and ${{\,\mathrm{rank}\,}}{\tilde{A}}= {{\,\mathrm{rank}\,}}A$ if and only if $B=AW$ for some $W\in {\mathbb {C}}^{n\times m}$ and $C= W^*AW.$

Definition 2.2

Let $(v_{\gamma })_{\gamma \in \Gamma _{m, d}},$ where $v_{\gamma }\in {\mathbb {C}}^{p \times q}$ for $\gamma \in \Gamma _{m, d}.$ We let

$$\begin{aligned} {{\,\mathrm{col}\,}}(v_{\gamma })_{\gamma \in \Gamma _{m, d}}:= \begin{pmatrix} v_{0,0, \dots , 0} \\ v_{1,0,\ldots , 0} \\ \vdots \\ v_{0,0,\ldots , 1} \\ \vdots \\ v_{m,0, \dots , 0}\\ \vdots \\ v_{0, \dots , 0,m} \end{pmatrix}. \end{aligned}$$

Definition 2.3

Let ${\mathcal {B}}({\mathbb {R}}^d)$ denote the collection of Borel sets on ${\mathbb {R}}^d$ and $\langle u, v \rangle = v^* u$ for $u, v \in {\mathbb {C}}^p$. A function $T: {{\mathcal {B}}({\mathbb {R}}^d)}\rightarrow {\mathcal {H}}_p$ is called a positive ${\mathcal {H}}_p$-valued Borel measure on ${\mathbb {R}}^d,$ if for each $u\in {\mathbb {C}}^p$, $\langle T(\sigma )u, u\rangle$ defines a positive Borel measure on ${\mathbb {R}}^d$ for all $\sigma \in {{\mathcal {B}}({\mathbb {R}}^d)},$ or, equivalently,

$$\begin{aligned} T(\sigma ):=\big (T_{ab}(\sigma )\big )_{a, b=1}^{p}=\begin{pmatrix} T_{11}(\sigma ) &{} \dots &{}T_{1p}(\sigma )\\ \vdots &{}\ddots &{}\vdots \\ \overline{T_{1p}(\sigma )} &{} \dots &{} T_{pp}(\sigma ) \end{pmatrix}\succeq 0 \quad \mathrm{for} \quad \sigma \in {{\mathcal {B}}({\mathbb {R}}^d)}. \end{aligned}$$

(2.1)

The support of an ${\mathcal {H}}_p$-valued measure T,  denoted by ${{\,\mathrm{supp}\,}}T,$ is defined as the smallest closed subset ${\mathcal {S}}\subseteq {\mathcal {B}}({\mathbb {R}}^d)$ such that $T({\mathbb {R}}^d{\setminus }{\mathcal {S}})=0_{p \times p}.$

Definition 2.4

For a measurable function $f: {\mathbb {R}}^d\rightarrow {\mathbb {C}}$, we let its integral

$$\begin{aligned} \int _{{\mathbb {R}}^d} f(x)\ dT(x)\in {\mathcal {H}}_p \end{aligned}$$

be given by

$$\begin{aligned} \left\langle \int _{{\mathbb {R}}^d} f(x)\;dT(x)u, v\right\rangle = \int _{{\mathbb {R}}^d} f(x)\; d\langle T(x)u, v\rangle \end{aligned}$$

for all $u, v \in {\mathbb {C}}^p$, provided all integrals on the right-hand side converge.

Remark 2.5

If an ${\mathcal {H}}_p$-valued measure T is of the form

$$\begin{aligned} T=\sum \limits _{a=1}^{\kappa } Q_a \delta _{w^{(a)}}, \end{aligned}$$

then

$$\begin{aligned} \int _{{\mathbb {R}}^d}f(x)\ dT(x)= \sum \limits _{a=1}^{\kappa } Q_a f(w^{(a)}). \end{aligned}$$

Definition 2.6

The power moments of a positive ${\mathcal {H}}_p$-valued measure $T = (T_{a,b})_{a,b=1}^p$ on ${\mathbb {R}}^d$ are given by

$$\begin{aligned} \int \limits _{{\mathbb {R}}^d} x^\lambda dT(x) \quad \text {for} \;\;\lambda \in {\mathbb {N}}_0^d, \end{aligned}$$

provided

$$\begin{aligned} \int \limits _{{\mathbb {R}}^d} |x^\lambda | \;d|T_{ab}(x)|< \infty \quad \text {for} \;\;\lambda \in {\mathbb {N}}_0^d \;\; \text {and}\;\; a,b=1, \ldots , p. \end{aligned}$$

Definition 2.7

For a measurable function $f: {\mathbb {R}}^d\rightarrow {\mathbb {C}}$, we let its integral

$$\begin{aligned} \int _{{\mathbb {R}}^d} f(x)\ dT(x)\in {\mathcal {H}}_p \end{aligned}$$

be given by

$$\begin{aligned} \left\langle \int _{{\mathbb {R}}^d} f(x)\;dT(x)u, v\rangle = \int _{{\mathbb {R}}^d} f(x)\; d\langle T(x)u, v\right\rangle \end{aligned}$$

for all $u, v \in {\mathbb {C}}^p$, provided all integrals on the right-hand side converge, that is,

$$\begin{aligned} \int _{{\mathbb {R}}^d} |f(x)|\ d|\langle T(x)u, v\rangle | < \infty , \end{aligned}$$

or, equivalently,

$$\begin{aligned} \int _{{\mathbb {R}}^d} f(x)\ dT(x)= \left( \int _{{\mathbb {R}}^d} f(x)\ dT_{ab}(x)\right) _{a, b=1}^{p}, \end{aligned}$$

where $T_{ab}$ is as in Definition 2.3.

Remark 2.8

If an ${\mathcal {H}}_p$-valued measure T is of the form

$$\begin{aligned} T=\sum \limits _{a=1}^{\kappa } Q_a \delta _{w^{(a)}}, \end{aligned}$$

then it is easy to check that

$$\begin{aligned} \int _{{\mathbb {R}}^d}f(x)\ dT(x)= \sum \limits _{a=1}^{\kappa } Q_a f(w^{(a)}). \end{aligned}$$

Definition 2.9

The power moments of a positive ${\mathcal {H}}_p$-valued measure T on ${\mathbb {R}}^d$ are given by

$$\begin{aligned} \int \limits _{{\mathbb {R}}^d} x^\lambda dT(x) \quad \text {for} \;\;\lambda \in {\mathbb {N}}_0^d, \end{aligned}$$

provided

$$\begin{aligned} \int \limits _{{\mathbb {R}}^d} |x^\lambda | \;d|T_{ab}(x)|< \infty \quad \text {for} \;\;\lambda \in {\mathbb {N}}_0^d \;\; \text {and}\;\; a,b=1, \ldots , p. \end{aligned}$$

Definition 2.10

Given distinct points $w^{(1)}, \dots , w^{(k)}\in {\mathbb {R}}^d$ and a subset $\Lambda =\{\lambda ^{(1)}, \dots , \lambda ^{(k)}\}$ of ${\mathbb {N}}_0^d,$ we define the multivariable Vandermonde matrix by

$$\begin{aligned} V(w^{(1)}, \dots , w^{(k)}; \Lambda ):=\begin{pmatrix} {\{w^{(1)}}\}^{\lambda ^{(1)}} &{} \dots &{} {\{w^{(1)}}\}^{\lambda ^{(k)}} \\ \vdots &{} &{}\vdots \\ {\{w^{(k)}}\}^{\lambda ^{(1)}} &{} \dots &{} {\{w^{(k)}}\}^{\lambda ^{(k)}} \end{pmatrix}. \end{aligned}$$

We now present [53, Theorem 2.13] which is based on [69, Algorithm 1] and provides a useful machinery when the invertibility of a multivariable Vandermonde matrix is needed to compute the weights of a representing measure.

Theorem 2.11

Given distinct points $w^{(1)}, \dots ,w^{(\kappa )} \in {\mathbb {R}}^d,$ there exists $\Lambda \subseteq {\mathbb {N}}_0^d$ such that ${{\,\mathrm{card}\,}}\Lambda =\kappa$ and $V(w^{(1)}, \dots ,w^{(\kappa )};\Lambda )$ is invertible.

Definition 2.12

Let ${\mathbb {C}}^{p \times p}[x_1,\dots , x_d]$ denote the set of $p\times p$ matrix-valued polynomials with real indeterminates $x_1,\dots , x_d,$ that is, ${\mathbb {C}}^{p \times p}[x_1,\dots , x_d]$ consists of matrix-valued polynomials of the form

$$\begin{aligned} P(x)= \sum \limits _{\lambda \in \Gamma _{n, d}} x^\lambda P_\lambda , \end{aligned}$$

where $P_\lambda \in {\mathbb {C}}^{p \times p},$ $x^\lambda = \prod \nolimits _{j=1}^{d} x_j^{ \lambda _j}$ for $\lambda \in \Gamma _{n, d}$ and $n\in {\mathbb {N}}_0$ is arbitrary.

Definition 2.13

Let ${\mathbb {C}}^{p \times p}_n[x_1,\dots , x_d]$ denote the set of $p\times p$ matrix-valued polynomials with degree at most n with real indeterminates $x_1,\dots , x_d,$ that is, ${\mathbb {C}}^{p \times p}_n[x_1,\dots , x_d]$ consists of matrix-valued polynomials of the form

$$\begin{aligned} P(x)= \sum \limits _{\lambda \in \Gamma _{n, d}} x^\lambda P_\lambda , \end{aligned}$$

where $P_\lambda \in {\mathbb {C}}^{p \times p},$ $x^\lambda = \prod \nolimits _{j=1}^{d} x_j^{ \lambda _j}$ for $\lambda \in \Gamma _{n, d}.$

3 d-Hankel Matrices

In this section we will define d-Hankel matrices and the variety of a d-Hankel matrix.

Definition 3.1

We order ${\mathbb {N}}_0^d$ by the graded lexicographic order $\prec _{\mathrm {grlex}},$ that is, $\gamma \prec _{\mathrm {grlex}} {\tilde{\gamma }}$ if $|\gamma |< |{\tilde{\gamma }}|,$ or, if $|\gamma |= |{\tilde{\gamma }}|$ then $x^{\gamma }\prec _{{{\,\mathrm{lex}\,}}} x^{\tilde{{\gamma }}}.$ We note that $\Gamma _{m, d}$ inherits the ordering of ${\mathbb {N}}_0^d$ and is such that

$$\begin{aligned} {{\,\mathrm{card}\,}}\Gamma _{m, d}= \left( {\begin{array}{c}m+d\\ d\end{array}}\right) :=\frac{(m+d)!}{m!d!}. \end{aligned}$$

Definition 3.2

Let $S:=(S_\gamma )_{\gamma \in \Gamma _{2n, d}}$ be a given truncated ${\mathcal {H}}_p$-valued multisequence and M(n) be the corresponding d-Hankel matrix based on S and defined as follows. We label the block rows and block columns by a family of monomials $(x^\gamma )_{\gamma \in \Gamma _{n, d}}$ ordered by $\prec _{\mathrm {grlex}}$ We let the entry in the block row indexed by $x^\gamma$ and in the block column indexed by $x^{{\tilde{\gamma }}}$ be given by

$$\begin{aligned} S_{\gamma + {\tilde{\gamma }}}. \end{aligned}$$

Definition 3.3

We will say that a representing measure T for a given truncated ${\mathcal {H}}_p$-valued multisequence $S:=(S_\gamma )_{\gamma \in \Gamma _{2n, d}}$ is minimal, if $\sum \nolimits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a$ (see Definition 2.3) is as small as possible.

Remark 3.4

It turns out that the corresponding d-Hankel matrix M(n) of S has the property that ${{\,\mathrm{rank}\,}}M(n) \le \sum \nolimits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a$ for any representing measure of S (see Lemma 5.57) and hence, any minimal representing measure T satisfies

$$\begin{aligned} {{\,\mathrm{rank}\,}}M(n) = \sum \limits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a. \end{aligned}$$

(3.1)

We next define the variety of a d-Hankel matrix in our matrix-valued setting. We introduce zeros of determinants of matrix-valued polynomials abstracting that way the notion of the variety of a d-Hankel matrix which can implicitly apeared first in Curto and Fialkow [16].

Definition 3.5

(variety of a d-Hankel matrix) Let $S:=(S_\gamma )_{\gamma \in \Gamma _{2n, d}}$ be a truncated ${\mathcal {H}}_p$-valued multisequence and let M(n) be the corresponding d-Hankel matrix. Let $P(x)= \sum _{\lambda \in \Gamma _{n, d}} x^\lambda P_\lambda \in {\mathbb {C}}^{p \times p}_n[x_1,\dots , x_d]$ such that $P(X)\in C_{M(n)}.$ The variety of M(n),  denoted by ${\mathcal {V}}(M(n)),$ is given by

$$\begin{aligned} {\mathcal {V}}(M(n)):=\bigcap _{{\mathop {P(X)={{\,\mathrm{col}\,}}( 0_{p\times p})_{\gamma \in \Gamma _{n, d}}}\limits ^{P\in {{\mathbb {C}}}^{p\times p}_n[x_1,\dots , x_d]}}} {\mathcal {Z}}(\det (P(x))). \end{aligned}$$

4 Matrix-Valued Polynomials

We introduce important definitions and notation while establishing several algebraic results involving matrix-valued polynomials with several real indeterminates which will be important for proving our flat extension theorem for matricial moments.

Definition 4.1

A set ${\mathscr {I}}\subseteq {\mathbb {C}}^{p \times p}[x_1,\dots , x_d]$ is a right ideal if it satisfies the following conditions:

• (i) $P+Q\in {\mathscr {I}}$ whenever $P, Q\in {\mathscr {I}}$.

• (ii) $PQ\in {\mathscr {I}}$ whenever $P\in {\mathscr {I}}$ and $Q\in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d].$

Definition 4.2

Let ${\mathscr {I}}\subseteq {\mathbb {C}}^{p \times p}[x_1,\dots , x_d]$ be a right ideal. We shall let

$$\begin{aligned} {\mathcal {V}}({\mathscr {I}}):= \{x\in {\mathbb {R}}^d: \det P(x)=0\quad \text {for all} \;\; P\in {\mathscr {I}} \} \end{aligned}$$

be the variety associated with the ideal ${\mathscr {I}}.$

Definition 4.3

A right ideal ${\mathscr {I}}\subseteq {\mathbb {C}}^{p \times p}[x_1,\dots , x_d]$ is real radical if

$$\begin{aligned} \sum _{a=1}^{\kappa } P^{(a)}(x) \{P^{(a)}(x)\}^*\in {\mathscr {I}} \Longrightarrow P^{(a)}(x) \in {\mathscr {I}}\quad \text {for} \;\; a=1, \dots , \kappa . \end{aligned}$$

Remark 4.4

We wish to justify the usage of the moniker real radical of Definition 4.3 when $p=1.$ We note that one usually says that a real ideal ${\mathscr {K}} \subseteq {\mathbb {R}}[x_1,\dots , x_d]$ is real radical if

$$\begin{aligned} \sum _{a=1}^\kappa (f^{(a)}(x))^2\in {\mathscr {K}}\Longrightarrow f^{(a)}\in {\mathscr {K}}\quad \text {for} \;\; a=1, \dots , \kappa \end{aligned}$$

(see, e.g., [60]). Suppose ${\mathscr {I}} ={\mathscr {I}}_1+{\mathscr {I}}_2\mathrm {i},$ where

$$\begin{aligned} {\mathscr {I}}_1=\{{{\,\mathrm{Re}\,}}(f(x)):f\in {\mathscr {I}}\}\quad \text {and}\quad {\mathscr {I}}_2=\{{{\,\mathrm{Im}\,}}(f(x)):f\in {\mathscr {I}}\} \end{aligned}$$

and let $f^{(a)}=q^{(a)}+r^{(a)}\mathrm {i},$ where

$$\begin{aligned} q^{(a)}(x)={{\,\mathrm{Re}\,}}(f(x))\quad \text {and}\quad r^{(a)}(x)= {{{\,\mathrm{Im}\,}}}(f(x)). \end{aligned}$$

We claim that

$$\begin{aligned} \sum _{a=1}^\kappa ((q^{(a)}(x))^2+(r^{(a)}(x))^2)\in {\mathscr {I}}_1\Longrightarrow q^{(a)}\in {\mathscr {I}}_1, \;r^{(a)}\in {\mathscr {I}}_2\quad \text {for} \;\; a=1, \dots , \kappa \end{aligned}$$

(4.1)

holds. We wish to demonstrate a connection between the notion of a real ideal ${\mathscr {K}}\subseteq {\mathbb {R}}[x_1,\dots , x_d]$ being real radical and our notion of a complex ideal ${\mathscr {I}}\subseteq {\mathbb {C}}[x_1,\dots , x_d]$ being real radical, that is,

$$\begin{aligned} \sum _{a=1}^\kappa |f^{(a)}(x)|^2\in {\mathscr {I}}\Longrightarrow f^{(a)}\in {\mathscr {I}}\quad \text {for} \;\; a=1, \dots , \kappa . \end{aligned}$$

Then

$$\begin{aligned}&\sum _{a=1}^\kappa |f^{(a)}(x)|^2=\sum _{a=1}^\kappa ((q^{(a)}(x))^2+(r^{(a)}(x))^2)\in {\mathscr {I}}\Longrightarrow q^{(a)}(x)+r^{(a)}(x)\in {\mathscr {I}}\quad \\&\text {for} \;\; a=1, \dots , \kappa . \end{aligned}$$

Notice that ${\mathscr {I}}_1, {\mathscr {I}}_2$ are closed under scalar addition and multiplication and so they are ideals in ${\mathbb {R}}[x_1,\dots , x_d].$ If $\sum \nolimits _{a=1}^\kappa |f^{(a)}(x)|^2\in {\mathscr {I}},$ then $q^{(a)}+r^{(a)}\mathrm {i} \in {\mathscr {I}}$ for all $a=1, \dots , \kappa .$ But then

$$\begin{aligned} q^{(a)}\in {\mathscr {I}}_1\quad \text {and}\quad r^{(a)}\in {\mathscr {I}}_2\quad \text {for} \;\; a=1, \dots , \kappa , \end{aligned}$$

since ${\mathscr {I}}={\mathscr {I}}_1+{\mathscr {I}}_2\mathrm {i}.$ However $|f^{(a)}(x)|^2=(q^{(a)}(x))^2+(r^{(a)}(x))^2$ and so

$$\begin{aligned} \sum _{a=1}^\kappa |f^{(a)}(x)|^2\in {\mathscr {I}}\Longrightarrow q^{(a)}\in {\mathscr {I}}_1, \; r^{(a)}\in {\mathscr {I}}_2\quad \text {for} \;\; a=1, \dots , \kappa \end{aligned}$$

can be written as

$$\begin{aligned} \sum _{a=1}^\kappa ((q^{(a)}(x))^2+(r^{(a)}(x))^2)\in {\mathscr {I}}\Longrightarrow q^{(a)}\in {\mathscr {I}}_1, \;r^{(a)}\in {\mathscr {I}}_2\quad \text {for} \;\; a=1, \dots , \kappa . \end{aligned}$$

Notice that $\sum \nolimits _{a=1}^\kappa ((q^{(a)}(x))^2+(r^{(a)}(x))^2)\in {\mathscr {I}}_1$ from which we conclude that the claim (4.1) holds.

In the following remark we will introduce an additional assumption on ${\mathscr {I}}\subseteq {\mathbb {C}}[x_1,\dots , x_d]$ which appears in Remark 4.4. As we noted in Remark 4.4, ${\mathscr {I}}={\mathscr {I}}_1+{\mathscr {I}}_2\mathrm {i},$ where ${\mathscr {I}}_1, {\mathscr {I}}_2$ are real ideals in ${\mathbb {R}}[x_1,\dots , x_d].$ Thus, it is clear that $f\in {\mathscr {I}}$ vanishes on a set $V\subseteq {\mathbb {R}}^d$ if and only if ${{\,\mathrm{Re}\,}}(f(x))$ and $\pm {{\,\mathrm{Im}\,}}(f(x))$ vanish on V. In view of the Real Nullstellensatz (see, e.g., [9]), any real radical ideal must agree with its vanishing ideal (that is, the set of polynomials which vanish on the variety). Therefore, if ${\mathscr {I}}\subseteq {\mathbb {C}}[x_1,\dots , x_d]$ is real radical, then $f\in {\mathscr {I}}$ implies that ${\bar{f}}\in {\mathscr {I}}.$

Remark 4.5

Let ${\mathscr {I}}\subseteq {\mathbb {C}}[x_1,\dots , x_d]$ and ${\mathscr {I}}_1, {\mathscr {I}}_2\subseteq {\mathbb {R}}[x_1,\dots , x_d]$ be as in Remark 4.4. Suppose ${\mathscr {I}}$ has the additional property that $f\in {\mathscr {I}}$ implies ${\bar{f}}\in {\mathscr {I}}.$ Then

• (i) ${\mathscr {I}}_1\subseteq {\mathbb {R}}[x_1,\dots , x_d]$ is real radical.

• (ii) ${\mathscr {I}}_2\subseteq {\mathbb {R}}[x_1,\dots , x_d]$ is real radical.

Since ${\mathscr {I}}$ is an ideal in ${\mathbb {C}}[x_1,\dots , x_d]$ which is closed under complex conjugation, we have that ${\mathscr {I}}_1$ and ${\mathscr {I}}_2$ are subideals of ${\mathscr {I}}$ over ${\mathbb {R}}[x_1,\dots , x_d].$ Hence, we may use the fact that ${\mathscr {I}}$ is real radical to deduce (i) and (ii).

Lemma 4.6

Fix $\gamma \in {\mathbb {N}}_0^d$ with $|\gamma |>n$ and let $P(x)= x^{\gamma }I_p + \sum \nolimits _{\lambda \in \Gamma _{n, d}} x^\lambda P_\lambda \in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d].$ Then

$$\begin{aligned} \det P(x) = x^{\gamma p} + \sum \limits _{\lambda \in \Gamma _{m, d}} x^\lambda h_\lambda , \end{aligned}$$

where $\gamma p:= (\gamma _1 p, \dots , \gamma _d p)\in {\mathbb {N}}_0^d$ and $m<|\gamma |p.$

Proof

We proceed by induction on p. For $p=2,$ $P(x) =\begin{pmatrix} x^{\gamma } + \beta _{11}(x) &{} \beta _{12}(x)\\ \beta _{21}(x) &{} x^{\gamma } + \beta _{22}(x) \end{pmatrix},$ where $\beta _{ab}(x)= \sum \nolimits _{\lambda \in \Gamma _{n, d}} x^\lambda P_\lambda ^{(a, b)} \in {\mathbb {C}}[x_1,\dots , x_d]$ with $P_\lambda ^{(a, b)}$ the (a, b)-th entry of $P_\lambda$ and $1\le a, b \le 2.$ We also have

$$\begin{aligned} \det P(x)= & {} (x^{\gamma }+\beta _{11}(x))(x^{\gamma } + \beta _{22}(x))- \beta _{12}(x)\beta _{21}(x)\\= & {} x^{2\gamma }+x^{\gamma }\beta _{22}(x) +x^{\gamma }\beta _{11}(x) + \beta _{11}(x)\beta _{22}(x)- \beta _{12}(x)\beta _{21}(x) \\= & {} x^{2\gamma } +L(x)+ C(x), \end{aligned}$$

where $L(x)=x^{\gamma }\beta _{22}(x) + +x^{\gamma }\beta _{11}(x),\;C(x)= \beta _{11}(x)\beta _{22}(x)- \beta _{12}(x)\beta _{21}(x)\in {\mathbb {C}}[x_1,\dots , x_d].$ Suppose the claim holds for $p>2.$ We have

$$\begin{aligned} P(x) =\begin{pmatrix} x^{\gamma } + \beta _{11}(x) &{} \dots &{} \beta _{1p}(x)\\ \vdots &{} \ddots &{} \vdots \\ \beta _{p1}(x) &{} \dots &{} x^{\gamma } + \beta _{pp}(x) \end{pmatrix} \end{aligned}$$

and so

$$\begin{aligned} \det P(x)= & {} (x^{\gamma } + \beta _{11}(x))\det \begin{pmatrix} x^{\gamma } + \beta _{22}(x) &{} \dots &{} \beta _{2p}(x)\\ \vdots &{} \ddots &{} \vdots \\ \beta _{p2}(x) &{} \dots &{} x^{\gamma } + \beta _{pp}(x) \end{pmatrix}+ \dots \\&\quad +(-1)^{1+p}\beta _{1p}(x)\det \begin{pmatrix} \beta _{21}(x) &{} \dots &{} \beta _{2,p-1}(x)\\ \vdots &{} \ddots &{} \vdots \\ \beta _{p1}(x) &{} \dots &{} \beta _{p,p-1}(x) \end{pmatrix} \\= & {} (x^{\gamma } + \beta _{11}(x))\left[ (x^{\gamma } + \beta _{22}(x))\begin{pmatrix} x^{\gamma } + \beta _{33}(x) &{} \dots &{} \beta _{3p}(x)\\ \vdots &{} \ddots &{} \vdots \\ \beta _{p3}(x) &{} \dots &{} x^{\gamma } + \beta _{pp}(x) \end{pmatrix}+ \dots \right. \\&\quad \left. +(-1)^{1+(2+p-1)}\beta _{2,p-1}(x)\det \begin{pmatrix} \beta _{31}(x) &{} \dots &{} \beta _{3,p-2}(x)\\ \vdots &{} \ddots &{} \vdots \\ \beta _{p1}(x) &{} \dots &{} \beta _{p-1,p-1}(x) \end{pmatrix}\right] . \end{aligned}$$

Let ${\widetilde{L}}(x)$ be the sum of the terms of $\det P(x)$ of degree up to $\gamma (p-1)$ with $|\gamma |>0$ and ${\widetilde{C}}(x)$ the sum of the terms of $\det P(x)$ of degree up to $\gamma p$ with $|\gamma |=0.$ Then

$$\begin{aligned} {\widetilde{L}}(x)+ {\widetilde{C}}(x)=\sum \limits _{\lambda \in \Gamma _{m, d}} x^\lambda h_\lambda , \end{aligned}$$

where $m<|\gamma |p.$ Thus

$\square$

We order the monomials in ${\mathbb {C}}[x_1,\dots , x_d]$ by the graded lexicographic order $\prec _{\mathrm {grlex}}.$

Remark 4.7

Fix $\gamma \in {\mathbb {N}}_0^d$ with $|\gamma |>n$ and let $P(x)= x^{\gamma }I_p + \sum \nolimits _{\lambda \in \Gamma _{n, d}} x^\lambda P_\lambda \in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d].$ For a polynomial $\varphi (x) \in {\mathbb {C}}[x_1,\dots , x_d]$ given by

$$\begin{aligned} \varphi (x):=\det P(x)= x^{\gamma p} + \sum \limits _{\lambda \in \Gamma _{m, d}} x^\lambda h_\lambda , \end{aligned}$$

where $\gamma p:= (\gamma _1 p, \dots , \gamma _d p)\in {\mathbb {N}}_0^d$ and $m<|\gamma |p,$ the leading term of $\varphi (x)$ is

$$\begin{aligned} \mathrm {LT}(\varphi (x))=x^{\gamma p}. \end{aligned}$$

Definition 4.8

We define the basis of ${\mathbb {C}}^{p \times p}$ viewed as a vector space over ${\mathbb {C}}$

$$\begin{aligned} {\mathcal {A}}^{p \times p}:=\{E_{11}, E_{12}, \ldots , E_{1p}, E_{21}, \ldots , E_{2p}, \ldots , E_{p1}, \ldots , E_{pp} \}, \end{aligned}$$

where $E_{jk} \in {\mathbb {C}}^{p \times p}$ is the matrix with 1 in the (j, k)-th entry and 0 in the rest of the entries, $j, k= 1, \dots , p.$

Definition 4.9

Given a right ideal ${\mathscr {I}}\subseteq {\mathbb {C}}^{p \times p}[x_1,\dots , x_d],$ we define

$$\begin{aligned} {\mathscr {I}}_{jk}:= & {} \{f\in {\mathbb {C}}[x_1,\dots , x_d]: \text {there}\; \text {exists}\; F \in {\mathscr {I}} \; \text {such}\; \text {that}\; F(x)E_{jk}=f(x)E_{jk} \} \subseteq {\mathbb {C}}\\&\times [x_1,\dots , x_d], \end{aligned}$$

where $E_{jk}\in {\mathbb {C}}^{p \times p}$ is as in Definition 4.8 for all $j, k= 1, \dots , p.$

Lemma 4.10

Suppose ${\mathscr {I}}\subseteq {\mathbb {C}}^{p \times p}[x_1,\dots , x_d]$ is a right ideal. Then ${\mathscr {I}}_{jk}\subseteq {\mathbb {C}}[x_1,\dots , x_d]$ is an ideal for all $j, k= 1, \dots , p.$

Proof

If $f, g \in {\mathscr {I}}_{jk},$ then

$$\begin{aligned} f(x)E_{jk}=F(x)E_{jk} \;\;\text {for}\;\; F\in {\mathscr {I}} \end{aligned}$$

and

$$\begin{aligned} g(x)E_{jk}=G(x)E_{jk}\;\;\text {for}\;\; G\in {\mathscr {I}}. \end{aligned}$$

Since $(f+g)(x)E_{jk}=(F+G)(x)E_{jk},$ we have

$$\begin{aligned} f+g \in {\mathscr {I}}_{jk}. \end{aligned}$$

If $f\in {\mathscr {I}}_{jk}$ and $h \in {\mathbb {C}}[x_1,\dots , x_d],$ then

$$\begin{aligned} (fh)(x) E_{jk}= (Fh)(x) E_{jk} \end{aligned}$$

and thus $fh \in {\mathscr {I}}_{jk}.$ $\square$

Lemma 4.11

Suppose ${\mathscr {I}}\subseteq {\mathbb {C}}^{p \times p}[x_1,\dots , x_d]$ is a right ideal. If ${\mathscr {I}}$ is real radical, then ${\mathscr {I}}_{jj}$ is real radical for all $j= 1, \dots , p.$

Proof

We need to show

$$\begin{aligned} \sum _{a=1}^{\kappa } |f^{(a)} (x)|^2 \in {\mathscr {I}}_{jj} \Longrightarrow f^{(a)}(x) \in {\mathscr {I}}_{jj}\quad \text {for} \;\; a=1, \dots , \kappa . \end{aligned}$$

Let $f(x)=\sum \nolimits _{a=1}^{\kappa } |f^{(a)} (x)|^2 \in {\mathscr {I}}_{jj}.$ Then there exists $F\in {\mathscr {I}}$ such that

$$\begin{aligned} f(x)E_{jj}=F(x)E_{jj}. \end{aligned}$$

Without loss of generality, we may assume that $F(x)=f(x)E_{jj}.$ If we let $F^{(a)}(x)= f^{(a)}(x)E_{jj},$ then

$$\begin{aligned} \sum _{a=1}^{\kappa } F^{(a)}(x) \{F^{(a)}(x)\}^* = \sum _{a=1}^{\kappa } |f^{(a)} (x)|^2 E_{jj} = f(x) E_{jj}. \end{aligned}$$

Thus

$$\begin{aligned} \sum _{a=1}^{\kappa } F^{(a)}(x) \{F^{(a)}(x)\}^* = F(x) \end{aligned}$$

and hence

$$\begin{aligned} \sum _{a=1}^{\kappa } F^{(a)}(x) \{F^{(a)}(x)\}^* \in {\mathscr {I}}, \end{aligned}$$

which implies that $F^{(a)}(x) \in {\mathscr {I}}\; \text {for all} \; a=1, \dots , \kappa ,$ since ${\mathscr {I}}$ is real radical. Consequently,

$$\begin{aligned} f^{(a)}(x)\in {\mathscr {I}}_{jj}\;\; \text {for} \;\; a=1, \dots , \kappa \end{aligned}$$

and ${\mathscr {I}}_{jj}$ is real radical. $\square$

5 Positive Infinite d-Hankel Matrices with Finite Rank

We shall study positive infinite d-Hankel matrices with finite rank, necessary conditions for a truncated ${\mathcal {H}}_p$-valued multisequence to have a representing measure and extension results for positive d-Hankel matrices.

5.1 Infinite d-Hankel Matrices

In this subsection we define d-Hankel matrices associated with an ${\mathcal {H}}_p$-valued multisequence. We investigate positive infinite d-Hankel matrices with finite rank and a right ideal of matrix-valued polynomials generated by column relations.

Definition 5.1

Let $(V_\lambda )_{\lambda \in {\mathbb {N}}_0^d},$ where $V_\lambda \in {\mathbb {C}}^{p\times p}$ for $\lambda \in {\mathbb {N}}_0^d.$ We let

$$\begin{aligned} {{\,\mathrm{col}\,}}(V_\lambda )_{\lambda \in {\mathbb {N}}_0^d}:=\begin{pmatrix} V_{0,0, \dots , 0} \\ \vdots \\ V_{m,0, \dots , 0}\\ \vdots \\ V_{0, \dots , 0,m} \\ \vdots \\ \end{pmatrix}. \end{aligned}$$

Definition 5.2

Let

$$\begin{aligned}&({\mathbb {C}}^{p \times p})_{0}^{\omega }:=\{V={{\,\mathrm{col}\,}}(V_\lambda )_{\lambda \in {\mathbb {N}}_0^d}: V_\lambda \in {\mathbb {C}}^{p \times p}\; \text {and}\; V_\lambda = 0_{p\times p}\; \text{ for } \text{ all } \text{ but } \text{ finitely } \text{ many }\;\\&\quad \lambda \in {\mathbb {N}}_0^d \}. \end{aligned}$$

Lemma 5.3

$({\mathbb {C}}^{p \times p})_{0}^{\omega }$ is a right module over ${\mathbb {C}}^{p \times p},$ under the operation of addition given by

$$\begin{aligned} A+B={{\,\mathrm{col}\,}}(A_\lambda +B_\lambda )_{\lambda \in {\mathbb {N}}_0^d}\in ({\mathbb {C}}^{p \times p})_{0}^{\omega } \end{aligned}$$

for $A={{\,\mathrm{col}\,}}(A_\lambda )_{\lambda \in {\mathbb {N}}_0^d}, B={{\,\mathrm{col}\,}}(B_\lambda )_{\lambda \in {\mathbb {N}}_0^d}\in ({\mathbb {C}}^{p \times p})_{0}^{\omega },$ together with the right multiplication given by

$$\begin{aligned} A\cdot C:= {{\,\mathrm{col}\,}}(A_\lambda C)_{\lambda \in {\mathbb {N}}_0^d}\in ({\mathbb {C}}^{p \times p})_{0}^{\omega } \end{aligned}$$

for $A={{\,\mathrm{col}\,}}(A_\lambda )_{\lambda \in {\mathbb {N}}_0^d}\in ({\mathbb {C}}^{p \times p})_{0}^{\omega }$ and $C \in {\mathbb {C}}^{p \times p}.$

Proof

The verification that $({\mathbb {C}}^{p \times p})_{0}^{\omega }$ is a right module over ${\mathbb {C}}^{p \times p}$ can be carried out in a very straight-forward manner. $\square$

We now give the definition of an infinite d-Hankel matrix based on $S^{(\infty )}:=(S_\gamma )_{\gamma \in {\mathbb {N}}_0^d},$ where $S_\gamma \in {\mathcal {H}}_p$ for all $\gamma \in {\mathbb {N}}_0^d.$

Definition 5.4

(infinite d-Hankel matrix) Let $S^{(\infty )}:=(S_\gamma )_{\gamma \in {\mathbb {N}}_0^d}$ be a given ${\mathcal {H}}_p$-valued multisequence. We define $M(\infty )$ to be the corresponding moment matrix based on $S^{(\infty )}$ as follows. We label the block rows and block columns by a family of monomials $(x^\gamma )_{\gamma \in {\mathbb {N}}_0^d}$ ordered by $\prec _{\mathrm {grlex}}.$ We let the entry in the block row indexed by $x^\gamma$ and in the block column indexed by $x^{{\tilde{\gamma }}}$ be given by

$$\begin{aligned} S_{\gamma + {\tilde{\gamma }}}. \end{aligned}$$

Let $X^\lambda :={{\,\mathrm{col}\,}}(S_{\lambda +\gamma })_{\gamma \in {\mathbb {N}}_0^d},\; \lambda \in \Gamma _{n, d}$ and $C_{M(\infty )}=\{M(\infty )V: V \in ({\mathbb {C}}^{p \times p})_{0}^{\omega }\}.$ We notice that $X^\lambda \in C_{M(\infty )}.$

For $S:=(S_\gamma )_{\gamma \in \Gamma _{2n, d}}$ a given truncated ${\mathcal {H}}_p$-valued multisequence and M(n) the corresponding d-Hankel matrix, we let $X^\lambda :={{\,\mathrm{col}\,}}(S_{\lambda +\gamma })_{\gamma \in \Gamma _{n, d}}$ for $\lambda \in \Gamma _{n, d}$ and $C_{M(n)}$ be the column space of M(n).

Remark 5.5

Let $S^{(\infty )}:=(S_\gamma )_{\gamma \in {\mathbb {N}}_0^d}$ be a given ${\mathcal {H}}_p$-valued multisequence. Then we can view $M(\infty ): ({\mathbb {C}}^{p \times p})_{0}^{\omega }\rightarrow C_{M(\infty )}$ as a right linear operator, that is,

$$\begin{aligned} M(\infty )(VQ+V)=M(\infty )VQ+M(\infty )V, \end{aligned}$$

for $V={{\,\mathrm{col}\,}}(V_\lambda )_{\lambda \in {\mathbb {N}}_0^d}\in ({\mathbb {C}}^{p \times p})_{0}^{\omega }\;\text {and}\; Q={{\,\mathrm{col}\,}}(Q_\lambda )_{\lambda \in {\mathbb {N}}_0^d}\in ({\mathbb {C}}^{p \times p})_{0}^{\omega }.$

Definition 5.6

Let $S^{(\infty )}:=(S_\gamma )_{\gamma \in {\mathbb {N}}_0^d}$ be a given ${\mathcal {H}}_p$-valued multisequence and let $M(\infty )$ be the corresponding d-Hankel matrix. Suppose $M(\infty ) \succeq 0$. We define

$$\begin{aligned} {{\,\mathrm{rank}\,}}M(\infty ):= \sup _{n \in {\mathbb {N}}} {{\,\mathrm{rank}\,}}M(n), \end{aligned}$$

where M(n) the corresponding d-Hankel matrix based on $S:=(S_\gamma )_{\gamma \in \Gamma _{2n, d} }.$

Definition 5.7

Let $S^{(\infty )}:=(S_\gamma )_{\gamma \in {\mathbb {N}}_0^d}$ be a given ${\mathcal {H}}_p$-valued multisequence and let $M(\infty )$ be the corresponding d-Hankel matrix. Suppose $M(\infty ) \succeq 0$. We define the right linear map

$$\begin{aligned} \Phi : {\mathbb {C}}^{p \times p}[x_1,\dots , x_d]\rightarrow C_{M(\infty )} \end{aligned}$$

to be given by

$$\begin{aligned} \Phi (P)= \sum \limits _{\lambda \in \Gamma _{n, d}} X^\lambda P_\lambda , \end{aligned}$$

where $P(x)= \sum \nolimits _{\lambda \in \Gamma _{n, d}} x^\lambda P_\lambda \in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d].$

Definition 5.8

Given $P(x)= \sum \nolimits _{\lambda \in \Gamma _{n, d}} x^\lambda P_\lambda \in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d],$ we let

$$\begin{aligned} P(X):= \sum \limits _{\lambda \in \Gamma _{n, d}} X^\lambda P_\lambda \end{aligned}$$

and

$$\begin{aligned} {\widehat{P}}:= {{\,\mathrm{col}\,}}(P_{\lambda })_{\lambda \in \Gamma _{n, d}} \oplus {{\,\mathrm{col}\,}}( 0_{p\times p})_{\gamma \in {\mathbb {N}}_0^d} \in ({\mathbb {C}}^{p \times p})_{0}^{\omega }. \end{aligned}$$

Remark 5.9

Let $S^{(\infty )}:=(S_\gamma )_{\gamma \in {\mathbb {N}}_0^d}$ be a given ${\mathcal {H}}_p$-valued multisequence and let $M(\infty )\succeq 0$ be the corresponding d-Hankel matrix. Given $P(x)= \sum \nolimits _{\lambda \in \Gamma _{n, d}} x^\lambda P_\lambda \in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d],$ we observe that

$$\begin{aligned} \Phi (P)=M(\infty ){\widehat{P}}. \end{aligned}$$

Indeed, notice that

$$\begin{aligned} M(\infty ){\widehat{P}} = {{\,\mathrm{col}\,}}\left( \sum \limits _{\lambda \in \Gamma _{n, d}} S_{\gamma +\lambda } P_\lambda \right) _{\gamma \in {\mathbb {N}}_0^d} = \sum \limits _{\lambda \in \Gamma _{n, d}} X^\lambda P_\lambda =P(X) =\Phi (P). \end{aligned}$$

Definition 5.10

Let $S^{(\infty )}:=(S_\gamma )_{\gamma \in {\mathbb {N}}_0^d}$ be a given ${\mathcal {H}}_p$-valued multisequence and let $M(\infty )$ be the corresponding infinite d-Hankel matrix. Suppose $M(\infty ) \succeq 0$ and

$$\begin{aligned} P(x)= \sum \limits _{\lambda \in \Gamma _{n, d}} x^\lambda P_\lambda \in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d]. \end{aligned}$$

We will write $M(\infty )\succeq 0$ if

$$\begin{aligned} {\widehat{P}}^*M(\infty ){\widehat{P}}\succeq 0_{p\times p}\quad \text {for}\;\; P \in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d], \end{aligned}$$

or, equivalently, $M(n)\succeq 0$ for all $n\in {\mathbb {N}}_0^d.$

Definition 5.11

Let ${\mathbb {C}}^p[x_1,\dots , x_d]$ be the set of vector-valued polynomials, that is,

$$\begin{aligned} q(x)=\sum \limits _{\lambda \in \Gamma _{n, d}} q_\lambda x^\lambda , \end{aligned}$$

where $q_\lambda \in {\mathbb {C}}^p,$ $x^\lambda = \prod \nolimits _{j=1}^{d} x_j^{ \lambda _j}$ for $\lambda \in \Gamma _{n, d}$ and n is arbitrary.

We shall proceed with a result on positivity when $M(\infty )$ is treated as a linear operator $M(\infty ): ({\mathbb {C}}^p)_{0}^{\omega } \rightarrow {\tilde{C}}_{M(\infty )}.$

Lemma 5.12

Let $S^{(\infty )}:=(S_\gamma )_{\gamma \in {\mathbb {N}}_0^d}$ be a given ${\mathcal {H}}_p$-valued multisequence and let $M(\infty )$ be the corresponding d-Hankel matrix. Suppose

$$\begin{aligned} q(x)=\sum \limits _{\lambda \in \Gamma _{n, d}} q_\lambda x^\lambda \in {\mathbb {C}}^p[x_1,\dots , x_d]. \end{aligned}$$

If $M(\infty )\succeq 0,$ then

$$\begin{aligned} {\hat{q}}^*M(\infty ){\hat{q}}\ge 0\quad \text {for}\;\; q \in {\mathbb {C}}^p[x_1,\dots , x_d]. \end{aligned}$$

Proof

Let $P(x)= \sum \nolimits _{\lambda \in \Gamma _{n, d}} x^\lambda P_\lambda \in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d].$ Then by Definition 5.10, $M(\infty )\succeq 0$ if

$$\begin{aligned} {\widehat{P}}^*M(\infty ){\widehat{P}}\succeq 0_{p\times p}\quad \text {for}\;\; P \in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d]. \end{aligned}$$

If $e_{1}$ is a standard basis vector in ${\mathbb {C}}^p,$ then

$$\begin{aligned} e_{1}^*{\widehat{P}}^*M(\infty ){\widehat{P}}e_{1}\ge 0. \end{aligned}$$

Let $q(x):= P(x)e_{1}.$ Notice that

$$\begin{aligned} q\in {\mathbb {C}}^p[x_1,\dots , x_d]\quad \text { and}\quad {\hat{q}}^*M(\infty ){\hat{q}}\ge 0. \end{aligned}$$

Since $P \in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d]$ is arbitrary, so is $q\in {\mathbb {C}}^p[x_1,\dots , x_d].$ Thus

$\square$

Definition 5.13

Suppose $M(\infty )\succeq 0.$ Let $P \in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d].$ We define the set

$$\begin{aligned} {\mathcal {I}}:= \{P \in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d]: {\widehat{P}}^*M(\infty ){\widehat{P}} = 0_{p\times p} \}\subseteq {\mathbb {C}}^{p \times p}[x_1,\dots , x_d] \end{aligned}$$

and the kernel of the map $\Phi : {\mathbb {C}}^{p \times p}[x_1,\dots , x_d]\rightarrow C_{M(\infty )}$ by

$$\begin{aligned} \ker \Phi :=\{P\in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d]:M(\infty ){\widehat{P}}={{\,\mathrm{col}\,}}( 0_{p\times p})_{\lambda \in {\mathbb {N}}_0^d}\}. \end{aligned}$$

Lemma 5.14

Suppose $M(\infty )\succeq 0.$ Then

$$\begin{aligned} {\mathcal {I}}=\ker \Phi , \end{aligned}$$

where ${\mathcal {I}}$ and $\ker \Phi$ are as in Definition 5.13.

Proof

By Definition 5.10, $M(\infty )\succeq 0$ if ${\widehat{P}}^*M(\infty ){\widehat{P}}\succeq 0_{p\times p}\;\text {for}\; P \in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d]$ and thus by Lemma 5.12, the corresponding d-Hankel matrixM(m) based on $S:=(S_\gamma )_{\gamma \in \Gamma _{2m, d} }$ is positive semidefinite for all $m\in {\mathbb {N}}.$ Hence $M(m)^{\frac{1}{2}}$ exists and we let $A:= M(m)^{\frac{1}{2}}{{\,\mathrm{col}\,}}(P_\lambda )_{\lambda \in \Gamma _{m, d}},$ for $P(x)= \sum \nolimits _{\lambda \in \Gamma _{m, d}} x^\lambda P_\lambda .$ Since $P\in {\mathcal {I}},$

$$\begin{aligned} {\widehat{P}}^*M(\infty ){\widehat{P}}=0_{p\times p}. \end{aligned}$$

But ${\widehat{P}}^*M(\infty ){\widehat{P}}=A^*A$ and hence $A^*A=0_{p\times p}.$ Thus, all singular values of A are 0 and so ${{\,\mathrm{rank}\,}}A=0,$ which forces

$$\begin{aligned} A={{\,\mathrm{col}\,}}(0_{p\times p})_{\lambda \in \Gamma _{m, d}}. \end{aligned}$$

Therefore

$$\begin{aligned} M(m)^{\frac{1}{2}}{{\,\mathrm{col}\,}}(P_\lambda )_{\lambda \in \Gamma _{m, d}}={{\,\mathrm{col}\,}}(0_{p\times p})_{\lambda \in \Gamma _{m, d}} \end{aligned}$$

and

$$\begin{aligned} M(m){{\,\mathrm{col}\,}}(P_\lambda )_{\lambda \in \Gamma _{m, d}}={{\,\mathrm{col}\,}}(0_{p\times p})_{\lambda \in \Gamma _{m, d}}. \end{aligned}$$

(5.1)

We have to show

$$\begin{aligned} M(\infty ){\widehat{P}}={{\,\mathrm{col}\,}}( 0_{p\times p})_{\gamma \in {\mathbb {N}}_0^d}. \end{aligned}$$

We will show that for all $\ell \ge m,$

$$\begin{aligned} M(\ell )\{{{\,\mathrm{col}\,}}(P_\lambda )_{\lambda \in \Gamma _{m, d}}\oplus {{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in \Gamma _{l, d}\setminus \Gamma _{m, d}}\}={{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in \Gamma _{\ell , d}}. \end{aligned}$$

(5.2)

First notice

$$\begin{aligned} {{\,\mathrm{card}\,}}\Gamma _{m, d}= \left( {\begin{array}{c}m+d\\ d\end{array}}\right) ,\;\; {{\,\mathrm{card}\,}}\Gamma _{\ell , d}= {\left( {\begin{array}{c}\ell +d\\ d\end{array}}\right) } \end{aligned}$$

and

$$\begin{aligned} {{\,\mathrm{card}\,}}( \Gamma _{\ell , d}\setminus \Gamma _{m, d}) = \left( {\begin{array}{c}\ell +d\\ d\end{array}}\right) -\left( {\begin{array}{c}m+d\\ d\end{array}}\right) . \end{aligned}$$

We write

$$\begin{aligned} M(\ell )=\begin{pmatrix} M(m) &{} B \\ B^* &{} C \\ \end{pmatrix}\succeq 0, \end{aligned}$$

where

$$\begin{aligned} M(m)\in {\mathbb {C}}^{({{\,\mathrm{card}\,}}\Gamma _{m, d})p \times ({{\,\mathrm{card}\,}}\Gamma _{m, d})p}, \quad B \in {\mathbb {C}}^{({{\,\mathrm{card}\,}}\Gamma _{m, d})p \times ({{\,\mathrm{card}\,}}( \Gamma _{\ell , d}\setminus \Gamma _{m, d}))p} \end{aligned}$$

and

$$\begin{aligned} C \in {\mathbb {C}}^{( {{\,\mathrm{card}\,}}\Gamma _{\ell , d}\setminus \Gamma _{m, d})p \times ({{\,\mathrm{card}\,}}(\Gamma _{\ell , d}\setminus \Gamma _{m, d}))p}. \end{aligned}$$

Since $M(\ell )\succeq 0,$ by Lemma 2.1, there exists $W\in {\mathbb {C}}^{({{\,\mathrm{card}\,}}\Gamma _{m, d})p \times ({{\,\mathrm{card}\,}}( \Gamma _{\ell , d}\setminus \Gamma _{m, d}))p}$ such that $M(m)W=B\quad \text {and}\quad C \succeq W^*M(m) W.$ Then

$$\begin{aligned} \begin{array}{clll}M(\ell )\{{{\,\mathrm{col}\,}}(P_\lambda )_{\lambda \in \Gamma _{m, d}}\oplus {{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in \Gamma _{\ell , d}\setminus \Gamma _{m, d}}\} &{}= \begin{pmatrix} M(m){{\,\mathrm{col}\,}}(P_\lambda )_{\lambda \in \Gamma _{m, d}} \\ B^*{{\,\mathrm{col}\,}}(P_\lambda )_{\lambda \in \Gamma _{m, d}} \\ \end{pmatrix}\\ &{}=\begin{pmatrix} {{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in \Gamma _{m, d}} \\ W^*M(m){{\,\mathrm{col}\,}}(P_\lambda )_{\lambda \in \Gamma _{m, d}} \\ \end{pmatrix}\\ &{}={{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in \Gamma _{\ell , d}},\end{array} \end{aligned}$$

by Eq. (5.1).

Thus, Eq. (5.2) holds for all $\ell \ge m$ and we obtain

$$\begin{aligned} M(\infty ){\widehat{P}}={{\,\mathrm{col}\,}}( 0_{p\times p})_{\gamma \in {\mathbb {N}}_0^d}, \end{aligned}$$

which implies $P \in \ker \Phi .$

Conversely, if $P \in \ker \Phi$ then

$$\begin{aligned} M(\infty ){\widehat{P}}={{\,\mathrm{col}\,}}( 0_{p\times p})_{\lambda \in {\mathbb {N}}_0^d} \end{aligned}$$

and so ${\widehat{P}}^*M(\infty ){\widehat{P}}=0_{p\times p},$ that is, $P \in {\mathcal {I}}.$ $\square$

Lemma 5.15

Suppose $M(\infty )\succeq 0.$ Then ${\mathcal {I}}=\ker \Phi$ is a right ideal.

Proof

Let $P, Q\in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d].$ We have to show the following:

(i) If $P\in \ker \Phi$ and $Q\in \ker \Phi ,$ then $P+Q\in \ker \Phi .$

(ii) If $P\in \ker \Phi$ and $Q\in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d],$ then $PQ\in \ker \Phi .$

To prove (i) notice that since $P\in \ker \Phi ,$

$$\begin{aligned} M(\infty ){\widehat{P}}={{\,\mathrm{col}\,}}(0_{p\times p})_{\lambda \in {\mathbb {N}}_0^d} \end{aligned}$$

and similarly, since $Q\in \ker \Phi ,$

$$\begin{aligned} M(\infty ){\widehat{Q}}={{\,\mathrm{col}\,}}(0_{p\times p})_{\lambda \in {\mathbb {N}}_0^d}. \end{aligned}$$

We then have

$$\begin{aligned} M(\infty ){\widehat{Q}}+ M(\infty ){\widehat{P}}=M(\infty )\widehat{(P+Q)}={{\,\mathrm{col}\,}}(0_{p\times p})_{\lambda \in {\mathbb {N}}_0^d}, \end{aligned}$$

that is, $P+Q\in \ker \Phi .$

To prove (ii) we need to show that if $P\in \ker \Phi$ and $Q\in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d],$ then

$$\begin{aligned} M(\infty )\widehat{(PQ)}={{\,\mathrm{col}\,}}(0_{p\times p})_{\lambda \in {\mathbb {N}}_0^d}. \end{aligned}$$

For

$$\begin{aligned} P(x)= \sum \limits _{\lambda \in \Gamma _{n, d}} x^\lambda P_\lambda \;\;\text {and}\; \;Q(x)= \sum \limits _{\lambda \in \Gamma _{n, d}} x^\lambda Q_\lambda , \end{aligned}$$

we let

$$\begin{aligned} R(x)=P(x)Q(x)=\sum \limits _{{\lambda '}\in \Gamma _{n, d}} P(x) x^{\lambda '} Q_{\lambda '}. \end{aligned}$$

We will show

$$\begin{aligned} M(\infty )(\widehat{x^{\lambda '}P})= {{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in {\mathbb {N}}_0^d}. \end{aligned}$$

(5.3)

We have

$$\begin{aligned} M(\infty )(\widehat{x^{\lambda '}P})={{\,\mathrm{col}\,}}\left( \sum \limits _{\lambda \in \Gamma _{n, d}} S_{\gamma +\lambda ' +\lambda } P_\lambda \right) _{\gamma \in {\mathbb {N}}_0^d}. \end{aligned}$$

But since $P\in \ker \Phi ,$

$$\begin{aligned} M(\infty ){\widehat{P}}={{\,\mathrm{col}\,}}(0_{p\times p})_{{\tilde{\gamma }}\in {\mathbb {N}}_0^d}, \end{aligned}$$

which means that

$$\begin{aligned} {{\,\mathrm{col}\,}}\left( \sum \limits _{\lambda \in \Gamma _{n, d}} S_{ \lambda +{\tilde{\gamma }}} P_\lambda \right) _{{\tilde{\gamma }}\in {\mathbb {N}}_0^d}={{\,\mathrm{col}\,}}(0_{p\times p})_{{\tilde{\gamma }}\in {\mathbb {N}}_0^d}. \end{aligned}$$

For ${\tilde{\gamma }}=\gamma +\lambda ',$ we have

$$\begin{aligned} {{\,\mathrm{col}\,}}\left( \sum \limits _{\lambda \in \Gamma _{n, d}} S_{\gamma +\lambda ' +\lambda } P_\lambda \right) _{\gamma \in {\mathbb {N}}_0^d}=M(\infty )(\widehat{x^{\lambda '}P})={{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in {\mathbb {N}}_0^d} \end{aligned}$$

and Eq. (5.3) holds. For any fixed $\lambda '\in \Gamma _{n, d},$ by Eq. (5.3),

$$\begin{aligned} M(\infty )(\widehat{x^{\lambda '}P)}\cdot Q_{\lambda '} ={{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in {\mathbb {N}}_0^d} \cdot Q_{\lambda '} \end{aligned}$$

and so

$$\begin{aligned} M(\infty )(\widehat{x^{\lambda '}P})\cdot Q_{\lambda '}={{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in {\mathbb {N}}_0^d}. \end{aligned}$$

Hence

$$\begin{aligned} \sum \limits _{\lambda '\in \Gamma _{n, d}} M(\infty )(\widehat{x^{\lambda '}P})\cdot Q_{\lambda '}= \sum \limits _{\lambda '\in \Gamma _{n, d}} {{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in {\mathbb {N}}_0^d}={{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in {\mathbb {N}}_0^d}. \end{aligned}$$

Finally, since

$$\begin{aligned} {\widehat{R}}= \sum \limits _{\lambda '\in \Gamma _{n, d}} \widehat{ x^{\lambda '}P} Q_{\lambda '}, \end{aligned}$$

we have

$$\begin{aligned} M(\infty ) \sum \limits _{\lambda '\in \Gamma _{n, d}}\widehat{x^{\lambda '}P} Q_{\lambda '}=M(\infty ){\widehat{R}}={{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in {\mathbb {N}}_0^d}, \end{aligned}$$

as desired and we derive that $\ker \Phi$ is a right ideal. By Lemma 5.14, ${\mathcal {I}}=\ker \Phi$ and so ${\mathcal {I}}$ is a right ideal as well. $\square$

Definition 5.16

Suppose $M(\infty )\succeq 0$ and let ${\mathcal {I}}$ be as in Definition 5.13. We define the right quotient module

$$\begin{aligned} {\mathbb {C}}^{p \times p}[x_1,\dots , x_d]/{\mathcal {I}}:=\{P+{\mathcal {I}}: P \in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d] \} \end{aligned}$$

of equivalence classes modulo ${\mathcal {I}},$ that is, we will write

$$\begin{aligned} P+ {\mathcal {I}}=P'+ {\mathcal {I}}, \end{aligned}$$

whenever

$$\begin{aligned} P-P'\in {\mathcal {I}}\quad \text {for}\;\; P, P' \in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d]. \end{aligned}$$

Lemma 5.17

Suppose $M(\infty ) \succeq 0$. Then ${\mathbb {C}}^{p \times p}[x_1,\dots , x_d]/{\mathcal {I}}$ is a right module over ${\mathbb {C}}^{p \times p},$ under the operation of addition $(+)$ given by

$$\begin{aligned} (P+ {\mathcal {I}}) + (P'+ {\mathcal {I}}):= (P+P')+ {\mathcal {I}} \end{aligned}$$

for $P, P' \in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d],$ together with the right multiplication $(\cdot )$ given by

$$\begin{aligned} (P+{\mathcal {I}})\cdot R:=PR+ {\mathcal {I}} \end{aligned}$$

for $P \in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d]$ and $R\in {\mathbb {C}}^{p \times p}.$

Proof

Let $P, Q\in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d].$ The following properties can be easily checked:

• (i) $((P+{\mathcal {I}})+(Q+{\mathcal {I}}))R=(P+{\mathcal {I}})R+(Q+{\mathcal {I}})R \quad \text {for all}\; R\in {\mathbb {C}}^{p \times p}.$

• (ii) $(P+{\mathcal {I}})(R+S)=(P+{\mathcal {I}})R+(P+{\mathcal {I}})S\quad \text {for all}\; R,S\in {\mathbb {C}}^{p \times p}.$

• (ii) $(P+{\mathcal {I}})(SR)=((P+{\mathcal {I}})S)R\quad \text {for all}\; R,S\in {\mathbb {C}}^{p \times p}.$

• (iv) $(P+{\mathcal {I}})I_p=P+{\mathcal {I}}.$

$\square$

Definition 5.18

Suppose $M(\infty ) \succeq 0$. For every $P, Q \in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d],$ we define the form

$$\begin{aligned}{}[\cdot ,\cdot ]: {\mathbb {C}}^{p \times p}[x_1,\dots , x_d]/{\mathcal {I}} \times {\mathbb {C}}^{p \times p}[x_1,\dots , x_d]/{\mathcal {I}} \rightarrow {\mathbb {C}}^{p \times p}\end{aligned}$$

given by

$$\begin{aligned}{}[P+ {\mathcal {I}}, Q +{\mathcal {I}}]:= {\widehat{Q}}^*M(\infty ){\widehat{P}}. \end{aligned}$$

The following lemma shows that the form in Definition 5.18 is a well-defined positive semidefinite sesquilinear form.

Lemma 5.19

Suppose $M(\infty )\succeq 0$ and let $P, Q \in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d].$ Then $[P+ {\mathcal {I}}, Q +{\mathcal {I}}]$ is well-defined, sesquilinear and positive semidefinite.

Proof

We first show that the form $[P+ {\mathcal {I}}, Q +{\mathcal {I}}]$ is well-defined. We need to prove that if $P+ {\mathcal {I}}=P'+ {\mathcal {I}}\;\;\text {and}\;\; Q+ {\mathcal {I}}=Q'+ {\mathcal {I}},$ then

$$\begin{aligned}{}[P+ {\mathcal {I}}, Q +{\mathcal {I}}]=[P'+ {\mathcal {I}}, Q' +{\mathcal {I}}], \end{aligned}$$

where $P,P',Q,Q'\in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d].$ We have

$$\begin{aligned}{}[P+ {\mathcal {I}}, Q +{\mathcal {I}}]={\widehat{Q}}^*M(\infty ){\widehat{P}}\quad \text {and}\quad [P'+ {\mathcal {I}}, Q' +{\mathcal {I}}]=\widehat{Q'}^*M(\infty )\widehat{P'}. \end{aligned}$$

Since $P-P'\in {\mathcal {I}},$

$$\begin{aligned} {\widehat{Q}}^*M(\infty )\widehat{(P-P')}= 0_{p\times p} \end{aligned}$$

and since $Q-Q'\in {\mathcal {I}},$

$$\begin{aligned} \widehat{(Q-Q')}^*M(\infty )\widehat{P'}= 0_{p\times p}. \end{aligned}$$

We write

$$\begin{aligned} {\widehat{Q}}^*M(\infty )\widehat{(P-P')}= {\widehat{Q}}^*M(\infty ){\widehat{P}}- {\widehat{Q}}^*M(\infty )\widehat{P'}= 0_{p\times p} \end{aligned}$$

(5.4)

and

$$\begin{aligned} \widehat{(Q-Q')}^*M(\infty )\widehat{P'}={\widehat{Q}}^*M(\infty )\widehat{P'}-\widehat{Q'}^*M(\infty )\widehat{P'}= 0_{p\times p}. \end{aligned}$$

(5.5)

We sum both hand sides of Eqs. (5.4) and (5.5) and we obtain

$$\begin{aligned} \widehat{(Q-Q')}^*M(\infty )\widehat{(P-P')}= 0_{p\times p}, \end{aligned}$$

that is,

$$\begin{aligned} {\widehat{Q}}^*M(\infty ){\widehat{P}}=\widehat{Q'}^*M(\infty )\widehat{P'}. \end{aligned}$$

Therefore

$$\begin{aligned}{}[P+ {\mathcal {I}}, Q +{\mathcal {I}}]=[P'+ {\mathcal {I}}, Q' +{\mathcal {I}}]. \end{aligned}$$

We now show that $[P+ {\mathcal {I}}, Q +{\mathcal {I}}]$ is sesquilinear. Let $A, {\tilde{A}} \in {\mathbb {C}}^{p \times p}.$ If

$$\begin{aligned} P(x)= \sum \limits _{\lambda \in \Gamma _{m, d}} x^\lambda P_\lambda \quad \text {and}\quad Q(x)= \sum \limits _{\lambda \in \Gamma _{n, d}} x^\lambda Q_\lambda , \end{aligned}$$

then

$$\begin{aligned} P(x)A=\sum \limits _{\lambda \in \Gamma _{m, d}} x^\lambda P_\lambda A\quad \text {and}\quad Q(x)A=\sum \limits _{\lambda \in \Gamma _{n, d}} x^\lambda Q_\lambda A. \end{aligned}$$

Let ${\tilde{m}}:=\max (m,n).$ Without loss of generality suppose ${\tilde{m}}=m.$ For $\lambda \in \Gamma _{m, d} {\setminus }\Gamma _{n, d},$ let $Q_\lambda :=0_{p\times p}.$ We may view Q as $Q(x)= \sum \nolimits _{\lambda \in \Gamma _{m, d}} x^\lambda Q_\lambda .$ We have

$$\begin{aligned}{}[(P+ {\mathcal {I}})A+ ({\tilde{P}}+ {\mathcal {I}}){\tilde{A}}, Q +{\mathcal {I}}]= & {} {\widehat{Q}}^*M(\infty )({\widehat{P}}A+ \widehat{{\tilde{P}}}{\tilde{A}})\\= & {} ({\widehat{Q}}^*M(\infty ){\widehat{P}})A+({\widehat{Q}}^*M(\infty ) \widehat{{\tilde{P}}}){\tilde{A}}\\= & {} [P+ {\mathcal {I}}, Q +{\mathcal {I}}]A+[{\tilde{P}}+ {\mathcal {I}}, Q +{\mathcal {I}}]{\tilde{A}} \end{aligned}$$

and

$$\begin{aligned}{}[Q+{\mathcal {I}}, (P+{\mathcal {I}})A+({\tilde{P}}+ {\mathcal {I}}){\tilde{A}}]= & {} {({\widehat{P}}A+\widehat{{\tilde{P}}}{\tilde{A}})}^*M(\infty ){\widehat{Q}}\\= & {} A^*({\widehat{P}}^*M(\infty ){\widehat{Q}})+{\tilde{A}}^*(\widehat{{\tilde{P}}}^*M(\infty ){\widehat{Q}})\\= & {} A^*[Q+{\mathcal {I}}, P+{\mathcal {I}}]+{\tilde{A}}^*[Q+{\mathcal {I}},{\tilde{P}}+ {\mathcal {I}}] \end{aligned}$$

and so $[P+ {\mathcal {I}}, Q +{\mathcal {I}}]$ is sesquilinear. Finally, we show that $[P+ {\mathcal {I}}, Q +{\mathcal {I}}]$ is positive semidefinite. By definition,

$$\begin{aligned}{}[P+ {\mathcal {I}}, P +{\mathcal {I}}]=0_{p\times p}\quad \text {if and only if} \quad P \in {\mathcal {I}}. \end{aligned}$$

Moreover, it follows from the definition of $M(\infty )\succeq 0$ (see Definition 5.10) that

$$\begin{aligned}{}[P+ {\mathcal {I}}, P +{\mathcal {I}}]= {\widehat{P}}^*M(\infty ){\widehat{P}}\succeq 0_{p\times p}. \end{aligned}$$

Thus $[P+ {\mathcal {I}}, Q +{\mathcal {I}}]$ is positive semidefinite. $\square$

In analogy to Definition 3.5, we define the variety associated with the right ideal ${\mathcal {I}}.$

Definition 5.20

Suppose $M(\infty ) \succeq 0$. Let ${\mathcal {I}}$ be the right ideal as in Definition 5.13 and let the matrix-valued polynomial $P(x)= \sum \nolimits _{\lambda \in \Gamma _{n, d}} x^\lambda P_\lambda \in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d].$ We define the variety associated with ${\mathcal {I}}$ by

$$\begin{aligned} {\mathcal {V}}({\mathcal {I}}):= \bigcap _{P\in {\mathcal {I}}} {\mathcal {Z}}(\det P(x)). \end{aligned}$$

Lemma 5.21

Let $S:=(S_\gamma )_{\gamma \in \Gamma _{2n, d}}$ be a given truncated ${\mathcal {H}}_p$-valued multisequence and M(n) the corresponding d-Hankel matrix. Suppose $M(n)\succeq 0$ has an extension $M(n+1)\succeq 0.$ If there exists $P(x)= \sum \nolimits _{\lambda \in \Gamma _{n, d}} x^\lambda P_\lambda \in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d]$ such that $P(X)={{\,\mathrm{col}\,}}( 0_{p\times p})_{\gamma \in \Gamma _{n, d}}\in C_{M(n)},$ then

$$\begin{aligned} P(X)={{\,\mathrm{col}\,}}( 0_{p\times p})_{\gamma \in \Gamma _{n+1, d}}\in C_{M(n+1)}. \end{aligned}$$

Proof

If there exists $P\in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d]$ such that $P(X)={{\,\mathrm{col}\,}}( 0_{p\times p})_{\gamma \in \Gamma _{n, d}}\in C_{M(n)},$ then since $M(n)\succeq 0,$ we have

$$\begin{aligned} M(n){{\,\mathrm{col}\,}}(P_\lambda )_{\lambda \in \Gamma _{n, d}}={{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in \Gamma _{n, d}}.\qquad \quad \end{aligned}$$

(5.6)

We will show

$$\begin{aligned} M(n+1)\{{{\,\mathrm{col}\,}}(P_\lambda )_{\lambda \in \Gamma _{n, d}}\oplus {{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in \Gamma _{n+1, d}\setminus \Gamma _{n, d}}\}={{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in \Gamma _{n+1, d}}.\qquad \end{aligned}$$

(5.7)

Notice that

$$\begin{aligned} {{\,\mathrm{card}\,}}\Gamma _{n, d}=\left( {\begin{array}{c}n+d\\ d\end{array}}\right) ,\;\; {{\,\mathrm{card}\,}}\Gamma _{n+1, d}= \left( {\begin{array}{c}n+1+d\\ d\end{array}}\right) \end{aligned}$$

and

$$\begin{aligned} {{\,\mathrm{card}\,}}( \Gamma _{n+1, d}\setminus \Gamma _{n, d}) = \left( {\begin{array}{c}n+1+d\\ d\end{array}}\right) -\left( {\begin{array}{c}n+d\\ d\end{array}}\right) . \end{aligned}$$

We write

$$\begin{aligned} M(n+1)=\begin{pmatrix} M(n) &{} B \\ B^* &{} C \\ \end{pmatrix}\succeq 0, \end{aligned}$$

where

$$\begin{aligned}&M(n)\in {\mathbb {C}}^{({{\,\mathrm{card}\,}}\Gamma _{n, d})p \times ({{\,\mathrm{card}\,}}\Gamma _{n, d})p}, \\&B \in {\mathbb {C}}^{({{\,\mathrm{card}\,}}\Gamma _{n, d})p \times ({{\,\mathrm{card}\,}}( \Gamma _{n+1, d}\setminus \Gamma _{n, d}))p} \end{aligned}$$

and

$$\begin{aligned} C \in {\mathbb {C}}^{( {{\,\mathrm{card}\,}}\Gamma _{n+1, d}\setminus \Gamma _{n, d})p \times ({{\,\mathrm{card}\,}}(\Gamma _{n+1, d}\setminus \Gamma _{n, d}))p}. \end{aligned}$$

Since $M(n+1)\succeq 0,$ by Lemma 2.1, there exists $W\in {\mathbb {C}}^{({{\,\mathrm{card}\,}}\Gamma _{n, d})p \times ({{\,\mathrm{card}\,}}( \Gamma _{n+1, d}\setminus \Gamma _{n, d}))p}$ such that

$$\begin{aligned} M(n)W=B\quad \text {and}\quad C \succeq W^*M(n) W. \end{aligned}$$

Then

$$\begin{aligned} \begin{array}{clll} M(n+1)\{{{\,\mathrm{col}\,}}(P_\lambda )_{\lambda \in \Gamma _{n, d}}\oplus {{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in \Gamma _{n+1, d}\setminus \Gamma _{n, d}}\} &{}= \begin{pmatrix} M(n){{\,\mathrm{col}\,}}(P_\lambda )_{\lambda \in \Gamma _{n, d}} \\ B^*{{\,\mathrm{col}\,}}(P_\lambda )_{\lambda \in \Gamma _{n, d}} \\ \end{pmatrix}\\ &{}=\begin{pmatrix} {{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in \Gamma _{n, d}} \\ W^*M(n){{\,\mathrm{col}\,}}(P_\lambda )_{\lambda \in \Gamma _{n, d}} \\ \end{pmatrix}\\ &{}={{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in \Gamma _{n+1, d}},\end{array} \end{aligned}$$

by Eq. (5.6). Thus, Eq. (5.7) holds and the proof is complete. $\square$

The following lemma is well-known, see, e.g., Horn and Johnson [47]. However, for the convenience of the reader, we provide a statement.

Lemma 5.22

Let $A \in {\mathbb {C}}^{n \times n}$ and $B\in {\mathbb {C}}^{m \times m}$ be given. Then

$$\begin{aligned} (\det A)^m(\det B)^n =\det (A \otimes B)=\det (B \otimes A). \end{aligned}$$

$A \otimes B$ and $B \otimes A$ are invertible if and only if A and B are both invertible.

Remark 5.23

By Lemma 5.22, the multivariable Vandermonde matrix $V^{p \times p}(w^{(1)}, \dots , w^{(k)}; \Lambda )$ is invertible if and only if $V(w^{(1)}, \dots , w^{(k)}; \Lambda )$ is invertible and $I_p$ is invertible. However, since $I_p$ is obviously invertible, we have $V^{p \times p}(w^{(1)}, \dots , w^{(k)}; \Lambda )$ is invertible if and only if $V(w^{(1)}, \dots , w^{(k)}; \Lambda )$ is invertible.

5.2 Existence of a Representing Measure for a Positive Infinite d-Hankel Matrix with Finite Rank

In this subsection we shall see that if $M(\infty )\succeq 0$ and ${{\,\mathrm{rank}\,}}M(\infty )<\infty ,$ then the associated ${\mathcal {H}}_p$-valued multisequence has a representing measure T.

Definition 5.24

We define the vector space

$$\begin{aligned} ({\mathbb {C}}^p)_{0}^{\omega }:=\{v={{\,\mathrm{col}\,}}(v_\lambda )_{\lambda \in {\mathbb {N}}_0^d}: v_\lambda \in {\mathbb {C}}^p \quad \text {and } v_\lambda = 0_p \text{ for } \text{ all } \text{ but } \text{ finitely } \text{ many } \lambda \in {\mathbb {N}}_0^d \}. \end{aligned}$$

Definition 5.25

We let ${\tilde{C}}_{M(\infty )}$ be the complex vector space

$$\begin{aligned} {\tilde{C}}_{M(\infty )}=\{M(\infty )v: v\in ({\mathbb {C}}^p)_{0}^{\omega } \}. \end{aligned}$$

Remark 5.26

We note that

$$\begin{aligned} {\tilde{C}}_{M(\infty )}=\{M(\infty )v: v\in ({\mathbb {C}}^p)_{0}^{\omega } \}= \left\{ \sum \limits _{\lambda \in \Gamma _{n, d}} X^\lambda v^{(\lambda )}: v\in ({\mathbb {C}}^p)_{0}^{\omega }, \quad \lambda \in \Gamma _{n, d} \right\} . \end{aligned}$$

Definition 5.27

Given $q(x)=\sum \nolimits _{\lambda \in \Gamma _{n, d}} q_\lambda x^\lambda \in {\mathbb {C}}^p[x_1,\dots , x_d],$ we let

$$\begin{aligned} {\hat{q}}:= {{\,\mathrm{col}\,}}(q_{\lambda })_{\lambda \in \Gamma _{n, d}} \oplus {{\,\mathrm{col}\,}}( 0_p)_{\gamma \in {\mathbb {N}}_0^d} \in ({\mathbb {C}}^p)_{0}^{\omega }. \end{aligned}$$

Lemma 5.28

Suppose $M(\infty )\succeq 0$ and $r={{\,\mathrm{rank}\,}}M(\infty )<\infty .$ Then $r=\dim {\tilde{C}}_{M(\infty )}.$

Proof

If $\dim {\tilde{C}}_{M(\infty )}=m$ and $m\ne r,$ then there exists a basis

$$\begin{aligned} {\mathcal {B}}:=\{X^{\lambda ^{(1)}}e_{k_1}, \dots , X^{\lambda ^{(m)}}e_{k_m}\} \end{aligned}$$

of ${\tilde{C}}_{M(\infty )}$ for $1\le k_a\le p,$ where $e_{k_a}$ is a standard basis vector in ${\mathbb {C}}^p$ and $a=1, \dots , m.$ We will show that

$$\begin{aligned} \tilde{{\mathcal {B}}}:=\{{\tilde{X}}^{\lambda ^{(1)}}e_{k_1}, \dots , {\tilde{X}}^{\lambda ^{(m)}}e_{k_m}\} \end{aligned}$$

is a basis of ${\tilde{C}}_{M(\kappa )},$ where

$$\begin{aligned} {\tilde{X}}^{\lambda ^{(a)}}={{\,\mathrm{col}\,}}(S_{\lambda ^{(a)}+\gamma })_{\gamma \in \Gamma _{ \kappa , d}}\quad \text {and}\quad \kappa \ge \max _{a=1, \dots , m} {\big (|\lambda ^{(a)}|\big )}. \end{aligned}$$

First we need to show that $\tilde{{\mathcal {B}}}$ is linearly independent in ${\tilde{C}}_{M(\kappa )}.$ For this, suppose that there exist $c_1, \dots , c_m \in {\mathbb {C}}$ not all zero such that

$$\begin{aligned} \sum \limits _{a=1}^{m}c_{a} {\tilde{X}}^{\lambda ^{(a)}}e_{k_a}={{\,\mathrm{col}\,}}(0_p)_{\gamma \in \Gamma _{\kappa , d}} \in {\tilde{C}}_{M(\kappa )}. \end{aligned}$$

(5.8)

Let $v={{\,\mathrm{col}\,}}(v_{\lambda })_{\lambda \in \Gamma _{\kappa , d}}$ be a vector in ${\mathbb {C}}^{({{\,\mathrm{card}\,}}\Gamma _{\kappa , d} )p}$ with

$$\begin{aligned} v_\lambda = {\left\{ \begin{array}{ll} 0_p, &{} \text {when }\lambda \in \Gamma _{\kappa , d}\setminus {\lambda ^{(a)}} \\ c_a, &{} \text {when }\lambda =\lambda ^{(a)} \end{array}\right. }\quad \text {for} \;\; a=1, \ldots , m. \end{aligned}$$

Then by Eq. (5.8), $M(\kappa )v={{\,\mathrm{col}\,}}(0_p)_{\gamma \in \Gamma _{\kappa , d}} \in {\tilde{C}}_{M(\kappa )}.$ Since $M(\kappa +\ell )\succeq 0$ for all $\ell =1, 2, \dots ,$ we have

$$\begin{aligned} M(\kappa +\ell )\{v\oplus {{\,\mathrm{col}\,}}( 0_p)_{\gamma \in \Gamma _{\kappa +\ell , d}\setminus \Gamma _{ \kappa , d}}\} ={{\,\mathrm{col}\,}}(0_p)_{\gamma \in \Gamma _{\kappa +\ell , d}} \in {\tilde{C}}_{M(\kappa )}. \end{aligned}$$

For $\eta \in {\mathbb {C}}^p[x_1,\dots , x_d]$ with ${\hat{\eta }}:=v\oplus {{\,\mathrm{col}\,}}( 0_p)_{{\gamma \in {\mathbb {N}}_0^d} \setminus \Gamma _{ \kappa , d}},$ we have

$$\begin{aligned} M(\infty ){\hat{\eta }} ={{\,\mathrm{col}\,}}(0_p)_{\gamma \in {\mathbb {N}}_0^d} \in {\tilde{C}}_{M(\infty )}, \end{aligned}$$

that is, there exist $c_1, \dots , c_m \in {\mathbb {C}}$ not all zero such that

$$\begin{aligned} \sum \limits _{a=1}^{m}c_{a} X^{\lambda ^{(a)}}e_{k_a}={{\,\mathrm{col}\,}}(0_p)_{\gamma \in {\mathbb {N}}_0^d } \in {\tilde{C}}_{M(\infty )}. \end{aligned}$$

However, this contradicts the fact that ${\mathcal {B}}$ is linear independent. Hence $\tilde{{\mathcal {B}}}$ is linearly independent in ${\tilde{C}}_{M(\kappa )}.$ It remains to show that $\tilde{{\mathcal {B}}}$ spans ${\tilde{C}}_{M(\kappa )}.$ Since ${\mathcal {B}}$ is a basis of ${\tilde{C}}_{M(\infty )},$ for any ${{\,\mathrm{col}\,}}(d_\gamma )_{\gamma \in {\mathbb {N}}_0^d }\in {\tilde{C}}_{M(\infty )}$ with $d_\gamma \in {\mathbb {C}}^p,$ there exists $c_1, \dots , c_m \in {\mathbb {C}}$ such that

$$\begin{aligned} \sum \limits _{a=1}^{m}c_{a} {X}^{\lambda ^{(a)}}e_{k_a}={{\,\mathrm{col}\,}}(d_\gamma )_{\gamma \in {\mathbb {N}}_0^d}. \end{aligned}$$

We next let ${\mathcal {X}}^{\lambda ^{(a)}}={{\,\mathrm{col}\,}}(S_{\lambda ^{(a)}+\gamma })_{\gamma \in {\mathbb {N}}_0^d{\setminus }\Gamma _{ \kappa , d}}.$ We have

$$\begin{aligned} \sum \limits _{a=1}^{m}c_{a} \{ {\tilde{X}}^{\lambda ^{(a)}}\oplus {\mathcal {X}}^{\lambda ^{(a)}} \}e_{k_a} ={{\,\mathrm{col}\,}}(d_\gamma )_{\gamma \in \Gamma _{ \kappa , d}}\oplus {{\,\mathrm{col}\,}}(d_\gamma )_{\gamma \in {\mathbb {N}}_0^d\setminus \Gamma _{ \kappa , d} } \end{aligned}$$

and so

$$\begin{aligned} \sum \limits _{a=1}^{m}c_{a} {\tilde{X}}^{\lambda ^{(a)}}e_{k_a}={{\,\mathrm{col}\,}}(d_\gamma )_{\gamma \in \Gamma _{\kappa , d}}. \end{aligned}$$

Hence $\tilde{{\mathcal {B}}}$ spans ${\tilde{C}}_{M(\kappa )}.$ Therefore $\tilde{{\mathcal {B}}}$ is a basis of ${\tilde{C}}_{M(\kappa )},$ which forces ${{\,\mathrm{rank}\,}}M(\kappa )=m\; \text {for all}\;\kappa .$ Thus $\sup _{\kappa } {{\,\mathrm{rank}\,}}M(\kappa )=\sup _{\kappa } m\;\text {for all}\;\kappa ,$ that is, $r=m,$ a contradiction. Consequently $\dim {\tilde{C}}_{M(\infty )}=r.$ $\square$

Remark 5.29

Presently, we shall view $M(\infty )$ as a linear operator

$$\begin{aligned} M(\infty ): ({\mathbb {C}}^p)_{0}^{\omega } \rightarrow {\tilde{C}}_{M(\infty )} \end{aligned}$$

and not as a linear operator

$$\begin{aligned} M(\infty ): ({\mathbb {C}}^{p \times p})_{0}^{\omega }\rightarrow C_{M(\infty )} \end{aligned}$$

as in Sect. 3.1.

Remark 5.30

Assume $r={{\,\mathrm{rank}\,}}M(\infty )$ (or, equivalently, $\dim {\tilde{C}}_{M(\infty )}<\infty$). Suppose

$$\begin{aligned} {\mathcal {B}}:=\{X^{\lambda ^{(1)}}e_{k_1}, \dots , X^{\lambda ^{(r)}}e_{k_r}\}\quad \text {for}\;\;1\le k_a\le p, \end{aligned}$$

is a basis for ${\tilde{C}}_{M(\infty )},$ where $e_{k_a}$ is a standard basis vector in ${\mathbb {C}}^p$ and $a=1, \dots , r.$ Then there exist $c_1, \dots , c_r \in {\mathbb {C}}$ such that any $w \in {\tilde{C}}_{M(\infty )}$ can be written as

$$\begin{aligned} w= \sum \limits _{a=1}^{r}c_{a} X^{\lambda ^{(a)}}e_{k_a} \in {\tilde{C}}_{M(\infty )}. \end{aligned}$$

In analogy to results from Section 3.1, we move on to the following.

Definition 5.31

We define the map $\phi : {\mathbb {C}}^p[x_1,\dots , x_d]\rightarrow {\tilde{C}}_{M(\infty )}$ given by

$$\begin{aligned} \phi ( v)= \sum \limits _{a=1}^{r}c_a{ X^{\lambda }}^{(a)}e_{k_a}, \end{aligned}$$

where $v(x)=\sum \nolimits _{\lambda \in \Gamma _{n, d}} v_\lambda x^\lambda \in {\mathbb {C}}^p[x_1,\dots , x_d].$

Definition 5.32

Suppose $M(\infty )\succeq 0.$ Let $q \in {\mathbb {C}}^p[x_1,\dots , x_d].$ We define the subspace of ${\mathbb {C}}^p[x_1,\dots , x_d]$

$$\begin{aligned} {\mathcal {J}}:= \{q \in {\mathbb {C}}^p[x_1,\dots , x_d]: \langle M(\infty ){\hat{q}}, {\hat{q}} \rangle = 0 \} \end{aligned}$$

and the kernel of the map $\phi$

$$\begin{aligned} \ker \phi :=\{q\in {\mathbb {C}}^p[x_1,\dots , x_d]:\phi (q)={{\,\mathrm{col}\,}}(0_p)_{\gamma \in {\mathbb {N}}_0^d } \}, \end{aligned}$$

where $\phi$ is as in Definition 5.31.

Lemma 5.33

Suppose $M(\infty )\succeq 0.$ Then

$$\begin{aligned} {\mathcal {J}}=\ker \phi , \end{aligned}$$

where ${\mathcal {J}}$ and $\ker \phi$ are as in Definition 5.32.

Proof

If $q(x)=\sum \nolimits _{\lambda \in \Gamma _{n, d}} q_\lambda x^\lambda \in \ker \phi ,$ then

$$\begin{aligned} \phi (q)= \sum \limits _{a=1}^{r}c_a{ X^{\lambda }}^{(a)}e_{k_a} ={{\,\mathrm{col}\,}}(0_p)_{\gamma \in {\mathbb {N}}_0^d }, \end{aligned}$$

that is, $M(\infty ){\hat{q}}={{\,\mathrm{col}\,}}(0_p)_{\gamma \in {\mathbb {N}}_0^d },$ where ${\hat{q}} \in ({\mathbb {C}}^p)_{0}^{\omega }.$ Thus $\langle M(\infty ){\hat{q}}, {\hat{q}} \rangle = 0$ and so $q\in {\mathcal {J}}.$

Conversely, let $q(x)=\sum _{\lambda \in \Gamma _{n, d}} q_\lambda x^\lambda \in {\mathcal {J}}.$ Then $\langle M(\infty ){\hat{q}}, {\hat{q}} \rangle = 0.$ It suffices to show that for every $\eta (x)=\sum _{\lambda \in \Gamma _{m, d}} \eta _\lambda x^\lambda \in {\mathbb {C}}^p[x_1,\dots , x_d],$

$$\begin{aligned} \langle M(\infty ){\hat{q}}, {\hat{\eta }} \rangle = 0. \end{aligned}$$

Let ${\tilde{m}}=\max (n,m).$ Without loss of generality suppose ${\tilde{m}}=m.$ Let $\eta _\lambda =0_p$ for $\lambda \in \Gamma _{n, d} {\setminus }\Gamma _{m, d}.$ We may view $\eta$ as $\eta (x)=\sum \nolimits _{\lambda \in \Gamma _{n, d}} \eta _\lambda x^\lambda .$ Since $\langle M(\infty ){\hat{q}}, {\hat{q}} \rangle = 0,$ we have ${\hat{q}}^* M(\infty ) {\hat{q}}=0$ and so

$$\begin{aligned} {{\,\mathrm{col}\,}}(q_\lambda )_{\lambda \in \Gamma _{m, d}}^* M(m){{\,\mathrm{col}\,}}(q_\lambda )_{\lambda \in \Gamma _{m, d}}=0. \end{aligned}$$

Moreover, since $M(\infty )\succeq 0,$ $M(m)\succeq 0$ and hence, the square root of M(m) exists. Next, $\langle M(m)^{\frac{1}{2}}{\hat{q}}, {\hat{q}} \rangle = 0$ implies $\langle M(m)^{\frac{1}{2}}{\hat{q}}, M(m)^{\frac{1}{2}}{\hat{q}} \rangle = 0,$ that is,

$$\begin{aligned} \parallel M(m)^{\frac{1}{2}}{\hat{q}}\parallel =0. \end{aligned}$$

Then $M(m)^{\frac{1}{2}}{\hat{q}}= {{\,\mathrm{col}\,}}(0_p)_{\lambda \in \Gamma _{m, d}}$ and

$$\begin{aligned} M(m)^{\frac{1}{2}}M(m)^{\frac{1}{2}}{\hat{q}}= M(m)^{\frac{1}{2}}{{\,\mathrm{col}\,}}(0_p)_{\lambda \in \Gamma _{m, d}}, \end{aligned}$$

which implies

$$\begin{aligned} M(m){\hat{q}}={{\,\mathrm{col}\,}}(0_p)_{\lambda \in \Gamma _{m, d}}. \end{aligned}$$

(5.9)

If $q(x)=\sum \nolimits _{\lambda \in \Gamma _{n, d}} q_\lambda x^\lambda \in {\mathcal {J}}$ and $\eta (x)=\sum \nolimits _{\lambda \in \Gamma _{n, d}} \eta _\lambda x^\lambda \in {\mathcal {J}}$ with ${\hat{q}}, {\hat{\eta }} \in ({\mathbb {C}}^p)_{0}^{\omega },$ then

$$\begin{aligned} \langle M(\infty ){\hat{q}}, {\hat{\eta }} \rangle= & {} {\hat{\eta }}^* M(\infty ) {\hat{q}}\\= & {} {{\,\mathrm{col}\,}}(\eta _\lambda )_{\lambda \in \Gamma _{m, d}}^* M(m){{\,\mathrm{col}\,}}(q_\lambda )_{\lambda \in \Gamma _{m, d}}\\= & {} \langle M(m){\hat{q}}, {\hat{\eta }} \rangle \\= & {} 0, \end{aligned}$$

by Eq. (5.9). $\square$

Definition 5.34

Let $M(\infty )\succeq 0$ and ${\mathcal {J}}$ be as in Definition 5.32. We define the quotient space

$$\begin{aligned} {\mathbb {C}}^p[x_1,\dots , x_d]/{\mathcal {J}}=\{q+{\mathcal {J}}: q \in {\mathbb {C}}^p[x_1,\dots , x_d] \} \end{aligned}$$

of equivalence classes modulo ${\mathcal {J}},$ that is, if

$$\begin{aligned} q+ {\mathcal {J}}=q'+ {\mathcal {J}}, \end{aligned}$$

then

$$\begin{aligned} q-q'\in {\mathcal {J}}\quad \text {for}\;\; q, q' \in {\mathbb {C}}^p[x_1,\dots , x_d]. \end{aligned}$$

Definition 5.35

For every $h,q \in {\mathbb {C}}^p[x_1,\dots , x_d],$ we define the inner product

$$\begin{aligned} \langle \cdot ,\cdot \rangle : {\mathbb {C}}^p[x_1,\dots , x_d]/{\mathcal {J}} \times {\mathbb {C}}^p[x_1,\dots , x_d]/{\mathcal {J}} \rightarrow {\mathbb {C}} \end{aligned}$$

given by

$$\begin{aligned} \langle h+ {\mathcal {J}}, q +{\mathcal {J}}\rangle = {\hat{q}}^*M(\infty ){\hat{h}}. \end{aligned}$$

Lemma 5.36

Suppose $M(\infty )\succeq 0$ and let $h, q \in {\mathbb {C}}^p[x_1,\dots , x_d].$ Then $\langle h+ {\mathcal {J}}, q +{\mathcal {J}}\rangle$ is well-defined, linear and positive semidefinite.

Proof

We first show that the inner product $\langle h+ {\mathcal {J}}, q +{\mathcal {J}}\rangle$ is well-defined. We need to prove that if $h+ {\mathcal {J}}=h'+ {\mathcal {J}}\;\;\text {and}\;\; q+ {\mathcal {J}}=q'+ {\mathcal {J}},$ then

$$\begin{aligned} \langle h+ {\mathcal {J}}, q +{\mathcal {J}}\rangle =\langle h'+ {\mathcal {J}}, q' +{\mathcal {J}}\rangle , \end{aligned}$$

where $h,h',q,q'\in {\mathbb {C}}^p[x_1,\dots , x_d].$ We write

$$\begin{aligned} \langle h+ {\mathcal {J}}, q +{\mathcal {J}}\rangle ={\hat{q}}^*M(\infty ){\hat{h}}\quad \text {and}\quad \langle h'+ {\mathcal {J}}, q' +{\mathcal {J}}\rangle =\hat{q'}^*M(\infty )\hat{h'}. \end{aligned}$$

Since $h-h'\in {\mathcal {J}},$

$$\begin{aligned} {\hat{q}}^*M(\infty )\widehat{(h-h')}= 0 \end{aligned}$$

and since $q-q'\in {\mathcal {J}},$

$$\begin{aligned} \widehat{(q-q')}^*M(\infty )\hat{h'}= 0. \end{aligned}$$

We write

$$\begin{aligned} {\hat{q}}^*M(\infty )\widehat{(h-h')}= {\hat{q}}^*M(\infty ){\hat{h}}- {\hat{q}}^*M(\infty )\hat{h'}= 0 \end{aligned}$$

(5.10)

and

$$\begin{aligned} \widehat{(q-q')}^*M(\infty )\hat{h'}={\hat{q}}^*M(\infty )\hat{h'}-\hat{q'}^*M(\infty )\hat{h'}= 0. \end{aligned}$$

(5.11)

We sum both hand sides of Eqs. (5.10) and (5.11) and we obtain

$$\begin{aligned} \widehat{(q-q')}^*M(\infty )\widehat{(h-h')}= 0, \end{aligned}$$

that is,

$$\begin{aligned} {\hat{q}}^*M(\infty ){\hat{h}}=\hat{q'}^*M(\infty )\hat{h'}, \end{aligned}$$

and hence

$$\begin{aligned} \langle h+ {\mathcal {J}}, q +{\mathcal {J}}\rangle =\langle h'+ {\mathcal {J}}, q' +{\mathcal {J}}\rangle . \end{aligned}$$

We now show that the inner product $\langle h+ {\mathcal {J}}, q +{\mathcal {J}} \rangle$ is linear. We must prove that for every $h, {\tilde{h}}, q \in {\mathbb {C}}^p[x_1,\dots , x_d]$ and $a, {\tilde{a}} \in {\mathbb {C}},$

$$\begin{aligned} \langle a(h +{\mathcal {J}})+{\tilde{a}}({\tilde{h}}+{\mathcal {J}}), q+ {\mathcal {J}} \rangle = a \langle h+ {\mathcal {J}}, q +{\mathcal {J}} \rangle + {\tilde{a}}\langle {\tilde{h}}+ {\mathcal {J}}, q +{\mathcal {J}} \rangle . \end{aligned}$$

Let

$$\begin{aligned} h(x)=\sum \limits _{\lambda \in \Gamma _{n, d}} h_\lambda x^\lambda \quad \text {and} \quad q(x)=\sum \limits _{\lambda \in \Gamma _{m, d}} q_\lambda x^\lambda . \end{aligned}$$

Then

$$\begin{aligned} ah(x)=\sum \limits _{\lambda \in \Gamma _{n, d}} a h_\lambda x^\lambda . \end{aligned}$$

Let ${\tilde{m}}=\max (n,m).$ Without loss of generality suppose ${\tilde{m}}=m.$ Let $q_\lambda =0_h$ for $\lambda \in \Gamma _{n, d} {\setminus }\Gamma _{m, d}.$ We may view q as $q(x)=\sum \nolimits _{\lambda \in \Gamma _{n, d}} q_\lambda x^\lambda$ and we have

$$\begin{aligned} \langle a(h +{\mathcal {J}})+{\tilde{a}}({\tilde{h}}+{\mathcal {J}}), q+ {\mathcal {J}} \rangle= & {} {\hat{q}}^*M(\infty )\widehat{(ah+{\tilde{a}}{\tilde{h}})}\\= & {} {\hat{q}}^*M(\infty )\widehat{(ah)}+{\hat{q}}^*M(\infty )\widehat{({\tilde{a}} {\tilde{h}})}\\= & {} a{\hat{q}}^*M(\infty ){\hat{h}}+{\tilde{a}}{\hat{q}}^*M(\infty )\hat{{\tilde{h}}}\\= & {} a \langle h+ {\mathcal {J}}, q +{\mathcal {J}} \rangle + {\tilde{a}}\langle {\tilde{h}}+ {\mathcal {J}}, q +{\mathcal {J}} \rangle . \end{aligned}$$

Finally, we show $\langle h+ {\mathcal {J}}, q +{\mathcal {J}} \rangle$ is positive semidefinite. By definition,

$$\begin{aligned} \langle h+ {\mathcal {J}}, h +{\mathcal {J}}\rangle =0 \quad \text {if and only if} \quad h \in {\mathcal {J}}. \end{aligned}$$

Since $M(\infty )\succeq 0,$ by Lemma 5.12,

$$\begin{aligned} \langle h+ {\mathcal {J}}, h +{\mathcal {J}}\rangle = {\hat{h}}^*M(\infty ){\hat{h}}\ge 0. \end{aligned}$$

Hence $\langle h+ {\mathcal {J}}, h +{\mathcal {J}}\rangle$ is positive semidefinite. $\square$

Definition 5.37

We define the map $\Psi : {\tilde{C}}_{M(\infty )} \rightarrow {\mathbb {C}}^p[x_1,\dots , x_d]/{\mathcal {J}}$ given by

$$\begin{aligned} \Psi (w )=\sum \limits _{a=1}^{r}c_a{ x^{\lambda }}^{(a)}e_{k_a}+{\mathcal {J}}, \end{aligned}$$

where

$$\begin{aligned} w= \sum \limits _{a=1}^{r}c_{a} X^{\lambda ^{(a)}}e_{k_a} \in {\tilde{C}}_{M(\infty )}. \end{aligned}$$

Lemma 5.38

$\Psi$ as in Definition 5.37 is an isomorphism.

Proof

We consider the map $\phi : {\mathbb {C}}^p[x_1,\dots , x_d]\rightarrow {\tilde{C}}_{M(\infty )}$ is as in Definition 5.31 and we first show that $\phi$ is an homomorphism. For $\sum \nolimits _{a=1}^{r}d_a{ x^{\lambda }}^{(a)}e_{k_a} \in {\mathbb {C}}^p[x_1,\dots , x_d],$ where $d_1, \dots , d_r \in {\mathbb {C}},$ we have

$$\begin{aligned} \phi \bigg (\displaystyle \sum \limits _{a=1}^{r}d_a{ x^{\lambda }}^{(a)}e_{k_a} + \displaystyle \sum \limits _{a=1}^{r}c_a{ x^{\lambda }}^{(a)}e_{k_a}\bigg )= & {} \phi \bigg (\displaystyle \sum \limits _{a=1}^{r}d_a{ x^{\lambda }}^{(a)}e_{k_a} \bigg )+\phi \bigg (\displaystyle \sum \limits _{a=1}^{r}c_a{ x^{\lambda }}^{(a)}e_{k_a} \bigg )\\= & {} \displaystyle \sum \limits _{a=1}^{r}d_a{ X^{\lambda }}^{(a)}e_{k_a} + \displaystyle \sum \limits _{a=1}^{r}c_a{ X^{\lambda }}^{(a)}e_{k_a}. \end{aligned}$$

Moreover, we shall see that $\phi$ is surjective. Indeed, for every $\sum \nolimits _{a=1}^{r}c_a{ X^{\lambda }}^{(a)}e_{k_a} \in {\tilde{C}}_{M(\infty )},$ there exists $\sum \nolimits _{a=1}^{r}c_a{ x^{\lambda }}^{(a)}e_{k_a} \in {\mathbb {C}}^p[x_1,\dots , x_d]$ such that

$$\begin{aligned} \phi \bigg (\sum \limits _{a=1}^{r}c_a{ x^{\lambda }}^{(a)}e_{k_a} \bigg ) = \sum \limits _{a=1}^{r}c_a{ X^{\lambda }}^{(a)}e_{k_a}. \end{aligned}$$

By the Fundamental homomorphism theorem (see, e.g., [41, Theorem 1.11]), ${\tilde{C}}_{M(\infty )}$ is isomorphic to ${\mathbb {C}}^p[x_1,\dots , x_d]/\ker \phi$ and thus to ${\mathbb {C}}^p[x_1,\dots , x_d]/{\mathcal {J}},$ by Lemma 5.33. Hence, the map $\Psi$ is an isomorphism. $\square$

Remark 5.39

By Lemma 5.28, $r={{\,\mathrm{rank}\,}}M(\infty )=\dim {\tilde{C}}_{M(\infty )}<\infty .$ Since $\Psi$ is an isomorphism, we derive that $r=\dim ({\mathbb {C}}^p[x_1,\dots , x_d]/{\mathcal {J}} ).$

In this setting, we present the multiplication operators $M_{x_j},\;j=1, \dots , d,$ as defined below.

Definition 5.40

Let $q\in {\mathbb {C}}^p[x_1,\dots , x_d].$ We define the multiplication operators

$$\begin{aligned} M_{x_j}: {\mathbb {C}}^p[x_1,\dots , x_d]/{\mathcal {J}} \rightarrow {\mathbb {C}}^p[x_1,\dots , x_d]/{\mathcal {J}} \quad \text {for} \;\; j=1, \dots , d \end{aligned}$$

given by

$$\begin{aligned} M_{x_j}(q+ {\mathcal {J}}):= \sum \limits _{k=1}^{p}M_{x_j}^{(k)}\bigg (\sum \limits _{\lambda \in \Gamma _{m, d}} q_\lambda ^{(k)}x^{\lambda }e_k + {\mathcal {J}}\bigg ), \end{aligned}$$

where

$$\begin{aligned} M_{x_j}^{(k)}: {\mathbb {C}}^p[x_1,\dots , x_d]/{\mathcal {J}} \rightarrow {\mathbb {C}}^p[x_1,\dots , x_d]/{\mathcal {J}} \end{aligned}$$

is the multiplication operator defined by

$$\begin{aligned} M_{x_j}^{(k)}\bigg (\sum \limits _{\lambda \in \Gamma _{m, d}} q_\lambda ^{(k)}x^{\lambda }e_k + {\mathcal {J}}\bigg ):= \sum \limits _{\lambda \in \Gamma _{m, d}} q_\lambda ^{(k)}x^{\lambda + \varepsilon _j}e_k + {\mathcal {J}} \end{aligned}$$

for all $j=1, \dots , d$ and $\varepsilon _j \in {\mathbb {N}}_0^d,$ $j=1, \dots , d.$

Let us now continue with lemmas on properties of the multiplication operators $M_{x_j}$.

Lemma 5.41

Let $M_{x_j},$ $j=1, \dots , d,$ be the multiplication operators as in Definition 5.40. Then $M_{x_j}$ is well-defined for all $j=1, \dots , d.$

Proof

Let $q(x)=\sum \nolimits _{\lambda \in \Gamma _{m, d}} q_\lambda x^\lambda$ and $h(x)=\sum \nolimits _{\lambda \in \Gamma _{m, d}} h_\lambda x^\lambda .$ If $q+{\mathcal {J}}=h+{\mathcal {J}},$ then

$$\begin{aligned} M_{x_j}(q+{\mathcal {J}})=M_{x_j}(h+{\mathcal {J}}), \end{aligned}$$

that is,

$$\begin{aligned} \sum \limits _{k=1}^{p}M_{x_j}^{(k)}\bigg (\sum \limits _{\lambda \in \Gamma _{m, d}} q_\lambda ^{(k)}x^{\lambda }e_k + {\mathcal {J}}\bigg )= \sum \limits _{k=1}^{p}M_{x_j}^{(k)}\bigg (\sum \limits _{\lambda \in \Gamma _{m, d}} h_\lambda ^{(k)}x^{\lambda }e_k + {\mathcal {J}}\bigg ), \end{aligned}$$

or equivalently,

$$\begin{aligned} \sum \limits _{\lambda \in \Gamma _{m, d}} \sum \limits _{k=1}^{p} q_\lambda ^{(k)}x^{\lambda }x^{\varepsilon _j}e_k + {\mathcal {J}} = \sum \limits _{\lambda \in \Gamma _{m, d}} \sum \limits _{k=1}^{p} h_\lambda ^{(k)}x^{\lambda }x^{\varepsilon _j}e_k + {\mathcal {J}}, \end{aligned}$$

which is equivalent to

$$\begin{aligned} x^{\varepsilon _j} \sum \limits _{\lambda \in \Gamma _{m, d}} q_\lambda x^{\lambda } + {\mathcal {J}} =x^{\varepsilon _j} \sum \limits _{\lambda \in \Gamma _{m, d}} h_\lambda x^{\lambda } + {\mathcal {J}}, \end{aligned}$$

that is,

$$\begin{aligned} x^{\varepsilon _j} q + {\mathcal {J}}=x^{\varepsilon _j} h + {\mathcal {J}}, \end{aligned}$$

and hence

$$\begin{aligned} x_j (q-h) \in {\mathcal {J}} \end{aligned}$$

as required. $\square$

Lemma 5.42

Let $M_{x_j},$ $j=1, \dots , d,$ be as in Definition 5.40. Then $M_{x_j}(q+ {\mathcal {J}})=x^{\varepsilon _j}q+ {\mathcal {J}}$ for all $j=1, \dots , d.$

Proof

For all $j=1, \dots , d,$

$$\begin{aligned} M_{x_j}(q+ {\mathcal {J}})= & {} \sum \limits _{k=1}^{p}M_{x_j}^{(k)}\bigg (\sum \limits _{\lambda \in \Gamma _{m, d}} q_\lambda ^{(k)}x^{\lambda }e_k + {\mathcal {J}}\bigg )\\= & {} \sum \limits _{k=1}^{p}\sum \limits _{\lambda \in \Gamma _{m, d}} q_\lambda ^{(k)}x^{\lambda +\varepsilon _j}e_k + {\mathcal {J}} \\= & {} \sum \limits _{\lambda \in \Gamma _{m, d}} \sum \limits _{k=1}^{p} q_\lambda ^{(k)}x^{\lambda }x^{\varepsilon _j}e_k + {\mathcal {J}} \\= & {} x^{\varepsilon _j} \sum \limits _{\lambda \in \Gamma _{m, d}} q_\lambda x^{\lambda } + {\mathcal {J}} \\= & {} x^{\varepsilon _j} q + {\mathcal {J}} \\= & {} x_j q + {\mathcal {J}} \end{aligned}$$

as required. $\square$

Lemma 5.43

Let $M_{x_j},$ $j=1, \dots , d,$ be as in Definition 5.40. Then $M_{x_j}M_{x_\ell }=M_{x_\ell }M_{x_j}$ for all $j, \ell =1, \dots , d.$

Proof

We need to show that for every $q, f \in {\mathbb {C}}^p[_1,\dots , x_d],$

$$\begin{aligned} \langle M_{x_j}M_{x_\ell } (q+ {\mathcal {J}}), f+ {\mathcal {J}}\rangle = \langle M_{x_\ell }M_{x_j} (q+ {\mathcal {J}}), f+ {\mathcal {J}}\rangle , \end{aligned}$$

that is, $\langle x^{\varepsilon _j} x^{\varepsilon _\ell } (q+ {\mathcal {J}}), f+ {\mathcal {J}}\rangle = \langle x^{\varepsilon _\ell }x^{\varepsilon _j} (q+ {\mathcal {J}}), f+ {\mathcal {J}}\rangle .$ We have

$$\begin{aligned} \langle x^{\varepsilon _j} x^{\varepsilon _\ell } (q+ {\mathcal {J}}), f+ {\mathcal {J}}\rangle= & {} \langle x_j x_\ell (q+ {\mathcal {J}}), f+ {\mathcal {J}}\rangle \\= & {} {\hat{f}}^* M(\infty ) \widehat{(x_j x_\ell q)} \\= & {} {\hat{f}}^* M(\infty ) \widehat{(x_\ell x_j q)} \\= & {} \langle x_\ell x_j(q+ {\mathcal {J}}), f+ {\mathcal {J}}\rangle \\= & {} \langle x^{\varepsilon _\ell }x^{\varepsilon _j} (q+ {\mathcal {J}}), f+ {\mathcal {J}}\rangle . \end{aligned}$$

Thus $M_{x_j}M_{x_\ell }=M_{x_\ell }M_{x_j}\;\text {for all}\; j, \ell =1, \dots , d.$ $\square$

Lemma 5.44

Let $M_{x_j},$ $j=1, \dots , d,$ be as in Definition 5.40. Then $M_{x_j}$ is self-adjoint for all $j=1, \dots , d.$

Proof

We need to show that

$$\begin{aligned}&\bigg \langle \sum \limits _{k=1}^{p}M_{x_j}^{(k)}\bigg (\sum \limits _{\lambda \in \Gamma _{m, d}} q_\lambda ^{(k)}x^{\lambda }e_k + {\mathcal {J}}\bigg ), \sum \limits _{\ell =1}^{p}\sum \limits _{\lambda \in \Gamma _{m, d}} f_\lambda ^{(\ell )}x^{\lambda }e_\ell + {\mathcal {J}} \bigg \rangle \\&\quad = \bigg \langle \sum \limits _{k=1}^{p}\sum \limits _{\lambda \in \Gamma _{m, d}} q_\lambda ^{(k)}x^{\lambda }e_k + {\mathcal {J}}, \sum \limits _{\ell =1}^{p}M_{x_j}^{(\ell )}\bigg (\sum \limits _{\lambda \in \Gamma _{m, d}} f_\lambda ^{(\ell )}x^{\lambda }e_\ell + {\mathcal {J}}\bigg )\bigg \rangle , \end{aligned}$$

that is,

$$\begin{aligned} \langle M_{x_j}(q+ {\mathcal {J}}), f+ {\mathcal {J}}\rangle = \langle q+ {\mathcal {J}}, M_{x_j}(f+ {\mathcal {J}})\rangle . \end{aligned}$$

We have

$$\begin{aligned}&\bigg \langle \sum \limits _{k=1}^{p}M_{x_j}^{(k)}\bigg (\sum \limits _{\lambda \in \Gamma _{m, d}} q_\lambda ^{(k)}x^{\lambda }e_k + {\mathcal {J}}\bigg ), \sum \limits _{\ell =1}^{p}\sum \limits _{\lambda \in \Gamma _{m, d}} f_\lambda ^{(\ell )}x^{\lambda }e_\ell + {\mathcal {J}} \bigg \rangle \nonumber \\&\quad = \bigg \langle \sum \limits _{k=1}^{p}\sum \limits _{\lambda \in \Gamma _{m, d}} q_\lambda ^{(k)}x^{\lambda +\varepsilon _j}e_k + {\mathcal {J}}, \sum \limits _{\ell =1}^{p}\sum \limits _{\lambda \in \Gamma _{m, d}} f_\lambda ^{(\ell )}x^{\lambda }e_\ell + {\mathcal {J}} \bigg \rangle \end{aligned}$$

(5.12)

and

$$\begin{aligned}&\bigg \langle \sum \limits _{k=1}^{p}\sum \limits _{\lambda \in \Gamma _{m, d}} q_\lambda ^{(k)}x^{\lambda }e_k + {\mathcal {J}}, \sum \limits _{\ell =1}^{p}M_{x_j}^{(\ell )}\bigg (\sum \limits _{\lambda \in \Gamma _{m, d}} f_\lambda ^{(\ell )}x^{\lambda }e_\ell + {\mathcal {J}}\bigg )\bigg \rangle \nonumber \\&\quad = \bigg \langle \sum \limits _{k=1}^{p}\sum \limits _{\lambda \in \Gamma _{m, d}} q_\lambda ^{(k)}x^{\lambda }e_k + {\mathcal {J}}, \sum \limits _{\ell =1}^{p}\sum \limits _{\lambda \in \Gamma _{m, d}} f_\lambda ^{(\ell )}x^{\lambda +\varepsilon _j}e_\ell + {\mathcal {J}}\bigg \rangle . \end{aligned}$$

(5.13)

Equation (5.12) is equal to

$$\begin{aligned} \sum \limits _{k,\ell =1}^{p} {\hat{f}}^* M(\infty ) \widehat{(x_j q)}, \end{aligned}$$

where ${\hat{f}} \in ({\mathbb {C}}^p)_{0}^{\omega }$ and $\widehat{(x_j q)}\in ({\mathbb {C}}^p)_{0}^{\omega }$ and equation (5.13) is equal to

$$\begin{aligned} \sum \limits _{\ell , k=1}^{p} \widehat{(x_j f)}^* M(\infty ) {\hat{q}}, \end{aligned}$$

where $\widehat{(x_j f)} \in ({\mathbb {C}}^p)_{0}^{\omega }$ and ${\hat{q}}\in ({\mathbb {C}}^p)_{0}^{\omega }.$ It remains to show that ${\hat{f}}^* M(\infty ) \widehat{(x_j q)} = \widehat{(x_j f)}^* M(\infty ) {\hat{q}}.$ We have

$$\begin{aligned} {\hat{f}}^* M(\infty ) \widehat{(x_j q)}= & {} {\hat{f}}^* {{\,\mathrm{col}\,}}(\sum \limits _{\lambda \in \Gamma _{m, d}}S_{\gamma +\lambda } \widehat{(x_j q)})_{\gamma \in {\mathbb {N}}_0^d} \\= & {} {\hat{f}}^* {{\,\mathrm{col}\,}}(\sum \limits _{\lambda \in \Gamma _{m, d}}S_{\gamma +\lambda +\varepsilon _j} {\hat{q}})_{\gamma \in {\mathbb {N}}_0^d} \\= & {} \widehat{(x_j f)}^* M(\infty ){\hat{q}} \end{aligned}$$

and the proof is now complete. $\square$

Next, we shall use spectral theory involving the preceding multiplication operators. First, we denote by ${\mathcal {P}}$ the set of the orthogonal projections on ${\mathbb {C}}^p[x_1,\dots , x_d]/{\mathcal {J}}.$

Remark 5.45

$M_{x_j}$ is self-adjoint for all $j=1, \dots ,d$ and so by the spectral theorem for bounded self-adjoint operators on a Hilbert space (see, e.g., [71, Theorem 5.1]), there exists a unique spectral measure $E_j: {{\mathcal {B}}(\sigma (E_j))} \rightarrow {\mathcal {P}},\; \sigma (E_j)\subseteq {\mathcal {B}}({\mathbb {R}}^d),$ such that

$$\begin{aligned} M_{x_j}(q+ {\mathcal {J}})= \int _{\sigma (E_j)} x d E_j(x) (q+ {\mathcal {J}})\quad \text {for} \;\; j=1, \dots ,d. \end{aligned}$$

$E_j$ is unique, in the sense that if $F_j: {\mathcal {B}}({\mathbb {R}}) \rightarrow {\mathcal {P}}$ is another spectral measure such that

$$\begin{aligned} M_{x_j}(q+ {\mathcal {J}})= \int _{\sigma (E_j)} x d F_j(x) (q+ {\mathcal {J}})\quad \text {for} \;\; j=1, \dots ,d, \end{aligned}$$

then we have

$$\begin{aligned} E_j\big ( \alpha \cap \sigma (E_j) \big ) =F_j(\alpha )\quad \text {for }\; \alpha \in {{\mathcal {B}}({\mathbb {R}})},\; j=1, \dots ,d. \end{aligned}$$

By [71, Lemma 4.3], $E_j(\alpha )E_j(\beta )=E_j(\alpha \cap \beta )\;\text {for}\; \alpha , \beta \in {{\mathcal {B}}(\sigma (E_j))},$ which implies that

$$\begin{aligned} E_j(\alpha )E_k(\beta )=E_k(\beta )E_j(\alpha )\;\;\text {for}\; \alpha \in {\mathcal {B}}(\sigma (E_j)),\; \beta \in {\mathcal {B}}(\sigma (E_k),\; j, k= 1, \dots , d. \end{aligned}$$

Since $M_{x_j}$ is self-adjoint and pairwise commute, that is, $M_{x_j}M_{x_k}=M_{x_k}M_{x_j}$ for all $j, k=1, \dots , d$ (see Lemma 5.43), we have that for all Borel sets $\alpha , \beta \in {{\mathcal {B}}({\mathbb {R}}^d)},$

$$\begin{aligned} M_{x_j}(\alpha )M_{x_k}(\beta )=M_{x_k}(\beta )M_{x_j}(\alpha )\quad \text {for}\;\; j, k= 1, \dots , d. \end{aligned}$$

Thus, by [71, Theorem 4.10], there exists a unique spectral measure E on the Borel algebra ${\mathcal {B}}(\Omega )$ of the product space $\Omega = \sigma (E_1) \times \dots \times \sigma (E_d)$ such that

$$\begin{aligned} E(\alpha _1 \times \dots \times \alpha _d )= E_{x_1}(\alpha _1)\cdots E_{x_d}(\alpha _d)\quad \text {for}\;\; \alpha _j \in {\mathcal {B}}(\Omega ),\; j=1, \ldots , d. \end{aligned}$$

Remark 5.46

[71, Theorem 5.23] For $M_{x_j},$ $j=1, \dots ,d,$ commuting self-adjoint operators on the quotient space ${\mathbb {C}}^p[x_1,\dots , x_d]/{\mathcal {J}},$ there exists a joint spectral measure $E: {{\mathcal {B}}({\mathbb {R}}^d)} \rightarrow {\mathcal {P}}$ such that for every $q, f \in {\mathbb {C}}^p,$

$$\begin{aligned}&\langle M_{x_1}^{\gamma _1}\cdots M_{x_d}^{\gamma _d}(q+ {\mathcal {J}}), f+ {\mathcal {J}}\rangle = \int _{{\mathbb {R}}^d} x_1^{\gamma _1}\cdots x_d^{\gamma _d} d\langle E(x_1,\ldots , x_d) (q+ {\mathcal {J}}), f+ {\mathcal {J}}\rangle ,\\&\quad j=1, \dots ,d. \end{aligned}$$

Definition 5.47

[71, Definition 5.3] The support of the spectral measure E is called the joint spectrum of $M_{x_1},\dots , M_{x_d}$ and is denoted by $\sigma (M_x)=\sigma (M_{x_1},\dots , M_{x_d}).$

Lemma 5.48

If $r={{\,\mathrm{rank}\,}}M(\infty )=\dim ( {\mathbb {C}}^p[x_1,\dots , x_d]/{\mathcal {J}})< \infty ,$ then

$$\begin{aligned} {{\,\mathrm{card}\,}}\sigma (M_x)\le r, \end{aligned}$$

where $\sigma (M_x)$ is as defined in Definition 5.47.

Proof

Since $M_{x_j}$ $j=1, \dots ,d$ are self-adjoint operators on the finite dimensional Hilbert space ${\mathbb {C}}^p[x_1,\dots , x_d]/{\mathcal {J}},$ we have

$$\begin{aligned} \sigma (M_{x_j}) \subseteq {\mathbb {R}} \end{aligned}$$

with

$$\begin{aligned} {{\,\mathrm{card}\,}}\sigma (M_{x_j}) \le \dim ( {\mathbb {C}}^p[x_1,\dots , x_d]/{\mathcal {J}}) =r< \infty . \end{aligned}$$

We next fix a basis ${\mathcal {D}}$ of ${\mathbb {C}}^p[x_1,\dots , x_d]/{\mathcal {J}}$ and let $A_j\in {\mathbb {C}}^{r\times r}$ be the matrix representation of $M_{x_j}$ with respect to ${\mathcal {D}}.$ Then since $M_{x_j}$ are commuting self-adjoint operators we get

$$\begin{aligned} A_j^*=A_j\;\; \text {for}\;\; j=1, \dots , d. \end{aligned}$$

By [47, Theorem 2.5.5], there exists unitary $U \in {\mathbb {C}}^{r\times r}$ such that

$$\begin{aligned} A_j= U \mathrm {diag}(\nu _1^{(j)}, \ldots , \nu _r^{(j)})U^* \;\; \text {for}\;\; j=1, \dots , d \end{aligned}$$

and $\mathrm {diag}(\nu _1^{(j)}, \ldots , \nu _r^{(j)})\in {\mathbb {C}}^{r\times r}$ with $\nu _1^{(j)}, \ldots , \nu _r^{(j)}$ the eigenvalues of $A_j.$ Therefore

$$\begin{aligned} \sigma (M_x)=\{ (\nu _1^{(1)}, \dots , \nu _1^{(d)}), \dots , (\nu _r^{(1)}, \dots , \nu _r^{(d)}) \}, \end{aligned}$$

from which we derive

$\square$

The following proposition proves the existence of a representing measure T for a given ${\mathcal {H}}_p$-valued multisequence $S^{(\infty )}:=(S_\gamma )_{\gamma \in {\mathbb {N}}_0^d}$ which gives rise to an infinite d-Hankel matrix with finite rank. In Sect. 5.4 we will obtain additional information on the representing measure T.

Proposition 5.49

Let $S^{(\infty )}:=(S_\gamma )_{\gamma \in {\mathbb {N}}_0^d}$ be a given ${\mathcal {H}}_p$-valued multisequence with corresponding d-Hankel matrix $M(\infty )\succeq 0.$ Suppose $r:={{\,\mathrm{rank}\,}}M(\infty )< \infty .$ Then $S^{(\infty )}$ has a representing measure T.

Proof

First we show

$$\begin{aligned} v^*S_\gamma v =\langle M_{x_1}^{\gamma _1}\cdots M_{x_d}^{\gamma _d} (v+ {\mathcal {J}}), v+ {\mathcal {J}}\rangle= & {} \int _{{\mathbb {R}}^d} x_1^{\gamma _1}\cdots x_d^{\gamma _d} d \langle E(x_1,\ldots , x_d)(v+ {\mathcal {J}}),\nonumber \\&v+ {\mathcal {J}}\rangle , \end{aligned}$$

(5.14)

that is,

$$\begin{aligned} v^*S_\gamma v =\langle M_{x_1}^{\gamma _1}\cdots M_{x_d}^{\gamma _d} (v+ {\mathcal {J}}), v+ {\mathcal {J}}\rangle = \int _{{\mathbb {R}}^d} x^\gamma d \langle E(x_1,\ldots , x_d)(v+ {\mathcal {J}}), v+ {\mathcal {J}}\rangle \end{aligned}$$

(5.15)

for all $v\in {\mathbb {C}}^p$ and $\gamma \in {\mathbb {N}}_0^d.$ For all $v\in {\mathbb {C}}^p,$ we have

$$\begin{aligned} \langle M_{x_1}^{\gamma _1}\cdots M_{x_d}^{\gamma _d} (v+ {\mathcal {J}}), v+ {\mathcal {J}}\rangle= & {} \langle x_1^{\gamma _1}\cdots x_d^{\gamma _d} v + {\mathcal {J}}, v+ {\mathcal {J}}\rangle \\= & {} {\hat{v}}^* M(\infty )\widehat{(x^\gamma v)}\\= & {} {\hat{v}}^*{{\,\mathrm{col}\,}}(S_{{\tilde{\gamma }}+\gamma } {\hat{v}})_{{\tilde{\gamma }}\in {\mathbb {N}}_0^d} \\= & {} v^*S_\gamma v \end{aligned}$$

Therefore, we have obtained the left hand side of the equation (5.14). The right hand side is implied by Remark 5.46. Indeed we have

$$\begin{aligned}&\left\langle \int _{{\mathbb {R}}^d} x_1^{\gamma _1}\cdots x_d^{\gamma _d} dE(x_1,\ldots , x_d)(v+ {\mathcal {J}}), (v+ {\mathcal {J}}) \right\rangle \\&\quad = \int _{{\mathbb {R}}^d} x_1^{\gamma _1}\cdots x_d^{\gamma _d} d\langle E(x_1,\ldots , x_d)(v+ {\mathcal {J}}), v+ {\mathcal {J}}\rangle \\&\quad =\langle M_{x_1}^{\gamma _1}\cdots M_{x_d}^{\gamma _d} (v+ {\mathcal {J}}), v+ {\mathcal {J}}\rangle , \end{aligned}$$

for $\gamma \in {\mathbb {N}}_0^d$ and Eq. (5.15) holds. Let $v^*T(\alpha )v:=\langle E(\alpha )(v+ {\mathcal {J}}), v+ {\mathcal {J}}\rangle$ for every $\alpha \in {{\mathcal {B}}({\mathbb {R}}^d)}.$ We rewrite Eq. (5.15) as

$$\begin{aligned} v^*S_\gamma v =\langle M_{x_1}^{\gamma _1}\cdots M_{x_d}^{\gamma _d} (v+ {\mathcal {J}}), v+ {\mathcal {J}}\rangle = \int _{{\mathbb {R}}^d} x^\gamma d\langle T(x)v, v\rangle \end{aligned}$$

and let $T_{v, v}(\alpha ):= v^*T(\alpha )v,$ where $\alpha \in {{\mathcal {B}}({\mathbb {R}}^d)}.$ Notice that $T_{v, v}(\alpha ) \succeq 0.$ We need to show

$$\begin{aligned} v^*S_\gamma w=\int _{{\mathbb {R}}^d} x^\gamma dT_{w, v}(x) \quad \text {for}\;\; \gamma \in {\mathbb {N}}_0^d. \end{aligned}$$

Fix $\alpha \in {\mathcal {B}}({\mathbb {R}}^d)$ and define

$$\begin{aligned} T_{w, v}(\alpha ):=\frac{1}{4}( T_{w+ v}(\alpha )- T_{w- v}(\alpha ) + i T_{w+i v}(\alpha )-iT_{w-iv}(\alpha ))\quad \text {for}\;v, w\in {\mathbb {C}}^p. \end{aligned}$$

(5.16)

We observe

$$\begin{aligned} 4\int _{{\mathbb {R}}^d} x^\gamma dT_{w, v}(x)= & {} \int _{{\mathbb {R}}^d} x^\gamma dT_{w+ v}(x) -\int _{{\mathbb {R}}^d} x^\gamma dT_{w- v}(x) \\&+i \int _{{\mathbb {R}}^d} x^\gamma dT_{w+i v}(x) -i \int _{{\mathbb {R}}^d} x^\gamma dT_{w-iv}(x) \\= & {} (w+v)^*S_\gamma (w+v)- (w-v)^*S_\gamma (w-v) \\&+i(w+iv)^*S_\gamma (w+iv)-i(w-iv)^*S_\gamma (w-iv) \\= & {} 4v^*S_\gamma w \end{aligned}$$

for all $\gamma \in {\mathbb {N}}_0^d$ and $v, w \in {\mathbb {C}}^p.$ Thus

$$\begin{aligned} v^*S_\gamma w = \int _{{\mathbb {R}}^d} x^\gamma dT_{w, v}(x) \quad \text {for} \;\; v, w\in {\mathbb {C}}^p\;\text { and}\;\gamma \in {\mathbb {N}}_0^d. \end{aligned}$$

(5.17)

Let $\beta (w, v):{\mathbb {C}}^p \times {\mathbb {C}}^p \rightarrow {\mathbb {C}}$ be given by $\beta (w, v ):=T_{w, v}(\alpha )$ where $\alpha \in {\mathcal {B}}({\mathbb {R}}^d)$ is fixed. Using the assumption (1.3) we have

$$\begin{aligned} T_{v, v}(\alpha ) \le T_{v, v}( {\mathbb {R}}^d) = v^* S_{0_d} v = v^* I_p v \le \max \frac{v^*I_p v}{v^*v}v^*v = || v ||^2, \end{aligned}$$

by the Rayleigh-Ritz Theorem (see, e.g., [47, Theorem 4.2.2]), where $\max \frac{v^*I_pv}{v^*v},$ $v\ne 0_p,$ is the maximum eigenvalue of the matrix $I_p$. For all $w, v \in {\mathbb {C}}^p,$ formula (5.16) yields

$$\begin{aligned} |\beta (w, v )|= & {} |T_{w, v}(\alpha )|\\\le & {} \left| \frac{1}{4}\bigg (||w+v||^2 -||w-v||^2+i||w+iv||^2-i||w-iv||^2 \bigg )\right| \\= & {} \left| \frac{1}{4}\bigg (||w||^2+||v||^2+2\mathrm {Re}(\langle w, v \rangle )-(||w||^2+||v||^2-2\mathrm {Re}(\langle w, v \rangle ))\right. \\&\left. +i(||w||^2+||v||^2-2i\mathrm {Re}(\langle w, v \rangle ) ) -i(||w||^2+||v||^2+2i\mathrm {Re}(\langle w, v \rangle )) \bigg )\right| \\= & {} |2\mathrm {Re}(\langle w, v \rangle )|\\\le & {} 2 ||w||\;||v||, \end{aligned}$$

by the Cauchy-Schwarz inequality. Hence $\beta$ is a bounded sesquilinear form. For every $v \in {\mathbb {C}}^p,$ the linear functional $L_{v}: {\mathbb {C}}^p\rightarrow {\mathbb {C}}$ given by $L_{v}(w)= \beta (w, v)$ is such that

$$\begin{aligned} |L_{v}(w)|= |\beta (w, v)|\le ||\beta ||\; ||w ||\; || v ||. \end{aligned}$$

By the Riesz Representation Theorem for Hilbert spaces (see, e.g., [62, Theorem 4, Section 6.3]), there exists a unique $\varphi \in {\mathbb {C}}^p$ such that $L_{v}(w)= \langle \varphi , v \rangle \; \text {for all}\; v \in {\mathbb {C}}^p.$ Let $T: {{\mathcal {B}}({\mathbb {R}}^d)}\rightarrow {\mathcal {H}}_p$ be given by

$$\begin{aligned} v^*T(\alpha )w=\beta (w, v)= T_{w, v}(\alpha ) \quad \text {for}\;\; w,v \in {\mathbb {C}}^p, \end{aligned}$$

for which $T(\alpha ) w =\varphi ,$ $\alpha \in {{\mathcal {B}}({\mathbb {R}}^d)}.$ Since

$$\begin{aligned} w^*T(\alpha )w= T_{w, w}(\alpha )\ge 0\;\; \text {for}\; w\in {\mathbb {C}}^p, \end{aligned}$$

we have $T(\alpha )\succeq 0\;\;\text {for} \;\;\alpha \in {{\mathcal {B}}({\mathbb {R}}^d)}.$ Therefore, formula (5.17) implies

$$\begin{aligned} S_\gamma = \int _{{\mathbb {R}}^d} x^\gamma dT(x)\; \text { for}\; \gamma \in {\mathbb {N}}_0^d \end{aligned}$$

and so, $S^{(\infty )}$ has a representing measure T. $\square$

5.3 Necessary Conditions for the Existence of a Representing Measure

Throughout this subsection a series of lemmas are shown on the variety of the d-Hankel matrix and its connection with the support of the representing measure.

Lemma 5.50

Let $S:=(S_\gamma )_{\gamma \in \Gamma _{2n, d}}$ be a given truncated ${\mathcal {H}}_p$-valued multisequence and M(n) the corresponding d-Hankel matrix. If S has a representing measure T,  then $M(n)\succeq 0.$

Proof

For $\eta = {{\,\mathrm{col}\,}}(\eta _{\lambda })_{\lambda \in \Gamma _{n, d}},$ we have

$$\begin{aligned} \eta ^*M(n)\eta =\int _{{\mathbb {R}}^d} \zeta (x)^*dT(x) \zeta (x) \ge 0, \end{aligned}$$

where $\zeta (x)=\sum \nolimits _{\lambda \in \Gamma _{n, d}} x^\lambda \eta _\lambda .$ $\square$

Definition 5.51

Let T be a representing measure for $S:=(S_\gamma )_{\gamma \in \Gamma _{2n, d}},$ where $S_\gamma \in {\mathcal {H}}_p$ for $\gamma \in \Gamma _{2n, d}$ and $P(x)= \sum \nolimits _{\lambda \in \Gamma _{n, d}} x^\lambda P_{\lambda } \in {\mathbb {C}}^{p \times p}_n[x_1, \dots ,x_d].$ We define

$$\begin{aligned} \int _{{\mathbb {R}}^d} P(x)^*dT(x) P(x):= \sum \limits _{{\lambda , \gamma }\in \Gamma _{n, d}} P_{\lambda } ^* S_{\gamma +\lambda } P_{\gamma }. \end{aligned}$$

Remark 5.52

In view of [51, Theorem 2], if S has a representing measure T,  then we can always find a representing measure ${\tilde{T}}$ for S of the form ${\tilde{T}}=\sum \nolimits _{a=1}^{\kappa } Q_a \delta _{w^{(a)}}$ with $\kappa \le \left( {\begin{array}{c}2n+d\\ d\end{array}}\right) p.$ Then we may let

$$\begin{aligned} \int _{{\mathbb {R}}^d} P(x)^*d{\tilde{T}}(x) P(x):=\sum \limits _{a=1}^{\kappa } P({w^{(a)}}) ^* Q_a P({w^{(a)}}). \end{aligned}$$

The following lemma will connect the support of a representing measure of an ${\mathcal {H}}_p$-valued truncated multisequence and the variety of the d-Hankel matrix M(n) and is a matricial generalisation of Proposition 3.1 in [16] (albeit in an equivalent complex moment problem setting). As we will see in Example 5.54, unlike the scalar setting (i.e., when $p = 1$), we only have one direction of the implication. Moreover, the proof of Lemma 5.53 is more cumbersome than the scalar case.

Lemma 5.53

Let $S:=(S_\gamma )_{\gamma \in \Gamma _{2n, d}}$ be a given truncated ${\mathcal {H}}_p$-valued multisequence with a representing measure T. Suppose M(n) is the corresponding d-Hankel matrix. If

$$\begin{aligned} {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{\lambda \in \Gamma _{n, d}} S_{\gamma +\lambda } P_{\lambda }\bigg )_{\gamma \in \Gamma _{n, d}}={{\,\mathrm{col}\,}}(0_{p \times p})_{\gamma \in \Gamma _{n, d}}, \end{aligned}$$

then

$$\begin{aligned} {{\,\mathrm{supp}\,}}T\subseteq {\mathcal {Z}}(\det P(x)), \end{aligned}$$

where $P(x)= \sum \nolimits _{\lambda \in \Gamma _{n, d}} x^\lambda P_{\lambda } \in {\mathbb {C}}^{p \times p}_n[x_1, \dots ,x_d].$

Proof

If ${{\,\mathrm{col}\,}}\bigg ( \sum \nolimits _{\lambda \in \Gamma _{n, d}} S_{\gamma +\lambda } P_{\lambda }\bigg )_{\gamma \in \Gamma _{n, d}}={{\,\mathrm{col}\,}}(0_{p \times p})_{\gamma \in \Gamma _{n, d}},$ then

$$\begin{aligned} {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{\lambda \in \Gamma _{n, d}} S_{\gamma +\lambda } P_{\lambda }\bigg )_{\gamma \in \Gamma _{n, d}}^*{{\,\mathrm{col}\,}}\bigg ( \sum \limits _{\lambda \in \Gamma _{n, d}} S_{\gamma +\lambda } P_{\lambda }\bigg )_{\gamma \in \Gamma _{n, d}}=0_{p \times p}, \end{aligned}$$

that is, $\sum \nolimits _{{\lambda , \gamma }\in \Gamma _{n, d}} P_{\lambda } ^* S_{\gamma +\lambda } P_{\gamma } = 0_{p \times p},$ which is equivalent to $\int _{{\mathbb {R}}^d} P(x)^*dT(x) P(x)= 0_{p \times p}.$ Indeed

$$\begin{aligned} {{\,\mathrm{col}\,}}(P_\lambda )_{\lambda \in \Gamma _{n, d}}^*{{\,\mathrm{col}\,}}\bigg ( \sum \limits _{\gamma \in \Gamma _{n, d}} S_{\gamma +\lambda } P_{\gamma }\bigg )_{\lambda \in \Gamma _{n, d}}=0_{p \times p} \end{aligned}$$

and so

$$\begin{aligned} {{\,\mathrm{col}\,}}(P_\lambda )_{\lambda \in \Gamma _{n, d}}^*M(n){{\,\mathrm{col}\,}}(P_\lambda )_{\lambda \in \Gamma _{n, d}}= & {} \displaystyle \sum \limits _{{\lambda , \gamma }\in \Gamma _{n, d}} P_{\lambda } ^* S_{\gamma +\lambda } P_{\gamma }\\= & {} \displaystyle \int _{{\mathbb {R}}^d} P(x)^*dT(x) P(x) \\= & {} 0_{p \times p}. \end{aligned}$$

Suppose to the contrary that

$$\begin{aligned} {{\,\mathrm{supp}\,}}T \nsubseteq {\mathcal {Z}}(\det P(x)). \end{aligned}$$

Then there exists a point $u^{(0)}\in {{\,\mathrm{supp}\,}}T$ such that $u^{(0)} \notin {\mathcal {Z}}(\det P(x))$ and

$$\begin{aligned} B_{\varepsilon }(u^{(0)})=\{x\in {\mathbb {R}}^d: ||x-u^{(0)}||<\varepsilon \}\quad \text {for}\;\; \varepsilon >0\;\; \text {small enough}, \end{aligned}$$

has the property $T(\overline{B_{\varepsilon }(u^{(0)})})\ne 0_{p\times p}$ and $\overline{B_{\varepsilon }(u^{(0)})}\cap {\mathcal {Z}}(\det P(x))=\emptyset .$ We write

$$\begin{aligned} \int _{{\mathbb {R}}^d} P(x)^*d{T}(x) P(x)=\int _{\overline{B_{\varepsilon }(u^{(0)})}} P(x)^*d{T}(x) P(x)+ \int _{{\mathbb {R}}^d\setminus \overline{B_{\varepsilon }(u^{(0)})}} P(x)^*d{T}(x) P(x) \end{aligned}$$

and we note that both terms on the right hand side are positive semidefinite.

Let $Y:=T|_{\overline{B_{\varepsilon }(u^{(0)})}}=T(\sigma \cap \overline{B_{\varepsilon }(u^{(0)})} )$ for $\sigma \in {\mathcal {B}}({\mathbb {R}}^d).$ Consider ${\tilde{S}}:=({\tilde{S}}_\gamma )_{\gamma \in \Gamma _{2n, d}},$ where

$$\begin{aligned} \tilde{S_\gamma }= \int _{{\mathbb {R}}^d} x^\gamma dY(x) \quad \text {for} \;\;\gamma \in \Gamma _{2n, d} \end{aligned}$$

and note that ${\tilde{S}}_{0_{d}}=\int _{{\mathbb {R}}^d} dY(x)=Y(\overline{B_{\varepsilon }(u^{(0)})})\ne 0_{p\times p}.$ Applying [51, Theorem 2] we obtain a representing measure for ${\tilde{S}}$ of the form ${\widetilde{Y}}= \sum \nolimits _{a=1}^{\kappa } Q_a \delta _{u^{(a)}},$ with nonzero $Q_a \succeq 0,$ $\kappa \le \left( {\begin{array}{c}2n+d\\ d\end{array}}\right) p$ and $u^{(1)}, \dots , u^{(\kappa )}\in \overline{B_{\varepsilon }(u^{(0)})}.$ But then

$$\begin{aligned} 0_{p\times p}= \displaystyle \int _{\overline{B_{\varepsilon }(u^{(0)})}} P(x)^*d{T}(x) P(x)= & {} \displaystyle \int _{{\mathbb {R}}^d} P(x)^*d{Y}(x) P(x)\\= & {} \displaystyle \int _{{\mathbb {R}}^d} P(x)^*d {\widetilde{Y}}(x) P(x)\\= & {} \displaystyle \sum \limits _{a=1}^{\kappa } P(u^{(a)}) ^* Q_a P(u^{(a)}), \end{aligned}$$

by Remark 5.52. Since $P(u^{(a)}) ^* Q_a P(u^{(a)}) \succeq 0_{p \times p} \;\;\text {for} \; a=1,\dots \kappa ,$ we derive

$$\begin{aligned} P(u^{(a)}) ^* Q_a P(u^{(a)}) = 0_{p \times p} \;\;\text {for} \;\;a=1,\dots \kappa . \end{aligned}$$

(5.18)

But $P(u^{(a)})$ is invertible and therefore formula (5.18) implies $Q_a= 0_{p \times p}$ for $a=1,\dots \kappa ,$ a contradiction. $\square$

The next example illustrates that the converse of Lemma 5.53 does not hold.

Example 5.54

Let $S:=(S_\gamma )_{\gamma \in \Gamma _{2, 2}}$ be a truncated ${\mathcal {H}}_2$-valued bisequence with $S_{00}=I_2,$ $S_{10}=\frac{1}{2}\begin{pmatrix} 1&{}0\\ 0&{}0 \end{pmatrix}=S_{20},$ $S_{01}=\frac{1}{2}\begin{pmatrix} 0&{}0\\ 0&{}1 \end{pmatrix}=S_{02}$ and $S_{11}=0_{2\times 2}.$ Then S has a representing measure T given by

$$\begin{aligned} T=\frac{1}{2} \bigg (I_2\delta _{(0,0)} +\begin{pmatrix} 1&{}0\\ 0&{}0 \end{pmatrix}\delta _{(1,0)} +\begin{pmatrix} 0&{}0\\ 0&{}1 \end{pmatrix}\delta _{(0,1)} \bigg ). \end{aligned}$$

Choose the matrix-valued polynomial in ${\mathbb {C}}^{2 \times 2}_1[x,y]$

$$\begin{aligned} \begin{array}{clll} P(x, y)&{}=\begin{pmatrix} x&{}1\\ 0&{}y \end{pmatrix}\\ &{}=\begin{pmatrix} 0&{}1\\ 0&{}0 \end{pmatrix}+x\begin{pmatrix} 1&{}0\\ 0&{}0 \end{pmatrix}+y\begin{pmatrix} 0&{}0\\ 0&{}1 \end{pmatrix} \end{array} \end{aligned}$$

and notice that $\det P(x, y)=xy$ and

$$\begin{aligned} \det P(x, y)|_{{{\,\mathrm{supp}\,}}T}=0. \end{aligned}$$

We have

$$\begin{aligned} \begin{array}{clll} P(X,Y)&{}= \begin{pmatrix} S_{00}\\ S_{10}\\ S_{01} \end{pmatrix}\begin{pmatrix} 0&{}1\\ 0&{}0 \end{pmatrix}+\begin{pmatrix} S_{10}\\ S_{20}\\ S_{11} \end{pmatrix}\begin{pmatrix} 1&{}0\\ 0&{}0 \end{pmatrix}+\begin{pmatrix} S_{01}\\ S_{11}\\ S_{02} \end{pmatrix}\begin{pmatrix} 0&{}0\\ 0&{}1 \end{pmatrix}\ne {{\,\mathrm{col}\,}}(0_{2 \times 2})_{\gamma \in \Gamma _{1, 2}} \end{array}, \end{aligned}$$

which asserts that the converse of Lemma 5.53 does not hold.

We continue with results on the variety of a d-Hankel matrix and its connection with the support of a representing measure T.

Lemma 5.55

Suppose $S:=(S_\gamma )_{\gamma \in \Gamma _{2n, d}}$ is a given truncated ${\mathcal {H}}_p$-valued multisequence with a representing measure T. Let M(n) be the corresponding d-Hankel matrix and let ${\mathcal {V}}(M(n))$ be the variety of M(n) (see Definition 3.5). Let $P(x)= \sum \nolimits _{\lambda \in \Gamma _{n, d}} x^\lambda P_{\lambda } \in {\mathbb {C}}^{p \times p}_n[x_1, \dots ,x_d].$ If

$$\begin{aligned} {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{\lambda \in \Gamma _{n, d}} S_{\gamma +\lambda } P_{\lambda }\bigg )_{\gamma \in \Gamma _{n, d}}={{\,\mathrm{col}\,}}(0_{p \times p})_{\gamma \in \Gamma _{n, d}}, \end{aligned}$$

then

$$\begin{aligned} {{\,\mathrm{supp}\,}}T\subseteq {\mathcal {V}}(M(n)). \end{aligned}$$

Proof

By Lemma 5.53, for any $P(x) \in {\mathbb {C}}^{p \times p}_n[x_1, \dots ,x_d]$ with

$$\begin{aligned} P(X)={{\,\mathrm{col}\,}}\bigg ( \sum \limits _{\lambda \in \Gamma _{n, d}} S_{\gamma +\lambda } P_{\lambda }\bigg )_{\gamma \in \Gamma _{n, d}}={{\,\mathrm{col}\,}}(0_{p \times p})_{\gamma \in \Gamma _{n, d}}, \end{aligned}$$

we have ${{\,\mathrm{supp}\,}}T\subseteq {\mathcal {Z}}(\det P(x)).$ Thus

$$\begin{aligned} \bigcap _{{\mathop {P\in {{\mathbb {C}}}^{p\times p}_n[x_1,\dots , x_d]}\limits ^{P(X)={{\,\mathrm{col}\,}}( 0_{p\times p})_{\gamma \in \Gamma _{n, d}}}}}{{\,\mathrm{supp}\,}}T\subseteq \bigcap _{{\mathop {P\in {{\mathbb {C}}}^{p\times p}_n[x_1,\dots , x_d]}\limits ^{P(X)={{\,\mathrm{col}\,}}( 0_{p\times p})_{\gamma \in \Gamma _{n, d}}}}} {\mathcal {Z}}(\det P(x)), \end{aligned}$$

which implies that

$\square$

Lemma 5.56

Let $S:=(S_\gamma )_{\gamma \in \Gamma _{2n, d}}$ be a given truncated ${\mathcal {H}}_p$-valued multisequence and let M(n) be the corresponding d-Hankel matrix. If S has a representing measure T and $w^{(1)}, \dots , w^{(\kappa )}\in {\mathbb {R}}^d$ are given such that

$$\begin{aligned} {{\,\mathrm{supp}\,}}T=\{ w^{(1)}, \dots , w ^{(\kappa )} \}, \end{aligned}$$

then there exists $P(x) \in {\mathbb {C}}^{p \times p}_n[x_1, \dots ,x_d]$ such that

$$\begin{aligned} {\mathcal {Z}}(\det P(x))= \{ w^{(1)}, \dots , w ^{(\kappa )} \}. \end{aligned}$$

Moreover

$$\begin{aligned} {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{\lambda \in \Gamma _{n, d}} S_{\gamma +\lambda } P_{\lambda }\bigg )_{\gamma \in \Gamma _{n, d}}={{\,\mathrm{col}\,}}(0_{p \times p})_{\gamma \in \Gamma _{n, d}}, \end{aligned}$$

and

$$\begin{aligned} {\mathcal {V}}(M(n))\subseteq {{\,\mathrm{supp}\,}}T, \end{aligned}$$

where ${\mathcal {V}}(M(n))$ the variety of M(n) (see Definition 3.5).

Proof

If we let $P(x):= \prod _{a=1}^{\kappa } \prod _{j=1}^{d} (x_j -w_{j} ^{(a)})I_p,$ then $\det P(x)= \prod _{a=1}^{\kappa } \prod _{j=1}^{d} (x_j -w_{j} ^{(a)})^p$ and so

$$\begin{aligned} \det P(w^{(a)})= \prod _{a=1}^{\kappa } \prod _{j=1}^{d} (w_{j} ^{(a)} -w_{j} ^{(a)})^p=0. \end{aligned}$$

Thus

$$\begin{aligned} \{ w^{(1)}, \dots , w ^{(\kappa )} \}\subseteq {\mathcal {Z}}(\det P(x)). \end{aligned}$$

(5.19)

If we let ${P}(x):= \prod _{a=1}^{\kappa } \bigg ( \sum _{j=1}^{d} (x_j -w_{j} ^{(a)})^2 \bigg )I_p,$ then $\det {P}(x)= \prod _{a=1}^{\kappa } \bigg ( \sum _{j=1}^{d} (x_j -w_{j} ^{(a)})^2 \bigg )^p$ and hence

$$\begin{aligned} \det {P}(w^{(a)})= \prod _{a=1}^{\kappa } \bigg ( \sum _{j=1}^{d} (w_j^{(a)} -w_{j} ^{(a)})^2 \bigg )^p=0, \end{aligned}$$

which yields

$$\begin{aligned} {\mathcal {Z}}(\det P(x))\subseteq \{ w^{(1)}, \dots , w ^{(\kappa )} \}. \end{aligned}$$

(5.20)

Then by inclusions (5.19) and (5.20), we obtain

$$\begin{aligned} {\mathcal {Z}}(\det P(x))= \{ w^{(1)}, \dots , w ^{(\kappa )} \}. \end{aligned}$$

Hence ${\mathcal {Z}}(\det P(x))= \{ w^{(1)}, \dots , w ^{(\kappa )} \}= {{\,\mathrm{supp}\,}}T,$ where $T=\sum \nolimits _{a=1}^{\kappa } Q_a \delta _{w^{(a)}}.$ We will next show that for both choices of $P\in {\mathbb {C}}^{p \times p}_{n}[x_1, \dots ,x_d],$ one obtains

$$\begin{aligned} {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{\lambda \in \Gamma _{n, d}} S_{\gamma +\lambda } P_{\lambda }\bigg )_{\gamma \in \Gamma _{n, d}}={{\,\mathrm{col}\,}}(0_{p \times p})_{\gamma \in \Gamma _{n, d}} \end{aligned}$$

and thus ${\mathcal {V}}(M(n))\subseteq {{\,\mathrm{supp}\,}}T.$ For the choice of $P(x):= \prod _{a=1}^{\kappa } \prod _{j=1}^{d} (x_j -w_{j} ^{(a)})I_p\in {{\mathbb {C}}}^{p\times p}_n[x_1,\dots , x_d],$

$$\begin{aligned} {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{\lambda \in \Gamma _{n, d}} S_{\gamma +\lambda } P_{\lambda }\bigg )_{\gamma \in \Gamma _{n, d}}={{\,\mathrm{col}\,}}(0_{p \times p})_{\gamma \in \Gamma _{n, d}}. \end{aligned}$$

Consider $P(X)\in C_{M(n)}.$ We have ${\mathcal {Z}}(\det P(x))= {{\,\mathrm{supp}\,}}T$ and we shall see $P(X)= {{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in \Gamma _{n, d}}.$ We notice

$$\begin{aligned} P(X)= & {} {{\,\mathrm{col}\,}}\left( \sum \limits _{\lambda \in \Gamma _{n, d}} X^{\gamma +\lambda } P_\lambda \right) _{\gamma \in \Gamma _{n, d}}\\= & {} {{\,\mathrm{col}\,}}\bigg ( \int _{{\mathbb {R}}^d} x^\gamma dT(x) P(x) \bigg )_{\gamma \in \Gamma _{n, d}}\\= & {} {{\,\mathrm{col}\,}}\bigg ( \int _{{\mathbb {R}}^d} x^\gamma dT(x) \prod \limits _{a=1}^{\kappa } \prod \limits _{j=1}^{d} (x_j -w_{j} ^{(a)})I_p \bigg )_{\gamma \in \Gamma _{n, d}}\\= & {} {{\,\mathrm{col}\,}}\bigg ( \int _{{\mathbb {R}}^d} x^\gamma \varphi (x) dT(x) \bigg )_{\gamma \in \Gamma _{n, d}}, \end{aligned}$$

where $\varphi (x)= \prod _{a=1}^{\kappa } \prod _{j=1}^{d} (x_j -w_{j} ^{(a)}) \in {\mathbb {R}}[x_1, \dots ,x_d].$ Since $T=\sum \nolimits _{a=1}^{\kappa } Q_a \delta _{w^{(a)}},$ P(X) becomes

$$\begin{aligned} {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{a=1}^{\kappa } \{w^{(a)}\}^\gamma \varphi (w^{(a)}) Q_a \bigg )_{\gamma \in \Gamma _{n, d}}= & {} {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{a=1}^{\kappa } \{w^{(a)}\}^\gamma \prod \limits _{a=1}^{\kappa } \prod \limits _{j=1}^{d} (w_{j} ^{(a)} -w_{j} ^{(a)}) Q_a \bigg )_{\gamma \in \Gamma _{n, d}}\\= & {} {{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in \Gamma _{n, d}} \end{aligned}$$

and hence $P(X)={{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in \Gamma _{n, d}}.$ Since there exists matrix-valued polynomial P(x) such that $P(X)={{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in \Gamma _{n, d}}$ and ${\mathcal {Z}}(\det P(x))= {{\,\mathrm{supp}\,}}T,$ we then have

$$\begin{aligned} \bigcap _{{\mathop {P\in {{\mathbb {C}}}^{p\times p}_n[x_1,\dots , x_d]}\limits ^{P(X)={{\,\mathrm{col}\,}}( 0_{p\times p})_{\gamma \in \Gamma _{n, d}}}}}{\mathcal {Z}}(\det P(x))\subseteq \bigcap _{{\mathop {P\in {{\mathbb {C}}}^{p\times p}_n[x_1,\dots , x_d]}\limits ^{P(X)={{\,\mathrm{col}\,}}( 0_{p\times p})_{\gamma \in \Gamma _{n, d}}}}} {{\,\mathrm{supp}\,}}T, \end{aligned}$$

which implies

$$\begin{aligned} {\mathcal {V}}(M(n))\subseteq {{\,\mathrm{supp}\,}}T. \end{aligned}$$

Next, for the choice of $P(x):= \prod _{a=1}^{\kappa } \bigg ( \sum _{j=1}^{d} (x_j -w_{j} ^{(a)})^2 \bigg )I_p \in {\mathbb {C}}^{p \times p}_{n}[x_1, \dots ,x_d],$ we will show that

$$\begin{aligned} {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{\lambda \in \Gamma _{n, d}} S_{\gamma +\lambda } P_{\lambda }\bigg )_{\gamma \in \Gamma _{n, d}}={{\,\mathrm{col}\,}}(0_{p \times p})_{\gamma \in \Gamma _{n, d}}. \end{aligned}$$

We have ${\mathcal {Z}}(\det P(x))= {{\,\mathrm{supp}\,}}T$ and we consider $P(X)\in C_{M(n)}$. We need to show that for this choice of P(x),  $P(X)= {{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in \Gamma _{n, d}}.$ Notice that

$$\begin{aligned} P(X)= & {} {{\,\mathrm{col}\,}}\left( \sum \limits _{\lambda \in \Gamma _{n, d}} X^{\gamma +\lambda } P_\lambda \right) _{\gamma \in \Gamma _{n, d}}\\= & {} {{\,\mathrm{col}\,}}\bigg ( \int _{{\mathbb {R}}^d} x^\gamma dT(x) P(x) \bigg )_{\gamma \in \Gamma _{n, d}}\\= & {} {{\,\mathrm{col}\,}}\bigg ( \int _{{\mathbb {R}}^d} x^\gamma dT(x) \prod \limits _{a=1}^{\kappa } \bigg ( \sum \limits _{j=1}^{d} (x_j -w_{j} ^{(a)})^2 \bigg )I_p \bigg )_{\gamma \in \Gamma _{n, d}}\\= & {} {{\,\mathrm{col}\,}}\bigg ( \int _{{\mathbb {R}}^d} x^\gamma {\tilde{\varphi }}(x) dT(x) \bigg )_{\gamma \in \Gamma _{n, d}}, \end{aligned}$$

where ${\tilde{\varphi }}(x)= \prod _{a=1}^{\kappa } \sum _{j=1}^{d} (x_j -w_{j} ^{(a)})^2 \in {\mathbb {R}}[x_1, \dots ,x_d].$ Since $T=\sum \nolimits _{a=1}^{\kappa } Q_a \delta _{w^{(a)}},$ P(X) becomes

$$\begin{aligned} {{\,\mathrm{col}\,}}\bigg ( \sum _{a=1}^{\kappa } \{w^{(a)}\}^\gamma {\tilde{\varphi }}(w^{(a)}) Q_a \bigg )_{\gamma \in \Gamma _{n, d}}&= {{\,\mathrm{col}\,}}\bigg ( \sum _{a=1}^{\kappa } \{w^{(a)}\}^\gamma \prod _{a=1}^{\kappa } \bigg ( \sum _{j=1}^{d} (w_{j} ^{(a)} -w_{j} ^{(a)})^2 \bigg ) Q_a \bigg )_{\gamma \in \Gamma _{n, d}}\\&= {{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in \Gamma _{n, d}} \end{aligned}$$

and so $P(X)={{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in \Gamma _{n, d}}.$ We thus conclude that there exists a matrix-valued polynomial P(x) such that $P(X)={{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in \Gamma _{n, d}}$ and ${\mathcal {Z}}(\det P(x))= {{\,\mathrm{supp}\,}}T$ and thus we obtain

$$\begin{aligned} \bigcap _{{\mathop {P\in {{\mathbb {C}}}^{p\times p}_n[x_1,\dots , x_d]}\limits ^{P(X)={{\,\mathrm{col}\,}}( 0_{p\times p})_{\gamma \in \Gamma _{n, d}}}}}{\mathcal {Z}}(\det P(x))\subseteq \bigcap _{{\mathop {P\in {{\mathbb {C}}}^{p\times p}_n[x_1,\dots , x_d]}\limits ^{P(X)={{\,\mathrm{col}\,}}( 0_{p\times p})_{\gamma \in \Gamma _{n, d}}}}} {{\,\mathrm{supp}\,}}T, \end{aligned}$$

which asserts

$\square$

Lemma 5.57

Let $S:= (S_\gamma )_{\gamma \in \Gamma _{2n, d}}$ be truncated ${\mathcal {H}}_p$-valued multisequence and let M(n) be the corresponding d-Hankel matrix. If T is a representing measure for S,  then

$$\begin{aligned} {{\,\mathrm{rank}\,}}M(n) \le \sum \limits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a. \end{aligned}$$

Proof

If ${{\,\mathrm{supp}\,}}T$ is infinite, then ${{\,\mathrm{rank}\,}}M(n) \le \sum \nolimits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a$ holds trivially. If ${{\,\mathrm{supp}\,}}T$ is finite, that is, T is of the form $T=\sum \nolimits _{a=1}^{\kappa } Q_a \delta _{w^{(a)}},$ then

$$\begin{aligned} M(n)= V^T R V, \end{aligned}$$

where $V:= V^{p\times p}(w^{(1)}, \dots , w^{(\kappa )}; \Lambda )\in {\mathbb {C}}^{\kappa p\times \kappa p}$ with $\Lambda \subseteq {\mathbb {N}}_0^d$ and ${{\,\mathrm{card}\,}}\Lambda =\kappa$ and

$$\begin{aligned} R:=Q_1\oplus \dots \oplus Q_\kappa = \begin{pmatrix} Q_1 &{} &{}0 \\ &{}\ddots &{}\\ 0 &{} &{}Q_\kappa \end{pmatrix} \in {\mathbb {C}}^{\kappa p\times \kappa p}. \end{aligned}$$

Hence

$$\begin{aligned} {{\,\mathrm{rank}\,}}M(n)\le & {} \min ({{\,\mathrm{rank}\,}}V^T, {{\,\mathrm{rank}\,}}RV)\\\le & {} \min ({{\,\mathrm{rank}\,}}V^T, {{\,\mathrm{rank}\,}}R, {{\,\mathrm{rank}\,}}V)\\\le & {} \min ({{\,\mathrm{rank}\,}}V, {{\,\mathrm{rank}\,}}R)\\\le & {} {{\,\mathrm{rank}\,}}R\\= & {} \sum \limits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a \end{aligned}$$

and the proof is complete. $\square$

Proposition 5.58

Let $S^{(\infty )}:=(S_\gamma )_{\gamma \in {\mathbb {N}}_0^d}$ be a given ${\mathcal {H}}_p$-valued multisequence with a representing measure T which has $\sum \nolimits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a < \infty$ and $M(\infty )$ be the corresponding d-Hankel matrix. Then

$$\begin{aligned} r:= {{\,\mathrm{rank}\,}}M(\infty )=\sum \limits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a. \end{aligned}$$

Proof

By Theorem 2.11, there exists $\Lambda \subseteq {\mathbb {N}}_0^d$ such that ${{\,\mathrm{card}\,}}\Lambda =\kappa$ and $V(w^{(1)}, \dots ,w^{(\kappa )};\Lambda )$ is invertible. If $S^{(\infty )}$ has a representing measure $T=\sum \nolimits _{a=1}^{\kappa } Q_a \delta _{w^{(a)}},$ then

$$\begin{aligned} {{\,\mathrm{rank}\,}}M_{\Lambda }(\infty ) \le {{\,\mathrm{rank}\,}}M(\infty )\le \sum \limits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a, \end{aligned}$$

(5.21)

where $M_{\Lambda }(\infty )$ is a principal submatrix of $M(\infty )$ with block rows and block columns indexed by $\Lambda .$ Notice that since $V(w^{(1)}, \dots ,w^{(\kappa )};\Lambda )$ is invertible, by Remark 5.23 we deduce that $V:=V^{p\times p}(w^{(1)}, \dots ,w^{(\kappa )}; \Lambda )\in {\mathbb {C}}^{\kappa p\times \kappa p}$ is invertible. Moreover, since $V \in {\mathbb {R}}^{\kappa p\times \kappa p},$ $M_{\Lambda }(\infty )$ can be written as

$$\begin{aligned} M_{\Lambda }(\infty )= V^T R V = V^* R V, \end{aligned}$$

where

$$\begin{aligned} R:=Q_1\oplus \dots \oplus Q_\kappa = \begin{pmatrix} Q_1 &{} &{}0 \\ &{}\ddots &{}\\ 0 &{} &{}Q_\kappa \end{pmatrix} \in {\mathbb {C}}^{\kappa p\times \kappa p}. \end{aligned}$$

By Sylvester’s law of inertia (see, e.g., [48, Theorem 4.5.8]), we have $i_{+}(M_{\Lambda }(\infty ))=i_{+}(R),$ where $i_{+}$ indicates the number of positive eigenvalues. So ${{\,\mathrm{rank}\,}}M_{\Lambda }(\infty ) = {{\,\mathrm{rank}\,}}R.$ However ${{\,\mathrm{rank}\,}}R= \sum \nolimits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a.$ By inequality (5.21),

$$\begin{aligned} \sum \limits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a \le {{\,\mathrm{rank}\,}}M(\infty ) \le \sum \limits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a, \end{aligned}$$

which implies

$\square$

Lemma 5.59

Suppose $S:=(S_\gamma )_{\gamma \in \Gamma _{2n, d}}$ is a truncated ${\mathcal {H}}_p$-valued multisequence with a representing measure T. Let M(n) be the corresponding d-Hankel matrix and ${\mathcal {V}}(M(n))$ be the variety of M(n) (see Definition 3.5). Then

$$\begin{aligned} {{\,\mathrm{rank}\,}}M(n)\le {{\,\mathrm{card}\,}}{\mathcal {V}}(M(n)). \end{aligned}$$

Proof

Lemma 5.57 asserts that ${{\,\mathrm{rank}\,}}M(n) \le \sum \nolimits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a$ and by Lemma 5.55,

$$\begin{aligned} {{\,\mathrm{supp}\,}}T \subseteq {\mathcal {V}}(M(n)), \end{aligned}$$

which implies $\sum \nolimits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a \le {{\,\mathrm{card}\,}}{\mathcal {V}}(M(n)).$ Hence

$\square$

In analogy to Lemma 5.56, we proceed to Lemmas 5.60 and 5.61 for $P \in {\mathbb {C}}^{p \times p}[x_1, \dots ,x_d].$

Lemma 5.60

Let $S^{(\infty )}:=(S_\gamma )_{\gamma \in {\mathbb {N}}_0^d }$ be a given ${\mathcal {H}}_p$-valued multisequence. If $S^{(\infty )}$ has a representing measure T and $w^{(1)}, \dots , w^{(\kappa )}\in {\mathbb {R}}^d$ are given, then there exists $P \in {\mathbb {C}}^{p \times p}[x_1, \dots ,x_d]$ such that

$$\begin{aligned} {\mathcal {Z}}(\det P(x))= \{ w^{(1)}, \dots , w ^{(\kappa )} \}. \end{aligned}$$

Moreover, $P \in {\mathcal {I}}$ and

$$\begin{aligned} {\mathcal {V}}({\mathcal {I}})\subseteq {{\,\mathrm{supp}\,}}T \end{aligned}$$

where ${\mathcal {I}}$ is as in Definition 5.13 and ${\mathcal {V}}({\mathcal {I}})$ the variety of ${\mathcal {I}}$ (see Definition 5.20).

Proof

Let the matrix-valued polynomial $P(x):= \prod _{a=1}^{\kappa } \prod _{j=1}^{d} (x_j -w_{j} ^{(a)})I_p\in {\mathbb {C}}^{p \times p}[x_1, \dots ,x_d].$ Then $\det P(x)= \prod _{a=1}^{\kappa } \prod _{j=1}^{d} (x_j -w_{j} ^{(a)})^p$ and so

$$\begin{aligned} \det P(w^{(a)})= \prod _{a=1}^{\kappa } \prod _{j=1}^{d} (w_{j} ^{(a)} -w_{j} ^{(a)})^p=0. \end{aligned}$$

Thus $\{ w^{(1)}, \dots , w ^{(\kappa )} \}\subseteq {\mathcal {Z}}(\det P(x)).$ To show the other inclusion, choose the matrix-valued polynomial ${P}(x):= \prod _{a=1}^{\kappa } \bigg ( \sum _{j=1}^{d} (x_j -w_{j} ^{(a)})^2 \bigg )I_p\in {\mathbb {C}}^{p \times p}[x_1, \dots ,x_d].$ Then we shall obtain $\det {P}(x)= \prod _{a=1}^{\kappa } \bigg ( \sum _{j=1}^{d} (x_j -w_{j} ^{(a)})^2 \bigg )^p$ and so

$$\begin{aligned} \det {P}(w^{(a)})= \prod _{a=1}^{\kappa } \bigg ( \sum _{j=1}^{d} (w_j^{(a)} -w_{j} ^{(a)})^2 \bigg )^p=0, \end{aligned}$$

which implies that ${\mathcal {Z}}(\det P(x))\subseteq \{ w^{(1)}, \dots , w ^{(\kappa )} \}.$ Thus

$$\begin{aligned} {\mathcal {Z}}(\det P(x))= \{ w^{(1)}, \dots , w ^{(\kappa )} \}. \end{aligned}$$

Let ${{\,\mathrm{supp}\,}}T=\{ w^{(1)}, \dots , w ^{(\kappa )} \}$ where $T=\sum \nolimits _{a=1}^{\kappa } Q_a \delta _{w^{(a)}}.$ In the following, we shall see that for both choices of the matrix-valued polynomial $P\in {\mathbb {C}}^{p \times p}[x_1, \dots ,x_d],$ one obtains $P\in {\mathcal {I}}$ and this in turn yields the inclusion ${\mathcal {V}}({\mathcal {I}})\subseteq {{\,\mathrm{supp}\,}}T.$ Consider first the matrix-valued polynomial $P(x):= \prod _{a=1}^{\kappa } \prod _{j=1}^{d} (x_j -w_{j} ^{(a)})I_p$ such that $P(X)\in C_{M(\infty )}.$ We have ${\mathcal {Z}}(\det P(x))= {{\,\mathrm{supp}\,}}T$ and we shall show that $P(X)= {{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in {\mathbb {N}}_0^d}.$ Notice that

$$\begin{aligned} P(X)= & {} {{\,\mathrm{col}\,}}\left( \sum \limits _{\lambda \in \Gamma _{n, d}} X^{\gamma +\lambda } P_\lambda \right) _{\gamma \in {\mathbb {N}}_0^d}\\= & {} {{\,\mathrm{col}\,}}\bigg ( \int _{{\mathbb {R}}^d} x^\gamma dT(x) P(x) \bigg )_{\gamma \in {\mathbb {N}}_0^d}\\= & {} {{\,\mathrm{col}\,}}\bigg ( \int _{{\mathbb {R}}^d} x^\gamma dT(x) \prod \limits _{a=1}^{\kappa } \prod \limits _{j=1}^{d} (x_j -w_{j} ^{(a)})I_p \bigg )_{\gamma \in {\mathbb {N}}_0^d}\\= & {} {{\,\mathrm{col}\,}}\bigg ( \int _{{\mathbb {R}}^d} x^\gamma \varphi (x) dT(x) \bigg )_{\gamma \in {\mathbb {N}}_0^d}, \end{aligned}$$

where $\varphi (x)= \prod _{a=1}^{\kappa } \prod _{j=1}^{d} (x_j -w_{j} ^{(a)}) \in {\mathbb {R}}[x_1, \dots ,x_d].$ Since $T=\sum \nolimits _{a=1}^{\kappa } Q_a \delta _{w^{(a)}},$ P(X) becomes

$$\begin{aligned} {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{a=1}^{\kappa } \{w^{(a)}\}^\gamma \varphi (w^{(a)}) Q_a \bigg )_{\gamma \in {\mathbb {N}}_0^d}= & {} {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{a=1}^{\kappa } \{w^{(a)}\}^\gamma \prod \limits _{a=1}^{\kappa } \prod \limits _{j=1}^{d} (w_{j} ^{(a)} -w_{j} ^{(a)}) Q_a \bigg )_{\gamma \in {\mathbb {N}}_0^d}\\= & {} {{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in {\mathbb {N}}_0^d} \end{aligned}$$

and hence $P \in {\mathcal {I}}.$ Since there exists $P \in {\mathcal {I}}$ such that ${\mathcal {Z}}(\det P(x))= {{\,\mathrm{supp}\,}}T,$

$$\begin{aligned} {\mathcal {V}}({\mathcal {I}}):=\bigcap _{P\in {\mathcal {I}}}{\mathcal {Z}}(\det P(x))\subseteq \bigcap _{P\in {\mathcal {I}}} {{\,\mathrm{supp}\,}}T \end{aligned}$$

and thus ${\mathcal {V}}({\mathcal {I}})\subseteq {{\,\mathrm{supp}\,}}T.$ We continue on showing that for the choice of the matrix-valued polynomial $P(x):= \prod _{a=1}^{\kappa } \bigg ( \sum _{j=1}^{d} (x_j -w_{j} ^{(a)})^2 \bigg )I_p,$ one obtains that $P\in {\mathcal {I}}$ as well. Consider $P(X)\in C_{M(\infty )}.$ We have ${\mathcal {Z}}(\det P(x))= {{\,\mathrm{supp}\,}}T$ and we shall see $P(X)={{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in {\mathbb {N}}_0^d}.$ Indeed

$$\begin{aligned} P(X)= & {} {{\,\mathrm{col}\,}}\left( \sum \limits _{\lambda \in \Gamma _{n, d}} X^{\gamma +\lambda } P_\lambda \right) _{\gamma \in {\mathbb {N}}_0^d}\\= & {} {{\,\mathrm{col}\,}}\bigg ( \int _{{\mathbb {R}}^d} x^\gamma dT(x) P(x) \bigg )_{\gamma \in {\mathbb {N}}_0^d}\\= & {} {{\,\mathrm{col}\,}}\bigg ( \int _{{\mathbb {R}}^d} x^\gamma dT(x) \prod \limits _{a=1}^{\kappa } \bigg ( \sum \limits _{j=1}^{d} (x_j -w_{j} ^{(a)})^2 \bigg )I_p \bigg )_{\gamma \in {\mathbb {N}}_0^d}\\= & {} {{\,\mathrm{col}\,}}\bigg ( \int _{{\mathbb {R}}^d} x^\gamma {\tilde{\varphi }}(x) dT(x) \bigg )_{\gamma \in {\mathbb {N}}_0^d}, \end{aligned}$$

where ${\tilde{\varphi }}(x)= \prod _{a=1}^{\kappa } \sum _{j=1}^{d} (x_j -w_{j} ^{(a)})^2 \in {\mathbb {R}}[x_1, \dots ,x_d].$ Since $T=\sum \limits _{a=1}^{\kappa } Q_a \delta _{w^{(a)}},$ P(X) becomes

$$\begin{aligned} {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{a=1}^{\kappa } \{w^{(a)}\}^\gamma {\tilde{\varphi }}(w^{(a)}) Q_a \bigg )_{\gamma \in {\mathbb {N}}_0^d}= & {} {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{a=1}^{\kappa } \{w^{(a)}\}^\gamma \prod \limits _{a=1}^{\kappa } \bigg ( \sum \limits _{j=1}^{d} (w_{j} ^{(a)} -w_{j} ^{(a)})^2 \bigg ) Q_a \bigg )_{\gamma \in {\mathbb {N}}_0^d}\\= & {} {{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in {\mathbb {N}}_0^d} \end{aligned}$$

and so $P \in {\mathcal {I}}.$ Since there exists $P \in {\mathcal {I}}$ such that ${\mathcal {Z}}(\det P(x))= {{\,\mathrm{supp}\,}}T,$ we again obtain

$$\begin{aligned} {\mathcal {V}}({\mathcal {I}})\subseteq {{\,\mathrm{supp}\,}}T \end{aligned}$$

as desired. $\square$

Lemma 5.61

Let T be a representing measure for $S^{(\infty )}:=(S_\gamma )_{\gamma \in {\mathbb {N}}_0^d },$ where $S_\gamma \in {\mathcal {H}}_p,$ $\gamma \in {\mathbb {N}}_0^d$ and $w^{(1)}, \dots , w^{(\kappa )}\in {\mathbb {R}}^d$ be such that

$$\begin{aligned} {{\,\mathrm{supp}\,}}T=\{ w^{(1)}, \dots , w ^{(\kappa )} \}. \end{aligned}$$

If there exists $P \in {\mathbb {C}}^{p \times p}[x_1, \dots ,x_d]$ with $P\in {\mathcal {I}},$ then

$$\begin{aligned} {{\,\mathrm{supp}\,}}T\subseteq {\mathcal {V}}({\mathcal {I}}), \end{aligned}$$

where ${\mathcal {I}}$ is as in Definition 5.13 and ${\mathcal {V}}({\mathcal {I}})$ the variety of ${\mathcal {I}}$ (see Definition 5.20).

Proof

By Lemma 5.60, if we choose $P(x):= \prod _{a=1}^{\kappa } \prod _{j=1}^{d} (x_j -w_{j} ^{(a)})I_p\in {\mathbb {C}}^{p \times p}[x_1, \dots ,x_d],$ then $P\in {\mathcal {I}}$ and

$$\begin{aligned} \{ w^{(1)}, \dots , w ^{(\kappa )} \}\subseteq {\mathcal {Z}}(\det P(x)), \end{aligned}$$

that is,

$$\begin{aligned} {{\,\mathrm{supp}\,}}T\subseteq {\mathcal {Z}}(\det P(x)). \end{aligned}$$

Therefore

$$\begin{aligned} \bigcap _{P\in {\mathcal {I}}}{{\,\mathrm{supp}\,}}T\subseteq \bigcap _{P\in {\mathcal {I}}} {\mathcal {Z}}(\det P(x)) \end{aligned}$$

and so

$\square$

In the next lemma we treat the multiplication operators of Definition 5.40 to provide a connection between the joint spectrum of $M_{x_1},\dots , M_{x_d}$ and a representing measure T.

Lemma 5.62

If T is a representing measure for $S^{(\infty )}:= (S_\gamma )_{\gamma \in {\mathbb {N}}_0^d },$ where $S_\gamma \in {\mathcal {H}}_p,$ $\gamma \in {\mathbb {N}}_0^d,$ then

$$\begin{aligned} {{\,\mathrm{supp}\,}}T \subseteq \sigma (M_x), \end{aligned}$$

where $\sigma (M_x)$ is as in Definition 5.47.

Proof

Since $M_{x_j},$ $j=1, \dots ,d,$ are commuting self-adjoint operators on ${\mathbb {C}}^p[x_1,\dots , x_d]/{\mathcal {J}},$ by Remark 5.46, there exists a joint spectral measure $E: {{\mathcal {B}}({\mathbb {R}}^d)} \rightarrow {\mathcal {P}}$ such that for every $q, f \in {\mathbb {C}}^p,$

$$\begin{aligned}&\langle M_{x_1}^{\gamma _1}\dots M_{x_d}^{\gamma _d}(q+ {\mathcal {J}}), f+ {\mathcal {J}}\rangle = \int _{{\mathbb {R}}^d} x_1^{\gamma _1}\dots x_d^{\gamma _d} d\langle E(x_1,\ldots , x_d) (q+ {\mathcal {J}}), f+ {\mathcal {J}}\rangle ,\\&\quad j=1, \dots ,d. \end{aligned}$$

Moreover

$$\begin{aligned} v^*T(\alpha )v=\langle E(\alpha )(v+ {\mathcal {J}}), v+ {\mathcal {J}}\rangle \;\; \text {for every}\;\; \alpha \in {{\mathcal {B}}({\mathbb {R}}^d)}. \end{aligned}$$

If $\alpha \subseteq {{\,\mathrm{supp}\,}}T,$ then $T(\alpha )\ne 0_{p\times p}.$ Thus, there exists $v \in {\mathbb {C}}^p$ such that $v^*T(\alpha )v > 0.$ Hence

$$\begin{aligned} \langle E(\alpha )(v+ {\mathcal {J}}), v+ {\mathcal {J}}\rangle > 0 \end{aligned}$$

and so $E(\alpha ) \ne 0_{p\times p}.$ $\square$

The next lemma describes the block column relations of an infinite d-Hankel matrix in terms of the variety of a right ideal built from matrix-valued polynomials.

Lemma 5.63

Let $S^{(\infty )}:=(S_\gamma )_{\gamma \in {\mathbb {N}}_0^d}$ be a given ${\mathcal {H}}_p$-valued multisequence with a representing measure T. Let $M(\infty )$ be the corresponding d-Hankel matrix with $r:={{\,\mathrm{rank}\,}}M(\infty ).$ If there exists $P \in {\mathbb {C}}^{p \times p}[x_1, \dots ,x_d]$ such that $P \in {\mathcal {I}}$ then

$$\begin{aligned} {{\,\mathrm{card}\,}}{\mathcal {V}}({\mathcal {I}}) = r, \end{aligned}$$

where ${\mathcal {I}}$ is as in Definition 5.13 and ${\mathcal {V}}({\mathcal {I}})$ the variety of ${\mathcal {I}}$ (see Definition 5.20).

Proof

By Lemma 5.60, there exists $P \in {\mathcal {I}}$ with ${\mathcal {V}}({\mathcal {I}})\subseteq {{\,\mathrm{supp}\,}}T$ such that

$$\begin{aligned} {\mathcal {Z}}(\det P(x))= {{\,\mathrm{supp}\,}}T \end{aligned}$$

and by Lemma 5.62, ${{\,\mathrm{supp}\,}}T \subseteq \sigma (M_x).$ Then

$$\begin{aligned} {{\,\mathrm{supp}\,}}T = {\mathcal {Z}}(\det P(x)) \subseteq \sigma (M_x) \end{aligned}$$

and thus

$$\begin{aligned} \bigcap _{P\in {\mathcal {I}}}{\mathcal {Z}}(\det P(x)) \subseteq \sigma (M_x), \end{aligned}$$

which is equivalent to ${\mathcal {V}}({\mathcal {I}}) \subseteq \sigma (M_x).$ Therefore

$$\begin{aligned} {{\,\mathrm{card}\,}}{\mathcal {V}}({\mathcal {I}}) \le {{\,\mathrm{card}\,}}\sigma (M_x) \le \dim ( {\mathbb {C}}^p[x_1,\dots , x_d]/{\mathcal {J}}) =r. \end{aligned}$$

Moreover, by Remark 5.55, ${{\,\mathrm{supp}\,}}T\subseteq {\mathcal {V}}({\mathcal {I}})$ and so $\sum \nolimits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a \le {{\,\mathrm{card}\,}}{\mathcal {V}}({\mathcal {I}}).$ Then Proposition 5.58 implies ${{\,\mathrm{card}\,}}{\mathcal {V}}({\mathcal {I}}) \ge r.$ Finally

$\square$

We next state and prove an algebraic result involving an ideal (see Definition 5.13) associated to an positive infinite d-Hankel matrix.

Proposition 5.64

If $M(\infty ) \succeq 0$ and ${\mathcal {I}}\subseteq {\mathbb {C}}^{p\times p}[x_1,\dots , x_d]$ is the associated right ideal (see Definition 5.13), then ${\mathcal {I}}$ is real radical.

Proof

We need to show that $\sum _{a=1}^{\kappa } P^{(a)} \{P^{(a)}\}^*\in {\mathcal {I}} \Rightarrow P^{(a)} \in {\mathcal {I}}\;\;\text {for all}\; a=1, \dots , \kappa .$ Let

$$\begin{aligned} {\widehat{R}}^{(a)}:= {{\,\mathrm{col}\,}}\big ( I_{p,\lambda }^{(a)}\big )_{\lambda =(0, \dots , 0)} \oplus {{\,\mathrm{col}\,}}(0_{p \times p})_{\gamma \in \Gamma _{n+1, d} \setminus \gamma =(0, \dots , 0) } \end{aligned}$$

and

$$\begin{aligned} {\widehat{P}}^{(a)}:= {{\,\mathrm{col}\,}}\big ( P_{\lambda }^{(a)}\big )_{\lambda \in \Gamma _{n, d}} \oplus {{\,\mathrm{col}\,}}(0_{p \times p})_{\gamma \in \Gamma _{n+1, d} \setminus \Gamma _{n, d} }\quad \text {for}\;\; a=1, \dots , \kappa . \end{aligned}$$

Since $\sum \nolimits _{a=1}^{\kappa } \{{\widehat{R}}^{(a)}\}^* M(n+1) {\widehat{P}}^{(a)} = 0_{p\times p},$ we may write

$$\begin{aligned} \sum _{a=1}^{\kappa } {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{\lambda \in \Gamma _{n, d}} S_{\gamma +\lambda } P^{(a)}_{\lambda }\bigg )_{\gamma \in \Gamma _{n+1, d}}{{\,\mathrm{col}\,}}\big (\{P^{(a)}_{\lambda }\}^*\big )_{\lambda \in \Gamma _{n, d}}=0_{p \times p} \end{aligned}$$

and so

$$\begin{aligned} \sum _{a=1}^{\kappa } {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{\lambda \in \Gamma _{n, d}} S_{\gamma +\lambda } P^{(a)}_{\lambda } \{P^{(a)}_{\lambda }\}^*\bigg )_{\gamma \in \Gamma _{n+1, d}} =0_{p \times p}. \end{aligned}$$

We then have

$$\begin{aligned} \sum _{a=1}^{\kappa } {{\,\mathrm{tr}\,}}\bigg ({{\,\mathrm{col}\,}}\bigg ( \sum \limits _{\lambda \in \Gamma _{n, d}} S_{\gamma +\lambda } P^{(a)}_{\lambda } \{P^{(a)}_{\lambda }\}^*\bigg )\bigg )_{\gamma \in \Gamma _{n, d}} ={{\,\mathrm{tr}\,}}(0_{p \times p})_{\gamma \in \Gamma _{n, d}}, \end{aligned}$$

which by properties of the trace is equivalent to

$$\begin{aligned} \sum _{a=1}^{\kappa } {{\,\mathrm{tr}\,}}\bigg ( {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{\lambda \in \Gamma _{n, d}} \{P^{(a)}_{\lambda }\}^* S_{\gamma +\lambda } P^{(a)}_{\lambda }\bigg ) \bigg )_{\gamma \in \Gamma _{n, d}} ={{\,\mathrm{tr}\,}}(0_{p \times p})_{\gamma \in \Gamma _{n, d}}, \end{aligned}$$

that is,

$$\begin{aligned} \sum _{a=1}^{\kappa } {{\,\mathrm{tr}\,}}\bigg ( {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{\lambda \in \Gamma _{n, d}} \{P^{(a)}_{\lambda }\}^* S_{\gamma +\lambda } P^{(a)}_{\lambda }\bigg ) \bigg )_{\gamma \in \Gamma _{n, d}} =0 \end{aligned}$$

and thus

$$\begin{aligned} \sum _{a=1}^{\kappa } {{\,\mathrm{col}\,}}\big (\{P^{(a)}_{\lambda }\}^*\big )^*_{\lambda \in \Gamma _{n, d}} {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{\lambda \in \Gamma _{n, d}} S_{\gamma +\lambda } P^{(a)}_{\lambda }\bigg )_{\gamma \in \Gamma _{n, d}}=0_{p \times p}. \end{aligned}$$

Hence

$$\begin{aligned} \sum _{a=1}^{\kappa } \{{\widehat{P}}^{(a)}\}^* M(n) {\widehat{P}}^{(a)}= 0_{p \times p}, \end{aligned}$$

which implies ${P^{(a)}}\in {\mathcal {I}}\;\text {for all}\; a=1, \dots , \kappa$ as desired. $\square$

5.4 Characterisation of Positive Infinite d-Hankel Matrices with Finite Rank

In this subsection we will characterise positive infinite d-Hankel matrices with finite rank via an integral representation. Moreover, we will connect the variety of the associated right ideal of the d-Hankel matrix with the support of the representing measure and also make a connection between the rank of the positive infinite d-Hankel matrix and the cardinality of the support of the representing measure.

We next state and prove the main theorem of this section. We shall see that if $M(\infty )\succeq 0$ with ${{\,\mathrm{rank}\,}}M(\infty )<\infty$, then the associated ${\mathcal {H}}_p$-valued multisequence has a unique representing measure T and one can extract information on the support of the representing measure in terms of the variety of the right ideal associated with $M(\infty ).$

Theorem 5.65

Let $S^{(\infty )}:=(S_\gamma )_{\gamma \in {\mathbb {N}}_0^d}$ be a given ${\mathcal {H}}_p$-valued multisequence. The following conditions are equivalent:

• (i) $M(\infty )\succeq 0$ and $r:={{\,\mathrm{rank}\,}}M(\infty )< \infty .$

• (ii) $S^{(\infty )}$ has a representing measure, i.e., there exists a ${\mathcal {H}}_p$-valued measure T on ${\mathbb {R}}^d$ such that

  $$\begin{aligned} S_{\gamma } = \int _{{\mathbb {R}}^d} x^{\gamma } \, dT(x) \quad \quad \mathrm{for} \quad \gamma \in {\mathbb {N}}_0^d. \end{aligned}$$

In this case,

$$\begin{aligned} {{\,\mathrm{supp}\,}}T = {\mathcal {V}} ({\mathcal {I}}), \end{aligned}$$

where ${\mathcal {I}}$ is as in Definition 5.13,

$$\begin{aligned} {{\,\mathrm{card}\,}}{\mathcal {V}}({\mathcal {I}})=r \end{aligned}$$

and the $S^{(\infty )}$ has a unique representing measure.

Proof

If condition (ii) holds, then condition (i) follows from Smuljan’s lemma (see Lemma 2.1) and Lemma 5.50.

Suppose condition (i) holds. By Proposition 5.49, if $S^{(\infty )}$ gives rise to $M(\infty )\succeq 0$ and $r:={{\,\mathrm{rank}\,}}M(\infty )< \infty ,$ then $S^{(\infty )}$ has a representing measure T. Moreover, by Lemma 5.61, we have ${{\,\mathrm{supp}\,}}T \subseteq {\mathcal {V}}({\mathcal {I}})$ and by Lemma 5.60, ${\mathcal {V}}({\mathcal {I}})\subseteq {{\,\mathrm{supp}\,}}T.$ Thus

$$\begin{aligned} {{\,\mathrm{supp}\,}}T = {\mathcal {V}} ({\mathcal {I}}). \end{aligned}$$

Next, Proposition 5.58 yields $\sum \nolimits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a = r= {{\,\mathrm{rank}\,}}M(\infty ).$ Since $\sum \nolimits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a = r<\infty ,$ the measure T is of the form $T=\sum \nolimits _{a=1}^{\kappa } Q_a \delta _{w^{(a)}},$ with

$$\begin{aligned} \sum \limits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a =r\;\; \text {and}\;\; Q_1, \dots , Q_\kappa \succeq 0. \end{aligned}$$

To prove T is unique, suppose ${\widetilde{T}}$ is another representing measure for $S^{(\infty )}.$ By Remark 5.55, we have ${{\,\mathrm{supp}\,}}{\widetilde{T}} \subseteq {\mathcal {V}}({\mathcal {I}})$ and by Remark 5.60, ${\mathcal {V}}({\mathcal {I}})\subseteq {{\,\mathrm{supp}\,}}{\widetilde{T}}.$ As before ${{\,\mathrm{supp}\,}}{\widetilde{T}} = {\mathcal {V}}(\mathcal {I)},$ and moreover, $\sum \nolimits _{b=1}^{{\widetilde{\kappa }}} {{\,\mathrm{rank}\,}}{\widetilde{Q}}_b = r< \infty ,$ by Proposition 5.58. So ${\widetilde{T}}$ is of the form ${\widetilde{T}}=\sum \nolimits _{b=1}^{{\widetilde{\kappa }}} {\widetilde{Q}}_b \delta _{{{\tilde{w}}}^{(b)}}$ with

$$\begin{aligned} \sum \limits _{b=1}^{{\widetilde{\kappa }}} {{\,\mathrm{rank}\,}}{\widetilde{Q}}_b =r\quad \text {and}\quad {\widetilde{Q}}_1, \dots , {\widetilde{Q}}_\kappa \succeq 0. \end{aligned}$$

Since ${{\,\mathrm{supp}\,}}T= {\mathcal {V}} ({\mathcal {I}})= {{\,\mathrm{supp}\,}}T,$ we have $\{ w^{(a)} \}_{a=1}^{\kappa }=\{ {\tilde{w}}^{(b)} \}_{b=1}^{{{\widetilde{\kappa }}}}.$ Thus $\kappa ={{\widetilde{\kappa }}}$ and $w^{(a)} = {\tilde{w}}^{(b)}={\tilde{w}}^{(a)}$ for all $a=1, \dots , \kappa .$ By Theorem 2.11, there exists $\Lambda =\{\lambda ^{(1)}, \dots , \lambda ^{(\kappa )}\}\subseteq {\mathbb {N}}_0^d$ such that ${{\,\mathrm{card}\,}}\Lambda =\kappa$ and $V(w^{(1)}, \dots ,w^{(\kappa )};\Lambda )$ is invertible. Remark 5.23 implies then that $V^{p \times p}(w^{(1)}, \dots , w^{(\kappa )}; \Lambda )$ is invertible. The positive semidefinite matrices $Q_{1}, \dots , Q_\kappa \in {\mathbb {C}}^{p \times p}$ are computed by the Vandermonde equation

$$\begin{aligned} {{{\,\mathrm{col}\,}}(Q_a)_{a=1}^{\kappa }} = V^{p \times p}(w^{(1)}, \dots , w^{(\kappa )}; \Lambda )^{-1} {{\,\mathrm{col}\,}}(S_{ \lambda })_{\lambda \in \Lambda }, \end{aligned}$$

where $Q_1, \dots , Q_\kappa \succeq 0.$ Moreover, the positive semidefinite matrices ${\widetilde{Q}}_1, \dots , {\widetilde{Q}}_{\kappa } \in {\mathbb {C}}^{p \times p}$ are computed by the Vandermonde equation

$$\begin{aligned} {{{\,\mathrm{col}\,}}({{\widetilde{Q}}}_a)_{a=1}^{\kappa }} = V^{p \times p}(w^{(1)}, \dots , w^{({\kappa })}; \Lambda )^{-1} {{\,\mathrm{col}\,}}(S_{ \lambda })_{\lambda \in \Lambda }, \end{aligned}$$

where ${\widetilde{Q}}_{1}, \dots , {\widetilde{Q}}_{\kappa } \succeq 0.$ Hence ${{{\,\mathrm{col}\,}}(Q_a)_{a=1}^{\kappa }}={{{\,\mathrm{col}\,}}({\widetilde{Q}}_a)_{a=1}^{\kappa }}$ and $(Q_a)_{a=1}^{\kappa }=({\widetilde{Q}}_a)_{a=1}^{\kappa }$ which asserts that the positive semidefinite matrices $Q_1, \dots , Q_\kappa$ are uniquely determined for all $a=1, \dots , \kappa .$ Consequently, the representing measure T is unique and the proof is complete. $\square$

In analogy to Theorem 5.65, we formulate the next corollary for a given truncated ${\mathcal {H}}_p$-valued multisequence $S:=(S_\gamma )_{\gamma \in \Gamma _{2n, d}}.$

Corollary 5.66

Let $S:=(S_\gamma )_{\gamma \in \Gamma _{2n, d}}$ be a given truncated ${\mathcal {H}}_p$-valued multisequence. Suppose there exist moments $(S_\gamma )_{\gamma \in \Gamma _{2n+2, d}\setminus \Gamma _{2n, d} }$ such that $M(n+1)\succeq 0$ and

$$\begin{aligned} {{\,\mathrm{rank}\,}}M(n)= {{\,\mathrm{rank}\,}}M(n+1). \end{aligned}$$

Then $(S_\gamma )_{\gamma \in \Gamma _{2n+2, d}}$ has a unique representing measure T. In this case,

$$\begin{aligned} {{\,\mathrm{supp}\,}}T = {\mathcal {V}} (M(n+k))\quad \text {for}\;\; k=1,2, \ldots , \end{aligned}$$

where ${\mathcal {V}} (M(n+k))$ denotes the variety of $M(n+k)$ for $P(x) \in {\mathbb {C}}^{p \times p}[x_1, \dots ,x_d]$ such that $M(n+k) {{\,\mathrm{col}\,}}(P_\lambda )_{\lambda \in \Gamma _{n+k, d}}={{\,\mathrm{col}\,}}(0_{p\times p})_{{\lambda }\in \Gamma _{n+k, d}}\; \text {for all}\; k=1, 2, \dots ,$ and moreover,

$$\begin{aligned} {{\,\mathrm{card}\,}}{\mathcal {V}}(M(n+k))=r. \end{aligned}$$

Proof

By Lemma 5.68, there exist moments $(S_\gamma )_{\gamma \in {\mathbb {N}}_0^d\setminus \Gamma _{2n+2, d} }$ which give rise to a unique sequence of extensions

$$\begin{aligned} M(n+k)\succeq 0\quad \text {for}\;\; k=2,3, \dots \end{aligned}$$

and thus to $M(\infty )\succeq 0.$ Hence, by Proposition 5.49, $(S_\gamma )_{\gamma \in {\mathbb {N}}_0^d}$ has a representing measure T and its uniqueness follows from Theorem 5.65. So if S gives rise to $M(n+1)\succeq 0$ and $r:={{\,\mathrm{rank}\,}}M(n+1)={{\,\mathrm{rank}\,}}M(n)< \infty ,$ then $(S_\gamma )_{\gamma \in \Gamma _{2n+2, d}}$ has a unique representing measure T. Moreover, Lemma 5.55 applied for $P(x) \in {\mathbb {C}}^{p \times p}_{n+1}[x_1, \dots ,x_d]$ with

$$\begin{aligned} {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{\lambda \in \Gamma _{n, d}} S_{\gamma +\lambda } P_{\lambda }\bigg )_{\gamma \in \Gamma _{n+1, d}}={{\,\mathrm{col}\,}}(0_{p \times p})_{\gamma \in \Gamma _{n+1, d}} \end{aligned}$$

yields

$$\begin{aligned} {{\,\mathrm{supp}\,}}T \subseteq {\mathcal {V}}(M(n+1)). \end{aligned}$$

(5.22)

Notice that since $(S_\gamma )_{\gamma \in \Gamma _{2n+2, d}}$ has a representing measure T,  for $P(x)\in {\mathbb {C}}^{p \times p}_{n+1}[x_1, \dots ,x_d],$ Lemma 5.56 asserts

$$\begin{aligned} {\mathcal {V}}(M(n+1))\subseteq {{\,\mathrm{supp}\,}}T, \end{aligned}$$

(5.23)

By inclusions (5.22) and (5.23),

$$\begin{aligned} {{\,\mathrm{supp}\,}}T = {\mathcal {V}} (M(n+1)). \end{aligned}$$

We need to show ${{\,\mathrm{supp}\,}}T = {\mathcal {V}} (M(n+k))\; \text {for all}\; k=1,2, \ldots$ We apply Lemma 5.61 for $P(x) \in {\mathbb {C}}^{p \times p}[x_1, \dots ,x_d]$ such that $M(n+k) {{\,\mathrm{col}\,}}(P_\lambda )_{\lambda \in \Gamma _{n+k, d}}={{\,\mathrm{col}\,}}(0_{p\times p})_{{\lambda }\in \Gamma _{n+k, d}}.$ Then

$$\begin{aligned} {{\,\mathrm{supp}\,}}T \subseteq {\mathcal {V}} (M(n+k))\quad \text {for}\;\; k=1,2, \ldots \end{aligned}$$

(5.24)

Next, since $(S_\gamma )_{\gamma \in {\mathbb {N}}_0^d}$ has a representing measure T,  $(S_\gamma )_{\gamma \in \Gamma _{2n+2k, d}}$ has a representing measure T for all $k=1,2, \ldots ,$ and thus, Lemma 5.60 applied for $P(x)\in {\mathbb {C}}^{p \times p}[x_1, \dots ,x_d]$ implies

$$\begin{aligned} {\mathcal {V}}(M(n+k))\subseteq {{\,\mathrm{supp}\,}}T \quad \text {for} \;\; k=1,2, \ldots \end{aligned}$$

(5.25)

We shall derive ${{\,\mathrm{supp}\,}}T = {\mathcal {V}} (M(n+k)) \; \text {for all} \; k=1,2, \ldots ,$ by inclusions (5.24) and (5.25). Furthermore, since T is a representing measure for $(S_\gamma )_{\gamma \in {\mathbb {N}}_0^d},$ then T is a representing measure for $(S_\gamma )_{\gamma \in \Gamma _{2n+2k, d}}$ and Lemma 5.63 implies ${{\,\mathrm{card}\,}}{\mathcal {V}} (M(n+k))=r \; \text {for all} \; k=1,2, \ldots$ Hence $\sum \nolimits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a = r< \infty$ and the measure T is of the form $T=\sum \nolimits _{a=1}^{\kappa } Q_a \delta _{w^{(a)}}$ with

$\square$

5.5 Positive Extensions of d-Hankel Matrices

We investigate positive extensions of a d-Hankel matrix based on a truncated ${\mathcal {H}}_p$-valued multisequence. Both results provided in this subsection are important for obtaining the flat extension theorem for matricial moments stated and proved in Sect. 6.

Lemma 5.67

(extension lemma) Let $S:=(S_\gamma )_{\gamma \in \Gamma _{2n,d}}$ be a given truncated ${\mathcal {H}}_p$-valued multisequence and let M(n) be the corresponding d-Hankel matrix. If $M(n)\succeq 0$ has an extension $M(n+1)$ such that $M(n+1)\succeq 0$ and ${{\,\mathrm{rank}\,}}M(n+1)={{\,\mathrm{rank}\,}}M(n),$ then there exist $(S_\gamma )_{\gamma \in {\mathbb {N}}_0^d{\setminus }\Gamma _{2n, d} }$ such that

$$\begin{aligned} M(n+k)\succeq 0 \end{aligned}$$

and

$$\begin{aligned} {{\,\mathrm{rank}\,}}M(n+k)={{\,\mathrm{rank}\,}}M(n+k-1)\quad \text {for}\;\; k=2,3, \ldots \end{aligned}$$

Proof

See Appendix A. $\square$

Lemma 5.68

Let $S:=(S_\gamma )_{\gamma \in \Gamma _{2n, d}}$ be a given truncated ${\mathcal {H}}_p$-valued multisequence and let $M(n)\succeq 0$ be the corresponding d-Hankel matrix. Suppose that M(n) has a positive extension $M(n+1)$ with

$$\begin{aligned} {{\,\mathrm{rank}\,}}M(n+1)={{\,\mathrm{rank}\,}}M(n). \end{aligned}$$

Then there exists a unique sequence of extensions

$$\begin{aligned} M(n+k)\succeq 0 \end{aligned}$$

with

$$\begin{aligned} {{\,\mathrm{rank}\,}}M(n+k)={{\,\mathrm{rank}\,}}M(n+k-1)\quad \text {for}\;\; k=2,3, \ldots \end{aligned}$$

Proof

See Appendix A for a proof. $\square$

6 The Flat Extension Theorem for a Truncated Matricial Multisequence

In this section, we will formulate and prove our flat extension theorem for matricial moments. We will see that a given truncated ${\mathcal {H}}_p$-valued multisequence $S:=(S_\gamma )_{\gamma \in \Gamma _{2n, d}}$ has a minimal representing measure (see Definition 3.3) if and only if the corresponding d-Hankel matrix M(n) has a flat extension $M(n+1).$ In this case, one can find a minimal representing measure such that the support of the minimal representing measure is the variety of the d-Hankel matrix $M(n+1).$

The definition that follows is an adaptation of the notion of flatness introduced by Curto and Fialkow [16] to our matricial setting.

Definition 6.1

Let $S:=(S_\gamma )_{\gamma \in \Gamma _{2n, d}}$ be a given truncated ${\mathcal {H}}_p$-valued multisequence and $M(n)\succeq 0$ be the corresponding d-Hankel matrix. Then M(n) has a flat extension if there exist $(S_\gamma )_{\gamma \in \Gamma _{2n+2, d}{\setminus }\Gamma _{2n, d} },$ where $S_\gamma \in {\mathcal {H}}_p$ for $\gamma \in \Gamma _{2n+2, d}\setminus \Gamma _{2n, d}$ such that $M(n+1)\succeq 0$ and

$$\begin{aligned} {{\,\mathrm{rank}\,}}M(n)= {{\,\mathrm{rank}\,}}M(n+1). \end{aligned}$$

For the convenience of the reader, please note that Assumption 1.3 is in force.

Theorem 6.2

(flat extension theorem for matricial moments) Let $S:=(S_\gamma )_{\gamma \in \Gamma _{2n,d}}$ be a given truncated ${\mathcal {H}}_p$-valued multisequence, $M(n)\succeq 0$ be the corresponding d-Hankel matrix and $r:={{\,\mathrm{rank}\,}}M(n).$ S has a representing measure

$$\begin{aligned} T=\sum \limits _{a=1}^{\kappa } Q_a \delta _{w^{(a)}} \end{aligned}$$

with

$$\begin{aligned} \sum \limits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a = r \end{aligned}$$

if and only if the matrix M(n) admits an extension $M(n+1)\succeq 0$ such that

$$\begin{aligned} {{\,\mathrm{rank}\,}}M(n)= {{\,\mathrm{rank}\,}}M(n+1). \end{aligned}$$

Moreover,

$$\begin{aligned} {{\,\mathrm{supp}\,}}T= {\mathcal {V}}(M(n+1)), \end{aligned}$$

and there exists $\Lambda = \{\lambda ^{(1)}, \dots , \lambda ^{(\kappa )}\}\subseteq {\mathbb {N}}_0^d$ with ${{\,\mathrm{card}\,}}\Lambda =\kappa$ such that the multivariable Vandermonde matrix $V^{p \times p}(w^{(1)}, \dots , w^{(\kappa )}; \Lambda )\in {\mathbb {C}}^{\kappa p\times \kappa p}$ is invertible. Then the positive semidefinite matrices $Q_1, \dots , Q_\kappa \in {\mathbb {C}}^{p \times p}$ are given by the Vandermonde equation

$$\begin{aligned} {{{\,\mathrm{col}\,}}(Q_a)_{a=1}^{\kappa }} = V^{p \times p}(w^{(1)}, \dots , w^{(\kappa )}; \Lambda )^{-1} {{\,\mathrm{col}\,}}(S_{ \lambda })_{\lambda \in \Lambda }. \end{aligned}$$

Proof

Suppose the matrix $M(n)\succeq 0$ admits an extension $M(n+1)\succeq 0$ such that

$$\begin{aligned} {{\,\mathrm{rank}\,}}M(n+1)= {{\,\mathrm{rank}\,}}M(n)=r. \end{aligned}$$

By Corollary 5.66, $(S_\gamma )_{\gamma \in \Gamma _{2n+2, d}}$ has a unique representing measure T such that

$$\begin{aligned} {{\,\mathrm{supp}\,}}T= {\mathcal {V}}(M(n+1))\quad \text {and}\quad {{\,\mathrm{card}\,}}{\mathcal {V}}(M(n+1))=r, \end{aligned}$$

that is,

$$\begin{aligned} \sum \limits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a=r. \end{aligned}$$

Consequently, T is of the form

$$\begin{aligned} T=\sum \limits _{a=1}^{\kappa } Q_a \delta _{w^{(a)}} \end{aligned}$$

with $\sum \nolimits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a=r.$

Conversely, suppose that S has a representing measure $T=\sum \nolimits _{a=1}^{\kappa } Q_a \delta _{w^{(a)}}$ with

$$\begin{aligned} \sum \limits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a=r. \end{aligned}$$

Consider the matrix $M(n+1)$ built from the moments $(S_\gamma )_{\gamma \in \Gamma _{2n+2, d}\setminus \Gamma _{2n, d} }.$ T is a representing measure for $M(n+1)$ and so, by Lemma 5.57 we obtain

$$\begin{aligned} {{\,\mathrm{rank}\,}}M(n+1)\le \sum \limits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a = {{\,\mathrm{rank}\,}}M(n). \end{aligned}$$

The extension lemma (see Lemma 5.67) asserts that $M(n+1)$ is a flat extension of M(n). $\square$

7 Abstract Solution for the Truncated ${\mathcal {H}}_p$-Valued Moment Problem

In this section we will formulate an abstract criterion for a truncated ${\mathcal {H}}_p$-valued multisequence to have a representing measure.

Theorem 7.1

Let $S:=(S_\gamma )_{\gamma \in \Gamma _{2n,d}}$ be a given truncated ${\mathcal {H}}_p$-valued multisequence and M(n) be the corresponding d-Hankel matrix based on S. S has a representing measure if and only if the d-Hankel matrix M(n) has an eventual extension $M(n+k)$ such that $M(n+k)$ admits a flat extension.

Proof

If S has an eventual extension $M(n+k)$ such that $M(n+k)$ admits a flat extension, then we may use Theorem 6.2 to see that S has a representing measure. Conversely, if S has a representing measure, then we may use the first author’s ${\mathcal {H}}_p$-valued generalisation of Bayer and Teichmann’s generalisation of Tchakaloff’s theorem (see [51]) to see that we can always find a finitely atomic representing measure for S. One can argue much in the same way as in the proof of Theorem 6.2 to see that M(n) has an eventual extension $M(n+k)$ which in turn has a flat extension. $\square$

8 The Bivariate Quadratic Matrix-Valued Moment Problem

Given a truncated ${\mathcal {H}}_p$-valued bisequence $S:=(S_\gamma )_{\gamma \in \Gamma _{2, 2}}=(S_{00}, S_{10}, S_{01}, S_{20}, S_{11}, S_{02}),$ we wish to determine when S has a minimal representing measure. In the scalar case (i.e., when $p=1)$, Curto and Fialkow [16] showed that every $S=(S_\gamma )_{\gamma \in \Gamma _{2, 2}}$ with $S_{00}>0$ and $M(1)\succeq 0$ has a minimal representing measure.

We shall see that a direct analogue of Curto and Fialkow’s results on the bivariate quadratic moment problem does not hold when $p \ge 2$ (see Example 8.12). However, we shall see that if M(1) is positive semidefinite and certain block column relations hold, then $S=(S_\gamma )_{\gamma \in \Gamma _{2, 2}},$ $S_{00}\succ 0,$ has a minimal representing measure.

8.1 General Solution of the Bivariate Quadratic Matrix-Valued Moment Problem

The next theorem illustrates necessary and sufficient conditions for a given quadratic ${\mathcal {H}}_p$-valued bisequence to have a minimal representing measure. We observe that the positivity and flatness conditions are key to obtain a minimal solution to the bivariate quadratic matrix-valued moment problem.

Theorem 8.1

Let $S:=(S_\gamma )_{\gamma \in \Gamma _{2, 2}}$ be a given truncated ${\mathcal {H}}_p$-valued bisequence and

be the corresponding d-Hankel matrix. S has a minimal representing measure if and only if the following conditions hold:

(i) $M(1)\succeq 0.$

(ii) There exist $S_{30}, S_{21}, S_{12}, S_{03}\in {\mathcal {H}}_p$ such that

$$\begin{aligned} {{\,\mathrm{Ran}\,}}\begin{pmatrix} S_{20}&{} S_{11} &{}S_{02} \\ S_{30}&{}S_{21} &{}S_{12}\\ S_{21}&{}S_{12}&{}S_{03} \end{pmatrix} \subseteq {{\,\mathrm{Ran}\,}}M(1) \end{aligned}$$

(hence, there exists $W={(W_{ab})}_{a,b=1}^{3}\in {\mathbb {C}}^{3p \times 3p}$ such that $M(1)W=B,$ where

$$\begin{aligned} B=\begin{pmatrix} S_{20}&{} S_{11} &{}S_{02} \\ S_{30}&{}S_{21} &{}S_{12}\\ S_{21}&{}S_{12}&{}S_{03} \end{pmatrix}) \end{aligned}$$

and moreover, the following matrix equations hold:

$$\begin{aligned} W_{11}^*S_{11}+ W_{21}^*S_{21}+ W_{31}^*S_{12}&= S_{11}W_{11}+S_{21}W_{21}+S_{12}W_{31}, \end{aligned}$$

(8.1)

$$\begin{aligned} W_{13}^*S_{20}+ W_{23}^*S_{30}+ W_{33}^*S_{21}&= W_{12}^*S_{11}+ W_{22}^*S_{21}+ W_{32}^*S_{12} \end{aligned}$$

(8.2)

and

$$\begin{aligned} W_{12}^*S_{02}+ W_{22}^*S_{12}+ W_{32}^*S_{03}= S_{02}W_{12}+S_{12}W_{22}+S_{03}W_{32}. \end{aligned}$$

(8.3)

Proof

Since

$$\begin{aligned} {{\,\mathrm{Ran}\,}}\begin{pmatrix} S_{20}&{} S_{11} &{}S_{02} \\ S_{30}&{}S_{21} &{}S_{12}\\ S_{21}&{}S_{12}&{}S_{03} \end{pmatrix} \subseteq {{\,\mathrm{Ran}\,}}M(1), \end{aligned}$$

there exists $W={(W_{ab})}_{a,b=1}^{3}\in {\mathbb {C}}^{3p \times 3p}$ such that

$$\begin{aligned} B:=\begin{pmatrix} S_{20}&{} S_{11} &{}S_{02} \\ S_{30}&{}S_{21} &{}S_{12}\\ S_{21}&{}S_{12}&{}S_{03} \end{pmatrix}=M(1)W. \end{aligned}$$

Let $W:= \begin{pmatrix} W_{11}&{} W_{12} &{}W_{13} \\ W_{21}&{}W_{22} &{}W_{23}\\ W_{31}&{}W_{32}&{}W_{33} \end{pmatrix}.$ Then

$$\begin{aligned} S_{20}&=W_{11}+S_{10}W_{21}+S_{01}W_{31}, \end{aligned}$$

(8.4)

$$\begin{aligned} S_{30}&=S_{10}W_{11}+S_{20}W_{21}+S_{11}W_{31}, \end{aligned}$$

(8.5)

$$\begin{aligned} S_{21}&=S_{01}W_{11}+S_{11}W_{21}+S_{02}W_{31} \nonumber \\&=S_{10}W_{12}+S_{20}W_{22}+S_{11}W_{32}, \end{aligned}$$

(8.6)

$$\begin{aligned} S_{11}&=W_{12}+S_{10}W_{22}+S_{01}W_{32} , \end{aligned}$$

(8.7)

$$\begin{aligned} S_{12}&=S_{01}W_{12}+S_{11}W_{22}+S_{02}W_{32} \nonumber \\&=S_{10}W_{13}+S_{20}W_{23}+S_{11}W_{33}, \end{aligned}$$

(8.8)

$$\begin{aligned} S_{02}&=W_{13}+S_{10}W_{23}+S_{01}W_{33} \end{aligned}$$

(8.9)

and

$$\begin{aligned} S_{03}=S_{01}W_{13}+S_{11}W_{23}+S_{02}W_{33}. \end{aligned}$$

(8.10)

Let $C:= W^*M(1)W=W^*B$ and write $C= \begin{pmatrix} C_{11}&{} C_{12} &{}C_{13} \\ C_{21}&{}C_{22} &{}C_{23}\\ C_{31}&{}C_{32}&{}C_{33} \end{pmatrix}.$ By formulas (8.6), (8.7) and (8.8), we have

$$\begin{aligned} C_{12}= & {} W^*_{11}S_{11}+ W^*_{21}S_{21}+W^*_{31}S_{12}\\= & {} W^*_{11}(W_{12}+S_{10}W_{22}+S_{01}W_{32})+ W^*_{21}(S_{10}W_{12}+S_{20}W_{22}+S_{11}W_{32})\\&+W^*_{31}(S_{01}W_{12}+S_{11}W_{22}+S_{02}W_{32}). \end{aligned}$$

Since the matrix equation (8.1) holds, $C_{12}=C_{12}^*=C_{21}.$ Next, by formulas (8.6), (8.7) and (8.8),

$$\begin{aligned} C_{22}= & {} W^*_{12}S_{11}+ W^*_{22}S_{21}+W^*_{32}S_{12}\\= & {} W^*_{12}(W_{12}+S_{10}W_{22}+S_{01}W_{32})+ W^*_{22}(S_{10}W_{12}+S_{20}W_{22}+S_{11}W_{32})\\&+W^*_{32}(S_{01}W_{12}+S_{11}W_{22}+S_{02}W_{32}) \end{aligned}$$

and by formulas (8.4), (8.5) and (8.6),

$$\begin{aligned} C_{31}= & {} W^*_{13}S_{20}+ W^*_{23}S_{30}+W^*_{33}S_{21}\\= & {} W^*_{13}(W_{11}+S_{10}W_{21}+S_{01}W_{31})+ W^*_{23}(S_{10}W_{11}+S_{20}W_{21}+S_{11}W_{31})\\&+W^*_{33}(S_{01}W_{11}+S_{11}W_{21}+S_{02}W_{31}). \end{aligned}$$

Since the matrix equation (8.2) holds, $C_{22}=C_{31}.$ Moreover, by formulas (8.8), (8.9) and (8.10),

$$\begin{aligned} C_{23}= & {} W^*_{12}S_{02}+ W^*_{22}S_{12}+W^*_{32}S_{03}\\= & {} W^*_{12}(W_{13}+S_{10}W_{23}+S_{01}W_{33})+ W^*_{22}(S_{10}W_{13}+S_{20}W_{23}+S_{11}W_{33})\\&+W^*_{32}(S_{01}W_{13}+S_{11}W_{23}+S_{02}W_{33}). \end{aligned}$$

Since the matrix equation (8.3) holds, $C_{23}=C_{23}^*=C_{32}.$ Thus, by Lemma 2.1,

$$\begin{aligned} M(2):=\begin{pmatrix} M(1) &{} B \\ B^* &{} C \\ \end{pmatrix}\succeq 0 \end{aligned}$$

is a flat extension of M(1). By the flat extension theorem for matricial moments (see Theorem 6.2), there exists a minimal representing measure T for S.

Conversely, if S has a minimal representing measure, then by the flat extension theorem for matricial moments (see Theorem 6.2), there exists a flat extension $M(2):=\begin{pmatrix} M(1) &{} B \\ B^* &{} C \\ \end{pmatrix}\succeq 0$ of M(1) such that ${{\,\mathrm{rank}\,}}M(1)={{\,\mathrm{rank}\,}}M(2).$ By Lemma 2.1, $C=W^*M(1)W$ for some $W\in {\mathbb {C}}^{3p \times 3p}$ such that

$$\begin{aligned} B:=\begin{pmatrix} S_{20}&{} S_{11} &{}S_{02} \\ S_{30}&{}S_{21} &{}S_{12}\\ S_{21}&{}S_{12}&{}S_{03} \end{pmatrix}=M(1)W \end{aligned}$$

and consequently, ${{\,\mathrm{Ran}\,}}B \subseteq {{\,\mathrm{Ran}\,}}M(1).$ Hence there exists $W:= \begin{pmatrix} W_{11}&{} W_{12} &{}W_{13} \\ W_{21}&{}W_{22} &{}W_{23}\\ W_{31}&{}W_{32}&{}W_{33} \end{pmatrix}$ satisfying $B=M(1)W.$ Since $C=\begin{pmatrix} S_{40}&{} S_{31} &{}S_{22} \\ S_{31}&{}S_{22} &{}S_{13}\\ S_{22}&{}S_{13}&{}S_{04} \end{pmatrix}=W^*M(1)W,$ we have

$$\begin{aligned} S_{31}&=W_{11}^*S_{11}+W_{21}^*S_{21}+W_{31}^*S_{12}, \\ S_{22}&=W_{13}^*S_{20}+W_{23}^*S_{30}+W_{33}^*S_{21} \\&=W_{12}^*S_{11}+W_{22}^*S_{21}+W_{32}^*S_{12} \end{aligned}$$

and

$$\begin{aligned} S_{13}=W_{12}^*S_{02}+W_{22}^*S_{12}+W_{32}^*S_{03}. \end{aligned}$$

We derive the matrix equations (8.1), (8.2) and (8.3), respectively. $\square$

8.2 The Block Diagonal Case of the Bivariate Quadratic Matrix-Valued Moment Problem

In the next theorem we shall see that every truncated ${\mathcal {H}}_p$-valued bisequence $S:=(S_\gamma )_{\gamma \in \Gamma _{2, 2}}$ with $M(1)\succ 0$ being block diagonal has a minimal representing measure.

In what follows, given $A, B \in {\mathbb {C}}^{n \times n}$, we shall let $\sigma (A,B)$ denote the set of generalised eigenvalues of A and B, i.e.,

$$\begin{aligned} \sigma (A,B):= \{ \lambda \in {\mathbb {C}}: \det (A - \lambda B) = 0 \}. \end{aligned}$$

The reader is encouraged to see [40] for results on generalised eigenvalues.

Theorem 8.2

Let $S:=(S_\gamma )_{\gamma \in \Gamma _{2, 2}}$ be a given truncated ${\mathcal {H}}_p$-valued bisequence with moments $S_{10}=S_{01}=S_{11}=0_{p \times p}.$ Suppose Then S has a minimal representing measure T with

$$\begin{aligned} {{\,\mathrm{supp}\,}}T = \{ (x,0): x \in \sigma (S_{20}^{-1}S_{02},-S_{02}) \} \cup \{ (1,y): y^2 \in \sigma (S_{02} + S_{20}^{-1} S_{02}) \}, \end{aligned}$$

where $\sigma (S_{20}^{-1}S_{02},-S_{02})$ is the set of generalised eigenvalues of $\{S_{20}^{-1}S_{02}, -S_{02}\}.$

Proof

Let $B:=\begin{pmatrix} S_{20}&{} 0 &{}S_{02} \\ S_{30}&{}S_{21} &{}S_{12}\\ S_{21}&{}S_{12}&{}S_{03} \end{pmatrix}.$ We have

$$\begin{aligned} W:= M(1)^{-1}B=\begin{pmatrix} S_{20}&{}\quad 0 &{}\quad S_{02}\\ S_{20}^{-1}S_{30}&{}\quad S_{20}^{-1}S_{21} &{}\quad S_{20}^{-1}S_{12}\\ S_{02}^{-1}S_{21}&{}\quad S_{02}^{-1}S_{12}&{}\quad S_{02}^{-1}S_{03} \end{pmatrix}. \end{aligned}$$

We then let $C:=W^*M(1)W=W^*B$ and we write $\begin{pmatrix} C_{11}&{} C_{12} &{}C_{13} \\ C_{21}&{}C_{22} &{}C_{23}\\ C_{31}&{}C_{32}&{}C_{33} \end{pmatrix}.$ Notice that

$$\begin{aligned} C_{12}&=S_{30}S_{20}^{-1}S_{21}+S_{21}S_{02}^{-1}S_{21}, \\ C_{13}&= S_{20}S_{02}+S_{30}S_{20}^{-1}S_{12}+S_{21}S_{02}^{-1}S_{03}, \\ C_{22}&=S_{21}S_{20}^{-1}S_{21}+S_{12}S_{02}^{-1}S_{12} \end{aligned}$$

and

$$\begin{aligned} C_{23}=S_{21}S_{20}^{-1}S_{12}+S_{12}S_{02}^{-1}S_{03}. \end{aligned}$$

Let $S_{21}:=0_{p \times p}\; \text {and}\; S_{03}:=0_{p \times p}.$ Then $C_{12}=0_{p \times p}= C_{23}\in {\mathcal {H}}_p$ and

$$\begin{aligned} C_{22}= C_{13} \end{aligned}$$

(8.11)

if and only if

$$\begin{aligned} S_{12}S_{02}^{-1}S_{12}=S_{20}S_{02}+S_{30}S_{20}^{-1}S_{12}. \end{aligned}$$

(8.12)

We assume $S_{12}$ is invertible and we solve equation (8.12) for $S_{30}$. We obtain

$$\begin{aligned} S_{30}= (S_{12}S_{02}^{-1}S_{12}-S_{20}S_{02})S_{12}^{-1}S_{20}. \end{aligned}$$

Hence

$$\begin{aligned} S_{30}=S_{12}S_{02}^{-1}S_{20}-S_{20}S_{02} S_{12}^{-1}S_{20}. \end{aligned}$$

Let $S_{12}:=S_{02}\succ 0$ and $S_{30}:=S_{20}-S_{20}^2.$ Then $S_{30}\in {\mathcal {H}}_p$ and equation (8.11) holds. Hence, by Lemma 2.1$M(2):=\begin{pmatrix} M(1) &{} B \\ B^* &{} C \\ \end{pmatrix}\succeq 0$ is a flat extension of M(1). By the flat extension theorem for matricial moments (see Theorem 6.2), there exists a minimal representing measure T for S. We now write

$$\begin{aligned} B=\begin{pmatrix} S_{20}&{} 0 &{}S_{02} \\ S_{30}&{}0 &{}S_{02}\\ 0&{}S_{02}&{}0 \end{pmatrix} \end{aligned}$$

and W becomes

$$\begin{aligned} W= {M(1)^{-1}}{B}=\begin{pmatrix} {S_{20}}&{} 0 &{}{S_{02}}\\ I_p-{S_{20}}&{}0&{}{S_{20}^{-1}}{S_{02}}\\ 0&{}I_p&{}0 \end{pmatrix}. \end{aligned}$$

Consider the following matrix-valued polynomials in ${\mathbb {C}}^{p\times p}[x, y]$:

$$\begin{aligned} P^{(2, 0)}(x,y)&=x^2 I_p - {S_{20}}-x(I_p-{S_{20}}),\\ P^{(1,1)}(x, y)&= xyI_p-yI_p \end{aligned}$$

and

$$\begin{aligned} P^{(0,2)}(x,y)=y^2I_p-{S_{02}}-x({S_{20}^{-1}}{S_{02}}). \end{aligned}$$

Let ${\mathcal {Z}}_{20}:={\mathcal {Z}}(\det (P^{(2,0)}(x, y))),\;{\mathcal {Z}}_{11}:={\mathcal {Z}}(\det (P^{(1,1)}(x, y)))$ and $\mathcal {Z}_{02}\nonumber :=\mathcal {Z}(\det (P^{(0,2)}(x, y)))$. Then

$$\begin{aligned} {{\,\mathrm{supp}\,}}{T} = {\mathcal {Z}}_{20}\bigcap {\mathcal {Z}}_{11}\bigcap {\mathcal {Z}}_{02}. \end{aligned}$$

We observe that $(x,y) \in Z_{20}$ if and only if $P^{(2,0)}(x,y)$ is singular, i.e., there exists a nonzero vector $\xi \in {\mathbb {C}}^p\setminus \{0\}$ such that

$$\begin{aligned} \{ x^2 I_p - S_{20} - x(I_p - S_{20}) \} \xi = 0, \end{aligned}$$

that is,

$$\begin{aligned} x(x-1) \xi = -(x-1) S_{20} \xi . \end{aligned}$$

(8.13)

We have ${\mathcal {Z}}_{11}=\{(1,y):y\in {\mathbb {R}} \}\cup \{ (x, 0):x \in {\mathbb {R}} \}$ and, in view of equation (8.13), we get

$$\begin{aligned} {\mathcal {Z}}_{11}\cap {\mathcal {Z}}_{20} = \{ (x,0): -x \in \sigma (S_{20}) \}\cup \{(1,y):y\in {\mathbb {R}} \}. \end{aligned}$$

Notice that $P^{(0,2)}(x,y)$ is singular if and only if

$$\begin{aligned} y^2 \xi = (S_{02} + S_{20}^{-1} S_{02}x )\xi \quad \quad {\mathrm for} \quad \xi \in {\mathbb {C}}^p \setminus \{ 0 \}. \end{aligned}$$

(8.14)

By equations (8.13) and (8.14) we see that

$$\begin{aligned} Z_{11} \cap Z_{20} \cap Z_{02}&= \{ (x,0): \xi \in {\mathbb {C}}^p {\setminus }\{ 0 \} \;\;\text {such that}\;\;xS_{20}^{-1}S_{02}\xi =-S_{02}\xi \}\\&\cup \{ (1,y): \xi \in {\mathbb {C}}^p {\setminus }\{ 0 \} \;\;\text {such that}\;\; y^2 \xi = (S_{02} + S_{20}^{-1} S_{02} )\xi \}, \end{aligned}$$

that is,

$$\begin{aligned} Z_{11} \cap Z_{20} \cap Z_{02} = \{ (x,0): x \in \sigma (S_{20}^{-1}S_{02},-S_{02}) \} \cup \{ (1,y): y^2 \in \sigma (S_{02} + S_{20}^{-1} S_{02}) \}, \end{aligned}$$

where $\sigma (S_{20}^{-1}S_{02},-S_{02})$ is the set of generalised eigenvalues of $\{S_{20}^{-1}S_{02}, -S_{02}. \}$ $\square$

Remark 8.3

We note that the set $\{ (x,0): x \in \sigma (S_{20}^{-1}S_{02},-S_{02}) \}$ describing the support of the representing measure in Theorem 8.2 is finite. Notice that both $S_{20}^{-1}S_{02}$ and $-S_{02}$ are invertible and thus the upper triangular matrices appearing in the respective generalised Schur decomposition are invertible. Hence the set of generalised eigenvalues of $\{S_{20}^{-1}S_{02}, -S_{02}\}$ $\sigma (S_{20}^{-1}S_{02},-S_{02})$ is finite. We refer the reader to [40, Theorem 7.7.1] for further details.

Theorem 8.4

Let $S:=(S_\gamma )_{\gamma \in \Gamma _{2, 2}}$ be a given truncated ${\mathcal {H}}_p$-valued bisequence with $S_{20}S_{02}=0_{p \times p}.$ Suppose

Then S has a minimal representing measure T with

$$\begin{aligned} {{\,\mathrm{supp}\,}}T \subseteq \{(x,y)\in {\mathbb {R}}^2:y(y-1)\in \sigma (S_{02}) \}&\cap \{ (x,0): x\in {\mathbb {R}}\}\cup \{ (0,y): y\in {\mathbb {R}}\}\\&\cap \{(x,y)\in {\mathbb {R}}^2:y(y-1)\in \sigma (S_{02}) \}. \end{aligned}$$

Proof

Let $S_{30}=S_{20},$ $S_{03}=S_{02}$ and $S_{21}=S_{12}=0_{p \times p}.$ Then $W:=\begin{pmatrix} S_{20}&{} 0 &{}S_{02} \\ I_p&{}0 &{}0\\ 0&{}0&{}I_p \end{pmatrix}$ will satisfy

$$\begin{aligned} B:=M(1)W=\begin{pmatrix} S_{20}&{} 0 &{}S_{02} \\ S_{20}&{}0 &{}0\\ 0&{}0&{}S_{02} \end{pmatrix}\quad \text {and}\quad C:=W^*M(1)W=\begin{pmatrix} S_{20}^2+S_{20}&{} 0 &{}0 \\ 0&{}0 &{}0\\ 0&{}0&{}S_{02}^2+S_{02} \end{pmatrix}, \end{aligned}$$

since $S_{20}S_{02}=0_{p \times p}.$ Lemma 2.1 asserts that $M(2):=\begin{pmatrix} M(1) &{} B \\ B^* &{} C \\ \end{pmatrix}\succeq 0$ is a flat extension of M(1). By the flat extension theorem for matricial moments (see Theorem 6.2), there exists a minimal representing measure T for S with ${{\,\mathrm{supp}\,}}T={\mathcal {V}}(M(2)).$ We next let the following matrix-valued polynomials in ${\mathbb {C}}^{p\times p}[x, y]$:

$$\begin{aligned} P^{(2, 0)}(x, y)&=x^2I_p -S_{20}-xI_p,\\ P^{(1,1)}(x, y)&= xyI_p \end{aligned}$$

and

$$\begin{aligned} P^{(0,2)}(x,y)=y^2I_p-S_{02}-yI_p. \end{aligned}$$

Let ${\mathcal {Z}}_{20}:={\mathcal {Z}}(\det (P^{(2,0)}(x, y))),\;{\mathcal {Z}}_{11}:={\mathcal {Z}}(\det (P^{(1,1)}(x, y))) \; \text {and}\;{\mathcal {Z}}_{02}:={\mathcal {Z}}(\det (P^{(0,2)}(x, y))).$ Then

$$\begin{aligned} {{\,\mathrm{supp}\,}}{T} = {\mathcal {Z}}_{20}\cap {\mathcal {Z}}_{11}\cap {\mathcal {Z}}_{02}. \end{aligned}$$

Since $P^{(2, 0)}(x, y)$ is not invertible, there exists $\eta \in {\mathbb {C}}^{p}{\setminus }\{0\}$ such that $x^2\eta -x\eta =S_{20}\eta .$ Thus $x(x-1)\eta =S_{20}\eta$ and

$$\begin{aligned} {\mathcal {Z}}_{20}=\{(x,y)\in {\mathbb {R}}^2:x(x-1)\in \sigma (S_{20}) \}. \end{aligned}$$

Notice that ${\mathcal {Z}}_{11}=\{ (x,0): x\in {\mathbb {R}}\}\cup \{ (0,y): y\in {\mathbb {R}}\}.$ Moreover, since $P^{(0, 2)}(x, y)$ is not invertible, there exists $\xi \in {\mathbb {C}}^{p}{\setminus }\{0\}$ such that $y^2\xi -y\xi =S_{02}\xi .$ Hence $y(y-1)\xi =S_{02}\xi$ and

$$\begin{aligned} {\mathcal {Z}}_{02}=\{(x,y)\in {\mathbb {R}}^2:y(y-1)\in \sigma (S_{02}) \}. \end{aligned}$$

Finally,

$$\begin{aligned} {{\,\mathrm{supp}\,}}T \subseteq {\mathcal {Z}}_{20}\cap {\mathcal {Z}}_{11}\cap {\mathcal {Z}}_{02}, \end{aligned}$$

that is,

$$\begin{aligned}&{{\,\mathrm{supp}\,}}T \subseteq \{(x,y)\in {\mathbb {R}}^2:y(y-1)\in \sigma (S_{02}) \}\bigcap \{ (x,0): x\in {\mathbb {R}}\}\cup \{ (0,y): y\in {\mathbb {R}}\}\\&\quad \bigcap \{(x,y)\in {\mathbb {R}}^2:y(y-1)\in \sigma (S_{02}) \}. \end{aligned}$$

$\square$

8.3 Some Singular Cases of the Bivariate Quadratic Matrix-Valued Moment Problem

In the following theorem we obtain a minimal representing measure for a given truncated ${\mathcal {H}}_p$-valued bisequence when then associated d-Hankel matrix has certain block column relations. Moreover, we extract information on the support of the representing measure observing its connection with the aforementioned block column relations. Theorem 8.5 can be thought of as an analogue of [16, Proposition 6.2] for $p\ge 1.$

Theorem 8.5

Let $S:=(S_\gamma )_{\gamma \in \Gamma _{2, 2}}$ be a given truncated ${\mathcal {H}}_p$-valued bisequence. Suppose

and $X=1 \cdot \Phi$ and $Y=1 \cdot \Psi$ for $\Phi , \Psi \in {\mathbb {C}}^{p\times p}.$ Then $\Phi =S_{10}$ and $\Psi =S_{01}$ and there exists a minimal (that is, $\sum \nolimits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a=p$) representing measure T for S of the form

$$\begin{aligned} T=\sum \limits _{a=1}^{\kappa } Q_a \delta _{w^{(a)}}, \end{aligned}$$

where $1 \le \kappa \le p$ and

$$\begin{aligned} {{\,\mathrm{supp}\,}}T = \{w^{(1)}, \ldots , w^{(\kappa )}\}\subseteq \sigma (\Phi ) \times \sigma (\Psi ). \end{aligned}$$

Proof

Since $X=1 \cdot \Phi$ and $Y=1 \cdot \Psi$ for $\Phi , \Psi \in {\mathbb {C}}^{p\times p},$ we have

$$\begin{aligned} S_{10}&=\Phi =\Phi ^* , \end{aligned}$$

(8.15)

$$\begin{aligned} S_{20}&=S_{10}\Phi =\Phi ^2 , \end{aligned}$$

(8.16)

$$\begin{aligned} S_{01}&=\Psi =\Psi ^* ,\nonumber \\ S_{02}&=S_{01}\Psi =\Psi ^2 \end{aligned}$$

(8.17)

and

$$\begin{aligned} S_{11}=S_{10}\Psi =\Phi \Psi . \end{aligned}$$

(8.18)

Let

$$\begin{aligned} S_{30}:= & {} S_{10}\Phi =S_{20},\nonumber \\ S_{21}:= & {} S_{01}\Phi =\Psi \Phi ,\; S_{12}:=S_{10}\Psi =\Phi \Psi =S_{11} \end{aligned}$$

(8.19)

and

$$\begin{aligned} S_{03}:=S_{01}\Psi =S_{02}. \end{aligned}$$

(8.20)

Then $S_{30}, S_{12}\in {\mathcal {H}}_p$ and $S_{03}\in {\mathcal {H}}_p.$ Moreover, $S^*_{21}=\Phi ^*\Psi ^*=S^*_{12}=S_{12}=S_{11}$ and so $S_{21}\in {\mathcal {H}}_p$ and

$$\begin{aligned} S_{12}=S_{11}=S_{21}, \end{aligned}$$

(8.21)

that is,

$$\begin{aligned} \Phi \Psi = \Psi \Phi . \end{aligned}$$

(8.22)

If we let $W:=\begin{pmatrix} 0&{} 0 &{}0 \\ \Phi &{}\Psi &{}0\\ 0&{}0&{}\Psi \end{pmatrix},$ then $B:=\begin{pmatrix} S_{20}&{} S_{11} &{}S_{02} \\ S_{30}&{}S_{21} &{}S_{12}\\ S_{21}&{}S_{12}&{}S_{03} \end{pmatrix}=M(1)W.$ Notice that

$$\begin{aligned} B=\begin{pmatrix} S_{20}&{} S_{11} &{}S_{02} \\ S_{20}&{}S_{11} &{}S_{11}\\ S_{11}&{}S_{11}&{}S_{02} \end{pmatrix}, \end{aligned}$$

by formulas (8.19), (8.20) and (8.21). Let

$$\begin{aligned} C:=W^*M(1)W=W^*B=\begin{pmatrix} \Phi ^*S_{20}&{}\quad \Phi ^*S_{11} &{}\quad \Phi ^*S_{11} \\ \Psi ^*S_{20}&{}\quad \Psi ^*S_{11} &{}\quad \Psi ^*S_{11}\\ \Psi ^*S_{11}&{}\quad \Psi ^*S_{11}&{}\quad \Psi ^*S_{02} \end{pmatrix} \end{aligned}$$

and write $C=\begin{pmatrix} C_{11}&{} C_{12} &{}C_{13} \\ C_{21}&{}C_{22} &{}C_{23}\\ C_{31}&{}C_{32}&{}C_{33} \end{pmatrix}.$ In order for C to have the appropriate block Hankel structure we need to show

$$\begin{aligned} \Psi ^*S_{20}=\Phi ^*S_{11}\;\; \text {and}\;\; \Psi ^*S_{11}=\Phi ^*S_{11}. \end{aligned}$$

By formulas (8.15), (8.16) and (8.22),

$$\begin{aligned} \Psi ^*S_{20}=\Psi ^*\Phi ^2=\Psi \Phi ^2=\Psi \Phi \Phi =\Phi \Psi \Phi . \end{aligned}$$

By formulas (8.17), (8.18) and (8.22), we have

$$\begin{aligned} \Phi ^*S_{11}=\Phi ^*\Phi \Psi =\Phi ^2\Psi =\Phi \Phi \Psi =\Phi \Psi \Phi =\Psi ^*S_{20} \end{aligned}$$

as desired. Furthermore, we have $C_{22} = C_{31}=\Psi ^*S_{11}.$ Thus $C_{31}=\Psi ^*S_{11}\in {\mathcal {H}}_p.$ However $C_{31} = C^*_{13}$ forces $C_{13} = C_{22} = C_{31}.$ Hence

$$\begin{aligned} M(2):=\begin{pmatrix} M(1) &{}\quad B \\ B^* &{}\quad C \\ \end{pmatrix}\succeq 0 \end{aligned}$$

is a flat extension of M(1) by Lemma 2.1. By the flat extension theorem for matricial moments (see Theorem 6.2), there exists a minimal representing measure T for S of the form

$$\begin{aligned} T=\sum \limits _{a=1}^{\kappa } Q_a \delta _{w^{(a)}} \end{aligned}$$

such that

$$\begin{aligned} {{\,\mathrm{supp}\,}}T= {\mathcal {V}}(M(2)), \end{aligned}$$

where

$$\begin{aligned} {{\,\mathrm{card}\,}}{{\,\mathrm{supp}\,}}T= \sum \limits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a={{\,\mathrm{card}\,}}{\mathcal {V}}(M(2)) = {{\,\mathrm{rank}\,}}M(1)=p. \end{aligned}$$

Since $X=1 \cdot \Phi$ and $Y=1 \cdot \Psi ,$ the matrix-valued polynomials

$$\begin{aligned} P_1(x,y)=xI_p -\Phi \quad \text {and}\quad P_2(x,y)=yI_p -\Psi \end{aligned}$$

are such that $P_1(X, Y)=P_2(X, Y)={{\,\mathrm{col}\,}}(0_{p\times p})_{\gamma \in \Gamma _{1, 2}}\in C_{M(2)}.$ Lemma 5.55 implies that

$$\begin{aligned} {{\,\mathrm{supp}\,}}T= & {} {\mathcal {V}}(M(2))\subseteq {\mathcal {Z}}(\det (P_1(x, y)))\bigcap {\mathcal {Z}}(\det (P_2(x, y))) \\= & {} \{(x,y)\in {\mathbb {R}}^2:\det (xI_p -\Phi )=0 \}\\&\bigcap&\{(x,y)\in {\mathbb {R}}^2:\det (yI_p- \Psi )=0 \}\\= & {} \sigma (\Phi ) \times \sigma (\Psi ). \end{aligned}$$

Thus

$$\begin{aligned} {{\,\mathrm{supp}\,}}T =\{w^{(1)}, \ldots , w^{(\kappa )}\}\subseteq {\mathcal {V}}(M(2))= \sigma (\Phi ) \times \sigma (\Psi ) \end{aligned}$$

and

$$\begin{aligned} T=\sum \limits _{a=1}^{\kappa } Q_a \delta _{w^{(a)}} \end{aligned}$$

is a representing measure for S with $\sum \nolimits _{a=1}^{\kappa } {{\,\mathrm{rank}\,}}Q_a =p.$ Since $1 \le {{\,\mathrm{rank}\,}}Q_a \le p,$ we must have $1 \le \kappa \le p.$ $\square$

Theorem 8.6

Let $S:=(S_\gamma )_{\gamma \in \Gamma _{2, 2}}$ be a given truncated ${\mathcal {H}}_p$-valued bisequence with moments $S_{10}=S_{01}=S_{11}=S_{20}=0_{p \times p}.$ Suppose

Then S has a minimal representing measure T with

$$\begin{aligned} {{\,\mathrm{supp}\,}}T \subseteq \{(x,y)\in {\mathbb {R}}^2:y^2\in \sigma (S_{02}) \}. \end{aligned}$$

Proof

Let $S_{30}=S_{21}=S_{12}=S_{03}=0_{p \times p}.$ Then $W:=\begin{pmatrix} 0&{} 0 &{}S_{02} \\ 0&{}0 &{}0\\ 0&{}0&{}0 \end{pmatrix}$ will satisfy

$$\begin{aligned} B:=M(1)W=\begin{pmatrix} 0&{}\quad 0 &{}\quad S_{02} \\ 0&{}\quad 0 &{}\quad 0\\ 0&{}\quad 0&{}\quad 0 \end{pmatrix}\quad \text {and}\quad C:=W^*M(1)W=\begin{pmatrix} 0&{}\quad 0 &{}\quad 0 \\ 0&{}\quad 0 &{}\quad 0\\ 0&{}\quad 0&{}\quad S_{02}^2 \end{pmatrix}. \end{aligned}$$

Lemma 2.1 asserts that $M(2):=\begin{pmatrix} M(1) &{} B \\ B^* &{} C \\ \end{pmatrix}\succeq 0$ is a flat extension of M(1). By the flat extension theorem for matricial moments (see Theorem 6.2), there exists a minimal representing measure T for S with ${{\,\mathrm{supp}\,}}T={\mathcal {V}}(M(2)).$ Let $P^{(0, 2)}(x, y)=y^2I_p -S_{02}\in {\mathbb {C}}^{p \times p}[x, y]$ and notice that

$$\begin{aligned} \begin{array}{clll} {\mathcal {V}}(M(2))&{}\subseteq {\mathcal {Z}}(\det (P^{(2, 0)}(x, y))) \\ &{}= \{(x,y)\in {\mathbb {R}}^2:\det (y^2I_p -S_{02})=0 \} \end{array}. \end{aligned}$$

Since $P^{(0, 2)}(y, 0)$ is not invertible, there exists $\eta \in {\mathbb {C}}^{p} {\setminus }\{0\}$ such that $y^2\eta =S_{02}\eta .$ Thus $y^2\in \sigma (S_{02})$ and

$\square$

Definition 8.7

Let $P(x)= \sum \nolimits _{\lambda \in \Gamma _{n, 2}} x^\lambda P_\lambda \in {\mathbb {C}}^{p\times p}_2[x, y]$ and consider the matrix $J\in {\mathbb {C}}^{6p\times 6p}.$ Suppose the map $\Psi (x, y):{\mathbb {R}}^2\rightarrow ({\mathbb {C}}^{p \times p}, {\mathbb {C}}^{p \times p})$ is given by $\Psi (x, y)=(\Psi _1(x, y), \Psi _2(x, y))$ with

$$\begin{aligned} \Psi _1(x, y)={J}_{00}+{J}_{10}x+{J}_{01}y\quad \text {and}\quad \Psi _2(x, y)={K}_{00}+{K}_{10}x+{K}_{01}y \end{aligned}$$

for some ${J}_{00}, {J}_{10}, {J}_{01}, {K}_{00}, {K}_{10}, {K}_{01}\in {\mathbb {C}}^{p\times p}.$ J is defined as a transformation matrix given by

$$\begin{aligned} J{\widehat{P}}={\widehat{P}}_{00}+\Psi _1{\widehat{P}}_{10} +\Psi _2{\widehat{P}}_{01}+\Psi _1^2{\widehat{P}}_{20} +\Psi _1\Psi _2{\widehat{P}}_{11}+\Psi _2^*\Psi _2{\widehat{P}}_{02}. \end{aligned}$$

If J is invertible, then we may view $J^{-1}$ as the matrix given by

$$\begin{aligned} J^{-1}{\widehat{P}}={\widehat{P}}_{00}+\Psi _1^{-1}{\widehat{P}}_{10} +\Psi _2^{-1}{\widehat{P}}_{01}+(\Psi _1^{-1})^2{\widehat{P}}_{20} +\Psi _1^{-1}\Psi _2^{-1}{\widehat{P}}_{11}+\Psi _2^{-*}\Psi _2^{-1}{\widehat{P}}_{02}, \end{aligned}$$

where

$$\begin{aligned} \Psi _1^{-1}(x, y)={\tilde{J}}_{00}+{\tilde{J}}_{10}x+{\tilde{J}}_{01}y\quad \text {and}\quad \Psi _2^{-1}(x, y)={\tilde{K}}_{00}+{\tilde{K}}_{10}x+{\tilde{K}}_{01}y \end{aligned}$$

for some ${\tilde{J}}_{00}, {\tilde{J}}_{10}, {\tilde{J}}_{01}, {\tilde{K}}_{00}, {\tilde{K}}_{10}, {\tilde{K}}_{01}\in {\mathbb {C}}^{p\times p}.$

In the next theorem we will consider the bivariate quadratic matrix-valued moment problem when the given truncated ${\mathcal {H}}_p$-valued bisequence gives rise to a d-Hankel matrix M(1) which is positive semidefinite, has a certain block column relation and obeys a certain condition which is automatically satisfied when $p=1$. Theorem 8.8 can be considered as an analogue of [16, Proposition 6.3] for $p\ge 1.$

Theorem 8.8

Let $S:=(S_\gamma )_{\gamma \in \Gamma _{2, 2}}$ be a given truncated ${\mathcal {H}}_p$-valued bisequence and suppose

and $Y =1 \cdot W_1 + X\cdot W_2$ for $W_1, W_2 \in {\mathbb {C}}^{p\times p}.$ Then the following statements hold:

• (i) There exist ${J}_{00}, {J}_{10}, {J}_{01}, {K}_{00}, {K}_{10}, {K}_{01}\in {\mathbb {C}}^{p\times p}$ such that J (as in Definition 8.7) is invertible, and if we write $J=\begin{pmatrix} {\mathfrak {J}}_{11}&{} {\mathfrak {J}}_{12}\\ {\mathfrak {J}}_{12}&{} {\mathfrak {J}}_{22} \end{pmatrix},$ where ${\mathfrak {J}}_{11}\in {\mathbb {C}}^{3p\times 3p},$ then ${\mathfrak {J}}_{11}^*M(1){\mathfrak {J}}_{11}=\begin{pmatrix} I_p &{} 0 &{} 0 \\ 0 &{}0 &{} 0 \\ 0 &{}0 &{} {\tilde{S}}_{02} \end{pmatrix},$ where ${\tilde{S}}_{02}=S_{20}-S_{10}^2\in {\mathcal {H}}_p.$

• (ii) Let J be as in (i). Let ${\tilde{S}}=({\tilde{S}}_\gamma )_{\gamma \in \Gamma _{2, 2}}$ be a truncated ${\mathcal {H}}_p$-valued bisequence given by ${\tilde{S}}_{10}={\tilde{S}}_{01}={\tilde{S}}_{11}=0_{p \times p}={\tilde{S}}_{20},$ and let ${\tilde{M}}(1)=\begin{pmatrix} I_p &{} 0 &{} 0 \\ 0 &{}0 &{} 0 \\ 0 &{}0 &{} {\tilde{S}}_{02} \end{pmatrix}$ be the corresponding d-Hankel matrix. If ${\tilde{M}}(2)$ is a flat extension of ${\tilde{M}}(1)$ such that $J^{-*}{\tilde{M}}(2)J^{-1}$ is of the form $M(2):=\begin{pmatrix} M(1) &{} B \\ B^* &{} C \\ \end{pmatrix},$ for some choice of $(S_\gamma )_{\gamma \in \Gamma _{2, 4}\setminus \Gamma _{2, 2}}$ with $S_\gamma \in {\mathcal {H}}_p$ for $\gamma \in \Gamma _{2, 4}\setminus \Gamma _{2, 2},$ then S has a minimal representing measure.

Proof

We will first prove (i). Let $J\in {\mathbb {C}}^{6p\times 6p}$ be the transformation matrix given in Definition 8.7 determined by

$$\begin{aligned} \Psi _1(x, y)={J}_{00}+{J}_{10}x+{J}_{01}y,\quad \Psi _2(x, y)={K}_{00}+{K}_{10}x+{K}_{01}y, \end{aligned}$$

where

$$\begin{aligned} J_{00}&=-S_{10}(S_{20}-S_{10}^2)^{-1}(S_{10}S_{01}-S_{11})-S_{01}, \\ J_{10}&=(S_{20}-S_{10}^2)^{-1}(S_{10}S_{01}-S_{11}), J_{01}=I_p,\\ K_{00}&=-S_{10}, K_{10}=I_p \;\; \text {and}\;\; K_{01}=0_{p\times p}. \end{aligned}$$

One can check that J is invertible and if we write $J=\begin{pmatrix} {\mathfrak {J}}_{11}&{} {\mathfrak {J}}_{12}\\ {\mathfrak {J}}_{12}&{} {\mathfrak {J}}_{22} \end{pmatrix},$ where ${\mathfrak {J}}_{11}\in {\mathbb {C}}^{3p\times 3p}$, then ${\mathfrak {J}}_{11}^{-1}=\begin{pmatrix} I_p &{} {\tilde{J}}_{00} &{} {\tilde{K}}_{00} \\ 0 &{} {\tilde{J}}_{10} &{} {\tilde{K}}_{10} \\ 0 &{}{\tilde{J}}_{01} &{} {\tilde{K}}_{01} \end{pmatrix},$ where ${\tilde{J}}_{00}= S_{10},$ ${\tilde{J}}_{10}=0_{p\times p},$ ${\tilde{J}}_{01}= I_p,$ ${\tilde{K}}_{00}=S_{01},$ ${\tilde{K}}_{10}=I_p,$ and ${\tilde{K}}_{01}=-(S_{20}-S_{10}^2)^{-1}(S_{10}S_{01}-S_{11})$ and

$$\begin{aligned} \mathfrak {J}_{11}^* M(1) \mathfrak {J}_{11}. =\begin{pmatrix} I_p &{} 0 &{} 0 \\ 0 &{}0 &{} 0 \\ 0 &{}0 &{} {\tilde{S}}_{02} \end{pmatrix}, \end{aligned}$$

where ${\tilde{S}}_{02}=S_{20}-S_{10}^2\in {\mathcal {H}}_p.$

We will now prove (ii). Let J be as in (i). Since ${\tilde{M}}(2)$ is a flat extension of ${\tilde{M}}(1)$ and

$$\begin{aligned} J^{-*}{\tilde{M}}(2)J^{-1}=M(2):=\begin{pmatrix} M(1) &{} B \\ B^* &{} C \\ \end{pmatrix}, \end{aligned}$$

we have that ${M}(2)\succeq 0$ and

$$\begin{aligned} 2p={{\,\mathrm{rank}\,}}M(1)\le {{\,\mathrm{rank}\,}}{M}(2)={{\,\mathrm{rank}\,}}{\tilde{M}}(2)={{\,\mathrm{rank}\,}}{\tilde{M}}(1)=2p. \end{aligned}$$

Thus M(2) is a flat extension of M(1) and so by the flat extension theorem for matricial moments (see Theorem 6.2), there exists a minimal representing measure T for S. $\square$

8.4 The Invertible Case of the Bivariate Quadratic Matrix-Valued Moment Problem

We shall see in the next theorem that every truncated ${\mathcal {H}}_p$-valued bisequence $S:=(S_\gamma )_{\gamma \in \Gamma _{2, 2}}$ such that $M(1)\succ 0$ and M(1) obeys an extra condition (which is automatically satisfied when $p=1$) has a minimal representing measure. Theorem 8.9 can be viewed as an analogue of [16, Proposition 6.5] when $p \ge 1$.

Theorem 8.9

Let $S:=(S_\gamma )_{\gamma \in \Gamma _{2, 2}}$ be a given truncated ${\mathcal {H}}_p$-valued bisequence and suppose

Then the following conditions hold:

• (i) There exist ${J}_{00}, {J}_{10}, {J}_{01}, {K}_{00}, {K}_{10}, {K}_{01}\in {\mathbb {C}}^{p\times p}$ such that J (as in Definition 8.7) is invertible, and if we write ${J} = \begin{pmatrix} \mathfrak {J}_{11} &{} \mathfrak {J}_{12} \\ \mathfrak {J}_{21} &{} \mathfrak {J}_{22} \end{pmatrix},$ where $\mathfrak {J}_{11}\in {\mathbb {C}}^{3p\times 3p},$ then $\mathfrak {J}_{11}^* M(1) \mathfrak {J}_{11} = \begin{pmatrix} I_p &{} 0 &{} 0 \\ 0 &{} I_p &{} 0 \\ 0 &{} 0 &{} I_p \end{pmatrix}.$

• (ii) Let J be as in (i). Let ${\tilde{S}}=({\tilde{S}}_\gamma )_{\gamma \in \Gamma _{2, 2}}$ be a truncated ${\mathcal {H}}_p$-valued bisequence given by ${\tilde{S}}_{10}={\tilde{S}}_{01}={\tilde{S}}_{11}=0_{p \times p}$ and let ${\tilde{M}}(1)=\begin{pmatrix} I_p &{} 0 &{} 0 \\ 0 &{} I_p &{} 0 \\ 0 &{}0 &{} I_p \end{pmatrix}$ be the corresponding d-Hankel matrix. If ${\tilde{M}}(2)$ is a flat extension of ${\tilde{M}}(1)$ such that $J^{-*}{\tilde{M}}(2)J^{-1}$ is of the form $M(2):=\begin{pmatrix} M(1) &{} B \\ B^* &{} C \\ \end{pmatrix},$ for some choice of $(S_\gamma )_{\gamma \in \Gamma _{2, 4}\setminus \Gamma _{2, 2}}$ with $S_\gamma \in {\mathcal {H}}_p$ for $\gamma \in \Gamma _{2, 4}\setminus \Gamma _{2, 2},$ then S has a minimal representing measure.

Proof

We will prove (i). Suppose $\Theta =S_{20}-S_{10}^2.$ $\Theta \succ 0,$ by a Schur complement argument applied to $M(1)\succ 0.$ Let

$$\begin{aligned} \Omega = -(S_{10}S_{01}-S_{11})^*(S_{20}-S_{10}^2)^{-1}(S_{10}S_{01}-S_{11})+S_{02}- S_{01}^2 \end{aligned}$$

and ${\mathcal {J}}\in {\mathbb {C}}^{6p \times 6p}$ be as in Definition 8.7 with

$$\begin{aligned} {\mathcal {J}}_{00}&=-S_{10}(S_{20}-S_{10}^2)^{-1}(S_{10}S_{01}-S_{11})-S_{01}, \\ {\mathcal {J}}_{10}&=(S_{20}-S_{10}^2)^{-1}(S_{10}S_{01}-S_{11}), {\mathcal {J}}_{01}=I_p,\\ {\mathcal {K}}_{00}&=-S_{10}, {\mathcal {K}}_{10}=I_p\;\; \text {and}\;\; {\mathcal {K}}_{01}=0_{p\times p}. \end{aligned}$$

Then ${\mathcal {J}}$ is invertible and if we write $\mathcal {J} = \begin{pmatrix} \mathcal {J}_{11} &{} \mathcal {J}_{12} \\ \mathcal {J}_{21} &{} \mathcal {J}_{22} \end{pmatrix},$ where ${\mathcal {J}}_{11}\in {\mathbb {C}}^{3p\times 3p},$ then ${\mathcal {J}}_{11}$ is invertible and the (2, 2) block of ${\mathcal {J}}_{11}^*M(1){\mathcal {J}}_{11}\succ 0$ is given by $\Omega ,$ and hence $\Omega \succ 0.$

Next we let $J\in {\mathbb {C}}^{6p\times 6p}$ be the transformation matrix given in Definition 8.7 determined by

$$\begin{aligned} \Psi _1(x, y)={J}_{00}+{J}_{10}x+{J}_{01}y,\quad \Psi _2(x, y)={K}_{00}+{K}_{10}x+{K}_{01}y, \end{aligned}$$

where

$$\begin{aligned} J_{00}&=\{-S_{10}(S_{20}-S_{10}^2)^{-1}(S_{10}S_{01}-S_{11})-S_{01}\}\Omega ^{-1/2},\\ J_{10}&=(S_{20}-S_{10}^2)^{-1}(S_{10}S_{01}-S_{11})\Omega ^{-1/2}, J_{01}=\Omega ^{-1/2},\\ K_{00}&=-S_{10}\Theta ^{-1/2}, K_{10}=\Theta ^{-1/2} \;\; \text {and}\;\; K_{01}=0_{p\times p}. \end{aligned}$$

One can check that J is invertible and if we write $J=\begin{pmatrix} {\mathfrak {J}}_{11}&{} {\mathfrak {J}}_{12}\\ {\mathfrak {J}}_{12}&{} {\mathfrak {J}}_{22} \end{pmatrix},$ where ${\mathfrak {J}}_{11}\in {\mathbb {C}}^{3p\times 3p}$, then ${\mathfrak {J}}_{11}^{-1}=\begin{pmatrix} I_p &{} {\tilde{J}}_{00} &{} {\tilde{K}}_{00} \\ 0 &{} {\tilde{J}}_{10} &{} {\tilde{K}}_{10} \\ 0 &{}{\tilde{J}}_{01} &{} {\tilde{K}}_{01} \end{pmatrix},$ where ${\tilde{J}}_{00}=S_{10}, {\tilde{J}}_{10}=0_{p\times p}, {\tilde{J}}_{01}=\Theta ^{1/2},$ ${\tilde{K}}_{00}=S_{01}, {\tilde{K}}_{10}=\Omega ^{1/2}, {\tilde{K}}_{01}=-\Theta ^{-1/2}(S_{10}S_{01}-S_{11}).$ We then have $\mathfrak {J}_{11}^*M(1)\mathfrak {J}_{11}=\begin{pmatrix} I_p &{} 0 &{} 0 \\ 0 &{}I_p &{} 0 \\ 0 &{}0 &{} I_p \end{pmatrix}.$

We will now prove (ii). Let J be as in (i). Since ${\tilde{M}}(2)$ is a flat extension of ${\tilde{M}}(1)$ and

$$\begin{aligned} J^{-*}{\tilde{M}}(2)J^{-1}=M(2):=\begin{pmatrix} M(1) &{} B \\ B^* &{} C \\ \end{pmatrix}, \end{aligned}$$

we have that ${M}(2)\succeq 0$ and

$$\begin{aligned} 3p={{\,\mathrm{rank}\,}}M(1)\le {{\,\mathrm{rank}\,}}{M}(2)={{\,\mathrm{rank}\,}}{\tilde{M}}(2)={{\,\mathrm{rank}\,}}{\tilde{M}}(1)=3p. \end{aligned}$$

Hence M(2) is a flat extension of M(1) and so by the flat extension theorem for matricial moments (see Theorem 6.2), there exists a minimal representing measure T for S. $\square$

8.5 Examples

The following example showcases Theorem 8.5 for an explicit truncated ${\mathcal {H}}_2$-valued bisequence.

Example 8.10

Let $S:=(S_\gamma )_{\gamma \in \Gamma _{2, 2}}$ be a truncated ${\mathcal {H}}_2$-valued bisequence given by

and suppose $X=1 \cdot \Phi$ and $Y=1 \cdot \Psi$ for $\Phi =S_{10}$ and $\Psi =S_{01}.$ The matrix-valued polynomials $P_1(x,y)=xI_2 -\Phi \;\;\text {and}\;\; P_2(x,y)=yI_2 -\Psi$ are such that

$$\begin{aligned} P_1(X, Y)=P_2(X, Y)={{\,\mathrm{col}\,}}(0_{2\times 2})_{\gamma \in \Gamma _{1, 2}}\in C_{M(1)} \end{aligned}$$

and we have $\det (P_1(x, y))=x(x-1)$ and $\det (P_2(x, y))=y(y-1).$ By Theorem 8.5, M(1) has a flat extension of the form

and there exists a minimal representing measure $T=\sum \nolimits _{a=1}^{\kappa } Q_a \delta _{w^{(a)}},$ where $1 \le \kappa \le 2$ and

$$\begin{aligned} \begin{array}{clll} {{\,\mathrm{supp}\,}}T &{}\subseteq \sigma (\Phi ) \times \sigma (\Psi )\\ {} &{}= {\mathcal {Z}}(\det (P_1(x, y)))\bigcap {\mathcal {Z}}(\det (P_2(x, y)))\\ &{}=\{(0, 0) (1, 0), (0, 1), (1,1) \}. \end{array} \end{aligned}$$

We note that M(2) is also described by the block column relation $X+Y=1$ and so the matrix-valued polynomial $P_3(x,y)=I_2-xI_2 -yI_2$ is such that

$$\begin{aligned} P_3(X, Y)=P_1(X, Y)=P_2(X, Y)={{\,\mathrm{col}\,}}(0_{2\times 2})_{\gamma \in \Gamma _{1, 2}}\in C_{M(2)}. \end{aligned}$$

Then $\det (P_3(x, y))=(1-x-y)^2$ and hence ${\mathcal {V}}(M(2))\subseteq \{ (1, 0), (0, 1) \}.$ We will show

$$\begin{aligned} {\mathcal {V}}(M(2))=\{ (1, 0), (0, 1) \}. \end{aligned}$$

Indeed, if ${\mathcal {V}}(M(2))\ne \{ (1, 0), (0, 1) \},$ then since $1\le \kappa \le 2,$

$$\begin{aligned} {\mathcal {V}}(M(2))= \{ (1, 0)\}\;\text {or}\; {\mathcal {V}}(M(2))= \{ (0, 1)\}. \end{aligned}$$

If ${\mathcal {V}}(M(2))= \{ (1, 0)\},$ then

$$\begin{aligned} T=Q_1\delta _{(1,0)} \end{aligned}$$

is a representing measure for S,  where ${{\,\mathrm{rank}\,}}Q_1=2.$ But then ${{\,\mathrm{rank}\,}}Q_1= {{\,\mathrm{rank}\,}}S_{20}=2,$ a contradiction. Similarly, if ${\mathcal {V}}(M(2))= \{ (0, 1)\},$ then

$$\begin{aligned} T=Q_1\delta _{(0,1)} \end{aligned}$$

is a representing measure for S,  where ${{\,\mathrm{rank}\,}}Q_1=2.$ However ${{\,\mathrm{rank}\,}}Q_1= {{\,\mathrm{rank}\,}}S_{01}=2,$ a contradiction. Hence $\kappa \ne 1$ and

$$\begin{aligned} {\mathcal {V}}(M(2))=\{ (1, 0), (0, 1) \}. \end{aligned}$$

We will now compute a representing measure for S. Remark 5.23 for $\Lambda = \{(0,0), (1,0)\}\subseteq {\mathbb {N}}_0^2$ asserts that the multivariable Vandermonde matrix

$$\begin{aligned} V^{2\times 2}((1, 0), (0, 1); \Lambda )=\begin{pmatrix} 1&{}\quad 0&{}\quad 1&{}\quad 0 \\ 0&{}\quad 1 &{}\quad 0&{}\quad 1\\ 1&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 1&{}\quad 0&{}\quad 0 \\ \end{pmatrix} \end{aligned}$$

is invertible. By the flat extension theorem for matricial moments (see Theorem 6.2), the positive semidefinite matrices $Q_1, Q_2 \in {\mathbb {C}}^{2 \times 2}$ are given by the Vandermonde equation

$$\begin{aligned} {{{\,\mathrm{col}\,}}(Q_a)_{a=1}^{2}} = V^{2 \times 2}((1, 0), (0, 1); \Lambda )^{-1} {{\,\mathrm{col}\,}}(S_{ \lambda })_{\lambda \in \Lambda }. \end{aligned}$$

(8.23)

We have

$$\begin{aligned} V^{2\times 2}((1, 0), (0, 1); \Lambda )^{-1}=\begin{pmatrix} 0&{}\quad 0&{}\quad 1&{}\quad 0 \\ 0&{}\quad 0 &{}\quad 0&{}\quad 1\\ 1&{}\quad 0&{}\quad -1&{}\quad 0 \\ 0&{}\quad 1&{}\quad 0&{}\quad -1 \\ \end{pmatrix} \end{aligned}$$

and thus by equation (8.23),

$$\begin{aligned} Q_1=\begin{pmatrix} 1&{}\quad 0 \\ 0&{}\quad 0 \\ \end{pmatrix}\quad \text {and}\quad Q_2=\begin{pmatrix} 0&{}\quad 0 \\ 0&{}\quad 1 \\ \end{pmatrix}, \end{aligned}$$

where ${{\,\mathrm{rank}\,}}Q_1={{\,\mathrm{rank}\,}}Q_2=1.$ Hence $T=\sum \nolimits _{a=1}^{2} Q_a \delta _{w^{(a)}}$ is a representing measure for S with ${{\,\mathrm{rank}\,}}Q_1+{{\,\mathrm{rank}\,}}Q_2 =2.$

The following example showcases Theorem 8.8 for an explicit truncated ${\mathcal {H}}_2$-valued bisequence.

Example 8.11

Let $S:=(S_\gamma )_{\gamma \in \Gamma _{2, 2}}$ be a truncated ${\mathcal {H}}_2$-valued bisequence given by

M(1) is described by the block column relation $Y=1 \cdot P_{00} \in C_{M(1)},$ where

Thus $P_1(X, Y)={{\,\mathrm{col}\,}}(0_{2\times 2})_{\gamma \in \Gamma _{1, 2}},$ where

$$\begin{aligned} P_1(x, y)=yI_2-P_{00}. \end{aligned}$$

(8.24)

Since $\det (P_1(x, y))=y(y-1),$ we obtain

$$\begin{aligned} {\mathcal {V}}(M(1))={\mathcal {Z}}(\det (P_1(x, y))) =\{ (x,0): x\in {\mathbb {R}}\}\cup \{ (x,1): x\in {\mathbb {R}}\}. \end{aligned}$$

Since $P_1(X, Y)={{\,\mathrm{col}\,}}(0_{2\times 2})_{\gamma \in \Gamma _{1, 2}}\in C_{M(1)},$ where $P_1$ as described in formula (8.24), Lemma 5.21 implies that any positive extension must have the block column relation

$$\begin{aligned} P_1(X, Y)={{\,\mathrm{col}\,}}(0_{2\times 2})_{\gamma \in \Gamma _{2, 2}}\in C_{M(2)}. \end{aligned}$$

Thus

$$\begin{aligned} \begin{pmatrix} S_{21} \\ S_{12} \\ S_{03} \end{pmatrix}= \begin{pmatrix} S_{20} \\ S_{11} \\ S_{02} \end{pmatrix} P_{00}. \end{aligned}$$

If we let

$$\begin{aligned} \begin{pmatrix} S_{22} \\ S_{13} \\ S_{04} \end{pmatrix}= \begin{pmatrix} S_{21} \\ S_{12} \\ S_{03} \end{pmatrix} P_{00}\quad \text {and}\quad S_{40}=2 S_{20}, \end{aligned}$$

then one can check that

$$\begin{aligned} X^2&= 1\cdot (2 I_2)\in C_{M(2)},\\ XY&=X\cdot P_{00}\in C_{M(2)} \end{aligned}$$

and

$$\begin{aligned} Y^2=Y\in C_{M(2)}. \end{aligned}$$

Let $W=\begin{pmatrix} 2 I_2 &{}0&{}0 \\ 0&{}P_{00} &{}0\\ 0&{}0&{}I_2 \end{pmatrix}\in {\mathbb {C}}^{6\times 6}.$ Then

$$\begin{aligned} \begin{pmatrix} S_{20}&{}\quad S_{11} &{}\quad S_{02} \\ S_{30}&{}\quad S_{21} &{}\quad S_{12}\\ S_{21}&{}\quad S_{12}&{}\quad S_{03} \end{pmatrix}=M(1)W \;\;\text {and}\;\; \begin{pmatrix} S_{40}&{}\quad S_{31} &{}\quad S_{22} \\ S_{31}&{}\quad S_{22} &{}\quad S_{13}\\ S_{22}&{}\quad S_{13}&{}\quad S_{04} \end{pmatrix} =W^*M(1)W. \end{aligned}$$

Lemma 2.1 asserts that $M(2)\succeq 0$ and

$$\begin{aligned} {{\,\mathrm{rank}\,}}M(1)={{\,\mathrm{rank}\,}}M(2). \end{aligned}$$

We have the following matrix-valued polynomials in ${\mathbb {C}}^{2\times 2}[x, y]$:

$$\begin{aligned} P_1(x, y)= & {} yI_2-P_{00}, \quad P_2(x, y)= x^2I_2-2I_2, \\ P_3(x, y)= & {} xyI_2-xP_{00},\quad P_4(x, y)= y^2I_2-yI_2, \end{aligned}$$

with

$$\begin{aligned} \det (P_1(x, y))= & {} y(y-1),\quad \det (P_2(x, y))=(x^2-2)^2,\\ \det (P_3(x, y))= & {} x^2y(y-1), \quad \det (P_4(x, y))=y^2(y-1)^2. \end{aligned}$$

We obtain

$$\begin{aligned} {\mathcal {V}}(M(2))=\{(\sqrt{2}, 0), (-\sqrt{2}, 0), (\sqrt{2}, 1), (-\sqrt{2}, 1)\}. \end{aligned}$$

We wish now to compute a representing measure for S. Remark 5.23 asserts that for a subset $\Lambda =\{(0,0), (1, 0), (0, 1), (1, 1)\}\subseteq {\mathbb {N}}_0^2,$ the matrix

is invertible. The positive semidefinite matrices $Q_1, Q_2, Q_3, Q_4 \in {\mathbb {C}}^{2\times 2}$ are given by the Vandermonde equation

$$\begin{aligned} \normalsize {{\,\mathrm{col}\,}}(Q_a)_{a=1}^{4} = V^{2\times 2}((\sqrt{2}, 0), (-\sqrt{2}, 0), (\sqrt{2}, 1), (-\sqrt{2}, 1); \Lambda )^{-1} {{\,\mathrm{col}\,}}(S_{ \lambda })_{\lambda \in \Lambda }. \end{aligned}$$

(8.25)

We then get

and so, Eq. (8.25) yields

where ${{\,\mathrm{rank}\,}}Q_a= 1$ and $Q_a \succeq 0$ for $a=1, \dots , 4.$ We note that

$$\begin{aligned} \sum \limits _{a=1}^{4}{{\,\mathrm{rank}\,}}Q_{a}= {{\,\mathrm{rank}\,}}M(1)= 4. \end{aligned}$$

Finally, a representing measure T for S with $\sum \nolimits _{a=1}^{4} {{\,\mathrm{rank}\,}}Q_a=4$ is $T= \sum \nolimits _{a=1}^{4} Q_a \delta _{w^{(a)}}.$

In the following example, we will see a bivariate quadratic ${\mathcal {H}}_2$-valued bisequence which does not have a minimal representing measure.

Example 8.12

Let $S:=(S_\gamma )_{\gamma \in \Gamma _{2, 2}}$ be a truncated ${\mathcal {H}}_2$-valued bisequence given by

Then S does not have a minimal representing measure.

For this, consider $S_{30}, S_{21}, S_{12}, S_{03}\in {\mathcal {H}}_2.$ Any $W:= \begin{pmatrix} 1 &{}1 &{} 0 &{}0 &{} 0 &{}0 \\ 1&{} 1 &{}0 &{} 0 &{} 0 &{} 1 \\ a_1 &{}a_2 &{} a_3 &{} a_4 &{} a_5 &{}a_6 \\ b_1 &{} b_2 &{}b_3 &{} b_4 &{} b_5 &{} b_6 \\ c_1 &{}c_2 &{} c_3 &{}c_4 &{} c_5 &{} c_6 \\ d_1 &{} d_2 &{}d_3 &{}d_4 &{} d_5 &{} d_6 \end{pmatrix}$ such that $B:=M(1)W=\begin{pmatrix} S_{20}&{} S_{11} &{}S_{02} \\ S_{30}&{}S_{21} &{}S_{12}\\ S_{21}&{}S_{12}&{}S_{03} \end{pmatrix}$ will satisfy $\begin{pmatrix} I_2&S_{10}&S_{01}\end{pmatrix} W=\begin{pmatrix} S_{20}&S_{11}&S_{02}\end{pmatrix}.$ Let $C:=W^*M(1)W=W^*B$ and write $C= \begin{pmatrix} C_{11}&{} C_{12} &{}C_{13} \\ C_{21}&{}C_{22} &{}C_{23}\\ C_{31}&{}C_{32}&{}C_{33} \end{pmatrix}.$ For any $W \in {\mathbb {C}}^{6\times 6}$ described as above, C does not have the appropriate block Hankel structure, since $C_{13}=\begin{pmatrix} 0&{} 1\\ 0&{}1 \end{pmatrix}$ is not ${\mathcal {H}}_2$-valued. Then Lemma 2.1 asserts that M(1) does not have a flat extension $M(2)\succeq 0$ and hence, by the flat extension theorem for matricial moments (see Theorem 6.2), S does not have a minimal representing measure.

$\square$

9 The Bivariate Cubic Matrix-Valued Moment Problem

Given a truncated ${\mathcal {H}}_p$-valued bisequence

$$\begin{aligned} S:=(S_\gamma )_{\gamma \in \Gamma _{3, 2}}=(S_{00}, S_{10}, S_{01}, S_{20}, S_{11}, S_{02}, S_{30}, S_{21}, S_{12}, S_{03}), \end{aligned}$$

we wish to determine when S has a minimal representing measure. In the scalar case (i.e., when $p=1)$, there is a concrete criterion for S to have a minimal representing measure (see Curto, Lee and Yoon [24], the first author [50], and Curto and Yoo [26]).

In what follows, we shall say that $T = \sum _{a=1}^{\kappa } Q_a \delta _{(x_a,y_a)}$ is a minimal representing measure for $S = (S_{\gamma })_{\gamma \in \Gamma _{3,2}}$ if $\sum _{a=1}^{\kappa } \mathrm{rank} Q_a = \mathrm{rank} M(1)$. In our matricial setting, we have the following result.

Theorem 9.1

Let $S:=(S_\gamma )_{\gamma \in \Gamma _{3, 2}}$ be a given truncated ${\mathcal {H}}_p$-valued bisequence and suppose

Let $B = \begin{pmatrix} S_{20} &{} S_{11} &{} S_{02} \\ S_{30} &{} S_{21} &{} S_{12} \\ S_{21} &{} S_{12} &{} S_{03} \end{pmatrix}$. If

$$\begin{aligned} B^* M(1)^{-1} B\text { is of the form }\begin{pmatrix} C_{11} &{}\quad C_{12} &{}\quad C_{13} \\ C_{12} &{}\quad C_{13} &{}\quad C_{23} \\ C_{13} &{}\quad C_{23} &{}\quad C_{33} \end{pmatrix}, \end{aligned}$$

then S has a minimal representing measure.

Proof

Notice that $M(1)W = B$ has the unique solution $W = M(1)^{-1}B$ and that $B^* M(1)^{-1} B = W^* M(1) W$, in which case Smuljan’s lemma (see Lemma 2.1) ensures that M(1) has a flat extension of M(2). We may then use Theorem 6.2 to construct a minimal representing measure for S. $\square$

Appendix A. Positive Extensions of a d-Hankel Matrix

The goal of this Appendix is to provide proofs for Lemmas 5.67 and 5.68, which deal with extensions of d-Hankel based on truncated ${\mathcal {H}}_p$-valued multisequence.

Proof of Lemma 5.67

We first consider the case when $d=2,$ while the general case $d>2$ can be proved similarly. We have

$$\begin{aligned} M(n)\succeq 0\quad \text {and} \quad {{\,\mathrm{rank}\,}}M(n)={{\,\mathrm{rank}\,}}M(n-1). \end{aligned}$$

We wish to choose moments $(S_\gamma )_{\gamma \in {\mathbb {N}}_0^2\setminus \Gamma _{2n, 2} }$ such that $M(n+1)\succeq 0$ and

$$\begin{aligned} {{\,\mathrm{rank}\,}}M(n+1)={{\,\mathrm{rank}\,}}M(n). \end{aligned}$$

There exist matrix-valued polynomials in ${\mathbb {C}}^{p \times p}_n[x, y]$

$$\begin{aligned} P^{(a, b)}(x, y)= x^a y^b I_p - \sum \limits _{(j, k)\in \Gamma _{n-1, 2}} x^j y^k P_{jk}^{(a, b)}, \end{aligned}$$

with $(a,b)\in \Gamma _{n, 2}$

$$\begin{aligned} P^{(n, 0)}(x, y)= x^n I_p - \sum \limits _{(j, k)\in \Gamma _{n-1, 2}} x^j y^k P_{jk}^{(n, 0)} \end{aligned}$$

and

$$\begin{aligned} P^{(0, n)}(x, y)= y^n I_p - \sum \limits _{(j, k)\in \Gamma _{n-1, 2}} x^j y^k P_{jk}^{(0, n)} \end{aligned}$$

such that

$$\begin{aligned} P^{(a, b)}(X, Y)=P^{(n, 0)}(X, Y)=P^{(0, n)}(X, Y)= {{\,\mathrm{col}\,}}(0_{p \times p})_{\gamma \in \Gamma _{n, d}}. \end{aligned}$$

(A.0.1)

Let the new moments in $M(n+1)$ be defined by

$$\begin{aligned} X^{n+1}=(xP^{(n, 0)})(X, Y)\quad \text {and}\quad Y^{n+1}=(yP^{(0, n)})(X, Y). \end{aligned}$$

Write $X^{n+1}\in C_{M(n+1)}$ as

$$\begin{aligned} X^{n+1}= & {} (xP^{(n, 0)})(X, Y) \\= & {} {{\,\mathrm{col}\,}}\bigg (S_{n+1+c, d}\bigg )_{(c, d)\in \Gamma _{n+1, 2}} \\= & {} {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}S_{c+j+1, d+k} P_{jk}^{(n, 0)}\bigg )_{(c, d)\in \Gamma _{n+1, 2}} \end{aligned}$$

and $Y^{n+1}\in C_{M(n+1)}$ as

$$\begin{aligned} Y^{n+1}= & {} (yP^{(0, n)})(X, Y) \\= & {} {{\,\mathrm{col}\,}}\bigg (S_{c, d+n+1}\bigg )_{(c, d)\in \Gamma _{n+1, 2}} \\= & {} {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}S_{c+j, d+k+1} P_{jk}^{(0, n)}\bigg )_{(c, d)\in \Gamma _{n+1, 2}}. \end{aligned}$$

We shall proceed by following certain steps to check that there exists a rank preserving extension $M(n+1).$ We write

$$\begin{aligned} M(n+1)=\begin{pmatrix} M(n) &{} B \\ B^* &{} C \\ \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned}&M(n)\in {\mathbb {C}}^{({{\,\mathrm{card}\,}}\Gamma _{n, 2})p \times ({{\,\mathrm{card}\,}}\Gamma _{n, 2})p}, \\&B \in {\mathbb {C}}^{({{\,\mathrm{card}\,}}\Gamma _{n, 2})p \times ({{\,\mathrm{card}\,}}( \Gamma _{n+1, 2}\setminus \Gamma _{n, 2}))p} \end{aligned}$$

and

$$\begin{aligned} C \in {\mathbb {C}}^{( {{\,\mathrm{card}\,}}\Gamma _{n+1, 2}\setminus \Gamma _{n, 2})p \times ({{\,\mathrm{card}\,}}(\Gamma _{n+1, 2}\setminus \Gamma _{n, 2}))p}. \end{aligned}$$

Step 1: We need to show that

$$\begin{aligned} S_{n+1+c, d}= \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}S_{c+j+1, d+k} P_{jk}^{(n, 0)} \end{aligned}$$

(A.0.2)

for all $(n+1+c, d)\in \Gamma _{2n, 2},$ that is, $(c, d)\in \Gamma _{n-1, 2}.$ Similarly, we must prove

$$\begin{aligned} S_{c, d+n+1}= \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}S_{c+j, d+k+1} P_{jk}^{(0, n)} \end{aligned}$$

(A.0.3)

for all $(c,d+n+1)\in \Gamma _{2n, 2},$ that is, $(c, d)\in \Gamma _{n-1, 2}.$

We have $X^n =P^{(n, 0)}(X, Y) \in C_{M(n)},$ which is equivalent to

$$\begin{aligned} {{\,\mathrm{col}\,}}\bigg (S_{n+\ell , m}\bigg )_{(\ell , m)\in \Gamma _{n, 2}} = {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}S_{\ell +j, m+k} P_{jk}^{(n, 0)}\bigg )_{(\ell , m)\in \Gamma _{n, 2}}. \end{aligned}$$

Thus $S_{n+\ell , m}= \sum \nolimits _{(j, k)\in \Gamma _{n-1, 2}}S_{\ell +j, m+k} P_{jk}^{(n, 0)}$ for all $(\ell , m)\in \Gamma _{n, 2}.$ Let $\ell = c+1$ and $m=d.$ We then have $(\ell , m)\in \Gamma _{n, 2}$ and so the Eq. (A.0.2) holds for all $(c, d)\in \Gamma _{n-1, 2}.$ Similarly, since

$$\begin{aligned} Y^n =P^{(0, n)}(X, Y) \in C_{M(n)}, \end{aligned}$$

that is,

$$\begin{aligned} {{\,\mathrm{col}\,}}\bigg (S_{\ell , m+n}\bigg )_{(\ell , m)\in \Gamma _{n, 2}} = {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}S_{\ell +j, m+k} P_{jk}^{(0, n)}\bigg )_{(\ell , m)\in \Gamma _{n, 2}}, \end{aligned}$$

we obtain $S_{\ell , m+n}= \sum \nolimits _{(j, k)\in \Gamma _{n-1, 2}}S_{\ell +j, m+k} P_{jk}^{(0, n)}$ for all $(\ell , m)\in \Gamma _{n, 2}.$ Let $\ell = c$ and $m=d+1.$ Then $(\ell , m)\in \Gamma _{n, 2}$ and thus the Eq. (A.0.3) holds for all $(c, d)\in \Gamma _{n-1, 2}.$ Notice that the moments

$$\begin{aligned} {{\,\mathrm{col}\,}}\bigg (S_{c+n+1, d}\bigg )_{(c, d)\in \Gamma _{n+1, 2}\setminus \Gamma _{n, 2}} = {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}S_{c+j+1, d+k} P_{jk}^{(n, 0)}\bigg )_{(c, d)\in \Gamma _{n+1, 2}\setminus \Gamma _{n, 2}} \end{aligned}$$

are already defined. We wish to show that for all $(c, d)\in \Gamma _{n, 2},$

$$\begin{aligned} S_{n+1+c, d}:= \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}S_{c+j+1, d+k} P_{jk}^{(n, 0)}\in {\mathcal {H}}_p, \end{aligned}$$

which are new moments. For this, consider ${\mathcal {M}}$ as the submatrix of $M(n+1)$ with block columns indexed by $\{(j+c+1, d+k):(j, k)\in \Gamma _{n-1, 2}\}$ and block rows indexed by $(j, k) \in \Gamma _{n-1, 2}.$ Notice that ${\mathcal {M}}$ is Hermitian. We have

$$\begin{aligned} \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}S_{c+j+1, d+k} P_{jk}^{(n, 0)}= & {} {{\,\mathrm{col}\,}}\bigg (S_{c+j+1, d+k} \bigg )_{(j, k)\in \Gamma _{n-1, 2}}^* {{\,\mathrm{col}\,}}\bigg (P_{jk}^{(n, 0)}\bigg )_{(j, k)\in \Gamma _{n-1, 2}} \\= & {} {{\,\mathrm{col}\,}}\bigg (P_{jk}^{(n, 0)}\bigg )_{(j, k)\in \Gamma _{n-1, 2}}^*{\mathcal {M}}{{\,\mathrm{col}\,}}\bigg (P_{jk}^{(n, 0)}\bigg )_{(j, k)\in \Gamma _{n-1, 2}} \\= & {} {{\,\mathrm{col}\,}}\bigg (P_{jk}^{(n, 0)}\bigg )_{(j, k)\in \Gamma _{n-1, 2}}^* {{\,\mathrm{col}\,}}\bigg (S_{c+j+1, d+k}\bigg )_{(j, k)\in \Gamma _{n-1, 2}} \\= & {} \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}{P_{jk}^{(n, 0)}}^* S_{c+j+1, d+k} \\= & {} S_{n+1+c, d}^*. \end{aligned}$$

Similarly, we shall note that

$$\begin{aligned} {{\,\mathrm{col}\,}}\bigg (S_{c, n+1+d}\bigg )_{(c, d)\in \Gamma _{n+1, 2}\setminus \Gamma _{n, 2}} = {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}S_{c+j, d+k+1} P_{jk}^{(0, n)}\bigg )_{(c, d)\in \Gamma _{n+1, 2}\setminus \Gamma _{n, 2}} \end{aligned}$$

are already defined and we need to show that the new moments

$$\begin{aligned} S_{c, n+1+d}:= \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}S_{c+j, d+k+1} P_{jk}^{(0, n)}\in {\mathcal {H}}_p \end{aligned}$$

for all $(c, d)\in \Gamma _{n, 2}.$ As before

$$\begin{aligned} \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}S_{c+j, d+k+1} P_{jk}^{(0, n)}= & {} {{\,\mathrm{col}\,}}\bigg (S_{c+j, d+k+1} \bigg )_{(j, k)\in \Gamma _{n-1, 2}}^* {{\,\mathrm{col}\,}}\bigg (P_{jk}^{(0, n)}\bigg )_{(j, k)\in \Gamma _{n-1, 2}} \\= & {} {{\,\mathrm{col}\,}}\bigg (P_{jk}^{(0, n)}\bigg )_{(j, k)\in \Gamma _{n-1, 2}}^*{\mathcal {M}}{{\,\mathrm{col}\,}}\bigg (P_{jk}^{(0, n)}\bigg )_{(j, k)\in \Gamma _{n-1, 2}} \\= & {} {{\,\mathrm{col}\,}}\bigg (P_{jk}^{(0, n)}\bigg )_{(j, k)\in \Gamma _{n-1, 2}}^* {{\,\mathrm{col}\,}}\bigg (S_{c+j, d+k+1}\bigg )_{(j, k)\in \Gamma _{n-1, 2}} \\= & {} \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}{P_{jk}^{(0, n )}}^* S_{c+j, d+k+1} \\= & {} S_{c, n+1+d}^*. \end{aligned}$$

Step 2: In this step, we need to show

$$\begin{aligned} X^{a+1}Y^b=(xP^{(n, 0)})(X, Y) \in C_{M(n+1)} \end{aligned}$$

for all $a+b=n$ with $a\ne n$ and $b\ne 0,$ and moreover,

$$\begin{aligned} X^{a}Y^{b+1}=(yP^{(0, n)})(X, Y) \in C_{M(n+1)} \end{aligned}$$

for all $a+b=n$ with $a\ne 0$ and $b\ne n,$ where $X^{a+1}Y^b$ and $X^{a}Y^{b+1}$ are block columns of the B block.

We first consider the case when $(c, d) \in \Gamma _{n, 2}.$ We have

$$\begin{aligned} X^{a+1}Y^b= {{\,\mathrm{col}\,}}\bigg (S_{a+1+c, b+d}\bigg )_{(c, d)\in \Gamma _{n-1, 2}} \end{aligned}$$

and

$$\begin{aligned} (xP^{(n, 0)})(X, Y) = {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}S_{c+j+1, d+k} P_{jk}^{(n, 0)}\bigg )_{(c, d)\in \Gamma _{n-1, 2}}. \end{aligned}$$

By condition (A.0.1), $X^n =P^{(n, 0)}(X, Y) \in C_{M(n)},$ that is,

$$\begin{aligned} {{\,\mathrm{col}\,}}\bigg (S_{n+\ell , m}\bigg )_{(\ell , m)\in \Gamma _{n, 2}} = {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}S_{\ell +j, m+k} P_{jk}^{(n, 0)}\bigg )_{(\ell , m)\in \Gamma _{n, 2}} \end{aligned}$$

and thus $S_{n+\ell , m}= \sum \nolimits _{(j, k)\in \Gamma _{n-1, 2}}S_{\ell +j, m+k} P_{jk}^{(n, 0)}$ for all $(\ell , m)\in \Gamma _{n, 2}.$ If we let $\ell = c+1$ and $m=d,$ then $(a+1+c, b+d)\in \Gamma _{2n, 2}.$

Similarly, we have

$$\begin{aligned} X^a Y^{b+1}= {{\,\mathrm{col}\,}}\bigg (S_{a+c, b+d+1}\bigg )_{(c, d)\in \Gamma _{n-1, 2}} \end{aligned}$$

and

$$\begin{aligned} (yP^{(0, n)})(X, Y) = {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}S_{c+j, d+k+1} P_{jk}^{(0, n)}\bigg )_{(c, d)\in \Gamma _{n-1, 2}}. \end{aligned}$$

Furthermore, by condition (A.0.1), $Y^n =P^{(0, n)}(X, Y) \in C_{M(n)},$ that is,

$$\begin{aligned} {{\,\mathrm{col}\,}}\bigg (S_{\ell ,n+ m}\bigg )_{(\ell , m)\in \Gamma _{n, 2}} = {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}S_{\ell +j, m+k} P_{jk}^{(0, n)}\bigg )_{(\ell , m)\in \Gamma _{n, 2}} \end{aligned}$$

and hence

$$\begin{aligned} S_{\ell ,n+ m}= \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}S_{\ell +j, m+k} P_{jk}^{(0, n)} \end{aligned}$$

for all $(\ell , m)\in \Gamma _{n, 2}.$ If we let $\ell = c$ and $m=d+1,$ then $(a+c, b+d+1)\in \Gamma _{2n, 2}.$ We continue with the case when $(c, d) \in \Gamma _{n+1, 2}\setminus \Gamma _{n, 2}.$ We have defined

$$\begin{aligned} {{\,\mathrm{col}\,}}\bigg (S_{n+\ell +1, m}\bigg )_{(\ell , m)\in \Gamma _{n+1, 2}\setminus \Gamma _{n, 2}} = {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}S_{\ell +j +1, m+k} P_{jk}^{(n, 0)}\bigg )_{(\ell , m)\in \Gamma _{n+1, 2}\setminus \Gamma _{n, 2}}. \end{aligned}$$

We have to show

$$\begin{aligned} {{\,\mathrm{col}\,}}\bigg (S_{a+ c +1, b+d}\bigg )_{(c, d)\in \Gamma _{n+1, 2}\setminus \Gamma _{n, 2}} = {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}S_{c+j +1, d+k} P_{jk}^{(n, 0)}\bigg )_{(c, d)\in \Gamma _{n+1, 2}\setminus \Gamma _{n, 2}}. \end{aligned}$$

For $\ell = c$ and $m=d,$ we obtain $(a+c+1, b+d)\in \Gamma _{2n+2, 2}.$ We have also defined

$$\begin{aligned} {{\,\mathrm{col}\,}}\bigg (S_{\ell , m+n+1}\bigg )_{(\ell , m)\in \Gamma _{n+1, 2}\setminus \Gamma _{n, 2}} = {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}S_{\ell +j, m+k+1} P_{jk}^{(0, n)}\bigg )_{(\ell , m)\in \Gamma _{n+1, 2}\setminus \Gamma _{n, 2}}. \end{aligned}$$

As before, we need to prove

$$\begin{aligned} {{\,\mathrm{col}\,}}\bigg (S_{a+ c, b+d+1}\bigg )_{(c, d)\in \Gamma _{n+1, 2}\setminus \Gamma _{n, 2}} = {{\,\mathrm{col}\,}}\bigg ( \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}S_{c+j, d+k+1} P_{jk}^{(0, n)}\bigg )_{(c, d)\in \Gamma _{n+1, 2}\setminus \Gamma _{n, 2}}. \end{aligned}$$

For $\ell = c$ and $m=d,$ we derive $(a+c, b+d+1)\in \Gamma _{2n+2, 2}.$

Step 3: Let the following moment of the C block $S_{n+1, n+1}:= \sum \nolimits _{(j, k)\in \Gamma _{n-1, 2}}S_{j+1, k+n+1} P_{jk}^{(n, 0)}.$ We must show

$$\begin{aligned} S_{n+1, n+1}= \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}S_{j+n+1, k+1} P_{jk}^{(0, n)}. \end{aligned}$$

Consider the submatrix ${\mathcal {M}}$ of $M(n+1)$ as described in Step 1.

We compute

$$\begin{aligned} \sum \limits _{(j, k)\in \Gamma _{n-1, 2}}S_{j+n+1, k+1} P_{jk}^{(0, n)}= & {} {{\,\mathrm{col}\,}}\bigg (S_{j+n+1, k+1} \bigg )_{(j, k)\in \Gamma _{n-1, 2}}^* {{\,\mathrm{col}\,}}\bigg (P_{jk}^{(0, n)}\bigg )_{(j, k)\in \Gamma _{n-1, 2}} \\= & {} {{\,\mathrm{col}\,}}\bigg (P_{jk}^{(0, n)}\bigg )_{(j, k)\in \Gamma _{n-1, 2}}^*{\mathcal {M}}{{\,\mathrm{col}\,}}\bigg (P_{jk}^{(0, n)}\bigg )_{(j, k)\in \Gamma _{n-1, 2}}\\= & {} {{\,\mathrm{col}\,}}\bigg (P_{jk}^{(0, n)}\bigg )_{(j, k)\in \Gamma _{n-1, 2}}^* {{\,\mathrm{col}\,}}\bigg (S_{j+1, k+n+1}\bigg )_{(j, k)\in \Gamma _{n-1, 2}}\\= & {} S_{n+1, n+1}^* \end{aligned}$$

by the definition of $S_{n+\ell , m}$ in Step 2 for $\ell =1$ and $m =n+1.$

Step 4: In the final step of this proof, we shall consider the case when $d>2.$ If $M(n)\succeq 0$ and ${{\,\mathrm{rank}\,}}M(n)={{\,\mathrm{rank}\,}}M(n-1),$ then we must choose moments $(S_\gamma )_{\gamma \in {\mathbb {N}}_0^d\setminus \Gamma _{2n, d} }$ such that

$$\begin{aligned} M(n+1)\succeq 0\quad \text {and} \quad {{\,\mathrm{rank}\,}}M(n+1)={{\,\mathrm{rank}\,}}M(n). \end{aligned}$$

There exist matrix-valued polynomials of the form

$$\begin{aligned} P(x)= x^{\gamma }I_p - \sum \limits _{\lambda \in \Gamma _{n, d}} x^\lambda P_\lambda \in {\mathbb {C}}^{p \times p}_n[x_1,\dots , x_d] \end{aligned}$$

with $|\gamma |>0$ such that

$$\begin{aligned} P(X)= {{\,\mathrm{col}\,}}(0_{p \times p})_{\gamma \in \Gamma _{n, d}}. \end{aligned}$$

Application of Steps 1–3 (for $d>2$) will yield the existence of moments $(S_\gamma )_{\gamma \in {\mathbb {N}}_0^d{\setminus }\Gamma _{2n, d} }$ such that

$$\begin{aligned} M(n+k)\succeq 0 \end{aligned}$$

and

$$\begin{aligned} {{\,\mathrm{rank}\,}}M(n+k)={{\,\mathrm{rank}\,}}M(n+k-1)\quad \text {for}\;\; k=2,3, \ldots \end{aligned}$$

as desired. $\square$

Proof of Lemma 5.68

Suppose there exists a choice of moments $(S_\gamma )_{\gamma \in {\mathbb {N}}_0^d\setminus \Gamma _{2n+2, d} }$ which gives rise to a sequence of extensions $M(n+k)\succeq 0$ for all $k=2,3, \ldots$ and thus to $M(\infty )\succeq 0.$ Consider a matrix-valued polynomial $P \in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d]$ and let ${\mathcal {I}}$ be the right ideal associated with $M(\infty )$ (see Definition 5.13 for the precise definition of ${\mathcal {I}}$). Suppose there exists another choice of moments $({\tilde{S}}_\gamma )_{\gamma \in {\mathbb {N}}_0^d{\setminus }\Gamma _{2n+2, d} }$ which gives rise to ${\tilde{M}}(\infty )\succeq 0$ and is such that ${\tilde{S}}_{ \gamma }=S_{\gamma } \;\text {for all} \; \gamma \in \Gamma _{2n+2, d}.$ Let $\mathcal {{\tilde{I}}}$ be the right ideal associated with ${\tilde{M}}(\infty ).$ Since M(n) has a positive extension $M(n+1)$ with

$$\begin{aligned} {{\,\mathrm{rank}\,}}M(n+1)={{\,\mathrm{rank}\,}}M(n), \end{aligned}$$

there exist matrix-valued polynomials of the form

$$\begin{aligned} P^{(\gamma )}(x)= x^{\gamma }I_p + \sum \limits _{\lambda \in \Gamma _{n, d}} x^\lambda P^{(\gamma )}_\lambda \in {\mathbb {C}}^{p \times p}[x_1,\dots , x_d] \end{aligned}$$

with $\gamma \in \Gamma _{n+1, d}\setminus \Gamma _{n, d}$ such that $P^{(\gamma )}(X)= {{\,\mathrm{col}\,}}(0_{p\times p})_{{\tilde{\gamma }}\in {\mathbb {N}}_0^d}\in C_{M{(\infty )}}.$ Thus for $\varepsilon _j \in {\mathbb {N}}_0^d,$

$$\begin{aligned} {{\,\mathrm{col}\,}}\left( S_{ (n+1)\varepsilon _{j}+\tilde{{\gamma }}} \right) _{{\tilde{\gamma }}\in {\mathbb {N}}_0^d}=-{{\,\mathrm{col}\,}}\left( \sum \limits _{\lambda \in \Gamma _{n, d}} S_{ \lambda +{\tilde{\gamma }}} P_\lambda ^{(\gamma )}\right) _{{\tilde{\gamma }}\in {\mathbb {N}}_0^d}\quad \text {for}\;\; j=1, \dots , d. \end{aligned}$$

(A.0.4)

We need to show first that

$$\begin{aligned} \{P^{(\gamma )}\}_{\gamma \in \Gamma _{n+1, d}\setminus \Gamma _{n, d}}\subseteq \mathcal {{\tilde{I}}}. \end{aligned}$$

Since ${\tilde{S}}_{ \gamma }=S_{\gamma }\; \text {for all}\; \gamma \in \Gamma _{2n+2, d},$ we have

$$\begin{aligned} {\tilde{S}}_{ (n+1)\varepsilon _{j}+\tilde{{\gamma }}}=S_{(n+1)\varepsilon _{j}+\tilde{{\gamma }}} \;\; \text {for} \;\; {\tilde{\gamma }}\in \Gamma _{n+1, d}. \end{aligned}$$

By equation (A.0.4),

$$\begin{aligned} {{\,\mathrm{col}\,}}\left( {\tilde{S}}_{ (n+1)\varepsilon _{j}+\tilde{{\gamma }}} \right) _{{\tilde{\gamma }}\in \Gamma _{n+1, d}}= -{{\,\mathrm{col}\,}}\left( \sum \limits _{\lambda \in \Gamma _{n, d}} {\tilde{S}}_{ \lambda +{\tilde{\gamma }}} P_\lambda ^{(\gamma )}\right) _{{\tilde{\gamma }}\in \Gamma _{n+1, d}} \end{aligned}$$

and

$$\begin{aligned} {\tilde{M}}(n+1){{\,\mathrm{col}\,}}(P_\lambda ^{(\gamma )})_{\lambda \in \Gamma _{n+1, d}}= & {} M(n+1){{\,\mathrm{col}\,}}(P_\lambda ^{(\gamma )})_{\lambda \in \Gamma _{n+1, d}}\nonumber \\= & {} {{\,\mathrm{col}\,}}(0_{p\times p})_{\tilde{{\gamma }}\in \Gamma _{n+1, d}}. \end{aligned}$$

(A.0.5)

To show $\{P^{(\gamma )}\}_{\gamma \in \Gamma _{n+1, d}{\setminus }\Gamma _{n, d}}\subseteq \mathcal {{\tilde{I}}},$ we need to prove

$$\begin{aligned}&s{\tilde{M}}(n+k)\{{{\,\mathrm{col}\,}}(P_\lambda ^{(\gamma )})_{\lambda \in \Gamma _{n+1, d}}\oplus {{\,\mathrm{col}\,}}(0_{p\times p})_{{\tilde{\gamma }}\in \Gamma _{n+k, d}\setminus \Gamma _{n+1, d}}\}={{\,\mathrm{col}\,}}(0_{p\times p})_{{\tilde{\gamma }}\in \Gamma _{n+k, d}}\;\nonumber \\&\text {for} \;\; k=2,3, \ldots \end{aligned}$$

(A.0.6)

Write

$$\begin{aligned} {\tilde{M}}(n+k)=\begin{pmatrix} {\tilde{M}}(n+1) &{} B \\ B^* &{} C \\ \end{pmatrix}\succeq 0, \end{aligned}$$

where

$$\begin{aligned}&{\tilde{M}}(n+1)\in {\mathbb {C}}^{({{\,\mathrm{card}\,}}\Gamma _{n+1, d})p \times ({{\,\mathrm{card}\,}}\Gamma _{n+1, d})p}, \\&B \in {\mathbb {C}}^{({{\,\mathrm{card}\,}}\Gamma _{n+1, d})p \times ({{\,\mathrm{card}\,}}( \Gamma _{n+k, d}\setminus \Gamma _{n+1, d}))p} \end{aligned}$$

and

$$\begin{aligned} C \in {\mathbb {C}}^{( {{\,\mathrm{card}\,}}\Gamma _{n+k, d}\setminus \Gamma _{n+1, d})p \times ({{\,\mathrm{card}\,}}(\Gamma _{n+k, d}\setminus \Gamma _{n+1, d}))p}. \end{aligned}$$

Since ${\tilde{M}}(n+k)\succeq 0,$ by Lemma 2.1, there exists $W\in {\mathbb {C}}^{({{\,\mathrm{card}\,}}\Gamma _{n+1, d})p \times ({{\,\mathrm{card}\,}}( \Gamma _{n+k, d}\setminus \Gamma _{n+1, d}))p}$ such that

$$\begin{aligned} {\tilde{M}}(n+1)W=B\quad \text {and} \quad C \succeq W^*{\tilde{M}}(n+1) W. \end{aligned}$$

Then

$$\begin{aligned}&{\tilde{M}}(n+k)\{{{\,\mathrm{col}\,}}(P_\lambda ^{(\gamma )})_{\lambda \in \Gamma _{n+1, d}}\oplus {{\,\mathrm{col}\,}}(0_{p\times p})_{\tilde{{\gamma }}\in \Gamma _{n+k, d}\setminus \Gamma _{n+1, d}}\}\\&\quad = \begin{pmatrix} {\tilde{M}}(n+1){{\,\mathrm{col}\,}}(P_\lambda ^{(\gamma )})_{\lambda \in \Gamma _{n+1, d}}\\ B^*{{\,\mathrm{col}\,}}(P_\lambda ^{(\gamma )})_{\lambda \in \Gamma _{n+1, d}} \\ \end{pmatrix}\\&\quad = \begin{pmatrix} M(n+1){{\,\mathrm{col}\,}}(P_\lambda ^{(\gamma )})_{\lambda \in \Gamma _{n+1, d}}\\ B^*{{\,\mathrm{col}\,}}(P_\lambda ^{(\gamma )})_{\lambda \in \Gamma _{n+1, d}} \\ \end{pmatrix}\\&\quad =\begin{pmatrix} {{\,\mathrm{col}\,}}(0_{p\times p})_{\tilde{{\gamma }}\in \Gamma _{n+1, d}} \\ W^*M(n+1){{\,\mathrm{col}\,}}(P_\lambda )_{\lambda \in \Gamma _{n+1, d}} \\ \end{pmatrix}\\&\quad ={{\,\mathrm{col}\,}}(0_{p\times p})_{\tilde{{\gamma }}\in \Gamma _{n+k, d}} \end{aligned}$$

for all $k=2,3, \ldots ,$ by equation (A.0.5). Thus, equation (A.0.6) holds as desired and so

$$\begin{aligned} \{P^{(\gamma )}\}_{\gamma \in \Gamma _{n+1, d}\setminus \Gamma _{n, d}}\subseteq \mathcal {{\tilde{I}}}. \end{aligned}$$

This in turn will yield $x^{\varepsilon _j} P^{(\gamma )} \in \mathcal {{\tilde{I}}}.$ Indeed

$$\begin{aligned} {\tilde{M}}(\infty )\left( x^{\varepsilon _j} {{\,\mathrm{col}\,}}(P_\lambda ^{(\gamma )})_{\lambda \in \Gamma _{n, d}}\right) ={{\,\mathrm{col}\,}}\left( \sum \limits _{\lambda \in \Gamma _{n, d}} {\tilde{S}}_{\lambda '+\varepsilon _j +\lambda } P_\lambda ^{(a)}\right) _{\lambda '\in {\mathbb {N}}_0^d}. \end{aligned}$$

But since $P^{(\gamma )}\in \mathcal {{\tilde{I}}},$

$$\begin{aligned} {\tilde{M}}(\infty ) {{\,\mathrm{col}\,}}(P_\lambda ^{(\gamma )})_{\lambda \in \Gamma _{n, d}}={{\,\mathrm{col}\,}}(0_{p\times p})_{{\tilde{\gamma }}\in {\mathbb {N}}_0^d}, \end{aligned}$$

that is,

$$\begin{aligned} {{\,\mathrm{col}\,}}\left( \sum \limits _{\lambda \in \Gamma _{n, d}} {\tilde{S}}_{ \lambda +{\tilde{\gamma }}} P_\lambda ^{(\gamma )}\right) _{{\tilde{\gamma }}\in {\mathbb {N}}_0^d}={{\,\mathrm{col}\,}}(0_{p\times p})_{{\tilde{\gamma }}\in {\mathbb {N}}_0^d}, \end{aligned}$$

For ${\tilde{\gamma }}=\lambda '+\varepsilon _j, \; j=1, \dots , d,$

$$\begin{aligned} {{\,\mathrm{col}\,}}\left( \sum \limits _{\lambda \in \Gamma _{n, d}} {\tilde{S}}_{\lambda '+\varepsilon _j +\lambda } P_\lambda ^{(\gamma )}\right) _{\lambda '\in {\mathbb {N}}_0^d}={{\,\mathrm{col}\,}}(0_{p\times p})_{\lambda '\in {\mathbb {N}}_0^d} \end{aligned}$$

and so

$$\begin{aligned} {\tilde{M}}(\infty )\left( x^{\varepsilon _j} {{\,\mathrm{col}\,}}(P_\lambda ^{(\gamma )})_{\lambda \in \Gamma _{n, d}}\right) ={{\,\mathrm{col}\,}}(0_{p\times p})_{{\tilde{\gamma }}\in {\mathbb {N}}_0^d}. \end{aligned}$$

Since $x^{\varepsilon _j} P^{(\gamma )} \in \mathcal {{\tilde{I}}},$ we have

$$\begin{aligned} {{\,\mathrm{col}\,}}\left( S_{ (n+2)\varepsilon _{j}+\tilde{{\gamma }}} \right) _{{\tilde{\gamma }}\in \Gamma _{n, d}}=-{{\,\mathrm{col}\,}}\left( \sum \limits _{\lambda \in \Gamma _{n, d}} S_{ \lambda +{\tilde{\gamma }}+\varepsilon _{j}} P_\lambda ^{(\gamma )}\right) _{{\tilde{\gamma }}\in \Gamma _{n, d}}\quad \text {for}\;\; j=1, \dots , d. \end{aligned}$$

Moreover

$$\begin{aligned} {{\,\mathrm{col}\,}}\left( {\tilde{S}}_{ (n+2)\varepsilon _{j}+\tilde{{\gamma }}} \right) _{{\tilde{\gamma }}\in \Gamma _{n+1, d}\setminus \Gamma _{n, d}}=-{{\,\mathrm{col}\,}}\left( \sum \limits _{\lambda \in \Gamma _{n, d}} S_{ \lambda +{\tilde{\gamma }}+\varepsilon _{j}} P_\lambda ^{(\gamma )}\right) _{{\tilde{\gamma }}\in \Gamma _{n+1, d} \setminus \Gamma _{n, d}}\nonumber \\ \end{aligned}$$

(A.0.7)

and

$$\begin{aligned} {{\,\mathrm{col}\,}}\left( {\tilde{S}}_{ (n+2)\varepsilon _{j}+\tilde{{\gamma }}} \right) _{{\tilde{\gamma }}\in {\mathbb {N}}_0^d\setminus \Gamma _{n+1, d}}=-{{\,\mathrm{col}\,}}\left( \sum \limits _{\lambda \in \Gamma _{n, d}} {\tilde{S}}_{ \lambda +{\tilde{\gamma }}+\varepsilon _{j}} P_\lambda ^{(\gamma )}\right) _{{\tilde{\gamma }}\in {\mathbb {N}}_0^d\setminus \Gamma _{n+1, d}} \end{aligned}$$

(A.0.8)

for all $j=1, \dots , d.$ In view of equation (A.0.4),

$$\begin{aligned} {\tilde{S}}_{ (n+2)\varepsilon _{j}+\tilde{{\gamma }}}=S_{ (n+2)\varepsilon _{j}+\tilde{{\gamma }}} \;\;\text {for}\;\; {\tilde{\gamma }}\in \Gamma _{n+1, d}\setminus \Gamma _{n, d}\quad \text {and}\quad j=1, \dots , d. \end{aligned}$$

Hence ${\tilde{S}}_{ {\tilde{\lambda }}}=S_{{\tilde{\lambda }}} \;\; \text {for} \;\; {\tilde{\lambda }}\in \Gamma _{2n+3, d}.$ We next rewrite the equations (A.0.7) and (A.0.8) as

$$\begin{aligned} {{\,\mathrm{col}\,}}\left( {\tilde{S}}_{ (n+2)\varepsilon _{j}+\tilde{{\gamma }}} \right) _{{\tilde{\gamma }}\in \Gamma _{n+2, d}\setminus \Gamma _{n+1, d}}=-{{\,\mathrm{col}\,}}\left( \sum \limits _{\lambda \in \Gamma _{n, d}} S_{ \lambda +{\tilde{\gamma }}+\varepsilon _{j}} P_\lambda ^{(\gamma )}\right) _{{\tilde{\gamma }}\in \Gamma _{n+2, d} \setminus \Gamma _{n+1, d}} \end{aligned}$$

and

$$\begin{aligned} {{\,\mathrm{col}\,}}\left( {\tilde{S}}_{ (n+2)\varepsilon _{j}+\tilde{{\gamma }}} \right) _{{\tilde{\gamma }}\in {\mathbb {N}}_0^d\setminus \Gamma _{n+2, d}}=-{{\,\mathrm{col}\,}}\left( \sum \limits _{\lambda \in \Gamma _{n, d}} {\tilde{S}}_{ \lambda +{\tilde{\gamma }}+\varepsilon _{j}} P_\lambda ^{(\gamma )}\right) _{{\tilde{\gamma }}\in {\mathbb {N}}_0^d\setminus \Gamma _{n+2, d}} \end{aligned}$$

for all $j=1, \dots , d.$ Thus

$$\begin{aligned} {\tilde{S}}_{ (n+2)\varepsilon _{j}+\tilde{{\gamma }}}=S_{ (n+2)\varepsilon _{j}+\tilde{{\gamma }}} \;\; \text {for} \;\; {\tilde{\gamma }}\in \Gamma _{n+2, d}\setminus \Gamma _{n+1, d}\quad \text {and}\quad j=1, \dots , d. \end{aligned}$$

Hence ${\tilde{S}}_{ {\tilde{\lambda }}}=S_{{\tilde{\lambda }}} \;\; \text {for all}\;\; {\tilde{\lambda }}\in \Gamma _{2n+4, d}.$ Continuing inductively we conclude that

$$\begin{aligned} {\tilde{S}}_{ {\tilde{\lambda }}}=S_{{\tilde{\lambda }}} \;\; \text {for}\;\; {\tilde{\lambda }}\in {\mathbb {N}}_0^d, \end{aligned}$$

from which we derive uniqueness for the sequence of extensions

$$\begin{aligned} M(n+k)\succeq 0 \end{aligned}$$

with

$\square$