Abstract
In this article we establish first and second order sufficient optimality conditions for a class of single-input control-affine problems, in presence of a scalar state constraint. We consider strong-local optimality (that is, the \(C^0\) topology in the state space). The minimum-time and the Mayer problem are addressed. We restrict our analysis to extremals containing a bang arc, a single boundary arc, followed by a finite number of bang arcs. The sufficient conditions are expressed as a strengthened version of the necessary ones, plus the coerciveness of a suitable finite-dimensional quadratic form. The sufficiency of the given conditions is proven via Hamiltonian methods.
Similar content being viewed by others
Notes
See, e.g., Chapter 1 in [11] for the regularity of measures defined via monotone right-continuous functions.
The function
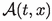 was defined in (2.8)
was defined in (2.8)This is a consequence of the fact that weak convergence of the controls implies strong convergence of the trajectories, see [21].
With a little abuse of language, when we say that \({\mathbb {R}}f_1({\widehat{x}}_2)\) is contained in \({\widetilde{W}}\) we mean that \(f_1({\widehat{x}}_2)\) is an admissible value of \(\zeta ({{\widehat{t}}}_1)\)
In the sense of Withney flat forms, as defined in [17].
References
Agrachev, A.A., Gamkrelidze, R.V.: Symplectic geometry for optimal control. In: Sussmann, H.J. (ed.) Nonlinear Controllability and Optimal Control, Pure and Applied Mathematics, vol. 133. Marcel Dekker (1990)
Agrachev, A.A., Gamkrelidze, R.V.: Symplectic methods for optimization and control. In: Jacubczyk, B., Respondek, W. (eds.) Geometry of Feedback and Optimal Control. Pure and Applied Mathematics, pp. 1–58. Marcel Dekker, New York (1997)
Agrachev, A.A., Sachkov, Y.L.: Control Theory from the Geometric Viewpoint. Springer (2004)
Agrachev, A.A., Stefani, G., Zezza, P.: An invariant second variation in optimal control. Int. J. Control 71(5), 689–715 (1998)
Agrachev, A.A., Stefani, G., Zezza, P.: Strong optimality for a bang–bang trajectory. SIAM J. Control. Optim. 41(4), 991–1014 (2002)
Aronna, M.S., Bonnans, J.F., Goh, B.S.: Second order analysis of state-constrained control-affine problems. Math. Program. Ser. A 160(1), 115–147 (2016)
Arutyunov, A.V., Karamzin, DYu.: On some continuity properties of the measure Lagrange multiplier from the maximum principle for state constrained problems. SIAM J. Control. Optim. 53(4), 2514–2540 (2015)
Bonnans, J.F., Hermant, A.: No-gap second-order optimality conditions for optimal control problems with a single state constraint and control. Math. Program. 117, 21–50 (2009)
Bonnard, B., Faubourg, L., Launay, G., Trélat, E.: Optimal control with state constraints and the space shuttle re-entry problem. J. Dyn. Control Syst. 9(2), 155–199 (2003)
Clarke, F.H.: On the inverse function theorem. Pac. J. Math. 64(1), 97–102 (1976)
Cohn, D.L.: Measure Theory. Birkhäuser Advanced Texts Basler Lehrbücher (BAT), 2nd edn. Birkhäuser
Cots, O.: Geometric and numerical methods for a state constrained minimum time control problem of an electric vehicle. ESAIM: COCV 23(4), 1715–1749 (2017)
Cots, O., Gergaud, J., Goubinat, D.: Direct and indirect methods in optimal control with state constraints and the climbing trajectory of an aircraft. Optim. Control Appl. Methods 39(1), 281–301 (2018)
do Rosario de Pinho, M., Margarida Ferreira, M., Ledzewicz, U., Schaettler, H.: A model for cancer chemotherapy with state-space constraints. Nonlinear Anal. Theory Methods Appl. 63(5), e2591–e2602 (2005). (Invited Talks from the Fourth World Congress of Nonlinear Analysts (WCNA 2004))
Fehér, M., Straka, O., Šmídl, V.: Constrained time-optimal control of double-integrator system and its application in MPC. J. Phys. Conf. Ser. 783, 012024 (2017)
Hartl, R.F., Sethi, S.P., Vickson, R.G.: A survey of the maximum principles for optimal control problems with state constraints. SIAM Rev. 37(2), 181–218 (1995)
Heinonen, J.M.: Lectures on Lipschitz Analysis (2005)
Hestenes, M.R.: Calculus of Variations and Optimal Control Theory. Wiley, New York (1966)
Jurdjevic, V.: Geometric Control Theory, Cambridge Studies in Advanced Mathematics, vol. 52. Cambridge University Press (1997)
Keller, J.B.: Optimal velocity in a race. Am. Math. Mon. 81(5), 474–480 (1974)
Liu, W., Sussmann, H.J.: Continuous dependence with respect to the input of trajectories of control-affine systems. SIAM J. Control. Optim. 37(3), 777–803 (1999)
Malanowski, K.: On normality of Lagrange multipliers for state constrained optimal control problems. Optimization 52(1), 75–91 (2003)
Maurer, H.: On optimal control problems with bounded state variables and control appearing linearly. SIAM J. Control. Optim. 15(3), 345–362 (1977)
Maurer, H., Kim, J.-H.R., Vossen, G.: On a State-Constrained Control Problem in Optimal Production and Maintenance, pp. 289–308. Springer (2005)
Pitcher, A.B.: Optimal strategies for a two-runner model of middle-distance running. SIAM J. Appl. Math. 70(4), 1032–1046 (2009)
Poggiolini, L., Stefani, G.: State-local optimality of a bang–bang trajectory: a Hamiltonian approach. Syst. Control Lett. 53, 269–279 (2004)
Poggiolini, L., Stefani, G.: Bang-singular-bang extremals: sufficient optimality conditions. J. Dyn. Control Syst. 17, 469–514 (2011). https://doi.org/10.1007/s10883-011-9127-y
Russak, I.B.: Second order necessary conditions for problems with state inequality constraints. SIAM J. Control 13, 372–388 (1975)
Schättler, H.: Local fields of extremals for optimal control problems with state constraints of relative degree 1. J. Dyn. Control Syst. 12, 563–599 (2006)
Seywald, H., Cliff, E.M.: Goddard problem in presence of a dynamic pressure limit. J. Guid. Control. Dyn. 16(4), 776–781 (1993)
Stefani, G.: Minimum–time optimality of a singular arc: second order sufficient conditions. In: 43th IEEE Conference on Decision and Control (2004)
Stefani, G.: Strong optimality of singular trajectories. In: Ancona, F., Bressan, A., Cannarsa, P., Clarke, F., Wolenski, P. (eds.) Geometric Control and Nonsmooth Analysis, Series on Advances in Mathematics for Applied Sciences, vol. 76, pp. 300–326. World Scientific Publishing Co. Pte. Ltd, Hackensack. ISBN: 978-981-277-606-8 (2008)
Stefani, G., Zezza, P.: Constrained regular LQ-control problems. SIAM J. Control. Optim. 35(3), 876–900 (1997)
Stefani, G., Zezza, P.: Time-optimality of a bang–bang trajectory with maple. In: 2nd IFAC Workshop on Lagrangian and Hamiltonian Methods for Nonlinear Control (2003)
Stefani, G., Zezza, P.: Variational Methods in Imaging and Geometric Control, Chapter A Hamiltonian Approach to Sufficiency in Optimal Control with Minimal Regularity Conditions: Part I. De Gruyter (2016)
Taitler, A., Ioslovich, I., Karpas, E., Gutman, P.-O.: Minimum time optimal control of second order system with quadratic drag and state constraints. In: 2019 IEEE 58th Conference on Decision and Control (CDC), pp. 523–528 (2019)
Acknowledgements
This work was completed with the support of Appel à projet “Enseignants-Chercheurs invités”, Université de Toulon, and by Progetto Internazionalizzazione, Università degli Studi di Firenze.
Author information
Authors and Affiliations
Contributions
FCC and LP contributed equally to the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: On the computation of first and second variation
Appendix A: On the computation of first and second variation
In this section, we provide more details on the constructions of the first and second variations of the functional J. As in Sect. 4, we focus on the minimum-time problem.
We start by recalling the coordinate expression of the reference extremal. Choosing any (local) coordinate chart on \(T^*M\) and setting \({\widehat{\lambda }}(t) = \big ({\widehat{\mu }}(t), {\widehat{\xi }}(t)\big )\), Eq. (2.5c) implies that \({\widehat{\mu }}(t)\) is a solution to the following linear ODE
Then, for every \(t \in [0,T]\), we have
where we recall that \(\widehat{\eta }\) is supported on \([{{\widehat{t}}}_1,{{\widehat{t}}}_2]\).
Let us now prove that the first variation, with respect to  and u, of the cost (4.5) is null. Using (A.1), we can see that
and u, of the cost (4.5) is null. Using (A.1), we can see that
Then we have that

Thanks to (4.3), the first variation of J with respect to u boils down to

which is null by PMP. Finally

where we recall that the \(\delta _k\) are defined in Eq. (4.6). The first addendum is null because of the constraint (4.9), and the second addendum is null since \(F_0({\widehat{\ell }}_k) = p_0\) for any k, so that
Differentiating twice the cost J with respect to  and u, we obtain an expression which depends on \(\delta u_0\) only by means of the quantities \(\delta _3, \ldots , \delta _{N+1}\), i.e. we get
and u, we obtain an expression which depends on \(\delta u_0\) only by means of the quantities \(\delta _3, \ldots , \delta _{N+1}\), i.e. we get





with \((\delta y,\delta u,\varvec{\delta })\in W\).
Exchanging the order of integration and relabeling the variables, we remark that

so (A.2) can be written as

Also, we have that
noticing that  , we obtain that
, we obtain that

Analogous computations show that

Summing up the addenda, we obtain the expression (4.10).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Chittaro, F.C., Poggiolini, L. On the strong local optimality for state-constrained control-affine problems. Nonlinear Differ. Equ. Appl. 30, 60 (2023). https://doi.org/10.1007/s00030-023-00870-y
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00030-023-00870-y



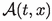 was defined in (
was defined in (