Abstract
We consider a class of generally non-self-adjoint eigenvalue problems which are nonlinear in the solution as well as in the eigenvalue parameter (“doubly” nonlinear). We prove a bifurcation result from simple isolated eigenvalues of the linear problem using a Lyapunov–Schmidt reduction and provide an expansion of both the nonlinear eigenvalue and the solution. We further prove that if the linear eigenvalue is real and the nonlinear problem \({\mathcal {PT}}\)-symmetric, then the bifurcating nonlinear eigenvalue remains real. These general results are then applied in the context of surface plasmon polaritons (SPPs), i.e. localized solutions for the nonlinear Maxwell’s equations in the presence of one or more interfaces between dielectric and metal layers. We obtain the existence of transverse electric SPPs in certain \({\mathcal {PT}}\)-symmetric configurations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We study the nonlinear problem
where \(A:L^2({\mathbb {R}}^d,{\mathbb {C}})\supset D(A)\rightarrow L^2({\mathbb {R}}^d,{\mathbb {C}})\) is a densely defined, closed (possibly non-self-adjoint) operator with a non-empty resolvent set. Throughout the paper the space \(L^2({\mathbb {R}}^d,{\mathbb {C}})\) and all other function spaces are complex vector spaces, i.e. defined over the complex field \({\mathbb {C}}\). The potential W is generally nonlinear in the spectral parameter \(\omega \) and typically complex valued. The function f is nonlinear in both \(\omega \) and \(\varphi \) and is asymptotically equivalent to a monomial near \(\varphi =0\). Moreover, we suppose that f is Lipschitz continuous in a neighbourhood of an eigen-pair \((\omega _0,\varphi _0)\), where \(\omega _0 \in {\mathbb {C}}\) is a simple isolated eigenvalue of \(L(x,\cdot )\). We prove the bifurcation from \(\omega _0\) using a fixed point argument and a Lyapunov–Schmidt decomposition. Bifurcation from simple eigenvalues is a well studied problem even in the non-selfadjoint case [6, 7, 15, 18]. In particular, bifurcation in complex Banach spaces (as relevant in our problem) is investigated in [7, 15] by means of a Lyapunov–Schmidt reduction coupled with topological degree techniques. However, our result includes also an asymptotic expansion of \((\omega ,\varphi )\) depending on the behaviour of f for small \(\varphi \) and for \(\omega \) near \(\omega _0\). More precisely, we find a solution \((\omega ,\varphi )\in {\mathbb {C}}\times D(A)\) of the form
where \(\varepsilon >0\) is small, \(\omega \) is the spectral parameter, \(\alpha \) is related to the degree of homogeneity of \(f(x,\omega ,\cdot )\) near 0, \(\tau \) is a positive parameter, and \(\nu ,\sigma \in {\mathbb {C}}\) as well as \(\phi ,\psi \in D(A)\cap \langle \varphi _0^*\rangle ^\perp \) are uniquely determined. Moreover, \(\nu \) is explicit, see (16), and \(\phi \) satisfies the linear equation (20).
In [11] the bifurcation was proved (and an asymptotic expansion of \((\omega ,\varphi )\) was provided) for
with A as above. This problem clearly has a linear dependence on the spectral parameter \(\omega \). The coefficient \(\varepsilon \) in (2) is the bifurcation parameter and one studies the bifurcation from an eigenvalue \(\omega _0\) at \(\varepsilon =0\). As the bifurcation parameter appears explicitly in the equation, the form of the asymptotic expansion of \((\omega ,\varphi )\) is unique. Note that (2) can be rescaled to \((A-\omega )\psi =f(\psi )\) only for the case of homogeneous nonlinearities f. Therefore, our result extends that of [11] to the case of more general nonlinearities f and a nonlinear dependence of both f and W on the spectral parameter.
An important application of non-selfadjoint problems which are nonlinear in \(\omega \) is the propagation of electromagnetic waves in dispersive media, in particular in structures that include a metal. Interfaces of two different media can support localized waves. A typical example is a surface plasmon polariton (SPP) at the interface of a dielectric and a metal, see e.g. [19, 20] or, when more layers of dielectrics and/or metals are considered, [14, 24, 26]. The general case is, of course, described by Maxwell’s equations. Assuming the absence of free charges, we have
where \({{\mathcal {E}}}\) and \({{\mathcal {H}}}\) is the electric and magnetic field respectively, \({{\mathcal {D}}}={{\mathcal {D}}}({{\mathcal {E}}})\) is the electric displacement field and \(\epsilon _0\) and \(\mu _0\) are respectively the permittivity and the permeability of the free space. The displacement field \({\mathcal {D}}\) is generally nonlinear in \({\mathcal {E}}\) and non-local in time. For odd (e.g. Kerr) nonlinearities and a monochromatic field \(({\mathcal {E}},{\mathcal {H}},{\mathcal {D}})(x,y,z,t)=(E,H,D)(x,y,z)e^{\mathrm{i}\omega t}+ \text {c.c.}\) (with a real frequency \(\omega \)) a nonlinear eigenvalue problem in \((\omega , (E,H))\) is obtained if higher harmonics are neglected, for details see Sect. 4. Equation (3) as well as the eigenvalue problem have to be accompanied by interface conditions if an interface of two media is present. Assuming that the interface is planar and parallel to the yz-plane, the interface conditions are
where we define (for the interface located at \(x=x_0\)), \(\llbracket E_2\rrbracket :=E_2(x\rightarrow x_0^+)-E_2(x\rightarrow x_0^-),\) etc., see Sect. 4.
A simple example in the cubically nonlinear case is obtained in structures independent of the y, z-variables by choosing the transverse electric (TE) ansatz
with \(k\in {\mathbb {R}}\). It leads to the scalar nonlinear problem
with functions \(W,\Gamma :{\mathbb {R}}^2\rightarrow {\mathbb {C}}\). The interface conditions here boil down to the continuity condition on \(\varphi \) and \(\varphi '\), see Sect. 4.
The bifurcation result provides a curve \(\varepsilon \mapsto \big (\omega (\varepsilon ),\varphi (\varepsilon )\big )\) with \(\omega (0)=\omega _0\) and \(\varphi (0)=0\). Even if \(\omega _0\) is real, the curve can lie in \({\mathbb {C}}{\setminus } {\mathbb {R}}\) for all \(\varepsilon \ne 0\). In order for \(\omega \) to correspond to the (real) frequency of an electromagnetic field, one needs to ensure that the curve lies in \({\mathbb {R}}\). As we show in Sect. 3, this is possible by restricting the fixed point argument to a symmetric subspace, namely the \({\mathcal {PT}}\)-symmetric subspace. \({\mathcal {PT}}\)-symmetry has been studied extensively in quantum mechanics, see e.g. [4, 5]. Recently, a number of physics papers have studied nonlinear \({\mathcal {PT}}\)-symmetric problems from a phenomenological point of view mainly with emphasis on localized solutions, e.g. [5, 21, 27]. In the context of SPPs, where metals normally lead to a lossy propagation, \({\mathcal {PT}}\)-symmetry has been applied to obtain lossless propagation, see [2, 3]. Mathematically, the restriction of a fixed point argument to a \({\mathcal {PT}}\)-symmetric (or more generally antilinearly symmetric) subspace has been used to obtain real nonlinear eigenvalues, see, e.g., [9, 11, 22].
This article is organized as follows. In Sect. 2 we state and prove our main bifurcation result (Theorem 2.1). The realness of the nonlinear eigenvalue is ensured in the case of \({\mathcal {PT}}\)-symmetry in Sect. 3. Applications to SPPs are then given in Sect. 4, where 2- and 3-layer-configurations are investigated.
2 Bifurcation of nonlinear eigenvalues
In this section we study problem (1), where A, W and f satisfy assumptions (A1)–(f4) below. We prove the existence of a branch of solutions starting from an eigenpair \((\omega _0,\varphi _0)\in {\mathbb {C}}\times D(A)\), i.e. \(L(x,\omega _0)\varphi _0=0\), such that
-
i)
\(\omega _0\) is algebraically simple: \(\ker (L(\cdot ,\omega _0)^2)=\ker (L(\cdot ,\omega _0))=\langle \varphi _0\rangle \),
-
ii)
\(\omega _0\) is isolated: there exists \(\rho >0\) such that \(0\in \sigma (L(\cdot ,\omega ))\) for \(\omega \in B_\rho (\omega _0)\subset {\mathbb {C}}\) if and only if \(\omega =\omega _0\).
Notation: Henceforth, the norm and the inner product in the underlying Hilbert space \(L^2({\mathbb {R}}^d,{\mathbb {C}})\) will be denoted by \(\Vert \cdot \Vert \) and \(\langle \cdot ,\cdot \rangle \) respectively. Moreover, \(\Vert \cdot \Vert _\infty \) stands for the \(L^\infty ({\mathbb {R}}^d)\) norm and \(\Vert \cdot \Vert _A\) for the graph norm, i.e. \(\Vert u\Vert _A:=\Vert u\Vert +\Vert Au\Vert \). Note that \(D(A)=D(L)\) due to assumptions (A2) and (W1).
We define \(\varphi _0^*\) as theFootnote 1 eigenfunction of \(\big (L(\cdot ,\omega _0)\big )^*\) and we suppose that the normalizations of the eigenfunctions \(\varphi _0\) and \(\varphi _0^*\) are chosen such that
The latter normalization is allowed since the simplicity of \(\omega _0\) ensures that \(\langle \varphi _0,\varphi _0^*\rangle \ne 0\). Indeed, if \(\langle \varphi _0,\varphi _0^* \rangle =0\), then \(\varphi _0 \in \mathrm{Ker}(L(\cdot ,\omega _0)) \cap \mathrm{Ran}(L(\cdot ,\omega _0))\) since \(\mathrm{Ker}(L(\cdot ,\omega _0)^*)^\perp = \mathrm{Ran}(L(\cdot ,\omega _0))\). From \(L(\cdot ,\omega _0)\psi =\varphi _0\) for some \(\psi \in \mathrm{D}(A)\) we get \(L(\cdot ,\omega _0)^2\psi =0\) and the algebraic simplicity in i) implies \(\psi = c\varphi _0\) and hence \(\varphi _0=0\), which is a contradiction.
We consider the following assumptions on the operator A and the potential W: there exists \(\delta >0\) such that
- A1):
-
\(A: D(A)\rightarrow L^2({\mathbb {R}}^d,{\mathbb {C}})\) is a densely defined, closed operator with a non-empty resolvent set;
- A2):
-
\(D(A)\hookrightarrow L^\infty ({\mathbb {R}}^d,{\mathbb {C}})\), where the embedding is continuous;
- W1):
-
\(W:{\mathbb {R}}^d\times {\mathbb {C}}\rightarrow {\mathbb {C}}\) satisfies that \(W(x,\cdot )\) is holomorphic on \(B_\delta (\omega _0)\subset {\mathbb {C}}\) for a.e. \(x\in {\mathbb {R}}^d\) and there exists \(c>0\) such that
$$\begin{aligned} \Vert W(\cdot ,\omega )\Vert _\infty \le c \quad \forall \omega \in B_\delta (\omega _0); \end{aligned}$$
and the technical assumption
- Wt):
-
\(\langle \partial _\omega W(\cdot ,\omega _0)\varphi _0,\varphi _0^*\rangle \not =0\).
Regarding the nonlinearity \(f=f(x,\omega ,\varphi )\), we assume that there are \(\delta ,\alpha ,\lambda _0>0\) such that
- f1):
-
\(f(\cdot ,\omega ,\varphi (\cdot ))\in L^2({\mathbb {R}}^d,{\mathbb {C}})\) for all \(\omega \in B_\delta (\omega _0)\) and \(\varphi \in B_\delta (0)\subset D(A)\),
- f2):
-
there exists a constant \(K_f^\omega (\varphi _0)>0\) such that for any \(\lambda \in (0,\lambda _0)\) there holds
$$\begin{aligned}&\Vert f(\cdot ,\omega _1,\lambda \varphi )-f(\cdot ,\omega _2,\lambda \varphi )\Vert \\&\quad \le K_f^\omega (\varphi _0)\lambda ^{\frac{1}{\alpha }+1}|\omega _1-\omega _2|,\quad \forall \omega _1,\omega _2\in B_\delta (\omega _0)\;,\forall \varphi \in B_\delta (\varphi _0); \end{aligned}$$ - f3):
-
there exists a constant \(K_f^\varphi (\omega _0)>0\) such that for any \(\lambda \in (0,\lambda _0)\) there holds
$$\begin{aligned}&\Vert f(\cdot ,\omega ,\lambda \varphi _1)-f(\cdot ,\omega ,\lambda \varphi _2)\Vert \\&\quad \le K_f^\varphi (\omega _0)\lambda ^{\frac{1}{\alpha }+1}\Vert \varphi _1-\varphi _2\Vert ,\quad \forall \varphi _1,\varphi _2\in B_\delta (\varphi _0)\;,\forall \omega \in B_\delta (\omega _0); \end{aligned}$$ - f4):
-
for any \(\omega \in B_\delta (\omega _0)\) there exists \(g_\omega \in L^\infty ({\mathbb {R}}^d,{\mathbb {C}}){\setminus }\{0\}\) such that
$$\begin{aligned} f(\cdot ,\omega ,\varphi )-g_\omega (\cdot )|\varphi |^\frac{1}{\alpha }\varphi ={\mathcal {O}}(|\varphi |^{\frac{1}{\alpha }+1+\beta })\quad \text{ as }\quad {\mathbb {C}}\ni \varphi \rightarrow 0 \end{aligned}$$(7)for some \(\beta >0\), uniformly wrt \(\omega \in B_\delta (\omega _0)\). Moreover, we assume that \(g_\omega \) is Lipschitz in \(\omega \) for \(\omega \in B_\delta (\omega _0)\) uniformly wrt \(x\in {\mathbb {R}}^d\), i.e. there exists a constant \(K_g>0\) such that
$$\begin{aligned} \Vert g_{\omega _1}-g_{\omega _2}\Vert _\infty \le K_g|\omega _1-\omega _2| \quad \forall \omega _1,\omega _2\in B_\delta (\omega _0). \end{aligned}$$
Theorem 2.1
Suppose that \(\omega _0\) is an algebraically simple and isolated eigenvalue of L with eigenfunction \(\varphi _0\) and that A, W and f satisfy assumptions (A1)–(f4). Let also \(\tau \in (0,\min \{1,\alpha \beta \}]\). Then there exists \(\varepsilon _0>0\) such that for any \(\varepsilon \in (0,\varepsilon _0)\) there is a unique solution \((\omega ,\varphi )\) of the nonlinear eigenvalue problem (1) with the constraint \(\langle \varphi ,\varphi _0^*\rangle =\varepsilon ^\alpha \). It can be written as
with \(\nu ,\sigma \in {\mathbb {C}}\) and \(\phi ,\psi \in D(A)\cap \langle \varphi _0^*\rangle ^\perp \).
Before going into the details of the proof, let us give some remarks and examples of applications.
Remark 1
The proof of Theorem (2.1) is constructive. Therefore, we also know which problems the constants \(\nu ,\sigma \) and the functions \(\phi ,\psi \) satisfy. In particular, \(\nu \) and \(\phi \) are uniquely determined by (16), (20) and \((\sigma ,\psi )\) uniquely solves the nonlinear system (17), (21) in \(B_{r_1}(0)\times B_{r_2}(0)\subset {\mathbb {C}}\times D(A)\), for suitable \(r_1,r_2=O(1)\) as \(\varepsilon \rightarrow 0\).
Remark 2
When D(A) is the Sobolev space \(H^s({\mathbb {R}}^d,{\mathbb {C}})\), assumption (A2) is equivalent to the requirement \(s>d/2\).
Remark 3
Note that assumption (W1) ensures that
Indeed, by Taylor’s theorem for holomorphic functions (see Chapt. 4, Sect. 3.1 in [1]) we have
where
for all \(\omega \in B_r(\omega _0)\) and any \(0<r<\delta \). One can easily estimate
where
Note that \(\omega \in B_{r/2}(\omega _0)\) is satisfied if \(\varepsilon >0\) is small enough. To estimate \(\Vert \partial _\omega ^kW(\cdot ,\omega _0)\Vert _{\infty }, k \in {\mathbb {N}}\), one proceeds by induction using (10), assumption (W1), and (11).
Remark 4
Assumption (Wt) is the classical transversality condition for the bifurcation from a simple eigenvalue [6, Theorem 1], [8, Theorem 28.6] in the case
However, note that in our setting the nonlinearity \(f(\cdot ,\omega ,\varphi )\sim g_\omega (\cdot )|\varphi |^\frac{1}{\alpha }\varphi \) for \(\varphi \rightarrow 0\) (and with \(\varphi \in D(A)\) with a suitable D(A), e.g. \(D(A)=H^2({\mathbb {R}},{\mathbb {C}})\) for \(d=1\)) is differentiable only at zero. This is due to the fact that our function spaces are defined over the complex field.
Nevertheless, given the differentiability property, if (12) holds, (Wt) is equivalent to \(F_{\omega \varphi }(\omega _0,0)[\varphi _0]\notin \text {Ran}(F_\varphi (\omega _0,0))\), where \(F(\omega ,\varphi ):=L(\cdot ,\omega )\varphi -f(\cdot ,\omega ,\varphi )\). To see this, first note that
since \(\partial _\varphi f(\cdot ,\omega ,0)=0\) for all \(\omega \in B_\delta (\omega _0)\) by (f4), and
By the closed range theorem is \((A-W(\cdot ,\omega _0))u=-\partial _\omega W(\cdot ,\omega _0)\varphi _0\) solvable if and only if (Wt) is violated. Here we have used the fact that \(A-W(\cdot ,\omega _0)\) is a Fredholm operator (in particular, \(\text {Ran}(A)\) is closed), see [16, Theorem IV.5.28].
Remark 5
(Example of the potential and the nonlinearity.) Assumptions (A1)–(f4) are satisfied for instance by equation (6) with \(D(A)=H^2({\mathbb {R}},{\mathbb {C}})\) provided (W1) and (Wt) hold and \(\Gamma \) satisfies
for some \(L>0\) and all \(\omega _{1,2}\in B_\delta (\omega _0)\). An example corresponding to the Drude model for metals (see Sect. 4) is
with parameters \(\gamma ,\omega _p,k\in {\mathbb {R}}\) and \(\hat{\chi }^{(3)}\) a bounded function, Lipschitz continuous in \(\omega \). This choice will be important for modelling SPPs. Note that, with such potential W, the operator \(L(\cdot ,\omega ):=\partial _x^2+W(\cdot ,\omega )\) is non-selfadjoint and also nonlinear in \(\omega \).
Remark 6
Let us discuss the role of the parameter \(\tau \) in the expansion (8). Clearly, \(\tau \) determines the accuracy of the expansion given by the first two terms. According to Theorem 2.1, if \(\alpha \beta \le 1\), then the optimal value is \(\tau =\alpha \beta \), which is proportional to the difference of the degree of the lowest degree term in f and the next term. Notice also that higher order terms in the nonlinearity do not play any role in the choice of \(\tau \). To give an example, consider the nonlinearities in the table below.
f(x) | \(\alpha \) | \(\beta \) | \(\tau _{\max }\) | \(\omega \) |
|---|---|---|---|---|
\(|\varphi |^2\varphi \) | \(\frac{1}{2}\) | \(+\infty \) | 1 | \(\omega _0+\varepsilon \nu +\varepsilon ^2\sigma \) |
\(|\varphi |^2\varphi +|\varphi |^4\varphi \) | \(\frac{1}{2}\) | 2 | 1 | \(\omega _0+\varepsilon \nu +\varepsilon ^2\sigma \) |
\(|\varphi |^2\varphi +|\varphi |^3\varphi \) | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | \(\omega _0+\varepsilon \nu +\varepsilon ^{\frac{3}{2}}\sigma \) |
\(|\varphi |^2\varphi +|\varphi |^3\varphi +|\varphi |^4\varphi \) | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | \(\omega _0+\varepsilon \nu +\varepsilon ^{\frac{3}{2}}\sigma \) |
As explained in Sect. 4, in the applications of Theorem 2.1 to time harmonic electromagnetic waves, the relevant nonlinearities are odd. In the case of a cubic nonlinearity (\(\alpha = 1/2\)) the first correction term in f is of the kind \(|\varphi |^4\varphi \) and therefore we have \(\beta =2\) such that we are in the optimal case \(\tau =1\).
The strategy of the proof of Theorem 2.1 may be summarized as follows. We employ a Lyapunov–Schmidt reduction making use of spectral projections (here the simplicity of the eigenvalue \(\omega _0\) is used) to decompose the problem into a system in which one rather easily determines \(\nu \) and \(\phi \). Then, the rest becomes a system for the unknowns \(\sigma \) and \(\psi \), which will be solved by means of a nested fixed-point argument. In particular, the assumption that \(\omega _0\) be isolated is exploited to invert the operator \(L(\cdot ,\omega _0)\) restricted to \(\langle \varphi _0^*\rangle ^\perp \).
Proof of Theorem 2.1
Lyapunov–Schmidt decomposition.
In this initial step we reformulate problem (1) with the ansatz in (8) as a system of two equations using the Lyapunov–Schmidt decomposition.
Let us first introduce the projections \(P_0: u\mapsto \langle u,\varphi _0^*\rangle \varphi _0\) and \(Q_0:=Id-P_0\). Clearly, \(P_0:L^2({\mathbb {R}}^d,{\mathbb {C}})\rightarrow \langle \varphi _0\rangle \) and \(Q_0:L^2({\mathbb {R}}^d,{\mathbb {C}})\rightarrow \langle \varphi _0^*\rangle ^\perp \). Using our constraint \(\langle \varphi ,\varphi _0^*\rangle = \varepsilon ^\alpha \), it is easy to see that \(P_0(\phi +\varepsilon ^\tau \psi )=0\). Applying then \(P_0\) to our Eq. (1), we get
Notice that the first term is of higher-order in \(\varepsilon \), mainly because of our assumption (f4), see the forthcoming computations (27)–(31).
On the other hand, Taylor expanding \(W(\cdot ,\omega )\) in \(\omega _0\) up to order two and using assumption (W1), we have
where
for any \(r<\delta \), see (10). Inserting now the expansions of \(\omega \) and \(\varphi \) from (8), i.e.
we obtain
where v collects all other terms of higher-order in \(\varepsilon \), namely
Comparing now (13) and (14), the terms of order \(\alpha +1\) in \(\varepsilon \) match if and only if we take
which is well-defined thanks to assumption (Wt). From the rest of (13)–(14) we obtain
Let us now apply \(Q_0\) to (1). On the one hand we have
and on the other hand
Therefore, we obtain
An expansion of the last term as in (14)–(15) yields
Rewriting (16) as
and using (18), we obtain
Again, imposing that the terms of the lowest-order in \(\varepsilon \) match, we get a linear equation for \(\phi \):
Notice that, with our choice of \(\nu \), Eq. (20) is uniquely solvable in \(Q_0D(A)=D(A)\cap \langle \varphi _0^*\rangle ^\perp \) by the closed range theorem. Indeed, the operator on the left hand side is Fredholm (see [16, Theorem IV.5.28], where the fact that \(\omega _0\) is a simple isolated eigenvalue in the above sense is used) and the right hand side is orthogonal to the kernel of the adjoint operator, i.e. to \(\varphi _0^*\), due to (16).
The rest of (19) produces the following equation for \((\sigma ,\psi )\):
Fixed Point Argument
In order to solve our initial problem (1), we now need to solve system (17), (21) for \((\sigma ,\psi )\in {\mathbb {C}}\times D(A)\). Inserting then \(\sigma \) and \(\psi \) into (8) produces a solution \((\omega ,\varphi )\) of (1).
We proceed by a fixed point argument. Note that although a direct fixed point argument for \((\sigma ,\psi )\) is possible, we opt for a nested version, where we first solve for \(\psi \) as a function of \(\sigma \) and subsequently solve for \(\sigma \). This approach is arguably more transparent.
Let us first address Eq. (21) and write it as a fixed point equation for \(\psi \), exploiting our assumptions on the eigenvalue \(\omega _0\), which is assumed simple and isolated. This actually means that \(Q_0L(\omega _0)Q_0:Q_0D(A)\rightarrow Q_0L^2({\mathbb {R}}^d)\) is boundedly invertible in \(Q_0D(A)\) and its norm is bounded by a constant \(C(\omega _0)\):
In our nested fixed point argument for (17), (22) we first solve (22) for \(\psi \in B_{r_2}(0)\subset D(A)\) for all \(\sigma \in B_{r_1}(0)\subset {\mathbb {C}}\) fixed with \(r_1>0\) arbitrary. To this aim we need to show that for each \(\sigma \in B_{r_1}(0)\) there exists \(r_2>0\) so thatFootnote 2
- (i):
-
\(\psi \in B_{r_2}(0)\) \(\Rightarrow \) \(G(\psi )\in B_{r_2}(0)\),
- (ii):
-
\(\exists \rho \in (0,1):\ \Vert G(\psi _1)-G(\psi _2)\Vert _A\le \rho \Vert \psi _1-\psi _2\Vert _A\) for all \(\psi _1,\psi _2\in B_{r_2}(0)\)
if \(\varepsilon >0\) is small enough.
Then, having obtained \(\psi =\psi (\sigma )\in B_{r_2}(0)\), we shall solve Eq. (17) for \(\sigma \) and finally find a suitable \(r_1\). Note that the fixed point argument for equation (17) requires the Lipschitz continuity of \(\sigma \mapsto \psi (\sigma )\), which we verify below.
To ensure (i), we need to estimate \(\Vert R(\psi )\Vert \). The second and the third term in (21) are easy to handle. Henceforth, we track the dependence of all constants on \(\sigma \) and \(\psi \) via \(r_1,r_2\).
using (9). Let us now deal with \(R_4\). Inspecting (15), we obtain
where \(h_1\) is polynomial in \(r_1\), linear in \(\Vert \psi \Vert \) and satisfies \(h_1(0,\Vert \psi \Vert )=0.\) Actually, all terms appearing in (15) are easy to estimate, so here we just briefly justify the one for the integral rest \(I(x,\omega )\), for later use too. Indeed, using (11) for \(n=3\), we have
for any \(0<r<\delta \) and all \(\omega \in B_{r/2}(\omega _0)\), i.e. for all \(\varepsilon >0\) small enough. Recall that \(M=\sup \limits _{\omega \in B_\delta (\omega _0)}\Vert W(\cdot ,\omega )\Vert _\infty .\) Finally, we need to estimate \(R_1\), which involves the nonlinearity. We split it as
and estimate term by term. First,
for \(\varepsilon >0\) small enough. In Eq. (28) we used the embedding \(D(A)\hookrightarrow L^\infty ({\mathbb {R}}^d)\). The dependence \(r_2\mapsto C_1(r_2)\) is of power type; in detail,
for some \(r_*\in [0,r_2]\). For each \(r_2>0\) there exists \(\varepsilon _0=\varepsilon _0(r_2)\) such that
for all \(\varepsilon \in (0,\varepsilon _0).\) In conclusion
for all \(\varepsilon \in (0,\varepsilon _0).\)
Next,
where we used the fact that the map \(z\mapsto |z|^\frac{1}{\alpha }z\) is locally Lipschitz as well as estimates of the type \(\Vert |\varphi |^{1/\alpha }\phi \Vert \le \Vert \varphi \Vert ^{1/\alpha }_{\infty }\Vert \phi \Vert \le c\Vert \varphi \Vert ^{1/\alpha }_{D(A)}\Vert \phi \Vert =C\). Finally, since \(g_\omega \) is Lipschitz in \(\omega \) by (f4),
and therefore, from (23)–(25) and (32), that
Using (29) and \(\tau \le \alpha \beta \), we may further estimate
for \(\varepsilon >0\) small enough. This follows because for \(\varepsilon \) small enough we have \(\varepsilon ^{1+\tau }h_1(r_1,r_2) <C_0\). Setting now \(r_2=r_2(r_1) := 4C_0 + {\tilde{C}}r_1\), we get (i) provided \(\varepsilon \in (0,{\overline{\varepsilon }}_0)\) with some \({\overline{\varepsilon }}_0={\overline{\varepsilon }}_0(r_1)>0.\)
Let us now address the contraction property (ii). We take \(\psi _1,\psi _2\in B_{r_2}(0)\) and define \(\varphi _{1,2}:=\varepsilon ^\alpha (\varphi _0+\varepsilon \phi +\varepsilon ^{1+\tau }\psi _{1,2})\). By (22), we need to estimate \(\Vert R(\psi _1)-R(\psi _2)\Vert \), with R defined in (21). First notice that \(R_2\) and \(R_3\) do not depend on \(\psi \), so they will vanish in the difference and we have to handle just the nonlinear term and v.
where \(C_2\) is polynomial in \(r_1\). Here, estimate (26) was used. Next, by (f3),
Hence, by (22), (34) and (35), we get
which yields (ii) if \(\varepsilon \) is small enough. Therefore, applying Banach’s fixed point theorem, we infer the existence of a solution \(\psi \) of Eq. (21). More precisely, for any \(r_1>0\) and for any \(\sigma \in B_{r_1}(0)\subset {\mathbb {C}}\) there exists \(r_2=r_2(r_1)\) and \(\varepsilon _0>0\) such that for each \(\varepsilon \in (0,\varepsilon _0)\) there is a unique \(\psi =\psi (\sigma )\in B_{r_2}(0)\subset D(A)\) such that \((\sigma ,\psi )\) solves (21).
Let us now address Eq. (17). Inserting \(\psi =\psi (\sigma )\) and dividing by the factor \(\varepsilon ^{\alpha +1+\tau }\langle \partial _\omega W(\cdot ,\omega _0)\varphi _0,\varphi _0^*\rangle \), which is nonzero by (Wt), this becomes a fixed point equation for \(\sigma \):
where \(\varphi (\sigma )\) is given by (8) with \(\psi =\psi (\sigma ).\) We need to show that for some \(r_1>0\)
- (i’):
-
\(S:B_{r_1}(0)\rightarrow B_{r_1}(0)\),
- (ii’):
-
there exists \(\rho \in (0,1)\) so that
$$\begin{aligned} |S(\sigma _1)-S(\sigma _2)|\le \rho |\sigma _1-\sigma _2|\quad \hbox {for all}\quad \sigma _1,\sigma _2\in B_{r_1}(0) \end{aligned}$$
if \(\varepsilon >0\) is small enough.
Notice that the first term on the right-hand side of (17’) is independent of \(\sigma \) and \(\psi \), therefore its norm can be simply estimated by a constant. Decomposing the nonlinear term as in (27), according to estimates (28)–(31), we get
Moreover, similarly to (25) we have
Therefore, combining (17’), (36) and (37), we obtain
For each \(r_1>0\) there is \({\tilde{\varepsilon }}_0={\tilde{\varepsilon }}_0(r_1)>0\) such that
for all \(|\sigma |<r_1\) and all \(\varepsilon \in (0,{\tilde{\varepsilon }}_0)\). Recalling that \(r_2=r_2(r_1)=4C_0+{\tilde{C}}r_1\) and that \(\tau \le \min \{1,\alpha \beta \}\), this implies that
i.e. \(\varepsilon \in (0,\varepsilon _0)\) with \(\varepsilon _0=\varepsilon _0(r_1).\) Setting \(r_1:=4C_0+2C+1\), we have property (i’).
Finally, let us address the contraction property (ii’). For \(\sigma _{1,2}\in B_{r_1}(0)\) we define \(\psi _{1,2}=\psi (\sigma _{1,2})\) and analogously \(\omega _{1,2}\) and \(\varphi _{1,2}\). We need to estimate \(|S(\sigma _1)-S(\sigma _2)|\). Recalling the form of v in (15), we get
with \(C_3(r_1)\) cubic in \(r_1\). Here the estimates are rather standard and quite similar to the ones used in (37), so we just point out how to deal with the rest term I. We have, as in Remark 3,
First, we estimate
which holds for all \(\varepsilon >0\) small enough with \(C_4(r_1)\) quadratic in \(r_1\) using an estimate analogous to (26). Second, we have
for \(\varepsilon >0\) small enough, where in the second step we have used \(\omega _1-\omega _2=\varepsilon ^{1+\tau }(\sigma _1-\sigma _2)\) and estimated \(|z-\omega _1|\ge \tfrac{1}{2}|z-\omega _0|\) for all \(z\in \partial B_r(\omega _0)\), which holds for \(\varepsilon >0\) small enough. In the last step estimate (11) was used again. The constants \(C_5(r_1),{\tilde{C}}_5(r_1)\) are cubic in \(r_1\). Consequently, by (39)–(41) we get
with \(C_6(r_1)\) cubic in \(r_1\).
Now we have to deal with the third term in (17’) involving the nonlinearity. However, this is easily estimated using its Lipschitz behaviour in \(\omega \) and \(\varphi \) as in (f2)–(f3). Indeed,
where the first term is estimated as in (35), whereas
Therefore, combining (38) and (42)–(43), we infer
with \(C_3(r_1)\) cubic in \(r_1\). Hence, it remains to show now that the map \(\sigma \mapsto \psi (\sigma )\) is Lipschitz continuous. Taking \(|\sigma _{1,2}|\le r_1\), we shall estimate the difference \(\Vert \psi _1-\psi _2\Vert \) starting from the fixed-point equation (22) for \(\psi \), where as before we define \(\psi _{1,2}:=\psi (\sigma _{1,2})\) and similarly for \(\omega _{1,2}\) and \(\varphi _{1,2}\). Indeed, exploiting the above estimates (38) and (42)–(43), we have
if \(\varepsilon >0\) is small enough.
This, together with (22), yields \(\Vert \psi (\sigma _1)-\psi (\sigma _2)\Vert _A\le 3C|\sigma _1-\sigma _2|\) for \(\sigma _{1,2}\in B_{r_1}(0)\) and \(\varepsilon >0\) small enough. As a consequence we may conclude the fixed point argument for \(\sigma \) because from (44) and (45) and from the fact that \(r_2=r_2(r_1)\) we obtain
with \({\tilde{C}}(r_1)>0\), which is the desired contraction property for suitably small values of \(\varepsilon \). Hence, for small \(\varepsilon >0\) the fixed point argument yields the sought solution for the system (17)–(21) and the proof of Theorem 2.1 is complete. \(\square \)
3 Bifurcation of real nonlinear eigenvalues: the \({\mathcal {PT}}\)-symmetric case
In applications one often starts from a real eigenvalue of the linear problem and seeks a bifurcation branch \((\omega ,\varphi )\) where the realness of the nonlinear eigenvalue is preserved, i.e. \(\omega \in {\mathbb {R}}\). This is required also for the applications to SPPs in Sect. 4. However, the solution \(\omega \) obtained by Theorem 2.1 is a-priori just complex. In this section we provide a symmetric situation in which the realness of \(\omega \) is preserved in the bifurcation. This is based on [11, Section III], whereby we adapt the analysis for our more general context. For the sake of completeness and since Sect. 4 is based on these results, we present most of the details here again.
Definition 3.1
A function \(\psi :{\mathbb {R}}^d\rightarrow {\mathbb {C}}\) (\(d\ge 1\)) is called \({\mathcal {PT}}\)-symmetric if \(\mathcal {B}\psi (x):=\overline{\psi (-x)}=\psi (x)\) for all \(x\in {\mathbb {R}}^d\). Moreover, an operator L acting on a Hilbert space with domain D(L) is \({\mathcal {PT}}\)-symmetric when it commutes with \(\mathcal {B}\), namely \(L\mathcal {B}=\mathcal {B}L\) in D(L).
The above operator \(\mathcal {B}\) is in fact the composition of the operator \({\mathcal {P}}\), the space reflection (parity), and \({\mathcal {T}}\), the complex conjugation, which corresponds the time-reversal in quantum mechanics.
Notice that the Schrödinger operator \(-\Delta +W\) with a complex potential W is \({\mathcal {PT}}\)-symmetric if and only if the real and the imaginary parts of W satisfy respectively \({{\,\mathrm{Re}\,}}W(-x)={{\,\mathrm{Re}\,}}W(x)\) and \({{\,\mathrm{Im}\,}}W(-x)=-{{\,\mathrm{Im}\,}}W(x)\) for all x. Moreover, general polynomial nonlinearities
are \({\mathcal {PT}}\)-symmetric if and only if the coefficients are so: \(\overline{a_{pq}}(-x)=a_{pq}(x)\), see [11, Sections III-IV]. An example is \(f(\varphi )=|\varphi |^{2m+1}\varphi , m \in {\mathbb {N}}\).
Proposition 3.1
Let A, W, f and \(g_\omega \) be as in Theorem 2.1 and suppose that they are \({\mathcal {PT}}\)-symmetric. If \(\omega _0\in {\mathbb {R}}\) is an algebraically simple eigenvalue, then for all \(\varepsilon \in (0,\varepsilon _0)\) the nonlinear eigenpair \((\omega ,\varphi )\) from Theorem 2.1 satisfies \(\omega \in {\mathbb {R}}\) and \(\mathcal {B}\varphi =\varphi \).
Remark 7
Under the assumptions on A, W, f, and \(g_\omega \) as in Prop. 3.1 and under the simplicity assumption on \(\omega _0\), the eigenfunction \(\varphi _0\) may always be chosen \({\mathcal {PT}}\)-symmetric. Indeed, \(L(\cdot ,\omega _0)=A+W(\cdot ,\omega _0)\) is \({\mathcal {PT}}\)-symmetric and, applying \(\mathcal {B}\) to \(L(\cdot ,\omega _0)\varphi _0=0\), we get \(L(\cdot ,\omega _0)\big (\mathcal {B}\varphi _0)=0\) and we conclude by the simplicity of \(\omega _0\).
Similarly, we obtain \(\mathcal {B}\varphi _0^*=\varphi _0^*\) because \(\mathcal {B}L^*(\cdot ,\overline{\omega _0})=L^*(\cdot ,\overline{\omega _0}) \mathcal {B}\). Indeed,
for all \(v,\phi \in D(A)\).
Proof
According to our expansions (8), we need to prove that \(\nu ,\sigma \) are real and that \(\phi ,\psi \) are \({\mathcal {PT}}\)-symmetric. First, \(\nu \) in (16) satisfies \(P_0(\nu \partial _\omega W(\cdot ,\omega _0)\varphi _0)=P_0(g_{\omega _0}(\cdot )|\varphi _0|^\frac{1}{\alpha }\varphi _0)\), where we recall that \(P_0\) is the spectral projection onto the eigenspace \(\langle \varphi _0\rangle \) and that with our assumptions \(P_0\) commutes with \(\mathcal {B}\). Indeed,
Therefore, on the one hand,
On the other hand,
This yields \(\nu \in {\mathbb {R}}\). Next, let us analyze \(\phi \), i.e. the solution of (20) in \(Q_0D(A)\). Notice that if \(P_0\) commutes with \(\mathcal {B}\), then the same holds for \(Q_0=Id-P_0\), too. Therefore, applying a similar argument, we get that \(\mathcal {B}(\phi )\) satisfies (20) too. Moreover, since \(\mathcal {B}(\phi )\in D(A)\cap \langle \varphi _0^*\rangle ^\perp \), we get \(\mathcal {B}(\phi )=\phi \) because (20) has a unique solution in \(P_0D(A)\). Let us now address \(\sigma \) and \(\psi \). We will show that the coupled fixed point problem (17),(21) preserves the realness of \(\sigma \) and the \({\mathcal {PT}}\)-symmetry of \(\psi \). First, given \(\sigma \in {\mathbb {R}}\) with \(\sigma \in (-r_1,r_1)\), we prove that
where G is defined in (22). If (46) holds, then the fixed point \(\psi =\psi (\sigma )\) of \(\psi =G(\sigma ,\psi )\) lies in \(B_{r_2}(0)\cap \{\eta \in L^2({\mathbb {R}}^d)\,|\,\mathcal {B}\eta =\eta \}\). To this aim, first we notice that for \(u\in Q_0L^2({\mathbb {R}}^d)\) it holds
Next, recalling that \(\varphi _0\), \(\phi \), and \(\psi \) are now \({\mathcal {PT}}\)-symmetric, we get for R (defined in (21))
Inspecting all terms in v appearing in (15) and exploiting \(\sigma \in {\mathbb {R}}\) (and therefore \(\omega \in {\mathbb {R}}\)), we obtain that \(\mathcal {B}v(\cdot ,\omega ,\varphi )=v(\cdot ,\omega ,\varphi )\), so (46) is proved. Finally, with similar manipulations one proves that \(\mathcal {B}(\psi )=\psi \) implies \(\mathcal {B}S(\sigma )=S(\sigma )\), where S is defined in (17’), obtaining thus \(S(\sigma )\in {\mathbb {R}}\) since \(\mathcal {B}S(\sigma )=\overline{S(\sigma )}\). Therefore, for a given \({\mathcal {PT}}-\)symmetric \(\psi (\sigma )\) the fixed point \(\sigma \) of \(S(\sigma )\) must be real. This completes the proof. \(\square \)
4 Applications to nonlinear surface plasmons
As mentioned in the introduction, we are interested in surface plasmon polaritons (SPPs) localized at one or more interfaces between different dielectric and metal layers. We consider the time harmonic and z-independent ansatz (5) for the Maxwell system (3). A simple nonlinear, non-local relation for the displacement field is
where \(\chi ^{(1,3)}:{\mathbb {R}}^3\times {\mathbb {R}}\rightarrow {\mathbb {R}}\) and \(\chi ^{(1,3)}(\cdot ,\tau )=0\) for \(\tau <0\). The functions \(\chi ^{(1)}\) and \(\chi ^{(3)}\) are the linear and the cubic electric susceptibilities of the material, respectively. In general, \(\chi ^{(1)}\) and \(\chi ^{(3)}\) are tensors but in the isotropic case, which we assume, the relation in (47) with scalar \(\chi ^{(1)}\) and \(\chi ^{(3)}\) holds, see [17, Section 2d].
Substituting a monochromatic ansatz \({{\mathcal {E}}}(x,y,z,t)=E(x,y,z)e^{\mathrm{i}\omega t} + \text {c.c.}\) in (3) and neglecting higher harmonics (terms proportional to \(e^{3\mathrm{i}\omega t}\) and \(e^{-3\mathrm{i}\omega t}\)), we get \({{\mathcal {D}}}(x,y,z,t)=D(x,y,z)e^{\mathrm{i}\omega t}+\text {c.c.}\) with
Here \(|E|^2=E\cdot {\overline{E}}\) and \({\hat{f}}(\omega )\) is the Fourier-transform of f. Neglecting higher harmonics is a common approach in theoretical studies of weakly nonlinear optical waves [23]. Using (3), we get that both H and D are curl-fields such that the divergence conditions \(\nabla \cdot D=0, \nabla \cdot H=0\) hold automatically. Defining \(c:=(\epsilon _0\mu _0)^{-1/2}\), in the second order formulation we have \(\frac{\omega ^2}{c^2}D=\nabla \times \nabla \times E,\) i.e.
Recall again only odd nonlinearities are allowed in \({{\mathcal {D}}}\) when studying time harmonic waves. Even nonlinearities do not produce terms proportional to \(e^{\mathrm{i}\omega t}\).
We consider structures independent of y and z, i.e. \(\chi ^{(1,3)}=\chi ^{(1,3)}(x,\omega )\). Interfaces between layers are thus parallel to the yz-plane.
For the TE-ansatz in (5), with only one nontrivial component, Eq. (48) reduces to the scalar problem
with
We study layers of x-periodic (including homogeneous) media. When a metal layer is homogeneous, we choose the simplest Drude model of the linear susceptibility in that layer [19]
where \(\omega _p\in {\mathbb {R}}^+\) and \(\gamma \in {\mathbb {R}}\). For dielectric layers we choose a periodic (possibly constant) and generally complex \({{\hat{\chi }}}^{(1)}(\cdot ,\omega )\). The imaginary part of \({{\hat{\chi }}}^{(1)}\) is related to the loss or gain of energy of an electromagnetic wave propagating inside the medium. For most of the materials, and in particular for metals, it is negative, corresponding to a lossy material. However, in active (doped) materials the energy of an electromagnetic wave is amplified (energy gain), and therefore the imaginary part of \({{\hat{\chi }}}^{(1)}\) is positive. Materials with a real \({{\hat{\chi }}}^{(1)}(\cdot ,\omega )\) are called conservative.
To make Eq. (49) dimensionless, as well as in order to use the physical values of the parameters involved in the numerical study in Sect. 4.1.2, we introduce the new rescaled spatial variable, frequency, and wave number
where \(\omega _p\) is the bulk plasma frequency of a prescribed metal layer. Defining then \({{\tilde{\varphi }}}({{\tilde{x}}}):=\varphi (x)\), we obtain the same equation as (49) but in the tilde variables and with W and \(\Gamma \) respectively replaced by
Note that for the Drude model the susceptibility is
where \({{\tilde{\gamma }}}:=\gamma /\omega _p\).
For the sake of a simpler notation henceforth we will simply write \(x,\omega ,\gamma ,k,W\), and \(\Gamma \) instead of \({{\tilde{x}}}, {{\tilde{\omega }}},{{\tilde{\gamma }}},{{\tilde{k}}}, {{\tilde{W}}}\), and \({{\tilde{\Gamma }}}\).
Due to the presence of material interface(s), solutions of the Maxwell’s equations (3) are not smooth. However, they satisfy the interface conditions that the tangential component of \({{\mathcal {E}}}\), the normal component of \({{\mathcal {D}}}\) and the whole vector \({{\mathcal {H}}}\) be continuous across each interface, see Sect. 33-3 in [13]. For our interfaces parallel to the yz-plane we get (4). For the ansatz (5) the interface conditions reduce to a \(C^1\)-continuity condition on \(\varphi \)
Our nonlinear problem (1) is thus Eq. (49) with W and \(\Gamma \) respectively replaced by (52)–(53) and coupled with the (IFCs).
To apply our bifurcation result to (49) with (IFCs), a real, linear eigenvalue is needed. We show that such an eigenvalue exists in some \({\mathcal {PT}}\)-symmetric choices of the layers. SPPs in \({\mathcal {PT}}\)-symmetric structures have been studied in the physics literature before by employing active materials, see e.g. [2, 3, 14, 25]. Nevertheless, we are not aware of a rigorous mathematical existence proof of the asymptotic expansion of nonlinear SPPs in the frequency dependent case.
Theorem 2.1 can be applied to (49) with finitely many interfaces (at \(x=x_1,\dots ,x_N\)) using the following natural choice of A, D(A), and f:
and
where \(\llbracket \varphi \rrbracket _j:=\lim _{x\rightarrow x_j+}\varphi (x)-\lim _{x\rightarrow x_j-}\varphi (x)\) and \(x_0:=-\infty \), \(x_{N+1}:=\infty \). It is easy to see that \(D(A)=H^2({\mathbb {R}},{\mathbb {C}})\) using the definition of the second weak derivative and the fact that at the interfaces any \(\varphi \in D(A)\) is of class \(C^1\). Note that assumptions (A1)–(A2), (f1)–(f4) are satisfied for any \(\omega \in {\mathbb {C}}{\setminus } \{0,-\mathrm{i}\gamma \}\).
4.1 The linear eigenvalue problem
In order to apply Theorem 2.1, we need to find an eigen-pair \((\omega _0,\varphi _0)\) of the linear problem
coupled with IFCs, with a simple and isolated \(\omega _0\in {\mathbb {C}}{\setminus }\{0\}\). To ensure the realness of the frequency we need, in fact, \(\omega _0\in {\mathbb {R}}{\setminus }\{0\}\) as well as the \({\mathcal {PT}}\)-symmetry of \(W(\cdot ,\omega )\), such that Proposition 3.1 can be applied. We shall see that the existence of a simple and isolated eigenvalue \(\omega _0\in {\mathbb {R}}{\setminus }\{0\}\) strongly depends on the choice of the layers. As we show in Sect. 4.1.1, the choice of two layers (\(N=1\)) of periodic materials with one being conservative and the other a non-conservative homogeneous material (i.e. with a complex \({\hat{\chi }}^{(1)}\)) leads to no real eigenvalues \(\omega _0\). On the other hand, in Sect. 4.1.2 we find two \({\mathcal {PT}}\)-symmetric settings with three homogeneous layers (\(N=2\)) leading to the existence of an isolated simple eigenvalue \(\omega _0\in {\mathbb {R}}\) in (54). These settings are: (active dielectric—conservative Drude metal—lossy dielectric) and a hypothetical setting of (Drude metal with gain—lossless dielectric—lossy Drude metal).
4.1.1 Two periodic layers
We consider first the case of two layers, each being either a periodic metal or a periodic dielectric, where we set the interface at \(x=0\). Hence
where the functions \(W_\pm (x,\omega )=\omega ^2(1+\hat{\chi }^{(1)}_{\pm }(x,\omega ))-k^2\) are periodic in x with periods \(\nu _\pm >0\). The governing linear problem (54) has two linearly independent Bloch wave solutions \(\psi ^\pm _{1,2}\) on the half line \(\pm x>0\) respectively. The Bloch wave theory for the Hill’s equation (54) can be found in [12]. A necessary condition for the existence of an \(L^2({\mathbb {R}},{\mathbb {C}})\)-solution of (54) is
Otherwise (if \(0\in S)\), on at least one of the half lines there is no decaying solution. If \(0\notin S\), the solutions \(\psi ^\pm _{1,2}\) have the form
where \({{\,\mathrm{Re}\,}}(\lambda _\pm ) >0, p^\pm _j(x+\nu _\pm )=p^\pm _j(x)\) for all \(x\in {\mathbb {R}}\) and both \(j=1,2\). If, say, \(W_+\) is real, then \(p^+_j\) and \(\lambda _+\) can be chosen real but \(p_j^+\) is generally \(2\nu _+\)-periodic, see [12].
An \(L^2({\mathbb {R}})\)-solution is given by
Due to the linearity of (54) the \(C^1\)-matching condition (IFCs) is equivalent to the condition
Note that by varying the parameters \(\omega ,k\in {\mathbb {R}}\) we get \(R_\pm =R_\pm (\omega ,k)\).
In [10] the case of real, periodic \(W_\pm \), i.e. the one of two periodic conservative materials, was considered and eigenvalues were found by varying k and searching for zeros of \(R_+(k)-R_-(k)\).
In the presence of non-conservative materials the respective potential W is complex. It is easy to see that the single interface of a conservative material (e.g. a classical dielectric) with a real W and non-conservative homogeneous material (e.g. a Drude metal) with a complex W does not support any eigenvalues of (54). Note that this does not contradict the existence of SPPs at such single metal/dielectric interfaces in general because this existence holds for TM-polarisations, see [19]. Without loss of generality we assume that the conservative material is on the half line \(x>0\), i.e. \(W_+(x,\omega )\) is real. The non-conservative material in \(x<0\) is homogeneous (described, e.g. by (50)) such that \(W_-(x,\omega )=W_-(\omega )\) is complex and independent of x. Hence \(\varphi _-(x)=ce^{\lambda _- x}\) withFootnote 3\(\lambda _-=\sqrt{W_-(\omega )}\in {\mathbb {C}}{\setminus } {\mathbb {R}}\), such that
and \(\varphi _+(x)=p_1^+(x)e^{-\lambda _+ x}\) with \(\lambda _+\in {\mathbb {R}}\) and \(p_1^+(x)\) real and \(2\nu _+-\)periodic, such that
Note that \(p_1^+(0)=0\) implies \(c=0\) due to (IFCs) such that only the trivial solution \(\varphi \equiv 0\) is produced in that case.
Because \(R_-\in {\mathbb {C}}{\setminus } {\mathbb {R}}\) and \(R_+\in {\mathbb {R}}\), condition (55) is not satisfied and no eigenvalue exists.
4.1.2 Three homogeneous layers
Next we consider three homogeneous material layers with interfaces at \(x=0\) and \(x=d>0\), i.e. a sandwich geometry with two unbounded layers,
where \(\eta _\pm ,\eta _*\in {\mathbb {C}}\). A localized solution of (54) is possible only if
Note that if the semi-infinite layers are conservative, then \(\eta _+,\eta _-\in {\mathbb {R}}\) and (57) is equivalent to
Under assumption (57) we have
where \(\mu :=\sqrt{-W_*}\), \(\lambda _\pm :=\sqrt{- W_\pm }\), \({{\,\mathrm{Re}\,}}(\lambda _\pm )>0\), and where \(A,B,C,D\in {\mathbb {C}}\) are constants to be determined. We can normalize such that \(D=1\). Then the \(C^1\)-matching at \(x=0\) and \(x=d\) is equivalent to
This system has the unique solution
together with a condition on the parameter d:
The term \(2\pi \mathrm{i}m\) appears due the fact that \(z=\log (b)+2\pi \mathrm{i}m\) solves \(e^z=b\) for any \(m\in \mathbb {Z}\). Condition (60) means that under assumption (57) there is a width \(d>0\) supporting a real eigenvalue if and only if \({{\tilde{d}}}_m={{\tilde{d}}}_m(\omega )\) is positive for some value of \(\omega \in {\mathbb {R}}\) and some \(m\in \mathbb {Z}\). If all the layers are homogeneous conservative materials, (60) cannot be satisfied because \(\mu >0\) and the argument of the logarithm on the right hand side of (60) lies in (0, 1) such that \(\text{ Re }({{\tilde{d}}}_m)<0\) for all \(m\in \mathbb {Z}\).
Next, we consider three sandwich settings, out of which the last two are \({\mathcal {PT}}\)-symmetric. As the numerical evaluation of \({\tilde{d}}_m\) suggests, both of these apparently lead to the existence of linear eigenvalues \(\omega _0\in {\mathbb {R}}\) and hence to real bifurcating nonlinear eigenvalues \(\omega \). The first one of these \({\mathcal {PT}}\)-symmetric cases has been taken from the physics literature [2, 3] while the second one corresponds to a hypothetical material.
Case 1: conservative dielectric—Drude metal—conservative dielectric
Note that a Drude metal layer being sandwiched between two conservative dielectrics does not produce a \({\mathcal {PT}}\)-symmetric potential W. Hence, we do not expect a real eigenvalue \(\omega \).
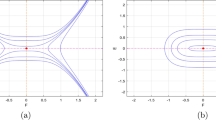
We have \(\eta _\pm >0\) and \(\eta _*=-\frac{1}{\omega ^2+\mathrm{i}\gamma \omega }\in {\mathbb {C}}\). Our numerical study of \({{\tilde{d}}}_m\) shows that for any choice of the constants \(\eta _+,\eta _-,\gamma \in {\mathbb {R}}\) and \(m\in \mathbb {Z}\) we cannot find a frequency \(\omega \) for which \({{\tilde{d}}}_m(\omega )\in (0,\infty )\). Figure 1a, b shows as an example the behaviour of the maps \(\omega \mapsto {{\,\mathrm{Re}\,}}({{\tilde{d}}}_0(\omega ))\) and \(\omega \mapsto {{\,\mathrm{Im}\,}}({{\tilde{d}}}_0(\omega ))\) for different choices of \(\gamma ,\eta _+,\eta _-\).
The graph of \(\omega \mapsto {{\,\mathrm{Re}\,}}({{\tilde{d}}}_m(\omega ))\) (full blue line) and \(\omega \mapsto {{\,\mathrm{Im}\,}}({{\tilde{d}}}_m(\omega ))\) (dashed red line). a, b Case 1 with \(k=1\), \(\gamma ={\mp }0.5\), \(\eta _+=5\), \(\eta _-=0.05\), and \(m=0\). c Case 2 with \(k=2\), \(\eta _\pm =9.2\pm 1.28\mathrm{i}\), \(\gamma =0\) and \(m=1\). d Case 3 with \(k=2\), \(\gamma ^+=-\gamma ^-=0.5\), \(\eta _*=0.2\) and \(m=-1\). In c (resp. d) the chosen value \(d=1\), attained at \(\omega \approx 3.8275\) (resp. \(d=0.5\), attained at \(\omega \approx 2.8096\)), is highlighted in the graph (colour figure online)
Case 2: \({\mathcal {PT}}\)-symmetric (dielectric—metal—dielectric) setting
For the case of a homogeneous Drude metal sandwiched between two homogeneous non-conservative dielectric layers, we have
This setting leads to a \({\mathcal {PT}}\)-symmetric W (with respect to \(x=d/2\), i.e. \(W(\frac{d}{2}-x,\omega )=\overline{W(\frac{d}{2}+x,\omega )}\) for all \(x\in {\mathbb {R}}\) and \(\omega \in {\mathbb {R}}{\setminus }\{0\}\)) if we choose
Hence, one of the dielectric layers is lossy while the other is active and generates energy gain.
Note that in this example the simple transformation \(\omega ':=\omega ^2\) leads to a linear dependence on the spectral parameter \(\omega '\).
This configuration of a conservative metal sandwiched between a couple of well-prepared active and lossy dielectrics was considered, e.g., in [2, 3]. As the active material we consider titanium dioxide (\(\hbox {TiO}_2\)), with refractive index \(n=3.2+0.2\mathrm{i}\), and as the metal we choose silver with the bulk plasma frequency \(\omega _p(\text {Ag})=8,85\cdot 10^{15}\text{ s}^{-1}\). We use \(\omega _p(\text {Ag})\) as the rescaling parameter in (51). Recalling the relation \(W(x)=\omega ^2n(x)^2-k^2\) between the refractive index and the potential W, we choose \(k=2\) and obtain \(\eta _\pm =9.2\pm 1.28\mathrm{i}\).
Our numerical tests show that this \({\mathcal {PT}}\)-symmetric setting leads to \({{\tilde{d}}}(\omega )>0\) for all \(\omega >\omega _{DMD}\approx 2.23\), see Fig. 1c. For the computation of the bifurcation we choose the point \(\omega _0\approx 3.8275\), for which \(d={\tilde{d}}_{-1}(3.8275) \approx 1\).
As the graph in Fig. 1c suggests, \(\frac{d}{d\omega }{{\,\mathrm{Re}\,}}({{\tilde{d}}}_{-1}(\omega ))\ne 0\) for all \(\omega >\omega _{DMD}\). Hence, for any width \(d\in {{\tilde{d}}}_{-1}((\omega _{DMD},\infty ))\) there is only one \(\omega _0\) for which \(d={{\tilde{d}}}_{-1}(\omega _0)\), i.e. for which (60) holds, i.e. there is only one eigenvalue \(\omega _0\). Because
and \(\eta _\pm \in {\mathbb {C}}{\setminus } {\mathbb {R}}\), we have \(\omega _0\notin \sigma _\text {ess}\left( -\frac{d^2}{dx^2}-W\right) \). Moreover, the constants A, B, C, D are unique (up to normalization of \(\varphi _0\)). Hence, \(\omega _0\) is an isolated simple eigenvalue.
Case 3: \({\mathcal {PT}}\)-symmetric (metal—dielectric—metal) setting.
For the case of a homogeneous conservative dielectric sandwiched between two homogeneous Drude metal layers we have
This setting leads to a \({\mathcal {PT}}\)-symmetric W with respect to \(x=d/2\) if we choose \(\omega \in {\mathbb {R}}{\setminus }\{0\}\) and \(\gamma ^+=-\gamma ^-.\) Note that this setting (with \(\gamma _+\ne 0\)) is hypothetical as materials with \(\chi ^{(1)}(\omega ) = - 1/(\omega ^2+\mathrm{i}\gamma \omega )\) and a negative \(\gamma \) may not exist.
Also notice that here, unlike the previous example, the dependence of W on \(\omega \) is truly nonlinear. We retrieve numerically again a similar plot for the function \(\omega \mapsto {{\tilde{d}}}(\omega )\), as shown in Fig. 1d: \({{\tilde{d}}}(\omega )>0\) for all \(\omega >\omega _{MDM}\) with some \(\omega _{MDM}>0\). For \(k=2,\gamma ^+=0.5\) and \(\eta _*=0.2\) we get \(\omega _{MDM}\approx 1.83\). For the computation of the bifurcation we choose the point \(\omega _0\approx 2.8096\) for which \(d={\tilde{d}}_{-1}(\omega _0)\approx 0.5\). Analogously to Case 2, such \(\omega _0\) is an isolated simple eigenvalue.
4.2 Bifurcation of a nonlinear eigenvalue
We are now in a position to apply the bifurcation result of Theorem 2.1 in its symmetric version provided by Proposition 3.1 in both settings given by Case 2 and Case 3 and find a bifurcating branch of solutions to the reduced Maxwell’s equation (49). In both cases we choose the cubic susceptibility \(\chi ^{(3)}\equiv 1\).
The numerical computations below were obtained using a centered finite difference discretization of fourth order on an equispaced grid and with the condition that \(\varphi (x)=0\) for x outside the computational interval. The linear eigenfunction \(\varphi _0\) was computed using Matlab’s built in eigenvalue solver \(\mathrm{eigs}\). The computation of the nonlinear solution \(\varphi \) was done via the standard Newton’s iteration.
Case 2 In this case the linear susceptibility \(\chi ^{(1)}\) is chosen as in (56), (61) with parameters as in Sect. 4.1.2 (\(k=2\), \(\gamma =0\) and \(\eta _\pm =9.2\pm 1.28\mathrm{i}\)). The linear eigenvalue is selected as \(\omega _0=3.8275\). The last condition to check is (Wt). A numerical approximation produces \(\langle \partial _\omega W(\cdot ,\omega _0)\varphi _0,\varphi _0^*\rangle \approx 7.602.\)
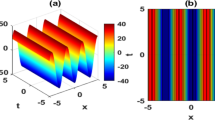
Equations (49), (56), (61) with the parameters: \(d=1\), \(\eta _\pm =9.2\pm 1.28\mathrm{i}\), and \(k=2\). a The potential \(W(\cdot ,\omega _0)\) at \(\omega _0\approx 3.8275\). b The eigenfunction \(\varphi _0\) of (54) at \(\omega _0\). c The solution of (49) at \(\omega =3.2\). d The bifurcation diagram \((\omega , \Vert \varphi \Vert )\) (dashed blue) and the approximation \((\omega _0+\varepsilon \nu , \Vert \varepsilon ^{1/2}\varphi _0\Vert )\) (full red) starting at \(\omega _0\) (colour figure online)
Equations (49), (56), (62) with the parameters: \(d=0.5\), \(\gamma ^+=-\gamma ^-=0.5\), and \(\eta _*=0.2\). a The potential \(W(\cdot ,\omega _0)\) at \(\omega _0\approx 2.8096\). b The eigenfunction \(\varphi _0\) of (54) at \(\omega _0\). c The solution of (49) for \(\omega =1.5\). d The bifurcation diagram \((\omega , \Vert \varphi \Vert )\) (dashed blue) and the approximation \((\omega _0+\varepsilon \nu , \Vert \varepsilon ^{1/2}\varphi _0\Vert )\) (full red) starting at \(\omega _0\) (colour figure online)
Figure 2a shows the resulting potential \(W(\cdot ,\omega _0)\). In Fig. 2d the bifurcation diagram is shown, where the actual (numerically computed) branch is plotted with the dashed blue line for \(\omega \in (3.2,\omega _0)\), while the first order approximation \((\omega _0+\varepsilon \nu , \Vert \varepsilon ^{1/2}\varphi _0\Vert _{L^2})\) for \(\varepsilon \in (0,(\omega _0-3.2)/|\nu |)\) is plotted in full red. The numerical value of \(\nu \) is \(\nu \approx -7.4226\). A good agreement is observed between the asymptotic and the numerical curves in the vicinity of \(\omega _0\). The eigenfunction \(\varphi _0\) related to the eigenvalue \(\omega _0\) is plotted in Fig. 2b. Finally, Fig. 2c shows the solution \(\varphi \) at \(\omega = 3.2,\) i.e. at the last \(\omega \) in the continuation procedure.
Case 3 Here we choose \(\chi ^{(1)}\) as in (56), (62) with parameters as in Sect. 4.1.2 (\(k=2\), \(\gamma ^+=-\gamma ^-=0.5\), and \(\eta _*=0.2\)). The linear eigenvalue is selected as \(\omega _0=2.8096\). Again we have to check condition (Wt): a numerical approximation produces \(\langle \partial _\omega W(\cdot ,\omega _0)\varphi _0,\varphi _0^*\rangle \approx 6.202.\)
The resulting bifurcation diagram is shown in Fig. 3d, where again the actual branch is plotted with the dashed blue line, while the first order approximation \((\omega _0+\varepsilon \nu , \Vert \varepsilon ^{1/2}\varphi _0\Vert )\) for \(\varepsilon \in (0,(\omega _0-1.5)/|\nu |)\) is plotted in full red. We get numerically \(\nu \approx -2.7233\). Once again, a good agreement is observed between the asymptotic and the numerical curves. The eigenfunction \(\varphi _0\) related to the eigenvalue \(\omega _0\) is plotted in Fig. 3b. Figure 3c shows the solution \(\varphi \) at \(\omega = 1.5,\) i.e. at the last \(\omega \) in the continuation procedure.
Change history
19 November 2022
A Correction to this paper has been published: https://doi.org/10.1007/s00030-022-00815-x
Notes
Recall that if 0 is a simple isolated eigenvalue of \(L(\cdot ,\omega _0)\), then it is also a simple isolated eigenvalue of \(L(\cdot ,\omega _0)^*\), cf. [16, Chap.III.6.5-6]
With a little abuse of notation, henceforth we write \(G(\psi ):=G(\sigma ,\psi )\) and similarly for R when \(\sigma \) is assumed to be fixed.
Henceforth, for any \(z\in {\mathbb {C}}\) we choose the square root \(\sqrt{z}\) as the one solution a of \(a^2=z\) with \(\text {arg}(a)\in (-\pi /2,\pi /2]\).
References
Ahlfors, L.V.: Complex Analysis. An Introduction to the Theory of Analytic Functions of One Complex Variable. McGraw-Hill Book Company, Inc., New York (1953)
Alaeian, H., Dionne, J.A.: Parity-time-symmetric plasmonic metamaterials. Phys. Rev. A 89, 033829 (2014)
Barton, D., Lawrence, M., Alaeian, H., Baum, B., Dionne, J.: Parity-Time Symmetric Plasmonics. In: Christodoulides, D., Yang, J. (eds.) Parity-Time Symmetry and Its Applications, pp. 301–349. Springer, Singapore (2018)
Bender, C.M.: PT Symmetry in Quantum and Classical Physics. World Scientific Publishing Co. Pte. Ltd., Hackensack, (2019)
Christodoulides, D., Yang, J.: Parity-Time Symmetry and Its Applications. Springer Tracts in Modern Physics. Springer, Singapore (2018)
Crandall, M.G., Rabinowitz, P.H.: Bifurcation from simple eigenvalues. J. Funct. Anal. 8(2), 321–340 (1971)
Dancer, E.N.: Bifurcation theory for analytic operators. Proc. Lond. Math. Soc. 3(26), 359–384 (1973)
Deimling, K.: Nonlinear Functional Analysis. Dover Books on Mathematics. Dover Publications, Mineola (2013)
Dohnal, T., Pelinovsky, D.: Bifurcation of nonlinear bound states in the periodic Gross-Pitaevskii equation with PT-symmetry. Proc. Roy. Soc. Edinburgh Sect. A 150(1), 171–204 (2020)
Dohnal, T., Plum, M., Reichel, W.: Localized modes of the linear periodic Schrödinger operator with a nonlocal perturbation. SIAM J. Math. Anal. 41(5), 1967–1993 (2009)
Dohnal, T., Siegl, P.: Bifurcation of eigenvalues in nonlinear problems with antilinear symmetry. J. Math. Phys. 57(9), 093502, 18 (2016)
Eastham, M.S.P.: The Spectral Theory of Periodic Differential Equations. Texts in Mathematics. Scottish Academic Press, London (1973)
Feynman, R.P., Leighton, R.B., Sands, M.: The Feynman Lectures on Physics, Vol. II: Mainly Electromagnetism and Matter. Feynman Lectures on Physics. California Institute of Technology, (1964)
Han, J., Fan, Y., Jin, L., Zhang, Z., Wei, Z., Wu, C., Qiu, J., Chen, H., Wang, Z., Li, H.: Mode propagation in a PT-symmetric gain–metal–loss plasmonic system. J. Opt. 16(4), 045002 (2014)
Ize, J.: Bifurcation theory for Fredholm operators. Mem. Am. Math. Soc. 7(174), 128 (1976)
Kato, T.: Perturbation Theory for Linear Operators. Classics in Mathematics. Springer, Berlin (1995)
Moloney, J., Newell, A.: Nonlinear Optics. Advanced Book Program. Westview Press, Boulder, CO (2004)
Nirenberg, L.: Topics in nonlinear functional analysis. Courant Institute of Mathematical Sciences. New York University, New York (1974)
Pitarke, J.M., Silkin, V.M., Chulkov, E.V., Echenique, P.M.: Theory of surface plasmons and surface-plasmon polaritons. Rep. Progress Phys. 70(1), 1–87 (2006)
Raether, H.: Surface Plasmons on Smooth and Rough Surfaces and on Gratings, vol. 111. Springer, Berlin (1988)
Rubinstein, J., Sternberg, P., Ma, Q.: Bifurcation diagram and pattern formation of phase slip centers in superconducting wires driven with electric currents. Phys. Rev. Lett. 99, 167003 (2007)
Rubinstein, J., Sternberg, P., Zumbrun, K.: The resistive state in a superconducting wire: bifurcation from the normal state. Arch. Rat. Mech. Anal. 195, 117–158 (2010)
Shen, Y.R.: The Principles of Nonlinear Optics. Pure & Applied Optics Series: 1-349. Wiley, Hoboken (1984)
Walasik, W., Renversez, G., Kartashov, Y.V.: Stationary plasmon-soliton waves in metal-dielectric nonlinear planar structures: modeling and properties. Phys. Rev. A 89, 023816 (2014)
Wang, W., Wang, L.-Q., Xue, R.-D., Chen, H.-L., Guo, R.-P., Liu, Y., Chen, J.: Unidirectional excitation of radiative-loss-free surface plasmon polaritons in \(\cal{P}\cal{T}\)-symmetric systems. Phys. Rev. Lett. 119, 077401 (2017)
Yin, H., Xu, C., Hui, P.M.: Exact surface plasmon dispersion relations in a linear-metal-nonlinear dielectric structure of arbitrary nonlinearity. Appl. Phys. Lett. 94(22), 221102 (2009)
Zezyulin, D.A., Konotop, V.V.: Nonlinear modes in the harmonic \(\cal{PT}\)-symmetric potential. Phys. Rev. A 85, 043840 (2012)
Acknowledgements
This research is supported by the German Research Foundation, DFG Grant No. DO1467/4-1.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dohnal, T., Romani, G. Eigenvalue bifurcation in doubly nonlinear problems with an application to surface plasmon polaritons. Nonlinear Differ. Equ. Appl. 28, 9 (2021). https://doi.org/10.1007/s00030-020-00668-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00030-020-00668-2