The Burgers’ equation with stochastic transport: shock formation, local and global existence of smooth solutions

Abstract

In this work, we examine the solution properties of the Burgers’ equation with stochastic transport. First, we prove results on the formation of shocks in the stochastic equation and then obtain a stochastic Rankine–Hugoniot condition that the shocks satisfy. Next, we establish the local existence and uniqueness of smooth solutions in the inviscid case and construct a blow-up criterion. Finally, in the viscous case, we prove global existence and uniqueness of smooth solutions.

1 Introduction

We prove the well-posedness of a stochastic Burgers’ equation of the form

$$\begin{aligned} {{\,\mathrm{d\!}\,}}u(t,x) + u(t,x)\partial _x u (t,x) \,{{\,\mathrm{d\!}\,}}t + \sum _{k=1}^\infty \xi _k(x) \partial _x u(t,x) \circ {{\,\mathrm{d\!}\,}}W_t^k = \nu \partial _{xx} u(t,x) {{\,\mathrm{d\!}\,}}t, \end{aligned}$$

(1.1)

where $x \in {\mathbb {T}}$ or ${\mathbb {R}},$ $\nu \ge 0$ is constant, $\{W_t^k\}_{k \in {\mathbb {N}}}$ is a countable set of independent Brownian motions, $\{\xi _k(\cdot )\}_{k \in {\mathbb {N}}}$ is a countable set of prescribed functions depending only on the spatial variable, and $\circ$ means that the stochastic integral is interpreted in the Stratonovich sense. If the set $\{\xi _k(\cdot )\}_{k \in {\mathbb {N}}}$ forms a basis of some separable Hilbert space ${\mathcal {H}}$ (for example $L^2({\mathbb {T}})$), then the process ${{\,\mathrm{d\!}\,}}W := \sum _{k=1}^\infty \xi _k(x) \circ {{\,\mathrm{d\!}\,}}W_t^k$ is a cylindrical Wiener process on ${\mathcal {H}}$, generalising the notion of a standard Wiener process to infinite dimensions.

The multiplicative noise in (1.1) makes the transport velocity stochastic, which allows the Burgers’ equation to retain the form of a transport equation $\partial _t u + \tilde{u} \,\partial _x u = 0,$ where $\tilde{u}(t,x) := u(t,x) + \dot{W}$ is a stochastic vector field with noise $\dot{W}$ that is smooth in space and rough in time. Compared with the well-studied Burgers’ equation with additive noise, where the noise appears as an external random forcing, this type of noise arises by taking the diffusive limit of the Lagrangian flow map regarded as a composition of a slow mean flow and a rapidly fluctuating one [9]. In several recent works, this type of noise, which we call stochastic transport, has been used to stochastically parametrise unresolved scales in fluid models while retaining the essential physics of the system [6, 7, 32]. On the other hand, it has also been shown to have a regularising effect on certain PDEs that are ill-posed [17, 20, 21, 25]. Therefore, it is of interest to investigate how the stochastic transport in (1.1) affects the Burgers’ equation, which in the inviscid case $\nu =0$ is a prototypical model for shock formation. In particular, we ask whether this noise can prevent the system from developing shocks or, on the contrary, produce new shocks. We also ask whether this system is well-posed or not. In this paper, we will show that:

• (1) For $\nu = 0$, Eq. (1.1) has a unique solution of class $H^s$ for $s > 3/2$ until some stopping time $\tau > 0$.

• (2) However, shock formation cannot be avoided a.s. in the case $\xi (x) = \alpha x + \beta$ and for a broader class of $\{\xi _k(\cdot )\}_{k \in {\mathbb {N}}}$, we can prove that it occurs in expectation.

• (3) For $\nu > 0$, we have global existence and uniqueness in $H^2$.

On top of this, we prove a continuation criterion for the inviscid equation ($\nu =0$), which generalises the result for the deterministic case. The above results are not immediately evident for reasons we will discuss below. Although we cannot prove this here, we believe that shocks in Burgers’ equation are too robust and ubiquitous to be prevented by noise, regardless of what $\{\xi _k(\cdot )\}_{k \in {\mathbb {N}}}$ is chosen. Our results provide rigorous evidence to support this claim.

The question of whether noise can regularise PDEs is not new. In finite dimensions, it is well-known that additive noise can restore the well-posedness of ODEs whose vector fields are merely bounded and measurable (see [41]). For PDEs, a general result is not known; however, there has been a significant effort in recent years to generalise this celebrated result to PDEs. In a remarkable paper, Flandoli et al. [20] demonstrated that the linear transport equation $\partial _t u + b(t,x) \nabla u = 0$, which is ill-posed if b is sufficiently irregular, can recover existence and uniqueness of $L^\infty$ solutions that is strong in the probabilistic sense, by the addition of a “simple” transport noise,

$$\begin{aligned} {{\,\mathrm{d\!}\,}}u + b(t,x) \nabla u {{\,\mathrm{d\!}\,}}t + \nabla u \circ {{\,\mathrm{d\!}\,}}W_t = 0, \end{aligned}$$

(1.2)

where the drift b is bounded, measurable, Hölder continuous, and satisfies an integrability condition on the divergence $\nabla \cdot b \in L^p([0,T] \times {\mathbb {R}}^d)$. In a subsequent paper [17], the same noise was shown to retain some regularity of the initial condition, thus restoring well-posedness of strong solutions, and a selection principle based on taking the zero-noise limit as opposed to the inviscid limit was considered in [1].

However, for nonlinear transport equations such as Burgers’, the same type of noise ${{\,\mathrm{d\!}\,}}u + u\,\partial _xu {{\,\mathrm{d\!}\,}}t + \partial _x u \circ {{\,\mathrm{d\!}\,}}W_t = 0$ does not help, since a simple change of variables $v(t,x) := u(t,x-W_t)$ will lead us back to the original equation $\partial _t v + v \,\partial _x v = 0$. Hence, if noise were to prevent shock formation, a more general class would be required, such as the cylindrical transport noise $\sum _{k=1}^\infty \xi _k(x) \partial _x u \circ {{\,\mathrm{d\!}\,}}W_t^k$ that we consider in this paper. In [21] and [12], it was shown that collapse in Lagrangian point particle solutions of certain nonlinear PDEs (point vortices in 2D Euler and point charges in the Vlasov–Poisson system), can be prevented by this cylindrical transport noise with $\xi _k(x)$ satisfying a certain hypoellipticity condition, thus providing hope for regularisation of nonlinear transport equation by noise. More recently, Gess and Maurelli [25] showed that adding a simple stochastic transport term into a nonlinear transport equation

$$\begin{aligned} {{\,\mathrm{d\!}\,}}u + b(x,u(t,x)) \nabla u {{\,\mathrm{d\!}\,}}t + \nabla u \circ {{\,\mathrm{d\!}\,}}W_t = 0, \end{aligned}$$

(1.3)

which in the deterministic case admits non-unique entropy solutions for sufficiently irregular b, can restore uniqueness of entropy solutions, providing a first example of a nonlinear transport equation that becomes well-posed when adding a suitable noise.

We should now stress the difference between the present work and previous works. First, we acknowledge that in Flandoli [23], Chapter 5.1.4, it is argued that shock formation does not occur even with the most general cylindrical transport noise, by writing the characteristic equation as an Itô SDE

$$\begin{aligned} X_t = X_0 + u(0,X_0) t + \sum _{k=1}^\infty \int ^t_0 \xi _k(X_s) {{\,\mathrm{d\!}\,}}W_s^k, \end{aligned}$$

(1.4)

which is a martingale perturbation of straight lines that will cross without noise. Thus, using the property that a martingale $M_t$ grows slower than t almost surely as $t \rightarrow \infty$, it is shown that the characteristics cross almost surely. However, the characteristic equation for the system (1.1) is in fact a Stratonovich SDE,

$$\begin{aligned} X_t = X_0 + u(0,X_0) t + \sum _{k=1}^\infty \int ^t_0 \xi _k(X_s) \circ {{\,\mathrm{d\!}\,}}W_s^k, \end{aligned}$$

(1.5)

and therefore Flandoli’s argument can be applied to the martingale term, but not to the additional drift term, which may disrupt shock formation. The techniques we use here apply to Stratonovich equations; however, due to the difficulty caused by the additional drift term, we were only able to prove that the characteristics cross almost surely in the very particular case $\xi (x) = \alpha x + \beta$, leaving the general case open for future investigation. By using a different strategy, where instead we look at how the slope $\partial _x u$ evolves along a characteristic (1.5), we manage to show that for a wider class of $\{\xi _k(\cdot )\}_{k=1}^\infty$ such that the infinite sum $\sum _{k\in {\mathbb {N}}} ((\partial _x \xi _k)^2 - \xi _k \partial _{xx}\xi _k)$ is pointwise bounded, we have that

• if $\partial _x u(0,X_0) > 0$, then $\partial _x u(t,X_t) < \infty$ almost surely for all $t>0$ and

• if $\partial _x u(0,X_0)$ is sufficiently negative, then there exists $0< t_* < \infty$ such that $\lim _{t \rightarrow t_*} {\mathbb {E}}[\partial _x u (t,X_t)] = -\infty$.

In summary, shock formation occurs in expectation if the initial profile has a sufficiently negative slope and no new shocks can form from a positive slope.

We finally address the question of well-posedness. We will prove that by choosing a sufficiently regular initial condition, equation (1.1) admits a unique local solution that is smooth enough, such that the arguments employed in the previous section on shock formation are valid (in fact, we show this for a noise of the type $Qu \circ {{\,\mathrm{d\!}\,}}W_t,$ where $Qu = a(x) \partial _x u + b(x) u,$ which generalises the one considered in (1.1)). For Burgers’ equation with additive space-time white noise, however, there have been many previous works showing well-posedness [3, 11, 15, 16]. The techniques used in these works are primarily based on reformulating the equations by a change of variable or by studying its linear part. The main difference in our work is that the multiplicative noise we consider depends on the solution and its gradient. Therefore, the effect of the noise hinges on its spatial gradient and the solution, giving rise to several complications. For instance, when deriving a priori estimates, certain high order terms appear, which need to be treated carefully. Recently, the same type of multiplicative noise has been treated for the Euler equation [8, 22] and the Boussinesq system [2], whose techniques we follow closely in our proof. We note that the well-posedness analysis of a more general stochastic conservation law, which includes the inviscid stochastic Burgers’ equation as a special case, has also been considered, for instance in [18, 19, 27]. However, these works deal with the well-posedness analysis of weak kinetic and entropy solutions, in contrast to classical solutions, which we consider here. There is also the recent work [31] showing the local well-posedness of weak solutions in the viscous Burgers’ equation ($\nu > 0$) driven by rough paths in the transport velocity. An important contribution of this paper is showing the global well-posedness of strong solutions in the viscous case by proving that the maximum principle is retained under perturbation by stochastic transport of type $Qu \circ {{\,\mathrm{d\!}\,}}W_t$.

1.1 Main results

Let us state here the main results of the article:

Theorem 1.1

(Shock formation in the stochastic Burgers’ equation) In the following, we use the notation $\psi (x) := \frac{1}{2}\sum _{k=1}^\infty \left( (\partial _x \xi _k(x))^2 - \xi _k(x) \partial _{xx} \xi _k(x)\right)$. The main results regarding shock formation in (1.1) are as follows:

• (1) Let $\xi _1(x) = \alpha x + \beta$, $x \in {\mathbb {R}}$ and $\xi _k \equiv 0$ for $k=2,3,\ldots$ and assume that u(0, x) has a negative slope. Then, there exists two characteristics satisfying (1.5) with different initial conditions that cross in finite time almost surely.

• (2) Let $X_t$ be a characteristic solving (1.5) with $\{\xi _k(\cdot )\}_{k \in {\mathbb {N}}}$ satisfying the conditions in Assumption A1 below and let $\partial _x u(0,X_0) \ge 0$. Then, if $\psi (x) < \infty$ for all $x \in {\mathbb {T}}$ or ${\mathbb {R}}$, we have that $\partial _t u(t,X_t) < \infty$ almost surely for all $t>0$.

• (3) Again, let $X_t$ be a characteristic solving (1.5) with $\{\xi _k(\cdot )\}_{k \in {\mathbb {N}}}$ satisfying the conditions in Assumption A1 and let $\partial _x u(0,X_0) < 0$. Also assume that $\partial _x u(0,X_0) < \psi (x)$ for all $x \in {\mathbb {T}}$ or ${\mathbb {R}}$. Then there exists $0<t_*<\infty$ such that $\lim _{t \rightarrow t_*} {\mathbb {E}} [\partial _x u(t,X_t)] = - \infty$.

Theorem 1.2

(Stochastic Rankine–Hugoniot condition) The curve of discontinuity $(t,s(t)) \in [0,\infty ) \times {\mathbb {T}}$ (or ${\mathbb {R}}$) of the stochastic Burgers’ equation (1.1) satisfies the following:

$$\begin{aligned} {{\,\mathrm{d\!}\,}}s_t = \frac{1}{2} \left[ (u_-(t,s(t)) + u_+(t,s(t))\right] \,{{\,\mathrm{d\!}\,}}t + \sum _{k=1}^\infty \xi _k(s(t)) \circ {{\,\mathrm{d\!}\,}}W_t^k, \end{aligned}$$

(1.6)

where $u_\pm (t,s(t)) := \lim _{x \rightarrow s(t)^\pm } u(t,x)$ are the left and right limits of u.

Theorem 1.3

(Well-posedness in the inviscid case) Let $u_{0}\in H^{s} (\mathbb {T},\mathbb {R}),$ for $s>3/2$ fixed. Then there exists a unique maximal solution $(\tau _{max},u)$ of the 1D stochastic Burgers’ equation (1.1) with $\nu = 0$. Therefore, if $(\tau ',u')$ is another maximal solution, then necessarily $\tau _{max}=\tau '$, $u=u'$ on $[0,\tau _{max})$. Moreover, either $\tau _{max}=\infty$ or $\displaystyle \lim \sup _{s\nearrow \tau _{max}} ||u(s)||_{H^{s}}= \infty$.

Theorem 1.4

(Global well-posedness in the viscous case) Let $u_{0} \in H^{2} (\mathbb {T},\mathbb {R}).$ Then there exists a unique maximal strong global solution $u:[0,\infty ) \times \mathbb {T} \times \Xi \rightarrow \mathbb {R}$ of the viscous stochastic Burgers’ equation (1.1) with $\nu > 0$ in $H^{2} (\mathbb {T},\mathbb {R})$.

Remark 1.5

Theorems 1.3 and 1.4 can be extended in a straightforward manner to the full line ${\mathbb {R}}$ and to higher dimensions.

Remark 1.6

We prove Theorems 1.3 and 1.4 for a more general noise ${\mathcal {Q}} u \circ dW_t$, where ${\mathcal {Q}}$ is a first order linear differential operator, which includes the transport noise as a special case. For the sake of clarity, our proof deals only with one noise term $\mathcal {Q}u \circ dW_t$, however, we can readily extend this to cylindrical noise with countable set of first order linear differential operators

$$\begin{aligned} \displaystyle \sum _{k=1}^{\infty }\mathcal {Q}_{k}(u) \circ {{\,\mathrm{d\!}\,}}W^{k}_{t}, \end{aligned}$$

by imposing certain smoothness and boundedness conditions for the sum of the coefficients.

1.2 Structure of the paper

This manuscript is organised as follows. In Sect. 2 we review some classical mathematical deterministic and stochastic background. We also fix the notations we will employ and state some definitions. Section 3 contains the main results regarding shock formation in the stochastic Burgers’ equation. Using a characteristic argument, we show that noise cannot prevent shocks from occurring for certain classes of $\{\xi _k(\cdot )\}_{k \in {\mathbb {N}}}$. Moreover, we prove that these shocks satisfy a Rankine–Hugoniot type condition in the weak formulation of the problem. In Sect. 4, we show local well-posedness of the stochastic Burgers’ equation in Sobolev spaces and a blow-up criterion. We also establish global existence of smooth solutions of a viscous version of the stochastic Burgers’ equation, which is achieved by proving a stochastic analogue of the maximum principle. In Sect. 5, we provide conclusions, propose possible future research lines, and comment on several open problems that are left to study.

2 Preliminaries and notation

Let us begin by reviewing some standard functional spaces and mathematical background that will be used throughout this article. Sobolev spaces are given by

$$\begin{aligned} W^{s,p}:=\lbrace f\in L^{p}(\mathbb {T},\mathbb {R}): (I-\partial _{xx})^{s/2}f\in L^{p}(\mathbb {T},\mathbb {R}) \rbrace , \end{aligned}$$

for any $s\ge 0$ and $p\in [1,\infty ),$ equipped with the norm $||f||_{W^{s,p}}=||(I-\partial _{xx})^{s/2}f||_{L^{p}}$. We will also use the notation $\Lambda ^{s}=(-\partial _{xx})^{s/2}$. Recall that $L^{2}$ based spaces are Hilbert spaces and may alternatively be denoted by $H^{s}=W^{s,2}$. For $s>0$, we also define $H^{-s}:=(H^{s})^{\star }$, i.e. the dual space of $H^s$. Let us gather here some well-known Sobolev embedding inequalities:

$$\begin{aligned} \left\| f \right\| _{L^{4}}\lesssim & {} \left\| f \right\| ^{1/2}_{L^{2}} \left\| \partial _{x} f \right\| ^{1/2}_{L^{2}}, \end{aligned}$$

(2.1)

$$\begin{aligned} \left\| \partial _{x} f \right\| _{L^{4}}\lesssim & {} \left\| f \right\| _\infty ^{1/2} \left\| \partial _{xx} f \right\| ^{1/2}_{L^{2}}, \end{aligned}$$

(2.2)

$$\begin{aligned} \left\| f \right\| _\infty\lesssim & {} \left\| f \right\| _{H^{1/2+\epsilon }}, \ \ \text {for every } \epsilon >0. \end{aligned}$$

(2.3)

Let us also recall the well-known commutator estimate of Kato and Ponce:

Lemma 2.1

[34] If $s\ge 0$ and $1<p<\infty$, then

$$\begin{aligned} \left| \left| \Lambda ^{s}(fg)-f\Lambda ^{s}(g)\right| \right| _{L^{p}} \le C_{p}\left( \left\| \partial _x f \right\| _\infty ||\Lambda ^{s-1}g||_{L^{p}}+||\Lambda ^{s}f||_{L^{p}} \left\| g \right\| _\infty \right) .\quad \end{aligned}$$

(2.4)

We will also use the following result as main tool for proving the existence results and blow-up criterion:

Theorem 2.2

[2] Let $\mathcal {Q}$ be a linear differential operator of first order

$$\begin{aligned} \mathcal {Q}= a(x) \partial _{x} + b(x) \end{aligned}$$

where the coefficients are smooth and bounded. Then for $f\in H^{2}(\mathbb {T},\mathbb {R})$ we have

$$\begin{aligned} \langle \mathcal {Q}^2 f, f \rangle _{L^2} + \langle \mathcal {Q} f, \mathcal {Q} f \rangle _{L^2} \lesssim ||f||_{L^2}^2. \end{aligned}$$

(2.5)

Moreover, if $f\in H^{2+s}(\mathbb {T},\mathbb {R})$, and $\mathcal {P}$ is a pseudodifferential operator of order s,  then

$$\begin{aligned} \langle \mathcal {P} \mathcal {Q}^2 f, \mathcal {P} f \rangle _{L^2} + \langle \mathcal {P} \mathcal {Q} f, \mathcal {P} \mathcal {Q} f \rangle _{L^2} \lesssim ||f||_{H^s}^2, \end{aligned}$$

(2.6)

for every $s\in [1, \infty )$.

Remark 2.3

Theorem 2.2 is fundamental for closing the energy estimates when showing well-posedness of the stochastic Burgers’ equation. It permits reducing the order of a sum of terms which in principle seems hopelessly singular.

Next, we briefly recall some aspects of the theory of stochastic analysis. Fix a stochastic basis $\mathcal {S}=(\Xi ,\mathcal {F},\lbrace \mathcal {F}_{t}\rbrace _{t\ge 0}, \mathbb {P},\lbrace W^{k}\rbrace _{k\in \mathbb {N}}),$ that is, a filtered probability space together with a sequence $\lbrace W^{k} \rbrace _{k\in \mathbb {N}}$ of scalar independent Brownian motions relative to the filtration $\lbrace \mathcal {F}_{t}\rbrace _{t\ge 0}$ satisfying the usual conditions.

Given a stochastic process $X\in L^{2}(\Xi ;L^{2}([0,\infty );L^{2}(\mathbb {T},\mathbb {R}))),$ the Burkholder–Davis–Gundy inequality is given by

$$\begin{aligned} \mathbb {E}\left[ \displaystyle \sup _{s \in [0,T]}\left| \int _{0}^{t} X_{s} {{\,\mathrm{d\!}\,}}W_ {s}\right| ^{p} \right] \le C_p \mathbb {E} \left[ \int _{0}^{T} |X_s|^{2} {{\,\mathrm{d\!}\,}}t \right] ^{p/2}, \end{aligned}$$

(2.7)

for any $p\ge 1$ and $C_{p}$ an absolute constant depending on p.

We also state the celebrated Itô–Wentzell formula, which we use throughout this work.

Theorem 2.4

[36, Theorem 1.2] For $0\le t<\tau$, let $u(t,\cdot )$ be $C^3$ almost surely, and $u(\cdot ,x)$ be a continuous semimartingale satisfying the SPDE

$$\begin{aligned} u(t,x) = u(0,x) + \sum ^\infty _{j=0} \int _{0}^{t} \sigma _j(s,x) \circ {{\,\mathrm{d\!}\,}}N_s^j, \end{aligned}$$

(2.8)

where $\{N_t^j\}_{j = 0}^\infty$ is a family of continuous semimartingales and $\{\sigma _j(t,x)\}_{j=0}^\infty$ is also a family of continuous semimartingales that are $C^2$ in space for $0\le t<\tau$. Also, let $X_t$ be a continuous semimartingale. Then, we have the following

$$\begin{aligned} u(t,X_t) = u(0,X_0) + \sum ^\infty _{j=0} \int ^t_0 \sigma _j(s,X_s) \circ {{\,\mathrm{d\!}\,}}N^j_s + \int ^t_0 \partial _x u (s,X_s) \circ {{\,\mathrm{d\!}\,}}X_s. \end{aligned}$$

(2.9)

Let us also introduce three different notions of solutions:

Definition 2.5

(Local solution) A local solution $u\in H^s(\mathbb {T},\mathbb {R})$ for $s>3/2$ of the Burgers’ equation (1.1) is a random variable $u:[0,\tau ] \times \mathbb {T} \times \Xi \rightarrow \mathbb {R},$ with trajectories of class $C([0,\tau ]; H^{s}(\mathbb {T}^{2},\mathbb {R}))$, together with a stopping time $\tau : \Xi \rightarrow [0, \infty ],$ such that $u(t \wedge \tau ),$ is adapted to $\lbrace \mathcal {F}_{t}\rbrace _{t\ge 0},$ and (1.1) holds in the $L^2$ sense. This is

$$\begin{aligned} u_{\tau '} - u_0+ & {} \int _0^{\tau '} u\partial _{x}u {{\,\mathrm{d\!}\,}}s + \displaystyle \sum _{k=1}^{\infty }\int _0^{\tau '} \xi _{k}(x)\partial _{x}u {{\,\mathrm{d\!}\,}}W^{k}_{s}\\ {}= & {} \dfrac{1}{2}\displaystyle \sum _{k=1}^{\infty }\int _{0}^{\tau '}\left( \xi _{k}(x)\partial _{x}\right) ^{2}u {{\,\mathrm{d\!}\,}}s, \end{aligned}$$

for finite stopping times $\tau ' \le \tau$.

Definition 2.6

(Maximal solution) A maximal solution of (1.1) is a stopping time $\tau _{max}:\Xi \rightarrow [0,\infty ]$ and random variable $u:[0,\tau _{max})\times \mathbb {T} \times \Xi \rightarrow \mathbb {R}$, such that:

• $\mathbb {P} (\tau _{max} >0) = 1, \ \tau _{max} = lim_{n \rightarrow \infty } \tau _n,$ where $\tau _n$ is an increasing sequence of stopping times, i.e. $\tau _{n+1}\ge \tau _{n}$, $\mathbb {P}$ almost surely.

• $(\tau _{n},u)$ is a local solution for every $n\in \mathbb {N}$.

• If $(\tau ',u')$ is another pair satisfying the above conditions and $u'=u$ on $[0,\tau '\wedge \tau _{max} )$, then $\tau '\le \tau _{max}$, $\mathbb {P}$ almost surely.

• A maximal solution is said to be global if $\tau _{max}=\infty$, $\mathbb {P}$ almost surely.

Definition 2.7

(Weak solution) We say that a random variable $u \in L^2( \Xi ; L^\infty ([0, \infty ) \times {\mathbb {T}}))$ that satisfies the following integral equation

$$\begin{aligned}&0 = \iint _{[0, \infty ) \times {\mathbb {T}}} \left( \left( u \,\partial _t \varphi + \frac{1}{2} u^2 \partial _x \varphi \right) {{\,\mathrm{d\!}\,}}t \right. \nonumber \\&\qquad \quad \left. + \sum _{k=1}^\infty u \,\partial _x \left( \varphi (t,x) \xi _k(x) \right) \circ {{\,\mathrm{d\!}\,}}W_t^k \right) {{\,\mathrm{d\!}\,}}x, \end{aligned}$$

(2.10)

${\mathbb {P}}$ almost surely for any test function $\varphi \in C_0^\infty ([0,\infty ) \times {\mathbb {T}})$ is a weak solution to the problem (3.1). It is easy to show that a local solution in the sense of Definition 2.5 is indeed a weak solution.

Notations: Let us stress some notations that we will use throughout this work. We will denote the Sobolev $L^{2}$ based spaces by $H^{s}(\text {domain}, \text {target space})$. However, we will sometimes omit the domain and target space and just write $H^s$, when these are clear from the context. $a\lesssim b$ means there exists C such that $a \le Cb$, where C is a positive universal constant that may depend on fixed parameters and constant quantities. Note also that this constant might differ from line to line. It is also important to remind that the condition “almost surely” is not always indicated, since in some cases it is obvious from the context.

3 Shocks in Burgers’ equation with stochastic transport

Recall that we are dealing with a stochastic Burgers’ equation of the form

$$\begin{aligned} {{\,\mathrm{d\!}\,}}u + \left( u(t,x) {{\,\mathrm{d\!}\,}}t + \sum _{k=1}^\infty \xi _k(x) \circ {{\,\mathrm{d\!}\,}}W_t^k \right) \cdot \partial _x u = \nu \partial _{xx} u {{\,\mathrm{d\!}\,}}t, \end{aligned}$$

for $x \in {\mathbb {T}}$ or ${\mathbb {R}},$ where $\nu \ge 0$ is constant, $\{\xi _k(x)\}_{k \in {\mathbb {N}}}$ is an orthonormal basis of some separable Hilbert space ${\mathcal {H}},$ and $\circ$ means that the integration is carried out in the Stratonovich sense. In this section, we study the problem of whether shocks can form in the inviscid Burgers’ equation with stochastic transport. By using a characteristic argument, we prove that for some classes $\{\xi _k(x)\}_{k \in {\mathbb {N}}}$, the transport noise cannot prevent shock formation. We also consider a weak formulation of the problem and prove that the shocks satisfy a stochastic version of the Rankine–Hugoniot condition.

3.1 Inviscid Burgers’ equation with stochastic transport

The inviscid Burgers’ equation with stochastic transport is given by

$$\begin{aligned} {{\,\mathrm{d\!}\,}}u + \left( u(t,x) \,{{\,\mathrm{d\!}\,}}t + \sum _{k=1}^\infty \xi _k(x) \circ {{\,\mathrm{d\!}\,}}W_t^k\right) \cdot \partial _x u = 0, \end{aligned}$$

(3.1)

which in integral form is interpreted as

$$\begin{aligned} u(t,x) = u(0,x) - \int _0^t \left( u(s,x) \partial _x u(s,x) \,{{\,\mathrm{d\!}\,}}s + \sum _{k=1}^\infty \xi _k(x) \partial _x u(s,x) \circ {{\,\mathrm{d\!}\,}}W_s^k \right) , \end{aligned}$$

(3.2)

for all $x \in {\mathbb {T}}$ or ${\mathbb {R}}$. Also, we will assume throughout this paper that the initial condition is positive, that is, $u(0,x) > 0$ for all $x \in {\mathbb {T}}$ or ${\mathbb {R}}$.

Consider a process $X_t$ that satisfies the Stratonovich SDE

$$\begin{aligned} {{\,\mathrm{d\!}\,}}X_t&= u(t,X_t) {{\,\mathrm{d\!}\,}}t + \sum _{k=1}^\infty \xi _k(X_t) \circ {{\,\mathrm{d\!}\,}}W_t^k, \end{aligned}$$

(3.3)

which in Itô form, reads

$$\begin{aligned} {{\,\mathrm{d\!}\,}}X_t = \left( u(t,X_t) + \frac{1}{2} \sum _{k=1}^\infty \xi _k(X_t) \partial _x\xi _k(X_t) \right) {{\,\mathrm{d\!}\,}}t + \sum _{k=1}^\infty \xi _k(X_t) {{\,\mathrm{d\!}\,}}W_t^k. \end{aligned}$$

(3.4)

We call this process the characteristic of (3.1), analogous to the characteristic lines in the deterministic Burgers’ equation. We assume the following conditions on $\{\xi _k(\cdot )\}_{k \in {\mathbb {N}}}$.

Assumption A1

$\xi _k$ is smooth for all $k \in {\mathbb {N}}$ and together with the Stratonovich-to-Itô correction term $\varphi (x):=\frac{1}{2} \sum _{k=1}^\infty \xi _k(x) \partial _x\xi _k(x)$, satisfy the following:

• Lipschitz continuity

  $$\begin{aligned} |\varphi (x) - \varphi (y)| \le C_0 |x-y|, \quad |\xi _k(x) - \xi _k(y)| \le C_k |x-y|, \quad k \in {\mathbb {N}}, \end{aligned}$$

  (3.5)

• Linear growth condition

  $$\begin{aligned} |\varphi (x)| \le D_0 (1 + |x|), \quad |\xi _k(x)| \le D_k (1+|x|), \quad k \in {\mathbb {N}} \end{aligned}$$

  (3.6)

for real constants $C_0, C_1, C_2, \ldots$ and $D_0, D_1, D_2, \ldots$ with

$$\begin{aligned} \sum _{k=1}^\infty C_k^2< \infty , \quad \sum _{k=1}^\infty D_k^2 < \infty . \end{aligned}$$

(3.7)

Provided $u(t,\cdot )$ is sufficiently smooth and bounded (hence satisfying Lipschitz continuity and linear growth) until some stopping time $\tau$, and $\{\xi _k(\cdot )\}_{k \in {\mathbb {N}}}$ satisfies the conditions in Assumption A1, the characteristic equation (3.4) is locally well-posed. One feature of the multiplicative noise in (3.1) is that u is transported along the characteristics, that is, we can show that $u(t,x) = (\Phi _t)_*u_0(x)$ for $0\le t < \tau _{max},$ where $\Phi _t$ is the stochastic flow of the SDE (3.4), $(\Phi _t)_*$ represents the pushforward by $\Phi _t,$ and $(\tau _{max}, X_t)$ is the maximal solution of (3.4). This is an easy corollary of the Itô-Wentzell formula (2.9).

Corollary 3.0.1

Let $u(t,\cdot )$ be $C^3 \cap L^\infty$ in space for $0<t<\tau$. Assume also that $u(\cdot ,x)$ is a continuous semimartingale satisfying (3.2), $\partial _x u (\cdot ,x)$ is a continuous semimartingale satisfying the spatial derivative of (3.2), and $\{\xi _k(\cdot )\}_{k \in {\mathbb {N}}}$ satisfies the conditions in Assumption A1. If $(\tau _{max},X_t)$ is a maximal solution to (3.4), then $u(t,X_t) = u(0,X_0)$ almost surely for $0<t<\tau _{max}$.

Remark 3.1

Notice that due to our local well-posedness result (Theorem 1.3) and the maximum principle (Proposition 4.10), one has $u_t \in C^3 \cap L^\infty$ for $t < \tau _{max}$ provided $u_0$ is smooth enough and bounded. For instance, $u_0 \in H^4 \cap L^\infty$ is sufficient.

Proof of Corollary 3.0.1

Note that under the given assumptions, $\sigma _0(t,x) := u(t,x)\partial _x u (t,x),$ and $\sigma _k(t,x) := \xi _k(x)\partial _x u(t,x)$ for all $k \in {\mathbb {N}},$ satisfy the conditions in Theorem 2.4. We take $N_t^0 = t$ and $N_t^k = W_t^k$ for $k \in {\mathbb {N}}$. Using the Itô-Wentzell formula (2.9) for the stochastic field u(t, x) satisfying (3.2), and the semimartingale $X_t$, we obtain

$$\begin{aligned} u(t,X_t)&= u(0,X_0) - \int _0^t \left( u(s,X_s)\partial _x u (s,X_s) {{\,\mathrm{d\!}\,}}s \right. \\&\quad \left. + \sum _{k=1}^\infty \xi _k(X_s)\partial _x u (s,X_s) \circ {{\,\mathrm{d\!}\,}}W_s^k \right) \\&\quad + \int _0^t \partial _x u (s,X_s) \circ {{\,\mathrm{d\!}\,}}X_s \\&= u(0,X_0) - I_1 + I_2. \end{aligned}$$

Now, we have $I_1 = I_2$ almost surely so indeed, $u(t,X_t) = u(0,X_0)$ almost surely for $0<t<\tau _{max}$. $\square$

3.2 Results on shock formation

In order to investigate the crossing of characteristics in the stochastic Burgers’ equation (3.1) with transport noise, we define the first crossing time $\tau$ as

$$\begin{aligned} \tau := \inf _{\begin{array}{c} a,b \in {\mathbb {R}} \\ a \ne b \end{array}} \left\{ \inf \left\{ t>0 : X_t^a = X_t^b \right\} \right\} , \end{aligned}$$

(3.8)

where $X_t^a, X_t^b$ are two characteristics that solve the SDE (3.3) with initial conditions $X_0^a = a$ and $X_0^b = b$. This gives us the first time when two characteristics intersect. In the following, we will show that in the special case $\xi _1(x) = \alpha x + \beta$ (where we only consider one noise term and the other terms $\xi _k$ are identically zero for $k = 2,3,\ldots$), the first crossing time is equivalent to the first hitting time of the integrated geometric Brownian motion. We note that in this case, Eq. (3.4) is explicitly solvable, where the general solution is given by

$$\begin{aligned} X_t^\gamma&= e^{\alpha W_t} \left( \gamma + \left( u_0(\gamma ) - \alpha \beta \right) \int ^t_0 e^{-\alpha W_s} {{\,\mathrm{d\!}\,}}s + \beta \int ^t_0 e^{-\alpha W_s} {{\,\mathrm{d\!}\,}}W_s \right) . \end{aligned}$$

(3.9)

Proposition 3.2

The first crossing time of the inviscid stochastic Burgers’ equation (3.1) with $\xi _1(x) = \alpha x + \beta$ for constants $\alpha , \beta \in {\mathbb {R}}$ and $\xi _k(\cdot ) \equiv 0$ for $k = 2,3,\ldots$ is equivalent to the first hitting time for the integrated geometric Brownian motion $I_t := \int ^t_0 e^{-\alpha W_s}ds$.

Proof

Consider two arbitrary characteristics $X_t^a$ and $X_t^b$ with $X_0^a = a$ and $X_0^b = b$. From (3.9), one can check that $X_t^a = X_t^b$ if and only if

$$\begin{aligned} I_t := \int ^t_0 e^{-\alpha W_s} {{\,\mathrm{d\!}\,}}s = -\frac{b-a}{u_0(b)-u_0(a)}. \end{aligned}$$

Now, since the left-hand side is continuous, strictly increasing with $I_0 = 0,$ and independent of a and b, we have

$$\begin{aligned} \tau&= \inf _{\begin{array}{c} a,b \in {\mathbb {R}} \\ a \ne b \end{array}} \left\{ \inf \left\{ t>0 : I_t = - \frac{b-a}{u_0(b)-u_0(a)} \right\} \right\} \nonumber \\&= {\left\{ \begin{array}{ll} \inf \left\{ t>0 : I_t = \theta (u_0)^{-1} \right\} , \quad &{} \text { if } \theta (u_0) > 0 \\ \infty , \quad &{} \text { if } \theta (u_0) = 0 \end{array}\right. }, \end{aligned}$$

(3.10)

where

$$\begin{aligned} \theta (u_0) := \sup _{\begin{array}{c} a,b \in {\mathbb {R}} \\ a \ne b \end{array}} \left\{ \zeta (a,b) \right\} , \quad \zeta (a,b) = {\left\{ \begin{array}{ll} \frac{|u_0(a)-u_0(b)|}{|a - b|}, \quad &{}\text {if } \frac{u_0(a)-u_0(b)}{a - b} < 0 \\ 0, \quad &{}\text {otherwise} \end{array}\right. }, \end{aligned}$$

is the steepest negative slope of $u_0$. Hence, the first crossing time is equivalent to the first hitting time of the process $I_t$. $\square$

Remark 3.3

Note that the constant $\beta$ does not affect the first crossing time, hence we can set $\beta =0$ without loss of generality. Also in the following, we simply write $\xi (\cdot )$ without the index when we only consider one noise term.

As an immediate consequence of Proposition 3.2, we prove that the transport noise with $\xi (x) = \alpha x$ cannot prevent shocks from forming almost surely in the stochastic Burgers’ equation (3.1).

Corollary 3.3.1

Let $\xi (x) = \alpha x$ for some $\alpha \in {\mathbb {R}}$. If the initial profile $u_0$ has a negative slope, then $\tau < \infty$ almost surely.

Proof

To prove this, it is enough to show that

$$\begin{aligned} \lim _{t \rightarrow \infty } \int ^t_0 e^{\alpha W_s} {{\,\mathrm{d\!}\,}}s = \infty \quad a.s. \end{aligned}$$

where we have assumed $\alpha > 0,$ without loss of generality, and $W_{\bullet } : {\mathbb {R}}_{\ge 0} \times \Xi \rightarrow {\mathbb {R}}$ is the standard Wiener process on the Wiener space $(\Xi , {\mathcal {F}}, {\mathbb {P}}),$ adapted to the natural filtration ${\mathcal {F}}_t$. This implies that $\tau < \infty$ a.s. by Proposition 3.2.

First, define the set

$$\begin{aligned} A = \left\{ \omega \in \Xi : \lim _{t \rightarrow \infty } \int ^t_0 e^{\alpha W_s(\omega )} {{\,\mathrm{d\!}\,}}s < \infty \right\} \subset \Xi . \end{aligned}$$

Fixing $\omega \in A$, choose $t_1, t_2, \ldots \in {\mathbb {R}}_{\ge 0}$ with $t_n < t_{n+1},$ such that $\lim _{n \rightarrow \infty } t_n = \infty$ and $\liminf _{n \rightarrow \infty } (t_{n+1}-t_n) > 0$, and consider the sequence

$$\begin{aligned} I_n(\omega ) = \int ^{t_n}_0 e^{\alpha W_s(\omega )} {{\,\mathrm{d\!}\,}}s, \quad n=1, 2, \ldots \end{aligned}$$

Clearly, $\{I_n(\omega )\}_{n \in {\mathbb {N}}}$ is monotonic increasing, and it is also bounded since $\omega \in A$. Hence, it is convergent by the monotone convergence theorem, and in particular, it is a Cauchy sequence. Therefore we have

$$\begin{aligned} \lim _{n \rightarrow \infty } |I_{n+1}(\omega ) - I_n(\omega )| = \lim _{n \rightarrow \infty } \int ^{t_{n+1}}_{t_n} e^{\alpha W_s(\omega )}{{\,\mathrm{d\!}\,}}s = 0. \end{aligned}$$

Since the integrand is strictly positive, this implies $\lim _{t \rightarrow \infty } e^{\alpha W_t(\omega )} = 0,$ and hence $W_t(\omega ) \rightarrow -\infty$. On the other hand, for $\omega \in \Xi$ such that $W_t(\omega ) \rightarrow -\infty$, it is easy to see that $\omega \in A$. This implies that under the identification $\Xi \cong C([0,\infty );{\mathbb {R}})$, the set A is equivalent to the set of Wiener processes $W_t$ with $W_t \rightarrow -\infty$, which is open in $C([0,\infty ); {\mathbb {R}})$ endowed with the norm $\Vert \cdot \Vert _{\infty }$ and therefore measurable. In particular, for $\omega \in A$, we have

$$\begin{aligned} \limsup _{t \rightarrow \infty } W_t(\omega ) = -\infty , \end{aligned}$$

but since $\limsup _{t \rightarrow \infty } W_t = +\infty ,$ a.s., this implies ${\mathbb {P}}(A) = 0$. $\square$

In the following, we show that for a broader class of $\{\xi _k(\cdot )\}_{k \in {\mathbb {N}}}$, shock formation occurs in expectation provided the initial profile has a sufficiently negative slope. Moreover, no new shocks can develop from positive slopes. We show this by looking at how the slope $\partial _x u$ evolves along the characteristics $X_t$, which resembles the argument given in [10] for the stochastic Camassa–Holm equation.

Theorem 3.4

Consider a characteristic $X_t,$ and a smooth initial profile $u(0,x)=u_0(x)$ such that $\partial _x u(0,X_0) = - \sigma < 0$. If

$$\begin{aligned} \frac{1}{2}\sum _{k=1}^\infty \left( (\partial _x \xi _k(x))^2 - \xi _k(x) \partial _{xx} \xi _k(x)\right) > -\sigma , \quad \forall x \in {\mathbb {R}}, \end{aligned}$$

then there exists $0<t_*<\infty$ such that $\lim _{t \rightarrow t_*} {\mathbb {E}} [\partial _x u(t,X_t)] = - \infty$. On the other hand, if $\partial _x u(0,X_0) \ge 0$ and

$$\begin{aligned} \frac{1}{2}\sum _{k=1}^\infty \left( (\partial _x \xi _k(x))^2 - \xi _k(x) \partial _{xx} \xi _k(x)\right) < \infty , \quad \forall x \in {\mathbb {R}}, \end{aligned}$$

then $\partial _x u(t,X_t) < \infty$ almost surely for all $t > 0$.

Proof

Taking the spatial derivative of (3.2), and evaluating the stochastic field $\partial _x u(t,x)$ along the semimartingale $X_t$ by the Ito–Wentzell formula (2.9) (again, this is valid due to the local well-posedness result, Theorem 1.3), the process $Y_t := \partial _x u(t,X_t)$ together with $X_t$ satisfy the following coupled Stratonovich SDEs

$$\begin{aligned} {{\,\mathrm{d\!}\,}}X_t&= u(t,X_t){{\,\mathrm{d\!}\,}}t + \sum _{k=1}^\infty \xi _k(X_t) \circ {{\,\mathrm{d\!}\,}}W_t^k , \end{aligned}$$

(3.11)

$$\begin{aligned} {{\,\mathrm{d\!}\,}}Y_t&= -Y_t^2{{\,\mathrm{d\!}\,}}t - \sum _{k=1}^\infty \partial _x \xi _k (X_t) Y_t \circ {{\,\mathrm{d\!}\,}}W_t^k. \end{aligned}$$

(3.12)

In Itô form, this reads

$$\begin{aligned} {{\,\mathrm{d\!}\,}}X_t&= \left( u(t,X_t) + \frac{1}{2} \sum _{k=1}^\infty \xi _k(X_t) \partial _x \xi _k(X_t)\right) {{\,\mathrm{d\!}\,}}t + \sum _{k=1}^\infty \xi _k(X_t) {{\,\mathrm{d\!}\,}}W_t^k, \end{aligned}$$

(3.13)

$$\begin{aligned} {{\,\mathrm{d\!}\,}}Y_t&= \left( -Y_t^2 + \frac{1}{2} Y_t \sum _{k=1}^\infty \left( (\partial _x \xi _k(x))^2 - \xi _k(x) \partial _{xx} \xi _k(x)\right) \right) {{\,\mathrm{d\!}\,}}t \nonumber \\&\quad - \sum _{k=1}^\infty \partial _x \xi _k(X_t) Y_t {{\,\mathrm{d\!}\,}}W_t^k. \end{aligned}$$

(3.14)

Taking the expectation of (3.14) on both sides, we obtain

$$\begin{aligned} \frac{{{\,\mathrm{d\!}\,}}{\mathbb {E}}[Y_t]}{{{\,\mathrm{d\!}\,}}t} = -{\mathbb {E}}[Y_t^2] + \frac{1}{2} {\mathbb {E}}\left[ Y_t\sum _{k=1}^\infty \left( (\partial _x \xi _k(x))^2 - \xi _k(x) \partial _{xx} \xi _k(x)\right) \right] . \end{aligned}$$

(3.15)

Now, assume that there exists a constant $C \in {\mathbb {R}}$ such that

$$\begin{aligned} C \le \sum _{k=1}^\infty \left( (\partial _x \xi _k(x))^2 - \xi _k(x) \partial _{xx} \xi _k(x)\right) , \end{aligned}$$

(3.16)

for all $x \in {\mathbb {R}}$. If $Y_0 = -\sigma < 0$, we have $Y_t < 0$ for all $t > 0,$ since $Y = 0$ is a fixed line in the phase space (X, Y) and therefore cannot be crossed. Hence from (3.16), we have

$$\begin{aligned} {\mathbb {E}}\left[ Y_t\sum _{k=1}^\infty \left( (\partial _x \xi _k(X_t))^2 - \xi _k(X_t) \partial _{xx} \xi _k(X_t)\right) \right] \le C {\mathbb {E}}[Y_t], \end{aligned}$$

and (3.15) becomes,

$$\begin{aligned} \frac{{{\,\mathrm{d\!}\,}}{\mathbb {E}}[Y_t]}{{{\,\mathrm{d\!}\,}}t}&\le -{\mathbb {E}}[Y_t^2] + \frac{C}{2} {\mathbb {E}}\left[ Y_t\right] \\&= -({\mathbb {E}}[Y_t^2] - {\mathbb {E}}[Y_t]^2) - {\mathbb {E}}[Y_t]^2 + \frac{C}{2} {\mathbb {E}}\left[ Y_t\right] \\&\le - {\mathbb {E}}[Y_t]^2 + \frac{C}{2} {\mathbb {E}}\left[ Y_t\right] , \end{aligned}$$

since ${\mathbb {E}}[Y_t^2] - {\mathbb {E}}[Y_t]^2 = {\mathbb {E}}\left[ (Y_t - {\mathbb {E}}[Y_t])^2\right] \ge 0$.

Solving this differential inequality, we get

$$\begin{aligned} {\mathbb {E}}[Y_t] \le {\left\{ \begin{array}{ll} \frac{-\sigma e^{Ct/2}}{1 - \frac{2\sigma }{C} \left( e^{Ct/2} - 1\right) }, \quad &{}\text {if } C \ne 0 \\ \frac{1}{t - \frac{1}{\sigma }}, \quad &{}\text {if } C=0 \end{array}\right. }. \end{aligned}$$

The right-hand side tends to $-\infty$ in finite time provided $-\sigma < C/2$.

Hence, if

$$\begin{aligned} -\sigma < C/2 \le \frac{1}{2} \sum _{k=1}^\infty \left( (\partial _x \xi _k(x))^2 - \xi _k(x) \partial _{xx} \xi _k(x)\right) , \end{aligned}$$

for all $x \in {\mathbb {R}}$, then there exists $t_* < \infty$ such that $\lim _{t \rightarrow t_*} {\mathbb {E}} [u_x(t, X_t)] = - \infty$.

Similarly, if $\frac{1}{2}\sum _{k=1}^\infty \left( (\partial _x \xi _k(x))^2 - \xi _k(x) \partial _{xx} \xi _k(x)\right) < D$ for some $D \in {\mathbb {R}}$, then for $Y_0 > 0$ we have again

$$\begin{aligned} \frac{{{\,\mathrm{d\!}\,}}{\mathbb {E}}[Y_t]}{{{\,\mathrm{d\!}\,}}t} \le -{\mathbb {E}}[Y_t]^2 + D {\mathbb {E}}[Y_t]. \end{aligned}$$

One can check that ${\mathbb {E}}[Y_t] < \infty$ for all $t>0,$ which implies $Y_t < \infty$ almost surely. $\square$

Remark 3.5

Blow-up in expectation does not imply pathwise blow-up. It is merely a necessary condition, which suggests that the law of $\partial _x u$ becomes increasingly fat-tailed with time, making it more likely for it to take extreme values. Nonetheless, it is a good indication of blow-up occurring with some probability.

Example 3.6

Consider the set $\{\xi _k(x)\}_{k \in {\mathbb {N}}} = \left\{ \frac{1}{k^2}\sin (kx), \frac{1}{k^2}\cos (kx)\right\} _{k \in {\mathbb {N}}}$, which forms an orthogonal basis for $L^2({\mathbb {T}})$. Then, one can easily check that

$$\begin{aligned} 0< \sum _{k=1}^\infty \left( (\partial _x \xi _k(x))^2 - \xi _k(x) \partial _{xx} \xi _k(x)\right) < \infty , \end{aligned}$$

for all $x \in {\mathbb {T}},$ so blow-up occurs in expectation for any initial profile with negative slope, but no new shocks can form from positive slopes.

3.3 Weak solutions

We saw that if the initial profile $u_0$ has a negative slope, then shocks may form in finite time (almost surely in the linear case $\xi (x) = \alpha x$), so solutions to (3.1) cannot exist in the classical sense. This motivates us to consider weak solutions to (3.1) in the sense of Definition 2.7.

Suppose that the profile u is differentiable everywhere except for a discontinuity along the curve $\gamma = \left\{ (t,s(t)) \in [0,\infty ) \times M \right\}$, where $M = {\mathbb {T}}$ or ${\mathbb {R}}$. Then the curve of discontinuity must satisfy the following for u to be a solution of the integral equation (2.10).

Proposition 3.7

(Stochastic Rankine–Hugoniot condition) The curve of discontinuity s(t) of the stochastic Burgers’ equation in weak form (2.10) satisfies the following SDE

$$\begin{aligned} {{\,\mathrm{d\!}\,}}s_t = \frac{1}{2} \left[ (u_-(t,s(t)) + u_+(t,s(t))\right] \,{{\,\mathrm{d\!}\,}}t + \sum _{k=1}^\infty \xi _k(s(t)) \circ {{\,\mathrm{d\!}\,}}W_t^k, \end{aligned}$$

(3.17)

where $u_\pm (t,s(t)) := \lim _{x \rightarrow s(t)^\pm } u(t,x)$ are the left and right limits of u.

The main obstacle here is that the curve s(t) is not piecewise smooth and therefore we cannot apply the standard divergence theorem, which is how the Rankine–Hugoniot condition is usually derived. Extending classical calculus identities such as Green’s theorem on domains with non-smooth boundaries is a tricky issue, but fortunately, there have been several works that extend this result to non-smooth but rectifiable boundaries in [40], and to non-rectifiable boundaries in [28,29,30, 38].

Lemma 3.8

Green’s theorem for non-smooth boundaries Let $\Omega$ be a bounded domain in the (x, y)-plane such that its boundary $\partial \Omega$ is a Jordan curve and let u, v be sufficiently regular functions in $\Omega$ (see Remark 3.9 below). Then

$$\begin{aligned} \int _\Omega \text {div}(u,v) {{\,\mathrm{d\!}\,}}x {{\,\mathrm{d\!}\,}}y = \oint _{\partial \Omega } \left( u {{\,\mathrm{d\!}\,}}y - v {{\,\mathrm{d\!}\,}}x \right) , \end{aligned}$$

(3.18)

where the contour integral on the right-hand side can be understood as a limit of a standard contour integral along a smooth approximation of the boundary. Here, the integral is taken in the anti-clockwise direction of the contour.

Remark 3.9

For the above to hold, there must be a pay-off between the regularity of $\partial \Omega$ and the functions u, v (i.e. the less regular the boundary, the more regular the integrand). In particular, the following condition is known:

• $\partial \Omega$ has box-counting dimension $d < 2$ and u, v is $\alpha$-Hölder continuous for any $\alpha > d-1$ (Harrison and Norton [30]).

Proof of Theorem 3.7

We provide a proof in the case $M = {\mathbb {T}}$ with only one noise term. Extending it to the case $M={\mathbb {R}}$ and countably many noise terms is straightforward. Take the atlas $\{(U_1,\varphi _1),(U_2,\varphi _2)\}$ on ${\mathbb {T}} ={\mathbb {R}}/{\mathbb {Z}},$ where $U_1 := (0,1)$, $\varphi _1:(0,1) \rightarrow U_1$ and $U_2 := (-\frac{1}{2},\frac{1}{2})$, $\varphi _2 : (0,1) \rightarrow U_2$. Without loss of generality, assume that the shock $s(\cdot )$ starts at time $t=0$.

Fig. 1

In the proof of the stochastic Rankine–Hugoniot condition (3.17), the domain $\Omega _n := [\tau _{n-1},\tau _n) \times (0,1) \subset [0,\infty ) \times {\mathbb {T}}$ is split up into two parts: $\Omega _-^n$, which is on the left of the shock curve (t, s(t)) and $\Omega _+^n$, which is on the right

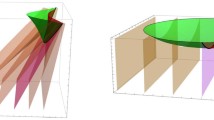
Now, consider a sequence $0 = \tau _0< \tau _1< \tau _2 < \cdots ,$ with $\lim _{n \rightarrow \infty } \tau _n = \infty$ such that for all $n \in \mathbb {N}$, the curve $\gamma _n := \{s(t) : t \in [\tau _{n-1}, \tau _n)\}$ is contained in either one of the charts $U_1$ or $U_2$. For convenience, we denote by $(U_n, \varphi _n)$ to mean the chart $(U_1,\varphi _1)$ or $(U_2,\varphi _2)$ that contains $\gamma _n$. In local coordinates, we split the domain $\Omega _n := [\tau _{n-1},\tau _n) \times \varphi _n^{-1}(U_n)$ into two regions (see Fig. 1)

$$\begin{aligned}&\Omega _-^n := \left\{ (t, x) \in \mathbb [\tau _{n-1},\tau _n) \times (0,1) : x \in (0, s(t)) \right\} , \end{aligned}$$

(3.19)

$$\begin{aligned}&\Omega _+^n := \left\{ (t, x) \in \mathbb [\tau _{n-1},\tau _n) \times (0,1) : x \in (s(t), 1) \right\} . \end{aligned}$$

(3.20)

For $n \in {\mathbb {N}}$, consider the following integrals

$$\begin{aligned} I_n&= \iint _{\Omega _-^n} \left( \left( u \partial _t \varphi + \frac{1}{2} u^2 \partial _x \varphi \right) {{\,\mathrm{d\!}\,}}t + u \partial _x \left( \varphi (t,x) \xi (x) \right) \circ {{\,\mathrm{d\!}\,}}W_t \right) {{\,\mathrm{d\!}\,}}x \\&=\iint _{\Omega _-^n} \text {div}_{x,t} \left( \frac{1}{2} \varphi u(t,x)^2, \, \varphi (t,x) u(t,x) \right) {{\,\mathrm{d\!}\,}}x {{\,\mathrm{d\!}\,}}t \\&\quad + \int _{\tau _{n-1}}^{\tau _n}\left( \int _0^{s(t)} \partial _x \left( \varphi (t,x) \xi (x) u(t,x) \right) {{\,\mathrm{d\!}\,}}x\right) \circ {{\,\mathrm{d\!}\,}}W_t \\&\quad - \underbrace{\iint _{\Omega _-^n} \varphi \left( {{\,\mathrm{d\!}\,}}u + u\partial _x u {{\,\mathrm{d\!}\,}}t + \xi (x) \partial _x u \circ {{\,\mathrm{d\!}\,}}{W_t} \right) {{\,\mathrm{d\!}\,}}x}_{=0}, \text { and}\\ J_n&= \iint _{\Omega _+^n} \left( \left( u \partial _t \varphi + \frac{1}{2} u^2 \partial _x \varphi \right) {{\,\mathrm{d\!}\,}}t + u \partial _x \left( \varphi (t,x) \xi (x) \right) \circ {{\,\mathrm{d\!}\,}}W_t \right) {{\,\mathrm{d\!}\,}}x \\&= \iint _{\Omega _+^n} \text {div}_{x,t} \left( \frac{1}{2} \varphi u(t,x)^2, \, \varphi (x,t) u(t,x) \right) {{\,\mathrm{d\!}\,}}x {{\,\mathrm{d\!}\,}}t \\&\quad + \int _{\tau _{n-1}}^{\tau _n}\left( \int ^1_{s(t)} \partial _x \left( \varphi (t,x) \xi (x) u(t,x) \right) {{\,\mathrm{d\!}\,}}x\right) \circ {{\,\mathrm{d\!}\,}}W_t \\&\quad - \underbrace{\iint _{\Omega _+^n} \varphi \left( {{\,\mathrm{d\!}\,}}u + u\partial _x u {{\,\mathrm{d\!}\,}}t + \xi (x) \partial _x u \circ {{\,\mathrm{d\!}\,}}{W_t} \right) {{\,\mathrm{d\!}\,}}x}_{=0}. \end{aligned}$$

Then by Lemma 3.8, we have

$$\begin{aligned} I_n&= \oint _{\partial \Omega _-^n} \left( \frac{1}{2} \varphi u(t,x)^2 {{\,\mathrm{d\!}\,}}t - \varphi (t,x) u(t,x) {{\,\mathrm{d\!}\,}}x \right) \\&\quad + \int ^{\tau _n}_{\tau _{n-1}} \varphi (t,s(t)) \xi (s(t)) u_-(t,s(t)) \circ {{\,\mathrm{d\!}\,}}W_t \\&= -\int ^{\tau _n}_{\tau _{n-1}} \varphi (t,s(t)) \left( u_-(t,s(t)) {{\,\mathrm{d\!}\,}}s_t - \frac{1}{2} u_-(t,s(t))^2 {{\,\mathrm{d\!}\,}}t \right. \\&\quad \left. - \xi (s(t)) u_-(t,s(t)) \circ {{\,\mathrm{d\!}\,}}W_t\right) \\&\quad + \left( \int _A-\int _B-\int _C\right) \left( \frac{1}{2} \varphi u(t,x)^2 {{\,\mathrm{d\!}\,}}t - \varphi (t,x) u(t,x) {{\,\mathrm{d\!}\,}}x \right) , \end{aligned}$$

where

$$\begin{aligned} A&:=\{(\tau _{n-1},x) : x \in (0,s(\tau _{n-1}))\},\, B:=\{(\tau _{n},x) : x \in (0,s(\tau _{n}))\}, \, \\ C&:=\{(t,0) : t \in (\tau _{n-1},\tau _n)\}, \end{aligned}$$

and

$$\begin{aligned} J_n&= \oint _{\partial \Omega _+^n} \left( \frac{1}{2} \varphi u(t,x)^2 {{\,\mathrm{d\!}\,}}t - \varphi (x,t) u(t,x) {{\,\mathrm{d\!}\,}}x \right) \\&\quad - \int ^{\tau _n}_{\tau _{n-1}} \varphi (t,s(t)) \xi (s(t)) u_+(t,s(t)) \circ {{\,\mathrm{d\!}\,}}W_t \\&= \int _{\tau _{n-1}}^{\tau _n} \varphi (t,s(t)) \left( u_+(t,s(t)) {{\,\mathrm{d\!}\,}}s_t - \frac{1}{2} u_+(t,s(t))^2 {{\,\mathrm{d\!}\,}}t \right. \\&\quad \left. - \xi (s(t)) u_+(t,s(t)) \circ {{\,\mathrm{d\!}\,}}W_t\right) \\&\quad + \left( \int _D+\int _E+\int _F\right) \left( \frac{1}{2} \varphi u(t,x)^2 {{\,\mathrm{d\!}\,}}t - \varphi (t,x) u(t,x) {{\,\mathrm{d\!}\,}}x \right) , \end{aligned}$$

where

$$\begin{aligned} D&:=\{(\tau _{n-1},x) : x \in (s(\tau _{n-1}),1)\},\, E:=\{(\tau _{n},x) : x \in (s(\tau _{n}),1)\}, \, \\ F&:=\{(t,1) : t \in (\tau _{n-1},\tau _n)\}. \end{aligned}$$

One can check by direct calculation that

$$\begin{aligned} \sum _{n=1}^N (I_n + J_n)&= - \int _{{\mathbb {T}}} \varphi (\tau _N,x) u(\tau _N,x) {{\,\mathrm{d\!}\,}}x \\&\quad + \int _0^{\tau _N} \varphi (t,s(t)) \left[ u_+(t,s(t)) - u_-(t,s(t)) \right] \\&\qquad \left( {{\,\mathrm{d\!}\,}}s_t - \frac{1}{2} \left[ u_-(t,s(t)) + u_+(t,s(t)) \right] {{\,\mathrm{d\!}\,}}t - \xi (s(t)) \circ {{\,\mathrm{d\!}\,}}W_t \right) , \end{aligned}$$

where we used the assumption that $\varphi (0,\cdot ) \equiv 0$.

Now, from (2.10), we have $\lim _{N\rightarrow \infty }\sum _{n=1}^N (I_n + J_n) = 0$ and since $\varphi$ has compact support, there exists $N > 0$ such that $\varphi (\tau _{N'},\cdot ) \equiv 0$ for all $N' \ge N$. Hence,

$$\begin{aligned} 0&= \lim _{N \rightarrow \infty }\sum _{n=1}^N (I_n + J_n) \\&= \int _0^{\infty } \varphi (t,s(t)) \left[ u_+(t,s(t)) - u_-(t,s(t)) \right] \\&\quad \left( {{\,\mathrm{d\!}\,}}s_t - \frac{1}{2} \left[ u_-(t,s(t)) + u_+(t,s(t)) \right] {{\,\mathrm{d\!}\,}}t - \xi (s(t)) \circ {{\,\mathrm{d\!}\,}}W_t \right) , \end{aligned}$$

and since $\varphi$ is arbitrary, we have

$$\begin{aligned} {{\,\mathrm{d\!}\,}}s_t = \frac{1}{2} \left[ u_-(t,s(t)) + u_+(t,s(t)) \right] {{\,\mathrm{d\!}\,}}t + \xi (s(t)) \circ {{\,\mathrm{d\!}\,}}W_t, \end{aligned}$$

for all $t > 0$. $\square$

4 Well-posedness results

4.1 Local well-posedness of a stochastic Burgers’ equation

Now, we prove local well-posedness of the stochastic Burgers’ equation (1.1) with $\nu =0$. In fact, since the techniques used in the proof are essentially the same, we prove local well-posedness of a more general equation, which includes (1.1) as a special case. The stochastic Burgers’ equation we treat is given by

$$\begin{aligned} {{\,\mathrm{d\!}\,}}u + u\partial _{x}u {{\,\mathrm{d\!}\,}}t+ \mathcal {Q} u {{\,\mathrm{d\!}\,}}W_{t}= \frac{1}{2} \mathcal {Q}^{2}u {{\,\mathrm{d\!}\,}}t. \end{aligned}$$

(4.1)

Here $\mathcal {Q}$ represents a first order differential operator

$$\begin{aligned} \mathcal {Q}u=a(x)\partial _{x}u+b(x)u, \end{aligned}$$

where the coefficients a(x), b(x) are smooth and bounded. We state the main result of this section:

Theorem 4.1

Let $u_{0}\in H^{s} (\mathbb {T},\mathbb {R}),$ for $s>3/2$ fixed, then there exists a unique maximal solution $(\tau _{max},u)$ of the 1D stochastic Burgers’ equation (4.1). Therefore, if $(\tau ',u')$ is another maximal solution, then necessarily $\tau _{max}=\tau '$, $u=u'$ on $[0,\tau _{max})$. Moreover, either $\tau _{max}=\infty$ or $\displaystyle \lim \sup _{s\nearrow \tau _{max}} ||u(s)||_{H^{s}}= \infty$.

We will provide a sketch of the proof, which follows closely the approach developed in [2, 8]. For clarity of exposition, let us divide the argument into several steps.

• Step 1: Uniqueness of local solutions. To show uniqueness of local solutions, one argues by contradiction. More concretely, one can prove that any two different solutions to (4.1) defined up to a stopping time must coincide, as explained in the following Proposition.

Proposition 4.2

Let $\tau$ be a stopping time, and $u^1,u^2: [0,\tau ] \times \mathbb {T}\times \Xi \rightarrow \mathbb {R}$ be two solutions with same initial data $u_{0}$ and continuous paths of class $C\left( [0,\tau ]; H^{s}(\mathbb {T},\mathbb {R})\right)$. Then $u^{1}=u^{2}$ on $[0,\tau ],$ almost surely.

Proof

For this, we refer the reader to [2, 8]. It suffices to define $\bar{u} = u^1 - u^2,$ and perform standard estimates for the evolution of the $L^2$ norm of $\bar{u}$. $\square$

• Step 2: Existence and uniqueness of truncated maximal solutions. Consider the truncated stochastic Burgers’ equation

  $$\begin{aligned} {{\,\mathrm{d\!}\,}}u_{r} + \theta _{r}(||\partial _{x}u||_\infty )u_{r}\partial _{x}u_{r} {{\,\mathrm{d\!}\,}}t+ \mathcal {Q}u_{r} {{\,\mathrm{d\!}\,}}W_{t}= \frac{1}{2} \mathcal {Q}^{2}u_{r} {{\,\mathrm{d\!}\,}}t, \end{aligned}$$

  (4.2)

  where $\theta _{r}:[0,\infty )\rightarrow [0,1]$ is a smooth function such that

  $$\begin{aligned} \theta _{r}(x)= {\left\{ \begin{array}{ll} 1, \ \text {for } |x| \le r, \\ 0, \ \text {for } |x| \ge 2r, \end{array}\right. } \end{aligned}$$

  for some $r>0$. Let us state the result which is the cornerstone for proving existence and uniqueness of maximal local solutions of the stochastic Burgers’ equation (4.1).

Proposition 4.3

Given $r>0$ and $u_{0}\in H^{s}(\mathbb {T},\mathbb {R})$ for $s>3/2$, there exists a unique global solution u in $H^{s}$ of the truncated stochastic Burgers’ equation (4.2).

It is very easy to check that once Proposition 4.3 is proven, Theorem 4.1 follows immediately (cf. [8]). Therefore, we focus our efforts on showing Proposition 4.3.

• Step 3: Global existence of solutions of the hyper-regularised truncated stochastic Burgers’ equation. Let us consider the following hyper-regularisation of our truncated equation

  $$\begin{aligned} {{\,\mathrm{d\!}\,}}u^{\nu }_{r} + \theta _{r}(||\partial _{x}u||_\infty )u^{\nu }_{r}\partial _{x}u^{\nu }_{r} {{\,\mathrm{d\!}\,}}t+\mathcal {Q}u^{\nu }_{r} {{\,\mathrm{d\!}\,}}W_{t}= \nu \partial ^{s'}_{xx} u^{\nu }_{r} {{\,\mathrm{d\!}\,}}t +\frac{1}{2} \mathcal {Q}^{2}u^{\nu }_{r} {{\,\mathrm{d\!}\,}}t, \end{aligned}$$

  (4.3)

  where $\nu >0$ is a positive parameter and $s'= 2s+1$. Notice that we have added dissipation in order to be able to carry out the calculations rigorously. Equation (4.3) is understood in the mild sense, i.e., as a solution to an integro-differential equation (see (4.4)).

Proposition 4.4

For every $\nu ,r >0$ and initial data $u_{0}\in H^{s}(\mathbb {T},\mathbb {R})$ for $s>3/2$, there exists a unique global strong solution $u^{\nu }_{r}$ of Eq. (4.3) in the class $L^{2}(\Xi ; C([0,T]; H^{s}(\mathbb {T},\mathbb {R})))$, for all $T>0$. Moreover, its paths will gain extra regularity, namely $C([\delta ,T]; H^{s+2}(\mathbb {T},\mathbb {R}) )$, for every $T>\delta >0$.

Proof of Proposition 4.4

The proof is based on a simple fixed point iteration argument which uses Duhamel’s principle. We will also omit the subscripts $\nu$ and r throughout the proof. Given $u_{0}\in L^{2}(\Xi ; H^{s}(\mathbb {T},\mathbb {R}))$, consider the mild formulation of the hyper-regularised truncated equation (4.3).

$$\begin{aligned} u(t)= (\Upsilon u)(t), \end{aligned}$$

(4.4)

where

$$\begin{aligned} (\Upsilon u)(t)=&e^{tA}u_{0} -\int _{0}^{t}e^{\left( t-s\right) A}B_{\theta }(u)(s) \ {{\,\mathrm{d\!}\,}}s +\int _{0}^{t}e^{\left( t-s\right) A} Lu(s) {{\,\mathrm{d\!}\,}}s \\&\quad - \int _{0}^{t}e^{\left( t-s\right) A}Ru(s) \ {{\,\mathrm{d\!}\,}}W_{s},\\ A:=&\nu \partial ^{s'}_{xx}, \quad B_{\theta }u:=\theta (||\partial _{x} u||_\infty )(u\partial _{x}u), \quad Lu:=\dfrac{1}{2}\mathcal {Q}^{2}u, \text { and } Ru:= \mathcal {Q}u. \end{aligned}$$

Now, consider the space $\mathcal {W}_{T}:=L^{2}(\Xi ; C([0,T];H^{s}(\mathbb {T},\mathbb {R})))$. One can show that $\Upsilon$ is a contraction on $\mathcal {W}_{T}$ by following the same arguments in [2, 8]. Therefore, by applying Picard’s iteration argument, one can construct a local solution. To extend it to a global one, it is sufficient to show that for a given $T>0$ and initial data $u_{0}\in H^{s}(\mathbb {R},\mathbb {T})$, we have

$$\begin{aligned} \sup _{t\in [0,T]} \mathbb {E}\left[ ||u(t)||^{2}_{H^{s}} \right] \le C(T), \end{aligned}$$

(4.5)

so we could glue together each local solution to cover any time interval. Furthermore, by standard properties of the semigroup $e^{tA}$ (cf. [26]), one can prove that for positive times $T>\delta >0$, each term in the mild equation (4.4) enjoys higher regularity, namely, $u\in L^{2}(\Xi ; C([\delta ,T];H^{s+2}))$ for every $T>\delta >0$. All the computations can be carried out easily by mimicking the same ideas as in [2, 8]. $\square$

• Step 4: Limiting and compactness argument. The main objective of this step is to show that the family of solutions $\{u^{\nu }_{r} \}_{\nu >0}$ of the hyper-regularised stochastic Burgers’ equation (4.3) is compact in a particular sense and therefore we are able to extract a subsequence converging strongly to a solution of the truncated stochastic Burgers’ equation (4.2). The main idea behind this argument relies on proving that the probability laws of this family are tight in some metric space. Once this is proven, one only needs to invoke standard stochastic partial differential equations arguments based on the Skorokhod’s representation and Prokhorov’s theorem. A more thorough approach can be found in [8, 24]. In the next Proposition, we present the main argument to show that the sequence of laws are indeed tight.

Proposition 4.5

Assume that for some $\alpha >0,$ $N \in \mathbb {N},$ there exist constants $C_1(T)$ and $C_2(T)$ such that

$$\begin{aligned}&\mathbb {E} \left[ \sup _{t \in [0,T]} ||u_r^\nu (t)||^2_{H^{s}} \right] \le C_1(T), \end{aligned}$$

(4.6)

$$\begin{aligned}&\mathbb {E} \left[ \int _0^T \int _0^T \frac{||u_r^\nu (t) - u_r^\nu (s)||^2_{H^{-N}}}{|t-s|^{1+2\alpha }} {{\,\mathrm{d\!}\,}}t {{\,\mathrm{d\!}\,}}s \right] \le C_2(T), \end{aligned}$$

(4.7)

uniformly in $\nu$. Then $\{u_{r}^{\nu }\}_{\nu >0}$ is tight in the Polish space E given by

$$\begin{aligned} E=L^{2}([0,T];H^{\beta }(\mathbb {T},\mathbb {R}))\cap C_{w}([0,T];H^{s}(\mathbb {T},\mathbb {R})), \end{aligned}$$

with $\beta >\frac{1}{2}$ and $s>3/2$.

Proof of Proposition 4.5

It is enough to imitate the techniques in [2, 8]. $\square$

• Step 5: Hypothesis estimates. We are left to show that hypothesis (4.6)–(4.7) hold. First, we will show that condition (4.6) implies condition (4.7). Applying Minkowski’s and Jensen’s inequalities, and carrying out some standard computations, we obtain

  $$\begin{aligned} \mathbb {E} [ ||u^{\nu }_{r}(t)-u^{\nu }_{r}(s)||^2_{H^{-N}} ]&\lesssim (t-s) \int _s^t \mathbb {E} [\theta _{r}(||\partial _{x}u||_\infty )||u^{\nu }_{r}\partial _{x}u^{\nu }_{r}(\gamma )||^2_{H^{-N}}] {{\,\mathrm{d\!}\,}}\gamma \\&\quad + (t-s)\int _s^t \mathbb {E} [||\nu \partial ^{s'}_{xx} u^{\nu }_{r} (\gamma )||^2_{H^{-N}}] {{\,\mathrm{d\!}\,}}\gamma \\&\quad + (t-s) \int _s^t \mathbb {E} [|| {}^{\mathrm{a}}\mathcal {Q}^{2}u^{\nu }_{r} (\gamma )||^2_{H^{-1}}] {{\,\mathrm{d\!}\,}}\gamma \\&\quad + \mathbb {E} \left[ \left| \left| \int _s^t \mathcal {Q} u^{\nu }_{r} (\gamma ) {{\,\mathrm{d\!}\,}}W_{\gamma } \right| \right| ^2_{L^2} \right] . \end{aligned}$$

It is easy to infer that

$$\begin{aligned} \int _s^t \mathbb {E} \left[ \theta _{r}(||\partial _{x}u||_\infty )||u^{\nu }_{r}\partial _{x}u^{\nu }_{r}(\gamma )||^{2}_{H^{-N}}\right] {{\,\mathrm{d\!}\,}}\gamma \lesssim \int _{s}^{t} \mathbb {E}\left[ ||u^{\nu }_{r}(\gamma )||^{2}_{H^{s}}\right] {{\,\mathrm{d\!}\,}}\gamma \le C(T),\nonumber \\ \end{aligned}$$

(4.8)

since

$$\begin{aligned} ||u^{\nu }_{r}\partial _{x}u^{\nu }_{r}||_{H^{-N}} \lesssim ||\partial _{x}u_r^\nu ||_\infty ||u_r^\nu ||_{H^{s}}, \end{aligned}$$

and hypothesis (4.6). In the same way, one can check that for $N=3s+2$,

$$\begin{aligned} \int _s^t \mathbb {E} [||\nu \partial ^{s'}_{xx} u^{\nu }_{r} (\gamma )||^2_{H^{-N}}] {{\,\mathrm{d\!}\,}}\gamma \lesssim \int _s^t \mathbb {E}\left[ ||u_r^\nu (\gamma )||^{2}_{H^s}\right] {{\,\mathrm{d\!}\,}}\gamma \le C(T). \end{aligned}$$

(4.9)

since

$$\begin{aligned} ||\partial ^{s'}_{xx} u_r^\nu ||_{H^{-N}} \lesssim ||u_r^\nu ||_{H^s}. \end{aligned}$$

Similarly,

$$\begin{aligned} \int _{s}^{t}\mathbb {E}\left[ ||\mathcal {Q}^{2}u^{\nu }_{r} (\gamma )||^2_{H^{-1}}\right] {{\,\mathrm{d\!}\,}}\gamma \lesssim \int _{s}^{t}\mathbb {E}\left[ ||u^{\nu }_{r}(\gamma )||^{2}_{H^{s}}\right] {{\,\mathrm{d\!}\,}}\gamma \le C(T), \end{aligned}$$

(4.10)

since $\left| \left| \mathcal {Q}^{2}u^{\nu }_{r} \right| \right| ^{2}_{H^{-1}} \lesssim ||u^{\nu }_{r}||^{2}_{H^{s}}$. We also have that the stochastic term can be controlled by

$$\begin{aligned} \mathbb {E} \left[ \left| \left| \int _s^t \mathcal {Q}u^{\nu }_{r} (\gamma ) {{\,\mathrm{d\!}\,}}W_{\gamma } \right| \right| ^2_{L^2} \right]&= \int _s^t \mathbb {E} \left[ ||\mathcal {Q} u^{\nu }_{r} (\gamma ) ||^2_{L^2} \right] {{\,\mathrm{d\!}\,}}\gamma \nonumber \\&\lesssim \int _s^t \mathbb {E} \left[ || u^{\nu }_{r} (\gamma ) ||^2_{H^{s}} \right] {{\,\mathrm{d\!}\,}}\gamma \le C(T). \end{aligned}$$

(4.11)

Combining estimates (4.8)–(4.11), we deduce that

$$\begin{aligned} \mathbb {E} \left[ ||u^{\nu }_{r}(t)-u^{\nu }_{r}(s)||^2_{H^{-N}} \right] \le C(t-s). \end{aligned}$$

Hence for $0<\alpha < 1/2,$

$$\begin{aligned} \mathbb {E} \left[ \int _0^T \int _0^T \frac{||u_r^\nu (t) - u_r^\nu (s)||^2_{H^{-N}}}{|t-s|^{1+2\alpha }} {{\,\mathrm{d\!}\,}}t {{\,\mathrm{d\!}\,}}s \right]&\le \mathbb {E} \left[ \int _0^T \int _0^T \frac{C}{|t-s|^{2 \alpha }} {{\,\mathrm{d\!}\,}}t {{\,\mathrm{d\!}\,}}s \right] \\&\le C(T). \end{aligned}$$

We are left to prove that hypothesis (4.6) holds true, i.e., there exists a constant C such that

$$\begin{aligned} \mathbb {E} \left[ \sup _{t \in [0,T]} ||u_r^\nu (t)||^2_{H^{s}} \right] \le C(T). \end{aligned}$$

(4.12)

Indeed, the evolution of the $L^{2}$ norm of $\Lambda ^{s}u$ is given by

$$\begin{aligned} \frac{1}{2} \int _{\mathbb {T}} |\Lambda ^{s} u^{\nu }_{r} (t)|^2 \ {{\,\mathrm{d\!}\,}}V&= \frac{1}{2}\int _{\mathbb {T}} |\Lambda ^{s} u^{\nu }_{r} (0)|^2 \ {{\,\mathrm{d\!}\,}}V \\&\quad - \int _0^t \langle \theta _{r}(||\partial _{x}u||_\infty ) \Lambda ^{s} \left( u^{\nu }_{r}\partial _{x}u^{\nu }_{r}(s)\right) , \Lambda ^{s} u^\nu _r (s) \rangle _{L^2} {{\,\mathrm{d\!}\,}}s \\&\quad - \int _0^t \langle \Lambda ^{s} \mathcal {Q} u^{\nu }_{r} (s), \Lambda ^{s} u_r^\nu (s) \rangle _{L^2} {{\,\mathrm{d\!}\,}}W_{s}\\&\quad + \int _0^t \langle \nu \Lambda ^{s} \partial ^{s'}_{xx} u^{\nu }_{r} (s), \Lambda ^{s} u^\nu _r (s) \rangle _{L^2} {{\,\mathrm{d\!}\,}}s \\&\quad + \frac{1}{2} \int _0^t \langle \Lambda ^{s} \mathcal {Q}^{2} u^{\nu }_{r} (s), \Lambda ^{s} u^\nu _r (s) \rangle _{L^2} {{\,\mathrm{d\!}\,}}s\\&\quad +\frac{1}{2} \int _0^t \langle \Lambda ^{s} \mathcal {Q} u^\nu _r(s), \Lambda ^{s} \mathcal {Q}u^\nu _r (s) \rangle _{L^2} {{\,\mathrm{d\!}\,}}s. \end{aligned}$$

The estimate of the nonlinear term is done via the Kato–Ponce commutator estimate (2.4),

$$\begin{aligned} \left| \int _{\mathbb {T}} \Lambda ^{s} (u^{\nu }_{r}\partial _{x}u^{\nu }_{r})\Lambda ^{s} u^\nu _r \ {{\,\mathrm{d\!}\,}}V \right| \lesssim ||\partial _{x}u^{\nu }_{r}||_\infty || u^{\nu }_{r}||^{2}_{H^{s}}. \end{aligned}$$

(4.13)

Applying integration by parts in the dissipative term, we see that it has the correct sign so we can drop it:

$$\begin{aligned} \langle \nu \Lambda ^{s} \partial ^{s'}_{xx} u^{\nu }_{r} (s), \Lambda ^{s} u^\nu _r (s) \rangle _{L^2}= -\nu ||\Lambda ^{3s+1}u^{\nu }_{r}||^{2}_{L^{2}}<0. \end{aligned}$$

The last two terms can be bounded using the general estimates (2.6) recently derived in [2].

To conclude this proof, we only need to bound the local martingale terms. This is effected by estimating their quadratic variation and using Burkholder–Davis–Gundy inequality (2.7). Indeed, let us denote

$$\begin{aligned} M_t = \int _0^t \left( \langle \mathcal {Q} u^{\nu }_{r} (s), u_r^\nu (s) \rangle _{L^2} + \langle \Lambda ^{s} \mathcal {Q} u^{\nu }_{r} (s), \Lambda ^{s} u_r^\nu (s) \rangle _{L^2} \right) {{\,\mathrm{d\!}\,}}W_s. \end{aligned}$$

We will denote $u_{r}^{\nu }$ by u to make the notation in the following estimates simpler, but implicitly taking into account that they indeed depend $\nu$ and r. Therefore we get that

$$\begin{aligned} ||u(t)||^{2}_{H^{s}} \lesssim ||u_0||^{2}_{H^{s}} + |M_t| + \int _0^t ||u(s)||^{2}_{H^{s}} {{\,\mathrm{d\!}\,}}s. \end{aligned}$$

Applying Grönwall’s inequality and taking expectation,

$$\begin{aligned} \mathbb {E} \left[ \sup _{s \in [0,t]}||u(s)||_{H^{s}}^4 \right] \lesssim \text {exp}\left( t\right) \left( ||u_0||^4_{H^{s}}+ \mathbb {E} \left[ \sup _{s \in [0,t]} |M_s|^2 \right] \right) . \end{aligned}$$

(4.14)

Invoking Burkholder–Davis–Gundy inequality (2.7), the term $|M_s|^{2}$ can be bounded as

$$\begin{aligned} \mathbb {E} \left[ \sup _{s \in [0,t]} |M_{s}|^{2} \right] \lesssim \mathbb {E} \left[ [M]_{t}\right] , \end{aligned}$$

(4.15)

where $[M]_t$ is the quadratic variation of $M_t,$ given by

$$\begin{aligned}{}[M]_t = \int _0^t \left( \langle \mathcal {Q}u(s), u(s) \rangle _{L^2} + \langle \Lambda ^{s} \mathcal {Q}u(s), \Lambda ^{s} u(s) \rangle _{L^2} \right) ^2 {{\,\mathrm{d\!}\,}}s. \end{aligned}$$

One can check that

$$\begin{aligned} \left| \langle \mathcal {Q}u(s), u(s) \rangle _{L^2} + \langle \Lambda ^{s} \mathcal {Q}u(s), \Lambda ^{s} u(s) \rangle _{L^2} \right| \lesssim ||u||^{2}_{H^{s}}, \end{aligned}$$

(4.16)

as in the proof of Theorem 2.2 in [2]. Therefore, the above equation can be bounded as

$$\begin{aligned} \mathbb {E} \left[ [M]_t\right] \lesssim \int _0^t \mathbb {E} \left[ \sup _{\gamma \in [0,s] } || u (\gamma ) ||^{4}_{H^{s}}\right] {{\,\mathrm{d\!}\,}}s. \end{aligned}$$

(4.17)

Hence, combining (4.14)–(4.17), and Grönwall’s inequality yield

$$\begin{aligned} \mathbb {E} \left[ \sup _{t \in [0,T]} ||u (t)||^4_{H^{s}} \right] \le C(T). \end{aligned}$$

Finally, the bound (4.12) follows from a simple application of Jensen’s inequality, concluding the proof.

4.2 Blow-up criterion

We are now interested in deriving a blow-up criterion for the stochastic Burgers’ equation (1.1) with $\nu =0$. However, we keep working with the generalised version (4.1), since the techniques needed are essentially the same. First of all, we we note that for the deterministic Burgers’ equation

$$\begin{aligned} u_t + u \partial _x u = 0, \end{aligned}$$

(4.18)

there exists a well-known blow-up criterion. For this one-dimensional PDE, local existence and uniqueness of strong solutions is guaranteed for initial data in $H^s(\mathbb {T},\mathbb {R}),$ for $s>3/2.$ This can be concluded by deriving a priori estimates and then applying a Picard iteration type theorem. Assume that u is a local solution to (4.18) in $H^s,$ and let $T^*>0.$ The deterministic blow-up criterion states that if

$$\begin{aligned} \int _{0}^{T^{\star }} ||\partial _x u(t)||_\infty \ {{\,\mathrm{d\!}\,}}t < \infty , \end{aligned}$$

(4.19)

then the local solution u can be extended to $[0,T^{\star }];$ and vice versa. We show an identical result for the stochastic case, which reads as follows.

Theorem 4.6

Blow-up criterion for stochastic Burgers’ Let us define the stopping times $\tau ^2$ and $\tau ^{\infty }$ by

$$\begin{aligned} \tau ^2= & {} \lim _{n \rightarrow \infty } \tau _n^2, \qquad \tau _n^2 = \inf \left\{ t \ge 0: ||u(t, \cdot )||_{H^2} \ge n \right\} , \\ \tau ^{\infty }= & {} \lim _{n \rightarrow \infty } \tau _n^{\infty }, \qquad \tau _n^{\infty } = \inf \left\{ t \ge 0: \int _0^t ||\partial _x u(s, \cdot )||_\infty \ {{\,\mathrm{d\!}\,}}s\ge n \right\} . \end{aligned}$$

Then $\tau ^2 = \tau ^{\infty },$ $\mathbb {P}$ almost surely.

Remark 4.7

The norm in the definition of $\tau _n^2$ in Theorem 4.6 could be replaced with $||u(t, \cdot )||_{H^s},$ for any $s> 3/2,$ but we choose $s=2$ for the sake of simplicity.

Proof of Theorem 4.6

We show both $\tau ^{2}\le \tau ^{\infty }$ and $\tau ^{\infty }\le \tau ^{2}$ in two steps.

Step 1: $\tau ^{2}\le \tau ^{\infty }$. This is straight-forward to establish, since it follows from the well-known Sobolev embedding inequality (2.3) that

$$\begin{aligned} ||\partial _x u||_\infty \lesssim ||u||_{H^2}. \end{aligned}$$

Step 2: $\tau ^{\infty }\le \tau ^{2}$. Consider the hyper-regularised Burgers’ truncated equation introduced in (4.3), which is given by

$$\begin{aligned} {{\,\mathrm{d\!}\,}}u^{\nu }_{r} + \theta _{r}(||\partial _{x}u||_\infty )u^{\nu }_{r}\partial _{x}u^{\nu }_{r} {{\,\mathrm{d\!}\,}}t+\mathcal {Q}u^{\nu }_{r} {{\,\mathrm{d\!}\,}}W_{t}= \nu \partial _{xx}^{5} u^{\nu }_{r} {{\,\mathrm{d\!}\,}}t +\frac{1}{2} \mathcal {Q}^{2}u^{\nu }_{r} {{\,\mathrm{d\!}\,}}t.\qquad \end{aligned}$$

(4.20)

For the sake of simplifying notation, we omit the subscripts $\nu$ and r throughout the proof. We proceed now to compute the evolution of the $H^{2}$ norm of u. First, we obtain

$$\begin{aligned} \frac{1}{2} {{\,\mathrm{d\!}\,}}||u||^{2}_{L^{2}}&+ \theta (||\partial _{x}u||_\infty )\langle u \partial _{x} u, u\rangle _{L^{2}} {{\,\mathrm{d\!}\,}}t + \langle \mathcal {Q} u, u \rangle _{L^{2}} \ {{\,\mathrm{d\!}\,}}W_{t} \\&= \nu \langle \partial _{xx}^{5}u,u \rangle _{L^{2}} {{\,\mathrm{d\!}\,}}t +\frac{1}{2} \langle \mathcal {Q}^2 u, u \rangle _{L^2} {{\,\mathrm{d\!}\,}}t + \frac{1}{2} \displaystyle \langle \mathcal {Q} u, \mathcal {Q} u \rangle _{L^2} {{\,\mathrm{d\!}\,}}t. \end{aligned}$$

Integrating the dissipative term by parts, applying Hölder’s inequality in the nonlinear term, and using the cancellation property (2.5), we derive the inequality

$$\begin{aligned} {{\,\mathrm{d\!}\,}}||u||^{2}_{L^{2}} + 2 \langle \mathcal {Q} u, u \rangle _{L^{2}} {{\,\mathrm{d\!}\,}}W_{t} \lesssim ||u||^{2}_{L^{2}} \ {{\,\mathrm{d\!}\,}}t. \end{aligned}$$

(4.21)

The $L^2$ norm of $\partial _{xx} u$ evolves as follows:

$$\begin{aligned}&\frac{1}{2} {{\,\mathrm{d\!}\,}}||\partial _{xx} u||^{2}_{L^{2}} + \theta (||\partial _{x}u||_\infty )\langle \partial _{xx} (u \partial _{x}u), \partial _{xx} u\rangle _{L^{2}} {{\,\mathrm{d\!}\,}}t + \langle \partial _{xx} \mathcal {Q} u, \partial _{xx} u \rangle _{L^{2}} \ {{\,\mathrm{d\!}\,}}W_{t} \\&\quad = \nu \langle \partial _{xx}^{6} u, \partial _{xx} u \rangle _{L^{2}} {{\,\mathrm{d\!}\,}}t +\frac{1}{2} \langle \partial _{xx} \mathcal {Q}^2 u, \partial _{xx} u \rangle _{L^2} {{\,\mathrm{d\!}\,}}t + \frac{1}{2} \langle \partial _{xx} \mathcal {Q} u, \partial _{xx} \mathcal {Q} u \rangle _{L^2} {{\,\mathrm{d\!}\,}}t. \end{aligned}$$

Again, applying standard estimates for the nonlinear term, dropping the dissipative term, and invoking inequality (2.6), one obtains

$$\begin{aligned} {{\,\mathrm{d\!}\,}}||\partial _{xx} u||^{2}_{L^{2}} + 2 \langle \partial _{xx} \mathcal {Q} u, \partial _{xx} u \rangle _{L^{2}} \ {{\,\mathrm{d\!}\,}}W_{t} \lesssim \left( ||\partial _{x}u||_\infty +1 \right) ||\partial _{xx}u||^{2}_{L^{2}} \ {{\,\mathrm{d\!}\,}}t.\qquad \quad \end{aligned}$$

(4.22)

Hence, combining inequalities (4.21) and (4.22), we get

$$\begin{aligned} {{\,\mathrm{d\!}\,}}||u||^{2}_{H^{2}} +2 \left( \langle \mathcal {Q} u, u \rangle _{L^2} + \langle \partial _{xx} \mathcal {Q} u,\partial _{xx}u \rangle _{L^2} \right) {{\,\mathrm{d\!}\,}}W_{t} \lesssim \left( ||\partial _{x}u||_\infty +1 \right) ||u||^{2}_{H^{2}} \ {{\,\mathrm{d\!}\,}}t.\nonumber \\ \end{aligned}$$

(4.23)

To finish the argument, one has to treat the stochastic term. To do so, apply Itô’s formula for the logarithmic function, in a similar fashion as carried out in [8]. Without loss of generality, we assume $||u||_{H^2} \ne 0$ and obtain

$$\begin{aligned} {{\,\mathrm{d\!}\,}}\ \text {log } \left( ||u||^{2}_{H^2} \right) = \frac{{{\,\mathrm{d\!}\,}}||u||^{2}_{H^2} }{||u||^{2}_{H^2}}-\frac{{{\,\mathrm{d\!}\,}}N_{t}}{\left( ||u||^{2}_{H^2}\right) ^{2}}, \end{aligned}$$

(4.24)

where $N_t$ is the local martingale

$$\begin{aligned} N_{t}:= 2 \int _{0}^{t} \left( \langle \mathcal {Q} u (s), u(s) \rangle _{L^2} + \langle \partial _{xx} \mathcal {Q} u(s), \partial _{xx} u(s) \rangle _{L^2} \right) ^2 {{\,\mathrm{d\!}\,}}W_{s}. \end{aligned}$$

By making use of (4.23), we can estimate the derivative of the logarithm as

$$\begin{aligned} {{\,\mathrm{d\!}\,}}\ \text {log} \left( ||u||^{2}_{H^2}\right) \lesssim \frac{\left( 1+||\partial _{x}u||_\infty \right) ||u||^{2}_{H^2}}{||u||^{2}_{H^2}} {{\,\mathrm{d\!}\,}}t+ {{\,\mathrm{d\!}\,}}M_{t}, \end{aligned}$$

where $M_t$ is a local martingale defined as

$$\begin{aligned} M_t = 2 \int _0^t \frac{\langle \mathcal {Q} u(s), u(s) \rangle _{L^2} +\langle \partial _{xx} \mathcal {Q} u(s), \partial _{xx} u(s) \rangle _{L^2} }{||u(s)||^{2}_{H^2}} \ {{\,\mathrm{d\!}\,}}W_{s}. \end{aligned}$$

Integrating in time, we derive

$$\begin{aligned} \text {log} \left( ||u(t)||^{2}_{H^2} \right) \lesssim \text {log } \left( ||u(0)||^{2}_{H^2}\right) + \int _0^t \left( 1+||\partial _{x}u(s)||_\infty \right) {{\,\mathrm{d\!}\,}}s + \int _{0}^{t} {{\,\mathrm{d\!}\,}}M_{s}.\nonumber \\ \end{aligned}$$

(4.25)

We need a good control of the semimartingale term in (4.25), which can done by invoking Burkholder–Davis–Gundy inequality (2.7). Hence, it suffices to estimate the quadratic variation of the stochastic process

$$\begin{aligned} \left[ \int _{0}^{t} \ {{\,\mathrm{d\!}\,}}M_{s} \right] _{t}= & {} 4 \int _{0}^{t} \frac{\left( \langle \mathcal {Q} u(s), u(s) \rangle _{L^2} +\langle \partial _{xx} \mathcal {Q} u(s), \partial _{xx} u(s) \rangle _{L^2} \right) ^{2}}{||u(s)||^{4}_{H^2} } {{\,\mathrm{d\!}\,}}s \\\lesssim & {} \int _{0}^{t} \frac{||u(s)||^{4}_{H^{2}} }{||u(s)||^{4}_{H^2} } \ {{\,\mathrm{d\!}\,}}s \lesssim t. \end{aligned}$$

Here, we have used estimation (4.16) to bound the numerator term in the integral above. Finally, applying Burkholder–Davis–Gundy inequality (2.7), we obtain

$$\begin{aligned} \mathbb {E} \left[ \displaystyle \sup _{s\in [0,t]} \left| \int _{0}^{s} \ {{\,\mathrm{d\!}\,}}M_{\tau } \right| \right] \lesssim \sqrt{t}. \end{aligned}$$

(4.26)

Taking expectation on (4.25) and using estimate (4.26), we establish

$$\begin{aligned} \mathbb {E}\left[ \displaystyle \sup _{s\in [0,\tau ^{\infty }_{n}\wedge m ]} \displaystyle \log \left( ||u||^{2}_{H^{2}} \right) \right] \lesssim \displaystyle \log \left( ||u_{0}||^{2}_{H^{2}} \right) + m(n+1) + \sqrt{m} < \infty ,\qquad \end{aligned}$$

(4.27)

for any $n, m \in \mathbb {N}$. Therefore

$$\begin{aligned} \mathbb {E} \left[ \text {log} \left( \displaystyle \sup _{s\in [0,\tau ^{\infty }_{n}\wedge m ]} \left( ||u(s)||_{H^2} \right) ^{2} \right) \right] < \infty , \end{aligned}$$

which in particular means that for $n,m \in \mathbb {N},$ $\displaystyle \sup _{s\in [0,\tau ^{\infty }_{n}\wedge m ]} ||u(s)||_{H^2}$ is a finite random measure $\mathbb {P}$ almost surely. To conclude the proof, one just needs to notice that if

$$\begin{aligned} \mathbb {P}\left( \displaystyle \sup _{s\in [0,\tau ^{\infty }_{n}\wedge m ]} ||u(s)||^{2}_{H^{2}} < \infty \right) =1, \end{aligned}$$

for every $n,m\in \mathbb {N}$, then $\tau ^{\infty }\le \tau ^{2}$ (cf. [8]). Note that we have omitted subscripts. Nevertheless, Fatou’s Lemma enables us to take limits on $u^{\nu }_{r}$ as $\nu$ tends to zero and r to infinity, recovering our result in the limit. $\square$

4.3 Global well-posedness of a viscous stochastic Burgers’ equation

The viscous stochastic Burgers’ equation is given by

$$\begin{aligned} {{\,\mathrm{d\!}\,}}u + u \partial _x u {{\,\mathrm{d\!}\,}}t + \mathcal {Q} u \circ {{\,\mathrm{d\!}\,}}W_t = \nu \partial _{xx}u {{\,\mathrm{d\!}\,}}t \end{aligned}$$

(4.28)

in the Stratonovich sense, supplemented with initial condition $u(x,0)=u_{0}(x)$. In the Itô sense, this can be rewritten as

$$\begin{aligned} {{\,\mathrm{d\!}\,}}u + u \partial _xu {{\,\mathrm{d\!}\,}}t + \mathcal {Q} u {{\,\mathrm{d\!}\,}}W_t = \frac{1}{2} \mathcal {Q}^2 u {{\,\mathrm{d\!}\,}}t +\nu \partial _{xx}u {{\,\mathrm{d\!}\,}}t. \end{aligned}$$

(4.29)

The main result of this section establishes the global regularity of solutions of (4.29).

Theorem 4.8

Let $u_{0} \in H^{2} (\mathbb {T},\mathbb {R}).$ Then there exists a unique maximal strong global solution $u:[0,\infty ) \times \mathbb {T} \times \Xi \rightarrow \mathbb {R}$ of the viscous stochastic Burgers’ equation (4.29) with $\nu > 0$ in $H^{2} (\mathbb {T},\mathbb {R})$.

For our purpose, we prove the following result:

Proposition 4.9

Let $u_{0}\in H^{2}(\mathbb {T},\mathbb {R}),$ $T>0,$ and u(t, x) be a smooth enough solution to Eq. (4.29) defined for $t \in [0,T]$. Then there exists a constant C(T), only depending on $||u_{0}||_{H^2}$ and T,  such that

$$\begin{aligned} \mathbb {E} \left[ \sup _{t \in [0,T]} ||u (t)||^2_{H^{2}} \right] \le C(T). \end{aligned}$$

(4.30)

Once we have proven the a priori estimate (4.30) we can repeat the arguments in Sect. 4.1 to obtain Theorem 4.8. However, since this is repetitive and tedious, we do not explicitly carry out these arguments here. Hence, we just provide a proof of Proposition 4.9.

Proof

Let us start by computing the evolution of the $L^{2}$ norm of the solution u. First note that

$$\begin{aligned} \nu \langle \partial _{xx} u, u \rangle _{L^2} = - \nu ||\partial _{x}u||^{2}_{L^2}. \end{aligned}$$

By taking this into account and applying the same techniques as in Sect. 4.1 (use estimate (2.5)), we obtain

$$\begin{aligned} {{\,\mathrm{d\!}\,}}||u||_{L^2}^2 + 2 \langle \mathcal {Q} u, u \rangle _{L^2} {{\,\mathrm{d\!}\,}}W_t + 2 \nu ||\partial _{x}u||^{2}_{L^2} {{\,\mathrm{d\!}\,}}t \lesssim ||u||^{2}_{L^2} {{\,\mathrm{d\!}\,}}t, \end{aligned}$$

and therefore, by following techniques in Sect. 4.1, we get

$$\begin{aligned} \mathbb {E} \left[ \sup _{t \in [0,T]} ||u(t,\cdot )||^{2}_{L^{2}} \right] \le C_1(T), \ \ \mathbb {E} \left[ \nu \int _{0}^{T} ||\partial _{x}u(s, \cdot )||^{2}_{L^{2}} {{\,\mathrm{d\!}\,}}s \right] \le C_2(T). \end{aligned}$$

The evolution of $||\partial _{x}u||_{L^{2}}$ can be estimated as

$$\begin{aligned} \frac{1}{2} {{\,\mathrm{d\!}\,}}||\partial _{x}u||^{2}_{L^{2}} + \langle \partial _x ( \mathcal {Q} u), \mathcal {Q} u \rangle _{L^2} {{\,\mathrm{d\!}\,}}W_t&= -\langle \partial _{x}(u\partial _{x}u), \partial _{x}u \rangle _{L^2} {{\,\mathrm{d\!}\,}}t \\&\quad + \nu \langle \partial _{x} (\partial _{xx} u), \partial _{x}u \rangle _{L^2} {{\,\mathrm{d\!}\,}}t \\&\quad + \frac{1}{2} \langle \partial _x (\mathcal {Q} u), \partial _x (\mathcal {Q} u) \rangle _{L^2} {{\,\mathrm{d\!}\,}}t \\&\quad + \frac{1}{2} \langle \partial _x (\mathcal {Q}^2 u), \partial _x u \rangle _{L^2} {{\,\mathrm{d\!}\,}}t. \end{aligned}$$

Integrating by parts on the first term of the RHS, using Hölder’s inequality, and Young’s inequality we have that

$$\begin{aligned} -\langle \partial _{x}(u\partial _{x}u), \partial _{x}u \rangle _{L^2}&= \langle u\partial _{x}u,\partial _{xx}u \rangle _{L^{2}} \nonumber \\&\lesssim ||u||_\infty ||\partial _{x}u||_{L^2}||\partial _{xx} u||_{L^{2}}\nonumber \\&\le \frac{1}{2\nu } ||u||_\infty ^{2}||\partial _{x}u||^{2}_{L^2}+\dfrac{\nu }{2} ||\partial _{xx}u||^{2}_{L^{2}}. \end{aligned}$$

(4.31)

The second term on the RHS can be rewritten as

$$\begin{aligned} \nu \langle \partial _{x} (\partial _{xx} u), \partial _{x}u \rangle _{L^2} = -\nu \langle \partial _{xx} u, \partial _{xx} u \rangle _{L^2} = -\nu ||\partial _{xx}u||^{2}_{L^2}. \end{aligned}$$

(4.32)

Finally, the sum in the last line can be estimated (thanks to inequality (2.6) for $\mathcal {P}=\partial _{x}$) as

$$\begin{aligned} \left| \langle \partial _x (\mathcal {Q} u), \partial _x (\mathcal {Q} u) \rangle _{L^2} + \langle \partial _x (\mathcal {Q}^2 u), \partial _x u \rangle _{L^2} \right| \lesssim ||u||^2_{H^1}. \end{aligned}$$

(4.33)

Notice that to bound rigorously the local martingale terms, we should introduce a sequence of stopping times and then by taking expectation those term should vanish. However we don’t repeat this same argument, in order to simplify the exposition. Putting together (4.31–4.33), one derives

$$\begin{aligned}&{{\,\mathrm{d\!}\,}}||\partial _{x}u||^{2}_{L^{2}} + 2 \langle \partial _x (\mathcal {Q} u), \mathcal {Q} u \rangle _{L^2} {{\,\mathrm{d\!}\,}}W_t + \nu ||\partial _{xx}u||^{2}_{L^2} {{\,\mathrm{d\!}\,}}t \\&\quad \le \frac{1}{\nu } \left( ||u||_\infty ^{2} + 1\right) ||\partial _{x}u||^{2}_{L^2} {{\,\mathrm{d\!}\,}}t. \end{aligned}$$

Therefore, mimicking the arguments in Sect. 4.1, one obtains

$$\begin{aligned}&\mathbb {E} \left[ \sup _{t \in [0,T]} ||\partial _{x}u(t)||^{2}_{L^2} \right] \le \mathbb {E} \left[ \sup _{t \in [0,T]} ||\partial _{x}u_{0}||^{2}_{L^2} \right] \nonumber \\&\quad + \frac{1}{\nu } \mathbb {E} \left[ \int _{0}^{T} ||u(s)||_\infty ^{2}||\partial _{x}u(s)||^{2}_{L^{2}} {{\,\mathrm{d\!}\,}}s \right] , \end{aligned}$$

(4.34)

and

$$\begin{aligned}&\nu \mathbb {E} \left[ \int _{0}^{T} ||\partial _{xx} u(s)||^{2}_{L^{2}} {{\,\mathrm{d\!}\,}}s \right] \le \mathbb {E} \left[ \sup _{t \in [0,T]} ||\partial _{x}u_{0}||^{2}_{L^2} \right] \nonumber \\&\quad + \frac{1}{\nu } \mathbb {E} \left[ \int _{0}^{T} ||u(s)||_\infty ^{2}||\partial _{x}u(s)||^{2}_{L^{2}} {{\,\mathrm{d\!}\,}}s \right] . \end{aligned}$$

(4.35)

Now we claim that the following maximum principle holds true

$$\begin{aligned} ||u_t||_{\infty } \le C(T) ||u_0||_{\infty }, \end{aligned}$$

(4.36)

for some positive constant C(T),  which we show in Lemma 4.10. By taking into account (4.36), it is easy to infer that by (4.34) and (4.35), together with Grönwall’s lemma, the quantities

$$\begin{aligned} \mathbb {E} \left[ \sup _{t \in [0,T] } ||\partial _x u(t, \cdot )||^{2}_{L^2} \right] , \quad \nu \mathbb {E} \left[ \int _{0}^{T} ||\partial _{xx} u(s, \cdot )||^{2}_{L^{2}} {{\,\mathrm{d\!}\,}}s \right] , \end{aligned}$$

are bounded by constants depending only on T and $u_0$. Finally, when carrying out the estimates for the $H^2$ norm of u,  one can apply once again similar arguments, realising that thanks to (4.36) the quantities

$$\begin{aligned} \mathbb {E} \left[ \sup _{t \in [0,T] } ||u(t, \cdot )||^{2}_{H^{2}} \right] , \quad \nu \mathbb {E} \left[ \int _{0}^{T} ||\partial ^3_{x} u(s, \cdot )||^{2}_{L^{2}} {{\,\mathrm{d\!}\,}}s \right] , \end{aligned}$$

can be bounded by constants depending only on T and $u_0.$ This concludes the proof. $\square$

Lemma 4.10

The maximum principle (4.36) is satisfied.

Proof

Let Q be of the form $Qu = a(x) \partial _xu + b(x) u,$ where a, b are assumed to be smooth and bounded. We perform the following change of variables: $v(t,x) = e^{b(x)W_t} u(t,x)$, and by Itô’s formula in Stratonovich form we obtain

$$\begin{aligned} {{\,\mathrm{d\!}\,}}v(t,x)&= b(x) v(t,x) \circ {{\,\mathrm{d\!}\,}}W_t + e^{b(x)W_t} \circ {{\,\mathrm{d\!}\,}}u(t,x) \\&= b(x) v(t,x) \circ {{\,\mathrm{d\!}\,}}W_t - u(t,x) \partial _x v(t,x) {{\,\mathrm{d\!}\,}}t - b(x)v(t,x) \circ {{\,\mathrm{d\!}\,}}W_t \\&\quad - a(x) \partial _x v(t,x) \circ {{\,\mathrm{d\!}\,}}W_t + \nu \partial _{xx} v(t,x) {{\,\mathrm{d\!}\,}}t \\&= - u(t,x) \partial _x v(t,x) {{\,\mathrm{d\!}\,}}t - a(x) \partial _x v(t,x) \circ {{\,\mathrm{d\!}\,}}W_t + \nu \partial _{xx} v(t,x) {{\,\mathrm{d\!}\,}}t. \end{aligned}$$

Next, following a similar type of argument used in [4], consider the SDE

$$\begin{aligned} {{\,\mathrm{d\!}\,}}X_t = a(X_t)\circ {{\,\mathrm{d\!}\,}}W_t, \end{aligned}$$

(4.37)

and let $\psi _t(X_0)$ be the corresponding flow of (4.37), which is a diffeomorphism provided a(x) is smooth and satisfies conditions (3.5) and (3.6) (see [37]). By the Itô–Wentzell formula (2.9), we evaluate v along $X_t := \psi _t(X_0)$, getting

$$\begin{aligned} v(t,X_t)&= v(0,X_0) - \int _0^t u(s,X_s) \partial _x v (s,X_s) {{\,\mathrm{d\!}\,}}s + \nu \int _0^t \partial _{xx} v(s,X_s) {{\,\mathrm{d\!}\,}}s \nonumber \\&\quad \underbrace{- \int _0^t a(X_s)\partial _x v (s,X_s) \circ {{\,\mathrm{d\!}\,}}W_s + \int ^t_0 \partial _x v (s,X_s) \circ {{\,\mathrm{d\!}\,}}X_s}_{=0, \,\, a.s.}, \end{aligned}$$

(4.38)

so the stochastic term cancels almost surely. Consider the change of variables $w(t,X_0) := v(t, \psi _t(X_0))$ and by chain rule, obtain

$$\begin{aligned} \partial _x v (t,X_t)&= \frac{\partial \psi _t^{-1}}{\partial x} (\psi _t(X_0)) \frac{\partial w}{\partial X_0}(t,X_0), \\ \partial _{xx} v (t,X_t)&= \frac{\partial ^2 \psi _t^{-1}}{\partial x^2} (\psi _t(X_0))\frac{\partial w}{\partial X_0}(t,X_0) + \left( \frac{\partial \psi _t^{-1}}{\partial x} (\psi _t(X_0))\right) ^2 \frac{\partial ^2 w}{\partial X_0^2}(t,X_0). \end{aligned}$$

Hence, (4.38) is equivalent to a PDE with random coefficients

$$\begin{aligned} \frac{\partial w}{\partial t} + \tilde{w} \frac{\partial w}{\partial X_0} = \tilde{\nu } \frac{\partial ^2 w}{\partial X_0^2}, \end{aligned}$$

(4.39)

where

$$\begin{aligned} \tilde{w}&:= \frac{\partial \psi _t^{-1}}{\partial x} (\psi _t(X_0)) u(t,\psi _t(X_0)) - \nu \frac{\partial ^2 \psi _t^{-1}}{\partial x^2} (\psi _t(X_0)), \\ \tilde{\nu }&:= \nu \cdot \left( \frac{\partial \psi _t^{-1}}{\partial x} (\psi _t(X_0))\right) ^2. \end{aligned}$$

We claim that w satisfies the maximum principle $\Vert w_t\Vert _\infty \le \Vert w_0\Vert _\infty$. Indeed, we perform the change of variables $f(t,X_0) = e^{-\alpha t}w(t,X_0)$ for any $\alpha > 0$. We obtain

$$\begin{aligned} \frac{\partial f}{\partial t} + \tilde{w}\frac{\partial f}{\partial X_0} = -\alpha f(t,X_0) + \tilde{\nu }\frac{\partial ^2 f}{\partial X_0^2}. \end{aligned}$$

(4.40)

Now, assume by contradiction that f attains a maximum at $(t^*, X_0^*) \in [0,T] \times {\mathbb {T}}$ such that $t^* > 0$. Then we have $\partial _t f(t^*, X_0^*) \ge 0$, $\partial _{X_0} f(t^*, X_0^*) = 0,$ and $\partial _{X_0}^2 f(t^*, X_0^*) \le 0$. However, since $f(t,\cdot ) > 0$ for all $t>0$, we obtain $-\alpha f(t,\cdot ) < 0$. Also since $\tilde{\nu } > 0$, the left-hand side of (4.40) is nonnegative but the right-hand side is strictly negative which is a contradiction. Taking $\alpha \rightarrow 0$, the claim follows.

Since $\psi _t$ is a diffeomorphism, we have $||v(t,\cdot )||_\infty = ||w(t,\cdot )||_\infty$ so the maximum principle also follows for v. Hence, we have shown

$$\begin{aligned} \left\| e^{b(x)W_t} u_t \right\| _\infty = \Vert v_t\Vert _\infty \le \Vert v_0\Vert _\infty = \Vert u_0\Vert _\infty , \end{aligned}$$

for all $t>0$. Now, let $c>0$ be a constant such that $|b(x)| > c$ for all $x \in {\mathbb {R}}$. Then we have

$$\begin{aligned} \Vert u_t\Vert _\infty \le e^{-cW_t} \Vert u_0\Vert _\infty \le C(T) \Vert u_0\Vert _\infty , \end{aligned}$$

where $C(T) = \sup _{0\le t \le T} e^{-cW_t} < \infty$. With this, we conclude the proof. $\square$

5 Conclusion and outlook

In this paper, we studied the solution properties of a stochastic Burgers’ equation on the torus and the real line, with the noise appearing in the transport velocity. We have shown that this stochastic Burgers’ equation is locally well-posed in $H^s(\mathbb {T},\mathbb {R}),$ for $s>3/2,$ and furthermore, found a blow-up criterion which extends to the stochastic case. We also proved that if the noise is of the form $\xi (x)\partial _x u \circ dW_t$ where $\xi (x) = \alpha x + \beta$, then shocks form almost surely from a negative slope. Moreover, for a more general type of noise, we showed that blow-up occurs in expectation, which follows from the previously mentioned stochastic blow-up criterion. Also, in the weak formulation of the problem, we provided a Rankine–Hugoniot type condition that is satisfied by the shocks, analogous to the deterministic shocks. Finally, we also studied the stochastic Burgers’ equation with a viscous term, which we proved to be globally well-posed in $H^2$.

Let us conclude by proposing some future research directions and open problems that have emerged during the course of this work:

• Regarding shock formation, it is natural to ask whether our results can be extended to show that shock formation occurs almost surely for more general types of noise.

• Another possible question is whether our global well-posedness result can be extended for the viscous Burgers’ equation with the Laplacian replaced by a fractional Laplacian $(-\Delta )^{\alpha },$ $\alpha \in (0,1)$. The main difficulty here is that in the stochastic case, the proof of the maximum principle (Proposition (4.10)) does not follow immediately since the pointwise chain rule for the fractional Laplacian is not available. In the deterministic case, this question has been settled and it is known that the solution exhibits a very different behaviour depending on the value of $\alpha$: for $\alpha \in [1/2,1]$, the solution is global in time, and for $\alpha \in [0,1/2)$, the solution develops singularities in finite time [33, 35]. Interestingly, when an Itô noise of type $\beta u {{\,\mathrm{d\!}\,}}W_t$ is added, it is shown in [39] that the probability of solutions blowing up for small initial conditions tends to zero when $\beta > 0$ is sufficiently large. It would be interesting to investigate whether the transport noise considered in this paper can also have a similar regularising effect on the equation.

• Similar results could be derived for other one-dimensional equations with non-local transport velocity [5, 13, 14]. For instance, the so called CCF model [5] is also known to develop singularities in finite time, although by a different mechanism to that of Burgers’. To our knowledge, investigating these types of equations with transport noise is new.