Homogenization in perforated domains with mixed conditions

Abstract.

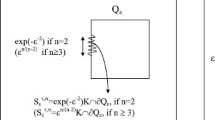
In this paper we study the asymptotic behaviour of the Laplace equation in a periodically perforated domain of R ⁿ, where we assume that the period is ε and the size of the holes is of the same order of greatness. An homogeneous Dirichlet condition is given on the whole exterior boundary of the domain and on a flat portion of diameter $\varepsilon ^{ \frac{n}{n-2}}$ if $n>2$ ($\exp (-\varepsilon ^{-2})$, if n=2) of the boundary of every hole, while we take an homogeneous Neumann condition elsewhere.