Oriented matroids from triangulations of products of simplices

Abstract

We introduce a construction of oriented matroids from a triangulation of a product of two simplices. For this, we use the structure of such a triangulation in terms of polyhedral matching fields. The oriented matroid is composed of compatible chirotopes on the cells in a matroid subdivision of the hypersimplex, which might be of independent interest. In particular, we generalize this using the language of matroids over hyperfields, which gives a new approach to construct matroids over hyperfields. A recurring theme in our work is that various tropical constructions can be extended beyond tropicalization with new formulations and proof methods.

1 Introduction

1.1 Oriented matroids and matching fields

An oriented matroid is a combinatorial object abstracting linear dependence over ${{\mathbb {R}}}$, and can be thought as a matroid with sign data, i.e., with signs attached to its bases that satisfy certain exchange axioms. The standard example of an oriented matroid is given by the signs of the maximal minors of a real matrix, but not all oriented matroids are realizable, meaning they arise this way. Oriented matroids play an important role in discrete and computational geometry as well as optimization, ranging from the study of geometric configurations to linear programming; they also make appearances in algebraic geometry and topology [14, Chapter 1 & 2].

A matching field is a collection of matchings of the complete bipartite graph $K_{\textsf{R},\textsf{E}}\cong K_{d,n}$, one perfect matching between $\textsf{R}$ and $\sigma$ for every subset $\sigma \subset \textsf{E}$ of size d; here $\textsf{R}$ is a set of size d,¹ and $\textsf{E}$ is a set of size $n\ge d$ which we refer to as the ground set. A systematic construction of matching fields is to take all weight-maximal $(d\times d)$ matchings selected by a generic matrix on the complete bipartite graph, yielding a coherent matching field. They were introduced by Sturmfels and Zelevinsky in [47] to study determinantal ideals: a matching field is essentially given by choosing a term from each maximal minor of a generic matrix, and a coherent matching field corresponds to choosing the leading term with respect to some monomial order. Along with follow-up works [13, 32], it was demonstrated that much of the Gröbner theory of maximal minors can be deduced from the more general linkage property that is analogous to the exchange property of matroids.

Signed tropicalization shows that coherent matching fields induce realizable oriented matroids. Sturmfels and Zelevinsky noted this in their paper, which illustrates the aforementioned analogy between linkage property and matroid exchange axiom. Motivated by their remarks, we note that the linkage property is not enough to guarantee an oriented matroid in Example 3.13. Nevertheless, our first main result is that the statement is true for polyhedral matching fields, which arise from triangulations of the product of two simplices. Every coherent matching field is polyhedral while every polyhedral matching field is linkage, so our result extends the relation between coherent matching fields and realizable oriented matroids to an appropriate generality. We elaborate more on why polyhedral matching fields form an interesting and important intermediate class of matching fields in the next subsections, but first we state our main theorem.

By fixing an arbitrary ordering for $\textsf{R}$ and $\textsf{E}$, every matching can be thought as a permutation. We define the sign of the matching as the sign of the permutation.

Theorem A

(Theorem 3.7) Given a polyhedral matching field $(M_\sigma )$ and a full $d\times n$ sign matrix A, the sign map $\upchi :\left( {\begin{array}{c}\textsf{E}\\ d\end{array}}\right) \rightarrow \{+,-\}$ defined by

$$\begin{aligned} \sigma \mapsto \text {sign}(M_\sigma )\prod _{e\in M_\sigma }A_e \hspace{5.0pt}\end{aligned}$$

(1)

is the chirotope of a uniform oriented matroid (Definition 2.1).

Conceptually, the theorem says that instead of taking maximal minors, we can pick out one term per determinant (carefully) and still obtain an oriented matroid. Hence, in some sense, the matchings take the role of signed bases of an oriented matroid. We show that this correspondence goes even further by considering other special graphs associated with a polyhedral matching field, such as linkage pd-graphs and Chow pd-graphs, and describe how these graphs directly yield objects such as signed circuits and signed cocircuits of the oriented matroid in Theorem A. We also develop a notion of duality for matching fields that descends to the duality of oriented matroids via Theorem A.

1.2 Connections to complexity questions

Our work adds a new piece to the connection between two major open complexity questions. On one hand, Smale’s 9th problem asks for a strongly polynomial algorithm in linear programming. Oriented matroids play an important role for this as it is the framework for the simplex method [22] which is still a natural candidate for such a strongly polynomial algorithm. On the other hand, determining the winning states of a mean payoff game is a problem in NP $\cap$ co-NP [27] but no polynomial time algorithm is known. The latter problem is also equivalent to deciding feasibility of a tropical linear program [1] and it turns out that matching fields are the combinatorial framework for describing tropical linear programming [31]. From the viewpoint of mean payoff games, the matchings can be considered as partial strategies. While the tropicalization of the simplex method [2, 12] based on sign patterns already gave a connection between pivoting and strategy iteration, we directly derive the correspondence on the level of oriented matroids. The interplay between classical and tropical linear programming has already lead to a proof that a wide class of interior point methods can not be strongly polynomial [3].

An indicator on the hardness of tropical linear programming comes from the richness of the oriented matroids arising for coherent matching fields. If only a subclass of uniform oriented matroids arises from coherent matching fields, this would exhibit a deep structural difference between linear programming and tropical linear programming. On the other hand, if all realizable uniform oriented matroids arise from coherent matching fields, then a combinatorial algorithm for tropical linear programming would already solve linear programming efficiently. Hence, our work leads to the following open question.

Question 1 Which oriented matroids are realizable from a coherent matching field or a polyhedral matching field? Numerically, what is the asymptotic fraction of realizable chirotopes one gets from polyhedral matching fields?

1.3 Triangulations of $\triangle _{d-1}\times \triangle _{n-1}$ and matroid subdivisions, with signs

Triangulations of a product of two simplices are fundamental in combinatorics and algebraic geometry [7, 17, 24], and via the connection explained in Sect. 1.2 also in computer science, just to name a few references. Matroid subdivisions are fundamental objects emerging from the context of valuated matroids and tropical linear spaces [19, 43], K-theory [46], and discrete convex analysis [36].

Drawing various motivations from the literature, we take a crucial new point of view and directly connect triangulations of products of simplices, matroid subdivisions and oriented matroids. Besides questions from complexity, we were inspired by the connection between regular subdivisions of products of simplices and tropical convexity established in [18]. This already lead to the concept of a tropical oriented matroid by Ardila and Develin [9], which is equivalent to the (not-necessarily regular) subdivisions of a product of two simplices [29, 37]. Polyhedral matching fields, or more precisely the pointed version thereof, give yet another equivalent description in the generic case of triangulations [32, 38].

In Section 5 of their seminal paper, Ardila and Develin asked for a connection between oriented matroids and tropical oriented matroids, especially for exploring questions related to non-realizability. The extraction of a realizable oriented matroid from a regular triangulation of $\triangle _{d-1}\times \triangle _{n-1}$ with signs is implicit in [12], but with our perspective, we finally manage to formalize such speculated connection in full generality. As asymptotically almost every triangulation of the product of two simplices is non-regular [41], our work allows a vast generalization. In particular, we derive Ringel’s non-realizable oriented matroid of rank 3 on 9 elements from a non-regular triangulation of $\triangle _2 \times \triangle _5$ in Example 4.19, breaking new ground for the study of realizability of oriented matroids.

Now we sketch our proof of Theorem A. Every triangulation of $\triangle _{d-1}\times \triangle _{n-1}$ gives rise to a matroid subdivision of the hypersimplex. Considering matroid polytopes allows us to manipulate the sign map $\upchi$ geometrically; in particular, the restriction of $\upchi$ to each subpolytope is a chirotope. Finally, we establish a general principle (Theorem 3.9) to show $\upchi$ is a chirotope from local information. The interaction between oriented matroids and matroid subdivisions seems to be largely unexplored, although some recent works on positive Dressians and positive tropical Grassmannians [10, 34, 44] share some common ideas with ours: whenever the uniform oriented matroid produced from Theorem A is positively oriented, the matroid subdivision above is a positroid subdivision.

1.4 Matroids over hyperfields

In [11], Baker and Bowler introduced the theory of matroids over hyperfields, which provides a common framework for many “matroids with extra data” theories. The base of the theory is the notion of hyperfields, which can be thought as ordinary fields with multi-valued addition. Besides unifying parallel notions and propositions among these theories, the new language allows one to explain features in a particular matroid theory using the property of its base hyperfield, which we do so here by classifying all hyperfields in which Theorem A is valid: they satisfy the inflation property [5, 35]. Unlike the case of oriented matroids, such an extension to hyperfields is new even for coherent matching fields.

Taking maximal minors of a matrix over a field yields a Grassmann–Plücker function, but as taking determinant over hyperfields is usually multi-valued, this standard method no longer works. While one can still construct matroids over some common hyperfields by pushing forward matroids over fields, the approach does not works when the hyperfield is not an image of a field either. Hence, as a contribution to the theory, our work gives a new way to construct matroids over hyperfields, which works for all hyperfields up to inflation (Corollary 5.11).

1.5 Organization of the paper

In Sect. 2, we collect essential definitions and background for the central objects in this paper. We prove Theorem A in Sect. 3. More axiomatic connections between matching fields and oriented matroids are introduced in Sect. 4. We extend our work to matroids over hyperfields in Sect. 5, where we also give a brief introduction to the theory.

This paper focuses primarily on the combinatorial aspects of the oriented matroid constructed in Theorem A. On the other hand, the celebrated Topological Representation Theorem of Folkman and Lawrence [21] states that there is a correspondence between oriented matroids and pseudosphere arrangements up to cellular homeomorphism. In a follow-up paper [16], we explain how this correspondence can be realized in our setting using the technique of Viro’s patchworking. This work makes heavy use of the results in Sect. 4.3, and makes precise the illustrations of Example 4.19.

2 Background

Throughout the paper, we fix a ground set $\textsf{E}$ of size n and a set $\textsf{R}$ of size $d \le n$. We often identify $\textsf{E},\textsf{R}$ with $[n] = \{1,2,\dots ,n\}$ and [d], hence fixing an ordering for them; we use $\{+,-,0\}$ and $\{1,-1,0\}$ for signs interchangeably, and we adopt the ordering $+,->0$ of signs.

2.1 Oriented matroids

We refer the reader to [14] for a comprehensive survey on oriented matroids. As in the case of matroids, there are multiple equivalent axiom systems for oriented matroids, but we mainly use the following definition.

Definition 2.1

A chirotope on $\textsf{E}$ of rank d is a non-zero, alternating map $\upchi :\textsf{E}^d\rightarrow \{+,-,0\}$ that satisfies the Grassmann–Plücker (GP) relation:

For any $x_1,\ldots ,x_{d-1},y_1,\ldots , y_{d+1}\in \textsf{E}$, the $d+1$ expressions

$$\begin{aligned} (-1)^k \upchi (x_1,\ldots ,x_{d-1},y_k)\upchi (y_1,\ldots ,\widehat{y_k},\ldots ,y_{d+1}), \qquad k=1,\ldots , d+1, \end{aligned}$$

either contain both a positive and a negative term, or are all zeros. An oriented matroid on $\textsf{E}$ of rank d is specified by a chirotope up to global sign change.

With the ordering on $\textsf{E}$, we can specify a chirotope by its values over $\left( {\begin{array}{c}\textsf{E}\\ d\end{array}}\right)$ using the alternating property, here $\upchi (\sigma ):=\upchi (\sigma _1,\ldots ,\sigma _d)$ where $\sigma =\{\sigma _1<\cdots <\sigma _d\}$.

Example 2.2

A chirotope is the generalization of the signs of maximal minors of a real matrix (oriented matroids coming from this way are said to be realizable). More precisely, let $A \in {{\mathbb {R}}}^{d \times n}$ be a rectangular matrix with rank d. Then

$$\begin{aligned} \upchi (j_1,j_2,\dots ,j_d):= \text {sign}\det \left( a^{(j_1)},a^{(j_2)},\dots ,a^{(j_d)}\right) , \end{aligned}$$

where $a^{(j_k)}$ denotes columns of A, is the chirotope of an oriented matroid of rank d. Note that we can normalize A to the form $(I_{d,d}|B)$ for some $B \in {{\mathbb {R}}}^{d \times (n-d)}$ by multiplying with the inverse of a full-rank submatrix of A. This incurs only a global sign change of the chirotope.

To state an important characterization of chirotopes, we briefly recall the definition of a matroid.

Definition 2.3

Let $\mathcal {B}(M)$ be a non-empty subset of $\left( {\begin{array}{c}\textsf{E}\\ d\end{array}}\right)$. Setting $\textbf{e}_B:=\sum _{i\in B}{} \textbf{e}_i\in \mathbb {R}^\textsf{E}$ for each $B\in \mathcal {B}(M)$, M is a matroid with bases $\mathcal {B}(M)$ if the convex hull of $\{\textbf{e}_B:B\in \mathcal {B}(M)\}$ has only edge directions $\textbf{e}_i -\textbf{e}_j$ for unit vectors $\textbf{e}_i, \textbf{e}_j$. The polytope itself is the matroid polytope of M and the rank of M is d.

$\left( {\begin{array}{c}\textsf{E}\\ d\end{array}}\right)$ itself is the collection of bases of a matroid, known as the uniform matroid $U_{d,n}$; in such case the matroid polytope is the hypersimplex.

Now if we know in advance that there is a matroid underneath, we can check whether a sign map is a chirotope locally [14, Theorem 3.6.2].

Proposition 2.4

Suppose $\upchi :\textsf{E}^d\rightarrow \{+,-,0\}$ is an alternating map. Then $\upchi$ satisfies the GP relation if and only if ${\underline{\upchi }}:=\{\sigma \in \left( {\begin{array}{c}\textsf{E}\\ d\end{array}}\right) : \upchi (\sigma )\ne 0\}$ is the collection of bases of some matroid and that $\upchi$ satisfies the 3-term GP relation:

For any $x_1,x_2,y_1,y_2\in \textsf{E},X:=\{x_3,\ldots ,x_d\}\subset \textsf{E}$, the three expressions

$$\begin{aligned} \upchi (x_1,x_2,X)\upchi (y_1,y_2,X), \upchi (x_1,y_1,X)\upchi (y_2,x_2,X), \upchi (x_1,y_2,X)\upchi (x_2,y_1,X), \end{aligned}$$

(2)

either contain both a positive and a negative term, or are all zeros.

2.2 Matching fields

A (d, n)-matching field is a collection of perfect matchings $M_\sigma$’s on bipartite node sets $\textsf{R}\sqcup \sigma$, one for each d-subset $\sigma$ of $\textsf{E}$. We use the terminology pd-graphs to denote subgraphs of $K_{d,n}$ which are composed of edges of the matchings.²

Example 2.5

(Diagonal matching field [47]) The diagonal matching field has exactly the edges $\{(1,j_1),\dots ,(d,j_d)\}$ in the matching on the ordered subset $j_1< j_2< \cdots < j_d$ of $\textsf{E}$. For $d=2$ and $n=4$ this is depicted in Fig. 1.

Fig. 1

The diagonal (2, 4)-matching field

Example 2.6

(Coherent matching field) A (d, n)-matching field is coherent if there is a generic matrix $M \in {{\mathbb {R}}}^{d \times n}$ such that the matching on $\textsf{R}\sqcup \sigma$ is the weight-maximal perfect matching induced by the entries of M as weights on $K_{d,n}$. The genericity here means that the weight-maximal matching is unique. A diagonal matching field is coherent as it is induced by the weight matrix $((i-1) \cdot (j-1))_{(i,j) \in [d] \times [n]}$.

Example 2.7

(Linkage matching field) A matching field is linkage if it fulfills a local compatibility condition. Namely, for every $(d+1)$-subset $\tau$ of $\textsf{E}$, the union of the matchings on $\tau$ is a spanning tree on $\textsf{R}\sqcup \tau$; such a tree is a linkage pd-graph. These graphs were called ‘linkage covectors’ in [32] but we show later that they can give rise to signed circuits. Note that each node in $\textsf{R}$ of a linkage pd-graph has to have degree 2 by a counting argument. Figure 3 shows a linkage matching field which is the pointed extension (see Sect. 3.1) of the non-linkage matching field depicted in Fig. 2. It was used in [47, Proposition 2.3] to show the existence of non-coherent linkage matching fields.

Fig. 2

This is the smallest matching field which is not linkage

Fig. 3

This is the smallest linkage matching field which is not polyhedral

2.3 Triangulations of $\triangle _{d-1}\times \triangle _{n-1}$ and polyhedral matching fields

We give a brief introduction to the necessary polyhedral notions and refer the reader to [17] for more details. We denote the $(k-1)$-simplex by $\triangle _{k-1}$, that is the convex hull of k affinely independent points. Even if we are mainly interested in combinatorial properties, we use the standard embedding $\triangle _{k-1} = \text {conv}\{\textbf{e}_i :i \in [k]\} \subset {{\mathbb {R}}}^k$. The product $\triangle _{d-1}\times \triangle _{n-1}$ of a $(d-1)$-simplex and an $(n-1)$-simplex is the convex hull

$$\begin{aligned} \triangle _{d-1}\times \triangle _{n-1} = \text {conv}\{ (\textbf{e}_i,\textbf{e}_j) :i \in [d],j \in [n] \}\subset \mathbb {R}^d\times \mathbb {R}^n \hspace{5.0pt}. \end{aligned}$$

A triangulation of $\triangle _{d-1}\times \triangle _{n-1}$ is a collection of full-dimensional simplices $\mathcal {T}$ whose vertices form a subset of the vertices of $\triangle _{d-1}\times \triangle _{n-1}$, such that

• 1. (Union) the union of all simplices in $\mathcal {T}$ is $\triangle _{d-1}\times \triangle _{n-1}$,

• 2. (Intersection) two simplices in $\mathcal {T}$ intersect in a common face.

Each simplex in $\mathcal {T}$ gives rise to a subgraph of the complete bipartite graph on the vertex set $\textsf{R}\sqcup \textsf{E}$ by identifying a vertex $(\textbf{e}_i,\textbf{e}_j)$ with an edge. Rephrasing the definition of a triangulation in terms of graphs leads to the following characterization.

Proposition 2.8

([7, Proposition 7.2]) A set of graphs on the bipartite node set $\textsf{R}\sqcup \textsf{E}$ encodes the maximal simplices of a triangulation of $\triangle _{d-1}\times \triangle _{n-1}$ if and only if:

• 1. Each graph is a spanning tree.

• 2. For each tree G and each edge e of G, either $G - e$ has an isolated node or there is another tree H containing $G - e$.

• 3. If two trees G and H contain perfect matchings on $I \sqcup J$ for $I \subseteq \textsf{R}$ and $J \subseteq \textsf{E}$ with $|J| = |I|$, then the matchings agree.

Starting from a triangulation of $\triangle _{d-1}\times \triangle _{n-1}$, we collect all $\textsf{R}$-saturating matchings (those covering all nodes in $\textsf{R}$) that appear as subgraphs of the trees corresponding to the simplices. By (3) of Proposition 2.8, there is at most one matching for each d-subset of $\textsf{E}$. Considering the barycentre of the subpolytope corresponding to $K_{\textsf{R},\sigma }$ shows that there is indeed a matching for each d-subset [32, Proposition 2.5].

Definition 2.9

(Polyhedral matching field) A polyhedral matching field is the collection of all $\textsf{R}$-saturating matchings appearing in the trees encoding a triangulation of $\triangle _{d-1}\times \triangle _{n-1}$.

Every coherent matching field is the polyhedral matching field extracted from a regular triangulation of $\triangle _{d-1}\times \triangle _{n-1}$, induced by the same weight matrix. On the other hand, all polyhedral matching fields are linkage [32, Section 3.1]. We see in Example 3.13 that the linkage matching field in Fig. 3 is not polyhedral.

Example 2.10

Fig. 4 depicts four trees comprising a triangulation of $\triangle _{1}\times \triangle _{3}$. The $2 \times 2$ matchings arising in these trees yield the matching field shown in Fig. 1.

Fig. 4

Trees corresponding to maximal simplices in a triangulation of $\triangle _{1}\times \triangle _{3}$

Using the iterated amalgamation construction of [32, Theorem 3.16], one can construct the collection $\mathcal {I}:=\mathcal {I}(\mathcal {T})$ of trees such that each node in $\textsf{R}$ has degree at least 2 by iteratively taking linkage pd-graphs. On the other hand, for $n > d$, all the matchings of the matching field occur in at least one of these trees since we can start this construction with a linkage pd-graph containing a fixed matching. These trees have another nice property which will be useful later.

Lemma 2.11

Every tree T in $\mathcal {I}$ contains an $\textsf{R}$-saturating matching.

Proof

Since each node in $\textsf{R}$ has degree bigger than 1, there is a leaf $\ell$ of T in $\textsf{E}$. Include the incident edge $(i,\ell )$ in the matching and iterate the procedure with $T-\{i,\ell \}$. This is possible as all remaining nodes in $\textsf{R}$ are still of degree at least 2. $\square$

A special class of polyhedral matching fields are the pointed ones (following the terminology in [47]), which comprise the full information of a triangulation of $\triangle _{d-1}\times \triangle _{n-1}$. We augment the ground set $\textsf{E}$ by a copy ${\widetilde{\textsf{R}}}$ of $\textsf{R}$ to obtain a ground set $\widetilde{\textsf{E}}$ of size $n+d$, and we set all elements of ${\widetilde{\textsf{R}}}$ to be smaller than all elements of $\textsf{E}$. To take the full information of all trees into account, for each tree in $\mathcal {T}$ we add edges between each node in $\textsf{R}$ to its copy ${\widetilde{\textsf{R}}}$, yielding a set $\widetilde{\mathcal {T}}$ of trees on $\textsf{R}\sqcup \widetilde{\textsf{E}}$ (Fig. 5).

Definition 2.12

The pointed polyhedral matching field associated with a triangulation $\mathcal {T}$ of $\triangle _{d-1}\times \triangle _{n-1}$ is the collection of $\textsf{R}$-saturating matchings on $\textsf{R}\sqcup \widetilde{\textsf{E}}$ in the trees in $\widetilde{\mathcal {T}}$.

Fig. 5

The pointed polyhedral matching field encoding the triangulation of the prism in Fig. 6 as visualization of Definition 2.12

The discussion after [32, Theorem 3.16] shows that the latter construction actually yields a correspondence between triangulations and matching fields.

One can see that pointed polyhedral matching fields are actually polyhedral matching fields by extending the original triangulation of $\triangle _{d-1}\times \triangle _{n-1}$ to a triangulation of $\triangle _{d-1}\times \triangle _{n+d-1}$ by using a placing triangulation as in [17, Lemma 4.3.2]. Note that, on the other hand, each polyhedral matching field is a sub-matching field of a pointed polyhedral matching field. We use both points of view as they allow different constructions as we see in Sect. 4.3 and the follow-up of our paper. It is similar to the relation between transversal matroids and fundamental transversal matroids, and it is reminiscent of the correspondence between matroids and linking systems [42].

Cutting appropriately through a triangulation of $\triangle _{d-1}\times \triangle _{n-1}$ yields a fine mixed subdivision of $n\triangle _{d-1}$. This is formalized as the Cayley trick, see [41]. A direct way to identify the polyhedral pieces in such a subdivision of $n\triangle _{d-1}$ is the following. For each tree G corresponding to a simplex in the triangulation $\mathcal {T}$, we form the Minkowski sum

$$\begin{aligned} \sum _{j \in \textsf{E}} \text {conv}\{ \textbf{e}_i :i \in \mathcal {N}_G(j) \} , \end{aligned}$$

where $\mathcal {N}_G(j)$ is the neighbourhood of an element $j \in \textsf{E}$ in G. The collection of these Minkowski sums tiles the dilated simplex $n\triangle _{d-1}$.

The dual polyhedral complexes to these mixed subdivisions were introduced as tropical pseudohyperplane arrangements in [9]. This draws from the correspondence between tropical hyperplane arrangements and regular subdivisions of products of simplices established in [18]. After starting from an axiomatic study of tropical oriented matroids in [9], it was subsequently shown that these combinatorial objects are indeed cryptomorphic to subdivisions of $\triangle _{d-1}\times \triangle _{n-1}$ and tropical pseudohyperplane arrangements, partially in [37] and finished in [29].

Fig. 6

A triangulation of $\triangle _1\times \triangle _2$. The vertices are labeled by the corresponding edges in $K_{2,3}$. This picture was created with polymake [23]

3 Polyhedral matching fields induce oriented matroids

3.1 Matroid subdivisions from triangulations

We first briefly recall the definition of a matroid subdivision.

Definition 3.1

A collection of matroids is a matroid subdivision of a matroid M if they have the same ground set and rank as M, and their matroid polytopes (together with their faces) form a subdivision of the matroid polytope of M.

In [45, Proposition 2.2], Speyer shows that a subdivision of a matroid polytope is a matroid subdivision if and only if the subdivision does not contain any additional edges beyond those already present in the matroid polytope. Although he proves this result only in the context of regular subdivisions of hypersimplices, his argument readily generalizes to our setting. His argument shows that any matroid subdivision which contains additional edges must contain at least one edge joining two vertices of distance 2 apart in the 1-skeleton of the matroid polytope, which is not possible. Hence, one might reformulate the result as follows, in a manner similar in spirit to the proof of our main theorem in the next section:

Proposition 3.2

A polyhedral subdivision of matroid polytope is a matroid subdivision if and only if the induced subdivision of each face of dimension at most three is a matroid subdivision.

The construction of matroid subdivisions from triangulations of products of simplices goes back to [30] and was further refined in [20, 28, 40]. We take a more combinatorial point of view described in [32]. Given a subgraph G of $K_{\textsf{R},\textsf{E}}$, the transversal matroid $\mathcal {M}(G)$ is the matroid whose bases are the subsets of $\textsf{E}$ which are matched by some $\textsf{R}$-saturating matching of G. Starting from the set of all trees corresponding to the full-dimensional simplices in a triangulation of $\triangle _{d-1}\times \triangle _{n-1}$, we restrict to the subset $\mathcal {I}$ of all trees where each node in $\textsf{R}$ has degree at least 2. By Lemma 2.11, the transversal matroid of each such tree has rank d.

Theorem 3.3

([20, §5.2], [28, §2], [30, 40]) The matroids $\mathcal {M}(T)$ ranging over all $T \in \mathcal {I}$ form a matroid subdivision of $U_{d,n}$.

Note that the subdivision of $U_{d,n}$ is regular if and only if the corresponding subdivision of $\triangle _{d-1}\times \triangle _{n-1}$ is regular, see [28, §2] for more details.

Example 3.4

(Matroid subdivisions of an octahedron) An octahedron is the matroid polytope of the uniform matroid $U_{2,4}$. There are exactly two types of matroid subdivisions of an octahedron. The trivial subdivision has only the octahedron as a cell. Apart from that, one can subdivide it into two pyramids as depicted in Fig. 7; there are three such subdivisions. While one can also subdivide the octahedron into four tetrahedra, it is not a matroid subdivision by the edge direction criterion.

The non-trivial subdivision in Fig. 7 arises through the construction of Theorem 3.3 from Example 2.9 and Fig. 4. We restrict our attention to the two trees with $\textsf{R}$-degree vector (2, 3) and (3, 2). The combinatorial Stiefel map gives the two sets $\{12,13,14,23,24\}$ and $\{13,14,23,24,34\}$, which form a matroid subdivision of $U_{2,4}$.

Fig. 7

The matroid subdivision described in Example 3.4

Recall from Sect. 2.3 the construction of the set $\widetilde{\mathcal {T}}$ of trees on $\textsf{R}\sqcup \widetilde{\textsf{E}}$. For each tree T in $\widetilde{\mathcal {T}}$, we get an induced transversal matroid $\widetilde{\mathcal {M}}(T)$ on $\widetilde{\textsf{E}}= {\widetilde{\textsf{R}}} \cup \textsf{E}$. In particular, the trees give rise to a matroid subdivision of $U_{d,d+n}$.

Corollary 3.5

The matroids $\widetilde{\mathcal {M}}(T)$ ranging over all trees T comprising a triangulation of $\triangle _{d-1}\times \triangle _{n-1}$ form the maximal cells for a matroid subdivision of $U_{d,d+n}$.

There is another way to think about this subdivision more geometrically. Following [40, §4], all cells in this subdivision are principal (or fundamental) transversal matroids with fundamental basis ${\widetilde{\textsf{R}}}$. Indeed, one can obtain this subdivision concretely as follows: In the matroid polytope of $U_{d,d+n}$, the vertices adjacent to ${\textbf {e}}_{{\widetilde{\textsf{R}}}}$ are in natural bijection with the vertices of $\triangle _{d-1}\times \triangle _{n-1}$ and their convex hull is $\left( -\triangle _{d-1}\right) \times \triangle _{n-1}$ up to translation. Triangulate the convex hull as the initial triangulation, and cone over the cells from ${\textbf {e}}_{{\widetilde{\textsf{R}}}}$. The matroid subdivision in Corollary 3.5 is the intersection of these cones with the matroid polytope.

3.2 Proof of Theorem A

Fix a triangulation of $\triangle _{d-1}\times \triangle _{n-1}$, and as before let $\mathcal {I}$ denote the trees of the triangulation of whose nodes in $\textsf{R}$ each have degree at least 2. Let $(M_{\sigma })$ denote the polyhedral matching field extracted from $\mathcal {I}$. Fix a sign matrix $A\in \{+,-,0\}^{\textsf{R}\times \textsf{E}}$ such that an entry is non-zero whenever the corresponding edge appears in some matching from $(M_{\sigma })$ (the collection of edges appearing in the matchings is the support of the matching field).

Definition 3.6

(Sign of a matching) Let $M_{\sigma }$ be a perfect matching between $\textsf{R}$ and $\sigma \subset \textsf{E}$ in $K_{\textsf{R},\textsf{E}}$. Define $\text {sign}(M_{\sigma })$ to be the sign of the permutation

$$\begin{aligned}{}[d]\longrightarrow \textsf{R}\longrightarrow \sigma \longrightarrow [d], \end{aligned}$$

where the first and last map are order-preserving bijections, with $\sigma$ inheriting the order from $\textsf{E}$, and the middle map is the bijection determined by $M_{\sigma }$.

With the terminology in place we restate our first main Theorem A.

Theorem 3.7

The sign map $\upchi :\left( {\begin{array}{c}\textsf{E}\\ d\end{array}}\right) \rightarrow \{+,-\}$ given by

$$\begin{aligned} \sigma \mapsto \text {sign}(M_\sigma )\prod _{e\in M_\sigma }A_e , \end{aligned}$$

(3)

is the chirotope of a uniform oriented matroid.

Let T be a tree in $\mathcal {I}$ and let A(T) be any matrix obtained by setting every entry of A not in T to 0 and replacing every remaining non-zero entry by an arbitrary real number of the same sign. Furthermore, let $\upchi _{T}$ be the map $\upchi$ restricted to the bases of the transversal matroid $\mathcal {M}(T)$.

Lemma 3.8

The map $\upchi _{T}$ is the chirotope of the rank d oriented matroid realized by A(T).

Proof

By Lemma 2.11, $\upchi _T$ is non-zero. If $\sigma \in \left( {\begin{array}{c}\textsf{E}\\ d\end{array}}\right)$ is not a basis of the transversal matroid, then there are no perfect matchings between $\textsf{R}$ and $\sigma$ in T, thus $\det (A(T)_{|\sigma })$ is 0. Otherwise there is a unique matching, namely $M_\sigma$, between $\textsf{R}$ and $\sigma$ in T. This matching corresponds to the unique non-zero term in the expansion of $\det (A(T)_{|\sigma })$, whose sign coincides with $\upchi (\sigma )$ by definition. $\square$

Theorem 3.9

Let $M_1,\ldots , M_k$ be a matroid subdivision of some matroid M. Let $\upchi$ be an alternating sign map supported on the bases $\mathcal {B}(M)$. Suppose each restriction $\upchi _i:\mathcal {B}(M_i)\rightarrow \{+,-\}$ is a chirotope. Then $\upchi$ itself is a chirotope.

Proof

Suppose $\upchi$ is not a chirotope. Since ${\underline{\upchi }}$ is by assumption a matroid, by Proposition 2.4, there exist $x_1,x_2,y_1,y_2,x_3,\ldots ,x_d\in \textsf{E}$ such that (2) is violated. It is routine to check that all $d+2$ elements must be distinct here, and the six d-element subsets involved in (2) form three “antipodal” pairs. Moreover, at least one such pair consists of bases of M as at least a term in (2) is non-zero.

Construct a vector $\textbf{c}\in \mathbb {R}^{\textsf{E}}$ where $\textbf{c}(x_1)=\textbf{c}(x_2)=\textbf{c}(y_1)=\textbf{c}(y_2)=1$, $\textbf{c}(x_i)=0, \forall i=3,\ldots ,d$, and $\textbf{c}(\ell )$’s are sufficiently large numbers for every other $\ell \in \textsf{E}$. Consider the face $F_\textbf{c}$ of the matroid polytope of M that minimizes $\textbf{x}\mapsto \textbf{c}^{\top }{} \textbf{x}$. A vertex of the matroid polytope of M achieves the minimum if and only if it corresponds to one of the aforementioned subsets while being a basis of M. $F_\textbf{c}$ is a matroid polytope and the global matroid subdivision restricts to a matroid subdivision of it. We distinguish two cases depending on the shape of $F_\textbf{c}$:

Case I: $F_\textbf{c}$ is an octahedron, i.e., all three terms of (2) are non-zero. There are four possible matroid subdivisions of an octahedron as discussed in Ex. 3.4, the trivial one and three that subdivide it into two pyramids. In either case, there is a 3-dimensional cell $C'$ that contains at least two pairs of antipodal vertices, pick a full-dimensional cell $C:=C_{M_i}$ of the global matroid subdivision that contains $C'$. Then restricting $\upchi$ to $M_i$ means that we are setting at most one term out of the three terms in (2) to zero, which still yields a violation of the 3-term GP relation in $\upchi _{M_i}$.

Case II: $F_\textbf{c}$ is not an octahedron (thus either a square or a pyramid). The only possible matroid subdivision of $F_\textbf{c}$ is the trivial one. Similar to Case I, we pick a cell $C:=C_{M_i}$ containing $F_\textbf{c}$, and $\upchi _{M_i}$ will violate (2) exactly like $\upchi$. $\square$

Proof of Theorem 3.7

By Theorem 3.3, there is a matroid subdivision of the uniform matroid $U_{d,n}$ consisting of transversal matroids, one for each spanning tree in $\mathcal {I}$. By Lemma 3.8, the sign maps $\upchi _T$’s are chirotopes. Hence $\upchi$ itself is a chirotope by Theorem 3.9. $\square$

Example 3.10

The diagonal matching field depicted in Fig. 1 with the sign-matrix

$$\begin{aligned} \begin{pmatrix} + &{} - &{} + &{} -\\ + &{} - &{} - &{} + \end{pmatrix} \end{aligned}$$

gives rise to the chirotope

$$\begin{aligned} (12,-),(13,-),(14,+),(23,+),(24,-),(34,+) \hspace{5.0pt}. \end{aligned}$$

This is shown in Fig. 8.

Fig. 8

A matroid subdivision with signs induced by the trees and signs from Example 3.10

Remark 3.11

Instead of the full polytope $\triangle _{d-1} \times \triangle _{n-1}$, one could equally start with a subpolytope of it. The whole construction then yields a chirotope for the transversal matroid of the subgraph of $K_{d,n}$ corresponding to the subpolytope. However, it is no restriction to study only the full polytope as each triangulation can be extended to the full product of simplices. This is further explained in [17] and (also with signs) in [31].

Example 3.12

The assumption in Theorem 3.7 that the support of A contains the support of the matching field is important. Consider the following sign matrix together with the (3, 5)-diagonal matching field:

$$\begin{aligned} \begin{pmatrix} + &{} + &{} 0 &{} 0 &{} 0\\ 0 &{} + &{} 0 &{} + &{} 0\\ 0 &{} 0 &{} + &{} 0 &{} + \end{pmatrix}. \end{aligned}$$

The support of the induced $\upchi$ is $\{123, 125, 145, 245\}$, which is not the collection of bases of any matroid.

Example 3.13

As the linkage property was introduced in [47] in analogy with the basis exchange axiom for matroids, it is tempting to assume that a linkage matching field gives rise to an oriented matroid, generalizing our construction for polyhedral matching fields. However, the linkage but not polyhedral matching field depicted in Fig. 3 shows that this is not correct. Take the sign matrix to be all positive. We have the following matchings (each tuple is a subset $\{i_1<i_2<i_3\}\in \left( {\begin{array}{c}[5]\\ 3\end{array}}\right)$ followed by the permutation $\sigma (i_1),\sigma (i_2),\sigma (i_3)$ of [3] and the sign of the permutation):

$$\begin{aligned} \begin{array}{lll} 125&{} 123&{} +\\ 135&{} 132&{} -\\ 145&{} 123&{} +\\ 235&{} 231&{} +\\ 245&{} 231&{} +\\ 345&{} 231&{} +.\\ \end{array} \end{aligned}$$

Take $(x_1,x_2,y_1,y_2,X)=(1,2,3,4,\{5\})$ in (2). Since all products

$$\begin{aligned} \upchi (1,2,5)\cdot \upchi (3,4,5)=+\cdot + = + \\ \upchi (1,3,5)\cdot \upchi (4,2,5)=-\cdot - = + \\ \upchi (1,4,5)\cdot \upchi (2,3,5)=+\cdot + = + \end{aligned}$$

are positive, this contradicts the 3-term GP relation.

We elaborate more on this. A linkage matching field also determines a collection of spanning trees [32], but those trees might contain new matchings. For example, in [32, Fig. 11], the top tree and the left tree contain different matchings on 3456. In such a case, while each tree still yields a chirotope, their values need not agree. The values on some of the bases correspond to distinct matchings which means geometrically that these chirotopes can not be “glued” together.

3.3 Compatibility of chirotopes

In this section, we discuss when does the converse of Theorem 3.9 hold. That is, starting with a matroid polytope whose vertices are labeled by the signs from a chirotope, for a given matroid subdivision, whether the restriction of this chirotope to every piece also forms a chirotope. If so, we say the matroid subdivision is compatible with the chirotope. For example, in the recent works on positive Dressians and positive tropical Grassmannians [10, 34, 44], their central notion of positroid subdivision is a special case of our problem with all signs being $+$. We provide a local criterion using a similar approach as in the proof of Theorem 3.9, which extends [44, Theorem 4.3].

Let $\upchi$ be a chirotope supported on $U_{2,4}$. There are exactly two terms among $\upchi (1,2)\upchi (3,4), -\upchi (1,3)\upchi (2,4), \upchi (1,4)\upchi (2,3)$ having the same sign, hence exactly one matroid subdivision of $U_{2,4}$ is not compatible, which is the subdivision into two pyramids that separates the two antipodal vertices corresponding to the minority sign.

Proposition 3.14

Let $\upchi$ be a chirotope supported on some matroid M and let $M_1,\ldots , M_k$ be a matroid subdivision of M. The restrictions $\upchi _i$’s of $\upchi$ to $M_i$’s are all chirotopes if and only if the restriction of the matroid subdivision to every octahedron face is compatible.

Proof

Suppose the restriction of the matroid subdivision to an octahedron face is not compatible with (3-dimensional) cells $C, C'$. Pick a full-dimensional cell $M_i$ that contains C, then the 3-term GP relation corresponding to the vertices of C is violated in $M_i$.

Conversely, suppose some 3-term GP relation (2) is violated in $M_i$; denote by F and $F'$ the faces of (the matroid polytopes of) M and $M_i$ that contain bases involved in (2), respectively. Since $\upchi$ is a chirotope but $\upchi _i$ is not, some bases of M involved in (2) must be non-bases of $M_i$, so we have $F'\subsetneq F$. Suppose F is an octahedron. $F'$ is either a pyramid or a square, and F must have been subdivided in the matroid subdivision. If $F'$ is a pyramid, then the subdivision of F is by definition not compatible; if $F'$ is a square, pick any pyramid of the subdivision and the 3-term GP relation is still violated there, so the subdivision is also not compatible. Now suppose F is a pyramid. $F'$ must be a square, but in such case F would have violated the 3-term GP relation as $F'$ does. $\square$

4 Dictionary between matching fields and oriented matroids

There are several cryptomorphic ways to describe an oriented matroid: by chirotopes, circuits, cocircuits, topes and covectors. Furthermore, a crucial notion for oriented matroids is duality. Knowing that $\upchi$ in Theorem A is a chirotope, one can use the equivalence of axiom systems as described in [14, Chapter 3] to convert $\upchi$ into these objects or notions. However, it is also possible to provide a direct correspondence between these descriptions of an oriented matroid and their incarnations in triangulations. The correspondences are summarized as follows:

Polyhedral notion	Matroidal notion
Matchings	Chirotope
Linkage pd-graphs	Signed circuits
(Trees identifying) Chow pd-graphs	Signed cocircuits
Covector pd-graphs	Covectors
Inner tope pd-graphs	Topes
(Pointed) Matching field duality	Oriented matroid duality

4.1 Duality

An important concept for oriented matroids is duality. Recall from Example 2.2 that an oriented matroid arising from a rectangular matrix can be represented in the form $(I_{d,d}|B)$, where we let B be a $d \times n$ matrix for now. Following [25, §7.2.5], its dual oriented matroid is represented by $(-{B}^{\top }|I_{n \times n})$. We mimic this by fixing a triangulations $\mathcal {T}$ of $\triangle _{d-1} \times \triangle _{n-1}$ as well as a sign matrix $A \in \{-1,+1\}^{d \times n}$, and constructing a pair of pointed polyhedral matching fields that gives a dual pair of oriented matroids. This illustrates an advantage of considering pointed matching fields: they allow a more satisfactory duality theory.³

The paragraph on “Duality” in [14, §3.5] gives the following condition for two chirotopes to be dual.

Lemma 4.1

Let $\textsf{E}$ be a ground set of size $d + n$. Let $\upchi :\textsf{E}^d \rightarrow \{+,-,0\}$ and $\upchi ' :\textsf{E}^n\rightarrow \{+,-,0\}$ be two chirotopes of a uniform oriented matroid of rank d and n, respectively. They are dual if and only if for each ordering $(x_1,\dots ,x_{d+n})$ of the ground set $\textsf{E}$ we have

$$\begin{aligned} \upchi (x_1,\dots ,x_d) \cdot \upchi '(x_{d+1},\dots ,x_{d+n}) = \text {sign}(x_1,\dots ,x_{d+n}), \end{aligned}$$

where the latter sign is the sign of the permutation represented by the ordering of the $x_k$.

As mentioned for the definition of a pointed polyhedral matching field (Definition 2.12), one has to take the information of all matchings occurring in the trees of $\mathcal {T}$ into account. This corresponds to looking at all minors of B. Equally, one can associate two different pointed polyhedral matching fields with $\mathcal {T}$ by swapping the factors of the product of simplices. This leads to a pointed polyhedral matching field $(M_{\sigma })$ of size $(d,n+d)$ and $(N_{\sigma })$ of size $(n,d+n)$.

$(M_{\sigma })$ and $(N_{\sigma })$ are related combinatorially as follows. Let $\mu$ be a matching on $\textsf{R}\sqcup \textsf{E}$. Augment $\textsf{R}$ by another copy ${\overline{\textsf{E}}}$ of $\textsf{E}$ and $\textsf{E}$ by another copy ${\overline{\textsf{R}}}$ of $\textsf{R}$. This leads to the two nodes sets $U = \textsf{R}\cup {\overline{\textsf{E}}}$ and $V = {\overline{\textsf{R}}} \cup \textsf{E}$, each union in this order. Next, introduce another copy ${\overline{\mu }}$ between ${\overline{\textsf{E}}}$ and ${\overline{\textsf{R}}}$ by adding the edge $({\overline{j}},{\overline{i}})$ for each edge (i, j) in $\mu$. Then, connect each isolated node to its copy. We obtain a perfect matching $\tau$ on $U \sqcup V$, which can be thought as a permutation in $S_{d+n}$. The two restricted matchings $\tau _{|\textsf{R}}$ and $\tau _{|{\overline{\textsf{E}}}}$ form a dual pair of matchings in $(M_{\sigma })$ and $(N_{\sigma })$, respectively. The terminology is justified as they have complementary supports in V. The notation is visualized in Fig. 9.

Finally, we let $\upchi _1$ be the chirotope induced by the matching field $(M_{\sigma })$ on $\textsf{R}\sqcup V = \textsf{R}\sqcup ({\overline{\textsf{R}}} \cup \textsf{E})$ with the sign matrix $(I_{d,d} | A)$ and let $\upchi _2$ be the chirotope induced by the matching field $(N_{\sigma })$ on ${\overline{\textsf{E}}} \sqcup V = {\overline{\textsf{E}}} \sqcup ({\overline{\textsf{R}}} \cup \textsf{E})$ with the sign matrix $(-{A}^{\top } | I_{n,n})$. This can also be interpreted as the sign matrix

$$\begin{aligned} H = \begin{pmatrix} I_{d,d} &{} A \\ -{A}^{\top } &{} I_{n,n} \end{pmatrix} \end{aligned}$$

on the bipartite graph $K_{d+n,d+n}$.

Fig. 9

The matchings arising in the proof of Proposition 4.2. In this picture, we have $|\textsf{R}| = 3$ and $|\textsf{E}| = 4$

Proposition 4.2

The two chirotopes $\upchi _1$ and $\upchi _2$ describe a dual pair of oriented matroids.

Proof

Let an arbitrary partition of $V\cong [d+n]$ into two ordered sets $P_1:= \{x_1< \cdots < x_d\}$ and $P_2:= \{x_{d+1}< \cdots < x_{d+n}\}$ be given. This defines the bijection $\pi$ in $S_{d+n}$ which maps $(x_1,\dots ,x_d,x_{d+1},\dots ,x_{d+n})$ to $(1,2,\dots ,d+n)$.

Let $\mu _1$ be the matching in $(M_{\sigma })$ on $P_1$ and let $\mu _2$ be the matching in $(N_{\sigma })$ on $P_2$. By construction, their union is a perfect matching $\tau$ on $U\sqcup V$, coming from a matching $\mu$ on $\textsf{R}\sqcup \textsf{E}$. Using Definition 3.6 and (3), we obtain

$$\begin{aligned} \upchi _1(P_1) = \text {sign}(\pi \cdot \tau _{|\textsf{R}})\prod _{e\in \tau _{|\textsf{R}}}H_e \quad \text { and } \quad \upchi _2(P_2) = \text {sign}(\pi \cdot \tau _{|{\overline{\textsf{E}}}})\prod _{e\in \tau _{|{\overline{\textsf{E}}}}}H_e \;. \end{aligned}$$

As the concatenation $\pi \cdot \tau$ of the matchings $\tau$ and $\pi$ is disjoint on $\textsf{R}$ and ${\overline{\textsf{E}}}$, we obtain

$$\begin{aligned} \upchi _1(P_1)\cdot \upchi _2(P_2) = \text {sign}(\pi ) \text {sign}(\tau )\prod _{e\in \tau _{|{\overline{\textsf{E}}}}}H_e\prod _{e\in \tau _{|\textsf{R}}}H_e . \end{aligned}$$

Using the definition of $\tau$ based on $\mu$, we get

$$\begin{aligned} \prod _{e\in \tau _{|{\overline{\textsf{E}}}}}H_e\prod _{e\in \tau _{|\textsf{R}}}H_e = \prod _{e\in \mu }(-A_e)\prod _{e\in \mu }A_e = (-1)^{|\mu |}. \end{aligned}$$

Now we compute the sign of $\tau$ by counting inversions. Every inversion within $\mu$ is paired up with an inversion within ${\overline{\mu }}$ and vice versa, while there are $|\mu |^2$ ($\equiv |\mu | \mod 2$) many inversions between $\mu$ and ${\overline{\mu }}$, so $\text {sign}(\tau ) = (-1)^{|\mu |}$. Since $\pi$ is just the inverse of the permutation encoded by $(x_1,\dots ,x_d,x_{d+1},\dots ,x_{d+n})$, the proposition follows from Lemma 4.1. $\square$

4.2 Signed circuits and cocircuits

We show that linkage pd-graphs form the analogue of signed circuits and Chow pd-graphs form the analogue of signed cocircuits. Observe that a matching field can be recovered from linkage pd-graphs and equally well from Chow pd-graphs, see [32], in analogy to the cryptomorphic description of an oriented matroid by signed circuits or signed cocircuits. Let $\tau \subset \textsf{E}$ be a $(d+1)$-subset. Recall from Example 2.7 that the linkage pd-graph $T_{\tau }:=\bigcup _{\sigma \subset \tau } M_\sigma$ is a spanning tree of $K_{\textsf{R},\tau }$ in which every node in $\textsf{R}$ has degree 2. One can then define an auxiliary tree ${\widetilde{T}}_\tau$ whose node set is $\tau$ and two nodes are connected by an edge if they are both incident to the same $r\in \textsf{R}$ in $T_{\tau }$. Note that this is the same as identifying a node j in $\tau$ with the matching on $\textsf{R}\sqcup (\tau {\setminus } \{j\})$ and connecting two matchings if they only differ by one edge. Such a tree ${\widetilde{T}}_\tau$, together with an edge labeling using $\textsf{R}$, is a linkage tree in [47]. We equip ${\widetilde{T}}_\tau$ with a sign labeling in the following way. To the edge $(u,v) \in {\widetilde{T}}_\tau$ associated to the two edges $(u,r),(v,r)\in T_\tau$, we assign the negative of the product of the signs on (u, r) and (v, r).

Proposition 4.3

For any $\tau$, there exist precisely two sign assignments of $\tau$ such that two adjacent nodes in ${\widetilde{T}}_\tau$ are of the same sign if and only if the edge between them is positive. These are the two signed circuits supported on $\tau$.

Proof

Pick an arbitrary root for ${\widetilde{T}}_\tau$ and choose a sign for it, then the sign of every other node is uniquely determined by its parent. We show that a signed circuit with respect to $\upchi$ satisfies the constraint described in the statement.

Let C be a signed circuit supported on $\tau$. Write $\textsf{R}=\{r_1<\cdots<r_d\},\tau =\{e_1<\cdots <e_{d+1}\}$ and let $x=e_i, y=e_j$ be two nodes. We assume that x, y are adjacent in ${\widetilde{T}}_\tau$ as the general case follows from an induction on their distance; in particular, $M_{\tau {\setminus }\{e_j\}}=M_{\tau {\setminus }\{e_i\}}{\setminus }\{r_ke_j\}\cup \{r_ke_i\}$ for some k. By [14, Lemma 3.5.7] and the alternating property of $\upchi$, we have

$$\begin{aligned} C(e_j)=C(e_i)\cdot (-1)^{j-i}\upchi (e_1,\ldots ,\widehat{e_i},\ldots ,e_{d+1})\upchi (e_1,\ldots ,\widehat{e_j}, \ldots ,e_{d+1}). \end{aligned}$$

(4)

Permuting $\textsf{R}$ imposes a uniform sign change to the sign of the matchings and leaves (4) invariant, so we may assume $M_{\tau {\setminus }\{e_i\}}$ is order preserving between $\textsf{R}$ and $\tau {\setminus }\{e_i\}$, thus $M_{\tau {\setminus }\{e_j\}}$ is of sign $(-1)^{j-i-1}$. Now the products of the signs of the edges of $M_{\tau {\setminus }\{e_i\}}$ and $M_{\tau {\setminus }\{e_j\}}$ differ by a factor of $A_{r_ke_i}A_{r_ke_j}$, together with the discussion on the signs of the matchings,

$$\begin{aligned} (-1)^{j-i}\upchi (e_1,\ldots ,\widehat{e_i},\ldots ,e_{d+1})\upchi (e_1,\ldots ,\widehat{e_j},\ldots ,e_{d+1}) \end{aligned}$$

is equal to $-A_{r_ke_i}A_{r_ke_j}$ as wanted. $\square$

Now we consider signed cocircuits of our oriented matroid. Recall that cocircuits correspond to vertices in an arrangement encoding an oriented matroid. These appear in the framework of abstract tropical linear programming [31] as certain trees with prescribed degree sequence, see also Remark 4.18. The statement of [39, Theorem 12.9] identifies the correct tree for our purpose.

Proposition 4.4

For any $(n-d+1)$-subset $\rho$, there exists a unique spanning tree $T_\rho$, encoding a cell in the triangulation, such that every node in $\rho$ is of degree 1 and every node in $\textsf{E}{\setminus }\rho$ is of degree 2.

We say we flip a node in $\textsf{R}$ if we negate the row of A indexed by the node. A flipping of $\textsf{R}$ is a result of multiple flips of nodes in $\textsf{R}$.

Proposition 4.5

For any $\rho$, there exist precisely two flippings of $\textsf{R}$ such that every node of $\textsf{E}{\setminus }\rho$ is incident to edges of different signs in $T_\rho$. In each case, the signs of the edges incident to $\rho$ together give a signed cocircuit supported on $\rho$.

It is possible to give a combinatorial proof in the same vein of Proposition 4.3, but as cocircuits are special instances of covectors, we apply the result in Sect. 4.3 (with no circular argument). In particular, we give a more formal definition of flips there. We put a separate discussion here because of the extra structural properties of cocircuits.

Proof

We construct an auxiliary tree ${\widetilde{T}}_\rho$ whose node set is $\textsf{R}$. Two nodes are connected by an edge if they are both incident to some node in $\textsf{E}{\setminus }\rho$ in $T_\rho$ and we label the edge by the said node in $\textsf{E}{\setminus }\rho$. Pick an arbitrary root for ${\widetilde{T}}_\rho$ and choose a flip decision for it, then the flip decision of every other node is uniquely determined by its parent. Apply Corollary 4.16 to $T_\rho$ and any of the two flip decisions, we know that the signs of the edges incident to $\rho$ is a covector of the oriented matroid supported on $\rho$, i.e., it is a cocircuit. $\square$

Remark 4.6

Perhaps a more intuitive way to understand Proposition 4.5 is to use the geometric picture in the follow-up of our paper (see Example 4.19 for a rank 3 example). The mixed cell representing $T_\rho$, reflected to the correct orthant in the patchworking complex specified by the flipping, is dual to the intersection of $d-1$ pseudohyperplanes. Thus it recovers the intuition from classical hyperplane arrangements.

Example 4.7

We illustrate the construction of the signed circuits and cocircuits by continuing Example 3.10. The left graph in Fig. 10 shows the linkage pd-graph $T_{\tau }$ for $\tau = \{1,2,3\}$ used in Proposition 4.3. The signs on the nodes in $\textsf{R}$ are chosen negative so that one can think of multiplying the signs along paths instead of forming a signed linkage tree as constructed before Proposition 4.3.

The right graph in Fig. 10 depicts the spanning tree $T_{\rho }$ for $\rho = \{1,2,4\}$ as constructed in Proposition 4.5. The sign vector on $\textsf{R}$ corresponds to the flippings. Note that the two sign vectors $(+,+)$ and $(-,-)$ on the nodes in $\textsf{R}$ correspond to the two orthants in which the (pseudo-)spheres corresponding to the elements in $\textsf{E}{\setminus } \rho$ intersect.

Fig. 10

Two pd-graphs corresponding to a signed circuit and a signed cocircuit

We give a further interpretation of the trees from Proposition 4.4 in terms of Chow pd-graphs. Each Chow pd-graph is a minimal subset of the edges of $K_{d,n}$ intersecting all matchings of the matching field. These graphs were introduced in [47, Eqn. 5.1] and they were called ‘Chow covectors’ in [32].

Proposition 4.8

The collection $\Omega _\rho$ of edges incident to $\rho$ in $T_\rho$ is the Chow pd-graph supported on $\rho$.

Proof

We claim that there is a (unique) perfect matching ${\widetilde{M}}_{\textsf{R}'}$ between any $(d-1)$-subset $\textsf{R}'\subset \textsf{R}$ and $\textsf{E}{\setminus }\rho$ in $T_\rho$: set the missing node of $\textsf{R}'$ as the root of ${\widetilde{T}}_\rho$ in the proof of Proposition 4.5, and match every other node with (the label of) the edge towards its parent. From this, for any $x\in \rho$ with adjacent node r, ${\widetilde{M}}_{\textsf{R}{\setminus } r}\cup \{xr\}$ is a perfect matching between $\textsf{R}$ and $\textsf{E}{\setminus }\rho \cup \{x\}$. This gives rise to the matchings required in the definition [47, Eqn. 5.1] of a Chow pd-graph. $\square$

4.3 Topes and covectors

In the development of tropical oriented matroids, the tropical analogue of topes and covectors played an important role. We adapt the notion to our terminology and provide the connection with the oriented matroid $\mathcal {M}$ represented by the chirotope $\upchi$.

Fix a polyhedral matching field $(M_{\sigma })$ extracted from the special trees $\mathcal {I}$ of a triangulation $\mathcal {T}$ of $\triangle _{d-1}\times \triangle _{n-1}$, and a sign matrix $A\in \{-1,1\}^{\textsf{R}\times \textsf{E}}$. A covector pd-graph is a subgraph of a tree in $\mathcal {T}$ with no isolated node in $\textsf{E}$. A tope pd-graph is a covector pd-graph for which each node in $\textsf{E}$ has degree 1; it is called inner tope pd-graph, if it is actually a subgraph of a tree in $\mathcal {I}$. Note that linkage pd-graphs and the trees identifying Chow pd-graphs of a polyhedral matching field are special cases of covector pd-graphs.

Definition 4.9

Given $S\in \{-1,0,1\}^{\textsf{R}}$ and $F\subseteq \textsf{R}\times \textsf{E}$, we define the sign matrices $A_F\in \left\{ -1,0,1\right\} ^{\textsf{R}\times \textsf{E}}$ and $SA_{F}\in \left\{ -1,0,1\right\} ^{\textsf{R}\times \textsf{E}}$ by

$$\begin{aligned} (A_{F})_{i,j}={\left\{ \begin{array}{ll} A_{i,j}, &{} (i,j)\in F,\\ 0, &{} \text {otherwise} \end{array}\right. }\qquad \text {and}\qquad (SA_{F})_{i,j}=S_{i}A_{i,j}. \end{aligned}$$

Definition 4.10

Given a subgraph F of $K_{\textsf{R},\textsf{E}}$ and a sign vector $S\in \{-1,0,1\}^{\textsf{R}}$, define the sign vector $\psi _A(S,F)= Z \in \{-1,0,1\}^{\textsf{E}}$, where

$$\begin{aligned} Z_{j}= {\left\{ \begin{array}{ll} 0, &{} \text {column } j \text {of } SA_{F} \text {has positive and negative entries, or all zeros}\\ 1, &{} \text {column } j \text {of } SA_{F} \text {has only non-negative entries, and is non-zero}\\ -1, &{} \text {column } j \text {of } SA_{F} \text {has only non-positive entries, and is non-zero.} \end{array}\right. } \end{aligned}$$

Note that $\psi _A(S,F)$ is the greatest lower bound of all sign vectors obtained from vectors of the form $y^{\top } A_F$ where $y\in {{\mathbb {R}}}^R$ and S share the same sign pattern.

Example 4.11

The graphs in Fig. 11 together with the sign vector $S = (0,-1,1)$ and sign matrix ${\widetilde{A}} = (I_{3,3} | A)$ with

$$\begin{aligned} A = \begin{pmatrix} 1 &{} 1 &{} -1 \\ -1 &{} -1 &{} 1 \\ -1 &{} -1 &{} -1 \end{pmatrix} \end{aligned}$$

give rise to the matrices

$$\begin{aligned} S{\widetilde{A}}_F = \begin{pmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} -1 &{} 0 &{} 1 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 &{} -1 &{} 0 &{} -1 \end{pmatrix} \; \text { and } \; S{\widetilde{A}}_T = \begin{pmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} -1 &{} 0 &{} 1 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} -1 \end{pmatrix}. \end{aligned}$$

Their images are

$$\begin{aligned} X = \psi _{{\widetilde{A}}}(S,F) = (0,-1,1,0,1,-1) \text { and } Y = \psi _{{\widetilde{A}}}(S,T) = (0,-1,1,1,1,-1). \end{aligned}$$

These sign vectors fulfill $Y \ge X$ and highlight the construction used in the proof of Proposition 4.15.

Fig. 11

On the left is a graph F on $\textsf{R}\sqcup {\widetilde{\textsf{E}}}$ with $|\textsf{R}| = |\textsf{E}| = 3$ and on the right is a related inner tope pd-graph T discussed in Example 4.11

For an oriented matroid $\mathcal {M}$, let $\mathcal {V}^*(\mathcal {M})$ denote the poset of covectors of $\mathcal {M}$. There is a weak map $\mathcal {M}\rightsquigarrow \mathcal {N}$ between two oriented matroids $\mathcal {M},\mathcal {N}$ on $\textsf{E}$, if for all covectors X of $\mathcal {N}$, there exists a covector Y of $\mathcal {M}$ such that $Y\ge X$.⁴

If $\mathcal {M}$ and $\mathcal {N}$ have the same rank, then this is the same as saying that, up to a global sign change, $\upchi _{\mathcal {M}}\ge \upchi _{\mathcal {N}}$ by [14, Proposition 7.7.5]. In particular, if $\upchi _{\mathcal {N}}$ is a chirotope obtained by restricting $\upchi _{\mathcal {M}}$ to a cell in some matroid subdivision of $\mathcal {M}$, such as in Lemma 3.8, then $\mathcal {M}\rightsquigarrow \mathcal {N}$ is a weak map.

Proposition 4.12

For each sign vector $S\in \{-1,1\}^{\textsf{R}}$ and each inner tope pd-graph F, $\psi _A(S,F)$ is a tope of the oriented matroid given by the chirotope $\upchi$.

Proof

Pick a tree $T \in \mathcal {I}$ that contains F and denote by $\mathcal {N}$ the oriented matroid representing $\upchi _T$. By Lemma 3.8, $\mathcal {N}$ is realized by any matrix of the form A(T), in which we choose $\pm 1$ for entries in T but not F, and $\pm 2d$ for entries in F. This ensures that the sign pattern of the row space element ${S}^{\top } \cdot A(T)$ equals $\psi _A(S,F)$, hence $\psi _A(S,F)$ is a tope of $\mathcal {N}$. From the discussion above, there is a weak map $\mathcal {M}\rightsquigarrow \mathcal {N}$, so $\psi _A(S,F)$ is a tope of $\mathcal {M}$ as well. $\square$

To extend this correspondence to more general covectors, we make use of a result by Mandel. Recall that for $X,Y \in \{-1,0,1\}^{\textsf{E}}$, the composition $X \circ Y$ agrees with X in all positions $e \in \textsf{E}$ with $X_e \ne 0$, and agrees with Y otherwise.

Theorem 4.13

([14, Thm. 4.2.13]) Let $\mathcal {T}\!\!o$ be the set of topes of the oriented matroid $\mathcal {M}$. Then $X \in \{-1,0,1\}^{\textsf{E}}$ is a covector of $\mathcal {M}$ exactly if $X \circ \mathcal {T}\!\!o\subseteq \mathcal {T}\!\!o$.

Corollary 4.14

Let $X\in \{-1,0,1\}^{\textsf{E}}$ be a sign vector such that every $Y\in \{-1,1\}^{\textsf{E}}$ satisfying $Y\ge X$ is a tope of $\mathcal {M}$. Then X is a covector of $\mathcal {M}$.

We now consider the pointed polyhedral matching field $\widetilde{(M_{\sigma })}$ encoding the starting triangulation, as well as the sign matrix ${\widetilde{A}}:= (I_{d,d} | A)$. By Theorem 3.7, they induce an oriented matroid ${\widetilde{\mathcal {M}}}$. Let F be a subgraph of a tree in $\widetilde{\mathcal {T}}$ without isolated nodes in $\textsf{E}\subset {\widetilde{\textsf{E}}}$ and such that a node in ${\widetilde{\textsf{R}}} \subset {\widetilde{\textsf{E}}}$ is isolated only if the corresponding node in $\textsf{R}$ is isolated as well. Furthermore, let $S \in \{-1,0,1\}^{\textsf{R}}$ be a sign vector whose support contains the set of non-isolated nodes of F in $\textsf{R}$.

Proposition 4.15

The sign vector $\psi _{{\widetilde{A}}}(S,F)$ is a covector of ${\widetilde{\mathcal {M}}}$.

Proof

By Corollary 4.14, it suffices to show that every full sign vector $Y\ge \psi _{{\widetilde{A}}}(S,F)$ is a tope of ${\widetilde{\mathcal {M}}}$. This amounts to finding a full sign vector $S'$ and an inner tope pd-graph T such that $Y=\psi _{{\widetilde{A}}}(S',T)$ by Proposition 4.12, since the extended trees in $\widetilde{\mathcal {T}}$ have degree at least 2 everywhere in $\textsf{R}$. We first construct $S'$ by setting each zero coordinate $i\in \textsf{R}$ of S to $Y_i$, and we include those missing edges between $\textsf{R}$ and its copy ${\widetilde{\textsf{R}}}$. Now for each coordinate $j\in \textsf{E}$ of $\psi _{{\widetilde{A}}}(S,F)$, the j-th column of $S{\widetilde{A}}_{F}$ must contain an entry whose sign equals $Y_j$, so we remove all edges incident to j except the one corresponding to that entry. This results in an inner tope pd-graph T, and from our construction it is easy to see that $Y=\psi _{{\widetilde{A}}}(S',T)$ as desired. $\square$

Restricting the covectors to $\textsf{E}$ yields the following.

Corollary 4.16

For a covector pd-graph F, $\psi _A(S,F)$ is a covector of $\mathcal {M}$ for every sign vector S.

Remark 4.17

It is a consequence of the Borsuk–Ulam theorem together with the Topological Representation Theorem that this map is surjective. See [16] for details.

Remark 4.18

Now that we can transfer the covector pd-graphs to covectors of the oriented matroid $\mathcal {M}$, we give a brief overview on the connection with simplex-like algorithms for tropical linear programming.

The iteration in the framework of abstract tropical linear programming [31] is described in the language of trees encoding a triangulation. The main object in each iteration is a basic covector, which represents the analogue of a basic point in the simplex method. These are formed by a subclass of those trees from Proposition 4.4 and, from our new perspective, give rise to certain cocircuits of $\mathcal {M}$.

One can go even further and consider the tropicalization of the simplex method [2]. Using their genericity assumption, one sees that the covector pd-graph of the basic point defined in [2, Proposition-Definition 3.8] is also such a tree. Their pivoting depends on the signs of the tropical reduced costs, which are deduced from a “Cramer digraph” [2, §5]. The latter can also be considered as covector pd-graphs and hence give rise to covectors for $\upchi$.

Example 4.19

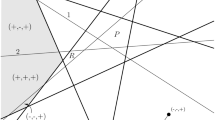
Ringel’s non-realizable oriented matroid $\texttt {Rin}(3,9)$ is the smallest (by rank) non-realizable uniform oriented matroid [14, §8.3], and is depicted as a pseudoline arrangement in Fig. 12a. We sketch a proof that the oriented matroid ${\widetilde{\mathcal {M}}}$, defined using the fine mixed subdivision of Fig. 12b and the sign matrix

is isomorphic to $\texttt {Rin}(3,9)$.

Fig. 12

Constructing $\texttt {Rin}(3,9)$. a Ringel’s pseudoline arrangement. This figure appears in [26, p. 42]. b A fine mixed subdivision of $6\Delta _{2}$. Also found in [8, Conjecture 5.7]

Fig. 13

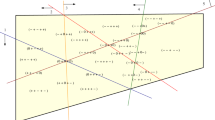
All pairs (S, F) satisfying the conditions of Proposition 4.15. Each maximal cell is labelled by its Minkowski summands, which in turn are specified by F

It follows from Proposition 4.5 that a pair (S, F) is mapped to a cocircuit of ${\widetilde{\mathcal {M}}}$ under $\psi _{{\widetilde{A}}}$ if and only if there are exactly $\left| \text {supp}(S)\right| -1$ Minkowski summands of F that are segments with oppositely signed vertices. In Figs. 13 and 14, these are depicted as white cells. Figure 14 also shows a pseudoline arrangement, which we assume is oriented so that the black dot is on the positive side of each pseudoline. The pairwise intersections of the pseudolines are shown to be in bijection with the cocircuits of ${\widetilde{\mathcal {M}}}$, and, indeed, by writing out the sign vectors explicitly, one can check by hand using this bijection that the cocircuits of ${\widetilde{\mathcal {M}}}$ and the cocircuits of the pseudoline arrangement agree. Therefore, this pseudoline arrangement must therefore be a representation of ${\widetilde{\mathcal {M}}}$.

The last step now is to verify that this pseudoline arrangement also represents Ringel’s oriented matroid $\texttt {Rin}(3,9)$. One may check these pseudoline arrangements are homeomorphic by considering their pseudoline sequences. Each pseudoline is intersected by all other pseudolines, giving rise to a (circular) sequence of elements of the oriented matroid for each pseudoline. In [15, Thm. 5.2], it was shown that the set of these sequences determines the oriented matroid.

Using the starting dots and directions indicated, it can be verified that the sequences for Figs. 12a and 14 agree. For example, the pseudoline sequence associated to $\textsf{a}$ in both figures is $1\textsf{ecb}3\textsf{f}2\textsf{d}$.

Fig. 14

The pseudoline arrangement derived from Fig. 12

5 Extension to matroids over hyperfields

We first provide the necessary background of matroids over hyperfields, then illustrate how the construction in this paper can be useful for the theory.

5.1 Introduction to matroids over hyperfields

Definition 5.1

A hyperfield $(\mathbb {H},\boxplus ,\otimes ,0,1)$ consists of a set $\mathbb {H}$ with distinguished elements $0\ne 1$, together with a possibly multi-valued hyperoperation $\boxplus :\mathbb {H}\times \mathbb {H}\rightarrow 2^{\mathbb H}{\setminus }\{\emptyset \}$ and an operation $\otimes :\mathbb {H}\times \mathbb {H}\rightarrow \mathbb {H}$, such that:

• $(\mathbb {H},\boxplus ,0)$ is a commutative hypergroup, i.e., $\boxplus$ is commutative and associative, with $0\boxplus x=\{x\},\forall x\in \mathbb {H}$. Moreover, for any $x\in \mathbb {H}$, there exists a unique $-x\in \mathbb {H}$ such that $0\in x\boxplus (-x)$; such an inverse element also satisfies the property that $x\in y\boxplus z$ if and only if $z\in x\boxplus (-y)$.

• $(\mathbb {H}{\setminus }\{0\},\otimes , 1)$ is an abelian group, and $0\otimes x=x\otimes 0=0, \forall x\in \mathbb {H}$.

• $a\otimes (x\boxplus y)=(a\otimes x)\boxplus (a\otimes y), \forall a,x,y\in \mathbb {H}$.

Definition 5.2

Let $\mathbb {H}$ be a hyperfield. A non-zero alternating function $\upchi :\textsf{E}^d\rightarrow \mathbb {H}$ specifies a weak matroid over $\mathbb {H}$ (on $\textsf{E}$ and of rank d) if ${\underline{\upchi }}$ is a matroid and that for any $x_1,x_2,y_1,y_2 \in \textsf{E},X:=\{x_3,\ldots ,x_d\}\subseteq \textsf{E}$,

$$\begin{aligned} 0\in \upchi (x_1,x_2,X)\upchi (y_1,y_2,X)\boxplus \upchi (x_1,y_1,X)\upchi (y_2,x_2,X)\boxplus \upchi (x_1,y_2,X)\upchi (x_2,y_1,X). \end{aligned}$$

$\upchi$ specifies a strong matroid over $\mathbb {H}$ if for any $x_1,\ldots ,x_{d-1},y_1,\ldots , y_{d+1}\in \textsf{E}$,

$$\begin{aligned} 0\in \boxplus _{k=1}^{d+1} (-1)^k \upchi (x_1,\ldots ,x_{d-1},y_k)\upchi (y_1,\ldots ,\widehat{y_k},\ldots ,y_{d+1}). \end{aligned}$$

In both cases, two functions differing by a non-zero scalar multiple represent the same matroid.

Example 5.3

The sign hyperfield $\mathbb {S}$ has three elements $0,1,-1$, with $1\boxplus 1=\{1\}, -1\boxplus -1=\{-1\}, 1\boxplus -1=\{0,1,-1\}$ (other arithmetics can be deduced from the axioms quite easily and are omitted). An oriented matroid is a (strong or weak) matroid over $\mathbb {S}$.

We refer the reader to [11] for more examples, in particular their Examples 3.37 and 3.38, which show that in general, the notions of strong and weak matroids do not coincide.

The theory of matroids over hyperfields is functorial, here a map $\varphi :\mathbb {H}\rightarrow \mathbb {H}'$ between hyperfields $(\mathbb {H},\boxplus ,\otimes ,0,1)$ and $(\mathbb {H}',\boxplus ',\otimes ',0',1')$ is a hyperfield morphism if it is a morphism between the multiplicative groups of $\mathbb {H}$ and $\mathbb {H}'$, takes 0 to $0'$, and $\varphi (x\boxplus y)\subset \varphi (x)\boxplus ' \varphi (y),\forall x,y\in \mathbb {H}$.

Proposition 5.4

([11, Lemma 3.40]) Let $\varphi :\mathbb {H}\rightarrow \mathbb {H}'$ be a hyperfield morphism, and $\upchi$ be a (strong, respectively weak) matroid over $\mathbb {H}$. Then $\varphi _*\upchi :=\varphi \circ \upchi$ is a (strong, respectively weak) matroid over $\mathbb {H}'$.

Remark 5.5

There is a straightforward extension of our work at the generality in [11], namely, matroids over tracts. However, the exposition of such theory is more complicated, so we stick with hyperfields here.

5.2 Hyperfields with the inflation property

The following definition was probably first considered by Massouros [35] under the name of monogene hyperfields, but we follow the terminology of Anderson [5].

Definition 5.6

A hyperfield $\mathbb {H}$ has the inflation property (IP) if $1\boxplus (-1)=\mathbb {H}$.

We refer the reader to [35] and [11, Example 2.14] for examples and constructions of hyperfields that have the IP.

Proposition 5.7

([5, Proposition 6.10]) $\mathbb {H}$ having the IP is equivalent to any of the following properties:

• (1) $a\boxplus (-a)=\mathbb {H}$ for any $a\ne 0$;

• (2) $a\in a\boxplus b$ for any $a\ne 0$;

• (3) if $0\in \boxplus _{i=1}^{k} a_i$ for some $a_1,\ldots ,a_k$ that are not all zero, then $0\in (\boxplus _{i=1}^{k} a_i)\boxplus a_{k+1}$ for any $a_{k+1}\in \mathbb {H}$.

We show that Theorem A can be extended to (weak) matroids over hyperfields with the IP.

Theorem 5.8

Let $(M_\sigma )$ be a polyhedral matching field. Let $\mathbb {H}$ be a hyperfield with the IP and A be an $\mathbb {H}$-matrix with no zero entries. Then $\upchi :\textsf{E}^d\rightarrow \mathbb {H}$ given by $\sigma \mapsto \text {sign}(M_\sigma )\otimes \bigotimes _{e\in M_\sigma }A_e$ is a weak matroid over $\mathbb {H}$.

Proof

We show that the proof in Sect. 3 can be adapted to this setting. Theorem 3.3 is a pure polyhedral geometric statement which requires no modification.

Next, concerning Lemma 3.8, we first temporarily replace the non-zero entries of A(T) by algebraically independent indeterminates. Now (i) every maximal minor of A(T) is either 0 or a monomial with coefficient $\pm 1$, and thus (ii) in an instance of the ordinary 3-term GP relation for A(T), the three terms involved must either be all zeros, or one term is zero while the other two are the same monomial with opposite coefficients. (i) implies that the maximal minors of A(T) are well-defined over $\mathbb {H}$, and their values coincide with $\upchi _T$; (ii) implies that $\upchi _T$ satisfies the hyperfield version of the 3-term GP relation.

Finally, the only part in the proof of Theorem 3.9 involving signs is to show that the restriction of a violation of the 3-term GP relation in the ambient matroid polytope to a subpolytope is still a violation, and the only non-trivial restriction is from an octahedron face to a pyramid/square cell. In the language of hyperfields, this means that if $0\not \in a\boxplus b\boxplus c$ with $a,b,c\ne 0$, then 0 is also not in the sum if we set one of the terms to zero. But this is (3) of Proposition 5.7. $\square$

Remark 5.9

The statement of Theorem 5.8 actually characterizes hyperfields with the IP. Suppose $\mathbb {H}$ does not have the IP, pick $a\in \mathbb {H}$ such that $-a\not \in 1\boxplus (-1)$, i.e., $0\not \in 1\boxplus (-1)\boxplus a$. Take the diagonal (2, 4)-matching field of the corresponding size depicted in Fig. 1. Also take the $\mathbb {H}$-matrix to be

$$\begin{aligned} \begin{pmatrix} 1 &{} 1 &{} 1 &{} 1\\ 1 &{} a &{} 1 &{} 1 \end{pmatrix}. \end{aligned}$$

The induced $\upchi$ is not a (weak) matroid over $\mathbb {H}$, as the 3-term GP relations involves the terms $\upchi (12)\upchi (34)=a, \upchi (13)\upchi (42)=-1,\upchi (14)\upchi (23)=1$.

The proof of Theorem 5.8 (as well as many results in the literature on matroid subdivisions) relies crucially on the reduction to the 3-term GP relation, hence is only enough to guarantee a weak matroid. This poses the obvious question of whether $\upchi$ is actually always a strong matroid; and the question provides a polyhedral angle to the differences between strong and weak matroids.

We elaborate on a construction of hyperfields with the IP from an arbitrary hyperfield $\mathbb {H}=(\mathbb {H},\boxplus ,\otimes ,0,1)$ [35]. It allows one to turn a $\upchi$ constructed in Theorem 5.8 over $\mathbb {H}$ into a (weak) matroid by pushforward. This is similar to the strategy of perfection of tracts that turns a weak matroid into a strong one, as proposed by Lorscheid et al. [33].

The new hyperfield $\widetilde{{\mathbb {H}}}$ has the same underlying set and multiplicative structure as $\mathbb {H}$, but with the new hyperoperation ${\widetilde{\boxplus }}$ where $a{\widetilde{\boxplus }} b=(a\boxplus b)\cup \{a,b\}$ for $a,b\ne 0$ and $a\ne -b$, and $a{\widetilde{\boxplus }} (-a)=\mathbb {H}$ for non-zero a. We suggest the name canonical inflation for the construction, as the (set-theoretic) identity map $\iota :\mathbb {H}\rightarrow \widetilde{{\mathbb {H}}}$ is a hyperfield morphism with the following universal property:

Proposition 5.10

Let $\varphi :\mathbb {H}\rightarrow \mathbb {H}'$ be a hyperfield morphism with $\mathbb {H}'$ having the IP. Then we have the factorization $\mathbb {H}\xrightarrow {\iota }\widetilde{\mathbb H}\xrightarrow {\varphi }\mathbb {H}'$ of hyperfield morphisms.

Proof

The only non-trivial part is that $\widetilde{\mathbb H}\xrightarrow {\varphi }\mathbb {H}'$ preserves addition of two non-zero values. Denote by $\boxplus , {\widetilde{\boxplus }}, \boxplus '$ the addition hyperoperators of $\mathbb {H}, \widetilde{{\mathbb {H}}}, \mathbb {H}'$, respectively. Suppose $a\ne -b$ are non-zero. Then $\varphi (a)\boxplus '\varphi (b)$ contains $\varphi (a\boxplus b)$ (as $\mathbb {H}\xrightarrow {\varphi }\mathbb {H}'$ is a hyperfield morphism) as well as $\{\varphi (a), \varphi (b)\}$ (as $\mathbb {H}'$ has the IP), so $\varphi (a)\boxplus '\varphi (b)$ contains $\varphi (a{\widetilde{\boxplus }} b)$. For $a\ne 0$, we have $\varphi (a{\widetilde{\boxplus }} (-a))=\varphi (\mathbb {H})\subset \mathbb {H}'=\varphi (a)\boxplus ' \varphi (-a)$. $\square$

Corollary 5.11

Let $(M_\sigma )$ be a polyhedral matching field. Let $\mathbb {H}$ be an arbitrary hyperfield and A be an $\mathbb {H}$-matrix with no zero entries. Then $\upchi :\sigma \mapsto \text {sign}(M_\sigma )\otimes \bigotimes _{e\in M_\sigma }A_e$ is a weak matroid over the canonical inflation $\widetilde{{\mathbb {H}}}$ of $\mathbb {H}$.

By Proposition 5.10 and Proposition 5.4, given a hyperfield morphism $\varphi :\mathbb {H}\rightarrow \mathbb {H}'$ with $\mathbb {H}'$ having the IP, $\varphi _*\upchi$ is a weak matroid over $\mathbb {H}'$.

Proof

Note that $\upchi$ does not involve the additive structure of $\mathbb {H}$ (respectively $\widetilde{{\mathbb {H}}}$), so we can simply interpret A as a $\widetilde{{\mathbb {H}}}$-matrix and apply Theorem 5.8 to $\upchi$. $\square$

We end with an example of canonical inflation that has a meaningful topological interpretation as a “closure” operation, and its connection with the theory of Grassmannians over hyperfields (see [6] for further discussion).

Example 5.12

The phase hyperfield $\mathbb {P}$ has underlying set $\{z\in \mathbb {C}:|z|=1\}\cup \{0\}$, with $w\boxplus z$ consists of the open minor arc between w, z if $w\ne -z$ are non-zero, $w\boxplus (-w)=\{w,-w,0\}$, and $w\otimes z=wz$. The tropical phase hyperfield $\Phi$ is the canonical inflation of $\mathbb {P}$, i.e., $w\boxplus z$ consists of the closed minor arc between w, z if $w\ne -z$ are non-zero, and $w\boxplus (-w)=\Phi$ if $w\ne 0$.

Let $ph:\mathbb {C}\rightarrow \mathbb {P}$ be given by $z\mapsto z/|z|$ if $z\ne 0$ and $0\mapsto 0$. Then we have the hyperfield morphisms $\mathbb {C}\xrightarrow {ph}\mathbb {P}\xrightarrow {\iota }\Phi$. Consider the diagonal (2, 4)-matching field together with the $\mathbb {P}$- (or $\Phi$-) matrix

$$\begin{aligned} \begin{pmatrix} 1 &{} 1 &{} 1 &{} 1\\ 1 &{} i &{} 1 &{} 1 \end{pmatrix}. \end{aligned}$$

Since $0\not \in 1\boxplus (-1)\boxplus i$ over $\mathbb {P}$, the function $\upchi$ such datum induces is not a matroid over $\mathbb {P}$, but it is a (weak) matroid over $\Phi$. However, $\upchi$ can be thought as a limit point of the Grassmannian $\textrm{Gr}_{\mathbb {P}}(2,4)\subset \mathbb {C}P^5$: we have $\upchi =\lim _{R\rightarrow \infty } ph_*\upchi _R$, where $\upchi _R$ is the matroid over $\mathbb {C}$ realized by the matrix

$$\begin{aligned} \begin{pmatrix} e^R &{} e^R &{} e^R &{} e^R\\ 1 &{} ie^R &{} e^{2R} &{} e^{3R} \end{pmatrix}. \end{aligned}$$