Abstract
On every closed contact manifold there exist contact forms with volume one whose Reeb flows have arbitrarily small topological entropy. In contrast, for many closed manifolds there is a uniform positive lower bound for the topological entropy of (not necessarily reversible) normalized Finsler geodesic flows.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Main results
The main results of this paper are the following two theorems.
Theorem 1.1
Let \((M,\xi )\) be a closed co-orientable contact manifold. For every \(\varepsilon >0\) there exists a contact form \(\alpha \) on \((M,\xi )\) with volume one such that the topological entropy \(h_{{\text {top}}}(\alpha )\) of its Reeb flow is smaller than \(\varepsilon \).
Given a closed manifold Q let \(h_{{\text {vol}}} (Q)\) be the infimum of the volume entropies of Riemannian metrics on Q that have volume one. This number is equal to \(2 \sqrt{\pi (k-1)}\) for a closed orientable surface of genus \(k \ge 2\), and it is positive for instance if Q admits a Riemannian metric of negative curvature. Given a Finsler metric F on Q we denote by \(h_{{\text {top}}} (F)\) the topological entropy of the time-one map of the geodesic flow of F. Define the dimension constants
where \(\omega _n\) is the volume of the Euclidean unit ball in \(\mathbb {R}^n\). For instance \(c_2 = \frac{1}{\sqrt{2\pi }}\), and asymptotically \(c_n \sim \sqrt{\frac{e}{2\pi }} \frac{1}{\sqrt{n}}\).
Theorem 1.2
Let Q be a closed connected n-dimensional manifold. Then for every Finsler metric F on Q of Holmes–Thompson volume one it holds that
and if F is symmetric that
In the rest of this introduction, we recall the notions appearing in these theorems, describe in more detail the results proved in this paper, put them into context, and formulate a few open problems they give rise to. We first tell our story for the special case of unit circle bundles over closed orientable surfaces of higher genus. Most ideas are present already for these simple spaces. We keep the presentation informal, referring to the subsequent sections for the precise definitions and arguments.
1.2 The case of unit circle bundles over higher genus surfaces
Let \(Q_k\) be the closed orientable surface of genus \(k \ge 2\). For every Riemannian metric g on \(Q_k\) we consider the geodesic flow \(\phi _g^t\) on the unit circle bundle
A good numerical measure for the complexity of the flow \(\phi _g^t\) is the topological entropy \(h_{{\text {top}}} (g):= h_{{\text {top}}} (\phi _g^1)\). A definition can be found in Appendix A. This is an interesting invariant because it is related to many other complexity measurements of \(\phi ^t_g\), see [60].
For which Riemannian metrics g is \(h_{{\text {top}}} (g)\) minimal? Such a g could then rightly be considered as a best Riemannian metric from a dynamical point of view. Since the topological entropy scales like
the problem is meaningful only if one imposes a normalization. We normalize by the Riemannian area and consider the scale invariant quantity
It is a classical theorem of Dinaburg [42] and Manning [69] that the geodesic flow of any Riemannian metric on \(Q_k\) has positive topological entropy (cf. Appendix A below). Their results do not give a uniform positive lower bound on \({\widehat{h}}_{{\text {top}}}(g)\) nor do they say anything about the minimizers, however. This was achieved in the following remarkable result of Katok [64].
Theorem 1.3
(Katok 1983) For every Riemannian metric g on \(Q_k\) it holds that
Moreover, equality holds if and only if g has constant curvature.
Geodesic flows are very special Reeb flows. For our unit circle bundle over \(Q_k\), Reeb flows can be described as follows. We look at the cotangent bundle \(T^*Q_k\) instead of the tangent bundle, endowed with its usual symplectic form \(\omega = d \lambda \), where \(\lambda = \sum _{j=1}^2 p_j dq_j\). Let \(H :T^*Q_k \rightarrow \mathbb {R}\) be a continuous function that is smooth and positive away from the zero-section and fiberwise positively homogenous of degree one: \(H(q, r p) = r H(q,p)\) for all \(r \ge 0\). Then \(S^*(H):= H^{-1} (1)\) is a smooth hypersurface of \(T^*Q_k\) with the property that for each point \(q \in Q_k\) the intersection \(S_q^* (H):= S^*(H) \cap T_q^*Q_k\) with the cotangent plane at q is the smooth boundary of a domain which is starshaped with respect to the origin \(0_q\), see the left drawing in Fig. 1. Denote by \(\phi _H^t\) the restriction of the Hamiltonian flow of H to \(S^*(H)\). The class of these flows are the Reeb flows on our unit circle bundle. This flow is a co-geodesic flow exactly if H restricts on each fiber to the square root of a positive quadratic form. Special shapes of the fibers \(S_q^* (H)\) in \(T_q^*Q_k\) correspond to special Reeb flows:
 :
:-
\(\phi _H^t\) is a Riemannian geodesic flow if and only if each \(S_q^* (H)\) is a centrally symmetric ellipse.
 :
:-
\(\phi _H^t\) is a reversible Finsler geodesic flow if and only if each \(S_q^* (H)\) is a centrally symmetric closed smooth curve with strictly positive curvature.
- (\(\triangle \)):
-
\(\phi _H^t\) is a Finsler geodesic flow if and only if each \(S_q^* (H)\) is a closed smooth curve with strictly positive curvature.
Here we identified co-Finsler geodesic flows with Finsler geodesic flows via the Legendre transform.
Based on [49] it was shown in [68] that the above result of Dinaburg and Manning about Riemannian geodesic flows extends to all Reeb flows:
Theorem 1.4
Every Reeb flow \(\phi _H^t\) on \(S^*(H)\subset T^* Q_k\), \(k\ge 2\), has positive topological entropy.
Does Katok’s theorem also extend to Reeb flows? To make the question meaningful, we again need to normalize. We do this by the symplectic volume of the bounded domain \(D^*(H)\) in \(T^*Q_k\) with boundary \(S^* (H)\), and define the Holmes–Thompson volume of \(Q_k\) associated with H by
Then the normalized topological entropy
is invariant under scalings of H. In the Riemannian case, this definition agrees with (1.2), since then \({\text {vol}}_H^{{\text {HT}}} (Q_k) = \textrm{area}_g (Q_k)\). The following question was asked in [48, §7.2].
Question 1.5
Is there a positive constant c(k) such that \(\widehat{h}_{{\text {top}}}^{{\text {HT}}} (H) \ge c(k)\) for every Reeb flow on the co-circle bundle over \(Q_k\)?
Let us first try to answer this question in the affirmative for Finsler geodesic flows. Given a Finsler metric F on \(Q_k\), an obvious idea is to find a lower bound for \(\widehat{h}_{{\text {top}}}^{{\text {HT}}}(F)\) by choosing a larger Riemannian metric \(\sqrt{g} \ge F\), cf. (1.1). In general, the topological entropy of geodesic flows is not monotone with respect to the order relation on metrics, however. We therefore pass to a more geometric version of entropy, which is indeed monotone: The volume entropy of F is defined as the exponential growth rate of balls in the universal cover \({\widetilde{Q}}_k\) (which is the plane),
where \({\tilde{q}}\) is any fixed point in \({\widetilde{Q}}_k\), \(B_{\tilde{q}} (R)\) is the ball of radius R about \({\tilde{q}}\) with respect to the lifted Finsler metric, and \({\text {Vol }}\) is the volume with respect to the lift of any smooth area form on \(Q_k\) (see Appendix A for details). It is clear that \(F_1 \ge F_2\) implies
In the case of a Riemmannian metric g, denoting \(h_{{\text {vol}}}(\sqrt{g})\) simply by \(h_{{\text {vol}}}(g)\), we have that
with equality if g has non-positive curvature, as proven by Manning in [69]. His proof of (1.6) readily generalizes to all Finsler metrics, see Appendix A:
Let g be a Riemannian metric such that \(\sqrt{g}\ge F\). Using (1.7) and (1.5) we can now estimate
In [64], Katok actually proved Theorem 1.3 for the normalized volume entropy \({\widehat{h}}_{{\text {vol}}}\) (which by Manning’s theorem implies Theorem 1.3). Hence we obtain
To get a uniform lower bound for \({\widehat{h}}_{{\text {top}}}^{{\text {HT}}} (F)\) we therefore look for a Riemannian metric g with \(\sqrt{g} \ge F\) that is as close as possible to F in the sense of the Holmes–Thompson volume. We best do this directly in the cotangent bundle \(T^*Q_k\). We thus look at each \(q \in Q_k\) for a centrally symmetric ellipse in \(T_q^* Q_k\) such that, denoting by \(E_q\) the region bounded by it, we have \(E_q \supset D_q^* (F)\) and \(E_q\) is as close to \(D_q^*(F)\) in volume as possible.
If \(D_q^*(F)\) is centrally symmetric, the best choice is Loewner’s outer ellipse. This is the unique centrally symmetric ellipse enclosing \(D_q^*(F)\) which minimizes the value of the area of the region bounded by it, which we denote by \(E(D_q^*(F))\). Here the area \(| \; |\) is taken with respect to any translation invariant measure on the plane \(T_q^*Q_k\). Loewner’s ellipse depends continuously on q, and the largest area ratio
is \(\frac{\pi }{2}\), which is attained exactly when \(D_q^*(F)\) is a parallelogram. If we take the Riemannian metric g on \(Q_k\) that has the sets \(E(D_q^*(F))\) as unit co-disks, we therefore obtain
Together with (1.8) this yields
If \(D_q^* (F)\) is not centrally symmetric, we observe that the convex hull
is centrally symmetric. It is not hard to see that for every convex body \(K \subset \mathbb {R}^2\) that contains the origin,
with equality attained exactly by the triangles with one vertex at the origin. Therefore,
Note that the constant \(2\pi \) is sharp and is attained exactly by the triangles with one vertex at the origin, see Fig. 2 (b).
Since the two maps
are continuous, we can take as g the Riemannian metric with unit co-disks
and obtain
Summarizing, we obtain Theorem 1.2 for orientable surfaces:
How sharp are these lower bounds? It is still unknown whether the constants \(\frac{1}{\sqrt{2\pi }}\) and \(\sqrt{\frac{2}{\pi }}\) can be replaced by 1. In other words, it is unknown whether there exist Finsler metrics F on \(Q_k\) such that \({\widehat{h}}_{{\text {vol}}}^{{\text {HT}}} (F) < h_{{\text {vol}}} (Q_k)\). We shall say more on this “minimal entropy problem" in Sect. 1.7.
Recall that for the closed orientable surfaces \(Q_k\) of genus k one has
For the non-orientable surface \(P_k\) whose orientation cover is \(Q_k\) this implies
For the other four closed surfaces (the sphere, the torus, the real projective plane and the Klein bottle) Theorem 1.2 is not useful since \(h_{{\text {vol}}}\) vanishes, and in fact there exist geodesic flows on these surfaces with vanishing topological entropy.
We now look at general Reeb flows on the co-circle bundle over \(Q_k\). As said earlier, these flows correspond to Hamiltonian flows on \(S^*(H) = H^{-1}(1)\) of Hamiltonian functions \(H :T^*Q_k \rightarrow \mathbb {R}\) that are fiberwise homogeneous of degree one. Looking for a lower bound for \({\widehat{h}}_{{\text {top}}}^{{\text {HT}}} (\phi _H)\), we proceed as in the case of Finsler geodesic flows, but knowing already (1.9) we now compare H with any Finsler metric. Choose a Finsler Hamiltonian \(F :T^*Q_k \rightarrow \mathbb {R}\) such that \(D^*(H) \subset D^*(F)\), i.e., \(F \le H\).
Definition (1.4) can be extended to Reeb flows: Fix a point \(q \in Q_k\), take a lift \({\tilde{q}} \in {\widetilde{Q}}_k\) of q and the lift \({\widetilde{H}} :T^*{\widetilde{Q}}_k \rightarrow \mathbb {R}\) of H, and then define \(h_{{\text {vol}}}(H,q)\) as the exponential growth rate of the volume of the set \(B_{{\tilde{q}}}({\widetilde{H}}, T)\) of those points \(z \in {\widetilde{Q}}_k\) for which the fiber \(S^*_z(\widetilde{H})\) can be reached in time \(\le T\) by a flow line of \(\phi _{{\widetilde{H}}}^t\) that starts at the fiber \(S^*_{\tilde{q}}({\widetilde{H}})\). As we shall show in Appendix A one then still has Manning’s inequality,
We now wish to show that there is a constant \(c>0\) depending only on H and F such that \(h_{{\text {vol}}}(H,q) \ge c\, h_{{\text {vol}}}(F)\). The existence of such a constant for non-convex H does not follow from geometric considerations, since it is not true in general that \(F \le H\) implies the inclusion of balls \(B_{{\tilde{q}}} (\widetilde{F},T) \subset B_{{\tilde{q}}}({\widetilde{H}}, T)\). However, using Lagrangian Floer homology in \(T^*Q_k\) one can avoid passing through \(h_{{\text {vol}}}(H, q)\) and prove directly that
where \(\sigma (H;F)\) is the smallest real number such that \(\frac{1}{\sigma (H;F)} D^*(F) \subset D^*(H)\), cf. Fig. 3. This is explained in Sect. 3, using the proof of the above Theorem 1.4 from [68].
The number \(\sigma (H):= \inf \{ \sigma (H;F) \mid F \le H \}\) is a measure for how far the fibers of \(D^*(H)\) are from being convex. Inequalities (1.10) and (1.9) and Katok’s inequality imply
Proposition 1.6
For every Reeb flow \(\phi _H\) on the co-circle bundle over \(Q_k\),
The following special case of Theorem 1.1 shows that the lower bound in (1.11) cannot be made uniform, that the answer to Question 1.5 is ‘no’, and that there is no way to extend Katok’s rigidity theorem to Reeb flows.
Theorem 1.7
For every \(\varepsilon >0\) there exists a Reeb flow \(\phi _H^t\) on \(S^*(H)\) with \({\widehat{h}}_{{\text {top}}}^{{\text {HT}}} (H) \le \varepsilon \).
Proposition 1.6 shows that this entropy collapse cannot happen unless at least some of the co-disks \(D_q^*(H) = D^*(H) \cap T_q^*Q_k\) are very far from convex. Writing down explicitely such star fields on \(T^*Q_k\) that lead to small \({\widehat{h}}_{{\text {top}}}^{{\text {HT}}}\) seems difficult, however. In fact, our proof of Theorem 1.7 does not use the special fibration structure of \(S^*(H)\), but uses the existence of open book decompositions valid for all closed 3-manifolds, see the beginning of Sect. 4.2 for an outline and Sect. 4 for the proof.
1.3 Entropy rigidity for Finsler geodesic flows
Proceeding as in the previous section, one readily arrives at Theorem 1.2 for Finsler geodesic flows on closed manifolds Q of arbitrary dimension n,
Here the normalization \({\widehat{h}}_{{\text {top}}}^{{\text {HT}}} (F) = \left( {\text {vol}}_F^{{\text {HT}}}(Q)\right) ^{1/n} \, h_{{\text {top}}}(F)\) is done in terms of the Holmes–Thompson volume
which extends definition (1.3). The proof of (1.12) uses Loewner’s outer ellipsoids and the Roger–Shephard volume bounds for symmetrized convex bodies. Similar arguments appear in [6], where they are used to derive systolic inequalities for Finsler metrics from the analogous inequalities for Riemannian metrics.
For Finsler metrics there is another natural volume, the Busemann–Hausdorff volume. For reversible Finsler metrics, this volume is at least the Holmes–Thompson volume, see Sect. 2. The second inequality in (1.12) thus also holds true if we normalize by the Busemann–Hausdorff volume. For irreversible Finsler metrics, however, we do not know whether the first inequality in (1.12) holds true for the Busemann–Hausdorff volume.
For manifolds of dimension \(n \ge 3\), it is more difficult to understand the volume entropy \(h_{{\text {vol}}}(Q)\) than for surfaces. The only sharp result is the following extension of Katok’s theorem.
Theorem 1.8
(Besson–Courtois–Gallot [20, 21]) If Q is a closed manifold of dimension at least 3 that admits a locally symmetric Riemannian metric \(g_0\) of negative curvature, then
for every Riemannian metric g on Q, and equality holds if and only if g is also locally symmetric. In particular, \(h_{{\text {vol}}}(Q) = {\widehat{h}}_{{\text {vol}}} (g_0) >0\).
Note that the space of minimizers up to isometry in Katok’s theorem is the \(6k-6\) dimensional Teichmüller space, while the minimizers in Theorem 1.8 are all isometric up to scaling, by Mostow’s theorem.
In the context of Theorem 1.2 we wish to know when \(h_{{\text {vol}}} (Q) >0\). The main tool for proving \(h_{{\text {vol}}} (Q) >0\) is the simplicial volume \(\Vert Q\Vert \). If Q is orientable, it is defined as \(\inf \sum _i |r_i|\) where the infimum is taken over those sums \(\sum _i r_i \sigma _i\) that represent the fundamental class \([Q] \in H_n (Q;\mathbb {R})\) with real coefficients. If Q is not orientable, pass to the orientation double covering \({\widehat{Q}}\) and put \(\Vert Q\Vert = \frac{1}{2} \Vert {\widehat{Q}}\Vert \). Gromov proved in [59] that
for an explicit dimension constant \(C_n\).
There are many more manifolds Q with positive simplicial volume \(\Vert Q\Vert \) than those in Theorem 1.8. Indeed, \(\Vert Q\Vert >0\) for all manifolds that admit a Riemannian metric of negative curvature, and positivity of the simplicial volume is preserved under taking the product with any other closed manifold of positive simplicial volume and under taking the connected sum with any other closed manifold of the same dimension. We refer to [59] and [66] for more examples and information on simplicial volume.
1.4 Entropy collapse for Reeb flows
Reeb flows are flows naturally associated to contact manifolds. A contact structure \(\xi \) on a (\(2n-1\))-dimensional manifold M is a maximally non-integrable hyperplane field of the tangent bundle TM. We assume throughout that \(\xi \) is co-orientable, i.e., \(\xi = \ker \alpha \) for a 1-form \(\alpha \) on M. In terms of such a form \(\alpha \), called a contact form for \(\xi \), the maximal non-integrability means that \(\alpha \wedge (d\alpha )^{n-1}\) is a volume form on M. For any non-vanishing function f on M the 1-form \(f \alpha \) is also a contact form on \((M,\xi )\). Each contact form \(\alpha \) gives rise to the Reeb flow \(\phi _\alpha ^t\), which is generated by the Reeb vector field \(R_\alpha \) implicitly defined by the two conditions
For every closed manifold Q the so-called spherization \((S^*Q,\xi _{\textrm{can}\,})\) is a contact manifold whose Reeb flows are exactly the flows \(\phi _H^t\) on \(S^*(H)\) described in Sect. 1.2 in the case of closed surfaces \(Q_k\), see Appendix B.1. Every closed 3-manifold admits infinitely many non-isotopic contact structures, and an odd-dimensional closed manifold M admits a contact structure if and only if its stabilized tangent bundle \(TM \oplus \mathbb {R}\) admits a complex structure [22].
Theorem 1.4 has been extended to many contact manifolds: First, for many closed manifolds Q every Reeb flow on \((S^*Q,\xi _{\textrm{can}\,})\) has positive topological entropy, [68]. Second, there are many closed 3-dimensional manifolds M such that for every contact structure \(\xi \) on M every Reeb flow has positive topological entropy, [7,8,9,10, 74]. For a recent result for non-degenerate Reeb flows see [33].
While in these results the underlying manifolds have rich loop space topology, there are also examples where the positivity of topological entropy of all Reeb flows does not come from the topological complexity of the loop space. For instance, it is shown in [11] that the standard smooth sphere of dimension \(2n-1 \ge 5\) admits a contact structure for which every Reeb flow has positive topological entropy.
Nevertheless, for none of these contact manifolds there can be a uniform bound for the normalized topological entropy: The contact volume of the co-oriented contact manifold \((M,\alpha )\) of dimension \(2n-1\) is defined as
Now define the normalized topological entropy of the Reeb flow \(\phi _\alpha ^t\) by
This normalization extends the normalizations (1.3) and (1.13) to all contact manifolds, see Appendix B.1. The following result implies Theorem 1.1.
Theorem 1.9
Let \((M,\xi )\) be a closed co-orientable contact manifold of dimension at least three. Then for every real number \(c >0\) there exists a contact form \(\alpha \) for \(\xi \) such that \(\widehat{h}_{{\text {top}}}(\alpha ) = c\).
We shall in fact prove the flexibility expressed in Theorem 1.9 for a larger growth rate: Given a \(C^1\)-diffeomorphism \(\phi \) of a compact manifold M, we define the two real numbers
Here \(\Vert \cdot \Vert _{\infty }\) denotes the supremum norm induced by a Riemannian metric on M, but the above limit, whose existence follows from the subadditivity of the sequence \(\log \Vert d\phi ^n\Vert _{\infty }\), is clearly independent of the choice of the metric.
The quantity \(\Gamma _+\) was used by Yomdin [96] to measure the difference between topological entropy and volume growth, and the study of the growth type of the sequence \(\Vert d \phi ^n \Vert _\infty \) for various classes of diffeomorphisms was proposed in [39, §7.10]. The more symmetric invariant \(\Gamma \) and its polynomial version were investigated, for instance, in [82, 83]. For Hamiltonian flows and Reeb flows, where uniform measurements (like the Hofer metric) turned out to capture symplectic rigidity, it is particularly natural to look at these two growth rates.
The norm growths \(\Gamma _+\) and \(\Gamma \) are related to the topological entropy by
see [60, Corollary 3.2.10] for the first inequality. The numbers \(\Gamma _+ (\phi )\) and \(\Gamma (\phi )\) are upper bounds for several other invariants of \(\phi \), and hence the collapsibility of \(\Gamma \) for Reeb flows also implies the collapsibility of these other invariants. For instance, \(\Gamma _+ (\phi )\) is not less than the largest Lyapunov exponent \(\chi _{\max } (p)\) at every point \(p \in M\). With
the sum of the positive Lyapunov exponents \(\chi _i^+(p)\) at p counted with their multiplicities \(k_i^+(p)\), we then also have \(\Sigma (p) \le (\dim M) \, \Gamma _+ (\phi )\). Together with the Margulis–Ruelle inequality (see [60, Theorem S.2.13]) we obtain that the metric entropy \(h_{\mu }(\phi )\) with respect to any invariant Borel probability measure \(\mu \) has the upper bound
Applying the variational principle for the topological entropy, we obtain again (1.15).
From now on we focus on \(\Gamma \). For a flow \(\phi ^t\) we set \(\Gamma (\phi ) = \Gamma (\phi ^1)\), and for a Reeb flow \(\phi _\alpha ^t\) we set \(\Gamma (\alpha ) = \Gamma (\phi _\alpha )\). For \(c>0\) we have \(\phi _{c \alpha }^t = \phi _\alpha ^{t/c}\) and hence \(\Gamma (c \alpha ) = \frac{1}{c} \Gamma (\alpha )\). Like for the topological entropy, the invariant
where \(\dim M = 2n-1\), is therefore invariant under scaling. In view of (1.15), the following result improves Theorem 1.1.
Theorem 1.10
Let \((M,\xi )\) be a closed co-orientable contact manifold of dimension at least three. Then for every real number \(c>0\) there exists a contact form \(\alpha \) for \(\xi \) such that \(\widehat{\Gamma }(\alpha ) = c\).
We shall prove Theorems 1.9 and 1.10 along the following lines. The main step is to show that for every \(\varepsilon >0\) there exists a contact form \(\alpha _{\varepsilon }\) for \(\xi \) such that \({\widehat{\Gamma }}(\alpha _{\varepsilon }) \le \varepsilon \). We do this with the help of an open book decomposition of M and an inductive construction, in which the induction step \(\dim 2n-1 \leadsto \dim 2n+1\) is carried out by applying the induction hypothesis to the binding of the open book decomposition of M. We can start the induction in dimension 1 at the circle, for which \({\widehat{\Gamma }} (d\theta ) =0\). We nevertheless present the 3-dimensional case separately in Sect. 4 because we believe that after understanding the geometric ideas in this particular situation it is easier to follow the general argument. The induction step is done in Sect. 6. It uses results of Giroux on the correspondence between contact structures and supporting open books, that we recollect in Sect. 5.
Given contact forms \(\alpha _{\varepsilon }\) as above, Theorems 1.9 and 1.10 follow from (1.15) and from a simple modification of \(\alpha _{\varepsilon }\) that increases \({\widehat{h}}_{{\text {top}}}\) and \({\widehat{\Gamma }}\), see Sect. 7.
1.5 Collapsing the growth rate of symplectic invariants
In the works [9, 11, 74] it is shown that the exponential growth rate of certain symplectic topological invariants provides a lower bound for the topological entropy of Reeb flows. These invariants are linearised Legendrian contact homology [9], wrapped Floer homology [11], and Rabinowitz–Floer homology [74]. Combining these results with Theorem 1.1 we obtain that the growth rate of these invariants can be made arbitrarily small. Details are given in Sect. 8.
1.6 Relations to systolic inequalities
Consider a closed co-orientable contact manifold \((M,\xi )\) of dimension \(2n-1\). Given a contact form \(\alpha \) for \(\xi \) that has at least one periodic Reeb orbit, take the smallest period \(T_{\min }(\alpha )\). The so-called systolic ratio
is then invariant under scalings of \(\alpha \).
While for spherizations \(S^*Q\) of many closed manifolds Q there are famous uniform upper bounds on the systolic ratios of Riemannian Reeb flows, in the full class of Reeb flows one has the following flexibility result.
Theorem 1.11
For any closed co-orientable contact manifold \((M,\xi )\) and every positive number c there exists a contact form \(\alpha \) such that \(\rho _{\textrm{sys}} (\alpha ) > c\).
This result was shown for the tight 3-sphere in [1] and for all contact 3-manifolds in [2] by a plug construction in open book decompositions. The idea in this paper to use open book decompositions for proving entropy collapse came from these works. Theorem 1.11 in dimension \(\ge 5\) was proved in [88]. That proof was later on much simplified [89] by using our inductive construction in Sect. 6. Interestingly, our construction in dimension 3 does not yield a proof of Theorem 1.11. This suggests that at least in the smallest interesting dimension, one has more flexibility to collapse the topological entropy of Reeb flows than to increase their systolic ratio.
1.7 Minimal entropy problems for Finsler and Reeb flows
Given a class \({{\mathcal {C}}}\) of maps on a compact manifold M, it is interesting to understand which maps in class \({{\mathcal {C}}}\) minimize the (normalized) topological entropy. Since topological entropy is a measure for the complexity, these maps can then be considered as the simplest, or the best, maps on M in class \({{\mathcal {C}}}\).
For the class of Riemannian geodesic flows on the spherization SQ of a compact manifold Q, the minimal entropy problem consists of three parts.
-
(P1)
Compute the minimal entropy
$$\begin{aligned} h_{{\text {top}}}(Q, {{\mathcal {G}}}) :=\, \inf \left\{ {\widehat{h}}_{{\text {top}}} ( \phi _g) \mid g\text { a Riemannian metric on } Q \right\} . \end{aligned}$$ -
(P2)
Decide whether the infimum is attained or not.
-
(P3)
If the infimum is attained, describe the minimizers g.
For manifolds admitting a locally symmetric Riemannian metric of negative curvature, Theorems 1.3 and 1.8 completely solve the minimal entropy problem. Among the many further interesting works on the minimal entropy problem are [65, 81].
The minimal entropy problem can also be formulated for the larger classes of Finsler and Reeb flows. Define three more numbers
by taking the infimum in the definition of \(h_{{\text {top}}} (Q,{{\mathcal {G}}})\) over all contact forms on \((S^*Q,\xi _{\textrm{can}\,})\) for \(h_{{\text {top}}}^{{\text {HT}}} (Q,{{\mathcal {R}}})\), over all Finsler metrics for \(h_{{\text {top}}}^{{\text {HT}}} (Q,{{\mathcal {F}}})\), and over all reversible Finsler metrics for \(h_{{\text {top}}}^{{\text {HT}}} (Q,{{\mathcal {F}}}_{{\text {rev}}})\), respectively, where as in (1.13) and (1.14) we normalize by the Holmes–Thompson volume.
Theorem 1.1 shows that \(h_{{\text {top}}}^{{\text {HT}}} (Q,{{\mathcal {R}}}) =0\) for all compact manifolds Q. This settles (P1) for the class \({{\mathcal {R}}}\). Furthermore, for many manifolds, like those with fundamental group of exponential growth, the answer to (P2) is ‘no’ by the general version of Theorem 1.4 from [68].
We now turn to the invariants \(h_{{\text {top}}}^{{\text {HT}}} (Q,{{\mathcal {F}}})\) and \(h_{{\text {top}}}^{{\text {HT}}} (Q,{{\mathcal {F}}}_{{\text {rev}}})\). By Theorems 1.2 and A.2 we have
For manifolds admitting a locally symmetric Riemannian metric of negative curvature (for which \(h_{{\text {top}}} (Q, {{\mathcal {G}}}) = h_{{\text {vol}}}(Q)\)) nothing more seems to be known about the values of \(h_{{\text {top}}}^{{\text {HT}}} (Q,{{\mathcal {F}}})\) and \(h_{{\text {top}}}^{{\text {HT}}} (Q,{{\mathcal {F}}}_{{\text {rev}}})\), so already (P1) in the entropy problem is wide open for the classes \({{\mathcal {F}}}\) and \({{\mathcal {F}}}_{{\text {rev}}}\).
Addressing (P3) we note that in the Finsler setting one cannot expect metrics of minimal normalized topological entropy to be unique, or even to be characterised in terms of curvature-like invariants. Indeed, any exact symplectomorphism of \(T^*Q\) that is \(C^2\)-close to the identity maps the unit cotangent sphere bundle \(S^*(F)\) of the Finsler metric F to the unit cotangent sphere bundle \(S^*(F')\) of some Finsler metric \(F'\) whose geodesic flow is conjugated to the one of F by a smooth time-preserving conjugacy. In particular, the new Finsler metric \(F'\) has the same normalized topological entropy as F, but need not be isometric to it. See Appendix D for a discussion of this.
Higher rank. More can be said in higher rank. The following result is proved in Sect. 2.6 using Verovic’s work [93].
Proposition 1.12
Let (Q, g) be a compact locally symmetric space of non-compact type and of rank \(\ge 2\). Then there exists a constant \(c<1\) such that
The constant c only depends on the globally symmetric space \(({\widetilde{Q}}, {\widetilde{g}})\), and it can be computed from its Weyl data. See Proposition 2.7 below for a more precise statement.
Let \(h_{{\text {vol}}}^{{\text {sym}}}(Q)\) be the minimum of \({\widehat{h}}_{{\text {vol}}}(g)\) taken over all locally symmetric Riemannian metrics g on Q. This number is easy to compute, see [35, §2]. Unfortunately it is still not known whether Theorem 1.8 also holds in higher rank, that is, whether \(h_{{\text {vol}}} (Q) = h_{{\text {vol}}}^{{\text {sym}}}(Q)\). However, this is known if (Q, g) is locally isometric to a product of negatively curved symmetric spaces of dimension \(\ge 3\), [35], and for quotients of the k-fold product \((\mathbb {H}^2)^k = \mathbb {H}_2 \times \dots \times \mathbb {H}_2\) of the real hyperbolic plane, [75]. For these spaces, (1.16) can thus be written as
We shall compute the constant c for quotients of \((\mathbb {H}^2)^k\) in Sect. 2.6. For instance, \(c (\mathbb {H}^2 \times \mathbb {H}^2) = \root 4 \of {2} \approx 0.841\). This should be compared with the constant \(2 c_4 = \sqrt{\frac{2}{\pi }} \approx 0.61\) for the lower bound in Theorem 1.1.
The minimal entropy problem can also be studied for the volume entropies \(h_{{\text {vol}}}\) instead of \(h_{{\text {top}}}\), and by normalizing either entropy by the Busemann–Hausdorff volume. Much of the above discussion applies also to these minimal entropies.
1.8 Topological pressure
In view of Theorem 1.1, there is no minimal entropy program for Reeb flows. Furthermore, the situation cannot be salvaged by looking at subexponential growth rates, since replacing \(\lim _{n \rightarrow \infty } \frac{1}{n} \log \dots \) in the definition of topological entropy by \(\lim _{n \rightarrow \infty } \frac{1}{n^c} \log \dots \) for some \(c \in (0,1)\) yields \(+ \infty \) for all Reeb flows on many contact manifolds by Theorem 1.4.
However, increasing topological entropy in terms of topological pressure leads to a meaningful problem. Given a closed contact manifold \((M,\xi )\) associate with every continuous function \(f \in C^0(M,\mathbb {R})\) and every contact form \(\alpha \) for \(\xi \) the topological pressure \(P(\alpha , f) = P (\phi _{\alpha },f)\), see [95, Chapter 9] for the definition and basic results on topological pressure. We recall that \(P(\alpha ,0) = h_{{\text {top}}}(\alpha )\) and that the variational principle for topological pressure says
where \({{\mathcal {M}}}(\alpha )\) denotes the set of \(\phi _{\alpha }^t\)-invariant Borel probability measures on M and \(h_\mu \ge 0\) is the entropy of the measure \(\mu \). Define
Since \(P(\alpha , f+c) = P(\alpha , f) +c\) for all \(c \in \mathbb {R}\), we can assume that \(\min f = 0\). Together with Theorem 1.1 we then obtain
It would be interesting to see if these bounds can be sharpened for functions f that do not identically vanish. Our proof of Theorem 1.1 does not help with this problem, since the maximal measures in (1.17) (the so-called equilibrium states) may not be related in any way to the open book decomposition in our proof.
2 Volume entropy for Finsler geodesic flows
2.1 Finsler metrics and their volumes
By a Finsler metric on an n-dimensional manifold Q we mean in this paper a continuous function \(F :TQ \rightarrow [0,+\infty )\) which is fiberwise convex, fiberwise positively homogeneous of degree 1, and positive outside of the zero section. The Finsler metric F is said to be reversible if \(F(v)=F(-v)\) for all \(v \in TQ\).
For \(q \in Q\) the unit disk in \(T_q Q\) determined by the Finsler metric F is the set
This is a convex compact neighborhood of the origin in \(T_q Q\). The function \(F|_{T_q Q}\) is precisely the Minkowski gauge of \(D_q(F)\). The unit co-disk in \(T_q^* Q\) is the polar set of \(D_q(F)\):
where \(\langle \cdot ,\cdot \rangle \) denotes the duality pairing between tangent vectors and co-vectors. This is a compact convex neighborhood of the origin in \(T_q^* Q\).
On compact Finsler manifolds there are two different notions of volume that are used in the literature. From the point of view of this paper, the most natural one is the Holmes–Thompson volume, which can be defined as
where
is the unit co-disk bundle of Q, where \(\omega ^n\) denotes the standard volume form on \(T^*Q\) induced by integrating the n-fold exterior power of the canonical symplectic form \(\omega = \sum _j dq_j \wedge dp_j\), and where \(\omega _n\) is the volume of the Euclidean unit ball in \(\mathbb {R}^n\), \(n=\dim Q\). The normalization factor \(n! \,\omega _n\) makes \({\text {vol}}_F^{{\text {HT}}}(Q)\) coincide with the Riemannian volume of Q when \(F(v) = \sqrt{g(v,v)}\) is a Riemannian metric on Q.
Alternatively, the Holmes–Thompson volume can be defined as the integral over Q of a suitable volume density \(\rho _F^*\). Here by volume density we mean a norm on the line bundle \(\Lambda ^n(TQ)\), whose fiber at \(q \in Q\) is the top degree component of the exterior algebra of \(T_q Q\), that is, the 1-dimensional space spanned by \(v_1\wedge \dots \wedge v_n\), where \(v_1,\dots ,v_n\) is a basis of \(T_q Q\). When Q is orientable, a volume density is just the absolute value of a nowhere vanishing differential n-form. A volume density can be integrated over any non-empty open subset of Q, producing a positive number. The volume density \(\rho _F^*\) is defined as follows: Given any volume density \(\rho \) on Q set
where \(|\! \cdot \!|^*_{\rho }\) denotes the Lebesgue measure on \(T_q^* Q\) that is normalized to 1 on the n-dimensional parallelogram spanned by the covectors that are dual to basis vectors \(v_1,\dots ,v_n\) in \(T_q Q\) such that \(\rho (q)[v_1 \wedge \dots \wedge v_n]=1\). We then have
Another common choice is to consider the Busemann–Hausdorff volume, which is defined as
where the volume density \(\rho _F\) is given by
Here \(\rho \) is again an arbitrary volume density on Q and \(| \! \cdot \! |_{\rho }\) is the Lebesgue measure on \(T_q Q\) normalized to 1 on the parallelogram spanned by vectors \(v_1,\dots ,v_n\) in \(T_q Q\) with \(\rho (q)[v_1 \wedge \dots \wedge v_n]=1\). When F is reversible, the Busemann–Hausdorff volume of Q coincides with the n-dimensional Hausdorff measure of Q with respect to the distance induced by F.
Both volumes reduce to the standard Riemannian volume when the Finsler metric F is Riemannian. If F is reversible, then
with equality holding if and only if F is Riemannian. This follows from the Blaschke–Santaló inequality, see e.g. [43]. In the non-reversible case, the Holmes–Thompson volume can be much larger than the Busemann–Hausdorff volume. Note that both the Holmes–Thompson and the Busemann–Hausdorff volume depend monotonically on the Finsler metric, meaning that
and rescale as
when the Finsler metric F is multiplied by a positive constant c.
2.2 Volume entropy
Let F be a Finsler metric on a compact n-dimensional manifold Q. This Finsler metric lifts to a Finsler metric on the universal cover \(\widetilde{Q}\) of Q, and we denote the lifted metric by the same symbol F. The R-ball centered at \(q \in \widetilde{Q}\) that is induced by F is the following compact subset of \(\widetilde{Q}\):
When F is reversible, \(B_q(F,R)\) is the ball of the distance on \(\widetilde{Q}\) that is induced by F; in general, it is the forward ball of an asymmetric distance.
The volume entropy of F is the non-negative number
Here \({\text {Vol }}\) denotes the volume of Borel subsets of \(\widetilde{Q}\) with respect to the lift to \(\widetilde{Q}\) of an arbitrary Riemannian metric on Q. A minor modification of Manning’s argument from [69] shows that the above limit exists and is independent of the choice of the point \(q \in \widetilde{Q}\) and of the Riemannian metric on Q, see Proposition A.1. In the case of the Finsler metric \(G=\sqrt{g(\cdot ,\cdot )}\) that is induced by a Riemannian metric g, we use interchangeably the notations
The volume entropy is monotonically decreasing in F, meaning that
Indeed, if \(F_1 \le F_2\) on Q then the same inequality holds on \(\widetilde{Q}\) and hence (2.4) implies
from which (2.6) follows. Let c be a positive number. From the identity
we deduce that the volume entropy rescales as
Together with (2.3), this suggests to consider the normalized volume entropies
These quantities are now invariant under scaling:
Since the Holmes–Thompson and the Busemann–Hausdorff volumes coincide when \(F=G=\sqrt{g}\) is Riemannian, there is just one normalized volume entropy in the Riemannian case, and we denote it by
In the next two subsections, we study how the two different normalized volume entropies of an arbitrary Finsler metric can be bounded from below and from above in terms of the normalized volume entropy of suitable Riemannian metrics. Our arguments follow [6], where similar techniques are used in order to derive bounds for the systolic ratio.
2.3 From reversible Finsler to Riemannian
Let F be a reversible Finsler metric on the compact n-dimensional manifold Q. Denote by \(E_q\) the inner Loewner ellipsoid of the symmetric convex body \(D_q(F)\), i.e. the ellipsoid centered at the origin which is contained in \(D_q(F)\) and has maximal volume among all ellipsoids with this property. Here by volume we mean any translation invariant measure on \(T_q Q\) (which is unique up to multiplication by a positive constant). It is well known that the inner Loewner ellipsoid is unique, and John proved that it satisfies
See [62], or [12] for a modern proof of these results. Denote by \(G :TQ \rightarrow [0,+\infty )\) the function which in each tangent space \(T_q Q\) is the Minkowski gauge of \(E_q\). The function G is the square root of a Riemannian metric: \(G(v) = \sqrt{g(v,v)}\) for some continuous Riemannian metric g on Q. Indeed, the continuity of G easily follows from the uniqueness of the inner Loewner ellipsoid. From the inclusions (2.8) we deduce the inequalities
which thanks to (2.6) and (2.7) imply the bounds
By (2.2) and the second inequality in (2.9) the Busemann–Hausdorff volume of (Q, F) has the upper bound
In order to get a lower bound for the Holmes–Thompson volume of (Q, F) we can use (2.2), (2.3) and the first inequality in (2.9) and obtain
However, we get a better bound by the following argument. The polar set \(E_q^*=D_q^*(G)\) of \(E_q=D_q(G)\) satisfies
and is the outer Loewner ellipsoid of \(D_q^*(F)\), i.e. the centrally symmetric ellipsoid of minimal volume among those containing \(D_q^*(F)\). Then we have
This follows from the fact that the ratio between the volume of the outer Loewner ellipsoid of a symmetric convex body K and the volume of K is maximal for the cross-polytope, a result that Ball deduced from the inverse Brascamp–Lieb inequality of Barthe in [13, Theorem 5]. Therefore, we obtain
which is a better bound than (2.12) for every \(n \ge 2\), and also asymptotically because
by the Stirling formula. By putting together (2.1), (2.10), (2.11) and (2.13) we obtain the following result.
Proposition 2.1
Let F be a reversible Finsler metric on the compact n-dimensional manifold Q and let \(G = \sqrt{g}\) be the Riemannian metric on Q whose unit disks are the inner Loewner ellipsoids of the unit disks of F. Then
2.4 From irreversible to reversible Finsler
Let F be an arbitrary Finsler metric on the compact n-dimensional manifold Q. We symmetrize the metric F by the following procedure: We define \(S :TQ \rightarrow [0,+\infty )\) to be the reversible Finsler metric on Q whose unit co-disk at each \(q \in Q\) is the reflection body of \(D_q^*(F)\), i.e. the centrally symmetric convex body
Note that
where \(\theta \) is the irreversibility ratio of F, i.e. the number
which is at least 1, and equal to 1 if and only if F is reversible. Indeed, the second inclusion in (2.14) follows from the fact that \(\theta \) is an upper bound for the norm of minus the identity on \(T_q Q\) with the asymmetric norm F, and hence also for the norm of minus the identity on \(T_q^* Q\) with the asymmetric norm that is dual to F. Moreover, the volume of \(D^*_q(S)\) has the upper bound
as proven by Rogers and Shephard in [86, Theorem 3]. From (2.14) we deduce
and hence (2.6) and (2.7) imply
On the other hand, from (2.16) and the second inequality in (2.17) we obtain the following inequalities for the Holmes–Thompson volume
The bounds (2.18) and (2.19) imply the following result.
Proposition 2.2
Let F be a Finsler metric on the compact n-dimensional manifold Q with irreversibility ratio \(\theta \) and let S be the reversible Finsler metric whose dual disks are the reflection bodies of the dual disks of F:
Then
The lower bounds of Propositions 2.1 and 2.2, together with Stirling’s formula, have the following consequence:
Corollary 2.3
Let Q be a compact n-dimensional manifold and denote by \(h_{{\text {vol}}}(Q)\) the infimum of \(\widehat{h}_{{\text {vol}}}(g)\) over all Riemannian metrics g on Q. Then the Holmes–Thompson normalized volume entropy of an arbitrary Finsler metric F on Q has the lower bound
where
Moreover, if the Finsler metric F is reversible, we have
Remark 2.4
If we symmetrize \(D_q^*(F)\) by considering the difference body \(D_q^*(F)-D_q^*(F)\) instead of the reflection body, then we get a worse bound, because in this case the factor \(2^n\) in (2.16) must be replaced by the middle binomial coefficient \(\left( {\begin{array}{c}2n\\ n\end{array}}\right) \), in view of the Rogers–Shephard inequality for the volume of the difference body, see [85]. By using the reflection body instead of the difference body, the systolic upper bounds of Theorem 4.13 and Corollary 4.14 in [6] can be improved by replacing the dimension dependent quantity \(\root n \of {(2n)!/(n!)^2}\) by the constant factor 2.
If the volume entropy is normalized by the Busemann–Hausdorff volume, we do not get a lower bound that is independent of the irreversibility ratio. From (2.2), (2.3), (2.17) and (2.18) we obtain
We do not have a lower bound that is independent of \(\theta \) because, unlike the volume ratio \(|D_q^*(S)|_{\rho }^*/ |D_q^*(F)|_{\rho }^*\), the ratio \(|D_q(F)|_{\rho }/|D_q(S)|_{\rho }\) can be arbitrarily large.
On the other hand, the upper bound can be made independent of the irreversibility ratio \(\theta \) by symmetrizing, this time, directly in TQ: We consider the reversible Finsler metric T whose unit ball at q is the set
For this metric, we have
from which we obtain
Moreover, the Rogers–Shephard inequality for the reflection body gives
and we deduce the following result.
Proposition 2.5
Let F be a Finsler metric on the compact n-dimensional manifold Q with irreversibility ratio \(\theta \) and let T be the reversible Finsler metric whose unit disk at each q is the reflection body
of the disk of F at q. Then
2.5 Lower bounds on the normalized topological entropy
We now assume that the (possibly irreversible) Finsler metric F on Q has better regularity and convexity properties: Outside of the zero section, \(F :TQ \rightarrow \mathbb {R}\) is of class \(C^{2}\) and the fiberwise second differential of \(F^2\) is positive definite. We will refer to such an F as to a regular Finsler metric. Under these assumptions, the geodesic flow of F is well defined. We denote by \(h_{{\text {top}}}(F)\) the topological entropy of this flow, and by
the Holmes–Thompson and Busemann–Hausdorff normalizations of this entropy. Manning’s inequality
from [69] holds also in the Finsler setting, as shown in Theorem A.2. Then Corollary 2.3 has the following immediate consequence.
Corollary 2.6
Let Q be a compact n-dimensional manifold and denote by \(h_{{\text {vol}}}(Q)\) the infimum of \(\widehat{h}_{{\text {vol}}}(g)\) over all Riemannian metrics g on Q. Then the Holmes–Thompson normalized topological entropy of any regular Finsler metric F on Q has the lower bound
where
Moreover, if the Finsler metric F is reversible, we have
2.6 Finsler metrics with small topological entropy
The following result is more precise than Proposition 1.12.
Proposition 2.7
Let \(({\widetilde{Q}}, {\widetilde{g}})\) be a Riemannian globally symmetric space of non-compact type and of rank \(\ge 2\). Let G be the connected component of the identity of the isometry group of \(({\widetilde{Q}}, {\widetilde{g}})\). Then there exist computable constants \(c^{{\text {HT}}}< c^{{\text {BH}}} < 1\) that depend only on \((\widetilde{Q}, {\widetilde{g}})\) with the following property: For every discrete co-compact subgroup \(\Gamma \) of G that acts without fixed points on \({\widetilde{Q}}\) and for every \(\varepsilon >0\) there exists a smooth reversible G-invariant Finsler metric F on \(Q = {\widetilde{Q}} / \Gamma \) such that
In particular, \({\widehat{h}}_{{\text {top}}}^{{\text {HT}}}(Q, {{\mathcal {F}}}_{{\text {rev}}}) \le c^{{\text {HT}}} \; {\widehat{h}}_{{\text {vol}}} ({\widetilde{g}})\) and \({\widehat{h}}_{{\text {top}}}^{{\text {BH}}}(Q, {{\mathcal {F}}}_{{\text {rev}}}) \le c^{{\text {BH}}} \; {\widehat{h}}_{{\text {vol}}} ({\widetilde{g}})\).
Proof
Fix a point \(x_0 \in G\), let \(K \subset G\) be the stabilizer of \(x_0\), let \({\mathfrak {g}}\) and \({\mathfrak {k}}\) be the Lie algebras of G and K, and let \({\mathfrak {g}} = {\mathfrak {k}} \oplus {\mathfrak {p}}\) be the Cartan decomposition associated with \(x_0\). (Then \({\mathfrak {p}} \cong T_{x_0} {\widetilde{Q}}\).) Choose a maximal abelian subalgebra \({\mathfrak {a}} \subset {\mathfrak {p}}\), and let \(W_{{\mathfrak {a}}}\) be its Weyl group.
The set of G-invariant Finsler metrics on \({\widetilde{Q}}\) is in bijection with the set
In general, the Finsler metric assoiated with \(C \in {{\mathcal {C}}}\) is only continuous, and it is smooth if and only if the boundary of C is smooth. Let \(C_0\) be “the least convex" body in \({{\mathcal {C}}}\) of \({\widetilde{g}}\)-volume one. (For details we refer to [93], but it should become clear from Examples 2.8 below how to construct \(C_0\).) Since \(\dim {\mathfrak {a}} = \mathrm {rank\,}(G/K) \ge 2\), \(C_0\) is not just a segment, and hence not an ellipsoid, i.e., the Finsler metric \(F_0\) associated with \(C_0\) is not Riemannian. In fact, \(F_0\) is not smooth. Verovic shows that \(F_0\) is the unique minimizer of \({\widehat{h}}_{{\text {vol}}} (F)\) among all G-invariant continuous Finsler metrics on \({\widetilde{Q}}\). In particular, the constant \(c^{{\text {BH}}}\) defined by
is strictly less than 1. There is a simple formula computing this constant in terms of the Weyl data of \({\mathfrak {a}}\).
Fix \(\varepsilon >0\), choose a smooth body C from \({{\mathcal {C}}}\) such that
and let F be the associated Finsler metric. Then
cf. Sect. 2.2. Since \({\widetilde{Q}}\) is of non-compact type, G is semi-simple, see for instance [99, Proposition 6.38 (d)]. It thus follows from [40, Theorem 6.3 (2)] that F has negative flag curvature. Therefore, the extension of Manning’s equality to reversible Finsler metrics in [44, Theorem 6.1] implies that
The line (2.21) follows from (2.24), (2.23), and (2.22).
Define the constant \(c^{{\text {HT}}}\) by
By (2.1) and the Santaló inequality, \(c^{{\text {HT}}} < c^{{\text {BH}}}\). Repeating the above arguments we obtain (2.20). \(\square \)
Example 2.8
1. Let Q be a compact quotient of the symmetric space \((\mathbb {H}^2)^k\) of rank k. The maximal abelian subalgebra \(\mathfrak a\) is \(\mathbb {R}^k\), with Weyl chamber \({\mathfrak {a}}^+ = \mathbb {R}_{>0}^k\). The set of positive roots is given by the dual basis \(\varepsilon _1, \dots , \varepsilon _k\) of the standard basis \(e_1, \dots , e_k\) of \(\mathbb {R}^k\).
The standard Riemannian metric g on Q corresponds, up to to scaling, to the closed unit ball B in \({\mathfrak {a}} = \mathbb {R}^k\), and we take \(F_0\) to be the non-smooth Finsler metric corresponding to the cross-polytope \(C_0\) in \({\mathfrak {a}}\) with vertices \(\pm e_1, \dots , \pm e_k\). Now Proposition 2.2 in [93] shows that
Let \(D_{x_0}(F_0)\) resp. \(D_{x_0}(g)\) be the unit ball of \(F_0\) resp. g in \(T_{x_0}{\widetilde{Q}} \sim {\mathfrak {p}}\). By G-invariance of \(F_0\) and g, and in view of the definition of the Busemann–Hausforff volume in Sect. 2.1,
Lemma 2.9
The quotient on the right of (2.25) is equal to \(\frac{(2k)!}{2^k k!}\).
Proof
We have \(D_{x_0}(F_0) = {\text {Ad}}(K) (C_0)\) and \(D_{x_0}(g) = {\text {Ad}}(K) (B)\). For \(k=1\), when \(G = \textrm{SL}(2;\mathbb {R})\) and \(K = \textrm{SO}(2;\mathbb {R})\), a computation in the orthogonal basis \({ \bigl ( {\begin{matrix} 1&{}0\\ 0&{}-1 \end{matrix}} \bigr )}\), \({ \bigl ( {\begin{matrix} 0&{}1\\ 1&{}0 \end{matrix}} \bigr )}\) of \({\mathfrak {p}}\) shows that the orbit \({\text {Ad}}(K) p\) of a point \(p \in {\mathfrak {p}}\) is the circle through p. For general \(k \ge 1\), the \({\text {Ad}}(K)\)-orbit of \(p = (p_1, \dots , p_k) \in {\mathfrak {p}}\) is the k-torus made of circles of radius \(|p_i|\). Since the restrictions of \(F_0\) and g to \({\mathfrak {p}}\) are \({\text {Ad}}(K)\)-invariant, it follows that the quotient on the right of (2.25) is equal to the quotient of the two integrals
The first integral equals \(\frac{1}{2^k k!}\) and the second equals \(\frac{1}{(2k)!}\) as one finds using Fubini’s theorem and induction. \(\square \)
Together with the lemma we conclude that
We next compute the Holmes–Thompson volumes \({\text {vol}}_{F_0}^{{\text {HT}}}(Q)\) and \({\text {vol}}_{g}^{{\text {HT}}}(Q)\). Denote by \(C_0^*\) and \(B^*\) the polar sets of \(C_0\) and B in \({\mathfrak {p}}^*\), respectively, and by \(g^*\) the dual Riemannian metric on \({\mathfrak {p}}^*\). By G-invariance of \(F_0\) and g, and in view of the definition of the Holmes–Thompson volume in Sect. 2.1,
Using that \(D_{x_0}^*(F_0) = {\text {Ad}}^* (K) (C_0^*)\) and \(D_{x_0}^*(g) = {\text {Ad}}^* (K) (B^*)\), that the polar set \(C_0^*\) of the cross-polytope \(C_0\) is the unit cube, and the computations
we find that the right quotient in (2.26) is k!. Therefore,
It is shown in [75] that
Together with Theorem 1.2 and Proposition 1.12 we obtain
The sequence \(c_k^{{\text {BH}}}\), \(k \ge 2\), is monotone decreasing to \(\sqrt{\frac{2}{e}} \approx 0.858\), starting with
The sequence \(c_k^{{\text {HT}}}\) is monotone decreasing to \(\sqrt{\frac{1}{e}} \approx 0.616\), starting with
In contrast, the sequence \(2 c_{2k} = \frac{2}{\bigl ( (2k)! \, \omega _{2k} \bigr )^{1/(2k)}}\) is monotone decreasing like \(\sqrt{\frac{e}{2\pi }} \frac{1}{\sqrt{2k}}\), starting with
The constant \(h_{{\text {vol}}}(Q)\) can be computed as follows. On \((\mathbb {H}^2)^k\) the minimum of the volume entropies among symmetric metrics is attained exactly by multiples of \(g^k:= g \times \dots \times g\), where g is the metric on \(\mathbb {H}\) of constant curvature \(-1\), see [35, §2]. Since \(h_{{\text {vol}}}(g) =1\), we have \(h_{{\text {vol}}}(g^k) = \sqrt{\sum (h_{{\text {vol}}}(g))^2} = \sqrt{k}\). Hence
For instance, if Q is the product of orientable surfaces of genus \(k_j\), then
2. Take the 5-dimensional symmetric space \(\textrm{SL}(3;\mathbb {R}) / \textrm{SO}(3;\mathbb {R})\) of rank 2. The “least convex” body \(C_0\) from \({{\mathcal {C}}}\) is a regular hexagon. We scale this hexagon such that it is the hexagon \(H_{{\textrm{in}}}\) inscribed the unit disc B of \(\mathbb {R}^2 = {\mathfrak {a}}\). Verovic computed in [93, p. 1644] that for the Finsler metric corresponding to \(\sqrt{\frac{2}{3}} \, H_{{\textrm{in}}}\), the volume growth is 2. Hence the volume growth of the Finsler metric corresponding to \(H_{{\textrm{in}}}\) is \(\sqrt{\frac{3}{2}} \,2\). Further, the volume growth of the Riemannian metric corresponding to B is \(2 \sqrt{2}\).
To compute the volumes, since \(\textrm{SO}(3;\mathbb {R})\) is 3-dimensional we now have to take \(r^3 dx dy\) as density on \({\mathfrak {a}}\). The integral of \(r^3\) over B and over \(H_{{\textrm{in}}}\) are, respectively, \(\frac{2\pi }{5}\) and
With this we find along the lines of the previous examples that
The polar set of \(H_{{\textrm{in}}}\) is a regular hexagon \(H_{{\textrm{out}}}\) circumscribed the unit co-disc. After identifying \({\mathfrak {a}}\) with \({\mathfrak {a}}^*\) by the inner product, we have that \(H_{{\textrm{out}}}\) is obtained from \(H_{{\textrm{in}}}\) by dilation by \(\frac{2}{\sqrt{3}}\) and rotation by \(\frac{\pi }{6}\). Hence the integral of \(r^3\) over \(H_{{\textrm{out}}}\) is
Therefore,
These two constants should be compared with the constant \(2 c_5 \approx 0.551\) for the lower bound in Corollary 2.6.
Question 2.10
Recall that the non-smooth Finsler metric \(F_0\) is the unique minimizer of \({\widehat{h}}_{{\text {vol}}}^{{\text {BH}}}(F)\) among G-invariant continuous Finsler metrics on Q. This Finsler metric has a high degree of symmetry: Its restriction to \({\mathfrak {a}}\) is invariant under the Weyl group, and it is G-invariant. Since in Theorems 1.3 and 1.8 the Riemannian minimizers are the locally symmetric metrics, one may expect that \(F_0\) minimizes \({\widehat{h}}_{{\text {vol}}}^{{\text {BH}}}(F)\) and \({\widehat{h}}_{{\text {vol}}}^{{\text {HT}}}(F)\) among all continuous Finsler metrics on Q. Would this imply that there are no smooth minimizers?
3 A lower entropy bound for Reeb flows on spherizations
Recall from Theorem 1.1 that there cannot be a uniform lower bound for the normalized topological entropy of Reeb flows. In this section we show that for many base manifolds Q, one nevertheless has a control on the entropy collapse of Reeb flows on the spherization \(S^*Q\) in terms of the geometry of their defining star fields: Entropy collapse can only happen if some fibers are far from convex. The proof relies on Floer homology.
We consider a closed manifold Q and two Reeb flows on \(S^*Q\), one arbitrary and one Finsler. As in the previous section and as in Appendix B.1 we work in \(T^*Q\). We then have two Hamiltonian functions \(H,F :T^*Q \rightarrow \mathbb {R}\) that are fiberwise positively homogeneous of degree one and smooth and positive away from the zero section. Again we denote by \(\phi _H^t\) the flow of H on \(S^*(H) = H^{-1}(1)\), and similarly for F. Let \(\sigma _-\) and \(\sigma _+\) be the smallest positive numbers such that
For the co-disk bundles we then have
see Fig. 4.
The number
does not change under rescalings of H or F. We have \(\sigma (H;F) \ge 1\) with equality if and only if \(H=cF\) for some positive number c. Moreover, \(\sigma (H;F) \le \sqrt{n}\) if H is a reversible Finsler Hamiltonian and F is chosen to be the Riemannian Hamiltonian associated with the outer Loewner ellipsoids of \(D^*(H)\), see (2.8).
Proposition 3.1
Let F be a (possibly irreversible) \(C^\infty \)-regular Finsler metric on the closed manifold Q. Then for every \(C^\infty \)-smooth Reeb flow \(\phi _H^t\) on \(S^*Q\) we have
Proof
After scaling F we can assume that \(\sigma _- \!=\!1\). We abbreviate \(\sigma (H;F) \!=\! \sigma _+ \!=: \!\sigma \).
Lemma 3.2
\(h_{{\text {top}}}(\phi _H) \ge h_{{\text {vol}}}(F)\).
Proof
The lemma can be extracted from [68]. We briefly review the proof. Instead of working with \(\phi _H\) and \(\phi _F\), we work with the Hamiltonian flows \(\Phi _H\) and \(\Phi _F\) on \(T^*Q\) of the functions \(H^2\) and \(F^2\). Then \(\Phi _H = \phi _H\) on \(S^*(H)\). Using the variational principle for topological entropy and the homogeneity of \(H^2\) one finds
Fixing a point \(q \in Q\) we can further estimate, using Yomdin’s theorem from [96] and the \(C^\infty \)-smoothness of \(\Phi _H\),
Here \(\mu _{g^*} (S)\) denotes the Riemannian volume of the submanifold \(S \subset T^*Q\) with respect to the restriction to S of the Riemannian metric on \(T^*Q\) induced by a Riemannian metric g on Q. In Theorem 4.6 and Section 5.1 of [68] it is shown by Lagrangian Floer homology that for every \(\varepsilon >0\) there exists \(N(\varepsilon )\) such that
where \(\gamma (F)\) is the exponential growth rate of the number of elements in the fundamental group of Q that can be represented by a loop of F-length \(\le R\). It is easy to see that \(\gamma (F) = h_{{\text {vol}}} (F)\). (The proof in [60, Prop. 9.6.6] given for a Riemannian F applies without changes to a general Finsler metric.) The lemma follows. \(\square \)
In view of the inclusion \(\frac{1}{\sigma }D^*(F) \subset D^*(H)\) we infer from Lemma 3.2 that
as claimed. \(\square \)
We now define the module of starshapedness of H by
While an individual \(\sigma (H;F)\) can be large even for a Riemannian Hamiltonian H, the number \(\sigma (H)\) is a measure for the maximal starshapedness, or non-convexity, of the fibers of \(D^*(H)\). For instance, \(\sigma (H) = 1\) if and only if H is Finsler. From Proposition 3.1 and Corollary 2.3 we obtain the following result.
Corollary 3.3
Let Q be a closed manifold. For every \(C^\infty \)-smooth Reeb flow \(\phi _H^t\) on \(S^*Q\) we have
Remark 3.4
-
(1)
In the special case that \(H=F\) is a \(C^\infty \)-regular reversible Finsler Hamiltonian, Proposition 3.1 applied to Riemannian metrics and the Loewner bound (2.8) yield the uniform lower bound
$$\begin{aligned} {\widehat{h}}_{{\text {top}}}^{{\text {HT}}}(F) \,\ge \, \tfrac{1}{\sqrt{n}} \, \widehat{h}_{{\text {vol}}} (Q). \end{aligned}$$Even in this special case, this lower bound for \(\widehat{h}_{{\text {top}}}^{{\text {HT}}}(F)\) coming from Floer homology and from the Loewner bound is only slightly weaker than the lower bound
$$\begin{aligned} {\widehat{h}}_{{\text {top}}}^{{\text {HT}}}(F) \,\ge \, 2 c_n \, {\widehat{h}}_{{\text {vol}}} (Q) \end{aligned}$$from Corollary 2.6 that comes from Manning’s inequality and the Loewner bound. Indeed, recalling that \(c_n = \frac{1}{ (n! \, \omega _n)^{1/n} }\), the function \(f(n) = 2 c_n \sqrt{n} :\mathbb {N}\rightarrow [1, \infty )\) is strictly monotone increasing, with
$$\begin{aligned} f(2) = \tfrac{2}{\sqrt{\pi }} \approx 1.13 \quad \text{ and } \quad \lim _{n \rightarrow + \infty } f(n) = \sqrt{\tfrac{2e}{\pi }} \approx 1.315. \end{aligned}$$ -
(2)
In the case that H is a Finsler Hamiltonian and F is a Riemannian Hamiltonian, we have obtained the inequality in Lemma 3.2 in Sect. 2.5 by estimating
$$\begin{aligned} h_{{\text {top}}}(\phi _H) \ge h_{{\text {vol}}}(\phi _H) \ge h_{{\text {vol}}}(F). \end{aligned}$$The first inequality, which is Manning’s inequality, also holds for \(C^\infty \)-smooth Reeb flows, see Theorem A.8. The second inequality holds in the Finsler case in view of the inclusion of balls (2.6), which follows from the triangle inequality. But in the Reeb case there is no triangle inequality. Floer homology (or, more precisely: properties of Floer continuation maps that stem from the Floer–Gromov compactness theorem for J-holomorphic strips) makes up for this.
-
(3)
Proposition 3.1 and Corollary 3.3 are interesting only if \({\widehat{h}}_{{\text {vol}}}(F)\) and \(h_{{\text {vol}}}(Q)\) are positive, which is possible only if the fundamental group of Q has exponential growth. The results in [68] imply meaningful variations of Proposition 3.1 and Corollary 3.3 for many other manifolds. For instance, assume that Q is a simply connected manifold such that the exponential growth rate \(\gamma (\Omega Q)\) of the dimension of the \(\mathbb {Z}_2\)-homology of degree \(\le k\) of the based loop space \(\Omega Q\) is positive. Then
$$\begin{aligned} {\widehat{h}}_{{\text {top}}}^{{\text {HT}}} (\phi _H) \,\ge \, \frac{1}{\sigma (H;F)} \; C(F) \, \gamma (\Omega Q) \end{aligned}$$with a positive constant C(F) that does not change under rescalings of F.
-
(4)
We refer to [38] for a thorough study of continuity properties of topological entropy implied by Floer homological techniques.
4 Entropy collapse for Reeb flows in dimension 3
In this section we prove Theorem 1.1 in dimension 3.
4.1 Recollections on open books
In this paragraph we collect results on open books needed in our proof. For more information and details we refer to [46] and [52, §4.4].
Let M be a closed connected orientable 3-manifold. An open book for M is a triple \((\Sigma ,\psi ,\Psi )\), where \(\Sigma \) is a compact oriented surface with non-empty boundary \(\partial \Sigma \) and \(\psi \) is a diffeomorphism of \(\Sigma \) that is the identity near the boundary such that there is a diffeomorphism \(\Psi \) from
to M. Here \(\Sigma (\psi )\) denotes the mapping torus
where \((2\pi ,p) \sim (0,\psi (p))\) for each \(p \in \Sigma \), and \({\overline{\mathbb {D}}}\) is the closed unit disk. Viewing \(S^1\) as the interval \([0,2\pi ]\) with endpoints identified, we write \(\partial (\Sigma (\psi ))\) as \(S^1 \times \partial \Sigma \). The manifold M is thus presented as the union of the mapping torus \(\Sigma (\psi )\) and finitely many full tori, one for each boundary component of \(\Sigma \), glued along their boundaries by the identity map
We remark that the diffeomorphism
is part of the definition of the open book. If \(\psi '\) is another diffeomorphism of \(\Sigma \) that is the identity near the boundary and is isotopic to \(\psi \) via an isotopy that fixes each point of \(\partial \Sigma \), then \(M(\psi ')\) is diffeomorphic to \(M(\psi )\). We also remark that what we call an open book is usually called an abstract open book decomposition in the literature.
For each \(\theta \in S^1\) denote by \(\Sigma _{\theta }^\circ \) the image under the diffeomorphism \(\Psi \) of the union of \(\{\theta \} \times \Sigma \) with the union of half-open annuli
The closure \(\Sigma _{\theta }\) of \(\Sigma _{\theta }^\circ \), called a page, is diffeomorphic to \(\Sigma \), and the common boundary of the pages \(\Sigma _{\theta }\), called the binding of the open book, is the image under \(\Psi \) of \( \{0\} \times \partial \Sigma \subset \mathbb {D}\times \partial \Sigma \). The orientation of \(\Sigma \) induces orientations on the pages and the binding.
There are several different beautiful constructions proving the existence of an open book for every 3-manifold M as above. The first of these constructions was given by J. W. Alexander [5] as early as 1920, who used his findings that every such M is a branched covering of the 3-sphere branching along a link and that every link in \(\mathbb {R}^3\) can be obtained as the closure of a braid, see also [87, p. 340]. Alexander’s construction in fact provides an open book such that \(\Sigma \) has just one boundary component.
Contact structures. Let M be a closed connected oriented 3-manifold and \((\Sigma , \psi ,\Psi )\) be an open book for M.
Definition 4.1
A contact form \(\alpha \) on M is said to be adapted to the open book \((\Sigma ,\psi ,\Psi )\) if
-
\(\alpha \) is positive on the binding,
-
\(d\alpha \) is a positive area form on the interior of every page.
It is not hard to see that a contact form \(\alpha \) is adapted to an open book if and only if
-
the Reeb vector field \(R_\alpha \) is positively transverse to the interior of the pages,
-
the Reeb vector field is tangent to the binding and induces the positive orientation on the binding.
Definition 4.2
A contact 3-manifold \((M,\xi )\) is said to be supported by an open book \((\Sigma ,\psi ,\Psi )\) if there exists a contact form \(\alpha \) on \((M,\xi )\) adapted to this open book.
Remark 4.3
If a contact 3-manifold \((M,\xi )\) is supported by an open book \((\Sigma ,\psi ,\Psi )\) and if \(\psi '\) is another diffeomorphism of \(\Sigma \) that is the identity near \(\partial \Sigma \) and that is isotopic to \(\psi \) via an isotopy that fixes \(\partial \Sigma \) pointwise, then \((M,\xi )\) is also supported by an open book \((\Sigma ,\psi ',\Psi ')\). This follows easily from the fact that for such a \(\psi '\) there exists a diffeomorphism from \(M(\psi )\) to \(M(\psi ')\) that takes pages to pages.
The following result of Giroux shows the central role played by open books in 3-dimensional contact topology.
Theorem 4.4
(Giroux) Given a closed connected oriented contact 3-manifold \((M,\xi )\), there exists an open book for M supporting \((M,\xi )\). Moreover, the open book can be chosen to have connected binding. Two contact structures supported by the same open book are diffeomorphic.
For the proof of the first and the third assertion we refer to [53, Theorem 3 and Proposition 2] and to [46, Theorem 4.6 and Proposition 3.18]. That the binding can be assumed to be connected is shown in [46, Corollary 4.25] and in [34].
4.2 Proof of entropy collapse in dimension 3
We now proceed with the proof of the main result of this section.
Theorem 4.5
Let \((M,\xi )\) be a closed co-orientable contact manifold of dimension 3. Then for every \(\varepsilon > 0\) there exists a contact form \(\alpha \) on \((M,\xi )\) such that \({\text {vol}}_{\alpha } (M) =1\) and \(h_{{\text {top}}}(\alpha ) \le \varepsilon \).
While our proof works verbatim when \(\partial \Sigma \) is not connected, the geometry in our argument is easier to visualize for connected \(\partial \Sigma \), so we assume this property.
The structure of the proof is as follows.
-
Given \((M,\xi )\) as in Theorem 4.5 we use the first statement in Theorem 4.4 to obtain an open book \((\Sigma ,\psi ,\Psi )\) for M that supports \((M,\xi )\).
-
We then apply a classical recipe due to Thurston–Winkelnkemper to construct for each \(\varepsilon >0\) a contact form \({\widetilde{\alpha }}_\varepsilon \) adapted to \((\Sigma ,\psi ,\Psi )\) with \({\text {vol}}_{\widetilde{\alpha }_\varepsilon }(M) = 1\) and \(h_{{\text {top}}}({\widetilde{\alpha }}_\varepsilon ) \le \varepsilon \).
-
By the second statement of Theorem 4.4, \(\ker \Psi _* {\widetilde{\alpha }}_\varepsilon \) is diffeomorphic to \(\xi \) by a diffeomorphism \(\rho _\varepsilon \). Hence \((\rho _\varepsilon \circ \Psi )_* ({\widetilde{\alpha }}_\varepsilon )\) is a contact form on \((M,\xi )\) with the properties asserted in Theorem 4.5.
For the construction of \({\widetilde{\alpha }}_{\varepsilon }\), we first construct on the mapping torus \(\Sigma (\psi )\) for all small \(s>0\) contact forms \(\alpha _s\) with \({\text {vol}}_{\alpha _s}(\Sigma (\psi )) = O(s)\) and \(h_{{\text {top}}}(\alpha _s) = O(1)\). Crucially, near the boundary of \(\Sigma (\psi )\) these contact forms are such that they extend to contact forms (also denoted \(\alpha _s\)) on the full torus \(\overline{\mathbb {D}}\times \partial \Sigma \) in such a way that the Reeb flows are linear on each torus \(S^1(r) \times \partial \Sigma \). Therefore, even though the Reeb vector fields “explode" in the interior of the full torus as \(s \rightarrow 0\) (see Fig. 7), the topological entropy on the full torus vanishes for all s. Since also \({\text {vol}}_{\alpha _s}({\overline{\mathbb {D}}} \times \partial \Sigma ) = O(s)\), we find that \({\text {vol}}_{\alpha _s}(M) = O(s)\) and \(h_{{\text {top}}}(\alpha _s) = O(1)\) for all small \(s >0\). The form \({\widetilde{\alpha }}_\varepsilon \) is now obtained by taking s small and rescaling \(\alpha _s\).
Proof of Theorem 4.5
Step 1: A family of contact forms \(\alpha _s\) on \(\Sigma (\psi )\). By Theorem 4.4 there exists an open book \((\Sigma ,\psi ,\Psi )\) for M that supports \((M,\xi )\). We first choose a collar neighbourhood \(N \subset \Sigma \) of \(\partial \Sigma \) on which \(\psi \) is the identity. Thus N is diffeomorphic to \([1,1+\delta ] \times \partial \Sigma \), and we have polar coordinates (r, x) for N, where x is the angular coordinate for \(\partial \Sigma \), such that the boundary of \(\partial \Sigma \) corresponds to \(r=1\).
Choose an area form \(\omega \) on \(\Sigma \) such that \(\omega = dx \wedge dr\) on N. By Remark 4.3 and by Moser’s isotopy theorem we can assume that the diffeomorphism \(\psi \) is a symplectomorphism of \((\Sigma , \omega )\). Since \(H^2(\Sigma ,\partial \Sigma ;\mathbb {R})\) vanishes, there exists a primitive \(\lambda \) of \(\omega \) that equals \((2-r) dx\) on N.
We now construct for each sufficiently small \(s>0\) a contact form \(\alpha _s\) on the mapping torus \(\Sigma (\psi )\). For this, let \(\chi :[0,2\pi ] \rightarrow [0,1]\) be a smooth monotone function such that \(\chi (0)=0\), \(\chi (2\pi )=1\), and \(\chi '\) has support in \((0,2\pi )\). On \([0,2\pi ] \times \Sigma \) define the 1-form
By the properties of \(\chi \), each 1-form \(\alpha _s\) descends to a 1-form on \(\Sigma (\psi )\), that we still denote by \(\alpha _s\). Using that \(\psi \) is a symplectomorphism of \((\Sigma , \omega )\) we compute that
Hence there exists \(s_0>0\) such that \(\alpha _s\) is a contact form for all \(s \in (0,s_0]\).
We now compute the Reeb vector field \(R_{\alpha _s}\). With \(\lambda _{\theta }:= (1-\chi (\theta )) \lambda + \chi (\theta ) \psi ^*\lambda \) one checks that
where Y is the vector field that is tangent to \(\{\theta \} \times \Sigma \) for all \(\theta \in S^1\) and satisfies
The formula (4.3) shows that \(R_{\alpha _s}\) is positively transverse to each surface \(\{\theta \} \times \Sigma \).
The next lemma gives an upper bound for \(h_{{\text {top}}}(\phi _{\alpha _s})\) when s is sufficiently small. Notice that it makes sense to talk about \(h_{{\text {top}}}(\phi _{\alpha _s})\), since \(\Sigma (\psi )\) is compact and \(R_{\alpha _s}\) is tangent to \(\partial \Sigma (\psi )\).
Lemma 4.6
There exists \(s_1 \in (0,s_0)\) and a constant \(E>0\) such that for every \(s \in (0,s_1]\),
Proof
Choose \(s_1 >0\) such that \(\frac{1}{2} \le \frac{1}{1+ s \lambda _\theta (Y)} \le 2\) on \(\Sigma (\psi )\) for every \(s \in (0,s_1]\). For each such s define the function \(f_s = \frac{1}{1+ s \lambda _\theta (Y)}\) on \(\Sigma (\psi )\). Then for every \(s \in (0,s_1]\) we have \(R_{\alpha _s} = f_s \, (\partial _{\theta } + Y)\) with \(\frac{1}{2} \le f_s \le 2\). By Ohno’s result from [79], for a non-vanishing vector field X and a positive function f on a compact manifold,
It follows that \(h_{{\text {top}}} (\phi _{\alpha _s}) \le 2 h_{{\text {top}}} (\phi _{\partial _{t} + Y }) =:E\). \(\square \)
Step 2: A family of contact forms \(\sigma _s\) on \(\overline{\mathbb {D}} \times \partial \Sigma \). We have constructed a family of contact forms \(\alpha _s\) on the mapping torus \(\Sigma (\psi )\). We now wish to extend these forms to contact forms on \(M(\psi )\). For this let V be the collar neighbourhood of \(\partial \Sigma (\psi )\) defined by
where \( (2\pi ,p) \sim (0,p)\) for each \(p \in \Sigma \). On V the contact form \(\alpha _s\) reads
where (r, x) are the coordinates on N introduced above and \(\theta \in S^1\).
We proceed to construct for each \(s \in (0,s_1)\) a contact form \(\sigma _s\) on \({\overline{\mathbb {D}}} \times \partial \Sigma \), where \(\overline{\mathbb {D}}\) is again the closed unit disk in \(\mathbb {R}^2\). Consider polar coordinates \((\varvec{\uptheta }, {{\textbf {r}}}) \in S^1 \times (0,1]\) on \(\overline{\mathbb {D}} \setminus \{0\}\) and the coordinate \({{\textbf {x}}}\) on \(\partial \Sigma \). We can then consider coordinates \((\varvec{\uptheta }, {{\textbf {r}}}, {{\textbf {x}}})\) on \(\overline{\mathbb {D}} {\setminus } \{0\} \times \partial \Sigma \). We pick a smooth function \(f :(0,1] \rightarrow \mathbb {R}\) such that
-
\(f'<0\),
-
\(f({{\textbf {r}}}) = 2-{{\textbf {r}}}\) on a neighbourhood of 1,
-
\(f({{\textbf {r}}}) = 2 -{{\textbf {r}}}^4\) on a neighbourhood of 0,
and we pick another smooth function \(g :(0,1]\rightarrow \mathbb {R}\) satisfying
-
\(g'>0\) on (0, 1),
-
\(g(1) =1\) and all derivatives of g vanish at 1,
-
\(g({{\textbf {r}}}) = \frac{{{\textbf {r}}}^2}{2}\) on a neighbourhood of 0 see Fig. 6.
Define the 1-form
on \(\overline{\mathbb {D}} \setminus \{0\} \times \partial \Sigma \). Then
where \(h({{\textbf {r}}}) = (fg'-f'g)({{\textbf {r}}})\). It follows that \(\sigma _s\) is a contact form on \(\overline{\mathbb {D}} {\setminus } \{0\} \times \partial \Sigma \). For \({{\textbf {r}}}\) near 0 we have \(h({{\textbf {r}}}) = {{\textbf {r}}}(2+{{\textbf {r}}}^4)\), whence \(\sigma _s\) extends to a smooth contact form on \(\overline{\mathbb {D}} \times \partial \Sigma \), that we also denote by \(\sigma _s\). The Reeb vector field of \(\sigma _s\) is given by
It follows that \(R_{\sigma _s}\) is tangent to the tori \(\mathbb {T}_{{{\textbf {r}}}}:= \{ {{\textbf {r}}}= \text {const} \}\) and that for each \({{\textbf {r}}}\in (0,1]\) the flow of \(R_{\sigma _s}\) is linear:
In particular, using our choices of f and g we see that \(R_{\sigma _s} = \partial _{\varvec{\uptheta }}\) on the boundary torus \(\mathbb {T}_1\), and that \(R_{\sigma _s} = \frac{1}{2 s} \partial _{{{\textbf {x}}}}\) is tangent along the core circle \(C= \{ {{\textbf {r}}}=0 \}\) of the full torus, and gives the positive orientation to \(\partial \Sigma \). Furthermore, (4.8) shows that \(R_{\sigma _s}\) is positively transverse to the half-open annuli see Fig. 7
The Reeb flow \(\phi _{\sigma _s}^t\) on the full torus \({\overline{\mathbb {D}}} \times \partial \Sigma \) is integrable. More precisely, the core circle C of \({\overline{\mathbb {D}}} \times \partial \Sigma \) is the trace of a periodic orbit of \(\phi _{\sigma _s}^t\), and \(({\overline{\mathbb {D}}} \times \partial \Sigma ) {\setminus } C\) is foliated by the flow-invariant tori \(\mathbb {T}_{{\textbf {r}}}\), on which \(\phi _{\sigma _s}^t\) is the linear flow (4.9). The topological entropy of these linear flows of course vanishes. By the variational principle for topological entropy we therefore find that
Step 3: A family of contact forms on M. We first observe that the coordinates \(\theta \) and \(\varvec{\uptheta }\), r and \({{\textbf {r}}}\), x and \({{\textbf {x}}}\) are glued via the identification map used to glue \(\Sigma (\psi )\) and \({\overline{\mathbb {D}}} \times \partial \Sigma \). It follows that they extend to coordinates on
In view of the expressions (4.5) and (4.6) for the contact forms \(\alpha _s\) on V, and \(\sigma _s\) on \({\overline{\mathbb {D}}} \times \partial \Sigma \), these two contact forms are glued to a smooth contact form \(\tau _s\) on \(M(\psi )\).
As mentioned above, the Reeb vector field \(R_{\tau _s}\) is positively transverse to the surfaces \(\{\theta \} \times \Sigma \) in \(\Sigma (\psi )\) and to the annuli \(A_{\varvec{\uptheta }}\) in \({\overline{\mathbb {D}}} \times \partial \Sigma \). Also, \(R_{\tau _s}\) is tangent to the core circle C of \({\overline{\mathbb {D}}} \times \partial \Sigma \), giving the positive orientation. It follows that the Reeb vector field of \(\Psi _* \tau _s\) is positively transverse to the interior of the pages of the open book \((\Sigma , \psi ,\Psi )\), and positively tangent to the binding of the open book. By Theorem 4.4 the contact structure \(\ker \Psi _* \tau _s\) is diffeomorphic to \(\xi \), by some diffeomorphism \(\rho _s :M \rightarrow M\). Summarizing, there are diffeomorphisms \(\Psi \) and \(\rho _s\) such that
with \(\ker ( (\rho _s \circ \Psi )_* \tau _s) = \xi \).
Step 4: Estimating the volume and the topological entropy of \(\tau _s\). The Reeb flow \(\phi _{\tau _s}^t\) of \(\tau _s\) leaves the compact sets \(\Sigma (\psi )\) and \(\overline{\mathbb {D}} \times \partial \Sigma \) invariant. Since these compact sets cover M and since \(\phi _{\tau _s}^t |_{\Sigma (\psi )} = \phi _{\alpha _s}^t\) and \(\phi _{\tau _s}^t |_{\overline{\mathbb {D}} \times \partial \Sigma } = \phi _{\sigma _s}^t\), it follows from [60, Proposition 3.1.7 (2)] and from Lemma 4.6 and (4.10) that
We decompose the integral of \(\tau _s \wedge d \tau _s\) as
For the first summand we have by (4.2) that
To estimate the second term in (4.13) we use (4.7):
Since the right integral is finite, it follows that also
Together with (4.13) and (4.14) we conclude that
Step 5: End of proof. By (4.16) we know that given \(\varepsilon >0\) there exists \(s \in (0,s_1]\) such that
Defining \(\widetilde{\tau }:= \left( {\text {vol}}_{\tau _s} \bigl ( M(\psi ) \bigr ) \right) ^{-\frac{1}{2}} \, \tau _s\) we obtain
Together with (4.11) and in view of the conjugacy invariance of topological entropy if follows that \((\rho _s \circ \Psi )_* {\widetilde{\tau }}\) is a contact form on \((M,\xi )\) of volume 1 and topological entropy at most \(\varepsilon \). \(\square \)
Question 4.7
It would be interesting to see how in the case of a spherization \(S^*Q_2\) over the closed orientable surface of genus 2 the open book decomposition used in the above proof looks like. Since our construction of the contact form \({\widetilde{\tau }}\) is explicit, one could then maybe understand the star field \(\{ D_q^*(H) \}\) corresponding to \({\widetilde{\tau }}\). In view of (1.11) some of the stars must be very spiky. How many spikes appear in these stars?
5 Generalities on Giroux’s correspondence in higher dimensions
In this section, we summarize those concepts and results on the Giroux correspondence between contact structures and supporting open books in higher dimensions that we shall use in the proof of Theorem 1.1. While we reprove those parts that we use in a somewhat different form, we refer to [53] and [54] for the parts that we can cite and for further results.
5.1 Ideal Liouville domains
Let F be a 2n-dimensional compact manifold with non-empty boundary K, and denote by \(F^\circ \) the interior of F. A symplectic form \(\omega \) on \(F^\circ \) is called an ideal Liouville structure on F (abbreviated ILS) if \(\omega \) admits a primitive \(\lambda \) on \(F^\circ \) such that for some (and then any) smooth function
the 1-form \(u \lambda \) on \(F^\circ \) extends to a smooth 1-form \(\beta \) on F which is a contact form along K.
If such a 2-form \(\omega \) exists, the pair \((F,\omega )\) is called an ideal Liouville domain (ILD), and any primitive \(\lambda \) with the above property is called an ideal Liouville form (ILF). Given an ILD \((F,\omega )\), the contact structure
depends on the 2-form \(\omega \) but neither on \(\lambda \) nor u, see Proposition 2 in [54]. Moreover, once \(\lambda \) is chosen, one can recover every (positive) contact form on \((K,\xi )\) as the restriction to K of the extension of \(u\lambda \) for some function u with property (5.1). This is why the pair \((K,\xi )\) is called the ideal contact boundary of \((F,\omega )\). We note that the orientation of K that is determined by the co-oriented contact structure \(\xi \) coincides with the orientation of K as the boundary of \((F,\omega )\).
A very useful feature of an ILD is that a neighborhood of its boundary admits an explicit parametrization in which any ILF has a very nice form.
Lemma 5.1
Let \((F,\omega )\) be an ILD and \(\lambda \) be an ILF. Let u be a function satisfying (5.1) and let \(\beta \) be the extension of \(u\lambda \). Then for any contact form \(\alpha _0\) on \((K,\xi )\), there exists an embedding
such that
where \(r \in [0,+\infty )\). In particular,
and for all \(q\in K\),
Proof
The above statement is a reformulation of Proposition 3 in [54]. We give a similar but more explicit proof.
Let \(\dim F=2n\). Since \(\beta \) is by assumption a positive contact form on K, \(\beta \wedge (d\beta )^{n-1}\) is a positive volume form on K. Using \(\omega = d \lambda = d(\beta / u)\) on \(F^\circ \) we compute
where \(\mu \) is the 2n-form
The above expression shows that \(\mu \) is smooth on F and, together with (5.2) and the fact that 0 is a regular value of u, that it is a positive volume form on F. Define the smooth vector field X on F by
Recall that the Liouville vector field Y of \(\lambda \) is the vector field on \(F^\circ \) defined by \(\iota _Y d\lambda = \lambda \). Using \(\beta = u \lambda \) on \(F^\circ \) we compute
Comparing with (5.3) we find \(Y = -u X\). Then
on \(F^{\circ }\), and by continuity \(\beta (X)=0\) on F. Hence on \(F^\circ \),
This shows that \(du (X) =1\) along K and that the function \(\frac{1}{u} (du(X)-1)\) is smooth on F. In particular, X points inwards on \(K=\partial F\) and hence the flow \(\phi _X^t\) of X on the compact manifold F is well-defined for every \(t\ge 0\). We define the smooth embedding
By construction we have \(\Phi ^*X=\partial _t\). Put \(\hat{\beta }:= \Phi ^*\beta \), \(\hat{u}:= \Phi ^*u\), and \(\hat{\lambda }:= \Phi ^*\lambda \). The identities \(\beta (X)=0\) and (5.4) say that on \([0,+\infty ) \times K\),
Here the function \(\frac{\partial _t {\hat{u}} -1}{{\hat{u}}}\) is smooth and bounded on \([0,+\infty ) \times K\) since by (5.4) the function \(\frac{1}{u} (du(X)-\!1)\) is smooth on F. Define the smooth function \(v_0 :[0,+\!\infty ) \!\times \! K \rightarrow \mathbb {R}\) by
The solution of the problem (5.5) with initial condition \(\beta _0(q) = \beta (0,q)\) is then
and therefore
Now let \(\alpha _0\) be a positive contact form on \((K,\xi )\). Then there is a positive function \(\kappa \) on K such that \(\beta _0 = \kappa \alpha _0\). On \((0,+\infty )\times K\) define the function
Then \(\hat{\lambda } = \Lambda \alpha _0\). It is clear that \(\Lambda >0\), and \(\lim _{t \rightarrow 0} \Lambda (t,q) = +\infty \) for all \(q \in K\). We note that
and therefore
On \([0,+\infty ) \times K\), \(\hat{u}\) is bounded from above since F is compact. Therefore \(\lim _{t \rightarrow +\infty } \Lambda (t,q)=0\) for all \(q \in K\). It follows that \(\Lambda (\cdot ,q)\) is an orientation reversing diffeomorphism from \((0,+\infty )\) onto \((0,+\infty )\) for all q. Hence there exists a positive smooth function f on \((0,+\infty ) \times K\) such that
and for every \(q\in K\) the function \(f(\cdot ,q)\) is an orientation preserving diffeomorphism from \((0,+\infty )\) onto \((0,+\infty )\). Define the embedding
By construction \(\Psi ^*\hat{\lambda }=\frac{1}{r}\alpha _0\). We claim that \(\Psi \) extends to a smooth embedding
Postponing the proof of the claim, we note that \(\imath = \Phi \circ \Psi \) is then the desired embedding. The rest of the statement of the lemma follows immediately from the identity \(\imath ^*\lambda = \frac{1}{r} \alpha _0\).
We now show that the extension of \(\Psi \) given by \(\Psi (0,q) = (0,q)\) is smooth. Combining (5.6) and (5.7) we get
We consider the function
on \((0,+\infty ) \times K\) and we define
Then we have
on \((0,+\infty )\times K\). We claim that \(\widetilde{\Psi }\) extends smoothly to \([0,+\infty )\times K\) by \(\widetilde{\Psi }(0,q)=q\) for all \(q\in K\). To see this we define the function \(v_1 :[0,+\infty ) \times K \rightarrow \mathbb {R}\) by
We recall that the above integrand is smooth and bounded on \([0,+\infty ) \times K\) and so is the function \(v_1\). For every \(t \in (0,+\infty )\) and \(q \in K\),
and so
Note that \(\Lambda (1,q)\ne 0\). The above expression says that g extends smoothly to \([0,+\infty ) \times K\) by \(g(0,q)=0\) for \(q \in K\). For \(t>0\) we compute
By the smoothness of g, this expression also holds true for \(t=0\). In particular, \(\partial _t g(t,q) >0\) for all \((t,q) \in [0,+\infty ) \times K\). It follows that \(D \widetilde{\Psi }(t,q)\) is invertible for all \((t,q) \in [0,+\infty ) \times K\). By the inverse function theorem, the extension of \(\Psi \) over \([0,+\infty )\times K\) is \(C^1\) and in fact \(C^\infty \)-smooth since \(\widetilde{\Psi }\) is smooth. \(\square \)
5.2 Ideal Liouville domains and contact structures
Ideal Liouville domains are particularly useful for clarifying the existence and uniqueness of contact structures supported by open books in higher dimensions. We first recollect some facts about open books.
An open book in a closed manifold M is a pair \((K,\Theta )\) where
-
(ob1)
\(K\subset M\) is a closed submanifold of co-dimension two with trivial normal bundle;
-
(ob2)
\(\Theta :M \setminus K \rightarrow S^1= \mathbb {R}/2 \pi \mathbb {Z}\) is a locally trivial smooth fibration that on a deleted neighbourhood \((\mathbb {D}\setminus \{0\}) \times K\) of K reads \(\Theta (re^{i\theta },q) = \theta \).
The submanifold K is called the binding of the open book, and the closures of the fibres of \(\Theta \) are called the pages. The pages are compact submanifolds with common boundary K. The canonical orientation of \(S^1\) induces co-orientations of the pages. Hence if M is oriented, then so are the pages, and then also the binding as the boundary of a page.
Another way of defining an open book is as follows. Let \(h :M \rightarrow \mathbb {C}\) be a smooth function such that 0 is a regular value. Set \(K:= h^{-1}(0)\), and assume that \(\Theta :=h/|h| :M {\setminus } K \rightarrow S^1\) has no critical points. Then the pair \((K,\Theta )\) is an open book in M. Moreover, any open book in M can be recovered via a defining function h as above, and such a defining function is unique up to multiplication by a positive function on M.
Given an open book \((K,\Theta )\) in a closed manifold M, one finds a vector field X on M, called a spinning vector field, such that
-
(m1)
X lifts to a smooth vector field on the manifold with boundary obtained from M by real oriented blow-up along K, in which each disk \(\mathbb {D}\times \{q\}\) of the neighbourhood \(\mathbb {D}\times K\) is replaced by the annulus \(S^1 \times [0,1] \times \{q\}\);
-
(m2)
\(X=0\) on K and \(d\Theta (X) = 1\) on \(M {\setminus } K\).
Then the time-\(2\pi \) map of the flow of X is a diffeomorphism
of the 0-page \(F:= \Theta ^{-1}(0)\cup K\), which fixes K pointwise. The isotopy class \([\phi ]\) of \(\phi \) among the diffeomorphisms of F that fix K pointwise is called the monodromy of the open book. It turns out that the open book is characterized by the pair \((F,[\phi ])\). Namely, given the pair \((F,\phi )\), one defines the mapping torus
This is a manifold with boundary. One has the natural fibration
with fibres diffeomorphic to F, and there is a natural parametrization of the fibre \(\widehat{\Theta }^{-1}(0)\) via the restriction of the above quotient map to \(\{0\} \times F\). For every \(\phi '\in [\phi ]\) there is a diffeomorphism between \({\text {MT}}(F,\phi )\) and \({\text {MT}}(F,\phi ')\) that respects the fibrations over \(S^1\) and the natural parametrizations of the 0-fibres. Now, given \({\text {MT}}(F,\phi )\) one collapses its boundary, which is diffeomorphic to \(S^1 \times K\), to K and obtains the so-called abstract open book \({\text {OB}}(F,\phi )\). In fact, the closed manifold \({\text {OB}}(F,\phi )\) admits an open book given by the pair \((K,\Theta )\), where \(\Theta \) is induced by \(\widehat{\Theta }\). Moreover, for \(\phi ' \in [\phi ]\), the diffeomorphism between \({\text {MT}}(F,\phi )\) and \({\text {MT}}(F,\phi ')\) descends to a diffeomorphism between the corresponding abstract open books. In particular, M and \({\text {OB}}(F,\phi )\) may be identified together with their open book structures. We note that one can choose the spinning vector field X smooth on M and such that its flow is \(2\pi \)-periodic near K. However, not every representative of the monodromy class can be obtained via a smooth spinning vector field, see Remark 12 in [54]. To obtain all representatives of the monodromy class, one needs to use the whole affine space of spinning vector fields.
Open books meet with contact topology via the following definition. Let M be a compact manifold with a co-oriented contact structure \(\xi \). We say that \(\xi \) is supported by an open book \((K,\Theta )\) on M or that the open book \((K,\Theta )\) supports \(\xi \) if there exists a contact form \(\alpha \) on \((M,\xi )\), that is \(\xi =\ker \alpha \), such that
-
\(\alpha \) restricts to a positive contact form on K;
-
\(d\alpha \) restricts to a positive symplectic form on each fibre of \(\Theta \).
It turns out that given a closed manifold M, the isotopy classes of co-oriented contact structures on M are in one-to-one correspondence with equivalence classes of supporting open books. This statement is a very rough summary of what is called the Giroux correspondence. We will recall certain pieces of this celebrated statement in detail.
Theorem 5.2
(Theorem 10 in [53]) Any contact structure on a compact manifold is supported by an open book with Weinstein pages.
This result is the core of the correspondence between supporting open books and contact structures. The existence statement of the opposite direction of the correspondence is relatively easy to achieve, especially in dimension three. Namely, given an open book in a 3-dimensional compact manifold, it is not hard to construct a contact form on the corresponding abstract open book whose kernel is supported. In higher dimensions, however, one needs that the pages are exact symplectic and that the monodromy is symplectic in order to construct a contact form on an abstract open book whose kernel is supported, see Proposition 9 in [53] and Proposition 17 in [54]. We will carry out such a construction in Sects. 6.1 and 6.2. Concerning the uniqueness features of the Giroux correspondence, we are mainly interested in one side, namely the “uniqueness” of supported contact structures. This result is again more involved in higher dimensions. Heuristically, given an open book, the symplectic geometry of the pages determines the supported contact structures. In dimension three, any two symplectic structures on a page are isotopic since they are just area forms on a given surface, but in higher dimensions this is not the case.
In [54] Giroux introduced the notion of a Liouville open book, which clears out the technicalities to which we pointed above.
A Liouville open book (LOB) in a closed manifold M is a triple \((K,\Theta ,(\omega _\theta )_{\theta \in S^1})\) where
-
(lob1)
\((K,\Theta )\) is an open book on M with pages \(F_\theta =\Theta ^{-1}(\theta )\cup K\), \(\theta \in S^1\);
-
(lob2)
\((F_\theta ,\omega _\theta )\) is an ILD for all \(\theta \in S^1\) and the following holds: there is a defining function \(h :M \rightarrow \mathbb {C}\) for \((K,\Theta )\) and a 1-form \(\beta \) on M such that the restriction of \(d(\beta /|h|)\) to each page is an ILF. More precisely,
$$\begin{aligned} \omega _\theta =d(\beta /|h|) |_{TF_\theta ^\circ } \end{aligned}$$for all \(\theta \in S^1\).
The 1-form \(\beta \) is called a binding 1-form associated to h. If \(h'\) is another defining function for \((K,\Theta )\), then \(h'=\kappa h\) for a positive function \(\kappa \) on M, and \(\beta ':= \kappa \beta \) is a binding 1-form associated to \(h'\). We also note that for a fixed defining function, the set of associated binding 1-forms is an affine space.
Similar to the case of classical open books, LOBs are characterized by their monodromy, which now has to be symplectic: One considers symplectically spinning vector fields, namely vector fields X satisfying (m1) and (m2) and generating the kernel of a closed 2-form on \(M \setminus K\) which restricts to \(\omega _\theta \) for all \(\theta \in S^1\). Given such a vector field, the time-\(2\pi \) map of its flow, say \(\phi \), is a diffeomorphism of \(F:= F_0\) which fixes K and preserves \(\omega := \omega _0\). The isotopy class \([\phi ]\), among the symplectic diffeomorphisms that fix K, is called the symplectic monodromy and characterizes the given LOB. For the construction of a LOB in the abstract open book \({\text {OB}}(F,\phi )\), where \(\phi ^*\omega =\omega \), we refer to Proposition 17 in [54] and to our construction at the end of the next section.
Again, symplectically spinning vector fields form an affine space, and all representatives of the symplectic monodromy can be obtained by sweeping out this affine space. The obvious choice of a symplectically spinning vector field X is smooth, and by suitably modifying a given binding 1-form without affecting its restriction to the kernel of \(d\Theta \) one can arrange that the flow of X is \(2\pi \)-periodic near the binding.
Lemma 5.3
(Lemma 15 in [54]) Let \((K, \Theta ,(\omega _\theta )_{\theta \in S^1})\) be a LOB in a closed manifold M, and let \(h :M \rightarrow \mathbb {C}\) be a defining function for \((K,\Theta )\). Then for every binding 1-form \(\beta \), the vector field X on \(M {\setminus } K\) spanning the kernel of \(d(\beta /|h|)\) and satisfying \(d \Theta (X) = 1\) extends to a smooth vector field on M which is zero along K. Furthermore, \(\beta \) can be chosen such that the flow of X is \(2\pi \)-periodic near K.
Natural sources of LOBs are contact manifolds:
Proposition 5.4
(Proposition 18 in [54]) Let \((M, \xi )\) be a closed contact manifold, and let \((K, \Theta )\) be a supporting open book with defining function \(h :M \rightarrow \mathbb {C}\). Then the contact forms \(\alpha \) on \((M,\xi )\) such that \(d(\alpha /|h|)\) induces an ideal Liouville structure on each page form a non-empty convex cone.
Let \((K,\Theta ,(\omega _\theta )_{\theta \in S^1})\) be a LOB in a closed manifold M with a defining function h. A co-oriented contact structure \(\xi \) on M is said to be symplectically supported by \((K,\Theta ,(\omega _\theta )_{\theta \in S^1})\) if there exists a contact form \(\alpha \) on \((M,\xi )\) such that \(\alpha \) is a binding 1-form of the LOB associated to h.
By our remark following the definition of a binding 1-form, the property of being symplectically supported is independent of the given defining function. But the crucial fact is that once a defining function is fixed, a contact binding 1-form is unique whenever it exists, see Remark 20 in [54]. Hence, once a defining function h is fixed, there is a one-to-one correspondence between contact structures supported by \((K,\Theta ,(\omega _\theta )_{\theta \in S^1})\) and contact binding 1-forms associated to h.
Given two contact structures \(\xi _0\) and \(\xi _1\) supported by \((K,\Theta ,(\omega _\theta )_{\theta \in S^1})\), after fixing h we therefore have unique contact binding 1-forms \(\alpha _0\) and \(\alpha _1\), respectively. Since the set of binding 1-forms associated to h is affine, there is a path \((\beta _t)_{t\in [0,1]}\) of binding 1-forms such that \(\beta _0 = \alpha _0\) and \(\beta _1 = \alpha _1\). Now it is not hard to explicitely deform the forms \(\beta _t\) without affecting their restrictions to \(\ker d\Theta \) in such a way that
-
for all \(s \ge 0\) and \(t \in [0,1]\), \(\beta ^s_t\) is a binding 1-form for \((K,\Theta ,(\omega _\theta )_{\theta \in S^1})\) associated to h (since the deformation of \(\beta _t\) leaves unchanged the restriction to the pages);
-
\(\beta _t^s\) is a contact form for s large enough, uniformly in \(t \in [0,1]\);
-
if \(\beta _t\) is already a contact form, then \(\beta _t^s\) is a contact form for all \(s \ge 0\).
By the first property of these deformations and by the uniqueness discussed above, whenever \(\beta ^s_t\) is a contact form then \(\ker \beta ^s_t\) is symplectically supported by \(\left( K,\Theta ,(\omega _\theta )_{\theta \in S^1}\right) \) and \(\beta _t^s\) is the unique contact binding 1-form associated to h. Together with the other two properties we see that there exists \(c>0\) such that the concatenation of the paths \((\ker \beta _0^s)_{s\in [0,c]}\), \((\ker \beta ^c_t)_{t\in [0,1]}\) and \((\ker \beta ^{c-s}_1)_{s\in [0,c]}\) gives an isotopy between \(\xi _0\) and \(\xi _1\) along contact structures that are symplectically supported by \((K,\Theta ,(\omega _\theta )_{\theta \in S^1})\) (cf. Fig. 8).
In fact the following more general statement holds.
Proposition 5.5
(Proposition 21 in [54]) On a closed manifold, contact structures supported by a given Liouville open book form a non-empty and weakly contractible subset in the space of all contact structures.
6 Entropy collapse for Reeb flows in dimension \(\ge 3\)
This section is devoted to the proof of the following main result.
Theorem 6.1
Let \((M,\xi )\) be a closed co-orientable contact manifold. Then for every real number \(\varepsilon >0\) there exists a contact form \(\alpha \) for \(\xi \) such that \({\widehat{\Gamma }}(\alpha ) \le \varepsilon \).
We prove the statement by induction on n, where \(\dim M=2n+1\). The initial case \(n=0\) is clear: Then M is a circle, and the Reeb flow generated by the vector field \(\partial _\theta \) has vanishing norm growth. It may be interesting to read the subsequent proof for \(n=0\) and to compare the line of argument with the one of Sect. 4.
We now assume by induction that Theorem 6.1 holds for \(n-1 \ge 0\) and fix a contact manifold \((M,\xi )\) of dimension \(2n+1\). By Theorem 5.2 there exists an open book \((K,\Theta )\) in M supporting \(\xi \). Let \(F_\theta := \Theta ^{-1}(\theta ) \cup K\), \(\theta \in S^1=\mathbb {R}/2\pi \mathbb {Z}\), denote the pages of the open book and let \(h :M \rightarrow \mathbb {C}\) be a defining function for \((K,\Theta )\). We wish to construct a contact form on the abstract open book defined via the 0-page
By Proposition 5.4, there exists a contact form \(\alpha \) on \((M,\xi )\) such that the triple \((K,\Theta , d(\alpha /|h|)|_{TF_\theta ^\circ })\) is a LOB which supports \(\xi \) symplectically. By Lemma 5.3, we can modify the contact binding 1-form \(\alpha \) without affecting its restriction to the kernel of \(d\Theta \), to obtain a binding 1-form \({\widehat{\alpha }}\), not necessarily contact, such that the flow of the associated symplectically spinning vector field X is \(2\pi \)-periodic near K. Hence the time-\(2\pi \) map of the flow of X gives us a diffeomorphism \(\psi :F \rightarrow F\) such that
where \(\lambda \in \Omega ^1(F^\circ )\) is the ILF
and \(\psi =\textrm{id}\) on some neighbourhood of K in F. Now our aim is to recover M as the abstract open book induced by the pair \((F,\psi )\) and to define a contact form on the abstract open book with small norm growth. We first consider the mapping torus
Since \(\psi =\textrm{id}\) on some neighbourhood of K, the boundary \(\partial {\text {MT}}(F,\psi )\) has an open neighbourhood given as a product of K with an annulus, in which we collapse the boundary and get the abstract open book \({\text {OB}}(F,\psi )\). We postpone the precise collapsing procedure since it will involve choices of coordinates, but note that the abstract open book is independent of these choices, and that we can make the identifications
6.1 A family of contact forms away from the binding
On \([0,2 \pi ]\times F^\circ \) with \(\theta \) the coordinate on \([0,2\pi ]\), we define the family of 1-forms
where \(\lambda _\psi := \psi ^*\lambda -\lambda \) and \(\chi :[0,2\pi ] \rightarrow [0,1]\) is a smooth function such that \(\chi (0)=0\), \(\chi (2\pi )=1\) and \(\chi '\) has support in \((0,2\pi )\). By the choice of \(\chi \), each 1-form \(\alpha _s\) descends to a 1-form on \({\text {MT}}(F^\circ ,\psi )\), that we still denote by \(\alpha _s\).
Lemma 6.2
There exists \(s_0>0\), depending on \(\psi , \lambda , \chi \), such that \(\alpha _s\) is a contact form on \({\text {MT}}(F^\circ ,\psi )\) for all \(s \in (0,s_0]\).
Proof
Since \(d\lambda _\psi =0\), we get \(d\alpha _s = s \left( \chi ' d\theta \wedge \lambda _\psi +d\lambda \right) \) and
Since \(d\theta \wedge (d\lambda )^n\) is a volume form and since with \(\lambda _\psi \) also \(\lambda \wedge d\theta \wedge \lambda _\psi \wedge (d\lambda )^{n-1}\) is compactly supported in \({\text {MT}}(F^\circ ,\psi )\), there exists \(s_0>0\) such that \(\alpha _s \wedge (d\alpha _s)^{n}\) is a positive volume form for all \(s \in (0,s_0]\). \(\square \)
Next, we study the Reeb vector field \(R_{\alpha _s}\) of \(\alpha _s\) on \({\text {MT}}(F^\circ ,\psi )\). Let Y be the vector field on \({\text {MT}}(F^\circ ,\psi )\) that is tangent to \(\{\theta \}\times F^\circ \) for each \(\theta \) and along each \(\{\theta \} \times F^\circ \) satisfies
Since \(\chi '=0\) near 0 and \(\pi \), Y is well defined, and since \(\psi \) is compactly supported in \(F^\circ \), Y is compactly supported in \({\text {MT}}(F^\circ ,\psi )\). We compute
Hence on \({\text {MT}}(F^\circ ,\psi )\) the Reeb vector field of \(\alpha _s\) is
Note that \(R_{\alpha _s} = \partial _\theta \) near K. Since the \(\partial _\theta \) component of \(R_{\alpha _s}\) never vanishes and since Y is tangent to the pages, \(R_{\alpha _s}\) is transverse to \(F^\circ \times \{\theta \}\) for all \(\theta \). Hence \(F^\circ \) is a global hypersurface of section for \(R_{\alpha _s}\) on \({\text {MT}}(F^\circ ,\psi )\). We have the first return time map
and the first return map
Remark 6.3
Since \(R_{\alpha _s}\) is a multiple of the vector field \(\partial _\theta +Y\) that does not depend on s, the return map \(\Upsilon \) is independent of s. This justifies the absence of the subscript in (6.7).
We note that for all \(s \in (0,s_0]\),
Recall that we write \(\Gamma (\alpha _s)\) for the norm growth \(\Gamma (\phi _{\alpha _s})\) of the Reeb flow \(\phi _{\alpha _s}^t\).
Lemma 6.4
There exists \(s_1 \in (0,s_0)\) such that for every \(s \in (0,s_1]\),
and such that
for some constant \(E >0\) that depends only on \(\psi , \lambda , \chi \).
Proof
We compute
Since Y is compactly supported, we find \(s_1 \in (0,s_0)\) such that for every \(s \in (0,s_1]\),
The inequality (6.9) follows. For the second claim, we apply Proposition C.2 to the vector field \(\partial _\theta + Y\) and the positive function \(\frac{1}{\alpha _s(\partial _\theta +Y)}\), and in view of (6.5) and (6.11) find that \(\Gamma (\alpha _s) \le 2 \, \Gamma (\phi _{\partial _\theta +Y}) =:E\). \(\square \)
6.2 A family of contact forms near the binding
Let \(E>0\) be the constant from Lemma 6.4. By our inductive hypothesis, for any \(\varepsilon >0\) there exists a contact form \(\sigma _\varepsilon \) on \((K, \xi |_K)\) such that
Indeed, there is a contact form \(\alpha _0\) on \((K, \xi |_K)\) such that
We can thus take \(\sigma _\varepsilon := \varepsilon ^{1/n} \, \alpha _0\).
Applying Lemma 5.1 to \(\sigma _\varepsilon \) we obtain an embedding
and \(\imath _\varepsilon (0,q)=q\) for every \(q \in K\). This embedding induces the smooth coordinate \(r \in [0,+\infty )\) on a neighborhood of \(K=\partial F\) in F. There exists \(r_{\varepsilon } > 0\) that depends only on \(\psi \) and \(\sigma _\varepsilon \) such that
We define
and note that near the boundary of \({\text {MT}}(F_\varepsilon ,\psi )\) the expression (6.4) for \(\alpha _s\) reads
Lemma 6.5
For every \(\varepsilon >0\) and \(s \in (0,r_\varepsilon /2)\) there exist smooth functions
with the following properties.
-
(f1)
\(f(r)=s/r\) near \(r=r_\varepsilon \) and \(f(r)=1\) near \(r=0\).
-
(f2)
\(f(r_\varepsilon /2)=1/2\).
-
(f3)
\(-2/r_\varepsilon \le f' \le 0 \) on \([0,r_\varepsilon ]\) and \(f'<0\) on \([r_\varepsilon /2, r_\varepsilon ]\).
-
(g1)
\(g=1\) on \([r_\varepsilon /2,r_\varepsilon ]\) and \(g(r)=r^2/2\) near \(r=0\).
-
(g2)
\(0\le g'\le 4/r_\varepsilon \) on \([0,r_\varepsilon ]\) and \(0 < g'\) on \((0,r_\varepsilon /2]\).
See Fig. 9. The easy proof is left to the reader. For later use we note that the function.
is positive on \((0,r_\varepsilon ]\), satisfies \(h(r)=r\) near \(r=0\), and
Furthermore,
Indeed, for \(r \in [r_\varepsilon / 2, r_\varepsilon ]\) we have \(( \frac{g'}{h} )(r) =0\) by (g1). In 0 we have \(\frac{g'}{h} =0\). Further, for \(r \in (0, \frac{r_\varepsilon }{2}]\) property (g2) shows that \(g'(r) >0\), and hence \(-f' \frac{g}{g'} \ge 0\). Since \(f(r) \ge \frac{1}{2}\) by (f2) and (f3), we conclude that
as claimed.
Given \(\varepsilon >0\) and \(s \in (0,r_\varepsilon /2)\), we define the 1-form
on \(S^1 \times [0,r_\varepsilon ] \times K\). We note that by (f1) and (g1),
By considering \(\theta \) and r as angular and radial coordinates on the disk \(r_\varepsilon \mathbb {D}\), we thus see that the 1-form \(\alpha _{s,\varepsilon }\) is smooth on \( r_\varepsilon \mathbb {D}\times K\).
Lemma 6.6
For \(\varepsilon >0\) and \(s \in (0,r_\varepsilon /2)\), \(\alpha _{s,\varepsilon }\) is a contact form on \(r_\varepsilon \mathbb {D}\times K\).
Proof
We compute
where \(h =fg'-f'g\). Since \(f^{n-1}h>0\) on \((0,r_\varepsilon ]\), it follows that \(\alpha _{s,\varepsilon }\) is a contact form away from K. Near K we have \(h(r)=r\), so that there \(\alpha _{s,\varepsilon } \wedge (d\alpha _{s,\varepsilon })^{n}\) reads
which is a positive volume form at any point on K. \(\square \)
Away from K the Reeb vector field is
and has the flow
where \(\phi _{\sigma _\varepsilon }^t\) is the flow of \(R_{\sigma _\varepsilon }\).
Lemma 6.7
For \(s \in (0,r_{\varepsilon }/2)\) we have \(\Gamma (\alpha _{s,\varepsilon } |_{r_\varepsilon \mathbb {D}\times K}) \le 2 E\).
Proof
By continuity it suffices to estimate the differentials of \(\phi _{\alpha _{s,\varepsilon }}^{\pm n}\) away from K. We choose a basis \(\partial _\theta , \partial _r, \partial _{q_1}, \dots , \partial _{q_{2n-1}}\) of the tangent space at \((\theta ,r,q)\). In view of (6.21), the images of these vectors under \(d \phi ^{\pm n}_{\alpha _{s,\varepsilon }}(\theta ,r,q)\) are
The size of the functions \(\bigl ( \frac{f'}{h} \bigr )'\) and \(\bigl ( \frac{g'}{h} \bigr )'\) plays no role when we apply \(\displaystyle \lim _{n \rightarrow \infty } \frac{1}{n} \log \), and together with (6.18) we find that
The lemma follows together with assumption (6.12). \(\square \)
6.3 A family of contact forms on \({\text {OB}}(F,\psi )\)
For every \(\varepsilon >0\) and \(s \in (0,r_\varepsilon /2)\), we define
on the abstract open book
where \(\alpha _s\) on \({\text {MT}}(F_{\varepsilon },\psi )\) is defined by (6.4) and f and g are given in Lemma 6.5. By (6.16) and the properties (f1) and (g1), each \(\alpha _{s,\varepsilon }\) is a well-defined contact form on \({\text {OB}}(F,\psi )\).
We first estimate the volume.
For \(s \in (0,s_1]\), where the positive number \(s_1\) is given by Lemma 6.4, we have
where we used (6.9) in the last inequality. For the second term we use (6.20), the assumption (6.12), and \(f \le 1\) and (6.17) to estimate
Together we get
Next we estimate the norm growth \(\Gamma \). The bound (6.10) also applies to the subset \({\text {MT}}(F_\varepsilon ,\psi )\) of \({\text {MT}}(F^\circ ,\psi )\) since \(\Gamma \) is monotone with respect to inclusion of compact invariant subsets. Since \({\text {MT}}(F_\varepsilon ,\psi )\) and \(r_\varepsilon \mathbb {D}\times K\) are invariant under the flow, we conclude together with assertion (3) of Proposition C.1 and Lemma 6.7 that
Now given any \(\varepsilon _0 >0\), we choose \(\varepsilon >0\) such that \(12 \pi n \varepsilon \le \varepsilon _0 /2\). Once \(\varepsilon \) is fixed, so are \(r_\varepsilon \) and \(\int _{F_{\varepsilon }}(d\lambda )^n\). If we choose \(s>0\) such that
then the right-hand side of (6.23) is \(\le \varepsilon _0\). Since \(n! \omega _n \ge 1\) we thus get a contact form \(\alpha _{s,\varepsilon }\) on \({\text {OB}}(F,\psi )\) such that
The last step of the proof consists of pushing the contact form \(\alpha _{s,\varepsilon }\) to M in such a way that the contact structure \(\ker \alpha _{s,\varepsilon }\) is mapped to \(\xi \). This is possible thanks to the following lemma.
Lemma 6.8
There exists a diffeomorphism \(\rho \) of M such that \(\rho _* (\xi ) = \ker \alpha _{s,\varepsilon }\).
Postponing the proof, we use the lemma to complete the proof of Theorem 6.1. Thanks to the lemma, the 1-form
is a contact form on \((M,\xi )\), and \({\text {vol}}_\tau (M) = 1\). By the elementary properties (1) and (4) in Proposition C.1 and by (6.25),
Since the constant E from Lemma 6.4 depends only on \(\psi , \lambda , \chi \), which are fixed data associated with \((M,\xi )\), and since \(\varepsilon _0 >0\) is arbitrarily small, we obtain \(\tau \) with \({\widehat{\Gamma }} (\tau )\) as small as we like.
6.4 Proof of Lemma 6.8
We first show that the obvious open book structure on \({\text {OB}}(F,\psi )\) is a Liouville open book with contact binding form \(\alpha _{s,\varepsilon }\). Let
be the fibration induced by the projection \({\text {MT}}(F,\psi ) \rightarrow S^1\). We construct a defining function \({\tilde{h}}\) as follows. As before, we consider the variable \(r \in [0,+\infty )\) on a neighborhood of \(K=\partial F\) in F that is induced by the embedding (6.13). Let
be a smooth function and \(d>0\) and \(\delta >0\) be constants such that
-
(df1)
\({\tilde{u}} (r,q)=r\) for \((r,q) \in [0,r_\varepsilon ] \times K\),
-
(df2)
\({\tilde{u}} \equiv d\) on \(([0,r_\varepsilon +\delta ) \times K)^c\) and \(\mathrm {supp\,}\psi \subset ([0,r_\varepsilon +\delta ] \times K)^c\),
-
(df3)
\(\tilde{u}\) depends only on r and \(\partial _r {\tilde{u}} \ge 0\) on \([0,r_\varepsilon +\delta ] \times K\).
See Fig. 10. Since \({\tilde{u}}\) is constant on \(\mathrm {supp\,}\psi \), the \(S^1\)-invariant extension of \({\tilde{u}}\) is a well-defined smooth function on \({\text {MT}}(F,\psi )\), which constitutes the function \(|{\tilde{h}}|\). Pairing \(|{\tilde{h}}|\) with \({\widetilde{\Theta }}\) leads to a well-defined defining function \({\tilde{h}}\) for the open book \((K,{\widetilde{\Theta }})\) on \({\text {OB}}(F,\psi )\). Note that on \(r_\varepsilon \mathbb {D}\times K\), \({\tilde{h}}\) is simply the projection to the disk \(r_\varepsilon \mathbb {D}\), which is smooth.
Claim 1
\(d \bigl ( \alpha _{s,\varepsilon }/|\tilde{h}| \bigr )\) induces an ideal Liouville structure on each fibre of \(\widetilde{\Theta }\).
Proof
For each \(\theta \in S^1\) we abbreviate
We need to check that \(d{{\tilde{\lambda }}}_\theta \) is a positive symplectic form on \(\{\theta \} \times F^\circ = \widetilde{\Theta }^{-1}(\theta )\). We do this on the three regions separately:
\(\underline{\hbox {On}\, \{\theta \} \times (0,r_\varepsilon ] \times K}\): By (6.22) and (df1) we have
and so
In view of the parametrization (6.13), \(d (\frac{1}{r} \sigma _{\varepsilon })\) is a positive symplectic form on \(\{\theta \} \times F^\circ \), whence \((d(\frac{1}{r} \sigma _{\varepsilon }))^n = - \frac{n}{r^{n+1}} \, dr \wedge \sigma _{\varepsilon } \wedge (d\sigma _{\varepsilon })^{n-1}\) is a positive volume form. Since \(f'r-f<0\) by (f1) and (f3), it follows that \((d {\tilde{\lambda }}_\theta )^n\) is a positive volume form, i.e., \(d {\tilde{\lambda }}_\theta \) is a positive symplectic form.
\(\underline{\hbox {On}\, \{\theta \} \times [r_\varepsilon ,r_\varepsilon +\delta ]\times K}\): By (df2) we have \(\psi = \textrm{id}\) on this set. Hence, by (6.16),
By (df3), \({\tilde{u}}\) depends only on r. We thus obtain
Also by (df3), \(\tilde{u} + r \partial _r \tilde{u}>0\), and the claim follows as in the previous case.
\(\underline{\hbox {On}\, \{\theta \} \times ([0,r_\varepsilon +\delta )\times K)^c}\): By (df2), \({\tilde{u}} \equiv d\) and
Hence \(d {\tilde{\lambda }}_\theta =\frac{s}{d} d\lambda \), which is a positive symplectic form. \(\square \)
Now we are in the following situation. On \({\text {OB}}(F,\psi )\) we have the Liouville open book
which symplectically supports the contact structure \(\xi = \ker \alpha \). Here \(\alpha \), \(\xi \), and h stand for the objects induced by the correspondence between M and \({\text {OB}}(F,\psi )\) given by the symplectically spinning vector field X on M. Moreover, by Claim 1 we have a second Liouville open book
which symplectically supports the contact structure \(\ker \alpha _{s,\varepsilon }\). By the identities (6.28), (6.29), and (6.30), the ideal Liouville structures \(\bigl ( d \bigl ( \alpha _{s,\varepsilon }/|\tilde{h}| \bigr ) |_{T(\{\theta \} \times F^\circ )} \bigr )_{\theta \in S^1}\) are invariant under the flow of the vector field \(\partial _\theta \). Although \({{\tilde{\lambda }}}_\theta \) in (6.30) is not invariant under this flow, the symplectic form \(d {{\tilde{\lambda }}}_\theta = \frac{s}{d} \, d\lambda \) is. The vector field \(\partial _\theta \) is therefore a symplectically spinning vector field on the LOB (6.32). Note that the symplectically spinning vector field X on M also reads \(\partial _\theta \) on the LOB (6.31).
Claim 2
There exists a diffeomorphism
such that \(\Phi \circ {\widetilde{\Theta }} = {\widetilde{\Theta }} \circ \Phi \) and the restriction of \(\Phi \) to each fibre is symplectic, that is,
If such a diffeomorphism exists, then \(\ker \Phi ^*\alpha _{s,\varepsilon }\) and \(\ker \alpha \) are two contact structures on \({\text {OB}}(F,\psi )\) which symplectically support the Liouville open book (6.31). Hence they are isotopic by Proposition 5.5. By Gray’s stability theorem we then find a diffeomorphism \({\hat{\rho }}\) of M such that \({\hat{\rho }}_* (\ker \alpha ) = \ker \Phi ^* \alpha _{s,\varepsilon }\). Set \(\rho = \Phi \circ {\hat{\rho }}\). Since \(\ker \Phi ^* \alpha _{s,\varepsilon } = \Phi _*^{-1} (\ker \alpha _{s,\varepsilon })\), we conclude that \(\rho _* (\ker \alpha ) = \ker \alpha _{s,\varepsilon }\), as claimed in Lemma 6.8.
Proof of Claim 2
We have the following ideal Liouville structures on the 0-page:
We first show that
is symplectic on \(F^\circ \) for all \(t\in [0,1]\). In fact, we claim that
is a Liouville form on \(F^\circ \) for all \(t \in [0,1]\), where \(\lambda \) is the primitive of \(\omega \) given by (6.3) and \({{\tilde{\lambda }}}\) is the primitive of \({\widetilde{\omega }}\) given by (6.27). Again, we compute \(d\lambda _t\) on different subsets of \(F^\circ \):
\(\underline{\hbox {On}\, \{\theta \} \times (0,r_\varepsilon ]\times K}\): By (6.28) we have
where \(\kappa =(1-t)+tf\). We have \(\kappa >0\) and \(\kappa '<0\), so that \(\kappa 'r-\kappa <0\). Hence the claim follows as in the first case of Claim 1.
\(\underline{\hbox {On}\, \{\theta \}\times [r_\varepsilon ,r_\varepsilon +\delta ]\times K}\): By (6.29) we have
where \(\kappa = (1-t) + t s/ {\tilde{u}}\). We have \(\kappa >0\) and \(\kappa ' \le 0\), so that \(\kappa 'r-\kappa <0\). The claim follows as above.
\(\underline{\hbox {On}\, \{\theta \} \times ([0,r_\varepsilon +\delta )\times K)^c}\): By (6.30) we have
Hence \(\omega _t = d\lambda _t\) is symplectic on \(F^\circ \) for all \(t \in [0,1]\).
Recall that by (6.13) and (f1),
Hence this identity holds on the same deleted neighbourhood of K for all the symplectic forms \(\omega _t\), \(t \in [0,1]\). Applying the standard Moser argument to the path \(\omega _t\), we obtain a smooth isotopy \((\psi _t)_{t\in [0,1]}\) of F such that
- (\(\Psi \)1):
-
\(\psi _0 = \textrm{id}\);
- (\(\Psi \)2):
-
\(\psi _t = \textrm{id}\) near K for all \(t \in [0,1]\);
- (\(\Psi \)3):
-
\(\psi _t^* \, \omega _t = \omega _0 = \omega \) for all \(t \in [0,1]\).
Now we define \(\Phi :[0,2\pi ] \times F \rightarrow [0,2\pi ] \times F\) by
where \(\psi \) is the monodromy that we fixed at the outset of the proof. We note that
and by (\(\Psi \)1),
Hence \(\Phi \) descends to a diffeomorphism on \({\text {MT}}(F,\psi )\). Since \(\psi = \textrm{id}\) near K and \(\psi _t = \textrm{id}\) near K for each t by (\(\Psi \)2), we have that \(\Phi = \textrm{id}\) on a neighbourhood of \(\partial {\text {MT}}(F,\psi )\). Hence \(\Phi \) descends to a diffeomorphism on \({\text {OB}}(F,\psi )\). By definition, \(\Phi \) commutes with \(\widetilde{\Theta }\).
Now recall that \(\partial _{\theta }\) is a symplectically spinning vector field for both LOBs (6.31) and (6.32). In view of (6.34) and (6.35) and identifying \(\{\theta \} \times F^\circ \) with \(\{0\} \times F^\circ \) via the flow of \(\partial _\theta \), we can therefore identify
Also recall that \(\psi ^* \omega = \omega \). Since \(\partial _\theta \) generates the monodromy \(\psi \) and preserves \({\widetilde{\omega }}\), we also have \(\psi ^* {\widetilde{\omega }} = {\widetilde{\omega }}\). Therefore, \(\psi ^*\omega _t = \omega _t\) for all \(t \in [0,1]\). Inserting (6.37) and using (\(\Psi \)3) we obtain, with the abbreviation \(F_\theta ^\circ = T (\{\theta \} \times F^\circ )\),
This concludes the proof of Lemma 6.8, and hence of Theorem 6.1.
7 Full entropy spectrum
By Theorem 6.1 every closed contact manifold \((M,\xi )\) admits normalized contact forms with arbitrarily small topological entropy. On the other hand, one can always find normalized contact forms \(\alpha \) on \((M,\xi )\) with arbitrarily large topological entropy. We first sketch a direct proof of this fact. A proof of a stronger statement relying on our previous construction is given thereon.
Existence of contact forms with large entropy. Choose a transverse knot \(\gamma \), that is, a simple closed curve \(\gamma :S^1 \rightarrow M\) such that \({\dot{\gamma }}\) is everywhere transverse to \(\xi \). Let \(B^{2n}\) be the closed ball in \(\mathbb {R}^{2n}\) of radius 1. By the normal form theorem for transverse knots [52, Example 2.5.16], we find a full torus \({{\mathcal {T}}}= B^{2n} \times S^1\) around \(\gamma \) with coordinates \((\theta _1, \dots , \theta _n, r_1, \dots , r_n, q)\) such that \(\gamma \) is parametrized by \(r_j = 0\) and q and such that on \({{\mathcal {T}}}\) the contact structure \(\xi \) is the kernel of \(\tau := d q + \sum _j r_j d \theta _j\).
Next, take a second such full torus \(({{\mathcal {T}}}_2, \tau _2)\) that is disjoint from \({{\mathcal {T}}}\), perturb \(\tau _2\) in the interior of \({{\mathcal {T}}}_2\) to a contact form \(\tau _2'\) with positive topological entropy, and take a contact form \(\alpha \) on \((M,\xi )\) that agrees with \(\tau \) on \({{\mathcal {T}}}\) and with \(\tau _2'\) on \({{\mathcal {T}}}_2\). Now for \(\delta >0\) let \(F :M \rightarrow \mathbb {R}\) be a positive smooth function that is equal to \(\delta \) outside \({{\mathcal {T}}}\), on \({{\mathcal {T}}}\) depends only on the coordinates \(r_1, \dots , r_n\), and is such that \({\text {vol}}_{F\tau } ({{\mathcal {T}}}) = 1\). Take the smooth contact form \(\alpha _{\delta , F}\) on M that is equal to \(F\tau \) on \({{\mathcal {T}}}\) and to \(\delta \alpha \) on \(M {\setminus } {{\mathcal {T}}}\). Then \(h_{{\text {top}}} (\alpha _{\delta , F}|_{{\mathcal {T}}}) = 0\) whence
With this one then readily finds
Varying \(\delta \) on \((0,\infty )\) we obtain a normalized contact form with topological entropy c for every \(c > {\widehat{h}}_{{\text {top}}}(\alpha |_{M {\setminus } {{\mathcal {T}}}})\). \(\square \)
Remark 7.1
For spherizations \(S^*Q_k\) of closed orientable surfaces of genus \(k \ge 2\) this result has been obtained in [45] inside the much smaller class of geodesic flows of negatively curved Riemannian metrics: For every \(c \ge 2\pi \sqrt{2(k-1)}\) there exists a negatively curved Riemannian metric g on \(Q_k\) such that \({\widehat{h}}_{{\text {top}}}(g) =c\). In the class of all Riemannian metrics, geodesic flows with arbitrarily large \({\widehat{h}}_{{\text {top}}}\) were constructed on all closed manifolds of dimension at least two already in [70].
We shall now combine the above argument with the construction in the proof of Theorem 6.1 to prove the following more precise result.
Proposition 7.2
Let \((M,\xi )\) be a closed co-orientable contact manifold of dimension \(2n+1 \ge 3\). Then for every \(c>0\) there exist normalized contact forms \(\alpha \) and \(\alpha '\) on \((M,\xi )\) such that \(h_{{\text {top}}}(\alpha ) = c\) and \(\Gamma (\alpha ') =c\).
Proof
We give the proof for the topological entropy. The proof for the norm growth \(\Gamma \) is similar. Fix \(c>0\) as in the proposition. As in (6.26) let
be a contact form with \(h_{{\text {top}}}(\tau ) \le c\) and \({\text {vol}}_\tau (M) = 1\). Here we abbreviated \(v:= {\text {vol}}_{\alpha _{s,\varepsilon }} \bigl ( {\text {OB}}(F,\psi ) \bigr )\). In view of (6.25) we can assume that
Recall that \(\alpha _{s,\varepsilon }\) on \(r_\varepsilon \mathbb {D}\times K\) was constructed recursively, starting from the circle \(S^1\). For \(j=1, \dots , n\) let \(f_j,g_j,h_j\) be the functions from Lemma 6.5 that we used in (6.19) to construct \(\alpha _{s,\varepsilon _j}\) on \(r_{\varepsilon _j} \mathbb {D}\times K_j\). Set \(r = \min \{ r_{\varepsilon _1}, \dots , r_{\varepsilon _n} \} >0\). Let \(B^{2n}(r)\) be the closed r-ball in \(\mathbb {R}^{2n}\) with polar coordinates \((\varvec{\uptheta }, {{\textbf {r}}}) \equiv (\theta _1, \dots , \theta _n, r_1, \dots , r_n)\), and abbreviate \({{\mathcal {T}}}_r = B^{2n}(r) \times S^1\).
For \(\delta >0\) choose a positive smooth function \(F :{\text {OB}}(F,\psi ) \rightarrow \mathbb {R}\) with the following properties:
-
(F1)
\(F = \delta \) on \({{\mathcal {T}}}_r^c:= {\text {OB}}(F,\psi ) {\setminus } {{\mathcal {T}}}_r\).
-
(F2)
F only depends on \({{\textbf {r}}}\) on \({{\mathcal {T}}}_r\).
-
(F3)
\({\text {vol}}_{F \alpha _{s,\varepsilon }} ({{\mathcal {T}}}_r) = 1\).
Lemma 7.3
\(h_{{\text {top}}} ( F \alpha _{s,\varepsilon } |_{{{\mathcal {T}}}_r}) =0\).
Proof
The full torus \({{\mathcal {T}}}_r\) is foliated by the tori
with \(r_1, \dots , r_n \ge 0\) constant, of dimension \(k+1 \le n+1\). By (f1) and (g1),
Writing out (6.21) recursively and using (7.2) we see that the Reeb flow of \(\alpha _{s,\varepsilon }\) leaves the tori \(\mathbb {T}_{{{\textbf {r}}}}\) invariant and on each \(\mathbb {T}_{{{\textbf {r}}}}\) is a Kronecker flow.
Applying now (6.19) recursively we see that on \({{\mathcal {T}}}_r\),
with smooth functions \(\rho _j, \rho \). The Reeb flow of any 1-form of this form leaves the tori \(\mathbb {T}_{{\textbf {r}}}\) invariant and there restricts to a Kronecker flow. This is clear at \({{\textbf {r}}}\) if the Jacobian determinant of \(\left( \frac{\partial \rho _i}{\partial r_j} ({{\textbf {r}}}) \right) \) does not vanish, and in general follows by approximation. Therefore, for each \({{\textbf {r}}}\) the Reeb flow of \(F \alpha _{s,\varepsilon }\) is a Kronecker flow on \(\mathbb {T}_{{\textbf {r}}}\), and hence \(h_{{\text {top}}} (F \alpha _{s,\varepsilon } |_{\mathbb {T}_{{{\textbf {r}}}}}) =0\). The variational principle for topological entropy now implies that
as claimed. \(\square \)
By Lemma 7.3 the topological entropy of \(\alpha _{s,\varepsilon }\) and \(F \alpha _{s,\varepsilon }\) on \({{\mathcal {T}}}_r\) vanishes. Together with (F1) we obtain
Now consider the contact form
on \((M,\xi )\). By (7.4) and (7.3),
By (7.1), \({\underline{v}}:= {\text {vol}}_{\alpha _{s,\varepsilon }} ({{\mathcal {T}}}_r^c) \in (0,1)\), and by (F1) and (F3),
whence
Assume first that \(h_{{\text {top}}} (\alpha _{s,\varepsilon }) >0\). Then the range of the function \(f :(0,\infty ) \rightarrow \mathbb {R}\) is \(\left( {\underline{v}}^{1/(n+1)} \, h_{{\text {top}}} (\alpha _{s,\varepsilon }), \infty \right) \). Since \({\underline{v}}<1\) and \(h_{{\text {top}}} (\alpha _{s,\varepsilon }) \le c\), we in particular find \(\delta \) such that \({\widehat{h}}_{{\text {top}}} \bigl ( (F \circ \rho ) \tau \bigr ) =c\). If \(h_{{\text {top}}} (\alpha _{s,\varepsilon }) =0\), Proposition 7.2 follows from the following result.
Lemma 7.4
We can assume that \(h_{{\text {top}}}(\alpha _{s,\varepsilon } |_{{\text {MT}}(F_\varepsilon , \psi )}) >0\).
Proof
Assume that \(h_{{\text {top}}}(\alpha _{s,\varepsilon } |_{ {\text {MT}}(F_\varepsilon , \psi )}) =0\). By Theorem 6.2 in [76] there exists a contact form \(\alpha _{s,\varepsilon }'\) on \({\text {MT}}(F_\varepsilon ,\psi )\) that is \(C^1\)-close to \(\alpha _{s,\varepsilon }\) and equal to \(\alpha _{s,\varepsilon }\) near the boundary, and whose Reeb flow has a generic 1-elliptic periodic orbit. Hence this flow contains a hyperbolic basic set, and therefore \(h_{{\text {top}}} (\alpha _{s,\varepsilon }') >0\). Further, the \(C^1\)-closeness of \(\alpha _{s,\varepsilon }\) and \(\alpha _{s,\varepsilon }'\) implies that all the 1-forms
are contact forms. Gray’s stability theorem therefore shows that there exists a diffeomorphism \(\zeta \) of \({\text {MT}}(F_\varepsilon , \psi )\) that is the identity near the boundary such that the kernel of \(\zeta ^* \alpha _{s,\varepsilon }'\) is \(\xi \). The contact form on \((M,\xi )\) that agrees with \(\alpha _{s,\varepsilon }\) on \(M {\setminus } {\text {MT}}(F_\varepsilon , \psi )\) and with \(\zeta ^* \alpha _{s,\varepsilon }'\) on \({\text {MT}}(F_\varepsilon , \psi )\) is the contact form we were looking for.
Newhouse’s full Theorem 6.2 starts with the \(C^1\)-closing lemma, and holds in all dimensions. We do not need to appeal to the closing lemma in our situation, and we only need the easier 3-dimensional result: Assume that \(\dim M = 3\). By (6.8) we can choose a flow-invariant neighbourhood \(U \subset {\text {MT}}(F_\varepsilon , \psi )\) of the boundary of \({\text {MT}}(F_\varepsilon , \psi )\) such that all orbits in U are closed. Let \(\gamma \) be one of these orbits that is not on the boundary of \({\text {MT}}(F_\varepsilon ,\psi )\), and choose a flow-invariant open neighbourhood \(N(\gamma )\) whose closure is also disjoint from the boundary of \({\text {MT}}(F_\varepsilon ,\psi )\). Since \(N(\gamma )\) is foliated by closed orbits, \(\gamma \) is elliptic. Using the Birkhoff normal form theorem and the KAM theorem, one can \(C^1\)-perturb \(\alpha _{s,\varepsilon }\) to a contact form \(\alpha _{s,\varepsilon }'\) that agrees with \(\alpha _{s,\varepsilon }\) outside \(N(\gamma )\) and whose Reeb flow has a transverse homoclinic connection near \(\gamma \), see [97]. This Reeb flow therefore contains a horse-shoe and thus has positive topological entropy. As above we can isotope \(\alpha _{s,\varepsilon }'\) without changing it outside \(N(\gamma )\) to a contact form \(\alpha _{s,\varepsilon }''\) for \((M^3,\xi )\). Proceeding from this contact form with positive topological entropy, our inductive construction in Sect. 6.2 shows that \(\sigma _\varepsilon \) on \(M^{2n+1}\) also has positive topological entropy. Hence this also holds true for \(\alpha _{s,\varepsilon }\) on the boundary of \({\text {MT}}(F_\varepsilon , \psi )\) and therefore, by the monotonicity of topological entropy, also on \({\text {MT}}(F_\varepsilon , \psi )\). \(\square \)
8 Collapsing the growth rate of symplectic invariants
Theorem 1.1 on the collapse of topological entropy of Reeb flows implies the collapse of the growth rate of two symplectic invariants: symplectic homology and wrapped Floer homology.
8.1 Liouville domains and fillings
Recall that a Liouville domain is a compact exact symplectic manifold \({\varvec{W}}=(W,\varvec{\omega },\varvec{\lambda })\) with boundary \(\Sigma = \partial W\) and a primitive \(\varvec{\lambda }\) of \(\varvec{\omega }\) such that \(\varvec{\alpha }_W = \varvec{\lambda }|_{\Sigma }\) is a contact form on \(\Sigma \). The Liouville 1-form \(\varvec{\lambda }\) also induces the contact structure \(\xi _W = \ker \varvec{\alpha }_W\) on \(\Sigma \). The Liouville domain \({\varvec{W}}\) is called an exact symplectic filling for the contact form \(\varvec{\alpha }_W\), and we say that the contact form \(\varvec{\alpha }_W\) is exactly filled by \({\varvec{W}}\).
A standard construction (see for example [11, Section 2.2.1]) shows that if a contact form \(\alpha \) on a contact manifold \((\Sigma ,\xi )\) is exactly filled by a Liouville domain \({\varvec{W}}_{\!\!\, \alpha }\), then we can construct for any other contact form \(\alpha '\) on \((\Sigma ,\xi )\) a Liouville domain \({\varvec{W}}_{\!\!\, \alpha '}\) that fills \(\alpha '\). It therefore makes sense to say that a contact manifold is fillable by Liouville domains.
8.2 Symplectic homology and collapse of its exponential growth
Let \({\varvec{W}}_{\!\!\, \alpha }\) be a Liouville domain filling the contact form \(\alpha \) on the contact manifold \((\Sigma ,\xi )\). The symplectic homology \({\text {SH}}({\varvec{W}}_{\!\!\, \alpha })\) is a homology theory associated to \({\varvec{W}}_{\!\!\, \alpha }\). While there are various versions of symplectic homology, we here consider the one originally developed by Viterbo [94].
Geometrically, one can think of the chain complex associated to \({\text {SH}}({\varvec{W}}_{\!\!\, \alpha })\) as the \(\mathbb {Z}_2\)-vector space generated by the periodic orbits of the Reeb flow of \(\alpha \) and by the critical points of a \(C^2\)-small non-positive Morse–Smale function \(f :{\varvec{W}}_{\!\!\, \alpha } \rightarrow \mathbb {R}\) such that \(f^{-1}(0) = \Sigma \) is a regular energy level. The differential of \({\text {SH}}({\varvec{W}}_{\!\!\, \alpha })\) counts Floer cylinders connecting generators. We refer the reader to [24, 78] for details.
There is a filtration of \({\text {SH}}({\varvec{W}}_{\!\!\, \alpha })\) by the action of its generators. For the Reeb orbits the action equals the period. For each real number \(a>0\) let \({\text {SH}}^{<a}({\varvec{W}}_{\!\!\, \alpha })\) be the homology of the subcomplex generated by the Reeb orbits of action \(<a\) and the critical points of f. The inclusion of this subcomplex induces the homomorphism of \(\mathbb {Z}_2\)-vector spaces
We define the exponential growth rate of \({\text {SH}}({\varvec{W}}_{\!\!\, \alpha })\) by
The following remarkable result is due to Meiwes [74].
Theorem
If \({\varvec{W}}_{\!\!\, \alpha }\) is a Liouville domain filling a contact form \(\alpha \) on \((\Sigma ,\xi )\), then
Together with Theorem 1.1 we obtain the following result.
Corollary 8.1
Let \((\Sigma ,\xi )\) be a contact manifold fillable by Liouville domains. Then for every \(\varepsilon >0 \) there exists a contact form \(\alpha \) with \({\text {vol}}_\alpha (\Sigma ) = 1\) such that
for any Liouville filling \({\varvec{W}}_{\!\!\, \alpha }\) of \(\alpha \).
It follows that one cannot, in general, recover the volume of a contact form \(\alpha \) from the exponential growth rate of \({\text {SH}}({\varvec{W}}_{\!\!\, \alpha })\) of a Liouville filling \({\varvec{W}}_{\!\!\, \alpha }\). To obtain a better geometric formulation of the corollary, we notice that if \({\varvec{W}}_{\!\!\, \alpha }=(W^{2n}_\alpha , \varvec{\omega }_{\alpha }, \varvec{\lambda }_\alpha )\) is a Liouville filling of \(\alpha \), then the symplectic volume \( \int _{W_{\!\!\, \alpha }} (\varvec{\omega }_\alpha )^n \) equals the contact volume of \({\text {vol}}_\alpha (\Sigma )\). Corollary 8.1 thus says that every Liouville fillable contact manifold admits fillings by Liouville domains of symplectic volume 1 and arbitrarily small growth of symplectic homology.
In the opposite direction, one can ask if for a fixed contact manifold \((\Sigma ,\xi )\) there exists a constant \(\textrm{K}_{\Sigma ,\xi }\) such that
for every Liouville domain \({\varvec{W}}\) that fills some normalized contact form on \((\Sigma ,\xi )\). A partial negative answer to this question is given by the following result. Recall that the spherization of a closed manifold Q is the contact manifold \((S^*Q,\xi _{\textrm{can}\,})\) whose Reeb flows comprise the co-geodesic flows of Riemannian metrics on Q.
Lemma 8.2
Let \(Q_k\) be the closed orientable surface of genus \(k \ge 2\). Then for every real number \(c \ge 2 \pi \sqrt{2(k-1)}\) there exists a contact form \(\alpha \) of volume 1 on \((S^*Q_k, \xi _{\textrm{can}\,})\) and a Liouville domain \({\varvec{W}}_{\!\!\, \alpha }\) filling \(\alpha \) such that
Proof
It follows from [45, Theorem A] that for any real number \(c \ge 2 \pi \sqrt{2(k-1)}\) there exists a negatively curved Riemannian metric g with area \(1/(2\pi )\) such that the topological entropy of the geodesic flow \(\phi _g\) is equal to c. Let \(\alpha \) be the contact form on \((S^*Q_k,\xi _{\textrm{can}\,})\) whose Reeb flow is the co-geodesic flow of g. Then \({\text {vol}}_\alpha (S^*Q_k) = 1\) and \(h_{{\text {top}}} (\phi _\alpha ) = h_{{\text {top}}}(\phi _g) = c\).
Let \({\varvec{W}}_{\!\!\, \alpha } = D^*(g) \subset (T^* Q_k, \lambda _{\textrm{can}\,})\) be the unit co-disk bundle associated to the Riemannian metric g, where \(\lambda _{\textrm{can}\,}\) is the Liouville form on the cotangent bundle \(T^*Q_k\). Then \({\varvec{W}}_{\!\!\, \alpha }\) is a Liouville domain filling \(\alpha \).
Since the Riemannian metric g is negatively curved, a theorem of Margulis [71] shows that
where \(P^t(\phi _\alpha )\) denotes the number of periodic orbits of the flow \(\phi _\alpha \) of length \(<t\), see also [25]. Since all periodic Reeb orbits have Morse index zero and are non-contractible, there are no Floer cylinders starting or ending at these orbits. Hence there is a bijection between the Reeb orbits of action \(<a\) and the generators of \({\text {SH}}^a ({\varvec{W}}_{\!\!\, \alpha })\), up to a finite error coming from the finitely many critical points of the function f. It follows that
see [7, 67] for details. Combining these two equalities we get
while as noted above \({\text {vol}}_\alpha (S^*Q_k) = 1\). \(\square \)
8.3 Wrapped Floer homology and collapse of its exponential growth
In a similar way we obtain a collapse result for the exponential growth of another symplectic invariant called wrapped Floer homology. The wrapped Floer homo- logy \({\text {WH}}({\varvec{W}},L)\) is an invariant associated to a Liouville domain \({\varvec{W}}\) and an asymptotically conical exact Lagrangian submanifold L of \({\varvec{W}}\). One of several references giving the precise definition of \({\text {WH}}({\varvec{W}},L)\) is [11].
With \(\alpha \) the contact form on the boundary of a Liouville domain \({\varvec{W}}_{\!\!\, \alpha }\), one can think of the chain complex associated to \({\text {WH}}({\varvec{W}}_{\!\!\, \alpha },L)\) as the \(\mathbb {Z}_2\)-vector space generated by the Reeb chords of \(\alpha \) that start and end on \(\partial L\), and by the intersection points of L and a \(C^2\)-small perturbation of L. The differential of \({\text {WH}}({\varvec{W}}_{\!\!\, \alpha },L)\) counts Floer strips connecting generators.
As in the case of symplectic homology there is a filtration of \({\text {WH}}({\varvec{W}}_{\!\!\, \alpha },L)\) by the action of the generators, and again the action of Reeb chords is equal to their time. For each real number \(a>0\) let \({\text {WH}}^{<a}({\varvec{W}}_{\!\!\, \alpha },L)\) be the homology of the subcomplex generated by Reeb chords and intersection points of action \(<a\). Again there are natural homomorphisms
and we define the exponential growth rate of \({\text {WH}}({\varvec{W}}_{\!\!\, \alpha },L)\) by
The following result was obtained in [11].
Theorem
Let \({\varvec{W}}_{\!\!\, \alpha }\) be a Liouville domain filling a contact form \(\alpha \) on \((\Sigma ,\xi )\), and let L be an asymptotically conical exact Lagrangian submanifold of \({\varvec{W}}_{\!\!\, \alpha }\) whose intersection with \(\partial {\varvec{W}}_{\!\!\, \alpha }\) is a sphere.Footnote 1 Then
Together with Theorem 1.1 we obtain
Corollary 8.3
Let \((\Sigma ,\xi )\) be a contact manifold fillable by Liouville domains. Then for every \(\varepsilon >0\) there exists a contact form \(\alpha \) with \({\text {vol}}_\alpha (\Sigma ) = 1\) such that
for any Liouville filling \({\varvec{W}}_{\alpha }\) of \(\alpha \) and any asymptotically conical Lagrangian submanifold L of \({\varvec{W}}_{\alpha }\) whose intersection with \(\partial {\varvec{W}}_{\alpha }\) is a sphere.
Classical examples of pairs \(({\varvec{W}}_{\!\!\, \alpha }, L)\) are the unit co-disk bundles \(D^*(g)\) over a closed Riemannian manifold Q, with L a co-disk \(D_q^*(g)\) over a point \(q \in Q\). Here is the analogue of Lemma 8.2.
Lemma 8.4
Let \(Q_k\) be the closed orientable surface of genus \(k \ge 2\). Then for every real number \(c \ge 2 \pi \sqrt{2(k-1)}\) there exists a Riemannian metric g on \(Q_k\) of area \(1/(2\pi )\) such that
Proof
As in the proof of Lemma 8.2 we appeal to [45] and take a negatively curved Riemannian metric g on \(Q_k\) of area \(1/(2\pi )\) whose geodesic flow has topological entropy
Since g is negatively curved, Manning’s inequality in Theorem A.2 is an equality,
On the other hand, it is clear that
where \(C^t(\phi _g,q)\) denotes the number of geodesics from q to q of length \(<t\). Furthermore, since the Morse indices of all geodesics vanish, we have as for the symplectic homology that
These four identities prove the lemma. \(\square \)
Notes
In Sect. II.1 of his text, page 259 of [84], he writes: “Unter diesen Annahmen wird das Linienelement eine beliebige homogene Function ersten Grades der Grössen dx sein können, welche ungeändert bleibt, wenn sämmtliche Grössen dx ihr Zeichen ändern”. He then readily specializes to the convex (Finsler) case, mentioning just an example, and then restricts to Riemannian metrics, since “die Untersuchung dieser allgemeinern Gattung würde zwar keine wesentlich andere Principien erfordern, aber ziemlich zeitraubend sein”.
References
Abbondandolo, A., Bramham, B., Hryniewicz, U., Salomão, P.A.S.: Sharp systolic inequalities for Reeb flows on the three-sphere. Invent. Math. 211, 687–778 (2018)
Abbondandolo, A., Bramham, B., Hryniewicz, U., Salomão, P.A.S.: Contact forms with large systolic ratio in dimension three. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 19, 1561–1582 (2019)
Abbondandolo, A., Majer, P.: A non-squeezing theorem for convex symplectic images of the Hilbert ball. Calc. Var. Partial Differ. Equ. 54, 1469–1506 (2015)
Abbondandolo, A., Schwarz, M.: On the Floer homology of cotangent bundles. Commun. Pure Appl. Math. 59, 254–316 (2006)
Alexander, J.W.: Note on Riemann spaces. Bull. Am. Math. Soc. 26, 370–372 (1920)
Álvarez Paiva, J.C., Balacheff, F., Tzanev, K.: Isosystolic inequalities for optical hypersurfaces. Adv. Math. 301, 934–972 (2016)
Alves, M.R.R.: Cylindrical contact homology and topological entropy. Geom. Topol. 20, 3519–3569 (2016)
Alves, M.R.R.: Positive topological entropy for Reeb flows on \(3\)-dimensional Anosov contact manifolds. J. Mod. Dyn. 10, 497–509 (2016)
Alves, M.R.R.: Legendrian contact homology and topological entropy. J. Topol. Anal. 11, 53–108 (2019)
Alves, M.R.R., Colin, V., Honda, K.: Topological entropy for Reeb vector fields in dimension three via open book decompositions. J. Éc. polytech. Math. 6, 119–148 (2019)
Alves, M.R.R., Meiwes, M.: Dynamically exotic contact spheres in dimensions \(\ge 7\). Comment. Math. Helv. 94, 569–622 (2019)
Ball, K.: An elementary introduction to modern convex geometry. Flavors of geometry, Math. Sci. Res. Inst. Publ., vol. 31, pp. 1–58. Cambridge University Press, Cambridge (1997)
Ball, K.: Convex geometry and functional analysis. In: Handbook of the Geometry of Banach Spaces, Vol. I, pp. 161–194. North-Holland, Amsterdam (2001)
Bangert, V.: On the existence of closed geodesics on two-spheres. Int. J. Math. 4, 1–10 (1993)
Bao, D., Chern, S. S., Shen, Z.: An introduction to Riemann–Finsler geometry. Graduate Texts in Mathematics, vol. 200. Springer, New York (2000)
Barthelmé, T.: On deformations of the spectrum of a Finsler–Laplacian that preserve the length spectrum. Bull. Soc. Math. France 145, 421–448 (2017)
Barthelmé, T., Colbois, B.: Eigenvalue control for a Finsler–Laplace operator. Ann. Global Anal. Geom. 44, 43–72 (2013)
Berger, M.: A Panoramic View of Riemannian Geometry. Springer, Berlin (2003)
Besse, A.: Manifolds all of whose geodesics are closed. Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 93. Springer, Berlin (1978)
Besson, G., Courtois, G., Gallot, S.: Entropies et rigidités des espaces localement symétriques de courbure strictement négative. Geom. Funct. Anal. 5, 731–799 (1995)
Besson, G., Courtois, G., Gallot, S.: Minimal entropy and Mostow’s rigidity theorems. Ergod. Theory Dyn. Syst. 16, 623–649 (1996)
Borman, M.S., Eliashberg, Ya., Murphy, E.: Existence and classification of overtwisted contact structures in all dimensions. Acta Math. 215, 281–361 (2015)
Bott, R.: On manifolds all of whose geodesics are closed. Ann. Math. 60, 375–382 (1954)
Bourgeois, F., Oancea, A.: An exact sequence for contact-and symplectic homology. Invent. Math. 175, 611–680 (2009)
Bowen, R.: Periodic points and measures for Axiom A diffeomorphisms. Trans. Am. Math. Soc. 154, 377–397 (1971)
Burns, K., Paternain, G.: Anosov magnetic flows, critical values and topological entropy. Nonlinearity 15, 281–314 (2002)
Busemann, H.: The Geometry of Geodesics. Academic Press Inc., New York (1955)
Busemann, H.: Metrizations of projective spaces. Proc. Am. Math. Soc. 8, 387–390 (1957)
Cannas da Silva, A.: Lectures on Symplectic Geometry. Lecture Notes in Mathematics, vol. 1764. Springer, Berlin (2001)
Chern, S.S.: Finsler geometry is just Riemannian geometry without the quadratic restriction. Not. Am. Math. Soc. 43, 959–963 (1996)
Cineli, E., Ginzburg, V. L., Gürel, B. Z.: Topological entropy of Hamiltonian diffeomorphisms: a persistence homology and Floer theory perspective. arXiv:2111.03983
Colbois, B., Newberger, F., Verovic, P.: Some smooth Finsler deformations of hyperbolic surfaces. Ann. Global Anal. Geom. 35, 191–226 (2009)
Colin, V., Dehornoy, P., Rechtman, A.: On the existence of supporting broken book decompositions for contact forms in dimension \(3\). Invent. Math. 231, 1489–1539 (2023)
Colin, V., Honda, K.: Stabilizing the monodromy of an open book decomposition. Geom. Dedicata 132, 95–103 (2008)
Connell, C., Farb, B.: Minimal entropy rigidity for lattices in products of rank one symmetric spaces. Commun. Anal. Geom. 11, 1001–1026 (2003)
Dahinden, L.: Lower complexity bounds for positive contactomorphisms. Isr. J. Math. 224, 367–383 (2018)
Dahinden, L.: The Bott-Samelson theorem for positive Legendrian isotopies. Abh. Math. Semin. Univ. Hambg. 88, 87–96 (2018)
Dahinden, L.: \(C^0\)-stability of topological entropy for contactomorphisms. Commun. Contemp. Math. 23, Paper No. 2150015 (2021)
D’Ambra, G., Gromov, M.: Lectures on transformation groups: geometry and dynamics. Surveys in differential geometry (Cambridge, MA, 1990), pp. 19–111, Lehigh University, Bethlehem (1991)
Deng, S., Hou, Z.: On symmetric Finsler spaces. Isr. J. Math. 162, 197–219 (2007)
De Philippis, G., Marini, M., Mazzucchelli, M., Suhr, S.: Closed geodesics on reversible Finsler 2-spheres. J. Fixed Point Theory Appl. 24, 64 pp (2022)
Dinaburg, E.I.: A connection between various entropy characterizations of dynamical systems. Izv. Akad. Nauk SSSR Ser. Mat. 35, 324–366 (1971)
Durán, C.E.: A volume comparison theorem for Finsler manifolds. Proc. Am. Math. Soc. 126, 3079–3082 (1998)
Egloff, D.: On the dynamics of uniform Finsler manifolds of negative flag curvature. Ann. Global Anal. Geom. 15, 101–116 (1997)
Erchenko, A., Katok, A.: Flexibility of entropies for surfaces of negative curvature. Isr. J. Math. 232, 631–676 (2019)
Etnyre, J.: Lectures on open book decompositions and contact structures. Floer homology, gauge theory, and low-dimensional topology, pp. 103–141, Clay Math. Proc. 5. AMS, Providence (2006)
Fender, E., Lee, S., Sohn, B.: Barcode entropy for Reeb flows on contact manifolds with Liouville fillings. arXiv:2305.04770
Frauenfelder, U., Labrousse, C., Schlenk, F.: Slow volume growth for Reeb flows on spherizations and contact Bott–Samelson theorems. J. Topol. Anal. 7, 407–451 (2015)
Frauenfelder, U., Schlenk, F.: Fiberwise volume growth via Lagrangian intersections. J. Symplectic Geom. 4, 117–148 (2006)
Frauenfelder, U., Schlenk, F.: Filtered Hopf algebras and counting geodesic chords. Math. Ann. 360, 995–1020 (2014)
Freire, A., Mañé, R.: On the entropy of the geodesic flow in manifolds without conjugate points. Invent. Math. 69, 375–392 (1982)
Geiges, H.: An Introduction to Contact Topology. Cambridge Studies in Advanced Mathematics, vol. 109. Cambridge University Press, Cambridge (2008)
Giroux, E.: Géométrie de contact : de la dimension trois vers les dimensions supérieures. Proceedings of the International Congress of Mathematicians, Vol. II (Beijing, 2002), pp. 405–414. Higher Ed. Press, Beijing (2002)
Giroux, E.: Ideal Liouville domains, a cool gadget. J. Symplectic Geom. 18, 769–790 (2020)
Glasmachers, E., Knieper, G., Ogouyandjou, C., Schröder, J.-P.: Topological entropy of minimal geodesics and volume growth on surfaces. J. Mod. Dyn. 8, 75–91 (2014)
Green, L.: Auf Wiedersehensflächen. Ann. Math. 78, 289–299 (1963)
Gromoll, D., Grove, K.: On metrics on \(S^2\) all of whose geodesics are closed. Invent. Math. 65, 175–177 (1981/82)
Gromoll, D., Meyer, W.: Periodic geodesics on compact Riemannian manifolds. J. Differ. Geom. 3, 493–510 (1969)
Gromov, M.: Volume and bounded cohomology. Inst. Hautes Études Sci. Publ. Math. 56, 5–99 (1982)
Hasselblatt, B., Katok, A.: Introduction to the Modern Theory of Dynamical Systems. Encyclopedia of Mathematics and Its Applications, vol. 54. Cambridge University Press, Cambridge (1995)
Hopf, E.: Closed surfaces without conjugate points. Proc. Nat. Acad. Sci. USA 34, 47–51 (1948)
John, F.: Extremum problems with inequalities as subsidiary conditions. Studies and essays presented to R. Courant on his 60th birthday, January 8, 1948. Interscience Publishers, Inc., New York (1948)
Katok, A.: Ergodic perturbations of degenerate integrable Hamiltonian systems. Izv. Akad. Nauk SSSR Ser. Mat. 37, 539–576 (1973)
Katok, A.: Entropy and closed geodesics. Ergod. Theory Dyn. Syst. 2 (1982), 339–365 (1983)
Katok, A., Knieper, G., Weiss, H.: Formulas for the derivative and critical points of topological entropy for Anosov and geodesic flows. Commun. Math. Phys. 138, 19–31 (1991)
Löh, C.: Simplicial volume. www.map.mpim-bonn.mpg.de/Simplicial_volume
Macarini, L., Paternain, G.P.: Equivariant symplectic homology of Anosov contact structures. Bull. Braz. Math. Soc. 43, 513–527 (2012)
Macarini, L., Schlenk, F.: Positive topological entropy of Reeb flows on spherizations. Math. Proc. Camb. Philos. Soc. 151, 103–128 (2011)
Manning, A.: Topological entropy for geodesic flows. Ann. Math. 110, 567–573 (1979)
Manning, A.: More topological entropy for geodesic flows. Dynamical systems and turbulence, Warwick 1980 (Coventry, 1979/1980), pp. 243–249. Lecture Notes in Math. 898, Springer, Berlin (1981)
Margulis, G.A.: Certain applications of ergodic theory to the investigation of manifolds of negative curvature. Funkcional. Anal. i Priloz̆en. 3, 89–90 (1969)
McDuff, D., Salamon, D.: Introduction to Symplectic Topology. Oxford Mathematical Monographs, 3rd edn. The Clarendon Press, New York (2015)
McLean, M.: Local Floer homology and infinitely many simple Reeb orbits. Algebr. Geom. Topol. 12, 1901–1923 (2012)
Meiwes, M.: Rabinowitz Floer homology, leafwise intersections and topological entropy. Ph.D. Thesis, Universität Heildelberg (2018)
Merlin, L.: Minimal entropy for uniform lattices in product of hyperbolic planes. Comment. Math. Helv. 91, 107–129 (2016)
Newhouse, S.: Quasi-elliptic periodic points in conservative dynamical systems. Am. J. Math. 99, 1061–1087 (1977)
Newhouse, S.: Entropy and volume. Ergodic Theory Dyn. Syst. 8\(^{*}\) (1988), Charles Conley Memorial Issue, 283–299
Oancea, A.: A survey of Floer homology for manifolds with contact type boundary or symplectic homology. In: Symplectic Geometry and Floer Homology, pp. 51–91, Ensaios Mat. 7, Soc. Brasil. Mat., Rio de Janeiro (2004)
Ohno, T.: A weak equivalence and topological entropy. Publ. Res. Inst. Math. Sci. 16, 289–298 (1980)
Paternain, G.: Geodesic flows. Progress in Mathematics, vol. 180. Birkhäuser Boston, Inc., Boston (1999)
Paternain, G., Petean, J.: Minimal entropy and collapsing with curvature bounded from below. Invent. Math. 151, 415–450 (2003)
Polterovich, L.: Growth of maps, distortion in groups and symplectic geometry. Invent. Math. 150, 655–686 (2002)
Polterovich, L., Sodin, M.: A growth gap for diffeomorphisms of the interval. J. Anal. Math. 92, 191–209 (2004)
Riemann, B.: Über die Hypothesen, welche der Geometrie zu Grunde liegen. Pages 254–269 of Bernhard Riemann’s gesammelte mathematische Werke und wissenschaftlicher Nachlass. Herausgegeben unter Mitwirkung von R. Dedekind von H. Weber. Teubner Verlag, Leipzig (1876)
Rogers, C.A., Shephard, G.C.: The difference body of a convex body. Arch. Math. (Basel) 8, 220–233 (1957)
Rogers, C.A., Shephard, G.C.: Convex bodies associated with a given convex body. J. Lond. Math. Soc. 33, 270–281 (1958)
Rolfsen, D.: Knots and links. Mathematics Lecture Series, No. 7. Publish or Perish, Berkeley (1976)
Sağlam, M.: Contact forms with large systolic ratio in arbitrary dimensions. Ann. Sc. Norm. Super. Pisa Cl. Sci. 22, 1265–1308 (2021)
Sağlam, M.: Reeb flows with small contact volume and large return time to a global section. arXiv:2003.04729
Samelson, H.: On manifolds with many closed geodesics. Portugal. Math. 22, 193–196 (1963)
Skornyakov, L.A.: Metrization of a projective plane in connection with a given system of curves. Izv. Akad. Nauk SSSR. Ser. Mat. 19, 471–482 (1955)
Spivak, M.: A comprehensive introduction to differential geometry, vol. II. Third edition. Publish or Perish, Houston (1999)
Verovic, P.: Problème de l’entropie minimale pour les métriques de Finsler. Ergodic Theory Dyn. Syst. 19, 1637–1654 (1999)
Viterbo, C.: Functors and computations in Floer homology with applications. I. Geom. Funct. Anal. 9, 985–1033 (1999)
Walters, P.: An Introduction to Ergodic Theory. Graduate Texts in Mathematics, vol. 79. Springer, Berlin (1982)
Yomdin, Y.: Volume growth and entropy. Isr. J. Math. 57, 285–300 (1987)
Zehnder, E.: Homoclinic points near elliptic fixed points. Commun. Pure Appl. Math. 26, 131–182 (1973)
Ziller, W.: Geometry of the Katok examples. Ergodic Theory Dyn. Syst. 3, 135–157 (1983)
Ziller, W.: Lie Groups. Representation Theory and Symmetric Spaces. www2.math.upenn.edu/~wziller/math650/LieGroupsReps.pdf
Acknowledgements
We wish to thank Viktor Ginzburg for several useful discussions, that in particular led to the results in Sect. 7, Leonid Polterovich who asked us whether the collapse of topological entropy can be extended to the collapse of norm growth, and Patrick Verovic for explaining to us his work [93]. We also thank the referee for many useful comments and the careful reading. A.A., M.A. and M.S. are partially supported by the SFB/TRR 191 ‘Symplectic Structures in Geometry, Algebra and Dynamics’, funded by the DFG (Projektnummer 281071066 - TRR 191). M.A. is also supported by the ERC consolidator grant 646649 ‘SymplecticEinstein’ and by the Senior Postdoctoral fellowship of the Research Foundation - Flanders (FWO) in fundamental research 1286921N. F.S. is partially supported by the SNF grant 200020-144432/1.
Funding
Open access funding provided by University of Neuchâtel
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Dedicated to the memory of Will Merry, 1984–2022.
Appendices
Appendix A. Volume entropy and Manning’s inequality for Finsler metrics
In this appendix we first give an elementary proof of Manning’s inequality for regular Finsler geodesic flows. We then use Yomdin’s theorem to prove a generalization of Manning’s inequality to arbitrary \(C^\infty \)-smooth flows on compact fiber bundles whose fibers are of dimension one less than the base.
1.1 A.1. The volume entropy of a Finsler metric
Let F be a Finsler metric on the closed n-dimensional connected manifold Q: F is a continuous real function on the tangent bundle TQ which is positive away from the zero section, fiberwise positively one-homogeneous and fiberwise convex. The Finsler metric F induces the length functional
on the space of Lipschitz curves \(\gamma :[a,b] \rightarrow Q\) and the function \(d_F :Q \times Q \rightarrow [0,+\infty )\),
By the Arzelà–Ascoli theorem, the above infimum is actually a minimum: There is a Lipschitz curve \(\gamma \) from x to y such that \(\ell _F(\gamma ) = d_F(x,y)\). The function \(d_F\) is positive away from the diagonal and satisfies the triangle inequality
In general, \(d_F\) is not symmetric because we are not assuming F to be reversible, i.e. to satisfy \(F(-v)=F(v)\) for every \(v \in TQ\). By the compactness of Q, the irreversibility ratio of F, i.e. the number
is well-defined and we have
The Finsler metric F lifts to a Finsler metric \({\widetilde{F}}\) on the universal cover \(\widetilde{Q}\) of Q. We denote by \(\ell _{{\widetilde{F}}}\) and \(d_{{\widetilde{F}}}\) the induced length functional and asymmetric distance on \(\widetilde{Q}\). Note that the lifted Finsler metric has the same irreversibility ratio \(\theta \) and (A.1) holds also for the lifted asymmetric distance \(d_{\widetilde{F}}\). The closed forward R-ball centered at \(x \in \widetilde{Q}\) is the set
which is easily seen to be compact also when \({\widetilde{Q}}\) is not compact. The compactness of the forward balls and the Arzelà–Ascoli theorem imply the existence of a Lipschitz curve \(\gamma \) of \({\widetilde{F}}\)-length \(\ell _{{\widetilde{F}}}(\gamma ) = d_{\widetilde{F}}(x,y)\) joining two arbitrary points x and y on \({\widetilde{Q}}\). This in turn implies the following characterization of forward balls:
We fix an arbitrary Riemannian metric on Q, lift it to \(\widetilde{Q}\), and denote by \(\textrm{Vol}\) the induced volume (i.e. n-dimensional Hausdorff measure) of Borel subsets of \(\widetilde{Q}\). The volume entropy of F is the number
Proposition A.1
The limit (A.3) exists, is finite, and is independent of the point \(x \in {\widetilde{Q}}\) and of the choice of the Riemannian metric on Q.
Proof
The independence of the choice of the Riemannian metric on Q is clear because by the compactness of Q the volume \(\textrm{Vol}'\) induced by another Riemannian metric satisfies
for a suitable positive number c. Given \(x\in \widetilde{Q}\) and \(R\ge 0\) we abbreviate
Choose a closed fundamental domain N in \({\widetilde{Q}}\) and set
By the triangle inequality we have
and hence
Let \(\tau \) be a deck transformation of \({\widetilde{Q}}\). Since \(\tau \) preserves the \({\widetilde{F}}\)-length of oriented curves,
Since \(\tau \) also preserves \(\textrm{Vol}\), we have
Applying this to deck transformations that bring points into N we can upgrade the inequalities (A.4) to
This implies that the limit (A.3) is independent of x, if it exists. Set
Fix \(R>0\), and let Y be a maximal subset of \(B_x(R)\) such that the balls \(B_y(1)\), \(y\in Y\), are pairwise disjoint. If z belongs to \(B_y(1)\) for some \(y\in Y\) then
Therefore,
and from the fact that the balls on the left-hand side are pairwise disjoint and from the definition of v we obtain
and so
From the maximality property of Y we deduce that for every \(z\in B_x(R)\) there is a point \(y\in Y\) such that \(B_z(1)\) intersects \(B_y(1)\). If w is a point in this non-empty intersection, we find
where \(\theta \) is the irreversibility ratio of F and we have used (A.1). This proves the inclusion
Let \(S\ge 0\) and \(z \in B_x(R+S)\). By (A.2), \(z=\gamma (R+S)\) where \(\gamma :[0,R+S] \rightarrow \widetilde{Q}\) is a Lipschitz curve satisfying \(\gamma (0)=x\) and \({\widetilde{F}}\circ \dot{\gamma }\le 1\) a.e.. Then \(\gamma (R)\) belongs to \(B_x(R)\), and from the above inclusion we find \(y \in Y\) such that \(d_{{\widetilde{F}}}(y,\gamma (R)) \le 1+\theta \). With this,
and hence (A.7) can be upgraded to
From this, together with (A.6) and (A.4), we obtain
Abbreviating \(b:= 1+\theta +a\), this implies
Taking logarithms, we find
This inequality implies that the function
is subadditive, i.e. \(f(R+S)\le f(R) + f(S)\) for every \(R,S\ge 0\). Therefore, f(R)/R converges to its infimum for \(R \rightarrow \infty \), which is a non-negative finite number because f is monotonically increasing. From the identity
we deduce that the limit (A.3) exists and is a non-negative finite number. Proposition A.1 is proven. \(\square \)
1.2 A.2. The topological entropy
We shall use the following definition of the topological entropy \(h_{{\text {top}}}(\phi )\) of a continuous flow \(\phi ^t\) on a compact metrizable space X: Choose a metric d which generates the topology of X. For \(T >0\) define a new metric \(d_T\) on X by
For \(\delta >0\), a subset Y of X is called \((T,\delta )\)-separated if \(d_T(y,y') \ge \delta \) for all \(y \ne y'\) in Y. Abbreviate
Then the function \(\delta \mapsto \nu (T,\delta )\) is monotonically decreasing for every \(T>0\), and one possible definition of \(h_{{\text {top}}}(\phi )\) is
This number represents the exponential growth rate of the number of orbit segments that can be distinguished with arbitrary fine but finite precision. As the notation suggests, one obtains the same number if one starts with another metric which generates the topology of X. We refer to [60, §3.1] and [95, §7] for this fact and for much information on topological entropy. We here only mention that for a Lipschitz-continuous flow on a compact manifold, \(h_{{\text {top}}} (\phi )\) is finite, see [60, Theorem 3.2.9].
1.3 A.3. Manning’s inequality
We now assume the Finsler metric F to be regular: F is of class \(C^2\) away from the zero section and the second fiberwise differential of \(F^2\) is positive definite at every non-zero tangent vector. Under these assumptions, the Euler–Lagrange equations for the energy functional
define a well-posed second order Cauchy problem on Q. Solutions of this Cauchy problem are \(C^2\)-curves defined on the whole \(\mathbb {R}\) and are called Finsler F-geodesics. The function \(F\circ \dot{\gamma }\) is constant for every Finsler F-geodesic \(\gamma \). After an orientation preserving reparametrization making \(F\circ \dot{\gamma }\) constant, any minimizer \(\gamma \) of \(\ell _F\) among Lipschitz curves from x to y is an arc of a Finsler F-geodesic.
The Cauchy problem for Finsler F-geodesics defines a \(C^1\)-flow \(\phi ^t\) on the unit sphere bundle
Denoting by \(\pi :S Q \rightarrow Q\) the footpoint projection, \(\gamma (t):= \pi \circ \phi ^t(v)\) is the unique Finsler F-geodesic starting at \(\pi (v)\) with velocity v for \(t=0\), and \(\phi ^t(v) = {\dot{\gamma }}(t)\).
We denote by \(h_{{\text {top}}}(F)\) the topological entropy of the flow \(\phi ^t\) defined above. Manning’s celebrated inequality from [69] states that for any Riemannian metric \(F=\sqrt{g}\) on the closed manifold Q, the topological entropy is bounded from below by the volume growth,
where we are writing the argument of both \(h_{{\text {top}}}\) and \(h_{{\text {vol}}}\) as g instead of \(\sqrt{g}\), as this is the standard notation when dealing with Riemannian geodesic flows. It is well-known that this inequality persists to hold for Finsler metrics:
Theorem A.2
Let F be a regular Finsler metric on a closed connected manifold Q. Then the topological entropy of the Finsler geodesic flow of F is at least the volume entropy of F:
The above theorem is stated for instance in [16, Theorem 15] as well as [44, Theorem 6.1] and [93, Remarque 3.3]. Since there does not seem to be a proof in the literature, we give one here, by a straightforward adaptation of Manning’s proof.
We will use the following standard property of functions having exponential growth:
Lemma A.3
Assume that the function \(f :(0,+\infty ) \rightarrow (0,+\infty )\) satisfies
for some \(h\in (0,+\infty )\). Then for every \(\varepsilon >0\) and every \(\delta >0\) there exists a sequence \((R_n)\subset (0,+\infty )\) tending to \(+\infty \) such that
Proof
The assumption on f is equivalent to
where the function \(R\mapsto \sigma (R)\) tends to zero for \(R\rightarrow +\infty \). We claim that
belongs to \([0,+\infty ]\). Indeed, if by contradiction L is negative or \(-\infty \), then we can find \(R_0>0\) and \(\mu >0\) such that
This inequality can be rewritten as
which implies
But then the divergence of the harmonic series implies that \(\sigma (R_0+ n\delta )\) tends to \(-\infty \), contradicting the fact that this sequence is infinitesimal.
Let \((R_n)\) be a sequence of positive numbers that diverges to \(+\infty \) and such that
Then we have
where we are using the notation \(e^{+\infty }:=+\infty \) in the case \(L=+\infty \). The identity (A.10) and a simple algebraic manipulation produce the identity
By (A.11) and the fact that \(\sigma (R_n+\delta )\) is infinitesimal, the expression in brackets on the right-hand side of this identity tends to
which belongs to \((0,+\infty ]\) because \(\delta h>0\) and \(L\in [0,+\infty ]\). This, together with the positivity of \(\varepsilon \) and the fact that \(\sigma (R_n)\) is infinitesimal, implies that the right-hand side of (A.12) tends to \(+\infty \). \(\square \)
Proof of Theorem A.2
We can assume that \(h:= h_{{\text {vol}}}(F) > 0\). Fix \(\varepsilon \in (0,h)\). We must show that
We use the following notation from the proof of Proposition A.1: Given x in the universal cover \(\widetilde{Q}\) of Q and \(R\ge 0\), \(B_x(R):= B_x(R,{\widetilde{F}})\) denotes the closed forward ball of radius R centered at x in \(\widetilde{Q}\), see (A.2), and \(V_x(R):= {\text {Vol }}(B_x(R))\) denotes its volume with respect to a Riemannian metric on Q which has been lifted to \(\widetilde{Q}\).
Fix \(x_0 \in {\widetilde{Q}}\). By Proposition A.1, there exists \(R_0(\varepsilon )\) such that
Fix some \(\delta >0\). By Lemma A.3, we find a diverging sequence of positive numbers \((R_n) \subset [R_0(\varepsilon ),+\infty )\) that satisfies
The F-distance function \(d_{{\widetilde{F}}}\) on \(\widetilde{Q}\) is not necessarily symmetric, because we are not assuming F to be reversible, but we can symmetrize it and obtain the genuine distance function
If \(\theta \in [1,+\infty )\) denotes the irreversibility ratio of F, then we have
For every \(n \in \mathbb {N}\), we take a maximal subset \(X_n\) of the annulus \(B_{x_0}(R_n+ \delta /2) \setminus B_{x_0}(R_n)\) such that
Since \(X_n\) is maximal, for every point \(z \in B_{x_0}(R_n+ \delta /2) {\setminus } B_{x_0}(R_n)\) there exists \(x \in X_n\) such that \({\widetilde{d}}(x,z) \le (2\theta +1)\, \delta \). A fortiori, \(d_{{\widetilde{F}}}(x,z) \le (2\theta +1) \delta \) and hence
If we set
we therefore find
and hence, by (A.14),
Given \(x\in X_n\), we denote by
an F-geodesic segment from \(x_0\) to x realizing the minimal distance \(d_{{\widetilde{F}}}(x_0,x)\) and such that \({\widetilde{F}}\circ {\dot{\gamma }}_x=1\). Since \(X_n \subset B_{x_0}(R_n+\delta /2) {\setminus } B_{x_0}(R_n)\), we have
Now comes the crux of the proof: Consider the subset
of the F-unit sphere \(S_{x_0} {\widetilde{Q}} \subset T_{x_0} {\widetilde{Q}}\), See Fig 11. Choose any metric \({\widetilde{d}}_S\) on \(S \widetilde{Q}\) such that the footpoint projection \({\widetilde{\pi }} :S {\widetilde{Q}} \rightarrow {\widetilde{Q}}\) is distance decreasing:
For instance, one can take \({\widetilde{d}}_S \bigl ( v,v' \bigr ):= {\widetilde{d}} \bigl ( {\widetilde{\pi }}(v),{\widetilde{\pi }}(v') \bigr ) + \overline{d} \bigl ( v,v')\), where \(\overline{d}\) is any metric on \(S {\widetilde{Q}}\).
Lemma A.4
The set \(Y_n\) is \((R_n,\delta )\)-separated for the Finsler geodesic flow \({\widetilde{\phi }}^t\) of F on the metric space \((S \widetilde{Q},{\widetilde{d}}_S)\), and \({\text {card}}Y_n = {\text {card}}X_n\).
Proof
We first show that the surjective map \(X_n \rightarrow Y_n\), \(x \mapsto \dot{\gamma }_x (0)\), that defines the set \(Y_n\), is a bijection. Assume that \(x,x' \in X_n\) give the same point \({\dot{\gamma }}_x(0) = \dot{\gamma }_{x'}(0)\) of \(Y_n\). We can assume that \(d_{\widetilde{F}}(x_0,x') \le d_{{\widetilde{F}}}(x_0,x)\). Then the fact that the vectors \(\gamma _x'(0)\) and \(\gamma _{x'}'(0)\) coincide implies that \(\gamma _{x'}\) is the restriction of \(\gamma _x\) to the interval \([0,d_{{\widetilde{F}}}(x_0,x')]\). The restriction of \(\gamma _x\) to the interval \([d_{{\widetilde{F}}}(x_0,x'),d_{{\widetilde{F}}}(x_0,x)]\) is a curve of \({\widetilde{F}}\)-length \(d_{{\widetilde{F}}}(x_0,x) - d_{{\widetilde{F}}}(x_0,x')\) from \(x'\) to x, and by (A.18) we have
Therefore, (A.15) implies
Our choice (A.16) now implies that \(x=x'\).
By the definition of \((R_n,\delta )\)-separated, for the first assertion it suffices to show that
Let \(x,x'\) be the points in \(X_n\) with \(y={\dot{\gamma }}_x(0)\) and \(y'={\dot{\gamma }}_{x'}(0)\). Then \(x = \gamma _x (d_{\widetilde{F}}(x_0,x))\) and \({\widetilde{\pi }} \bigl ( {\widetilde{\phi }}^{R_n}(y) \bigr ) = \gamma _x(R_n)\), and so, by (A.18) again,
In the same way, \(d_{{\widetilde{F}}} \bigl ( {\widetilde{\pi }} ({\widetilde{\phi }}^{R_n}(y')), x' \bigr ) \le \delta /2\). Together with (A.16), we can now estimate
Hence
The proof of Lemma A.4 is complete. \(\square \)
We now consider the projection \({\textrm{pr}}_S :S {\widetilde{Q}} \rightarrow S Q\) induced by the covering map \({\textrm{pr}}:{\widetilde{Q}} \rightarrow Q\) and we look at the set \({\textrm{pr}}_S (Y_n)\). Since \(Y_n \subset S_{x_0} \widetilde{Q}\), we have \({\text {card}}{\textrm{pr}}_S (Y_n) = {\text {card}}Y_n\), and so by the previous lemma and by (A.17),
As for \({\widetilde{Q}}\), we symmetrize the asymmetric distance \(d_F\) on Q and obtain the genuine metric
and we choose a metric \(d_S\) on SQ such that the projection \(\pi :(SQ, d_S) \rightarrow (Q,d)\) is distance decreasing. Note that the covering map \({\textrm{pr}}:\bigl ( {\widetilde{Q}}, {\widetilde{d}} \bigr ) \rightarrow (Q,d)\) is a local isometry. Therefore, there exists \(\delta _1>0\) such that for all \(z,z' \in \widetilde{Q}\) with \({\widetilde{d}} (z,z') \le \delta _1\) we have \(d \bigl ( {\textrm{pr}}(z),{\textrm{pr}}(z') \bigr ) = {\widetilde{d}}(z,z')\).
Lemma A.5
For every \(\delta >0\) smaller than \(\delta _1\) the set \({\textrm{pr}}_S (Y_n)\) is \((R_n,\delta )\)-separated for the Finsler geodesic flow \(\phi ^t\) of F on the metric space \((S Q,d_S)\).
Proof
Let \(v = {\textrm{pr}}_S (y)\) and \(v' = {\textrm{pr}}_S (y')\) be two different points of \({\textrm{pr}}_S (Y_n)\). Recall from the previous proof that \({\widetilde{d}} \bigl ( {\widetilde{\pi }} ( {\widetilde{\phi }}^{R_n}(y)),\widetilde{\pi }({\widetilde{\phi }}^{R_n}(y')) \bigr ) \ge \delta \). This does not imply that the same lower bound holds for \(d \bigl ( \pi (\phi ^{R_n}(v)), \pi (\phi ^{R_n}(v')) \bigr )\), because \({\textrm{pr}}\) is only a local isometry.
Since \({\widetilde{d}} \bigl ( {\widetilde{\pi }} (\widetilde{\phi }^{R_n}(y)),{\widetilde{\pi }} ({\widetilde{\phi }}^{R_n}(y')) \bigr ) \ge \delta \), we can look at
Since \({\textrm{pr}}_S \circ {\widetilde{\phi }}^t = \phi ^t \circ {\textrm{pr}}_S\) and \({\textrm{pr}}\circ {\widetilde{\pi }} = \pi \circ {\textrm{pr}}_S\), we have \({\textrm{pr}}\circ {\widetilde{\pi }} \circ {\widetilde{\phi }}^t = \pi \circ \phi ^t \circ {\textrm{pr}}_S\). Hence, by the fact that \(\delta <\delta _1\) and by the local isometry property of \({\textrm{pr}}\),
For the dynamical metric \((d_S)_{R_n}\) on SQ defined in (A.8) we therefore find
Hence \({\textrm{pr}}_S (Y_n)\) is \((R_n,\delta )\)-separated. \(\square \)
Using a \(\delta _0 < \delta _1\) as in Lemma A.5, the sequence \(R_n \rightarrow \infty \) satisfying (A.14) for \(\delta =\delta _0\), and the estimate (A.19), and noting that \(w = \sup _{z \in {\widetilde{Q}}} V_z(\delta _0(2\theta +1))\) depends only on \(\delta _0\) but not on \(R_n\), we can conclude:
as we wished to show. \(\square \)
Remark A.6
Manning’s inequality \(h_{{\text {top}}}(g) \ge h_{{\text {vol}}}(g)\) for Riemannian geodesic flows has several improvements:
-
(1)
Let \({{\mathcal {M}}}_g \subset SQ\) be the set of minimal vectors, namely those vectors v for which the lifts to \(\widetilde{Q}\) of the geodesic determined by v are shortest paths between any of their points. The set \({{\mathcal {M}}}_g\) is invariant under the geodesic flow. Then \(h_{{\text {top}}} (\phi _g |_{{{\mathcal {M}}}_g}) \ge h_{{\text {vol}}}(g)\), see [60, Theorem 9.6.7] and [55, Theorem 1.1]. This follows from a modification of Manning’s proof of \(h_{{\text {top}}}(g) \ge h_{{\text {vol}}}(g)\), and the same modification of our proof above shows that this stronger inequality generalizes to regular Finsler geodesic flows:
$$\begin{aligned} h_{{\text {top}}} (\phi _F |_{{{\mathcal {M}}}_F}) \ge h_{{\text {vol}}}(F). \end{aligned}$$ -
(2)
Manning also showed in [69] that \(h_{{\text {top}}}(g) = h_{{\text {vol}}}(g)\) if g has non-positive sectional curvature. This hypothesis was weakened by Freire and Ma\(\tilde{\text{ n }}\)é [51], who only need to assume that the geodesic flow has no conjugate points. Manning’s equality extends to Finsler geodesic flows if F has non-positive flag curvature, see [16, Theorem 15]. On the other hand, it is not known if the improvement of Freire–Ma\(\tilde{\text{ n }}\)é extends to Finsler geodesic flows. We thank Thomas Barthelmé for pointing out this open problem.
1.4 A.4. A proof via Yomdin’s theorem
Given a \(C^1\) flow \(\phi ^t\) on a closed manifold M, define the volume growth of \(\phi \) by
Here the supremum is taken over all compact smooth submanifolds S of M of any dimension and \({\mathcal {H}}(S)\) denotes the Riemannian volume of the submanifold S with respect to the restriction of a fixed Riemannian metric on M or, equivalently, the k-dimensional Hausdorff measure \({\mathcal {H}}^k(S)\) of S in the metric space M, where \(k=\dim S\). The Riemannian metric is not specified, since \(v(\phi )\) does not depend on its choice. Yomdin proved in [96] that if the flow \(\phi :\mathbb {R}\times M \rightarrow M\) is smooth, i.e. \(C^{\infty }\), then
Actually, equality holds in (A.20), since by a result of Newhouse [77], \(h_{{\text {top}}}(\phi ) \le v(\phi )\) for \(C^{1+\varepsilon }\) flows. Hence the volume growth \(v(\phi )\) is another way to think of the topological entropy of smooth flows.
Gabriel Paternain noticed in [80, p. 72] that Yomdin’s theorem yields a quick proof of Mannings’ inequality for smooth Riemannian geodesic flows. We conclude this appendix by showing that a variant of his argument applies to general smooth flows on the total space of a fiber bundle and in particular implies Theorem A.2 in the case of smooth Finsler metrics.
Consider the following setting: \(\phi ^t\) is an arbitrary smooth flow on the total space E of a smooth fiber bundle
over the closed n-dimensional manifold Q with typical fiber a closed manifold of dimension \(k<n\). The universal cover of Q is denoted by
and the pull-back bundle of E by the map \(\textrm{pr}\) is denoted by
Therefore, we have the commutative diagram of smooth maps

where \(\textrm{pr}_E\) is a covering map. We choose Riemannian metrics on Q, \({\widetilde{Q}}\), E and \({\widetilde{E}}\) such that the horizontal maps are local isometries and the vertical projections are Riemannian submersions. The d-dimensional Hausdorff measures induced by these metrics are denoted \({{\mathcal {H}}}^d\). The flow \(\phi ^t\) on E lifts to a smooth flow \({\widetilde{\phi }}^t\) on \({\widetilde{E}}\) such that
We shall prove the following result:
Proposition A.7
For any \({\widetilde{x}}_0\) in \({\widetilde{Q}}\) let \({\widetilde{E}}_{{\widetilde{x}}_0}:= \widetilde{\pi }^{-1} ( \widetilde{x}_0)\) be the fiber of \({\widetilde{E}}\) at \(\widetilde{x}_0\) and \(E_{x_0}:= \pi ^{-1}(x_0)\) the fiber of E at \(x_0:= \widetilde{\pi }( {\widetilde{x}}_0 )\). Then
where on the left-hand side we are using the convention \(\log 0:= - \infty \).
Postponing the proof, we specialize to the case \(k+1 = n\), and for \(x_0 \in Q\) define the volume entropy of \(\phi \) by the left-hand side of (A.21):
Note that the right-hand side indeed does not dependent on the lift \({\widetilde{x}}_0\) of \(x_0\) nor on the Riemannian metric used to define the Hausforff measure. The set \(\widetilde{\pi } (\widetilde{\phi } ([0,T] \times \widetilde{E}_{{\widetilde{x}}_0} ))\) is the set of points \({\widetilde{x}} \in {\widetilde{Q}}\) for which the fiber \({\widetilde{E}}_{{\widetilde{x}}}\) can be reached in time \(\le T\) by a \({\widetilde{\phi }}\)-flow line starting at \(\widetilde{E}_{{\widetilde{x}}_0}\). In the case of a Finsler geodesic flow, when E is an \(S^{n-1}\)-bundle, this set is the forward ball \(B_{{\widetilde{x}}_0}({\widetilde{F}}, T)\). Hence (A.22) generalizes (2.5).
The right-hand side of (A.21) is, by definition, a lower bound for the volume growth \(v(\phi )\) of \(\phi \). Together with Yomdin’s inequality (A.20) we obtain
We have shown the following result.
Theorem A.8
Assume that \(\phi \) is a \(C^\infty \)-smooth flow on the compact fiber bundle E over Q with fibers of dimension \(\dim Q -1\). Then
In the case of Finsler geodesic flows, Theorem A.8 together with Proposition A.1 imply Theorem A.2. This proof is less satisfactory than the one in the previous paragraphs, however: It needs the Finsler geodesic flow to be \(C^\infty \)-smooth and it is less elementary, as it relies on Yomdin’s theorem whose proof is highly non-trivial. On the other hand, this proof shows that the special features of Finsler geodesic flows which are given by the underlying length functional and the triangle inequality are needed only to guarantee that the limit defining the volume entropy exists and is independent of the center of the balls, whereas for a general flow on the total space of a fiber bundle the limit superior in definition (A.22) cannot be replaced by a limit and may depend on the choice of \(x_0\). These special features of a Finsler geodesic flow are instead not needed for proving that the volume entropy does not exceed the topological entropy.
Theorem A.8 in particular applies to Reeb flows on spherizations \(S^*Q\) and to magnetic flows on SQ. In the latter situation, Theorem A.8 improves the first statement in [26, Theorem D].
Proof of Proposition A.7
As it intertwines the flows \({\widetilde{\phi }}^t\) and \(\phi ^t\), the projection \({\textrm{pr}}_E\) maps \({\widetilde{\phi }}^T({\widetilde{E}}_{\widetilde{x}_0})\) bijectively to \(\phi ^T (E_{x_0})\) for every T, and since \({\textrm{pr}}_E\) is a local isometry we have
By the area formula, we have
where \(J\psi (t,\xi ):= \det \bigl ( d\psi (t,\xi )^T d \psi (t,\xi ) \bigr )^{\frac{1}{2}}\) is the Jacobian of the map
and \(d\xi \) denotes the Riemannian volume form on the compact manifold \({\widetilde{E}}_{{\widetilde{x}}_0}\). If X denotes the vector field on \(\widetilde{E}\) generating the flow \({\widetilde{\phi }}^t\) and \(\psi ^t\) is the map
we easily see that the symmetric linear endomorphism
has the form
By the Schur determinant identity, this implies the bound
where c is the supremum norm of the vector field X, which is bounded being the lift of a vector field on the compact manifold E. Together with (A.24) and using the area formula for injective maps, we find
and hence
It is easy to see that if f is a positive function on \([0,+\infty )\) then
see [80, Lemma 3.24.2], so using also (A.23) we obtain the bound
The desired bound (A.21) now follows from the fact that the projection \({\widetilde{\pi }}\) is 1-Lipschitz, by our choice of the Riemannian metrics. \(\square \)
Remark A.9
If one replaces the inequality (A.24) in the above proof by the equality
which is given by the area formula, one gets the more precise bound
For \(k+1=n\), this inequality and the argument leading to Theorem A.8, applied to Q instead of the universal cover \({\widetilde{Q}}\), yield the bound
where \(n_T(x_0,x)\) denotes the number of \(\phi \)-flow lines of time at most T from \(E_{x_0}\) to \(E_x\). For Finsler geodesic flows, \(n_T(x_0,x)\) is the number of F-geodesics arcs from \(x_0\) to x, and (A.25) is a Finsler generalization of [80, Corollary 3.28].
Appendix B. From Riemannian geodesic flows to Reeb flows
In this appendix we first recall from a historical and geometric perspective how Finsler and Reeb flows are successive generalizations of Riemannian geodesic flows. We then give for each of the four circles below at least two results on Riemannian geodesic flows that stop to hold exactly at \({\textcircled {1}}\) or at \({\textcircled {2}}\) or at \({\textcircled {3}}\), or extends all the way to Reeb flows (\({\textcircled {4}}\)).

1.1 B.1. Reeb flows on spherizations as a generalization of Riemannian geodesic flows
Fix an n-dimensional manifold Q. Consider a smooth star field along Q: At every point \(q \in Q\) there is a set \(S_qQ \subset T_qQ\) that is the smooth boundary of a subset \(D_qQ\) of \(T_qQ\) that is strictly starshaped with respect to the origin of \(T_qQ\), and \(S_qQ\) varies smoothly with q. The star field \(\{S_qQ\}_{q \in Q}\) can be used to define the length of oriented curves in Q: For a smooth curve \(\gamma :[a,b] \rightarrow Q\) with non-vanishing derivative, set
where \(\ell ({\dot{\gamma }} (t)) = s\) if \(\frac{1}{s} {\dot{\gamma }} (t) \in S_{\gamma (t)}Q\). The number \({\text {length}}(\gamma )\) does not change under orientation preserving reparametrisations of \(\gamma \). Given \(q,q' \in Q\) set
where the infimum is taken over all curves as above from q to \(q'\). The function \(d_S\) is non-degenerate in the sense that \(d_S (q,q') = 0\) if and only if \(q=q'\). Furthermore, \(d_S\) satisfies the ordered triangle inequality
The function \(d_S\) is symmetric if and only if each star \(S_qQ\) is symmetric, that is \(-S_qQ=S_qQ\) for all \(q \in Q\). If each \(S_qQ\) is strictly convex, then there are unique shortest curves between sufficiently nearby points, see e.g. [15, §6.3].
A star field \(\{S_qQ\}\) as above is called a Finsler structure if each \(D_q Q\) is strictly convex, and a Finsler structure is called reversible if each \(S_q Q\) is symmetric, and irreversible otherwise. A reversible Finsler structure is a Riemannian structure if each \(S_q Q\) is an ellipsoid, i.e., the level set of an inner product on \(T_qQ\).
Riemannian structures were introduced in 1854 by Riemann in his Habilitationsvortrag [84]. Both Berger [18, p. 708] and Chern [30] pointed out that what Riemann really had in mind are Finsler structures. However, from his textFootnote 2 and given that Riemann’s main conceptual point was to do intrinsic measurements, that were all based on length measurements, one may at least as well argue that what he meant is “reversible star field geometry”, see also Spivak [92, p. 167 and p. 202]. In contrast to Riemannian geometry, Finsler geometry developed only slowly, see [15], and “star field geometry” developed only in the setting of Lorentzian and semi-Riemannian geometry (and their Finsler generalizations), in which however the stars \(S_q Q\) are not compact.
If each \(D_qQ\) is strictly convex, one can pass from TQ to \(T^*Q\) by the Legendre transform. In geometric terms, each convex body \(D_q Q \subset T_qQ\) is replaced by its dual body
in \(T_q^*Q\). The dual body \(D_q^*Q\) is strictly convex, or is symmetric, or is an ellipsoid, if and only if \(D_qQ\) has this property, cf. Fig. 12.
In more dynamical terms, we associate to the field of strictly convex disks \(\{D_qQ\}\) and its dual field \(\{D_q^*Q\}\) the functions
that are homogenous of degree one in each fiber and satisfy
The Legendre transform
is a diffeomorphism that maps fibers to fibers and \(D_qQ\) to \(D_q^*Q\). This diffeomorphism conjugates the Finsler geodesic flow of F on SQ with the Hamiltonian flow of \(F^*\) restricted to \(S^*Q\),
For strictly convex starfields, one can therefore freely switch between Finsler geodesic flows on tangent bundles and co-Finsler geodesic flows on cotangent bundles.
For non-convex star fields \(\{ S_qQ \}\) along Q there is no Legendre transform. However, a smooth star field \(\{ S^*_qQ \}\) in \(T^*Q\) is the same thing as a Reeb flow on the spherization \(S^*Q\) of Q, as we shall recall below. We conclude that while Riemann’s concept of a star field geometry in TQ led to nothing, the same picture in \(T^*Q\) describes the main example of contact geometry and Reeb flows, a by now huge and thriving theory! This is one more instance for the fact that it is always worthwhile and often crucial to work in \(T^*Q\) instead of TQ.
The flows \(\phi _H\) on \(S^*(H)\) are Reeb flows. For every function \(H :T^* Q \rightarrow \mathbb {R}\) that is fiberwise homogenous of degree one and smooth and positive off the zero-section we consider the regular hypersurface \(S^*(H) = H^{-1}(1)\) in \(T^*Q\) and the restriction \(\phi _H^t\) of the Hamiltonian flow of H to \(S^*(H)\). The flows \(\phi _H^t\) live on different spaces. To have a class of flows on one manifold, we consider the spherization, or positive projectivization, of the cotangent bundle
While the 1-form \(\lambda = \sum _j p_j dq_j\) on \(T^*Q\) does not descend to this quotient, the kernel of \(\lambda \) does descend. The resulting hyperplane field \(\xi _{\textrm{can}\,}\) is the canonical contact structure on \(S^*Q\). If for every function H as above we abbreviate \(\lambda _H = \lambda |_{S^* (H)}\) and \(\xi _H = \ker (\lambda _H)\), we have that \((S^*(H),\xi _H)\) is diffeomorphic to \((S^*Q, \xi _{\textrm{can}\,})\) under the map \((q,p) \mapsto [(q,p)]\).
We wish to show that the set of flows \(\phi _H^t\) is in bijection with the set of Reeb flows on \((S^*Q, \xi _{\textrm{can}\,})\). For this we first recall that \(\phi _H^t\) is the Reeb flow of the contact form \(\lambda _H\) on \((S^*(H), \xi _H)\), see [48, Lemma 4.2] for the short proof. To identify the Reeb flows of the contact forms \(\lambda _H\) with the Reeb flows on \((S^*Q, \xi _{\textrm{can}\,})\), we fix a representative \((S^*(H_0), \xi _{H_0})\) of \((S^*Q, \xi _{\textrm{can}\,})\), and for an arbitrary H consider the diffeomorphism \(\Psi _H :S^*(H) \rightarrow S^*(H_0)\) given by fiberwise radial projection,
A computation shows that the differential of \(\Psi _H\) takes the Reeb vector field of \(\lambda _H\) to the Reeb vector field of \(\frac{H_0}{H} \lambda _{H_0}\). Therefore, the map \(\Psi _H\) conjugates the Reeb flows of \(\lambda _H\) and of \(\frac{H_0}{H} \lambda _{H_0}\). In conclusion, each Reeb flow on \((S^*Q,\xi _{\textrm{can}\,})\) corresponds to the Reeb flow of \(f \lambda _{H_0}\) on \((S^*(H_0), \xi _{H_0})\) for a positive smooth function f on \(S^*(H_0)\), and this Reeb flow is conjugate to the Hamiltonian flow \(\phi _H^t\) on \(S^*(H)\), where \(H = H_0 / {\tilde{f}}\) and \({\tilde{f}}\) is the extension of f to \(T^*Q \setminus Q\) that is fiberwise homogenous of degree zero.
For a Hamiltonian H as above, the Holmes–Thompson volume is defined as
and for a contact form \(\alpha \) on \(S^*Q\) we defined the contact volume in Sect. 1.4 as
Under the above identification of \((S^*(H), \lambda _H)\) with \((S^*Q, \alpha )\) we obtain, using \(\lambda _H = \lambda |_{S^*(H)}\) and \(d \lambda = \omega \) and Stokes’ theorem,
Therefore,
1.2 B.2. A few generalizations of Riemannian results to Finsler geodesic flows and Reeb flows
Given a result in Riemannian geometry or dynamics, it is interesting to see whether this result extends to reversible or even irreversible Finsler metrics, or even to Reeb flows. In this way it becomes clear to which geometry the Riemannian result belongs properly. In this section we state a few such results from dynamics. For (non-)extensions of results from Riemannian geometry, involving for instance curvatures and spectra, we refer to [16, 17, 32, 93].
\({\textcircled {1}}\) (i) Riemannian 2-tori without conjugate points are flat, [61], but there are many reversible and irreversible Finsler 2-tori without conjugate points that are not flat [27, §33].
(ii) There is (up to scaling) only one Riemannian metric on \(\mathbb{R}\mathbb{P}^2\) all of whose geodesics are simple closed and of the same length, [56], but there are many such Finsler metrics on \(\mathbb{R}\mathbb{P}^2\), among them reversible ones, see [91] and also [28].
\({\textcircled {2}}\) (i) Every Riemannian 2-sphere carries infinitely many geometrically distinct closed geodesics [14]. This result extends to reversible Finsler metrics [41], but not to all Finsler metrics: Katok [63] gave a simple example of a Finsler metric on \(S^2\) with only two geometrically distinct geodesics (where the reverse geodesic is counted, since it has different period).
(ii) For reversible Finsler geodesic flows on \(S^2\) that are periodic all orbits have the same period [57], but there exist irreversible periodic Finsler geodesic flows on \(S^2\) whose orbits have different minimal periods, [98, p. 143].
\({\textcircled {3}}\) (i) For many compact manifolds Q (namely so-called essential ones and all surfaces), there exists a constant \(C>0\) such that every normalized Finsler metric F on Q has a closed geodesic of F-length at most C, cf. Sect. 1.6. This was shown by Loewner, Pu, Croke, and Gromov in the Riemannian case and was extended to the Finsler case by Álvarez Paiva–Balacheff–Tzanev [6]. The generalization of length to closed orbits of Reeb flows is the period \(\int _\gamma \alpha \). It is shown in [2, 88] that every spherization \(S^*Q\) of a compact manifold Q admits for every \(C>0\) a normalized contact form \(\alpha \) whose Reeb flow has periodic orbits, but none of period \(\le C\).
(ii) Theorems 1.2 and 1.1 of this paper show that there is a positive lower bound for the topological entropy of all normalized Finsler geodesic flows on compact surfaces of genus at least two, but not for Reeb flows.
\({\textcircled {4}}\) (i) Most of the existence and multiplicity results for closed geodesics on compact Riemannian manifolds Q extend to Reeb flows on spherizations. For instance, the isomorphism in [4] implies that every Reeb flow on \(S^*Q\) has a closed orbit in every component of the free loop space \(\Lambda Q\). Also the Gromoll–Meyer theorem, according to which every Riemannian metric has infinitely many prime closed geodesics provided that the Betti numbers of \(\Lambda Q\) are unbounded [58], extends to Reeb flows on spherizations [73].
(ii) The exponential growth of the fundamental group of a compact manifold Q or of the rank of the homology of the based loop space of a simply connected compact manifold Q implies that the topological entropy of every Riemannian geodesic flow on Q is positive, see [42] and [80, §5.3]. This result generalizes to all Reeb flows on the spherization \(S^*Q\), see [50, 68], and in fact to time-dependent Reeb flows, namely contact isotopies that are everywhere transverse to the contact distribution \(\xi \), see [36].
(iii) According to the Bott–Samelson theorem [23, 90], the cohomology ring of a Riemannian manifold all of whose geodesics are simple closed and of equal length must be generated by one element. Finer versions are proven in [19, Chapter 7]. All these results hold true for Reeb flows on spherizations, even time-dependent ones, see [37, 48].
Appendix C. Properties of the norm growth
Given a \(C^1\)-diffeomorphism \(\phi \) of a compact manifold M, we define the two real numbers
Here \(\Vert \cdot \Vert _{\infty }\) denotes the supremum norm induced by the operator norm on endomorphisms of TM that is determined by any Riemannian metric on M. The limit defining \(\Gamma _+\) exists because the sequence \(\left( \log \Vert d \phi ^n \Vert _{\infty } \right) \) is subadditive. Clearly, \(\Gamma _+\) and \(\Gamma \) do not depend on the choice of the Riemannian metric on M.
For a \(C^1\)-flow \(\phi =\{\phi ^t\}_{t\in \mathbb {R}}\), we set \(\Gamma _+(\phi ):= \Gamma _+(\phi ^1)\) and \(\Gamma (\phi ):= \Gamma (\phi ^1)\), or equivalently
The following properties of \(\Gamma _+\) and \(\Gamma \) are analogous to those of the topological entropy, cf. [60, Prop. 3.1.7], except for (5) (the topological entropy of a product is the sum of the topological entropies of the factors). The proofs are somewhat easier, since in contrast to the case of topological entropy, which is defined in metrical terms, we can use differential calculus.
Proposition C.1
Let \(\phi \) be a \(C^1\)-diffeomorphism of the compact manifold M. The norm growths \(\Gamma _+\) and \(\Gamma \) have the following properties.
-
(1)
(Conjugacy invariance) If \(\psi \) is another \(C^1\)-diffeomorphism of M, then
$$\begin{aligned} \Gamma _+ (\psi ^{-1} \phi \psi ) = \Gamma _+ (\phi ), \qquad \Gamma (\psi ^{-1} \phi \psi ) = \Gamma (\phi ). \end{aligned}$$ -
(2)
(Monotonicity) If K is a compact submanifold of M that is invariant under \(\phi \), then
$$\begin{aligned} \Gamma _+ (\phi |_K) \le \Gamma _+ (\phi ), \qquad \Gamma (\phi |_K) \le \Gamma (\phi ). \end{aligned}$$ -
(3)
(Decomposition) If \(M = \bigcup _{i=1}^m K_i\), where \(K_1, \dots , K_m\) are compact \(\phi \)-invariant submanifolds, then
$$\begin{aligned} \Gamma _+ (\phi ) = \max _{1 \le i \le m} \Gamma _+ (\phi |_{K_i}), \qquad \Gamma (\phi ) = \max _{1 \le i \le m} \Gamma (\phi |_{K_i}). \end{aligned}$$ -
(4)
(Elementary time change) \(\Gamma _+ (\phi ^m) = m \Gamma _+ (\phi )\) for all \(m\in \mathbb {N}\) and \(\Gamma (\phi ^m) = |m| \Gamma (\phi )\) for all \(m \in \mathbb {Z}\). For a flow,
$$\begin{aligned} \Gamma _+ \bigl ( \{\phi ^{st}\}_{t\in \mathbb {R}} \bigr ) = s \, \Gamma _+ \bigl ( \{\phi ^t\}_{t \in \mathbb {R}} \bigr ) \quad \forall \, s \ge 0, \qquad \Gamma \bigl ( \{\phi ^{st}\}_{t\in \mathbb {R}} \bigr ) = |s| \, \Gamma \bigl ( \{\phi ^t\}_{t \in \mathbb {R}} \bigr ) \quad \forall \, s \in \mathbb {R}. \end{aligned}$$ -
(5)
(Product) If \(\phi = \phi _1 \times \phi _2\) on \(M_1 \times M_2\), then \(\Gamma _+ (\phi ) = \max \left\{ \Gamma _+ (\phi _1), \Gamma _+ (\phi _2) \right\} \) and \(\Gamma (\phi ) = \max \left\{ \Gamma (\phi _1), \Gamma (\phi _2) \right\} \).
Proof
Properties (2) and (4) are clear, and (1) follows from the chain rule.
For (3) it suffices to show that \(\Gamma _+ (\phi ) \le \max _{1 \le i \le m} \Gamma _+ (\phi |_{K_i})\) in view of (2). For each \(n \in \mathbb {N}\) choose \(i_n \in \{1, \dots , m\}\) such that
There exists \(j \in \{1, \dots , m \}\) such that \(i_n = j\) for infinitely many n. For such a j it holds that \(\Gamma _+ (\phi ) = \Gamma _+ (\phi _j)\). The result for \(\Gamma \) follows.
For (5), given norms \(\Vert \cdot \Vert _1\) on \(TM_1\) and \(\Vert \cdot \Vert _2\) on \(TM_2\), we choose the norm \(\Vert (v_1,v_2) \Vert = \max \{ \Vert v_1\Vert _1, \Vert v_2\Vert _2 \}\) on TM. With this choice,
The equality \(\Gamma _+ (\phi ) = \max \{ \Gamma _+ (\phi _1), \Gamma _+ (\phi _2)\}\) now follows by arguing as in the proof of (3) for \(m=2\). The result for \(\Gamma \) follows. \(\square \)
The following result improves property (4) above. It is an analogue of the time change estimate for the topological entropy in [79].
Proposition C.2
Let X be a smooth vector field on a compact manifold M, and let \(f :M \rightarrow \mathbb {R}\) be a positive smooth function. Then
Proof
Fix some positive number \(\gamma >\Gamma _+(\phi _X)\). By the definition of \(\Gamma _+(\phi _X)\) and the continuity of \(t\mapsto \Vert \phi _X^t\Vert _{\infty }\), there exists a positive number \(C_{\gamma }\) such that
The smooth function \(F :\mathbb {R}\times M \rightarrow \mathbb {R}\) that is defined by
is the time change function relating the two flows:
We have
and from (C.1) we find
Here and in the following equations, d denotes differentiation with respect to the spatial variables. By differentiating the identity
we obtain
Let \(v\in T_p M\) be a vector of norm one and set
Multiplying both sides of this inequality by \(1/\alpha (t)\), which is bounded from above by \(1/\min f\), we obtain
Since \(u(0)=0\), integration on the interval [0, t] and multiplication by \(\alpha (t)\), which is bounded from above by \(\Vert f\Vert _{\infty }\), yields
Recalling that \(u(t)= d F(t,p)[v]\) where v is an arbitrary unit tangent vector at p, we have proven the bound
where \(C_{\gamma }'= \frac{C_{\gamma } \Vert df\Vert _{\infty }}{\gamma \min f}\). Thanks to the identity
and hence
Since \(\gamma \) is an arbitrary number that is larger than \(\Gamma _+(\phi _X)\), we deduce the desired bound
The analogous bound for \(\Gamma \) immediately follows. \(\square \)
Appendix D. Dynamically trivial deformations of Finsler metrics
The aim of this section is to show that it is always possible to deform any given regular Finsler metric on a closed manifold of dimension at least two into a new Finsler metric which is not isometric to the original one but whose geodesic flow is nevertheless conjugate to the one of the original metric by a smooth time-preserving conjugacy.
Let Q be a closed manifold and \(\lambda = \sum _j p_j dq_j\) be the canonical Liouville one-form on \(T^*Q\). A diffeomorphism \(\varphi :T^*Q \rightarrow T^*Q\) is a symplectomorphism, i.e. preserves the symplectic form \(d\lambda \), if and only if the one-form \(\varphi ^* \lambda - \lambda \) is closed. When this form is exact, \(\varphi \) is called an exact symplectomorphism.
Any diffeomorphism \(\theta :Q \rightarrow Q\) lifts to an exact symplectomorphism \(T^*\theta \) of \(T^* Q\) by setting
where the symbol \(-*\) denotes the inverse of the adjoint. Indeed, \(T^* \theta \) preserves the Liouville form \(\lambda \). Actually, every diffeomorphism of \(T^*Q\) preserving \(\lambda \) is the lift of some diffeomorphism of Q, see for instance Proposition 2.1 and Homework 3.3 in [29].
Therefore, the diffeomorphism group of Q embeds naturally into the group of exact symplectomorphisms of \(T^* Q\). The latter group is much larger, though. For instance, any symplectomorphism \(\varphi :T^* Q \rightarrow T^* Q\) which is compactly supported is exact: The exactness of \(\varphi ^* \lambda - \lambda \) is equivalent to the fact that this closed one-form has vanishing integral on any closed curve in \(T^*Q\), and if \(\varphi \) is compactly supported this is certainly true since every closed curve in \(T^* Q\) is freely homotopic to a closed curve taking values in the complement of any given compact subset of \(T^* Q\). Producing non-trivial compactly supported symplectomorphisms of \(T^* Q\) is very easy, as one can integrate the vector field that is induced by a compactly supported Hamiltonian function. Actually, the time-one map of any possibly time-dependent Hamiltonian vector field with globally defined flow is exact even without assuming the support to be compact. Indeed, denoting by \(X_t\) the Hamiltonian vector field of the time-dependent function \(H_t\) and by \(\phi _H^t\) its flow, we compute with the help of Cartan’s identity
and hence
If Q has non-trivial de-Rham cohomology in degree one, then any closed one-form \(\eta \) on Q that is not exact induces a symplectomorphism
which is symplectically isotopic to the identity but not exact.
Recall from Sect. B.1 that to a fiberwise starshaped hypersurface \(S \subset T^*Q\) we associate the Reeb flow \(\phi _{\alpha }\) of \(\alpha := \lambda |_S\), namely the flow generated by the vector field \(R_\alpha \) defined by
Equivalently, \(\phi _\alpha \) is the restriction to S of the Hamiltonian flow on \(T^*Q\) of the function \(T^*Q \rightarrow \mathbb {R}\) that is fiberwise positively homogeneous of degree 1 and equal to 1 on S.
The next result tells us that the Reeb dynamics on fiberwise starshaped hypersurfaces does not change when we transform them by exact symplectomorphisms.
Proposition D.1
Let Q be a closed manifold, S a fiberwise starshaped hypersurface of \(T^*Q\) and \(\varphi : T^* Q \rightarrow T^* Q\) an exact symplectomorphism such that \(S':= \varphi (S)\) is also fiberwise starshaped. Then there exists a diffeomorphism \(\psi :S \rightarrow S'\) such that
In particular, the diffeomorphism \(\psi \) is a smooth time-preserving conjugacy between the Reeb flows of S and \(S'\).
The above proposition is proven at the end of this appendix. We now discuss its consequences concerning Finsler geodesic flows. Let F be a regular Finsler metric on Q and denote by \(S^*(F)\subset T^* Q\) the corresponding unit cotangent sphere bundle, which we here consider as the domain of the geodesic flow of F. The push-forward \(\theta _* F\) of this Finsler metric by a diffeomorphism \(\theta :Q \rightarrow Q\) is another Finsler metric on Q. By construction, the Finsler manifolds (Q, F) and \((Q,\theta _* F)\) are isometric, and their geodesic flows are smoothly conjugate. Indeed, the cotangent lift \(T^* \theta \) restricts to a diffeomorphism from \(S^*(F)\) to \(S^*(\theta _* F)\) conjugating the two geodesic flows. Diffeomorphisms of Q induce “metrically trivial deformations” of F.
Now consider a more general exact symplectomorphism \(\varphi :T^* Q \rightarrow T^* Q\). If \(\varphi \) is \(C^2\)-close to the identity, then the image of \(S^*(F)\) under \(\varphi \) is still fiberwise strictly convex and hence can be seen as the unit cotangent sphere bundle of another Finsler metric \(F'\):
The fact that \(\varphi \) is volume preserving implies that the Finsler metrics F and \(F'\) have the same Holmes–Thompson volume. By Proposition D.1 above, the geodesic flows of the Finsler metrics F and \(F'\) are conjugate by a smooth time-preserving conjugacy. Therefore, the exact symplectomorphism \(\varphi \) induces a “dynamically trivial deformation” \(F'\) of F. However, F and \(F'\) need not be isometric. For instance, F could be a Riemannian metric, meaning that \(S^*(F)\) is a field of centrally symmetric ellipsoids. In the special case in which \(\varphi \) is the cotangent lift of a diffeomorphism of Q, \(\varphi \) maps fibers into fibers and acts linearly on them, so \(\varphi (S^*(F))\) is still a field of centrally symmetric ellipsoids and the metric \(F'\) is still Riemannian. But for a more general exact symplectomorphism \(\varphi \), there is no reason why \(\varphi (S^*(F))\) should still be a field of ellipsoids, so the new Finsler metric \(F'\) is in general not Riemannian.
Let F again be an arbitrary regular Finsler metric on Q and let q be a point in Q. By acting just by diffeomorphisms of Q, we obtain Finsler metrics \(F'\) on Q which are isometric to F and whose unit sphere \(S_q^*(F')\) at q is the image of some \(S^*_{q'}(F)\) by some linear isomorphism. Therefore, all the possible cotangent unit spheres at q of Finsler metrics which are constructed in this way belong to the finite dimensional family of sets
Instead, by acting by more general exact symplectomorphisms, we can get a new Finsler metric \(F'\) whose geodesic flow is still conjugate to the one of F but such that \(S^*_q(F')\) is an arbitrary convex hypersurface which is sufficiently close to \(S^*_q(F)\). When \(S^*_q(F')\) does not belong to the above finite dimensional family, the metric \(F'\) cannot be isometric to F.
Let us prove this fact. Let \(S'_q\) be a strictly convex hypersurface in \(T^*_q Q\). Using a cotangent local chart, we identify \(\pi ^{-1}(U)\), where U is a neighborhood of q in Q and \(\pi :T^* Q \rightarrow Q\) denotes the footpoint projection, with \(T^* \mathbb {R}^n = \mathbb {R}^n \times (\mathbb {R}^n)^*\) in such a way that \(T^*_q Q\) is identified with \(\{0\} \times (\mathbb {R}^n)^*\). Then both \(S_q^*(F)\) and \(S'_q\) are subsets of \(\{0\} \times (\mathbb {R}^n)^* \cong (\mathbb {R}^n)^*\). Let \(\xi :(\mathbb {R}^n)^* \rightarrow (\mathbb {R}^n)^*\) be a compactly supported smooth vector field whose flow at time one maps \(S_q^*(F)\) to \(S'_q\) (one easily achieves this by a radial vector field). Consider the Hamiltonian function
where \(\langle \cdot ,\cdot \rangle \) denotes the duality pairing and \(\chi :\mathbb {R}^n \rightarrow \mathbb {R}\) is a smooth compactly supported function taking the value 1 near 0. This function extends to a compactly supported smooth function on \(T^*Q\) and the corresponding Hamiltonian flow leaves \(T_q^*Q\) invariant and restricts to the flow of \(\xi \) on it. Therefore, denoting by \(\varphi :T^* Q \rightarrow T^* Q\) the time-one map of this Hamiltonian flow, we obtain an exact symplectomorphism \(\varphi \) such that \(\varphi (S_q^*(F))=S'_q\). If \(S_q'\) is \(C^3\)-close to \(S_q^*(F)\), meaning that
for some \(C^3\)-small function f on \(S_q^*(F)\), then the vector field \(\xi \) can be chosen to be \(C^3\)-small, the Hamiltonian vector field of H is \(C^2\)-small and hence \(\varphi \) is \(C^2\)-close to the identity. Under this closeness assumption, \(\varphi (S^*(F))\) is fiberwise strictly convex and hence is the unit cotangent sphere bundle of a Finsler metric \(F'\) such that \(S_q^*(F') = S_q'\).
Note that if the Finsler metric F is reversible and \(S_q'\) is centrally symmetric, then the dynamically equivalent Finsler metric \(F'\) as above can be chosen to be reversible by requiring \(\xi \) to be an odd map.
Summarizing: Given any regular (reversible) Finsler metric F, we obtain a large family of non-isometric (reversible) Finsler metrics \(F'\) having the same Holmes–Thompson volume and whose geodesic flows are smoothly conjugate to the one of F; \(F'\) can be chosen to be non-Riemannian even if F is Riemannian. The topological entropy, the volume growth used in Appendix A.4, the norm growth from Appendix C, the length spectrum and all the dynamical invariants of \(F'\) coincide with those of F. If one uses exact symplectomorphisms that are isotopic to the identity, then also the marked length spectrum is preserved, and if one starts with a reversible Finsler metric F of negative flag curvature and deforms it to a reversible Finsler metric \(F'\) that still has negative flag curvature, then also the volume entropy of F and \(F'\) agrees, since for Finsler metrics of negative flag curvature the volume entropy is equal to the topological entropy by the equality case in Manning’s theorem, see [16, Theorem 15]. One deformation to Finsler metrics with equal marked length spectrum and equal volume entropy was constructed in [32] for the Riemannian metrics of constant curvature on hyperbolic surfaces. Our discussion here shows that this is a general phenomenon and is a manifestation of the fact that a neighborhood of the identity on the group of exact symplectomorphisms of \(T^*Q\) can transform a Finsler metric in ways in which diffeomorphisms of Q cannot.
Proof of Proposition D.1
The proof is given in [3, §8] for the case of convex hypersurfaces in a Hilbert space. That proof is readily adapted to our situation. We give the proof for the reader’s convenience.
Since the symplectomorphism \(\varphi \) is assumed to be exact, there exists a smooth function \(h :T^*Q \rightarrow \mathbb {R}\) such that
We abbreviate \(\alpha = \lambda |_S\) and \(\alpha ' = \lambda |_{S'}\). The pull-back of \(\alpha '\) to S, that is the 1-form
is a contact form on S, and its Reeb vector field is
Since \(\alpha \) and \(\alpha + dh |_S\) have the same differential, we have
for a nowhere vanishing function f on S. If \(Y= p\, \partial _p\) denotes the canonical Liouville vector field on \(T^*Q\), the identity \(\imath _Y d\lambda = \lambda \) implies that for every \(x\in S\) the one-form \((\imath _{R_{\alpha }} d\lambda ) (x)\), whose kernel is the tangent space \(T_x S\), is negative on tangent vectors which are pointing outwards, i.e. belong to the half-space containing Y(x). Similarly, \(\imath _{R_{\alpha '}} d\lambda \) is negative on outward pointing vectors based at \(S'\). By the identity
and by the fact that the differential of \(\varphi \) maps outward pointing vectors based at S to outward pointing vectors based at \(S'\), we deduce that the above one-form is negative on outward pointing vectors based at S. Since also \(\imath _{R_{\alpha }} d\lambda \) is negative on these vectors, the function f appearing in (D.2) is everywhere positive.
By applying the 1-form \(\alpha + dh|_S\) to (D.2) we obtain \(1 = f \bigl ( 1 + dh (R_\alpha ) \bigr )\). Therefore,
We now apply Moser’s homotopy method: We look for a smooth time-dependent vector field \(X_t\) on S of the form \(X_t = \chi _t R_\alpha \), where \(\chi _t\) is a family of functions on S, such that the flow \(\eta _t\) of \(X_t\) satisfies
Since \(\eta _0^* \alpha = \alpha \), this identity is equivalent to
Using Cartan’s identity we compute
Since \(\imath _{X_t} d\alpha = \chi _t \, \imath _{R_{\alpha }} d\alpha = 0\), it follows that (D.5) holds if and only if
Since \(\imath _{X_t} (\alpha + t\, d h) = \chi _t \bigl ( 1 + t \,dh (R_{\alpha }) \bigr )\), equation (D.6) is satisfied if we take
By (D.3) the functions \(\chi _t\) are well-defined.
In view of (D.1) and (D.4), the diffeomorphism \(\psi := \varphi \circ \eta _1 :S \rightarrow S'\) satisfies
as required. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Abbondandolo, A., Alves, M.R.R., Sağlam, M. et al. Entropy collapse versus entropy rigidity for Reeb and Finsler flows. Sel. Math. New Ser. 29, 67 (2023). https://doi.org/10.1007/s00029-023-00865-8
Accepted:
Published:
DOI: https://doi.org/10.1007/s00029-023-00865-8



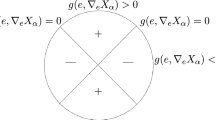
 :
: :
:










