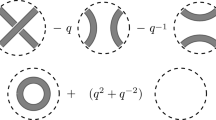Abstract
In this paper we will present a homological model for Coloured Jones Polynomials. For each colour \(N \in {\mathbb {N}}\), we will describe the invariant \(J_N(L,q)\) as a graded intersection pairing of certain homology classes in a covering of a configuration space on the punctured disc. This construction is based on the Lawrence representation and a result due to Kohno that relates quantum representations and homological representations of the braid groups.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The theory of quantum invariants of knots started with the discovery of the Jones polynomial and continued with Reshetikhin and Turaev’s construction that having as input any ribbon category leads to link invariants. This method is purely algebraic and combinatorial. The coloured Jones polynomials \(\{J_N(L,q) \in {\mathbb {Z}}[q^{\pm 1}]\}_{N \in {\mathbb {N}}}\) are a family of quantum link invariants, constructed in this manner from the representation theory of \(U_q(sl(2))\). The first invariant of this sequence, corresponding to \(N=2\), is the original Jones polynomial. The geometric and topological meaning of quantum invariants is an important problem in quantum topology.
1.1 Main result
We give a topological model for the family of coloured Jones polynomials \(J_N(L,q)\), showing that they are graded intersection pairings between homology classes in coverings of configuration spaces on the punctured disc. The colour N of the invariant will be seen in the number of particles in the configuration space. This work, together with the further development from [1, 2] provides a new framework for understanding these invariants directly from graded intersections of submanifolds in configuration spaces.
1.2 Jones polynomial
The Jones polynomial is a quantum invariant but it can also be characterised by skein relations. However, its relation with the topology of the knot complement is a mysterious question. On the topological side, Lawrence [18] constructed a sequence of representations of braid groups on the homology of certain coverings of configuration spaces. Later on, Bigelow [4] and Lawrence [19] gave a homological model for the original Jones polynomial, describing it as a graded intersection pairing between homology classes in a covering of a configuration space on the punctured disc. They used the skein nature of the invariant for the proof.
1.3 Coloured Jones polynomials
At the moment there are conjectures that coloured Jones polynomials contain topological information of knot complements [11, 21]. In 2012, Kohno [8, 14] proved that quantum representations on highest weight spaces of the Verma module for \(U_q(sl(2))\) are isomorphic to the homological Lawrence representations. This identification used the work due to Schechtman and Varchenko which describes solutions of the KZ equations by means of hypergeometric integrals [22, 23]. Also, Ito [9] gave a homological formula for the loop expansion of the coloured Jones polynomials, as an infinite sum of traces of specialised Lawrence representations. In [9], it was mentioned that the highest weight spaces corresponding to finite dimensional \(U_q(sl(2))\)-representations do not yet have a homological counterpart and this is one of the reasons why there were no known topological models for coloured Jones polynomials. We present a topological model for all coloured Jones polynomials. Unlike the original case, they cannot be described directly by skein relations. Our strategy is to use their definition as quantum invariants, to study the Reshetikhin-Turaev functor and to construct step by step homological counterparts.
1.4 Description of the topological tools
Let \(n,m \in {\mathbb {N}}\) and consider \(C_{n,m}\) to be the unordered configuration space of m points in the n-punctured disc. We define \({\tilde{C}}_{n,m}\) to be a \({\mathbb {Z}}\oplus {\mathbb {Z}}\) covering of this configuration space. Then, the Borel–Moore homology of this covering \({\mathcal {H}}^{\text {lf}}_{m}({\tilde{C}}_{n,m}, {\mathbb {Z}})\) is a \({\mathbb {Z}}[x^{\pm 1},d^{\pm 1}]\)-module (using the deck transformations) and carries an action of the braid group \(B_n\).
1.5 I. Lawrence representation
We define certain subspaces in these homology groups. Let the indexing set \( E_{n,m}=\{e=(e_1,\ldots ,e_{n-1})\in {\mathbb {N}}^{n-1} | e_1+\cdots +e_{n-1}=m \}.\) For each such partition e, one associates an m-dimensional disc \({\mathbb {F}}_{e}\) in the base space \(C_{n,m}\) and then lifts it to a submanifold \({\tilde{{\mathbb {F}}}}_e\) in \({\tilde{C}}_{n,m}\). We consider the subspace generated by the classes given by these submanifolds, as in Definition 3.2.2:
1.6 II. The dual Lawrence representation
We consider a dual space, defined from the homology of the covering relative to its boundary, which is generated by classes of submanifolds which are also prescribed by partitions (Definition 4.1.2):
1.7 III. Topological pairing
These homology groups are related by a non-degenerate intersection pairing (which is a certain type of Poincaré–Lefschetz duality):
1.8 The specific model
Let \(N \in {\mathbb {N}}\) be the colour of the invariant. We look at oriented links as closures of braids with \(n \in {\mathbb {N}}\) strands. For the topological model, we use the Lawrence representation and its dual, with the following parameters:
We change the coefficients using certain specialisations presented in Sect. 7.1:

Theorem 1.0.1
(Topological model with specialised homology classes)
Let \(n \in {\mathbb {N}}\). Then, for any colour \(N \in \mathbb N\), there exist two homology classes
such that for any oriented link L for which there exists a braid \(\beta _{n} \in B_{n}\) with \(L={\hat{\beta }}_{n} \) (braid closure), the \(N^{th}\)coloured Jones polynomial of L has the formula:
Here, \(\mathbb I_{n}\) is the trivial braid with n strands and \(w(\beta _n)\) is the writhe of the braid.
The classes \(\tilde{\mathscr {F}}_n^N\) and \(\tilde{\mathscr {G}}_n^N\) are intrinsic and they do not depend on the link. The link plays a role in the action of the associated braid on the homological representation.

1.9 Colour that goes to infinity
We are interested in the parts of this model that depend on the colour. In Theorem 1.0.1, the colour N appears in two places:
-
The number of points in the configuration spaces: \({\text {Conf}}_{n(N-1)}(\mathbb D_{2n})\).
-
The specialisation of the coefficients \(\alpha _{N-1}\).
We show that the homology classes which lead to the coloured invariants, can be lifted to the homology groups before specialising with respect to the colour:
(here \(\gamma \) is just a morphism which enlarges the ring \({\mathbb {Z}}[x^{\pm 1},d^{\pm 1}]\) to the field \({\mathbb {Q}}(q,s)\)).
Theorem 1.0.2
(Topological model with globalised homology classes)
For \(n,N \in {\mathbb {N}}\) there exist homology classes
such that if an oriented link \(L={\hat{\beta }}_{n}\) with \(\beta _n \in B_n\), we have the formula:
1.10 Further development-new framework, towards categorifications
This is the first topological model for coloured Jones polynomials, as intersection pairings between homology classes, which appeared in 2017. The tools that we use are highest weight space representations and their identifications with homological representations due to Kohno’s Theorem. This research direction has since developed further- in 2020 Martel [20] provided an expicit version of Kohno’s Theorem, and using that, the author showed a unified topological model for the coloured Jones and coloured Alexander polynomials as intersections of explicit Lagrangians in configuration spaces [1, 2]. The precise form of these Lagrangians makes the latter model a proper starting point for investigating categorification questions. Also, in [3] we present a topological model for the Witten-Reshetikhin-Turaev invariants for 3-manifolds, as state sums of Lagrangian intersections in a fixed configuration space in the punctured disc.
1.11 Structure of the paper
The paper has six main parts. In Sect. 2, we present the quantum group that we use and the definition of the coloured Jones polynomials. Sect. 3 contains the definition of the Lawrence representation. Then, in Sect. 4 we define the dual Lawrence representation and present a graded intersection form that relates the two representations. In Sect. 5, we present identifications between quantum and homological representations of the braid group and discuss in detail the specialisation at natural parameters. Section 6 is devoted to the construction of the topological model for \(J_N(L,q)\) where the homology classes are defined in the specialised homology. In Sect. 7 we show that we can lift the homology classes from this topological model to the non-specialised homology groups.
2 Representation theory of \(U_q(sl(2))\)
2.1 \(U_q(sl(2))\) and its representations
Let \(q, s\) be parameters and consider the ring
We will use the following notations: \(\overline{1,n}=\{1,\ldots ,n\}\)
Definition 2.1.1
Let the quantum enveloping algebra \(U_q(sl(2))\) be the algebra over \({\mathbb {L}}_s\) generated by the elements \(\{ E,F^{(n)}, K^{\pm 1} | \ n \in \mathbb N^{*} \}\) with the following relations:

The generators \(F^{(n)}\) correspond to the “divided powers” of the generator F, from the version of the quantum group \(U_q(sl(2))\) with generators \( \{ E,F,K^{\pm 1} \}\).
Then, one has that \(U_q(sl(2))\) is a Hopf algebra with the following comultiplication, counit and antipode:
Now we describe the representation theory of \(U_q(sl(2))\). In the following part the abstract variable s will be thought of as being the weight of the Verma module.
Definition 2.1.2
(The Verma module) Let \(\hat{V}\) be the \({\mathbb {L}}_s\)-module generated by an infinite family of vectors \(\{v_0, v_1,\ldots \}\). The following relations define an \(U_q(sl(2))\) action on \(\hat{V}\):
2.2 Specialisations
In order to arrive at the definition of the coloured Jones polynomials we consider certain specialisations of this quantum group and its Verma modules.
Definition 2.2.1
We consider two types of specialisations of coefficients, as below.
Let \(h, \lambda \in {\mathbb {C}}\) and \(\mathbf{q} =e^h\). In the following, we have \(e^{\lambda h}=\mathbf{q} ^{\lambda }\):
Let q be a parameter and specialise the highest weight to a natural number \(\lambda =N-1 \in {\mathbb {N}}\):
Using these specialisations, we consider the associated specialised quantum groups and their representations, as below.
Ring | Quantum group | Representations | Specialisations |
|---|---|---|---|
\( {\mathbb {L}}_s={\mathbb {Z}}[q^{\pm 1},s^{\pm 1}] \) | \( U_q(sl(2))\) | \(\hat{V}\) | (1) \(q,s \text { param} \ \ \ \ \ \ \ \) |
\( {\mathbb {C}}\) | \(\mathscr {U}_\mathbf{q ,\lambda }=\) \(U_q(sl(2))\otimes _{\eta _\mathbf{q ,\lambda }}{\mathbb {C}}\) | \(\hat{V}_\mathbf{q ,\lambda }=\hat{V}\otimes _{\eta _{q,\lambda }}{\mathbb {C}}\) | (2) \((\mathbf{q} =e^h, \lambda )\in {\mathbb {C}}^2\) \( \eta _\mathbf{q ,\lambda } \) |
\( {\mathbb {L}}={\mathbb {Z}}[q^{\pm 1}] \) | \(\mathscr {U}=\mathscr {U}_{\lambda }=\) \(U_q(sl(2))\otimes _{\eta _{\lambda }}{\mathbb {Z}}[q^{\pm 1}]\) | \(\hat{V}_{\lambda }=\hat{V}\otimes _{\eta _{\lambda }}{\mathbb {Z}}[q^{\pm 1}]\) \(V_N\subseteq \hat{V}_{\lambda }\) | \((q \text { param,} \ \ \ \ \ \ \ \ \ \) \(\lambda =N-1 \in {\mathbb {N}})\) \(\eta _{\lambda }\) |
Following this procedure \(\mathscr {U}_\mathbf{q ,\lambda }\) and \(\mathscr {U}_{\lambda }\) become Hopf algebras and \(\hat{V}_\mathbf{q ,\lambda }\) a \(\mathscr {U}_\mathbf{q , \lambda }\)-representation and \(\hat{V}_{\lambda }\) a \(\mathscr {U}_{\lambda }\)-representation.
Lemma 2.2.2
If \(\lambda =N-1 \in {\mathbb {N}}\), then \( \{ v_{0},\ldots ,v_{N-1} \} \) span an N-dimensional \(\mathscr {U}_{\lambda }\)-submodule inside \(\hat{V}_{N-1}\). Denote this module by
Proof
This can be seen easily by looking at the actions of the generators on the basis. The only part that needs to be checked is that \(F^{(n)}v_i=0\) if \(n \ge N-i\) and this comes from the coefficient that appears in the \(F^{(n)}\)-action, which will vanish when we specialise \(\lambda =N-1\).
\(\square \)
2.3 The Reshetikhin–Turaev functor
In this section we present the construction due to Reshetikhin and Turaev (which starts with a ribbon category and gives link invariants) for the case given by representations of \(\mathscr {U}\).
Notation 2.3.1
For any representations V and W, we define the twist:
For the next part we denote by \(U_q(sl(2)) {\hat{\otimes }} U_q(sl(2))\) a completion of the module \(U_q(sl(2)) \otimes U_q(sl(2))\), where we allow infinite formal sums of tensor products.
Proposition 2.3.2
(Braid group action [8, 10]) There exists an R-matrix \(R \in U_q(sl(2)){\hat{\otimes }} U_q(sl(2))\), which is given by the formula:
Then, for any representation V of the quantum group (finite dimensional or the Verma module) one has the following well-defined action of the braid group:
Here, we use the notation \({\mathscr {R}}=C \circ R\) where \(C(v_i \otimes v_j)=s^{-(i+j)}q^{2ij}v_j \otimes v_i\).
For the next part, we are interested in finite dimensional representations of the quantum group \(\mathscr {U}\).
Proposition 2.3.3
[12] (1) The braid group action on the subcategory of \(\mathscr {U}\)-representations \(Rep({\mathscr {U}})\) (finite dimensional or the Verma module) comes from the specialisation of the R-matrix, which we denote by:
(2) The category of finite dimensional \({\mathscr {U}}\)-representations has the dualities:
for all \(V_N \in Rep(\mathscr {U})\) finite dimensional, where \(\{v_j\}\) is a basis of \(V_N\) and \(\{v_j^*\}\) the dual basis of \(V_N^*\).
The action of \(\mathscr {R}\) on the standard basis of \(\hat{V}\otimes \hat{V}\) is given in [8] (Sect. 4.1):
where \(F_{i,j,n}(q)\in {\mathbb {Z}}[q^{\pm 1}]\) has the expression:
Definition 2.3.4
The category of oriented tangles \({\mathscr {T}}\) is defined as follows:
The tangles T have to preserve the signs \(\epsilon _i\) which are on their boundaries. Also, the orientation of T should follow the convention \((-) \ \downarrow , \ \ (+) \ \uparrow .\)
Theorem 2.3.5
(Reshetikhin–Turaev) For any finite dimensional \(\mathscr {U}\)-representation V, there exists a unique monoidal functor \({\mathbb {F}}_V: {\mathscr {T}}\rightarrow Rep(\mathscr {U})\) that respects a set of local relations, out of which we recall:

2.4 The coloured Jones polynomial \(J_N(L,q)\)
Now we present how the Reshetikhin-Turaev construction leads to quantum invariants for knots and links.
Notation 2.4.1
We denote the evaluation \( {\mathop {{\text {ev}}}\limits ^{\longrightarrow }}^{\otimes n}_{V_N}:V_N^{\otimes n}\otimes (V_N^{*})^{\otimes n}\rightarrow {\mathbb {Z}}[q^{\pm 1}]\) and coevaluation \( {{\mathop {{\text {coev}}}\limits ^{\longleftarrow }}}^{\otimes n}_{V_N}: {\mathbb {Z}}[q^{\pm 1}] \rightarrow V_N^{\otimes n} \otimes (V_N^{*})^{\otimes n}\) as below:
Notation 2.4.2
Let \(\mathbb I_n\) be the trivial braid with n strands, all oriented upwards. Also, we consider \(\bar{\mathbb I}_n\) to be the trivial braid with n strands, all oriented downwards.
Proposition 2.4.3
(Coloured Jones polynomial from a braid presentation [9]) Let us fix \(N \in {\mathbb {N}}\). Consider L to be an oriented link and \(\beta \in B_n\) such that \(L={\hat{\beta }}\) (braid closure). We denote by \(w:B_n\rightarrow {\mathbb {Z}}\) the map given by the abelianisation. Then, the Reshetikhin-Turaev construction leads to the following formula:
As we have seen so far, the construction of \(J_N(L,q)\) is purely algebraic and combinatorial. We are interested in a geometrical interpretation for this invariant. For this purpose, we study the Reshetikhin-Turaev functor on certain intermediate levels of the link diagram. More precisely, we start with L as a closure of a braid \(\beta \in B_{n}\) and split the diagram into three main parts as follows:

We investigate the functor \({\mathbb {F}}_{V_N}\) on each of these main levels. The starting point in our description is the fact that at the level of the braid, there is a homological counterpart for the quantum representation, called Lawrence representation [14, 19]. This relation is established using the notion of highest weight spaces.
2.5 Highest weight spaces
Now we discuss properties of certain vector subspaces included in tensor powers of a fixed representation of the quantum group.
Definition 2.5.1
For two natural numbers \(n,m \in {\mathbb {N}}\) and a fixed parameter \(N \in {\mathbb {N}}\), consider the following indexing sets:
Also, for an element \(e=(e_1,\ldots ,e_n)\in {\mathbb {N}}^n\), let us denote \(v_e:= \hat{v}_{e_1}\otimes \cdots \otimes \hat{v}_{e_n}\).
The elements of the set \(E_{n,m}\) are partitions of the natural number m into \(n-1\) natural numbers. Its cardinality is well-known and we denote it as:
We define highest weight spaces as follows.
Definition 2.5.2
(Highest weight spaces) Let us fix \(n,m\in {\mathbb {N}}\).
(1) The case of two parameters (q, s)
The \(n^{th}\)-weight space of the generic Verma module \(\hat{V}\) corresponding to the weight m is defined by:
The highest weight space of the generic Verma module \(\hat{V}^{\otimes n}\) corresponding to the weight m:
(2) Specialisation with two complex numbers Let \(h, \lambda \in {\mathbb {C}}\) and \(\mathbf{q} =e^h\).
The weight space of \( \hat{V}^{\otimes n}_\mathbf{q ,\lambda }\) corresponding to the weight m is:
The highest weight space of the Verma module \(\hat{V}^{\otimes n}_\mathbf{q ,\lambda }\) corresponding to the weight m:
(3) The case where q is a parameter and \(\lambda \)a natural number (\(\lambda =N-1 \in {\mathbb {N}}\))
(a) Inside the Verma module \(\hat{V}_{N-1} ^{\otimes n}\)
The weight space of \( \hat{V}^{\otimes n}_{N-1}\) of weight m:
The highest weight space for Verma module \(\hat{V}^{\otimes n}_{N-1}\) corresponding to the weight m:
(b) Inside the finite dimensional module \(V_{N} ^{\otimes n}\)
The weight space for the finite dimensional representation \(V^{\otimes n}_{N}\) of weight m:
The highest weight space of the finite dimensional representation \(V^{\otimes n}_{N}\) corresponding to the weight m:
We remark that since \(V_N \subseteq \hat{V}_{N-1}\), we have \(v_e \in V^{\otimes n}_N\) if and only if \(e \in E^N_{n,m}\). This will happen also for the following (highest) weight spaces:
Remark 2.5.3
One can easily see that the weight spaces of Verma modules have the bases:
Using these bases, we conclude that we have a basis for the weight space of the finite dimensional module \(V_N\):
Moreover, if we denote \(V^{\ge N}_{n,m}:= \langle v_e | e \in E^{\ge N}_{n+1,m}\rangle _{{\mathbb {L}}_s}\subseteq \hat{V}^{\otimes n}_{N-1}\) then we have the following splitting as vector spaces \( \hat{V}^{N-1}_{n,m}= V^N_{n,m} \oplus V^{\ge N}_{n,m}.\) Also, from (14) we have:
2.6 Bases for heighest weight spaces
As we have seen, there is a straightforward definition of bases in weight spaces. However, for highest weight spaces this becomes a subtle question. In [10], bases in the highest weight spaces of the Verma module were presented, as well as connections between highest weight spaces and weight spaces, which correspond to different parameters n and m. Moreover, Jackson and Kerler proved that for the parameter \(m=2\), the braid group action on the highest weight space \(\hat{W}_{n,m}\) corresponds to the homological Lawrence-Bigelow-Krammer representation [5, 16,17,18]. They conjectured that this identification is true for any natural number m and Kohno [8, 14] proved this conjecture. Now, we present following [8] bases for the highest weight spaces.
Definition 2.6.1
(Basis for \(\hat{W}_{n,m}\)) For \(e \in E_{n+1,m}\), we denote by:
Notice that \({\mathscr {B}}_{{{\hat{V}}}_{n,m}}:=\{ v_e^s | e \in E_{n+1,m} \}\) forms a basis for \(\hat{V}_{n,m}\).
In this part the highest weight spaces \(\hat{W}_{n,m}\) will be identified with a certain subspace of the weight spaces \(\hat{V}_{n,m}\). Let \(\iota : E_{n,m} \rightarrow E_{n+1,m}\) be the inclusion:
Denote by \(\hat{V}'_{n,m}:={\mathbb {L}}_s \hat{v}_0 \oplus \hat{V}_{n-1,m}\subseteq \hat{V}_{n,m}\). Then, the set \({\mathscr {B}}_{\hat{V}'_{n,m}}:= \{ \hat{v}^s_{\iota (e)} | e \in E_{n,m} \}\) gives a basis for the space \(\hat{V}'_{n,m}\).
Proposition 2.6.2
[8] Consider the function \(\phi : \hat{V}'_{n,m}\rightarrow \hat{W}_{n,m}\) given by:
Then \(\phi \) is an isomorphism of \({\mathbb {L}}_s\)-modules. Moreover, the set
gives a basis for the generic highest weight space \(\hat{W}_{n,m}\). Using the remarks from (14) and (15), it follows that: \(\dim (\hat{W}_{n,m} )=d_{n,m}={n+m-2 \atopwithdelims ()m}.\)
2.7 Quantum representations of the braid groups
In the following part, we will see that the braid group action on tensor powers of the (generic) Verma module and the finite dimensional module passes to the level of highest weight spaces.
Remark 2.7.1
Since \(\varphi ^{\hat{V}}_n\) gives an action on \(\hat{V}^{\otimes n}\) over the quantum group (Proposition 2.3.2), it commutes with the actions of the generators K and E. Hence, it induces a well-defined action on the generic highest weight spaces \( \hat{W}_{n,m}\).
Proposition 2.7.2
(1) This action in the basis \({\mathscr {B}}_{\hat{W}_{n,m}}\) leads to a representation called the generic quantum representation on highest weight spaces of the Verma module:
Similarly, using specialisations we get induced braid group actions as follows.
(2) A well-defined action induced by \(\varphi ^{\hat{V}_\mathbf{q ,\lambda }}_n\):
(3) (a) A well-defined action induced by \(\varphi ^{\hat{V}_{N-1}}_n\), called the quantum representation on highest weight spaces of the Verma module:
(3) (b) An action induced by \(\varphi ^{V_N}_n\), called the quantum representation on highest weight spaces of the finite dimensional module:
As a summary, we have highest weights spaces, which carry braid group actions and live inside the \(n^{th}\) tensor power of specialisations of the Verma module \(\hat{V}\):
Braid group action | Highest weight space | Representation | Specialisation |
|---|---|---|---|
\( {{\varphi }^{\hat{W}}_{n,m}}\) | \( \hat{W}_{n,m} \) | \( \hat{V}^{\otimes n}\) | (1) \(q,s\text { param} \ \ \ \ \ \) |
\({\varphi }^{\hat{W}^{ \mathbf{q} ,\lambda }}_{n,m}\) | \( \hat{W}^\mathbf{q ,\lambda }_{n,m} \) | \( \hat{V}^{\otimes n}_\mathbf{q ,\lambda }\) | (2) \(\mathbf{q} =e^h,\lambda \in {\mathbb {C}}\) \( \eta _\mathbf{q ,\lambda } \) |
\({\varphi }^{\hat{W}^{N-1}}_{n,m}\) | \(\hat{W}^{N-1}_{n,m} \) | \(\hat{V}^{\otimes n}_{N-1} \) | (3) (a) q; \(\lambda =N-1 \in {\mathbb {N}}\) \(\eta _{\lambda }\) |
\({\varphi }^{W^N}_{n,m}\) | \(W^{N}_{n,m} \) | \( V^{\otimes n}_N \) | (3) (b) q; \(\lambda =N-1 \in {\mathbb {N}}\) \(\eta _{\lambda }\) |
3 Lawrence representation
3.1 Local system
In this section we present certain braid group representations, called homological Lawrence representations, introduced by Lawrence [19]. Let \(n \in {\mathbb {N}}\). Let \({\mathcal {D}}^2\subseteq {\mathbb {C}}\) be the unit disc including its boundary and \(\{ p_1,\ldots ,p_n\}\) be n points in its interior, on the real axis. Let \({\mathcal {D}}_n:={\mathcal {D}}^2 \setminus \{p_1,\ldots ,p_n \} \) and fix \(m\in {\mathbb {N}}\) a natural number. Let \(C_{n,m}\) be the unordered configuration space of m points in the n-punctured disc:
Here, \(Sym_m\) is the symmetric group of order m. Let us fix \(d_1,\ldots ,d_m \in \partial {\mathcal {D}}_n\).

Definition 3.1.1
(Local system on \(C_{n,m}\)) Let us denote the abelianisation map by
Then, it is known that for any \(m\ge 2\) one has that:
The generators of \({\mathbb {Z}}^{n}\) are classes of loops whose first component goes around one of the punctures \(p_i\) and the others are constant: \(\Sigma _i(t):=\{ \left( \sigma _i(t), d_2,\ldots ,d_m \right) \}, t \in [0,1].\) The last component is generated by the class of a loop \(\Delta \) which swaps two points between them: \(\Delta (t):=\{ \left( \delta (t), d_3,\ldots ,d_m \right) \}, t \in [0,1].\) Let the augmentation map be:
Consider the local system defined by the composition of the previous maps:
Definition 3.1.2
(Covering space) Let \({\tilde{C}}_{n,m}\) be the covering of \(C_{n,m}\) corresponding to \({\text {Ker}}(\phi )\) and its associated projection map \(\pi : {\tilde{C}}_{n,m} \rightarrow C_{n,m}\).
The deck transformations of the covering are \({\text {Deck}}({\tilde{C}}_{n,m})={\mathbb {Z}}\oplus {\mathbb {Z}}\) and this induces a \({\mathbb {Z}}[{\mathbb {Z}}\oplus {\mathbb {Z}}]\simeq {\mathbb {Z}}[x^{\pm 1}, d^{\pm 1}]\)-action on the homology groups of the covering. It follows that the homology groups \(H^{\text {lf}}_m({\tilde{C}}_{n,m}, {\mathbb {Z}})\) and \(H_m({\tilde{C}}_{n,m}, {\mathbb {Z}}; \partial )\) are \({\mathbb {Z}}[x^{\pm 1}, d^{\pm 1}]\)-modules (here \(H^{\text {lf}}\) is the Borel–Moore homology, the homology of locally finite chains).
3.2 Basis of multiforks
In order to define the Lawrence representation, we consider certain subspaces in these homologies of the covering \({\tilde{C}}_{n,m}\).
Definition 3.2.1
(1) Submanifolds Let \(e=(e_1,\ldots ,e_{n-1}) \in E_{n,m}\) as in the Definition 2.5.1. We will construct an associated m-dimensional submanifold in \({\tilde{C}}_{n,m}\), which gives a homology class in the Borel Moore homology of the covering. For each \(i \in \{ 1,\ldots ,n-1 \} \), consider \(e_i\) disjoint horizontal segments in \({\mathcal {D}}_n\), between \(p_i\) and \(p_{i+1}\) (which meet just at their boundary), as in the Fig. 1. Denote those segments by \(I^{e}_1,\ldots ,I^{e}_{e_1},\ldots , I^{e}_{m}\). Also, for each \(k \in \{ 1,\ldots ,m \} \), choose a vertical path \({\gamma }^{e}_k\) between the segment \(I^{e}_k\) and \(d_k\). The product of these segments gives a map as below:
Composing this map with the quotient map to the unordered configuration space we obtain an m-dimensional disc:
(2) Base Points The paths \({\gamma }^{e}_1,\ldots ,{\gamma }^{e}_m\), which start on the segments \(I^{e}_{1},\ldots ,I^{e}_{m}\) and end at the base points \(d_1,..,d_m\), will prescribe a lift of the submanifold \({\mathbb {F}}_{e}\) to the covering. Let \(\mathbf{d} \in C_{n,m} \) be the point defined by the m-tuple \((d_1,\ldots ,d_m)\). Then, let us fix a lift of this point \(\tilde{ \mathbf{d}} \in \pi ^{-1} ({ \mathbf{d}}) \). The set of the paths \(\{\gamma ^e_k, 1 \le k\le m\}\) defines a path in the configuration space: \(\gamma ^e := (\gamma ^{e}_1, \ldots , \gamma ^{e}_m ) : [0,1] \rightarrow C_{n,m}.\) Consider \({\tilde{\gamma }}^e\) to be the unique lift of the path \(\gamma ^e\) such that:
(3) Multiforks Let \({\tilde{{\mathbb {F}}}}_{e}\) be the unique lift of the submanifold \({\mathbb {F}}_e\) to the covering, which passes through the point \({\tilde{\gamma }}^e (1)\):
Then \({\tilde{{\mathbb {F}}}}_{e}\) gives a well-defined homology class \([{\tilde{{\mathbb {F}}}}_{e}] \in H^{\text {lf}}_m({\tilde{C}}_{n,m}, {\mathbb {Z}})\) called the multifork corresponding to the element \(e \in E_{n,m}\).
The Lawrence representation is the subspace of this Borel–Moore homology of the covering, spanned by the multiforks.
Definition 3.2.2
Denote by \({\mathscr {B}}_{{\mathcal {H}}_{n,m}}:= \{ [{\tilde{{\mathbb {F}}}}_e] | e\in E_{n,m} \}\) the set of all multiforks and consider the subspace generated by it:
Proposition 3.2.3
([8], Prop 3.1) \({\mathcal {H}}_{n,m}\) is a free module over \({\mathbb {Z}}[x^{\pm 1}, d^{\pm 1}]\) and \({\mathscr {B}}_{{\mathcal {H}}_{n,m}}\) gives a basis for it, called the multifork basis.
As we have seen, the cardinality of \(E_{n,m}\) is known (relation (14)), so we have:
3.3 Braid group action
In this part we present a braid group action on the homology of the covering of the configuration space. Following [13] (chap. I.6) it is known that:
Using the definition of the local system one can conclude that there is a well-defined action of the braid group on the homology of the covering, as follows:
Definition 3.3.1
(Lawrence representation [8]-Prop 3.1) The subspace in the homology group \({\mathcal {H}}_{n,m}\subseteq H^{\text {lf}}_m({\tilde{C}}_{n,m}, {\mathbb {Z}})\) is invariant under the action of \(B_n\). The braid group action on the homology \({\mathcal {H}}_{n,m}\) written in the multifork basis \({\mathscr {B}}_{{\mathcal {H}}_{n,m}}\), leads to a representation which is called the Lawrence representation:
4 Blanchfield pairing
In this section, we will present a non-degenerate duality between the Lawrence representation \({\mathcal {H}}_{n,m}\) and a “dual” space, which we will denote by \({\mathcal {H}}^{\partial }_{n,m}\). This dual space lives in the homology of the covering relative to its boundary. Using this form, we will be able to express any element in the dual of \({\mathcal {H}}_{n,m}\), as a certain geometric pairing with an element from the dual space. This property will play an important role in the homological model from Sect. 6.
4.1 Dual space
We start by defining a certain subset in the homology of the covering relative to its boundary \(H_m({\tilde{C}}_{n,m},\partial ;{\mathbb {Z}})\), by specifying a generating set.
Definition 4.1.1
(Barcodes [7]) For each \(e=(e_1,\ldots ,e_{n-1}) \in E_{n,m}\) we will define an m-dimensional submanifold in \({\tilde{C}}_{n,m}\) and consider its homology class in \(H_{m}({\tilde{C}}_{n,m}, \partial ;{\mathbb {Z}})\).
(1) Submanifolds For each \(i \in \{ 1,\ldots ,n-1 \} \), consider \(e_i\) disjoint vertical segments in \({\mathcal {D}}_n\), between \(p_i\) and \(p_{i+1}\) as in the Fig. 1. Denote those segments by \(J^{e}_1,\ldots ,J^{e}_{e_1},\ldots , J^{e}_{m}\). Also, for each \(k \in \{ 1,\ldots ,m \} \), we choose a vertical path \({\delta }^{e}_k\) between the segment \(J^{e}_k\) and the base point \(d_k\). The product of these segments leads to a map to the configuration space as follows:
(2) Base Points As in the case of multiforks, the collection of paths from these vertical segments to the base points \(d_1,\ldots ,d_m\) gives a path in the configuration space: \(\delta ^e: [0,1] \rightarrow C_{n,m}.\) Define \({\tilde{\delta }}^e\) to be the unique lift of the path \(\delta ^e\) such that:
(3) Barcodes Consider \({\tilde{{\mathbb {D}}}}_{e}\) to be the unique lift of \({\mathbb {D}}_e\) to the covering which passes through \({\tilde{\delta }}^e (1)\):
Then \({\tilde{{\mathbb {D}}}}_{e}\) defines a class in the homology relative to the boundary \([{\tilde{{\mathbb {D}}}}_{e}] \in H_m({\tilde{C}}_{n,m}, {\mathbb {Z}}; \partial )\) called the barcode corresponding to the element \(e \in E_{n,m}\).
Definition 4.1.2
(The “dual” representation) Let us denote the set given by all barcodes by \({\mathscr {B}}_{{\mathcal {H}}^{\partial }_{n,m}}:= \{ [{\tilde{{\mathbb {D}}}}_e] | e \in E_{n,m}\}\) and consider the submodule in the homology generated by this:
We call \({\mathcal {H}}^{\partial }_{n,m}\) the “dual” representation of \({\mathcal {H}}_{n,m}\).
4.2 Graded intersection pairing
In this part, we will describe how the Borel–Moore homology and the homology relative to the boundary of \({\tilde{C}}_{n,m}\) are related by an intersection form, a Poincaré-Lefschetz type duality, which relates homologies of the covering with respect to differents parts of its boundary. This will lead to a pairing between \({\mathcal {H}}_{n,m}\) and \({\mathcal {H}}^{\partial }_{n,m}\). We follow [6, 7] for the computations of the pairing in the case where the homology classes are given by geometric submanifolds.
Definition 4.2.1
(Graded intersection [4]) Let us consider \(F \in H^{\text {lf}}_m({\tilde{C}}_{n,m}, {\mathbb {Z}}) \) and \(G \in H_m({\tilde{C}}_{n,m}, \partial ;{\mathbb {Z}})\). Suppose that there exist \(M,N \subseteq C_{n,m}\) transverse submanifolds of dimension m which intersect in a finite number of points such that there exist lifts in the covering \({\tilde{M}}, {\tilde{N}}\) with \(F=[{\tilde{M}}]\) and \(G=[{\tilde{N}}]\). The graded intersection between the submanifolds in the covering is defined by the formula:
where \(( \cdot \cap \cdot )\) means the geometric intersection number between submanifolds.
In the next part we will see that even if a priori the graded intersection between \({\tilde{M}}\) and \({\tilde{N}}\) is defined in the covering space \({\tilde{C}}_{n,m}\), it can be computed in the base space using M and N and the local system.
Proposition 4.2.2
For \(x \in M \cap N\) there exists a unique \(\varphi _x \in {\text {Deck}}({\tilde{C}}_{n,m})\) with:
Now we present the formula for computing the pairing following [4]. Let us fix a basepoint \(d \in C_{n,m}\) and \({\tilde{d}}\in \pi ^{-1}(d)\). Let \(x \in M \cap N\) and \(\varphi _x \in {\text {Deck}}({\tilde{C}}_{n,m})\) as in proposition 4.2.2. Denote by \({\tilde{x}}=(\varphi _x{\tilde{M}} \cap {\tilde{N}})\cap \pi ^{-1}(x).\) We will describe \(\varphi _x\) using just the local system \(\phi \) and the point x. We notice that we have the same sign of the intersection in the covering and in the base space: \((\varphi _x {\tilde{M}} \cap {\tilde{N}})_{{\tilde{x}}}= (M \cap N)_x\), which we denote by \(c_x\).
Suppose that we have two paths \(\gamma _M, \delta _N: [0,1]\rightarrow C_{n,m}\) such that their unique lifts which start at \({\tilde{d}}\), denoted by \({\tilde{\gamma }}_M, {\tilde{\delta }}_N:[0,1] \rightarrow {\tilde{C}}_{n,m}\), have the properties:
Let us consider two paths \({\hat{\gamma }}_M,{\hat{\delta }}_N: [0,1]\rightarrow C_{n,m}\) such that:
We denote the loop: \(l_x:=\delta _N {\hat{\delta }}_N {\hat{\gamma }}^{-1}_M\gamma _M^{-1}.\) Following [4], one has that \(\varphi _x= \phi (l_x).\)
Corollary 4.2.3
The pairing can be computed using the intersection points in the base space \(C_{n,m}\) and the local system as follows:
Lemma 4.2.4
[7] The pairing \(\ll , \gg \) can be extended for classes \(F \in H^{\text {lf}}_m({\tilde{C}}_{n,m}, {\mathbb {Z}}) \) and \(G \in H_m({\tilde{C}}_{n,m},\partial ;{\mathbb {Z}})\) that are represented as linear combinations of classes of lifts of submanifolds as above. Then, the pairing \(\ll F,G \gg \) does not depend on the choice of representatives for the homology classes.
4.3 Pairing between \({\mathcal {H}}_{n,m}\) and \({\mathcal {H}}^{\partial }_{n,m}\)
Definition 4.3.1
Let us denote the pairing \(\langle ~,~\rangle : {\mathcal {H}}_{n,m} \otimes {\mathcal {H}}^{\partial }_{n,m}\rightarrow {\mathbb {Z}}[x^{\pm 1},d^{\pm 1}]\):
This is a sesquilinear form (with respect to the transformations \(x\leftrightarrow x^{-1}, d\leftrightarrow d^{-1}\)).
Proposition 4.3.2
(Computing the local signs in the base configuration space [4])
The submanifolds \({{\mathbb {F}}}_e\) and \({\mathbb {D}}_f\) in \(C_{n,m}\) are constructed from products of arcs in the punctured disc. For an intersection point \(x=(x_1,\ldots ,x_m)\in {{\mathbb {F}}}_e\cap {\mathbb {D}}_f \) let \(\alpha _x:=\epsilon _1 \cdot \cdots \cdot \epsilon _m\) where \(\epsilon _i\) is the sign of the intersection between the red arc and green arc that contain the point \(x_i\) at this point, in the punctured disc. Then we can compute the pairing using these signs. Let \(g: {\mathbb {Z}}[x^{\pm 1},d^{\pm 1}]\rightarrow {\mathbb {Z}}[x^{\pm 1},d'^{\pm 1}]\) be given by \(g(x)=x\) and \(g(d)=d'\). We consider the intersection:
Let \(S:{\mathbb {Z}}[x^{\pm 1}, d'^{\pm 1}]\rightarrow {\mathbb {Z}}[x^{\pm 1}, d^{\pm 1}]\) be given by \(S(x)=x\) and \(S(d')=-d\). Then:
Lemma 4.3.3
For any \(e,f \in E_{n,m}\), the pairing has the following form:
where \(p_e\in {\mathbb {Z}}[d^{\pm 1}]\left( \subseteq {\mathbb {Z}}[x^{\pm 1},d^{\pm 1}]\right) \) is a non-zero polynomial.
Proof
Since we are working in the configuration space, we remark that:
Let us fix a partition \(e \in E_{n,m}\). Following formula (28), the intersection pairing can be computed using the intersections “supported” between punctures i and \(i+1\) between \({\mathbb {F}}_{e_i}:= {\mathbb {F}}_{(0,0,\ldots ,e_i,\ldots ,0)}\) and \({\mathbb {D}}_{e_i}:={\mathbb {D}}_{(0,0,\ldots ,e_i,\ldots ,0)}\) in the following manner:
Now we compute the pairing \(\langle {\tilde{{\mathbb {F}}}}_{e_i},{\tilde{{\mathbb {D}}}}_{e_i}\rangle \). Each intersection point \(x \in {\mathbb {F}}_{e_i}\cap {\mathbb {D}}_{e_i}\) is characterised by an \(e_i\)-tuple which pairs a horizontal line from the multifork with a vertical line from the barcode. In other words \(x=x_{\sigma }= \left( x_{(1,\sigma (1))},\ldots ,x_{(e_i, \sigma (e_i))} \right) \) where \(\sigma \in Sym_{e_i}\) is a permutation. It follows:
Since all red segments which give the multifork are oriented in the same way and all parts of the barcode have the same orientation we get that \(\alpha _{x_\sigma }=1\). Now we construct the loop \(l_{x_{\sigma }}\). For any \(k\in \{1,\ldots ,m\}\) we consider:
Let \(a_i:=e_1+\cdots +e_{i-1}\) and the paths in the configuration space of \(e_i\) points:
From formula (26) we have: \(l_{x_{\sigma }}=\Delta _{e_i} {{\hat{\Delta }}}_{e_i} { {{\hat{\Gamma }}_{e_i}} }^{-1}\Gamma _{e_i}^{-1} \subseteq C_{n,e_i}.\) We follow the loop \(l_{x_{\sigma }}\) using Fig. 1 and notice that none of its components go around any of the punctures. So, the variable x will not appear in \((g\circ \phi )(l_{x_{\sigma }})\). Also, for \(\sigma =\text {Id}\) we have \(l_{x_{\text {Id}}}\) as the union of trivial loops, so: \((g\circ \phi )(l_{x_{\text {Id}}})=1.\) Putting the previous remarks together in the formula (31), we conclude that \(\langle {\tilde{{\mathbb {F}}}}_{e_i},{\tilde{{\mathbb {D}}}}_{e_i}\rangle _{d'} \in {\mathbb {N}}[d'^{\pm 1}]\) and it has a nontrivial free term. Combining this with the Eq. (30), we obtain that:
with a non trivial free part. Then, since S is injective we obtain that:
is also non-zero which concludes the proof. \(\square \)
Lemma 4.3.4
The family of barcodes \(\{ [{\tilde{{\mathbb {D}}}}_e] | e\in E_{n,m} \} \) is linearly independent and it gives a basis for \({\mathcal {H}}^{\partial }_{n,m}\).
Proof
This follows directly from the computation of the pairing between \([{\tilde{{\mathbb {F}}}}_e]\) and \([{\tilde{{\mathbb {D}}}}_e]\) and the fact that \(p_e \in {\mathbb {Z}}[x^{\pm 1}, d^{\pm 1}]\) are non-zero divisors. \(\square \)
Notation 4.3.5
The set \({\mathscr {B}}_{{\mathcal {H}}^{\partial }_{n,m}}\) will be called the barcodes basis for \({\mathcal {H}}^{\partial }_{n,m}\).
By an analogous argument, we re-obtain also a proof for the fact that the multiforks \( \{ [{\tilde{{\mathbb {F}}}}_e] | e \in E_{n,m} \}\) are linearly independent in \(H^{\text {lf}}_m({\tilde{C}}_{n,m},{\mathbb {Z}})\) ([8] Sect. 3.1). We conclude that the matrix of the graded intersection pairing \(\langle ~,~\rangle \) in the bases of multiforks \( {\mathscr {B}}_{{\mathcal {H}}_{n,m}}\) and barcodes \({\mathscr {B}}_{{\mathcal {H}}^{\partial }_{n,m}}\) is a diagonal matrix:
where \(p_1,\ldots ,p_{e_{d_{n,m}}}\in {\mathbb {Z}}[x^{\pm 1}, d^{\pm 1}]\) are all non-zero divisors.
Corollary 4.3.6
The pairing \(\langle ~,~\rangle : {\mathcal {H}}_{n,m} \otimes {\mathcal {H}}^{\partial }_{n,m}\rightarrow {\mathbb {Z}}[x^{\pm 1},d^{\pm 1}]\) is non-degenerate.
4.4 Specialisations
Our aim is to describe the coloured Jones polynomials in a homological way. For this purpose, our starting point is the deep connection proved by Kohno, that relates quantum representations of the braid groups and certain specializations of the Lawrence representations. In this part we will focus on those specializations of the Lawrence representation which are used in Kohno’s Theorem. Our aim is to obtain non-degenerate intersection forms between these specialisations.
Definition 4.4.1
(Specialisation of coefficients) Let \(\lambda =N-1 \in {\mathbb {N}}\) be a parameter. Consider the specialization of the coefficients:
Definition 4.4.2
Let us define the specialised Lawrence representation:
These multiforks and barcodes define bases of \({\mathcal {H}}_{n,m}|_{\psi _{ \lambda }}\) and \({\mathcal {H}}_{n,m}|_{\psi _{\lambda }}\) over \({\mathbb {Z}}[q^{\pm 1}]\).
Definition 4.4.3
Let us consider the specialised Blanchfield pairing, obtained from the generic pairing \(\langle ~,~\rangle \) by specialising its coefficients using \(\psi _{\lambda }\):
We notice that \( \{ p_{e} | e \in E_{n,m} \} \cap {\text {Ker}}(\psi _{\lambda })= \varnothing \). At this point we see that the choice of barcodes on the dual side of \({\mathcal {H}}_{n,m}\) has an important role. The geometric intersection pairing between multiforks and these barcodes, has a corresponding matrix \(M_{\langle ~,~\rangle }\) which is diagonal with non-zero polynomials \(p \in {\mathbb {Z}}[d^{\pm 1}]\) on the diagonal. This fact ensures that these polynomials become non-zero elements in \({\mathbb {Z}}[q^{\pm 1}]\) through the specialization \(\psi _{ \lambda }\).
Corollary 4.4.4
The form \(\langle ~,~\rangle |_{\psi _{\lambda }}\) is sesquilinear and non-degenerate over \({\mathbb {Z}}[q^{\pm 1}]\).
4.5 Dualizing the algebraic evaluation
This part is motivated by the fact that we are interested in describing the third level of a braid closure (the union of “caps”), viewed through the Reshetikhin-Turaev functor, in a geometrical way using the geometric intersection pairing. We will see the details in the following Sect. 6, but for this part the aim is to be able to understand an element of the dual of \({\mathcal {H}}_{n,m}|_{\psi _{\lambda }}\), as a geometric intersection \(\langle \cdot , {\mathscr {G}}\rangle \) for some \(G \in {\mathcal {H}}_{n,m}|_{\psi _{\lambda }}\).
Remark 4.5.1
The non-degenerate pairing \(\langle ~,~\rangle |_{\psi _{\lambda }}: {\mathcal {H}}_{n,m}|_{\psi _{\lambda }} \otimes {\mathcal {H}}^{\partial }_{n,m}|_{\psi _{\lambda }}\rightarrow {\mathbb {Z}}[q^{\pm 1}]\) has the following matrix:
Here \(\psi _{\lambda }(p_1),\ldots ,\psi _{\lambda }(p_{e_{d_{n,m}}}) \in {\mathbb {Z}}[q^{\pm 2}]\) are polynomials with non-zero free terms. In particular, the diagonal coefficients are not necessarily invertible elements in \({\mathbb {Z}}[q^{\pm 1}]\).
Following this remark, we notice that a priori not any element of \( \mathcal {F} \in ({\mathcal {H}}_{n,m}|_{\psi _{\lambda }})^{*}\) can be described as a geometric intersection pairing \(\langle \cdot , \mathscr {G}_{\mathcal {F}}\rangle \) for some \(G_{\mathcal {F}}\in {\mathcal {H}}^{\partial }_{n,m}|_{\psi _{ \lambda }}\). This issue comes from the fact that we are working over a ring and not over a field. In order to overcome this problem, we will change the ring of coefficients from \({\mathbb {Z}}[q^{\pm 1}]\) to the field of fractions \({\mathbb {Q}}(q)\). Let us consider the embedding \(i: {\mathbb {Z}}[q^{\pm 1}]\hookrightarrow {\mathbb {Q}}(q)\) and use \({\mathbb {Q}}(q)\) as field of coefficients.
Definition 4.5.2
(New Specialisation) Let us consider the specialization of coefficients \(\alpha _{\lambda }: {\mathbb {Z}}[x^{\pm 1},d^{\pm 1}] \rightarrow {\mathbb {Q}}(q)\) defined by: \(\alpha _{\lambda }=i \circ \psi _{\lambda }\). Also, we define the specialised Lawrence representations:
These multiforks and barcodes define bases for \({\mathcal {H}}_{n,m}|_{\alpha _{\lambda }}\) and \({\mathcal {H}}^{\partial }_{n,m}|_{\alpha _{\lambda }}\) over \({\mathbb {Q}}(q)\).
We notice that the previous specialisations are related in the following manner:
Notation 4.5.3
Let us denote the corresponding change of the coefficients at the homological level by: \(p_{\lambda }: {\mathcal {H}}_{n,m}|_{\psi _{\lambda }} \xrightarrow {( \ \cdot \ \otimes _{i}1)} {\mathcal {H}}_{n,m}|_{\alpha _{\lambda }}.\)
Definition 4.5.4
Consider the Blanchfield pairing constructed from the pairing \(\langle ~,~\rangle \) using the specialisation \(\alpha _{\lambda }\):
We notice that for any partition \(e\in E_{n,m}\), the evaluation \(\alpha _{\lambda }(p_{e})\in {\mathbb {Q}}(q)\) is a non-zero element, so it is invertible. This shows that \(\langle ~,~\rangle |_{\alpha _{\lambda }}\) is a non-degenerate sesquilinear form. Moreover, working over a field, we conclude that any element in the dual of the first homology group, can be described as a pairing with a fixed element from the dual homology. More precisely, we obtain the following description.
Corollary 4.5.5
For any \(\mathscr {G} \in ({\mathcal {H}}_{n,m}|_{\alpha _{\lambda }})^{*}\), there exists a corresponding homology class \(\tilde{{\mathscr {G}}}\in {\mathcal {H}}^{\partial }_{n,m}|_{\alpha _{\lambda }} \) such that:
Definition 4.5.6
(Construction of geometric duals) Let us start with an element
We construct the following element:
Then, taking the pairing with the dual element \(\tilde{{\mathscr {G}}}\) of \(\mathscr {G}\) given by relation (39), we obtain \(\mathscr {G}_0\) in a topological way, as below:
5 Identifications between quantum representations and homological representations
So far, we have presented two important constructions that lead to representations of the braid group: the quantum representation and the Lawrence representation. We will discuss relations between these representations using a result due to Kohno. The identifications over two parameters were presented in [8] based on a continuity procedure. The results from this section follow from this identification, however, we explain in more detail the continuity argument. For \(h, \lambda \in {\mathbb {C}}\) and \(\mathbf{q} =e^h\), consider the following specialisations of coefficients:
We recall that the quantum representation \(\hat{W}\) is defined over \({\mathbb {Z}}[q^{\pm 1}, s^{\pm 1}]\) and the Lawrence representation \({\mathcal {H}}_{n,m}\) is defined over \({\mathbb {Z}}[x^{\pm 1},d^{\pm 1}]\). Kohno relates these two representations, by connecting each of them with a monodromy representation of the braid group which arises using the theory of KZ-connections (Knizhnik-Zamolodchikov). We will shortly describe these relations, following [8].
5.1 KZ-Monodromy representation
Consider the Lie algebra \(sl_2({\mathbb {C}})\) and consider an orthonormal basis \( \{ I_{\mu } \}_{\mu }\) for its Cartan-Killing form. Denote
Definition 5.1.1
For \(\lambda \in {\mathbb {C}}^*\) consider \(M_{\lambda }\) to be the Verma module of sl(2) defined as: \(M_{\lambda }=\langle v_0,v_1,\ldots \rangle _{{\mathbb {C}}}\) with the following actions:
For \(n \in {\mathbb {N}}\) and \(i,j \in \{1,\ldots ,n\}\) we define the endomorphism \(\Omega _{i,j} \in {\text {End}}(M_{\lambda }^{\otimes n})\) to be the action of \(\Omega \) on the i th and j th components. The monodromy representation is constructed from the complement of a hyperplane arrangement. We consider the spaces \(X_n:= {\mathbb {C}}^n \setminus \left( \bigcup _{1\le i,j \le n} {\text {Ker}}(z_i=z_j) \right) \) and \(Y_n:= X_n /Sym_n\). For \(h \in {\mathbb {C}}^*\), the KZ-connection \(\omega _h\) is a 1-form defined over \(Y_n\) with values in \({\text {End}}(M^{\otimes n}_{\lambda })\) defined using the endomorphisms \(\Omega _{i,j}\). This gives a flat connection with values in the trivial bundle \(Y_n \times M^{\otimes n}_{\lambda }\). The monodromy of this connection leads to a representation:
Definition 5.1.2
For \(m \in {\mathbb {N}}\), the space of null vectors in \(M^{\otimes n}_{\lambda }\) of weight m is:
Definition 5.1.3
(Monodromy representation) For \(m \in {\mathbb {N}}\), the monodromy of the KZ-connection induces a braid group action on the spaces of null vectors:
Proposition 5.1.4
Following [8], for \(e \in E_{n,m}\), consider the vector:
Then, for any \(\lambda \in {\mathbb {C}}^* \setminus {\mathbb {N}}\), the set \({\mathscr {B}}_{N[n \lambda -2m]}:= \{w_e| e \in E_{n,m} \}\) describes a basis for the space of null vectors \(N[n \lambda -2m].\)
Theorem 5.1.5
(Kohno’s Theorem [8, 14, 15]) There exists an open dense set \(U \subseteq {\mathbb {C}}^* \times {\mathbb {C}}^*\) such that for any \((h,\lambda ) \in U\) there is the following identification between representations of the braid group:
More precisely, the quantum representation \({\varphi }^{\hat{W}^{ \mathbf{q} ,\lambda }}_{n,m}\) and Lawrence representation \(l_{n,m}|_{{\psi }_\mathbf{q ,\lambda }}\) are the same in the above bases (see Proposition 2.7.1, Definition 3.2.2).
5.2 Identifications with q and \(\lambda \) complex numbers
We are interested in quantum representations with natural parameter \(\lambda =N-1 \in {\mathbb {N}}\). This case does not belong to the situation with “generic parameters”. In the next part we study the relation between these braid group representations specialised with any parameters.
Remark 5.2.1
Let R be a ring and M a free R-module with a fixed basis \({\mathscr {B}}\) of cardinality d. Consider a group action \(G \curvearrowright M\) and a representation of G using the basis \({\mathscr {B}}\): \(\rho : G \rightarrow GL(d,R).\) Suppose that S is another ring and we have a specialisation of the coefficients, given by a ring morphism: \(\psi : R \rightarrow S.\)
Let us denote \(M^{\psi }:=M \otimes _{R} S\) and \({\mathscr {B}}_{M^{\psi }}:={\mathscr {B}} \otimes _{R}1 \in M^{\psi } \). The specialisation \(\psi \) leads to an induced group action \(G\curvearrowright M^{\psi }\). Then, the following properties hold:
(1) \({\mathscr {B}}_{M^\psi }\) is a basis for \(M^{\psi }\).
(2) Let \(\rho ^{\psi }: G\rightarrow GL(d,S)\) be the representation of G on \(M^{\psi }\) coming from the induced action, in the basis \({\mathscr {B}}_{M^{\psi }}\). In this way, the two actions, before and after specialisation give the same action: \(\rho ^{\psi }(g)=\rho (g)|_{\psi }, \forall g \in G.\) Here if \(f: M \rightarrow M\), we denote by \(f|_{\psi }: M^{\psi }\rightarrow M^{\psi }\) the specialisation \(f|_{\psi }=f \otimes _{R}Id_{S}\).
Theorem 5.2.2
Let \((h,\lambda ) \in {\mathbb {C}}^*\times {\mathbb {C}}\) be any fixed complex parameters. Then the following braid group representations are isomorphic, using the following corresponding bases:
Proof
In the proof of the previous Theorem 5.1.5, this correspondence is stated for any parameters in a dense open subset in \({\mathbb {C}}^* \times {\mathbb {C}}\). The relation between quantum representations and the Lawrence representations is established by relating both of them with the monodromy of the KZ-connection. More precisely, two isomorphisms of braid group representations are constructed:
These isomorphisms are constructed using correspondences between the bases below:
From this, Kohno proved that for all \((h, \lambda ) \in U\) there is the relation:
Let us denote by \(\Theta _\mathbf{q , \lambda }: {\mathcal {H}}_{n,m}|_{\psi _\mathbf{q ,\lambda }}\rightarrow \hat{W}_{n,m}^\mathbf{q ,\lambda }\) the function given by:
This function is defined for all \((h,\lambda ) \in {\mathbb {C}}^* \times {\mathbb {C}}\). We notice that the functions \(f^{WN}_\mathbf{q ,\lambda }, f^{NH}_\mathbf{q ,\lambda }\) are continuous with respect to the parameters \((h,\lambda )\in U\) and then \(\Theta _\mathbf{q , \lambda }\) is also continuous with respect to the two complex parameters.
Now we investigate the case of non-generic parameters. We recall that \({\mathscr {B}}_{\hat{W}_{n,m}}\) is a basis for \(\hat{W}_{n,m}\). Following the definition of a specialisation, we obtain that \( {\mathscr {B}}_{\hat{W}_{n,m}^\mathbf{q ,\lambda }}:={\mathscr {B}}_{\hat{W}_{n,m}}|_{\eta _\mathbf{q ,\lambda }}\) is a well-defined basis for \(\hat{W}_{n,m}^\mathbf{q ,\lambda }\), for any \((h,\lambda )\in {\mathbb {C}}^* \times {\mathbb {C}}\).
Since the specialisation \(\eta _\mathbf{q ,\lambda }\) is well-defined for any complex parameters \((h, \lambda ) \in {\mathbb {C}}^* \times {\mathbb {C}}\), all the coefficients from \({{\varphi }^{\hat{W}}_{n,m}}|_{\eta _\mathbf{q ,\lambda }}\) are well-defined complex numbers. In particular, the action \({\varphi }^{\hat{W}^{ \mathbf{q} ,\lambda }}_{n,m}\) in the basis \({\mathscr {B}}_{\hat{W}_{n,m}}|_{\eta _\mathbf{q ,\lambda }}\) has all coefficients well-defined.
We conclude that for any braid \(\beta \in B_n\), the specialisation of the matrix obtained from the initial action \({{\varphi }^{\hat{W}}_{n,m}}\) on \(\hat{W}_{n,m}\) in the basis \({\mathscr {B}}_{\hat{W}_{n,m}}\) is the matrix of the specialised action \({\varphi }^{\hat{W}^{ \mathbf{q} ,\lambda }}_{n,m}\) in the specialised basis \({\mathscr {B}}_{\hat{W}_{n,m}^\mathbf{q ,\lambda }}\):
On the homological side, the specialisation \({\mathscr {B}}_{{\mathcal {H}}_{n,m}|_{\psi _\mathbf{q ,\lambda }}}\) is a well-defined basis for \({\mathcal {H}}_{n,m}|_{\psi _\mathbf{q ,\lambda }}\) for any parameters \( (h, \lambda )\in {\mathbb {C}}^* \times {\mathbb {C}}\).
This shows that for every \(\beta \in B_n\), the specialisations of the matrices from the action on \({\mathcal {H}}_{n,m}\) in the multifork basis, are actually the same as the matrices of the specialised Lawrence action, in the specialised multifork basis \({\mathscr {B}}_{{\mathcal {H}}_{n,m}}|_{\psi _\mathbf{q ,\lambda }}\):
We obtain that for any parameters \((q, \lambda ) \in {\mathbb {C}}^* \times {\mathbb {C}}\), the following identification holds:
\(\square \)
5.3 Identifications with q indeterminate
Following Theorem 5.2.2, quantum representations and Lawrence representations are isomorphic after appropriate identifications of coefficients, if we fix \((\mathbf{q} ,\lambda )\) any complex numbers. In this part, we will state a similar result for the case where we keep q an indeterminate and \(\lambda =N-1 \in {\mathbb {N}}\). We recall the specialisations of the coefficients:
For \(\mathbf{q} \in {\mathbb {C}}\), let \(f_\mathbf{q }: {\mathbb {Z}}[q^{\pm 1}]\rightarrow {\mathbb {C}}\) be the evaluation given by \(f_\mathbf{q }(q)=\mathbf{q} .\) Then:
We recall the notations:
Theorem 5.3.1
The braid group representations with respect to the specialisation with one complex number are isomorphic over \({\mathbb {Z}}[q^{\pm 1}]\):
Proof
Let \(\Theta _{\lambda }: {\mathcal {H}}_{n,m}|_{\psi _{\lambda }}\rightarrow \hat{W}_{n,m}|_{\eta _{\lambda }}\) be given by \(\Theta _{\lambda }([{\tilde{{\mathbb {F}}}}_e ])=\phi \left( v^s_{\iota (e)}\right) |_{\eta _{\lambda }}, \forall e \in E_{n,m}.\) We have that \({\mathscr {B}}_{\hat{W}_{n,m}}|_{\eta _{\lambda }}\) is a basis for \(\hat{W}_{n,m}^{\lambda }\) and \({\mathscr {B}}_{{\mathcal {H}}_{n,m}}|_{\psi _{\lambda }}\) is a basis for \({\mathcal {H}}_{n,m}|_{\psi _{\lambda }}\). Also, we have the following relations between specialisations:
For \(\beta \in B_n\), we notice that for any \(\mathbf{q} \in {\mathbb {C}}\) we have the relations:
Using Theorem 5.2.2 we obtain that \( {{\varphi }^{\hat{W}}_{n,m}}(\beta ) |_{\eta _{\lambda }}=l_{n,m}(\beta )|_{\psi _{\lambda }}, \forall \beta \in B_n.\) These matrices correspond to well-defined actions in the previous bases, so we have:
We conclude that the braid group actions from the statement are isomorphic.
\(\square \)
6 Homological model for the coloured Jones polynomial
In this section, we present a topological model for the coloured Jones polynomials. We will start with an oriented link and consider a braid that leads to the link by braid closure. In the first part, we study the Reshetikhin-Turaev functor on a link diagram that leads to the invariant, by separating it on three main levels. Secondly, for each of these levels we construct step by step a homological counterpart in the Lawrence representation and its dual. Finally, we show that the evaluation of the Reshetikhin–Turaev functor on the whole knot corresponds to the geometric intersection pairing between the homological counterparts.
Let \(N \in \mathbb N\) be the colour. Let the parameter \(\lambda = N-1\) and the specialisations \( \eta _{N-1}, \psi _{ N-1}\) be defined as in formula (42). In the next part, we will use the braid group actions corresponding to the quantum representations:
We recall the change of coefficients \(\alpha _{\lambda }\) from definition 4.5.2:
Using these notations, we will prove the following model.
Theorem 6.0.2
(Topological model for coloured Jones polynomials with specialised homology classes) Let \(n \in {\mathbb {N}}\). Then, there exist two homology classes
such that for any oriented link L with \(L={\hat{\beta }}_n\) for \(\beta _n \in B_n\), the \(N^{th}\) coloured Jones polynomial has the formula:
Proof
Consider the planar diagram for the link L which is associated to the closure of the braid \(\beta _{n}\). It has the following three main levels:

We use the formula for the coloured Jones polynomial from proposition 2.4.3:
6.1 (Step I)-Coevaluation corresponding to the cups
Looking at the bottom part of the diagram, we notice that the properties of the quantum group actions on its representations imply that the first morphism \({\mathop {{\text {coev}}}\limits ^{\longleftarrow }}^{\otimes n}_{V_N}\) naturally arrives in particular subspace in \(V_N^{\otimes n} \otimes \left( V_N^*\right) ^{\otimes n}\). This subspace would correspond to a certain highest weight space if it was inside the tensor power of the same representation.
Lemma 6.1.1
One has the following:
Proof
From the fact that \({{\mathop {{\text {coev}}}\limits ^{\longleftarrow }}}^{\otimes n}_{V_N}: {\mathbb {Z}}[q^{\pm 1}] \rightarrow V_N^{\otimes n} \otimes \left( V_N^*\right) ^{\otimes n}\) is a morphism of \(\mathscr {U}\)-modules (Definition 2.4.1) it follows that it commutes with the E and K-actions. Since \({\mathbb {Z}}[q^{\pm 1}]\) is the trivial representation, this shows that:
\(\square \)
From this remark, one gets that for any vector \(v \in {\text {Im}}\left( {{\mathop {{\text {coev}}}\limits ^{\longleftarrow }}}^{\otimes n} _{V_N}\right) \):
Having in mind the notion of weight spaces, we write \(q^0=q^{\mathbf{2n}(N-1)- 2 \mathbf{(N-1)n}}\) and conclude that:
Notation 6.1.2
Let us consider the vector:
More precisely, it has the form:
6.2 (Step II)-Arriving in a highest weight space
As we have seen in Sect. 5, quantum representations of the braid group encode homological information. This means that for the braid part of the diagram, we could create a bridge towards a homological action if all the strands had the same orientation. Therefore, we are interested in arriving at a formula for \(J_N(L,q)\) which contains in the middle the action of \(B_{2n}\) on \(V_N^{\otimes 2n}\). For the moment, corresponding to the braid group action, we have the Reshetikhin-Turaev functor as follows:
The second idea is to insert additional isomorphisms at the first and the third level, which transform \((V_{N}^*)^{\otimes n}\) into \(V_N^{\otimes n}\) and act non-trivially just on the last n components of the tensor product, corresponding to the last n strands of the diagram. Then, in the middle, we will have the Reshetikhin-Turaev functor evaluated on the braid, which is exactly the quantum representation:
We will make this precise in the next part. Following the first step, we notice that the bottom part of the diagram – corresponding to the cups – leads towards an analogue of the highest weight space of weight \(n(N-1)\). Now we show that we can arrive in the corresponding highest weight space inside \(V_N^{\otimes 2n}\).
Lemma 6.2.1
For \(n \in {\mathbb {N}}\) there exists an isomorphism of vector spaces such that:
Proof
We search for a function \(\alpha _{n,N}\) of the form:
where \(f_i:V_N^{*}\rightarrow V_N\) are isomorphisms of \({\mathbb {Z}}[q^{\pm 1}]\)- modules, for all \(i \in \{1,\ldots ,n\}\). We prove the statement by induction on the number of strands. For \(n \in {\mathbb {N}}\), let us consider the following statement:
\(\mathbf{P(n)}\) There exists a sequence of isomorphisms of \({\mathbb {L}}\)-modules \(\{f_k | k\in \overline{1,n} \}\) such that:
We recall the Definition 2.5.2 of highest weight spaces inside finite dimensional modules, more precisely the fact that these subspaces come as specialisations from highest weight spaces over two variables:
On the other hand, having in mind the type of isomorphisms that occur in the case of the usual version of the quantum group \(U_q(sl(2))\) – between the N-dimensional representation and its dual – it would be natural to search for a sequence of coefficients \(\{c^i_k \in {\mathbb {L}}\} \) such that the functions from \(\mathbf{P}(n)\) have the form:
This combined with the definition of highest weight spaces from above suggests an extra requirement, namely the existence of a sequence of lifts of the coefficients over two variables \(\{ {\tilde{c}}^i_k \in {\mathbb {L}}_s\}\):
Having in mind this requirement and the definition of \(w_n^N\) from Eq. (58), we restate the induction hypothesis that we prove.
\(\mathbf{P(n)}\): There exists a sequence of coefficients in two variables:
such that if one considers the following vector in \(\hat{V}^{\otimes 2n}\):
then it belongs to the \(n(N-1)^{th}\) highest weight space: \({\tilde{v}}_n^N \in \hat{W}_{2n,n(N-1)}.\)
In other words, one requires the following conditions:
We start with the requirement concerning the K-action. Since the vector \({\tilde{v}}_n^N\) has the property that all its monomials have a constant sum of indices, then for any choice of coefficients the following relation holds:
In order to see this, we recall the comultiplication of the quantum group:
Then for any indices \(i_1,\ldots ,i_n \in \{1,\ldots ,N-1\}\), we have:
This shows that \(\forall i_1,\ldots ,i_n \in \{1,\ldots ,n\}\):
Therefore the first requirement from Eq. (64) is fulfilled: \({\tilde{v}}_n^N \in \hat{V}_{2n,n(N-1)}.\) So, the only condition that we require for \(\mathbf{P}(n)\) concerns the E-action. This action is done using the comultiplication, given by:
The requirement concerning the coefficients in two variables from Eq. (64) becomes:
We will show by induction that this condition can be fulfilled.
(I) Base case n=1
We search for a sequence of coefficients \(\{ {\tilde{c}}_1^i \in {\mathbb {L}}_s | i \in \overline{0,N-1}\}\) such that:
This is equivalent to:
By changing the variable i to \(i+1\) in the first sum, the equation becomes:
We consider the sequence of coefficients that satisfies the condition below, which implies Eq. (70):
This concludes the base case.
(II) The inductive step: \(\mathbf{P}(\mathbf{n})\Rightarrow \mathbf{P(n+1)}\)
Let us suppose that \(\mathbf{P(n)}\) is true and aim to prove \(\mathbf{P(n+1)}\), by searching for a sequence of coefficients \(\{ {\tilde{c}}_{n+1}^{i_{n+1}} \in {\mathbb {L}}_s | i_{n+1} \in \overline{0,N-1}\}\) such that:
Notation 6.2.2
Let us consider the following notation:
Then, \(\mathbf{P(n)}\) is equivalent to:
We will study the condition for \(\mathbf{P(n+1)}\) from Eq. (72), by splitting the coevaluation of E into two parts: one part which is associated to the first and the last strand, and another part which corresponds to all the other strands in the middle. This means that there is the first part, which has one term with E on the first component and another term with E on the last component and a second part, which contains all the other terms with E in the middle.
Separating the two parts of the sum, we get:
Using the induction hypothesis reformulated as in Eq. (73), we conclude that the second sum from this formula vanishes. In other words, the conditions for the sequence \(\{ {\tilde{c}}_{n+1}^{i_{n+1}}\}\) are given by:
This is equivalent to the following requirements:
By changing the parameter \(i_{n+1}-1\) to \(i_{n+1}\) and denoting it by i in the first sum and then gluing together the previous two terms, we obtain the condition:
Then, let us consider the coefficients given by the following conditions, which imply Eq. (77):
This concludes the induction step \(\mathbf{P(n+1)}\). Then, the set of coefficients \(\{c_{i}^{k} \in {\mathbb {L}}\}\) is given by the evaluation of the previous sequence using the specialisation \(\eta _{N-1}\):
We notice that these sequences of coefficients do not actually depend on the strand to which they correspond, namely \(n+1\). This shows that all the functions are the same:
However, their lifts towards the generic highest weight space are different and depend on the strand. We obtain the normalising function \(\alpha _{n,N}\) as in Eq. (59), given by:
\(\square \)
We conclude that using this normalising function \(\alpha _{n,N}\), we arrive in the following highest weight space:
6.3 (Step III)-The invariant seen through highest weight spaces
So far, we have seen that if we compose the extra normalising function with the coevaluation, we arrive in a highest weight space. Pursuing this idea, we introduce \(\alpha _{n,N}\) and its inverse to the first and third level of the associated diagram. The interesting part is that this procedure does not modify the invariant that we get. More precisely, we have the following:
Lemma 6.3.1
The coloured Jones polynomial has the following description:
Proof
This is the formula from Eq. (53), with the two extra terms that contain the normalisation function. The key point is the fact that this function acts nontrivially just on the last n components, where we act with \(\mathbb I_n\) at the braid level, whereas the normalising function is the identity on the first n components, where we have a non-trivial action at the braid level, coming from \(\beta _n\). So, the two functions \(\alpha _{n,N}\) and its inverse cancel out with each other.
Then, replacing this relation in Eq. (53), we conclude the lemma. \(\square \)
Then, we conclude that we can obtain the invariant by composing the morphisms corresponding to the following diagram:

In the following part, we aim to show that we can see the whole coloured Jones polynomial through the highest weight space from Step II. We introduce the following notation.
Notation 6.3.2
(Normalising the evaluation and coevaluation)
Consider the following morphisms:
given by:
The formula for \(J_N(L,q)\) presented in Lemma 6.3.1 together with the definition of the quantum representation given in proposition 2.7.2 lead to the following description:
Putting together notation (58), the properties of the normalising function \(\alpha _{n,N}\) given in (59) and notation (85), we obtain that:
On the other hand, we know that the action:
preserves the highest weight spaces, in particular preserves \(W^N_{2n,n(N-1)}\). Using this invariance together with formula (86), we notice that actually we can obtain \(J_N(L,q)\) using just highest weight spaces, by composing the morphisms from the second column (2) from Fig. 2. We conclude the following formula for the coloured Jones invariant:
6.4 (Step IV)-Change of the highest weight space
We have seen that \(J_N(L,q)\) is encoded by the action through highest weight spaces corresponding to the finite dimensional module \(V_N\). On the other hand, these highest weight spaces \(W^N_{2n,m}\) inside \(V^{\otimes 2n}_N\) do not yet have a known geometric counterpart. This is one of the reasons why there were no known topological interpretations for these invariants. On the other hand, Kohno’s Theorem provides a geometric correspondent of the bigger highest weight spaces \(\hat{W}^{N-1}_{2n, n(N-1)}\), which live inside the tensor power of the Verma module \(\hat{V}_{N-1}\). Having this in mind, we look at the inclusion:
In the next part, we show that the quantum representation behaves well with respect to \(\iota \).
Lemma 6.4.1
The \(B_n\)-action on the highest weight spaces from the Verma module leaves invariant the highest weight spaces of the finite dimensional module and we have:
Proof
The action of the R-matrix on \(\hat{V} \otimes \hat{V}\) is given in relation (9). We are interested in the specialisation of this action by the function \(\eta _{N-1}\), which corresponds to the identifications: \(\lambda = N-1; s=q^\lambda .\) It follows that the action on \(\hat{V}_{N-1} \otimes \hat{V}_{N-1}\) has the following form:
We prove that this action preserves \(V_N \otimes V_N\) inside \(\hat{V}_{N-1} \otimes \hat{V}_{N-1}\) (see Lemma 2.2.2). We show this by checking the action on the following basis of \(V_N \otimes V_N\):
Let \(0 \le i,j\le N-1 \). We notice that in formula (90) all the indices of the second components decrease and so the vectors \(v_{i-n}\) will remain in \(V_N\). For the first components, let us suppose that we pass over \(V_N\) inside \(\hat{V}_{N-1}\), in other words we have a term corresponding to the index
We prove that in this situation the coefficient vanishes. We notice that for \(k=N-1-j\), the following term vanishes:
Moreover, for \(j+n \ge N\), it follows that \(N-1-j \le n-1\), so the term from relation (91) will appear in the product which is part of the coefficient of the vector \(v_{j+n} \otimes v_{i-n}\). We conclude that this coefficient vanishes.
Secondly, we show that the action of the braid group preserves the inclusion \(W^N_{n,m}\subseteq \hat{W}^{N-1}_{n,m}\). For this, we prove that each generator \(\sigma _i\) of the braid group preserves \(W^N_{n,m}\). Let \(w\in W^N_{n,m}\) and since \(W^N_{n,m} \subseteq V^N_{n,m}\) there exist \(\alpha _e \in {\mathbb {Z}}[q^{\pm 1}]\) such that:
We recall the action: \(\sigma _i w= (Id^{\otimes (i-1)} \otimes {\mathscr {R}} \otimes Id^{\otimes (n-i-1)})w\). So \(\sigma _i w\) will modify just the components i and \(i+1\) of w. Using that the braid action preserves the inclusion of weight spaces, as we proved above, the indices of all vectors that appear in this action remain strictly smaller than N. This shows that:
Since the action of \(B_n\) is an action of \(\mathscr {U}\)-modules, this commutes with the action of the generators E and K, so it preserves the weights and the kernel of E. Using this remark and relation (92), we conclude that:
\(\square \)
Up to this moment, we focused on the phenomenon that occurs at the bottom part of the diagram, with the cups and the braid. Now, we study the upper part given by the caps, which correspond to the algebraic evaluation.
First, we will use the finite dimensional submodule \(V_N\) inside the Verma module \(\hat{V}_{N-1}\), which has a well-defined evaluation from Eq. (8) and define an evaluation type map on \(\hat{V}_{N-1}\), supported on this submodule.
Definition 6.4.2
(Normalised evaluation on the Verma module)
Consider \({\mathop {{\text {Ev}}}\limits ^{\longrightarrow }}^{\otimes n}_{\hat{V}_{N-1}}: \hat{V}_{N-1}^{\otimes n} \rightarrow {\mathbb {Z}}[q^{\pm 1}] \) given by the expression:
and extended it by linearity.
6.5 (Step V)-The invariant through highest weight spaces in the Verma module
In the following part, our strategy is to use the highest weight spaces from the Verma module and show that we can see the coloured Jones polynomial through these subspaces.
We start with the normalised coevaluation which arrives in the highest weight spaces \(W^N_{2n,n(N-1)}\) from \(V_N\) and then follow the inclusion into \(\hat{W}^{N-1}_{2n,n(N-1)}\). Now, we continue with the braid group action on these bigger highest weight spaces and finally close with the evaluation \({\mathop {{\text {Ev}}}\limits ^{\longrightarrow }}^{\otimes n}_{\hat{V}_{N-1}}\). We conclude that the coloured Jones polynomial can be obtained through the highest weight spaces of weight \(n(N-1)\) from the Verma module, following column (3) from Fig. 2:
6.6 (Step VI)-Construction of the first homology class
Now, we start the construction of the homology classes. The advantage of the bigger highest weight spaces \(\hat{W}^{N-1}_{2n,n(N-1)}\) consists in the fact that they have homological correspondents, given by the Lawrence representation \({\mathcal {H}}_{2n,n(N-1)}\), due to Kohno’s relation. In this part, we encode the cups of the diagram using the Lawrence representation. More precisely, we consider the element corresponding to the image of 1 through the normalised coevaluation, seen inside the highest weight space \(\hat{W}^{N-1}_{2n,n(N-1)}\). After that, we reverse it using Khono’s function to obtain a topological class in the Lawrence representation, as follows.
Definition 6.6.1
(The first homology class \( {\mathscr {F}}_0\), over \({\mathbb {Z}}[q^{\pm 1}]\))
Let us define the vector \(v \in \hat{W}^{N-1}_{2n, n(N-1)}\) given by:
Then, using the isomorphism between quantum and homological representations from Theorem 5.3.1, we consider the homology class in the Lawrence representation given by the following relation:
Proposition 6.6.2
(Braid group action) The correspondence between the vector v and the homology class \({\mathscr {F}}_0\) is preserved under the braid group action, so we have:
Proof
This comes from the identification between braid group actions from Theorem 5.3.1 and definition of the homology class \({\mathscr {F}}_0\) given in Eq. (96). \(\square \)
Up to this point, we found the first homology class \({\mathscr {F}}_0\) which encodes homologically the algebraic coevaluation \({{\mathop {{\text {Coev}}}\limits ^{\longleftarrow }}}^{\otimes n}_{V_N}\). Moreover, the braid part of the diagram corresponds to the homological braid group action applied to this class.
6.7 (Step VII)-Construction of the second homology class
Now we are interested in finding the second homology class \(\tilde{{\mathscr {G}}}_n^N\), which will be a geometric counterpart for the part of the diagram given by the caps. The main ingredient that we use is the non-degenerate intersection form between the Lawrence representation and its dual. More precisely, our aim is to encode homologically the evaluation
Even if we are interested in this function, in practice we will use the extended evaluation
which encodes the evaluation on the highest weight spaces of the finite dimensional module, but it is defined on the bigger highest weight space. This is an element of the dual space:
Following the identification between quantum and homological braid group representations, it corresponds to an element from the dual space:
Our aim is to encode this map by a geometric element from the dual Lawrence representation \({\mathcal {H}}^{\partial }_{2n,n(N-1)}|_{\psi _{N-1}}\), using the intersection pairing. We refer to the discussion from Sect. 4.5 concerning different specialisations of the Blanchfield pairing.
At this point we notice a subtlety about the coefficients that we work with. So far, on the homological side, we needed the specialisation \(\psi _{N-1}: {\mathbb {Z}}[x^{\pm 1},d^{\pm 1}]\rightarrow {\mathbb {Z}}[q^{\pm 1}].\) Corresponding to these coefficients, one has the non-degenerate intersection form:
However, the non-degenerancy does not ensure that the evaluation can be seen as the intersection with a dual element. The issue comes from the fact that we are working over a ring and not a field. Now we change all these coefficients, passing to the field of fractions, to arrive in the situation where the dualising procedure is more convenient. We recall the change of coefficients from Definition 4.5.2:
Using this specialisation, there is the following non-degenerate sesquilinear form:
Definition 6.7.1
(The second homology class \(\tilde{ {\mathscr {G}}}_n^N\)) Let us define the element:
Then, let us consider the associated dual class given by Definition 4.5.6:
Remark 6.7.2
This means that \(\forall {\mathscr {E}} \in {\mathcal {H}}_{2n,n(N-1)}|_{\alpha _{N-1}}\) we have:
Since the construction of the second homology class needed this change of coefficients, we consider the element which corresponds to the first homology class over this field as below.
Definition 6.7.3
(The first homology class \(\tilde{{\mathscr {F}}}_n^N\)) We consider the homology class corresponding to \({\mathscr {F}}_0\) over the field \({\mathbb {Q}}(q)\), using the map \(p_{N-1}\) from notation 4.5.3 :
6.8 (Step VIII)-Proof of the intersection formula
Now we prove that the coloured Jones polynomial can be obtained from the intersection formula from Eq. (52). Putting all the previous steps together, we obtain the following:
We remark that the morphism \(p_{N-1}\) commutes with the braid group actions on the two specialisations of the Lawrence representations as below:

Also, using the properties of the geometric duals from relation (39), we have:
Following the two previous remarks about the change of coefficients over the field of fractions and the braid group actions together with Eq. (103) we obtain:
Simplifying the notations in the last equality, we obtain the desired interpretation which concludes the proof. \(\square \)
7 Topological model with non-specialised homology classes
For the homological model for \(J_N(L,q)\), we have constructed homology classes
which lead to the invariant through the topological intersection pairing. We notice that the colour N appears in two places. The first part where it appears is the number of points from the configuration space (since we are using configuration spaces of \( n(N-1)\) particles in a fixed punctured disc). Secondly, the specialisation \(\alpha _{N-1}\) depends on the colour N.
In this section we show that \( \tilde{{\mathscr {F}}}_n^N \) and \(\tilde{{\mathscr {G}}}_n^N\) come from two homology classes that live in the unspecialised Lawrence representation (more precisely, they belong to the homology of the configuration space \({\tilde{C}}_{2n,n(N-1)}\) over a larger ring of coefficients). The feature of this model is that the colour now appears just in the number of points from the configuration space, but no longer in the specialisation. We will prove the statement from Theorem 1.0.2, showing that we can construct two classes
so that the \(N^{th}\) coloured Jones polynomial has the formula:
Here \(\gamma \) is a specialisation over the field \({\mathbb {Q}}(s,q)\) which does not depend on N, whereas \(\delta _{N-1}\) is a change of coefficients towards \({\mathbb {Q}}(q)\), defined using the colour.
7.1 Identifications with q, s indeterminates
In Sect. 5 we have studied identifications between quantum and homological representations which are specialised with two complex parameters or using a natural number and an indeterminate. In this section we will show that, if we enlarge the ring of coefficients, the identification holds also over a ring with two indeterminates.
We recall that the quantum representation \(\hat{W}\) is defined over \({\mathbb {Z}}[q^{\pm 1}, s^{\pm 1}]\) and the Lawrence representation \({\mathcal {H}}_{n,m}\) is defined over \({\mathbb {Z}}[x^{\pm 1},d^{\pm 1}]\). We have the following specialisations:
Also, the inclusion \(i:{\mathbb {Z}}[q^{\pm 1}] \rightarrow {\mathbb {Q}}(q)\) and \(\alpha _{\lambda }=i \circ \psi _{\lambda }\).
Definition 7.1.1
Consider the specialisation which enlarges the ring of coefficients in the following manner:
As before, we need to work over a field. Let us consider the inclusion map:
Then, let us define the extension of the initial ring by:
In order to make the connection to the specialisation from Theorem 6.0.2, let us consider the change of coefficients:
We have the following commutative diagrams between these specialisations of coefficients (Fig. 3).
Using a similar argument as the one that we discussed in Sect. 5.3, one concludes that the identification between quantum and homological representations works over a ring with two indeterminates. This was also briefly discussed in [8].
Theorem 7.1.2
The braid group representations over \({\mathbb {Z}}[s^{\pm 1}, q^{\pm 1}]\) are isomorphic:
7.2 Lifts of the homology classes \(\tilde{\mathscr {F}}_n^N\) and \( \tilde{\mathscr {G}}_n^N\)
Having in mind this identification between the braid group actions, a natural question would be to lift the homology classes constructed in Theorem 6.0.2, which live a priori in the homology groups specialised by \(\alpha _{N-1}\), towards two elements belonging to the Lawrence representation specialised over two variables by the specialisation \(\xi \). However, in our arguments we need to work over a field in order to be able to interpret the elements from the dual of the homology by the pairing with dual elements. So, we will use the specialisation \(\gamma \) and prove the following.
Lemma 7.2.1
There exist two homology classes
such that under the specialisation \(\delta _{N-1}\) one has:
Proof
(1) We start with the definition of the class \(\tilde{{\mathscr {F}}}_n^N\) and aim to lift it over two variables. Following the discussion from Step 6.2, the normalising function can be lifted over two variables. From relation (62) there exists \({\tilde{v}}_n^N\in \hat{W}_{2n,n(N-1)}\) such that:
Following the definition of the normalised coevaluation we have:
We remark that the function \(\phi \) from Proposition 2.6.2 is also defined over the ring with two parameters, so the isomorphisms from Theorem 5.3.1 and Theorem 7.1.2 are related as below:
Definition 7.2.2
Using the isomorphism from (111), let us consider the class:
From relations (113), (114) and the construction of the homology class from (96) we obtain:
Definition 7.2.3
(Lift of the first homology class) Following the construction of the first homology class over a field from (102) and relation (115), let us consider:
We remark that there is the following commutativity of the specialisations:
Putting together the definitions of the first class from (102) and the globalised class from (116) with the properties (115) and (117) we conclude the first relation from the statement:
(2) We remark that the action of the quantum group, in particular the generator K, can be seen over \({\mathbb {Z}}[q^{\pm 1},s^{\pm 1}]\) and the evaluation from (8) can be defined over \({\mathbb {Z}}[s^{\pm 1},q^{\pm 1}]\) as well. On the other hand, we have seen that the coefficients of \(\alpha _{n,N}\) can be lifted over two variables. We conclude that there exists a normalised evaluation over two variables:
which specialises to the normalised evaluation:
Definition 7.2.4
Using this evaluation and Kohno’s function over two variables, let us consider the elements:
We notice that the Blanchfield pairing remains non-degenerate when we specialise the coefficients using the function \(\gamma \):
Definition 7.2.5
(Globalisation of the second homology class) Dualising the globalised evaluation \(\mathscr {G}_n\) using the non-degenerate pairing \(\langle ~,~\rangle |_{\gamma }\) we get a homology class \({\mathscr {G}}_n^N \in H^{\partial }_{2n, n(N-1)}|_{\gamma }\) such that:
Following the construction from Definition 6.7.1, the definition of the globalised class from (121) and the commutativity property of specialisations from (117), we obtain the second specialisation property:
\(\square \)
Now we will finish the proof of the main Theorem 1.0.2. Using that the braid group action commutes with the specialisation of the coefficients, the intersection pairings are related with one another as follows:
Following the homological model from Theorem 6.0.2, the construction of lifts of the homology classes from Lemma 7.2.1 and the previous relation between intersection pairings we conclude the topological model for \(J_N(L,q)\) with globalised homology classes.
References
Anghel, C.: Coloured Jones and Alexander polynomials as topological intersections of cycles in configuration spaces. math.GT Submitted, 47 p (2020) arXiv: 2002.09390
Anghel, C.: \(U_q(sl(2))-\)quantum invariants unified via intersections of embedded Lagrangians. math.GT, Submitted, 24 p (2020). arXiv: 2010.05890
Anghel, C.: Witten–Reshetikhin–Turaev invariants for \(3\)-manifolds from Lagrangian intersections in configuration spaces. Submitted, 24 p (2021). arXiv: 2104.02049
Bigelow, S.: A homological definition of the Jones polynomial. In: Invariants of knots and 3-manifolds (Kyoto, 2001), volume 4 of Geom. Topol. Monogr., pp. 29–41. Geom. Topol. Publ., Coventry (2002)
Bigelow, S.: Braid groups are linear. J. Am. Math. Soc. 14, 471–486 (2001)
Bigelow, S.: Homological representations of the Iwahori–Hecke algebra. In: Geometry and Topology Monographs, Volume 7: Proceedings of the Casson Fest, pp. 493–507 (2004)
Bigelow, S.: A homological definition of the HOMFLY polynomial. Algebr. Geom. Topol. 7, 1409–1440 (2007)
Ito, T.: Reading the dual Garside length of braids from homological and quantum representations. Commun. Math. Phys. 335(1), 345–367 (2015)
Ito, T.: Topological formula of the loop expansion of the colored Jones polynomials. Trans. Am. Math. Soc. 372, 53–70 (2019)
Jackson, C., Kerler, T.: The Lawrence–Krammer–Bigelow representations of the braid groups via \(U_q(sl_2)\). Adv. Math. 228, 1689–1717 (2011)
Kashaev, R.: The hyperbolic volume of knots from the quantum dilogarithm. Lett. Math. Phys. 39, 269–275 (1997)
Kassel, C.: Quantum Groups. Springer, Berlin (1995)
Kassel, C., Turaev, V.: Braid Groups. Springer, Berlin (2008)
Kohno, T.: Homological representations of braid groups and KZ connections. J. Singul. 5, 94–108 (2012)
Kohno, T.: Quantum and homological representations of braid groups. In: Configuration Spaces—Geometry, Combinatorics and Topology, Edizioni della Normale, pp. 355–372 (2012)
Krammer, D.: The braid group B4 is linear. Invent. Math. 142, 451–486 (2000)
Krammer, D.: Braid groups are linear. Ann. Math. 2(155), 131–156 (2002)
Lawrence, R.J.: Homological representations of the Hecke algebra. Commun. Math. Phys. 135, 141–191 (1990)
Lawrence, R.J.: A functorial approach to the one-variable Jones polynomial. J. Differ. Geom. 37(3), 689–710 (1993)
Martel, J.: A homological model for \(U_q(sl(2)\) Verma-modules and their braid representations (2020). arXiv:2002.08785
Murakami, H., Murakami, J.: The colored Jones polynomials and the simplicial volume of a knot. Acta Math. 186, 85–104 (2001)
Schechtman, V., Varchenko-, A.: Hypergeometric solutions of the Knizhnik–Zamolodchikov equation. Lett. Math. Phys. 20, 93–102 (1990)
Varchenko, A.: Multidimensional hypergeometric functions and representation theory of Lie algebras and quantum groups. Adv. Math. Phys. vol. 21. World Scientific (1995). https://www.maths.ox.ac.uk/people/cristina.palmer-anghel
Acknowledgements
I would like to thank very much my advisor, Professor Christian Blanchet for posing this beautiful problem of finding homological interpretations for quantum invariants, at the beginning of my Ph.D. I am very grateful for many useful and nice discussions and for his continuous support. Also, I am thankful to Dr Martin Palmer for discussions about homology with twisted coefficients and Lawrence representations. This research was supported by Grants from Région Ile-de-France. I would also like to thank the Isaac Newton Institute for support and hospitality during the programme “Homology theories in low dimensional topology” where work on this paper was undertaken between 12 February–28 March 2017 and supported also by EPSRC Grant No EP/K032208/1. The second version of this paper was prepared at the University of Oxford, and I acknowledge the support of the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement No 674978).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.