Abstract
We consider the Hodge filtration on the sheaf of meromorphic functions along free divisors for which the logarithmic comparison theorem holds. We describe the Hodge filtration steps as submodules of the order filtration on a cyclic presentation in terms of a special factor of the Bernstein–Sato polynomial of the divisor and we conjecture a bound for the generating level of the Hodge filtration. Finally, we develop an algorithm to compute Hodge ideals of such divisors and we apply it to some examples.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
For a reduced divisor D in a complex manifold X of dimension n, we consider the sheaf \({\mathcal {O}}_X(*D)\) of meromorphic functions along D. It is well-known that this is a coherent and holonomic left \({\mathcal {D}}_X\)-module, which underlies a mixed Hodge module on X (see [37, 38] and more specifically [39]). The latter can be constructed in a functorial way as  , where \(U:=X\backslash D\), \(j:U\hookrightarrow X\) is the canonical embedding, and
, where \(U:=X\backslash D\), \(j:U\hookrightarrow X\) is the canonical embedding, and  denotes the constant pure Hodge module on U. The aim of this paper is to describe the Hodge filtration on the mixed Hodge module
denotes the constant pure Hodge module on U. The aim of this paper is to describe the Hodge filtration on the mixed Hodge module  for certain divisors and to compute it explicitly in some examples. This question has some history, but has recently been reconsidered in a series of articles (see [28,29,30,31]) by Mustaţă and Popa (in the algebraic setting though), from a birational point of view. The authors of these papers introduce the so-called Hodge ideals: these are coherent sheaves of ideals \({\mathcal {I}}_k(D)\subset {\mathcal {O}}_X\) measuring the difference between the Hodge filtration \(F^H_\bullet {\mathcal {O}}(*D)\) and the pole order filtration \(P_\bullet {\mathcal {O}}_X(*D)\). The latter consists of locally free \({\mathcal {O}}_X\)-modules of rank one given by \(P_k {\mathcal {O}}_X(*D):={\mathcal {O}}_X((k+1)D)\). Indeed, by a classical result of Saito ([39, Proposition 0.9]) we always have \(F^H_k {\mathcal {O}}_X(*D) \subset P_k{\mathcal {O}}_X(*D)\), with equality if and only if D is smooth (the “only if” part of the latter statement is also due to Mustaţă and Popa, see [28, Theorem A]) and then one puts
for certain divisors and to compute it explicitly in some examples. This question has some history, but has recently been reconsidered in a series of articles (see [28,29,30,31]) by Mustaţă and Popa (in the algebraic setting though), from a birational point of view. The authors of these papers introduce the so-called Hodge ideals: these are coherent sheaves of ideals \({\mathcal {I}}_k(D)\subset {\mathcal {O}}_X\) measuring the difference between the Hodge filtration \(F^H_\bullet {\mathcal {O}}(*D)\) and the pole order filtration \(P_\bullet {\mathcal {O}}_X(*D)\). The latter consists of locally free \({\mathcal {O}}_X\)-modules of rank one given by \(P_k {\mathcal {O}}_X(*D):={\mathcal {O}}_X((k+1)D)\). Indeed, by a classical result of Saito ([39, Proposition 0.9]) we always have \(F^H_k {\mathcal {O}}_X(*D) \subset P_k{\mathcal {O}}_X(*D)\), with equality if and only if D is smooth (the “only if” part of the latter statement is also due to Mustaţă and Popa, see [28, Theorem A]) and then one puts
It is known (see [28, Proposition 10.1] as well as [41, Theorem 0.4]) that the zeroth Hodge ideal \({\mathcal {I}}_0(D)\) coincides with the multiplier ideal \({\mathcal {J}}((1-\varepsilon )D)\). Notice that the latter, although originally defined either analytically or via birational methods (see, e.g., [23, Section 9] and the references given therein) was already known to have a description via \({\mathcal {D}}\)-modules, see [5, Theorem 0.1]. For X projective, there is the celebrated Nadel vanishing theorem for multiplier ideals, and one looks for similar statements for the higher Hodge ideals (see [28, §§ G and H] and also [15]); these have applications e.g. if  or if X is an abelian variety.
or if X is an abelian variety.
The known results on Hodge ideals are mostly either global in nature, or concern the case of isolated singularities, see e.g. [21, 49]. In this paper, we are interested in a specific class of divisors with highly non-isolated singular loci (namely, we will have \(\text {codim}_D(D_{\text {sing}})=1\), in particular, these divisors are not normal). These are the so-called free divisors, introduced and first studied by K. Saito almost 40 years ago (see [36]). They often appear as discriminants in a generalized sense, e.g., discriminants of singularities of maps (e.g. isolated hypersurface or complete intersection singularities, see, e.g. [24], or of reduced space curves [48]) or discriminants in quiver representation spaces (see, e.g., [17]). Another important class of free divisors are free hyperplane arrangements (see, e.g., [12, Chapter 8]); we will perform some computations for Hodge ideals for low-dimensional examples of free arrangements in section 5 below.
Although our methods are adapted to the special situation of free divisors, we believe that they have the potential to give insights into the structure of the Hodge filtration steps on \({\mathcal {O}}_X(*D)\) in more general situations. As an example, we consider cases of divisors that are not free, but close to it at the very end of the paper. More generally, it is clear that the Hodge filtration on \({\mathcal {O}}_X(*D)\) can always be accessed using the approach of our paper, that is, by some non-trivial use of the V-filtration along this divisor (see below), however, the concrete calculation of this V-filtration might sometimes be difficult. A related, though different approach, also using the V-filtration, is found in [30, 31]. In concrete classes of examples, such as hyperplane arrangements, we hope that our results, and more generally the study of Hodge ideals will be useful for classical questions, like Terao’s conjecture, or the homological characterization of freeness ( [14]).
Let us briefly recall the definition of free divisors. For a complex manifold X, we denote by \(\Omega ^p_X\) resp. by \(\Theta _X\) the locally free \({\mathcal {O}}_X\)-module of holomorphic p-forms resp. the locally free \({\mathcal {O}}_X\)-module of tangent vector fields or of  -derivations of \({\mathcal {O}}_X\). If \(D\subset X\) is a reduced divisor, then we write \(\Omega ^1_X(\log \, D)\) resp. \(\Theta _X(-\log \,D)\) for the sheaf of logarithmic one-forms resp. of logarithmic vector fields on X, that is:
-derivations of \({\mathcal {O}}_X\). If \(D\subset X\) is a reduced divisor, then we write \(\Omega ^1_X(\log \, D)\) resp. \(\Theta _X(-\log \,D)\) for the sheaf of logarithmic one-forms resp. of logarithmic vector fields on X, that is:
where \({\mathcal {I}}(D)\subset {\mathcal {O}}_X\) is the ideal sheaf of D. These are coherent and reflexive \({\mathcal {O}}_X\)-modules. The examples of divisors that we are studying in this paper are given by the following condition.
Definition 1.1
(see [36]) A divisor \(D\subset X\) is called free if the sheaf \(\Omega ^1_X(\log \,D)\) (or, equivalently, the sheaf \(\Theta _X(-\log \,D)\)) is a locally free \({\mathcal {O}}_X\)-module.
If D is free, then we have the equality
Hence the terms of the so-called logarithmic de Rham complex of (X, D), i.e., the complex \((\Omega ^\bullet _X(\log \,D),d)\), are locally free \({\mathcal {O}}_X\)-modules. Notice that the most basic example of a free divisor is a divisor with simple normal crossings, in which case the logarithmic de Rham complex is a well studied object. It is particularly useful for the construction (due to Deligne, see, e.g., [33, II.4]) of a mixed Hodge structure on the cohomology of the complement \(U=X\backslash D\), in case it is quasi-projective. If D has simple normal crossings, then it is classical that the logarithmic de Rham complex computes the cohomology of U, in other words, we have a quasi-isomorphism  . This is not always true for any free divisor, but if it is, we say that the logarithmic comparison theorem holds for D (see [11]). This is in particular the case under a condition called strongly Koszul (see [32, Corollary 4.5]), which we recall in the next section (see Definition 2.3 below). Strongly Koszul free divisors are the objects of study of this paper. Many interesting free divisors, such as free hyperplane arrangements, or more generally locally quasi-homogeneous free divisors satisfy the strong Koszul hypothesis. A nice feature of divisors in this class is that we have a natural isomorphism \({\mathcal {D}}_X \otimes _{{\mathcal {V}}_X^D} {\mathcal {O}}_X(D) \cong {\mathcal {O}}_X(*D)\), where \({\mathcal {V}}_X^D\) is the sheaf of logarithmic differential operators with respect to D, from which we obtain an explicit representation of \({\mathcal {O}}_X(*D)\cong {\mathcal {D}}_X/{\mathcal {I}}\), where \({\mathcal {I}}\) is a left ideal in \({\mathcal {D}}_X\). As a consequence, we can consider another filtration (besides the Hodge filtration) \(F_\bullet ^{{\text {ord}}}{\mathcal {O}}_X(*D)\), called the order filtration, which is simply given by the image of \(F_\bullet {\mathcal {D}}_X\) (the filtration by order of differential operators) under the isomorphism \({\mathcal {D}}_X \otimes _{{\mathcal {V}}_X^D} {\mathcal {O}}_X(D) {\mathop {\rightarrow }\limits ^{\cong }} {\mathcal {O}}_X(*D)\) (or, equivalently, is induced from \(F_\bullet {\mathcal {D}}_X\) when writing \({\mathcal {O}}_X(*D)\cong {\mathcal {D}}_X/{\mathcal {I}}\) for the ideal \({\mathcal {I}}\) mentioned above).
. This is not always true for any free divisor, but if it is, we say that the logarithmic comparison theorem holds for D (see [11]). This is in particular the case under a condition called strongly Koszul (see [32, Corollary 4.5]), which we recall in the next section (see Definition 2.3 below). Strongly Koszul free divisors are the objects of study of this paper. Many interesting free divisors, such as free hyperplane arrangements, or more generally locally quasi-homogeneous free divisors satisfy the strong Koszul hypothesis. A nice feature of divisors in this class is that we have a natural isomorphism \({\mathcal {D}}_X \otimes _{{\mathcal {V}}_X^D} {\mathcal {O}}_X(D) \cong {\mathcal {O}}_X(*D)\), where \({\mathcal {V}}_X^D\) is the sheaf of logarithmic differential operators with respect to D, from which we obtain an explicit representation of \({\mathcal {O}}_X(*D)\cong {\mathcal {D}}_X/{\mathcal {I}}\), where \({\mathcal {I}}\) is a left ideal in \({\mathcal {D}}_X\). As a consequence, we can consider another filtration (besides the Hodge filtration) \(F_\bullet ^{{\text {ord}}}{\mathcal {O}}_X(*D)\), called the order filtration, which is simply given by the image of \(F_\bullet {\mathcal {D}}_X\) (the filtration by order of differential operators) under the isomorphism \({\mathcal {D}}_X \otimes _{{\mathcal {V}}_X^D} {\mathcal {O}}_X(D) {\mathop {\rightarrow }\limits ^{\cong }} {\mathcal {O}}_X(*D)\) (or, equivalently, is induced from \(F_\bullet {\mathcal {D}}_X\) when writing \({\mathcal {O}}_X(*D)\cong {\mathcal {D}}_X/{\mathcal {I}}\) for the ideal \({\mathcal {I}}\) mentioned above).
The main tool to describe the Hodge filtration \(F^H_\bullet {\mathcal {O}}_X(*D)\) is to look at the graph embedding  , where h is a local defining equation of D, and to consider \(i_{h,+} {\mathcal {O}}_X(*D)\). It also underlies a mixed Hodge module (on
, where h is a local defining equation of D, and to consider \(i_{h,+} {\mathcal {O}}_X(*D)\). It also underlies a mixed Hodge module (on  ), and it is well-known that the Hodge filtration on \({\mathcal {O}}_X(*D)\) can be deduced from the one on \(i_{h,+} {\mathcal {O}}_X(*D)\) (up to a shift by one), and vice versa. More precisely, recall that \(i_{h,+}{\mathcal {O}}_X(*D) \cong {\mathcal {O}}_X(*D)[\partial _t]\) (we recall the
), and it is well-known that the Hodge filtration on \({\mathcal {O}}_X(*D)\) can be deduced from the one on \(i_{h,+} {\mathcal {O}}_X(*D)\) (up to a shift by one), and vice versa. More precisely, recall that \(i_{h,+}{\mathcal {O}}_X(*D) \cong {\mathcal {O}}_X(*D)[\partial _t]\) (we recall the  -module structure on \({\mathcal {O}}_X(*D)[\partial _t]\) in Formula (19) on page 22 below), and that under this isomorphism, we have
-module structure on \({\mathcal {O}}_X(*D)[\partial _t]\) in Formula (19) on page 22 below), and that under this isomorphism, we have
Hence we are reduced to determine \(F^H_\bullet i_{h,+} {\mathcal {O}}_X(*D)\). In order to do so, we use a key property of mixed Hodge modules, which is known as strict specializability. It can be rephrased as a formula (see [39, Proposition 4.2]) describing the Hodge filtration on a module which is the extension of its restriction outside a smooth divisor (which is the hyperplane  in our case). In order to use it, we have to compute some steps of the canonical V-filtration along
\(\{t=0\}\) of the module
\(i_{h,+}{\mathcal {O}}_X(*D)\), denoted by
\(V^\bullet _{{\text {can}}} i_{h,+}{\mathcal {O}}_X(*D)\). Here we rely crucially on a previous result of the second named author ([32, Theorem 4.1]), namely, that the roots of the Bernstein–Sato polynomial
\(b_h(s)\) of h are contained in \((-2,0)\) and that they are symmetric around \(-1\). As we will see below, the set of roots of \(b_h(s)\) bigger than \(-1\) plays a particular role, and we put
in our case). In order to use it, we have to compute some steps of the canonical V-filtration along
\(\{t=0\}\) of the module
\(i_{h,+}{\mathcal {O}}_X(*D)\), denoted by
\(V^\bullet _{{\text {can}}} i_{h,+}{\mathcal {O}}_X(*D)\). Here we rely crucially on a previous result of the second named author ([32, Theorem 4.1]), namely, that the roots of the Bernstein–Sato polynomial
\(b_h(s)\) of h are contained in \((-2,0)\) and that they are symmetric around \(-1\). As we will see below, the set of roots of \(b_h(s)\) bigger than \(-1\) plays a particular role, and we put

for later reference. For an element
\(\alpha _i\in B_h'\), we write
\(l_i\) for the multiplicity of the root \(\alpha _i-1\) in \(b_h\). The polynomial  is the special factor of the Bernstein–Sato polynomial \(b_h(s)\) mentioned in the abstract.
is the special factor of the Bernstein–Sato polynomial \(b_h(s)\) mentioned in the abstract.
We can consider another V-filtration on the module \(i_{h,+}{\mathcal {O}}_X(*D)\), induced from  for a cyclic presentation
for a cyclic presentation  of \(i_{h,+}{\mathcal {O}}_X(*D)\) obtained from the cyclic presentation \({\mathcal {D}}_X/{\mathcal {I}}\) of \({\mathcal {O}}_X(*D)\) mentioned above. We will denote it by \(V^\bullet _{{\text {ind}}} i_{h,+}{\mathcal {O}}_X(*D)\). Knowing that \(b_h(s)\) is closely related to the b-function of such filtration (see Lemma 3.2 below), we can describe \(V^k_{{\text {can}}} i_{h,+}{\mathcal {O}}_X(*D)\) at least for integer values of k as a submodule of \(V^k_{{\text {ind}}} i_{h,+}{\mathcal {O}}_X(*D)\).
of \(i_{h,+}{\mathcal {O}}_X(*D)\) obtained from the cyclic presentation \({\mathcal {D}}_X/{\mathcal {I}}\) of \({\mathcal {O}}_X(*D)\) mentioned above. We will denote it by \(V^\bullet _{{\text {ind}}} i_{h,+}{\mathcal {O}}_X(*D)\). Knowing that \(b_h(s)\) is closely related to the b-function of such filtration (see Lemma 3.2 below), we can describe \(V^k_{{\text {can}}} i_{h,+}{\mathcal {O}}_X(*D)\) at least for integer values of k as a submodule of \(V^k_{{\text {ind}}} i_{h,+}{\mathcal {O}}_X(*D)\).
Our main result can then be summarized as follows:
Theorem
(see Proposition 3.3 and Theorem 4.4 below) Let \(D\subset X\) be a strongly Koszul free divisor, and suppose that it is globally given by a reduced equation \(h\in {\mathcal {O}}_X\). Then:
-
1.
We have the following inclusions of coherent \({\mathcal {O}}_X\)-modules:
$$\begin{aligned} F^H_\bullet {\mathcal {O}}_X(*D) \subset F^{{\text {ord}}}_\bullet {\mathcal {O}}_X(*D) \subset P_\bullet {\mathcal {O}}_X(*D). \end{aligned}$$ -
2.
The zeroth step of the canonical V-filtration on \(i_{h,+}{\mathcal {O}}_X(*D)\) can be described as follows:
$$\begin{aligned} V^0_{{\text {can}}} i_{h,+} {\mathcal {O}}_X(*D) \cong \displaystyle V_{{\text {ind}}}^1 i_{h,+} {\mathcal {O}}_X(*D) + \prod _{\alpha _i\in B'_h} (\partial _t t +\alpha _i)^{l_i} V_{{\text {ind}}}^0 i_{h,+} {\mathcal {O}}_X(*D). \end{aligned}$$ -
3.
For all
 , we have the following recursive formula for the Hodge filtration on \({\mathcal {O}}_X(*D)\) (recall the shift convention between \(F_\bullet ^H{\mathcal {O}}_X(*D)\) and \(F_\bullet ^H i_{h,+}{\mathcal {O}}_X(*D)\)): $$\begin{aligned}&F_k^H {\mathcal {O}}_X(*D) \cong \nonumber \\&\quad \left[ \partial _t F^H_k i_{h,+}{\mathcal {O}}_X(*D)+V^0_{{\text {can}}} i_{h,+}{\mathcal {O}}_X(*D)\right] \cap \left( F_k^{{\text {ord}}}{\mathcal {O}}_X(*D)\otimes 1\right) . \end{aligned}$$(3)
, we have the following recursive formula for the Hodge filtration on \({\mathcal {O}}_X(*D)\) (recall the shift convention between \(F_\bullet ^H{\mathcal {O}}_X(*D)\) and \(F_\bullet ^H i_{h,+}{\mathcal {O}}_X(*D)\)): $$\begin{aligned}&F_k^H {\mathcal {O}}_X(*D) \cong \nonumber \\&\quad \left[ \partial _t F^H_k i_{h,+}{\mathcal {O}}_X(*D)+V^0_{{\text {can}}} i_{h,+}{\mathcal {O}}_X(*D)\right] \cap \left( F_k^{{\text {ord}}}{\mathcal {O}}_X(*D)\otimes 1\right) . \end{aligned}$$(3)
Notice that part 2 actually holds under weaker assumptions on D, see Proposition 3.3 below for more details.
Combining these three results and taking into account equation (1) allow us to determine the Hodge ideals of D. Theorem 5.2 below (and specifically Formula (48)) gives a concrete and explicit way to calculate the Hodge filtration steps on \(i_{h,+}{\mathcal {O}}_X(*D)\) resp. on \({\mathcal {O}}_X(*D)\) and the Hodge ideals of D. In the second part of section 5, we apply our method to certain interesting examples.
In applications, it is sometimes useful to study the behaviour of a Hodge module under the duality functor. It is defined for objects of the category \({\text {MHM}}\), but it restricts to the usual holonomic dual of the underlying \({\mathcal {D}}\)-module. We give (see Theorem 4.10) some statements estimating the Hodge filtration on the dual Hodge module with underlying \({\mathcal {D}}_X\)-module  , following standard convention, this \({\mathcal {D}}_X\)-module is denoted by \({\mathcal {O}}_X(!D)\). Interestingly, our results on the dual Hodge filtration also involve the cardinality of the set \(B'_h\), i.e. the number of roots (counted with multiplicity) of \(b_h\) lying strictly in the interval \((-1,0)\). Finally, we state a conjecture (see Conjecture 4.12) estimating the generating level of the Hodge filtration \(F^H_\bullet {\mathcal {O}}_X(*D)\), namely, we expect that it is always generated at level \(|B'_h|\). Computation of examples in section 5 supports this conjecture.
, following standard convention, this \({\mathcal {D}}_X\)-module is denoted by \({\mathcal {O}}_X(!D)\). Interestingly, our results on the dual Hodge filtration also involve the cardinality of the set \(B'_h\), i.e. the number of roots (counted with multiplicity) of \(b_h\) lying strictly in the interval \((-1,0)\). Finally, we state a conjecture (see Conjecture 4.12) estimating the generating level of the Hodge filtration \(F^H_\bullet {\mathcal {O}}_X(*D)\), namely, we expect that it is always generated at level \(|B'_h|\). Computation of examples in section 5 supports this conjecture.
The paper is organized as follows: In section 2, we first introduce rigorously the class of divisors we are interested in, and define the order filtration on \({\mathcal {O}}_X(*D)\) globally. We prove an important fact for the filtered module \(({\mathcal {O}}_X(*D),F_\bullet ^{{\text {ord}}})\), which is known as the Cohen-Macaulay property (see Proposition 2.9). It is known from Saito’s theory that the same property holds for \(({\mathcal {O}}_X(*D),F_\bullet ^H)\), i.e., the filtered module underlying the mixed Hodge module  . We are using the Cohen-Macaulay property of both filtrations to give the estimation of the Hodge filtration on the dual module of \({\mathcal {O}}_X(*D)\) (see Theorem 4.10) referred to above.
. We are using the Cohen-Macaulay property of both filtrations to give the estimation of the Hodge filtration on the dual module of \({\mathcal {O}}_X(*D)\) (see Theorem 4.10) referred to above.
In section 3, we recall some general facts on V-filtrations and then describe (see Proposition 3.3) the canonical V-filtration on the graph embedding module of \({\mathcal {O}}_X(*D)\). In the subsequent section 4, we use these results to prove formula (3) (see Theorem 4.4). Finally, in section 5, we develop techniques for the computation of Hodge ideals, and perform them for some significant examples.
2 Filtration by order on \({\mathcal {O}}_X(*D)\)
The purpose of this section is to introduce the class of divisors we are going to study in this paper, these are free divisors satisfying the strong Koszul hypothesis. In that case, we can define a particular good filtration \(F_\bullet ^{{\text {ord}}}\) on the sheaf \({\mathcal {O}}_X(*D)\). We call it order filtration, because if locally we choose a reduced equation h for D, then the strong Koszul hypothesis implies that there is a canonical representation of \({\mathcal {O}}_X(*D)\) as a cyclic left \({\mathcal {D}}_X\)-module (generated by \(h ^{-1}\)) \({\mathcal {D}}_X/{\mathcal {I}}(h)\), and then our order filtration is the filtration on \({\mathcal {D}}_X/{\mathcal {I}}(h)\) induced by the filtration on \({\mathcal {D}}_X\) by the order of differential operators. Nevertheless, as we will see below, \(F_\bullet ^{{\text {ord}}} {\mathcal {O}}_X(*D)\) is globally well defined. As mentioned in the introduction, one of our main results is that for each  the Hodge filtration \(F_k^H {\mathcal {O}}_X(*D)\) is a coherent \({\mathcal {O}}_X\)-submodule of \(F_k^{{\text{ ord }}}{\mathcal {O}}_X(*D)\) as well as a precise description of the inclusion \(F_k^H {\mathcal {O}}_X(*D) \subset F_k^{{\text{ ord }}}{\mathcal {O}}_X(*D)\) (see Theorem 4.4 below). We will also show in this section that the order filtration \(F^{{\text {ord}}}_\bullet {\mathcal {O}}_X(*D)\) shares a key feature with \(F_\bullet ^H {\mathcal {O}}_X(*D)\), known as the Cohen-Macaulay property. This is used in section 4 (see the proof of Theorem 4.10) to give some statement about the dual Hodge filtration.
the Hodge filtration \(F_k^H {\mathcal {O}}_X(*D)\) is a coherent \({\mathcal {O}}_X\)-submodule of \(F_k^{{\text{ ord }}}{\mathcal {O}}_X(*D)\) as well as a precise description of the inclusion \(F_k^H {\mathcal {O}}_X(*D) \subset F_k^{{\text{ ord }}}{\mathcal {O}}_X(*D)\) (see Theorem 4.4 below). We will also show in this section that the order filtration \(F^{{\text {ord}}}_\bullet {\mathcal {O}}_X(*D)\) shares a key feature with \(F_\bullet ^H {\mathcal {O}}_X(*D)\), known as the Cohen-Macaulay property. This is used in section 4 (see the proof of Theorem 4.10) to give some statement about the dual Hodge filtration.
For the remainder of this paper (except in subsection 5.4, where we explicitly relax these assumptions), we will assume X to be an n-dimensional complex manifold, and \(D\subset X\) a free divisor. We will be specifically working with those free divisors satisfying an additional hypothesis called strongly Koszul, that we define now.
Denote as before by \(\Theta _X\) the locally free \({\mathcal {O}}_X\)-module of rank n of vector fields and by \({\mathcal {D}}_X\) the sheaf of linear differential operators with holomorphic coefficients, endowed with the filtration \(F_\bullet {\mathcal {D}}_X\) by the order of differential operators. For each divisor \(D\subset X\) we write \({\mathcal {O}}_X(*D)\) for the sheaf of meromorphic functions with poles along D and \(\Omega _X^\bullet (*D)\) the meromorphic de Rham complex. If D is a free divisor, we denote by \(\Theta _X(-\log D) \subset \Theta _X\) the locally free \({\mathcal {O}}_X\)-module of rank n of logarithmic vector fields and by \(\Omega _X^\bullet (\log \,D)\) the logarithmic de Rham complex. Moreover, we let

be the sheaf of rings of logarithmic differential operators with respect to D. It is filtered by the order of differential operators as well, namely \(F_k {\mathcal {V}}_X^D := {\mathcal {V}}_X^D \cap F_k {\mathcal {D}}_X\) for all  , and there is a canonical isomorphism of graded \({\mathcal {O}}_X\)-algebras (see [7, Remark 2.1.5])
, and there is a canonical isomorphism of graded \({\mathcal {O}}_X\)-algebras (see [7, Remark 2.1.5])
The sheaf \({\mathcal {O}}_X(D)\subset {\mathcal {O}}_X(*D)\) of meromorphic functions with poles of order \(\le 1\) is a left \({\mathcal {V}}_X^D\)-module by the definition of \({\mathcal {V}}_X^D\) and we have a canonical \({\mathcal {D}}_X\)-linear map ( [9, §4])
We quote the following result (see [9, Corollaire 4.2]):
Theorem 2.1
Let \(D\subset X\) be a free divisor. The following properties are equivalent:
-
(i)
The logarithmic comparison theorem (LCT) holds for D (i.e. the inclusion \(\Omega _X^\bullet (\log \,D) \hookrightarrow \Omega _X^\bullet (*D)\) is a quasi-isomorphism of complexes of sheaves of
 -vector spaces).
-vector spaces). -
(ii)
The map (4) is a quasi-isomorphism of complexes of left \({\mathcal {D}}_X\)-modules.
Let us notice that property (ii) in the above theorem means that the complex \({\mathcal {D}}_X {\mathop {\otimes }\limits ^{{\mathbf {L}}}}_{{\mathcal {V}}_X^D} {\mathcal {O}}_X(D)\) is concentrated in degree 0 and the canonical \({\mathcal {D}}_X\)-linear map
is an isomorphism of left \({\mathcal {D}}_X\)-modules.
Definition 2.2
Assume that \(D\subset X\) is free and that the logarithmic comparison theorem holds for D. We define the order filtration \(F_\bullet ^{{\text {ord}}} {\mathcal {O}}_X(*D)\) by
which by definition is a filtration by \({\mathcal {O}}_X\)-coherent submodules.
Let us give a more explicit local description. Let \(p\in D\), and take a basis \(\delta _1,\dots ,\delta _n\) of \(\Theta _X(-\log D)_p\) as well as a local equation \(h\in {\mathcal {O}}_{X,p}\) of D around p, such that \(\delta _i(h)=\alpha _i h\). Assume that the LCT holds for D, then we have the following explicit local presentation
where the class [1] is send to \(h^{-1}\) (see the explanation after Corollaire 4.2 in [9]). Under this isomorphism, the filtration \(F_\bullet ^{{\text {ord}}} {\mathcal {O}}_X(*D)_p\) is the induced filtration on \( {\mathcal {D}}_{X,p}/{\mathcal {D}}_{X,p}(\delta _1+\alpha _1,\dots ,\delta _n+\alpha _n)\) by \(F_\bullet {\mathcal {D}}_{X,p}\), which explains its name.
We now introduce the strong Koszul hypothesis. It implies that the LCT holds for \(D\subset X\), but it is stronger. Its additional assumptions will be needed in the next section.
Definition 2.3
Let \(D\subset X\) be a free divisor and let \(p\in D\). Let \(h\in {\mathcal {O}}_{X,p}\) be a local reduced equation of (D, p) and let \(\delta _1,\ldots , \delta _n\) be any \({\mathcal {O}}_{X,p}\)-basis of \(\Theta _{X,p}(-\log \,D)\) with \( \delta _i(h) = \alpha _i h\).
-
1.
We say that D is Koszul at \(p\in D\) if the sequence
$$\begin{aligned} \sigma (\delta _1),\ldots , \sigma (\delta _n) \end{aligned}$$is regular in \(\text {Gr}^F_\bullet {\mathcal {D}}_{X,p}\). (Here and at later occasions, for an element P in a filtered ring, we denote by \(\sigma (P)\) its symbol, i.e. its class in the associated graded ring.)
-
2.
We say that D is strongly Koszul at \(p\in D\) if the sequence
$$\begin{aligned} h, \sigma (\delta _1)-\alpha _1 s,\dots , \sigma (\delta _n)-\alpha _n s \end{aligned}$$is regular in \(\text {Gr}^T_\bullet {\mathcal {D}}_{X,p}[s]\) (where \(T_\bullet {\mathcal {D}}_{X,p}[s]\) is the filtration on \({\mathcal {D}}_{X,p}[s]\) for which vector fields on X as well as the variable s have order 1, we will call it the total order filtration on \({\mathcal {D}}_{X,p}[s]\)).
We say that D is Koszul resp. strongly Koszul if it is so at any \(p\in D\). Since the strong Koszul assumption will be our main hypothesis later, we will sometimes abbreviate it by saying that D is an SK-free divisor.
Let us notice that, in the above definition, the ordering of the sequences is not relevant because their elements are homogeneous. Let us also notice that if D has an Euler local equation \(h\in {\mathcal {O}}_{X,p}\), i.e. h belongs to its gradient ideal (with respect to some local coordinates), then there is a basis \(\delta _1,\dots ,\delta _{n-1},\chi \) of \(\Theta _X(-\log D)_p\) with \(\delta _i(h)=0\) and \(\chi (h)=h\). In such a case, D is strongly Koszul at p if and only if \( h, \sigma (\delta _1),\dots , \sigma (\delta _{n-1})\) is a regular sequence in \(\text {Gr}^F_\bullet {\mathcal {D}}_{X,p}\) (compare with Definition 7.1 and Proposition 7.2 of [18] in the case of linear free divisors). For D to be strongly Koszul is equivalent to be of “linear Jacobian type”, i.e. the ideal \((h,h'_{x_1},\dots ,h'_{x_1})\) is of linear type, and any strongly Koszul free divisor is Koszul (see Propositions (1.11) and (1.14) of [32]).
Any plane curve is a Koszul free divisor. Any locally quasi-homogeneous free divisor is strongly Koszul [9, Theorem 5.6], and so are free hyperplane arrangements or discriminants of stable maps in Mather’s “nice dimensions”. In particular, any normal crossing divisor is strongly Koszul free.
Let us recall the following properties of SK-free divisors.
Proposition 2.4
If D is a strongly Koszul free divisor, then we have:
-
1.
D is locally strongly Euler homogeneous, that is, for each \(p\in D\) there is a vector field \(\chi \in \Theta _{X,p}\) which vanishes at p and such that \(\chi (h)=h\) for some reduced local equation h of D at p.
-
2.
The LCT holds for D, in particular, we have the local cyclic presentation of \({\mathcal {O}}_X(*D)\) from formula (5) above. More specifically, if for each \(p\in D\), we take h and \(\chi \) as in point 1 and if we let \(\delta _1,\dots ,\delta _{n-1}\) to be a basis of germs at p of vector fields vanishing on h, in such a way that \( \delta _1,\dots ,\delta _{n-1},\chi \) is a basis of \(\Theta _X(-log\,D)_p\), then there is an isomorphism of left \({\mathcal {D}}_{X,p}\)-modules
$$\begin{aligned} \frac{{\mathcal {D}}_{X,p}}{{\mathcal {D}}_{X,p}\left( \delta _1,\ldots ,\delta _{n-1},\chi +1\right) } \cong {\mathcal {O}}_{X,p}(*D), \end{aligned}$$(6)sending the class of \(1\in {\mathcal {D}}_{X,p}\) to \(h^{-1}\in {\mathcal {O}}_{X,p}(*D)\).
-
3.
Let \(p\in D\) be a point, \(h\in {\mathcal {O}}_{X,p}\) be a reduced local equation of D at p and \(b_h(s)\) the Bernstein–Sato polynomial of h (i.e., the monic generator of the ideal of polynomials
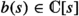 satisfying \(P(s) h^{s+1} = b(s) h^s\) for some \(P(s)\in {\mathcal {D}}_{X,p}[s]\)). Then we have \(b_h(-s-2) = \pm b_h(s)\). In particular, if
satisfying \(P(s) h^{s+1} = b(s) h^s\) for some \(P(s)\in {\mathcal {D}}_{X,p}[s]\)). Then we have \(b_h(-s-2) = \pm b_h(s)\). In particular, if  is the set of roots of \(b_h(s)\), with \(\alpha _1\le \cdots \le \alpha _k\), we have \(\alpha _i\in (-2,0)\) and \(\alpha _i+\alpha _{k+1-i}=-2\) for all i.
is the set of roots of \(b_h(s)\), with \(\alpha _1\le \cdots \le \alpha _k\), we have \(\alpha _i\in (-2,0)\) and \(\alpha _i+\alpha _{k+1-i}=-2\) for all i.
Proof
Part 1 is a consequence of Propositions (1.9) and (1.11) of [32]. Part 2 is a consequence of Corollary (4.5) of [32]. Part 3 is a consequence of Corollary (4.2) of [32]. \(\square \)
Remark 2.5
Definition 2.3 is purely algebraic and makes sense in rings other than analytic local rings \({\mathcal {O}}_{X,p}\), for instance in polynomial rings  , algebraic local rings of polynomial rings at maximal ideals or formal power series rings. Under this scope, if
, algebraic local rings of polynomial rings at maximal ideals or formal power series rings. Under this scope, if  is a non-constant reduced polynomial, \(D= {\mathcal {V}}(h) \) is the affine algebraic hypersurface with equation \(h=0\) and
is a non-constant reduced polynomial, \(D= {\mathcal {V}}(h) \) is the affine algebraic hypersurface with equation \(h=0\) and  is the corresponding analytic hypersurface, we know that D is a (algebraic) free divisor if and only if \(D^{an}\) is a (analytic) free divisor, and if so, the following properties are equivalent:
is the corresponding analytic hypersurface, we know that D is a (algebraic) free divisor if and only if \(D^{an}\) is a (analytic) free divisor, and if so, the following properties are equivalent:
-
(a)
The (affine algebraic) divisor D is strongly Koszul, i.e. for some (and hence for any) basis \(\delta _1,\dots ,\delta _n\) of
 , the sequence $$\begin{aligned} h, \sigma (\delta _1)-a_1 s,\ldots , \sigma (\delta _n)-a_n s,\quad \text {with}\quad \delta _i(h) = a_i h,\quad a_i\in R, \end{aligned}$$
, the sequence $$\begin{aligned} h, \sigma (\delta _1)-a_1 s,\ldots , \sigma (\delta _n)-a_n s,\quad \text {with}\quad \delta _i(h) = a_i h,\quad a_i\in R, \end{aligned}$$is regular in
 , where
, where 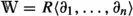 is the Weyl algebra and
is the Weyl algebra and  is the graded ring of
is the graded ring of  with respect to the total order filtration.
with respect to the total order filtration. -
(b)
For each maximal ideal \({\mathfrak {m}}\subset R\) containing h, D is strongly Koszul at \({\mathfrak {m}}\), i.e. for some (and hence for any) basis \(\delta _1,\dots ,\delta _n\) of

the sequence
$$\begin{aligned} h, \sigma (\delta _1)-a_1 s,\ldots , \sigma (\delta _n)-a_n s,\quad \text {with}\quad \delta _i(h) = a_i h, \quad a_i\in R_{\mathfrak {m}}, \end{aligned}$$is regular in
 , where
, where  , and
, and  is the graded ring of
is the graded ring of  with respect to the total order filtration.
with respect to the total order filtration. -
(c)
The (analytic) divisor \(D^{an}\) is strongly Koszul (in the sense of Definition 2.3 above).
The next step is to discuss some of the deeper properties of the order filtration \(F^{{\text {ord}}}_\bullet {\mathcal {O}}_X(*D)\). The main result is Proposition 2.9 below, which is concerned with the dual filtered module  . In order to do this, we need to recall a few facts about the duality theory of filtered modules. The original reference is [37, Section 2.4], but for what follows below, [43, § 29] provides enough background information.
. In order to do this, we need to recall a few facts about the duality theory of filtered modules. The original reference is [37, Section 2.4], but for what follows below, [43, § 29] provides enough background information.
For any complex manifold X, we consider the (sheaf of) Rees ring(s) \({\mathcal {R}}_F {\mathcal {D}}_X\) of the filtered ring \(({\mathcal {D}}_X,F_\bullet )\), that is  . In local coordinates \(x_1,\ldots ,x_n\) on \(U\subset X\), we have
. In local coordinates \(x_1,\ldots ,x_n\) on \(U\subset X\), we have
The ring \({\mathcal {R}}_F {\mathcal {D}}_X\) will be denoted by \({\widetilde{{\mathcal {D}}}}_X\). For what follows, we will need an interpretation of this sheaf in terms of Lie algebroids, more precisely, we will use the fact that \({\widetilde{{\mathcal {D}}}}_X\) is the enveloping algebra of the Lie algebroid  of rank \(n=\dim X\) over the
of rank \(n=\dim X\) over the  -algebra \({\mathcal {O}}_X[z]\).
-algebra \({\mathcal {O}}_X[z]\).
Lie algebroids are the sheaf version of Lie-Rinehart algebras (see [34]). They were originally studied in the setting of Differential Geometry (the book [25] is a complete reference here), and for instance in [6] the complex analytic case is considered.
For the ease of the reader, let us recall the notions of Lie-Rinehart algebras and Lie algebroids. Let us take a commutative base ring k and a commutative k-algebra A (resp. a sheaf of commutative k-algebras \({\mathcal {A}}\) over a topological space X). A Lie-Rinehart algebra over (k, A) is a (left) A-module L which is also a k-Lie algebra, endowed with an anchor map \(\varrho : L \rightarrow {\mathcal {D}}{} \textit{er}_k(A)\): a (left) A-linear morphism of k-Lie algebras such that
for all \(\lambda ,\lambda '\in L\) and \(a\in A\). Respectively, a Lie algebroid over \((k,{\mathcal {A}})\) is a (left) \({\mathcal {A}}\)-module \({\mathcal {L}}\) which is also a sheaf of k-Lie algebras, endowed with an anchor map \(\varrho : {\mathcal {L}}\rightarrow {\mathcal {D}}{} \textit{er}_k({\mathcal {A}})\): a (left) \({\mathcal {A}}\)-linear morphism of sheaves of k-Lie algebras such that
for all local sections \(\lambda ,\lambda '\) of \({\mathcal {L}}\) and a of \({\mathcal {A}}\).
We usually assume that L is a projective A-module (resp. \({\mathcal {L}}\) is a locally free \({\mathcal {A}}\)-module) of finite rank. It is clear that for each point \(p\in X\), by using the natural morphism \({\mathcal {D}}{} \textit{er}_k({\mathcal {A}})_p \rightarrow {\mathcal {D}}{} \textit{er}_k({\mathcal {A}}_p)\), any Lie algebroid \({\mathcal {L}}\) over \((k,{\mathcal {A}})\) gives rise to a Lie-Rinehart algebra \({\mathcal {L}}_p\) over \((k,{\mathcal {A}}_p)\).
For any Lie-Rinehart algebra L over (k, A) (resp. for any Lie algebroid \({\mathcal {L}}\) over \((k,{\mathcal {A}})\)), there is a universal k-algebra \({\mathcal {U}}( L)\) (resp. sheaf of k-algebras \({\mathcal {U}}({\mathcal {L}})\)), endowed with canonical maps \(A\rightarrow {\mathcal {U}}(L)\) and \(L\rightarrow {\mathcal {U}}( L)\) (resp. \({\mathcal {A}}\rightarrow {\mathcal {U}}({\mathcal {L}})\) and \({\mathcal {L}}\rightarrow {\mathcal {U}}( {\mathcal {L}})\)), called the enveloping algebra of L (resp. of \({\mathcal {L}}\)). One easily proves that for each \(p\in X\), there is a canonical isomorphism \({\mathcal {U}}({\mathcal {L}}_p) \cong {\mathcal {U}}({\mathcal {L}})_p\). Enveloping algebras are naturally (positively) filtered.
Over a complex analytic manifold X, our basic example is  , \({\mathcal {A}}={\mathcal {O}}_X\) and
, \({\mathcal {A}}={\mathcal {O}}_X\) and  , where the anchor is the identity. In this case, the corresponding enveloping algebra is the sheaf of differential operators \({\mathcal {D}}_X\) (cf. [6, § 2]). The fact that \({\mathcal {R}}_F {\mathcal {D}}_X\) is the enveloping algebra of the Lie algebroid \(z\Theta _X[z]\) over
, where the anchor is the identity. In this case, the corresponding enveloping algebra is the sheaf of differential operators \({\mathcal {D}}_X\) (cf. [6, § 2]). The fact that \({\mathcal {R}}_F {\mathcal {D}}_X\) is the enveloping algebra of the Lie algebroid \(z\Theta _X[z]\) over  , where the anchor map is given by the inclusion
, where the anchor map is given by the inclusion  , is easy (it is basically [46, Exercise 8.7]). In general, the enveloping algebra of any Lie algebroid comes equipped with a natural filtration, but in the case of \({\mathcal {R}}_F {\mathcal {D}}_X\), we have an additional structure: the grading by z. All the objects
, is easy (it is basically [46, Exercise 8.7]). In general, the enveloping algebra of any Lie algebroid comes equipped with a natural filtration, but in the case of \({\mathcal {R}}_F {\mathcal {D}}_X\), we have an additional structure: the grading by z. All the objects  are graded by the powers of z, and the enveloping algebra of \(z\Theta _X[z]\) inherits a graded structure which coincides with the original one in \({\mathcal {R}}_F {\mathcal {D}}_X\). Later, we will come back to the role of graded structures on our Lie algebroid (or our Lie-Rinehart algebra).
are graded by the powers of z, and the enveloping algebra of \(z\Theta _X[z]\) inherits a graded structure which coincides with the original one in \({\mathcal {R}}_F {\mathcal {D}}_X\). Later, we will come back to the role of graded structures on our Lie algebroid (or our Lie-Rinehart algebra).
On the other hand, the natural filtration on \({\widetilde{{\mathcal {D}}}}_X\) as enveloping algebra of \(z\Theta _X[z]\) can be derived from its graded structure in the following way (notice that it is not the usual filtration associated to the grading):
We have a canonical commutative diagram of graded \({\mathcal {O}}_X[z]\)-algebras

where \(F_\bullet ({\mathcal {D}}_X[z]):=(F_\bullet {\mathcal {D}}_X)[z]\) and where the horizontal arrows are isomorphisms by the Poincaré-Birkhoff-Witt theorem for Lie algebroids resp. Lie-Rinehart algebras (see, e.g., [34, Theorem 3.1]). Let us notice that all objects in the above diagram are bigraded (where the additional grading is given by the z-degree), and all maps in the diagram are morphisms of bigraded algebras.
For a filtered left (resp. right) \({\mathcal {D}}_X\)-module \(({\mathcal {M}},F_\bullet )\), we write  for its associated Rees module, which is naturally a graded (by degree in z) left (resp. right) \({\widetilde{{\mathcal {D}}}}_X\)-module. A graded left (or right) \({\widetilde{{\mathcal {D}}}}_X \)-module \({\widetilde{{\mathcal {M}}}}\) is called strict if it has no z-torsion. Associating \({\mathcal {R}}({\mathcal {M}},F_\bullet )\) to \(({\mathcal {M}},F_\bullet )\) defines a faithful functor from the category of filtered left (resp. right) \({\mathcal {D}}_X\)-modules to the category of graded left (resp. right) \({\widetilde{{\mathcal {D}}}}_X \)-modules. It is readily verified that a graded left (resp. right) \({\widetilde{{\mathcal {D}}}}_X \)-module \({\widetilde{{\mathcal {M}}}}\) is the Rees module of a filtered left (resp. right) \({\mathcal {D}}_X\)-module \(({\mathcal {M}},F_\bullet )\) iff it has no z-torsion. Notice that in this case we naturally have
for its associated Rees module, which is naturally a graded (by degree in z) left (resp. right) \({\widetilde{{\mathcal {D}}}}_X\)-module. A graded left (or right) \({\widetilde{{\mathcal {D}}}}_X \)-module \({\widetilde{{\mathcal {M}}}}\) is called strict if it has no z-torsion. Associating \({\mathcal {R}}({\mathcal {M}},F_\bullet )\) to \(({\mathcal {M}},F_\bullet )\) defines a faithful functor from the category of filtered left (resp. right) \({\mathcal {D}}_X\)-modules to the category of graded left (resp. right) \({\widetilde{{\mathcal {D}}}}_X \)-modules. It is readily verified that a graded left (resp. right) \({\widetilde{{\mathcal {D}}}}_X \)-module \({\widetilde{{\mathcal {M}}}}\) is the Rees module of a filtered left (resp. right) \({\mathcal {D}}_X\)-module \(({\mathcal {M}},F_\bullet )\) iff it has no z-torsion. Notice that in this case we naturally have
Moreover, for a sequence of filtered \({\mathcal {D}}_X\)-modules
the following properties are equivalent:
-
1.
The underlying sequence of \({\mathcal {D}}_X\)-modules \({\mathcal {M}}' \xrightarrow {i} {\mathcal {M}}\xrightarrow {p} {\mathcal {M}}''\) is exact and strict with respect to \(F_\bullet \) (i.e. \(F_k {\mathcal {M}}\cap (\ker p) = i(F'_k {\mathcal {M}}')\) for all
 ).
). -
2.
The associated sequence of \({\widetilde{{\mathcal {D}}}}_X\)-modules \({\mathcal {R}}_{F'} {\mathcal {M}}' \xrightarrow {{\mathcal {R}}\,i} {\mathcal {R}}_{F} {\mathcal {M}}\xrightarrow {{\mathcal {R}}\,p} {\mathcal {R}}_{F''} {\mathcal {M}}''\) is exact.
-
3.
The associated sequence of \(\text {Gr}_\bullet ^F {\mathcal {D}}_X\)-modules \(\text{ Gr}^{F'}_\bullet {\mathcal {M}}' \xrightarrow {\text{ Gr }\,i} \text{ Gr}^{F}_\bullet {\mathcal {M}}\xrightarrow {\text{ Gr }\,p} \text{ Gr}^{F''}_\bullet {\mathcal {M}}''\) is exact.
The left \({\mathcal {D}}_X\)-module \({\mathcal {O}}_X\) will be always endowed with the trivial filtration
such that \({\mathcal {R}}_F {\mathcal {O}}_X = {\mathcal {O}}_X[z]\) is a graded left \({\widetilde{{\mathcal {D}}}}_X \)-module with the usual z-grading, that will be denoted by \({\widetilde{{\mathcal {O}}}}_X\).
The canonical right \({\widetilde{{\mathcal {D}}}}_X \)-module (see [46, Example 8.1.9])
can also be seen as the Rees module \({\mathcal {R}}_F \omega _X\) associated with the canonical right \({\mathcal {D}}_X\)-module \(\omega _X\) endowed with the filtration
The main advantage to work with (graded) \({\widetilde{{\mathcal {D}}}}_X\)-modules rather than with filtered \({\mathcal {D}}_X\)-modules is that the former category is abelian whereas the latter is not.
Let k be a commutative graded ring (e.g.,  ) and \({\widetilde{{\mathcal {B}}}}\) a sheaf of graded k-algebras over a topological space X (e.g., \({\widetilde{{\mathcal {B}}}}={\widetilde{{\mathcal {D}}}}_X\) or \({\widetilde{{\mathcal {B}}}}={\widetilde{{\mathcal {O}}}}_X\) for X a complex manifold). We recall the sheaf version of some well-known definitions for graded modules over graded rings (cf. [16, §1]).
) and \({\widetilde{{\mathcal {B}}}}\) a sheaf of graded k-algebras over a topological space X (e.g., \({\widetilde{{\mathcal {B}}}}={\widetilde{{\mathcal {D}}}}_X\) or \({\widetilde{{\mathcal {B}}}}={\widetilde{{\mathcal {O}}}}_X\) for X a complex manifold). We recall the sheaf version of some well-known definitions for graded modules over graded rings (cf. [16, §1]).
For any graded left resp. right \({\widetilde{{\mathcal {B}}}}\)-modules \({\widetilde{{\mathcal {M}}}}\), \({\widetilde{{\mathcal {N}}}}\), let us denote by \({^*}{\mathcal {H}}{} \textit{om}_{{\widetilde{{\mathcal {B}}}}}({\widetilde{{\mathcal {M}}}},{\widetilde{{\mathcal {N}}}})\) the sheaf of graded k-modules

where the \({\widetilde{{\mathcal {N}}}}(i)\) is the shifted graded module defined as \({\widetilde{{\mathcal {N}}}}(i)_j = {\widetilde{{\mathcal {N}}}}(i+j) \) for all  . The above inclusion is an equality whenever \({\widetilde{{\mathcal {M}}}}\) is locally of finite presentation.
. The above inclusion is an equality whenever \({\widetilde{{\mathcal {M}}}}\) is locally of finite presentation.
For any graded right \({\widetilde{{\mathcal {B}}}}\)-module \({\widetilde{{\mathcal {Q}}}}\) and any left \({\widetilde{{\mathcal {B}}}}\)-module \({\widetilde{{\mathcal {M}}}}\), the graded tensor product \({\widetilde{{\mathcal {Q}}}}{^*}{\otimes }_{{\widetilde{{\mathcal {B}}}}} {\widetilde{{\mathcal {M}}}}\) is the sheaf of k-modules \({\widetilde{{\mathcal {Q}}}}\otimes _{{\widetilde{{\mathcal {B}}}}} {\widetilde{{\mathcal {M}}}}\) endowed with the grading
Clearly,
and
for all integers i, j. If \({\widetilde{{\mathcal {M}}}}\) is a left resp. right \({\widetilde{{\mathcal {B}}}}\)-module, then \({^*}{\mathcal {H}}{} \textit{om}_{{\widetilde{{\mathcal {B}}}}}({\widetilde{{\mathcal {M}}}},{\widetilde{{\mathcal {B}}}})\) is a graded right resp. left \({\widetilde{{\mathcal {B}}}}\)-module.
The complex \({\mathbf {R}}{^*}{\mathcal {H}}{} \textit{om}_{{\widetilde{{\mathcal {D}}}}_X}({\widetilde{{\mathcal {O}}}}_X,{\widetilde{{\mathcal {D}}}}_X)\) can be computed by means of the Spencer resolution of \({\widetilde{{\mathcal {O}}}}_X\)
graded by
The complex \({\mathbf {R}}{^*}{\mathcal {H}}{} \textit{om}_{{\widetilde{{\mathcal {D}}}}_X}({\widetilde{{\mathcal {O}}}}_X,{\widetilde{{\mathcal {D}}}}_X)\) is concentrated in homological degree n and we have a canonical isomorphism of graded right \({\widetilde{{\mathcal {D}}}}_X\)-modules
As for the non-graded case, we have natural equivalences of categories between graded left \({\widetilde{{\mathcal {D}}}}_X\)-modules and graded right \({\widetilde{{\mathcal {D}}}}_X\)-modules:
-
1.
For any graded left \({\widetilde{{\mathcal {D}}}}_X\)-module \({\widetilde{{\mathcal {M}}}}\), we define
$$\begin{aligned} {\widetilde{{\mathcal {M}}}}^{\text{ right }} := {\widetilde{\omega }}_X {^*}\!\!\otimes _{{\widetilde{{\mathcal {O}}}}_X} {\widetilde{{\mathcal {M}}}} \cong \omega _X \otimes _{{\mathcal {O}}_X} {\widetilde{{\mathcal {M}}}} \end{aligned}$$with grading \(\left[ {\widetilde{{\mathcal {M}}}}^{\text {right}}\right] _i = \omega _X \otimes _{{\mathcal {O}}_X} {\widetilde{{\mathcal {M}}}}_{i+n}. \)
-
2.
For any graded right \({\widetilde{{\mathcal {D}}}}_X\)-module \({\widetilde{{\mathcal {M}}}}\), we define
$$\begin{aligned} {\widetilde{{\mathcal {M}}}}^{\text {left}} := {^*}{\mathcal {H}}{} \textit{om}_{{\widetilde{{\mathcal {O}}}}_X}({\widetilde{\omega }}_X,{\widetilde{{\mathcal {M}}}}) \cong {\mathcal {H}}{} \textit{om}_{{\mathcal {O}}_X}(\omega _X,{\widetilde{{\mathcal {M}}}}) \end{aligned}$$with grading \(\left[ {\widetilde{{\mathcal {M}}}}^{\text {left}}\right] _i = {\mathcal {H}}{} \textit{om}_{{\mathcal {O}}_X}(\omega _X,{\widetilde{{\mathcal {M}}}}_{i-n})\).
For a complex of graded left or right \({\widetilde{{\mathcal {D}}}}_X \)-modules \({\widetilde{{\mathcal {M}}}}\) (which may not come from a complex of filtered \({\mathcal {D}}_X\)-modules \(({\mathcal {M}},F_\bullet )\)), we define its dual complex to be


respectively. We have canonical isomorphisms of graded left (resp. right) \({\widetilde{{\mathcal {D}}}}_X\)-modules (actually, complexes concentrated in degree 0)

We also have canonical isomorphisms

for all  .
.
Given a filtered holonomic module, one can consider the dual of its Rees module. However, this is not in general the Rees module of a filtered module. The next lemma gives a criterion to know when this is the case.
Lemma 2.6
(see, e.g., [46, 8.8.22]) Let \(({\mathcal {M}},F_\bullet )\) be a filtered left or right holonomic \({\mathcal {D}}_X\)-module, and \({\widetilde{{\mathcal {M}}}}:={\mathcal {R}}({\mathcal {M}},F_\bullet )\) its associated Rees module. Then we have that  for all \(i\ne 0\) and
for all \(i\ne 0\) and  has no z-torsion iff \(({\mathcal {M}},F_\bullet )\) has the Cohen-Macaulay property, that is, iff \(\text {Gr}^F_\bullet {\mathcal {M}}\) is a Cohen-Macaulay \(\text {Gr}^F_\bullet {\mathcal {D}}_X\)-module.
has no z-torsion iff \(({\mathcal {M}},F_\bullet )\) has the Cohen-Macaulay property, that is, iff \(\text {Gr}^F_\bullet {\mathcal {M}}\) is a Cohen-Macaulay \(\text {Gr}^F_\bullet {\mathcal {D}}_X\)-module.
In this case,  is the Rees module of a filtered module, the underlying \({\mathcal {D}}_X\)-module of which is
is the Rees module of a filtered module, the underlying \({\mathcal {D}}_X\)-module of which is  and we denote the filtration thus defined by
and we denote the filtration thus defined by  . We call
. We call  the dual filtered module, and
the dual filtered module, and  the dual filtration on \(F_\bullet {\mathcal {M}}\).
the dual filtration on \(F_\bullet {\mathcal {M}}\).
From (13), the canonical left (resp. right) \({\mathcal {D}}_X\)-module \({\mathcal {O}}_X\) (resp. \(\omega _X\)) is self-dual as filtered module with the trivial filtration (resp. with the filtration (10)).
It is clear that if \(({\mathcal {M}},F_\bullet )\) is a filtered holonomic \({\mathcal {D}}_X\)-module having the Cohen-Macaulay property, then \(({\mathcal {M}},F(i)_\bullet )\) also has the Cohen-Macaulay property and (see (14) above)

for any integer i.
Let us come back to the situation of a free divisor \(D\subset X\). The sheaf of logarithmic differential operators \({\mathcal {V}}_X^D \subset {\mathcal {D}}_X\) is the enveloping algebra of the Lie algebroid \(\Theta _X(-\log D) \subset \Theta _X\) over the  -algebra \({\mathcal {O}}_X\) (this is basically [7, Corollary 2.2.6]). The Rees ring \({\widetilde{{\mathcal {V}}}}_X^D\) of the filtered ring \(({\mathcal {V}}_X^D, F_\bullet )\) turns out to be the enveloping algebra of the Lie algebroid
-algebra \({\mathcal {O}}_X\) (this is basically [7, Corollary 2.2.6]). The Rees ring \({\widetilde{{\mathcal {V}}}}_X^D\) of the filtered ring \(({\mathcal {V}}_X^D, F_\bullet )\) turns out to be the enveloping algebra of the Lie algebroid  of rank n over the
of rank n over the  .
.
The Lie algebroids \(z\Theta _X[z]\) and \(z\Theta _X(-\log D)[z]\) with their z-grading are graded Lie algebroids in the sense that they are graded as \({\mathcal {O}}_X[z]\)-modules and as sheaves of  -Lie algebras, and that their anchor maps
-Lie algebras, and that their anchor maps

are graded too. Moreover, the inclusion \( z\Theta _X(-\log D)[z]\subset z\Theta _X[z]\) is graded and so is a map of graded Lie algebroids in the sense we leave the reader to write down.
We know that the relative dualizing module (see Definition (A.28) of [32]) for the inclusion of Lie algebroids \({\mathcal {L}}_0:=\Theta _X(-\log D) \subset {\mathcal {L}}:=\Theta _X\) is \(\omega _{{\mathcal {L}}/{\mathcal {L}}_0} = {\mathcal {H}}{} \textit{om}_{{\mathcal {O}}_X}\left( \omega _{\mathcal {L}},\omega _{{\mathcal {L}}_0}\right) \) with \(\omega _{\mathcal {L}}= \bigwedge ^n {\mathcal {L}}^* = \omega _X \), \(\omega _{{\mathcal {L}}_0} = \bigwedge ^n {\mathcal {L}}_0^* = \omega _X(\log D) \), and so \( \omega _{{\mathcal {L}}/{\mathcal {L}}_0} = {\mathcal {O}}_X(D)\).
In a completely similar way, the relative dualizing module of the inclusion \({\widetilde{{\mathcal {L}}}}_0:=z\Theta _X(-\log D)[z] \subset {\widetilde{{\mathcal {L}}}}:=z\Theta _X[z]\) is \(\omega _{{\widetilde{{\mathcal {L}}}}/{\widetilde{{\mathcal {L}}}}_0} = {\mathcal {H}}{} \textit{om}_{{\widetilde{{\mathcal {O}}}}_X}\left( \omega _{{\widetilde{{\mathcal {L}}}}},\omega _{{\widetilde{{\mathcal {L}}}}_0}\right) \) with \(\omega _{{\widetilde{{\mathcal {L}}}}} = \bigwedge ^n {\widetilde{{\mathcal {L}}}}^* = z^{-n} \omega _X[z] = {\widetilde{\omega }}_X \), \(\omega _{{\widetilde{{\mathcal {L}}}}_0} = \bigwedge ^n {\widetilde{{\mathcal {L}}}}_0^* = z^{-n}\omega _X(\log D)[z]) =: {\widetilde{\omega }}_X(\log D)\), and so we have a canonical isomorphism \( \omega _{{\widetilde{{\mathcal {L}}}}/{\widetilde{{\mathcal {L}}}}_0} = {\mathcal {O}}_X(D)[z]\), but in this case, due to the graded structures, this relative dualizing module is also naturally graded since it can be defined by using \({^*}{\mathcal {H}}{} \textit{om}_{{\widetilde{{\mathcal {O}}}}_X}\) instead of \({\mathcal {H}}{} \textit{om}_{{\widetilde{{\mathcal {O}}}}_X}\), and of course, this grading coincides with the z-grading of \({\mathcal {O}}_X(D)[z]\).
We have seen before (see Theorem 2.1) that if \(D \subset X\) is such that the LCT holds (e.g. if D is strongly Koszul), then there is an isomorphism of left \({\mathcal {D}}_X\)-modules \({\mathcal {D}}_X\otimes _{{\mathcal {V}}_X^D} {\mathcal {O}}_X(D) \cong {\mathcal {O}}_X(*D)\). Clearly, \({\mathcal {O}}_X(D)\) is a left \({\mathcal {V}}_X^D\)-module that is locally free (actually, of rank one) over \({\mathcal {O}}_X\).
This situation can be generalized by replacing \({\mathcal {O}}_X(D)\) by an integrable logarithmic connection (ILC) \({\mathcal {E}}\) with respect to D, which by definition is a locally free \({\mathcal {O}}_X\)-module of finite rank endowed with a left \({\mathcal {V}}_X^D\)-module structure. This notion is useful when one aims at studying the cohomology of \(X\backslash D\) with respect to some local coefficient system (i.e., the local system of horizontal sections of \({\mathcal {E}}\)). The next two results will be stated and proved in this greater generality. Although we will use them in this paper only for the case \({\mathcal {E}}={\mathcal {O}}_X(D)\), we believe that they may be useful for future applications. Moreover, for the final proof of Proposition 2.9 below (even if we are only interested in the case \({\mathcal {E}}={\mathcal {O}}_X(D)\)) some intermediate steps need to be carried out for an arbitrary ILC.
Given an ILC \({\mathcal {E}}\) with respect to D, we define (in complete analogy to Definition 2.2) the order filtration on \({\mathcal {D}}_X \otimes _{{\mathcal {V}}_X^D} {\mathcal {E}}\) to be:
In other words, \(({\mathcal {D}}_X \otimes _{{\mathcal {V}}_X^D} {\mathcal {E}}, F_\bullet ^{{\text {ord}}})\) is the filtered tensor product of \({\mathcal {D}}_X\) with its order filtration and \({\mathcal {E}}\) with its trivial filtration given by \(F_k {\mathcal {E}}= {\mathcal {E}}\) for \(k\ge 0\) and \(F_k {\mathcal {E}}= 0\) for \(k< 0\).
We have a natural \({\widetilde{{\mathcal {D}}}}_X\)-linear graded map
induced by the \({\widetilde{{\mathcal {V}}}}_X^D\)-linear graded map
Notice that \({\mathcal {R}}({\mathcal {D}}_X \otimes _{{\mathcal {V}}_X^D} {\mathcal {E}}, F_\bullet ^{{\text {ord}}})\) is a left graded \({\widetilde{{\mathcal {V}}}}_X^D\)-module through the inclusion \({\widetilde{{\mathcal {V}}}}_X^D\subset {\widetilde{{\mathcal {D}}}}_X\).
Lemma 2.7
Let D be a Koszul free divisor, and let \({\mathcal {E}}\) be an ILC with respect to D. Then:
-
1.
The map (16) is an isomorphism of graded \({\widetilde{{\mathcal {D}}}}_X\)-modules
-
2.
The complex \({\widetilde{{\mathcal {D}}}}_X {\mathop {{^*}{\otimes }}\limits ^{{\mathbf {L}}}}_{{\widetilde{{\mathcal {V}}}}_X^D} {\widetilde{{\mathcal {E}}}}\) is concentrated in degree 0 and so we have an isomorphism in the derived category of complexes of left graded \({\widetilde{{\mathcal {D}}}}_X\)-modules
$$\begin{aligned} {\widetilde{{\mathcal {D}}}}_X {\mathop {{^*}{\otimes }}\limits ^{{\mathbf {L}}}}_{{\widetilde{{\mathcal {V}}}}_X^D} {\widetilde{{\mathcal {E}}}}{\mathop {\longrightarrow }\limits ^{\cong }} {\widetilde{{\mathcal {D}}}}_X {^*}{\otimes }_{{\widetilde{{\mathcal {V}}}}_X^D} {\widetilde{{\mathcal {E}}}}. \end{aligned}$$
Proof
Both properties can be proved by forgetting the graded structures. It is easy to see that under the Koszul hypothesis on D, the inclusion of Lie algebroids (over the  -algebra \({\mathcal {O}}_X[z]\))
-algebra \({\mathcal {O}}_X[z]\))
is a Koszul pair in the sense of [10, Definition 1.16], i.e., some (or any) local \({\mathcal {O}}_X[z]\)-basis of \(z\Theta _X(-\log \,D)[z]\) forms a regular sequence in \(\text {Sym}^\bullet _{{\mathcal {O}}_X[z]} (z\Theta _X[z])\), namely, by using the inclusion \(\text {Sym}^\bullet _{{\mathcal {O}}_X[z]}(z\Theta _X[z]) \hookrightarrow \text {Sym}^\bullet _{{\mathcal {O}}_X}(\Theta _X)[z])\) (see diagram (8) above) and the fact that the Koszul property means exactly that the inclusion of Lie algebroids (over \({\mathcal {O}}_X\)) \(\Theta _X(-\log \,D)\subset \Theta _X\) is a Koszul pair.
Following [10, § 1.1.2], we can define for both inclusions of Lie algebroids \(\Theta _X(-\log \,D) \subset \Theta _X\) and \(z\Theta _X(-\log \,D)[z] \subset z\Theta _X[z]\), for an ILC \({\mathcal {E}}\) (which is a left \({\mathcal {V}}_X^D\)-module) and the corresponding Rees module \({\widetilde{{\mathcal {E}}}}\) (which is a \({\widetilde{{\mathcal {V}}}}_X^D\)-module) the Spencer complexes \(\text {Sp}^\bullet _{{\mathcal {V}}_X^D}({\mathcal {E}})\) and \(\text {Sp}^\bullet _{{\widetilde{{\mathcal {V}}}}_X^D}({\widetilde{{\mathcal {E}}}})\), which are, respectively,
and
They have augmentations to \({\mathcal {E}}\) resp. to \({\widetilde{{\mathcal {E}}}}\) and are a locally free \({\mathcal {V}}_X^D\)- resp. \({\widetilde{{\mathcal {V}}}}_X^D\)-resolution of \({\mathcal {E}}\) resp. \({\widetilde{{\mathcal {E}}}}\).
We can also consider the complex
which are
resp.
According to [10, Proposition 1.18], since both inclusions of Lie algebroids are Koszul pairs, the cohomology of both complexes is concentrated in degree 0, and equal to \({\mathcal {D}}\otimes _{{\mathcal {V}}_X^D} {\mathcal {E}}\) and \({\widetilde{{\mathcal {D}}}}\otimes _{{\widetilde{{\mathcal {V}}}}_X^D} {\widetilde{{\mathcal {E}}}}\), respectively. This proves in particular the second statement.
But actually the proof of this result in loc. cit. gives us an additional strictness property for \(\text {Sp}^\bullet _{{\mathcal {V}}_X^D,{\mathcal {D}}_X}({\mathcal {E}})\). Namely, if we filter this complex as
for \(i=0,\dots ,n\), we obtain that
and this complex is concentrated in degree 0 by the Koszul hypothesis (and so is \(\text {Sp}^\bullet _{{\mathcal {V}}_X^D,{\mathcal {D}}_X}({\mathcal {E}})\)), but this result also implies that the differentials
for \(i=1,\dots ,n\), are strict for the above filtrations. In particular, the right exact sequence
is strict, or equivalently, the sequence
is exact. Notice also that we clearly have
for all \(i\in \{0,\ldots , n\}\), since \(F_k{\mathcal {D}}_X\), \(\Theta _X(-\log D)\) as well as \({\mathcal {E}}\) are \({\mathcal {O}}_X\)-locally free (hence, flat over \({\mathcal {O}}_X\)).
To finish, consider the commutative diagram of graded left \({\widetilde{{\mathcal {D}}}}_X\)-modules

The first row is exact since \(\text {Sp}^\bullet _{{\widetilde{{\mathcal {V}}}}_X^D,{\widetilde{{\mathcal {D}}}}_X}({\widetilde{{\mathcal {E}}}})\) is a resolution of \({\widetilde{{\mathcal {D}}}}_X\otimes _{{\widetilde{{\mathcal {V}}}}_X^D}{\widetilde{{\mathcal {E}}}}\), the second row is so as we have just explained (sequence (17) above). By (18), the first and second vertical arrows are isomorphisms and so is the third one. \(\square \)
To prove our main result in this section, we will use a graded (and Lie-algebroid) version of Theorem (A.32) of [32]. However, instead of stating it in full generality (for general graded Lie algebroids or Lie-Rinehart algebras), we will only state it for the case we need, namely, the inclusion of graded Lie algebroids \({\widetilde{{\mathcal {L}}}}_0=z\Theta _X(-\log \,D)[z]\subset {\widetilde{{\mathcal {L}}}}=z\Theta _X[z]\) and the corresponding map of graded enveloping algebras \({\widetilde{{\mathcal {V}}}}_X^D \subset {\widetilde{{\mathcal {D}}}}_X\).
Proposition 2.8
Let \({\mathcal {F}}\) be a graded locally free \({\widetilde{{\mathcal {O}}}}_X\)-module of finite rank endowed with a graded left module structure over \({\widetilde{{\mathcal {V}}}}_X^D\). We have a canonical isomorphism in the derived category of graded \({\widetilde{{\mathcal {D}}}}_X\)-modules

where \({\mathcal {F}}^*= {^*}{\mathcal {H}}{} \textit{om}_{{\widetilde{{\mathcal {O}}}}_X}({\mathcal {F}},{\widetilde{{\mathcal {O}}}}_X)\) as graded left \({\widetilde{{\mathcal {V}}}}_X^D\)-module.
Proof (Outline)
This proof is a straightforward translation of the proof of Theorem (A.32) of [32] to the graded case. It essentially consists of replacing functors \({\mathcal {H}}{} \textit{om}\) and \(\otimes \) by \({^*}{\mathcal {H}}{} \textit{om}\) and \({^*}{\otimes }\) in all the constructions in the Appendix of loc. cit., as well as the fact that the relative dualizing module \(\omega _{{\widetilde{{\mathcal {L}}}}/{\widetilde{{\mathcal {L}}}}_0}\) is naturally graded. We sketch it for the convenience of the reader, and, actually, we propose a shorter and slightly different approach.
Let us recall that \(\omega _{{\widetilde{{\mathcal {L}}}}/{\widetilde{{\mathcal {L}}}}_0} = {^*}{\mathcal {H}}{} \textit{om}_{{\widetilde{{\mathcal {O}}}}_X}\left( {\widetilde{\omega }}_X,{\widetilde{\omega }}_X(\log D)\right) \cong {\mathcal {O}}_X(D)[z] \). For each left graded \({\widetilde{{\mathcal {V}}}}_X^D\)-module \({\mathcal {N}}\), the natural graded \({\widetilde{{\mathcal {O}}}}_X\)-linear map
where \(i:{\widetilde{{\mathcal {V}}}}_X^D \rightarrow {\widetilde{{\mathcal {D}}}}_X\) is the inclusion, turns out to be left \({\widetilde{{\mathcal {V}}}}_X^D\)-linear. It induces a natural graded \({\widetilde{{\mathcal {D}}}}_X\)-linear map from \( {\widetilde{{\mathcal {D}}}}_X {^*}{\otimes }_{{\widetilde{{\mathcal {V}}}}_X^D} \left( \omega _{{\widetilde{{\mathcal {L}}}}/{\widetilde{{\mathcal {L}}}}_0} {^*}{\otimes }_{{\widetilde{{\mathcal {O}}}}_X} \left[ {^*}{\mathcal {H}}{} \textit{om}_{{\widetilde{{\mathcal {V}}}}_X^D}({\mathcal {N}},{\widetilde{{\mathcal {V}}}}_X^D)\right] ^\text {left} \right) \) to \(\left[ {^*}{\mathcal {H}}{} \textit{om}_{{\widetilde{{\mathcal {V}}}}_X^D}({\mathcal {N}},{\widetilde{{\mathcal {D}}}}_X)\right] ^\text {left} = \left[ {^*}{\mathcal {H}}{} \textit{om}_{{\widetilde{{\mathcal {D}}}}_X}({\widetilde{{\mathcal {D}}}}_X {^*}{\otimes }_{{\widetilde{{\mathcal {V}}}}_X^D}{\mathcal {N}},{\widetilde{{\mathcal {D}}}}_X)\right] ^\text {left}\), and so a natural map in the derived category of left graded \({\widetilde{{\mathcal {D}}}}_X\)-modules

which, by standard reasons, is an isomorphism whenever \({\mathcal {N}}\) is coherent. To finish, notice that if \({\mathcal {N}}\) is a graded locally free \({\widetilde{{\mathcal {O}}}}_X\)-module, then we have a canonical isomorphism

(cf. Corollary (A.24) of [32]). \(\square \)
We are now ready to prove the announced result on the dual of the filtered module \(({\mathcal {D}}_X\otimes _{{\mathcal {V}}_X^D}{\mathcal {E}},F^{{\text{ ord }}}_\bullet )\).
Proposition 2.9
Assume that \(D\subset X\) is a Koszul free divisor and that \({\mathcal {E}}\) is an ILC with respect to D. Consider the filtered holonomic \({\mathcal {D}}_X\)-module \({\mathcal {M}}:=({\mathcal {D}}_X \otimes _{{\mathcal {V}}_X^D} {\mathcal {E}}, F_\bullet ^{{\text {ord}}})\), and its corresponding Rees module \({\widetilde{{\mathcal {M}}}}:={\mathcal {R}}({\mathcal {D}}_X \otimes _{{\mathcal {V}}_X^D} {\mathcal {E}}, F_\bullet ^{{\text {ord}}})\). Then the dual module  is strict, that is,
is strict, that is,  for \(i\ne 0\) and
for \(i\ne 0\) and  has no z-torsion. Moreover, we have an isomorphism of graded left \({\mathcal {D}}_X\)-modules
has no z-torsion. Moreover, we have an isomorphism of graded left \({\mathcal {D}}_X\)-modules

In particular, the filtered module \(({\mathcal {D}}_X \otimes _{{\mathcal {V}}_X^D} {\mathcal {E}}, F_\bullet ^{{\text {ord}}})\) satisfies the Cohen-Macaulay property and its dual filtered module is isomorphic to \(({\mathcal {D}}_X \otimes _{{\mathcal {V}}_X^D} {\mathcal {E}}^*(D), F_\bullet ^{{\text {ord}}})\).
Proof
By Lemma 2.7, we have
and so we have

Notice that we write \({\mathcal {E}}^*={\mathcal {H}}{} \textit{om}_{{\mathcal {O}}_X}({\mathcal {E}},{\mathcal {O}}_X)\) and similarly \({\widetilde{{\mathcal {E}}}}^*={\mathcal {H}}{} \textit{om}_{{\widetilde{{\mathcal {O}}}}_X}({\widetilde{{\mathcal {E}}}},{\widetilde{{\mathcal {O}}}}_X)\).
In conclusion, the dual \({\widetilde{{\mathcal {D}}}}_X\)-module of \({\widetilde{{\mathcal {M}}}}\) is strict, and the dual filtration  is given as the order filtration \(F^{{\text {ord}}}_\bullet \) on
is given as the order filtration \(F^{{\text {ord}}}_\bullet \) on  . \(\square \)
. \(\square \)
Remark 2.10
For the case \({\mathcal {E}}={\mathcal {O}}_X(D)\), we can directly deduce from the local representation
(see formula (6)) that \(\text {Gr}^{F^{{\text {ord}}}}_\bullet \left( {\mathcal {D}}_X\otimes _{{\mathcal {V}}^D}{\mathcal {O}}(D)\right) \) is a Cohen-Macaulay \(\text {Gr}^F_\bullet {\mathcal {D}}_X\)-module, since the symbols in \(\text {Gr}^F_\bullet {\mathcal {D}}_X\) of the operators \(\delta _1,\ldots ,\delta _{n-1},\chi +1\) form a regular sequence. However, later (see the proof of Theorem 4.10 below) we need to know that the dual filtration  is \(F_\bullet ^{{\text {ord}}} ({\mathcal {D}}_X\otimes _{{\mathcal {V}}_X^D}{\mathcal {O}}_X)\), which is provided by the proof above.
is \(F_\bullet ^{{\text {ord}}} ({\mathcal {D}}_X\otimes _{{\mathcal {V}}_X^D}{\mathcal {O}}_X)\), which is provided by the proof above.
The following is an easy variant of Proposition 2.9 which we will need later in section 4.
Corollary 2.11
Let, as above, \(D\subset X\) be a Koszul free divisor and \({\mathcal {E}}\) be an ILC. Then for any  , the filtered holonomic module \(({\mathcal {D}}\otimes _{{\mathcal {V}}_X^D}{\mathcal {E}}, F^{{\text {ord}}}_{\bullet +k})\) has the Cohen-Macaulay property, and its dual filtered module is given by \(({\mathcal {D}}_X \otimes _{{\mathcal {V}}_X^D} {\mathcal {E}}^*(D), F^{{\text {ord}}}_{\bullet -k})\).
, the filtered holonomic module \(({\mathcal {D}}\otimes _{{\mathcal {V}}_X^D}{\mathcal {E}}, F^{{\text {ord}}}_{\bullet +k})\) has the Cohen-Macaulay property, and its dual filtered module is given by \(({\mathcal {D}}_X \otimes _{{\mathcal {V}}_X^D} {\mathcal {E}}^*(D), F^{{\text {ord}}}_{\bullet -k})\).
Proof
The statement of the corollary follows simply by combining the proof of Proposition 2.9 with formula (15) and the remark that surrounds it. \(\square \)
3 Canonical and induced V-filtration
In this section we are discussing in detail the V-filtration on \(i_{h,+} {\mathcal {O}}_X(*D)\), where \(i_h\) is the graph embedding for some local reduced equation h of \(D\subset X\). This will be used in the next section in order to obtain information on the Hodge filtration on \(i_{h,+} {\mathcal {O}}_X(*D)\), and on \({\mathcal {O}}_X(*D)\) itself.
Recall that for any complex manifold M, and for a divisor \(H \subset M\) with \({\mathcal {I}}={\mathcal {I}}(H)\), we have the filtration \(V^\bullet {\mathcal {D}}_M\) defined by
\(V^0{\mathcal {D}}_M\) is a sheaf of rings, notice that it equals the sheaf of logarithmic differential operators (with respect to H), which was denoted by \({\mathcal {V}}_X^H\) in the previous chapter. Moreover, all \(V^k{\mathcal {D}}_M\) are sheaves of \(V^0{\mathcal {D}}_M\)-modules. We will usually suppose that H is smooth, and moreover that it is given by a globally defined equation \(t\in \Gamma (M,{\mathcal {O}}_M)\).
For any holonomic \({\mathcal {D}}_M\)-module \({\mathcal {M}}\), and any section \(m\in {\mathcal {M}}\), we write \(b^{{\mathcal {M}}}_m(s)\) for the unique monic polynomial of minimal degree satisfying \(b^{{\mathcal {M}}}_m(\partial _t t)m\in t V^0{\mathcal {D}}_M \cdot m\). Moreover, if \(U^\bullet {\mathcal {M}}\) is a good V-filtration on \({\mathcal {M}}\), then it has (locally) a Bernstein polynomial denoted by \(b^{{\mathcal {M}}}_{U^\bullet }(s)\), which is the minimal monic polynomial satisfying
We start by recalling the canonical V-filtration on a holonomic \({\mathcal {D}}_M\)-module. In general, it is indexed by the complex numbers, and in order to define it, one needs to choose an ordering on  such that for all
such that for all  , we have \(\alpha < \alpha +1\), \(\alpha< \beta \Longleftrightarrow \alpha +1<\beta +1\) and \(\alpha <\beta +m\) for some
, we have \(\alpha < \alpha +1\), \(\alpha< \beta \Longleftrightarrow \alpha +1<\beta +1\) and \(\alpha <\beta +m\) for some  . Notice however that for Hodge modules, only rational indices can occur. Moreover, we will later only use the integer parts of this filtration.
. Notice however that for Hodge modules, only rational indices can occur. Moreover, we will later only use the integer parts of this filtration.
Definition-Lemma 3.1
Let M and \(H=\{t=0\}\) as above, and let \({\mathcal {M}}\) be a holonomic \({\mathcal {D}}_M\)-module.
-
1.
(See [37, Definition 3.1.1], [40, Section 1.2] and [27, § 4]) Then there exists a filtration
 uniquely defined by the following properties:
uniquely defined by the following properties: -
(a)
 ,
, -
(b)
\((V^k{\mathcal {D}}_M)\cdot (V^\alpha _{{\text{ can }}}{\mathcal {M}})\subset V^{\alpha +k}_{{\text{ can }}}{\mathcal {M}}\),
-
(c)
For all
 , the module \(V^\alpha _{{\text {can}}}{\mathcal {M}}\) is \(V^0{\mathcal {D}}_M\)-coherent,
, the module \(V^\alpha _{{\text {can}}}{\mathcal {M}}\) is \(V^0{\mathcal {D}}_M\)-coherent, -
(d)
\(t\cdot V_{{\text {can}}}^\alpha {\mathcal {M}}=V_{{\text {can}}}^{\alpha +1}{\mathcal {M}}\) for \(\alpha >0\),
-
(e)
The action of the operator \(\partial _t\cdot t -\alpha \) on \(\text {Gr}^\alpha _{V_{{\text {can}}}} {\mathcal {M}}:= V_{{\text {can}}}^\alpha {\mathcal {M}}/ V_{{\text {can}}}^{>\alpha } {\mathcal {M}}\) is nilpotent, where \(V_{{\text {can}}}^{>\alpha } {\mathcal {M}}:=\cup _{\beta >\alpha } V_{{\text {can}}}^\beta {\mathcal {M}}\).
\(V^\bullet _{{\text {can}}}{\mathcal {M}}\) is called the canonical V-filtration or Kashiwara-Malgrange filtration on \({\mathcal {M}}\) with respect to H or to t. It can be characterized by
$$\begin{aligned} V^\alpha _{{\text {can}}} {\mathcal {M}}=\left\{ m\in {\mathcal {M}}\,|\, \text {roots of }b^{\mathcal {M}}_m(s) \,\subset \,[\alpha ,\infty \}\right\} , \end{aligned}$$where
 .
. -
(a)
-
2.
If \({\mathcal {M}}= {\mathcal {D}}_M/{\mathcal {I}}\) is a cyclic \({\mathcal {D}}_M\)-module, where \({\mathcal {I}}\) is a sheaf of left ideals of \({\mathcal {D}}_M\), then we put for any
 $$\begin{aligned} V^k_{{\text {ind}}} {\mathcal {M}}:= \frac{V^k {\mathcal {D}}_M}{{\mathcal {I}}\cap V^k {\mathcal {D}}_M} \cong \frac{V^k {\mathcal {D}}_M+{\mathcal {I}}}{{\mathcal {I}}}, \end{aligned}$$
$$\begin{aligned} V^k_{{\text {ind}}} {\mathcal {M}}:= \frac{V^k {\mathcal {D}}_M}{{\mathcal {I}}\cap V^k {\mathcal {D}}_M} \cong \frac{V^k {\mathcal {D}}_M+{\mathcal {I}}}{{\mathcal {I}}}, \end{aligned}$$and we call the filtration \(V^\bullet _{{\text {ind}}} {\mathcal {M}}\) the induced V-filtration on \({\mathcal {M}}\). In particular, if \({\mathcal {M}}\) is holonomic, then \(V^\bullet _{{\text {ind}}} {\mathcal {M}}\) has a (minimal and monic) Bernstein polynomial
 .
.
We will mainly use the above definitions for the case where H is the divisor  and where \({\mathcal {M}}= i_{h,+}{\mathcal {O}}_X(*D)\), \(i_h\) being the graph embedding of a defining equation for a divisor \(D\subset X\). Using a construction that goes back to Malgrange (see [26]), one can find a cyclic generator for this module, so that it has an induced V-filtration. It is essentially well-known that the Bernstein polynomial of this filtration is given by the Bernstein polynomial \(b_h(s)\) of the equation h defining D, up to a change of variables. However, we recall the proof for the convenience of the reader. Notice also that this result holds quite generally for any divisor, and does not depend on freeness or any Koszul assumption.
and where \({\mathcal {M}}= i_{h,+}{\mathcal {O}}_X(*D)\), \(i_h\) being the graph embedding of a defining equation for a divisor \(D\subset X\). Using a construction that goes back to Malgrange (see [26]), one can find a cyclic generator for this module, so that it has an induced V-filtration. It is essentially well-known that the Bernstein polynomial of this filtration is given by the Bernstein polynomial \(b_h(s)\) of the equation h defining D, up to a change of variables. However, we recall the proof for the convenience of the reader. Notice also that this result holds quite generally for any divisor, and does not depend on freeness or any Koszul assumption.
We therefore let \(D\subset X\) be a divisor defined locally at a point \(p\in X\) by a reduced equation \(h=0\), and we denote by  its graph embedding. We put
its graph embedding. We put
then N(h) is a holonomic  -module. Since \(i_h\) is a closed immersion, we have that
-module. Since \(i_h\) is a closed immersion, we have that
as  -modules. It becomes an isomorphism of
-modules. It becomes an isomorphism of  -modules when equipping the right hand side with the
-modules when equipping the right hand side with the  -structure given by
-structure given by
for any \(i=1,\ldots ,n\), any \(m\in {\mathcal {O}}_{X,p}(*D)\) and any \(a\in {\mathcal {O}}_{X,p}\).
Lemma 3.2
In the above situation, write  for the negative of the smallest integer root of \(b_h(s)\). Then we have
for the negative of the smallest integer root of \(b_h(s)\). Then we have
Proof
Following the constructions in [26, § 4], one can show that \(N(h) \cong (i_{h,*}{\mathcal {O}}_X(*D))_{(0,p)}[s]\cdot h^s\), using that \(t=h\) is invertible in N(h) and substituting \(-\partial _t t\) by s, where \(h^s\) is a symbol on which tangent fields \(\xi \) act as \(\xi (h^s)=sh^{-1}\xi (h)\cdot h^s\).
The fact that \(-j\) is the smallest integer root of \(b_h(s)\) is equivalent to say that \({\mathcal {O}}_{X,p}(*D)\) is generated as a \({\mathcal {D}}_{X,p}\)-module by \(h^{-j}\). Therefore, N(h) is generated by \(h^{-j}\cdot h^s\), that we will write \(h^{s-j}\) from now on. Hence we can consider the filtration  . The V-filtration on
. The V-filtration on  can be written as
can be written as  ,
,  for \(k\ge 0\) and
for \(k\ge 0\) and  for \(k\le 0\). Therefore, we obtain that
for \(k\le 0\). Therefore, we obtain that
where we have used that \(s=-\partial _tt\) and \(t=h\) in our alternative representation of N(h).
As a consequence, we have isomorphisms
for every \(k\ge 0\). On the other hand, for \(k\le 0\), we have that
so we obtain surjections
Since
we see that \(\varphi _k\left( (i_{h,*}{\mathcal {D}}_X)_{(0,p)}[s]s^{-k+1}h^{s-j+k}\right) =0\). As a consequence, we obtain a surjection
for any \(k\le 0\).
We finally obtain surjections
for any \(k\le 0\), where the first isomorphism holds because for any \(l\ge 0\) and any  , s is a non-zero divisor on the modules \((i_{h,*}{\mathcal {D}}_X)_{(0,p)}[s] s^l h^{s+l'}\).
, s is a non-zero divisor on the modules \((i_{h,*}{\mathcal {D}}_X)_{(0,p)}[s] s^l h^{s+l'}\).
By the Bernstein functional equation, we know that \(b_h(s)\) sends \(h^s\) to \({\mathcal {D}}_{X,p}[s]h^{s+1}\), hence \(b_h(-\partial _tt-j+k)\) annihilates the left-hand side of equation (20) and \(b_h(-\partial _tt-j+k-1)\) annihilates the left-hand side of the surjection (21), so they annihilate the respective right-hand sides as well. In other words, \(b_h(-\partial _tt-j+k)\) kills the quotient \(V_{{\text {ind}}}^k N(h)/V_{{\text {ind}}}^{k+1} N(h)\) for any  . This means precisely that \(b_h(-s-j)=b_{V_{{\text {ind}}}^\bullet }^{N(h)}(s)\), as desired. \(\square \)
. This means precisely that \(b_h(-s-j)=b_{V_{{\text {ind}}}^\bullet }^{N(h)}(s)\), as desired. \(\square \)
The next result gives a precise description of the canonical V-filtration for N(h) for divisors satisfying the additional assumption that the roots of \(b_h\) are included in the open interval \((-2,0)\).
Proposition 3.3
Let X, D, h and N(h) be as in the previous lemma. Assume moreover that the roots of \(b_h(s)\) are contained in \((-2,0)\). Then for all  , we have
, we have
recall from the introduction (see Formula (2)) that

In particular, we have
for all  .
.
Proof
Since the roots of \(b_h(s)\) are in \((-2,0)\), we know thanks to Lemma 3.2 that the roots of \(b^{N(h)}_{V_{{\text {ind}}}^\bullet }(s)=b_h(-s-1)\) are contained in \((-1,1)\). Now we argue as in the proof of [22, Theorem I] (cf. also [27, Proposition 4.2-6]): Let \(\lambda _1< \ldots <\lambda _c\) be the set of roots of \(b^{N(h)}_{V_{{\text {ind}}}^\bullet }(s)\) with \(-1<\lambda _i<0\), with respective multiplicities \(l_1,\ldots ,l_c\). We write
with \(b'(\lambda _i)\ne 0\) for all \(i\in \{1,\ldots ,c\}\). Then for each  put
put
Then \({\overline{V}}^\bullet N(h)\) is a good V-filtration on N(h) and moreover, \(\prod _{i=1}^c(s-(\lambda _i+1))^{l_i}\cdot b'(s)\) is a Bernstein polynomial for \({\overline{V}}^\bullet N(h)\), namely we have that
and
where the two inclusions marked as \({\mathop {\subset }\limits ^{*}}\) are due to the definition of the filtration \({\overline{V}}^\bullet N(h)\), i.e., due to formula (23). Hence we obtain that
that is, \(\prod _{i=1}^c(s-(\lambda _i+1))^{l_i}\cdot b'(s)\) is a Bernstein polynomial for \({\overline{V}}^\bullet N(h)\). We conclude that \({\overline{V}}^\bullet N(h)\) is a good V-filtration on N(h) such that its Bernstein polynomial has all its roots in the interval [0, 1).
Now by [27, Proposition 4.3-5] we conclude that
holds for all  , and this shows Formula (22). \(\square \)
, and this shows Formula (22). \(\square \)
Remark 3.4
Without the assumption that the roots of \(b_h(s)\) are in \((-2,0)\) (i.e., for general \(h\in {\mathcal {O}}_{X,p}\)) the previous result is no longer true in general. Namely, since in general the roots of \(b_h(s)\) are negative rational numbers, we know by Lemma 3.2 that the roots of \(b_{V_{{\text {ind}}}^\bullet }^{N(h)}\) are contained in \((-j,\infty )\), where \(-j\) is the smallest integer root of \(b_h(s)\). It can thus happen that \(b_{V_{{\text {ind}}}^\bullet }^{N(h)}\) has roots bigger than 1, and this prevents the inclusion \(V^k_{{\text {can}}} N(h) \subset V^k_{{\text {ind}}} N(h)\) to hold in general. The roots of \(b_h(s)\) are contained in \((-2,0)\) for the class of SK free divisors (see point 3 of Proposition 2.4 and [32, Theorem 4.1]), but it also holds for instance when h defines a central hyperplane arrangement by [42, Theorem 1] (which is not necessarily a free divisor).
In the remaining part of this section, we restrict our attention to SK free divisors. We study more in detail the induced V-filtration on the module N(h), since as we have seen, it helps to understand (at least the integer steps of) the canonical V-filtration on that module. In particular, we will prove (see Proposition 3.10 below) a compatibility property between the induced V-filtration and the order filtration on that module (which is similar to the order filtration \(F^{{\text {ord}}}_\bullet {\mathcal {O}}_X(*D)\) studied in section 2). Its statement is similar to [35, Proposition 4.9]), although the presentation of the proof is slightly different.
We first give a concrete cyclic presentation of the graph embedding module for equations defining an SK free divisor, starting from the presentation for \({\mathcal {O}}_X(*D)\) discussed in the previous section (see Equation (5) above).
Lemma 3.5
Let \(D\subset X\) be a free divisor and let \(p\in D\) be such that D is strongly Koszul at p. Let \(h\in {\mathcal {O}}_{X,p}\) be a reduced equation for D near p. Let  , \(x\mapsto (h(x),x)\) be the graph embedding of h, then we have an isomorphism of
, \(x\mapsto (h(x),x)\) be the graph embedding of h, then we have an isomorphism of  -modules
-modules

We still denote this module (resp. this cyclic presentation) by N(h).
Proof
This is a consequence of the logarithmic comparison theorem, as stated in point 2 of Proposition 2.4. Namely, we know that
Now we consider the direct image of this object under the graph embedding. Then we have

by taking into account that \(\delta _i(h)=0\) for every \(i=1,\ldots ,n-1\) and \(\chi (h)=h\). The claim now follows from the fact that in N(h) we have \(h\partial _t=\partial _t h=\partial _t t\) (here and later on, we sometimes denote operators and their classes in a cyclic quotient module by the same symbol). \(\square \)
We will be later interested in calculating the Hodge filtration on a mixed Hodge module which has \(i_{h,+}{\mathcal {O}}_{X.x}(*D)\) as underlying  -module. For that purpose, we consider the filtration \(F_\bullet ^{{\text {ord}}} N(h)\) which is induced on N(h) by the filtration
-module. For that purpose, we consider the filtration \(F_\bullet ^{{\text {ord}}} N(h)\) which is induced on N(h) by the filtration  by the order of differential operators.
by the order of differential operators.
For the sake of brevity, let us write  and
and  . Consider the ring
. Consider the ring

Then we have \({\mathcal {G}}=\text {Gr}_\bullet ^F {\mathcal {D}}\) (where, as before, \(F_\bullet {\mathcal {D}}\) is the filtration on \({\mathcal {D}}\) by the order). Obviously, \({\mathcal {G}}\) is graded by the degree of the variables \(T,X_1,\ldots ,X_n\), and we write \({\mathcal {G}}_l\) for the degree l part.
Lemma 3.6
Let \(D\subset X\) be a free divisor and let \(p\in D\) such that D is strongly Koszul at p and locally defined by some \(h\in {\mathcal {O}}_{X,p}\). Write
so that \(N(h)={\mathcal {D}}/ I(h)\). Then the set \(\{t-h,\delta _1,\ldots ,\delta _{n-1}, \chi +\partial _t t +1\}\) is an involutive basis of the ideal I(h), that is, we have the equality
of ideals in \({\mathcal {G}}\). Recall that we denote for an element \(P\in {\mathcal {D}}\) its symbol in \({\mathcal {G}}\) by \(\sigma (P)\) and by \(\sigma (I(h))\) the ideal \(\{\sigma (P)\,|\,P\in I(h)\}\) in \({\mathcal {G}}\).
Proof
The proof basically follows the argument in [7, Proposition 4.1.2] once we know that symbols of the generators of I(h), i.e., the elements
form a regular sequence in the ring \({\mathcal {G}}\). Notice also that Lemma 3.7 below is a similar statement (in a commutative ring though), and we will give some indications of the proof there.
In order to show this regularity statement, first recall that since D is strongly Koszul at p by assumption, it is in particular Koszul (see Definition 2.3 and the subsequent remarks). Hence we know that
is a regular sequence in the ring  . Then clearly the sequence
. Then clearly the sequence
is regular in the ring  . On the other hand, we have the following equality of ideals of
. On the other hand, we have the following equality of ideals of  :
:
so that also the sequence
is regular in  . Since we have an isomorphism of rings
. Since we have an isomorphism of rings

we obtain that the sequence
is regular in  . Then again by equality of ideals
. Then again by equality of ideals
in \({\mathcal {G}}\) we get that
is a regular sequence in \({\mathcal {G}}\), but then also the shorter sequence
must be regular in \({\mathcal {G}}\). \(\square \)
We denote by \({\widetilde{V}}^\bullet {\mathcal {G}}\) the filtration induced by \(V^\bullet {\mathcal {D}}\) (the V-filtration on \({\mathcal {D}}\) with respect to the divisor  ) on the ring \({\mathcal {G}}\). It can be described as
) on the ring \({\mathcal {G}}\). It can be described as

For any \(f\in {\mathcal {G}}\), we write \({\text {ord}}^{{\widetilde{V}}}\) for the maximal  such that \(f\in {\widetilde{V}}^b {\mathcal {G}}\). The graded ring of \({\mathcal {G}}\) with respect to the filtration \({\widetilde{V}}\) looks quite similar to \({\mathcal {G}}\) itself, namely, we have
such that \(f\in {\widetilde{V}}^b {\mathcal {G}}\). The graded ring of \({\mathcal {G}}\) with respect to the filtration \({\widetilde{V}}\) looks quite similar to \({\mathcal {G}}\) itself, namely, we have

since \({\widetilde{V}}^\bullet \) induces the t-adic filtration on the ring  .
.
As usual, for \(f\in {\mathcal {G}}\) we denote by \(\sigma ^{{\widetilde{V}}}(f)\in \text {Gr}^\bullet _{{\widetilde{V}}} {\mathcal {G}}\) the symbol with respect to \({\widetilde{V}}\), i.e., the class of f in  . Now consider an ideal \(I=(f_1,\ldots ,f_k)\subset {\mathcal {G}}\). We write
. Now consider an ideal \(I=(f_1,\ldots ,f_k)\subset {\mathcal {G}}\). We write
Then we have the following fact (which is analogous to the statement of Lemma 3.6 above, and in fact holds in a more general setting for certain filtered rings, although we do not consider such a generality here).
Lemma 3.7
Suppose that \(\sigma ^{{\widetilde{V}}}(f_1),\ldots , \sigma ^{{\widetilde{V}}}(f_k)\) is a regular sequence in \(\text {Gr}^\bullet _{{\widetilde{V}}} {\mathcal {G}}\). Then we have the equality
of ideals in \(\text {Gr}^\bullet _{{\widetilde{V}}} {\mathcal {G}}\).
Proof
We follow the argument given (in a more algebraic situation though) in [47, Proposition 4.3.2]. We obviously have \(\sigma ^{{\widetilde{V}}}(I) \supset \left( \sigma ^{{\widetilde{V}}}(f_1),\ldots , \sigma ^{{\widetilde{V}}}(f_k)\right) \) and we need to show the converse inclusion. Assume that it does not hold, that is, take \(f\in I\) (so that \(\sigma ^{{\widetilde{V}}}(f)\in \sigma ^{{\widetilde{V}}}(I)\)) such that \(\sigma ^{{\widetilde{V}}}(f) \notin \left( \sigma ^{{\widetilde{V}}}(f_1),\ldots , \sigma ^{{\widetilde{V}}}(f_k)\right) \). For a representation
write
then clearly \(o({\underline{g}})\le {\text {ord}}^{{\widetilde{V}}}(f)\). Choose a representation \(f=\sum _{i=1}^k g_i\cdot f_i\) such that \(o({\underline{g}})\) is maximal. Since \(\sigma ^{{\widetilde{V}}}(f) \notin \left( \sigma ^{{\widetilde{V}}}(f_1),\ldots , \sigma ^{{\widetilde{V}}}(f_k)\right) \), we have \({\text {ord}}^{{\widetilde{V}}}(f) > o({\underline{g}})\). We conclude that
Now by assumption the symbols \(\sigma ^{{\widetilde{V}}}(f_1),\ldots ,\sigma ^{{\widetilde{V}}}(f_k)\) form a regular sequence in \(\text {Gr}^\bullet _{{\widetilde{V}}}{\mathcal {G}}\), and this implies that the module of syzygies between these elements of \({\mathcal {G}}\) is generated by the so-called Koszul relations, i.e.,
In other words, we have an equality
of elements of \({\mathcal {G}}^k\) (where \(e_i\) is the i-th canonical generator of \({\mathcal {G}}^k\)). Reordering the right hand side of the above equation yields
and hence
for all \(i\in \{1,\ldots ,k\}\) such that \({\text {ord}}^{{\widetilde{V}}}(g_i)+{\text {ord}}^{{\widetilde{V}}}(f_i)=o({\underline{g}})\). Hence if we replace those \(g_i\) in equation (24) by \(g'_i:=g_i-\left( \sum _{l<i} h_{li} f_l -\sum _{i<j} h_{ij}f_j\right) \) (and collect all the \(f_i\)), we obtain a new expression \(f=\sum _{i=1}^k g'_i f_i\) such that
which contradicts the above choice of a relation \({\underline{g}}\) with maximal \(o({\underline{g}})\). Hence we must have that \(\sigma ^{{\widetilde{V}}}(f) \in \left( \sigma ^{{\widetilde{V}}}(f_1),\ldots , \sigma ^{{\widetilde{V}}}(f_k)\right) \) and therefore
as required. \(\square \)
We apply the previous lemma in the situation where I is given as the ideal \(\sigma (I(h))\subset {\mathcal {G}}\) (recall that \(\sigma \) denotes the usual symbol with respect to the order filtration \(F_\bullet {\mathcal {D}}\)). For notational convenience, put \(G_0:=t-h\), \(G_1:=\delta _1,\ldots , G_{n-1}:=\delta _{n-1}\) and \(G_n:=\chi +\partial _t t +1\), so that \(I(h)=(G_0,\ldots ,G_n) \subset {\mathcal {D}}\). Then we obtain the following consequence.
Corollary 3.8
Let \(D\subset X\) be a free divisor and let \(x\in D\) such that D is strongly Koszul at x and locally defined by some \(h\in {\mathcal {O}}_{X,p}\). Then the set
is an involutive basis of the ideal \(\sigma (I(h))\subset {\mathcal {G}}\) with respect to the filtration \({\widetilde{V}}^\bullet {\mathcal {G}}\) induced from the filtration \(V^\bullet {\mathcal {D}}\), that is, we have
As a consequence, any \(f\in \sigma (I(h))\subset {\mathcal {G}}\) has a standard representation with respect to \({\widetilde{V}}^\bullet \), that is, there are elements \(k_0,k_1,\ldots ,k_n\in {\mathcal {G}}\) with \(f=\sum _{i=0}^n k_i\cdot \sigma (G_i) =k_0\cdot (t-h)+\sum _{i=1}^{n-1} k_i \cdot \sigma (\delta _i)+k_n\cdot (\sigma (\chi )+T\cdot t)\) such that \({\text {ord}}^{{\widetilde{V}}}(k_i)+{\text {ord}}^{{\widetilde{V}}}(\sigma (G_i)) \ge {\text {ord}}^{{\widetilde{V}}}(f)\) holds for all \(i\in \{0,\ldots ,n\}\).
For the last statement, we remind the reader that the filtration \({\widetilde{V}}^\bullet {\mathcal {G}}\) is descending, and that consequently, for \(g\in {\mathcal {G}}\), \({\text {ord}}^{{\widetilde{V}}}(g)\) denotes the maximum of all l such that \(g\in {\widetilde{V}}^l {\mathcal {G}}\).
Proof
Consider the ring extension

sending s to \(-T\cdot t\). Then clearly \(\text {Gr}^\bullet _{{\widetilde{V}}}({\mathcal {G}})\) is a flat \(\text {Gr}^T_\bullet ({\mathcal {D}}[s])\)-module, since for any ring R, we have that R[t, T] is a flat (and even free) \(R[-T\cdot t]\)-module.
From the very definition of the strongly Koszul property (see again Definition 2.3), we know that
is a regular sequence in \(\text {Gr}^T_\bullet ({\mathcal {D}}[s])\). Now notice that the elements \(\sigma (\delta _1),\ldots ,\sigma (\delta _{n-1})\), \(\sigma (\chi )\) lie in the ring  , which is a subring of both \({\mathcal {G}}\) and of \(\text {Gr}^\bullet _{{\widetilde{V}}}({\mathcal {G}})\). Clearly, for
, which is a subring of both \({\mathcal {G}}\) and of \(\text {Gr}^\bullet _{{\widetilde{V}}}({\mathcal {G}})\). Clearly, for  we have \(\sigma ^{{\widetilde{V}}}(p)=p\), therefore, we know that
we have \(\sigma ^{{\widetilde{V}}}(p)=p\), therefore, we know that
is a regular sequence in \(\text {Gr}_\bullet ^T({\mathcal {D}}[s])\). Since the ring extension \(\text {Gr}_\bullet ^T({\mathcal {D}}[s])\subset \text {Gr}^\bullet _{{\widetilde{V}}}({\mathcal {G}})\) is flat, it follows (see, e.g., [4, Proposition 9.6.7 and remark right after it]) that the elements
form a regular sequence in \(\text {Gr}^\bullet _{{\widetilde{V}}}({\mathcal {G}})\). Now the assertion of the Corollary follows from Lemma 3.7 above. \(\square \)
The next statement is a rather direct consequence of the previous results. We include it here since it will be used in section 5 where we discuss techniques for computation of Hodge ideals.
Corollary 3.9
Let \(D\subset X\) be a free divisor, let \(p\in D\) such that D is strongly Koszul at p and locally defined by some \(h\in {\mathcal {O}}_{X,p}\). Then
Proof
Since the generators of I(h) belong all to \(V^0{\mathcal {D}}\), which is a ring, the inclusion \(I(h)\cap V^0{\mathcal {D}}\supset V^0{\mathcal {D}}( t-h,\delta _1,\ldots ,\delta _{n-1},\chi +\partial _t t+1)\) is trivial. Let us show the reverse one.
Let P be an operator in \(I(h)\cap V^0{\mathcal {D}}\) and let us prove that it lies within \(V^0{\mathcal {D}}( t-h,\delta _1,\ldots ,\delta _{n-1},\chi +\partial _tt+1)\) by induction on the order of P with respect to \(F_\bullet {\mathcal {D}}\), written \({\text {ord}}^F(P)\).
If \({\text {ord}}^F(P)=-1\), the claim is trivial, for then \(P=0\). Let us now assume that the statement is true for all \(Q\in F_{d-1}{\mathcal {D}}\) for a given non-negative integer d, and let us prove it for any \(P\in F_d{\mathcal {D}}\). Since \(P\in I(h)\), we have the expression
Thanks to Lemma 3.6, we know that \(A\in F_d{\mathcal {D}}\) and the \(B_i\) and C are in \(F_{d-1}{\mathcal {D}}\) and also that \(\sigma (P)\), which belongs to \(\widetilde{V}^0{\mathcal {G}}\), can be written as
On the other hand, we know after Corollary 3.8 that we can choose \({\tilde{A}}\in \text {Gr}^F_d({\mathcal {D}})\cap \widetilde{V}^0{\mathcal {G}}\) and some \({{\tilde{B}}}_i,{{\tilde{C}}}\in \text {Gr}^F_{d-1}({\mathcal {D}})\cap \widetilde{V}^0{\mathcal {G}}\) such that
Then we have that
is a syzygy of the tuple \((t-h,\sigma (\delta _1),\ldots ,\sigma (\delta _{n-1}),\sigma ({{\tilde{\chi }}})+Tt).\) By Lemma 3.6 again, since this tuple is a regular sequence in \({\mathcal {G}}\), \(\varsigma \) will be a sum of Koszul syzygies (i.e., those of the form \(a_ie_j-a_je_i\in {\mathcal {G}}^{n+1}\) for some elements \(a_i, a_j\) of the regular sequence, \(e_i\) and \(e_j\) being the corresponding unit vectors).
Now notice that for all k, l, the canonical map
is surjective. Hence, we can choose \(A'\in F_d{\mathcal {D}}\cap V^0{\mathcal {D}}\) and \(B'_i,C'\in F_{d-1}{\mathcal {D}}\cap V^0{\mathcal {D}}\) such that \(\sigma (A')={{\tilde{A}}}\), \(\sigma (B'_i)={{\tilde{B}}}_i\) for every i and \(\sigma (C')={{\tilde{C}}}\). Then the tuple \((A-A',B_1-B'_1,\ldots ,B_{n-1}-B'_{n-1},C-C')\) can be written as a sum of Spencer syzygies of \((t-h,\delta _1,\ldots ,\delta _{n-1},\chi +\partial _tt+1)\) (that is, the respective lifts of the Koszul ones in \({\mathcal {G}}\) that come from the expression of the \([G_i,G_j]\), for any i, j, as a linear combination of the form \(\sum _k\alpha _kG_k\) with coefficients in \({\mathcal {O}}\)) plus another tuple \((A'',B''_1,\ldots ,B''_{n-1},C'')\), where now \(A''\in F_{d-1}{\mathcal {D}}\) and \(B''_i,C''\in F_{d-2}{\mathcal {D}}\).
Let us call now
Consequently,
Summing up, we obtain that \(P''\in F_{d-1}{\mathcal {D}}\cap V^0{\mathcal {D}}\cap I(h)\), so by the induction hypothesis, it can be written as a linear combination of \(t-h,\delta _1,\ldots ,\delta _{n-1},\chi +\partial _tt+1\) with coefficients in \(V^0{\mathcal {D}}\) and thus P too. \(\square \)
Now we can show the following result expressing a certain compatibility between the induced V-filtration and the order filtration on N(h).
Proposition 3.10
For all  , the canonical morphism
, the canonical morphism
is surjective.
Proof
We reformulate the surjectivity we want to prove as a compatibility property between three filtrations on \({\mathcal {D}}\), the first two being \(F_\bullet {\mathcal {D}}\) and \(V^\bullet {\mathcal {D}}\). The third one is defined (somewhat artificially) as
It is clear that the statement of the proposition is equivalent to the surjectivity of the map
for \(r=0\), where we denote by \({'}F_\bullet \) resp. by \({'}V^\bullet \) the filtrations induced by \(F_\bullet {\mathcal {D}}\) resp. \(V^\bullet {\mathcal {D}}\) on \(\text {Gr}_r^J{\mathcal {D}}\) (notice that for \(r=0\), these are nothing but \(F^{{\text {ord}}}_\bullet N(h)\) resp. \(V^\bullet _{{\text {ind}}}N(h)\)). Since both the J- and the F-filtration are exhaustive, we can now apply [37, Corollaire 1.2.14] from which we conclude that surjectivity of the map (25) holds (for all l, k, r) if and only if the map
is surjective for all l, k, r. Again, \({\widetilde{J}}_\bullet {\mathcal {G}}_l\) is the filtration induced by \(J_\bullet {\mathcal {D}}\) on \({\mathcal {G}}_l\), i.e., \({\widetilde{J}}_r {\mathcal {G}}_l={\mathcal {G}}_l\) if \(r\ge 0\) and \({\widetilde{J}}_r {\mathcal {G}}_l=\sigma _l(I(h)\cap F_l{\mathcal {D}})\) if \(r< 0\), where, as usual, \(\sigma _l:F_l{\mathcal {D}}\twoheadrightarrow {\mathcal {G}}_l\) denotes the map sending an operator of degree l to its symbol in \({\mathcal {G}}_l\). However, the surjectivity of (26) is a nontrivial condition only for \(r<0\) (and it is the same condition for all negative r): For \(r\ge 0\), it means that the map \(F_l {\mathcal {D}}\cap V^k {\mathcal {D}}\longrightarrow {\widetilde{V}}^k {\mathcal {G}}_l\) is surjective, which is true, as we have already noticed in the proof of Corollary 3.9. If \(r<0\), the map (26) is nothing but
We will see that the surjectivity of the latter map follows from the involutivity properties proved above. Namely, let \(\sigma (P)=\sigma _l(P) \in {\widetilde{V}}^k{\mathcal {G}}_l\) be given, where \(P\in I(h)\cap F_l{\mathcal {D}}\). Then by Lemma 3.6 we have an expression
recall that we had put \(G_0:=t-h\), \(G_1:=\delta _1,\ldots , G_{n-1}:=\delta _{n-1}\) and \(G_n:=\chi +\partial _t t +1\) for the involutive basis of I(h). Since obviously the symbols \(\sigma (G_i)\) are homogeneous elements in the ring \({\mathcal {G}}=\text {Gr}_\bullet ^F {\mathcal {D}}\), we have that \(\deg (k_i) = l-\deg (\sigma (G_i)) = l-{\text {ord}}(G_i)\). On the other hand, we know by Corollary 3.8 that \({\text {ord}}^{{\widetilde{V}}}(k_i)\ge {\text {ord}}^{{\widetilde{V}}}(\sigma (P))-{\text {ord}}^{{\widetilde{V}}}(\sigma (G_i))\), that is,
Moreover, it follows from the concrete form of the operators \(G_0,\ldots , G_n\) that \({\text {ord}}^{{\widetilde{V}}}(\sigma (G_i))={\text {ord}}^{V}(G_i)=0\), hence \(k_i\in {\widetilde{V}}^{{\text {ord}}^{{\widetilde{V}}}(\sigma (P))}{\mathcal {G}}\). Now choose any lift of \(k_i\) to an operator \(K_i\in F_{l-{\text {ord}}(G_i)}{\mathcal {D}}\cap V^{{\text {ord}}^{{\widetilde{V}}}(\sigma (P))}{\mathcal {D}}\). Such a lift exists since, as we have already noticed above, the map
is surjective for all l, k. Then the element \(P':=\sum _{i=0}^n K_i \cdot G_i\in I(h)\) is the preimage we are looking for, i.e., \(\sigma (P')=\sigma (P)\) and we have
recall that we had chosen \(\sigma (P)\in {\widetilde{V}}^k {\mathcal {G}}_l \cap \sigma _l(I(h)\cap F_l{\mathcal {D}})\), meaning that \(k \le {\text {ord}}^{{\widetilde{V}}}(\sigma (P))\). Hence we have shown the surjectivity of
and as we said at the beginning of the proof, using [37, Corollaire 1.2.14], the surjectivity of
as required. \(\square \)
4 Description of the Hodge filtration
This section is the central piece of the article. We apply the results on the canonical V-filtration from the last section to compute the Hodge filtration on the mixed Hodge module which has \({\mathcal {O}}_X(*D)\) as underlying \({\mathcal {D}}_X\)-module. The main result is Theorem 4.4, which gives a precise description of \(F^H_\bullet {\mathcal {O}}_X(*D)\). We also complement it with some statements about the Hodge filtration on the dual module \({\mathcal {O}}_X(!D)\), see Theorem 4.10, which we expect to be useful for future applications. We conjecture (see Conjecture 4.12) some bound for the so-called generating level of the Hodge filtration (see Definition 4.11 for this notion), which is supported by computation of examples in section 5 below.
Notice that some of the results in this section (first part of Theorem 4.4 or Theorem 4.12) hold globally on X, however, for most of the proofs we will need to require that \(D\subset X\) is defined by an equation h. As already indicated, we will determine the Hodge filtration using the graph embedding  and by considering extensions of Hodge modules from
and by considering extensions of Hodge modules from  to
to  .
.
Hence, let again X be an n-dimensional complex manifold and \(D\subset X\) a reduced free divisor, which is strongly Koszul at each point \(p\in D\). We assume for now (until and including Corollary 4.3) that D is given by a reduced equation \(h\in \Gamma (X,{\mathcal {O}}_X)\). Notice also that contrary to the last section, we will consider all the objects as sheaves since this is more convenient when applying the functorial constructions from the theory of mixed Hodge modules.
Put \(U:=X\backslash D\), and consider the following basic diagram:

Here j and \(j'\) are open embeddings, whereas \(i_h\) and \(i'_h\) (both are given by \({\underline{x}} \mapsto ({\underline{x}},h({\underline{x}}))\) and may be called graph embeddings) are closed.
We are considering the pure Hodge module  on U. By the functorial properties of the category of mixed Hodge modules, we know that there is an object
on U. By the functorial properties of the category of mixed Hodge modules, we know that there is an object  , whose underlying \({\mathcal {D}}_X\)-module is the module \({\mathcal {O}}_X(*D)\) of meromorphic functions. We are interested in describing the Hodge filtration \(F^H_\bullet \) on \({\mathcal {O}}_X(*D)\).
, whose underlying \({\mathcal {D}}_X\)-module is the module \({\mathcal {O}}_X(*D)\) of meromorphic functions. We are interested in describing the Hodge filtration \(F^H_\bullet \) on \({\mathcal {O}}_X(*D)\).
The \({\mathcal {D}}_U\)-module underlying  is simply the structure sheaf \({\mathcal {O}}_U\) and we have \(F^H_k{\mathcal {O}}_U=0\) for all \(k<0\) and \(F^H_k{\mathcal {O}}_U={\mathcal {O}}_U\) for all \(k\ge 0\). We obviously have
is simply the structure sheaf \({\mathcal {O}}_U\) and we have \(F^H_k{\mathcal {O}}_U=0\) for all \(k<0\) and \(F^H_k{\mathcal {O}}_U={\mathcal {O}}_U\) for all \(k\ge 0\). We obviously have
recall from Proposition 2.4 that the basis \(\delta _1,\ldots ,\delta _{n-1},\chi \) of \({\mathcal {D}}{} \textit{er}_X(-\log D)\) was chosen such that \(\delta _i(h)=0\) for \(i=1,\ldots ,n-1\) and \(\chi (h)=h\). Hence we have the following presentation
identifying the class of \(1\in {\mathcal {D}}_U\) on the right-hand side with the function \(h^{-1}\in {\mathcal {O}}_U\). Under this isomorphism, \(F^H_\bullet {\mathcal {O}}_U \cong F^{{\text {ord}}}_\bullet {\mathcal {D}}_U/(\delta _1,\ldots ,\delta _{n-1},\chi +1)\), here \(F^{{\text {ord}}}_\bullet \) denotes the filtration induced on a cyclic \({\mathcal {D}}\)-module by the filtration on \({\mathcal {D}}\) by the order of differential operators.
From this presentation, we deduce the following statement.
Lemma 4.1
The pure Hodge module  has the underlying
has the underlying  -module
-module

where \({\widetilde{\chi }}:=\chi +\partial _t t\). Under this isomorphism, we have the following description of the Hodge filtration on  :
:

where again \(F^{{\text {ord}}}_\bullet \) is the filtration induced from  .
.
Proof
We rewrite the morphism \(i'_h\) as the composition \(i'_h={^{(2)}}i'_h\circ {^{(1)}}i'_h\), where  is the graph embedding of the restricted morphism
is the graph embedding of the restricted morphism  (in particular, it is closed) and where
(in particular, it is closed) and where

is the canonical open embedding. Notice however that the composed morphism  is closed, since the closure of its image is contained in \({\mathbb {C}}^*_t \times U\).
is closed, since the closure of its image is contained in \({\mathbb {C}}^*_t \times U\).
We can extend the above diagram (27) as follows:

We have

and (see [39, Formula 1.8.6])

Again, since

we obtain

Now we consider the Hodge filtration on the module

We use once more the inclusion in formula (29), which gives, when applying [39, Formula 4.2.1] to the module  and the morphism \({^{(2)}i'_h}\), that
and the morphism \({^{(2)}i'_h}\), that

where the second equality follows since the closure of

in  is contained in
is contained in  , i.e., from formula (29). \(\square \)
, i.e., from formula (29). \(\square \)
Next we will deduce from this result a description of the Hodge filtration on the Hodge module  . This is the crucial step towards our first main result (Theorem 4.4 below). We will use the results from the last section concerning the canonical V-filtration of the graph embedding module \(i_{h,+}{\mathcal {O}}_X(*D)\) in an essential way. The result we are after can be stated as follows.
. This is the crucial step towards our first main result (Theorem 4.4 below). We will use the results from the last section concerning the canonical V-filtration of the graph embedding module \(i_{h,+}{\mathcal {O}}_X(*D)\) in an essential way. The result we are after can be stated as follows.
Proposition 4.2
The mixed Hodge module  has \(i_{h,+}{\mathcal {O}}_X(*D)\) as underlying
has \(i_{h,+}{\mathcal {O}}_X(*D)\) as underlying  -module. Under the isomorphism
-module. Under the isomorphism

from Lemma 3.5 (which, as indicated at the beginning of this section, we write here as an isomorphism of sheaves of  -modules rather than of germs) we have the following inclusion of coherent
-modules rather than of germs) we have the following inclusion of coherent  -modules for all
-modules for all  :
:
Proof
First put for notational convenience

Now it is known (see [39, Proposition 4.2]) that the Hodge filtration on the Hodge module  has the following description (this is due to the construction of the open direct image for mixed Hodge modules, see [38, Section 2.7-2.8]):
has the following description (this is due to the construction of the open direct image for mixed Hodge modules, see [38, Section 2.7-2.8]):
but since
we are left to show that we have
Since
holds for all  , it is sufficient to show the inclusion
, it is sufficient to show the inclusion
for all  . We have seen in Proposition 3.3 that \(V_{{\text {can}}}^k {\mathcal {N}}(h) \subset V_{{\text {ind}}}^k {\mathcal {N}}(h)\) holds for all
. We have seen in Proposition 3.3 that \(V_{{\text {can}}}^k {\mathcal {N}}(h) \subset V_{{\text {ind}}}^k {\mathcal {N}}(h)\) holds for all  (recall that since we assume in this section that D is SK free, we know that the roots of \(b_h(s)\) are included in \((-2,0)\) by [32, Theorem 4.1], so that the assumptions of Proposition 3.3 are satisfied). Thus it suffices to show that we have
(recall that since we assume in this section that D is SK free, we know that the roots of \(b_h(s)\) are included in \((-2,0)\) by [32, Theorem 4.1], so that the assumptions of Proposition 3.3 are satisfied). Thus it suffices to show that we have
for all  . Let an element \(m\in V_{{\text {ind}}}^0 {\mathcal {N}}(h) \cap j'_* F^{{\text {ord}}}_r {\mathcal {N}}'(h) \) be given. Then there is some
. Let an element \(m\in V_{{\text {ind}}}^0 {\mathcal {N}}(h) \cap j'_* F^{{\text {ord}}}_r {\mathcal {N}}'(h) \) be given. Then there is some  such that \(t^p \cdot m \in V^p_{{\text {ind}}} {\mathcal {N}}(h) \cap F_r^{{\text {ord}}} {\mathcal {N}}(h)\) (see also the proof of [37, Proposition 3.2.2], especially the implication (3.2.1.2) \(\Rightarrow \) (3.2.2.1)): Since the filtration \(F^{{\text {ord}}}_\bullet \) is exhaustive on \(V^0_{{\text {ind}}} {\mathcal {N}}(h)\) we know that there is some
such that \(t^p \cdot m \in V^p_{{\text {ind}}} {\mathcal {N}}(h) \cap F_r^{{\text {ord}}} {\mathcal {N}}(h)\) (see also the proof of [37, Proposition 3.2.2], especially the implication (3.2.1.2) \(\Rightarrow \) (3.2.2.1)): Since the filtration \(F^{{\text {ord}}}_\bullet \) is exhaustive on \(V^0_{{\text {ind}}} {\mathcal {N}}(h)\) we know that there is some  such that \(m\in F^{{\text {ord}}}_l {\mathcal {N}}(h) \cap V^0_{{\text {ind}}}{\mathcal {N}}(h)\), if \(l\le r\), we are done by putting \(p=0\). Otherwise, since \(m\in j'_*F^{{\text {ord}}}_r {\mathcal {N}}'(h)\) (which means by definition that
such that \(m\in F^{{\text {ord}}}_l {\mathcal {N}}(h) \cap V^0_{{\text {ind}}}{\mathcal {N}}(h)\), if \(l\le r\), we are done by putting \(p=0\). Otherwise, since \(m\in j'_*F^{{\text {ord}}}_r {\mathcal {N}}'(h)\) (which means by definition that  ) it follows that the class of m in the quotient \(F^{{\text {ord}}}_l {\mathcal {N}}(h)/ F^{{\text {ord}}}_r {\mathcal {N}}(h)\) is a t-torsion element in that module. Notice that \(F^{{\text {ord}}}_l {\mathcal {N}}(h)/ F^{{\text {ord}}}_r {\mathcal {N}}(h)\) is
) it follows that the class of m in the quotient \(F^{{\text {ord}}}_l {\mathcal {N}}(h)/ F^{{\text {ord}}}_r {\mathcal {N}}(h)\) is a t-torsion element in that module. Notice that \(F^{{\text {ord}}}_l {\mathcal {N}}(h)/ F^{{\text {ord}}}_r {\mathcal {N}}(h)\) is  -coherent, hence there is some p such that the class of \(t^p\cdot m\) is zero in this quotient, that is \(t^p\cdot m \in F^{{\text {ord}}}_r {\mathcal {N}}(h)\), and obviously we have \(t^p\cdot m \in V_{{\text {ind}}}^p {\mathcal {N}}(h)\) since \(m\in V^0_{{\text {ind}}} {\mathcal {N}}(h)\).
-coherent, hence there is some p such that the class of \(t^p\cdot m\) is zero in this quotient, that is \(t^p\cdot m \in F^{{\text {ord}}}_r {\mathcal {N}}(h)\), and obviously we have \(t^p\cdot m \in V_{{\text {ind}}}^p {\mathcal {N}}(h)\) since \(m\in V^0_{{\text {ind}}} {\mathcal {N}}(h)\).
Now by Proposition 3.10 we know that there exists an operator  projecting to \(t^p\cdot m \in V^p_{{\text {ind}}} {\mathcal {N}}(h) \cap F_r^{{\text {ord}}} {\mathcal {N}}(h)\). By definition, \(P'\) can be written as \(P'=t^p\cdot P\), where
projecting to \(t^p\cdot m \in V^p_{{\text {ind}}} {\mathcal {N}}(h) \cap F_r^{{\text {ord}}} {\mathcal {N}}(h)\). By definition, \(P'\) can be written as \(P'=t^p\cdot P\), where  . Then the class [P] of P in \({\mathcal {N}}(h)\) satisfies \([P]\in F^{{\text {ord}}}_r {\mathcal {N}}(h)\) and obviously we have \([P]=m\). Hence the inclusion \(V_{{\text {ind}}}^0 {\mathcal {N}}(h) \cap j'_* F^{{\text {ord}}}_r {\mathcal {N}}'(h) \subset F^{{\text {ord}}}_r {\mathcal {N}}(h)\) is proved. \(\square \)
. Then the class [P] of P in \({\mathcal {N}}(h)\) satisfies \([P]\in F^{{\text {ord}}}_r {\mathcal {N}}(h)\) and obviously we have \([P]=m\). Hence the inclusion \(V_{{\text {ind}}}^0 {\mathcal {N}}(h) \cap j'_* F^{{\text {ord}}}_r {\mathcal {N}}'(h) \subset F^{{\text {ord}}}_r {\mathcal {N}}(h)\) is proved. \(\square \)
Using the description of the canonical V-filtration on the module \({\mathcal {N}}(h)\) along the divisor \(\{t=0\}\) from Corollary 3.3, we can give a more precise description of the Hodge filtration on that module. We also recall from such corollary that  , and for \(\alpha \in B'_h\), we write \(l_\alpha \) for the multiplicity of \(\alpha -1\) in \(b_h(s)\).
, and for \(\alpha \in B'_h\), we write \(l_\alpha \) for the multiplicity of \(\alpha -1\) in \(b_h(s)\).
For the sake of brevity, we will sometimes write in the following \(F^H{\mathcal {N}}(h)\), translating the Hodge filtration on \(i_{h,+}{\mathcal {O}}_X(*D)\) using the isomorphism \({\mathcal {N}}(h)\cong i_{h,+}{\mathcal {O}}_X(*D)\).
Corollary 4.3
Under the isomorphism \(i_{h,+}{\mathcal {O}}_X(*D)\cong {\mathcal {N}}(h)\), we have the following (equivalent) descriptions of the Hodge filtration steps \(F^H_k {\mathcal {O}}_X(*D)\) for all  :
:
Proof
From the proof of the last lemma we know already that
so that in particular \(F^H_k i_{h,+}{\mathcal {O}}_X(*D) =0\) for all \(k<1\) since \(F^{{\text {ord}}}_l {\mathcal {N}}'(h)=0\) for negative l. The same holds for \(F^{{\text {ord}}}_l{\mathcal {N}}(h)\), hence, the above formulas are proved when \(k<1\). We rewrite formula (35) in a recursive way, namely
where the last equality uses again formula (35).
Now we conclude using Proposition 4.2: Thanks to equation (30), we can claim that \(F^H_k(i_{h,+}{\mathcal {O}}_X(*D)) \subset F^{{\text {ord}}}_{k-1} {\mathcal {N}}(h)\), hence we obtain
since we clearly have \(F^{{\text {ord}}}_{k-1} {\mathcal {N}}(h) \subset j'_* F^{{\text {ord}}}_{k-1} {\mathcal {N}}'(h)\) by the very definition of the functor \((j')_*\) and where the inclusion \({\mathop {\subset }\limits ^{*}}\) follows from equation (36) above. As a consequence, the first inclusion \(V_{{\text {can}}}^0 {\mathcal {N}}(h) \cap F^{{\text {ord}}}_{k-1} {\mathcal {N}}(h) \subset V_{{\text {can}}}^0 {\mathcal {N}}(h) \cap j'_* F^{{\text {ord}}}_{k-1} {\mathcal {N}}'(h)\) is in fact an equality, and therefore equation (36) becomes
so that the recursive Formula (33) is shown. Formula (34) follows by replacing the term \(V^0_{{\text {can}}} {\mathcal {N}}(h)\) with the expression from Proposition 3.3. Moreover, it is clear that the non-recursive Formula (32) follows from the recursive one (33) by induction. \(\square \)
Our main purpose is to describe the Hodge filtration on \({\mathcal {O}}_X(*D)\). This description will be obtained as a consequence of Proposition 4.2 and Corollary 4.3. Recall that the graph embedding module \({\mathcal {N}}(h)\) can be alternatively described as \({\mathcal {M}}(h)[\partial _t]\), where the left action by  on \({\mathcal {M}}(h)[\partial _t]\) is given by Formula (19).
on \({\mathcal {M}}(h)[\partial _t]\) is given by Formula (19).
We then have the following result.
Theorem 4.4
Consider a strongly Koszul free divisor \(D\subset X\). Then we have the following inclusion of coherent \({\mathcal {O}}_X\)-modules (which holds globally on X and does not require that D is given by a global equation)
where \(F^H_\bullet {\mathcal {O}}_X(*D)\) is the filtration such that the filtered \({\mathcal {D}}_X\)-module \(({\mathcal {O}}_X(*D),F^H_\bullet )\) underlies the mixed Hodge module  .
.
If \(h=0\) is a local reduced equation for D and using the local isomorphism \({\mathcal {M}}(h)\cong {\mathcal {O}}_X(*D)\), we have the recursive formula
where the intersection takes place in \({\mathcal {M}}(h)[\partial _t] \cong {\mathcal {N}}(h)\).
Formula (37) is recursive despite the appearance of the same index k on both sides: in order to calculate (locally) the k-th filtration step of the Hodge filtration on \({\mathcal {O}}_X(*D)\), we need to know the k-th filtration step of the Hodge filtration on \({\mathcal {N}}(h)\), the knowledge of which is equivalent to the knowledge of \(F^H_{k-1} {\mathcal {M}}(h)\cong F^H_{k-1} {\mathcal {O}}_X(*D)\) (see the discussion in the proof below, in particular, Formula (39)).
Proof
It is sufficient to prove the second statement, since locally, where D is defined by an equation \(h=0\), formula (37) exhibits \(F_k^H{\mathcal {O}}_X(*D)\) as a submodule of \(F_k^{{\text {ord}}}{\mathcal {M}}(h)\). However, the statement \(F^H_k {\mathcal {O}}_X(*D) \subset F_k^{{\text {ord}}} {\mathcal {O}}_X(*D)\) (where \(F^{{\text {ord}}}_\bullet {\mathcal {O}}_X(*D)\) is as in Definition 2.2) holds globally on X, once it is shown at each \(p\in D\).
First notice that we have the equality

of objects in  . It follows that the filtered module \(({\mathcal {N}}(h),F_\bullet ^H)\) (where \(F^H_\bullet \) is the filtration considered in Proposition 4.2 and Corollary 4.3) underlies the mixed Hodge module
. It follows that the filtered module \(({\mathcal {N}}(h),F_\bullet ^H)\) (where \(F^H_\bullet \) is the filtration considered in Proposition 4.2 and Corollary 4.3) underlies the mixed Hodge module  . Then [39, Formula (1.8.6)] yields the following relation between the filtration \(F^H_\bullet {\mathcal {N}}(h)\) and the Hodge filtration on
. Then [39, Formula (1.8.6)] yields the following relation between the filtration \(F^H_\bullet {\mathcal {N}}(h)\) and the Hodge filtration on  (which is \(F_\bullet ^H {\mathcal {O}}_X(*D)\), and again we will freely denote it by \(F^H_\bullet {\mathcal {M}}(h)\) using the isomorphism \({\mathcal {M}}(h)\cong {\mathcal {O}}_X(*D)\)):
(which is \(F_\bullet ^H {\mathcal {O}}_X(*D)\), and again we will freely denote it by \(F^H_\bullet {\mathcal {M}}(h)\) using the isomorphism \({\mathcal {M}}(h)\cong {\mathcal {O}}_X(*D)\)):
in other words, we obtain
for all \(k>1\). As we have noticed in Corollary 4.3, we have the inclusion
and since obviously \(F^{{\text {ord}}}_{k-1} {\mathcal {N}}(h) \cap \left( {\mathcal {M}}(h)\otimes 1\right) = F^{{\text {ord}}}_{k-1} {\mathcal {N}}(h) \cap \left( F^{{\text {ord}}}_{k-1}{\mathcal {M}}(h)\otimes 1\right) \), we obtain by plugging in formula (34) that \(F_{k-1}^H{\mathcal {O}}_X(*D)\) is isomorphic to
Shifting the indices by one, the inclusion
is then clear. But we also have the inclusion in the other direction: Let \(a\in \partial _t F_k^H{\mathcal {N}}(h)\) and \(b\in V_{{\text {ind}}}^1{\mathcal {N}}(h) + \prod _{\alpha \in B'_h}(\partial _t t +\alpha )^{l_\alpha } V_{{\text {ind}}}^0 {\mathcal {N}}(h)\) and assume that \(a+b\in F^{{\text {ord}}}_k{\mathcal {M}}(h)\otimes 1\subset F^{{\text {ord}}}_k{\mathcal {N}}(h)\). Then since \(\partial _t F_k^H{\mathcal {N}}(h)\subset \partial _t F_{k-1}^{{\text {ord}}}{\mathcal {N}}(h)\subset F_k^{{\text {ord}}}{\mathcal {N}}(h)\), we must necessarily have \(b\in F_k^{{\text {ord}}}{\mathcal {N}}(h)\), so that \(a+b\) belongs to
that is, to \(F^H_k{\mathcal {O}}_X(*D)\), as required. \(\square \)
Remark 4.5
(see also subsection 5.1below) As shown in [39, Proposition 0.9] we have
for any reduced divisor, where \(P_k {\mathcal {O}}_X(*D) := {\mathcal {O}}_X((k+1)D)\) is the pole order filtration. In our situation of a strongly Koszul free divisor, we obviously have
with \(F^H_0 {\mathcal {O}}_X(*D)\subset F^{{\text {ord}}}_0 {\mathcal {O}}_X(*D) = P_0 {\mathcal {O}}_X(*D)\). Therefore, one can consider \(F^{{\text {ord}}}_k {\mathcal {O}}_X(*D)\), in the current situation, as a better approximation to the Hodge filtration than the pole order filtration \(P_\bullet {\mathcal {O}}_X(*D)\) (though both are equal at level \(k=0\)) . A very special example is the case where D has normal crossings, then for any local reduced equation \(h=0\) for D the only root of \(b_h(s)\) is \(-1\), and one easily obtains \(F_k^H{\mathcal {O}}_X(*D)= F_k^{{\text {ord}}} {\mathcal {O}}_X(*D)\). Correspondingly, we have \(F_0^H{\mathcal {O}}_X(*D) = F_0^{{\text {ord}}} {\mathcal {O}}_X(*D)=P_0 {\mathcal {O}}(*D) = {\mathcal {O}}(D)\), so that \({\mathcal {I}}_0(D)={\mathcal {O}}_X\), but the higher Hodge ideals are non-trivial even for the normal crossing case, precisely because we have \(F_k^{{\text {ord}}} {\mathcal {O}}_X(*D)\subsetneq P_k {\mathcal {O}}(*D)\) for \(k>0\).
We have seen so far that \(F^H_\bullet {\mathcal {O}}_X(*D) \subset F^{{\text {ord}}}_\bullet {\mathcal {O}}_X(*D)\), with equality iff \(-1\) is the only root of \(b_h(s)\) for any local reduced equation h of D. However, we can actually give an inclusion in the reverse direction, but with a specific shift, which we conjecture to be the generating level of the Hodge filtration on \({\mathcal {O}}_X(*D)\) (see Conjecture 4.12 below). As a preparation, we need the following result.
Lemma 4.6
Let \((D,p) \subset (X,p)\) be a germ of strongly Koszul free divisor with reduced equation \(h=0\), let \(\beta (s)=\prod _{\alpha \in B'_h}(s +\alpha )^{l_\alpha }\), where \(l_\alpha \) is the multiplicity of \(\alpha -1\) in \(b_h(s)\) and put \(r := \deg \beta (s)\). Consider the generator \([1]\in {\mathcal {N}}(h)\), then we have
Proof
Write \(\beta (s)=\sum _{i=0}^r a_i s^i\) with  . We have \([t\cdot (\partial _t t)^{i-1}]\in V^1_{{\text {ind}}}{\mathcal {N}}(h)\cap F^{{\text {ord}}}_{i-1}{\mathcal {N}}(h)\) for all \(i\in \{1,\ldots ,r\}\). Now we may rewrite Formula (34) as
. We have \([t\cdot (\partial _t t)^{i-1}]\in V^1_{{\text {ind}}}{\mathcal {N}}(h)\cap F^{{\text {ord}}}_{i-1}{\mathcal {N}}(h)\) for all \(i\in \{1,\ldots ,r\}\). Now we may rewrite Formula (34) as
Then we have for all \(i\in \{1,\ldots ,r\}\)
On the other hand, we have \(\beta (\partial _t t) \cdot [1] \in \beta (\partial _t t)V^0_{{\text {ind}}}{\mathcal {N}}(h)\cap F^{{\text {ord}}}_r{\mathcal {N}}(h) \subset F^H_{r+1}{\mathcal {N}}(h)\). Since \(\beta (\partial _t t)- \sum _{i=1}^r a_i (\partial _t t)^i=a_0\) we find that \(a_0[1]\in F^H_{r+1}{\mathcal {N}}(h)\). By definition of the set \(B'_h\), we have \(\beta (0)\ne 0\) and hence \(a_0\ne 0\), so that finally \([1]\in F^H_{r+1} {\mathcal {N}}(h)\), as required. \(\square \)
We obtain the following two consequences that we will use below to discuss the dual Hodge filtration.
Corollary 4.7
With the aforementioned notations, we have
-
1.
\([1]\in F^H_r {\mathcal {M}}(h)\),
-
2.
For all
 , we have the inclusion of coherent \({\mathcal {O}}_X\)-modules \(F^{{\text {ord}}}_{k-r} {\mathcal {M}}(h) \subset F^H_k {\mathcal {M}}(h)\).
, we have the inclusion of coherent \({\mathcal {O}}_X\)-modules \(F^{{\text {ord}}}_{k-r} {\mathcal {M}}(h) \subset F^H_k {\mathcal {M}}(h)\).
Proof
-
1.
Recall Formula (39), which says that
$$\begin{aligned} F^H_{k-1} {\mathcal {M}}(h) \cong F^H_k {\mathcal {N}}(h)\cap \left( {\mathcal {M}}(h)\otimes 1\right) . \end{aligned}$$Now obviously the element \([1]\in {\mathcal {N}}(h)\) belongs to the submodule \({\mathcal {M}}(h)\otimes 1\subset {\mathcal {N}}(h)\), hence we obtain from Lemma 4.6 that the element \([1]\in {\mathcal {M}}(h)\) lies in \(F^H_r{\mathcal {M}}(h)\).
-
2.
The statement is trivial for \(k<r\). On the other hand, we have by definition that for any \(k\ge r\) any class \([P]\in F^{{\text {ord}}}_{k-r} {\mathcal {M}}(h)\) can be represented by an operator \(P\in {\mathcal {D}}_X\) of order \(k-r\). Moreover, \(F^H_\bullet {\mathcal {M}}(h)\) is a good filtration (in particular, compatible with \(F_\bullet {\mathcal {D}}_X\)), so \([P]=P\cdot [1]\in F_{k-r}{\mathcal {D}}_X\cdot [1]\subset F_{k-r}{\mathcal {D}}_X\cdot F^H_r{\mathcal {M}}(h)\subset F^H_k{\mathcal {M}}(h)\). Hence \(F^{{\text {ord}}}_{k-r} {\mathcal {M}}(h) \subset F^H_k {\mathcal {M}}(h)\), as required.
\(\square \)
Let us call \(b_D(s)\) the least common multiple of the local b-functions of all reduced local equations of D at p, for \(p\in D\), whenever it exists (it always exists if \(D\subset X\) is algebraic or if X is compact),  and \(\beta _D(s)=\prod _{\alpha \in B'_D}(s +\alpha )^{l_\alpha }\), where \(l_\alpha \) is the multiplicity of \(\alpha -1\) in \(b_D(s)\) and put \(r := \deg \beta _D(s)\). The strong Koszul hypothesis on D then implies the symmetry property \(b_D(-s-2) = \pm b_D(s)\) and so \(r=\frac{1}{2}\left( \deg (b_D(s))-\text {mult}_{b_D(s)}(-1)\right) \). The following global result about the divisor \(D\subset X\) is a consequence of the first point of Theorem 4.4 and of Corollary 4.7.
and \(\beta _D(s)=\prod _{\alpha \in B'_D}(s +\alpha )^{l_\alpha }\), where \(l_\alpha \) is the multiplicity of \(\alpha -1\) in \(b_D(s)\) and put \(r := \deg \beta _D(s)\). The strong Koszul hypothesis on D then implies the symmetry property \(b_D(-s-2) = \pm b_D(s)\) and so \(r=\frac{1}{2}\left( \deg (b_D(s))-\text {mult}_{b_D(s)}(-1)\right) \). The following global result about the divisor \(D\subset X\) is a consequence of the first point of Theorem 4.4 and of Corollary 4.7.
Corollary 4.8
Under the above conditions, we have:
We will finish this section by showing some results about the Hodge filtration on the dual Hodge module  . Its underlying \({\mathcal {D}}_X\)-module is
. Its underlying \({\mathcal {D}}_X\)-module is  , which we denote by \({\mathcal {O}}_X(!D)\). From the logarithmic comparison theorem we know that \({\mathcal {D}}_X \otimes _{{\mathcal {V}}_X^D} {\mathcal {O}}_X(D) \cong {\mathcal {O}}_X(*D)\), and so we can apply Proposition 2.9 (for the case \({\mathcal {E}}={\mathcal {O}}_X(D)\)) to obtain that the holonomic filtered module \(({\mathcal {O}}_X(*D),F_\bullet ^{{\text {ord}}})\) has the Cohen-Macaulay property and moreover that the dual filtered module of \(({\mathcal {O}}_X(*D),F_\bullet ^{{\text {ord}}})\) is isomorphic to \(({\mathcal {O}}_X(!D)\cong {\mathcal {D}}_X \otimes _{{\mathcal {V}}_X^D} {\mathcal {O}}_X, F_\bullet ^{{\text {ord}}})\). We recall that a similar property holds for the Hodge filtration, more precisely, we have the following.
, which we denote by \({\mathcal {O}}_X(!D)\). From the logarithmic comparison theorem we know that \({\mathcal {D}}_X \otimes _{{\mathcal {V}}_X^D} {\mathcal {O}}_X(D) \cong {\mathcal {O}}_X(*D)\), and so we can apply Proposition 2.9 (for the case \({\mathcal {E}}={\mathcal {O}}_X(D)\)) to obtain that the holonomic filtered module \(({\mathcal {O}}_X(*D),F_\bullet ^{{\text {ord}}})\) has the Cohen-Macaulay property and moreover that the dual filtered module of \(({\mathcal {O}}_X(*D),F_\bullet ^{{\text {ord}}})\) is isomorphic to \(({\mathcal {O}}_X(!D)\cong {\mathcal {D}}_X \otimes _{{\mathcal {V}}_X^D} {\mathcal {O}}_X, F_\bullet ^{{\text {ord}}})\). We recall that a similar property holds for the Hodge filtration, more precisely, we have the following.
Theorem 4.9
([37, Section 2.4], [37, Lemme 5.1.13], see also [43, Theorem 29.3]) Let \(({\mathcal {M}},F_\bullet )\) be a filtered left or right \({\mathcal {D}}_X\)-module underlying a pure Hodge module M of weight w, then \(({\mathcal {M}},F_\bullet )\) has the Cohen-Macaulay property. In particular, its dual module is strict, and underlies a pure Hodge module  of weight \(-w\). Similarly, if \((M,W_\bullet M)\) is a mixed Hodge module, then so is the object
of weight \(-w\). Similarly, if \((M,W_\bullet M)\) is a mixed Hodge module, then so is the object  . In particular, if \(({\mathcal {M}},F_\bullet )\) underlies a mixed Hodge module M, then it also fulfills the Cohen-Macaulay property. Its dual filtration
. In particular, if \(({\mathcal {M}},F_\bullet )\) underlies a mixed Hodge module M, then it also fulfills the Cohen-Macaulay property. Its dual filtration  is the Hodge filtration
is the Hodge filtration  of
of  up to a shift, i.e., we have
up to a shift, i.e., we have

With these preparations, we obtain the following result concerning the Hodge filtration on the dual module \({\mathcal {O}}_X(!D)\).
Theorem 4.10
Let, as above, \(D\subset X\) be a strongly Koszul free divisor, then we have the following inclusions of coherent \({\mathcal {O}}_X\)-submodules of \({\mathcal {O}}_X(!D)\):

In particular, since \(F^{{\text {ord}}}_{-1}{\mathcal {O}}(!D)=0\), we obtain the vanishing

Proof
Equation (40) from Corollary 4.8 says
Applying the Rees functor \({\mathcal {R}}(-)\) defined on page 11 to the first inclusion yields a short exact sequence of graded \({\widetilde{{\mathcal {D}}}}_X\)-modules
recall that for a graded \({\widetilde{{\mathcal {D}}}}_X\)-module \({\widetilde{{\mathcal {M}}}}\), we write \({\widetilde{{\mathcal {M}}}}(l)\) for the same module with grading \({\widetilde{{\mathcal {M}}}}(l)_k={\widetilde{{\mathcal {M}}}}_{k+l}\). Notice that the cokernel \({\mathcal {C}}\) is a z-torsion module, since, e.g., for any section \(s\in F_k^H {\mathcal {O}}_X(*D)\) we have \(s \in F^{{\text {ord}}}_k {\mathcal {O}}_X(*D)\) (due to the second inclusion from Formula (4.8)). Hence \([s]\cdot z^k\in ({\mathcal {R}}_{F^{{\text {ord}}}}{\mathcal {O}}_X(*D))_k= ({\mathcal {R}}_{F^{{\text {ord}}}}{\mathcal {O}}_X(*D)(-r))_{k+r}\) and therefore \([s]\cdot z^k\) maps to 0 in \({\mathcal {C}}\).
Now apply the duality functor for graded left \({\widetilde{{\mathcal {D}}}}_X\)-modules (defined by formula (11)) to the short exact sequence (42). From Corollary 2.11 we deduce that

On the other hand, by Theorem 4.9 we know that the filtered module \(({\mathcal {O}}_X(*D), F_\bullet ^H)\) satisfies the Cohen-Macaulay property as well, and we write as before  for its dual filtered module.
for its dual filtered module.
Hence, the triangle resulting from applying  to the sequence (42) has the following long exact cohomology sequence:
to the sequence (42) has the following long exact cohomology sequence:

The \({\widetilde{{\mathcal {D}}}}_X\)-module \({\mathcal {C}}\) is a z-torsion module, which implies that  is so (since z is a central element in \({\widetilde{{\mathcal {D}}}}_X\)). The \({\widetilde{{\mathcal {D}}}}_X\)-module
is so (since z is a central element in \({\widetilde{{\mathcal {D}}}}_X\)). The \({\widetilde{{\mathcal {D}}}}_X\)-module  (and analogously \(({\mathcal {R}}_{F^{{\text {ord}}}}{\mathcal {O}}_X(!D))(r)\)) has no z-torsion, since it is the Rees module of a filtered \({\mathcal {D}}_X\)-module, hence
(and analogously \(({\mathcal {R}}_{F^{{\text {ord}}}}{\mathcal {O}}_X(!D))(r)\)) has no z-torsion, since it is the Rees module of a filtered \({\mathcal {D}}_X\)-module, hence  . Notice however that
. Notice however that  does not necessarily vanish, since the homological dimension of the rings \(R_U\) defined in Formula (7) is bounded from above by \(2n+1\) only (which is the global homological dimension of \(\text {Gr}_\bullet ^F R_U={\mathcal {O}}_U[z,\xi _1,\ldots ,\xi _n]\), where \(\xi _i\) is the symbol of \(z\partial _{x_i}\)), see [20, Theorem D.2.6 and Theorem D.4.3 (ii)]. Summing up, the exact sequence (43) yields the injective morphism
does not necessarily vanish, since the homological dimension of the rings \(R_U\) defined in Formula (7) is bounded from above by \(2n+1\) only (which is the global homological dimension of \(\text {Gr}_\bullet ^F R_U={\mathcal {O}}_U[z,\xi _1,\ldots ,\xi _n]\), where \(\xi _i\) is the symbol of \(z\partial _{x_i}\)), see [20, Theorem D.2.6 and Theorem D.4.3 (ii)]. Summing up, the exact sequence (43) yields the injective morphism  of graded \({\widetilde{{\mathcal {D}}}}_X\)-modules, which gives an inclusion
of graded \({\widetilde{{\mathcal {D}}}}_X\)-modules, which gives an inclusion

of coherent \({\mathcal {O}}_X\)-modules for any  .
.
The very same argument, starting from the inclusion \(F^H_\bullet {\mathcal {O}}_X(*D)\subset F^{{\text {ord}}}_\bullet {\mathcal {O}}_X(*D)\) (and using the Cohen-Macaulay property of \(({\mathcal {O}}_X(*D),F^{{\text {ord}}}_\bullet )\) proved in Proposition 2.9 instead of the one of \(({\mathcal {O}}_X(*D),F^H_\bullet )\) as above) yields that

for all  , which completes the proof. \(\square \)
, which completes the proof. \(\square \)
Finally, we will state a conjecture about the so-called generating level of the Hodge filtration. Let us recall the following definition from [41].
Definition 4.11
Let X be a complex manifold and let a well filtered module \(({\mathcal {M}},F_\bullet )\) be given. Then we say that the filtration \(F_\bullet {\mathcal {M}}\) is generated at level k if
holds for all \(l\ge 0\), or, equivalently, if for all \(k'\ge k\), we have
The smallest integer k with this property is called the generating level of \(F_\bullet {\mathcal {M}}\).
Based on our calculations in section 5, we conjecture the following bound for the generating level of \(F^H_\bullet \) on \({\mathcal {O}}_X(*D)\).
Conjecture 4.12
Under the assumptions of Theorem 4.4 and Corollary 4.8, the Hodge filtration \(F^H_\bullet {\mathcal {O}}(*D)\) is generated at level \(r:=\frac{1}{2}\left( \deg (b_D(s))-\text {mult}_{b_D(s)}(-1)\right) \).
Remark 4.13
-
1.
As we will see in section 5, this bound for the generating level is not always better than the known general bound, which is \(n-2\) (see [28, Theorem B]). For the specific class of linear free divisors, it is known however that \(\deg (b_h(s))=n\), and in this case the bound r would be a drastic improvement, see subsection 5.3 below. Notice also that the general bound \(n-1-\lceil {\widetilde{\alpha }}_D \rceil \) from [30, Theorem A] is not helpful in our situation, since the minimal exponent \({\widetilde{\alpha }}_D\), which is the negative of the biggest root of the reduced Bernstein polynomial \(b_h(s)/(s+1)\), lies in (0, 1), so that this bound is again \(n-2\).
-
2.
There is a criterion in [40, Lemma 2.5] that guarantees generating level smaller or equal to k for a filtered module \(({\mathcal {M}}, F_\bullet )\) satisfying the Cohen-Macaulay property in terms of vanishing of the dual filtration. It cannot, however, directly be applied in our situation since for this we would need the vanishing
 instead of
instead of 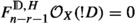 , which is provided by Theorem 4.10. One may hope though that some refinement of this argument (see, e.g., [30, Proposition 3.3] for a statement in a related situation) can give the desired result.
, which is provided by Theorem 4.10. One may hope though that some refinement of this argument (see, e.g., [30, Proposition 3.3] for a statement in a related situation) can give the desired result. -
3.
As an immediate consequence of the conjecture, we would obtain a local vanishing result for a log resolution of an SK-free divisor, as provided by [28, Theorem 17.1]. Namely, for a log resolution \(\pi :{\widetilde{X}}\longrightarrow X\) which is an isomorphism over \(X\backslash D\) and where \(E:=(\pi ^{-1}(D))_{\text {red}}\) (a reduced normal crossing divisor on \({\widetilde{X}}\)) we would have (provided that Conjecture 4.12 holds true)
$$\begin{aligned} R^k\pi _* \Omega ^{n-k}_{{\widetilde{X}}}(\log \, E) = 0 \end{aligned}$$for all \(k>r\).
5 Computations of Hodge ideals and examples
The purpose of this section is to develop some techniques to calculate Hodge ideals of a strongly Koszul free divisor using our main result (Theorem 4.4). We will illustrate these methods by concrete computations of Hodge ideals and of the generating level of the Hodge filtration for some interesting examples. We start with the following preliminary result.
Lemma 5.1
Let \(D\subset X\) be a free divisor, let \(p\in D\) such that D is strongly Koszul at p and take a reduced local defining equation \(h\in {\mathcal {O}}_{X,p}\) of \((D,p)\subset (X,p)\). Consider the vector fields \(\delta _1,\ldots , \delta _{n-1},{{\tilde{\chi }}}\) as in Lemma 4.1. Let \(\beta (s)\) be any polynomial in  . Then
. Then

Proof
For the sake of simplicity, let us denote  just by \({\mathcal {D}}\). Before starting the proof, let us explain something we will take for granted throughout it: we know that
just by \({\mathcal {D}}\). Before starting the proof, let us explain something we will take for granted throughout it: we know that  and that any \(P\in V^0{\mathcal {D}}\) can be expressed in a unique way as a series
and that any \(P\in V^0{\mathcal {D}}\) can be expressed in a unique way as a series
with constant coefficients, and for each \((\beta , m)\), the series \(\sum _{\alpha , \ell } a_{\alpha ,\ell }^{\beta ,m} x^\alpha t^\ell \) is convergent. Now, by using the identity \(t^\ell (\partial _t t)^m = (\partial _t t -\ell )^m t^\ell \) we find another unique formal representation
with
and one easily sees that for fixed \(\beta ,i,\ell \) the series \(\sum _\alpha c_{\alpha ,\ell }^{\beta ,i} x^\alpha \) is convergent. So we have a unique formal expression
and it makes sense to consider \(P\in {\mathcal {D}}_{X,p}[\partial _tt][[t]]\), where the last ring is the completion of \({\mathcal {D}}_{X,p}[\partial _tt][t]\) with respect to the (t)-adic topology. Here one has to use that the left ideal generated by t coincides with the right ideal generated by t, and so it is a bilateral ideal, and also that the monomials \(t^\ell , \ell \ge 0\), form a basis of \({\mathcal {D}}_{X,p}[\partial _tt][t]\) as a left and as a right \({\mathcal {D}}_{X,p}[\partial _tt]\)-module.
Let us now begin with the actual proof and denote by \(\widetilde{\mathcal {I}}\) the ideal \(( t,\beta (\partial _tt),t-h,\delta _1,\ldots ,\delta _{n-1},{{\tilde{\chi }}}+1)\) of \(V^0{\mathcal {D}}\). The inclusion \(\supset \) in equation (45) is trivial, let us show the reverse one. We will use a more suitable set of generators of \(\widetilde{\mathcal {I}}\), namely \(\{t,{{\tilde{\beta }}},h,\delta _1,\ldots ,\delta _{n-1},\chi +\partial _tt+1\}\), where \({{\tilde{\beta }}}=\beta (-\chi -1)\).
Let then \(P\in \widetilde{\mathcal {I}}\cap {\mathcal {D}}_{X,p}[\partial _t t]\). Then there exist operators \(Q,R,A,B^1,\ldots ,B^{n-1},C\in V^0{\mathcal {D}}\) such that
Our goal is to show that Q must vanish and that the other operators belong actually to \({\mathcal {D}}_{X,p}[\partial _tt]\). Let us write \(Q=\sum _kQ_kt^k\), with \(Q_k\in {\mathcal {D}}_{X,p}[\partial _tt]\), and analogously for R, A, the \(B_i\) and C. We can express the right-hand side of equation (46) as a new operator \(S=\sum _kS_kt^k\), where again \(S_k\in {\mathcal {D}}_{X,p}[\partial _t t]\). Moreover, since t, \({{\tilde{\beta }}}\), h, \(\delta _1,\ldots , \delta _{n-1}\) and \(\widetilde{\chi }+1\), when seen as elements of \({\mathcal {D}}_{X,p}[\partial _t t][[t]]\), are homogeneous in t, we have for every \(k\ge 0\) that
Comparing the \(S_k\in {\mathcal {D}}_{X,p}[\partial _tt]\) with the terms of degree k in t at the left-hand side (recall that \(P\in {\mathcal {D}}_{X,p}[\partial _t t]\)), we find that \(S_k=0\) for every \(k>0\).
Let us write now \({{\bar{R}}}=R-R_0\) and similarly with the other operators. Each of them can be written as a series in t and we have checked that
Therefore, since \(\sum _{k>0}C_k(\widetilde{\chi }-k+1)t^k={{\bar{C}}}(\widetilde{\chi }+1)\),
Summing up, we have been able to write P as a linear combination of h, \({{\tilde{\beta }}}\), the \(\delta _i\) and \(\widetilde{\chi }+1\) with coefficients in \({\mathcal {D}}_{X,p}[\partial _tt]\), as we wanted. \(\square \)
Theorem 5.2
Let \(D\subset X\) be a free divisor, let \(p\in D\) such that D is strongly Koszul at p and let \(h\in {\mathcal {O}}_{X,p}\) be a reduced local equation of D. Let as before \(\beta (s)=\prod _{\alpha \in B'_h}(s+\alpha )^{l_\alpha }\), where \(l_\alpha \) is the multiplicity of \(\alpha -1\) in \(b_h(s)\), \(N(h)={\mathcal {N}}(h)_{(0,p)}\) and \(\pi _p:{\mathcal {D}}_{X,p}[s]\rightarrow N(h)\) the morphism of \({\mathcal {D}}_{X,p}[s]\)-modules given by \(P(s)\mapsto [P(-\partial _tt)]\) (where we give N(h) the \({\mathcal {D}}_{X,p}[s]\)-module structure coming from the inclusion  sending s to \(-\partial _t t\)). Consider also the ideal \({\mathcal {J}}_p\) of \({\mathcal {D}}_{X,p}[s]\) defined as
sending s to \(-\partial _t t\)). Consider also the ideal \({\mathcal {J}}_p\) of \({\mathcal {D}}_{X,p}[s]\) defined as
Then,
-
1.
\({\mathcal {D}}_{X,p}[s]\) can be endowed with a structure of
 -module such that \(\pi _p\) becomes
-module such that \(\pi _p\) becomes  -linear. As a consequence, the terms of the total order filtration \(T_\bullet {\mathcal {D}}_{X,p}[s]\) (see Definition 2.3) are
-linear. As a consequence, the terms of the total order filtration \(T_\bullet {\mathcal {D}}_{X,p}[s]\) (see Definition 2.3) are  -modules.
-modules. -
2.
For any \(k\ge 0\), we have the following equality of
 -modules: $$\begin{aligned} \left( V_{{\text {can}}}^0 {\mathcal {N}}(h)\cap F^{{\text {ord}}}_k {\mathcal {N}}(h)\right) _{(0,p)} =\pi _p({\mathcal {J}}_p\cap T_k{\mathcal {D}}_{X,p}[s]), \end{aligned}$$(47)
-modules: $$\begin{aligned} \left( V_{{\text {can}}}^0 {\mathcal {N}}(h)\cap F^{{\text {ord}}}_k {\mathcal {N}}(h)\right) _{(0,p)} =\pi _p({\mathcal {J}}_p\cap T_k{\mathcal {D}}_{X,p}[s]), \end{aligned}$$(47)and so
$$\begin{aligned} \begin{aligned} F_k^H {\mathcal {N}}(h)_{(0,p)}&=\partial _t F^H_{k-1}{\mathcal {N}}(h)_{(0,p)} + \pi _p({\mathcal {J}}_p\cap T_{k-1}{\mathcal {D}}_{X,p}[s]) \\&=\displaystyle \sum _{i=0}^{k-1} \partial _t^k\left( \pi _p({\mathcal {J}}_p\cap T_{k-1-i}{\mathcal {D}}_{X,p}[s])\right) . \end{aligned} \end{aligned}$$(48)
Proof
Following the same convention as in Lemma 5.1 above, we will write \({\mathcal {O}}\) and \({\mathcal {D}}\) for  and
and  , respectively.
, respectively.
We will define on \({\mathcal {D}}_{X,p}[s]\) an action of \({\mathcal {O}}\) by putting \(t\cdot P(s):=P(s+1)h\) and extending it by linearity. Let us check that such an action is well-defined. Indeed, let \(a(x,t)=\sum _{\alpha ,k}a_{\alpha k} x^\alpha t^k\) be a series in \({\mathcal {O}}\) and let us show that we can multiply by a in \({\mathcal {D}}_{X,p}[s]\). As a first step, we will restrict ourselves to consider an element \(P\in {\mathcal {D}}_{X,p}\). In order to show that \(a\cdot P\) lies within \({\mathcal {D}}_{X,p}[s]\), it is equivalent by linearity to show it for \(P=\partial ^\beta \), with  . Then we will have
. Then we will have
where we use the common componentwise partial ordering and the standard multi-index notation for the factorial and the binomial numbers. Therefore, \(a\cdot \partial ^\beta \) is a finite sum of monomials in the \(\partial _i\) times certain convergent series, so it belongs to \({\mathcal {D}}_{X,p}\subset {\mathcal {D}}_{X,p}[s]\).
Consider now \(Ps^j\in {\mathcal {D}}_{X,p}[s]\). Then,
which is another finite sum of elements in \({\mathcal {D}}_{X,p}[s]\). Thus \(a\cdot Ps^j\) belongs clearly to \({\mathcal {D}}_{X,p}[s]\), as we wanted to show.
Now the action of \({\mathcal {O}}\) on \({\mathcal {D}}_{X,p}[s]\) can be extended to an action of \(V^0{\mathcal {D}}\). Indeed, we have \([t,s]\cdot P(s)=P(s+1)h=t\cdot P(s)\) for any \(P(s)\in {\mathcal {D}}_{X,p}[s]\), so we can take the action of \(\partial _tt\) as that of \(-s\). Now using that \(V^0{\mathcal {D}}\cong {\mathcal {D}}_{X,p}[s]\otimes _{{\mathcal {O}}_{X,p}}{\mathcal {O}}\) as \({\mathcal {O}}_{X,p}\)-modules, we can extend both actions by linearity to get the desired one of \(V^0{\mathcal {D}}\).
Let us check now that \(\pi _p\) becomes \(V^0{\mathcal {D}}\)-linear with the new structure on \({\mathcal {D}}_{X,p}[s]\). Indeed, consider an operator \(P(s)\in {\mathcal {D}}_{X,p}[s]\) and a series \(a=\sum _{\alpha ,k}a_{\alpha k}x^\alpha t^k\in {\mathcal {O}}\) as before. Then,
Note that we are replacing the powers of t by those of h in the third equality. To justify this step, let us rewrite
the \(p_{\beta ,m}\) being convergent functions in \({\mathcal {O}}\). Now dividing all such functions by \(t-h\) we can write them as \(p_{\beta m}(x,t)=q_{\beta m}(x,t)(t-h)+r_{\beta m}(x)\). (This is a very particular instance of the Weierstraß division theorem for convergent power series whose proof is elementary in this case.) Consequently,
For every \(\beta \) and m we know that \(r_{\beta m}(x)=p_{\beta m}(x,h)\), hence, we have an expression
and thus \([{\overline{P}}]=[{\overline{P}}']\) in N(h) which shows the third equality in Formula (51).
Let us show the second point of the theorem. Take an element \(\xi \in V_{{\text {can}}}^0N(h)\cap F_k^{{\text {ord}}}N(h)\). Since by Proposition 3.3 we have \(V_{{\text {can}}}^0N(h)=V_{{\text {ind}}}^1N(h) + \beta (\partial _tt) V_{{\text {ind}}}^0 N(h)\), we know that there is a representative \({\widetilde{P}}\in {\mathcal {D}}\) of \(\xi \) and that there are operators \(\widetilde{Q},\widetilde{R}\in V^0{\mathcal {D}}\) and \({\widetilde{A}},{\widetilde{B}}_1,\ldots ,{\widetilde{B}}_{n-1},{\widetilde{C}}\in {\mathcal {D}}\) such that
It is clear that \(t\widetilde{Q}\) can be rewritten as \(Q't\) for a suitable \(Q'\in V^0{\mathcal {D}}\). Regarding \(\beta (\partial _tt)\widetilde{R}\), let us expand \(\widetilde{R}\) as \(\sum _k\widetilde{R}_kt^k\) with \(\widetilde{R}_k\in V^0{\mathcal {D}}\) in an analogous fashion as in the proof of Lemma 5.1. Then,
where \(R'\in V^0{\mathcal {D}}\). Therefore, renaming \(Q'+R'\) as \(\widetilde{Q}\in V^0{\mathcal {D}}\), we have a new expression
Notice that since
it follows from Proposition 3.10 that we can pick a new representative \({\widehat{P}} \in F_k{\mathcal {D}}\cap V^0{\mathcal {D}}\) of \(\xi \), that is, we have \({\widehat{P}}-{\widetilde{P}}\in I(h)\). Moreover, when writing \({\widehat{P}}\) as an element in \({\mathcal {D}}_{X,p}[\partial _t t][[t]]\), we can replace any positive power of t by h, and this will not change the order. Hence, there exists an operator \(P \in F_k{\mathcal {D}}\cap {\mathcal {D}}_{X,p}[\partial _t t]\) with \(P-{\widehat{P}}={\widehat{A}}(t-h)\). It follows that \(P-{\widetilde{P}}\in I(h)\), or, said otherwise, there are coefficients \(A',B'_1,\ldots ,B'_{n-1}, C' \in {\mathcal {D}}\) such that
Hence (by replacing \({\widetilde{P}}\) with the expression from equation (52)) we obtain that the class \(\xi \in V^0_{{\text {can}}}N(h)\cap F_k^{{\text {ord}}}N(h)\) can be represented by an operator \(P\in F_k{\mathcal {D}}\cap {\mathcal {D}}_{X,p}[\partial _t t]\) which has an expression
where \(A:={\widetilde{A}}+A'\), \(B_i:={\widetilde{B}}_i+B'_i\) and \(C:={\widetilde{C}}+C'\). By construction, the operators P, Q and R are elements in \(V^0{\mathcal {D}}\). Then we apply Corollary 3.9 and conclude that A, \(B_1,\ldots ,B_{n-1}\) and C belong to \(V^0{\mathcal {D}}\) as well.
Summing up, we can choose P inside
Applying Lemma 5.1 above, we obtain that
and replacing \(\partial _tt\) by \(-s\) provides the desired claim. For the last part, Formula (48), we combine Formula (33) (or its non-recursive version, Formula (32)) with Formula (47). \(\square \)
As a first application of Theorem 5.2 and Theorem 4.4, we can give a formula to calculate the zeroth Hodge ideal \({\mathcal {I}}_0(D)_p\).
Corollary 5.3
Under the assumptions of the previous Proposition, let \(({\mathcal {J}}_0)_p\) be the ideal of \({\mathcal {O}}_{X,p}\) defined as
Then
-
1.
\(F_1^H N(h)=\{[f]\in N(h)\,:\,f\in ({\mathcal {J}}_0)_p\}\).
-
2.
\(F_0^H M(h)=\{[f]\in M(h)\,:\,f\in ({\mathcal {J}}_0)_p\}\).
-
3.
\( {\mathcal {I}}_0(D)_p= ({\mathcal {J}}_0)_p\).
Proof
Point 1 is a consequence of Corollary 4.3 and Theorem 5.2 above. For the second point we use formula (39). We know that \(F_0^H M(h)=F_1^H N(h)\cap ( M(h)\otimes 1)\), where M(h) is seen as a \({\mathcal {O}}_{X,p}\)-submodule of N(h). However, since \( ({\mathcal {J}}_0)_p\subset {\mathcal {O}}_{X,p}\), there is actually no proper intersection and the claim follows.
In order to obtain the formula for the zeroth Hodge ideal we just need to recall its definition and the isomorphism between \({\mathcal {O}}_{X,p}(*D)\) and M(h) (see point 2 of Proposition 2.4). Since \(F_0^H{\mathcal {O}}_{X,p}(*D)={\mathcal {I}}_0(D)_p\cdot {\mathcal {O}}_{X,p}(D)\), we just need to multiply by h the elements of \(({\mathcal {J}}_0)_p\cdot h^{-1}\subset {\mathcal {O}}_{X,p}(*D)\), but again, \(({\mathcal {J}}_0)_p\subset {\mathcal {O}}_{X,p}\), so \(I_0(D)_p=({\mathcal {J}}_0)_p\) and we are done. \(\square \)
Remark 5.4
Notice that the ideal \({\mathcal {J}}_p\) from Theorem 5.2 equals, up to changing s by \(s+1\) the ideal
where \({{\widehat{\beta }}}(s)=\prod _{\alpha \in B_h}(s-\alpha )^{l_\alpha }\), with \(B_h\) and \(l_\alpha \) being, respectively, the set of roots of \(b_h\) in the interval \((-1,0)\) and the multiplicity of each root \(\alpha \). Then we have
and it is known (see, e.g., [10, Theorem 1.24] and [32, § 4])) that \({\widehat{{\mathcal {J}}}}'_p\) is the annihilator of the class \(h^s\) in \({\mathcal {D}}_{X,p}[s]\cdot h^s/{\mathcal {D}}_{X,p}[s]\cdot h^{s+1}\). Hence, by the Bernstein functional equation, we know that \(b_h(s) \in {\widehat{{\mathcal {J}}}}'_p\). The polynomial \({\widehat{\beta }}(s)\), which is a proper factor of \(b_h(s)\), is not an element of \({\widehat{{\mathcal {J}}}}'_p\) in general.
Our next aim is to describe an algorithm to calculate effectively the filtration steps \(F_k^H{\mathcal {O}}_X(*D)\) resp. the Hodge ideals \(I_k(D)\) for an SK-free divisor. The starting point is Formula (48). Recall (see the explanation before Lemma 3.2) that there is a left  -linear isomorphism
-linear isomorphism
which we need to make explicit in order to describe our algorithmic procedure to obtain the modules \(F_k^H {\mathcal {O}}_X(*D)\).
Let us consider the  -algebra automorphism
-algebra automorphism  defined as
defined as
It is clear that \(\varphi (\delta )=\delta -\delta (h)\partial _t\) and \(\varphi ^{-1}(\delta )=\delta +\delta (h)\partial _t\) for each \(\delta \in \Theta _{X,p}\), and \(\varphi ^{-1}(t)=t-h\). Now given a class \([Q]\in N(h)\), by division by t we find unique operators  and \(Q'\in {\mathcal {O}}_{X,p}\langle \partial _{x_1},\dots , \partial _{x_n}, \partial _t \rangle \) such that
and \(Q'\in {\mathcal {O}}_{X,p}\langle \partial _{x_1},\dots , \partial _{x_n}, \partial _t \rangle \) such that
Then we write
and taking classes in M(h) we obtain the element \(\sum _{k=0}^{{\text {ord}}(Q)} [Q_k]\partial _t^k=:\Psi ([Q]) \in M(h)[\partial _t]\) which is readily verified to be well-defined. Notice that the inverse map \(\Psi ^{-1}\) sends an element \(\sum _{k=0}^d [Q_k] \partial _t^k \in M(h)[\partial _t]\), with \(Q_k\in {\mathcal {D}}_{X,p}\), to
Let us define \(F^{{\text {ord}}}_\bullet \left( M(h)[\partial _t]\right) := \Psi \left( F^{{\text {ord}}}_\bullet N(h) \right) \). Then we clearly have

Similarly, put \(F^H_\bullet \left( M(h)[\partial _t]\right) := \Psi \left( F^H_\bullet N(h) \right) \). Formula (48) becomes:
where we put \({\overline{\Psi }}= \Psi \circ \pi _p\).
We denote \(\Phi :M(h) \xrightarrow {\sim } {\mathcal {O}}_{X,p}(* D)\) the isomorphism of left \({\mathcal {D}}_{X,p}\)-modules given by \(\Phi ([Q]) = Q(h^{-1})\), for each \(Q\in {\mathcal {D}}_{X,p}\) (see formula (5)), and by \({\overline{\Phi }}: M(h)[\partial _t] \xrightarrow {\sim } {\mathcal {O}}_{X,p}(* D)[\partial _t]\) the induced isomorphism of  -modules:
-modules:
We recall from Formulas (38) and (39) that the relationship between the Hodge filtrations on \({\mathcal {O}}_{X,p}(* D)[\partial _t]\cong N(h)\cong (i_{h,+} {\mathcal {O}}(*D))_{(0,p)}\) and on \({\mathcal {O}}_{X,p}(* D)\) is given by
for all  . We obviously have \(\Phi (F^H_\bullet M(h)) = F^H_\bullet {\mathcal {O}}_{X,p}(*D)\) and
. We obviously have \(\Phi (F^H_\bullet M(h)) = F^H_\bullet {\mathcal {O}}_{X,p}(*D)\) and
The pole order filtration \(P_k {\mathcal {O}}_{X,p}(*D) = {\mathcal {O}}_{X,p}((k+1)D) \), \(k\ge 0\), induces a filtration on \({\mathcal {O}}_{X,p}(*D)[\partial _t]\):
With these preliminary remarks, we can now explain an effective procedure to compute a system of generators of the \({\mathcal {O}}_{X,p}\)-modules \(F_k^H {\mathcal {O}}_{X,p}(*D) \), \(k\ge 0\):
- Step 1::
-
We compute an involutive basis \({\mathcal {B}}= \{P_1,\dots ,P_N \}\) of \({\mathcal {J}}_p\) with respect to the total order filtration T on \({\mathcal {D}}_{X,p}[s]\), i.e. \(P_1,\ldots ,P_N\) are such that
$$\begin{aligned} \text {Gr}_\bullet ^T ({\mathcal {J}}_p) = \text {Gr}_\bullet ^T({\mathcal {D}}_{X,p}[s])(\sigma ^T(P_1),\ldots ,\sigma ^T(P_N)), \end{aligned}$$where for \(P\in {\mathcal {D}}_{X,p}[s]\), \(\sigma ^T(P)\) denotes the symbol of P in \(\text {Gr}_\bullet ^T({\mathcal {D}}_{X,p}[s])\). Let us write \({\text {ord}}_T(P_j) = d_j\). Consequently, for each \(k\ge 0\), a system of generators of the \({\mathcal {O}}_{X,p}\)-module \({\mathcal {J}}_p\cap T_k{\mathcal {D}}_{X,p}[s]\) is given by
$$\begin{aligned} \left\{ s^l {\underline{\partial }}_x^\alpha P_j\ |\ l + |\alpha | + d_j \le k \right\} . \end{aligned}$$ - Step 2::
-
After equation (54), a system of generators of \(F_{k+1}^H \left( M(h)[\partial _t]\right) \) as an \({\mathcal {O}}_{X,p}\)-module is
$$\begin{aligned} \left\{ \partial _t^i\, {\overline{\Psi }}(s^l {\underline{\partial }}_x^\alpha P_j)\ |\ l + |\alpha | + d_j + i\le k \right\} . \end{aligned}$$ - Step 3::
-
By means of the isomorphism \({\overline{\Phi }}\), we obtain a system of generators of the \({\mathcal {O}}_{X,p}\)-module \(F_{k+1}^H \left( {\mathcal {O}}_{X,p}(*D)[\partial _t]\right) \), that we call \(\xi _e\), \(e=1,\dots ,R\). Since \(F_{k+1}^H \left( {\mathcal {O}}_{X,p}(*D)[\partial _t]\right) \) is a submodule of the rank \((k+1)\) free \({\mathcal {O}}_{X,p}\)-module \(P_k \left( {\mathcal {O}}_{X,p}(*D)[\partial _t]\right) \), we have
$$\begin{aligned} \xi _e = \sum _{i=0}^k \xi _{e,i} \partial _t^i \in {\mathcal {O}}_{X,p}((k+1)D) \oplus {\mathcal {O}}_{X,p}(kD) \partial _t \oplus \cdots \oplus {\mathcal {O}}_{X,p}(D) \partial _t^k, \end{aligned}$$for any \(e=1,\dots ,R\). Finally, a syzygy computation allows us to compute a system of generators of the \({\mathcal {O}}_{X,p}\)-module
$$\begin{aligned} {\mathcal {O}}_{X,p}\langle \xi _1,\dots ,\xi _R\rangle \cap {\mathcal {O}}_{X,p}((k+1)D) = F_{k+1}^H \left( {\mathcal {O}}_{X,p}(*D)[\partial _t]\right) \cap {\mathcal {O}}_{X,p}(*D) = F_k^H {\mathcal {O}}_{X,p}(*D). \end{aligned}$$
In the following subsections we apply this algorithm to calculate the Hodge ideals and the generating level for some interesting classes of examples. Since it is known ([28, Proposition 10.1]) that \({\mathcal {I}}_0(D)={\mathcal {J}}((1-\varepsilon )D)\), and since an algorithm for the calculation of multiplier ideals exists already (see [2]), our approach first of all provides an alternative way to compute these multiplier ideals. In some cases our methods yield results whereas the algorithm in loc. cit. does not terminate. Moreover, we can effectively calculate higher Hodge ideals, and we indicate them below in some of the cases for which the generating level of the Hodge filtration \(F^H_\bullet {\mathcal {O}}_X(*D)\) is positive.
We also determine the generating level of the Hodge filtration, always confirming Conjecture 4.12. In many cases, the Hodge filtration is even generated at level zero. This is not always true, however, and we show in particular that for linear free divisors, the conjectured bound from 4.12 is sharp. Examples with low generating level are interesting because of the local vanishing conjecture (see point 3 of Remark 4.13 as well as [28, Theorem 17.1]). Notice that only plane curves, normal crossing divisors (cf. the introduction of [28]) and surfaces with rational singularities ( [30, Corollary B]) were previously known to have generating level equal to zero.
5.1 Divisors with normal crossings
If X is any complex manifold and \(D\subset X\) is a reduced divisor with only normal crossings, then it is elementary to check that D is free and strongly Koszul at each of its points. As we have already pointed out in Remark 4.5, it easily follows from the fact that \(-1\) is the only root of \(b_D(s)\) that we have
Consequently, since obviously the order filtration is generated at level 0, so is the Hodge filtration (a fact that is of course well known from Saito’s theory). For the Hodge ideals themselves, we obtain that \({\mathcal {I}}_k(D)\cdot F_k^{{\text {ord}}} {\mathcal {O}}_X(*D) = P_k {\mathcal {O}}_X(*D)\), and an easy local calculation shows that this coincides with [28, Proposition 8.2].
Summarizing, if the divisor D has only normal crossings, then our results easily imply the known facts about the Hodge filtration resp. the Hodge ideals for such divisors.
5.2 Surfaces
We consider two kinds of free surfaces in  , namely (two-dimensional hyper-)plane arrangements and Sekiguchi’s free divisors ([44]). Let D be a central hyperplane arrangement
, namely (two-dimensional hyper-)plane arrangements and Sekiguchi’s free divisors ([44]). Let D be a central hyperplane arrangement  . It is a longstanding question to detect when an arrangement is a free divisor; for a recent account, see [12, Chapter 8]. However, if D is free, then it is strongly Koszul since it is locally quasi-homogeneous (see, e.g., [8] for this implication), so that the methods from this paper do apply.
. It is a longstanding question to detect when an arrangement is a free divisor; for a recent account, see [12, Chapter 8]. However, if D is free, then it is strongly Koszul since it is locally quasi-homogeneous (see, e.g., [8] for this implication), so that the methods from this paper do apply.
Below are some results for low-dimensional free arrangements:
Name | Equation | \({\mathcal {I}}_\mathbf {0}\mathbf {(D)}\) |
|---|---|---|
\(A_2\) | \((x-y)(x-z)(y-z)\) | \((y-z,x-z)\) |
\(D_3\) | \((x^2-y^2)(x^2-z^2)(y^2-z^2)\) | \(\Big (y^2z-z^3,x^2z-z^3,y^3-yz^2, xy^2-xz^2,x^2y-yz^2,x^3-xz^2\Big )\) |
In both cases the Hodge filtration on \({\mathcal {O}}_X(*D)\) is generated at level zero. Of course, these results do not depend on the fact that \(\dim (D)=2\), similar calculations are possible for other arrangements, but the ideal \({\mathcal {I}}_0(D)\) becomes difficult to print.
Let us consider now the examples of divisors in  that are discussed in the paper [44]. We refer to loc. cit. for details on their construction and only produce the results of the calculation of \({\mathcal {I}}_0(D)\) here. All these examples are given by weighted homogeneous equations in three variables, and we write \((d;d_x,d_y,d_z)\) for a weight vector, where \(d_x\), \(d_y\) and \(d_z\) are the weights of x, y and z and d is the degree of the defining equation for the divisor
that are discussed in the paper [44]. We refer to loc. cit. for details on their construction and only produce the results of the calculation of \({\mathcal {I}}_0(D)\) here. All these examples are given by weighted homogeneous equations in three variables, and we write \((d;d_x,d_y,d_z)\) for a weight vector, where \(d_x\), \(d_y\) and \(d_z\) are the weights of x, y and z and d is the degree of the defining equation for the divisor  .
.
Name | Weight vector | Equation/\(\mathbf {{\mathcal {I}}_0(D)}\) |
|---|---|---|
\(A_1\) | (12; 2, 3, 4) | \(\begin{aligned} h&=16x^4z-4x^3y^2-128x^2z^2+144xy^2z\\&\quad -27y^4+256z^3\end{aligned}\) |
\({\mathcal {I}}_\mathbf {0}\mathbf {(D)}:(9y^2-32xz,x^2+12z)\) | ||
\(A_2\) | (12; 2, 3, 4) | \(h = 2x^6-3x^4z+18x^3y^2-18xy^2z+27y^4+z^3\) |
\({\mathcal {I}}_\mathbf {0}\mathbf {(D)}: (y^2,x^2-z)\) | ||
\(B_1\) | (9; 1, 2, 3) | \(h = z(x^2y^2-4y^3-4x^3z+18xyz-27z^2)\) |
\({\mathcal {I}}_\mathbf {0}\mathbf {(D)}: (y^2-3xz,xy-9z,x^2z-3yz)\) | ||
\(B_3\) | (9; 1, 2, 3) | \(h = z(-2y^3+9xyz+45z^2)\) |
\(\mathbf {{\mathcal {I}}_0(D)}: (z,y^2)\) | ||
\(H_2\) | (15; 1, 3, 5) | \(\begin{aligned} h&=100x^3y^4+y^5+40x^4y^2z-10xy^3z+4x^5z^2\\&\quad -15x^2yz^2+z^3\end{aligned}\) |
\({\mathcal {I}}_\mathbf {0}\mathbf {(D)}: (y^2-xz,12x^2yz-z^2,12x^3z-yz)\) | ||
\(H_5\) | (15; 1, 3, 5) | \(h = x^3y^4-y^5+3xy^3z+z^3\) |
\({\mathcal {I}}_\mathbf {0}\mathbf {(D)}: (y^2,yz,z^2)\) |
We have managed to perform the analogous calculations for all of Sekiguchi’s examples but \(H_1\). The Hodge filtration on  is generated at level 0 for all of them.
is generated at level 0 for all of them.
5.3 Linear free divisors
The paper [3] introduced a large class of examples of free divisors which appear as discriminants in pre-homogenous vector spaces. Since the module \(\Theta (-\log \, D)\) has a basis of linear (in the global coordinates) vector fields in these examples, the divisor D is called linear free. A rich source of linear free divisors comes from representation of quivers. It can be shown that the strong Koszul assumption is satisfied in these cases if the underlying graph of the quiver is of ADE-type. Quivers of type A yield free divisors with normal crossings, so the first non-trivial example is the discriminant in the representation space of the \(D_4\)-quiver. Here we have

where \(D=V(h)\) and \(h=\Delta _1\cdot \Delta _2\cdot \Delta _3\), with \(\Delta _1\), \(\Delta _2\) and \(\Delta _3\) being the three maximal minors of an element of  (hence, h is a homogenous equation of degree 6). In this case, we have \(b_h(s)=(s+1)^4(s+2/3)(s+4/3)\) and hence we consider
(hence, h is a homogenous equation of degree 6). In this case, we have \(b_h(s)=(s+1)^4(s+2/3)(s+4/3)\) and hence we consider

The intersection with  (which can also be calculated as
(which can also be calculated as  ) is
) is
The Hodge filtration on \({\mathcal {O}}_X(D)\) is generated at level 1, and the first Hodge ideal is minimally generated by 13 polynomials in the variables \(a_{ij}\) of degree 7 at most (for typsetting reasons, we refrain to print it here).
This discriminant is a first example of the series where the underlying graph of the quiver is of \(D_n\)-type. The next example is the \(D_5\)-quiver, where the discriminant in the 10-dimensional representation space yields a hypersurface of degree 10. A defining equation  for D is given by
for D is given by
and we obtain
Notice that for this example, the computation of the multiplier ideal \({\mathcal {J}}((1-\varepsilon )D)\) with the methods from [2] does not terminate. The generating level of the Hodge filtration on \({\mathcal {O}}_X(*D)\) is two here. The first Hodge ideal \({\mathcal {I}}_1(D)\) has a minimal generating set consisting of 24 polynomials of degree 13 at most, whereas \({\mathcal {I}}_2(D)\) is minimally generated by 124 polynomials, their maximal degree being 22.
In fact, Conjecture 4.12 would yield the following estimate for the generating level of the full \(D_n\)-series.
Conjecture 5.5
Let  be the linear free divisor \(D_n\). Then, the Hodge filtration on \({\mathcal {O}}_X(*D)\) is generated at level \(n-3\).
be the linear free divisor \(D_n\). Then, the Hodge filtration on \({\mathcal {O}}_X(*D)\) is generated at level \(n-3\).
Proof assuming Conjecture 4.12
The dimension of the divisors \(D_n\) can be found in [13, p. 1347]. The result then is just a consequence of applying the statement of Conjecture 4.12, once we know a general formula for the Bernstein–Sato polynomials of the divisors \(D_n\). It can be found at [45, Table 4.1] that they are, respectively,
\(\square \)
Note that this conjecture, if true, would give a bound for the generating level which is exactly a quarter of the general one given in [28, Theorem B]. We also believe that such bounds are attained for all of the \(D_n\) (i.e. that the generating level is exactly \(n-3\)), as we have checked for \(n=4,5\).
Another typical example of a linear free divisor in low dimensions is the discriminant in the space of binary cubics (see, e.g., [17, Examples 1.4. (2)]). Here we have \(D={\mathcal {V}}(h)\), where  , and we obtain that
, and we obtain that
In this case the Hodge filtration on  is generated in level one, with first Hodge ideal
is generated in level one, with first Hodge ideal
Notice that similar computations are possible up to some extent for other linear free divisors of SK-type, such as those given by the \(E_6\)- and \(E_7\)-quivers. Under the assumption of Conjecture 4.12, one could give generating level bounds, using the calculation of Bernstein polynomials from [1].
We finish this subsection with some examples of non-reductive linear free divisors in low dimension, as found in [17, Example 5.1, Table 6.1], that we summarize in the table below.
Name | Equation | \({\mathcal {I}}_\mathbf {0}\mathbf {(D)}\) |
|---|---|---|
\(\dim 3\) | \((y^2+xz)z\) | (y, z) |
\(\dim 4\text {, case }1\) | \((y^2+xz)zw\) | (y, z) |
\(\dim 4\text {, case }2\) | \((yz+xw)zw\) | (z, w) |
\(\dim 4\text {, case }3\) | \(x(y^3-3xyz+3x^2w)\) | \((x,y^2)\) |
| \(x\begin{vmatrix}x&y\\y&u\end{vmatrix}\begin{vmatrix}x&y&z\\y&u&v\\z&v&w\end{vmatrix}\) | \((xv-yz,xu-y^2,xzu-xyv)\) |
In all those cases, the Hodge filtration on the corresponding ring of meromorphic functions is generated at level 0.
5.4 The Whitney umbrella and the cross caps
We finish this section by mentioning two examples that slightly fall out of the general setup of this paper. Namely, consider the Whitney umbrella  . This is not a free divisor, indeed, we have
. This is not a free divisor, indeed, we have  where
where
so that \(\Theta (-\log \,D)\) is not  -locally free. However, the isomorphism
-locally free. However, the isomorphism

of left  -modules still holds true, and we find that \(b_h(s)=(s+1)^2(s+3/2)\). According to Lemma 3.2 from above, we have \(b_{V_{{\text {ind}}}^\bullet }^{N(h)}=s^2(s-1/2)\). One checks that the main results of this paper can also be applied to this example. In particular, it follows that the integer r appearing in Lemma 4.6 is zero, and hence we deduce from Corollary 4.7 that
-modules still holds true, and we find that \(b_h(s)=(s+1)^2(s+3/2)\). According to Lemma 3.2 from above, we have \(b_{V_{{\text {ind}}}^\bullet }^{N(h)}=s^2(s-1/2)\). One checks that the main results of this paper can also be applied to this example. In particular, it follows that the integer r appearing in Lemma 4.6 is zero, and hence we deduce from Corollary 4.7 that

In particular, in this example the generating level of the Hodge filtration is zero since  is generated at level 0.
is generated at level 0.
A similar reasoning applies to the higher dimensional example  , where
, where
called cross-cap, which again is not free (the module of logarithmic vector fields has 9 generators), here we have
As a conclusion, we obtain that for both the Whitney umbrella and the cross-cap we have \({\mathcal {I}}_0(D)={\mathcal {O}}_X\), but \({\mathcal {I}}_k(D) \subsetneq {\mathcal {O}}_X\) for all \(k>1\).
Actually, these two examples are the first two of a whole series, which is discussed in [19]. However, it is unclear at this point whether we always have the equality  since this needs the fact that the roots of \(b_h(s)\) are contained in \((-2,-1]\), and a general formula for the Bernstein polynomial for the elements in this series is not known (actually, it seems computational impossible to obtain \(b_h(s)\) even for the next example, which is a divisor in
since this needs the fact that the roots of \(b_h(s)\) are contained in \((-2,-1]\), and a general formula for the Bernstein polynomial for the elements in this series is not known (actually, it seems computational impossible to obtain \(b_h(s)\) even for the next example, which is a divisor in  ).
).
References
Barz, C.: Differential invariants of prehomogeneous vector spaces, Ph.D. thesis, Technische Universität Chemnitz (2018). https://www.logos-verlag.de/cgi-bin/engbuchmid?isbn=4894 &lng=deu &id=
Berkesch, C., Leykin, A.: Algorithms for Bernstein–Sato polynomials and multiplier ideals. In: ISSAC 2010—Proceedings of the 2010 International Symposium on Symbolic and Algebraic Computation, pp. 99–106. ACM, New York (2010)
Buchweitz, R.-O., Mond, D.: Linear free divisors and quiver representations, Singularities and computer algebra, London Math. Soc. Lecture Note Ser., vol. 324, pp. 41–77. Cambridge University Press, Cambridge (2006)
Bourbaki, N.: Éléments de mathématique. Algèbre. Chapitre 10. Algèbre homologique, Springer-Verlag, Berlin (2007). Reprint of the 1980 original
Budur, N., Saito, M.: Multiplier ideals, $V$-filtration, and spectrum. J. Algebraic Geom. 14(2), 269–282 (2005)
Chemla, S.: A duality property for complex Lie algebroids. Math. Z. 232(2), 367–388 (1999)
Calderón Moreno, F.L.: Logarithmic differential operators and logarithmic de Rham complexes relative to a free divisor. Ann. Sci. École Norm. Sup. 32(5), 701–714 (1999)
Calderón-Moreno, F., Narváez-Macarro, L.: The module ${\cal{D}}f^s$ for locally quasi-homogeneous free divisors. Compositio Math. 134(1), 59–74 (2002)
Calderón-Moreno, F.J., Narváez-Macarro, L.: Dualité et comparaison sur les complexes de de Rham logarithmiques par rapport aux diviseurs libres. Ann. Inst. Fourier (Grenoble) 55(1), 47–75 (2005)
Calderón-Moreno, F.J., Narváez-Macarro, L.: On the logarithmic comparison theorem for integrable logarithmic connections. Proc. Lond. Math. Soc. 98(3), 585–606 (2009)
Castro-Jiménez, F., Narváez-Macarro, L., Mond, D.: Cohomology of the complement of a free divisor. Trans. Am. Math. Soc. 348(8), 3037–3049 (1996)
Dimca, A.: Hyperplane Arrangements. An introduction. Universitext, Springer, Cham (2017)
de Gregorio, I., Mond, D., Sevenheck, C.: Linear free divisors and Frobenius manifolds. Compos. Math. 145(5), 1305–1350 (2009)
Denham, G., Schenck, H., Schulze, M., Wakefield, M., Walther, U.: Local cohomology of logarithmic forms. Ann. Inst. Fourier (Grenoble) 63(3), 1177–1203 (2013)
Dutta, Y.: Vanishing for Hodge ideals on toric varieties. Math. Nachr. 293(1), 79–87 (2020)
Fossum, R., Foxby, H.-B.: The category of graded modules. Math. Scand. 35, 288–300 (1974)
Granger, M., Mond, D., Nieto, A., Schulze, M.: Linear free divisors and the global logarithmic comparison theorem. Ann. Inst. Fourier (Grenoble) 59(1), 811–850 (2009)
Granger, M., Schulze, M.: On the symmetry of $b$-functions of linear free divisors. Publ. Res. Inst. Math. Sci. 46(3), 479–506 (2010)
Houston, K., Littlestone, D.: Vector fields liftable over corank 1 stable maps (2009). Preprint arXiv:0905.0556
Hotta, R., Takeuchi, K., Tanisaki, T.: ${\cal{D}}$-modules, perverse sheaves, and representation theory, Progress in Mathematics, vol. 236, Birkhäuser Boston Inc., Boston, MA (2008). Translated from the 1995 Japanese edition by Takeuchi
Jung, S.-J., Kim, I.-K., Yoon, Y., Saito, M.: Hodge ideals and spectrum of isolated hypersurface singularities (2019). Preprint arXiv:1904.02453, to appear in “Annales de l’Institut Fourier”
Kashiwara, M.: Vanishing cycle sheaves and holonomic systems of differential equations. In: Raynaud, M., Shioda, T. (eds.) Algebraic geometry (Tokyo/Kyoto, 1982), Lecture Notes in Math., vol. 1016, pp. 134–142. Springer, Berlin (1983)
Lazarsfeld, R.: Positivity in algebraic geometry. II, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics, Positivity for vector bundles, and multiplier ideals, vol. 49. Springer-Verlag, Berlin (2004)
Looijenga, E.J.N.: Isolated singular points on complete intersections, London Mathematical Society Lecture Note Series, vol. 77. Cambridge University Press, Cambridge (1984)
Mackenzie, K.C.H.: General theory of Lie groupoids and Lie algebroids, London Mathematical Society Lecture Note Series, vol. 213. Cambridge University Press, Cambridge (2005)
Malgrange, B.: Le polynôme de Bernstein d’une singularité isolée, Fourier integral operators and partial differential equations (Colloq. Internat., Univ. Nice, Nice, 1974). Lecture Notes in Math., vol. 459, pp. 98–119. Springer, Berlin (1975)
Maisonobe, P., Mebkhout, Z.: Le théorème de comparaison pour les cycles évanescents, Éléments de la théorie des systèmes différentiels géométriques, Sémin. Congr., vol. 8, pp. 311–389. Soc. Math. France, Paris (2004)
Mustaţă, M., Popa, M.: Hodge ideals. Mem. Amer. Math. Soc. 262(1268), v+80 (2019)
Mustaţă, M., Popa, M.: Hodge ideals for ${ Q}$-divisors: birational approach. J. Éc. polytech. Math. 6, 283–328 (2019)
Mustaţă, M., Popa, M.: Hodge filtration, minimal exponent, and local vanishing. Invent. Math. 220(2), 453–478 (2020)
Mustaţă, M., Popa, M.: Hodge ideals for ${ Q}$-divisors, $V$-filtration, and minimal exponent. Forum Math. Sigma 8, e19, 41 (2020)
Narváez Macarro, L.: A duality approach to the symmetry of Bernstein-Sato polynomials of free divisors. Adv. Math. 281, 1242–1273 (2015)
Peters, C.A.M., Steenbrink, J.H.M.: Mixed Hodge structures, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics, vol. 52. Springer-Verlag, Berlin (2008)
Rinehart, G.S.: Differential forms on general commutative algebras. Trans. Amer. Math. Soc. 108, 195–222 (1963)
Reichelt, T., Sevenheck, C.: Hypergeometric Hodge modules. Algebr. Geom. 7(2), 263–345 (2020)
Saito, K.: Theory of logarithmic differential forms and logarithmic vector fields. J. Fac. Sci. Univ. Tokyo Sect. IA Math. 27(2), 265–291 (1980)
Saito, M.: Modules de Hodge polarisables. Publ. Res. Inst. Math. Sci. 24(6), 849–995 (1988) (1989)
Saito, M.: Mixed Hodge modules. Publ. Res. Inst. Math. Sci. 26(2), 221–333 (1990)
Saito, M.: On $b$-function, spectrum and rational singularity. Math. Ann. 295(1), 51–74 (1993)
Saito, M.: On microlocal $b$-function. Bull. Soc. Math. France 122(2), 163–184 (1994)
Saito, M.: On the Hodge filtration of Hodge modules. Mosc. Math. J. 9(1), 161–191 (2009)
Saito, M.: Bernstein-Sato polynomials of hyperplane arrangements. Selecta Math. (N.S.) 22(4), 2017–2057 (2016)
Schnell, C.: An overview of Morihiko Saito’s theory of mixed Hodge modules (2014). Preprint arXiv:1405.3096
Sekiguchi, J.: A classification of weighted homogeneous Saito free divisors. J. Math. Soc. Jpn. 61(4), 1071–1095 (2009)
Sevenheck, C.: Bernstein polynomials and spectral numbers for linear free divisors. Ann. Inst. Fourier (Grenoble) 61(1), 379–400 (2011)
Sabbah, C., Schnell, C.: The MHM Project (2019). http://www.cmls.polytechnique.fr/perso/sabbah/MHMProject/mhm.html
Saito, M., Sturmfels, B., Takayama, N.: Gröbner deformations of hypergeometric differential equations, Algorithms and Computation in Mathematics, vol. 6. Springer-Verlag, Berlin (2000)
van Straten, D.: A note on the discriminant of a space curve. Manuscr. Math. 87(2), 167–177 (1995)
Zhang, M.: Hodge filtration and Hodge ideals for ${\mathbb{Q}}$-divisors with weighted homogeneous isolated singularities (2018). Preprint arXiv:1810.06656, to appear in “Asian Journal of Mathematics”
Acknowledgements
We would like to thank the anonymous referee for valuable suggestions to improve the readability, as well as for pointing out a mistake in the proof of Corollary 3.8 in a former version of this paper.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The first two authors are partially supported by the ERDF, PID2020-114613GB-I00, P20_01056 and US-1262169. The first author is also partially supported by VI PPIT US-2018-II.5. The third author is partially supported by the DFG Project Se 1114/3-2. The third author would like to thank the Institute of Mathematics of the University of Seville for its hospitality during his visit in 2019.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Castaño Domínguez, A., Narváez Macarro, L. & Sevenheck, C. Hodge ideals of free divisors. Sel. Math. New Ser. 28, 57 (2022). https://doi.org/10.1007/s00029-022-00767-1
Accepted:
Published:
DOI: https://doi.org/10.1007/s00029-022-00767-1




 , we have the following recursive formula for the Hodge filtration on
, we have the following recursive formula for the Hodge filtration on  -vector spaces).
-vector spaces).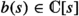 satisfying
satisfying  is the set of roots of
is the set of roots of  , the sequence
, the sequence  , where
, where 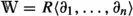 is the Weyl algebra and
is the Weyl algebra and  is the graded ring of
is the graded ring of  with respect to the total order filtration.
with respect to the total order filtration.
 , where
, where  , and
, and  is the graded ring of
is the graded ring of  with respect to the total order filtration.
with respect to the total order filtration. ).
). uniquely defined by the following properties:
uniquely defined by the following properties:  ,
, , the module
, the module  .
.
 .
. , we have the inclusion of coherent
, we have the inclusion of coherent  instead of
instead of 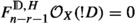 , which is provided by Theorem
, which is provided by Theorem  -module such that
-module such that  -linear. As a consequence, the terms of the total order filtration
-linear. As a consequence, the terms of the total order filtration  -modules.
-modules. -modules:
-modules: 