Abstract
The generalized Miller–Morita–Mumford classes of a manifold bundle with fiber M depend only on the underlying \(\tau _M\)-fibration, meaning the family of vector bundles formed by the tangent bundles of the fibers. This motivates a closer study of the classifying space for \(\tau _M\)-fibrations, \(Baut(\tau _M)\), and its cohomology ring, i.e., the ring of characteristic classes of \(\tau _M\)-fibrations. For a bundle \(\xi \) over a simply connected Poincaré duality space, we construct a relative Sullivan model for the universal \(\xi \)-fibration with holonomy in a given connected monoid, together with explicit cocycle representatives for the characteristic classes of the canonical bundle over its total space. This yields tools for computing the rational cohomology ring of \(Baut(\xi )\) as well as the subring generated by the generalized Miller–Morita–Mumford classes. To illustrate, we carry out sample computations for spheres and complex projective spaces. We discuss applications to tautological rings of simply connected manifolds and to the problem of deciding whether a given \(\tau _M\)-fibration comes from a manifold bundle.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The generalized Miller–Morita–Mumford classes, or tautological classes, are characteristic classes of manifold bundles that play an important role in the study of the cohomology of moduli spaces of manifolds [14, 26]. The tautological class \(\kappa _c\), associated to a characteristic class c of oriented vector bundles, is defined by its evaluation on an oriented manifold bundle,
namely
i.e., the class \(\kappa _c(\pi )\) is obtained by integration along the fiber of the characteristic class c evaluated on the fiberwise tangent bundle \(T_\pi E\).
This paper studies characteristic classes that, like the tautological classes, are defined using only homotopy theory and tangential data, viz. the fiberwise tangent bundle and its characteristic classes. For a bundle \(\xi \) over a space X, we define a \(\xi \)-fibration to be a pair \((\pi ,\zeta )\), where
-
\(\pi :E\rightarrow B\) is a fibration whose fibers are homotopy equivalent to X, and
-
\(\zeta \) is a bundle over E, the ‘total bundle’, whose restriction to each fiber is equivalent to \(\xi \) in an appropriate sense.
In other words, a \(\xi \)-fibration is a family of bundles \(\{\zeta _b\}\) parameterized by the space B such that \(\zeta _b \sim \xi \) for every \(b\in B\). Every smooth manifold bundle \(\pi :E\rightarrow B\) with fiber M gives rise to a \(\tau _M\)-fibration \((\pi ,\zeta )\) where \(\zeta \) is the fiberwise tangent bundle.
The base of the universal \(\xi \)-fibration may be identified with \(Baut(\xi )\), the classifying space of the topological monoid \(aut(\xi )\) of automorphisms of \(\xi \) that cover a self-homotopy equivalence of X. Therefore, the cohomology ring of \(Baut(\xi )\) may be thought of as the ring of characteristic classes of \(\xi \)-fibrations.
The main result of the paper, Theorem 3.8, is the construction of a relative Sullivan model for the universal \(\xi \)-fibration with holonomy in a given connected monoid, together with explicit formulas for cocycle representatives of the characteristic classes of its total bundle. This can be used to compute \(H^*(Baut(\xi );{\mathbb {Q}})\), and the subring \(R^*(\xi )\) generated by the tautological classes, for bundles \(\xi \) over simply connected Poincaré duality spaces.
We will spend the rest of this introduction discussing sample calculations done using Theorem 3.8 and some applications. Full details are given in Sect. 4.
Theorem 1.1
Consider the oriented tangent bundle \(\tau _{S^m}\) of an even dimensional sphere \(S^m\). The ring of characteristic classes of \(\tau _{S^{m}}\)-fibrations may be identified with the polynomial ring
where \(m = 2k\) and r is the smallest integer such that \(4r>m\). In particular, all characteristic classes of \(\tau _{S^{m}}\)-fibrations are tautological.
Our calculation for odd dimensional spheres, to be presented next, informs the following definition. For a class \(c\in H^*(BSO(m))\) of degree \(<m\), we define a characteristic class \(\alpha _c\) of \(\tau _{S^m}\)-fibrations \((\pi :E\rightarrow B,\zeta )\) by
This uniquely defines \(\alpha _c(\pi ,\zeta )\in H^*(B)\), because \(\pi ^*:H^*(B) \rightarrow H^*(E)\) is an isomorphism in degrees \(<m\).
Next, recall that every spherical fibration \(S^{m}\rightarrow E\xrightarrow {\pi } B\) has an associated Euler class \(e(\pi )\in H^{m+1}(B)\). The Euler class is a characteristic class of spherical fibrations and in particular of \(\tau _{S^{m}}\)-fibrations.
Let \(A^*(\tau _{S^{m}})\) denote the subring of \(H^*(Baut(\tau _{S^{m}});{\mathbb {Q}})\) generated by the \(\alpha \)-classes and the Euler class.
Theorem 1.2
Consider the oriented tangent bundle \(\tau _{S^{m}}\) of an odd dimensional sphere \(S^m\). Let \(m=2k+1\ge 3\) and let r be the smallest integer such that \(4r>m\).
-
(1)
The cohomology ring \(H^*(Baut(\tau _{S^{m}});{\mathbb {Q}})\) is additively the direct sum
$$\begin{aligned} A^*(\tau _{S^{m}}) \oplus R^*(\tau _{S^{m}}), \end{aligned}$$and the multiplication is determined by
$$\begin{aligned} \alpha _a \kappa _b&= \kappa _{ab}, \\ e \kappa _b&= 0, \end{aligned}$$for all \(a,b\in H^*(BSO(m))\) with \(|a|<m\). In particular, the ring of characteristic classes of \(\tau _{S^{m}}\)-fibrations is generated by the \(\alpha \)-classes, the Euler class, and the \(\kappa \)-classes.
-
(2)
The ring generated by the \(\alpha \)-classes and the Euler class may be identified with the polynomial ring
$$\begin{aligned} A^*(\tau _{S^{m}}) = {\mathbb {Q}}[\alpha _{p_1},\ldots ,\alpha _{p_{r-1}},e]. \end{aligned}$$ -
(3)
The tautological ring is isomorphic to the ring of exact Kähler differential forms on \({\mathbb {Q}}[p_1,\ldots ,p_k]\), with respect to a formal differential d of degree \(-m\) which is linear over \({\mathbb {Q}}[p_1,\ldots ,p_{r-1}]\),
$$\begin{aligned} R^*(\tau _{S^{m}}) \cong d \Omega _{{\mathbb {Q}}[p_1,\ldots , p_k]|{\mathbb {Q}}[p_1,\ldots ,p_{r-1}]}^*, \end{aligned}$$through an isomorphism that sends \(\kappa _c\) to dc for all \(c\in {\mathbb {Q}}[p_1,\ldots ,p_k]\).
For concreteness, let us look closer at what this means for \(S^3\).
Corollary 1.3
The tautological ring \(R^*(\tau _{S^3})\) of the tangent bundle of \(S^3\) is spanned by the \(\kappa \)-classes associated to the Hirzebruch L-classes,
The multiplication is trivial.
Proof
The ring of exact Kähler forms over a polynomial ring has a non-trivial algebraic structure in general, but for \(m =3\) the ring
has basis \(p_1^{i-1}dp_1\) for \(i=1,2,\ldots \) and the multiplication is trivial. The Hirzebruch L-classes in the cohomology of BSO(3) are given by \({\mathcal {L}}_i = b_i p_1^i\), for certain non-zero rational numbers \(b_i\). Through the isomorphism in the theorem, \(\kappa _{{\mathcal {L}}_i}\) corresponds to \(d{\mathcal {L}}_i = i b_i p_1^{i-1}dp_i\), showing the classes \(\kappa _{{\mathcal {L}}_i}\) are non-zero and span \(R^*(\tau _{S^3})\). \(\square \)
As we will discuss next, the classes \(\kappa _{{\mathcal {L}}_i}\) are obstructions for extending a given \(\tau _{S^m}\)-fibration to a fiber bundle and, rationally, they turn out to be the only obstructions. It is a consequence of the family signature theorem that \(\kappa _{{\mathcal {L}}_i}(\pi ,\zeta ) = 0\) for all \(i>m/4\) if \((\pi ,\zeta )\) is the \(\tau _{S^m}\)-fibration associated to a smooth manifold bundle with fiber \(S^m\) (see [20, Theorem A.2]). Define \(Baut(\tau _{S^m})_L\) to be the homotopy fiber of the map
that records the classes \(\kappa _{{\mathcal {L}}_i}\) in the indicated range. It may be thought of as the classifying space of \(\tau _{S^m}\)-fibrations with trivializations of the classes \(\kappa _{{\mathcal {L}}_i}\). Every oriented vector bundle \(E\rightarrow B\) of dimension \(m+1\) has an associated sphere bundle
This is an \(SO(m+1)\)-bundle, so it can be equipped with a fiberwise tangent bundle \(\zeta \rightarrow S(E)\) making it into a \(\tau _{S^m}\)-fibration, and the map that classifies it factors through \(Baut(\tau _{S^m})_L\).
While the calculations for m even and m odd are quite different, they both lead to the following result (for m odd we do not suggest that it is an obvious consequence of the statement of Theorem 1.2 but it follows from the methods that prove it).
Theorem 1.4
The map
induced by taking the oriented sphere bundle of the universal oriented vector bundle, is a rational homotopy equivalence.
As an application, this implies that the classes \(\kappa _{{\mathcal {L}}_i}\) are the only obstructions for a given \(\tau _{S^m}\)-fibration \((\pi ,\zeta )\) to be rationally equivalent to an \(SO(m+1)\)-bundle with fiber \(S^m\). By the latter we mean that there exists a rational homotopy equivalence \(f:B' \rightarrow B\) such that the pulled back \(\tau _{S^m}\)-fibration \(f^*(\pi ,\zeta )\) is equivalent to the underlying \(\tau _{S^m}\)-fibration of an \(SO(m+1)\)-bundle over \(B'\) with fiber \(S^m\).
Corollary 1.5
A \(\tau _{S^m}\)-fibration
is rationally equivalent to an \(SO(m+1)\)-bundle if and only if
for \(m/4<i\le m/2\).
Proof
Given a \(\tau _{S^m}\)-fibration \((\pi ,\zeta )\) such that \(\kappa _{{\mathcal {L}}_i}(\pi ,\zeta ) = 0\) for \(m/4<i\le m/2\), the classifying map factors through \(B\rightarrow Baut(\tau _{S^m})_L\). Forming the homotopy pullback

yields the desired data, as rational equivalences are stable under homotopy pullbacks. \(\square \)
As another application, we note that computations over \(Baut(\tau _M)\) can yield information about the tautological ring of M in the sense of [13], i.e., the subring \(R^*(M)\) of \(H^*(B\,{\mathrm{Diff}}^+(M);{\mathbb {Q}})\) generated by the \(\kappa \)-classes. Indeed, the map
that classifies the \(\tau _M\)-fibration associated to the universal smooth oriented M-bundle induces a surjective ring homomorphism
Thus, in principle, the ring \(R^*(M)\) can be carved out of \(R^*(\tau _M)\) by imposing further relations. As a simple illustration of this point, we give an alternative calculation of the tautological ring of \(S^m\) for m even, cf. [13, Theorem 1.1(i)].
Corollary 1.6
The ring homomorphism
is split injective. For \(m=2k\) even, the image is the tautological ring \(R^*(S^{m})\), and
Proof
The map (1) factors as
inducing
The composite is a ring isomorphism by Theorem 1.4. This proves the first claim.
Now assume m is even. Since all characteristic classes of \(\tau _{S^m}\)-fibrations are tautological, the image is \(R^*(S^m)\). As will be clear from the proof, one can replace the Pontryagin classes by the Hirzebruch L-classes in Theorem 1.1, so that
Since \(\kappa _{{\mathcal {L}}_r},\ldots ,\kappa _{{\mathcal {L}}_k}\) is a regular sequence, it follows that
\(\square \)
For another sample calculation, we turn to complex projective spaces. Consider a fibration
which is orientable in the sense that \(\pi _1(B)\) acts trivially on the cohomology of the fiber. For every choice of generator \(\omega \in H^2({\mathbb {C}}\mathrm {P}^n;{\mathbb {Q}})\), there is a unique cohomology class \(\omega _{fw}(\pi ) \in H^2(E;{\mathbb {Q}})\) (the ‘coupling class’) such that \(\omega _{fw}(\pi )|_{{\mathbb {C}}\mathrm {P}^n} = \omega \) and
For definiteness, we fix the generator \(\omega = -c_1(\gamma ^1)\), the negative of the first Chern class of the canonical line bundle \(\gamma ^1\).
By a standard argument, it follows that \(H^*(E;{\mathbb {Q}})\) is a free \(H^*(B;{\mathbb {Q}})\)-module with basis \(1,\, \omega _{fw}(\pi ), \ldots ,\, \omega _{fw}(\pi )^n\). A key observation is that \(\omega _{fw}(\pi )\) is natural in the fibration \(\pi \) (see Lemma 4.1). Inspired by Grothendieck’s approach to Chern classes (cf. [16] or [7, §20]), we can then define characteristic classes of orientable \({\mathbb {C}}\mathrm {P}^n\)-fibrations \(\pi :E\rightarrow B\),
by postulating the equality
in the cohomology of the total space (we set \(a_0(\pi ) =1\) and \(a_1(\pi ) = 0\)).Footnote 1
Similarly, if \(\xi \) is a bundle over \({\mathbb {C}}\mathrm {P}^n\) with structure group G, then for every class \(x\in H^\ell (BG;{\mathbb {Q}})\) we can define characteristic classes
of orientable \(\xi \)-fibrations
by postulating the equality
in the cohomology of the total space.
Theorem 1.7
Let \(\xi \) be a bundle over \({\mathbb {C}}\mathrm {P}^n\) with structure group G. Assume that G is connected and that the cohomology of BG is an evenly graded polynomial ring, say \(H^*(BG;{\mathbb {Q}}) = {\mathbb {Q}}[p_1,p_2,\ldots ]\) with \(|p_i|=2r_i\).
-
(1)
The ring of characteristic classes of orientable \(\xi \)-fibrations,
$$\begin{aligned} H^*(Baut_\circ (\xi );{\mathbb {Q}}), \end{aligned}$$may be identified with the polynomial ring
$$\begin{aligned} {\mathbb {Q}}[a_2,\ldots ,a_{n+1},p_{i|j}], \end{aligned}$$generated by \(a_2,\ldots , a_{n+1}\) and \(p_{i|j}\) for all i and all j such that \(0\le j < r_i\).
-
(2)
The ring of characteristic classes of \(\xi \)-fibrations may be identified with the invariant subring
$$\begin{aligned} H^*(Baut(\xi );{\mathbb {Q}}) = {\mathbb {Q}}[a_2,\ldots ,a_{n+1},p_{i|j}]^{\Gamma (\xi )}, \end{aligned}$$where
$$\begin{aligned} \Gamma (\xi ) \cong \left\{ \begin{array}{cc} {\mathbb {Z}}/2{\mathbb {Z}}, &{} c^*(\xi )\cong \xi , \\ 0, &{} c^*(\xi ) \not \cong \xi , \end{array} \right. \end{aligned}$$where \(c:{\mathbb {C}}\mathrm {P}^n \rightarrow {\mathbb {C}}\mathrm {P}^n\) denotes complex conjugation, and where the non-trivial element of \(\Gamma (\xi )\) acts by
$$\begin{aligned} a_k\mapsto (-1)^k a_k, \quad p_{i|j}\mapsto (-1)^j p_{i|j}, \end{aligned}$$in the case when \(c^*(\xi ) \cong \xi \).
For example, since complex conjugation is an orientation preserving diffeomorphism of \({\mathbb {C}}\mathrm {P}^2\) we have \(c^*(\tau _{{\mathbb {C}}\mathrm {P}^2}^{\mathbb {R}}) \cong \tau _{{\mathbb {C}}\mathrm {P}^2}^{{\mathbb {R}}}\), where the latter denotes the underlying oriented vector bundle of the complex tangent bundle, whence
This ring is abstractly isomorphic to
In particular, it is a complete intersection of Krull dimension 6 and embedding dimension 9.
By counting dimensions, one quickly realizes that there are not enough tautological classes to generate \(H^*(Baut_\circ (\xi );{\mathbb {Q}})\) in general. However, if we extend the set of tautological classes by defining
for \(n\ge 0\) and \(c\in H^*(BG;{\mathbb {Q}})\), then we have the following.
Theorem 1.8
With hypotheses as in Theorem 1.7, the ring of characteristic classes of orientable \(\xi \)-fibrations is a polynomial ring in the classes
In particular, all such characteristic classes are tautological in the extended sense.
Remark 1.9
For the \(\tau _{{\mathbb {C}}\mathrm {P}^n}\)-fibration \((\pi ,\zeta )\) associated to a symplectic \({\mathbb {C}}\mathrm {P}^n\)-bundle, the class \(\kappa _{\omega ^{n+k}c^I}(\pi ,\zeta )\), where \(c^I = c_1^{m_1}\ldots c_n^{m_n}\) for a multi-index \(I=(m_1,\ldots ,m_n)\), agrees with the class \(\mu _{k,I}\) defined by Kȩdra-McDuff [19, p.147].
Remark 1.10
By letting \(\xi \) be the trivial bundle with fiber a point, we recover a result of Kuribayashi [22] on the ring of characteristic classes of orientable \({\mathbb {C}}\mathrm {P}^n\)-fibrations as a special case of Theorem 1.8: \(H^*(Baut_\circ ({\mathbb {C}}\mathrm {P}^n);{\mathbb {Q}}) = {\mathbb {Q}}[\mu _2,\ldots ,\mu _{n+1}]\).
As an application of Theorem 1.7, we establish necessary and sufficient conditions for a \(\tau _{{\mathbb {C}}\mathrm {P}^n}\)-fibration to be rationally equivalent to a \(PU(n+1)\)-bundle. To do this, we first equip every orientable \({\mathbb {C}}\mathrm {P}^n\)-fibration with a cohomological stand-in for a fiberwise tangent bundle. The following definition is based on the observation that the Chern classes of the fiberwise tangent bundle of the projectivization of a complex vector bundle can be expressed in terms of the classes \(a_i(\pi )\) and \(\omega _{fw}(\pi )\) and hence only depend on the underlying \({\mathbb {C}}\mathrm {P}^n\)-fibration (see Proposition 4.8).
Definition 1.11
For an orientable fibration
we define the fiberwise Chern classes \(c_1^{fw}(\pi ),\ldots , c_n^{fw}(\pi )\) by the formula
Let \(Baut(\tau _{{\mathbb {C}}\mathrm {P}^n})^c\) denote the classifying space for \(\tau _{{\mathbb {C}}\mathrm {P}^n}\)-fibrations \((\pi ,\zeta )\) with a trivialization of the ‘Chern difference’
for every i. By design, the Chern differences of \(\tau _{{\mathbb {C}}\mathrm {P}^n}\)-fibrations arising from projectivizations of complex vector bundles are trivial. Somewhat surprisingly, it turns out that the Chern differences are the only obstructions for a \(\tau _{{\mathbb {C}}\mathrm {P}^n}\)-fibration to be rationally equivalent to a \(PU(n+1)\)-bundle.
Theorem 1.12
Every \(PU(n+1)\)-bundle with fiber \({\mathbb {C}}\mathrm {P}^n\) has trivial Chern differences and the induced map
is a rational homotopy equivalence.
Corollary 1.13
A \(\tau _{{\mathbb {C}}\mathrm {P}^n}\)-fibration is rationally equivalent to a \(PU(n+1)\)-bundle if and only if its Chern differences are trivial.
Remark 1.14
Since \(c_1^{fw}(\pi ) = (n+1)\omega _{fw}(\pi )\), it follows immediately from Theorem 1.8 that all characteristic classes of \(\tau _{{\mathbb {C}}\mathrm {P}^n}\)-fibrations with trivial first Chern difference are tautological.
There are similar results for \(\tau _{{\mathbb {C}}\mathrm {P}^n}^{\mathbb {R}}\)-fibrations \((\pi ,\zeta )\), where the total bundle \(\zeta \) is an oriented vector bundle instead of a complex vector bundle. We define fiberwise Pontryagin classes and a fiberwise Euler class by
We remark that \(e^{fw}(\pi )\) as defined here agrees with the fiberwise Euler class in the sense of [17], as follows from [29, Theorem 5.6]. Let \(Baut(\tau _{{\mathbb {C}}\mathrm {P}^n}^{\mathbb {R}})^{p,e}\) denote the classifying space for \(\tau _{{\mathbb {C}}\mathrm {P}^n}^{\mathbb {R}}\)-fibrations \((\pi ,\zeta )\) with trivializations of the Pontryagin differences and the Euler difference,
and let \(\,{\mathrm{Isom}}^+({\mathbb {C}}\mathrm {P}^n)\) denote the group of orientation preserving isometries of \({\mathbb {C}}\mathrm {P}^n\) with respect to the Fubini-Study metric.
Theorem 1.15
The universal \(\,{\mathrm{Isom}}^+({\mathbb {C}}\mathrm {P}^n)\)-bundle with fiber \({\mathbb {C}}\mathrm {P}^n\) has trivial Pontryagin and Euler differences, and the induced map
is a rational homotopy equivalence.
Corollary 1.16
A \(\tau _{{\mathbb {C}}\mathrm {P}^n}^{{\mathbb {R}}}\)-fibration is rationally equivalent to an \(\,{\mathrm{Isom}}^+({\mathbb {C}}\mathrm {P}^n)\)-bundle if and only if its Pontryagin and Euler differences are trivial.
Theorem 1.17
Consider the ring \(H^*\big (B\,{\mathrm{Isom}}^+({\mathbb {C}}\mathrm {P}^n);{\mathbb {Q}}\big )\) of characteristic classes of \(\,{\mathrm{Isom}}^+({\mathbb {C}}\mathrm {P}^n)\)-bundles with fiber \({\mathbb {C}}\mathrm {P}^n\).
-
(1)
For odd \(n=2k+1\), the ring may be identified with the polynomial ring in the n generators
$$\begin{aligned} \kappa _{ep_1},\ldots ,\kappa _{ep_1^{k+1}},\kappa _{p_1^{k+2}},\ldots ,\kappa _{p_1^{2k+1}}. \end{aligned}$$ -
(2)
For even \(n=2k\), the ring is a complete intersection of Krull dimension n and embedding dimension \(n + \left( {\begin{array}{c}k\\ 2\end{array}}\right) \). A minimal set of generators is given by
$$\begin{aligned} \kappa _{p_1^{k+1}},\ldots ,\kappa _{p_1^{2k}},\quad \kappa _{p_1^{3k+1}}, \end{aligned}$$and
$$\begin{aligned} \kappa _{p_1^{k+s-1}\beta _s},\ldots , \kappa _{p_1^{2k}\beta _s}, \end{aligned}$$for \(s=2,\ldots , k\), where
$$\begin{aligned} \beta _s = (n+1)^s p_s - \left( {\begin{array}{c}n+1\\ s\end{array}}\right) p_1^s. \end{aligned}$$
In particular, all characteristic classes of \(\,{\mathrm{Isom}}^+({\mathbb {C}}\mathrm {P}^n)\)-bundles with fiber \({\mathbb {C}}\mathrm {P}^n\) are tautological.
Remark 1.18
In view of Theorem 1.15, Theorem 1.17 could also be read as a statement about the ring of characteristic classes of \(\tau _{{\mathbb {C}}\mathrm {P}^n}^{\mathbb {R}}\)-fibrations with trivialized Pontryagin and Euler differences. The displayed generators are by no means canonical, there are other options.
The above results have interesting consequences for the tautological ring of \({\mathbb {C}}\mathrm {P}^n\). For an orientable \(\tau _{{\mathbb {C}}\mathrm {P}^n}^{\mathbb {R}}\)-fibration \((\pi ,\zeta )\) over B, let \({\mathfrak {d}}\subseteq H^*(B;{\mathbb {Q}})\) denote the ideal generated by the coefficients \(pd_{i|j}\), \(ed_{|i}\), of the Pontryagin and Euler differences,
If \((\pi ,\zeta )\) is not orientable, we define \({\mathfrak {d}}\) by pullback along \(H^*(B;{\mathbb {Q}}) \rightarrow H^*(B_\circ ;{\mathbb {Q}})\), where \(B_\circ \rightarrow B\) is the cover corresponding to the kernel of the action of \(\pi _1(B)\) on the cohomology of the fiber. Let us call elements of \({\mathfrak {d}}\subseteq H^*(B;{\mathbb {Q}})\) ‘difference classes’. We let \(R^*(B) \subseteq H^*(B;{\mathbb {Q}})\) denote the subring of tautological classes.
Theorem 1.19
Consider a \(\tau _{{\mathbb {C}}\mathrm {P}^n}^{\mathbb {R}}\)-fibration over a space B whose classifying map fits in a homotopy commutative diagram

The induced ring homomorphism
is surjective and the kernel is the ideal \(R^*(B)\cap {\mathfrak {d}}\) of tautological difference classes.
For a \({\mathbb {C}}\mathrm {P}^2\)-fibration \(\pi :E\rightarrow B\), the fiberwise Pontryagin and Euler classes are
A recent result of Baraglia [1, Theorem 1.3(ii)] implies that every smooth oriented \({\mathbb {C}}\mathrm {P}^2\)-bundle \(\pi :E\rightarrow B\) has trivial Pontryagin and Euler differences,
We remark in passing that triviality of the Euler difference makes sense—and holds—more generally for any oriented manifold bundle by [17, §3.2.1]. Baraglia uses [1, Theorem 1.3(ii)] as one of several ingredients in a computation of the tautological ring of \({\mathbb {C}}\mathrm {P}^2\). Theorem 1.19 applied to \(B=B\,{\mathrm{Diff}}^+({\mathbb {C}}\mathrm {P}^2)\) gives a direct path from (5) to the computation that circumvents the other ingredients: triviality of the Pontryagin and Euler differences means that \({\mathfrak {d}}= 0\) so
is an isomorphism. The target may be identified with \({\mathbb {Q}}[\kappa _{p_1^2},\kappa _{p_1^4}]\) by Theorem 1.17. (Incidentally, this is the only even n for which the target of (4) is a polynomial ring.)
It is interesting to compare with Randal-Williams’ computations [32, §4.4]; they inspire the following observations. For a closed oriented smooth manifold M, the conditions on \(\kappa _{{\mathcal {L}}_i}\) that come from the family signature theorem give relations among the generators for \(R^*(M)\). These relations are sometimes sufficient for determining \(R^*(M)\) (as in Corollary 1.6). The following shows they are not sufficient in general.
Theorem 1.20
-
(1)
For every \(\tau _{{\mathbb {C}}\mathrm {P}^2}^{\mathbb {R}}\)-fibration
$$\begin{aligned} {\mathbb {C}}\mathrm {P}^2 \rightarrow E \xrightarrow {\pi } B,\quad \zeta \rightarrow E, \end{aligned}$$such that
$$\begin{aligned} e(\zeta ) = e^{fw}(\pi ),\quad \kappa _{{\mathcal {L}}_i}(\pi ,\zeta ) = 0,\quad i>1, \end{aligned}$$(6)the difference class \(pd_{1|0}\) is tautological and generates the ideal \(R^*(B)\cap {\mathfrak {d}}\).
-
(2)
There exist \(\tau _{{\mathbb {C}}\mathrm {P}^2}^{\mathbb {R}}\)-fibrations satisfying (6) such that \(pd_{1|0} \ne 0\). In particular, for such \(\tau _{{\mathbb {C}}\mathrm {P}^2}^{\mathbb {R}}\)-fibrations, \(R^*(B) \rightarrow R^*({\mathbb {C}}\mathrm {P}^2)\) is not injective.
Remark 1.21
The difference class \(pd_{1|0}\) is directly related to the class \(4\kappa _{p_1^2} - 7\kappa _{ep_1}\) featured in the computations of [32, §4.4]: for every \(\tau _{{\mathbb {C}}\mathrm {P}^2}^{\mathbb {R}}\)-fibration satisfying (6),
In particular, vanishing of the Pontryagin difference for smooth \({\mathbb {C}}\mathrm {P}^2\)-bundles explains why
answering the question posed after Theorem D in [32], but we stress that (7) should be viewed as a corollary of [1, Theorem 1.3(ii)].
Remark 1.22
For a closed oriented smooth manifold M, triviality of the Euler difference together with the conditions on \(\kappa _{{\mathcal {L}}_i}\) that come from the family signature theorem are necessary for being able to reduce the ‘structure group’ of a \(\tau _M\)-fibration from \(aut(\tau _M)\) to \(\,{\mathrm{Diff}}^+(M)\) rationally. For \(S^m\) these conditions are sufficient (Corollary 1.5), but they are not sufficient in general. Indeed, the \(\tau _{{\mathbb {C}}\mathrm {P}^2}^{\mathbb {R}}\)-fibration in Theorem 1.20(2) has a non-trivial Pontryagin difference, so cannot be rationally equivalent to a smooth \({\mathbb {C}}\mathrm {P}^2\)-bundle.
Remark 1.23
Theorem 1.19 shows that the structure of the tautological ring \(R^*({\mathbb {C}}\mathrm {P}^n)\) is intimately linked to the behavior of the Pontryagin differences of smooth oriented \({\mathbb {C}}\mathrm {P}^n\)-bundles. For \(n=2\), the Pontryagin difference vanishes, but this turns out to be a low-dimensional phenomenon. For n sufficiently large, there are smooth oriented \({\mathbb {C}}\mathrm {P}^n\)-bundles with non-trivial Pontryagin differences. We thank Oscar Randal-Williams for suggesting a way to construct such bundles in a comment to an earlier version of this paper.
The rational homotopy groups of the space \(aut({\mathbb {C}}\mathrm {P}^n)/{\widetilde{\,{\mathrm{Diff}}}}({\mathbb {C}}\mathrm {P}^n)\), which classifies homotopically trivial block bundles with fiber \({\mathbb {C}}\mathrm {P}^n\), can be computed using the surgery exact sequence (see e.g. [4, §3] for a review). After a few manipulations, this assumes the form of an exact sequence
where the first map sends the equivalence class of a homotopically trivial block bundle \(\pi :E\rightarrow S^k\), with fiber \({\mathbb {C}}\mathrm {P}^n\) and stable fiberwise tangent bundle \(\zeta \), to the sequence of cohomology classes \(w^{-1}({\mathcal {L}}d_i(\pi ,\zeta )) \in H^{4i-k}({\mathbb {C}}\mathrm {P}^n;{\mathbb {Q}})\), where \({\mathcal {L}}d_i(\pi ,\zeta )\) is the ith ‘L-class difference’ and \(w:H^{*-k}({\mathbb {C}}\mathrm {P}^n;{\mathbb {Q}}) \rightarrow H^*(E;{\mathbb {Q}})\) comes from the Wang sequence associated to \(\pi \). In particular, this shows the existence of block bundles over spaces within the rational homotopy type of \(S^k\) with non-trivial L-differences and hence Pontryagin differences. To promote such block bundles to smooth bundles, [10, Corollary D] implies that
is surjective as long as k is in the pseudoisotopy stable range for \({\mathbb {C}}\mathrm {P}^n\), which holds if \(2n \ge \max (2k+7,3k+4)\) by [18].
The applicability of Theorem 3.8 is not limited to the examples presented here. Further computations and applications using Theorem 3.8 are worked out in the PhD thesis of Nils Prigge [30].
The original motivation for this work was to understand the relation between the generalized Miller–Morita–Mumford classes and certain classes defined using graph complexes in the cohomology of the classifying space of the block diffeomorphism group of the manifold \(\#^g S^d\times S^d\setminus \,{\mathrm{int}}D^{2d}\), see [5]. This application will be treated in a separate paper.
Remark 1.24
In [3], we constructed a different rational model for \(Baut_\circ (\xi )\), but this model is insufficient for the applications presented here, because it does not say anything about the universal \(\xi \)-fibration or the classifying map for the total bundle. Theorem 3.8, on the other hand, does this. A precursor to Theorem 1.2 was obtained in [3], but it lacks an interpretation in terms of characteristic classes.
2 Families of bundles and characteristic classes
In this section, we discuss the notion of a family of bundles and, more generally, fibrations with extra structure on the total space that restrict to a given structure on the fiber. We review different models for universal fibrations and define tautological classes in this context, and we discuss the relation to smooth manifold bundles.
2.1 Fibrations with extra structure
The following definition distills the relevant homotopical information carried by a family of bundles.
Definition 2.1
Let \(g:X\rightarrow Z\) be a map. A \(g\)-fibration over a space B is a pair \((\pi ,h)\) consisting of
-
a fibration \(\pi :E\rightarrow B\),
-
a map \(h:E\rightarrow Z\),
such that \(h|_{E_b}:E_b\rightarrow Z\) is weakly equivalent to \(g:X\rightarrow Z\) as a space over Z, for every \(b\in B\), where \(E_b = \pi ^{-1}(b)\).
There are mainly two types of g-fibrations that will interest us:
Families of bundles. Let \(\xi \) be a bundle over X with structure group G and let \(g:X\rightarrow BG\) be a map that classifies \(\xi \). In this case, a \(g\)-fibration may be interpreted as a \(\xi \)-fibration as in the introduction, i.e., a fibration \(\pi :E\rightarrow B\) together with a bundle \(\zeta \) over E such that \(\zeta |_{E_b}\) is weakly equivalent to \(\xi \) through bundle maps that cover weak homotopy equivalences, for every \(b\in B\).
Fiberwise cohomology classes. Let \(c_i \in H^{\ell _i}(X)\) a sequence of cohomology classes, represented by a map
Letting Z denote the product of Eilenberg–Mac Lane spaces, a \(g\)-fibration
may be thought of as a fibration \(\pi :E\rightarrow B\) with fiber X together with cohomology classes \(c_i(h)\in H^{\ell _i}(E)\) that restrict to \(c_i\) in the fiber.
2.2 Universal fibrations with extra structure
Let X be a CW complex equipped with a map \(g:X\rightarrow Z\). Let \(map(X,Z)_{g}\) denote the connected component of the space of maps from X to Z that contains \(g\), and let \(aut(X)_{[g]}\) denote the topological monoid of homotopy equivalences \(f:X\rightarrow X\) such that \(g\circ f \simeq g\). For a topological monoid \({\mathcal {H}}\), a right \({\mathcal {H}}\)-space M, and a left \({\mathcal {H}}\)-space N, we let \(B\big (M,{\mathcal {H}},N\big )\) denote the geometric bar construction [27, §7]. Recall that \(B\big (M,{\mathcal {H}}) = B\big (M,{\mathcal {H}},*)\) is a model for the homotopy orbit space  .
.
Theorem 2.2
The universal \(g\)-fibration is weakly equivalent to the map
and the reference map from the total space to Z is equivalent to the map
induced by the evaluation map \(map(X,Z)_{g} \times X \rightarrow Z\).
Proof
The notion of a \(g\)-fibration fits into May’s framework of ‘fibrations with a Y-structure’, and the result is a consequence of [27, Theorem 11.1] (the statement about the reference map is implicit in the proof). \(\square \)
In the case when the map \(g\) classifies a bundle \(\xi \), there is a model for the universal \(g\)-fibration of a more geometric flavor, which will be useful when we study manifold bundles. Suppose \(\xi \) is a fiber bundle over a CW complex X with fiber F, structure group G, and projection \(T\rightarrow X\). Let \(aut(\xi )\) denote the topological monoid of self-equivalences of \(\xi \), i.e., bundle maps

such that f is a homotopy equivalence and \(\varphi \) is a fiberwise isomorphism. The classifying space of this monoid, \(Baut(\xi )\), is a model for the base of the universal \(\xi \)-fibration, cf. [3, Corollary 2.4] or [5, Proposition 4.11]. The following enhances this result by giving a model, expressed in terms of \(\xi \), for the fibration and the total bundle as well. Clearly, the monoid \(aut(\xi )\) acts on both T and X, and the projection \(T\rightarrow X\) is a map of \(aut(\xi )\)-spaces.
Proposition 2.3
Let \(\xi \) be a bundle classified by \(g:X\rightarrow BG\). The underlying fibration of the universal \(\xi \)-fibration is weakly equivalent to the map
and the total bundle is equivalent to
Proof
We highlight two key properties of spaces of bundle maps that we will use:
-
(Covering homotopy property) For bundles \(\xi \) and \(\xi '\) over X and \(X'\), the forgetful map \(map(\xi ,\xi ') \rightarrow map(X,X')\) is a fibration.
-
(Existence of a universal bundle) There is a bundle \(\gamma \) such that \(map(\xi ,\gamma )\) is weakly contractible for every bundle \(\xi \).
That these properties hold for vector bundles over CW complexes should be well-known. See Remark 2.4 below for a discussion and generalizations.
We may assume that \(\xi = g^*(\gamma )\), where \(\gamma \) is the universal bundle over BG, so that we have a bundle map \(\xi \rightarrow \gamma \) given by a pullback square

We then have an induced pullback square

The vertical maps are fibrations by the covering homotopy property, so it is a homotopy pullback square. It follows from [5, Lemma 4.10] that the induced map
is a weak homotopy equivalence. The map
is a weak homotopy equivalence since \(map(\xi ,\gamma )\) is weakly contractible. Thus, the bottom horizontal maps in the following diagram are weak homotopy equivalences.

The squares are homotopy cartesian by Theorem 7.6 and Proposition 7.8 of [27]. It follows that the top horizontal maps are weak homotopy equivalences. This proves the first claim.
The second claim can be proved by considering the diagram

where the rightmost square is the pullback of the universal bundle along the map ev, the map \({\overline{ev}}\) is induced by the map
and the dashed arrow exists by the universal property of the pullback. \(\square \)
Remark 2.4
Our main applications are to vector bundles over CW complexes, but Proposition 2.3 remains valid for more general interpretations of the terms ‘bundle’ and ‘bundle map’. Indeed, these can be taken to mean ‘\({\mathcal {F}}\)-fibration’ and ‘\({\mathcal {F}}\)-map’, respectively, in the sense of May [27], for \({\mathcal {F}}\) a category of fibers that satisfies the hypotheses of the classification theorem [27, Theorem 9.2] (the ‘structure group’ G should then be interpreted as the grouplike monoid of \({\mathcal {F}}\)-self-maps of the typical fiber F as in [27, Definition 4.3]). The covering homotopy property as stated here is equivalent to the covering homotopy property for \(\xi '\) in the definition of \({\mathcal {F}}\)-fibrations [27, Definition 2.1]. That \(map(\xi ,\gamma )\) is weakly contractible is implicitly verified in the course of the proof of [27, Theorem 9.2] (see the bottom of p. 50). Numerable fiber bundles (in the sense of Dold [11, §7]) with structure group G and fiber F are \({\mathcal {F}}\)-fibrations for a suitable choice of \({\mathcal {F}}\) (see Theorem 3.8 and Example 6.11 of [27]), but ‘bundle’ could also be taken to mean e.g. ‘fibration with fiber weakly homotopy equivalent to F’ for a fixed CW complex F (see [27, Example 6.6]).
Remark 2.5
Replacing \(g:X\rightarrow Z\) by a fibration if necessary, and letting \(aut(g)\) denote the topological monoid of self-equivalences of X as a space over Z, the universal \(g\)-fibration can be seen to be weakly equivalent to
with structure map \(B\big (aut(g),X\big ) \rightarrow Z\) induced by \(g:X\rightarrow Z\). One way to see this is to apply [5, Lemma 4.10] to the homotopy cartesian square

This justifies writing \(Baut(\xi )\) for the classifying space of \(\xi \)-fibrations, regardless of whether \(\xi \) denotes a bundle over X or a map from X to a space Z.
2.3 Fibrations with prescribed holonomy
Let \({\mathcal {H}}\) be a grouplike topological monoid that acts on the CW complex X by homotopy equivalences and let \({\mathcal {H}}_{[g]}\) denote the stabilizer of the homotopy class of the map \(g:X\rightarrow Z\) under the induced action of \({\mathcal {H}}\) on [X, Z]. The homotopy orbit space
classifies \(g\)-fibrations such that the underlying fibration \(\pi :E \rightarrow B\) has ‘holonomy in \({\mathcal {H}}\)’, in the sense that there is a lift up to homotopy,

where the horizontal map is the classifying map for the fibration \(\pi \). This can be deduced from Theorem 2.2 by contemplating the homotopy pullback square

If \(g\) is the classifying map for a bundle \(\xi \) over X, then a model for the universal \(g\)-fibration with holonomy in \({\mathcal {H}}\) is obtained by replacing \(aut(\xi )\) in Proposition 2.3 by the monoid \(aut_{{\mathcal {H}}}(\xi )\) of pairs \((f,\varphi )\) such that \(f\in {\mathcal {H}}\) and \(\varphi :\xi \rightarrow \xi \) is a bundle map covering the map \(X\rightarrow X\) given by the action of f.
Examples of \({\mathcal {H}}\) that we have in mind are:
-
\(aut_\circ (X)\) self-equivalences homotopic to the identity,
-
\(aut_+(X)\) orientation preserving self-equivalences (if X is oriented),
-
\(aut_A(X)\) self-equivalences that fix a given subset \(A\subseteq X\) pointwise.
If \({\mathcal {H}}= aut_\circ (X)\), we will write \(aut_\circ (\xi )\) for \(aut_{{\mathcal {H}}}(\xi )\). Similarly for \(aut_+(X)\), etc.
2.4 Families of bundles from manifold bundles
Let M be a smooth compact manifold of dimension m and let \(\tau _M = (TM, p, M)\) denote its tangent bundle. Consider a smooth M-bundle,
i.e., a fiber bundle with fiber M and structure group \(\,{\mathrm{Diff}}(M)\). Recall that the fiberwise tangent bundle, or vertical tangent bundle, \(T_\pi E\) is a vector bundle over E that may be defined as follows. If E and B are smooth compact manifolds and \(\pi \) is a surjective submersion, then \(T_\pi E\) can be defined as the kernel of the differential \(D\pi :TE \rightarrow \pi ^*(TB)\). More generally, \(T_\pi E\) may be defined as the vector bundle over E with projection
where \(P\rightarrow B\) is the principal \(\,{\mathrm{Diff}}(M)\)-bundle associated to \(\pi \). Thus, every smooth M-bundle has an underlying \(\tau _M\)-fibration with fibration \(\pi \) and total bundle \(T_\pi E\).
There is an evident map of monoids \(D:\,{\mathrm{Diff}}(M) \rightarrow aut(\tau _M)\) that sends a diffeomorphism \(f:M\rightarrow M\) to its differential \(Df:\tau _M\rightarrow \tau _M\).
Proposition 2.6
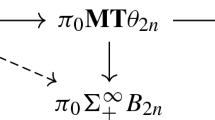
The \(\tau _M\)-fibration underlying the universal smooth M-bundle is classified by the map \(B\,{\mathrm{Diff}}(M) \rightarrow Baut(\tau _M)\) induced by the differential.
Proof
The space of embeddings \(\,{\mathrm{Emb}}(M,{\mathbb {R}}^\infty )\) is contractible and carries a free right action of \(\,{\mathrm{Diff}}(M)\), so
may be taken as a model for the universal principal \(\,{\mathrm{Diff}}(M)\)-bundle. Hence, a model for the universal M-bundle is
Given an embedding \(f:M\rightarrow {\mathbb {R}}^{m+k}\) and a point \(x\in M\), the image of the differential \(Df_x:T_x M \rightarrow T_{f(x)}{\mathbb {R}}^{m+k} = {\mathbb {R}}^{m+k}\) is an m-dimensional linear subspace of \({\mathbb {R}}^{m+k}\). This defines a map into the Grassmannian, the generalized Gauss map,
It is covered by a bundle map \(\tau _M \rightarrow \gamma ^m({\mathbb {R}}^{m+k})\), into the canonical m-dimensional vector bundle over \(G_{m}({\mathbb {R}}^{m+k})\), cf. [28, p.60–61]. Varying the embedding, the Gauss maps give rise to a map
This map is \(\,{\mathrm{Diff}}(M)\)-equivariant and the action on the target factors through the differential \(D:\,{\mathrm{Diff}}(M)\rightarrow aut(\tau _M)\). Letting \(k\rightarrow \infty \), we obtain a bundle map

We recognize the left vertical map as a model for the fiberwise tangent bundle of the universal M-bundle and the right vertical map as a model for the total bundle of the universal \(\tau _M\)-fibration as in Proposition 2.3. This shows that the fiberwise tangent bundle of the universal M-bundle is pulled back from the total bundle of the universal \(\tau _M\)-fibration. \(\square \)
Remark 2.7
In the classifying space interpretation, the map
may be identified with the forgetful map that sends the equivalence class of a smooth M-bundle over B to the equivalence class of its underlying \(\tau _M\)-fibration.
2.5 Tautological classes
Definition 2.8
Let X be an oriented Poincaré duality space of formal dimension m equipped with a map \(g:X\rightarrow Z\), and let
be a \(g\)-fibration such that \(\pi _1(B)\) acts on X by orientation preserving homotopy equivalences. For a cohomology class \(c\in H^{k+m}(Z)\), we define
where
denotes integration along the fiber. We will also write \(\kappa _c(\pi ,\zeta )\) for \(\kappa _c(\pi ,h)\) if \(h\) classifies a bundle \(\zeta \). We will often denote \(\kappa _c(\pi ,h)\) simply by \(\kappa _c\) when there is no risk of confusion.
Remark 2.9
Recall that the pushforward map, or integration along the fiber, may be defined as the composite
where the first two maps arise from the fact that the Serre spectral sequence of the fibration satisfies \(E_2^{k,\ell } = 0\) for \(\ell >m\), and the last map comes from the orientation. This only requires the fiber to be an oriented Poincaré duality space of dimension m and the action of \(\pi _1(B)\) on the fiber to be through orientation preserving homotopy equivalences. See e.g. [15] and the references therein for a further discussion.
The following is immediate from the definitions and Proposition 2.6, but it is a key observation and we record it as a theorem for reference.
Theorem 2.10
Let M be a closed oriented smooth manifold of dimension m and let \(\vartheta \) be a smooth oriented M-bundle, i.e., a fiber bundle \(\pi :E\rightarrow B\) with fiber M and structure group \(\,{\mathrm{Diff}}^+(M)\).
The generalized Miller–Morita–Mumford classes of \(\vartheta \) agree with those of the underlying \(\tau _M\)-fibration, i.e.,
for all \(c\in H^{*+m}(BSO(m))\).
In particular, the universal classes \(\kappa _c\in H^*(B\,{\mathrm{Diff}}^+(M))\) lift to \(H^*(Baut(\tau _M))\) under the map
induced by the differential \(\,{\mathrm{Diff}}^+(M) \rightarrow aut(\tau _M)\). \(\square \)
The tautological ring \(R^*(M)\), in the sense of [13], can be defined as the subring of the cohomology ring of \(B\,{\mathrm{Diff}}^+(M)\) generated by the \(\kappa \)-classes. It is clear how to define an analog of the tautological ring for bundles.
Definition 2.11
For a bundle \(\xi \) with structure group G over an oriented Poincaré duality space X, we define \(R^*(\xi )\) to be the subring of the cohomology ring of \(Baut_+(\xi )\) generated by the classes \(\kappa _c\), for all \(c\in H^*(BG)\).
Corollary 2.12
For every closed oriented smooth manifold M, the differential induces a surjective ring homomorphism \(R^*(\tau _M) \rightarrow R^*(M)\).
3 Rational homotopy theory of fibrations with extra structure
Let X be a simply connected finite CW-complex equipped with a map \(g:X\rightarrow Z\) and let \({\mathcal {H}}\) be a connected topological monoid acting on X by homotopy equivalences. The aim of this section is to construct a relative Sullivan model, in the sense of rational homotopy theory (see e.g. [12, §14]), for the universal \(g\)-fibration with holonomy in \({\mathcal {H}}\).
3.1 The Chevalley–Eilenberg cochain complex
Let L be a differential graded Lie algebra over \({\mathbb {Q}}\) with differential \(\delta \). For \(n\in {\mathbb {Z}}\), we define \(L\langle n \rangle \) by
Recall that a Maurer–Cartan element is an element \(\tau \in L_{-1}\) such that
If \(\tau \) is a Maurer–Cartan element, then one can form the twisted dg Lie algebra \(L^\tau \). It has the same underlying graded Lie algebra as L but the differential is \(\delta + [\tau ,-]\).
The Chevalley–Eilenberg complex is the differential graded coalgebra
where the differential is characterized by
By definition, the Chevalley–Eilenberg cochain complex is the dual differential graded algebra \(C^*(L) = C_*(L)^\vee \).
If M is a differential graded left L-module, the Chevalley–Eilenberg complex with coefficients in M is defined by
The differential is the sum \(\partial + t\), where
Here \(\tau _L \cdot f\) denotes the action of the universal twisting function \(\tau _L \in \,{\mathrm{Hom}}(C_*(L),L)\) on \(f\in \,{\mathrm{Hom}}(C_*(L),M)\). Explicitly,
We call a cochain \(f\in C^*(L,M)\) an n-cochain if \(f(sx_1\wedge \cdots \wedge sx_k) = 0\) unless \(k=n\). Elements of M may be identified with 0-cochains. If \(\alpha _i\) is a graded vector space basis for L, then the dual 1-cochains \(x_i\in C^*(L)\) are characterized by
Remark 3.1
Our sign convention agrees with that of [36], but differs from that of [12]. The signs are dictated by wanting the 1-cochain \(\tau _L\in C_*(L,L)\) defined by \(\tau _L(sx) = x\) to be a twisting function in the sense of [31].
3.2 Characteristic cochains
Fix a map \(g:X\rightarrow Z\). We assume that Z is nilpotent and of finite \({\mathbb {Q}}\)-type. Let A be cdga model for X and let \(\Pi \) be a Lie model for Z in the sense that A and \(C^*(\Pi )\) are quasi-isomorphic to \(A_{PL}^*(X)\) and \(A_{PL}^*(Z)\), respectively, as cdgas. The rational homotopy class of \(g\) is recorded by either
-
the homotopy class of a morphism of cdgas
$$\begin{aligned} \varphi _{g} :C^*(\Pi ) \rightarrow A,\quad \text{ or } \end{aligned}$$ -
the gauge equivalence class of a Maurer–Cartan element
$$\begin{aligned} \tau (g) \in A {\widehat{\otimes }}\Pi , \end{aligned}$$in a certain completed tensor product.
For the latter, see e.g. [2, Theorem 1.5]. For A of finite type, the completed tensor product can be taken to be \((A {\widehat{\otimes }}\Pi )_n = \prod _{i} A^i \otimes \Pi _{i+n}\). If A or \(\Pi \) is finite dimensional, then \(A{\widehat{\otimes }}\Pi \cong A\otimes \Pi \). Concretely, if we fix a basis \(\{q_i\}\) for \(\Pi \) and we let \(p_i\in C^*(\Pi )\) denote the dual 1-cochains, then \(\varphi _{g}\) and \(\tau (g)\) are determined by certain cochains \(p_i(g) \in A\), namely
We will refer to \(p_i(g)\) as characteristic cochains of \(g:X\rightarrow Z\). The characteristic cochains are not unique, but the equivalence classes of \(\varphi _{g}\) or \(\tau (g)\) are.
In the special case when Z is simply connected and \(H^*(Z;{\mathbb {Q}})\) is a free graded commutative algebra (e.g., if \(Z=BG\) for G a connected compact Lie group), the rational homotopy groups \(\Pi = \pi _*(\Omega Z)\otimes {\mathbb {Q}}\), with trivial differential and Lie bracket, is a dg Lie algebra model for Z, and the cochains \(p_i\) are cocycles. In this case, the homotopy class of \(\varphi _{g}\), or the gauge equivalence class of \(\tau (g)\), determines and is determined by the cohomology classes of the cocycles \(p_i(g) \in A\).
3.3 Lie models for monoid actions
Let \({\mathfrak {h}}\) be a positively graded dg Lie algebra. Following [3] we associate a simplicial group \(\exp _\bullet ({\mathfrak {h}})\) to \({\mathfrak {h}}\) as follows. In simplicial degree n it is the nilpotent group associated to the nilpotent Lie algebra \(Z_0(\Omega _n \otimes {\mathfrak {h}})\) of 0-cycles in the dg Lie algebra \(\Omega _n \otimes {\mathfrak {h}}\), where \(\Omega _n = A_{PL}^*(\Delta ^n)\) is the cdga of polynomial differential forms on the standard n-simplex.
Remark 3.2
If \({\mathfrak {h}}\) is of finite type, then the simplicial group \(\exp _\bullet ({\mathfrak {h}})\) is isomorphic to the simplicial realization of the dg commutative Hopf algebra \(\Gamma {\mathfrak {h}}= U {\mathfrak {h}}^\vee \), studied in [12, §25], see [3, Proposition 3.8].
Next, if \({\mathfrak {h}}\) acts on a cdga \(\Lambda \) by derivations, then the simplicial group \(\exp _\bullet ({\mathfrak {h}})\) acts on the simplicial set \(\langle \Lambda \rangle = \,{\mathrm{Hom}}_{cdga}(\Lambda ,\Omega _\bullet )\). Indeed, the Lie algebra \(Z_0(\Omega _\bullet \otimes {\mathfrak {h}})\) acts on \(\Omega _\bullet \otimes \Lambda \) by \(\Omega _\bullet \)-linear chain derivations. In each simplicial degree the action is nilpotent (since \({\mathfrak {h}}\) is assumed to be positively graded), so induces an action of the group \(\exp Z_0(\Omega _\bullet \otimes {\mathfrak {h}})\) on \(\Omega _\bullet \otimes \Lambda \) by cdga automorphisms, and this induces an action on \(\langle \Lambda \rangle \cong \,{\mathrm{Hom}}_{cdga(\Omega _\bullet )}(\Omega _\bullet \otimes \Lambda ,\Omega _\bullet )\).
Remark 3.3
If \({\mathfrak {h}}\) is of finite type, then the action can alternatively be constructed as follows. That \({\mathfrak {h}}\) acts on \(\Lambda \) by derivations means that the map
is a cdga morphism, where \(\,{\mathrm{Hom}}(U{\mathfrak {h}},\Lambda )\) is given the convolution product. If \({\mathfrak {h}}\) is of finite type, then the natural cdga morphism
is an isomorphism. The composite map
defines the group action.
Definition 3.4
We will say that the action of \({\mathfrak {h}}\) on \(\Lambda \) models the action of a topological monoid \({\mathcal {H}}\) on a space X if \(({\mathcal {H}},X)\) is rationally equivalent to \((|\exp _\bullet ({\mathfrak {h}})|, |\Lambda |)\) in the category of pairs \(({\mathcal {G}},M)\) of topological monoids \({\mathcal {G}}\) and \({\mathcal {G}}\)-spaces M, where morphisms \((g,m):({\mathcal {G}},M)\rightarrow ({\mathcal {G}}',M')\) are pairs where \(g:{\mathcal {G}}\rightarrow {\mathcal {G}}'\) is a map of topological monoids and \(m:M\rightarrow M'\) is a map of \({\mathcal {G}}\)-spaces, and where (g, m) is a rational equivalence if both g and m induce isomorphisms in rational homology.
Remark 3.5
Since the action of a grouplike monoid \({\mathcal {G}}\) on a space X can be recovered, up to homotopy, as the holonomy action of \(\Omega B{\mathcal {G}}\) on X associated to the fibration  , we have that \(({\mathcal {G}},X)\) is weakly equivalent to \(({\mathcal {H}},Y)\) if and only if the associated fibrations
, we have that \(({\mathcal {G}},X)\) is weakly equivalent to \(({\mathcal {H}},Y)\) if and only if the associated fibrations  and
and  are weakly equivalent.
are weakly equivalent.
Proposition 3.6
Suppose that \(\Lambda \) is a Sullivan algebra of finite type. If the action of \({\mathfrak {h}}\) on \(\Lambda \) models the action of \({\mathcal {H}}\) on X, then the fibration

is modeled by the relative Sullivan algebra
Proof
The realization of the universal \(U{\mathfrak {h}}\)-coalgebra bundle
is a universal \(\langle U{\mathfrak {h}}\rangle \cong \exp _\bullet ({\mathfrak {h}})\)-bundle, cf. [3, Theorem 3.9] and [12, §25]. It follows that the fibration  is rationally equivalent to
is rationally equivalent to
The latter map isomorphic to the realization of the morphism of dg coalgebras \(C_*({\mathfrak {h}},\Lambda ^\vee ) \rightarrow C_*({\mathfrak {h}})\), the dual of which is isomorphic to (8). \(\square \)
For a simply connected finite CW-complex X with Sullivan model \(\Lambda \), a well-known and widely used result is that \(\,{\mathrm{Der}}\Lambda \langle 1 \rangle \), the positive truncation of the dg Lie algebra of derivations on \(\Lambda \), is a Lie model for \(Baut_\circ (X)\). This is sketched in [35, p.313]. See also [23, 29, 34, 36] for this and related results. We will here give a short proof that shows the slightly stronger statement that the action of \(aut_\circ (X)\) on X is modeled by the action of \(\,{\mathrm{Der}}\Lambda \langle 1 \rangle \) on \(\Lambda \).
Proposition 3.7
For a simply connected finite CW-complex X with Sullivan model \(\Lambda \), the action of \(\,{\mathrm{Der}}\Lambda \langle 1 \rangle \) on \(\Lambda \) models the action of \(aut_\circ (X)\) on X.
Proof
The action of \({\mathfrak {h}}= \,{\mathrm{Der}}\Lambda \langle 1 \rangle \) on \(\Lambda \) gives rise to an action of the connected group \(\exp _\bullet ({\mathfrak {h}})\) on \(\langle \Lambda \rangle \), which yields map of monoids
The pairs \((aut_\circ (X),X)\) and \((aut_\circ \langle \Lambda \rangle , \langle \Lambda \rangle )\) are easily seen to be rationally equivalent (see, e.g., [3, p.6]), so we are done if we can show that (9) is a weak homotopy equivalence. For \(k\ge 1\), the map
that sends the homology class of a cycle \(\theta \in {\mathfrak {h}}_k\) to the homotopy class of the k-simplex \(\omega \otimes \theta \in Z_0(\Omega ^*(\Delta ^k) \otimes {\mathfrak {h}})\), where \(\omega \) is the fundamental form \(k!dt_1\wedge \cdots \wedge dt_k\), is an isomorphism. This can be checked directly by using the normalized chain complex for computing the homotopy groups of a simplicial vector space (the underlying simplicial set of \(\exp _\bullet ({\mathfrak {h}})\) is the simplicial vector space \(Z_0(\Omega _\bullet \otimes {\mathfrak {h}})\)), or by using the isomorphism of simplicial sets \(\exp _\bullet ({\mathfrak {h}}) \cong \mathsf {MC}_\bullet (s^{-1}{\mathfrak {h}})\) (where the desuspension \(s^{-1}{\mathfrak {h}}\) is viewed as an abelian dg Lie algebra) and invoking [2, Theorem 4.6].
On the other hand, it is well-known that the homotopy groups of the target of (9) are computable in terms of derivations of \(\Lambda \), cf. [6, 9, 24, 35]. This goes as follows (cf. [24, Theorem 2.1]): by the equivalence of homotopy categories between finite type Sullivan algebras and rational nilpotent spaces of finite \({\mathbb {Q}}\)-type,
The set \([\Lambda , H^*(S^k)\otimes \Lambda ]^\Lambda \) of homotopy classes of cdga morphisms \(f:\Lambda \rightarrow H^*(S^k)\otimes \Lambda \) over \(\Lambda \) is in bijection with the set of homology classes of degree k chain derivations \(\theta :\Lambda \rightarrow \Lambda \) via \(f(x) = 1\otimes x + z \otimes \theta (x)\), where \(z\in H^k(S^k)\) is a generator.
The final step is to check that the composite map
is the identity map. We leave this as an exercise to the reader. \(\square \)
3.4 A relative Sullivan model for the universal \(g\)-fibration
Let X be a simply connected finite CW complex, let \(g:X\rightarrow Z\) be a map, and let \({\mathcal {H}}\) be a connected monoid acting on X by homotopy equivalences. Assume that the space Z is nilpotent and of finite \({\mathbb {Q}}\)-type.
Let \(\Lambda \) be a Sullivan model for X of finite type, let \({\mathfrak {h}}\) be a positively graded dg Lie algebra acting on \(\Lambda \) by derivations, modeling the action of \({\mathcal {H}}\) on X as in the previous section, and let \(\Pi \) be a degreewise nilpotent finite type Lie model for Z. Fix characteristic cochains \(p_i(g)\in \Lambda \) for \(g:X\rightarrow Z\) and let
denote the corresponding Maurer–Cartan element in \(\Lambda {\widehat{\otimes }}\Pi \).
The dg Lie algebra \({\mathfrak {h}}\) acts by derivations on the dg Lie algebra \(\Lambda {\widehat{\otimes }}\Pi \) by
so we may form the semi-direct product dg Lie algebra \({\mathfrak {h}}\ltimes \Lambda {\widehat{\otimes }}\Pi \). The element \(\tau (g)\) may be viewed as a Maurer–Cartan element in this semi-direct product. Define
i.e., the dg Lie algebra \({\mathfrak {h}}^{g}\) is obtained by twisting \({\mathfrak {h}}\ltimes \Lambda {\widehat{\otimes }}\Pi \) by the Maurer–Cartan element \(\tau (g)\) and then taking the non-negative truncation. We note that \({\mathfrak {h}}^{g}\) acts on \(\Lambda \) by derivations via the evident map to \({\mathfrak {h}}\).
Theorem 3.8
The universal \(g\)-fibration with holonomy in \({\mathcal {H}}\) admits the following rational model.
-
(1)
The underlying fibration has relative Sullivan model
$$\begin{aligned} C^*({\mathfrak {h}}^{g}) \rightarrow C^*({\mathfrak {h}}^{g},\Lambda ). \end{aligned}$$ -
(2)
Characteristic cochains \(p_i(h)\in C^*({\mathfrak {h}}^{g},\Lambda )\) of the structure map from the total space to Z are given by
$$\begin{aligned} p_i(h) = p_i(g) + P_i, \end{aligned}$$where \(p_i(g)\in \Lambda \) is viewed as a 0-cochain in \(C^*({\mathfrak {h}}^{g},\Lambda )\) and \(P_i\in C^*({\mathfrak {h}}^{g},\Lambda )\) is the 1-cochain determined by
$$\begin{aligned} P_i(s x\otimes q) = (-1)^{|x||q|} p_i(sq) x, \end{aligned}$$for \(x\in \Lambda \) and \(q\in \Pi \), and \(P_i(s\theta ) = 0\) for \(\theta \in {\mathfrak {h}}\).
Remark 3.9
If \(g\) is the classifying map for a bundle \(\xi \), then the first part of the theorem can be read as saying that the action of \({\mathfrak {h}}^{g}\) on \(\Lambda \) models the action of \(aut_{\mathcal {H}}(\xi )\) on X.
Proof
We use the model for the universal \(g\)-fibration with holonomy in \({\mathcal {H}}\) described in Sect. 2.3. Since \({\mathcal {H}}\) is connected \({\mathcal {H}}= {\mathcal {H}}_{[g]}\). Let \(C = \Lambda ^\vee \) be the dual dg coalgebra and let \(\mathfrak {hom}\) denote the dg Lie algebra \(\,{\mathrm{Hom}}(C,\Pi ) \cong \Lambda {\widehat{\otimes }}\Pi \). An adaptation of the argument of [3] (with C replacing \({\mathcal {C}} L\) and \({\mathfrak {h}}\) replacing \((\,{\mathrm{Der}}L \ltimes _{\,{\mathrm{ad}}} sL)\langle 1 \rangle \), and using \(\tau =\tau (g)\)) shows that the map
is modeled by the map of dg coalgebras
Now observe that there is an isomorphism of dg coalgebras
natural in \(U{\mathfrak {h}}\)-module coalgebras M. It follows that the fibration (10) is rationally equivalent to the fibration constructed from the action of \({\mathfrak {h}}^{g}\) on \(\Lambda \). To establish the formula for the characteristic cochains, it is enough to understand how to model evaluation maps. This will be dealt with in the next section. \(\square \)
Remark 3.10
For a more explicit description of the cochain \(P_i\), choose a basis \(\{x_\ell \}\) for \(\Lambda \) and let \(p_i^{x_\ell } \in C^*({\mathfrak {h}}^{g})\) denote 1-cochain characterized by
and \(p_i^{x_\ell }(s\theta ) = 0\) for all \(\theta \in {\mathfrak {h}}\). The cochain \(P_i\) then assumes the form
where we view \(x_\ell \in \Lambda \) as a 0-cochain in \(C^*({\mathfrak {h}}^{g},\Lambda )\). The sum is finite because of the truncation in the definition of \({\mathfrak {h}}^{g}\) and because \(\Lambda \) is of finite type. Indeed, this implies that for i fixed, the cochain \(p_i^{x_{\ell }}\) is zero for all but finitely many \(\ell \).
3.5 Rational models for evaluation maps
Theorem 3.11
Let X be a simply connected finite CW complex, let Z be a nilpotent space of finite \({\mathbb {Q}}\)-type and let \(g:X\rightarrow Z\) be a map. If C is a fibrant cdgc model for X of finite type, \(\Pi \) is a degreewise nilpotent Lie model for Z of finite type and \(\tau :C\rightarrow \Pi \) is a twisting function that models the map \(g:X\rightarrow Z\), then the map
determined by
is a twisting function that models the evaluation map
Proof
First, we show that the map is a twisting function. For a cdgc \({\mathcal {C}}\), a dg Lie algebra \({\mathfrak {g}}\) and a Maurer–Cartan element \(\tau \in \mathsf {MC}({\mathfrak {g}})\), there is a bijection between sets of twisting functions,
where \(\epsilon :{\mathcal {C}} \rightarrow {\mathbb {Q}}\) is the counit. If we apply this observation to \({\mathfrak {g}}= \,{\mathrm{Hom}}(C,\Pi )\) and \({\mathcal {C}} = C_*({\mathfrak {g}}^\tau \langle 0 \rangle )\), the universal twisting function composed with the inclusion, \(\pi :C_*({\mathfrak {g}}^\tau \langle 0 \rangle ) \rightarrow {\mathfrak {g}}^\tau \langle 0 \rangle \rightarrow {\mathfrak {g}}^\tau \), gives rise to a twisting function \(\pi + \tau \circ \epsilon :{\mathcal {C}} \rightarrow {\mathfrak {g}}.\) Under the adjunction isomorphism,
this corresponds to the map in the statement of the theorem, showing it is a twisting function.
Next, we will argue that the twisting function just constructed is a model for the evaluation map. To simplify the exposition, we will go through the argument in the case when \(\Pi \) is finite dimensional. For the general case, one writes \(\Pi \) as an inverse limit of finite dimensional nilpotent dg Lie algebras \(\Pi /\Pi \langle r \rangle \) and works with the inverse system, cf. [3, Remark 3.17].
As in [3, §3.2–§3.3], we write \(\mathsf {MC}_\bullet (\Pi ) = \mathsf {MC}(\Pi \otimes \Omega _\bullet )\) for the nerve of \(\Pi \) and \(\langle C \rangle = {\mathcal {G}}(C\otimes \Omega _\bullet )\) for the simplicial realization of C, where \(\mathsf {MC}\) stands for Maurer–Cartan elements and \({\mathcal {G}}\) for group-like elements. By a slight variation of [3, Theorem 3.16] the natural map
defined as the adjoint of the map
that sends \((\rho ,\xi )\) to \(\rho (\xi )\), is a weak equivalence. Indeed, the proof of [3, Theorem 3.16] goes through after using the natural identifications \(\mathsf {MC}_\bullet (L) \cong \langle {\mathcal {C}} L \rangle \) and \({\mathcal {C}}_{\Omega _\bullet }(L\otimes \Omega _\bullet ) \cong {\mathcal {C}}(L)\otimes \Omega _\bullet \), and then replacing \({\mathcal {C}} L\) with C throughout. This implies that \(\epsilon \) is a model for the evaluation map
Because of the simplifying assumption that \(\Pi \) is finite dimensional, the left factor in the source of \(\epsilon \) may be identified with \(\mathsf {MC}_\bullet ({\mathfrak {g}})\) where \({\mathfrak {g}}= \,{\mathrm{Hom}}(C,\Pi )\). Let
denote the map \(\epsilon \) after making this identification.
Next, the map \(\lambda _\tau :\mathsf {MC}_\bullet ({\mathfrak {g}}^\tau \langle 0 \rangle ) \rightarrow \mathsf {MC}_\bullet ({\mathfrak {g}})\) that adds \(\tau \) is a weak equivalence to the component that is determined by \(\tau \), cf. [2, Corollary 4.11]. Also, note that the universal twisting function \(\alpha :C_*({\mathfrak {g}}^\tau \langle 0 \rangle )\rightarrow {\mathfrak {g}}^\tau \langle 0 \rangle \) induces an isomorphism \(\langle C_*({\mathfrak {g}}^\tau \langle 0 \rangle ) \rangle \rightarrow \mathsf {MC}_\bullet ({\mathfrak {g}}^\tau \langle 0 \rangle )\). Now compose:
By writing out definitions, one sees that this composite may be identified with the map induced by the twisting function in the statement of the theorem. By the above, the composite map models the evaluation map \(map(X,Z_{\mathbb {Q}})_{rg} \times X\rightarrow Z_{\mathbb {Q}}\), where \(r:Z\rightarrow Z_{\mathbb {Q}}\) is the rationalization. Since X is a finite complex and Z is nilpotent, this is rationally equivalent to \(map(X,Z)_{g} \times X \rightarrow Z\). \(\square \)
Remark 3.12
Rational models for evaluation maps have been studied before by many authors, see e.g. [8, 21, 24, 25], but our approach of using twisting functions appears to be new.
To finish the proof of Theorem 3.8(2), note that since \({\mathfrak {h}}\) acts on \(C = \Lambda ^\vee \) by coderivations, the twisting function of Theorem 3.11 is \({\mathfrak {h}}\)-equivariant (cf. [3, Proposition 3.18]). This implies that it induces a twisting function
given by essentially the same formula, and that this models the evaluation map
Observing, as before, that
it is an exercise to see that the Maurer–Cartan element in \(C^*({\mathfrak {h}}^{g},\Lambda ) {\widehat{\otimes }}\Pi \) corresponding to (12) is given by the formula in Theorem 3.8(2).
4 Sample calculations and applications
4.1 Even spheres
We consider the oriented tangent bundle \(\xi = \tau _{S^m}\) of an even dimensional sphere \(S^m\) for \(m=2k \ge 2\) and compute a model for the universal \(\xi \)-fibration over \(Baut(\xi )\) using Theorem 3.8.
Thus, \(G = SO(2k)\) in this case and we have
where \(p_i\) are the Pontryagin classes and e the Euler class.
where \(q_i\) is dual to \(p_i\) and \(\epsilon \) to e under the Hurewicz pairing.
The minimal Sullivan model for \(S^{2k}\) has the form
with x and y in cohomological degrees 2k and \(4k-1\), respectively. The dg Lie algebra \(\,{\mathrm{Der}}\Lambda \langle 1 \rangle \) has basis
and the only non-trivial differential is given by
Therefore, if we let \({\mathfrak {h}}\subset \,{\mathrm{Der}}\Lambda \) be the abelian dg Lie subalgebra spanned by \(\frac{\partial }{\partial y}\), then the inclusion \({\mathfrak {h}}\rightarrow \,{\mathrm{Der}}\Lambda \langle 1\rangle \) is a quasi-isomorphism.
If we equip the cohomology \(H = H^*(S^{2k};{\mathbb {Q}}) = {\mathbb {Q}}[x]/(x^2)\) with the trivial \({\mathfrak {h}}\)-action, then the section \(i:H\rightarrow \Lambda \) of p sending 1 to 1 and the class of x to x is a quasi-isomorphism of dg \({\mathfrak {h}}\)-modules (but not of algebras). The characteristic classes of \(\xi \) are \(p_i(\xi ) = 0\) and \(e(\xi ) = 2x\) and as cocycle representatives in \(\Lambda \) we may choose their images under i. The Maurer–Cartan element is \(\tau (\xi ) = 2x\otimes \epsilon \).
The section i induces a quasi-isomorphism of dg Lie algebras
Thus, a Lie model for \(Baut(\xi )\) is given by
This is the abelian dg Lie algebra with trivial differential and basis
where \(r = \lceil \frac{k+1}{2} \rceil \). Thus,
where a is the dual 1-cochain of \(\frac{\partial }{\partial y}\) and \(p_i^x\) is dual to \(x\otimes q_i\), and so forth. The differential is zero, so
The relative Sullivan model \(C^*({\mathfrak {g}}) \rightarrow C^*({\mathfrak {g}},\Lambda )\) may be identified with
where the differential is given by \(dy = x^2 + a\). Clearly, the map
is a quasi-isomorphism of dg R-algebras. Thus, the universal \(\tau _{S^{2k}}\)-fibration over \(Baut(\tau _{S^{2k}})\) is formal and in cohomology it is given by
It follows from Theorem 3.8 that the characteristic classes of the total bundle \(\zeta \) over  are given by
are given by
where \(p_i^x\) should be interpreted as 0 for \(1\le i \le r-1\).
The pushforward map \(\pi _!:R[x]/(x^2+a) \rightarrow R\) is determined by R-linearity and \(\pi _!(x) = 1\). The \(\kappa \)-classes can now be computed explicitly as elements of the polynomial ring R:
A look at the linear terms of these expressions shows that the classes
where we write \(p_k\) for \(e^2\), are algebraically independent and generate R. This proves Theorem 1.1.
To prove Theorem 1.4 for m even, observe that the sphere bundle associated to the universal oriented vector bundle may be identified the fibration
induced by the inclusion \(SO(m) \rightarrow SO(m+1)\), and the fiberwise tangent bundle may be identified with the universal oriented vector bundle \(\gamma ^m\) over BSO(m). For this \(\tau _{S^m}\)-fibration, we have that
so it follows that \(H^*(BSO(m+1);{\mathbb {Q}})\) is a polynomial ring in the classes
The computation of \(H^*(Baut(\tau _{S^m})_L;{\mathbb {Q}})\) in the proof of Corollary 1.6 (which does not use Theorem 1.4) then shows that \( BSO(m+1)\rightarrow Baut(\tau _{S^m})_L\) induces an isomorphism in rational cohomology.
4.2 Odd spheres
Consider the sphere \(S^m\), for \(m=2k+1\) odd, and its tangent bundle \(\xi = \tau _{S^m}\) viewed as an oriented vector bundle. The structure group is \(G = SO(2k+1)\) and the cohomology of its classifying spaces is \(H^*(BSO(2k+1);{\mathbb {Q}}) = {\mathbb {Q}}[p_1,\ldots ,p_k]\).
The minimal model for \(S^{2k+1}\) has the form
The dg Lie algebra \({\mathfrak {h}}= \,{\mathrm{Der}}\Lambda \) is one-dimensional and spanned by
We have that \(p_i(S^{2k+1}) = 0\) for all i, so we may take \(\tau (\xi ) = 0\).
The dg Lie algebra model \({\mathfrak {h}}^\xi \) for \(Baut(\tau _{S^{2k+1}})\) from Theorem 3.8 then has basis
where \(r = \lceil \frac{k+1}{2} \rceil \). The differential is zero and the only non-trivial Lie brackets are
for \(i=r,\ldots ,k\). Writing z, \(p_i\) and \(p_i^x\) for the dual 1-cochains of \(\frac{\partial }{\partial x}\), \(q_i\) and \(xq_i\), respectively, and setting \(p_i^x = 0\) for \(i<r\), we see that
where the non-trivial differentials are given by \(dp_i= p_i^x z\). The model for the universal \(\tau _{S^m}\)-fibration then assumes the form
where x is adjoined as an exterior generator and \(dx = z\).
Let \(\Omega \) be a graded commutative algebra equipped with a degree \(-(2k+1)\) derivation D such that \(D^2 =0\). We may adjoin a polynomial generator z of degree \(2k+2\) and form the cdga
There is a natural isomorphism of algebras
where the right hand side denotes the ring of polynomials \(\sum _i a_i z^i\) where \(a_0\) a cycle in \((\Omega ,D)\) and the coefficients \(a_i\) for \(i\ge 1\) are cohomology classes with respect to D.
We observe that R may be identified with \(\big (\Omega [z],zD\big )\) if we let
equipped with the derivation D defined by \(D(p_i) = p_i^x\) and \(D(p_i^x) =0\). In other words,
is the cdga of Kähler differential forms on the polynomial ring \({\mathbb {Q}}[p_1,\ldots ,p_k]\) that are linear over the subring \({\mathbb {Q}}[p_1,\ldots ,p_{r-1}]\), with differential D of degree \(-(2k+1)\). Moreover, R[x] may be identified with the same construction applied to \(\Omega [x]\) with derivation D defined as above and extended by \(D(x) =1\).
Observe that \(H^*(\Omega [x],D) = 0\) since \(xD + Dx = 1\). Furthermore, the projection \(Z(\Omega [x],D) \rightarrow \Omega \) sending \(a+bx\) to a is an isomorphism, with inverse \(a\mapsto a + (-1)^{|a|}D(a)x\). By naturality of the isomorphism (13), we can therefore identify the map \(\pi ^*:H^*(R) \rightarrow H^*(R[x])\) with the map \(Z(\Omega ,D) \ltimes \overline{H^*(\Omega ,D)[z]} \rightarrow \Omega \) that sends \(\sum _i a_i z^i\) to \(a_0\). The pushforward map \(\pi _!:H^*(R[x]) \rightarrow H^*(R)\) is induced by the dg R-module map \(R[x]\rightarrow R\) that sends x to 1. Tracing this through the isomorphisms discussed above, one sees that the map \(\pi _!\) may be identified with the map \(\Omega \rightarrow Z(\Omega ,D) \ltimes \overline{H^*(\Omega ,D)[z]}\) that sends a to \(-D(a)\).
For our particular \(\Omega \), we obviously have
so we can rewrite the cohomology of \((\Omega [z],zD)\) as
where z acts trivially on the second factor.
Since \(p_i(\xi ) = 0\) for all i, the characteristic cochains for the total bundle \(\zeta \) are given by
Observe that \(p_i^x = D(p_i)\), so \(p_i(\zeta ) = p_i + D(p_i) x\). Since D is a derivation, this implies that
for every \(c\in {\mathbb {Q}}[p_1,\ldots ,p_k]\). Hence,
The class represented by \(z\in R\) may be identified with the Euler class of the underlying spherical fibration. The fact that \(p_i(\zeta ) = p_i\) for \(1\le i \le r-1\) allows us to identify the class represented by the cocycle \(p_i\in R\) with the class we called \(\alpha _{p_i}\) in the introduction. Thus, Theorem 1.2 is proved. (Concerning the statement about \(R^*(\tau _{S^m})\), the above yields an isomorphism where \(\kappa _c\) corresponds \(-dc\), but the sign can be removed by composing with the algebra automorphism \(a\mapsto (-1)^{|a|}a\).)
To prove Theorem 1.4 in the case m odd, use the Hirzebruch L-classes as generators for \(H^*(BSO(m);{\mathbb {Q}})\) when constructing the model, so that
with differential \(d{\mathcal {L}}_i = {\mathcal {L}}_i^x z\) for \(r\le i \le k\). As above, we have
A model \(R_L\) for the homotopy fiber \(Baut(\tau _{S^m})_L\) is then obtained by adding new generators \(M_i\) to kill the cocycles \(-{\mathcal {L}}_i^x\) for \(i=r,\ldots ,k\);
There is an evident cdga quasi-isomorphism \(R_L\rightarrow {\mathbb {Q}}[{\mathcal {L}}_1,\ldots ,{\mathcal {L}}_k,z]\). In particular, the spaces \(Baut(\tau _{S^m})_L\) and \(BSO(n+1)\) have abstractly isomorphic minimal models, whence abstractly isomorphic rational homotopy groups. The map
is injective on rational homotopy groups, because its composite with the evident map to \(Baut(F(\tau _{S^m}))\) is, where \(F(\tau _{S^m})\) denotes the frame bundle, see (5) on p.242 of [3]. An injection between finite dimensional isomorphic vector spaces must be an isomorphism, so (14) is a rational equivalence. By that, the proof of Theorem 1.4 is complete.
4.3 Complex projective spaces
Characteristic classes are often defined as cohomology classes in the base space, but one can also consider characteristic classes in the total space. Let \({\mathcal {F}}\) be a class of fibrations, e.g., the class of orientable X-fibrations for a given space X. By a total-space characteristic class for \({\mathcal {F}}\) we will mean the assignment of a cohomology class \(\chi (\pi ) \in H^*(E)\) to each fibration \(\pi :E \rightarrow B\) in \({\mathcal {F}}\) such that
for every homotopy cartesian square

such that \(\pi \) and \(\pi '\) belong to \({\mathcal {F}}\).
Lemma 4.1
For every generator \(\omega \in H^2({\mathbb {C}}\mathrm {P}^n;{\mathbb {Q}})\) there is a unique total-space characteristic class for orientable \({\mathbb {C}}\mathrm {P}^n\)-fibrations \(\omega _{fw}\) such that \(\omega _{fw}({\mathbb {C}}\mathrm {P}^n \rightarrow *) = \omega \).
The class \(\omega _{fw}(\pi )\) is characterized by \(\pi _!(\omega _{fw}(\pi )^{n+1}) = 0\) and \(\omega _{fw}(\pi )|_{{\mathbb {C}}\mathrm {P}^n} = \omega \).
Remark 4.2
The last statement means that \(\omega _{fw}(\pi )\) may be identified with the ‘coupling class’. That the coupling class admits a homotopy theoretical definition has been observed in [19, Proposition 3.1]. Lemma 4.1 shows that the coupling class is the only total-space characteristic class for orientable \({\mathbb {C}}\mathrm {P}^n\)-fibrations that restricts to \(\omega \) in the fiber.
Proof
Consider the universal orientable \({\mathbb {C}}\mathrm {P}^n\)-fibration,
Since \(H^k(Baut_\circ ({\mathbb {C}}\mathrm {P}^n);{\mathbb {Q}}) = 0\) for \(k=2,3\), an application of the Serre spectral sequence shows that the restriction map
is an isomorphism. Define \(\omega _{fw}\) to be the preimage of \(\omega \) under this map.
Since the classifying map for an orientable \({\mathbb {C}}\mathrm {P}^n\)-fibration \(\pi :E\rightarrow B\) factors through \(Baut_\circ ({\mathbb {C}}\mathrm {P}^n)\), there is a homotopy cartesian square

which is uniquely determined up to homotopy by \(\pi \). Define \(\omega _{fw}(\pi ) = f_\pi ^*(\omega _{fw})\). We note that \(\pi _!^{univ}(\omega _{fw}^{n+1}) = 0\) simply because \(H^2(Baut_\circ ({\mathbb {C}}\mathrm {P}^n);{\mathbb {Q}}) = 0\). By naturality of the pushforward map, it then follows that \(\pi _!(\omega _{fw}(\pi )^{n+1}) = 0\). The property \(\omega _{fw}(\pi )|_{{\mathbb {C}}\mathrm {P}^n} = \omega \) holds because it holds in the universal orientable fibration by definition. \(\square \)
The classes
form a basis for \(H^*(E;{\mathbb {Q}})\) as a \(H^*(B;{\mathbb {Q}})\)-module, and yield an isomorphism of \(H^*(B;{\mathbb {Q}})\)-modules
which is natural in \(\pi \). The basis of course depends on the choice of generator \(\omega \), but the decomposition (15) does not. In what follows we fix the standard generator \(\omega = -c_1(\gamma ^1)\), which has the convenient property \(\pi _!(\omega _{fw}(\pi )^n) = 1\) (cf. [28, p.170]).
We now proceed to prove Theorem 1.7.
The minimal Sullivan model for \({\mathbb {C}}\mathrm {P}^n\) has the form
where x is a cocycle that represents \(\omega \) and \(dy = x^{n+1}\). Let
The map \(p :\Lambda \rightarrow H\) defined by \(p(x) = \omega \) and \(p(y) = 0\) is a quasi-isomorphism of cdgas. It admits a section \(\iota :H\rightarrow \Lambda \), which is a quasi-isomorphism of cochain complexes (but which does not respect the multiplication).
Now consider a bundle \(\xi \) over \({\mathbb {C}}\mathrm {P}^n\), with structure group G as in the statement of Theorem 1.7. As a dg Lie model for BG we may take the rational homotopy groups
with trivial Lie bracket and differential. It has basis
where \(q_i \in \pi _{*}(G) \cong \pi _{*+1}(BG)\) is dual to the generator \(p_i\in H^*(BG;{\mathbb {Q}})\) under the Hurewicz pairing between cohomology and homotopy.
If we let \(p_i(\xi )\in H\) denote the characteristic classes of \(\xi \), then we may choose \(\iota (p_i(\xi )) \in \Lambda \) as characteristic cochains of the bundle, so that
One checks that the subspace \({\mathfrak {a}}\subset \,{\mathrm{Der}}\Lambda \langle 1 \rangle \) spanned by the derivations
forms an abelian dg Lie subalgebra with trivial differential, and that the inclusion \({\mathfrak {a}}\rightarrow \,{\mathrm{Der}}\Lambda \langle 1\rangle \) is a quasi-isomorphism. This means that the action of \({\mathfrak {a}}\) on \(\Lambda \) models the action of \(aut_\circ ({\mathbb {C}}\mathrm {P}^n)\) on \({\mathbb {C}}\mathrm {P}^n\).
If we equip the cohomology H with trivial \({\mathfrak {a}}\)-action, then \(\iota :H \rightarrow \Lambda \) is a quasi-isomorphism of dg \({\mathfrak {a}}\)-modules, and the induced map
is a quasi-isomorphism of dg Lie algebras (\(\iota \) is not a morphism of algebras, but this does not matter since we tensor with the abelian dg Lie algebra \(\Pi \)). It follows from Theorem 3.8 that the dg Lie algebra
is a model for \(Baut_\circ (\xi )\). Explicitly, the dg Lie algebra \({\mathfrak {g}}\) has trivial Lie bracket and trivial differential, and a basis is given by
Since \({\mathfrak {g}}\) is concentrated in odd degrees, the Chevalley–Eilenberg construction \(C^*({\mathfrak {g}})\) is a polynomial algebra with trivial differential,
generated by the 1-cochains \(v_k\) and \(p_{i,k}\) dual to \(x^k \frac{\partial }{\partial y}\) and \(x^k \otimes q_i\), respectively. It follows that we have an isomorphism of graded algebras
This is as far as we get from knowing a model for the base \(Baut_\circ (\xi )\). To identify which characteristic classes \(v_k\) and \(p_{i,k}\) represent, we must use the full force of Theorem 3.8.
The relative Sullivan model \(C^*({\mathfrak {g}}) \rightarrow C^*({\mathfrak {g}},\Lambda )\) for the universal \(\xi \)-fibration from Theorem 3.8 may in the case at hand be identified with
where the only non-trivial differential is given by
The evident map \(R \otimes \Lambda (x,y) \rightarrow R[x]/I\), where I is the ideal generated by the element \(x^{n+1} + \sum _{\ell =0}^{n-1} v_{\ell } x^{\ell }\) and where R[x]/I is equipped with the zero differential, is a quasi-isomorphism of cdgas over R. Thus, the universal \(\xi \)-fibration over \(Baut_{\circ }(\xi )\) is formal and modeled by the morphism of algebras
The R-algebra R[x]/I is free as an R-module with basis \(1,x,\ldots ,x^n\). The multiplication is determined by R-linearity and the relation
The pushforward map in cohomology is the degree \(-2n\) map
determined by R-linearity and \(\pi _!(x^n) = 1\) (note that \(\pi _!(x^k) = 0\) for \(k<n\) for degree reasons). Since (16) contains no \(x^n\)-term, we have \(\pi _!(x^{n+1}) = 0\), and by construction x represents \(\omega \) when restricted to the fiber, so the cocycle x represents the class \(\omega _{fw}\) by Lemma 4.1. This in turn implies that the class \(v_i\) in the model represents the characteristic class \(a_{n+1-i}\) featured in Theorem 1.7.
From Theorem 3.8 and Remark 3.10, one sees that the characteristic classes of the total bundle \(\zeta \) of the universal \(\xi \)-fibration over \(Baut_{\circ }(\xi )\) are given by
This implies that the class \(p_{i,j}\) in the model R represents the characteristic class \(p_{i|j}\). This finishes the proof of the first part of Theorem 1.7.
We now proceed to the second part of Theorem 1.7. For a bundle \(\xi \) over a CW complex X, there is a homotopy fiber sequence
where
is the group of homotopy classes of self-homotopy equivalences of X that fix the isomorphism class of the bundle \(\xi \). For \(X={\mathbb {C}}\mathrm {P}^n\), the group \(\pi _0 aut({\mathbb {C}}\mathrm {P}^n)\) of homotopy classes of self-homotopy equivalences is cyclic of order two, generated by complex conjugation \(c:{\mathbb {C}}\mathrm {P}^n\rightarrow {\mathbb {C}}\mathrm {P}^n\). For a bundle \(\xi \) over \({\mathbb {C}}\mathrm {P}^n\), it follows that
For example, \(\Gamma (\tau _{{\mathbb {C}}\mathrm {P}^n}) = 0\) for the complex tangent bundle \(\tau _{{\mathbb {C}}\mathrm {P}^n}\), but for the underlying oriented vector bundle \(\tau _{{\mathbb {C}}\mathrm {P}^n}^{\mathbb {R}}\) we have
because complex conjugation is a diffeomorphism of \({\mathbb {C}}\mathrm {P}^n\) which is orientation preserving if n is even and orientation reversing if n is odd.
Whenever \(\Gamma (\xi )\) is finite, the rational Serre spectral sequence of the fibration (17) collapses at the second page, which allows us to identify
where the latter denotes the invariant subring. Complex conjugation is modeled by the involution on the minimal model \((\Lambda (x,y),d)\) given by
Using this, one can work out that the action on R is determined by
With that, the second part of Theorem 1.7 is proved.
Remark 4.3
If \(H^*(BG;{\mathbb {Q}})\) is concentrated in degrees divisible by 4, then the action agrees with the action given by multiplication by \((-1)\) in degrees \(4\ell +2\) and by the trivial action in degrees \(4\ell \). Thus, if this is the case, and if \(c^*(\xi ) \cong \xi \), then the cohomology of \(Baut(\xi )\) may be identified with the subring \(R^{(4)} \subset R\) of elements in degrees divisible by 4. For example, this is the case for \(\tau _{{\mathbb {C}}\mathrm {P}^n}^{\mathbb {R}}\) for n even.
The proof of Theorem 1.12 will depend on an analysis of the universal \(U(n+1)\)- bundle with fiber \({\mathbb {C}}\mathrm {P}^n\). This in turn may be identified with the projectivization of the universal complex vector bundle of rank \(n+1\), so we proceed to discuss projectivizations.
Let \(p:E\rightarrow B\) be a complex vector bundle of rank \(n+1\). By taking fiberwise projectivization, we obtain a \(U(n+1)\)-bundle with fiber \({\mathbb {C}}\mathrm {P}^n\),
There are two distinguished vector bundles over \({\mathbb {P}}(E)\), the fiberwise canonical line bundle L and the fiberwise tangent bundle \(\zeta \). These make (18) into a \(\gamma ^1\)-fibration and a \(\tau _{{\mathbb {C}}\mathrm {P}^n}\)-fibration, respectively.
Proposition 4.4
The following equation relates the Chern classes of the \((n+1)\)-dimensional complex vector bundle \(p:E\rightarrow B\) and the Chern classes of the fiberwise tangent bundle \(\zeta \) and the line bundle L over the projectivization \({\mathbb {P}}(E)\). For all i,
where \({\overline{L}}\) denotes the conjugate bundle.
Proof
The proof is essentially a fiberwise version of the classical computation of the Chern classes of \({\mathbb {C}}\mathrm {P}^n\) [28, Theorem 14.10]. The pullback of the vector bundle E along \(\pi :{\mathbb {P}}(E) \rightarrow B\) can be written as
where \(L'\) is the fiberwise orthogonal complement to L, and the fiberwise tangent bundle is given by
Since \(\,{\mathrm{Hom}}(L,L)\) may be identified with the trivial line bundle \(\epsilon ^1\), we have
Since \(c_i(\zeta ) = c_i(\epsilon ^1 \oplus \zeta )\), the formula (19) now follows from the well-known formula for the Chern classes of a tensor product of a line bundle and a vector bundle. \(\square \)
Remark 4.5
The fiberwise tangent bundle \(\zeta \) is n-dimensional, so \(c_{n+1}(\zeta ) = 0\). Hence, a special case of (19) is
By an application of Theorem 1.7 to the canonical line bundle \(\gamma ^1\) over \({\mathbb {C}}\mathrm {P}^n\), for which the structure group is U(1) with \(H^*(BU(1);{\mathbb {Q}})\) equal to the polynomial ring in \(e=c_1\) and \(c^*(\gamma ^1) \not \cong \gamma ^1\), we see that the ring of characteristic classes of \(\gamma ^1\)-fibrations may be identified with
Proposition 4.6
Consider a complex \((n+1)\)-dimensional vector bundle,
and the \(\gamma ^1\)-fibration formed by its projectivization,
The following equations express the Chern classes of the vector bundle E in terms of the characteristic classes of the \(\gamma ^1\)-fibration \((\pi ,L)\), and vice versa.
For \(i=1,\ldots ,n+1\), we have that
On the other hand
and
for \(i=2,\ldots , n+1\).
Proof
By definition of the classes \(e_{|j}\),
Since both \(\omega _{fw}(\pi )\) and \(-e(L)\) restrict to \(\omega = - c_1(\gamma ^1)\) in the fiber, it follows that \(e_{|1}(\pi ,L) = - 1\). Next, insert \(\omega _{fw}(\pi ) = -e(L) + e_{|0}(\pi ,L) = e({\overline{L}}) + e_{|0}(\pi ,L)\) in the defining equation for the characteristic classes \(a_i\),
compare with (20) (remember that \(c_1({\overline{L}}) = e({\overline{L}})\)), and use that \(1,e({\overline{L}}),\ldots ,e({\overline{L}})^n\) form a \(H^*(B;{\mathbb {Q}})\)-module basis for the cohomology. This yields the formula (21). The formula (23) is derived in a similar fashion by inserting \(e({\overline{L}}) = \omega _{fw}(\pi ) - e_{|0}(\pi ,L)\) in (20) and by observing that (21) in particular shows that
\(\square \)
Corollary 4.7
The map \(BU(n+1)\rightarrow Baut(\gamma ^1)\) that classifies the \(\gamma ^1\)-fibration obtained by projectivizing the universal complex vector bundle of rank \(n+1\) is a rational homotopy equivalence.
Proof
The Eqs. (22), (23), and (21) give explicit formulas for the induced map in rational cohomology and its inverse. \(\square \)
Proposition 4.8
Consider a \(U(n+1)\)-bundle with fiber \({\mathbb {C}}\mathrm {P}^n\),
The Chern classes of the fiberwise tangent bundle \(\zeta = T_\pi P\) satisfy the equation
In particular, they only depend on the underlying \({\mathbb {C}}\mathrm {P}^n\)-fibration \(\pi \).
Proof
Every \(U(n+1)\)-bundle with fiber \({\mathbb {C}}\mathrm {P}^n\) is equivalent to the projectivization of some complex \((n+1)\)-dimensional vector bundle \(p:E\rightarrow B\) (e.g. the complex vector bundle constructed from the associated principal \(U(n+1)\)-bundle), so we may without loss of generality assume that the bundle is of the form
Let \(\zeta = T_\pi {\mathbb {P}}(E)\) denote the fiberwise tangent bundle over \({\mathbb {P}}(E)\) and let L be the canonical line bundle over \({\mathbb {P}}(E)\). By inserting
in the formula (19), we obtain
Using the identity
and changing the order of summation, the above may be written as
By (23) and (22), we recognize the inner sum as \(a_{i-k}(\pi )\), so we conclude that
as claimed. \(\square \)
As discussed in the introduction, this justifies defining fiberwise Chern classes \(c_i^{fw}(\pi )\), for arbitrary orientable \({\mathbb {C}}\mathrm {P}^n\)-fibrations \(\pi \), in terms of the right hand side of (24). An equivalent formulation of Proposition 4.8 is then that every \(U(n+1)\)-bundle with fiber \({\mathbb {C}}\mathrm {P}^n\) has trivial Chern differences. By using that \(BSU(n+1)\rightarrow BPU(n+1)\) is a rational equivalence, one can deduce the stronger statement that every \(PU(n+1)\)-bundle with fiber \({\mathbb {C}}\mathrm {P}^n\) has trivial Chern differences (this is also verified in Theorem 4.9 below).
Fix a map that represents the rational Chern classes of \({\mathbb {C}}\mathrm {P}^n\),
and let \(Baut(\xi _c)\) denote the classifying space for \(\xi _c\)-fibrations. We define the classifying space of \(\tau _{{\mathbb {C}}\mathrm {P}^n}\)-fibrations with trivialized Chern differences as the homotopy pullback

where \(c^{fw}\) arises by taking the fiberwise Chern classes of an orientable \({\mathbb {C}}\mathrm {P}^n\)-fibration and \(c^{tot}\) by taking the Chern classes of the total bundle of a \(\tau _{{\mathbb {C}}\mathrm {P}^n}\)-fibration.
A consequence of the next result is that the Chern differences are the only obstructions for a \(\tau _{{\mathbb {C}}\mathrm {P}^n}\)-fibration to be rationally equivalent to a \(PU(n+1)\)-bundle.
Theorem 4.9
Every \(PU(n+1)\)-bundle with fiber \({\mathbb {C}}\mathrm {P}^n\) has trivial Chern differences and the induced map
is a rational homotopy equivalence.
Proof
By Theorem 1.7, the ring of characteristic classes of \(\tau _{{\mathbb {C}}\mathrm {P}^n}\)-fibrations is the polynomial ring
where we have one generator \(c_{i|j}\) for each pair of integers (i, j) such that \(1\le i \le n\) and \(0\le j<i\). By definition of the characteristic classes \(c_{i|j}\), we have
for every \(\tau _{{\mathbb {C}}\mathrm {P}^n}\)-fibration \((\pi ,\zeta )\). By comparing coefficients, we see that the equation \(c_i(\zeta ) = c_i^{fw}(\pi )\) is equivalent to the equations
for \(0\le j < i\). It follows that the cohomology ring of \(Baut(\tau _{{\mathbb {C}}\mathrm {P}^n})^c\) is isomorphic to
where I is the ideal generated by the linear polynomials
for \(1\le i \le n\) and \(0\le j < i\). We note in passing that this implies that the map \(Baut(\tau _{{\mathbb {C}}\mathrm {P}^n})^c \rightarrow Baut_\circ ({\mathbb {C}}\mathrm {P}^n)\) is a rational equivalence.
By (23), Proposition 4.8 and (26) applied to the universal \(U(n+1)\)-bundle with fiber \({\mathbb {C}}\mathrm {P}^n\), the map in rational cohomology induced by
may be identified with
where
It follows that
Now, observe that q factors as

The map f is injective in rational cohomology, so
This implies that the universal \(PU(n+1)\)-bundle with fiber \({\mathbb {C}}\mathrm {P}^n\) has trivial Chern differences, and that the induced map
is injective. Since both source and target are abstractly isomorphic to a polynomial ring with generators in degrees \(4,6,\ldots ,2n+2\), the map must be an isomorphism. \(\square \)
Remark 4.10
The above shows in particular that each map in
is a rational equivalence. (That \(BPU(n+1) \rightarrow Baut_{\circ }({\mathbb {C}}\mathrm {P}^n)\) is a rational equivalence has been observed before, cf. [19, 21, 29, 33].) These rational equivalences together with Remark 1.10 imply that the ring of characteristic classes of \(\tau _{{\mathbb {C}}\mathrm {P}^n}\)-fibrations with trivialized Chern differences, or equivalently the ring of characteristic classes of \(PU(n+1)\)-bundles with fiber \({\mathbb {C}}\mathrm {P}^n\), may be identified with the polynomial ring in the classes \(\kappa _{c_1^{n+2}},\ldots ,\kappa _{c_1^{2n+1}}\).
In the calculations that follow, we will use the abbreviations \(\omega _{fw} = \omega _{fw}(\pi )\), \(a_i= a_i(\pi )\), \(p_{i|j} = p_{i|j}(\pi ,\zeta )\), etc, when there is no risk of confusion.
Lemma 4.11
For every orientable \({\mathbb {C}}\mathrm {P}^n\)-fibration \(\pi :E \rightarrow B\) we have
for \(1\le k \le n+1\), and
for \(k>n+1\). Here, \({\mathfrak {a}}\subseteq H^*(B;{\mathbb {Q}})\) is the ideal generated by \(a_2,\ldots ,a_{n+1}\).
Proof
Multiply both sides of the equation
with suitable powers of \(\omega _{fw}\) and apply \(\pi _!\). We omit the details. \(\square \)
Proof of Theorem 1.8
Let \((\pi ,\zeta )\) be the universal \(\xi \)-fibration over \(Baut_\circ (\xi )\). By Lemma 4.11, the class \(\kappa _{\omega ^{n+k}}\) is a polynomial in \(a_2,\ldots ,a_{n+1}\) with linear term \(-a_k\). This implies that the classes \(\kappa _{\omega ^{n+2}},\ldots , \kappa _{\omega ^{2n+1}}\) are algebraically independent and that they generate the same subring as \(a_2,\ldots ,a_{n+1}\). Say \(|p_i|=2r_i\). By definition of \(p_{i|j}\), we have
where \(p_{i|j} = 0\) if \(j>r_i\) for degree reasons and \(p_{i|r_i}\) is a rational number. By multiplying the above with \(\omega _{fw}^{n-j}\) and applying \(\pi _!\), we obtain the equality
This can be used to express \(p_{i|j}\) in terms of the extended \(\kappa \)-classes by descending induction on \(j=r_i-1,r_i-2,\ldots , 0\). The equality can also be used to show algebraic independence of the extended \(\kappa \)-classes by observing that the linear term of \(\kappa _{\omega ^{n-j} p_i}\) is \(p_{i|j}\), modulo the subspace spanned by \(a_2,\ldots , a_{n+1}\). \(\square \)
We now turn to the proof of Theorem 1.17. The first step is to reduce this to a statement about \(\tau _{{\mathbb {C}}\mathrm {P}^n}^{{\mathbb {R}}}\)-fibrations with trivialized Pontryagin and Euler differences and prove Theorem 1.15.
Observe that the fiberwise Pontryagin classes and the fiberwise Euler class can be defined for every \({\mathbb {C}}\mathrm {P}^n\)-fibration \(\pi :E\rightarrow B\) such that \(\pi _1(B)\) acts on the fiber by orientation preserving homotopy equivalences (this is weaker than “orientability” of the fibration for n even, but equivalent to it for n odd). The reason is that we may identify

where \({\mathbb {Z}}/2{\mathbb {Z}}\) acts by \((-1)\) in degrees congruent to 2 modulo 4 (cf. Remark 4.3). The classes \(p_i^{fw}(\pi )\) and \(e^{fw}(\pi )\) are invariant since their degrees are divisible by 4 when n is even.
Now, let us be more precise about the definition of the classifying space for \(\tau _{{\mathbb {C}}\mathrm {P}^n}^{\mathbb {R}}\)-fibrations with trivialized Pontryagin and Euler differences; we define it as a homotopy pullback

similar to (25), where \(\xi _{p,e}\) is the map
that records the Pontryagin and Euler classes of \(\tau _{{\mathbb {C}}\mathrm {P}^n}^{\mathbb {R}}\).
Proof of Theorem 1.15
Vanishing of the Pontryagin differences and the Euler difference for \(\,{\mathrm{Isom}}_\circ ({\mathbb {C}}\mathrm {P}^n)\)-bundles follows from Corollary 1.13, because \(\,{\mathrm{Isom}}_\circ ({\mathbb {C}}\mathrm {P}^n) \cong PU(n+1)\). One can show that the map \(\,{\mathrm{Isom}}_\circ ({\mathbb {C}}\mathrm {P}^n)\cong PU(n+1) \rightarrow Baut_\circ (\tau _{{\mathbb {C}}\mathrm {P}^n}^{\mathbb {R}})^{p,e}\) is a rational equivalence as in the proof of Theorem 4.9. For n odd, \(\,{\mathrm{Isom}}^+({\mathbb {C}}\mathrm {P}^n) = \,{\mathrm{Isom}}_\circ ({\mathbb {C}}\mathrm {P}^n)\) and \(Baut(\tau _{{\mathbb {C}}\mathrm {P}^n}^{\mathbb {R}})^{p,e} = Baut_\circ (\tau _{{\mathbb {C}}\mathrm {P}^n}^{\mathbb {R}})^{p,e}\) so nothing more needs to be said. For n even, one uses that \(\,{\mathrm{Isom}}^+({\mathbb {C}}\mathrm {P}^n) \cong \,{\mathrm{Isom}}_\circ ({\mathbb {C}}\mathrm {P}^n)\rtimes {\mathbb {Z}}/2{\mathbb {Z}}\), and similarly for \(Baut(\tau _{{\mathbb {C}}\mathrm {P}^n}^{\mathbb {R}})^{p,e}\). \(\square \)
Next, we relate the space \(Baut(\tau _{{\mathbb {C}}\mathrm {P}^n}^{\mathbb {R}})^{p,e}\) to self-homotopy equivalences.
Proposition 4.12
The map \(Baut(\tau _{{\mathbb {C}}\mathrm {P}^n}^{\mathbb {R}})^{p,e} \rightarrow Baut_+({\mathbb {C}}\mathrm {P}^n)\) is a rational equivalence.
Proof
The bottom horizontal map in (29) is a rational equivalence, because it may be identified with the map

induced by the map \(BSO(2n)\rightarrow K_{p,e}\) that records the universal Pontryagin and Euler classes, which is a rational equivalence. It follows that the top horizontal map in (29) is a rational equivalence. \(\square \)
We proceed to make computations over \(Baut_+({\mathbb {C}}\mathrm {P}^n)\) using the fiberwise Pontryagin and Euler classes. By Theorem 1.7 applied to the orientation bundle,
where \(\Gamma \) is trivial if n is odd and cyclic of order 2, acting by \(a_k\mapsto (-1)^k a_k\), if n is even.
Lemma 4.13
Let \(\pi :E\rightarrow B\) be a \({\mathbb {C}}\mathrm {P}^n\)-fibration such that \(\pi _1(B)\) acts by orientation preserving homotopy equivalences on the fiber. Let \({\mathfrak {a}}\subseteq H^*(B;{\mathbb {Q}})\) denote the ideal generated by \(a_2,\ldots ,a_{n+1}\). We have that
Proof
We have that
It is a simple matter to expand \(\left( p_1^{fw}\right) ^\ell \) and \(e^{fw}\left( p_1^{fw}\right) ^\ell \) and then use Lemma 4.11 to calculate their pushforwards. We omit the details. \(\square \)
Assume n is odd, say \(n=2k+1\). Lemma 4.13 shows that, modulo \({\mathfrak {a}}^2\) and up to multiplication by non-zero scalars, the classes
agree with the classes
This implies that the displayed \(\kappa \)-classes are algebraically independent and that they generate \(H^*(Baut_+({\mathbb {C}}\mathrm {P}^n);{\mathbb {Q}}) = {\mathbb {Q}}[a_2,\ldots ,a_{n+1}]\).
Now assume n is even, say \(n=2k\). By what we said above, the ring
may be identified with the subring of \({\mathbb {Q}}[a_2,\ldots ,a_{n+1}]\) consisting of all elements in degrees divisible by 4. This ring is generated by the following \(n + \left( {\begin{array}{c}k\\ 2\end{array}}\right) \) elements:
-
\(a_{\ell }\) for all even \(\ell \), and
-
\(a_{i,j} = a_i a_j\) for all odd i and j with \(i\le j\).
It is easy to see that the kernel of the map
is generated by the \(\left( {\begin{array}{c}k\\ 2\end{array}}\right) \) polynomials
and these clearly form a regular sequence. Hence, the ring \(H^*(Baut_+({\mathbb {C}}\mathrm {P}^n);{\mathbb {Q}})\) is a complete intersection of Krull dimension n and embedding dimension \(n + \left( {\begin{array}{c}k\\ 2\end{array}}\right) \).
We will now show that all classes are tautological. Clearly, it suffices to prove that the generators \(a_\ell \) and \(a_{i,j}\) are tautological.
For \(n=2\), the computation is very easy. The expressions
show that \(\kappa _{p_1^2},\kappa _{p_1^4}\) generate the same subring as \(a_2,a_3^2\).
The idea in the general case is the same but more care is required.
Lemma 4.14
Let n be even, say \(n=2k\). Let \(\beta _2,\ldots ,\beta _{k+1}\in H^*(BSO(2n);{\mathbb {Q}})\) be classes of degree \(|\beta _s| = 4s\) such that \(\beta _{s|2s} =0\) for \(s\le k\) and \(\beta _{s|1} \not \in {\mathfrak {a}}^2\) for all s. Then \(H^*(Baut_+({\mathbb {C}}\mathrm {P}^n);{\mathbb {Q}})\) is minimally generated by the classes
for \(2\le s \le k+1\) and \(s-1\le i \le k\).
Proof
Let \(A=H^*(Baut_\circ ({\mathbb {C}}\mathrm {P}^n);{\mathbb {Q}}) = {\mathbb {Q}}[a_2,\ldots ,a_{n+1}]\). We have that
is the subring of elements in degrees divisible by 4. Let R denote the subring of A generated by the classes (30). Clearly, \(R\subseteq A^{(4)}\). We will prove that \(A^{4\ell } = R^{4\ell }\) for all \(\ell \) by induction.
In degree 0 there is nothing to prove. In degree 4, Lemma 4.13 shows that
so \(a_2\in R\), and hence \(A^4 = R^4\).
Let \(\ell >1\) and assume by induction that \(A^{4\ell '} = R^{4\ell '}\) for all \(\ell '<\ell \). To show that \(A^{4\ell } = R^{4\ell }\), it is enough to show that the generators in degree \(4\ell \) belong to R. These are
for all odd i such that \(\max (3,2\ell -n-1)\le i \le \ell \) and, if \(2\ell \le n+1\),
Let us use the convention that \(a_m=0\) for \(m>n+1\). Lemma 4.11 shows that
for all \(i\le \ell \) All elements of \({\mathfrak {a}}^3\) of degree \(4\ell \) belong to R by induction. Hence,
for all odd \(i\le \ell \).
We will now show that \(a_ia_{2\ell -i} \in R\), or equivalently \(\pi _!(a_i \omega _{fw}^{n+2\ell -i})\in R\), for all odd \(i\le \ell \) by induction on i, starting with the vacuous case \(a_1a_{2\ell -1} = 0 \in R\). Thus, let i be odd with \(3\le i \le \ell \) and assume that \(a_ja_{2\ell -j} \in R\) for all odd \(j<i\). We may also assume \(2\ell -n-1\le i\le n+1\), because otherwise \(a_i=0\) or \(a_{2\ell -i} = 0\) and there is nothing to prove. Say \(i=2s-1\). We have \(s\le k+1\) because \(i\le n+1\). By the assumption \(\beta _{s|2s} = 0\) for \(s\le k\) (and the fact that \(A^2 = 0\)) we may write
where \(b_j \in A^{2j}\). Multiplying by \(\omega _{fw}^{2k+2\ell -2s}\) yields
Now note that since
for non-zero rational numbers \(\mu \), \(\nu \), it follows that
where c is a non-zero rational number and K is a sum of products of \(\kappa \)-classes of lower degree, whence \(K\in R\) by induction (this only uses that the \(\kappa \)-classes have degree divisible by four, not their specific form). Also note that \(\kappa _{\beta _s p_1^{k+\ell -s}}\) is one of the generators for R. Indeed, \(s-1\le \ell -s\) holds because \(2s-1=i \le \ell \) by assumption, and \(\ell -s \le k\) holds because we have assumed \(2\ell -i\le n+1\).
Turning to the pushforward of the right hand side of (32), consider
The inequality \(j\le 2s=i+1\le \ell +1\) implies \(|b_j|= 2j <4\ell \) since \(\ell >1\), so \(b_j\in R\) for all even j. Also, for \(j=2j'\) even and positive, the class \(\pi _!(\omega _{fw}^{2k+2\ell -j})\) has degree \(4(\ell -j') < 4\ell \), so it belongs to R by induction. Thus, \(\pi _!(b_j\omega _{fw}^{2k+2\ell -j}) \in R\) for all even j.
Now for odd j, we may write
where \(f_{j-q} \in A^{2(j-q)}\). Hence,
For \(q<j\), both factors \(f_{j-q}\) and \(\pi _!(a_q\omega _{fw}^{2k+2\ell -j})\) have degrees that are smaller than \(4\ell \) and divisible by 4, so they belong to R by induction. For \(q=j\), we have \(f_0 \in {\mathbb {Q}}\) and \(\pi _!(a_j\omega _{fw}^{2k+2\ell -j})\in R\) by the inductive hypothesis that \(a_ja_{2\ell -j} \in R\) for odd \(j<i\).
Thus, we have shown that \(\pi _!(b_j\omega _{fw}^{2k+2\ell -j}) \in R\) for all \(j<i\) and that, for \(j=i\), all terms in the right hand side of (34), except possibly the one corresponding to \(q=i\), belong to R. But applying \(\pi _!\) to (32) and using our above observation that \(\pi _!(\beta _s \omega _{fw}^{2k+2\ell -2s}) \in R\), we can conclude that also this last term,
belongs to R. The assumption that \(\beta _{s|1} \not \in {\mathfrak {a}}^2\) means that \(b_i\) must contain a term of the form \(f_0 a_i\) with \(f_0\) a non-zero rational number. Therefore, \(\pi _!(a_i \omega _{fw}^{2k+2\ell -i})\) belongs to R as well, and this finishes the induction on i.
To show that \(a_{2\ell }\in R\), we use Lemma 4.13. It shows that
All elements of \({\mathfrak {a}}^2\) in degree \(4\ell \) belong to R by induction or by the now proved statement that \(a_ia_{2\ell -i} \in R\) for all odd i. Also, \(\kappa _{p_1^{k+\ell }}\) is one of the generators for R since we may assume \(\ell \le k\) (otherwise \(a_{2\ell } =0\) and there is nothing to prove). This finishes the induction on \(\ell \) and concludes the proof. \(\square \)
We have that
We do not need a general formula for \(p_s^{fw}\), but we record the following properties when \(2s\le n\): the leading term is
and
These facts imply that we may use
for \(s=2,3\ldots ,k\). Finally, we have that
This implies that we can use \(\beta _{k+1} = \left( p_1^{fw}\right) ^{k+1}\). By that, Theorem 1.17 is proved.
Proof of Theorem 1.19
Theorem 1.15 and Theorem 1.17 show that all characteristic classes of \(\,{\mathrm{Isom}}^+({\mathbb {C}}\mathrm {P}^n)\)-bundles with fiber \({\mathbb {C}}\mathrm {P}^n\) are tautological, so the map (4) is surjective.
As in the proof of Theorem 4.9, the map in cohomology induced by
may be identified with the homomorphism
where \({\mathfrak {d}}^{univ}\) is the ideal generated by the coefficients of the Pontryagin and Euler differences of the universal orientable \(\tau _{{\mathbb {C}}\mathrm {P}^n}^{\mathbb {R}}\)-fibration. It follows that the map
has kernel \(R^*(\tau _{{\mathbb {C}}\mathrm {P}^n}^{\mathbb {R}})\cap {\mathfrak {d}}^{univ}\). The hypotheses on the given \(\tau _{{\mathbb {C}}\mathrm {P}^n}^{\mathbb {R}}\)-fibration over B imply a factorization of (35) into surjective ring homomorphisms
This implies that \(\ker (f) = g(\ker (fg))\), which is seen to be equal to \(R^*(B)\cap {\mathfrak {d}}\) by the above. \(\square \)
Proof of Theorem 1.20
The ring \(H^*(Baut(\tau _{{\mathbb {C}}\mathrm {P}^2}^{\mathbb {R}})^e;{\mathbb {Q}})\) may be identified with the subring of \({\mathbb {Q}}[a_2,a_3,p_{1|0},p_{1|1}]\) generated by the elements
If \((\pi ,\zeta )\) denotes the universal \(\tau _{{\mathbb {C}}\mathrm {P}^2}^{\mathbb {R}}\)-fibration with trivialized Euler difference, then
With the above expressions at hand, it is straightforward to compute the following.
Setting \(\lambda = p_{1|1}^2\), the first two equations show that \(\lambda \), \(\kappa _{p_1^2}\), \(\kappa _{{\mathcal {L}}_2}\) span the same subspace as \(a_2\), \(p_{1|0}\), \(p_{1|1}^2\). The last two can then be used in turn to express \(a_3p_{1|1}\) and \(a_3^2\) in terms of \(\kappa _{p_1^2},\kappa _{p_1^4},\kappa _{{\mathcal {L}}_2},\kappa _{{\mathcal {L}}_3},\lambda \). All algebraic relations among the generators (36) are consequences of the single relation
It follows that
where J is the principal ideal generated by the element \((a_3p_{1|1})^2 - (a_3^2)(p_{1|1}^2)\) rewritten in the new generators. Let \(Baut(\tau _{{\mathbb {C}}\mathrm {P}^2}^{\mathbb {R}})_L^e\) denote the classifying space of \(\tau _{{\mathbb {C}}\mathrm {P}^2}^{\mathbb {R}}\)-fibrations with trivializations of the Euler difference and the classes \(\kappa _{{\mathcal {L}}_2},\kappa _{{\mathcal {L}}_3}\). The classes \(\kappa _{{\mathcal {L}}_2},\kappa _{{\mathcal {L}}_3}\) form a regular sequence in the cohomology of \(Baut(\tau _{{\mathbb {C}}\mathrm {P}^2}^{\mathbb {R}})^e\), so
where I is the reduction of J modulo \((\kappa _{{\mathcal {L}}_2}, \kappa _{{\mathcal {L}}_3})\). By rewriting \((a_3p_{1|1})^2 - (a_3^2)(p_{1|1}^2)\) in the new generators and multiplying with a suitable scalar, we find that I is generated by the element
In particular, this shows that the kernel of the surjective map
is the principal ideal generated by \(\lambda \).
We have that \(pd_{1|1} = -p_{1|1}\) and \(pd_{1|0} = -2a_2-p_{1|0}\). The equations
show that \(pd_{1|0}\) and \(\lambda \) are tautological and that \(\lambda = 6pd_{1|0}\) if \(\kappa _{{\mathcal {L}}_2} = 0\).
For an arbitrary \(\tau _{{\mathbb {C}}\mathrm {P}^n}^{\mathbb {R}}\)-fibration over a space B with trivial Euler difference and trivial \(\kappa _{{\mathcal {L}}_2}, \kappa _{{\mathcal {L}}_3}\), the above shows that the kernel of
is the principal ideal generated by \(pd_{1|0}\).
Imposing trivializations of \(\kappa _{{\mathcal {L}}_i}\) for \(i>3\) by taking the homotopy fiber of a suitable map from \(Baut(\tau _{{\mathbb {C}}\mathrm {P}^2}^{\mathbb {R}})_L^e\) to a product of Eilenberg–Mac Lane spaces will not change the cohomology in degree 4, so the resulting space will have a \(\tau _{{\mathbb {C}}\mathrm {P}^2}^{\mathbb {R}}\)-fibration over it with trivial Euler difference and \(\kappa _{{\mathcal {L}}_i} = 0\) for all \(i>1\), but with \(pd_{1|0}\ne 0\). In particular, it has a non-vanishing Pontryagin difference. \(\square \)
Notes
For the precise relation between the classes \(a_i\) and the Chern classes in the case when the fibration arises through projectivization of a complex vector bundle, see Proposition 4.6.
References
Baraglia, D.: Tautological classes of definite 4-manifolds. Geom. Topol. arXiv:2008.04519 [math.DG] (to appear)
Berglund, A.: Rational homotopy theory of mapping spaces via Lie theory for \(L_\infty \)-algebras. Homol. Homotopy Appl. 17(2), 343–369 (2015)
Berglund, A.: Rational models for automorphisms of fiber bundles. Doc. Math. 25, 239–265 (2020)
Berglund, A., Madsen, I.: Homological stability of diffeomorphism groups. Pure Appl. Math. Q. 9(1), 1–48 (2013)
Berglund, A., Madsen, I.: Rational homotopy theory of automorphisms of manifolds. Acta Math. 224, 67–185 (2020)
Block, J., Lazarev, A.: André–Quillen cohomology and rational homotopy of function spaces. Adv. Math. 193(1), 18–39 (2005)
Bott, R., Tu, L.W.: Differential Forms in Algebraic Topology. Graduate Texts in Mathematics, vol. 82. Springer, New York (1982)
Buijs, U., Murillo, A.: Basic constructions in rational homotopy theory of function spaces. Ann. Inst. Fourier (Grenoble) 56(3), 815–838 (2006)
Buijs, U., Murillo, A.: The rational homotopy Lie algebra of function spaces. Comment. Math. Helv. 83(4), 723–739 (2008)
Burghelea, D., Lashof, R.: Geometric transfer and the homotopy type of the automorphism groups of a manifold. Trans. Am. Math. Soc. 269(1), 1–38 (1982)
Dold, A.: Partitions of unity in the theory of fibrations. Ann. Math. (2) 78, 223–255 (1963)
Félix, Y., Halperin, S., Thomas, J.-C.: Rational Homotopy Theory. Graduate Texts in Mathematics, vol. 205. Springer, Berlin (2001)
Galatius, S., Grigoriev, I., Randal-Williams, O.: Tautological rings for high-dimensional manifolds. Compos. Math. 153(4), 851–866 (2017)
Galatius, S., Randal-Williams, O.: Stable moduli spaces of high-dimensional manifolds. Acta Math. 212(2), 257–377 (2014)
Grigoriev, I.: Relations among characteristic classes of manifold bundles. Geom. Topol. 21(4), 2015–2048 (2017)
Grothendieck, A.: La théorie des classes de Chern. Bull. Soc. Math. France 86, 137–154 (1958)
Hebestreit, F., Land, M., Lück, W., Randal-Williams, O.: A vanishing theorem for tautological classes of aspherical manifolds. Geom. Topol. 25(1), 47–110 (2021)
Igusa, K.: The stability theorem for smooth pseudoisotopies. K-Theory 2(1–2), 1–355 (1988)
Kȩdra, J., McDuff, D.: Homotopy properties of Hamiltonian group actions. Geom. Topol. 9, 121–162 (2005)
Kupers, A., Randal-Williams, O.: On diffeomorphisms of even-dimensional discs. arXiv:2007.13884 [math.AT]
Kuribayashi, K.: A rational model for the evaluation map. Georgian Math. J. 13(1), 127–141 (2006)
Kuribayashi, K.: On the rational cohomology of the total space of the universal fibration with an elliptic fibre. Contemp. Math. 519, 165–179. Homotopy theory of function spaces and related topics. American Mathematical Society, Providence (2010)
Lazarev, A.: Models for classifying spaces and derived deformation theory. Proc. Lond. Math. Soc. (3) 109(1), 40–64 (2014)
Lupton, G., Smith, S.B.: Rationalized evaluation subgroups of a map. I. Sullivan models, derivations and G-sequences. J. Pure Appl. Algebra 209(1), 159–171 (2007)
Lupton, G., Smith, S.B.: Rationalized evaluation subgroups of a map. II. Quillen models and adjoint maps. J. Pure Appl. Algebra 209(1), 173–188 (2007)
Madsen, I., Weiss, M.: The stable moduli space of Riemann surfaces: Mumford’s conjecture. Ann. Math. (2) 165(3), 843–941 (2007)
May, J.P.: Classifying spaces and fibrations. Mem. Am. Math. Soc. 1(1), 155 (1975)
Milnor, J.W., Stasheff, J.D.: Characteristic classes. Annals of Mathematics Studies, vol. 76. Princeton University Press (1974)
Prigge, N.: Tautological rings of fibrations. arXiv:1905.02676 [math.AT]
Prigge, N.: On tautological classes of fibre bundles and self-embedding calculus. PhD thesis, University of Cambridge (2020)
Quillen, D.: Rational homotopy theory. Ann. Math. (2) 90, 205–295 (1969)
Randal-Williams, O.: Some phenomena in tautological rings of manifolds. Sel. Math. (N.S.) 24(4), 3835–3873 (2018)
Sasao, S.: The homotopy of \({{\rm Map}}({{\mathbb{C}}{{\rm P}}}^{m},{{\mathbb{C}}{{\rm P}}}^{n})\). J. Lond. Math. Soc. (2) 8, 193–197 (1974)
Schlessinger, M., Stasheff, J.: Deformation theory and rational homotopy type. arXiv:1211.1647 [math.QA]
Sullivan, D.: Infinitesimal computations in topology. Inst. Hautes Études Sci. Publ. Math. 47(1977), 269–331 (1978)
Tanré, D.: Homotopie rationnelle: modèles de Chen, Quillen, Sullivan. Lecture Notes in Mathematics, vol. 1025. Springer, Berlin (1983)
Acknowledgements
We are grateful to Nils Prigge for his interest in this work and for numerous discussions. We thank Oscar Randal-Williams for useful conversations and for bringing our attention to the account of the family signature theorem found in [20, Appendix A]. We thank the anonymous referee for several pertinent remarks. The author was supported by the Swedish Research Council through grant no. 2015-03991.
Funding
Open access funding provided by Stockholm University.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.