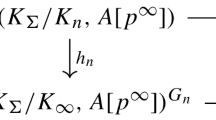Abstract
We completely calculate the Fitting ideal of the classical p-ramified Iwasawa module for any abelian extension K/k of totally real fields, using the shifted Fitting ideals recently developed by the second author. This generalizes former results where we had to assume that only p-adic places may ramify in K/k. One of the important ingredients is the computation of some complexes in appropriate derived categories.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
One of the most important themes in Iwasawa theory is to study the relationship between p-adic analytic objects and p-adic algebraic objects, usually formulated as “main conjectures,” in which the algebraic objects are described by characteristic ideals of suitable arithmetic modules. However, more recent research has given us a better understanding of closer relationships between analytic and algebraic objects beyond characteristic ideals. For example, such relationship can be described by using Fitting ideals.
In certain cases, using the p-adic L-functions corresponding to the arithmetic objects, we can describe the Fitting ideals of certain arithmetic modules, which give more information than the characteristic ideals. But in those cases it has always been necessary to use modified versions of the relevant Iwasawa modules instead of the modules themselves; see for example, [3, 11], etc.
In this paper we study a much more difficult and subtle object, the Fitting ideals of non-modified classical Iwasawa modules. We prove that they can be described by the analytic objects and certain ideals constructed from simple objects. We think it is remarkable that the Fitting ideals of classical Iwasawa modules can be also described by some variants of p-adic L-functions.
In order to explain this in slightly more detail, we introduce the notation we will use in this paper. Throughout this paper, we fix an odd prime number p. We consider a finite abelian extension K/k of totally real number fields and the cyclotomic \(\mathbb {Z}_p\)-extension \(K_\infty \) of K. Let \(S_p\) be the set of p-adic places of k. For any algebraic extension F/k, let \(S_{{{\,\mathrm{ram}\,}}}(F/k)\) be the set of finite places of k which are ramified in F. For any finite set S of primes of k, let \(X_{K_\infty ,S}\) be the S-ramified Iwasawa module, which is by definition the Galois group of the maximal pro-p-abelian extension of \(K_{\infty }\) unramified outside S. Recall that \(X_{K_\infty ,S}\) is a module over the Iwasawa algebra \(\mathcal {R}=\mathbb {Z}_p[[{\mathcal {G}}]]\), where \({\mathcal {G}}= {{\,\mathrm{Gal}\,}}(K_{\infty }/k)\) is the profinite Galois group in this setting. We simply write \(X_{S}\) for \(X_{K_\infty ,S}\) when no confusion arises.
The main theme in this paper is to compute \({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}(X_{S_p})\), the Fitting ideal of the Iwasawa module \(X_{S_{p}}\). The module \(X_{S_p}\) has been important in Iwasawa theory and is related to class groups as follows. Let \(A_{K(\mu _{p^{\infty }})}^{\omega }\) be the Teichmüller character component of the inductive limit \(A_{K(\mu _{p^{\infty }})}\) of the p-parts of the ideal class groups (full class groups) of \(K(\mu _{p^{n}})\) (for the definition of the character component, see Sect. 1.4). Then, assuming that K/k is a p-extension, we have the Kummer duality between \(X_{S_p}\) and \(A_{K(\mu _{p^{\infty }})}^{\omega }\):
Here, \((-)^{\vee }\) denotes the Pontryagin dual of a module and (1) denotes the Tate twist. The Fitting ideals of (the duals of) the minus components of class groups are studied in [7, 16], etc. Moreover, after the authors finished writing the first version of this paper, Dasgupta and Kakde [5] unconditionally proved a description of the Fitting ideals of (the duals of) the minus components of T-modified class groups. However, our objects of study in this paper are much more subtle, roughly because we do not allow T-modifications. See Sect. 1.5 for more discussion on this issue. We finally remark here that the Kummer duality plays practically no role in the proof of the main theorem in this paper.
In the papers [8, 9] by the first and the third author, and in the paper [10] with Tokio, we determined \({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}(X_{S})\) when S contains \(S_{{{\,\mathrm{ram}\,}}}(K_{\infty }/k) = S_{{{\,\mathrm{ram}\,}}}(K/k) \cup S_p\). Therefore, \({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}(X_{S_{p}})\) was determined in [8,9,10] under the assumption that \(S_{{{\,\mathrm{ram}\,}}}(K/k) \subset S_{p}\), that is, K/k is unramified outside p. But the assumption \(S_{{{\,\mathrm{ram}\,}}}(K/k) \subset S_p\), is a pretty severe constraint. In the present paper we completely remove the assumption \(S_{{{\,\mathrm{ram}\,}}}(K/k) \subset S_p\), and determine \({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}(X_{S_p})\) for any finite abelian extension K/k of totally real fields. Thus we are mainly concerned with the case \(S_{{{\,\mathrm{ram}\,}}}(K_{\infty }/k) \supsetneq S_{p}\).
The main result of this paper is the following.
Theorem 0.1
Let S be a finite set of finite places of k such that \(S \supset S_p \cup S_{{{\,\mathrm{ram}\,}}}(K/k)\) and \(S \ne S_p\). Put \(S'=S \setminus S_{p} \ne \emptyset \). Then we have
The definitions of the \(\mathcal {R}\)-module \(Z_{S'}^0\), of the element \(\theta _{S}^{{{\,\mathrm{mod}\,}}}\), and of \({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}^{[1]}\) will be given in Sect. 1. We introduce in this paper an integral element \(\theta _{S}^{{{\,\mathrm{mod}\,}}} \in \mathcal {R}\), which is a kind of (modified) equivariant Iwasawa power series. This is an integral Stickelberger element, but different from the so-called “T-modified Stickelberger elements” which appear in the theory of the Stark conjecture. The shifted Fitting ideal \({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}^{[1]}\) was introduced by the second author in [13]. It is defined by using a certain type of resolutions and the syzygies produced by them. The main point of the theorem is that all quantities on the right hand side are computable in principle.
Using the above-mentioned work of Dasgupta-Kakde [5], Johnston and Nickel proved in [12] the abelian equivariant main conjecture unconditionally, more precisely without assuming the condition \(\mu =0\) (under \(\mu =0\), the abelian equivariant main conjecture was known to be true, for example, by the work [19] of Ritter and Weiss). We use the result of Johnston and Nickel in Theorem 3.11 to prove our Theorem 0.1 above. Even if we do not use the theorem by Johnston and Nickel, we can prove our main theorem under the assumption of \(\mu =0\). In that case, the only place where we use \(\mu =0\) is Theorem 3.11.
The crucial point in this study is the case when \({{\,\mathrm{Gal}\,}}(K/k)\) is a p-group. In fact, the ring \(\mathcal {R}=\mathbb {Z}_p[[{\mathcal {G}}]]\) is semi-local, and decomposed into direct product of local rings. Let \({\mathcal {G}}={\mathcal {G}}^{(p')} \times {\mathcal {G}}^{(p)}\) be the decomposition of \({\mathcal {G}}\) such that \({\mathcal {G}}^{(p')}\) is a finite group of order prime to p and \({\mathcal {G}}^{(p)}\) is a pro-p group. Then each local component of \(\mathcal {R}\) corresponds to an equivalence class of characters of \({\mathcal {G}}^{(p')}\) (see Sect. 1.4), and accordingly the statement of Theorem 0.1 can be decomposed. On the one hand, the trivial character component is the most difficult, and the statement is equivalent to that for the pro-p extension \((K_{\infty })^{{\mathcal {G}}^{(p')}}/k\) with Galois group \({\mathcal {G}}^{(p)}\). (In fact, the trivial character component corresponds to the the Teichmüller character component by Kummer duality.) On the other hand, the non-trivial character components are easier to handle; for example, those components of \({{\,\mathrm{Fitt}\,}}^{[1]}_{\mathcal {R}}(Z_{S'}^0)\) can be computed easily (see Corollary 1.10). In that sense the case that \({{\,\mathrm{Gal}\,}}(K/k)\) is a p-group is essential. However, the proof of Theorem 0.1 does not involve an explicit reduction to that case.
The proof of our main result occupies Sects. 2 and 3; indeed the proof splits naturally into an algebraic part and an arithmetic part. The former constructs a certain complex \(C_S\) via an exact triangle, whose other two terms come from complexes that arise in global and local Galois cohomology respectively. This produces a short exact sequence
as in Proposition 2.11. Since the middle term turns out to be cohomologically trivial, this already gives a formula for \({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}(X_{S_p})\) in terms of \({{\,\mathrm{Fitt}\,}}^{[1]}_{\mathcal {R}}(Z_{S'}^0)\): these two quantities differ by a principal factor governed by the complex \(C_S\). In the second part of the proof, this factor is then identified with the (equivariant, modified) p-adic L-function \(\theta _{S}^{{{\,\mathrm{mod}\,}}}\).
In Sect. 2.4, we also discuss the natural question under what circumstances \({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}(X_{S_p})\) is principal. The rough answer is: very rarely (see Proposition 2.14).
In Sect. 4 we will present several attempts to make our determination of \({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}(X_{S_p})\) really explicit. The module \(Z^0_{S'}\) that occurs in the main result appears to be fairly explicit, but a closer look quickly shows that (unless the extension K/k is very small in a way) an honestly explicit description of its first shifted Fitting ideal is not obvious at all, and in fact turns out to be pretty hard in general. We present a general method to attack the problem, and show that it produces in some nice cases a truly explicit result, that is, a concrete list of generators for \({{\,\mathrm{Fitt}\,}}^{[1]}(Z^0_{S'})\).
In the final Sect. 5 we compute \({{\,\mathrm{Fitt}\,}}^{[1]}_{\mathcal {R}}(Z_{S'}^0)\) explicitly to determine the Fitting ideal of \(X_{S_{p}}\) in the case that K/k is cyclic and satisfies some mild conditions (see Theorems 5.1 and 5.4). Especially, these results give generalizations of the main result in [15] by the third author where only the case that K/k is of degree p was treated. We think that this new look at the third author’s previous result is a good way to use our main result and to test the techniques of Sect. 4.
Remark 0.2
Large parts of this paper, as they are written now, make an essential use of homological algebra. More precisely speaking, we need the theory of complexes including the cone construction, and some theory of derived categories. We would like to mention here that in the earliest stages of this manuscript we used different and more elementary methods. Actually, as far as the proof of the main result is concerned, one might call those other methods old-fashioned, since they mimicked and partially repeated ingenious arguments of Tate [21], which are over fifty years old. It is interesting to note that already in those old arguments one can perceive some central ideas of homological algebra like the use of Ext groups, but the theory of complexes was not used in the way we know it today. Anyway, it may be reassuring to know that alternative arguments exist, but we think that using the framework of Galois cohomology and complexes leads to shorter arguments and to a better logical structure, so this is what the reader will actually see in the body of this paper.
2 Ingredients for the main result
Our main result in this paper is Theorem 0.1 in the Introduction. In this section we define the \(\mathcal {R}\)-module \(Z_{S'}^0\), the element \(\theta _S^{{{\,\mathrm{mod}\,}}} \in \mathcal {R}\), and \({{\,\mathrm{Fitt}\,}}^{[1]}_{\mathcal {R}}\) which appeared in the statement of Theorem 0.1, and also give detailed explanation of several statements mentioned in the Introduction.
We recall some important notation from the Introduction.
Let p be an odd prime number, K/k a finite abelian extension of totally real fields, and \(K_{\infty }\) the cyclotomic \(\mathbb {Z}_p\)-extension of K. Put \({\mathcal {G}}= {{\,\mathrm{Gal}\,}}(K_{\infty }/k)\) and \(\mathcal {R}= \mathbb {Z}_p[[{\mathcal {G}}]]\). We denote by \(S_p\) the set of p-adic primes of k, and by \(S_{{{\,\mathrm{ram}\,}}}(K/k)\) the set of primes of k which are ramified in K/k. Let \(X_{S_p} = X_{K_{\infty }, S_p}\) be the \(S_p\)-ramified Iwasawa module for \(K_{\infty }\).
2.1 Definition of \(Z_{S'}^0\)
As in Theorem 0.1, let S be a finite set of finite places of k such that \(S \supset S_p \cup S_{{{\,\mathrm{ram}\,}}}(K/k)\) and \(S \ne S_p\). Put \(S' = S \setminus S_p \ne \emptyset \).
For each finite place v of k outside p, let \({\mathcal {G}}_v\) be the decomposition subgroup of \({\mathcal {G}}\) at v. Then \({\mathcal {G}}_v\) is an open subgroup of \({\mathcal {G}}\). Put
which is regarded as an \(\mathcal {R}\)-module; note that it is a finitely generated free \(\mathbb {Z}_p\)-module. Moreover, put
Finally, define an \(\mathcal {R}\)-module \(Z_{S'}^0\) by the exact sequence
where the map \(Z_{S'} \rightarrow \mathbb {Z}_p\) is defined to be the augmentation map on each summand \(Z_v\). Note that this map is onto for the precise reason that we assume \(S'\) to be nonempty.
2.2 Definition of \(\theta _{S}^{{{\,\mathrm{mod}\,}}}\)
Again let S be a finite set of finite places of k such that \(S \supset S_p \cup S_{{{\,\mathrm{ram}\,}}}(K/k)\), but we do not assume \(S \ne S_p\) in this subsection.
Definition 1.1
Let v be a finite place of k outside p. We denote by N(v) the cardinality of the residue field of k at v. Let \(\mathcal {T}_v \subset {\mathcal {G}}_v\) be the inertia group, which is finite. Let \(\sigma _v \in {\mathcal {G}}/\mathcal {T}_v\) be the N(v)-th power Frobenius automorphism.
Definition 1.2
For a finite character \(\psi : {\mathcal {G}}= {{\,\mathrm{Gal}\,}}(K_{\infty }/k) \rightarrow \mathbb {C}^{\times }\), we have the S-imprimitive L-function
where v runs over the finite places of k that are not in S. This infinite product converges on the half plane \(\Re (s) > 1\) and \(L_S(\psi , s)\) has a meromorphic continuation to the whole plane \(\mathbb {C}\).
We fix embeddings \(\overline{\mathbb {Q}} \hookrightarrow \overline{\mathbb {Q}_p}\) and \(\overline{\mathbb {Q}} \hookrightarrow \mathbb {C}\). Then each finite character \(\psi : {\mathcal {G}}\rightarrow \mathbb {C}^{\times }\) can be regarded to have values in \(\overline{\mathbb {Q}_p}^{\times }\). Thus \(\psi \) induces a continuous \(\mathbb {Z}_p\)-algebra homomorphism \(\mathcal {R}= \mathbb {Z}_p[[{\mathcal {G}}]] \rightarrow \overline{\mathbb {Q}_p}\), which we again denote by \(\psi \).
Let
denote the cyclotomic character, and
denote the Teichmüller character. The \(\mathbb {Z}_p\)-algebra homomorphisms induced by them are also written by the same letters.
The S-truncated p-adic L-functions \(\theta _{S}\) are defined via interpolation properties, as follows.
Definition 1.3
Let \(\theta _S = \theta _{S, K_{\infty }/k} \in {{\,\mathrm{Frac}\,}}(\mathcal {R})^{\times }\) be the element characterized by
for each finite character \(\psi \) of \({\mathcal {G}}\) and positive integers n. The existence of \(\theta _S\) follows from Deligne-Ribet [6]. Moreover, it is known that \(\theta _S\) is a pseudo-measure in the sense of Serre [20], that is, we have \({{\,\mathrm{Ann}\,}}_{\mathcal {R}}(\mathbb {Z}_p) \theta _S \subset \mathcal {R}\).
We will define a modification \(\theta _S^{{{\,\mathrm{mod}\,}}}\) of \(\theta _S\) below. We denote by \(N_{\mathcal {T}_{v}}=\sum _{\sigma \in \mathcal {T}_{v}} \sigma \) the norm element of the inertia group \(\mathcal {T}_{v}\) in a group ring, and put \(e_{v}=N_{\mathcal {T}_{v}}/\# \mathcal {T}_{v}\), which we regard as an element of \({{\,\mathrm{Frac}\,}}(\mathcal {R})\). We take a lift \(\widetilde{\sigma _v} \in {\mathcal {G}}\) of \(\sigma \in {\mathcal {G}}/\mathcal {T}_{v}\) and consider \(\widetilde{\sigma _v}e_{v}\), which is independent of the choice of \(\widetilde{\sigma _v}\). We simply write \(\sigma _{v}e_{v}\) for \(\widetilde{\sigma _v}e_{v}\).
Definition 1.4
We define \(\theta _S^{{{\,\mathrm{mod}\,}}}= \theta _{S, K_{\infty }/k}^{{{\,\mathrm{mod}\,}}} \in {{\,\mathrm{Frac}\,}}(\mathcal {R})^{\times }\) by
By definition \(\theta _S^{{{\,\mathrm{mod}\,}}}\) satisfies the interpolation properties
for \(\psi \) and n as in Definition 1.3, where v runs over the elements in \(S'\) such that \(\psi \) is unramified at v.
We will prove later in Sect. 2.1 the following.
Theorem 1.5
Our modified p-adic L-function \(\theta _S^{{{\,\mathrm{mod}\,}}}\) is integral, namely \(\theta _S^{{{\,\mathrm{mod}\,}}} \in \mathcal {R}\).
We note that a variant of this element \(\theta _{S}^\mathrm{mod}\) was called “Greither’s Stickelberger element” in [15, Theorem 0.1], and its integrality was proved in [15, Lemma 2.1] for a special type of extension K/k studied there.
We also note that we do not use Theorem 1.5 in the proof of Theorem 0.1.
Let us first discuss some basic properties of \(\theta _S^{{{\,\mathrm{mod}\,}}}\).
Lemma 1.6
-
(1)
Let \(S_1\) be a finite set which contains S. Then we have
$$\begin{aligned} \theta _{S_1}^\mathrm{mod} = \theta _S^\mathrm{mod} \prod _{v \in S_1 \setminus S} (1 - \sigma _v). \end{aligned}$$ -
(2)
We also have an element \(\theta _{S, M_{\infty }/k}^{{{\,\mathrm{mod}\,}}} \in {{\,\mathrm{Frac}\,}}(\mathbb {Z}_p[[{{\,\mathrm{Gal}\,}}(M_{\infty }/k)]])\) for any intermediate field \(M_{\infty }\) of \(K_{\infty }/k_{\infty }\), as in Definition 1.4. Then the image of \(\theta _{S, K_{\infty }/k}^{{{\,\mathrm{mod}\,}}}\) in \({{\,\mathrm{Frac}\,}}(\mathbb {Z}_{p}[[{{\,\mathrm{Gal}\,}}(M_{\infty }/k)]])\) coincides with \(\theta _{S, M_{\infty }/k}^{{{\,\mathrm{mod}\,}}}\).
Proof
(1) We note that \(v \in S_{1} \setminus S\) is unramified in \(K_{\infty }/k\) because S contains all ramifying primes. By the definition of \(\theta _{S}\), we have
Then by the definition of \(\theta _S^{{{\,\mathrm{mod}\,}}}\), we obtain
The claim in (2) follows from the interpolation properties of \(\theta _{S, K_{\infty }/k}^{{{\,\mathrm{mod}\,}}}\) and \(\theta _{S, M_{\infty }/k}^{{{\,\mathrm{mod}\,}}}\). \(\square \)
2.3 Shifted Fitting ideals
We review the theory of the second author [13] on Fitting invariants. Let \({{\,\mathrm{pd}\,}}_{\mathcal {R}}(P)\) be the projective dimension of an \(\mathcal {R}\)-module P. By [13, Theorem 2.6] and [13, Proposition 2.7], we have the following.
Theorem 1.7
Let n be a non-negative integer and X a finitely generated torsion \(\mathcal {R}\)-module. Take an n-step resolution \(0 \rightarrow Y \rightarrow P_1 \rightarrow \cdots \rightarrow P_n \rightarrow X \rightarrow 0\) of X, in which all modules are finitely generated torsion over \(\mathcal {R}\) and such that \({{\,\mathrm{pd}\,}}_{\mathcal {R}}(P_i) \le 1\) for \(i=1,\ldots ,n\). If we put
then the fractional ideal \({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}^{[n]}(X)\) of \(\mathcal {R}\) is independent of the choice of the n-step resolution. In this sense, \({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}^{[n]}(X)\) is well defined.
2.4 Decomposition of group rings
In general, suppose that \(\Delta \) is a finite abelian group of order prime to p. Then we have a decomposition
where \(\chi \) runs over equivalence classes of p-adic characters of \(\Delta \) (two characters \(\chi _1\), \(\chi _2\) are equivalent if and only if \(\sigma \chi _1=\chi _2\) for some \(\sigma \in {{\,\mathrm{Gal}\,}}(\overline{\mathbb {Q}}_{p}/\mathbb {Q}_{p})\)), and \({\mathcal O}_{\chi }=\mathbb {Z}_{p}[{{\,\mathrm{Im}\,}}(\chi )]\) is a \(\mathbb {Z}_{p}[\Delta ]\)-module on which \(\Delta \) acts via \(\chi \). According to this decomposition, each \(\mathbb {Z}_p[\Delta ]\)-module M can be decomposed as
with \(\mathcal {O}_{\chi }\)-modules \(M^{\chi }\).
Now we consider \({\mathcal {G}}={{\,\mathrm{Gal}\,}}(K_{\infty }/k)\). We decompose it into \({\mathcal {G}}={\mathcal {G}}^{(p')} \times {\mathcal {G}}^{(p)}\) where \({\mathcal {G}}^{(p')}\) is a finite group of order prime to p and \({\mathcal {G}}^{(p)}\) is a pro-p group. Since \(\mathbb {Z}_{p}[[{\mathcal {G}}]]=\mathbb {Z}_{p}[{\mathcal {G}}^{(p')}][[{\mathcal {G}}^{(p)}]]\), applying the above decomposition of \(\mathbb {Z}_{p}[\Delta ]\) to \(\Delta ={\mathcal {G}}^{(p')}\), we have
We also have
where the first component of the right hand side corresponds to the trivial character \(\chi =1\).
Here we give a description of \({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}^{[1]}(Z_v)\). Let v be a finite place of k outside p. Recall (Definition 1.1) that \(\mathcal {T}_v\) is the inertia group in \(K_{\infty }/k\), and \(\sigma _v \in {\mathcal {G}}/\mathcal {T}_v\) is the Frobenius automorphism. Let
be the map induced by the multiplication by the norm element \(N_{\mathcal {T}_v}=\sum _{\sigma \in \mathcal {T}_v} \sigma \).
Proposition 1.8
For each finite place v of k outside p, we have
as fractional ideals of \(\mathcal {R}\).
Proof
The statement of the lemma can be decomposed according to characters \(\chi \) of \({\mathcal {G}}^{(p')}\). We consider the decomposition \(\mathcal {T}_v = \mathcal {T}_v^{(p')} \times \mathcal {T}_v^{(p)}\) where the order of \(\mathcal {T}_v^{(p')}\) is prime to p and \(\mathcal {T}_v^{(p)}\) is a pro-p group. If \(\chi \) is non-trivial on \(\mathcal {T}_v^{(p')}\), we have \(Z_v^{\chi } = 0\) and \(\chi (\nu _v) = 0\), so the equation holds. Therefore, we only have to deal with \(\chi \) which is trivial on \(\mathcal {T}_v^{(p')}\). Thus we may assume \(\mathcal {T}_v = \mathcal {T}_v^{(p)}\) from the start.
Assume \(\mathcal {T}_v = \mathcal {T}_v^{(p)}\). Note that, by local class field theory, \(\mathcal {T}_v\) is a quotient of the unit group \(\mathcal {O}_{k_v}^{\times }\), so in particular \(\mathcal {T}_v^{(p)}\) is a cyclic group. Hence we can take a generator \(\delta _v\) of \(\mathcal {T}_v\). Take a lift \(\widetilde{\sigma _v} \in {\mathcal {G}}\) of \(\sigma _v \in {\mathcal {G}}/\mathcal {T}_v\). Then \({\mathcal {G}}_v\) is topologically generated by \(\widetilde{\sigma _v}\) and \(\delta _v\), so we have \(Z_v \simeq \mathcal {R}/(\widetilde{\sigma _v} - 1, \delta _v-1)\). Thus we have an exact sequence
Observe that the cokernel of \(N_{\mathcal {T}_v}\) here has a presentation \((N_{\mathcal {T}_v}, \widetilde{\sigma _v}-1)\) as an \(\mathcal {R}\)-module. Hence we obtain
\(\square \)
Now we give an explicit description of \({{\,\mathrm{Fitt}\,}}^{[1]}_{\mathcal {R}}(Z_{S'}^0)\) for non-trivial character components.
Proposition 1.9
For any non-trivial character \(\chi \) of \({\mathcal {G}}^{(p')}\), we have
as fractional ideals of \(\mathcal {R}^{\chi }\).
Proof
Since \(\chi \) is non-trivial, we have \((\mathbb {Z}_p)^{\chi } = 0\), so \((Z_{S'}^0)^{\chi } = (Z_{S'})^{\chi }\). Then the assertion follows from Proposition 1.8 immediately. \(\square \)
Note that \(N_{\mathcal {T}_v} \in \mathcal {R}\) goes to 0 in \(\mathcal {R}^{\chi }\) unless \(\chi \) is trivial on \(\mathcal {T}_v\), that is, \(\chi (v) = 1\). Therefore, only places \(v \in S'\) with \(\chi (v) = 1\) contribute in the product.
Using Theorem 0.1 and the Proposition 1.9, we get a complete description of the Fitting ideal of the non-trivial character component of \(X_{S_{p}}\).
Corollary 1.10
For any non-trivial character \(\chi \) of \({\mathcal {G}}^{(p')}\), we have
2.5 Relation with minus class groups
In this short subsection, we compare our results on \(X_{S_p}\) with related work on the minus components of class groups.
As recalled in the Introduction: Assuming that K/k is a p-extension, we have the Kummer duality between \(X_{S_p}\) and \(A_{K(\mu _{p^{\infty }})}^{\omega }\), the Teichmüller character component of \(A_{K(\mu _{p^{\infty }})}\). Therefore, our results in this paper can be translated into results on \((A_{K(\mu _{p^{\infty }})}^{\omega })^{\vee }\).
The Fitting ideals of the minus part \((A_{K(\mu _{p^{\infty }})}^{-})^{\vee }\) are known outside the Teichmüller character component. For example, the method of the first author [7] can be applied to the Iwasawa theoretic situation without assuming the ETNC, the equivariant Tamagawa number conjecture.
The third author made a conjecture in [16] on a complete description of the Fitting ideal of \((A_{K(\mu _{p^n})}^{T, -})^{\vee }\), the dual of the minus component of the T-modified class group \(A_{K(\mu _{p^n})}^{T}\) for certain finite sets T of primes, and proved it assuming the ETNC. Very recently, Dasgupta and Kakde proved in [5] the Brumer-Stark conjecture, and more strongly, the above conjecture by the third author unconditionally. From that result, one can get information on the full class group outside the Teichmüller character component. However, the Teichmüller character component is a much more subtle and difficult object than the other components, and is still mysterious even if we know the Brumer-Stark conjecture. For this reason, the results of [5] do not seem to impact directly on our main theorems.
We now explain briefly the difficulty in computing the Fitting ideal of the \(\omega \)-component, and the difference from the computation of the T-modified class groups in Dasgupta and Kakde [5], and in [16] by the third author, etc. In [5] and [16] a kind of Tate sequences are used to study the T-modified class group \(A_{K(\mu _{p^n})}^{T}\). An important fact is that the class group appears in the final term of some 4 term exact sequence. In a different terminology, it is well-known that the class group of \(\mathcal {O}_{K(\mu _{p^{n}}),S}\) appears in \(H^2\) of the étale cohomology complex \(\mathcal {R}\Gamma _{et}(\mathrm{Spec} \ {\mathcal O}_{{K(\mu _{p^n})},S}, \mathbb {Z}_{p}(1))\). In the T-modification \(\mathcal {R}\Gamma _{T}(\mathrm{Spec} \ {\mathcal O}_{{K(\mu _{p^n})},S}, \mathbb {Z}_{p}(1))\) introduced in [3], \(H^i=0\) if \(i \ne 1, \ 2\), and \(H^2\) is related to the T-modified class group. On the other hand, in the study of the \(\omega \)-component of the full class group, T-modification is not allowed, and \(H^3\) of \(\mathcal {R}\Gamma _{et}(\mathrm{Spec} \ {\mathcal O}_{{K(\mu _{p^n})},S}, \mathbb {Z}_{p}(1))\) does not vanish. So for this one would require an argument totally different from the one used for \(A_{K(\mu _{p^n})}^{T}\). We hope that the approach of the present paper provides some steps in this direction.
3 Proof of main result (I)
3.1 Integrality of \(\theta _{S}^\mathrm{mod}\)
Before proving the main theorem, let us give a proof of Theorem 1.5 in this subsection. (We remark that this result is not used in the proof of the main theorem.)
For a subset J of \(S'\), we define \(K_{J}/k\) to be the maximal subextension of \(K_{\infty }/k\) that is unramified in J. Since \(J \cap S_{p}\) is empty, \(K_{J}\) contains the cyclotomic \(\mathbb {Z}_{p}\)-extension \(k_{\infty }\) of k, which implies that \(K_{\infty }/K_{J}\) is a finite extension. We put \({\mathcal {G}}_{K_{J}}={{\,\mathrm{Gal}\,}}(K_{J}/k)\). Let
be the norm homomorphism which is induced by the multiplication by the norm element \(N_{{{\,\mathrm{Gal}\,}}(K_{\infty }/K_{J})}=\sum _{\sigma \in {{\,\mathrm{Gal}\,}}(K_{\infty }/K_{J})} \sigma \). We extend \(\nu _{K_{\infty }/K_{J}}\) to the total quotient rings of both sides.
We first prove two lemmas.
Lemma 2.1
In \({{\,\mathrm{Frac}\,}}(\mathcal {R})\) we have
where J runs over all subsets of \(S'\) and \(\sigma _{v, K_{J}}\) is the Frobenius automorphism of v in \({\mathcal {G}}_{K_{J}}\).
Proof
We compute the right hand side of the definition of \(\theta _{S, K_{\infty }/k}^\mathrm{mod}\) (see Definition 1.4). Choosing a lift \(\widetilde{\sigma _v} \in {\mathcal {G}}\) of \(\sigma _v \in {\mathcal {G}}/\mathcal {T}_v\) and putting \(\xi _{v}=\frac{N(v)^{-1}-1}{\# \mathcal {T}_{v}}\widetilde{\sigma _v}\), we get
Therefore, we have
On the other hand, for any element \(\alpha \) of \({{\,\mathrm{Frac}\,}}(\mathcal {R})\), we know
where
is the natural restriction map. For a subset J of \(S'\) and \(v \in J\), put
Using \(\pi _{K_{\infty }/K_{J}}(\theta _{S, K_{\infty }/k}) =\theta _{S, K_{J}/k}\) and
we apply (2.2) to \(\alpha = \theta _{S, K_{\infty }/k} \prod _{v \in J}(\xi _{v}/ (1-\sigma _{v}e_{v}N(v)^{-1}))\) to get
The equation (2.1) together with the above equation implies that
This completes the proof of Lemma 2.1. \(\square \)
Lemma 2.2
The modified p-adic L-function \(\theta _{S, K_{\infty }/k}^\mathrm{mod}\) is a pseudo-measure of \({\mathcal {G}}_{K_{\infty }}\) in the sense of Serre [20].
Proof
We know that \(\theta _{S \setminus J, K_{J}/k}\) is a pseudo-measure of \({\mathcal {G}}_{K_{J}}\). Since \([K_{\infty }:K_{J}]\) divides \(\prod _{v \in J} \# \mathcal {T}_{v}\) and \(\# \mathcal {T}_{v}\) p-adically divides \(N(v)-1\), Lemma 2.2 is a consequence of Lemma 2.1. \(\square \)
Now we prove Theorem 1.5. By Lemma 2.2, \(\theta _{S, K_{\infty }/k}^\mathrm{mod}\) is holomorphic at any characters of \({\mathcal {G}}\) except the trivial character. The rest of our task is to show that it is holomorphic also at the trivial character.
Let \(\gamma \in {\mathcal {G}}={{\,\mathrm{Gal}\,}}(K_{\infty }/k)\) be a lift of a generator of \({{\,\mathrm{Gal}\,}}(k_{\infty }/k)\). Since \(\theta _{S, K_{\infty }/k}\) is a pseudo-measure, as in [20] one can write
for some \(c \in \mathbb {Z}_{p}\) and some \(\alpha \in \mathbb {Z}_{p}[[{\mathcal {G}}]]\) (we are writing \(N_{H}\) for the norm element in a group ring for any finite group H). We know that c can be expressed by the class number of k, the p-adic regulator, etc. by Colmez’s theorem, but we do not need it.
We also write
for some \(c_{J} \in \mathbb {Z}_{p}\) and some \(\alpha _{K_{J}} \in \mathbb {Z}_{p}[[{\mathcal {G}}_{K_{J}}]]\). Let \(\pi _{K_{\infty }/K_{J}}\) be the map in the proof Lemma 2.1. Since
we have
so
By Lemma 2.2, \(\theta _{S, K_{\infty }/k}^\mathrm{mod}\) is also a a pseudo-measure. So we can write
for some \(c^\mathrm{mod} \in \mathbb {Z}_{p}\) and some \(\alpha ^\mathrm{mod} \in \mathbb {Z}_{p}[[{\mathcal {G}}_{K_{\infty }}]]\). In order to prove Theorem 1.5, it is enough to show \(c^\mathrm{mod}=0\). By Lemma 2.1 and (2.3), we have
Put \(n=\#S'\). We note that n is positive since \(S'\) is non-empty. Counting the subsets J with \(\# J=k\), we deduce from the above equation that
This completes the proof of Theorem 1.5.
3.2 Some facts on arithmetic complexes
We collect some facts on local and global arithmetic complexes. A comprehensive reference is Nekovář [17].
Let \(k_S/k\) be the maximal S-ramified algebraic extension. For each finite place v of k, let \(k_v\) be the completion at v. Fix an algebraic closure \(\overline{k_v}\) of \(k_v\) and an inclusion \(k_S \hookrightarrow \overline{k_v}\) over k. Then any representation of \({{\,\mathrm{Gal}\,}}(k_S/k)\) will yield a representation of \({{\,\mathrm{Gal}\,}}(\overline{k_v}/k_v)\).
We denote by \((-)^{\vee }\) the Pontryagin dual of a module. This symbol will also be used for the corresponding construction in derived categories. As usual, we denote by \(\mu _{p^m}\) the group of \(p^m\)-th roots of unity. Let \(\mathbb {Z}_p(1) = \varprojlim _m \mu _{p^m}\) be the Tate module. Let \(\chi _{{\mathcal {G}}}: {{\,\mathrm{Gal}\,}}(k_S/k) \twoheadrightarrow {{\,\mathrm{Gal}\,}}(K_{\infty }/k) = {\mathcal {G}}\hookrightarrow \mathcal {R}^{\times }\) be the tautological representation. We consider
which is an \(\mathcal {R}\)-module of rank one with a certain action of \({{\,\mathrm{Gal}\,}}(k_S/k)\).
We shall study the complexes
which are defined using the continuous cochain complexes for the profinite groups \({{\,\mathrm{Gal}\,}}(k_S/k)\) and \({{\,\mathrm{Gal}\,}}(\overline{k_v}/k_v)\) (see [17, (3.4.1)]).
We denote by \(D^{{{\,\mathrm{perf}\,}}}(\mathcal {R})\) the derived category of perfect complexes of \(\mathcal {R}\)-modules, and by \(D^{{{\,\mathrm{perf}\,}}}_{{{\,\mathrm{tor}\,}}}(\mathcal {R})\) the subcategory of objects whose cohomology groups are torsion as \(\mathcal {R}\)-modules. We will see that most of the complexes we treat in this paper are objects of \(D^{{{\,\mathrm{perf}\,}}}_{{{\,\mathrm{tor}\,}}}(\mathcal {R})\). First we recall the following fact.
Proposition 2.3
([17, Proposition (4.2.9)]) The “global complex”
as well as the “local complexes”
for any finite place v of k, are objects of \(D^{{{\,\mathrm{perf}\,}}}(\mathcal {R})\).
The following two propositions are interpretations of the local Tate duality and the global Poitou-Tate exact sequence, respectively. It would be certain that they have been known since Grothendieck’s works, and are explicitly mentioned in Nekovář [17]. We use [17, (2.9.1)] to identify the Pontryagin dual and the Matlis dual [17, (2.3)].
Proposition 2.4
([17, Proposition (5.2.4)(i)]) We have an isomorphism
Proposition 2.5
([17, Proposition (5.4.3)(i)]) We have a distinguished triangle
where the first morphism is obtained by the localization, and the second morphism by the localization and the duality in Proposition 2.4.
Remark 2.6
It should also be possible to deduce this exact triangle from the paper [1]. The notation there is closer in spirit to ours than Nekovář’s, but there is the disadvantage that everything is formulated at finite level, and we have not checked whether the transition to the projective limit offers problems. A little more precisely: The definition of the cone in [1], formula (3) on p.1345, gives an exact triangle
where \(\mathcal C\) denotes the cone. Then with the method of loc.cit. p.1357, see equation (36) in particular, it should be possible to identify \(\mathcal C\) with \(\mathcal {R}\Gamma (k_S/k, \mathbb {Z}_p(1)^\vee (1))^\vee [-2]\). Again, we gloss over some technical problems and we do not try to discuss the passage from \(\mathbb {Z}_p(1)\) (finite level) to \(\mathbb {T}\) (infinite level).
Next we compute the cohomology groups of the global and local complexes.
Definition 2.7
Let v be a finite place of k outside p. Put
where \(\mu _{p^{\infty }}(K_n \otimes _k k_v)\) denotes the p-primary subgroup of \((K_n \otimes _k k_v)^{\times }\) and the inverse limit is taken with respect to the norm maps. Then \(J_v\) is naturally an \(\mathcal {R}\)-module and its structure is as in Remark 2.8. Put
Let \(X_S = X_{K_{\infty }, S}\) be the S-ramified Iwasawa module. From global class field theory, we have an exact sequence
where the injectivity of \(J_{S'} \rightarrow X_{S}\) follows from the weak Leopoldt conjecture.
Remark 2.8
Take a place w of \(K_{\infty }\) above v, and put
Here \(K_{n,w}\) denotes the completion of \(K_n\) at the place below w. Then we have \(J_v \simeq \mathcal {R}\otimes _{\mathcal {R}_v} J_w\), where \(\mathcal {R}_v = \mathbb {Z}_p[[{\mathcal {G}}_v]]\).
If \(\mu _{p^{\infty }}(K_{\infty , w}) = 0\), then we have \(J_w = 0\) and thus \(J_v = 0\). Otherwise, we have \(\mu _{p^{\infty }} \subset (K_{\infty , w})^{\times }\) and \(J_w \simeq \mathbb {Z}_p\). In the latter case, the action of \({\mathcal {G}}_v\) on \(J_w\) is given by the cyclotomic character \(\kappa _v: {\mathcal {G}}_v \rightarrow \mathbb {Z}_p^{\times }\) at v, and we have \(J_v \simeq \mathbb {Z}_p[{\mathcal {G}}/{\mathcal {G}}_v]\) as a \(\mathbb {Z}_p\)-module.
Proposition 2.9
We have
and
for \(v \not \mid p\) where \(Z_v\) was defined in Sect. 1.1.
Proof
We feel that it should also be possible to assemble a proof from suitable references to Nekovář’s book [17], but we will write out a direct proof for the reader’s convenience.
We have
where \(\chi _{{\mathcal {G}}_n}: {{\,\mathrm{Gal}\,}}(k_S/k) \twoheadrightarrow {{\,\mathrm{Gal}\,}}(K_n/k) \hookrightarrow \mathbb {Z}_p[{{\,\mathrm{Gal}\,}}(K_n/k)]^{\times }\) is the tautological representation. Then
where the third isomorphism follows from Shapiro’s lemma. The weak Leopoldt conjecture, which says that \(H^2(k_S/K_{\infty }, \mathbb {Q}_p/\mathbb {Z}_p)\) vanishes, is known to be true. This implies the first assertion of Proposition 2.9.
For the second assertion, we use Proposition 2.4 to see that \(H^i(k_v, \mathbb {T}) \simeq H^{2-i}(k_v, \mathbb {T}^{\vee }(1))^{\vee }\). Take a place w of \(K_{\infty }\) above v. A computation similar to the global case that we just have done shows (\(G_{v,n}\) is an ad hoc abbreviation for \({{\,\mathrm{Gal}\,}}(K_{n, w}/k_v)\)):
This implies the assertion for \(i \ne 1\). For \(i = 1\), the above computation implies
For each positive integer m, the exact sequence \(0 \rightarrow \mu _{p^m} \rightarrow \overline{k_v}^{\times } \overset{(-)^{p^m}}{\rightarrow } \overline{k_v}^{\times } \rightarrow 0\) induces an isomorphism \(K_{n, w}^{\times } / (K_{n, w}^{\times })^{p^m} \simeq H^1(K_{n, w}, \mu _{p^m})\). By taking the inverse limit with respect to m and n, we obtain \(\varprojlim _n H^1(K_{n,w}, \mathbb {Z}_p(1)) \simeq J_w\). This completes the proof. \(\square \)
Corollary 2.10
The complexes \(\mathcal {R}\Gamma (k_S/k, \mathbb {T}^{\vee }(1))^{\vee }\) and \(\mathcal {R}\Gamma (k_v, \mathbb {T})\) for \(v \not \mid p\) are objects of \(D^{{{\,\mathrm{perf}\,}}}_{{{\,\mathrm{tor}\,}}}(\mathcal {R})\).
Proof
Propositions 2.3 and 2.5 imply that these complexes are objects of \(D^{{{\,\mathrm{perf}\,}}}(\mathcal {R})\). By Proposition 2.9, the cohomology groups are torsion. \(\square \)
3.3 The algebraic part of the proof
We define a complex \(C_S = C_S(K_{\infty }/k)\) as a mapping cone of \(\bigoplus _{v \in S'} \mathcal {R}\Gamma (k_v, \mathbb {T}) \rightarrow \mathcal {R}\Gamma (k_S/k, \mathbb {T}^{\vee }(1))^{\vee }[-2]\), namely define it such that it fits into a distinguished triangle
where the first morphism is induced by the restriction, using Proposition 2.4. By Corollary 2.10, \(C_S\) is actually an object of \(D^{{{\,\mathrm{perf}\,}}}_{{{\,\mathrm{tor}\,}}}(\mathcal {R})\).
Proposition 2.11
We have \(H^i(C_S) = 0\) unless \(i = 1\), and an exact sequence
of \(\mathcal {R}\)-modules.
Proof
Taking the long exact sequence associated to (2.5) and using Proposition 2.9, we obtain an exact sequence
Then the assertion follows from the exact sequences (1.1) and (2.4). \(\square \)
Corollary 2.12
The projective dimension of \(H^1(C_S)\) is at most one, and we have
Proof
Since \(C_S\) is perfect, the first statement of Proposition 2.11 tells us that \({{\,\mathrm{pd}\,}}_{\mathcal {R}}(H^1(C_S)) < \infty \). By the exact sequence (2.6), \(H^1(C_S)\) does not contain any non-trivial finite submodule. Hence we have \({{\,\mathrm{pd}\,}}_{\mathcal {R}}(H^1(C_S)) \le 1\). The formula (2.7) is therefore a consequence of (2.6) and the definition of \({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}^{[1]}\). \(\square \)
3.4 Principality of \({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}(X_{S_p})\)
At the end of this section we put the preceding result into perspective by discussing the exact conditions under which the ideal \({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}(X_{S_p})\) is principal. Keep the setup of preceding sections.
Lemma 2.13
Suppose that there is a place \(v^* \in S'\) such that \({\mathcal {G}}_{v*} \supset {\mathcal {G}}_v\) for any \(v \in S'\). Then we have an isomorphism
Proof
Put \(Z_{S' \setminus \{v^*\}} = \bigoplus _{v \in S', v \ne v^*} Z_v\). Consider the commutative diagram with exact rows and columns

We shall show that the left vertical sequence splits. Pick any \(v \in S'\) with \(v \ne v^*\). Then since \({\mathcal {G}}_{v^*} \supset {\mathcal {G}}_v\), we have a natural surjective homomorphism
Using these homomorphisms, define a homomorphism \(s: Z_{S' \setminus \{v^*\}} \rightarrow Z_{S'}\) as follows. For \(x = (x_v)_{v \in S', v \ne v^*} \in Z_{S' \setminus \{v^*\}}\), put \(s(x)_v = x_v\) if \(v \ne v^*\) and put
Then define \(s(x) = (s(x)_v)_{v \in S'} \in Z_{S'}\). By construction, s is a section of the natural projection \(Z_{S'} \rightarrow Z_{S' \setminus \{v^*\}}\), and moreover the image of s is contained in \(Z_{S'}^0\). Therefore s gives a splitting of the left vertical sequence, which completes the proof. \(\square \)
Proposition 2.14
Suppose K/k is a p-extension. Put \(S = S_p \cup S_{{{\,\mathrm{ram}\,}}}(K/k)\) and suppose that \(S' = S \setminus S_p \ne \emptyset \) (note that this implies \(K_{\infty } \ne k_{\infty }\)). Then the following are equivalent.
-
(i)
\({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}(X_{S_p})\) is a principal ideal.
-
(ii)
\({{\,\mathrm{pd}\,}}_{\mathcal {R}}(X_{S_p}) \le 1\).
-
(iii)
\({{\,\mathrm{pd}\,}}_{\mathcal {R}}(Z^0_{S'}) \le 1\).
-
(iv)
\(Z^0_{S'} = 0\).
-
(v)
\(S'\) consists of only one place \(v^*\), and this place satisfies \({\mathcal {G}}_{v^*} ={\mathcal {G}}\). In other words, \(v^*\) must be totally inert in \(k_\infty /k\) and totally ramified in \(K_\infty /k_\infty \).
Proof
The equivalence (i) \(\Leftrightarrow \) (ii) follows from the argument of [4, Proposition 4]. The equivalence (ii) \(\Leftrightarrow \) (iii) follows from the short exact sequence (2.6) and the first line of Corollary 2.12. The equivalence (iv) \(\Leftrightarrow \) (v) is clear, and the implication (iv) \(\Rightarrow \) (iii) is trivial.
Now we show the implication (iii) \(\Rightarrow \) (iv). Put \(H={{\,\mathrm{Gal}\,}}(K_\infty /k_\infty )\), which is a non-trivial p-group by assumption. We note that, for any \(\mathcal {R}\)-module M which is free of finite rank over \(\mathbb {Z}_p\), we have \({{\,\mathrm{pd}\,}}_{\mathcal {R}}(M) \le 1\) if and only if M is a free \(\mathbb {Z}_p[H]\)-module.
First suppose that all quotients \({\mathcal {G}}/{\mathcal {G}}_v\) with \(v\in S'\) are non-trivial. Then the \(\mathbb {Z}_p\)-rank of every \(Z_v = \mathbb {Z}_p[{\mathcal {G}}/{\mathcal {G}}_v]\) is a p-power \(>1\), so that we have \({{\,\mathrm{rank}\,}}_{\mathbb {Z}_p}(Z^0_{S'}) \equiv -1 (\bmod p)\). Hence \(Z^0_{S'}\) cannot be free over \(\mathbb {Z}_p[H]\).
Consequently, if \({{\,\mathrm{pd}\,}}_{\mathcal {R}}(Z^0_{S'}) \le 1\), then we have at least one \(v^* \in S'\) such that \({\mathcal {G}}/{\mathcal {G}}_{v^*}\) is trivial. Then by Lemma 2.13, we obtain
It is easy to check that, for each \(v \in S'\) with \(v \ne v^*\), we have \(Z_v = \mathbb {Z}_p[{\mathcal {G}}/{\mathcal {G}}_v]\) is free over \(\mathbb {Z}_p[H]\) if and only if \({\mathcal {G}}_v \cap H = 1\). But \({\mathcal {G}}_v \cap H\) is the decomposition group of (a prime above) v in \(K_\infty /k_\infty \), and by the assumption \(S' = S_{{{\,\mathrm{ram}\,}}}(K/k) \setminus S_p\), the prime v must ramify in \(K_\infty /k_\infty \). Hence we must have \(S' = \{v^*\}\). \(\square \)
For completeness, we note the following.
Lemma 2.15
Suppose that K/k is a p-extension and that \(S_{{{\,\mathrm{ram}\,}}}(K/k) \subset S_p\). Then \({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}(X_{S_p})\) is a principal ideal if and only if \(K_{\infty } = k_{\infty }\).
Proof
As already used in the proof of Proposition 2.14, the ideal \({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}(X_{S_p})\) is principal if and only if \({{\,\mathrm{pd}\,}}_{\mathcal {R}}(X_{S_p}) \le 1\). By Propositions 2.3 and 2.9, we see that \({{\,\mathrm{pd}\,}}_{\mathcal {R}}(X_{S_p}) \le 1\) is equivalent to \({{\,\mathrm{pd}\,}}_{\mathcal {R}}(\mathbb {Z}_p) \le 1\), which is true exactly when \(K_{\infty } = k_{\infty }\). \(\square \)
4 Proof of main result (II)
In this section, we complete the proof of Theorem 0.1 by determining the ideal \({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}(H^1(C_S))\). This is in a certain way the arithmetic part of the proof. We need a few preliminaries concerning determinants and Fitting ideals.
4.1 The determinant homomorphism
This subsection is devoted to the homological algebra related to the determinant functor. Let \(\mathcal {I}(\mathcal {R})\) be the commutative group of invertible fractional ideals of \(\mathcal {R}\). We shall introduce a group homomorphism, called the determinant,
Here \(K_0\) denotes the Grothendieck group of a triangulated category. We refer to Knudsen-Mumford [14] for more on the theory of determinants.
Let \(Ch^{{{\,\mathrm{perf}\,}}}(\mathcal {R})\) be the abelian category of perfect complexes of \(\mathcal {R}\)-modules. More precisely, \(Ch^{{{\,\mathrm{perf}\,}}}(\mathcal {R})\) consists of bounded complexes F of \(\mathcal {R}\)-modules such that \(F^i\) is finitely generated and projective for all i. Let \(Ch^{{{\,\mathrm{perf}\,}}}_{{{\,\mathrm{tor}\,}}}(\mathcal {R})\) be the subcategory of complexes with torsion cohomology groups.
Definition 3.1
A graded invertible \(\mathcal {R}\)-module is a pair \((L, \alpha )\) where L is an invertible \(\mathcal {R}\)-module and \(\alpha : {{\,\mathrm{Spec}\,}}(\mathcal {R}) \rightarrow \mathbb {Z}\) is a locally constant map. Two graded invertible \(\mathcal {R}\)-modules \((L, \alpha )\) and \((L', \alpha ')\) are said to be isomorphic if \(\alpha = \alpha '\) and L and \(L'\) are isomorphic as \(\mathcal {R}\)-modules. For two graded invertible \(\mathcal {R}\)-modules \((L, \alpha ), (L', \alpha ')\), we define
Then \(({{\,\mathrm{Hom}\,}}_{\mathcal {R}}(L, \mathcal {R}), -\alpha )\) is the inverse of \((L, \alpha )\).
Definition 3.2
For a finitely generated projective \(\mathcal {R}\)-module F, let \({{\,\mathrm{rank}\,}}(F)\) denote the (locally constant) rank of F, and define the determinant of F by
which is a graded invertible \(\mathcal {R}\)-module. Let \({{\,\mathrm{Det}\,}}_{\mathcal {R}}^{-1}(F)\) be the inverse of \({{\,\mathrm{Det}\,}}_{\mathcal {R}}(F)\). \(\square \)
Lemma 3.3
The following statements hold true.
(1) Let \(0 \rightarrow F' \rightarrow F \rightarrow F'' \rightarrow 0\) be an exact sequence of finitely generated projective \(\mathcal {R}\)-modules. Then we have a canonical isomorphism \({{\,\mathrm{Det}\,}}_{\mathcal {R}}(F) \simeq {{\,\mathrm{Det}\,}}_{\mathcal {R}}(F') \otimes {{\,\mathrm{Det}\,}}_{\mathcal {R}}(F'')\).
(2) Let F and \(F'\) be finitely generated projective \(\mathcal {R}\)-modules. Then we have a canonical isomorphism
which is locally given by
Here r and \(r'\) denote the local rank of F and \(F'\), respectively.
The appearance of the sign is the reason of introducing the information of the rank in the definition of the determinant.
Definition 3.4
For each complex \(F \in Ch^{{{\,\mathrm{perf}\,}}}(\mathcal {R})\), we define its determinant by
Thanks to Lemma 3.3(2), this is independent from the ordering of \(\mathbb {Z}\). We denote by \({{\,\mathrm{Det}\,}}_{\mathcal {R}}^{-1}(F)\) its inverse.
Lemma 3.5
The following hold true.
(1) Let \(0 \rightarrow F' \rightarrow F \rightarrow F'' \rightarrow 0\) be an exact sequence in \(Ch^{{{\,\mathrm{perf}\,}}}(\mathcal {R})\). Then we have a natural isomorphism \({{\,\mathrm{Det}\,}}_{\mathcal {R}}(F) \simeq {{\,\mathrm{Det}\,}}_{\mathcal {R}}(F') \otimes _{\mathcal {R}} {{\,\mathrm{Det}\,}}_{\mathcal {R}}(F'')\).
(2) If F is acyclic, then we have a natural isomorphism \({{\,\mathrm{Det}\,}}_{\mathcal {R}}(F) \simeq (\mathcal {R}, 0)\).
(3) Every quasi-isomorphism \(F' \rightarrow F\) induces an isomorphism \({{\,\mathrm{Det}\,}}_{\mathcal {R}}(F') \simeq {{\,\mathrm{Det}\,}}_{\mathcal {R}}(F)\).
Proof
(1) and (2) follow from Lemma 3.3(1).
(3) Consider the mapping cone \(F''\) of \(F' \rightarrow F\). Then we have an exact sequence \(0 \rightarrow F \rightarrow F'' \rightarrow F'[1] \rightarrow 0\). Since \(F''\) is acyclic, (1) and (2) imply
Now the observation \({{\,\mathrm{Det}\,}}_{\mathcal {R}}(F'[1]) \simeq {{\,\mathrm{Det}\,}}_{\mathcal {R}}^{-1}(F')\) completes the proof. \(\square \)
Definition 3.6
Suppose \(F \in Ch^{{{\,\mathrm{perf}\,}}}_{{{\,\mathrm{tor}\,}}}(\mathcal {R})\). Since \({{\,\mathrm{Frac}\,}}(\mathcal {R}) \otimes _{\mathcal {R}} F\) is acyclic, Lemma 3.5(2) gives a natural isomorphism \({{\,\mathrm{Det}\,}}_{{{\,\mathrm{Frac}\,}}(\mathcal {R})}({{\,\mathrm{Frac}\,}}(\mathcal {R}) \otimes _{\mathcal {R}} F) \simeq ({{\,\mathrm{Frac}\,}}(\mathcal {R}), 0)\). Therefore, we have a natural map
Here we disregard the degree since it is zero. From now on, we identify \({{\,\mathrm{Det}\,}}_{\mathcal {R}}(F)\) with its image in \({{\,\mathrm{Frac}\,}}(\mathcal {R})\). This defines a mapping \({{\,\mathrm{Det}\,}}_{\mathcal {R}}\) from the set of isomorphism classes of objects of \(D^{{{\,\mathrm{perf}\,}}}_{{{\,\mathrm{tor}\,}}}(\mathcal {R})\) to the set of fractional ideals of \(\mathcal {R}\).
Lemma 3.7
The map \({{\,\mathrm{Det}\,}}_{\mathcal {R}}\) that was just defined induces a group homomorphism \({{\,\mathrm{Det}\,}}_{\mathcal {R}}: K_0(D^{{{\,\mathrm{perf}\,}}}_{{{\,\mathrm{tor}\,}}}(\mathcal {R})) \rightarrow \mathcal {I}(\mathcal {R})\).
Proof
This follows from Lemma 3.5 (1) and (3). \(\square \)
As a preparation for the main arguments, we now formulate two lemmas, relating determinants to Fitting ideals.
Lemma 3.8
Let \(F \in D^{{{\,\mathrm{perf}\,}}}_{{{\,\mathrm{tor}\,}}}(\mathcal {R})\) be a complex and n be an integer. Suppose that we have \(H^i(F) = 0\) for any \(i \ne n\) and \({{\,\mathrm{pd}\,}}_{\mathcal {R}}(H^n(F)) \le 1\). Let \(\mathbb Q\) be the foll ring of quotients of \(\mathcal {R}\) and let \(\lambda =\lambda _{F_{\mathbb Q}}\) be the canonical trivialization \({{\,\mathrm{Det}\,}}_{\mathbb Q}(F_{\mathbb Q}) \rightarrow \mathbb Q\). Then we have
in \(\mathcal {I}(\mathcal {R})\).
Proof
By translation, we may and will assume that \(n = 0\). By using truncations, we see that the complex F is quasi-isomorphic to the complex \(H^0(F)[0]\). Taking a projective resolution of \(H^0(F)\) of length 2, we can construct a perfect complex \(F' \in Ch^{{{\,\mathrm{perf}\,}}}_{{{\,\mathrm{tor}\,}}}(\mathcal {R})\) which is quasi-isomorphic to F such that \((F')^i = 0\) for \(i \ne -1, 0\). We can assume that both \((F')^{-1}\) and \((F')^0\) are free \(\mathcal {R}\)-modules of the same rank a.
We take bases \(e_1, \ldots , e_a\) of \((F')^{-1}\) and \(f_1, \ldots , f_a\) of \((F')^{0}\). Then we can identify the homomorphism \(d: (F')^{-1} \rightarrow (F')^0\) with a matrix \(A \in M_a(\mathcal {R})\), and we have \({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}(H^0(\mathcal {R})) = (\det (A))\).
On the other hand, one may verify \({{\,\mathrm{Det}\,}}_{\mathcal {R}}(F')^{-1} = (\det (A))\). This is a standard fact, but we give a sketch of the proof for completeness. Let \(f_1^*, \ldots , f_a^*\) be the dual basis of \(f_1, \ldots , f_a\). Put \(\mathcal {Q}= {{\,\mathrm{Frac}\,}}(\mathcal {R})\) for notational simplicity. Then we have a natural isomorphism
under which the trivialization \({{\,\mathrm{Det}\,}}_{\mathcal {Q}}^{-1}(\mathcal {Q}\otimes _{\mathcal {R}} F') \simeq \mathcal {Q}\) is given by
for \(x_1, \dots , x_a \in \mathcal {Q}\otimes _{\mathcal {R}} (F')^{-1}\) and \(\varphi _1, \dots , \varphi _a \in {{\,\mathrm{Hom}\,}}_{\mathcal {Q}}((\mathcal {Q}\otimes _{\mathcal {R}} (F')^{0}) ,\mathcal {Q})\). Now
has \((e_1 \wedge \dots \wedge e_a) \otimes (f_1^* \wedge \dots \wedge f_a^*)\) as a basis over \(\mathcal {R}\) and it goes to
by the trivialization. This proves \({{\,\mathrm{Det}\,}}_{\mathcal {R}}(F')^{-1} = (\det (A))\). \(\square \)
Lemma 3.9
Let \(F \in D^{{{\,\mathrm{perf}\,}}}_{{{\,\mathrm{tor}\,}}}(\mathcal {R})\) be a complex and n be an integer. Suppose that we have \(H^i(F) = 0\) for \(i \ne n, n+1\) and \(H^i(F)\) does not contain any nonzero finite submodule for \(i = n, n+1\). Then we have
where the superscript \((-)^*\) denotes the Iwasawa adjoint.
Proof
By translation, we may assume that \(n = 0\). By using truncations, we see that the complex F is quasi-isomorphic to a complex \(F'\) such that \((F')^i = 0\) for \(i \ne 0, 1\). Moreover, the construction of the truncations allows us to assume \((F')^1\) is a projective \(\mathcal {R}\)-module. Then we have an exact sequence
We can construct a projective \(\mathcal {R}\)-module \(\overline{F}\) and a homomorphism \(\overline{F} \rightarrow (F')^0\) such that the composition \(\overline{F} \rightarrow (F')^0 \rightarrow (F')^1\) is an injective homomorphism with torsion cokernel. Then, by defining \(P_1\) and \(P_2\) as the cokernel of \(\overline{F} \rightarrow (F')^0\) and \(\overline{F} \rightarrow (F')^1\) respectively, we have an exact sequence
By the assumption, none of these modules contain any nonzero finite submodule. Then by the construction, we deduce that \({{\,\mathrm{pd}\,}}_{\mathcal {R}}(P^i) \le 1\) for \(i = 0, 1\). By a purely algebraic result (see [2, Lemma 5] or [13, Remark 4.8]), we have
On the other hand, by construction, the complex F is quasi-isomorphic to the complex \([P^0 \rightarrow P^1]\) located at degrees 0 and 1. Hence the distinguished triangle
shows that
The final equation follows from Lemma 3.8. This completes the proof. \(\square \)
4.2 Description of \(C_S\) by p-adic L-functions
Let us now go back to the arithmetic situation. Recall that it is our goal to determine the Fitting ideal of \(H^1(C_S)\). We first express it as a combination of determinants of one global and some local complexes.
Lemma 3.10
We have
Proof
By Lemma 3.8, we have
But the definition (2.5) of \(C_S\) and Lemma 3.7 imply
This completes the proof, since the shift by \(-2\) does not change the determinant. \(\square \)
Now we deal with the global term in the preceding lemma. The following is a formulation of an abelian equivariant main conjecture.
Theorem 3.11
We have
Proof
This is now a theorem of Johnston and Nickel. They have proved this theorem unconditionally in [12], using a recent celebrated theorem by Dasgupta and Kakde [5] on the strong Brumer-Stark conjecture. More precisely, the equivariant main conjecture was known to be true under the assumption of \(\mu =0\) by Ritter and Weiss [19], and Johnston and Nickel have succeeded in removing this condition.
For context, let us also explain how the equality in Theorem 3.11 can be deduced from the result of Ritter and Weiss in [19, §4] if one is willing to make the assumption \(\mu =0\). They constructed a certain exact sequence
of finitely generated torsion \(\mathcal {R}\)-modules with \({{\,\mathrm{pd}\,}}_{\mathcal {R}}({{\,\mathrm{Cok}\,}}(\Psi )) \le 1, {{\,\mathrm{pd}\,}}_{\mathcal {R}}({{\,\mathrm{Cok}\,}}(\psi )) \le 1\) (we do not give the definitions of \(\Psi \) and \(\psi \) here), and proved the equality
assuming the vanishing of the \(\mu \)-invariant. By Nickel [18, Theorem 2.4], the complex \(\mathcal {R}\Gamma (k_S/k, \mathbb {T}^{\vee }(1))^{\vee }\) is isomorphic in \(D^{{{\,\mathrm{perf}\,}}}_{{{\,\mathrm{tor}\,}}}(\mathcal {R})\) to the complex
located at degrees \(-1, 0\). So similarly as in the final paragraph of the proof of Lemma 3.9, we have
Thus we get Theorem 3.11 under the assumption of \(\mu =0\). \(\square \)
In preparation for the final part of the proof, we state another lemma, which by now seems to be well known. Recall \(\Gamma _K = {{\,\mathrm{Gal}\,}}(K_{\infty }/K)\) and put \(\Lambda = \mathbb {Z}_p[[\Gamma _K]]\), which is a subring of \(\mathcal {R}= \mathbb {Z}_p[[{\mathcal {G}}]]\). For a prime ideal \(\mathfrak {q}\) of \(\Lambda \), let \(\mathcal {R}_{\mathfrak {q}}\) be the localization of \(\mathcal {R}\) with respect to the multiplicative set \(\Lambda \setminus \mathfrak {q}\).
Lemma 3.12
Let \(f, g \in \mathcal {R}\) be non-zero-divisors and \(\mathcal {I}\) an ideal of \(\mathcal {R}\). Suppose that \(\mathcal {I}\mathcal {R}_{p\Lambda } = \mathcal {R}_{p\Lambda }\). If \(f\mathcal {I}= g\mathcal {I}\) holds, then \(f\mathcal {R}= g\mathcal {R}\) holds.
Now we compute the local contributions in Lemma 3.10.
Proposition 3.13
For every finite place v of k outside p, there exists a unique element \(f_v \in {{\,\mathrm{Frac}\,}}(\mathcal {R})^{\times }\) satisfying the following.
(1) We have
(2) For any continuous character \(\psi : {\mathcal {G}}\rightarrow \overline{\mathbb {Q}_p}^{\times }\) such that \(\psi |_{{\mathcal {G}}_v}\) is non-trivial, we have
Proof
Observe that property (2) ensures the uniqueness of \(f_v\).
Let \(\mathcal {R}_v = \mathbb {Z}_p[[{\mathcal {G}}_v]] \subset \mathcal {R}\) and \(\mathbb {T}_v = \mathbb {Z}_p(1) \otimes \mathcal {R}_v(\chi _{{\mathcal {G}}_v}^{-1})\), which is a local counterpart of \(\mathbb {T}\). Then \(\mathcal {R}\Gamma (k_v, \mathbb {T})\) is induced by \(\mathcal {R}\Gamma (k_v, \mathbb {T}_v)\), so
This reduces the problem to a completely local statement. We will in fact find \(f_v\) in the ring \({{\,\mathrm{Frac}\,}}(\mathcal {R}_v)\). Fix a place w of \(K_{\infty }\) above v so that \({\mathcal {G}}_v = {{\,\mathrm{Gal}\,}}(K_{\infty , w}/k_v)\).
Put \(n_v = {{\,\mathrm{ord}\,}}_p(N(v)-1) \ge 0\), which is the maximal integer such that \(\mu _{p^{n_v}} \subset k_v^{\times }\). Recall that \(\mathcal {T}_v\) is the inertia subgroup of v in \({\mathcal {G}}\). Since \(\mathcal {T}_v\) is a quotient of \(\mathcal {O}_{k_v}^{\times }\) by local class field theory, the p-Sylow subgroup \(\mathcal {T}_v^{(p)}\) of \(\mathcal {T}_v\) is a cyclic p-group of order at most \(p^{n_v}\). Fix a generator \(\delta _v\) of \(\mathcal {T}_v^{(p)}\).
We decompose \({\mathcal {G}}_v\) into \({\mathcal {G}}_v={\mathcal {G}}_{v}^{(p)} \times {\mathcal {G}}_{v}^{(p')}\) such that \({\mathcal {G}}_{v}^{(p)}\) is pro-p and \({\mathcal {G}}_v^{(p')}\) is of order prime to p. Then as in Sect. 1.4 we have \(\mathcal {R}_v=\mathbb {Z}_{p}[[{\mathcal {G}}_{v}]]=\bigoplus _{\chi } {\mathcal O}_{\chi } [[{\mathcal {G}}_{v}^{(p)}]]\) where \(\chi \) runs over equivalence classes of p-adic characters of \({\mathcal {G}}_{v}^{(p')}\). We also decompose \(\mathcal {T}_v = \mathcal {T}_{v}^{(p)} \times \mathcal {T}_{v}^{(p')}\) where \(\mathcal {T}_{v}^{(p)}\) is pro-p and \(\mathcal {T}_{v}^{(p')}\) is of order prime to p. Put \(\mathcal {T}_{v}'=\mathcal {T}_{v}^{(p')}\) and \(\mathcal {R}_{v}'=\mathbb {Z}_p[[{\mathcal {G}}_v/\mathcal {T}_{v}']]\). Then we decompose \(\mathcal {R}_v=\mathbb {Z}_p[[{\mathcal {G}}_v]]\) as
where \(\chi \) runs over the equivalent classes of characters of \({\mathcal {G}}_{v}^{(p')}\), which are non-trivial on \(\mathcal {T}_{v}'\). We define an element \(f_v\) of \({{\,\mathrm{Frac}\,}}(\mathcal {R}_v)\) such that
using the identification (3.1).
We shall show that this element satisfies the desired properties (1) and (2); let us begin with the latter.
Property (2): Let \(\psi : {\mathcal {G}}_v \rightarrow \overline{\mathbb {Q}_p}^{\times }\) be a non-trivial continuous character.
First suppose that \(\psi \) is unramified at v. Then \(\psi \) is trivial on \(\mathcal {T}_{v}'\), \(\psi (\delta _v) = 1\), and \(\psi (N_{\mathcal {T}_v^{(p)}}) = \sharp \mathcal {T}_v^{(p)}\). Hence
Now suppose that \(\psi \) is ramified at v. If \(\psi \) is non-trivial on \(\mathcal {T}_{v}'\), then \(\psi (f_v) = 1\) by the definition of \(f_v\). Otherwise, \(\psi \) is non-trivial on \(\mathcal {T}_v^{(p)}\) and hence we have \(\psi (\delta _v) \ne 1\) and \(\psi (N_{\mathcal {T}_v^{(p)}}) = 0\). Therefore
Property (1): By Proposition 2.9 and Remark 2.8, we can apply Lemma 3.9 to obtain
Note that we have \((J_w)^* \simeq J_w\) by the simple description in Remark 2.8. By Lemma 3.12, this formula characterizes \({{\,\mathrm{Det}\,}}_{\mathcal {R}_v}(\mathcal {R}\Gamma (k_v, \mathbb {T}_v))\). Hence it is enough to show that
Recall the identification (3.1). Since the actions of \(\mathcal {T}_{v}'\) on \(\mathbb {Z}_p\) and \(J_w\) are trivial, the Eq. (3.2) for the \(\chi \)-part with \(\chi _{\mid \mathcal {T}_{v}'} \ne 1\) holds trivially. Thus we have only to worry about the \(\mathcal {R}_{v}'=\mathbb {Z}_p[[{\mathcal {G}}_v/\mathcal {T}_{v}']]\)-component.
First we suppose \(\mu _p \not \subset k_v^{\times }\), namely \(n_v = 0\). Since \(\mathcal {T}_v^{(p)}=1\), we have \(\mathcal {T}_v=\mathcal {T}_{v}'\) and \(\mathcal {R}_{v}' = \mathbb {Z}_p[[{\mathcal {G}}_v/\mathcal {T}_v]]\), whose augmentation ideal is generated by \(1 - \sigma _v\). Then the \(\mathcal {R}_{v}'\)-component of the Eq. (3.2) says
as ideals. Here we used Remark 2.8 and \(\kappa _v(\sigma _v) = N(v)\) in the latter case.
We shall show that \(\sigma _v - N(v)\) is a unit of \(\mathcal {R}_{v}'\) when \(\mu _{p^{\infty }}(K_{\infty , w}) = 0\). To do this, by Nakayama’s lemma, it is enough to show \(\chi (\sigma _v) - N(v) \in {\mathcal O}_{\chi }^{\times }\) for every character \(\chi \) of \({\mathcal {G}}_{v}^{(p')}\) which is trivial on \(\mathcal {T}_{v}'\). Put \(f=\#({\mathcal {G}}_{v}^{(p')}/\mathcal {T}_{v}')\). Since \(\chi (\sigma _v)^{f}=1\), it suffices to show \(N(v)^f \not \equiv 1 \pmod {p}\). Let M be the maximum intermediate field of \(K_{\infty , w}/k_v\) such that \(M/k_v\) is a finite unramified extension of degree prime to p, so \({{\,\mathrm{Gal}\,}}(M/k_v)={\mathcal {G}}_{v}^{(p')}/\mathcal {T}_{v}'\). Our assumption \(\mu _{p^{\infty }}(K_{\infty , w}) = 0\) implies \(\mu _p \not \subset M^{\times }\). Since the residue field of M is \(\mathbb {F}_{N(v)^f}\), it follows that \(N(v)^f \not \equiv 1 \pmod {p}\).
Next we suppose \(\mu _p \subset k_v^{\times }\). Take a lift \(\widetilde{\sigma _v} \in {\mathcal {G}}_v\) of \(\sigma _v\). Then we have
Hence the Eq. (3.2) on \(\mathcal {R}_{v}'\) says
By \(N_{\mathcal {T}_v^{(p)}}(\delta _v - 1) = 0\), the each side is generated by \((\delta _v-1)^2\) and
respectively. Thus, it is enough to show that the difference of these elements,
is contained in the ideal \((\delta _v-1)^2\). By \(\delta _v^{p^{n_v}} = 1\), we have
Since \(N(v) - 1\) is an element of \(p^{n_v}\mathbb {Z}_p\) by the definition of \(n_v\), this implies \((N(v)-1)(\delta _v-1) \in (\delta _v-1)^2\). This completes the proof. \(\square \)
4.3 Proof of Theorem 0.1
By comparing the values given by the respective interpolation formulas, we have
where \(f_v\) is introduced in Proposition 3.13. Therefore, Lemma 3.10, Theorem 3.11, and Proposition 3.13 imply
Then Theorem 0.1 follows immediately from Corollary 2.12.
Remark 3.14
Let us give a direct argument showing that the right hand side of Theorem 0.1 is actually independent of the choice of S. Since this independence is a logical consequence of our main result, this verification is not strictly necessary, but we think that doing it anyway gives a nice consistence check for our result.
Let \(S_1 \supset S\) be another finite set and put \(S_1' = S_1 \setminus S_p\). By the exact sequence
we have an exact sequence
Note that all \(v \in S_1 \setminus S\) are unramified in \(K_{\infty }\). Since \({{\,\mathrm{pd}\,}}_{\mathcal {R}}(Z_v) \le 1\) for \(v \in S_1 \setminus S\), we obtain
(recall that \({{\,\mathrm{Fitt}\,}}^{[1]}_{\mathcal {R}}\) is again a Fitting invariant by [13, Theorem 2.6]). For \(v \in S_1 \setminus S\), the description \(Z_v = \mathcal {R}/ (1 - \sigma _v)\) shows
Hence, using Lemma 1.6(1), we obtain
This completes the proof of independence from the choice of S.
5 A strategy for computing \({{\,\mathrm{Fitt}\,}}^{[1]}_{\mathcal {R}}(Z_{S'}^0)\)
In this section, we look at methods of computing \({{\,\mathrm{Fitt}\,}}^{[1]}_{\mathcal {R}}(Z_{S'}^0)\). The motivation for this is fairly obvious: without any concrete information on this Fitting ideal, our main result would remain rather abstract and impractical. As one application among others, we will reprove in Sect. 5 a previous result of the third author [15].
Throughout this section, we assume that K/k is a p-extension.
5.1 The algebraic problem
We propose an algebraic problem whose full understanding (if it can be achieved) will help a lot in computing \({{\,\mathrm{Fitt}\,}}^{[1]}_{\mathcal {R}}(Z_{S'}^0)\).
Let p be a prime number and G a finite abelian p-group. We denote the group ring by \(R = \mathbb {Z}_p[G]\). Take subgroups \(G_1, \dots , G_r\) of G with \(r \ge 1\). We consider the R-module
and the R-submodule \(Z^0\) of Z, defined by the exact sequence
where the surjective map is the augmentation map. Now the algebraic problem is the following.
Problem 4.1
How can we construct a free R-resolution of \(Z^0\)?
In the subsequent sections, we will try to solve this problem. Before that, we explain how to utilize a solution of Problem 4.1 for a computation of \({{\,\mathrm{Fitt}\,}}^{[1]}_{\mathcal {R}}(Z_{S'}^0)\).
In the arithmetic situation as in Theorem 0.1, let \(K_n\) be the n-th layer of \(K_{\infty }/K\). Take n sufficiently large such that no places in \(S'\) split in \(K_{\infty }/K_n\). With this choice, put \(G = {{\,\mathrm{Gal}\,}}(K_n/k)\) and let \(G_v\) be the decomposition group of v in G. Then we can identify
Let us moreover put \(R = \mathbb {Z}_p[G]\), and note that \({{\,\mathrm{pd}\,}}_{\mathcal {R}}(R) \le 1\), since \(R = \mathcal {R}/ (\gamma _K^{p^n}-1)\mathcal {R}\) with \(\gamma _K \in \Gamma _K = {{\,\mathrm{Gal}\,}}(K_{\infty }/K)\) a topological generator.
For a matrix B over a commutative ring and a non-negative integer e, let \({{\,\mathrm{Min}\,}}_e(B)\) denote the ideal generated by the e-minors of B.
Proposition 4.2
In the above situation, let
be an exact sequence over R. We identify A with a matrix and take a lift \(\widetilde{A}\) of A over \(\mathcal {R}\). Then we have
Proof
The short exact sequence
provides an equality
Furthermore there is an exact sequence
By the definition of Fitting ideals, we obtain
\(\square \)
5.2 How to attack Problem 4.1: an idea
We explain a very general idea which will be essential in the subsequent sections. We shall construct a homological complex D of R-modules such that:
-
(a)
the components of D are finitely generated free R-modules;
-
(b)
D is located in degrees \(\ge 0\), that is, all components in degree \(\le -1\) are zero (remember that the numbering is homological, so the degrees increase when we go to the left);
-
(c)
D is exact except in degree 1, and
$$\begin{aligned} H_1(D) \simeq Z^0. \end{aligned}$$
We have to warn our readers right away that we have to write the degrees as superscripts, not as subscripts (which would be much more customary), in our homological complexes. We will need the subscript position later, to distinguish different complexes of similar type.
Such a complex D gives a way to compute \({{\,\mathrm{Fitt}\,}}^{[1]}_{\mathcal {R}}(Z^0_{S'})\) from a complex D as follows.
Proposition 4.3
Consider the arithmetic situation as in Proposition 4.2. Let
be a complex over R satisfying the above conditions (a)(b)(c). Put \(t_n = {{\,\mathrm{rank}\,}}_{R}(D^n)\) for \(n \ge 0\). We regard A as a matrix over R by choosing bases of \(D^3\) and \(D^2\), and take a lift \(\widetilde{A}\) over \(\mathcal {R}\). Then we have
Proof
By the properties (b) and (c), we have exact sequences
and
By the first sequence, the module \({{\,\mathrm{Ker}\,}}(d_1)\) is free of rank \(t_1-t_0\). Now Proposition 4.2 implies the assertion. \(\square \)
In order to construct such a complex D, we will first construct complexes C and \(C_i\) (\(i=1,\ldots ,r\)) which have similar properties. More precisely, (a) and (b) will hold without change; and (c) is modified to (c\('\)): C and \(C_i\) are exact except in degree 0, satisfying
Moreover, we will construct a morphism of complexes
which induces the augmentation homomorphism in degree 0 homology. Then, roughly speaking, D can be constructed by either taking the mapping cone of f or the cokernel of f; the choice between these two options will depend on the precise setting.
5.3 The most general situation
Let us describe a completely general method, even though its usefulness is limited because it produces modules with far too large ranks. The main ingredient is the standard resolution of finite groups, which we recall now.
Definition 4.4
Let G be a finite group. For each \(n \ge 0\), let \(B_n(G)\) be the free \(\mathbb {Z}_p[G]\)-module on the set \(\{(g_1, \dots , g_n) \mid g_1, \dots , g_n \in G\}\). For \(n \ge 1\), define a \(\mathbb {Z}_p[G]\)-homomorphism \(B_n(G) \rightarrow B_{n-1}(G)\) by
Moreover, define \(\varepsilon : B_0(G) \rightarrow \mathbb {Z}_p\) by sending the empty tuple (which is by definition the only basis element of \(B_0(G)\)) to 1.
The following is well known.
Proposition 4.5
The sequence
is exact.
Therefore, the complex
satisfies the conditions described above. Similarly, for each \(1 \le i \le r\), the complex
satisfies the required conditions, because then \(H_0(C_i) = \mathbb {Z}_p \otimes _{\mathbb {Z}_p[G_i]} \mathbb {Z}_p[G] = \mathbb {Z}_p[G/G_i]\).
For every \(i\in \{1,\ldots ,r\}\) there is a natural morphism \(C_i \rightarrow C\) induced by

where the vertical arrow in degree n sends the basis element \((g_1, \dots , g_n) \in B_n(G_i)\) to the “same” basis element \((g_1, \dots , g_n) \in B_n(G)\). Thus we have a morphism f as claimed in (4.1).
Let \(D = {{\,\mathrm{Cone}\,}}(f)\) be the mapping cone of f, so we have an exact sequence
Then the conditions (a)(b)(c) for D hold by construction.
5.4 A first special setting
As we said above, the above construction tends to lead to a free resolution of \(Z^0\) with extremely unwieldy terms. Motivated by this, we consider in this subsection the (fairly rare) case where
and moreover \(G_i\) is cyclic for each i. In this case, we shall obtain an alternative construction of \(C, C_i\), and D involving much smaller modules.
5.4.1 Definition of C
The construction of C will closely follow the approach of the first and the third author in [8]. For all i, we choose a generator \(\sigma _i\) of \(G_i\), and we denote by \(N_{G_i}\) the norm element of \(\mathbb {Z}_p[G_i]\). Define a complex \(E_i\) by
Then \(E_i\) is exact except for degree 0, and \(H_0(E_i) = \mathbb {Z}_p\). We define
which satisfies the conditions (a)(b)(c), since \(H_0(C) = \mathbb {Z}_p \otimes _{\mathbb {Z}_p} \dots \otimes _{\mathbb {Z}_p} \mathbb {Z}_p = \mathbb {Z}_p\).
The structure of C is fully described in [8]. In particular, for each \(n \ge 0\), the n-th component of C is the free R-module on the set of monomials
5.4.2 Definition of \(C_i\)
For each \(1 \le j \le r\), define
Thus, \(\mathbb {Z}_p[G_j]\) is placed in degree zero. Define \(C_i\) by
(Here, only the i-th component is \(E_i\), and all other components are \(E_j'\).) Then the conditions (a)(b)(c) hold because
Note that the structure of \(C_i\) is quite easy to understand. In a way, \(C_i\) arises from \(E_i\) via base change from the smaller group ring \(\mathbb {Z}_p[G_i]\) to the big group ring \(\mathbb {Z}_p[G]\). For each \(n \ge 0\), the n-th component of \(C_i\) is a free R-module of rank one, and the differentials are “the same” as in the complex \(E_i\). The definition of the complexes \(C_i\) is arranged in this particular way in order to make it possible to construct a map f of complexes below.
5.4.3 Definition of f
For each \(j \ne i\), we have a unique morphism \(E_j' \rightarrow E_j\) which is identity in degree 0. Together with the identity morphism \(E_i \rightarrow E_i\), we get a morphism \(C_i \rightarrow C\). Thus we obtain a morphism f as claimed in (4.1).
It is not hard to see that in degree n, the morphism f sends the canonical basis element of \(C_i\) to the basis element \(x_{i}^n\) of \(C^n\). This is a very special basis element, labeled by a power of one single variable \(x_i\); recall that the general basis element of \(C^n\) is labeled by a general monomial of degree n in \(x_1,\ldots , x_r\).
5.4.4 Definition of D
We can take the mapping cone of f to construct D as in Sect. 4.3. However, in our special case, it is much more efficient to consider the “cokernel” of f. The quotation marks are supposed to draw attention to the minor problem that f is not injective in degree 0. In fact, in degree 0, the morphism f looks like
On the other hand, in all strictly positive degrees, the morphism \(f: \bigoplus _{i=1}^r C_i \rightarrow C\) is fortunately injective and the cokernel is free over \(R = \mathbb {Z}_p[G]\). These facts can be read off from the description of f just given, in terms of the bases.
To avoid the minor problem in degree 0, we modify C to
where the acyclic complex \(Y = [\dots \rightarrow 0 \rightarrow \bigoplus _{i=1}^r \mathbb {Z}_p[G] \overset{{{\,\mathrm{id}\,}}}{\rightarrow } \bigoplus _{i=1}^r \mathbb {Z}_p[G] \rightarrow 0]\) is concentrated in degrees 1 and 0. Then we can extend f to an injective morphism \(f': \bigoplus _{i=1}^r C_i \rightarrow C'\) such that the cokernel \(D = {{\,\mathrm{Cok}\,}}(f': \bigoplus _{i=1}^r C_i \rightarrow C')\) satisfies the conditions (a)(b)(c). More precisely, we stipulate that in degree 0, the new component of \(f'\), that is, the additional morphism of complexes \(\bigoplus _{i=1}^{r} C_i \rightarrow Y\), is simply the identity morphism on \(\bigoplus _{i=1}^{r} \mathbb {Z}_p[G]\).
This completes the construction of D. Moreover the construction gives us a nice description of D at no expense at all. Indeed, the component \(D^n\) of D in any degree \(n \ge 2\) is the free R-module on the set
(Here is a catch phrase describing this set: Take all monomials of degree n and throw out the pure powers.) The structure morphisms of D are canonically induced by those of C.
5.4.5 Arithmetic situation
Let us get back to the arithmetic situation.
We assume \(K \cap k_{\infty } = k\) and also that every \(v \in S'\) is inert in \(K_{\infty }/K\). By this assumption, we can put \(G = {{\,\mathrm{Gal}\,}}(K/k)\) (see the text before Proposition 4.2). We label \(S' = \{v_1, \dots , v_r\}\), put the decomposition groups \(G_i = G_{v_i}\) for \(i = 1, \dots , r\), and we suppose that \(G = G_1 \times \dots \times G_r\) and each \(G_i\) is cyclic. Then, using the above information, it is possible to obtain much more precise information on \({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}(Z^0_{S'})\).
Example 4.6
Here is a modest numerical example. We take \(p=3\), \(k=\mathbb {Q}\) and K the compositum of the cubic extensions of \(\mathbb {Q}\) with conductor 7 and 223 respectively. The primes 7 and 223 stay inert in \(k_\infty \) because they are congruent to 1 modulo 3 but not modulo 9. We take \(S'=\{7,223\}\). The group \(G={{\,\mathrm{Gal}\,}}(K/\mathbb {Q})\) is the product of the two decomposition groups at 7 and 223, since these two primes are cubic residues modulo each other. This shows that we are indeed in the setting considered in this subsection with \(r = 2\). We have not made any effort to determine the modified Stickelberger element (even approximately), but this should be possible, in principle, by going over to the minus side and using classical cyclotomic Stickelberger elements.
Returning to the general case, we construct the complex D as above. Then the ranks \(t_n = {{\,\mathrm{rank}\,}}_R(D^n)\) satisfy \(t_0 = 1, t_1 = r, t_2 = r(r-1)/2\). Let A be the matrix that describes the differential \(d_3: D^3 \rightarrow D^2\) in the complex D constructed above, in the canonical bases. Then the rows (columns) of A are indexed by the monomials in \(x_1,\ldots ,x_r\) of degree 3 (degree 2 respectively), with the extra restriction that the pure powers \(x_i^3\) (\(x_i^2\) resp.) are omitted. In [8] and [10], the differential \(C^3 \rightarrow C^2\) was studied. It was described by a matrix \(\tilde{M}_r\), whose rows and columns were indexed in exactly the same fashion, with the only difference that the pure cubes and squares were still present as labels. Since D is obtained as a homomorphic image of C as discussed above, it is very simple to describe the new matrix A. It is obtained from \(\tilde{M}_r\) in [8, 10] by eliminating all rows with labels \(x_i^3\) and all columns with labels \(x_j^2\) (with \(1\le i,j \le r\)).
The entries of A are all of the form \(\nu _i\) or \(\tau _i\) (neglecting signs), where we put \(\nu _i = N_{G_i}\), the norm element, and \(\tau _i = \sigma _i-1\) for compatibility with [8]. Note that \(\tau _i\nu _i=0\). Since we are assuming \(K \cap k_{\infty } = k\), the natural map \(H = {{\,\mathrm{Gal}\,}}(K_{\infty }/k_{\infty }) \rightarrow G = {{\,\mathrm{Gal}\,}}(K/k)\) is an isomorphism, so the matrix A can be lifted to a matrix \(\widetilde{A}\) uniquely as a matrix over \(\mathbb {Z}_p[H]\). We denote this matrix \(\widetilde{A}\) simply by A. Similarly by abuse of notation, we use the same symbols \(\sigma _i, \nu _i, \tau _i\) in H, which are the canonical lifts from G. Then the entries of the lifted matrix \(A = \widetilde{A}\) have the same description in terms of \(\nu _i\) and \(\tau _i\). Now by Proposition 4.3, we have
where we put \(T = \gamma _K - 1\).
Let us first give examples where \(r = 2\) or \(r = 3\). When we write presentation matrices in this section, we use the row vector convention.
Example 4.7
Suppose that \(r=2\). Then we have
which shows that
Example 4.8
Suppose \(r = 3\). We then get:
Let us compute the 3-minors of A. To begin with, we easily see that neither \(\nu _{1}^2\tau _{2}\) nor \(\nu _{1}^2\tau _{3}\) appears as a minor. But \(\nu _{1}\nu _{2}\tau _{3}\) does appear. By a not overly tedious complete verification, one obtains the following result. Let
be the ideal of \(\mathcal {R}\) generated by the given list of elements. Then we find that
Thus we obtain in the case \(r=3\):
Let us now go back to general r. In the situation of the paper [10], which deals with the somewhat larger matrix \(\tilde{M}_r\) instead of A, the minors of \(\tilde{M}_r\) are completely determined for general r. Since A is a submatrix of \(\tilde{M}_r\), this certainly gives an upper bound for \({{\,\mathrm{Fitt}\,}}^{[1]}_{\mathcal {R}}(Z^0)\), which is already something to start with. We will be a little more ambitious and state a conjectural equality in a moment.
Our conjectural decription involves the notion of “admissible” \(\nu \)-monomials, which was already crucial in [10]. We quickly review the definition here and refer to that paper ([10, Section 1.2]) for more information.
A \(\nu \)-monomial is, by definition, any expression \(\nu _1^{f_1}\ldots \nu _r^{f_r}\) with exponents \(f_1, \dots , f_r \ge 0\). Similarly, one defines \(\tau \)-monomials. A \((\tau , \nu )\)-monomial is, by definition, a product \(z=xy\) with x a \(\tau \)-monomial and y a \(\nu \)-monomial. We also demand that the events \(\tau _i\) appears in x, and \(\nu _i\) appears in y do not happen simultaneously for any i (because if that happens, we get \(z=0\)). The \(\nu \)-part of such a \((\tau , \nu )\)-monomial z is simply y; we write \(\nu (z) = y\).
Definition 4.9
We say that a \(\nu \)-monomial \(y = \nu _1^{f_1}\ldots \nu _r^{f_r}\) is admissible if there is a permutation \(\sigma \) of \(\{1, 2, \dots , r\}\) satisfying
and
for any \(1 \le i \le r\).
Putting it very roughly: to be an admissible monomial, the exponents must not be distributed too unevenly.
Example 4.10
For \(r=3\), a \(\nu \)-monomial of degree 3 is admissible if and only if it is not the cube of one \(\nu _i\).
Suppose \(r=4\) and let us look at \(\nu \)-monomials of degree 6. Then for instance no exponent in an admissible monomial can exceed 3; but this does not suffice, since for example \(\nu _1^3\nu _2^3\) is not admissible either. On the other hand, \(\nu _1^3\nu _2^2\nu _3\) is admissible, and many other \(\nu \)-monomials as well.
The following is proved in [10].
Theorem 4.11
[10] For all \(e \ge 0\), the eth minor ideal \({{\,\mathrm{Min}\,}}_d(\tilde{M}_r)\) is generated by all \((\tau , \nu )\)-monomials of degree e whose \(\nu \)-part is admissible.
To state our conjecture, a little extra notation will be useful. For any \(\nu \)-monomial y, let n(y) denote the number of indices i such that \(\nu _i\) occurs in y. Define \(M(d,\ell )\) to be the set of \((\tau , \nu )\)-monomials z of degree d such that \(\nu (z)\) is admissible and \(n(\nu (z))\ge \ell \) (more simply put: which contain at least \(\ell \) different \(\nu _i\)). Finally, recall that \(t_2=r(r-1)/2\).
Conjecture 4.12
For all \(e\ge 0\), the e-th minor ideal \({{\,\mathrm{Min}\,}}_e(A)\) is generated by \(M(e, r-1-t_2+e)\).
Note that for all \(e\ge t_2-r-1\), the second argument of \(M(e,-)\) occurring here is non-positive, so the restricting condition concerning the number of \(\nu _i\) that must show up in the monomials is vacuously satisfied.
By the Eq. (4.3), this conjecture implies the following statement. We could call it the weak form of the above conjecture (which then would be called the strong form):
Conjecture 4.13
We keep the same notation and assumptions. Then the union of the following sets generates the ideal \({{\,\mathrm{Fitt}\,}}^{[1]}_{\mathcal {R}}(Z^0_{S'})\):
Here the last exponent \(t_2+1-r\) can be rewritten \((r-1)(r-2)/2\), and the last set \(M(0,r-1-t_2)\) only consists of the trivial monomial 1.
It is not difficult to see that these conjectures agree with the result of our calculations in the cases \(r = 2\) (Example 4.7) or \(r=3\) (Example 4.8). We think that we have verified it completely for \(r=4\) as well. However, a general proof for all r would probably require to revisit most of the technical arguments in [10], and we haven’t tried to do this.
We point out that while the latter conjecture seems logically weaker than the former, it is hard to image a proof (even partial) of the weaker conjecture which does not pass through a proof of the strong one.
5.5 Another special setting
In this subsection, apart from the setting in Sect. 4.4, we suppose that \(r=1\), so we are given only one subgroup \(G_1 \subset G\). In this case, we can decompose G as an abelian group into
where all factors \(G^{(j)}\) are non-trivial cyclic. Hence s is the p-rank of G. Moreover, we can arrange the decomposition so that
with subgroups \(G_1^{(j)} \subset G^{(j)}\). Note that this is where we use \(r=1\); in the general case, we cannot expect a decomposition of G into cyclic factors that is compatible with all subgroups \(G_i\).
Remark 4.14
An important remark is in order. In our arithmetical setting for abelian p-extension K/k, \(G_1\) is always the decomposition group \(G_v\) of a tamely ramified prime v in some abelian extension \(K_n/k\) with group G. Since the ramification group of such a prime is always cyclic, \(G_v\) is always generated by at most two elements as an abelian p-group. Thus in the last formula we can arrange things so as to have \(G_1 = G_1^{(1)} \times G_1^{(2)}\). But in practice, this reduction is possibly not too helpful, see a further comment below, where we do some calculations for the case \(s=2\).
5.5.1 Definition of \(C, C_1, f, D\)
Exactly as in Sect. 4.4.1, we fix a generator \(\sigma ^{(j)}\) of \(G^{(j)}\), for \(1\le j \le s\). We define a complex \(E^{(j)}\) for every j by (4.2), with \(G_i\) replaced by \(G^{(j)}\), and a complex \(C = E^{(1)} \otimes \dots \otimes E^{(s)}\). Moreover, we may define \(E_1^{(j)}\) exactly as \(E^{(j)}\), just replacing \(G^{(j)}\) by \(G_1^{(j)}\) and taking \((\sigma ^{(j)})^{m_j}\) as the chosen generator of \(G_1^{(j)}\), where we put \(m_j = (G^{(j)}: G_1^{(j)})\). Then we may put \(C_1 = (E_1^{(1)} \otimes \dots \otimes E_1^{(s)}) \otimes _{\mathbb {Z}_p[G_1]} \mathbb {Z}_p[G]\). It can be checked that C and \(C_1\) again satisfy the conditions (a)(b)(c). (Note that there is only one value of the index i now; \(i=1\).)
We can define a morphism \(f: E_1^{(j)} \rightarrow E^{(j)}\) explicitly. We stipulate that f is identity in every even degree, and f is multiplication by \(\mu ^{(j)} = 1 + \sigma ^{(j)} + \dots + (\sigma ^{(j)})^{m_j-1}\) in every odd degree. We omit some easy verifications that certain squares commute, making f into a morphism of complexes.
Hence we obtain a morphism \(f: C_1 \rightarrow C\). By taking the mapping cone of f, it is again possible to construct a complex D satisfying the conditions (a)(b)(c). However, the matrices representing the maps \(C_1^n \rightarrow C^n\) in each degree n will contain entries involving factors \(\mu ^{(j)}\). Since these elements are in general neither zero nor units in R, it cannot be expected (and indeed does not happen in general) that the degree-wise cokernels of f are again free over R. So it does not seem possible to replace the cone of f by the cokernel, and this makes the calculations more difficult.
5.5.2 Arithmetic situation
As in Sect. 4.4.5, we assume \(K \cap k_{\infty } = k\) and that every \(v \in S'\) is inert in \(K_{\infty }/K\). Put \(G = {{\,\mathrm{Gal}\,}}(K/k)\), which admits an isomorphism from \(H = {{\,\mathrm{Gal}\,}}(K_{\infty }/k_{\infty })\). Suppose that \(S'\) consists of a single place \(v_1\) and put \(G_1 = G_{v_1}\). Let s be the p-rank of G.
Example 4.15
First suppose \(s = 1\); we omit all super- and subscripts j, since \(j=1\) is the only value. For example, \(\sigma \) is a generator of G, \(\tau = \sigma - 1\), and \(m = (G: G_1)\). Let \(\widetilde{\nu }\) be the norm element of \(G_1\).
One can check that the ranks \(t_n\) of \(D^n\) are given by \(t_n = 2\) for \(n \ge 1\) and \(t_0 = 1\). The differential from \(D^3\) to \(D^2\) is given by the square matrix \(\begin{pmatrix} \tilde{\nu }&{} 1 \\ 0 &{} \tau \end{pmatrix}\). Let \(T = \gamma _K - 1\) be defined as in Sect. 4.4.5. By Proposition 4.3 again, we obtain:
For this case it is quite possible (and actually quicker) to calculate the left hand side directly, by finding a simple resolution of \(Z^0\) by hand; we did it, and the results agree.
Example 4.16
Next suppose \(s=2\). This case should be prototypical in a certain way, since (as pointed out in Remark 4.14) we can always assume that \(G_1\) has only two cyclic summands \(G_1^{(1)}\) and \(G_1^{(2)}\); of course s can be larger than 2. Even letting \(s=2\), we found the calculation rather cumbersome. Again, we need to take the cone, not the cokernel.
The R-ranks \(t_n\) of \(D^n\) are given by \(t_n = 2n + 1\) for \(n \ge 0\). We determined the matrix A of the differential \(D^3 \rightarrow D^2\). To write it down we have to review notation: For \(j = 1, 2\), \(\sigma ^{(j)}\) is a generator of \(G^{(j)}\) and \(m_j = (G^{(j)}: G_1^{(j)})\); we put
where \(n_j=ord(\sigma ^{(j)}) = \sharp G^{(j)}\). The outcome is the following 7 times 5 matrix:
up to sign. Using ideals generated by the minors of this matrix A, it is again possible to write down an expression that gives \({{\,\mathrm{Fitt}\,}}^{[1]}_{\mathcal {R}}(Z^0)\). But we have strong doubts whether such an expression would be very enlightening. All 5-minors are 0 (unless we made an error), but the minors of degree 4 and less seem to be so numerous and hard-to-describe that it is not really helpful to write them all down; in fact we gave up somewhere along the way.
6 Description of the Fitting ideal in the case that \({{\,\mathrm{Gal}\,}}(K/k)\) is cyclic
In this section, we concentrate on cyclic p-extensions K/k and we describe \({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}(X_{S_p})\) more explicitly from Theorem 0.1. We deduce two results from Theorem 0.1 (see Theorems 5.1 and 5.4). Both are a generalization of the main result of the third author in [15] where the case \([K:k] = p\) was studied. We keep the notations of Theorem 0.1. We assume throughout \(K \cap k_{\infty } = k\).
For each finite place v of k outside p, as in Sect. 1.4, \(\nu _{v}{:} {{\,\mathrm{Frac}\,}}(\mathbb {Z}_p[[{\mathcal {G}}/\mathcal {T}_v]])\) \(\rightarrow \) \({{\,\mathrm{Frac}\,}}(\mathbb {Z}_p[[{\mathcal {G}}]])\) is the map induced by the multiplication by \(N_{\mathcal {T}_v}=\sum _{\sigma \in \mathcal {T}_v} \sigma \). Recall that \(\sigma _v \in {\mathcal {G}}/\mathcal {T}_v\) is the Frobenius automorphism (Definition 1.1).
Put \(\Gamma _k = {{\,\mathrm{Gal}\,}}(k_{\infty }/k)\) and \(H = {{\,\mathrm{Gal}\,}}(K_{\infty }/k_{\infty })\). Then \(N_H = \sum _{h \in H} h\) also induces a map \({{\,\mathrm{Frac}\,}}(\mathbb {Z}_p[[\Gamma _k]]) \rightarrow {{\,\mathrm{Frac}\,}}(\mathbb {Z}_p[[{\mathcal {G}}]])\), which we denote by \(\nu _H\). Choose a topological generator \(\gamma \) of \(\Gamma _k\).
Theorem 5.1
Suppose that K/k is a cyclic p-extension and \(K \cap k_{\infty } = k\). Assume that we have a place \(v^* \in S'\) such that \(v^*\) is totally ramified in K/k and that \({\mathcal {G}}_{v^*} \supset {\mathcal {G}}_v\) holds for all \(v\in S'\). Then we have
Note that, since \(v^*\) is totally ramified in K/k, we have \(\nu _H = \nu _{v^*}\).
Before we prove this theorem, let us deduce a corollary which is exactly Theorem 0.1 (1) in [15].
In general, for the cyclotomic \(\mathbb {Z}_p\)-extension \(k_{\infty }/k\), let \(k_n\) denote its n-th layer. For each finite place v of k outside p, let \(n_v\) be the non-negative integer such that the decomposition field of v in \(k_{\infty }/k\) is \(k_{n_v}\). This use of \(n_v\) cancels an earlier meaning of \(n_v\) in the proof of Proposition 3.13. Note that, if v is totally ramified in \(K_{\infty }/k_{\infty }\), then \(\sigma _v\) is an element of \(\Gamma _k = {{\,\mathrm{Gal}\,}}(k_{\infty }/k)\) which generates the same subgroup as \(\gamma ^{p^{n_v}}\).
Corollary 5.2
[15, Theorem 0.1(1)] Suppose that K/k is a cyclic extension of degree p and that \(K \cap k_{\infty } = k\). Take \(S = S_p \cup S_{{{\,\mathrm{ram}\,}}}(K/k)\) and suppose that \(S' = S \setminus S_p \ne \emptyset \).Footnote 1 Then we have
Proof
In this situation, any \(v \in S'\) is totally ramified in K/k since its degree is p. Therefore, we have \(\nu _{v}=\nu _{H}\). Moreover, if we take \(v^* \in S'\) such that \(n_{v^*}\) is the minimum of the \(n_v\), \(v\in S'\), then \(v^*\) satisfies the condition in Theorem 5.1. Then it is not hard to see that
Thus Theorem 5.1 implies the corollary. \(\square \)
Remark 5.3
The equivalence of Theorem 5.2 and [15, Theorem 0.1] can be seen in the following way. First, the statement of [15] concerns \((A_{K(\mu _{p^{\infty }})}^{\omega })^{\vee }\), which is connected to \(X_{S_p}\) via the Kummer duality as we recalled in the Introduction. Second, the modified Stickelberger element \(\vartheta _{K(\mu _{p^{\infty }})}\) is defined in [15, (2.3.4)], using a modifying factor \(\xi \). This factor \(\xi \) corresponds to our modifying factor \(\prod _{v \in S'} f_v^{-1}\). Finally we remark that we removed the assumption \(\mu =0\) in [15], using Johnston and Nickel [12].
Proof of Theorem 5.1
By Theorem 0.1, it is enough to show
By Lemma 2.13, we have
since shifted Fitting ideals are multiplicative on direct sums. The second term in the right hand side is computed in Proposition 1.8. For the first term, it is enough to show
for any non-negative integer n.
In the rest of this calculation we will neglect some signs; this will play no role in the calculation of Fitting ideals via minors of certain matrices, and it spares us the effort of being precise about the signs of morphisms in the tensor product of complexes. These sign questions are certainly important in many settings, but for us they are inessential and would mess up some arguments.
We apply the arguments of Sects. 4.4 and 4.5 to
Take a generator \(\delta \) of \(H = {{\,\mathrm{Gal}\,}}(K_{\infty }/k_{\infty })\), which is identified with \({{\,\mathrm{Gal}\,}}(K_n/k_n) \subset G\). Let \(\gamma _K \in {{\,\mathrm{Gal}\,}}(K_{\infty }/K)\) be the lift of \(\gamma \in \Gamma _k\). As in Sect. 4.4, define complexes
and
where
with \(N_n = 1 + \gamma _K + \gamma _K^2 + \dots \gamma _K^{p^n-1}\) We have a natural injective homomorphism \(C_1 \rightarrow C\) whose cokernel D looks like
where \(d_2', d_3', \dots \) are obtained by removing both the final row and the final column of \(d_2, d_3, \dots \). From this complex D, we obtain an exact sequence
where \(\widetilde{d_3'}\) is any lift of \(d_3'\). Explicitly we can write down
and it is easy to see that the ideal generated by its \(2 \times 2\) minors is
Hence
This completes the proof. \(\square \)
Finally there is another variant, where there is no privileged place \(v^*\) and still the degree of the cyclic p-extension K/k can be arbitrary. The proof again uses the techniques of Sect. 4; but this time the reduction lemma 2.13 cannot be used. So one has to work with the full direct sum of “local” complexes \(C_i\), not just one of them, and this makes it inevitable to work with the cone, not the cokernel, of the map \(\bigoplus _i C_i \rightarrow C\) of complexes. This makes the proof more complicated, but it will be given in very explicit terms.
Theorem 5.4
Suppose that K/k is a cyclic p-extension with \(K \cap k_{\infty } = k\) as before, and let \(\delta \) denote a generator of \(H = {{\,\mathrm{Gal}\,}}(K_{\infty }/k_{\infty })\). Assume that the inertial degrees of all \(v\in S'\) in K/k are all 1 (that is, there is only ramification and splitting). Then \({{\,\mathrm{Fitt}\,}}^{[1]}_{\mathcal {R}}(X_{S_p})\) is generated by the following list of quantities:
and
where J runs through all proper subsets of \(S'\). The quantity corresponding to \(J=\emptyset \) is to be understood as 1.
Proof
We use the lift \(\gamma _K \in \Gamma _K\) of \(\gamma \in \Gamma \) to define \(T = \gamma _K - 1 \in \mathcal {R}\). We number \(S'=\{v_1,...,v_r\}\) and put \({\mathcal {G}}_i = {\mathcal {G}}_{v_i}\), \(\mathcal {T}_i = \mathcal {T}_{v_i}\), and \(\nu _i = \nu _{v_i} = \nu _{\mathcal {T}_i}\) for simplicity. By the assumption that the inertial degree of \(v_i\) in K/k is one, the decomposition field of \(v_i\) in \(K_{\infty }/k\) is an intermediate field of the cyclotomic \(\mathbb {Z}_p\)-extension \((K_{\infty })^{\mathcal {T}_i}/ K^{\mathcal {T}_i}\). Hence there is a unique lift \(\widetilde{\sigma _i} \in \Gamma _K\) of \(\sigma _i = \sigma _{v_i} \in {\mathcal {G}}/\mathcal {T}_i\). Put \(\delta _i = \delta ^{[H: \mathcal {T}_i]}\), which is a generator of \(\mathcal {T}_i\). Then \({\mathcal {G}}_v\) is generated by \(\delta _i\) and \(\widetilde{\sigma _i}\).
We have two exact sequences involving \(\mathbb {Z}_{p}\) and \(Z_{S'} = \bigoplus _{i=1}^{r} \mathbb {Z}_{p}[{\mathcal {G}}/{\mathcal {G}}_i]\), aligning in a commutative ladder as follows:

The second and the fourth vertical arrows from the right are the canonical maps, whose existence follow from the fact that T divides \(\widetilde{\sigma _i}-1\). (This would not have worked without assuming that \(v_i\) has no inertia in K/k.) The third vertical arrow from the right on the i-th component comes from multiplication by \(\mu _i = 1 + \delta + \dots + \delta ^{[H: \mathcal {T}_i]-1}\).
By the cone construction, we obtain a complex D of the form
where the term \(\mathcal {R}/(T)\) is located at degree 0. Here,
Recall that the degree n component of D is denoted by \(D^n\). By a property of the cone, the complex D is exact except in degree 1, and \(H_1(D) \simeq Z_{S'}^0\). Then as in the proof of Proposition 4.3, we have short exact sequences
and
Since we have \({{\,\mathrm{pd}\,}}_{\mathcal {R}}(D^n) \le 1\) for any degree n, the first exact sequence implies \({{\,\mathrm{pd}\,}}_{\mathcal {R}}({{\,\mathrm{Ker}\,}}(d_1)) \le 1\) and
Then the second exact sequence implies
By the description of \(d_3\) above, we easily see that the module \({{\,\mathrm{Cok}\,}}(d_3)\) has a presentation as an \(\mathcal {R}\)-module
(all blank entries being zero). To obtain \({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}({{\,\mathrm{Cok}\,}}(d_3))\), we have to compute the maximal minors of B. As a consequence, we shall show that \({{\,\mathrm{Fitt}\,}}_{\mathcal {R}}({{\,\mathrm{Cok}\,}}(d_3))\) is generated by the following elements:
where J runs through all proper subsets of \(\{1, 2, \dots , r\}\).
Let V run through all subsets of \(\{1, 2, \dots , 2r+2\}\) of cardinality \(r+1\), and let \(d_V\) be the determinant of the submatrix of B picking up the v-th rows for \(v \in V\) (we ignore the sign throughout). For each \(1 \le i \le r\), the i-th column in B is zero except for the i-th and \((r+1+i)\)-th rows. Hence \(d_V \ne 0\) only if, for each \(1 \le i \le r\), we have either \(i \in V\) or \(r+1+i \in V\). We divide the argument into two cases.
Case 1. There is (a unique) \(1 \le l \le r\) such that both \(l \in V\) and \(r+1+l \in V\) hold. In this case, putting \(J = (V \cap \{1, 2, \dots , r\}) \setminus \{l\}\), we can see that
where \(i \not \in J\) means i runs through \(\{1, 2, \dots , r\} \setminus J\). In this way, we obtain the third family of elements in (5.2).
Case 2. For each \(1 \le i \le r\), exactly one of \(i \in V\) or \(r+1+i \in V\) holds. Put \(J = \{1, 2, \dots , r\} \cap V\). Then exactly one of \(r+1 \in V\) or \(2r+2 \in V\) holds, and accordingly we obtain4
These elements are in the ideal generated by (5.2). Moreover, if we choose V to be \(\{1, 2, \dots , r, r+1\}\) and \(\{1, 2, \dots , r, 2r+2\}\) respectively, we can produce the first two elements in (5.2) among the \(d_V\).
We obtain Theorem 5.4 from (5.1), (5.2), and Theorem 0.1. \(\square \)
References
Burns, D., Flach, M.: On Galois structure invariants associated to Tate motives. Am. J. Math. 120, 1343–1397 (1998)
Burns, D., Greither, C.: Equivariant Weierstrass preparation and values of \(L\)-functions at negative integers. Doc. Math., 157–185 (2003). Kazuya Kato’s fiftieth birthday
Burns, D., Kurihara, M., Sano, T.: On zeta elements for \(\mathbb{G}_m\). Doc. Math. 21, 555–626 (2016)
Cornacchia, P., Greither, C.: Fitting ideals of class groups of real fields with prime power conductor. J. Number Theory 73, 459–471 (1998)
Dasgupta, S., Kakde, M.: On the Brumer–Stark Conjecture. arXiv:2010.00657 (2020)
Deligne, P., Ribet, K.A.: Values of abelian \(L\)-functions at negative integers over totally real fields. Invent. Math. 59(3), 227–286 (1980)
Greither, C.: Determining Fitting ideals of minus class groups via the equivariant Tamagawa number conjecture. Compos. Math. 143(6), 1399–1426 (2007)
Greither, C., Kurihara, M.: Tate sequences and Fitting ideals of Iwasawa modules. Algebra i Analiz 27(6), 117–149 (2015)
Greither, C., Kurihara, M.: Fitting ideals of Iwasawa modules and of the dual of class groups. Tokyo J. Math. 39(3), 619–642 (2017)
Greither, C., Kurihara, M., Tokio, H.: The second syzygy of the trivial \(g\)-module, and an equivariant main conjecture. In: Advanced Studies in Pure Mathematics vol. 86, Development of Iwasawa Theory – the Centennial of K. Iwasawa’s Birth, 317–349 (2020)
Greither, C., Popescu, C.D.: An equivariant main conjecture in Iwasawa theory and applications. J. Algebraic Geom. 24(4), 629–692 (2015)
Johnston, H., Nickel, A.: An unconditional proof of the abelian equivariant Iwasawa main conjecture and applications. (2020). arXiv:2010.03186
Kataoka, T.: Fitting invariants in equivariant Iwasawa theory. In: Advanced Studies in Pure Mathematics vol. 86, Development of Iwasawa Theory – the Centennial of K. Iwasawa’s Birth, 413–465 (2020)
Knudsen, F.F., Mumford, D.: The projectivity of the moduli space of stable curves. I. Preliminaries on “det” and “Div”. Math. Scand. 39(1), 19–55 (1976)
Kurihara, M.: On stronger versions of Brumer’s conjecture. Tokyo J. Math. 34(2), 407–428 (2011)
Kurihara, M.: Notes on the dual of the ideal class groups of CM-fields. J. Théor. Nombres Bordeaux (to appear)
Nekovář, J.: Selmer complexes. Astérisque 310, viii+559 (2006)
Nickel, A.: Equivariant Iwasawa theory and non-abelian Stark-type conjectures. Proc. Lond. Math. Soc. (3) 106 6, 1223–1247 (2013)
Ritter, J., Weiss, A.: Toward equivariant Iwasawa theory. II. Indag. Math. (N.S.) 15 4, 549–572 (2004)
Serre, J..-P.: Sur le résidu de la fonction zêta \(p\)-adique d’un corps de nombres. C. R. Acad. Sci. Paris Sér. A-B 287 4, A183–A188 (1978)
Tate, J.: The cohomology group of tori in finite Galois extensions of number fields. Nagoya Math. J. 27, 709–719 (1966)
Acknowledgements
The second-named author acknowledges support by JSPS KAKENHI Grant Number 19J00763.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Greither, C., Kataoka, T. & Kurihara, M. Fitting ideals of p-ramified Iwasawa modules over totally real fields. Sel. Math. New Ser. 28, 14 (2022). https://doi.org/10.1007/s00029-021-00731-5
Accepted:
Published:
DOI: https://doi.org/10.1007/s00029-021-00731-5