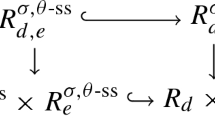K-theoretic Hall algebras, quantum groups and super quantum groups

Abstract

We prove that the K-theoretic Hall algebra of a preprojective algebra of affine type is isomorphic to the positive half of a quantum toroidal quantum group. We also compare super toroidal quantum groups of type A with some K-theoretic Hall algebras of quivers with potential introduced recently by Padurariu using categories of singularities of some Landau–Ginzburg models. The proof uses both a deformation of the K-theoretic Hall algebra and a dimensional reduction which allows us to compare the KHA of preprojective algebras to the K-theoretic Hall algebras of a quiver with potential.

Appendices

Proof of Lemma 2.4.3

We fix a total order on the set $\Pi$ such that the subset $X_{\leqslant O}=\bigcup _{O'\leqslant O}\mathcal {X}_{O'}$ is closed in X for each O. We have $\mathrm {G}_1(\mathcal {X}_O)^{\mathop {\text {top}}\nolimits }=\{0\}$ and the cycle map ${\mathop {\text {c}}\nolimits }_O:\mathrm {G}_0(\mathcal {X}_O)\rightarrow \mathrm {G}_0(\mathcal {X}_O)^{\mathop {\text {top}}\nolimits }$ is invertible. Thus, the localization exact sequence in topological and algebraic equivariant K-theory yields the following commutative diagram

The upper row and the lower rectangle are exact. Now, assume that ${\mathop {\text {c}}\nolimits }_{<O}$ is invertible and $\mathrm {G}_1(\mathcal {X}_{<O})^{\mathop {\text {top}}\nolimits }=\{0\}$. Then $\mathrm {G}_1(\mathcal {X}_{\leqslant O})^{\mathop {\text {top}}\nolimits }=\{0\}$. Further, the map $b_O$ is injective and ${\mathop {\text {c}}\nolimits }_{\leqslant O}$ is invertible by the five lemma. An induction implies that for each orbit O the following holds

• the maps ${\mathop {\text {c}}\nolimits }_{<O}$ and ${\mathop {\text {c}}\nolimits }_{\leqslant O}$ are invertible,

• $\mathrm {G}_1(\mathcal {X}_{<O})^{\mathop {\text {top}}\nolimits }=\mathrm {G}_1(\mathcal {X}_{\leqslant O})^{\mathop {\text {top}}\nolimits }=\{0\}.$

We deduce that the map $b_O$ is injective for each O, proving the lemma.

Proof of Lemma 2.5.2

We must check that the defining relations of $\mathbf {U}^+_{\mathrm {T},\mathrm {K}}$ hold in $\mathop {\text {SH}}\nolimits ^\diamond _{\mathrm {T},\mathrm {K}}$. Since Condition (2.6) holds, the kernel $\zeta ^\diamond _{\alpha ,\gamma }$ in (2.35) takes the following form

$$\begin{aligned} \zeta ^\diamond _{\alpha ,\gamma }= \prod _{\begin{array}{c} i,j\in Q_0\\ i<j \end{array}} \prod _{\begin{array}{c} 0<r\leqslant a_i\\ b_j\geqslant s>a_j \end{array}}\frac{q^{-a_{ij}}x_{i,r}-tx_{j,s}}{x_{i,r}-q^{-a_{ij}}tx_{j,s}} \cdot \prod _{i\in Q_0}\prod _{\begin{array}{c} 0<r\leqslant a_i\\ b_i\geqslant s>a_i \end{array}} \frac{q^{-2}x_{i,r}-x_{i,s}}{x_{i,r}-x_{i,s}}. \end{aligned}$$

Relations (a) and (b) are straightforward. Let us concentrate on (c). The proof of the relation (d) is similar way and is left to the reader. By the same argument as in [14], see also [27, § 10.4], it is enough to prove the following relation

$$\begin{aligned} \sum _{h+k=l}(-1)^h\, \psi ({\mathop {\text {e}}\nolimits }_{i,0})^{\diamond (h)}\diamond \psi ({\mathop {\text {e}}\nolimits }_{j,0})\diamond \psi ({\mathop {\text {e}}\nolimits }_{i,0})^{\diamond (k)}=0 ,\quad i\ne j ,\quad l=1-a_{i,j}, \end{aligned}$$

where $a^{\diamond (h)}$ is the q-divided power of a relative to the multiplication $\diamond$. We may assume that $i<j$. We’ll abbreviate $x_r=x_{i,r}$, $y=tx_{j,1}$. We have

$$\begin{aligned} \psi ({\mathop {\text {e}}\nolimits }_{i,0})^{\diamond (h)}=\frac{1}{[h]_q!}\mathop {\text {Sym}}\nolimits _x(\Delta _h) ,\quad \Delta _h=\prod _{0<r<s\leqslant h}\frac{q^{-2}x_r-x_s}{x_r-x_s}. \end{aligned}$$

We deduce that

$$\begin{aligned} \psi ({\mathop {\text {e}}\nolimits }_{i,0})^{\diamond (h)}\diamond \psi ({\mathop {\text {e}}\nolimits }_{j,0})=\frac{1}{[h]_q!} \mathop {\text {Sym}}\nolimits _x\Big (\Delta _h\cdot \prod _{r=1}^h\frac{q^{-a_{ij}}x_r-y}{x_r-q^{-a_{ij}}y}\Big )\,\Big . \end{aligned}$$

Hence, we have

$$\begin{aligned} \psi ({\mathop {\text {e}}\nolimits }_{i,0})^{\diamond (h)}\diamond \psi ({\mathop {\text {e}}\nolimits }_{j,0})\diamond \psi ({\mathop {\text {e}}\nolimits }_{i,0})^{\diamond (k)}= \frac{1}{[h]_q![k]_q!} \mathop {\text {Sym}}\nolimits _x\Big (\Delta _{k+h}\cdot \prod _{r=1}^h\frac{q^{-a_{ij}}x_r-y}{x_r-q^{-a_{ij}}y}\Big )\,\Big . \end{aligned}$$

We define

$$\begin{aligned}&F(x_1,\dots ,x_l,n)\\&\quad = \sum _{h=0}^l(-1)^hq^{nh}\left[ \begin{matrix}l\\ h\end{matrix}\right] _q\, \mathop {\text {Sym}}\nolimits _x\Big (\Delta _l\cdot \prod _{r=1}^h(q^{l-1-n}x_r-1)\cdot \prod _{s=h+1}^l(x_s-q^{l-1-n})\Big ). \end{aligned}$$

We must prove that $F(x_1,\dots ,x_l,0)$ vanishes. The Pascal identity for the q-Gaussian binomial coefficient implies that

$$\begin{aligned} F(x_1,\dots ,x_l,n)&=\mathop {\text {Sym}}\nolimits _x\left( \sum _{h=0}^{l-1}(-1)^hq^{(n-1)h}\left[ \begin{matrix}l-1\\ h\end{matrix}\right] _q\cdot \Delta _l\cdot \prod _{r=1}^h(q^{l-1-n}x_r-1)\right. \\&\quad \cdot \prod _{s=h+1}^l(x_s-q^{l-1-n})-\\&\quad \sum _{h=0}^{l-1}(-1)^hq^{n+l-1+(n-1)h}\left[ \begin{matrix}l-1\\ h\end{matrix}\right] _q\cdot \Delta _l\cdot \prod _{r=1}^{h+1}(q^{l-1-n}x_r-1)\\&\quad \left. \cdot \prod _{s=h+2}^l(x_s-q^{l-1-n}) \right) . \end{aligned}$$

We first check that $F(x_1,\dots ,x_l,n)$ does not depend on $x_1,\dots ,x_l$ by induction on l. Set $F(l-1,n-1)=F(x_1,\dots ,x_{l-1},n-1)$. The induction hypothesis implies that

$$\begin{aligned} F(x_1,\dots ,x_l,n)&=F(l-1,n-1)\sum _{k=1}^l\Bigg ( \prod _{\begin{array}{c} 0<r\leqslant l\\ r\ne k \end{array}}\frac{q^{-2}x_r-x_k}{x_r-x_k}(x_k-q^{l-1-n})-\\&\quad q^{n+l-1}\prod _{\begin{array}{c} 0<s\leqslant l\\ s\ne k \end{array}}\frac{q^{-2}x_k-x_s}{x_k-x_s} (q^{l-1-n}x_k-1)\Bigg ). \end{aligned}$$

We define

$$\begin{aligned} A=\prod _{r=1}^l\frac{q^{-2}x_r-z}{x_r-z}(z-q^{l-1-n})\frac{dz}{z} ,\quad B=-q^{n+l-1}\prod _{s=1}^l\frac{q^{-2}z-x_s}{z-x_s}(q^{l-1-n}z-1)\frac{dz}{z}. \end{aligned}$$

We have

$$\begin{aligned} (1-q^{-2})\,F(x_1,\dots ,x_l,n)&=F(l-1,n-1)\sum _{k=1}^l\big (\mathrm {res}_{x_k}A+\mathrm {res}_{x_k}B\big )\\&=-F(l-1,n-1)\big (\mathrm {res}_0A+\mathrm {res}_\infty A+\mathrm {res}_0B+\mathrm {res}_\infty B\big )\\&=F(l-1,n-1)(q^{-n-l-1}+q^{n+l-1}-q^{n-l-1}-q^{-n+l-1})\\&=q^{-1}F(l-1,n-1)(q^n-q^{-n})(q^{l}-q^{-l}). \end{aligned}$$

This proves our claim, and that

$$\begin{aligned} (1-q^{-2})\,F(l,n)=q^{-1}F(l-1,n-1)(q^n-q^{-n})(q^{l}-q^{-l}). \end{aligned}$$

Hence $F(l,0)=0$, proving the lemma.

Cohomological Hall algebra

We define the rational Borel–Moore homology $H_\bullet (-\!\,,\mathbb {Q})$ of a stack as in [20]. It is the dual of the cohomology with compact support $H^\bullet _c(-\!\,,\mathbb {Q})$. By the Borel–Moore homology of a dg-stack we’ll mean the Borel—Moore homology of its truncation. Similarly, the fundamental class of a dg-stack in Borel–Moore homology will mean the fundamental class of its truncation. The results in the previous sections have an analogue by replacing everywhere the rational Grothendieck group $\mathrm {G}_0(\text {-})\otimes \mathbb {Q}$ by the rational Borel–Moore homology $H_\bullet (\text {-},\mathbb {Q})$. Let us explain this briefly. For each linear algebraic group G we set $H_G^\bullet =H^\bullet (BG,\mathbb {Q})$. If $G=\mathbb {C}^\times$ then $H_G^\bullet =\mathbb {Q}[\hbar ]$ where $\hbar ={\mathop {\text {c}}\nolimits }_{1,G}$ is the first Chern class of the linear character q. If $G=\mathrm {T}=\mathbb {C}^\times \times \mathbb {C}^\times$ then $H_\mathrm {G}^\bullet =\mathbb {Q}[\hbar ,\varepsilon ]$ where $\hbar$, $\varepsilon$ are the first Chern classes of the characters q,  t of weight (1, 0) and (0, 1). We abbreviate $\mathrm {A}=H^\bullet _{\mathbb {C}^\times }$.

1.1 The Yangian of $\mathfrak {g}_Q$

Given an homogeneous weight function ${\bar{Q}}_1\rightarrow \mathrm {X}^*(\mathrm {T})$, we consider the dg-moduli stack $T^*\mathcal {X}$ of representations of the preprojective algebra $\Pi _Q$. The $\mathrm {R}$-algebra structure on $H_\bullet (T^*\mathcal {X},\mathbb {Q})$ and $H_\bullet (T^*\mathcal {X},\mathbb {Q})_\Lambda$ is as in [33], see also [20, 39]. The first algebra is called the cohomological Hall algebra of $\Pi _Q$, and the second one the nilpotent cohomological Hall algebra of $\Pi _Q$. Let us denote them by $\mathbf {H}(\Pi _Q)$ and $\mathbf {N}\mathbf {H}(\Pi _Q)$.

Given a $\mathrm {T}$-invariant potential potential W on a quiver Q, the deformed cohomological Hall algebras $\mathbf {H}(Q)_\mathrm {T}$ and $\mathbf {H}(Q,W)_\mathrm {T}$ of the quiver Q, with and without potential, are defined in [23] in the particular case where $\mathrm {T}=\{1\}$. They are studied further in several works, in particular in [5] in the triple quiver case.

Now, let the quiver Q be of Kac–Moody type. We define $\mathbf {Y}^+$ to be the positive part of the Yangian of $\mathfrak {g}_Q$. It is an $\mathrm {R}$-algebra generated by elements ${\mathop {\text {e}}\nolimits }_{i,r}$ with $i\in Q_0$ and $r\in \mathbb {N}$ modulo some relations which are analoguous to the relations (a) to (c) in Sect. 2.3.1. Let $[T^*\mathcal {X}_{\alpha _i}]$ be the fundamental class in $\mathbf {N}\mathbf {H}(\Pi _Q)_{\alpha _i}=H_\bullet (T^*\mathcal {X}_{\alpha _i}\,,\,\mathbb {Q}).$

The following theorem is analogous to Theorem 2.3.2.

Theorem C.1

Fix a normal weight function on ${\bar{Q}}$ in $\mathrm {X}^*(\mathbb {C}^\times )$.

• (a) There is a surjective $\mathbb {N}^{Q_0}$-graded $\mathrm {R}$-algebra homomorphism $\phi :\mathbf {Y}^+\rightarrow \mathbf {N}\mathbf {H}(\Pi _Q)$ such that $\phi ({\mathop {\text {e}}\nolimits }_{i,r})=({\mathop {\text {c}}\nolimits }_{1,G_{\alpha _i}})^r\cup [T^*\mathcal {X}_{\alpha _i}]$ for all $i\in Q_0$ and $r\in \mathbb {N}.$

• (b) If $Q$ is of finite or affine type but not of type $A^{(1)}$, then the map $\phi$ is injective. $\square$

The proof of Theorem 2.3.2 relies on two types of arguments : the geometric lemmas in Sect. 2.4, and the combinatorial Lemma 2.5.2 proved in Appendix B. The proof of Theorem C.1 is similar : the geometric lemma are proved in [5, 33], and the analogue of the computation in Appendix B is done in [39, App. A].

1.2 The Yangian of $\widehat{\mathfrak {s}\mathfrak {l}}(m|n)$

Let the quiver Q, the potential W and the $\mathrm {T}$-action on the representation space of Q be as in Sect. 3. Let $\varvec{\mathcal {Y}}^+_\mathrm {T}$ be the positive part of the affine Yangian of type $\mathfrak {s}\mathfrak {l}(m|n)$ with $(m,n)\ne (0,0)$ and $mn\ne 1,2$. It is the $H_\mathrm {T}^\bullet$-algebra generated by ${\mathop {\text {e}}\nolimits }_{i,r}$ with $i\in Q_0$ and $r\in \mathbb {N}$, subject to the defining relations $\mathrm {(a)}$ to $\mathrm {(d)}$ below, see [38].

• (a) if $a_{i,j}\ne 0$, then we have the Drinfeld relation

  $$\begin{aligned}{}[{\mathop {\text {e}}\nolimits }_{i,r}\,,\,{\mathop {\text {e}}\nolimits }_{j,s+1}]-[{\mathop {\text {e}}\nolimits }_{i,r+1}\,,\,{\mathop {\text {e}}\nolimits }_{j,s}]= -a_{i,j}\hbar \,\{{\mathop {\text {e}}\nolimits }_{i,r}\,,\,{\mathop {\text {e}}\nolimits }_{j,s}\} +m_{i,j}\varepsilon \,[{\mathop {\text {e}}\nolimits }_{i,r}\,,\,{\mathop {\text {e}}\nolimits }_{j,s}], \end{aligned}$$

• (b) if $a_{i,j}=0$, then we have the Drinfeld relation

  $$\begin{aligned}{}[\,{\mathop {\text {e}}\nolimits }_{i,r}\,,\,{\mathop {\text {e}}\nolimits }_{j,s}\,]=0, \end{aligned}$$

• (c) if i even and $j-i=\pm 1$, then we have the cubic Serre relation

  $$\begin{aligned} \mathop {\text {Sym}}\nolimits _r[\,{\mathop {\text {e}}\nolimits }_{i,r_1}\,,\,[\,{\mathop {\text {e}}\nolimits }_{i,r_2}\,,\,{\mathop {\text {e}}\nolimits }_{j,s}\,]]=0, \end{aligned}$$

• (d) if i odd and $i-1$, $i+1$ even, then we have the quartic Serre relation

  $$\begin{aligned} \mathop {\text {Sym}}\nolimits _r[\,{\mathop {\text {e}}\nolimits }_{i,r_1}\,,\,[\,{\mathop {\text {e}}\nolimits }_{i+1,s_1}\,,\,[{\mathop {\text {e}}\nolimits }_{i,r_2}\,,\,{\mathop {\text {e}}\nolimits }_{i-1,s_2}\,]]]=0. \end{aligned}$$

We used the following commutators

$$\begin{aligned}{}[\,a\,,\,b\,]=ab-(-1)^{|a|\,|b|}ba ,\quad \{\,a\,,\,b\,\}=ab+(-1)^{|a|\,|b|}ba. \end{aligned}$$

Let ${\mathop {\text {gr}}\nolimits }(-\!\,)$ denote the associated graded for the topological filtration, see below for more details. By [29, prop.5.3, cor.5.6] there is a Riemann–Roch map

$$\begin{aligned} {\mathop {\text {gr}}\nolimits }\mathbf {K}(Q,W)_\mathrm {T}\rightarrow \mathbf {H}(Q,W)_\mathrm {T},\quad {\mathop {\text {gr}}\nolimits }\mathbf {K}(Q)_\mathrm {T}\rightarrow \mathbf {H}(Q)_\mathrm {T}. \end{aligned}$$

It is a ring homomorphism. We have a decomposition

$$\begin{aligned} \mathbf {H}(Q)_\mathrm {T}=\bigoplus _\beta \mathbf {H}(Q)_{\beta ,\mathrm {T}} ,\quad \mathbf {H}(Q)_{\beta ,\mathrm {T}}=H_\bullet (\mathcal {X}_{\beta ,\mathrm {T}}\,,\mathbb {Q}). \end{aligned}$$

Let $[\mathcal {X}_{\beta ,\mathrm {T}}]$ be the fundamental class in $\mathbf {H}(Q)_{\beta ,\mathrm {T}}$. Let $i:\pi _0(\mathcal {W}_{\beta ,\mathrm {T}})\rightarrow \mathcal {X}_{\beta ,\mathrm {T}}$ be the inclusion of the zero fiber (underived) of the map $w_\beta :\mathcal {X}_{\beta ,\mathrm {T}}\rightarrow \mathbb {C}$. Let $\psi _{w_\beta },\varphi _{w_\beta }[-1]: D^{\mathop {\text {b}}\nolimits }_c(\mathcal {X}_{\beta ,\mathrm {T}})\rightarrow D^{\mathop {\text {b}}\nolimits }_c(\mathcal {X}_{\beta ,\mathrm {T}})$ be the nearby-cycle and vanishing-cycle functors. By definition of the cohomological Hall algebra of the quiver with potential (Q, W), see, e.g., [6], we have the decomposition

$$\begin{aligned} \mathbf {H}(Q,W)_\mathrm {T}=\bigoplus _\beta \mathbf {H}(Q,W)_{\beta ,\mathrm {T}} ,\quad \mathbf {H}(Q,W)_{\beta ,\mathrm {T}}=H_\bullet (\mathcal {X}_{\beta ,\mathrm {T}}\,,\,\varphi _{w_\beta }\mathbb {Q}[-1]). \end{aligned}$$

There are canonical morphisms of functors

$$\begin{aligned} \psi _{w_\beta }[-1]\rightarrow \varphi _{w_\beta }[-1]\rightarrow i^*, \end{aligned}$$

see [21, (8.6.7)]. It yields a map

$$\begin{aligned} H^\bullet _c(\mathcal {X}_{\beta ,\mathrm {T}}\,,\,\varphi _{w_\beta }\mathbb {Q}[-1])\rightarrow H^\bullet _c(\pi _0(\mathcal {W}_{\beta ,\mathrm {T}})\,,\,\mathbb {Q}). \end{aligned}$$

Recall that we defined

$$\begin{aligned} H_\bullet (\mathcal {W}_{\beta ,\mathrm {T}}\,,\,\mathbb {Q})=H_\bullet (\pi _0(\mathcal {W}_{\beta ,\mathrm {T}})\,,\,\mathbb {Q}). \end{aligned}$$

Taking the dual, we get a map

$$\begin{aligned} b:H_\bullet (\mathcal {W}_{\beta ,\mathrm {T}}\,,\,\mathbb {Q})\rightarrow H_\bullet (\mathcal {X}_{\beta ,\mathrm {T}}\,,\,\varphi _{w_\beta }\mathbb {Q}[-1])=\mathbf {H}(Q,W)_{\beta ,\mathrm {T}}. \end{aligned}$$

Let $[\mathcal {W}_{\beta ,\mathrm {T}}]$ denote both the fundamental class of $\pi _0(\mathcal {W}_{\beta ,\mathrm {T}})$ in $H_\bullet (\mathcal {W}_{\beta ,\mathrm {T}}\,,\,\mathbb {Q})$ and its image in $\mathbf {H}(Q,W)_{\beta ,\mathrm {T}}$ by the map b. The following theorem is analogous to Lemma 3.2.2 and Theorem 3.2.1.

Theorem C.2

• (a) There is an $\mathbb {N}^{Q_0}$-graded $H_\mathrm {T}^\bullet$-algebra homomorphism $\psi _0:\varvec{\mathcal {Y}}^+_\mathrm {T}\rightarrow \mathbf {H}(Q)_\mathrm {T}$ such that $\psi _0({\mathop {\text {e}}\nolimits }_{i,r})=({\mathop {\text {c}}\nolimits }_{1,G_{\alpha _i}})^r\cup [\mathcal {X}_{\alpha _i,\mathrm {T}}]$ for all $i\in Q_0$ and $r\in \mathbb {N}$.

• (b) There is an $\mathbb {N}^{Q_0}$-graded $H_\mathrm {T}^\bullet$-algebra homomorphism $\psi :\varvec{\mathcal {Y}}^+_\mathrm {T}\rightarrow \mathbf {H}(Q,W)_\mathrm {T}$ such that $\psi ({\mathop {\text {e}}\nolimits }_{i,r})=({\mathop {\text {c}}\nolimits }_{1,G_{\alpha _i}})^r\cup [\mathcal {W}_{\alpha _i,\mathrm {T}}]$ for all $i\in Q_0$ and $r\in \mathbb {N}$.

Proof

The proof of (a) is similar to the proof of Lemma 3.2.2. Let us concentrate on (b).

Given a linear algebraic group G, let $I_G$ be the augmentation ideal of $\mathrm {R}_G$. Let X be a quasi-projective G-scheme and $\mathcal {X}=[X\,/\,G]$ the quotient stack. The $I_G$-adic filtration of the $\mathrm {R}_G$-module $\mathrm {G}_0(\mathcal {X})$ is called the topological filtration, see, e.g., [8, §6]. Let $\widehat{\mathrm {G}_0(\mathcal {X})}$ be the completion with respect to this filtration. Assume that $\mathcal {X}$ is pure of dimension n. We define

$$\begin{aligned} \widehat{H_\bullet (\mathcal {X},\mathbb {Q})}=\prod _{a\geqslant 0}H_{2n-a}(\mathcal {X},\mathbb {Q}). \end{aligned}$$

Composing the Riemann–Roch isomorphism in (2.54) with the cycle map we get a map

$$\begin{aligned} {\widehat{\tau }}_\mathcal {X}:\widehat{\mathrm {G}_0(\mathcal {X})}\rightarrow \widehat{H_\bullet (\mathcal {X},\mathbb {Q})} \end{aligned}$$

which satisfies the usual properties, see [8, thm. 3.1] and [11, thm. 18.3]. Taking the associated graded with respect to the topological filtration, we get a map

$$\begin{aligned} \tau _\mathcal {X}:{\mathop {\text {gr}}\nolimits }{\mathrm {G}_0(\mathcal {X})}\rightarrow H_\bullet (\mathcal {X},\mathbb {Q})\end{aligned}$$

(C.1)

which is covariant for proper morphisms, contravariant for l.c.i. morphisms and which takes the class of $\mathcal {O}_\mathcal {Y}$ to the fundamental class $[\mathcal {Y}]$ for any pure dimensional closed substack $\mathcal {Y}$ of $\mathcal {X}$. The singularity K-theory group fits into an exact sequence

The topological filtration on $\mathrm {G}_0(\mathcal {X})$ induces a filtration on the quotient $\mathrm {G}_0^{\mathop {\text {sg}}\nolimits }(\mathcal {X})$. Let ${\mathop {\text {gr}}\nolimits }\,\mathrm {G}_0^{\mathop {\text {sg}}\nolimits }(\mathcal {X})$ be the associated graded.

Coming back to the setting of the theorem, we define

$$\begin{aligned} {\mathop {\text {gr}}\nolimits }\,\mathbf {K}(Q,W)_\mathrm {T}=\bigoplus _\beta {\mathop {\text {gr}}\nolimits }\,\mathrm {G}_0^{\mathop {\text {sg}}\nolimits }(\mathcal {W}_{\beta ,\mathrm {T}}). \end{aligned}$$

The map (C.1) yields a map

$$\begin{aligned} \tau _{\mathcal {W}_{\beta ,\mathrm {T}}}:{\mathop {\text {gr}}\nolimits }{\mathrm {G}_0(\mathcal {W}_{\beta ,\mathrm {T}})}\rightarrow H_\bullet (\mathcal {W}_{\beta ,\mathrm {T}},\mathbb {Q}). \end{aligned}$$

By [29, cor 5.6] there is an algebra homomorphism $\tau :{\mathop {\text {gr}}\nolimits }\,\mathbf {K}(Q,W)_\mathrm {T}\rightarrow \mathbf {H}(Q,W)_\mathrm {T}$ such that the following square commutes

There is a filtration on the algebra $\varvec{\mathcal {U}}^+_\mathrm {T}$ with associated graded ${\mathop {\text {gr}}\nolimits }\,\varvec{\mathcal {U}}^+_\mathrm {T}$ and an algebra homomorphism $\varvec{\mathcal {Y}}^+_\mathrm {T}\rightarrow {\mathop {\text {gr}}\nolimits }\,\varvec{\mathcal {U}}^+_\mathrm {T}$ such that the map $\psi :\varvec{\mathcal {U}}^+_\mathrm {T}\rightarrow \mathop {\mathbf {K}}\nolimits (Q,W)_\mathrm {T}$ in Theorem 3.2.1 is compatible with the filtrations. Composing $\tau$ with the associated graded ${\mathop {\text {gr}}\nolimits }\psi :{\mathop {\text {gr}}\nolimits }\,\varvec{\mathcal {U}}^+_\mathrm {T}\rightarrow {\mathop {\text {gr}}\nolimits }\mathop {\mathbf {K}}\nolimits (Q,W)_\mathrm {T}$ we get a map

$$\begin{aligned} \psi :\varvec{\mathcal {Y}}^+_\mathrm {T}\rightarrow \mathbf {H}(Q,W)_\mathrm {T}\end{aligned}$$

such that

$$\begin{aligned} \psi ({\mathop {\text {e}}\nolimits }_{i,0})=\tau \big ([\mathcal {O}_{\mathcal {W}_{\alpha _i,\mathrm {T}}}]\big ) =[\mathcal {W}_{\alpha _i,\mathrm {T}}],\quad \forall i\in Q_0. \end{aligned}$$

The map $\psi$ is the required algebra homomorphism. $\square$

We also have the following analogue of Conjecture 3.2.4.

Conjecture C.3

There is an $H_\mathrm {T}^\bullet$-algebra homomorphism $\rho :\mathbf {H}(Q,W)_\mathrm {T}\rightarrow \mathbf {H}(Q)_\mathrm {T}.$ The $H_\mathrm {T}^\bullet$-algebra homorphism $\psi _0:\varvec{\mathcal {Y}}^+_\mathrm {T}\rightarrow \mathbf {H}(Q)_\mathrm {T}$ factorizes through the map $\rho$ into the $H_\mathrm {T}^\bullet$-algebra homorphism $\psi :\varvec{\mathcal {Y}}^+_\mathrm {T}\rightarrow \mathbf {H}(Q,W)_\mathrm {T}$ and the latter is injective. $\square$

Mayer–Vietoris in equivariant K-theory

Let X be a T-equivariant quasi-projective variety with a covering $X=A\cup B$ where A, B are closed T-equivariant subsets of X. Let $Y=A\cap B$. The following lemma is a consequence of the Mayer–Vietoris long exact sequence for the K-theory of T-equivariant coherent sheaves. A well-known proof which goes back to Quillen and Thomason uses the K-theory spectrum of T-equivariant coherent sheaves. Let us indicate a simpler proof using only the localization exact sequence in equivariant K-theory. It is enough for our purpose.

Lemma D.1

There is an exact sequence

$$\begin{aligned} \mathrm {G}_0([Y\,/\,T])\rightarrow \mathrm {G}_0([A\,/\,T])\oplus \mathrm {G}_0([B\,/\,T])\rightarrow \mathrm {G}_0([X\,/\,T])\rightarrow 0. \end{aligned}$$

Proof

Set $U=X\setminus A$ and $V=X\setminus B$. We have $U=B\setminus Y$ and $V=A\setminus Y$. We consider the following commutative diagram

The localization long exact sequence yields the following commutative diagram with exact rows

We consider the maps

$$\begin{aligned} \alpha :\mathrm {G}_0([Y\,/\,T])\rightarrow \mathrm {G}_0([A\,/\,T])\oplus \mathrm {G}_0([B\,/\,T]),\quad \beta :\mathrm {G}_0([A\,/\,T])\oplus \mathrm {G}_0([B\,/\,T])\rightarrow \mathrm {G}_0([X\,/\,T]) \end{aligned}$$

by

$$\begin{aligned} \alpha =\begin{pmatrix}\ \ i^1_*\!i^2_*\end{pmatrix},\quad \beta =(i^3_*\ i^4_*). \end{aligned}$$

The map $\beta$ is surjective because for each element $x\in \mathrm {G}_0([X/T])$ there is an element $a\in \mathrm {G}_0([A/T])$ such that $j_2^*(a)=j_1^*(x)$. Hence $j_1^*(x-i^3_*(a))=0$. Thus, there is an element $b\in \mathrm {G}_0([B/T])$ such that $i_*^4(b)=x-i^3_*(a)$. We also have $\beta \circ \alpha =0$. Thus, it is enough to check that $\mathop {\text {Ker}}\nolimits (\beta )\subset \mathop {\text {Im}}\nolimits (\alpha )$. To do that, fix an element (a, b) in the kernel. Then, we have $i_*^3(a)=-i_*^4(b)$. Thus $j_2^*(a)=j^*_1i_*^3(a)=-j_1^*i_*^4(b)=0$. Hence $a=i_*^1(y)$ for some element $y\in \mathrm {G}_1([Y\,/\,T])$. We deduce that $i_*^4(b+i_*^2(y))=i_*^4(b)-i_*^3(a)=0$. So $b+i_*^2(y)=\partial (v)=i_*^2\delta (v)$ for some $v\in \mathrm {G}_1([V\,/\,T])$. Thus $b=i_*^2(-y+\delta (v))$. Hence

$$\begin{aligned} (a,b)=(i_*^1(y), i_*^2(-y+\delta (v)))=\alpha (y-\delta (z)). \end{aligned}$$

$\square$