Abstract
Let E/K be a finite Galois extension of totally real number fields with Galois group G. Let p be an odd prime and let \(r>1\) be an odd integer. The p-adic Beilinson conjecture relates the values at \(s=r\) of p-adic Artin L-functions attached to the irreducible characters of G to those of corresponding complex Artin L-functions. We show that this conjecture, the equivariant Iwasawa main conjecture and a conjecture of Schneider imply the ‘p-part’ of the equivariant Tamagawa number conjecture for the pair \((h^0(\mathrm {Spec}(E))(r), \mathbb {Z}[G])\). If \(r>1\) is even we obtain a similar result for Galois CM-extensions after restriction to ‘minus parts’.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let E/K be a finite Galois extension of number fields with Galois group G and let r be an integer. The equivariant Tamagawa number conjecture (ETNC) for the pair \((h^0(\mathrm {Spec}(E))(r), \mathbb {Z}[G])\) as formulated by Burns and Flach [17] asserts that a certain canonical element \(T\Omega (E/K,r)\) in the relative algebraic K-group \(K_0(\mathbb {Z}[G], \mathbb {R})\) vanishes. This element relates the leading terms at \(s=r\) of Artin L-functions to natural arithmetic invariants.
If \(r=0\) this might be seen as a vast generalization of the analytic class number formula for number fields, and refines Stark’s conjecture for E/K as discussed by Tate in [75] and the ‘Strong Stark conjecture’ of Chinburg [25, Conjecture 2.2]. It is known to imply a whole bunch of conjectures such as Chinburg’s ‘\(\Omega _3\)-conjecture’ [25, 26], the Rubin–Stark conjecture [68], Brumer’s conjecture, the Brumer–Stark conjecture (see [75, Chapitre IV, Sect. 6]) and generalizations thereof due to Burns [13] and the author [57]. If r is a negative integer, the ETNC refines a conjecture of Gross [42] and implies (generalizations of) the Coates–Sinnott conjecture [28] and a conjecture of Snaith [71] on annihilators of the higher K-theory of rings of integers (see [56]). If \(r>1\) the ETNC likewise predicts constraints on the Galois module structure of p-adic wild kernels [62].
The functional equation of Artin L-functions suggests that the ETNC at r and \(1-r\) are equivalent. This is not known in general, but leads to a further conjecture which is sometimes referred to as the local ETNC. Except for the validity of the local ETNC it therefore suffices to consider the (global) ETNC for either odd or even integers r. Note that the local ETNC is widely believed to be easier to settle. For instance, the ‘global epsilon constant conjecture’ of Bley and Burns [6] measures the compatibility of the closely related ‘leading term conjectures’ at \(s=0\) [12] and \(s=1\) [10] and is known to hold for arbitrary tamely ramified extensions [6, Corollary 7.7] and also for certain weakly ramified extensions [7].
Now suppose that E/K is a Galois extension of totally real number fields and let p be an odd prime. If \(r<0\) is odd Burns [14] and the author [60] independently have shown that the ‘p-part’ of the ETNC for the pair \((h^0(\mathrm {Spec}(E))(r), \mathbb {Z}[G])\) holds provided that a certain Iwasawa \(\mu _p\)-invariant vanishes (which conjecturally is always true). The latter condition is mainly present because the equivariant Iwasawa main conjecture (EIMC) for totally real fields then holds by independent work of Ritter and Weiss [67] and of Kakde [51].
The case \(r \ge 0\) is more subtle. Burns and Venjakob [22, 23] (see also [14, Corollary 2.8]) proposed a strategy for proving the p-part of the ETNC for the pair \((h^0(\mathrm {Spec}(E))(1), \mathbb {Z}[G])\). More precisely, this special case of the ETNC is implied by the vanishing of the relevant \(\mu _p\)-invariant, Leopoldt’s conjecture for E at p and the ‘p-adic Stark conjecture at \(s=1\)’. The latter conjecture relates the leading terms at \(s=1\) of the complex and p-adic Artin L-functions attached to characters of G by certain comparison periods. Note that Burns and Venjakob actually assume these conjectures for all odd primes p and then deduce the ETNC for the pair \((h^0(\mathrm {Spec}(E))(1), \mathbb {Z}[{\textstyle \frac{1}{2}}][G])\), but their approach has recently been refined by Johnston and the author [49] so that one can indeed work prime-by-prime.
There are similar results on minus parts if L/K is a Galois CM-extension with Galois group G, i.e. K is totally real and L is a totally complex quadratic extension of a totally real field \(L^+\). Namely, if \(r<0\) is even and \(\mu _p\) vanishes, then the minus p-part of the ETNC for the pair \((h^0(\mathrm {Spec}(L))(r), \mathbb {Z}[G])\) holds [14, 60]. Burns [15] recently proposed a strategy for proving the minus p-part of the ETNC in the case \(r=0\). In comparison with the strategy in the case \(r=1\), Leopoldt’s conjecture is replaced with the conjectural non-vanishing of Gross’s regulator [41], and the p-adic Stark conjecture is replaced with the ‘weak p-adic Gross–Stark conjecture’ [41, Conjecture 2.12b] (now a theorem for linear characters by work of Dasgupta, Kakde and Ventullo [32]). For an approach that only relies upon the validity of the EIMC we refer the reader to [58, 61].
The aim of this article is to propose a similar strategy in the remaining cases, i.e. we will consider the ETNC for Tate motives \(h^0(\mathrm {Spec}(L))(r)\) where \(r>1\) and L is a CM-field. Note that we can treat all integers \(r>1\) simultaneously as the ‘plus p-part’ of the ETNC for the pair \((h^0(\mathrm {Spec}(L))(r), \mathbb {Z}[G])\) naturally identifies with the corresponding conjecture for the extension \(L^+/K\) of totally real fields. We show that the p-adic Beilinson conjecture at \(s=r\), a conjecture of Schneider [69] and the EIMC imply the plus (resp. minus) p-part of the ETNC for the pair \((h^0(\mathrm {Spec}(L))(r), \mathbb {Z}[G])\) if r is odd (resp. even).
We follow the formulation of the p-adic Beilinson conjecture in [5]. It relates the values at \(s=r\) of the complex and p-adic Artin L-functions by certain comparison periods involving Besser’s syntomic regulator [4]. For absolutely abelian extensions variants of the p-adic Beilinson conjecture have been formulated and proved by Coleman [29], Gros [39, 40] and Kolster and Nguyen Quang Do [52]. Thus the p-adic Beilinson conjecture holds for absolutely abelian characters (see Sect. 3.13 for a precise statement).
Let us compare our approach to the earlier work mentioned above. The formulation of both the p-adic Beilinson conjecture and the p-adic Stark conjecture involves the choice of a field isomorphism \(j: \mathbb {C}\simeq \mathbb {C}_p\). We show in Sect. 3.12 that the p-adic Beilinson conjecture does not depend upon this choice if and only if a conjecture of Gross [42] holds. The latter is revisited in Sect. 3.8 and might be seen as a higher analogue of Stark’s conjecture; a similar result in the case \(r=1\) has recently been established by Johnston and the author in [49]. In both cases the independence of j is therefore equivalent to the rationality part of the appropriate special case of the ETNC. This eventually allows us to establish a prime-by-prime descent result analogous to [49, Theorem 8.1].
In a little more detail, we formulate conjectural ‘higher refined p-adic class number formulae’ analogous to [15, Conjecture 3.5] (where \(r=0\)), and show that these follow from the EIMC and Schneider’s conjecture in Sect. 4.6. Here, as will be shown in Sect. 4.5, the latter conjecture ensures that the relevant complexes are semisimple at all Artin characters as Leopoldt’s conjecture does in the case \(r=1\) and the non-vanishing of Gross’s regulator does in the case \(r=0\). This is a necessary condition in order to apply the descent formalism of Burns and Venjakob [23]. A second condition is the vanishing of the aforementioned Iwasawa \(\mu _p\)-invariant, but given recent progress of Johnston and the author [47, 50] on the EIMC without assuming \(\mu _p=0\), we wish to circumvent this hypothesis. For this purpose, we develop a different descent argument that makes no use of this assumption, but requires a more delicate analysis of the relevant complexes. The higher refined p-adic class number formula at \(s=r\) may then be combined with the p-adic Beilinson conjecture at \(s=r\) to deduce the plus, respectively minus, p-part of the ETNC for the pair \((h^0(\mathrm {Spec}(L))(r), \mathbb {Z}[G])\) in Sect. 4.7. For this, it is crucial to relate Besser’s syntomic regulators to Soulé’s p-adic Chern class maps [72] and the Bloch–Kato exponential maps [8] that appear in the formulation of the ETNC. This is carried out in Sect. 3.9 (in particular see Proposition 3.16). The formulation of the ETNC that is most suitable for our purposes is a reformulation due to the author [62]. This has primarily been introduced in order to construct (conjectural) annihilators of p-adic wild kernels.
Our prime example are totally real Galois extensions \(E/\mathbb {Q}\) with Galois group isomorphic to \(\mathrm {Aff}(q)\), where \(q = \ell ^n\) is a prime power and \(\mathrm {Aff}(q)\) denotes the group of affine transformations on the finite field \(\mathbb {F}_q\) with q elements. We show that Gross’s conjecture holds in this case (Theorem 3.14 (iv)). Moreover, the relevant cases of the EIMC hold unconditionally by recent work of Johnston and the author [47] (see also [50]) and the p-adic Beilinson conjecture reduces to the case of the trivial extension \(E^H/E^H\) where H denotes the subgroup \(\mathrm {GL}_1(\mathbb {F}_q)\) of \(\mathrm {Aff}(q)\). See Example 4.24 for more details.
Finally, we note that the ETNC for the pair \((h^0(\mathrm {Spec}(L))(r), \mathbb {Z}[G])\) has been verified for any integer r whenever L is abelian over the rationals by work of Burns, Greither and Flach [19, 20, 35]. However, if \(r>1\) and L is not absolutely abelian, then we are not aware of any previous (conditional) results that establish the (p-part of the) ETNC for the pair \((h^0(\mathrm {Spec}(L))(r), \mathbb {Z}[G])\).
1.1 Notation and conventions
All rings are assumed to have an identity element and all modules are assumed to be left modules unless otherwise stated. Unadorned tensor products will always denote tensor products over \(\mathbb {Z}\). For a ring \(\Lambda \) we write \(\zeta (\Lambda )\) for its center and \(\Lambda ^{\times }\) for the group of units in \(\Lambda \). For every field F we fix a separable closure \(F^c\) of F and write \(G_F := \mathrm {Gal}(F^c/F)\) for its absolute Galois group. If \(n>0\) is an integer coprime to the characteristic of F, we let \(\zeta _n\) denote a primitive nth root of unity in \(F^c\).
A finite Galois extension of totally real number fields will usually be denoted by E/K, whereas L/K denotes an arbitrary Galois extension of number fields. Galois CM-extensions will usually be denoted by L/K as well.
2 Algebraic preliminaries
2.1 Derived categories and Galois cohomology
Let \(\Lambda \) be a noetherian ring and let \(\mathrm {PMod}(\Lambda )\) be the category of all finitely generated projective \(\Lambda \)-modules. We write \({\mathcal {D}}(\Lambda )\) for the derived category of \(\Lambda \)-modules and \(\mathcal C^b(\mathrm {PMod}(\Lambda ))\) for the category of bounded complexes of finitely generated projective \(\Lambda \)-modules. Recall that a complex of \(\Lambda \)-modules is called perfect if it is isomorphic in \({\mathcal {D}}(\Lambda )\) to an element of \(\mathcal C^b(\mathrm {PMod}(\Lambda ))\). We denote the full triangulated subcategory of \({\mathcal {D}}(\Lambda )\) comprising perfect complexes by \({\mathcal {D}}^{\mathrm {perf}}(\Lambda )\).
If M is a \(\Lambda \)-module and n is an integer, we write M[n] for the complex
where M is placed in degree \(-n\). Note that this is compatible with the usual shift operator on cochain complexes.
Let L be an algebraic extension of the number field K. For a finite set S of places of K containing the set \(S_{\infty }\) of all archimedean places we let \(G_{L,S}\) be the Galois group over L of the maximal extension of L that is unramified outside S(L); here we write S(L) for the set of places of L lying above those in S. We let \({\mathcal {O}}_{L,S}\) be the ring of S(L)-integers in L. For any topological \(G_{L,S}\)-module M we write \(R\Gamma ({\mathcal {O}}_{L,S}, M)\) for the complex of continuous cochains of \(G_{L,S}\) with coefficients in M. If F is a field and M is a topological \(G_{F}\)-module, we likewise define \(R\Gamma (F,M)\) to be the complex of continuous cochains of \(G_{F}\) with coefficients in M.
If F is a global or a local field of characteristic zero, and M is a discrete or a compact \(G_F\)-module, then for \(r \in \mathbb {Z}\) we denote the rth Tate twist of M by M(r). Now fix a prime p and suppose that S also contains all p-adic places of K. Then for each integer i the cohomology group in degree i of \(R\Gamma ({\mathcal {O}}_{L,S}, \mathbb {Z}_p(r))\) naturally identifies with \(H^i_{\acute{\mathrm {e}}\mathrm {t}} ({\mathcal {O}}_{L,S}, \mathbb {Z}_p(r))\), the ith étale cohomology group of the affine scheme \(\mathrm {Spec}({\mathcal {O}}_{L,S})\) with coefficients in the étale p-adic sheaf \(\mathbb {Z}_p(r)\). We set \(H^i_{\acute{\mathrm {e}}\mathrm {t}} ({\mathcal {O}}_{L,S}, \mathbb {Q}_p(r)) := \mathbb {Q}_p \otimes _{\mathbb {Z}_{p}} H^i_{\acute{\mathrm {e}}\mathrm {t}} ({\mathcal {O}}_{L,S}, \mathbb {Z}_p(r))\).
2.2 Representations and characters of finite groups
Let G be a finite group and let F be a field of characteristic zero. We write \(R_{F}^{+}(G)\) for the set of characters attached to finite-dimensional F-valued representations of G, and \(R_{F}(G)\) for the ring of virtual characters generated by \(R_{F}^{+}(G)\). Moreover, we denote the subset of irreducible characters in \(R_{F}^{+}(G)\) and the ring of F-valued virtual characters of G by \(\mathrm {Irr}_{F}(G)\) and \(\mathrm {Char}_{F}(G)\), respectively.
For a subgroup H of G and \(\psi \in R_{F}^{+}(H)\) we write \(\mathrm {ind}_{H}^{G} \psi \in R_{F}^{+}(G)\) for the induced character; for a normal subgroup N of G and \(\chi \in R_{F}^{+}(G/N)\) we write \(\mathrm {infl}_{G/N}^{G} \chi \in R_{F}^{+}(G)\) for the inflated character. For \(\sigma \in \mathrm {Aut}(F)\) and \(\chi \in \mathrm {Char}_{F}(G)\) we set \(\chi ^{\sigma } := \sigma \circ \chi \) and note that this defines a group action from the left even though we write exponents on the right of \(\chi \). We denote the trivial character of G by \(\mathbbm {1}_{G}\).
2.3 \(\chi \)-twists
Let G be a finite group and let F be a field of characteristic zero. If M is a \(\mathbb {Z}[G]\)-module we let \(M^G\) be the maximal submodule of M upon which G acts trivially. Likewise we write \(M_G\) for the maximal quotient module with trivial G-action. For any \(\chi \in R_{F}^{+}(G)\) we fix a (left) F[G]-module \(V_{\chi }\) with character \(\chi \). For any F[G]-module M and any \(\alpha \in \mathrm {End}_{F[G]}(M)\) we write \(M^{\chi }\) for the F-vector space
and \(\alpha ^{\chi }\) for the induced map \((f \mapsto \alpha \circ f) \in \mathrm {End}_{F}(M^{\chi })\). We note that \(\det _{F}(\alpha ^{\chi })\) is independent of the choice of \(V_{\chi }\). The following is [49, Lemma 2.1] and very similar to [75, Chapitre I, 6.4].
Lemma 2.1
Let M be an F[G]-module and let \(\alpha \in \mathrm {End}_{F[G]}(M)\). Let H be a subgroup of G and let \(M |_{H}\) denote M considered as an F[H]-module. Let N be a normal subgroup of G and view \(M^N\) as an F[G/N]-module in the obvious way.
-
(i)
For \(\chi _{1},\chi _{2} \in R_{F}^{+}(G)\) one has \({\det }_{F}(\alpha ^{\chi _{1} + \chi _{2}}) = {\det }_{F}(\alpha ^{\chi _{1}}) {\det }_{F}(\alpha ^{\chi _{2}})\).
-
(ii)
For \(\chi \in R^{+}_{F}(H)\) there is an isomorphism \(M^{\mathrm {ind}^{G}_{H} \chi } \simeq (M |_{H})^{\chi }\) and an equality \({\det }_{F}(\alpha ^{\mathrm {ind}^{G}_{H} \chi }) = {\det }_{F}(\alpha ^{\chi })\).
-
(iii)
For \(\chi \in R^{+}_{F}(G/N)\) there is an isomorphism \(M^{\mathrm {infl}^{G}_{G/N} \chi } \simeq (M^{N})^{\chi }\) and an equality \({\det }_{F}(\alpha ^{\mathrm {infl}^{G}_{G/N} \chi }) = {\det }_{F}( (\alpha |_{M^{N}})^{\chi })\).
Let p be a prime. For each \(\chi \in \mathrm {Irr}_{\mathbb {C}_{p}}(G)\) we fix a subfield \(F_{\chi }\) of \(\mathbb {C}_p\) which is both Galois and of finite degree over \(\mathbb {Q}_p\) and such that \(\chi \) can be realized over \(F_{\chi }\). We write \(e_{\chi } := |G|^{-1} \chi (1) \sum _{g \in G} \chi (g) g^{-1}\) for the associated primitive central idempotent in \(\mathbb {C}_p[G]\) and choose an indecomposable idempotent \(f_{\chi }\) of \(F_{\chi }[G]e_{\chi }\). Let \({\mathcal {O}}_{\chi }\) be the ring of integers in \(F_{\chi }\) and choose a maximal \({\mathcal {O}}_{\chi }\)-order \({\mathcal {M}}_{\chi }\) in \(F_{\chi }[G]\) containing \(f_{\chi }\). Then \(T_{\chi } := f_{\chi } {\mathcal {M}}_{\chi }\) is an \({\mathcal {O}}_{\chi }\)-free right \({\mathcal {O}}_{\chi }[G]\)-module.
For any (left) \(\mathbb {Z}_p[G]\)-module M we define a (left) \({\mathcal {O}}_{\chi }[G]\)-module \(M[\chi ] := T_{\chi } \otimes _{\mathbb {Z}_{p}} M\), where \(g \in G\) acts upon \(t \otimes m\) by the rule \(g(t \otimes m) = t g^{-1} \otimes gm\) for all \(t \in T_{\chi }\) and \(m \in M\). We define \({\mathcal {O}}_{\chi }\)-modules \(M^{(\chi )} := M[\chi ]^G\) and \(M_{(\chi )} := M[\chi ]_G \simeq T_{\chi } \otimes _{\mathbb {Z}_p[G]} M\). We thereby obtain left, respectively right exact functors \(M \mapsto M^{(\chi )}\) and \(M \mapsto M_{(\chi )}\) from the category of \(\mathbb {Z}_p[G]\)-modules to the category of \({\mathcal {O}}_{\chi }\)-modules. Note that there is an isomorphism \(F_{\chi } \otimes _{{\mathcal {O}}_{\chi }} M^{(\chi )} \simeq (F_{\chi } \otimes _{\mathbb {Z}_{p}} M)^{\chi }\) for every finitely generated \(\mathbb {Z}_p[G]\)-module M.
Since multiplication by the trace \(\mathrm {Tr}_G := \sum _{g \in G} g\) gives rise to an isomorphism \(P_{(\chi )} \simeq P^{(\chi )}\) for each projective \(\mathbb {Z}_p[G]\)-module P (in fact for each cohomologically trivial G-module P), these functors extend to naturally isomorphic exact functors \({\mathcal {D}}^{\mathrm {perf}}(\mathbb {Z}_p[G]) \rightarrow {\mathcal {D}}^{\mathrm {perf}}({\mathcal {O}}_{\chi })\) (and \({\mathcal {D}}^{\mathrm {perf}}(\mathbb {Q}_p[G]) \rightarrow {\mathcal {D}}^{\mathrm {perf}}(F_{\chi })\)).
Lemma 2.2
Let \(\chi \in \mathrm {Irr}_{\mathbb {C}_{p}}(G)\) and let \(a \le b\) be integers. If \(C^{\bullet } \in {\mathcal {D}}^{\mathrm {perf}}(\mathbb {Z}_p[G])\) is acyclic outside [a, b], then \(C^{\bullet }_{(\chi )}\) is also acyclic outside [a, b] and there are natural isomorphisms of \({\mathcal {O}}_{\chi }\)-modules
For \(C^{\bullet } \in {\mathcal {D}}^{\mathrm {perf}}(\mathbb {Q}_p[G])\) we have isomorphisms \(H^i(C^{\bullet }_{(\chi )}) \simeq H^i(C^{\bullet })_{(\chi )} \simeq H^i(C^{\bullet })^{(\chi )}\) for every \(i \in \mathbb {Z}\).
Proof
Since (finitely generated) \(\mathbb {Q}_p[G]\)-modules are cohomologically trivial, the functors \(M \mapsto M^{(\chi )}\) and \(M \mapsto M_{(\chi )}\) are naturally isomorphic exact functors on the category of finitely generated \(\mathbb {Q}_p[G]\)-modules. The final assertion of the lemma is therefore clear.
Now suppose that \(C^{\bullet } \in {\mathcal {D}}^{\mathrm {perf}}(\mathbb {Z}_p[G])\) is acyclic outside [a, b]. If \(b-a \le 1\) the claim is [15, Lemma 5.1]. We repeat the short argument for convenience. Choose a complex \(A \rightarrow B\) of cohomologically trivial \(\mathbb {Z}_p[G]\)-modules that is isomorphic to \(C^{\bullet }\) in \({\mathcal {D}}(\mathbb {Z}_p[G])\). Here A and B are placed in degrees a and \(a+1\), respectively. Then we obtain a commutative diagram of \({\mathcal {O}}_{\chi }\)-modules

which implies the claim. If \(b-a \ge 2\) we choose a complex \(P^{\bullet } \in {\mathcal {C}}^b(\mathrm {PMod}(\mathbb {Z}_p[G]))\) that is isomorphic to \(C^{\bullet }\) in \({\mathcal {D}}(\mathbb {Z}_p[G])\) and consider the exact sequence of perfect complexes
where \(\tau _{\ge b-1}\) and \(\tau _{\le b-2}\) denote naive truncation. Note that the complexes \(\tau _{\ge b-1} P^{\bullet }\) and \(\tau _{\le b-2} P^{\bullet }\) are acyclic outside \([b-1,b]\) and \([a,b-2]\), respectively. It follows by induction that \(C^{\bullet }_{(\chi )}\) is acyclic outside [a, b] and, since \(H^b(C^{\bullet }) = H^b(\tau _{\ge b-1} P^{\bullet })\), that we have an isomorphism \(H^b(C^{\bullet }_{(\chi )}) \simeq H^b(C^{\bullet })_{(\chi )}\). If \(b-a \ge 3\) then we likewise have that \(H^a(C^{\bullet }) = H^a(\tau _{\le b-2} P^{\bullet })\) and we may again conclude by induction that we have an isomorphism \(H^a(C^{\bullet }_{(\chi )}) \simeq H^a(C^{\bullet })^{(\chi )}\). If \(b-a=2\) we may alternatively consider the exact sequence of perfect complexes
and deduce as above. \(\square \)
3 The p-adic Beilinson conjecture
3.1 Setup and notation
Let L/K be a finite Galois extension of number fields with Galois group G. For any place v of K we choose a place w of L above v and write \(G_w\) and \(I_w\) for the decomposition group and inertia subgroup of L/K at w, respectively. We denote the completions of L and K at w and v by \(L_w\) and \(K_v\), respectively, and identify the Galois group of the extension \(L_w / K_v\) with \(G_w\). For each non-archimedean place w we let \({\mathcal {O}}_w\) be the ring of integers in \(L_w\). We identify \(\overline{G_w} := G_w / I_w\) with the Galois group of the corresponding residue field extension which we denote by L(w) /K(v). Finally, we let \(\phi _w \in \overline{G_w}\) be the Frobenius automorphism, and we denote the cardinality of K(v) by N(v). We let S be a finite set of places of K containing the set \(S_{\infty }\) of archimedean places. If a prime p is fixed, we will usually assume that the set \(S_p\) of all p-adic places is also contained in S.
By a Galois CM-extension of number fields we shall mean a finite Galois extension L/K such that K is totally real and L is a CM-field. Thus complex conjugation induces a unique automorphism \(\tau \) in the center of G and we denote the maximal totally real subfield of L by \(L^+\). Then \(L^+/K\) is also Galois with group \(G^+ := G / \langle \tau \rangle \).
3.2 Higher K-theory
For an integer \(n \ge 0\) and a ring R we write \(K_n(R)\) for the Quillen K-theory of R. In the cases \(R = {\mathcal {O}}_{L,S}\) and \(R=L\) the groups \(K_n({\mathcal {O}}_{L,S})\) and \(K_n(L)\) are equipped with a natural G-action and for every integer \(r>1\) the inclusion \({\mathcal {O}}_{L,S} \subseteq L\) induces an isomorphism of \(\mathbb {Z}[G]\)-modules
Moreover, if \(S'\) is a second finite set of places of K containing S, then for every \(r>1\) there is a natural exact sequence of \(\mathbb {Z}[G]\)-modules
Both results (3.1) and (3.2) are due to Soulé [72]; see [77, Chapter V, Theorem 6.8]. We also note that sequence (3.2) remains left-exact in the case \(r=1\). The structure of the finite \(\mathbb {Z}[\overline{G_w}]\)-modules \(K_{2r-1}(L(w))\) has been determined by Quillen [63] (see also [77, Chapter IV, Theorem 1.12 and Corollary 1.13]) to be
3.3 The regulators of Borel and Beilinson
Let \(\Sigma (L)\) be the set of embeddings of L into the complex numbers; we then have \(|\Sigma (L)| = r_1 + 2 r_2\), where \(r_1\) and \(r_2\) are the number of real embeddings and the number of pairs of complex embeddings of L, respectively. For an integer \(k \in \mathbb {Z}\) we define a finitely generated \(\mathbb {Z}\)-module
which is endowed with a natural \(\mathrm {Gal}(\mathbb {C}/ \mathbb {R})\)-action, diagonally on \(\Sigma (L)\) and on \((2\pi i)^{-k}\). The invariants of \(H_k(L)\) under this action will be denoted by \(H_k^+(L)\), and it is easily seen that we have
The action of G on \(\Sigma (L)\) endows \(H_k^+(L)\) with a natural G-module structure.
Let \(r>1\) be an integer. Borel [9] has proved that the even K-groups \(K_{2r-2}({\mathcal {O}}_L)\) (and thus \(K_{2r-2}({\mathcal {O}}_{L,S})\) for any S as above by (3.2) and (3.3)) are finite, and that the odd K-groups \(K_{2r-1}({\mathcal {O}}_L)\) are finitely generated abelian groups of rank \(d_r\). More precisely, for each \(r>1\) Borel constructed an equivariant regulator map
with finite kernel. Its image is a full lattice in \(H_{1-r}^+(L) \otimes \mathbb {R}\). The covolume of this lattice is called the Borel regulator and will be denoted by \(R_r^{\mathrm {Bor}}(L)\). Moreover, Borel showed that
where \(\zeta _L^{*}(1-r)\) denotes the leading term at \(s=1-r\) of the Dedekind zeta function \(\zeta _L(s)\) attached to the number field L.
In the context of the ETNC, however, it is more natural to work with Beilinson’s regulator map [3]. By a result of Burgos Gil [11] Borel’s regulator map is twice the regulator map of Beilinson. Hence we will work with \(\rho _r := {\textstyle \frac{1}{2}}\rho _r^{\mathrm {Bor}}\) in the following.
Remark 3.1
We will sometimes refer to [62] where we have worked with Borel’s regulator map. However, if we are interested in rationality questions or in verifying the p-part of the ETNC for an odd prime p, the factor 2 essentially plays no role. In contrast, the p-adic Beilinson conjecture below predicts an equality of two numbers in \(\mathbb {C}_p\) so that this factor indeed matters.
3.4 The Quillen–Lichtenbaum conjecture
Fix an odd prime p and assume that S contains \(S_{\infty }\) and the set \(S_p\) of all p-adic places of K. Then for any integer \(r > 1\) and \(i=1,2\) Soulé [72] has constructed canonical G-equivariant p-adic Chern class maps
We need the following deep result.
Theorem 3.2
(Quillen–Lichtenbaum Conjecture) Let p be an odd prime. Then for every integer \(r > 1\) and \(i=1,2\) the p-adic Chern class maps \(ch^{(p)}_{r, i}\) are isomorphisms.
Proof
Soulé [72] proved surjectivity. Building on work of Rost and Voevodsky, Weibel [76] completed the proof of the Quillen–Lichtenbaum Conjecture. \(\square \)
Let p be a prime. For an integer \(n \ge 0\) and a ring R we write \(K_n(R; \mathbb {Z}_p)\) for the K-theory of R with coefficients in \(\mathbb {Z}_p\). The following result is due to Hesselholt and Madsen [43].
Theorem 3.3
Let p be an odd prime and let w be a finite place of L. Then for every integer \(r > 1\) and \(i=1,2\) there are canonical isomorphisms of \(\mathbb {Z}_p[G_w]\)-modules
3.5 Local Galois cohomology
We keep the notation of Sect. 3.1. In particular, L/K is a Galois extension of number fields with Galois group G. Let p be an odd prime. We denote the (finite) set of places of K that ramify in L/K by \(S_{\mathrm {ram}}\) and let S be a finite set of places of K containing \(S_{\mathrm {ram}}\) and all archimedean and p-adic places (i.e. \(S_{\infty } \cup S_p \cup S_{\mathrm {ram}} \subseteq S\)).
Let M be a topological \(G_{L,S}\)-module. Then M becomes a topological \(G_{L_w}\)-module for every \(w \in S(L)\) by restriction. For any \(i \in \mathbb {Z}\) we put
For any integers r and i we define \(P^i({\mathcal {O}}_{L,S}, \mathbb {Q}_p(r))\) to be \(P^i({\mathcal {O}}_{L,S}, \mathbb {Z}_p(r)) \otimes _{\mathbb {Z}_p} \mathbb {Q}_p\).
Lemma 3.4
Let \(r>1\) be an integer. Then we have isomorphisms of \(\mathbb {Q}_p[G]\)-modules
Proof
This is [62, Lemma 3.3] (see also [1, Lemma 5.2.4]). The case \(i=1\) will be crucial in the following so that we briefly recall its proof. Let \(w \in S_p(L)\) and put \(D_{dR}^{L_w}(\mathbb {Q}_p(r)) := H^0(L_w, B_{dR} \otimes _{\mathbb {Q}_p} \mathbb {Q}_p(r))\), where \(B_{dR}\) denotes Fontaine’s de Rham period ring. Then the Bloch–Kato exponential map
is an isomorphism for every \(w \in S_p(L)\) as follows from [8, Corollary 3.8.4 and Example 3.9]. Since the groups \(H^1_{\acute{\mathrm {e}}\mathrm {t}}(L_w, \mathbb {Z}_p(r))\) are finite for \(w \not \in S_p(L)\), we obtain isomorphisms of \(\mathbb {Q}_p[G]\)-modules
\(\square \)
3.6 Schneider’s conjecture
Let M be a topological \(G_{L,S}\)-module. For any integer i we denote the kernel of the natural localization map
by  . We call
. We call  the Tate–Shafarevich group of M in degree i. We recall the following conjecture of Schneider [69, p. 192].
the Tate–Shafarevich group of M in degree i. We recall the following conjecture of Schneider [69, p. 192].
Conjecture 3.5
(\(\mathrm {Sch}(L,p,r)\)) Let \(r \not =0\) be an integer. Then the Tate–Shafarevich group  vanishes.
vanishes.
Remark 3.6
It is not hard to show that Conjecture 3.5 does not depend on the choice of the set S.
Remark 3.7
Schneider originally conjectured that \(H^2_{\acute{\mathrm {e}}\mathrm {t}}({\mathcal {O}}_{L,S}, \mathbb {Q}_p / \mathbb {Z}_p (1-r))\) vanishes. Both conjectures are in fact equivalent (see [62, Proposition 3.8 (ii)]).
Remark 3.8
It can be shown that Schneider’s conjecture for \(r=1\) is equivalent to Leopoldt’s conjecture (see [54, Chapter X, Sect. 3]).
Remark 3.9
For a given number field L and a fixed prime p, Schneider’s conjecture holds for almost all r. This follows from [69, Sect. 5, Corollar 4] and [69, Sect. 6, Satz 3].
Remark 3.10
Schneider’s conjecture \(\mathrm {Sch}(L,p,r)\) holds whenever \(r<0\) by work of Soulé [72]; see also [54, Theorem 10.3.27].
For an integer r we let  .
.
Lemma 3.11
Let \(r\not =0\) be an integer and let p be an odd prime. Then the Tate–Shafarevich group  is torsion-free. In particular, Schneider’s conjecture \(\mathrm {Sch}(L,p,r)\) holds if and only if
is torsion-free. In particular, Schneider’s conjecture \(\mathrm {Sch}(L,p,r)\) holds if and only if  vanishes.
vanishes.
Proof
The first claim is [62, Proposition 3.8 (i)]. The second claim is immediate. \(\square \)
3.7 Artin L-series
Let L/K be a finite Galois extension of number fields with Galois group G and let S be a finite set of places of K containing all archimedean places. For any irreducible complex-valued character \(\chi \) of G we denote the S-truncated Artin L-series by \(L_S(s, \chi )\), and the leading coefficient of \(L_S(s, \chi )\) at an integer r by \(L_S^{*}(r, \chi )\). We shall sometimes use this notion even if \(L_S^{*}(r, \chi ) = L_S(r, \chi )\) (which will happen frequently in the following).
Recall that there is a canonical isomorphism \(\zeta (\mathbb {C}[G]) \simeq \prod _{\chi \in \mathrm {Irr}_{\mathbb {C}}(G)} \mathbb {C}\). We define the equivariant S-truncated Artin L-series to be the meromorphic \(\zeta (\mathbb {C}[G])\)-valued function
For any \(r \in \mathbb {Z}\) we also put
3.8 A conjecture of Gross
Let \(r>1\) be an integer. Since Borel’s regulator map (3.5) induces an isomorphism of \(\mathbb {R}[G]\)-modules, the Noether–Deuring Theorem (see [54, Lemma 8.7.1] for instance) implies the existence of \(\mathbb {Q}[G]\)-isomorphisms
Let \(\chi \) be a complex character of G and let \(V_{\chi }\) be a \(\mathbb {C}[G]\)-module with character \(\chi \). Composition with \(\rho _r \circ \phi _{1-r}\) induces an automorphism of \(\mathrm {Hom}_G(V_{{\check{\chi }}}, H_{1-r}^+(L) \otimes \mathbb {C})\). Let \(R_{\phi _{1-r}}(\chi ) = \det _{\mathbb {C}}((\rho _r \circ \phi _{1-r})^{\check{\chi }}) \in \mathbb {C}^{\times }\) be its determinant. If \(\chi '\) is a second character, then \(R_{\phi _{1-r}}(\chi + \chi ') = R_{\phi _{1-r}}(\chi ) \cdot R_{\phi _{1-r}}(\chi ')\) by Lemma 2.1 so that we obtain a map
where \(R(G) := R_{\mathbb {C}}(G)\) denotes the ring of virtual complex characters of G. We likewise define
Gross [42, Conjecture 3.11] conjectured the following higher analogue of Stark’s conjecture.
Conjecture 3.12
(Gross) We have \(A_{\phi _{1-r}}^S(\chi ^{\sigma }) = A_{\phi _{1-r}}^S(\chi )^{\sigma }\) for all \(\sigma \in \mathrm {Aut}(\mathbb {C})\).
Remark 3.13
It is not hard to see that Gross’s conjecture does not depend on S and the choice of \(\phi _{1-r}\) (see also [56, Remark 6]). A straightforward substitution shows that if it is true for \(\chi \) then it is true for \(\chi ^{\tau }\) for every choice of \(\tau \in \mathrm {Aut}(\mathbb {C})\).
We record some cases where Gross’s conjecture is known and deduce a few new cases. If \(q = \ell ^n\) is a prime power, we let \(\mathrm {Aff}(q)\) be the group of affine transformations on \(\mathbb {F}_q\). Thus we may write \(\mathrm {Aff}(q)\) as a semi-direct product \(N \rtimes H\), where \(H = \{ x \mapsto ax \mid a \in \mathbb {F}_{q}^{\times }\} \simeq \mathbb {F}_q^{\times }\) acts on \(N =\{ x \mapsto x+b \mid b \in \mathbb {F}_{q} \} \simeq \mathbb {F}_q\) in the natural way. Note that N is the commutator subgroup of \(\mathrm {Aff}(q)\).
Theorem 3.14
Let L/K be a finite Galois extension of number fields with Galois group G and let \(\chi \in R(G)\) be a virtual character. Let \(r>1\) be an integer. Then Gross’s conjecture (Conjecture 3.12) holds in each of the following cases.
-
(i)
\(\chi \) is absolutely abelian, i.e. there is a normal subgroup N of G such that \(\chi \) factors through \(G/N \simeq \mathrm {Gal}(L^N/K)\) and \(L^N/\mathbb {Q}\) is abelian;
-
(ii)
\(\chi = \mathbbm {1}_{G}\) is the trivial character;
-
(iii)
\(\chi \) is a virtual permutation character, i.e. a \(\mathbb {Z}\)-linear combination of characters of the form \(\mathrm {ind}_{H}^G \mathbbm {1}_H\) where H ranges over subgroups of G;
-
(iv)
\(G \simeq \mathrm {Aff}(q) = N \rtimes H\) and \(L^N/\mathbb {Q}\) is abelian;
-
(v)
\(L^{\ker (\chi )}\) is totally real and r is even;
-
(vi)
\(L^{\ker (\chi )} / K\) is a CM-extension, \(\chi \) is an odd character and r is odd.
Proof
We first note that (ii) is Borel’s result (3.6) above. Since Gross’s conjecture is invariant under induction and respects addition of characters, (ii) implies (iii). For (i), (v) and (vi) we refer the reader to [62, Theorem 5.2] and the references given therein. We now prove (iv). It suffices to show that Gross’s conjecture holds for every \(\chi \in \mathrm {Irr}_{\mathbb {C}}(G)\). If \(\chi \) is linear, it factors through G/N so that \(\chi \) is indeed absolutely linear. Thus Gross’s conjecture holds by (i). It has been shown in the proof of [49, Theorem 10.5] that there is a unique non-linear irreducible character \(\chi _{\mathrm {nl}}\) of G and that this character can be expressed as a \(\mathbb {Z}\)-linear combination of \(\mathrm {ind}_H^G \mathbbm {1}_H\) and linear characters in \(\mathrm {Irr}_{\mathbb {C}}(G)\). As Gross’s conjecture holds for the linear characters and for \(\mathrm {ind}_H^G \mathbbm {1}_H\) by (iii), it also holds for \(\chi _{\mathrm {nl}}\). \(\square \)
For any integer k we write
for the canonical \(\mathbb {C}[G \times \mathrm {Gal}(\mathbb {C}/ \mathbb {R})]\)-equivariant isomorphism which is induced by mapping \(l \otimes z\) to \((\sigma (l)z)_{\sigma \in \Sigma (L)}\) for \(l \in L\) and \(z \in \mathbb {C}\). Now fix an integer \(r>1\). We define a \(\mathbb {C}[G]\)-isomorphism
Here, the first isomorphism is induced by \(\rho _r \oplus \mathrm {id}_{H_{-r}^+(L)}\), whereas the second isomorphism is \(\iota _r^{-1}\). As above, there exist \(\mathbb {Q}[G]\)-isomorphisms
We now define maps
and
Proposition 3.15
Fix an integer \(r>1\) and a character \(\chi \). Then Gross’s conjecture 3.12 holds if and only if we have \(A_{\phi _{r}}^S(\chi ^{\sigma }) = A_{\phi _{r}}^S(\chi )^{\sigma }\) for all \(\sigma \in \mathrm {Aut}(\mathbb {C})\).
Proof
This is [62, Proposition 5.5]. \(\square \)
3.9 The comparison period
We henceforth assume that p is an odd prime and that L/K is a Galois CM-extension. Recall that \(\tau \in G\) is the unique automorphism induced by complex conjugation. For each \(n \in \mathbb {Z}\) we define a central idempotent \(e_n := \frac{1- (-1)^n \tau }{2}\) in \(\mathbb {Z}[{\textstyle \frac{1}{2}}][G]\). Now let \(r>1\) be an integer. Since L is CM, the idempotent \(e_r\) acts trivially on \(H_{1-r}^+(L) \otimes \mathbb {C}\), whereas \(e_r(H_{-r}^+(L) \otimes \mathbb {C})\) vanishes. Thus (3.10) induces a \(\mathbb {C}[G]\)-isomorphism
We likewise define a \(\mathbb {C}_p[G]\)-homomorphism
as follows. For each \(w \in S_p(L)\) we let \(H^i_{\mathrm {syn}}({\mathcal {O}}_w, r)\) be the ith syntomic cohomology group as considered by Besser [4]. We let \(\mathrm {reg}_r^w: K_{2r-1}({\mathcal {O}}_w) \rightarrow H^1_{\mathrm {syn}}({\mathcal {O}}_w, r)\) be the syntomic regulator [4, Theorem 7.5]. By [5, Lemma 2.15] (which heavily relies on [4, Proposition 8.6]) we have canonical isomorphisms \(H^1_{\mathrm {syn}}({\mathcal {O}}_w, r) \simeq L_w\) for each \(w \in S_p(L)\). The map \(\mu _p(r)\) is induced by the following chain of homomorphisms
The map \(\mu _p(r)\) shows up in the formulation of the p-adic Beilinson conjecture. However, the following map will be more suitable for the relation to the ETNC. We define a \(\mathbb {C}_p[G]\)-homomorphism
Here, the first map is induced by the p-adic Chern class map \(ch_{r,1}^{(p)}\) which is an isomorphism by Theorem 3.2; the arrow is the natural localization map, and the last isomorphism is induced by the Bloch–Kato exponential maps (see Lemma 3.4).
The following result will be crucial for relating the p-adic Beilinson conjecture to the ETNC.
Proposition 3.16
For each \(r>1\) we have \(\mu _p(r) = {\tilde{\mu }}_p(r)\).
Proof
For any abelian group A we write \({\widehat{A}}\) for its p-completion, that is \({\widehat{A}} := \varprojlim _n A / p^n A\). The localization maps (3.12) induce a map
For each \(w \in S_p(L)\) the Universal Coefficient Theorem [77, Chapter IV, Theorem 2.5] implies that there is a natural (injective) map
By [4, Corollary 9.10] there is a natural map \(H^1_{\mathrm {syn}}({\mathcal {O}}_w, r) \rightarrow H^1_{\acute{\mathrm {e}}\mathrm {t}}(L_w, \mathbb {Q}_p(r))\) such that the diagram

commutes. Here, the left-hand vertical arrow is induced by the syntomic regulator, and the map on the right by the isomorphism in Theorem 3.3. Moreover, the composite map
is the Bloch–Kato exponential map (3.7) by [4, Proposition 9.11]. Unravelling the definitions we now see that the maps \(\mu _p(r)\) and \({\tilde{\mu }}_p(r)\) coincide. \(\square \)
We will henceforth often not distinguish between the maps \(\mu _p(r)\) and \({\tilde{\mu }}_p(r)\). Since the Tate–Shafarevich group  is torsion-free by Lemma 3.11, the following result is now immediate.
is torsion-free by Lemma 3.11, the following result is now immediate.
Lemma 3.17
The map \(\mu _p(r)\) is a \(\mathbb {C}_p[G]\)-isomorphism if and only if \(\mathrm {Sch}(L,p,r)\) holds.
Definition 3.18
Let \(j: \mathbb {C}\simeq \mathbb {C}_{p}\) be a field isomorphism and let \(\rho \in R_{\mathbb {C}_{p}}^{+}(G)\). Let \(r>1\) be an integer. We define the comparison period attached to j, \(\rho \) and r to be
We record some basic properties of \(\Omega _{j}(r,-)\).
Lemma 3.19
Let H, N be subgroups of G with N normal in G.
-
(i)
Let \(\rho _{1}, \rho _{2} \in R_{\mathbb {C}_{p}}^{+}(G)\). Then \(\Omega _{j}(r, \rho _{1} + \rho _{2}) = \Omega _{j}(r, \rho _{1}) \Omega _{j}(r, \rho _{2})\).
-
(ii)
Let \(\rho \in R_{\mathbb {C}_{p}}^{+}(H)\). Then \(\Omega _{j}(r, \mathrm {ind}_{H}^{G} \rho ) = \Omega _{j}(r,\rho )\).
-
(iii)
Let \(\rho \in R_{\mathbb {C}_{p}}^{+}(G / N)\). Then \(\Omega _{j}(r, \mathrm {infl}_{G / N}^{G} \rho ) = \Omega _{j}(r,\rho )\).
Proof
Each part follows from the corresponding part of Lemma 2.1. \(\square \)
Remark 3.20
Since \(\mu _{\infty }(r)\) is an isomorphism, for any two choices of field isomorphism \(j,j': \mathbb {C}\simeq \mathbb {C}_{p}\) we have that \(\Omega _{j}(r,\rho )=0\) if and only if \(\Omega _{j'}(r,\rho )=0\).
Remark 3.21
For any fixed choice of field isomorphism \(j:\mathbb {C}\simeq \mathbb {C}_{p}\) we have
where the first equivalence is Lemma 3.17. Thus the non-vanishing of \(\Omega _{j}(r,\rho )\) can be thought of as the ‘\(\rho \)-part’ of \(\mathrm {Sch}(L,p,r)\). Moreover, if \(\Omega _{j}(r,\rho ) \ne 0\) then we may set \(\Omega _{j}(r, -\rho ) := \Omega _{j}(r,\rho )^{-1}\) and so if we assume \(\mathrm {Sch}(L,p,r)\) then Lemma 3.19 (i) shows that the definition of \(\Omega _{j}(r,\rho )\) naturally extends to any virtual character \(\rho \in R_{\mathbb {C}_{p}}(G)\).
Remark 3.22
Assume that G is abelian. For each integer r, Burns, Kurihara and Sano [21, Sect. 2.2] define canonical period-regulator isomorphisms
Here \(\varepsilon _r \in \mathbb {Z}_p[G]\) are certain idempotents such that the \(\varepsilon _r\)-parts of both \(\mathbb {C}_p[G]\)-modules in the exterior products are free of the same rank \(r_j^{\varepsilon }\). If \(r>1\) and \(\mathrm {Sch}(L,p,r)\) holds, then one may take \(\varepsilon _r = e_r\) and \(r_j^{\epsilon } = 0\). In this case the diagram [21, p. 125] gives an exact sequence of \(\mathbb {C}_p[G]\)-modules
where \((-)^{*}\) denotes \(\mathbb {C}_p\)-linear duals (note also that their \(H_L(r-1)^+\) is \(H_{1-r}^+(L)\) in our notation). The non-trivial map is (up to sign) the dual of \(\mu _p(r) \circ \rho _r^{-1}\). Hence the exterior product on the left of (3.13) canonically identifies with
and the isomorphisms \(\mu _p(r) \circ \rho _r^{-1}\) and \(\iota _r\) induce a map to \(\det _{\mathbb {C}_{p}[G]}(H_{-r}^+(L) \otimes \mathbb {C}_p)\) which can be identified with the exterior power on the right by a variant of Lemma 3.4. For more details we refer the interested reader to [21, Sect. 2.2.4].
The authors then use the isomorphism (3.13) to define generalized Stark elements and to state [21, Conjecture 3.6] which might be seen as an analogue and refinement of a conjecture of Rubin [68] in the case \(r=0\). It is then shown in [21, Sect. 4] that their conjecture is implied by the appropriate special case of the ETNC. As the formulation of the latter involves the Bloch–Kato exponential map rather than the syntomic regulator, a variant of Proposition 3.16 is already implicit in their work (for instance, see [21, Remark 2.7])
3.10 p-adic Artin L-functions
Let E/K be a finite Galois extension of totally real number fields and let \(G=\mathrm {Gal}(E/K)\). Let p be an odd prime and let S be a finite set of places of K containing \(S_{p} \cup S_{\infty }\). For each \(\rho \in R_{\mathbb {C}_{p}}(G)\) the S-truncated p-adic Artin L-function attached to \(\rho \) is the unique p-adic meromorphic function \(L_{p,S}(s, \rho ) : \mathbb {Z}_{p} \rightarrow \mathbb {C}_{p}\) with the property that for each strictly negative integer n and each field isomorphism \(j: \mathbb {C}\simeq \mathbb {C}_{p}\) we have
where \(\omega : G_K \rightarrow \mathbb {Z}_{p}^{\times }\) is the Teichmüller character and we view \(\rho \otimes \omega ^{n-1}\) as a character of \(\mathrm {Gal}(E(\zeta _p)/K)\). By a result of Siegel [70] the right-hand side does indeed not depend on the choice of j. In the case that \(\rho \) is linear, \(L_{p,S}(s, \rho )\) was constructed independently by Deligne and Ribet [33], Barsky [2] and Cassou-Nogués [24]. Greenberg [37] then extended the construction to the general case using Brauer induction.
3.11 Statement of the p-adic Beilinson conjecture
We now formulate our variant of the p-adic Beilinson conjecture.
Conjecture 3.23
(The p-adic Beilinson conjecture) Let E/K be a finite Galois extension of totally real number fields and let \(G=\mathrm {Gal}(E/K)\). Let p be an odd prime and let S be a finite set of places of K containing \(S_{p} \cup S_{\infty }\). Let \(\rho \in R_{\mathbb {C}_{p}}^{+}(G)\) and let \(r>1\) be an integer. Then for every choice of field isomorphism \(j: \mathbb {C}\cong \mathbb {C}_{p}\) we have
Remark 3.24
It is straightforward to show that Conjecture 3.23 does not depend on the choice of S.
Remark 3.25
One can show (see Theorem 4.12 below) that \(L_{p, S}(r,\rho ) \not = 0\) if and only if \(\Omega _{j}(r, \rho \otimes \omega ^{r-1}) \not = 0\). In this case (and thus in particular if \(\mathrm {Sch}(E(\zeta _p),p,r)\) holds) the statement of Conjecture 3.23 naturally extends to all virtual characters \(\rho \in R_{\mathbb {C}_p}(G)\).
Remark 3.26
It is clear from the definitions that Conjecture 3.23 is compatible with the p-adic Beilinson conjecture as considered by Besser, Buckingham, de Jeu and Roblot [5, Conjecture 3.18]. More concretely, the equality (3.14) is equivalent to the appropriate special case of [5, Conjecture 3.18 (i)–(iii)], whereas [5, Conjecture 3.18 (iv)] then is equivalent to the non-vanishing of \(\Omega _{j}(r, \rho \otimes \omega ^{r-1})\) as follows from Remark 3.25.
Remark 3.27
Since both complex and p-adic Artin L-functions satisfy properties analogous to those of \(\Omega _{j}(r, -)\) given in Lemma 3.19, the truth of Conjecture 3.23 is invariant under induction and inflation; moreover, if it holds for \(\rho _{1}, \rho _{2} \in R_{\mathbb {C}_{p}}(G)\) then it holds for \(\rho _{1}+\rho _{2}\).
3.12 The relation to Gross’s conjecture
The following results are the analogues of [49, Theorem 4.16 and Corollary 4.18], respectively.
Theorem 3.28
Let E/K be a finite Galois extension of totally real number fields and let \(G=\mathrm {Gal}(E/K)\). Let p be an odd prime and let S be a finite set of places of K containing \(S_{p} \cup S_{\infty }\). Let \(\rho \in R_{\mathbb {C}_{p}}^{+}(G)\) and let \(r>1\) be an integer. We put \(\psi := \rho \otimes \omega ^{r-1}\). If \(\Omega _{j}(r,\psi ) \ne 0\) for some (and hence every) choice of field isomorphism \(j:\mathbb {C}\cong \mathbb {C}_{p}\) then the following statements are equivalent.
-
(i)
\(\Omega _{j}(r,\psi ) \cdot j ( L_{S}(r, \psi ^{j^{-1}}) )\) is independent of the choice of \(j:\mathbb {C}\cong \mathbb {C}_{p}\).
-
(ii)
Gross’s conjecture at \(s=1-r\) holds for \({\check{\psi }}^{j^{-1}} \in R_{\mathbb {C}}^{+}(\mathrm {Gal}(E(\zeta _p)/K)\) and some (and hence every) choice of \(j:\mathbb {C}\cong \mathbb {C}_{p}\).
Proof
The first and second occurrence of ‘and hence every’ in the statement of the theorem follow from Remarks 3.13 and 3.20, respectively.
Let \(j,j': \mathbb {C}\cong \mathbb {C}_{p}\) be field isomorphisms and let \(\chi := \psi ^{j^{-1}}\). Then \(j = j' \circ \sigma \) for some \(\sigma \in \mathrm {Aut}(\mathbb {C})\) and so \(\psi ^{j'^{-1}} = \chi ^{\sigma }\). For every \(\mathbb {Q}[G]\)-isomorphism \(\phi _r\) as in (3.11) we have
which does not depend on j. Hence we have
By Proposition 3.15 the last expression is equal to 1 if and only if Gross’s conjecture at \(s=1-r\) (Conjecture 3.12) holds for the character \({\check{\chi }}\). \(\square \)
Corollary 3.29
Let E/K be a finite Galois extension of totally real number fields and let \(G=\mathrm {Gal}(E/K)\). Fix a prime p and let \(r>1\) be an integer. Assume that \(\mathrm {Sch}(E(\zeta _p),p,r)\) holds. If the p-adic Beilinson conjecture at \(s=r\) holds for all \(\rho \in R_{\mathbb {C}_{p}}^{+}(G)\) then Gross’s conjecture at \(s=1-r\) holds for \(\chi \otimes \omega ^{r-1}\) for all \(\chi \in R_{\mathbb {C}}^{+}(G)\).
3.13 Absolutely abelian characters
Since our conjecture is compatible with that of [5] by Remark 3.26 and invariant under induction and inflation of characters by Remark 3.27, we deduce the following result from work of Coleman [29] (see [5, Proposition 4.17]).
Theorem 3.30
Let E/K be a finite Galois extension of totally real number fields and let \(G=\mathrm {Gal}(E/K)\). Let p be a prime and let \(r>1\) be an integer. Suppose that \(\rho \in R_{\mathbb {C}_{p}}^+(G)\) is an absolutely abelian character, i.e., there exists a normal subgroup N of G such that \(\rho \) factors through \(G/N \cong \mathrm {Gal}(E^{N}/K)\) and \(E^{N}/\mathbb {Q}\) is abelian. Then the p-adic Beilinson conjecture (Conjecture 3.23) holds for \(\rho \).
4 Equivariant Iwasawa theory
4.1 Bockstein homomorphisms
We recall some background material regarding Bockstein homomorphisms. The reader may also consult [22, Sect. 3.1–Sect. 3.2].
Let \({\mathcal {G}}\) be a compact p-adic Lie group that contains a closed normal subgroup H such that \(\Gamma := {\mathcal {G}}/H\) is isomorphic to \(\mathbb {Z}_p\). We fix a topological generator \(\gamma \) of \(\Gamma \). The Iwasawa algebra of \({\mathcal {G}}\) is
where the inverse limit is taken over all open normal subgroups \({\mathcal {N}}\) of \({\mathcal {G}}\). If F is a finite field extension of \(\mathbb {Q}_{p}\) with ring of integers \({\mathcal {O}}={\mathcal {O}}_{F}\), we put \(\Lambda ^{{\mathcal {O}}}({\mathcal {G}}) := {\mathcal {O}} \otimes _{\mathbb {Z}_{p}} \Lambda ({\mathcal {G}}) = {\mathcal {O}}\llbracket {\mathcal {G}}\rrbracket \). We consider continuous homomorphisms
where \(T_{\pi }\) is a finitely generated free \({\mathcal {O}}\)-module. For \(g \in {\mathcal {G}}\) we denote its image in \(\Gamma \) under the canonical projection by \({\overline{g}}\). We view \(\Lambda ^{{\mathcal {O}}}(\Gamma ) \otimes _{{\mathcal {O}}} T_{\pi }\) as a \((\Lambda ^{{\mathcal {O}}}(\Gamma ), \Lambda ({\mathcal {G}}))\)-bimodule, where \(\Lambda ^{{\mathcal {O}}}(\Gamma )\) acts by left multiplication and \(\Lambda ({\mathcal {G}})\) acts on the right via
for \(\lambda \in \Lambda ^{{\mathcal {O}}}(\Gamma )\), \(t \in T_{\pi }\) and \(g \in {\mathcal {G}}\). For each complex \(C^{\bullet } \in {\mathcal {D}}^{\mathrm {perf}}(\Lambda ({\mathcal {G}}))\) we define a complex \(C^{\bullet }_{\pi } \in {\mathcal {D}}^{\mathrm {perf}}(\Lambda ^{{\mathcal {O}}}(\Gamma ))\) by
Given an open normal subgroup U of \({\mathcal {G}}\) we set \(C_U^{\bullet } := \mathbb {Z}_p[{\mathcal {G}}/U] \otimes _{\Lambda ({\mathcal {G}})}^{{\mathbb {L}}} C^{\bullet }\) and, if U is contained in the kernel of \(\pi \), we furthermore obtain a complex
which does actually not depend on U. The natural exact triangles
in \({\mathcal {D}}({\mathcal {O}})\) induce short exact sequences of \({\mathcal {O}}\)-modules
for each \(i \in \mathbb {Z}\). The Bockstein homomorphism in degree i is defined to be the composite homomorphism
where the middle arrow is the tautological map. We obtain a bounded complex of \({\mathcal {O}}\)-modules
where the term \(H^i(C^{\bullet }_{U,(\pi )})\) is placed in degree i. Note that the Bockstein homomorphisms and the complex \(\Delta _{C^{\bullet },\pi }\) actually depend on the choice of \(\gamma \), though our notation does not reflect this. The complex \(C^{\bullet }\) is called semisimple at \(\pi \) if \(\mathbb {Q}_p \otimes _{\mathbb {Z}_p}\Delta _{C^{\bullet },\pi }\) is acyclic (for any and hence every choice of \(\gamma \)).
For any \(\Lambda ({\mathcal {G}})\)-module M we put \(M_{\pi } := (\Lambda ^{{\mathcal {O}}}(\Gamma ) \otimes _{{\mathcal {O}}} T_{\pi }) \otimes _{\Lambda ({\mathcal {G}})} M\).
Lemma 4.1
Assume that \({\mathcal {G}}\) is a compact p-adic Lie group of dimension 1 and let \(C^{\bullet } \in {\mathcal {D}}^{\mathrm {perf}}(\Lambda ({\mathcal {G}}))\) be acyclic outside degree a for some \(a \in \mathbb {Z}\). Further assume that the \(\Lambda ({\mathcal {G}})\)-module \(H^a(C^{\bullet })\) has projective dimension at most 1. Then for every continuous homomorphism \(\pi : {\mathcal {G}} \rightarrow \mathrm {Aut}_{{\mathcal {O}}}(T_{\pi })\) the complex \(C^{\bullet }_{\pi }\) is acyclic outside degree a and there is a canonical isomorphism of \(\Lambda ^{{\mathcal {O}}}(\Gamma )\)-modules \(H^a(C^{\bullet }_{\pi }) \simeq H^a(C^{\bullet })_{\pi }\).
Proof
This has been shown in the course of the proof of [15, Lemma 5.6]. We repeat the short argument for convenience.
We may assume that \(a=0\). Then \(C^{\bullet }\) may be represented by a complex \(P^{-1} {\mathop {\rightarrow }\limits ^{d}} P^0\), where \(P^{-1}\) and \(P^0\) are projective \(\Lambda ({\mathcal {G}})\)-modules placed in degrees \(-1\) and 0, respectively, and the homomorphism d is injective. Then \(C^{\bullet }_{\pi }\) is represented by
where \(d'\) is injective since d is. The result follows. \(\square \)
4.2 Algebraic K-theory
Let R be a noetherian integral domain with field of fractions E. Let A be a finite-dimensional semisimple E-algebra and let \({\mathfrak {A}}\) be an R-order in A. For any field extension F of E we set \(A_F := F \otimes _E A\). Let \(K_0({\mathfrak {A}}, F) = K_{0}({\mathfrak {A}}, A_F)\) denote the relative algebraic K-group associated to the ring homomorphism \({\mathfrak {A}} \hookrightarrow A_F\). We recall that \(K_{0}({\mathfrak {A}}, A_F)\) is an abelian group with generators [X, g, Y] where X and Y are finitely generated projective \({\mathfrak {A}}\)-modules and \(g:F \otimes _{R} X \rightarrow F \otimes _{R} Y\) is an isomorphism of \(A_F\)-modules; for a full description in terms of generators and relations, we refer the reader to [74, p. 215]. Moreover, there is a long exact sequence of relative K-theory (see [74, Chapter 15])
The reduced norm map \(\mathrm {Nrd} = \mathrm {Nrd}_{A_F}: A_F \rightarrow \zeta (A_F)\) is defined componentwise on the Wedderburn decomposition of \(A_F\) and extends to matrix rings over \(A_F\) (see [31, Sect. 7D]); thus it induces a map \(K_{1}(A_F) \longrightarrow \zeta (A_F)^{\times }\), which we also denote by \(\mathrm {Nrd}\).
In the case \(E = F\) the relative K-group \(K_{0}({\mathfrak {A}}, A)\) identifies with the Grothendieck group whose generators are \([C^{\bullet }]\), where \(C^{\bullet }\) is an object of the category \({\mathcal {C}}^{b}_{\mathrm {tors}}(\mathrm {PMod}({\mathfrak {A}}))\) of bounded complexes of finitely generated projective \({\mathfrak {A}}\)-modules whose cohomology modules are R-torsion, and the relations are as follows: \([C^{\bullet }] = 0\) if \(C^{\bullet }\) is acyclic, and \([C_{2}^{\bullet }] = [C_{1}^{\bullet }] + [C_{3}^{\bullet }]\) for every short exact sequence
in \({\mathcal {C}}^{b}_{\mathrm {tors}}(\mathrm {PMod}({\mathfrak {A}}))\) (see [77, Chapter 2] or [73, Sect. 2], for example).
We denote the full triangulated subcategory of \({\mathcal {D}}^{\mathrm {perf}} ({\mathfrak {A}})\) comprising perfect complexes whose cohomology modules are R-torsion by \({\mathcal {D}}^{\mathrm {perf}}_{\mathrm {tors}} ({\mathfrak {A}})\). Then every object \(C^{\bullet }\) of \({\mathcal {D}}^{\mathrm {perf}}_{\mathrm {tors}} ({\mathfrak {A}})\) defines a class \([C^{\bullet }]\) in \(K_{0}({\mathfrak {A}}, A)\).
Let p be an odd prime and let \({\mathcal {G}}\) be a one-dimensional compact p-adic Lie group that surjects onto \(\mathbb {Z}_p\). Then \({\mathcal {G}}\) may be written as \({\mathcal {G}} = H \rtimes \Gamma \) with a finite normal subgroup H of \({\mathcal {G}}\) and a subgroup \(\Gamma \simeq \mathbb {Z}_p\). Let \({\mathcal {O}}\) be the ring of integers in some finite extension F of \(\mathbb {Q}_p\). We consider \({\mathfrak {A}} = \Lambda ^{{\mathcal {O}}}({\mathcal {G}}) = \mathcal O\llbracket {\mathcal {G}}\rrbracket \) as an order over \(R := \Lambda ^{{\mathcal {O}}}(\Gamma _0)\), where \(\Gamma _{0}\) is an open subgroup of \(\Gamma \) that is central in \({\mathcal {G}}\). We denote the fraction field of \(\Lambda ^{{\mathcal {O}}}(\Gamma _0)\) by \({\mathcal {Q}}^F(\Gamma _0)\) and let \(A = {\mathcal {Q}}^F({\mathcal {G}}) := {\mathcal {Q}}^F(\Gamma _0) \otimes _R \Lambda ^{{\mathcal {O}}}({\mathcal {G}})\) be the total ring of fractions of \(\Lambda ^{{\mathcal {O}}}({\mathcal {G}})\). Then [78, Corollary 3.8] shows that the map \(\partial \) in (4.3) is surjective; thus the sequence
is exact. If \(\xi \in K_{1}({\mathcal {Q}}^F({\mathcal {G}}))\) is a pre-image of some \(x \in K_{0}(\Lambda ^{{\mathcal {O}}}({\mathcal {G}}),{\mathcal {Q}}^F({\mathcal {G}}))\), we say that \(\xi \) is a characteristic element for x. We also set \({\mathcal {Q}}({\mathcal {G}}) := {\mathcal {Q}}^{\mathbb {Q}_p}({\mathcal {G}})\).
We include the following consequence of (4.4) for later use.
Lemma 4.2
Let M be a finitely generated \(\Lambda ^{{\mathcal {O}}}({\mathcal {G}})\)-module of projective dimension at most one. Assume that M is torsion as an R-module. Then M admits a free resolution of the form
for some positive integer m.
Let \(\Gamma ' \simeq \mathbb {Z}_p\) be an open normal subgroup of \({\mathcal {G}}\) and set \(G := {\mathcal {G}}/\Gamma '\). If in addition \(M_{\Gamma '}\) is finite, then \(M^{\Gamma '}\) vanishes and (4.5) induces a short exact sequence of \(\mathbb {Z}_p[G]\)-modules
Proof
Choose a surjective \(\Lambda ^{{\mathcal {O}}}({\mathcal {G}})\)-homomorphism \(\Lambda ^{{\mathcal {O}}}({\mathcal {G}})^m \rightarrow M\). Its kernel is a projective \(\Lambda ^{{\mathcal {O}}}({\mathcal {G}})\)-module P by assumption. Since M is R-torsion, we see that the classes of P and \(\Lambda ^{{\mathcal {O}}}({\mathcal {G}})^m\) in \(K_0(\Lambda ^{{\mathcal {O}}}({\mathcal {G}}))\) have the same image in \(K_0({\mathcal {Q}}^F({\mathcal {G}}))\). Hence they coincide by (4.4). In other words, P and \(\Lambda ^{{\mathcal {O}}}({\mathcal {G}})^m\) are stably isomorphic. By enlarging m if necessary, we may assume that P is free of rank m and we have established the existence of (4.5). By [54, Lemma 5.3.11] this sequence induces an exact sequence of \(\mathbb {Z}_p[G]\)-modules
It follows that \(M^{\Gamma '}\) is a free \(\mathbb {Z}_p\)-module of the same rank as \(M_{\Gamma '}\). This proves the remaining claims. \(\square \)
Now let \(\pi : {\mathcal {G}} \rightarrow \mathrm {Aut}_{{\mathcal {O}}}(T_{\pi })\) be a continuous homomorphism as in (4.1) and set \(n := \mathrm {rank}_{{\mathcal {O}}}(T_{\pi })\). There is a ring homomorphism \(\Phi _{\pi }: \Lambda ({\mathcal {G}}) \rightarrow M_{n\times n}(\Lambda ^{{\mathcal {O}}}(\Gamma ))\) induced by the continuous group homomorphism
where \({\overline{g}}\) denotes the image of g in \({\mathcal {G}} / H \simeq \Gamma \). By [27, Lemma 3.3] this homomorphism extends to a ring homomorphism \({\mathcal {Q}}({\mathcal {G}}) \rightarrow M_{n\times n}({\mathcal {Q}}^{F}(\Gamma ))\) and this in turn induces a homomorphism
For \(\xi \in K_{1}({\mathcal {Q}}({\mathcal {G}}))\) we set \(\xi (\pi ) := \Phi _{\pi }(\xi )\). If \(\pi = \pi _{\rho }\) is an Artin representation with character \(\rho \), we also write \(\Phi _{\rho }\) and \(\xi (\rho )\) for \(\Phi _{\pi _{\rho }}\) and \(\xi (\pi _{\rho })\), respectively, and let
be the map defined by Ritter and Weiss in [66]. By [60, Lemma 2.3] (choose \(r=0\)) we have a commutative triangle

We shall also write \(\xi ^{*}(\rho )\) for the leading term at \(T=0\) of the power series \(\Phi _{\rho }(\xi )\).
We choose a maximal \(\Lambda (\Gamma _0)\)-order \({\mathfrak {M}}({\mathcal {G}})\) in \({\mathcal {Q}}({\mathcal {G}})\) such that \(\Lambda ({\mathcal {G}})\) is contained in \({\mathfrak {M}}({\mathcal {G}})\).
Lemma 4.3
Let \(C^{\bullet } \in {\mathcal {D}}^{\mathrm {perf}}_{\mathrm {tors}}(\Lambda ({\mathcal {G}}))\) be a complex and let \(\xi \) be a characteristic element for \(C^{\bullet }\). Let \(\pi _{\rho }\) be an Artin representation with character \(\rho \). Then \(\xi (\rho ) \cdot j_{\rho }(x)\) is a characteristic element for \(C^{\bullet }_{\rho }\) for every \(x \in \zeta ({\mathfrak {M}}({\mathcal {G}}))^{\times }\).
Proof
In the case that \(x = 1\) this is [15, Lemma 5.4 (vii)] (and follows from the naturality of connecting homomorphisms). By [66, Remark H] the image of \(\zeta ({\mathfrak {M}}({\mathcal {G}}))^{\times }\) under \(j_{\rho }\) is contained in \(\Lambda ^{{\mathcal {O}}}(\Gamma )^{\times }\). This proves the claim. \(\square \)
4.3 Cohomology with compact support
Let p be an odd prime. We denote the cyclotomic \(\mathbb {Z}_p\)-extension of a number field K by \(K_{\infty }\) and set \(\Gamma _K := \mathrm {Gal}(K_{\infty }/K)\). Let S be a finite set of places of K containing the set \(S_{\infty } \cup S_p\). Let M be a topological \(G_{K,S}\)-module. Following Burns and Flach [17] we define the compactly supported cohomology complex to be
where the arrow is induced by the natural restriction maps. For any integers i and r we abbreviate \(H^iR\Gamma _c({\mathcal {O}}_{K,S}, M)\) to \(H^i_c({\mathcal {O}}_{K,S}, M)\) and set \(H^i_c({\mathcal {O}}_{K,S}, \mathbb {Q}_p(r)) := \mathbb {Q}_p \otimes _{\mathbb {Z}_p} H^i_c({\mathcal {O}}_{K,S}, \mathbb {Z}_p(r))\).
Let E/K be a finite Galois extension of totally real fields and set \(L := E(\zeta _p)\). Then L is a CM-field and we denote its maximal totally real subfield by \(L^+\) as in Sect. 3.9. Set \({\mathcal {G}}:= \mathrm {Gal}(L_{\infty }/K)\) and let
be the p-adic cyclotomic character defined by \(\sigma (\zeta ) = \zeta ^{\chi _{\mathrm {cyc}}(\sigma )}\) for any \(\sigma \in {\mathcal {G}}\) and any p-power root of unity \(\zeta \). The composition of \(\chi _{\mathrm {cyc}}\) with the projections onto the first and second factors of the canonical decomposition \(\mathbb {Z}_{p}^{\times } = \langle \zeta _{p-1} \rangle \times (1+p\mathbb {Z}_{p})\) are given by the Teichmüller character \(\omega \) and a map that we denote by \(\kappa \).
Assume in addition that S contains all places that ramify in \(L_{\infty }/K\). For each integer r we define a complex of \(\Lambda ({\mathcal {G}})\)-modules
where \(\Lambda ({\mathcal {G}})^{\sharp }(r)\) denotes the \(\Lambda ({\mathcal {G}})\)-module \(\Lambda ({\mathcal {G}})\) upon which \(\sigma \in G_K\) acts on the right via multiplication by the element \(\chi _{\mathrm {cyc}}^r(\sigma ){\overline{\sigma }}^{-1}\); here \({\overline{\sigma }}\) denotes the image of \(\sigma \) in \({\mathcal {G}}\). Note that the complexes \(C_{r,S}^{\bullet }\) are perfect by [36, Proposition 1.6.5] and we have natural isomorphisms
for every integer r.
Each \(\Lambda ({\mathcal {G}})\)-module M naturally decomposes as a direct sum \(M^+ \oplus M^-\) with \(M^{\pm } = \frac{1 \pm \tau }{2} M\). Similarly, each complex \(C^{\bullet }\) of \({\mathcal {D}}^{\mathrm {perf}}(\Lambda ({\mathcal {G}}))\) gives rise to subcomplexes \((C^{\bullet })^+\) and \((C^{\bullet })^-\). Moreover, we let \((C^{\bullet })^{\vee } := R\mathrm {Hom}(C^{\bullet }, \mathbb {Q}_p/\mathbb {Z}_p)\) be the Pontryagin dual of \(C^{\bullet }\). By a Shapiro Lemma argument and Artin–Verdier duality we then have isomorphisms
in \({\mathcal {D}}(e_r\Lambda ({\mathcal {G}}))\). We let \(M_{S}\) be the maximal abelian pro-p-extension of \(L_{\infty }^+\) unramified outside S. Then \(X_{S} := \mathrm {Gal}(M_{S}/L_{\infty }^+)\) is a finitely generated \(\Lambda ({\mathcal {G}}^+)\)-module, where we put \({\mathcal {G}}^+ := {\mathcal {G}}/\langle \tau \rangle = \mathrm {Gal}(L^+_{\infty }/K)\). Iwasawa [45] has shown that \(X_{S}\) is in fact torsion as a \(\Lambda (\Gamma _{L^+})\)-module. We let \(\mu _{p}(L^+)\) denote the Iwasawa \(\mu \)-invariant of \(X_{S}\) and note that this does not depend on the choice of S (see [54, Corollary 11.3.6]). Hence \(\mu _{p}(L^+)\) vanishes if and only if \(X_{S}\) is finitely generated as a \(\mathbb {Z}_{p}\)-module. It is conjectured that we always have \(\mu _{p}(L^+)=0\) and as explained in [47, Remark 4.3], this is closely related to the classical Iwasawa ‘\(\mu =0\)’ conjecture for L at p. Thus a result of Ferrero and Washington [34] on this latter conjecture implies that \(\mu _{p}(L^+)=0\) whenever \(E/\mathbb {Q}\) and thus \(L/\mathbb {Q}\) is abelian.
The only non-trivial cohomology groups of \(R\Gamma ({\mathcal {O}}_{L^+_{\infty },S}, \mathbb {Q}_p/\mathbb {Z}_p)^{\vee }\) occur in degrees \(-1\) and 0 and canonically identify with \(X_{S}\) and \(\mathbb {Z}_p\), respectively. Hence (4.7) with \(r=1\) and (4.6) imply that for each integer r the cohomology of \(C_{r,S}^{\bullet }\) is concentrated in degrees 2 and 3 and we have
4.4 The main conjecture
The following is an obvious reformulation of the equivariant Iwasawa main conjecture for the extension \(L^+_{\infty }/K\) (without its uniqueness statement).
Conjecture 4.4
(equivariant Iwasawa main conjecture) Let L/K be a Galois CM-extension such that L contains a primitive pth root of unity. Let S be a finite set of places of K containing \(S_{\infty }\) and all places that ramify in \(L^+_{\infty }/K\). Then there exists an element \(\zeta _{S} \in K_{1}({\mathcal {Q}}({\mathcal {G}}^+))\) such that \(\partial (\zeta _{S}) = [C_{1,S}^{\bullet }]\) and for every irreducible Artin representation \(\pi _{\rho }\) of \({\mathcal {G}}^+\) with character \(\rho \) and for each integer \(n \ge 1\) divisible by \(p-1\) we have
for every field isomorphism \(j: \mathbb {C}\cong \mathbb {C}_p\).
Part (i) of the following theorem has been shown by Ritter and Weiss [67] and by Kakde [51] independently. Part (ii) is due to Johnston and the present author [50].
Theorem 4.5
Conjecture 4.4 holds for \(L_{\infty }^+/K\) in each of the following cases.
-
(i)
The \(\mu \)-invariant \(\mu _{p}(L^+)\) vanishes.
-
(ii)
The Galois group \({\mathcal {G}}^+\) has an abelian Sylow p-subgroup.
By starting out from the work of Deligne and Ribet [33], Greenberg [37] has shown that for each topological generator \(\gamma \) of \(\Gamma \) there is a unique element \(f_{\rho , S}(T)\) in the quotient field of \(\mathbb {Q}_p^c \otimes _{\mathbb {Z}_p} \mathbb {Z}_p \llbracket T \rrbracket \) (which we will identify with \(\mathbb {Q}_p^c \otimes _{\mathbb {Z}_p} \Lambda (\Gamma )\) via the usual map that sends \(\gamma \) to \(1+T\)) such that
where \(u := \kappa (\gamma )\). For each integer a we let \(x \mapsto t_{\mathrm {cyc}}^a(x)\) be the automorphisms on \({\mathcal {Q}}^c({\mathcal {G}})\) induced by \(g \mapsto \chi _{\mathrm {cyc}}(g)^a g\) for \(g \in {\mathcal {G}}\). We use the same notation for the induced group homomorphisms on \(K_1({\mathcal {Q}}({\mathcal {G}}))\) and \(K_1(e_r{\mathcal {Q}}({\mathcal {G}}))\), \(r \in \mathbb {Z}\).
Proposition 4.6
Suppose that Conjecture 4.4 holds for \(L_{\infty }^+/K\). Then for each \(r \in \mathbb {Z}\) there exists an element \(\zeta _{r,S} \in K_{1}(e_r{\mathcal {Q}}({\mathcal {G}}))\) such that \(\partial (\zeta _{r,S}) = [C_{r,S}^{\bullet }]\) and for every irreducible Artin representation \(\pi _{\rho }\) of \({\mathcal {G}}^+\) with character \(\rho \) we have
Proof
When \(r=1\) we may take \(\zeta _{1,S} = \zeta _S\) by [49, Proposition 7.5]. Then \(\zeta _{r,S} := t_{\mathrm {cyc}}^{1-r}(\zeta _{1,S})\) is a characteristic element for \(C_{r,S}^{\bullet }\) by (4.6) and (4.9) follows from [15, Lemma 5.4 (v)] (see also [14, Lemma 9.5]). \(\square \)
Corollary 4.7
Let \(r \in \mathbb {Z}\) be an integer and let \(\pi _{\rho }\) be an irreducible Artin representation of \({\mathcal {G}}^+\) with character \(\rho \). Then \(f_{\rho , S}(u^{1-r}(1+T)-1)\) is a characteristic element of \(C^{\bullet }_{r, \rho \otimes \omega ^{r-1}}\).
Proof
Since the main conjecture (Conjecture 4.4) holds ‘over the maximal order’ by [47, Theorem 4.9] (this result is essentially due to Ritter and Weiss [66]), the equality (4.9) holds unconditionally up to a factor \(j_{\rho }(x)\) for some \(x \in \zeta ({\mathfrak {M}}({\mathcal {G}}))^{\times }\). Thus the claim follows from Lemma 4.3. \(\square \)
4.5 Schneider’s conjecture and semisimplicity
We recall the following result from [62, Propositions 3.11 and 3.12]. Part (i) is a special case of [16, Proposition 1.20] and of [36, Proposition 1.6.5].
Proposition 4.8
Let L/K be a Galois extension of number fields with Galois group G. Let \(r>1\) be an integer and let p be an odd prime. Then the following hold.
-
(i)
The complex \(R\Gamma _c({\mathcal {O}}_{L,S}, \mathbb {Z}_p(r))\) belongs to \({\mathcal {D}}^{\mathrm {perf}} (\mathbb {Z}_p[G])\) and is acyclic outside degrees 1, 2 and 3.
-
(ii)
We have an exact sequence of \(\mathbb {Z}_p[G]\)-modules

-
(iii)
We have an isomorphism of \(\mathbb {Z}_p[G]\)-modules
$$\begin{aligned} H^3_c({\mathcal {O}}_{L,S}, \mathbb {Z}_p(r)) \simeq \mathbb {Z}_p(r-1)_{G_L}. \end{aligned}$$ -
(iv)
The \(\mathbb {Z}_{p}[G]\)-module
 is finite.
is finite. -
(v)
The \(\mathbb {Z}_p\)-rank of \(H^2_c({\mathcal {O}}_{L,S}, \mathbb {Z}_p(r))\) equals \(d_{r+1}\) if and only if Schneider’s conjecture \(\mathrm {Sch}(L,p,r)\) holds.
We now return to the situation considered in Sect. 4.3. Before proving the next result we recall that for a finitely generated \(\Lambda ^{{\mathcal {O}}}(\Gamma )\)-torsion module M the following are equivalent: (i) \(M^{\Gamma }\) is finite; (ii) \(M_{\Gamma }\) is finite; (iii) \(f_M(0) \not = 0\), where \(f_M\) denotes a characteristic element for M. Moreover, by [54, Proposition 5.3.19] we have that \(M=0\) if and only if \(M_{\Gamma } = M^{\Gamma } = 0\).
Proposition 4.9
Let \(r>1\) be an integer and let \(\rho \) be an irreducible Artin character of \({\mathcal {G}}^+\) such that \(\ker (\rho )\) contains \(\Gamma _{L^+}\). Set \(\psi := \rho \otimes \omega ^{r-1}\). Then we have that \(H^i(C^{\bullet }_{r,S,\psi }) = 0\) for \(i \not = 2,3\) and natural isomorphisms of \({\mathcal {O}}_{\psi }\)-modules

and
and a short exact sequence of \({\mathcal {O}}_{\psi }\)-modules
In particular, the \({\mathcal {O}}_{\psi }\)-modules \(H^3(C^{\bullet }_{r,S,\psi })_{\Gamma }\) and \(H^3(C^{\bullet }_{r,S,\psi })^{\Gamma }\) are finite.
Proof
We put \({\mathcal {O}} := {\mathcal {O}}_{\psi }\) for brevity. Since the complex \(C_{r,S}^{\bullet }\) is acyclic outside degrees 2 and 3 and the functor \(M \mapsto M_{\psi } = (\Lambda ^{{\mathcal {O}}}(\Gamma ) \otimes _{{\mathcal {O}}} T_{\psi }) \otimes _{\Lambda ({\mathcal {G}})} M\) is right exact, it is clear that \(H^i(C^{\bullet }_{r,S,\psi })\) vanishes for \(i\ge 4\). We let \(U = \Gamma _L =\mathrm {Gal}(L_{\infty }/L)\). Then U is contained in the kernel of \(\psi \), and by [36, Proposition 1.6.5] we have an isomorphism
in \({\mathcal {D}}(e_r\mathbb {Z}_p[G])\). We now consider the exact sequence (4.2) for the case at hand and various integers i. We will repeatedly apply Lemma 2.2. In particular, the complex \(C_{r,S,U,(\psi )}^{\bullet }\) is acyclic outside degrees 1, 2 and 3 by Proposition 4.8 (i). For \(i\le 0\) we find that \(H^{i}(C^{\bullet }_{r,S,\psi })_{\Gamma }\) and \(H^{i+1}(C^{\bullet }_{r,S,\psi })^{\Gamma }\) vanish. Thus \(H^i(C^{\bullet }_{r,S,\psi })\) vanishes for \(i \le 0\) and even for \(i=1\) once we show that the \({\mathcal {O}}\)-module \(H^{1}(C^{\bullet }_{r,S,\psi })_{\Gamma }\) is trivial. We already know that it is finite. Sequence (4.2) in the case \(i=1\) and Lemma 2.2 now give rise to a short exact sequence
Since the central idempotent \(e_r\) annihilates \(H_{-r}^+(L) \otimes \mathbb {Z}_p\) and \(e_r e_{\psi } = e_{\psi }\) we have an isomorphism

by Proposition 4.8 (ii). Since the Tate–Shafarevich group  is torsion-free by Lemma 3.11, the \({\mathcal {O}}\)-module
is torsion-free by Lemma 3.11, the \({\mathcal {O}}\)-module  is free. Therefore \(H^{1}(C^{\bullet }_{r,S,\psi })_{\Gamma }\) vanishes as desired and we have established (4.10). Proposition 4.8 (iii), Lemma 2.2 and the case \(i=3\) of sequence (4.2) imply (4.11). Finally, sequence (4.12) is the case \(i=2\) of sequence (4.2). \(\square \)
is free. Therefore \(H^{1}(C^{\bullet }_{r,S,\psi })_{\Gamma }\) vanishes as desired and we have established (4.10). Proposition 4.8 (iii), Lemma 2.2 and the case \(i=3\) of sequence (4.2) imply (4.11). Finally, sequence (4.12) is the case \(i=2\) of sequence (4.2). \(\square \)
Lemma 4.10
Let r be an arbitrary integer. Then there are finitely generated \(e_r\Lambda ({\mathcal {G}})\)-modules \(Y_{r,S}\) and \(Z_r\) with all of the following properties:
-
(i)
The projective dimension of both \(Y_{r,S}\) and \(Z_r\) is at most 1;
-
(ii)
both \(Y_{r,S}\) and \(Z_r\) are torsion as R-modules;
-
(iii)
there is an exact triangle
$$\begin{aligned} Z_r[-3] \longrightarrow C_{r,S}^{\bullet } \longrightarrow Y_{r,S}[-2] \end{aligned}$$in \({\mathcal {D}}(e_r\Lambda ({\mathcal {G}}))\);
-
(iv)
we have that \(Y_{r,S} = Y_{0,S}(r)\) and \(Z_r = Z_0(r)\);
-
(v)
the coinvariants \((Z_r)_{\Gamma _L}\) are finite if \(r \not =1\).
Proof
We first consider the case \(r=0\). It is shown in [48, Proposition 8.5] that the complex \(C_{0,S}^{\bullet }\) is isomorphic in \({\mathcal {D}}(e_0 \Lambda ({\mathcal {G}}))\) to a complex
where \(Y_{0,S}\) is placed in degree 2. More precisely, in the notation of [48] we have
where T is a finite set of places of K disjoint from S with certain properties, and \({\mathcal {G}}_{w_{\infty }}\) denotes the decomposition group at a chosen place \(w_{\infty }\) of \(L_{\infty }\) above v for each \(v \in T\); moreover, we write \(\mathrm {ind}_{{\mathcal {U}}}^{{\mathcal {G}}} M := \Lambda ({\mathcal {G}}) \otimes _{\Lambda ({\mathcal {U}})} M\) for any open subgroup \({\mathcal {U}}\) of \({\mathcal {G}}\) and any \(\Lambda ({\mathcal {U}})\)-module M. By [48, Lemmas 8.4 and 8.5] the modules \(Z_0\) and \(Y_{0,S}\) are R-torsion and of projective dimension at most 1. Thus (i) and (ii) also hold for \(Y_{r,S} := Y_{0,S}(r) = Y_S^T(r-1)\) and \(Z_r := Z_0(r) = e_r \bigoplus _{v \in T} \mathrm {ind}_{{\mathcal {G}}_{w_{\infty }}}^{{\mathcal {G}}} \mathbb {Z}_p(r-1)\). It is now clear that (iv) holds and that \(C_{r,S}^{\bullet }\) is isomorphic to the complex
in \({\mathcal {D}}(e_r \Lambda ({\mathcal {G}}))\). Hence (iii) also holds. Moreover, the coinvariants \((Z_r)_{\Gamma _L}\) are clearly finite for \(r \not =1\). \(\square \)
Remark 4.11
We point out that similar constructions repeatedly appear in the literature. In fact, by [60, Theorem 2.4] the complex \(C_S^{\bullet }(L_{\infty }^+/K)\) naturally identifies with the complex constructed by Ritter and Weiss [65]. Choosing their maps \(\Psi \) and \({\tilde{\psi }}\) in [66, p.562 f.] suitably one can take \(Y_{1,S} = \mathrm {coker}(\Psi )\) and \(Z_1 = \mathrm {coker}({\tilde{\psi }})\). Moreover, Burns [15, Sect. 5.3.1] constructed an exact triangle in \({\mathcal {D}}(e_0 \Lambda ({\mathcal {G}}))\) of the form
where the set T is as in the proof of Lemma 4.10. For each \(v \in T\) the complex \(R\Gamma (K(v), e_0 \Lambda ({\mathcal {G}})^{\sharp }(1))\) is acyclic outside degree 1 and we have an \(e_0 \Lambda ({\mathcal {G}})\)-isomorphism
For each \(\Lambda ({\mathcal {G}})\)-module M and \(i \in \mathbb {Z}\) we set \(E^i(M) := \mathrm {Ext}^i_{\Lambda ({\mathcal {G}})}(M, \Lambda ({\mathcal {G}}))\). We then have an isomorphism of \(e_0 \Lambda ({\mathcal {G}})\)-modules
If \(C^{\bullet }\) is a complex in \({\mathcal {D}}(e_0\Lambda ({\mathcal {G}}))\), we denote the complex \(R\mathrm {Hom}_{e_0\Lambda ({\mathcal {G}})}(C^{\bullet }, e_0 \Lambda ({\mathcal {G}}))\) by \((C^{\bullet })^{*}\). If M is an R-torsion \(e_0\Lambda ({\mathcal {G}})\)-module of projective dimension at most 1, then we have isomorphisms \(M[-n]^{*} \simeq E^1(M)[n-1]\) in \({\mathcal {D}}(e_0\Lambda ({\mathcal {G}}))\) for every \(n \in \mathbb {Z}\). This yields
The complex \(R\Gamma _T({\mathcal {O}}_{K,S}, e_0 \Lambda ({\mathcal {G}})^{\sharp }(1))\) is acyclic outside degree 2 and its second cohomology group \(H^2_T({\mathcal {O}}_{K,S}, e_0 \Lambda ({\mathcal {G}})^{\sharp }(1))\) is of projective dimension at most 1 by [15, Proposition 5.5]. Since we have an isomorphism
by Artin–Verdier duality, it follows that we have an isomorphism
in \({\mathcal {D}}(e_0\Lambda ({\mathcal {G}}))\) and an isomorphism of \(e_0 \Lambda ({\mathcal {G}})\)-modules
Finally, the minus Tate module \(T_p(\mathcal {M_{S,T}^K})^-\) of the Iwasawa-theoretic 1-motive \(\mathcal {M_{S,T}^K}\) constructed by Greither and Popescu [38] plays the role of \(E^1(Y_S^T(-1))\); the \(e_0 \Lambda ({\mathcal {G}})\)-module \(T_p(\Delta _{\mathcal {K,T}})^-\) is our \(E^1(I_T)\). See in particular [38, Remark 3.10].
Theorem 4.12
Let \(r>1\) be an integer and let \(\rho \) be an irreducible Artin character of \({\mathcal {G}}^+\) such that \(\ker (\rho )\) contains \(\Gamma _{L^+}\). Set \(\psi := \rho \otimes \omega ^{r-1}\). Then the following conditions are equivalent.
-
(i)
We have that
 vanishes.
vanishes. -
(ii)
We have that
 vanishes.
vanishes. -
(iii)
We have that \(H^2_c({\mathcal {O}}_{L, S}, \mathbb {Q}_p(r))^{(\psi )}\) vanishes.
-
(iv)
The period \(\Omega _j (r, \psi )\) is non-zero for any (and hence every) choice of \(j: \mathbb {C}\simeq \mathbb {C}_p\).
-
(v)
We have that \(L_{p, S}(r, \rho ) \not = 0\).
If these equivalent conditions hold (in particular if \(\mathrm {Sch}(L,p,r)\) holds), then the complex \(C_{r,S}^{\bullet }\) is semisimple at \(\psi \).
Proof
We again set \({\mathcal {O}} := {\mathcal {O}}_{\psi }\) for brevity. We have already observed in the proof of Proposition 4.9 that  is a free \({\mathcal {O}}\)-module. The equivalence of (i) and (ii) is therefore clear. We have an exact sequence of \(\mathbb {Z}_{p}[G]\)-modules
is a free \({\mathcal {O}}\)-module. The equivalence of (i) and (ii) is therefore clear. We have an exact sequence of \(\mathbb {Z}_{p}[G]\)-modules

Since  is finite by Proposition 4.8 (iv) and the \(e_r\mathbb {Q}_p[G]\)-modules \(e_r H^1_{\acute{\mathrm {e}}\mathrm {t}}({\mathcal {O}}_{L, S}, \mathbb {Q}_p(r)) \simeq e_r K_{2r-1}({\mathcal {O}}_L) \otimes \mathbb {Q}_p\) and \(e_r P^1({\mathcal {O}}_{L, S}, \mathbb {Q}_p(r)) \simeq e_r(L \otimes _{\mathbb {Q}} \mathbb {Q}_p)\) are (non-canonically) isomorphic, there is a (non-canonical) isomorphism of \(e_r \mathbb {Q}_p[G]\)-modules
is finite by Proposition 4.8 (iv) and the \(e_r\mathbb {Q}_p[G]\)-modules \(e_r H^1_{\acute{\mathrm {e}}\mathrm {t}}({\mathcal {O}}_{L, S}, \mathbb {Q}_p(r)) \simeq e_r K_{2r-1}({\mathcal {O}}_L) \otimes \mathbb {Q}_p\) and \(e_r P^1({\mathcal {O}}_{L, S}, \mathbb {Q}_p(r)) \simeq e_r(L \otimes _{\mathbb {Q}} \mathbb {Q}_p)\) are (non-canonically) isomorphic, there is a (non-canonical) isomorphism of \(e_r \mathbb {Q}_p[G]\)-modules

Thus also  and \(H^2_c({\mathcal {O}}_{L, S}, \mathbb {Q}_p(r))^{(\psi )}\) are (non-canonically) isomorphic and so (ii) and (iii) are indeed equivalent. The equivalence of (ii) and (iv) is easy (see Remark 3.21).
and \(H^2_c({\mathcal {O}}_{L, S}, \mathbb {Q}_p(r))^{(\psi )}\) are (non-canonically) isomorphic and so (ii) and (iii) are indeed equivalent. The equivalence of (ii) and (iv) is easy (see Remark 3.21).
We next establish the equivalence of (i) and (v). By Lemma 4.1 the triangle of Lemma 4.10 (iii) induces an exact triangle
in \({\mathcal {D}}(\Lambda ^{{\mathcal {O}}}(\Gamma ))\). Let \(h_{r, \psi }(T)\) and \(g_{r,S, \psi }(T)\) be characteristic elements of \(Z_{r,\psi }\) and \(Y_{r,S,\psi }\), respectively. Corollary 4.7 implies that we may assume that
Since \((Z_{r,\psi })_{\Gamma }\) is finite by Lemma 4.10 (v) we have \(h_{r,\psi }(0) \not = 0\). Thus \(L_{p,S}(r, \rho ) = f_{\rho ,S}(u^{1-r}-1)\) is non-zero if and only if \(g_{r,S,\psi }(0) \not = 0\) if and only if \(Y_{r,S,\psi }^{\Gamma }\) vanishes, where the latter equivalence uses Lemma 4.2 (with \(M = Y_{r,S,\psi }\) and \({\mathcal {G}} = \Gamma \)) and Lemma 4.10 (i) and (ii). By (4.13) we have an exact sequence of \(\Lambda ^{{\mathcal {O}}}(\Gamma )\)-modules
Since taking \(\Gamma \)-invariants is left exact and \(Z_{r,\psi }^{\Gamma }\) vanishes by another application of Lemma 4.2, it follows that there is an isomorphism \(Y_{r,S,\psi }^{\Gamma } \simeq H^2(C^{\bullet }_{r,S,\psi })^{\Gamma }\). The latter identifies with  by Proposition 4.9 which proves the claim.
by Proposition 4.9 which proves the claim.
Finally, if these equivalent conditions all hold, then Proposition 4.9 implies that the \({\mathcal {O}}\)-modules \(H^i(C^{\bullet }_{r,S,\psi })^{\Gamma }\) and \(H^i(C^{\bullet }_{r,S,\psi })_{\Gamma }\) are finite for all \(i \in \mathbb {Z}\). It follows from the short exact sequences (4.2) that \(H^i(C^{\bullet }_{r,S,U})\) is finite for all \(i \in \mathbb {Z}\), where we set \(U = \Gamma _L\) as before. Thus the whole complex \(\mathbb {Q}_p \otimes _{\mathbb {Z}_{p}} \Delta _{C_{r,S}^{\bullet },\psi }\) vanishes. In particular, the complex \(C_{r,S}^{\bullet }\) is semisimple at \(\psi \). \(\square \)
Remark 4.13
By specializing \(K = L^+\) in the above argument, we see that Schneider’s conjecture \(\mathrm {Sch}(L,p,r)\) implies that \(Y_{r,S}^{\Gamma _L}\) vanishes and that \((Y_{r,S})_{\Gamma _L}\) is finite.
4.6 Higher refined p-adic class number formulae
We keep the notation of Sect. 4.3. We let \(\partial _p: \zeta (\mathbb {C}_p[G])^{\times } \simeq K_1(\mathbb {C}_{p}[G]) \rightarrow K_0(\mathbb {Z}_p[G], \mathbb {C}_p)\) be the composition of the inverse of the reduced norm and the connecting homomorphism to relative K-theory. By abuse of notation we shall use the same symbol for the induced maps on ‘\(e_r\)-parts’. We recall that G denotes \(\mathrm {Gal}(L/K)\) and that \(G^+ = G / \langle \tau \rangle = \mathrm {Gal}(L^+/K)\). We define
Let us assume that Schneider’s conjecture \(\mathrm {Sch}(L,p,r)\) holds. Then we actually have that \(L_{p,S}(r) \in \zeta (e_r\mathbb {Q}_p[G])^{\times }\) and the cohomology groups of the complex \(e_r R\Gamma _c({\mathcal {O}}_{L,S}, \mathbb {Z}_p(r))\) are finite by Proposition 4.8 and Theorem 4.12. This complex therefore is an object in \({\mathcal {D}}^{\mathrm {perf}}_{\mathrm {tors}}(e_r \mathbb {Z}_p[G])\). We now state our conjectural higher refined p-adic class number formula.
Conjecture 4.14
Let \(r>1\) be an integer and assume that \(\mathrm {Sch}(L,p,r)\) holds. Then in \(K_0(e_r\mathbb {Z}_p[G], \mathbb {Q}_p)\) one has
Remark 4.15
In the case \(r=1\) Burns [15, Conjecture 3.5] has formulated a conjectural refined p-adic class number formula. Conjecture 4.14 might be seen as a higher analogue of his conjecture. Accordingly, Theorem 4.17 below is the higher analogue of [15, Theorem 3.6].
Lemma 4.16
Let \(r>1\) be an integer and assume that \(\mathrm {Sch}(L,p,r)\) holds. Then
does not depend on the set S.
Proof
Let \(S'\) be a second sufficiently large finite set of places of K. By embedding S and \(S'\) into the union \(S \cup S'\) we may and do assume that \(S \subseteq S'\). By induction we may additionally assume that \(S' = S \cup \left\{ v \right\} \), where v is not in S. In particular, v is unramified in L/K and \(v \not \mid p\). By [17, (30)] we have an exact triangle
where \(R\Gamma _f(L_w, \mathbb {Z}_p(r))\) is a perfect complex of \(\mathbb {Z}_p[G_w]\)-modules which is naturally quasi-isomorphic to

with terms in degree 0 and 1. We set
We compute
where the first and second equality follow from (4.14) and (4.15), respectively. This implies the claim. \(\square \)
Our main evidence for Conjecture 4.14 is provided by the following result which, crucially, does not depend upon the vanishing of \(\mu _p(L^+)\).
Theorem 4.17
Let \(r>1\) be an integer and assume that \(\mathrm {Sch}(L,p,r)\) holds. If the equivariant Iwasawa main conjecture (Conjecture 4.4) holds for \(L^+_{\infty }/K\) (and so in particular if \(\mu _p(L^+) = 0\) or if \({\mathcal {G}}^+\) has an abelian Sylow p-subgroup), then Conjecture 4.14 holds.
Proof
We first observe that the complex \(C_{r,S}^{\bullet }\) is semisimple at \(\rho \otimes \omega ^{r-1}\) for all \(\rho \in \mathrm {Irr}_{\mathbb {C}_{p}}(G^+)\) by Theorem 4.12. Moreover, if we put \(U = \Gamma _L\) as above, then we have an isomorphism
in \({\mathcal {D}}(e_r \mathbb {Z}_p[G])\). If Conjecture 4.4 holds, then by Proposition 4.6 there is a characteristic element \(\zeta _{r,S}\) of \([C_{r,S}^{\bullet }]\) such that \(\zeta _{r,S}(\rho \otimes \omega ^{r-1}) = f_{\rho ,S}(u^{1-r}(1+T)-1)\). Since \(f_{\rho ,S}(u^{1-r}-1) = L_{p,S}(r, \rho ) \not =0\) we have that \(\zeta _{r,S}^{*}(\rho \otimes \omega ^{r-1}) = L_{p,S}(r, \rho )\). If \(\mu _p(L^+)\) vanishes or p does not divide the cardinality of \(G^+\), then [23, Theorem 2.2] implies the claim (as noted above the complexes \(\mathbb {Q}_p \otimes _{\mathbb {Z}_{p}} \Delta _{C_{r,S}^{\bullet },\rho \otimes \omega ^{r-1}}\) all vanish).
In order to avoid these assumptions, we proceed as follows. Observe that both \((Z_r)_{\Gamma _L}\) and \((Y_{r,s})_{\Gamma _L}\) are finite by Lemma 4.10 (v) and Theorem 4.12 (or rather Remark 4.13), respectively, since Schneider’s conjecture holds by assumption. Recall from Lemma 4.10 (iii) that we have an exact triangle
in \({\mathcal {D}}(e_r\Lambda ({\mathcal {G}}))\). It now follows from (4.16) and Lemma 4.2 for both \(Z_r\) and \(Y_{r,S}\) that we likewise have an exact triangle
in \({\mathcal {D}}(e_r\mathbb {Z}_p[G])\). Let \(H_r\) and \(G_{r,S}\) in \(\zeta (e_r{\mathcal {Q}}({\mathcal {G}}))^{\times }\) be the reduced norms of characteristic elements of \(Z_r\) and \(Y_{r,S}\), respectively. Note that both \(H_r\) and \(G_{r,S}\) are actually reduced norms of matrices with coefficients in \(e_r \Lambda ({\mathcal {G}})\). Since Conjecture 4.4 holds by assumption, we may assume that \(\mathrm {Nrd}(\zeta _{r,S}) = G_{r,S} / H_r\), where \(\zeta _{r,S}\) is the characteristic element of \([C_{r,S}^{\bullet }]\) that occurs in Proposition 4.6. Now by (the proof of) [55, Theorem 6.4] one has
where
and \(\overline{H_r}\) is defined similarly. Hence we obtain
It remains to justify the last equality \((*)\). For this we compute
Here the first and second equality follow from [59, Lemma 2.3] and (4.9), respectively. This finishes the proof of \((*)\). \(\square \)
Let us write \(K_0(e_r\mathbb {Z}_p[G], \mathbb {Q}_p)_{\mathrm {tors}}\) for the torsion subgroup of \(K_0(e_r\mathbb {Z}_p[G], \mathbb {Q}_p)\).
Corollary 4.18
Let \(r>1\) be an integer and assume that \(\mathrm {Sch}(L,p,r)\) holds. Then we have that \(HR_p(L/K,r) \in K_0(e_r\mathbb {Z}_p[G], \mathbb {Q}_p)_{\mathrm {tors}}\).
Proof
Let \(K' \subseteq L^+\) be a totally real field containing K. Denote the Galois group \(\mathrm {Gal}(L/K')\) by \(G'\). Then \(HR_p(L/K,r)\) maps to \(HR_p(L/K',r)\) under the natural restriction map \(K_0(e_r\mathbb {Z}_p[G], \mathbb {Q}_p) \rightarrow K_0(e_r\mathbb {Z}_p[G'], \mathbb {Q}_p)\). If \(L' \subseteq L\) is a Galois CM-extension of K, then likewise \(HR_p(L/K,r)\) maps to \(HR_p(L'/K,r)\) under the natural quotient map \(K_0(e_r\mathbb {Z}_p[G], \mathbb {Q}_p) \rightarrow K_0(e_r\mathbb {Z}_p[\mathrm {Gal}(L'/K)], \mathbb {Q}_p)\). Since \(HR(L'/K',r)\) vanishes for each intermediate Galois CM-extension of degree prime to p by Theorem 4.17, we deduce the result by a slight modification of the argument given in [64, Proof of Proposition 11] (also see [58, Proof of Corollary 2]). \(\square \)
4.7 An application to the equivariant Tamagawa number conjecture
Let r be an integer and let L/K be a finite Galois extension of number fields with Galois group G. We set \(\mathbb {Q}(r)_L := h^0(\mathrm {Spec}(L))(r)\) which we regard as a motive defined over K and with coefficients in the semisimple algebra \(\mathbb {Q}[G]\). The ETNC [17, Conjecture 4 (iv)] for the pair \((\mathbb {Q}(r)_L, \mathbb {Z}[G])\) asserts that a certain canonical element \(T\Omega (\mathbb {Q}(r)_L, \mathbb {Z}[G])\) in \(K_0(\mathbb {Z}[G], \mathbb {R})\) vanishes. Note that in this case the element \(T\Omega (\mathbb {Q}(r)_L, \mathbb {Z}[G])\) is indeed well-defined as observed in [18, Sect. 1]. If \(T\Omega (\mathbb {Q}(r)_L, \mathbb {Z}[G])\) is rational, i.e. belongs to \(K_0(\mathbb {Z}[G], \mathbb {Q})\), then by means of the canonical isomorphism
we obtain elements \(T\Omega (\mathbb {Q}(r)_L, \mathbb {Z}[G])_p\) in \(K_0(\mathbb {Z}_p[G], \mathbb {Q}_p)\).
If \(r>1\) is an integer and L/K is a Galois CM-extension, the following result provides a strategy for proving the ETNC for the pair \((\mathbb {Q}(r)_L, e_r \mathbb {Z}[\frac{1}{2}][G])\). We let \(T\Omega (\mathbb {Q}(r)_L, e_r\mathbb {Z}[{\textstyle \frac{1}{2}}][G])\) be the image of \(T\Omega (\mathbb {Q}(r)_L, \mathbb {Z}[G])\) under the canonical maps
induced by extension of scalars. We define \(T\Omega (\mathbb {Q}(r)_L, e_r\mathbb {Z}[{\textstyle \frac{1}{2}}][G])_p\) similarly.
Theorem 4.19
Let \(r>1\) be an integer and let p be an odd prime. Let L/K be a Galois CM-extension with Galois group G and set \({\tilde{L}} := L(\zeta _p)\). Assume that both Schneider’s conjecture \(\mathrm {Sch}({\tilde{L}},p,r)\) and the p-adic Beilinson conjecture (Conjecture 3.23) for \({\tilde{L}}^+/K\) hold. Then \(T\Omega (\mathbb {Q}(r)_L, e_r\mathbb {Z}[{\textstyle \frac{1}{2}}][G])\) is rational and we have that
If we assume in addition that the equivariant Iwasawa main conjecture (Conjecture 4.4) holds for \(\tilde{L}^+_{\infty }/K\), then the p-part of the ETNC for the pair \((\mathbb {Q}(r)_L, e_r \mathbb {Z}[\frac{1}{2}][G])\) holds, i.e. the element \(T\Omega (\mathbb {Q}(r)_L, e_r \mathbb {Z}[{\textstyle \frac{1}{2}}][G])_p\) vanishes.
Proof
Since \(T\Omega (\mathbb {Q}(r)_{{\tilde{L}}}, e_r\mathbb {Z}[{\textstyle \frac{1}{2}}][\mathrm {Gal}({\tilde{L}} / K)])\) maps to \(T\Omega (\mathbb {Q}(r)_L, e_r\mathbb {Z}[{\textstyle \frac{1}{2}}][G])\) under the canonical quotient map \(K_0(e_r \mathbb {Z}[{\textstyle \frac{1}{2}}][\mathrm {Gal}({\tilde{L}} / K)], \mathbb {R}) \rightarrow K_0(e_r \mathbb {Z}[{\textstyle \frac{1}{2}}][G], \mathbb {R})\) by [17, Theorem 4.1], we may and do assume that \({\tilde{L}} = L\). Since both Schneider’s conjecture and the p-adic Beilinson conjecture hold, Corollary 3.29 implies that Gross’s conjecture at \(s=1-r\) holds for all even (odd) irreducible characters of G if r is even (odd). By [62, Proposition 5.5 and Theorem 6.5] (or rather the ‘\(e_r\)-parts’ of these results) this is indeed equivalent to the rationality of \(T\Omega (\mathbb {Q}(r)_L, e_r\mathbb {Z}[{\textstyle \frac{1}{2}}][G])\).
Let us define
By the validity of the p-adic Beilinson conjecture we have that
We clearly have that \(\Omega _j(r) = \mathrm {Nrd} ([e_r(L \otimes _{\mathbb {Q}} \mathbb {C}_p) \mid \mu _p(r) \circ (\mathbb {C}_p \otimes _{\mathbb {C},j} \mu _{\infty }(r))^{-1}])\). Moreover, by Proposition 3.16 the automorphism
coincides with the ‘\(e_r\)-part’ of the trivialization of the same name in [62, Sect. 6.2] (up to an insignificant factor 2; cf. Remark 3.1). Since we have that
the object
is equal to the \(e_r\)-part of the object denoted by \(\Omega _{r,S}^j\) in [62, Sect. 6.2]. We now compute
Here, the first equality holds by definition of \(HR_p(L/K,r)\), the second and third equality follow from (4.17) (essentially the p-adic Beilinson conjecture) and (4.18), respectively, and the last equality follows from [62, Proposition 6.4 and Theorem 6.5]. Now Corollary 4.18 and Theorem 4.17 give the result. \(\square \)
Remark 4.20
Fix an integer \(r>1\). We have assumed throughout that \({\tilde{L}}\) contains a pth root of unity. What was actually needed in the above considerations, however, is that \(\omega ^{r-1}\) restricted to \(G_{{\tilde{L}}}\) is trivial. Let \(E \subseteq {\tilde{L}}_r \subseteq {\tilde{L}}\) be the smallest intermediate field such that \(\omega ^{r-1}\) restricted to \(G_{{\tilde{L}}_r}\) is trivial. Then we can replace \({\tilde{L}}\) by \({\tilde{L}}_r\) throughout. Note that \(\tilde{L}_r\) is totally real and thus \({\tilde{L}}_r^+ = {\tilde{L}}_r\) whenever r is odd, whereas we have \({\tilde{L}}_r = {\tilde{L}}\) otherwise. In particular, we can replace \({\tilde{L}}\) by E whenever \(r \equiv 1 \mod (p-1)\).
Corollary 4.21
Let p be an odd prime and let \(r>1\) be an integer such that \(r \equiv 1 \mod (p-1)\). Let E/K be a Galois extension of totally real fields with Galois group G. Assume that Schneider’s conjecture \(\mathrm {Sch}(E,p,r)\), the p-adic Beilinson conjecture (Conjecture 3.23) for E/K and the equivariant Iwasawa main conjecture (Conjecture 4.4) for \(E_{\infty }/K\) all hold. Then \(T\Omega (\mathbb {Q}(r)_E, \mathbb {Z}[{\textstyle \frac{1}{2}}][G])\) is rational and the p-part of the ETNC for the pair \((\mathbb {Q}(r)_E, \mathbb {Z}[\frac{1}{2}][G])\) holds.
Proof
This follows from Theorem 4.19 and Remark 4.20. \(\square \)
Corollary 4.22
Let L/K be a Galois extension of number fields with Galois group G and let p be an odd prime. Assume in addition that \(L/\mathbb {Q}\) is abelian. Then \(T\Omega (\mathbb {Q}(r)_L, e_r\mathbb {Z}[{\textstyle \frac{1}{2}}][G])\) is rational and the p-part of the ETNC for the pair \((\mathbb {Q}(r)_L, e_r\mathbb {Z}[\frac{1}{2}][G])\) holds for all but finitely many \(r>1\).
Proof
We may assume that \(K = \mathbb {Q}\) by functoriality. As \(L(\zeta _p)\) is abelian over the rationals, the relevant Iwasawa invariant \(\mu _p(L(\zeta _p)^+)\) vanishes by the aforementioned result of Ferrero and Washington [34] (see the discussion following (4.7)). Hence Conjecture 4.4 holds for \(L(\zeta _p)^+_{\infty }/\mathbb {Q}\) by either part of Theorem 4.5 (but note that in this case a variant of the equivariant Iwasawa main conjecture can be deduced from work of Mazur and Wiles [53] as in [65, Theorem 8] for example). The p-adic Beilinson conjecture holds for \(L(\zeta _p)^+/\mathbb {Q}\) by Theorem 3.30. Finally, Schneider’s conjecture \(\mathrm {Sch}(L(\zeta _p), p, r)\) holds for all but finitely many r by Remark 3.9. Thus the result follows from Theorem 4.19. \(\square \)
Remark 4.23
Of course, the result of Corollary 4.22 is not new. In fact, the ETNC for the pair \((\mathbb {Q}(r)_L, \mathbb {Z}[G])\) holds for every integer r whenever \(L/\mathbb {Q}\) is abelian. If \(r \le 0\) this is the main result of Burns and Greither in [20] (important difficulties with the prime 2 have subsequently been resolved by Flach [35]). The case \(r>0\) is due to Burns and Flach [19]. A slightly weaker variant of the ETNC, where the integral group ring \(\mathbb {Z}[G]\) is essentially replaced by a maximal order containing it, has been studied earlier by Huber and Kings [44].
Example 4.24
Let \(E/\mathbb {Q}\) be a Galois extension of totally real fields with Galois group \(G \simeq \mathrm {Aff}(q)\), where \(q = \ell ^n\) is a prime power. Let \(r>1\) be an integer. Since Gross’s conjecture holds for all \(\chi \in R(G)\) by Theorem 3.14 (iv), we have that \(T\Omega (\mathbb {Q}(r)_L, \mathbb {Z}[{\textstyle \frac{1}{2}}][G])\) is rational by [62, Theorem 6.5 (i)]. Let us write \(\mathrm {Aff}(q) \simeq N \rtimes H\), where N denotes the commutator subgroup of \(\mathrm {Aff}(q)\). Then the p-adic group ring \(\mathbb {Z}_p[\mathrm {Aff}(q)]\) is ‘N-hybrid’ in the sense of [46, Definition 2.5] by [46, Example 2.16] for every prime \(p \not = \ell \). Since every p-adic group ring is \(\{1\}\)-hybrid, we deduce from [48, Theorem 10.2] (or just as well from Theorem 4.5 (ii)) that the equivariant Iwasawa main conjecture holds unconditionally for \(E(\zeta _p)^+_{\infty }/\mathbb {Q}\) for every odd prime p. Thus Conjecture 4.14 holds by Theorem 4.17 whenever \(\mathrm {Sch}(E(\zeta _p),p,r)\) holds. In particular, this conjecture holds for almost all \(r>1\) for a fixed prime p.
We now assume for simplicity that \(r \equiv 1 \mod (p-1)\). The p-adic Beilinson conjecture holds for all linear characters of G by Theorem 3.30. As we have already observed in the proof of Theorem 3.14 (iv) there is only one non-linear character \(\chi _{\mathrm {nl}}\) of \(\mathrm {Aff}(q)\) which is a \(\mathbb {Z}\)-linear combination of linear characters and of \(\mathrm {ind}_H^G \mathbbm {1}_H\). Hence it suffices to show Conjecture 3.23 for the trivial character \(\mathbbm {1}_H\), i.e. for the trivial extension \(E^H/E^H\). Assuming this we can apply Corollary 4.21 to deduce that the p-part of the ETNC for the pair \((\mathbb {Q}(r)_E, e_r\mathbb {Z}[\frac{1}{2}][G])\) holds. So what is missing here (apart from Schneider’s conjecture) is a higher analogue of Colmez’s p-adic analytic class number formula [30] and its complex analytic counterpart. (A closer analysis of the proof of Theorem 4.19 shows that similar observations indeed hold for arbitrary \(r>1\).)
References
Barrett, J.P.: Annihilating the Tate-Shafarevic groups of Tate motives. Ph.D. thesis, King’s College London (2009)
Barsky, D.: Fonctions zeta \(p\)-adiques d’une classe de rayon des corps de nombres totalement réels, in Groupe d’Etude d’Analyse Ultramétrique (5e année: 1977/78), Secrétariat Math., Paris, pp. Exp. No. 16, 23 (1978)
Beĭlinson, A.A.: Higher regulators and values of \(L\)-functions. In: Current Problems in Mathematics, Vol. 24, Itogi Nauki i Tekhniki, Akad. Nauk SSSR, Vsesoyuz. Inst. Nauchn. i Tekhn. Inform., Moscow, pp. 181–238 (1984)
Besser, A.: Syntomic regulators and \(p\)-adic integration. I. Rigid syntomic regulators. Israel J. Math. 120, 291–334 (2000)
Besser, A., Buckingham, P., de Jeu, R., Roblot, X.-F.: On the \(p\)-adic Beilinson conjecture for number fields. Pure Appl. Math. Q. 5, 375–434 (2009)
Bley, W., Burns, D.: Equivariant epsilon constants, discriminants and étale cohomology. Proc. Lond. Math. Soc. 3(87), 545–590 (2003)
Bley, W., Cobbe, A.: Equivariant epsilon constant conjectures for weakly ramified extensions. Math. Z. 283, 1217–1244 (2016)
Bloch, S., Kato, K.: \(L\)-functions and Tamagawa numbers of motives, in The Grothendieck Festschrift, Vol. I, vol. 86 of Progr. Math., Birkhäuser Boston, Boston, MA, pp. 333–400 (1990)
Borel, A.: Stable real cohomology of arithmetic groups. Ann. Sci. École Norm. Sup. (4) 7(1974), 235–272 (1975)
Breuning, M., Burns, D.: Leading terms of Artin \(L\)-functions at \(s=0\) and \(s=1\). Compos. Math. 143, 1427–1464 (2007)
Burgos Gil, J.I.: The Regulators of Beilinson and Borel. CRM Monograph Series, vol. 15. American Mathematical Society, Providence (2002)
Burns, D.: Equivariant Tamagawa numbers and Galois module theory. I. Compos. Math. 129, 203–237 (2001)
Burns, D.: On derivatives of Artin \(L\)-series. Invent. Math. 186, 291–371 (2011)
Burns, D.: On main conjectures in non-commutative Iwasawa theory and related conjectures. J. Reine Angew. Math. 698, 105–159 (2015)
Burns, D.: On derivatives of \(p\)-adic \(L\)-series at \(s\) = 0. J. Reine Angew. Math. 762, 53–104 (2020)
Burns, D., Flach, M.: Motivic \(L\)-functions and Galois module structures. Math. Ann. 305, 65–102 (1996)
Burns, D., Flach, M.: Tamagawa numbers for motives with (non-commutative) coefficients. Doc. Math. 6, 501–570 (2001)
Burns, D., Flach, M.: Tamagawa numbers for motives with (noncommutative) coefficients. II. Am. J. Math. 125, 475–512 (2003)
Burns, D., Flach, M.: On the equivariant Tamagawa number conjecture for Tate motives. II, Doc. Math., pp. 133–163 (2006)
Burns, D., Greither, C.: On the equivariant Tamagawa number conjecture for Tate motives. Invent. Math. 153, 303–359 (2003)
Burns, D., Kurihara, M., Sano, T.: On Stark elements of arbitrary weight and their \(p\)-adic families, in Development of Iwasawa Theory—The Centennial of K. Iwasawa’s Birth, vol. 86 of Adv. Stud. Pure Math., Math. Soc. Japan, Tokyo, pp. 113–140 (2020)
Burns, D., Venjakob, O.: On the leading terms of zeta isomorphisms and \(p\)-adic \(L\)-functions in non-commutative Iwasawa theory. Doc. Math., pp. 165–209 (2006)
Burns, D., Venjakob, O.: On descent theory and main conjectures in non-commutative Iwasawa theory. J. Inst. Math. Jussieu 10, 59–118 (2011)
Cassou-Noguès, P.: Valeurs aux entiers négatifs des fonctions zêta et fonctions zêta \(p\)-adiques. Invent. Math. 51, 29–59 (1979)
Chinburg, T.: On the Galois structure of algebraic integers and \(S\)-units. Invent. Math. 74, 321–349 (1983)
Chinburg, T.: Exact sequences and Galois module structure. Ann. Math. 2(121), 351–376 (1985)
Coates, J., Fukaya, T., Kato, K., Sujatha, R., Venjakob, O.: The \(\rm GL_2\) main conjecture for elliptic curves without complex multiplication. Publ. Math. Inst. Hautes Études Sci. 101, 163–208 (2005)
Coates, J., Sinnott, W.: An analogue of Stickelberger’s theorem for the higher \(K\)-groups. Invent. Math. 24, 149–161 (1974)
Coleman, R.F.: Dilogarithms, regulators and \(p\)-adic \(L\)-functions. Invent. Math. 69, 171–208 (1982)
Colmez, P.: Résidu en \(s=1\) des fonctions zêta \(p\)-adiques. Invent. Math. 91, 371–389 (1988)
Curtis, C.W., Reiner, I.: Methods of Representation Theory. Pure and Applied Mathematics. With applications to finite groups and orders, vol. I. Wiley, New York (1981)
Dasgupta, S., Kakde, M., Ventullo, K.: On the Gross–Stark conjecture. Ann. Math. 2(188), 833–870 (2018)
Deligne, P., Ribet, K.A.: Values of abelian \(L\)-functions at negative integers over totally real fields. Invent. Math. 59, 227–286 (1980)
Ferrero, B., Washington, L.C.: The Iwasawa invariant \(\mu _{p}\) vanishes for abelian number fields. Ann. Math. 2(109), 377–395 (1979)
Flach, M.: On the cyclotomic main conjecture for the prime 2. J. Reine Angew. Math. 661, 1–36 (2011)
Fukaya, T., Kato, K.: A formulation of conjectures on \(p\)-adic zeta functions in noncommutative Iwasawa theory, in Proceedings of the St. Petersburg Mathematical Society. Vol. XII, vol. 219 of Amer. Math. Soc. Transl. Ser. 2, pp. 1–85. Amer. Math. Soc., Providence, RI (2006)
Greenberg, R.: On \(p\)-adic Artin \(L\)-functions. Nagoya Math. J. 89, 77–87 (1983)
Greither, C., Popescu, C.D.: An equivariant main conjecture in Iwasawa theory and applications. J. Algebraic Geom. 24, 629–692 (2015)
Gros, M.: Régulateurs syntomiques et valeurs de fonctions L p-adiques I. Invent. Math. 99, 293–320 (1990). (With an appendix by M. Kurihara)
Gros, M.: Régulateurs syntomiques et valeurs de fonctions \(L~p\)-adiques. II. Invent. Math. 115, 61–79 (1994)
Gross, B.H.: \(p\)-adic \(L\)-series at \(s=0\). J. Fac. Sci. Univ. Tokyo Sect. IA Math. 28, 979–994 (1982)
Gross, B.H.: On the values of Artin \(L\)-functions. Q. J. Pure Appl. Math. 1, 1–13 (2005)
Hesselholt, L., Madsen, I.: On the \(K\)-theory of local fields. Ann. Math. 2(158), 1–113 (2003)
Huber, A., Kings, G.: Bloch-Kato conjecture and main conjecture of Iwasawa theory for Dirichlet characters. Duke Math. J. 119, 393–464 (2003)
Iwasawa, K.: On \({{ Z}} _{l}\)-extensions of algebraic number fields. Ann. Math. 2(98), 246–326 (1973)
Johnston, H., Nickel, A.: On the equivariant Tamagawa number conjecture for Tate motives and unconditional annihilation results. Trans. Am. Math. Soc. 368, 6539–6574 (2016)
Johnston, H., Nickel, A.: Hybrid Iwasawa algebras and the equivariant Iwasawa main conjecture. Am. J. Math. 140, 245–276 (2018)
Johnston, H., Nickel, A.: On the non-abelian Brumer–Stark conjecture and the equivariant Iwasawa main conjecture. Math. Z. 292, 1233–1267 (2019)
Johnston, H., Nickel, A.: On the \(p\)-adic Stark conjecture at \(s = 1\) and applications. J. Lond. Math. Soc. 101, 1320–1354 (2020). (With an appendix by T. Hofmann, Johnston and Nickel)
Johnston, H., Nickel, A.: An unconditional proof of the abelian equivariant Iwasawa main conjecture and applications. arXiv:2010.03186 (2020)
Kakde, M.: The main conjecture of Iwasawa theory for totally real fields. Invent. Math. 193, 539–626 (2013)
Kolster, M., Nguyen Quang Do, T.: Syntomic regulators and special values of \(p\)-adic \(L\)-functions. Invent. Math. 133, 417–447 (1998)
Mazur, B., Wiles, A.: Class fields of abelian extensions of \( { Q}\). Invent. Math. 76, 179–330 (1984)
Neukirch, J., Schmidt, A., Wingberg, K.: Cohomology of Number Fields. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 323, 2nd edn. Springer, Berlin (2008)
Nickel, A.: Non-commutative Fitting invariants and annihilation of class groups. J. Algebra 323, 2756–2778 (2010)
Nickel, A.: Leading terms of Artin \(L\)-series at negative integers and annihilation of higher \(K\)-groups. Math. Proc. Camb. Philos. Soc. 151, 1–22 (2011)
Nickel, A.: On non-abelian Stark-type conjectures. Ann. Inst. Fourier (Grenoble) 61(2011), 2577–2608 (2012)
Nickel, A.: On the equivariant Tamagawa number conjecture in tame CM—extensions. Math. Z. 268, 1–35 (2011)
Nickel, A.: On the equivariant Tamagawa number conjecture in tame CM—extensions. II. Compos. Math. 147, 1179–1204 (2011)
Nickel, A.: Equivariant Iwasawa theory and non-abelian Stark-type conjectures. Proc. Lond. Math. Soc. 3(106), 1223–1247 (2013)
Nickel, A.: Integrality of Stickelberger elements and the equivariant Tamagawa number conjecture. J. Reine Angew. Math. 719, 101–132 (2016)
Nickel, A.: Annihilating wild kernels. Doc. Math. 24, 2381–2422 (2019)
Quillen, D.: On the cohomology and \(K\)-theory of the general linear groups over a finite field. Ann. Math. 2(96), 552–586 (1972)
Ritter, J., Weiss, A.: Cohomology of units and \(L\)-values at zero. J. Am. Math. Soc. 10, 513–552 (1997)
Ritter, J., Weiss, A.: Toward equivariant Iwasawa theory. Manuscr. Math. 109, 131–146 (2002)
Ritter, J., Weiss, A.: Toward equivariant Iwasawa theory. II. Indag. Math. (N.S.) 15, 549–572 (2004)
Ritter, J., Weiss, A.: On the "main conjecture" of equivariant Iwasawa theory. J. Am. Math. Soc. 24, 1015–1050 (2011)
Rubin, K.: A Stark conjecture "over \( {Z}\)" for abelian \(L\)-functions with multiple zeros. Ann. Inst. Fourier (Grenoble) 46, 33–62 (1996)
Schneider, P.: Über gewisse Galoiscohomologiegruppen. Math. Z. 168, 181–205 (1979)
Siegel, C.L.: Über die Fourierschen Koeffizienten von Modulformen. Nachr. Akad. Wiss. Göttingen Math.-Phys. Kl. II 1970, 15–56 (1970)
Snaith, V.: Stark’s conjecture and new Stickelberger phenomena. Canad. J. Math. 58, 419–448 (2006)
Soulé, C.: \(K\)-théorie des anneaux d’entiers de corps de nombres et cohomologie étale. Invent. Math. 55, 251–295 (1979)
Sujatha, R.: Reductions of the main conjecture, in Noncommutative Iwasawa Main Conjectures Over Totally Real Fields, vol. 29 of Springer Proc. Math. Stat., pp. 23–50. Springer, Heidelberg (2013)
Swan, R. G.: Algebraic \(K\)-Theory. Lecture Notes in Mathematics, No. 76. Springer, Berlin (1968)
Tate, J.: Les conjectures de Stark sur les fonctions \(L\) d’Artin en \(s=0\), vol. 47 of Progress in Mathematics. Lecture notes edited by Dominique Bernardi and Norbert Schappacher. Birkhäuser Boston Inc., Boston, MA (1984)
Weibel, C.: The norm residue isomorphism theorem. J. Topol. 2, 346–372 (2009)
Weibel, C.: The \(K\)-Book, vol. 145 of Graduate Studies in Mathematics. An Introduction to Algebraic \(K\)-Theory. American Mathematical Society, Providence, RI (2013)
Witte, M.: On a localisation sequence for the K-theory of skew power series rings. J. K-Theory 11, 125–154 (2013)
Acknowledgements
The author acknowledges financial support provided by the Deutsche Forschungsgemeinschaft (DFG) within the Heisenberg programme (Project No. 334383116).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nickel, A. On the p-adic Beilinson conjecture and the equivariant Tamagawa number conjecture. Sel. Math. New Ser. 28, 3 (2022). https://doi.org/10.1007/s00029-021-00717-3
Accepted:
Published:
DOI: https://doi.org/10.1007/s00029-021-00717-3





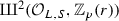 is finite.
is finite. vanishes.
vanishes. vanishes.
vanishes.