Abstract
We study the affine schemes of modules over gentle algebras. We describe the smooth points of these schemes, and we also analyze their irreducible components in detail. Several of our results generalize formerly known results, e.g. by dropping acyclicity, and by incorporating band modules. A special class of gentle algebras are Jacobian algebras arising from triangulations of unpunctured marked surfaces. For these we obtain a bijection between the set of generically \(\tau \)-reduced decorated irreducible components and the set of laminations of the surface. As an application, we get that the set of bangle functions (defined by Musiker–Schiffler–Williams) in the upper cluster algebra associated with the surface coincides with the set of generic Caldero-Chapoton functions (defined by Geiß–Leclerc–Schröer).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and main results
1.1 Overview
We study some geometric aspects of the representation theory of gentle algebras. This class of finite-dimensional algebras was defined by Assem and Skowroński [5], who were classifying the iterated tilted algebras of path algebras of extended Dynkin type \({\widetilde{A}}\). Gentle algebras are special biserial, which implies that their module categories can be described combinatorially, see [56] and also [11].
The irreducible components of the affine schemes of modules over gentle algebras are easy to classify (see Proposition 7.1). As a first main result, we describe all smooth points of these schemes, and we show that most components are generically reduced.
A special class of gentle algebras are Jacobian algebras arising from triangulations of unpunctured marked surfaces \(({{\mathbb {S}}},{{\mathbb {M}}})\). For these we obtain a bijection between the set of generically \(\tau \)-reduced decorated irreducible components and the set of laminations of the surface. This bijection is compatible with the parametrization of these two sets via g-vectors and shear coordinates. This bijection has some application to cluster algebras, a class of combinatorially defined commutative algebras discovered by Fomin and Zelevinsky [27]. Initially meant as a tool to describe parts of Lusztig’s dual canonical basis of quantum groups in a combinatorial way, cluster algebras turned out to appear at numerous different places of mathematics and mathematical physics. The generically \(\tau \)-reduced decorated components parametrize the generic Caldero-Chapoton functions, which belong to the coefficient-free upper cluster algebra \({{\mathcal {U}}}_{({{\mathbb {S}}},{{\mathbb {M}}})}\) associated with \(({{\mathbb {S}}},{{\mathbb {M}}})\). In many cases, these generic Caldero-Chapoton functions are known to form a basis, called the generic basis, of \({{\mathcal {U}}}_{({{\mathbb {S}}},{{\mathbb {M}}})}\), see for example [30] and [49]. We use the bijection mentioned above to show that the generic basis coincides with Musiker–Schiffler–Williams’ bangle basis (see [45, Corollary 1.3]) of the coefficient-free cluster algebra \({{\mathcal {A}}}_{({{\mathbb {S}}},{{\mathbb {M}}})}\) associated with \(({{\mathbb {S}}},{{\mathbb {M}}})\). It is known in most cases (for example, if \(|{{\mathbb {M}}}| \ge 2\)) that \({{\mathcal {A}}}_{({{\mathbb {S}}},{{\mathbb {M}}})} = {{\mathcal {U}}}_{({{\mathbb {S}}},{{\mathbb {M}}})}\), see [42, 43].
In the following subsections we describe our results in more detail.
1.2 Gentle algebras
Let \(Q = (Q_0,Q_1,s,t)\) be a quiver. Thus by definition, \(Q_0\) and \(Q_1\) are finite sets, where the elements of \(Q_0\) and \(Q_1\) are the vertices and arrows of Q, respectively. Furthermore, s and t are maps \(s,t:Q_1 \rightarrow Q_0\), where s(a) and t(a) are the starting vertex and terminal vertex of an arrow \(a \in Q_1\), respectively. A loop in Q is an arrow \(a \in Q_1\) with \(s(a) = t(a)\).
A basic algebra \(A = KQ/I\) is a gentle algebra provided the following hold:
-
(i)
For each \(i \in Q_0\) we have \(|\{ a \in Q_1 \mid s(a) = i \}| \le 2\) and \(|\{ a \in Q_1 \mid t(a) = i \}| \le 2\).
-
(ii)
The ideal I is generated by a set \(\rho \) of paths of length 2.
-
(iii)
Let \(a,b,c \in Q_1\) such that \(a \not = b\) and \(t(a) = t(b) = s(c)\). Then exactly one of the paths ca and cb is in I.
-
(iv)
Let \(a,b,c \in Q_1\) such that \(a \not = b\) and \(s(a) = s(b) = t(c)\). Then exactly one of the paths ac and bc is in I.
A gentle algebra \(A = KQ/I\) is a Jacobian algebra in the sense of [22] if and only if the following hold:
-
(v)
Q is connected.
-
(vi)
Q does not have any loops.
-
(vii)
Let \(a,b \in Q_1\) such that \(s(a) = t(b)\) and \(ab \in I\). Then there exists an arrow \(c \in Q_1\) with \(s(c) = t(a)\) and \(t(c) = s(b)\) such that \(bc,ca \in I\).
The gentle Jacobian algebras are exactly the Jacobian algebras associated to triangulations of unpunctured marked surfaces. This follows from [4, Section 2].
1.3 Smooth locus and generic reducedness of module schemes
Let Q be a quiver with \(Q_0 = \{ 1,\ldots ,n \}\), and let \(A = KQ/I\) be a basic algebra. For \({\mathbf {d}}\in {\mathbb {N}}^n\) let \({\text {Irr}}(A,{\mathbf {d}})\) be the set of irreducible components of the affine scheme \({\text {mod}}(A,{\mathbf {d}})\) of A-modules with dimension vector \({\mathbf {d}}\). For \(Z \in {\text {Irr}}(A,{\mathbf {d}})\) we write \({\underline{\dim }}(Z) := {\mathbf {d}}\). Let
The group
acts on the K-rational points of \({\text {mod}}(A,{\mathbf {d}})\) by conjugation, where \({\mathbf {d}}= (d_1,\ldots ,d_n)\). The orbit of \(M \in {\text {mod}}(A,{\mathbf {d}})\) is denoted by \({{\mathcal {O}}}_M\). The orbits in \({\text {mod}}(A,{\mathbf {d}})\) correspond bijectively to the isomorphism classes of A-modules with dimension vector \({\mathbf {d}}\).
For \(Z \in {\text {Irr}}(A,{\mathbf {d}})\) let \(Z^\circ \) be the interior of Z. These are all \(M \in Z\) such that M is not contained in any other irreducible component of \({\text {mod}}(A,{\mathbf {d}})\). Obviously \(Z^\circ \) is a non-empty, open, irreducible subset of \({\text {mod}}(A,{\mathbf {d}})\).
A module \(M \in {\text {mod}}(A,{\mathbf {d}})\) is smooth, if
where \(T_M\) is the tangent space of M at the affine scheme \({\text {mod}}(A,{\mathbf {d}})\). Otherwise, M is singular. Let \({\text {smooth}}(A,{\mathbf {d}})\) denote the set of smooth points of \({\text {mod}}(A,{\mathbf {d}})\).
For each gentle algebra A we obtain a complete description of smooth points of \({\text {mod}}(A,{\mathbf {d}})\) for all \({\mathbf {d}}\), see Theorem 7.6. As a consequence we get the following neat characterization for the case of gentle Jacobian algebras.
Theorem 1.1
(Smooth points) Let A be a gentle Jacobian algebra. For each dimension vector \({\mathbf {d}}\) we have
Note that the inclusion \(\subseteq \) in Theorem 1.1 is true for arbitrary basic algebras A. The other inclusion \(\supseteq \) is wrong in general. For example, it fails for most gentle algebras which are not Jacobian algebras.
A module \(M \in {\text {mod}}(A,{\mathbf {d}})\) is reduced if
where \(T_M^\mathrm{red}\) is the tangent space of M at the reduced affine scheme \({\text {mod}}(A,{\mathbf {d}})^\mathrm{red}\) associated with \({\text {mod}}(A,{\mathbf {d}})\). We call \({\text {mod}}(A,{\mathbf {d}})\) reduced if \({\text {mod}}(A,{\mathbf {d}}) = {\text {mod}}(A,{\mathbf {d}})^\mathrm{red}\). This is the case if and only if M is reduced for all \(M \in {\text {mod}}(A,{\mathbf {d}})\).
An irreducible component \(Z \in {\text {Irr}}(A)\) is generically reduced provided Z contains a dense open subset U such that each \(M \in U\) is reduced.
Theorem 1.2
(Generic reducedness) Let A be a gentle algebra without loops. Then each \(Z \in {\text {Irr}}(A)\) is generically reduced.
We prove a slightly more general version of Theorem 1.2 where we characterize all generically reduced components for arbitrary gentle algebras, see Theorem 7.4.
For acyclic gentle algebras, Theorem 1.2 is a consequence of [21].
1.4 Generically \(\tau \)-reduced components
For \(M \in {\text {mod}}(A,{\mathbf {d}})\) let
Here \(\tau _A\) denotes the Auslander-Reiten translation of A.
For each \(Z \in {\text {Irr}}(A)\) there is a dense open subset \(U \subseteq Z\) such that the maps \(c_A\), \(e_A\) and \(h_A\) are constant on U. These generic values are denoted by \(c_A(Z)\), \(e_A(Z)\) and \(h_A(Z)\).
It follows that
Voigt’s Lemma 2.2 and the Auslander-Reiten formulas (see Theorem 5.4) imply that
Clearly, an irreducible component Z is generically reduced if and only if \(c_A(Z) = e_A(Z)\). We say that Z is generically \(\tau \)-reduced provided
Such irreducible components were first defined and studied in [30], where they ran under the name strongly reduced components.
Let \({\text {Irr}}^\tau (A)\) be the subset of \({\text {Irr}}(A)\) consisting of the generically \(\tau \)-reduced components.
Recall that an A-module M is rigid (resp. \(\tau \)-rigid) if \({\text {Ext}}_A^1(M,M) = 0\) (resp. \({\text {Hom}}_A(M,\tau _A(M)) = 0\)). By the Auslander-Reiten formulas, any \(\tau \)-rigid module is rigid, wheras the converse is wrong in general. Each rigid A-module M yields a generically reduced component \(Z = \overline{{{\mathcal {O}}}_M}\). If M is \(\tau \)-rigid, then this Z is generically \(\tau \)-reduced.
The next result says that for gentle Jacobian algebras, the generically \(\tau \)-reduced components are determined by their dimension vectors.
Theorem 1.3
Let A be a gentle Jacobian algebra. For \(Z_1,Z_2 \in {\text {Irr}}^\tau (A)\) the following are equivalent:
-
(i)
\({\underline{\dim }}(Z_1) = {\underline{\dim }}(Z_2)\);
-
(ii)
\(Z_1 = Z_2\).
Let \(A = KQ/I\) be a gentle Jacobian algebra with \(Q_0 = \{ 1,\ldots ,n \}\). Recall that the ideal I is generated by a set \(\rho \) of paths of length 2. We denote the standard idempotents of A by \(e_1,\ldots ,e_n\). Let \(a \in Q_1\). Then we are in one of the following two cases:
-
(i)
There is no arrow \(b \in Q_1\) with \(s(a) = t(b)\) such that \(ab \in I\). In this case, the 3-dimensional subalgebra of A spanned by \(e_{s(a)}\), \(e_{t(a)}\) and a is called a 2-block of A.
-
(ii)
There are arrows \(b,c \in Q_1\) with \(s(a) = t(b)\), \(s(c) = t(a)\) and \(s(b) = t(c)\) such that \(ab,ca,bc \in I\). In this case, the 6-dimensional subalgebra of A spanned by \(e_{s(a)}\), \(e_{s(b)}\), \(e_{s(c)}\), a, b and c is called a 3-block of A.
In the special case where the quiver Q consists just of a single vertex, we call A itself a 1-block. A \(\rho \)-block of A is a subalgebra which is either a 1-block, 2-block or 3-block. (Note that the \(\rho \)-blocks are not necessarily unital subalgebras, i.e. the unit of a \(\rho \)-block of A does in general not coincide with the unit of A.)
We say that a vertex \(j \in Q_0\) or an arrow \(a \in Q_1\) belongs to a \(\rho \)-block \(A_i\) of A if \(e_j \in A_i\) or \(a \in A_i\), respectively. Note that each arrow of Q belongs to exactly one \(\rho \)-block of A, and each vertex of Q belongs to at most two \(\rho \)-blocks.
The restriction of representations of a gentle Jacobian algebra A to its \(\rho \)-blocks \(A_1,\ldots ,A_t\) yields a bijection
In Sect. 4 we extend this observation to arbitrary basic algebras \(A = KQ/I\). This reduces the study of schemes of modules over gentle algebras to schemes of complexes.
Our next result characterizes the generically \(\tau \)-reduced components of a gentle Jacobian algebra in terms of the generically \(\tau \)-reduced components of its \(\rho \)-blocks.
The fact that the generic reducedness or the smooth locus of a component Z relate to the generic reducedness or the smooth locus of the components \(\pi _i(Z)\) does not come as a surprise. The following result however is somewhat unexpected, since the Auslander-Reiten translation for A is quite different from the Auslander-Reiten translations for the \(\rho \)-blocks of A.
Theorem 1.4
Let \(A = KQ/I\) be a gentle Jacobian algebra, and let \(A_1,\ldots ,A_t\) be its \(\rho \)-blocks. For an irreducible component \(Z \in {\text {Irr}}(A)\) the following are equivalent:
-
(i)
\(Z \in {\text {Irr}}^\tau (A)\);
-
(ii)
\(\pi _i(Z) \in {\text {Irr}}^\tau (A_i)\) for all \(1 \le i \le t\).
One might ask if Theorem 1.4 holds for arbitrary finite-dimensional K-algebras using of course a generalized definition for \(\rho \)-blocks.
1.5 Band components
The indecomposable modules over a gentle algebra A (or more generally, over a string algebra) are either string modules or band modules, see [11, 56] for details. The band modules occur naturally in \(K^*\)-parameter families. An irreducible component \(Z \in {\text {Irr}}(A)\) is a string component if it contains a string module whose orbit is dense in Z, and Z is a band component if it contains a \(K^*\)-parameter family of band modules whose union of orbits is dense in Z.
An irreducible component \(Z \in {\text {Irr}}(A)\) is a brick component if it contains a brick, i.e. an A-module M with \(\dim {\text {End}}_A(M) = 1\). In this case, by upper semicontinuity the bricks in Z form a dense open subset of Z.
Theorem 1.5
Let A be a gentle algebra. Then each band component is a brick component.
Using the terminology of [20], each irreducible component \(Z \in {\text {Irr}}(A)\) is a direct sum of uniquely determined indecomposable irreducible components. The string and band components are the only indecomposable components for string algebras.
The generically \(\tau \)-reduced string components are exactly the components containing an indecomposable \(\tau \)-rigid module, which is then automatically a string module.
Theorem 1.6
Let A be a gentle algebra. For \(Z \in {\text {Irr}}(A,{\mathbf {d}})\) the following are equivalent:
-
(i)
Z is a direct sum of band components.
-
(ii)
\(\dim (Z) = \dim ({\text {GL}}_{\mathbf {d}}(K))\).
In this case, Z is generically \(\tau \)-reduced.
Theorem 1.6 is closely related to the seemingly different [15, Proposition 4.3]. The proofs follow the same line of arguments. We thank Ryan Kinser for pointing this out to us.
For acyclic gentle algebras, Theorems 1.5 and 1.6 can be extracted from Carroll and Chindris [14, Corollary 10] and [14, Proposition 11], see also [13, Theorem 2]. As a consequence of Theorem 1.5, one gets the known result that a gentle algebra A is representation-finite if and only if \({\text {mod}}(A)\) contains just finitely many bricks, compare [48, Theorem 1.1].
1.6 Laminations of marked surfaces and generically \(\tau \)-reduced components
A lamination of an unpunctured marked surface \(({{\mathbb {S}}},{{\mathbb {M}}})\) is a set of homotopy classes of curves and loops in \(({{\mathbb {S}}},{{\mathbb {M}}})\), which do not intersect each other, together with a positive integer attached to each class. Let \({\text {Lam}}({{\mathbb {S}}},{{\mathbb {M}}})\) be the set of such laminations. (For more precise definitions, we refer to Sect. 10.)
Let T be a triangulation of \(({{\mathbb {S}}},{{\mathbb {M}}})\), and let \(A_T\) be the associated gentle Jacobian algebra. A decorated irreducible component is roughly speaking an irreducible component of \({\text {mod}}(A_T,{\mathbf {d}})\) equipped with a certain integer datum. Similarly as before, one defines generically \(\tau \)-reduced decorated irreducible components. Let \({\text {decIrr}}^\tau (A_T)\) be the set of all generically \(\tau \)-reduced decorated components of \({\text {decmod}}(A_T,({\mathbf {d}},{{\mathbf {v}}}))\), where \(({\mathbf {d}},{{\mathbf {v}}})\) runs over all dimension vectors. A precise definition can be found in Sect. 9.
Theorem 1.7
Let \(({{\mathbb {S}}},{{\mathbb {M}}})\) be an unpunctured marked surface, and let T be a triangulation of \(({{\mathbb {S}}},{{\mathbb {M}}})\). Let \(A = A_T\) be the associated Jacobian algebra. Then there is a natural bijection
In their ground breaking work, Fomin, Shapiro and Thurston [25] proved that the laminations of \(({{\mathbb {S}}},{{\mathbb {M}}})\) consisting of curves are in bijection with the cluster monomials of a cluster algebra \({{\mathcal {A}}}_{({{\mathbb {S}}},{{\mathbb {M}}})}\) associated with \(({{\mathbb {S}}},{{\mathbb {M}}})\). Note that Fomin, Shapiro and Thurston work with cluster algebras with arbitrary coefficient systems, whereas we always assume that \({{\mathcal {A}}}_{({{\mathbb {S}}},{{\mathbb {M}}})}\) is a coefficient-free cluster algebra.
Musiker, Schiffler and Williams [45] defined a set
of bangle functions, whose elements are parametrized by \({\text {Lam}}({{\mathbb {S}}},{{\mathbb {M}}})\), and which (by results in [44]) contains all cluster monomials. They show that \({{\mathcal {B}}}_T\) forms a basis of \({{\mathcal {A}}}_{({{\mathbb {S}}},{{\mathbb {M}}})}\) provided \(|{{\mathbb {M}}}| \ge 2\), see [45, Corollary 1.3].
A result by W. Thurston (see [26, Theorem 12.3]) says that there is a bijection
sending a lamination to its shear coordinate. Combining a theorem by Brüstle and Zhang [10, Theorem 1.6] with a result by Adachi, Iyama and Reiten [1, Theorem 4.1], one gets a bijection between the laminations in \({\text {Lam}}({{\mathbb {S}}},{{\mathbb {M}}})\) which consist only of curves, and the set of generically \(\tau \)-reduced decorated components in \({\text {decIrr}}^\tau (A_T)\), which contain a dense orbit. On the other hand, Plamondon [47] proved that there is a bijection
sending a component to its g-vector. Theorem 1.7 extends Brüstle-Zhang’s bijection mentioned above to a bijection
such that \({\mathbf {g}}_T \circ \eta _T = {{\mathbf {s}}}_T\).
Let
be the set of generic Caldero-Chapoton functions as defined in [30]. As a consequence of more general results in [23], the set \({{\mathcal {G}}}_T\) is contained in the upper cluster algebra \({{\mathcal {U}}}_{({{\mathbb {S}}},{{\mathbb {M}}})}\) and contains all cluster monomials. Furthermore, by [47, Theorem 1.3], the set \({{\mathcal {G}}}_T\) is (in a certain sense) independent of the choice of the triangulation T of \(({{\mathbb {S}}},{{\mathbb {M}}})\).See also [29]
The proof of the next theorem is based on the bijection from Theorem 1.7.
Theorem 1.8
\({{\mathcal {B}}}_T = {{\mathcal {G}}}_T\).
The diagram in Fig. 1 summarizes the situation.
1.7 Overall structure of the article
The article is organized as follows. After the introduction (Sect. 1), we recall in Sect. 2 some fundamentals on schemes of modules over basic algebras. Section 3 contains a characterization of generically \(\tau \)-reduced components for tame algebras. In Section 4 we introduce \(\rho \)-block decompositions of schemes of modules and derive some consequences on tangent spaces. Section 5 contains a few facts on the representation theory of gentle algebras. We also recall the definition of rank functions of modules over gentle algebras. Section 6 consists of a detailed study of schemes of complexes. We determine their smooth points, and we describe all rigid and \(\tau \)-rigid modules over the associated basic algebras. In Sect. 7 we apply the results obtained in Sect. 6 and prove Theorems 1.1, 1.2, 1.6 and 1.5. The proofs of Theorems 1.3 and 1.4 can be found in Sect. 8. In Sect. 9 we recall some basics on decorated modules and schemes of decorated modules over finite-dimensional algebras. Section 10 contains the proof of Theorem 1.7, and also the proof that under the bijection in Theorem 1.7, shear coordinates and g-vectors are compatible. Theorem 1.8 is proved in Sect. 11. In Sect. 12 we illustrate the combinatorics used in Sect. 11 by an example.
2 Scheme of modules
In this section, we recall some definitions and elementary facts on the representation theory of basic algebras and on schemes of modules over such algebras. Throughout, let K be an algebraically closed field.
2.1 Orbits, tangent spaces and Voigt’s Lemma
Let \(Q = (Q_0,Q_1,s,t)\) be a quiver. If not mentioned otherwise, we always assume that \(Q_0 = \{ 1,\ldots ,n \}\).
A path in Q is a tuple \(p = (a_1,\ldots ,a_m)\) of arrows \(a_i \in Q_1\) such that \(s(a_i) = t(a_{i+1})\) for all \(1 \le i \le m-1\). Then \({\text {length}}(p) := m\) is the length of p, and we set \(s(p) := s(a_m)\) and \(t(p) := t(a_1)\). Additionally, for each vertex \(i \in Q_0\) there is a path \(e_i\) of length 0, and let \(s(e_i) = t(e_i) = i\). We often just write \(a_1 \cdots a_m\) instead of \((a_1,\ldots ,a_m)\). A path \(p = (a_1,\ldots ,a_m)\) of length \(m \ge 1\) is a cycle in Q, or more precisely an m-cycle in Q, if \(s(p) = t(p)\).
Let KQ be the path algebra of Q, and let \({\mathfrak {m}}\) be the ideal generated by the arrows of Q. An ideal I of KQ is admissible if there exists some \(m \ge 2\) such that \({\mathfrak {m}}^m \subseteq I \subseteq {\mathfrak {m}}^2\). In this case, we call \(A := KQ/I\) a basic algebra. Clearly, basic algebras are finite-dimensional. By a Theorem of Gabriel, each finite-dimensional K-algebra is Morita equivalent to a basic algebra.
A relation in KQ is a linear combination
where the \(p_i\) are pairwise different paths of length at least 2 in Q with \(s(p_i) = s(p_j)\) and \(t(p_i) = t(p_j)\) for all \(1 \le i,j \le s\) and \(\lambda _i \in K^*\) for all i.
Each admissible ideal is generated by a finite set of relations.
Let \(A = KQ/I\) be a basic algebra. Up to isomorphism, there are n simple A-modules \(S_1,\ldots ,S_n\) corresponding to the vertices of Q. Let \(P_1,\ldots ,P_n\) (resp. \(I_1,\ldots ,I_n\)) be the projective covers (resp. injective envelopes) of the simple modules \(S_1,\ldots ,S_n\).
A representation of a quiver \(Q = (Q_0,Q_1,s,t)\) is a tuple \(M = (M_i,M_a)_{i \in Q_0,a \in Q_1}\), where \(M_i\) is a finite-dimensional K-vector space for each \(i \in Q_0\), and \(M_a:M_{s(a)} \rightarrow M_{t(a)}\) is a K-linear map for each arrow \(a \in Q_1\).
For a path \(p = (a_1,\ldots ,a_m)\) in Q and a representation M as above, let
We call
the dimension vector of M, and let
be the dimension of M. The ith entry \(\dim (M_i)\) of \({\underline{\dim }}(M)\) equals the Jordan-Hölder multiplicity \([M:S_i]\) of \(S_i\) in M.
A representation of a basic algebra \(A = KQ/I\) is a representation M of Q, which is annihilated by the ideal I, i.e. for each relation
in I we demand that
In the usual way, we identify the category \({\text {rep}}(A)\) of representations of A with the category \({\text {mod}}(A)\) of finite-dimensional left A-modules.
For \({\mathbf {d}}= (d_1,\ldots ,d_n) \in {\mathbb {N}}^n\) let \({\text {mod}}(A,{\mathbf {d}})\) be the affine scheme of representations of A with dimension vector \({\mathbf {d}}\). By definition the K-rational points of \({\text {mod}}(A,{\mathbf {d}})\) are the representations \(M = (M_i,M_a)_{i \in Q_0,a \in Q_1}\) of A with \(M_i = K^{d_i}\) for all \(i \in Q_0\). When there is no danger of confusion, we will just write \({\text {mod}}(A,{\mathbf {d}})\) for the set of K-rational points of \({\text {mod}}(A,{\mathbf {d}})\). One can regard \({\text {mod}}(A,{\mathbf {d}})\) as a Zariski closed subset of the affine space
The group \({\text {GL}}_{\mathbf {d}}(K)\) acts on the K-rational points of \({\text {mod}}(A,{\mathbf {d}})\) by conjugation. More precisely, for \(g = (g_1,\ldots ,g_n) \in {\text {GL}}_{\mathbf {d}}(K)\) and \(M \in {\text {mod}}(A,{\mathbf {d}})\) let
For \(M \in {\text {mod}}(A,{\mathbf {d}})\) let \({{\mathcal {O}}}_M\) be the \({\text {GL}}_{\mathbf {d}}(K)\)-orbit of M. The \({\text {GL}}_{\mathbf {d}}(K)\)-orbits are in bijection with the isomorphism classes of representations of A with dimension vector \({\mathbf {d}}\).
For \(M \in {\text {mod}}(A,{\mathbf {d}})\) we denote the tangent space of M at \({\text {mod}}(A,{\mathbf {d}})\) by \(T_M\). Let \(T_M({{\mathcal {O}}}_M)\) be the tangent space of M at \({{\mathcal {O}}}_M\). Since the \({\text {GL}}_{\mathbf {d}}(K)\)-orbit \({{\mathcal {O}}}_M\) is smooth, we have
The following lemma is obvious.
Lemma 2.1
For \(M \in {\text {mod}}(A,{\mathbf {d}})\) the following are equivalent:
-
(i)
\({{\mathcal {O}}}_M\) is open.
-
(ii)
The Zariski closure \(\overline{{{\mathcal {O}}}_M}\) is an irreducible component of \({\text {mod}}(A,{\mathbf {d}})\).
For the following proposition we refer to Gabriel [28, Proposition 1.1] and Voigt [55].
Lemma 2.2
(Voigt’s Lemma) For \(M \in {\text {mod}}(A,{\mathbf {d}})\) there is an isomorphism
of K-vector spaces.
Corollary 2.3
Let \(M \in {\text {mod}}(A,{\mathbf {d}})\) be rigid. Then \({{\mathcal {O}}}_M\) is open.
The converse of Corollary 2.3 is in general wrong.
Corollary 2.4
Let \(M \in {\text {mod}}(A,{\mathbf {d}})\) be rigid. Then M is smooth.
Corollary 2.5
For \(M \in {\text {mod}}(A,{\mathbf {d}})\) the following are equivalent:
-
(i)
M is rigid.
-
(ii)
The Zariski closure of \({{\mathcal {O}}}_M\) is a generically reduced component of \({\text {mod}}(A,{\mathbf {d}})\).
Lemma 2.6
Let \(M \in {\text {mod}}(A,{\mathbf {d}})\) be smooth. Then M is reduced.
Proof
This is clear, since for each irreducible component Z with \(M \in Z\) we have
\(\square \)
The following three results are well known and can be extracted e.g. from [35, 52, 53].
Proposition 2.7
Let \(Z \in {\text {Irr}}(A,{\mathbf {d}})\). Then there is a dense open subset \(U \subseteq Z\) such that
for all \(M \in U\).
Proposition 2.8
Let \(Z \in {\text {Irr}}(A,{\mathbf {d}})\). Then the smooth points in Z form a (possibly empty) open subset of Z.
Proposition 2.9
Let \(M \in {\text {mod}}(A,{\mathbf {d}})\) be contained in at least two different irreducible components. Then M is singular.
The following statement is proved in [31, Proposition 3.7]. It relies on results from [32].
Proposition 2.10
Let \(M \in {\text {mod}}(A,{\mathbf {d}})\) with \({\text {Ext}}_A^2(M,M) = 0\). Then M is smooth.
2.2 Canonical decompositions of irreducible components
An irreducible component \(Z \in {\text {Irr}}(A,{\mathbf {d}})\) is indecomposable if
is dense in Z. Let \({\mathbf {d}}\) and \({\mathbf {d}}_1,\ldots ,{\mathbf {d}}_t\) be dimension vectors with \({\mathbf {d}}= {\mathbf {d}}_1 + \cdots + {\mathbf {d}}_t\). For \(Z_i \in {\text {Irr}}(A,{\mathbf {d}}_i)\) with \(1 \le i \le t\) let
be the image of the morphism
For each \(Z \in {\text {Irr}}(A)\) there are uniquely determined (up to renumbering) indecomposable irreducible components \(Z_1,\ldots ,Z_t \in {\text {Irr}}(A)\) such that
see [20, Theorem 1.1]. This is called the canonical decomposition of Z. For \(Z \in {\text {Irr}}(A,{\mathbf {d}})\) set \({\underline{\dim }}(Z) := {\mathbf {d}}\). For \(Z_1,Z_2 \in {\text {Irr}}(A)\) let
Theorem 2.11
([20, Theorem 1.2]) Let A be a finite-dimensional K-algebra. For \(Z_1,\ldots ,Z_t \in {\text {Irr}}(A)\) the following are equivalent:
-
(i)
\(\overline{Z_1 \oplus \cdots \oplus Z_t} \in {\text {Irr}}(A)\);
-
(ii)
\({\text {ext}}_A^1(Z_i,Z_j) = 0\) for all \(i \not = j\).
For each \(Z \in {\text {Irr}}^\tau (A)\) there are uniquely determined (up to renumbering) indecomposable components \(Z_1,\ldots ,Z_t \in {\text {Irr}}^\tau (A)\) such that
Theorem 2.12
([17, Theorem 5.11]) Let A be a finite-dimensional K-algebra. For \(Z_1,\ldots ,Z_t \in {\text {Irr}}^\tau (A)\) the following are equivalent:
-
(i)
\(\overline{Z_1 \oplus \cdots \oplus Z_t} \in {\text {Irr}}^\tau (A)\);
-
(ii)
\(h_A(Z_i,Z_j) = 0\) for all \(i \not = j\).
3 Generically \(\tau \)-reduced components for tame algebras
In this section, we characterize the indecomposable \(\tau \)-reduced components for tame algebras. The proof consists basically of combining some known results in a straightforward manner.
Let A be a finite-dimensional K-algebra. Then A is a tame algebra if for each dimension d there exists a finite number \(M_1,\ldots ,M_t\) of A-K[X]-bimodules \(M_i\), which are free of rank d as K[X]-modules, such that all but finitely many d-dimensional A-modules are isomorphic to
for some \(1 \le i \le t\) and some \(\lambda \in K\).
The following lemma is well known folklore. A proof can be found in [14, Section 2.2].
Lemma 3.1
Let A be a tame algebra, and let \(Z \in {\text {Irr}}(A)\) be an indecomposable irreducible component. Then \(c_A(Z) \in \{ 0,1 \}\). Furthermore, the following hold:
-
(i)
\(c_A(Z) = 0\) if and only if Z contains an indecomposable module M with
$$\begin{aligned} Z = \overline{{{\mathcal {O}}}_M}. \end{aligned}$$ -
(ii)
\(c_A(Z) = 1\) if and only if Z contains a rational curve C such that the points of C are pairwise non-isomorphic indecomposable modules with
$$\begin{aligned} Z = \overline{\bigcup _{M \in C} {{\mathcal {O}}}_M}. \end{aligned}$$
Theorem 3.2
Let A be a tame algebra, and let \(Z \in {\text {Irr}}(A)\) be an indecomposable irreducible component. Then the following hold:
-
(i)
For \(c_A(Z) = 0\) the following are equivalent:
-
(a)
Z is generically \(\tau \)-reduced.
-
(b)
Z contains an indecomposable \(\tau \)-rigid module M.
In this case,
$$\begin{aligned} Z = \overline{{{\mathcal {O}}}_M}. \end{aligned}$$ -
(a)
-
(ii)
For \(c_A(Z) = 1\) the following are equivalent:
-
(a)
Z is generically \(\tau \)-reduced.
-
(b)
Z contains a rational curve C such that the points of C are pairwise non-isomorphic bricks.
-
(c)
Z contains infinitely many pairwise non-isomorphic bricks.
In this case,
$$\begin{aligned} Z = \overline{\bigcup _{M \in C} {{\mathcal {O}}}_M}. \end{aligned}$$ -
(a)
Proof
Part (i) follows directly from the definitions. Thus assume \(c_A(Z) = 1\). By Lemma 3.1, Z contains a rational curve C such that the points of C are pairwise non-isomorphic indecomposable modules with
Now a deep result by Crawley-Boevey [19, Theorem D] says that \(\tau _A(M) \cong M\) for all but finitely many \(M \in C\). Thus Z is generically \(\tau \)-reduced if and only if \(h_A(Z) = 1\) if and only if \(\dim {\text {Hom}}_A(M,\tau _A(M)) = \dim {\text {End}}_A(M) = 1\) for all but finitely many \(M \in C\). Thus (a) and (b) are equivalent. In a brick component, the bricks always form a dense open subset. Keeping in mind Lemma 3.1, this implies the equivalence of (b) and (c). \(\square \)
For an arbitrary finite-dimensional K-algebra A, each generically \(\tau \)-reduced component \(Z \in {\text {Irr}}(A)\) is a direct sum of indecomposable generically \(\tau \)-reduced components. This is explained in Sect. 9.5.
4 \(\rho \)-block decomposition and tangent spaces
Let \(A = KQ/I\), where KQ is a path algebra and I is an admissible ideal generated by a set \(\rho = \{ \rho _1,\ldots ,\rho _m \}\) of relations.
For each
with \(1 \le k \le m\) let \(Q(\rho _k)\) be the smallest subquiver of Q containing the paths \(p_i\). Of course, these subquivers might overlap for different relations.
For arrows \(a,b \in Q_1\) write \(a \sim b\) if there is some k with \(a,b \in Q(\rho _k)\). Let \(\sim \) be the smallest equivalence relation on \(Q_1\) respecting this rule. In particular, each \(a \in Q_1\) which is not contained in any of the \(Q(\rho _k)\) forms its own equivalence class.
Each equivalence class in \(Q_1\) with respect to \(\sim \) gives rise to a subquiver of Q and also to a subalgebra of A. These subalgebras are the \(\rho \)-blocks of A. Each vertex \(i \in Q_0\), which has no arrow attached to it yields a 1-dimensional subalgebra (with basis \(e_i\)). Such subalgebras are also called \(\rho \)-blocks of A.
Not under this name and for a different purpose (tameness proofs), \(\rho \)-blocks appear already in [9], see also [3]. We thank Thomas Brüstle for pointing this out.
Let us remark that each arrow of Q belongs to exactly one \(\rho \)-block, whereas a standard idempotent \(e_i\) can belong to several \(\rho \)-blocks. For an arrow a which does not appear in any of the relations in \(\rho \), the path algebra of the quiver

is a \(\rho \)-block. For example, let Q be the quiver

and let \(A = KQ\). (In this trivial example, we have \(I = 0\) and \(\rho = \varnothing \).) For \(n \ge 2\) the \(\rho \)-blocks of A are the path algebras of the subquivers

where \(1 \le i \le n-1\). For \(n=1\) there is only one \(\rho \)-block, namely A itself.
As another example, let Q be the quiver

and let I be the ideal in KQ generated by \(\rho = \{ a_1a_3,a_2a_1,a_3a_2,b_1b_3,b_2b_1,b_3b_2 \}\). Then KQ/I is a gentle Jacobian algebra, and there are two \(\rho \)-blocks with three vertices and one \(\rho \)-block with two vertices. (This algebra arises from a torus with one boundary component and one marked point on the boundary.)
Our \(\rho \)-blocks are in general very different from the classically defined blocks of an algebra. However, on the geometric level there is at least some resemblance. This will be explained at the end of this subsection.
Now let \(A_1,\ldots ,A_t\) be the \(\rho \)-blocks of A. For each dimension vector \({\mathbf {d}}\in {\mathbb {N}}^n\) and \(1 \le i \le t\) let \(\pi _i({\mathbf {d}})\) denote the corresponding dimension vector for \(A_i\). Each \(M \in {\text {mod}}(A,{\mathbf {d}})\) induces via restriction modules \(\pi _i(M) \in {\text {mod}}(A_i,\pi _i({\mathbf {d}}))\) for \(1 \le i \le t\) in the obvious way.
For each \({\mathbf {d}}\) we obtain an isomorphism
of affine schemes and therefore a bijection
Proposition 4.1
Let A and \(A_1,\ldots ,A_t\) be defined as above. For \(M \in {\text {mod}}(A,{\mathbf {d}})\) the following hold:
-
(i)
\(T_M \cong \prod _{i=1}^n T_{\pi _i(M)}\);
-
(ii)
\(T_M^\mathrm{red}\cong \prod _{i=1}^n T_{\pi _i(M)}^\mathrm{red}\).
Proof
(i): Obvious.
(ii): For a ring R let \({\text {nil}}(R)\) be its ideal of nilpotent elements. For R commutative and finitely generated, let \({\text {Spec}}(R)\) be as usual its prime ideal spectrum, which is an affine scheme.
We have an isomorphism of affine schemes
Let \(R_i\) be the coordinate algebra of \({\text {mod}}(A_i,\pi _i({\mathbf {d}}))\) for \(1 \le i \le t\). We get an isomorphism of affine schemes
Furthermore, we have
Let B and C be finitely generated commutative K-algebras. Then one easily shows that
This yields
Applying this via induction to the situation above, we get
We get
which implies (ii). \(\square \)
Proposition 4.1 allows us to study the tangent spaces of \({\text {mod}}(A,{\mathbf {d}})\) in terms of the often easier to compute tangent spaces of \({\text {mod}}(A_i,\pi _i({\mathbf {d}}))\).
Corollary 4.2
Let \(M \in {\text {mod}}(A,{\mathbf {d}})\). Then the following are equivalent:
-
(i)
M is smooth.
-
(ii)
\(\pi _i(M)\) is smooth for all \(1 \le i \le t\).
Corollary 4.3
Let \(M \in {\text {mod}}(A,{\mathbf {d}})\). Then the following are equivalent:
-
(i)
M is reduced.
-
(ii)
\(\pi _i(M)\) is reduced for all \(1 \le i \le t\).
Corollary 4.4
Let \(Z \in {\text {Irr}}(A)\). Then the following are equivalent:
-
(i)
Z is generically reduced.
-
(ii)
\(\pi _i(Z)\) is generically reduced for all \(1 \le i \le t\).
For the basic algebra \(A = KQ/I\), let \(Q(1),\ldots ,Q(m)\) be the connected components of the quiver Q. For \(1 \le i \le m\) let \(I(i) := I \cap KQ(i)\). Then I(i) is generated by a subset \(\rho (i)\) of \(\rho \). With \(B_i := KQ(i)/I(i)\) we get an algebra isomorphism
The \(B_i\) are indecomposable algebras, i.e. they are not isomorphic to the product of two algebras of smaller dimension. In other words, the \(B_i\) are the classical blocks of A. For a dimension vector \(\mathbf{d} \in {\mathbb {N}}^n\) let \({\mathbf {d}}(i)\) be the corresponding dimension vector for \(B_i\). We get an isomorphism
of affine schemes. The \(\rho \)-blocks of A are the disjoint union of the \(\rho (i)\)-blocks of the \(B_i\).
5 Modules over gentle algebras
Throughout this section, let \(A = KQ/I\) be a gentle algebra with \(Q = (Q_0,Q_1,s,t)\).
5.1 The maps \(\sigma \) and \(\varepsilon \)
We need two maps
satisfying the following properties:
-
(i)
If \(a_1,a_2 \in Q_1\) with \(a_1 \not = a_2\) and \(s(a_1) = s(a_2)\), then \(\sigma (a_1) = - \sigma (a_2)\).
-
(ii)
If \(b_1,b_2 \in Q_1\) with \(b_1 \not = b_2\) and \(t(b_1) = t(b_2)\), then \(\varepsilon (b_1) = - \varepsilon (b_2)\).
-
(iii)
If \(a,b \in Q_1\) with \(s(a) = t(b)\) and \(ab \notin I\), then \(\sigma (b) = -\varepsilon (\gamma )\).
It is straightforward to see that such maps \(\sigma \) and \(\varepsilon \) exist. We fix \(\sigma \) and \(\varepsilon \) for the rest of this section.
Later on we will define 1-sided and 2-sided standard homomorphisms. To make this anambiguous, we need the functions \(\sigma \) and \(\varepsilon \).
5.2 Strings
For each arrow \(a \in Q_1\) we introduce a formal inverse \(a^-\). We extend the maps s, t by defining \(s(a^-) := t(a)\) and \(t(a^-) := s(a)\). We also set \((a^-)^- = a\). Let \(Q_1^- = \{ a^- \mid a \in Q_1 \}\) be the set of inverse arrows. Now a string C of length \(l(C) := m \ge 1\) is an m-tuple
such that the following hold:
-
\(c_i \in Q_1 \cup Q_1^-\) for all \(1 \le i \le m\);
-
\(s(c_i) = t(c_{i+1})\) for all \(1 \le i \le m-1\);
-
\(c_i \not = c_{i+1}^-\) for all \(1 \le i \le m-1\).
-
\(\{ c_ic_{i+1},\; c_{i+1}^-c_i^- \mid 1 \le i \le m-1 \} \cap I = \varnothing \).
We often just write \(C = c_1 \cdots c_m\) instead of \(C = (c_1,\ldots ,c_m)\). Let \(C^- := (c_m^-,\ldots ,c_1^-)\) be the inverse of C, which is obviously again a string.
Additionally, for each vertex \(i \in Q_0\) there are two strings \(1_{i,t}\) with \(t = \pm 1\) of length \(l(1_{i,t}) := 0\). We set \(s(1_{i,t}) = t(1_{i,t}) = i\) and \(1_{i,t}^- = 1_{i,-t}\).
Sometimes we will just write \(1_i\) instead of \(1_{(i,t)}\).
We extend the maps \(\sigma \) and \(\varepsilon \) to strings as follows:
-
(i)
For \(a \in Q_1\) define \(\sigma (a^-) := \varepsilon (a)\) and \(\varepsilon (a^-) := \sigma (a)\).
-
(ii)
For a string \(C = (c_1,\ldots ,c_m)\) of length \(m \ge 1\), let \(\sigma (C) := \sigma (c_m)\) and \(\varepsilon (C) := \varepsilon (c_1)\).
-
(iii)
\(\sigma (1_{i,t}) := -t\) and \(\varepsilon (1_{i,t}) := t\).
For strings \(C = (c_1,\ldots ,c_p)\) and \(D = (d_1,\ldots ,d_q)\) of length \(p,q \ge 1\), the composition of C and D is defined, provided \((c_1,\ldots ,c_p,d_1,\ldots ,d_q)\) is again a string. We write then \(CD = c_1 \cdots c_pd_1 \cdots d_q\).
Now let C be any string. The composition of \(1_{(u,t)}\) and C is defined if \(t(C) = i\) and \(\varepsilon (C) = t\). In this case, we write \(1_{(i,t)}C = C\). The composition of C and \(1_{(i,t)}\) is defined if \(s(C) = i\) and \(\sigma (C) = -t\). In this case we write \(C1_{(i,t)} = C\).
If C and D are arbitrary strings such that the composition CD is defined, then \(\sigma (C) = - \varepsilon (D)\).
For a string C we write \(C \sim C^-\). This defines an equivalence relation on the set of all strings. Let \({{\mathcal {S}}}\) denote a set of representatives of all equivalence classes of strings for A.
A string C is a direct string if C is of length 0 or if it does not contain any inverse arrows. A direct string C is right-bounded (resp. left-bounded) if \(Ca \in I\) (resp. \(aC \in I\)) for all \(a \in Q_1\).
When visualizing a string we draw an arrow \(a \in Q_1\) often pointing from northeast to southwest:

Instead of the bullets one often displays the numbers \(i := s(a)\) and \(j := t(a)\):

On the other hand, an inverse arrow \(a^- \in Q_1^-\) is pointing from northwest to southeast:

Note that in this picture the arrow \(a^-\) carries just the label a.
5.3 Example
Let again \(A = KQ/I\), where Q is the quiver

and I is the ideal in KQ generated by \(a_1a_3,a_2a_1,a_3a_2,b_1b_3,b_2b_1,b_3b_2\). Then
is a string, which looks as follows:

5.4 String modules
Let \(C = (c_1,\ldots ,c_m)\) be a string of length \(m \ge 1\). We define a string module M(C) as follows: The module M(C) has a standard basis \((b_1,\ldots ,b_{m+1})\). The generators of the algebra A act on this basis as follows: For \(i \in Q_0\) and \(1 \le j \le m+1\) we have
and for \(a \in Q_1\) and \(1 \le j \le m+1\) we have
For strings \(E_1\) and \(E_2\) with \(E_1 \sim E_2\), let
be the obvious canonical isomorphism. (If \(E_1 = E_2\), then \(\phi _{E_1,E_2}\) is just the identity. Let \(E_1 = E_2^-\), and let \((b_1,\ldots ,b_m)\) (resp. \((b_1',\ldots ,b_m')\)) be the standard basis of \(M(E_1)\) (resp. \(M(E_2)\)). Then \(\phi _{E_1,E_2}(b_i) = b_{m-i+1}'\) for \(1 \le i \le m\).)
5.5 Bands
A band for A is a string B such that the following hold:
-
\(l(B) \ge 2\);
-
\(B^t\) is a string for all \(t \ge 1\);
-
B is not of the form \(C^s\) for some string C and some \(s \ge 2\).
Let B be a band, and let C and D be strings such that \(B = CD\). Then DC is a rotation of B. Obviously, any rotation of B is again a band. We write
This yields an equivalence relation on the set of all bands for A. Let \({{\mathcal {B}}}\) be a set of representatives of all equivalence classes of bands for A.
As an example, let \(A = KQ/I\) as in Sect. 5.3. Then
is a band.
5.6 Band modules
Now let \(B = (c_1,\ldots ,c_m)\) be a band, and let \(\lambda \in K^*\). We define a band module \(M(B,\lambda ,1)\) as follows: The module \(M(B,\lambda ,1)\) has a standard basis \((b_1,\ldots ,b_{m})\). The generators of the algebra A act on this basis as follows: For \(i \in Q_0\) and \(1 \le j \le m\) we have
and for \(a \in Q_1\) and \(1 \le j \le m\) we have
For \(q \ge 2\) and \(\lambda \in K^*\) there are also band modules \(M(B,\lambda ,q)\). They do not play a major role in this article, so we omit their definition. Let us just mention that they form Auslander-Reiten sequences
and
for \(q \ge 2\). For \(q \ge 1\), we say that \(M(B,\lambda ,q)\) has quasi-length q.
5.7 Classification of modules
The following classification theorem was first proved by Wald and Waschbüsch [56] using covering techniques. There is an alternative proof by Butler and Ringel [11] using functorial filtrations. Both articles [11] and [56] also contain a combinatorial description of all Auslander-Reiten sequences for string algebras. Recall that all gentle algebras are string algebras.
Theorem 5.1
Let \(A = KQ/I\) be a gentle algebra. The modules M(C) and \(M(B,\lambda ,q)\) with \(C \in {{\mathcal {S}}}\), \(B \in {{\mathcal {B}}}\), \(\lambda \in K^*\) and \(q \ge 1\) are a complete set of pairwise non-isomorphic representatives of isomorphism classes of indecomposable modules in \({\text {mod}}(A)\).
For string modules we have \(M(C_1) \cong M(C_2)\) if and only if \(C_1 \sim C_2\), and for band modules we have \(M(B_1,\lambda _1,q_1) \cong M(B_2,\lambda _2,q_2)\) if and only if \(B_1 \sim _b B_2\), \(\lambda _1 = \lambda _2\) and \(q_1 = q_2\).
5.8 Homomorphisms
For a string C we define \({{\mathcal {S}}}(C)\) as the set of triples (D, E, F) such that the following hold:
-
(i)
\(C = DEF\);
-
(ii)
Either \(l(D) = 0\), or \(D = D'a^-\) for some \(a \in Q_1\) and some string \(D'\);
-
(iii)
Either \(l(F) = 0\), or \(F = bF'\) for some \(b \in Q_1\) and some string \(F'\).
Following our convention for displaying strings, a triple \((D,E,F) \in {{\mathcal {S}}}(C)\) with \(l(D),l(F) \ge 1\) yields the following picture, where the left (resp. right) hand red line stands for the string \(D'\) (resp. \(F'\)), and the blue line stands for E.

We clearly see that M(C) has a submodule isomorphic to M(E) and that the corresponding factor module is isomorphic to \(M(D') \oplus M(F')\). Let
be the obvious canonical inclusion.
Dually, for a string C we define \({{\mathcal {F}}}(C)\) as the set of triples (D, E, F) such that the following hold:
-
(i)
\(C = DEF\);
-
(ii)
Either \(l(D) = 0\), or \(D = D'a\) for some \(a \in Q_1\) and some string \(D'\);
-
(iii)
Either \(l(F) = 0\), or \(F = b^-F'\) for some \(b \in Q_1\) and some string \(F'\).
For such a \((D,E,F) \in {{\mathcal {F}}}(C)\) with \(l(D),l(F) \ge 1\) we get the following picture, where the left (resp. right) hand green line stands for the string \(D'\) (resp. \(F'\)), and the blue line stands for E.

Then M(C) has a submodule isomorphic to \(M(D') \oplus M(F')\) and the corresponding factor module is isomorphic to M(E). Let
be the obvious canonical projection.
For a pair \((C_1,C_2)\) of strings we call a pair
admissible if \(E_1 = E_2\) or \(E_1 = E_2^-\).
Suppose that h is admissible. For \(E_1=E_2\), h is 2-sided if \(l(D_i) \ge 1\) and \(l(F_j) \ge 1\) for at least one \(i \in \{1,2\}\) and at least one \(j \in \{1,2\}\). For \(E_1 = E_2^-\), h is 2-sided if \(((D_1,E_1,F_1),(F_2^-,E_2^-,D_2^-))\) is 2-sided.
Let h be admissible as above, and let
be the associated standard homomorphism. We call \(f_h\) oriented if \(E_1 = E_2\). Furthermore, \(f_h\) is 2-sided if h is 2-sided. Otherwise, \(f_h\) is 1-sided.
The following picture describes \(f_h\) for the case \(E_1 = E_2\) and \(l(D_i),l(F_i) \ge 1\) for \(i=1,2\).

Thus we have \(C_1 = D_1'a_1E_1b_1^-F_1'\) and \(C_2 = D_2'a_2^-E_2b_2F_2'\). Furthermore, it follows that \(a_1a_2, b_1b_2 \in I\).
Depending if some of the four strings \(D_1,F_1,D_2,F_2\) are of length 0 or not, there are 16 different types of oriented standard homomorphisms.
Theorem 5.2
([18]) For M and N string modules, the set of standard homomorphisms \(M \rightarrow N\) is a basis of \({\text {Hom}}_A(M,N)\).
In this article, we are mainly concerned with the question if certain homomorphism spaces \({\text {Hom}}_A(M,N)\) are zero or not. The actual dimension of these spaces does not matter.
For a band module \(M = M(B,\lambda ,q)\) and an arbitrary indecomposable A-module N, the conditions \({\text {Hom}}_A(M,N) \not = 0\) and \({\text {Hom}}_A(N,M) \not = 0\) do not depend on the quasi-length q. (This follows from the description of the Auslander-Reiten sequences involving band modules, see for example [11].) Therefore we can restrict our attention to band modules of quasi-length 1.
Krause [37] extended Theorem 5.2 to homomorphisms also involving band modules. We just recall a special case here, where we only consider band modules of quasi-length 1.
For a band B let
Let \(B_1\) and \(B_2\) be bands, and let C be a string. Let
be an element in \({{\mathcal {F}}}^\infty (B_1) \times {{\mathcal {S}}}(C)\), \({{\mathcal {F}}}(C) \times {{\mathcal {S}}}^\infty (B_1)\) or \({{\mathcal {F}}}^\infty (B_1) \times {{\mathcal {S}}}^\infty (B_2)\). Then h is admissible if \(E_1 = E_2\) or \(E_1 = E_2^-\). In this case, one can again define a standard homomorphism \(f_h:M(B_1,\lambda _1,1) \rightarrow M(C)\), \(f_h:M(C) \rightarrow M(B_1,\lambda _1,1)\) or \(f_h:M(B_1,\lambda _1,1) \rightarrow M(B_2,\lambda _2,1)\), respectively. All of these are 2-sided. This involves of course a choice of scalars \(\lambda _1\) and/or \(\lambda _2\), in case we deal with \(B_1\) and/or \(B_2\). For a band module \(M(B,\lambda ,1)\), the identity is also called a standard homomorphism. Similarly as before, we call \(f_h\) oriented if \(E_1 = E_2\). For further details we refer to [37].
Theorem 5.3
([37]) For M and N string modules or band modules of quasi-length 1, the set of standard homomorphisms \(M \rightarrow N\) is a basis of \({\text {Hom}}_A(M,N)\).
5.9 Auslander-Reiten translation of string modules
Let A be a gentle algebra, and let \(M \in {\text {mod}}(A)\) be a non-projective string module. It follows that \(\tau _A(M)\) is also a string module, and that we are in one of the five situations displayed in Fig. 2, see [11, Section 3]. (We use here the same way of illustrating strings and string modules as in [51, Section 3].) The subfactor of M and \(\tau _A(M)\) defined by the string between the two red points is called the core of M. (In the 5th case, the core is just the 0-module.) The core of M does not change under the Auslander-Reiten translation.
The strings \(E_i\) in Fig. 2 are left-bounded direct strings, and the strings \(F_i\) are right-bounded direct strings. The strings \(E_1a_1^-\) and \(a_2E_2^-\) are hooks in the sense of [11], and the strings \(F_1^-b_1\) and \(b_2^-F_2\) are cohooks in the sense of [11].
For each arrow \(a = a_1 = b_2 \in Q_1\) there is exactly one Auslander-Reiten sequence of type 5. In this case, there is a string

which yields the middle term of an Auslander-Reiten sequence
All other Auslander-Reiten sequences involving string modules are of types \(1,\ldots ,4\), and their middle terms are a direct sum of two indecomposable string modules. For details we refer to [11].
5.10 Auslander-Reiten formulas
The following is a well known statement from Auslander-Reiten theory, see for example [6, 7, 50].
Theorem 5.4
(Auslander, Reiten) Let A be a finite-dimensional basic algebra. For \(M,N \in {\text {mod}}(A)\) the following hold:
-
(i)
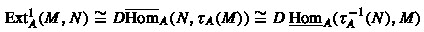 .
. -
(ii)
If \({\text {proj.dim}}(M) \le 1\), then \({\text {Ext}}_A^1(M,N) \cong D{\text {Hom}}_A(N,\tau _A(M))\).
-
(iii)
If \({\text {inj.dim}}(N) \le 1\), then \({\text {Ext}}_A^1(M,N) \cong D{\text {Hom}}_A(\tau ^{-1}(N),M)\).
Lemma 5.5
Let A be a gentle algebra. For any band module \(M \in {\text {mod}}(A)\) the following hold:
-
(i)
\({\text {proj.dim}}(M) \le 1\) and \({\text {inj.dim}}(M) \le 1\);
-
(ii)
\(\tau _A(M) \cong M\).
Proof
(i): This is well known, see for example [8, Corollary 3.6].
(ii): This is proved for example in [11, Section 3]. \(\square \)
Note that part (ii) of the above lemma holds also for all string algebras A.
Corollary 5.6
Let A be a gentle algebra, and let \(M,N \in {\text {mod}}(A)\). If M is a band module, then

and
5.11 Rank functions for gentle algebras
Let \(A = KQ/I\) be a gentle algebra, and let \({\mathbf {d}}\in {\mathbb {N}}^n\) be a dimension vector. A map \(r:Q_1 \rightarrow {\mathbb {N}}\) is a rank function for \((A,{\mathbf {d}})\) if the following hold:
-
(i)
\(r(a) \le \min \{ d_{s(a)},d_{t(a)} \}\) for all \(a \in Q_1\);
-
(ii)
Let \(a,b \in Q_1\) with \(s(a) = t(b)\) and \(ab \in I\). Then \(r(a) + r(b) \le d_{s(a)}\).
(Using a slightly different wording, this definition appears in [14, Section 5].)
For \(M \in {\text {mod}}(A)\) the rank function of M is defined by
One easily checks that \(r_M\) is a rank function for \((A,{\mathbf {d}})\) where \({\mathbf {d}}= {\underline{\dim }}(M)\). Furthermore, each rank function for \((A,{\mathbf {d}})\) is obtained in this way.
The following lemma is well known and follows directly from the definitions of string and band modules.
Lemma 5.7
Let A be a gentle algebra. The number of string modules in a direct sum decomposition of \(M \in {\text {mod}}(A)\) into indecomposable modules is
Proof
It follows directly from the definition of a string module M that
For a band module M we have
Since each A-module is isomorphic to a direct sum of string modules and band modules, the claim follows. \(\square \)
Let r and \(r'\) be rank functions for \((A,{\mathbf {d}})\). We write \(r \le r'\) if \(r(a) \le r'(a)\) for all \(a \in Q_1\). This defines a partial order on the set of rank functions for \((A,{\mathbf {d}})\).
For a rank function r for \((A,{\mathbf {d}})\) let
This is a non-empty closed subset of \({\text {mod}}(A,{\mathbf {d}})\).
6 Schemes of complexes
As already mentioned in the introduction, the study of schemes of modules over gentle algebras can (to a large extent) be reduced to schemes of complexes. This section deals with all necessary results on schemes of complexes.
6.1 Definition of schemes of complexes
For \(n \ge 1\) let
where Q is the quiver

and I is the ideal generated by all paths of length 2. (For \(n=1\), Q has just one vertex and no arrows. For \(n=1,2\), we set \(I = 0\).)
For \(n \ge 1\) let
where Q is the quiver

and I is the ideal generated by all paths of length 2. For \({\widetilde{C}}_n\) we adopt the convention that all indices are meant modulo n.
Let A be one of the algebras \(C_n\) or \({\widetilde{C}}_n\). By scheme of complexes we mean the affine schemes \({\text {mod}}(A,{\mathbf {d}})\) with \({\mathbf {d}}\in {\mathbb {N}}^n\). This definition is a bit more general than the one used by De Concini and Strickland [21], who consider only the case \(C_n\).
The representation theory of A is extremely well understood. Obviously, A is a representation-finite gentle algebra. So all its indecomposable modules are string modules. For each vertex \(i \in Q_0\) there is a simple module \(S_i\) and an indecomposable projective modules \(P_i\), and these are all indecomposable A-modules up to isomorphism. The modules \(S_1,\ldots ,S_n,P_1,\ldots ,P_n\) are pairwise non-isomorphic, with the exception of \(P_n\) being equal to \(S_n\) in case \(A = C_n\). Using the usual notation for string modules, for each \(i \in Q_0\) we have \(S_i = M(e_i)\) and
It is straightforward to compute homomorphism spaces and extension groups between A-modules. All this can be proved in an elementary fashion using mainly Linear Algebra. The next two lemmas contain all the homological data we need.
Lemma 6.1
Let A be one of the algebras \(C_n\) or \({\widetilde{C}}_n\). The only pairs (X, Y) of indecomposable A-modules with \({\text {Hom}}_A(X,Y) \not = 0\) are
where \(i \in Q_0\) and \(a \in Q_1\). In these cases, we have \(\dim {\text {Hom}}_A(X,Y) = 1\) with only one exception for \(A = {\widetilde{C}}_1\), where we have \(\dim {\text {Hom}}_A(P_1,P_1) = 2\).
Lemma 6.2
Let A be one of the algebras \(C_n\) or \({\widetilde{C}}_n\). The only pairs (X, Y) of indecomposable A-modules with \({\text {Ext}}_A^1(X,Y) \not = 0\) are
where \(a \in Q_1\). In these cases, we have \(\dim {\text {Ext}}_A^1(X,Y) = 1\).
Let A be one of the algebras \(C_n\) or \({\widetilde{C}}_n\). Let \({\mathbf {d}}= (d_1,\ldots ,d_n) \in {\mathbb {N}}^n\) be a dimension vector, and let r be a rank function for \((A,{\mathbf {d}})\). Then there exists a unique (up to isomorphism) A-module \(M = M_{{\mathbf {d}},r}\) with \({\underline{\dim }}(M) = {\mathbf {d}}\) and \(r_M = r\). More precisely, we have
where
Proposition 6.3
Let A be one of the algebras \(C_n\) or \({\widetilde{C}}_n\), and let \({\mathbf {d}}\in {\mathbb {N}}^n\). For each rank function r for \((A,{\mathbf {d}})\) we have
Proof
For \(M \in {\text {mod}}(A,{\mathbf {d}})\) and \(a \in Q_1\) we have
Now the claim follows from [57, Theorem 1 and its Corollary]. \(\square \)
Corollary 6.4
Let A be one of the algebras \(C_n\) or \({\widetilde{C}}_n\), and let \({\mathbf {d}}\in {\mathbb {N}}^n\). For each \(M = M_{{\mathbf {d}},r}\) the following are equivalent:
-
(i)
\({{\mathcal {O}}}_M\) is open;
-
(ii)
The rank function r is maximal.
Corollary 6.5
Let A be one of the algebras \(C_n\) or \({\widetilde{C}}_n\), and let \({\mathbf {d}}\in {\mathbb {N}}^n\). Then
Lemma 6.6
Let \(A = KQ/I\) be one of the algebras \(C_n\) or \({\widetilde{C}}_n\). For \(M \in {\text {mod}}(A)\) we have
Furthermore, this becomes an equality if and only if M does not have a simple direct summand.
Proof
We have
for some \(m_a,m_i \ge 0\). Thus for \(a \in Q_1\) we have \(r_M(a) = m_a\). This implies
The claim follows. \(\square \)
6.2 Rigid and \(\tau \)-rigid modules
Proposition 6.7
(Rigid modules) Let A be one of the algebras \(C_n\) or \({\widetilde{C}}_n\), and let \({\mathbf {d}}\in {\mathbb {N}}^n\). For \(M \in {\text {mod}}(A,{\mathbf {d}})\) the following are equivalent:
-
(i)
M is rigid;
-
(ii)
M does not have a direct summand isomorphic to
$$\begin{aligned} S_a := \bigoplus _{i \in \{ s(a),t(a) \}} S_i \end{aligned}$$for some \(a \in Q_1\).
For \(A = {\widetilde{C}}_1\) we assume now additionally that \({\mathbf {d}}= (d_1)\) with \(d_1\) even. Then the two conditions above are equivalent to the following:
-
(iii)
\({{\mathcal {O}}}_M\) is open.
Proof
The equivalence (i) \(\iff \) (ii) follows from Lemma 6.2. The implication (i) \(\implies \) (iii) is true in general and follows from Voigt’s Lemma 2.2.
(iii) \(\implies \) (ii): Assume that (ii) does not hold. Thus there is an arrow a such that \(S_a\) is isomorphic to a direct summand of M. For \(A \not = {\widetilde{C}}_1\) there is a non-split short exact sequence
Thus M is properly contained in the orbit closure of
For \(A = {\widetilde{C}}_1\) and \({\mathbf {d}}= (d_1)\) with \(d_1\) even, we get that M has a direct summand isomorphic to \(S_{s(a)} \oplus S_{s(a)}\). (Here we used that \(d_1\) is even.) We get a non-split short exact sequence
Thus M is properly contained in the orbit closure of
In both case, this shows that \({{\mathcal {O}}}_M\) is not open. \(\square \)
The module \(S_a\) in Proposition 6.7(ii) is a critical summand of type I of M. In Proposition 6.7(ii) we have
Consequently, we have
Recall that a \(\tau \)-rigid module is automatically rigid. Thus to get a decription of all \(\tau \)-rigid modules, it suffices to look at rigid modules.
Proposition 6.8
(\(\tau \)-rigid modules) Let A be one of the algebras \(C_n\) or \({\widetilde{C}}_n\), and let \({\mathbf {d}}\in {\mathbb {N}}^n\). For a rigid \(M \in {\text {mod}}(A,{\mathbf {d}})\) the following are equivalent:
-
(i)
M is \(\tau \)-rigid;
-
(ii)
M has no direct summand isomorphic to
$$\begin{aligned} P_a := P_{t(a)} \oplus S_{s(a)} \end{aligned}$$for some \(a \in Q_1\).
Proof
We have \(\tau _A(P_i) = 0\) for \(i \in Q_0\) and \(\tau _A(S_{s(a)}) = S_{t(a)}\) for \(a \in Q_1\).
(i) \(\implies \) (ii): Assume that M has a direct summand isomorphic to \(P_a\). Then
(ii) \(\implies \) (i): Assume that \({\text {Hom}}_A(M,\tau _A(M)) \not = 0\). Thus there are indecomposable direct summands X and Y of M with \({\text {Hom}}_A(X,\tau _A(Y)) \not = 0\). We get \(Y \cong S_{s(a)}\) and \(\tau _A(Y) \cong S_{t(a)}\) for some \(a \in Q_1\). This implies \(X \cong S_{t(a)}\) or \(X \cong P_{t(a)}\). If \(X \cong S_{t(a)}\), then the rigid module M has a direct summand isomorphic to \(S_a\), a contradiction to Proposition 6.7. If \(X \cong P_{t(a)}\), then \(X \oplus Y \cong P_a\). This proves the claim. \(\square \)
The module \(P_a\) in Proposition 6.8(ii) is a critical summand of type II of M.
6.3 Generic reducedness and singular locus
Proposition 6.9
Let \(A = KQ/I\) be one of the algebras \(C_n\) or \({\widetilde{C}}_n\), and let \({\mathbf {d}}= (d_1,\ldots ,d_n) \in {\mathbb {N}}^n\). For \(Z \in {\text {Irr}}(A,{\mathbf {d}})\) the following are equivalent:
-
(i)
Z is not generically reduced.
-
(ii)
\(A = {\widetilde{C}}_1\) and \(d_1\) is odd.
Proof
(i) \(\implies \) (ii): Suppose that (ii) does not hold. Then it follows from Proposition 6.7 that Z contains a rigid module M. Then \(Z = \overline{{{\mathcal {O}}}_M}\) and Z is generically reduced by Corollary 2.5.
(ii) \(\implies \) (i): Assume that (ii) holds. Then
with \(M = S_1 \oplus P_1^{(d_1-1)/2}\). In particular, M is not rigid and therefore Z is not generically reduced, again by Corollary 2.5. \(\square \)
Proposition 6.9 is not really original. Using very different methods, it is shown in [21, Theorem 1.7] that \({\text {mod}}(C_n,{\mathbf {d}})\) is reduced for all \({\mathbf {d}}\). Reducedness is in general a much stronger and harder to prove property than being generically reduced. Also the schemes \({\text {mod}}({\widetilde{C}}_n,{\mathbf {d}})\) should be reduced provided \(n \ge 2\). A proof for \(n=2\) is in [54, Proposition 1.3].
Proposition 6.10
Let \(A = KQ/I\) be one of the algebras \(C_n\) or \({\widetilde{C}}_n\), and let \({\mathbf {d}}\in {\mathbb {N}}^n\). For \(M \in {\text {mod}}(A,{\mathbf {d}})\) the following are equivalent:
-
(i)
M is singular;
-
(ii)
There exist arrows \(a,b \in Q_1\) with \(s(a) = t(b)\) such that the module
$$\begin{aligned} S_{ab}:= \bigoplus _{k \in \{ s(a),t(a),s(b) \}} S_k \end{aligned}$$is isomorphic to a direct summand of M.
Proof
Let r be a rank function for \((A,{\mathbf {d}})\) and let
For \(A = C_n\) we adopt the convention that \(P_j = S_j = 0\) and \(r_j = q_j = 0\) for all \(j \notin Q_0\), and for \(A = {\widetilde{C}}_n\) we use all indices modulo n.
Case 1: \(A = C_1\) or \(A = C_2\). In this case, \({\text {mod}}(A,{\mathbf {d}})\) is always an affine space. Therefore all modules M are smooth. On the other hand condition (ii) is never satisfied. This proves (i) \(\iff \) (ii).
Case 2: \(A = {\widetilde{C}}_1\). In this case, M is of the form
We have \(\dim {\text {Ext}}_A^1(M,M) = q_1^2\) and \(\dim {{\mathcal {O}}}_M = 2r_1^2 + 2r_1q_1\). Thus
Now \(Z = \overline{{{\mathcal {O}}}_N} = {\text {mod}}(A,{\mathbf {d}})\) is irreducible, where
We get
This shows that M is smooth if and only if \(q_1 = 0\). (Thus if \({\mathbf {d}}= (d_1)\) is odd, then \({\text {mod}}(A,{\mathbf {d}})\) does not contain any smooth module, and if \({\mathbf {d}}\) is even, then there is only one smooth module up to isomorphism, namely \(M = P_1^{d_1/2}\).) Note that (ii) holds if and only if \(q_1 \ge 1\). This proves (i) \(\iff \) (ii).
Case 3: \(A = {\widetilde{C}}_2\). In this case, M is of the form
Assume that \(q_1 = 0\) or \(q_2 = 0\). Then M is rigid and therefore smooth. Next, assume that \(q_1,q_2 \ge 1\). Then M is contained in the intersection of at least two different irreducible components \(Z_1\) and \(Z_2\), with maximal rank functions \(r_1\) and \(r_2\), respectively, which are defined by
Thus M is singular.
This shows that M is singular if and only if \(q_1,q_2 \ge 1\). But this condition is equivalent to (ii).
Case 4: \(n \ge 3\). Let
Case 4(a): Assume that \(q_i,q_{i+1},q_{i+2} \ge 1\) and \(q_i+q_{i+2} > q_{i+1}\) for some i. Similarly as in Case 3 one shows that M is contained in at least two different irreducible components of \({\text {mod}}(A,{\mathbf {d}})\). Thus M is singular.
Case 4(b): Assume that for all i with \(q_i,q_{i+1},q_{i+2} \ge 1\) we have \(q_i+q_{i+2} \le q_{i+1}\). It follows immediately that \(q_{i-1} = q_{i+3} = 0\) for all such i. In other words, we have \(i \in H_3\).
We get that M is contained in exactly one irreducible component \(Z = \overline{{{\mathcal {O}}}_N}\), where N is obtained from M as follows: For each \(i \in H_2\) replace
Furthermore, for each \(i \in H_3\) replace
The module N is rigid and therefore smooth.
Now M is smooth if and only if
(Note that the first and third equality always hold.) Thus M is smooth if and only if
We have
Now a straightforward but lengthy calculation shows that Equation (6.1) holds if and only if \(H_3 = \varnothing \). More precisely, one gets that
Thus M is smooth if and only if \(H_3 = \varnothing \). This finishes the proof. \(\square \)
In Proposition 6.10(ii) we have
Consequently, we have
The singularities of the closures of the \({\text {GL}}_{\mathbf {d}}(K)\)-orbits of the schemes \({\text {mod}}(C_n,{\mathbf {d}})\) have been described by Lakshmibai [40] for \(n=3\) and by Gonciulea [33] for arbitrary n. Note the difference to Proposition 6.10, where we look at the singularities of the whole scheme.
6.4 \(\rho \)-blocks of gentle Jacobian algebras
Let \(A = KQ/I\) be a gentle Jacobian algebra. It follows from the definitions that the \(\rho \)-blocks of A are isomorphic to \(C_1\), \(C_2\) or \({\widetilde{C}}_3\). We call them 1-blocks, 2-blocks or 3-blocks, respectively.
A 1-block can only occur if \(A = C_1\). Here we used that gentle Jacobian algebras are by definition connected.
Now let \(A_s\) be a 1-block or 2-block. Then the schemes \({\text {mod}}(A_s,{\mathbf {d}})\) are obviously just affine spaces. In particular, they are irreducible, and all modules \(M \in {\text {mod}}(A_s,{\mathbf {d}})\) are smooth and reduced. Furthermore, \({\text {mod}}(A_s,{\mathbf {d}})\) contains a unique \(\tau \)-rigid module. In particular, \({\text {mod}}(A_s,{\mathbf {d}})\) is generically \(\tau \)-reduced.
Next, let \(A_s\) be a 3-block of A. For convenience, we assume that \(A = {\widetilde{C}}_3 = KQ/I\), where Q is the quiver

and I is generated by the paths \(a_2a_1\), \(a_3a_2\) and \(a_1a_3\).
For later use, we define
Lemma 6.11
Let A be a 1-block, 2-block or 3-block as above. For \(\tau \)-rigid A-modules M and N the following are equivalent:
-
(i)
\(M \cong N\);
-
(ii)
\({\underline{\dim }}(M) = {\underline{\dim }}(N)\).
Proof
By the discussion above, the statement is clear for 1-blocks and 2-block. Thus assume A is a 3-block as above.
(i) \(\implies \) (ii): This is trivial.
(ii) \(\implies \) (i): By Proposition 6.8 there are four types of \(\tau \)-rigid A-modules:
where \(r_i \ge 0\) and \(s_i \ge 1\) for all i.
First, let M be of type 0 with \({\underline{\dim }}(M) = {\mathbf {d}}= (d_1,d_2,d_3)\). It follows that
For a fixed \({\mathbf {d}}\), this system of linear equations has exactly one solution. This proves (ii) \(\implies \) (i) for modules of type 0.
Next, let M be of type i for some \(1 \le i \le 3\) with \({\underline{\dim }}(M) = {\mathbf {d}}= (d_1,d_2,d_3)\). It follows that
For a fixed \({\mathbf {d}}\), this system of linear equations has exactly one solution. This proves (ii) \(\implies \) (i) for modules of type i.
Finally, we observe that modules of different types have always different dimension vectors. This finishes the proof. \(\square \)
Lemma 6.12
Let A be a 1-block, 2-block or 3-block as above. For \(M \in {\text {mod}}(A,{\mathbf {d}})\) the following are equivalent:
-
(i)
M is singular;
-
(ii)
M is contained in at least two different irreducible components of \({\text {mod}}(A,{\mathbf {d}})\).
Proof
By the discussion above, the statement is clear for 1-blocks and 2-block. Thus assume A is a 3-block as above.
(i) \(\implies \) (ii): Assume M is singular. Now Proposition 6.10 implies that
with \(q_1,q_2,q_3 \ge 1\). Without loss of generality assume that
It follows that \(q_2 + q_3 > q_1\). Now one proceeds as in the proof of Proposition 6.10 to show that M is contained in at least two different irreducible components.
(ii) \(\implies \) (i): This holds for arbitrary finite-dimensional K-algebras, see Proposition 2.9. \(\square \)
7 Irreducible components for gentle algebras
7.1 Irreducible components
Finding the irreducible components of schemes of modules over gentle algebras is rather easy, since each of these schemes is isomorphic to a product of schemes of complexes.
Let \(A = KQ/I\) be a gentle algebra, and let \(A_1,\ldots ,A_t\) be its \(\rho \)-blocks. For each \(\rho \)-block \(A_s\) there is a unique
such that there exists an algebra homomorphism
with the following properties:
-
(i)
\(f_s\) sends vertices to vertices and arrows to arrows.
-
(ii)
\(f_s\) is bijective on the sets of arrows.
(In (i) we think of the vertices as standard idempotents.) This follows directly from the definition of a gentle algebra and from the definition of a \(\rho \)-block. We say that \(A_s\) is of type \(A_s'\). Let \(n_s\) (resp. \(n_s'\)) be the number of vertices of \(A_s\) (resp. \(A_s'\)). For each dimension vector \({\mathbf {d}}= (d_1,\ldots ,d_{n_s})\), the homomorphism \(f_s\) induces an isomorphism
of affine schemes, where
For example, let \(A = KQ\), where Q is the quiver

So here we have \(I = 0\) and \(\rho = \varnothing \). There are two \(\rho \)-blocks \(A_1\) and \(A_2\) of type \(C_2\), i.e. \(A_1' = A_2' = C_2\). Define \(f_1:A_1' \rightarrow A_1\) by \(1 \mapsto 1\), \(2 \mapsto 2\), \(a_1 \mapsto a\), and define \(f_2:A_2' \rightarrow A_2\) by \(1 \mapsto 2\), \(2 \mapsto 3\) and \(a_1 \mapsto b\). For \(s=1,2\) and a dimension vector \({\mathbf {d}}\) for \(A_s\) we have \({\mathbf {d}}' = {\mathbf {d}}\).
As a less trivial example, let \(A = KQ/I\), where Q is the quiver

and I is generated by the paths \(\{ a_{i+1}a_i \mid 1 \le i \le 6 \}\). Then A has only one \(\rho \)-block, namely \(A_1 = A\), which is of type \(C_8\). Define \(f_s:A_1' \rightarrow A_1\) by
and \(f_s(a_i) := a_i\) for \(1 \le i \le 7\).
For \({\mathbf {d}}= (d_1,d_2,d_3,d_4,d_5) \in {\mathbb {N}}^5\) we get an isomorphism
of affine schemes, where \({\mathbf {d}}' = (d_1,d_2,d_3,d_4,d_5,d_3,d_1,d_5)\).
The following result follows almost immediately from [21], see also [16, Propositions 3.4 and 5.2]. Note that Carroll and Weyman [16] only consider the class of gentle algebras admitting a colouring. However, the result holds in general.
Proposition 7.1
([16, 21]) Let A be a gentle algebra, and let \({\mathbf {d}}\in {\mathbb {N}}^n\). Then we have
Proof
Let \(A_1,\ldots ,A_t\) be the \(\rho \)-blocks of A. Recall that for each \({\mathbf {d}}\) we have an isomorphism
which yields a bijection
Now the isomorphisms
and the description of irreducible components of varieties of complexes (see Corollary 6.5) yield the result. \(\square \)
7.2 String and band components and generic decompositions
Let \(A = KQ/I\) be a gentle algebra. An indecomposable irreducible component Z of \({\text {mod}}(A,{\mathbf {d}})\) is a string component provided there is a string C such that the orbit \({{\mathcal {O}}}_{M(C)}\) is dense in Z. In this case, C is (up to equivalence of strings) uniquely determined by Z, and we write \(Z = Z(C)\).
An indecomposable component \(Z \in {\text {Irr}}(A,{\mathbf {d}})\) is a band component provided there is a band B such that the union
is dense in Z. In this case, B is (up to equivalence of bands) uniquely determined by Z, and we write \(Z = Z(B)\). (The band modules \(M(B,\lambda ,q)\) are contained in the closure of the union
so they do no play a role here.)
Any indecomposable component \(Z \in {\text {Irr}}(A)\) is either a string or a band component.
For \(Z \in {\text {Irr}}(A,{\mathbf {d}})\) let
be the canonical decomposition of Z. Then M is generic in Z, if
with pairwise different \(\lambda _1,\ldots ,\lambda _q \in K^*\).
Lemma 7.2
Let A be a gentle algebra. For \(Z \in {\text {Irr}}(A,{\mathbf {d}})\) let
be the canonical decomposition of Z. Then \(c_A(Z) = q\).
Proof
Let \(f:{\text {GL}}_{\mathbf {d}}(K) \times (K^*)^q \rightarrow {\text {mod}}(A,{\mathbf {d}})\) be defined by
For \(M \in {\text {Im}}(f)\) the fibre \(f^{-1}(M)\) is obviously isomorphic to the automorphism group \(\mathrm{Aut}_A(M)\) of M. This implies
Thus we have
By definition
where M is generic in Z. By Chevelley’s Theorem we have
where M is again generic in Z. Combining these equations yields \(c_A(Z) = q\). \(\square \)
Corollary 7.3
Let A be a gentle algebra. For \(Z \in {\text {Irr}}(A,{\mathbf {d}})\) the following hold:
-
(i)
If Z is a string component, then \(c_A(Z) = 0\).
-
(ii)
If Z is a band component, then \(c_A(Z) = 1\).
Note that Corollary 7.3 is just a special case of Lemma 3.1.
7.3 Generically reduced components
Theorem 7.4
Let A be a gentle algebra, and let \(A_1,\ldots ,A_t\) be its \(\rho \)-blocks. For \({\mathbf {d}}= (d_1,\ldots ,d_n) \in {\mathbb {N}}^n\) and \(Z \in {\text {Irr}}(A,{\mathbf {d}})\) the following are equivalent:
-
(i)
Z is generically reduced;
-
(ii)
For each loop \(a \in Q_1\), the number \(d_{s(a)}\) is even.
Proof
We know from Corollary 4.4 that Z is generically reduced if and only if \(\pi _i(Z)\) is generically reduced for all \(1 \le i \le t\). Now the result follows from Proposition 6.9. \(\square \)
Corollary 7.5
Let A be a gentle algebra without loops. Then each \(Z \in {\text {Irr}}(A)\) is generically reduced.
Note that Corollary 7.5 is exactly the statement of Theorem 1.2.
7.4 Singular locus
The following theorem describes the singular locus of schemes of modules over gentle algebras. It turns out that the rank function of a module determines completely if this module is singular or not.
Theorem 7.6
Let \(A = KQ/I\) be a gentle algebra. Let \(M \in {\text {mod}}(A,{\mathbf {d}})\), and let \(r = r_M:Q_1 \rightarrow Q_0\) be the rank function of M. The following are equivalent:
-
(i)
M is singular;
-
(ii)
There exist \(a,b \in Q_1\) with \(s(a) = t(b)\) and \(ab \in I\) such that the following hold:
-
(1)
\(r(a) < d_{t(a)}\), \(r(b) < d_{s(b)}\) and \(r(a) + r(b) < d_{s(a)}\).
-
(2)
If \(a' \in Q_1\) with \(s(a') = t(a)\) and \(a'a \in I\), then \(r(a') + r(a) < d_{t(a)}\).
-
(3)
If \(b' \in Q_1\) with \(t(b') = s(b)\) and \(bb' \in I\), then \(r(b) + r(b') < d_{s(b)}\).
-
(1)

Proof
Let \(A_1,\ldots ,A_t\) be the \(\rho \)-blocks of A. For \(M \in {\text {mod}}(A,{\mathbf {d}})\) we know from Corollary 4.2 that M is smooth if and only if \(\pi _i(M)\) is smooth for all \(1 \le i \le t\). Now for each \(\rho \)-block \(A_i\) and each dimension vector \({\mathbf {d}}\) there is an algebra \(A_i' = C_{n_i'}\) or \(A_i' = {\widetilde{C}}_{n_i'}\) and an isomorphism
of affine schemes. In particular, \(\pi _i(M)\) is singular if and only if \(f_{s,\pi _i({\mathbf {d}})}(\pi _i(M))\) is singular.
By Proposition 6.10 we know all singular points of \({\text {mod}}(A_i',\pi _i({\mathbf {d}})')\). The conditions Theorem 7.6(ii) and Proposition 6.10(ii) are equivalent. More precisely, let \(A_i\) be the \(\rho \)-block containing the arrows a and b. Then \(f_{i,\pi _i({\mathbf {d}})}(\pi _i(M))\) has a direct summand isomorphic to \(S_{ab}\) if and only if condition Theorem 7.6(ii) holds. This finishes the proof. \(\square \)
Theorem 7.7
Let A be a gentle Jacobian algebra. For \(M \in {\text {mod}}(A,{\mathbf {d}})\) the following are equivalent:
-
(i)
M is singular;
-
(ii)
M is contained in at least two different irreducible components of \({\text {mod}}(A,{\mathbf {d}})\).
Proof
Let \(A_1,\ldots ,A_t\) be the \(\rho \)-blocks of A. We know that M is singular if and only if \(\pi _i(M)\) is singular for some \(1 \le i \le t\).
We also know that M is contained in two different components if and only if \(\pi _i(M)\) is contained in two different components.
Now the claim follows from Lemma 6.12. \(\square \)
Corollary 7.8
Let A be a gentle Jacobian algebra. For each \({\mathbf {d}}\) we have
Note that Corollary 7.8 is exactly the statement of Theorem 1.1.
7.5 Band components
Proposition 7.9
Let A be a gentle algebra, and let \(M \in {\text {mod}}(A,{\mathbf {d}})\) be a direct sum of band modules. Then M is smooth.
Proof
By Lemma 5.5(i) we have \({\text {proj.dim}}(M) \le 1\). This implies \({\text {Ext}}_A^2(M,M) = 0\). Now Proposition 2.10 yields that M is smooth. \(\square \)
Corollary 7.10
Let A be a gentle algebra, and let \(Z \in {\text {Irr}}(A)\) be a direct sum of band components. Then Z is generically reduced.
Proof
In a direct sum of band components, the direct sums of band modules form a dense open subset. Now the statement follows from Proposition 7.9 combined with Lemma 2.6. \(\square \)
Proposition 7.11
Let A be a gentle algebra. For any band component \(Z \in {\text {Irr}}(A)\) we have
In particular, Z is a brick component.
Proof
Let Z be a band component. Thus there is a band B such that the union
forms a dense subset of Z. Let \(M = M(B,\lambda ,1)\) for some \(\lambda \in K^*\).
By Corollary 7.3 we have \(c_A(Z) = 1\). Now Corollary 7.10 implies \(e_A(Z) = 1\). In other words, we have
Now Lemma 5.5(ii) together with Corollary 5.6 imply that
In other words, \(h_A(Z) = 1\) and M is a brick. It follows that Z is a brick component. \(\square \)
Note that Proposition 7.11 yields Theorem 1.5.
Corollary 7.12
Let A be a gentle algebra, and let \(Z \in {\text {Irr}}(A)\) be a direct sum of band components. Then Z is generically \(\tau \)-reduced.
Proof
We have
for some band components \(Z_i = Z(B_i)\), \(1 \le i \le m\). By Lemma 7.2 we have \(c_A(Z) = m\).
By Theorem 2.11 we get \(\mathrm{ext}_A^1(Z_i,Z_j) = 0\) for all \(i \not = j\). Let
with pairwise different \(\lambda _1,\ldots ,\lambda _m\). In other words, M is generic in Z. For brevity we set \(M_i := M(B_i,\lambda _i,1)\). It follows that
for all \(i \not = j\). For the last equality we used again Corollary 5.6. By Proposition 7.11 we have
for all i. Combining this, we get
In other words, \(c_A(Z) = h_A(Z)\), thus Z is generically \(\tau \)-reduced. \(\square \)
Theorem 7.13
Let A be a gentle algebra. For \(Z \in {\text {Irr}}(A,{\mathbf {d}})\) the following are equivalent:
-
(i)
Z is a direct sum of band components.
-
(ii)
\(\dim (Z) = \dim ({\text {GL}}_{\mathbf {d}}(K))\).
Proof
(i) \(\implies \) (ii): Let
be a direct sum of band components, and let
be generic in Z. It follows from Proposition 7.11 and the proof of Corollary 7.12 that
By Proposition 7.9, M is smooth. Thus
(ii) \(\implies \) (i): Let
be a direct sum of string and band components. For a generic \(M \in Z\) we get \(c_A(Z) = q\), see Lemma 7.2. In other words,
Clearly \(\dim {\text {End}}_A(M) \ge p+q\). So \(\dim (Z) = \dim ({\text {GL}}_{\mathbf {d}}(K))\) implies \(p=0\). In other words, Z is a direct sum of band components. This finishes the proof. \(\square \)
Combining Corollary 7.12 and Theorem 7.13 proves Theorem 1.6.
The following theorem is a combination of [14, Corollary 10] and [14, Proposition 11], see also [13, Theorem 2]. Proposition 7.11 generalizes Theorem 7.14(ii) to arbitrary gentle algebras, whereas Theorem 7.14(i) fails in general.
Theorem 7.14
([14]) Let A be an acyclic gentle algebra. Then the following hold:
-
(i)
For each dimension vector \({\mathbf {d}}\) there exists at most one band component Z in \({\text {Irr}}(A,{\mathbf {d}})\).
-
(ii)
Each band component \(Z \in {\text {Irr}}(A,{\mathbf {d}})\) is a brick component.
For acyclic gentle algebras A, a combinatorial construction of generic modules for each irreducible component of \({\text {mod}}(A,{\mathbf {d}})\) is described in [13].
7.6 Examples
7.6.1. Let \(A = KQ/I\), where Q is the quiver

and I is generated by \(\{ a^2 \}\). Obviously, A is gentle. Let \({\mathbf {d}}= (1)\). Then \({\text {mod}}(A,{\mathbf {d}})\) has just one K-rational point, corresponding to the simple A-module \(M = S_1\). Clearly, M is not smooth and not reduced.
7.6.2. Let \(A = KQ/I\), where Q is the quiver

and I is generated by \(\{ ab \}\). Clearly, A is a gentle algebra. Let \({\mathbf {d}}= (1,1,1)\). Then \({\text {mod}}(A,{\mathbf {d}})\) has 2 irreducible components. The module \(M = S_1 \oplus S_2 \oplus S_3 \in {\text {mod}}(A,{\mathbf {d}})\) is reduced, but not smooth. For \({\mathbf {d}}= (1,2,1)\), the affine scheme \({\text {mod}}(A,{\mathbf {d}})\) is irreducible, reduced, but not smooth.
7.6.3. Let \(A = KQ/I\), where Q is the quiver

and I is generated by \(\{ ab \}\). Then A is a gentle algebra, which does not admit a colouring in the sense of [14].
7.6.4. Let \(A = KQ/I\), where Q is the quiver

and I is generated by \(\{ a^2,\; e^2,\; c_1c_2,\; c_2c_1 \}\). This is a gentle algebra admitting a colouring. For \({\mathbf {d}}= (2,2,2,2)\), the affine scheme \({\text {mod}}(A,{\mathbf {d}})\) has 3 irreducible components, and all of these are band components.
8 Generically \(\tau \)-reduced components for gentle Jacobian algebras
In this section, we concentrate on the description of generically \(\tau \)-reduced components for gentle Jacobian algebras. Some of this can be generalized to arbitrary gentle algebras. We leave this endeavor to the reader.
8.1 Simple summands of restrictions
Let \(A = KQ/I\) be a gentle Jacobian algebra and let \(A_1,\ldots ,A_t\) be its \(\rho \)-blocks. For \(a \in Q_0 \cup Q_1\) and \(1 \le s \le t\) let
Lemma 8.1
Let \(A = KQ/I\) be a gentle Jacobian algebra and let \(A_1,\ldots ,A_t\) be its \(\rho \)-blocks. For a string module \(M = M(C) \in {\text {mod}}(A)\) and any \(\rho \)-block \(A_s\), the \(A_s\)-module \(\pi _s(M)\) has a simple direct summand if and only if one of the following hold:
-
\(C = 1_i\) and \(i \in A_s\);
-
\(C = (c_1,\ldots ,c_r)\) with \(s(C) \in A_s\) and \(c_r \notin A_s\);
-
\(C = (c_1,\ldots ,c_r)\) with \(t(C) \in A_s\) and \(c_1 \notin A_s\).
Proof
For \(C = 1_i\) the claim is clear. Thus let \(C = (c_1,\ldots ,c_r)\). For each \(1 \le i \le r\) we have \(c_i = a_i^\pm \) for some \(a_i \in Q_1\). For \(M = M(C)\) we get
This follows directly from the definition of a string module. The claim follows. \(\square \)
Lemma 8.2
Let \(A = KQ/I\) be a gentle Jacobian algebra, and let \(A_1,\ldots ,A_t\) be its \(\rho \)-blocks. For a band module \(M \in {\text {mod}}(A)\) and any \(\rho \)-block \(A_s\), the module \(\pi _s(M)\) has no simple direct summand. In particular, \(\pi _s(M)\) is a projective \(A_s\)-module.
Proof
Let \(M = M(B,\lambda ,q)\) be a band module where \(B = (c_1,\ldots ,c_r)\). For each \(1 \le i \le r\) we have \(c_i = a_i^\pm \) for some \(a_i \in Q_1\). We get
This follows directly from the definition of a band module. The claim follows. \(\square \)
8.2 Non-vanishing of \({\text {Hom}}_A(M,\tau _A(M))\)
Let A be a gentle Jacobian algebra, and let \(A_1,\ldots ,A_t\) be its \(\rho \)-blocks. Recall from Sect. 6.2 the definition of critical summands of type I or II for modules over \(C_n\) or \({\widetilde{C}}_n\). We say that \(M \in {\text {mod}}(A,{\mathbf {d}})\) has a critical summand of type I (resp. type II) if there exists some \(1 \le i \le t\) such that \(\pi _i(M)\) has a critical summand of type I (resp. of type II).
Lemma 8.3
Let A be a gentle Jacobian algebra, and let \(A_1,\ldots ,A_t\) be its \(\rho \)-blocks. For \(M \in {\text {mod}}(A)\) the following are equivalent:
-
(i)
M does not have a critical summand of type I or II.
-
(ii)
\(\pi _i(M)\) is \(\tau \)-rigid for all \(1 \le i \le t\).
Proof
This follows from Propositions 6.7 and 6.8\(\square \)
Lemma 8.4
Let A be a gentle Jacobian algebra, and let \(A_1,\ldots ,A_t\) be its \(\rho \)-blocks. Let \(M_1,M_2 \in {\text {mod}}(A)\) such that the following hold: There exists a \(\rho \)-block \(A_i\) containing an arrow \(a \in Q_1\) such that \(S_{s(a)}\) is (up to isomorphism) a direct summand of \(\pi _i(M_1)\), and \(S_{t(a)}\) is (up to isomorphism) a direct summand of \(\pi _i(M_2)\). Then \({\text {Ext}}_A^1(M_1,M_2) \not = 0\).
Proof
We can assume that \(M_1\) and \(M_2\) are both indecomposable. By Lemma 8.2 we know that \(M_1 = M(C_1)\) and \(M_2 = M(C_2)\) are both string modules. By Lemma 8.1 we can assume without loss of generality that \(s(C_1) = s(a)\) and \(t(C_2) = t(a)\) and that \(C_1a^{-1}C_2\) is a string. We obtain a non-split short exact sequence
Thus \({\text {Ext}}_A^1(M_1,M_2) \not = 0\). \(\square \)
Corollary 8.5
Let A be a gentle Jacobian algebra, and let \(A_1,\ldots ,A_t\) be its \(\rho \)-blocks. Let \(M_1,M_2 \in {\text {mod}}(A)\) such that \({\text {Ext}}_A^1(M_1,M_2) = 0\). Then
for all \(1 \le i \le t\).
Proof
Combine Lemma 8.4 with Proposition 6.7. \(\square \)
Lemma 8.6
Let A be a gentle Jacobian algebra, and let \(A_1,\ldots ,A_t\) be its \(\rho \)-blocks. Let \(M_1,M_2 \in {\text {mod}}(A)\) such that the following hold: There exists a 3-block \(A_s\) containing an arrow \(a \in Q_1\) such that \(S_{s(a)}\) is (up to isomorphism) a direct summand of \(\pi _s(M_1)\), and \(P_{t(a)}\) is (up to isomorphism) a direct summand of \(\pi _s(M_2)\). Then
Proof
We can assume that \(M_1\) and \(M_2\) are both indecomposable. We know that \(M_1 = M(C_1)\) for some string \(C_1\) (see Lemma 8.2) and \(M_2 = M(C_2)\) or \(M_2 = M(C_2,\lambda ,q)\) for some string or band \(C_2\), respectively.
If \(M_2\) is a band module, then there is a surjective homomorphism \(M(C_1,\lambda ,q) \rightarrow M(C_1,\lambda ,1)\). Thus in this case we can assume without loss of generality that \(q=1\).
We can assume that the 3-block \(A_s\) is of the form

with \(a_2a_1, a_3a_2, a_1a_3 \in I\) and \(a = a_1\).
Without loss of generality we can assume that \(s(C_1) = 1\) and that either \(l(C_1) = 0\) or \(C_1 = (c_1,\ldots ,c_m)\) such that \(c_m \notin A_2\). We can also assume that \(C_2 = C'a_2C''\) for some strings \(C'\) and \(C''\) and we can assume that \(C' = (c_1',\ldots ,c_r')\) with \(c_1' \in Q_1^{-1}\).
We want to construct a non-zero homomorphism
Let E be a path of maximal length such that \(a_1^{-1}E\) is a string. It follows that \(\tau _A(M(C_1)) = M(E'E)\) for some string \(E'\), where \(E'\) is either of length 0 or of the form \(E' = E''a_1^{-1}\) for some string \(E''\), compare Sect. 5.9.
Let F be a path of maximal length such that \(FF' = C''\). Thus \(C_2 = C'a_2FF'\). It follows that \(F'\) is of length 0 or of the form \(F' = b^{-1}F''\) for some \(b \in Q_1\) and some string \(F''\). This yields a surjective homomorphism
Furthermore, we have \(E = FG'\) for some direct string \(G'\). We get a standard homomorphism
Thus
is the desired non-zero homomorphism. This finishes the proof. \(\square \)
Corollary 8.7
Let A be a gentle Jacobian algebra, and let \(A_1,\ldots ,A_t\) be its \(\rho \)-blocks. Let \(M_1,M_2 \in {\text {mod}}(A)\) such that \({\text {Hom}}_A(M_2,\tau _A(M_1)) = 0\). Then
for all \(1 \le i \le t\).
Proof
Combine Lemma 8.6, Corollary 8.5 and Proposition 6.8. \(\square \)
Corollary 8.8
Let A be a gentle Jacobian algebra, and assume that \(M \in {\text {mod}}(A)\) has a critical summand of type I or II. Then
8.3 Proof of Theorem 1.4
Let \(A = KQ/I\) be a gentle Jacobian algebra, and let \(A_1,\ldots ,A_t\) be its \(\rho \)-blocks. Let \(Z \in {\text {Irr}}(A)\). We want to show that the following are equivalent:
-
(i)
\(Z \in {\text {Irr}}^\tau (A)\);
-
(ii)
\(\pi _s(Z) \in {\text {Irr}}^\tau (A_s)\) for all \(1 \le s \le t\).
Throughout, let
be generic in Z.
For \(1 \le i \le p\) let \(N_i := M(C_i)\), and for \(1 \le j \le q\) let \(N_{p+j} := M(B_j,\lambda _j,1)\).
(i) \(\implies \) (ii): Assume that \(Z \in {\text {Irr}}^\tau (A)\). Then Theorem 9.2 yields that \({\text {Hom}}_A(N_i,\tau _A(N_j)) = 0\) for all \(i \not = j\). Furthermore we have
Now it follows from Corollary 8.7 that
for all \(i \not = j\), and also for all \(i=j\) with \(1 \le i \le p\). Since \(N_{p+1},\ldots ,N_{p+q}\) are band modules, we get from Lemma 8.2 that also in this case
This proves that \(\pi _s(M)\) is a \(\tau \)-rigid \(A_s\)-module for all s. Thus \(\pi _s(Z) \in {\text {Irr}}^\tau (A_s)\).
(ii) \(\implies \) (i): Assume that \(\pi _s(Z) \in {\text {Irr}}^\tau (A_s)\) for all \(1 \le s \le t\).
We have
for all \(1 \le j \le q\) and \(1 \le k \le p+q\). For the third equality we used Corollary 5.6.
Thus Z is generically \(\tau \)-reduced if and only if \({\text {Hom}}_A(N_k,\tau _A(N_i)) = 0\) for all \(1 \le i \le p\) and \(1 \le k \le p+q\). To get a contradiction, assume that
for some \(1 \le i \le p\) and some \(1 \le k \le p+q\). On the other hand, we know that
Let
be a non-zero homomorphism. We know that f factors through some injective A-module. Without loss of generality, we can assume that this injective module equals \(I_r\) for some \(r \in Q_0\). Thus we have \(f = f_1 \circ f_2\) with \(f_1 \in {\text {Hom}}_A(I_r,\tau _A(N_i))\) and \(f_2 \in {\text {Hom}}_A(N_k,I_r)\). Again without loss of generality we can assume that
is a standard homomorphism. (Here we use the same notation and terminology as in [51].)
The module \(I_r\) is of the form
where C and D are direct strings in Q such that \(C\gamma ,D\gamma \in I\) for all \(\gamma \in Q_1\). Since \(\tau _A(M_i)\) is not injective, we know that \(f_1\) cannot be a monomorphism. Thus \(I_r\) is not simple and we can assume without loss of generality that \(C = \alpha _1 \cdots \alpha _v\) and that
for some \(1 \le k \le v\). Thus we have
Since A is a gentle algebra, we also know that \(\alpha _v\gamma \in I\) for all \(\gamma \in Q_1\). This implies \(E' = 1_{s(\alpha )}\). Set \(a := \alpha _k\).
The following picture shows \(I_r\), where \(I_r/{\text {Ker}}(f_1)\) is given by the string F between the blue vertices.

By the properties of \(f_1\) discussed above, we see that we must be in the 2nd, 4th or 5th case and that F coincides with the subfactor of \(\tau _A(M)\) marked by the two rightmost blue points. Here we refer to Sect. 5.9 for the description of \(\tau _A(M)\).
We get \(ab \in I\). Thus there exists a third arrow \(c \in Q_1\) with \(s(c) = t(a)\) and \(t(c) = s(b)\). So the arrows a, b, c form a 3-block, say \(A_s\), of A. So we are in the following situation:

(In the 5th case, the red bullet in this picture should be green.)
Clearly \(\pi _s(N_k)\) contains M(a) as a direct summand, and \(\pi _s(N_i)\) contains \(S_{s(b)}\) as a direct summand.
It follows that \(\pi _s(N_k \oplus N_i)\) has a direct summand isomorphic to \(S_{s(b)} \oplus P_{s(a)}\). Now Proposition 6.8 implies that \(\pi _s(N_k \oplus N_i)\) and therefore also \(\pi _s(M)\) is not \(\tau \)-rigid in \({\text {mod}}(A_s)\). This finishes the proof.
8.4 Proof of Theorem 1.3
Let A be a gentle Jacobian algebra, and let \(A_1,\ldots ,A_t\) be its \(\rho \)-blocks. Let \(Z_1,Z_2 \in {\text {Irr}}^\tau (A)\). We want to show that the following are equivalent:
-
(i)
\({\underline{\dim }}(Z_1) = {\underline{\dim }}(Z_2)\);
-
(ii)
\(Z_1 = Z_2\).
(ii) \(\implies \) (i): This direction is trivial.
(i) \(\implies \) (ii): Assume that \({\underline{\dim }}(Z_1) = {\underline{\dim }}(Z_2)\). We know from Theorem 1.4 that \(\pi _i(Z_1)\) and \(\pi _i(Z_2)\) are generically \(\tau \)-reduced for all \(1 \le i \le t\). In particular, \(\pi _i(Z_1)\) and \(\pi _i(Z_2)\) both contain a \(\tau \)-rigid \(A_i\)-module. We clearly have \({\underline{\dim }}(\pi _i(Z_1)) = {\underline{\dim }}(\pi _i(Z_2))\) for all i. Note that for gentle Jacobian algebras, we have \(A_i = A_i'\) for all i. Now the statement follows from Lemma 6.11.
9 Schemes of decorated modules
9.1 Decorated modules
Let \(A = KQ/I\) be a basic algebra. A decorated A-module is a pair \({{\mathcal {M}}}= (M,V)\), where \(M \in {\text {mod}}(A)\) and \(V = (V_1,\ldots ,V_n)\) is a tuple of finite-dimensional K-vector spaces.
One defines morphisms and direct sums of decorated modules in the obvious way. Let \({\text {decmod}}(A)\) be the abelian category of decorated A-modules.
For \(1 \le i \le n\) set \({{\mathcal {S}}}_i := (S_i,0)\), and let \({{\mathcal {S}}}_i^- := (0,V)\), where \(V_i = K\) and \(V_j = 0\) for all \(j \not = i\). The decorated modules \({{\mathcal {S}}}_i\) and \({{\mathcal {S}}}_i^-\) are the simple and negative simple decorated A-modules, respectively.
9.2 Schemes of decorated modules
For \(({\mathbf {d}},{{\mathbf {v}}}) \in {\mathbb {N}}^n \times {\mathbb {N}}^n\) let \({\text {decmod}}(A,({\mathbf {d}},{{\mathbf {v}}}))\) be the affine scheme of decorated A-modules \({{\mathcal {M}}}= (M,V)\) with \(M \in {\text {mod}}(A,{\mathbf {d}})\) and \(V = K^{{\mathbf {v}}}:= (K^{v_1},\ldots ,K^{v_n})\), where \({{\mathbf {v}}}= (v_1,\ldots ,v_n)\). Note that \({\text {mod}}(A,{\mathbf {d}}) \cong {\text {decmod}}(A,({\mathbf {d}},{{\mathbf {v}}}))\) for all \(({\mathbf {d}},{{\mathbf {v}}})\).
For \({{\mathcal {M}}}= (M,V) \in {\text {decmod}}(A,({\mathbf {d}},{{\mathbf {v}}}))\) let \(g.{{\mathcal {M}}}:= (g.M,V)\). This defines a \({\text {GL}}_{\mathbf {d}}(K)\)-action on \({\text {decmod}}(A,({\mathbf {d}},{{\mathbf {v}}}))\). The \({\text {GL}}_{\mathbf {d}}(K)\)-orbit of \({{\mathcal {M}}}\) is denoted by \({{\mathcal {O}}}_{{\mathcal {M}}}\).
9.3 E-invariants and g-vectors of decorated modules
Let \({{\mathcal {M}}}= (M,V)\) be a decorated A-module, and let
be a minimal projective presentation of M. The g-vector of \({{\mathcal {M}}}\) is defined as
with
for \(1 \le i \le n\).
For decorated A-modules \({{\mathcal {M}}}= (M,V)\) and \({{\mathcal {N}}}= (N,W)\) let
For finite-dimensional Jacobian algebras A arising from quivers with potentials, \(E_A({{\mathcal {M}}},{{\mathcal {N}}})\) coincides with \(E^\mathrm{proj}({{\mathcal {M}}},{{\mathcal {N}}})\) as defined in [23, Section 10].
The E-invariant of \({{\mathcal {M}}}\) is defined as \(E_A({{\mathcal {M}}}) := E_A({{\mathcal {M}}},{{\mathcal {M}}})\). The decorated module \({{\mathcal {M}}}\) is called E-rigid if \(E_A({{\mathcal {M}}}) = 0\).
For \({{\mathcal {M}}}= (M,0)\) we also write \({\mathbf {g}}_A(M)\) and \(E_A(M)\) instead of \({\mathbf {g}}_A({{\mathcal {M}}})\) and \(E_A({{\mathcal {M}}})\), respectively.
Dualizing the results from [23, Section 10] (for Jacobian algebras A) and [17, Section 3] (for arbitrary A), for decorated A-modules \({{\mathcal {M}}}= (M,V)\) and \({{\mathcal {N}}}= (N,W)\) we have
Note that in [23] and [17], this equation is used as a definition.
9.4 Generically \(\tau \)-reduced decorated components
Let \(A = KQ/I\) be a basic algebra, and let \(({\mathbf {d}},{{\mathbf {v}}}) \in {\mathbb {N}}^n \times {\mathbb {N}}^n\). By \({\text {decIrr}}(A,({\mathbf {d}},{{\mathbf {v}}}))\) we denote the set of irreducible components of \({\text {decmod}}(A,({\mathbf {d}},{{\mathbf {v}}}))\). For \(Z \in {\text {decIrr}}(A,({\mathbf {d}},{{\mathbf {v}}}))\) we write \({\underline{\dim }}(Z) := ({\mathbf {d}},{{\mathbf {v}}})\). Let
For \(Z \in {\text {decIrr}}(A,({\mathbf {d}},{{\mathbf {v}}}))\) set \(Z' := \{ M \in {\text {mod}}(A,{\mathbf {d}}) \mid (M,K^{{\mathbf {v}}}) \in Z \}\). We clearly have \(Z' \in {\text {Irr}}(A,{\mathbf {d}})\), and write \(Z = (Z',K^{{\mathbf {v}}})\). Define \(c_A(Z) := c_A(Z')\) and \(e_A(Z) := e_A(Z')\).
For \(Z,Z_1,Z_2 \in {\text {decIrr}}(A)\) there are dense open subsets \(U \subseteq Z\) and \(U' \subseteq Z_1 \times Z_2\) such that the maps \({\mathbf {g}}_A(-)\), \(E_A(-)\) and \(E_A(-,-)\) are constant on U and \(U'\), respectively. These generic values are denoted by \({\mathbf {g}}_A(Z)\), \(E_A(Z)\) and \(E_A(Z_1,Z_2)\), respectively.
For \(Z \in {\text {decIrr}}(A)\) we have
An irreducible component \(Z \in {\text {decIrr}}(A)\) is generically reduced if \(c_A(Z) = e_A(Z)\) and generically \(\tau \)-reduced provided
Let \({\text {decIrr}}^\tau (A,({\mathbf {d}},{{\mathbf {v}}}))\) be the set of all generically \(\tau \)-reduced components of \({\text {decmod}}(A,({\mathbf {d}},{{\mathbf {v}}}))\), and let
It follows from the definitions that
where \({\mathbf {d}}= (d_1,\ldots ,d_n)\) and \({{\mathbf {v}}}= (v_1,\ldots ,v_n)\).
The following beautiful result due to Plamondon shows that the generic g-vectors parametrize the generically \(\tau \)-reduced decorated components.
Theorem 9.1
([47, Theorem 1.2]) Let A be a basic algebra. Then the map
is bijective.
9.5 Decomposition of generically \(\tau \)-reduced components
An irreducible component \(Z \in {\text {decIrr}}(A,({\mathbf {d}},{{\mathbf {v}}}))\) is called indecomposable if there exists a dense open subset \(U \subseteq Z\), which contains only indecomposable decorated modules. This is the case if and only if \(Z = (Z',0)\) with \(Z' \in {\text {Irr}}(A,{\mathbf {d}})\) indecomposable or \(Z = \{ {{\mathcal {S}}}_i^- \}\) for some i. In particular, if \(Z \in {\text {decIrr}}(A,({\mathbf {d}},{{\mathbf {v}}}))\) is indecomposable, then either \({\mathbf {d}}= 0\) or \({{\mathbf {v}}}= 0\).
Given irreducible components \(Z_i\) of \({\text {decmod}}(A,({\mathbf {d}}_i,{{\mathbf {v}}}_i))\) for \(1 \le i \le t\), let \(({\mathbf {d}},{{\mathbf {v}}}) := ({\mathbf {d}}_1,{{\mathbf {v}}}_1) + \cdots + ({\mathbf {d}}_t,{{\mathbf {v}}}_t)\), and let
be the image of the morphism
The Zariski closure \(\overline{Z_1 \oplus \cdots \oplus Z_t}\) of \(Z_1 \oplus \cdots \oplus Z_t\) is an irreducible closed subset of \({\text {decmod}}(A,({\mathbf {d}},{{\mathbf {v}}}))\) and is called the direct sum of \(Z_1,\ldots ,Z_t\). Note that \(\overline{Z_1 \oplus \cdots \oplus Z_t}\) is in general not an irreducible component.
Theorem 9.2
([17, Theorem 1.3]) For \(Z_1,\ldots ,Z_t \in {\text {decIrr}}(A)\) the following are equivalent:
-
(i)
\(\overline{Z_1 \oplus \cdots \oplus Z_t}\) is a generically \(\tau \)-reduced component.
-
(ii)
Each \(Z_i\) is generically \(\tau \)-reduced and \(E_A(Z_i,Z_j) = 0\) for all \(i \not = j\).
Each \(Z \in {\text {decIrr}}^\tau (A)\) is a direct sum of indecomposable generically \(\tau \)-reduced components, which are uniquely determined up to reordering.
10 Laminations and generically \(\tau \)-reduced decorated components
10.1 Marked surfaces
By an unpuntured marked surface \(({{\mathbb {S}}},{{\mathbb {M}}})\) we mean a connected, compact, oriented surface \({{\mathbb {S}}}\) with non-empty boundary \(\partial {{\mathbb {S}}}\) together with a finite set \({{\mathbb {M}}}\) of marked points on the boundary. We set \({{\mathbb {S}}}^\circ := {{\mathbb {S}}}\setminus \partial {{\mathbb {S}}}\). We assume that there is at least one marked point on each boundary component. We also require that \(({{\mathbb {S}}},{{\mathbb {M}}})\) is not a monogon, digon or triangle. (This ensures the existence of non-trivial triangulations.)
10.2 Curves and loops
A curve in \(({{\mathbb {S}}},{{\mathbb {M}}})\) is a map
of differentiability class \(C^1\), with derivative vanishing in at most finitely many points of [0, 1], such that the following hold:
-
(A1)
\(\gamma (0)\) and \(\gamma (1)\) are in \({{\mathbb {M}}}\);
-
(A2)
\({\text {Im}}(\gamma ) \setminus \{ \gamma (0),\gamma (1) \}\) is disjoint from \(\partial {{\mathbb {S}}}\);
-
(A3)
\({\text {Im}}(\gamma )\) does not cut out a monogon or digon.
A curve \(\gamma \) in \(({{\mathbb {S}}},{{\mathbb {M}}})\) is simple if additionally the following holds:
-
(A4)
\(\gamma \) is injective on the open interval (0, 1), i.e. \(\gamma \) does not intersect itself, except that \(\gamma (0)\) and \(\gamma (1)\) may coincide.
Simple curves in \(({{\mathbb {S}}},{{\mathbb {M}}})\) are also called arcs.
Let \(S^1\) be the unit circle in \({\mathbb {C}}\). A loop in \(({{\mathbb {S}}},{{\mathbb {M}}})\) is a map
of differentiability class \(C^1\), with derivative vanishing in at most finitely many points of \(S^1\), such that the following hold:
-
(L1)
\({\text {Im}}(\gamma )\) is disjoint from \(\partial {{\mathbb {S}}}\);
-
(L2)
\({\text {Im}}(\gamma )\) is non-contractible.
A loop \(\gamma \) in \(({{\mathbb {S}}},{{\mathbb {M}}})\) is simple if additionally the following holds:
-
(L3)
\(\gamma \) is injective, i.e. \(\gamma \) does not intersect itself.
Let \(A({{\mathbb {S}}},{{\mathbb {M}}})\) be the set of curves in \(({{\mathbb {S}}},{{\mathbb {M}}})\) up to homotopy (relative to \(\gamma (0)\) and \(\gamma (1)\)) and up to the equivalence \(\gamma \sim \gamma ^{-1}\). For a curve \(\gamma \) let \([\gamma ]\) be its class in \(A({{\mathbb {S}}},{{\mathbb {M}}})\).
Let \(L({{\mathbb {S}}},{{\mathbb {M}}})\) be the set of loops in \(({{\mathbb {S}}},{{\mathbb {M}}})\) up to homotopy and up to the equivalence \(\gamma \sim \gamma ^{-1}\). For a loop \(\gamma \) let \([\gamma ]\) be its class in \(L({{\mathbb {S}}},{{\mathbb {M}}})\).
For a curve or loop \(\gamma \) in \(({{\mathbb {S}}},{{\mathbb {M}}})\) we just write \(\gamma \) for the image \({\text {Im}}(\gamma )\).
For
let
Note that for a simple curve or loop \(\gamma \) we get \({\text {Int}}([\gamma ],[\gamma ]) = 0\).
From now on we will not distinguish between a curve or loop \(\gamma \) and its class \([\gamma ]\).
A loop \(\gamma \) is primitive of it is not of the form \(\gamma = \theta ^m\) for some loop \(\theta \) and some \(m \ge 2\). Here \(\theta ^m(z) := \theta (z^m)\) for all \(z \in S^1\). Let
be the subset of primitive loops.
Let \(\pi :{\widetilde{S}}^1 \rightarrow S^1\) be the universal cover of \(S^1\). For a loop \(\gamma :S^1 \rightarrow {{\mathbb {S}}}\) in \(({{\mathbb {S}}},{{\mathbb {M}}})\) let
We call this the periodic curve associated with \(\gamma \).
For later convenience, for \(\gamma \in A({{\mathbb {S}}},{{\mathbb {M}}})\) we set \({\widetilde{\gamma }}:= \gamma \).
For \(\gamma _1,\gamma _2 \in A({{\mathbb {S}}},{{\mathbb {M}}})\cup L({{\mathbb {S}}},{{\mathbb {M}}})\), define \({\text {Int}}({\widetilde{\gamma }}_1,\gamma _2)\) and \({\text {Int}}({\widetilde{\gamma }}_1,{\widetilde{\gamma }}_2)\) similarly as above. Note that the value \(\infty \) might occur in this situation.
The following lemma is straightforward
Lemma 10.1
For \(\gamma _1,\gamma _2 \in A({{\mathbb {S}}},{{\mathbb {M}}})\cup L({{\mathbb {S}}},{{\mathbb {M}}})^\mathrm{prim}\) the following are equivalent:
-
1.
\({\text {Int}}(\gamma _1,\gamma _2) = 0\);
-
2.
\({\text {Int}}({\widetilde{\gamma }}_1,\gamma _2) = 0\);
-
3.
\({\text {Int}}({\widetilde{\gamma }}_1,{\widetilde{\gamma }}_2) = 0\).
10.3 Laminations and triangulations
By a lamination of \(({{\mathbb {S}}},{{\mathbb {M}}})\) we mean a pair \(L = (\gamma ,m)\), where \(\gamma \) is a (finite) subset of \(A({{\mathbb {S}}},{{\mathbb {M}}})\cup L({{\mathbb {S}}},{{\mathbb {M}}})\) such that \({\text {Int}}(\gamma _i,\gamma _j) = 0\) for all \(\gamma _i,\gamma _j \in \gamma \), and \(m:\gamma \rightarrow {\mathbb {Z}}_{>0}\) is a map. Instead of \(L = (\gamma ,m)\) we also write \(L = \{ (\gamma _1,m_1),\ldots ,(\gamma _t,m_t) \}\), where \(\gamma = \{ \gamma _1,\ldots ,\gamma _t \}\) and \(m_i = m(\gamma _i)\) for \(1 \le i \le t\). By abuse of terminology, we also say that \(\gamma \) is a lamination. Note that each element in \(\gamma \) is a simple curve or a simple loop. We think of \(m_i\) as the multiplicity of \(\gamma _i\) in the lamination L. Let \({\text {Lam}}({{\mathbb {S}}},{{\mathbb {M}}})\) be the set of laminations of \(({{\mathbb {S}}},{{\mathbb {M}}})\). Note that in [45, Definition 3.17], the set \({\text {Lam}}({{\mathbb {S}}},{{\mathbb {M}}})\) is denoted by \({{\mathcal {C}}}^\circ ({{\mathbb {S}}},{{\mathbb {M}}})\).
Each boundary component of \(({{\mathbb {S}}},{{\mathbb {M}}})\) with m marked points has m boundary segments, each connecting two consecutive marked points.
Next, a curve in \({{\mathbb {S}}}\setminus {{\mathbb {M}}}\) is a map
of differentiability class \(C^1\), with derivative vanishing in at most finitely many points of [0, 1], such that the following hold:
-
(A1)
\(\gamma (0)\) and \(\gamma (1)\) are in \(\partial {{\mathbb {S}}}\setminus {{\mathbb {M}}}\);
-
(A2)
\({\text {Im}}(\gamma ) \setminus \{ \gamma (0),\gamma (1) \}\) is disjoint from \(\partial {{\mathbb {S}}}\);
-
(A3)
\({\text {Im}}(\gamma )\) is non-contractible (with respect to the relative homotopy described below) and does not cut out a monogon, see Fig. 3.
A curve \(\gamma \) in \({{\mathbb {S}}}\setminus {{\mathbb {M}}}\) is simple if additionally the following holds:
-
(A4)
\(\gamma \) is injective, i.e. \(\gamma \) does not intersect itself.
Let \(A({{\mathbb {S}}}\setminus {{\mathbb {M}}})\) be the set of curves in \({{\mathbb {S}}}\setminus {{\mathbb {M}}}\) up to homotopy, such that \(\gamma (0)\) and \(\gamma (1)\) never leave their respective boundary segment, and up to the equivalence \(\gamma \sim \gamma ^{-1}\). More precisely, we consider here homotopies
such that for each \(t \in [0,1]\) the map \(H_t := H(t,-)\) is a curve in \({{\mathbb {S}}}\setminus {{\mathbb {M}}}\) with \(H_t(0)\) (resp. \(H_t(1)\)) belonging to the same boundary segment as \(\gamma (0)\) (resp. \(\gamma (1)\)) and such that \(H_0 = \gamma \).
As before, we just write \(\gamma \) for the class of \(\gamma \) in \(A({{\mathbb {S}}}\setminus {{\mathbb {M}}})\).
By a classical lamination of \(({{\mathbb {S}}},{{\mathbb {M}}})\) we mean a pair \(L = (\gamma ,m)\), where \(\gamma \) is a (finite) subset of \(A({{\mathbb {S}}}\setminus {{\mathbb {M}}}) \cup L({{\mathbb {S}}},{{\mathbb {M}}})\) such that \({\text {Int}}(\gamma _i,\gamma _j) = 0\) for all \(\gamma _i,\gamma _j \in \gamma \), and \(m:\gamma \rightarrow {\mathbb {Z}}_{>0}\) is a map. Here \({\text {Int}}(\gamma _i,\gamma _j)\) is defined in the obvious way. Again by abuse of terminology, we also say that \(\gamma \) is a classical lamination. Let \({\text {Lam}}({{\mathbb {S}}}\setminus {{\mathbb {M}}})\) be the set of classical laminations of \(({{\mathbb {S}}},{{\mathbb {M}}})\).
Given a curve \(\gamma \in A({{\mathbb {S}}},{{\mathbb {M}}})\), let \(\tau ^{1/2}(\gamma ) \in A({{\mathbb {S}}}\setminus {{\mathbb {M}}})\) be the curve obained from \(\gamma \) by rotating its endpoints in clockwise direction to the adjacent boundary segment. This yields a bijection
A triangulation T of \(({{\mathbb {S}}},{{\mathbb {M}}})\) consists of all boundary segments together with a maximal collection \(T^\circ \) of curves in \(({{\mathbb {S}}},{{\mathbb {M}}})\) such that \({\text {Int}}(\gamma _i,\gamma _j) = 0\) for all \(\gamma _i,\gamma _j \in T^\circ \). In this case, we have
where g is the genus of \({{\mathbb {S}}}\) and b is the number of boundary components of \({{\mathbb {S}}}\), see for example [25, Proposition 2.10].
Note that the classical laminations defined above correspond to the \({{\mathcal {X}}}\)-laminations in the sense of Fock and Goncharov [24]. Let T be a triangulation of \(({{\mathbb {S}}},{{\mathbb {M}}})\), and let \(A_T\) be the associated gentle Jacobian algebra. We refer to Sect. 10.5 for a precise definition of \(A_T\). To a lamination L of \(({{\mathbb {S}}},{{\mathbb {M}}})\) we will associate a certain generic decorated \(A_T\)-module, which is a direct sum of indecomposable \(\tau \)-rigid modules, of certain band modules of quasi-length 1, and of negative simples. In Sect. 11, we will look at the Caldero-Chapoton functions of these modules, which can be thought of as generating functions of Euler characteristics of quiver Grassmannians. In contrast, Allegretti [2] works with certain \({{\mathcal {A}}}\)-laminations (see [2, 24] for a definition), and he associates \(A_T\)-modules, which are direct sums of indecomposable \(\tau \)-rigid modules, of band modules with arbitrary quasi-length, and of negative simples. He then looks at certain generating functions of Euler characteristics of transversal quiver Grassmannians.
10.4 Curves and loops as combinatorial objects
A triangulation cuts the surface into triangles. Each triangle has exactly three sides. (Recall that we work here with unpunctured marked surfaces, i.e. we do not have any marked points in the interior of \({{\mathbb {S}}}\).)
Let T be a fixed triangulation of \(({{\mathbb {S}}},{{\mathbb {M}}})\) with \(T^\circ = \{ \tau _1,\ldots ,\tau _t \}\). Let \(\gamma :[0,1] \rightarrow {{\mathbb {S}}}\) be a curve in \(({{\mathbb {S}}},{{\mathbb {M}}})\), and let
We assume that \(\gamma \) is minimal in the sense that
To \(\gamma \) we associate a sequence
where \(a = \gamma (0)\) and \(b = \gamma (1)\), and there exist \(0< t_1< \cdots< t_m < 1\) such that \(\gamma (t_i) \in \tau _{j_i}\). We illustrate this in Fig. 4. Note that the curves \(\tau _{i_1},\ldots ,\tau _{i_m}\) do not have to be pairwise different. We do have, however, \(\tau _{i_j} \not = \tau _{i_{j+1}}\) for all \(1 \le i \le m-1\). The curve \(\gamma ^{-1}\) yields \((b,\tau _{j_m},\ldots ,\tau _{j_1},a)\).
Analogously, with a loop \(\gamma :S^1\rightarrow {{\mathbb {S}}}\) in \(({{\mathbb {S}}},{{\mathbb {M}}})\) we associate a sequence
where \(a = \gamma (1)\). Starting in \(1 \in S^1\) in clockwise orientation, we assume that \(\gamma \) first passes through \(\tau _{j_1}\), then through \(\tau _{j_2}\) etc. We can assume here that \(a \in \tau _{j_1}\). This is illustrated in Fig. 5.
The periodic curve \({\widetilde{\gamma }}:{\mathbb {R}} \rightarrow {{\mathbb {S}}}\) associated with \(\gamma \) is represented by the infinite sequence
Arguing similarly as in [4, Section 4.2], we can identify each \(\gamma \in A({{\mathbb {S}}},{{\mathbb {M}}})\cup L({{\mathbb {S}}},{{\mathbb {M}}})\) with its associated sequence \((a,\tau _{j_1},\ldots ,\tau _{j_m},b)\) modulo the equivalence
10.5 From triangulations to gentle Jacobian algebras
Let T be a triangulation of an unpunctured marked surface \(({{\mathbb {S}}},{{\mathbb {M}}})\). Assume that \(T^\circ \) consists of n curves \(\tau _1,\ldots ,\tau _n\). Then \(Q = Q_T\) is by definition the quiver with vertices \(1,\ldots ,n\). The arrows of Q are defined as follows: As displayed in Fig. 6, there are three types of triangles defined by T, and two of these yield arrows in Q, as indicated in the picture. Note that the non-labelled sides of the triangles are meant to be boundary segments of \(({{\mathbb {S}}},{{\mathbb {M}}})\), and note that our arrows point in clockwise direction. Other authors might choose the opposite convention. The algebra associated to T is then \(A_T := KQ/I\), where I is generated by the paths \(a_2a_1,\; a_3a_2,\; a_1a_3\) arising from triangles with all three sides in \(T^\circ \).
The algebra \(A_T\) was first studied by [4] and [38], where it was defined as the Jacobian algebra \({{\mathcal {P}}}_{\mathbb {C}}(Q_T,W_T)\) of a quiver with potential.
Theorem 10.2
([4, Section 2]) The Jacobian algebras \(A_T\) arising from triangulations of unpunctured marked surfaces are exactly the gentle Jacobian algebras.
10.6 From curves and loops to string and band modules
Let \(({{\mathbb {S}}},{{\mathbb {M}}})\) be an unpunctured marked surface, and let T be a fixed triangulation of \(({{\mathbb {S}}},{{\mathbb {M}}})\).
Theorem 10.3
([4, Propositions 4.2 and 4.3]) For \(({{\mathbb {S}}},{{\mathbb {M}}})\) and T as above the following hold:
-
(i)
There is a bijection \(\gamma \mapsto M_\gamma \) between \(A({{\mathbb {S}}},{{\mathbb {M}}})\setminus T^\circ \) and the set of isoclasses of string modules in \({\text {mod}}(A_T)\).
-
(ii)
There is a bijection \((\gamma ,\lambda ) \mapsto M_{\gamma ,\lambda }\) between \(L({{\mathbb {S}}},{{\mathbb {M}}})\times K^*\) and the set of isoclasses of band modules in \({\text {mod}}(A_T)\).
The arcs in \(T^\circ \) correspond bijectively to the negative simple decorated \(A_T\)-modules. Thus the isoclasses of indecomposable decorated \(A_T\)-modules are in bijection with \(A({{\mathbb {S}}},{{\mathbb {M}}})\cup L({{\mathbb {S}}},{{\mathbb {M}}})\times K^*\).
For an indecomposable decorated \(A_T\)-module \({{\mathcal {M}}}\) let \(\gamma _{{{\mathcal {M}}}}\) be the corresponding curve or loop in \(A({{\mathbb {S}}},{{\mathbb {M}}})\cup L({{\mathbb {S}}},{{\mathbb {M}}})\). For \({{\mathcal {M}}}= (M,0)\) we set \(\gamma _M := \gamma _{{{\mathcal {M}}}}\).
The string associated with the curve in Fig. 4 looks as follows:

The band associated with the curve in Fig. 5 looks as in the following picture, where the two blue vertices have to be identified:

Note that for an arbitrary gentle algebra A there is also a geometric model for the derived category \(D^b({\text {mod}}(A))\) (see [34, 41, 46]), which differs substantially from the one for \({\text {mod}}(A)\) used in this article.
Theorem 10.4
([10, Corollary 5.4]) Let \(A = A_T\) as above, and let \(M,N \in {\text {mod}}(A)\) be string modules. Then the following are equivalent:
-
(i)
\({\text {Int}}(\gamma _M,\gamma _N) = 0\);
-
(ii)
\({\text {Hom}}_A(N,\tau _A(M)) = 0 = {\text {Hom}}_A(M,\tau _A(N)) = 0\).
Note that the results in [10] are formulated in terms of the cluster category associated with \(({{\mathbb {S}}},{{\mathbb {M}}})\). Theorem 10.4 is a straightforward reformulation in terms of decorated \(A_T\)-modules.
In Sect. 10.9 we reprove and generalize Theorem 10.4 by also including band modules.
10.7 Rotation of curves and the Auslander-Reiten translation
Let T be a triangulation of \(({{\mathbb {S}}},{{\mathbb {M}}})\), and let \(A = A_T\). Let \(M \in {\text {mod}}(A)\) be a string module, and let \(\gamma _M = (a,\tau _{j_1},\ldots ,\tau _{j_t},b)\) be the associated curve in \(A({{\mathbb {S}}},{{\mathbb {M}}})\setminus T^\circ \).
For the following two statements we refer to [10, Theorem 3.6]. (Note that the orientation of our \(Q_T\) is opposite to the one used in [10].)
We orient each boundary component of \({{\mathbb {S}}}\) by requiring that when following the orientation, the surface lies to the left. We call this the induced orientation of the boundary component.
If M is non-projective, then \( \gamma _{\tau _A(M)} = \tau (\gamma ), \) where \(\tau (\gamma )\) is obtained from \(\gamma \) by rotating the points \(a = \gamma (0)\) and \(b = \gamma (1)\) of \(\gamma \) to the next marked point on their respective boundary component, following the induced orientation.
Dually, if M is non-injective, then \( \gamma _{\tau _A^{-1}(M)} = \tau ^{-1}(\gamma ), \) where \(\tau ^{-1}(\gamma )\) is obtained from \(\gamma \) by rotating a and b to the next marked points on their respective boundary component, following the opposite induced orientation.
The proof of these statements uses the combinatorial descriptions of \(\tau _A(M)\) and \(\tau _A^{-1}(M)\) given in [11] and [56].
For more details we refer to [10, Section 3].
10.8 Three types of intersections
Let \(({{\mathbb {S}}},{{\mathbb {M}}})\) be an unpunctured marked surface. We fix a triangulation T of \(({{\mathbb {S}}},{{\mathbb {M}}})\). Now let \(\gamma _1, \gamma _2 \in A({{\mathbb {S}}},{{\mathbb {M}}})\cup L({{\mathbb {S}}},{{\mathbb {M}}})\). Then the intersections of \({\widetilde{\gamma }}_1\) and \({\widetilde{\gamma }}_2\) can be divided into three different types: Type I (resp. II) are displayed on the left (resp. right) in Fig. 7. Up to symmetry there are 6 different kinds of Type III intersections, which are pictured in the left hand column of Fig. 8. (Note that the definition of intersection types depend here on our fixed triangulation T.)
10.9 Proof of Theorem 1.7
Throughout, we fix a triangulation T of \(({{\mathbb {S}}},{{\mathbb {M}}})\). Let \(A = A_T\).
Lemma 10.5
Let \(M = M(B,\lambda ,q) \in {\text {mod}}(A)\) be a band module with \(q \ge 2\). Then \({\text {Int}}(\gamma _M,\gamma _M) \not = 0\).
Proof
Since \(q \ge 2\), we have \(\gamma _M = \gamma ^q\) for some primitive loop \(\gamma \). It follows that \({\text {Int}}(\gamma _M,\gamma _M) \not = 0\). \(\square \)
Lemma 10.6
Let \({{\mathcal {S}}}_i^-\) be a negative simple decorated A-module, and let \({{\mathcal {M}}}\) be an indecomposable decorated A-module. Then the following are equivalent:
-
(i)
\({\text {Int}}(\gamma _{{{\mathcal {S}}}_i^-},\gamma _{{{\mathcal {M}}}}) = 0\);
-
(ii)
\(E_A({{\mathcal {S}}}_i^-,{{\mathcal {M}}}) = E_A({{\mathcal {M}}},{{\mathcal {S}}}_i^-) = 0\).
Proof
Suppose that \({{\mathcal {M}}}= {{\mathcal {S}}}_j^-\) is also negative simple. Then the equivalence of (i) and (ii) follows directly from the definitions. Next, assume that \({{\mathcal {M}}}= (M,0)\). Let \({\mathbf {d}}= (d_1,\ldots ,d_n) = {\underline{\dim }}(M)\). Then \(d_i = 0\) if and only if the simple A-module \(S_i\) is not a composition factor of M if and only if (i) holds. By the definition of \(E_A(-,-)\), condition (ii) holds if and only if \(d_i = 0\). This finishes the proof. \(\square \)
In view of Lemma 10.6, we can now restrict to indecomposable A-modules and curves in \(A({{\mathbb {S}}},{{\mathbb {M}}})\setminus T^\circ \).
Recall that the notions of \(\rho \)-blocks and of the associated restriction maps \(\pi _i\) were defined in Sect. 4.
Lemma 10.7
Let M and N be indecomposable A-modules such that \({\widetilde{\gamma }}_M\) and \({\widetilde{\gamma }}_N\) have a Type I or Type II intersection as shown in Fig. 7. Then
Proof
Assume we are in Type I: Let \(A_i\) be the \(\rho \)-block of A containing the arrow \(2 \rightarrow 1\). Then \(\pi _i(M) = S_1\) and \(\pi _i(N) = S_2\). By Lemma 8.4 we get \({\text {Ext}}_A^1(N,M) \not = 0\), which implies
Next, assume we are in Type II: Let \(A_i\) be the \(\rho \)-block of A containing the arrow \(1 \rightarrow 2\). Thus \(A_i\) also contains the arrows \(2 \rightarrow 3\) and \(3 \rightarrow 1\). We get \(\pi _i(M) = P_2\) and \(\pi _i(N) = S_1\). By Lemma 8.6 this implies
\(\square \)
Lemma 10.8
Let \(A_1,\ldots ,A_t\) be the \(\rho \)-blocks of A. Let M and N be indecomposable A-modules. Then the following are equivalent:
-
(i)
\({\widetilde{\gamma }}_M\) and \({\widetilde{\gamma }}_N\) have an intersection of type I or II.
-
(ii)
For some \(1 \le i \le t\), \(\pi _i(M \oplus N)\) is not \(\tau \)-rigid.
Proof
This is a direct consequence of Propositions 6.7 and 6.8. \(\square \)
Lemma 10.9
Let M and N be indecomposable A-modules. Then the following are equivalent:
-
(i)
\({\widetilde{\gamma }}_M\) and \({\widetilde{\gamma }}_N\) have a Type III intersection, as shown in the left column of Fig. 8 with \({\widetilde{\gamma }}_M\) green and \({\widetilde{\gamma }}_N\) red.
-
(ii)
There exists a 2-sided standard homomorphism in \({\text {Hom}}_A(M,N)\).
Proof
This follows by a case by case inspection, which is carried out in Figs. 8 and 9. \(\square \)
Lemma 10.10
Let M and N be indecomposable A-modules. If there exists a 2-sided standard homomorphism in \({\text {Hom}}_A(M,N)\), then \({\text {Hom}}_A(M,\tau _A(N)) \not = 0\).
Proof
Assume that M and N are string modules. It follows from [51, Proposition 4.9] that the existence of a 2-sided standard homomorphism in \({\text {Hom}}_A(M,N)\) implies \({\text {Ext}}_A^1(N,M) \not = 0\). By Theorem 5.4(i), this yields \({\text {Hom}}_A(M,\tau _A(N)) \not = 0\).
If N is a band module, then \(\tau _A(N) \cong N\), which implies the claim.
Finally, let M be a band module and assume that \({\text {Hom}}_A(M,N) \not = 0\). Since \(\tau _A(M) \cong M\) and \({\text {inj.dim}}(M) \le 1\) (see Lemma 5.5), we get from Theorem 5.4(iii) that
By Theorem 5.4(i), this implies \({\text {Hom}}_A(M,\tau _A(N)) \not = 0\). \(\square \)
For indecomposable A-modules M and N, let \({\text {rad}}_A(M,N)\) be the non-invertible homomorphisms in \({\text {Hom}}_A(M,N)\). These form a subspace of \({\text {Hom}}_A(M,N)\).
Lemma 10.11
Let M and N be indecomposable A-modules. Then the following hold:
-
(i)
Let N be a string module. If \({\text {Hom}}_A(M,\tau _A(N)) \not = 0\), then \({\text {Int}}({\widetilde{\gamma }}_M,{\widetilde{\gamma }}_N) \not = 0\).
-
(ii)
Let N be a band module of quasi-length 1. If \({\text {rad}}_A(M,\tau _A(N)) \not = 0\), then \({\text {Int}}({\widetilde{\gamma }}_M,{\widetilde{\gamma }}_N) \not = 0\).
Proof
(i) Let \(N = M(C)\) be a string module, and let \(f:M \rightarrow \tau _A(N)\) be a standard homomorphism. Thus, up to symmetry, f is given by one of the ten pictures in Fig. 8 and 9. The green curves in these pictures stand now for \({\widetilde{\gamma }}_M\) and the red curves for \({\widetilde{\gamma }}_{\tau _A(N)}\). Now \(\tau ^{-1}({\widetilde{\gamma }}_{\tau _A(N)}) = {\widetilde{\gamma }}_N\) is obtained by a rotation in the direction opposite to the induced orientation. By a straightforward case by case analysis we obtain \({\text {Int}}({\widetilde{\gamma }}_M,{\widetilde{\gamma }}_N) \not = 0\) in all ten cases.
(ii) Let N be a band module of quasi-length 1. Then \(\tau _A(N) \cong N\). Let \(f_h \in {\text {rad}}_A(M,N)\) be a standard homomorphism. Since N is a band module, we know that h is of the form
with \(l(D_2),l(F_2) \ge 1\). Thus f is described by one of the six cases in Figs. 8, where the green curves in these pictures stand for \({\widetilde{\gamma }}_M\) and the red curves for \({\widetilde{\gamma }}_N\). (Actually we are then in 1st, 3rd or 5th case, where we count from top to bottom.) This implies \({\text {Int}}({\widetilde{\gamma }}_M,{\widetilde{\gamma }}_N) \not = 0\). \(\square \)
Theorem 10.12
Let M and N be indecomposable A-modules. If M and N are both band modules, then we assume that \(M \not \cong N\). Then the following are equivalent:
-
(i)
\({\text {Int}}(\gamma _M,\gamma _N) = 0\);
-
(ii)
\({\text {Hom}}_A(M,\tau _A(N)) = 0\) and \({\text {Hom}}_A(N,\tau _A(M)) = 0\).
Proof
(ii) \(\implies \) (i): This follows by combining Lemmas 10.7, 10.9 and 10.10.
(i) \(\implies \) (ii): Assume that (ii) does not hold. Without loss of generality let \({\text {Hom}}_A(M,\tau _A(N)) \not = 0\). If N is a string module, then the result follows from Lemma 10.11(i). Next, suppose \(N = M(B,\lambda ,q)\) is a band module. The periodic curve \({\widetilde{\gamma }}_N\) and also the condition \({\text {Hom}}_A(M,\tau _A(N)) \not = 0\) are independent of t. So we can assume that \(q=1\). By assumption we have \(M \not \cong N\). Thus \({\text {rad}}_A(M,\tau _A(N)) \not = 0\). Now the result follows from Lemma 10.11(ii). \(\square \)
The following theorem corresponds to Theorem 1.7.
Theorem 10.13
There is a bijection
which is natural in the sense that
for each lamination \(L = (\gamma ,m)\) with \(\gamma = \{ \gamma _1,\ldots ,\gamma _t \}\) and \(m(\gamma _i) = m_i\).
Proof
(a): Let \(M = M(C) \in {\text {mod}}(A)\) be a string module, and let
where \({\mathbf {d}}:= {\underline{\dim }}(M)\). By Theorem 10.12 we have \({\text {Int}}(\gamma _M,\gamma _M) = 0\) if and only if \({\text {Hom}}_A(M,\tau _A(M)) = 0\) if and only if \(Z_C\) is a generically \(\tau \)-reduced decorated indecomposable irreducible component containing a dense orbit.
(b): Next, let \(M = M(B,\lambda ,q) \in {\text {mod}}(A)\) be a band module, and let
where \({\mathbf {d}}:= {\underline{\dim }}(M)\). If \(q \ge 2\), then \({\text {Int}}(\gamma _M,\gamma _M) \not = 0\). Furthermore,
where \(Z_{B,1} \oplus \cdots \oplus Z_{B,1}\) consists of all decorated modules in \({\text {decmod}}(A,({\mathbf {d}},0))\) which are isomorphic to \((M(B,\lambda _1,1),0) \oplus \cdots \oplus (M(B,\lambda _q,1),0)\) for some \((\lambda _1,\ldots ,\lambda _q) \in (K^*)^q\).
Thus, we assume that \(t=1\) and set \(Z_B := Z_{B,1}\). Let \(N = M(B,\mu ,1)\) for some \(\mu \in K^*\) with \(\mu \not = \lambda \). Note that \(\gamma _M = \gamma _N\). By Theorem 10.12 we have \({\text {Int}}(\gamma _M,\gamma _N) = 0\) if and only if \({\text {Hom}}_A(M,N) = 0\) if and only if \(Z_B\) is a generically \(\tau \)-reduced decorated indecomposable irreducible component not containing a dense orbit. Note here that \(\tau _A(M) \cong M\) and \(\tau _A(N) \cong N\) and that the condition \({\text {Hom}}_A(M,N) = 0\) is equivalent to the condition \({\text {End}}_A(M) \cong K\).
(c): The considerations in (a) and (b) show that there is a bijection between the set of indecomposable components in \({\text {Irr}}^\tau (A)\) and the set of laminations of the form \(L = (\{ \gamma _1 \},m)\) with \(m(\gamma _1) = 1\) and \(\gamma _1 \notin T^\circ \).
(d): Now the Theorem follows from Lemma 10.6 (which takes care of the negative simple decorated modules) and Theorem 10.12 combined with the Decomposition Theorem 9.2. \(\square \)
10.10 Shear coordinates and g-vectors
Let \(A = A_T\) as above. As mentioned before, a result by W. Thurston (see [26, Theorem 12.3]) says that there is a bijection \({{\mathbf {s}}}_T:{\text {Lam}}({{\mathbb {S}}},{{\mathbb {M}}})\rightarrow {\mathbb {Z}}^n\) sending a lamination to its shear coordinate. We briefly and informally recall the construction of \({{\mathbf {s}}}_T\).
First, consider an arc
Then
where \(a',b' \in \partial {{\mathbb {S}}}\setminus {{\mathbb {M}}}\), and \((\tau _{j_{11}},\ldots ,\tau _{j_{1t_a}})\) and \((\tau _{j_{m1}},\ldots ,\tau _{j_{mt_b}})\) are possibly empty sequences of curves in \(T^\circ \) which are incident with a and b, respectively. Let \(\tau _{a'}\) and \(\tau _{b'}\) the boundary segments, which contain \(a'\) and \(b'\), respectively.
For each \(1 \le k \le m\), we look at the triple \((\tau ',\tau _{j_k},\tau '')\), where \(\tau '\) and \(\tau ''\) are the left and right neighbour, respectively, of \(\tau _{j_k}\) in the sequence
Then we are in one of the four cases displayed in Fig. 10, where the red line is a segment of the curve \(\tau ^{1/2}(\gamma )\) and the dotted arrows indicate possible arrows of A. (There is an arrow on the left if and only if \(\tau ' \not = \tau _{a'}\), and there is an arrow on the right if and only if \(\tau '' \not = \tau _{b'}\).)
Next, consider a simple loop
For each \(1 \le k \le m\), we look at the triple
In both cases (i.e. \(\gamma \in A({{\mathbb {S}}},{{\mathbb {M}}})\) and \(\gamma \in L({{\mathbb {S}}},{{\mathbb {M}}})\)), the shear coordinate of \(\gamma \) (with respect to T) is defined as \({{\mathbf {s}}}_T(\gamma ) := (s_1,\ldots ,s_n)\), where
for \(1 \le i \le n\). Here \(\delta _{j_k,i}\) denotes the Kronecker delta and
Finally, let \(L = (\gamma ,m)\) be a lamination. Then
Recall that by Plamondon [47, Theorem 1.2], there is a bijection \({\mathbf {g}}_T:{\text {decIrr}}(A)^\tau \rightarrow {\mathbb {Z}}^n\) sending a generically \(\tau \)-reduced decorated component to its g-vector.
The proof of the following result is a bit tedious but straightforward. It follows essentially the ideas from Labardini-Fragoso [39, Theorem 10.0.5]. Note that [39] deals with a dual situation and only considers curves. The case of loops is however easier than the curve case and uses the same arguments. Note also that [39] uses a different (but equivalent) definition of g-vectors.
Proposition 10.14
With \(A = A_T\) as above, the diagram

commutes.
11 Bangle functions and generic Caldero-Chapoton functions
We will assume throughout that our surface with marked points \(({{\mathbb {S}}},{{\mathbb {M}}})\) is connected and has no punctures. We fix a triangulation T with internal edges \(T^\circ =(\tau _1, \tau _2,\ldots ,\tau _n)\).
11.1 Strings and bands
Recall from Sect. 10.4 that we identify each curve \(\gamma \in A({{\mathbb {S}}},{{\mathbb {M}}})\setminus T^\circ \) with a certain sequence \((a,\tau _{j_1},\ldots ,\tau _{j_m},b)\), where \(a,b\in {{\mathbb {M}}}\) and the \(\tau _{j_i}\) are the sequence of arcs of \(T^\circ \) which are crossed by \(\gamma \) in a minimal way, up to homotopy. Denote by \(\Delta _i\) the triangle of T, which contains the arcs \(\tau _{j_i}\) and \(\tau _{j_{i+1}}\), and which contains the segment \([\gamma (t_i),\gamma (t_{i+1})]\) of \(\gamma \) for \(1 \le i \le m-1\). This sequence can be coded into a (decorated) quiver \(Q^T_\gamma \) of type \({\mathsf {A}}_m\) with vertices \(\{1,2, \ldots , m\}\). Now, in \(\Delta _i\) there exists an unique arrow \(a_i\) of the quiver \(Q_T\) (see Sect. 10.5), which goes either from \(\tau _{j_i}\) to \(\tau _{j_{i+1}}\), or from \(\tau _{j_{i+1}}\) to \(\tau _{j_i}\). In the first case we draw an arrow with label \(a_i\) from i to \(i+1\). In the second case, we draw an arrow with the same label from \(i+1\) to i. We call \(Q^T_\gamma \) the string of \(\gamma \) with respect to the triangulation T.
Analogously, we associate with a loop \(\gamma =(a,\tau _{j_1},\ldots ,\tau _{j_m},\tau _{j_1},a)\in L({{\mathbb {S}}},{{\mathbb {M}}})\) a quiver of type \(\widetilde{{\mathsf {A}}}_{m-1}\) with vertices \(\{1,2,\ldots , m\}\). The only difference is that now we have an additional triangle \(\Delta _m\), which contains the edges \(\tau _{j_m}\), \(\tau _{j_1}\), and the segment \([\gamma (t_m),\gamma (t_1)]\) of \(\gamma \). In this case \(\Delta _m\) determines the direction of the arrow between \(a_m\) between 1 and m. We call in this case \(Q^T_\gamma \) the band of \(\gamma \) with respect to T.
11.2 MSW-functions
In this section we will use the conventions and definitions from [45, Section 3] without further reference.
Musiker, Schiffler and Williams [45] assign to each homotopy class \(\gamma \in A({{\mathbb {S}}},{{\mathbb {M}}})\) (resp. \(\gamma \in L({{\mathbb {S}}},{{\mathbb {M}}})\)) a snake graph (resp. band graph) \(G=G_{T,\gamma }\). We assume that in each tile \(G_1, G_2,\ldots G_l\) of G, the diagonal goes from SE to NW, and we always think that G is drawn from SW to NE.
Remark 11.1
The graph G comes with a distinguished good resp. perfect matching \(P_-\) which consists of the external edges of G which are either vertical and belong to a negatively oriented tile, or are horizontal and belong to a positively oriented tile. On the other hand, the tile \(G_j\) and the position of its two neighbours record how \(\gamma \) crosses the quadrilateral surrounding \(\tau _{j_i}\) in the neighbourhood of \(\gamma (t_i)\). With these two observations it is an easy exercise to show that
where \({{\mathbf {s}}}_T(\gamma )\) is the shear coordinate vector (see Sect. 10.10) of \(\gamma \) with respect to T.
Remark 11.2
Following Derksen-Weyman-Zelevinsky [22, p. 60] each skew-symmetric matrix \(B\in {\mathbb {Z}}^{n\times n}\) corresponds to a 2-acyclic quiver Q(B) with vertices \(\{1,2,\ldots , n\}\) and \(b_{ij}\) arrows from j to i whenever \(b_{ij}>0\).
In [45, Definition 2.19] the (skew-symmetric) signed adjacency matrix \(B_T \in {\mathbb {Z}}^{n\times n}\) of a triangulation T of \(({{\mathbb {S}}},{{\mathbb {M}}})\) is introduced. With these conventions in place we have \(Q_T=Q(-B_T)\) for our quiver \(Q_T\) from Sect. 10.5. The (coefficient-free) cluster algebra \({{\mathcal {A}}}(B_T)\) associated with \(B_T\) is just \({{\mathcal {A}}}_{({{\mathbb {S}}},{{\mathbb {M}}})}\). Let \({{\mathcal {A}}}_\bullet (B_T)\) be the corresponding cluster algebra with principal coefficients.
Remark 11.3
In [45, Definitions 5.3 and 5.6] the authors associate to their graph \(G=G_{T,\gamma }\) a poset structure \(Q_G\) on the set \(\{1,2,\ldots , m\}\) by describing its Hasse quiver. We leave it as an exercise that our quiver \(Q_\gamma ^T\) from Sect. 11.1 is opposite to the Hasse quiver in [45]. Thus, the poset ideals of \(Q_G\) are precisely the subsets I of vertices of \(Q_\gamma ^T\) which are closed under predecessors. We call such subsets order coideals of \(Q_\gamma ^T\).
In [45, Definition 3.4] a Laurent polynomial
is defined, where the sum runs over the perfect resp. good matchings of G. We agree that \(X^T_{\gamma _i}=x_i\) for \(\gamma _i\in T^\circ \) and for \(L=(\xi , m)\in {\text {Lam}}({{\mathbb {S}}},{{\mathbb {M}}})\) one sets
The following result is implicit in [45, Sections 5 and 6]:
Lemma 11.4
For each \(\gamma \in A({{\mathbb {S}}},{{\mathbb {M}}})\cup L({{\mathbb {S}}},{{\mathbb {M}}})\) holds
where the summation runs over the order coideals I of \(Q_\gamma ^T\) and
for \(j=1,2,\ldots ,n\).
Proof
According to [45, Theorem 5.7] the lattice L(G) of good matchings of G is in natural bijection with the distributive lattice of order coideals of \(Q_\gamma ^T\). More precisely, to a good matching corresponds the coideal I(P), which consists of the labels of the tiles of G which are enclosed by \(P\ominus P_-\).
On the other hand, by [45, Proposition 6.2] \(x_\gamma \in R\) is homogeneous of degree
if we agree that \(\deg {x_j}={\mathbf {e}}_j\in {\mathbb {Z}}^n\) and \(\deg {y_j} = -\sum _{i=1}^n b_{ij}{\mathbf {e}}_i \in {\mathbb {Z}}^n\).
Thus in view of (11.1) we have to show that
In order to show (11.3) we proceed by induction on the Hasse diagram of the distributive lattice L(G) as in the proof of [45, Theorem 5.1] at the end of [45, Section 5]. \(\square \)
11.3 Dual CC-functions and MSW-functions
We introduce the anti principal ice quiver \({\widetilde{Q}}_T\), which is obtained from \(Q_T\) by adding an additional set of frozen vertices \(\{1',2',\ldots ,n'\}\), and an additional arrow \(p_i:i'\rightarrow i\) for \(i=1,2,\ldots , n\). The potential \(W_T\) mentioned in Sect. 10.5 can be naturally viewed as a potential for \({\widetilde{Q}}_T\) and it is not hard to see that \(({\widetilde{Q}}_T,W_T)\) is a non-degenerate QP with finite-dimensional Jacobian algebra \({\widetilde{A}}_T = {{\mathcal {P}}}_{\mathbb {C}}({\widetilde{Q}}_T,W_T)\).
Definition 11.5
The dual Caldero-Chapoton function with respect to \({\widetilde{A}}_T\) of a decorated representation \({{\mathcal {M}}}=(M,V)\) of \(A_T\) is the Laurent polynomial
where \({\text {Gr}}_{A_T}^{\mathbf {e}}(M)\) is the quiver Grassmannian of factor modules with dimension vector \({\mathbf {e}}\) of the \(A_T\)-module M, and \(\chi \) is the topological Euler characteristic.
Note that for a decorated representation \({{\mathcal {M}}}\) of \(A_T\) we have in fact \({\mathbf {g}}_{{\widetilde{A}}_T}({{\mathcal {M}}}) = ({\mathbf {g}}_{A_T},0,\ldots , 0)\). This is so, since for each \(A_T\)-module M with minimal projective presentation
the same sequence can be taken as a minimal projective presentation of M viewed as an \({\widetilde{A}}_T\)-module, due to the shape of \({\widetilde{Q}}_A\).
Remark 11.6
Obviously, the dual Caldero-Chapoton-function is the same as the usual Caldero-Chapoton-function for the corresponding dual module, more precisely
where \(D{{\mathcal {M}}}=(DM,DV)\) is the \({\mathbb {C}}\)-dual decorated \(A_T^{{\text {op}}}\)-module,
is the classical g-vector, calculated in terms of the minimal injective copresentation \(0\rightarrow DM\rightarrow DP_0\rightarrow DP_1\), and \({\text {Gr}}^{A_T^{{\text {op}}}}_{\mathbf {e}}(DM)\) is the quiver Grassmannian of \({\mathbf {e}}\)-dimensional \(A_T^{{\text {op}}}\)-submodules of DM.
Thus we have in particular
for decorated representations \({{\mathcal {M}}}_1\) and \({{\mathcal {M}}}_2\).
Moreover the \({\text {CC}}({{\mathcal {M}}})\) for decorated reachable E-rigid \(A_T\)-modules \({{\mathcal {M}}}\) are precisely the cluster monomials for the cluster algebra \({{\mathcal {A}}}_\bullet (B_T) \subset R\) with principal coefficients, see for example [23].
Remark 11.7
For a curve \(\gamma \in A({{\mathbb {S}}},{{\mathbb {M}}})\setminus T^\circ \) let \({{\mathcal {M}}}_\gamma := (M_\gamma ,0)\) be the corresponding decorated \(A_T\)-module. For a primitive \(\gamma \in L({{\mathbb {S}}},{{\mathbb {M}}})\) let \({{\mathcal {M}}}_\gamma := (M_{\gamma ,\lambda },0)\) for some \(\lambda \in {\mathbb {C}}^*\). Note that \(M_{\gamma ,\lambda }\) is a band module of quasi-length 1. In these two cases, the quiver \(Q_\gamma ^T\) is the coefficient quiver of the string module \(M_\gamma \) (resp. of the band module \(M_{\gamma ,\lambda }\)). Moreover, the order coideals of \(Q_\gamma ^T\) can be identified with the coordinate factor modules of \({{\mathcal {M}}}_\gamma \), see also [45, Remark 5.8]. Finally, for \(\gamma \in T^\circ \) let \({{\mathcal {M}}}_\gamma \) be the associated negative simple decorated \(A_T\)-module.
Proposition 11.8
For a curve or primitive loop \(\gamma \in A({{\mathbb {S}}},{{\mathbb {M}}})\cup L({{\mathbb {S}}},{{\mathbb {M}}})\) we have
Proof
We use Lemma 11.4 to compare both expressions. As a consequence of Proposition 10.14, we get \({{\mathbf {s}}}_T(\gamma ) = {\mathbf {g}}_{A_T}({{\mathcal {M}}}_\gamma ) = {\mathbf {g}}_{{\widetilde{A}}_T}({{\mathcal {M}}}_\gamma )\). In view of Remark 11.7 our claim follows now from [36, Theorem 1.2]. \(\square \)
11.4 Bangle functions are generic
Recall that our set of laminations \({\text {Lam}}({{\mathbb {S}}},{{\mathbb {M}}})\) from Sect. 10.3 is the same as the set of \({{\mathcal {C}}}^\circ ({{\mathbb {S}}},{{\mathbb {M}}})\) of \({{\mathcal {C}}}^\circ \)-compatible collection of arcs and simple (= essential) loops in [45, Def. 3.17].
Recall also that each irreducible component \(Z\in {\text {decIrr}}^\tau (A_T)\) we can consider the map
as a constructible function, which indeed has a finite image. Thus there exists an open dense subset \(U \subseteq Z\) where \({\text {CC}}'_Z\) takes a constant value, say \({\text {CC}}'_{{\widetilde{A}}_T}(Z)\). We define
and
With this definition we can state now the main result of this section:
Theorem 11.9
For each lamination \(L\in {\text {Lam}}({{\mathbb {S}}},{{\mathbb {M}}})\) we have
where \(\eta _T:{\text {Lam}}({{\mathbb {S}}},{{\mathbb {M}}})\rightarrow {\text {decIrr}}^\tau (A_T)\) is the bijection from Theorem 10.13. In particular, we have
Proof
If an irreducible component \(Z\in {\text {decIrr}}(A_T)\) decomposes as \(Z=\overline{Z_1\oplus Z_2}\) then it follows from (11.4) and the above definition that
Let \(L=(\xi , m)\in {\text {Lam}}({{\mathbb {S}}},{{\mathbb {M}}})\) be a lamination,
In Theorem 10.13 we assign to \((\xi , m)\) a generically \(\tau \)-reduced decorated irreducible component
Since on the other hand, we have by definition
it is sufficient to prove
for \(\gamma \) an arc or a simple loop. This is trivial if \(\gamma \in T^\circ \), thus we have to distinguish only two cases:
Case 1: \(\gamma \) is an arc which does not belong to T. In this case, the string module \(M_\gamma \) is \(\tau \)-rigid and therefore
compare Theorem 10.13. So our claim follows directly from Proposition 11.8.
Case 2: \(\gamma \) is a simple loop. In this case \(\eta _T(\gamma )\) is the closure of the union of a the orbits of a family of modules, namely
In this case we have again by Proposition 11.8\(X^T_\gamma = {\text {CC}}'_{{\widetilde{A}}_T}((M_{\gamma ,\lambda },0))\) for all \(\lambda \in {\mathbb {C}}^*\), and we are done. \(\square \)
By specializing the coefficients to 1, the equality \({\widetilde{{{\mathcal {B}}}}}_T = {\widetilde{{{\mathcal {G}}}}}_T\) from Theorem 11.9 yields
Thus Theorem 1.8 is proved.
12 An example
Let \(({{\mathbb {S}}},{{\mathbb {M}}})\) be the sphere with three disks cut out, and one marked point on each boundary component. In Fig. 11 we display a triangulation T of \(({{\mathbb {S}}},{{\mathbb {M}}})\), where the arcs of T are marked in green, together with a loop \(\sigma \) in \(({{\mathbb {S}}},{{\mathbb {M}}})\).
It is easy to read off the quiver \(Q_T\) (following our convention) and the signed adjacency matrix \(B_T\) (following the convention of [45]). Both are shown in Fig. 12. Recall that with these convention in place we have \(Q_T=Q(-B_T)\).
Musiker, Williams and Schiffler [45] associate to each loop \(\sigma \) a band graph \(G=G_{T,\sigma }\) with respect to a triangulation T. In our example, we obtain the band graph G displayed in Fig. 13. Note that G has \(m=7\) tiles, corresponding to the 7 intersections of \(\sigma \) with the edges of T. The thick edges of G correspond to the distinguished good matching \(P_-\). Note that the two extremal edges have to be identified along the corresponding arrows.
Recall from Sect. 11.3 that Musiker, Schiffler and Williams associate to G a Hasse quiver \(Q_G\), which is opposite to our coefficient quiver \(Q_\sigma ^T\) of the band module \(M_{\sigma ,\lambda }\) for \(\lambda \in {\mathbb {C}}^*\), see Remarks 11.1 and 11.7. We display the coefficient quiver \(Q_\sigma ^T\) in Fig. 14. Note that the two encircled vertices have to be identified.
Thus the order coideals of \(Q_\sigma ^T\) (i.e. coordinate factor modules of \(M_{\sigma ,\lambda }\)) are in bijection with the good matchings of G. More precisely, the tiles which are enclosed by the symmetric difference \(P\ominus P_-\) for a good matching P are identified with a basis of the corresponding coordinate factor module. Finally we display in Fig. 15, three of the 27 good matchings of G. In each case the edges of the matching P are highlighted in orange, whilst the tiles which are enclosed by \(P\ominus P_-\) are highlighted in yellow. Moreover, we show in each case the contribution of P to \(X_\sigma ^T\).
The relation between perfect matchings and coordinate submodules of string modules has been also studied in a more general setup by Canakci and Schroll [12].
References
Adachi, T., Iyama, O., Reiten, I.: \(\tau \)-tilting theory. Compos. Math. 150(3), 415–452 (2014)
D. Allegretti, ategorified canonical bases and framed BPS states. Sel. Math. New Ser. 25, 69 (2019). https://doi.org/10.1007/s00029-019-0518-3
C. Amiot, T. Brüstle, Derived equivalences between skew-gentle algebras using orbifolds. Preprint (2019), 46 pp., arXiv:1912.04367
Assem, I., Brüstle, T., Charbonneau-Jodoin, G., Plamondon, P.-G.: Gentle algebras arising from surface triangulations. Algebra Number Theory 4(2), 201–229 (2010)
Assem, I., Skowroński, A.: Iterated tilted algebras of type \({\widetilde{A}}_n\). Math. Z. 195(2), 269–290 (1987)
I. Assem, D. Simson, A. Skowroński, Elements of the representation theory of associative algebras, Vol. 1. Techniques of representation theory. London Mathematical Society Student Texts, 65. Cambridge University Press, Cambridge, 2006. x+458 pp
M. Auslander, I. Reiten, S. Smalø, Representation theory of Artin algebras. Corrected reprint of the 1995 original. Cambridge Studies in Advanced Mathematics, 36. Cambridge University Press, Cambridge, 1997. xiv+425 pp
K. Baur, S. Schroll, Higher extensions for gentle algebras.Bulletin des Sciences Mathématiques, Vol. 170 (2021), [103010], https://doi.org/10.1016/j.bulsci.2021.103010
Brüstle, T.: Kit algebras. J. Algebra 240(1), 1–24 (2001)
Brüstle, T., Zhang, J.: On the cluster category of a marked surface without punctures. Algebra Number Theory 5(4), 529–566 (2011)
Butler, M.C.R., Ringel, C.M.: Auslander-Reiten sequences with few middle terms and applications to string algebras. Comm. Algebra 15(1–2), 145–179 (1987)
I. Canakci, S. Schroll, Lattice bijections for string modules, snake graphs and the weak Bruhat order. Advances in Applied Mathematics, 126, 1-22. [102094]. https://doi.org/10.1016/j.aam.2020.102094
Carroll, A.: Generic modules for string algebras. J. Algebra 437, 177–201 (2015)
Carroll, A., Chindris, C.: On the invariant theory for acyclic gentle algebras. Trans. Amer. Math. Soc. 367(5), 3481–3508 (2015)
Carroll, A., Chindris, C., Kinser, R., Weyman, J.: Moduli Spaces of Representations of Special Biserial Algebras. Int. Math. Res. Not. IMRN 2, 403–421 (2020)
A. Carroll, J. Weyman, Semi-invariants for gentle algebras. Noncommutative birational geometry, representations and combinatorics, 111–136, Contemp. Math., 592, Amer. Math. Soc., Providence, RI, 2013
Cerulli Irelli, G., Labardini-Fragoso, D., Schröer, J.: Caldero-Chapoton algebras. Trans. Amer. Math. Soc. 367(4), 2787–2822 (2015)
Crawley-Boevey, W.: Maps between representations of zero-relation algebras. J. Algebra 126(2), 259–263 (1989)
W. Crawley-Boevey, On tame algebras and bocses. In: Proc. London Math. Soc. (3) 56 (1988), 451–483
Crawley-Boevey, W., Schröer, J.: Irreducible components of varieties of modules. J. Reine Angew. Math. 553, 201–220 (2002)
De Concini, C., Strickland, E.: On the variety of complexes. Adv. Math. 41(1), 57–77 (1981)
Derksen, H., Weyman, J., Zelevinsky, A.: Quivers with potentials and their representations. I. Mutations. Selecta Math. (N.S.) 14(1), 59–119 (2008)
Derksen, H., Weyman, J., Zelevinsky, A.: Quivers with potentials and their representations II: applications to cluster algebras. J. Amer. Math. Soc. 23(3), 749–790 (2010)
V. Fock, A. Goncharov, Dual Teichmüller and lamination spaces. Handbook of Teichmüller theory. Vol. I, 647–684, IRMA Lect. Math. Theor. Phys., 11, Eur. Math. Soc., Zürich, 2007
Fomin, S., Shapiro, M., Thurston, D.: Cluster algebras and triangulated surfaces. I. Cluster complexes. Acta Math. 201(1), 83–146 (2008)
Fomin, S., Thurston, D.: Cluster algebras and triangulated surfaces Part II Lambda lengths. Mem. Amer. Math. Soc. 255(1223), v+97 (2018)
Fomin, S., Zelevinsky, A.: Cluster algebras. I. Foundations. J. Amer. Math. Soc. 15(2), 497–529 (2002)
P. Gabriel, Finite representation type is open. Proceedings of the International Conference on Rep- resentations of Algebras (Carleton Univ., Ottawa, Ont., 1974), Paper No. 10, 23pp. Carleton Math. Lecture Notes, No. 9, Carleton Univ., Ottawa, Ont., 1974
C. Geiß, D. Labardini-Fragoso, J. Schröer, Generic Caldero-Chapoton functions with coefficients and applications to surface cluster algebras, Preprint (2020), 45 pp., arXiv:2007.05483
Geiß, C., Leclerc, B., Schröer, J.: Generic bases for cluster algebras and the chamber Ansatz. J. Amer. Math. Soc. 25(1), 21–76 (2012)
C. Geiß, Geometric methods in representation theory of finite-dimensional algebras. Representation theory of algebras and related topics (Mexico City, 1994), 53–63, CMS Conf. Proc., 19, Amer. Math. Soc., Providence, RI, 1996
Geiß, C., de la Peña, J.A.: On the deformation theory of finite-dimensional algebras. Manuscripta Math. 88(2), 191–208 (1995)
Gonciulea, N.: Singular Loci of Varieties of Complexes. II. J. Algebra 235(2), 547–558 (2001)
Haiden, F., Katzarkov, L., Kontsevich, M.: Flat surfaces and stability structures. Publ. Math. Inst. Hautes Études Sci. 126, 247–318 (2017)
Hartshorne, R.: Algebraic geometry. Graduate Texts in Mathematics, vol. 52, p. xvi+496. Springer, New York (1977)
Haupt, N.: Euler characteristics of quiver Grassmannians and Ringel-Hall algebras of string algebras. Algebr. Represent. Theory 15(4), 755–793 (2012)
Krause, H.: Maps between tree and band modules. J. Algebra 137(1), 186–194 (1991)
Labardini-Fragoso, D.: Quivers with potentials associated to triangulated surfaces. Proc. London Math. Soc 98, 797–839 (2009)
Labardini-Fragoso, D.: Quivers with potentials associated with triangulations of Riemann surfaces. Northeastern University (2010). Ph.D. thesis
V. Lakshmibai, Singular loci of varieties of complexes. Commutative algebra, homological algebra and representation theory (Catania/Genoa/Rome, 1998). J. Pure Appl. Algebra 152 (2000), no. 1-3, 217–230
Y. Lekili, A. Polishchuk, Derived equivalences of gentle algebras via Fukaya categories. Math. Ann. 376, 187–225 (2020). https://doi.org/10.1007/s00208-019-01894-5
Muller, G.: Locally acyclic cluster algebras. Adv. Math. 233, 207–247 (2013)
G. Muller, \({\cal{A}}={\cal{U}}\)for locally acyclic cluster algebras. SIGMA Symmetry Integrability Geom. Methods Appl. 10 (2014), Paper 094, 8 pp
Musiker, G., Schiffler, R., Williams, L.: Positivity for cluster algebras from surfaces. Adv. Math. 227, 2241–2308 (2011)
Musiker, G., Schiffler, R., Williams, L.: Bases for cluster algebras from surfaces. Compos. Math. 149(2), 217–263 (2013)
S. Opper, P.-G. Plamondon, S. Schroll, A geometric model for the derived category of gentle algebras. Preprint (2018), 41 pp., arXiv:1801.09659v5
Plamondon, P.-G.: Generic bases for cluster algebras from the cluster category. Int. Math. Res. Not. IMRN 10, 2368–2420 (2013)
P.-G. Plamondon, \(\tau \)-tilting finite gentle algebras are representation-finite. Pacific J. Math. Vol. 302 (2019), No. 2, 709–716. https://doi.org/10.2140/pjm.2019.302.709
F. Qin, Bases for upper cluster algebras and tropical points. Journal of the European Mathematical Society, to appear
Ringel, C.M.: Tame algebras and integral quadratic forms. Lecture Notes in Mathematics, vol. 1099. Springer, Berlin (1984)
Schröer, J.: Modules without self-extensions over gentle algebras. J. Algebra 216(1), 178–189 (1999)
Shafarevich, I.: Basic algebraic geometry. 1. Varieties in projective space. Third edition. Translated from the 2007 third Russian edition. Springer, Heidelberg. xviii+310 pp. (2013)
Shafarevich, I.: Basic algebraic geometry. 2. Schemes and complex manifolds. Third edition. Translated from the 2007 third Russian edition by Miles Reid. Springer, Heidelberg. xiv+262 pp. (2013)
Strickland, E.: On the conormal bundle of the determinantal variety. J. Algebra 75(2), 523–537 (1982)
Voigt, D.: Induzierte Darstellungen in der Theorie der endlichen, algebraischen Gruppen. Lecture Notes in Mathematics, vol. 592. Springer, New York (1977)
Wald, B., Waschbüsch, J.: Tame biserial algebras. J. Algebra 95(2), 480–500 (1985)
Zwara, G.: Degenerations for modules over representation-finite algebras. Proc. Amer. Math. Soc. 127, 1313–1322 (1999)
Acknowledgements
The first named author acknowledges partial support from CONACyT grant no. 239255. The second author gratefully acknowledges the support he received from a Cátedra Marcos Moshinsky and the grants CONACyT-238754 and PAPIIT-IN112519. The third author thanks the Sonderforschungsbereich/Transregio SFB 45 for support. He was also funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy - GZ 2047/1, Projekt-ID 390685813. He thanks the Instituto de Matemátics of the UNAM (Mexico City) for two weeks of hospitality in September 2019, where part of this work was done. The first and second author thank the Mathematical Institute of the University of Bonn for two weeks of hospitality in January 2020. We thank Ryan Kinser for helpful comments on an earlier version of this article. We are indepted to the anonymous referee for suggesting improvements of the proofs of Proposition 6.3 and Lemma 6.6.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Geiß, C., Labardini-Fragoso, D. & Schröer, J. Schemes of modules over gentle algebras and laminations of surfaces. Sel. Math. New Ser. 28, 8 (2022). https://doi.org/10.1007/s00029-021-00710-w
Accepted:
Published:
DOI: https://doi.org/10.1007/s00029-021-00710-w




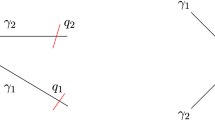


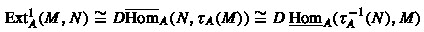 .
.








 of
of 



