Abstract
Relying on recent advances in the theory of motives we develop a general formalism for derived categories of motives with \({\mathbf{Q}}\)-coefficients on perfect \(\infty \)-prestacks. We construct Grothendieck’s six functors for motives over perfect (ind-)schemes perfectly of finite presentation. Following ideas of Soergel–Wendt, this is used to study basic properties of stratified Tate motives on Witt vector partial affine flag varieties. As an application we give a motivic refinement of Zhu’s geometric Satake equivalence for Witt vector affine Grassmannians in this set-up.
Similar content being viewed by others
1 Introduction
1.1 Motivation
The Satake isomorphism [23] plays a foundational rôle in several branches of the Langlands program. Let p be a prime number, and fix \(p^{1/2}\in \overline{{\mathbf{Q}}}\). For a split reductive group G and a non-archimedean local field like \({\mathbf{Q}}_p\) or  , this isomorphism relates spherical functions pertaining to G to the representation theory of the Langlands dual group \(\widehat{G}\):
, this isomorphism relates spherical functions pertaining to G to the representation theory of the Langlands dual group \(\widehat{G}\):

The so-called spherical Hecke algebras at the right and left consist of finitely supported \(\mathbf{Z}[p^{\pm 1/2}]\)-valued functions on the \(G(\mathbf{Z}_p)\)- (resp.  -)double cosets in \(G(\mathbf{Q}_p)\) (resp.
-)double cosets in \(G(\mathbf{Q}_p)\) (resp.  ). In the middle, \(\widehat{G}\) denotes the Langlands dual group formed over \({\mathbf{Q}}\) using a fixed pinning (T, B, X) of G. By the classification of split reductive groups in terms of their root data, it can be described by switching characters and cocharacters, as well as roots and coroots. For example [13], \(\widehat{\mathrm{GL}}_n=\mathrm{GL}_n\), \(\widehat{\mathrm{SL}}_n = \mathrm{PGL}_n\) and \(\widehat{{\text {Sp}}}_{2g} ={\text {SO}}_{2g+1}\). The ring \(R(\widehat{G})\) is the Grothendieck \(\mathbf{Z}[p^{\pm 1/2}]\)-algebra of algebraic representations of this dual group.
). In the middle, \(\widehat{G}\) denotes the Langlands dual group formed over \({\mathbf{Q}}\) using a fixed pinning (T, B, X) of G. By the classification of split reductive groups in terms of their root data, it can be described by switching characters and cocharacters, as well as roots and coroots. For example [13], \(\widehat{\mathrm{GL}}_n=\mathrm{GL}_n\), \(\widehat{\mathrm{SL}}_n = \mathrm{PGL}_n\) and \(\widehat{{\text {Sp}}}_{2g} ={\text {SO}}_{2g+1}\). The ring \(R(\widehat{G})\) is the Grothendieck \(\mathbf{Z}[p^{\pm 1/2}]\)-algebra of algebraic representations of this dual group.
The chain of isomorphisms (1.1) is an instance of the resemblance [35] between \(\mathbf{Q}_p\) and  , in which the uniformizer p corresponds to the uniformizer t. Despite being only a superficial similarity –given that the addition and multiplication in the two fields are severely different– the kinship is strong enough so that the characteristic functions of the double cosets \(G(\mathbf{Z}_p)p^{\mu } G(\mathbf{Z}_p)\) and
, in which the uniformizer p corresponds to the uniformizer t. Despite being only a superficial similarity –given that the addition and multiplication in the two fields are severely different– the kinship is strong enough so that the characteristic functions of the double cosets \(G(\mathbf{Z}_p)p^{\mu } G(\mathbf{Z}_p)\) and  correspond to each other under (1.1). Here \(\mu :\mathbf{G} _{\mathrm{m}}\rightarrow T\) is any dominant cocharacter.
correspond to each other under (1.1). Here \(\mu :\mathbf{G} _{\mathrm{m}}\rightarrow T\) is any dominant cocharacter.
The geometric Satake equivalence might be regarded, at the same time, as a geometrization and a categorification of the right hand isomorphism above: the right-most term is geometrized by means of the affine Grassmannian, whose \(\mathbf{F}_p\)-points are the quotient  . The categorification is achieved by relating the entire category of algebraic \(\widehat{G}\)-representations (as opposed to its Grothendieck ring) to certain equivariant perverse sheaves on the affine Grassmannian. This circle of ideas has been worked on by various authors including Lusztig [26], Ginzburg [21], Belinson–Drinfeld [5] and Mirković–Vilonen [27]. For the relation with (1.1) the reader is referred to [32, 38].
. The categorification is achieved by relating the entire category of algebraic \(\widehat{G}\)-representations (as opposed to its Grothendieck ring) to certain equivariant perverse sheaves on the affine Grassmannian. This circle of ideas has been worked on by various authors including Lusztig [26], Ginzburg [21], Belinson–Drinfeld [5] and Mirković–Vilonen [27]. For the relation with (1.1) the reader is referred to [32, 38].
In analogy to the function field case, a geometrization and categorification of the left hand isomorphism in (1.1) was proven by Zhu [37]. To begin with, such an endeavour is made possible by [37] and Bhatt–Scholze [9] who have shown that the cosets \(G(\mathbf{Q}_p) / G(\mathbf{Z}_p)\) are the \(\mathbf{F}_p\)-points of an algebro-geometric object known as the Witt vector affine Grassmannian, and denoted \(\mathrm{Gr}_G\rightarrow \mathrm{Spec}(\mathbf{F}_p)\) in this paper. For a fixed prime nubmer \(\ell \not = p\) and a choice of half twist \(\overline{{\mathbf{Q}}}_{\ell }({1\over 2})\), Zhu proves an equivalence of Tannakian categories
between semi-simple perverse \(\overline{{\mathbf{Q}}} _{\ell }\)-sheaves on \(\mathrm{Gr}_{G}\) of weight 0 which are furthermore equivariant with respect to the action of the positive loop group \(L^+G\). This positive loop group has as \(\mathbf{F}_p\)-points the group \(G(\mathbf{Z}_p)\); it lies inside the full loop group LG, whose \(\mathbf{F}_p\)-points are \(G(\mathbf{Q}_p)\).
Building upon our earlier work [30, 31], the goal of the present paper is to refine (1.2) into an equivalence between the category of mixed Tate motives on the double quotient \(L^+G\backslash LG/ L^+G\) and representations of Deligne’s extended dual group \(\widehat{G}_1\), a certain extension of \(\mathbf{G} _{\mathrm{m}}\) (which records the weights) by \(\widehat{G}\). This equivalence is independent of the choice of \(\ell \not = p \) present in (1.2) via the use of \(\ell \)-adic cohomology. We refer to Remark 5.8 for the relation with (1.1). Also we remark that Zhu [39] has explained the construction of a motivic Satake equivalence using numerical motives. This approach is based on an explicit enumeration of algebraic cycles on affine Grassmannians. By comparison, the approach taken in this paper is more strongly relying on the general framework of motives given by Ayoub [2, 3] and Cisinski–Déglise [11].
1.2 Results
A prestack over \(\mathbf{F}_p\) is a functor from affine \(\mathbf{F}_p\)-algebras to anima (called spaces in [25], Kan complexes, or \(\infty \)-groupoids or, in classical terminology, simplicial sets up to weak equivalences). Examples of prestacks include (ordinary) presheaves such as \(\mathbf{F}_p\)-schemes and ind-schemes (via their functor of points), but also homotopy quotients of such objects by group actions, and more general geometric objects such as higher stacks over \(\mathbf{F}_p\). In [31] we have constructed a stable \(\infty \)-category \(\mathrm{DM}(X)\) of motives with \({\mathbf{Q}}\)-coefficients on any prestack X. For example, we can speak of and conveniently work with \(\mathrm{DM}(L^+G \backslash LG / L^+G)\), the category of motives on the indicated double quotient.
In order to state our results, we first need to deal with the general process of perfection, see §6 in the first arXiv version of [31], and also [17], or the recent preprint of Bouthier–Kazhdan–Varshavsky [8, §2.3.5]. There are two ways to turn a \(\mathbf{F}_p\)-prestack X perfect, i.e., to ensure that pullback along the absolute Frobenius \(\sigma \) is an isomorphism: the limit perfection
and the colimit perfection \(X^{\mathrm{perf}} :={\text {colim}}_{T\rightarrow X} \lim _{\sigma } T\). The latter is constructed by glueing the perfections of all affine \(\mathbf{F}_p\)-schemes covering the prestack (see Definition 2.3).
Proposition 1.1
(Corollary 2.6) For any \(\mathbf{F}_p\)-prestack X, there are maps
inducing equivalences on categories of motives
Recall from [9, 37] (or see Sect. 2.3 for a brief recapitulation) that perfectly finitely presented (pfp) \(\mathbf{F}_p\)-schemes are precisely those \(\mathbf{F}_p\)-schemes X which arise as \(X \simeq \lim _{\sigma } X_0\) for some finite-type \(\mathbf{F}_p\)-scheme \(X_0\). Such a scheme \(X_0\) is called a model of X. We have \(\mathrm{DM}(X_0) \simeq \mathrm{DM}(X)\) by the previous proposition. A typical example of a pfp scheme is \((\mathbf{A}^1_{\mathbf{F}_p})^{\mathrm{perf}} = \mathrm{Spec}\mathbf{F}_p[t^{p^{-\infty }}]\), the perfection of \(\mathbf{A}^1_{\mathbf{F}_p}\).
Theorem 1.2
(Theorems 2.10 and 2.12) The equivalences of Proposition 1.1 can be used to endow motives on pfp schemes over \(\mathbf{F}_p\) with a six functor formalism obeying all the standard properties including base change, localization, h-descent, duality and homotopy invariance with respect \(({\mathbf{A}}^1_{\mathbf{F}_p})^{\mathrm{perf}}\).
Similar results also hold for motives on ind-(pfp schemes), i.e., objects presented as \(\mathbf{N}\)-indexed colimits \(X = \mathrm{colim}X_i\), where the \(X_i\) are pfp schemes and the transition maps \(X_i \rightarrow X_{i+1}\) are closed immersions. An example is the Witt vector affine Grassmannian \(\mathrm{Gr}_G=(LG/L^+G)^{\acute{\mathrm{e}}\mathrm{t}}\) which is shown to be an ind-(pfp scheme) in [9].
Such a convenient formalism lends itself to applications in geometric representation theory. Extending previous work of Soergel–Wendt [34] for finite type schemes and of [31] for ind-schemes of ind-(finite type) to the (ind-)pfp case, we say that a stratification on an ind-(pfp scheme) X is Whitney–Tate if the derived categories of Tate motives on the individual strata “glue” in a meaningful manner (see Definition 3.3 for the precise condition).
Theorem 1.3
(special case of Theorem 4.5)
-
(i)
The stratification on the Witt vector affine Grassmannian \(\mathrm{Gr}_G\) by \(L^+G\)-orbits is Whitney–Tate. Accordingly, the stable \(\infty \)-category \(\mathrm{DTM}(\mathrm{Gr}_G)\) of stratified Tate motives is well-defined: such motives are characterized by the property that their restriction to the \(L^+G\)-orbits are Tate, i.e., generated (under shifts and extensions) by motives of the form 1(n), \(n\in \mathbf{Z}\) on the \(L^+G\)-orbits.
-
(ii)
The category \(\mathrm{DTM}(\mathrm{Gr}_G)\) admits a “motivic” t-structure whose heart \(\mathrm{MTM}(\mathrm{Gr}_G)\) is generated by intersection motives \(\mathrm{IC}_{\mu }(n)\), \(n\in \mathbf{Z}\) as simple objects, where \(\mu :\mathbf{G} _{\mathrm{m}}\rightarrow T\) ranges over the dominant cocharacters of the fixed maximal torus \(T\subset G\).
In fact, this result is as a special case of Theorem 4.5 where we prove the same result more generally for stratifications on Witt vector (partial) affine flag varieties \(\mathrm{Fl}_{\mathbf{f }} =(LG/{\mathcal {P}}_{\mathbf{f }})^{\acute{\mathrm{e}}\mathrm{t}}\) associated to any parahoric subgroup \({\mathcal {P}}_{\mathbf{f }} \subset L G\), in place of \(L^+G\). An example is the Iwahori subgroup \({\mathcal {B}}\subset LG\) associated to the choice of the Borel subgroup \(B\subset G\).
The convolution product of functions in the Hecke algebra is enhanced by the convolution product (Sect. 4.3)
By étale descent, motives on \(LG / L^+ G\) are equivalent to motives on the étale sheafification \(\mathrm{Gr}_G = (LG / L^+ G)^{\acute{\mathrm{e}}\mathrm{t}}\). Therefore, motives on the double quotient \(L^+G \backslash LG / L^+ G\) are equivalent to \(L^+ G\)-equivariant motives on \(\mathrm{Gr}_G\).
We define a category of equivariant stratified Tate motives
by requiring that the underlying (non-equivariant) motive on \(\mathrm{Gr}_G\) is stratified Tate in the sense above. By Theorem 4.6, the category \(\mathrm{DTM}(L^+ G \backslash LG / L^+G)\) inherits a t-structure from the t-structure on \(\mathrm{DTM}(\mathrm{Gr}_G)\). The heart of this t-structure is denoted \(\mathrm{MTM}(L^+ G \backslash LG / L^+G)\). In relation to the outline in Sect. 1.1, this category is an independent-of-\(\ell \) version of perverse \(L^+G\)-equivariant \(\ell \)-adic sheaves on \(\mathrm{Gr}_G\) subject to the condition that their restriction to the strata are Tate twists of the (possibly shifted) constant sheaf.
Theorem 1.4
(special case of Theorem 4.8) The convolution product functor \(\star \) preserves the subcategory (1.3).
Again, this statement is shown in Theorem 4.8 in the greater generality for Witt vector (partial) affine flag varieties as above. The following statements, however, are specific to the choice of \(L^+ G\). In Proposition 5.3 we prove, as a consequence of the semi-simplicity of \(\mathrm{MTM}(\mathbf{F}_q)\) and Kazhdan–Lusztig’s parity vanishing, that the forgetful functor
is an equivalence of semi-simple (abelian) categories whose generators are the simple objects \(\mathrm{IC}_{\mu }(n)\) mentioned in Theorem 1.3(ii). This category is stable under the convolution product \(\star \) and hence inherits a monoidal structure by Theorem 4.8(iii).
We write \(\widehat{G}_1\) for the modification of the Langlands dual group introduced by Frenkel and Gross [19] following a suggestion of Deligne [15]. If G is simply connected, \(\widehat{G}_1\) is the (direct) product of \(\widehat{G}\) and \(\mathbf{G} _{\mathrm{m}}\), where the \(\mathbf{G} _{\mathrm{m}}\)-factor arises from the presence of Tate twists. In general, \(\widehat{G}_1\) is a not necessarily split extension of \(\mathbf{G} _{\mathrm{m}}\) by \(\widehat{G}\), a phenomenon which is related to the necessity of fixing \(p^{1/2}\in \overline{{\mathbf{Q}}}\) in the Satake isomorphisms (1.1). Our main result is the motivic Satake equivalence for Witt vector affine flag varieties.
Theorem 1.5
(Theorems 5.2 and 5.7) The monoidal structure on (1.4) given by the convolution product is part of the structure of a \({\mathbf{Q}}\)-linear Tannakian category, and as such there is, after extending scalars to \(\overline{{\mathbf{Q}}}\), an equivalence
This statement is independent of \(\ell \) since no category of \(\ell \)-adic (perverse) sheaves is required for its formulation. Furthermore, this equivalence is uniquely determined by its compatibility with (the appropriate version of) the \(\ell \)-adic equivalence (1.2). As mentioned in Sect. 1.1 a similar result was also obtained in [39] using a different route, namely an explicit enumeration of algebraic cycles on the Witt vector affine Grassmannian, and working with the category of numerical motives. As is explained by the material in the sections below, working with the six functor formalism of motives as in this paper offers more flexibility including, say, handling the derived categories \(\mathrm{DTM}({\mathcal {B}}\backslash LG / {\mathcal {B}})\) of doubly Iwahori-equivariant stratified Tate motives on the loop group: the convolution product on this category does not respect the abelian subcategory of equivariant mixed Tate motives, so that working with numerical motives is prohibitive in such a situation.
2 Motives on perfect (ind-)schemes
2.1 Recollections on prestacks
In order to treat motives on the Witt vector affine Grassmannian and to relate them to motives on ordinary affine Grassmannians, it is very useful to use the definition of a category of motives on arbitrary prestacks developed in [31, §2]. We briefly recall the rudiments in this subsection. A very similar theory, for \(\ell \)-adic sheaves instead of motives, has been developed very recently in [8].
For a field k, \(\mathrm{AffSch}_k^{\mathrm{ft}}\) is the category of affine k-schemes of finite type. We denote by \(\mathrm{AffSch}_k\) its \(\kappa \)-pro-completion, i.e., the category of affine k-schemes whose underlying k-algebra is generated by at most \(\kappa \) elements. Here \(\kappa \) is a large enough regular cardinal fixed once and for all. For all purposes in this paper, we may choose \(\kappa \) to be the countable cardinal. The \(\infty \)-category of prestacks is defined as the \(\infty \)-categorical presheaf category, i.e.,
Here, following the terminology and discussion in [14, §5.1.4], \(\mathrm{Ani}\) denotes the \(\infty \)-category of anima, i.e., the free completion of the category of finite sets under sifted homotopy colimits, or, equivalently, the \(\infty \)-category of spaces [25, §1.2.16], also called \(\infty \)-groupoids. Prestacks are an extremely general class of algebro-geometric objects: by means of its functor of points, any k-scheme defines a prestack. In addition, prestacks are closed under all (homotopy) limits and colimits. In particular, any strict ind-scheme \(X = \mathrm{colim}X_i\) is a prestack, as is a quotient (always understood in the \(\infty \)-categorical sense, otherwise also known as a homotopy quotient) Y/G, where G is a group-valued presheaf acting on a presheaf Y.
We denote by \(\mathrm{DGCat}_{\mathrm{cont}}\) the \(\infty \)-category of presentable, stable dg-\(\infty \)-categories with continuous (i.e., colimit-preserving) functors.
Construction 2.1
In [31, Definition 2.2.1], we have defined a category \(\mathrm{DM}(X)\) in \(\mathrm{DGCat}_{\mathrm{cont}}\) of motives on any prestack X with the following features:
-
(i)
For a scheme X of finite type over k, the homotopy category of \(\mathrm{DM}(X)\) (which is a triangulated category) recovers the usual triangulated category of motives with rational coefficients due to Ayoub and Cisinski–Déglise [2, 3, 11, §14].
-
(ii)
If \(X = \lim _{n \in \mathbf{N}} X_n\) is an affine pro-algebraic scheme, i.e., \(X_i / k\) is affine and of finite type and so are the transition maps \(X_n {\mathop {\longrightarrow }\limits ^{p_n}}X_{n-1}\), then
$$\begin{aligned} \mathrm{DM}(X) = \mathrm{colim}\left( \mathrm{DM}(X_0) {\mathop {\longrightarrow }\limits ^{(p_0)^!}} \mathrm{DM}(X_1) {\mathop {\longrightarrow }\limits ^{(p_1)^!}} \dots \right) \end{aligned}$$where the colimit is taken in \(\mathrm{DGCat}_{\mathrm{cont}}\) (we emphasize that this category consists of colimit-preserving functors only).
-
(iii)
If a prestack X admits a presentation \(X = \mathrm{colim}X_i\), where \(X_i \in \mathrm{AffSch}_k\), then
$$\begin{aligned} \mathrm{DM}(X) = \lim \big (\mathrm{DM}(X_i), (f_{ij})^!\big ) \end{aligned}$$where the maps \(X_i {\mathop {\longrightarrow }\limits ^{f_{ij}}}X_j\) are the ones in the colimit diagram defining X. More colloquially speaking, a motive on X is a family of motives on all the “covers” \(X_i\) compatible with the system defining the colimit diagram.
-
(iv)
For any map of prestacks \(f:X \rightarrow Y\), there is a functor \(f^!:\mathrm{DM}(Y) \rightarrow \mathrm{DM}(X)\). These yield a presheaf \(\mathrm{DM}:\mathrm{PreStk}^{\mathrm{op}} \rightarrow \mathrm{DGCat}_{\mathrm{cont}}\) which is shown to be a sheaf in Voevodsky’s h-topology in [31, Theorem 2.2.16]. If we need to emphasize the nature of the pullback functors, we also write \(\mathrm{DM}^!\) for this (pre)sheaf.
-
(v)
In both preceding items, we use !-pullback instead of the more easily defined \(*\)-pullback in order to obtain the desired categories \(\mathrm{DM}(X)\) for ind-schemes X, see [31, Corollary 2.3.4]. For \(X = Y / G\), the quotient of an action of a smooth algebraic group G on a finite type k-scheme Y, the approach with \(*\)- and !-pullback yields equivalent categories, though, cf. the discussion in [31, Remark 2.2.2] and after [31, Lemma 2.2.7]
2.2 Perfection of prestacks
In this section we develop a general formalism of colimit perfections for \(\infty \)-prestacks, and compare it to the limit perfection as used in [37, Appendix A], [9] (cf. also [7]) and [36, Appendix A].
Let p be a prime, and let k be a perfect field of characteristic p. For each \(T = \mathrm{Spec}R\in \mathrm{AffSch}_k\), let \(\sigma _T:T\rightarrow T\) be the absolute Frobenius morphism given by \(R\rightarrow R, x\mapsto x^p\). This defines an endofunctor \(\sigma \) of the identity transformation on \(\mathrm{AffSch}_k\). Let \(\mathrm{AffSch}_k^{\mathrm{perf}}\) be the full subcategory of objects \(T\in \mathrm{AffSch}_k\) such that \(\sigma _T\) is an automorphism. These are called perfect affine k-schemes. The inclusion \(\mathrm{AffSch}_k^{\mathrm{perf}}\subset \mathrm{AffSch}_k\) admits a right adjoint given by \(T\mapsto \lim _{\sigma } T=\mathrm{Spec}(\mathrm{colim}_{r\mapsto r^p}R)\).
Precomposition with \(\sigma \) defines a (co-)limit preserving endofunctor of the identity on \(\mathrm{PreStk}_k\), denoted by the same letter. The category of perfect prestacksFootnote 1 is the \(\infty \)-category
The natural restriction functor \({\text {res}}:\mathrm{PreStk}_k\rightarrow \mathrm{PreStk}_k^{\mathrm{perf}}\) clearly preserves limits and colimits.
Lemma 2.2
There is an adjunction
which under the Yoneda embedding extends the adjunction \(\mathrm{AffSch}_k^{\mathrm{perf}}\leftrightarrows \mathrm{AffSch}_k\). Both functors \(\mathrm{incl}\) and \(\mathrm{res}\) preserve colimits, and satisfy \({\text {res}}\circ {\text {incl}} =\mathrm{id}\). In particular, \({\text {incl}}\) is a full embedding, and \(\sigma \) is an equivalence on objects in the essential image.
Proof
The adjunction \((\mathrm{incl},\mathrm{res})\) exists by [25, Proposition 5.2.6.3]. Here \(\mathrm{incl}\) is the colimit preserving functor constructed in [25, Theorem 5.1.5.6]. Hence, the claim \(\mathrm{res}\circ \mathrm{incl}= \mathrm{id}\) follows, by continuity of both functors, from the corresponding fact for affine schemes. \(\square \)
Definition 2.3
The (colimit) perfection is the endofunctor on \(\mathrm{PreStk}_k\) defined by
For \(X\in \mathrm{PreStk}_k\), \(X=\mathrm{colim}_{T\rightarrow X} T\) with \(T\in \mathrm{AffSch}_k\), it is computed as \(X^{\mathrm{perf}}=\mathrm{colim}_{T\rightarrow X} \lim _{\sigma } T\).
In the following, we identify \(\mathrm{PreStk}_k^{\mathrm{perf}}\simeq {\text {incl}}(\mathrm{PreStk}_k^{\mathrm{perf}})\subset \mathrm{PreStk}_k\). This is the full subcategory of all objects X such that the counit of the adjunction \(X^{\mathrm{perf}}\rightarrow X\) is an equivalence. Note that the perfection of ind-objects produces ind-(perfect objects), so that the functor \((\text {-})^{\mathrm{perf}}\) is well-suited for working with ind-schemes.
The following lemma appeared in an early arxiv version of [31]. A more refined statement for \(\mathrm{SH}[\frac{1}{p}]\), the stable \(\mathbf{A}^1\)-homotopy category localized at the characteristic (as opposed to \(\mathrm{DM}\) with rational coefficients) is due to Elmanto and Khan [17].
Lemma 2.4
Let \(X\in \mathrm{PreStk}_k\) be any prestack.
-
(i)
The pullback \(\sigma ^!:\mathrm{DM}(X)\rightarrow \mathrm{DM}(X)\) is equivalent to the identity.
-
(ii)
The counit of the adjunction \(\pi :X^{\mathrm{perf}}\rightarrow X\) induces an equivalence \(\pi ^!:\mathrm{DM}(X)\simeq \mathrm{DM}(X^{\mathrm{perf}})\).
Proof
For (i), first let \(X\in \mathrm{AffSch}_k^{\mathrm{ft}}\). Invariance of \(\mathrm{DM}\) under pullback along finite surjective radicial maps [11, Proposition 2.1.9] shows that the natural map \(\mathrm{id}\rightarrow \sigma _*\) is invertible. Thus, we get \(\mathrm{id}\simeq \sigma ^!\) by adjunction (using \(\sigma _*=\sigma _!\)). This equivalence extends to \(\mathrm{PreStk}_k\) by continuity.
For (ii), we reduce to the case \(X\in \mathrm{AffSch}_k\) by continuity. Then \(X^{\mathrm{perf}}=\lim _{\sigma } X=\lim _{X\rightarrow T}\lim _{\sigma } T\) for \(T\in \mathrm{AffSch}_k^{\mathrm{ft}}\), and we reduce further to the case \(X=T\in \mathrm{AffSch}_k^{\mathrm{ft}}\). In this case, \(\pi ^!:\mathrm{DM}(X)\rightarrow \mathrm{DM}(X^{\mathrm{perf}})=\mathrm{colim}_{\sigma ^!}\mathrm{DM}(X)\) is the natural map which is an equivalence by (i). \(\square \)
Definition 2.5
The (limit) perfection is the endofunctor on \(\mathrm{PreStk}_k\) defined by
where the limit is indexed by the positive integers.
Restricted to schemes, this functor is used in [9, 37]. It gives another way of constructing prestacks on which \(\sigma \) acts as an equivalence. In general, the natural map
is not an equivalence. For a counter-example, take the ind-scheme \(\mathbf{A}^{\infty } = \mathrm{colim}(\mathbf{A}^0 {\mathop {\rightarrow }\limits ^{0}} \mathbf{A}^1 {\mathop {\rightarrow }\limits ^{\mathrm{id}\times 0}}\mathbf{A}^2 \dots )\). For a k-algebra R, the natural map
is bijective if R is reduced (so that Frobenius is injective), but not in general (e.g., take \(R=k[\varpi ^{1\over {p^{\infty }}}]/ (\varpi )\)). However, as \(\mathrm{DM}\) is invariant under Nil-thickenings, the categories of motives on these two prestacks are equivalent:
Corollary 2.6
For any prestack \(X\in \mathrm{PreStk}_k\), there is a commutative diagram of prestacks

where \(\pi \) is the natural projection. In particular by Lemma 2.4(ii), the !-pullback induces equivalences \(\mathrm{DM}(X)\simeq \mathrm{DM}(\lim _{\sigma } X)\simeq \mathrm{DM}(X^{\mathrm{perf}})\).
Proof
We have to show that \(\pi ^{\mathrm{perf}}\) is an equivalence, and we claim that \(\mathrm{res}\circ \pi \) is already an equivalence. Namely, \(\mathrm{Hom}(T,\lim _{\sigma } X)\simeq \mathrm{Hom}(T,X)\) for any \(T\in \mathrm{AffSch}_k^{\mathrm{perf}}\). Indeed, for any map \(f:T\rightarrow X\) and any \(r\ge 0\), the diagram

commutes up to equivalence. \(\square \)
Remark 2.7
If X is a scheme, then the canonical map \(X^{\mathrm{perf}}\rightarrow \lim _{\sigma } X\) induces an isomorphism after Zariski sheafification. Indeed, if \(U\rightarrow X\) is an open affine subscheme, then \(U^{\mathrm{perf}}=\lim _{\sigma } U\rightarrow \lim _{\sigma } X\) is an open affine subscheme by [9, Lemma 3.4 (ix)]. This easily implies \((X^{\mathrm{perf}})^{\mathrm{Zar}}\cong \lim _{\sigma } X\).
2.3 Motives on perfect schemes
In order to obtain a six functor formalism, we need to put suitable finiteness assumptions on the objects.
Definition 2.8
([37, Definition A.13], [9, Proposition 3.11]) A map \(f:X \rightarrow Y\) of perfect qcqs schemes is called perfectly of finite presentation or just pfp if the induced map \(\mathrm{Spec}A \rightarrow \mathrm{Spec}B\) of any open affines in X, resp. Y factors as \(\mathrm{Spec}A \simeq \lim _{\sigma } (\mathrm{Spec}A_0)\rightarrow \mathrm{Spec}A_0 \rightarrow \mathrm{Spec}B\), where \(A_0\) is a finitely presented B-algebra. The full subcategory of \(\mathrm{Sch}_k\) spanned by the qcqs pfp perfect k-schemes, or just pfp schemes, is denoted by \(\mathrm{Sch}_k^{\mathrm{pfp}}\).
Lemma 2.9
-
(i)
([37, Proposition A.17]) The functor \(\mathrm{Sch}_k^{\mathrm{ft}}\rightarrow \mathrm{Sch}_k^{\mathrm{pfp}}\), \(X\mapsto \lim _{\sigma } X\) is full and essentially surjective. Thus, each object \(X\in \mathrm{Sch}_k^{\mathrm{pfp}}\) and similarly each morphism f admits a model, i.e., a finite type k-scheme \(X_0\) such that \(X=\lim _{\sigma } X_0\).
-
(ii)
It induces an equivalence of categories \(\mathrm{Sch}_k^{\mathrm{ft}}[{\mathcal {S}}^{-1}]\cong \mathrm{Sch}_k^{\mathrm{pfp}}\) on the localization with respect to the class \({\mathcal {S}}\) of finite radicial surjective maps in \(\mathrm{Sch}_k^{\mathrm{ft}}\).
-
(iii)
The equivalence in ii) induces an equivalence on small étale sites.
-
(iv)
If \(Z \subset X \supset U\) is a diagram consisting of a closed and complementary open immersion in \(\mathrm{Sch}_k^{\mathrm{pfp}}\), then there is a model \(Z_0 \subset X_0 \supset U_0\) again consisting of a closed and open immersion.
Proof
Part (iii) follows from (ii), see [33, Tag 04DZ]. A map f in \(\mathrm{Sch}_k^{\mathrm{ft}}\) lies in \({\mathcal {S}}\) iff it is a universal homeomorphism, cf. [33, Tags 04DF, 01WJ, 01S4] or, equivalently by [9, Lemma 3.8], iff \(\lim _{\sigma } f\) is an isomorphism. It remains to show that any functor \(\varphi :\mathrm{Sch}_k^{\mathrm{ft}} \rightarrow C\) to a category C that sends maps in \({\mathcal {S}}\) to isomorphisms factors uniquely over the perfection functor. By Zhu’s result in (i) \(\psi :\mathrm{Sch}^{\mathrm{pfp}}_k \rightarrow C\) is unique if it exists. Also, to show the existence we may replace \(\mathrm{Sch}^{\mathrm{pfp}}_k\) by the full subcategory of \(\mathrm{Sch}_k^{\mathrm{pfp}}\) spanned by the image of the perfection functor. We define \(\psi \) on objects by fixing a model \(X = \lim _{\sigma } X_0\) for each X, and set \(\psi (X) := \varphi (X_0)\). By definition [9, Proposition 3.11], given any pfp map \(f: X \rightarrow Y\), there is some \(n \gg 0\) such that we have the diagram below, where \(X_0^{(n)}\) is the n-th stage of the limit defining X (it is abstractly isomorphic to \(X_0\), but the structural map to k differs by \(\sigma ^n\)):

We define \(\psi (f)\) as the composite \(\varphi (f_0^{(n)}) \circ \varphi (\sigma ^n)^{-1}\). This is well-defined independently of n. One immediately checks that it is also compatible with composition. This shows the existence of a factorization, hence (ii).
For (iv), let \(X_0\) be a reduced model of X. Then \(|X|=|X_0|\) on the underlying topological spaces, and we define \(Z_0\) (resp. \(U_0\)) as the reduced closed (resp. open) subscheme \(X_0\) defined by the closed subset |Z| (resp. open subset |U|) in \(|X|=|X_0|\). The limit perfection preserves open and closed immersions by [9, Lemma 3.4], so that \(Z_0 \subset X_0 \supset U_0\) is a model for \(Z \subset X \supset U\). \(\square \)
Theorem 2.10
Motives on pfp schemes enjoy a six-functor formalism with the following properties. Throughout, let X, Y denote objects, resp. f a morphism in \(\mathrm{Sch}^{\mathrm{pfp}}_k\). Let \(X_0\), \(Y_0\), resp. \(f_0\) be models thereof.
-
(i)
The presheaves \(\mathrm{DM}^*\) and \(\mathrm{DM}^!\) on \(\mathrm{Sch}^{\mathrm{ft}}_k\) (given on objects by \(X \mapsto \mathrm{DM}(X)\), and on morphisms by \(f \mapsto f^*\), resp. \(f^!\)) factor uniquely over functors
$$\begin{aligned} \mathrm{DM}^*, \mathrm{DM}^!:(\mathrm{Sch}^{\mathrm{pfp}}_k)^{\mathrm{op}} \rightarrow \mathrm{DGCat}_{\mathrm{cont}}. \end{aligned}$$On objects \(X \in \mathrm{Sch}^{\mathrm{pfp}}_k\), these two presheaves take the same values, denoted simply \(\mathrm{DM}(X)\). The functor \(\mathrm{DM}^!\) agrees with the restriction of the presheaf \(\mathrm{DM}\) in Construction 2.1(iv) from \(\mathrm{PreStk}_k\) to \(\mathrm{Sch}^{\mathrm{pfp}}_k\).
-
(ii)
The natural map \(p :X \rightarrow X_0\) induces an equivalence of \(\infty \)-categories
$$\begin{aligned} p^! :\mathrm{DM}(X_0) {\mathop {\longrightarrow }\limits ^{\cong }} \mathrm{DM}(X), \end{aligned}$$(2.1)which preserves the monoidal unit 1 and is compatible with all functors below. In particular, if X has a regular model \(X_0 / k\), then

where the terms at the right are the n-th Adams eigenspace in the algebraic K-theory of X and Bloch’s higher Chow group, both tensored with \(\mathbf{Q}\).
-
(iii)
There are adjunctions
$$\begin{aligned}&f^* : \mathrm{DM}(Y) \rightleftarrows \mathrm{DM}(X) : f_*.\\&f_! : \mathrm{DM}(X) \rightleftarrows \mathrm{DM}(Y): f^!. \end{aligned}$$If f has a smooth model, there is an adjunction
$$\begin{aligned} f_{\sharp } : \mathrm{DM}(X) \rightleftarrows \mathrm{DM}(Y): f^*. \end{aligned}$$These functors are functorial in f. Under the equivalence (2.1), they correspond to \((f_0)^*\) etc.
-
(iv)
If f has a proper model, then \(f_! = f_*\); if f has an étale model, then \(f^! = f^*\). More generally, if f has a smooth model \(f_0\) of relative dimension n, there is a functorial equivalence (called relative purity)
$$\begin{aligned} f^! \simeq f^* (n)[2 n]. \end{aligned}$$(2.2)Yet more generally, the latter equivalence holds if f is a perfectly smooth map of relative dimension n in the sense of [37, Definition A.25].
-
(v)
For the projection \(p:(\mathbf{G} _{\mathrm{m}})^{\mathrm{perf}} \times _k X \rightarrow X\), and any \(M \in \mathrm{DM}(X)\), the map \(p_{\sharp } p^* M[-1] \rightarrow M[-1]\) in \(\mathrm{DM}(X)\) is a split monomorphism. The complementary summand is denoted by M(1). The functor \(M \mapsto M(1)\) is an equivalence with inverse denoted by \(M \mapsto M(-1)\).
-
(vi)
The category \(\mathrm{DM}(X)\) is compactly generated by the objects \(t_{\sharp } 1(n)\), \(t:T \rightarrow X\) pfp smooth and \(n \in \mathbf{Z}\). In particular, the monoidal unit \(1_X \in \mathrm{DM}(X)\) is compact. The functors \(f_{\sharp }\), \(f_*\), \(f^*\), \(f_!\), and \(f^!\) preserve compact objects and preserve arbitrary (homotopy) colimits.
-
(vii)
For any pfp map f, there is a projection formula
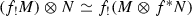 .
. -
(viii)
If \(p:X\rightarrow \mathrm{Spec}k\) denotes the structural map, the dualising functor
$$\begin{aligned} \mathrm{D}_X {\mathop {=}\limits ^{\mathrm{def}}} \underline{\mathrm{Hom}}(-, p^! 1) \end{aligned}$$(2.3)is a contravariant involution on the subcategory \(\mathrm{DM}(X)^{\mathrm{c}}\) of compact objects, i.e., \(\mathrm{D}_X \circ \mathrm{D}_X = \mathrm{id}\). Furthermore, on compact objects, there are equivalences
$$\begin{aligned} \mathrm{D}_Y f_! = f_* \mathrm{D}_X,\;\; f^* \mathrm{D}_Y = \mathrm{D}_X f^!. \end{aligned}$$ -
(ix)
For a pfp closed immersion \(i:Z \rightarrow X\) with open complement \(j:U \rightarrow X\), there are equivalences
$$\begin{aligned}&\mathrm{DM}(X) = \mathrm{laxlim} \left( \mathrm{DM}(U) {\mathop {\longrightarrow }\limits ^{i^! j_!}}\mathrm{DM}(Z) \right) ,\\&\mathrm{DM}(X) = \mathrm{laxlim} \left( \mathrm{DM}(U) {\mathop {\longrightarrow }\limits ^{i^* j_*}}\mathrm{DM}(Z) \right) . \end{aligned}$$Here \(\mathrm{laxlim}\) denotes the lax limit [20] whose objects can be colloquially described as triples \((M \in \mathrm{DM}(U), N \in \mathrm{DM}(Z), \alpha : i^! j_! M \rightarrow N)\), where \(\alpha \) is any map (and the non-lax limit would be the subcategory where this map is an isomorphism). Equivalently, the (co)units of the adjunctions above assemble into so-called localization homotopy fiber sequences
$$\begin{aligned}&i_! i^! \rightarrow \mathrm{id}\rightarrow j_* j^* {\mathop {\rightarrow }\limits ^{[1]\;}}, \end{aligned}$$(2.4)$$\begin{aligned}&j_! j^! \rightarrow \mathrm{id}\rightarrow i_* i^*{\mathop {\rightarrow }\limits ^{[1]\;}}. \end{aligned}$$(2.5) -
(x)
For a cartesian diagram in \(\mathrm{Sch}_S^{\mathrm{pfp}}\) (necessarily consisting of pfp maps)

there are natural equivalences
$$\begin{aligned} g^! f_*&{\mathop {\longrightarrow }\limits ^{\cong }} f'_* g'^!, \end{aligned}$$(2.6)$$\begin{aligned} f^* g_!&{\mathop {\longrightarrow }\limits ^{\cong }} g'_! f'^*. \end{aligned}$$(2.7) -
(xi)
The category \(\mathrm{DM}\) is perfectly homotopy-invariant in the sense that for the projection map \(p:(\mathbf{A}^n)^{\mathrm{perf}} \times _k X \rightarrow X\) for any \(n\in \mathbf{Z}_{\ge 0}\), the counit and unit maps \(p_{\sharp } p^* \rightarrow \mathrm{id}\) and \(\mathrm{id}\rightarrow p_* p^*\) are functorial equivalences in \(\mathrm{DM}(X)\) [11, 2.1.3].
-
(xii)
The presheaves \(\mathrm{DM}^*\) and \(\mathrm{DM}^!\) are sheaves for the h-topology on pfp schemes, i.e., if \(f:X \rightarrow Y\) admits a model which is an h-covering in \(\mathrm{Sch}_k^{\mathrm{ft}}\), then the natural map
$$\begin{aligned} \mathrm{DM}(Y) \;\rightarrow \; \lim \left( \mathrm{DM}(X) \mathop {\rightrightarrows } \limits _{(p_2)^*}^{(p_1)^*} \mathrm{DM}(X \times _Y X) \dots \right) \end{aligned}$$is an equivalence, and likewise with !-pullbacks instead. We refer to this property as h-descent.
-
(xiii)
Suppose X is separated. The category \(\mathrm{DM}(X)\) is equipped with a weight structure
$$\begin{aligned} (\mathrm{DM}(X)^{\mathrm{w}\le 0}, \mathrm{DM}(X)^{\mathrm{w}\ge 0}). \end{aligned}$$If X admits a regular model, \(1_X\) is in the heart \(\mathrm{DM}(X)^{\mathrm{w}= 0} = \mathrm{DM}(X)^{\mathrm{w}\le 0} \cap \mathrm{DM}(X)^{\mathrm{w}\ge 0}\) of this weight structure. Moreover, \(f^*\) and \(f_!\) are weight-left exact (preserve “\(\mathrm{w}\le 0\)”) while \(f_*\) and \(f^!\) are weight-right exact (preserve “\(\mathrm{w}\ge 0\)”).
-
(xiv)
Let \(\ell \) be a prime number different from \(p = \mathrm{char}k\). There is a \(\ell \)-adic realization functor
$$\begin{aligned} \rho _{\ell }:\mathrm{DM}(X) \rightarrow \mathrm{D}_{\acute{\mathrm{e}}\mathrm{t}}(X, {\mathbf{Q}_{\ell }}) := \mathrm{Ind}(\mathrm{D}^{\mathrm{b}}_{\mathrm{cons}}(X, {\mathbf{Q}_{\ell }})) \end{aligned}$$taking values in the ind-completion of the bounded derived category of constructible \({\mathbf{Q}_{\ell }}\)-adic étale sheaves constructed in [37, §A.3]. It commutes with the six functors
 .
.
Proof
(i) follows from Lemma 2.9 and the above-mentioned fact that \(f^*\) and \(f^!\) are equivalences for any finite radicial surjective map f [11, Proposition 2.1.9].
(ii) The prestack approach to \(\mathrm{DM}(X)\) yields \(\mathrm{DM}(X) \simeq \mathrm{DM}(X_0)\) by Corollary 2.6.
With (i) and (ii) in hand, the remaining statements mostly follow directly from the classical assertions for finite-type k-schemes, which for the large majority are due to Ayoub and Cisinski–Déglise and, for functoriality for non-separated maps and h-descent proven in [31, Theorem 2.1.13, Proposition 2.1.14]. We will use these classical properties below without further comment, and refer to [31, Synopsis 2.1.1] for a detailed list of references.
The equivalence (2.1) is immediate from Lemma 2.9 using invariance of \(\mathrm{DM}\) under finite radicial surjective maps (hence \(\mathrm{DM}\) is well-defined on the localization) and Corollary 2.6. The statements in (iii)–(vi), (x), (xi) are then direct consequences of the corresponding assertions for finite type k-schemes.
For (vii) note that the functoriality \(f_!\) and \(f^*\) and also the tensor product are induced, by definition, from \((f_0)_!\), \((f_0)_*\) and the tensor product on \(\mathrm{DM}(X_0)\) etc. Similarly for the internal Hom in (viii).
The purity equivalence in the case of a perfectly smooth map f follows from the smooth case and the étale descent property in (xii).
In the definition of \(\mathrm{D}_X\) as stated in (2.3), note that the pullback functor \(p^!\) exists by virtue of the general formalism of motives on prestacks. Under the equivalence \(\mathrm{DM}(X) = \mathrm{DM}(X_0)\), it can also be computed as \(\underline{\mathrm{Hom}}(-, p_0^! 1)\), where \(p_0 : X_0 \rightarrow k\) is the structural map. This again reduces all the assertions to the classical duality statements for motives on finite type k-schemes.
In the situation of (ix), apply Lemma 2.9(iv) to get the localization fiber sequences (2.4), (2.5) from the corresponding statements for \(\mathrm{DM}\) on \(\mathrm{Sch}_k^{\mathrm{ft}}\) due to Ayoub. In the presence of the base change equivalence in (x), these fiber sequences are equivalent to the formulation involving the lax limit, cf. the argument in [1, Example 4.1.6].
For (xiii) note that X is separated iff it admits a separated model \(X_0\), so that the weight structure on \(\mathrm{DM}(X_0)\) can be used.
In the same vein, (xiv) follows from the equivalence (2.1) and its \(\ell \)-adic counterpart \(\mathrm{D}^{\mathrm{b}}_{\mathrm{cons}}(X) = \mathrm{D}^{\mathrm{b}}_{\mathrm{cons}}(X_0)\) [37, §A.3.1]. \(\square \)
2.4 Motives on perfect ind-schemes
As an extension of Definition 2.8, we consider the full subcategory \(\mathrm{IndSch}_k^{\mathrm{pfp}}\) of ordinary presheaves consisting of strict \(\aleph _0\)-ind-(pfp schemes), i.e., objects are countable filtered colimits of pfp schemes with transition maps being closed immersions. See for example [31, §A.1], or the notes [29, §1] for details on ind-schemes.
For brevity, the objects of \(\mathrm{IndSch}_k^{\mathrm{pfp}}\) are called ind-(pfp schemes). Similarly to [29, Lemma 1.10] one shows that this category has final object \(\mathrm{Spec}(k)\), is closed under fibre product and countable disjoint unions. As an example we note that if \(X=\mathrm{colim}X_i\) is an ind-scheme of ind-(finite type) over k, then the Zariski sheafification of the perfection \((X^{\mathrm{perf}})^{\mathrm{Zar}}=\mathrm{colim}\lim _{\sigma } X_i\) is an ind-(pfp scheme) by Remark 2.7. We have the following basic lemma.
Lemma 2.11
Every quasi-compact map between ind-(pfp schemes) is schematic and pfp.
Proof
Let \(X\rightarrow Y\) be a quasi-compact map of ind-(pfp schemes). Choosing a presentation \(Y={\text {colim}} Y_i\) by pfp schemes, it is enough to show that each \(X\times _YY_i\) is a pfp scheme. We reduce to the case where \(Y=Y_i\) is a pfp scheme, and in particular quasi-compact. By assumption \(X=\mathrm{colim}X_i\) is quasi-compact as well. Being an object in \(\mathrm{IndSch}_k^{\mathrm{pfp}}\) the underlying topological space \(|X|=\mathrm{colim}|X_i|\) is Jacobson. Hence, the sequence of reduced schemes \(X_{i}=X_{i,\mathrm{red}}\) stabilizes by [29, Corollary 1.24] which shows that \(X=X_i\), \(i>>0\) is a pfp scheme. \(\square \)
Theorem 2.12
Motives on ind-(pfp schemes) \(X \in \mathrm{IndSch}_k^{\mathrm{pfp}}\) satisfy the properties listed in Theorem 2.10, with the following adjustments:
-
The statement in (ii) has no analogue for ind-(pfp schemes), since they need not have models among ind-schemes of ind-(finite type).
-
The description of compact generators (cf. (vi) above) is as follows: the category \(\mathrm{DM}(X)\) is compactly generated by the images of the compact objects in \(\mathrm{DM}(X_i)\), where \(X = \mathrm{colim}X_i\) is a presentation.
-
The weight structure on \(\mathrm{DM}(X)\) exists if there is a presentation \(X = \mathrm{colim}X_i\), where the \(X_i \in \mathrm{Sch}_k^{\mathrm{pfp}}\) are separated.
-
The functor \(f^*\) exists (and satisfies the properties as stated in the remaining items) if f is quasi-compact (hence schematic and pfp).
-
If X is componentwise quasi-compact, then \(p^* 1\) is a monoidal unit, for the structural map \(p:X \rightarrow \mathrm{Spec}k\). In general, \(\mathrm{DM}(X)\) only carries a non-unital symmetric monoidal structure.
-
The condition that f has a smooth model (resp. is a pfp closed immersion, pfp open immersion) has to be replaced with “f has a schematic smooth model \(f_0\)” (has a model which is a schematic pfp closed, resp. open immersion). The h-covering in xii) has to be schematic. The term “proper” has to be replaced by “ind-(perfectly proper)” in (iv).
Proof
Recall from [31, Theorem 2.4.2] that the corresponding assertions hold for motives on ind-schemes. From there, the theorem as stated follows from Lemma 2.9, in the same way as the assertions for motives on pfp schemes follow from those on finite-type k-schemes. \(\square \)
3 Stratified Tate motives for perfect ind-schemes
With this convenient extension of the six functor formalism for the categories \(\mathrm{DM}\) of motives on pfp schemes and their ind-variants, we can quickly adapt the contents of [31, §§3–5].
Definition 3.1
A stratified ind-(pfp scheme) is a map of ind-(pfp schemes)
where \(\iota \) is bijective on the level of underlying sets, each \(X_w\) is a pfp scheme, each restriction \(\iota |_{X_w}\) is an immersion and the topological closure of each \(\iota (X_w)\) is a union of strata. Here W is a countable index set which is partially ordered by the closure relations on the strata, i.e., \(\iota (X_v)\) lies in the closure of \(\iota (X_w)\) if and only if \(v\le w\).
Since each \(X_w\) is pfp (hence quasi-compact), each restriction \(\iota |_{X_w}:X_w\rightarrow X\) is a quasi-compact map of ind-(pfp schemes) and hence schematic and pfp by Lemma 2.11. A map of stratified ind-(pfp schemes) is required to be quasi-compact (hence, again, schematic and pfp), and to map strata to strata.
Definition 3.2
A perfect cell is a k-scheme isomorphic to the perfection of a cell \(\mathbf{A}^n_k \times \mathbf{G} _{\mathrm{m}, {k}}^r\). A pfp scheme X is perfectly cellular if it admits a smooth model over k, and admits a stratification into perfect cells. (We do not require that the smooth model admits a stratification into cells.) A perfectly cellular stratified, or just pcs ind-scheme is a stratified ind-(pfp scheme) X where each \(X_w\), \(w\in W\) is a perfectly cellular k-scheme.
For a pfp scheme X, or a disjoint union of those, the category of Tate motives \(\mathrm{DTM}(X)\subset \mathrm{DM}(X)\) is the full subcategory generated under arbitrary shifts and colimits by \(1_X(n)\), \(n \in \mathbf{Z}\). By Theorem 2.10(ii), it is equivalent to \(\mathrm{DTM}(X_0)\) as defined in [31, Definition 3.1.8], where \(X_0\) is any model of X. Indeed, the equivalence \(\sigma ^!:\mathrm{DM}(X_0) \rightarrow \mathrm{DM}(X_0)\) restricts to an equivalence of the \(\mathrm{DTM}\)-subcategories by Theorem 2.10(ii).
For the next definition, we note that by quasi-compactness of \(\iota \) the pullback \(\iota ^*\) is well-defined, cf. Theorem 2.12.
Definition 3.3
A stratified ind-(pfp scheme) X is Whitney–Tate if \(\iota ^* \iota _*:\mathrm{DM}(X^+) \rightarrow \mathrm{DM}(X^+)\) preserves the subcategory \(\mathrm{DTM}(X^+)\), i.e., \((\iota _w)^* (\iota _v)_*\) induces \(\mathrm{DTM}(X_v)\rightarrow \mathrm{DTM}(X_w)\) for all \(v,w\in W\). In this case, the category of stratified Tate motives
is well-defined. Here the transition functors used to form the lax limit is \((\iota _w)^* (\iota _v)_*\). Since \(\mathrm{DM}(X)\) is equivalent to the lax limit of the categories \(\mathrm{DM}(X_w)\), the category \(\mathrm{DTM}(X, X^+)\) is a full subcategory of \(\mathrm{DM}(X)\). A map \(\pi \) between stratified ind-(pfp schemes) is a Whitney–Tate map if \(\pi _*\) preserves stratified Tate motives.
The characterization of Whitney–Tate stratifications in [31, Definition and Lemma 3.1.11] holds literally. Also the perfection of a cellular stratified k-scheme of finite type in the sense of [31, Definition 3.1.5] is pcs. Conversely, every pcs scheme \(\sqcup X_w\rightarrow X\) admits a model \(\sqcup X_{w,0}\rightarrow X_0\) where each \(X_{w,0}\) is smooth. We now show that the t-structures on the individual strata \(X_w\), which are induced from a model \(X_{w,0}\), glue together for any pcs (ind-)scheme.
Recall from [24] that the Beilinson–Soulé vanishing conjecture for k is equivalent to the existence of a t-structure on \(\mathrm{DTM}(\mathrm{Spec}k)\) such that \(1_{\mathrm{Spec}k}(r)\) is in the heart for all \(r \in \mathbf{Z}\). By Quillen’s work, this conjecture holds for \(k = \mathbf{F}_q\). By Harder’s work, it holds for a function field \(\mathbf{F}_q(t)\) and therefore, by the compatibility of algebraic K-theory with filtered colimits of rings, it also holds for its perfection \(k=\mathbf{F}_q(t)^{\mathrm{perf}}\).
Definition and Lemma 3.4
Suppose k satisfies the Beilinson–Soulé vanishing conjecture. Let X be a pcs Whitney–Tate ind-scheme over k. Then each \(\mathrm{DTM}(X_w)\) carries a unique t-structure such that \(1_{X_w}(n)[d_w]\), \(d_w:=\dim (X_w)\) is in the heart.
The subcategories
define a compactly generated t-structure on \(\mathrm{DTM}(X, X^+)\). The heart of this t-structure is denoted by \(\mathrm{MTM}(X, X^+)\) or just by \(\mathrm{MTM}(X)\) if the stratification is clear from the context.
Proof
By assumption there exists a finite stratification \(\sqcup _iX_w^{(i)}\rightarrow X_w\) into perfect cells. We may choose a model \(\sqcup _i X_{w,0}^{(i)}\rightarrow X_{w,0}\) where both source and target are smooth. (Here the schemes \(X_{w,0}^{(i)}\) are cells, but this map is only a stratification after perfection.) Then the first claim follows from [31, Lemma 3.2.4] using that the equivalence \(\mathrm{DTM}(X_w) = \mathrm{DTM}(X_{w,0})\) in Theorem 2.10(ii) commutes with the six functors (by construction). The second statement is also shown similarly as in op. cit.: for any \(w \in W\), the t-structure on \(\mathrm{DTM}(X_{\le w}, X^+)^{\mathrm{c}}\) arises by glueing the t-structures on the strata \(X_v\), \(v \le w\). Given that the compact objects in \(\mathrm{DM}(X,X^+)\) are supported on some finite union of \(X_{\le w}\), this gives a t-structure on \(\mathrm{DTM}(X,X^+)^{\mathrm{c}}\) and therefore a compactly generated t-structure on \(\mathrm{DTM}(X,X^+)\). \(\square \)
Restricting the \(\ell \)-adic realization functor to Tate motives continues to have the pleasant properties—such as conservativity and faithfulness—we know from the case of cellular Whitney–Tate stratified ind-schemes. The proof of the following statement is a verbatim copy of [31, Lemma 3.2.8] and [30, Corollary 2.20].
Proposition 3.5
Let X be a pcs Whitney–Tate ind-scheme over k and suppose that k satisfies the Beilinson–Soulé vanishing conjecture. The restriction of the \(\ell \)-adic realization functor \(\rho _{\ell }\) from \(\mathrm{DM}(X)\) to \(\mathrm{DTM}(X) := \mathrm{DTM}(X, X^+)\) has the following properties:
-
(i)
it is conservative,
-
(ii)
it creates the motivic t-structure in the sense that \(M \in \mathrm{DTM}(X)^{\mathrm{c}}\) is in positive (resp. negative) degrees of the motivic t-structure iff \(\rho _{\ell }(M)\) has the corresponding property for the perverse t-structure. In particular, it restricts to a functor
$$\begin{aligned} \rho _{\ell }:\mathrm{MTM}(X)^{\mathrm{c}} \rightarrow \mathrm{Perv}(X, {\mathbf{Q}_{\ell }}). \end{aligned}$$(3.1)Furthermore, this latter functor is faithful.
4 Motives on Witt vector affine flag varieties
Let \(K/{\mathbf{Q}}_p\) be a finite extension with uniformizer \(\varpi \in {\mathcal {O}}_K\) and residue field \(k/\mathbf{F}_p\). Let G be a split reductive group over \({\mathcal {O}}_K\). In this section, we introduce Tate motives on the Witt vector affine flag varieties for G and prove basic properties thereof.
4.1 Loop groups and their affine flag varieties
For any k-algebra R, we denote by \(W_{{\mathcal {O}}_K}(R)\) the ring of ramified Witt vectors, cf. e.g. [18, §1.2]. If R is perfect, then
where \(W(k)\rightarrow {\mathcal {O}}_K\) is the unique map, and where \([\cdot ]:R\rightarrow W(R)\) is the Teichmüller lift. The (Witt vector) loop group is the group-valued functor on the category of perfect k-algebras given by
For any smooth, affine \({\mathcal {O}}_K\)-group scheme \({\mathcal {G}}\), the Witt vector positive loop group is the group-valued functor on the category of perfect k-algebras given by
If \({\mathcal {G}}\otimes K=G\otimes K\), then \(L^+{\mathcal {G}}\subset LG\) defines a closed subgroup functor, cf. [37, Lemma 1.2 (i)]. Being presheaves on \(\mathrm{AffSch}^{\mathrm{perf}}_k\), LG and \(L^+ {\mathcal {G}}\) are also perfect prestacks, so that we can consider categories such as \(\mathrm{DM}(LG)\) etc.
Fix a Borel pair \(T\subset B\) in G over \({\mathcal {O}}_K\). Denote by \({\mathscr {A}}={\mathscr {A}}(G,T,K)\) the associated apartment of the Bruhat–Tits building of G(K) equipped with the base point 0 corresponding to \(G/{\mathcal {O}}_K\). The choice of B induces a unique alcove \(\mathbf{a }_0\subset {\mathscr {A}}\) in the dominant chamber whose closure contains 0. For each facet \(\mathbf{f }\subset {\mathscr {A}}\), there is a parahoric group scheme \({\mathcal {G}}_{\mathbf{f }}\) over \({\mathcal {O}}_K\) with generic fibre \(G\otimes K\) by [10, §5.2]. Recall that \({\mathcal {G}}_{\mathbf{f }}\) is a smooth, affine \({\mathcal {O}}_K\)-group scheme with connected fibers such that \({\mathcal {G}}_{\mathbf{f }}({\mathcal {O}}_K)\subset G(K)\) fixes \(\mathbf{f }\) pointwise.
Lemma 4.1
-
(i)
The functor LG is representable by a group ind-(perfect affine scheme).
-
(ii)
For every smooth, affine \({\mathcal {O}}_K\)-group scheme \({\mathcal {G}}\), the functor \(L^+{\mathcal {G}}=\lim _{i\ge 0}{\mathcal {G}}_{i}\) is representable by the perfection of an inverse system of smooth, affine group schemes with smooth, surjective transition maps. For each \(i\ge 0\), the kernel \(\ker ({\mathcal {G}}_{i+1}\rightarrow {\mathcal {G}}_{i})\) is the perfection of a vector group. In particular, every \(L^+{\mathcal {G}}\)-torsor in the fpqc-topology admits sections étale locally. If \({\mathcal {G}}={\mathcal {G}}_{\mathbf{f }}\) for some facet \(\mathbf{f }\subset {\mathscr {A}}\), then each \({\mathcal {G}}_{i}={\mathcal {G}}_{\mathbf{f },i}\) is moreover the perfection of a cellular k-scheme, i.e., the perfection of a smooth (finite type) k-scheme which can be stratified by pieces isomorphic to \(\mathbf{A}^r_k \times \mathbf{G} _{\mathrm{m}, {k}}^s\).
Proof
For the representability statements see [9, Proposition 9.2], and the references cited therein. For the étale local triviality, we note that \(L^+{\mathcal {G}}\) is already representable as a functor on the category of all k-algebras by the same formula by Greenberg [22] (cf. also [37, §1.1.1], [9, Remark 9.3]). It is the perfection of the pro-algebraic group \(\lim _{i\ge 0}{\mathcal {H}}_i\) where \({\mathcal {H}}_i:R\mapsto {\mathcal {G}}(W_{{\mathcal {O}}_K}(R)/V_{\varpi }^iW_{{\mathcal {O}}_K}(R))\) and \(V_{\varpi }\) denotes the Verschiebung on the ramified Witt vectors. Consequently, \(L^+{\mathcal {G}}=\lim _{i\ge 0}{\mathcal {G}}_i\) where \({\mathcal {G}}_i={\mathcal {H}}_i^{\mathrm{perf}}\). For any k-algebra R, there is a short exact sequence
By [31, Proposition A.4.9] we have \({\mathbb {V}}({\mathcal {E}}_i)=\ker ({\mathcal {H}}_{i+1}\rightarrow {\mathcal {H}}_{i})\) where \({\mathcal {E}}_i\) is the vector space given by the formula [31, (A.4.11)] applied with \(X=\mathrm{Spec}(W_{{\mathcal {O}}_K}(R))\), \(\hat{D}=\mathrm{colim}_{i\ge 0}D_i\) for \(D_i=\mathrm{Spec}(W_{{\mathcal {O}}_K}(R)/V_{\varpi }^i W_{{\mathcal {O}}_K}(R))\). Restricting back to perfect k-algebras, we see that \({\mathbb {V}}({\mathcal {E}}_i)^{\mathrm{perf}}=\ker ({\mathcal {G}}_{i+1}\rightarrow {\mathcal {G}}_{i})\) is the perfection of a vector group. Now by [37, Lemma A.9] a torsor under \({\mathcal {G}}_i={\mathcal {H}}_i^{\mathrm{perf}}\) is trivial if and only if its pushout along \({\mathcal {G}}_i\rightarrow {\mathcal {H}}_i\) is trivial. In particular, each \({\mathcal {G}}_i\)-torsor is étale locally trivial, and each affine \(\ker ({\mathcal {G}}_{i+1}\rightarrow {\mathcal {G}}_{i})\)-torsor is trivial. Thus, [31, Lemma A.4.3, Corollary A.4.8] applies to show that each fpqc-\(L^+{\mathcal {G}}\)-torsor is étale locally trivial. Finally, let \({\mathcal {G}}={\mathcal {G}}_{\mathbf{f }}\) for some facet \(\mathbf{f }\). By the same argument as in [31, Lemma 4.2.7] each \({\mathcal {H}}_{\mathbf{f },i}\) is cellular, and thus \({\mathcal {G}}_{\mathbf{f },i} ={\mathcal {H}}_{\mathbf{f },i}^{\mathrm{perf}}\) is perfectly cellular. \(\square \)
For any facet \(\mathbf{f }\subset {\mathscr {A}}\), we denote by \({\mathcal {P}}_{\mathbf{f }}:=L^+{\mathcal {G}}_{\mathbf{f }}\subset LG\) the associated parahoric subgroup. The Iwahori subgroup is denoted \({\mathcal {B}}:={\mathcal {P}}_{\mathbf{a }_0}\), and the positive loop group is denoted \(L^+G:={\mathcal {P}}_{\{0\}}\).
Definition 4.2
The Witt vector (partial) affine flag variety is the étale sheaf quotient
i.e., the étale sheaf associated with the (ordinary) presheaf \(LG/{\mathcal {P}}_{\mathbf{f }}\) in \(\mathrm{PreStk}_k^{\mathrm{perf}}\).
By Lemma 4.1, the étale sheaf \(\mathrm{Fl}_{\mathbf{f }}\) is an fpqc sheaf, so the definition agrees with [37, §1.1.2] and [9, Definition 9.4]. In particular, it is representable by an ind-scheme \(\mathrm{Fl}_{\mathbf{f }}=\mathrm{colim}_i X_i\) where each \(X_i\) is the perfection of a projective k-scheme [9, Corollary 9.6]. In particular, it is a strict ind-(pfp scheme) over k.
Now fix two facets \(\mathbf{f },\mathbf{f }'\subset {\mathscr {A}}\) contained in the closure of the base alcove. The definitions and arguments in [31, §4] translate (almost) literally: the left action of \({\mathcal {P}}_{\mathbf{f }'}\) on \(\mathrm{Fl}_{\mathbf{f }}\) induces a presentation
where w ranges through the double quotient \(W_{\mathbf{f }'}\backslash W/W_{\mathbf{f }}\) of the Iwahori–Weyl group by the reflection subgroups associated with the facets, defined analogously to [31, (4.2.9)]. Here the Schubert varieties \(\mathrm{Fl}_{\mathbf{f }, \le w}\) are defined as the scheme-theoretic image of the orbit map \({\mathcal {P}}_{\mathbf{f }'}\rightarrow \mathrm{Fl}_{\mathbf{f }}, p'\mapsto p'\cdot \dot{w}\cdot e\) analogously to [31, Definition 4.4.1]. Then each \(\mathrm{Fl}_{\mathbf{f },\le w}\) is the perfection of a projective k-variety by [9, Corollary 9.6]. The étale sheaf image \(\mathrm{Fl}_{\mathbf{f },w}\subset \mathrm{Fl}_{\mathbf{f }, \le w}\) of the orbit map is representable by the perfection of a smooth k-variety, and identifies with the étale sheaf quotient \({\mathcal {P}}_{\mathbf{f }'}/{\mathcal {P}}_{\mathbf{f }'\cup w\mathbf{f }}\) (combine the argument of [31, Lemma 4.3.7] with [37, Proposition A.32].) Here \({\mathcal {P}}_{\mathbf{f }'\cup w\mathbf{f }}:=L^+{\mathcal {G}}_{\mathbf{f }'\cup w\mathbf{f }}\) where \({\mathcal {G}}_{\mathbf{f }'\cup w\mathbf{f }}\) is the Bruhat-Tits \({\mathcal {O}}_K\)-group scheme with geometrically connected fibers determined by the subset \({\mathbf{f }'\cup w\mathbf{f }}\subset {\mathscr {A}}\).
There is a stratification
where the closure relations of the strata are given by the Bruhat order on \(W_{\mathbf{f }'}\backslash W/W_{\mathbf{f }}\). This follows from the existence of Demazure resolutions [37, (1.4.1)] using the method in [28, Proposition 2.8]. If \(\mathbf{f }'=\mathbf{a }_0\), we refer to this stratification as the Iwahori stratification. We summarize important properties in the following lemma.
Lemma 4.3
Let \(\mathbf{f },\mathbf{f }'\subset {\mathscr {A}}\) be contained in the closure of the base alcove.
-
(i)
The stratification (4.2) is a pcs stratification in the sense of Definition 3.2.
-
(ii)
The stabilizers of the \({\mathcal {P}}_{\mathbf{f }'}\)-left action on \(\mathrm{Fl}_{\mathbf{f }}\) are geometrically connected.
-
(iii)
If \({\mathcal {P}}_{\mathbf{f }'}\subset {\mathcal {P}}_{\mathbf{f }}\), the projection \(\pi :\mathrm{Fl}_{\mathbf{f }'}\rightarrow \mathrm{Fl}_{\mathbf{f }}\) is schematic, perfectly proper, and étale locally on the target isomorphic to the projection \({\mathcal {P}}_{\mathbf{f }}/{\mathcal {P}}_{\mathbf{f }'}\times \mathrm{Fl}_{\mathbf{f }}\rightarrow \mathrm{Fl}_{\mathbf{f }}\). The induced map on the Iwahori strata \(\pi ^+:\mathrm{Fl}_{\mathbf{f }'}^+\rightarrow \mathrm{Fl}_{\mathbf{f }}^+\) is a Whitney–Tate map and admits a section \(s^+:\mathrm{Fl}_{\mathbf{f }}^+\rightarrow \mathrm{Fl}_{\mathbf{f }'}^+\) which is an open and closed immersion.
-
(iv)
In iii), the étale quotient \({\mathcal {P}}_{\mathbf{f }}/{\mathcal {P}}_{\mathbf{f }'}\) is the perfection of an homogenous space.
Proof
Part (i) follows from the discussion above, and the following observation: For each \(w\in W_{\mathbf{f }'}\backslash W/W_{\mathbf{f }}\), we have the Iwahori stratification \({\mathrm{Fl}}{_{\mathbf{f },w}} = \bigsqcup _{v} {}^{\mathbf{a }_0}{\mathrm{Fl}}{_{\mathbf{f },v}}\), where v runs through \(W_{\mathbf{f }'}wW_{\mathbf{f }}/W_{\mathbf{f }}\), cf. [37, §1.4]. Each Iwahori orbit \({}^{\mathbf{a }_0}{\mathrm{Fl}}{_{\mathbf{f },v}}\) is isomorphic to \(({\mathbf{A}}^{l(v)}_k)^{\mathrm{perf}}\) where l(v) is the length in \(W/W_{\mathbf{f }}\). This is proven as in [31, (4.3.10)], but working with perfections everywhere: for each affine root \(\alpha \), there is a root subgroup \(U_{\alpha }\subset LG\), \(U_{\alpha }\simeq ({\mathbf{A}}^1_k)^{\mathrm{perf}}\), and an isomorphism

where the product (taken in any order) ranges over all affine roots \(\alpha \) such that \((w\alpha )|_{\mathbf{a }_0}\) takes positive values and \(\alpha |_{\mathbf{f }}\) takes negative values. Part (ii) follows from the presentation \({\mathrm{Fl}}{_{\mathbf{f },w}}={\mathcal {P}}_{\mathbf{f }}/{\mathcal {P}}_{\mathbf{f }'\cup w\mathbf{f }}\) and the geometrical connectedness of \({\mathcal {P}}_{\mathbf{f }'\cup w\mathbf{f }}\) explained above. Part (iii) is proven analogously to [31, Proposition 4.3.13]; note that \(s^+\) is open since it is an inclusion of a disjoint union of certain Iwahori strata. For (iv), let \({\mathcal {P}}_{\mathbf{f },0}={\mathcal {H}}_0^{\mathrm{perf}}\), \({\mathcal {P}}_{\mathbf{f }',0}=({\mathcal {H}}_0')^{\mathrm{perf}}\) be the Greenberg realization as in the proof of Lemma 4.1. Let \(\bar{{\mathcal {P}}}_{\mathbf{f }',0}=\mathrm{im}({\mathcal {P}}_{\mathbf{f }',0}\rightarrow {\mathcal {P}}_{\mathbf{f },0})\), and let \(\bar{{\mathcal {H}}}_0'=\mathrm{im}({\mathcal {H}}_0'\rightarrow {\mathcal {H}}_0)\) which is a parabolic subgroup of \({\mathcal {H}}_0\). Then on étale quotients
For the second isomorphism, we use that these étale quotients are already fpqc sheaves, and that taking perfections preserves faithfully flat maps [9, Lemma 3.4 (xii)], hence \(\bar{{\mathcal {P}}}_{\mathbf{f }',0}\cong (\bar{{\mathcal {H}}}_0')^{\mathrm{perf}}\). See also [7, Theorem 6.1]. \(\square \)
Example 4.4
Let \(s\in {\mathbb {S}}\) be a simple affine reflection. Let \(\mathbf{f }_s\) be the unique facet of maximal dimension in the closure of \(\mathbf{a }_0\) such that \(s(\mathbf{f }_s)=\mathbf{f }_s\), i.e., \(W_{\mathbf{f }_s}\) is the subgroup of W generated by s. We specialize Lemma 4.3(iii) to the case \(\mathbf{f }'=\mathbf{a }_0\), and \(\mathbf{f }=\mathbf{f }_s\), so that \(\pi :\mathrm{Fl}:=\mathrm{Fl}_{\mathbf{a }_0}\rightarrow \mathrm{Fl}_{\mathbf{f }_s}\) is the projection from the full affine flag variety. In this case, \(\pi \) has general fiber \({\mathcal {P}}_{\mathbf{f }_s}/{\mathcal {B}}=\lim _{\sigma }{} \mathbf{P} _{k}^{1}\) by Lemma 4.3(iv) (cf. also [37, above (1.4.1)]). If \(w\in W\), and \(w=v\cdot s\) is a reduced decomposition, then
Here \(\pi ^+|_{\mathrm{Fl}_v}\) is an isomorphism, and \(\pi ^+|_{\mathrm{Fl}_{vs}}\) is isomorphic to the projection \(({\mathbf{A}}^1_k)^{\mathrm{perf}}\times \mathrm{Fl}_v\rightarrow \mathrm{Fl}_v\).
4.2 Motives on affine flag varieties
All results from [31, §§5.1–5.3] except [31, Corollary 5.3.6] (there seems to be no such \(\mathbf{G} _{\mathrm{m}}\)-action on Witt vector loop groups) translate to the setting of Witt vector affine flag varieties. For the purposes of this paper, the salient features are as follows:
Theorem 4.5
Let \(\mathbf{f },\mathbf{f }'\subset {\mathscr {A}}\) be contained in the closure of the base alcove.
-
(i)
The pcs stratification (4.2) into \({\mathcal {P}}_{\mathbf{f }'}\)-orbits on \(\mathrm{Fl}_{\mathbf{f }}\) is Whitney–Tate. In particular, by Definition 3.3 and Lemma 3.4 there are well-defined categories of motives
$$\begin{aligned} \mathrm{MTM}(\mathrm{Fl}_{\mathbf{f }})\;\subset \; \mathrm{DTM}(\mathrm{Fl}_{\mathbf{f }})\;\subset \; \mathrm{DM}(\mathrm{Fl}_{\mathbf{f }}). \end{aligned}$$The \({\mathbf{Q}}\)-linear abelian category \(\mathrm{MTM}(\mathrm{Fl}_{\mathbf{f }})\) is generated (by means of extensions and direct sums) by the simple objects called intersection motives
$$\begin{aligned} \mathrm{IC}_w(n) := (\iota _w)_{!*} (1 (n)) \end{aligned}$$for \(n\in \mathbf{Z}\), \(w\in W_{\mathbf{f }'}\backslash W/W_{\mathbf{f }}\). These objects are defined as the Tate twists of intermediate extensions along the inclusions \(\iota _w : \mathrm{Fl}_{\mathbf{f },w} \rightarrow \mathrm{Fl}_{\mathbf{f }}\). (Note that the dependency of the categories \(\mathrm{DTM}(\mathrm{Fl}_{\mathbf{f }})\) and \(\mathrm{MTM}(\mathrm{Fl}_{\mathbf{f }})\) on the choice of \(\mathbf{f }'\) is suppressed in the notation.)
-
(ii)
Let \(\ell \) be a prime number \(\ne p\). The \(\ell \)-adic realization functor \(\rho _{\ell }\) (cf. (3.1)) maps \(\mathrm{IC}_w(n)\) to the \(\ell \)-adic intersection complexes on the Schubert varieties \(\mathrm{Fl}_{\mathbf{f }, \le w}\). A compact object \(M\in \mathrm{DTM}(\mathrm{Fl}_{\mathbf{f }})^{\mathrm{c}}\) lies in \(\mathrm{MTM}(\mathrm{Fl}_{\mathbf{f }})^{\mathrm{c}}\) iff \(\rho _{\ell }(M)\) is a perverse \(\ell \)-adic sheaf.
Proof
The proofs in [31, §§5.1–5.3] carry over literally, as we briefly indicate. The Whitney–Tate property is shown in three steps: First, for \(\mathbf{f }' = \mathbf{f }=\mathbf{a }_0\), the Whitney–Tate condition in (i) is a consequence of the geometric properties listed in Example 4.4 together with an induction on the length of w. Second, the case \(\mathbf{f }' = \mathbf{a }_0\) and arbitrary \(\mathbf{f }\) follows from a general criterion [31, Lemma 3.1.19] that allows to carry over the Whitney–Tate property along the projection map \(\mathrm{Fl}_{\mathbf{a }_0} \rightarrow \mathrm{Fl}_{\mathbf{f }}\), using the geometric properties of this map listed in Lemma 4.3(iii). Third, for both \(\mathbf{f }, \mathbf{f }'\) arbitrary, we use [31, Proposition 3.1.23]: a \({\mathcal {P}}_{\mathbf{f }}\)-equivariant motive is Tate with respect to the stratification by \({\mathcal {P}}_{\mathbf{f }}\)-orbits as soon as it is Tate with respect to the finer stratification by Iwahori-orbits (i.e. \({\mathcal {P}}_{\mathbf{a }_0}\)-orbits). This latter property holds by the second step.
The category \(\mathrm{DTM}(\mathrm{Fl}_{\mathbf{f },w})\) of (unstratified) Tate motives on the strata \(\mathrm{Fl}_{\mathbf{f },w}\) carries a t-structure whose heart \(\mathrm{MTM}(\mathrm{Fl}_{\mathbf{f },w})\) is an abelian category whose simple objects are of the form \(1(n)[\dim \mathrm{Fl}_{\mathbf{f },w}]\) (Lemma 3.4). These t-structures are glued together, as is classical in the context of perverse sheaves [4, §1.4]; see also [34, Theorem 10.3] for an application of this idea in the context of stratified Tate motives.
The description of the simple generators then follows from the description of the simple generators in the categories that are glued together [31, Theorem 5.2.3].
ii) is then a direct consequence of Proposition 3.5. \(\square \)
Theorem 4.6
-
(i)
The full subcategories of \(\mathrm{DM}({\mathcal {P}}_{\mathbf{f }'}\backslash LG/{\mathcal {P}}_{\mathbf{f }})\),
$$\begin{aligned} \mathrm{DM}({\mathcal {P}}_{\mathbf{f }'}\backslash LG/{\mathcal {P}}_{\mathbf{f }}) \times _{\mathrm{DM}(\mathrm{Fl}_{\mathbf{f }})} \mathrm{DTM}(\mathrm{Fl}_{\mathbf{f }}) \;\;\;\text {and}\;\;\; \mathrm{DM}({\mathcal {P}}_{\mathbf{f }'}\backslash LG/{\mathcal {P}}_{\mathbf{f }}) \times _{\mathrm{DM}(\mathrm{Fl}^{\mathrm{op}}_{\mathbf{f }'})} \mathrm{DTM}(\mathrm{Fl}^{\mathrm{op}}_{\mathbf{f }'}) \end{aligned}$$agree where \(\mathrm{Fl}^{\mathrm{op}}_{\mathbf{f }'} := ({\mathcal {P}}_{\mathbf{f }} \backslash LG)^{\acute{\mathrm{e}}\mathrm{t}}\). (For example, the first category consists of those motives on \({\mathcal {P}}_{\mathbf{f }'}\backslash LG/{\mathcal {P}}_{\mathbf{f }}\) whose underlying, i.e., non-equivariant motive on \(\mathrm{Fl}_{\mathbf{f }}\) is a stratified Tate motive with respect to the stratification by \({\mathcal {P}}_{\mathbf{f }'}\)-orbits.) This category is denoted \(\mathrm{DTM}({\mathcal {P}}_{\mathbf{f }'}\backslash LG/{\mathcal {P}}_{\mathbf{f }})\).
-
(ii)
For \(\mathbf{f }=\mathbf{f }'\), there is a t-structure on \(\mathrm{DTM}({\mathcal {P}}_{\mathbf{f }'}\backslash LG/{\mathcal {P}}_{\mathbf{f }})\) such that the forgetful functors to \(\mathrm{DTM}(\mathrm{Fl}_{\mathbf{f }})\) (and also to \(\mathrm{DTM}(\mathrm{Fl}^{\mathrm{op}}_{\mathbf{f }})\)) are t-exact. The heart of this t-structure is the category of mixed Tate motives on the double quotient, denoted \(\mathrm{MTM}({\mathcal {P}}_{\mathbf{f }'}\backslash LG/{\mathcal {P}}_{\mathbf{f }})\). The functor forgetting the \({\mathcal {P}}_{\mathbf{f }}\)-equivariance of a mixed Tate motive,
$$\begin{aligned} \mathrm{MTM}({\mathcal {P}}_{\mathbf{f }}\backslash LG/{\mathcal {P}}_{\mathbf{f }})\rightarrow \mathrm{MTM}(\mathrm{Fl}_{\mathbf{f }}), \end{aligned}$$is fully faithful, and induces a bijection of isomorphism classes of simple objects as described in Theorem 4.5(i).
Proof
(i) is shown by exhibiting an explicit set of generators, in the same way as in [31, Theorem 5.3.4]. (ii) The t-structure on \(\mathrm{DTM}({\mathcal {P}}_{\mathbf{f }'}\backslash LG/{\mathcal {P}}_{\mathbf{f }})\) is an instance of a t-structure on a limit of a diagram of stable \(\infty \)-categories equipped with t-structures and t-exact transition functors [31, Lemma 3.2.18]. For \(\mathbf{f }=\mathbf{f }'\) (but not in general, because of the shift by the dimension of \(\mathrm{Fl}_{\mathbf{f }}^w\)), this t-structure is identical to the one obtained by using the underlying non-equivariant motive on \(\mathrm{Fl}_{\mathbf{f }}^{\mathrm{op}}\) [31, Theorem 5.3.4].
The full faithfulness of the forgetful functor is a general consequence of [31, Proposition 3.2.20]: the key point is that the stabilizers of the \({\mathcal {P}}_{\mathbf{f }}\)-action on \(\mathrm{Fl}_{\mathbf{f }}\) are connected by Lemma 4.3(ii) and that for the perfection of a connected algebraic group H, the pullback functor \(\mathrm{MTM}(X) \rightarrow \mathrm{MTM}(X \times H)\) is fully faithful [31, Lemma 3.2.12], which implies that the forgetful functor
is fully faithful as well. Finally, the intersection motives \(\mathrm{IC}_w(n)\) are \({\mathcal {P}}_{\mathbf{f }}\)-equivariant by construction and therefore also generate the subcategory \(\mathrm{MTM}({\mathcal {P}}_{\mathbf{f }}\backslash LG/{\mathcal {P}}_{\mathbf{f }})\subset \mathrm{MTM}(\mathrm{Fl}_{\mathbf{f }})\) (again, by means of extensions and direct sums). \(\square \)
4.3 The convolution product
In this section, we discuss the convolution product on the category \(\mathrm{MTM}({\mathcal {P}}_{\mathbf{f }} \backslash LG / {\mathcal {P}}_{\mathbf{f }})\) by indicating how the corresponding arguments in the equi-characteristic situation carry over to the case considered here.
We define the convolution product by the same formula as in [30, Definition 3.1]:
where p and m are the projection and multiplication maps:

As in [31, Proposition 2.4.4], the exterior product
is defined using that the kernels of \({\mathcal {P}}_{\mathbf{f }} \rightarrow {\mathcal {P}}_{\mathbf{f }, i}\) are perfectly split pro-unipotent (i.e., of the form \(\lim G_i\), where the underlying schemes of \(G_0\) and all of the \(\ker (G_{i+1} \rightarrow G_i)\) are perfections of vector groups, cf. the proof of Lemma 4.1) and the perfect homotopy invariance of \(\mathrm{DM}\) (Theorem 2.10(xi)). The pushforward \(m_!\) exists by Theorem 2.12 (and the descent of functoriality expressed in [31, Lemma 2.2.9]) since the multiplication map induces a schematic map of ind-schemes \(\mathrm{Fl}_{\mathbf{f }} \widetilde{\times }\mathrm{Fl}_{\mathbf{f }} := (LG \times ^{{\mathcal {P}}_{\mathbf{f }}} LG/{\mathcal {P}}_{\mathbf{f }})^{\acute{\mathrm{e}}\mathrm{t}} \rightarrow \mathrm{Fl}_{\mathbf{f }}\). Note that the convolution of two compact objects is again compact.
Remark 4.7
The exterior product for motives on \(\mathrm{Fl}_{\mathbf{f }}^{\mathrm{op}} / {\mathcal {P}}_{\mathbf{f }}\) can be used to define another convolution product functor. At least on the level of the homotopy categories \(\mathrm{Ho}(\mathrm{DM}({\mathcal {P}}_{\mathbf{f }} \backslash LG / {\mathcal {P}}_{\mathbf{f }}))\), these two functors are isomorphic as can be shown like in [30, Proposition 3.4], using that \(LG_{\le w} ={\mathcal {P}}_{\mathbf{f }} w {\mathcal {P}}_{\mathbf{f }}\) is perfectly placid, i.e., a countable filtered limit of affine pfp schemes whose transition maps are perfections of smooth maps.
Theorem 4.8
The convolution product \(\star \) has the following properties:
-
(i)
It is compatible with the convolution product defined in the \(\ell \)-adic situation [37, p. 432] under the \(\ell \)-adic realization functor \(\rho _{\ell }:\mathrm{DM}({\mathcal {P}}_{\mathbf{f }} \backslash LG / {\mathcal {P}}_{\mathbf{f }})^{\mathrm{c}} \rightarrow \mathrm{D}^{\mathrm{b}}_{\mathrm{cons}, {\mathcal {P}}_{\mathbf{f }}}(\mathrm{Fl}_{\mathbf{f }})\) (taking values in the bounded derived \({\mathcal {P}}_{\mathbf{f }}\)-equivariant category of constructible sheaves on \(\mathrm{Fl}_{\mathbf{f }}\)).
-
(ii)
It admits an associativity isomorphism.
-
(iii)
It preserves the subcategory \(\mathrm{DTM}({\mathcal {P}}_{\mathbf{f }} \backslash LG / {\mathcal {P}}_{\mathbf{f }}) \subset \mathrm{DM}({\mathcal {P}}_{\mathbf{f }} \backslash LG / {\mathcal {P}}_{\mathbf{f }})\). For \({\mathcal {P}}_{\mathbf{f }} = L^+ G\), it also preserves the abelian subcategory \(\mathrm{MTM}(L^+G \backslash LG / L^+G)\).
Proof
Part (i) holds since both convolution product functors are defined as the concatenation of the same functors (motivic, resp. \(\ell \)-adic) and Theorem 2.10(xiv). Part (ii) results from the base-change isomorphism for proper maps of ind-(pfp schemes) (cf. (2.6)) as in [30, Lemma 3.7].
For (iii), we review the key geometric arguments in case \({\mathcal {P}}_{\mathbf{f }}\) is the Iwahori group \({\mathcal {B}}\), and refer to [30, Proposition 3.26] for the reduction to this case and for further details concerning the case \({\mathcal {P}}_{\mathbf{f }} = {\mathcal {B}}\). Writing \(\iota _w : \mathrm{Fl}_w \rightarrow \mathrm{Fl}:= \mathrm{Fl}_{\mathbf{a }_0}\) for the inclusion of the stratum, the claim \((\iota _w)_! 1 \star (\iota _{w'})_! 1 \in \mathrm{DTM}(\mathrm{Fl})\) is first shown in case \(w=w'\) is a simple reflection s. In this case the map
is an isomorphism because it is a closed immersion of 2-dimensional irreducible perfectly proper schemes. There is a stratification of \(\mathrm{Fl}_{\le s} = \mathrm{Fl}_s \sqcup \mathrm{Fl}_e \cong (\mathbf{A}^1)^{\mathrm{perf}} \sqcup \mathrm{Spec}k\). Furthermore, the multiplication map \(\tilde{m} : \mathrm{Fl}_{\le s} \widetilde{\times }\mathrm{Fl}_{\le s} \rightarrow \mathrm{Fl}_{\le s}\) is a Whitney–Tate map with respect to the this stratification. This can be seen as in loc. cit., except that all the affine lines (intervening as strata) are replaced by their perfections. The second step uses the isomorphism (see loc. cit.) \(\mathrm{Fl}_w \widetilde{\times }\mathrm{Fl}_{w'} \rightarrow \mathrm{Fl}_{ww'}\) for \(w, w' \in W\) such that \(l(ww')=l(w)+l(w')\). This isomorphism is a consequence of (4.3) and Bruhat–Tits theory, applied to the Witt vector affine flag variety. The remaining steps (still for \({\mathcal {P}}_{\mathbf{f }} = {\mathcal {B}}\)) are then formal consequences.
The preservation of \(\mathrm{MTM}\) as stated holds because of the corresponding assertion in the \(\ell \)-adic case [37, Proposition 2.2] together with (i). Here we use Theorem 4.5(ii) to reduce to \(\ell \)-adic (perverse) sheaves. \(\square \)
5 The motivic Satake equivalence
We keep the notation from Sect. 4: \(K/{\mathbf{Q}}_p\) is a finite extension with ring of integers \({\mathcal {O}}_K\) and finite residue field \(k/\mathbf{F}_p\). Let G be a split reductive group over \({\mathcal {O}}_K\). Fix a maximal split torus contained in a Borel subgroup \(T\subset B\subset G\) over \({\mathcal {O}}_K\).
Let \(\widehat{G}\) denote the Langlands dual group over \(\mathbf{Q}\) formed with respect to the pair (T, B) and a fixed pinning \(X\in {\text {Lie}}(B)\). Recall that \((\widehat{G},\widehat{T}, \widehat{B}, \widehat{X})\) is a split reductive \(\mathbf{Q}\)-group scheme equipped with a pinning whose root datum is dual to the root datum of (G, T, B). Denote by \(\widehat{T}_{\mathrm{ad}}\) the image of \(\widehat{T}\) in the adjoint group \(\widehat{G}_{\mathrm{ad}}\). Via \(X_*(T)=X^*(\widehat{T})\), we can view the half-sum of the B-positive roots in G as a cocharacter \(\rho :\mathbf{G} _{\mathrm{m}, {\mathbf{Q}}}\rightarrow \widehat{T}_{\mathrm{ad}}\). Then \(\mathbf{G} _{\mathrm{m}, {\mathbf{Q}}}\) acts from the right on \(\widehat{G}\) via conjugation as \({\text {Ad}}_{\rho }:(g,\lambda )\mapsto \rho (\lambda )^{-1}g\rho (\lambda )\). This action preserves the pair \((\widehat{T}, \widehat{B})\).
Definition 5.1
The extended Langlands dual group is the \(\mathbf{Q}\)-group scheme \(\widehat{G}_1:=\widehat{G}\rtimes ^{{\text {Ad}}_{\rho }} \mathbf{G} _{\mathrm{m}, {\mathbf{Q}}}\) equipped with the pinning \((\widehat{T}_1, \widehat{B}_1, \widehat{X}_1)\).
Here \(\widehat{T}_1:=\widehat{T}\rtimes ^{{\text {Ad}}_{\rho }} \mathbf{G} _{\mathrm{m}, {\mathbf{Q}}}\subset \widehat{B}\rtimes ^{{\text {Ad}}_{\rho }}\mathbf{G} _{\mathrm{m}, {\mathbf{Q}}}=:\widehat{B}_1\) and \(\widehat{X}_1:=(\widehat{X}, 0)\) is the principal nilpotent element in \({\text {Lie}}(\widehat{B}_1)={\text {Lie}}(\widehat{B})\times \mathbf{G} _{\mathrm{a}, {\mathbf{Q}}}\). We note that \(\widehat{G}_1\) is a split reductive \({\overline{\mathbf{Q}}}\)-group scheme with split maximal torus \(\widehat{T}_1= \widehat{T}\times \mathbf{G} _{\mathrm{m}, {\mathbf{Q}}}\), since \({\text {Ad}}_{\rho }\) acts trivially on \(\widehat{T}\). One easily verifies that the map \((g, \lambda )\mapsto (g\cdot 2\rho (\lambda ),\lambda ^2)\) induces a short exact sequence of \({\overline{\mathbf{Q}}}\)-group schemes
where \({\varvec{\mu }}_2\) is generated by \((\epsilon , -1)\) with \(\epsilon :=(2\rho )(-1)\in \widehat{G}(\mathbf{Q})\). Thus \(\widehat{G}_1\) is the same as the group constructed in [19, §2] following [15], cf. also [6, Proposition 5.39 ff.] for further examples. We denote by \(d:\widehat{G}_1\rightarrow \mathbf{G} _{\mathrm{m}, {\mathbf{Q}}}/{\varvec{\mu }}_2\simeq \mathbf{G} _{\mathrm{m}, {\mathbf{Q}}}\) the character where the isomorphism is induced from the square map \(\lambda \mapsto \lambda ^2\). As an example take \(G={\text {PGL}}_2\) in which case \(\widehat{G}_1={\text {SL}}_2\times ^{{\varvec{\mu }}_2}\mathbf{G} _{\mathrm{m}, {\mathbf{Q}}}=\mathrm{GL}_2\), and the character d identifies with the determinant.
We write \(\mathrm{Rep}_{\mathbf{Q}}(\widehat{G}_1)\) for the category of algebraic \(\widehat{G}_{1}\)-representations on \(\mathbf{Q}\)-vector spaces. The subcategory \({\text {Rep}}_{\mathbf{Q}}^{{\text {fd}}} (\widehat{G}_1)\) of finite-dimensional representations is a semi-simple abelian category with (absolutely) simple objects
where \(\widehat{B}_1^{\mathrm{op}}\subset \widehat{G}_1\) denotes the Borel opposite to \(\widehat{B}_1\), and \(\mu _n:\widehat{B}_1^{\mathrm{op}}\rightarrow \widehat{T}_1\rightarrow \mathbf{G} _{\mathrm{m}, {\mathbf{Q}}}\) is the composition of the projection with the character \((\mu ,n)\in X_*(T)^+\times \mathbf{Z}=X^*(\widehat{T}_1)^+\). Note that the restriction of \(V_{\mu }(n)\) along \(\widehat{G}\times \mathbf{G} _{\mathrm{m}, {\mathbf{Q}}}\rightarrow \widehat{G}_1\) is the representation \(V_{\mu }\otimes d^{\otimes n}\) where \(V_{\mu }\) is the \(\widehat{G}\)-representation of highest weight \(\mu \).
Extending scalars from \(\mathbf{Q}\) to \({\overline{\mathbf{Q}}}\) we obtain the categories
of algebraic \(\widehat{G}_{1,{\overline{\mathbf{Q}}}}\)-representations on \({\overline{\mathbf{Q}}}\)-vector spaces which have the same simple objects (5.1).
The aim of this section is to prove the following theorem due to Zhu [37] in the context of \(\ell \)-adic sheaves and in the context of numerical motives [39, §2]. It will be stated and proven in a slightly sharper form in Theorem 5.7 and Remark 5.9 below.
Theorem 5.2
There is an equivalence of \({\overline{\mathbf{Q}}}\)-linear abelian tensor categories
under which \(\mathrm{IC}_{\mu }(n)\mapsto V_{\mu }(n)\) for all \(\mu \in X_*(T)^+\), \(n\in \mathbf{Z}\). For each prime number \(\ell \ne p\), this equivalence is compatible under the \(\ell \)-adic realization with the geometric Satake equivalence constructed in [37].
At the left hand side, \(\mathrm{MTM}\big (L^+G\backslash LG/L^+G\big )\) denotes the category of stratified mixed Tate motives on the loop group double quotient constructed in Theorems 4.5 and 4.6. The subscript \({\overline{\mathbf{Q}}}\) indicates that we consider this category with \({\overline{\mathbf{Q}}}\)-coefficients (as opposed to \(\mathbf{Q}\)-coefficients like in the preceding sections). The simple objects \(\mathrm{IC}_{\mu }(n)\), \(\mu \in X_*(T)^+\), \(n\in \mathbf{Z}\) are Tate twists of intersection cohomology motives of the Schubert varieties. We already know that the convolution product \(\star \) for motives on \(L^+G\backslash LG/L^+G\) preserves mixed Tate motives (Theorem 4.8). In order to prove the above theorem, we will perform the following steps: we show in Theorem 5.6 that
is a neutral Tannakian category. The fiber functor \(\omega \) is given by taking global motivic cohomology. We show that the Tannaka dual group is reductive by showing that the category is semi-simple (Proposition 5.3). This step relies on the Kazhdan–Lusztig parity vanishing and on the semisimplicity of \(\mathrm{MTM}(k)\). In particular, every object in \(\mathrm{MTM}\left( L^+G\backslash LG/L^+G\right) \) is a (possibly infinite) direct sum of \(\mathrm{IC}_{\mu }(n)\)’s. We further identify, at least over \({\overline{\mathbf{Q}}}\), the Tannaka dual group \(\widetilde{G}_1 := \mathrm{Aut}^{\star }(\omega )\) of \(\mathrm{MTM}\left( L^+G\backslash LG/L^+G\right) ^{\mathrm{c}}\) with \(\widehat{G}_1\), by relying on the \(\ell \)-adic Satake equivalence for the Witt vector affine Grassmannian due to Zhu. Once this is done, we obtain Theorem 5.2 by passing to ind-completions, cf. Remark 5.9.
5.1 Semisimplicity
The Witt vector affine Grassmannian \(\mathrm{Gr}_G=(LG/L^+G)^{\acute{\mathrm{e}}\mathrm{t}}\) admits a stratification by left \(L^+G\)-orbits which yields a presentation as ind-(perfectly proper pfp k-schemes) by Witt vector Schubert varieties:
Here \(\mu \) ranges of the partially ordered semigroup \(X_*(T)^+\) of B-dominant cocharacters. Recall that \(\mathrm{Gr}_{G,\le \lambda }\subset \mathrm{Gr}_{G,\le \mu }\) if and only if \(\lambda \le \mu \) in the dominance order, i.e., \(\mu -\lambda \) is a sum of positive coroots with non-negative integral coefficients. The dense open stratum \(\mathrm{Gr}_{G, \mu }\subset \mathrm{Gr}_{G,\le \mu }\) is an irreducible perfectly smooth pfp k-scheme of dimension \(\langle 2\rho ,\mu \rangle \). Here \(\rho \) denotes the half-sum of the positive roots in B and \(\langle \text {-},\text {-}\rangle \) is the natural pairing between the characters and cocharacters. In particular, the \(L^+G\)-orbit stratification satisfies the parity property
because \(\langle 2\rho ,\mu -\lambda \rangle =2\langle \rho ,\mu -\lambda \rangle \) is an even integer. Recall from Theorem 4.5 the abelian category \(\mathrm{MTM}(\mathrm{Gr}_G)\) of mixed stratified Tate motives with respect to the \(L^+G\)-orbit stratification. Its simple objects are the Tate twists of the intersection motives \(\mathrm{IC}_{\mu }(n)\), \(\mu \in X_*(T)^+\), \(n\in \mathbf{Z}\) of the Schubert varieties \(\mathrm{Gr}_{G,\le \mu }\). By Theorem 4.6 the forgetful functor
is fully faithful and yields a bijection on simple objects. The following proposition is analogous to [27, Proposition 2.1].
Proposition 5.3
The forgetful functor (5.4) is an equivalence of abelian categories. Both categories are semisimple with simple objects \(\mathrm{IC}_{\mu }(n)\), \(\mu \in X_*(T)^+\), \(n\in \mathbf{Z}\).
Proof
The argument follows closely [30, §5.1]. We outline the key steps for the reader’s convenience. If \(\mathrm{MTM}(\mathrm{Gr}_G)\) is semisimple, then \(\mathrm{MTM}(L^+G\backslash LG/L^+G)\) is semisimple as well by the full faithfulness of (5.4). In this case (5.4) is an equivalence because the simple objects agree.
To prove the semisimplicity of \(\mathrm{MTM}(\mathrm{Gr}_G)\) it is enough to show that all extensions between simple objects vanish, i.e., that
for all \(\lambda ,\mu \in X_*(T)^+\), \(m, n\in \mathbf{Z}\). By the conservativity and t-exactness of the \(\ell \)-adic realization (Proposition 3.5) and (5.3), the Kazhdan–Lustig parity vanishing holds, i.e.,
where \(A\in \mathrm{MTM}(\mathrm{Gr}_G)\) and \(\iota :X\subset \mathrm{Gr}_G\) is a finite union of Schubert varieties and where \({{}^{\mathrm{m}}\mathrm{H}}^i\) denotes the truncation with respect to the motivic t-structure on X. This formally implies
where we have used that \(\mathrm{MTM}(\mathrm{Gr}_{\mu })=\mathrm{MTM}(k)\), cf. the argument in [30, Lemma 6.3]. Finally, the higher algebraic K-groups of the finite field k are torsion (i.e., their rationalizations vanish), so that \(\mathrm{MTM}(k)\) is semisimple. This shows (5.5). \(\square \)
5.2 The tensor structure
By Theorem 4.8 the category \(\mathrm{MTM}(L^+G\backslash LG/ L^+G)\) is stable under the convolution product \(\star \) compatible with the \(\ell \)-adic realization, i.e., for each pair of such motives A, B, there is a functorial isomorphism of \(\ell \)-adic perverse sheaves
where
denotes the \(\ell \)-adic realization taking values in the category of \(L^+G\)-equivariant perverse \(\ell \)-adic sheaves on \(\mathrm{Gr}_G\) (cf. Theorem 4.8), and where \(\star _{\ell }\) denotes the convolution of \(\ell \)-adic complexes.
Proposition 5.4
The convolution product \(\star \) can be upgraded to a unique symmetric monoidal structure on \(\mathrm{MTM}(L^+ G \backslash LG / L^+ G)\) such that the \(\ell \)-adic realization functor
is a symmetric monoidal functor, where the target category carries the symmetric monoidal structure established in the geometric Satake equivalence [37, Proposition 2.21].
Proof
There exist functorial commutativity and associativity constraints
which are uniquely determined by the following two properties:
-
(i)
The isomorphisms are colimit-preserving in each argument.
-
(ii)
The constraints map under the \(\ell \)-adic realization (5.7) to the constraints used in geometric Satake as in [37, Proposition 2.21].
The uniqueness follows from the faithfulness of the \(\ell \)-adic realization (Proposition 3.5). The associativity constraint is constructed in Theorem 4.8. The construction of the (correct) commutativity constraint is the most subtle part and follows [37, §2.4.3]. For details the reader is referred to [30, Proposition 5.9]. Here we only sketch the main ideas. The anti-involution \(\theta :G\rightarrow G\) is defined by \(g\mapsto (g^*)^{-1}=(g^{-1})^*\), where \((\text {-})^*\) denotes the Cartan involution. By functoriality, we obtain an anti-involution on LG preserving \(L^+G\), and thus an equivalence of prestacks, still denoted
Then for \(A,B\in \mathrm{MTM}(L^+G\backslash LG/L^+G)\) we have a functorial isomorphism \(\theta ^!(A\star B)\cong (\theta ^!B)\star (\theta ^!A)\). Also we have a (carefully chosen) equivalence \(\theta ^!\simeq \mathrm{id}\) of endofunctors on \(\mathrm{MTM}(L^+G\backslash LG/L^+G)\). The point being that \(\theta \) preserves Schubert varieties and hence also intersection motives. However, to obtain the correct equivalence \(\theta ^!\simeq \mathrm{id}\) compatible with the \(\ell \)-adic realization one needs to introduce a carefully chosen sign, cf. the aforementioned references. Combining the above equivalences leads to the commutativity constraint \(c'_{A, B}:A\star B\cong B\star A\). We finally define
and extend it linearly to all objects in \(\mathrm{MTM}(L^+G\backslash LG/L^+G)\) using the semisimplicity, cf. Proposition 5.3. \(\square \)
5.3 The Tannakian structure
Next we equip the \({\mathbf{Q}}\)-linear, abelian, symmetric monoidal, semisimple category \((\mathrm{MTM}(L^+G\backslash LG/L^+G), \star )\) with a tensor functor valued in vector spaces \((\mathrm{Vect}_{{\mathbf{Q}}},\otimes )\) leading to the aforementioned Tannakian structure. Following [30, §5.3] we define the fibre functor as the composition
of the forgetful functor (which is an equivalence by Proposition 5.3; note that mixed Tate motives are with respect to the stratification by \(L^+ G\)-orbits), the pushforward along the structural map \(\epsilon :\mathrm{Gr}_G \rightarrow \mathrm{Spec}(k)\) (which preserves Tate motives by [31, Lemma 3.1.19], using that the stratification of \(\mathrm{Gr}_G\) by \(L^+G\)-orbits is perfectly cellular), followed by the grading functors for the classical (which agrees in this case with the motivic) t-structure \(\mathrm{gr}^{\mathrm{cl}}\) and the weight structure \(\mathrm{gr}^{\mathrm{W}}\), and finally the equivalence [24] of pure Tate motives of weight 0 with the category of \(\mathbf{Q}\)-vector spaces.
Lemma 5.5
The fibre functor \(\omega :\mathrm{MTM}(L^+G\backslash LG/L^+G)\rightarrow \mathrm{Vect}_{{\mathbf{Q}}}\) has a natural monoidal structure with respect to the convolution product on the source and the ordinary tensor product on the target which is compatible with the \(\ell \)-adic realization.
Proof
At least on the level of homotopy categories the composition of functors
has a natural monoidal structure with respect to convolution on the source and the tensor product on the target, cf. [30, Proposition 5.13] whose arguments translate literally. Next the conservativity of the \(\ell \)-adic realization implies the Kazdhan–Lusztig parity vanishing \({^{\mathrm{cl}}\mathrm{H}^i}(\epsilon _!\mathrm{IC}_{\mu }(n))=0\) whenever \(i\not \equiv \langle 2\rho ,\mu \rangle \mod 2\). Hence, the composition
admits a natural monoidal structure as well. The vanishing is needed in order to obtain a monoidal structure as opposed to a \(\mathbf{Z}/2\)-graded monoidal structure coming from a sign in the formation of tensor products of complexes. Using the natural monoidal structure on the weight graduation functor \(\mathrm{gr}^W\) we obtain a monoidal structure on \(\omega \). The compatibility with the \(\ell \)-adic realization follows from Theorem 2.10(xiv) and the fact that the \(\ell \)-adic fiber functor is defined by the analogous functors. \(\square \)
Theorem 5.6
The category \(\mathrm{MTM}(L^+G\backslash LG/L^+G)^{\mathrm{c}}\) of compact mixed Tate motives on the double quotient, endowed with the convolution product, the constraints from Proposition 5.4 and \(\omega \) as fibre functor is a neutral Tannakian category over \({\mathbf{Q}}\) [16, Chapter II, Definition 2.19].
Proof
Note that the restriction of \(\omega \) to compact objects takes values in finite-dimensional vector spaces. As in [30, Theorem 5.14] we check the conditions in [16, Chapter II, Proposition 1.20]:
-
(i)
The functor \(\omega \) has the structure of a tensor functor. This is Lemma 5.5.
-
(ii)
The functor \(\omega \) is \({\mathbf{Q}}\)-linear, exact and faithful. The functor \(\omega \) is clearly \(\mathbf{Q}\)-linear and additive. Hence, it is exact because \(\mathrm{MTM}(L^+G\backslash LG/L^+G)^{\mathrm{c}}\) is semi-simple. The faithfulness follows from the compatibility with the \(\ell \)-adic realization, the faithfulness of the latter, and the faithfulness of the \(\ell \)-adic fiber functor \(\omega _{\ell }\) [37, Corollary 2.10].
-
(iii)
The constraints constructed in Proposition 5.4give the usual constraints in \(\mathrm{Vect}_{\mathbf{Q}}\) after applying \(\omega \). This is immediate from Lemma 5.5 and the \(\ell \)-adic case, cf. [37, Proposition 2.21].
-
(iv)
Neutral object. This is the skyscraper \(\mathrm{IC}_0\) supported at the base point.
-
(v)
Any \(M\in \mathrm{MTM}(L^+G\backslash LG/L^+G)^{\mathrm{c}}\) with \(\dim _{{\mathbf{Q}}} \omega (M)=1\) admits a dual object \(M^{-1}\) such that \(M \star M^{-1} = \mathrm{IC}_0\). Any such object is necessarily of the form \(M=\mathrm{IC}_{\mu }\) with 0-dimensional support, in which case \(M^{-1}=\mathrm{IC}_{-\mu }\).
\(\square \)
5.4 The Tannakian group
Theorem 5.7
There is an equivalence of Tannakian categories

where the subscript \({\overline{\mathbf{Q}}}\) indicates the category with the same objects, but \(\mathrm{Hom}\)-spaces are tensored with \({\overline{\mathbf{Q}}}\). At the right, \(v:\mathrm{Rep}_{{\overline{\mathbf{Q}}}}^{{\text {fd}}}(\widehat{G}_1)\rightarrow {\text {Vec}}_{{\overline{\mathbf{Q}}}}\) denotes the forgetful functor. The intersection motives \(\mathrm{IC}_{\mu }(n)\) correspond to the simple \(\widehat{G}_1\)-representations \(V_{\mu }(n)\) for \((\mu ,n)\in X_*(T)^+\times \mathbf{Z}=X^*(\widehat{T}_1)^+\).
Proof
The argument is very similar to the proof of [30, Theorem 6.8]; it relies on the \(\ell \)-adic geometric Satake equivalence proven in [37]. Let us recall the key points. Denote by \(\widetilde{G}_1:=\mathrm{Aut}^{\star }(\omega )\) the affine \({\overline{\mathbf{Q}}}\)-group scheme of tensor automorphisms provided by Theorem 5.6. We need to prove an isomorphism \(\widetilde{G}_1\simeq \widehat{G}_1\) of \({\overline{\mathbf{Q}}}\)-group schemes.
For a prime number \(\ell \not \mid p\), the \(\ell \)-adic realization induces an equivalence of Tannakian categories
where \({\text {Sat}}_{G,\ell }\) denotes the full semi-simple subcategory of \(L^+G\)-equivariant \({\overline{\mathbf{Q}}}_{\ell }\)-adic perverse sheaves sheaves on \(\mathrm{Gr}_G\) generated by the Tate twisted intersection complexes \(\mathrm{IC}_{\mu ,\ell }(n)\), \(\mu \in X_*(T)^+\), \(n\in \mathbf{Z}\). The affine \({\overline{\mathbf{Q}}}\)-group scheme of tensor automorphisms \(\mathrm{Aut}^{\star }(\omega _{\ell })\) is isomorphic to \(\widehat{G}_1\otimes {\overline{\mathbf{Q}}}_{\ell }\) by the \(\ell \)-adic geometric Satake equivalence as in [37]. This reference is for the ordinary affine Grassmannian, but the arguments carry over to the case of Witt vectors, see also [39, §2]. Hence, (5.8) implies that there is an isomorphism of \({\overline{\mathbf{Q}}}_{\ell }\)-group schemes
for all prime numbers \(\ell \not \mid p\). In particular, \(\widetilde{G}_1\) is a reductive \({\overline{\mathbf{Q}}}\)-group scheme by fpqc descent along the extension \({\overline{\mathbf{Q}}}_{\ell }/{\overline{\mathbf{Q}}}\) for one fixed prime number \(\ell \not \mid p\). We conclude \(\widetilde{G}_1\simeq \widehat{G}_1\) by the isomorphism theorem for split reductive groups. \(\square \)
Remark 5.8
The relation with the classical Satake isomorphism [23] is as follows, cf. also [30, §6.4] for a detailed discussion in the (completely analogous) equal characteristic case. Consider the spherical Hecke ring
of functions \(G({\mathcal {O}}_K)\backslash G(K)/G({\mathcal {O}}_K)\rightarrow \mathbf{Z}\) supported on finitely many double cosets with ring structure given by the convolution product. Taking the trace of geometric Frobenius on motives as in [12] induces a surjective ring homomorphism from the Grothendieck ring
with kernel generated by the class \([\mathrm{IC}_0(-1)]-q[\mathrm{IC}_0]\) (the trace of geometric Frobenius on \({\overline{\mathbf{Q}}}(-1)\) is given by multiplication with q). Hence, under Theorem 5.7 the map \([\mathrm{IC}_{\mu }(n)]\mapsto [V_{\mu }(n)]\) induces an isomorphism of rings
where \(R(\widehat{G}_1)=K_0\mathrm{Rep}_{{\overline{\mathbf{Q}}}}^{{\text {fd}}} (\widehat{G}_1)\). This is immediate from the preceding discussion using \([V_0(-1)]=[d^{-1}]\) in \(R(\widehat{G}_1)\). Now choosing a square root \(q^{1/2}\in {\overline{\mathbf{Q}}}\) the composition gives the classical Satake isomorphism as in [23, Proposition 3.6, (3.12)],
where the last isomorphism is induced from \([V_{\mu }(0)]\mapsto q^{\langle \rho ,\mu \rangle }[V_{\mu }]\).
Remark 5.9
Theorem 5.7 implies Theorem 5.2 by passing to ind-completions. Indeed, the category of algebraic representations \(\mathrm{Rep}_{{\overline{\mathbf{Q}}}}(\widehat{G}_1)\) is compactly generated by its subcategory \(\mathrm{Rep}_{{\overline{\mathbf{Q}}}}^{{\text {fd}}}(\widehat{G}_1)\) of finite-dimensional representations. Similarly, \(\mathrm{MTM}(L^+G\backslash LG/L^+G)\) is compactly generated by \(\mathrm{MTM}(L^+G\backslash LG/L^+G)^{\mathrm{c}}\).
Remark 5.10
We expect that the analogue of Theorem 5.7 for \(\mathbf{Q}\)-coefficients (as opposed to \({\overline{\mathbf{Q}}}\)-coefficients) holds as well. For this, one needs to show that the Tannakian group \(\widetilde{G}_1=\mathrm{Aut}^{\star }(\omega )\) is \(\mathbf{Q}\)-split. It will then be automatically isomorphic to \(\widehat{G}_1\) by the isomorphism theorem. In order to obtain a more canonical identification \(\widetilde{G}_1\simeq \widehat{G}_1\) it would be interesting to construct constant term functors in this setting.
Also, we expect that Theorem 5.7 admits, similarly to [37], a generalization from split reductive groups to unramified reductive groups. For this a key input is the existence of motivic t-structures on categories of stratified Artin–Tate motives (as opposed to Tate motives). Here we expect the methods of [31, § 3] to carry over.
Notes
Recall that we fixed a regular cardinal \(\kappa \) in Sect. 2.1.
References
Arinkin, D., Gaitsgory, D.: The category of singularities as a crystal and global Springer fibers. J. Am. Math. Soc. 31(1), 135–214 (2018). https://doi.org/10.1090/jams/882
Ayoub, J.: Les six opérations de Grothendieck et le formalisme des cycles évanescents dans le monde motivique. I. Astérisque, (314):x+466 pp. (2008), 2007
Ayoub, J.: Les six opérations de Grothendieck et le formalisme des cycles évanescents dans le monde motivique. II. Astérisque, (315):vi+364 pp. (2008), 2007
Beĭlinson, A.A., Bernstein, J., Deligne, P.: Faisceaux pervers. In: Analysis and Topology on Singular Spaces, I (Luminy, 1981). Astérisque. vol. 100, pp. 5–171. Société mathématique de France, Paris (1982)
Beilinson, A., Drinfeld, V.: Quantization of Hitchin’s integrable system and Hecke eigensheaves (1999). http://www.math.utexas.edu/users/benzvi/Langlands.html
Buzzard, K., Gee, T.: The conjectural connections between automorphic representations and Galois representations. In: Automorphic Forms and Galois representations. London Mathematical Society Lecture Note Series 414. vol. 1, pp. 135–187. Cambridge University Press, Cambridge (2014). https://doi.org/10.1017/CBO9781107446335.006
Bertapelle, A., González-Avilés, C.D.: On the perfection of schemes. Expo. Math. 36(2), 197–220 (2018). https://doi.org/10.1016/j.exmath.2017.08.001
Bouthier, A., Kazhdan, D., Varshavsky, Y.: Perverse sheaves on infinite-dimensional stacks, and affine springer theory (2020). arXiv:2003.01428
Bhatt, B., Scholze, P.: Projectivity of the Witt vector affine Grassmannian. Invent. Math. 209(2), 329–423 (2017). https://doi.org/10.1007/s00222-016-0710-4
Bruhat, F., Tits, J.: Groupes réductifs sur un corps local. II. Schémas en groupes. Existence d’une donnée radicielle valuée. Inst. Hautes Études Sci. Publ. Math. (60):197–376 (1984). http://www.numdam.org/item?id=PMIHES_1984__60__5_0
Cisinski, D.-C., Déglise, F.: Triangulated Categories of Mixed Motives. Springer Monographs in Mathematics, Springer, Cham (2019). https://doi.org/10.1007/978-3-030-33242-6 . arXiv:0912.2110
Cisinski, D.-C.: Cohomological Methods in Intersection Theory (2019). arXiv:1905.03478
Cogdell, J.W.: Dual groups and Langlands functoriality. In: An Introduction to the Langlands Program (Jerusalem, 2001), pp. 251–268. Birkhäuser, Boston (2003)
Česnavičius, K., Scholze, P.: Purity for flat cohomology (2019). arXiv:1912.10932
Deligne, P.: Letter to Serre (2007). https://publications.ias.edu/sites/default/files/2007%20Serre_0.pdf
Deligne, P., Milne, J.S., Ogus, A., Shih, K.: Hodge Cycles, Motives, and Shimura Varieties. Lecture Notes in Mathematics, vol. 900. Springer, Berlin (1982)
Elmanto, E., Khan, A.A.: Perfection in motivic homotopy theory. Proc. Lond. Math. Soc. 120(1), 28–38 (2020). https://doi.org/10.1112/plms.12280. arXiv:1812.07506
Fargues, L., Fontaine, J.M.: Courbes et fibrés vectoriels en théorie de Hodge \(p\)-adique. Astérisque (406):xiii+382 (2018). With a preface by Pierre Colmez
Frenkel, E., Gross, B.: A rigid irregular connection on the projective line. Ann. Math. (2) 170(3), 1469–1512 (2009). https://doi.org/10.4007/annals.2009.170.1469
Gepner, D., Haugseng, R., Nikolaus, T.: Lax colimits and free fibrations in \(\infty \)-categories. Doc. Math. 22, 1225–1266 (2017)
Ginzburg, V.: Perverse sheaves on a Loop group and Langlands’ duality (2000). arXiv:9511007 [alg-geom]
Greenberg, M.J.: Schemata over local rings. Ann. Math. 2(73), 624–648 (1961). https://doi.org/10.2307/1970321
Gross, B.H.: On the Satake isomorphism. In: Galois Representations in Arithmetic Algebraic Geometry (Durham, 1996), London Mathematical Society Lecture Note Series, vol. 254, pp. 223–237. Cambridge University Press, Cambridge (1998). https://doi.org/10.1017/CBO9780511662010.006
Levine, M.: Tate motives and the vanishing conjectures for algebraic \(K\)-theory. In: Algebraic \(K\)-theory and algebraic topology (Lake Louise, AB, 1991), NATO Advanced Science Institutes Series C: Mathematical and Physical Sciences, vol. 407, pp. 167–188. Kluwer Academic Publications, Dordrecht (1993)
Lurie, J.: Higher Topos Theory. Annals of Mathematics Studies, vol. 170. Princeton University Press, Princeton (2009)
Lusztig, G.: Singularities, character formulas, and a \(q\)-analog of weight multiplicities. In: Analysis and Topology on Singular Spaces, II, III (Luminy, 1981). Astérisque. vol. 101, pp. 208–229. Société mathématique de France, Paris (1983)
Mirković, I., Vilonen, K.: Geometric Langlands duality and representations of algebraic groups over commutative rings. Ann. Math. (2) 166(1), 95–143 (2007)
Richarz, T.: Schubert varieties in twisted affine flag varieties and local models. J. Algebra 375, 121–147 (2013). https://doi.org/10.1016/j.jalgebra.2012.11.013
Richarz, T.: Basics on affine Grassmannians. (2019). https://timo-richarz.com/teaching/
Richarz, T., Scholbach, J.: The motivic Satake equivalence (2019). arXiv:1909.0832
Richarz, T., Scholbach, J.: The intersection motive of the moduli stack of shtukas. Forum Math. (Sigma) 8, e8 (2020). https://doi.org/10.1017/fms.2019.32. arXiv:1901.04919
Richarz, T., Zhu, X.: Appendix to: the geometric Satake correspondence for ramified groups. Ann. Sci. Éc. Norm. Supér. (4) 48(2), 409–451 (2015). https://doi.org/10.24033/asens.2248
The Stacks Project Authors. Stacks Project (2017). http://stacks.math.columbia.edu
Soergel, W., Wendt, M.: Perverse motives and graded derived category \({\cal{O}}\). J. Inst. Math. Jussieu 17(2), 347–395 (2018). https://doi.org/10.1017/S1474748016000013. arXiv:1404.6333v3
Weil, A.: Sur l’analogie entre les corps de nombres algébriques et les corps de fonctions algébriques. In: Oeuvres Scientifiques, Collected papers. vol. I, pp. 236–240. Springer, New York (1979)
Xiao, L., Zhu, X.: Cycles on Shimura varieties via geometric Satake (2017). arXiv:1707.05700
Zhu, X.: Affine Grassmannians and the geometric Satake in mixed characteristic. Ann. Math. (2) 185(2), 403–492 (2017). https://doi.org/10.4007/annals.2017.185.2.2
Zhu, X.: An introduction to affine Grassmannians and the geometric Satake equivalence. In: Geometry of moduli spaces and representation theory. IAS/Park City Mathematics Series, vol. 24, pp. 59–154. American Mathematical Society, Providence (2017)
Zhu, X.: Geometric Satake, categorical traces, and arithmetic of Shimura varieties. In: Current Developments in Mathematics 2016, pp. 145–206. International Press, Somerville (2018)
Acknowledgements
We thank Eugen Hellmann and Thomas Nikolaus for helpful discussions, and the anonymous referee for many suggestions that improved the quality of the manuscript. The authors thank the University of Münster, the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation; under Germany’s Excellence Strategy EXC 2044–390685587, Mathematics Münster: Dynamics–Geometry–Structure) and the Technical University of Darmstadt for financial and logistical support which made this research possible.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Richarz, T., Scholbach, J. Tate motives on Witt vector affine flag varieties. Sel. Math. New Ser. 27, 44 (2021). https://doi.org/10.1007/s00029-021-00665-y
Accepted:
Published:
DOI: https://doi.org/10.1007/s00029-021-00665-y





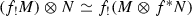 .
.
 .
.