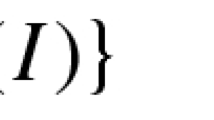Abstract
We study the evolution of curves with fixed length and clamped boundary conditions moving by the negative \(L^2\)-gradient flow of the elastic energy. For any initial curve lying merely in the energy space we show existence and parabolic smoothing of the solution. Applying previous results on long-time existence and proving a constrained Łojasiewicz–Simon gradient inequality we furthermore show convergence to a critical point as time tends to infinity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and main results
For an immersed curve \(f:I:=[0,1]\rightarrow {\mathbb {R}}^d\), \(d\ge 2\), its Euler–Bernoulli energy or simply elastic energy is defined by
Here \(\textrm{d}s:=\gamma \!\textrm{d}x\), where \(\gamma :=|\partial _x f|\) denotes the arc-length element, and \(\vec {\kappa }:=\partial _s^2 f\) is the curvature vector field, where \(\partial _s :=\gamma ^{-1}\partial _x\) is the arc-length derivative.
In this article, we deform an initial curve \(f_0\) in such a way that its elastic energy decreases as fast as possible, while keeping the (total) length \({\mathcal {L}}(f):=\int \nolimits _I\!\textrm{d}s\) fixed. This yields the geometric evolution equation
Here \(\nabla _s\) denotes the connection on the normal bundle along f, i.e. \(\nabla _s :=P^{\perp }\partial _s\), where \(P^{\perp }X :=X^{\perp _f}:=X-\langle X,\partial _s f\rangle \partial _s f\) denotes the orthogonal projection along f of any vector field X along f. The Lagrange multiplier \(\lambda \) depends on the solution f and is given by
Here \(\langle \cdot , \cdot \rangle \) denotes the Euclidean inner product. Note that the evolution (1.1) is geometric, i.e. if a smooth f satisfies (1.1), then for any smooth family of reparametrizations \(\Phi :[0,T)\times I\rightarrow I\) so does \({\hat{f}}(t,x) :=(f\circ \Phi )(t,x):=f(t, \Phi (t,x))\). In addition to the evolution (1.1), we prescribe clamped boundary conditions, fixing position and the unit tangent of the curve at the endpoints of I. For an immersed curve \(f_0\) we hence study the following initial boundary value problem.
where the unknown \(\theta :[0,T)\times I\rightarrow {\mathbb {R}}\), \(\theta = \langle \partial _t f, \partial _s f\rangle \) is the tangential velocity. By the integral representation of \(\lambda \), (1.3) becomes a nonlocal quasilinear system which is also degenerate parabolic by its geometric nature. We assume that the boundary data \(p_y\in {\mathbb {R}}^d, \tau _y\in {\mathbb {S}}^{d-1}\subset {\mathbb {R}}^d\) satisfy the compatibility conditions
Note that (1.3) is preserved under a smooth family of reparametrizations \(\Phi \) which keeps the boundary \(\partial I\) fixed, where the tangential velocity might change.
It is not difficult to see that \(\lambda \) is chosen exactly in such a way that the length remains fixed during the flow, since along any sufficiently smooth solution of (1.3) we have
whereas the energy indeed decreases since by (1.5)
using that the \(L^2(\!\textrm{d}s_f)\)-gradient of \({\mathcal {E}}\) is given by \(\nabla {\mathcal {E}}(f) = \nabla _s^2 \vec {\kappa }+ \frac{1}{2} |\vec {\kappa }| ^2 \vec {\kappa }\). In the above calculations, we also used the fact that all boundary terms vanish due to the boundary conditions. In order for \(\lambda \) to be well-defined, we need to ensure that \(f(t):=f(t, \cdot )\) is not a piece of a straight line. This can be guaranteed with no restrictions on \(\tau _0, \tau _1\) by requiring
so \({\mathcal {E}}(f_0)>0\), see Sect. 2.1 for a more detailed analysis of \(\lambda \).
In [10], long-time existence for smooth solutions of (1.3) with tangential velocity \(\theta \equiv 0\) under assumption (1.7) was shown with the help of interpolation inequalities. For the short-time existence the authors of [10] refer to the beginning of Section 3 in [17], where the short-time existence in the setting of Hölder spaces is only sketched for the case of closed curves. Moreover, the uniform bounds in [10, Theorem 1.1] imply subconvergence after reparametrization as \(t\rightarrow \infty \). However, different sequences could still have different limits.
The contribution of this paper is twofold: First, we give a rigorous and fairly concise proof of short-time existence and parabolic smoothing for the elastic flow (1.3). Compared to the previous classical existence results for elastic flows, where the initial datum is assumed to be smooth [10, 17, 42] or at least with Hölder continuous second derivative [50], one major improvement is that we allow for rough initial values, lying merely in the natural energy space, see Remark 2.11 for a detailed discussion. In contrast to existence theorems relying on the minimizing movement scheme (cf. [5, 6, 33, 39, 41]), our methods rely on maximal regularity, yielding here smooth solutions, cf. Theorem 1.1 below, while still allowing for rough initial data. The price for this substantial improvement is that the necessary contraction estimates become quite technical and rely delicately on the precise structure of (1.3). This is the first existence result for an elastic flow with general initial data of such weak regularity.
Theorem 1.1
Let \(f_0\in W^{2,2}(I;{\mathbb {R}}^d)\) be immersed, let \({p_0, p_1\in {\mathbb {R}}^d}\) and \(\tau _0, \tau _1 \in {\mathbb {S}}^{d-1}\) satisfy (1.4) and (1.7). Then, there exist \(T\!>\!0\) and a solution \({f\!\in \! W^{1,2}(0,T;L^2}{(I,{\mathbb {R}}^d))}{\cap L^2(0,T;W^{4,2}(I;{\mathbb {R}}^d))}\) of (1.3).
Moreover, we show that under the assumptions (1.4) and (1.7), the solution in Theorem 1.1 instantaneously becomes smooth, both in space and time, cf. Theorem 3.1.
Secondly we prove and apply a constrained Łojasiewicz–Simon gradient inequality (cf. [45]) to deduce convergence of the flow, where a new estimate (see Lemma 4.10) substantially simplifies the argument for the convergence result compared to previous works, cf. [8, 13].
Theorem 1.2
Let \(f_0\in W^{2,2}(I;{\mathbb {R}}^d)\) be an immersed curve and suppose \({p_0, p_1\in {\mathbb {R}}^d}\) and \(\tau _0, \tau _1 \in {\mathbb {S}}^{d-1}\) satisfy (1.4) and (1.7). Then, there exists a smooth family of curves \(f:(0,\infty )\times I\rightarrow {\mathbb {R}}^d\) solving (1.3), such that
-
(i)
\(f(t)\rightarrow f_0\) in \(W^{2,2}(I;{\mathbb {R}}^d)\) as \(t\rightarrow 0\);
-
(ii)
\(f(t)\rightarrow f_{\infty }\) smoothly after reparametrization as \(t\rightarrow \infty \), where \(f_\infty \) is a constrained clamped elastica, i.e. a solution of
$$\begin{aligned} \left\{ \begin{array}{rll} - \nabla _s^2 \vec {\kappa }-\frac{1}{2} |\vec {\kappa }| ^2 \vec {\kappa }+ \lambda \vec {\kappa }&{}= 0&{} \text { on } I\\ f(y)&{}=p_y &{}\text { for }y\in \partial I \\ \partial _s f(y) &{}= \tau _y &{}\text { for } y\in \partial I \end{array} \right. \end{aligned}$$(1.8)for some \(\lambda \in {\mathbb {R}}\).
Together with the previously mentioned work [10] this paper completes the study of the existence and convergence of the elastic flow of clamped curves with fixed length. Unfortunately, due to the low regularity of the initial curves considered here, we are not able to show uniqueness for the solution of the geometric evolution equation (1.3).
In the smooth category, one can show uniqueness “up to reparametrization” by a PDE argument similar to [22]. However, due to our low regularity we were not able to prove sufficient contraction estimates. The reason for that is the rigid characterization of Lipschitz properties of Nemytskii operators, see for instance [4, Theorem 3.10, Theorem 7.9].
The elastic energy of curves has already been studied by Bernoulli. The analysis of the elastic flow, i.e. the one-dimensional analogue of the Willmore flow, started with [42] and [17]. The boundary value problem for the elastic flow was considered in [25] for clamped curves and in [9] for natural second-order boundary conditions, see also [26, 27, 52] for related second-order evolutions. For further related literature on elastic flows, we refer to [5, 6, 35, 39, 41, 50]. Recent research has also studied the geometric evolution of networks and previously achieved results were applied to the elastic flow of networks, see e.g. [11, 15, 20, 21, 37]. Moreover, the elastic flow with different ambient geometries has been considered in [14, 34, 43], especially, the case of hyperbolic space [34] is of interest, cf. [12, 24]. Additionally, we mention the elastic flow of closed curves under a length and area constraint [38].
The Łojasiewicz–Simon gradient inequality is a remarkable result on (real) analytic functions which was first proven in \({\mathbb {R}}^d\) [28] and later generalized to infinite dimensions [49], see also [7]. Nowadays, it is the fundamental tool for investigating the asymptotic properties of gradient flows with analytic energies, which has been used for many geometric evolution equations, see for instance [8, 13, 19, 30, 31, 40, 47, 48] and also [36] for a different approach. The fixed-length constraint in (1.3) and (1.5) obstructs the use of [7] to deduce the gradient inequality, which is why we apply a recent extension to constrained energies [45]. We emphasize that this article is the first application of the constrained Łojasiewicz–Simon gradient inequality for a constrained gradient flow.
This article is structured as follows. In Sect. 2, we pick a specific tangential velocity such that (1.3) becomes a parabolic system, which we reduce to a fixed point equation. The existence of a fixed point is then established on a small time interval, using the concept of maximal \(L^p\)-regularity together with appropriate contraction estimates. Section 3 is devoted to show instantaneous smoothing of our solution, both in space and in time. After that, we prove long-time existence and a refined Łojasiewicz–Simon gradient inequality to finally prove Theorem 1.2 in Sect. 4. For the sake of readability, some details on the contraction estimates and the parabolic smoothing have been moved to the appendix or can be found in the first author’s dissertation [46, Chapter 3].
2 Short-time existence
The goal of this section is to prove Theorem 1.1. As in [20], we prescribe an explicit tangential motion to transform (1.3) into a quasilinear parabolic system. We then perform a linearization and use the theory of maximal \(L^p\)-regularity and suitable contraction estimates to prove Theorem 1.1 using a fixed point argument. We consider an initial datum merely lying in \(W^{2,2}_{Imm}(I;{\mathbb {R}}^d)\), the space of \(W^{2,2}\)-immersions. This is a natural space for the elastic energy, since it is the roughest Sobolev space where \({\mathcal {E}}\) remains finite.
2.1 On the Lagrange multiplier
To ensure that the Lagrange multiplier is well-defined, one needs to prevent the denominator from vanishing. Write \(\lambda (f) =:\frac{N(f)}{2{\mathcal {E}}(f)}\), where N(f) denotes the numerator in (1.2) and observe that for a solution of (1.3) we have
using the boundary conditions, (1.7) and (1.5). In particular, f(t) cannot be part of a straight line, so \({\mathcal {E}}(f(t))>0\) for all \(t\in [0,T)\). Moreover, we observe that after integration by parts we have
Note that in (2.1), no derivatives of second order of the curvature appear, which means that the Lagrange multiplier is formally of lower order compared to \(\nabla {\mathcal {E}}(f)\). This is extremely useful later on, since we can rely on the well-studied property of maximal \(L^p\)-regularity for a local operator in the linearization and treat the Lagrange multiplier as a nonlinearity in the fixed point argument.
2.2 From the geometric problem to a quasilinear PDE
As a next step, we explicitly compute the right-hand side of (1.1). By Proposition A.1
where
In order to solve (1.3), we study the following evolution problem, prescribing an explicit tangential motion \(\theta =\mu \) to make the problem parabolic. We want to find a family of immersions \(f:[0,T)\times I\rightarrow {\mathbb {R}}^d\) satisfying
with \(\lambda \) as in (1.2) and \(\mu =\mu (f):[0,T)\times I\rightarrow {\mathbb {R}}\) given by \(\mu :=- \langle {\mathcal {A}}(f), \partial _s f\rangle \). Note that the first-order boundary conditions are a linear version of the general boundary conditions in (1.3) and thus easier to handle. The system (2.3) is often referred to as the analytic problem.
For \(1<p<\infty \) and \(T>0\), we consider the space of solutions
and the space of data
The space of initial data is given by the Besov space
see for instance [16, Section 2]. We also consider the solution space with vanishing trace at time \(t=0\) given by
For convenience, we also set \({\mathbb {Y}}_{T,p} :={\mathbb {Y}}_{T,p}^1 \times {\mathbb {Y}}_p^2\).
2.3 Linearization of the analytic problem
If we linearize (2.3) for \(\lambda \equiv 0\), we obtain a linear parabolic system. This system is a local PDE which we can apply maximal regularity theory to. First, assuming \(\lambda \equiv 0\) and using (2.2), the evolution in (2.3) has the form
with \({\mathcal {A}}\) as in (2.2). If we freeze coefficients for the highest order term at the initial datum \(f_0\) we get
where \(\gamma _0 :=\gamma (0, \cdot ) = |\partial _x f_0|\) and \({\tilde{F}}\) is as in (2.2). The linearized system we associate to (2.3) with \(\lambda \equiv 0\) is
We can now apply the general \(L^p\)-theory for parabolic systems to obtain the following classical maximal regularity result, whose proof can be found in [46, Chapter 3, Section 2.3]. For the definition of the spaces for the boundary data \({\mathcal {D}}^{i}_{T,p}\) with \(i=0,1,\) see (B.2).
Theorem 2.1
Let \(p\in (\frac{5}{3},\infty )\), \(0<T\le T_0\). Suppose \(a\in {\mathcal {C}}([0,T_0]\times I;{\mathbb {R}})\) such that \(a(t,x)\ge \alpha \) for some \(\alpha >0\) and all \(t\in [0,T_0], x\in I\). Let \((\psi ,f_0) \in {\mathbb {Y}}_{T,p}\), \(b^0 \in {\mathcal {D}}^0_{T,p}\) and \(b^1\in {\mathcal {D}}^1_{T,p}\) such that the following compatibility conditions are satisfied:
Then, there exists a unique \(f\in {\mathbb {X}}_{T,p}\) such that
and there exists \(C=C(p, T, a)>0\) such that
Moreover, if \(b^0=0\) and \(b^1=0\), then we may choose \(C=C(p,T_0,a)\) independent of \(T\le T_0\).
Now, we want to solve (2.3) for initial data \(f_0\in W^{2,2}(I;{\mathbb {R}}^d)\) using a fixed point argument. Note that \(B^{2}_{2,2}(I;{\mathbb {R}}^d)=W^{2,2}(I;{\mathbb {R}}^d)\) by (B.1), so \(p=2\) is a fine setup to deal with the desired initial data, see Remark 2.11 for a more detailed discussion. We observe that the linearized system (2.5) can be viewed as a special case of Theorem 2.1 with \(a= \frac{1}{\gamma _0^4}\), \(b^0 = (p_0, p_1)\), \(b^1 = (\tau _0, \tau _1)\) and \(\psi =F\).
Throughout the rest of this section, we exclusively work with \(p= 2\). To simplify notation the spaces \({\mathbb {X}}_{T}, {\mathbb {Y}}_T, {\mathcal {D}}^0, {\mathcal {D}}^1\) denote the respective spaces with \(p=2\).
2.4 Contraction estimates
The key ingredient in the proof of the short-time existence is a contraction estimate for the nonlinearity in (2.3). We fix an initial datum \(f_0\in W^{2,2}_{Imm}(I;{\mathbb {R}}^d)\) and boundary conditions \(p_0, p_1\in {\mathbb {R}}^d\) and \(\tau _0, \tau _1\in {\mathbb {S}}^{d-1}\) satisfying (1.4) and (1.7). For a reference flow \({\bar{f}}\in {\mathbb {X}}_{T=1}\) with \({\bar{f}}(0)=f_0\), and some M and \(T\in (0,1]\) we define
We denote by T the existence time and by M the contraction radius. Since we take \(T,M>0\) small later on, it is no restriction to only consider \(T,M\le 1\). Later, we choose a specific reference flow \({\bar{f}}\), see Definition 2.5.
First, the following lemma yields uniform bounds from below on the arc-length element and the elastic energy for small times, ensuring that the system (2.3) does not immediately become singular. A detailed proof can be found in [46, Chapter 3, Section 2.4.1].
Lemma 2.2
For \(T=T({\bar{f}})\in (0,1]\) small enough and \(M\in (0, 1]\), any \(f\in {{\bar{B}}_{T,M}}\) satisfies \(\gamma (t,x)\ge \inf _{I}\frac{\gamma _0}{2}\) for all \((t,x)\in [0,T)\times I\). In particular, all curves \(f(t,\cdot )\) are immersed.
Lemma 2.3
For \(T=T({\bar{f}})\in (0,1]\) small enough and \(M\in (0,1]\), any \(f\in {{\bar{B}}_{T,M}}\) satisfies \({\mathcal {E}}(f(t)) \ge \frac{{\mathcal {E}}(f_0)}{3}>0\) (cf. (1.7)) for all \(t\in [0,T)\),.
We now state the crucial contraction property of the nonlinearities. Since the space of initial data is the energy space, cf. Remark 2.11, the necessary estimates are quite involved and rely on the special structure of (1.1). For the sake of readability, some of the details and the proof of the following lemma are moved to Appendix C.
Lemma 2.4
Let \(q\in (0,1)\). Then the following maps
are well-defined q-contractions (i.e. Lipschitz continuous with Lipschitz constant q) for \(T=T(q,{\bar{f}})\), \(M=M(q, {\bar{f}})\in (0,1]\) small enough, with F as in (2.4) and \(\lambda \) as in (1.2).
2.5 The fixed point argument
We now reduce the analytic problem (2.3) to a fixed point equation and show local existence and uniqueness via the contraction principle. To that end, we first choose a specific reference solution \({\bar{f}}\) in (2.9) on the time interval \([0,1]\supset [0,T]\) for \(0<T\le 1\).
Definition 2.5
We define the reference solution \({\bar{f}}\) to be the unique solution of the following initial boundary value problem.
Existence and uniqueness in the class
follows from Theorem 2.1. Note that the restriction of the solution to any time interval [0, T] is the unique solution in the class \({\mathbb {X}}_{T}\) for all \(0<T\le {1}\).
Fix \(q\in (0,1)\) and take \({T}={T}(q,{\bar{f}})\in (0,1],M=M(q,{\bar{f}})\in (0,1]\) small enough such that Lemmas 2.2 to 2.4 hold. Let \(f\in {{\bar{B}}_{T,M}}\). Then, we have \({\mathcal {N}}(f) \in {\mathbb {Y}}_{{T}}^{1}\), cf. Lemma 2.4. For \(\psi :={\mathcal {N}}(f), b^0 :=(p_0,p_1)\), \(b^1 :=(\tau _0, \tau _1)\), \(a:=\gamma _0^{-4}\in {\mathcal {C}}([0,{1}]\times I)\) the compatibility conditions (2.6) are satisfied, since by (1.4) we have
Hence, by Theorem 2.1, there exists a unique solution \(g\in {\mathbb {X}}_T\) of the linear initial boundary value problem
Definition 2.6
We define the map \(\Phi :{{\bar{B}}_{T,M}} \rightarrow {\mathbb {X}}_T, \Phi (f):=g\), where \(g\in {\mathbb {X}}_T\) is the unique solution to (2.10).
Remark 2.7
Finding a solution of (2.3) in the ball \({{\bar{B}}_{T,M}} \subset {\mathbb {X}}_T\) is equivalent to finding a fixed point of the map \(\Phi \) in Definition 2.6.
We now show that \(\Phi \) is a contraction on \({{\bar{B}}_{T,M}}\) for \(T,M>0\) small enough.
Proposition 2.8
Let \(q\in (0,1)\). Then there exist \(M=M(q,{\bar{f}})\in (0,1]\), \(T=T(q,M,{\bar{f}})\in (0,1]\) such that \(\Phi :{{\bar{B}}_{T,M}} \rightarrow {{\bar{B}}_{T,M}}\) is well-defined and a q-contraction, i.e.
for all \(f,{\tilde{f}} \in {{\bar{B}}_{T,M}}\).
Proof
The contraction property: Let \(q\in (0,1)\) and \(f, {\tilde{f}}\in {{\bar{B}}_{T,M}}\) and let \(g=\Phi (f)\), \({\tilde{g}}=\Phi ({\tilde{f}})\). We observe that \(g-{\tilde{g}}\) vanishes at \(t=0\) and at the boundary \(\partial I\) up to first order. Hence, by Definition 2.6 and (2.8), for some \(C=C(f_0)=C({\bar{f}})>0\), independent of \(T\in (0,1]\), we have
Taking \(T=T(q,{\bar{f}}),M=M(q,{\bar{f}})\in (0,1]\) small enough so that Lemma 2.4 can be applied with q replaced by q/(2C), we have
Equations (2.12) and (2.13) imply (2.11).
Well-definedness: Let \(f\in {{\bar{B}}_{T,M}, g=\Phi (f)}\). Again by (2.8) we find
where we applied (2.13) with \({\tilde{f}}={\bar{f}}\) in the third step. Now, by dominated convergence we have \(\Vert {\mathcal {N}}({\bar{f}}) \Vert _{L^2(0,T;L^2)} \le \frac{M}{2C}\) reducing \(T=T(q,M, {\bar{f}})\in (0,1]\) if necessary. Then, from (2.14) we conclude \(\Vert \Phi (f)-{\bar{f}} \Vert _{{\mathbb {X}}_T}\le M\). \(\square \)
Theorem 2.9
Let \(f_0\in W^{2,2}_{Imm}(I;{\mathbb {R}}^{d})\), \(p_0, p_1\in {\mathbb {R}}^d\), \(\tau _0, \tau _1\in {\mathbb {S}}^{d-1}\) satisfying (1.4) and (1.7). Then there exist \(M>0\) and \(T>0\) such that the system (2.3) has a unique solution \(f\in {{\bar{B}}_{T,M}}\subset W^{1,2}\left( 0,T; L^2(I;{\mathbb {R}}^d)\right) \cap L^2\left( 0,T; W^{4,2}(I;{\mathbb {R}}^d)\right) \).
Proof
For \(T,M>0\) as in Proposition 2.8 with \(q=\frac{1}{2}\), the map \(\Phi :{{\bar{B}}_{T,M}}\rightarrow {{\bar{B}}_{T,M}}\) is a contraction in the complete metric space \({{\bar{B}}_{T,M}}\) and hence has a unique fixed point \(f\in {{\bar{B}}_{T,M}}\) by the contraction principle. Since any fixed point of \(\Phi \) is a solution of (2.3) in \({{\bar{B}}_{T,M}}\) and vice versa, the claim follows. \(\square \)
Remark 2.10
By the construction of our solution and Lemma 2.2 and Lemma 2.3 the arc-length element \(|\partial _x f|\) and the elastic energy of the solution f in Theorem 2.9 are bounded from below and above, uniformly in \(t\in [0,T)\).
This immediately implies Theorem 1.1.
Proof of Theorem 1.1
By Theorem 2.9, there exist \(T>0\) and a solution f of (2.3) such that \(f\in W^{1,2}(0,T;L^2(I;{\mathbb {R}}^d))\cap L^2(0,T;W^{4,2}(I;{\mathbb {R}}^d))\). Consequently, f solves (1.3), since at the boundary we have
\(\square \)
Remark 2.11
Our assumption on the regularity of the initial datum is very natural. On the one hand, the space \(W^{2,2}_{Imm}(I;{\mathbb {R}}^d)\) is the correct energy space associated to the elastic energy, so we would like to obtain short-time existence for an initial datum in \(W^{2,2}_{Imm}(I;{\mathbb {R}}^d)\). In view of the linear problem in Theorem 2.1, working in the Sobolev scale one would hence need to pick \(p\in (1,\infty )\) such that \(W^{2,2}(I;{\mathbb {R}}^d)\hookrightarrow B^{4(1-\frac{1}{p})_{p,p}}(I;{\mathbb {R}}^d) ={\mathbb {Y}}_p^2\).
However, in order to estimate the denominator of the Lagrange multiplier \(\lambda \), we want continuity of our solution with values in \(W^{2,2}(I;{\mathbb {R}}^d)\). Using Proposition B.1 (i), this can be achieved if \(B^{4(1-\frac{1}{p})_{p,p}}(I;{\mathbb {R}}^d) \hookrightarrow W^{2,2}(I;{\mathbb {R}}^d)\).
Clearly, this can only work for \(p=2\). Moreover, for the same reason as above, even the introduction of time-weighted Sobolev spaces would not provide solutions with lower initial regularity.
Theorem 2.12
The solution \(f \in {{\bar{B}}_{T,M}} \) in Theorem 2.9 is the unique solution of (2.3) in the whole space \(W^{1,2}\left( 0,T; L^2(I;{\mathbb {R}}^d)\right) \cap L^2\left( 0,T; W^{4,2}(I;{\mathbb {R}}^d)\right) \).
Proof
First we note that any restriction of the solution \(f \in {{\bar{B}}}_M \) to a smaller time interval \([0,{{\tilde{T}}}]\) is again the unique solution of (2.3) in \({{\bar{B}}}_M\) on \([0,{{\tilde{T}}}]\) by Theorem 2.9. Now, we let \(T_1, T_2 > 0\) and assume that \(f_i \in W^{1,2}\left( 0,T_i; L^2(I;{\mathbb {R}}^d)\right) \cap L^2\left( 0,T_i; W^{4,2}(I;{\mathbb {R}}^d)\right) \), \(i = 1,2\) are two families of immersions satisfying (2.3) with \(f_0 \in W^{2,2}_{{Imm}}(I)\). Without loss of generality we may assume that \(T_1 \le T_2\). We claim that \(f_2 |_{[0,T_1]} = f_1\).
To show the claim we define \({\bar{t}} = \sup \{t \in [0,T_1): f_1(s) = f_2(s) \, \forall \, 0 \le s \le t\}\). Note that \({\bar{t}}\) is well-defined by Proposition B.1 (i). We need to show that \({\bar{t}} = T_1\). To do so we first prove that \({\bar{t}} > 0\). Indeed, for \(T \searrow 0\), we have \(\Vert f_i|_{[0,T]} \Vert _{{\mathbb {X}}_T} \rightarrow 0\) by the dominated convergence theorem, and the same holds for the reference flow \({{\overline{f}}}\) from Definition 2.5. Thus, for \(T > 0\) small enough, \(f_i|_{[0,T]} \in {{\bar{B}}}_M\) for \(i = 1,2\). Further decreasing \(T>0\) if necessary we obtain from Theorem 2.9 that \(f_1|_{[0,T]} = f_2|_{[0,T]}\) is the unique solution \(f \in {{\bar{B}}}_M\). Thus, \(f_1(s) = f(s) = f_2(s)\) for all \(0 \le s \le T\), showing that \({\bar{t}} \ge T > 0\).
We now assume that \({\bar{t}} < T_1\). Since \(f_i \in {\mathbb {X}}_{T_1} \hookrightarrow BUC([0,T_1],W^{2,2}(I;{\mathbb {R}}^d))\) and both solutions are immersed for all times, we find that \(f_0 :=f_1({\bar{t}}) \in W^{2,2}_{Imm}(I;{\mathbb {R}}^d)\). Whence, by Theorem 2.9, there exist \(M >0\), \(T > 0\) such that (2.3) has a unique solution \(f \in {{\bar{B}}}_M\). Observing that \(f_i({\bar{t}} + t, \cdot )|_{0 \le t \le T_1-{\bar{t}}}\), \(i = 1,2\) are both solutions to (2.3) with the same initial value \(f_0\), we find by similar arguments as above that \(f_1({\bar{t}} + \cdot ) = f = f_2({\bar{t}} + \cdot ) \) on [0, T), contradicting the definition of \({\bar{t}}\). \(\square \)
3 Parabolic smoothing
The goal of this section is to show that our solution f from Theorem 2.9 instantaneously becomes smooth.
Theorem 3.1
Let \(f_0\in W^{2,2}_{Imm}(I;{\mathbb {R}}^d)\) such that (1.4) and (1.7) are satisfied. Then, there exists \(0<T_1\le T\) such that the solution f in Theorem 1.1 is smooth on \((0,T_1)\), i.e. \(f\in {\mathcal {C}}^{\infty }((0,T_1)\times I;{\mathbb {R}}^d)\).
A close examination of the contraction estimates in Appendix C reveals that the critical embeddings are used, for instance in (C.12), (C.14) and (C.15). Thus, higher integrability of the nonlinearity cannot be obtained by standard estimates relying on Hölder’s inequality. Therefore, we cannot directly start the usual bootstrap argument to show smoothness. Instead, we use an instantaneous gain of regularity in the time variable, relying on Angenent’s parameter trick [2, 3], see also [18] and [44, Chapter 9]. Since we want to conclude smoothness in space up to the boundary, we first show increased regularity in time before deducing global smoothness up to the boundary by using parabolic Schauder theory. For the sake of readability, we omit the proof of the following proposition and refer to [46, Chapter 3, Section 3.1].
Proposition 3.2
Let \(f\in W^{1,2}(0,T;L^2(I;{\mathbb {R}}^d))\cap L^2(0,T;W^{4,2}(I;{\mathbb {R}}^d))\) be the unique solution of (2.3), given by Theorem 2.9. Then there exists \(0<T_1<T\) such that \(f\in {\mathcal {C}}^{\omega }((0,T_1); W^{2,2}(I,{\mathbb {R}}^d))\).
Next, we use the higher time regularity to improve the integrability of \(\lambda \), which then allows us to start a bootstrap argument. First, we recall the following modification of [10, Lemma 4.3].
Lemma 3.3
Let \(f\in {\mathbb {X}}_{T,2}\) be a solution of (1.3). Then, we have
Proof
We proceed as in [10, Lemma 4.3]. Let \(l:[0,T)\times I\rightarrow {\mathbb {R}}^d\) be the parametrization of the line segment from \(p_0\) to \(p_1\) given by
with \(\varphi (t, \xi ):=\int \nolimits _{0}^\xi |\partial _x f|\,\!\textrm{d}x\) for \((t,\xi )\in [0,T)\times I\). Then \(l(t,0)=p_0\), \(l(t,1)=p_1\) and \(\partial _{s } l(t, \cdot ) = \frac{1}{\ell }(p_1-p_0)\). Therefore, using \(\nabla _s^2\vec {\kappa }+ \frac{1}{2}|\vec {\kappa }|^2\vec {\kappa }= \nabla _s\left( \nabla _s\vec {\kappa }+ \frac{1}{2}|\vec {\kappa }|^2\partial _s f\right) \) (cf. [10, p. 1048]), we find after integrating by parts
Consequently, since \(f=l\) on the boundary, we have
Using (1.7) and the simple estimate \(\Vert f-l \Vert _{\infty } \le 2\ell \) yields the claim. \(\square \)
Note that a priori, the Lagrange multiplier \(\lambda \) is only \(L^2(0,T)\) for \(f\in {\mathbb {X}}_{T,2}\). The next proposition improves this integrability, at least on a small timescale bounded away from zero.
Lemma 3.4
Let f be the solution of (2.3) from Theorem 2.9 and let \(T_1>0\) as in Proposition 3.2. Then, for any \(0<\varepsilon <T_1\) we have \(\lambda (f)\in L^4(\varepsilon ,T_1)\).
Proof
As a consequence of Proposition 3.2, we have \(\partial _t f\in {\mathcal {C}}^{\omega }((0,T_1);W^{2,2}(I;{\mathbb {R}}^d))\) and thus we get \(\partial _t f\in {\mathcal {C}}^{0}([\varepsilon ,T_1]\times I;{\mathbb {R}}^d)\). Hence, Lemma 3.3 and (1.7) yield that \(\lambda \) has the same integrability on \((\varepsilon , T_1)\) as \(\int \nolimits _I |\nabla _s\vec {\kappa }|\,\!\textrm{d}s\). By Proposition A.1 (ii) and the uniform bounds on the arc-length element, cf. Remark 2.10, it suffices to show \(\partial _x^3 f \in L^4(\varepsilon ,T_1;L^1(I;{\mathbb {R}}^d))\), since \(\partial _x^2f\in {\mathcal {C}}^{0}([\varepsilon ,T_1];L^2(I;{\mathbb {R}}^d))\). In fact using Proposition B.3 (i) as in (C.12), we even get \(\partial _x^3 f\in L^4(\varepsilon , T_1; L^2(I;{\mathbb {R}}^d))\). \(\square \)
The improved integrability of \(\lambda \) in Lemma 3.4 enables us to start a bootstrap argument to increase the Sobolev regularity of our solution in Theorem 2.9. Note that by Sobolev embeddings, in order to prove smoothness of our solution it suffices to reach \({\mathbb {X}}_{T,p}\) with \(p>5\), see Lemma 3.6.
Lemma 3.5
Let f be as in Theorem 2.9, let \(T_1>0\) be as in Proposition 3.2 and let \(0<\varepsilon <T_1\). Then \(f\in W^{1,20}(\varepsilon , T_1; L^{20}(I;{\mathbb {R}}^d))\cap L^{20}(\varepsilon ,T_1;W^{4,20}(I;{\mathbb {R}}^d))\).
Proof
See [46, Chapter 3, Section 3.3]. \(\square \)
Finally, Theorem 3.1 follows from parabolic Schauder theory and the following
Lemma 3.6
Let f be the solution of (2.3) constructed in Theorem 2.9. If there exist \(p>5\) and \(\varepsilon >0\) such that \(f \in W^{1,p}\left( \varepsilon ,T_1; L^p(I;{\mathbb {R}}^d)\right) \cap L^p\left( \varepsilon ,T_1; W^{4,p}(I;{\mathbb {R}}^d)\right) \) then \(f \in {\mathcal {C}}^\infty ((\varepsilon , T_1) \times I;{\mathbb {R}}^d)\).
Proof
See [46, Chapter 3, Section 3.4]. \(\square \)
Now, Theorem 3.1 is immediate.
Proof of Theorem 3.1
The solution f in Theorem 1.1 is exactly the solution f in Theorem 2.9. By Lemma 3.5 we have \(f\in W^{1,20}(\varepsilon ,T_1;L^{20}(I;{\mathbb {R}}^d))\cap L^{20}(\varepsilon ,T_1;L^{20}(I;{\mathbb {R}}^d))\) for any \(0<\varepsilon <T_1\). Hence, by Lemma 3.6, we find that \(f\in {\mathcal {C}}^{\infty }((\varepsilon ,T_1)\times I;{\mathbb {R}}^d))\). \(\square \)
4 Long-time behaviour and the proof of Theorem 1.2
In this section, we use the long-time existence result in [10] to show the existence of a global solution of (1.3). Moreover, we prove and use a refined Łojasiewicz–Simon gradient inequality to conclude convergence after reparametrization.
4.1 Long-time existence after reparametrization
As a first step towards proving Theorem 1.2, we establish long-time existence and subconvergence after reparametrization for our solution. The key ingredient is the smoothness of our solution and [10, Theorem 1.1].
Theorem 4.1
Let \(f\in W^{1,2}(0,T;L^2(I;{\mathbb {R}}^d))\cap L^2(0,T;W^{4,2}(I;{\mathbb {R}}^d))\) be as in Theorem 2.9 and let \(0<\varepsilon <T\). Then, there exist \({\bar{\varepsilon }}\in (\varepsilon , T)\) and \({\hat{f}}\in {\mathcal {C}}^{\infty }((0,\infty )\times I;{\mathbb {R}}^d)\) satisfying (1.3) such that
-
(i)
\({\hat{f}}(t,x) = f(t,x)\) for all \(0\le t\le \varepsilon , x\in I\);
-
(ii)
\({\hat{f}}(t, \cdot )\) has zero tangential velocity for all \(t\ge {\bar{\varepsilon }}\);
-
(iii)
\({\hat{f}}\) subconverges smoothly as \(t\rightarrow \infty \), after reparametrization with constant speed, to a constrained elastica, i.e. a solution (1.8).
Proof
By Theorem 3.1, the solution f in Theorem 2.9 is instantaneously smooth. Thus, to simplify notation we may assume \(f\in {\mathcal {C}}^{\infty }([\varepsilon , T]\times I;{\mathbb {R}}^d)\) for some \(\varepsilon >0\) after possibly reducing \(T>0\). Moreover, we may also assume a uniform bound from below on the arc-length element using Remark 2.10.
Let \(\theta :=\langle \partial _t {f}, \partial _{s_{{f}}} {f}\rangle \) be the tangential velocity of f. By the smoothness of f and the bound on the arc-length element, the function \((t,r)\mapsto \frac{\theta (t,r)}{|\partial _x f(t,r)|}\) is globally Lipschitz continuous on \([\varepsilon , T]\times I\). For each \(x\in I\), we consider the initial value problem
By classical ODE theory, there exist \(\varepsilon < {\hat{T}}\le T\) and a smooth family of reparametrizations \(\Phi :[\varepsilon ,{\hat{T}}]\times I\rightarrow I\) satisfying (4.1) and
Therefore, \(\Phi (t, \cdot )\) is strictly increasing and a diffeomorphism of I for each \(t\in [\varepsilon , {\hat{T}}]\). A direct computation yields that the reparametrization \({f}_1(t,x):={f}(t, \Phi (t,x))\) satisfies
using that f solves (1.3) and the transformation of the geometric quantities. For the boundary conditions, let \(t\in [\varepsilon ,{\hat{T}}]\), \(y\in \partial I\) and note that \(f_1(t,y)=f(t,y)=p_y\) and \( \partial _{s_{f_1}} f_1(t,y) =\partial _{s_f}f(t,y) =\tau _y\) by (4.2). Consequently, \(f_1\) is a smooth solution of (1.3) on \([\varepsilon , {\hat{T}}]\) with tangential velocity zero and smooth initial datum \(f(\varepsilon )\). By [10, Theorem 1.1], \(f_1\) can be extended to a global smooth solution \({\bar{f}}\) on \([\varepsilon , \infty )\) which subconverges, after reparametrization with constant speed, to a constrained elastica as \(t\rightarrow \infty \).
In particular, we have the identity
Now, let \(\varepsilon<{\bar{\varepsilon }}<{\hat{T}}\) and \(\Psi :[0, {\hat{T}}]\times I \rightarrow I\) be a smooth family of reparametrizations with
The existence of such a \(\Psi \) is proven in Lemma D.1. We now define
Note that \({\hat{f}}\) is clearly smooth in x for every \(t\ge 0\) fixed. It is also smooth in t for fixed \(x\in I\), by (4.3) and (4.4). Property (i) follows from (4.4). Furthermore, by definition of \({\hat{f}}\) on \([{\bar{\varepsilon }},\infty )\times I\) we find that \({\hat{f}}={\bar{f}}\) has zero tangential velocity and hence (ii) is satisfied. The last property follows since the asymptotic behaviour of \({\hat{f}}\) is inherited from \({\bar{f}}\). \(\square \)
4.2 The length-preserving elastic flow as a gradient flow on a Hilbert manifold
In this section, we show that the flow (1.3) is in fact a gradient flow on a suitable submanifold of curves.
Proposition 4.2
Let \(p_0,p_1 \in {\mathbb {R}}^d, \tau _0, \tau _1 \in {\mathbb {S}}^{d-1}\) and \(\ell \in {\mathbb {R}}\) such that (1.7) holds. Then
is a weak Riemannian splitting analytic submanifold of \(W^{4,2}(I;{\mathbb {R}}^d)\) with codimension \(4d-1\).
Proof
By the Sobolev embedding \(W^{4,2}(I;{\mathbb {R}}^d)\hookrightarrow {\mathcal {C}}^{1}(I;{\mathbb {R}}^{d})\), the set of \(W^{4,2}\)-immersions denoted by \(W^{4,2}_{Imm}(I;{\mathbb {R}}^d)\) is open in \(W^{4,2}(I;{\mathbb {R}}^{d})\). The function
is an analytic map. Moreover, its differential is given by
for \(f\in W^{4,2}_{Imm}(I;{\mathbb {R}}^{d})\) and \(u \in W^{4,2}(I;{\mathbb {R}}^{d})\). It is not difficult to see that \(d{\mathcal {G}}_f\) is surjective if \(f\in {\mathcal {X}} = {\mathcal {G}}^{-1}\left( \{(\ell , p_0, p_1, \tau _0, \tau _1)^T\}\right) \). Indeed, let \(\alpha \in {\mathbb {R}}\), \(q_y\in {\mathbb {R}}^{d}\), \(z_y \in T_{\partial _{s}f(y)}{\mathbb {S}}^{d-1}\) for \(y=0,1\). We have \({ {\mathcal {T}}_{\partial _s f(y)}{\mathbb {S}}^{d-1} = \{z\in {\mathbb {R}}^{d} \mid \langle z, \partial _x f(y)\rangle =0 \}}\). Clearly, we can find an immersed curve \(u\in W^{4,2}(I;{\mathbb {R}}^{d})\) with \(u(y)=q_y\) and \(\frac{\partial _x u(y)}{|\partial _x f(y)|} = z_y\) for \(y=0,1\). Now, using the characterization of the tangent space, for \(v\in {\mathcal {C}}^{\infty }_0(I;{\mathbb {R}}^d)\) we find
since adding v does not change the boundary behaviour. Moreover, as \(\vec {\kappa }_{f}\not \equiv 0\) using \(f\in {\mathcal {X}}\) and (1.7), we can choose v such that \(\int \nolimits _{I}\langle \vec {\kappa }_f, v\rangle \,\!\textrm{d}s_{f} =\varepsilon \ne 0\). Setting \(\beta :=\int \nolimits _{I}\langle \vec {\kappa }_f, u\rangle \,\!\textrm{d}s_{f}\) and \(w:=u -\frac{\alpha +\beta }{\delta } v\), we find \(\int \nolimits _{I} \langle \vec {\kappa }_f, w\rangle \,\!\textrm{d}s_{f} = \beta - (\alpha + \beta ) = -\alpha \); hence, we have shown \(d{\mathcal {G}}_f(w) = (\alpha , q_0, q_1, z_0, z_1)\), so \(d{\mathcal {G}}_f\) is surjective.
Consequently, \({\mathcal {X}}\subset W^{4,2}(I;{\mathbb {R}}^{d})\) is a splitting submanifold by [1, Theorem 3.5.4] with codimension \(1+2d+2(d-1)=4d-1\). Like in [45], the analytic form of the implicit function theorem can be used to show that \({\mathcal {X}}\) is in fact analytic. The tangent space is given by
Since (1.3) is a \(L^2(\,\!\textrm{d}s_f)\) gradient flow, it is natural to endow \({\mathcal {X}}\) with the Riemannian metric \(\langle u,v\rangle _{L^2(\,\!\textrm{d}s_f)} = \int \nolimits _{I} \langle u,v\rangle \,\!\textrm{d}s_{f}\) for \(u,v \in {\mathcal {T}}_f {\mathcal {X}}\). Note that since \({\mathcal {T}}_f{\mathcal {X}}\) is certainly not complete with respect to the induced norm, the metric is only weakly Riemannian (cf. [1, Definition 5.2.12]). \(\square \)
It is not difficult to see that by (4.5) the right-hand side of the evolution (1.1) is the projection of the full \(L^2 (\,\!\textrm{d}s_f)\)-gradient \(\nabla {\mathcal {E}}(f)\) onto the \(L^2(\,\!\textrm{d}s_f)\)-closure of the tangent space \({\mathcal {T}}_f{\mathcal {X}}\). This implies that (1.1) is the gradient flow of \({\mathcal {E}}\) on the manifold \({\mathcal {X}}\).
4.3 The constrained Łojasiewicz–Simon gradient inequality
In this subsection, we establish a Łojasiewicz–Simon inequality for \({\mathcal {E}}\) on \({\mathcal {X}}\). To do so, we have to deal with the invariance of both energies \({\mathcal {E}}\) and \({\mathcal {G}}\), which unfortunately creates large kernels for their first and second variations. Like in [8, 13], we work around this issue by restricting the energy to normal directions and using the implicit function theorem.
In the following, we always assume that the assumptions (1.4) and (1.7) are satisfied.
Definition 4.3
Fix \({\bar{f}}\in {\mathcal {X}}\) and define \(V_c:=W^{4,2}(I;{\mathbb {R}}^d)\cap W^{2,2}_{0}(I;{\mathbb {R}}^d)\). We define the space of normal vector fields along \({\bar{f}}\) by
Moreover, we define \(H^{\perp }:=L^{2,\perp }(I;{\mathbb {R}}^d):=\{ u\in L^{2}(I;{\mathbb {R}}^d)\mid \langle u, \partial _x {\bar{f}} \rangle = 0 \text { a.e.}\}\) and \(V_c^{\perp } :=V_c \cap W^{4,2,\perp }(I;{\mathbb {R}}^d)\). Both are Hilbert spaces and the \(L^2\)-orthogonal projection onto \(H^{\perp }\) is given by the pointwise projection \(P^{\perp }(f) :=f - \langle f, \partial _s {\bar{f}}\rangle \partial _s {\bar{f}}\).
Moreover, by the embedding \(W^{4,2}(I;{\mathbb {R}}^d)\hookrightarrow {\mathcal {C}}^{1}(I;{\mathbb {R}}^d)\) there exists \(\varepsilon >0\) small enough such that for all \(u\in W^{4,2,\perp }(I;{\mathbb {R}}^d)\) with \(\Vert u \Vert _{W^{4,2}}<\varepsilon \), the curve \(f={\bar{f}}+u\) is immersed. Defining \(U_\varepsilon :=\{ u\in V_c^{\perp } \mid \Vert u \Vert _{W^{4,2}}<\varepsilon \}\) we consider the energies
We have the following result.
Proposition 4.4
(cf. [13, Proof of Theorem 3.1, Remark 3.3]) The energy E satisfies the following properties.
-
(1)
\(E:U_\varepsilon \rightarrow {\mathbb {R}}\) is analytic;
-
(2)
its gradient \(\nabla E :U_\varepsilon \rightarrow H^{\perp }\) is analytic;
-
(3)
the derivative \((\nabla E)^{\prime }(0):V^{\perp }_{c} \rightarrow H^{\perp }\) is Fredholm with index zero.
It is well known that this is sufficient to prove a Łojasiewicz–Simon gradient inequality for E (cf. [7, Corollary 3.11]), [13, Theorem 3.1], [45, Theorem 1.2], [43, Corollary 2.6]). However, in order to conclude a constrained or refined Łojasiewicz–Simon gradient inequality, cf. (16) in [45], we also need to analyse the length functional.
Proposition 4.5
The energy L satisfies the following properties.
-
(1)
\(L:U_\varepsilon \rightarrow {\mathbb {R}}\) is analytic.
-
(2)
The gradient map \(\nabla L :U_\varepsilon \rightarrow H^{\perp }\) is analytic.
-
(3)
The derivative \((\nabla L)^{\prime }(0):V_{c}^{\perp }\rightarrow H^{\perp }\) is compact.
-
(4)
\(L(0)=\ell \) and \(\nabla L(0)\ne 0\).
Proof
-
(1)
The map \(U_{\varepsilon }\rightarrow {\mathcal {C}}(I;{\mathbb {R}}^d), u \mapsto |\partial _x({\bar{f}}+u)|\) is analytic by [13, Lemma 3.4, 1.], and hence so is L.
-
(2)
The \(H^{\perp }\)-gradient of L is given by \(\nabla L(u) = -P^{\perp } \left( \vec {\kappa }_{{\bar{f}}+u}|\partial _{x}({\bar{f}}+u)|\right) \). Note that the map \(U_{\varepsilon }\rightarrow L^{2}(I;{\mathbb {R}}^d), u \mapsto \vec {\kappa }_{{\bar{f}}+u}\) is analytic by [13, Lemma 3.4, 3.]. Since the multiplication \(L^2(I;{\mathbb {R}}^d)\times L^{\infty }(I;{\mathbb {R}}) \rightarrow L^2(I;{\mathbb {R}}^d), (f,\phi )\mapsto f\phi \) is analytic, so is the map \(U_{\varepsilon }\rightarrow L^2(I;{\mathbb {R}}^d), u\mapsto \vec {\kappa }_{{\bar{f}}+u}|\partial _{x}({\bar{f}}+u)|\). The continuity and linearity of \(P^{\perp }:L^2(I;{\mathbb {R}}^d)\rightarrow H^{\perp }\) yield the claim.
-
(3)
We compute the second derivative using standard formulas for the variation of geometric quantities (see for instance [17, Lemma 2.1]). We have
$$\begin{aligned} (\nabla L)^{\prime }(0) u&= \left. \frac{\!\textrm{d}}{\!\textrm{d}t}\right| _{t=0}\nabla L(tu) = -\left. \frac{\!\textrm{d}}{\!\textrm{d}t}\right| _{t=0}P^{\perp } \left( \vec {\kappa }_{{\bar{f}}+u}|\partial _{x}({\bar{f}}+u)|\right) \\&= -P^{\perp } \left. \frac{\!\textrm{d}}{\!\textrm{d}t}\right| _{t=0}\vec {\kappa }_{{\bar{f}}+tu} |\partial _{x}{\bar{f}}| - P^{\perp } \vec {\kappa }_{{\bar{f}}} \left. \frac{\!\textrm{d}}{\!\textrm{d}t}\right| _{t=0}|\partial _x ({\bar{f}}+tu)|\\&= -\left( \nabla _{s_{{\bar{f}}}}^2 u + \langle u, \vec {\kappa }_{{\bar{f}}}\rangle \vec {\kappa }_{{\bar{f}}}\right) |\partial _{x}{\bar{f}}| + \vec {\kappa }_{{\bar{f}}}\langle u, \vec {\kappa }_{{\bar{f}}}\rangle |\partial _x {\bar{f}}|. \end{aligned}$$In particular, the operator \((\nabla L)^{\prime }(0):V_c^{\perp }\rightarrow H^{\perp }\) is only of second order in u, hence compact by the Rellich–Kondrachov Theorem [23, Theorem 7.26].
-
(4)
\(L(0)={\mathcal {L}}({\bar{f}})=\ell \) since \({\bar{f}}\in {\mathcal {X}}\). Since we have \(|{\bar{f}}(1)-{\bar{f}}(0)| = |p_1-p_0| < \ell \), \({\bar{f}}\) cannot be part of a straight line; hence, \(\vec {\kappa }_{{\bar{f}}}\not \equiv 0\) and also \(|\partial _x {\bar{f}}|\ne 0\) since \({\bar{f}}\) is immersed.
\(\square \)
This enables us to conclude the inequality in normal directions.
Theorem 4.6
Suppose \({\bar{f}}\in {\mathcal {X}}\) is a constrained elastica. Then, there exist \(C, \sigma >0\) and \(\theta \in (0,\frac{1}{2}]\) such that for all \(f={\bar{f}}+u\in {\mathcal {X}}\) with \(u\in V_c^{\perp }\) and \(\Vert u \Vert _{W^{4,2}}\le \sigma \) we have
Proof
First, we verify the conditions of [45, Corollary 5.2] for the energy E and the constraint \({\mathcal {G}}(u)=L(u)-\ell \) on the spaces \(V=V_{c}^{\perp }, H=H^{\perp }\). Note that \(\nabla {\mathcal {G}} = \nabla {L}\). Clearly, \(V_c^{\perp }\hookrightarrow H^{\perp }\) densely. Assumptions (ii) and (iii) follow from Proposition 4.4, whereas assumptions (iv)–(-vi) are satisfied by Proposition 4.5. Note that \(u=0\) is a constrained critical point of E on \({\mathcal {M}}={\mathcal {G}}^{-1}(\{0\})\) since \({\bar{f}}\) is a constrained elastica.
Then, by [45, Corollary 5.2] \(E\vert _{{\mathcal {M}}}\) satisfies a constrained Łojasiewicz–Simon gradient inequality, i.e. there exist \(C, \sigma >0\) and \(\theta \in (0,\frac{1}{2}]\) such that for all \(u\in {\mathcal {M}}\) with \(\Vert u \Vert _{W^{4,2}}\le \sigma \) we have
where \(P(u):H^{\perp }\rightarrow H^{\perp }\) denotes the orthogonal projection onto the closure of the tangent space \(\overline{T_u {\mathcal {M}}} = \{ y\in H^{\perp }\mid \langle \nabla L(u), y\rangle _{L^2} = 0\}\) (cf. [45, Proposition 3.3]). Therefore, for
as in (1.2) with \(f={\bar{f}}+u\) we have the estimate
Moreover, we have \(\nabla E(u) = \nabla _{L^2(\,\!\textrm{d}s_{f})} {\mathcal {E}}(f) |\partial _x f|\) and \(\nabla L(u) = \nabla _{L^2(\,\!\textrm{d}s_{f})} {\mathcal {L}}(f) |\partial _x f|\). Consequently,
Reducing \(\sigma >0\) if necessary, we may assume that \(\Vert \partial _x f \Vert _{L^{\infty }}\) is uniformly bounded for \(\Vert f-{\bar{f}} \Vert _{W^{4,2}}\le \sigma \) by the Sobolev embedding theorem. This proves the claim. \(\square \)
We use this to prove the full constrained Łojasiewicz–Simon gradient inequality for not necessarily normal variations via the following reparametrization argument.
Lemma 4.7
([13, Lemma 4.1]) Let \({\bar{f}}\in W^{5,2}(I;{\mathbb {R}}^d)\) be a regular curve. Then, there exists \(\sigma >0\) such that for all \(\psi \in V_c\) with \(\Vert \psi \Vert _{W^{4,2}}\le \sigma \), there exists a \(W^{4,2}\)-diffeomorphism \(\Phi :I\rightarrow I\) such that
for some \(\eta \in V_c^{\perp }\). Moreover, given \(\sigma >0\) there exists \({\tilde{\sigma }}={\tilde{\sigma }}({\bar{f}}, \sigma )>0\) such that for all \(\psi \in V_c\) with \(\Vert \psi \Vert _{W^{4,2}}\le {\tilde{\sigma }}\) we have the above representation with \(\Vert \eta \Vert _{W^{4,2}}\le \sigma \).
Theorem 4.8
Let \({\bar{f}}\in {\mathcal {X}}\cap W^{5,2}(I;{\mathbb {R}}^d)\) be a constrained elastica. Then there exist \(C, \sigma >0\) and \(\theta \in (0,\frac{1}{2}]\) such that
for all \(f\in {\mathcal {X}}\) such that \(\Vert f-{\bar{f}} \Vert _{W^{4,2}}\le \sigma \).
Proof
Let \(C, \sigma >0, \theta \in (0,\frac{1}{2}]\) as in Theorem 4.6, \({\bar{f}}\in {\mathcal {X}}\) be a constrained critical point of \({\mathcal {E}}\) on \({\mathcal {X}}\). By the regularity assumption on \({\bar{f}}\), we may use Lemma 4.7.
Thus, we find \({\tilde{\sigma }}>0\) such that (4.6) holds for all \(\psi \in V_c\) with \(\Vert \psi \Vert _{W^{4,2}}\le {\tilde{\sigma }}\) for some \(\eta \in V_c^{\perp }\) with \(\Vert \eta \Vert _{W^{4,2}}\le \sigma \). Let \(f\in {\mathcal {X}}\) such that \(\Vert f-{\bar{f}} \Vert _{W^{4,2}}\le {\tilde{\sigma }}\). Then by Lemma 4.7, there exist a diffeomorphism \(\Phi :I \rightarrow I\) and \(\eta \in V_c^{\perp }\) such that \(f\circ \Phi = {\bar{f}}+\eta \).
Note that with \(f, {\bar{f}}\in {\mathcal {X}}\) we also get \(f\circ \Phi = {\bar{f}}+\eta \in {\mathcal {X}}\), since \({\mathcal {L}}(f) = {\mathcal {L}}(f\circ \Phi ) = \ell \). Since the elastic energy is invariant under reparametrization, we hence get using Theorem 4.6
Since \(\lambda \) and the gradients are geometric, i.e. transform correctly under reparametrizations, we have
Consequently, we obtain
Together with (4.7), this implies the Łojasiewicz–Simon gradient inequality for the elastic energy on \({\mathcal {X}}\). \(\square \)
4.4 Convergence
In previous works (see e.g. [8, p. 358 – 359] and [13, p. 2188 – 2191]), a lot of PDE theory and a priori parabolic Schauder estimates are needed to apply the Łojasiewicz–Simon gradient inequality to conclude convergence for geometric problems. In this section, we introduce a novel inequality (see Lemma 4.10) which enables us to significantly shorten this lengthy argument in the proof of Theorem 1.2. We exploit the explicit structure of the constant speed reparametrization and the length bound to control the full velocity of the constant speed parametrization by the purely normal velocity of the original evolution.
Definition 4.9
Let \(T\in (0, \infty ]\) and let \(f:[0,T)\times I\rightarrow {\mathbb {R}}^d\) be a family of immersed curves in \({\mathbb {R}}^d\). The constant speed \({\mathcal {L}}(f(t))\) reparametrization \({\tilde{f}}(t)\) of f(t) is given by \({\tilde{f}}(t,x):=f(t, \psi (t,x))\) where \(\psi (t, \cdot ):{I}\rightarrow {I}\) is the inverse of \(\varphi (t,\cdot ):{I}\rightarrow {I}\) given by
Lemma 4.10
Suppose \(T\in (0, \infty ]\) and \(f:[0,T)\times I\rightarrow {\mathbb {R}}^d\) is a family of curves in \({\mathbb {R}}^d\), such that \(f(t,0)=p_0, f(t,1)=p_1\) and \({\mathcal {L}}(f(t)) >0\) for all \(t\in (0,T]\). Then, if \({\tilde{f}}(t)\) is the constant speed \({\mathcal {L}}(f(t))\) reparametrization of f(t), for all \(t\in [0,T)\) we have
In particular, if f evolves by the length-preserving elastic flow (1.3), we have
for all \(t\in (0,T]\), where \(C=\sqrt{\frac{2}{\ell }+16{\mathcal {E}}(f_0)}\).
Proof
Recall that by Definition 4.9 we have
For the derivatives of \(\varphi \) and \(\psi \) we thus obtain
-
(i)
\(\partial _t \varphi (t,x)=-\frac{\partial _t {\mathcal {L}}(f(t))}{{\mathcal {L}}(f(t))^2} \int \nolimits _0^{x} \!\textrm{d}s_{f(t)} - \frac{1}{{\mathcal {L}}(f(t))}\int \nolimits _0^{x}\langle \partial _t f, \vec {\kappa }_{f(t)}\rangle \,\, \!\textrm{d}s_{f(t)}\);
-
(ii)
\(\partial _x \varphi (t,x) = \frac{|\partial _x f(t,x)|}{{\mathcal {L}}(f(t))}\);
-
(iii)
\(\partial _x \psi (t,\varphi (t,x)) = \left( \partial _x \varphi (t,x)\right) ^{-1} = \frac{{\mathcal {L}}(f(t))}{|\partial _x f(t,x)|}\);
-
(iv)
$$\begin{aligned} \partial _t \psi (t, \varphi (t,x))&= - \partial _x \psi (t,{\varphi (t,x)})~ \partial _t\varphi (t,x)\\&= \frac{{\mathcal {L}}(f(t))}{|\partial _x f(t,x)|}\left( \frac{\partial _t {\mathcal {L}}(f(t))}{{\mathcal {L}}(f(t))^2} \int \nolimits _0^{x} \!\textrm{d}s_{f(t)} \right. \\&\quad \left. + \frac{1}{{\mathcal {L}}(f(t))}\int \nolimits _0^{x}\langle \partial _t f, \vec {\kappa }_{f(t)}\rangle \,\,\!\textrm{d}s_{f(t)}\right) . \end{aligned}$$
Now, we estimate
Taking \(y=\psi (t,x)\) and using \(\psi (t,0)=0\), \(\psi (t,1)=1\), we find
For the first integral, we clearly have
For the second part, note that by (iv), we have
Now, using the boundary conditions, we have \(\partial _t {\mathcal {L}}(f(t)) = -\int \nolimits _{I}\langle \vec {\kappa }_{f(t)}, \partial _t f(t)\rangle \,\!\textrm{d}s_{f(t)}\) and the Cauchy–Schwarz inequality yields
\(\square \)
Remark 4.11
Note that in the proof of Lemma 4.10, we only used the boundary conditions to conclude that no boundary terms appear when integrating by parts. In particular, Lemma 4.10 also holds in the case of closed curves.
Finally, we can prove our main convergence result.
Proof of Theorem 1.2
Let \(\varepsilon >0\) and let \({\hat{f}}\in {\mathcal {C}}^{\infty }((0, \infty )\times I;{\mathbb {R}}^d)\), \({\bar{\varepsilon }}>\varepsilon \) be as in Theorem 4.1. The first statement of Theorem 1.2 follows from property (i) in Theorem 4.1, and the fact that the solution f in Theorem 2.9 lies in \({\mathbb {X}}_{T,2}\hookrightarrow BUC([0,T];W^{2,2}(I;{\mathbb {R}}^d))\) by Proposition B.1 and (B.1).
For the convergence statement, let \({\tilde{f}}\) be the constant speed \(\ell \) reparametrization of \({\hat{f}}\), cf. Definition 4.9, and note that \({\tilde{f}}\in {\mathcal {C}}^{\infty }((0,\infty )\times I;{\mathbb {R}}^d)\). By Theorem 4.1 (iii), there exist a sequence \(t_n\rightarrow \infty \) and a smooth regular curve \(f_{\infty }:I\rightarrow {\mathbb {R}}^{n}\), such that \({\tilde{f}}(t_n)\rightarrow f_\infty \) in \({\mathcal {C}}^{k}(I;{\mathbb {R}}^{n})\) for all \(k\in {\mathbb {N}}_0\). Moreover, as a consequence of Theorem 4.1, \(f_{\infty }\) is a smooth constrained elastica, i.e. a smooth solution of (1.8).
Recall from Theorem 4.1 (ii) that \({\hat{f}}\) has tangential velocity zero for t sufficiently large. Thus, we can without loss of generality assume \({\mathcal {E}}({\hat{f}}(t))= {\mathcal {E}}({\tilde{f}}(t)) >{\mathcal {E}}(f_\infty )\), since otherwise \({\hat{f}}(t)\) would be eventually constant by (1.6), and hence convergent. Moreover, since \({\mathcal {E}}({\hat{f}}(t))\) is nonincreasing, we have that \(\lim _{t\rightarrow \infty }{\mathcal {E}}({\hat{f}}(t)) = \lim _{n\rightarrow \infty }\) \({\mathcal {E}}({\tilde{f}}(t_n))= {\mathcal {E}}(f_\infty )\).
Since \(f_{\infty }\) is smooth, by Theorem 4.8, there exist \(\sigma , C_{LS}>0\) and \(\theta \in (0,\frac{1}{2}]\) such that we have a refined Łojasiewicz–Simon inequality, i.e. for all \(g\in {\mathcal {X}}\) satisfying \(\Vert g-f_{\infty } \Vert _{W^{4,2}}\le \sigma \) we have
Passing to a subsequence, we can assume \(\Vert {\tilde{f}}(t_n,\cdot )-f_{\infty } \Vert _{W^{4,2}}<\sigma \) for all n. Define
and note that \(s_n>t_n\) since \({\tilde{f}}\) is smooth. Define \(G(t):= \left( {\mathcal {E}}({\tilde{f}}(t))-{\mathcal {E}}(f_\infty )\right) ^{\theta }\). By our assumption \({\mathcal {E}}({\tilde{f}}(t))>{\mathcal {E}}(f_\infty )\), so we can compute on \([t_n, s_n)\) using that \({\hat{f}}\) solves (1.3) with \(\theta \equiv 0\), so \(\partial _t {\hat{f}} = -\nabla {\mathcal {E}}({\hat{f}})-\lambda \nabla {\mathcal {L}}({\hat{f}})\) and the fact that \({\mathcal {E}}\) is geometric, i.e. invariant under reparametrization
However, the quantity \(\Vert \nabla _{L^2(\,\!\text {d}s_{{\hat{f}} })} {\mathcal {E}}({\hat{f}} ) +\lambda ({\hat{f}} )\nabla _{L^2(\,\!\text {d}s_{{\hat{f}} })} {\mathcal {L}}({\hat{f}} ) \Vert _{L^2(\,\!\text {d}s_{{\hat{f}} })}\) is geometric, too. Thus
on \([t_n, s_n)\) by (4.8) and our choice of \(s_n\). Therefore, by Lemma 4.10 we have
for all \(t\in [t_n, s_n)\), where \({C} = C(\ell , {\mathcal {E}}(f_0), \theta , C_{LS})>0\). Let \(t\in [t_n, s_n)\). Then
using (4.9) and \({\mathcal {E}}({\tilde{f}}(t_n)) \rightarrow {\mathcal {E}}(f_\infty )\) as \(n\rightarrow \infty \). We now assume that all of the \(s_n\) are finite. Then, by continuity (4.10) also holds for \(t=s_n\). By the subconvergence result in Theorem 4.1, passing to a subsequence we have \({\tilde{f}}(s_{n})\rightarrow \psi \) smoothly as \(n \rightarrow \infty \). Moreover, by continuity and the definition of \(s_n\), we have that \(\Vert \psi - f_\infty \Vert _{W^{4,2}}=\sigma \), whereas \(\Vert \psi -f_\infty \Vert _{L^2(\,\!\text {d}x)} = \lim _{n\rightarrow \infty }\Vert {\tilde{f}}(s_{n})-{\tilde{f}}(t_{n}) \Vert _{L^2(\,\!\text {d}x)} = 0\) by (4.10), a contradiction.
Consequently, there has to exist some \(n_0\in {\mathbb {N}}\) such that \(s_{n_0}=\infty \), and this yields \(\Vert {\tilde{f}}(t)-f_\infty \Vert _{W^{4,2}}<\sigma \) for all \(t\ge t_{n_0}\). This means that (4.9) holds for any \(t\ge t_{n_0}\); thus, \(t\mapsto \Vert \partial _t {\tilde{f}}(t) \Vert _{L^2(\,\!\text {d}x)}\in L^1([0,\infty );{\mathbb {R}})\). Hence, for all \(t_{n_0}\le t\le t^{\prime }\) we have
as \(t,t'\rightarrow \infty \) by the dominated convergence theorem. Therefore, \(\lim _{t\rightarrow \infty }{\tilde{f}}(t)\) exists in \(L^2(\,\!\text {d}x)\) and thus equals \(f_\infty \). A subsequence argument shows that for any \(k\in {\mathbb {N}}_0\) we have \(\Vert {\tilde{f}}(t)-f_\infty \Vert _{{\mathcal {C}}^{k}(I;{\mathbb {R}}^d)}\rightarrow 0\) as \(t\rightarrow \infty \), i.e. the convergence is smooth. \(\square \)
Data availability
Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.
References
R. Abraham, J. E. Marsden, and T. S. Ratiu. Manifolds, tensor analysis, and applications. Springer, New York, 2004.
S. Angenent. Parabolic equations for curves on surfaces. I. Curves with \(p\)-integrable curvature. Ann. of Math. (2), 132(3):451–483, 1990.
S. B. Angenent. Nonlinear analytic semiflows. Proc. Roy. Soc. Edinburgh Sect. A, 115(1-2):91–107, 1990.
J. Appell and P. P. Zabrejko. Nonlinear superposition operators, volume 95 of Cambridge Tracts in Mathematics. Cambridge University Press, Cambridge, 1990.
R. Badal. Curve-shortening of open elastic curves with repelling endpoints: a minimizing movements approach. Interfaces Free Bound., 24(3):389–430, 2022.
S. Blatt, C. P. Hopper, and N. Vorderobermeier. A minimising movement scheme for the \(p\)-elastic energy of curves. J. Evol. Equ., 22(2):Paper No. 41, 25, 2022.
R. Chill. On the Łojasiewicz-Simon gradient inequality. J. Funct. Anal., 201(2):572–601, 2003.
R. Chill, E. Fašangová, and R. Schätzle. Willmore blowups are never compact. Duke Math. J., 147(2):345–376, 2009.
A. Dall’Acqua, C.-C. Lin, and P. Pozzi. Evolution of open elastic curves in \(\mathbb{R}^n\) subject to fixed length and natural boundary conditions. Analysis (Berlin), 34(2):209–222, 2014.
A. Dall’Acqua, C.-C. Lin, and P. Pozzi. A gradient flow for open elastic curves with fixed length and clamped ends. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5), 17(3):1031–1066, 2017.
A. Dall’Acqua, C.-C. Lin, and P. Pozzi. Elastic flow of networks: short-time existence result. J. Evol. Equ., 21(2):1299–1344, 2021.
A. Dall’Acqua, M. Müller, R. Schätzle, and A. Spener. The Willmore flow of tori of revolution, 2020. arXiv:2005.13500. To appear in Anal. PDE.
A. Dall’Acqua, P. Pozzi, and A. Spener. The Łojasiewicz-Simon gradient inequality for open elastic curves. J. Differential Equations, 2016.
A. Dall’Acqua, T. Laux, C.-C. Lin, P. Pozzi, and A. Spener. The elastic flow of curves on the sphere. Geom. Flows, 3(1):1 – 13, 2018.
A. Dall’Acqua, C.-C. Lin, and P. Pozzi. Elastic flow of networks: long-time existence result. Geom. Flows, 4(1):83 – 136, 2019.
R. Denk, M. Hieber, and J. Prüss. Optimal \(L^p\)-\(L^q\)-estimates for parabolic boundary value problems with inhomogeneous data. Math. Z., 257(1):193–224, 2007.
G. Dziuk, E. Kuwert, and R. Schätzle. Evolution of elastic curves in \({\mathbb{R}}^n\): existence and computation. SIAM J. Math. Anal., 33(5):1228–1245, 2002.
J. Escher, J. Prüss, and G. Simonett. A new approach to the regularity of solutions for parabolic equations. In Evolution equations, volume 234 of Lecture Notes in Pure and Appl. Math., pages 167–190. Dekker, New York, 2003.
P. M. N. Feehan and M. Maridakis. Łojasiewicz–Simon gradient inequalities for analytic and Morse–Bott functions on Banach spaces. J. Reine Angew. Math., 765:35–67, 2020.
H. Garcke, J. Menzel, and A. Pluda. Willmore flow of planar networks. J. Differential Equations, 266(4):2019–2051, 2019.
H. Garcke, J. Menzel, and A. Pluda. Long time existence of solutions to an elastic flow of networks. Comm. Partial Differential Equations, 45(10):1253–1305, 2020.
H. Garcke and A. Novick-Cohen. A singular limit for a system of degenerate Cahn-Hilliard equations. Adv. Differential Equations, 5(4-6):401–434, 2000.
D. Gilbarg and N. S. Trudinger. Elliptic partial differential equations of second order. Classics in Mathematics. Springer, Berlin, 2001.
J. Langer and D. Singer. Curves in the hyperbolic plane and mean curvature of tori in \(3\)-space. Bull. London Math. Soc., 16(5):531–534, 1984.
C.-C. Lin. L2-flow of elastic curves with clamped boundary conditions. J. Differential Equations, 252(12):6414 – 6428, 2012.
C.-C. Lin and Y.-K. Lue. Evolving inextensible and elastic curves with clamped ends under the second-order evolution equation in \(\mathbb{R}^2\). Geom. Flows, 3(1):14–18, 2018.
C.-C. Lin, Y.-K. Lue, and H. R. Schwetlick. The second-order \(L^2\)-flow of inextensible elastic curves with hinged ends in the plane. J. Elasticity, 119(1-2):263–291, 2015.
S. Łojasiewicz. Sur les ensembles semi-analytiques. I.H.E.S., Bures-sur-Yvette, 1965.
A. Lunardi. Interpolation theory, volume 16 of Appunti. Scuola Normale Superiore di Pisa (Nuova Serie). Edizioni della Normale, Pisa, 2018.
C. Mantegazza and M. Pozzetta. The Łojasiewicz-Simon inequality for the elastic flow. Calc. Var. Partial Differential Equations, 60(1):Paper No. 56, 17, 2021.
C. Mantegazza and M. Pozzetta. Asymptotic convergence of evolving hypersurfaces. Rev. Mat. Iberoam., 38(6):1927–1944, 2022.
M. Meyries and R. Schnaubelt. Interpolation, embeddings and traces of anisotropic fractional Sobolev spaces with temporal weights. J. Funct. Anal., 262(3):1200–1229, 2012.
M. Müller. On gradient flows with obstacles and Euler’s elastica. Nonlinear Anal., 192:111676, 48, 2020.
M. Müller and A. Spener. On the convergence of the elastic flow in the hyperbolic plane. Geom. Flows, 5(1):40–77, 2020.
M. Novaga and S. Okabe. Curve shortening-straightening flow for non-closed planar curves with infinite length. J. Differential Equations, 256(3):1093–1132, 2014.
M. Novaga and S. Okabe. Convergence to equilibrium of gradient flows defined on planar curves. J. Reine Angew. Math., 733:87–119, 2017.
M. Novaga and P. Pozzi. A second order gradient flow of \(p\)-elastic planar networks. SIAM J. Math. Anal., 52(1):682–708, 2020.
S. Okabe. The motion of elastic planar closed curves under the area-preserving condition. Indiana Univ. Math. J., 56(4):1871–1912, 2007.
S. Okabe, P. Pozzi, and G. Wheeler. A gradient flow for the \(p\)-elastic energy defined on closed planar curves. Math. Ann., 378(1-2):777–828, 2020.
S. Okabe and P. Schrader. Convergence of Sobolev gradient trajectories to elastica, 2023.
S. Okabe and G. Wheeler. The \(p\)-elastic flow for planar closed curves with constant parametrization. J. Math. Pures Appl. (9), 173:1–42, 2023.
A. Polden. Curves and Surfaces of Least Total Curvature and Fourth Order Flows. PhD thesis, Universität Tübingen, 1996.
M. Pozzetta. Convergence of elastic flows of curves into manifolds. Nonlinear Anal., 214:Paper No. 112581, 53, 2022.
J. Prüss and G. Simonett. Moving interfaces and quasilinear parabolic evolution equations, volume 105 of Monographs in Mathematics. Birkhäuser/Springer, [Cham], 2016.
F. Rupp. On the Łojasiewicz–Simon gradient inequality on submanifolds. J. Funct. Anal., 279(8):108708, 2020.
F. Rupp. Constrained gradient flows for Willmore-type functionals. PhD thesis, Universität Ulm, 2022.
F. Rupp. The volume-preserving Willmore flow. Nonlinear Anal., 230:Paper No. 113220, 30, 2023.
F. Rupp. The Willmore flow with prescribed isoperimetric ratio. Comm. Partial Differential Equations, 49(1-2):148–184, 2024.
L. Simon. Asymptotics for a class of nonlinear evolution equations, with applications to geometric problems. Ann. of Math. (2), 118(3):525–571, 1983.
A. Spener. Short time existence for the elastic flow of clamped curves. Math. Nachr., 290(13):2052–2077, 2017.
H. Triebel. Interpolation theory, function spaces, differential operators. VEB Deutscher Verlag der Wissenschaften, Berlin, 1978.
Y. Wen. \(L^2\) flow of curve straightening in the plane. Duke Math. J., 70(3):683–698, 1993.
Acknowledgements
Fabian Rupp has been supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)-Projektnummer: 404870139 and by the Austrian Science Fund (FWF), grant numbers 10.55776/P32788 and 10.55776/ESP557. The authors would like to thank Anna Dall’Acqua, Marius Müller and Rico Zacher for helpful discussions and comments. Moreover, the authors are grateful to the referees for their valuable feedback on the original manuscript.
Funding
Open access funding provided by University of Vienna.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that there is no conflict of interest regarding the publication of this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Explicit formulas in coordinates
In this section, we present the explicit representation of the geometric quantities appearing in this article. They can be obtained by a straight forward calculation, see e.g. [20, (2.3)].
Proposition A.1
Suppose \(f:I \rightarrow {\mathbb {R}}^{d}\) is a smooth immersion. With the arc-length element \(\gamma = |\partial _x f|\) we have
-
(i)
\(\vec {\kappa }_f = \partial _s^{2} f = \frac{\partial ^2_x f}{\gamma ^{2}} - \frac{\langle \partial _x^{2}f, \partial _x f\rangle }{\gamma ^{4}} \partial _x f = \frac{(\partial _x^2 f)^{\perp }}{\gamma ^4}\);
-
(ii)
\(\nabla _{s_f} \vec {\kappa }_f = \frac{\partial _x^{3}f}{\gamma ^{3}} - \frac{\langle \partial _x^{3}f, \partial _x f\rangle }{\gamma ^{5}}\partial _x f - 3 \frac{\langle \partial _x^{2} f, \partial _{x} f\rangle }{\gamma ^{5}} \partial _x^{2} f + 3 \frac{\langle \partial _x^{2}f, \partial _{x}f\rangle ^{2}}{\gamma ^{7}}\partial _x f\);
-
(iii)
$$\begin{aligned} \nabla _{s_f}^2 \vec {\kappa }_f&= \Bigg [ \frac{\partial _x^{4}f}{\gamma ^{4}} -6 \frac{\langle \partial _{x}^{2} f, \partial _x f\rangle }{\gamma ^{6}}\partial _x^{3}f - 4 \frac{\langle \partial _x^{3}f, \partial _x f\rangle }{\gamma ^{6}}\partial _x^{2}f \\&\quad - 3 \frac{|\partial _x^{2} f|^{2}}{\gamma ^{6}} \partial _x^{2} f + 18 \frac{\langle \partial _x^{2}f, \partial _x f\rangle ^{2}}{\gamma ^{8}} \partial _x^{2}f\Bigg ]^{\perp _f}; \end{aligned}$$
-
(iv)
$$\begin{aligned} \nabla {\mathcal {E}}(f)&=\Bigg [\frac{\partial _x^{4}f}{\gamma ^{4}} -6 \frac{\langle \partial _{x}^{2} f, \partial _x f\rangle }{\gamma ^{6}}\partial _x^{3}f - 4 \frac{\langle \partial _x^{3}f, \partial _x f\rangle }{\gamma ^{6}}\partial _x^{2}f \\&\quad - \frac{5}{2} \frac{|\partial _x^{2} f|^{2}}{\gamma ^{6}} \partial _x^{2} f + \frac{35}{2} \frac{\langle \partial _x^{2}f, \partial _x f\rangle ^{2}}{\gamma ^{8}} \partial _x^{2}f\Bigg ]^{\perp _f}.\end{aligned}$$
Here \(\nabla {\mathcal {E}}(f)\) denotes the \(L^2(\!\textrm{d}s_f)\)-gradient of \({\mathcal {E}}\) at f.
Lemma A.2
Let f be a smooth immersed curve with arc-length element \(\gamma \). Then
-
(i)
\(|\vec {\kappa }_{f}|^{4} = \gamma ^{-8} |\partial _x^2 f|^{4} - 2\gamma ^{-10} |\partial _x^{2}f|^{2}\langle \partial _x^{2}f, \partial _x f\rangle ^{2} + \gamma ^{-12} \langle \partial _x^{2}f, \partial _x f\rangle ^{4}\);
-
(ii)
$$\begin{aligned} |\nabla _{s_f}\vec {\kappa }_{f}|^{2}&= \gamma ^{-6}|\partial _x^{3} f|^{2} - \gamma ^{-8} \langle \partial _x^{3}f, \partial _x f\rangle ^{2} - 6\gamma ^{-8}\langle \partial _x^{3}f, \partial _x^{2}f\rangle \langle \partial _x^{2}f, \partial _x f\rangle \\&\quad + 6 \gamma ^{-10} \langle \partial _x^{3}f, \partial _x f\rangle \langle \partial _x^{2}f, \partial _x f\rangle ^{2} + 9 \gamma ^{-10}\langle \partial _x^{2}f, \partial _x f\rangle ^{2} |\partial _x^{2}f|^{2} \\&\quad - 9 \gamma ^{-12}\langle \partial _x^{2}f, \partial _x f\rangle ^{4}; \end{aligned}$$
-
(iii)
$$\begin{aligned} \langle \nabla _{s_f}\vec {\kappa }_{{f}}, \vec {\kappa }_f\rangle&= \gamma ^{-5} \langle \partial _x^{3}f, \partial _x^{2}f\rangle - \gamma ^{-7} \langle \partial _x^{3}f, \partial _x f\rangle \langle \partial _x^{2}f, \partial _x f\rangle \\&\quad - 3\gamma ^{-7}\langle \partial _x^{2}f, \partial _x f\rangle |\partial _x^{2} f|^2 + 3\gamma ^{-9} \langle \partial _x^{2}f, \partial _x f\rangle ^{3}. \end{aligned}$$
Appendix B: Function spaces
In this section, we collect all relevant information on the function spaces for maximal \(L^p\)-regularity. Most of the embedding results are collected in [16], see also [32], where even a polynomial weight \(t^{1-\mu }\) in time is allowed. As discussed in Remark 2.11, time weights do not allow to prove short-time existence with weaker initial data, and hence we restrict ourselves to the case \(\mu =1\).
Let \(J\subset {\mathbb {R}}\) be an interval, \(1\le p<\infty \). For any \(s\in (0,\infty ){\setminus }{\mathbb {N}}\) and a Banach space E, the (E-valued) Sobolev–Slobodetskii space and the Bessel potential space, respectively, are given by real and complex interpolation
where \(W^{k,p}(J;E)\) denotes the usual Bochner–Sobolev space for \(k\in {\mathbb {N}}_0\). Recall from [51, Theorem 2.4.1 (a), Definition 4.2.1] that the Besov spaces are given by
where \(s=(1-\theta )m_1+\theta m_2\), \(\theta \in (0,1), m_1, m_2\in {\mathbb {N}}_0, m_1<m_2, p,q\in [1,\infty )\). By [51, Definition 2.3.1 (d) and Theorem 2.3.2 (d)] we have the relation
Moreover, recall from [16, Section 2], that in the setting of the maximal regularity spaces \({\mathbb {X}}_{T,p}\), the spaces of zeroth- and first-order boundary data are given by
We now recall the Sobolev embeddings for the maximal regularity space \({\mathbb {X}}_{T,p}\). We emphasize that the operator norms of the embeddings below might blow up as \(T\rightarrow 0+\). However, in the solution space with vanishing trace, i.e. the space \( {}_{0}{{\mathbb {X}}_{T,p}}\), they are bounded independently of T.
Proposition B.1
Let \(0<T\le \infty \), let \(p\ge 2\) and let \(k\in \{0,\dots ,4\}\).
-
(i)
\({\mathbb {X}}_{T,p} \hookrightarrow BUC([0,T], B^{4(1-\frac{1}{p})}_{p,p})(I;{\mathbb {R}}^d))\) with the estimate
$$\begin{aligned} \Vert f \Vert _{BUC([0,T];B^{4(1-\frac{1}{p})}_{p,p}(I;{\mathbb {R}}^d))} \le {C(p)}\Vert f \Vert _{{\mathbb {X}}_{T,p}} \quad \text {for }f\in {}_{0}{{\mathbb {X}}_{T,p}}. \end{aligned}$$ -
(ii)
\({\mathbb {X}}_{T,p} \hookrightarrow {\mathcal {C}}^{\alpha }([0,T];{\mathcal {C}}^{1,\alpha }(I;{\mathbb {R}}^d))\) for some \(\alpha \in (0,1)\) with the estimate
$$\begin{aligned} \Vert f \Vert _{{\mathcal {C}}^{\alpha }([0,T]; {\mathcal {C}}^{1,\alpha }(I;{\mathbb {R}}^d))}\le {C(p,\alpha )} \Vert f \Vert _{{\mathbb {X}}_{T,p}}\quad \text {for }f\in {}_{0}{{\mathbb {X}}_{T,p}}. \end{aligned}$$ -
(iii)
The k-th spatial derivative is continuous as a map
$$\begin{aligned} \partial _x^k :{\mathbb {X}}_{T,p}&\rightarrow H^{\frac{4-k}{4}, p}(0,T;L^p(I;{\mathbb {R}}^d)) \cap L^p(0,T; H^{4-k,p}(I;{\mathbb {R}}^d)) \\&\hookrightarrow W^{\frac{(4-k)\theta }{4}, p}(0,T;W^{(4-k)(1-\theta ),p}(I;{\mathbb {R}}^d)) \text { for all } \theta \in (0,1), \end{aligned}$$with the estimate
$$\begin{aligned} \Vert \partial _x^k f \Vert _{H^{\frac{4-k}{4}, p}(0,T;L^p(I;{\mathbb {R}}^d)) \cap L^p(0,T; H^{4-k,p}(I;{\mathbb {R}}^d))}\le {C(k,p)} \Vert f \Vert _{{\mathbb {X}}_{T,p}}\quad \text {for }f\in {}_{0}{{\mathbb {X}}_{T,p}}. \end{aligned}$$ -
(iv)
The spatial trace of the k-th spatial derivative is continuous as a map
$$\begin{aligned} {{\,\textrm{tr}\,}}_{\partial I}\partial _x^k :{\mathbb {X}}_T&\rightarrow W^{\frac{4-k}{4} - \frac{1}{8}, p}(0,T;L^p(\partial I;{\mathbb {R}}^d)) \cong W^{\frac{4-k}{4} - \frac{1}{8}, p}(0,T;({\mathbb {R}}^d)^2), \end{aligned}$$with the estimate
$$\begin{aligned} \Vert {{\,\textrm{tr}\,}}_{\partial I}\partial _x^k f \Vert _{W^{\frac{4-k}{4} - \frac{1}{8}, p}(0,T;({\mathbb {R}}^d)^2)}\le {C(k,p)} \Vert f \Vert _{{\mathbb {X}}_{T,p}}\quad \text {for }f\in {}_{0}{{\mathbb {X}}_{T,p}}. \end{aligned}$$
Proof
For \(T=\infty \) and I replaced by \({\mathbb {R}}\), the statements follow from the corresponding results in [16, Section 3]. The statements in our case can then be obtained by considering appropriate temporal and spatial extension operators, see for instance [32, Lemma 2.5 and (3.2)]. When restricted to \({}_{0}{{\mathbb {X}}_{T,p}}\), the operator norm of the temporal extension does not depend on T by [32, Lemma 2.5], which implies the above T-independent estimates. \(\square \)
Remark B.2
For a Hilbert space E and \(s\in (0,\infty ),p=2\), the Bessel potential spaces coincide with the Slobodetskii spaces, i.e. \(H^{s,2}(0,T;E) = W^{s,2}(0,T;E)\) with equivalence of norms, cf. [29, Corollary 4.37]. A particular consequence of this is that in the case \(p=2\) we get from Proposition B.1 (iii) that for \(k\in {\mathbb {N}}\), \(k\le 4\), and \(T\in (0,1]\) we have
is continuous, with the estimate
A crucial tool in proving the contraction estimates in Sect. 2.4 is the precise control of the integrability of the spatial derivatives and their spatial trace, with operator norm bounded independent of T. As in Sect. 2.4, we restrict to the case \(p=2\) here.
Proposition B.3
Let \(T\in (0,1]\), \(k\in {\mathbb {N}}\), \(k\le 4\), \(\rho _1, \rho _2 \in [1, \infty )\).
-
(i)
If there exists \(\theta \in [0,1]\) such that \(\frac{4-k}{4}\theta - \frac{1}{2}\ge -\frac{1}{\rho _1}\) and \((4-k)(1-\theta )-\frac{1}{2}\ge -\frac{1}{\rho _2}\) then \(\partial _x^k :{{\mathbb {X}}_{T,2}}\rightarrow L^{\rho _1}(0,T;L^{\rho _2}(I;{\mathbb {R}}^d))\) with the estimate
$$\begin{aligned} \Vert \partial _x^k f \Vert _{L^{\rho _1}(0,T;L^{\rho _2}(I;{\mathbb {R}}^d))} \le {C(k,\theta , \rho _1, \rho _2)}\Vert f \Vert _{{\mathbb {X}}_{T,2}} \quad \text { for all }f\in {}_{0}{{\mathbb {X}}_{T,2}}. \end{aligned}$$ -
(ii)
If \(\frac{4-k}{4}-\frac{5}{8}\ge -\frac{1}{\rho _1}\), then \({{\,\textrm{tr}\,}}_{\partial I} \partial _x^k :{{\mathbb {X}}_{T,2}}\rightarrow L^{\rho _1}(0,T;({\mathbb {R}}^d)^2)\) with the estimate
$$\begin{aligned} \Vert {{\,\textrm{tr}\,}}_{\partial I}\partial _x^k f \Vert _{L^{\rho _1}(0,T;({\mathbb {R}}^d)^2} \le {C(k, \rho _1)}\Vert f \Vert _{{\mathbb {X}}_{T,2}} \quad \text { for all }f\in {}_{0}{{\mathbb {X}}_{T,2}}. \end{aligned}$$
Proof
We first prove the estimates.
-
(i)
Using first Proposition B.1 (iii) and Remark B.2, then interpolation, and in the last line the usual Sobolev embedding both in the temporal and spatial variable, we find
$$\begin{aligned} \partial _x^k :{}_{0}{{\mathbb {X}}_{{1},2}}&\rightarrow W^{\frac{4-k}{4},2}(0,{1};L^2(I;{\mathbb {R}}^d)) \cap L^2(0,{1}, W^{4-k, 2}(I;{\mathbb {R}}^d)) \nonumber \\&\hookrightarrow W^{\frac{4-k}{4}\theta ,2}(0,{1};W^{(4-k)(1-\theta ),2}(I;{\mathbb {R}}^d)) \nonumber \\&\hookrightarrow L^{\rho _1}(0, {1}; L^{\rho _2}(I;{\mathbb {R}}^d)). \end{aligned}$$(B.3)Now, by [32, Lemma 2.5], there exists an extension operator \(E_T\) from (0, T) to \((0,{1})\) such that \(E_T :{}_{0}{{\mathbb {X}}_{T,2}} \rightarrow {}_{0}{{\mathbb {X}}_{{1},2}}\) has operator norm independent of T. Then, for any \(f\in {}_{0}{{\mathbb {X}}_{T,2}}\) we have using (B.3)
$$\begin{aligned} \Vert \partial _x^k f \Vert _{L^{\rho _1}(0,T;L^{\rho _2}(I;{\mathbb {R}}^d))}&\le \Vert \partial _x^k(E_T f) \Vert _{L^{\rho _1}(0,{1};L^{\rho _2}(I;{\mathbb {R}}^d))} \\&\le {C(k, \theta , \rho _1, \rho _2)} \Vert E_T f \Vert _{{\mathbb {X}}_{{1},2}} \\&\le {C(k, \theta , \rho _1, \rho _2)} \Vert f \Vert _{{\mathbb {X}}_{T,2}}. \end{aligned}$$ -
(ii)
Since \({{\,\textrm{tr}\,}}_{\partial I}\partial _k f\) only depends on the temporal variable, we first use Proposition B.1 (iv) and Remark B.2 and then the Sobolev embedding to find
$$\begin{aligned} {{\,\textrm{tr}\,}}_{\partial I}\partial _x^k :{}_{0}{{\mathbb {X}}_{{1},2}}&\rightarrow W^{\frac{4-k}{4}-\frac{1}{8},2}(0,{1};({\mathbb {R}}^d)^2)\nonumber \\&\hookrightarrow L^{\rho _1}(0, {1}; ({\mathbb {R}}^d)^2). \end{aligned}$$(B.4)Again, using the extension operator, we find for any \(f\in {}_{0}{{\mathbb {X}}_{T,2}}\)
$$\begin{aligned} \Vert {{\,\textrm{tr}\,}}_{\partial I}\partial _x^k f \Vert _{L^{\rho _1}(0,T;({\mathbb {R}}^d)^2)}&\le \Vert {{\,\textrm{tr}\,}}_{\partial I}\partial _x^k(E_T f) \Vert _{L^{\rho _1}(0,{1};({\mathbb {R}}^d)^2)} \\&\le {C(k, \rho _1)} \Vert E_T f \Vert _{{\mathbb {X}}_{{1},2}} \\&\le {C(k, \rho _1)} \Vert f \Vert _{{\mathbb {X}}_{T,2}}. \end{aligned}$$
The mapping properties follow from (B.3) and (B.4). \(\square \)
Appendix C: Details of the contraction estimates
First, the following definition describes the structure of the nonlinearities in (2.3) which guarantees the desired contraction properties.
Definition C.1
Let \((a,b)\in {\mathbb {N}}_0^{2}\). We denote by \(A^{(a,b)}\) the set of bounded multilinear maps
for some \(w\in {\mathbb {N}}\), \(m\in {\mathbb {N}}_0\). Then, we define the set \({\mathcal {A}}^{(a,b)}\) of multilinear maps of type (a, b) as the set of all maps \(f\mapsto \Phi (f)\) acting via
for almost every \((t,x)\in (0,T)\times I\) where \(\varphi \in A^{(a,b)}\).
Remark C.2
Note that we do not keep track of m, the number of first-order derivatives appearing in \(\Phi \in {\mathcal {A}}^{(a,b)}\). This is justified since by Proposition B.1 (ii), the derivatives of first order of \(f\in {\mathbb {X}}_{T}\) are in \({\mathcal {C}}([0,T]\times I;{\mathbb {R}}^d)\) and hence do not affect the integrability of \(\Phi (f)\).
Example C.3
The map \(f\mapsto \Phi (f) = {\langle \partial _x^2f, \partial _x f\rangle } \partial _x^3 f\) is in \({\mathcal {A}}^{(1,1)}\), since the derivatives of second and third order only appear linearly.
The following proposition yields for which parameters (a, b) we get a contraction. Note that nonlinearities with this structure appear in \({\tilde{F}}\) in (2.2) and \(\lambda \) in (2.1). As in Sect. 2.4, we assume \(T,M\le 1\) and set \({\mathbb {X}}_T = {\mathbb {X}}_{T,2}\) to simplify notation.
Proposition C.4
Let \(q\in (0,1)\) and let \(\Phi \in {\mathcal {A}}^{(a,b)}\). Then, for \(T=T(q,{\bar{f}}),M=M(q,{\bar{f}})\in (0,1] \) small enough, each of the following nonlinear maps is a well-defined q-contraction, i.e. Lipschitz continuous with Lipschitz constant q.
-
(i)
\({{\bar{B}}_{T,M}}\rightarrow L^2(0,T;L^2), f\mapsto \Phi (f)\), if \((a,b)=(1,1)\) or \((a,b)=(3,0)\).
-
(ii)
\({{\bar{B}}_{T,M}} \rightarrow L^2(0,T), f\mapsto \int \nolimits _{I} \Phi (f)\!\textrm{d}x\), if \((a,b)=(0,2), (a,b)=(2,1)\) or \((a,b)=(4,0)\).
-
(iii)
\({{\bar{B}}_{T,M}} \rightarrow L^2(0,T;({\mathbb {R}}^{d})^2), f\mapsto {{\,\textrm{tr}\,}}_{\partial I} \Phi (f)\), if \((a,b)=(1,1)\) or \((a,b)=(3,0)\).
-
(iv)
\({{\bar{B}}_{T,M}} \rightarrow L^2(0,T;L^2), f\mapsto \left( \gamma _0^{-4}-\gamma ^{-4}\right) \partial _x^4f\).
The following general functional analytic result gives sufficient conditions for a multilinear map to be a q-contraction for \(T>0\) small. It is the key ingredient in the proof of Proposition C.4.
Lemma C.5
Let \(1\le q_1\le \infty \) and suppose \((f_1, \dots , f_r)\mapsto \mu (f_1, \dots , f_r)\) is a multilinear map such that for all \(f_1, \dots , f_r\in {\mathbb {X}}_{T,2}\) we have
Here, we have \(d_1, \dots , d_r \in \{0,\dots , 3\}\), \(S\in \{{{\,\textrm{Id}\,}}, {{\,\textrm{tr}\,}}_{\partial I}\}\) and \(Z,X_1, \dots , X_r\) are Banach spaces such that there exists \(C\in (0,\infty )\) independent of T with
-
(i)
\(\partial _x^{d_i} :{\mathbb {X}}_T \rightarrow X_i\) and for \(f\in {}_{0}{{\mathbb {X}}_T}\) we have \(\Vert S \partial _x^{d_i}f \Vert _{X_i}\le {C}\Vert f \Vert _{{\mathbb {X}}_T}\) for all \(i=1, \dots ,r\).
-
(ii)
for all \(j=1, \dots r\) one of the following conditions is satisfied.
-
(a)
There exists \(\alpha >0\) with \(\Vert S\partial _x^{d_j}f \Vert _{X_j}\le {C} T^{\alpha } \Vert f \Vert _{{\mathbb {X}}_T}\) for all \(f\in {}_{0}{{\mathbb {X}}}_T\).
-
(b)
There exists \(k\ne j\) with \(\Vert S\partial _x^{d_k}f \Vert _{X_k}\rightarrow 0\) as \(T\rightarrow 0\) for all \(f\in {\mathbb {X}}_T\).
-
(a)
Then, setting \(\mu (f) = \mu (f, \dots , f)\), we have \(\mu (f)\in L^{q_1}(0,T;Z)\) for all \(f\in {\mathbb {X}}_T\) and for any \(q\in (0,1)\), there exist \(M = M(q,r,{\bar{f}}),T = T(q,r, {\bar{f}})\in (0,1]\) small enough, such that for all \(f,{\tilde{f}}\in {{\bar{B}}_{T,M}}\) we have
Remark C.6
When applying Lemma C.5, we always work with Banach spaces of the type \(X_j=L^{p_j}(0,T;L^{q_j})\) and \(Z=L^{p_0}\), for some \(p_0, p_j, q_j \in [1,\infty ]\). Note that (ii) b) is always satisfied if there exists \(k\ne j\) with \(p_k<\infty \), since then \(\lim _{T\rightarrow 0} \Vert f \Vert _{L^{p_k}(0,T;L^{q_k})}\rightarrow 0\) by dominated convergence.
Proof of Lemma C.5
Let \(f, {\tilde{f}}\in {{\bar{B}}_{T,M}}\). Adding and subtracting zeroes and using the multilinearity, we get
Thus, using (C.2), we get
We now show that the contraction property is valid for each summand in (C.3). Note that for all \(k\in \{1, \dots ,r\}\) by (i) we have
In particular, for \(T\le 1\), \(M\le 1\) we find
Now, let \(j\in \{1, \dots , r\}\). If (ii) a) is satisfied, using \(f(0)={\tilde{f}}(0)=f_0\), we find
for \(T = T(\alpha , {\bar{f}})>0\) small enough. Otherwise, if (ii) b) is satisfied, we estimate using (i) for the j-th factor, (C.4) for the k-th factor and (C.5) for the remaining factors, to get
By (ii) b), \(\lim _{T\rightarrow 0}\Vert S\partial _x^{d_k}{\bar{f}} \Vert _{X_k} = 0\). Consequently, for \({T = T(q,r,{\bar{f}}), M =}\) \( {M(q,r, {\bar{f}}) \in (0,1]}\) small enough we find
All in all, we have proven
\(\square \)
Together with the embedding results in Proposition B.1 and Proposition B.3, we can now prove Proposition C.4.
Proof of Proposition C.4
Let \(f, {\tilde{f}}\in {{\bar{B}}_{T,M}}\subset {\mathbb {X}}_T\) with \({T=T(q,{\bar{f}}), M=M(q,{\bar{f}})} \) \( {\in (0,1]}\) small enough such that Lemma 2.2 is satisfied. The strategy for the proof of cases (i)–(iii) is to apply Lemma C.5. To that end, we use Hölder’s inequality in time and space and then verify the assumptions of Lemma C.5 using Proposition B.3. In the following, we denote by \(f_1,\dots ,f_m\), \(g,g_1, g_2, g_3, g_4, h, h_1, h_2\) general functions in \({{\bar{B}}_{T,M}}\).
Case (i): If \((a,b)=(1,1)\), by Hölder’s inequality we have
Using Proposition B.1 (ii) we have
Therefore, we find
such that (ii) a) in Lemma C.5 is satisfied. Next, using Proposition B.3 (i) with \(k=2\) and \(\theta =\frac{3}{4}\) yields
since \(\frac{4-2}{4}\cdot \frac{3}{4}-\frac{1}{2}\ge -\frac{1}{8}\) and \((4-2)(1-\frac{3}{4}) - \frac{1}{2}\ge -\frac{1}{4}\). Similarly for the third derivative with \(\theta =\frac{1}{2}\) we get
Thus, condition (ii) a) in Lemma C.5 is satisfied for the fist m factors in (C.6) by (C.7), whereas for the remaining factors condition (ii) b) holds. More precisely, for \(j=m+1\) choosing \(k=m+2\) works and conversely \(j=m+2,k=m+1\), using Remark C.6.
The case \((a,b)=(3,0)\) can be treated similarly, using Hölder to obtain
and then Proposition B.3 (i) with \(k=2\), \(\theta =\frac{2}{3}\) to get
Case (ii): First, we have the following basic estimate
It hence suffices to show that \({\mathbb {X}}_T\rightarrow L^2(0,T;L^1), f\mapsto \Phi (f)\) is a q-contraction. To that end, we use Lemma C.5 with \(Z=L^1, S={{\,\textrm{Id}\,}}\).
If \((a,b)=(0,2)\), we have by Hölder’s inequality
Now, using Proposition B.3 (i) with \(k=3\) and \(\theta =1\), we have
Consequently, the last two factors in (C.11) satisfy condition (i) and (ii) b) in Lemma C.5, cf. Remark C.6. For the first m factors, we may once again use (C.7) to deduce that conditions (i) and (ii) a) in Lemma C.5 are satisfied.
If \((a,b)=(2,1)\), we proceed similarly, first using Hölder to get
and then applying (C.7), (C.8) and (C.12). For \((a,b)=(4,0)\), we may apply Hölder’s inequality to obtain
Case (iii): Again, we use Lemma C.5, now with \(Z=({\mathbb {R}}^d)^2\) and \(S={{\,\textrm{tr}\,}}_{\partial I}\). If \((a,b)=(1,1)\) we obtain by Hölder’s inequality
Note that by Proposition B.3 (ii), we have
whereas for the third derivative, we obtain
As in cases (i) and (ii), we then use the mapping properties and the estimates in (C.7), (C.14) and (C.15) together with Remark C.6 to verify that the assumptions of Lemma C.5 are satisfied.
If \((a,b)=(3,0)\), we proceed similarly, first using Hölder to obtain
and then (C.7) for the first-order terms and Proposition B.3 (ii) with \(k=2\), yielding
Case (iv): Let \(q\in (0,1)\). For \(f, {\tilde{f}}\in {{\bar{B}}_{T,M}}\), we have
Thus, we may estimate
For the first term, we use the mean value theorem and Lemma 2.2 to conclude
Consequently, using Proposition B.1 (ii) we may estimate
Combined with the simple estimate \(\Vert \partial _x^4 f -\partial _x^{4}{\tilde{f}} \Vert _{L^2(0,T;L^2)}\le \Vert f-{\tilde{f}} \Vert _{{\mathbb {X}}_T}\) this yields a \(\frac{q}{2}\)-contraction estimate for the first part of (C.16), taking \({T=T(q, {\bar{f}})\in (0,1]}\) small enough. For the remaining part, we use (C.17) with \(\gamma _0\) replaced by \({\tilde{\gamma }}\) to conclude
and \(\Vert \partial _x^4 f \Vert _{L^2(0,T;L^2)} \le \Vert f-{\bar{f}} \Vert _{{\mathbb {X}}_T} + \Vert \partial _x^4 {\bar{f}} \Vert _{L^2(0,T;L^2)} \le {C({\bar{f}})}\). Consequently, if \({T=T(q, {\bar{f}})\in (0,1]}\) is small enough, the second part of (C.16) is a \(\frac{q}{2}\)-contraction. \(\square \)
It is not difficult to see that the statement of Proposition C.4 remains true if one allows multiplication by powers of the arc-length element.
Corollary C.7
Let \(q\in (0,1),\ell \in {\mathbb {N}}\), \(\Phi \in {\mathcal {A}}^{(a,b)}\). For \({T=T(q,\ell ) \in (0,1]}\), \({M=}\) \({M(q, \ell )\in (0,1]}\) small enough, each of the following maps is a well-defined q-contraction.
-
(i)
\({{\bar{B}}_{T,M}}\rightarrow L^2(0,T;L^2), f\mapsto \gamma ^{-\ell }\Phi (f)\), if \((a,b)=(1,1)\) or \((a,b)=(3,0)\).
-
(ii)
\({{\bar{B}}_{T,M}} \rightarrow L^2(0,T), f\mapsto \int \nolimits _{I} \gamma ^{-\ell }\Phi (f)\!\textrm{d}x\), if \((a,b)=(0,2), (a,b)=(2,1)\) or \((a,b)=(4,0)\).
-
(iii)
\({{\bar{B}}_{T,M}} \rightarrow L^2(0,T({\mathbb {R}}^{d})^2), f\mapsto {{\,\textrm{tr}\,}}_{\partial I}\gamma ^{-\ell } \Phi (f)\), if \((a,b)=(1,1)\) or \((a,b)=(3,0)\).
Proof
Well-definedness: By Lemma 2.2 we can estimate \(|\gamma ^{-\ell } \Phi (f)|\le \frac{\inf \gamma _0}{2} |\Phi (f)|\) for all \(T,M>0\) small enough. Thus \(f\mapsto \gamma ^{-\ell }\Phi (f)\) maps into the correct space by Lemma C.5.
Contraction: Let \(q\in (0,1)\) and let \(f, {\tilde{f}}\in {{\bar{B}}_{T,M}}\). For the first case, taking \(T,M>0\) small enough, we have
using Proposition C.4 for \(q_2\in (0,1)\) to be chosen. With similar estimates one finds
and
We now prove that for any \(q\in (0,1)\) the map \({{\bar{B}}_{T,M}}\rightarrow L^{\infty }((0,T)\times I)\), \(f\mapsto \gamma ^{-\ell }\) is a q-contraction for \(T,M>0\) small enough. We find as in (C.17)
for \({T=T(q, \ell , {\bar{f}})\in (0,1]}\) small enough using Proposition B.1 (ii) and the fact that \(f(0)={\tilde{f}}(0)=f_0\). Thus, we find
choosing first \({q_2 = q_2 (q, \ell , {\bar{f}}) \in (0,1)}\) sufficiently small and passing to a smaller \({T = T(q, \ell , {\bar{f}})}\) and \({M= M(q, \ell , {\bar{f}})\in (0,1]}\) if necessary. \(\square \)
Proof of Lemma 2.4
First, taking \({T=T({\bar{f}}),M\in (0,1]}\) small enough such that Lemmas 2.2 and 2.3 hold, all terms are defined almost everywhere. We observe that \({\mathcal {F}}(f)\) is a sum of terms as in Corollary C.7 (i) and Proposition C.4 (iv) by (2.2), hence well-defined and a q-contraction for all \(q\in (0,1)\), if \({T=T(q, {\bar{f}})}\), \({M=M(q, {\bar{f}})\in (0,1]}\) are small enough.
For \(\Lambda \) we need to do one additional estimate. For \(f\in {{\bar{B}}_{T,M}}\) and \(T,M>0\) the scalar-valued function \(\lambda \) is in \(L^{2}(0,T)\), since by Lemma 2.3 the energy \({\mathcal {E}}(f)\) in the denominator of \(\lambda \) (cf. Sect. 2.1) is bounded from below uniformly in t, whereas the nominator N(f) is in \(L^2(0,T)\) by Corollary C.7 (ii) and (iii) and by the explicit formulas in Lemma A.2 and (2.1). The term \(\vec {\kappa }_{{f}}\) is in \(L^{\infty }(0,T)\) by the embedding \({\mathbb {X}}_T\hookrightarrow BUC([0,T]; W^{2,2}(I;{\mathbb {R}}^d))\), cf. Proposition B.1 (i),(B.1) and Proposition A.1.
Now, the crucial step is the proof of the contraction estimate for \(\Lambda \). To that end, let \(f, {\tilde{f}}\in {{\bar{B}}_{T,M}}\). Then, writing \(\lambda (f)=\frac{N(f)}{2{\mathcal {E}}(f)}\) as in Sect. 2.1, we find for almost every (t, x)
using that by Lemma 2.3 the elastic energy is bounded from below. Taking the \(L^2L^2\)-norm in (C.18), we are left with three terms. The first one is
Now, note that N(f) is a sum of terms as in Corollary C.7 (ii) and (iii) by (2.1) and the explicit formulas in Lemma A.2. Therefore, for any \(q\in (0,1)\), we have
if we take \({T=T(q, {\bar{f}}),M=M(q, {\bar{f}})\in (0,1]}\) small enough. In particular, we can assume that \(f\mapsto N(f)\) is 1-Lipschitz.
For the elastic energy term, note that \({\mathcal {E}}\) is analytic, hence \({\mathcal {C}}^{1}\) on the space of \(W^{2,2}\)-immersions, cf. Proposition 4.4, in particular it is locally Lipschitz continuous in a neighbourhood of \(f_0\in W^{2,2}_{Imm}(I;{\mathbb {R}}^d)\). Hence, there exists \(C(f_0)>0\) such that \(|{\mathcal {E}}(h)-{\mathcal {E}}({\tilde{h}})|\le C(f_0)\Vert h-{\tilde{h}} \Vert _{W^{2,2}(I;{\mathbb {R}}^d)}\) for all h and \({\tilde{h}}\) satisfying \(\Vert h-f_0 \Vert _{W^{2,2}}<\delta \) and \(\Vert {\tilde{h}}-f_0 \Vert _{W^{2,2}}\le \delta \).
By Proposition B.1(i), we have \({}_{0}{{\mathbb {X}}}_T \hookrightarrow BUC(0,T;W^{2,2})\) with operator norm independent of \(T\in (0,1]\). Consequently, we have
for \({ T=T({\bar{f}}), M\in (0,1]}\) small enough, and similarly \(\Vert {\tilde{f}}(t)-f_0 \Vert _{W^{2,2}}\le \delta \). But then, using Proposition B.1(i), we have the estimate
For the curvature term \(\vec {\kappa }_f\), note that \(W^{2,2}_{Imm}(I;{\mathbb {R}}^d)\rightarrow L^2(I;{\mathbb {R}}^d), f\mapsto \vec {\kappa }_{f} = \partial _{s_f}^2 f\) is analytic (cf. Proposition 4.4), in particular Lipschitz continuous near \(f_0\). The same argument as above yields
Now, we estimate
and using (C.20), we obtain the bound
If we now combine (C.21), (C.23) and (C.24), we obtain from (C.19)
if we take \({T=T(q,{\bar{f}}), M=M(q,{\bar{f}})\in (0,1]}\) small enough.
For the second term in (C.18), using (C.20) and (C.23) we have
taking \({q_2=q_2(q, {\bar{f}})\in (0,1)}\) small enough and possibly reducing \({T=T(q,{\bar{f}})}\), \({M=}\) \({M(q, {\bar{f}})\in (0,1]}\) if necessary.
For the last term in (C.18), using Lemma 2.3, (C.24) and (C.22), we have
taking \({M=M(q,{\bar{f}}),T=T(q,{\bar{f}})\in (0,1]}\) small enough. All in all, we have now shown that taking \({T=T(q,{\bar{f}}), M=M(q,{\bar{f}})\in (0,1]}\) small enough, we have
which proves that \(\Lambda :{{\bar{B}}_{T,M}}\rightarrow L^2(0,T;L^2)\) is a \(\frac{3q}{4}\)-contraction. Reducing \({T=} \) \( {T(q,{\bar{f}})}\in (0,1]\), \({M=M(q,{\bar{f}}) \in (0,1]}\) if necessary, we may assume that \({\mathcal {F}}\) is a \(\frac{q}{4}\)-contraction; hence, \({\mathcal {N}}:{{\bar{B}}_{T,M}}\rightarrow {\mathbb {Y}}_T^{1}\) is a q-contraction for \(T=T(q, {\bar{f}}),M=M(q,{\bar{f}})\in (0,1]\) small enough. \(\square \)
Appendix D: A gluing lemma for reparametrizations
In Theorem 4.1, we used the fact that two smooth reparametrizations can be interpolated by another smooth reparametrization. We state this gluing result here in a slightly more general form for possible future reference.
Lemma D.1
Let \(0<t_1<t_2<T\) and \(\Phi _1:[0,t_2]\times I\rightarrow I\), \(\Phi _2:[t_1, T]\times I\rightarrow I\) be smooth families of reparametrizations, such that \(\Phi _i(t, \cdot )\) is strictly increasing for all suitable t and \(i=1,2\). Then, there exists a smooth family of strictly increasing reparametrizations \(\Psi :[0,T]\times I\rightarrow I\) satisfying
Proof
Let \(\delta >0\) be sufficiently small and \(\eta :[0,T]\rightarrow {\mathbb {R}}, 0\le \eta \le 1\) be a smooth cut-off function, satisfying
Then it is not difficult to check that the function \(\Psi :[0,T]\times I\rightarrow {\mathbb {R}}\) given by
is smooth and satisfies all the desired properties. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rupp, F., Spener, A. Existence and convergence of the length-preserving elastic flow of clamped curves. J. Evol. Equ. 24, 59 (2024). https://doi.org/10.1007/s00028-024-00988-1
Accepted:
Published:
DOI: https://doi.org/10.1007/s00028-024-00988-1
Keywords
- Nonlocal geometric evolution equation
- Clamped boundary conditions
- Elastic energy
- Willmore functional
- Łojasiewicz–Simon gradient inequality