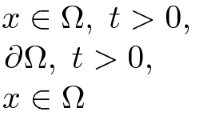Fujita exponent for non-local parabolic equation involving the Hardy–Leray potential

Abstract

In this paper, we analyse the existence and non-existence of non-negative solutions to a non-local parabolic equation with a Hardy–Leray-type potential. More precisely, we consider the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} (w_t-\Delta w)^s=\frac{\lambda }{|x|^{2s}} w+w^p +f, &{}\quad \text {in }\mathbb {R}^N\times (0,+\infty ),\\ w(x,t)=0, &{}\quad \text {in }\mathbb {R}^N\times (-\infty ,0], \end{array}\right. } \end{aligned}$$

where $N> 2s$, $0<s<1$ and $0<\lambda <\Lambda _{N,s}$, the optimal constant in the fractional Hardy–Leray inequality. In particular, we show the existence of a critical existence exponent $p_{+}(\lambda , s)$ and of a Fujita-type exponent $F(\lambda ,s)$ such that the following holds:

• Let $p>p_+(\lambda ,s)$. Then there are not any non-negative supersolutions.

• Let $p<p_+(\lambda ,s)$. Then there exist local solutions, while concerning global solutions we need to distinguish two cases:

  • Let $1< p\le F(\lambda ,s)$. Here we show that a weighted norm of any positive solution blows up in finite time.

  • Let $F(\lambda ,s)<p<p_+(\lambda ,s)$. Here we prove the existence of global solutions under suitable hypotheses.

1 Introduction

The main goal of this work is to analyse the existence or non-existence of positive global solutions to the non-local parabolic equation given by

$$\begin{aligned} {\left\{ \begin{array}{ll} (w_t-\Delta w)^s=\dfrac{\lambda }{|x|^{2s}} w+w^p+f, &{}\quad \text {in } \mathbb {R}^N \times (0,\infty ),\\ w(x,t)=0 &{}\quad \text {in } \mathbb {R}^N \times (-\infty ,0], \end{array}\right. } \end{aligned}$$

(1)

where $s \in (0,1)$, $N\ge 2$, $\lambda \in (0,\Lambda _{N,s})$ (see (3)), $p>1$, and f is a non-negative function satisfying suitable integrability hypothesis.

The operator $H^s (w):=(w_t-\Delta w)^s$ is the fractional heat operator. In the literature there are many possible ways to define $H^s$, see, for example, [3] for an overview. Among the papers concerning the operators $H^s$ and its properties, we cite [28] for regularity results, a Harnack inequality, an extension result and a monotonicity formula for solution to the equation $H^s (w)=0$. The more general case of smooth potentials has been treated by [4], where the authors obtain a monotonicity formula by the means of a suitable Hölder regularity results and an extension theorem.

In the presence of an Hardy-type potential, a monotonicity formula and the asymptotic behaviour near the singular point 0 were investigated in [15]. A detailed analysis of local solutions to the extended problem has been carried out in [3]. Furthermore, a more general extension theorem for a vast class of parabolic fractional operators, including $H^s$, has been obtained in [5]. We will give a precise definition of the operator $H^s$ by means of the Fourier transform in Sect. 2.1.

The study of existence of global solutions to problem (1), is related to the study of the so called Fujita-type exponent, see [19]. Furthermore, the presence of an Hardy-type potential obstructs even the existence of local solutions for large p. Before stating our main results, let us make a brief overview of the literature concerning Fujita exponents and non-existence results when there is a Hardy-type potential.

In the semi-linear case, $s=1$ and $\lambda =0$, Fujita proved, in his fundamental work [19], the existence of a critical exponent $F=1+\frac{2}{N}$ such that if $1<p<F$, then any solution to the semi-linear problem

$$\begin{aligned}\left\{ \begin{array}{l} u_t=\Delta u+u^p,\, x\in \mathbb {R}^n,\, t>0,\\ u(x,0)=u_0(x)\ge 0,\,x\in \mathbb {R}^n, \end{array}\right. \end{aligned}$$

blows up in finite time. The critical case $p=F$ was considered later in [34]. It is proved that in that case, a suitable norm of the solution goes to infinity in a finite time.

In the case of fractional diffusion, the author in [29] considered the equation

$$\begin{aligned} \left\{ \begin{array}{ll} u_t+(-\Delta )^{s} u= u^p &{}\quad \text {in } \mathbb {R}^N\times (0,T),\\ u(x,0)= u_0(x) &{}\quad \text {if }x\in \mathbb {R}^N, \end{array} \right. \end{aligned}$$

where $N> 2s$ and $0<s<1$. Notice that $(-\Delta )^s$ is the fractional Laplacian defined by

$$\begin{aligned} (-\Delta )^{s}u(x):=a_{N,s}\text { P.V.}\int _{\mathbb {R}^{N}}{\frac{u(x)-u(y)}{|x-y|^{N+2s}}\, dy},\,s\in (0,1), \end{aligned}$$

where

$$\begin{aligned} a_{N,s}=2^{2s-1}\pi ^{-\frac{N}{2}}\frac{\Gamma \left( \frac{N+2s}{2}\right) }{|\Gamma (-s)|} \end{aligned}$$

is the normalization constant. See [11, 18, 23] and the references therein for additional properties of the fractional Laplacian. In this case, the Fujita critical exponent takes the form $F(s)=1+\frac{2s}{N}$.

Now, in the case $\lambda >0$, the problem is related to the following Hardy–Leray-type inequality:

Theorem 1.1

For all $\varphi \in \mathcal {C}^{\infty }_{0}(\mathbb {R}^n)$, we have

$$\begin{aligned} \Lambda _{N,s}\,\int _{\mathbb {R}^N} \frac{\varphi ^2(x)}{|x|^{2s}}\,dx\le \int _{\mathbb {R}^N}\int _{\mathbb {R}^N} \frac{(\varphi (x)-\varphi (y))^2}{|x-y|^{N+2s}}dxdy, \end{aligned}$$

(2)

with

$$\begin{aligned} \Lambda _{N,s}=2^{2s}\dfrac{\Gamma ^2\left( \frac{N+2s}{4}\right) }{\Gamma ^2\left( \frac{N-2s}{4}\right) }. \end{aligned}$$

(3)

The constant $\Lambda _{N,s}$ is optimal and is not attained. Moreover, $\Lambda _{N,s}\rightarrow \Lambda _{N,1}:=\left( \dfrac{N-2}{2}\right) ^2$, the classical Hardy constant, when s tends to 1.

This inequality was first proved in [20]. See also [27] for a direct proof.

Notice that elliptic and parabolic problems related to the Hardy potential have received much attention and have been studied by several authors, see, for example, [6,7,8, 22, 32, 33] and the references therein.

The case $s=1$ and $\lambda >0$ was treated in [1]. More precisely, if we consider the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t-\Delta u=\lambda \dfrac{u}{|x|^{2}}+u^{p}, &{}\quad \text { in }\mathbb {R}^N\times (0,\infty ),\\ u(x,0)=u_{0}(x), &{}\quad \text { in }\mathbb {R}^N, \end{array}\right. } \end{aligned}$$

(4)

setting $\mu (\lambda )=\frac{N-2}{2}-\sqrt{\Big (\frac{N-2}{2}\Big )^2-\lambda }$, then if $p\ge p_+(\lambda ):=1+\frac{2}{\mu (\lambda )}$ there are no local positive supersolutions.

Due to the presence of the Hardy potential, then it is possible to show that any positive solution of (4) satisfies

$$\begin{aligned} u(x,t)\ge C(t,r)|x|^{-\mu (\lambda )} \text{ in } B_r(0), t>0. \end{aligned}$$

See, for instance, [1].

Furthermore, in the spirit of Fujita blow-up exponent, it is proved in [1] that if $1<p<1+\frac{2}{N-\mu (\lambda )}$, there exists $T^*>0$, independent of the initial datum, such that the solution u to Eq. (4) satisfies

$$\begin{aligned} \lim \limits _{t\rightarrow T^{*}}\int _{B_{r}(0)}|x|^{-\mu (\lambda )}u(x,t)\,dx=\infty , \end{aligned}$$

for any ball $B_{r}(0)$. Finally, if $1+\dfrac{2}{N-\mu (\lambda )}<p<1+\dfrac{2}{\mu (\lambda )}$, if the initial datum is small enough, there exists a global solution to (4).

Hence, we can define the Fujita-type exponent in this case by setting $F(\lambda )= 1+\dfrac{2}{N-\mu (\lambda )}$. Under fractional diffusion, Eq. (4) takes the form

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t+(-\Delta )^s u=\lambda \dfrac{u}{|x|^{2}}+u^{p}, &{}\quad \text {in }\mathbb {R}^N\times (0,\infty ),\\ u(x,0)=u_{0}(x), &{}\quad \text {in }\mathbb {R}^N. \end{array}\right. } \end{aligned}$$

(5)

In this case, it was proved in [2] that if $p\ge \tilde{p}_+(\lambda ,s):=1+\frac{2s}{\mu (\lambda )}$, there are no local positive supersolutions, while the Fujita critical exponent is given by $\tilde{F}(\lambda ,s)= 1+\dfrac{2s}{N-\mu (\lambda )}$ where

$$\begin{aligned} \mu (\lambda )= \dfrac{N-2s}{2}-\alpha _{\lambda } \end{aligned}$$

(6)

and $\alpha _{\lambda }$ is defined by the implicit formula

$$\begin{aligned} \Upsilon (\alpha _{\lambda })=\dfrac{2^{2s}\,\Gamma \left( \frac{N+2s+2\alpha _{\lambda }}{4}\right) \Gamma \left( \frac{N+2s-2\alpha _{\lambda }}{4}\right) }{\Gamma \left( \frac{N-2s+2\alpha _{\lambda }}{4}\right) \Gamma \left( \frac{N-2s-2\alpha _{\lambda }}{4}\right) }, \end{aligned}$$

see also Proposition 3.1.

Going back to the operator $H^s$, in the case $\lambda =0$, the author in [30, 31] considers the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} 0\le (w_t-\Delta w)^s\le w^p, &{}\quad \text {in } \mathbb {R}^N \times (0,\infty ),\\ w(x,t)=0, &{}\quad \text {in } \mathbb {R}^N \times (-\infty ,0]. \end{array}\right. } \end{aligned}$$

(7)

Using an integral representation formula for the inverse of $H^s$, he was able to show the existence of a critical Fujita exponent given by $F(s)=1+\frac{2s}{N+2-2s}$. The proof is deeply based on some convolution properties of Gaussian functions.

The situation when $\lambda >0$ is more delicate. The argument used in [31] seems to be directly not applicable in our situation. Our approach is instead based on the extension result proved for fractional powers of the heat operator in [5].

Let us define the critical non-existence exponent $p_+(\lambda ,s)$ and the Fujita exponent $F(\lambda ,s)$, respectively, as:

$$\begin{aligned} p_+(\lambda ,s):=1+\frac{2s}{\mu (\lambda )} \quad \text { and } F(\lambda ,s):=1+\frac{2s}{N+2-2s-\mu (\lambda )}, \end{aligned}$$

with $\mu (\lambda )$ as in (6). We distinguish different cases according to the value of the exponent p. Our main results are the following.

• The case $p>p_+(\lambda ,s)$. Here, as in the elliptic case, using the local behaviour of the solution near the origin obtained in Proposition 5.6, and thanks to a Picone-type inequality (see Proposition 6.1 below), we are able to show that there is not any weak non-trivial solution to problem (1). In particular, if $f\not \equiv 0$, there are not any non-negative weak supersolutions.

• The case $p<p_+(\lambda ,s)$. Here it is possible to show the existence of local solutions, see Remark 6.3. On the other hand, concerning global solutions we distinguish two cases:

  • The case $F(\lambda ,s)<p<p_+(\lambda ,s)$. Here we prove the existence of a very weak supersolution. Thanks to Proposition 4.8, we get the existence of a very weak solution to Eq. (1).

  • The case $1< p\le F(\lambda ,s)$. Here we show that any positive weak or very weak solution of (1) blows up, in a suitable sense, in finite time. See Theorem 6.4.

We remark that our results are coherent with [31]. Indeed, $\mu (\lambda ) \rightarrow 0^+$, $p_+(\lambda ,s)\rightarrow \infty$ and $F(\lambda ,s)\rightarrow F(s)$ as $\lambda \rightarrow 0^+$, where F(s) is the Fujita exponent of problem (7). Furthermore, the technique that we used to prove Theorem 6.4 can be easily adapted to the case $\lambda =0$, see Remark 6.5 and also [31].

It is also interesting to notice that the critical non-existence exponent $p_+(\lambda ,s)$ is the same for problems (5) and (1) and that $p_+(\lambda ,s) \rightarrow p_+(\lambda )$ as $s \rightarrow 1^+$, where $p_+(\lambda )$ is the critical non-existence exponent of problem (4). This is due to the fact the exponent $p_+(\lambda ,s)$ is determined only by the elliptic part of the operator and the presence of the Hardy-type potential, which induces a singular behaviour near 0 for any non-negative supersolutions.

On the other hand, the Fujita exponents $F(\lambda ,s)$ and $\tilde{F}(\lambda ,s)$ of problems (5) and (1) are different and in particular $F(\lambda ,s) <\tilde{F}(\lambda ,s)$ for any $s \in (0,1)$ and $\lambda \in (0,\Lambda _{N,s})$. Nevertheless, we have that $F(\lambda ,s) \rightarrow F(\lambda )$ and $\tilde{F}(\lambda ,s) \rightarrow F(\lambda )$ as $s \rightarrow 1^-$, where $F(\lambda )$ is the Fujita exponent of (4).

Fig. 1

Fujita exponent for the fractional heat equation with Hardy potential

This paper is organized as follows. In Sect. 2 we introduce some definitions and useful tools about the fractional power of the heat equation, the sense for which solution is defined, some representation formulas and preliminary results.

In Sect. 3 we consider the operator $H^s$ perturbed by the Hardy potential and prove ground state representation formula for $H^s(\cdot )-\lambda \frac{\cdot }{|x|^{2s}}$. In Sect. 4 we obtain a comparison principle for weak solutions using the extension procedure developed in [5]. As a consequence, we show the existence of weak solutions in a suitable sense of problem (1), if there exists a supersolution of the same problem. In Sect. 5, we analyse the local behaviour of weak supersolutions. In particular, we are able to obtain pointwise estimates from below and a strong maximum principle as consequence.

Finally, our main results are proved in Sect. 6, while in Sect. 7, we discuss some remaining open problems and possible further developments.

2 Preliminaries

2.1 Functional setting

For any real Hilbert space X, we denote with $X^*$ its dual space and with $_{X^*}\mathop {{\mathop {\mathop {\left\langle \cdot , \cdot \right\rangle }}\nolimits _{X}}}\limits$ the duality between $X^*$ and X; $\left( \cdot , \cdot \right) _{X}$ denotes the scalar product in X.

We define the operator $H^s$ by means of the Fourier transform as follows:

$$\begin{aligned} \widehat{ H^s (w)}(\xi ,\theta ):=(i\theta +|\xi |^2)^s\widehat{w}(\xi ,\theta ), \end{aligned}$$

(8)

where the Fourier transform of w is defined as

$$\begin{aligned} \mathcal {F}(w)(\xi ,\theta )=\widehat{w}(\xi ,\theta ):=\int _{\mathbb {R}^{N+1}}e^{-i(x \cdot \xi +t \theta )}w(x,t) \, dx\,dt. \end{aligned}$$

Then the natural domain for a pointwise definition of $H^s$ is the set

$$\begin{aligned} \left\{ w \in L^2(\mathbb {R}^{N+1}):|i\theta +|\xi |^2|^s\widehat{w} \in L^2(\mathbb {R}^{N+1})\right\} . \end{aligned}$$

Furthermore, if $\phi \in \mathcal {S}(\mathbb {R}^N)$, then by [28, Theorem 1.1], we have the following pointwise formula for the operator $H^s$

$$\begin{aligned} H^s\phi (x,t)= \frac{1}{(4\pi )^{\frac{N}{2}}\Gamma (-s)}\int _{-\infty }^t\int _{\mathbb {R}^N}\frac{\phi (x,t)-\phi (y,\sigma )}{(t-\sigma )^{\frac{N}{2}+s+1}} e^{-\frac{|x-y|^2}{4(t-\sigma )}}dyd\sigma . \end{aligned}$$

(9)

Note that we have stated the previous formula for $\phi \in \mathcal {S}(\mathbb {R}^N)$ for the sake of simplicity, see [28, Theorem 1.1] for less restrictive regularity assumption on $\phi$.

We can extend $H^s$ on

$$\begin{aligned} \mathrm{{Dom}}(H^s):=\left\{ w \in L^2(\mathbb {R}^{N+1}):\int _{\mathbb {R}^{N+1}}|i\theta +|\xi |^2|^s|\widehat{w}(\xi ,\theta )|^2 \,d\xi \, d\theta <+\infty \right\} , \end{aligned}$$

endowed with the norm

$$\begin{aligned} \left\Vert w\right\Vert _{\mathrm{{Dom}}(H^s)}:=\left( \int _{\mathbb {R}^{N+1}} w^2(x,t) \,dx\,dt\right) ^{\frac{1}{2}}+\left( \int _{\mathbb {R}^{N+1}}|i\theta +|\xi |^2|^{s}|\widehat{w}(\xi ,\theta )|^2d\xi \,d\theta \right) ^{\frac{1}{2}}, \end{aligned}$$

as the map from $\mathrm{{Dom}}(H^s)$ into its dual space $(\mathrm{{Dom}}(H^s))^*$, defined as

$$\begin{aligned} _{({\textrm{Dom}}(H^s))^*}\mathop {{\mathop {\mathop {\left\langle H^s(w), v \right\rangle }}\nolimits _{{\textrm{Dom}}(H^s)}}}\limits :=\int _{\mathbb {R}^{N+1}}(i\theta +|\xi |^2)^s\widehat{w}(\xi ,\theta )\overline{\widehat{v}(\xi ,\theta )} d \xi d\eta , \end{aligned}$$

for any $w, v \in \mathrm{{Dom}}(H^s)$. We remark that $\mathrm{{Dom}}(H^s)$ coincides with the set of pointwise definition for the operator $H^{\frac{s}{2}}$.

The space $\mathrm{{Dom}}(H^s)$ can be characterized more explicitly. Let

$$\begin{aligned} X^s:=L^2(\mathbb {R},W^{s,2}(\mathbb {R}^N)) \cap L^2\left( \mathbb {R}^N, W^{\frac{s}{2},2}(\mathbb {R})\right) , \end{aligned}$$

where we are identifying a function $u:\mathbb {R}^{N+1}\rightarrow \mathbb {R}$ with variables $(x,t) \in \mathbb {R}^{N}\times \mathbb {R}$ with the map $t \mapsto u(\cdot ,t)$ or with the map $x \mapsto u(x,\cdot )$, respectively. We can endow $X^s$ with the natural norm

$$\begin{aligned} \left\Vert \phi \right\Vert _{X^s}:= & {} \left\Vert \phi \right\Vert _{L^2(\mathbb {R},W^{s,2}(\mathbb {R}^N))}+\left\Vert \phi \right\Vert _{L^2\left( \mathbb {R}^N, W^{\frac{s}{2},2}(\mathbb {R})\right) }\\= & {} \left( \int _{\mathbb {R}^{N+1}}|\xi |^{2s}|\mathcal {F}_x(w)(\xi ,t)|^2 d \xi dt\right) ^\frac{1}{2}+ \left( \int _{\mathbb {R}^{N+1}}|\theta |^s|\mathcal {F}_t(w)(x,\theta )|^2dx d\theta \right) ^\frac{1}{2}, \end{aligned}$$

where $\mathcal {F}_x$ and $\mathcal {F}_t$ denote the Fourier transforms in the variables x and t, respectively.

Proposition 2.1

For any $s \in (0,1)$,

$$\begin{aligned} X^s=\mathrm{{Dom}}(H^s) \end{aligned}$$

(10)

with equivalent norms. In particular, the natural embedding

$$\begin{aligned} \mathrm{{Dom}}(H^s) \hookrightarrow L^2(\mathbb {R},W^{s,2}(\mathbb {R}^N)) \end{aligned}$$

(11)

is linear and continuous.

Proof

It is clear that $|\xi |^{2s}\le |i\theta +|\xi |^2|^{s}$ and $|\theta |^{s}\le |i\theta +|\xi |^2|^{s}$ for any $(\theta ,\xi ) \in \mathbb {R}^{N+1}$. Furthermore, it is easy to see that there exists a constant $C>0$, depending on s, such that for any $a,b \in [0,+\infty )$

$$\begin{aligned} (a+b)^s \le C (a^s +b^s). \end{aligned}$$

Indeed, the function $f(\tau ):=\frac{(\tau +1)^s}{1+\tau ^s}$ is bounded in $[0,+\infty )$. Hence, $|i\theta +|\xi |^2|^{s}\le C (|\theta |^s +|\xi |^{2s})$ for any $(\theta ,\xi ) \in \mathbb {R}^{N+1}$. Then (10) follows from the Plancherel identity.

$\square$

We also have an inversion formula for the operator $H^s$.

Definition 2.2

Let $q \in [1,2]$ and $g \in L^q(\mathbb {R}^N \times (-\infty , T))$, for any $T \in \mathbb {R}$, be fixed. We define the operator

$$\begin{aligned} J_s g (x,t):=\frac{1}{\Gamma (s)(4\pi )^{\frac{N}{2}}}\int _0^\infty \int _{\mathbb {R}^N} \frac{e^{-\frac{|z|^2}{4\tau }}}{\tau ^{\frac{N}{2}+1-s}} g(x-z,t-\tau )\, dz \, d\tau . \end{aligned}$$

(12)

By [30], the operator $J_s$ has the following properties:

$$\begin{aligned}&H^s(\phi )=g \text { if and only if } J_s(g)=\phi , \quad \text{ for } \text{ any } \phi \in \mathcal {S}(\mathbb {R}^{N+1}), \end{aligned}$$

(13)

$$\begin{aligned}&J_s (g) \in L^q_{loc}(\mathbb {R}^{N+1}),\nonumber \\&J_s= J_\alpha J_\beta \text { for any } \alpha , \beta >0 \text{ such } \text{ that } \alpha +\beta =s. \nonumber \\&\text { If } g \text { is non-negative, then } J_s(g) =0 \text { in } (-\infty ,0) \text{ if } \text{ and } \text{ only } \text{ if } g=0 \text { in } (-\infty ,0). \end{aligned}$$

(14)

In view of (2.1), we say that $J_s$ is the inverse of the operator $H^s$.

In the spirit of [30, 31], it makes sense to give the following definitions for weak supersolution, subsolutions and solutions of the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} H^s(w)=g &{}\quad \text {in }\mathbb {R}^N\times (0,+\infty ),\\ w=0 &{}\quad \text {in }\mathbb {R}^N\times (-\infty ,0]. \end{array}\right. } \end{aligned}$$

(15)

Definition 2.3

Let $q \in [1,2]$, $g \in L^q(\mathbb {R}^N \times (-\infty , T))$ for any $T \in \mathbb {R}$ and suppose that $g(t,x)=0$ a.e. in $(-\infty ,0)\times \mathbb {R}^{N}$. Then, we say that w is a very weak supersolution (subsolution) of (15) if $w \in L^q_{loc}(\mathbb {R}^{N+1})$ and

$$\begin{aligned} w\ge (\le ) \, J_s(g) \text { a.e. in }\mathbb {R}^{N+1}. \end{aligned}$$

If w is both a supersolution and a subsolution of (15), then, we say that w is a solution of (15).

The definition above already encodes that condition $w=0$ in $\mathbb {R}^N\times (-\infty ,0]$ by (14).

We can also define energy solutions to (15) for a suitable class of data g.

Definition 2.4

Let $g \in L^1_{loc}(\mathbb {R}^{N+1})$ be non-negative, and suppose that $g(t,x)=0$ a.e. in $(-\infty ,0)\times \mathbb {R}^{N}$. Assume that

$$\begin{aligned} \phi \mapsto \int _{0}^{\infty }\left( \int _{\mathbb {R}^N}g \phi \, dx \right) dt \end{aligned}$$

belongs to $(\mathrm{{Dom}}(H^s))^*$. Then we say that w is a energy or weak supersolution (subsolution) of (15) if $w \in \mathrm{{Dom}}(H^s)$,

$$\begin{aligned} _{(\mathrm{{Dom}}(H^s))^*}\mathop {{\mathop {\mathop {\left\langle H^s(w), \phi \right\rangle }}\nolimits _{\mathrm{{Dom}}(H^s)}}}\limits \ge (\le )\int _{0}^{\infty }\left( \int _{\mathbb {R}^N}g \phi \, dx \right) dt, \end{aligned}$$

for any non-negative $\phi \in \mathcal {S}(\mathbb {R}^{N+1})$ and $w=0$ in $\mathbb {R}^N\times (-\infty ,0]$. If w is a supersolution and a subsolution of the equation in (15), we say that w is a solution of Eq. (15).

To deal with (1), we recall the following fractional Sobolev inequality (see [11, Theorem 6.5])

$$\begin{aligned} \left( \int _{\mathbb {R}^N} |\phi |^\frac{2N}{N-2s} \, dx \right) ^\frac{N-2s}{N} \le S_{N,s} \int _{\mathbb {R}^N}\int _{\mathbb {R}^N} \frac{|\phi (x)-\phi (y)|^2}{|x-y|^{N+2s}} \, dx dy \quad \text{ for } \text{ any } \phi \in C^{\infty }_c(\mathbb {R}^N). \end{aligned}$$

(16)

Let $f \in L^2(\mathbb {R}^{N+1})$ and suppose that $f(t,x)=0$ a.e. in $(-\infty ,0)\times \mathbb {R}^{N}$. Let $w \in \mathrm{{Dom}}(H^s)$ be such that

$$\begin{aligned} \int _{0}^{+\infty }\left( \int _{\mathbb {R}^N}|w|^{\frac{2Np}{N+2s}}\, dx \right) ^{\frac{N+2s}{N}} \, dt <+\infty \quad \text { or } \quad w \in L^{2p}(\mathbb {R}^{N+1}), \end{aligned}$$

(17)

$w=0$ in $\mathbb {R}^N\times (-\infty ,0]$, and

$$\begin{aligned} _{(\mathrm{{Dom}}(H^s))^*}\mathop {{\mathop {\mathop {\left\langle H^s(w), \phi \right\rangle }}\nolimits _{\mathrm{{Dom}}(H^s)}}}\limits \ge (\le )\int _{0}^{\infty }\left( \int _{\mathbb {R}^N}\left( \frac{\lambda }{|x|^{2s}} w\phi +w^p\phi +f \phi \right) \, dx \right) dt, \end{aligned}$$

(18)

for any non-negative $\phi \in \mathcal {S}(\mathbb {R}^{N+1})$. Then w is a weak supersolution (subsolution) of problem (1). Indeed, in view of (2), (11), (16), (17), and the Hölder inequality, the right-hand side of (18), as a function of $\phi$, belongs to $(\mathrm{{Dom}}(H^s))^*$.

2.2 Properties of the operators $J_s$ and $H^s$

In this section we prove some preliminary results about the operators $J_s$ and $H^s$.

Lemma 2.5

Suppose that $g \in L^1(\mathbb {R}^{N+1})\cap L^2(\mathbb {R}^{N+1})$. Then $J_s(g) \in L^2(\mathbb {R}^{N+1})$.

Proof

We proceed in the spirit of [30]. Let

$$\begin{aligned} Y(z,\tau ):=\frac{1}{\Gamma (s)(4\pi )^{\frac{N}{2}}} \frac{e^{-\frac{|z|^2}{4\tau }}}{\tau ^{\frac{N}{2}+1-s}} \text{ where } \tau >0 \text{ and } z\in \mathbb {R}^n. \end{aligned}$$

We can write $J_s(g)$ as

$$\begin{aligned} J_s(g)= (Y\chi _{(0,1)}) *g +(Y\chi _{(1,+\infty )}) *g, \end{aligned}$$

where for any measurable set $E\subseteq \mathbb {R}$

$$\begin{aligned} \chi _E(t):= {\left\{ \begin{array}{ll} 1, &{}\text { if } t \in E,\\ 0, &{}\text { if } t \not \in E. \end{array}\right. } \end{aligned}$$

By the proof of [30, Theorem 2.1], we know that $Y\chi _{(0,1)} \in L^1(\mathbb {R}^{N+1})$ and so by the Young inequality $(Y\chi _{(0,1)}) *g \in L^2(\mathbb {R}^{N+1})$, since $g \in L^2(\mathbb {R}^{N+1})$. Furthermore, by the Young inequality

$$\begin{aligned} \left\Vert (Y\chi _{(1,+\infty )}) *h_n\right\Vert _{L^2(\mathbb {R}^{N+1})} \le \left\Vert h_n\right\Vert _{L^1(\mathbb {R}^{N+1})}\left\Vert Y\chi _{(1,+\infty )}\right\Vert _{L^2(\mathbb {R}^{N+1})} \end{aligned}$$

and by a change of variables

$$\begin{aligned}{} & {} \left\Vert Y\chi _{(1,+\infty )}\right\Vert _{L^2(\mathbb {R}^{N+1})} ^2= \frac{1}{(\Gamma (s))^2(4\pi )^{N}} \int _{1}^{+\infty } \int _{\mathbb {R}^N} \frac{e^{-\frac{|z|^2}{2\tau }}}{\tau ^{N+2-2s}} \, dz d \tau \\{} & {} \quad =\frac{1}{(\Gamma (s))^2(4\pi )^{N}} \int _{1}^{+\infty } \tau ^{-\frac{N}{2}-2+2s} \,d \tau \int _{\mathbb {R}^N}e^{-\frac{|z|^2}{2}} \, dz <+\infty , \end{aligned}$$

since $N\ge 2$ and $s \in (0,1)$. In conclusion, $J_s(g) \in L^2(\mathbb {R}^{N+1})$. $\square$

Lemma 2.6

Let $g \in L^2(\mathbb {R}^{N+1})$ and suppose that $J_s(g) \in L^2(\mathbb {R}^{N+1})$. Then

$$\begin{aligned} \int _{\mathbb {R}^{N+1}}|i\theta +|\xi |^2|^{2s}|\widehat{J_s(g)}(\xi ,\theta )|^2d\xi \,d\theta <+\infty . \end{aligned}$$

(19)

In particular, $J_s(g) \in \mathrm{{Dom}}(H^s)$ and $H^s(J_s(g))$ is well defined pointwise.

Proof

Since

$$\begin{aligned} \mathcal {F}(J_{\frac{s}{2}} g)=\frac{1}{\Gamma (s)(4\pi )^{\frac{N}{2}}}\mathcal {F}\left( \chi _{[0,+\infty )}(\tau )\frac{e^{-\frac{|z|^2}{4\tau }}}{\tau ^{\frac{N}{2}+1-s}}\right) \widehat{g}, \end{aligned}$$

we need to compute the Fourier transform of $\chi _{(0,+\infty )}(\tau ) \frac{e^{-\frac{|z|^2}{4\tau }}}{\tau ^{\frac{N}{2}+1-s}}$, where

$$\begin{aligned} \chi _{[0,+\infty )}(\tau )= {\left\{ \begin{array}{ll} 1, &{}\text { if } \tau \in (0,+\infty ),\\ 0, &{}\text { if } \tau \in (-\infty ,0). \end{array}\right. } \end{aligned}$$

We make this computation in detail for the sake of completeness, see [30] and the references within. The Fourier transform of Gaussian function and a change of variables yield

$$\begin{aligned}{} & {} \int _{\mathbb {R}^{N+1}}e^{-i(z\cdot \xi +\tau \theta )}\chi _{[0,+\infty )}(\tau ) \frac{e^{-\frac{|z|^2}{4\tau }}}{\tau ^{\frac{N}{2}+1-s}} \, dz d\tau \\{} & {} \quad =\int _0^\infty \tau ^{-\frac{N}{2}-1+s}e^{-i\tau \theta } \int _{\mathbb {R}^N} e^{-i z \cdot \xi } e^{-\frac{|z|^2}{4\tau }} \, dz d\tau \\{} & {} \quad =2^N \pi ^{\frac{N}{2}}\int _0^\infty \tau ^{-1+s}e^{-\tau (i \theta +|\xi |^2)} \, d\tau = 2^N \pi ^{\frac{N}{2}} \Gamma (s)(i \theta +|\xi |^2)^{-s}. \end{aligned}$$

Hence, since $g \in L^2(\mathbb {R}^{N+1})$, we have proved (19) and the last claim follows from (19). $\square$

Lemma 2.7

For any $\phi ,\psi \in \mathcal {S}(\mathbb {R}^{N+1})$, we have that

$$\begin{aligned}&\int _{\mathbb {R}^{N+1}}H^s(\phi ) \psi \, dx dt=\int _{\mathbb {R}^{N+1}}\phi (-x,-t) H^s(\psi (-\cdot )) \, dx dt \nonumber \\&=\int _{\mathbb {R}^{N+1}}H^{\frac{s}{2}}(\phi )(-x,-t) H^{\frac{s}{2}}(\psi (-\cdot )) \, dx dt, \end{aligned}$$

(20)

$$\begin{aligned}&\int _{\mathbb {R}^{N+1}}J_s(\phi ) \psi \, dx dt=\int _{\mathbb {R}^{N+1}}\phi (-x,-t) J_s(\psi (-\cdot )) \, dx dt. \end{aligned}$$

(21)

Proof

By (8) and the Plancherel identity

$$\begin{aligned} \int _{\mathbb {R}^{N+1}}H^s(\phi ) \psi \, dx dt=\int _{\mathbb {R}^{N+1}}(i\theta +|\xi |^2)^s\widehat{\phi }(\xi ,\theta )\overline{\widehat{\psi }(\xi ,\theta )} d \xi d\eta \end{aligned}$$

and so the first equality in (20) follows from $\overline{\widehat{\psi }}=\widehat{\psi (-\cdot )}$ and the Plancherel identity. The second identity is an easy consequence of the first one. On the other hand by (12), the Fubini–Tonelli theorem and a change of variables

$$\begin{aligned}{} & {} \int _{\mathbb {R}^{N+1}}J_s(\phi ) \psi \, dx dt =\frac{1}{\Gamma (s)(4\pi )^{\frac{N}{2}}} \int _0^\infty \int _{\mathbb {R}^N} \int _{\mathbb {R}^{N+1}}\frac{e^{-\frac{|z|^2}{4\tau }}}{\tau ^{\frac{N}{2}+1-s}}\\{} & {} \quad \phi (x-z,t-\tau )\psi (x,t)\, dx \, dt \, dz \, d\tau \\{} & {} \quad =\frac{1}{\Gamma (s)(4\pi )^{\frac{N}{2}}}\int _{\mathbb {R}^{N+1}}\int _0^\infty \int _{\mathbb {R}^N}\frac{e^{-\frac{|z|^2}{4\tau }}}{\tau ^{\frac{N}{2}+1-s}}\psi (x+z,t+\tau ) \, dz \, d\tau \phi (x,t)\, dx \, dt, \end{aligned}$$

which yields (21). $\square$

Lemma 2.8

Suppose that $g \in L^2(\mathbb {R}^{N+1})$, $g(t,x)=0$ a.e. in $(-\infty ,0)\times \mathbb {R}^{N}$ and that $w \in \mathrm{{Dom}}(H^s)$ is a weak supersolution of the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} H^s(w)= g, &{}\quad \text {in } \mathbb {R}^N\times (0,\infty ),\\ w=0, &{}\quad \text {in } \mathbb {R}^N\times (-\infty ,0), \end{array}\right. } \end{aligned}$$

in the sense given by Definition 2.4. Then

$$\begin{aligned} H^{\frac{s}{2}}(w) \ge J_{\frac{s}{2}}(g)\quad \text { a.e. in } \mathbb {R}^{N+1}. \end{aligned}$$

(22)

Proof

By (21) and a change of variables for any positive $\phi \in \mathcal {S}(\mathbb {R}^{N+1})$,

$$\begin{aligned} \int _{0}^{\infty }\left( \int _{\mathbb {R}^N}g \phi \, dx \right) dt =\int _{\mathbb {R}^{N+1}}J_{\frac{s}{2}}(g)(-x,-t)H^{\frac{s}{2}}(\phi (-\cdot ))\, dx\, dt. \end{aligned}$$

Hence, by (20) we deduce that for any positive $\phi \in \mathcal {S}(\mathbb {R}^{N+1})$

$$\begin{aligned} \int _{\mathbb {R}^{N+1}}[H^{\frac{s}{2}}(w)(-x,-t)- J_{\frac{s}{2}}(g)(-x,-t)] H^{\frac{s}{2}}(\phi (-\cdot )) \, dx dt \ge 0. \end{aligned}$$

For any positive $\psi \in \mathcal {S}(\mathbb {R}^{N+1})$ let

$$\begin{aligned} \phi :=J_{\frac{s}{2}}(\psi )(-\cdot ). \end{aligned}$$

Then $H^{\frac{s}{2}}(\phi (-\cdot ))=\psi$, and $\phi \in \mathcal {S}(\mathbb {R}^{N+1})$. It follows that

$$\begin{aligned} H^{\frac{s}{2}}(w)(-x,-t)- J_{\frac{s}{2}}(g)(-x,-t) \ge 0 \text { a.e. in } \mathbb {R}^{N+1}, \end{aligned}$$

which is equivalent to (22). $\square$

3 Ground state transformation for the operator $H^s-\frac{\lambda }{|x|^{2s}}$

We start by recalling the following proposition.

Proposition 3.1

([18, Lemma 3.2], [14, Proposition 3.2]) Let $\Lambda _{N,s}$ be as in (3). Then the function $\Upsilon :\Big [0,\frac{N-2s}{2}\Big ) \rightarrow (0,\Lambda _{N,s}]$ defined as

$$\begin{aligned} \Upsilon (\alpha ):=2^{2s}\frac{\Gamma \left( \frac{N+2s+2\alpha }{4}\right) \Gamma \left( \frac{N+2s-2\alpha }{4}\right) }{\Gamma \left( \frac{N-2s-2\alpha }{4}\right) \Gamma \left( \frac{N-2s+2\alpha }{4}\right) } \end{aligned}$$

is well-defined, continuous, surjective, decreasing, $\Upsilon (0)=\Lambda _{N,s}$ and $\lim _{\alpha \rightarrow (\frac{N-2s}{2})^-}\Upsilon (\alpha )=0$.

Let us define for any $\lambda \in (0,\Lambda _{N,s}]$

$$\begin{aligned} \mu (\lambda ):=\frac{N-2s}{2}-\Upsilon ^{-1}(\lambda ). \end{aligned}$$

(23)

Then clearly

$$\begin{aligned} 0<{\mu (\lambda )}<\frac{N-2s}{2} \quad \text { for any } \lambda \in (0,\Lambda _{N,s}). \end{aligned}$$

(24)

The most important result of this section is a ground state transformation for the operator $H^s-\frac{\lambda }{|x|^{2s}}$, in the spirit of [18, Proposition 4.1] where a similar representation was computed for the elliptic operator $(-\Delta )^s-\frac{\lambda }{|x|^{2s}}$. We need a preliminary lemma about radial functions.

Lemma 3.2

Let $f \in L^1(\mathbb {R}^N)$ be radial. Then there exists a constant $K_{N,s,\lambda }>0$ depending only on N, s and $\lambda$ such that

$$\begin{aligned} \int _{\mathbb {R}^N}\frac{|f(y)|}{|x-y|^{\mu (\lambda )}} dy \le K_{N,s, \lambda } |x|^{-\mu (\lambda )} \int _{\mathbb {R}^N}|f(y)| \, dy,\quad \text { for any } x \in \mathbb {R}^N \setminus \{0\}. \end{aligned}$$

(25)

Proof

Passing in polar coordinates and letting $y'=\frac{y}{\rho }$ and $x'=\frac{y}{r}$, we obtain

$$\begin{aligned}{} & {} \int _{\mathbb {R}^N}\frac{|f(y)|}{|x-y|^{\mu (\lambda )}} dy = \int _0^{+\infty }\rho ^{N-1}|f(\rho )|\int _{\mathbb {S}^{N-1}}|x'r-\rho y'|^{-\mu (\lambda )}dS_{y'} \, d\rho \\{} & {} \quad = r^{-\mu (\lambda )}\int _0^{+\infty }(r\sigma )^{N-1}|f(r\sigma )|\left( \int _{\mathbb {S}^{N-1}}|x'-\sigma y'|^{-\mu (\lambda )}dS_{y'}\right) r \,d\sigma , \end{aligned}$$

by the change of variables $\sigma =\frac{\rho }{r}$. Let us define

$$\begin{aligned} K(\sigma ):=\int _{\mathbb {S}^{N-1}}|x'-\sigma y'|^{-\mu (\lambda )}dS_{y'}. \end{aligned}$$

Since $|x'-\sigma y|^2=1-2\sigma x'\cdot y' +\sigma ^2$, with a change of variables, we deduce that

$$\begin{aligned} K(\sigma )=\int _{\mathbb {S}^{N-1}}|1-2\sigma y_1+\sigma ^2|^{-\frac{\mu (\lambda )}{2}}dS_{y'}, \end{aligned}$$

and so K does not depends on x. Using spherical coordinates, see also [17], we obtain

$$\begin{aligned} K(\sigma )=C\int _0^\pi \frac{\sin (\theta )^{N-2}}{|1-2\sigma \cos (\theta )+\sigma ^2|^{\frac{\mu (\lambda )}{2}}}d\theta , \end{aligned}$$

where $C>0$ is a positive constant depending only on N. Since for $\sigma =1$ the singularity in 0 is integrable in view of (24), we conclude that K is bounded. It follows that, thanks to the change of variables $\rho = r \sigma$,

$$\begin{aligned}{} & {} \int _{\mathbb {R}^N}\frac{|f(y)|}{|x-y|^{\mu (\lambda )}} dy \le r^{-\mu (\lambda )}\left\Vert K\right\Vert _{L^\infty (0,+\infty )} \int _0^{+\infty }(r\sigma )^{N-1}|f(r\sigma )|r \,d\sigma \\{} & {} \quad =r^{-\mu (\lambda )}\left\Vert K\right\Vert _{L^\infty (0,+\infty )} \int _0^{+\infty }\rho ^{N-1}|f(\rho )| \,d\rho =r^{-\mu (\lambda )}\left\Vert K\right\Vert _{L^\infty (0,+\infty )}\int _{\mathbb {R}^N}|f(y)| dy, \end{aligned}$$

and so we have proved (25). $\square$

Proposition 3.3

Let $\lambda \in (0,\Lambda _{N,s})$ and let, for any $(x,t) \in \mathbb {R}^{N}\setminus \{0\}\times \mathbb {R}$, and $\phi \in \mathcal {S}(\mathbb {R}^{N+1})$,

$$\begin{aligned} L^s\phi (x,t):=\frac{1}{(4\pi )^{\frac{N}{2}}\Gamma (-s)} \int _{-\infty }^t\int _{\mathbb {R}^N}\frac{\phi (x,t)-\phi (y,\sigma )}{|y|^{{\mu (\lambda )}}(t-\sigma )^{\frac{N}{2}+s+1}}e^{-\frac{|x-y|^2}{4(t-\sigma )}}dyd\sigma . \end{aligned}$$

Then there exists $C>0$, depending only on N, s and $\lambda$, such that for any $(x,t) \in \mathbb {R}^{N}\setminus \{0\}\times \mathbb {R}$

$$\begin{aligned} |L^s\phi (t,x)|\le C|x|^{-\mu (\lambda )}\left( \left\Vert \phi \right\Vert _{L^\infty (\mathbb {R}^{N+1})}+\left\Vert |\nabla _{(x,t)}\phi |\right\Vert _{L^\infty (\mathbb {R}^{N+1})}+\left\Vert |\nabla ^2_{x}\phi |\right\Vert _{L^\infty (\mathbb {R}^{N+1})}\right) , \end{aligned}$$

(26)

for any $\phi \in \mathcal {S}(\mathbb {R}^{N+1})$, where $\nabla _x^2$ denotes the matrix of the second derivates of $\phi$ with respect to the spatial variable x. Furthermore, for any $\phi \in \mathcal {S}(\mathbb {R}^{N+1})$

$$\begin{aligned} H^s(\phi )-\frac{\lambda }{|x|^{2s}}\phi =L^s(|x|^{\mu (\lambda )}\phi ), \end{aligned}$$

(27)

where ${\mu (\lambda )}$ is as in (23).

Proof

By a change of variables, it is clear that

$$\begin{aligned} |L^s\phi (x,t)|= & {} \left| \frac{1}{(4\pi )^{\frac{N}{2}}\Gamma (-s)}\int _0^{+\infty }\int _{\mathbb {R}^N}\frac{\phi (x,t)-\phi (x-z,t-\tau )}{|x-z|^{{\mu (\lambda )}}\tau ^{\frac{N}{2}+s+1}}e^{-\frac{|z|^2}{4\tau }}dzd\tau \right| \\\le & {} \frac{1}{(4\pi )^{\frac{N}{2}}|\Gamma (-s)|}\left| \int _0^1\int _{\mathbb {R}^N}\frac{\phi (x,t)-\phi (x-z,t-\tau )}{|x-z|^{{\mu (\lambda )}}\tau ^{\frac{N}{2}+s+1}}e^{-\frac{|z|^2}{4\tau }}dzd\tau \right| \\{} & {} +C_1\left\Vert \phi \right\Vert _{L^\infty (\mathbb {R}^{N+1})}\int _1^{+\infty }\int _{\mathbb {R}^N}\frac{e^{-\frac{|z|^2}{4\tau }}}{|x-z|^{{\mu (\lambda )}}\tau ^{\frac{N}{2}+s+1}}dzd\tau \end{aligned}$$

for some constant positive $C_1$ depending on N and s. In view of Lemma 3.2,

$$\begin{aligned} \int _1^{+\infty }\int _{\mathbb {R}^N}\frac{e^{-\frac{|z|^2}{4\tau }}}{|x-z|^{{\mu (\lambda )}}\tau ^{\frac{N}{2}+s+1}}dzd\tau \le C_2 |x|^{-\mu (\lambda )} \end{aligned}$$

for some positive constant $C_2$ depending on N, s and $\lambda$. Furthermore, letting

$$\begin{aligned} B'_1:=\{x\in \mathbb {R}^N:|x|<1\}, \end{aligned}$$

we have that

$$\begin{aligned}{} & {} \int _0^1\int _{\mathbb {R}^N}\frac{\phi (x,t)-\phi (x-z,t-\tau )}{|x-z|^{{\mu (\lambda )}}\tau ^{\frac{N}{2}+s+1}}e^{-\frac{|z|^2}{4\tau }}dzd\tau \\{} & {} \quad =\int _0^1\int _{\mathbb {R}^N\setminus B'_1}\frac{\phi (x,t)-\phi (x-z,t-\tau )}{|x-z|^{{\mu (\lambda )}}\tau ^{\frac{N}{2}+s+1}} e^{-\frac{|z|^2}{4\tau }}dzd\tau \\{} & {} \qquad +\int _0^1\int _{B'_1}\frac{\phi (x,t) -\phi (x-z,t-\tau )}{|x-z|^{{\mu (\lambda )}}\tau ^{\frac{N}{2}+s+1}}e^{-\frac{|z|^2}{4\tau }}dzd\tau . \end{aligned}$$

We will estimate the last two integrals. We start by noticing that

$$\begin{aligned}{} & {} \int _0^1\int _{\mathbb {R}^N\setminus B'_1}\frac{\phi (x,t)-\phi (x-z,t-\tau )}{|x-z|^{{\mu (\lambda )}}\tau ^{\frac{N}{2}+s+1}}e^{-\frac{|z|^2}{4\tau }}dzd\tau \\{} & {} \quad =\int _0^1\int _{\mathbb {R}^N\setminus B'_1}\frac{\phi (x,t)-\phi (x-z,t)}{|x-z|^{{\mu (\lambda )}}\tau ^{\frac{N}{2}+s+1}}e^{-\frac{|z|^2}{4\tau }}dzd\tau \\{} & {} \qquad +\int _0^1\int _{\mathbb {R}^N\setminus B'_1}\frac{\phi (x-z,t)-\phi (x-z,t-\tau )}{|x-z|^{{\mu (\lambda )}}\tau ^{\frac{N}{2}+s+1}}e^{-\frac{|z|^2}{4\tau }}dzd\tau . \end{aligned}$$

Then the change of variables $z=-z$ yields

$$\begin{aligned}{} & {} 2\int _0^1\int _{\mathbb {R}^N\setminus B'_1}\frac{\phi (x,t)-\phi (x-z,t)}{|x-z|^{{\mu (\lambda )}}\tau ^{\frac{N}{2}+s+1}}e^{-\frac{|z|^2}{4\tau }}dzd\tau \\{} & {} \quad =\int _0^1\int _{\mathbb {R}^N\setminus B'_1}\frac{\phi (x,t)-\phi (x-z,t)}{|x-z|^{{\mu (\lambda )}}\tau ^{\frac{N}{2}+s+1}}e^{-\frac{|z|^2}{4\tau }}dzd\tau +\\{} & {} \qquad \int _0^1\int _{\mathbb {R}^N\setminus B'_1}\frac{\phi (x,t)-\phi (x+z,t)}{|x+z|^{{\mu (\lambda )}}\tau ^{\frac{N}{2}+s+1}}e^{-\frac{|z|^2}{4\tau }}dzd\tau \\{} & {} \quad \le \int _0^1\int _{\mathbb {R}^N\setminus B'_1}\frac{|2\phi (x,t)-\phi (x+z,t)-\phi (x-z,t)|}{|x-z|^{{\mu (\lambda )}}\tau ^{\frac{N}{2}+s+1}}e^{-\frac{|z|^2}{4\tau }}dzd\tau \\{} & {} \qquad +\int _0^1\int _{\mathbb {R}^N\setminus B'_1}\frac{|\phi (x,t)-\phi (x+z,t)|}{\tau ^{\frac{N}{2}+s+1}} e^{-\frac{|z|^2}{4\tau }}\left| \frac{1}{|z+x|^{\mu (\lambda )}}-\frac{1}{|x-z|^{\mu (\lambda )}}\right| dzd\tau \\{} & {} \quad \le \int _0^1\int _{\mathbb {R}^N\setminus B'_1}\frac{|2\phi (x,t)-\phi (x+z,t)-\phi (x-z,t)|}{|x-z|^{{\mu (\lambda )}}\tau ^{\frac{N}{2}+s+1}}e^{-\frac{|z|^2}{4\tau }}dzd\tau \\{} & {} \qquad +\int _0^1\int _{\mathbb {R}^N\setminus B'_1}|z|\frac{|\phi (x,t)-\phi (x+z,t)|}{\tau ^{\frac{N}{2}+s+1}} e^{-\frac{|z|^2}{4\tau }}\left( \frac{1}{|z+x|^{\mu (\lambda )}}+\frac{1}{|x-z|^{\mu (\lambda )}}\right) dzd\tau . \end{aligned}$$

Since $\phi \in \mathcal {S}(\mathbb {R}^N)$, we have that

$$\begin{aligned}&|\phi (x,t)-\phi (x+z,t)| \le \left\Vert |\nabla _x \phi |\right\Vert _{L^\infty (\mathbb {R}^{N+1})} |z|,\\&|2\phi (x,t)-\phi (x+z,t)-\phi (x-z,t)| \le \left\Vert |\nabla ^2_x \phi |\right\Vert _{L^\infty (\mathbb {R}^{N+1})} |z|^2. \end{aligned}$$

Hence, in view of Lemma 3.2 and a change of variables we conclude that there exists a positive constant $C_3>0$, depending only on N, s, and $\lambda$ such that

$$\begin{aligned}{} & {} \int _0^1\int _{\mathbb {R}^N\setminus B'_1}\frac{\phi (x-z,t)-\phi (x-z,t)}{|x-z|^{{\mu (\lambda )}}\tau ^{\frac{N}{2}+s+1}}e^{-\frac{|z|^2}{4\tau }}dzd\tau \\{} & {} \quad \le C_3|x|^{-\mu (\lambda )} (\left\Vert |\nabla _x \phi |\right\Vert _{L^\infty (\mathbb {R}^{N+1})}+\left\Vert |\nabla ^2_x \phi |\right\Vert _{L^\infty (\mathbb {R}^{N+1})}). \end{aligned}$$

Moreover, we note that

$$\begin{aligned} |\phi (x,t)-\phi (x,t-\tau )| \le \tau \left\Vert \frac{\partial \phi }{\partial t}\right\Vert _{L^\infty (\mathbb {R}^{N+1})} \end{aligned}$$

and so by Lemma 3.2 and a change of variables there exists a constant $C_4>0$, depending only on N, s, and $\lambda$, such that

$$\begin{aligned} \int _0^1\int _{\mathbb {R}^N\setminus B'_1}\frac{\phi (x,t)-\phi (x,t-\tau )}{|x-z|^{{\mu (\lambda )}}}dzd\tau \le C_4\left\Vert \frac{\partial \phi }{\partial t}\right\Vert _{L^\infty (\mathbb {R}^N\setminus B'_1)}|x|^{-\mu (\lambda )}. \end{aligned}$$

By [28, Corollary 1.4] there exists a positive constant $C_5>0$, depending only on N, s, such that

$$\begin{aligned} \frac{e^{-\frac{|z|^2}{4\tau }}}{\tau ^{\frac{N}{2}+s+1}} \le \frac{C_5}{|z|^{N + 2+2s}+ \tau ^{\frac{N + 2+2s}{2}}} \quad \text { for any } z \in \mathbb {R}^{N+1}, \tau \in (0,\infty ). \end{aligned}$$

Then arguing, as in Lemma 3.2, we have that there exist positive constants $C_6,C_7,C_8$ and $C_9$ depending only on N, s, and $\lambda$, such that

$$\begin{aligned}{} & {} \int _0^1\int _{B'_1}\frac{|\phi (x,t)-\phi (x-z,t-\tau )|}{|x-z|^{\mu (\lambda )}\tau ^ {\frac{N}{2}+s+1}}e^{-\frac{|z|^2}{4\tau }}dzd\tau \le C_6 \left\Vert |\nabla \phi |\right\Vert _{L^\infty (\mathbb {R}^{N+1})}\\{} & {} \quad \int _0^1\int _{B'_1}\frac{(|z|+\sqrt{\tau })^{-N-2s}}{|x-z|^{\mu (\lambda )}}dzd\tau \\{} & {} \quad \le C_7 \left\Vert |\nabla \phi |\right\Vert _{L^\infty (\mathbb {R}^{N+1})} \int _0^1\int _{B'_1}\frac{|z|^{-N-2s}+\tau ^{-\frac{N+2s}{2}}}{|x-z|^{\mu (\lambda )}}dzd\tau \\{} & {} \quad \le C_8 \left\Vert |\nabla \phi |\right\Vert _{L^\infty (\mathbb {R}^{N+1})} |x|^{-\mu (\lambda )}\int _0^1\int _{B'_1}(|z|+\sqrt{\tau })^{-N-2s} dzd\tau \le C_9 |x|^{-\mu (\lambda )}. \end{aligned}$$

To see that the last integral is convergent, it is enough to consider polar coordinates in $B'_1 \times (0,1)$ taking $\rho ^2$ instead of $\rho$ as radial coordinate in the time coordinate. Hence, we have proved (26).

For any $\phi \in \mathcal {S}(\mathbb {R}^{N+1})$ by (9) and [28, Remark 2.2]

$$\begin{aligned}{} & {} H^s(|x|^{-\mu (\lambda )}\phi )\\{} & {} \quad =\frac{1}{(4\pi )^{\frac{N}{2}}\Gamma (-s)} \int _{-\infty }^t\int _{\mathbb {R}^N}\frac{|x|^{-{\mu (\lambda )}}\phi (x,t)-|y|^{-{\mu (\lambda )}}\phi (y,\sigma )}{(t-\sigma )^{\frac{N}{2}+s+1}}e^{-\frac{|x-y|^2}{4(t-\sigma )}}dyd\sigma \\{} & {} \quad =\frac{1}{(4\pi )^{\frac{N}{2}}\Gamma (-s)}\left[ \phi (x,t)\int _{-\infty }^t\int _{\mathbb {R}^N}\frac{|x|^{-{\mu (\lambda )}}-|y|^{-{\mu (\lambda )}}}{(t-\sigma )^{\frac{N}{2}+s+1}}e^{-\frac{|x-y|^2}{4(t-\sigma )}}dyd\sigma + L^s(\phi )\right] . \end{aligned}$$

Since in view of [13, Lemma 4.1] and [28, Corollary 1.4],

$$\begin{aligned} \frac{1}{(4\pi )^{\frac{N}{2}}\Gamma (-s)} \int _{-\infty }^t\int _{\mathbb {R}^N}\frac{|x|^{-{\mu (\lambda )}}-|y|^{-{\mu (\lambda )}}}{(t-\sigma )^{\frac{N}{2}+s+1}}e^{-\frac{|x-y|^2}{4(t-\sigma )}}dyd\sigma =(-\Delta )^s|x|^{-\mu (\lambda )}=\frac{\lambda }{|x|^{2s+{\mu (\lambda )}}}, \end{aligned}$$

we conclude that (27) holds. $\square$

As a direct application of the ground state representation, we get the next Kato-type inequality for the operator $\bigg (H^s-\frac{\lambda }{|x|^{2s}}\bigg )$.

Proposition 3.4

Assume that $\phi \in \mathcal {S}(\mathbb {R}^{N+1})$ is a non-negative function. Then, for any $m>1$, we have

$$\begin{aligned} L^s(\phi ^m)(x,t)\le m\phi ^{m-1}(x,t)L^s(\phi )(x,t). \end{aligned}$$

(28)

Proof

We start by showing the next algebraic inequality

$$\begin{aligned} a^m-b^m\le ma^{m-1}(a-b) \quad \text { for any } a,b\ge 0. \end{aligned}$$

(29)

To this end, let $\gamma (x)=1-x^m-m(1-x)$ for any $x \in [0,+\infty )$. Since $\gamma '(x)=m(1-x^{m-1})$, it is clear that $\gamma (x)\le \gamma (1)=0$ for any $x \in [0,+\infty )$. Taking $x=b/a$, we obtain (29). Hence,

$$\begin{aligned}{} & {} L^s(\phi ^m)(x,t)= \frac{1}{(4\pi )^{\frac{N}{2}}\Gamma (-s)}\int _{-\infty }^t\int _{\mathbb {R}^N}\frac{\phi ^m(x,t)-\phi ^m(y,\sigma )}{|y|^{{\mu (\lambda )}} (t-\sigma )^{\frac{N}{2}+s+1}}e^{-\frac{|x-y|^2}{4(t-\sigma )}}dyd\sigma \\{} & {} \quad \le m\phi ^{m-1}(x,t)\displaystyle \frac{1}{(4\pi )^{\frac{N}{2}}\Gamma (-s)}\int _{-\infty }^t\int _{\mathbb {R}^N}\frac{\phi (x,t)-\phi (y,\sigma )}{|y|^{{\mu (\lambda )}} (t-\sigma )^{\frac{N}{2}+s+1}}e^{-\frac{|x-y|^2}{4(t-\sigma )}}dyd\sigma \\{} & {} \quad =m\phi ^{m-1}(x,t)L^s(\phi )(x,t), \end{aligned}$$

and so we have proved (28). $\square$

Remark 3.5

It is an open and interesting problem to obtain an inversion formula for the operator $L^s$. It is object of current investigation by the authors. The main difficulty is the loss of stability using the Fourier transform of convolutions as in [30], under the presence of singular kernels.

Hence, we will follow a different approach, based on the extension results proved in [5], to construct positive solutions and supersolutions of problem (1).

4 A comparison principle

In this section, we are going to prove a comparison principle for weak solutions using the extension procedure developed in [5].

4.1 An extension result

We will use the extension procedure of [5] (see also [4, 25, 28]) to localize the problem. We denote as $(z,t)=(x,y,t)$ the variable in $\mathbb {R}^{N} \times (0,+\infty ) \times \mathbb {R}$ and $\mathbb {R}^{N+1}_+:=\mathbb {R}^{N} \times (0,+\infty )$. Furthermore, we use the symbols $\nabla$ and $\mathrm{{div}}$ to denote the gradient, respectively, the divergence, with respect to the space variable $z=(x,y)$.

For any $p \in [1,\infty )$ and any open set $E \subseteq \mathbb {R}^{N+1}_+$, let

$$\begin{aligned} L^p(E,y^{1-2s}):=\left\{ V:E\rightarrow \mathbb {R}\text { measurable}: \int _{E} y^{1-2s}|V|^p \, dz<+\infty \right\} . \end{aligned}$$

If E is an open Lipschitz set contained in $\mathbb {R}^{N+1}_+$, $H^1(E,y^{1-2s})$ is defined as the completion of $C_c^{\infty }(\overline{E})$ with respect to the norm

$$\begin{aligned} \left\Vert \phi \right\Vert _{H^1(E,y^{1-2s})}:=\left( \int _{E} y^{1-2s}(\phi ^2 +|\nabla \phi |^2)\, dz\right) ^{\frac{1}{2}}. \end{aligned}$$

In view of [26, Theorem 11.11, Theorem 11.2, 11.12 Remarks(iii)] and the extension theorems for weighted Sobolev spaces with weights in the Muckenhoupt’s $\mathcal {A}_2$ class proved in [10], the space $H^1(E,y^{1-2s})$ admits a concrete characterization as

$$\begin{aligned} H^1(E,y^{1-2s})=\left\{ V \in W^{1,1}_{loc}(E):\int _{E} y^{1-2s} (V^2+|\nabla V|^2)\, dz< +\infty \right\} . \end{aligned}$$

By [24] there exists a linear and continuous trace operator

$$\begin{aligned} \mathrm{{Tr}}:H^1(\mathbb {R}_+^{N+1},y^{1-2s}) \rightarrow W^{2,s}(\mathbb {R}^{N}). \end{aligned}$$

(30)

For any $w \in \mathrm{{Dom}}(H^s)$ and any $(x,y,t) \in \mathbb {R}^{N+1}_+ \times \mathbb {R}$, let

$$\begin{aligned} W(x,y,t):=\frac{y^{2s}}{4^{\frac{N}{2}+s} \pi ^{\frac{N}{2}}\Gamma (s)}\int _{0}^\infty \int _{\mathbb {R}^N} \frac{e^{-\frac{|\xi |^2+y^2}{4\tau }}}{\tau ^{\frac{N}{2}+1+s}} w(x-\xi ,t-\tau ) \, d\xi d\tau . \end{aligned}$$

(31)

The function W is an extension of w which possesses good properties, as it has been proved in [4] and [5], see also [25, Theorem 1], [28, Theorem 1.7] and [4, Section 3, Section 4]. More precisely, there holds the following theorem.

Theorem 4.1

([5, Theorem 4.1, Remark 4.3], [4, Corollary 3.2]) Let $w \in \mathrm{{Dom}}(H^s)$ and let W be as in (31). Then $W \in L^2(\mathbb {R},H^1(\mathbb {R}^{N+1}_+,y^{1-2s}))$ and weakly solves

$$\begin{aligned} {\left\{ \begin{array}{ll} y^{1-2s}W_t-\mathrm{{div}}(y^{1-2s}\nabla W)=0, &{}\quad \text { in } \mathbb {R}_+^{N+1} \times \mathbb {R},\\ \mathrm{{Tr}}(W(\cdot ,t))=w(\cdot ,t), &{}\quad \text { on }\mathbb {R}^N, \text { for a.e. } t \in \mathbb {R},\\ -\lim \limits _{y \rightarrow 0^+}y^{1-2s}\frac{\partial W}{\partial y}= \kappa _s H^s(w), &{}\quad \text {on }\mathbb {R}^N\times \mathbb {R}, \end{array}\right. } \end{aligned}$$

in the sense that for a.e. $T>0$ and any $\phi \in C^\infty _c (\overline{\mathbb {R}_+^{N+1}} \times [0,T])$

with $\kappa _s:=\frac{\Gamma (1-s)}{2^{2s-1} \Gamma (s)}$.

4.2 A comparison principle

Let us begin by proving a weak maximum principle for the extended problem.

Proposition 4.2

Let $T>0$ and suppose that $W \in L^2((0,T),H^1(\mathbb {R}^{N+1}_+,y^{1-2s}))$ is a weak positive subsolution of the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} y^{1-2s}W_t-\mathrm{{div}}(y^{1-2s}\nabla W)= 0, &{}\text { in } \mathbb {R}_+^{N+1} \times (0,T),\\ -\lim \limits _{y \rightarrow 0^+}y^{1-2s}\frac{\partial W}{\partial y}= 0, &{}\text { on }\mathbb {R}^N\times (0,T),\\ W(z,0)=0, &{}\text { on }\mathbb {R}_+^{N+1}, \end{array}\right. } \end{aligned}$$

(32)

in the sense that for any positive $\phi \in C^\infty _c (\overline{\mathbb {R}_+^{N+1}} \times [0,T])$

$$\begin{aligned}{} & {} \int _{0}^{T}\left( \int _{\mathbb {R}_+^{N+1}}y^{1-2s} \nabla W \cdot \nabla \phi \, dz \, \right) dt-\int _{0}^{T}\left( \int _{\mathbb {R}_+^{N+1}}y^{1-2s} W\phi _t \, dz \, \right) dt\nonumber \\{} & {} \quad +\int _{\mathbb {R}_+^{N+1}}y^{1-2s} W(z,T)\phi (z,T) \, dz \le 0. \end{aligned}$$

(33)

Then $W\equiv 0$ a.e. in $\mathbb {R}^{N+1}_+\times (0,T)$.

Proof

By an approximated procedure, for example the Faedo–Galerkin method, we may suppose that $W_t \in L^2((0,+\infty ),L^2(\mathbb {R}^{N+1}_+,y^{1-2s}))$. Hence, we may test (33) with W. Since

$$\begin{aligned} \int _{0}^{T}\left( \int _{\mathbb {R}_+^{N+1}}y^{1-2s} W W_t \, dz \, \right) dt=\frac{1}{2}\int _{\mathbb {R}^{N+1}_+}y^{1-2s} W^2(z,T)\, dz \end{aligned}$$

we obtain

$$\begin{aligned} \int _{0}^{T}\left( \int _{\mathbb {R}_+^{N+1}}y^{1-2s} |\nabla W |^2 \, dz \, \right) dt +\frac{1}{2}\int _{\mathbb {R}^{N+1}_+}y^{1-2s} W^2(z,T)\, dz \le 0, \end{aligned}$$

in view of (33). We conclude that $W\equiv 0$ in $\mathbb {R}^{N+1}_+$. $\square$

Corollary 4.3

Let $T>0$ and suppose that $V,W \in L^2((0,T),H^1(\mathbb {R}^{N+1}_+,y^{1-2s}))$ satisfy the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} y^{1-2s}W_t-\mathrm{{div}}(y^{1-2s}\nabla W)\le y^{1-2s}V_t-\mathrm{{div}}(y^{1-2s}\nabla V), &{}\text { in } \mathbb {R}_+^{N+1} \times (0,T),\\ -\lim \limits _{y \rightarrow 0^+}y^{1-2s}\frac{\partial W}{\partial y}\le -\lim \limits _{y \rightarrow 0^+}y^{1-2s}\frac{\partial V}{\partial y}, &{}\text { on }\mathbb {R}^N\times (0,T),\\ W(z,0) \le V(z,0) &{}\text { a.e. } z \in \mathbb {R}_+^{N+1}, \end{array}\right. } \end{aligned}$$

(34)

in a weak sense. Then $W\le V$ a.e. in $\mathbb {R}^{N+1}_+\times (0,T)$. Furthermore, letting $v:=\mathrm{{Tr}}(V)$ and $w:=\mathrm{{Tr}}(W)$, we have that $w\le v$ a.e. in $\mathbb {R}^{N} \times (0,+\infty )$.

Proof

Let $U:=W-V$. By the Kato inequality, and (34), it is easy to see that $U^+$ satisfies (32). Hence, $U^+\equiv 0$ in $\mathbb {R}^{N+1}_+\times (0,T)$ thanks to Proposition 4.2, that is $W\le V$ a.e. in $\mathbb {R}^{N+1}_+\times (0,T)$. Let us define

$$\begin{aligned} \widetilde{U}(z,t)=\widetilde{U}(x,y,t):= {\left\{ \begin{array}{ll} U(x,y,t), &{} \text{ if } y>0,\\ U(x,-y,t), &{} \text{ if } y<0, \end{array}\right. } \end{aligned}$$

and let $\{\rho _\varepsilon \}_{\varepsilon >0}$ be a family of standard mollifiers on $\mathbb {R}^{N+1}$. By [21, Lemma 1.5], $\rho _\varepsilon *\widetilde{U} \rightarrow \widetilde{U}$ in $H^1(\mathbb {R}^{N+1},|y|^{1-2s})$ and $\rho _\varepsilon *\widetilde{U} \ge 0$ in $\mathbb {R}^{N+1}\times (0,+\infty )$. Since $\rho _\varepsilon *\widetilde{U}$ is smooth, in particular $\mathrm{{Tr}}(\rho _\varepsilon *\widetilde{U})\ge 0$ in $\mathbb {R}^{N}\times (0,+\infty )$. Up to a subsequence, we may pass to the limit as $\varepsilon \rightarrow 0^+$ and deduce that $\mathrm{{Tr}}(U) \ge 0$ a.e. in $\mathbb {R}^{N} \times (0,+\infty )$ thanks to the continuity of the trace operator defined in (30). We conclude that $w\le v$ in $\mathbb {R}^{N} \times (0,+\infty )$.

$\square$

From Corollary 4.3 and Theorem 4.1, we can deduce the following weak comparison principle for $H^s$.

Corollary 4.4

Suppose that $w,v \in \mathrm{{Dom}}(H^s)$ solve

$$\begin{aligned} {\left\{ \begin{array}{ll} H^s(w)\le H^s(v), &{} \text{ in } \mathbb {R}^N \times (0,+\infty ),\\ w=v=0, &{} \text{ on } \mathbb {R}^N \times (-\infty ,0], \end{array}\right. } \end{aligned}$$

in the sense that $w= v=0$ on $\mathbb {R}^N \times (-\infty ,0]$ and

$$\begin{aligned} _{(\mathrm{{Dom}}(H^s))^*}\mathop {{\mathop {\mathop {\left\langle H^s(w), \phi \right\rangle }}\nolimits _{\mathrm{{Dom}}(H^s)}}}\limits \le _{(\mathrm{{Dom}}(H^s))^*}\mathop {{\mathop {\mathop {\left\langle H^s(v), \phi \right\rangle }}\nolimits _{\mathrm{{Dom}}(H^s)}}}\limits \end{aligned}$$

for any positive $\phi \in \mathcal {S}(\mathbb {R}^{N+1})$. Then $w\le v$ a.e. in $\mathbb {R}^{N+1}$.

Comparing a weak supersolution of problem (1) with 0, from Corollary 4.4 we have the following.

Corollary 4.5

Suppose that $f \in L^2(\mathbb {R}^{N+1})$, $f(t,x)=0$ a.e. in $(-\infty ,0)\times \mathbb {R}^{N}$ and that f is non-negative. Then any weak supersolution w of problem (1) in the sense given by Definition 2.4 satisfies $w\ge 0$ a.e. in $\mathbb {R}^{N+1}$.

4.3 An existence result

In this subsection we show how to deduce the existence of solutions of problem (1) from the existence of supersolutions by the means of the comparison principle proved in Sect. 4.2.

Suppose that $f \in L^2(\mathbb {R}^{N+1})$, $f(t,x)=0$ a.e. in $(-\infty ,0)\times \mathbb {R}^{N}$. Let us define for any $n \in \mathbb {N}$ a cut-off function $\eta _n\in C^{\infty }_c(\mathbb {R}^{N+1})$ such that $\eta _n=1$ in $B'_{n} \times (\frac{1}{n+1},n+1)$ and $\eta _n=0$ in $(\mathbb {R}^{N}\setminus B'_{n+2}) \times \mathbb {R}$ and in $\mathbb {R}^{N} \times [(-\infty ,\frac{1}{n+2})\cup (n+2,+\infty )]$. Let us consider the approximating problems

$$\begin{aligned} {\left\{ \begin{array}{ll} H^s(w_0)=\eta _0 \frac{f}{1+f}, &{}\quad \text {in } \mathbb {R}^{N}\times (0,+\infty ),\\ w_0=0, &{}\quad \text {in } \mathbb {R}^{N}\times (-\infty ,0], \end{array}\right. } \end{aligned}$$

(35)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} H^s(w_{n+1})=\eta _n\left( \lambda \dfrac{w_n}{1+\frac{1}{n}w_n} \dfrac{1}{\left( |x|+\frac{1}{n}\right) ^{2s}} + \dfrac{w^p_n}{1+\frac{1}{n} w^p_n} +\dfrac{f}{1+\frac{1}{n}f}\right) , &{}\quad \text { in } \mathbb {R}^{N}\times (0,+\infty ),\\ w_{n+1}=0, &{}\quad \text {in } \mathbb {R}^{N}\times (-\infty ,0], \end{array}\right. } \end{aligned}$$

(36)

for any $n \in \mathbb {N}\setminus \{0\}$. To simplify the notations, we define

$$\begin{aligned}&h_0:=\eta _0 f_0,&h_n:=\eta _n\left( \lambda \frac{w_n}{1+\frac{1}{n}w_n} \frac{1}{\left( |x|+\frac{1}{n}\right) ^{2s}} + \frac{w^p_n}{1+\frac{1}{n} w^p_n} +\frac{f}{1+\frac{1}{n}f}\right) . \end{aligned}$$

Lemma 4.6

For any $n\in \mathbb {N}$, the function

$$\begin{aligned} w_n:=J_s\left( h_n\right) , \end{aligned}$$

(37)

belongs to $\mathrm{{Dom}}(H^s)$, and it is pointwise solutions to the problem (35) if $n=0$ or (36) if $n>0$. Furthermore, $w_n$ solves problem (35) if $n=0$ or (36) if $n>0$ in the sense given by Definition 2.4 and

$$\begin{aligned} 0\le w_n\le w_{n+1} \text { a.e. in } \mathbb {R}^{N+1} \quad \text { for any } n \in \mathbb {N}. \end{aligned}$$

(38)

Proof

By Lemma 2.5 and by Lemma 2.6, it follows that $w_n \in \mathrm{{Dom}}(H^s)$ for any $n \in \mathbb {N}$ and that $H^s(w_n)=h_n$ pointwise. Then for any $\phi \in \mathcal {S}(\mathbb {R}^{N+1})$, by the Plancherel identity,

$$\begin{aligned} \int _{\mathbb {R}^{N+1}}(i\theta +|\xi |^2)^s \widehat{w}_n \overline{\widehat{\phi }} \, d\xi \, d \theta = \int _{\mathbb {R}^{N+1}}H^s(w_n)\phi \, d\xi \, d \theta =\int _{0}^\infty \int _{\mathbb {R}^{N}} h_n \phi \, dx \, dt. \end{aligned}$$

Thanks to the Hölder inequality, $\phi \mapsto \int _{\mathbb {R}^{N+1}} h_n \phi \, dx \, dt$ belongs to $(\mathrm{{Dom}}(H^s))^*$ while $w_n=0$ in $\mathbb {R}^{N} \times (-\infty ,0]$ in view of (14).

In conclusion, $w_n$ is a solution of problem (35) if $n=0$ or (36) if $n>0$, in the sense given by Definition 2.4. Finally, (38) follows from Corollary 4.4 or directly by (12) and (37). $\square$

In the next proposition, we prove the existence of a weak solution of problem (1) starting from a weak supersolution of the same problem.

Proposition 4.7

Suppose that $f \in L^2(\mathbb {R}^{N+1})$, $f(t,x)=0$ a.e. in $(-\infty ,0)\times \mathbb {R}^{N}$ and that $u \in \mathrm{{Dom}}(H^s)$ is a weak supersolution of problem (1) in the sense given by Definition 2.4. Let ${w_n}$ be as in Lemma 4.6. Then there exists a function $w \in \mathrm{{Dom}}(H^s)$ such that $w_n(x,t) \rightarrow w(x,t)$ as $n \rightarrow \infty$ a.e. in $\mathbb {R}^{N+1}$ and w weakly solves problem (1).

Proof

In view of Corollary 4.4 and (38), we conclude that $w:=\lim _{n \rightarrow \infty } w_n$ is well-defined, that $w \le u$ a.e. in $\mathbb {R}^{N+1}$, and in particular that $w \in L^2(\mathbb {R}^{N+1})$. Let us prove that $\{w_n\}_{n \in \mathbb {N}}$ is bounded in $\mathrm{{Dom}}(H^s)$. To this end, notice that u is a weak supersolution of the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} H^s(u) \ge h_n, &{}\quad \text {in } \mathbb {R}^{N+1} \times (0,+\infty ),\\ u=0 &{}\quad \text {in }\mathbb {R}^{N+1} \times (-\infty ,0), \end{array}\right. } \end{aligned}$$

since $w_n \le w \le u$ a.e. in $\mathbb {R}^{N+1}$. Then by the Plancherel identity and Lemma 2.8

$$\begin{aligned}{} & {} \int _{\mathbb {R}^{N+1}}|(i\theta +|\xi |^2)^\frac{s}{2} \widehat{w}_n|^2 \, d\xi \, d \theta = \int _{\mathbb {R}^{N+1}}|\mathcal {F}^{-1}((i\theta +|\xi |^2)^\frac{s}{2} \widehat{w}_n)|^2 \, d\xi \, d\theta \\{} & {} \quad =\int _{\mathbb {R}^{N+1}}|J_{\frac{s}{2}}(h_n)|^2 \, d\xi \, d \theta \\{} & {} \quad \le \int _{\mathbb {R}^{N+1}}|H^{\frac{s}{2}}(u)|^2 \, d\xi \, d \theta =\int _{\mathbb {R}^{N+1}}|(i\theta +|\xi |^2)^\frac{s}{2} \widehat{u}|^2 \, d\xi \, d \theta <+\infty . \end{aligned}$$

We conclude that, up to a subsequence, $w_n \rightarrow w$ weakly in $\mathrm{{Dom}}(H^s)$ as $n \rightarrow \infty$. Thus, thanks to the Dominated Convergence Theorem,

$$\begin{aligned}{} & {} \int _{\mathbb {R}^{N+1}}(i\theta +|\xi |^2)^s \widehat{w} \overline{\widehat{\phi }} \, d\xi \, d \theta = \lim _{n \rightarrow \infty }\int _{\mathbb {R}^{N+1}}(i\theta +|\xi |^2)^s \widehat{w}_n \overline{\widehat{\phi }} \, d\xi \, d \theta \\{} & {} \quad =\lim _{n \rightarrow \infty }\int _{0}^\infty \int _{\mathbb {R}^{N}} h_n \phi \, dx \, dt= \int _{0}^\infty \int _{\mathbb {R}^{N}} \left( \frac{\lambda }{|x|^{2s}}w+w^p+f\right) \phi \, dx \, dt, \end{aligned}$$

for any $\phi \in \mathcal {S}(\mathbb {R}^{N+1})$.

It is also clear that $\phi \mapsto \int _{\mathbb {R}^{N+1}}(\frac{\lambda }{|x|^{2s}}w+w^p+f) \phi \, dx \, dt$ belongs to $(\mathrm{{Dom}}(H^s))^*$ since $w \le u$ a.e. in $\mathbb {R}^{N+1}$. In conclusion, w is a weak solution of problem (1) in the sense given by Definition 2.4. $\square$

We can also prove the existence of a very weak solution of problem (1) starting from a very weak supersolution of the same problem.

Proposition 4.8

Let $q \in [1,2]$, $f\in L^q(\mathbb {R}^N \times (-\infty , T))$ for any $T \in \mathbb {R}$ and suppose that $f(x,t)=0$ a.e. in $(-\infty ,0)\times \mathbb {R}^{N}$. Let u be a weak supersolution of problem (1) in the sense given by Definition 2.3. Let ${w_n}$ be as in Lemma 4.6. Then there exists a function $w \in L^q_{loc} (\mathbb {R}^{N+1})$ such that $w_n(x,t) \rightarrow w(x,t)$ as $n \rightarrow \infty$ a.e. in $\mathbb {R}^{N+1}$ and w is a very weak solution of problem (1).

Proof

By (12) and (37), it is clear that $w_n \le u$ a.e. in $\mathbb {R}^{N+1}$ for any $n \in \mathbb {N}$. Hence, $w:=\lim _{n \rightarrow \infty } u_n$ is well-defined and $w \le u$ a.e. in $\mathbb {R}^{N+1}$, in particular $w \in L^q_{loc}(\mathbb {R}^{N+1})$. Furthermore, by the Dominated Converge Theorem

$$\begin{aligned} w =\lim _{n \rightarrow \infty } w_n =\lim _{n \rightarrow \infty } J_s(h_n) = J_s\left( \frac{\lambda }{|x|^{2s}}w+w^p+f\right) , \end{aligned}$$

that is, w is a very weak solution of (1). $\square$

5 Local behaviour of weak solutions

In this section, we will study the local behaviour near the singular point 0 of non-negative weak supersolutions of the equation

$$\begin{aligned} H^s(w)=\lambda \frac{w}{|x|^{2s}} \quad \text { in } \mathbb {R}^N\times (0,\infty ). \end{aligned}$$

(39)

The initial datum plays no role in the results proved in this section; hence, we consider the following definition of weak solutions.

Definition 5.1

We say that w is weak supersolution (subsolution) of (39) if $w \in \mathrm{{Dom}}(H^s)$,

$$\begin{aligned} _{(\mathrm{{Dom}}(H^s))^*}\mathop {{\mathop {\mathop {\left\langle H^s(w), \phi \right\rangle }}\nolimits _{\mathrm{{Dom}}(H^s)}}}\limits \ge (\le )\int _{0}^{\infty }\left( \int _{\mathbb {R}^N} \frac{\lambda }{|x|^{2s}}w\phi \, dx \right) dt, \end{aligned}$$

(40)

for any non-negative $\phi \in \mathcal {S}(\mathbb {R}^{N+1})$ such that $\phi =0$ in $\mathbb {R}^N\times (-\infty ,0]$. If w is a supersolution and a subsolution of the equation in (40), we say that w is a solution of (40).

We start by fixing some notations and recalling some useful preliminary results.

Proposition 5.2

([14, Section 2]) For any $\phi \in C^\infty _c(\overline{\mathbb {R}^{N+1}_+})$

$$\begin{aligned} k_s \Lambda _{N,s} \int _{\mathbb {R}^N}\frac{|\phi (x,0)|^2}{|x|^{2s}} \, dx \le \int _{\mathbb {R}^{N+1}_+} y^{1-2s}|\nabla \phi |^2\, dz, \end{aligned}$$

(41)

with $\Lambda _{N,s}$ as in (3) and $k_s$ as in Theorem 4.1.

For $r>0$ let us define

$$\begin{aligned}{} & {} B_r:=\{z \in \mathbb {R}^{N+1}:|z|<r\}, \quad B_r^+:=\{z \in \mathbb {R}_+^{N+1}:|z|<r\}, \quad \text { and } \quad \\{} & {} \quad B_r':=\{x \in \mathbb {R}^{N}:|x|<r\}. \end{aligned}$$

Proposition 5.3

([13, Lemma 4.1]) For any $\lambda \in (0,\Lambda _{N,s})$, there exists a positive, continuous function $\Phi _\lambda :\mathbb {R}^{N+1}_+\setminus \{0\} \rightarrow \mathbb {R}$ such that $\Phi _\lambda \in H^1(B_r^+,y^{1-2s})$ for any $r>0$ and $\Phi _\lambda$ weakly solves the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathrm{{div}}(y^{1-2s} \nabla \Phi _\lambda )=0, &{}\quad \text {in } \mathbb {R}^{N+1}_+,\\ \Phi _\lambda (x,0)=|x|^{-\mu (\lambda )}, &{}\quad \text {on } \mathbb {R}^N, \\ -\lim _{y \rightarrow 0^+}y^{1-2s}\frac{\partial \Phi _\lambda }{\partial y}= \kappa _s \frac{\lambda }{|x|^{2s}} |x|^{-\mu (\lambda )}, &{}\quad \text {on } \mathbb {R}^N, \end{array}\right. } \end{aligned}$$

(42)

in the sense that for any $\varphi \in C_c^{\infty }(\overline{\mathbb {R}^{N+1}_+})$

$$\begin{aligned} \int _{\mathbb {R}^{N+1}_+}y^{1-2s} \nabla \Phi _\lambda \nabla \varphi \, dz =\kappa _s \int _{\mathbb {R}^N}\frac{\lambda }{|x|^{2s}} |x|^{-\mu (\lambda )} \varphi \, dz. \end{aligned}$$

Furthermore,

$$\begin{aligned}&\Phi _\lambda (\tau z)=\tau ^{-\mu (\lambda )}\Phi _\lambda (z), \quad \text { for any } \tau \in [0,\infty ) \text { and any } z \in \mathbb {R}^{N+1}_+\setminus \{0\},\nonumber \\&C_1 |z|^{-\mu (\lambda )}\le \Phi _\lambda (z)\le C_2 |z|^{-\mu (\lambda )}, \quad \text { for any } \tau \in (0,\infty ) \text { and any } z \in \mathbb {R}^{N+1}_+\setminus \{0\}, \end{aligned}$$

(43)

$$\begin{aligned}&\nabla \Phi _\lambda (z)\cdot z = -\mu (\lambda ) \Phi _\lambda (z), \quad \text { for any } z \in \mathbb {R}^{N+1}_+\setminus \{0\}, \end{aligned}$$

(44)

for some positive constants $C_1,C_2>0$.

We recall the definition of the class $\mathcal {A}_2$ of Muckenhoupt weights.

Definition 5.4

We say that a measurable function $\rho :\mathbb {R}^{N+1} \rightarrow [0,+\infty )$ belongs to $\mathcal {A}_2$ if

$$\begin{aligned} \sup _{r>0}\left\{ r^{-2N-2}\left( \int _{B_r} \rho \, dz\right) \left( \int _{B_r} \rho ^{-1} \, dz\right) \right\} < +\infty . \end{aligned}$$

(45)

Let

$$\begin{aligned} \widetilde{\Phi }_\lambda (z)=\widetilde{\Phi }_\lambda (x,y):= {\left\{ \begin{array}{ll} \Phi _\lambda (x,y), &{} \text{ if } y>0,\\ \Phi _\lambda (x,-y), &{} \text{ if } y<0. \end{array}\right. } \end{aligned}$$

(46)

Proposition 5.5

We have that $|y|^{1-2s}\widetilde{\Phi }_\lambda ^2 \in \mathcal {A}_2$, that is $|y|^{1-2s}\widetilde{\Phi }_\lambda ^2$ is a Muckenhoupt weight.

Proof

For any $r>0$, passing in polar coordinates,

$$\begin{aligned}{} & {} \int _{B_r}|y|^{1-2s}\widetilde{\Phi }_\lambda ^2 \, dz \int _{B_r}|y|^{2s-1}\widetilde{\Phi }_\lambda ^{-2} \, dz \\{} & {} \quad \le \mathrm{{const}\,}\int _0^r \rho ^{N+1-2s-2{{\mu (\lambda )}}} \, d\rho \int _0^r \rho ^{N+2s-1+2{{\mu (\lambda )}}} \, d\rho = \mathrm{{const}\,}r^{2N+2}, \end{aligned}$$

in view of (23), (43) and (46). Hence, the claim follows from (45). $\square$

For any $r>0$ let us define the Hilbert spaces

$$\begin{aligned}&L^2(B_r^+,y^{1-2s}\Phi _\lambda ^2):=\{U \in L^1_{loc}(B_r^+):\int _{B_r^+} y^{1-2s}\Phi _\lambda ^2 |U|^2 \, dz<+\infty \}, \\&H^1(B_r^+,y^{1-2s}\Phi _\lambda ^2):=\{U \in W^{1,1}_{loc}(B_r^+):\int _{B_r^+} y^{1-2s}\Phi _\lambda ^2(|U|^2+|\nabla U|^2 )\, dz <+\infty \}, \end{aligned}$$

endowed with the natural norms

$$\begin{aligned}&\left\Vert U\right\Vert _{L^2(B_r^+,y^{1-2s}\Phi _\lambda ^2)}:=\int _{B_r^+} y^{1-2s}\Phi _\lambda ^2 |U|^2 \, dz, \\&\left\Vert U\right\Vert _{H^1(B_r^+,y^{1-2s}\Phi _\lambda ^2)}:=\int _{B_r^+} y^{1-2s}\Phi _\lambda ^2(|U|^2+|\nabla U|^2 ) \, dz. \end{aligned}$$

In the next proposition we estimate the behaviour of weak solutions of (39) near the origin.

Proposition 5.6

Assume that w is a non-negative, non-trivial, weak supersolution of

$$\begin{aligned} H^s(w)= \frac{\lambda }{|x|^{2s}}w \quad \text { in } \mathbb {R}^N \times (0,+\infty ). \end{aligned}$$

Then for $r>0$ small and for all $(t_1,t_2)\subset \subset (0,\infty )$, there exists a positive constant $C(r,t_1,t_2,w)$ depending only on $r,t_1,t_2$ and w, such that

$$\begin{aligned} w(x,t)\ge C(r,t_1,t_2,w) |x|^{-\mu (\lambda )} \quad \text { for a.e. } (x,t)\in B_r(0)\times (t_1,t_2). \end{aligned}$$

(47)

In particular,

$$\begin{aligned} w>0 \quad \text { a.e. in } \mathbb {R}^{N}\times (0,+\infty ). \end{aligned}$$

Proof

Let W be the extension of w as in Theorem 4.1. Then, by (31), $W>0$ in $\mathbb {R}^{N+1}_+$ while by classical parabolic regularity theory W is continuous in $\mathbb {R}^{N+1}_+$. Let $r>0$ and $(t_1,t_2)\subset \subset (0,\infty )$. For any $\rho >0$ there exists $\delta >0$ such that $W>\rho$ on $S_{4r,\delta }\times (t_1,t_2)$ where for any $r>0$ and any $\delta \in [0,4r)$

$$\begin{aligned} S_{4r,\delta }:=\{z=(x,y) \in \mathbb {R}^{N+1}_+:|z|=4r, y > \delta \}. \end{aligned}$$

Let $\eta \in C^{\infty }(\mathbb {R}^{N+1})$ be a cut-off function such that $\eta (x,y)=0$ if $y <\delta$ and $\eta (x,y)=1$ if $y >\frac{4r+\delta }{2}$ for any $x \in \mathbb {R}^{N}$. Let us consider the elliptic problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -\mathrm{{div}}(y^{1-2s}\nabla U)=0, &{}\quad \text {in } B^+_{4r},\\ U=\rho \eta &{}\quad \text {on } S^+_r, \\ -\lim \limits _{y \rightarrow 0^+}y^{1-2s}\frac{\partial U}{\partial y}= \kappa _s \frac{\lambda }{|x|^{2s}}u, &{}\quad \text {on }B_{4r}', \end{array}\right. } \end{aligned}$$

where $u=\mathrm{{Tr}}(U)$. In view of (41), by standard minimization technique it is easy to see that there exists a unique weak solution $u \in H^1(B_r^+,y^{1-2s})$, that is u solves the equation

$$\begin{aligned} \int _{B_{4r}^+}y^{1-2s}\nabla U \cdot \nabla \phi \, dz=\kappa _s \lambda \int _{B'_{4r}}y^{1-2s}\frac{u}{|x|^{2s}} \phi (x,0) \, dx \end{aligned}$$

for any $\phi \in C^{\infty }(\overline{B_{4r}^+})$ such that $\phi =0$ on $S_{4r}^+$. Furthermore, since $\rho \eta$ is positive, it is clear that $U^-=0$ on $S_{4r}^+$. Hence, we may test with $U^-$ the equation above and conclude that U is non-negative. Since $U=\rho \eta$ on $S^+_r$, it is also clear that $U\not \equiv 0$.

Let us define $V:=U \Phi _\lambda ^{-1}$ and $v:=u|\cdot |^{-\mu (\lambda )}$. Then with a direct computation we see that $V \in H^1(B_{4r}^+,y^{1-2s}\Phi _\lambda ^2)$ and weakly solves the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -\mathrm{{div}}(y^{1-2s}\Phi _\lambda ^2\nabla V)=0, &{}\quad \text {in } B^+_{4r},\\ V=\rho \eta \Phi _\lambda ^{-1} &{}\quad \text {on } S^+_{4r}, \\ -\lim \limits _{y \rightarrow 0^+}y^{1-2s}\frac{\partial V}{\partial y}= 0, &{}\quad \text {on }B_{4r}'. \end{array}\right. } \end{aligned}$$

Let us define $\widetilde{V}$ as

$$\begin{aligned} \widetilde{V}(x,y):= {\left\{ \begin{array}{ll} V(x,y), &{}\quad \text {if } y>0,\\ V(x,-y), &{}\quad \text {if } y<0. \end{array}\right. } \end{aligned}$$

Then $\widetilde{V}\in H^1(B_{4r},|y|^{1-2s}\Phi _\lambda ^2)$ is a weak solution of the equation

$$\begin{aligned} -\mathrm{{div}}(|y|^{1-2s}\Phi _\lambda ^2\nabla \widetilde{V})=0 \quad \text { in } B_{2r}. \end{aligned}$$

Then there exists a positive constant $C>0$ such that $V\ge C$ a.e. in $B_{2r}$ thanks to Proposition 5.5 and the Harnack inequality proved in [9]. It follows that $U\ge C \Phi _\lambda$ a.e. in $B_{2r}$.

Let us define for any $t\in \mathbb {R}$ the function $\overline{U}(t,z):=U(z)$ for any $z \in B_{4r}^+$. Since $W\ge \overline{U}$ on $S_{4r}^+ \times (t_1,t_2)$, arguing as in Sect. 4.2, we can show that $W \ge \overline{U}$ a.e. in $B_{4r}^+$. It follows that there exists a positive constant $C(r,t_1,t_2,w)>0$ depending only on $r,t_1,t_2$ and w such that

$$\begin{aligned} W \ge C(r,t_1,t_2,w) \Phi _\lambda \quad \text { a.e. in } B_{2r}^+. \end{aligned}$$

Let us define

$$\begin{aligned} \widetilde{W}(x,y,t):= {\left\{ \begin{array}{ll} W(x,y,t), &{}\quad \text {if }y>0, \\ W(x,-y,t), &{} \quad \text {if }y<0,\\ \end{array}\right. } \end{aligned}$$

and let $\widetilde{\Phi _\lambda }$ be as in (46). Furthermore, let $\varphi \in C^\infty _c(\mathbb {R}^{N+1})$ be a cut-off function such that $\varphi = 1$ in $B_{r}$ and $\varphi =0$ in $\mathbb {R}^{N+1}\setminus B_{2r}$. Then

$$\begin{aligned} \varphi (x,y) \widetilde{W}(x,y,t)\ge C(r,t_1,t_2,w) \, \varphi (x,y) \widetilde{\Phi }_\lambda (x,y) \quad \text { a.e. in } \mathbb {R}^{N+1} \times (t_1,t_2) \end{aligned}$$

and so

$$\begin{aligned} \rho _\varepsilon *(\varphi \widetilde{W} )\ge C(r,t_1,t_2,w) \, \rho _\varepsilon *(\varphi \widetilde{\Phi _\lambda }), \quad \text { in } \mathbb {R}^{N+1} \times (t_1,t_2), \end{aligned}$$

where $\{\rho _\varepsilon \}_{\varepsilon >0}$ is a family of standard mollifier on $\mathbb {R}^{N+1}$.

It is clear that $\varphi \widetilde{W} \in H^1(\mathbb {R}^{N+1},|y|^{1-2s})$ and also $\varphi \widetilde{\Phi _\lambda } \in H^1(\mathbb {R}^{N+1},|y|^{1-2s})$, in view of Proposition 5.3. Then by [21, Lemma 1.5], $\rho _\varepsilon *(\phi \widetilde{W} ) \rightarrow \varphi \widetilde{W}$ and $\rho _\varepsilon *(\phi \widetilde{\Phi _\lambda }) \rightarrow \phi \widetilde{\Phi _\lambda }$ strongly in $H^1(\mathbb {R}^{N+1},|y|^{1-2s})$ as $\varepsilon \rightarrow 0^+$. Hence, up to a subsequence,

$$\begin{aligned}{} & {} \mathrm{{Tr}}(\varphi W))(x,t)= \lim _{\varepsilon \rightarrow 0^+}(\rho _\varepsilon *(\phi \widetilde{W}))(x,0,t) \ge \lim _{\varepsilon \rightarrow 0^+} \\{} & {} \quad C(r,t_1,t_2,w) (\rho _\varepsilon *(\varphi \Phi _\lambda ))(x,0) =C(r,t_1,t_2,w)\mathrm{{Tr}}(\varphi \Phi _\lambda )) \end{aligned}$$

a.e. in $\mathbb {R}^{N} \times (t_1,t_2)$. It follows that

$$\begin{aligned} w(x,t)\ge C(r,t_1,t_2,w)|x|^{-\mu (\lambda )} \quad \text { in } B'_{r} \times (t_1,t_2), \end{aligned}$$

since

$$\begin{aligned} \mathrm{{Tr}}(\varphi W)(x,0,t)=\varphi (x,0) w(x,t) \quad \text { and }\quad \mathrm{{Tr}}(\varphi \Phi _\lambda )(x,0)=\varphi (x,0) |x|^{-\mu (\lambda )}. \end{aligned}$$

Hence, we have proved (47). $\square$

6 Non-existence result and Fujita-type behaviour

In this section, we analyse the existence and behaviour of solutions to problem (1) according to the value of the parameter p.

6.1 A non-existence result

In order to prove Theorem 6.2, we need a version of the Picone-type inequality for the extended problem.

Proposition 6.1

Let $r>0$ and assume $W \in H^1(B_r^+,y^{1-2s})$ is such that $W>\delta$ for some positive constant $\delta >0$ and W weakly solves the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -\mathrm{{div}}(y^{1-2s}\nabla W)=y^{1-2s}g, &{}\text { in } B_r^+,\\ -\lim \limits _{y \rightarrow 0^+}y^{1-2s}\frac{\partial W}{\partial y}= f(x), &{}\text { on } B_r', \end{array}\right. } \end{aligned}$$

in the sense that for any $\phi \in C^\infty _c(B_r^+\cup B_r')$

$$\begin{aligned} \int _{B_r^+} y^{1-2s} \nabla W \cdot \nabla \phi \, dz = \int _{B_r^+} y^{1-2s} g \phi \, dz+ \int _{B_r'}f \phi (x,0) \, dx, \end{aligned}$$

where $g \in L^2(B_r^+,y^{1-2s})$, $f \in L^1_{loc}(B_r')$ with $f \ge 0$, $f \ne 0$. Then for any $\phi \in C_c^\infty (B_r^+\cup B_r')$

$$\begin{aligned} \int _{B_r^+}y^{1-2s} |\nabla \phi |^2 \, dz \ge \int _{B_r'}\frac{f(x)}{\mathrm{{Tr}}(W)}\phi ^2(x,0)dx+\int _{B_r^+} y^{1-2s} \frac{ g}{W}\phi ^2 \, dz. \end{aligned}$$

(48)

Proof

Let $\phi \in C_c^\infty (B_r^+\cup B_r')$. Then

$$\begin{aligned} y^{1-2s}|\nabla \phi (x,y)|^2\ge y^{1-2s}\nabla \left( \frac{\phi ^2(x,y)}{W(x,y)}\right) \nabla W(x,y)\quad \text { a.e. in }B_r^+. \end{aligned}$$

Hence, by integration, since $\phi ^2 W^{-1} \in H^1(B_r^+,y^{1-2s})$, we obtain

$$\begin{aligned} \displaystyle \int _{B_r^+}y^{1-2s} |\nabla \phi |^2\, dz\ge & {} \int _{B_r^+}y^{1-2s}\nabla \left( \frac{\phi ^2(x,y)}{W(x,y)}\right) \nabla W(x,y) \,dz \\= & {} \int _{B_r^+} y^{1-2s} g \frac{\phi ^2(x,y)}{W(x,y)} \, dz +\int _{B_r'}f \frac{\phi ^2(x,0)}{\mathrm{{Tr}}(W)} \, dx \end{aligned}$$

which proves (48). $\square$

We have the following non-existence theorem for weak supersolutions.

Theorem 6.2

Assume that $p>1+\frac{2s}{{\mu (\lambda )}}$. Let $f \in L^2(\mathbb {R}^{N+1})$ be such that $f(x,t)=0$ a.e. in $\mathbb {R}^N\times (-\infty ,0)$. Then any non-negative weak supersolution w of problem (1) is trivial. In particular, if $f\not \equiv 0$, there are not any non-negative weak supersolutions.

Proof

We argue by contradiction. Let $p>1+\frac{2s}{{\mu (\lambda )}}$ and suppose that (18) has a non-negative supersolution w. Then there exists a solution of (18) and a sequence $\{w_n\}_{n \in \mathbb {N}}$ as in Proposition 4.7. For any $r>0$ and any $(t_1,t_2) \subset (0,+\infty )$ by standard abstract parabolic elliptic theory, see, for example, [12], letting $W_n$ be the extension of $w_n$ as in Theorem 4.1, it follows that $(W_n)_t \in L^2((t_1,t_2),B_r^+)$. Fix $r>0$ and $(t_1,t_2) \subset (0,+\infty )$. Then for any $\phi \in C_c^{\infty }(B_r^+ \cup B_r')$ by (1), Proposition 6.1, Theorem 4.1, and the regularity of $(W_n)_t$ it follows that

$$\begin{aligned} \int _{B^+_r} y^{1-2s}|\nabla \phi |^2 dz \ge \kappa _s \int _{B'_r}\frac{w^p_{n-1}}{\left( 1+\frac{1}{n}w^p_{n-1}\right) w_n}\phi ^2(x,0)dx + \int _{B^+_r}y^{1-2s}\phi ^2\frac{(W_n)_t}{W_n}dz. \end{aligned}$$

Furthermore, $\{w_n\}_{n \in \mathbb {N}}$ is bounded in ${\mathrm{{Dom}}(H^s)}$ and so for any $\sigma >1$ there exists a constant C that does not depend on n, such that for any $n \in \mathbb {N}$

$$\begin{aligned} \int _{B^+_r}y^{1-2s}|\log W_n(x,y,t_i)|^{\sigma }dz \le C \end{aligned}$$

for $i=1,2$, see [5]. It is also clear that

$$\begin{aligned} \int _{t_1}^{t_2}\int _{B^+_r}y^{1-2s}\phi ^2\frac{(W_n)_t}{W_n}dx=\int _{B^+_r}y^{1-2s}\phi ^2(\log (W_n(z,t_1))- \log (W_n(z,t_2))dz. \end{aligned}$$

Then, letting

$$\begin{aligned} 2^{**}_s:=\min \left\{ \frac{N+2-2s}{N-2s},2\frac{N+1}{N-1}\right\} \end{aligned}$$

and $\sigma$ its conjugate exponent, that is $\frac{1}{2^{**}_s} +\frac{1}{\sigma }=1$, by the Hölder inequality and [16, Lemma 4.2],

$$\begin{aligned}{} & {} \int _{B_r^+}y^{1-2s}\phi ^2|\log W_n(x,y,t_i)|dz\\{} & {} \quad \le \bigg (\int _{B_r^+}y^{1-2s}|\phi |^{2^{**}_s}dz\bigg )^{\frac{2}{2^{**}_s}}\bigg (\int _{B^+_r}y^{1-2s}|\log W_n(x,y,t_i)|^{\sigma }dz\bigg )^{\frac{1}{\sigma }}\\{} & {} \quad \le C^\frac{1}{\sigma } \int _{B^+_r} y^{1-2s} |\nabla \phi |^2\, dz, \end{aligned}$$

for $i=1,2$. Hence, combining the above estimates and integrating over $(t_1,t_2)$, we obtain that there exists a constant $C_1>0$, that does not depend on $\phi$, such that

$$\begin{aligned} (t_2-t_1)\int _{B^+_r} y^{1-2s}|\nabla \phi |^2 dz \ge C_1 \int _{t_1}^{t_2}\int _{B'_r}\frac{w^p_{n-1}}{\left( 1+\frac{1}{n}w^p_{n-1}\right) w_n}\phi ^2(x,0)dx \, dt. \end{aligned}$$

Passing to the limit as $n \rightarrow \infty$ by the Dominated Converge Theorem, we conclude that

$$\begin{aligned} \int _{B^+_r} y^{1-2s} |\nabla \phi |^2dz \ge C_1\int _{B'_r}|x|^{-(p-1){\mu (\lambda )}}\phi ^2(x,0)dx, \end{aligned}$$

in view of Proposition 5.6. Since $(p-1){\mu (\lambda )}>2s$, then we have reached a contradiction with the optimality of the power $|x|^{2s}$ in the Hardy-type inequality (41).

$\square$

Remark 6.3

If $p<p_+(\lambda ,s)$, we get the existence of a local pointwise positive supersolution to (1) in any bounded domain $\Omega \times (T_1,T_2)$. Indeed, using [28, Corollary 1.4.], there exists positive supersolution to the correspondent elliptic problem

$$\begin{aligned} {\left\{ \begin{array}{ll} (-\Delta )^s\psi =\frac{\lambda }{|x|^{2s}} \psi +\psi ^p +h, &{}\quad \text {in }\Omega ,\\ \psi (x)=0, &{}\quad \text {in }\mathbb {R}^N\setminus \Omega , \end{array}\right. } \end{aligned}$$

where h, depending only on x, satisfies some additional assumptions.

6.2 A blow-up result

In the case $1<p\le 1+\frac{2s}{N+2-2s-\mu (\lambda )}$, we have the following blow-up result.

Theorem 6.4

Assume that $1 < p \le 1+\frac{2s}{N+2-2s-{\mu (\lambda )}}$ and that w is a non-negative, non-trivial solution of (1) either in the sense of Definition 2.3 or in the sense of Definition 2.4. Then there exists $T^*<\infty$ such that

$$\begin{aligned} \lim \limits _{t\rightarrow T^{*}}\int _{\mathbb {R}^N}|x|^{-\mu (\lambda )}w^p(x,t)\,dx=\infty . \end{aligned}$$

Proof

Let w be a positive non-trivial solution of (1) in the sense of Definition 2.3 or in the sense of Definition 2.4. Let us define

$$\begin{aligned} v(x,t):=|x|^{\mu (\lambda )}w(x,t), \end{aligned}$$

so that $|x|^{-\mu (\lambda )}w^p(x,t)=|x|^{-(p+1)\mu (\lambda )}v^p(x,t)$. We argue by contradiction assuming that

$$\begin{aligned} \limsup _{t\rightarrow T}\int _{\mathbb {R}^N}|x|^{-\mu (\lambda )}w^p(x,t)\,dx<+\infty \quad \text { for all }T\ge 0. \end{aligned}$$

Then in particular

$$\begin{aligned} \int _0^{T}\int _{\mathbb {R}^N}|x|^{-(p+1)\mu (\lambda )}v^p(x,t) \,dx dt<\infty \quad \text { for all }T>0. \end{aligned}$$

If w is a solution of (1) in the sense of Definition 2.3 then for any even $\phi \in C^{\infty }_c(\mathbb {R}^{N+1})$

$$\begin{aligned}{} & {} \int _{\mathbb {R}^{N+1}} w(x,t) H^s(\phi )(-x,-t) \, dx \, dt \\{} & {} \quad = \int _{\mathbb {R}^{N+1}}J_s\left( \frac{\lambda }{|x|^{2s}}w +w^p+f\right) H^s(\phi )(-x,-t)\, dx \, dt \\{} & {} \quad =\int _{\mathbb {R}^{N+1}}\left( \frac{\lambda }{|x|^{2s}}w +w^p+f\right) \phi (x,t)\, dx \, dt \end{aligned}$$

by Lemma 2.7 and a change of variables. If w is a solution of (1) in the sense of Definition 2.3, then the equation above still holds in view of Lemma 2.7 and (18). Then, by Proposition 3.3, in both cases we have that

$$\begin{aligned} \int _{\mathbb {R}^{N+1}}v(x,t)^p |x|^{-\mu (\lambda )(p+1)}\phi (x,t)\, dx dt\le \int _{\mathbb {R}^{N+1}} v(-x,-t) |x|^{-\mu (\lambda )}L^s(\phi )\, dx dt \end{aligned}$$

(49)

for any even $\phi \in C^{\infty }_c(\mathbb {R}^{N+1})$.

Let $\varphi \in C^{\infty }_c(B_2')$ be an even cut-off function such that $0\le \varphi \le 1$, $\varphi \equiv 1$ in $B_1'$. For any $R \ge 1$ let us define

$$\begin{aligned} \varphi _R(x,t):=\varphi \left( \frac{x}{R},\frac{t}{R^2}\right) . \end{aligned}$$

Fix $m > p'$. Then testing (49) with $\varphi _R^m$, we obtain

$$\begin{aligned}{} & {} \int _{\mathbb {R}^{N+1}}v(x,t)^p |x|^{-\mu (\lambda )(p+1)}\varphi ^m_R(x,t)\, dx dt\\{} & {} \quad \le \int _{\mathbb {R}^{N+1}} v(-x,-t) |x|^{-\mu (\lambda )}L^s(\varphi ^m_R)(x,t)\, dx dt \\{} & {} \quad \le m \int _{\mathbb {R}^{N+1}} v(-x,-t) |x|^{-\mu (\lambda )}\varphi ^{m-1}_R(x,t)L^s(\varphi _R)(x,t)\, dx dt, \end{aligned}$$

in view of Proposition 3.4. Letting $p'$ be such that $1/p+1/p'=1$, from the Hölder inequality it follows that

$$\begin{aligned}{} & {} \int _{\mathbb {R}^{N+1}}v(x,t)^p |x|^{-\mu (\lambda )(p+1)}\varphi _R^m(x,t)\, dx dt\\{} & {} \quad \le m \left( \int _{\mathbb {R}^{N+1}}v(-x,-t)^p |x|^{-\mu (\lambda )(p+1)}\varphi ^m_R(x,t)\, dx dt\right) ^\frac{1}{p}\\{} & {} \qquad \times \left( \int _{\mathbb {R}^{N+1}} |x|^{\mu (\lambda )(p'-1)}\varphi _R^{m-p'}(x,t)(L^s(\varphi _R)(x,t))^{p'}\, dx dt\right) ^\frac{1}{p'}. \end{aligned}$$

Then by a change of variables, we deduce that

$$\begin{aligned}{} & {} \int _{\mathbb {R}^{N+1}}v(x,t)^p |x|^{-\mu (\lambda )(p+1)}\varphi ^m_R(x,t)\, dx dt\nonumber \\{} & {} \quad \le \int _{\mathbb {R}^{N+1}} |x|^{\mu (\lambda )(p'-1)}\varphi _R^{m-p'}(x,t)(L^s(\varphi _R)(x,t))^{p'}\, dx dt. \end{aligned}$$

(50)

Furthermore, the change of variables $\tilde{y}=R^{-1} y$ and $\tilde{\sigma }=R^{-2} \sigma$ yields

$$\begin{aligned}{} & {} L^s(\varphi _R)(x,t)=\frac{1}{(4\pi )^{\frac{N}{2}}\Gamma (-s)} \int _{-\infty }^t\int _{\mathbb {R}^N}\frac{\varphi _R(x,t)-\varphi _R(y,\sigma )}{|y|^{{\mu (\lambda )}}(t-\sigma )^{\frac{N}{2}+s+1}}e^{-\frac{|x-y|^2}{4(t-\sigma )}}dyd\sigma \\{} & {} \quad =\frac{1}{(4\pi )^{\frac{N}{2}}\Gamma (-s)}R^{-\mu (\lambda )-2s} \int _{-\infty }^{\frac{t}{R^2}}\int _{\mathbb {R}^N}\frac{\varphi (R^{-1}x,R^{-2}t)-\varphi (\tilde{y},\tilde{\sigma })}{|\tilde{y}|^{{\mu (\lambda )}}(R^{-2}t-\tilde{\sigma })^{\frac{N}{2}+s+1}} e^{-\frac{|R^{-1}x-\tilde{y}|^2}{4(R^{-2}t-\tilde{\sigma })}}d\tilde{y}d\tilde{\sigma }\\{} & {} \quad \le C_1 R^{-2s} |x|^{-\mu (\lambda )}, \end{aligned}$$

for some positive constant $C_1>0$ depending only on $N,s, \lambda$ and $\varphi$, by Proposition 3.3. Hence,

$$\begin{aligned}{} & {} \int _{\mathbb {R}^{N+1}}v(x,t)^p |x|^{-\mu (\lambda )(p+1)}\varphi ^m_R(x,t)\, dx dt\\{} & {} \quad \le C_2 R^{-2sp'}\int _{\mathbb {R}^{N+1}} |x|^{-\mu (\lambda )}\varphi _R^{m-p'}(x,t)\, dx dt, \end{aligned}$$

for some positive constant $C_2>0$. The change of variables $\tilde{x}=R^{-1} x$ and $\tilde{t}=R^{-2} t$ yields

$$\begin{aligned}{} & {} \int _{\mathbb {R}^{N+1}}v(x,t)^p |x|^{-\mu (\lambda )(p+1)}\varphi _R^m(x,t)\, dx dt\\{} & {} \quad \le C_2 R^{N+2-\mu (\lambda )-2sp'}\int _{\mathbb {R}^{N+1}} |x|^{-\mu (\lambda )}\varphi ^{m-p'}(\tilde{x},\tilde{t})\, d\tilde{x} d\tilde{t}. \end{aligned}$$

Thanks to Fatou’s Lemma, we can pass to the limit as $R \rightarrow \infty$ and conclude that

$$\begin{aligned} \int _{\mathbb {R}^{N+1}}v(x,t)^p |x|^{-\mu (\lambda )(p+1)}\, dx dt <+\infty . \end{aligned}$$

In particular, if $p<1+\frac{2s}{N+2-2s-\mu (\lambda )}$, we obtain

$$\begin{aligned} \int _{\mathbb {R}^{N+1}}v(x,t)^p |x|^{-\mu (\lambda )(p+1)}\, dx dt=0, \end{aligned}$$

and thus $v\equiv 0$. Since $w(x,t)=v(x,t)|x|^{-\mu (\lambda )}$, then $w \equiv 0$ in $\mathbb {R}^N\times \mathbb {R}$, a contradiction.

We deal now with the critical case $p=1+\frac{2s}{N+2-2s-\mu (\lambda )}$. Let $\delta \in (0,\frac{1}{p'-1})$. Then

$$\begin{aligned}{} & {} \int _{\mathbb {R}^{N+1}} v(x,t) |x|^{-\mu (\lambda )}\varphi ^{m-1}_R(x,t)L^s(\varphi _R(x,t))\, dx dt \nonumber \\{} & {} \quad =\int _{\mathbb {R}^{N+1}} v(x,t) |x|^{-\mu (\lambda )}\varphi ^{m-1}_R(x,t)(1-\varphi _R(x,t))^\delta (1-\varphi _R(x,t))^{-\delta } L^s(\varphi _R(x,t))\, dx dt\nonumber \\{} & {} \quad \le \left( \int _{\mathbb {R}^{N+1}} |x|^{\mu (\lambda )(p'-1)}\varphi _R^{m-p'}(x,t)(1-\varphi _R(x,t))^{\delta (1-p')}(L^s(\varphi _R(x,t)))^{p'}\, dx dt\right) ^\frac{1}{p'}\nonumber \\{} & {} \qquad \times \left( \int _{\mathbb {R}^{N+1}}v(x,t)^p |x|^{-\mu (\lambda )(p+1)}\varphi ^m_R(x,t)(1-\varphi _R(x,t))^{\delta }\, dx dt\right) ^\frac{1}{p}. \end{aligned}$$

(51)

Furthermore, arguing as above, we can show that

$$\begin{aligned}{} & {} \int _{\mathbb {R}^{N+1}} |x|^{\mu (\lambda )(p'-1)}\varphi _R^{m-p'}(x,t)(1-\varphi _R(x,t))^{\delta (1-p')}(L^s(\varphi _R(x,t)))^{p'}\, dx dt \nonumber \\{} & {} \quad \le C_2 \int _{\mathbb {R}^{N+1}} |x|^{-\mu (\lambda )}\varphi ^{m-p'}(x,t)(1-\varphi (x,t))^{\delta (1-p')}\, dx dt. \end{aligned}$$

(52)

Since we have chosen $\delta \in (0,\frac{1}{p'-1})$, we conclude that the integral in the right-hand side of (52) is finite. In conclusion, from (51) and (52) we deduce that there exists a constant $C_3>0$ such that

$$\begin{aligned}{} & {} \int _{\mathbb {R}^{N+1}} v(x,t) |x|^{-\mu (\lambda )}\varphi ^{m-1}_R(x,t)L^s(\varphi _R(x,t))\, dx dt\\{} & {} \quad \le C_3\left( \int _{\mathbb {R}^{N+1}\setminus B'_R}v(x,t)^p |x|^{-\mu (\lambda )(p+1)}\, dx dt\right) ^\frac{1}{p} \end{aligned}$$

for any $R\ge 1$. Passing to the limit as $R \rightarrow \infty$, we conclude that

$$\begin{aligned} \lim _{R\rightarrow \infty }\int _{\mathbb {R}^{N+1}} v(x,t) |x|^{-\mu (\lambda )}\varphi ^{m-1}_R(x,t)L^s(\varphi _R(x,t))\, dx dt =0. \end{aligned}$$

Then from (6.2) and Fatou’s Lemma, we deduce that $v\equiv 0$ and so $w\equiv 0$. $\square$

Remark 6.5

It is easy to see that, if $\lambda =0$, then proceeding as in Theorem 6.4, we can show that there exists $T^*<\infty$ such that

$$\begin{aligned} \lim \limits _{t\rightarrow T^{*}}\int _{\mathbb {R}^N}w^p(x,t)\,dx=\infty , \end{aligned}$$

see also [31].

6.3 Existence of supersolutions

We start by proving the following result.

Proposition 6.6

Let $p \in \left( 1+\frac{2s}{N-\mu (\lambda )+2-2s}, 1+\frac{2s}{\mu (\lambda )}\right)$. Then there exist $\varepsilon _0>0$ and $\delta >0$ such that for any $\varepsilon \in (0,\varepsilon _0]$ and any $\lambda _1 \in (\lambda ,\lambda +\delta ]$ the function

$$\begin{aligned} U_{\varepsilon , \lambda _1}(x,y,t):= \varepsilon (1+t)^{\frac{\mu (\lambda _1)}{2}-\frac{s}{p-1}} \Phi _{\lambda _1}(z) e^{-\frac{|z|^2}{4(t+1)}} \end{aligned}$$

is a positive classical solution of the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} y^{1-2s}(U_{\varepsilon , \lambda _1})_t-\mathrm{{div}}(y^{1-2s}\nabla U_{\varepsilon , \lambda _1})\ge 0, &{}\quad \text {in } \mathbb {R}_+^{N+1}\setminus \{0\} \times (0,+\infty ),\\ -\lim \limits _{y \rightarrow 0^+}y^{1-2s}\frac{\partial U_{\varepsilon , \lambda _1}}{\partial y}\ge \kappa _s \left( \frac{\lambda }{|x|^{2s}}u_{\varepsilon , \lambda _1}+u_{\varepsilon , \lambda _1}^p\right) , &{}\quad \text {on }(\mathbb {R}^N\setminus \{0\}) \times (0,+\infty ),\\ U_{\varepsilon , \lambda _1}(z,0)\ge 0, &{}\quad \text { on }\mathbb {R}_+^{N+1}\setminus \{0\}, \end{array}\right. } \end{aligned}$$

(53)

where $u_{\varepsilon , \lambda _1}(x,t):=U_{\varepsilon , \lambda _1}(x,0,t)=\varepsilon (1+t)^{\frac{s}{p-1}-\frac{\mu (\lambda _1)}{2}} |x|^{-\mu (\lambda _1)} e^{-\frac{|x|^2}{4(t+1)}}$ and $k_s$ is as in Theorem 4.1. Furthermore for any $T>0$, we have that $U_{\varepsilon , \lambda _1} \in L^2((0,T),H^1(\mathbb {R}^{N+1}_+,y^{1-2s}))$ and $(U_{\varepsilon , \lambda _1})_t \in L^2((0,T),L^2(\mathbb {R}^{N+1}_+,y^{1-2s})$ .

Proof

Let us consider the family of functions

$$\begin{aligned} U(x,y,t):=\varepsilon (1+t)^{-\theta } \Phi _{\lambda _1}(z) e^{-\frac{|z|^2}{4(t+1)}}, \end{aligned}$$

with $\varepsilon >0$, $\theta >0$ and $\lambda _1 \in (\lambda ,\Lambda _{N,s})$. With a direct computation we can see that

$$\begin{aligned}&U_t(z,t)=\varepsilon \left[ -\theta +\frac{1}{4}t^{-1}|z|^2\right] (1+t)^{-\theta -1} \Phi _{\lambda _1}(z) e^{-\frac{|z|^2}{4(1+t)}}, \\&\mathrm{{div}}(y^{1-2s}\nabla U)(z,t)= \varepsilon y^{1-2s}\\&\left[ -\mu (\lambda _1)-\frac{1}{2}(N+2-2s) +\frac{1}{4}t^{-1}|z|^2\right] (1+t)^{-\theta -1} \Phi _{\lambda _1}(z) e^{-\frac{|z|^2}{4(1+t)}}, \end{aligned}$$

thanks to (42) and (44). Hence,

$$\begin{aligned}{} & {} y^{1-2s}U_t(z,t)-\mathrm{{div}}(y^{1-2s}\nabla U)(z,t)\\{} & {} \quad =\varepsilon y^{1-2s} \left[ -\theta -\mu (\lambda _1)+\frac{1}{2}(N+2-2s)\right] (1+t)^{-\theta -1} \Phi _{\lambda _1}(z) e^{-\frac{|z|^2}{4(1+t)}}. \end{aligned}$$

On the other hand by (42),

$$\begin{aligned} -\lim _{y \rightarrow 0^+}y^{1-2s} \frac{\partial U}{\partial y}= \varepsilon (1+t)^{-\theta } \kappa _s\frac{\lambda _1}{|x|^{2s}}|x|^{-\mu (\lambda _1)}e^{-\frac{|x|^2}{4(1+t)}}. \end{aligned}$$

Then $-\lim \limits _{y \rightarrow 0^+}y^{1-2s}\frac{\partial U_{\varepsilon , \lambda _1}}{\partial y}\ge k_s \left( \frac{\lambda }{|x|^{2s}}u_{\varepsilon , \lambda _1}+u_{\varepsilon , \lambda _1}^p\right)$ if and only if

$$\begin{aligned} (1+t)^{-\theta } (\lambda _1-\lambda )|x|^{-\mu (\lambda _1)-2s} e^{-\frac{|x|^2}{4(1+t)}} \ge \varepsilon ^{p-1} (1+t)^{-\theta p} |x|^{-p\mu (\lambda _1)} e^{-p\frac{|x|^2}{4(1+t)}}. \end{aligned}$$

The change of variables $x:=(1+t)^{\frac{1}{2}}\xi$ yields

$$\begin{aligned} (1+t)^{-\theta -\frac{\mu (\lambda _1)}{2}-s} (\lambda _1-\lambda )|\xi |^{-\mu (\lambda _1)-2s} \ge \varepsilon ^{p-1} (1+t)^{-\theta p-\frac{p\mu (\lambda _1)}{2}} |\xi |^{-p\mu (\lambda _1)} e^{-(p-1)\frac{|\xi |^2}{4}}. \end{aligned}$$

Choosing $\theta :=\frac{s}{p-1}-\frac{\mu (\lambda _1)}{2}$, we obtain

$$\begin{aligned} (\lambda _1-\lambda )|\xi |^{p\mu (\lambda _1)-\mu (\lambda _1)-2s} \ge \varepsilon ^{p-1} e^{-(p-1)\frac{|\xi |^2}{4}}. \end{aligned}$$

(54)

With this choice of $\theta$ and a direct computation, we can see that

$$\begin{aligned} -\theta -\mu (\lambda _1)+\frac{1}{2}(N+2-2s) >0 \end{aligned}$$

if and only if

$$\begin{aligned} p> 1+\frac{2s}{N+2-2s-\mu (\lambda _1)}. \end{aligned}$$

Hence, choosing $\lambda _1$ close enough to $\lambda$,

$$\begin{aligned} y^{1-2s}U_t(z,t)-\mathrm{{div}}(y^{1-2s}\nabla U)(z,t) \ge 0. \end{aligned}$$

Finally, up to choosing $\lambda _1$ closer to $\lambda$, we also have that

$$\begin{aligned} p< 1+\frac{2s}{\mu (\lambda _1)} \end{aligned}$$

and so (54) holds for any $\xi \in \mathbb {R}^{N}$ if $\varepsilon >0$ is small enough. In conclusion, we have proved that $U_{\varepsilon ,\lambda _1}$ is a classical solution of problem (53). Since $\Phi _{\lambda _1} \in H^1(B^+_1,y^{1-2s})$, the last claim is clear. $\square$

Theorem 6.7

Let $p \in \left( 1+\frac{2s}{N-\mu (\lambda )+2-2s}, 1+\frac{2s}{\mu (\lambda )}\right)$ and $\delta ,\varepsilon _0$ as in Proposition 6.6. Let f be a measurable non-negative, non-trivial function such that $f(x,t)=0$ a.e. in $\mathbb {R}^N \times (-\infty ,0)$. Assume that for some $\delta _1 \in (0,\delta )$

$$\begin{aligned} f(x,t) \le \delta _1 (1+t)^{\frac{\mu (\lambda _1)}{2}-\frac{s}{p-1}} |x|^{-\mu (\lambda _1)-2s} e^{-\frac{|x|^2}{4(1+t)}}. \end{aligned}$$

Then for some a small enough $\varepsilon \in (0,\varepsilon _0)$ and $\lambda _1 \in (\lambda ,\lambda +\delta )$ close enough to $\lambda$, the function

$$\begin{aligned}{} & {} w(x,t):=\frac{\Gamma (1-s)}{2^{2s-1}\Gamma (s)^2(4\pi )^{\frac{N}{2}}}\int _0^\infty \int _{\mathbb {R}^N} \frac{e^{-\frac{|z|^2}{4\tau }}}{\tau ^{\frac{N}{2}+1-s}} \, \,\\{} & {} \quad \Big [\varepsilon \lambda (1+t-\tau )^{\frac{s}{p-1}-\frac{\mu (\lambda _1)}{2}} |x-z|^{-\mu (\lambda _1)-2s} e^{-\frac{|x-z|^2}{4(t-\tau +1)}}\\{} & {} \quad +\varepsilon ^p(1+t-\tau )^{\frac{ps}{p-1}-\frac{p\mu (\lambda _1)}{2}} |x-z|^{-p\mu (\lambda _1)} e^{-p\frac{|x-z|^2}{4(t-\tau +1)}} +f(x-z,t-\tau )\Big ]\, dz \, d\tau , \end{aligned}$$

is a non-trivial, non-negative, very weak supersolution of problem (1) and $w\in L^1_{loc}(\mathbb {R}^{N+1})$.

Proof

We start by observing that for any $p \in \left( 1+\frac{2s}{N-\mu (\lambda )+2-2s}, 1+\frac{2s}{\mu (\lambda )}\right)$ and $\lambda _1 \in (\lambda ,\lambda +\delta )$ the function

$$\begin{aligned} \varphi (t,x)=(1+t)^{(p-1)\frac{\mu (\lambda _1)}{2}-s}|x|^{-p\mu (\lambda _1)+\mu (\lambda _1)+2s}e^{-(p-1)\frac{|x|^2}{4(t+1)}} \end{aligned}$$

is bounded on $\mathbb {R}^N \times (0,+\infty )$. It follows that, if f is as above, taking for example $\lambda _1:= \lambda +\frac{\delta _1}{2}$, there exists an $\varepsilon >0$ such that the function $U_{\varepsilon ,\lambda _1}$ is a classical supersolution of the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} y^{1-2s}(U_{\varepsilon , \lambda _1})_t-\mathrm{{div}}(y^{1-2s}\nabla U_{\varepsilon , \lambda _1})\ge 0, &{}\text { in } \mathbb {R}_+^{N+1}\setminus \{0\} \times (0,+\infty ),\\ -\lim \limits _{y \rightarrow 0^+}y^{1-2s}\frac{\partial U_{\varepsilon , \lambda _1}}{\partial y}\ge k_s(\frac{\lambda }{|x|^{2s}}u_{\varepsilon , \lambda _1}+u_{\varepsilon , \lambda _1}^p+f), &{}\text { on }(\mathbb {R}^N\setminus \{0\}) \times (0,+\infty ),\\ U_{\varepsilon , \lambda _1}(z,0)\ge 0, &{}\text { on }\mathbb {R}_+^{N+1}\setminus \{0\}. \end{array}\right. } \end{aligned}$$

Let us extend trivially the function $u_{\varepsilon , \lambda _1}$ to $\mathbb {R}^{N+1}$ and still denote, with a slight abuse of notation, the extended function with $u_{\varepsilon , \lambda _1}$. Then $\frac{\lambda }{|x|^{2s}}u_{\varepsilon , \lambda _1}+u_{\varepsilon , \lambda _1}^p+f \in L^1(\mathbb {R}^{N}\times (-\infty ,T))$ for any $T>0$ and $\frac{\lambda }{|x|^{2s}}u_{\varepsilon , \lambda _1}+u_{\varepsilon , \lambda _1}^p+f\equiv 0$ on $\mathbb {R}^N \times (-\infty ,0)$. It follows that, letting $k_s$ be as in Theorem 4.1,

$$\begin{aligned} w:=k_sJ_s\left( \frac{\lambda }{|x|^{2s}}u_{\varepsilon , \lambda _1}+u_{\varepsilon , \lambda _1}^p+f\right) \end{aligned}$$

is well-defined, $w \in L^1_{loc}(\mathbb {R}^{N+1})$ and $w \equiv 0$ on $\mathbb {R}^N \times (-\infty ,0)$ by (14). Let $\eta _n$ be as in Sect. 4.3 and let us define for any $n \in \mathbb {N}$

$$\begin{aligned} w_n:=k_sJ_s\left( \eta _n\left[ \frac{\lambda }{(|x|+\frac{1}{n})^{2s}}\frac{u_{\varepsilon , \lambda _1}}{1+\frac{1}{n}u_{\varepsilon , \lambda _1}} +\frac{u^p_{\varepsilon , \lambda _1}}{1+\frac{1}{n}u^p_{\varepsilon , \lambda _1}}+\frac{f}{1+\frac{1}{n}f}\right] \right) . \end{aligned}$$

Then $w_n \in \mathrm{{Dom}}(H^s)$ thanks to Lemmas 2.5 and 2.6. Hence, we may define its extension $W_n$ as in Theorem 4.1 and notice that $W_n$ weekly solves the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} y^{1-2s}(W_n)_t-\mathrm{{div}}(y^{1-2s}\nabla W_n)=0, &{}\quad \text {in } \mathbb {R}_+^{N+1} \times (0,+\infty ),\\ -\lim \limits _{y \rightarrow 0^+}y^{1-2s}\frac{\partial W_n}{\partial y}= \kappa _s \eta _n\left[ \frac{\lambda }{(|x|+\frac{1}{n})^{2s}}\frac{u_{\varepsilon , \lambda _1}}{1+\frac{1}{n}u_{\varepsilon , \lambda _1}} +\frac{u^p_{\varepsilon , \lambda _1}}{1+\frac{1}{n}u^p_{\varepsilon , \lambda _1}}+\frac{f}{1+\frac{1}{n}f}\right] , &{}\quad \text {on }\mathbb {R}^N\times \times (0,+\infty ),\\ W_n(z,0)=0 &{}\quad \text { on }\mathbb {R}^{N+1}_+. \end{array}\right. } \end{aligned}$$

By Corollary 4.3, it follows that $w_n \le w_{n+1}\le u_{\varepsilon ,\lambda _1}$ for any $n \in \mathbb {N}$. Then, by the Dominated Convergence Theorem,

$$\begin{aligned} w= & {} k_sJ_s\left( \frac{\lambda }{|x|^{2s}}u_{\varepsilon , \lambda _1}+u_{\varepsilon , \lambda _1}^p+f\right) \\= & {} \lim _{n\rightarrow \infty }k_sJ_s\left( \eta _n\left( \frac{\lambda }{(|x|+\frac{1}{n})^{2s}}\frac{u_{\varepsilon , \lambda _1}}{1+\frac{1}{n}u_{\varepsilon , \lambda _1}} +\frac{u^p_{\varepsilon , \lambda _1}}{1+\frac{1}{n}u^p_{\varepsilon , \lambda _1}}+\frac{f}{1+\frac{1}{n}f}\right) \right) \\= & {} \lim _{n\rightarrow \infty }w_n \le u_{\varepsilon ,\lambda _1}, \end{aligned}$$

a.e. in $\mathbb {R}^{N+1}$. We conclude that

$$\begin{aligned} w=k_sJ_s\left( \frac{\lambda }{|x|^{2s}}u_{\varepsilon , \lambda _1}+u_{\varepsilon , \lambda _1}^p+f\right) \ge J_s\left( \frac{\lambda }{|x|^{2s}}w+w^p+f\right) . \end{aligned}$$

Hence, w is a very weak supersolution of (1), that is, is a supersolution in the sense of Definition 2.3. $\square$

From Theorem 6.7 and Proposition 4.8, we can immediately deduce the existence of very weak solutions of problem (1) for small datum.

Corollary 6.8

Let $p \in \left( 1+\frac{2s}{N-\mu (\lambda )+2-2s}, 1+\frac{2s}{\mu (\lambda )}\right)$ and suppose that f satisfies the assumptions of Theorem 6.7. Then (1) has a non-negative, non-trivial very weak solution $w\in L^1_{loc}(\mathbb {R}^{N+1})$.

7 Open problems and subjects of further investigation

In this last section, we make a brief overview over remaining questions and further developments concerning existence and non-existence results for the operator $H^s-\frac{\lambda }{|x|^{2s}}$ and other fractional parabolic operators.

As already stated in Remark 3.5, it is an interesting open problem to obtain an inversion formula for the operator $H^s-\frac{\lambda }{|x|^{2s}}$. Furthermore in the case $p=p_+(\lambda ,s)$ it is still not known if there exists or not weak supersolution of (1). It is reasonable to think that a non-existence result may hold, coherently with the classical case $s=1$, but to obtain such a result seems to be technically demanding.

Further possible subject of investigation includes considering different nonlinearities in problem (1), for example of the form $|\nabla u|^p$ or $|(-\Delta )^{\frac{s}{2}}u|^p$, which, to the best of the authors knowledge, have yet to be studied with or without the presence of an Hardy-type potential. It may also be interesting to study similar questions for more general parabolic fractional operators, for example $(w_t- \Delta -\frac{\lambda }{|x|^2})^s$, under assumption of positivity of the elliptic part $- \Delta -\frac{\lambda }{|x|^2}$. Finally, the critical case $\lambda =\Lambda _{N_s}$ is yet to be studied for the operator $H^s-\frac{\lambda }{|x|^{2s}}$ and could be of interest.

All the subjects mentioned above are object of current investigation by the authors.