Semilinear damped wave equations on the Heisenberg group with initial data from Sobolev spaces of negative order

Abstract

In this paper, we focus on studying the Cauchy problem for semilinear damped wave equations involving the sub-Laplacian $\mathcal {L}$ on the Heisenberg group $\mathbb {H}^n$ with power type nonlinearity $|u|^p$ and initial data taken from Sobolev spaces of negative order homogeneous Sobolev space $\dot{H}^{-\gamma }_{\mathcal {L}}(\mathbb {H}^n), \gamma >0$, on $\mathbb {H}^n$. In particular, in the framework of Sobolev spaces of negative order, we prove that the critical exponent is the exponent $p_{\text {crit}}(Q, \gamma )=1+\frac{4}{Q+2\gamma },$ for $\gamma \in (0, \frac{Q}{2})$, where $Q:=2n+2$ is the homogeneous dimension of $\mathbb {H}^n$. More precisely, we establish

• A global-in-time existence of small data Sobolev solutions of lower regularity for $p>p_{\text {crit}}(Q, \gamma )$ in the energy evolution space;

• A finite time blow-up of weak solutions for $1<p<p_{\text {crit}}(Q, \gamma )$ under certain conditions on the initial data by using the test function method.

Furthermore, to precisely characterize the blow-up time, we derive sharp upper bound and lower bound estimates for the lifespan in the subcritical case.

1 Introduction and discussion on main results

1.1 Description of problem and background

In this study, our main aim is to determine a new critical exponent for the Cauchy problem for a semilinear damped wave equation with the power type nonlinearities as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{tt}-\mathcal {L}u +u_{t} =|u|^p, &{} g\in \mathbb {H}^n,~t>0,\\ u(0,g)=\varepsilon u_0(g), &{} g\in \mathbb {H}^n,\\ u_t(0, g)=\varepsilon u_1(g), &{} g\in \mathbb {H}^n, \end{array}\right. } \end{aligned}$$

(1.1)

where $\mathcal {L}$ is the sub-Laplacian on the Heisenberg group $\mathbb {H}^n$, $1<p<\infty$, and the initial data $(u_0, u_1)$ with its size parameter $\varepsilon >0$ belongs to subelliptic (or Folland–Stein) homogeneous Sobolev spaces of negative order $\left( u_0, u_1\right) \in {\dot{H}}_\mathcal {L}^{-\gamma }(\mathbb {H}^n) \times \dot{H}_\mathcal {L}^{-\gamma }(\mathbb {H}^n)$ with $\gamma >0$. In other words, we study the global-in-time existence of small data solutions and the blow-up in finite time of solutions to the Cauchy problem (1.1).

To discuss the classical Euclidean scenario, let us consider the semilinear damped wave equation on $\mathbb {R}^n$ with the power type nonlinearities as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{tt}-\Delta u+ u_t=|u|^p,&{} x \in \mathbb {R}^n, ~t>0, \\ u( 0,x)=u_0(x), &{} x \in \mathbb {R}^n,\\ u_t( 0,x)=u_1(x), &{} x \in \mathbb {R}^n, \end{array}\right. } \end{aligned}$$

(1.2)

where $1<p<\infty$ and $\Delta$ is the Laplacian on $\mathbb {R}^n$. When the initial data belongs additionally to $L^1$-space, the global existence or a blow-up result to (1.2), depending on the critical exponent has been studied in [21, 25, 38, 40] and references therein. The critical exponent signifies the threshold condition on the exponent p for the global-in-time Sobolev solutions and the blow-up of local-in-time weak solutions with small data. The critical exponent for solutions to (1.2) is the so-called Fujita exponent given by $p_{\text {Fuji}}(n):=1+\frac{2}{n}$ (see [21, 25, 38, 40]). More precisely,

• When $n=1, 2$, Matsumura in his seminal paper [25] proved the global-in-time existence of small data solutions for $p>p_{\text{ Fuji }}(n)$.

• For any $n \geqslant 1$, a global existence for $p>p_{\text{ Fuji }}(n)$ (by assuming compactly supported initial data) and blow-up of the local-in-time solutions in the subcritical case $1<p<p_{\text{ Fuji }}(n)$ was explored by Todorova and Yordanov [38].

• For $p=p_{\text{ Fuji }}(n),$ the blow-up result was obtained by Zhang [40].

Later, Ikehata and Tanizawa [21] removed the restriction of compactly supported data for the supercritical case $p>p_{\text{ Fuji }}(n)$. Moreover, the sharp lifespan estimates for the Cauchy problem (1.2) with additional $L^1$-data assumption are given by

$$\begin{aligned} T_\varepsilon \left\{ \begin{array}{ll} =\infty &{} \text{ if } p>p_{\textrm{Fuji}}(n), \\ \simeq \exp \left( C \varepsilon ^{-(p-1)}\right) &{} \text{ if } p=p_{\textrm{Fuji}}(n), \\ \simeq C \varepsilon ^{-\frac{2(p-1)}{2-n(p-1)}} &{} \text{ if } p<p_{\textrm{Fuji}}(n), \end{array}\right. \end{aligned}$$

where C is a positive constant independent of $\varepsilon$. We cite [17,18,19, 23, 24] for a detailed study on the sharp lifespan estimates for the Cauchy problem (1.2). We also refer to the excellent book [7] for the global-in-time small data solutions for the semilinear damped wave equations in the Euclidean framework.

In recent years, considerable attention has been devoted by numerous researchers to finding new critical exponents for the classical semilinear damped wave equations on $\mathbb {R}^n$ in different contexts. For instance, considering the Cauchy problem (1.2) with initial data additionally belonging to $L^m$-spaces with $m \in (1,2)$, the critical exponent is changed and the new modified Fujita exponent becomes

$$\begin{aligned} p_{\text{ Fuji }}(n):=p_{\text{ Fuji } }\left( \frac{n}{m}\right) =1+\frac{2 m}{n}. \end{aligned}$$

Unlike the $L^1$-data case, here with additional $L^m$-regular data, the global-in-time solution exists uniquely at the critical point $p_{\text{ Fuji }}\left( \frac{n}{m}\right) =1+\frac{2 m}{n}$. This is the main difference between $L^1$ and $L^m$ regular data. We refer to [16, 20, 27] and references therein for a detailed study related to the critical exponent $p_{\text{ Fuji }}\left( \frac{n}{m}\right)$ for the solutions to the semilinear wave equations with the $L^m$-regular data.

The study of the semilinear damped wave equation has also been extended in the non-Euclidean framework. Several papers have studied nonlinear PDEs in non-Euclidean settings in the last decades. For example, the semilinear wave equation with or without damping has been investigated for the Heisenberg group in [12, 26, 34]. In the case of graded groups, we refer to the recent works [13, 33, 34, 36]. We refer to [3, 6, 10, 28, 30, 31] concerning the wave equation on compact Lie groups and [1, 2, 22, 39] on a Riemannian symmetric space of noncompact type. In particular, for the semilinear damped wave equation on the Heisenberg group $\mathbb {H}^n$, namely

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{tt}-\mathcal {L}u +u_t =|u|^p, &{} g\in \mathbb {H}^n,~t>0,\\ u(0,g)=u_0(g), &{} g\in \mathbb {H}^n,\\ u_t(0,g)=u_1(g), &{} g\in \mathbb {H}^n, \end{array}\right. } \end{aligned}$$

(1.3)

where $p>1$, $\mathcal {L}$ is the sub-Laplacian on the Heisenberg group $\mathbb {H}^n$, it was shown in [12] that the critical exponent is given by

$$\begin{aligned} p_{\text {Fuji}}(Q):=1+\frac{2}{Q}, \end{aligned}$$

(1.4)

where $Q:=2n+2$ represents the homogeneous dimension of $\mathbb {H}^n$. It is interesting to note that (1.4) is also the Fujita exponent for the semilinear heat equation

$$\begin{aligned} {\left\{ \begin{array}{ll} u_t-\mathcal {L}u =|u|^p, &{} g\in \mathbb {H}^n,~t>0,\\ u(0,g)=u_0(g), &{} g\in \mathbb {H}^n,\\ \end{array}\right. } \end{aligned}$$

on $\mathbb {H}^n,$ where $p>1$. This topic has been discussed in [12, 13, 35]. However, in the case of a compact Lie group $\mathbb {G}$, it has been shown in [28] that $p_{\text{ Fuji }}(0):=\infty$ is the critical exponent for the solution to the semilinear damped wave equation on $\mathbb {G}$. We cite [34] for a global existence result with small data in the more general setting of graded Lie groups for the semilinear damped wave equation involving a Rockland operator with an additional mass term.

Recently, Chen and Reissig [5] considered the following semilinear damped wave equation

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{tt}-\Delta u+ u_t= |u|^p,&{} x \in \mathbb {R}^n, ~t>0, \\ u( 0, x)=u_0(x), &{} x \in \mathbb {R}^n,\\ u_t( 0,x)=u_1(x), &{} x \in \mathbb {R}^n, \end{array}\right. } \end{aligned}$$

(1.5)

on $\mathbb {R}^n,$ where $p>1$ and the initial data additionally belonging to homogeneous Sobolev spaces of negative order $\dot{H}^{-\gamma }(\mathbb {R}^n)$ with $\gamma >0$. They obtained a new critical exponent $p = p_{\text {crit}}(n, \gamma ):= 1+ \frac{4}{n+2\gamma }$ for some $\gamma \in (0, \frac{n}{2})$ in this framework. More specifically, the authors proved that:

• For $p>p_{\text {crit}}(n, \gamma )$, the problem (1.5) admits a global-in-time Sobolev solution for sufficiently small data of lower regularity.

• For $1<p<p_{\text {crit}}(n, \gamma )$, the solutions to (1.5) blow-up in a finite time. In other words, there exists $T>0$ such that the solution to (1.5) satisfies $\left\| u\left( \cdot , t_m\right) \right\| _{\infty } \rightarrow \infty$ as $t_m \rightarrow T$.

Further, the authors also investigated sharp lifespan estimates for weak solutions to (1.5), in which the sharpness of lifespan estimates is given by

$$\begin{aligned} T_\varepsilon \left\{ \begin{array}{ll} =\infty &{} \text{ if } p>p_{\text{ crit } }(n, \gamma ), \\ \simeq C \varepsilon ^{-\frac{2}{2 p^{\prime }-2-\frac{n}{2}-\gamma }} &{} \text{ if } p<p_{\text{ crit } }(n, \gamma ), \end{array}\right. \end{aligned}$$

where C is a positive constant independent of $\varepsilon$ and $p^{\prime }$ is the Lebesgue exponent conjugate of p such that $\frac{1}{p}+\frac{1}{p^{\prime }}=1$. We remark that some other technical assumptions on p and $\gamma$ are also required to find the sharp lifespan estimate in the subcritical case.

To the best of our knowledge, in the non-Euclidean framework, the subelliptic damped wave equation on the Heisenberg group with initial data localized in Sobolev spaces of negative order has not been considered in the literature so far, even for the linear Cauchy problem. Therefore, an interesting and viable problem is to study several qualitative properties such as global-in-time well-posedness, blow-up criterion, decay rate, asymptotic profiles to solutions for the subelliptic damped wave equations on the Heisenberg group $\mathbb {H}^n$ with initial data additionally belonging to subelliptic Sobolev space ${\dot{H}}_\mathcal {L}^{-\gamma }(\mathbb {H}^n)$ with $\gamma >0$.

The main aim of this paper is to investigate and determine a critical exponent for the Cauchy problem for semilinear damped wave equation (1.1) with the initial data additionally belonging to subelliptic homogeneous Sobolev spaces $\dot{H}_\mathcal {L}^{-\gamma }(\mathbb {H}^n)$ of negative order $-\gamma$. More specifically,

• Under additional assumptions for the initial data in ${\dot{H}}_\mathcal {L}^{-\gamma }(\mathbb {H}^n)$, we obtain a new critical exponent to (1.1) given by

  $$\begin{aligned} p_{\text{ crit } }(Q, \gamma ):=1+\frac{4}{Q+2 \gamma }, \end{aligned}$$

  (1.6)

  with $\gamma \in { \left( 0, \frac{\sqrt{Q^2+16 Q}-Q}{4}\right) . }$

• We derive sharp lifespan estimates for weak solutions to the semilinear Cauchy problem (1.1). Define the lifespan $T_\varepsilon$ as the maximal existence time for solution of (1.1), i.e.,

  $$\begin{aligned} T_\varepsilon \,:\,=\,\Big \{ T>0~&:~ \text {there exists a unique local-in-time solution to the Cauchy} \nonumber \\&\text { problem}\, (1.1) \,\text {on}\, [0, T)\, \text {with a fixed parameter}~\varepsilon >0\Big \}. \end{aligned}$$

  (1.7)

  If the initial data is from $\dot{H}_\mathcal {L}^{-\gamma }(\mathbb {H}^n)$ with $\gamma \in \left( 0, {\tilde{\gamma }}\right)$ and the exponent p satisfies $1+\frac{2 \gamma }{Q} \leqslant p \leqslant \frac{Q}{Q-2}$, then the new sharp lifespan estimates are given by

  $$\begin{aligned} T_\varepsilon \left\{ \begin{array}{ll} =\infty &{} \text{ if } p>p_{\text{ crit } }(Q, \gamma ), \\ \simeq C \varepsilon ^{-\left( \frac{1}{p-1}-\left( \frac{Q}{4}+\frac{\gamma }{2}\right) \right) ^{-1}} &{} \text{ if } p<p_{\text{ crit } }(Q, \gamma ), \end{array}\right. \end{aligned}$$

  where the positive constant C is independent of $\varepsilon .$

1.2 Main results: comprehensive review

Throughout the paper, we denote $L^{q}(\mathbb {H}^n), 1 \leqslant q<\infty$, the space of q-integrable functions on $\mathbb {H}^n$ with respect to the Haar measure dg on $\mathbb {H}^n,$ which is nothing but the Lebesgue measure of $\mathbb {R}^{2n+1},$ and the space of all essentially bounded functions on $\mathbb {H}^n$ for $q=\infty$. The fractional subelliptic (Folland–Stein) Sobolev space $H_{\mathcal {L}}^s(\mathbb {H}^n), s \in \mathbb {R}$, associated to the sub-Laplacian $\mathcal {L}$ on $\mathbb {H}^n$, is defined as

$$\begin{aligned} H_{\mathcal {L}}^s\left( \mathbb {H}^n\right) :=\left\{ f \in \mathcal {D}^{\prime }\left( \mathbb {H}^n\right) :(I-\mathcal {L})^{s / 2} f \in L^2\left( \mathbb {H}^n\right) \right\} , \end{aligned}$$

equipped with the norm

$$\begin{aligned} \Vert f\Vert _{H_{\mathcal {L}}^s\left( \mathbb {H}^n\right) }:=\left\| (I-\mathcal {L})^{s / 2} f\right\| _{L^2\left( \mathbb {H}^n\right) }. \end{aligned}$$

Similarly, we denote by ${\dot{H}}_{\mathcal {L}}^{ s}(\mathbb {H}^n),$ the homogeneous Sobolev defined as the space of all $f\in \mathcal {D}^{\prime }(\mathbb {H}^n)$ such that $(-\mathcal {L})^{{s}/{2}}f\in L^2(\mathbb {H}^n)$. At times, we also write $H_{\mathcal {L}}^s$ and ${\dot{H}}_{\mathcal {L}}^s$ for $H_{\mathcal {L}}^s\left( \mathbb {H}^n\right)$ and ${\dot{H}}_{\mathcal {L}}^s\left( \mathbb {H}^n\right) ,$ respectively from here on.

For $(u_0, u_1)\in { \mathcal {A}_{\mathcal {L}}^{s, -\gamma }}:= (H^s_{\mathcal {L}} \cap {\dot{H}}^{-\gamma }_\mathcal {L} ) \times (L^2 \cap {\dot{H}}^{-\gamma }_\mathcal {L} )$, we denote $\left\| \left( u_0, u_1\right) \right\| _{{ \mathcal {A}_{\mathcal {L}}^{s, -\gamma }}}$ as

$$\begin{aligned} \left\| \left( u_0, u_1\right) \right\| _{{ \mathcal {A}_{\mathcal {L}}^{s, -\gamma }}}:=\Vert u_0\Vert _{H^s_{\mathcal {L}} \cap {\dot{H}}^{-\gamma }_\mathcal {L}}+\Vert u_1\Vert _{ L^2 \cap \dot{H}^{-\gamma }_\mathcal {L} }. \end{aligned}$$

Utilizing techniques derived from the noncommutative Fourier analysis on the Heisenberg group $\mathbb {H}^n$, we present our initial finding regarding time decay estimates in the ${\dot{H}}_\mathcal {L}^s$-norm of solutions to the homogeneous version of the Cauchy problem (1.1). This result is detailed below.

Theorem 1.1

Let $\mathbb {H}^n$ be the Heisenberg group with the homogeneous dimension Q. Let $\left( u_0, u_1\right) \in \left( H_\mathcal {L}^s \cap \dot{H}_\mathcal {L}^{-\gamma }\right) \times \left( H_\mathcal {L}^{s-1} \cap {\dot{H}}_\mathcal {L}^{-\gamma }\right)$ with $s \geqslant 0$ and $\gamma \in \mathbb {R}$ such that $s+\gamma \geqslant 0$. Consider the following linear Cauchy problem

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{tt}-\mathcal {L}u+u_t =0, &{} g\in \mathbb {H}^n,t>0,\\ u(0,g)= u_0(g), &{} g\in \mathbb {H}^n,\\ u_t(0,g)= u_1(g), &{} g\in \mathbb {H}^n. \end{array}\right. } \end{aligned}$$

(1.8)

Then, the solution u satisfies the following ${\dot{H}}_\mathcal {L}^s$-decay estimate

$$\begin{aligned} \Vert u(t, \cdot )\Vert _{ {\dot{H}}_\mathcal {L}^s} \lesssim (1+t)^{-\frac{s+\gamma }{2}}\left( \left\| u_0\right\| _{H^s_\mathcal {L} \cap {\dot{H}}^{-\gamma }_\mathcal {L}}+\left\| u_1\right\| _{H_\mathcal {L}^{s-1} \cap {\dot{H}}_\mathcal {L}^{-\gamma }}\right) , \end{aligned}$$

(1.9)

for any $t\geqslant 0$.

The next result is about the global-in-time well-posedness of the Cauchy problem (1.1) in the energy evolution space ${\mathcal {C}}\left( [0,T], H^s_{\mathcal {L}}\right) , s\in (0, 1]$. In this case, a version of a Gagliardo–Nirenberg type inequality on $\mathbb {H}^n$ (see Sect. 2) will play a crucial role in estimating the power type nonlinearity in $L^2(\mathbb {H}^n)$. Let us first make clear what do we mean by a solution of (1.1). For the global existence result, we will work with the mild solutions of (1.1).

We say that a function u is a mild solution to (1.1) on [0, T] if u is a fixed point for the integral operator $N: u \in X_s(T) \mapsto N u(t, g),$ given by

$$\begin{aligned} N u(t, g):=u^{\text {lin}}(t, g) + u^{\text {non}}(t, g), \end{aligned}$$

(1.10)

in the energy evolution space $X_s(T) \doteq \mathcal {C}\left( [0, T], H_{\mathcal {L}}^{s}(\mathbb {H}^n)\right) , s\in (0, 1]$, equipped with the norm

$$\begin{aligned} \Vert u\Vert _{X_s(T)}&:=\sup \limits _{t\in [0,T]}\left( (1+t)^{\frac{\gamma }{2}} \Vert u(t,\cdot )\Vert _{L^2}+(1+t)^{\frac{s+\gamma }{2}}\Vert u(t,\cdot )\Vert _{ \dot{H}^s_{\mathcal {L}}}\right) , \end{aligned}$$

with $\gamma >0,$ where

$$\begin{aligned} u^{\text {lin}}(t, g)= u_{0}(g) *_{(g)} E_{0}(t, g)+ u_{1}(g) *_{(g)} E_{1}(t, g) \end{aligned}$$

is the solution to the corresponding linear Cauchy problem (1.8) and

$$\begin{aligned} u^{\text {non}}(t, g)= \int _{0}^{t}|u(s, g)|^{p} *_{(g)} E_{1}(t-s, g) \;ds. \end{aligned}$$

Here, $*_{(g)}$ is the group convolution product on $\mathbb {H}^n$ with respect to the g variable and $E_{0}(t, g)$ and $E_{1}(t, g)$ represent the fundamental solutions to the homogeneous problem (1.8) with initial data $\left( u_{0}, u_{1}\right) =\left( \delta _{0}, 0\right)$ and $\left( u_{0}, u_{1}\right) =$ $\left( 0, \delta _{0}\right)$, respectively.

We prove the global-in-time existence and uniqueness of small data Sobolev solutions to the semilinear damped wave equation (1.1) of low regularity by finding a unique fixed point to the operator N, i.e., $Nu\in X_s(T)$ for all $T>0$. It means that there exists a unique global solution u to the equation $N u=u\in X_s(T)$ which also gives the solution to (1.1). In order to prove that N has a uniquely determined fixed point, we use Banach’s fixed point argument on the space $X_s(T)$ defined above.

Keeping $p_{\text{ crit } }(Q, \gamma ) =1+\frac{4}{Q+2\gamma }$ in mind, we state the following global-in-time existence result.

Theorem 1.2

Let $s \in (0,1]$ and $\gamma \in \left( 0, \frac{Q}{2}\right)$. Assume that the exponent p satisfies $1<p \leqslant \frac{Q}{Q-2 s}$ and

$$\begin{aligned} p\left\{ \begin{array}{ll}>p_{\text{ crit } }(Q, \gamma ) &{} \text{ if } \gamma \leqslant {\tilde{\gamma }}, \\ \geqslant 1+\frac{2 \gamma }{Q} &{} \text{ if } \gamma >{\tilde{\gamma }}, \end{array}\right. \end{aligned}$$

(1.11)

where ${\tilde{\gamma }}$ denotes the positive root of the quadratic equation $2 {\tilde{\gamma }}^2+Q {\tilde{\gamma }}-2 Q=0$. Then, there exists a small positive constant $\varepsilon _0$ such that for any $\left( u_0, u_1\right) \in \mathcal {A}_{\mathcal {L}}^{s,-\gamma }$ satisfying $\left\| \left( u_0, u_1\right) \right\| _{\mathcal {A}_{\mathcal {L}}^{s,-\gamma }}=\varepsilon \in \left( 0, \varepsilon _0\right]$, the Cauchy problem for the semilinear damped wave equation (1.1) has a uniquely determined Sobolev solution

$$\begin{aligned} u \in \mathcal {C}\left( [0, \infty ), H_{\mathcal {L}}^s\right) . \end{aligned}$$

Therefore, the lifespan of the solution is given by $T_\varepsilon =\infty$. Moreover, the solution satisfies the following two estimates listed below:

$$\begin{aligned} \Vert u(t, \cdot )\Vert _{L^2} \lesssim (1+t)^{-\frac{\gamma }{2}}\left\| \left( u_0, u_1\right) \right\| _{{ \mathcal {A}_{\mathcal {L}}^{s, -\gamma }}}, \end{aligned}$$

and

$$\begin{aligned} \Vert u(t, \cdot )\Vert _{\dot{H}^s_{\mathcal {L}}} \lesssim (1+t)^{-\frac{s+\gamma }{2}}\left\| \left( u_0, u_1\right) \right\| _{{ \mathcal {A}_{\mathcal {L}}^{s, -\gamma }}}. \end{aligned}$$

It is crucial to emphasize that there is no loss in the decay of the solution when transitioning from the linear to the nonlinear problem. In other words, the decay rates outlined in the preceding theorem align precisely with the decay rates established for the corresponding linearized damped wave equation, as presented in Theorem 1.1. However, the restriction $1< p\leqslant \frac{Q}{Q-2\,s}$ in the above theorem is necessary in order to apply a Gagliardo–Nirenberg type inequality on $\mathbb {H}^n$.

Remark 1.3

Some examples for the admissible range of exponents p for the global-in-time existence result in the low dimensions Heisenberg group $\mathbb {H}^n$ with $n=1$ and 2, that is, $Q=4$ and 6, respectively, are as follows:

• When $Q=4$, we take $s \in (0,1]$ and $\gamma \in (0, 2 )$ and the exponent satisfies

  $$\begin{aligned} \begin{array}{l} 1+\frac{2}{2+ \gamma }<p \leqslant \frac{2}{2- s} ~\quad \text{ if } ~0<\gamma \leqslant {\tilde{\gamma }}={ \sqrt{5}-1}, \\ 1+\frac{ \gamma }{2} \leqslant p \leqslant \frac{2}{2- s} ~\quad \quad \text{ if } ~ { \sqrt{5}-1}<\gamma <2. \end{array} \end{aligned}$$

• When $Q=6$, we take $s \in (0,1]$ and $\gamma \in (0, 3)$ and the exponent satisfies

  $$\begin{aligned} \begin{array}{l} 1+\frac{2}{3+ \gamma }<p \leqslant \frac{3}{3- s} ~\quad \text{ if } ~0<\gamma \leqslant {\tilde{\gamma }}={ \frac{\sqrt{33}-3}{2}}, \\ 1+\frac{ \gamma }{3} \leqslant p \leqslant \frac{3}{3- s} ~\quad \quad \text{ if } ~ { \frac{\sqrt{33}-3}{2}}<\gamma <3. \end{array} \end{aligned}$$

Note that the positive root ${\tilde{\gamma }}$ of $2 {\tilde{\gamma }}^2+Q {\tilde{\gamma }}-2 Q=0$ is always strictly less than 2 for any homogeneous dimension Q.

Based on the aforementioned illustrations, it is clear that the global existence result, as stated in Theorem 1.2, is only pertinent to specific lower homogeneous dimensions. This constraint is due to the technical stipulation that $1 < p \leqslant \frac{Q}{Q-2\,s}$. For global existence results in higher homogeneous dimensions, one can study Sobolev solutions by considering initial data from subelliptic Sobolev spaces with an appropriate degree of higher/large regularity.

Our next result is about a blow-up (in-time) result in the subcritical case to the Cauchy problem (1.1) for certain values of p, regardless of the size of the initial data. Before the blow-up result, we first introduce a suitable notion of a weak solution to the Cauchy problem (1.1).

Definition 1.4

For any $T>0$, a weak solution of the Cauchy problem (1.1) in $[0, T) \times \mathbb {H}^n$ is a function $u \in L_{\text{ loc } }^p\left( [0, T) \times \mathbb {H}^n\right)$ that satisfies the following integral relation:

$$\begin{aligned}&\int _0^T \int _{\mathbb {H}^n} u(t, g)\left( \partial _t^2 \phi (t, g)-\mathcal {L} \phi (t, g)-\partial _t \phi (t, g)\right) \;\hbox {d}g \;\hbox {d}t -\varepsilon \int _{\mathbb {H}^n} u_0(g) \phi (0, g) \;\hbox {d}g \nonumber \\&\qquad -\varepsilon \int _{\mathbb {H}^n} u_1(g) \phi (0, g) \;\hbox {d}g +\varepsilon \int _{\mathbb {H}^n} u_0(g) \partial _t \phi (0, g) \;\hbox {d}g \nonumber \\&\quad = \int _0^T \int _{\mathbb {H}^n}|u(t, g)|^p \phi (t, g) \;\hbox {d}g \;\hbox {d}t, \end{aligned}$$

(1.12)

for any $\phi \in \mathcal {C}_{0}^{\infty }([0, T) \times \mathbb {H}^n)$. If $T=\infty$, we call u to be a global-in-time weak solution to (1.1), otherwise u is said to be a local-in-time weak solution to (1.1).

Let $|\cdot |$ be any homogeneous norm on the Heisenberg group $\mathbb {H}^n$, while we denote $\left( 1+|g|^2\right) ^{\frac{1}{2}}$ by the Japanese bracket $\langle g\rangle$ for $g \in \mathbb {H}^n$. Then, under some additional assumptions on the initial data, we have the following blow-up result.

Theorem 1.5

Let $\gamma \in \left( 0, \frac{Q}{2}\right)$ and let the exponent p satisfy $1<p<p_{\text{ crit } }(Q, \gamma )$. We also assume that the nonnegative initial data $\left( u_0, u_1\right) \in {\dot{H}}_\mathcal {L}^{-\gamma } \times {\dot{H}}_\mathcal {L}^{-\gamma }$ satisfies

$$\begin{aligned} u_0(g)+u_1(g)&\geqslant C_0 \langle g \rangle ^{-Q\left( \frac{1}{2}+\frac{\gamma }{Q}\right) }(\log (e+|g|))^{-1}, \quad g\in \mathbb {H}^n, \end{aligned}$$

(1.13)

where $C_0>0$ is a fixed constant. Then, there is no global (in time) weak solution to the Cauchy problem (1.1).

Moreover, the lifespan $T_{w,\varepsilon }$ of local (in time) weak solutions to the Cauchy problem (1.1) satisfies the following upper bound estimate

$$\begin{aligned} {T_{w, \varepsilon } \leqslant C \varepsilon ^{-\left( \frac{1}{p-1}-\left( \frac{Q}{4}+\frac{\gamma }{2}\right) \right) ^{-1}},} \end{aligned}$$

where C is a positive constant independent of $\varepsilon$.

From Theorems 1.2 and 1.5, we can conclude that the critical exponent for the semilinear damped wave equation (1.1) is $p_{\text{ crit } }(Q, \gamma ):=1+\frac{4}{Q+2 \gamma }$ (see (1.6)) when initial data are additionally taken from the negative order Sobolev space ${\dot{H}}_\mathcal {L}^{-\gamma }, \gamma >0$. It gives us a new way to look at the critical exponent for the semilinear damped wave equation in Sobolev space with a negative order. Indeed, we can interpret the exponent $p_{\text{ crit } }(Q, \gamma )$ as a modification of the exponent $p_{\text{ Fujita } }\left( \frac{Q}{2}\right) =1+\frac{4}{Q}$ (which would correspond to the critical exponent with only $L^2$ regularity for the Cauchy data) by working with even weaker regularity ($H_{\mathcal {L}}^{-\gamma }$ regularity), the critical exponent becomes even smaller $p_{\text{ crit } }(Q, \gamma )=1+\frac{4}{Q+2 \gamma }$. Since, we are working with less regularity for the data, the decay rates in the estimates for the solutions of the homogeneous problem improve and the Banach fixed point theorem holds for a larger range of p.

The behavior of the Cauchy problem at the critical case $p=p_{\text{ crit } }(Q, \gamma )$ remains uncertain, as it is unclear whether a global (in time) small data Sobolev solutions exist or the weak solutions will blow-up.

In the next remark, particularly, we consider $s=1$ for Theorem 1.2 and 1.5 to give a rough idea about the critical exponent.

Remark 1.6

Due to the applications of Gagliardo–Nirenberg inequality, we have the technical restriction on the exponent $1<p \leqslant \frac{Q}{Q-2}$. Consequently, the ranges of exponent p for global-in-time existence and blow-up are as follows.

• When $Q=4,6$

  • blow-up of weak solutions if $1<p<p_{\text{ crit } }(Q, \gamma )$,

  • and global-in-time existence of Sobolev solutions if

    $$\begin{aligned} p_{\text{ crit } }(Q, \gamma )<p \leqslant \frac{Q}{Q-2}, \qquad \text {for}~0<\gamma \leqslant {\tilde{\gamma }}, \end{aligned}$$

    as well as

    $$\begin{aligned} 1+\frac{2 \gamma }{Q} \leqslant p \leqslant \frac{Q}{Q-2}, \qquad \text {for}~{\tilde{\gamma }}<\gamma <\frac{Q}{2}. \end{aligned}$$

• When $Q\geqslant 8$, from Theorem 1.2, the set of admissible exponents p is completely empty.

Fig. 1

Description of the critical exponent in the $(\gamma , p)$ plane

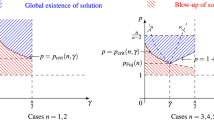
For a detailed analysis of the critical exponent which depends on the parameter $\gamma$ and Q, we can describe it by the $(\gamma , p)$ plane in Fig. 1. In Fig. 1, with an increase of the homogeneous dimension Q of $\mathbb {H}^n$, the curve $p=p_{\text{ crit } }(Q, \gamma )$ and the segment $p=1+\frac{2 \gamma }{Q}$ will move following the direction of $\nearrow$ and $\nwarrow$ lines arrows, respectively.

The formulations of Theorems 1.2 and 1.5 for $s=1$ also give the critical index for regularity of initial data that belongs additionally to ${\dot{H}}_\mathcal {L}^{-\gamma }$ with $0<\gamma <{\tilde{\gamma }}$. Specifically, for $1+\frac{2}{Q}<p<1+\frac{4}{Q}$, the critical index is given by $\gamma _{\text{ crit } }(p, Q):=\frac{2}{p-1}-\frac{Q}{2}$. Regarding the initial data that also additionally belongs to ${\dot{H}}_\mathcal {L}^{-\gamma }$ with $\gamma >0$,

• then local (in-time) weak solutions in general blow-up in finite time for $0<\gamma <\gamma _{\text{ crit } }(p, Q)$;

• then the global (in-time) small data Sobolev solutions exists uniquely for $\gamma _{\text{ crit } }(p, Q)<\gamma <\min \{{\tilde{\gamma }}, \frac{Q}{2} \}$.

From Theorem 1.5, for $1< p < p_{\text{ crit } }(Q, \gamma )$, we know that the non-trivial local (in time) weak solution blow-up in finite time and we have the following upper bound estimates for the lifespan

$$\begin{aligned} T_\varepsilon \leqslant T_{w,\varepsilon } \leqslant C \varepsilon ^{-\left( \frac{1}{p-1}-\left( \frac{Q}{4}+\frac{\gamma }{2}\right) \right) ^{-1}}. \end{aligned}$$

Now, it is important to investigate the lower bound estimates for the lifespan.

To thoroughly examine the lifespan, it is essential to consider the precise definition of mild solutions to the Cauchy problem (1.1) on [0, T) with $T > 0$ for $u \in C([0,T),H_\mathcal {L}^1)$. Let $T_{m,\varepsilon }$ be the lifespan of a mild solution u. Then, we have the following result regarding the lower bound for the lifespan.

Theorem 1.7

Let $\gamma \in (0, {\tilde{\gamma }} )$ and let the exponent p satisfy $1<p<p_{\text{ crit } }(Q, \gamma )$ such that

$$\begin{aligned} 1+\frac{2 \gamma }{Q} \leqslant p \leqslant \frac{Q}{Q-2 }. \end{aligned}$$

(1.14)

We also assume that $\left( u_0, u_1\right) \in \mathcal {A}_1^{\mathcal {L}}$. Then, there exists a constant $\varepsilon _0$ such that for every $\varepsilon \in \left( 0, \varepsilon _0 \right]$, the lifespan $T_{m, \varepsilon }$ of mild solutions u to the Cauchy problem (1.1) satisfies the following lower bound condition:

$$\begin{aligned} T_{m,\varepsilon } \geqslant D \varepsilon ^{-\left( \frac{1}{p-1}-\left( \frac{Q}{4}+\frac{\gamma }{2}\right) \right) ^{-1}}, \end{aligned}$$

where D is a positive constant independent of $\varepsilon$, but may depends on $p, Q, \gamma$ as well as $\left\| \left( u_0, u_1\right) \right\| _{\mathcal {A}_1^{\mathcal {L}}}$.

Since u in Theorem 1.2 is a mild solution to (1.1), this mild solution is also a weak solution to (1.1) (according to a density argument) with timespan $T_{m,\varepsilon }\leqslant T_\varepsilon$. Once more drawing on Theorems 1.5 and 1.7, for $1<p<p_{\text{ crit } }(Q, \gamma )$, we claim a sharp estimate for the lifespan $T_\varepsilon$ as stated below

$$\begin{aligned} T_\varepsilon \simeq C \varepsilon ^{-\left( \frac{1}{p-1}-\left( \frac{Q}{4}+\frac{\gamma }{2}\right) \right) ^{-1}}, \end{aligned}$$

for $\gamma \in (0, \min \{2, \frac{Q}{2} \} )$. Moreover, the lifespan estimate mentioned above agrees with the one for additional $L^1$-regular data when particularly we consider $\gamma =\frac{Q}{2}$.

Remark 1.8

One interesting observation is to discuss the acceptable ranges for p so that we can get sharp lifespan estimates. This can be summed up as follows:

• when $Q=4$, for $1+\frac{2 \gamma }{Q} \leqslant p<p_{\text{ crit } }(Q, \gamma )$ and $0<\gamma \leqslant \frac{-Q+\sqrt{Q^2+16 Q}}{4}$, we can achieve sharp lifespan estimates;

• When $Q=6$, for $1+\frac{2 \gamma }{Q} \leqslant p<p_{\text{ crit } }(Q, \gamma )$ with $p \leqslant \frac{Q}{Q-2}$ and $0<\gamma \leqslant \frac{-Q+\sqrt{Q^2+16 Q}}{4}$, sharp lifespan estimates can be achieved;

• when $Q \geqslant 8$, for $1+\frac{2 \gamma }{Q} \leqslant p \leqslant \frac{Q}{Q-2}$ and $0<\gamma \leqslant \frac{Q}{Q-2}$, we can achieve sharp lifespan estimates.

We conclude the introduction with a brief outline of the organization of the paper. In Sect. 1, we discuss the main results and their explanations related to the critical exponent $p_{\text {crit}}(Q, \gamma )$ and sharp lifespan estimates for weak solutions to Cauchy problem (1.1) when initial data taken additionally from $\dot{H}_\mathcal {L}^{-\gamma }$. Section 2 is devoted to recalling some basics of the Fourier analysis on the Heisenberg group $\mathbb {H}^n$ to make the paper self-contained. Using the Fourier analysis on the Heisenberg group $\mathbb {H}^n$, we derive $\dot{H}^s_{\mathcal {L}}(\mathbb {H}^n)$-decay estimates for the solution to the linear damped wave equation (1.1) with vanishing right-hand side in Sect. 3. Using the $\dot{H}^s_{\mathcal {L}}(\mathbb {H}^n)$-decay estimates for the solution to a linear damped wave equation, we demonstrate global-in-time well-posedness for the semilinear Cauchy problem (1.1) if $p>p_{\text{ crit } }(Q, \gamma )$ with the help of Banach’s fixed point argument in Sect. 4. In order to estimate the nonlinear term in ${\dot{H}}_\mathcal {L}^{-\gamma }(\mathbb {H}^n)$, we use Sobolev inequality and the Gagliardo–Nirenberg inequality on the Heisenberg group $\mathbb {H}^n$. In Sect. 5, by employing the test function method, we conclude the optimality by showing the blow-up of weak solutions even for small data for the range $1<p<p_{\text{ crit } }(Q, \gamma )$. As a byproduct, we also obtain upper bound estimates for the lifespan. We conclude our paper by deriving the sharp lower bound estimates for the lifespan of mild solutions in Sect. 6 by using the method of contradiction.

2 Preliminaries: analysis on the Heisenberg group $\mathbb {H}^n$

In this section, we recall some basics of the Fourier analysis on the Heisenberg groups $\mathbb {H}^n$ to make the manuscript self-contained. A complete account of the representation theory on $\mathbb {H}^n$ can be found in [8, 12, 13, 32, 34, 37]. However, we mainly adopt the notation and terminology given in [8] for convenience. We commence this section by establishing the notations that will be employed consistently throughout the paper.

2.1 Notations

Throughout the article, we use the following notations:

• $f \lesssim g:$   There exists a positive constant C (whose value may change from line to line in this manuscript) such that $f \leqslant C g.$

• $f \simeq g$: Means that $f \lesssim g$ and $g \lesssim f$.

• $\mathbb {H}^n:$ The Heisenberg group.

• Q: The homogeneous dimension of $\mathbb {H}^n$.

• dg: The Haar measure on the Heisenberg group $\mathbb {H}^n.$

• $\mathcal {L}:$ The sub-Laplacian on $\mathbb {H}^n.$

• ${H}_\mathcal {L}^{-\gamma }$: The subelliptic Sobolev spaces of negative order with $\gamma >0$ on $\mathbb {H}^n$.

2.2 The Hermite operator

In this subsection, we recall some definitions and properties of Hermite functions which we will use frequently in order to study Schrödinger representations and sub-Laplacian on the Heisenberg group $\mathbb {H}^n$. We start with the definition of Hermite polynomials on $\mathbb {R}.$

Let $H_k$ denote the Hermite polynomial on $\mathbb {R}$, defined by

$$\begin{aligned} H_k(x)=(-1)^k \frac{\hbox {d}^k}{\hbox {d}x^k}(e^{-x^2} )e^{x^2}, \quad k=0, 1, 2, \ldots , \end{aligned}$$

and $h_k$ denote the normalized Hermite functions on $\mathbb {R}$ defined by

$$\begin{aligned} h_k(x)=(2^k\sqrt{\pi } k!)^{-\frac{1}{2}} H_k(x)e^{-\frac{1}{2}x^2}, \quad k=0, 1, 2, \ldots , \end{aligned}$$

The Hermite functions $\{h_k \}$ are the eigenfunctions of the Hermite operator (or the one-dimensional harmonic oscillator) $H=-\frac{\hbox {d}^2}{\hbox {d}x^2}+x^2$ with eigenvalues $2k+1, k=0, 1, 2, \cdots$. These functions form an orthonormal basis for $L^2(\mathbb {R})$. The higher-dimensional Hermite functions denoted by $e_{k}$ are then obtained by taking tensor products of one-dimensional Hermite functions. Thus for any multi-index $k=(k_1, \ldots , k_n) \in \mathbb {N}_0^n$ and $x =(x_1, \ldots , x_n)\in \mathbb {R}^n$, we define $e_{k}(x)=\prod _{j=1}^{n}h_{k_j}(x_j).$ The family $\{e_{k}\}_{k\in \mathbb {N}^n_0}$ is then an orthonormal basis for $L^2(\mathbb {R}^n)$. They are eigenfunctions of the Hermite operator $\textrm{H}=-\Delta +|x|^2$, namely, we have an ordered set of natural numbers $\{\mu _k\}_{k \in \mathbb {N}_0^n}$ such that

$$\begin{aligned} \textrm{H} e_{k}(x)=\mu _ke_{k}(x), \quad x\in \mathbb {R}^n, \end{aligned}$$

for all $k\in \mathbb {N}_0^n$ and $x\in \mathbb {R}^n$. More precisely, $\textrm{H}$ has eigenvalues

$$\begin{aligned} \mu _k=\sum _{j=1}^{n}(2k_j+1)=2|k|+n, \end{aligned}$$

corresponding to the eigenfunction $e_{k}$ for $k\in \mathbb {N}_0^n.$

Given $f \in L^{2}(\mathbb {R}^{n})$, we have the Hermite expansion

$$\begin{aligned} f=\sum _{k \in \mathbb {N}_0^{n}}\left( f, e_{k}\right) e_{k}=\sum _{m=0}^\infty \sum _{|k|=m}\left( f, e_{k}\right) e_{k}= \sum _{m=0}^\infty P_mf, \end{aligned}$$

where $P_{m}$ denotes the orthogonal projection of $L^{2}(\mathbb {R}^{n})$ onto the eigenspace spanned by $\{e_{k}:|k|=m\}.$ Then, the spectral decomposition of H on $\mathbb {R}^n$ is given by

$$\begin{aligned} Hf=\sum _{m=0}^{+\infty }(2 m+n) P_mf, \end{aligned}$$

Since 0 is not in the spectrum of H, for any $s \in \mathbb {R}$, we can define the fractional powers $H^s$ by means of the spectral theorem, namely

$$\begin{aligned} H^s f=\sum _{m=0}^{\infty }(2 m+n)^s P_m f. \end{aligned}$$

(2.1)

2.3 The Heisenberg group

One of the simplest examples of a noncommutative and noncompact group is the famous Heisenberg group $\mathbb {H}^n$. The theory of the Heisenberg group plays a crucial role in several branches of mathematics and physics. The Heisenberg group $\mathbb {H}^n$ is a nilpotent Lie group whose underlying manifold is $\mathbb {R}^{2n+1}$ and the group operation is defined by

$$\begin{aligned} (x, y, t)\circ (x^{\prime }, y^{\prime }, t^{\prime })=(x+x^{\prime }, y+y^{\prime }, t+t^{\prime }+ \frac{1}{2}(xy^{\prime }-x^{\prime }y)), \end{aligned}$$

where (x, y, t), $(x^{\prime }, y^{\prime }, t^{\prime })$ are in $\mathbb {R}^n \times \mathbb {R}^n \times \mathbb {R}$ and $xy^{\prime }$ denotes the standard scalar product in $\mathbb {R}^n$. Moreover, $\mathbb {H}^n$ is a unimodular Lie group on which the left-invariant Haar measure dg is the usual Lebesgue measure $\, \hbox {d}x \, \hbox {d}y \,\hbox {d}t$.

The canonical basis for the Lie algebra $\mathfrak {h}_n$ of $\mathbb {H}^n$ is given by the left-invariant vector fields:

$$\begin{aligned} X_j&=\partial _{x_j}-\frac{y_j}{2} \partial _{t},&Y_j=\partial _{y_j}+\frac{x_j}{2} \partial _{t}, \quad j=1, 2, \ldots n, ~ \textrm{and} ~ T=\partial _{t}, \end{aligned}$$

(2.2)

which satisfy the commutator relations $[X_{i}, Y_{j}]=\delta _{ij}T, \quad \text {for} ~i, j=1, 2, \dotsc n.$

Moreover, the canonical basis for $\mathfrak {h}_n$ admits the decomposition $\mathfrak {h}_n=V\oplus W,$ where $V={\text {span}}\{X_j, Y_j\}_{j=1}^n$ and $W={\text {span}} \{T\}$. Thus, the Heisenberg group $\mathbb {H}^n$ is a step 2 stratified Lie group and its homogeneous dimension is $Q:=2n +2$. The sublaplacian $\mathcal {L}$ on $\mathbb {H}^n$ is defined as

$$\begin{aligned} \mathcal {L}&=\sum _{j=1}^{n}(X_j^2+Y_j^2)=\sum _{j=1}^{n}\bigg (\bigg (\partial _{x_j}-\frac{y_j}{2} \partial _{t}\bigg )^2+\bigg (\partial _{y_j}+\frac{x_j}{2} \partial _{t}\bigg )^2\bigg )\\ {}&=\Delta _{\mathbb {R}^{2n}}+\frac{1}{4}(|x|^2+|y|^2) \partial _t^2+\sum _{j=1}^n\left( x_j \partial _{y_j t}^2-y_j \partial _{x_j t}^2\right) , \end{aligned}$$

where $\Delta _{\mathbb {R}^{2n}}$ is the standard Laplacian on $\mathbb {R}^{2n}.$

2.4 Fourier analysis on the Heisenberg group $\mathbb {H}^n$

We start this subsection by recalling the definition of the operator-valued group Fourier transform on $\mathbb {H}^n$. By Stone–von Neumann theorem, the only infinite-dimensional unitary irreducible representations (up to unitary equivalence) are given by $\pi _{\lambda }$, $\lambda$ in $\mathbb {R}^*$, where the mapping $\pi _{\lambda }$ is a strongly continuous unitary representation defined by

$$\begin{aligned} \pi _{\lambda }(g)f(u)=e^{i \lambda (t+\frac{1}{2}xy)} e^{i \sqrt{\lambda }yu} { f(u+\sqrt{|\lambda |}x)}, \quad g=(x, y, t)\in \mathbb {H}^n, \end{aligned}$$

for all $f \in L^2(\mathbb {R}^n).$ We use the convention

$$\begin{aligned} \sqrt{\lambda }:=\textrm{sgn}(\lambda )\sqrt{|\lambda |} = {\left\{ \begin{array}{ll} \sqrt{\lambda },&{}\lambda >0,\\ -\sqrt{|\lambda |}, &{}\lambda <0.\end{array}\right. } \end{aligned}$$

For each ${\lambda } \in \mathbb {R}^*$, the group Fourier transform of $f\in L^1(\mathbb {H}^n)$ is a bounded linear operator on $L^2(\mathbb {R}^n)$ defined by

$$\begin{aligned} {\widehat{f}}(\lambda ) \equiv \pi _{\lambda }(f)=\int _{\mathbb {H}^n}f(g)\pi _{\lambda }^*(g)\, \hbox {d}g. \end{aligned}$$

Let $B(L^2(\mathbb {R}^n))$ be the set of all bounded operators on $L^2(\mathbb {R}^n)$. As the Schrödinger representations are unitary, for any $\lambda \in \mathbb {R}^*$, we have

$$\begin{aligned} \Vert {\widehat{f}}\Vert _{B(L^2(\mathbb {R}^n))}\leqslant \Vert f\Vert _{L^1(\mathbb {H}^n)}. \end{aligned}$$

If $f \in L^2(\mathbb {H}^n)$, then ${\widehat{f}}(\lambda )$ is a Hilbert–Schmidt operator on $L^2(\mathbb {R}^n)$ and satisfies the following Plancherel formula

$$\begin{aligned} \Vert {f}\Vert _{L^2(\mathbb {H}^n)}^2=\int _{\mathbb {R}^*}\Vert {\widehat{f}}(\lambda )\Vert _{S_2}^{2} \, \hbox {d}\mu ( \lambda ), \end{aligned}$$

where $\Vert . \Vert _{S_2}$ stands for the norm in the Hilbert space $S_2$, the set of all Hilbert–Schmidt operators on $L^2(\mathbb {R}^n)$ and $\hbox {d}\mu (\lambda )=c_n {|\lambda |}^n \, d\lambda$ with $c_n$ being a positive constant.

Therefore, with the help of the orthonormal basis $\left\{ e_k\right\} _{k \in \mathbb {N}_0^n}$ for $L^2\left( \mathbb {R}^n\right)$ and the definition of the Hilbert–Schmidt norm, we have

$$\begin{aligned} \begin{aligned} \Vert {\widehat{f}}(\lambda )\Vert _{S_2}^2&\doteq {\text {Tr}}\left[ (\pi _\lambda (f) )^* \pi _\lambda (f)\right] \\&=\sum _{k \in \mathbb {N}_0^n} \Vert {\widehat{f}}(\lambda ) e_k \Vert _{L^2\left( \mathbb {R}^n\right) }^2=\sum _{k, \ell \in \mathbb {N}^n_0} | ({\widehat{f}}(\lambda ) e_k, e_{\ell } )_{L^2\left( \mathbb {R}^n\right) } |^2. \end{aligned} \end{aligned}$$

The above expression allows us to write the Plancherel formula in the following way:

$$\begin{aligned} \Vert {f}\Vert _{L^2(\mathbb {H}^n)}^2=\int _{\mathbb {R}^*}\sum _{k, \ell \in \mathbb {N}^n_0} | ({\widehat{f}}(\lambda ) e_k, e_{\ell } )_{L^2\left( \mathbb {R}^n\right) } |^2 \, \hbox {d}\mu ( \lambda ). \end{aligned}$$

For $f \in \mathcal {S}(\mathbb {H}^n)$, the space of all Schwartz class functions on $\mathbb {H}^n,$ the Fourier inversion formula takes the form

$$\begin{aligned} f(g)&:= \int _{\mathbb {R}^*}{\text {Tr}}[\pi _{\lambda }(g){\widehat{f}}(\lambda )]\,\hbox {d}\mu (\lambda ), \quad g\in \mathbb {H}^n, \end{aligned}$$

where ${\text {Tr(A)}}$ denotes the trace of the operator A.

Furthermore, the action of the infinitesimal representation $d\pi _\lambda$ of $\pi _\lambda$ on the generators of the first layer of the Lie algebra $\mathfrak {h}_n$ is given by

$$\begin{aligned} \begin{aligned} \;d \pi _\lambda \left( X_j\right)&=\sqrt{|\lambda |} \partial _{x_j}&\text{ for } j=1, \ldots , n, \\ \mathrm {~d} \pi _\lambda \left( Y_j\right)&=i {\text {sign}}(\lambda ) \sqrt{|\lambda |} x_j&\text{ for } j=1, \ldots , n. \end{aligned} \end{aligned}$$

Since the action of $\;\hbox {d}\pi _\lambda$ can be extended to the universal enveloping algebra of $\mathfrak {h}_n$, combining the above two expressions, we obtain

$$\begin{aligned} \;\hbox {d}\pi _\lambda \left( \mathcal {L}\right) =\;d \pi _\lambda \bigg (\sum _{j=1}^n(X_j^2+Y_j^2)\bigg )=|\lambda | \sum _{j=1}^n\big (\partial _{x_j}^2-x_j^2\big )=-|\lambda | \textrm{H}, \end{aligned}$$

where $\textrm{H} =-\Delta +|x|^2$ is the Hermite operator on $\mathbb {R}^n$. Thus, the operator-valued symbol $\sigma _\mathcal {L}(\lambda )$ of $\mathcal {L}$ acting on $L^2(\mathbb {R}^n)$ takes the form $\sigma _\mathcal {L}(\lambda )=-|\lambda | \textrm{H}.$ Furthermore, for $s \in \mathbb {R}$, using the functional calculus, the symbol of $(-\mathcal {L})^s$ is $|\lambda |^s \textrm{H}^s,$ where the notion of $\textrm{H}^s$ is defined in (2.1).

The Sobolev spaces $H_{\mathcal {L}}^s, s \in \mathbb {R}$, associated to the sublaplacian $\mathcal {L}$, are defined as

$$\begin{aligned} H_{\mathcal {L}}^s\left( \mathbb {H}^n\right) :=\left\{ f \in \mathcal {D}^{\prime }\left( \mathbb {H}^n\right) :(I-\mathcal {L})^{s / 2} f \in L^2\left( \mathbb {H}^n\right) \right\} , \end{aligned}$$

with the norm

$$\begin{aligned} \Vert f\Vert _{H_{\mathcal {L}}^s\left( \mathbb {H}^n\right) }:=\left\| (I-\mathcal {L})^{s / 2} f\right\| _{L^2\left( \mathbb {H}^n\right) }. \end{aligned}$$

Similarly, we denote by ${\dot{H}}_{\mathcal {L}}^{ s}(\mathbb {H}^n),$ the homogeneous Sobolev defined as the space of all $f\in \mathcal {D}^{\prime }(\mathbb {H}^n)$ such that $(-\mathcal {L})^{{s}/{2}}f\in L^2(\mathbb {H}^n)$. More generally, we define ${\dot{H}}_{\mathcal {L}}^{p, s}(\mathbb {H}^n)$ as the homogeneous Sobolev defined as the space of all $f\in \mathcal {D}^{\prime }(\mathbb {H}^n)$ such that $(-\mathcal {L})^{{s}/{2}}f\in L^p(\mathbb {H}^n)$ for $s <\frac{Q}{p}$. Then, we recall the following important inequalities, see, e.g., [4, 8, 14, 15, 34] for a more general graded Lie group framework. However, we will state those in the Heisenberg group setting.

Theorem 2.1

(Hardy–Littlewood–Sobolev inequality) Let $\mathbb {H}^n$ be the Heisenberg group with the homogeneous dimension $Q:=2n+2$. Let $a\geqslant 0$ and $1<p\leqslant q<\infty$ be such that

$$\begin{aligned} \frac{a}{Q}= \frac{1}{p}-\frac{1}{q}. \end{aligned}$$

Then we have the following inequality

$$\begin{aligned} \Vert f\Vert _{{\dot{H}}_{\mathcal {L}}^{q, -a}(\mathbb {H}^n)} \lesssim \Vert f\Vert _{L^p(\mathbb {H}^n)}. \end{aligned}$$

We have the Gagliardo–Nirenberg inequality on $\mathbb {H}^n$ as follows:

Theorem 2.2

(Gagliardo–Nirenberg inequality) Let Q be the homogeneous dimension on the Heisenberg group $\mathbb {H}^n$. Assume that

$$\begin{aligned} s\in (0,1], 1<r<\frac{Q}{s}, \text{ and } ~ 2 \leqslant q \leqslant \frac{rQ}{Q-sr}. \end{aligned}$$

Then, we have the following Gagliardo–Nirenberg type inequality,

$$\begin{aligned} \Vert u\Vert _{L^q(\mathbb {H}^n)} \lesssim \Vert u\Vert _{{\dot{H}}_{\mathcal {L}}^{r,s}(\mathbb {H}^n)}^\theta \Vert u\Vert _{L^2(\mathbb {H}^n)}^{1-\theta }, \end{aligned}$$

for $\theta =\left( \frac{1}{2}-\frac{1}{q}\right) /{\left( \frac{s}{Q}+\frac{1}{2}-\frac{1}{r}\right) }\in [0,1]$, provided $\frac{s}{Q}+\frac{1}{2}\ne \frac{1}{r}$.

3 Linear damped wave equations: ${\dot{H}}_{\mathcal {L}}^s(\mathbb {H}^n)$-norm estimates

In this section, as a preliminary step in preparing to investigate the local and global well-posedness of the nonlinear Cauchy problem (1.1), we examine its associated linear counterpart, which involves a vanishing right-hand side. Specifically, our attention is directed toward the decay properties of solutions, in which our proofs are slightly different from the known results. Let us consider the Cauchy problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial ^2_tu-\mathcal {L}u+ \partial _tu =0, &{} g\in \mathbb {H}^n,t>0,\\ u(0,g)= u_0(g), &{} g\in \mathbb {H}^n,\\ \partial _tu(0, g)= u_1(g), &{} g\in \mathbb {H}^n, \end{array}\right. } \end{aligned}$$

(3.1)

where $u_{0}(g)$ and $u_{1}(g)$ are the initial data additionally belonging to subelliptic Sobolev space $\dot{H}_{\mathcal {L}}^{-\gamma }(\mathbb {H}^n)$ of negative order. We will derive $\dot{H}_{\mathcal {L}}^s(\mathbb {H}^n)$-norm estimates for the solution $u(t, \cdot )$ to the homogeneous problem (3.1). We make use of the group Fourier transform on the Heisenberg group $\mathbb {H}^n$, specifically with respect to the spatial variable g, and combine it with the Plancherel identity to estimate the $\dot{H}_{\mathcal {L}}^s(\mathbb {H}^n)$-norm. We refer to [29], where a similar approach has been carried out for the $L^2$-estimates of the solution to the damped wave equation (3.1) on the Heisenberg group $\mathbb {H}^n$.

Given that the group Fourier transform of a function $f \in L^2\left( \mathbb {H}^n\right)$ is no longer a function but a family of bounded linear operators $\{{\widehat{f}}(\lambda )\}_{\lambda \in \mathbb {R}^*}$ on $L^2\left( \mathbb {R}^n\right)$, the proofs are more involved and do not follow as in the Euclidean setup. We overcome this obstacle by using a trick to project these operators by using the orthonormal basis $\left\{ e_k\right\} _{k \in \mathbb {N}^n}$ of $L^2(\mathbb {R}^n)$, namely, by working with the Fourier coefficients $\left\{ \left( {\widehat{f}}(\lambda ) e_k, e_{\ell }\right) _{L^2\left( \mathbb {R}^n\right) }\right\} _{k, \ell \in \mathbb {N}^n}$ for the Fourier transform ${\widehat{f}}(\lambda )$ for each $\lambda \in \mathbb {R}^*.$

Invoking the group Fourier transform with respect to g on (3.1), we get a Cauchy problem related to a parameter-dependent functional differential equation for ${\widehat{u}}(t,\lambda ),$ namely,

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial ^2_t{\widehat{u}}(t,\lambda )- \sigma _{\mathcal {L}}(\lambda ) {\widehat{u}}(t,\lambda ) +\partial _t {\widehat{u}}(t,\lambda )=0,&{} \lambda \in \mathbb {R}^*,~t>0,\\ {\widehat{u}}(0,\lambda )={\widehat{u}}_0(\lambda ), &{}\lambda \in \mathbb {R}^*,\\ \partial _t{\widehat{u}}(0,\lambda )={\widehat{u}}_1(\lambda ), &{}\lambda \in \mathbb {R}^*, \end{array}\right. } \end{aligned}$$

(3.2)

where $\sigma _{\mathcal {L}}(\lambda )$ is the symbol of the sub-Laplacian $\mathcal {L}$ on $\mathbb {H}^n$. In fact, we know that $\sigma _{\mathcal {L}}(\lambda )=-|\lambda | \textrm{H}$. For any $k, \ell \in \mathbb {N}^n$, let us introduce the notation

$$\begin{aligned} {{\widehat{u}}(t, \lambda )_{k, \ell } \doteq \left( {\widehat{u}}(t, \lambda ) e_\ell , e_{k}\right) _{L^2\left( \mathbb {R}^n\right) },} \end{aligned}$$

where $\left\{ e_k\right\} _{k \in \mathbb {N}^n}$ is the system of Hermite functions forming an orthonormal basis of $L^2(\mathbb {R}^n)$. Since $\textrm{H} e_k=\mu _k e_k$, ${\widehat{u}}(t, \lambda )_{k, \ell }$ solves an ordinary differential equation with respect to the variable t depending on parameters $\lambda \in \mathbb {R}^*$ and $k, \ell \in \mathbb {N}^n,$

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial ^2_t{\widehat{u}}(t,\lambda )_{kl}+ \partial _t{\widehat{u}}(t,\lambda )_{kl}+ \beta _{k, \lambda }^{2 } {\widehat{u}}(t,\lambda )_{kl}= 0,&{} \lambda \in \mathbb {R}^*,~t>0,\\ {\widehat{u}}(0,\lambda )_{kl}={\widehat{u}}_0(\lambda )_{kl}, &{}\lambda \in \mathbb {R}^*,\\ \partial _t{\widehat{u}}(0,\lambda )_{kl}={\widehat{u}}_1(\lambda )_{kl}, &{}\lambda \in \mathbb {R}^*, \end{array}\right. } \end{aligned}$$

(3.3)

where $\beta _{k, \lambda }^{2 } =|\lambda |\mu _k.$ Then, the characteristic equation of (3.3) is given by

$$\begin{aligned} m^2+ m+\beta _{k, \lambda }^{2 } =0, \end{aligned}$$

and so the characteristic roots $m_1$ and $m_2$ are $\frac{-1- \sqrt{1-4\beta _{k, \lambda }^{2 }}}{2}$ and $\frac{-1+ \sqrt{1-4\beta _{k, \lambda }^{2 }}}{2},$ respectively.

Observe that, for $|\beta _{k, \lambda }| \ll 1$, we get

$$\begin{aligned}&m_1=\frac{-1- \sqrt{1-4\beta _{k, \lambda }^{2 }}}{2} =\frac{-1- (1-4{\beta _{k, \lambda }}^2 )^{\frac{1}{2}}}{2}=-1+\mathcal {O}\left( \beta _{k, \lambda }^{2 }\right) ,\\&m_2= \frac{-1+ (1-4{\beta _{k, \lambda }}^2 )^{\frac{1}{2}}}{2}=-\beta _{k, \lambda }^{2 }+\mathcal {O}\left( \beta _{k, \lambda }^4\right) . \end{aligned}$$

Again, for $|\beta _{k, \lambda }| \gg 1$, we obtain

$$\begin{aligned} m_{1}= \frac{-1- (1-4\beta _{k, \lambda }^2 )^{\frac{1}{2}}}{2}&=\frac{-1- 2i|\beta _{k, \lambda }| (1-(4\beta _{k, \lambda }^2)^{-1})^{\frac{1}{2}}}{2}\\&=- i|\beta _{k, \lambda }|-\frac{1}{2}+\mathcal {O}\left( |\beta _{k, \lambda }|^{-1}\right) ,\\ m_{2}= \frac{-1+(1-4\beta _{k, \lambda }^2 )^{\frac{1}{2}}}{2}&=\frac{-1+ 2i|\beta _{k, \lambda }| (1-(4\beta _{k, \lambda }^2)^{-1})^{\frac{1}{2}}}{2} \\ {}&= i|\beta _{k, \lambda }|-\frac{1}{2}+\mathcal {O}\left( |\beta _{k, \lambda }|^{-1}\right) .\end{aligned}$$

We collect the above easy observations as the following relations:

• $m_1=-1+\mathcal {O}\left( \beta _{k, \lambda }^{2 }\right) , m_2=-\beta _{k, \lambda }^{2 }+\mathcal {O}\left( \beta _{k, \lambda }^4\right)$ for $|\beta _{k, \lambda }|<\varepsilon \ll 1$;

• $m_{1}= - i|\beta _{k, \lambda }|-\frac{1}{2}+\mathcal {O}\left( |\beta _{k, \lambda }|^{-1}\right)$ and $m_{2}= i|\beta _{k, \lambda }|-\frac{1}{2}+\mathcal {O}\left( |\beta _{k, \lambda }|^{-1}\right)$ for $|\beta _{k, \lambda }|>N \gg 1$;

• $\text {Re}( m_{1})<0$ and $\text {Re}( m_{2})<0$ for $\varepsilon \leqslant |\beta _{k, \lambda }| \leqslant N$.

Therefore, the solution to the homogeneous problem (3.3) is given by

$$\begin{aligned} {\widehat{u}}(t,\lambda )_{kl}&= A_0(t, \lambda )_{k\ell } {\widehat{u}}_0(\lambda )_{kl}+ A_1(t, \lambda )_{k\ell }{\widehat{u}}_1(\lambda )_{k\ell }, \end{aligned}$$

(3.4)

where

$$\begin{aligned}&A_0(t, \lambda )_{k\ell }=\frac{m_1{e}^{m_2 t}-m_2{e}^{m_1 t}}{m_1-m_2} \end{aligned}$$

(3.5)

$$\begin{aligned}&\quad ={\left\{ \begin{array}{ll} \frac{\left( -1+\mathcal {O}(\beta _{k, \lambda }^2)\right) {e}^{\left( -\beta _{k, \lambda }^{2 }+\mathcal {O} (\beta _{k, \lambda }^{4} )\right) t}-\left( -\beta _{k, \lambda }^{2 }+\mathcal {O} (\beta _{k, \lambda }^{4})\right) {e}^{\left( -1 +\mathcal {O} (\beta _{k, \lambda }^{2} )\right) t}}{-1+\mathcal {O}\left( \beta _{k, \lambda }^{2 }\right) } &{} \text{ for } |\beta _{k, \lambda }|<\varepsilon , \\ \\ \frac{\left( i|\beta _{k, \lambda }|-\frac{1}{2}+\mathcal {O}\left( |\beta _{k, \lambda }|^{-1}\right) \right) {e}^{\left( -i|\beta _{k, \lambda }|-\frac{1}{2}+\mathcal {O}\left( |\beta _{k, \lambda }|^{-1}\right) \right) t}}{2 i|\beta _{k, \lambda }|+\mathcal {O}(1)} &{} \\ \\ \qquad -\frac{\left( -i|\beta _{k, \lambda }|-\frac{1}{2}+\mathcal {O}\left( |\beta _{k, \lambda }|^{-1}\right) \right) {e}^{\left( i|\beta _{k, \lambda }|-\frac{1}{2}+\mathcal {O}\left( |\beta _{k, \lambda }|^{-1}\right) \right) t}}{2 i|\beta _{k, \lambda }|+\mathcal {O}(1)} &{} \text{ for } |\beta _{k, \lambda }|>N . \end{array}\right. } \end{aligned}$$

(3.6)

and

$$\begin{aligned}&A_1(t, \lambda )_{k\ell }=\frac{ {e}^{m_1 t}-{e}^{m_2 t}}{m_1-m_2} \end{aligned}$$

(3.7)

$$\begin{aligned}&\quad =\left\{ \begin{array}{ll} \frac{ {e}^{\left( -1+\mathcal {O}\left( \beta _{k, \lambda }^2\right) \right) t}- {e}^{\left( -\beta _{k, \lambda }^2+\mathcal {O}\left( \beta _{k, \lambda }^4\right) \right) t}}{-1+\mathcal {O}\left( \beta _{k, \lambda }^2\right) } &{} \text{ for } |\beta _{k, \lambda }|<\varepsilon , \\ \\ \frac{ {e}^{\left( i|\beta _{k, \lambda }|-\frac{1}{2}+\mathcal {O}\left( |\beta _{k, \lambda }|^{-1}\right) \right) t}- {e}^{\left( -i|\beta _{k, \lambda }|-\frac{1}{2}+\mathcal {O}\left( |\beta _{k, \lambda }|^{-1}\right) \right) t}}{2 i|\beta _{k, \lambda }|+\mathcal {O}(1)} &{} \text{ for } |\beta _{k, \lambda }|>N . \end{array}\right. \end{aligned}$$

(3.8)

Thus from the above collected observations and asymptotic expression, we deduce the following pointwise estimates

$$\begin{aligned} \left| A_0(t,\lambda )_{k\ell }\right| \lesssim \left\{ \begin{array}{ll} |\beta _{k, \lambda }|^2 {e}^{-c t}+ {e}^{-ct\beta _{k, \lambda }^2 } &{} \text{ for } |\beta _{k, \lambda }|<\varepsilon \ll 1, \\ \\ \textrm{e}^{-c t} &{} \text{ for } \varepsilon \leqslant |\beta _{k, \lambda }| \leqslant N, \\ \\ \textrm{e}^{-c t} &{} \text{ for } |\beta _{k, \lambda }|>N \gg 1, \end{array}\right. \end{aligned}$$

(3.9)

and

$$\begin{aligned} \left| A_1(t,\lambda )_{k\ell }\right| \lesssim \left\{ \begin{array}{ll} {e}^{-c t}+ {e}^{-ct\beta _{k, \lambda }^2 } &{} \text{ for } |\beta _{k, \lambda }|<\varepsilon \ll 1, \\ \\ {e}^{-c t} &{} \text{ for } \varepsilon \leqslant |\beta _{k, \lambda }| \leqslant N, \\ \\ |\beta _{k, \lambda }|^{-1} {e}^{-c t} &{} \text{ for } |\beta _{k, \lambda }|>N \gg 1, \end{array}\right. \end{aligned}$$

(3.10)

for some suitable positive constant c.

Before finding the Sobolev norm of $u(t, \cdot )$, first we notice that, for $\beta _{k, \lambda }^2 = |\lambda | \mu _k<\varepsilon ^2$, we have

$$\begin{aligned} \left| (|\lambda | \mu _k)^{s+\gamma } {e}^{-ct|\lambda | \mu _k}\right| \lesssim (1+t)^{-(s+\gamma )}, \qquad \text {for~} s+\gamma \geqslant 0. \end{aligned}$$

(3.11)

Now by using the Plancherel formula and the fact that $\{e_k\}_{k\in \mathbb {N}^n}$ is an orthonormal basis of $L^2(\mathbb {R}^n)$, we have

$$\begin{aligned}&\Vert u(t, \cdot )\Vert _{\dot{H}^s_{\mathcal {L}}}^2=\int _{\mathbb {R}^*}\Vert (-\sigma _{\mathcal {L}}(\lambda ))^{\frac{s}{2}} {\widehat{u}}(t, \lambda )\Vert _{S_2}^2 \,\hbox {d}\mu (\lambda ) \nonumber \\&\qquad =\int _{\mathbb {R}^*} \sum _{k, \ell \in \mathbb {N}^n} (|\lambda | \mu _k)^{s} |{\widehat{u}}(t, \lambda )_{k\ell }|^2 \,\hbox {d}\mu (\lambda ) \nonumber \\&\qquad \lesssim \int _{\mathbb {R}^*} \sum _{k, \ell \in \mathbb {N}^n} (|\lambda | \mu _k)^{s}\left[ |A_0(t, \lambda )_{k\ell }|^2 |{\widehat{u}}_0(\lambda )_{kl}|^2 + |A_1(t, \lambda )_{k\ell }|^2 |{\widehat{u}}_1(\lambda )_{k\ell } |^2 \right] \hbox {d}\mu (\lambda ) \nonumber \\&\qquad = (I)+(II), \end{aligned}$$

(3.12)

where

$$\begin{aligned} (I):=\int _{\mathbb {R}^*} \sum _{k, \ell \in \mathbb {N}^n} (|\lambda | \mu _k)^{s} |A_0(t, \lambda )_{k\ell }|^2 |{\widehat{u}}_0(\lambda )_{kl}|^2 \hbox {d}\mu (\lambda ), \end{aligned}$$

and

$$\begin{aligned} (II):=\int _{\mathbb {R}^*} \sum _{k, \ell \in \mathbb {N}^n} (|\lambda | \mu _k)^{s} |A_1(t, \lambda )_{k\ell }|^2 |{\widehat{u}}_1(\lambda )_{k\ell } |^2 \hbox {d}\mu (\lambda ). \end{aligned}$$

Case 1: When $|\beta _{k, \lambda }|<\varepsilon \ll 1$: Recalling that $\beta _{k, \lambda }^2=|\lambda | \mu _k$ and using (3.9) and (3.11), we get

$$\begin{aligned} (I)&= \sum _{k, \ell \in \mathbb {N}^n} \int _{|\lambda |<\frac{\varepsilon ^2}{\mu _k}} (|\lambda | \mu _k)^{s+\gamma } |A_0(t, \lambda )_{k\ell }|^2 (|\lambda | \mu _k)^{-\gamma }|{\widehat{u}}_0(\lambda )_{kl}|^2 \hbox {d}\mu (\lambda ) \nonumber \\ {}&\leqslant \sum _{k, \ell \in \mathbb {N}^n} \int _{|\lambda |<\frac{\varepsilon ^2}{\mu _k}} (|\lambda | \mu _k)^{s+\gamma } \{ |\beta _{k, \lambda }|^2 {e}^{-c t}+ {e}^{-ct\beta _{k, \lambda }^2 }\}^2 (|\lambda | \mu _k)^{-\gamma }|{\widehat{u}}_0(\lambda )_{kl}|^2 \hbox {d}\mu (\lambda )\nonumber \\ {}&\leqslant \sum _{k, \ell \in \mathbb {N}^n} \int _{|\lambda |<\frac{\varepsilon ^2}{\mu _k}} (|\lambda | \mu _k)^{s+\gamma } {e}^{-2ct\beta _{k, \lambda }^2} \{ |\beta _{k, \lambda }|^2 {e}^{-c t (1-\beta _{k, \lambda }^2)}+ 1\}^2\nonumber \\&\qquad \times (|\lambda | \mu _k)^{-\gamma }|{\widehat{u}}_0(\lambda )_{kl}|^2 \hbox {d}\mu (\lambda )\nonumber \\&\lesssim (1+t)^{-(s+\gamma )} \sum _{k, \ell \in \mathbb {N}^n} \int _{|\lambda |<\frac{\varepsilon ^2}{\mu _k}} (|\lambda | \mu _k)^{-\gamma }|{\widehat{u}}_0(\lambda )_{kl}|^2 \hbox {d}\mu (\lambda ) \nonumber \\&\lesssim (1+t)^{-(s+\gamma )} \Vert {u}_0 \Vert _{\dot{H}^{-\gamma }_{\mathcal {L}}}^2 . \end{aligned}$$

(3.13)

Similarly, using (3.10) and (3.11) we can find that

$$\begin{aligned} (II)&=\sum _{k, \ell \in \mathbb {N}^n}\int _{|\lambda |<\frac{\varepsilon ^2}{\mu _k}} (|\lambda | \mu _k)^{s} |A_1(t, \lambda )_{k\ell }|^2 |{\widehat{u}}_1(\lambda )_{k\ell } |^2 \hbox {d}\mu (\lambda )\nonumber \\&\lesssim (1+t)^{-(s+\gamma )} \Vert {u}_1 \Vert _{ \dot{H}^{-\gamma }_{\mathcal {L}}}^2 . \end{aligned}$$

(3.14)

Case 2: When $|\beta _{k, \lambda }|>N \gg 1$: Again using (3.9) we get

$$\begin{aligned} (I)&= \sum _{k, \ell \in \mathbb {N}^n} \int _{|\lambda |>\frac{N^2}{\mu _k}} (|\lambda | \mu _k)^{s} |A_0(t, \lambda )_{k\ell }|^2 |{\widehat{u}}_0(\lambda )_{kl}|^2 \hbox {d}\mu (\lambda )\nonumber \\&\lesssim {e}^{-2c t} \sum _{k, \ell \in \mathbb {N}^n} \int _{|\lambda |>\frac{N^2}{\mu _k}} (1+|\lambda | \mu _k)^{s } |{\widehat{u}}_0(\lambda )_{kl}|^2 \hbox {d}\mu (\lambda ) \nonumber \\&\lesssim {e}^{-2c t} \Vert {u}_0 \Vert _{H_\mathcal {L}^{-s}}^2 . \end{aligned}$$

(3.15)

Also, with the help of (3.10) we find that

$$\begin{aligned} (II)&= \sum _{k, \ell \in \mathbb {N}^n} \int _{|\lambda |>\frac{N^2}{\mu _k}} (|\lambda | \mu _k)^{s} |A_1(t, \lambda )_{k\ell }|^2 |{\widehat{u}}_1(\lambda )_{k\ell } |^2 \hbox {d}\mu (\lambda ) \nonumber \\ {}&\lesssim \sum _{k, \ell \in \mathbb {N}^n} \int _{|\lambda |>\frac{N^2}{\mu _k}} (|\lambda | \mu _k)^{s} |\beta _{k, \lambda }|^{-2} {e}^{-2c t} |{\widehat{u}}_1(\lambda )_{k\ell } |^2 \hbox {d}\mu (\lambda ) \nonumber \\&= {e}^{-2c t} \sum _{k, \ell \in \mathbb {N}^n} \int _{|\lambda |>\frac{N^2}{\mu _k}} (1+|\lambda | \mu _k)^{s-1} \left( \frac{|\lambda | \mu _k }{1+|\lambda | \mu _k}\right) ^{s-1} |{\widehat{u}}_1(\lambda )_{k\ell } |^2 \hbox {d}\mu (\lambda ) \nonumber \\&\lesssim {e}^{-2c t} \Vert {u}_1 \Vert _{H_\mathcal {L}^{s-1}}^2. \end{aligned}$$

(3.16)

Case 3: When $\varepsilon \leqslant |\beta _{k, \lambda }|\leqslant N$: From (3.9) and (3.10), we get

$$\begin{aligned} (I)&=\sum _{k, \ell \in \mathbb {N}^n} \int _{\frac{N^2}{\mu _k}\leqslant |\lambda |\leqslant \frac{\varepsilon ^2}{\mu _k} } (|\lambda | \mu _k)^{s} |A_0(t, \lambda )_{k\ell }|^2 |{\widehat{u}}_0(\lambda )_{kl}|^2 \hbox {d}\mu (\lambda ) \nonumber \\ {}&\lesssim {e}^{-2c t} \sum _{k, \ell \in \mathbb {N}^n} \int _{\frac{N^2}{\mu _k}\leqslant |\lambda |\leqslant \frac{\varepsilon ^2}{\mu _k} } (|\lambda | \mu _k)^{s} |{\widehat{u}}_0(\lambda )_{kl}|^2 \hbox {d}\mu (\lambda )\nonumber \\ {}&\lesssim {e}^{-2c t} \sum _{k, \ell \in \mathbb {N}^n} \int _{\frac{N^2}{\mu _k}\leqslant |\lambda |\leqslant \frac{\varepsilon ^2}{\mu _k} } |{\widehat{u}}_0(\lambda )_{kl}|^2 \hbox {d}\mu (\lambda )\nonumber \\&\lesssim {e}^{-2c t} \Vert {u}_0 \Vert _{L^2}^2, \end{aligned}$$

(3.17)

and

$$\begin{aligned} (II)&= \sum _{k, \ell \in \mathbb {N}^n} \int _{\frac{N^2}{\mu _k}\leqslant |\lambda |\leqslant \frac{\varepsilon ^2}{\mu _k} } (|\lambda | \mu _k)^{s} |A_1(t, \lambda )_{k\ell }|^2 |{\widehat{u}}_1(\lambda )_{k\ell } |^2 \hbox {d}\mu (\lambda )\nonumber \\ {}&\lesssim {e}^{-2c t} \sum _{k, \ell \in \mathbb {N}^n} \int _{\frac{N^2}{\mu _k}\leqslant |\lambda |\leqslant \frac{\varepsilon ^2}{\mu _k} } (1+|\lambda | \mu _k)^{s} |{\widehat{u}}_0(\lambda )_{kl}|^2 \hbox {d}\mu (\lambda )\nonumber \\&\lesssim {e}^{-2c t} \sum _{k, \ell \in \mathbb {N}^n} \int _{\frac{N^2}{\mu _k}\leqslant |\lambda |\leqslant \frac{\varepsilon ^2}{\mu _k} } (1+|\lambda | \mu _k)^{s-1} |{\widehat{u}}_0(\lambda )_{kl}|^2 \hbox {d}\mu (\lambda ) \nonumber \\&\lesssim {e}^{-2c t} \Vert {u}_1 \Vert _{H_\mathcal {L}^{s-1}}^2. \end{aligned}$$

(3.18)

Proof of Theorem 1.1

Combining above Case 1 [(3.13) and (3.14)], Case 2 [(3.15) and (3.16)], and Case 3 [(3.17) and (3.18)], we obtain the following $\dot{H}_\mathcal {L}^s$-decay estimate

$$\begin{aligned} \Vert u(t, \cdot )\Vert _{ {\dot{H}}_\mathcal {L}^s} \lesssim (1+t)^{-\frac{s+\gamma }{2}}\left( \left\| u_0\right\| _{H^s_\mathcal {L} \cap {\dot{H}}^{-\gamma }_\mathcal {L}}+\left\| u_1\right\| _{H_\mathcal {L}^{s-1} \cap {\dot{H}}_\mathcal {L}^{-\gamma }}\right) , \end{aligned}$$

for any $t\geqslant 0$. $\square$

4 Global-in-time well-posedness

In this section, we will prove Theorem 1.2, that is, the global-in-time well-posedness of the Cauchy problem (1.1) in the energy evolution space $\mathcal C\left( [0,T], H^s_{\mathcal {L}}(\mathbb {H}^n)\right)$.

Proof of Theorem 1.2

Recall that for $s \geqslant 0$ and $\gamma \in \mathbb {R}$ such that $s+\gamma \geqslant 0$, from the estimate (1.9) of Theorem 1.1, we have

$$\begin{aligned} \Vert u(t, \cdot )\Vert _{\dot{{H}}_\mathcal {L}^s(\mathbb {H}^n)} \lesssim (1+t)^{-\frac{s+\gamma }{2}}\left( \left\| u_0\right\| _{H^s_{\mathcal {L}} \cap \dot{{H}}_\mathcal {L}^{-\gamma } }+\left\| u_1\right\| _{H_\mathcal {L}^{s-1} \cap \dot{{H}}_\mathcal {L}^{-\gamma } }\right) . \end{aligned}$$

(4.1)

In particular, for $\gamma =0$ and $s \geqslant 0,$ we get

$$\begin{aligned} \Vert u(t, \cdot )\Vert _{{{\dot{H}}}_\mathcal {L}^s} \lesssim (1+t)^{-\frac{s}{2}}\left( \left\| u_0\right\| _{H_\mathcal {L}^s }+\left\| u_1\right\| _{L^2}\right) . \end{aligned}$$

(4.2)

From (4.1), in particular for $s \in [0, 1]$ and $\gamma >0$ we have the following estimate for the Sobolev solutions of the linear Cauchy problem

$$\begin{aligned} \Vert u(t, \cdot )\Vert _{\dot{{H}}_\mathcal {L}^s} \lesssim (1+t)^{-\frac{s+\gamma }{2}}\left( \left\| u_0\right\| _{ H^s_{\mathcal {L}} \cap {{\dot{H}}}_\mathcal {L}^{-\gamma }}+\left\| u_1\right\| _{L^2 \cap {{\dot{H}}}_\mathcal {L}^{-\gamma }}\right) , \end{aligned}$$

(4.3)

where we have used the Sobolev embedding $L^2\subset H_\mathcal {L}^{s-1}$ for $s\leqslant 1$. Particularly, for $s=0$ in (4.3), using the Sobolev embedding $H_\mathcal {L}^{s} \subset L^2$ for $s\geqslant 0$, we obtain

$$\begin{aligned} \Vert u(t, \cdot )\Vert _{L^2}&\lesssim (1+t)^{-\frac{\gamma }{2}}\left( \left\| u_0\right\| _{ L^2 \cap {{\dot{H}}}_\mathcal {L}^{-\gamma }}+\left\| u_1\right\| _{L^2 \cap {{\dot{H}}}_\mathcal {L}^{-\gamma }}\right) \nonumber \\ {}&\lesssim (1+t)^{-\frac{\gamma }{2}}\left( \left\| u_0\right\| _{ H^s_{\mathcal {L}} \cap {{\dot{H}}}_\mathcal {L}^{-\gamma }}+\left\| u_1\right\| _{L^2 \cap {{\dot{H}}}_\mathcal {L}^{-\gamma }}\right) . \end{aligned}$$

(4.4)

Now from (4.3) and (4.4), for $s\in (0, 1]$, we can write

$$\begin{aligned} (1+t)^{\frac{s+\gamma }{2}}\Vert u(t, \cdot )\Vert _{{{\dot{H}}}_\mathcal {L}^s}&+(1+t)^{\frac{\gamma }{2}}\Vert u(t, \cdot )\Vert _{L^2}\\ {}&\lesssim \left( \left\| u_0\right\| _{H^s_{\mathcal {L}} \cap {{\dot{H}}}_\mathcal {L}^{-\gamma }}+\left\| u_1\right\| _{L^2 \cap {\dot{H}}_\mathcal {L}^{-\gamma }}\right) =\left\| \left( u_{0}, u_{1}\right) \right\| _{ { \mathcal {A}_{\mathcal {L}}^{s, -\gamma }}}. \end{aligned}$$

Thus from above, we can claim that $u \in X_s(T)$ and

$$\begin{aligned} \Vert u^{\text {lin}}\Vert _{X_s(T)} \lesssim \left\| \left( u_{0}, u_{1}\right) \right\| _{ { \mathcal {A}_{\mathcal {L}}^{s, -\gamma }}}. \end{aligned}$$

(4.5)

Our next aim is to prove

$$\begin{aligned} \Vert u^{\text {non}}\Vert _{X_s(T)} \lesssim \left\| u\right\| _{ X_s(T)}^p, \end{aligned}$$

under some conditions for p. First we will estimate $L^2$ and $\dot{H}^{-\gamma }_{\mathcal {L}}$ norm of $|u(t, \cdot )|^p$. Applying Gagliardo–Nirenberg inequality (Theorem 2.2), we have

$$\begin{aligned}&\left\| |u(\sigma , \cdot )|^p\right\| _{L^2}\nonumber \\ {}&\quad = \left\| u(\sigma , \cdot )\right\| _{L^{2p}}^p \lesssim \Vert u(\sigma , \cdot )\Vert _{{\dot{H}}_\mathcal {L}^s(\mathbb {H}^n)}^{p\theta _1} \Vert u(\sigma , \cdot )\Vert _{L^2(\mathbb {H}^n)}^{p(1-\theta _1)}\nonumber \\&\quad = (1+\sigma )^{-\frac{p}{2} (s\theta _1+\gamma )} \left\{ (1+\sigma )^{\frac{(s+\gamma )}{2} } \Vert u(\sigma , \cdot )\Vert _{{\dot{H}}_\mathcal {L}^s(\mathbb {H}^n)} \right\} ^{p\theta _1} \nonumber \\ {}&\qquad \times \left\{ (1+\sigma )^{\frac{\gamma }{2} } \Vert u(\sigma ,\cdot )\Vert _{L^2(\mathbb {H}^n)}\right\} ^{p(1-\theta _1)}\nonumber \\ {}&\quad = (1+\sigma )^{-\frac{p}{2}\left[ \gamma +\frac{Q}{2}\left( 1-\frac{1}{p}\right) \right] } \left\{ (1+\sigma )^{\frac{(s+\gamma )}{2} } \Vert u(\sigma , \cdot )\Vert _{{\dot{H}}_\mathcal {L}^s(\mathbb {H}^n)} \right\} ^{p\theta _1}\nonumber \\ {}&\qquad \times \left\{ (1+\sigma )^{\frac{\gamma }{2} } \Vert u(\sigma , \cdot )\Vert _{L^2(\mathbb {H}^n)}\right\} ^{p(1-\theta _1)}\nonumber \\&\quad \lesssim (1+\sigma )^{- p\left( \frac{\gamma }{2}+\frac{Q}{4}\right) +\frac{Q}{4}} \left\| u\right\| _{ X_s(T)}^p, \end{aligned}$$

(4.6)

for $\sigma \in [0, T]$ with $\theta _1=\frac{Q}{2\,s}(1-\frac{1}{p})\in [0, 1]$, provided that

$$\begin{aligned} 1\leqslant p\leqslant \frac{Q}{Q-2s}, \quad \text {if} ~~Q>2s. \end{aligned}$$

(4.7)

On the other hand, using the Hardy–Littlewood–Sobolev inequality (Theorem 2.1), we have

$$\begin{aligned} \left\| |u(\sigma , \cdot )|^p\right\| _{\dot{H}^{-\gamma }_{\mathcal {L}}} \lesssim \left\| |u(\sigma , \cdot )|^p\right\| _{L^{m}} = \left\| u(\sigma , \cdot )\right\| _{L^{mp}}^p \end{aligned}$$

with $\frac{1}{m}-\frac{1}{2}=\frac{\gamma }{Q}$ provided that $0<\gamma <Q$ and $1<m<2$. Since $m \in (1,2)$, we have to restrict $0<\gamma <\frac{Q}{2}$. Again, the Gagliardo–Nirenberg inequality (Theorem 2.2) implies that

$$\begin{aligned}&\left\| |u(\sigma , \cdot )|^p\right\| _{\dot{H}^{-\gamma }_{\mathcal {L}}}\nonumber \\ {}&\quad \lesssim \left\| u(\sigma , \cdot )\right\| _{L^{mp}}^p\lesssim \Vert u(\sigma , \cdot )\Vert _{{\dot{H}}_\mathcal {L}^s(\mathbb {H}^n)}^{p\theta _2} \Vert u(\sigma , \cdot )\Vert _{L^2(\mathbb {H}^n)}^{p(1-\theta _2)}\nonumber \\&\quad = (1+\sigma )^{-\frac{p}{2} (s\theta _2+\gamma )} \left\{ (1+\sigma )^{\frac{(s+\gamma )}{2} } \Vert u(\sigma , \cdot )\Vert _{\dot{H}_\mathcal {L}^s(\mathbb {H}^n)} \right\} ^{p\theta _1}\nonumber \\ {}&\qquad \times \left\{ (1+\sigma )^{\frac{\gamma }{2} } \Vert u(\sigma , \cdot )\Vert _{L^2(\mathbb {H}^n)}\right\} ^{p(1-\theta _1)}\nonumber \\ {}&= (1+\sigma )^{-\frac{p}{2} \left[ \gamma +Q(\frac{1}{2}-\frac{1}{mp})\right] } \left\{ (1+\sigma )^{\frac{(s+\gamma )}{2} } \Vert u(\sigma , \cdot )\Vert _{\dot{H}_\mathcal {L}^s(\mathbb {H}^n)} \right\} ^{p\theta _1}\nonumber \\ {}&\qquad \times \left\{ (1+\sigma )^{\frac{\gamma }{2} } \Vert u(\sigma , \cdot )\Vert _{L^2(\mathbb {H}^n)}\right\} ^{p(1-\theta _1)}\nonumber \\&\quad = (1+\sigma )^{-p ( \frac{\gamma }{2}+\frac{Q}{4} )+ \frac{\gamma }{2}+\frac{Q}{4} } \left\{ (1+\sigma )^{\frac{(s+\gamma )}{2} } \Vert u(\sigma , \cdot )\Vert _{{\dot{H}}_\mathcal {L}^s(\mathbb {H}^n)} \right\} ^{p\theta _2}\nonumber \\ {}&\qquad \times \left\{ (1+\sigma )^{\frac{\gamma }{2} } \Vert u(\sigma , \cdot )\Vert _{L^2(\mathbb {H}^n)}\right\} ^{p(1-\theta _2)}\nonumber \\&\quad \lesssim (1+\sigma )^{-p ( \frac{\gamma }{2}+\frac{Q}{4} )+ \frac{\gamma }{2}+\frac{Q}{4} } \left\| u\right\| _{ X_s(T)}^p, \end{aligned}$$

(4.8)

for $\sigma \in [0, T]$ with $\theta _2=\frac{Q}{s}(\frac{1}{2}-\frac{1}{mp})\in [0, 1]$. Using the fact that $\theta _2\in [0, 1]$, we get

$$\begin{aligned} p\geqslant \frac{2}{m} \quad \text {and}\quad p\leqslant \frac{2Q}{m(Q-2s)}, \quad \text {if} ~Q>2s. \end{aligned}$$

(4.9)

Since $m=\frac{2Q}{Q+2\gamma }\in (1, 2)$, from (4.9), we obtain

$$\begin{aligned} 1< 1+\frac{2\gamma }{Q} \leqslant p \leqslant { \frac{Q+2\gamma }{(Q-2s)}}\quad \text{ if } Q>2s. \end{aligned}$$

(4.10)

Therefore, from (4.7) and (4.10), if we consider

$$\begin{aligned} 1+\frac{2\gamma }{Q} \leqslant p \left\{ \begin{array}{ll} <\infty &{} \text{ if } Q \leqslant 2s, \\ \leqslant \frac{Q}{(Q-2s)}&{} \text{ if } Q>2s, \end{array}\right. \end{aligned}$$

then from (4.6) and (4.8), for $\sigma \in [0, T]$, we assert that

$$\begin{aligned} \left\| |u(\sigma , \cdot )|^p\right\| _{L^2\cap \dot{H}^{-\gamma }_{\mathcal {L}}}\lesssim (1+\sigma )^{-p ( \frac{\gamma }{2}+\frac{Q}{4} )+ \frac{\gamma }{2}+\frac{Q}{4} } \left\| u\right\| _{ X_s(T)}^p. \end{aligned}$$

(4.11)

Using the $(L^2 \cap {\dot{H}}_\mathcal {L}^{-\gamma } )-L^2$ estimate given in (4.3) (with $u_0=0$, $u_1= |u(\sigma ,\cdot )|^p$) as well as from the statement (4.11), we have the following $L^2$-estimate of the solution

$$\begin{aligned} \left\| u^{\textrm{non}}(t, \cdot )\right\| _{L^2}&=\bigg \Vert \int \limits _0^t |u(\sigma ,\cdot )|^p*_{(g)} E_1(t-\sigma , \cdot ) \hbox {d}\sigma \bigg \Vert _{L^2 }\nonumber \\&\leqslant \int \limits _0^t (1+t-\sigma )^{-\frac{\gamma }{2}} \Vert |u(\sigma ,\cdot )|^p\Vert _{L^2 \cap \dot{H}^{-\gamma }_{\mathcal {L}}} \hbox {d}\sigma \nonumber \\ {}&\lesssim \int _0^t(1+t-\sigma )^{-\frac{\gamma }{2}}(1+\sigma )^{-p ( \frac{\gamma }{2}+\frac{Q}{4} )+ \frac{\gamma }{2}+\frac{Q}{4} }\hbox {d}\sigma ~ \left\| u\right\| _{ X_s(T)}^p \nonumber \\&\lesssim (1+t)^{-\frac{\gamma }{2}} \int _0^{\frac{t}{2}}(1+\sigma )^{-p ( \frac{\gamma }{2}+\frac{Q}{4} )+ \frac{\gamma }{2}+\frac{Q}{4} }\hbox {d}\sigma ~ \left\| u\right\| _{ X_s(T)}^p \end{aligned}$$

(4.12)

$$\begin{aligned}&\qquad +(1+t)^{-p ( \frac{\gamma }{2}+\frac{Q}{4} )+ \frac{\gamma }{2}+\frac{Q}{4} } \int _{\frac{t}{2}}^t(1+t-\sigma )^{-\frac{\gamma }{2}} \mathrm {~d} \sigma \Vert u\Vert _{X_s(T)}^p . \end{aligned}$$

(4.13)

For $p>1+\frac{4}{Q+2 \gamma },$ the integral given in (4.12) converges uniformly over $\left[ 0, \frac{t}{2}\right]$. Now we will compute the integral given in (4.13) precisely. Now

$$\begin{aligned} \int _{\frac{t}{2}}^t(1+t-\sigma )^{-\frac{\gamma }{2}} \mathrm {~d} \sigma \lesssim \left\{ \begin{array}{ll} (1+t)^{1-\frac{\gamma }{2}} &{} \text{ if } \gamma <2, \\ \ln (\textrm{e}+t) &{} \text{ if } \gamma =2, \\ 1 &{} \text{ if } \gamma >2. \end{array}\right. \end{aligned}$$

(4.14)

Thus by considering $p>1+\frac{4}{Q+2 \gamma }$ if $\gamma \leqslant 2$ and using the integral estimate (4.14), we get

$$\begin{aligned}&(1+t)^{-\left( \frac{\gamma }{2}+\frac{Q}{4}\right) p+\frac{\gamma }{2}+\frac{Q}{4}} \int _{\frac{t}{2}}^t(1+t-\sigma )^{-\frac{\gamma }{2}} {~d} \sigma \\&\quad \leqslant (1+t)^{-1} \int _{\frac{t}{2}}^t(1+t-\sigma )^{-\frac{\gamma }{2}} {~d} \sigma \lesssim (1+t)^{-\frac{\gamma }{2}}. \end{aligned}$$

Again by considering $p>1+\frac{2 \gamma }{Q+2 \gamma }$ if $\gamma >2$ and using the integral estimate (4.14), a simple calculation yields

$$\begin{aligned} (1+t)^{-\left( \frac{\gamma }{2}+\frac{Q}{4}\right) p+\frac{\gamma }{2}+\frac{Q}{4}} \int _{\frac{t}{2}}^t(1+t-\sigma )^{-\frac{\gamma }{2}} {~d} \sigma \lesssim (1+t)^{-\frac{\gamma }{2}} . \end{aligned}$$

Summarizing all the estimates, it holds that

$$\begin{aligned} (1+t)^{\frac{\gamma }{2}} \Vert u^{\text {non}}(t, \cdot )\Vert _{L^2} \lesssim \left\| u\right\| _{ X_s(T)}^p. \end{aligned}$$

(4.15)

Now we will estimate ${\dot{H}}_\mathcal {L}^s$-norm of the solution. Similar to the previous argument, we use $\left( L^2 \cap \dot{H}_\mathcal {L}^{-\gamma }\right) -{\dot{H}}_\mathcal {L}^s$ estimate (4.3) in $\left[ 0, \frac{t}{2}\right]$ and the $L^2-\dot{H}_\mathcal {L}^s$ estimate (4.2) in $\left[ \frac{t}{2}, t\right]$ to estimate the solution itself in $\dot{H}_\mathcal {L}^s$. Thus,

$$\begin{aligned} \left\| u^{\textrm{non}}(t, \cdot )\right\| _{{\dot{H}}_\mathcal {L}^s}&\leqslant \int \limits _0^t \Vert |u(\sigma ,\cdot )|^p*_{(g)} E_1(t-\sigma , \cdot ) \Vert _{{\dot{H}}_\mathcal {L}^s} \hbox {d}\sigma \nonumber \\&\lesssim \int _0^{\frac{t}{2}}(1+t-\sigma )^{-\frac{(s+\gamma )}{2}} (1+\sigma )^{-p ( \frac{\gamma }{2}+\frac{Q}{4} )+ \frac{\gamma }{2}+\frac{Q}{4} }\hbox {d}\sigma ~ \left\| u\right\| _{ X_s(T)}^p\nonumber \\ {}&\qquad + \int _{\frac{t}{2}}^t (1+t-\sigma )^{-\frac{s}{2}} (1+\sigma )^{-p ( \frac{\gamma }{2}+\frac{Q}{4} )+\frac{Q}{4} } \mathrm {~d} \sigma \Vert u\Vert _{X_s(T)}^p \nonumber \\ {}&\lesssim (1+t)^{-\frac{(s+\gamma )}{2}} \int _0^{\frac{t}{2}}(1+\sigma )^{-p ( \frac{\gamma }{2}+\frac{Q}{4} )+ \frac{\gamma }{2}+\frac{Q}{4} }\hbox {d}\sigma ~ \left\| u\right\| _{ X_s(T)}^p \nonumber \\ {}&\qquad +(1+t)^{-p ( \frac{\gamma }{2}+\frac{Q}{4} )+\frac{Q}{4} } \int _{\frac{t}{2}}^t(1+t-\sigma )^{-\frac{s}{2}} \mathrm {~d} \sigma \Vert u\Vert _{X_s(T)}^p . \end{aligned}$$

(4.16)

For $p>1+\frac{4}{Q+2 \gamma }$, summarizing as previously, we have

$$\begin{aligned} (1+t)^{\frac{s+\gamma }{2}}\left\| u^{ \text {non}}(t, \cdot )\right\| _{{\dot{H}}_\mathcal {L}^s} \lesssim \Vert u\Vert _{X_s(T)}^p . \end{aligned}$$

(4.17)

Therefore from (4.17) and (4.15), we obtain

$$\begin{aligned} \left\| u^{ \text {non}}(t, \cdot )\right\| _{X_s(T)} \lesssim \Vert u\Vert _{X_s(T)}^p, \end{aligned}$$

under the conditions on p as follows:

• $1< p \leqslant \frac{Q}{Q-2\,s}$, from the application of the Gagliardo–Nirenberg inequality,

• $p>1+\frac{4}{Q+2 \gamma }$ if $\gamma \leqslant 2$,

• $p>1+\frac{2 \gamma }{Q+2 \gamma }$ if $\gamma >2$, from the integrability and decay estimates of solution.

• $p \geqslant 1+\frac{2 \gamma }{Q}$, from the application of the Gagliardo–Nirenberg inequality.

First, we consider the case $\gamma >2.$ Then, we observe that

$$\begin{aligned} \max \left\{ 1+\frac{2 \gamma }{Q+2 \gamma }, 1+\frac{2 \gamma }{Q}\right\} =1+\frac{2 \gamma }{Q}. \end{aligned}$$

Now for $\gamma \leqslant 2$, we have to compare between $1+\frac{4}{Q+2 \gamma }$ and $1+\frac{2 \gamma }{Q}$. Notice that $1+\frac{4}{Q+2 \gamma }$ and $1+\frac{2 \gamma }{Q}$ intersects at a point $\tilde{\gamma }$, which is the positive root of the quadratic equation $2\gamma ^2+Q\gamma -2Q=0$. Moreover, it is easy to check that the positive root ${{\tilde{\gamma }}}<2$ for all $Q\geqslant 4.$ This shows that

• $\max \left\{ 1+\frac{4}{Q+2 \gamma }, 1+\frac{2 \gamma }{Q} \right\} =1+\frac{4}{Q+2 \gamma }$ for $\gamma \leqslant {\tilde{\gamma }}$,

• $\max \left\{ 1+\frac{4}{Q+2 \gamma }, 1+\frac{2 \gamma }{Q} \right\} =1+\frac{2 \gamma }{Q}$ for ${\tilde{\gamma }}<\gamma \leqslant 2$.

Finally, for any $\gamma \in (0, \frac{Q}{2})$, the condition for the exponent p is reduced to

$$\begin{aligned} p\left\{ \begin{array}{ll}>1+\frac{4}{Q+2 \gamma } =p_{\text{ crit } }(Q, \gamma ) &{} \text{ if } \gamma \leqslant {\tilde{\gamma }}, \\ \geqslant 1+\frac{2 \gamma }{Q} &{} \text{ if } \gamma >{\tilde{\gamma }}. \end{array}\right. \end{aligned}$$

Furthermore, we have

$$\begin{aligned} \Vert N u\Vert _{X_s(T)} \lesssim \left\| \left( u_{0}, u_{1}\right) \right\| _{ { \mathcal {A}_{\mathcal {L}}^{s, -\gamma }}}+\Vert u\Vert _{X_s(T)}^{p}. \end{aligned}$$

(4.18)

Now we will calculate $\Vert N u-N {\bar{u}}\Vert _{X_s(T)}$. In order to do that, we first notice that

$$\begin{aligned} \Vert N u-N {\bar{u}}\Vert _{X_s(T)}=\left\| \int _0^t E_1(t-\sigma , \cdot )*_{(g)}\left( |u(\sigma , \cdot )|^p-|{\bar{u}}(\sigma , \cdot )|^p\right) {d} \sigma \right\| _{X_s(T)}. \end{aligned}$$

Similar to (4.11), using the Hardy–Littlewood–Sobolev inequality (Theorem 2.1), we have

$$\begin{aligned} \left\| |u(\sigma , \cdot )|^p-|{\bar{u}}(\sigma , \cdot )|^p \right\| _{\dot{H}^{-\gamma }_{\mathcal {L}}} \lesssim \left\| |u(\sigma , \cdot )|^p-|{\bar{u}}(\sigma , \cdot )|^p\right\| _{L^{m}} \end{aligned}$$

with $\frac{1}{m}-\frac{1}{2}=\frac{\gamma }{Q}$ provided that $0<\gamma <Q$ and $1<m<2$. An application of Hölder’s inequality yields

$$\begin{aligned} \left\| |u(\sigma , \cdot )|^p-|{\bar{u}}(\sigma , \cdot )|^p\right\| _{L^m} \lesssim \Vert u(\sigma , \cdot )-{\bar{u}}(\sigma , \cdot )\Vert _{L^{m p}}\left( \Vert u(\sigma , \cdot )\Vert _{L^{m p}}^{p-1}+\Vert {\bar{u}}(\sigma , \cdot )\Vert _{L^{m p}}^{p-1}\right) . \end{aligned}$$

(4.19)

Again, the Gagliardo–Nirenberg inequality (Theorem 2.2) implies that

$$\begin{aligned}&\left\| u(\sigma , \cdot )-{\bar{u}}(\sigma , \cdot )\right\| _{L^{mp}}\nonumber \\ {}&\lesssim \Vert u(\sigma , \cdot )-{\bar{u}}(\sigma , \cdot )\Vert _{\dot{H}_\mathcal {L}^s(\mathbb {H}^n)}^{\theta _3} \Vert u(\sigma , \cdot )-{\bar{u}}(\sigma , \cdot )\Vert _{L^2(\mathbb {H}^n)}^{(1-\theta _3)}\nonumber \\&= (1+\sigma )^{-\left( \frac{\gamma }{2}+\frac{s\theta _3}{2}\right) } \left\{ (1+\sigma )^{\frac{(s+\gamma )}{2} } \Vert u(\sigma , \cdot )-{\bar{u}}(\sigma , \cdot )\Vert _{{\dot{H}}_\mathcal {L}^s(\mathbb {H}^n)} \right\} ^{\theta _3} \nonumber \\ {}&\qquad \times \left\{ (1+\sigma )^{\frac{\gamma }{2} } \Vert u(\sigma , \cdot )-{\bar{u}}(\sigma , \cdot )\Vert _{L^2(\mathbb {H}^n)}\right\} ^{(1-\theta _3)}\nonumber \\&\lesssim (1+\sigma )^{ -\left( \frac{\gamma }{2}+\frac{s\theta _3}{2}\right) } \left\| u(\sigma , \cdot )-{\bar{u}}(\sigma , \cdot )\right\| _{ X_s(T)}, \end{aligned}$$

(4.20)

and

$$\begin{aligned}&\left\| u(\sigma , \cdot )\right\| _{L^{mp}}^{p-1}\nonumber \\&\lesssim \Vert u(\sigma , \cdot )\Vert _{\dot{H}_\mathcal {L}^s(\mathbb {H}^n)}^{(p-1)\theta _3} \Vert u(\sigma , \cdot )\Vert _{L^2(\mathbb {H}^n)}^{(p-1)(1-\theta _3)}\nonumber \\&= (1+\sigma )^{-\frac{(p-1)}{2} (s\theta _3+\gamma )} \left\{ (1+\sigma )^{\frac{(s+\gamma )}{2} } \Vert u(\sigma , \cdot )\Vert _{{\dot{H}}_\mathcal {L}^s(\mathbb {H}^n)} \right\} ^{(p-1)\theta _3} \nonumber \\&\quad \times \left\{ (1+\sigma )^{\frac{\gamma }{2} } \Vert u(\sigma , \cdot )\Vert _{L^2(\mathbb {H}^n)}\right\} ^{(p-1)(1-\theta _3)}\nonumber \\&\lesssim (1+\sigma )^{-\frac{(p-1)}{2} (s\theta _3+\gamma )} \left\| u\right\| _{ X_s(T)}^{p-1}, \end{aligned}$$

(4.21)

for $\sigma \in [0, T]$ with $\theta _3=\frac{Q}{s}(\frac{1}{2}-\frac{1}{mp})\in [0, 1]$. Thus from (4.19), (4.20), and (4.21), we finally have

$$\begin{aligned}&\left\| |u(\sigma , \cdot )|^p-|{\bar{u}}(\sigma , \cdot )|^p \right\| _{\dot{H}^{-\gamma }_{\mathcal {L}}} \\&\quad \lesssim (1+\sigma )^{-\left( \frac{p-1}{2}+\frac{1}{2}\right) (\gamma {+}{Q}(\frac{1}{2}-\frac{1}{mp}))} \left\| u(\sigma , \cdot ){-}{\bar{u}}(\sigma , \cdot )\right\| _{ X_s(T)}\left( \Vert u\Vert _{X_s(T)}^{p-1}+\Vert {\bar{u}}\Vert _{X_s(T)}^{p-1}\right) \\&\quad \lesssim (1+\sigma )^{- \frac{p}{2}(1-\frac{1}{p})(\gamma +\frac{Q}{2}) } \left\| u(\sigma , \cdot )-{\bar{u}}(\sigma , \cdot )\right\| _{ X_s(T)}\left( \Vert u\Vert _{X_s(T)}^{p-1}+\Vert {\bar{u}}\Vert _{X_s(T)}^{p-1}\right) \\&\quad \lesssim (1+\sigma )^{-\left( \frac{\gamma }{2}+\frac{Q}{4}\right) p+\frac{\gamma }{2}+\frac{Q}{4}} \left\| u(\sigma , \cdot )-{\bar{u}}(\sigma , \cdot )\right\| _{ X_s(T)}\left( \Vert u\Vert _{X_s(T)}^{p-1}+\Vert {\bar{u}}\Vert _{X_s(T)}^{p-1}\right) . \end{aligned}$$

Now using the given range of p, we get

$$\begin{aligned} \Vert N u-N {\bar{u}}\Vert _{X_s(T)} \leqslant C \Vert u-{\bar{u}}\Vert _{X_s(T)}\left( \Vert u\Vert _{X_s(T)}^{p-1}+\Vert {\bar{u}}\Vert _{X_s(T)}^{p-1}\right) , \end{aligned}$$

(4.22)

for any $u, {{\bar{u}}} \in X_s(T)$ and for some $C>0.$ Also from (4.18), we obtain

$$\begin{aligned} \Vert N u\Vert _{X_s(T)} \leqslant D\left\| \left( u_{0}, u_{1}\right) \right\| _{ { \mathcal {A}_{\mathcal {L}}^{s, -\gamma }}}+D\Vert u\Vert _{X_s(T)}^{p}, \end{aligned}$$

(4.23)

for some $D>0$ with initial data space ${ \mathcal {A}_{\mathcal {L}}^{s, -\gamma }}: =(H^s_{\mathcal {L}}\cap \dot{H}^{-\gamma }_{\mathcal {L}}) \times (L^2\cap \dot{H}^{-\gamma }_{\mathcal {L}})$.

Therefore, by Banach’s fixed point theorem, there exists a uniquely determined fixed point $u^*$ of the operator N, which means $u^*=Nu^* \in X_s(T)$ for all positive T. This fixed point $u^*$ will be our mild solution to (1.1) on [0, T]. This implies that there exists a global (in-time) small data Sobolev solution $u^*$ of the equation $u^*=Nu^*$ in $X_s(T)$, which also gives the solution to the semilinear damped wave equation (1.1) and this completes the proof of the theorem. $\square$

5 Blow-up analysis of solutions: a test function method

Proof of Theorem 1.5

In order to prove this result, we apply the so-called test function method. By contradiction, we assume that there exists a global-in-time weak solution u to (1.1). Let us consider two bump functions $\alpha \in \mathcal {C}_0^{\infty }(\mathbb {R}^n)$ and $\beta \in \mathcal {C}_0^{\infty }(\mathbb {R})$ such that

$$\begin{aligned} \alpha =1 ~\text{ on }~ B_n\left( \frac{1}{2}\right) ~ \text{ with } ~{\text{ supp }}~ \alpha \subset B_n(1) \end{aligned}$$

and

$$\begin{aligned} \beta =1 ~\text{ on }~ \left[ -\frac{1}{4}, \frac{1}{4}\right] ~\text{ with }~ {\text{ supp }}~ \beta \subset (-1,1). \end{aligned}$$

If $R>1$ is a parameter, then, we define the test function $\varphi _R \in \mathcal {C}_0^{\infty }\left( [0, \infty ) \times \mathbb {R}^{2 n+1}\right)$ with separate variables as

$$\begin{aligned} \varphi _R(t, x, y, \tau ) \doteq \beta \left( \frac{t}{R^2}\right) \alpha \left( \frac{x}{R}\right) \alpha \left( \frac{y}{R}\right) \beta \left( \frac{\tau }{R^2}\right) , \quad (t, x, y, \tau ) \in [0, \infty ) \times \mathbb {R}^{2 n+1}. \end{aligned}$$

Let $\mathcal {D}_R:= B_{n}(R) \times B_{n}(R) \times \left[ -R^{2}, R^{2}\right]$. Then using support of $\alpha$ and $\beta$, we can conclude that ${\text{ supp }} ~\varphi _{R} \subset \left[ 0, R^{2}\right] \times \mathcal {D}_R$. Furthermore, a simple calculation yields

$$\begin{aligned} \partial _t \varphi _R(t, x, y, \tau )&=R^{-2} \beta ^{\prime }\left( \frac{t}{R^2}\right) \alpha \left( \frac{x}{R}\right) \alpha \left( \frac{y}{R}\right) \beta \left( \frac{\tau }{R^2}\right) , \\ \partial _t^2 \varphi _R(t, x, y, \tau )&=R^{-4} \beta ^{\prime \prime }\left( \frac{t}{R^2}\right) \alpha \left( \frac{x}{R}\right) \alpha \left( \frac{y}{R}\right) \beta \left( \frac{\tau }{R^2}\right) . \end{aligned}$$

Moreover, from the following expression of the sublaplacian

$$\begin{aligned} \mathcal {L}=\Delta +\frac{1}{4}(|x|^2+|y|^2) \partial _\tau ^2+\sum _{j=1}^n\left( x_j \partial _{y_j \tau }^2-y_j \partial _{x_j \tau }^2\right) , \end{aligned}$$

we have

$$\begin{aligned} \mathcal {L}\varphi _{R}(t, x, y, \tau )&= R^{-2} \beta \left( \frac{t}{R^{2}}\right) \Delta \alpha \left( \frac{x}{R}\right) \alpha \left( \frac{y}{R}\right) \beta \left( \frac{\tau }{R^{2}}\right) \\ {}&+R^{-2} \beta \left( \frac{t}{R^{2}}\right) \alpha \left( \frac{x}{R}\right) \Delta \alpha \left( \frac{y}{R}\right) \beta \left( \frac{\tau }{R^{2}}\right) \\&\quad +R^{-3} \sum _{j=1}^{n} x_{j} \beta \left( \frac{t}{R^{2}}\right) \alpha \left( \frac{x}{R}\right) \partial _{j} \alpha \left( \frac{y}{R}\right) \beta ^{\prime }\left( \frac{\tau }{R^{2}}\right) \\&\quad -R^{-3} \sum _{j=1}^{n} y_{j} \beta \left( \frac{t}{R^{2}}\right) \partial _{j} \alpha \left( \frac{x}{R}\right) \alpha \left( \frac{y}{R}\right) \beta ^{\prime }\left( \frac{\tau }{R^{2}}\right) \\&\quad +\frac{1}{4} R^{-4}\left( |x|^{2}+|y|^{2}\right) \beta \left( \frac{t}{R^{2}}\right) \alpha \left( \frac{x}{R}\right) \alpha \left( \frac{y}{R}\right) \beta ^{\prime \prime }\left( \frac{\tau }{R^{2}}\right) , \end{aligned}$$

where $\Delta$ denotes the Laplace operator on $\mathbb {R}^{n}$.

From the condition $0 \leqslant \alpha , \beta \leqslant 1$, we can get $\alpha \leqslant \alpha ^{\frac{1}{p}}$ and $\beta \leqslant \beta ^{\frac{1}{p}}$. Moreover, using the following bounds

$$\begin{aligned} \begin{aligned}&\left| \partial _j \alpha \right| \lesssim \alpha ^{\frac{1}{p}} \quad \quad \text{ for } \text{ any } 1 \leqslant j \leqslant n, \\ {}&\left| \partial _j \partial _k \alpha \right| \lesssim \alpha ^{\frac{1}{p}} \quad \text{ for } \text{ any } 1 \leqslant j, k \leqslant n, \\&\left| \beta ^{\prime }\right| \lesssim \beta ^{\frac{1}{p}}, \quad \left| \beta ^{\prime \prime }\right| \lesssim \beta ^{\frac{1}{p}}, \end{aligned} \end{aligned}$$

we immediately get

$$\begin{aligned} \begin{aligned} \left| \partial _{t} \varphi _{R}\right|&\lesssim R^{-2}\left( \varphi _{R}\right) ^{\frac{1}{p}}, \\ \left| \partial _{t}^{2} \varphi _{R}\right|&\lesssim R^{-4}\left( \varphi _{R}\right) ^{\frac{1}{p}} \lesssim R^{-2}\left( \varphi _{R}\right) ^{\frac{1}{p}}, \text {and}\\ \left| \mathcal {L}\varphi _{R}\right|&\lesssim R^{-2}\left( \varphi _{R}\right) ^{\frac{1}{p}}. \end{aligned} \end{aligned}$$

Let

$$\begin{aligned} I_R= \int _0^T \int _{\mathbb {H}^n}|u(t, \eta )|^p \varphi _R(t, \eta ) \;\hbox {d}\eta \;\hbox {d}t. \end{aligned}$$

Now from (1.12) with keeping in mind the fact $\partial _t \varphi _R \leqslant 0$ (by choosing the factor $\beta$ appropriately, for example, let $\beta$ be even and non-increasing in $[0, \infty )$), an application of Hölder’s and Young’s inequalities yields

$$\begin{aligned}&\int _0^T \int _{\mathbb {H}^n}|u(t, g)|^p \varphi _R(t, g) \;\hbox {d}g \;\hbox {d}t+ \varepsilon \int _{\mathbb {H}^n}\left( u_0(g)+u_1(g)\right) \varphi _R(0, g) \;\hbox {d}g \nonumber \\ {}&\quad \leqslant \int _0^T \int _{\mathbb {H}^n} |u(t, g)|\left( |\partial _t^2 \varphi _R(t, g)|+|\mathcal {L}\varphi _R(t, g)|+|\partial _t \varphi _R(t, g)|\right) \;\hbox {d}g \;\hbox {d}t\nonumber \\&\quad \lesssim R^{-2} \int _0^T \int _{\mathbb {H}^n} |u(t, g)||\varphi _R(t, g)|^{\frac{1}{p}} \;\hbox {d}g\;\hbox {d}t \nonumber \\&\quad \leqslant C R^{-2}\left( \int _{0}^{\infty } \int _{\mathbb {H}^{n}}|u(t, g)|^{p} \varphi _{R}(t, g) \;\hbox {d}g \;\hbox {d} t\right) ^{\frac{1}{p}}\left( \int _{\left[ 0, R^{2}\right] \times \mathcal {D}_R } \hbox {d}t\;\hbox {d}g \right) ^{\frac{1}{p^{\prime }}}\nonumber \\ {}&= CR^{-2} I_R^{\frac{1}{p}} R^{\frac{2+Q}{p^{\prime }}}=C R^{-2+\frac{Q+2}{p^{\prime }}}I_R^{\frac{1}{p}}\nonumber \\ {}&\quad \leqslant \frac{I_R}{p}+\frac{ C R^{Q+2-2p^{\prime }}}{p^{\prime }}, \end{aligned}$$

(5.1)

where in (5.1), we used the fact that ${\text {meas}} (\mathcal {D}_R) \approx R^Q$. Therefore,

$$\begin{aligned}&\int _0^T \int _{\mathbb {H}^n}|u(t, g)|^p \varphi _R(t, g) \;\hbox {d}g \;\hbox {d}t\nonumber \\&\quad \leqslant \frac{I_R}{p}+\frac{CR^{Q+2-2p^{\prime }}}{p^{\prime }}- \varepsilon \int _{\mathbb {H}^n}(u_0(g)+u_1(g) ) \varphi _R(0, g) \;\hbox {d}g. \end{aligned}$$

(5.2)

Now using our assumption (1.13), it remains to find estimate for

$$\begin{aligned} \int _{\mathbb {H}^n}\left( u_{0}(g)+u_{1}(g)\right) \varphi _{R}(0,g)\hbox {d}g. \end{aligned}$$

Before that, we have to justify that the set of all initial data $\left( u_0, u_1\right)$ in ${\dot{H}}_\mathcal {L}^{-\gamma } \times \dot{H}_\mathcal {L}^{-\gamma }$ with the assumptions (1.13), is non-empty. For that, we denote the set $\mathcal {D}_{Q, \gamma }$ as

$$\begin{aligned} \mathcal {D}_{Q, \gamma }&:=\{\left( u_{0}, u_{1}\right) \in { L^1_{\text {loc}}(\mathbb {H}^n) \times L^1_{\text {loc}}(\mathbb {H}^n)}: u_0(g)+u_1(g)\\&\geqslant C_0 \langle g \rangle ^{-Q\left( \frac{1}{2}+\frac{\gamma }{Q}\right) }(\log (e+|g|))^{-1}\}, \end{aligned}$$

then first we claim that $\mathcal {D}_{Q, \gamma } \cap \left( L^{\frac{2Q}{Q+2\gamma }} \times L^{\frac{2Q}{Q+2\gamma }} \right) \ne \emptyset$ for $\frac{2Q}{Q+2\gamma }>1$. In particular, consider the functions

$$\begin{aligned} u_{0}(g)=u_{1}(g)&= C_0 \langle g \rangle ^{-Q\left( \frac{1}{2}+\frac{\gamma }{Q}\right) }(\log (e+|g|))^{-1}. \end{aligned}$$

Then using the polar decomposition (see Proposition (1.15) in [9]) for $\mathbb {H}^n$, we have

$$\begin{aligned} \begin{aligned} \int _{\mathbb {H}^n}|u_{0}(g)| ^{\frac{2Q}{Q+2\gamma }} {d} g&= C_0^{\frac{2Q}{Q+2\gamma }} \int _{\mathbb {H}^n}\langle g \rangle ^{-Q\left( \frac{1}{2}+\frac{\gamma }{Q}\right) \times \frac{2Q}{Q+2\gamma }}(\log (e+|g|))^{-\frac{2Q}{Q+2\gamma }}\;\hbox {d}g\\&= C_0^{\frac{2Q}{Q+2\gamma }} \int _{\mathbb {H}^n}\langle g \rangle ^{-Q }(\log (e+|g|))^{-\frac{2Q}{Q+2\gamma }}\;\hbox {d}g\\&\lesssim C_0^{\frac{2Q}{Q+2\gamma }} \int _{0}^{\infty } \langle r \rangle ^{-Q} r^{Q-1}(\log (\textrm{e}+ r))^{-\frac{2Q}{Q+2\gamma }}\hbox {d}r\\&= C_0^{\frac{2Q}{Q+2\gamma }} \int _{0}^{\infty } \langle r \rangle ^{-1} (\log (\textrm{e}+ r))^{-\frac{2Q}{Q+2\gamma }}\hbox {d}r<\infty , \end{aligned} \end{aligned}$$

for $\frac{2Q}{Q+2\gamma }>1$. This implies that $u_{0}, u_{1} \in L^{\frac{2Q}{Q+2\gamma }}$. Since $\frac{Q+2 \gamma }{2 Q}-\frac{1}{2}=\frac{\gamma }{Q}$ with $\gamma \in \left( 0, \frac{Q}{2}\right)$, according to the Hardy–Littlewood–Sobolev inequality (Theorem 2.1), we have $L^{\frac{2Q}{Q+2\gamma }} \subset {\dot{H}}_\mathcal {L}^{-\gamma }$. Therefore, in every instance, we can deduce that

$$\begin{aligned} \mathcal {D}_{Q, \gamma } \cap \left( \dot{H}_\mathcal {L}^{-\gamma }\times {\dot{H}}_\mathcal {L}^{-\gamma } \right) \ne \emptyset , \quad \text {for} ~\gamma \in \left( 0, \frac{Q}{2}\right) . \end{aligned}$$

Now from our assumption (1.13), for $R \gg 1$, we obtain

$$\begin{aligned}&\int _{\mathbb {H}^n}\left( u_{0}(g)+u_{1}(g)\right) \varphi _{R}(0, g)\;\hbox {d}g \nonumber \\&\geqslant C_0 \int _{\mathcal {D}_R} \langle g \rangle ^{-Q\left( \frac{1}{2}+\frac{\gamma }{Q}\right) }(\log (e+|g|))^{-1} \,\hbox {d}g \nonumber \\&\geqslant C_0 R^{Q-Q(\frac{1}{2}+\frac{\gamma }{Q} )}(\log R)^{-1}= C_0 R^{\frac{Q}{2}-\gamma } (\log R)^{-1}. \end{aligned}$$

(5.3)

Thus from (5.2) and (5.3), we have

$$\begin{aligned} I_R= \int _0^T \int _{\mathbb {H}^n}|u(t, g)|^p \varphi _R(t, g) \;\hbox {d}g \;d t\leqslant \frac{I_R}{p}{+}\frac{CR^{Q+2-2p^{\prime }}}{p^{\prime }}{-} \varepsilon C_0 R^{\frac{Q}{2}-\gamma }(\log R)^{-1} , \end{aligned}$$

which further implies that

$$\begin{aligned} 0\leqslant \Big (1-\frac{1}{p}\Big ) I_R \leqslant \frac{CR^{Q+2-2p^{\prime }}}{p^{\prime }}- \varepsilon C_0 R^{\frac{Q}{2}-\gamma }(\log R)^{-1}. \end{aligned}$$

(5.4)

By the assumption $p \in \left( 1, 1+\frac{4}{Q+2\gamma }\right) ,$ we have $Q+2-2p^{\prime }-\frac{Q}{2}+\gamma <0$ and therefore, it is easy to see that

$$\begin{aligned} R^{Q+2-2p^{\prime }-\frac{Q}{2}+\gamma } \log R < \frac{\varepsilon C_0 p^{\prime }}{C}, \end{aligned}$$

(5.5)

for $R \gg 1.$

Hence, from (5.4) and (5.5), we obtain

$$\begin{aligned} 0\leqslant \Big (1-\frac{1}{p}\Big ) I_R \leqslant \frac{CR^{Q+2-2p^{\prime }}}{p^{\prime }}- \varepsilon C_0 R^{\frac{Q}{2}-\gamma }(\log R)^{-1}<0, \end{aligned}$$

which is a contradiction. This completes the proof of the blow-up result.

Since the scaling factor $R^2$, appeared in the bump function $\beta$ with respect to the time varibale, has to be dominated by the lifespan $T_{w,\varepsilon }$ of the weak solution in order to guarantee $\varphi _R \in \mathcal {C}_0^{\infty }([0, T) \times \mathbb {H}^n)$, to generate upper bound estimate for the lifespan, we consider $R \uparrow T_{w,\varepsilon }^{ \frac{1}{2}}$ in (5.4). As a result, a contradiction (similar to (5.4)) exists if

$$\begin{aligned} \frac{T_{w,\varepsilon }^{\frac{Q+2}{2}-p^{\prime }}}{p^{\prime }}<C \varepsilon T_{w,\varepsilon }^{\frac{Q-2\gamma }{4}}(\log T_{w,\varepsilon })^{-1}. \end{aligned}$$

In other words

$$\begin{aligned} T_{w,\varepsilon } \leqslant C\varepsilon ^{-\left( \frac{1}{p-1}-\left( \frac{Q}{4}+\frac{\gamma }{2}\right) \right) ^{-1}}, \end{aligned}$$

which is the desired lifespan for the local-in-time weak solutions to the Cauchy problem (1.1), where the constant C is positive and independent of $\varepsilon$ and p. $\square$

6 Sharp lifespan estimates of solutions

The aim of this section is to find the lower bound estimates of lifespan. We will make use of certain notations, specifically, the evolution space $X_1(T)$ and the data space $\mathcal {A}_1^{\mathcal {L}}$, introduced in Sect. 1. As we are now considering the case where $1< p < p_{\text {crit}}(Q, \gamma )$, in order to obtain lower limit estimates for the lifespan, we will use a different nonlinear inequality instead of (4.5).

Proof of Theorem 1.7

Here, we note that using the definition of mild solutions (1.10), we can estimate and express local-in-time mild solutions directly. Proceeding in a similar way as to establish (4.12)–(4.13) in Sect. 4, we get

$$\begin{aligned} (1+t)^{\frac{\gamma }{2}}\Vert u(t, \cdot )\Vert _{L^2} \lesssim&\varepsilon \left\| \left( u_0, u_1\right) \right\| _{\mathcal {A}_1^{\mathcal {L}}}+ \int _0^{\frac{t}{2}}(1+\sigma )^{-p ( \frac{\gamma }{2}+\frac{Q}{4} )+ \frac{\gamma }{2}+\frac{Q}{4} }\hbox {d}\sigma ~ \left\| u\right\| _{ X_1(T)}^p\nonumber \\&+(1+t)^{-p ( \frac{\gamma }{2}+\frac{Q}{4} )+ \frac{\gamma }{2}+\frac{Q}{4} +1} \Vert u\Vert _{X_1(T)}^p \end{aligned}$$

(6.1)

because of $\gamma \in (0, 2 )$, where we restricted p as

$$\begin{aligned} 1+\frac{2 \gamma }{Q} \leqslant p \leqslant \frac{Q}{Q-2}, \end{aligned}$$

for the application of the Gagliardo–Nirenberg inequality. Since $1<p<p_{\text{ crit } }(Q, \gamma )=1+\frac{4}{Q+2\gamma }$, this implies that

$$\begin{aligned} -p \left( \frac{\gamma }{2}+\frac{Q}{4} \right) + \frac{\gamma }{2}+\frac{Q}{4} > - \frac{2\gamma +Q}{4} \left( 1+\frac{4}{Q+2\gamma }\right) + \frac{2\gamma +Q}{4}=-1. \end{aligned}$$

Therefore, from (6.1), we have

$$\begin{aligned} (1+t)^{\frac{\gamma }{2}}\Vert u(t, \cdot )\Vert _{L^2} \lesssim \varepsilon \left\| \left( u_0, u_1\right) \right\| _{\mathcal {A}_1^{\mathcal {L}}}+(1+t)^{-p\left( \frac{\gamma }{2}+\frac{Q}{4}\right) +\frac{Q}{4}+\frac{\gamma }{2}+1}\Vert u\Vert _{X_1(T)}^p . \end{aligned}$$

(6.2)

Choosing $s=1$ in (4.16) leads to

$$\begin{aligned} (1+t)^{\frac{1+\gamma }{2}} \left\| u(t, \cdot )\right\| _{\dot{H}_\mathcal {L}^1} \lesssim \varepsilon \left\| \left( u_0, u_1\right) \right\| _{\mathcal {A}_1^{\mathcal {L}}} +(1+t)^{-p ( \frac{\gamma }{2}+\frac{Q}{4} )+\frac{Q}{4} +\frac{\gamma }{2}+1} \Vert u\Vert _{X_1(T)}^p . \end{aligned}$$

(6.3)

Thus from (6.2) and (6.3), we can say that

$$\begin{aligned} \Vert u\Vert _{X_1(T)} \leqslant \varepsilon C+D (1+t)^{\alpha (p, Q, \gamma )}\Vert u\Vert _{X_1(T)}^p, \end{aligned}$$

(6.4)

where $\alpha (p, Q, \gamma ):=-p ( \frac{\gamma }{2}+\frac{Q}{4} )+\frac{Q}{4} +\frac{\gamma }{2}+1\in (0,1)$, and C, D are two positive constants independent of $\varepsilon$ and T.

Now let us now introduce

$$\begin{aligned} T^*:=\sup \left\{ T \in \left[ 0, T_{m,\varepsilon }\right) \text{ such } \text{ that } \mathcal {G}(T):=\Vert u\Vert _{X_1(T)} \leqslant M \varepsilon \right\} \end{aligned}$$

with a large enough constant $M>0$, which we shall select later. As a result, from (6.4) and the fact that $\mathcal {G}\left( T^*\right) \leqslant M \varepsilon$, we obtain

$$\begin{aligned} \mathcal {G}\left( T^*\right)&=\Vert u\Vert _{X_1(T^*)} \nonumber \\&\leqslant \left( \varepsilon C+D\left( 1+T^*\right) ^{\alpha (p, Q, \gamma )} M^p \varepsilon ^{p}\right) \nonumber \\&= \varepsilon \left( C+D\left( 1+T^*\right) ^{\alpha (p, Q, \gamma )} M^p \varepsilon ^{p-1}\right) <M \varepsilon \end{aligned}$$

(6.5)

for large M, provided $2C<M$ and

$$\begin{aligned} 2D\left( 1+T^*\right) ^{\alpha (p,Q, \gamma )} M^{p-1} \varepsilon ^{p-1}<1. \end{aligned}$$

It is important to note that the function $\mathcal {G}=\mathcal {G}(T)$ is continuous for $T \in \left( 0, T_{m,\varepsilon }\right)$. Nonetheless, (6.5) demonstrates that there exists a time $T_0 \in \left( T^*, T_{m,\varepsilon } \right)$ such that $\mathcal {G}\left( T_0\right) \leqslant M \varepsilon$, which contradicts to the assumption that $T^*$ is the supremum. To put it another way, we must enforce the following condition:

$$\begin{aligned} D\left( 1+T^*\right) ^{\alpha (p, Q, \gamma )} M^{p-1} \varepsilon ^{p-1} \geqslant 1. \end{aligned}$$

This implies that

$$\begin{aligned} 1+T^* \geqslant D^{-\frac{1}{\alpha (p, Q, \gamma )}} M^{-\frac{p-1}{\alpha (p, Q, \gamma )}}\varepsilon ^{-\frac{p-1}{\alpha (p, Q, \gamma )}}. \end{aligned}$$

This implies that we can deduce the blow-up time estimate as

$$\begin{aligned} T_{m,\varepsilon } \geqslant D \varepsilon ^{-\left( \frac{1}{p-1}-\left( \frac{Q}{4}+\frac{\gamma }{2}\right) \right) ^{-1}}. \end{aligned}$$

This completes the proof of the theorem regarding lower bound estimates of lifespan. $\square$

Remark 6.1

We believe that the results obtained in this paper on the Heisenberg group can be generalized on a general stratified Lie group $\mathbb {G}$, where the formula for $p_{\text{ crit } }(Q, \gamma )$ will be the same as in the case of Heisenberg group, with Q now the homogeneous dimension of $\mathbb {G}$. The global existence result can be proved by following the approach of [34, Sect. 4], while the blow-up result can be proved using again the test function method considered in [11].