On the 3D Navier–Stokes equations with a linear multiplicative noise and prescribed energy

Abstract

For a prescribed deterministic kinetic energy, we use convex integration to construct analytically weak and probabilistically strong solutions to the 3D incompressible Navier–Stokes equations driven by a linear multiplicative stochastic forcing. These solutions are defined up to an arbitrarily large stopping time and have deterministic initial values, which are part of the construction. Moreover, by a suitable choice of different kinetic energies which coincide on an interval close to time 0, we obtain non-uniqueness.

1 Introduction

1.1 Motivation and previous works

Proving existence and smoothness of strong solutions to the incompressible Navier–Stokes equations is a longstanding open problem in the field of fluid dynamics. It is the subject of one of the Millennium Prize Problems and caused, especially in the recent years, worldwide much attention.

The method of convex integration played a particularly important role in the last developments. It was initially introduced by Nash and Kuiper in order to prove the celebrated Nash–Kuiper theorem [26, 27, 32] and further developed by Müller and Šverák [31]. De Lellis and Székelyhidi brought these ideas to fluid dynamics in a series of breakthrough works. First of all, they were able to construct infinitely many weak solutions to the incompressible Euler equations which dissipate the total kinetic energy and satisfy the global and local energy inequality [10,11,12]. Subsequently, the regularity of such solutions was gradually increased, see [2, 14] leading to the proof of Onsager’s conjecture by Isett [25] and a refinement by Buckmaster et al. [3].

These works led to a number of further important papers. One of the key groundbreaking results was the non-uniqueness of weak solutions to the incompressible Navier–Stokes equations with finite kinetic energy by Buckmaster and Vicol [6]. Let us also mention a similar result for power-law Navier–Stokes equations by Burczak et al. [7].

Meanwhile, the method of convex integration also found its way to the theory of stochastic partial differential equations. Perturbing deterministic systems of partial differential equations by a certain stochastic noise has a long tradition. The motivation can be for instance to model intrinsic uncertainties or chaotic behavior of the studied systems. Particularly in fluid dynamics, coming together with the obstacles related to the Millennium Prize Problem and the above mentioned negative results, the hope was that the noise may provide some regularizing effect.

Some positive results could indeed be achieved. For instance, considering in particular a linear multiplicative noise provides a certain stabilization effect on the three-dimensional Navier–Stokes equations see Röckner et al. [34]. Delayed blowup with large probability was obtained by Flandoli and Luo for the vorticity form of the three-dimensional Navier–Stokes equations perturbed by a suitable transport noise [17]. Flandoli et al. [16] then showed that the delayed blowup is also provided by deterministic but highly oscillatory vector fields.

Another idea how to use the noise might be to try to prove uniqueness in law. This could potentially be true even if pathwise uniqueness failed. Moreover, if additionally existence of probabilistically strong solutions could be established, one might hope to use the celebrated Yamada–Watanabe–Engelbert’s theorem (see [9, 19, 28]) to deduce pathwise uniqueness. These hopes were proved wrong in the setting of the three-dimensional Navier–Stokes equations in a series of works [19, 20, 22, 24], which developed a stochastic variant of the convex integration method.

The first result on convex integration for stochastic PDEs was published by Breit, Feireisl and Hofmanová [4], dealing with the ill-posedness of the stochastic barotropic Euler system. A stochastic counterpart to [6] was obtained by Hofmanová, Zhu and Zhu [19], who were able to show non-uniqueness in law for 3D Navier–Stokes equations driven by an additive, linear multiplicative as well as a certain nonlinear cylindrical noise. In [24], the same authors proved existence and non-uniqueness of analytically weak and probabilistically strong solutions to the stochastic 3D Navier–Stokes equations with a prescribed energy and driven by an additive noise.

Further stochastic versions of the convex integration were developed to prove non-uniqueness of dissipative martingale solutions to 3D stochastic Euler equations [21], global existence and non-uniqueness for 3D stochastic Navier–Stokes equations with space time white noise [20], non-unique ergodic solutions for 3D Navier–Stokes equations and Euler equations [22] as well as sharp non-uniqueness of solutions to stochastic Navier–Stokes equations [8]. Very recently first results regarding the 3D Euler equations with transport noise [18], power-law equations with additive noise [30] and surface quasi-geostrophic equations with irregular spatial perturbations could already be achieved [23].

A series of further results regarding non-uniqueness in law for several stochastic partial differential equations, such as the transport-diffusion equation, the 3D magnetohydrodynamics system or also the hypodissipative Navier–Stokes equations, were attained by Yamazaki [37, 38], Koley and Yamazaki [29] and Rehmeier and Schenke [33]. These equations are perturbed either by an additive or linear multiplicative noise.

Up to now, it has not been known whether the kinetic energy could be prescribed a priori for the case 3D Navier–Stokes equations with linear multiplicative noise. This is the main goal of the present paper. In particular, we follow the ideas of [19] and [24] to establish the existence and non-uniqueness of solutions to the 3D incompressible Navier–Stokes equations driven by a multiplicative noise up to an arbitrarily large stopping time. We are able to show that the kinetic energy of the constructed solutions equals a prescribed energy profile. To this end, we make use of a transformation to a random PDE and the convex integration technique and it was necessary to find the correct formulation of the main iteration.

1.2 Main result

We consider the three-dimensional incompressible Navier–Stokes equations perturbed by a linear multiplicative forcing

$$\begin{aligned} \begin{aligned} {\begin{matrix} du+{{\,\text {div}\,}}(u \otimes u) \,dt+ \nabla P \,dt&{}= \nu \Delta u \,dt+ u\,dB, \\ {{\,\text {div}\,}}u&{}=0, \end{matrix}} \end{aligned} \end{aligned}$$

(1.1)

posed on $[0,T]\times \mathbb {T}^3\times \Omega$ for some $T>0$, where $\left( B_t\right) _{t \in [0,T]}$ is a real-valued Brownian motion on an given probability space $\left( \Omega , \mathcal {F}, \mathcal {P}\right)$ and $\mathbb {T}^3= [0,2\pi ]^3$ denotes the three-dimensional torus. Moreover, let $\left( \mathcal {F}_{t}\right) _{t \in [0,T]}$ be the natural filtration generated by $\left( B_t\right) _{t \in [0,T]}$.

For some pressure $P:[0,T]\times \mathbb {T}^3\times \Omega \rightarrow \mathbb {R}$, the system governs the time evolution of the velocity $u :[0,T]\times \mathbb {T}^3\times \Omega \rightarrow \mathbb {R}^3$ of an incompressible fluid with viscosity $\nu$. Throughout the paper, the viscosity is, for the sake of simplicity, assumed to be 1, which physically corresponds to water of $20^\circ$C (cf. [1], p. 1238, Table 3) and moreover we will often deal with the $\mathbb {T}^3$-periodic extensions of u and P on $\mathbb {R}^3$, which can be identified with functions on the three-dimensional flat torus $\mathbb {R}^3\setminus \left( 2\pi \mathbb {Z}\right) ^3$.

In this paper, we are concerned with finding solutions in the following sense:

Definition 1.1

An $\left( \mathcal {F}_t\right) _{t \in [0,T]}$-adapted solution u to (1.1) is said to be probabilistically strong and analytically weak if

• (i) it belongs for some $\gamma \in (0,1)$ to $C\left( [0,T];H^\gamma \left( \mathbb {T}^3\right) \right)$ $\mathcal {P}$-a.s.,

• (ii) it satisfies

  $$\begin{aligned} \int _0^t \int _{\mathbb {T}^3} u(s,x,\omega )\cdot \varphi (x) \,dx \,dB_s=&\int _{\mathbb {T}^3} \Big (u(t,x,\omega )-u(0,x,\omega )\Big )\cdot \varphi (x)\,dx\\ {}&-\int _0^t \int _{\mathbb {T}^3} (u \otimes u)(s,x, \omega ): \nabla \varphi ^T(x)\,dx \,ds\\ {}&+ \int _0^t \int _{\mathbb {T}^3} u(s,x,\omega )\cdot \Delta \varphi (x)\,dx\,ds \end{aligned}$$

  for every divergence-free test function $\varphi \in C^\infty \left( \mathbb {T}^3;\mathbb {R}^3\right)$, any $t \in [0,T]$ and $\mathcal {P}$-almost all $\omega \in \Omega$,

• (iii) it is weakly divergence free, i.e., it obeys

  $$\begin{aligned} \int _{\mathbb {T}^3} \Big (u(t,x,\omega )\cdot \nabla \Big )\phi (x) \,dx = 0 \end{aligned}$$

  for all $\phi \in C^\infty \left( \mathbb {T}^3;\mathbb {R}\right)$, $\mathcal {P}$-almost all $\omega \in \Omega$ at any time $t \in [0,T]$.

Note that working with divergence-free test functions in the definition above allows to eliminate the pressure term, which can be reconstructed after a weak solution has been found. We can now formulate our main result:

Theorem 1.2

For any $L>0$ arbitrarily large and every energy $e\in C^1_b\big ( [0,L];$$\left. [\underline{e},\infty )\right)$, satisfying

$$\begin{aligned} \Vert e\Vert _{C}\le \bar{e}\quad \text{ and } \quad \Big \Vert \frac{d}{dt} e\Big \Vert _{C}\le \widetilde{e}\end{aligned}$$

for some constants $4< \underline{e}\le \bar{e}$ and $\widetilde{e}>0$ a probabilistically strong and analytically weak solution u to (1.1), depending explicitly on the given energy e, can be constructed up to a $\mathcal {P}$-a.s. strictly positive stopping time

$$\begin{aligned} \tau := \inf \{t>0: |B_t|\ge L\} \wedge \inf \{t>0: \Vert B\Vert _{C_{[0,t]}^{0,\iota }}\ge L \} \wedge L \end{aligned}$$

with $\iota \in \Big (\frac{1}{3}, \frac{1}{2}\Big )$. This solution has deterministic initial value $u_0$ and belongs to $C\left( [0,\tau ];H^\gamma \left( \mathbb {T}^3\right) \right)$ $\mathcal {P}$-a.s. for some $\gamma \in (0,1)$. It obeys

$$\begin{aligned} \mathop {\mathrm {ess\,sup}}\limits _{\omega \in \Omega } \sup _{t\in [0,\tau ]} \Vert u(t,\omega )\Vert _{H^\gamma }< \infty , \end{aligned}$$

and its kinetic energy is given by e, i.e.,

$$\begin{aligned} \Vert u(t)\Vert ^2_{L^2}=e(t), \end{aligned}$$

as long as $t \in [0,\tau ]$.

Moreover, the following consistency result holds:

If two energies with the same bounds $\underline{e}, \bar{e}, \widetilde{e}$ coincide for some $t \in [0,L]$ everywhere on [0, t], then so do the corresponding solutions on $[0,t \wedge \tau ]$.

The proof of 1.2 is based on a convex integration scheme. That is, after transforming (1.1) to a random PDE, we develop an iteration procedure and apply it to the just received equation.

More precisely, if u solves (1.1), the function $v:=e^{-B}u$ is by Itô’s formula a solution to the ensuing system

$$\begin{aligned} \begin{aligned} \partial _tv+\frac{1}{2} v- \Delta v+ \Theta {{\,\textrm{div}\,}}(v \otimes v)+\Theta ^{-1}\nabla P&=0,\\ {{\,\textrm{div}\,}}v&=0, \end{aligned} \end{aligned}$$

(1.2)

where $\Theta$ is the stochastic process given by

$$\begin{aligned} \Theta :[0,T]\times \Omega \rightarrow \mathbb {R}, \qquad \Theta (t,\omega ):=e^{B_t(\omega )} \end{aligned}$$

and the converse is also true. In fact, applying Itô’s formula to the smooth function $f:[0,T]\times \mathbb {R} \rightarrow \mathbb {R}$, $f(t,y):= e^{-y}$ yields $de^{-B_t}=\frac{1}{2}e^{-B_t}\, dt- e^{-B_t}\, dB_t$ and by Itô’s product rule and (1.1) we conclude (1.2).

1.3 Organization of the paper

We organize the present paper as follows: Chapter 2 is devoted to the collection of basic notations used throughout this paper. In Chapter 3, we outline the convex integration technique to prove Proposition 4.1. This is the core of the proof of our main Theorem 1.2, which is established in Chapter 4. “Appendix A” covers some lemmata used in the previous chapters.

2 Preliminaries

In order to define several function spaces and operators, we need the Fourier transform and the inverse Fourier transform of a function u on $\mathbb {T}^3$ given by

$$\begin{aligned} (\mathcal {F}u)(n):&=\hat{u}_n:=(2\pi )^{-3} \int _{\mathbb {T}^3} u(y)e^{-in\cdot y}\, dy\qquad \text{ and } \\ (\mathcal {F}^{-1}\hat{u}_n)(x)&=u(x)=\sum _{n \in \mathbb {Z}^3}\hat{u}_n e^{in\cdot x} \end{aligned}$$

for any $n \in \mathbb {Z}^3$ and $x\in \mathbb {T}^3$, respectively, where the series shall be understood as the limit of partial sums with square cutoff

$$\begin{aligned} u_N(x):=\sum _{n \in [-N,N]^3}\hat{u}_n e^{in\cdot x}. \end{aligned}$$

Moreover, for $d \in \mathbb {N}$ we will often deal with the spaces of symmetric or traceless $d \times d$-matrices A, designated by $\mathbb {R}_{\text {sym}}^{d\times d}$ and $\mathring{\mathbb {R}}^{d\times d}$, respectively. As usual we consider the Frobenius norm on them and in order to elucidate that the matrix itself is traceless we will frequently write $\mathring{A}$ instead of A.

2.1 Function spaces

For some $N\in \mathbb {N}_0\cup \{\infty \},\, T\in [0,\infty )$ and a Banach space $\left( Y,\Vert \cdot \Vert _Y\right)$, we denote the space of all N-times continuously differentiable functions from $X\in \{ \mathbb {T}^3,\mathbb {R}^3\}$ to Y by $C_{XY}^N$ and from $X=(-\infty ,T]$ to Y we shorten $C_{TY}^N$. Endowed with the natural norms

$$\begin{aligned}&\Vert u\Vert _{C_{XY}^N}:= \sum _{\begin{array}{c} 0 \le |\alpha | \le N\\ \alpha \in \mathbb {N}_0^3 \end{array}}\sup _{x\in X} \Vert D^\alpha u(x) \Vert _Y \qquad \text { and }\\&\Vert u\Vert _{C_{TY}^N}:= \sum _{\begin{array}{c} 0 \le n \le N\\ n \in \mathbb {N}_0 \end{array}}\sup _{t \in (-\infty ,T]}\Vert \partial _t^n u(t) \Vert _Y , \end{aligned}$$

respectively, it is well known that they become Banach spaces.

Sometimes we will omit writing X or Y if it is clear from the context which domain or codomain is considered, and moreover, we will frequently write $C_{XY}$ instead of $C^0_{XY}$. In particular, $\Vert u\Vert _C$ is the usual supremum norm, which will also be used for more general normed spaces X.

There should be no misunderstanding when we talk about $C_c^N$- and $C_b^N$-functions, meaning the N-times continuous differentiable ones with compact support and the ones that are either bounded from above, bounded from below or even both.

Besides it is customary to introduce the space of test functions

$$\begin{aligned} \mathcal {D}\left( X\right) :=\left\{ \begin{array}{ll} C^\infty \left( X \right) ,&{} X \text { is compact},\\ C_c^\infty \left( X\right) ,&{} \text {otherwise}, \end{array}\right. \end{aligned}$$

and we moreover label by $C_{T,x}^N$ the space of all N-times continuously differentiable functions on $(-\infty ,T]\times \mathbb {T}^3$, equipped with the corresponding norm

$$\begin{aligned} \Vert u\Vert _{C_{T,x}^N}:= \sum _{\begin{array}{c} 0 \le n+|\alpha | \le N\\ n \in \mathbb {N}_0, \alpha \in \mathbb {N}_0^3 \end{array}}\Vert \partial _t^n D^\alpha u\Vert _{C_TL^\infty }. \end{aligned}$$

We will speak of Hölder-continuous functions u on $X\in \{\mathbb {T}^3,\mathbb {R}^3\}$ of exponent $N+\iota$ with $N\in \mathbb {N}_0$ and $\iota \in (0,1]$, whenever

$$\begin{aligned} \Vert u\Vert _{C_{XY}^{N,\iota }}:=\sum _{\begin{array}{c} 0 \le |\alpha | \le N\\ \alpha \in \mathbb {N}_0^3 \end{array}}\Vert D^\alpha u\Vert _{C_{XY}}+\sum _{\begin{array}{c} |\alpha | = N\\ \alpha \in \mathbb {N}_0^3 \end{array}}\sup _{x \in X}[ D^\alpha u(x)]_{C_{XY}^{0,\iota }}<\infty \end{aligned}$$

holds, where

$$\begin{aligned} {[}u(x)]_{C_{XY}^{0,\iota }}:= \sup _{\begin{array}{c} x_1,x_2 \in X\\ x_1 \ne x_2 \end{array}} \frac{\Vert u(x_1)-u(x_2)\Vert _Y}{|x_1-x_2|^\iota }, \end{aligned}$$

is the $\iota ^\text {th}$-Hölder seminorm. For functions on $(-\infty ,T]$, we define the space in the same manner.

The space of Bochner-integrable functions $L^p\left( X;Y\right)$ consists of the equivalence classes of all functions $u:X \rightarrow Y$, which coincide $\mathcal {P}$-almost everywhere and for which the usual $L^p$-norm $\Vert \cdot \Vert _{L^p}$ is finite, whereas $\left( W^{k,p}\big ( X;\mathbb {R}^d\big ),\Vert \cdot \Vert _{W^{k,p}}\right)$ should be the usual Sobolev space for all $k \in \mathbb {N}_0$ and $1\le p\le \infty$. Moreover, we denote by $W^{k,p}_0\left( X\right)$ the closure of $\mathcal {D}\left( X\right)$ in $\left( W^{k,p}\big (X\big ),\Vert \cdot \Vert _{W^{k,p}}\right)$ and by $W^{-k,q}\left( X\right)$ the dual space of $W^{k,p}_0\left( X\right)$ with $\frac{1}{p}+ \frac{1}{q}=1$.

The Bessel potential spaces are for any $p,q\in (1,\infty )$, $\frac{1}{p}+\frac{1}{q}=1$ on $\mathbb {T}^3$ defined in the spirit of [35, 36]:

We set

$$\begin{aligned} W^{s,p}\left( \mathbb {T}^3\right)&:=\bigg \{u \in L^p\left( \mathbb {T}^3\right) : \Big \Vert \mathcal {F}^{-1}\big [(1+|\cdot |^2)^{s/2}\mathcal {F}u\big ] \Big \Vert _{L^p}<\infty \bigg \} \end{aligned}$$

for $s\ge 0$, whereas we define

$$\begin{aligned} W^{-s,p}\left( \mathbb {T}^3\right)&:=\bigg \{u ^\prime \in \left( \mathcal {D}\left( \mathbb {T}^3\right) \right) ^\prime : \Big \Vert \mathcal {F}^{-1}\big [(1+|\cdot |^2)^{-s/2}\mathcal {F}u^\prime \big ] \Big \Vert _{(L^q)^\prime }<\infty \bigg \} \end{aligned}$$

whenever $s>0$, which can be identified with the dual space of $W^{s,q}\left( \mathbb {T}^3\right)$ (see also [13]).

Endowed with the canonical norms

$$\begin{aligned}&\Vert u\Vert _{W^{s,p}}:= \Big \Vert \mathcal {F}^{-1}\big [(1+|\cdot |^2)^{s/2}\mathcal {F}u\big ] \Big \Vert _{L^p} \qquad \text{ and } \\ {}&\Vert u^\prime \Vert _{W^{-s,p}}:= \Big \Vert \mathcal {F}^{-1}\big [(1+|\cdot |^2)^{-s/2}\mathcal {F}u^\prime \big ] \Big \Vert _{(L^q)^\prime },\end{aligned}$$

respectively, these spaces become Banach spaces and furthermore we stipulate $\displaystyle H^s\left( X\right)$$:= W^{s,2}\left( X\right)$.

For $p\in [1,\infty ], \, d\in \mathbb {N}$ and $X\in \{\mathbb {N}^d, \mathbb {Z}^d\}$, we denote by $\ell ^p(X)$ the usual space of sequences for which the corresponding norm $\Vert \cdot \Vert _{\ell ^p}$ is finite.

We will often deal with functions of zero mean. So for convenience we set

$$\begin{aligned} X_{\ne 0}:=\mathbb {P}_{\ne 0} \left( X\right) , \end{aligned}$$

for any function space X, where $\mathbb {P}_{\ne 0}$ is the projection onto functions with nonzero frequencies, which will be introduced in 2.2.

2.2 Operators

We will deal with the extended Leray projection $\mathbb {P}={{\text {Id}}}-\nabla \Delta ^{-1}{{\text {div}}}$ on the Bessel potential spaces $W_{\ne 0}^{s,p}\left( \mathbb {T}^3\right)$ for every real $s\ge 0$ and $p \in (1,\infty )$, which enjoys the following useful property.

Lemma 2.1

The Leray projection commutes $\mathcal {P}$-almost everywhere with any partial derivative on $W_{\ne 0}^{1,p}\left( \mathbb {T}^3\right)$ and if we work with time depended functions u, satisfying

$$\begin{aligned} |\partial _t u(t,x)|\le g(x) \end{aligned}$$

for some $g\in L^1\left( \mathbb {T}^3\right)$ and all $x \in \mathbb {T}^3$, even on $C^1\left( (-\infty ,T];C_{\ne 0}\left( \mathbb {T}^3\right) \right)$ with $T>0$. In other words,

$$\begin{aligned} \partial _{x_j}(\mathbb {P}u)(t,x)=(\mathbb {P}\partial _{x_j} u)(t,x) \qquad \text { and } \qquad \partial _t(\mathbb {P}u)(t,x)=(\mathbb {P}\partial _t u)(t,x) \end{aligned}$$

holds for all $x\in \mathbb {T}^3$, each $t\in \mathbb {R}$ and $j=1,2,3$.

Moreover, it is very common and practical to introduce the Fourier multiplier operators, which project a function onto its null mean frequencies and onto its frequencies $\le \kappa$ in absolute value.

Definition 2.2

For any $u \in L^p\left( \mathbb {T}^3\right)$ with $1<p\le \infty$, we denote by

the projection onto its nonzero frequencies.

Furthermore, for all real $\kappa \ge 1$ we define the operators $\mathbb {P}_{\le \kappa }$ and $\mathbb {P}_{\ge \kappa }$ as

$$\begin{aligned} \left( \mathbb {P}_{\le \kappa }u\right) (x)&:= \mathcal {F}^{-1}\Big [ \chi _\kappa \, \mathcal {F}u\Big ](x)=\sum _{n \in \mathbb {Z}^3} \chi _\kappa (n)\hat{u}_n e^{in\cdot x} \end{aligned}$$

and

$$\begin{aligned} \left( \mathbb {P}_{\ge \kappa }u\right) (x)&:= \mathcal {F}^{-1}\Big [ \big (1-\chi _\kappa \big )\, \mathcal {F}u\Big ](x)=\sum _{n \in \mathbb {Z}^3} \big (1-\chi _\kappa (n)\big )\hat{u}_ne^{in\cdot x}, \end{aligned}$$

respectively, where we set $\chi _\kappa := \chi \left( \frac{\cdot }{\kappa }\right)$ for the smooth compactly supported function $\chi \in C_c^\infty \left( \mathbb {R}^3\right)$ given by

$$\begin{aligned} \chi (x):=\left\{ \begin{array}{ll} 1,&{}{} |x|\le \frac{1}{2}, \\ \frac{1}{\exp \left( \frac{1}{1/2-|x|}+\frac{1}{1-|x|} \right) +1},&{}{} \frac{1}{2}<|x|<1,\\ 0,&{}{} |x|\ge 1.\\ \end{array}\right. \end{aligned}$$

Lemma 2.3

The above operators $\mathbb {P}_{\ne 0},\, \mathbb {P}_{\le \kappa }$ and $\mathbb {P}_{\ge \kappa }$ are for each real $\kappa \ge 1$ and $1<p\le \infty$ continuous on $L^p\left( \mathbb {T}^3\right)$, where the implicit constants do not depend on $\kappa$.

Lemma 2.4

For all real $\kappa \ge 1$, it holds

$$\begin{aligned} \Vert \left( -\Delta \right) ^{-1/2} \mathbb {P}_{\ge \kappa }\Vert _{L^p\rightarrow L^p} \lesssim \frac{1}{\kappa } \end{aligned}$$

whenever $1<p<\infty$.

Lemma 2.5

For all $\Big (\frac{\mathbb {T}}{L}\Big )^3$-periodic functions $u \in L^p \left( \mathbb {T}^3\right)$ with $L \in \mathbb {N}$ and $1< p\le \infty$, the operators $\mathbb {P}_{\le \kappa }$ and $\mathbb {P}_{\ge \kappa }$ can be written as

$$\begin{aligned} \left( \mathbb {P}_{\le \kappa }u\right) (x)&= \sum _{n \in (L\mathbb {Z})^3} \chi _\kappa (n)\hat{u}_{n}e^{in\cdot x} \end{aligned}$$

and

$$\begin{aligned} \left( \mathbb {P}_{\ge \kappa }u\right) (x)&= \sum _{n \in (L\mathbb {Z})^3} \big (1-\chi _\kappa (n)\big )\hat{u}_{n}e^{in\cdot x}, \end{aligned}$$

respectively. If additionally $L>\kappa$, we have that

$$\begin{aligned} \mathbb {P}_{\ge \kappa }u=\mathbb {P}_{\ne 0}u. \end{aligned}$$

3 Outline of the convex integration scheme

The convex integration scheme is an iterative procedure giving rise to solutions to several deterministic and stochastic PDEs. Also in the present paper, we construct, based on a suitable starting point, a solution $v_q$ to (1.2) on $(-\infty ,\tau ]$ perturbed by an error term $\mathring{R}_q$, called Reynolds stress, on the level $q\in \mathbb {N}_0$. While the iterations $v_q$ approach the desired velocity v, solving (1.2) on $[0,\tau ]$, the stress tensor $\mathring{R}_q$ becomes step by step infinitesimally small. The convex integration technique provides typically a way to construct even an infinite number of such solutions, as it is also the case in the present paper.

For the construction of our sequence $(v_q,\mathring{R}_q)_{q\in \mathbb {N}_0}$, we previously have to fix some parameters, done in Sect. 3.1. Section 3.2 is concerned with the key bounds that each pair $(v_q,\mathring{R}_q)$ has to fulfill. In Sect. 3.3, we recall the definitions of intermittent jets used to give an explicit expression of $v_{q+1}$. Section 3.4 is then concerned with the verification of the key bounds of the next iteration step $v_{q+1}$, culminating in the proof of convergence of the sequence $\left( v_q\right) _{q\in \mathbb {N}_0}$. In Sect. 3.5, we decompose the Reynolds stress, and in Sect. 3.6, we verify the key bound for this tensor on the level $q+1$. We close this chapter in Sect. 3.7 by proving that our constructed sequence is adapted and deterministic at any time $t\le 0$.

3.1 Choice of parameters

To simplify the upcoming computations we assume $L=1$ in 1.2 and for sufficiently large $a \in \mathbb {N}, b\in 7\mathbb {N}$ and sufficiently small $\alpha ,\beta \in (0,1)$, we require

$$\begin{aligned} \begin{array}{ll} \bullet ~161\alpha <\frac{1}{7},&{}\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \bullet ~a\ge 3600,\\ \bullet ~\alpha \iota > 4\beta b^2,&{}\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \bullet ~a^{\beta b}\ge 2,\\ \bullet ~\alpha b\ge \frac{10}{\iota }-4,&{}\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \bullet ~a^{\frac{3\alpha }{2}b+2}\ge m^2\bar{e}\\ \end{array} \end{aligned}$$

and define

$$\begin{aligned} \begin{array}{ll} \lambda _q:=a^{(b^q)},&{}\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \ell := \lambda _{q+1}^{-\frac{3\alpha }{2}}\lambda _q^{-2},\\ \delta _q:=\lambda _1^{2\beta }\lambda _q^{-2\beta },&{}\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad m:=\exp {(4)}\\ \end{array} \end{aligned}$$

for $q\in \mathbb {N}_0$. As a consequence, the following estimates hold

$$\begin{aligned} \ell \lambda _q^{5/\iota }\le \lambda _{q+1}^{-\alpha }, \end{aligned}$$

(3.1a)

$$\begin{aligned} m^2\bar{e}\le \ell ^{-1}\le \lambda _{q+1}^{2\alpha }. \end{aligned}$$

(3.1b)

Particularly, that means $\ell \in (0,1)$ and we have developed an increasing and a decreasing sequence $\left( \lambda _q\right) _{q \in \mathbb {N}_0}\subseteq \mathbb {N}$, $\left( \delta _q\right) _{q\ge 2}\subseteq (0,1)$, which diverges to $\infty$ and converges to 0, respectively. We therefore find some $q_0 \in \mathbb {N}$ so that the above parameters additionally fulfill

$$\begin{aligned} \begin{array}{ll} \bullet ~10\, M_0 \bar{e}\lambda _{q+1}^{-\alpha /2+2\beta b^2}\le 1,&{}\bullet ~ 2K\frac{M}{4|\Lambda |} \lambda _{q{+}1}^{{-}12/7}{+}K\left( \frac{M}{4|\Lambda |}\right) ^2 \lambda _{q{+}1}^{{-}6/7} {\le } \frac{1}{2},\\ \bullet ~ \frac{M}{4|\Lambda |}\lambda _{q+1}^{33\alpha -1/7}\le 1,&{}\bullet ~ \widetilde{K}\lambda _q^5\lambda _{q+1}^{-5}\le \frac{1}{2},\\ \bullet ~ 33(2\pi )^{3/2}M_0 m^{9/4}(\bar{e}{+}\widetilde{e}) \lambda _{q{+}1}^{{-}\alpha \big (\frac{3}{2}\iota {-}\frac{1}{2}\big )} {\le } \frac{1}{1500m^{1/2}},&{} \bullet ~ \hat{K}\lambda _{q{+}1}^{{-}147\alpha }{\le } \frac{1}{80m^{3/4}},\\ \bullet ~ S\left( \frac{M}{4|\Lambda |}+\left( \frac{M}{4|\Lambda |}\right) ^2 \right) \lambda _{q+1}^{-100\alpha } \le \frac{1}{1500m^{1/2}},&{} \bullet ~ K^*\, 2\pi \, \frac{M}{4|\Lambda |} \lambda _{q+1}^{-5/21} \le \frac{1}{5m^{1/2}},\\ \bullet ~ 3\widetilde{S}\max \limits _{n\in \{2,3,4\}}\left( \frac{M}{4|\Lambda |}\right) ^n\lambda _{q+1}^{-68 \alpha }\le \frac{1}{1500m^{1/2}},&{}\bullet ~ K^\prime \left( M_0+\frac{M}{4|\Lambda |} \right) ^3 \lambda _{q+1}^{-\frac{1}{14}}\le \frac{1}{5m^{1/2}},\\ \bullet ~ \hat{S}\left( \frac{M}{4|\Lambda |}\right) ^2 \lambda _{q+1}^{-111 \alpha }\!\le \! \frac{1}{1500m^{1/2}},&{} \bullet ~ K^{\prime \prime } \left( \!\left( \frac{M}{4|\Lambda |} \right) ^2\!+\! \left( \frac{M}{4|\Lambda |} \right) ^4\right) \lambda _{q+1}^{-1/7}\!\le \! \frac{1}{5m^{1/2}}\\ \end{array} \end{aligned}$$

for every $q\ge q_0$, where $K, \,\widetilde{K}, \, \hat{K}, \, K^*, \, K^\prime , \, K^{\prime \prime }, \, S, \, \widetilde{S},\,\hat{S}, \, \frac{M}{4|\Lambda |}$ and $M_0\ge 1$ are universal constants determined by (3.28), (3.29), (3.38), (3.39), (3.40), (3.41), (3.45), (3.46), (3.7) and (3.26), respectively.

Note that the assumption $33(2\pi )^{3/2}M_0 m^{9/4}(\bar{e}+\widetilde{e}) \lambda _{q+1}^{-\alpha \big (\frac{3}{2}\iota -\frac{1}{2}\big )} \le \frac{1}{1500m^{1/2}}$ requires $\iota >\frac{1}{3}$. Choosing furthermore a, b sufficiently large and $\alpha ,\beta$ sufficiently small enough permits to suppose $q_0=1$.

3.2 Start of the iteration

In view of (1.2), we are concerned with an adapted velocity field $v_q$ and a symmetric traceless matrix $\mathring{R}_q$; solving the transformed Navier–Stokes–Reynolds system reads

$$\begin{aligned} \begin{aligned} \partial _t v_q+ \frac{1}{2}v_q-\Delta v_q+ \Theta {{\,\textrm{div}\,}}(v_q \otimes v_q)+\nabla p_q&={{\,\textrm{div}\,}}(\mathring{R}_q),\\ {{\,\textrm{div}\,}}v_q&=0 \end{aligned} \end{aligned}$$

(3.2)

and that obey

$$\begin{aligned}&\Vert v_q\Vert _{C_tL^2}\le M_0 \Big ( 1+\sum _{r=1}^q \delta _r^{1/2}\Big )m\bar{e}^{1/2}, \end{aligned}$$

(3.3a)

$$\begin{aligned}&\Vert v_q\Vert _{C_{t,x}^1}\le \lambda _q^5 m\bar{e}^{1/2}, \end{aligned}$$

(3.3b)

$$\begin{aligned}&\Vert \mathring{R}_q\Vert _{C_tL^1}\le \frac{1}{1500} \delta _{q+2}\Theta ^{-2}(t)e(t) \end{aligned}$$

(3.3c)

for $q\in \mathbb {N}_0$, any $t\in (-\infty ,\tau ]$ and some universal constant $M_0\ge 1$. Here, we have to include also negative times in order to avoid several problems by decomposing the Reynolds stress in Sect. 3.5. For this purpose, the energy e and the Brownian motion B are continuously extended to functions on $(-\infty ,\tau ]$ by taking them equal to the value at $t=0$. We furthermore set $\sum _{r=1}^0:=0$ and point out that $\sum _{r=1}^q \delta _r^{1/2}$ is bounded by 2. Indeed, thanks to the assumed $a^{\beta b} \ge 2$ it holds

$$\begin{aligned} \sum _{r=1}^q \delta _r^{1/2}\le \sum _{r=1}^\infty a^{\beta b-\beta rb}=\sum _{r=0}^\infty (a^{-\beta b})^r =\frac{1}{1-a^{-\beta b}}\le 2. \end{aligned}$$

(3.4)

Moreover, we require

$$\begin{aligned} \frac{3}{4}\delta _{q+1} \Theta ^{-2}(t)e(t)\le \Theta ^{-2}(t)e(t)- \Vert v_q(t)\Vert ^2_{L^2}\le \frac{5}{4}\delta _{q+1} \Theta ^{-2}(t)e(t) \end{aligned}$$

(3.5)

at any time t up to the stopping time $\tau$. In other words, the given energy e will be gradually approximated by the kinetic energies of the iterations $e^Bv_q$.

If we set $\mathcal {F}_t:=\mathcal {F}_0$ whenever $t<0$, the pair $\big (v_0,\mathring{R}_0\big ):=(0,0)$ is evidently a deterministic, hence $\left( \mathcal {F}_t\right) _{t\in \mathbb {R}}$-adapted, weak solution to (3.2), satisfying (3.3) as well as (3.5). Therefore, we may start our iteration procedure with this pair.

3.3 Construction of $v_{q+1}$

In order to obtain more regularity, we refrain in defining the next iteration $v_{q+1}$ in mere dependence of $v_q$. Instead we intend to define $v_{q+1}$ in terms of the mollified velocity field $v_\ell$ and a perturbation $w_{q+1}$, pointed out in the two subsequent sections. For short, the new velocity field will be given as

$$\begin{aligned} v_{q+1}:=v_{\ell }+w_{q+1}. \end{aligned}$$

3.3.1 Mollification

Let us start with the mollification of the velocity $v_q$. For this end, we consider the standard mollifier

$$\begin{aligned} \phi (x):=\left\{ \begin{array}{ll} C_{\text {space}} \exp {\left( \frac{1}{|x|^2-1}\right) }, &{}\text {if } |x|<1, \\ 0, &{} \text {if } |x| \ge 1, \end{array}\right. \end{aligned}$$

on $\mathbb {R}^3$ and the shifted mollifier

$$\begin{aligned} \varphi (t):=\left\{ \begin{array}{ll} C_{\text {time}} \exp {\left( \frac{1}{|t-1/2|^2-1/4}\right) }, &{}\text {if } t \in (0,1),\\ 0, &{} \text {if } t\notin (0,1), \end{array}\right. \end{aligned}$$

on $\mathbb {R}$, where $C_{\text {space}},C_{\text {time}}>0$ are chosen, such that $\int _{\mathbb {R}^3}\phi (x)\, dx=1$ and $\int _{\mathbb {R}}\varphi (t)\, dt=1$, as usual. Thus, the convolution of $v_q$ with the rescaled mollifiers $\phi _\ell :=\frac{1}{\ell ^3}\phi (\frac{\cdot }{\ell })$ and $\varphi _\ell :=\frac{1}{\ell }\varphi (\frac{\cdot }{\ell })$ yields a smooth function in space and time, and of $\Theta$ with $\varphi _\ell$ just in time.

For short, we consider

$$\begin{aligned} v_\ell :=(v_q *_t \varphi _\ell )*_x\phi _\ell , \quad \mathring{R}_\ell := (\mathring{R}_q *_t \varphi _\ell )*_x\phi _\ell , \quad \Theta _\ell :=\Theta *_t \varphi _\ell , \end{aligned}$$

where $\mathring{R}_\ell$ remains traceless, because the mollification acts only componentwise.

It is worth noting that the adaptedness of $v_\ell ,\, \mathring{R}_\ell$ and $\Theta _\ell$ follows from the fact that the support of $\varphi$ lives in $\mathbb {R}^+$. In fact, let $\Pi _\ell$ be the set that contains all partitions of $[0,\ell ]$ of the form $\{0=s_0<s_1<\ldots <s_n=\ell \}$ for some $n\in \mathbb {N}$. Then, for any $t\in (-\infty ,\tau ]$ and $x\in \mathbb {T}^3$ the function

$$\begin{aligned} \omega \mapsto (v_q *_t \varphi _\ell )(t,x,\omega )&=\int _0^\ell v_q(t-s,x,\omega )\varphi _\ell (s) \,ds\\&=\inf _{\Pi _\ell }\sum _{i=1}^n(s_i-s_{i-1})\sup _{s\in (s_{i-1},s_i)} \underbrace{v_q(t-s,x,\omega )}_{\mathcal {F}_{t-s}\subseteq \mathcal {F}_t\text {-meas.}}\overbrace{\varphi _\ell (s)}^{\text {deterministic}} \end{aligned}$$

is $\mathcal {F}_t$-measurable.

Taking into account that the convolution in space does not influence the behavior of $(v_q *_t \varphi _\ell )$ in time, $v_\ell$ inherits the $\left( \mathcal {F}_t\right) _{t\in \mathbb {R}}$-adaptedness and so do $\mathring{R}_\ell$ and $\Theta _\ell$.

It is easy to see that $v_\ell$ is close to $v_q$ w.r.t. $\Vert \cdot \Vert _{L^2}$ at any time up to the stopping time $\tau$ and fulfills (3.3) as well. More precisely, the subsequent Lemma from [24], p. 10 holds.

Lemma 3.1

The mollification $v_\ell$, defined above, enjoys the following bounds

$$\begin{aligned}&\Vert v_q-v_\ell \Vert _{C_tL^2}\le (2\pi )^{3/2}\ell \Vert v_q\Vert _{C^1_{t,x}}\le (2\pi )^{3/2} \delta _{q+1}^{1/2}m \bar{e}^{1/2}, \end{aligned}$$

(3.6a)

$$\begin{aligned}&\Vert v_\ell \Vert _{C_tL^2}\le \Vert v_q\Vert _{C_tL^2}\le M_0\Big (1+\sum _{r=1}^q \delta _r^{1/2}\Big )m\bar{e}^{1/2}, \end{aligned}$$

(3.6b)

$$\begin{aligned}&\Vert v_\ell \Vert _{C_{t,x}^N}\lesssim \ell ^{-N+1}\Vert v_q\Vert _{C_{t,x}^1}\lesssim \ell ^{-N}\lambda _{q+1}^{-\alpha } m \bar{e}^{1/2} \end{aligned}$$

(3.6c)

for any $t \in (-\infty ,\tau ]$ and $N\ge 1$.

The proof is rather straightforward, so that we do not pursue this here.

3.3.2 Perturbation

Let us now have a closer look at the perturbation $w_{q+1}$. We will decompose it into three parts: the principal part $w_{q+1}^{(p)}$, the incompressibility corrector $w_{q+1}^{(c)}$ and the temporal corrector $w_{q+1}^{(t)}$. Each of them will be defined in terms of the amplitude functions and the intermittent jets, introduced and worked out in [6] and [5], respectively. In what follows, we will give a short review of the necessary facts.

First, we recall the essential geometric lemma from [5].

Lemma 3.2

(Geometric Lemma) There exists a family of smooth real-valued functions $\left( \gamma _\xi \right) _{\xi \in \Lambda }$, where $\Lambda$ is a set of finite directions, contained in $\mathbb {S}^2\cap \mathbb {Q}^3$, so that each symmetric $3\times 3$ matrix R, satisfying $\Vert R-{{\,\textrm{Id}\,}}\Vert _F\le \frac{1}{2}$, admits the representation

$$\begin{aligned} R=\sum _{\xi \in \Lambda }\gamma _\xi ^2(R)(\xi \otimes \xi ). \end{aligned}$$

Second, based on this lemma, we define for all $N\in \mathbb {N}$ the constant

$$\begin{aligned} M:=8 |\Lambda |(1+8\pi ^3)^{1/2} \sup _{\xi \in \Lambda }\Big (\Vert \gamma _\xi \Vert _{C}+\sum _{|\alpha |\le N}\Vert D^\alpha \gamma _\xi \Vert _C\Big ). \end{aligned}$$

(3.7)

3.3.3 Amplitude Functions

The function $\gamma _\xi$ in the geometric Lemma 3.2 is used to define the amplitude functions as

$$\begin{aligned} a_{(\xi )}(t,x,\omega )&:=a_{\xi ,q+1}(t,x,\omega ):=(2\pi )^{3/2} \rho ^{1/2}(t,x,\omega )\gamma _\xi \left( {{\,\textrm{Id}\,}}-\frac{\mathring{R}_\ell (t,x,\omega )}{\rho (t,x,\omega )}\right) \end{aligned}$$

with

$$\begin{aligned} \rho (t,x,\omega )&:=2\sqrt{\ell ^2+\Vert \mathring{R}_\ell (t,x,\omega )\Vert _F^2}+\Theta _\ell (t,\omega )\eta _\ell (t,\omega ),\\ \eta _q(t,\omega )&:= \frac{1}{3 (2\pi )^3}\Big [\Theta ^{-2} (t,\omega )e(t)(1-\delta _{q+2})-\Vert v_q(t)\Vert ^2_{L^2}\Big ] \end{aligned}$$

for any $t \in (-\infty , \tau ],\, x\in \mathbb {R}^3,\, \omega \in \Omega$, where $\eta _\ell$ denotes the mollification in time of $\eta _q$.

Since we start our iteration procedure with $\mathring{R}_0=0$, we include a small perturbation $\ell$ in the definition of $\rho$ to avoid its degeneracy, whereas the function $\eta _q$ should pump energy into the system. This enables us to confirm the key bounds (3.3) at level $q+1$ in Sects. 3.4.2 and 3.6.1, respectively.

Moreover, we point out that (3.5) and our choice of parameters $a^{\beta b}\ge 2, b\ge 7$ (cf. Sect. 3.1) ensure

$$\begin{aligned} 3(2\pi )^3\eta _q&\ge \Theta ^{-2} e \left( \frac{3}{4}\delta _{q+1}-\delta _{q+2}\right) \ge \Theta ^{-2} e (a^{-2\beta b (b-1)}\delta ^b_{q+1}-\delta _{q+2})=0, \end{aligned}$$

which entails

$$\begin{aligned} \rho \ge 2 \ell \quad \text { and } \quad \rho \ge 2\Vert \mathring{R}_\ell \Vert _F. \end{aligned}$$

As a consequence, ${{\,\textrm{Id}\,}}-\frac{\mathring{R}_\ell }{\rho }$ fulfills the condition $\big \Vert {{\,\textrm{Id}\,}}-\frac{\mathring{R}_\ell }{\rho }-{{\,\textrm{Id}\,}}\big \Vert _F\le \frac{1}{2}$ in the geometric Lemma 3.2, so that the amplitude functions are actually well defined.

Now, we would already like to sum up some properties of these functions here.

Lemma 3.3

The amplitude functions enjoy the following bounds

$$\begin{aligned}&\Vert a_{(\xi )}\Vert _{C_tL^2}\lesssim \frac{M}{4 |\Lambda |} \delta _{q+1}^{1/2}m^{3/8}\bar{e}^{1/2}, \end{aligned}$$

(3.8a)

$$\begin{aligned}&\Vert a_{(\xi )}\Vert _{C_{t,x}^N}\lesssim \frac{M}{4 |\Lambda | } \ell ^{-8-7N} \delta _{q+1}^{1/2} m^{3/8}\bar{e}^{1/2} \end{aligned}$$

(3.8b)

for any $t \in (-\infty , \tau ]$ and $N\ge 0$.

The proofs of this lemma and of Lemma 3.6 are collected in Sect. 3.4.1.

In view of [19], one might heuristically think that it makes sense to define the amplitude function as

$$\begin{aligned} a_{(\xi )}(t,x,\omega ):=a_{\xi ,q+1}(t,x,\omega ):=(2\pi )^{3/2} \rho ^{1/2}(t,x,\omega )\gamma _\xi \left( {{\,\textrm{Id}\,}}-\frac{\mathring{R}_\ell (t,x,\omega )}{\rho (t,x,\omega )}\right) \end{aligned}$$

with

$$\begin{aligned} \rho (t,x,\omega ):=2\Theta _\ell ^{-1}\sqrt{\ell ^2+\Vert \mathring{R}_\ell (t,x,\omega )\Vert _F^2}+\Theta _\ell ^{-1}\eta _\ell (t) \end{aligned}$$

and

$$\begin{aligned} \eta _q(t,\omega ):= \frac{1}{3 (2\pi )^3}\Big [e(t)(1-\delta _{q+2})-\Vert v_q(t)\Vert ^2_{L^2}\Big ]. \end{aligned}$$

In this case, the first statement of 1.2 remains true, but there would appear several problems in order to deduce the energy equality later on.

The factor $\Theta ^{-2}$ in the definition of $\eta _q$ is thereby essential to make use of (3.5), so that we can derive practical bounds for amplitude functions later on (cf., e.g., (3.21)), whereas $\Theta _\ell$ in front of $\eta _\ell$ in the definition of $\rho$ is needed to get a suitable cancellation in the first term of (3.30).

3.3.4 Intermittent jets

Let us now proceed with the construction of the intermittent jets. To this end, consider two smooth functions

$$\begin{aligned} \Phi :\mathbb {R}^2 \rightarrow \mathbb {R}, \quad \quad \psi :\mathbb {R} \rightarrow \mathbb {R} \end{aligned}$$

with support in a ball of radius 1 and center 0, where $\Phi$ should solve the Poisson equation $\phi :=-\Delta \Phi$. We require $\phi$ and $\psi$ to admit the normalizations

$$\begin{aligned} \frac{1}{4 \pi ^2} \int _{B_1(0)} \phi ^2(x_1,x_2) \,d(x_1,x_2)=1, \qquad \frac{1}{2\pi } \int _{B_1(0)} \psi ^2(x_3) \,dx_3=1 \end{aligned}$$

(3.9)

and $\psi$ to have zero mean. Note that Green’s identity implies $\int _{\mathbb {T}^2} \phi \,dx$$=\int _{\mathbb {T}^2}-\Delta \Phi \,dx=0$ as well.

Moreover, we define

$$\begin{aligned} \lambda :=\lambda _{q+1}, \qquad r_\perp :=\lambda _{q+1}^{-6/7}, \qquad r_\parallel :=\lambda _{q+1}^{-4/7}, \qquad \mu :=\frac{r_\parallel }{r_\perp }\lambda _{q+1}=\lambda _{q+1}^{9/7}, \end{aligned}$$

so that we find by our choice of parameters (c.f. Sect. 3.1)

$$\begin{aligned} 0<\lambda ^{-1} \ll r_\perp \ll r_\parallel \ll 1,\quad \quad \quad \lambda r_\perp \in \mathbb {N},\quad \quad \quad \mu >0. \end{aligned}$$

Since the rescaled cutoff functions

$$\begin{aligned} \phi _{r_\perp }(x_1,x_2)&:=\frac{1}{r_\perp }\phi \left( \frac{x_1}{r_\perp }, \frac{x_2}{r_\perp } \right) ,\\ \Phi _{r_\perp }(x_1,x_2)&:=\frac{1}{r_\perp }\Phi \left( \frac{x_1}{r_\perp }, \frac{x_2}{r_\perp } \right) , \\\psi _{r_\parallel }(x_3)&:= \frac{1}{r_\parallel ^{1/2}}\psi \left( \frac{x_3}{r_\parallel }\right) \end{aligned}$$

remain compactly supported, we will henceforth identify them with their $\mathbb {T}^2, \mathbb {T}^2$ and $\mathbb {T}$-periodic versions.

The vectors $\xi \in \Lambda$ in the geometric Lemma 3.2 are used to construct the building blocks (3.10) of our intermittent jets. Strictly speaking, let us select $\left( \alpha _\xi \right) _{\xi \in \Lambda } \subseteq \mathbb {R}^3$ in such a way that

$$\begin{aligned} \sqrt{|\alpha _{\xi }\cdot A_{\xi }{-}\alpha _{\xi ^\prime }\cdot A_{\xi ^\prime }{-}2 \pi z_1|^2{+}|\alpha _{\xi }\cdot (\xi {\times } A_{\xi }){-}\alpha _{\xi ^\prime }\cdot (\xi ^\prime {\times } A_{\xi ^\prime }){-}2 \pi z_2|^2}{>}\frac{2}{n_*\lambda } \end{aligned}$$

for each $\xi ,\xi ^\prime \in \Lambda$ and $z_1,z_2 \in \mathbb {Z}$, which forces the families $\left( \phi _{(\xi )}\right) _{\xi \in \Lambda }$ and $\left( \Phi _{(\xi )}\right) _{\xi \in \Lambda }$ given by

$$\begin{aligned} \phi _{(\xi )}(x)&:=\phi _{\xi ,r_\perp ,\lambda }(x):= \phi _{r_\perp }(n_*r_\perp \lambda (x-\alpha _\xi )\cdot A_\xi ,n_*r_\perp \lambda (x-\alpha _\xi )\cdot (\xi \times A_\xi )), \end{aligned}$$

(3.10a)

$$\begin{aligned} \Phi _{(\xi )}(x)&:=\Phi _{\xi ,r_\perp ,\lambda }(x):= \Phi _{r_\perp }(n_*r_\perp \lambda (x-\alpha _\xi )\cdot A_\xi ,n_*r_\perp \lambda (x-\alpha _\xi )\cdot (\xi \times A_\xi )), \end{aligned}$$

(3.10b)

$$\begin{aligned} \psi _{(\xi )}(t,x)&:=\psi _{\xi ,r_\perp ,r_\parallel ,\lambda ,\mu }(t,x):=\psi _{r_\parallel }(n_*r_\perp \lambda (x\cdot \xi +\mu t)) \end{aligned}$$

(3.10c)

to have mutually disjoint support. Here, we consider $\psi _{(\xi )}$ at any time $t \in \mathbb {R}$. The vector $A_\xi \in \mathbb {S}^2 \cap \mathbb {Q}^3$ should be orthogonal to $\xi$, so that $\{\xi ,A_\xi ,\xi \times A_\xi \}\subseteq \mathbb {S}^2\cap \mathbb {Q}^3$ forms an orthonormal basis for $\mathbb {R}^3$ and $n_*\in \mathbb {N}$ denotes the least common multiple of the denominators of the rational numbers $\xi _i, (A_\xi )_i$ and $(\xi \times A_\xi )_i,\, i=1,2,3$, in other words $\big \{n_*\xi , n_*A_\xi ,n_*\big (\xi \times A_\xi \big )\big \}\subseteq \mathbb {Z}^3$.

With these preparations in hand, we introduce the intermittent jet

$$\begin{aligned} W_{(\xi )}(t,x):=W_{\xi ,r_\perp ,r_\parallel ,\lambda , \mu }(t,x):=\xi \psi _{(\xi )}(t,x)\phi _{(\xi )}(x) \end{aligned}$$

and its incompressibility corrector

$$\begin{aligned} W_{(\xi )}^{(c)}(t,x):&=\frac{1}{n_*^2 \lambda ^2} \nabla \psi _{(\xi )}(t,x) \times {{\,\text {curl}\,}}{(\Phi _{(\xi )}(t,x)\xi )}\nonumber \\ {}&={{\,\text {curl}\,}}{{{\,\text {curl}\,}}{V_{(\xi )}(t,x)}}-W_{(\xi )}(t,x),\end{aligned}$$

(3.11)

where $V_{(\xi )}(t,x):=\frac{1}{n_*^2\lambda ^2}\xi \psi _{(\xi )}(t,x)\Phi _{(\xi )}(x)$, so that $W_{(\xi )}+W_{(\xi )}^{(c)}$ becomes divergence free. Their spatial support is then contained in some cylinders of radius $\frac{r _\parallel +r_\perp }{n_*r_\perp \lambda }$ and axis being the line passing through $(-\mu t, \alpha _\xi \cdot A_\xi , \alpha _\xi \cdot (\xi \times A_\xi ))^T$ with direction $\xi$. More precisely, one has

$$\begin{aligned}&{{\,\textrm{supp}\,}}(W_{(\xi )}\,(t,\cdot ))\subseteq B_\frac{r_\parallel +r_\perp }{n_*r_\perp \lambda }(0)+ \left( \begin{matrix} -\mu t\\ \alpha _\xi \cdot A_\xi \\ \alpha _\xi \cdot (\xi \times A_\xi ) \end{matrix} \right) +\{s \xi \}_{s \in \mathbb {R}} + 2\pi \mathbb {Z}^3 \end{aligned}$$

at each time $t\in \mathbb {R}$. So by possibly shifting $\alpha _{\xi ^\prime }$ in direction of $A_\xi , \xi \times A_\xi$, Lemma A.1 guarantees that their supports are still disjoint for all distinct $\xi ,\, \xi ^\prime \in \Lambda$. As a consequence of the orthogonal directions of oscillations for the functions defined in (3.10), we may deduce

Lemma 3.4

The building blocks $\psi _{(\xi )}$ and $\phi _{(\xi )}$ obey

$$\begin{aligned} \Vert D^\alpha \partial _t^N \psi _{(\xi )}^n D^\beta \phi _{(\xi )}^m\Vert _{CL^p}= (2\pi )^{-3/p}\Vert D^\alpha \partial _t^N \psi _{(\xi )}^n\Vert _{CL^p} \Vert D^\beta \phi _{(\xi )}^m\Vert _{L^p} \end{aligned}$$

(3.12)

for each $n,m,N \in \mathbb {N}_0$, $p \in [1,\infty )$ and all multi-indices $\alpha ,\beta \in \mathbb {N}_0^3$.

as well as the following fundamental bounds (cf. [5], p. 57).

Lemma 3.5

For any $N,M \in \mathbb {N}_0$ and $p \in [1,\infty ]$, it holds

$$\begin{aligned}&\sum _{|\alpha |\le N}\Vert D^\alpha \partial _t^M\psi _{(\xi )}\Vert _{CL^p} \lesssim r_{\parallel }^{1/p-1/2}\left( \frac{r_\perp \lambda }{r_\parallel }\right) ^N \left( \frac{r_\perp \lambda \mu }{r_\parallel }\right) ^M \end{aligned}$$

(3.13a)

$$\begin{aligned}&\sum _{|\alpha |\le N}\Vert D^\alpha \phi _{(\xi )}\Vert _{L^p}+\sum _{|\beta |\le N}\Vert D^\beta \Phi _{(\xi )}\Vert _{L^p}\lesssim r_\perp ^{2/p-1}\lambda ^N \end{aligned}$$

(3.13b)

$$\begin{aligned} \sum _{|\alpha |\le N} \Vert D^\alpha \partial _t^M W_{(\xi )}\Vert _{CL^p}&+\frac{r_\parallel }{r_\perp }\sum _{|\beta |\le N} \Vert D^\beta \partial _t^M W_{(\xi )}^{(c)}\Vert _{CL^p}+\lambda ^2 \sum _{|\gamma |\!\le \! N} \Vert D^\gamma \partial _t^M V_{(\xi )}\!\Vert _{CL^p} \!\nonumber \\&\lesssim \! r_\perp ^{2/p-1}r_\parallel ^{1/p-1/2}\lambda ^N \!\left( \frac{r_\perp \lambda \mu }{r_\parallel }\right) ^M, \end{aligned}$$

(3.13c)

where the implicit constants merely depend on $M,\, N$ and p.

In the special case, $N=M=0,\, p=2$ Lemma 3.4 and the normalizations in (3.9) even entail $\Vert W_{(\xi )}\,\Vert _{CL^2}=1$.

Based on this, we are now able to define the principal part

$$\begin{aligned} w_{q+1}^{(p)}:= \Theta ^{-1/2}_\ell \sum _{\xi \in \Lambda } a_{(\xi )}W_{(\xi )}, \end{aligned}$$

the temporal corrector

$$\begin{aligned} w_{q+1}^{(t)}:&= - \mu ^{-1} \sum _{\xi \in \Lambda } \mathbb {P}\mathbb {P}_{\ne 0} \left( a^2_{(\xi )} \psi ^2_{(\xi )} \phi ^2_{(\xi )} \xi \right) ,\end{aligned}$$

which will provide a better handling of the oscillation error later on, and the incompressibility corrector

$$\begin{aligned} w_{q+1}^{(c)}:&= \Theta ^{-1/2}_\ell \sum _{\xi \in \Lambda } \Big ( {{\text {curl}}}\left( \nabla a_{(\xi )}\times V_{(\xi )}\right) + \nabla a_{(\xi )}\times {{\text {curl}}}V_{(\xi )}+a_{(\xi )}\,W^{(c)}_{(\xi )}\Big ),\end{aligned}$$

whose purpose is to ensure that $w_{q+1}^{(p)}+w_{q+1}^{(c)}$ is divergence free and to have zero mean. In fact, the expression

$$\begin{aligned} w_{q+1}^{(p)}+w_{q+1}^{(c)}= \Theta ^{-1/2}_\ell \sum _{\xi \in \Lambda } {{\text {curl} {curl}}}\left( a_{(\xi )}V_{(\xi )}\right) \end{aligned}$$

(3.14)

can be easily verified by a direct computation, so that $w_{q+1}^{(p)}+w_{q+1}^{(c)}$ is obviously divergence free and since $a_{(\xi )}V_{(\xi )}$ is a smooth function with periodic boundary conditions, it has additionally zero mean. Notably, these properties carry over to the total perturbation

$$\begin{aligned} w_{q+1}:=w_{q+1}^{(p)}+w_{q+1}^{(c)}+w_{q+1}^{(t)}\end{aligned}$$

and we may bound each part of it as follows.

Lemma 3.6

At any time $t \in (-\infty ,\tau ]$, each component of the perturbation $w_{q+1}$ can be estimated

• (a) in $C_tL^p$ for any $p \in (1,\infty )$ as

  $$\begin{aligned}&\Vert w_{q+1}^{(p)}\Vert _{C_tL^p}\lesssim \frac{M}{4|\Lambda |} \ell ^{-8} \delta _{q+1}^{1/2} m \bar{e}^{1/2} r_\perp ^{2/p-1}r_\parallel ^{1/p-1/2}, \end{aligned}$$

  (3.15a)
  $$\begin{aligned} ATA[&\Vert w_{q+1}^{(c)}\Vert _{C_tL^p}\lesssim \frac{M}{4|\Lambda |} \ell ^{-22} \delta _{q+1}^{1/2}m\bar{e}^{1/2} r_\perp ^{2/p} r_\parallel ^{1/p-3/2}, \end{aligned}$$

  (3.15b)
  $$\begin{aligned}&\Vert w_{q+1}^{(t)}\Vert _{C_tL^p}\lesssim \left( \frac{M}{4|\Lambda |}\right) ^2\ell ^{-16}\delta _{q+1}m^2\bar{e} r_\perp ^{2/p-1}r_\parallel ^{1/p-2} \lambda _{q+1}^{-1}. \end{aligned}$$

  (3.15c)

  In the specific case $p=2$, the principal part admits the stronger bound

  $$\begin{aligned} \Vert w_{q+1}^{(p)}\Vert _{C_tL^2}\lesssim \frac{M}{4|\Lambda |} \delta _{q+1}^{1/2}m\bar{e}^{1/2} .\end{aligned}$$

  (3.15d)

• (b) in $C_{t,x}^1$ as

  $$\begin{aligned}&\Vert w_{q+1}^{(p)}\Vert _{C_{t,x}^1}\lesssim \frac{M}{4|\Lambda |} \ell ^{-16}\delta _{q+1}^{1/2}m\bar{e}^{1/2}r_\perp ^{-1}r_\parallel ^{-1/2}\lambda _{q+1}^2, \end{aligned}$$

  (3.16a)
  $$\begin{aligned}&\Vert w_{q+1}^{(c)}\Vert _{C_{t,x}^1}\lesssim \frac{M}{4|\Lambda |} \ell ^{-30} \delta _{q+1}^{1/2}m\bar{e}^{1/2} r_\parallel ^{-3/2}\lambda _{q+1}^2, \end{aligned}$$

  (3.16b)
  $$\begin{aligned}&\Vert w_{q+1}^{(t)}\Vert _{C_{t,x}^1}\lesssim \bigg (\frac{M}{4 |\Lambda |}\bigg )^2 \ell ^{-30}\delta _{q+1}m^2\bar{e}r_\perp ^{-1}r_\parallel ^{-2} \lambda _{q+1}^2. \end{aligned}$$

  (3.16c)

• (c) in $C_tW^{1,p}$ for any $p\in (1,\infty )$ as

  $$\begin{aligned} \Vert w_{q+1}^{(p)}+w_{q+1}^{(c)}\Vert _{C_tW^{1,p}}&\lesssim \frac{M}{4|\Lambda |} \ell ^{-29}\delta _{q+1}^{1/2} m\bar{e}^{1/2} r_\perp ^{2/p-1}r_\parallel ^{1/p-1/2}\lambda _{q+1}, \end{aligned}$$

  (3.17a)
  $$\begin{aligned} \Vert w_{q+1}^{(t)}\Vert _{C_tW^{1,p}}&\lesssim \left( \frac{M}{4|\Lambda |}\right) ^2 \ell ^{-23}\delta _{q+1}m^2\bar{e} r_\perp ^{2/p-1} r_\parallel ^{1/p-2}. \end{aligned}$$

  (3.17b)

The proof is postponed to Sect. 3.4.1.

It is worth mentioning that the factor $\Theta _\ell ^{-1/2}$ in the principal part $w_{q+1}^{(p)}$ of the perturbation is needed to establish (3.31), which in turn is essential to deduce a handy expression of the oscillation error (3.43). We also define the incompressibility corrector $w_{q+1}^{(c)}$ with the factor $\Theta _\ell ^{-1/2}$ ahead, in order to guarantee (3.14), whereas the temporal corrector $w_{q+1}^{(t)}$ does not contain it.

3.4 Inductive estimates for $v_{q+1}$

So far we have developed a sequence $\left( v_q\right) _{q \in \mathbb {N}_0}$, solving (3.2) on the level $q \in \mathbb {N}_0$ and with the corresponding Reynolds stress constructed below, also on the level $q+1$. As we will see in Sect. 3.4.4, this sequence converges in $C\left( (-\infty ,\tau ];L^2\left( \mathbb {T}^3\right) \right)$, so that the limit function will be our desired weak solution to (1.2) on $[0,\tau ]$. However, let us take one step after the other. We start by aiming $\left( v_q\right) _{q \in \mathbb {N}_0}$ to admit the bounds (3.3a) and (3.3b) on the level $q+1$.

3.4.1 Preparations

For this purpose, we need to control the amplitude functions and intermittent jets, so that we go back to Lemmas 3.3, and 3.6. The key ingredient of the proof of Lemma 3.3 is the ensuing result from [2], p. 163, where we set $D_t^\alpha :=\partial ^{\alpha _1}_{x_1}\ldots \partial ^{\alpha _n}_{x_n} \partial _t^{\alpha _{n+1}}$ for all multi-indices $\alpha =(\alpha _1,\ldots ,\alpha _{n+1})\in \mathbb {N}_0^{n+1}$.

Proposition 3.7

For any $k \in \mathbb {N}$, the composition of $f \in C^\infty \left( {{\,\textrm{Im}\,}}(u); \mathbb {R} \right)$ and $u \in C^\infty \left( \mathbb {R}\times \mathbb {R}^n; \mathbb {R}^N\right)$ can be estimated as

$$\begin{aligned} \sum _{0<|\alpha |\le k} \Vert D_t^\alpha f(u)\Vert _{C_tL^\infty } \lesssim&\sum _{0<|\alpha |\le k} \Bigg (\max _{|\beta |=1} \Vert D_t^\beta f \Vert _{C_tL^\infty } \max _{|\beta |=|\alpha |}\Vert D_t^\beta u\Vert _{C_tL^\infty }\\&\quad +\sum _{j=0}^{|\alpha |-1} \max _{|\beta |=j+1}\Vert D_t^{\beta }f \Vert _{C_tL^\infty } \max _{|\beta |=1} \Vert D_t^\beta u\Vert ^{|\alpha |}_{C_tL^\infty }\Bigg ). \end{aligned}$$

Proof of Lemma 3.3

(3.8a): Keeping in mind that $\alpha>4\beta b^2>\frac{4}{3} \beta$ and $\bar{e}> 4$ imply

$$\begin{aligned} \ell \le \delta _{q+1}\bar{e}, \end{aligned}$$

(3.18)

and taking (3.7), (3.3c), $\eta _q \ge 0$ and (3.5) into account lead to

$$\begin{aligned} \Vert a_{(\xi )}\Vert _{C_tL^2}&\lesssim \sup _{\begin{array}{c} R \in \mathbb {R}_{\text {sym}}^{3\times 3}\\ \Vert R-{{\,\textrm{Id}\,}}\Vert _F\le 1/2 \end{array}}|\gamma _\xi (R)| \, \Vert \rho \Vert _{C_tL^1}^{1/2}\\&\lesssim \frac{M}{4|\Lambda |} \left( \delta _{q+1}\bar{e} +\Vert \mathring{R}_q\Vert _{C_tL^1} +m^{1/4} \Vert \eta _q\Vert _{C_t} \right) ^{1/2}\\&\lesssim \frac{M}{4|\Lambda |}\left( \delta _{q+1}\bar{e} + \delta _{q+2}m^{2/4} \bar{e}+m^{1/4} \Vert \Theta ^{-2} e-\Vert v_q\Vert _{L^2}^2\Vert _{C_t}\right) ^{1/2}\\&\lesssim \frac{M}{4|\Lambda |}\left( \delta _{q+1}\bar{e} + \delta _{q+2}m^{2/4}\bar{e}+\delta _{q+1}m^{3/4}\bar{e}\right) ^{1/2}\\&\lesssim \frac{M}{4 |\Lambda |}\delta _{q+1}^{1/2}m^{3/8}\bar{e}^{1/2}. \end{aligned}$$

(3.8b): To estimate the $C_{t,x}^N$-norm of $a_{(\xi )}$, we make use of Leibniz’s rule

$$\begin{aligned} \Vert a_{(\xi )}\Vert _{C_{t,x}^N}&\lesssim \sum _{|\alpha |\le N} \sum _{\beta \le \alpha } \Big \Vert D_t^\beta \big ( \rho ^{1/2}\big )\Big \Vert _{C_tL^\infty } \bigg \Vert D_t^{\alpha -\beta } \gamma _\xi \bigg ( {{\,\text {Id}\,}}- \frac{\mathring{R}_\ell }{\rho }\bigg )\bigg \Vert _{C_tL^\infty }\\ {}&\lesssim \sum _{k\le N} \big \Vert \rho ^{1/2}\big \Vert _{C^k_{t,x}} \bigg \Vert \gamma _\xi \bigg ( {{\,\text {Id}\,}}- \frac{\mathring{R}_\ell }{\rho }\bigg )\bigg \Vert _{C_{t,x}^{N-k}}. \end{aligned}$$

Let us proceed with a bound for $\big \Vert \rho ^{1/2}\big \Vert _{C_{t,x}^k}$. We will verify

$$\begin{aligned} \big \Vert \rho ^{1/2}\big \Vert _{C_{t,x}^k} \lesssim \left\{ \begin{array}{ll} \ell ^{-2} \delta ^{1/2}_{q+1}m^{3/8}\bar{e}^{1/2}, &{} \text{ if } k=0,\\ \ell ^{1-7k}\delta _{q+1}^{1/2}m^{3/8}\bar{e}^{1/2}, &{}{} \text{ if } k>0. \end{array}\right. \end{aligned}$$

(3.19)

For this purpose, we need

$$\begin{aligned} {\underline{1.\,Claim:}}\quad \Vert \mathring{R}_\ell \Vert _{C_{t,x}^k} \lesssim \ell ^{-4-k} \delta _{q+2}m^{1/2} \bar{e} \end{aligned}$$

(3.20)

$\square$

Proof

Owing to the embedding $W^{4,1}\subseteq L^\infty$ (cf. [15], p. 284, Theorem 6), Fubini’s theorem and (3.3c), we may deduce

$$\begin{aligned} \Vert \mathring{R}_\ell \Vert _{C_{t,x}^k}&\lesssim \sum _{n+|\alpha | \le k} \Vert \partial _t^n D^\alpha \mathring{R}_\ell \Vert _{C_tW^{4,1}}\\ {}&\lesssim \sum _{\begin{array}{c} n+|\alpha | \le k\\ |\beta | \le 4 \end{array}}\Big \Vert \Big ( \mathring{R}_q *_t \partial _t^n \varphi _\ell \Big ) *_x D^{\alpha +\beta } \phi _\ell \Big \Vert _{C_tL^1}\\ {}&\lesssim \sum _{\begin{array}{c} n+|\alpha | \le k\\ |\beta | \le 4 \end{array}} \sup _{s \in (-\infty ,t]} \int _{\mathbb {T}^3} \int _0^\ell \int _{|y|\le \ell } |\mathring{R}_q(s-u,x-y)| \ell ^{-n} \frac{1}{\ell } \varphi ^{(n)} \left( \frac{u}{\ell } \right) \\ {}& \cdot \ell ^{-(|\alpha |+|\beta |)} \frac{1}{\ell ^3} D_{\frac{y}{\ell }}^{\alpha +\beta } \phi \left( \frac{y}{\ell }\right) \,dy \,du \,dx\\ {}&\lesssim \ell ^{-4-k} \Vert \mathring{R}_q\Vert _{C_tL^1} \sum _{\begin{array}{c} n+|\alpha | \le k\\ |\beta | \le 4 \end{array}} \int _0^1 \varphi ^{(n)} \left( u \right) \,du \int _{|y|\le 1} D^{\alpha +\beta } \phi (y) \,dy \\ {}&\lesssim \ell ^{-4-k} \delta _{q+2} m^{2/4}\bar{e}. \end{aligned}$$

$\square$

to derive

$$\begin{aligned} {\underline{2.\,Claim:}}\quad \Vert \rho \Vert _{C_{t,x}^k} \lesssim \left\{ \begin{array}{ll} \ell ^{-4} \delta _{q+1}m^{3/4}\bar{e}, &{}\text{ if } k=0, \\ \ell ^{2-7k}\delta _{q+1}m^{3/4}\bar{e}, &{}{} \text{ if } k>0.\end{array}\right. \end{aligned}$$

(3.21)

Proof

Combining (3.18), (3.20) and $\eta _q\ge 0$ with (3.5) results in

$$\begin{aligned} \Vert \rho \Vert _{C_{t,x}^0} \lesssim \delta _{q+1}\bar{e}+\ell ^{-4}\delta _{q+2}m^{1/2}\bar{e} +m^{1/4}\big \Vert \Theta ^{-2} e-\Vert v_q\Vert _{L^2}^2 \big \Vert _{C_t}\lesssim \ell ^{-4}\delta _{q+1} m^{3/4}\bar{e}. \end{aligned}$$

For $k>0$, we introduce the smooth function

$$\begin{aligned} f :\mathbb {R} \rightarrow \mathbb {R}, \quad f(z):= \sqrt{\ell ^2+z^2}, \end{aligned}$$

satisfying

$$\begin{aligned} |f^{(k)}(z)| \lesssim \ell ^{-k+1}. \end{aligned}$$

(3.22)

Keeping (3.20) and (3.1b) in mind, Proposition 3.7 teaches us

$$\begin{aligned} \sum _{0<|\alpha |\le k}\Big \Vert D_t^\alpha \Big ( \sqrt{\ell ^2+\Vert \mathring{R}_\ell \Vert _F^2}\Big )\Big \Vert _{C_tL^\infty } \lesssim \ell ^{2-7k} \delta _{q+2}m^{1/2}\bar{e}. \end{aligned}$$

Moreover, we use Leibniz’s rule together with the fact $\eta _q \ge 0$ and (3.5) to calculate

$$\begin{aligned} \sum _{0<|\alpha |\le k} \Vert D_t^\alpha (\Theta _\ell \eta _\ell )\Vert _{C_tL^\infty }&\lesssim \sum _{0<n\le k} \sum _{j\le n}\Vert \partial _t^{n-j} \Theta _\ell \Vert _{C_t}\Vert \partial _t^j\eta _\ell \Vert _{C_t}\\ {}&\lesssim \sum _{0<n\le k} \sum _{j\le n}m^{1/4}\ell ^{-n+j+i} \int _0^1 \varphi ^{(n-j)}(u)\,du\, \Vert \eta _q\Vert _{C_t} \ell ^{-j} \\ {}&\int _0^1 \varphi ^{(j)}(u)\,du \lesssim \ell ^{-k}m^{1/4} \Vert \Theta ^{-2}e-\Vert v_q\Vert ^2_{L^2}\Vert _{C_t}\\ {}&\lesssim \ell ^{-k} \delta _{q+1} m^{3/4}\bar{e}.\end{aligned}$$

As a result of these three bounds

$$\begin{aligned} \Vert \rho \Vert _{C_{t,x}^k}&{\lesssim } \Vert \rho \Vert _{C_{t,x}^0}{+}\sum _{0<|\alpha |\le k}\Big \Vert D_t^\alpha \Big (\sqrt{\ell ^2+\Vert \mathring{R}_\ell \Vert ^2}\Big )\Big \Vert _{C_tL^\infty } {+}\sum _{0<|\alpha |\le k} \Vert D_t^\alpha (\Theta _\ell \eta _\ell )\Vert _{C_tL^\infty }\\ {}&\lesssim \ell ^{2-7k}\delta _{q+1}m^{3/4}\bar{e}. \end{aligned}$$

$\square$

In order to find a bound for $\Vert \rho ^{1/2}\Vert _{C_{t,x}^k}$, we intend to make use of Proposition 3.7 again. This time, however, applied to the function

$$\begin{aligned} \widetilde{f} :{{\,\textrm{Im}\,}}(\rho ) \rightarrow \mathbb {R}, \quad \widetilde{f}(z)=z^{1/2}. \end{aligned}$$

and $\rho$. Taking into account that $\rho \ge \ell$ entails $|\widetilde{f}^{(k)}(z)|\lesssim |z|^{1/2-k}\lesssim \ell ^{1/2-k}$, we deduce from (3.21) and (3.1b) that

$$\begin{aligned} \sum _{0<|\alpha |\le k}\Vert D_t^\alpha \big ( \rho ^{1/2}\big )\Vert _{C_tL^\infty }&\lesssim \ell ^{-1/2} \ell ^{2-7k} \delta _{q+1} m^{3/4}\bar{e}+\ell ^{1/2-k}\left( \ell ^{2-7} \delta _{q+1}m^{3/4}\bar{e}\right) ^k\\&\lesssim \ell ^{1-7k}\delta _{q+1}^{1/2} \bar{e}^{1/2} \end{aligned}$$

holds, provided $k>0$. As a consequence and accordingly (3.21)

$$\begin{aligned} \Vert \rho ^{1/2}\Vert _{C_{t,x}^k} \lesssim \left( \ell ^{-4}\delta _{q+1}m^{3/4}\bar{e}\right) ^{1/2}+\ell ^{1-7k}\delta _{q+1}^{1/2} \bar{e}^{1/2}\lesssim \ell ^{1-7k}\delta _{q+1}^{1/2} m^{3/8}\bar{e}^{1/2}. \end{aligned}$$

Let us now have a closer look at $\Big \Vert \gamma _\xi \left( {{\,\textrm{Id}\,}}- \frac{\mathring{R}_\ell }{\rho }\right) \Big \Vert _{C_{t,x}^{N-k}}$. Our aim is to verify

$$\begin{aligned} \Big \Vert \gamma _\xi \left( {{\,\textrm{Id}\,}}- \frac{\mathring{R}_\ell }{\rho }\right) \Big \Vert _{C_{t,x}^{N-k}} \lesssim \left\{ \begin{array}{ll} \frac{M}{4|\Lambda |}, &{} \text {if } k=N, \\ \frac{M}{4|\Lambda |}\ell ^{-6-7(N-k)} , &{} \text {if } 0\le k<N.\end{array}\right. \end{aligned}$$

(3.23)

The case $k=N$ is trivial, whereas Proposition 3.7 and (3.7) again imply

$$\begin{aligned}&\Big \Vert \gamma _\xi \left( {{\,\text {Id}\,}}- \frac{\mathring{R}_\ell }{\rho }\right) \Big \Vert _{C_{t,x}^{N-k}}-\Big \Vert \gamma _\xi \left( {{\,\text {Id}\,}}- \frac{\mathring{R}_\ell }{\rho }\right) \Big \Vert _{C_tL^\infty }\\ {}& {\lesssim } \sum _{0<|\alpha |{\le } N-k} \frac{M}{8 |\Lambda |(1{+}8 \pi ^3)^{1/2}}\left( \Vert {{\,\text {Id}\,}}\Vert _{C_{t,x}^{N-k}}{+} \bigg \Vert \frac{\mathring{R}_\ell }{\rho } \bigg \Vert _{C^{N-k}_{t,x}} {+}\Vert {{\,\text {Id}\,}}\Vert _{C_{t,x}^1}^{|\alpha |}{+}\bigg \Vert \frac{\mathring{R}_\ell }{\rho } \bigg \Vert ^{|\alpha |}_{C^1_{t,x}} \right) \end{aligned}$$

and we assert

$$\begin{aligned} {\underline{3.\,Claim:}}\quad \bigg \Vert \frac{\mathring{R}_\ell }{\rho }\bigg \Vert _{C_{t,x}^{N-k}} \lesssim \ell ^{-6-7(N-k)}.\end{aligned}$$

Proof

Thanks to Leibniz’s formula

$$\begin{aligned} \bigg \Vert \frac{\mathring{R}_\ell }{\rho }\bigg \Vert _{C_{t,x}^{N-k}}&\lesssim \sum _{|\alpha |\le N-k} \sum _{\beta \le \alpha } \Vert D_t^\beta \mathring{R}_\ell \Vert _{C_tL^\infty } \bigg \Vert D_t^{\alpha -\beta }\frac{1}{\rho }\bigg \Vert _{C_tL^\infty }\lesssim \sum _{j\le N-k} \Vert \mathring{R}_\ell \Vert _{C_{t,x}^{j}} \bigg \Vert \frac{1}{\rho } \bigg \Vert _{C_{t,x}^{N-k-j}}. \end{aligned}$$

Applying Proposition 3.7 to the functions

$$\begin{aligned} \hat{f} :{{\,\textrm{Im}\,}}(\rho ) \rightarrow \mathbb {R}, \quad \hat{f}(z)=\frac{1}{z}, \quad |\hat{f}^{(k)}(z)|\lesssim |z|^{-1-k}\lesssim \ell ^{-1-k} \end{aligned}$$

and $\rho$ yields according to (3.21) and (3.1b)

$$\begin{aligned} \sum _{0<|\alpha |\le N-k-j}\bigg \Vert D_t^\alpha \frac{1}{\rho }\bigg \Vert _{C_tL^\infty }&\lesssim \ell ^{-7(N-k-j)}\delta _{q+1}m^{3/4} \bar{e}+\ell ^{-1-6(N-k-j)} \delta _{q+1}m^{\frac{3(N-k-j)}{4}}\bar{e}^{N-k-j}\\ {}&\lesssim \ell ^{-1-7(N-k-j)}. \end{aligned}$$

Consequently,

$$\begin{aligned} \bigg \Vert \frac{\mathring{R}_\ell }{\rho }\bigg \Vert _{C_{t,x}^{N-k}}&\lesssim \sum _{j\le N-k-1} \Vert \mathring{R}_\ell \Vert _{C_{t,x}^{j}} \left( \bigg \Vert \frac{1}{\rho }\bigg \Vert _{C_tL^\infty }+\sum _{0<|\alpha |\le N-k-j} \bigg \Vert D_t^\alpha \frac{1}{\rho }\bigg \Vert _{C_tL^\infty } \right) \\ {}& +\Vert \mathring{R}_\ell \Vert _{C_{t,x}^{N-k}} \bigg \Vert \frac{1}{\rho }\bigg \Vert _{C_{t,x}^0}\\ {}&\lesssim \sum _{j\le N-k-1} \ell ^{-4-j}\delta _{q+2}m^{1/2}\bar{e}\left( \ell ^{-1}+ \ell ^{-1-7(N-k-j)}\right) \\ {}&\quad +\ell ^{-4-(N-k)}\delta _{q+2}m^{1/2}\bar{e}\ell ^{-1}\lesssim \ell ^{-6-7(N-k)}. \end{aligned}$$

The penultimate step additionally follows from (3.20) and $\rho \ge \ell$, whereas the last step also holds due to (3.1b). $\square$

If $k=N-1$, we obtain a stronger bound

$$\begin{aligned} \ \ {\underline{4.Claim:}}\ \quad \bigg \Vert \frac{\mathring{R}_\ell }{\rho }\bigg \Vert _{C_{t,x}^1} \lesssim \ell ^{-7}.\end{aligned}$$

Proof

Remembering that $\rho \ge \ell$ and $\rho \ge \Vert \mathring{R}_\ell \Vert _F$ holds and taking (3.20), (3.21) and (3.1b) into account, we compute

$$\begin{aligned} \bigg \Vert \frac{\mathring{R}_\ell }{\rho }\bigg \Vert _{C_{t,x}^1}&\lesssim \bigg \Vert \frac{\mathring{R}_\ell }{\rho }\bigg \Vert _{C_tL^\infty } +\bigg \Vert \frac{\partial _t \mathring{R}_\ell }{\rho }\bigg \Vert _{C_tL^\infty }+ \bigg \Vert \frac{\mathring{R}_\ell \partial _t \rho }{\rho ^2}\bigg \Vert _{C_tL^\infty }\\ {}&\quad + \sum _{k=1}^3 \left( \bigg \Vert \frac{\partial _{x_k}\mathring{R}_\ell }{\rho }\bigg \Vert _{C_tL^\infty }+\bigg \Vert \frac{\mathring{R}_\ell \partial _{x_k}\rho }{\rho ^2}\bigg \Vert _{C_tL^\infty }\right) \\ {}&\lesssim \ell ^{-1} \left( \Vert \mathring{R}_\ell \Vert _{C_tL^\infty }+ \Vert \partial _t \mathring{R}_\ell \Vert _{C_tL^\infty } +\sum _{k=1}^3 \Vert \partial _{x_k}\mathring{R}_\ell \Vert _{C_tL^\infty } \right) \\ {}&\quad + \ell ^{-1} \left( \Vert \partial _t \rho \Vert _{C_tL^\infty }+\sum _{k=1}^3 \Vert \partial _{x_k}\rho \Vert _{C_tL^\infty } \right) \\ {}&\lesssim \ell ^{-1} \left( \ell ^{-4-1} \delta _{q+2} m^{1/2}\bar{e} +\ell ^{2-7} \delta _{q+1}m^{3/4}\bar{e}\right) \\ {}&\lesssim \ell ^{-7}.\end{aligned}$$

As a result

$$\begin{aligned} \Big \Vert \gamma _\xi \bigg ( {{\,\text {Id}\,}}{-} \frac{\mathring{R}_\ell }{\rho }\bigg ) \Big \Vert _{C_{t,x}^{N-k}}&\lesssim \sum _{0<|\alpha |\le N-k} \frac{M}{8|\Lambda |(1{+}8\pi ^3)^{1/2}}\left( 1{+}\ell ^{-6-7(N-k)}{+}1{+}\ell ^{-7|\alpha |}\right) \\ {}& {+}\Big \Vert \gamma _\xi \left( {{\,\text {Id}\,}}- \frac{\mathring{R}_\ell }{\rho }\right) \Big \Vert _{C_tL^\infty }\\ {}&\lesssim \frac{M}{4|\Lambda |}\ell ^{-6-7(N-k)}. \end{aligned}$$

Altogether we therefore bound (3.8b) as

$$\begin{aligned} \Vert a_{(\xi )}\Vert _{C_{t,x}^N}&\lesssim \Vert \rho ^{1/2}\Vert _{C^0_{t,x}} \bigg \Vert \gamma _\xi \bigg ( {{\,\text {Id}\,}}- \frac{\mathring{R}_\ell }{\rho }\bigg )\bigg \Vert _{C_{t,x}^N} +\sum _{k=1}^{N-1} \Vert \rho ^{1/2}\Vert _{C^k_{t,x}} \bigg \Vert \gamma _\xi \bigg ( {{\,\text {Id}\,}}- \frac{\mathring{R}_\ell }{\rho }\bigg )\bigg \Vert _{C_{t,x}^{N-k}}\\ {}&\quad +\Vert \rho ^{1/2}\Vert _{C^N_{t,x}} \bigg \Vert \gamma _\xi \bigg ( {{\,\text {Id}\,}}- \frac{\mathring{R}_\ell }{\rho }\bigg )\bigg \Vert _{C_{t,x}^0}\\ {}&\lesssim \frac{M}{4 |\Lambda |}\delta _{q+1}^{1/2}m^{3/8}\bar{e}^{1/2}\left( \ell ^{-8-7N}+\ell ^{-5-7N}+\ell ^{1-7N} \right) \\ {}&\lesssim \frac{M}{4|\Lambda |}\ell ^{-8-7N} \delta _{q+1}^{1/2}m^{3/8}\bar{e}^{1/2},\end{aligned}$$

provided $N>0$. However, the final bound is due to (3.7) and (3.19) even valid for $N=0$. The proof of Lemma 3.3 is therefore complete. $\square$

Proof of Lemma 3.6

(3.15a): follows readily from (3.8b) and (3.13c).

(3.15b): Thanks to (3.8b) and (3.13c) again, we obtain

$$\begin{aligned} Vert w_{q+1}^{(c)}\Vert _{C_tL^p}&{\lesssim } m^{1/8}\sum _{\xi \in \Lambda } \bigg \{ \sum _{\ell ij=1}^3 \Big \Vert \partial _{x_\ell } \partial _{x_i} a_{(\xi )}V_{(\xi )}^j\Big \Vert _{C_tL^p}{+}\!\! \sum _{\ell ij=1}^3\Vert \partial _{x_i} a_{(\xi )}\partial _{x_\ell } V_{(\xi )}^j\Vert _{C_tL^p} \bigg \}\\ {}&\quad +m^{1/8}\sum _{\xi \in \Lambda } \bigg \{ \sum _{\ell ij=1}^3\Big \Vert \partial _{x_\ell } a_{(\xi )}\partial _{ x_i} V_{(\xi )}^j \Big \Vert _{C_tL^p}+ \Big \Vert a_{(\xi )}W^{(c)}_{(\xi )}\Big \Vert _{C_tL^p} \bigg \} \\ {}&{\lesssim } m^{1/8}\sum _{\xi \in \Lambda } \bigg \{ \Vert a_{(\xi )}\Vert _{C^2_{t,x}}\Vert V_{(\xi )}\Vert _{C_tL^p} {+}\Vert a_{(\xi )}\Vert _{C^1_{t,x}}\!\!\sum _{|\gamma |\le 1 } \Vert D^\gamma V_{(\xi )}\Vert _{C_tL^p}\bigg \}\\ {}&\quad +m^{1/8}\sum _{\xi \in \Lambda }\Vert a_{(\xi )}\Vert _{C^0_{t,x}}\Vert W^{(c)}_{(\xi )}\Vert _{C_tL^p}\\ {}&\lesssim \frac{M}{4 |\Lambda |} \ell ^{-22} \delta _{q+1}^{1/2} m \bar{e}^{1/2} r_\perp ^{2/p}r_\parallel ^{1/p-3/2}. \end{aligned}$$

(3.15c): Remembering that $\mathbb {P}\mathbb {P}_{\ne 0}$ is bounded on $L^p$ and keeping (3.12), (3.8b), (3.13a) and (3.13b) in mind, we may compute

$$\begin{aligned} \Vert w_{q+1}^{(t)}\Vert _{C_tL^p}&\lesssim \mu ^{-1} \sum _{\xi \in \Lambda } \Vert a_{(\xi )}^2\Vert _{C^0_{t,x}} \Vert \psi _{(\xi )}^2 \phi _{(\xi )}^2\Vert _{C_tL^p}\\ {}&\lesssim \mu ^{-1} \sum _{\xi \in \Lambda } \Vert a_{(\xi )}\Vert _{C_{t,x}^0}^2 \Vert \psi _{(\xi )}\Vert ^2_{C_tL^{2p}} \Vert \phi _{(\xi )}\Vert ^2_{L^{2p}}\\ {}&\lesssim \left( \frac{M}{4 |\Lambda |}\right) ^2 \ell ^{-16} \delta _{q+1} m^2 \bar{e} r_\perp ^{2/p-1} r_\parallel ^{1/p-2} \lambda _{q+1}^{-1}. \end{aligned}$$

(3.15d): Moreover, if $p=2$, we obtain according to (3.8a) and (3.8b)

$$\begin{aligned} \sum _{|\alpha |\le j}\Vert D^\alpha a_{(\xi )}\Vert _{C_tL^2} \lesssim \frac{M}{4|\Lambda |} \delta _{q+1}^{1/2}m^{3/8}\bar{e}^{1/2}\ell ^{-15j} \end{aligned}$$

for all $j\ge 0$. Choosing $N\in \mathbb {N}$ in such a way that $N \ge \frac{60\ln (\ell )-\ln (16)-12}{\ln (12\pi )+3-\ln (n_*r_\perp \lambda _{q+1})-15 \ln (\ell )}$ holds, ensures

$$\begin{aligned} 16 \exp (12)\ell ^{-60} \left( 3\frac{2 \pi }{n_*r_\perp \lambda _{q+1}} \,2\exp (3)\ell ^{-15} \right) ^N \le 1, \end{aligned}$$

whereas $a\ge 3600,\, b\ge 7,\, 161\alpha <\frac{1}{7 }$ and (3.1b) imply

$$\begin{aligned} 3\frac{2 \pi }{n_*r_\perp \lambda _{q+1}} \, \ell ^{-15}\le \frac{1}{41}. \end{aligned}$$

Here, we need in particular that $a\ge 3600$. Alternatively one could also chose a smaller a, but then we have to increase $b\in 7\mathbb {N}$.

So all requirements of Lemma 3.7 from [6], recalled in “Appendix A,” A.2, are satisfied. Invoking additionally (3.13c) entails

$$\begin{aligned} \Vert w_{q+1}^{(p)}\Vert _{C_tL^2} \lesssim m^{1/8} \frac{M}{4|\Lambda |} \delta _{q+1}^{1/2}m^{3/8}\bar{e}^{1/2}\sum _{\xi \in \Lambda } \Vert W_{(\xi )}\Vert _{C_tL^2}\lesssim \frac{M}{4|\Lambda |} \delta _{q+1}^{1/2}m\bar{e}^{1/2}. \end{aligned}$$

b)(3.16a): follows from (3.8b), (3.13c) and

$$\begin{aligned} \Vert \partial _t \Theta _\ell ^{-1/2}\Vert _{C_t}\lesssim \Vert \partial _t \Theta _\ell \Vert _{C_t}\Vert \Theta _\ell ^{-3/2}\Vert _{C_t}\lesssim \ell ^{-1}m^{1/4}m^{3/8}. \end{aligned}$$

(3.24)

Namely,

$$\begin{aligned} \Vert w_{q+1}^{(p)}\Vert _{C_{t,x}^1}&\lesssim \Vert \Theta _\ell ^{-1/2}\Vert _{C_t}\Vert \Theta _\ell ^{1/2}w_{q+1}^{(p)}\Vert _{C_tL^\infty } +\Vert \partial _t\Theta _\ell ^{-1/2}\Vert _{C_t}\Vert \Theta _\ell ^{1/2}w_{q+1}^{(p)}\Vert _{C_tL^\infty }\\ {}& +\Vert \Theta _\ell ^{-1/2}\Vert _{C_t}\Vert \partial _t (\Theta _\ell ^{1/2}w_{q+1}^{(p)})\Vert _{C_tL^\infty }\\ {}& +\Vert \Theta _\ell ^{-1/2}\Vert _{C_t}\sum _{|\alpha |= 1}\Vert \Theta _\ell ^{1/2}D^\alpha w_{q+1}^{(p)}\Vert _{C_tL^\infty } \\&{\lesssim }\ell ^{-1}m^{5/8} \sum _{\xi \in \Lambda } \bigg ( \Vert a_{(\xi )}\Vert _{C_tL^\infty }\Vert W_{(\xi )}\Vert _{C_tL^\infty }{+} \Vert \partial _t a_{(\xi )}\Vert _{C_tL^\infty } \Vert W_{(\xi )}\Vert _{C_tL^\infty }\bigg )\\& {+}\ell ^{-1}m^{5/8}\sum _{\xi \in \Lambda }\!\bigg (\Vert a_{(\xi )}\Vert _{C_tL^\infty }\Vert \partial _t W_{(\xi )}\Vert _{C_tL^\infty }{+}\sum _{|\alpha |=1}\Vert D^\alpha a_{(\xi )}\Vert _{C_tL^\infty }\Vert W_{(\xi )}\Vert _{C_tL^\infty }\bigg )\\& +\ell ^{-1}m^{5/8}\sum _{\xi \in \Lambda }\sum _{|\alpha |=1}\Vert a_{(\xi )}\Vert _{C_tL^\infty }\Vert D^\alpha W_{(\xi )}\Vert _{C_tL^\infty } \\&\lesssim \ell ^{-1}m^{5/8}\sum _{\xi \in \Lambda } \Vert a_{(\xi )}\Vert _{C_{t,x}^0} \bigg (\Vert W_{(\xi )}\Vert _{C_tL^\infty }+\Vert \partial _tW_{(\xi )}\Vert _{C_tL^\infty }\\&+\sum _{|\alpha |=1} \Vert D^\alpha W_{(\xi )}\Vert _{C_tL^\infty } \bigg )+\ell ^{-1}m^{5/8}\sum _{\xi \in \Lambda }\Vert a_{(\xi )}\Vert _{C_{t,x}^1}\Vert W_{(\xi )}\Vert _{C_tL^\infty } \\&\lesssim \frac{M}{4 |\Lambda |} \ell ^{-16}\delta _{q+1}^{1/2} m\bar{e}^{1/2} r_\perp ^{-1}r_\parallel ^{-1/2}\lambda _{q+1}^2. \end{aligned}$$

(3.16b): We will estimate each involved term of

$$\begin{aligned} \Vert w_{q+1}^{(c)}\Vert _{C_{t,x}^1}&\overset{(3.24)}{\le }\ \ell ^{-1}m^{5/8} \sum _{\xi \in \Lambda }\Vert {{\,\text {curl}\,}}(\nabla a_{(\xi )}\times V_{(\xi )})\Vert _{C_{t,x}^1} \\ {}&\quad +\ell ^{-1}m^{5/8} \sum _{\xi \in \Lambda }\Big (\Vert \nabla a_{(\xi )}\times {{\,\text {curl}\,}}V_{(\xi )}\Vert _{C_{t,x}^1}+\Vert a_{(\xi )}W^{(c)}_{(\xi )}\Vert _{C_{t,x}^1}\Big )\end{aligned}$$

by using (3.8b) and (3.13c) in order of their appearance.

Firstly, by using the Levi-Civita symbol,

$$\begin{aligned} \Vert {{\,\text {curl}\,}}(\nabla a_{(\xi )}&\times V_{(\xi )})\Vert _{C_{t,x}^1}\\ {}&\lesssim \sum _{\ell , k,m,i,j} \Vert \mathcal {E}_{\ell k m} \mathcal {E}_{ijk}\partial _{x_\ell } (\partial _{x_i} a_{(\xi )}V^j_{(\xi )}){\textbf {e}}_m\Vert _{C_{t,x}^1}\\ {}&\lesssim \sum _{\ell , i,j}\Big \{ \Vert \partial _{x_\ell } \partial _{x_i} a_{(\xi )}V^j_{(\xi )}\Vert _{C_{t,x}^1}+\Vert \partial _{x_i} a_{(\xi )}\partial _{x_\ell } V^j_{(\xi )}\Vert _{C_{t,x}^1}\Big \}\\ {}&\lesssim \sum _{|\alpha |\le 2} \sum _{|\beta |\le 1} \Vert D^\alpha a_{(\xi )}D^\beta V_{(\xi )}\Vert _{C_{t,x}^1}\\ {}&\lesssim \!\! \sum _{|\alpha |\le 2} \sum _{|\beta |\le 1} \bigg \{ \Vert D^\alpha a_{(\xi )}\Vert _{C_tL^\infty }\Vert D^\beta V_{(\xi )}\Vert _{C_tL^\infty }{+}\Vert \partial _t D^\alpha a_{(\xi )}\Vert _{C_tL^\infty }\Vert D^\beta V_{(\xi )}\Vert _{C_tL^\infty }\bigg \}\\ {}& +\sum _{|\alpha |\le 2} \sum _{|\beta |\le 1}\Vert D^\alpha a_{(\xi )}\Vert _{C_tL^\infty }\Vert \partial _t D^\beta V_{(\xi )}\Vert _{C_tL^\infty }\\ {}& +\sum _{|\alpha |\le 2} \sum _{|\beta |\le 1}\sum _{|\gamma |=1}\Vert D^{\alpha +\gamma }a_{(\xi )}\Vert _{C_tL^\infty }\Vert D^\beta V_{(\xi )}\Vert _{C_tL^\infty }\\ {}&+\sum _{|\alpha |\le 2} \sum _{|\beta |\le 1}\sum _{|\gamma |=1}\Vert D^\alpha a_{(\xi )}\Vert _{C_tL^\infty }\Vert D^{\beta +\gamma } V_{(\xi )}\Vert _{C_tL^\infty }\\ {}&\lesssim \Vert a_{(\xi )}\Vert _{C_{t,x}^3} \bigg ( \sum _{|\beta |\le 1} \Vert \partial _tD^\beta V_{(\xi )}\Vert _{C_tL^\infty }+ \sum _{|\beta |\le 2} \Vert D^\beta V_{(\xi )}\,\Vert _{C_tL^\infty } \bigg )\\ {}&\lesssim \frac{M}{4|\lambda |} \ell ^{-29} \delta _{q+1}^{1/2} m^{3/8}\bar{e}^{1/2} r_\perp ^{-1} r_\parallel ^{-1/2} \lambda _{q+1},\end{aligned}$$

secondly

$$\begin{aligned} \Vert \nabla a_{(\xi )}\times {{\,\text {curl}\,}}V_{(\xi )}\Vert _{C_{t,x}^1} \lesssim \frac{M}{4|\lambda |} \ell ^{-22} \delta _{q+1}^{1/2} m^{3/8} \bar{e}^{1/2} r_\perp ^{-1} r_\parallel ^{-1/2} \lambda _{q+1} \end{aligned}$$

and thirdly

$$\begin{aligned} \Vert a_{(\xi )}W^{(c)}_{(\xi )}\Vert _{C_{t,x}^1} \lesssim \frac{M}{4 |\Lambda |} \ell ^{-15} \delta _{q+1}^{1/2} m^{3/8}\bar{e}^{1/2} r_\parallel ^{-3/2} \lambda _{q+1}^2,\end{aligned}$$

verifying the claim.

(3.16c): Let $E_{n,\beta }\partial ^n_t D^\beta w_{q+1}^{(t)}$ for any $n\in \mathbb {N}_0,\, \beta \in \mathbb {N}_0^3$ be the canonical extension of $\partial _t^n D^\beta w_{q+1}^{(t)}$ to $\mathbb {R}^3$, meaning that $E_{n,\beta }:W^{1,p}\left( \mathbb {T}^3 \right) \rightarrow W^{1,p}\left( \mathbb {R}^3 \right)$ denotes a linear bounded operator with ${E_{n,\beta }\partial _t^n D^\beta w_{q+1}^{(t)}}_{|\mathbb {T}^3}=\partial _t^nD^\beta w_{q+1}^{(t)}$ $\mathcal {P}$-almost everywhere (see [15], p. 268, Theorem 1 for instance). It then holds according to Morrey’s inequality (see [15], p. 280, Theorem 4)

$$\begin{aligned} \Vert w_{q+1}^{(t)}\Vert _{C_{t,x}^1(\mathbb {T}^3)}&\lesssim \sum _{n+|\beta |\le 1} \Vert E_{n,\beta }\partial ^n_t D^\beta w_{q+1}^{(t)}\Vert _{C_tC^{0,\gamma }(\mathbb {R}^3)}\\ {}&\lesssim \sum _{n+|\beta |\le 1} \Vert E_{n,\beta }\partial ^n_t D^\beta w_{q+1}^{(t)}\Vert _{C_tW^{1,p}(\mathbb {R}^3)} \\ {}&\lesssim \mu ^{-1} \sum _{\xi \in \Lambda } \Vert \mathbb {P}\mathbb {P}_{\ne 0}(a_{(\xi )}^2\psi _{(\xi )}^2\phi _{(\xi )}^2\xi )\Vert _{C_tW^{1,p}(\mathbb {T}^3)}\\ {}&\quad +\mu ^{-1} \sum _{\xi \in \Lambda }\Vert \partial _t\mathbb {P}\mathbb {P}_{\ne 0}(a_{(\xi )}^2\psi _{(\xi )}^2\phi _{(\xi )}^2\xi )\Vert _{C_tW^{1,p}(\mathbb {T}^3)}\\ {}&\quad + \mu ^{-1} \sum _{\xi \in \Lambda }\sum _{|\beta |=1}\Vert D^\beta \mathbb {P}\mathbb {P}_{\ne 0} (a_{(\xi )}^2 \psi _{(\xi )}^2\phi _{(\xi )}^2\xi )\Vert _{C_tW^{1,p}(\mathbb {T}^3)} \end{aligned}$$

for any $p \in \big (3, \infty \big )$ and $\gamma :=1-\frac{3}{p}$.

Note that $x\mapsto (a_{(\xi )}^2\psi _{(\xi )}^2\phi _{(\xi )}^2 \xi )(x)$ and $x\mapsto \partial _t(a_{(\xi )}^2\psi _{(\xi )}^2\phi _{(\xi )}^2 \xi )(x)$ are as smooth functions on $\mathbb {T}^3$ bounded, so that they are particularly dominated by some integrable constant function. This allows us to compute

$$\begin{aligned} \partial _t \mathbb {P}_{\ne 0}\big (a_{(\xi )}^2\psi _{(\xi )}^2\phi _{(\xi )}^2 \xi \big )= \mathbb {P}_{\ne 0}\partial _t\big (a_{(\xi )}^2\psi _{(\xi )}^2\phi _{(\xi )}^2 \xi \big ),\end{aligned}$$

which implies together with Lemma 2.1

$$\begin{aligned} \partial _t \mathbb {P}\mathbb {P}_{\ne 0}\big (a_{(\xi )}^2\psi _{(\xi )}^2\phi _{(\xi )}^2 \xi \big )= \mathbb {P}\mathbb {P}_{\ne 0}\partial _t\big (a_{(\xi )}^2\psi _{(\xi )}^2\phi _{(\xi )}^2 \xi \big ) \end{aligned}$$

(3.25)

and

$$\begin{aligned} \partial _{x_i} \mathbb {P}\mathbb {P}_{\ne 0}\big (a_{(\xi )}^2\psi _{(\xi )}^2\phi _{(\xi )}^2 \xi \big )= \mathbb {P}\partial _{x_i} \mathbb {P}_{\ne 0} \big (a_{(\xi )}^2\psi _{(\xi )}^2\phi _{(\xi )}^2 \xi \big )=\mathbb {P}\partial _{x_i} \big (a_{(\xi )}^2\psi _{(\xi )}^2\phi _{(\xi )}^2 \xi \big ). \end{aligned}$$

for each $i=1,2,3$. Taking into account that the Leray projection is bounded on $W_{\ne 0}^{1,p}\left( \mathbb {T}^3\right)$ and the projection onto zero mean functions $\mathbb {P}_{\ne 0}$ is a bounded operator on $W^{1,p}\left( \mathbb {T}^3\right)$, the above expression amounts to

$$\begin{aligned} \Vert w_{q+1}^{(t)}\Vert _{C_{t,x}^1}&\lesssim \mu ^{-1} \sum _{\xi \in \Lambda } \bigg (\overbrace{\Vert a_{(\xi )}^2 \psi _{(\xi )}^2\phi _{(\xi )}^2\Vert _{C_tW^{1,p}}}^{=:\text{ I }}+\overbrace{\Vert \partial _t ( a_{(\xi )}^2 \psi _{(\xi )}^2 \phi _{(\xi )}^2)\Vert _{C_tW^{1,p}}}^{=:\text{ II }}\bigg )\\ {}& +\mu ^{-1} \sum _{\xi \in \Lambda } \underbrace{\sum _{|\beta |=1}\Vert D^\beta ( a_{(\xi )}^2 \psi _{(\xi )}^2\phi _{(\xi )}^2)\Vert _{C_tW^{1,p}}}_{=:\text{ III }}. \end{aligned}$$

Employing the formula

$$\begin{aligned} \Big \Vert \prod _{n=1}^N f_n\Big \Vert _{W^{1,p}} \lesssim \sum _{k=1}^N \prod _{\begin{array}{c} n=1\\ n\ne k \end{array}}^N \Vert f_n\Vert _{L^\infty } \Vert f_k\Vert _{W^{1,p}}, \end{aligned}$$

which holds for all functions $f_n \in W^{1,p}\left( \mathbb {T}^3\right) \cap L^\infty \left( \mathbb {T}^3\right) ,\,n=1,\ldots ,N,\, N\ge 2$, permits to deduce

$$\begin{aligned} \text{ I }&\lesssim \Vert a_{(\xi )}\Vert ^2_{C_tL^\infty }\Vert \psi _{(\xi )}\Vert _{C_tL^\infty }^2\Vert \phi _{(\xi )}\Vert _{L^\infty } \Vert \phi _{(\xi )}\Vert _{W^{1,p}}\\ {}&\quad +\Vert a_{(\xi )}\Vert ^2_{C_tL^\infty }\Vert \psi _{(\xi )}\Vert _{C_tL^\infty }\Vert \psi _{(\xi )}\Vert _{C_tW^{1,p}}\Vert \phi _{(\xi )}\Vert ^2_{L^\infty }\\ {}&\quad + \Vert a_{(\xi )}\Vert _{C_tL^\infty }\Vert a_{(\xi )}\,\Vert _{C_tW^{1,p}}\Vert \psi _{(\xi )}\Vert _{C_tL^\infty }^2\Vert \phi _{(\xi )}\Vert ^2_{L^\infty }. \end{aligned}$$

Due to the embedding $W^{1,\infty }\left( \mathbb {T}^3\right) \subseteq W^{1,p}\left( \mathbb {T}^3\right)$ and by invoking (3.8b), (3.13a), (3.13b), we obtain

$$\begin{aligned} \text {I} \lesssim \bigg (\frac{M}{4 |\Lambda |}\bigg )^2 \ell ^{-23}\delta _{q+1}m^{3/4}\bar{e}r_\perp ^{-2}r_\parallel ^{-1}\lambda _{q+1}. \end{aligned}$$

In the same manner, we estimate

$$\begin{aligned} \text{ II }&\lesssim \Vert \partial _t a_{(\xi )}a_{(\xi )}\psi _{(\xi )}^2\phi ^2_{(\xi )}\Vert _{C_tW^{1,p}}+ \Vert a_{(\xi )}^2\partial _t\psi _{(\xi )}\psi _{(\xi )}\phi _{(\xi )}^2\Vert _{C_tW^{1,p}}\\ {}&\lesssim \bigg (\frac{M}{4 |\Lambda |}\bigg )^2 \ell ^{-30}\delta _{q+1}m^{3/4}\bar{e}r_\perp ^{-2}r_\parallel ^{-1}\lambda _{q+1} +\bigg (\frac{M}{4 |\Lambda |}\bigg )^2 \ell ^{-23}\delta _{q+1}m^{3/4}\bar{e}r_\perp ^{-2}r_\parallel ^{-1}\lambda _{q+1}^3\\ {}&\lesssim \bigg (\frac{M}{4 |\Lambda |}\bigg )^2 \ell ^{-30}\delta _{q+1}m^{3/4}\bar{e}r_\perp ^{-2}r_\parallel ^{-1}\lambda _{q+1}^3 \end{aligned}$$

and

$$\begin{aligned} \text{ III }&\lesssim \sum _{|\beta |\le 1}\Big \{ \Vert D^\beta a_{(\xi )}a_{(\xi )}\psi _{(\xi )}^2\phi ^2_{(\xi )}\Vert _{C_tW^{1,p}}+ \Vert a_{(\xi )}^2D^\beta \psi _{(\xi )}\psi _{(\xi )}\phi _{(\xi )}^2\Vert _{C_tW^{1,p}}\Big \}\\ {}& +\sum _{|\beta |\le 1}\Vert a_{(\xi )}^2\psi _{(\xi )}^2 D^\beta \phi _{(\xi )}\phi _{(\xi )}\Vert _{C_tW^{1,p}}\\ {}&\lesssim \bigg (\frac{M}{4 |\Lambda |}\bigg )^2 \ell ^{-30}\delta _{q+1}m^{3/4}\bar{e} r_\perp ^{-2}r_\parallel ^{-1} \lambda _{q+1}+ \bigg (\frac{M}{4 |\Lambda |}\bigg )^2 \ell ^{-23}\delta _{q+1}m^{3/4}\bar{e}r_\perp ^{-1}r_\parallel ^{-2}\lambda _{q+1}^2\\ {}&+\bigg (\frac{M}{4 |\Lambda |}\bigg )^2 \ell ^{-23}\delta _{q+1}m^{3/4}\bar{e}r_\perp ^{-2}r_\parallel ^{-1} \lambda _{q+1}^2\\ {}&\lesssim \bigg (\frac{M}{4 |\Lambda |}\bigg )^2 \ell ^{-30}\delta _{q+1}m^{3/4}\bar{e} r_\perp ^{-2}r_\parallel ^{-1} \lambda _{q+1}^2. \end{aligned}$$

Therefore, we conclude

$$\begin{aligned} \Vert w_{q+1}^{(t)}\Vert _{C_{t,x}^1} \lesssim \bigg (\frac{M}{4 |\Lambda |}\bigg )^2 \ell ^{-30}\delta _{q+1}m^2\bar{e}r_\perp ^{-1}r_\parallel ^{-2} \lambda _{q+1}^2. \end{aligned}$$

(3.17a): In view of (3.14), (3.8b) and (3.13c), we infer again with help of Levi-Civita’s symbol

$$\begin{aligned} \Vert w_{q+1}^{(p)}+w_{q+1}^{(c)}\Vert _{C_tW^{1,p}}&\lesssim m^{1/8} \sum _{\xi \in \Lambda } \sum _{\ell , k, n, i, j=1}^3 \Vert \mathcal {E}_{\ell k n} \mathcal {E}_{i j k} \partial _{x_\ell } \big (\partial _{x_i} \big (a_{(\xi )}V_{(\xi )}^j\big )\big ){\textbf {e}}_n\Vert _{C_tW^{1,p}}\\ {}&\lesssim m^{1/8}\sum _{\xi \in \Lambda } \sum _{|\alpha |=2} \sum _{|\gamma |\le 1} \Vert D^\gamma \big (D^\alpha a_{(\xi )}V_{(\xi )}\big )\Vert _{C_tL^p}\\ {}&+ m^{1/8}\sum _{\xi \in \Lambda } \sum _{ |\alpha |=1}\sum _{ |\beta |=1} \sum _{|\gamma |\le 1} \Vert D^\gamma \big (D^\alpha a_{(\xi )}D^\beta V_{(\xi )}\big )\Vert _{C_tL^p}\\ {}& + m^{1/8}\sum _{\xi \in \Lambda }\sum _{|\beta |=2} \sum _{|\gamma |\le 1} \Vert D^\gamma \big ( a_{(\xi )}D^\beta V_{(\xi )}\big )\Vert _{C_tL^p}\\ {}&\lesssim m^{1/8} \sum _{\xi \in \Lambda } \bigg \{ \Vert a_{(\xi )}\Vert _{C_{t,x}^3} \Vert V_{(\xi )}\Vert _{C_tL^p}+ \Vert a_{(\xi )}\Vert _{C_{t,x}^2} \sum _{|\beta |\le 1} \Vert D^\beta V_{(\xi )}\Vert _{C_tL^p}\bigg \} \\ {}&+ m^{1/8} \sum _{\xi \in \Lambda }\bigg \{ \Vert a_{(\xi )}\Vert _{C_{t,x}^1} \sum _{|\beta | \le 2} \Vert D^\beta V_{(\xi )}\Vert _{C_tL^p} +\Vert a_{(\xi )}\Vert _{C_{t,x}^0} \sum _{|\beta |\le 3} \Vert D^\beta V_{(\xi )}\Vert _{C_tL^p} \bigg \}\\ {}&\lesssim \frac{M}{4|\Lambda |} \delta _{q+1}^{1/2} m^{1/2}\bar{e}^{1/2} r_\perp ^{2/p-1}r_\parallel ^{1/p-1/2} (\ell ^{-29}\lambda _{q+1}^{-2}+\ell ^{-22}\lambda _{q+1}^{-1}+ \ell ^{-15}+\ell ^{-8}\lambda _{q+1})\\ {}&\lesssim \frac{M}{4|\Lambda |} \ell ^{-29}\delta _{q+1}^{1/2} m \bar{e}^{1/2} r_\perp ^{2/p-1}r_\parallel ^{1/p-1/2} \lambda _{q+1}. \end{aligned}$$

(3.17b): Bearing in mind that $\mathbb {P}$ and $\mathbb {P}_{\ne 0}$ are both bounded operators on $W_{\ne 0}^{1,p}\left( \mathbb {T}^3\right)$ and $W^{1,p}\left( \mathbb {T}^3\right)$, respectively, we make use of Lemma 3.4 in order to obtain

$$\begin{aligned} \Vert w_{q+1}^{(t)}\Vert _{C_tW^{1,p}}&{\lesssim } \mu ^{-1} \sum _{\xi \in \Lambda } \bigg \{ \Vert a_{(\xi )}^2\psi _{(\xi )}^2\phi _{(\xi )}^2\Vert _{C_tL^p}+ \sum _{|\alpha |=1}\Vert D^\alpha a_{(\xi )}a_{(\xi )}\,\psi _{(\xi )}^2\phi _{(\xi )}^2\Vert _{C_tL^p}\bigg \}\\ {}& {+}\mu ^{-1} \sum _{\xi \in \Lambda }\bigg \{\!\sum _{|\alpha |=1}\Vert a_{(\xi )}^2 D^\alpha \psi ^2_{(\xi )}\phi _{(\xi )}^2\Vert _{C_tL^p}{+}\!\!\sum _{|\alpha |=1}\Vert a_{(\xi )}^2 \psi _{(\xi )}^2 D^\alpha \phi _{(\xi )}^2 \Vert _{C_tL^p} \bigg \}\\ {}&\lesssim \mu ^{-1} \sum _{\xi \in \Lambda } \Vert a_{(\xi )}\Vert ^2_{C_{t,x}^0} \Vert \psi _{(\xi )}\Vert _{C_tL^{2p}}^2 \Vert \phi _{(\xi )}\Vert _{L^{2p}}^2\\ {}& +\mu ^{-1} \sum _{\xi \in \Lambda }\Vert a_{(\xi )}\Vert _{C_{t,x}^1}\Vert a_{(\xi )}\Vert _{C_{t,x}^0} \Vert \psi _{(\xi )}\Vert _{C_tL^{2p}}^2\Vert \phi _{(\xi )}\Vert _{L^{2p}}^2\\ {}& +\mu ^{-1} \sum _{\xi \in \Lambda } \Vert a_{(\xi )}\Vert _{C_{t,x}^0}^2\sum _{|\alpha |\le 1 } \Vert D^\alpha \psi _{(\xi )}\psi _{(\xi )}\Vert _{C_tL^p}\Vert \phi _{(\xi )}\Vert _{L^{2p}}^2\\ {}& +\mu ^{-1} \sum _{\xi \in \Lambda }\Vert a_{(\xi )}\Vert _{C_{t,x}^0}^2 \Vert \psi _{(\xi )}\Vert _{C_tL^{2p}}^2 \sum _{|\alpha |\le 1}\Vert D^\alpha \phi _{(\xi )}\phi _{(\xi )}\Vert _{L^p}.\end{aligned}$$

Since Cauchy–Schwarz inequality implies

$$\begin{aligned} \sum _{|\alpha |\le 1} \Vert D^\alpha \psi _{(\xi )}\psi _{(\xi )}\Vert _{C_tL^p} \lesssim \sum _{|\alpha |\le 1} \Vert D^\alpha \psi _{(\xi )}\Vert _{C_tL^{2p}} \Vert \psi _{(\xi )}\Vert _{C_tL^{2p}}, \end{aligned}$$

and

$$\begin{aligned} \sum _{|\alpha |\le 1} \Vert D^\alpha \phi _{(\xi )}\phi _{(\xi )}\Vert _{L^p} \lesssim \sum _{|\alpha |\le 1} \Vert D^\alpha \phi _{(\xi )}\Vert _{L^{2p}} \Vert \phi _{(\xi )}\Vert _{L^{2p}}, \end{aligned}$$

respectively, we appeal to (3.8b), (3.13a) and (3.13b) to conclude

$$\begin{aligned} \Vert w_{q+1}^{(t)}\Vert _{C_tW^{1,p}} \lesssim \left( \frac{M}{4|\Lambda |}\right) ^2 \ell ^{-23}\delta _{q+1} m^2\bar{e}r_\perp ^{2/p-1}r_{\parallel }^{1/p-2}.\end{aligned}$$

$\square$

3.4.2 Verifying the key bounds on the level $q+1$

With these preparations in hands, we are now able to justify (3.3a) and (3.3b) on the level $q+1$.

3.4.3 First Key Bound (3.3a)

By (3.15d), (3.15b), (3.15c) and (3.1b), we find

$$\begin{aligned} \Vert w_{q{+}1}\Vert _{C_tL^2}{\le } \delta _{q+1}^{1/2} m \bar{e}^{1/2} \left( C\frac{M}{4|\Lambda |}{+}C\frac{M}{4|\Lambda |}\lambda _{q+1}^{44\alpha -2/7}{+}C\frac{M}{4|\Lambda |}\frac{M}{4|\Lambda |} \lambda _{q+1}^{33\alpha -1/7}\right) \end{aligned}$$

for some constant $C>\frac{4|\Lambda |}{3M}$. In order to absorb the subsequent implicit constants, we chose

$$\begin{aligned} M_0:= 3C\frac{M}{4|\Lambda |} . \end{aligned}$$

(3.26)

Recalling the requirements $\frac{M}{4|\Lambda |}\lambda _{q+1}^{33\alpha -1/7}\le 1$ and $161\alpha <\frac{1}{7},\, a\ge 3600,\, b\ge 7$, ensuring $\lambda _{q+1}^{44\alpha -2/7}\le 1$, permits to achieve

$$\begin{aligned} \Vert w_{q+1}\Vert _{C_tL^2} \le M_0 \delta _{q+1}^{1/2} m\bar{e}^{1/2}, \end{aligned}$$

(3.27)

which combined with (3.6b) actually confirms

$$\begin{aligned} \Vert v_{q+1}\Vert _{C_tL^2}\le \Vert v_\ell \Vert _{C_tL^2}+ \Vert w_{q+1}\Vert _{C_tL^2} \le M_0\left( 1+\sum _{r=1}^{q+1} \delta _r^{1/2}\right) m \bar{e}^{1/2}. \end{aligned}$$

3.4.4 Second Key Bound (3.3b)

In the same manner as above, (3.16a), (3.16b), (3.16c), (3.1b), the fact $161 \alpha <\frac{1}{7}$, (3.6c) and (3.3b) furnish the existence of some constants $K, \widetilde{K}>0$, so that

$$\begin{aligned} \Vert w_{q+1}\Vert _{C_{t,x}^1}&\le \lambda _{q+1}^5 m \bar{e}^{1/2}\left( K\frac{M}{4|\Lambda |} \lambda _{q+1}^{-12/7}+K\frac{M}{4|\Lambda |}\lambda ^{-2}_{q+1}+K\left( \frac{M}{4|\Lambda |}\right) ^2 \lambda _{q+1}^{-6/7} \right) \end{aligned}$$

(3.28)

and

$$\begin{aligned} \Vert v_\ell \Vert _{C_{t,x}^1}\le \widetilde{K} \Vert v_q\Vert _{C_{t,x}^1} \le \widetilde{K} \lambda _q^5 \lambda _{q+1}^{-5}\lambda _{q+1}^5 m \bar{e}^{1/2}, \end{aligned}$$

(3.29)

respectively. As pointed out in Sect. 3.1, we increase a and b in a fashion that $K\frac{M}{4|\Lambda |} \lambda _{q+1}^{-12/7}+K\frac{M}{4|\Lambda |}\lambda ^{-2}_{q+1}+K\left( \frac{M}{4|\Lambda |}\right) ^2 \lambda _{q+1}^{-6/7} \le \frac{1}{2}$ as well as $\widetilde{K}\lambda _q^5\lambda _{q+1}^{-5}\le \frac{1}{2}$. That means (3.3b) stays true on the level $q+1$.

3.4.5 Control of the energy

It remains to affirm (3.5) at level $q+1$, which is equivalent in showing

$$\begin{aligned} |\Theta ^{-2}(t) e(t)(1- \delta _{q+2})-\Vert v_{q+1}(t)\Vert _{L^2}^2|\le \frac{1}{4}\delta _{q+2}\Theta ^{-2}(t)e(t), \end{aligned}$$

or expressed in terms of the function $\eta _q$

$$\begin{aligned} |3(2\pi )^3\eta _q(t)+\Vert v_q(t)\Vert _{L^2}^2-\Vert v_{q+1}(t)\Vert _{L^2}^2|\le \frac{1}{4}\delta _{q+2}\Theta ^{-2}(t)e(t) \end{aligned}$$

whenever $t \in (-\infty , \tau ]$.

As we will see it is not enough to require only boundedness of the energy e here, rather it is necessary to ask for a uniform bound of its derivative $e^\prime$. From a physical point of view, it means that the change of kinetic energy and therefore the acceleration of a fluid cannot become arbitrary large. For example, if we consider a river that flows uphill, the gravity will influence its flow rate, so that the gradient can only attend limited values.

Anyway, lets come back to the mathematical computations:

$$\begin{aligned} |3&(2\pi )^3\eta _q(t)+\Vert v_q(t)\Vert _{L^2}^2-\Vert v_{q+1}(t)\Vert _{L^2}^2| \nonumber \\ {}&\le \Big \Vert 3(2\pi )^3\eta _q+\Vert v_q\Vert ^2_{L^2}-\Vert |v_\ell +w_{q+1}^{(p)}+w_{q+1}^{(c)}+w_{q+1}^{(t)}|^2\Vert _{L^1}\Big \Vert _{C_t} \nonumber \nonumber \\ {}&\le \overbrace{\Big \Vert 3(2\pi )^3\eta _q- \Vert w_{q+1}^{(p)}\Vert _{L^2}^2\Big \Vert _{C_t}}^{\text{=:I }} +\overbrace{\Big \Vert \Vert v_q\Vert ^2_{L^2}-\Vert v_\ell \Vert ^2_{L^2}\Big \Vert _{C_t}}^{\text{=:II }}+\overbrace{2\Vert v_\ell \cdot w_{q+1}^{(p)}\Vert _{C_tL^1}}^{\text{=:III }} \nonumber \\ {}&\quad +\underbrace{2\Vert v_\ell \cdot (w_{q+1}^{(c)}+w_{q+1}^{(t)})\Vert _{C_tL^1}+2\Vert w_{q+1}^{(p)}\cdot (w_{q+1}^{(c)}+w_{q+1}^{(t)})\Vert _{C_tL^1}}_{\text{=:IV }}\nonumber \\ {}&\quad +\underbrace{\Vert w_{q+1}^{(c)}+w_{q+1}^{(t)}\Vert ^2_{C_tL^2}}_{\text{=:V }}\end{aligned}$$

(3.30)

and we proceed with a bound for I.

For this purpose we first assert

$$\begin{aligned} {\underline{1.\ Claim:}}\quad \Theta _\ell \left( w_{q+1}^{(p)}\otimes w_{q+1}^{(p)}\right) =\sum _{\xi \in \Lambda } a_{(\xi )}^2 \mathbb {P}_{\ne 0}\big (W_{(\xi )}\otimes W_{(\xi )}\big )+\rho {{\,\text {Id}\,}}-\mathring{R}_\ell . \end{aligned}$$

(3.31)

Proof

Keeping in mind that the mutually disjoint supports of $\left( W_{(\xi )}\,\right) _{\xi \in \Lambda }$ causes $W_{(\xi )}\,\otimes W_{(\xi ^\prime )} \equiv 0$ for $\xi \ne \xi ^\prime$, we invoke Lemma 3.4 to deduce

$$\begin{aligned} w_{q+1}^{(p)}\otimes w_{q+1}^{(p)}&= \Theta _\ell ^{-1}\sum _{\xi \in \Lambda } a_{(\xi )}^2 \big (W_{(\xi )}\otimes W_{(\xi )}\big )\\ {}&= \Theta _\ell ^{-1}\sum _{\xi \in \Lambda } a_{(\xi )}^2 \mathbb {P}_{\ne 0}\big (W_{(\xi )}\otimes W_{(\xi )}\big ) +\Theta _\ell ^{-1}\sum _{\xi \in \Lambda } a_{(\xi )}^2 \big (\xi \otimes \xi \big ) (2\pi )^{-6}\Vert \psi _{(\xi )}^2\Vert _{L^1}\Vert \phi _{(\xi )}^2\Vert _{L^1}\end{aligned}$$

and appealing to the geometric Lemma 3.2 as well as to the normalizations (3.9), we find

$$\begin{aligned} w_{q+1}^{(p)}\otimes w_{q+1}^{(p)}=\Theta _\ell ^{-1} \sum _{\xi \in \Lambda } a_{(\xi )}^2 \mathbb {P}_{\ne 0}\big (W_{(\xi )}\otimes W_{(\xi )}\big )+\Theta _\ell ^{-1}\left[ \rho {{\,\text {Id}\,}}-\mathring{R}_\ell \right] .\end{aligned}$$

$\square$

to deduce

$$\begin{aligned} |w_{q+1}^{(p)}|^2-3\eta _q&= {{\,\text {tr}\,}}\Big (w_{q+1}^{(p)}\otimes w_{q+1}^{(p)}\Big )-3\eta _q\\ {}&= \Theta _\ell ^{-1}\bigg [\sum _{\xi \in \Lambda } a_{(\xi )}^2 \mathbb {P}_{\ne 0} {{\,\text {tr}\,}}\Big (W_{(\xi )}\otimes W_{(\xi )}\Big ) +{{\,\text {tr}\,}}({{\,\text {Id}\,}})\rho -{{\,\text {tr}\,}}(\mathring{R}_\ell )\bigg ]-3 \eta _q\\ {}&= 6 \Theta _\ell ^{-1}\sqrt{\ell ^2+\Vert \mathring{R}_\ell \Vert _F^2}+ 3(\eta _\ell -\eta _q)+ \Theta _\ell ^{-1}\sum _{\xi \in \Lambda } a_{(\xi )}^2 \mathbb {P}_{\ne 0}|W_{(\xi )}|^2, \end{aligned}$$

yielding

$$\begin{aligned} \Big \Vert \Vert w_{q+1}^{(p)}\Vert _{L^2}^2-3(2\pi )^3 \eta _q \Big \Vert _{C_t}&\le \int _{\mathbb {T}^3} \Big \Vert 6\Theta _\ell ^{-1}\sqrt{\ell ^2+\Vert \mathring{R}_\ell \Vert _F^2} \Big \Vert _{C_t} \,dx +3 \int _{\mathbb {T}^3} \Vert \eta _\ell -\eta _q\Vert _{C_t}\, dx\\ {}& +\bigg \Vert \Theta _\ell ^{-1}\sum _{\xi \in \Lambda }\int _{\mathbb {T}^3}a_{(\xi )}^2 \mathbb {P}_{\ne 0} |W_{(\xi )}|^2\,dx\bigg \Vert _{C_t}\\ {}&\le 6m^{1/4}(2\pi )^3 \ell {+}6m^{1/4}\Vert \mathring{R}_\ell \Vert _{C_tL^1}{+}3(2\pi )^3 \Vert \eta _\ell {-}\eta _q\Vert _{C_t}\\ {}&+m^{1/4} \sum _{\xi \in \Lambda }\bigg \Vert \int _{\mathbb {T}^3} a_{(\xi )}^2 \mathbb {P}_{\ne 0} |W_{(\xi )}|^2\,dx\bigg \Vert _{C_t}. \end{aligned}$$

We continue by proving

$$\begin{aligned} {\underline{2.\ Claim:}}\quad 6 m^{1/4}(2\pi )^3 \ell \le \frac{1}{80} \delta _{q+2} \Theta ^{-2}(t) e(t).&\end{aligned}$$

(3.32)

Proof

Using $2\beta b< \frac{3 \alpha }{2}$, implied by the assumptions $4 \beta b^2< \alpha$ and $b \ge 7$, together with $e(t)\ge \underline{e}> 4$ and $\Theta ^{-2}(t)\ge m^{-1/2}$ and also $\lambda _q>3600^7>\sqrt{120 }m^{3/4}\, (2\pi )^{3/2}$, we compute

$$\begin{aligned} 6m^{1/4}(2\pi )^3 \ell&\le \frac{3}{2} e(t)m^{1/4}(2\pi )^3 \lambda _{q+1}^{-2\beta b} \lambda _{q}^{-2}\le \frac{1}{80m^{1/2}} e(t)\lambda _{q+2}^{-2\beta }\le \frac{1}{80} \delta _{q+2} \Theta ^{-2}(t) e(t).\end{aligned}$$

$\square$

We further need

$$\begin{aligned} {\underline{3.\ Claim:}}\quad \Vert \mathring{R}_\ell \Vert _{C_tL^1} \le \frac{1}{480 m^{1/4}} \delta _{q+2}\Theta ^{-2}(t) e(t),&\end{aligned}$$

(3.33)

Proof

It follows immediately from Fubini’s theorem, the normalization of the mollifiers and (3.3c).

$$\begin{aligned} {\underline{4.\ Claim:}}\quad 3(2\pi )^3 \Vert \eta _\ell -\eta _q\Vert _{C_t} \le \frac{1}{80} \delta _{q+2}\Theta ^{-2}(t) e(t)&\end{aligned}$$

(3.34)

$\square$

Proof

Both terms of

$$\begin{aligned} 3(2\pi )^3 \Vert \eta _\ell&-\eta _q\Vert _{C_t} \nonumber \\ {}&\le (1-\delta _{q+2}) \Vert \Theta ^{-2} e-\left( \Theta ^{-2}e\right) *\varphi _\ell \Vert _{C_t}+ \Big \Vert \Vert v_q\Vert ^2_{L^2}-\Vert v_q\Vert _{L^2}^2*_t \varphi _\ell \Big \Vert _{C_t} \end{aligned}$$

(3.35)

will be estimated separately.

First, for any $s\in (-\infty ,t]$ and $u \in [0,\ell ]$ it holds

$$\begin{aligned} |\Theta ^{-2}(s)e(s)-\Theta ^{-2}(s-u)e(s-u)|&\le |e^{-2B_s}e(s)-e^{-2B_{s-u}}e(s)|+|e^{-2B_{s-u}}e(s)-e^{-2B_{s-u}}e(s-u)|\\ {}&\le \overline{e} \frac{|e^{-2B_{s}}-e^{-2B_{s-u}}|}{|2B_s-2B_{s-u}|}\frac{2|B_s-B_{s-u}|}{|s-(s-u)|^\iota }|s-(s-u)|^\iota \\ {}&\quad +m^{1/2}\frac{|e(s)-e(s-u)|}{|s-(s-u)|}|s-(s-u)|\\ {}&\le \overline{e}m^\frac{1}{2} 2 \Vert B\Vert _{C^{0,\iota }}\ell ^{\iota }+ m^{1/2} \widetilde{e} \ell \\ {}&\le 3m^{1/2}(\overline{e}+\widetilde{e})\ell ^\iota .\end{aligned}$$

Hence,

$$\begin{aligned} \Vert \Theta ^{-2}e-\left( \Theta ^{-2} e\right) *_t \varphi _\ell \Vert _{C_t}&\le \sup _{s\in (-\infty ,t]} \int _0^\ell |\Theta ^{-2}(s)e(s)\nonumber -\Theta ^{-2}(s-u)e(s-u)| \varphi _\ell (u) \,du \nonumber \\&\le 5 m^{1/2}(\bar{e}+\widetilde{e})\ell ^\iota ,\end{aligned}$$

(3.36)

where we exploited the normalization of $\varphi$ in both steps again.

Estimating the second term of (3.35) follows by standard mollification estimates

$$\begin{aligned} \Big \Vert \Vert v_q\Vert _{L^2}^2-\Vert v_q\Vert _{L^2}^2*_t \varphi _\ell \Big \Vert _{C_t}&\le \sup _{s \in (-\infty ,t]} \int _0^\ell \Big |\Vert v_q(s)\Vert ^2_{L^2}-\Vert v_q(s-u)\Vert ^2_{L^2} \Big | \varphi _\ell (u) \,du \\ {}&\le \sup _{s \in (-\infty ,t]} \int _0^\ell \bigg |\int _0^1 \partial _\theta \Vert v_q(s-\theta u)\Vert ^2_{L^2} \,d\theta \bigg | \varphi _\ell (u) \,du \\ {}&\le 2\sup _{s \in (-\infty ,t]}\int _0^\ell \bigg | \int _0^1 \Vert v_q(s-\theta u)\cdot \partial _\theta v_q(s-\theta u)\Vert _{L^1} \,d\theta \bigg | \varphi _\ell (u) \,du \\ {}&\le 2(2\pi )^{3/2}\sup _{s \in (-\infty ,t]}\int _0^\ell \bigg |\int _0^1 \Vert \partial _\theta v_q(s-\theta u)\Vert _{L^\infty } \,d\theta \bigg | \varphi _\ell (u) \,du \Vert v_q\Vert _{C_tL^2} \\ {}&=2(2\pi )^{3/2}\sup _{s \in (-\infty ,t]} \int _0^\ell \bigg | \int _0^1 u\, \Vert \partial _s v_q(s-\theta u)\Vert _{L^\infty } \,d\theta \bigg | \varphi _\ell (u)\, du \, \Vert v_q\Vert _{C_tL^2}\\ {}&\le 2(2\pi )^{3/2} \ell \Vert \partial _s v_q\Vert _{C_tL^\infty } \Vert v_q\Vert _{C_tL^2}. \end{aligned}$$

Therefore, it holds owing to (3.3a), (3.3b), (3.4) and (3.1a)

$$\begin{aligned} 3(2\pi )^3 \Vert \eta _\ell -\eta _q\Vert _{C_t}&\le (1-\delta _{q+2})5m^{1/2}(\bar{e}+\widehat{e})\ell ^\iota +6(2\pi )^{3/2}M_0 \ell \lambda _{q}^5m^2\bar{e}\\&\le 5\lambda _{q+1}^{-\frac{3\alpha }{2}\iota }m^{1/2}(\bar{e}+ \widetilde{e})+6(2\pi )^{3/2}M_0\lambda _{q+1}^{-\alpha }m^2\bar{e}\\&\le 12(2\pi )^{3/2}M_0 \lambda _{q+1}^{-\alpha \big (\frac{3}{2}\iota -\frac{1}{2}\big )}m^2(\bar{e}+\widetilde{e})\lambda _{q+1}^{-\frac{\alpha }{2}}. \end{aligned}$$

In view of $12(2\pi )^{3/2}M_0 \lambda _{q+1}^{-\alpha \big (\frac{3}{2}\iota -\frac{1}{2}\big )}m^2(\bar{e}+\widetilde{e})\le \frac{1}{20m^{1/2}} \le \frac{1}{80}\Theta ^{-2}(t) e(t)$ and $\alpha >4\beta b$, yielding $\lambda _{q+1}^{-\alpha /2}<\lambda _{q+1}^{-2\beta b}\le \delta _{q+2}$, we get the desired bound. and lastly

$$\begin{aligned} {\underline{5.\ Claim:}}\quad \sum _{\xi \in \Lambda } \Big \Vert \int _{\mathbb {T}^3}a_{(\xi )}^2 \mathbb {P}_{\ne 0} |W_{(\xi )}|^2 \, dx\Big \Vert _{C_t} \le \frac{1}{80m^{1/4}} \delta _{q+2} \Theta ^{-2}(t) e(t). \end{aligned}$$

(3.37)

$\square$

Proof

Applying Green’s identity $L>0$ times to the functions $a_{(\xi )}^2$ and $\Delta ^{-L}\mathbb {P}_{\ne 0}$$|W_{(\xi )}|^2$ furnishes

$$\begin{aligned} \sum _{\xi \in \Lambda } \Big \Vert \int _{\mathbb {T}^3}a_{(\xi )}^2 \mathbb {P}_{\ne 0} |W_{(\xi )}|^2 \, dx\Big \Vert _{C_t}\lesssim \sum _{\xi \in \Lambda } \Vert \Delta ^L a_{(\xi )}^2\Vert _{C_tL^\infty }\Big \Vert \int _{\mathbb {T}^3} \Delta ^{-L} \mathbb {P}_{\ne 0} |W_{(\xi )}|^2 \, dx\Big \Vert _{C_t}.\end{aligned}$$

Thanks to Leibniz rule, we get

$$\begin{aligned} \Vert \Delta ^L a_{(\xi )}^2\Vert _{C_tL^\infty }&\lesssim \sum _{|\alpha |=2L} \sum _{\beta \le \alpha } \Vert D^\beta a_{(\xi )}\Vert _{C_tL^\infty } \Vert D^{\alpha -\beta }a_{(\xi )}\Vert _{C_tL^\infty }\\&\lesssim \sum _{n=0}^{2L} \Vert a_{(\xi )}\Vert _{C^n_{t,x}} \Vert a_{(\xi )}\Vert _{C^{2L-n}_{t,x}}.\end{aligned}$$

Moreover, Lemma 2.5, Cauchy–Schwarz’s inequality and Lemma 2.4 entail

$$\begin{aligned} \Big \Vert \int _{\mathbb {T}^3} \Delta ^{-L} \mathbb {P}_{\ne 0} |W_{(\xi )}|^2 \,dx \Big \Vert _{C_t}&\le \int _{\mathbb {T}^3} \Big \Vert \Big ((-\Delta )^{-1/2} \mathbb {P}_{\ge \frac{r_\perp \lambda _{q+1}}{2}}\Big )^{2L}|W_{(\xi )}|^2\Big \Vert _{C_t}\,dx\\ {}&\lesssim \Big \Vert \Big ((-\Delta )^{-1/2} \mathbb {P}_{\ge \frac{r_\perp \lambda _{q+1}}{2}}\Big )^{2L}|W_{(\xi )}|^2\Big \Vert _{C_tL^2}\\ {}&\lesssim (r_\perp \lambda _{q+1})^{-2L} \Vert W_{(\xi )}\Vert ^2_{C_tL^4}.\end{aligned}$$

Therefore, by stipulating $L=5$, we conclude with help of (3.8b), (3.13c) and (3.1b)

$$\begin{aligned} \sum _{\xi \in \Lambda } \Big \Vert \int _{\mathbb {T}^3}a_{(\xi )}^2 \mathbb {P}_{\ne 0} |W_{(\xi )}|^2 \, dx\Big \Vert _{C_t}&{\lesssim } \left( \frac{M}{4|\Lambda |}\right) ^2 \ell ^{-86} \delta _{q+1} m^{3/4}\bar{e} (r_\perp \lambda _{q+1})^{-10}r_\perp ^{-1} r_\parallel ^{-1/2}\\ {}&\lesssim \lambda _{q+1}^{174\alpha -2/7} \lambda _1^{2 \beta }\\ {}&\lesssim \lambda _{q+1}^{-147\alpha - 2\beta b} \lambda _1^{2\beta } \\ {}&\lesssim \lambda _{q+1}^{-147\alpha } \delta _{q+2}e(t). \end{aligned}$$

Here, we used the fact $174\alpha -\frac{2}{7}<-148\alpha <-147 \alpha -2\beta b$, which follows from the constraint $161\alpha <\frac{1}{7}$ and $2 \beta b<4\beta b^2<\alpha$, in the penultimate and we employed $4 \le \underline{e}\le e(t)$ in the last step.

In order to absorb the implicit constant, we choose a, b sufficiently large and $\alpha ,\beta$ sufficiently small enough. In other words, we have ascertained the existence of some $\hat{K}>0$, so that

$$\begin{aligned} \sum _{\xi \in \Lambda } \Big \Vert \int _{\mathbb {T}^3}a_{(\xi )}^2 \mathbb {P}_{\ne 0} |W_{(\xi )}|^2 \, dx\Big \Vert _{C_t} \le \hat{K} \lambda _{q+1}^{-147\alpha }\delta _{q+2}e(t) \end{aligned}$$

(3.38)

holds. Imposing $\hat{K}\lambda _{q+1}^{-147\alpha }\le \frac{1}{80m^{3/4}}$ (cf. Sect. 3.1) yields the desired bound. $\square$

Armed with these statements, we are now able to bound I, i.e., taking (3.32), (3.33), (3.34) and (3.37) into account, we find

$$\begin{aligned}&\Big \Vert \Vert w_{q+1}^{(p)}\Vert _{L^2}^2-3(2\pi )^3 \eta _q \Big \Vert _{C_t}\le 4\cdot \frac{1}{80} \delta _{q+2}\Theta ^{-2}(t) e(t).\end{aligned}$$

The second term can according to Cauchy–Schwarz’s inequality, (3.6a), (3.3b), (3.3a), (3.6b), (3.4) and (3.1a) be bounded as

$$\begin{aligned} \Big \Vert \Vert v_q\Vert _{L^2}^2-\Vert v_\ell \Vert ^2_{L^2} \Big \Vert _{C_t}&\le \Vert v_q-v_\ell \Vert _{C_tL^2} \big (\Vert v_q\Vert _{C_tL^2}+\Vert v_\ell \Vert _{C_tL^2}\big ) \\&\le (2\pi )^{3/2} \ell \lambda _q^5 m\bar{e}^{1/2} 6M_0m\bar{e}^{1/2}\\&\le 6(2\pi )^{3/2} M_0\lambda _{q+1}^{-\alpha } m^2\bar{e}. \end{aligned}$$

Invoking the assumption $6(2\pi )^{3/2}M_0\lambda _{q+1}^{-\alpha /2}m^2\bar{e}\le \frac{1}{5m^{1/2}}$ together with $e(t)\ge \underline{e}\ge 4$, $\Theta ^{-2}(t)\ge m^{-1/2}$ and $\alpha >4\beta b^2$ permits to conclude

$$\begin{aligned} \Big \Vert \Vert v_q\Vert _{L^2}^2-\Vert v_\ell \Vert ^2_{L^2} \Big \Vert _{C_t}&\le \frac{1}{5m^{1/2}}\lambda _{q+1}^{-\alpha /2}\le \frac{1}{20m^{1/2}} \lambda _{q+1}^{-2\beta b}e(t)\le \frac{1}{20} \delta _{q+2}\Theta ^{-2}(t) e(t). \end{aligned}$$

For the third term, we employ Hölder’s inequality with exponents $r:=3$ and $p:=\frac{3^{}}{2}$ and appeal to (3.3b), (3.15a), (3.1a) and (3.1b) to deduce

$$\begin{aligned} \Vert v_\ell \cdot w_{q+1}^{(p)}\Vert _{C_tL^1}&\le \Vert v_q\Vert _{C_tL^\infty }(2 \pi )^{3/r}\Vert w_{q+1}^{(p)}\Vert _{C_tL^p}\lesssim 2\pi \frac{M}{4|\Lambda |} \lambda _{q+1}^{19\alpha -8/21}. \end{aligned}$$

Furthermore, it follows from the assumption $19\alpha -1/7<160\alpha -1/7<-\alpha$ and $\alpha>4\beta b^2>2\beta b$ that

$$\begin{aligned} 2 \Vert v_\ell \cdot w_{q+1}^{(p)}\,\Vert _{C_tL^1} \le K^*\,2\pi \frac{M}{4|\Lambda |}\lambda _{q+1}^{-5/21} \lambda _{q+1}^{-2\beta b} \end{aligned}$$

(3.39)

holds for some constant $K^*>0$. Imposing $K^*\, 2\pi \, \frac{M}{4|\Lambda |} \lambda _{q+1}^{-5/21} \le \frac{1}{5\,m^{1/2}}$ and remembering that $e(t)\ge \underline{e}\ge 4$ and $\Theta ^{-2}(t)\ge m^{-1/2}$, we find

$$\begin{aligned} 2\Vert v_\ell \cdot w_{q+1}^{(p)}\,\Vert _{C_tL^1} \le \frac{1}{20} \delta _{q+2} \Theta ^{-2}(t) e(t). \end{aligned}$$

Next, we aim at estimating IV also as $\text {IV}\le \frac{1}{20} \delta _{q+2}\Theta ^{-2}(t)e(t)$. Namely, after applying Cauchy–Schwarz’s inequality, we use (3.6b), (3.15d), (3.15b), (3.15c) and (3.1b) to obtain

$$\begin{aligned}&2\Vert v_\ell \cdot (w_{q+1}^{(c)}\,+w_{q+1}^{(t)}\,)\Vert _{C_tL^1}+2\Vert w_{q+1}^{(p)}\,\cdot (w_{q+1}^{(c)}\,+w_{q+1}^{(t)}\,)\Vert _{C_tL^1}\\&\le 2\Big (\Vert v_\ell \Vert _{C_tL^2}+\Vert w_{q+1}^{(p)}\,\Vert _{C_tL^2}\Big )\Big (\Vert w_{q+1}^{(c)}\,\Vert _{C_tL^2}+\Vert w_{q+1}^{(t)}\,\Vert _{C_tL^2}\Big )\\&\lesssim \left( M_0\lambda _{q+1}^\alpha +\frac{M}{4|\Lambda |}\lambda _{q+1}^\alpha \right) \left( \frac{M}{4|\Lambda |}\lambda _{q+1}^{45\alpha -2/7}+\left( \frac{M}{4|\Lambda |}\right) ^2\lambda _{q+1}^{34\alpha -1/7}\right) \\& \lesssim \left( M_0+\frac{M}{4|\Lambda |} \right) \left( \frac{M}{4|\Lambda |}+\left( \frac{M}{4|\Lambda |}\right) ^2\right) \lambda _{q+1}^{46\alpha -1/7}. \end{aligned}$$

Due to $46\alpha -\frac{1}{14}<-2\beta b$, entailing from $160 \alpha - 1/7<-\alpha$ and $\alpha >4\beta b^2$, it holds

$$\begin{aligned} \begin{aligned}&2\Vert v_\ell \cdot (w_{q+1}^{(c)}\,+w_{q+1}^{(t)}\,)\Vert _{C_tL^1}+2\Vert w_{q+1}^{(p)}\,\cdot (w_{q+1}^{(c)}\,+w_{q+1}^{(t)}\,)\Vert _{C_tL^1}\\& \le K^\prime \left( M_0+\frac{M}{4|\Lambda |} \right) \left( \frac{M}{4|\Lambda |}+\left( \frac{M}{4|\Lambda |}\right) ^2\right) \lambda _{q+1}^{-\frac{1}{14}} \lambda _{q+1}^{-2\beta b} \end{aligned} \end{aligned}$$

(3.40)

for some constant $K^\prime >0$. Similarly as above we achieve

$$\begin{aligned} 2\Vert v_\ell \cdot (w_{q+1}^{(c)}\,+w_{q+1}^{(t)}\,)\Vert _{C_tL^1}+2\Vert w_{q+1}^{(p)}\,\cdot (w_{q+1}^{(c)}\,+&w_{q+1}^{(t)}\,)\Vert _{C_tL^1}\le \frac{1}{20} \delta _{q+2}\Theta ^{-2}(t) e(t) \end{aligned}$$

by assuming $K^\prime \left( M_0+\frac{M}{4|\Lambda |} \right) \left( \frac{M}{4|\Lambda |}+\left( \frac{M}{4|\Lambda |}\right) ^2\right) \lambda _{q+1}^{-\frac{1}{14}}\le \frac{1}{5\,m^{1/2}}$.

To bound the last term, we proceed similarly as in IV. Namely, thanks to (3.15b), (3.15c), (3.1b) and to the required $160\alpha -1/7<-\alpha$ and $\alpha >4\beta b^2$ it holds

$$\begin{aligned} \Vert w_{q+1}^{(c)}+w_{q+1}^{(t)}\Vert ^2_{C_tL^2}&\lesssim \left( \frac{M}{4|\Lambda |} \right) ^2 \lambda _{q+1}^{90\alpha -4/7}+\left( \frac{M}{4|\Lambda |} \right) ^4 \lambda _{q+1}^{68\alpha -2/7}\lesssim \left( \left( \frac{M}{4|\Lambda |} \right) ^2\right. \\&\left. +\left( \frac{M}{4|\Lambda |} \right) ^4\right) \lambda _{q+1}^{-2\beta b -1/7}. \end{aligned}$$

Moreover, we already know about the existence of some $K^{\prime \prime }>0$, such that

$$\begin{aligned} \Vert w_{q+1}^{(c)}+w_{q+1}^{(t)}\Vert ^2_{C_tL^2} \le K^{\prime \prime } \left( \left( \frac{M}{4|\Lambda |} \right) ^2+\left( \frac{M}{4|\Lambda |} \right) ^4\right) \lambda _{q+1}^{-1/7} \delta _{q+2}. \end{aligned}$$

(3.41)

Choosing the parameters in such a way that $K^{\prime \prime } \left( \left( \frac{M}{4|\Lambda |} \right) ^2+\left( \frac{M}{4|\Lambda |} \right) ^4\right) \lambda _{q+1}^{-1/7}\le \frac{1}{5m^{1/2}}$ leads together with $e(t)\ge \underline{e}\ge 4$ and $\Theta ^{-2}(t)\ge m^{-1/2}$ to

$$\begin{aligned} \Vert w_{q+1}^{(c)}+w_{q+1}^{(t)}\Vert ^2_{C_tL^2}\le \frac{1}{20}\delta _{q+2}\Theta ^{-2}(t) e(t). \end{aligned}$$

Finally, plugging all the above estimates from I through to V into (3.30) proves (3.5) on the level $q+1$.

3.4.6 Convergence of the sequence

Moreover, we claim $\left( v_q\right) _{q \in \mathbb {N}_0}$ to be a Cauchy sequences in $C\left( (-\infty ,\tau ]; L^2\left( \mathbb {T}^3 \right) \right)$.

Thanks to (3.27) and (3.6a), we obtain

$$\begin{aligned} \Vert v_{q+1}-v_q\Vert _{C_tL^2}\le \Vert \omega _{q+1}\Vert _{C_tL^2}+\Vert v_\ell -v_q\Vert _{C_tL^2} \le \left( M_0+(2\pi )^{3/2}\right) \delta _{q+1}^{1/2}m\bar{e}^{1/2} \end{aligned}$$

(3.42)

for any $t \in (-\infty ,\tau ]$ and $q \in \mathbb {N}_0$, which results together with $a^{\beta b}\ge 2$ in

$$\begin{aligned} \sum _{q\ge 0} \Vert v_{q+1}-v_q\Vert _{C_tL^2}&\le \left( M_0+(2\pi )^{3/2}\right) m \bar{e}^{1/2}\sum _{q\ge 0} a^{\beta b-(q+1)\beta b}\\ {}&\overset{\text{ geom. }}{\underset{\text{ series }}{=}} \left( M_0+(2\pi )^{3/2}\right) m \bar{e}^{1/2}\frac{1}{1-a^{-\beta b}}\\ {}&\le 2\left( M_0+(2\pi )^{3/2}\right) m\bar{e}^{1/2}. \end{aligned}$$

As a consequence, the sequence $\left( \sum \limits _{q=0}^n \Vert v_{q+1}-v_q\Vert _{C_tL^2}\right) _{n\in \mathbb {N}_0}$ converges and is therefore in particular Cauchy in $\mathbb {R}$, i.e., for each $\varepsilon >0$ there exists some $N\in \mathbb {N}_0$, such that

$$\begin{aligned} \Vert v_n-v_k\Vert _{C_tL^2}\le \sum _{q=k}^{n-1} \Vert v_{q+1}-v_q\Vert _{C_tL^2} \le \varepsilon \end{aligned}$$

holds for every $n\ge k\ge N$, verifying the claim.

3.5 Decomposition of the Reynolds stress $\mathring{R}_{q+1}$

In order to find an expression for the Reynolds error at level $q+1$, we plug $v_{q+1}$ into (3.2) and exploit the formula ${{\text {div}}}\big (A \big )= {{\text {div}}}\big (\mathring{A} \big )+\frac{1}{3} \nabla {{\text {tr}}}\big (A\big )$ together with ${{\,\textrm{tr}\,}}(a \otimes b)=a \cdot b$, which holds for arbitrary quadratic matrices A and vectors $a,\, b$, respectively, to derive

$$\begin{aligned} {{\text {div}}}(&\mathring{R}_{q+1})-\nabla p_{q+1}\\ {}&:= \underbrace{\big [\partial _tv_q+\frac{1}{2}v_q-\Delta v_q+\Theta {{\,\text {div}}}(v_q \otimes v_q) \big ]}_{= {{\,\text {div}}}(\mathring{R}_q)-\nabla p_q}*_t \varphi _\ell *_x \phi _\ell \\ {}&\quad -[\Theta {{\,\text {div}}}(v_q \otimes v_q)]*_t \varphi _\ell *_x \phi _\ell +\partial _t w_{q+1}+\frac{1}{2} w_{q+1}\\ {}&\quad -\Delta w_{q+1}+ \Theta _\ell {{\,\text {div}}}(v_{q+1}\otimes v_{q+1})+(\Theta -\Theta _\ell ) {{\,\text {div}}}(v_{q+1}\otimes v_{q+1})\\ {}&=\underbrace{\partial _t (w_{q+1}^{(p)}+w_{q+1}^{(c)})+\frac{1}{2} w_{q+1}-\Delta w_{q+1} +\Theta _\ell {{\,\text {div}}}(v_\ell \mathring{\otimes }w_{q+1}+w_{q+1}\mathring{\otimes }v_\ell )}_{=:{{\text {div}}}(\mathring{R}_\text{ lin})}\\ {}& +\nabla \underbrace{\frac{2}{3}\Theta _\ell (v_\ell \cdot w_{q+1})}_{=:p_\text{ lin }}+\underbrace{\partial _t w_{q+1}^{(t)}+ {{\,\text {div}}}(\Theta _\ell w_{q+1}^{(p)}\otimes w_{q+1}^{(p)}+\mathring{R}_\ell )-\nabla p_\ell }_{=:{{\,\text {div}}}(\mathring{R}_\text{ osc})+\nabla p_\text{ osc }}\\ {}&\quad +{{\,\text {div}}}\bigg (\underbrace{\Theta _\ell \Big [(w_{q+1}^{(c)}+w_{q+1}^{(t)}) \mathring{\otimes } w_{q+1}+ w_{q+1}^{(p)}\mathring{\otimes }(w_{q+1}^{(c)}+w_{q+1}^{(t)}) \Big ]}_{=:\mathring{R}_\text{ cor }}\bigg )\\ {}&+\nabla \underbrace{ \frac{1}{3} \Theta _\ell \Big [(w_{q+1}^{(c)}+w_{q+1}^{(t)})\cdot w_{q+1}+w_{q+1}^{(p)}\cdot (w_{q+1}^{(c)}+w_{q+1}^{(t)})\Big ]}_{=:p_\text{ cor }}\\ {}& + {{\,\text {div}}}\bigg (\underbrace{(\Theta -\Theta _\ell )v_{q+1} \mathring{\otimes } v_{q+1}+\Theta _\ell v_\ell \mathring{\otimes }v_\ell -(\Theta v_q\mathring{\otimes } v_q)*_t \varphi _\ell *_x \phi _\ell }_{=: \mathring{R}_\text{ com }} \bigg ) \\ {}&+\nabla \underbrace{\frac{1}{3}\bigg [(\Theta -\Theta _\ell )|v_{q+1}|^2+\Theta _\ell |v_\ell |^2-(\Theta |v_q|^2)*_t\varphi _\ell *_x \phi _\ell \bigg ]}_{=:p_\text{ com }},\end{aligned}$$

where we have set $p_\ell := p_q*_t \varphi _\ell *_x \phi _\ell$.

Keeping in mind that ${{\text {div}}}\big (a_{(\xi )}^2 \mathbb {P}_{\ne 0}\big )$ $(W_{(\xi )}\otimes W_{(\xi )})\big )$ has zero mean, since $a_{(\xi )}^2 \mathbb {P}_{\ne 0} (W_{(\xi )}\otimes W_{(\xi )})$ is a smooth function with periodic boundary conditions, we invoke (3.31) to rewrite the oscillation error as

$$\begin{aligned} {{\,\text {div}}}(\mathring{R}_{\text{ osc }})+\nabla p_{\text{ osc }}&=\partial _t w_{q+1}^{(t)}+\sum _{\xi \in \Lambda } \mathbb {P}_{\ne 0}\Big [ \mathbb {P}_{\ne 0}(W_{(\xi )}\otimes W_{(\xi )})\nabla a_{(\xi )}^2\Big ]\nonumber \\ \quad&+\sum _{\xi \in \Lambda } \mathbb {P}_{\ne 0}\bigg [ a_{(\xi )}^2 {{\,\text {div}\,}}\Big (\mathbb {P}_{\ne 0}(W_{(\xi )}\otimes W_{(\xi )})\Big ) \bigg ] \!+\!\nabla (\rho -p_\ell ) , \end{aligned}$$

(3.43)

where

$$\begin{aligned} \big ({{\text {div}\,}}( W_{(\xi )}\otimes W_{(\xi )})\big )_i&=\sum _{j=1}^3 2n_*r_\perp \lambda \xi _j \psi _{r_\parallel }^{\prime } \psi _{(\xi )}\phi _{(\xi )}^2\xi _i\xi _j\\ {}&\quad +\sum _{j=1}^3 2 \psi _{(\xi )}^2 \big [n_*r_\perp \lambda (A_\xi )_j \partial _{y_1}\phi _{r_\perp }+n_*r_\perp \lambda (\xi \times A_\xi )_j \partial _{y_2}\phi _{r_\perp } \big ] \phi _{(\xi )}\xi _i\xi _j\\ {}&=\mu ^{-1} \partial _t(\psi _{(\xi )}^2\phi _{(\xi )}^2 \xi _i), \end{aligned}$$

with $y_1:=n_*r_\perp \lambda (x-\alpha _\xi )\cdot A_\xi$ and $y_2:=n_*r_\perp \lambda (x-\alpha _\xi )\cdot (\xi \times A_\xi )$. The second step follows from the fact that $\{\xi ,A_\xi ,\xi \times A_\xi \}$ form an orthonormal basis of $\mathbb {R}^3$.

Therefore, (3.43) boils, thanks to (3.25), down to

$$\begin{aligned}&{{\text {div}}}(\mathring{R}_{\text{ osc }})+\nabla p_{\text{ osc }} =-\mu ^{-1} \sum _{\xi \in \Lambda } \mathbb {P}\mathbb {P}_{\ne 0} \Big [ \partial _t \big (a_{(\xi )}^2\psi _{(\xi )}^2\phi _{(\xi )}^2 \xi \big ) \Big ]+ \sum _{\xi \in \Lambda } \mathbb {P}_{\ne 0} \Big [ \mathbb {P}_{\ne 0}\big (W_{(\xi )}\otimes W_{(\xi )}\big )\nabla a_{(\xi )}^2 \Big ]\\&\qquad \qquad \qquad + \mu ^{-1} \sum _{\xi \in \Lambda } \mathbb {P}_{\ne 0} \Big [\partial _t \big (a_{(\xi )}^2\psi _{(\xi )}^2\phi _{(\xi )}^2 \xi \big ) \Big ]-\mu ^{-1} \sum _{\xi \in \Lambda } \mathbb {P}_{\ne 0} \Big [\big (\partial _t a_{(\xi )}^2\big )\psi _{(\xi )}^2\phi _{(\xi )}^2 \xi \Big ] +\nabla (\rho -p_\ell ) \end{aligned}$$

and because of ${{\text {Id}}}- \mathbb {P}= \nabla \Delta ^{-1} {{\text {div}}}$ and Lemma 2.5 we may continue by writing

$$\begin{aligned} {{\,\textrm{div}\,}}(\mathring{R}_{\text {osc}})+\nabla p_{\text {osc}}&=\nabla \bigg [\Delta ^{-1} {{\,\textrm{div}\,}}\Big (\mu ^{-1}\sum _{\xi \in \Lambda } \mathbb {P}_{\ne 0} \big [\partial _t (a_{(\xi )}\,^2\psi _{(\xi )}^2\phi _{(\xi )}^2 \xi ) \big ]\Big )+\rho -p_\ell \bigg ]\\&+ \sum _{\xi \in \Lambda } \mathbb {P}_{\ne 0} \Big [ \mathbb {P}_{\ge \frac{r_\perp \lambda _{q+1}}{2} }\big (W_{(\xi )}\,\otimes W_{(\xi )}\,\big )\nabla a_{(\xi )}\,^2 \Big ]\\&-\mu ^{-1} \sum _{\xi \in \Lambda } \mathbb {P}_{\ne 0} \Big [ \big (\partial _t a_{(\xi )}\,^2\big )\psi _{(\xi )}^2\phi _{(\xi )}^2 \xi \Big ]. \end{aligned}$$

In order to find a specific representation of the stress terms $R_{\text {lin}}$ and $R_{\text {osc}}$, we need a right inverse of the divergence operator. We recall the one that emerged in [12], which acts on the space of smooth, $\mathbb {R}^3$-valued vector fields on $\mathbb {T}^3$ with zero mean and which takes values in $L^p\left( \mathbb {T}^3; \mathring{\mathbb {R}}_{\text {sym}}^{3\times 3}\right)$.

Lemma 3.8

The operator $\mathcal {R}$ defined by

$$\begin{aligned} \mathcal {R}:\left( C_{\ne 0}^\infty \left( \mathbb {T}^3; \mathbb {R}^3\right) ,\Vert \cdot \Vert _{L^p}\right)&\rightarrow \left( L^p\left( \mathbb {T}^3; \mathring{\mathbb {R}}_{\text{ sym }}^{3\times 3}\right) , \Vert \cdot \Vert _{L^p}\right) ,\\ \mathcal {R}u:= \nabla \otimes (\Delta ^{-1}u)+\Big (\nabla \otimes (\Delta ^{-1}u)\Big )^T&-\frac{1}{2} \Big ((\nabla \otimes \nabla ) \Delta ^{-1}+ {{\,\text {Id}\,}}\Big ){{\,\text {div}\,}}(\Delta ^{-1}u) \end{aligned}$$

is a right inverse of the divergence operator and is particularly bounded for $p \in (1,\infty )$.

We can moreover formulate the ensuing Lemma, which states that the composition of $\mathcal {R}$ with the differential operators $\Delta$, ${{\,\textrm{curl}\,}}$ and with the Fourier cutoff operator $\mathbb {P}_{\ge \kappa /2}$ is bounded operators as well.

Lemma 3.9

The composition of operators

• (i) $\mathcal {R}{{\,\textrm{curl}\,}}:\left( C^\infty \left( \mathbb {T}^3;\mathbb {R}^3\right) ,\Vert \cdot \Vert _{L^p}\right) \rightarrow \left( L^p\left( \mathbb {T}^3; \mathring{\mathbb {R}}_{\text {sym}}^{3\times 3}\right) , \Vert \cdot \Vert _{L^p}\right) ,$

• (ii) $\mathcal {R}\Delta :\left( C^\infty \left( \mathbb {T}^3;\mathbb {R}^3\right) ,\Vert \cdot \Vert _{W^{1,p}}\right) \rightarrow \left( L^p\left( \mathbb {T}^3; \mathring{\mathbb {R}}_{\text {sym}}^{3\times 3}\right) , \Vert \cdot \Vert _{L^p}\right) ,$

• (iii) $\mathcal {R}\mathbb {P}_{\ge \kappa }:\left( C^\infty \left( \mathbb {T}^3;\mathbb {R}^3\right) , \Vert \cdot \Vert _{L^p}\right) \rightarrow \left( L^p\left( \mathbb {T}^3; \mathring{\mathbb {R}}_{\text {sym}}^{3\times 3}\right) , \Vert \cdot \Vert _{L^p}\right)$

are for $p \in (1,\infty )$ continuous ones. More precisely, we find

$$\begin{aligned} \Vert \mathcal {R}\mathbb {P}_{\ge \kappa }\Vert _{L^p\rightarrow L^p} \lesssim \frac{1}{\kappa }. \end{aligned}$$

Equipped with this knowledge, it makes sense to define

$$\begin{aligned} \mathring{R}_{\text{ lin }}&:=\mathcal {R}\partial _t (w_{q+1}^{(p)}{+}w_{q+1}^{(c)}){+} \frac{1}{2}\mathcal {R} w_{q{+}1}{-}\mathcal {R}\Delta w_{q+1} {+}\Theta _\ell \Big (v_\ell \mathring{\otimes }w_{q+1}{+}w_{q+1}\mathring{\otimes }v_\ell \Big ),\\ \mathring{R}_{\text{ cor }}&:=\Theta _\ell \Big [(w_{q+1}^{(c)}+w_{q+1}^{(t)}) \mathring{\otimes } w_{q+1}+ w_{q+1}^{(p)}\mathring{\otimes }(w_{q+1}^{(c)}+w_{q+1}^{(t)}) \Big ],\\ \mathring{R}_{\text{ osc }}&:= \sum _{\xi \in \Lambda } \mathcal {R}\mathbb {P}_{\ne 0} \Big [ \mathbb {P}_{\ge \frac{ r_\perp \lambda _{q+1}}{2}}\big (W_{(\xi )}\otimes W_{(\xi )}\big )\nabla a_{(\xi )}^2 \Big ] -\mu ^{-1} \sum _{\xi \in \Lambda }\mathcal {R} \mathbb {P}_{\ne 0} \Big [ \big (\partial _t a_{(\xi )}^2\big )\psi _{(\xi )}^2\phi _{(\xi )}^2 \xi \Big ],\\ \mathring{R}_{\text{ com }}&:=(\Theta -\Theta _\ell )v_{q+1} \mathring{\otimes } v_{q+1}+\Theta _\ell v_\ell \mathring{\otimes }v_\ell -(\Theta v_q\mathring{\otimes } v_q)*_t \varphi _\ell *_x \phi _\ell \end{aligned}$$

with the corresponding pressure terms

$$\begin{aligned} p_{\text{ lin }}&:=\frac{2}{3}\Theta _\ell (v_\ell \cdot w_{q+1}),\\ p_{\text{ cor }}&:= \frac{1}{3} \Theta _\ell \Big [(w_{q+1}^{(c)}+w_{q+1}^{(t)})\cdot w_{q+1}+w_{q+1}^{(p)}\cdot (w_{q+1}^{(c)}+w_{q+1}^{(t)})\Big ],\\ p_{\text{ osc }}&:=\Delta ^{-1} {{\text {div}}}\Big (\mu ^{-1}\sum _{\xi \in \Lambda } \mathbb {P}_{\ne 0} \big [\partial _t (a_{(\xi )}^2\psi _{(\xi )}^2\phi _{(\xi )}^2 \xi ) \big ]\Big )+\rho -p_\ell , \\ p_{\text{ com }}&:=\frac{1}{3}\Big [(\Theta -\Theta _\ell )|v_{q+1}|^2+\Theta _\ell |v_\ell |^2-(\Theta |v_q|^2)*_t\varphi _\ell *_x \phi _\ell \Big ]. \end{aligned}$$

The Reynolds stress at level $q+1$ then becomes

$$\begin{aligned} \mathring{R}_{q+1}= \mathring{R}_\text {lin}+\mathring{R}_\text {cor}+\mathring{R}_\text {osc}+\mathring{R}_\text {com} \end{aligned}$$

and remains by construction symmetric and traceless.

3.6 Inductive estimates for the Reynolds stress $\mathring{R}_{q+1}$

3.6.1 Verifying the key bound on the level $q+1$

Next, we aim at verifying (3.3c) on the level $q+1$. To do so, we need $r_\perp ^{2/p-2}r_{\parallel }^{1/p-1}\le \lambda _{q+1}^{\alpha }$, which can be achieved by taking $p \in \Big (1,\frac{16}{16-7\alpha }\Big ]$. We start with a bound for the Linear error.

3.7 Linear Error

Remembering that $\mathcal {R}\Delta$ and $\mathcal {R}{{\,\textrm{curl}\,}}$ are according to Lemma 3.9 bounded operators on $C^\infty \left( \mathbb {T}^3;\mathbb {R}^3\right)$, we employ Hölder’s inequality, (3.14) and (3.24) to obtain

$$\begin{aligned} \Vert \mathring{R}_\text{ lin }\Vert _{C_tL^1}&\lesssim \sum _{\xi \in \Lambda } \ell ^{-1}m^{5/8}\Vert \mathcal {R} {{\,\text {curl}}}{{\,\text {curl}\,}}(a_{(\xi )}V_{(\xi )})\Vert _{C_tL^p} +m^{1/8}\sum _{\xi \in \Lambda } \Vert \mathcal {R} \partial _t{{\,\text {curl}}}{{\,\text {curl}\,}}(a_{(\xi )}V_{(\xi )})\Vert _{C_tL^p}\\ {}&\quad +\Vert w_{q+1}\Vert _{C_tL^p}+\Vert w_{q+1}\Vert _{C_tW^{1,p}}+m^{1/4}\Vert v_\ell \mathring{\otimes } w_{q+1}+w_{q+1} \mathring{\otimes } v_\ell \Vert _{C_tL^p}\\ {}&\lesssim \sum _{\xi \in \Lambda } \underbrace{\ell ^{-1} m^{5/8}\Vert {{\,\text {curl}\,}}(a_{(\xi )}V_{(\xi )})\Vert _{C_tL^p}}_{=:\text{ I }}+\sum _{\xi \in \Lambda } \underbrace{m^{1/8}\Vert \partial _t{{\,\text {curl}\,}}(a_{(\xi )}\,V_{(\xi )}\,)\Vert _{C_tL^p}}_{=:\text{ II }}\\ {}&\quad +\underbrace{\Vert w_{q+1}\Vert _{C_tW^{1,p}}}_{=:\text{ III }}+\underbrace{m^{1/4}\Vert v_\ell \mathring{\otimes } w_{q+1}+w_{q+1} \mathring{\otimes } v_\ell \Vert _{C_tL^p}}_{\text{=:IV }}. \end{aligned}$$

We combine (3.8b) and (3.13c) and (3.1b) with $r_\perp ^{2/p-2}r_\parallel ^{1/p-1}\le \lambda _{q+1}^\alpha$ to control the first term as follows

$$\begin{aligned} \ell ^{-1} m^{5/8}\Vert {{\,\text {curl}\,}}(a_{(\xi )}V_{(\xi )})\Vert _{C_tL^p}&\le \ell ^{-1} m^{5/8}\bigg ( \Vert a_{(\xi )}\Vert _{C_{t,x}^1}\Vert V_{(\xi )}\Vert _{C_tL^p} +\Vert a_{(\xi )}\,\Vert _{C_{t,x}^0} \sum _{|\gamma |=1}\Vert D^\gamma V_{(\xi )}\,\Vert _{C_tL^p}\bigg )\\ {}&\lesssim \frac{M}{4 |\Lambda |} \left( \lambda _{q+1}^{34 \alpha - 22/7}+\lambda _{q+1}^{20\alpha -15/7} \right) . \end{aligned}$$

A bound for the second term can be deduced in the same manner:

$$\begin{aligned} m^{1/8}\Vert \partial _t {{\,\text {curl}\,}}(a_{(\xi )}V_{(\xi )})\Vert _{C_tL^p}&\le m^{1/8}\big (\Vert a_{(\xi )}\Vert _{C_{t,x}^2}\Vert V_{(\xi )}\Vert _{C_tL^p} +\Vert a_{(\xi )}\Vert _{C_{t,x}^1}\Vert \partial _t V_{(\xi )}\Vert _{C_tL^p}\big )\\ {}&+m^{1/8}\big (\Vert a_{(\xi )}\Vert _{C_{t,x}^1} \sum _{|\gamma |=1}\Vert D^\gamma V_{(\xi )}\Vert _{C_tL^p}\\ {}&+\Vert a_{(\xi )}\Vert _{C_{t,x}^0} \sum _{|\gamma |=1}\Vert D^\gamma \partial _tV_{(\xi )}\Vert _{C_tL^p}\big )\\ {}&\lesssim \frac{M}{4|\Lambda |} \left( \lambda _{q+1}^{46\alpha -22/7}+\lambda _{q+1}^{32\alpha -8/7}+\lambda _{q+1}^{32\alpha -15/7}+\lambda _{q+1}^{18\alpha -1/7} \right) . \end{aligned}$$

Thanks again to the constrained $r_\perp ^{2/p-2}r_\parallel ^{1/p-1}\le \lambda _{q+1}^\alpha$, the third term can owing to (3.17a), (3.17b) and (3.1b) be estimated as

$$\begin{aligned} \sum _{0<|\alpha |\le k} \Vert D_t^\alpha f(u)\Vert _{C_tL^\infty }&\lesssim \sum _{0<|\alpha |\le k} \max _{|\beta |=1} \Vert D_t^\beta f \Vert _{C_tL^\infty } \max _{|\beta |=|\alpha |}\Vert D_t^\beta u\Vert _{C_tL^\infty } \\ {}&\quad +\sum _{0<|\alpha |\le k}\sum _{j=0}^{|\alpha |-1} \max _{|\beta |=j+1}\Vert D_t^{\beta }f \Vert _{C_tL^\infty } \max _{|\beta |=1} \Vert D_t^\beta u\Vert ^{|\alpha |}_{C_tL^\infty }.\end{aligned}$$

Keeping in mind that

$$\begin{aligned} \Vert v \mathring{\otimes } w\Vert _{\text {F}}=\sqrt{\Vert v \otimes w\Vert ^2_{\text {F}} -\frac{1}{3} {{\,\textrm{tr}\,}}\left( v \otimes w \right) ^2} \le \Vert v \otimes w\Vert _{\text {F}}= |v|\, |w| \end{aligned}$$

(3.44)

holds for any two vector fields v and w, the fourth term admits, according to (3.3b), (3.15a), (3.15b), (3.15c), (3.1a), (3.1b) and $r_\perp ^{2/p-2}r_\parallel ^{1/p-1}\le \lambda _{q+1}^\alpha$, the inequality

$$\begin{aligned} m^{1/4}\Vert v_\ell \mathring{\otimes } w_{q+1}+w_{q+1}\mathring{\otimes } v_\ell \Vert _{C_tL^p}&\lesssim m^{1/4}\Vert v_\ell \Vert _{C_{t,x}^0} \Vert w_{q+1}\Vert _{C_tL^p}\lesssim \frac{M}{4|\Lambda |} \lambda _{q+1}^{21\alpha -8/7}\\&\qquad +\frac{M}{4|\Lambda |}\lambda _{q+1}^{49 \alpha -10/7}+\left( \frac{M}{4|\Lambda |} \right) ^2 \lambda _{q+1}^{38\alpha -9/7} . \end{aligned}$$

Thus, remembering the assumptions $161 \alpha <\frac{1}{7}$, $\alpha >4 \beta b^2$, $e(t)\ge \underline{e}>4$ and $\Theta ^{-2}(t)\ge m^{-1/2}$ we can finally bound the linear error as

$$\begin{aligned} \Vert \mathring{R}_\text{ lin }\Vert _{C_tL^1}&\le S\left( \frac{M}{4|\Lambda |}+\left( \frac{M}{4|\Lambda |}\right) ^2 \right) \lambda _{q+1}^{60\alpha -1/7}\\&\le S\left( \frac{M}{4|\Lambda |}+\left( \frac{M}{4|\Lambda |}\right) ^2 \right) \lambda _{q+1}^{-100 \alpha -4\beta b^2}\\&\le \frac{1}{6000} \delta _{q+3}\Theta ^{-2}(t)e(t) , \end{aligned}$$

provided $S\left( \frac{M}{4|\Lambda |}+\left( \frac{M}{4|\Lambda |}\right) ^2 \right) \lambda _{q+1}^{-100\alpha }\le \frac{1}{1500m^{1/2}}$ for some constant $S>0$ (cf. Sect. 3.1).

3.7.1 Corrector Error

We apply (3.44) and Hölder’s inequality twice in order to obtain

$$\begin{aligned} \Vert R_{\text{ cor }}\Vert _{C_tL^1}&\le m^{1/4}\Vert w_{q+1}^{(c)}+w_{q+1}^{(t)}\Vert _{C_tL^{2p}}\Vert w_{q+1}\Vert _{C_tL^{2p}}+m^{1/4}\Vert w_{q+1}^{(c)} +w_{q+1}^{(t)}\Vert _{C_tL^{2p}}\Vert w_{q+1}^{(p)}\Vert _{C_tL^{2p}}\\ {}&\le m^{1/4}\Vert w_{q+1}^{(c)}+w_{q+1}^{(t)}\Vert _{C_tL^{2p}}^2 +2m^{1/4}\Vert w_{q+1}^{(c)}+w_{q+1}^{(t)}\Vert _{C_tL^{2p}}\Vert w_{q+1}^{(p)}\Vert _{C_tL^{2p}}. \end{aligned}$$

Appealing to (3.15b), (3.15c), (3.15a), (3.1b) and $r_\perp ^{2/p-2}r_\parallel ^{1/p-1}\le \lambda _{q+1}^{\alpha }$, it follows

$$\begin{aligned} \Vert w_{q+1}^{(c)}+w_{q+1}^{(t)}\Vert ^2_{C_tL^{2p}}\lesssim \left( \frac{M}{4|\Lambda |}\right) ^2 \lambda _{q+1}^{91\alpha -4/7}+\left( \frac{M}{4|\Lambda |}\right) ^4\lambda _{q+1}^{69\alpha -2/7} \end{aligned}$$

and

$$\begin{aligned} \Vert w_{q+1}^{(c)}+w_{q+1}^{(t)}\Vert _{C_tL^{2p}} \Vert w_{q+1}^{(p)}\Vert _{C_tL^{2p}}\lesssim \left( \frac{M}{4|\Lambda |}\right) ^2 \lambda _{q+1}^{63\alpha -2/7}+\left( \frac{M}{4|\Lambda |}\right) ^3\lambda _{q+1}^{52\alpha -1/7}. \end{aligned}$$

That means there exists a constant $\widetilde{S}>0$ such that

$$\begin{aligned} \Vert \mathring{R}_\text {cor}\Vert _{C_tL^1}&\le \widetilde{S}\left( \left( \frac{M}{4|\Lambda |}\right) ^2+\left( \frac{M}{4|\Lambda |}\right) ^3+\left( \frac{M}{4|\Lambda |}\right) ^4 \right) \lambda _{q+1}^{92\alpha -1/7}\nonumber \\&\le \widetilde{S}\left( \left( \frac{M}{4|\Lambda |}\right) ^2+\left( \frac{M}{4|\Lambda |}\right) ^3+\left( \frac{M}{4|\Lambda |}\right) ^4 \right) \lambda _{q+1}^{-69\alpha }, \end{aligned}$$

(3.45)

where we also took $m^{1/4}\le \lambda _{q+1}^\alpha$ and $161\alpha <\frac{1}{7}$ into account.

In view of our choice of parameters (cf. Sect. 3.1), it holds

$$\begin{aligned} \widetilde{S}\left( \left( \frac{M}{4|\Lambda |}\right) ^2+\left( \frac{M}{4|\Lambda |}\right) ^3+\left( \frac{M}{4|\Lambda |}\right) ^4 \right) \lambda _{q+1}^{-68 \alpha }\le \frac{1}{1500m^{1/2}}, \end{aligned}$$

so that together with $\alpha >4\beta b^2$, $e(t)\ge \underline{e}> 4$ and $\Theta ^{-2}(t)\ge m^{-1/2}$ again, we accomplish

$$\begin{aligned} \Vert \mathring{R}_\text {cor}\Vert _{C_tL^1}\le \frac{1}{1500m^{1/2}} \lambda _{q+1}^{-4\beta b^2}\le \frac{1}{6000} \delta _{q+3}\Theta ^{-2}(t)e(t). \end{aligned}$$

3.7.2 Oscillation Error

To control the first term of the oscillation error, we intend to apply Lemma A.3. Thanks to Leibniz’s formula, (3.8b) and (3.1b) we accomplish

$$\begin{aligned} \sum _{|\alpha |=n} \Vert D^\alpha (\nabla a_{(\xi )}^2)\Vert _{C_tL^\infty }&\lesssim \sum _{|\alpha |=n+1} \sum _{\beta \le \alpha } \Vert D^\beta a_{(\xi )}\Vert _{C_tL^\infty }\Vert D^{\alpha -\beta }a_{(\xi )}\Vert _{C_tL^\infty }\\ {}&\lesssim \sum _{k \le n+1} \Vert a_{(\xi )}\Vert _{C^{k}_{t,x}} \Vert a_{(\xi )}\Vert _{C^{n+1-k}_{t,x}}\\ {}&\lesssim \left( \frac{M}{4|\Lambda |}\right) ^2 \ell ^{-24}\ell ^{-7n} \end{aligned}$$

for any $n\ge 0$ and owing to the constraints $161\alpha <\frac{1}{7}$, $a\ge 3600$, $b\ge 7$ and (3.1b) also

$$\begin{aligned} \ell ^{-7}&\le \lambda _{q+1}^{14\alpha } < \lambda _{q+1}^{-3/23} \lambda _{q+1}^{1/7} \le 3600^{-7 \cdot \frac{3}{23}}r_\perp \lambda _{q+1} \le \frac{r_\perp \lambda _{q+1}}{2} \end{aligned}$$

and

$$\begin{aligned} \ell ^{-7N}&\le (\lambda _{q+1}^{14 \alpha })^{ N}\le \lambda _{q+1}^{3/7-\frac{3}{23} N} \lambda _{q+1}^{\frac{1}{7}(N-3)}\\ {}&\le 3600^{7 \cdot (3/7-\frac{3}{23} N)} (r_\perp \lambda _{q+1})^{N-3} \le \left( \frac{r_\perp \lambda _{q+1}}{2}\right) ^{N-3} , \end{aligned}$$

as long as $\frac{3 \ln (2^{-1}\cdot 3600)}{\ln (2^{-1}\cdot 3600^{21/23})}<4 \le N$. Therefore, all requirements of Lemma A.3 are fulfilled and together with (3.1b), (3.44) and (3.13c) it teaches us

$$\begin{aligned} \Big \Vert \sum _{\xi \in \Lambda } \mathcal {R}\mathbb {P}_{\ne 0}\big [ \mathbb {P}_{\ge \frac{r_\perp \lambda _{q+1}}{2}}(W_{(\xi )}\otimes W_{(\xi )})\nabla a_{(\xi )}^2\big ] \Big \Vert _{C_tL^p}&\lesssim \left( \frac{M}{4|\Lambda |}\right) ^2\lambda _{q+1}^{48 \alpha } \frac{\Vert W_{(\xi )}\otimes W_{(\xi )}\Vert _{C_tL^p}}{r_\perp \lambda _{q+1}}\\ {}&= \left( \frac{M}{4|\Lambda |}\right) ^2\lambda _{q+1}^{48 \alpha } \Vert W_{(\xi )}\Vert ^2_{C_tL^{2p}}r_\perp ^{-1}\lambda _{q+1}^{-1}\\ {}&\lesssim \left( \frac{M}{4|\Lambda |}\right) ^2\lambda _{q+1}^{49 \alpha -1/7}, \end{aligned}$$

where we make again use of $r_\perp ^{2/p-2}r_\parallel ^{1/p-1}\le \lambda _{q+1}^\alpha$ in the last step.

The second term of the oscillation error can according to the boundedness of $\mathcal {R}\mathbb {P}_{\ne 0}$ on $\left( C^\infty \left( \mathbb {T}^3; \mathbb {R}^3\right) ,\Vert \cdot \Vert _{L^p}\right)$, Lemma 3.4, (3.8b), (3.13a), (3.13b), (3.1b) and $r_\perp ^{2/p-2}r_\parallel ^{1/p-1}\le \lambda _{q+1}^\alpha$ be estimated as

$$\begin{aligned} \Big \Vert \mu ^{-1} \sum _{\xi \in \Lambda } \mathcal {R} \mathbb {P}_{\ne 0} \big [(\partial _t a_{(\xi )}^2) \psi _{(\xi )}^2 \phi _{(\xi )}^2 \xi \big ] \Big \Vert _{C_tL^p}&\lesssim \mu ^{-1} \sum _{\xi \in \Lambda } \Vert \partial _t a_{(\xi )}\Vert _{C_tL^\infty }\Vert a_{(\xi )}\Vert _{C_tL^\infty } \Vert \psi _{(\xi )}^2 \phi _{(\xi )}^2\Vert _{C_tL^p}\\ {}&\lesssim \mu ^{-1} \sum _{\xi \in \Lambda } \Vert a_{(\xi )}\Vert _{C_{t,x}^1}\Vert a_{(\xi )}\Vert _{C_{t,x}^0} \Vert \psi _{(\xi )}\Vert ^2_{C_tL^{2p}} \Vert \phi _{(\xi )}\Vert ^2_{L^{2p}}\\ {}&\lesssim \left( \frac{M}{4|\Lambda |}\right) ^2 \lambda _{q+1}^{49\alpha -9/7}. \end{aligned}$$

Under the assumptions $161\alpha <\frac{1}{7}$ and $\alpha >4\beta b^2$, we therefore get by Hölder’s inequality

$$\begin{aligned} \Vert \mathring{R}_\text {osc}\Vert _{C_tL^1}\le \hat{S}\left( \frac{M}{4|\Lambda |}\right) ^2 \lambda _{q+1}^{49 \alpha -1/7} \le \hat{S}\left( \frac{M}{4|\Lambda |}\right) ^2 \lambda _{q+1}^{-111 \alpha }\lambda _{q+1}^{-2\beta b^2} \end{aligned}$$

(3.46)

for some $\hat{S}>0$. To absorb this implicit universal constant, we impose $\hat{S}\left( \frac{M}{4|\Lambda |}\right) ^2 \lambda _{q+1}^{-111 \alpha }$$\le$ $\frac{1}{1500\,m^{1/2}}$ by possibly increasing a. Finally, $e(t)\ge \underline{e}> 4$ and $\Theta ^{-2}(t)\ge m^{-1/2}$ entail

$$\begin{aligned} \Vert \mathring{R}_\text {osc}\Vert _{C_tL^1}\le \frac{1}{1500m^{1/2}}\delta _{q+3}\le \frac{1}{6000} \delta _{q+3}\Theta ^{-2}(t) e(t). \end{aligned}$$

3.7.3 Commutator Error

We will estimate each term of

$$\begin{aligned} \Vert \mathring{R}_\text{ com }\Vert _{C_tL^1}&\le \underbrace{\Vert (\Theta -\Theta _\ell ) v_{q+1} \mathring{\otimes } v_{q+1}\Vert _{C_tL^1}}_{=:\text{ I }}+\underbrace{\Vert \Theta _\ell v_\ell \mathring{\otimes } v_\ell -\Theta _\ell v_q \mathring{\otimes } v_\ell \Vert _{C_tL^1}}_{=:\text{ II }}\nonumber \\ {}&\quad +\underbrace{\Vert \Theta _\ell v_q \mathring{\otimes } v_\ell -\Theta v_q \mathring{\otimes }v_\ell \Vert _{C_tL^1}}_{_{=:\text{ III }}}+\underbrace{\Vert \Theta v_q \mathring{\otimes }v_\ell -\Theta v_q \mathring{\otimes }v_q \Vert _{C_tL^1}}_{_{=:\text{ IV }}}\nonumber \\ {}&\quad +\underbrace{\Vert \Theta v_q \mathring{\otimes }v_q-(\Theta v_q \mathring{\otimes }v_q )*_t \varphi _\ell *_x \phi _\ell \Vert _{C_tL^1}}_{_{=:\text{ V }}} \end{aligned}$$

(3.47)

separately.

To find a bound for $\Vert \Theta - \Theta _\ell \Vert _{C_t}$, we proceed in a similar way as in (3.36) by using Itô’s formula. More precisely, we find

$$\begin{aligned} \Vert \Theta - \Theta _\ell \Vert _{C_t} \le \frac{3}{2}m^{1/4} \ell ^\iota . \end{aligned}$$

(3.48)

Together with (3.44), it furnishes

$$\begin{aligned} \text{ I }&\le \Vert \Theta - \Theta _\ell \Vert _{C_t} \sup _{s \in (-\infty ,t]} \int _{\mathbb {T}^3} |v_{q+1}(s,x)|^2\, dx \\ {}&\le \frac{3}{2}(2\pi )^{3/2}m^{1/4} \ell ^\iota \Vert v_{q+1}\Vert _{C_{t,x}^1} \Vert v_{q+1}\Vert _{C_tL^2}. \end{aligned}$$

Keeping Cauchy–Schwarz’s inequality in mind, we combine (3.44) with (3.6a) and (3.6b) to find

$$\begin{aligned} \text{ II }&\le m^{1/4} \sup _{s \in (-\infty ,t]} \int _{\mathbb {T}^3} |(v_\ell -v_q)(s,x)|\, |v_\ell (s,x) |\,dx\\ {}&\le m^{1/4} \Vert v_\ell -v_q\Vert _{C_tL^2}\Vert v_\ell \Vert _{C_tL^2}\\ {}&\le (2\pi )^{3/2}m^{1/4} \ell \Vert v_q\Vert _{C^1_{t,x}} \Vert v_q\Vert _{C_tL^2}. \end{aligned}$$

Note that the final bound is also valid for IV.

Moreover, we invoke (3.48), (3.44) and (3.6b) to get

$$\begin{aligned} \text{ III }&\le \Vert \Theta _\ell - \Theta \Vert _{C_t}\sup _{s\in (-\infty ,t]} \int _{\mathbb {T}^3} |v_q(s,x)|\, |v_\ell (s,x)| \,dx\\ {}&\le \frac{3}{2}(2\pi )^{3/2}m^{1/4} \ell ^\iota \Vert v_q\Vert _{C_{t,x}^1}\Vert v_q\Vert _{C_tL^2}. \end{aligned}$$

Thanks to the normalizations of mollifiers, we have

$$\begin{aligned} \text {V}&{\le } \underbrace{\sup _{s \in (-\infty ,t]} \sup _{u \in [0,\ell ]} \int _{\mathbb {T}^3}\Vert \Theta (s)(v_q \mathring{\otimes }v_q)(s,x)-\Theta (s-u)(v_q \mathring{\otimes }v_q)(s-u,x)\Vert _F \, dx }_{=:V_1}\\&\quad {+}\underbrace{\sup _{s \in ({-}\infty ,t]} \sup _{u \in [0,\ell ]} \sup _{|y|\le \ell }\int _{\mathbb {T}^3}\Vert \Theta (s{-}u)(v_q \mathring{\otimes }v_q)(s{-}u,x){-}\Theta (s{-}u)(v_q \mathring{\otimes }v_q)(s{-}u,x{-}y)\Vert _F \, dx }_{=:V_2}, \end{aligned}$$

where $V_1$ boils owing to (3.44) and Cauchy–Schwarz’s inequality down to

$$\begin{aligned} \text{ V}_1&\le \sup _{s \in (-\infty ,t]} \sup _{u \in [0,\ell ]} \int _{\mathbb {T}^3}\big \Vert [\Theta (s)v_q(s,x)- \Theta (s-u)v_q(s-u,x)] \mathring{\otimes }v_q(s,x)\big \Vert _F \, dx\\ {}&\quad {+}\sup _{s \in ({-}\infty ,t]} \sup _{u \in [0,\ell ]} \int _{\mathbb {T}^3}\big \Vert \Theta (s{-}u)v_q(s{-}u,x) \mathring{\otimes }[v_q(s,x){-}v_q(s-u,x)]\big \Vert _F \, dx\\ {}&\le \sup _{s \in ({-}\infty ,t]} \sup _{u \in [0,\ell ]} \int _{\mathbb {T}^3} \underbrace{|\Theta (s)v_q(s,x){-} \Theta (s{-}u)v_q(s{-}u,x)|}_{{\le } 3m^{1/4} \ell ^\iota \Vert v_q\Vert _{C_{t,x}^1} \, (*)} \, \,|v_q(s,x)| \, dx\\ {}&\quad +\sup _{s \in (-\infty ,t]} \sup _{u \in [0,\ell ]} \int _{\mathbb {T}^3} | \Theta (s-u)v_q(s-u,x)|\, |v_q(s,x)-v_q(s-u,x)| \, dx\\ {}&\le 3m^{1/4} \ell ^\iota \Vert v_q\Vert _{C_{t,x}^1} (2\pi )^{3/2} \Vert v_q\Vert _{C_tL^2}\\ {}&\quad +m^{1/4} \Vert v_q\Vert _{C_tL^2}\sup _{s \in (-\infty ,t]} \sup _{u \in [0,\ell ]} \left( \int _{\mathbb {T}^3} |v_q(s,x)-v_q(s-u,x)|^2 \, dx \right) ^{1/2}\\ {}&= 3(2\pi )^{3/2}m^{1/4} \ell ^\iota \Vert v_q\Vert _{C_{t,x}^1} \!\Vert v_q\Vert _{C_tL^2}\\ {}&\quad +\!m^{1/4} \!\Vert v_q\Vert _{C_tL^2}\sup _{s \in (-\!\infty ,t]} \!\sup _{u \in [0,\ell ]} \!\bigg (\int _{\mathbb {T}^3} \Big | \!\int _0^1 \underbrace{\partial _\varsigma v_q(s\!-\!\varsigma u,x)}_{\begin{array}{l} =\!-u\partial _s v_q(s\!-\varsigma u,x)\!\le \! \ell \Vert v_q\Vert _{C_{t,x}^1} \end{array}}\, d\varsigma \Big |^2 \, dx \bigg )^{1/2}\\ {}&\le 4(2\pi )^{3/2}m^{1/4} \ell ^\iota \Vert v_q\Vert _{C_{t,x}^1} \Vert v_q\Vert _{C_tL^2}. \end{aligned}$$

Here, ($*$) follows similarly to (3.36), this time, however, with e(s) replaced by $v_q(s,x)$ and $\bar{e}$, $\widetilde{e}$ by $\Vert v_q\Vert _{C_{t,x}^1}$.

One more time we employ (3.44) and stick to standard mollification estimates in order to control $\hbox {V}_2$ as follows

$$\begin{aligned} \text{ V}_2&\le m^{1/4} \sup _{s \in (-\infty ,t]} \sup _{|y|\le \ell }\int _{\mathbb {T}^3}\big \Vert [v_q(s,x)-v_q(s,x-y)] \mathring{\otimes }v_q(s,x)\big \Vert _F \, dx \\ {}&\quad + m^{1/4} \sup _{s \in (-\infty ,t]} \sup _{|y|\le \ell }\int _{\mathbb {T}^3}\big \Vert v_q(s,x-y) \mathring{\otimes }[v_q(s,x)-v_q(s,x-y)]\big \Vert _F \, dx \\ {}&\le m^{1/4} \sup _{s \in (-\infty ,t]} \sup _{|y|\le \ell }\int _{\mathbb {T}^3} |v_q(s,x)-v_q(s,x-y)| \, |v_q(s,x)| \, dx \\ {}&\quad + m^{1/4} \sup _{s \in (-\infty ,t]} \sup _{|y|\le \ell }\int _{\mathbb {T}^3}|v_q(s,x-y)|\,|v_q(s,x)-v_q(s,x-y)| \, dx \\ {}&\le 2m^{1/4} \Vert v_q\Vert _{C_tL^2}\sup _{s \in (-\infty ,t]} \sup _{|y|\le \ell }\left( \int _{\mathbb {T}^3} |v_q(s,x)-v_q(s,x-y)|^2 \, dx \right) ^{1/2}\\ {}&= 2m^{1/4} \Vert v_q\Vert _{C_tL^2}\sup _{s \in (-\infty ,t]} \sup _{|y|\le \ell }\left( \int _{\mathbb {T}^3} \Big | \int _0^1 \partial _\varsigma v_q(s,x-\varsigma y) \, d\varsigma \Big |^2 \, dx \right) ^{1/2}\\ {}&= 2m^{1/4} \Vert v_q\Vert _{C_tL^2}\sup _{s \in (-\infty ,t]} \sup _{|y|\le \ell }\left( \int _{\mathbb {T}^3} \Big | \int _0^1 \sum _{i=1}^3 y_i \partial _{x_i} v_q(s,x-\varsigma y) \, d\varsigma \Big |^2 \, dx \right) ^{1/2}\\ {}&\le 2 (2\pi )^{3/2}m^{1/4} \ell \Vert v_q\Vert _{C_{t,x}^1} \Vert v_q\Vert _{C_tL^2}. \end{aligned}$$

Thence,

$$\begin{aligned} \text {V}\le 6 (2\pi )^{3/2} m^{1/4}\ell ^\iota \Vert v_q\Vert _{C_{t,x}^1} \Vert v_q\Vert _{C_tL^2}. \end{aligned}$$

Plugging the above bounds into (3.47) and taking (3.3b), (3.3a), (3.4) and (3.1a) into account lead to

$$\begin{aligned} \Vert R_{\text{ com }}\Vert _{C_tL^1}&\le (2\pi )^{3/2}m^{1/4} \ell ^\iota \left( \frac{3}{2}\Vert v_{q+1}\Vert _{C_{t,x}^1} \Vert v_{q+1}\Vert _{C_tL^2}+\frac{19}{2}\Vert v_q\Vert _{C_{t,x}^1} \Vert v_q\Vert _{C_tL^2} \right) \\ {}&\le 33 (2\pi )^{3/2}M_0 m^{9/4} \bar{e} \lambda _{q+1}^{-\alpha \iota }. \end{aligned}$$

Finally, combining $33 (2\pi )^{3/2}M_0 m^{9/4} \bar{e} \lambda _{q+1}^{-\frac{\alpha \iota }{2}} \le \frac{1}{1500 m^{1/2}}$ with $\alpha \iota >4\beta b^2$, $e(t)\ge \underline{e}>4$ and $\Theta ^{-2}\ge m^{-1/2}$ permits to achieve

$$\begin{aligned} \Vert R_{\text {com}}\Vert _{C_tL^1} \le \frac{1}{1500m^{1/2}} \lambda _{q+1}^{-2\beta b^2} \le \frac{1}{6000} \delta _{q+3} \Theta ^{-2}(t)e(t). \end{aligned}$$

So altogether this proves (3.3c) at level $q+1$.

3.7.4 Convergence of the sequence

Furthermore, note that it follows instantly from (3.3c) that $\big (\mathring{R}_q \big )_{q \in \mathbb {N}_0}$ is a zero sequence in $C\left( (-\infty ,\tau ]; L^1\left( \mathbb {T}^3\right) \right)$.

3.8 Adapted and deterministic

3.8.1 Adaptedness of the iterates

Now, we aim at proving the adaptedness of the next iteration step $(v_{q+1},\mathring{R}_{q+1})$. As already mentioned in Sect. 3.3.1, we emphasize again that the mollified velocity field $v_\ell$ as well as $\mathring{R}_\ell$ and $\Theta _\ell$ remains $\left( \mathcal {F}_t\right) _{t\in (-\infty , \tau ]}$-adapted. Since the energy e is deterministic, the adaptedness of $\eta _\ell$ follows in the same way as for $v_\ell$.

These facts in turn yield the adaptedness of $\rho$ and thus also of the amplitude functions $a_{(\xi )}$ as composition of them.

Furthermore, note that the building blocks $\phi ,\, \Phi$ and $\psi$ of the intermittent jets do not depend on $\omega$, so consequently $V_{(\xi )},\, W^{(c)}_{(\xi )}$ and the intermittent jets themselves are deterministic as well. Taking additionally into account that any partial derivative of $a_{(\xi )}$ in space remains $\left( \mathcal {F}_t\right) _{t \in (-\infty , \tau ]}$-adapted, establishes the adaptedness of $w_{q+1}^{(p)}$ and $w_{q+1}^{(c)}$. Moreover, the Leray projection $\mathbb {P}$ and obviously also the projection $\mathbb {P}_{\ne 0}$ onto functions with zero mean preserve adaptedness, which confirms the adaptedness of the temporal corrector $w_{q+1}^{(t)}$.

To summarize our above considerations, we have proven that $v_\ell$ and the total perturbation $w_{q+1}=w_{q+1}^{(p)}+w_{q+1}^{(c)}+w_{q+1}^{(t)}$ are, at any time $t \in (-\infty , \tau ]$, $\mathcal {F}_t$-measurable, which finally verifies the adaptedness of $v_{q+1}=v_\ell +w_{q+1}$ and $\mathring{R}_{q+1}$.

3.8.2 Deterministic initial values

We will use an induction argument to verify that the constructed sequence $\big (v_q(t,x),\mathring{R}_q(t,x)\big )_{q\in \mathbb {N}_0}$ is deterministic for each $t\le 0$ and $x \in \mathbb {T}^3$.

Obviously, the starting point $\big (v_0,\mathring{R}_0 \big )=(0,0)$ does not depend on $\omega$ at any time.

So assuming $v_q(t,x)$ for all $t\le 0$ and $x \in \mathbb {T}^3$ to be deterministic, it can be easily seen that

$$\begin{aligned} v_\ell (t,x,\omega )=\int _0^\ell \int _{|y|\le \ell }v_q(t-s,x-y,\omega )\varphi _\ell (s) \phi _\ell (y)\,dy \,ds, \end{aligned}$$

$\mathring{R}_\ell (t,x)$ and $\Theta _\ell (t)$ are deterministic as well. Combined with the fact, that $\eta _q(t,\cdot )$ is deterministic, $\rho (t,\cdot )$ and hence $a_{(\xi )}(t,\cdot )$ does not depend on $\omega$ either. Based on this, we are able to conclude that each part of the total perturbation $w_{q+1}(t,\cdot )$ is deterministic, that is to say $w_{q+1}^{(p)},\, w_{q+1}^{(c)}$ and $w_{q+1}^{(t)}$ do not depend on $\omega$ at each time up to time 0. The functions $\phi ,\,\Phi$ and $\psi$ and hence the intermittent jets $W_{(\xi )}$ as well as its incompressibility corrector $W^{(c)}_{(\xi )}$ and $V_{(\xi )}$ are by definition deterministic.

On the one hand, this together with the independence of $v_\ell (t,\cdot )$ of $\omega$ results in the deterministic behavior of $v_{q+1}$ at time $t\le 0$. On the other hand, it also follows that $\mathring{R}_\text {lin}(t,\cdot )$, $\mathring{R}_\text {cor}(t,\cdot )$, $\mathring{R}_\text {osc}(t,\cdot )$, $\mathring{R}_\text {com}(t,\cdot )$ and thereby $\mathring{R}_{q+1}(t,\cdot )$ are deterministic as well, yielding the assertion.

4 End of the proof of Theorem 1.1

Summarizing our previous results, we formulate the following Proposition.

Proposition 4.1

(Main iteration) For an $(\mathcal {F}_t)_{t\in (-\infty ,\tau ]}$-adapted solution $\big (v_q,\mathring{R}_q\big )$ to (3.2) on $(-\infty ,\tau ]\times \mathbb {T}^3\times \Omega$, which admits the bounds in (3.3) and (3.5) for some $q\in \mathbb {N}_0$, an $\left( \mathcal {F}_t\right) _{t \in (-\infty ,\tau ]}$-adapted process $\big (v_{q+1},\mathring{R}_{q+1}\big )$ can be constructed, so that this pair also solves (3.2) on $(-\infty ,\tau ]\times \mathbb {T}^3\times \Omega$ and obeys (3.3) and (3.5) at level $q+1$. Moreover, the sequences $\left( v_q\right) _{q\in \mathbb {N}_0}$ and $\big (\mathring{R}_q\big )_{q\in \mathbb {N}_0}$ are Cauchy in $C\left( (-\infty ,\tau ];L^2\left( \mathbb {T}^3 \right) \right)$ and $C\left( (-\infty ,\tau ];L^1\left( \mathbb {T}^3 \right) \right)$, respectively; more precisely, $\big (\mathring{R}_q\big )_{q\in \mathbb {N}_0}$ converges to zero and (3.42) holds.

Additionally, $v_q(t,x)$ and $\mathring{R}_q(t,x)$ are deterministic for all $t\le 0,\, x \in \mathbb {T}^3$ and $q\in \mathbb {N}_0$.

Now, we have everything in hand to finish the proof of 1.2.

Proof of Theorem 1.2

Existence:

According to Proposition 4.1, there exists a sequence $\big (v_q,\mathring{R}_q \big )_{q\in \mathbb {N}_0}$, so that $\big (v_q(t),$$\mathring{R}_q(t) \big )$ is for every $q\in \mathbb {N}_0$ and $t\le 0$ deterministic and so that $\big (v_q, \mathring{R}_q \big )$ solves (3.2) on $(-\infty ,\tau ]\times \mathbb {T}^3\times \Omega$ in the weak sense. That means for any divergence-free test function $\varphi \in C^\infty \left( \mathbb {T}^3;\mathbb { R}^3\right)$ the pair $\big (v_q,\mathring{R}_q \big )$ satisfies

$$\begin{aligned}&\underbrace{\int _{\mathbb {T}^3}\Big (v_q(t,x)-v_q(0,x)\Big )\cdot \varphi (x) \,dx}_{=:\text{ I }}+\frac{1}{2}\underbrace{\int _0^t\int _{\mathbb {T}^3}v_q(s,x)\cdot \varphi (x)\,dx\,ds}_{=:\text{ II }}\nonumber \\ {}&\quad -\underbrace{\int _0^t \int _{\mathbb {T}^3} v_q(s,x)\cdot \Delta \varphi (x)\,dx\,ds}_{=:\text{ III }}\nonumber \\ {}&\quad +\underbrace{\int _0^t\Theta (s)\!\int _{\mathbb { T}^3}(v_q \!\otimes \! v_q)(s,x):\nabla \! \varphi ^T(x)\,dx ds}_{=: \text{ IV }}\!+\!\underbrace{\int _0^t\!\int _{\mathbb {T}^3} p_q(s,x)\!\cdot \! {{\text {div}}}(\varphi (x))\, dx \,ds}_{=:\text{ V }}\nonumber \\&=\underbrace{\int _0^t \int _{\mathbb {T}^3} \mathring{R}_q(s,x): \nabla \varphi ^T(x) \,dx \,ds}_{=:\text{ VI }} \end{aligned}$$

(4.1)

in particular for every $t\in [0,\tau ]$, where the fifth term vanishes due to the fact that we work with solenoidal test functions.

Moreover, the sequence can be chosen in such a way that $\big (\mathring{R}_q\big )_{q \in \mathbb {N}_0}$ converges to zero in $C\left( (-\infty ,\tau ];L^1\left( \mathbb {T}^3\right) \right)$ and such that $(v_q)_{q\in \mathbb {N}_0}$ is Cauchy in the Banach space $C\left( (-\infty ,\tau ];L^2\left( \mathbb {T}^3\right) \right)$. Integration by parts and Cauchy–Schwarz’s inequality permits therefore to deduce

$$\begin{aligned} \bigg |\int _0^t \!\!\int _{\mathbb {T}^3} \mathring{R}_q(s,x): \nabla \varphi ^T(x) dx ds \bigg |&\le \!\! \int _0^t\int _{\mathbb {T}^3}\! \left( \sum _{i,j=1}^3\big | \!\big (\mathring{R}_q(s,x) \big )_{i,j} \big |^2\right) ^{1/2} \!\!\left( \sum _{i,j=1}^3 \big |\partial _{ x_j} \varphi _i(x)\big |^2\right) ^{1/2} dx ds \\ {}&\le \sqrt{3}\int _0^t\int _{\mathbb {T}^3} \Vert \mathring{R}_q(s,x)\Vert _F\Vert \varphi \Vert _{C^1} \,dx \,ds\\ {}&\le \sqrt{3} \Vert \varphi \Vert _{C^1} \Vert \mathring{R}_q\Vert _{C_tL^1} \underbrace{\int _0^t\,ds}_{\le \tau \le 1} \overset{q \rightarrow \infty }{\longrightarrow }\ 0. \end{aligned}$$

Furthermore, we may assume the existence of a limit $\lim \limits _{q \rightarrow \infty }v_q=:v \in C\left( (-\infty ,\tau ];L^2\right.$$\left. \left( \mathbb {T}^3\right) \right)$, which causes that each term on the left-hand side of (4.1) will converge for $q \rightarrow \infty$ $\mathcal {P}$-a.s.. In fact integrating by parts again and Cauchy–Schwartz’s inequality furnish

$$\begin{aligned}&\bigg |\int _{\mathbb {T}^3}\big [ v_q(t,x)-v_q(0,x)\big ] \cdot \varphi (x) \,dx-\int _{\mathbb {T}^3}\big [v(t,x)-v(0,x)\big ]\cdot \varphi (x) \,dx \bigg |\\ {}&\quad \le (2\pi )^{3/2} \Vert \varphi \Vert _C\Big [\Vert v_q(t)-v(t)\Vert _{L^2} +\Vert v_q(0)-v(0)\Vert _{L^2}\Big ]\overset{q \rightarrow \infty }{\longrightarrow }\ 0, \end{aligned}$$

$$\begin{aligned}&\bigg |\int _0^t\int _{\mathbb {T}^3}v_q(s,x)\cdot \varphi (x)\,dx\,ds-\int _0^t\int _{\mathbb {T}^3}v(s,x)\cdot \varphi (x)\,dx\,ds\bigg |\\ {}&\quad \le (2\pi )^{3/2} \Vert \varphi \Vert _C\Vert v_q -v\Vert _{C_tL^2}\overset{q \rightarrow \infty }{\longrightarrow }\ 0, \end{aligned}$$

$$\begin{aligned}&\bigg |\int _0^t \int _{\mathbb {T}^3} v_q(s,x)\cdot \Delta \varphi (x)\,dx\,ds-\int _0^t \int _{\mathbb {T}^3} v(s,x)\cdot \Delta \varphi (x)\,dx\,ds \bigg |\\ {}&\quad \le (2\pi )^{3/2} \Vert \varphi \Vert _{C^2}\Vert v_q-v\Vert _{C_tL^2}\overset{q \rightarrow \infty }{\longrightarrow }\ 0 \end{aligned}$$

and by virtue of Cauchy–Schwartz’s inequality and (3.44) also

$$\begin{aligned}&\bigg |\int _0^t \Theta (s)\int _{\mathbb { T}^3}(v_q \otimes v_q)(s,x):\nabla \varphi ^T(x)\,dx \,ds\\ {}&-\int _0^t \Theta (s)\int _{\mathbb { T}^3}(v \otimes v)(s,x):\nabla \varphi ^T(x)dx ds\bigg |\\ {}&\le m^{1/4} \int _0^t \int _{\mathbb {T}^3} \left( \sum _{i,j=1}^3 \big |(v_q \otimes v_q{-}v\otimes v)_{ij}(s,x)\big |^2\right) ^{1/2}\!\! \left( \sum _{i,j=1}^3 \big |\partial _{x_j} \varphi _i(x)\big |^2\right) ^{1/2}\!\! dx ds \\ {}&\le \sqrt{3}m^{1/4} \Vert \varphi \Vert _{C^1} \underbrace{\int _0^t\,ds}_{\le \tau \le 1} \sup _{s \in [0,t]} \int _{\mathbb {T}^3} \Vert v_q \otimes (v_q-v)-(v-v_q)\otimes v\Vert _F(s,x)dx \\ {}&\le \sqrt{3}m^{1/4} \Vert \varphi \Vert _{C^1} \sup _{s \in [0,t]} \int _{\mathbb {T}^3} |v_q (s,x)|\, |v_q(s,x)-v(s,x)|\,dx\\ {}&+\sqrt{3}m^{1/4} \Vert \varphi \Vert _{C^1}\sup _{s \in [0,t]} \int _{\mathbb {T}^3}|v(s,x)-v_q(s,x)| \, | v(s,x)|\,dx \\ {}&\le \sqrt{3}m^{1/4} \Vert \varphi \Vert _{C^1} \Big ( \Vert v_q\Vert _{C_tL^2} \Vert v_q-v\Vert _{C_tL^2}+ \Vert v_q-v\Vert _{C_tL^2}\Vert v\Vert _{C_tL^2}\Big )\overset{q \rightarrow \infty }{\longrightarrow }\ 0. \end{aligned}$$

So passing to the limit on both sides of (4.1) shows that v is an analytically weak solution to (1.2) with deterministic initial condition. Therefore, $u:=e^Bv$ solves (1.1) on $[0,\tau ]$ in the probabilistically strong and analytically weak sense, of course also with a deterministic initial condition $u_0$.

Regularity:

It remains to verify that the convergence of $(v_q)_{q\in \mathbb {N}_0}$ to v even takes place in $C\left( (-\infty ,\tau ];H^\gamma \left( \mathbb {T}^3\right) \right)$. For this end, we combine Hölder’s inequality with exponents $\frac{1}{\gamma }$ and $\frac{1}{1-\gamma }$ with Plancherel’s theorem to accomplish

$$\begin{aligned} \sum _{q\ge 0}\Vert v_{q+1}(t)-v_q(t)\Vert _{H^\gamma }&=\sum _{q \ge 0} \big \Vert \mathcal {F}^{-1}\big [(1+|\cdot |^2)^{\gamma /2} \mathcal {F}(v_{q+1}(t)-v_q(t))\big ] \big \Vert _{L^2}\\ {}&\overset{\text{ Plancherel }}{=}\sum _{q \ge 0} \big \Vert (1+|\cdot |^2)^{\gamma /2} \mathcal {F}(v_{q+1}(t)-v_q(t)) \big \Vert _{\ell ^2(\mathbb {Z}^3)}\\ {}&=\sum _{q \ge 0} \big \Vert (1+|\cdot |^2)^{\gamma } \big [\mathcal {F}(v_{q+1}(t)-v_q(t))\big ]^2 \big \Vert ^{1/2}_{\ell ^1(\mathbb {Z}^3)}\\ {}&=\!\sum _{q \ge 0} \big \Vert (1{+}|\cdot |^2)^{\gamma }\! \big [\mathcal {F}(v_{q{+}1}(t){-}v_q(t))\big ]^{2\gamma } \big [\mathcal {F}(v_{q{+}1}(t){-}v_q(t))\big ]^{2(1{-}\gamma )} \big \Vert ^{1/2}_{\ell ^1(\mathbb {Z}^3)}\\ {}&\overset{\text{ H }\ddot{o}\text{ lder }}{\le } \sum _{q \ge 0} \big \Vert (1{+}|\cdot |^2)\big [ \mathcal {F}(v_{q{+}1}(t){-}v_q(t))\big ]^2 \big \Vert _{\ell ^1(\mathbb {Z}^3)}^{\gamma /2} \big \Vert \big [\mathcal {F}(v_{q{+}1}(t){-}v_q(t))\big ]^2\big \Vert _{\ell ^1(\mathbb {Z}^3)}^{(1{-}\gamma )/2}\\ {}&\overset{\text{ Plancherel }}{=} \sum _{q\ge 0} \Vert v_{q+1}(t)-v_q(t)\Vert _{H^1}^\gamma \Vert v_{q+1}(t)-v_q(t)\Vert ^{1-\gamma }_{L^2}\\ {}&\lesssim \sum _{q\ge 0} \Vert v_{q+1}-v_q\Vert _{C_{t,x}^1}^\gamma \Vert v_{q+1}-v_q\Vert ^{1-\gamma }_{C_tL^2}. \end{aligned}$$

for any $t \in (-\infty ,\tau ]$. Invoking (3.3b) and (3.42) then yields

$$\begin{aligned} \sum _{q\ge 0}\Vert v_{q+1}(t)\!-\!v_q(t)\Vert _{H^\gamma }\!\lesssim 2^\gamma \!\bigg (M_0\!+\!(2\pi )^{3/2} \bigg )^{1-\gamma }\!\!m\bar{e}^{1/2}\lambda _1^{\beta (1-\gamma )}\!\sum _{q\ge 0} a^{\big [5\gamma \!-\beta (1-\gamma )\big ]b^{q+1}}\!. \end{aligned}$$

So if we impose $\gamma \in \Big (0, \frac{\beta }{5+\beta } \Big )$, the above series will converge as it can be bounded by a geometric series. Thus, the sequence $\left( \sum \limits _{q\ge 0}^n \Vert v_{q+1}-v_q\Vert _{C_tH^\gamma }\right) _{n\in \mathbb {N}_0}$ is as a convergent sequence particularly Cauchy in $\mathbb {R}$, which means that for all $\varepsilon >0$ there exists some $N\in \mathbb {N}_0$ so that

$$\begin{aligned} \Vert v_n-v_k\Vert _{C_tH^\gamma }\le \sum _{q=k}^{n-1} \Vert v_{q+1}-v_q\Vert _{C_tH^\gamma } \le \varepsilon \end{aligned}$$

holds for every $n\ge k\ge N$. In other words, $\left( v_q\right) _{q \in \mathbb {N}_0}$ is also a Cauchy sequence in the Banach space $C\left( (-\infty ,\tau ];H^\gamma \left( \mathbb {T}^3\right) \right)$ for $\gamma \in \Big (0, \frac{\beta }{5+\beta } \Big )$, furnishing the existence of the limit in $C\left( (-\infty ,\tau ];H^\gamma \left( \mathbb {T}^3\right) \right)$, which equals, by virtue of the uniqueness of the limit, v.

Bounded:

Furthermore, it follows

$$\begin{aligned} \Vert v(t,\omega )\Vert _{H^\gamma }&\le \Vert v(t,\omega )-v_{q+1}(t,\omega )\Vert _{H^\gamma }+ \sum _{k=0}^q\Vert v_{k+1}(t,\omega )-v_k(t,\omega )\Vert _{H^\gamma }\\&\lesssim \varepsilon + 2^\gamma \bigg (M_0+(2\pi )^{3/2} \bigg )^{1-\gamma }m\bar{e}^{1/2}\lambda _1^{\beta (1-\gamma )} \left( 1-a^{\big [5\gamma -\beta (1-\gamma )\big ]b}\right) ^{-1} \end{aligned}$$

for any $\varepsilon >0$, sufficiently large $q\ge 0$ and every $t \in [0,\tau ]$ and $\omega \in \Omega$. Note that the constant on the right-hand side neither depends on t nor on $\omega$.

Kinetic Energy:

Moreover, remembering that $\left( v_q\right) _{q \in \mathbb {N}_0}$ is a Cauchy sequence in $C\big ( (-\infty ,\tau ];$$L^2\left( \mathbb {T}^3\right) \big )$, we may deduce

$$\begin{aligned} \Vert u(t)\Vert _{L^2}^2=e(t) \end{aligned}$$

from (3.5).

Consistency:

Let $e_1$ and $e_2$ be two energies in $C_b^1\left( (-\infty ,1];[\underline{e},\infty ) \right)$ respecting

$$\begin{aligned} \Vert e_i\Vert _{C}\le \bar{e}, \qquad \Big \Vert \frac{d}{dt} e_i\Big \Vert _{C}\le \widetilde{e} \end{aligned}$$

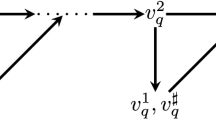
and $e_i(t)=e_i(0)$ for every $t\le 0$ and $i=1,2$, which coincide on [0, t] for some $t \in [0,1]$ and let $\left( v^1_q\right) _{q \in \mathbb {N}_0}$, $\left( v^2_q\right) _{q \in \mathbb {N}_0}$ be the corresponding sequences, constructed in Proposition 4.1. Then for each $q \in \mathbb {N}_0$ and $i=1,2$, $v^i_{q+1}$ consists of the previous, mollified iteration $v_\ell ^i:=v_q^i*_t\varphi _\ell *_x \phi _\ell$ and the perturbation $w_{q+1}^i$. If we decompose the perturbations $w_{q+1}^1$ and $w_{q+1}^2$ in a way that is presented in Fig. 1, one can see that they coincide on $(-\infty ,t \wedge \tau ]$, if $\mathring{R}_\ell ^1$ and $\mathring{R}_\ell ^2$ and also $\eta _\ell ^1$ and $\eta _\ell ^2$ do. The functions $\phi ,\, \Phi$ and $\psi$ can be chosen for both sequences in the same way.

Taking into account that $e_1=e_2$ on $(-\infty ,t]$ together with $v_q^1=v_q^2$ on $(-\infty ,t \wedge \tau ]$ implies $\eta _q^1=\eta _q^2$ on $(-\infty ,t \wedge \tau ]$, it indeed holds

$$\begin{aligned} \eta _\ell ^1(s,x,\omega )=\int _{|y|\le \ell }\int _{0}^{\ell } \eta _q^1(s-u,x-y,\omega )\varphi _\ell (u)\phi _\ell (y)\, du\, dy =\eta _\ell ^2(s,x,\omega ) \end{aligned}$$

for all $s\in (-\infty , t\wedge \tau ]$, $x \in \mathbb {T}^3$ and $\omega \in \Omega$.

Fig. 1

Implication scheme of the adaptedness of each process up to the desired iteration step $v_{q+1}$

In the same manner, we deduce $v_\ell ^1(s)=v_\ell ^2(s)$ and $\mathring{R}_\ell ^1(s)=\mathring{R}_\ell ^2(s)$, furnishing $v_{q+1}^1(s)=v_{q+1}^2(s)$ and thus also $\mathring{R}_{q+1}^1(s)=\mathring{R}_{q+1}^2(s)$ at any time $s\in (-\infty , t\wedge \tau ]$. That means by induction we have ascertained that the sequences $\left( v^1_q\right) _{q \in \mathbb {N}_0}$ and $\left( v^2_q\right) _{q \in \mathbb {N}_0}$ are the same on $(-\infty , t\wedge \tau ]$; hence so are their limits

$$\begin{aligned} v^1:=\lim _{q\rightarrow \infty }v_q^1=\lim _{q\rightarrow \infty }v_q^2=:v^2. \end{aligned}$$

As a consequence, the solutions $u_1:=e^Bv^1$ and $u_2:=e^Bv^2$ to (1.1) on $[0,\tau ]$, associated with the energies $e_1$ and $e_2$, respectively, coincide on $[0, t\wedge \tau ]$, completing the proof of 1.2. $\square$

Appendix

Lemma A.1

For $d\ge 3$ and a finite set of directions $\Lambda \subseteq \mathbb {R}^d$, there exists some $(\alpha _\xi )_{\xi \in \Lambda }$ and $\rho >0$ such that the periodic tubes

$$\begin{aligned} \left( B_\rho (0)+\alpha _\xi +\{s \xi \}_{s\in \mathbb {R}}+2\pi \mathbb {Z}^d\right) _{\xi \in \Lambda } \end{aligned}$$

are mutually disjoint.

Proof

See [7], p. 9, Lemma 3. $\square$

Lemma A.2

Take $p \in \{1,2\}$ and let g be a $\left( \frac{\mathbb {T}}{\kappa }\right) ^3$-periodic function with $\kappa \in \mathbb {N}$ and f be a $\mathbb {T}^3$-periodic function, satisfying

$$\begin{aligned} \sum _{|\alpha |\le n}\Vert D^\alpha f\Vert _{L^p} \le C_f \zeta ^{n} \end{aligned}$$

for some constants $C_f>0,\, \zeta \ge 1$ and every $0\le n\le N+4$ with $N\in \mathbb {N}$. Then, it holds

$$\begin{aligned} \Vert fg\Vert _{L^p}\lesssim C_f \Vert g\Vert _{L^p}, \end{aligned}$$

provided

$$\begin{aligned} 3\, \frac{2\pi }{\kappa }\zeta \le \frac{1}{41} \quad \text {and} \quad 16\exp (12)\zeta ^4 \left( 3\, \frac{2\pi }{\kappa }2\exp (3)\zeta \right) ^N \le 1. \end{aligned}$$

Proof

See [6], p. 12, Lemma 3.7. $\square$

Lemma A.3

Assume $1\le \zeta <\kappa$ to be parameters, satisfying $\kappa ^{3-N}\zeta ^N\le 1$ for some nonnegative integer $N \ge 2$, let $f\in L^p\left( \mathbb {T}^3 \right)$ with $p \in (1,2]$ and let $a \in C^N\left( \mathbb {T}^3\right)$ be a function which obeys

$$\begin{aligned} \sum _{|\alpha |= n}\Vert D^\alpha a\Vert _{L^\infty } \le C_a\zeta ^{n} \end{aligned}$$

for some constant $C_a>0$ and $n \in \{0,N\}$. It then holds that

$$\begin{aligned} \Vert \, \mathcal {R}\mathbb {P}_{\ne 0}(a \mathbb {P}_{\ge \kappa }f)\Vert _{L^p}\lesssim C_a\frac{\Vert f\Vert _{L^p}}{\kappa }, \end{aligned}$$

where the implicit constant depends on p and N.

Proof

See [6], p. 32, Lemma B.1. $\square$