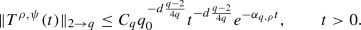On vector-valued Schrödinger operators with unbounded diffusion in $L^p$ spaces

Abstract

We prove generation results of analytic strongly continuous semigroups on $L^p({{\mathbb {R}}}^d,{{\mathbb {R}}}^m)$ ($1<p<\infty$) for a class of vector-valued Schrödinger operators with unbounded coefficients. We also prove Gaussian type estimates for such semigroups.

1 Introduction

Systems of elliptic and parabolic equations with (possibly) unbounded coefficients arise quite naturally in the study of mathematical models which describe physical phenomena such as Navier Stokes equations (see e.g. [17, 19, 20]). Differently from the scalar case, where the theory of elliptic and parabolic operators with unbounded coefficients is widely studied (see [24] and the reference therein), the interest on the vector-valued case is quite recent as the quoted references show.

In this paper, we consider realizations in $L^p$-spaces of Schrödinger type vector-valued elliptic operators defined on smooth functions ${\varvec{u}}:{\mathbb {R}}^d\rightarrow {\mathbb {R}}^m$, ($d,m \in {{\mathbb {N}}}$), by $\varvec{{\mathcal {A}}}{\varvec{u}}= \mathrm{div}(Q\nabla {\varvec{u}})-V{\varvec{u}}=:\varvec{{\mathcal {A}}}_0 {\varvec{u}}-V{\varvec{u}}$, where the diffusion matrix Q(x) is positive definite at each $x\in {\mathbb {R}}^d$ and V is a measurable matrix-valued function. The first problem is to find conditions on Q and V and identify a realization of the operator $\varvec{{\mathcal {A}}}$ in $L^p({\mathbb {R}}^d, {\mathbb {R}}^m)$ which generates a strongly continuous semigroup $({\varvec{T}}_p(t))_{t\ge 0}$; afterwards one is interested in regularity properties of the semigroup, such as analyticity, ultracontractivity and kernel estimates.

This type of operators have been recently studied in different settings. For an analysis in the space of bounded and continuous functions we refer the reader to the papers [1, 4, 12]. Also the $L^p$-context has been investigated. As shown by the scalar case, the $L^p$-spaces related to the invariant measure represent the most suitable $L^p$-spaces where to set problems associated with elliptic operators with unbounded coefficients, but, in the vector-valued case, only partial results in this direction are available so far (see [2, 3]). Nevertheless, the classical $L^p$-context is important in view of the applications. A perturbation method, due to Monniaux and Prüss, see [29], has been applied in the seminal paper [18], where generation results in $L^p({\mathbb {R}}^d;{\mathbb {R}}^m)$ are proved for a class of nondegenerate weakly coupled elliptic operators containing also a first-order diagonal term, and more recently in [22], where a class of vector-valued Schrödinger-type operators is considered, when the matrix-valued function Q is bounded and can degenerate neither at some $x\in {\mathbb {R}}^d$ nor at infinity, while the potential V is quasi accretive and locally Lipschitz continuous on ${\mathbb {R}}^d$, and $|D_j V(-V)^{-\alpha }|\in L^\infty ({\mathbb {R}}^d)$ for some $\alpha \in [0,1/2)$. In this case the domain of the $L^p$-realization of $\varvec{{\mathcal {A}}}$ is the intersection of the domains of the diffusion and the potential part of the operator. By perturbing V with a scalar potential $v \in W^{1,\infty }_\mathrm{loc}({\mathbb {R}}^d)$ satisfying the condition $|\nabla v|\le cv$ on ${\mathbb {R}}^d$ for some positive constant c (in the $L^2$-setting, actually even with more general matrix-valued perturbation), a larger class of potentials has been considered in [5, 25], by using perturbation results due to N. Okazawa [30]. In [23], assuming again strict ellipticity and boundedness for the diffusion coefficients, pointwise accretivity and local boundedness of the potential term, the authors prove that $\varvec{{\mathcal {A}}}$, endowed with its maximal domain, generates a strongly continuous semigroup in $L^p({\mathbb {R}}^d;{\mathbb {C}}^m)$.

A different approach has been adopted in [7] to deal with a class of vector-valued nondegenerate elliptic operators, coupled up to the first order. More precisely, using the semigroup, obtained in [1] in the space $C_b({\mathbb {R}}^d;{\mathbb {R}}^m)$, the authors of [7] provide sufficient conditions which allow to extend this semigroup to the $L^p$ scale. It is worth mentioning that this approach does not provide any sharp description of the domain of the generator of the semigroup.

A class of vector-valued elliptic operators $\varvec{{\mathcal {L}}}$, including also a first-order coupling term, has been considered very recently in [6]. This class contains the operator $\varvec{{\mathcal {A}}}$, but the presence of the drift term causes technical problems which prevent us from both analyzing the $L^1$-setting and proving an integral representation of the semigroup $({\varvec{T}}_p(t))_{t\ge 0}$ associated with the operator $\varvec{{\mathcal {L}}}$ in $L^p({\mathbb {R}}^d;{\mathbb {C}}^m)$. For this reason, it is of interest to consider the operator $\varvec{{\mathcal {A}}}$ on its own. We introduce assumptions on its coefficients that can be made independent of $p\in [1,\infty )$ and, as a consequence, allow to prove summability improving properties as ultracontractivity and the integral representation of the associated semigroup $({\varvec{T}}(t))_{t\ge 0}$ in terms of a kernel K. A domination with a scalar semigroup associated to a suitable form, allows us also to deduce some Gaussian type estimates satisfied by the kernel K, which are expressed in terms of a distance associated with the diffusion coefficients. To our knowledge, this result seems to be new and of interest even in the scalar case.

Notation. Throughout the paper ${\mathbb {K}}={\mathbb {R}}$ or ${\mathbb {K}}={\mathbb {C}}$. The Euclidean inner product in ${\mathbb {K}}^m$ and the associated norm are denoted by $\langle \cdot ,\cdot \rangle$ and $|\cdot |$ respectively. Given a function ${\varvec{u}}: \varOmega \subseteq {\mathbb {R}}^d\rightarrow {{\mathbb {K}}}^m$, we denote by $u_k$ its k-th component and we set $\mathrm{sign}({\varvec{u}})=|{\varvec{u}}|^{-1}{\varvec{u}}\chi _{\{{\varvec{u}}\not =0\}}$. For each $1\le p<\infty$, $L^p({\mathbb {R}}^d, {\mathbb {K}}^m)$ denotes the classical vector-valued Lebesgue space endowed with the norm $\Vert {\varvec{f}}\Vert _p=(\int _{{\mathbb {R}}^d} |{\varvec{f}}(x)|^p\mathrm{d}x)^{1/p}$. The pairing between $L^p({\mathbb {R}}^d, {\mathbb {K}}^m)$ and $L^{p'}({\mathbb {R}}^d, {\mathbb {K}}^m)$ , where $p'$ is the conjugate index of p, is defined by $\langle {\varvec{u}}, {\varvec{v}}\rangle _{p,p'}=\int _{{\mathbb {R}}^d} \langle {\varvec{u}}(x), {\varvec{v}}(x)\rangle \mathrm{d}x$ for every ${\varvec{u}}\in L^p({\mathbb {R}}^d, {\mathbb {K}}^m)$ and ${\varvec{v}}\in L^{p'}({\mathbb {R}}^d, \mathbb K^m)$. If $k\in {\mathbb {N}}$, $W^{k,p}({\mathbb {R}}^d, {\mathbb {K}}^m)$ is the classical vector-valued Sobolev space, namely the space of all functions ${\varvec{u}}\in L^p({\mathbb {R}}^d, {\mathbb {K}}^m)$ whose components have distributional derivatives up to the order k belonging to $L^p({{\mathbb {R}}}^d, {\mathbb {K}})$. The norm of $W^{k,p}({\mathbb {R}}^d, {\mathbb {K}}^m)$ will be denoted by $\Vert \cdot \Vert _{k,p}$. The spaces $W^{k,p}_{\mathrm{loc}}({\mathbb {R}}^d, {\mathbb {K}}^m)$ are defined analogously. $C({\mathbb {R}}^d,\mathbb K^m)$ stands for the space of functions ${\varvec{u}}:{\mathbb {R}}^d\rightarrow \mathbb K^m$ whose components belong to $C({\mathbb {R}}^d,{\mathbb {K}})$. A similar notation is used for the subspaces of $C({\mathbb {R}}^d,{\mathbb {K}}^m)$. The subscript “b“ (resp. “c”) stands for “bounded” (resp. “compactly supported”). When $m=1$ and ${\mathbb {K}}={\mathbb {R}}$, we simply write $C^k({\mathbb {R}}^d)$, $L^p({\mathbb {R}}^d)$ and $W^{1,2}({\mathbb {R}}^d)$ instead of $C^k({\mathbb {R}}^d;{\mathbb {R}})$, $L^p({\mathbb {R}}^d;{{\mathbb {R}}})$ and $W^{1,2}({\mathbb {R}}^d;{{\mathbb {R}}})$. Finally, by B(r) we denote the ball of ${\mathbb {R}}^d$ centered at 0 and with radius r.

2 Generation results

We are going to consider the elliptic operator $\varvec{{\mathcal {A}}}$ acting on vector-valued smooth functions ${\varvec{u}}$ as follows:

$$\begin{aligned} \varvec{{\mathcal {A}}}{\varvec{u}}&= \mathrm{div}(Q \nabla {\varvec{u}}) - V{\varvec{u}}=: \varvec{{\mathcal {A}}}_0{\varvec{u}}- V{\varvec{u}} \end{aligned}$$

(1)

where the coefficients $Q=(q_{ij})_{1\le i,j\le d}$ and $V=(v_{hk})_{1\le h,k\le m}$ satisfy the following assumptions:

Hypotheses 1

• (i) $q_{ij}=q_{ji}\in C^1 ({\mathbb {R}}^d)$ for each $i,j=1, \ldots , d$ and $\langle Q(x)\xi , \xi \rangle$ is positive for every $x\in {\mathbb {R}}^d$ and $0\ne \xi \in {\mathbb {R}}^d$;

• (ii) $v_{hk}:{\mathbb {R}}^d\rightarrow {{\mathbb {R}}}$ are measurable functions for every $h,k=1,\ldots ,m$;

• (iii) there exist a function $v\in C^1({\mathbb {R}}^d)$, with positive infimum $v_0$, and positive constants $c_1, \gamma$ and $C_\gamma$ such that

  $$\begin{aligned}&\text{(a) } \langle V(x)\xi , \xi \rangle \ge v(x)|\xi |^2, \qquad |V(x)\xi | \le c_1 v(x)|\xi |, \qquad \;\, x\in {\mathbb {R}}^d, \xi \in {\mathbb {R}}^m,\\&\text{(b) } \langle Q(x)\nabla v(x), \nabla v(x)\rangle ^{\frac{1}{2}} \le \gamma v(x)^{3/2}+ C_\gamma , \qquad \;\, x\in {\mathbb {R}}^d; \end{aligned}$$

• (iv) there exists a positive function $\psi \in C^1({\mathbb {R}}^d)$ such that $\lim _{|x|\rightarrow \infty }\psi (x)=\infty$ and $\displaystyle \frac{\langle Q\nabla \psi , \nabla \psi \rangle }{(\psi \log \psi )^2}\in L^\infty ({\mathbb {R}}^d)$.

Hypothesis 1(iii) goes back to the papers [8, 9], where the domain of the realization in $L^2({\mathbb {R}}^d)$ of the scalar Schrödinger operator $-\varDelta + v$ is characterized under suitable assumptions on v. Afterwards the same type of assumptions, but for more general diffusion matrices, have been considered in [26, 27]. On the other hand, Hypothesis 1(iv) allows us to apply to the operator $\varvec{{\mathcal {A}}}$ in (1) the following result which is a particular case of [6, Theorem 2.3].

Theorem 1

Let $p\in (1,\infty )$ and assume that Hypotheses 1(i) and 1(iv) are satisfied. Further, assume that $v_{hh} \in L^p_{\mathrm {loc}}({\mathbb {R}}^d)$ for every $h=1,\ldots ,m$, $v_{hk}\in L^\infty _{\mathrm {loc}}({\mathbb {R}}^d)$ for every $h,k=1, \dots , m$ with $h\not =k$ and V is pointwise accretive. Then, the realization in $L^p({\mathbb {R}}^d,{{\mathbb {R}}}^m)$ of the operator $\varvec{{\mathcal {A}}}$ with domain

$$\begin{aligned} D_{p,\mathrm{max}}=\{ {\varvec{u}}\in L^p({\mathbb {R}}^d;{\mathbb {R}}^m)\cap W_{\mathrm {loc}}^{2,p}({\mathbb {R}}^d;{\mathbb {R}}^m)\,\mid \, \varvec{{\mathcal {A}}}{\varvec{u}}\in L^p({\mathbb {R}}^d;{\mathbb {R}}^m)\} \end{aligned}$$

generates a contraction semigroup in $L^p({\mathbb {R}}^d;{\mathbb {R}}^m)$. Moreover $C_c^\infty ({\mathbb {R}}^d;{\mathbb {R}}^m)$ is a core for $(\varvec{{\mathcal {A}}}, D_{p,\mathrm{max}})$.

For every $\xi , \eta \in {\mathbb {C}}^m$, we set ${{\mathfrak {q}}}(\xi , \eta )=\langle Q(\cdot )\xi ,\eta \rangle$ and ${{\mathfrak {q}}}(\xi )=\langle Q(\cdot )\xi ,\xi \rangle$. We also recall that for every ${\varvec{u}}\in W^{1,p}({\mathbb {R}}^d, {\mathbb {C}}^m)$ it holds that

$$\begin{aligned} \nabla |{\varvec{u}}|^2= 2\mathrm{Re} \sum _{j=1}^m (\nabla u_j)\overline{u_j},\qquad \;\,{{\mathfrak {q}}}(\nabla |{\varvec{u}}|^2)\le 4 |{\varvec{u}}|^2 \sum _{j=1}^m {{\mathfrak {q}}}(\nabla u_j). \end{aligned}$$

(2)

For each $p\in (1,\infty )$, we consider the realization ${\varvec{A}}_p$ of the operator $\varvec{{\mathcal {A}}}$ in $L^p({\mathbb {R}}^d;{\mathbb {R}}^m)$ endowed with the minimal domain

$$\begin{aligned} D_p&=\{{\varvec{u}}\in W^{2,p}_{\mathrm{loc}}({\mathbb {R}}^d;{\mathbb {R}}^m): {\varvec{u}}, \varvec{{\mathcal {A}}}_0{\varvec{u}}, V{\varvec{u}}\in L^p({\mathbb {R}}^d;{\mathbb {R}}^m)\}\\&= \{{\varvec{u}}\in W^{2,p}_{\mathrm{loc}}({\mathbb {R}}^d;{\mathbb {R}}^m): \varvec{{\mathcal {A}}}_0{\varvec{u}}, v{\varvec{u}}\in L^p({\mathbb {R}}^d;{\mathbb {R}}^m)\}. \end{aligned}$$

On $D_p$ we consider the norm $\Vert {\varvec{u}}\Vert _{D_p}=\Vert \varvec{{\mathcal {A}}}_0{\varvec{u}}\Vert _p+\Vert v{\varvec{u}}\Vert _p$. By the assumptions on V and v, $\Vert \cdot \Vert _{D_p}$ is clearly equivalent to the norm ${\varvec{u}}\mapsto \Vert {\varvec{u}}\Vert _p+\Vert \varvec{{\mathcal {A}}}_0{\varvec{u}}\Vert _p+\Vert V{\varvec{u}}\Vert _p$. Moreover, $(D_p, \Vert \cdot \Vert _{D_p})$ is a Banach space, since $\varvec{{\mathcal {A}}}_0$ is a closed operator.

Proposition 1

Let Hypotheses 1(i), (ii), (iii)(a) be satisfied. Then, the operator $(\varvec{{\mathcal {A}}}, C_c^\infty ({\mathbb {R}}^d, {\mathbb {C}}^m))$ is regularly dissipative in $L^p({\mathbb {R}}^d, {\mathbb {C}}^m)$, i.e. there exists $\phi \in \left( 0,\frac{\pi }{2}\right)$ such that $e^{\pm i\phi }\varvec{{\mathcal {A}}}$ is dissipative.

Proof

It is well known that $\left( \varvec{{\mathcal {A}}}, C_c^\infty ({\mathbb {R}}^d, {\mathbb {C}}^m)\right)$ is regularly dissipative if and only if

$$\begin{aligned} \left| \int _{{\mathbb {R}}^d} \langle {\varvec{{\mathcal {A}}}}{\varvec{u}},{\varvec{u}}\rangle |{\varvec{u}}|^{p-2} \mathrm{d}x\right| \le -\delta \mathrm{Re} \int _{{\mathbb {R}}^d} \langle {\varvec{{\mathcal {A}}}}{\varvec{u}},{\varvec{u}}\rangle |{\varvec{u}}|^{p-2} \mathrm{d}x \end{aligned}$$

(3)

for some $\delta >0$ and all ${\varvec{u}}\in C_c^\infty ({\mathbb {R}}^d, {\mathbb {C}}^m)$, (see [14, Theorem II.4.6] and [16, Theorem 1.5.9]).

To prove (3), we fix ${\varvec{u}}\in C_c^\infty ({\mathbb {R}}^d, {\mathbb {C}}^m)$, $\varepsilon >0$ and consider the function $u_{\varepsilon }=(|{\varvec{u}}|^2+\varepsilon )^{1/2}$. Integrating by parts, we get

$$\begin{aligned}&\int _{{\mathbb {R}}^d} \langle {\varvec{{\mathcal {A}}}}{\varvec{u}},{\varvec{u}}\rangle u_\varepsilon ^{p-2} \mathrm{d}x\\&\quad = - \sum _{h=1}^m \int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla u_h)u_{\varepsilon }^{p-2} \mathrm{d}x - \frac{p-2}{2} \sum _{h=1}^m \int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla u_h,\nabla |u|^2) \overline{u_h} u_{\varepsilon }^{p-4}\mathrm{d}x\\&\qquad - \int _{{\mathbb {R}}^d} \langle V{\varvec{u}}, {\varvec{u}}\rangle u_\varepsilon ^{p-2}\mathrm{d}x. \nonumber \end{aligned}$$

Therefore, using Hypothesis 1(iii)(a), we obtain

$$\begin{aligned} -\mathrm{Re} \int _{{\mathbb {R}}^d} \langle {\varvec{{\mathcal {A}}}}{\varvec{u}},{\varvec{u}}\rangle u_\varepsilon ^{p-2} \mathrm{d}x \ge&\sum _{h=1}^m \int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla u_h)u_{\varepsilon }^{p-2} \mathrm{d}x +\frac{p-2}{4} \int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla |u|^2) u_{\varepsilon }^{p-4}\mathrm{d}x\\&+ \int _{{\mathbb {R}}^d} v |{\varvec{u}}|^2 u_\varepsilon ^{p-2}\mathrm{d}x \end{aligned}$$

and, using also both the two formulas in (2), we can estimate

$$\begin{aligned}&\bigg |\int _{{\mathbb {R}}^d} \langle \varvec{{\mathcal {A}}}{\varvec{u}},{\varvec{u}}\rangle u_{\varepsilon }^{p-2} \mathrm{d}x\bigg |\\&\quad \le \sum _{h=1}^m \int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla u_h)u_{\varepsilon }^{p-2} \mathrm{d}x + \frac{|p-2|}{2} \sum _{h=1}^m \int _{{\mathbb {R}}^d} |{{\mathfrak {q}}}(\nabla u_h,\nabla |u|^2)| \,|\overline{u_h}| u_{\varepsilon }^{p-4}\mathrm{d}x\\&\qquad +c_1\int _{{\mathbb {R}}^d}v|{\varvec{u}}|^2 u_\varepsilon ^{p-2}\mathrm{d}x \\&\quad \le \sum _{h=1}^m\int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla u_h)u_{\varepsilon }^{p-2} \mathrm{d}x +\frac{|p-2|}{4} \sum _{h=1}^m \int _{{\mathbb {R}}^d} {{\mathfrak {q}}}(\nabla u_h) |{\varvec{u}}|^2 u_\varepsilon ^{p-4}\mathrm{d}x\\&\qquad +\frac{|p-2|}{4} m \int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla |{\varvec{u}}|^2)u_\varepsilon ^{p-4}\mathrm{d}x +c_1\int _{{\mathbb {R}}^d}v|{\varvec{u}}|^2 u_\varepsilon ^{p-2}\mathrm{d}x\\&\quad \le \bigg (1+\frac{|p-2|}{4}\bigg ) \sum _{h=1}^m\int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla u_h)u_{\varepsilon }^{p-2} \mathrm{d}x + \frac{|p-2|}{4} m \int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla |{\varvec{u}}|^2)u_\varepsilon ^{p-4}\mathrm{d}x\\&\qquad + c_1\int _{{\mathbb {R}}^d}v|{\varvec{u}}|^2 u_\varepsilon ^{p-2}\mathrm{d}x\\&\quad \le \left( 1+\frac{|p-2|}{4} +|p-2|m \right) \sum _{h=1}^m\int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla u_h)u_{\varepsilon }^{p-2} \mathrm{d}x + c_1\int _{{\mathbb {R}}^d}v|{\varvec{u}}|^2 u_\varepsilon ^{p-2}\mathrm{d}x. \end{aligned}$$

If $p\ge 2$, then we get that

$$\begin{aligned} -\mathrm{Re} \int _{{\mathbb {R}}^d} \langle {\varvec{{\mathcal {A}}}}{\varvec{u}},{\varvec{u}}\rangle u_\varepsilon ^{p-2} \mathrm{d}x&\ge \sum _{h=1}^m \int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla u_h)u_{\varepsilon }^{p-2} \mathrm{d}x + \int _{{\mathbb {R}}^d} v |{\varvec{u}}|^2 u_\varepsilon ^{p-2}\mathrm{d}x\nonumber \\&\ge \delta \bigg |\int _{{\mathbb {R}}^d} \langle \varvec{{\mathcal {A}}}{\varvec{u}},{\varvec{u}}\rangle u_{\varepsilon }^{p-2} \mathrm{d}x\bigg | \end{aligned}$$

(4)

by choosing $\delta <\min \{(1+4^{-1}|p-2|+|p-2|m)^{-1}, c_1^{-1}\}$.

On the other hand, if $p\in (1,2)$, then, by applying the inequality in (2) and observing that $|{\varvec{u}}|^2\le u_\varepsilon ^2$, we obtain

$$\begin{aligned} -\mathrm{Re} \int _{{\mathbb {R}}^d} \langle {\varvec{{\mathcal {A}}}}{\varvec{u}},{\varvec{u}}\rangle u_{\varepsilon }^{p-2} \mathrm{d}x&\ge (p-1) \sum _{h=1}^m\int _{{\mathbb {R}}^d} {{\mathfrak {q}}}(\nabla u_h) u_\varepsilon ^{p-2}\mathrm{d}x+ \int _{{\mathbb {R}}^d} v|{\varvec{u}}|^2u_\varepsilon ^{p-2}\mathrm{d}x\nonumber \\&\ge \delta \bigg |\int _{{\mathbb {R}}^d} \langle \varvec{{\mathcal {A}}}{\varvec{u}},{\varvec{u}}\rangle u_{\varepsilon }^{p-2} \mathrm{d}x\bigg |, \end{aligned}$$

(5)

by choosing $\delta <\min \{(1+4^{-1}|p-2|+|p-2|m)^{-1}(p-1), c_1^{-1}\}$.

The assertion follows letting $\varepsilon$ tend to 0 in (4) and (5). $\square$

Theorem 2

Under Hypotheses 1, if $p<1+4\gamma ^{-2}$, then the operator ${\varvec{A}}_p$ generates an analytic contraction semigroup $({\varvec{T}}_p(t))_{t\ge 0}$ in $L^p({\mathbb {R}}^d;{\mathbb {R}}^m)$. Moreover, $C^{\infty }_c({\mathbb {R}}^d;{\mathbb {C}}^m)$ is a core of ${\varvec{A}}_p$.

Proof

We assume first that $C_\gamma =0$ and prove that there exists a constant $C=C(p,\gamma )>0$ such that $\Vert v{\varvec{u}}\Vert _p\le C \Vert \varvec{{\mathcal {A}}}{\varvec{u}}\Vert _p$ for every ${\varvec{u}}\in C^{\infty }_c({\mathbb {R}}^d;{{\mathbb {R}}}^m)$. For this purpose, we fix ${\varvec{u}}\in C_c^\infty ({\mathbb {R}}^d;{\mathbb {R}}^m)$, set ${\varvec{f}}=-\varvec{{\mathcal {A}}}{\varvec{u}}$ and, for every $\varepsilon >0$, consider the function $u_{\varepsilon }$ introduced in Proposition 1. By using both the formulas in (2) and integrating by parts, we obtain

$$\begin{aligned}&\int _{{\mathbb {R}}^d} \langle {\varvec{f}}, {\varvec{u}}\rangle u_{\varepsilon }^{p-2} v^{p-1} \mathrm{d}x\\&\quad =\sum _{h=1}^m \int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla u_h)u_{\varepsilon }^{p-2} v^{p-1} \mathrm{d}x + \frac{p-2}{4} \int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla |{\varvec{u}}|^2)u_{\varepsilon }^{p-4}v^{p-1}\mathrm{d}x \nonumber \\&\qquad ~~~~~~~+\frac{p-1}{2}\int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla |{\varvec{u}}|^2,\nabla v)u_{\varepsilon }^{p-2}v^{p-2}\mathrm{d}x + \int _{{\mathbb {R}}^d}\langle V{\varvec{u}}, {\varvec{u}}\rangle u_{\varepsilon }^{p-2}v^{p-1}\mathrm{d}x\\&\quad \ge \sum _{h=1}^m \int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla u_h)u_{\varepsilon }^{p-2} v^{p-1} \mathrm{d}x -\frac{1}{4}\int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla |{\varvec{u}}|^2)u_{\varepsilon }^{p-4}v^{p-1}\mathrm{d}x\\&\qquad -\frac{p-1}{4}\gamma ^2\int _{\mathrm{supp}\mathbf{(u)}}v^{p}u_\varepsilon ^p\mathrm{d}x +\int _{{\mathbb {R}}^d}v^p|{\varvec{u}}|^2u_{\varepsilon }^{p-2}\mathrm{d}x\\&\quad \ge -\frac{p-1}{4}\gamma ^2\int _{\mathrm{supp}\mathbf{(u)}}v^{p}u_\varepsilon ^p\mathrm{d}x +\int _{{\mathbb {R}}^d}v^p|{\varvec{u}}|^2u_{\varepsilon }^{p-2}\mathrm{d}x. \end{aligned}$$

By applying Young’s inequality, we get that for every $\delta >0$ there exists a positive constant $C=C(\delta , p)$ such that

$$\begin{aligned} \int _{{\mathbb {R}}^d}v^p|{\varvec{u}}|^2u_{\varepsilon }^{p-2}\mathrm{d}x\!-\!\frac{p-1}{4}\gamma ^2\int _{\mathrm{supp}\mathbf{(u)}}v^{p}u_\varepsilon ^p\mathrm{d}x&\le \int _{{\mathbb {R}}^d} \langle {\varvec{f}}, {\varvec{u}}\rangle u_{\varepsilon }^{p-2}v^{p-1}\mathrm{d}x \nonumber \\&\le \delta \!\int _{\mathrm{supp}\mathbf{(u)}} v^p u_{\varepsilon }^p \mathrm{d}x\!+\!C\int _{{\mathbb {R}}^d} |{\varvec{f}}|^p\mathrm{d}x. \end{aligned}$$

Letting $\varepsilon$ tend to 0 yields

$$\begin{aligned} \bigg (1-\frac{p-1}{4}\gamma ^2-\delta \bigg ) \int _{{\mathbb {R}}^d} v^p |{\varvec{u}}|^p \mathrm{d}x \le C\int _{{\mathbb {R}}^d} |{\varvec{f}}|^p\mathrm{d}x \end{aligned}$$

and we get the assertion by the assumptions on $\gamma$ and p, choosing $\delta$ sufficiently small.

As a consequence of the estimate that we have proved, we can show that there exist positive constants $M_1$ and $M_2$, depending on $c_0$, $c_1$ and $\gamma$ such that

$$\begin{aligned} M_1 \Vert {\varvec{u}}\Vert _{D_p}\le \Vert \varvec{{\mathcal {A}}}{\varvec{u}}- {\varvec{u}}\Vert _p \le M_2 \Vert {\varvec{u}}\Vert _{D_p},\qquad \;\,{\varvec{u}}\in C_c^\infty ({\mathbb {R}}^d;{\mathbb {R}}^m). \end{aligned}$$

(6)

Indeed, for every ${\varvec{u}}\in C_c^\infty ({\mathbb {R}}^d;{\mathbb {R}}^m)$, it holds that

$$\begin{aligned} \Vert {\varvec{u}}\Vert _{D_p}&= \Vert \varvec{{\mathcal {A}}}_0{\varvec{u}}\Vert _p + \Vert v{\varvec{u}}\Vert _p \le \Vert \varvec{{\mathcal {A}}}{\varvec{u}}\Vert _p +\Vert V{\varvec{u}}\Vert _p + \Vert v{\varvec{u}}\Vert _p\\&\le \Vert \varvec{{\mathcal {A}}}{\varvec{u}}\Vert _p +(1+c_1) \Vert v{\varvec{u}}\Vert _p \le \big ((1+c_1)C+1\big )\Vert \varvec{{\mathcal {A}}}{\varvec{u}}\Vert _p\\&\le 2\big ((1+c_1)C+1\big )\Vert \varvec{{\mathcal {A}}}{\varvec{u}}-{\varvec{u}}\Vert _p \end{aligned}$$

by the dissipativity of $\varvec{{\mathcal {A}}}$. Moreover,

$$\begin{aligned} \Vert \varvec{{\mathcal {A}}}{\varvec{u}}- {\varvec{u}}\Vert _p\le & {} \Vert \varvec{{\mathcal {A}}}_0{\varvec{u}}\Vert _p+\Vert v{\varvec{u}}\Vert _p + \Vert {\varvec{u}}\Vert _p\nonumber \\\le & {} \Vert \varvec{{\mathcal {A}}}_0{\varvec{u}}\Vert _p+(1+c_0^{-1}) \Vert v{\varvec{u}}\Vert _p\nonumber \\\le & {} M_2 \Vert {\varvec{u}}\Vert _{D_p}. \end{aligned}$$

(7)

If $C_\gamma \ne 0$, then we fix $\lambda >0$ such that $V+\lambda I$ and $v+\lambda$ satisfy Hypothesis 1(iii) with $C_\gamma =0$. Applying (6) to $\varvec{{\mathcal {A}}}-\lambda I$ and using the dissipativity of $\varvec{{\mathcal {A}}}$, we obtain

$$\begin{aligned} \Vert {\varvec{u}}\Vert _{D_p}\le {\widetilde{C}}\Vert \varvec{{\mathcal {A}}}{\varvec{u}}\!-\!\lambda {\varvec{u}}\!-\!{\varvec{u}}\Vert _p\le {\widetilde{C}}\Vert \varvec{{\mathcal {A}}}{\varvec{u}}\!-\!{\varvec{u}}\Vert _p\!+\!{\widetilde{C}}\lambda \Vert {\varvec{u}}\Vert _p\le (1+\lambda ){\widetilde{C}} \Vert \varvec{{\mathcal {A}}}{\varvec{u}}-{\varvec{u}}\Vert _p, \end{aligned}$$

while the other inequality follows as in (7).

Next, we show that $D_p=D_{p,\max }$. Clearly, we just need to prove that $D_{p,\max }\subset D_p$. We fix ${\varvec{u}}\in D_{p,\max }$ and a sequence $({\varvec{u}}_n)\subset C^{\infty }_c({\mathbb {R}}^d;{{\mathbb {R}}}^m)$ converging to ${\varvec{u}}$ in $L^p({\mathbb {R}}^d;{{\mathbb {R}}}^m)$ and such that $\varvec{{\mathcal {A}}}{\varvec{u}}_n$ converges to $\varvec{{\mathcal {A}}}{\varvec{u}}$ in $L^p({\mathbb {R}}^d;{{\mathbb {R}}}^m)$ as n tends to $\infty$ (see Theorem 1). By (6), $({\varvec{u}}_n)$ is a Cauchy sequence in the Banach space $D_p$ (endowed with the norm $\Vert \cdot \Vert _{D_p}$). Hence, ${\varvec{u}}\in D_p$ and the inclusion $D_{p,\max }\subset D_p$ follows. In particular, $C^{\infty }_c({\mathbb {R}}^d;{{\mathbb {R}}}^m)$ is dense in $D_p$ and, by Theorem 1, $(\varvec{{\mathcal {A}}}, D_p)$ generates a contraction semigroup. $\square$

Theorem 3

Under Hypotheses 1, suppose that v(x) blows up as |x| tends to $\infty$. Then, for every $p\in (1,1+4\gamma ^{-2})$, the operator ${\varvec{A}}_p$ has compact resolvent.

Proof

We have to show that the unit ball ${\mathcal {B}}$ of $D_p$ is totally bounded in $L^p({\mathbb {R}}^d; {\mathbb {R}}^m)$. First let observe that for every $\varepsilon >0$ there exists $R>0$ such that $v(x)>\varepsilon ^{-1}$ if $|x|>R$. Now, let us fix $\varepsilon \in (0,1)$. Then,

$$\begin{aligned} \int _{|x|\ge R} |{\varvec{u}}(x)|^p\mathrm{d}x \le \frac{1}{(\inf _{B(R)}v)^p} \int _{{\mathbb {R}}^d} v(x)^p|{\varvec{u}}(x)|^p \mathrm{d}x \le \varepsilon ^p \end{aligned}$$

(8)

for every ${\varvec{u}}\in {\mathcal {B}}$. Let ${\mathcal {B}}'$ be the set of the restrictions of the elements of ${\mathcal {B}}$ to B(R). By [15, Theorem 9.11], ${\mathcal {B}}'$ is a bounded subsets of $W^{2,p}(B(R), {\mathbb {C}}^m)$ and therefore is totally bounded in $L^p(B(R), {\mathbb {C}}^m)$. So, there exist functions ${\varvec{f}}_1,\ldots , {\varvec{f}}_n\in L^p(B(R), {\mathbb {C}}^m)$ such that ${{\mathcal {B}}'}$ is contained in the union of the balls of $L^p(B(R);{\mathbb {C}}^m)$ centered at ${\varvec{f}}_i$ $(i=1,\ldots ,n)$ with radius $\varepsilon$. Letting $\overline{{\varvec{f}}}_i$ be the trivial extension of ${\varvec{f}}_i$ to ${\mathbb {R}}^d$ and by taking (8) into account, we conclude that ${\mathcal {B}}$ is contained in the union of the ball of $L^p({\mathbb {R}}^d;{\mathbb {C}}^m)$, centered at ${\overline{{\varvec{f}}}}_i$ $(i=1,\ldots ,n)$ with radius $2\varepsilon$. $\square$

3 Consistency and summability properties

Let us define

$$\begin{aligned} D({\mathfrak {a}})=\{ {\varvec{u}}\in W^{1,2}_\mathrm{loc}({\mathbb {R}}^d, {\mathbb {C}}^m)\,\mid \, ({{\mathfrak {q}}}(\nabla {\varvec{u}}))^{\frac{1}{2}}, v^{\frac{1}{2}}|{\varvec{u}}|\in L^2({\mathbb {R}}^d)\} \end{aligned}$$

(9)

and ${\mathfrak {a}} : D({\mathfrak {a}})\times D({\mathfrak {a}})\rightarrow {\mathbb {C}}$ by

$$\begin{aligned} {\mathfrak {a}}({\varvec{u}},{\varvec{w}})=\int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla {\varvec{u}}, \nabla {\varvec{w}}) \mathrm{d}x + \int _{{\mathbb {R}}^d} \langle V{\varvec{u}}, {\varvec{w}}\rangle \mathrm{d}x. \end{aligned}$$

(10)

As usually, we denote by $\Vert \cdot \Vert _{{\mathfrak {a}}}=\sqrt{\mathrm{Re}\,{{\mathfrak {a}}}(\cdot ,\cdot )+\Vert \cdot \Vert _2^2}$ the norm of $D({\mathfrak {a}})$ associated with the form ${{\mathfrak {a}}}$. The following properties hold true:

• (i) ${\mathfrak {a}}$ is densely defined since $C_c^\infty ({\mathbb {R}}^d, {\mathbb {C}}^m)\subseteq D({{\mathfrak {a}}})$, it is also continuous and accretive;

• (ii) ${{\mathfrak {a}}}$ is closed: let $({\varvec{u}}_n)_{n\in {{\mathbb {N}}}}$ be a Cauchy sequence in $D({{\mathfrak {a}}})$. Then, $({\varvec{u}}_n)_{n\in {{\mathbb {N}}}}$ converges to a function ${\varvec{u}}\in W^{1,2}_\mathrm{loc}({\mathbb {R}}^d;{\mathbb {C}}^m)\cap L^p({\mathbb {R}}^d;{\mathbb {C}}^m)$ and, up to a subsequence, we can assume that $\nabla {\varvec{u}}_n$ converges to $\nabla {\varvec{u}}$ and ${\varvec{u}}_n$ converges to ${\varvec{u}}$ almost everywhere in ${\mathbb {R}}^d$. Since $\Vert {{\mathfrak {q}}}(\nabla {\varvec{u}}_n)\Vert _2+\Vert \langle V{\varvec{u}}_n, {\varvec{u}}_n\rangle \Vert _2 \le M$ for all $n\in {{\mathbb {N}}}$ and a positive constant M, by applying Fatou’s lemma we get that ${\varvec{u}}\in D({{\mathfrak {a}}})$ and $\lim _{n\rightarrow \infty }\Vert {\varvec{u}}_n-{\varvec{u}}\Vert _{{{\mathfrak {a}}}}=0$;

• (iii) $C_c^\infty ({\mathbb {R}}^d; {\mathbb {C}}^m)$ is a core for ${{\mathfrak {a}}}$: indeed, $D({{\mathfrak {a}}})$ is a Hilbert space with respect to the scalar product $\langle {\varvec{u}},{\varvec{w}}\rangle _{{\mathfrak {a}}}= \frac{1}{2}[{{\mathfrak {a}}}({\varvec{u}},{\varvec{w}})+{{\mathfrak {a}}}({\varvec{w}},{\varvec{u}})]+ ({\varvec{u}},{\varvec{w}})_{L^2({\mathbb {R}}^d;{\mathbb {C}})}$. Then, $C_c^\infty ({\mathbb {R}}^d;{\mathbb {C}}^m)$ is a core for ${{\mathfrak {a}}}$ if and only if $\langle {\varvec{u}},\varvec{\phi }\rangle _{{{\mathfrak {a}}}}=0$ for all ${\varvec{\phi }}\in C_c^\infty ({\mathbb {R}}^d;{\mathbb {C}}^m)$, implies that ${\varvec{u}}={\varvec{0}}$. The proof of this statement runs analogously to that of [6, Theorem 2.2].

Since the diffusion part in $\varvec{{\mathcal {A}}}$ is diagonal, integrating by parts, we deduce that the operator ${\varvec{B}}$ associated with ${{\mathfrak {a}}}$ coincides with $-{\varvec{A}}_2$ on $C_c^\infty ({\mathbb {R}}^d, {\mathbb {C}}^m)$. Thus, since $C_c^\infty ({\mathbb {R}}^d, {\mathbb {C}}^m)$ is a core for ${\varvec{A}}_2$ (see Theorem 2), ${\varvec{B}}=-{\varvec{A}}_2$ follows from the closedness of ${\varvec{B}}$.

Based on these remarks, we can prove the consistency of the semigroups $({\varvec{T}}_p(t))_{t\ge 0}$.

Theorem 4

For every $p,q\in (1,1+4\gamma ^{-2})$, the semigroups $({\varvec{T}}_p(t))_{t\ge 0}$ and $({\varvec{T}}_q(t))_{t\ge 0}$ coincide on $L^p({\mathbb {R}}^d;{{\mathbb {R}}}^m)\cap L^q({\mathbb {R}}^d;{{\mathbb {R}}}^m)$.

Proof

We begin the proof by observing that Hypotheses 1(ii) and (iii)(a) imply that, for every $r\in (1,\infty )$, the realization in $L^r({\mathbb {R}}^d;{{\mathbb {R}}}^m)$ of the multiplication operator ${\varvec{u}}\mapsto -V{\varvec{u}}$, with $D(V)=\{{\varvec{u}}\in L^r({\mathbb {R}}^d;{{\mathbb {R}}}^m): V{\varvec{u}}\in L^r({\mathbb {R}}^d;{{\mathbb {R}}}^m)\}$, generates the strongly continuous semigroup of contractions $({\varvec{S}}_r(t))_{t\ge 0}$, defined by $({\varvec{S}}_r(t){\varvec{f}})(x)=e^{-tV(x)}{\varvec{f}}(x)$ for every $t>0$, ${\varvec{f}}\in L^r({\mathbb {R}}^d;{{\mathbb {R}}}^m)$ and almost every $x\in {\mathbb {R}}^d$. These semigroups are clearly consistent.

Next, we denote by $({\widetilde{{\varvec{T}}}}(t))_{t\ge 0}$ the semigroup associated with the form ${{\mathfrak {a}}}$ in (10), where we take $V=0$. This semigroup coincides with the semigroup (that we denote by $({\varvec{T}}^0_2(t))_{t\ge 0}$) associated with the operator $\varvec{{\mathcal {A}}}_0$, provided by Theorem 2, since their generators coincide. Since $\varvec{{\mathcal {A}}}_0$ is diagonal, the semigroup $({\varvec{T}}^0_2(t))_{t\ge 0}$ is diagonal as well and it consists of m copies of the scalar semigroup $(T^0_2(t))_{t\ge 0}$ associated with the scalar version ${{\mathfrak {a}}}_s$ of the form ${{\mathfrak {a}}}$ (with $V=0$). The form ${{\mathfrak {a}}}_s$ satisfies the Beurling-Deny criterion. Thus, the semigroup $(T_2^0(t))_{t\ge 0}$ can be extended to the $L^r$-scale ($r\ge 2$) and these semigroups are consistent, see [11, Theorem 1.4.1]. As a byproduct, also the semigroup $({\varvec{T}}_2^0(t))_{t\ge 0}$ can be extended from $L^2({{\mathbb {R}}}^d,{{\mathbb {R}}}^m)\cap L^r({{\mathbb {R}}}^d,{{\mathbb {R}}}^m)$ to a strongly continuous semigroup $({\widetilde{{\varvec{T}}}}_r(t))_{t\ge 0}$ on $L^r({{\mathbb {R}}}^d, {{\mathbb {R}}}^m)$ for every $r\in [2,\infty )$. These semigroups are consistent. We claim that ${\varvec{T}}_r^0(t)={\widetilde{{\varvec{T}}}}_r(t)$ for every $r\in (2,\infty )$ and $t>0$. For this purpose, we observe that [13, Lemma 1.11] (applied to the scalar semigroup $(T^0_2(t))_{t\ge 0}$) shows that, if ${\varvec{f}}\in D(\varvec{{\mathcal {A}}}_2^0)$ is such that ${\varvec{f}}$ and $\varvec{{\mathcal {A}}}_2^0{\varvec{f}}\in L^r({\mathbb {R}}^d,{{\mathbb {R}}}^m)$, then ${\varvec{f}}$ belongs to the domain of the infinitesimal generator ${\widetilde{\varvec{{\mathcal {A}}}}}_r$ of the semigroup $({\widetilde{{\varvec{T}}}}_r(t))_{t\ge 0}$. In particular, ${\widetilde{\varvec{{\mathcal {A}}}}}_r{\varvec{f}}=\varvec{{\mathcal {A}}}_r^0{\varvec{f}}$ on $C^{\infty }_c({\mathbb {R}}^d;{{\mathbb {R}}}^m)$. This fact and Theorem 2 imply that $(\lambda I-{\widetilde{\varvec{{\mathcal {A}}}}}_r)(C^{\infty }_c({\mathbb {R}}^d;{{\mathbb {R}}}^m))=(\lambda I-\varvec{{\mathcal {A}}}_r^0)(C^{\infty }_c({\mathbb {R}}^d;{{\mathbb {R}}}^m))$ is dense in $L^p({\mathbb {R}}^d;{{\mathbb {R}}}^m)$. As a consequence $C^{\infty }_c({\mathbb {R}}^d;{{\mathbb {R}}}^m)$ is a core both for $\varvec{{\mathcal {A}}}_r^0$ and ${\widetilde{\varvec{{\mathcal {A}}}}}_r$ and this is enough to infer that the semigroups $({\varvec{T}}_r^0(t))_{t\ge 0}$ and $({\widetilde{{\varvec{T}}}}_r(t))_{t\ge 0}$ coincide.

Now, we fix p, q as in the statement and we first assume that $p,q\in [2,\infty )$. Applying Trotter product formula (see [14, Corollary III.5.8]), we conclude that

$$\begin{aligned} {\varvec{T}}_r(t){\varvec{f}}=\lim _{n\rightarrow \infty }\bigg ({\varvec{T}}_r^0\bigg (\frac{t}{n}\bigg ) \circ {\varvec{S}}_r\bigg (\frac{t}{n}\bigg )\bigg )^n{\varvec{f}},\qquad \;\,{\varvec{f}}\in L^r({\mathbb {R}}^d;{{\mathbb {R}}}^m), \end{aligned}$$

for every $t>0$ and $r\in \{p,q\}$. Fix $t>0$ and ${\varvec{f}}\in L^p({\mathbb {R}}^d;{{\mathbb {R}}}^m)\cap L^q({\mathbb {R}}^d;{{\mathbb {R}}}^m)$. Then, from the above arguments we infer that

$$\begin{aligned} {\varvec{T}}_p(t){\varvec{f}}=\lim _{n\rightarrow \infty }\bigg ({\varvec{T}}_q^0\bigg (\frac{t}{n}\bigg ) \circ {\varvec{S}}_q\bigg (\frac{t}{n}\bigg )\bigg )^n{\varvec{f}}, \end{aligned}$$

where the limit is taken in $L^p({\mathbb {R}}^d;{{\mathbb {R}}}^m)$. Then, up to a subsequence, we obtain that $({\varvec{T}}_q^0(t/n)\circ {\varvec{S}}_q(t/n))^n{\varvec{f}}$ converges pointwise both to ${\varvec{T}}_p(t){\varvec{f}}$ and to ${\varvec{T}}_q(t){\varvec{f}}$ as n tends to $\infty$, so that the equality ${\varvec{T}}_p(t){\varvec{f}}={\varvec{T}}_q(t){\varvec{f}}$ follows.

Next, we assume that $p,q\in (1,2]$ and observe that ${\varvec{T}}_p(t)={{\widehat{{\varvec{T}}}}}_{p'}(t)^*$ and ${\varvec{T}}_q(t)={{\widehat{{\varvec{T}}}}}_{q'}(t)^*$ for every $t>0$, where ${{\widehat{{\varvec{T}}}}}_{p'}(t)$ and ${{\widehat{{\varvec{T}}}}}_{q'}(t)$ denote the semigroup in $L^{p'}({\mathbb {R}}^d;{{\mathbb {R}}}^m)$ and $L^{q'}({\mathbb {R}}^d;{{\mathbb {R}}}^m)$, respectively, associated with the operator $\varvec{{\mathcal {A}}}^*$, adjoint to operator $\varvec{{\mathcal {A}}}$. Since the potential $V^*$ satisfies the same assumptions as the potential V and $p',q'\ge 2$, from the results so far proved we conclude that ${{\widehat{{\varvec{T}}}}}_{p'}(t)$ and ${{\widehat{{\varvec{T}}}}}_{q'}(t)$ coincide on $L^{p'}({\mathbb {R}}^d;{{\mathbb {R}}}^m)\cap L^{q'}({\mathbb {R}}^d;{{\mathbb {R}}}^m)$ for every $t>0$. Hence, for every $t>0$, ${\varvec{f}}\in L^p({\mathbb {R}}^d;{{\mathbb {R}}}^m)\cap L^q({\mathbb {R}}^d;{{\mathbb {R}}}^m)$ and $\varvec{\varphi }\in C^{\infty }_c({\mathbb {R}}^d;{{\mathbb {R}}}^m)$, we can write

$$\begin{aligned} \langle {\varvec{T}}_p(t){\varvec{f}},\varvec{\varphi }\rangle _{p,p'}=\langle {\varvec{f}},{{\widehat{{\varvec{T}}}}}_{p'}(t) \varvec{\varphi }\rangle _{p,p'} =\langle {\varvec{f}},{{\widehat{{\varvec{T}}}}}_{q'}(t)\varvec{\varphi }\rangle _{q,q'} =\langle {\varvec{T}}_q(t){\varvec{f}},\varvec{\varphi }\rangle _{q,q'} \end{aligned}$$

and the arbitrariness of $\varvec{\varphi }\in C^{\infty }_c({\mathbb {R}}^d;{{\mathbb {R}}}^m)$ yields the equality ${\varvec{T}}_p(t){\varvec{f}}={\varvec{T}}_q(t){\varvec{f}}$.

Finally, if $1<p<2<q$, then we observe that ${\varvec{T}}_p(t){\varvec{f}}={\varvec{T}}_2(t){\varvec{f}}={\varvec{T}}_q(t){\varvec{f}}$ for every $t>0$ and ${\varvec{f}}\in C^{\infty }_c({\mathbb {R}}^d;{{\mathbb {R}}}^m)$. Since every ${\varvec{f}}\in L^p({\mathbb {R}}^d;{{\mathbb {R}}}^m)\cap L^q({\mathbb {R}}^d;{{\mathbb {R}}}^m)$ is the limit (in $L^p({\mathbb {R}}^d;{{\mathbb {R}}}^m)\cap L^q({\mathbb {R}}^d;{{\mathbb {R}}}^m)$) of a sequence of functions which belong to $C^{\infty }_c({\mathbb {R}}^d;{{\mathbb {R}}}^m)$, the equality ${\varvec{T}}_p(t)={\varvec{T}}_q(t)$ on $L^p({\mathbb {R}}^d;{{\mathbb {R}}}^m)\cap L^q({\mathbb {R}}^d;{{\mathbb {R}}}^m)$ follows for every $t>0$. $\square$

Remark 1

As a straightforward consequence of Theorems 3 and 4, we deduce that if, Hypotheses 1 hold true for every $\gamma >0$ and $\langle Q(x)\xi ,\xi \rangle \ge q_0|\xi |^2$ for every $x,\xi \in {\mathbb {R}}^d$ and some positive constant $q_0$, then the spectrum of operator $\varvec{{\mathcal {A}}}_p$ is independent of p and consists of eigenvalues only.

Based on Theorem 3 we can now prove the following result.

Theorem 5

Assume that Hypotheses 1 hold true for some $\gamma >0$ and let $1<p<1+4\gamma ^{-2}$. Then the restriction of the semigroup $({\varvec{T}}_p(t))_{t\ge 0}$ to $L^p({\mathbb {R}}^d; {\mathbb {R}}^m)\cap L^1({\mathbb {R}}^d; {\mathbb {R}}^m)$ can be extended to a contraction $C_0$-semigroup $({\varvec{T}}_1(t))_{t\ge 0}$ on the space $L^1({\mathbb {R}}^d; {\mathbb {R}}^m)$, which is consistent with $({\varvec{T}}_q(t))_{t\ge 0}$ for each $q\in (1,p)$. The spaces $X_q=\{{\varvec{u}}\in D_q\cap L^1({\mathbb {R}}^d; {\mathbb {R}}^m)\mid {\varvec{A}}_q{\varvec{u}}\in L^1({\mathbb {R}}^d; {\mathbb {R}}^m)\}$ are cores for the generator ${\varvec{A}}_1$ of $({\varvec{T}}_1(t))_{t\ge 0}$ and ${\varvec{A}}_1{\varvec{u}}={\varvec{A}}_q{\varvec{u}}=\varvec{{\mathcal {A}}}{\varvec{u}}$ for every ${\varvec{u}}\in X_q$ and $q<1+4\gamma ^{-2}$. Finally, if Hypotheses 1 hold true for every $\gamma <2$ and

$$\begin{aligned} (Q(x)\xi , \xi )\ge q_0|\xi |^2,\qquad \;\, \xi , x\in {{\mathbb {R}}}^d, \end{aligned}$$

(11)

then, for every $t>0$, ${\varvec{T}}_1(t)$ is bounded from $L^1({\mathbb {R}}^d; {\mathbb {R}}^m)$ into $L^2({\mathbb {R}}^d; {\mathbb {R}}^m)$.

Proof

Fix ${\varvec{f}}\in L^p({\mathbb {R}}^d; {\mathbb {R}}^m)\cap L^1({\mathbb {R}}^d; {\mathbb {R}}^m)$ and $r>0$. Then, ${\varvec{f}}\in L^q({\mathbb {R}}^d;{{\mathbb {R}}}^m)$ for each $1<q<p$ and, since the semigroups $({\varvec{T}}_q(t))_{t\ge 0}$ are consistent, we can estimate

$$\begin{aligned} \Vert {\varvec{T}}_p(t){\varvec{f}}\Vert _{L^1(B(r), {\mathbb {R}}^m)}=&\lim _{q\rightarrow 1^+}\Vert {\varvec{T}}_q(t){\varvec{f}}\Vert _{L^q(B(r), {\mathbb {R}}^m)} \\ \le&\limsup _{q\rightarrow 1^+}\Vert {\varvec{f}}\Vert _{L^q({\mathbb {R}}^d; {\mathbb {R}}^m)} \le \Vert {\varvec{f}}\Vert _{L^1({\mathbb {R}}^d; {\mathbb {R}}^m)}. \end{aligned}$$

From this chain of inequalities and letting r tend to $\infty$, it follows that we can extend the restriction of the semigroup $({\varvec{T}}_p(t))_{t\ge 0}$ to $L^p({\mathbb {R}}^d;{\mathbb {R}}^m)\cap L^1({\mathbb {R}}^d; {\mathbb {R}}^m)$ with a contraction semigroup $({\varvec{T}}_1(t))_{t\ge 0}$ on $L^1({\mathbb {R}}^d; {\mathbb {R}}^m)$. This semigroup is strongly continuous. Indeed, since it is uniformly bounded, it suffices to prove that ${\varvec{T}}_1(t){\varvec{f}}$ converges to ${\varvec{f}}$ in $L^1({\mathbb {R}}^d;{\mathbb {R}}^m)$ when ${\varvec{f}}\in C^{\infty }_c({\mathbb {R}}^d;{\mathbb {R}}^m)$. For each ${\varvec{f}}\in C_c^{\infty }({\mathbb {R}}^d; {\mathbb {R}}^m)$ and $q\in (1,p)$, we can write

$$\begin{aligned} {\varvec{T}}_1(t){\varvec{f}}-{\varvec{f}}={\varvec{T}}_q(t){\varvec{f}}\\ -{\varvec{f}}=\int _0^t {\varvec{T}}_q(s)\varvec{{\mathcal {A}}}{\varvec{f}}\mathrm{d}s. \end{aligned}$$

and thus estimate $\Vert {\varvec{T}}_1(t){\varvec{f}}-{\varvec{f}}\Vert _{L^q(B(r), {\mathbb {R}}^m)} \le t\Vert \varvec{{\mathcal {A}}}{\varvec{f}}\Vert _q$. Letting q tend to 1 and then r tend to $\infty$, we infer that ${\varvec{T}}_1(t){\varvec{f}}$ converges to ${\varvec{f}}$ in $L^1({\mathbb {R}}^d;{\mathbb {R}}^m)$ as t tends to 0.

Next, we observe that

$$\begin{aligned} \frac{{\varvec{T}}_1(t){\varvec{u}}-{\varvec{u}}}{t} =\frac{{\varvec{T}}_q(t){\varvec{u}}-{\varvec{u}}}{t}=\frac{1}{t} \int _0^t {\varvec{T}}_q(s){\varvec{A}}_q {\varvec{u}}\mathrm{d}s=\frac{1}{t} \int _0^t {\varvec{T}}_1(s){\varvec{A}}_q {\varvec{u}}\mathrm{d}s \end{aligned}$$

for every ${\varvec{u}}\in X_q$. Thus, the ratio $t^{-1}({\varvec{T}}_1(t){\varvec{u}}-{\varvec{u}})$ converges to ${\varvec{A}}_q{\varvec{u}}$ in $L^1({\mathbb {R}}^d; {\mathbb {R}}^m)$, as t tends to 0. This shows that $X_q\subset D({\varvec{A}}_1)$ and ${\varvec{A}}_1{\varvec{u}}={\varvec{A}}_q{\varvec{u}}$ for ${\varvec{u}}\in X_q$. To conclude that the set $X_q$ is a core for ${\varvec{A}}_1$ for every $q<1+4\gamma ^{-2}$, it suffices to apply [14, Proposition II.1.7]. Indeed, the semigroup $({\varvec{T}}_1(t))_{t\ge 0}$ leaves $X_q$ invariant, since it is consistent with the semigroup $({\varvec{T}}_q(t))_{t\ge 0}$, and, clearly, $X_q$ is also dense in $L^1({\mathbb {R}}^d; {\mathbb {R}}^m)$ since it contains $C_c^\infty ({\mathbb {R}}^d; {\mathbb {R}}^m)$.

To prove the last part of the assertion, we assume that Hypotheses 1 hold true for every $\gamma <2$ and recall that $({\varvec{T}}_2(t))_{t\ge 0}$ is the semigroup associated with the quadratic form ${{\mathfrak {a}}}$. By (11) there exists $C>0$ such that ${{\mathfrak {a}}}({\varvec{f}},{\varvec{f}})\ge C\Vert {\varvec{f}}\Vert _{1,2}^2$ for every ${\varvec{f}}\in D({{\mathfrak {a}}})$. Since by a straightforward adaptation of Nash’s inequality to the vector-valued case, $\Vert {\varvec{f}}\Vert _2^{2+4/d} \le C_1\Vert {\varvec{f}}\Vert _{1,2}^2\Vert {\varvec{f}}\Vert _1^{4/d}$ for some constant $C_1>0$ and every ${\varvec{f}}\in W^{1,2}({\mathbb {R}}^d; {\mathbb {R}}^m)\cap L^1({\mathbb {R}}^d; {\mathbb {R}}^m)$, we get that $\Vert {\varvec{f}}\Vert _2^{2+4/d}\le K {{\mathfrak {a}}}({\varvec{f}}, {\varvec{f}})\Vert {\varvec{f}}\Vert _1^{4/d}$ for some constant $K>0$ and, therefore, ${\varvec{T}}_1(t)$ is bounded from $L^1({\mathbb {R}}^d; {\mathbb {R}}^m)$ into $L^2({\mathbb {R}}^d; {\mathbb {R}}^m)$ (see for instance the proof of [18, Lemma 4.1]). $\square$

If Hypotheses 1 hold true for each $\gamma >0$, then, by Theorem 4, the semigroups $({\varvec{T}}_p(t))_{t\ge 0}$ exist for each $p\in [1,\infty )$ and are consistent. In this case, we will write $({\varvec{T}}(t))_{t\ge 0}$ instead of $({\varvec{T}}_p(t))_{t\ge 0}$.

Theorem 6

Assume that Hypotheses 1 hold true for every $\gamma >0$ and that estimate (11) is satisfied too. Then, for every $t>0$ and $1\le p< q\le \infty$, $({\varvec{T}}(t))_{t\ge 0}$ is bounded from $L^p({\mathbb {R}}^d; {\mathbb {R}}^m)$ into $L^q({\mathbb {R}}^d; {\mathbb {R}}^m)$. Moreover, for every $t>0$ there exists a kernel $K(t, \cdot , \cdot )\in L^\infty ({\mathbb {R}}^d\times {\mathbb {R}}^d; {\mathbb {R}}^{m\times m})$ such that

$$\begin{aligned} ({\varvec{T}}(t){\varvec{f}})(x)= \int _{{\mathbb {R}}^d} K(t,x,y){\varvec{f}}(y)\mathrm{d}y, \qquad x\in {\mathbb {R}}^d,\ {\varvec{f}}\in L^p({\mathbb {R}}^d; {\mathbb {R}}^m). \end{aligned}$$

Proof

By observing that $\varvec{{\mathcal {A}}}^*{\varvec{u}}=\mathrm{div}(Q\nabla {\varvec{u}})-V^*{\varvec{u}}$ for each ${\varvec{u}}\in C_c^\infty ({\mathbb {R}}^d; {\mathbb {R}}^m)$ and that $V^*$ satisfies the same assumptions as V, we deduce that ${\varvec{T}}^*(t)$ is bounded from $L^1({\mathbb {R}}^d; {\mathbb {R}}^m)$ into $L^2({\mathbb {R}}^d; {\mathbb {R}}^m)$ for every $t>0$. Thus, by applying the usual duality argument and the semigroup law, it follows that ${\varvec{T}}(t)$ is bounded from $L^1({\mathbb {R}}^d; {\mathbb {R}}^m)$ into $L^\infty ({\mathbb {R}}^d; {\mathbb {R}}^m)$ and, hence, from $L^p({\mathbb {R}}^d; {\mathbb {R}}^m)$ into $L^q({\mathbb {R}}^d; {\mathbb {R}}^m)$ for every $p,q\in (1,\infty )\cup \{\infty \}$, with $p<q$.

To establish the existence of the kernel, observe that

$$\begin{aligned} {\varvec{T}}(t){\varvec{f}}=\sum _{i,j=1}^mT_{ij}(t)(f_j){\varvec{e}}_i,\qquad \;\,{\varvec{f}}=(f_1, \dots , f_m)\in L^p({\mathbb {R}}^d; {\mathbb {R}}^m), \end{aligned}$$

where $\{{\varvec{e}}_1, \dots , {\varvec{e}}_m\}$ is the canonical basis of ${\mathbb {R}}^m$ and $T_{ij}(t){\varvec{u}}= \langle {\varvec{T}}(t)(u{\varvec{e}}_j), {\varvec{e}}_i\rangle$ for every $u\in L^p({\mathbb {R}}^d)$. Since ${\varvec{T}}(t)$ maps $L^1({\mathbb {R}}^d; {\mathbb {R}}^m)$ into $L^\infty ({\mathbb {R}}^d; {\mathbb {R}}^m)$, also every $T_{ij}(t)$ maps $L^1({\mathbb {R}}^d)$ into $L^\infty ({\mathbb {R}}^d)$, and therefore, by the Dunford–Pettis theorem, there exists $k_{ij}(t, \cdot , \cdot )\in L^\infty ({\mathbb {R}}^d\times {\mathbb {R}}^d)$ such that

$$\begin{aligned} T_{ij}(t)u(x)= \int _{{\mathbb {R}}^d} k_{ij}(t,x,y)u(y)\mathrm{d}y, \qquad x\in {\mathbb {R}}^d,\ u\in L^1({\mathbb {R}}^d). \end{aligned}$$

We get the assertion by defining K(t, x, y) as the matrix with entries $k_{ij}(t,x,y)$ for every $t>0$ and almost every $x,y\in {\mathbb {R}}^d$. $\square$

Finally, we establish a domination property of the semigroup $({\varvec{T}}(t))_{t\ge 0}$ with the scalar semigroup generated by $\varvec{{\mathcal {A}}}_0-vI$.

Proposition 2

Assume Hypotheses 1 with $\gamma <2$ and that (11) holds true. Then, the semigroup $({\varvec{T}}(t))_{t\ge 0}$ is dominated by the analogous scalar semigroup $(T_2(t))_{t\ge 0}$ generated by the realization of the operator $\mathrm{div}(Q\nabla )-vI$ in $L^2({\mathbb {R}}^d)$, namely $|{\varvec{T}}(t){\varvec{f}}|\le T_2(t)|{\varvec{f}}|$ for every $t>0$ and ${\varvec{f}}\in L^2({\mathbb {R}}^d; {\mathbb {R}}^m)$.

Proof

As in the proof of Theorem 4, we denote by ${{\mathfrak {a}}}_s$ the sesquilinear form ${{\mathfrak {a}}}$ in the scalar case. Observe that for every ${\varvec{u}}\in D ({{\mathfrak {a}}})$, by the formulas in (2) and using also the formula $\nabla |{\varvec{u}}|=|{\varvec{u}}|^{-1}\mathrm{Re} \sum _{j=1}^m (\nabla u_j)\overline{u_j}\chi _{\{{\varvec{u}}\not =0\}}$, we can show that $|{\varvec{u}}|$ belongs to $D({{\mathfrak {a}}}_s)$ and $\sum _{k=1}^m {{\mathfrak {q}}}(\nabla u_k, \nabla (|{\varvec{u}}|^{-1}u_k))\ge 0$. Moreover, for every $f\in D({{\mathfrak {a}}}_s)$, $|f| \mathrm{sign}({\varvec{u}})$ belongs to $D({{\mathfrak {a}}})$ if $|f|\le |{\varvec{u}}|$ and

$$\begin{aligned} \mathrm{Re}\,{{\mathfrak {a}}}({\varvec{u}}, |f| \mathrm{sign} ({\varvec{u}}))&= \mathrm{Re}\sum _{j=1}^m \int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla u_j, \nabla (|f| \mathrm{sign} (u_j)))\mathrm{d}x\\&\quad + \int _{{\mathbb {R}}^d}\langle V{\varvec{u}}, {\varvec{u}}|{\varvec{u}}|^{-1}|f|\rangle \mathrm{d}x \\&\ge \int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla |{\varvec{u}}|, \nabla |f|) \mathrm{d}x + \sum _{k=1}^m \int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla u_k, \nabla (|{\varvec{u}}|^{-1}u_k)) |f|\mathrm{d}x\\&\quad + \int _{{\mathbb {R}}^d}v|{\varvec{u}}| |f|\mathrm{d}x\\&\ge {{\mathfrak {a}}}_s(|{\varvec{u}}|, |f|). \end{aligned}$$

Thus, the assertion follows by applying [31, Theorem 2.30]. $\square$

4 Gaussian estimates

In this section we mainly focus on the scalar operator ${\mathcal A}_0-v I$, where ${{\mathcal {A}}}_0=\mathrm{div}(Q\nabla )$, assuming that Hypotheses 1 hold true for some $\gamma \in (0,2)$ and that condition (11) is satisfied. We prove a sharp Gaussian estimate for the kernel of the semigroup generated by ${\mathcal A}_0-v I$, with explicit control on the constants appearing. Based on this result, we will prove a Gaussian estimate for the kernel of the semigroup $({\varvec{T}}(t))_{t\ge 0}$.

In the scalar case, we adapt the arguments in [31, Chapter 6] to our situation in which the matrix Q is allowed to be unbounded. As a consequence, the Gaussian estimate will be expressed in terms of a distance associated with the diffusion term, namely

$$\begin{aligned} d_Q(x,y)=\sup \{|\psi (x)-\psi (y)|\mid \psi \in C_b({\mathbb {R}}^d) \cap C^1({\mathbb {R}}^d), \Vert {{\mathfrak {q}}}(\nabla \psi )\Vert _\infty \le 1\} \end{aligned}$$

for every $x,y\in {\mathbb {R}}^d$.

It is well known (see e.g. [10, Theorem 7]), that this distance is equivalent to the Euclidean metric if there exist two positive constants $q_0$ and $q_1$ such that $q_0|\xi |^2 \le \langle Q(x)\xi , \xi \rangle \le q_1|\xi |^2$ for every $\xi ,x\in {\mathbb {R}}^d$. In our case, only the inequality

$$\begin{aligned} d_Q(x,y) \le \frac{1}{\sqrt{q_0}}|x-y|, \qquad \;\, x,y\in {\mathbb {R}}^d, \end{aligned}$$

(12)

holds true in general. We will provide an example at the end of the section.

Theorem 7

Assume Hypotheses 1 for every $\gamma >0$ and condition (11) hold true. Then there exist positive constants $H_d$, $K_d$ and $c_d$, depending only on the dimension d, such that the kernel of the semigroup generated by $A_2$ in $L^2({\mathbb {R}}^d)$ satisfies the estimate

$$\begin{aligned} k(t,x,y) \le H_d q_0^{-\frac{\mathrm{d}}{2} } t^{-\frac{\mathrm{d}}{2}}e^{-v_0K_\mathrm{d} t} e^{-\frac{\mathrm{d}_Q(x,y)^2}{4t}} \bigg (1+\frac{c_dd_Q(x,y)^2}{8t}\bigg )^{\frac{\mathrm{d}}{2}} \end{aligned}$$

for all $t>0$ and almost every $x,\,y\in {{\mathbb {R}}}^d$.

Proof

Observe first that the semigroup generated by $A_2$ in $L^2({\mathbb {R}}^d)$ is positive. Hence $k(t,x,y)\ge 0$ for all $t>0$ and a.e. $x,\,y\in {{\mathbb {R}}}^d$. Define $W=\{ \psi \in C_b({{\mathbb {R}}})\cap C^1({\mathbb {R}}^d)\mid \Vert {{\mathfrak {q}}}(\nabla \psi )\Vert _\infty \le 1\}$ and observe that for every $\psi \in W$ and every $\rho \in {{\mathbb {R}}}$ it holds that $e^{\rho \psi }u\in D({{\mathfrak {a}}})$ for every $u\in D({{\mathfrak {a}}})$, where ${{\mathfrak {a}}}$ denotes the sesquilinear form associated with $-{{\mathcal {A}}}_0+vI$, i.e., the scalar version of the form ${{\mathfrak {a}}}$ in (9) and (10). Fix $\rho \in {{\mathbb {R}}}$, $\psi \in W$ and consider the form ${{\mathfrak {a}}}_{\rho , \psi }:D({{\mathfrak {a}}})\times D({{\mathfrak {a}}})\rightarrow {\mathbb {C}}$, defined by ${{{\mathfrak {a}}}}_{\rho , \psi }(u,w)={{\mathfrak {a}}}(e^{-\rho \psi }u, e^{\rho \psi }w)$ for every $u,w\in D({{\mathfrak {a}}})$. Straightforward computations show that

$$\begin{aligned} {{{\mathfrak {a}}}}_{\rho , \psi }(u,w)&= {{\mathfrak {a}}}(u,w)- \rho \int _{{\mathbb {R}}^d} {{\mathfrak {q}}}(\nabla \psi , \nabla w) u \mathrm{d}x \\&+\rho \int _{{\mathbb {R}}^d} {{\mathfrak {q}}}(\nabla u, \nabla \psi ) {\overline{w}} \mathrm{d}x - \rho ^2\int _{{\mathbb {R}}^d} {{\mathfrak {q}}}(\nabla \psi ) u{\overline{w}}\mathrm{d}x \end{aligned}$$

for every $u,w\in D({{\mathfrak {a}}})$. It follows that ${{\mathfrak {a}}}_{\rho , \psi }$ is continuous with respect to $\Vert \cdot \Vert _{{\mathfrak {a}}}$. Indeed, taking into account that ${{\mathfrak {a}}}$ is a continuous form, we can estimate

$$\begin{aligned} |{{\mathfrak {a}}}_{\rho , \psi }(u,w)|&\le |{{\mathfrak {a}}}(u,w)| + |\rho | \int _{{\mathbb {R}}^d} \big ( {{\mathfrak {q}}}(\nabla u)^{\frac{1}{2}} |w| + {{\mathfrak {q}}}(\nabla w)^\frac{1}{2} |u|\big ) \mathrm{d}x + \rho ^2\int _{{\mathbb {R}}^d}|u\Vert w| \mathrm{d}x \\&\le |{{\mathfrak {a}}}(u,w)|+\rho ^2 \Vert u\Vert _2\Vert w\Vert _2\\&\quad +|\rho | \int _{{\mathbb {R}}^d}( {{\mathfrak {q}}}(\nabla u)+|u|^2)^\frac{1}{2}({{\mathfrak {q}}}(\nabla w)+|w|^2)^\frac{1}{2}\mathrm{d}x\\&\le C\Vert u\Vert _{{\mathfrak {a}}}\Vert w\Vert _{{\mathfrak {a}}}\end{aligned}$$

for every $u, w\in D({{\mathfrak {a}}})$, where C is a positive constant not depending on u, w. Moreover, by observing that

$$\begin{aligned} \mathrm{Re}\,{{\mathfrak {a}}}_{\rho ,\psi }(u,u) = {{\mathfrak {a}}}(u,u) - \int _{{\mathbb {R}}^d} \rho ^2{{\mathfrak {q}}}(\nabla \psi ) |u|^2 \mathrm{d}x \ge {{\mathfrak {a}}}(u,u)-\rho ^2 \Vert u\Vert _2^2, \end{aligned}$$

(13)

we get that ${{\mathfrak {a}}}_{\rho , \psi }$ is closed and quasi-accretive. Therefore, the opposite of the operator associated with ${{\mathfrak {a}}}_{\rho , \psi }$ generates a $C_0$-semigroup $(T^{\rho , \psi }(t))$ on $L^2({\mathbb {R}}^d, {\mathbb {C}})$. An easy calculation shows that $T^{\rho , \psi }(t)(\cdot )=e^{\rho \psi }T_2(t)(e^{-\rho \psi }\cdot )$ for $t\ge 0$, where $(T_2(t))_{t\ge 0}$ is the (contraction) $C_0$-semigroup associated with ${{\mathfrak {a}}}$ on $L^2({\mathbb {R}}^d, {\mathbb {C}})$.

We need to estimate the norm $\Vert T^{\rho , \psi }(t)\Vert _{1\rightarrow \infty }$ and we do this through several steps.

Step 1. Here, we show that, for every $p\in [2,\infty )$ and $t\ge 0$, the operator $T^{\rho , \psi }(t)$ is bounded on $L^p({\mathbb {R}}^d, {\mathbb {C}})$ and

$$\begin{aligned} \Vert T^{\rho , \psi }(t)\Vert _{p\rightarrow p}\le e^{-\alpha _{p,\rho }t},\qquad \;\, t\ge 0, \end{aligned}$$

(14)

where

$$\begin{aligned} \alpha _{q,\rho }= \frac{2v_0}{q}-\bigg (q+\frac{4}{ q} +1\bigg )\rho ^2,\qquad \;\,q\ge 2. \end{aligned}$$

(15)

This step is a bit trickier. To prove estimate (14) we decompose the form ${{\mathfrak {a}}}_{\rho ,\psi }$ into the sum of two forms, say ${\mathfrak {b}}_{\rho ,\psi }$ and $\widetilde{{\mathfrak {b}}}_{\rho ,\psi }$, which are defined on $D({{\mathfrak {a}}})\times D({{\mathfrak {a}}})$ as follows:

$$\begin{aligned} {\mathfrak {b}}_{\rho ,\psi }(u,w)&=\frac{1}{2} \int _{{\mathbb {R}}^d} {{\mathfrak {q}}}(\nabla u, \nabla w) \mathrm{d}x -\rho \int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla \psi ,\nabla (\overline{u}w))\mathrm{d}x+\frac{1}{2} \int _{{\mathbb {R}}^d}v u {\overline{w}} \mathrm{d}x \end{aligned}$$

and

$$\begin{aligned} \widetilde{{\mathfrak {b}}}_{\rho ,\psi }(u,w)&= \frac{1}{2} \int _{{\mathbb {R}}^d} {{\mathfrak {q}}}(\nabla u, \nabla w) \mathrm{d}x +2\rho \int _{{\mathbb {R}}^d} {{\mathfrak {q}}}(\nabla u, \nabla \psi ) {\overline{w}} \mathrm{d}x\\&\quad +\frac{1}{2} \int _{{\mathbb {R}}^d}v u {\overline{w}} \mathrm{d}x-\rho ^2\int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla \psi )u{\overline{w}}\mathrm{d}x \end{aligned}$$

for $u,w\in D({{\mathfrak {a}}})$. We prove that we can associate two semigroups $(T^{\rho ,\psi }_1(t))_{t\ge 0}$ and $(S^{\rho ,\psi }(t))_{t\ge 0}$ with these forms and they satisfy the estimates

$$\begin{aligned}&\Vert T^{\rho ,\psi }_1(t)\Vert _{p\rightarrow p}\le e^{\left( p\rho ^2 - \frac{v_0}{p}\right) t},\qquad \;\,t>0, \end{aligned}$$

(16)

$$\begin{aligned}&\Vert S^{\rho ,\psi }(t)\Vert _{p\rightarrow p} \le e^{-\frac{v_0}{p} t}e^{\rho ^2\left( \frac{4}{p} +1\right) t},\qquad \;\,t>0. \end{aligned}$$

(17)

Applying the Trotter product formula, we can write

$$\begin{aligned} T^{\rho ,\psi }(t)f=\lim _{n\rightarrow \infty }\bigg (T^{\rho ,\psi }_1\bigg (\frac{t}{n}\bigg ) \circ S^{\rho ,\psi }\bigg (\frac{t}{n}\bigg )\bigg )^n f,\qquad \;\,f\in L^p({\mathbb {R}}^d), \end{aligned}$$

so that, using (16) and (17), estimate (14) easily follows.

For every $z\in {\mathbb {C}}$, consider the form ${{\mathfrak {b}}}_{\rho z,\psi }:D({{\mathfrak {a}}})\times D({{\mathfrak {a}}})\rightarrow {\mathbb {C}}$ which is defined as the form ${{\mathfrak {b}}}_{\rho ,\psi }$, with $\rho$ being replaced by $\rho z$. Clearly ${{\mathfrak {b}}}_{\rho z,\psi }$ is densely defined, continuous with respect to $\Vert \cdot \Vert _{{\mathfrak {a}}}$ (this can be proved adapting the argument used to prove the continuity of the form ${{\mathfrak {a}}}_{\rho , \psi }$). Moreover, it is closed and quasi-accretive since for every $u\in D({{\mathfrak {a}}})$

$$\begin{aligned} \mathrm{Re}\,{{\mathfrak {b}}}_{\rho z,\psi }(u,u)=&\,\frac{1}{2} \int _{{\mathbb {R}}^d} {{\mathfrak {q}}}(\nabla u)\mathrm{d}x\nonumber \\&-\rho \mathrm{Re}\bigg (z \int _{{\mathbb {R}}^d} {{\mathfrak {q}}}(\nabla \psi ,{\overline{u}}\nabla u + u\nabla {\overline{u}} )\mathrm{d}x\bigg ) + \frac{1}{2} \int _{{\mathbb {R}}^d}v|u|^2 \mathrm{d}x\nonumber \\ \ge&\,\frac{1}{2} \int _{{\mathbb {R}}^d} {{\mathfrak {q}}}(\nabla u) \mathrm{d}x - 2 |\mathrm{Re}\,z\rho | \int _{{\mathbb {R}}^d} {{\mathfrak {q}}}(\nabla u)^\frac{1}{2}|u|\mathrm{d}x +\frac{1}{2} \int _{{\mathbb {R}}^d}v|u|^2 \mathrm{d}x\nonumber \\ \ge&\,\bigg (\frac{1}{2}-\varepsilon \bigg )\int _{{\mathbb {R}}^d} {{\mathfrak {q}}}(\nabla u) \mathrm{d}x - \varepsilon ^{-1}|\mathrm{Re}z|^2 \rho ^2 \Vert u\Vert _2^2 +\frac{1}{2} \int _{{\mathbb {R}}^d} v|u|^2 \mathrm{d}x \end{aligned}$$

(18)

for every $\varepsilon >0$. Taking $\varepsilon =1/4$, we deduce that

$$\begin{aligned} \mathrm{Re}\,{\mathfrak {b}}_{\rho z,\psi }(u,u)\ge \frac{1}{4} {{\mathfrak {a}}}(u,u) - 4|\mathrm{Re}z|^2 \rho ^2 \Vert u\Vert _2^2, \end{aligned}$$

so that the opposite of the operator associated with $b_\rho (z)$ generates a $C_0$-semigroup $(T^{\rho ,\psi }_z(t))_{t\ge 0}$ in $L^2({\mathbb {R}}^d,{\mathbb {C}})$. On the other hand, taking $\varepsilon =1/2$ yields

$$\begin{aligned} \mathrm{Re}\,{\mathfrak {b}}_{\rho z,\psi }(u,u)\ge \bigg (\frac{v_0}{2} -2{|\mathrm Re}z|^2 \rho ^2\bigg )\Vert u\Vert _2^2, \end{aligned}$$

which implies that $\Vert T^{\rho ,\psi }_z(t)\Vert _{2\rightarrow 2}\le e^{(2|\mathrm{Re}z |^2 \rho ^2-\frac{v_0}{2}) t}$ for every $t>0$.

Now, we prove that the semigroups $(T^{\rho ,\psi }_{is}(t))_{t\ge 0}$ are $L^\infty$-contractive for every $s\in {{\mathbb {R}}}$. By [31, Theorem 2.15], it suffices to show that the function $(|u|\wedge 1)\mathrm{sign}(u)$ belongs to $D({{\mathfrak {a}}})$ for every $u\in D({{\mathfrak {a}}})$ and

$$\begin{aligned} \mathrm{Re}\,{\mathfrak {b}}_{i\rho s,\psi }((|u|\wedge 1)\mathrm{sign}(u), (|u|-1)^+\mathrm{sign}(u))\ge 0. \end{aligned}$$

(19)

Indeed, observe that for every $u\in D({{\mathfrak {a}}})$, $(|u|\wedge 1)\mathrm{sign}(u)\in W^{1,2}_\mathrm{loc}({\mathbb {R}}^d, {\mathbb {C}})$ (see e.g. [31, Proposition 4.11]) and

$$\begin{aligned} \nabla ((|u|\wedge 1)\mathrm{sign}(u))= \frac{i \mathrm{Im}(\mathrm{sign}({\overline{u}})\nabla u)}{|u|} \mathrm{sign}(u) \chi _{\{|u|>1\}} + \chi _{\{|u|\le 1\}}\nabla u . \end{aligned}$$

It then follows that ${{\mathfrak {q}}}(\nabla ((|u|\wedge 1)\mathrm{sign}(u)))^{\frac{1}{2}}$, $v^{\frac{1}{2} } (|u|\wedge 1)\mathrm{sign}(u)$ belong to $L^2({\mathbb {R}}^d, {\mathbb {C}})$, and therefore $(|u|\wedge 1)\mathrm{sign}(u)\in D({{\mathfrak {a}}})$. Consequently, $(|u|-1)^+\mathrm{sign}(u) =u- (|u|\wedge 1) \mathrm{sign}(u)\in D({{\mathfrak {a}}})$ and

$$\begin{aligned} \nabla ((|u|-1)^+\mathrm{sign}(u))= \left( \nabla u- \frac{i \mathrm{Im}( \mathrm{sign}({\overline{u}})\nabla u)}{|u|} \mathrm{sign}(u)\right) \chi _{\{|u|>1\}}. \end{aligned}$$

Based on the above remarks, we can write

$$\begin{aligned}&\mathrm{Re}\,b_{i\rho s,\psi }\big ( (|u|\wedge 1)\mathrm{sign}(u), (|u|-1)^+\mathrm{sign}(u)\big )\nonumber \\&\quad =\frac{1}{2} \mathrm{Re} \int _{|u|>1} \bigg (Q \frac{ i\mathrm{Im}( \mathrm{sign}({\overline{u}})\nabla u)}{|u|} \mathrm{sign}(u)\bigg )\cdot \bigg ( \frac{i \mathrm{Im}( \mathrm{sign}({\overline{u}})\nabla u)}{|u|} \mathrm{sign} ({\overline{u}})\bigg )\mathrm{d}x\nonumber \\&\qquad +\frac{1}{2} \mathrm{Re} \int _{|u|>1} Q \frac{i \mathrm{Im}\, ( \mathrm{sign}({\overline{u}})\nabla u)}{|u|}\cdot \overline{\mathrm{sign}( {\overline{u}})\nabla u}\, \mathrm{d}x +\frac{1}{2} \int _{|u|>1}v(|u|-1) \mathrm{d}x\nonumber \\&\quad =\frac{1}{2} \int _{|u|>1} Q \frac{\mathrm{Im}\, ( \mathrm{sign}({\overline{u}})\nabla u)}{|u|} \mathrm{sign}(u)\cdot \bigg ( \frac{\mathrm{Im}\, ( \mathrm{sign}({\overline{u}})\nabla u)}{|u|} \mathrm{sign} ({\overline{u}})\bigg )(|u|-1)\mathrm{d}x\nonumber \\&\qquad + \frac{1}{2} \int _{|u|>1}v(|u|-1) \mathrm{d}x \ge 0, \end{aligned}$$

(20)

where $\xi \cdot \eta =\sum _{i=1}^d\xi _i\eta _i$ for every $\xi ,\eta \in {\mathbb {C}}^d$. This proves (19). Moreover, by [21, Theorems VII-4.2, IX-2.6], the operators $T^{\rho ,\psi }_z(t)$ depend analytically on z for every $t\ge 0$. Hence we can apply Stein’s interpolation theorem and, by interpolating the $L^2$- and $L^\infty$-estimates, we get

$$\begin{aligned} \Vert T^{\rho ,\psi }_{\frac{2}{p}}(t)\Vert _{p\rightarrow p}\le e^{\left( \frac{4}{p} \rho ^2-\frac{v_0}{p}\right) t},\qquad \;\,t>0, \end{aligned}$$

(21)

for every $p\ge 2$. Since ${\mathfrak {b}}_{\rho ,\psi }={\mathfrak {b}}_{\frac{2}{p}{\widetilde{\rho }},\psi }$, where ${\widetilde{\rho }}=\frac{p}{2}\rho$, we conclude that $T^{\rho ,\psi }_1(t)=T^{{\widetilde{\rho }},\psi }_{\frac{2}{p}}(t)$ for every $t>0$ and estimate (16) follows at once from (21).

Next, we consider the form $\widetilde{{\mathfrak {b}}}_{\rho ,\psi }:D({{\mathfrak {a}}})\times D({{\mathfrak {a}}})\rightarrow {\mathbb {C}}$, which is densely defined and continuous with respect to $\Vert \cdot \Vert _{{\mathfrak {a}}}$. Moreover, using Cauchy-Schwartz inequality as in (18), we can estimate

$$\begin{aligned} \widetilde{{\mathfrak {b}}}_{\rho ,\psi }(u,u)&\ge \frac{1}{2} \int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla u) \mathrm{d}x - 2|\rho |\int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla \psi )^\frac{1}{2} {{\mathfrak {q}}}(\nabla u)^\frac{1}{2} |u|\mathrm{d}x+\frac{1}{2} \int _{{\mathbb {R}}^d}v |u|^2 \mathrm{d}x\\&\quad -\rho ^2\int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla \psi )|u|^2\mathrm{d}x\\&\ge \bigg (\frac{1}{2}-\varepsilon \bigg )\int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla u) \mathrm{d}x-\bigg (1+\frac{1}{\varepsilon }\bigg )\rho ^2\int _{{\mathbb {R}}^d}|u|^2\mathrm{d}x+ \frac{1}{2} \int _{{\mathbb {R}}^d}v |u| \mathrm{d}x \end{aligned}$$

for every $u\in D({{\mathfrak {a}}})$ and $\varepsilon >0$. Taking $\varepsilon =1/4$ and $\varepsilon =1/2$, we get

$$\begin{aligned} \widetilde{{\mathfrak {b}}}_{\rho ,\psi }(u,u)\ge \frac{1}{4}{{\mathfrak {a}}}(u,u)-5\rho ^2\int _{{\mathbb {R}}^d}|u|^2\mathrm{d}x, \end{aligned}$$

so that $\widetilde{{\mathfrak {b}}}_{\rho ,\psi }$ is closed and quasi-accretive too and the opposite of its associated operator generates a $C_0$-semigroup $(S^{\rho ,\psi }(t))_{t\ge 0}$ in $L^2({\mathbb {R}}^d, {\mathbb {C}})$, and

$$\begin{aligned} \widetilde{{\mathfrak {b}}}_{\rho ,\psi }(u,u)\ge \Big (\frac{v_0}{2}-3\rho ^2\Big )\int _{{\mathbb {R}}^d}|u|^2 \mathrm{d}x, \end{aligned}$$

which shows that $\Vert S^{\rho ,\psi }(t)\Vert _{2\rightarrow 2} \le e^{(3\rho ^2-v_0/2) t}$ for every $t>0$.

Arguing as in the proof of (20) we can show that

$$\begin{aligned}&\mathrm{Re}\, \widetilde{{\mathfrak {b}}}_{\rho ,\psi }\big ( (|u|\wedge 1)\mathrm{sign}(u), (|u|-1)^+\mathrm{sign}(u)\big )\\&\quad =\frac{1}{2} \int _{|u|>1}Q \frac{\mathrm{Im}\, ( \mathrm{sign}({\overline{u}}) \nabla u)}{|u|} \mathrm{sign}(u)\cdot \bigg ( \frac{\mathrm{Im}\,( \mathrm{sign}({\overline{u}}) \nabla u)}{|u|} \mathrm{sign }({\overline{u}})\bigg )(|u|-1)\mathrm{d}x \\&\qquad + \frac{1}{2} \int _{|u|>1}v(|u|-1) \mathrm{d}x -\rho ^2 \int _{|u|>1} (|u|-1) \mathrm{d}x\\&\quad \ge -\rho ^2 \int _{|u|>1} (|u|-1) \mathrm{d}x \end{aligned}$$

for every $u\in D({{\mathfrak {a}}})$ Therefore, the semigroup $(e^{-\rho ^2 t }S^{\rho ,\psi }(t))_{t\ge 0}$ is $L^\infty$-contractive by [31, Theorem 2.15]. Hence, by interpolating between $L^2$ and $L^\infty$ using Riesz-Thorin’s theorem, estimate (17) easily follows.

Step 2. Here, we prove the following properties:

• (1) if $d\ge 3$, then $T^{\rho ,\psi }:L^2({\mathbb {R}}^d) \rightarrow L^{2^*}({\mathbb {R}}^d)$ continuously and

  $$\begin{aligned} \Vert T^{\rho ,\psi }(t)\Vert _{2\rightarrow 2^*} \le \sqrt{\frac{C_d}{2q_0}}t^{-\frac{1}{2}}e^{-\alpha _{2^*,\rho }t},\qquad \;\,t>0, \end{aligned}$$

  (22)

  where $2^*=2d(d-2)^{-1}$ and $C_d$ is the Sobolev constant such that $\Vert u\Vert _{2^*}\le C_d \Vert \nabla u\Vert _2$ for every $u\in W^{1,2}({\mathbb {R}}^d)$;

• (2) if $d\le 2$, then $T^{\rho ,\psi }(t): L^2({\mathbb {R}}^d) \rightarrow L^{q}({\mathbb {R}}^d)$ continuously for every $q> 2$ and there exists a positive constant $C_q$ such that

  

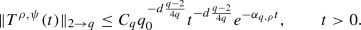  (23)

Let us begin by proving (22). Using Sobolev’s inequality, we can estimate

$$\begin{aligned} {{\mathfrak {a}}}_{\rho , \psi }(u,u)\ge \int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla u) \mathrm{d}x -(\rho ^2-v_0)\Vert u\Vert _2^2\ge \frac{q_0}{C_d} \Vert u\Vert _{2^*}^2- (\rho ^2-v_0)\Vert u\Vert _2^2 \end{aligned}$$

(24)

for every real-valued function $u\in D({{\mathfrak {a}}})\subseteq W^{1,2}({\mathbb {R}}^d)$. By Step 1, $T^{\rho , \psi }(t)$ maps $L^{2^*}({\mathbb {R}}^d)$ into itself and $\Vert T^{\rho , \psi }(t)\Vert _{2^*\rightarrow 2^*}\le e^{-\alpha _{2^*,\rho }t}$. For every $f\in L^2({\mathbb {R}}^d) \cap L^{2^*}({\mathbb {R}}^d)$, we set $\nu (t)=\Vert e^{\alpha _{2^*,\rho }t} T^{\rho , \psi }(t)f\Vert ^2_{2^*}$ for $t\ge 0$. The function $\nu$ is decreasing since $(e^{\alpha _{2^*,\rho }t}T^{\rho , \psi }(t))_{t\ge 0}$ is a contraction semigroup on $L^{2^*}({\mathbb {R}}^d)$, and therefore, taking (24) into account and observing that $\alpha _{2^*,\rho }+\rho ^2-v_0<0$, we get

$$\begin{aligned} t\nu (t)&\le \int _0^t \nu (s) \mathrm{d}s\\&\le \frac{C_d}{q_0}\bigg [\int _0^t {{\mathfrak {a}}}_{\rho , \psi }(e^{\alpha _{2^*,\rho }s}T^{\rho , \psi }(s)f,e^{\alpha _{2^*,\rho }s}T^{\rho , \psi }(s)f) \mathrm{d}s \!+\!(\rho ^2\!-\!v_0) \int _0^t\nu (s)\mathrm{d}s\bigg ]\\&= \frac{C_d}{q_0} \bigg [-\frac{1}{2}\int _0^te^{2\alpha _{2^*,\rho }s}\frac{\mathrm{d}}{\mathrm{d}s}\Vert T^{\rho , \psi }(s)f\Vert _2^2 \mathrm{d}s+(\rho ^2-v_0) \int _0^t\nu (s)\mathrm{d}s\bigg ]\\&= \frac{C_d}{q_0}\bigg [(\alpha _{2^*,\rho }+\rho ^2-v_0) \int _0^t\nu (s)\mathrm{d}s-\frac{1}{2}\int _0^t\nu '(s)\mathrm{d}s\bigg ] \\&\le \frac{C_d}{2q_0}\Vert f\Vert ^2_2 \end{aligned}$$

for every $t>0$. Estimate (22) easily follows.

If $d\le 2$, then, by the Gagliardo–Nirenberg interpolation inequality, for every $q> 2$ (which implies that $0<d\frac{q-2}{2q}<1$) there exists a positive constant $c_{q}>0$ such that, for every real-valued function $u\in D({{\mathfrak {a}}})\subseteq W^{1,2}({\mathbb {R}}^d)$,

$$\begin{aligned} c_{q} \Vert u\Vert _q\le \Vert u\Vert _2^{1-d\frac{q-2}{2q}}\Vert \nabla u\Vert _2^{d\frac{q-2}{2q}}, \end{aligned}$$

or equivalently

$$\begin{aligned} \Vert \nabla u\Vert _2^2\Vert u\Vert _2^{\frac{4q}{d(q-2)}-2} \ge c'_q \Vert u\Vert _q^{\frac{4q}{d(q-2)}}, \end{aligned}$$

where $c'_q=c_q^{\frac{4q}{d(q-2)}}$. Hence, taking (13) into account, we can write

$$\begin{aligned} {{\mathfrak {a}}}_{\rho , \psi }(u,u)\Vert u\Vert _2^{\frac{4q}{d(q-2)}-2}&\ge \Vert u\Vert _2^{\frac{4q}{d(q-2)}-2}\bigg (\int _{{\mathbb {R}}^d}{{\mathfrak {q}}}(\nabla u) \mathrm{d}x -(\rho ^2-v_0)\Vert u\Vert _2^2\bigg ) \nonumber \\&\ge q_0\Vert u\Vert _2^{\frac{4q}{d(q-2)}-2} \Vert \nabla u\Vert _2^2 - (\rho ^2-v_0)\Vert u\Vert _2^{\frac{4q}{d(q-2)}}\nonumber \\&\ge q_0 c_q'\Vert u\Vert _2^{\frac{4q}{d(q-2)}} -(\rho ^2-v_0)\Vert u\Vert _2^{\frac{4q}{d(q-2)}} . \end{aligned}$$

(25)

By Step 1, $\Vert T^{\rho , \psi }(t)\Vert _{q\rightarrow q}\le e^{-\alpha _{q,\rho }t}$, where $\alpha _{q,\rho }$ is given by (15). Hence, the function $\nu _q(t)=\Vert e^{\alpha _{q,\rho }t} T^{\rho , \psi }(t)f\Vert _{q}$ for $t\ge 0$, is decreasing for every $f\in L^2({\mathbb {R}}^d) \cap L^{q}({\mathbb {R}}^d)$ and, therefore, taking (25) into account, setting $\nu _{2,q}(t)=\Vert e^{\alpha _{q,\rho }t} T^{\rho , \psi }(t)f\Vert _2^2$ for every $t>0$ and arguing as in the case $d\ge 3$, we can show that

$$\begin{aligned} t\nu _q (t)^{\frac{4q}{d(q-2)}}&\le \frac{1}{c_q' q_0}\int _0^t \bigg [{{\mathfrak {a}}}_{\rho , \psi }(e^{\alpha _{q,\rho }s} T^{\rho , \psi }(s)f, e^{\alpha _{q,\rho }s} T^{\rho , \psi }(s)f ) \!+\!(\rho ^2\!-\!v_0)\nu _{2,q}(s)^2\bigg ]\\&~~~~~~~~\;\,\times \nu _{2,q}(s)^{\frac{2q}{\mathrm{d}(q-2)}-2} \mathrm{d}s\\&\le \frac{1}{c_q' q_0}\Vert f\Vert _2^{\frac{4q}{d(q-2)}-2} \int _0^t \bigg [{{\mathfrak {a}}}_{\rho , \psi }(e^{\alpha _{q,\rho }s} T^{\rho , \psi }(s)f, e^{\alpha _{q,\rho }s} T^{\rho , \psi }(s)f) \\&+(\rho ^2-v_0)\nu _{2,q}(s)\bigg ]\mathrm{d}s \\&\le \frac{1}{c_q' q_0}\Vert f\Vert _2^{\frac{4q}{d(q-2)}-2} \bigg [-\frac{1}{2}\int _0^t e^{2\alpha _{q,\rho }s} \frac{\mathrm{d}}{\mathrm{d}s}\Vert T^{\rho , \psi }(s)f\Vert _2^2 \mathrm{d}s\\&~~~~~~~~~~~~~~~~~~~~~+ (\rho ^2-v_0) \int _0^t\nu _{2,q}(s)\mathrm{d}s\bigg ]\\&= \frac{1}{c_q' q_0}\Vert f\Vert _2^{\frac{4q}{d(q-2)}-2} \bigg [\frac{1}{2}\Vert f\Vert _2^2\!-\!\frac{1}{2}\nu _{2,q}(t)\!+\!(\alpha _{q,\rho } \!+\!\rho ^2\!-\!v_0) \int _0^t\nu _{2,q}(s)\mathrm{d}s\bigg ]\\&\le \frac{1}{2c_q' q_0}\Vert f\Vert _2^{\frac{4q}{d(q-2)}} \end{aligned}$$

for every $t>0$. Estimate (23) follows since $\alpha _{q,\rho }+\rho ^2-v_0<0$.

Step 3. In this part we prove that there exist strictly positive constants $K_d, M_d, c_d$, depending only on d, such that for every $\rho \in {{\mathbb {R}}},\, \psi \in W$

$$\begin{aligned} \Vert T^{\rho , \psi }(t)\Vert _{2\rightarrow \infty } \le M_d q_0^{-\frac{d}{4} } t^{-\frac{d}{4}}e^{-v_0K_d t}e^{ \rho ^2 t} (1+c_d\rho ^2 t)^{\frac{d}{4}},\qquad \;\, t>0. \end{aligned}$$

(26)

If $d\ge 3$, then we interpolate between the estimates (14) and (22) to get

$$\begin{aligned} \Vert T^{\rho , \psi }(t)\Vert _{p\rightarrow \frac{pd}{d-1}}&\le \Vert T^{\rho , \psi }(t)\Vert _{2 \rightarrow 2^*}^{\frac{1}{p}} \Vert T^{\rho , \psi }(t)\Vert _{2(p-1) \rightarrow 2(p-1)}^{1-\frac{1}{p}}\\&\le \left( \sqrt{\frac{C_d}{2q_0}}t^{-\frac{1}{2}}e^{-\alpha _{2^*,\rho }t}\right) ^{\frac{1}{p}} \left( e^{-\alpha _{2(p-1),\rho }t}\right) ^{1-\frac{1}{p}}\\&=\left( \frac{C_d}{2q_0}\right) ^{\frac{1}{2p}} t^{-\frac{1}{2p}}e^{-\frac{v_0}{p}\left( \frac{2}{2^*}+1\right) t}e^{\rho ^2 \left( \frac{ 1}{p}\left( 2^*+\frac{4}{2^*}+1\right) + \frac{2(p-1)^2}{p} + 1 + \frac{1}{p}\right) t}. \end{aligned}$$

By applying the same bootstrap argument as in [31, Theorem 6.8], one gets that there exist positive constants $B_d$, $K_d$ and $c_d$ such that

Since $\Vert T^{\rho , \psi }(t)\Vert _{2\rightarrow 2} \le e^{\rho ^2 t}$ for every $t>0$, by (13), [31, Lemma 6.5] applied to the semigroup $(e^{-v_0 K_d t}T^{\rho , \psi }(t))_{t\ge 0}$ yields that

The assertion follows by taking $M_d=2^{-\frac{\mathrm{d}}{4}}C_d^{\frac{\mathrm{d}}{4}}B_d$.

If $d\le 2$, we fix a number $r>2$ and we apply Step 2 with $q=\frac{2r}{r-2}$. Hence

$$\begin{aligned} \Vert T^{\rho , \psi }(t)\Vert _{2\rightarrow q} \le \sqrt{\frac{C_q}{2q_0}} t^{-d\frac{q-2}{4q}}e^{-\alpha _{q,\rho }t},\qquad \;\, t>0. \end{aligned}$$

The same bootstrap argument as in the case $d\ge 3$ gives the assertion.

Step 4. Finally, we prove that

$$\begin{aligned} \Vert T^{\rho , \psi }(t)\Vert _{1\rightarrow \infty } \le H_d q_0^{-\frac{\mathrm{d}}{2} } t^{-\frac{\mathrm{d}}{2}}e^{-v_0K_d t}e^{ \rho ^2 t}\bigg (1+\frac{c_d}{2}\rho ^2 t\bigg )^{\frac{\mathrm{d}d}{2}},\qquad \;\, t>0, \end{aligned}$$

(27)

for some strictly positive constant $H_d$ depending only on d.

It is immediate to check that ${{\mathfrak {a}}}^{ \rho ,\psi }(w,u) = \overline{{{\mathfrak {a}}}^{ -\rho , \psi }(u,w)}$ for every $u, w\in D({{\mathfrak {a}}})$. Hence the adjoint operator of $T^{\rho , \psi }(t)$ is $T^{-\rho , \psi }(t)$ for every $t>0$ and, therefore,

$$\begin{aligned} \Vert T^{\rho , \psi }(t)\Vert _{1\rightarrow 2} \le M_d q_0^{-\frac{\mathrm{d}}{4}} t^{-\frac{d}{4}}e^{-v_0K_d t}e^{ \rho ^2 t} (1+c_d\rho ^2 t)^{\frac{d}{4}},\qquad \;\, t>0. \end{aligned}$$

From this estimate and (26), estimate (27) follows, with $H_d=2^{d/2}M_d^2$, if we write $\Vert T^{\rho , \psi }(t)\Vert _{1\rightarrow \infty } \le \Vert T^{\rho , \psi }(t/2)\Vert _{2\rightarrow \infty }\Vert T^{\rho , \psi }(t/2)\Vert _{1\rightarrow 2}$.

Now, we have all the tools to prove the assertion of the theorem. By (27), the kernel of $T^{\rho , \psi }(t)$ satisfies the estimate

$$\begin{aligned} 0\le e^{\rho \psi (x)} k(t,x,y)e^{-\rho \psi (y)} \le H_d q_0^{-\frac{\mathrm{d}}{2} } t^{-\frac{\mathrm{d}}{2}}e^{-v_0K_d t}e^{ \rho ^2 t}\bigg (1+\frac{c_d}{2}\rho ^2 t\bigg )^{\frac{\mathrm{d}}{2}} \end{aligned}$$

for every $t>0$, where k is the heat kernel of the semigroup $(T(t))_{t\ge 0}$ and therefore

$$\begin{aligned} k(t,x,y) \le H_d q_0^{-\frac{\mathrm{d}}{2} } t^{-\frac{\mathrm{d}}{2}}e^{-v_0K_d t}e^{\rho (\psi (y)-\psi (x))}e^{ \rho ^2 t}\bigg (1+\frac{c_d}{2}\rho ^2 t\bigg )^{\frac{\mathrm{d}}{2}},\qquad \;\, t>0. \end{aligned}$$

Minimizing the sum $\rho ^2t+\rho (\psi (y)-\psi (x))$ with respect to $\rho >0$, i.e., taking $\rho =(2t)^{-1}(\psi (x)-\psi (y))$, we get

$$\begin{aligned} k(t,x,y)&\le H_d q_0^{-\frac{\mathrm{d}}{2} } t^{-\frac{\mathrm{d}}{2}}e^{-v_0K_d t} e^{-\frac{(\psi (y)-\psi (x))^2}{4t}} \bigg (1+\frac{c_d(\psi (x)-\psi (y))^2}{8t}\bigg )^{\frac{\mathrm{d}}{2}}\\&\le H_d q_0^{-\frac{\mathrm{d}}{2} } t^{-\frac{\mathrm{d}}{2}}e^{-v_0K_d t} e^{-\frac{(\psi (y)-\psi (x))^2}{4t}} \bigg (1+\frac{c_dd_Q(x,y)^2}{8t}\bigg )^{\frac{\mathrm{d}}{2}} \end{aligned}$$

for every $t>0$. The assertion follows by minimizing over $\psi$. $\square$

Example 1

Let Q(x) be a diagonal matrix for every $x\in {\mathbb {R}}^d$, where $q_{ii}(x)=a_i(x_i)$ and $a_i\in C^1({{\mathbb {R}}})$ has positive infimum over ${\mathbb {R}}^d$ for every $i=1,\ldots ,d$. Set

$$\begin{aligned} \sigma _i(t)=\int _0^t \frac{1}{\sqrt{a_i(s)}}ds, \qquad \;\, i=1, \ldots , d,\;\, t\in {{\mathbb {R}}}, \end{aligned}$$

and $\sigma (x)=(\sigma _1(x_1), \dots , \sigma _n(x_n))$ for every $x\in {\mathbb {R}}^d$. Given $\phi \in C_b({\mathbb {R}}^d) \cap C^1({\mathbb {R}}^d)$ such that $\Vert \nabla \phi \Vert _\infty \le 1$, set $\psi = \phi \circ \sigma$. Then $\psi \in C_b({\mathbb {R}}^d) \cap C^1({\mathbb {R}}^d)$ and

$$\begin{aligned} {{\mathfrak {q}}}(\nabla \psi )(x)= \sum _{i=1}^da_i(x_i) (D_i\psi (x))^2 = \sum _{i=1}^d|D_i\phi (\sigma (x))|^2 \le 1,\qquad \;\, x\in {\mathbb {R}}^d. \end{aligned}$$

It follows that

$$\begin{aligned} d_Q(x,y)&=\sup \{|\psi (x)-\psi (y)|\mid \psi \in C_b({\mathbb {R}}^d) \cap C^1({\mathbb {R}}^d), \, {{\mathfrak {q}}}(\nabla \psi ) \le 1\}\\&\ge \sup \{ |\phi (\sigma (x))-\phi (\sigma (y))|\mid \phi \in C_b({\mathbb {R}}^d) \cap C^1({\mathbb {R}}^d), \Vert \nabla \phi \Vert _\infty \le 1\} \\&\ge |\sigma (x)-\sigma (y)|,\quad x,y\in {\mathbb {R}}^d. \end{aligned}$$

The last inequality is obtained by considering the function $\phi _{\varepsilon ,y}:{\mathbb {R}}^d\rightarrow {{\mathbb {R}}}$, defined by

$$\begin{aligned} \phi _{\varepsilon ,y}(x)=\frac{\sqrt{\varepsilon +|x-\sigma (y)|^2}}{1+\varepsilon \sqrt{\varepsilon +|x-\sigma (y)|^2}},\qquad \;\,x\in {\mathbb {R}}^d, \end{aligned}$$

for fixed $y\in {\mathbb {R}}^d$ and letting $\varepsilon \rightarrow 0$. Taking (12) into account, the Gaussian estimate becomes, in this case,

$$\begin{aligned} k(t,x,y) \le H_d q_0^{-\frac{\mathrm{d}}{2}} t^{-\frac{\mathrm{d}}{2}}e^{-v_0K_d t}e^{-\frac{ |\sigma (x)-\sigma (y)|^2}{4t}} \bigg (1+\frac{c_d}{q_0} \frac{|x-y|^2}{8t} \bigg )^{\frac{\mathrm{d}}{2}},\quad \;\, t>0. \end{aligned}$$

As a concrete example, we take $a_i(s)=1+s^2$ for every $s\in {{\mathbb {R}}}$ and $i=1,\ldots ,d$, and obtain that $\sigma _i(t)=\log (t+\sqrt{1+t^2})$ for every $t\in {{\mathbb {R}}}$.

As an immediate consequence of Proposition 2, Theorem 6 and Theorem 7, we can prove the following Gaussian type estimates for the matrix-valued kernel K which generalizes Theorem 5.4 in [25].

Corollary 1

Under the assumptions of Theorem 6, there exist constants $H_d$, $K_d$, $c_d>0$, depending only on the dimension d, such that

$$\begin{aligned} |k_{ij}(t,x,y)| \le H_d q_0^{-\frac{\mathrm{d}}{2}} t^{-\frac{\mathrm{d}}{2}}e^{-v_0K_d t} e^{-\frac{\mathrm{d}_Q(x,y)^2}{4t}} \bigg (1+\frac{c_dd_Q(x,y)^2}{8t}\bigg )^{\frac{\mathrm{d}}{2}} \end{aligned}$$

for every $t>0$, $i,j=1,\ldots ,m$ and almost every $x,y\in {\mathbb {R}}^d$.

Proof

From the proof of Theorem 6, we know that

$$\begin{aligned} {\varvec{T}}(t){\varvec{f}}=\sum \limits _{i,j=1}^mT_{ij}(t)(f_j){\varvec{e}}_i,\qquad \;\, {\varvec{f}}\in L^2({\mathbb {R}}^d,{{\mathbb {R}}}^m), \end{aligned}$$

where $\{{\varvec{e}}_1,\ldots ,{\varvec{e}}_m\}$ is the canonical basis of ${{\mathbb {R}}}^m$ and $T_{ij}(t)u=\langle {\varvec{T}}(t)(u{\varvec{e}}_j),{\varvec{e}}_i\rangle =\int _{{\mathbb {R}}^d}k_{ij}(t,x,y)u(y)\,dy$ for $t>0$, $i,j=1,\ldots ,m$, $u\in L^2({\mathbb {R}}^d)$. Moreover, Proposition 2 shows that $|T_{ij}(t)u(x)|\le (T(t)|u|)(x)$ and hence

$$\begin{aligned} \bigg |\int _{{\mathbb {R}}^d} k_{ij}(t,x,y)u(y)dy\bigg |\le \int _{{\mathbb {R}}^d}k(t,x,y)|u(y)|dy \end{aligned}$$

for all $t>0,\,u\in L^2({\mathbb {R}}^d)$ and a.e. $x\in {\mathbb {R}}^d$. Applying [28, Theorem 3.3.5] we deduce that $|k_{ij}(t,x,y)|\le k(t,x,y)$ holds true for all $t>0$, $i,j=1,\ldots ,m$ and almost every $x,y\in {\mathbb {R}}^d$. So, the assertion follows from Theorem 7. $\square$