Introduction

Climate warming is impacting surface waters worldwide (Woolway et al. 2020) and along with eutrophication is threatening water quality (Moss 2011). The direct effects of climate warming on lakes are increasing surface water temperature (O’Reilly et al. 2015; Piccolroaz et al. 2020), changes in stratification patterns (Ficker et al. 2017; Woolway and Merchant 2019; Woolway et al. 2021), and decreasing ice cover (Dibike et al. 2011; Gebre et al. 2014). But not all lakes are affected in the same way and the susceptibility of a specific lake is controlled by different factors. The rate of surface water temperature warming is influenced by geomorphic factors like maximum depth and the climatic region (O’Reilly et al. 2015; Piccolroaz et al. 2020). The susceptibility to changes in stratification is influenced by the morphology and average water temperature (Kraemer et al. 2015). Change in ice cover is sensitive to the mean depth and surface area (Magee and Wu 2017). To predict impacts of climate warming on a specific lake, it is crucial to understand its specific morphological, and hydrological characteristics as well as its mesoclimatic conditions. With this knowledge, mechanistic models can be used to produce estimates on ice cover properties (Magee et al. 2016) and stratification patterns (Butcher et al. 2015; Calamita et al. 2021).

Stratification duration and water temperature influence oxygen dynamics and can potentially cause or prolong anoxic periods (Missaghi et al. 2017; Darko et al. 2019; Ladwig et al. 2021). This effect is caused by inhibition of oxygen exchange between deeper water and the surface due to lower vertical diffusion rates and high water column stability (Zhang et al. 2015). In deep lakes, mixing can be even more important in controlling deep layer oxygen concentration than eutrophication (Schwefel et al. 2016). Under anoxic conditions, phosphorus release from the sediment can increase (North et al. 2014). However, anoxia is more important for controlling seasonal and sub-seasonal variations in phosphorus than for controlling its long-term release (Hupfer and Lewandowski 2008).

Compared to lakes, reservoirs react differently to changes in the climate, whereas catchment and management are more important mediators (Hayes et al. 2017). Especially, multipurpose reservoirs experience additional stress due to (often) contradictory management goals. For example, flood protection requires a reduced water volume in the reservoir, whereas for drinking water production, a larger water volume is preferable. With reduced volume and residence time, anoxic conditions can additionally be problematic, as changed redox conditions can cause the release of dissolved metals, e.g., iron or manganese, from the sediment (Davison 1993). When oxygen is reintroduced into the raw water during purification, metal ions are oxidized and precipitated. The precipitation can lead to clogging of pipes and filters, so iron and manganese need to be removed in an additional step at the treatment plant (Tobiason et al. 2016).

Changes in lake physics also impact lake ecology at different levels from phytoplankton community composition (Rühland et al. 2015) to trophic interactions due to warming in sensitive periods like winter or onset of stratification (Wagner et al. 2013). Changes in lake mixing can lead to increases of phytoplankton biomass, even in lakes where the nutrient loading is decreasing (see, e.g., Horn et al. 2015; Swann et al. 2020; Mesman et al. 2021). This effect can be caused by increased internal nutrient recycling and shifts in the phytoplankton community (bottom-up) or by predator–prey interaction (top-down, Anneville et al. 2019). The changes induced by climate warming are reported to favor cyanobacteria and thus increase the risk of cyanobacteria mass development (e.g., Jöhnk et al. 2008; Huisman et al. 2018), which is a problem for water quality.

To prepare and plan mitigation strategies, it is important to have impact predictions, which can be realized using process-based lake models fed with meteorological forcing of future conditions. There are different methods to generate such forcing: adapting observed data based on historic trends or general circulation models (Dibike et al. 2011; Jeznach and Tobiason 2015), applying weather generators—software that can generate forcing data with a given (shifted) distribution (Gal et al. 2020)—or using the output of regional climate models (RCM, Buccola et al. 2016; Ladwig et al. 2018). Whereas data from regional climate models are not precise enough to correctly simulate short stratification events, atmospheric reanalysis data can predict diurnal patterns and seasonal thermodynamics in large shallow lakes over the year (Frassl et al. 2018). Model studies using locally downscaled climate data have successfully been used to, e.g., evaluate the impact of climate warming on surface water temperature (Piccolroaz et al. 2020) or the possible change in water temperature for a drinking water reservoir (Mi et al. 2020). In addition, precipitation-runoff models can be coupled to obtain discharges as input for the lake model (Buccola et al. 2016) and inflow temperature or suspended sediment concentration of the inflow can be estimated by additional models (Råman Vinnå et al. 2018).

When communicating modeling results, especially if they are intended for decision support, it is important to address the associated uncertainties (Schuwirth et al. 2019; Saltelli et al. 2020). For lake models, sources of uncertainty are related to forcing data, initial conditions, model parameter values, and imperfect process representation in the model (Thomas et al. 2020). When dealing with these uncertainties, a possible solution is to use ensembles. In climate and weather forecasting, the use of model ensembles is state of the art (e.g., Gneiting and Raftery 2005; Parker 2010), but in lake modeling, use of ensembles is not yet common. An ensemble can be several realizations of the same model using different forcing data (Shatwell et al. 2019; Bartosiewicz et al. 2021; Piccolroaz et al. 2021), several realizations of the same model using different initial or parameter values (e.g., Gal et al. 2014; Nielsen et al. 2014), or different models fed with the same forcing data (Gal et al. 2020; Zhu et al. 2020). Especially, for simulating ice cover, there are some successful applications of ensembles in lakes (Yao et al. 2014; Kobler and Schmid 2019), and there are also ensembles of water quality models (Nielsen et al. 2014; Trolle et al. 2014). In a large international cooperation, the Lake Sector of the Inter-Sectoral Impact Model Intercomparison Project (ISIMIP) is working on a protocol for using an ensemble of lake models and climate change scenarios (Golub et al. 2022).

While using ensembles with different parametrization or different forcing is state of the art, applying the novel R package LakeEnsemblR (Moore et al. 2021), it is now also possible to analyze structural uncertainty, also called epistemic uncertainty (see, e.g., Efstratiadis and Koutsoyiannis 2010), introduced by different models using an unified interface. The current study exemplifies its application for the Lichtenberg drinking water reservoir, for which regional climate simulations and a calibrated precipitation-runoff model were available. As meteorological forcing, we use 10 realizations of a regional climate model following the A1B climate scenario, and for each of them, we ran the ensemble with 10 different parametrizations, thereby addressing uncertainties associated with forcing data, calibrated parameters, and model structure.

Methods

Study site

Fig. 1
figure 1

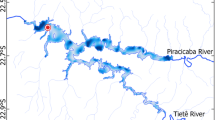
Location and catchment of the Lichtenberg reservoir and near by weather stations from the German weather service (DWD) Chemnitz (1), Zinnwald-Georgenfeld (2), and Freiberg (3). Reservoir data were measured close to the reservoir dam (red star) and provided by the State Reservoir Administration of Saxony (LTV). Meteorological forcing and climate simulations were taken from stations 1 and 2. \(\copyright \) OpenStreetMap and the OpenStreetMap Foundation 2021. Distributed under a Creative Commons BY-SA License. Additional data from GADM (https://gadm.org). Reservoir, river, and catchment shape data were obtained from the Saxon State Office for Environment, Agriculture and Geology (LfULG)

Full size image

The drinking water reservoir Lichtenberg is located in the low mountain range Erzgebirge in Germany next to the city of Freiberg (Fig. 1). It has a 46 m-high rock-fill embankment dam impounding the river Gimmlitz with a catchment area of about 39 km\(^2\) (LTV 2008). The reservoir water body has a length of about 3000 m, a maximum width of approximately 300 m, a mean depth of 15 m, and a maximum depth of 39 m. The reservoir bottom is located at an altitude of 455 m above sea level, and the water has a mean residence time of about 200 days. The reservoir is managed and maintained by the State Reservoir Administration of Saxony (LTV). In addition to drinking water production, the reservoir is used for flood protection.

Climate scenarios and data

The environmental agencies of the federal states Saxony, Thuringia, and Saxony-Anhalt, together with the Technische Universität Dresden, host a joint climate information system called ReKIS (https://rekis.hydro.tu-dresden.de/) that provides regionalized climate projections for different emission scenarios for the period 1961–2100 with up to daily resolution. The platform is intended to provide data for decision-makers, the interested public, and scientists to be used in climate impact analysis (e.g., Kronenberg et al. 2015). When preparing this study, regionalized data based on emission scenarios (SRES) as used in the fourth IPCC report (IPCC 2007) were available.

We forced our model ensemble with 10 realizations of a climate projection following the A1B scenario. This describes a world with rapid economic growth and a population that starts to decrease after the middle of the century and uses a balanced energy production between fossil and renewable (Nakicenovic et al. 2000). The projections were generated using the statistical downscaling method WETTREG2010 (Kreienkamp et al. 2010; Spekat et al. 2010) forced with data from the general circulation model (GCM) ECHAM5 (Roeckner et al. 2003). This approach applies an environment-to-circulation classification method (see Spekat et al. 2010) to generate data for specific weather stations based on observations and GCM. Using station-based data has the advantage that the same data processing steps can be used consistently for calibration, validation, and climate projections. The same work flow is also used for the precipitation discharge model, that inherently provides tools for automatic pre-processing of station-based meteorological forcing data.

For meteorological forcing, we used data from two of the close-by stations that provided all necessary model driver data (stations Chemnitz and Zinnwald, Fig. 1). We interpolated the data from the two stations using weights proportional to the altitude difference between the stations and the reservoir. We calibrated and validated the lake models using interpolated observational data from the same two weather stations. For calibration and validation, we used water temperature profiles provided by LTV, that were measured on a 2–4 week basis at the deepest point of the reservoir in front of the dam. The data were available from 01 January 2000 to 31 December 2016. Daily observations of ice thickness at the reservoir dam were available for the whole modeling period.

As hydrological forcing, we used observed discharge data from the gauge upstream the pre-dam, measured by the LTV. For the climate scenario, we used inflow data that were simulated using a site-specific rainfall–runoff model that was built using ECHSE, an open source framework for rapid development of hydrological catchment models (https://echse.github.io/). The rainfall–runoff model used in this study is an extension of the HYPSO-RR model engine included in the ECHSE framework (Kneis 2015) with additional state variables for stream water temperature (Zündorf 2018). The precipitation discharge model was fed with meteorological data from ReKIS and calculated daily inflow discharges and water temperature. After calibration, the fit of simulated to observed discharges had a mean absolute error (MAE) of 0.2 m\(^3\) s\(^{-1}\), a Nash Sutcliffe Efficiency Index (NSE) of 0.70 for the calibration phase, and an NSE of 0.81 for the validation phase. The fit of simulated to observed water temperature had an MAE of 1.2 K, NSE of 0.86 for the calibration phase, and NSE of 0.84 for the validation phase.

Lake model ensemble

The dynamics of water temperature and ice cover in the reservoir were simulated by five different one-dimensional lake models using the R package LakeEnsemblR (Moore et al. 2021). The five applied hydrodynamic models were: the General Lake Model (GLM—Hipsey et al. 2019), the General Ocean Turbulence Model (GOTM—Umlauf et al. 2005), Simstrat (Goudsmit et al. 2002), the Freshwater Lake model (FLake—Mironov 2008), and the Multi Year Lake model (MyLake—Saloranta and Andersen 2007). Out of the five models, only GLM, GOTM, and Simstrat can simulate outflows from depths different than the surface, whereas MyLake only simulates surface outflow and FLake simulates no outflow at all. FLake assumes a rectangular-shaped basin with constant mean depth instead of a hypsographic curve.

To avoid making assumptions about future water use and consumption, we assumed outflow to be equal to inflow for all simulations, including calibration and validation. This resulted in a constant water level of 36 m, which was the average water level in the period 1990–2010. For the models that can simulate withdrawal from below the surface, the outflow was split equally in two parts: 2 and 14 m above the reservoir bottom representing withdrawal for drinking water production and water released to the downstream river, respectively. The equal division of outflow between the two depths is close to the long-term average ratio of the two, which is 56:44.

For a qualitative evaluation, we calculated annual characteristic features for every realization, parametrization, and model, which are: annual average water temperature at 3 and 25 m depth, start, end, and duration of summer stratification, inverse stratification, and ice cover. As FLake uses the mean depth (about 15 m), water temperature at 25 m is omitted for FLake in the data analysis. The reservoir was assumed to be stratified if the difference between surface and bottom temperature exceeded the 1 K criterion (see Engelhardt and Kirillin 2014). We assumed inverse stratification when the surface water was more than 1 K cooler than the bottom temperature.

Calibration

All five models were calibrated using the Latin hypercube calibration method (see, e.g., Mckay et al. 2000) included in the LakeEnsemblR package. Therefore, upper and lower bounds for the selected parameters and meteorological scaling factors were supplied, and then, a given number (2000) of parameter sets were sampled from a Latin hypercube, so that they were equally distributed in the parameter space. Then, the models were run for every parameter set and performance metrics were calculated. We chose the Latin hypercube method, as it provides additional information about the sensitivity and thus identifiability of the calibrated parameters. Using the model runs, we performed a visual analysis of the identifiability of the parameters by plotting the parameter values against the root-mean-squared error (see, e.g., Beven 1993; the plots can be found in Fig. S1 to S5 in the Supplementary Information).

The parameters that were calibrated are: the scaling factors for wind speed and short-wave radiation as well as one model-specific parameters for each model (see Table S1 in the Supplementary Information). The model-specific parameters were chosen from parameters used for calibration in previous studies (Peeters et al. 2002; Saloranta 2006; Layden et al. 2016; Bruce et al. 2018; Ayala et al. 2020). We split the available observed temperature into a calibration phase (01 January 2000–31 December 2008) and a validation phase (01 January 2009–31 December 2015).

To evaluate the model performance in recreating water temperature, five different goodness-of-fit metrics were calculated for the whole depth profile using daily values: root-mean-squared error—RMSE, Pearson correlation coefficient—R, Nash Sutcliffe model efficiency index—NSE, normalized mean absolute error—NMAE, mean absolute error—MAE, and mean error or bias (c.f. Jachner et al. 2007). In addition to the individual models, also the performance of the ensemble mean was evaluated. The ensemble mean is calculated as the arithmetic mean of the simulated temperature (or ice cover thickness) values of the five models for every time step and depth (for water temperature). To evaluate the performance of the models to capture ice cover and summer stratification timing (start, end, duration), the MAE was calculated. We calculated the timings of the ensemble mean for summer stratification and ice cover by taking the average of the single models timings.

Data evaluation

To analyze the impact of climate warming on the investigated annual characteristic features, two regression models were fitted for every single lake model, a simple linear regression and a segmented linear regression with breakpoints using the R package segmented (Muggeo 2008). The best model, in terms of parsimony and explanatory power, was then selected as the model with minimum Bayesian Information Criterion (BIC; Schwarz 1978).

For the inverse stratification and ice cover, we also estimated the probability of occurrence for every year by logistic regression using a generalized linear model for binomial data

$$\begin{aligned} p = \frac{e^{\left( a + b \cdot t\right) }}{1 + e^{(a + b \cdot t)}}, \end{aligned}$$
(1)

where p is the probability of occurrence of ice cover or inverse stratification in a year t given our model results and a and b are the parameters of the generalized linear model. A similar approach was used by Wagner et al. (2012).

Uncertainty partitioning

There are different sources of uncertainty which we addressed in this study, namely the uncertainty from the forcing data (Meteorology), the uncertainty related to the calibrated parameters (Parameter), and the epistemic uncertainty which is the uncertainty related to the different model structures (Model). To quantify the contribution of these sources on the overall ensemble output, we used an analysis of variance (ANOVA) approach similar as applied by Bosshard et al. (2013), but without subsampling (for a detailed description of the method, see Yip et al. 2011). For each year of the simulation period, we estimated the contributions of the three sources of uncertainty as well as interactions between them to the total variance in the ensemble output. We estimated the fraction of variance as the fraction of the individual effect sum of squares to the total sum of squares and summarized all interaction terms into one term which we called Interactions.

Results

Observed trends

Fig. 2
figure 2

Observed annual air temperature at the reservoir (a), observed annual surface water temperature (b), and annual average air temperature of the used climate scenario (c). In a and b, years with observations missing for more than 1 month were removed from the analysis. For the climate scenario, 10 different realizations (members) of the regional climate model were used. The green lines in a and b show the fitted linear regression with confidence interval and prediction interval. The orange lines in c show the fitted segmented linear regression with confidence interval and prediction interval and the vertical dashed purple line in c shows the break point of the segmented linear regression

Full size image

For the period 1973–2016, the annual average air temperature, measured at the Lichtenberg reservoir (Fig. 1), showed a significant trend (Mann–Kendall test \(p<\) 0.05) of 0.47 K decade\(^{-1}\) (Fig. 2a). From observed surface water temperatures, an even larger significant (Mann–Kendall test \(p<\) 0.05) annual trend of 0.57 K decade\(^{-1}\) was estimated for the period 1977–2015 (Fig. 2b). This trend is in good agreement with earlier estimations for annual average water temperature trends at 3 m depth for the period 1992–2016 that were 0.5 K decade\(^{-1}\) (Feldbauer et al. 2020). For the 1992–2016 period, an increase of about 0.3 K decade\(^{-1}\) for the deep water temperature (25 m depth) and an earlier onset of summer stratification of about 4 d decade\(^{-1}\) were found. During the period 1975–2015, the ice cover break off advanced by 6 d decade\(^{-1}\).

For the annual average air temperature of the applied climate scenario, an increase of 0.42 K decade\(^{-1}\) was estimated. As in the A1B climate scenario, the world population starts to decrease at the middle of the century, we additionally applied a segmented linear regression and compared the results with the simple linear regression using the BIC. The segmented linear regression slightly outperforms the simple linear regression in terms of parsimony and explanatory power with a BIC of 811.30 and R\(^2\) of 0.93 compared to a BIC of 921.24 and R\(^2\) of 0.92. The segmented linear regression has a first slope of 0.45 K decade\(^{-1}\) and after the break point in 2082 a slope of 0.08 K decade\(^{-1}\) (Fig. 2c).

Model performance

Table 1 Model performance measures for whole column water temperature data in calibration (01 January 2000–31 December 2008) and validation (01 January 2009–31 December 2015) period
Full size table

For GLM, Simstrat, and MyLake, the model performance was not sensitive to their model-specific parameters (see Fig. S1 to S5 in the Supplementary Information). We choose the model-specific parameters based on previous studies, experience, and personal communication. For GLM (Bruce et al. 2018) and GOTM (Andersen et al. 2020), the sensitivity of model parameters differs between lakes and we would assume the same for the other models. Why the model-specific parameters were not sensitive cannot be explained from our study alone, but Bruce et al. (2018) found that most mixing parameters in GLM are not sensitive when using the whole temperature profile. For MyLake, Saloranta (2006) found C_shelter to be sensitive for the thermocline depth. In contrast, the parameter identified for our study site (an artificial reservoir) was quite insensitive within its range (see Fig. S5 in the Supplementary Information).

As the overall model performance was satisfactory compared to other studies (e.g., Bruce et al. 2018; Kobler and Schmid 2019; Ayala et al. 2020), we choose not to calibrate other parameters and re-run the calibration using only the meteorological scaling factors for these three models. After calibration, all models simulated the observed water temperature to a satisfactory level as all RMSE were below 2.0 K and all NSE were above 0.87 (Fig. S6 and S7 in the Supplementary Information, Table 1). In both the calibration and validation phase, Simstrat, GLM, and GOTM performed best from the single models, but the ensemble mean performed even better with a RMSE that was about 10% smaller than the best of the three (Table 1).

For the summer stratification timing, Simstrat, GLM, GOTM, and the ensemble mean performed best (Table 2). In all cases, the end of stratification was estimated with a larger error than the beginning. As the average sampling interval was about 14 days, the errors for GLM, GOTM, and Simstrat are in the range of the maximum margin of error of the observations. For the estimation of ice cover timing Simstrat, MyLake, GOTM, and the ensemble mean performed best. The least successful performance for ice cover was seen from GLM. The capability of the models in predicting inverse stratification could not be evaluated, as during winter and especially during ice cover, water temperature observations were sparse.

Table 2 Mean absolute error (MAE) for start, end, and duration (dur) of simulated summer stratification (sum) and ice cover (ice) for all five models, and the ensemble mean
Full size table

As evaluation of the different model runs in the LHC calibration showed possible problems with nonuniqueness of the calibrated parameter sets (Fig S1 to S5 in the Supplementary Information), we decided to run the ensemble with 10 different parameter sets instead of just using the single best one. We randomly selected these parameter sets from the 5% best sets (in terms of RMSE) for each model. The used parameter sets for each model are given in Table S1 in the Supplementary Information.

Climate predictions

Water temperature

Fig. 3
figure 3

Simulated annual average temperatures in 3 m depth (a–e) and 25 m depth (f–i) from the five models with the fitted linear regression and segmented linear regression. The dots represent average values of the 100 ensemble runs for each year, and the shaded gray areas give the area containing 50 and 90% of the ensemble runs. At 25 m depth, no data for FLake are available, as FLake uses the mean depth (approximately 15 m) and assumes a rectangular basin

Full size image

All five models predicted an increase of water temperature over time, for both surface (3 m) and deep water (25 m). There were some slight differences in the slope, intercept, and spread, but overall the five models gave similar results for the increase in water temperature (Fig. 3; Table 3). Especially, in the deeper water temperature, GLM and Simstrat showed a wider spread of simulated water temperature compared to GOTM and MyLake (Fig. 3f–i).

At 3 m depth, the segmented linear regression described the change in average water temperature better than the linear regression (in terms of parsimony—BIC) for all models and except for Simstrat, the break points occurred around the year 2080. The larger slope was similar between the models with an average of 0.34 K decade\(^{-1}\), whereas the average slope of the linear regression was slightly lower with 0.32 K decade\(^{-1}\) (Table 3).

At 25 m depth, the segmented regression for GOTM, Simstrat, and MyLake gave a break at around 2015 and for GLM at 2001. For GOTM, Simstrat, and MyLake, the segmented regression performed better than the linear regression (in terms of parsimony), whereas for GLM, the segmented regression performed inferior compared to the linear regression (Table 3). The average slope of the linear regression for the annual water temperature at 25 m depth was 0.11 K decade\(^{-1}\), whereas the average of the steeper part of the segmented regression was 0.12 K decade\(^{-1}\).

Table 3 Slope of linear regression (lr), slope of segmented linear regression before (slr 1) and after (slr 2) break point (BP), and Bayesian Information Criterion (BIC) for linear regression and segmented linear regression for water temperature at 3 and 25 m below the surface for all five models
Full size table

Stratification and ice cover

Fig. 4
figure 4

Annual summer stratification duration with the fitted linear regression and segmented linear regression for the five models. The dots represent average values of the 100 ensemble runs for each year and the shaded gray areas give the area containing 50 and 90% of the ensemble runs

Full size image

All five models predicted a prolongation of the summer stratification (Fig. 4), with an earlier onset of stratification and except for FLake, all models showed a later end of summer stratification (Table 4). For the sake of simplicity, we decided to focus on the slopes of the linear regression. However, except for FLake, the segmented regression performed better than the linear regressions (in therms of BIC). The values for both fitted regression models and their BIC can be found in the Supplementary Information (Table S2).

Table 4 Linear trend for duration (dur), start, and end of summer stratification (sum), inverse stratification (inv), and ice cover (ice) for each of the five models estimated from the simulations along with mean and standard error (se) of the ensemble estimate
Full size table

All five models predicted a decreasing number of days with ice cover, shorter inverse stratification, later start of the inverse stratification, and an earlier spring overturn (Table 4). Accordingly, all models predicted a decreasing probability of occurrence for both inverse stratification and ice cover (Fig. 5). Compared to the results for water temperature and summer stratification, the predicted changes in ice cover and inverse stratification were less consistent between the models. Still, all showed decreasing ice cover and inverse stratification duration.

Fig. 5
figure 5

Probability of occurrence of ice cover (a–f) and probability of occurrence of inverse stratification (g–l) for the five models individually and data from all models pooled (all) estimated by logistic regression (Eq. 1). The orange line shows the fitted generalized linear model. Each point represents a simulated year, where a value of 1 represents occurrence of ice or inverse stratification in this year, and 0 represents the absence of ice or inverse stratification. To improve visibility, the single data points are scattered around 0 and 1

Full size image

Uncertainty partitioning

From the three sources of uncertainty, the epistemic uncertainty (Model) can account for the largest fraction of variance in all characteristic features (Fig. 6). The second most important were the uncertainties in meteorological forcing (Meteorology) and interaction terms (Interactions). For summer stratification duration, epistemic uncertainty is even more dominant than the other sources. There is a small amount of variance over the simulation period, and especially at the end of the century, some changes in the fraction of variance can be seen. Especially, for ice cover duration, Parameters becomes more important at the end of the century.

Fig. 6
figure 6

Variance decomposition of the uncertainty for the annual average water temperature in 3 m depth (a), the annual average water temperature in 25 m depth (b), the summer stratification duration (c), and the duration of ice cover (d) over the simulation period. The yearly fractions of variance were smoothed using a loess filter with a smoothing parameter of 0.2

Full size image

Discussion

The simulated decrease in ice cover duration is in the range of values estimated from historic data for other German drinking water reservoirs (Wilmitzer et al. 2015) and lakes in Poland (Skowron 2009; Bartosiewicz et al. 2021). The simulated average decrease in ice cover duration of 5.6 d decade\(^{-1}\) is slightly larger than the empirically observed decrease of about 4.8 d decade\(^{-1}\) (for the period 1975–2015) in the Lichtenberg reservoir, but this rate has accelerated in the last decades. Compared to warming rates calculated from historic data that are about 0.5 K decade\(^{-1}\) (Fig. 2a), the average simulated surface water warming rates are lower (0.3 K decade\(^{-1}\)). Also, the estimated prolongation of summer stratification was lower than recently observed (Feldbauer et al. 2020). The SRES scenario A1B used in this study is comparable to the newer RCP 6.0 scenario, in terms of socio-economic development, radiative forcing, atmosphere composition, and climate (van Vuuren and Carter 2014). Recent climate impact simulations for another German drinking water reservoir (Rappbode) using the RCP 6.0 emission scenario showed similar warming rates (trend in 1 m depth: 0.32 K decade\(^{-1}\), in 50 m depth 0.06 K decade\(^{-1}\)) and larger warming rates for the RCP 8.5 emission scenario (Mi et al. 2020). Simulations for other European lakes under the RCP 4.5 and 8.5 scenario are in agreement with this, yielding weaker and stronger trends than our simulations, respectively (Shatwell et al. 2019; Piccolroaz et al. 2021). The difference between the simulated and observed warming rates could be explained by the fact that historically observed greenhouse gas emissions were larger than the predicted emissions from the A1B scenario, that we used in this study. This is in accordance with findings that the RCP 8.5 scenario is best capturing recent and historic greenhouse gas emissions, that were underestimated by other scenarios (Schwalm et al. 2020).

For water temperature and summer stratification both linear and segmented linear regression gave similar values for the rate of warming. In all cases for surface water temperature and in all except one case for summer stratification duration (FLake), the segmented regression performed better (in terms of parsimony and explanatory power) than the linear regression. In all, except two of these segmented regressions, the break point was estimated around the year 2080. When applying the segmented linear regression to the air temperature forcing data from the RCM, a break point around the same time was estimated (see Fig. 2c). We attribute this pattern to the A1B emission scenario that is assuming a decreasing population starting mid-twenty-first century. Nevertheless, the difference between the trends for water temperature and summer stratification estimated with the two regression methods was relatively small (see Table 3 and Table S2 in the Supplementary Information). However, the segmented linear regression shows another feature: The surface water temperature almost instantaneously responds to the change in air temperature as can be seen in the break points of the segmented linear regression (Figs. 2c, 3a–e), whereas no clear response of the deep water temperature can be seen within the time span of our simulations (Fig. 3f–i).

Surface water temperature trends are quite consistent between different lakes (O’Reilly et al. 2015), whereas deep water temperature trends show large variations and are generally less well understood (Pilla et al. 2020). Although the response of stratification to climate warming is dependent on the lake’s morphology and size (Kraemer et al. 2015; Butcher et al. 2015; Zhong et al. 2016), only little of the variation in deep water temperature trends can be explained by the lake characteristics (Pilla et al. 2020). To our knowledge, no study has shown differences in the response time to changing forcing between surface and deep water temperature. For a better understanding of this response, a larger scale modeling study with different lakes using similar forcing and evaluation would be needed.

As water temperature and mixing affect the water quality, reservoir managers are interested in their long-term trends. Along with increasing water temperature and stratification duration, we saw an increase in temperature difference between surface and bottom and thus an increase in stratification strength. This effect was also reported for other lakes and reservoirs (e.g., Mi et al. 2020). Increasing water temperature gradients (and therefore stability) and stratification duration can cause or promote the formation of anoxic zones (Foley et al. 2012; Zhang et al. 2015; Ladwig et al. 2021), which in terms can cause the release of nutrients (North et al. 2014) or heavy metals (Davison 1993). Also, increased stratification and temperature can lead to a change in the food web (Wagner et al. 2013) and are expected to favor cyanobacteria mass development (Huisman et al. 2018). Thus, the predicted changes in the thermal structure can lead to water quality challenges.

There are indications that loss of ice cover, as predicted by all five models, can also influence the water quality of reservoirs and lakes. Winter lake ecology has long been neglected, but is now getting more attention (Hampton et al. 2017; McMeans et al. 2020). The physical conditions under ice can potentially influence the oxygen concentrations in the next spring due to primary production in winter (Yang et al. 2020). A short ice cover period can increase spring mass development of phytoplankton (Horn et al. 2011). The ice cover period can additionally influence the composition of the spring phytoplankton bloom (Rühland et al. 2015) and shortening of the ice cover period can potentially result in changes of fish growth and reproduction (Shuter et al. 2012). There are strong hints that ice cover phenology can influence summer nutrients and zooplankton dynamics (Hampton et al. 2017) and that the different capacities of organisms to cope with under ice conditions help to promote species coexistence. Decreasing periods of ice cover could thus threaten biodiversity in lakes and reservoirs (McMeans et al. 2020).

Similar to another study (Kobler and Schmid 2019), all models using the MyLake ice module (MyLake, GOTM, and Simstrat) showed better performance in recreating ice cover phenology. In previous studies (Yao et al. 2014; Kobler and Schmid 2019), GLM was the least sensitive in terms of ice cover response to climate change. However, in our study, GLM was the most sensitive and predicted almost complete loss of ice cover. A reason for this distinction could be model code improvements in recent GLM versions. Altogether, the performance of ice cover simulation in our study (Table 4) was slightly worse than in previous studies that had mean average deviation (MAD) of about 6 days for both ice onset and break off (Dibike et al. 2011), or MAE between 8 and 15 days for ice onset and an MAE between 7 and 19 days for ice-off (Kobler and Schmid 2019).

We saw higher variance in simulated deep water temperature in GLM and Simstrat compared to GOTM and MyLake (Fig. 3). Compared to the range of annual average water temperature calculated from observations, the wider range of GLM and Simstrat seemed more realistic. However, evaluating the model performance in capturing deep water temperature in the calibration and validation phase did not show a large difference between GLM, GOTM, and Simstrat (validation RMSE at 25 m depth: GLM 1.17 K, GOTM 1.01 K, Simstrat 1.14 K, MyLake 1.81 K; calibration RMSE at 25 m: GLM 1.15 K, GOTM 0.96 K, Simstrat 0.93 K, MyLake 2.00 K). Therefore, it is not quite certain if the higher variance of deep water temperatures in GLM and Simstrat are to be expected in the future, if they show the higher sensitivity of simulated deep water temperatures toward meteorological forcing of the two models, or if they are caused by the different implementation of deep water withdrawal.

Using an ensemble approach, we were able to quantify the contribution of the considered sources of uncertainty to the total variance of the simulated variables. We highlight here that epistemic uncertainty was dominating for all characteristic features. Meteorology was less important as we were using different realizations of the same climate scenario. Additionally, using different climate scenarios, GCMs, or regionalization methods, we would expect Meteorology to be a more important factor (see, e.g., Her et al. 2019). Parameters were less important, because we were varying them within the range of values that were performing well in the calibration. Still, they were more important for ice cover duration, which could be caused by the fact that we did only calibrate for water temperature. The even larger dominance of epistemic uncertainty for summer stratification duration was probably caused by the low summer stratification duration simulated by FLake (see Fig, 4). The increasing contribution of epistemic uncertainty for water temperature at 25 m depth was reflecting the larger difference in the estimated deep water temperature trend from the five models (see Table 3). In this study, we only investigated annual characteristic features, but it would be interesting to also look at the uncertainties on seasonal or short scale periods like extreme events, where model errors are often larger (Mesman et al. 2020). Nevertheless, quantitative comparison of sources of uncertainty can help to put into perspective global modeling studies using a single model (e.g., Woolway and Merchant 2019). A larger comparative analysis of uncertainty partitioning over multiple lakes could further improve confidence in model predictions.

The better performance of GLM, GOTM, and Simstrat in simulating water temperature and stratification can be attributed to their ability to simulate water withdrawal from deeper layers, as the withdrawal depth influences the water temperature profiles (Weber et al. 2017; Mi et al. 2019). We confirmed this hypothesis by fitting the three models using surface outflows, which resulted in inferior performance for all three models (Table S3 in the Supplementary Information). In contrast to natural lakes, where the end of summer stratification is mostly caused by convective cooling, in reservoirs, the end of summer stratification can be caused by withdrawal from deeper layers. The withdrawal reduces or in some cases completely discharges the hypolimnetic volume, thereby decreasing water column stability which can trigger the start of autumn turnover (Feldbauer et al. 2020). This effect explains the better performance of the models with variable withdrawal depth and our results highlight that the ensemble approach can help to identify the best suited models for a research question of interest (Janssen et al. 2015). The superior performance of the ensemble mean in predicting water temperature, stratification, and ice cover additionally highlights the benefit of using an ensemble approach as also shown in other studies (Trolle et al. 2014). Regardless of their slightly inferior performance in simulating water temperatures, we still conclude that including MyLake and FLake in the ensemble was beneficial. The simulated trends in the observed characteristic features were coherent between all models and MyLake performed well in simulating ice cover.

Conclusions

We used an ensemble consisting of five vertical one-dimensional lake models to simulate future water temperature, stratification, and ice cover by example of a drinking water reservoir located in the low mountain range Erzgebirge, Germany. All models in the ensemble were able to recreate observed water temperature, stratification, and ice cover sufficiently well. To estimate the impact of climate warming, we used 10 realizations of WETTREG2010 following the A1B emission scenario as meteorological forcing for the lake models and ran each of them with 10 different parameter sets. Discharge and temperature of inflow were generated by a rainfall–runoff model and, for simplicity, the outflow was assumed to be same as the inflow.

Ensembles have not been used often in lake modeling studies, but in recent years are getting more attention (e.g., Yao et al. 2014; Kobler and Schmid 2019; Gal et al. 2020; Zhu et al. 2020; Bartosiewicz et al. 2021). With the recently released LakeEnsemblR software (Moore et al. 2021), applying lake ensemble in scientific studies became much more accessible. Out of the five used models, the three that can simulate water withdrawal from a chosen depth below the surface (GLM, GOTM, and Simstrat) performed best in recreating observed water temperatures and summer stratification patterns. Moreover, the ensemble mean outperformed all single models in predicting water temperatures. For all observed annual characteristic features, epistemic uncertainty was the dominant source of uncertainty.

All models showed coherent response to warming climate, with increasing water temperature, longer summer stratification, shorter ice cover duration, and decreased inverse stratification duration. The surface water temperature warming was estimated to be 0.34 ± 0.02 K decade\(^{-1}\) and the summer stratification duration was prolonged by about 3.2 ± 0.6 d per decade. The overall probability of ice cover formation at the end of the century, estimated from all models, was just below 25%. These findings are in accordance with simulations for another drinking water reservoir in Germany under the RCP 6.0 pathway (Mi et al. 2020), but are lower than rates estimated from historic observations.

We expect similar responses for other reservoirs, especially if comparable in terms of size and average temperature (Kraemer et al. 2015). In any case, the predicted changes are challenges for reservoir management, because they will potentially decrease water quality (Woolway et al. 2020). There are suggestions on how to mitigate these effects by adapting the reservoir management strategies. Most of them use dynamic adaptation of withdrawal depth and quantity (Weber et al. 2017; Mi et al. 2019; Weber et al. 2019; Feldbauer et al. 2020; Mi et al. 2020) to optimize water temperature or oxygen concentration in the reservoir. Most reservoir managers in Germany are already adapting their management strategies, but the amount of local mitigation that can be done is limited, whereas climate warming is accelerating. A global strategy to minimize and reduce greenhouse gas emissions is therefore needed to—among other things—sustain the water quality of drinking water reservoirs.