Dominance Regions for Rank Two Cluster Algebras

Abstract

We study the polygons defining the dominance order on ${\varvec{g}}$-vectors in cluster algebras of rank 2 as in Fig. 1.

1 Introduction

Cluster algebras were introduced by Fomin and Zelevinsky as a tool in the study of Lusztig’s dual canonical bases. Since their inception they have found application in a variety of different areas in mathematics, nevertheless a fundamental problem in the theory remains constructing bases with “good” properties.

Over time several bases for cluster algebras have been described in different generalities [1,2,3,4,5,6,7,8,9,10,11]. All of their elements share the property of being “pointed”; this turned out to be a desirable feature for a basis to have and a natural question is to find all bases enjoying this property. Recently Qin studied the deformability of pointed bases whenever the cluster algebra has full rank [12]. As no explicit calculation is carried out in his work, we aim here at describing explicitly the space of deformability for pointed bases in rank two, i.e. when clusters contain a pair of mutable cluster variables. By doing so we shed more light on the combinatorial structure of such bases. In this setting, frozen variables do not carry any additional information so we will work in the coefficient-free case.

Fix integers $b,c>0$. The cluster algebra ${\mathcal {A}}(b,c)$ is the ${\mathbb {Z}}$-subalgebra of ${\mathbb {Q}}(x_0,x_1)$ generated by the cluster variables $x_m$, $m\in {\mathbb {Z}}$, defined recursively by

$$\begin{aligned} x_{m-1}x_{m+1}= {\left\{ \begin{array}{ll} x_m^b+1 &{} \quad \text {if }m\text { is even;}\\ x_m^c+1 &{} \quad \text {if }m\text { is odd.} \end{array}\right. } \end{aligned}$$

By the Laurent Phenomenon [13], each $x_m$ is actually an element of ${\mathbb {Z}}[x_k^{\pm 1},x_{k+1}^{\pm 1}]$ for any $k\in {\mathbb {Z}}$. Moreover, these Laurent polynomials are known to have positive coefficients [6, 7, 14].

Fig. 1

The dominance region ${\mathcal {P}}_\lambda$, the opposite dominance region ${\mathcal {P}}'_\lambda$, and the maximal support region ${\mathcal {S}}_\lambda$ for $\lambda =(4,-3)$ when $b=3$ and $c=2$. Highlighted lattice points in the region bounded by solid black lines and dashed lines represent the maximal support of an element pointed at $\lambda$; the dotted lines indicate which lattice points are in the support of the corresponding greedy basis element

An element of ${\mathcal {A}}(b,c)$ has ${\varvec{g}}$-vector $\lambda =(\lambda _0,\lambda _1)\in {\mathbb {Z}}^2$, with respect to the embedding ${{\mathcal {A}}(b,c)\hookrightarrow {\mathbb {Z}}[x_0^{\pm 1},x_{1}^{\pm 1}]}$, if it can be written in the form

$$\begin{aligned} x_0^{\lambda _0}x_1^{\lambda _1}\sum \limits _{\alpha _0,\alpha _1 \ge 0} \rho _{\alpha _0,\alpha _1} x_0^{-b\alpha _0} x_1^{c\alpha _1} \end{aligned}$$

(1)

with $\rho _{0,0}=1$ and $\rho _{\alpha _0,\alpha _1}\in {\mathbb {Z}}$. This definition agrees with the notion of ${\varvec{g}}$-vector from [15] defined for cluster variables. An element of ${\mathcal {A}}(b,c)$ is pointed if an analogous structure reproduces after expanding in terms of any pair $\{x_k,x_{k+1}\}$; a basis is pointed if it consists entirely of pointed elements.

Important examples of pointed elements are the cluster monomials of ${\mathcal {A}}(b,c)$, i.e. the elements of the form $x_k^{\alpha _k}x_{k+1}^{\alpha _{k+1}}$ for some $k\in {\mathbb {Z}}$ and $\alpha _k,\alpha _{k+1}$ non-negative integers. Indeed, by [12, Lemma 3.4.12] cluster monomials are part of any pointed basis in any (upper) cluster algebra of full rank. We achieve the same conclusion in our setting by elementary calculations (cf. Lemma 4.1).

Elements of any pointed basis are parametrized by ${\mathbb {Z}}^2$ thought of as the collection of possible ${\varvec{g}}$-vectors. Qin introduced a partial order $\preceq$ on ${\varvec{g}}$-vectors called the dominance order, refining the order used in [16, Proposition 4.3], and showed that it provides a characterization of pointed bases. We restate his results in the generality needed for this paper and using our notation.

Theorem 1.1

[12, Theorem 1.2.1] Let $\{x_\lambda \}$ and $\{y_\lambda \}$ be pointed bases of ${\mathcal {A}}(b,c)$. Then for each $\lambda \in {\mathbb {Z}}^2$, there exist scalars $q_{\lambda ,\mu }$ for $\mu \prec \lambda$ such that

$$\begin{aligned} y_\lambda =x_\lambda +\sum _{\mu \prec \lambda } q_{\lambda ,\mu } x_\mu . \end{aligned}$$

Moreover, having fixed a reference pointed basis $\{x_\lambda \}$, any choice of scalars $q_{\lambda ,\mu }$ as above provides a pointed basis of ${\mathcal {A}}(b,c)$.

When $bc\le 3$, the cluster algebra ${\mathcal {A}}(b,c)$ will be of finite-type and cluster monomials form its only pointed basis. We therefore assume that $bc\ge 4$. Write ${\mathcal {I}}\subset {\mathbb {R}}^2$ for the imaginary cone (positively) spanned by the vectors $\big (2b,-bc\pm \sqrt{bc(bc-4)}\big )$. Lattice points outside of ${\mathcal {I}}$ are precisely the ${\varvec{g}}$-vectors of cluster monomials in ${\mathcal {A}}(b,c)$.

We give an explicit description of the dominance relation among ${\varvec{g}}$-vectors. Specifically, we show that the ${\varvec{g}}$-vector $\lambda$ dominates the collection of ${\varvec{g}}$-vectors of the form $\lambda +(b \alpha _0,c \alpha _1)$, $\alpha _0,\alpha _1\in {\mathbb {Z}}$, inside its dominance region ${\mathcal {P}}_\lambda$ (cf. Definition 3.1).

Theorem 1.2

If $\lambda$ lies outside of ${\mathcal {I}}$, then the dominance region ${\mathcal {P}}_\lambda$ is the point $\lambda$. Otherwise the dominance region ${\mathcal {P}}_\lambda$ of the ${\varvec{g}}$-vector $\lambda =(\lambda _0,\lambda _1)$ is the polygon consisting of those $\mu =(\mu _0,\mu _1)\in {\mathbb {R}}^2$ satisfying the following inequalities:

$$\begin{aligned} \begin{aligned}&0 \le \frac{b c-\sqrt{b c (b c-4)}}{2 b}(\mu _0-\lambda _0)+(\mu _1-\lambda _1) \le -c\lambda _0-\frac{b c+\sqrt{b c (b c-4)}}{2b}b\lambda _1;\\&0 \le -\frac{b c-\sqrt{b c (b c-4)}}{2 b}(\mu _0-\lambda _0)+(\mu _1-\lambda _1) \le c\lambda _0;\\&0 \le -(\mu _0-\lambda _0)-\frac{b c-\sqrt{b c (b c-4)}}{2 c}(\mu _1-\lambda _1) \le \frac{b c+\sqrt{b c (b c-4)}}{2c}c\lambda _0+b\lambda _1;\\&0 \le -(\mu _0-\lambda _0) + \frac{b c-\sqrt{b c (b c-4)}}{2 c} (\mu _1-\lambda _1) \le -b \lambda _1. \end{aligned} \end{aligned}$$

Remark 1.3

Empirical calculations reveal that for certain pairs of notable bases (e.g. greedy and triangular) most of the coefficients $q_{\lambda ,\mu }$ are zero. Understanding this phenomenon might be worth further study.

Corollary 1.4

There are six classes of dominance polygons.

• 1. If $\lambda$ lies outside of ${\mathcal {I}}$, then ${\mathcal {P}}_\lambda$ is the point $\lambda$.

• 2. If $\lambda$ lies in the cone spanned by the vectors $(2b,-bc-\sqrt{bc(bc-4)})$ and $(2,-c)$, then ${\mathcal {P}}_\lambda$ is the trapezoid with vertices $\lambda$, $\big (0,\frac{bc+\sqrt{bc(bc-4)}}{2b}\lambda _0+\lambda _1\big )$, $-\frac{bc+\sqrt{bc(bc-4)}}{2c}\big (\frac{bc+\sqrt{bc(bc-4)}}{2b}\lambda _0+\lambda _1,0\big )$, and $\frac{bc+\sqrt{bc(bc-4)}}{2\sqrt{bc(bc-4)}}\big (-(bc-2)\lambda _0 -b\lambda _1,c\lambda _0+2\lambda _1\big )$.

• 3. If $\lambda$ lies on the ray spanned by $(2,-c)$, then ${\mathcal {P}}_\lambda$ is the triangle with vertices $\lambda$, $\big (0,\frac{bc+\sqrt{bc(bc-4)}}{2b}\lambda _0+\lambda _1\big )$, and $\big (\lambda _0+\frac{bc+\sqrt{bc(bc-4)}}{2c}\lambda _1,0\big )$.

• 4. If $\lambda$ lies in the cone spanned by the vectors $(2,-c)$ and $(b,-2)$, then ${\mathcal {P}}_\lambda$ is the kite with vertices $\lambda$, $\big (0,\frac{bc+\sqrt{bc(bc-4)}}{2b}\lambda _0+\lambda _1\big )$, $\frac{bc+\sqrt{bc(bc-4)}}{2\sqrt{bc(bc-4)}}(2\lambda _0+b\lambda _1,c\lambda _0+2\lambda _1)$, and $\big (\lambda _0+\frac{bc+\sqrt{bc(bc-4)}}{2c}\lambda _1,0\big )$.

• 5. If $\lambda$ lies on the ray spanned by $(b,-2)$, then ${\mathcal {P}}_\lambda$ is the triangle with vertices $\lambda$, $\big (0,\frac{bc+\sqrt{bc(bc-4)}}{2b}\lambda _0+\lambda _1\big )$, and $\big (\lambda _0+\frac{bc+\sqrt{bc(bc-4)}}{2c}\lambda _1,0\big )$.

• 6. If $\lambda$ lies in the cone spanned by the vectors $(b,-2)$ and $(2b,-bc+\sqrt{bc(bc-4)})$, then ${\mathcal {P}}_\lambda$ is the trapezoid with vertices $\lambda$, $\frac{bc+\sqrt{bc(bc-4)}}{2\sqrt{bc(bc-4)}}\big (2\lambda _0+b\lambda _1,-c\lambda _0-(bc-2)\lambda _1\big )$, $-\frac{bc+\sqrt{bc(bc-4)}}{2b}\big (0,\lambda _0+\frac{bc+\sqrt{bc(bc-4)}}{2c}\lambda _1\big )$, and $\big (\lambda _0+\frac{bc+\sqrt{bc(bc-4)}}{2c}\lambda _1,0\big )$.

Remark 1.5

Note that the rays which separate the regions inside ${\mathcal {I}}$ correspond exactly to the columns of the associated Cartan matrix. Moreover the expression for the dominance regions along those rays coincide. These unexpected coincidences are one of our reasons for deciding to write down these results. Unfortunately, at the moment, we are unable to explain the reason behind it.

Given a Laurent polynomial in ${\mathbb {Z}}[x_0^{\pm 1},x_1^{\pm 1}]$, its support is the set of its exponent vectors inside ${\mathbb {Z}}^2$. Given a ${\varvec{g}}$-vector $\lambda$, in the next result we identify a polygon ${\mathcal {S}}_\lambda$ whose lattice points of the form $\lambda +(b \alpha _0,c \alpha _1)$ for $\alpha _0,\alpha _1\in {\mathbb {Z}}$ give the maximum possible support of a pointed basis element $x_\lambda$. See Fig. 2 for an illustration.

Theorem 1.6

Let $\lambda =(\lambda _0,\lambda _1)\in {\mathbb {Z}}^2$ be the ${\varvec{g}}$-vector for a pointed basis element $x_\lambda$.

• 1. If $\lambda$ lies outside of ${\mathcal {I}}$, then the support of $x_\lambda$ is precisely the points of the form $\lambda +(b \alpha _0,c \alpha _1)$, $\alpha _0,\alpha _1\in {\mathbb {Z}}$, inside the region ${\mathcal {S}}_\lambda$ given as follows:

  • (a) If $0\le \lambda _0,\lambda _1$, then ${\mathcal {S}}_\lambda$ is just the point $\lambda =\lambda '$.

  • (b) If $\lambda _1 < 0$ and $0\le \lambda _0+b\lambda _1$, then ${\mathcal {S}}_\lambda$ is the segment joining $\lambda$ and $\lambda '=(\lambda _0+b\lambda _1,\lambda _1)$.

  • (c) If $\lambda _0 < 0$ and $0\le \lambda _1$, then ${\mathcal {S}}_\lambda$ is the segment joining $\lambda$ and $\lambda '=(\lambda _0,-c\lambda _0+\lambda _1)$.

  • (d) If $\lambda _0,\lambda _1 < 0$, then ${\mathcal {S}}_\lambda$ has vertices $\lambda$, $(\lambda _0+b\lambda _1,\lambda _1)$, $\lambda '=\big (\lambda _0+b\lambda _1,-c\lambda _0-(bc-1)\lambda _1\big )$, and ${(\lambda _0,-c\lambda _0+\lambda _1)}$.

  • (e) If $\lambda _0 > 0$, $\lambda _0+b\lambda _1 < 0$, and $-c\lambda _0-(bc-1)\lambda _1\le 0$, then ${\mathcal {S}}_\lambda$ has vertices $\lambda$, $(\lambda _0+b\lambda _1,\lambda _1)$, $\lambda '=\big (\lambda _0+b\lambda _1,-c\lambda _0-(bc-1)\lambda _1\big )$, and $\big ((bc+1)\lambda _0-b^2c\lambda _1,-c\lambda _0-(bc-1)\lambda _1\big )$.

  • (f) If $\lambda _0 > 0$, $\lambda _0+b\lambda _1 < 0$, and $0 < -c\lambda _0-(bc-1)\lambda _1$, then ${\mathcal {S}}_\lambda$ has vertices $\lambda$, $(\lambda _0+b\lambda _1,\lambda _1)$, $\lambda '=\big (\lambda _0+b\lambda _1,-c\lambda _0-(bc-1)\lambda _1\big )$, and (0, 0). Here the point (0, 0) and its adjacent open segments are excluded from ${\mathcal {S}}_\lambda$ while both $\lambda$ and $\lambda '$ are included.

• 2. If $\lambda$ lies inside of ${\mathcal {I}}$, then the support of $x_\lambda$ is contained in ${\mathcal {S}}_\lambda$ with vertices $\lambda$, $(\lambda _0+b\lambda _1,\lambda _1)$, $\lambda '=\big (\lambda _0+b\lambda _1,-c\lambda _0-(bc-1)\lambda _1\big )$, and $\frac{bc+\sqrt{bc(bc-4)}}{2\sqrt{bc(bc-4)}}\big (2\lambda _0+b\lambda _1,-c\lambda _0-(bc-2)\lambda _1\big )$. This last point and its adjacent open segments are excluded from ${\mathcal {S}}_\lambda$ while both $\lambda$ and $\lambda '$ are included.

  Moreover, there is an element pointed at $\lambda$ whose support is precisely the points of the form $\lambda +(b \alpha _0,c \alpha _1)$, $\alpha _0,\alpha _1\in {\mathbb {Z}}$, inside ${\mathcal {S}}_\lambda$.

Fig. 2

The maximal supports ${\mathcal {S}}_\lambda$ as described in Theorem 1.6 with $\lambda$ marked by a black dot and $\lambda '$ by a white dot. Dashed edges indicate the maximal support of an element pointed at $\lambda$ while dotted edges indicate the support of the corresponding greedy basis element. The imaginary cone ${\mathcal {I}}$ is dashed; the shaded cones correspond to the cases in Theorem 1.6

The paper is organized as follows. In Sect. 2, we collect useful results related to two-parameter Chebyshev polynomials which support our main calculations. Section 3 contains calculations related to the transformation of ${\varvec{g}}$-vectors under mutations. Section 4 proves Theorem 1.2. Section 5 proves Corollary 1.4. Section 6 proves Theorem 1.6. The paper ends with Sect. 7 interpreting the dominance polygons in terms of generalized minors in the cases where $b=c=2$.

2 Chebyshev Polynomials

Define two-parameter Chebyshev polynomials $u_i^\varepsilon$ for $i\in {\mathbb {Z}}$ and $\varepsilon \in \{\pm \}$ recursively by $u_0^\varepsilon =0$, $u_1^\varepsilon =1$, and

$$\begin{aligned} u_{i+1}^\varepsilon = {\left\{ \begin{array}{ll} bu_i^- -u_{i-1}^+ &{} \text {if }\varepsilon =+;\\ cu_i^+-u_{i-1}^- &{} \text {if }\varepsilon =-. \end{array}\right. } \end{aligned}$$

Remark 2.1

Observe that, by easy inductions, we have $u_{-i}^\varepsilon =-u_i^\varepsilon$ for $i\in {\mathbb {Z}}$ and $u_{2j+1}^+=u_{2j+1}^-$ for $j\in {\mathbb {Z}}$.

Lemma 2.2

For $i,\ell \in {\mathbb {Z}}$ and $\varepsilon \in \{\pm \}$, we have

$$\begin{aligned} u_{i+\ell }^\varepsilon = {\left\{ \begin{array}{ll} u_{\ell +1}^\varepsilon u_i^{-\varepsilon }-u_\ell ^{-\varepsilon } u_{i-1}^\varepsilon &{}\quad \textrm{if}~\ell ~\mathrm {is~odd;}\\ u_{\ell +1}^{-\varepsilon } u_i^\varepsilon -u_\ell ^\varepsilon u_{i-1}^{-\varepsilon } &{}\quad \textrm{if}~\ell ~\mathrm {is~even.} \end{array}\right. } \end{aligned}$$

(2)

Proof

We work by induction on $\ell$ for all i simultaneously, the cases $\ell =0,1$ being tautological and reproducing the defining recursions, respectively. Using the claim for $\ell >0$ and then the defining recursion twice, $u_{i+\ell +1}^\varepsilon$ can be rewritten for $\ell$ odd as

$$\begin{aligned} u_{\ell +1}^\varepsilon u_{i+1}^{-\varepsilon }-u_\ell ^{-\varepsilon } u_i^\varepsilon&=u_{\ell +1}^\varepsilon (u_2^{-\varepsilon }u_i^\varepsilon -u_{i-1}^{-\varepsilon }) -u_\ell ^{-\varepsilon } u_i^\varepsilon \\&=(u_2^{-\varepsilon } u_{\ell +1}^\varepsilon -u_\ell ^{-\varepsilon }) u_i^\varepsilon -u_{\ell +1}^\varepsilon u_{i-1}^{-\varepsilon }\\&=u_{\ell +2}^{-\varepsilon } u_i^\varepsilon - u_{\ell +1}^\varepsilon u_{i-1}^{-\varepsilon } \end{aligned}$$

and for $\ell$ even as

$$\begin{aligned} u_{\ell +1}^{-\varepsilon } u_{i+1}^\varepsilon -u_\ell ^\varepsilon u_i^{-\varepsilon }&=u_{\ell +1}^{-\varepsilon }(u_2^\varepsilon u_i^{-\varepsilon }-u_{i-1}^\varepsilon ) -u_\ell ^\varepsilon u_i^{-\varepsilon }\\&=(u_2^\varepsilon u_{\ell +1}^{-\varepsilon }-u_\ell ^\varepsilon ) u_i^{-\varepsilon }-u_{\ell +1}^{-\varepsilon } u_{i-1}^\varepsilon \\&=u_{\ell +2}^\varepsilon u_i^{-\varepsilon }-u_{\ell +1}^{-\varepsilon } u_{i-1}^\varepsilon . \end{aligned}$$

This gives the claimed recursion for $\ell +1$. These calculations can be reversed to show the result for $\ell <0$. $\square$

Lemma 2.3

We have

$$\begin{aligned} \lim _{i\rightarrow \infty } \frac{u_i^-}{u_{i-1}^+}= & {} \frac{bc+\sqrt{bc(bc-4)}}{2b} =\lim _{i\rightarrow -\infty } \frac{u_{i-1}^-}{u_i^+}; \\ \lim _{i\rightarrow \infty } \frac{u_{i-1}^-}{u_i^+}= & {} \frac{bc-\sqrt{bc(bc-4)}}{2b} =\lim _{i\rightarrow -\infty } \frac{u_i^-}{u_{i-1}^+}. \end{aligned}$$

Moreover, the limits in the first line converge monotonically from above and the limits in the second line converge monotonically from below.

Remark 2.4

The analogous limits with $\varepsilon =+$ and $\varepsilon =-$ reversed are obtained from these by interchanging the roles of b and c.

Proof

When $bc=4$ it is easy to compute closed formulas for $u_i^\varepsilon$ and the claimed limits follow; we thus concentrate on the case $bc>4$.

The standard Chebyshev polynomials (normalized, of the second kind) are defined by the recursion $u_0=0$, $u_1=1$, $u_{i+1}=ru_i-u_{i-1}$, which can be computed explicitly as

$$\begin{aligned} u_i(r)=\frac{1}{2^i\sqrt{r^2-4}}\left( \big (r+\sqrt{r^2-4}\big )^i -\big (r-\sqrt{r^2-4}\big )^i\right) . \end{aligned}$$

An induction on i shows that

$$\begin{aligned} u_i^\varepsilon ={\left\{ \begin{array}{ll} \frac{\sqrt{b}}{\sqrt{c}}u_i(\sqrt{bc}) &{} \quad \text {if }i\text { is even and }\varepsilon =+;\\ \frac{\sqrt{c}}{\sqrt{b}}u_i(\sqrt{bc}) &{} \quad \text {if }i\text { is even and }\varepsilon =-;\\ u_i(\sqrt{bc}) &{} \quad \text {if }i\text { is odd.} \end{array}\right. } \end{aligned}$$

It follows that $u_i^\varepsilon$ can be computed explicitly as

$$\begin{aligned} u_i^\varepsilon ={\left\{ \begin{array}{ll} \frac{\sqrt{b}}{2^i\sqrt{c(bc-4)}}\left( \big (\sqrt{bc} +\sqrt{bc-4}\big )^i-\big (\sqrt{bc}-\sqrt{bc-4}\big )^i\right) &{}\quad \text {if }i\text { is even and }\varepsilon =+;\\ \frac{\sqrt{c}}{2^i\sqrt{b(bc-4)}}\left( \big (\sqrt{bc}+\sqrt{bc-4}\big )^i -\big (\sqrt{bc}-\sqrt{bc-4}\big )^i\right) &{}\quad \text {if }i\text { is even and }\varepsilon =-;\\ \frac{1}{2^i\sqrt{bc-4}}\left( \big (\sqrt{bc}+\sqrt{bc-4}\big )^i -\big (\sqrt{bc}-\sqrt{bc-4}\big )^i\right) &{} \quad \text {if }i\text { is odd.} \end{array}\right. } \end{aligned}$$

For any $i\ne 1$, we have

$$\begin{aligned}{} & {} \displaystyle \frac{\big (\sqrt{bc}+\sqrt{bc-4}\big )^i -\big (\sqrt{bc}-\sqrt{bc-4}\big )^i}{\big (\sqrt{bc}+\sqrt{bc-4}\big )^{i-1} -\big (\sqrt{bc}-\sqrt{bc-4}\big )^{i-1}}\\{} & {} \quad =\frac{\big (\sqrt{bc}+\sqrt{bc-4}\big )\cdot \left( 1-\left( \frac{\sqrt{bc}- \sqrt{bc-4}}{\sqrt{bc}+\sqrt{bc-4}}\right) ^i\right) }{1-\left( \frac{\sqrt{bc} -\sqrt{bc-4}}{\sqrt{bc}+\sqrt{bc-4}}\right) ^{i-1}}. \end{aligned}$$

It follows that

$$\begin{aligned} \lim _{i\rightarrow \infty } \frac{u_i^-}{u_{i-1}^+}&=\lim _{i\rightarrow \infty } \left( \frac{\sqrt{c}}{2\sqrt{b}}\cdot \frac{\big (\sqrt{bc}+\sqrt{bc-4}\big )\cdot \left( 1-\left( \frac{\sqrt{bc} -\sqrt{bc-4}}{\sqrt{bc}+\sqrt{bc-4}}\right) ^i\right) }{1-\left( \frac{\sqrt{bc}-\sqrt{bc-4}}{\sqrt{bc}+\sqrt{bc-4}}\right) ^{i-1}} \right) \\&=\frac{\sqrt{c}}{2\sqrt{b}}\cdot \big (\sqrt{bc}+\sqrt{bc-4}\big ), \end{aligned}$$

which is equivalent to the desired expression. Similarly, for $i\ne 0$ we have

$$\begin{aligned}{} & {} \displaystyle \frac{\big (\sqrt{bc}+\sqrt{bc-4}\big )^{i-1}-\big (\sqrt{bc} -\sqrt{bc-4}\big )^{i-1}}{\big (\sqrt{bc}+\sqrt{bc-4}\big )^i -\big (\sqrt{bc}-\sqrt{bc-4}\big )^i}\\{} & {} \quad =\frac{\big (\sqrt{bc} -\sqrt{bc-4}\big )\cdot \left( 1-\left( \frac{\sqrt{bc} -\sqrt{bc-4}}{\sqrt{bc}+\sqrt{bc-4}}\right) ^{i-1}\right) }{4\left( 1-\left( \frac{\sqrt{bc}-\sqrt{bc-4}}{\sqrt{bc} +\sqrt{bc-4}}\right) ^i\right) }, \end{aligned}$$

so that

$$\begin{aligned} \lim _{i\rightarrow \infty } \frac{u_{i-1}^-}{u_i^+}&=\lim _{i\rightarrow \infty } \left( \frac{2\sqrt{c}}{\sqrt{b}}\cdot \frac{\big (\sqrt{bc}-\sqrt{bc-4}\big )\cdot \left( 1-\left( \frac{\sqrt{bc} -\sqrt{bc-4}}{\sqrt{bc}+\sqrt{bc-4}}\right) ^{i-1}\right) }{4\left( 1-\left( \frac{\sqrt{bc}-\sqrt{bc-4}}{\sqrt{bc}+\sqrt{bc-4}}\right) ^i\right) } \right) \\&=\frac{\sqrt{c}}{2\sqrt{b}}\cdot \big (\sqrt{bc}-\sqrt{bc-4}\big ), \end{aligned}$$

which is again equivalent to the desired expression. This proves the claim for $i\rightarrow \infty$, the cases $i\rightarrow -\infty$ follow from these using $u_{-i}^\varepsilon =-u_i^\varepsilon$.

For the final claim, observe that $\frac{u_{i+1}^{-\varepsilon }}{u_i^\varepsilon }<\frac{u_i^{-\varepsilon }}{u_{i-1}^\varepsilon }$ and $\frac{u_{i-1}^{-\varepsilon }}{u_i^\varepsilon }<\frac{u_i^{-\varepsilon }}{u_{i+1}^\varepsilon }$ are both equivalent to $u_{i+1}^{-\varepsilon }u_{i-1}^\varepsilon <u_i^{-\varepsilon }u_i^\varepsilon$. This inequality is then immediate, for $i>0$, from the following inductions:

$$\begin{aligned} u_{i+1}^{-}u_{i-1}^+&=(cu_i^+-u_{i-1}^{-})u_{i-1}^+ =cu_i^+ u_{i-1}^+-u_{i-1}^{-} u_{i-1}^+\\&<cu_i^+ u_{i-1}^+-u_i^+ u_{i-2}^{-} =u_i^+(cu_{i-1}^+-u_{i-2}^{-}) =u_i^+ u_i^{-};\\ u_{i+1}^{+}u_{i-1}^-&=(bu_i^--u_{i-1}^{+})u_{i-1}^- =bu_i^- u_{i-1}^--u_{i-1}^{+} u_{i-1}^-\\&<bu_i^- u_{i-1}^--u_i^- u_{i-2}^{+} =u_i^-(bu_{i-1}^--u_{i-2}^{+}) =u_i^- u_i^{+}. \end{aligned}$$

Again the case $i<0$ then follows from $u_{-i}^\varepsilon =-u_i^\varepsilon$. $\square$

3 ${\varvec{g}}$-Vector Mutations

We begin by studying transformations of ${\mathbb {R}}^2$ which determine the change of ${\varvec{g}}$-vectors when expanding an expression of the form (1) in terms of a cluster $\{x_k,x_{k+1}\}$. This adapts the notation from [12, Definition 2.1.4] to our setting, see also [17, Definition 4.1].

Write $\phi _0:{\mathbb {R}}^2\rightarrow {\mathbb {R}}^2$ for the identity map and define piecewise-linear maps $\phi _{\pm 1}:{\mathbb {R}}^2\rightarrow {\mathbb {R}}^2$ as follows:

$$\begin{aligned} \phi _1(\lambda )&:= {\left\{ \begin{array}{ll} (-\lambda _0,c\lambda _0+\lambda _1) &{} \quad \text {if }\lambda _0 \ge 0;\\ (-\lambda _0,\lambda _1) &{} \quad \text {if }\lambda _0< 0; \end{array}\right. } \\ \phi _{-1}(\lambda )&:= {\left\{ \begin{array}{ll} (\lambda _0,-\lambda _1) &{} \quad \text {if }\lambda _1 \ge 0;\\ (\lambda _0+b\lambda _1,-\lambda _1) &{} \quad \text {if }\lambda _1 < 0. \end{array}\right. }\nonumber \end{aligned}$$

(3)

For $k\in {\mathbb {Z}}$ with $|k|>1$, define piecewise-linear maps

$$\begin{aligned} \phi _k:= {\left\{ \begin{array}{ll} (\phi _{-1}^{-1}\phi _1)^j &{} \quad \text {if }k=2j;\\ \phi _1(\phi _{-1}^{-1}\phi _1)^j &{} \quad \text {if }k=2j+1.\\ \end{array}\right. } \end{aligned}$$

These determine the dominance region as we paraphrase from [12, Section 3.1].

Definition 3.1

For $\lambda =(\lambda _0,\lambda _1)\in {\mathbb {Z}}^2$ and $k\in {\mathbb {Z}}$, define cones

$$\begin{aligned} {\mathcal {C}}_k(\lambda ):= {\left\{ \begin{array}{ll} \{(\lambda _0-r,\lambda _1+s):r,s\in {\mathbb {R}}_{\ge 0}\} &{} \quad \text {if }k=2j;\\ \{(\lambda _0+r,\lambda _1-s):r,s\in {\mathbb {R}}_{\ge 0}\} &{} \quad \text {if }k=2j+1. \end{array}\right. } \end{aligned}$$

The dominance region ${\mathcal {P}}_\lambda$ is the intersection $\bigcap _{k\in {\mathbb {Z}}}\phi _k^{-1}{\mathcal {C}}_k(\phi _k\lambda )$. When $\mu \in {\mathcal {P}}_\lambda$, we say $\lambda$ dominates $\mu$.

We record here a few useful calculations relating to the tropical transformations $\phi _k$. First observe the following explicit expression for $\phi _2$:

$$\begin{aligned} \phi _2(\lambda ) = {\left\{ \begin{array}{ll} \big ((bc-1)\lambda _0+b\lambda _1, -c\lambda _0-\lambda _1\big ) &{}\quad \text {if }\lambda _0\ge 0\text { and }c\lambda _0+\lambda _1\ge 0;\\ (-\lambda _0, -c\lambda _0-\lambda _1) &{} \quad \text {if }\lambda _0\ge 0\text { and }c\lambda _0+\lambda _1<0;\\ (-\lambda _0+b\lambda _1, -\lambda _1) &{} \quad \text {if }\lambda _0<0\text { and }\lambda _1\ge 0;\\ (-\lambda _0,-\lambda _1) &{}\quad \text {if }\lambda _0<0\text { and }\lambda _1<0. \end{array}\right. } \end{aligned}$$

(4)

By an eigenvector of a piecewise-linear map $\phi$, we will mean a vector $\lambda$ such that there exists a positive scalar $\nu$ so that $\phi (\lambda )=\nu \lambda$.

Lemma 3.2

Any nonzero eigenvector of $\phi _2$ is a positive multiple of one of the vectors $\big (2b,-bc\pm \sqrt{bc(bc-4)}\big )$.

Proof

First observe that, by equation (4), the equation $\phi _2(\lambda )=\nu \lambda$ cannot be satisfied with a positive $\nu$ unless $\lambda _0\ge 0$ and $c\lambda _0+\lambda _1\ge 0$. In this region, $\phi _2$ is linear with eigenvalue $\nu$ satisfying $\nu ^2-(bc-2)\nu +1=0$, i.e. $\nu =\frac{bc-2\pm \sqrt{bc(bc-4)}}{2}$. We thus require

$$\begin{aligned}{} & {} \frac{bc-2\pm \sqrt{bc(bc-4)}}{2}\lambda _0=(bc-1)\lambda _0+b\lambda _1\\{} & {} \quad \text {and}\,\,\,\frac{bc-2\pm \sqrt{bc(bc-4)}}{2}\lambda _1= -c\lambda _0-\lambda _1, \end{aligned}$$

or equivalently

$$\begin{aligned} \frac{-bc\pm \sqrt{bc(bc-4)}}{2b}\lambda _0=\lambda _1 \quad \text {and}\quad \frac{-bc\mp \sqrt{bc(bc-4)}}{2c}\lambda _1=\lambda _0. \end{aligned}$$

As these represent the same relationship, the result immediately follows by inspection. $\square$

Observe that the imaginary cone ${\mathcal {I}}$ is spanned by the eigenvectors of $\phi _{2}$ and that $\phi _{2}$ is linear in ${\mathcal {I}}$.

Lemma 3.3

For $j\in {\mathbb {Z}}$ and $\lambda \in {\mathcal {I}}$, we have $\phi _{2j}(\lambda )\in {\mathcal {I}}$.

Proof

Since $\phi _{2j}=\phi _2^j$, the result follows from the case $j=1$ which is immediate. $\square$

It will be useful to have explicit expressions for $\phi _k(\lambda )$ for $\lambda \in {\mathcal {I}}$.

Lemma 3.4

For $j\in {\mathbb {Z}}$ and $\lambda \in {\mathcal {I}}$, we have

$$\begin{aligned} \phi _{2j}(\lambda )&=(u_{2j+1}^-\lambda _0+u_{2j}^+\lambda _1,-u_{2j}^- \lambda _0-u_{2j-1}^+\lambda _1);\\ \phi _{2j+1}(\lambda )&=(-u_{2j+1}^-\lambda _0-u_{2j}^+\lambda _1,u_{2j+2}^- \lambda _0+u_{2j+1}^+\lambda _1). \end{aligned}$$

Proof

We work by induction on j, the case $j=0$ being clear from the definitions. For $\lambda \in {\mathcal {I}}$, the action of $\phi _2$ from (4) can be rewritten as

$$\begin{aligned} \phi _2(\lambda )=(u_3^-\lambda _0+u_2^+\lambda _1, -u_2^-\lambda _0-u_1^+\lambda _1). \end{aligned}$$

Therefore, after applying the equivalences for odd Chebyshev polynomials from Remark 2.1, we have

$$\begin{aligned} \phi _{2j+2}(\lambda )&=\phi _2\phi _{2j}(\lambda )\\&=\Big ( (u_3^- u_{2j+1}^+-u_2^+u_{2j}^-)\lambda _0+(u_3^-u_{2j}^+ -u_2^+u_{2j-1}^-)\lambda _1,\\&\quad -(u_2^-u_{2j+1}^+-u_1^+u_{2j}^-)\lambda _0-(u_2^-u_{2j}^+ -u_1^+u_{2j-1}^-)\lambda _1 \Big )\\&=(u_{2j+3}^+\lambda _0+u_{2j+2}^+\lambda _1, -u_{2j+2}^-\lambda _0-u_{2j+1}^-\lambda _1), \end{aligned}$$

where the last equality uses (2) with $i=2j+1$ and $\ell =2$. Using Remark 2.1 again, this is equivalent to the desired expression.

Similarly, using $\phi _1(\lambda )=(-\lambda _0,u_2^-\lambda _0+u_1^+\lambda _1)$ for $\lambda \in {\mathcal {I}}$ together with the basic Chebyshev recursion and the equality $\phi _{2j+1}=\phi _1\phi _2^j$ gives the claimed formula for $\phi _{2j+1}$ from that of $\phi _{2j}$. $\square$

4 Proof of Theorem 1.2

Here we explicitly compute the dominance regions ${\mathcal {P}}_\lambda$. The following Lemma proves Theorem 1.2 for $\lambda \not \in {\mathcal {I}}$.

Lemma 4.1

If $\lambda \in {\mathbb {Z}}^2{\setminus }{\mathcal {I}}$, then ${\mathcal {P}}_\lambda =\{\lambda \}$.

Proof

Any such $\lambda$ is the ${\varvec{g}}$-vector of a cluster monomial, say $x_k^{\alpha _k}x_{k+1}^{\alpha _{k+1}}$. In this case, the intersection

$$\begin{aligned} \phi _{k-1}^{-1}{\mathcal {C}}_{k-1}(\phi _{k-1}\lambda ) \cap \phi _{k+1}^{-1}{\mathcal {C}}_{k+1}(\phi _{k+1}\lambda ) \end{aligned}$$

is precisely $\{\lambda \}$. Indeed, for k odd, the cone ${\mathcal {C}}_{k-1}(\phi _{k-1}\lambda )$ lies entirely within a domain of linearity for $\phi _{k-1}^{-1}$. In particular, $\phi _{k-1}^{-1}{\mathcal {C}}_{k-1}(\phi _{k-1}\lambda )$ is a cone containing $\lambda$ directed away from the origin (with walls parallel to the boundary of the domain of linearity containing $\lambda$). Next, again for k odd, the cone ${\mathcal {C}}_{k+1}(\phi _{k+1}\lambda )$ intersects the domain of linearity for $\phi _{k+1}^{-1}$ containing $\phi _{k+1}\lambda$ in a (possibly degenerate) convex quadrilateral with corners at the origin and $\phi _{k+1}\lambda$. In particular, the intersection of $\phi _{k+1}^{-1}{\mathcal {C}}_{k+1}(\phi _{k+1}\lambda )$ with the cone containing $\lambda$ is a (possibly degenerate) convex quadrilateral with corners at the origin and $\lambda$. Combining these observations proves the result for k odd, the case of even k is similar. $\square$

Next we aim to understand how inequalities transform under the action of a piecewise-linear map. The following well known fact about linear maps will suffice.

Lemma 4.2

Let M be an invertible $2\times 2$ matrix. Under the left action of M, say $M\mu =\mu '$ for $\mu ,\mu '\in {\mathbb {R}}^2$, the region inside ${\mathbb {R}}^2$ defined by the inequality $\langle \alpha ,\mu \rangle \le t$ with $\alpha \in {\mathbb {R}}^2$ and $t\in {\mathbb {R}}$ is transformed into the region defined by the inequality

$$\begin{aligned} \langle M^{-T}\alpha ,\mu '\rangle \le t. \end{aligned}$$

Proof

This is immediate from the equalities

$$\begin{aligned} \langle \alpha ,\mu \rangle = \alpha ^T\mu = \alpha ^TM^{-1}M\mu = (M^{-T}\alpha )^TM\mu = \langle M^{-T}\alpha ,\mu '\rangle . \end{aligned}$$

$\square$

The following calculation is key to our main result.

Lemma 4.3

For $k\in {\mathbb {Z}}$, $k\ne 0$, and $\lambda \in {\mathcal {I}}$, the region $\phi _k^{-1}{\mathcal {C}}_k(\phi _k\lambda )\subset {\mathbb {R}}^2$ is determined by the following inequalities when $k>0$:

$$\begin{aligned} u_k^-\mu _0+u_{k-1}^+\mu _1&\le u_k^-\lambda _0+u_{k-1}^+\lambda _1; \end{aligned}$$

(5)

$$\begin{aligned} u_{k+1}^-\mu _0+u_k^+\mu _1&\le u_{k+1}^-\lambda _0+u_k^+\lambda _1; \end{aligned}$$

(6)

$$\begin{aligned} -u_{k-1}^-\mu _0+u_k^+\mu _1&\le u_{k+1}^-\lambda _0+u_k^+\lambda _1;\end{aligned}$$

(7)

$$\begin{aligned} -u_{k-1}^-\mu _0-u_{k-2}^+\mu _1&\le u_{k+1}^-\lambda _0+u_k^+\lambda _1; \end{aligned}$$

(8)

and by the following inequalities when $k<0$:

$$\begin{aligned} u_{k+1}^-\mu _0+u_k^+\mu _1&\le u_{k+1}^-\lambda _0+u_k^+\lambda _1;\\ u_k^-\mu _0+u_{k-1}^+\mu _1&\le u_k^-\lambda _0+u_{k-1}^+\lambda _1;\\ u_k^-\mu _0-u_{k+1}^+\mu _1&\le u_k^-\lambda _0+u_{k-1}^+\lambda _1;\\ -u_{k+2}^-\mu _0-u_{k+1}^+\mu _1&\le u_k^-\lambda _0+u_{k-1}^+\lambda _1. \end{aligned}$$

See Fig. 3 for an illustration.

Fig. 3

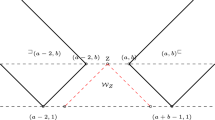
Two examples of the regions in Lemma 4.3. Each inequality is represented by a shaded halfspace, darker regions consist of points satisfying multiple inequalities

Proof

We prove the claim for $k>0$, the proof for $k<0$ is similar or can be deduced from the other case by a symmetry argument. Following Lemma 3.4, we consider even and odd sequences of mutations separately.

For $k=2j$, $j>0$, and $\lambda \in {\mathcal {I}}$, we observe that ${\mathcal {C}}_k(\phi _k\lambda )\subset {\mathbb {R}}^2$ is given by the inequalities

$$\begin{aligned} (\dagger )\ \mu _0 \le u_{2j+1}^-\lambda _0+u_{2j}^+\lambda _1 \qquad \text {and}\qquad (\ddagger )\ -\mu _1\le u_{2j}^-\lambda _0+u_{2j-1}^+\lambda _1. \end{aligned}$$

We compute the region $\phi _{2j}^{-1}{\mathcal {C}}_{2j}(\phi _{2j}\lambda )$ using Lemma 4.2 and the equality $\phi _{2j}^{-1}=\left( \phi _2^{-1}\right) ^{j}$. First observe that $\phi _2^{-1}=\phi _{-2}$ is given as follows:

$$\begin{aligned} \phi _{-2}(\lambda ) = {\left\{ \begin{array}{ll} \big (-\lambda _0-b\lambda _1, c\lambda _0+(bc-1)\lambda _1\big ) &{}\quad \text {if }\lambda _1\le 0\text { and }\lambda _0+b\lambda _1\le 0;\\ (-\lambda _0-b\lambda _1, -\lambda _1) &{} \quad \text {if }\lambda _1\le 0\text { and }\lambda _0+b\lambda _1>0;\\ (-\lambda _0, c\lambda _0-\lambda _1) &{} \quad \text {if }\lambda _1>0\text { and }\lambda _0\le 0;\\ (-\lambda _0,-\lambda _1) &{} \quad \text {if }\lambda _1>0\text { and }\lambda _0>0. \end{array}\right. } \end{aligned}$$

(9)

4.1 Claim:

For $i>0$, $\phi _{2i}^{-1}{\mathcal {C}}_{2j}(\phi _{2j}\lambda )$ is the region determined by the inequalities

$$\begin{aligned} u_{2i}^-\mu _0+u_{2i-1}^+\mu _1&\le u_{2j}^-\lambda _0+u_{2j-1}^+\lambda _1;\end{aligned}$$

(a)

$$\begin{aligned} u_{2i+1}^-\mu _0+u_{2i}^+\mu _1&\le u_{2j+1}^-\lambda _0+u_{2j}^+\lambda _1;\end{aligned}$$

(b)

$$\begin{aligned} -u_{2i-1}^-\mu _0+u_{2i}^+\mu _1&\le u_{2j+1}^-\lambda _0+u_{2j}^+\lambda _1;\end{aligned}$$

(c)

$$\begin{aligned} -u_{2i-1}^-\mu _0-u_{2i-2}^+\mu _1&\le u_{2j+1}^-\lambda _0+u_{2j}^+\lambda _1. \end{aligned}$$

(d)

We prove the claim by induction on i. We see from (9), that $\lambda \in {\mathcal {I}}$ implies the boundary ray for ${\mathcal {C}}_{2j}(\phi _{2j}\lambda )$ corresponding to ($\ddagger$) lies entirely in the region in which $\phi _2^{-1}$ acts according to the matrix $\left[ \begin{array}{cc} -1 &{}\quad -b\\ c &{}\quad bc-1 \end{array}\right]$. By Lemma 4.2, the inequality ($\ddagger$) transforms into the inequality $c\mu _0+\mu _1\le u_{2j}^-\lambda _0+u_{2j-1}^+\lambda _1$ which corresponds to (a) with $i=1$. Similarly, the boundary ray for ${\mathcal {C}}_{2j}(\phi _{2j}\lambda )$ corresponding to ($\dagger$) intersects the three domains of linearity in which $\phi _2^{-1}$ acts according to the matrices $\left[ \begin{array}{cc} -1 &{}\quad -b\\ c &{}\quad bc-1 \end{array}\right]$, $\left[ \begin{array}{cc} -1 &{}\quad -b\\ 0 &{}\quad -1 \end{array}\right]$, $\left[ \begin{array}{cc} -1 &{} \quad 0\\ 0 &{}\quad -1 \end{array}\right]$. By Lemma 4.2, the inequality ($\dagger$) can be seen to transform by these into each of inequalities (b), (c), (d) with $i=1$. This establishes the base of our induction.

Assuming the inequalities (a)–(d) hold for i, we apply Lemma 4.2 for $\phi _2^{-1}$. Both of the boundary rays corresponding to the inequalities (a) and (d) lie entirely in the region where $\phi _2^{-1}$ acts according to the matrix $\left[ \begin{array}{cc} -1 &{}\quad -b\\ c &{}\quad bc-1 \end{array}\right]$, also the boundary segment corresponding to (b) intersects this region. Thus applying Lemma 4.2 to (a) gives the inequality

$$\begin{aligned} u_{2i+2}^-\mu _0+u_{2i+1}^+\mu _1= & {} (u_3^+u_{2i}^--u_2^-u_{2i-1}^+) \mu _0+(u_2^+u_{2i}^--u_1^-u_{2i-1}^+)\mu _1\\\le & {} u_{2j}^-\lambda _0+u_{2j-1}^+\lambda _1, \end{aligned}$$

which is the inequality (a) for $i+1$ by Lemma 2; while applying this to (d) gives the inequality

$$\begin{aligned} -u_{2i+1}^-\mu _0-u_{2i}^+\mu _1&=(-u_3^+u_{2i-1}^-+u_2^-u_{2i-2}^+)\mu _0+(-u_2^+u_{2i-1}^-+u_1^-u_{2i-2}^+)\mu _1\\&\le u_{2j+1}^-\lambda _0+u_{2j}^+\lambda _1, \end{aligned}$$

which is the inequality (d) for $i+1$ again by Lemma 2; finally applying this to (b) gives the inequality

$$\begin{aligned} u_{2i+3}^-\mu _0+u_{2i+2}^+\mu _1=(u_3^+u_{2i+1}^--u_2^-u_{2i}^+) \mu _0+(u_2^+u_{2i+1}^--u_1^-u_{2i}^+)\mu _1\le u_{2j+1}^-\lambda _0+u_{2j}^+\lambda _1, \end{aligned}$$

which is the inequality (b) for $i+1$. Similarly, the boundary segment corresponding to (c) lies entirely in the region where $\phi _2^{-1}$ acts according to the matrix $\left[ \begin{array}{cc} -1 &{}\quad 0\\ c &{}\quad -1 \end{array}\right]$. Thus applying Lemma 4.2 to (c) gives the inequality

$$\begin{aligned} -u_{2i+1}^-\mu _0-u_{2i}^+\mu _1= & {} (u_1^+u_{2i-1}^--u_2^-u_{2i}^+) \mu _0+(-u_0^+u_{2i-1}^--u_1^-u_{2i}^+)\mu _1\\\le & {} u_{2j+1}^-\lambda _0+u_{2j}^+\lambda _1, \end{aligned}$$

which is the inequality (d) for $i+1$ by Lemma 2, in particular we see that the segment determined by (c) and the ray determined by (d) align in the image. Lastly, the boundary segment corresponding to (b) also intersects the regions where $\phi _2^{-1}$ acts according to the matrices $\left[ \begin{array}{cc} -1 &{}\quad -b\\ 0 &{}\quad -1 \end{array}\right]$ and $\left[ \begin{array}{cc} -1 &{}\quad 0\\ 0 &{}\quad -1 \end{array}\right]$ respectively. Applying Lemma 4.2 to (b) with the first matrix gives the inequality

$$\begin{aligned} -u_{2i+1}^-\mu _0+u_{2i+2}^+\mu _1&=(-u_1^+u_{2i+1}^-+u_0^-u_{2i}^+)\mu _0+(u_2^+u_{2i+1}^--u_1^-u_{2i,+})\mu _1\\&\le u_{2j+1}^-\lambda _0+u_{2j}^+\lambda _1, \end{aligned}$$

which is the inequality (c) for $i+1$ by Lemma 2, while applying Lemma 4.2 to (b) with the second matrix gives the inequality

$$\begin{aligned} -u_{2i+1}^-\mu _0-u_{2i}^+\mu _1\le u_{2j+1}^-\lambda _0+u_{2j}^+\lambda _1, \end{aligned}$$

which again reproduces the inequality (d) and aligns with the previous segment and ray in the image. This completes the induction on i, proving the Claim and the result for k even.

For $k=2j+1$, $j\ge 0$, and $\lambda \in {\mathcal {I}}$, we get ${\mathcal {C}}_{2j+1}(\phi _{2j+1}\lambda )\subset {\mathbb {R}}^2$ is given by the inequalities

$$\begin{aligned} (\dagger ')\ -\mu _0\le u_{2j+1}^-\lambda _0+u_{2j}^+\lambda _1 \qquad \text {and}\qquad (\ddagger ')\ \mu _1\le u_{2j+2}^-\lambda _0+u_{2j+1}^+\lambda _1. \end{aligned}$$

Using that $\phi _{2j+1}^{-1}=\left( \phi _2^{-1}\right) ^j\phi _1^{-1}$, we compute the image inductively as above. From (3) and Lemma 3.3, we see that the boundary ray for ${\mathcal {C}}_{2j+1}(\phi _{2j+1}\lambda )$ corresponding to ($\dagger '$) lies entirely in the region in which $\phi _1^{-1}$ acts according to the matrix $\left[ \begin{array}{cc} -1 &{}\quad 0\\ c &{}\quad 1 \end{array}\right]$. Thus applying Lemma 4.2, the inequality ($\dagger '$) is transformed by $\phi _1^{-1}$ into the inequality $\mu _0\le u_{2j+1}^-\lambda _0+u_{2j}^+\lambda _1$. The boundary ray corresponding to ($\ddagger '$) intersects both domains of linearity for $\phi _1^{-1}$ and thus produces the inequalities

$$\begin{aligned} c\mu _0+\mu _1\le u_{2j+2}^-\lambda _0+u_{2j+1}^+\lambda _1 \qquad \text {and}\qquad \mu _1\le u_{2j+2}^-\lambda _0+u_{2j+1}^+\lambda _1. \end{aligned}$$

4.2 Claim:

For $i\ge 0$, $\phi _{2i+1}^{-1}{\mathcal {C}}_{2j+1}(\phi _{2j+1}\lambda )$ is the region determined by the inequalities

By essentially the same calculations as above, these inequalities reproduce under the action of $\phi _2^{-1}$ and this completes the proof. $\square$

We are now ready to prove Theorem 1.2. The dominance region ${\mathcal {P}}_\lambda =\bigcap _{k\in {\mathbb {Z}}}\phi _k^{-1}{\mathcal {C}}_k(\phi _k\lambda )$ for $\lambda \in {\mathcal {I}}$ is obtained by imposing all of the inequalities from Lemma 4.3 together with $\mu _0 -\lambda _0 \le 0$ and $0 \le \mu _1 - \lambda _1$ coming from $k=0$.

We rewrite the inequalities from Lemma 4.3 using the Chebyshev recursion. For $k>0$, we get

$$\begin{aligned} u_k^-(\mu _0-\lambda _0)+u_{k-1}^+(\mu _1-\lambda _1)&\le 0;\\ u_{k+1}^-(\mu _0-\lambda _0)+u_k^+(\mu _1-\lambda _1)&\le 0;\\ -u_{k-1}^-(\mu _0-\lambda _0)+u_k^+(\mu _1-\lambda _1)&\le cu_k^+\lambda _0;\\ -u_{k-1}^-(\mu _0-\lambda _0)-u_{k-2}^+(\mu _1-\lambda _1)&\le cu_k^+\lambda _0+bu_{k-1}^-\lambda _1; \end{aligned}$$

and, for $k<0$, we get

$$\begin{aligned} u_{k+1}^-(\mu _0-\lambda _0)+u_k^+(\mu _1-\lambda _1)&\le 0;\\ u_k^-(\mu _0-\lambda _0)+u_{k-1}^+(\mu _1-\lambda _1)&\le 0;\\ u_k^-(\mu _0-\lambda _0)-u_{k+1}^+(\mu _1-\lambda _1)&\le bu_k^-\lambda _1;\\ -u_{k+2}^-(\mu _0-\lambda _0)-u_{k+1}^+(\mu _1-\lambda _1)&\le cu_{k+1}^+\lambda _0+bu_k^-\lambda _1. \end{aligned}$$

The first inequality in each list is redundant so we drop them. Moreover, for $k=1$ the third and fourth inequalities in the first list are the same so we can increment k in the last equality without losing any information and similarly for $k=-1$ in the second list. This gives

$$\begin{aligned}&0 \le -u_{k+1}^-(\mu _0-\lambda _0)+u_k^-(\mu _1-\lambda _1); \\&-u_{k-1}^-(\mu _0-\lambda _0)+u_k^+(\mu _1-\lambda _1) \le cu_k^+\lambda _0;\\&-u_k^-(\mu _0-\lambda _0)-u_{k-1}^+(\mu _1-\lambda _1) \le cu_{k+1}^+\lambda _0+bu_k^-\lambda _1; \end{aligned}$$

for $k>0$ and

$$\begin{aligned}&0 \le -u_k^-(\mu _0-\lambda _0)+u_{k-1}^-(\mu _1-\lambda _1); \\&u_k^-(\mu _0-\lambda _0)-u_{k+1}^+(\mu _1-\lambda _1) \le bu_k^-\lambda _1;\\&-u_{k+1}^-(\mu _0-\lambda _0)-u_k^+(\mu _1-\lambda _1) \le cu_k^+\lambda _0+bu_{k-1}^-\lambda _1; \end{aligned}$$

for $k<0$.

Then, using that $-u_k^\varepsilon <0$ for $k>0$ and $u_k^\varepsilon <0$ for $k<0$, we rewrite the inequalities again as

$$\begin{aligned}&0 \le -(\mu _0-\lambda _0)-\frac{u_k^+}{u_{k+1}^-}(\mu _1-\lambda _1); \end{aligned}$$

(10)

$$\begin{aligned}&-\frac{u_{k-1}^-}{u_k^+}(\mu _0-\lambda _0)+(\mu _1-\lambda _1) \le c\lambda _0;\end{aligned}$$

(11)

$$\begin{aligned}&-(\mu _0-\lambda _0)-\frac{u_{k-1}^+}{u_k^-}(\mu _1-\lambda _1) \le c\frac{u_{k+1}^+}{u_k^-}\lambda _0+b\lambda _1; \end{aligned}$$

(12)

for $k>0$ and

$$\begin{aligned}&0 \le (\mu _0-\lambda _0)+\frac{u_{k-1}^+}{u_k^-}(\mu _1-\lambda _1); \end{aligned}$$

(13)

$$\begin{aligned}&-(\mu _0-\lambda _0)+\frac{u_{k+1}^+}{u_k^-}(\mu _1-\lambda _1) \le -b\lambda _1;\end{aligned}$$

(14)

$$\begin{aligned}&-\frac{-u_{k+1}^-}{u_k^+}(\mu _0-\lambda _0)+(\mu _1-\lambda _1) \le -c\lambda _0 -b\frac{u_{k-1}^-}{u_k^+}\lambda _1; \end{aligned}$$

(15)

for $k<0$. We now study each sequence of inequalities in turn.

For $\mu _1-\lambda _1\ge 0$, the inequalities (10) become more restrictive as k gets larger since the sequence $\frac{-u_{k+1}^-}{u_k^+}$ of negative slopes is monotonically increasing (cf. Lemma 2.3). Thus, following Lemma 2.3, in the limit as $k\rightarrow \infty$, we obtain the inequality below determining a boundary of ${\mathcal {P}}_\lambda$:

$$\begin{aligned} 0 \le -(\mu _0-\lambda _0)-\frac{bc -\sqrt{bc(bc-4)}}{2c}(\mu _1-\lambda _1). \end{aligned}$$

Similarly, the inequalities (11) become more restrictive for $\mu _0\le 0$ and $\mu _1\ge 0$ as k gets larger since the sequence $\frac{u_{k-1}^-}{u_k^+}$ of positive slopes is monotonically increasing and the intersection with (10) moves lower on the $\mu _1$-axis as k increases. Thus, following Lemma 2.3, in the limit as $k\rightarrow \infty$, we obtain the inequality

$$\begin{aligned} -\frac{bc-\sqrt{bc(bc-4)}}{2b}(\mu _0-\lambda _0)+(\mu _1-\lambda _1) \le c\lambda _0 \end{aligned}$$

determining a boundary of ${\mathcal {P}}_\lambda$. Observe further that the inequalities $\mu _0-\lambda _0 \le 0$ and $0 \le \mu _1-\lambda _1$ allow to strengthen this as

$$\begin{aligned} 0 \le -\frac{bc-\sqrt{bc(bc-4)}}{2b}(\mu _0-\lambda _0)+(\mu _1-\lambda _1) \le c\lambda _0. \end{aligned}$$

Finally, the inequalities (12) become more restrictive for $\mu _1\le 0$ as k gets larger since the sequence $\frac{-u_k^-}{u_{k-1}^+}$ of negative slopes is monotonically increasing (cf. Lemma 2.3) and the intersection with (11) (for $k+1$) moves to the right on the $\mu _0$-axis as k increases. Thus, following Lemma 2.3, in the limit as $k\rightarrow \infty$, we obtain the inequality below determining a boundary of ${\mathcal {P}}_\lambda$:

$$\begin{aligned} -(\mu _0-\lambda _0)-\frac{bc-\sqrt{bc(bc-4)}}{2c}(\mu _1-\lambda _1) \le \frac{bc+\sqrt{bc(bc-4)}}{2c}c\lambda _0+b\lambda _1. \end{aligned}$$

Similar arguments using (13)–(15) lead to the remaining inequalities determining the boundary of ${\mathcal {P}}_\lambda$:

$$\begin{aligned}{} & {} 0 \le (\mu _0-\lambda _0)+\frac{bc+\sqrt{bc(bc-4)}}{2c}(\mu _1-\lambda _1);\\{} & {} 0 \le -(\mu _0-\lambda _0)+\frac{bc-\sqrt{bc(bc-4)}}{2c}(\mu _1-\lambda _1) \le -b\lambda _1;\\{} & {} 0 \le \frac{bc-\sqrt{bc(bc-4)}}{2b}(\mu _0-\lambda _0)+(\mu _1-\lambda _1) \le -c\lambda _0 -\frac{bc+\sqrt{bc(bc-4)}}{2b}b\lambda _1. \end{aligned}$$

These can easily be seen to be equivalent to the remaining inequalities from Theorem 1.2 and this complete the proof.

5 Proof of Corollary 1.4

This follows from basic manipulations finding the intersection points of the boundary segments determined by the inequalities from Theorem 1.2. Note that in each of the cases (2), (4), and (6) there are only four inequalities to consider while in cases (3) and (5) there are only three inequalities to consider. We leave the details as an exercise for the reader.

6 Proof of Theorem 1.6

We begin observing that, by Lemma 4.1, the dominance region ${\mathcal {P}}_\lambda$ of any ${\varvec{g}}$-vector $\lambda \not \in {\mathcal {I}}$ is just the point $\lambda$. Therefore, by Theorem 1.1 the corresponding pointed element is the cluster monomial whose ${\varvec{g}}$-vector is $\lambda$. The support of this element is exactly ${\mathcal {S}}_\lambda$ by [7, Proposition 4.1].

Every pointed basis element for ${\mathcal {A}}(b,c)$ admits an opposite ${\varvec{g}}$-vector arising by interchanging the roles of b, c and $x_0$, $x_1$ in (1). One can easily compute the following correspondence.

Lemma 6.1

Given a ${\varvec{g}}$-vector $\lambda$, the opposite ${\varvec{g}}$-vector $\lambda '$ is obtained as follows:

• if $\lambda _0,\lambda _1\ge 0$, then $\lambda '=\lambda$;

• if $\lambda _1\ge 0$ and $\lambda _0<0$, then $\lambda '=(\lambda _0,-c\lambda _0+\lambda _1)$;

• if $\lambda _0>0$ and $\lambda _0+b\lambda _1>0$, then $\lambda '=(\lambda _0+b\lambda _1,\lambda _1)$;

• otherwise, $\lambda '=(\lambda _0+b\lambda _1,-c\lambda _0-(bc-1)\lambda _1)$.

In particular, we get an opposite dominance region ${\mathcal {P}}'_\lambda$ for each ${\varvec{g}}$-vector $\lambda$.

Lemma 6.2

For $\lambda \in {\mathcal {I}}$, the opposite dominance polygon ${\mathcal {P}}'_\lambda$ pointed at its opposite ${\varvec{g}}$-vector $\lambda '=(\lambda '_0,\lambda '_1)$ is the region consisting of those $\mu \in {\mathbb {R}}^2$ satisfying $\mu _0 \ge \lambda '_0, \mu _1 \le \lambda '_1$, and the following inequalities:

$$\begin{aligned} \begin{aligned}&0 \le \frac{b c-\sqrt{b c (b c-4)}}{2 c}(\mu _1-\lambda '_1)+(\mu _0-\lambda '_0) \le -b\lambda '_1-\frac{b c+\sqrt{b c (b c-4)}}{2c}c\lambda '_0\\&0 \le -\frac{b c-\sqrt{b c (b c-4)}}{2 c}(\mu _1-\lambda '_1)+(\mu _0-\lambda '_0) \le b\lambda '_1\\&0 \le -(\mu _1-\lambda '_1)-\frac{b c-\sqrt{b c (b c-4)}}{2 b}(\mu _0-\lambda '_0) \le \frac{b c+\sqrt{b c (b c-4)}}{2b}b\lambda '_1+c\lambda '_0\\&0 \le (\mu _1-\lambda '_1) - \frac{b c-\sqrt{b c (b c-4)}}{2 b} (\mu _0-\lambda '_0) \le -c \lambda '_0 \end{aligned} \end{aligned}$$

Proof

As stated above, we obtain the opposite ${\varvec{g}}$-vector by interchanging b, c and swapping the roles of $\lambda _0,\lambda _1$. Translating from Theorem 1.2, it immediately follows that the opposite dominance region is given by the claimed inequalities.

$\square$

For $\lambda \in {\mathcal {I}}$, the region ${\mathcal {S}}_\lambda$ from Theorem 1.6 is determined by the following inequalities:

$$\begin{aligned} \lambda _1&\le \mu _1;\\ \lambda '_0&\le \mu _0;\\ 0&\le -\frac{b c+\sqrt{b c (b c-4)}}{2 b}(\mu _0-\lambda _0)-(\mu _1-\lambda _1);\\ 0&\le -\frac{b c-\sqrt{b c (b c-4)}}{2 b}(\mu _0-\lambda '_0) -(\mu _1-\lambda '_1). \end{aligned}$$

To begin proving that this is the maximal support we claim that ${\mathcal {P}}_\lambda ,{\mathcal {P}}'_\lambda \subset {\mathcal {S}}_\lambda$.

Observe that the last inequality can be rewritten as

$$\begin{aligned} \frac{b c-\sqrt{b c (b c-4)}}{2 b}(\mu _0-\lambda _0) + (\mu _1-\lambda _1) \le -c\lambda _0 - \frac{b c + \sqrt{b c (b c-4)}}{2 } \lambda _1, \end{aligned}$$

which together with the second to last inequality already gives two of the boundaries for the dominance region ${\mathcal {P}}_\lambda$. Note then that, under the assumption $\mu _0\le \lambda _0$, the inequality

$$\begin{aligned} 0 \le \frac{b c-\sqrt{b c (b c-4)}}{2 b}(\mu _0-\lambda _0)+(\mu _1-\lambda _1) \end{aligned}$$

defining another boundary of ${\mathcal {P}}_\lambda$ is more restrictive than the inequality $\lambda _1\le \mu _1$ bounding ${\mathcal {S}}_\lambda$.

It follows from Corollary 1.4 that the minimum value for $\mu _0$ inside ${\mathcal {P}}_\lambda$ occurs when $\mu _1=0$, i.e. either at the point $\big ( \lambda _0+\frac{bc+\sqrt{bc(bc-4)}}{2c}\lambda _1, 0 \big )$ when $0 \le c\lambda _0+2\lambda _1$ or at the point $-\frac{bc+\sqrt{bc(bc-4)}}{2c} \big ( \frac{bc+\sqrt{bc(bc-4)}}{2b}\lambda _0+\lambda _1, 0 \big )$ when $c\lambda _0+2\lambda _1<0$. The second point can be rewritten as

$$\begin{aligned} \left( \lambda _0 -\frac{bc+\sqrt{bc(bc-4)}}{2c} c\lambda _0-\frac{bc+\sqrt{bc(bc-4)}}{2c} \lambda _1, 0\right) \end{aligned}$$

but, since $c\lambda _0 < -2\lambda _1$, the first coordinate is greater than $\lambda _0+\frac{bc+\sqrt{bc(bc-4)}}{2c}\lambda _1$. Then, using $\frac{bc+\sqrt{bc(bc-4)}}{2c}<b$ and $\lambda _1<0$, we see that the minimum value of $\mu _0$ inside ${\mathcal {P}}_\lambda$ satisfies the inequality $\lambda '_0=\lambda _0+b\lambda _1 \le \mu _0$. In particular, combining with the observation above, we see that ${\mathcal {P}}_\lambda \subset {\mathcal {S}}_\lambda$.

Similarly, the second to last inequality can be rewritten as

$$\begin{aligned} \frac{b c-\sqrt{b c (b c-4)}}{2 c}(\mu _1-\lambda '_1)+(\mu _0-\lambda '_0) \le -b\lambda '_1-\frac{b c+\sqrt{b c (b c-4)}}{2c}c\lambda '_0, \end{aligned}$$

which together with the last inequality already gives two of the boundaries for the opposite dominance region ${\mathcal {P}}'_\lambda$. Note then that, under the assumption $\mu _1\le \lambda '_1$, the inequality

$$\begin{aligned} 0 \le \frac{b c-\sqrt{b c (b c-4)}}{2 c}(\mu _1-\lambda '_1)+(\mu _0-\lambda '_0) \end{aligned}$$

defining another boundary of ${\mathcal {P}}_\lambda$ is more restrictive than the inequality $\lambda '_0\le \mu _0$ bounding ${\mathcal {S}}_\lambda$. As above, the minimum value of $\mu _1$ inside ${\mathcal {P}}'_\lambda$ occurs when $\mu _0=0$, i.e. either at the point $\big (0, \frac{bc+\sqrt{bc(bc-4)}}{2b}\lambda '_0+\lambda '_1 \big )$ when $0 \le 2\lambda '_0+b\lambda '_1$ or at the point $-\frac{bc+\sqrt{bc(bc-4)}}{2b} \big (0, \lambda '_0+\frac{bc+\sqrt{bc(bc-4)}}{2c}\lambda '_1 \big )$ when $2\lambda '_0+b\lambda '_1<0$. The second point can be rewritten as

$$\begin{aligned} \left( 0, -\frac{bc+\sqrt{bc(bc-4)}}{2b} \lambda '_0-\frac{bc+\sqrt{bc(bc-4)}}{2b} b\lambda '_1+\lambda '_1 \right) \end{aligned}$$

but, since $b\lambda '_1\le -2\lambda '_0$, the first coordinate is greater than $\frac{bc+\sqrt{bc(bc-4)}}{2b}\lambda '_0+\lambda '_1$. Then, using $\frac{bc+\sqrt{bc(bc-4}}{2b}<c$ and $\lambda '_0<0$, we see that the minimum value of $\mu _1$ inside ${\mathcal {P}}'_\lambda$ satisfies the inequality $\lambda _1=c\lambda '_0+\lambda '_1\le \mu _1$ and so ${\mathcal {P}}'_\lambda \subset {\mathcal {S}}_\lambda$.

To continue, we compare the support for an arbitrary basis element pointed at $\lambda \in {\mathcal {I}}$ with the greedy basis elements having ${\varvec{g}}$-vector inside the dominance polygon ${\mathcal {P}}_\lambda$.

The support region ${\mathcal {G}}_\lambda$ of the greedy basis element with ${\varvec{g}}$-vector $\lambda$ is well-known [7, 18]. This is indicated by the solid and dotted lines in Figs. 1 and 2, where dotted lines indicate points that are excluded from the support. (The actual support of the greedy basis element consists of the points of the form $\lambda +(b \alpha _0,c \alpha _1)$, $\alpha _0,\alpha _1\in {\mathbb {Z}}$, inside ${\mathcal {G}}_\lambda$.) For our purposes, it is enough to observe the following closure property for the greedy support region which is evident from Fig. 2.

Definition 6.3

A subset ${\mathcal {S}}\subset {\mathbb {R}}^2$ is called -closed if $\lambda ,\mu \in {\mathcal {S}}$ implies the segments joining $\lambda$ and $\mu$ to $\big (\min (\lambda _0,\mu _0),\min (\lambda _1,\mu _1)\big )$ are contained in ${\mathcal {S}}$.

In particular, (an upper bound for) the greedy support region ${\mathcal {G}}_\lambda$ can be found using its ${\varvec{g}}$-vector $\lambda$ and its opposite ${\varvec{g}}$-vector $\lambda '$. Write ${\overline{{\mathcal {G}}}}_\lambda$ for the downward scaling of the -closure of $\{\lambda ,\lambda '\}$, that is ${\overline{{\mathcal {G}}}}_\lambda$ contains the segments joining $\lambda$ and $\lambda '$ with $\big (\min (\lambda _0,\lambda '_0),\min (\lambda _1,\lambda '_1)\big )$ and for any $\mu \in {\overline{{\mathcal {G}}}}_\lambda$ we have $t\mu \in {\overline{{\mathcal {G}}}}_\lambda$ for $0\le t\le 1$. Clearly, ${\mathcal {G}}_\lambda \subset {\overline{{\mathcal {G}}}}_\lambda$.

As we saw above, for any ${\varvec{g}}$-vector $\mu \in {\mathcal {P}}_\lambda$ its opposite ${\varvec{g}}$-vector $\mu '$ is also contained in ${\mathcal {S}}_\lambda$. But ${\mathcal {S}}_\lambda$ is -closed and closed under downward scaling. It follows that ${\overline{{\mathcal {G}}}}_\mu \subset {\mathcal {S}}_\lambda$ for any $\mu \in {\mathcal {P}}_\lambda$ and hence, following Theorem 1.1, the support of any basis element pointed at $\lambda$ is contained in ${\mathcal {S}}_\lambda$.

In particular, ${\mathcal {G}}_\lambda \subset {\mathcal {S}}_\lambda$. Note also that the dominance region ${\mathcal {P}}_\lambda$ contains the intersection of ${\mathcal {S}}_\lambda$ with the region ${\mathcal {R}}$ defined by the inequalities $\mu _0\ge 0$ and $\lambda _1\mu _0-\lambda _0\mu _1\ge 0$. Similarly, the opposite dominance region ${\mathcal {P}}'_\lambda$ contains the intersection of ${\mathcal {S}}_\lambda$ with the region ${\mathcal {R}}'$ defined by the inequalities $\mu _1\ge 0$ and $-\lambda '_1\mu _0+\lambda '_0\mu _1\ge 0$. But ${\mathcal {S}}_\lambda ={\mathcal {G}}_\lambda \cup ({\mathcal {S}}_\lambda \cap {\mathcal {R}})\cup ({\mathcal {S}}_\lambda \cap {\mathcal {R}}')$ so ${\mathcal {S}}_\lambda$ is the maximum possible support for an element pointed at $\lambda$.

7 The Untwisted Affine Case

In this section we compare our main result with the construction of [19] in the case $b=c=2$. To match conventions, in this section, we work over an algebraically closed field $\Bbbk$ of characteristic 0. Because the exchange matrix is full rank there is no loss of generality in continuing to work in the coefficient-free case. We will identify the family of bases in Theorem 1.1 with the continuous family of bases of ${\mathcal {A}}(2,2)$ constructed in [19] from generalized minors, which we recast here with the current notation.

Theorem 7.1

([19, Theorem 4.6]) Choose a point ${\varvec{a}}^{(n)}=(a_1,\dots ,a_n)\in (\Bbbk ^\times )^n$ for each $n\ge 1$. Then, together with all cluster monomials, the elements

$$\begin{aligned} x_{(n,-n)}^{{\varvec{a}}^{(n)}}:= x_0^{-n} x_1^{-n} \sum _{0 \le k \le \ell \le n} \sum _{r=0}^\ell {\ell -r\atopwithdelims ()k} {n-2r\atopwithdelims ()\ell -r} S_{{\varvec{a}}^{(n)},r} \, x_0^{2(\ell -k)} x_1^{2(n-\ell )} \end{aligned}$$

(16)

with

$$\begin{aligned} S_{{\varvec{a}}^{(n)},r}=\sum \limits _{\begin{array}{c} I,J\subseteq [1,n]\\ |I|=r=|J|\\ I\cap J=\varnothing \end{array}}\frac{\prod _{i\in I} a_i}{\prod _{j\in J} a_j} \end{aligned}$$

form a linear basis of ${\mathcal {A}}(2,2)$.

We begin by noting that when $b=c=2$ the imaginary cone ${\mathcal {I}}$ degenerates to the ray spanned by $(1,-1)$. For any $\lambda \in {\mathcal {I}}$, the dominance region ${\mathcal {P}}_\lambda$ is the segment connecting $\lambda$ to the origin. It follows that ${\varvec{g}}$-vectors dominated by $\lambda =(n,-n)$ are of the form $(n-2r,-n+2r)$ for $0\le r \le n/2$.

In order to use Theorem 1.1 we need to fix a reference pointed basis of ${\mathcal {A}}(2,2)$; to simplify our computations, we choose to work with the generic basis. This basis consists of the cluster monomials of ${\mathcal {A}}(2,2)$ together with the elements

$$\begin{aligned} x_{(n,-n)}^{ge}&:= \Big (x_0 x_1^{-1} + x_0^{-1}x_1^{-1} + x_0^{-1}x_1\Big )^n\\&= x_0^{-n} x_1^{-n} \sum _{0 \le k \le \ell \le n} {\ell \atopwithdelims ()k} {n\atopwithdelims ()\ell } \, x_0^{2(\ell -k)} x_1^{2(n-\ell )}. \end{aligned}$$

Proposition 7.2

For $n\ge 0$, we have

$$\begin{aligned} x_{(n,-n)}^{{\varvec{a}}^{(n)}} = \sum _{r=0}^{\lfloor n/2 \rfloor } S_{{\varvec{a}}^{(n)},r} \, x_{(n-2r,-n+2r)}^{ge}. \end{aligned}$$

Proof

To begin, we observe that (16) may be rewritten as

$$\begin{aligned} x_{(n,-n)}^{{\varvec{a}}^{(n)}} = x_0^{-n} x_1^{-n} \sum _{k=0}^n \sum _{\ell =k}^n \sum _{r=0}^\ell {\ell -r\atopwithdelims ()k} {n-2r\atopwithdelims ()\ell -r} S_{{\varvec{a}}^{(n)},r} \, x_0^{2(\ell -k)} x_1^{2(n-\ell )}. \end{aligned}$$

The first binomial coefficient above is zero if $0 \le \ell -r < k$ while the second is zero for $\ell < r \le \lfloor n/2\rfloor$ or if $n-r < \ell$, therefore $x_{(n,-n)}^{{\varvec{a}}^{(n)}}$ can be expressed as

$$\begin{aligned} x_{(n,-n)}^{{\varvec{a}}^{(n)}}&= x_0^{-n} x_1^{-n} \sum _{k=0}^n \sum _{r=0}^{\lfloor n/2\rfloor } \sum _{\ell =k+r}^{n-r} {\ell -r\atopwithdelims ()k} {n-2r\atopwithdelims ()\ell -r} S_{{\varvec{a}}^{(n)},r} \, x_0^{2(\ell -k)} x_1^{2(n-\ell )}. \end{aligned}$$

But then, rearranging terms and replacing $\ell$ by $\ell +r$, this becomes

$$\begin{aligned} x_{(n,-n)}^{{\varvec{a}}^{(n)}}&= \sum _{r=0}^{\lfloor n/2\rfloor } S_{{\varvec{a}}^{(n)},r}\, x_0^{-n +2r} x_1^{-n+2r} \sum _{k=0}^n \sum _{\ell =k}^{n-2r} {\ell \atopwithdelims ()k} {n -2r\atopwithdelims ()\ell } \, x_0^{2(\ell -k)} x_1^{2(n-2r-\ell )}\\&= \sum _{r=0}^{\lfloor n/2\rfloor } S_{{\varvec{a}}^{(n)},r}\, x_{n-2r,-n+2r}^{ge} \end{aligned}$$

as desired. $\square$

Remark 7.3

Observe that the expansion coefficients $S_{{\varvec{a}}^{(n)},r}$ can be expressed as the ratio of monomial symmetric functions $\frac{m_{2^{(r)},1^{(n-2r)}}}{m_{1^{(n)}}}$ evaluated at ${\varvec{a}}^{(n)}$. The analogous expansion coefficients when $x_{(n,-n)}^{{\varvec{a}}^{(n)}}$ is expressed in terms of the triangular basis (resp. greedy basis) are the ratios of Schur functions $\frac{s_{2^{(r)},1^{(n-2r)}}}{s_{1^{(n)}}}$ (resp. ratios of elementary symmetric functions $\frac{e_{n-r,r}}{e_n}$) evaluated at ${\varvec{a}}^{(n)}$. We leave the details to the reader.

Theorem 7.4

As the points ${\varvec{a}}^{(n)}$ vary in $(\Bbbk ^\times )^n$, the bases in Theorem 7.1 recover precisely all the pointed bases of ${\mathcal {A}}(2,2)$.

Proof

By Theorem 1.1, in view of Proposition 7.2 and the discussion immediately before it, it suffices to show that as ${\varvec{a}}^{(n)}$ vary in $(\Bbbk ^\times )^n$ the tuple of coefficients $\big (S_{{\varvec{a}}^{(n)},r}\big )_{1\le r \le \lfloor n/2\rfloor }$ assume all the values in $\Bbbk ^{\lfloor n/2\rfloor }$. (The fact that $S_{{\varvec{a}}^{(n)},0}=1$ is immediate from the definition.)

By Remark 7.3, this is equivalent to the fact that the monomial symmetric functions in n variables $m_{2^{(r)},1^{(n-2r)}}$ are algebraically independent. But this follows immediately from the observation that

$$\begin{aligned} m_{2^{(r)},1^{(n-2r)}} = \sum _{i=0}^r \gamma _i\, e_{n-i,i} \end{aligned}$$

for some coefficients $\gamma _i$ with $\gamma _r=1$, and the Fundamental Theorem of Symmetric Polynomials. $\square$