Boolean Complexes of Involutions

Abstract

Let (W, S) be a Coxeter system. We introduce the boolean complex of involutions of W which is an analogue of the boolean complex of W studied by Ragnarsson and Tenner. By applying discrete Morse theory, we determine the homotopy type of the boolean complex of involutions for a large class of (W, S), including all finite Coxeter groups, finding that the homotopy type is that of a wedge of spheres of dimension $\vert S\vert -1$. In addition, we find simple recurrence formulas for the number of spheres in the wedge.

1 Introduction

Let F be a finite alphabet. A word over F is injective if it is a sequence of distinct letters from F. The poset of all injective words over F ordered by the (not necessarily consecutive) subword relation is a simplicial poset, hence the face poset of a boolean cell complex. This is the well-studied complex of injective words. Farmer [2] showed that it is homotopy equivalent to a wedge of spheres of dimension $|F|-1$. Jonsson and Welker [12] proved the same conclusion for considerably more general classes of boolean cell complexes using shellability techniques.

Ragnarsson and Tenner [15] independently arrived at one of Jonsson and Welker’s families of complexes from a different starting point. Namely, Ragnarsson and Tenner considered the boolean elements of a Coxeter system (W, S), i.e. those elements whose Bruhat order ideals are boolean lattices. These elements were first considered by Tenner in [18]. Under Bruhat order, they generate the face poset of a boolean cell complex, the boolean complex of (W, S). Using discrete Morse theory, it was shown in [15] that this complex is homotopy equivalent to a wedge of spheres of dimension $|S|-1$, and a recurrence formula for the number of spheres was found.

In [9], the first named author and Vorwerk studied the boolean involutions of (W, S) as an involution analogue of Tenner’s boolean elements. In the Bruhat order on involutions, they too form the face poset of a boolean cell complex. In this paper, we study this boolean complex of involutions, $\Delta _{\textrm{inv}}(W)$. Such complexes are not special cases of Jonsson and Welker’s constructions.¹

For a large class of Coxeter systems, including all finite ones, we apply discrete Morse theory to show that $\Delta _{\textrm{inv}}(W)$ is also homotopy equivalent to a wedge of spheres of dimension $|S|-1$ and provide a recurrence formula for the number of spheres.

The remainder of this paper is organized in the following way. Section 2 contains preliminaries on cell complexes, acyclic matchings, and Coxeter group theory. Section 3 contains the main technical results of this paper. There we describe a way to recursively produce acyclic matchings on $\Delta _{\textrm{inv}}(W)$ for certain families of Coxeter systems. In Sect. 4, we provide applications by computing the homotopy type of $\Delta _{\textrm{inv}}(W)$ for many Coxeter systems, including all finite types.

2 Preliminaries

In this section, notions on simplicial posets, acyclic matchings and cell complexes are collected for being used in the sequel.

2.1 Posets, Matchings, and Cell Complexes

Let P be a poset and $x,y\in P$ such that $x<y$. We say that y covers x, written as $x\lessdot y$, if there is no $z\in P$ such that $x<z<y$.

Definition 2.1

Let P be a poset with cover relation $\lessdot$. An involution $M:P\rightarrow P$ (i.e., $M\circ M=id$) such that for each $x\in P$, $x\lessdot M(x)$ or $M(x)\lessdot x$ or $M(x)=x$ is called a matching. An element $x\in P$ such that $M(x)=x$ is called critical.

Definition 2.2

Let P be a poset and M be a matching on P. Consider the Hasse diagram of P as a directed graph with edges $x\leftarrow y$ if $x\lessdot y$ for $x,y\in P$. From the Hasse diagram of P construct a new directed graph $G_{M}(P)$ by reversing each arrow $x\leftarrow y$ to $x\rightarrow y$ if $y=M(x)$. The matching M on P is called acyclic if there are no directed cycles in $G_{M}(P)$.

In $G_{M}(P)$, the unchanged edge $x\leftarrow y$ is said to be downward while the edge $x\rightarrow M(x)$ is said to be upward. Since for any matching M, no two incident edges are directed upward in $G_{M}(P)$, the next lemma follows:

Lemma 2.3

If a matching M on a poset P is not acyclic, then any directed cycle in $G_{M}(P)$ is of the form

$$\begin{aligned} a_{1}\lessdot M(a_{1}) \gtrdot a_{2} \lessdot M(a_{2}) \cdots \gtrdot a_{k} \lessdot M(a_{k} )\gtrdot a_{1}, \end{aligned}$$

for pairwise distinct $a_{i}$ and some $k\ge 2$.

Let $\Delta$ be a finite regular cell complex. The face poset of $\Delta$, denoted by $P(\Delta )$, is the poset of all cells ordered by set inclusion of their closures where a minimum element (sometimes thought of as the empty cell) is also in $P(\Delta )$. For more on regular cell complexes, see [13].

Definition 2.4

Let $\Delta$ be a finite regular cell complex and $P(\Delta )$ its face poset. Then $\Delta$ is called a boolean cell complex if $P(\Delta )$ is a simplicial poset (i.e., a poset with a minimum element in which every principal order ideal is isomorphic to a boolean lattice).

Conversely, any finite simplicial poset is the face poset of a boolean cell complex which is unique (up to cellular isomorphism).

The following is one of the most useful consequences of discrete Morse theory. It will serve as our main topological tool.

Theorem 2.5

[3, Theorem 6.3] Let $\Delta$ be a boolean cell complex and let M be an acyclic matching on the face poset $P(\Delta )$. If there are c critical cells, all of the same dimension m, then $\Delta$ is homotopy equivalent to a wedge of c spheres of dimension m.

Corollary 2.6

If an acyclic matching M on $P(\Delta )$ does not have any critical cells, then $\Delta$ is contractible.

Lemma 2.7 has been discovered by Jonsson [11] and independently by Hersh [6]. It provides a way to patch together acyclic matchings.

Lemma 2.7

Let $\Delta$ be a boolean cell complex such that $\Delta =\bigcup _{\alpha \in Q} \Delta _{\alpha }$ where the index set Q is partially ordered. Assume that

• (1) Each cell $\gamma \in \Delta$ is only in one $\Delta _{\alpha }$ (i.e., the union is disjoint).

• (2) $\bigcup _{\beta \le \alpha \in Q}\Delta _{\beta }$ is an order ideal of $P(\Delta )$ for every $\alpha \in Q$.

For each $\alpha \in Q$, suppose that $M_{\alpha }$ is an acyclic matching on $P(\Delta _{\alpha })$ where $P(\Delta _{\alpha })$ is the subposet of $P(\Delta )$ induced by $\Delta _{\alpha }$. Then $\bigcup _{\alpha \in Q}M_{\alpha }$ is an acyclic matching on $P(\Delta )$.

2.2 Coxeter Systems

We review some facts on Coxeter groups for later use. For more, we refer the reader to [1] or [10].

Let W be a group generated by a finite set of involutions S, where $(ss')^{m(s,s')}=e$ for $m(s,s)=1$, $m(s,s')=m(s',s)\ge 2$ for all $s\ne s'$ in S and $m(s,s')\in \mathbb {Z}^{+}\cup \{\infty \}$. Here, e denotes the identity element in W. The group W as described above, together with its generating set S form a pair (W, S) which is called a Coxeter system. Any $w\in W$ is a product of generators in S. That is $w=s_{1}s_{2}\cdots s_{k}$ for some $s_{i}\in S$. If k is smallest among all such expressions for w, then k is called the length of w, denoted $\ell (w)=k$, and $s_{1}s_{2}\cdots s_{k}$ is called a reduced expression for w. Note that we do not distinguish notationally between an expression and the group element it represents.

A Coxeter system (W, S) is sometimes represented by its Coxeter graph. It is the edge-labeled (simple, undirected) graph with vertex set S and an edge-labeled $m(s,s')$ connecting two vertices s and $s'$ if $m(s,s')\ge 3$. By convention, the label is usually omitted if it is equal to 3, see Fig. 1.

If W is finite, it has a unique longest element $w_{0}$. A subgroup $W_{J}$ of W, generated by $J\subseteq S$ is called parabolic. If $W_{J}$ is finite, its longest element is denoted by $w_{0}(J)$.

A Coxeter system is irreducible if its Coxeter graph is connected. The Coxeter graphs in Fig. 1 indicate the classification of finite irreducible Coxeter groups. There are three classical families of types $A_{n}$ $(n\ge 1)$, $B_{n}$ $(n\ge 2)$, $D_{n}$ $(n\ge 4)$, six exceptional groups of types $E_{6}$, $E_{7}$, $E_{8}$, $F_{4}$, $H_{3}$ and $H_{4}$, and one family of dihedral groups of type $I_{2}(m)$ $(m\ge 3)$.

Fig. 1

The finite, irreducible Coxeter groups

Given $w\in W$, define the right descent set of w by

$$\begin{aligned} D_{R}(w)=\{s\in S| \ell (ws)<\ell (w)\}. \end{aligned}$$

For $s\in S$, $s \in D_{R}(w)$ if and only if w has a reduced expression that ends in s.

Let $T:=\{wsw^{-1}| w\in W, s\in S\}$ be the set of reflections in W.

Definition 2.8

For $u,w\in W$, let $u\rightarrow w$ if there is $t\in T$ such that $w=ut$ and $\ell (u)< \ell (w)$. The Bruhat order is the partial order relation on W which is defined by $u\le w$ if there is a sequence

$$\begin{aligned} u=u_{0}\rightarrow u_{1}\rightarrow \cdots u\rightarrow u_{n}=w. \end{aligned}$$

Definition 2.9

Let (W, S) be a Coxeter system and consider W as a poset under Bruhat order. An element $w\in W$ is called boolean if its lower principal order ideal is isomorphic to a boolean algebra.

The following lemma is a characterization of boolean elements. For W of type A, B, or D this lemma is [18, Proposition 7.3].

Lemma 2.10

[15] Let (W, S) be a Coxeter system and $w\in W$. Then w is boolean if and only if it has some reduced expression without repeated letters.

In fact, Lemma 2.10 is equivalent to the statement that “w is boolean if and only if no reduced expression for w has repeated letters.” Let $\mathbb {B}(W)$ denote the subposet of W induced by the boolean elements. The subposet $\mathbb {B}(W)$ is the boolean ideal. Note that $\mathbb {B}(W)$ is a simplicial poset.

Definition 2.11

For a Coxeter system (W, S), the boolean complex of (W, S) is the boolean cell complex $\Delta (W)$ whose face poset is $\mathbb {B}(W)$.

All maximal cells of $\Delta (W)$ have dimension $|S|-1$. Boolean complexes of Coxeter groups were studied by Ragnarsson and Tenner [15]. They showed that for every Coxeter system (W, S), there is a nonnegative integer $\beta (W)$ called boolean number such that $\Delta (W)$ is homotopy equivalent to a wedge of $\beta (W)$ spheres of dimension $\vert S \vert -1$. Moreover, they found a recurrence formula for computing $\beta (W)$ in terms of the (unlabeled) Coxeter graph. Note that the labels of the Coxeter graph have no effect in determining $\beta (W)$. That is, if W and $W'$ have isomorphic Coxeter graphs when ignoring all edge labels that are at least 4, then $\mathbb {B}(W) \cong \mathbb {B}(W')$. In particular, $\beta (W)=\beta (W')$ [15].

2.3 Reduced $\underline{S}$-Expressions

In this subsection we review some material on reduced $\underline{S}$-expressions and boolean involutions needed in Sects. 3 and 4.

For a Coxeter system (W, S), let $I=\{w\in W| w=w^{-1}\}$ denote the set of involutions. Consider an alphabet $\underline{S}=\{\underline{s} \, | \, s\in S\}$.

Definition 2.12

The free monoid $\underline{S}^{*}$ acts from the right on the set W by

$$\begin{aligned} w\underline{s}=\left\{ \begin{array}{ll} ws &{}\quad \text {if } sws=w,\\ sws&{}\quad \text {otherwise}, \end{array}\right. \end{aligned}$$

and $w\underline{s}_{1}\underline{s}_{2}\cdots \underline{s}_{k}= (\cdots ((w\underline{s}_{1})\underline{s}_{2})\cdots \underline{s}_{k})$.

Note that $w\underline{s}\,\underline{s}=w$ for all $w\in W$ and $s\in S$. For the identity element $e\in W$, write $\underline{s}_{1}\underline{s}_{2}\cdots \underline{s}_{k}$ for $e\underline{s}_{1}\underline{s}_{2}\cdots \underline{s}_{k}$.

For every $w\in I$ there are symbols $\underline{s}_{1}, \underline{s}_{2},\ldots ,\underline{s}_{k}$ such that $w=\underline{s}_{1} \underline{s}_{2}\cdots \underline{s}_{k}$ and, conversely, all such elements are involutions [16]. The minimal k such that $w=\underline{s}_{1}\underline{s}_{2}\cdots \underline{s}_{k}$ for some $\underline{s}_{1}, \underline{s}_{2}, \ldots , \underline{s}_{k}\in \underline{S}$ is called the rank of w, and is denoted $\rho (w)$. The expression $\underline{s}_{1}\underline{s}_{2}\cdots \underline{s}_{k}$ is then called a reduced $\underline{S}$-expression for w.

Reduced $\underline{S}$-expressions appear under various names in the literature. It is (the right-handed version of) what Richardson and Springer [16] call “admissible sequences” and Hamaker, Marberg, and Pawlowski [4] refer to as “involution words”. In this paper, the notation is taken from [7, 8].

Definition 2.13

Let $\alpha _{\underline{s},\underline{s}'}=\underline{s}\,\underline{s}' \underline{s}\cdots$ be the alternating word in $\underline{s}$ and $\underline{s}'$, where the number of letters $\underline{s}$ and $\underline{s}'$ in $\alpha _{\underline{s},\underline{s}'}$ is equal to $m(s,s')$. Operating on words in $\underline{S}^{*}$, we define a braid move as the replacement of $\alpha _{\underline{s},\underline{s}'}$ by $\alpha _{\underline{s}',\underline{s}}$.

In fact, braid moves in a reduced $\underline{S}$-expression for $w\in I$ preserve w (see [4]).

Definition 2.14

Let $\mathcal {\hat{R}}(w)$ denote the set of all reduced $\underline{S}$-expressions for $w\in I$. For $u,w\in I$, the replacement of one element in $\mathcal {\hat{R}}(u)$ by another in the beginning of a reduced $\underline{S}$-expression for $w\in I$ is called an initial move.

The following theorem provides a minimal list of initial moves that combined with braid moves suffice to connect all elements of $\mathcal {\hat{R}}(w)$.

Theorem 2.15

[5] Let (W, S) be a Coxeter system and $w\in I$. Any two reduced $\underline{S}$-expressions for w can be connected by a sequence of braid moves and initial moves that replace u with v if $u, v \in \mathcal {\hat{R}}(w_{0}(J))$ for some $J \subseteq S$. The following parabolic subgroups $W_{J}$ are necessary and sufficient:

• (1) $W_{J}$ of type $B_{3}$;

• (2) $W_{J}$ of type $D_{4}$;

• (3) $W_{J}$ of type $H_{3}$;

• (4) $W_{J}$ of type $I_{2}(m)$, for $m\ge 3$.

In other words, given $x,y\in \mathcal {\hat{R}}(w)$, there exist some $x_{0}, x_{1}, \ldots , x_{k}$ such that $x=x_{0}$, $x_{k}=y$ and for all i, $x_{i}$ differs from $x_{i+1}$ by a braid move or an initial move of the kind specified in Theorem 2.15.

Lemma 2.16

[7] Let $w\in I$. Then $s\in D_{R}(w)$ if and only if w has a reduced $\underline{S}$-expression that ends in $\underline{s}$. Moreover, $\rho (w\underline{s}) = \rho (w)+1$ if and only if $s\not \in D_R(w)$.

Let $\textrm{Br}(I)$ denote the subposet of the Bruhat order on W induced by I. The order relation on $\textrm{Br}(I)$ has been characterized in [7, 16, 17].

Lemma 2.17

(Subword property of I [7]) Suppose that $v,w\in I$ and $\underline{s}_{1}\underline{s}_{2}\cdots \underline{s}_{k}$ is a reduced $\underline{S}$-expression for w. Then $v\le w$ if and only if $v=\underline{s}_{i_{1}}\underline{s}_{i_{2}}\cdots \underline{s}_{i_{r}}$ for some $1\le i_{1}\le i_{2}\le \cdots \le i_{r}\le k$.

For $w\in I$, let B(w) denote the principal order ideal generated by w in $\textrm{Br}(I)$. Then we have

Definition 2.18

An element $w\in I$ is called a boolean involution if B(w) is isomorphic to a boolean algebra.

Analogously to the characterization of boolean elements (i.e., Theorem 2.10), we have

Proposition 2.19

[9] Let $w\in I$. Then the following are equivalent:

• (1) w is a boolean involution.

• (2) w has some reduced $\underline{S}$-expression without repeated letters.

In fact, Proposition 2.19 is equivalent to “w is a boolean involution if and only if no reduced $\underline{S}$-expression for w has repeated letters.”

Suppose $s,s'\in S$ satisfy $m(s,s')=3$. Let us say that a half-braid move is the replacement of $\underline{s}\,\underline{s}'$ by $\underline{s}'\underline{s}$ in the beginning of a reduced $\underline{S}$-expression.

Proposition 2.20

Any two reduced $\underline{S}$-expressions for a boolean involution $w\in I$ can be connected by a sequence of braid moves and half-braid moves.

Proof

In the list of parabolic subgroups given in Theorem 2.15, it is only in type $I_2(3)$ that the longest element is a boolean involution. It has only two reduced $\underline{S}$-expressions, and the initial move replacing one of them by the other is a half-braid move. $\square$

Let $P(\Delta _{\textrm{inv}}(W))$ denote the subposet of $\textrm{Br}(I)$ induced by all boolean involutions. It is a simplicial poset which we call the boolean involution ideal. We have the following definition:

Definition 2.21

Let $\Delta _{\textrm{inv}}(W)$ be the boolean cell complex whose face poset is $P(\Delta _{\textrm{inv}}(W))$.

By abuse of notation, we identify a boolean involution with the cell it represents. It follows from Proposition 2.20 together with Lemma 2.16 that every $\underline{S}$-expression without repeated letters is reduced. Hence, every maximal cell in $\Delta _{\textrm{inv}}(W)$ has dimension $\vert S\vert -1$. Let $\beta _I(W)$ denote the absolute value of the reduced Euler characteristic of $\Delta _{\textrm{inv}}(W)$.

Example 2.22

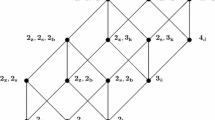
Figure 2 shows the Hasse diagram of $P(\Delta _{\textrm{inv}}(W))$ for W of type $F_4$. (The significance of the different styles of vertices and edges will become clear later.) Inspecting it shows that $\Delta _{\textrm{inv}}(W)$ has four 3-cells, eight 2-cells, seven 1-cells, and four 0-cells. Consequently, $\beta _I(W) = |-1 + 4 - 7 + 8 - 4| = 0$ in this case.

In contrast to the situation for the boolean complex $\Delta (W)$, it is not the case that $\Delta _{\textrm{inv}}(W)$ only depends on the unlabeled Coxeter graph. As the following lemma shows, it is, however, not necessary to keep track of the actual labels:

Lemma 2.23

If the Coxeter graph of a Coxeter system $(W',S)$ is obtained from that of another system (W, S) by increasing some edge labels which are at least 4, then $\Delta _{\textrm{inv}}(W') \cong \Delta _{\textrm{inv}}(W)$.

Proof

In a reduced $\underline{S}$-expression without repeated letters, the possible braid moves are provided by the vertices that are not adjacent in the Coxeter graph, and the half-braid moves come from the vertices that are connected by an edge-labeled 3 (i.e., with omitted label). It follows that the boolean involution ideals of W and $W'$ are isomorphic. $\square$

Fig. 2

A $\Gamma$-matching on $P(\Delta _{\textrm{inv}}(F_{4}))$

3 Acyclic Matchings on the Boolean Involution Ideal

Say that a Coxeter system (W, S) (with S finite) is ordered if the generating set S is endowed with a total order. For such a system, assume $S = \{s_1< \cdots < s_n\}$ and define

$$\begin{aligned} P_1(W) := \{a\in \Delta _{\textrm{inv}}(W)\mid \ \underline{s}_n \not \le a\text { or }s_n \in D_R(a)\}. \end{aligned}$$

Then, let

$$\begin{aligned} \begin{aligned} \Gamma (W) :&= \Delta _{\textrm{inv}}(W)\setminus P_1(W)\\&= \{a\in \Delta _{\textrm{inv}}(W)\mid \underline{s}_n \le a\text { and }s_n \not \in D_R(a)\}. \end{aligned} \end{aligned}$$

As an example, with W of type $F_4$ and S ordered as in Fig. 1, $\Gamma (W)$ consists of the two elements that appear in yellow circles in Fig. 2.

Definition 3.1

Suppose (W, S) is an ordered Coxeter system. A matching M on $P(\Delta _{\textrm{inv}}(W))$ is a $\Gamma$-matching if it satisfies the following properties:

• M is acyclic;

• All critical cells of M are of top dimension $|S| - 1$;

• M preserves $\Gamma (W)$, that is $w \in \Gamma (W)$ implies $M(w)\in \Gamma (W)$;

• All critical cells of M belong to $\Gamma (W)$.

In particular, by Theorem 2.5, if $P(\Delta _{\textrm{inv}}(W))$ has a $\Gamma$-matching, then $\Delta _{\textrm{inv}}(W)$ is homotopy equivalent to a wedge of spheres of dimension $\vert S \vert -1$. Since the reduced homology groups are then trivial in all other dimensions, this number is $\beta _I(W)$. It is also equal to the number of critical cells.

Example 3.2

A $\Gamma$-matching of $P(\Delta _{\textrm{inv}}(W))$ for W of type $F_4$ is indicated by the red, dotted edges in Fig. 2. Since there are no critical cells, in agreement with the Betti number calculation in Example 2.22, $\Delta _{\textrm{inv}}(W)$ is homotopy equivalent to a point in this case.

If (W, S) is ordered, we let $W_{-k}$ denote the parabolic subgroup which is generated by the first $|S|-k$ elements of S, i.e. $W_{-k} = \langle s_1, \ldots , s_{n-k}\rangle$ if $S = \{s_1< \cdots < s_n\}$. The corresponding subsystem is ordered with the order inherited from S.

Definition 3.3

Suppose (W, S) is an ordered Coxeter system with $S =\{s_1<\cdots <s_n\}$ where $n\ge 3$. We say that (W, S) is path ended if $s_n$ commutes with every $s_i$ for $i\le n-2$, $s_{n-1}$ commutes with every $s_i$ for $i\le n-3$, $s_ns_{n-1}s_n=s_{n-1}s_ns_{n-1}$ and $s_{n-1}s_{n-2}s_{n-1}=s_{n-2}s_{n-1}s_{n-2}$.

Definition 3.3 means that the Coxeter graph of a path ended system (W, S) is as illustrated in Fig. 3, where the parabolic subgroups $W_{-2}$ and $W_{-3}$ are also indicated; $W_{-2}$ is generated by all $s_{i}$ inside the thick blue circle, and $W_{-3}$ is generated by all $s_{i}$ inside the thin black circle, respectively.

Fig. 3

A Coxeter graph of a path ended system (W, S)

Now we have the following theorem.

Theorem 3.4

Let (W, S) be a path ended Coxeter system. Assume that $P(\Delta _{\textrm{inv}}(W_{-2}))$ and $P(\Delta _{\textrm{inv}}(W_{-3}))$ have $\Gamma$-matchings $M^{-2}$ and $M^{-3}$, respectively. Then, $P(\Delta _{\textrm{inv}}(W))$ has a $\Gamma$-matching M. Moreover, the number of critical elements of M equals the number of critical elements of $M^{-2}$ plus the number of critical elements of $M^{-3}$.

To prove Theorem 3.4, we first need to establish a couple of lemmas. Let (W, S) be as in Definition 3.3.

Lemma 3.5

Let $w\in W$ be a boolean involution. If $\underline{s}_{n-1}$ comes after both $\underline{s}_{n-2}$ and $\underline{s}_{n}$ in some reduced $\underline{S}$-expression for w, then $\underline{s}_{n-1}$ comes after both $\underline{s}_{n-2}$ and $\underline{s}_{n}$ in every reduced $\underline{S}$-expression for w.

Proof

Note that if $\underline{s}_{n-1}$ comes after both $\underline{s}_{n-2}$ and $\underline{s}_{n}$ in a reduced $\underline{S}$-expression for w, then this cannot be changed by a half-braid move or a braid move. Hence the result follows from Proposition 2.20. $\square$

Now define

$$\begin{aligned}P_2(W):=\{x\underline{s}_{n-2} \underline{s}_{n}\underline{s}_{n-1}: x\in \Delta _{\textrm{inv}}(W_{-3})\}.\end{aligned}$$

Lemma 3.6

We have $P_2(W) \subseteq \Gamma (W)$.

Proof

By Lemma 3.5, $\underline{s}_{n-1}$ comes after $\underline{s}_{n-2}$ and $\underline{s}_{n}$ in every reduced $\underline{S}$-expression for every element $a\in P_2(W)$. Hence by Lemma 2.16, $s_{n}\not \in D_{R}(a)$. $\square$

Define $P_3(W):=\Gamma (W)\backslash P_2(W)$. Note that $P_1(W)$, $P_2(W)$, and $P_3(W)$ are pairwise disjoint sets whose union is $\Delta _{\textrm{inv}}(W)$.

Lemma 3.7

$P_3(W)=\{y\underline{s}_{n}\underline{s}_{n-1}:y\in \Gamma (W_{-2})\}$.

Proof

For any $a\in \{y\underline{s}_{n}\underline{s}_{n-1}:y\in \Gamma (W_{-2})\}$ we have that $a\not \in P_2(W)$ since $s_{n-2}\not \in D_{R}(y)$. By Lemma 3.5, $\underline{s}_{n-1}$ comes after $\underline{s}_{n-2}$ and $\underline{s}_{n}$ in every reduced $\underline{S}$-expression for a, hence $\underline{s}_{n}\le a$ and $s_{n}\notin D_{R}(a)$. Thus $a\in \Gamma (W)\backslash P_2(W)=P_3(W)$.

Conversely, assume that $a\in P_3(W)$. Since $\underline{s}_{n}\le a$ and $s_n\not \in D_R(a)$, $\underline{s}_{n-1}$ comes after $\underline{s}_n$ in every reduced $\underline{S}$-expression for a. Hence, no reduced $\underline{S}$-expression for a can begin with $\underline{s}_n\underline{s}_{n-1}$, which means that $\underline{s}_{n-1}$ also comes after $\underline{s}_{n-2}$ in every reduced $\underline{S}$-expression for a. Therefore, $a = y\underline{s}_n\underline{s}_{n-1}$ for some $y\in \Delta _{\textrm{inv}}(W_{-2})$. Moreover, $y\in \Gamma (W_{-2})$ because $a\not \in P_2(W)$. $\square$

Proof of Theorem 3.4

Define matchings $M_{1}, M_{2}$ and $M_{3}$ on $P_1(W)$, $P_2(W)$, and $P_3(W)$ respectively as:

• (1) $M_{1}(a):=a\underline{s}_{n}$ for $a\in P_1(W)$;

• (2) $M_2(a):=M^{-3}(x)\underline{s}_{n-2}\underline{s}_{n} \underline{s}_{n-1}$ for $a=x\underline{s}_{n-2}\underline{s}_{n} \underline{s}_{n-1}\in P_2(W)$;

• (3) $M_{3}(a):=M^{-2}(y)\underline{s}_{n}\underline{s}_{n-1}$ for $a=y\underline{s}_{n}\underline{s}_{n-1}\in P_3(W)$.

Note that $M^{-2}(y)\in \Gamma (W_{-2})$ since $M^{-2}$ preserves $\Gamma (W_{-2})$. This ensures that $M_{3}$ is well defined.

Define also a matching

$$\begin{aligned} M(a):=\left\{ \begin{array}{ll} M_{1}(a) &{}\quad \text {if}\, a\in P_{1}(W),\\ M_{2}(a) &{}\quad \text {if}\, a\in P_{2}(W),\\ M_{3}(a) &{}\quad \text {if}\, a\in P_{3}(W) \end{array}\right. \end{aligned}$$

on $P(\Delta _{\textrm{inv}}(W))$. We shall show that M is a $\Gamma$-matching on $P(\Delta _{\textrm{inv}}(W))$.

A. M is an acyclic matching on $P(\Delta _{\textrm{inv}}(W))$: We will first show that the matchings $M_{1}$, $M_{2}$ and $M_{3}$ are acyclic on $P_{1}(W)$, $P_{2}(W)$ and $P_{3}(W)$ respectively and then use Lemma 2.7 to show that M is an acyclic matching on $P(\Delta _{\textrm{inv}}(W))$.

The matching $M_{1}$ is acyclic. To see it: By Lemma 2.3, if $M_{1}$ has a cycle on $P_{1}(W)$, then $a_{0}\lessdot M_{1}(a_{0})=a_{0}\underline{s}_{n} \gtrdot a_{1}$ and $a_{1} \lessdot M_{1}(a_{1})=a_{1} \underline{s}_{n}$ for some $a_{0}\ne a_{1}$. However since $\underline{s}_{n} \nleq a_{0}$ and $\underline{s}_{n}\nleq a_{1}$ we have that $a_{0}=a_{1}$, so there is no cycle. Hence $M_{1}$ is acyclic.

Define a map $g:P(\Delta _{\textrm{inv}}(W_{-3}))\rightarrow P_{2}(W)$ by $g(x)=x\underline{s}_{n-2}\underline{s}_{n}\underline{s}_{n-1}$. The subword property implies that g is a poset isomorphism. Since $M^{-3}$ is a $\Gamma$-matching, it is acyclic. Hence, $M_{2}$ is an acyclic matching.

Similarly, $\Gamma (W_{-2})$ and $P_{3}(W)$ are isomorphic. Since $M^{-2}$ is acyclic and $M^{-2}$ preserves $\Gamma (W_{-2})$, $M_{3}$ is an acyclic matching.

Our goal is to show that M is acyclic using Lemma 2.7. Let Q be the (total) order whose Hasse diagram is shown in Fig. 4.

Fig. 4

Hasse diagram of Q

We proceed to verify the hypotheses of the lemma.

• (1) As we have already seen, each cell belongs to only one $P_{i}(W)$ for $i=1,2,3$.

• (2) We show that $P_{1} (W)$ and $P_{1}(W)\cup P_{2}(W)$ are order ideals. To observe that $P_{1} (W)$ is an order ideal we let $a\in P_{1} (W)$ and $t\le a$. If $\underline{s}_{n}\nleq a$, then $\underline{s}_{n} \nleq t$ and hence $t\in P_{1} (W)$. If $s_{n} \in D_{R}(a)$, then either $\underline{s}_{n}\nleq t$ or $s_{n} \in D_{R}(t)$. So $t\in P_{1} (W)$. Thus $P_{1}(W)$ is an order ideal. Also $P_{1}(W)\cup P_{2} (W)$ is an order ideal. If $a\in P_{2} (W)$ and $t< a$, then we have $t<a=x\underline{s}_{n-2}\underline{s}_{n}\underline{s}_{n-1}$. If $\underline{s}_{n-2}\underline{s}_{n}\underline{s}_{n-1}\le t$ then $t\in P_{2} (W)$. If $\underline{s}_{n-2}\underline{s}_{n}\underline{s}_{n-1} \nleq t$ then $\underline{s}_{i} \nleq t$ for at least one of $i=n-2,n-1,n$. If $\underline{s}_{n-2}\nleq t$ then $t=x\underline{s}_{n} \underline{s}_{n-1}=x\underline{s}_{n-1} \underline{s}_{n}\in P_{1}(W)$. Similarly if $\underline{s}_{n}$ or $\underline{s}_{n-1}\nleq t$, then $t=x\underline{s}_{n-2} \underline{s}_{n-1}\in P_{1}(W)$ or $t=x\underline{s}_{n-2}\underline{s}_{n}\in P_{1}(W)$. Hence $P_{1}(W)\cup P_{2} (W)$ is an order ideal.

Now since $P_{1}(W), P_{1}(W)\cup P_{2}(W)$ and $P_{1}(W)\cup P_{2}(W)\cup P_{3} (W)$ are order ideals, and $M_{1}, M_{2}$ and $M_{3}$ are acyclic matchings on $P_{1}(W), P_{2} (W)$, and $P_{3} (W)$ respectively, then by Lemma 2.7, M is an acyclic matching on $P(\Delta _{\textrm{inv}}(W))$.

B. All critical cells are of top dimension $n-1$: Let a be a critical cell of M. Since $M_{1}$ is complete on $P_{1}(W)$, then either $a = x\underline{s}_{n-2}\underline{s}_{n}\underline{s}_{n-1}$ with x a critical cell of $M^{-3}$ or $a =y\underline{s}_{n}\underline{s}_{n-1}$ with y a critical cell of $M^{-2}$. By the assumptions on $M^{-2}$ and $M^{-3}$, $\text {dim}(a)=n-1$ in both cases.

C. M preserves $\Gamma (W)$: That the matching M preserves $\Gamma (W)$ follows by construction since $\Gamma (W) = P_{2}(W) \cup P_{3}(W)$.

D. All critical cells belong to $\Gamma (W)$: Since M is complete on $P_{1} (W)$, there are no critical cells in $P_{1} (W)$. So all critical cells of M are in $P(\Delta _{\textrm{inv}}(W))\backslash P_{1} (W)=\Gamma (W)$.

This completes the proof that M is a $\Gamma$-matching on $P(\Delta _{\textrm{inv}}(W))$. Finally, the assertion about the number of critical cells is immediate from part B above. $\square$

We proceed to apply Theorem 3.4 to prove Corollary 3.8 below, which is the main result of this paper.

For two ordered Coxeter systems (W, S) and $(Z,S')$, we say that $(Z,S')$ is a path extension of (W, S) if $S=\{s_1<\cdots <s_n\}$ and $S'=\{s_1<\cdots <s_N\}$ for some $N\ge n$, and for all $1\le i\le N$ and $n<j\le N$ with $i\ne j$, it holds that

$$\begin{aligned} m(s_i,s_j)={\left\{ \begin{array}{ll} 2 &{} \text {if }|i-j|\ge 2,\\ 3 &{} \text {if }|i-j| = 1. \end{array}\right. } \end{aligned}$$

In other words, we obtain the Coxeter graph of a path extension of (W, S) from that of (W, S) by attaching a (possibly empty) path at the maximum vertex $s_n$. Figure 5 illustrates this situation for a path ended system (W, S). This is the setting of the upcoming result.

Fig. 5

A Coxeter system $(Z,S')$ as a path extension of a path ended Coxeter system (W, S)

Corollary 3.8

Let (W, S) be a path ended Coxeter system such that $P(\Delta _{\textrm{inv}}(W_{-1}))$, $P(\Delta _{\textrm{inv}}(W_{-2}))$ and $P(\Delta _{\textrm{inv}}(W_{-3}))$ all have $\Gamma$-matchings. Then, for every path extension $(Z,S')$ of (W, S), $\Delta _{\textrm{inv}}(Z)$ is homotopy equivalent to a wedge of $(|S'|-1)$-dimensional spheres. The number of spheres satisfies the recurrence $\beta _I(Z) = \beta _I(Z_{-2}) + \beta _I(Z_{-3}).$

Proof

Since $(Z,S')$ is path ended, Theorem 3.4 together with Theorem 2.5 provide the desired conclusions if we are able to show that $Z_{-2}$ and $Z_{-3}$ have $\Gamma$-matchings. By induction on $|S'|$, it however follows from Theorem 3.4 that $Z_{-1}, Z_{-2}$, and $Z_{-3}$ all have $\Gamma$-matchings. $\square$

4 Applications of Corollary 3.8

In this section we shall calculate the homotopy types of some explicit boolean involution complexes, including all those of finite Coxeter groups. Barring some small examples that are easily computed by hand, we achieve this by identifying $\Gamma$-matchings of some suitably chosen ordered Coxeter systems, and then invoking Corollary 3.8.

Theorem 4.1

If W is irreducible and finite, the homotopy type of $\Delta _{\textrm{inv}}(W)$ is as specified in Table 1, where the Betti numbers in the classical types are determined by

• $\beta _I(A_{n})=\beta _I(A_{n-2})+\beta _I(A_{n-3})$ with $\beta _I(A_{1})=0, \beta _I(A_{2})=0$ and $\beta _I(A_{3})=1$,

• $\beta _I(B_{n})=\beta _I(B_{n-2})+\beta _I(B_{n-3})$ with $\beta _I(B_{2})=1, \beta _I(B_{3})=1$ and $\beta _I(B_{4})=1$,

• $\beta _I(D_{n})=\beta _I(D_{n-2})+\beta _I(D_{n-3})$ with $\beta _I(D_{4})=1, \beta _I(D_{5})=1$ and $\beta _I(D_{6})=2$.

Table 1 Homotopy type of $\Delta _{\textrm{inv}}(W)$ for finite, irreducible W

Remark 4.2

Recall that the Padovan sequence $P_{0}, P_{1}, \ldots$ is determined by $P_{0}=1, P_{1}=0, P_{2}=0$ and $P_{n}=P_{n-2}+P_{n-3}$ for $n\ge 3$. Hence, $\beta _I(A_{n})=P_{n}$ for $n\ge 1$, $\beta _I(B_{n})=P_{n+3}$ for $n\ge 2$, and $\beta _I(D_{n})=P_{n+2}$ for $n\ge 2$. For more information about the Padovan sequence, see [14] and the references cited there.

Proof of Theorem 4.1

Let us provide $\Gamma$-matchings of $P(\Delta _{\textrm{inv}}(W))$. In types A, B, D, and E, this is achieved using Corollary 3.8. Somewhat nonstandard type terminology will be employed to indicate specific ordered Coxeter systems. Their Coxeter graphs are collected in Fig. 6.

First, let us make a general observation. To verify that the boolean involution ideal of a certain ordered Coxeter system (W, S) has a $\Gamma$-matching, it is enough to verify that the subposet induced by $\Gamma (W)$ admits an acyclic matching with all critical cells of top dimension. Namely, just as in the proof of Theorem 3.4, the subposet $P_1(W)$ is an order ideal with a complete acyclic matching, and so the union of these two matchings is a $\Gamma$-matching. This is illustrated for W of type $F_{4}$ in Fig. 2. There, the entire acyclic matching on $P(\Delta _{\textrm{inv}}(W))$ is depicted. For the conclusion of the theorem, it is however enough to inspect $\Gamma (W)$, which consists of the two yellow, encircled elements.

Type A. Consider (W, S) of type $A_n$, $n \ge 4$, as an ordered Coxeter system with the natural order on the generators indicated in Fig. 1. Then, (W, S) is a path extension of the path ended system $A_4$. To obtain the desired result from Corollary 3.8, it therefore suffices to verify the hypotheses, namely that the boolean involution ideals of $A_{3}$, $A_{2}$, and $A_{1}$ have $\Gamma$-matchings. Concluding the proof in type A, one readily verifies that $\Gamma (A_{3}) = \{\underline{s}_1\underline{s}_3\underline{s}_2\}$ and $\Gamma (A_{2}) = \Gamma (A_{1}) = \emptyset$.

Type B. We proceed similarly to type A. This time, we begin with the ordered type B system in Fig. 1 which, for $n\ge 4$, is a path extension of $B_4$. Here, $\Gamma (B_{3}) = \{\underline{s}_1\underline{s}_3\underline{s}_2\}$, $\Gamma (B_{2}) = \{\underline{s}_2\underline{s}_1\}$, and $\Gamma (B_{1}) = \emptyset$.

Type D. Again, we argue in a similar way. Here, we begin with the ordered system of type $D_{n}$ as in Fig. 1, where $D_{n}$ is a path extension of $D_{5}$ for all $n\ge 5$. The hypotheses are verified by observing that $\Gamma (D_{2}) = \emptyset$, $\Gamma (D_{3}) = \{\underline{s}_1\underline{s}_3\underline{s}_2\}$, and $\Gamma (D_{4}) =\lbrace \underline{s}_1\underline{s}_4\underline{s}_3,$ $\underline{s}_2\underline{s}_4\underline{s}_3,$ $\underline{s}_1\underline{s}_4\underline{s}_3\underline{s}_2,$ $\underline{s}_1\underline{s}_2\underline{s}_4\underline{s}_3,$ $\underline{s}_2\underline{s}_4\underline{s}_3\underline{s}_1\rbrace$. Here, an acyclic matching on $\Gamma (D_{4})$ is depicted in Fig. 7 where the only critical cell is $\underline{s}_2\underline{s}_4\underline{s}_3\underline{s}_1$.

Type E. We proceed in a similar way as in types A, B, D above. We start with the ordered system of type E as in Fig. 1 where $E_{6}$, $E_{7}$, and $E_{8}$ are path extensions of $E_{6}$. The hypotheses are readily checked by observing that $\Gamma (E_{3}) = \emptyset$, $\Gamma (E_{4}) = \{\underline{s}_2\underline{s}_4\underline{s}_3$, $\underline{s}_1\underline{s}_4\underline{s}_2$, $\underline{s}_1\underline{s}_2\underline{s}_4\underline{s}_3$, $\underline{s}_1\underline{s}_4\underline{s}_2\underline{s}_3\}$ see Fig. 8, and $\Gamma (E_{5})$ is as depicted in Fig. 9 where an acyclic matching on $\Gamma (E_{5})$ with one critical cell, $\underline{s}_3\underline{s}_5\underline{s}_4\underline{s}_2\underline{s}_1$, is indicated.

Fig. 6

Ordered Coxeter systems that appear in the proof of Theorem 4.1

Fig. 7

An acyclic matching on $\Gamma (D_{4})$

Type H. The results in type H are the same as in type B by Lemma 2.23. $\square$

Fig. 8

An acyclic matching on $\Gamma (E_{4})$

Fig. 9

An acyclic matching on $\Gamma (E_{5})$

Some concluding remarks are in order:

First, the previous theorem concerns irreducible groups, but reducible groups are easily covered. Namely, taking products of Coxeter systems is readily seen to imply taking the join of their corresponding boolean complexes of involutions.

Second, there is of course nothing that prevents extending the approach of the previous proof to path extensions which are not finite. For example, $\tilde{F}_{4}$ is a path extension of $F_{4}$ and $\Delta _{\textrm{inv}}(\tilde{F}_{4})$ is homotopy equivalent to $S^{4}$, $\tilde{E}_{8}$ is a path extension of $E_{8}$ and $\Delta _{\textrm{inv}}(\tilde{E}_{8})$ is homotopy equivalent to $S^{8}$, etc.

Third, just as we did for type H in the proof above, we may apply Lemma 2.23 to obtain results for more Coxeter systems without additional effort.

Let us end with the natural question: Does the above result extend to all Coxeter systems? That is, is $\Delta _{\textrm{inv}}(W)$ homotopy equivalent to a wedge of spheres of dimension $|S|-1$ for every system (W, S)?