Abstract
A matching of the set \([2n]=\{1,2,\ldots ,2n\}\) is a partition of [2n] into blocks with two elements, i.e. a graph on [2n], such that every vertex has degree one. Given two matchings \(\sigma \) and \(\tau \), we say that \(\sigma \) is a \(pattern \) of \(\tau \) when \(\sigma \) can be obtained from \(\tau \) by deleting some of its edges and consistently relabelling the remaining vertices. This is a partial order relation turning the set of all matchings into a poset, which will be called the matching pattern poset. In this paper, we continue the study of classes of pattern avoiding matchings (see below for previous work on this subject). In particular, we work out explicit formulas to enumerate the class of matchings avoiding two new patterns, obtained by juxtaposition of smaller patterns, and we describe a recursive formula for the generating function of the class of matchings avoiding the lifting of a pattern and two additional patterns. Moreover, we introduce the notion of unlabeled pattern, as a combinatorial way to collect patterns, and we provide enumerative formulas for two classes of matchings avoiding an unlabeled pattern of order three. In one case, the enumeration follows from an interesting bijection between the matchings of the class and ternary trees. The last part of the paper initiates the study of the matching pattern poset, by providing some preliminary results about its Möbius functions and the structure of some simple intervals.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \(n\in {\mathbb {N}}^{*}\) and set as usual \([n]=\{1,2,\ldots ,n\}\). A \(matching \) of [2n] is a partition of [2n] into blocks having two elements. Note that a matching of [2n] is the same as a graph on [2n] such that every vertex has degree one; hence, we will borrow some standard terminology from graph theory, as well as the usual representation of graphs using diagrams consisting of dots and lines. In particular, every matching of [2n] will be represented either by a circular or by a linear chord diagram, as shown in Fig. 1.
Let \(\tau \) be a matching of [2n]. The integer n, i.e., the number of edges of \(\tau \), will be called the \(order \) of \(\tau \) and will be denoted by \(|\tau |\). The set of all matchings will be denoted by \({\mathcal {M}}\) and the set of all matchings of order n will be denoted by \({\mathcal {M}}_{n}\). Given \(e\in \tau \), the integers \(\min (e)\) and \(\max (e)\) will be called the \(left \) \(vertex \) and the \(right \) \(vertex \) of e, respectively. Given a subset S of \(\tau \) and \(e\in S\), we will say that e is the \(leftmost \) (respectively, \(rightmost \)) edge of S when \(\min (e)\le \min (f)\) (respectively, \(\max (e)\ge \max (f)\)) for every \(f\in S\). Following [23], we will represent \(\tau \) by means of the unique integer sequence \({\tilde{\tau }}\in [n]^{2n}\) such that \({\tilde{\tau }}_{\min (e)}={\tilde{\tau }}_{\max (e)}\) and \({\tilde{\tau }}_{\min (e)}<{\tilde{\tau }}_{\min (f)}\) for every \(e,f\in \tau \) such that \(\min (e)<\min (f)\). Using this encoding, the vertices of \(\tau \) are represented by the elements of \({\tilde{\tau }}\) and two vertices of \(\tau \) are connected by an edge when the corresponding components of \({\tilde{\tau }}\) are equal (see Fig. 2).
In the following, we will always identify matchings with their corresponding integer sequences. Let \(\sigma \) and \(\tau \) be matchings. The matching \(\sigma (\tau +|\sigma |)\) will be called the \(juxtaposition \) of \(\sigma \) and \(\tau \) (where \(\tau +|\sigma |\) denotes the sequence obtained from \(\tau \) by adding \(|\sigma |\) to each of its elements). Its linear chord diagram can be indeed represented by juxtaposing the linear chord diagrams of \(\sigma \) and \(\tau \), respectively. The matching \(1(\tau +1)1\) will be called the \(lifting \) of \(\tau \). Its linear chord diagram can be represented by nesting the linear chord diagram of \(\tau \) into an additional edge. The matching obtained from the sequence \(\tau _{n}\ldots \tau _{2}\tau _{1}\) by suitably renaming its elements so as to obtain a valid matching will be called the \(reversal \) of \(\tau \) and denoted by \({\overline{\tau }}\). Its linear chord diagram can be represented by reflecting the linear chord diagram of \(\tau \) along a vertical line.
Given \(k\in {\mathbb {N}}^{*}\), let \(\sigma \) be a matching of [2k] and \(i=(i_{1},\ldots ,i_{2k})\in [2n]^{2k}\). We say that i is an \(occurrence \) of \(\sigma \) in \(\tau \) when \(i_{1}<i_{2}<\cdots <i_{2k}\) and \(\{i_{p},i_{q}\}\in \tau \) if and only if \(\{p,q\}\in \sigma \), for every \(p,q\in [2k]\) (see Fig. 3).
We say that \(\sigma \) is a \(pattern \) of \(\tau \), and write \(\sigma \le \tau \), when there is an occurrence of \(\sigma \) in \(\tau \), and that \(\tau \) \(avoids \) \(\sigma \) otherwise. The relation \(\le \) is a partial order turning the set of all matchings into a poset, which we will call the \(matching \) \(pattern \) \(poset \). If S is a set of matchings, the class of all matchings avoiding every pattern in S will be denoted by \({\mathcal {M}}(S)\), the class of all matchings in \({\mathcal {M}}(S)\) of order n will be denoted by \({\mathcal {M}}_{n}(S)\), and the generating function of the sequence \(\{|{\mathcal {M}}_{n}(S)|\}_{n\in {\mathbb {N}}}\) will be denoted by \({\mathcal {M}}(S,z)\). We say that \(\sigma \) and \(\tau \) are \(Wilf-equivalent \) when \({\mathcal {M}}(\sigma ,z)={\mathcal {M}}(\tau ,z)\).
The study of pattern posets is nowadays a major trend in enumerative combinatorics. The notion of pattern for permutations [24], for instance, has proved incredibly prolific, giving rise to a great deal of research papers with applications to several disciplines. There are however many other combinatorial structures for which the notion of pattern has revealed very fruitful, such as set partitions [28], words [8], lattice paths [4, 11], trees (both labeled [14] and unlabeled [12, 27]), and polyominoes [3]. See also the article [30], which lays the groundwork for a general theory of pattern posets.
The goal of our paper is to continue the study of classes of pattern avoiding matchings, initiated in [6, 10, 23]. Our focus is mainly enumerative, aiming at extending some results and suggesting further lines of research concerning the enumeration of classes of pattern avoiding matchings. Moreover, we begin the investigation of the structure of the matching pattern poset, which appears to be highly nontrivial (for instance, it contains the permutation pattern poset as an induced subposet). More in detail, the paper is organized as follows.
In Sect. 3, we investigate classes of the form \({\mathcal {M}}(\sigma (\tau +|\sigma |))\) and \({\mathcal {M}}(1(\sigma +1)1,\chi ,{\overline{\chi }})\), providing a general approach which yields enumerative formulas for some patterns \(\sigma ,\tau \) and \(\chi \). Following a recursive approach already described in [23], we reduce the enumeration of \({\mathcal {M}}(\sigma (\tau +|\sigma |))\) to the enumeration of a specific class of matchings \(\mu (\sigma )\) (depending on \(\sigma \)) and the class \({\mathcal {M}}(\tau )\), finding an explicit answer for the prefix \(\sigma =1212\). Moreover, we introduce a suitable pattern \(\chi =123132\) to relate the generating function of \({\mathcal {M}}(1(\sigma +1)1,\chi ,{\overline{\chi }})\) to the generating function of \({\mathcal {M}}(\sigma ,\chi ,{\overline{\chi }})\).
In Sect. 4, we introduce the notion of unlabeled matching, which is an equivalence class of matchings having the same unlabeled circular chord diagram. This seems a reasonable and combinatorially meaningful way to collect patterns. As a first result concerning unlabeled pattern avoidance, we provide enumerative formulas for two classes of matchings avoiding an unlabeled pattern of order three, as well as a bijection between matchings avoiding a certain unlabeled pattern and ternary trees.
Section 5 is a first step towards the study of the structure of the matching pattern poset. Specifically, we find some properties of the Möbius function (which allow us to easily compute it in several cases, especially in the induced subposet of noncrossing matchings) and we illustrate some formulas for counting elements of specific intervals.
Finally, Sect. 6 provides some hints for further work.
2 Previous Work
Given a permutation \(\sigma \) of [n], we can construct a matching of [2n] by connecting the vertices \(\{1,\ldots ,n\}\) with the vertices \(\{n+1,\ldots ,2n\}\) in the order prescribed by \(\sigma \), thus obtaining the matching corresponding to the integer sequence \(12\ldots n\sigma _{1}\ldots \sigma _{n}\). A matching of this kind will be called a \(permutational \) \(matching \) and it is immediate to notice that a matching of [2n] is permutational if and only if it avoids the pattern 1122, so that \(|{\mathcal {M}}_{n}(1122)|=n!\). Two remarkable examples of permutational matchings are \(123\ldots n123\ldots n\) and \(123\ldots nn\ldots 321\), which will be called the \(totally \) \(crossing \) and the \(totally \) \(nesting \) matching of [2n], respectively. It is easy to see that the map sending every permutation to the corresponding permutational matching is a poset embedding; hence, we can regard the permutation pattern poset as a subposet of the matching pattern poset. Throughout this paper, we will denote by \(C_{n}=\frac{1}{n+1}\left( {\begin{array}{c}2n\\ n\end{array}}\right) \) the \(n^{th}\) Catalan number and by C(z) the generating function of Catalan numbers. As for other enumerative results on pattern avoidance, it is well known that noncrossing matchings have a Catalan structure; therefore, \(|{\mathcal {M}}_{n}(1212)|=C_{n}\), and it is also well known that nonnesting matchings are counted by the same sequence, that is, \(|{\mathcal {M}}_{n}(1221)|=C_{n}\). More surprisingly, it was proved in [10] that the matchings \(123\ldots k123\ldots k\) and \(123\ldots kk\ldots 321\) are Wilf-equivalent for every \(k\in {\mathbb {N}}^{*}\). No closed formula for the number of matchings avoiding these patterns is available in general, although it was proved in [21] that \(|{\mathcal {M}}_{n}(123123)|=C_{n}C_{n+2}-C_{n+1}^{2}\). Furthermore, Wilf-equivalences between several classes of patterns are established in [23] through bijective methods; for instance, as an immediate consequence of Lemmas 3.7 and 3.10 in that paper, one can deduce the following useful fact.
Proposition 2.1
If \(\sigma \) and \(\sigma '\) are two Wilf-equivalent matchings and \(\tau \) and \(\tau '\) are two Wilf-equivalent matchings, then \(\sigma (\tau +|\sigma |)\) and \(\sigma '(\tau '+|\sigma '|)\) are Wilf-equivalent.
Moreover, the same paper also contains an enumerative result which reduces the enumeration of \({\mathcal {M}}(11(\sigma +1))\) to the enumeration of \({\mathcal {M}}(\sigma )\) in a recursive fashion. Finally, aside for the classes of patterns mentioned above, the only (up to Wilf-equivalence) further class of matchings avoiding a small pattern has been enumerated in [6], proving that
In the same paper, some enumerative results are given for most of the classes of matchings avoiding a pair of permutational patterns of order three. Nevertheless, enumerating all the remaining classes of matchings avoiding a single patterns of order three remains an open problem and it is likely to be a hard one. Indeed, it is suggested in [6] that enumeration of the class of matchings avoiding the pattern 123231 could be related to the enumeration of the class of permutations avoiding 1324, which is considered to be a very hard problem.
3 Pattern Avoidance
3.1 The Juxtaposition of Two Patterns
Let \(\sigma \) and \(\tau \) be two matchings. In this section, we investigate the class of matchings avoiding the juxtaposition of \(\sigma \) and \(\tau \). To this purpose, we define a set of matchings depending on \(\sigma \). Let \(n\in {\mathbb {N}}\) and \(\lambda \) be a matching of order n. We will say that \(\lambda \) minimally contains \(\sigma \) when it contains \(\sigma \) and the matching obtained from \(\lambda \) by deleting its rightmost edge does not contain \(\sigma \). Denote by \(\mu (\sigma )\) the set of matchings minimally containing \(\sigma \), by \(\mu _{n}(\sigma )\) the set of elements in \(\mu (\sigma )\) with order n and by \(\mu (\sigma ,z)\) the corresponding generating function. Generalizing an approach already used in [23], the following formula allows us to relate the enumeration of \({\mathcal {M}}(\sigma (\tau +|\sigma |))\) to the enumeration of \({\mathcal {M}}(\sigma )\), \(\mu (\sigma )\) and \({\mathcal {M}}(\tau )\).
Proposition 3.1
Let \(\sigma \) and \(\tau \) be matchings and \(n\in {\mathbb {N}}\), with \(n\ge |\sigma |\). Then
Proof
Given \(\lambda \in {\mathcal {M}}_{n}(\sigma (\tau +|\sigma |))\), then either \(\lambda \in {\mathcal {M}}_{n}(\sigma )\) or \(\sigma \) is a pattern of \(\lambda \). From now on, we assume that the latter case occurs, since the former one is taken into account by the first summand in the right-hand side of (1). For \(h\in [2n]\), we denote by \(\lambda _{\le h}\) the pattern of \(\lambda \) consisting of all the edges of \(\lambda \) with both vertices smaller than or equal to h, by \(\lambda _{\ge h}\) the pattern of \(\lambda \) consisting of all the edges of \(\lambda \) with both vertices bigger than or equal to h and finally by \(\lambda _{h}\) the pattern of \(\lambda \) consisting of all the edges of \(\lambda \) that are neither in \(\lambda _{\le h}\) nor in \(\lambda _{\ge h}\). Note that an edge of \(\lambda \) belongs to \(\lambda _{h}\) if and only if its left vertex is smaller than or equal to h and its right vertex is bigger than or equal to h.

Now, let h denote the smallest integer such that \(\lambda _{\le h}\) contains an occurrence of \(\sigma \) (of course, such an h exists, because \(\lambda _{\le 2n}=\lambda \)) and let \(\ell \) be the order of \(\lambda _{\le h}\). Then, by definition, \(\lambda _{\le h}\in \mu _{\ell }(\sigma )\) and \(\ell \in \{|\sigma |,\ldots ,n\}\); hence, there are \(|\mu _{\ell }(\sigma )|\) possible choices for \(\lambda _{\le h}\). Furthermore, \(\lambda _{h}\in {\mathcal {M}}_{k}(1122)\) for some \(k\in \{0,\ldots ,n-\ell \}\); hence, there are \(|{\mathcal {M}}_{k}(1122)|=k!\) possible choices for \(\lambda _{h}\). Moreover, \(\lambda _{\ge h}\in {\mathcal {M}}_{n-\ell -k}(\tau )\), because \(\lambda \in {\mathcal {M}}_{n}(\sigma (\tau +|\sigma |))\); hence, there are \(|{\mathcal {M}}_{n-\ell -k}(\tau )|\) possible choices for \(\lambda _{\ge h}\). Finally, notice that \(h=2\ell +k\) and that the vertex h necessarily belongs to \(\lambda _{\le h}\); hence, the left vertices of the edges of \(\lambda _{h}\) can be chosen among the vertices of \(\lambda \) smaller than h in \(\left( {\begin{array}{c}2\ell +k-1\\ k\end{array}}\right) \) ways. Similarly, the right vertices of the edges of \(\lambda _{h}\) can be chosen among the vertices of \(\lambda \) bigger than h in \(\left( {\begin{array}{c}2n-2\ell -k\\ k\end{array}}\right) \) ways. Notice that all possible choices of the vertices of \(\lambda _{\le h}\) and \(\lambda _{h}\) satisfying the above constraints lead to valid matchings. This explains the factors in the remaining summands of the right-hand side of (1) and concludes the proof. \(\square \)
Unfortunately, Formula (1) is not very informative, as enumerating \(\mu (\sigma )\) is often as difficult as enumerating \({\mathcal {M}}(\sigma )\) itself. Nevertheless, one might still hope that this task can be achieved for some special prefixes \(\sigma \). For instance, note that, for \(\sigma =11\) and \(n\in {\mathbb {N}}^{*}\), we easily recover the formula
which can be found in [23]. The next proposition shows that the prefix \(\sigma =1212\) can be successfully addressed as well. We just need a couple of definitions. We say that a matching is \(connected \) when it is nonempty and it is not the juxtaposition of two nonempty matchings. A connected component of a matching \(\lambda \) is a maximal connected submatching of \(\lambda \) (where maximal refers to the number of edges). It is clear that every matching can be decomposed as the juxtaposition of its connected components.
Proposition 3.2
Let \(n\in {\mathbb {N}}\), with \(n\ge 2\), then
Proof
Let \(n\ge 1\). Note that any matching \(\lambda \in \mu _{n+1}(1212)\) can be obtained by inserting the left vertex \(\ell \) of the rightmost edge of \(\lambda \) in one of the available positions between the vertices of a noncrossing matching \({\hat{\lambda }}\) of order n. More specifically, \(\ell \) can be inserted in any position between the vertices of \({\hat{\lambda }}\) other than the positions between the connected components of \({\hat{\lambda }}\). Therefore, if \({\hat{\lambda }}\) has k connected components for some \(k\in [n]\), there are \(2n-k\) possible positions for the vertex \(\ell \) between the vertices of \({\hat{\lambda }}\). It follows that:
where \(C_{n,k}\) denotes the number of matchings of order n with k connected components. The triangle \(\{C_{n,k}\}_{1\le k\le n}\) is sometimes called the transposed Catalan triangle (sequence A033184 in [29]). A closed formula for its entries is given by
for every \(n,k\in {\mathbb {N}}\) such that \(1\le k\le n\). Plugging this expression into formula (2) and observing that \(\frac{2n-k}{n}\left( {\begin{array}{c}2n-k-1\\ n-k\end{array}}\right) =\left( {\begin{array}{c}2n-k\\ n-k\end{array}}\right) \) when \(k\in [n]\), we find
Now, when \(n,k\in {\mathbb {N}}\) and \(1\le k\le n\), it is not difficult to show by induction on n that
Indeed identity (4) is trivial for \(n=1\) and, when \(n\ge 2\), it follows by induction that:
From Eqs. (3) and (4), we thus get
as desired.
Unfortunately, we have not been able to provide a neat combinatorial argument to explain the appearance of the binomial coefficient in Proposition 3.2. However, observe that, as a byproduct, we also find the following identity:
which holds for every \(n\in {\mathbb {N}}\) such that \(n\ge 2\). Indeed, the left-hand side of the above equation counts all matchings in \(\mu _{n}(1212)\) by deleting the rightmost edge, and then counting the resulting \(1212-\)avoiding matchings according to the number of connected components. As an immediate consequence of Propositions 2.1, 3.1 and 3.2, we deduce the following.
Theorem 3.1
Let \(\sigma \in \{1212,1221\}\) and let \(\tau \) be a matching. Then, for \(n\ge 2\)
Specializing \(\tau \) in Theorem 3.1, we are able to enumerate a couple of new classes of matchings avoiding a single pattern (see also Table 1). Recall that, as we reported in Sect. 2, the patterns \(\tau \) appearing in the next corollary are among the very few ones whose avoiders have been enumerated.
Corollary 3.1
Let \(n\in {\mathbb {N}}\), with \(n\ge 2\), and \(\sigma \in \{1212,1221\}\).
-
(i)
If \(\tau \in \{1212,1221\}\), then
$$\begin{aligned} |{\mathcal {M}}_{n}(\sigma (\tau +2))|=C_{n} +\sum _{\ell =2}^{n}\sum _{k=0}^{n-\ell }\left( {\begin{array}{c}2\ell -1\\ \ell -2\end{array}}\right) \left( {\begin{array}{c}2\ell +k-1\\ k\end{array}}\right) \left( {\begin{array}{c}2n-2\ell -k\\ k\end{array}}\right) k!C_{n-\ell -k}. \end{aligned}$$ -
(ii)
If \(\tau \in \{123123,123321\}\), then
$$\begin{aligned}&|{\mathcal {M}}_{n}(\sigma (\tau +2))|=C_{n}\\&\quad +\sum _{\ell =2}^{n}\sum _{k=0}^{n-\ell }\left( {\begin{array}{c}2\ell -1\\ \ell -2\end{array}}\right) \left( {\begin{array}{c}2\ell +k-1\\ k\end{array}}\right) \left( {\begin{array}{c}2n-2\ell -k\\ k\end{array}}\right) k!(C_{n-\ell -k}C_{n-\ell -k+2}-C_{n-\ell -k+1}^{2}). \end{aligned}$$
3.2 The Lifting of a Pattern
In this section, we investigate classes of matchings avoiding the lifting of a given matching \(\sigma \). The enumeration of such classes seems to be a hard problem in general, since a special instance of it is the enumeration of matchings avoiding the pattern 123231, which is the lifting of 1212, and it was remarked in Sect. 1 that this is likely to be a hard problem. However, if we impose additional constraints, namely the avoidance of a special pattern \(\chi \) and its reversal \({\overline{\chi }}\), the description of the structure of matchings avoiding the lifting of \(\sigma \) becomes more accessible. We start by fixing some preliminary definitions. Let e and f be any two edges of \(\sigma \). We say that e is \(nested \) in f when \(\min (f)<\min (e)\) and \(\max (e)<\max (f)\). We say that e is a \(nested \) \(edge \) when it is nested in some edge of \(\sigma \) and that e is a \(top \) \(edge \) otherwise. The pattern of \(\sigma \) consisting of all the nested edges of \(\sigma \) will be called the \(core \) of \(\sigma \) and the pattern of \(\sigma \) consisting of all the top edges of \(\sigma \) will be called the \(roof \) of \(\sigma \). Note that, by definition, the roof of \(\sigma \) is a nonnesting matching. Recall that a matching is said to be \(connected \) when it is nonempty and it is not the juxtaposition of two nonempty matchings. Let S be a set of matchings and \(n\in {\mathbb {N}}\), we denote by \({\mathcal {M}}^{*}(S)\) the class of all connected matchings avoiding S, by \({\mathcal {M}}_{n}^{*}(S)\) the set of matchings in \({\mathcal {M}}^{*}(S)\) of order n and by \({\mathcal {M}}^{*}(S,z)\) the generating function of \({\mathcal {M}}^{*}(S)\). In the following, we will make some use of the so-called symbolic method, borrowing some standard constructions and notations from [18], such as disjoint union, cartesian product and composition of combinatorial classes (in particular, the operator \(\mathrm {Seq}\)), which will allow us to easily translate combinatorial descriptions into generating functions.
Remark 3.1
Note that, for a set of connected patterns S, \({\mathcal {M}}(S)=\mathrm {Seq}({\mathcal {M}}^{*}(S))\) and, therefore, \({\mathcal {M}}(S,z)=\frac{1}{1-{\mathcal {M}}^{*}(S,z)}\). In particular, \(C(z)={\mathcal {M}}(1221,z)=\frac{1}{1-{\mathcal {M}}^{*}(1221,z)}\), which leads to
which means that, for every \(n\in {\mathbb {N}}^{*}\), there are \(C_{n-1}\) connected nonnesting matchings of order n.
We are now in a position to state and prove the main result of this section.
Theorem 3.2
Let \(\sigma \) be a connected matching and set \(\chi =123132\), so that \({\overline{\chi }}=123213\). Then
Proof
Let \(n\in {\mathbb {N}}^{*}\), \(\lambda \in {\mathcal {M}}^{*}_{n}(1(\sigma +1)1,\chi ,{\overline{\chi }})\) and m be the order of its roof. The matching \(\lambda \) is required to avoid both \(\chi \) and \({\overline{\chi }}\), that are the matchings represented by the following linear chord diagrams:

This means that every nested edge of \(\lambda \) is forced to never cross a top edge of \(\lambda \). Therefore, the core of \(\lambda \) can be decomposed as the juxtaposition of \(2m-1\) (possibly empty) matchings \(\lambda _{1},\ldots ,\lambda _{2m-1}\in {\mathcal {M}}(\sigma ,\chi ,{\overline{\chi }})\); moreover, the occurrences of these factors in \(\lambda \) are separated by the vertices of the top edges of \(\lambda \). Conversely, every matching constructed as above belongs to the class \({\mathcal {M}}^{*}(1(\sigma +1)1,\chi ,{\overline{\chi }})\), because \(\sigma \) is connected, and so, no occurrence of \(\sigma \) can show up by juxtaposing two patterns in the class \({\mathcal {M}}(\sigma ,\chi ,{\overline{\chi }})\). Thus, \({\mathcal {M}}^{*}_{n}(1(\sigma +1)1,\chi ,{\overline{\chi }})\) is the set of matchings obtained by choosing some \(m\in {\mathbb {N}}^{*}\) and a matching in \({\mathcal {M}}_{m}^{*}(1221)\), then replacing its edges other than the rightmost one with structures and the rightmost edge with a structure. An instance of this decomposition is illustrated in the following figure, when the roof is 121323, and where each of the isolated points inside a box is one vertex of the edge of the roof incident to that box.

It follows that the combinatorial class \({\mathcal {M}}^{*}(1(\sigma +1)1,\chi ,{\overline{\chi }})\) is isomorphic to the combinatorial class:

and this isomorphism immediately translates into the following expression for the generating function:
Now, the claim follows from the above Remark. \(\square \)
Note that, at least in principle, iterating Theorem 3.2 allows us to find expressions for the generating function of \({\mathcal {M}}(12\ldots k(\sigma +k)k\ldots 21,\chi ,{\overline{\chi }})\) in terms of the generating function of \({\mathcal {M}}(\sigma ,\chi ,{\overline{\chi }})\), for every \(k\in {\mathbb {N}}^{*}\). As an immediate application, we are able to compute the generating function of two classes of matchings avoiding three patterns of order three.
Corollary 3.2
The following equalities hold:
and \(|{\mathcal {M}}_{n}(123231,123132,123213)|=|{\mathcal {M}}_{n}(123321,123132,123213)|\) is the \(n^{th}\) term of sequence \(\mathrm {A125188}\) in [29].
Proof
Let \(\sigma \in \{1212,1221\}\), then it follows from Theorem 3.2 that:
where \(\chi =123132\) and \({\overline{\chi }}=123213\). Moreover, \({\mathcal {M}}(\sigma ,\chi ,{\overline{\chi }},z)={\mathcal {M}}(\sigma ,z)=C(z)\) and the first claim follows. The generating function for sequence \(\mathrm {A125188}\) can be found in [29] and is given by
Applying the change of variable \(y=zC(z)\), so that \(z=y(1-y)\) and \(C(z)=\frac{1}{1-y}\), some routine computations show that \(f(z)=\frac{1}{1-zC(z)C(C(z)-1)}\); hence, the second claim also follows.
Sequence \(\mathrm {A125188}\) of [29] counts Dumont permutations of the first kind avoiding the patterns 2413 and 4132, but we have not been able to find any bijection with our classes of pattern avoiding matchings. Note that, for \(\sigma \in \{1212,1221\}\), iterating Theorem 3.2 allows us to prove that \({\mathcal {M}}(12\ldots k(\sigma +k)k\ldots 21,\chi ,{\overline{\chi }},z)\) is an algebraic function of C(z); hence, it is itself algebraic, for every \(k\in {\mathbb {N}}^{*}\).
4 Unlabeled Pattern Avoidance
In this section, we introduce the notion of unlabeled matching, which provides a way to collect patterns that are combinatorially equivalent, in a sense that is specified below. Given \(n\in {\mathbb {N}}^{*}\), let \(\gamma _{n}\) denote the \(2n-\)cycle \((1\ 2\ 3\ \ldots \ 2n)\) on [2n] and let \(\sigma \) and \(\tau \) be two matchings of order n. We say that \(\sigma \) and \(\tau \) are \(cyclically \) \(equivalent \) when there exists \(k\in [2n]\) such that \(\{i,j\}\in \sigma \) if and only if \(\{\gamma _{n}^{k}(i),\gamma _{n}^{k}(j)\}\in \tau \), for every \(i,j\in [2n]\). In other words, two matchings are cyclically equivalent when they have the same unlabeled circular chord diagram. An equivalence class of matchings is called an \(unlabeled \) \(matching \). For instance, \([112323]=\{112323,123231,123312,121233,121332,122313\}\). Thus, an unlabeled matching can be represented by an unlabeled circular chord diagram; for instance, the unlabeled matching [112323] can be represented by the following unlabeled chord diagram:

Note that a matching avoids an unlabeled pattern if and only if its circular chord diagram avoids the unlabeled chord diagram of the pattern.
The unlabeled matchings of order 2 are exactly \([1122]=\{1122,1221\}\) and \([1212]=\{1212\}\). Note that, for every \(n\in {\mathbb {N}}^{*}\), a matching \(\lambda \) of order n avoids [1122] if and only if it is permutational and nonnesting; hence, \({\mathcal {M}}_{n}([1122])=\{123\ldots n123\ldots n\}\). We thus have \({\mathcal {M}}([1212],z)=C(z)\) and \({\mathcal {M}}([1122],z)=\frac{1}{1-z}\). There are exactly five unlabeled matchings of order 3, namely
-
\([112323]=\{ 112323,123231,123312,121233,121332,122313 \},\)
-
\([123132]=\{ 121323,123213,121323\},\)
-
\([123321]=\{ 123321,122133,112332\},\)
-
\([112233]=\{ 112233,122331\},\)
-
\([123123]=\{ 123123\}.\)
Clearly, \(|{\mathcal {M}}_{n}([123123])|=C_{n}C_{n+2}-C_{n+1}^{2}\). In this section, we will work out explicit formulas to enumerate \({\mathcal {M}}([112323])\) and \({\mathcal {M}}([123132])\).
Proposition 4.1
The generating function of matchings avoiding the unlabeled pattern [112323] is given by
As a consequence, its coefficients have the following closed form:
for \(n\ge 2\).
Proof
Clearly, the noncrossing matchings in \({\mathcal {M}}_{n}([112323])\) are counted by the Catalan number \(C_{n}\); hence, it remains to count the crossing matchings in \({\mathcal {M}}_{n}([112323])\). Let \(\lambda \) be a crossing matching in \({\mathcal {M}}_{n}([112323])\). Let \(\sigma \) denote the pattern of \(\lambda \) consisting of all the edges intersecting the leftmost edge of \(\lambda \) and let \(\tau \) denote the pattern of \(\lambda \) consisting of all the remaining edges. Note that \(\sigma \) is nonempty; otherwise, since \(\lambda \) is assumed to be crossing, there would be a pair of crossing edges that do not cross the leftmost edge of \(\lambda \), thus forming an occurrence of [112323]. Observe that \(\sigma \) has to be permutational, because an occurrence of 1122 in \(\sigma \) should have at least one edge which does not cross the leftmost edge of \(\lambda \), against the definition of \(\sigma \). Moreover, since \(\sigma \) avoids [112323], the corresponding permutation has to avoid both the permutation patterns 231 and 312. Furthermore, \(\tau \) must be noncrossing; otherwise, any pair of crossing edges of \(\tau \) together with the leftmost edge of \(\lambda \) would form an occurrence of [112323]. Finally, using a similar argument, we deduce that each edge of \(\tau \) has to cross all the edges of \(\sigma \). We can thus conclude that \(\tau \) is the juxtaposition of two totally crossing matchings, such that the leftmost one is nonempty. In other words, \(\lambda \) has the form illustrated by the following linear chord diagram:

If we denote by \({\mathcal {A}}\) the class of crossing matchings in \({\mathcal {M}}_{n}([112323])\), by \({\mathcal {B}}\) the class of permutations avoiding the patterns 231 and 312 and by \({\mathcal {C}}\) the class of totally crossing matchings, the previous characterization of matchings in \({\mathcal {A}}\) amounts to a bijection between \({\mathcal {A}}\) and \( ({\mathcal {B}}\times \{\})\times {\mathcal {C}}\times ( {\mathcal {C}}\times \{\})\), which immediately translates into the functional equation
for the generating functions \({\mathcal {A}}(z), {\mathcal {B}}(z)\) and \({\mathcal {C}}(z)\) of \({\mathcal {A}}, {\mathcal {B}}\) and \({\mathcal {C}}\), respectively. Now, it is well known that \({\mathcal {B}}(z)=\frac{1-z}{1-2z}\) and \({\mathcal {C}}(z)=\frac{1}{1-z}\), and therefore
which is the generating function of sequence \(\mathrm {A000295}\) in [29], whose \(n^{th}\) term is called the \(n^{th}\) Eulerian number and can be written as \(2^{n}-n-1\), as desired.
\(\square \)
The sequence enumerating \({\mathcal {M}}([112323])\) begins \(1,1,1,3,9,25,68,189,\ldots \) and it has been recently added to [29] as sequence A338726.
Our last result concerns the unlabeled pattern [123132], which is represented by the following unlabeled chord diagram:

It turns out that matchings avoiding [123132] have a ternary tree structure and the following discussion is in fact devoted to describe a bijection between this class of matchings and ternary trees. To this purpose, recall that, for \(k\in {\mathbb {N}}^{*}\), a \(k-ary \) \(tree \) is an ordered rooted tree, such that every node has at most k children, each of which is labeled as the i-th child, for some i between 1 and k (and no two children having the same label). Notice that, according to such a definition, a node can have its i-th child without having its j-th child, for some \(j<i\). In the pictorial description of a k-ary tree, the children of a node are depicted in increasing order of their labels from left to right. Let \({\mathcal {T}}_{k}\) denote the combinatorial class of \(k-\)ary trees. Note that every \(k-\)ary tree is either empty or it can be decomposed as in the following figure:

where \(\bullet \) is the root and \(T_{1},\ldots ,T_{k}\in {\mathcal {T}}_{k}\). Therefore, the combinatorial classes \({\mathcal {T}}_{k}\) and \(\{\emptyset \}+\{\bullet \}\times ({\mathcal {T}}_{k})^{k}\) are isomorphic and the isomorphism translates into the functional equation \({\mathcal {T}}_{k}(z)=1+z{\mathcal {T}}_{k}(z)^{k}\) for the generating function \({\mathcal {T}}_{k}(z)\) of the class \({\mathcal {T}}_{k}\). This equation can be classically solved by Lagrange’s inversion as follows:
In particular, when \(k=3\), we thus get
for every \(n\in {\mathbb {N}}^{*}\). This is sequence A001764 in [29].
Now, we recursively define a map \(\varphi :\{\emptyset \}+\{\bullet \}\times ({\mathcal {T}}_{3})^{3}\longrightarrow {\mathcal {M}}([123132])\) as follows. Set \(\varphi (\emptyset )=\emptyset \); furthermore, for every \((T_{1},T_{2},T_{3})\in ({\mathcal {T}}_{3})^{3}\), let \(\varphi (\bullet ,T_{1},T_{2},T_{3})\) be the matching whose linear chord diagram \(\Gamma \) is constructed as follows:
-
1.
Denote by \(\Gamma ^{(i)}\) the linear chord diagram of \(\varphi (T_{i})\), for every \(i\in \{1,2,3\}\).
-
2.
If \(\Gamma ^{(1)}\) is empty, then:
-
1.
draw a vertex \(\ell '\) to the left of a vertex \(r'\) and connect them with an edge;
-
2.
draw \(\Gamma ^{(2)}\) between \(\ell '\) and \(r'\) and \(\Gamma ^{(3)}\) to the right of \(r'\).
-
1.
-
3.
If \(\Gamma ^{(1)}\) is nonempty, then:
-
1.
let \(\ell \) and r denote the left and right vertex of the leftmost edge of \(\Gamma ^{(1)}\), respectively; draw two vertices \(\ell '\) and \(r'\) to the left of \(\ell \) and r, respectively, and connect them with an edge.
-
2.
draw \(\Gamma _{2}\) between \(\ell '\) and \(\ell \) and \(\Gamma _{3}\) between \(r'\) and r.
-
1.
In other words, the map \(\varphi \) can be represented by the following diagram:

Conversely, define recursively a map \(\psi :{\mathcal {M}}([123132])\longrightarrow {\mathcal {T}}_{3}\) as follows. Set \(\psi (\emptyset )=\emptyset \). For every \(\lambda \in {\mathcal {M}}([123132])\setminus \{\emptyset \}\), let \(\psi (\lambda )\) be the ternary tree defined as follows:
-
1.
Suppose that the leftmost edge of \(\lambda \) does not cross any other edge. In this case, denote by \(\lambda _{2}\) the pattern of \(\lambda \) consisting of all the edges of \(\lambda \) which are nested below the leftmost edge of \(\lambda \) and denote by \(\lambda _{3}\) the pattern of \(\lambda \) consisting of all the remaining edges of \(\lambda \) other than the leftmost edge. We then define \(\psi (\lambda )=(\bullet ,\emptyset ,\psi (\lambda _{2}),\psi (\lambda _{3}))\).
-
2.
Suppose that the leftmost edge \(\ell \) of \(\lambda \) crosses some other edge of \(\lambda \) and let \(\ell '\) denote the leftmost edge of \(\lambda \) among those crossed by \(\ell \). Let \(\lambda _{2}\) denote the pattern of \(\lambda \) consisting of all \(e\in \lambda \) such that \(\min (\ell )<\min (e)<\max (e)<\min (\ell ')\) and let \(\lambda _{3}\) denote the pattern of \(\lambda \) consisting of all \(e\in \lambda \) such that \(\max (\ell )<\min (e)<\max (e)<\max (\ell ')\). Finally, let \(\lambda _{1}\) denote the pattern of \(\lambda \) consisting of all the remaining edges of \(\lambda \) other than \(\ell \). We then define \(\psi (\lambda )=(\bullet ,\psi (\lambda _{1}),\psi (\lambda _{2}),\psi (\lambda _{3}))\).
Proposition 4.2
The maps \(\varphi \) and \(\psi \) are well-defined mutually inverse bijections. In particular
for every \(n\in {\mathbb {N}}\).
Proof
The main thing we have to prove is that \(\varphi \) is well defined. Denote by \(\Lambda \) the unlabeled chord diagram of [123132]. Given \(T=(\bullet ,T_{1},T_{2},T_{3})\in \{\bullet \}\times ({\mathcal {T}}_{3})^{3}\), we now prove (by induction hypothesis on the number of nodes of T) that \(\varphi (T)\in {\mathcal {M}}([123132])\). Using the same notation as in the definition of \(\varphi \), we first observe that (by induction hypothesis) there is no occurrence of \(\Lambda \) in \(\Gamma ^{(1)}\). Furthermore, the edge \(\{\ell ',r'\}\) cannot be involved in any occurrence of \(\Lambda \). Suppose in fact that \(\Lambda _{0}\) is an occurrence of \(\Lambda \) involving \(\{\ell ',r'\}\). If \(\Gamma ^{(1)}\) is nonempty, then it is not difficult to realize that the leftmost edge \(\{\ell ,r\}\) of \(\Gamma ^{(1)}\) cannot occur in \(\Lambda _{0}\) (this is due to the choice of the specific pattern \(\Lambda \)). Thus, we can replace \(\{\ell ',r'\}\) with \(\{\ell ,r\}\) in \(\Lambda _{0}\) to get an occurrence of \(\Lambda \) in \(\Gamma ^{(1)}\), which is a contradiction. On the other hand, if \(\Gamma ^{(1)}\) is empty, it is easy to check that \(\{\ell ',r'\}\) cannot belong to any occurrence of \(\Lambda \) in \(\varphi (T)\). Finally, no edge in \(\Gamma ^{(2)}\) or \(\Gamma ^{(3)}\) can be involved in an occurrence of \(\Lambda \), because both \(\varphi (T_{2})\) and \(\varphi (T_{3})\) avoid [123132] (by induction) and each of the edges of their chord diagrams does not cross any of the remaining edges of \(\varphi (T)\). To conclude, it suffices to prove that \(\varphi \) and \(\psi \) are mutually inverse, which is immediate by their construction. An instance of the bijections \(\varphi \) and \(\psi \) is shown in Fig. 4. \(\square \)
5 A Glimpse into the Structure of the Matching Pattern Poset
As we have already observed in the Introduction, the poset structure of the set of all matchings of finite order associated with the notion of pattern appears to be rather complicated. This is witnessed, for example, by the fact that the subposet of permutational matchings is isomorphic to the permutation pattern poset, whose structure is still far from being completely understood. Here, we aim at laying the groundwork for the investigation of the matching pattern poset, with a particular emphasis on aspects such as the combinatorics of intervals and the Möbius function.
5.1 Combinatorics of Intervals: Preliminary Results
From a combinatorial point of view, typical questions on intervals of a poset concern the counting of elements or, more generally, the enumeration of (saturated) chains of a given interval. These are problems that have been classically studied for many combinatorial posets, such as Bruhat orders [31], Tamari lattices [9, 15], and Stanley (or Dyck) lattices [16, 17]. In this section, we just scratch the surface of this vast subject, by proposing a couple of relatively simple results concerning the enumeration of intervals of the form  , when \(\tau \) has a specific form. In particular, in all the cases, we will consider \(\tau \) to be noncrossing.
, when \(\tau \) has a specific form. In particular, in all the cases, we will consider \(\tau \) to be noncrossing.
Before starting, we point out that, when restricted to noncrossing matchings, the notion of pattern on matchings essentially reduces to that of non-contiguous pattern on plane trees, introduced in the case of binary (and m-ary) trees in [12, 19]. In fact, both noncrossing matchings and plane trees belong to the so-called “Catalan family” (of combinatorial objects counted by Catalan numbers), and it turns out that the classical bijection between noncrossing matchings and plane trees is more precisely an order isomorphism between the associated pattern posets. The relevance of the notion of pattern (or related ones) for trees can also be inferred by several articles exploiting it to address a wide range of problems (see for instance [25] for application to generalization of the secretary problem, [20] where the asymptotic of pattern occurrence is studied, and [2] for an application to database theory).
Given a matching \(\tau \), we say that an edge of \(\tau \) is small whenever its vertices are consecutive integers. If \(\tau (n,k)\) is a noncrossing matching of size n having k small edges, what is the cardinality of the interval  ? This may be a difficult problem in general. Here, we address only a few very simple cases.
? This may be a difficult problem in general. Here, we address only a few very simple cases.
First of all, it is immediate to see that
-
 , for all \(\tau (n,0)\) (since there are no noncrossing matchings having no small edges);
, for all \(\tau (n,0)\) (since there are no noncrossing matchings having no small edges); -
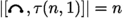 , for all \(\tau (n,1)\) (since, in this case, the interval is a chain having n elements, which are all totally nesting matchings).
, for all \(\tau (n,1)\) (since, in this case, the interval is a chain having n elements, which are all totally nesting matchings).
When \(k=2\), the generic noncrossing matching having two small edges has the following form:

where an edge labeled x stands for a totally nesting matching having x edges. In words, the above matching is the juxtaposition of two totally nesting matchings having r and s edges, respectively, enclosed in a totally nesting matching having k edges. To have easy inline notations, such a matching will be denoted \({\mathbf {k}}({\mathbf {r}};{\mathbf {s}})\). Assuming w.l.o.g. that \(r\ge s\), it is easy to see that  contains \(r+k\) matchings having 1 small edge and \(rs(k+1)\) matchings having two small edges. Therefore,
contains \(r+k\) matchings having 1 small edge and \(rs(k+1)\) matchings having two small edges. Therefore,  .
.
When \(k=3\), again w.l.o.g., the generic matching \(\tau (n,3)\) has the form

Similarly as before, we denote the above matching with \({\mathbf {k}}({\mathbf {h}}({\mathbf {a}};{\mathbf {b}});{\mathbf {c}})\). We can count the elements of  with respect to the number of small edges.
with respect to the number of small edges.
-
In order to count the number \(\chi _1\) of matchings having one small edge, we have to understand how many edges the largest totally nesting matching smaller than \({\mathbf {k}}({\mathbf {h}}({\mathbf {a}};{\mathbf {b}});{\mathbf {c}})\) has. To construct such a matching, we take the k external edges, and add the largest number between c and \(h+\max (a,b)\). Therefore \(\chi _1 =\max (k+h+a,k+h+b,k+c)\).
-
Matchings having two small edges can be obtained in two different ways from \({\mathbf {k}}({\mathbf {h}}({\mathbf {a}};{\mathbf {b}});{\mathbf {c}})\). First, we can remove the totally nesting matching having c edges, thus obtaining the matching \((\mathbf {h+k})({\mathbf {a}};{\mathbf {b}})\), which has \(ab(h+k+1)\) matchings with 2 small edges below. The second option is to remove one of the two totally nesting matchings with a and b edges, and precisely the smaller one, thus obtaining the matching \({\mathbf {k}}((\mathbf {\max (a,b)+h});{\mathbf {c}})\), which has \((\max (a,b)+h)c(k+1)\) matchings with 2 small edges below. However, there are matchings in common in the two above cases, which causes an overcount. Indeed, the matchings which can be obtained in both the above cases are precisely those lying below \({\mathbf {k}}({\mathbf {a}};\mathbf {\min (b,c)})\) and having 2 small edges, which are \(a\cdot \min (b,c)\cdot (k+1)\). From the above consideration, we can write the total number \(\chi _2\) of elements of the interval
 having 2 small edges, which is \(\chi _2 =ab(h+k+1)+(\max (a,b)+h)c(k+1)-a\cdot \min (b,c)\cdot (k+1)\).
having 2 small edges, which is \(\chi _2 =ab(h+k+1)+(\max (a,b)+h)c(k+1)-a\cdot \min (b,c)\cdot (k+1)\). -
Finally, the total number \(\chi _3\) of matchings in
 having 3 small edges is immediate to compute, and we get \(\chi _3 =abc(h+1)(k+1)\).
having 3 small edges is immediate to compute, and we get \(\chi _3 =abc(h+1)(k+1)\).
Summing up the above contributions, we then find the desired closed expression for  .
.
Our last example concerns a class of noncrossing matchings defined in a recursive fashion. Before introducing them, we state an easy, but useful, lemma whose proof is left to the reader.
Lemma 5.1
Let \(\sigma \) and \(\tau \) be any matchings. Then the following are equivalent:
-
(i)
\(\sigma \le \tau \);
-
(ii)

-
(iii)

Set \(\tau _0 =\emptyset \). For every \(n>0\), define
-
 , and
, and -
 .
.
Denote by \(f_{n}\) the cardinality of the interval  and by \(f_{n,k}\) the number of elements having k edges of the same interval, for \(k>0\). In particular, it is clear that \(f_{n,k}=0\) for \(n<k\) and whenever \(n\le 0\) or \(k\le 0\) (actually, when \(n=k=0\), we set \(f_{n,k}=0\) by convention). In the next proposition, we give closed formulas for such quantities.
and by \(f_{n,k}\) the number of elements having k edges of the same interval, for \(k>0\). In particular, it is clear that \(f_{n,k}=0\) for \(n<k\) and whenever \(n\le 0\) or \(k\le 0\) (actually, when \(n=k=0\), we set \(f_{n,k}=0\) by convention). In the next proposition, we give closed formulas for such quantities.
Proposition 5.1
Let \(n>0\) and \(0<k\le n\), and denote by \(\varphi _n\) the n-th Fibonacci number (with \(\varphi _0 =0\) and \(\varphi _1 =1\)). Then
-
(i)
\(f_{n,k}=\sum _{i=0}^{n-1}\left( {\begin{array}{c}k-1\\ i-k-1\end{array}}\right) \);
-
(ii)
\(f_n =\varphi _{n+2}-1\).
Proof
We use the following notations: \(A_{n,k}\) is the set of all matchings in  having k edges, \(B_{n,k}\) is the set of all matchings in
having k edges, \(B_{n,k}\) is the set of all matchings in  having k edges, and \(C_{n,k}\) is the set of all matchings of the form
having k edges, and \(C_{n,k}\) is the set of all matchings of the form  , with \(\sigma \in B_{n,k-1}\). We then have that \(f_{2n,k}=|A_{n,k}|=|B_{n,k}|+|C_{n,k}|-|B_{n,k}\cap C_{n,k}|\). By definition, we have \(|B_{n,k}|=f_{2n-1,k}\), and clearly, \(|C_{n,k}|=f_{2n-1,k-1}\). Furthermore, as a consequence of Lemma 5.1 and of the specific shape of the matchings under consideration, the set \(B_{n,k}\cap C_{n,k}\) is precisely the set of matchings of the form
, with \(\sigma \in B_{n,k-1}\). We then have that \(f_{2n,k}=|A_{n,k}|=|B_{n,k}|+|C_{n,k}|-|B_{n,k}\cap C_{n,k}|\). By definition, we have \(|B_{n,k}|=f_{2n-1,k}\), and clearly, \(|C_{n,k}|=f_{2n-1,k-1}\). Furthermore, as a consequence of Lemma 5.1 and of the specific shape of the matchings under consideration, the set \(B_{n,k}\cap C_{n,k}\) is precisely the set of matchings of the form  , with \(\sigma \in B_{n-1,k-1}\); hence, \(|B_{n,k}\cap C_{n,k}|=f_{2n-3,k-1}\). We thus get the recurrence relation \(f_{2n,k}=f_{2n-1,k}+f_{2n-1,k-1}-f_{2n-3,k-1}\). Using a completely similar argument, we can also prove the analogous recurrence \(f_{2n-1,k}=f_{2n-2,k}+f_{2n-2,k-1}-f_{2n-4,k-1}\). Summing up, we thus have the following recurrence relation, which holds for all \(n,k\ge 2\):
, with \(\sigma \in B_{n-1,k-1}\); hence, \(|B_{n,k}\cap C_{n,k}|=f_{2n-3,k-1}\). We thus get the recurrence relation \(f_{2n,k}=f_{2n-1,k}+f_{2n-1,k-1}-f_{2n-3,k-1}\). Using a completely similar argument, we can also prove the analogous recurrence \(f_{2n-1,k}=f_{2n-2,k}+f_{2n-2,k-1}-f_{2n-4,k-1}\). Summing up, we thus have the following recurrence relation, which holds for all \(n,k\ge 2\):
Together with the starting condition \(f_{1,1}=1\), formula (5) allows us to compute the generating function \(F(x,y)=\sum _{n,k\ge 0}f_{n,k}x^n y^k\). Indeed, using standard arguments, our recurrence translates into the functional equation
which gives
It turns out that \(F(x,y)=xyG(x,y)\), where G(x, y) is the generating function given in [29] for the number triangle A004070: from there, we deduce the desired closed form given in (i) for \(f_{n,k}\). Moreover, denoting with \(\Phi (x)=\sum _{n\ge 0}\varphi _n x^n\) the generating function of Fibonacci numbers, it is easy to see that
which proves (ii). \(\square \)
5.2 The Möbius Function: Preliminary Results
In the present section, we deal with the Möbius function of the matching pattern poset \({\mathcal {M}}\). For this reason, the symbol \(\mu \) here is reserved for the Möbius function (and so matchings will be denoted with different symbols).
For our purposes, we can define the Möbius function \(\mu :{\mathcal {P}}^2 \rightarrow {\mathbb {Z}}\) of a locally finite poset \({\mathcal {P}}\) in the following recursive way (for \(x\le y\)):
We now wish to exploit a powerful result that relates the Möbius functions of two posets, when one is the image of the other under a closure operator. To this aim, we first need some preliminary notations and results, and then, we need to define some “interesting” closure operators on \({\mathcal {M}}\).
A closure operator on a poset \({\mathcal {P}}\) [26] is a map \(c:{\mathcal {P}}\rightarrow {\mathcal {P}}\) such that, for all \(x,y\in {\mathcal {P}}\):
-
\(x\le c(x)\);
-
if \(x\le y\), then \(c(x)\le c(y)\);
-
\(c(c(x))=c(x)\).
An element \(x\in {\mathcal {P}}\) is said to be closed when \(c(x)=x\). Denote by \({\mathcal {P}}_c\) the set of closed elements of \({\mathcal {P}}\) (with respect to the closure operator c).
The proof of the following lemma is easy, and so, it is left to the reader.
Lemma 5.2
Let \({\mathcal {P}}\) be a poset with minimum 0 and let c be a closure operator on \({\mathcal {P}}\). Then, the map \(c'\) defined by setting \(c'(x)=c(x)\) for all \(x\ne 0\), and \(c'(0)=0\), is a closure operator.
The following important result (stated in a slightly different form) is due to Gian-Carlo Rota [26, Proposition 2 of Section 5].
Theorem 5.1
Let \(\mu \) be the Möbius function of a poset \({\mathcal {P}}\) and let c be a closure operator on \({\mathcal {P}}\). Moreover, denote by \(\mu _c\) the Möbius function of the subposet of closed elements of \({\mathcal {P}}\). For any \(x,y\in {\mathcal {P}}\), we have
Let \(\sigma \) be a connected matching. Given \(\alpha \in {\mathcal {M}}\), we express it as \(\alpha =M\rho \), where \(\rho \) is the longest suffix of connected components of \(\alpha \) such that \(\rho \le \sigma \). Notice that both \(\rho \) and M can be empty. This will be called the \(\sigma \)-decomposition of \(\alpha \). In the rest of this section, every matching will be tacitly assumed to be expressed by means of its \(\sigma \)-decomposition, for some given connected matching \(\sigma \).
Define the map \(k_\sigma :{\mathcal {M}}\rightarrow {\mathcal {M}}\) by setting \(k_\sigma (\alpha )=k_\sigma (M\rho )=M\sigma \). The following lemma is immediate.
Lemma 5.3
For a given matching \(\alpha = M \rho \), we have \(k_\sigma (\alpha )=M k_\sigma (\rho )\).
Proposition 5.2
The map \(k_\sigma \) is a closure operator on \({\mathcal {M}}\), for any connected matching \(\sigma \).
Proof
It is easy to see that, for any matching \(\alpha \), we have \(\alpha \le k_\sigma (\alpha )\) and \(k_\sigma (k_\sigma (\alpha ))=k_\sigma (\alpha )\).
Now, suppose that \(\alpha \le \beta \), and let \(\alpha = M \rho \), \(\beta = N \tau \) be the \(\sigma \)-decompositions of \(\alpha \) and \(\beta \), respectively. We start by observing that necessarily \(M\le N\). To prove this, consider the rightmost occurrence of \(\alpha \) into \(\beta \). If the rightmost connected component of M of such an occurrence were contained in \(\tau \), then \(\rho \) would not be the longest suffix of \(\alpha \) contained in \(\sigma \) (since \(\tau \le \sigma \)), which is a contradiction. Then, necessarily, the rightmost connected component of M is contained in N, which means that there exists an occurrence of M into N, that is \(M\le N\). Thanks to this fact, we then get
as desired. \(\square \)
Corollary 5.1
The map \(c_\sigma \) defined by setting  and, for any
and, for any  , \(c_\sigma (\alpha )=k_\sigma (\alpha )\) is a closure operator.
, \(c_\sigma (\alpha )=k_\sigma (\alpha )\) is a closure operator.
Proof
This is an immediate consequence of Lemma 5.2 and Proposition 5.2.
\(\square \)
Some special cases of the above corollary are particularly relevant.
-
1.
The closure operator
 maps a matching \(\alpha \) to the matching
maps a matching \(\alpha \) to the matching  , unless the rightmost connected component of \(\alpha \) is a single edge, in which case \(\alpha \) is left unchanged.
, unless the rightmost connected component of \(\alpha \) is a single edge, in which case \(\alpha \) is left unchanged. -
2.
Generalizing the previous example, for any \(k>0\), denote by \({\mathbf {k}}\) the totally nesting matching having k edges (observe that, with this notation,
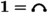 ). The closure operator \(c_{{\mathbf {k}}}\) maps a matching
). The closure operator \(c_{{\mathbf {k}}}\) maps a matching  to the matching \(\alpha {\mathbf {k}}\), unless the rightmost connected component of \(\alpha \) is \({\mathbf {h}}\), with \(0<h\le k\); in such a case, \(\alpha \) is mapped into the matching obtained by completing the rightmost connected component to \({\mathbf {k}}\).
to the matching \(\alpha {\mathbf {k}}\), unless the rightmost connected component of \(\alpha \) is \({\mathbf {h}}\), with \(0<h\le k\); in such a case, \(\alpha \) is mapped into the matching obtained by completing the rightmost connected component to \({\mathbf {k}}\).
The following corollary states some useful consequences of Corollary 5.1 in connection with Theorem 5.1.
Corollary 5.2
-
1.
If \(\alpha \) is a nonempty matching whose rightmost connected component is not a single edge, then
 ; moreover, for any matching \(\alpha \),
; moreover, for any matching \(\alpha \),  .
. -
2.
Let \(k\ge 2\). If \(\alpha \) is a nonempty matching whose rightmost connected component is different from \({\mathbf {h}}\), for all \(h\le k\), then
 .
. -
3.
If \(\alpha \) is a nonempty matching of order n, such that (1, 2n) is not an edge of \(\alpha \) (that is, \(\alpha \) is not lifted), then
 ; moreover, for any matching \(\alpha \),
; moreover, for any matching \(\alpha \),  .
.
Proof
-
1.
Suppose that the rightmost connected component of the matching \(\alpha \) is not a single edge and consider the closure operator
 . The set of matchings whose closure is equal to \(c_{{\mathbf {1}}}(\alpha )\) is
. The set of matchings whose closure is equal to \(c_{{\mathbf {1}}}(\alpha )\) is  . Using Theorem 5.1 (and recalling that
. Using Theorem 5.1 (and recalling that  is closed), we thus get
is closed), we thus get 
Now, observe that closed elements (with respect to \(c_{{\mathbf {1}}}\)) are precisely those matchings whose rightmost connected component is a single edge. Therefore, in the subposet \(P_{c_{{\mathbf {1}}}}\), the interval
 has a single atom (which is
has a single atom (which is  ), and so its Möbius function is 0. Using a similar argument, since the only matching whose closure is equal to
), and so its Möbius function is 0. Using a similar argument, since the only matching whose closure is equal to  is
is  itself, again Theorem 5.1 says that
itself, again Theorem 5.1 says that 
and the right-hand side is equal to 0 for the same reason as above.
-
2.
We proceed by induction on k. First, suppose that \(k=2\), and consider the closure operator \(c_{{\mathbf {2}}}\). Using Theorem 5.1 and the hypothesis on \(\alpha \) (that is, \(\alpha \)’s rightmost component is different from \({\mathbf {1}}\) and \({\mathbf {2}}\)), we get that

Similarly as before, we observe that the closed elements (with respect to \(c_{{\mathbf {2}}}\)) are those matchings whose rightmost connected component is \({\mathbf {2}}\); hence, the interval
 has exactly one atom (which is \({\mathbf {2}}\)); hence,
has exactly one atom (which is \({\mathbf {2}}\)); hence,  . Together with the result in the previous item, we thus have that
. Together with the result in the previous item, we thus have that  . Now, fix \(h\le k\) and suppose that
. Now, fix \(h\le k\) and suppose that  , for all \(t<h\), \(t\ge 2\). This time, we exploit the closure operator \(c_{{\mathbf {h}}}\), which allows us to apply Theorem 5.1 to get
, for all \(t<h\), \(t\ge 2\). This time, we exploit the closure operator \(c_{{\mathbf {h}}}\), which allows us to apply Theorem 5.1 to get 
Again, the summands in the left-hand side depend on the fact that \(\alpha \)’s rightmost connected component is not \({\mathbf {h}}\), and the usual argument shows that the right-hand side is 0. Moreover, for every \(2\le t<h\), we have
 (by inductive hypothesis, using the assumptions on the rightmost connected component of \(\alpha \)). Summing up, and using again the result of item 1, we thus get that
(by inductive hypothesis, using the assumptions on the rightmost connected component of \(\alpha \)). Summing up, and using again the result of item 1, we thus get that 
-
3.
This is not a direct consequence of Corollary 5.1; however, we use a closure operator whose definition is somewhat analogous to that of \(c_{{\mathbf {1}}}\). Consider the map \(c^{{\mathbf {1}}}\) defined by setting
 if \(\alpha \) is a matching of order n having at least two edges, such that (1, 2n) is not an edge; otherwise, \(c^{{\mathbf {1}}}(\alpha )=\alpha \). It is possible to prove that \(c^{{\mathbf {1}}}\) is a closure operator (and we leave this to the reader). Applying Theorem 5.1 in a way similar to what we did for \(c_{{\mathbf {1}}}\) then gives the desired result.
if \(\alpha \) is a matching of order n having at least two edges, such that (1, 2n) is not an edge; otherwise, \(c^{{\mathbf {1}}}(\alpha )=\alpha \). It is possible to prove that \(c^{{\mathbf {1}}}\) is a closure operator (and we leave this to the reader). Applying Theorem 5.1 in a way similar to what we did for \(c_{{\mathbf {1}}}\) then gives the desired result.
\(\square \)
The above results allow us to efficiently compute the Möbius functions in several cases, especially in the induced subposet of noncrossing matchings. Consider, for instance, the interval

Using Theorem 5.1 with the closure operator \(c=c_\sigma \), where  , we get
, we get

The interval I in the subposet of closed elements has a unique atom (which is \(\sigma \)); hence, the right-hand side is equal to 0. Moreover, thanks to Corollary 5.2, and the second and the third summand of the left-hand side are equal to 0, whereas the fourth and the fifth are opposite. As a consequence, we have that

Another interesting example concerns the matchings \(\tau _n\) introduced in the previous section. An immediate application of our results (whose details we omit) gives that \(\mu (\tau _n )=(-1)^{n-1}\), for all \(n\ge 1\).
6 Conclusion and Further Work
The enumerative combinatorics of the matching pattern poset remains still largely unknown. Although some major efforts to enumerate pattern avoiding matchings have already been spent, as mentioned in Sect. 2, the enumeration of most classes of matchings avoiding a single pattern of order three is still lacking. To this regard, in the present paper, we have introduced the notion of unlabeled pattern, and we have enumerated matchings avoiding the unlabeled patterns [123123], [112323], and [123132], respectively. However, we did not succeed in finding a formula for the number of matchings avoiding the remaining two unlabeled patterns of order three, namely [123321] and [112233], although matchings in the former class seem to have a rather neat combinatorial structure.
In Sect. 5, we have started the investigation of the combinatorial structure of intervals in the matching pattern poset, with special emphasis on enumerative issues. However, all important general questions concerning this topic are completely unanswered yet. How many elements does a generic interval contain? How many (saturated) chains of fixed length? What is the Möbius function of a generic interval? In which cases does an interval have a (possibly distributive) lattice structure? Notice that the subposet of noncrossing matchings is isomorphic to the pattern order on 231-avoiding permutations (this is rather easy to show, see also [1, 13]). This can be useful, for instance, in the computation of the Möbius function, since the results developed in [7] can be applied. However, it is possible (and maybe likely) that the specific combinatorial structure of matchings may help in finding neater formulas.
Data Availibility
Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.
References
M. Albert, M. Bouvel.A general theory of Wilf-equivalence for Catalan structures, Electron. J. Combin., 22 (2015) P4.45.
S. Amer-Yahia, S. Cho, L. V. S. Lakshmanan, D. Srivastava.Tree pattern query minimization, The VLDB Journal, 11 (2002) 315–331.
D. Battaglino, M. Bouvel, A. Frosini, S. Rinaldi.Permutation classes and polyomino classes with excluded submatrices, Math. Structures Comput. Sci., 27 (2017) 157–183.
A. Bacher, A. Bernini, L. Ferrari, B. Gunby, R. Pinzani, and J. West.The Dyck pattern poset, Discrete Math., 321 (2014) 12–23.
A. Bernini, L. Ferrari, M. Cervetti, E. Steingrímsson. Enumerative combinatorics of intervals in the Dyck pattern poset, Order, 38 (2021) 473–487.
J. Bloom, S. Elizalde.Pattern avoidance in matchings and partitions, Electron. J. Combin., 20 (2013) P5.
A. Burstein, V. Jelínek, E. Jelínková, E. Steingrímsson.The Möbius function of separable and decomposable permutations, J. Combin. Theory Ser. A, 118 (2011) 2346–2364.
A. Burstein, T. Mansour.Counting occurrences of some subword patterns, Discrete Math. Theoret. Comput. Sci., 6 (2003) 1–12.
F. Chapoton, G. Châtel, V. Pons.Two bijections on Tamari intervals, Discrete Math. Theoret. Comput. Sci. Proc., AT (2014) 241–252.
W. Y. C. Chen, E. Y. P. Deng, R. R. X. Du, R. P. Stanley, C. H. F. Yan. Crossings and nestings of matchings and partitions, Trans. Amer. Math. Soc., 359 (2007) 1555–1575.
L. Cioni, L. Ferrari.Enumerative results on the Schröder pattern poset, In Cellular Automata and Discrete Complex Systems, AUTOMATA 2017, Lecture Notes in Comput. Sci., vol 10248, pp. 56–67, 2017.
M. Dairyko, L. Pudwell, S. Tyner, C. Wynn.Non-contiguous pattern avoidance in binary trees, Electron. J. Combin., 19 (2012) P22.
F. Disanto, L. Ferrari, R. Pinzani, S. Rinaldi.Catalan pairs: a relational-theoretic approach to Catalan numbers, Adv. in Appl. Math., 45 (2010) 505–517.
V. Dotsenko.Pattern avoidance in labelled trees, Sem. Lothar. Combin., 67 (2012) B67b.
W. Fang.Planar triangulations, bridgeless planar maps and Tamari intervals, European J. Combin., 70 (2018) 75–91.
L. Ferrari, E. Munarini.Enumeration of edges in some lattices of paths, J. Integer Seq., 17 (2013) 14.1.5.
L. Ferrari, E. Munarini.Enumeration of chains and saturated chains in Dyck lattices, Adv. in Appl. Math., 62 (2015) 118–140.
P. Flajolet, R. Sedgewick.Analytic Combinatorics. Cambridge University Press, Cambridge (2009).
N. Gabriel, K. Peske, L. Pudwell, S. Tay.Pattern avoidance in ternary trees, J. Integer Seq., 15 (2012) 12.1.5.
B. Gittenberger, Z. Gołebiewski, I. Larcher, M. Sulkowska.Counting embeddings of rooted trees into families of rooted trees, at arXiv:2008.08312.
D. Gouyou–Beauchamps. Standard Young tableaux of height 4 and 5, European J. Combin. 10 (1989) 69 – 82.
V. Jelínek. Dyck paths and pattern–avoiding matchings, European J. Combin. 28 (2007) 202–213.
V. Jelínek, T. Mansour.Matchings and partial patterns, Electron. J. Combin., 20 (2010) R158.
D. E. Knuth.The Art of Computer Programming, Volume 1, Boston, Addison-Wesley, 1968.
G. Kubicki, J. Lehel, M. Morayne.An asymptotic ratio in the complete binary tree, Order, 20 (2003) 91–97.
G.-C. Rota.On the foundations of combinatorial theory I. Theory of Möbius Functions, Z. Wahrscheinlichkeitstheorie verw Gebiete 2 (1964) 340–368.
E. S. Rowland.Pattern avoidance in binary trees, J. Combin. Theory Ser. A, 117 (2010) 741–758.
B. E. Sagan.Pattern avoidance in set partitions, Ars. Combin., 94 (2010) 79–96.
N. J. A. Sloane. The On-line Encyclopedia of Integer Sequences, at oeis.org.
J. P. Smith.On the Möbius function and topology of general pattern posets, Electron. J. Combin., 26 (2019) P1.49.
B. E. Tenner.Intervals and factors in the Bruhat order, Discrete Math. Theoret. Comput. Sci., 17 (2015) 383–396.
Acknowledgements
The authors would like to express their gratitude to two anonymous referees for many suggestions which have improved the presentation of the paper.
Funding
Open access funding provided by Universitá degli Studi di Firenze within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors state that there is no conflict of interest.
Additional information
Communicated by Mathilde Bouvel.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Luca Ferrari is member of the INdAM research group GNCS; partially supported by the 2020 INdAM-GNCS project “Combinatoria delle permutazioni, delle parole e dei grafi: algoritmi e applicazioni”.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cervetti, M., Ferrari, L. Enumeration of Some Classes of Pattern Avoiding Matchings, with a Glimpse into the Matching Pattern Poset. Ann. Comb. 26, 971–995 (2022). https://doi.org/10.1007/s00026-022-00596-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00026-022-00596-1









 , for all
, for all 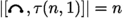 , for all
, for all  having 2 small edges, which is
having 2 small edges, which is  having 3 small edges is immediate to compute, and we get
having 3 small edges is immediate to compute, and we get 

 , and
, and .
. maps a matching
maps a matching  , unless the rightmost connected component of
, unless the rightmost connected component of  ). The closure operator
). The closure operator  to the matching
to the matching  ; moreover, for any matching
; moreover, for any matching  .
. .
. ; moreover, for any matching
; moreover, for any matching  .
. . The set of matchings whose closure is equal to
. The set of matchings whose closure is equal to  . Using Theorem
. Using Theorem  is closed), we thus get
is closed), we thus get 
 has a single atom (which is
has a single atom (which is  ), and so its Möbius function is 0. Using a similar argument, since the only matching whose closure is equal to
), and so its Möbius function is 0. Using a similar argument, since the only matching whose closure is equal to  is
is  itself, again Theorem
itself, again Theorem 

 has exactly one atom (which is
has exactly one atom (which is  . Together with the result in the previous item, we thus have that
. Together with the result in the previous item, we thus have that  . Now, fix
. Now, fix  , for all
, for all 
 (by inductive hypothesis, using the assumptions on the rightmost connected component of
(by inductive hypothesis, using the assumptions on the rightmost connected component of 
 if
if