1 Introduction

Let c be a coloring of the set \({\mathbb {N}}\) of positive integers. A finite non-empty subset of \({\mathbb {N}}\) consisting of consecutive integers is called an interval. For any subset \(A=\{a_1,a_2,\dots ,a_r\}\) (with a natural order), denote by \(c_A=(c(a_1),c(a_2),\dots ,c(a_r))\) the color sequence of the set A. Two intervals A and B of \({\mathbb {N}}\) are adjacent if \(A\cap B =\varnothing \) and \(A\cup B\) is an interval. More generally, we say that intervals \(A_1, A_2,\dots , A_k\) are consecutively adjacent if \(A_i\) is adjacent to \(A_{i+1}\), for every \(1\le i\le k-1\). A coloring c is nonrepetitive if no two adjacent intervals have the same color sequences, that is, \(c_A\ne c_B\) holds for any pair of adjacent intervals A and B.

In 1906, Thue [21] (see [6]) proved that there exists a nonrepetitive coloring of \({\mathbb {N}}\) using only three colors (it is easy to see that two colors are not sufficient). This result inspired a lot of further research. It is in particular the starting point of Combinatorics on Words, a wide discipline with lots of exciting problems, deep results, and important applications (see [1, 2, 4, 7, 13, 16, 17, 22]).

In this paper, we consider some generalizations of the result of Thue in the spirit of list colorings. Suppose that each positive integer n is assigned an arbitrary set L(n) with three different colors. Is it then true that there exists a nonrepetitive coloring c of \({\mathbb {N}}\) such that \(c(n)\in L(n)\) for every \(n\in {\mathbb {N}}\)?

At first glance, the question may seem trivial, as it is natural to expect that the hardest situation is when all sets L(n) are equal. However, this intuition appears to be completely wrong for analogous list coloring problem for graphs. In the paper by Erdős et al. [11], where the idea of list coloring was introduced, there are many examples showing that bad choice of lists may make the coloring of a graph impossible, even if the list sizes are much larger than the actual chromatic number of the graph.

The above question on nonrepetitive list coloring of \({\mathbb {N}}\) remains open, though it is known that 4-element lists are sufficient, as proved by Grytczuk et al.  [15] by the use of the probabilistic method. A different proof, based on the entropy compression argument, was provided by Grytczuk et al. [14]. Recently, a surprisingly simple refinement of this method was found by Rosenfeld [20], which additionally gives a stronger conclusion on the number of colorings. We shall apply here the approach based on the entropy compression to the following more general setting.

For a fixed \(r\ge 1\), let \(G_r\) be a graph whose vertex set \(V(G_r)\) is the collection of all intervals of length r in \({\mathbb {N}}\). We shall always assume that only disjoint intervals can be joined by en edge in \(G_r\). Let \(G=G_1\cup G_2\cup \cdots \) be the union of all graphs \(G_r\). Therefore, the vertex set of G is a family of all finite intervals in \({\mathbb {N}}\), with some pairs of disjoint intervals of the same length joined by an egde. We will call G an interval-constraint graph. For instance, in the case considered by Thue, each graph \(G_r\) consists of r infinite paths corresponding to r different sequences of consecutively adjacent intervals of length r. A coloring c of the set \(\mathbb N\) is called G-nonrepetitive if for a pair of intervals A and B, we have \(c_A\ne c_B\) whenever A and B are adjacent in G.

We will prove that graphs \(G_r\) can be much more dense and still allow for a G-nonrepetitive coloring with bounded list sizes. Indeed, let us define the back degree of a vertex \(A\in V(G)\), denoted by \(\deg (A)\), as the number of vertices adjacent to A in G and occurring earlier than A in the natural order. Let \(\Delta _r\) denote the maximum of all back degrees of the vertices in \(G_r\).

Our main result (Theorem 2) states that if \(\Delta _r \le \alpha ^r\) for some real \(\alpha >1\), then there exists a G-nonrepetitive coloring of \({\mathbb {N}}\) form arbitrary lists of size at least \(4\alpha \). We derive some consequences of this result connected to the famous Dejean’s Conjecture [10], turned finally into a theorem after a long battle with a major breakthrough achieved by Carpi [8] (see [9, 18, 19]). In terms of integer colorings, it states that for every \(k\ge 5\), there is a k-coloring of \({\mathbb {N}}\), such that any two intervals of length \(r\ge 1\) with the same color sequence are separated by at least \(r(k-2)\) integers (see [13]). We deduce in Corollary 2 that a similar statement holds in the list setting for \(r\ge 2\) and \(k\ge 30\). In another result (Theorem 3), we prove that a slight simplification of Dejean’s Conjecture holds asymptotically in the list setting. This result asserts that for every \(k\ge 1\), there is a coloring of \({\mathbb {N}}\) from lists of size \((1+o(1))k\), such that no two among any k consecutively adjacent intervals have the same color sequence.

Inspired by these results, we state two sharp conjectures in the final section of the paper. In the next section, we present the entropy compression method by giving a slightly simplified proof from [14] (see also [3]). Proofs of the stated results are found in Sect. 3. In the final section, we state some open problems.

2 The Entropy Compression Method

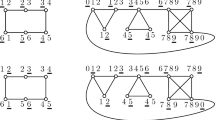
In this section, we give a flagship example of the use of the entropy compression method. Suppose that we want to produce a nonrepetitive coloring of \({\mathbb {N}}\) in a most primitive way, by choosing colors for consecutive integers randomly. Therefore, we have a set of colors, and at every step, we pick a random color for the next uncolored integer. Once we get two consecutive intervals A and B with the same color sequences, the so-called repetition, we erase colors from all elements in the later interval B, and continue from the first uncolored number. For instance, if in the first seven steps, we have got the following coloring:

then we erase all colors form the interval \(\{5,6,7\}\)

and then continue from the number 5. It is not hard to demonstrate that only one repetition may occur at each step of this procedure, which is located at the end of the colored segment.

We record the random coloring process with erasures in two sequences, R and S, defined as follows. The sequence R just records the randomly chosen colors, so R(n) is a color chosen in step n. The sequence S consists of two signs \(\{+,-\}\). We put \(S(n)=+\) whenever we make a step forward by coloring the leftmost uncolored integer, while \(S(n)=-\), when we make a step back by erasing color from the rightmost colored integer. For example, in the above situation, the sequences R and S look as follows:

Let m and M be fixed positive integers, where M is sufficiently large with respect to m. We shall demonstrate that after execution of M steps of the random coloring procedure, we will get a nonrepetitive coloring of the segment \(\{1,2,\dots ,m\}\), provided that the number of colors is at least five. By the compactness principle, this implies the existence of a nonrepetitive 5-coloring of the whole set \({\mathbb {N}}\).

Indeed, after execution of M steps of the procedure, we get a random sequence R of length M, a sequence of signs S of length at most 2M (since the number of minuses in S cannot exceed the number of pluses), and a color sequence C of some initial segment of \({\mathbb {N}}\).

Now, a crucial observation. First, obviously, the random sequence R uniquely determines a sequence of signs S and a final coloring C (one may think that the sequence R was produced before and then successively applied in the course of experiment). However, the other way around, given a resulting pair (S, C), one may uniquely reconstruct the random sequence R. Indeed, if the last symbol of S is plus, then the last color in R coincides with the last color in C. If S ends with a block of r minuses, then the last r colors of R also coincide with the last r colors of C, since the erased part was repeated. It is now not hard to prove the whole statement by induction. Thus, the number of resulting pairs (S, C) must be equal to the number of random sequences R.

Assume now, for the sake of contradiction, that the length of C is strictly smaller than m. Therefore, the number of color sequences C is at most \(5^m\). The number of sign sequences S is at most \(2^{2M}\). Hence, the total number of resulting pairs (S, C) cannot be greater than \(5^m4^M\). On the other hand, this number must be equal to the number of random sequences R, which is clearly equal to \(5^M\). This is not true for sufficiently large M.

Notice that the above argument works also for the list version of nonrepetitive colorings (we just encode a random sequence R by numerating colors in lists L(n)). Also, we may easily go down from 5 to 4 colors in a list, by noticing that the number of sign sequences S is actually asymptotically smaller than \(4^M\). Indeed, in any initial segment of S, the number of minuses cannot exceed the number of pluses. The number of such sequences of length 2M is equal to the Mth Catalan number \(C_M=\frac{1}{M+1}\left( {\begin{array}{c}2M\\ M\end{array}}\right) \), which is of order \(o(4^M)\).

In this way, we proved the following theorem form [15], reproved in [14].

Theorem 1

(Grytczuk et al. [15]). There exists a nonrepetitive coloring of \({\mathbb {N}}\) from lists of size 4.

As we mentioned in the introduction, it is not known if this result is optimal. The following conjecture was stated in [13].

Conjecture 1

There exists a nonrepetitive coloring of \({\mathbb {N}}\) from lists of size 3.

In the next section, we will prove a generalization of Theorem 1 for G-nonrepetitive colorings using the approach described above.

3 The Results

3.1 Decorated Dyck Words

We start with some simple observations concerning certain generalizations of signed sequences used in the entropy compression argument.

Recall that a Dyck word is a binary sequence S on symbols \(\{+,-\}\), such that the number of minuses never exceeds the number of pluses in any prefix of S, and these two numbers are equal in the whole sequence S. It is well known that the number of Dyck words of length 2n is the Catalan number \(C_n=\frac{1}{n+1}\left( {\begin{array}{c}2n\\ n\end{array}}\right) \). This is a consequence of a simple fact that every Dyck word S can be uniquely split into a prefix of k pluses and k shorter (possibly empty) Dyck words \(S_1,S_2,\dots ,S_k\) separated by single minuses

$$\begin{aligned} S=\underbrace{(++\cdots +)}_{k\,\text {signs}}(-)S_1(-)S_2(-)\cdots (-)S_k. \end{aligned}$$
(3.1)

Let F(x) be the generating function for the sequence \(C_n\) of Catalan numbers. It is well known that

$$\begin{aligned} C(x)=\frac{1-\sqrt{1-4x}}{2x}. \end{aligned}$$
(3.2)

This formula can be derived easily from the following equation, which is a direct consequence of the splitting property (3.1):

$$\begin{aligned} C(x)=1+xC(x)+x^2C(x)^2+\cdots . \end{aligned}$$
(3.3)

Suppose now that each maximal block of r pluses in a Dyck word is decorated by an element of some fixed set \(A_r\). Let \(|A_r|=a_r\), for all \(r\ge 0\). How many decorated Dyck words of a given length are there? If D(x) is the corresponding generating function, then, by the same splitting property (3.1), we get

$$\begin{aligned} D(x)=a_0+a_1xD(x)+a_2x^2D(x)^2+\cdots . \end{aligned}$$
(3.4)

Denoting the generating function for the sequence \((a_r)\) by \(A(x)=a_0+a_1x+a_2x^2+\cdots \), we may write it compactly as

$$\begin{aligned} D(x)=A(xD(x)). \end{aligned}$$
(3.5)

Notice that the same is true when we decorate maximal blocks of minuses instead of pluses. Indeed, there is a bijection between these two types of decorated Dyck words defined by reversal and sign switching. For instance, from a decorated Dyck word

we get

Therefore, if the generating function A(x) is sufficiently nice, we may recover the generating function D(x) for decorated Dyck words that occur in the coloring-erasure algorithm for a specific problem.

3.2 Interval-Constraint Graphs with Exponential Back Degrees

We give an application of the above tools to G-nonrepetitive colorings with the interval-constraint graphs G having exponentially large back degrees. To this end, we will need the following simple lemma.

Lemma 1

Let \(\alpha >1\) be a real number and let \(A_r\) be a set of decorations of size at most \(\alpha ^r\), for each \(r\ge 1\). Let \(D_n\) denote the number of Dyck words of length 2n decorated from sets \(A_r\). Then, \(D_n=o((4\alpha )^n)\).

Proof

Let \(A(x)=1+\alpha x+\alpha ^2x^2+\cdots \) be the generating function for the sequence \((\alpha ^r)\). Therefore, we have

$$\begin{aligned} A(x)=\frac{1}{1-\alpha x}. \end{aligned}$$

Let \(D(x)=d_0+d_1x+d_2x^2+\cdots \) be the generating function satisfying the relation (3.5). Therefore, we have

$$\begin{aligned} D(x)=\frac{1-\sqrt{1-4\alpha x}}{2\alpha x}. \end{aligned}$$
(3.6)

In much the same way as for the Catalan numbers, we get that

$$\begin{aligned} d_n=\frac{\alpha ^n}{n+1}\left( {\begin{array}{c}2n\\ n\end{array}}\right) =\alpha ^nC_n, \end{aligned}$$

for all \(n\ge 0\). Since \(C_n=o(4^n)\), it follows that \(d_n=o((4\alpha )^n)\). This completes the proof, since we obviously have \(D_n\le d_n\) for every \(n\ge 0\). \(\square \)

Using this lemma we may now prove the following result.

Theorem 2

Let \(\alpha >1\) be a real number and let G be an interval-constraint graph whose maximum back degree sequence satisfies \(\Delta _r\le \alpha ^r\), for every \(r\ge 1\). Then, there exists a G-nonrepetitive coloring of \({\mathbb {N}}\) from lists of size at least \(4\alpha \).

Proof

Let G be a fixed interval-constraint graph of maximum back degree sequence \(\Delta _r\). Let \(A_r=\{1,2,\dots , \Delta _r\}\) be a collection of decoration sets. For any interval X of length r, we may label all backward edges going to the left from X by numbers \(\{1,2,\dots , \deg (X)\}\subseteq A_r\). We will denote such labels by \(\ell (AX)\), where A is any backward neighbor of X.

Let \(k\in {\mathbb {N}}\) be a fixed natural number. For every integer \(n\ge 1\), let L(n) be a list of k colors assigned to n. Assume that colors in L(n) are numbered from 1 up to k.

We shall apply the entropy compression argument. Let M be a fixed number and let R be a random sequence of length M with elements chosen from the set \(\{1,2,\dots ,k\}\). Consider the random coloring-erasure process described in Sect. 2. In the nth step, we pick a color form the list L(n) whose number in the list is R(n), color the leftmost uncolored integer, and append \(+\) to the sequence S. If a G-repetition occurs, by which we mean a pair of intervals A and X with the same color sequence that are adjacent in some graph \(G_r\), then we erase all colors from the second interval of the repetition and append a block of r minuses at the end of the sign sequence S. If more than one G-repetition occurs, then we choose the one with the largest interval length and the smallest distance between the two intervals. Additionally, we decorate the block of appended r minuses by the number \(\ell (AX)\).

Now, let m be fixed positive integer and assume that M is sufficiently large with respect to m. Suppose that M steps of the above coloring-erasure process were executed. Therefore, we obtained a decorated sign sequence S and a color sequence C of some initial segment of \({\mathbb {N}}\). Notice also that, in a pretty much the same way as described in Sect. 2, the random sequence R can be uniquely reconstructed from the resulting pair (S, C). Indeed, if the last sign of S is \(+\), we look at the last color of C and put its list number as R(M). If there is a decorated block of r minuses at the end of S, we know that there was a block of r colors just deleted. The decoration number informs about location of the first interval of the repetition, which allows to recover the deleted sequence of colors from C. This sequence can now be turned into a corresponding block of numbers forming a suffix of the sequence R. This step can be repeated until the whole sequence R will be reconstructed. It follows that the number of all possible resulting pairs (S, C) must coincide with the number of random sequences R.

Assume for the sake of contradiction that the length of C is smaller than m. Hence, there are at most \(k^m\) such color sequences. By Lemma 1, the number of decorated sign sequences S is of order \(o((4\alpha )^M)\). Thus, the total number of the resulting pairs (S, C) is at most \(k^m\cdot o((4\alpha )^M)\). On the other hand, the number of random sequences R is obviously equal to \(k^M\). Therefore, we get a contradiction when \(k\ge 4\alpha \) and M is sufficiently large. The proof is complete.

\(\square \)

This theorem has many striking consequences. For instance, we get the following corollary.

Corollary 1

There exists a coloring of \({\mathbb {N}}\) from lists of size 8, such that in any collection of \(2^r\) consecutively adjacent intervals of length \(r\ge 1\), no two have the same color sequence.

Proof

Consider an interval-constraint graph G, such that in every part \(G_r\), any interval X of length r is joined to \(2^r-1\) earlier consecutively adjacent intervals. Hence, the maximum backward degree sequence satisfies \(\Delta _r \le 2^r\). Notice that every sequence of \(2^r\) consecutively adjacent intervals of length r forms a clique in \(G_r\). Thus, no two of them may have the same color sequence in any G-nonrepetitive coloring. The result follows by taking \(\alpha =2\) in Theorem 2.

\(\square \)

It would be interesting to know the exact number of colors needed for this property, also in a non-list version.

3.3 Dejean’s Conjecture

Another consequence of Theorem 2 is connected to the famous conjecture of Dejean [10] (now a Theorem [8, 9]). In coloring terminology, it states that for every \(k\ge 5\), there is a k-coloring of \({\mathbb {N}}\), such that any two intervals of length \(r\ge 1\) with the same color sequence are separated by an interval of length at least \(r(k-2)\). By Theorem 2, we get the following slightly weaker statement, though in a more general setting of list colorings.

Corollary 2

For every \(k\ge 30\), there exists a coloring of \({\mathbb {N}}\) from lists of size k, such that every pair of intervals of length \(r\ge 2\) with the same color sequence is separated by at least \(r(k-2)\) integers.

Proof

Let \(k\ge 30\) be fixed, and let \(\alpha = k/4\). It is not hard to check that the inequality \(r(k-2)\le (k/4)^r\) holds for all \(r\ge 2\). This gives the assertion for pairs of disjoint intervals. To handle the case of overlapping intervals, it is enough to guarantee that consecutive integers will be colored differently. This can be obtained by taking as \(G_1\) the infinite path on consecutive integers, as its back degree satisfies \(\Delta _1=1\le \alpha = k/4\). \(\square \)

This shows that the real difficulty in Dejean’s Conjecture is to handle even the shortest intervals. The result we are now going to prove suggests that perhaps the full conjecture holds also in the list version. It says that for every fixed k, there is a coloring of \({\mathbb {N}}\) from lists of size \((1+o(1))k\) in which no two out of any k consecutively adjacent intervals have the same color sequence. In the proof, we will make use of the following general lemma from [12].

Lemma 2

(Flajolet, Sedgewick [12]). Let f be a function analytic at 0, having non-negative Taylor coefficients, and satisfying \(f(0)\ne 0\). Let \(R\le +\infty \) be the radius of convergence of the series representing f at 0. Then, there exists a unique real number \(t\in (0,R)\) satisfying the characteristic equation

$$\begin{aligned} tf'(t)=f(t), \end{aligned}$$
(3.7)

provided that \(\lim \limits _{x\rightarrow R^-}\frac{xf'(x)}{f(x)}>1\). Moreover, the formal solution G(x) of the functional equation \(G(x)=xf(G(x))\) is analytic at 0 and its Taylor coefficients are of the asymptotic order \(\rho ^n\), where \(\rho = f'(t)\).

We will use this lemma to derive an upper bound on the asymptotic order of the number of corresponding decorated Dyck words.

Theorem 3

Let \(k\ge 2\) be a fixed integer. There exists a coloring of \({\mathbb {N}}\) form lists of size at least \(k+2\sqrt{k}\), such that among any k consecutively adjacent intervals no two have the same color sequence.

Proof

Let \(k\ge 2\) be a fixed integer. Let G be the corresponding interval-constraint graph with \(\Delta _r=k-1\) for all \(r\ge 1\). Therefore, the corresponding decoration sets satisfy\(A_r=\{1,2,\dots ,k-1\}\) for \(r\ge 1\). Let \(A(x)=1+(k-1)x+(k-1)x^2+\cdots \) be the generating function for the sizes of sets \(A_r\)

$$\begin{aligned} A(x)=\frac{1+(k-2)x}{1-x}. \end{aligned}$$
(3.8)

Thus, the generating function for the related sets of decorated Dyck words defined by the relation (3.5) satisfies

$$\begin{aligned} D(x)=\frac{1+(k-2)xD(x)}{1-xD(x)}, \end{aligned}$$
(3.9)

which transforms to the equation \(D(x)-1=xD(x)(D(x)+k-2)\). Substituting \(D(x)=G(x)+1\), we get the following functional equation:

$$\begin{aligned} G(x)=x(G(x)+1)(G(x)+k-1). \end{aligned}$$
(3.10)

Thus, we may take \(f(x)=(x+1)(x+k-1)=x^2+kx+k-1\) and apply Lemma 2. It is easy to find that \(t=\sqrt{k-1}\) and \(\rho =k+2\sqrt{k-1}\).

Suppose now that each list has q colors, and that we executed M steps of the coloring-erasure algorithm. Then, arguing as in the proof of Theorem 2, we get that there exists at most \(q^m\cdot O((k+2\sqrt{k-1})^M)\) resulting pairs (S, C), with the length of a final coloring sequence C strictly smaller than m. Taking \(q=k+2\sqrt{k}\), we get that the number \(q^M\) of random sequences R is bigger than the number of pairs (S, C), for M sufficiently large with respect to m. This contradiction proves the assertion of the theorem. \(\square \)

4 Open Problems

Let us conclude the paper with two sharp conjectures. First, motivated by Corollary 2, we propose the following strengthening of Dejean’s Conjecture.

Conjecture 2

For every \(k\ge 5\), there exists a coloring of \({\mathbb {N}}\) from lists of size k, such that every pair of intervals of length \(r\ge 1\) with the same color sequence is separated by at least \(r(k-2)\) integers.

Using the entropy compression, one may prove that this statement holds asymptotically, which means that lists of size \((1+o(1))k\) are sufficient. The conjecture seems very strong as even highly restricted versions resisted attempts so far. Below, we state one of such weaker versions, which still seems quite challenging.

The original solution of Dejean’s conjecture implies that for every \(k\ge 4\), there is a \((k+1)\)-coloring of \({\mathbb {N}}\), such that no two among any k consecutively adjacent intervals have the same color sequence. For \(k=2\), this statement coincides with the original theorem of Thue. For \(k=3\), it was proved in [5]. We suspect that the same is true in the list setting.

Conjecture 3

For every \(k\ge 2\), there is a coloring of \({\mathbb {N}}\) from lists of size \(k+1\), such that no two among any k consecutively adjacent intervals have the same color sequence.

Notice that this conjecture is open even for the smallest case \(k=2\), which corresponds to Conjecture 1.