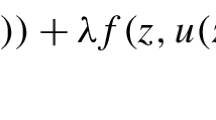Global Multiplicity of Positive Solutions for Nonlinear Robin Problems with an Indefinite Potential Term

Abstract

We consider a Robin problem driven by a nonlinear nonhomogeneous differential operator plus an indefinite potential term. The reaction is parametric and exhibits the competing effects of a concave (sublinear) and of a convex (superlinear) terms (“concave-convex” problem). The parameter multiplies the convex term. We prove an existence and multiplicity theorem which is global in parameter.

1 Introduction

Let $\Omega \subseteq {\mathbb {R}}^N$ be a bounded domain with a $C^2$-boundary $\partial \Omega$. In this paper, we study the following parametric, nonlinear, nonhomogeneous Robin problem:

$$\begin{aligned} {\left\{ \begin{array}{ll} -\text {div }a(D u(z)) + \xi (z)(u(z))^{p-1} = c(u(z))^{\tau -1}+\lambda f(z, u(z)) &{} \text {in } \Omega , \\ \frac{\partial u}{\partial n_{a}} + \beta (z)(u(z))^{p-1}= 0 \ \text {on } \partial \Omega , \ \lambda>0, \ u>0, \ 1<\tau <p. \end{array}\right. } \ \ \ (p_{\lambda }) \end{aligned}$$

In this problem, the map $a: {\mathbb {R}}^N \rightarrow {\mathbb {R}}^N$ involved in the differential operator of $(p_{\lambda })$, is strictly monotone and continuous (thus, maximal monotone too) and satisfies certain other regularity and growth conditions listed in hypotheses ${\widehat{H}}$ below. These conditions provide a general framework in which we can fit many differential operators of interest such as the p-Laplacian and the (p, q)-Laplacian.

In the boundary condition, $\frac{\partial u}{\partial n_a}$ denotes the conormal derivative corresponding to the map a(.). If $u\in C^{1}({\bar{\Omega }})$ then

$$\begin{aligned} \frac{\partial u}{\partial n_a}=\langle a(D(u)),n \rangle _{{\mathbb {R}}^N}, \end{aligned}$$

with n(.) being the outward unit normal. The boundary coefficient $\beta \in C^{0,\alpha }(\partial \Omega )$ with $0<\alpha <1$ and $\beta (z)\ge 0.$

The reaction term f(z, x) is a Caratheodory function (that is, for all $x\in {\mathbb {R}}$, $z\mapsto f(z,x)$ is measurable, while for almost all $z\in \Omega$, $x\mapsto f(z,x)$ is continuous). The potential term $\xi (z)(u(z))^{p-1}$ is indefinite, that is, $\xi (.)$ is sign-changing and this makes the differential operator (left-hand side of the $(p_{\lambda })$) non-coercive. In the reaction (right-hand side of $(p_{\lambda })$), we have the competing effects of a “concave” ($(p-1)$-sublinear) term $c(u(z))^{\tau -1}$ ($c>0, \ 1<\tau <p$) and of a parametric perturbation which is “convex” ($(p-1)$-superlinear). So, problem $(p_{\lambda })$ is a generalized version of the classical “concave-convex problem”. The study of such problems started with the seminal work of Ambrosetti–Brezis–Gerami [1], who considered semilinear Dirichlet equations driven by the Laplacian and with no potential term (that is, $\xi =0$). The concave and convex contributions in the reaction are of the power type, that is, the reaction in [1] has the form

$$\begin{aligned} x\rightarrow \lambda x^{\tau -1}+x^{r-1}, \ x\ge 0, \ 1<\tau<2<r<2^*=\frac{2N}{N-2}, \ N\ge 3, \ \lambda >0. \end{aligned}$$

Their work was extended to Dirichlet equations driven by the p-Laplacian, by Garcia Azorero–Peral Alonso–Manfredi [3] and by Guo–Zhang [6]. In these works the reaction is also of the power type as above. More general differential operators and reactions were considered by Papageorgiou–Radulescu–Repovs [12] (anisotropic p-Laplacian equations) and by Papageorgiou–Vetro [16] ((p, 2)-equations). In both works, the problem has Dirichlet boundary conditions, there is no potential term (thus the operator is coercive) and the parameter $\lambda$ multiplies the concave term. Only Marano–Marino–Papageorgiou [8], deal with a Dirichlet p-Laplacian equation with no potential term and a parametric convex (superlinear) term. The work of [8] was extended recently by Gasiniski–Papageorgiou–Zhang [5] to problems driven by the Robin p-Laplacian and with a positive potential term (thus, the differential operator is coercive). Recently Bai–Papageorgiou–Zeng [2], studied nonparametric Robin problems driven by a similar nonhomogeneous differential operator as $(p_{\lambda })$ plus an indefinite potential term. The authors proved a multiplicity result producing solutions with sign information (positive, negative and nodal (sign-changing) solutions). Finally, we should also mention the recent relevant work of Papageorgiou–Radulescu–Zhang [15], which examines a nonlinear eigenvalue problem for the Robin p-Laplacian plus a positive potential term. They proved a bifurcation-type result but for large values of the parameter $\lambda >0$.

Using variational tools combined with suitable truncation and comparison techniques, we prove an existence and multiplicity result for the positive solutions of $(p_{\lambda })$ which is global in $\lambda >0$ (a bifurcation-type result but for small values of $\lambda >0$).

2 Mathematical Background and Hypotheses

The main spaces in the analysis of the problem $(p_{\lambda })$ are the Sobolev space $W^{1,p}(\Omega )$ with $1<p<\infty$, the Banach space $C^1({\overline{\Omega }})$, and the boundary Lebesgue spaces $L^s(\partial \Omega )$ with $1\le s\le \infty$. By $\Vert \cdot \Vert$, we denote the norm of $W^{1,p}(\Omega )$, which is defined by

$$\begin{aligned} \Vert u\Vert = \left[ \Vert u\Vert _p^p + \Vert Du\Vert _p^p\right] ^{1/p} \end{aligned}$$

for all $u\in W^{1,p}(\Omega )$.

The Banach space $C^1({\overline{\Omega }})$ is an ordered with a positive (order) cone $C_+$ which is defined by;

$$\begin{aligned} C_+ = \{u\in C^1({\overline{\Omega }}): u(z)\ge 0 \text { for all } z\in {\overline{\Omega }}\}. \end{aligned}$$

This cone has a nonempty interior given by

$$\begin{aligned} \text {int} C_+ = \{u\in C_+: u(z)>0 \text { for all } z\in {\overline{\Omega }}\}. \end{aligned}$$

Also we use another cone in $C^1({\overline{\Omega }})$, namely,

$$\begin{aligned} D_+ = \left\{ u\in C^1({\overline{\Omega }}): u(z)>0 \text { for all } z\in \Omega , \frac{\partial u}{\partial n}|_{\partial \Omega \cap u^{-1}(0)}<0\right\} . \end{aligned}$$

On $\partial \Omega$ we consider the $(N-1)$-dimensional Hausdorff (surface) measure $\sigma (\cdot )$. Using this measure on $\partial \Omega$, we can define in the usual way the boundary Lebesgue spaces $L^s(\partial \Omega )$ with $1\le s\le \infty$. From the theory of Sobolev spaces, we know that there exists a unique bounded linear operator $\gamma _0: W^{1,p}(\Omega ) \rightarrow L^p(\partial \Omega )$, called the “trace operator”, such that

$$\begin{aligned} \gamma _0(u) = u|_{\partial \Omega }, \ \forall u\in W^{1,p}(\Omega ) \cap C({\overline{\Omega }}). \end{aligned}$$

Using $\gamma _0(.)$ we have a way to speak about the boundary values of a Sobolev function. The trace operator $\gamma _0(\cdot )$ is compact into $L^s(\partial \Omega )$ for all $s\in [1, \frac{(N-1)p}{N-p})$ if $p<N$, and into $L^s(\partial \Omega )$ for all $s\in [1,+\infty )$ if $N\le p$. Moreover, we know that:

$$\begin{aligned} \gamma _0(W^{1,p}(\Omega )) = W^{\frac{1}{p'},p}(\partial \Omega ) \ \text {with} \ \frac{1}{p} + \frac{1}{p'} = 1 \end{aligned}$$

and

$$\begin{aligned} \text {ker}\gamma _0 = W^{1,p}_0(\Omega ). \end{aligned}$$

In the sequel, for the sake of notation simplicity, we drop the use of the operator $\gamma _0(\cdot )$. All restrictions of Sobolev functions on $\partial \Omega$ are understood in the sense of traces.

Given $u:\Omega \rightarrow {\mathbb {R}}$ is measurable, then we define

$$\begin{aligned} u^+(z) = \max \{u(z),0\}, \quad u^-(z) = \max \{-u(z),0\} \text { for all } z\in \Omega . \end{aligned}$$

These are measurable functions and $u=u^+-u^-$, $|u|=u^++u^-$. Moreover, if $u\in W^{1,p}(\Omega )$, then $u^\pm \in W^{1,p}(\Omega )$. Suppose $u,v:\Omega \rightarrow {\mathbb {R}}$ are measurable functions with $u(z)\le v(z)$ for a.a. $z\in \Omega$. We define

$$\begin{aligned}{} & {} [u,v] = \{h\in W^{1,p}(\Omega ): u(z)\le h(z)\le v(z) \text { for a.a. } z\in \Omega \}, \\{} & {} \quad \text {int}_{ C^1({\overline{\Omega }})}[u,v] = \text {the interior in } C^1({\overline{\Omega }}) \text { of } [u,v]\cap C^1({\overline{\Omega }}), \\{} & {} \quad [u) = \{h\in W^{1,p}(\Omega )\mid u(z)\le h(z)\text { for a.a. } z\in \Omega \}. \end{aligned}$$

Let X be a Banach space and $\varphi \in C^1(X)$. We say that $\varphi (.)$ satisfies the “C-condition”, if it has the following property:

“Every sequence $\{u_n\}_{n\in {\mathbb {N}}}\subset X$ such that

• $\{\varphi (u_n)\}_{n\in {\mathbb {N}}}\subseteq {\mathbb {R}}$ is bounded,

• $(1+\Vert u_n\Vert _X)\varphi '(u_n)\rightarrow 0 \ \text {in} \ X^*$,

admits a strongly convergent subsequence.”

This is a compactness-type condition on $\varphi (.)$ which compensates for the fact that the ambient space X need not be locally compact (being in general infinite-dimensional). By $K_\varphi$ we denote the critical set of $\varphi (.)$, that is,

$$\begin{aligned} K_{\varphi } = \{u\in X: \varphi '(u) = 0\}. \end{aligned}$$

By $p^*$ we denote the critical Sobolev exponent corresponding to $p\in (1,\infty )$, defined by

$$\begin{aligned} p^*:= {\left\{ \begin{array}{ll} \frac{Np}{N-p} &{} \text {if } p<N, \\ +\infty &{} \text {if } N\le p. \end{array}\right. } \end{aligned}$$

Let ${\hat{l}}\in C^1(0,\infty )$ with ${\hat{l}}(t)>0$ for all $t>0$. We assume that there exist constants $c_1, \ c_2>0$ and $1<s<p$ such that

$$\begin{aligned} 0<{\hat{c}}\le \frac{t{\hat{l}}'(t)}{{\hat{l}}(t)}\le c_0 \quad \text {and} \quad c_1t^{p-1}\le {\hat{l}}(t)\le c_2(t^{s-1}+t^{p-1}) \end{aligned}$$

for all $t>0$.

We introduce the following conditions on the map $a:{\mathbb {R}}^N\rightarrow {\mathbb {R}}^N$ (see also Bai-Papageorgiou–Zeng [2]):

$\mathbf {{\hat{H}}:}$ $a(y)=a_0(|y|)y$ for all $y\in {\mathbb {R}}^N$ with $a_0(t)>0$ for all $t>0$ satisfies the following conditions:

• (i) $a_0\in C^1(0,\infty )$, $t\mapsto a_0(t)t$ is strictly increasing on ${\mathbb {R}}^+:= (0,\infty )$ and $a_0(t)t\rightarrow 0^+$ as $t\rightarrow 0^+$ such that $\lim _{t\rightarrow 0^+} \frac{ta'_0(t)}{a_0(t)}>-1$;

• (ii) $|\nabla a(y)|\le c_3\frac{{\hat{l}}(|y|)}{|y|}$ for all $y\in {\mathbb {R}}^N\backslash \{0\}$ for some $c_3>0$;

• (iii) $(\nabla a(y)\xi ,\xi )_{{\mathbb {R}}^N}\ge \frac{{\hat{l}}(|y|)}{|y|}|\xi |^2$ for all $y\in {\mathbb {R}}^N\backslash \{0\}$ and all $\xi \in {\mathbb {R}}^N$;

• (iv) if $G_0(t)=\int _0^t a_0(s)sds$ for all $t>0$, then for some $q\in (\tau ,p]$ we have $\lim _{t\rightarrow 0^+}\frac{ qG_0(t)}{t^q} \le c^*$ and $t\mapsto G_0(t^{1/q})$ is convex.

Remark 2.1

Hypotheses $\mathbf {{\hat{H}}}(i)$, (ii), (iii) are dictated by the nonlinear regularity theory of Lieberman [7] and the nonlinear maximum principle of Pucci and Serrin [17]. Hypothesis $\mathbf {{\hat{H}}}(iv)$ is an extra condition for the needs of our problem, but it is mild and it is satisfied in all cases of interest as the examples which follow illustrate.

Example 2.2

The following maps satisfy hypotheses $\mathbf {{\hat{H}}}$:

• (a.) $a(y)=|y|^{p-2}y$ with $1<p<\infty$.

• (b.) $a(y)=|y|^{p-2}y+|y|^{q-2}y$ with $1<q<p<\infty$.

• (c.) $a(y)=\big (1+|y|^2\big )^{\frac{p-2}{2}}y$ with $1<p<\infty$.

Note that the map in (a.) corresponds to the p-Laplacian while the map in (b.) corresponds to the (p, q)-Laplacian.

Using these hypotheses, we can prove the following properties of the map a(.) (see Papageorgiou–Radulescu [9]).

Lemma 2.3

If hypotheses $\mathbf {{\hat{H}}}(i)$, (ii), (iii) hold, then

• (a.) $y\rightarrow a(y)$ is continuous and strictly monotone, hence maximal monotone too;

• (b.) $|a(y)|\le c_4(|y|^{s-1}+|y|^{p-1})$ for all $y\in {\mathbb {R}}^N$, some $c_4>0$;

• (c.) $(a(y),y)_{{\mathbb {R}}^N}\ge \frac{c_1}{p-1}|y|^p$ for all $y\in {\mathbb {R}}^N$.

We set $G(y)=G_0(|y|)$ for all $y\in {\mathbb {R}}^N$. Then the map $G(\cdot )\in C^1({\mathbb {R}}^N,{\mathbb {R}})$ and we have

$$\begin{aligned} \nabla G(y)=G'_0(|y|)\frac{y}{|y|}=a_0(|y|)y=a(y), \ \ \forall y\in {\mathbb {R}}^N\backslash \{0\}, \ \nabla G(0)=0. \end{aligned}$$

So $G(\cdot )$ is the primitive of the map $a(\cdot )$ and on account of Lemma 2.3 (a), $G(\cdot )$ is strictly convex. Since $G(0)=0$, we have

$$\begin{aligned} G(y)\le (a(y),y)_{{\mathbb {R}}^N} \ \text {for all } y\in {\mathbb {R}}^N. \end{aligned}$$

(2.1)

Using Lemma 2.3 and (2.1), we deduce the following bilateral growth restrictions on G(.).

Corollary 2.4

If hypotheses $\mathbf {{\hat{H}}}(i)$, (ii), (iii) hold, then

$$\begin{aligned} \frac{c_1}{p(p-1)}|y|^p \le G(y) \le c_5(1+|y|^p) \ \text { for all } y\in {\mathbb {R}}^N, \ \text {some} \ c_5>0. \end{aligned}$$

Let $V:W^{1,p}(\Omega )\rightarrow W^{1,p}(\Omega )^*$ be the nonlinear operator defined by

$$\begin{aligned} \langle V(u),h\rangle = \int _{\Omega } \big (a(Du),Dh\big )_{{\mathbb {R}}^N} dz \ \text { for all} \ \ u,h\in W^{1,p}(\Omega ). \end{aligned}$$

This operator has the following properties (see Problem 2.192 of Gasinski–Papageorgiou [4]).

Proposition 2.5

If hypotheses $\mathbf {{\hat{H}}}(i)$, (ii), (iii) hold, then the operator $V(\cdot )$ is bounded (that is, maps bounded sets to bounded sets), continuous, monotone (hence, maximal monotone too) and of type $(S)_+$, that is, it has the following property, if $u_n \overset{w}{\rightarrow }\ u$ in $W^{1,p}(\Omega )$ and $\limsup \nolimits _{n\rightarrow \infty }\langle V(u_n),u_n-u\rangle \le 0$, then $u_n \rightarrow u$ in $W^{1,p}(\Omega )$.

The hypotheses on the potential function $\xi (.)$ and the boundary coefficient $\beta (.)$ are the following:

$\mathbf {H_0}$: $\xi \in L^{\infty }(\Omega )$, $\beta \in C^{0,\alpha }(\partial \Omega )$ with $\alpha \in (0, 1]$, $\beta (z) \ge 0$ for all $z \in \partial \Omega$ and $\xi \ne 0$ or $\beta \ne 0$.

The above hypotheses imply that

$$\begin{aligned} u\rightarrow \Vert Du\Vert _p^p+\int _{\Omega }|\xi (z)||u|^{p}dz+\int _{\partial \Omega }\beta (z)|u|^{p}dz \end{aligned}$$

is an equivalent norm on $W^{1,p}(\Omega )$.

In the boundary condition, $\frac{\partial u}{\partial n_a}$ denotes the conormal derivative of u corresponding to the map a(.) and it is interpreted using the nonlinear Green’s identity (see Paoageorgiou–Radulescu–Repovs [11], p.34).

The hypotheses on the perturbation f(z, x) are the following:

${\textbf{H}}$: $f:\Omega \times {\mathbb {R}}\rightarrow {\mathbb {R}}$ be a Caratheodory function such that $f(z, 0) = 0$ for almost every $z \in \Omega$, and satisfies the following conditions:

• (i) $0\le f(z, x) \le a(z)(1 + x^{r-1})$ for almost every $z \in \Omega$ and all $x\ge 0$, where $a \in L^{\infty }(\Omega )$ and $p<r<p^*$;

• (ii) if $F(z,x)=\int _{0}^{x}f(z,s)ds$, then $\lim _{x \rightarrow + \infty } \frac{F(z,x)}{x^{p}} = +\infty$ uniformly for almost every $z \in \Omega$;

• (iii) there exists $\theta \in \big (\max \{1,(r-p)\frac{N}{p}\},p^*\big )$ such that

  $$\begin{aligned} 0<\beta \le \liminf _{x \rightarrow \infty } \frac{f(z,x)x-pF(z,x)}{x^\theta } \ \text { uniformly for almost every } \ z \in \Omega ; \end{aligned}$$

• (iv) $\lim _{x\rightarrow 0^+}\frac{f(z,x)}{x^{q-1}}=0$ uniformly for almost every $z\in \Omega$;

• (v) for every $s>0$, there exists $\eta _{s} > 0$ such that $0<\eta _{s} \le f(z,x)$ for almost every $z\in \Omega$, all $x\ge s$ and for every $\rho >0$, there exists ${\hat{\xi }}_{\rho }>0$ such that for almost every $z\in \Omega$

  $$\begin{aligned} x\rightarrow f(z,x)+{\hat{\xi }}_{\rho }x^{p-1} \end{aligned}$$

  is nondecreasing on $[0,\rho ]$.

Remark 2.6

Since we look for positive solutions and all the above hypotheses concern the positive semiaxis, we may assume that $f(z,x)=0$ for almost every $z\in \Omega$, all $x\le 0$. Hypotheses H(ii), (iii) imply that

$$\begin{aligned} \lim _{x\rightarrow +\infty }\frac{f(z,x)}{x^{p-1}}=\infty \ \text { uniformly for almost every} \ z\in \Omega . \end{aligned}$$

So the perturbation f(z, x) is $(p-1)$-superlinear. However, this superlinearity is not formulated in terms of Ambrosetti–Rabinowitz condition, which is common in the literature when dealing with superlinear problems (see Struwe [18], p.102). Instead, we use a less restrictive condition (see H(iii)), which incorporates in our framework also superlinear functions with “slower” growth as $x\rightarrow \infty$. For example, the function

$$\begin{aligned} f(x)={\left\{ \begin{array}{ll} (x^+)^{s-1} \ \ \ \ \ \ \ \ \ \ \ \ \ \text {if } \ \ x\le 1, \\ x^{p-1}\ln x+x^{\eta -1} \ \ \text {if } \ \ 1<x \end{array}\right. } \end{aligned}$$

with $q<s\le p$ and $1<\eta \le p$, satisfies hypotheses H, but fails to satisfy the Ambrosetti–Rabinowitz condition.

In what follows $\gamma _{p}:W^{1,p}(\Omega )\rightarrow {\mathbb {R}}$ is the $C^1$-functional defined by

$$\begin{aligned} \gamma _p(u) = \int _{\Omega } pG(Du) dz + \int _{\Omega } \xi (z) |u|^p dz + \int _{\partial \Omega } \beta (z) |u|^p d\sigma \quad \text {for all } u \in W^{1,p}(\Omega ). \end{aligned}$$

Consider the following auxiliary Robin problem

$$\begin{aligned} {\left\{ \begin{array}{ll} -\text {div }a(D u(z)) + |\xi (z)|(u(z))^{p-1} = c (u(z))^{\tau -1}&{} \text {in } \Omega , \\ \frac{\partial u}{\partial n_{a}} + \beta (z)(u(z))^{p-1}= 0 &{} \text {on } \partial \Omega , \ \ u>0. \end{array}\right. } \ \ \ (2) \end{aligned}$$

Reasoning as in the proof of Proposition 3.3 of Bai–Papageorgiou–Zeng [2], we obtain the following result.

Proposition 2.7

If hypotheses ${\hat{H}}$, $H_{0}$ hold, then problem (2) admits a unique positive solution

$$\begin{aligned} {\bar{u}}\in intC_{+}. \end{aligned}$$

We introduce the following two sets:

$$\begin{aligned}{} & {} {\mathfrak {L}}=\{\lambda >0: \text {problem} \ (p_{\lambda }) \ \text {has a positive solution}\}, \\{} & {} S_{\lambda }=\text {set of positive solutions of} \ (p_{\lambda }). \end{aligned}$$

In the next section, we establish the properties of these two sets.

3 Positive Solutions

First, we prove the nonemptiness of ${\mathfrak {L}}$ and the regularity of the elements of $S_{\lambda }.$

Fix $\lambda >0$ and let $k>\frac{1}{\lambda }\Vert \xi \Vert _{\infty }$. We introduce the Caratheodory function $l_{\lambda }(z,x)$ defined by

$$\begin{aligned} l_{\lambda }(z,x)={\left\{ \begin{array}{ll} c({\bar{u}}(z))^{\tau -1}+\lambda f(z,{\bar{u}}(z))+\lambda k ({\bar{u}}(z))^{p-1} \ \ \ \ \text {if } \ x\le {\bar{u}}(z) \\ cx^{\tau -1}+\lambda f(z,x)+\lambda k x^{p-1} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text {if } {\bar{u}}(z)<x \end{array}\right. } \ \ \ \end{aligned}$$

(3.1)

with ${\bar{u}}\in int C_+$ being the unique positive solution of (2) (see Proposition 2.7).

We set $L_{\lambda }(z,x)=\int _{0}^{x}l_{\lambda }(z,s)ds$ and consider the $C^{1}$-functional $\psi _{\lambda }:W^{1,p}(\Omega )\rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned} \psi _{\lambda }(u)=\frac{1}{p}\gamma _{p}(u)+\frac{\lambda k}{p}\Vert u\Vert _{p}^p-\int _{\Omega }L_{\lambda }(z,u)dz \ \ \text {for all} \ u\in W^{1,p}(\Omega ). \end{aligned}$$

Proposition 3.1

If hypotheses ${\hat{H}}, H_{0},H$ hold, then ${\mathfrak {L}}\ne \emptyset$ and $S_{\lambda }\subseteq int C_{+}$ for every $\lambda >0$.

Proof

For every $u\in W^{1,p}(\Omega )$, we have

$$\begin{aligned} \psi _{\lambda }(u){} & {} \ge c_{6}\Vert u\Vert _{}^p-\int _{\{u\le {\bar{u}}\}}[c{\bar{u}}(z)^{\tau -1}+\lambda f(z,{\bar{u}})+\lambda k{\bar{u}}(z)^{p-1}]udz \\{} & {} \quad -\int _{\{u>{\bar{u}}\}}[c{\bar{u}}(z)^{\tau -1}+\lambda f(z,{\bar{u}})+\lambda k {\bar{u}}(z)^{p-1}]u dz\\{} & {} \quad -\int _{\{{\bar{u}}<u\}}[R_{\lambda }(z,u)-R_{\lambda }(z,{\bar{u}})]dz \ \ \ \text {for some} \ \ c_{5}>0 \end{aligned}$$

where

$$\begin{aligned} R_{\lambda }(z,x)=\int _{0}^{x}[cs^{\tau -1}+\lambda f(z,s)+\lambda k s^{p-1}]ds=\frac{c}{\tau }x^{\tau }+\lambda F(z,x)+\frac{\lambda k}{p}x^{p} \end{aligned}$$

for all $x\ge 0$. Note that $R_{\lambda }\ge 0$ and $c{\bar{u}}(.)^{\tau -1}+\lambda f(.,{\bar{u}}(.) )+\lambda k{\bar{u}}(.)^{p-1}\in L^{\infty }(\Omega )$. Hence we have

$$\begin{aligned} \psi _{\lambda }(u){} & {} \ge c_{6}\Vert u\Vert _{}^p-\int _{\Omega }[c{\bar{u}}(z)^{\tau -1}+\lambda f(z,{\bar{u}})+\lambda k{\bar{u}}(z)^{p-1}]|u|dz\\{} & {} \quad -\int _{\{{\bar{u}}<u\}}R_{\lambda }(z,u)dz \\{} & {} \ge c_{6}\Vert u\Vert ^p-c_{7}\Vert u\Vert -\int _{\Omega }\left[ \frac{c}{\tau }(u^+)^\tau +\lambda F(z,u^+)+\frac{\lambda k}{p}(u^+)^p\right] dz \\{} & {} \quad \ \text {for some} \ \ c_{7}>0 \end{aligned}$$

Hypotheses H(i), (iv) imply that

$$\begin{aligned} 0\le F(z,x)\le c_{8}[x^q+x^r] \ \text {for almost all } \ \ z\in \Omega , \ \text {all} \ x\ge 0, \ \text {some} \ c_{8}>0. \end{aligned}$$

Since $1<q<p<r$ we have $\Vert u\Vert ^p\le \Vert u\Vert ^q+\Vert u\Vert ^r.$ Therefore we can write that

$$\begin{aligned} \psi _{\lambda }(u)\ge c_{6}\Vert u\Vert _{}^r-c_{9}(\Vert u\Vert +\Vert u\Vert ^\tau )-\lambda c_{9}(\Vert u\Vert ^q+\Vert u\Vert ^r) \ \text {for some} \ c_{9}>0. \qquad \end{aligned}$$

(3.2)

Let $\rho =\Vert u\Vert$. If $\rho >1$ is large, then since $1<\tau <p$, we have

$$\begin{aligned} c_{6}\rho ^p-c_{9}(\rho +\rho ^{\tau })\ge \vartheta _{\rho }>0. \end{aligned}$$

We fix such a large $\rho >1$ and choose $\lambda _{0}>0$ small such that

$$\begin{aligned} \lambda c_{9}(\rho ^q+\rho ^r)<\vartheta _{\rho } \ \text {for all} \ \ 0<\lambda <\lambda _{0}. \end{aligned}$$

Then from (3.2) it follows that

$$\begin{aligned} \psi _{\lambda }(u)\ge m_{\lambda }>0 \ \text {for all} \ \Vert u\Vert =\rho , \ \text {all} \ \lambda \in (0,\lambda _{0}). \end{aligned}$$

(3.3)

On account of hypotheses ${\hat{H}}(iv)$, we can find $\delta >0$ such that

$$\begin{aligned} G(y)\le \frac{c_{10}}{q}|y|^{q} \ \text {for all} \ |y|\le \delta , \text {with} \ c_{10}>c^*. \end{aligned}$$

(3.4)

Let $u\in C^1(\bar{\Omega })$ with $u(z)>0$ for all $z\in \Omega$. Since ${\bar{u}}\in int C_+$ (see Proposition 2.7), using Proposition 4.1.22, p.274 of Papageorgiou–Radulescu–Repovs [11], we can find $t\in (0,1)$ small such that

$$\begin{aligned} 0\le tu(z)\le {\bar{u}}(z), \ t|Du(z)|\le \delta \ \text {for all} \ z\in {\bar{\Omega }}. \end{aligned}$$

From (3.1) and (3.4) we have

$$\begin{aligned} \psi _{\lambda }(tu)\le c_{11}t^{q}-c_{12}t \ \ \text {for some} \ c_{11}, c_{12}>0. \end{aligned}$$

Since $q>1$, choosing $t\in (0,1)$ even smaller if necessary, we see that

$$\begin{aligned} \psi _{\lambda }(tu)<0 \ \ \text {and} \ \ t\Vert u\Vert \le \rho . \end{aligned}$$

(3.5)

we consider the closed ball

$$\begin{aligned} {\bar{B}}_\rho =\{u\in W^{1,p}(\Omega ): \Vert u\Vert \le \rho \}. \end{aligned}$$

Since $W^{1,p}(\Omega )$ is reflexive, ${\bar{B}}_\rho$ is w-compact and by the Eberlein–Smulian theorem, it is sequently w-compact. Also, using the Sobolev embedding theorem, we see that $\psi _{\lambda }(.)$ is sequentially weakly lower semicontinuous. So, by the Weierstrass–Tonelli theorem, we can find ${\hat{u}}_{\lambda }\in {\bar{B}}_\rho$ such that

$$\begin{aligned} \psi _{\lambda }({\hat{u}}_{\lambda })=\underset{{\bar{B}}_{\rho }}{\min }\psi _{\lambda }. \end{aligned}$$

(3.6)

From (3.3) and (3.5), we infer that

$$\begin{aligned} 0<\Vert {\hat{u}}_{\lambda }\Vert <\rho . \end{aligned}$$

Then from (3.6) it follows that

$$\begin{aligned} \langle \psi _{\lambda }'({\hat{u}}_{\lambda }),h\rangle =0 \ \text {for all} \ h\in W^{1,p}(\Omega ). \end{aligned}$$

(3.7)

In (3.7), we use the test function $h=({\bar{u}}-{\hat{u}}_{\lambda })^+ \in W^{1,p}(\Omega )$. Then we have

$$\begin{aligned}{} & {} \langle V({\hat{u}}_{\lambda }), ({\bar{u}}-{\hat{u}}_{\lambda })^+\rangle + \int _{\Omega } [\xi (z)+\lambda k]|{\hat{u}}_{\lambda }|^{p-2}{\hat{u}}_{\lambda })({\bar{u}}-{\hat{u}}_{\lambda })^+dz\\{} & {} \quad +\int _{\partial \Omega } \beta (z)|{\hat{u}}_{\lambda })|^{p-2}{\hat{u}}_{\lambda }({\bar{u}}-{\hat{u}}_{\lambda })^+d\sigma \\{} & {} \quad =\int _{\Omega }l_{\lambda }(z,{\hat{u}}_{\lambda })({\bar{u}}-{\hat{u}}_{\lambda })^+dz \\{} & {} \quad =\int _{\Omega }[c{\bar{u}}^{\tau -1}+\lambda f(z,{\bar{u}})+\lambda k {\bar{u}}^{p-1}]({\bar{u}}-{\hat{u}}_{\lambda })^+ dz \ \ (\text {see } (3.1)) \\{} & {} \quad \ge \int _{\Omega }[c{\bar{u}}^{\tau -1}+\lambda k {\bar{u}}^{p-1}]({\bar{u}}-{\hat{u}}_{\lambda })^+ dz \ (\text {since} \ f\ge 0) \\{} & {} \quad =\langle V({\bar{u}}), ({\bar{u}}-{\hat{u}}_{\lambda })^+\rangle +\int _{\Omega }[|\xi (z)|+\lambda k]{\bar{u}}^{p-1}({\bar{u}}-{\hat{u}}_{\lambda })^+dz\\{} & {} \quad +\int _{\partial \Omega }\beta (z) {\bar{u}}^{p-1}({\bar{u}}-{\hat{u}}_{\lambda })^+d\sigma \end{aligned}$$

(by Proposition 2.7)

$$\begin{aligned}{} & {} \ge \langle V({\bar{u}}), ({\bar{u}}-{\hat{u}}_{\lambda })^+\rangle +\int _{\Omega }[\xi (z)+\lambda k]{\bar{u}}^{p-1}({\bar{u}}-{\hat{u}}_{\lambda })^+dz\\{} & {} \quad +\int _{\partial \Omega }\beta (z) {\bar{u}}^{p-1}({\bar{u}}-{\hat{u}}_{\lambda })^+d\sigma \end{aligned}$$

then

$$\begin{aligned} {\bar{u}}\le {\hat{u}}_{\lambda } \ \ \left( \text {see Proposition } 2.5\text { and recall} \ \ k>\frac{1}{\lambda }\Vert \xi \Vert _\infty , \ \beta \ge 0\right) . \end{aligned}$$

(3.8)

From (3.8), (3.1), (3.7) it follows that ${\hat{u}}_{\lambda }\in S_{\lambda }$ and hence $(0,\lambda _{0})\subset {\mathfrak {L}}\ne \emptyset$.

From Papageorgiou–Radulescu [10], we have that if $u\in S_{\lambda }$, then $u\in L^{\infty }(\Omega )$. Therefore nonlinear regularity theory of Lieberman [7] implies that $u\in C_{+}\backslash \{0\}$.

Let $k_{0}>\Vert \xi \Vert _\infty$. Then

$$\begin{aligned} -div a(Du)+(k_{0}+\xi (z))u^{p-1}\ge 0 \end{aligned}$$

with $k_{0}+\xi (.)\in L^{\infty }(\Omega )$, $k_{0}+\xi (z)>0$ for almost all $z\in \Omega$. Then from Pucci and Serrin [17] (p.120) we infer that

$$\begin{aligned} u\in int C_+ \ \ \text {and hence} \ \ S_{\lambda }\subseteq int C_+ \ \ \text {for all } \ \lambda >0. \end{aligned}$$

$\square$

In the next proposition, we show that ${\mathfrak {L}}$ is a connected set (an interval).

Proposition 3.2

If hypotheses ${\hat{H}}, H_{0},H$ hold, $\lambda \in {\mathfrak {L}}$ and $0<\mu <\lambda$ then $\mu \in {\mathfrak {L}}$.

Proof

Since $\lambda \in {\mathfrak {L}}$ we can find $u_{\lambda } \in S_{\lambda }\subseteq intC_+$. Let $k_0>\Vert \xi \Vert _\infty$ and introduce the Caratheodory function $\eta _\mu (z,x)$ defined by

$$\begin{aligned} \eta _\mu (z,x)={\left\{ \begin{array}{ll} c(x^+)^{\tau -1}+\mu f(z,x^+)+k_0 (x^+)^{p-1} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text {if } \ \ \ x\le u_{\lambda }(z), \\ c(u_{\lambda }(z))^{\tau -1}+\mu f(z,u_{\lambda }(z))+k_0 (u_{\lambda }(z))^{p-1}\ \ \ \ \ \text {if } \ \ u_{\lambda }(z)<x. \end{array}\right. }\nonumber \\ \end{aligned}$$

(3.9)

We set $H_{\mu }(z,x)=\int _{0}^{x}\eta _{\mu }(z,s)ds$ and consider the $C^1$-functional ${\hat{\psi }}_{\mu }:W^{1,p}(\Omega )\rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned} {\hat{\psi }}_{\mu }(u)=\frac{1}{p}\gamma _{p}(u)+\frac{k_{0}}{p}\Vert u\Vert _p^p-\int _{\Omega }H_{\mu }(z,u)dz \ \text {for all} \ u\in W^{1,p}(\Omega ). \end{aligned}$$

Since $k_{0}>\Vert \xi \Vert _{\infty }$, from (3.9) we see that ${\hat{\psi }}_{\mu }(.)$ is coercive. Also, it is sequentially weakly lower semicontinuous. So, we can find $u_{\mu }\in W^{1,p}(\Omega )$ such that

$$\begin{aligned} {\hat{\psi }}_{\mu } (u_\mu )=\inf \{{\hat{\psi }}_{\mu }(u): \ u\in W^{1,p}(\Omega )\} \end{aligned}$$

(3.10)

Let $u\in C^1({\bar{\Omega }})$ with $u(z)>0$ for all $z\in \Omega$. As before since $u_{\lambda }\in int C_+$, we can find $t\in (0,1)$ small such that

$$\begin{aligned} 0\le tu(z)\le u_{\lambda }(z), t|Du(z)|\le \delta \ \ \text {for all} \ \ z\in {\bar{\Omega }}. \end{aligned}$$

From (3.9) and (3.4) and since $\tau <q$ (see hypotheses H(iv)) we see that for $t\in (0,1)$ small

$$\begin{aligned} {\hat{\psi }}_{\lambda }(tu)<0 \end{aligned}$$

then

$$\begin{aligned} {\hat{\psi }}_{\lambda }(u_\mu )<0={\hat{\psi }}_{\lambda }(0) \end{aligned}$$

So, $u_{\mu }\ne 0.$

From (3.10) we have

$$\begin{aligned} \langle {\hat{\psi }}_{\lambda }'(u_\mu ),h \rangle =0 \ \ \text {for all} \ h\in W^{1,p}(\Omega ). \end{aligned}$$

(3.11)

In (3.11), first, we choose the test function $h=-u_{\mu }^-\in W^{1,p}(\Omega )$. Since $k_0>\Vert \xi \Vert _{\infty }$, we obtain

$$\begin{aligned} c_{13}\Vert u_{\mu }^-\Vert ^{p}\le 0 \ \ \text {for some} \ c_{13}>0 \ (\text {see }(3.9)) \end{aligned}$$

then $u_{\mu }\ge 0$, $u_{\mu }\ne 0.$

Next in (3.11), we choose the test function $h=(u_{\mu }-{u}_{\lambda })^+ \in W^{1,p}(\Omega )$. Using (3.9), we have

$$\begin{aligned}{} & {} \langle V(u_{\mu }), (u_{\mu }-u_{\lambda })^+\rangle + \int _{\Omega } [\xi (z)+k_{0}] u_{\mu }^{p-1}(u_{\mu }-u_{\lambda })^+dz\\{} & {} \qquad +\int _{\partial \Omega } \beta (z)u_{\mu }^{p-1}(u_{\mu }-u_{\lambda })^+d\sigma \\{} & {} \quad =\int _{\Omega }[cu_{\lambda }^{\tau -1}+\mu f(z,u_\lambda )+ k_{0} u_\lambda ^{p-1}](u_{\mu }-u_{\lambda })^+ dz\\{} & {} \quad \le \int _{\Omega }[cu_{\lambda }^{\tau -1}+\lambda f(z,u_\lambda )+ k_{0} u_\lambda ^{p-1}](u_{\mu }-u_{\lambda })^+ dz \\{} & {} \qquad (\text {since} \ \mu <\lambda , \ f\ge 0) \end{aligned}$$

Since $u_{\lambda }\in S_{\lambda }$

$$\begin{aligned}{} & {} =\langle V(u_\lambda ), (u_{\mu }-u_{\lambda })^+\rangle +\int _{\Omega }[|\xi (z)|+k_{0}]u_{\lambda }^{p-1}(u_{\mu }-u_{\lambda })^+dz\\{} & {} \quad +\int _{\partial \Omega }\beta (z) u_{\lambda }^{p-1}(u_{\mu }-u_{\lambda })^+d\sigma \end{aligned}$$

then

$$\begin{aligned} u_{\mu }\le u_{\lambda } \ \ (\text {see Proposition}~2.5\text { and recall} \ \ k_{0}>\Vert \xi \Vert _\infty )\ \end{aligned}$$

So, we have proved that

$$\begin{aligned} u_{\mu }\in [0,u_{\lambda }],\ u_{\mu }\ne 0 \end{aligned}$$

(3.12)

From (3.12), (3.9), (3.11), we see that

$$\begin{aligned} u_{\mu }\in S_{\mu }\subseteq intC_+ \end{aligned}$$

then

$$\begin{aligned} \mu \in {\mathfrak {L}}. \end{aligned}$$

$\square$

Hidden in the above proof is the following corollary.

Corollary 3.3

If hypotheses ${\hat{H}},H_{0},H$ hold, $\lambda \in {\mathfrak {L}}$, $u_{\lambda }\in S_{\lambda }$ and $0<\mu <\lambda$, then $\mu \in {\mathfrak {L}}$ and there exists $u_{\mu }\in S_{\mu }$ such that $u_{\mu }\le u_{\lambda }$.

We can improve this corollary.

Proposition 3.4

If hypotheses ${\hat{H}},H_{0},H$ hold, $\lambda \in {\mathfrak {L}}$, $u_{\lambda }\in S_{\lambda }$ and $0<\mu <\lambda$, then $\mu \in {\mathfrak {L}}$ and there exists $u_{\mu }\in S_{\mu }$ such that

$$\begin{aligned} u_\lambda -u_{\mu }\in D_+. \end{aligned}$$

Proof

From Corollary (3.3) we already know that $\mu \in {\mathfrak {L}}$ and there exists $u_{\mu }\in S_{\mu }\subseteq intC_{+}$ such that

$$\begin{aligned} 0\le u_{\mu }\le u_{\lambda }.\nonumber \\ \end{aligned}$$

(3.13)

Let $\rho =\Vert u_{\lambda }\Vert _{\infty }$ and let ${\hat{\xi }}_{\rho }>0$ be as postulated by hypotheses H(v). We can always take ${\hat{\xi }}_{\rho }>\frac{1}{\lambda }\Vert \xi \Vert _{\infty }$. We have

$$\begin{aligned}{} & {} -div a (Du_{\mu })+(\xi (z)+\lambda {\hat{\xi }}_{\rho })u_{\mu }^{p-1}=cu_{\mu }^{\tau -1}+\mu f(z,u_{\mu })+\lambda {\hat{\xi }}_{\rho }u_{\mu }^{p-1} \nonumber \\{} & {} \quad =cu_{\mu }^{\tau -1}+\lambda [ f(z,u_{\mu })+ {\hat{\xi }}_{\rho }u_{\mu }^{p-1}]-(\lambda -\mu )f(z,u_{\mu }) \nonumber \\{} & {} \quad \le cu_{\lambda }^{\tau -1}+\lambda f(z,u_{\lambda })+\lambda {\hat{\xi }}_{\rho }u_{\lambda }^{p-1} \ (\text {see }(3.13)\text {see and hypotheses H(v)})\nonumber \\{} & {} \quad =-div a(Du_{\lambda })+(\xi (z)+\lambda {\hat{\xi }}_{\rho }u_{\lambda }^{p-1} \ \text {in} \ \Omega \ \ (\text {since} \ \ u_{\lambda }\in S_{\lambda }). \end{aligned}$$

(3.14)

Since $u_{\mu }\in intC_{+}$, we have $u_{\mu }(z)\ge s>0$ for all $z\in {\bar{\Omega }}$. Therefore

$$\begin{aligned} 0<\eta _{s}\le f(z,u_{\mu }(z)) \ \text {for almost all} \ \ z\in \Omega \ (\text {see hypotheses H(v)}). \end{aligned}$$

Then from (3.14) and Proposition 6 of Papageorgiou–Radulescu–Repovs [13], we have that

$$\begin{aligned} u_\lambda -u_{\mu }\in D_+. \end{aligned}$$

$\square$

Let $\lambda ^{*}=\sup {\mathfrak {L}}.$

Proposition 3.5

If hypotheses ${\hat{H}},H_{0},H$ hold, then $\lambda ^{*}<\infty .$

Proof

Hypotheses H and the fact that $\xi \in L^{\infty }(\Omega )$, imply that we can find $\lambda _{0}>0$ such that

$$\begin{aligned} cx^{\tau -1}+\lambda _{0}f(z,x)\ge \Vert \xi \Vert _{\infty }x^{p-1} \ \text {for almost all} \ z\in \Omega , \ \text {all} \ x\ge 0.\qquad \end{aligned}$$

(3.15)

Let $\lambda > \lambda _{0}$ and suppose that $\lambda \in {\mathfrak {L}}$. We can find $u_{\lambda }\in S_{\lambda }\subseteq int C_+.$ Let $m=\underset{{\bar{\Omega }}}{min} \ u_{\lambda }>0$ and for $\delta >0$ let $m_{\delta }=m+\delta$. For $\rho =\Vert u_{\lambda }\Vert _{\infty }$, let ${\hat{\xi }}_{\rho }>0$ be as postulated by hypothesis H(v). We can always take ${\hat{\xi }}_{\rho }>\frac{1}{\lambda }\Vert \xi \Vert _{\infty }$. Then we have

$$\begin{aligned}{} & {} -div \ a(Dm_{\delta })+(\xi (z)+\lambda {\hat{\xi }}_{\rho })m_{\delta }^{p-1} \nonumber \\{} & {} \quad \le (\Vert \xi \Vert _{\infty }+\lambda {\hat{\xi }}_{\rho })m^{p-1}+\varepsilon (\delta ) \ \ \text {where} \ \ \varepsilon (\delta )\rightarrow 0^+ \ \ \text {as} \ \ \delta \rightarrow 0^+ \nonumber \\{} & {} \quad \le cm^{\tau -1}+\lambda _{0}f(z,m)+\lambda {\hat{\xi }}_{\rho }m^{p-1}+\varepsilon (\delta ) \ \ (\text {see } [17]) \nonumber \\{} & {} \quad =cm^{\tau -1}+\lambda [f(z,m)+ {\hat{\xi }}_{\rho }m^{p-1}]-(\lambda -\lambda _{0})f(z,m)+\varepsilon (\delta ) \nonumber \\{} & {} \quad \le cu_{\lambda }^{\tau -1}+\lambda f(z,u_{\lambda })+\lambda {\hat{\xi }}_{\rho } u_{\lambda }^{p-1} \ \ \text {for} \ \ \delta >0 \ \ \text {small} \ \ (\text {see hypothesis H(v)}).\nonumber \\{} & {} \quad = -div \ a(D u_{\lambda })+(\xi (z)+\lambda {\hat{\xi }}_{\rho })u_{\lambda }^{p-1} \ \ \text {in} \ \Omega . \end{aligned}$$

(3.16)

Since $0\le \eta _{m}\le f(z,m)$ (see hypothesis H(v)) as before using Proposition 6 of [13], from (3.16) we obtain that

$$\begin{aligned} m_{\delta }<u_{\lambda }(z) \ \ \text {for all} \ \ z\in \Omega \ \ \text {and for} \ \ \delta \in (0,1) \ \text {small}; \end{aligned}$$

a contradiction to the definition of m. Therefore $\lambda \notin {\mathfrak {L}}$ and so $\lambda ^*\le \lambda _{0}<\infty$. $\square$

Therefore we can say that ${\mathfrak {L}}\subset (0,\infty )$ is a bounded interval and $(0,\lambda ^{*})\subseteq {\mathfrak {L}}\subseteq (0,\lambda ^*]$.

Next, we show that for $\lambda \in (0,\lambda ^*)$, we have a multiplicity of positive solutions for problem $(p_{\lambda })$.

Proposition 3.6

If hypotheses ${\hat{H}}$, $H_{0}$, H hold, then problem $(p_{\lambda })$ has at least two positive solutions

$$\begin{aligned} u_{0},{\hat{u}}\in intC_{+}. \end{aligned}$$

Proof

Let $0<\mu<\lambda <\theta$. From Proposition (3.4), we know that we can find $u_{\theta }\in S_{\theta }$, $u_{0}\in S_{\lambda }$ and $u_{\mu }\in S_{\mu }$ such that

$$\begin{aligned} u_{\theta }-u_0\in D_+ \ \ \text {and} \ \ u_0-u_\mu \in D_+ \ \ \Rightarrow u_0\in int _{C^{1}({\bar{\Omega }})}[u_\mu ,u_{\theta }]. \end{aligned}$$

(3.17)

Let $k>\frac{1}{\lambda }\Vert \xi \Vert _{\infty }$ and introduce the Caratheodory function $j_{\lambda }(z,x)$ defined by

$$\begin{aligned} j_{\lambda }(z,x)={\left\{ \begin{array}{ll} cu_{\mu }(z)^{\tau -1}+\lambda f(z,u_{\mu }(z))+ \lambda k u_{\mu }(z)^{p-1} \ \ \ \ \text {if} \ \ x<u_{\mu }(z) \\ cx^{\tau -1}+\lambda f(z,x)+ \lambda k x^{p-1} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text {if} \ \ u_{\mu }(z)\le x\le u_{\theta }(z) \\ cu_{\theta }(z)^{\tau -1}+\lambda f(z,u_{\theta }(z))+ \lambda k u_{\theta }(z)^{p-1} \ \ \ \ \ \text {if} \ \ u_{\theta }(z)<x. \end{array}\right. }\nonumber \\ \end{aligned}$$

(3.18)

We set $J_{\lambda }(z,x)=\int _{0}^{x}j_{\lambda }(z,s)ds$ and consider the $C^{1}$-functional $\sigma _{\lambda }:W^{1,p}(\Omega )\rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned} {\sigma }_{\lambda }(u)=\frac{1}{p}\gamma _{p}(u)+\frac{\lambda k}{p}\Vert u\Vert _{p}^{p}-\int _{\Omega }J_{\lambda }(z,u)dz \ \ \text {for all} \ u\in W^{1,p}(\Omega ). \end{aligned}$$

Using (3.18) and the nonlinear regularity theory, we obtain that

$$\begin{aligned} K_{{\sigma }_{\lambda }}\subseteq [u_{\mu },u_{\theta }]\cap int C_{+}. \end{aligned}$$

(3.19)

(see also the proof of Proposition (3.2)). From (3.18) and since $k>\frac{1}{\lambda }\Vert \xi \Vert _{\infty }$, we see that ${\sigma }_{\lambda }(.)$ is coercive. Also, it is sequentially weakly lower semicontinuous. Therefore we can find ${\tilde{u}}_{0}\in W^{1,p}(\Omega )$ such that

$$\begin{aligned} {\sigma }_{\lambda }({\tilde{u}}_{0})=\inf \{{\sigma }_{\lambda }(u): \ \ u\in W^{1,p}(\Omega ) \}\Rightarrow \ {\tilde{u}}_{0} \in K_{{\sigma }_{\lambda }}. \end{aligned}$$

If ${\tilde{u}}_{0}\ne u_0$, then on account of (3.19), (3.18), we see that ${\tilde{u}}_{0}$ is the second positive smooth solution of ($p_{\lambda }$) and so we are done. Therefore, we assume that ${\tilde{u}}_{0}=u_{0}\in intC_+$. Hence $u_{0}$ is a minimizer of ${\sigma }_{\lambda }(.)$. We introduce another Caratheodory function ${\hat{j}}_{\lambda }(z,x)$ defined by

$$\begin{aligned} {\hat{j}}_{\lambda }(z,x)={\left\{ \begin{array}{ll} cu_{\mu }(z)^{\tau -1}+\lambda f(z,u_{\mu }(z))+ \lambda k u_{\mu }(z)^{p-1} \ \ \ \ \text {if} \ \ x\le u_{\mu }(z) \\ cx^{\tau -1}+\lambda f(z,x)+ \lambda k x^{p-1} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text {if} \ \ u_{\mu }(z)<x. \end{array}\right. }\nonumber \\ \end{aligned}$$

(3.20)

We set ${\hat{J}}_{\lambda }(z,x)=\int _{0}^{x}\hat{j}_{\lambda }(z,s)ds$ and consider the $C^{1}$-functional ${\hat{\sigma }}_{\lambda }:W^{1,p}(\Omega )\rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned} \hat{{\sigma }}_{\lambda }(u)=\frac{1}{p}\gamma _{p}(u)+\frac{\lambda k}{p}\Vert u\Vert _{p}^{p}-\int _{\Omega }{\hat{J}}_{\lambda }(z,u)dz \ \ \text {for all} \ u\in W^{1,p}(\Omega ). \end{aligned}$$

Using (3.20) and the nonlinear regularity theory, we obtain that

$$\begin{aligned} K_{{\hat{\sigma }}_{\lambda }}\subseteq [u_{\mu })\cap int C_{+}. \end{aligned}$$

(3.21)

From (3.18) and (3.20), we see that

$$\begin{aligned} \hat{{\sigma }}_{\lambda }|_{[u_{\mu },u_{\theta }]}=\sigma _{\lambda }|_{[u_{\lambda },u_{\theta }]}. \end{aligned}$$

(3.22)

Recall that $u_0$ is a minimizer of $\sigma _{\lambda }(.)$. Then from (3.22) and (3.17), we infer that

$$\begin{aligned}{} & {} u_{0} \text { is a local }\ \ C^1({\bar{\Omega }})-\text {minimizer of} \ \ \hat{{\sigma }}_{\lambda }(.),\nonumber \\{} & {} \quad \Rightarrow u_{0} \text { is a local }\ \ W^{1,p}(\Omega )-\text {minimizer of} \ \ \hat{{\sigma }}_{\lambda }(.), \end{aligned}$$

(3.23)

(see [10], Prpoposition 2.12). From (3.21) and (3.20), we see that we may assume that $K_{\sigma _{\lambda }}$ is finite or otherwise we already have an infinity of positive smooth solutions and so we are done. Then (3.23) and Theorem 5.76, p.449 of [11], imply that we can find $\rho \in (0,1)$ small such that

$$\begin{aligned} \hat{{\sigma }}_{\lambda }(u_{0})<\inf \{\hat{{\sigma }}_{\lambda }(u): \ \ \Vert u-u_0\Vert =\rho \}={\hat{m}}_{\lambda }. \end{aligned}$$

(3.24)

If $u\in intC_+$, then on account of hypotheses H(ii), we have

$$\begin{aligned} \hat{{\sigma }}_{\lambda }(tu)\rightarrow -\infty \ \text {as} \ \ t\rightarrow \infty \end{aligned}$$

(3.25)

Using hypotheses H(iii) and reasoning as in the proof of Proposition 4 in [14], we show that

$$\begin{aligned} \hat{{\sigma }}_{\lambda }(.) \ \ \text {satisfies the} \ \ C-\text {condition}. \end{aligned}$$

(3.26)

From (3.24), (3.25) and (3.26) and the mountain pass theorem we can find ${\hat{u}}\in W^{1,p}(\Omega )$ such that

$$\begin{aligned} {\hat{u}}\in K_{{\hat{\sigma }}_{\lambda }}\subseteq [u_{\mu })\cap int C_+ \ \ (\text {see }(3.21), \ {\hat{\sigma }}_{\lambda }(u_0)<{\hat{m}}_{\lambda }\le {\hat{\sigma }}_{\lambda }({\hat{u}}) \ (\text {see }(3.24))\nonumber \\ \end{aligned}$$

(3.27)

Therefore ${\hat{u}}\in intC_+$ is the second positive smooth solution of $(p_\lambda )$ ($\lambda \in (0,\lambda ^*)$), distinct from $u_{0}$. $\square$

We need to determine the status of the critical parameter $\lambda ^*>0$.

Proposition 3.7

If hypotheses ${\hat{H}},H_{0},H$ hold, then $\lambda ^* \in {\mathfrak {L}}$.

Proof

Let $\{\lambda _n\}_{n\in {\mathbb {N}}}\subseteq {\mathfrak {L}}$ be such that $\lambda _n \rightarrow \lambda ^*$. From the proof of Proposition (3.8), we know that we can find $u_n\in S_{\lambda _{n}}\subseteq intC_+, \ \ n\in {\mathbb {N}}$ such that

$$\begin{aligned} {\hat{\sigma }}_{{\lambda _n}}(u_n)\le {\hat{\sigma }}_{{\lambda _n}}(u_1). \end{aligned}$$

(3.28)

Note that in the definition of ${\hat{J}}_{\lambda _{n}}(.,.)$ (see (3.20)), we replace $u_{\mu }$ by $u_1$ and $k>\frac{1}{\lambda _{1}}\Vert \xi \Vert _{\infty }$. We have

$$\begin{aligned} {\hat{\sigma }}_{\lambda _{n}}(u_1){} & {} =\frac{1}{p}\gamma _{p}(u_1)+\frac{\lambda _n k}{p}\Vert u_1\Vert _{p}^p-\int _{\Omega }[cu_1^{\tau -1}+\lambda _{n}f(z,u_1)+\lambda _n ku_1^{p-1}]u_1dz \\{} & {} \le \frac{1}{p}\gamma _{p}(u_1)+\frac{\lambda _n k}{p}\Vert u_1\Vert _{p}^p-\int _{\Omega }[cu_1^{\tau -1}\\{} & {} \quad +\lambda _{1}f(z,u_1)+\lambda _1 ku_1^{p-1}]u_1dz \ (\text {since} \ \lambda _1\le \lambda _{n} \ \text {for all} \ n\in {\mathbb {N}}, f\ge 0) \\{} & {} =\left( \frac{1}{p}-1\right) \gamma _{p}(u_{1})+\frac{\lambda _n-\lambda _1}{p}\Vert u_1\Vert _p^p \ \ \ \ (\text {since} \ u_1\in S_{\lambda _1} \ \text {and using } (2.1)) \\{} & {} \le \frac{\lambda ^*-\lambda _1}{p}k\Vert u_1\Vert _p^p=c^* \ \ \text {for all} \ \ n\in {\mathbb {N}} \end{aligned}$$

$$\begin{aligned} \Rightarrow {\hat{\sigma }}_{\lambda _n}(u_n)\le c^* \ \ \text {for all} \ \ n\in {\mathbb {N}} \ \ (\text {see }(3.28)). \end{aligned}$$

(3.29)

Also we have

$$\begin{aligned} \langle {\hat{\sigma }}_{{\lambda _n}}'(u_n),h \rangle =0 \ \ \text {for all} \ \ h\in W^{1,p}(\Omega ), \ \text {all} \ \ n\in {\mathbb {N}}. \end{aligned}$$

(3.30)

From (3.29) and (3.30) and following the argument which shows that the functional ${\hat{\sigma }}_\lambda (.)$ satisfies the C-condition (see in [14] the proof of Proposition 4 and recall that $\lambda _n\rightarrow \lambda ^*$), we obtain that

$$\begin{aligned} u_n\rightarrow u^* \ \text {in} \ \ W^{1,p}(\Omega ). \end{aligned}$$

(3.31)

Passing to the limit as $n\rightarrow \infty$ in (3.30) and using (3.31), we obtain

$$\begin{aligned} \langle \gamma _p'(u^*), h\rangle= & {} \int _{\Omega }[c(u^*)^{\tau -1}+\lambda ^*f(z,u^*)]hdz \ \ \text {for all} \ \ h\in W^{1,p}(\Omega ),\nonumber \\\Rightarrow & {} u^*\in S_{\lambda ^*} \ \ \text {and so} \ \ \lambda ^*\in {\mathfrak {L}}. \end{aligned}$$

(3.32)

$\square$

Summarizing, we can state the following existence and multiplicity theorem for the problem $(p_{\lambda })$, which is global in the parameter $\lambda >0$ (a bifurcation-type theorem).

Theorem 3.8

If hypotheses ${\hat{H}},H_{0},H$ hold, then there exists $\lambda ^*$ such that

• (a) for all $\lambda \in (0,\lambda ^*)$, problem $(p_{\lambda })$ has at least two positive solutions

  $$\begin{aligned} u_{0},{\hat{u}}\in intC_{+}; \end{aligned}$$

• (b) for $\lambda =\lambda ^*$, problem $(p_{\lambda })$ has at least one positive solution

  $$\begin{aligned} u^{*}\in intC_{+}; \end{aligned}$$

• (c) for all $\lambda >\lambda ^*$, problem $(p_{\lambda })$ has no positive solutions.