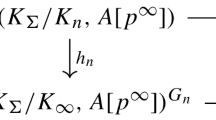Boundedness of Iwasawa Invariants of Fine Selmer Groups and Selmer Groups

Abstract

In this article we consider Selmer groups and fine Selmer groups of abelian varieties over a number field K. Following a classical approach of Monsky for Iwasawa modules from ideal class groups, we give sufficient conditions for the Iwasawa $\mu$-invariants of the fine Selmer groups and the $\mu$-invariants of the Selmer groups to be bounded as one runs over the $\mathbb {Z}_p$-extensions of K. Moreover, we describe a criterion for the boundedness of Iwasawa $\lambda$-invariants of Selmer groups and fine Selmer groups over multiple $\mathbb {Z}_p$-extensions which generalises a criterion of Monsky from dimension 2 to arbitrary dimension.

1 Introduction

Classical Iwasawa theory is concerned with the growth of class numbers in $\mathbb {Z}_p$-extensions of number fields. To be more precise, let $K_\infty /K$ be a $\mathbb {Z}_p$-extension, with intermediate fields $K_n$, ${n \in \mathbb {N}}$, and let $h_n$ denote the class number of $K_n$. By a famous result of Iwasawa (see [11]), we have

$$\begin{aligned} v_p(h_n) = \mu \cdot p^n + \lambda \cdot n + \nu \end{aligned}$$

(1)

for each sufficiently large ${n \in \mathbb {N}}$. The so-called Iwasawa invariants ${\mu \ge 0}$, ${\lambda \ge 0}$ and ${\nu \in \mathbb {Z}}$ do not depend on n, but they do depend on the chosen $\mathbb {Z}_p$-extension $K_\infty$ of K.

Having fixed K and p, Greenberg studied in [8] whether the Iwasawa invariants are bounded as one runs over the $\mathbb {Z}_p$-extensions of K, and he was able to obtain first partial results. A few years later, Monsky and independently Babaĭcev (see [1, 26]) proved that the $\mu$-invariants of the $\mathbb {Z}_p$-extensions of a fixed number field K are indeed bounded.

On the other hand, the corresponding question for the $\lambda$-invariants is still open. In [26, Theorem IV], Monsky obtained a necessary and sufficient criterion for the boundedness of the $\lambda$-invariants of the $\mathbb {Z}_p$-extensions of K which are contained in any fixed $\mathbb {Z}_p^2$-extension of K.

It is the main aim of this article to prove analogous results in a more general context. To be more precise, fix K and p, and let A be an abelian variety defined over K. We let $X_A^{(K_\infty )}$ and $Y_A^{(K_\infty )}$ denote the Pontryagin duals of the Selmer group and the fine Selmer group of A over a $\mathbb {Z}_p$-extension $K_\infty$ of K (see Sect. 2.2 for the definitions). The investigation of the Selmer groups (respectively, the fine Selmer groups) has been introduced into Iwasawa theory by Mazur (respectively, Coates and Sujatha), see [6, 24]. This is probably the most vital branch of modern Iwasawa theory.

One can attach $\mu$- and $\lambda$-invariants to each $X_A^{(K_\infty )}$ and $Y_A^{(K_\infty )}$. Some technical problems arise since these objects need not be torsion modules over the Iwasawa algebra ${\Lambda = \mathbb {Z}_p[[T]]}$. The following theorem is our first main result (see also Theorem 3.20 below).

Theorem 1.1

Let K be a number field. Suppose that $Y_A^{(K_\infty )}$ is $\Lambda$-torsion for all but finitely many $\mathbb {Z}_p$-extensions $K_\infty$ of K. Then $\mu (Y_A^{(K_\infty )})$ is bounded.

An analogous statement holds for the Selmer groups, provided that A has good ordinary reduction at the primes of K above p, and that the inertia subgroup of $\text{ Gal }(\mathbb {L}_\infty /K)$ of every prime of K above p has $\mathbb {Z}_p$-rank at least $d-1$.

In [5], Cuoco and Monsky proved a generalisation of Iwasawa’s growth formula (1) for multiple $\mathbb {Z}_p$-extensions: If $K_n$ now denotes the nth layer in a $\mathbb {Z}_p^d$-extension $\mathbb {L}_\infty /K$, then

$$\begin{aligned} v_p(h_n) = m_0 \cdot p^{dn} + l_0 \cdot n p^{n(d-1)} + O(p^{n(d-1)}). \end{aligned}$$

(2)

We call the leading coefficients $m_0, l_0 \ge 0$ of this asymptotic formula the generalised Iwasawa invariants of the $\mathbb {Z}_p^d$-extension $\mathbb {L}_\infty /K$.

In [26, Theorem IV], Monsky obtained the following criterion for the boundedness of $\lambda$-invariants: If $\mathbb {L}_\infty /K$ is a $\mathbb {Z}_p^2$-extension, then the $\lambda$-invariants of the $\mathbb {Z}_p$-extensions $K_\infty$ of K which are contained in $\mathbb {L}_\infty$ are bounded if and only if ${l_0(\mathbb {L}_\infty /K) = 0}$.

The definition of the $l_0$-invariant of an Iwasawa module is a bit complicated (see Sect. 2.2), and its meaning is mysterious. In this article we propose the definition of a slightly modified invariant $\widehat{l_0}$, which coincides with the original $l_0$-invariant of Cuoco and Monsky in the case of $\mathbb {Z}_p^2$-extensions (more precisely, for Iwasawa modules over the Iwasawa algebra ${\Lambda _2 = \mathbb {Z}_p[[T_1, T_2]]}$), but may differ from $l_0$ for $\mathbb {Z}_p^d$-extensions with ${d > 2}$. Using this invariant $\widehat{l_0}$, we can generalise Monsky’s criterion to the setting of $\mathbb {Z}_p^d$-extensions. For the sake of simplicity, we do not state here in the introduction the best possible formulation of our result (see also Theorem 3.22 below):

Theorem 1.2

Let $\mathbb {L}_\infty /K$ be a $\mathbb {Z}_p^d$-extension, ${d \ge 2}$, and suppose that $Y_A^{(K_\infty )}$ is $\Lambda$-torsion for each $\mathbb {Z}_p$-extension ${K_\infty \subseteq \mathbb {L}_\infty }$ of K. We assume that the decomposition subgroup in $\text{ Gal }(\mathbb {L}_\infty /K)$ of every prime of K above p is open, and that $Y_A^{(K_\infty )}$ does not contain any non-trivial pseudo-null $\Lambda _d$-submodules. Then $\lambda (Y_A^{(K_\infty )})$ is bounded as one runs over the $\mathbb {Z}_p$-extensions ${K_\infty \subseteq \mathbb {L}_\infty }$ of K if and only if ${\widehat{l_0}(Y_A^{(\mathbb {L}_\infty )}) = 0}$.

An analogous result holds for Selmer groups, provided that A has good ordinary reduction at the primes of K above p, and that each of these primes ramifies in $\mathbb {L}_\infty /K$.

In [18] the first-named author constructed an example of an imaginary-quadratic number field K such that $\lambda (X_A^{(K_\infty )})$ was unbounded as $K_\infty$ runs over the $\mathbb {Z}_p$-extensions of K (here A was a suitable elliptic curve defined over K). Since the composite of all $\mathbb {Z}_p$-extensions of K is a $\mathbb {Z}_p^2$-extension $\mathbb {L}_\infty$ of K, we may use Theorem 1.2 to deduce that ${l_0(X_A^{(\mathbb {L}_\infty )}) > 0}$. To the authors’ knowledge, this yields the first known example of an Iwasawa module with a non-trivial $l_0$-invariant over an Iwasawa algebra of a $\mathbb {Z}_p^d$-extension with ${d > 1}$. In the last section, we show how to derive examples of $\mathbb {Z}_p^d$-extensions $\mathbb {L}_\infty$ of K with arbitrarily large d and ${\widehat{l_0}(X_A^{(\mathbb {L}_\infty )}) > 0}$. (For more information on the relations between the invariants $l_0$ and $\widehat{l_0}$ we refer the reader to the definitions in Sect. 2.2 and to the end of Sect. 3.3, where we prove several results relating $l_0$ and $\widehat{l_0}$, see for example Proposition 3.25).

Let us briefly describe the structure of the article. In Sect. 2 we introduce the general background on Iwasawa modules, (generalised) Iwasawa invariants, Selmer groups and fine Selmer groups, and we describe a topology on the set of $\mathbb {Z}_p$-extensions of K which is due to Greenberg. Section 3 contains two preliminary subsections where we prove auxiliary results on Iwasawa modules, and the control theorems which we need. Section 3.3 is devoted to the proofs of our main results.

In Sect. 4, we derive several applications. First, we study the relations between the variation of $\mu$- and $\lambda$-invariants, and the weak Leopoldt conjecture. Finally, we construct examples of Iwasawa modules with non-trivial $l_0$- and $\widehat{l_0}$-invariant.

2 Notation

2.1 General Notation

Fix a number field K and a prime number p, and let $\Sigma$ be a finite set of primes of K. For any (possibly infinite) algebraic extension N of K, we denote by $\Sigma (N)$ the set of primes w of N which divide some $v \in \Sigma$. Moreover, $\Sigma _p(N)$ will denote the subset of $\Sigma (N)$ which consists of the primes above p (usually our set $\Sigma$ will contain all the primes of K above p).

We denote by ${G_K = \text{ Gal }({\overline{K}}/K)}$ the absolute Galois group of K, i.e. ${\overline{K}}$ is a fixed algebraic closure of K. Moreover, $K_\Sigma$ will denote the maximal algebraic (non-necessarily abelian) extension of K which is unramified outside of $\Sigma$.

For any abelian group G, we denote by $G[p^\infty ]$ the subgroup of p-power torsion elements of G.

2.2 Group Rings and Iwasawa Modules

For every $\mathbb {Z}_p^d$-extension $K_\infty /K$, ${d \in \mathbb {N}}$, the completed group ring $\mathbb {Z}_p[[\text{ Gal }(K_\infty /K)]]$ can be identified (non-canonically) with the ring

$$\begin{aligned} \Lambda _d:= \mathbb {Z}_p[[T_1, \ldots , T_d]] \end{aligned}$$

of formal power series in d variables over $\mathbb {Z}_p$. In [5], Cuoco and Monsky introduced, in this setting, the generalised Iwasawa invariants of any finitely generated and torsion $\Lambda _d$-module, $d > 1$, as follows: To each such module M, one can attach an elementary torsion $\Lambda _d$-module of the form

$$\begin{aligned} E_M = \bigoplus _{i=1}^s \Lambda _d/(p^{m_i}) \oplus \bigoplus _{j = 1}^t \Lambda _d/(g_j^{n_j}), \end{aligned}$$

where all the exponents are natural numbers and the $g_j$ are irreducible elements of $\Lambda _d$ which are coprime with p. Moreover, one has a $\Lambda _d$-module homomorphism $\varphi :M \longrightarrow E_M$, the kernel and cokernel of which are pseudo-null over $\Lambda _d$, i.e. annihilated by two relatively prime elements of the unique factorisation domain $\Lambda _d$. In fact, the kernel of any such homomorphism $\varphi$ is the maximal pseudo-null submodule of M, which we denote by $M^\circ$. The element $F_M = \prod _{i=1}^s p^{m_i} \cdot \prod _{j = 1}^t g_j^{n_j}$ is called the characteristic power series of M. It is determined uniquely by M up to multiplication by units of $\Lambda _d$. In particular, if ${E_M = \{0\}}$ (this happens if and only if ${M = M^\circ }$ is pseudo-null), then we set ${F_M = 1}$.

One then defines the generalised Iwasawa invariants of M as follows. First, $m_0(M) = \sum _{i=1}^s m_i$. The definition of the second invariant is more involved. Recall that $\Lambda _d$ has been identified with the completed group ring $\mathbb {Z}_p[[\text{ Gal }(K_\infty /K)]]$. We write ${F_M = p^{m_0(M)} \cdot G_M}$, and we consider the image $\overline{G_M}$ of $G_M$ in the quotient ring $\Lambda _d/p \Lambda _d$. We let $l_0(M)$ be the sum of the valuations $v_{\mathfrak {p}}(\overline{G_M})$, where ${\mathfrak {p}}$ runs over the primes of $\Lambda _d/p \Lambda _d$ of the form ${\overline{\gamma - 1}}$, with ${\gamma \in \text{ Gal }(K_\infty /K)}$ not a pth power (since $\Lambda _d/p \Lambda _d$ is again a unique factorisation domain, this sum is in fact finite). Note that ${l_0(M) = \lambda (M)}$ if ${d = 1}$.

In this paper, we will also use an alternative definition of the $l_0$-invariant, which might be more appropriate for $\Lambda _d$-modules, ${d > 2}$, than the classical $l_0$-invariant (this is motivated by some results in Sect. 3). To this purpose, we assume that ${d \ge 2}$, and we again write the characteristic power series ${F_M \in \Lambda _d}$ of a finitely generated $\Lambda _d$-module M as ${F_M = p^{m_0(M)} \cdot G_M}$, i.e. ${p \not \mid G_M}$. Now we define

$$\begin{aligned} \widehat{l_0}(M) = \sum _{{\mathfrak {p}}} v_{{\mathfrak {p}}}(\overline{G_M}), \end{aligned}$$

where $\overline{G_M} \in \Omega _d:= \Lambda _d/p \Lambda _d$, and where now ${\mathfrak {p}}$ runs over the prime ideals of $\Omega _d$ which are minimal over $(\overline{G_M})$ and contained in a prime ideal of the form

$$\begin{aligned} {\mathcal {P}} = (\overline{\sigma _1 - 1}, \ldots , \overline{\sigma _{d-1} - 1}), \end{aligned}$$

where ${\sigma _1, \ldots , \sigma _{d-1} \in \text{ Gal }(K_\infty /K)}$ generate a subgroup which is isomorphic to $\mathbb {Z}_p^{d-1}$. Note that this coincides with the original definition of $l_0$ in the case ${d =2}$ since the prime ideals of $\Omega _2$ of the form $(\overline{\gamma - 1})$ have height 1. It is important to restrict to minimal primes in the case ${d> 2}$ in order to guarantee that the sum $\widehat{l_0}(M)$ is finite.

In the special case of a $\mathbb {Z}_p$-extension, one has a more precise structure theory (see [11]). In this case, we usually abbreviate $\Lambda _1$ to $\Lambda$. In fact, to any (non-necessarily torsion) finitely generated $\Lambda _1$-module M, we can attach an elementary $\Lambda _1$-module of the form

$$\begin{aligned} E_M = \Lambda ^r \oplus \bigoplus _{i = 1}^s \Lambda /(p^{m_i}) \oplus \bigoplus _{j = 1}^t \Lambda /(g_j^{n_j}), \end{aligned}$$

where the $g_j$ are now so-called distinguished polynomials, i.e. they are monic polynomials, and each coefficient besides the leading one is divisible by p. We let $\mu (M) = \sum _{i=1}^s m_i$ (i.e. ${\mu (M) = m_0(M)}$ in the case of finitely generated and torsion $\Lambda _1$-modules) and ${\lambda (M) = \sum _{j = 1}^t \deg (g_j^{n_j})}$. Using the fact that the $g_j$ are distinguished, it is easy to see that ${\lambda (M) = l_0(M)}$ for finitely generated torsion $\Lambda _1$-modules. Again, one defines the characteristic power series ${F_M \in \Lambda }$ of M (which now differs from a polynomial only by some unit in $\Lambda ^\times$) to be the product of the powers of p and the distinguished polynomials $g_j^{n_j}$ occuring in the definition of $E_M$.

Using the Weierstraß Preparation Theorem (see [32, Theorem 7.3]), we can define Iwasawa invariants of any non-zero element ${f \in \Lambda }$, as follows: f can be written uniquely as

$$\begin{aligned} f = u \cdot p^m \cdot g, \end{aligned}$$

where $u \in \Lambda ^\times$, $m \in \mathbb {N}$, and ${g \in \Lambda }$ is a distinguished polynomial. Then we let ${\mu (F):= m}$ and ${\lambda (f):= \deg (g)}$. Under this point of view, the Iwasawa invariants of a finitely generated $\Lambda$-module M are just the Iwasawa invariants of the associated characteristic power series ${F_M \in \Lambda }$ of M.

We conclude the current subsection with some remarks on Fitting ideals. For a general summary on the properties of Fitting ideals, we refer to [32, Section 13.6], [28, Chapter 3] and [13, Appendix A]. In this article, we will restrict to the zero-th Fitting ideals of Iwasawa modules.

Let M be a finitely generated $\Lambda _d$-module, ${d \in \mathbb {N}}$. Recall the definition of the Fitting ideal ${\mathcal {F}}_{\Lambda _d}(M)$: Take a presentation

$$\begin{aligned} \Lambda _d^q {\mathop {\longrightarrow }\limits ^{\rho }} \Lambda _d^l \longrightarrow M, \end{aligned}$$

(3)

and let A be a ${q \times l}$-matrix with entries in $\Lambda _d$ which describes the map $\rho$. If M is torsion, then we must have ${q \ge l}$. Then we let ${\mathcal {F}}_{\Lambda _d}(M)$ be the ideal of $\Lambda _d$ generated by all the l-minors of A if M is torsion, and we define it to be the zero ideal if ${q < l}$. We summarise all the facts on the Fitting ideal which we will need in the following

Proposition 2.1

Let M be a finitely generated $\Lambda _d$-module, and let ${\text{ Ann }(M) \subseteq \Lambda _d}$ denote its annihilator ideal. Then the following statements hold.

• (1) The definition of ${\mathcal {F}}_{\Lambda _d}(M)$ does not depend on the choice of the presentation (3) of M.

• (2) If M can be generated over $\Lambda _d$ by l elements, then

  $$\begin{aligned} \text{ Ann }(M)^l \subseteq {\mathcal {F}}_{\Lambda _d}(M) \subseteq \text{ Ann }(M). \end{aligned}$$

  In particular, if M is not a torsion $\Lambda _d$-module, then ${{\mathcal {F}}_{\Lambda _d}(M) = (0)}$.

• (3) Suppose that M is $\Lambda _d$-torsion. Let ${M^\circ \subseteq M}$ be the maximal pseudo-null $\Lambda _d$-submodule, and let $E_M$ be an elementary $\Lambda _d$-module which is pseudo-isomorphic to M. If M can be generated over $\Lambda _d$ by l elements, then

  $$\begin{aligned} \text{ Ann }(M^\circ ) \text{ Ann }(E_M) \subseteq \text{ Ann }(M) \end{aligned}$$

  and

  $$\begin{aligned} \text{ Ann }(M^\circ )^l \text{ Ann }(E_M)^l \subseteq {\mathcal {F}}_{\Lambda _d}(M). \end{aligned}$$

• (4) If ${i < d}$ and $\pi : \Lambda _d \longrightarrow \Lambda _i$ denotes a surjective ring homomorphism, then

  $$\begin{aligned} {\mathcal {F}}_{\Lambda _i}(M/\ker (\pi )) = \pi ({\mathcal {F}}_{\Lambda _d}(M)). \end{aligned}$$

• (5) Suppose that M is $\Lambda _d$-torsion. Then we can write

  $$\begin{aligned} {\mathcal {F}}_{\Lambda _d}(M) = (F_M) \cdot J_M, \end{aligned}$$

  where the ideal $J_M$ of $\Lambda _d$ is not contained in any height one prime ideal of $\Lambda _d$.

• (6) Now suppose that $d = 1$, and that M is torsion. Then

  $$\begin{aligned} {\mathcal {F}}_{\Lambda _1}(M) = (F_M) \cdot {\mathcal {F}}_{\Lambda _1}(M^\circ ). \end{aligned}$$

Proof

The first statement follows from [7, Corollary 20.4], and (2) is [7, Proposition 20.7].

The first statement in (3) follows from the exact sequence

$$\begin{aligned} 0 \longrightarrow M^\circ \longrightarrow M \longrightarrow E_M, \end{aligned}$$

and the second part of (3) follows by combining the first part with (2).

Assertion (4) follows from [13, Lemma A.6]. Now we turn to the proof of (5). Choose a presentation as in (3) and let A be the corresponding matrix. We will show that the greatest common divisor of the ${l \times l}$-minors of A is equal to $F_M$; this proves the assertion.

To this purpose, we will argue prime-by-prime. Let g be an irreducible element of $\Lambda _d$ (which may or may not divide the characteristic power series $F_M$ of M). In the following, we localise at g. Note that $(\Lambda _d)_{(g)}$ is a flat $\Lambda _d$-module and that ${N_{(g)} \cong N \otimes _{\Lambda _d} (\Lambda _d)_{(g)}}$ for any finitely generated $\Lambda$-module N. Therefore we obtain from the exact sequence

$$\begin{aligned} 0 \longrightarrow M^\circ \longrightarrow M \longrightarrow E_M \longrightarrow C \longrightarrow 0, \end{aligned}$$

with $E_M$ elementary and C pseudo-null over $\Lambda _d$, an exact sequence

$$\begin{aligned} 0 \longrightarrow (M^\circ )_{(g)} \longrightarrow M_{(g)} \longrightarrow (E_M)_{(g)} \longrightarrow C_{(g)} \end{aligned}$$

of finitely generated $(\Lambda _d)_{(g)}$-modules. Since both $M^\circ$ and C are pseudo-null over $\Lambda _d$, there exists an element h which is coprime with g and annihilates both $M^\circ$ and C. Since h is a unit in $(\Lambda _d)_{(g)}$, we may conclude that both $(M^\circ )_{(g)}$ and $C_{(g)}$ are zero.

We therefore obtain an isomorphism

$$\begin{aligned} M_{(g)} \cong (E_M)_{(g)}. \end{aligned}$$

Note that $(\Lambda _d)_{(g)}$ is a discrete valuation ring with maximal ideal (g). Writing

$$\begin{aligned} E_M = \bigoplus _{i = 1}^s \Lambda _d/(f_i) \end{aligned}$$

with $f_i \in \Lambda _d$ (here $f_i$ may be equal to p), we obtain that

$$\begin{aligned} M_{(g)} \cong \bigoplus _{i = 1}^s (\Lambda _d)_{(g)}/(f_i). \end{aligned}$$

(4)

In particular, ${M_{(g)} = 0}$ if each $f_i$ is coprime with g.

On the other hand, it follows from the presentation (3) that we have an exact sequence

$$\begin{aligned} (\Lambda _d)_{(g)}^q {\mathop {\longrightarrow }\limits ^{\rho }} (\Lambda _d)^l_{(g)} \longrightarrow M_{(g)} \longrightarrow 0. \end{aligned}$$

Let A be the matrix representing the map $\rho$. Then ${\mathcal {F}}_{(\Lambda _d)_{(g)}}(M_{(g)})$ is the ideal generated by the images of the ${l \times l}$-minors of A under the natural map ${\Lambda _d \longrightarrow (\Lambda _d)_{(g)}}$.

It follows from [2, Theorem 2.9.6] that the greatest common divisor of the ${l \times l}$-minors of the matrix A (considered as a matrix over the principal ideal domain $(\Lambda _d)_{(g)}$) is equal to the product of the first l principal divisors of $M_{(g)}$. In view of (4), we may conclude that

$$\begin{aligned} v_{(g)}({\mathcal {F}}_{(\Lambda _d)_{(g)}}) = v_g(F_M). \end{aligned}$$

This concludes the proof of (5).

Now suppose that ${d = 1}$. The theory of Fitting ideals over ${\Lambda := \Lambda _1}$ is better understood. One of the reasons is that a finitely generated torsion $\Lambda$-module M has projective dimension 1 if and only if it does not contain any non-trivial pseudo-null (i.e. finite) $\Lambda$-submodules (see e.g. [29, Proposition 5.3.19]). We therefore may proceed as follows.

We start from the usual exact sequence

$$\begin{aligned} 0 \longrightarrow M^\circ \longrightarrow M \longrightarrow {\tilde{E}}_M \longrightarrow 0, \end{aligned}$$

where ${{\tilde{E}}_M \subseteq E_M}$. Since $E_M$ does not contain any non-trivial finite $\Lambda$-submod- ules, the submodule ${\tilde{E}}_M$ has projective dimension at most 1. Therefore we can use [28, Chapter 3, Theorem 22] in order to deduce from the exact sequence that

$$\begin{aligned} {\mathcal {F}}_{\Lambda }(M) = {\mathcal {F}}_{\Lambda }({\tilde{E}}_M) \cdot {\mathcal {F}}_\Lambda (M^\circ ). \end{aligned}$$

Moreover, since ${\tilde{E}}_M$ has projective dimension at most one, it follows from [13, Lemma A.7] that ${\mathcal {F}}_\Lambda ({\tilde{E}}_M)$ equals the characteristic ideal of ${\tilde{E}}_M$. As ${\tilde{E}}_M$ is pseudo-isomorphic to $E_M$ and M, we may conclude that

$$\begin{aligned} {\mathcal {F}}_\Lambda ({\tilde{E}}_M) = (F_M). \end{aligned}$$

This concludes the proof of the proposition. $\square$

2.3 Selmer Groups and Fine Selmer Groups

Fix a number field K, a prime number p, and let A be an abelian variety defined over K. Also fix a finite set $\Sigma$ of primes of K which contains the primes above p and the set $\Sigma _{\text{ br }}(A)$ of primes where A has bad reduction. If $p = 2$, then we assume that K is totally imaginary. For any number field L and a prime w of L, we denote by $L_w$ the completion of L at w.

Let $K_\infty$ be a $\mathbb {Z}_p^d$-extension of K, $d \ge 1$, with intermediate fields $K_n$ (i.e., ${\text{ Gal }(K_n/K)}$ is isomorphic to $(\mathbb {Z}/p^n\mathbb {Z})^d$ for every $n \in \mathbb {N}$). Then we define the Selmer group of A over $K_n$ as

$$\begin{aligned} \text{ Sel}_A(K_n):= \ker \left( H^1(K_\Sigma /K_n, A[p^\infty ]) \longrightarrow \prod \limits _{v \in \Sigma (K_n)} H^1(K_{n,v}, A)[p^\infty ] \right) , \end{aligned}$$

where $K_\Sigma$ is defined as in Sect. 2.1 (note that ${K_\infty \subseteq K_\Sigma }$ because $\Sigma$ contains the primes above p by assumption). This definition does not depend on the choice of $\Sigma$, as long as $\Sigma$ contains $\Sigma _p(K)$ and $\Sigma _{\text{ ram }}(A)$ (see [25, Corollary 6.6]).

Moreover, we define the fine Selmer group of A over $K_n$ as

$$\begin{aligned} \text{ Sel}_{A,0}(K_n):= \ker \left( H^1(K_\Sigma /K_n, A[p^\infty ]) \longrightarrow \prod \limits _{v \in \Sigma (K_n)} H^1(K_{n,v}, A[p^\infty ])\right) . \end{aligned}$$

This definition does not depend on the set $\Sigma$, for it can be seen that for any finite set $\Sigma$ containing the primes above p and the set $\Sigma _{\text{ br }}(A)$ we have an exact sequence

$$\begin{aligned} 0 \longrightarrow \text{ Sel}_{A,0}(K_n) \longrightarrow \text{ Sel}_A(K_n) \longrightarrow \prod \limits _{v \mid p} H^1(K_{n,v}, A[p^\infty ]). \end{aligned}$$

Now let

$$\begin{aligned} X_A^{(K_n)} = \text{ Sel}_A(K_n)^\vee \end{aligned}$$

and

$$\begin{aligned} Y_A^{(K_n)} = \text{ Sel}_{A,0}(K_n)^\vee \end{aligned}$$

be the Pontryagin duals. Finally, we define

$$\begin{aligned} X_A^{(K_\infty )} = \varprojlim _n X_A^{(K_n)} \end{aligned}$$

and

$$\begin{aligned} Y_A^{(K_\infty )} = \varprojlim _n Y_A^{(K_n)}, \end{aligned}$$

where the projective limits are taken with respect to the dual of the restriction maps from cohomology. It is well-known that both $X_A^{(K_\infty )}$ and $Y_A^{(K_\infty )}$ are finitely generated $\Lambda _d$-modules (as in the previous subsection, we identify $\mathbb {Z}_p[[\text{ Gal }(K_\infty /K)]]$ with $\Lambda _d$).

2.4 A Topology on the Set of $\mathbb {Z}_p$-Extensions of K

For any $\mathbb {Z}_p^d$-extension $\mathbb {L}_\infty$ of a number field K, we let ${\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)$ denote the set of $\mathbb {Z}_p$-extensions of K which are contained in $\mathbb {L}_\infty$. In the following we assume that ${d \ge 2}$, so that the set ${\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)$ is infinite. It follows from [8, p. 208] that this set is compact with respect to the following topology (which we will call Greenberg’s topology). A basis of this topology is given by the following sets: For any ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$ and every ${n \in \mathbb {N}}$, we define

$$\begin{aligned} {\mathcal {E}}(K_\infty ,n) = \left\{ {\tilde{K}}_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K) \, \Big | \, [({\tilde{K}}_\infty \cap K_\infty ): K] \ge p^n \right\} . \end{aligned}$$

In other words, ${\mathcal {E}}(K_\infty , n)$ contains the $\mathbb {Z}_p$-extensions of K which are subextensions of $\mathbb {L}_\infty$ and which coincide with $K_\infty$ at least up to the nth layer. Two $\mathbb {Z}_p$-extensions of K are close with respect to Greenberg’s topology if they have a large intersection, i.e. if they share a large number of common layers.

For any ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$, the restriction map ${\text{ Gal }(\mathbb {L}_\infty /K) \twoheadrightarrow \text{ Gal }(K_\infty /K)}$ on the Galois groups induces a canonical surjection

$$\begin{aligned} \pi _{K_\infty } :\Lambda _d = \mathbb {Z}_p[[T_1, \ldots , T_d]] \twoheadrightarrow \Lambda _1 = \mathbb {Z}_p[[S]], \end{aligned}$$

and the kernel of this map is the ideal of $\Lambda _d$ generated by the elements

$$\begin{aligned} \sigma _1 - 1, \ldots , \sigma _{d-1} - 1, \end{aligned}$$

where ${\sigma _1, \ldots , \sigma _{d-1}}$ are topological generators of the subgroup

$$\begin{aligned} \text{ Gal }(\mathbb {L}_\infty /K_\infty ) \subseteq \text{ Gal }(\mathbb {L}_\infty /K) \end{aligned}$$

fixing $K_\infty$. For every finitely generated $\Lambda _d$-module M, the quotient

$$\begin{aligned} M_{K_\infty } := M/(\sigma _1 -1, \ldots , \sigma _{d-1} - 1)M \end{aligned}$$

(5)

is a finitely generated $\mathbb {Z}_p[[S]]$-module.

Now we focus on the case $d = 2$. Fix topological generators $\sigma _1$ and $\sigma _2$ of ${G:= \text{ Gal }(\mathbb {L}_\infty /K) \cong \mathbb {Z}_p^2}$. For any $\mathbb {Z}_p$-extension ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$, let $\sigma _{K_\infty }$ be a topological generator of ${\text{ Gal }(K_\infty /K) \cong \mathbb {Z}_p}$. We consider the surjective map

$$\begin{aligned} \pi _{K_\infty } :\text{ Gal }(\mathbb {L}_\infty /K) \longrightarrow \text{ Gal }(K_\infty /K). \end{aligned}$$

Then

$$\begin{aligned} \pi _{K_\infty }(\sigma _1) = \sigma _{K_\infty }^{a_1}, \quad \pi _{K_\infty }(\sigma _2) = \sigma _{K_\infty }^{a_2} \end{aligned}$$

for suitable ${a_1, a_2 \in \mathbb {Z}_p}$, and not both of $a_1$ and $a_2$ are divisible by p (since $\pi _{K_\infty }$ is surjective). In fact, ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$ may be identified with the class ${[a_1: a_2]}$ of the pair $(a_1, a_2)$ in a projective space, since the topological generator of ${\text{ Gal }(K_\infty /K)}$ is unique only up to raising to a power with a unit exponent. Note that the tuple $[a_1: a_2]$ uniquely determines the kernel $\text{ Gal }(\mathbb {L}_\infty /K_\infty )$ of $\pi _{K_\infty }$. Therefore the set ${\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)$ can be identified with the projective one-dimensional space ${\mathbb {P}}^1(\mathbb {Z}_p)$ over $\mathbb {Z}_p$.

More generally, if $\mathbb {L}_\infty /K$ is a $\mathbb {Z}_p^d$-extension with ${d \ge 2}$ arbitrary and ${K_\infty \subseteq \mathbb {L}_\infty }$ is a $\mathbb {Z}_p$-extension of K, then the images of a fixed set of topological generators $\sigma _1, \ldots , \sigma _d$ of ${\text{ Gal }(\mathbb {L}_\infty /K) \cong \mathbb {Z}_p^d}$ under the map $\pi _{K_\infty }$ are of the form

$$\begin{aligned} \sigma _{K_\infty }^{a_1}, \ldots , \sigma _{K_\infty }^{a_d}, \end{aligned}$$

where ${a_1, \ldots , a_d \in \mathbb {Z}_p}$ are not all divisible by p. As in the special case ${d = 2}$, we can identify $K_\infty$ with the element ${[a_1: \cdots : a_d] \in {\mathbb {P}}^{d-1}(\mathbb {Z}_p)}$.

Let $T_i = \sigma _i - 1$ for each ${i \in \{1, \ldots , d\}}$. Moreover, we will use the notation

$$\begin{aligned} T_{K_\infty } = \sigma _{K_\infty } - 1. \end{aligned}$$

Then the restriction map

$$\begin{aligned} \pi _{K_\infty } :\Lambda _d \twoheadrightarrow \Lambda _1 \end{aligned}$$

maps $T_i$ to $(T_{K_\infty } + 1)^{a_i} - 1$, respectively. In [26], Monsky usually denotes the image of an element ${f \in \Lambda _d}$ under $\pi _{K_\infty }$ by $f_a$, where ${a = [a_1: \cdots : a_d] \in {\mathbb {P}}^{d-1}(\mathbb {Z}_p)}$ corresponds to the $\mathbb {Z}_p$-extension $K_\infty$ of K, as above.

In particular, if the topological generators $\sigma _1, \ldots , \sigma _d$ of $\text{ Gal }(\mathbb {L}_\infty /K)$ have been chosen such that $\sigma _1, \ldots , \sigma _{d-1}$ generate the subgroup $\text{ Gal }(\mathbb {L}_\infty /K_\infty )$ fixing $K_\infty$, then the kernel of $\pi _{K_\infty }$ is generated by ${T_1, \ldots , T_{d-1}}$, i.e. with this choice of topological generators of $\text{ Gal }(\mathbb {L}_\infty /K)$, the $\mathbb {Z}_p$-extension $K_\infty$ of K corresponds to

$$\begin{aligned} a = [0:\cdots :0:1] \in {\mathbb {P}}^{d-1}(\mathbb {Z}_p). \end{aligned}$$

Therefore

$$\begin{aligned} M_{K_\infty } = M/(\ker (\pi _{K_\infty }) \cdot M) \end{aligned}$$

for every finitely generated $\Lambda _d$-module M, where $M_{K_\infty }$ is defined as in (5).

Remark 2.2

Choosing a different topological generator of ${\text{ Gal }(K_\infty /K) \cong \mathbb {Z}_p}$ does not change the Iwasawa invariants of an element of ${\mathbb {Z}_p[[\text{ Gal }(K_\infty /K)]] \cong \Lambda _1}$. In particular, such a change of variables does not affect the $\mu$- or $\lambda$-invariant of a quotient module $M_{K_\infty }$.

Using the above notation, the $\mathbb {Z}_p$-extensions ${{\tilde{K}}_\infty \in {\mathcal {E}}(K_\infty ,n)}$, $n \in \mathbb {N}$, correspond to surjections $\pi _{{\tilde{K}}_\infty }$ that map the topological generators of $\text{ Gal }(\mathbb {L}_\infty /K_\infty )$ to elements in $\text{ Gal }({\tilde{K}}_\infty /K)^{p^n}$. Recall that in the above, ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$ has been identified with ${[a_1: \cdots : a_d] \in {\mathbb {P}}^{d-1}(\mathbb {Z}_p)}$. Then the $\mathbb {Z}_p$-extensions ${\tilde{K}}_\infty$ in the neighbourhood ${\mathcal {E}}(K_\infty ,n)$ of $K_\infty$ correspond to elements ${[b_1: \cdots : b_d] \in {\mathbb {P}}^{d-1}}{(\mathbb {Z}_p)}$ such that

$$\begin{aligned} b_i \equiv a_i \pmod {p^n} \end{aligned}$$

for every i.

3 Analogues of Monsky’s Boundedness Results

In [26], Monsky proved that the $\mu$-invariants of the $\mathbb {Z}_p$-extensions of a number field K are bounded, and he obtained sufficient criteria for the $\lambda$-invariants to be bounded as one runs over the $\mathbb {Z}_p$-extensions of K which are contained in some fixed $\mathbb {Z}_p^2$-extension of K.

In this section, we prove analogues of Monsky’s results in the setting of fine Selmer groups and Selmer groups. The module-theoretic results from [26, Sections 2 and 3] carry over immediately; we therefore state these results without proof in the first subsection. One of these results is then generalised from the ${d = 2}$ case to arbitrary ${d \ge 2}$. The second subsection contains the control theorems which we need, and in the final subsection we focus on the remaining parts of Monsky’s proof, which have to be adapted to the Selmer group setting.

3.1 Auxiliary Results on Iwasawa Modules Over $\mathbb {Z}_p^d$-Extensions

Fix a $\mathbb {Z}_p^d$-extension $\mathbb {L}_\infty /K$. As in Sect. 2.4, we write ${\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)$ for the set of $\mathbb {Z}_p$-extensions of K which are contained in $\mathbb {L}_\infty$. Let M be a finitely generated torsion $\Lambda _d$-module (as usual, we identify $\mathbb {Z}_p[[\text{ Gal }(\mathbb {L}_\infty /K)]]$ with $\Lambda _d$), and let $F_M$ be the characteristic power series of M. We recall that for every ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$, the quotient ${M_{K_\infty } = M/(\ker (\pi _{K_\infty }) \cdot M)}$ (see Sect. 2.4) is a finitely generated, but not necessarily torsion, $\mathbb {Z}_p[[\text{ Gal }(K_\infty /K)]]$-module.

Lemma 3.1

There exist non-trivial elements ${\sigma _1, \ldots , \sigma _l \in \text{ Gal }(\mathbb {L}_\infty /K)}$ such that for every $\mathbb {Z}_p$-extension ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$ of K such that $\sigma _i|_{K_\infty } \ne 1$ for each i, the quotient $M_{K_\infty }$ is a torsion $\Lambda _1$-module and satisfies

$$\begin{aligned} \mu (M_{K_\infty }) = m_0(M). \end{aligned}$$

Proof

This is [26, Theorem 3.2]. $\square$

In the next lemma we restrict to the case $d = 2$.

Lemma 3.2

Let $\mathbb {L}_\infty /K$ be a $\mathbb {Z}_p^2$-extension, let ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$ correspond to ${a = [a_1: a_2] \in {\mathbb {P}}^1(\mathbb {Z}_p)}$ (as in Sect. 2.4), and let $\pi _{K_\infty } = \pi _a :\Lambda _2 \longrightarrow \Lambda _1$ be the canonical surjection induced by the restriction map on the Galois groups. Choose a topological generator $\sigma$ of $\text{ Gal }(\mathbb {L}_\infty /K_\infty )$, and let ${T = \sigma - 1}$. We assume that ${M_{K_\infty } = M/(\ker (\pi _{K_\infty }) \cdot M)}$ is a torsion $\Lambda$-module, and we write ${F_M = p^{m_0(M)} \cdot G_M}$, where ${p \not \mid G_M}$.

Then

$$\begin{aligned} \lambda (M_{K_\infty }) = \lambda ((G_M)_a) \end{aligned}$$

is unbounded in any neighbourhood of $K_\infty$ if and only if the image ${\overline{G_M} \in \Lambda _2/ p \Lambda _2}$ of $G_M$ is divisible by ${\overline{T}}$.

Proof

See [26, Theorem 3.3]. $\square$

Monsky’s Lemma 3.2 can be generalised to $\mathbb {Z}_p^d$-extensions, ${d \ge 2}$ arbitrary (see Lemma 3.5 below). In order to prove this generalisation, we first prove two auxiliary lemmas.

Lemma 3.3

Let $\mathbb {L}_\infty /K$ be a $\mathbb {Z}_p^d$-extension, ${d \ge 2}$, and identify $\mathbb {Z}_p[[\text{ Gal }(\mathbb {L}_\infty /K)]]$ with $\Lambda _d$.Let M be a finitely generated and torsion $\Lambda _d$-module.Let ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }}{(K)}$ correspond to ${a = [a_1: \cdots : a_d] \in {\mathbb {P}}^{d-1}(\mathbb {Z}_p)}$, and let

$$\begin{aligned} \pi _{K_\infty } = \pi _a :\Lambda _d \longrightarrow \Lambda \end{aligned}$$

be the canonical surjective map induced by the restriction map on the Galois groups. If ${M_{K_\infty } = M/(\ker (\pi _{K_\infty }) \cdot M)}$ is a torsion $\Lambda$-module, then there exists a neighbourhood ${\mathcal {E}}(K_{\infty },n)$ such that for all $K'_{\infty } \in {\mathcal {E}}(K_{\infty },n)$, $M_{K'_{\infty }}$ is a torsion $\Lambda$-module.

Proof

It follows from Proposition 2.1(4) that the Fitting ideal of the quotient $M_{K_\infty }$ in ${\Lambda \cong \Lambda _d/\ker (\pi _{K_\infty })}$ is given by the image of ${\mathcal {F}}_{\Lambda _d}(M)$ under $\pi _{K_\infty }$. By hypothesis, there exists an element ${F \ne 0}$ in the annihilator ideal of $M_{K_\infty }$. If $M_{K_\infty }$ can be generated as a $\Lambda$-module by l elements, then ${H':= F^l }$ is contained in the Fitting ideal of $M_{K_\infty }$ by Proposition 2.1(2). Since

$$\begin{aligned} {\pi _{K_\infty } :{\mathcal {F}}_{\Lambda _d}(M) \longrightarrow }{ {\mathcal {F}}_\Lambda (M_{K_\infty })} \end{aligned}$$

is surjective, we can choose a pre-image ${H \in {\mathcal {F}}_{\Lambda _d}(M)}$ of $H'$ under the map $\pi _{K_\infty }$. In particular, ${H' = \pi _{K_\infty }(H)}$ is non-zero. By the Weierstrass Preparation Theorem, we may assume that ${H' = p^x \cdot G}$ for some distinguished polynomial G.

Let ${m \in \mathbb {N}}$ be large enough such that ${m > x}$ and ${p^m > \deg (G)}$, and choose ${n = 2\,m}$. Since

$$\begin{aligned} (T+1)^{p^n} - 1 \equiv 0 \mod (p^m, T^{p^m}), \end{aligned}$$

we may conclude that

$$\begin{aligned} \pi _{{\tilde{K}}_\infty }(H) \equiv H' \mod (p^m, T^{p^m}) \end{aligned}$$

is non-zero for each ${{\tilde{K}}_\infty \in {\mathcal {E}}(K_\infty ,n)}$ (we identify each quotient

$$\begin{aligned} \Lambda _d/\ker (\pi _{{\tilde{K}}_\infty }) \cong \mathbb {Z}_p[[\text{ Gal }({\tilde{K}}_\infty /K)]] \end{aligned}$$

with ${\Lambda = \mathbb {Z}_p[[T]]}$, and therefore this congruence makes sense as a statement in $\Lambda$). Since $\pi _{{\tilde{K}}_\infty }(H)$ is contained in ${{\mathcal {F}}_\Lambda (M_{{\tilde{K}}_\infty }) \subseteq \text{ Ann}_\Lambda (M_{{\tilde{K}}_\infty })}$, this proves the lemma. $\square$

Lemma 3.4

Let ${G \in \Lambda _d}$ be such that the coset ${\overline{G}}$ of G in the quotient algebra ${\Omega _d = \Lambda _d/p\Lambda _d = \mathbb {F}_p[[T_1, \ldots , T_d]]}$ is non-trivial (i.e., ${p \not \mid G}$), and recall that ${d \ge 2}$. Then $\lambda (G_a)$ is unbounded in any neighbourhood of $[0: \cdots : 0: 1]$ if and only if ${{\overline{G}} \in (T_1, \ldots , T_{d-1})}$ (recall that ${G_a = \pi _a(G)}$).

Proof

Let ${K_\infty = \mathbb {L}_\infty ^{\langle T_1 + 1, \ldots , T_{d-1}+1 \rangle }}$. Then

$$\begin{aligned} {\overline{G}} \in (T_1, \ldots , T_{d-1}) \quad \text{ if } \text{ and } \text{ only } \text{ if } \quad \pi _{K_\infty }(G) \equiv 0 \!\!\pmod {p}. \end{aligned}$$

Suppose first that ${{\overline{G}} \not \in (T_1, \ldots , T_{d-1})}$, and recall that

$$\begin{aligned} \mathbb {Z}_p[[\text{ Gal }(K_\infty /K)]] \cong \Lambda = \mathbb {Z}_p[[T]]. \end{aligned}$$

Then ${\pi _a(G) = G(0, \ldots , 0,T)}$ is not divisible by p, i.e. ${\overline{G}}(0, \ldots , 0, T)$ does not vanish identically. Let r be its T-order. It is then easy to see that ${\lambda (G_a) \le r}$ on any sufficiently small neighbourhood of $[0: \cdots : 0: 1]$.

Now suppose that ${{\overline{G}} \in (T_1, \ldots , T_{d-1})}$ and let U be a neighbourhood of $K_\infty$ as in Lemma 3.3, which we identify with a neighbourhood of ${[0: \cdots : 0: 1]}$. Choose ${a = [p^{j_1}: \cdots : p^{j_{d-1}}: 1] \in U}$, with $j_i$ large for all i. Since

$$\begin{aligned} (T+1)^{p^j} - 1 \equiv T^{p^j} \pmod {p} \end{aligned}$$

for every ${j \in \mathbb {N}}$, it follows that ${\pi _a(T_i) \in (p, T^{p^{j_i}})}$ for each ${i \in \{1, \ldots , d-1\}}$. Since G is a $\Lambda _d$-linear combination of p and ${T_1, \ldots , T_{d-1}}$ by assumption, it follows that

$$\begin{aligned} G_a = \pi _a(G) \in (p, T^{p^j}), \end{aligned}$$

where ${j = \min (j_1, \ldots , j_{d-1})}$. In particular, if ${{\overline{G}}_a \ne {\overline{0}}}$ in $\Omega _d$, then ${\lambda (G_a) \ge j}$.

It remains to prove that ${{\overline{G}}_a \ne {\overline{0}}}$ for ${a = [p^{j_1}: \cdots : p^{j_{d-1}}: 1]}$ and arbitrarily large $j_i$. We prove this claim via induction on ${d \ge 2}$. Let first ${d = 2}$, and let ${m > 0}$ be given (we look for some ${j \ge m}$ for which our claim holds true). We may write

$$\begin{aligned} {\overline{G}}(T_1, T_2) = T_1^t \cdot (F_1 + F_2), \end{aligned}$$

where $F_1$ is divisible by $T_1$ and $F_2 \in \mathbb {F}_p[[T_2]] {\setminus } \{{\overline{0}}\}$ (i.e. we are factoring out $T_1^t$, the largest power of $T_1$ dividing ${\overline{G}}$ in the unique factorisation domain $\Omega _d$).

If ${F_1 = {\overline{0}}}$, then clearly ${{\overline{G}}_a \ne {\overline{0}}}$ for any ${a = (p^j,1)}$. Now assume that ${F_1 \ne {\overline{0}}}$, and let s be the largest power of T dividing $(F_2)_{[0:1]}$, so that

$$\begin{aligned} (F_2)_{[0:1]} = c \cdot T^s + \text{ higher } \text{ order } \text{ terms }, \end{aligned}$$

with ${c \ne 0}$. Note that ${(F_2)_{[0:1]} = F_2}$ in the ring $\mathbb {F}_p[[T_2]]$. Let ${j \ge m}$ be arbitrary such that ${p^j > s}$, and let ${a = [p^j: 1]}$. Since $T_1$ divides $F_1$, the exponent of T in every term in ${(F_1)_a \in \mathbb {F}_p[[T]]}$ is larger than s. Moreover, since ${F_2 \in \mathbb {F}_p[[T_2]] \subseteq \mathbb {F}_p[[T_1, T_2]]}$ does not depend on the variable $T_1$, we have ${(F_2)_a = (F_2)_{[0:1]}}$. Therefore

$$\begin{aligned} (F_1)_a + (F_2)_a = (F_1)_a + (F_2)_{[0:1]} = c T^s + \text {higher order terms}, \end{aligned}$$

and thus ${{\overline{G}}_a \ne {\overline{0}}}$. This proves our claim for ${d = 2}$.

Now suppose that the claim holds for all ${i < d}$, and let ${m > 0}$ be given. As in the base step, we may write

$$\begin{aligned} {\overline{G}}(T_1, \ldots , T_{d}) = T_1^t \cdot (F_1 + F_2), \end{aligned}$$

where $F_1$ is divisible by $T_1$ and ${F_2 \in \mathbb {F}_p[[T_2, \ldots , T_d]] {\setminus } \{ {\overline{0}}\}}$. By the inductive step, we have ${(F_2)_a \ne {\overline{0}}}$ for ${a = [p^{j_2}: \cdots : p^{j_{d-1}}: 1] \in {\mathbb {P}}^{d-2}(\mathbb {Z}_p)}$ if all ${j_i \ge m}$ are sufficiently large.

If ${F_1 = {\overline{0}}}$, then we let ${b = [p^{j_1}: \cdots : p^{j_{d-1}}: 1] \in {\mathbb {P}}^{d-1}(\mathbb {Z}_p)}$ for any $j_1$. In this case we clearly have ${{\overline{G}}_b \ne {\overline{0}}}$, and we are done. Otherwise we have ${F_1 \ne {\overline{0}}}$. Let s be the largest power of T dividing $(F_2)_a$, so that

$$\begin{aligned} (F_2)_a = c \cdot T^s + \text{ higher } \text{ order } \text{ terms }, \end{aligned}$$

with ${c \ne 0}$. Now choose ${j_1 \ge \min (j_2, \ldots , j_{d-1})}$ large enough such that ${p^{j_1} > s}$. Let ${b = [p^{j_1}: \cdots : p^{j_{d-1}}: 1]}$. Since $T_1$ divides $F_1$, the exponent of T in each term of $(F_1)_b$ is larger than s. Therefore

$$\begin{aligned} (F_1)_b + (F_2)_b = (F_1)_b + (F_2)_a = c \cdot T^s + \text{ higher } \text{ order } \text{ terms }. \end{aligned}$$

It follows that ${{\overline{G}}_b \ne {\overline{0}}}$, which completes the proof. $\square$

Lemma 3.5

Let $\mathbb {L}_\infty /K$ be a $\mathbb {Z}_p^d$-extension, ${d \ge 2}$, and identify $\mathbb {Z}_p[[\text{ Gal }(\mathbb {L}_\infty /K)]]$ with $\Lambda _d$. Let $F_M$ be the characteristic power series of the finitely generated torsion $\Lambda _d$-module M, and write ${F_M = p^{m_0(M)} \cdot G_M}$ with ${p \not \mid G_M}$.

Let ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$ correspond to ${a = [a_1: \cdots : a_d] \in {\mathbb {P}}^{d-1}(\mathbb {Z}_p)}$, and let

$$\begin{aligned} \pi _{K_\infty } = \pi _a :\Lambda _d \longrightarrow \Lambda \end{aligned}$$

be the canonical surjective map induced by the restriction map on the Galois groups. We assume that ${M_{K_\infty } = M/(\ker (\pi _{K_\infty }) \cdot M)}$ is a torsion $\Lambda$-module.

• (a) If $\pi _{K_\infty }(G_M) \equiv 0 \pmod {p}$, then $\lambda (M_{K_\infty })$ is unbounded in any neighbourhood of $K_\infty$.

• (b) Suppose that there exists an element ${H \in \Lambda _d}$ such that $p^s \cdot H$ annihilates the maximal pseudo-null submodule $M^\circ$ of M for a sufficiently large ${s \in \mathbb {N}}$, and such that ${\pi _{K_\infty }(H) \not \equiv 0 \pmod {p}}$.

  Then the reverse conclusion also holds, i.e. if ${\pi _{K_\infty }(G_M) \not \equiv 0 \pmod {p}}$, then $\lambda (M_{K_\infty })$ is bounded in a sufficiently small neighbourhood of $K_\infty$.

Remark 3.6

If $d = 2$, then the additional assumption on the maximal pseudo-null submodule in Lemma 3.5 is always satisfied (cf. also the proof of [26, Theorem 3.3]).

Remark 3.7

In Lemmas 3.2 and 3.5 there is a statement that $\lambda (M_{K_{\infty }})$ is unbounded (or bounded) in a neighbourhood of $K_{\infty }$. Implicit in this statement is the fact that there is a neighbourhood of ${\mathcal {E}}(K_{\infty },n)$ such that $M_{K'_{\infty }}$ is a torsion $\Lambda$-module for all $K'_{\infty } \in {\mathcal {E}}(K_{\infty },n)$. This is true by Lemma 3.3.

Proof of lemma 3.5

Without loss of generality, we may choose the topological generators of ${\text{ Gal }(\mathbb {L}_\infty /K) \cong \mathbb {Z}_p^d}$ such that ${a = [0: \cdots : 0: 1]}$ (see also Sect. 2.4). As in [26], we work with the zero-th Fitting ideal ${\mathcal {F}}_{\Lambda _d}(M)$ of M. Recall from Proposition 2.1(4) that

$$\begin{aligned} {\mathcal {F}}_{\Lambda _1}(M_a) = \pi _a({\mathcal {F}}_{\Lambda _d}(M)). \end{aligned}$$

Suppose first that $\overline{G_M} \in (T_1, \ldots , T_{d-1})$. Assume that $M_a$ is a torsion $\Lambda$-module. Since $(G_M)$ divides ${\mathcal {F}}_{\Lambda _d}(M)$, the ideal $((G_M)_a)$ of $\Lambda$ divides ${{\mathcal {F}}_{\Lambda _d}(M)_a}{ = {\mathcal {F}}_{\Lambda _1}(M_a)}$. Therefore ${\lambda ((G_M)_a) \le \lambda (M_a)}$. It follows from Lemma 3.4 that $\lambda ((G_M)_a)$ and consequently also $\lambda (M_a)$ are unbounded in any neighbourhood U of $[0: \cdots : 0: 1]$ in which $M_a$ is a torsion $\Lambda$-module for each ${a \in U}$. Such a neighbourhood exists by Lemma 3.3.

Now suppose that we are in the setting of assertion (b), and that $\lambda (M_a)$ is unbounded in any neighbourhood of $[0: \cdots :0:1]$. Suppose that M is generated by l elements as a $\Lambda _d$-module. Then Proposition 2.1(3) implies that

$$\begin{aligned} p^{l \cdot m_0(M) + ls} \cdot H^l \cdot G_M^l \in {\mathcal {F}}_{\Lambda _d}(M), \end{aligned}$$

so ${p^{l m_0(M) + ls} H_a^l (G_M)_a^l \in {\mathcal {F}}_{\Lambda _1}(M_a)}$. It follows that ${\lambda (M_a) \le \lambda (H_a^l \cdot (G_M)_a^l)}$. Since ${\overline{H}}$ is not contained in the prime ideal $(T_1, \ldots , T_{d-1})$ of $\Omega _d$, it follows from Lemma 3.4 that ${{\overline{G}}_M \in (T_1, \ldots , T_{d-1})}$. $\square$

Remark 3.8

It follows from the proof of Lemma 3.5 that in the statement of Lemmas 3.5 and  3.2unbounded in any neighbourhood may be replaced by unbounded in some neighbourhood, i.e. these statements are equivalent.

Remark 3.9

The additional hypothesis on the existence of H in assertion (b) is also necessary, as the following example shows which we take from [17].

Suppose that ${d = 3}$ and ${M = \Lambda _3/(T_1, T_2 + p)}$. Then M is a pseudo-null $\Lambda _3$-module, and therefore ${F_M = G_M = 1}$, i.e. ${\overline{G}}_M$ is not contained in $(T_1, T_2)$. However, we have seen in [17, Example 6.3] that $\lambda (M_a)$ is unbounded in a neighbourhood of [0 : 0 : 1]. Each annihilator H of ${M^\circ = M}$ is contained in the ideal $(p, T_1, T_2)$ of $\Lambda _3$.

It will be one of our tasks in the next section to derive natural hypotheses which are sufficient for the existence of the element H in Lemma 3.5 (of course, it will be sufficient if M does not contain any non-trivial pseudo-null submodules, i.e. ${M^\circ = \{0\}}$, but we try to do better, so also Remark 3.23 below).

3.2 Control Theorems

For the remainder of this section, we fix a number field K and an abelian variety A of dimension g defined over K. If $p = 2$, then we assume that K is totally imaginary. Let $\Sigma$ be a finite set of primes of K which contains the primes above p and the primes where A has bad reduction.

Lemma 3.10

Let $G \cong \mathbb {Z}_p^d$ and let M be a discrete G-module that is cofinitely generated over $\mathbb {Z}_p$. Let $m= {{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(M)$. Then $H^1(G,M)$ and $H^2(G,M)$ are cofinitely generated over $\mathbb {Z}_p$ with

$$\begin{aligned} {{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(H^1(G,M)) \le md \end{aligned}$$

and

$$\begin{aligned} {{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(H^2(G,M)) \le md(d-1)/2. \end{aligned}$$

Proof

First we prove the result for $H^1(G,M)$ by induction on d. For $d=1$ we have that $H^1(G,M)=M/(\sigma -1)M$ where $\sigma$ is a topological generator of G. Therefore ${{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(H^1(G,M)) \le m$. Now assume that the result is true for $d-1$. Let H be a subgroup of G that is isomorphic to $\mathbb {Z}_p^{d-1}$ with $G/H \cong \mathbb {Z}_p$. The desired result then follows from the Hochschild-Serre spectral sequence ${H^i(G/H, H^j(H, M)) \Rightarrow H^{i+j}(G, M)}$.

Now we prove the result for $H^2(G,M)$ by induction on d. Since $cd_p(\mathbb {Z}_p)=1$, the result is true for $d=1$. Now assume that the result is true for $d-1$. Let H be a subgroup of G that is isomorphic to $\mathbb {Z}_p^{d-1}$ with $G/H \cong \mathbb {Z}_p$. By the Hochschild-Serre spectral sequence $H^i(G/H, H^j(H, M)) \Rightarrow H^{i+j}(G, M)$, it will suffice to show that

$$\begin{aligned}&{{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(H^2(G/H, H^0(H,M))+{{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(H^1(G/H, H^1(H,M))\\&\quad +{{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(H^0(G/H, H^2(H,M)) \le md(d-1)/2. \end{aligned}$$

The first term is zero because $cd_p(G/H)=1$. Using the result just proven for the first cohomology group we get that ${{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(H^1(G/H, H^1(H,M)) \le m(d-1)$. By the induction hypothesis we get ${{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(H^0(G/H, H^2(H,M)) \le m(d-1)(d-2)/2$. Therefore, as desired, the sum is at most $md(d-1)/2$. $\square$

Now we can prove a control theorem for fine Selmer groups.

Lemma 3.11

Let A be an abelian variety of dimension g defined over K. Let $\mathbb {L}_\infty /K$ be a $\mathbb {Z}_p^d$-extension $(d \ge 2)$, ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$ and write ${Y = Y_A^{(\mathbb {L}_\infty )}}$ for brevity. Consider the dual of the restriction map

$$\begin{aligned} f^\vee :Y_{K_\infty } \longrightarrow Y_A^{(K_\infty )}. \end{aligned}$$

We have

• (a) $\textrm{coker}f^{\vee }$ is a finitely generated $\mathbb {Z}_p$-module with

  $$\begin{aligned} {{\,\textrm{rank}\,}}_{\mathbb {Z}_p}(\textrm{coker}f^{\vee }) \le 2g(d-1) \end{aligned}$$

• (b) Let $m_p=\sum _{v | p} m_v$ where the sum runs over the primes of K above p and $m_v$ is defined to be zero if v splits completely in $K_{\infty }$ and equal to the number of primes of $K_{\infty }$ above v otherwise. Then $\ker f^{\vee }$ is a finitely generated torsion $\Lambda$-module with

  $$\lambda (\ker f^{\vee }) \le 2\,g(d-1)m_p +g(d-1)(d-2).$$

Proof

Let $\Gamma _{\infty }=\text{ Gal }(\mathbb {L}_{\infty }/K_{\infty })$ and consider the following canonical commutative diagram:

By the snake lemma we have an exact sequence

$$\begin{aligned} 0 \longrightarrow \ker f \longrightarrow \ker f' \longrightarrow \ker f'' \cap {{\,\textrm{img}\,}}\rho _0 \longrightarrow \textrm{coker}f \longrightarrow \textrm{coker}f'. \end{aligned}$$

(6)

According to the inflation-restriction exact sequence and Lemma 3.10 we have that

$$\begin{aligned} {{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(\ker f')={{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(H^1(\Gamma _{\infty }, A(\mathbb {L}_{\infty })[p^{\infty }])) \le 2g(d-1). \end{aligned}$$

Therefore from the exact sequence (6),

$$\begin{aligned} {{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(\ker f) \le {{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(\ker f') \le 2g(d-1). \end{aligned}$$

This proves (a).

By the inflation-restriction sequence and Shapiro’s lemma it follows that we can write $\ker f''=\oplus _{v \in \Sigma (K)} B_v$ where $B_v=\oplus _{w|v} H^1(\Gamma _{\infty ,w}, A(\mathbb {L}_{\infty ,w})[p^{\infty }])$. In the definition of $B_v$ the sum runs over all primes w of $K_{\infty }$ above v. For each such w we have also written w for a fixed prime of $\mathbb {L}_{\infty }$ so that $\Gamma _{\infty ,w}$ denotes the corresponding decomposition group.

Assume that $v \in \Sigma (K)$ splits completely in $K_{\infty }/K$. Then for any prime w of $\mathbb {L}_{\infty }$ above v we have that $H^0(\Gamma _{\infty ,w}, A(\mathbb {L}_{\infty ,w})[p^{\infty }])=A(K_v)[p^{\infty }]$ is finite. Therefore by [19, Lemma 6.2] we have that $H^1(\Gamma _{\infty ,w}, A(\mathbb {L}_{\infty ,w})[p^{\infty }])$ is finite and this order does not depend on the prime w of $\mathbb {L}_{\infty }$ above v. It follows that $p^n$ annihilates $B_v$ for some n.

Now assume that $v \in \Sigma (K)$ does not split completely in $K_{\infty }/K$. If v does not lie above p, then any prime w of $K_{\infty }$ above v splits completely in $\mathbb {L}_{\infty }/K_{\infty }$ so in this case $B_v=0$. Now suppose that $v \in \Sigma _p(K)$ and let w be a prime of $\mathbb {L}_{\infty }$ above v. According to Lemma 3.10$H^1(\Gamma _{\infty ,w}, A(\mathbb {L}_{\infty ,w})[p^{\infty }])$ is cofinitely generated over $\mathbb {Z}_p$ with corank at most $2\,g(d-1)$. It follows that $B_v$ is cofinitely generated over $\mathbb {Z}_p$ with ${{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(B_v) \le 2g(d-1)m_v$. Putting all of this together, we get that the Pontryagin dual of $\ker f''$ is $\Lambda$-torsion with $\lambda$-invariant at most $2g(d-1)m_p$.

By the inflation-restriction sequence $\textrm{coker}f'$ injects into $H^2(\Gamma _{\infty }, A[p^{\infty }])$. So by Lemma 3.10 we have

$$\begin{aligned} {{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(\textrm{coker}f') \le {{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(H^2(\Gamma _{\infty }, A[p^{\infty }])) \le 2g(d-1)(d-2)/2. \end{aligned}$$

It therefore follows from the exact sequence (6) and the above observations that $\ker f^{\vee }$ is a finitely generated torsion $\Lambda$-module with

$$\begin{aligned} \lambda (\ker f^{\vee }) \le 2g(d-1)m_p +2g(d-1)(d-2)/2. \end{aligned}$$

This completes the proof. $\square$

Corollary 3.12

Let $K_\infty$ be as in Lemma 3.11, then we have

• (a) $\text{ rank}_{\Lambda }(Y_{K_\infty }) = \text{ rank}_\Lambda (Y_A^{(K_\infty )})$

• (b) Let $\Sigma _s(K)$ be the set of all primes ${v \in \Sigma (K)}$ that split completely in $\mathbb {L}_\infty /K$. If $\text{ rank}_{\Lambda }(Y_{K_\infty })=\text{ rank}_\Lambda (Y_A^{(K_\infty )})=0$, then

  • (i) $\mu (Y_{K_\infty }) \ge \mu (Y_A^{(K_\infty )})$ with equality if no prime ${v \in \Sigma (K) \setminus \Sigma _s(K)}$ splits completely in $K_{\infty }/K$.

  • (ii) If no prime $v \in \Sigma _p(K)$ splits completely in $K_{\infty }/K$, then there exists a neighbourhood ${\mathcal {E}}(K_{\infty },n)$ such that

    • for all $K'_{\infty } \in {\mathcal {E}}(K_{\infty },n)$ we have

      $$\begin{aligned} \text{ rank}_{\Lambda }(Y_{K'_\infty })=\text{ rank}_\Lambda (Y_A^{(K'_\infty )})=0, \end{aligned}$$

    • $|\lambda (Y_{K'_\infty }) - \lambda (Y_A^{(K'_\infty )})|$ is bounded as $K'_\infty$ runs over ${\mathcal {E}}(K_{\infty },n)$.

Proof

Statement (a) follows directly from Lemma 3.11. Now assume that both $Y_{K_{\infty }}$ and $Y_A^{(K_{\infty })}$ are $\Lambda$-torsion. From Lemma 3.11 we see that $\mu (Y_{K_\infty }) \ge \mu (Y_A^{(K_\infty )})$. The proof reveals that $\mu (\ker f^{\vee })=0$ if no prime $v \in \Sigma (K) {\setminus } \Sigma _s(K)$ splits completely in $K_{\infty }/K$. This proves (b)-i.

Now assume that no prime $v \in \Sigma _p(K)$ splits completely in $K_{\infty }/K$. Then we can choose a neighbourhood ${\mathcal {E}}(K_{\infty },n)$ such that for any $K'_{\infty } \in {\mathcal {E}}(K_{\infty },n)$ we have $\#\Sigma _p(K'_{\infty })=\#\Sigma _p(K_{\infty })$. By Lemma 3.3 we can reduce our neighbourhood if necessary so that for all $K'_{\infty } \in {\mathcal {E}}(K_{\infty },n)$ we have $\text{ rank}_{\Lambda }(Y_A^{(K'_\infty )})=0$. Then (b)-ii follows from Lemma 3.11. $\square$

In fact, the cokernels of $f^\vee$ can be bounded in a more general setting (this will prove useful below).

Corollary 3.13

Let $\mathbb {L}_\infty /K$ be a $\mathbb {Z}_p^d$-extension, and let ${K_\infty \subseteq \mathbb {L}_\infty }$ be a $\mathbb {Z}_p^i$-extension of K, ${i \ge 1}$. We write ${Y = Y_A^{(\mathbb {L}_\infty )}}$ and ${H = \text{ Gal }(\mathbb {L}_\infty /K_\infty )}$ for brevity. Then the cokernel of the natural map

$$\begin{aligned} f^\vee :Y_H \longrightarrow Y_A^{(K_\infty )} \end{aligned}$$

is a finitely generated $\mathbb {Z}_p$-module of rank at most $2g(d-i)$.

Proof

The proof of the first part of Lemma 3.11, using Lemma 3.10, goes through without changes. $\square$

Now we turn to a control theorem for Selmer groups.

Lemma 3.14

Let A be an abelian variety of dimension g defined over K. Let $\mathbb {L}_\infty /K$ be a $\mathbb {Z}_p^d$-extension $(d \ge 2)$, ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$ and write ${X = X_A^{(\mathbb {L}_\infty )}}$. Assume that A has good ordinary reduction at the primes of K above p, and that each ${v \in \Sigma _p(K)}$ is ramified in $\mathbb {L}_{\infty }/K$. We define r to be zero if each ${v \in \Sigma _p(K)}$ is ramified in $K_{\infty }/K$ and equal to one otherwise. Consider the dual of the restriction map

$$\begin{aligned} f^\vee :X_{K_\infty } \longrightarrow X_A^{(K_\infty )}. \end{aligned}$$

We have

• (a) $\textrm{coker}f^{\vee }$ is a finitely generated $\mathbb {Z}_p$-module with

  $$\begin{aligned} {{\,\textrm{rank}\,}}_{\mathbb {Z}_p}(\textrm{coker}f^{\vee }) \le 2gr(d-1). \end{aligned}$$

• (b) Let $m_p=\sum _{v | p} m_v$ where the sum runs over the primes of K above p and $m_v$ is defined to be zero if either v splits completely or ramifies in $K_{\infty }/K$, and equal to the number primes of $K_{\infty }$ above v otherwise. Then $\ker f^{\vee }$ is a finitely generated torsion $\Lambda$-module with

  $$\begin{aligned} \lambda (\ker f^{\vee }) \le gdm_p +gr(d-1)(d-2). \end{aligned}$$

Proof

We proceed as in the proof of Lemma 3.11. Let $\Gamma _{\infty }=\text{ Gal }(\mathbb {L}_{\infty }/K_{\infty })$ and consider the following canonical commutative diagram:

By the snake lemma we have an exact sequence

$$\begin{aligned} 0 \longrightarrow \ker f \longrightarrow \ker f' \longrightarrow \ker f'' \cap {{\,\textrm{img}\,}}\rho _0 \longrightarrow \textrm{coker}f \longrightarrow \textrm{coker}f'. \end{aligned}$$

(7)

If every prime $v \in \Sigma _p(K)$ ramifies in $K_{\infty }/K$, then by [9, Prop. 3.2(ii)] we have that $A(K_{\infty })[p^{\infty }]$ is finite. Therefore by [19, Lemma 6.2] $H^1(\Gamma _{\infty }, A(\mathbb {L}_{\infty })[p^{\infty }])$ is finite. From this observation and Lemma 3.10 we conclude that

$$\begin{aligned} {{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(\ker f')={{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(H^1(\Gamma _{\infty }, A(\mathbb {L}_{\infty })[p^{\infty }])) \le 2gr(d-1). \end{aligned}$$

Therefore from the exact sequence (7),

$$\begin{aligned} {{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(\ker f) \le {{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(\ker f') \le 2gr(d-1). \end{aligned}$$

This proves (a).

Now we deal with (b). We can write $\ker f''=\oplus _{v \in \Sigma (K)} B_v$ where $B_v=\oplus _{w|v} \ker f''_w$ and $f''_w: H^1(K_{\infty ,w}, A)[p^{\infty }] \longrightarrow H^1(\mathbb {L}_{\infty ,w}, A)[p^{\infty }]$ is the restriction map. In the definition of $B_v$ the sum runs over all primes w of $K_{\infty }$ above v. For each such w we have also written w for a fixed prime of $\mathbb {L}_{\infty }$.

First, assume that $v \in \Sigma (K)$ does not lie above p. Let w be a prime of $K_{\infty }$ above v and fix a prime of $\mathbb {L}_{\infty }$ above it which we also denote by w. Since ${A(K_{\infty ,w})\otimes \mathbb {Q}_p/\mathbb {Z}_p=0}$ and ${A(\mathbb {L}_{\infty ,w})\otimes \mathbb {Q}_p/\mathbb {Z}_p=0}$ we have isomorphisms

$$\begin{aligned}{} & {} H^1(K_{\infty ,w}, A)[p^{\infty }] \cong H^1(K_{\infty ,w}, A[p^{\infty }]),\\{} & {} H^1(\mathbb {L}_{\infty ,w}, A)[p^{\infty }] \cong H^1(\mathbb {L}_{\infty ,w}, A[p^{\infty }]). \end{aligned}$$

It follows that $\ker f''_w \cong H^1(\Gamma _{\infty ,w}, A(\mathbb {L}_{\infty ,w})[p^{\infty }])$. Therefore the same observations as those in the proof of Lemma 3.11 apply to $B_v$.

Now let $v \in \Sigma _p(K)$ and let w be a prime of $K_{\infty }$ above v and fix a prime of $\mathbb {L}_{\infty }$ above it which we also denote by w. Let

$$\begin{aligned}{} & {} \kappa _{K_{\infty },w}: A(K_{\infty ,w})\otimes \mathbb {Q}_p/\mathbb {Z}_p \hookrightarrow H^1(K_{\infty ,w}, A[p^{\infty }]),\\{} & {} \kappa _{\mathbb {L}_{\infty },w}: A(\mathbb {L}_{\infty ,w})\otimes \mathbb {Q}_p/\mathbb {Z}_p \hookrightarrow H^1(\mathbb {L}_{\infty ,w}, A[p^{\infty }]) \end{aligned}$$

be the Kummer maps. Then the map $f''_w$ is

$$\begin{aligned} f''_w: H^1(K_{\infty ,w}, A[p^{\infty }])/{{\,\textrm{img}\,}}\kappa _{K_{\infty },w} \longrightarrow H^1(\mathbb {L}_{\infty ,w}, A[p^{\infty }])/{{\,\textrm{img}\,}}\kappa _{\mathbb {L}_{\infty ,w}} \end{aligned}$$

Now let $C_w={\mathcal {F}}(\bar{{\mathfrak {m}}})[p^{\infty }]$ where $\bar{{\mathfrak {m}}}$ is the maximal ideal of ${\bar{K}}_v$ and ${\mathcal {F}}$ is the formal group over $O_{K_v}$ attached to the Néron model of A over $O_{K_v}$. The inclusion $C_w \subseteq A[p^{\infty }]$ induces maps

$$\begin{aligned}{} & {} \lambda _{K_{\infty },w}: H^1(K_{\infty ,w}, C_w) \longrightarrow H^1(K_{\infty ,w}, A[p^{\infty }]),\\{} & {} \lambda _{\mathbb {L}_{\infty },w}: H^1(\mathbb {L}_{\infty ,w}, C_w) \longrightarrow H^1(\mathbb {L}_{\infty ,w}, A[p^{\infty }]). \end{aligned}$$

Since v ramifies in $\mathbb {L}_{\infty }/K$, the extension $\mathbb {L}_{\infty ,w}/K_v$ is deeply ramified in the sense of [4]. Therefore by [4, Proposition 4.3] and the discussion proceeding it we have ${{\,\textrm{img}\,}}\kappa _{\mathbb {L}_{\infty ,w}}={{\,\textrm{img}\,}}\lambda _{\mathbb {L}_{\infty ,w}}$ and ${{\,\textrm{img}\,}}\kappa _{K_{\infty ,w}} \subseteq {{\,\textrm{img}\,}}\lambda _{K_{\infty ,w}}$. Therefore $f''_w$ can be viewed as the composition of the following maps:

$$\begin{aligned}{} & {} a_w: H^1(K_{\infty ,w}, A[p^{\infty }])/{{\,\textrm{img}\,}}\kappa _{K_{\infty ,w}} \longrightarrow H^1(K_{\infty ,w}, A[p^{\infty }])/{{\,\textrm{img}\,}}\lambda _{K_{\infty ,w}},\\{} & {} b_w: H^1(K_{\infty ,w}, A[p^{\infty }])/{{\,\textrm{img}\,}}\lambda _{K_{\infty ,w}} \longrightarrow H^1(\mathbb {L}_{\infty ,w}, A[p^{\infty }])/{{\,\textrm{img}\,}}\lambda _{\mathbb {L}_{\infty ,w}}. \end{aligned}$$

We will now determine ${{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(\ker a_w)$ and ${{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(\ker b_w)$.

First we deal with $\ker b_w$. Let ${\tilde{A}}$ be the reduction of A over the residue field of an algebraic closure ${\bar{K}}_w$ of $K_w$. The exact sequence

$$\begin{aligned} 0 \longrightarrow C_w \longrightarrow A[p^{\infty }] \longrightarrow {\tilde{A}}[p^{\infty }] \longrightarrow 0 \end{aligned}$$

induces an exact sequence

$$\begin{aligned} 0 \longrightarrow {{\,\textrm{img}\,}}\lambda _{K_{\infty ,w}} \longrightarrow H^1(K_{\infty ,w}, A[p^{\infty }]) \longrightarrow H^1(K_{\infty ,w}, {\tilde{A}}[p^{\infty }]) \end{aligned}$$

Similarly, we have an exact sequence

$$\begin{aligned} 0 \longrightarrow {{\,\textrm{img}\,}}\lambda _{\mathbb {L}_{\infty ,w}} \longrightarrow H^1(\mathbb {L}_{\infty ,w}, A[p^{\infty }]) \longrightarrow H^1(\mathbb {L}_{\infty ,w}, {\tilde{A}}[p^{\infty }]) \end{aligned}$$

It follows that $\ker b_w$ is a subgroup of $H^1(\text{ Gal }(\mathbb {L}_{\infty ,w}/K_{\infty ,w}), {\tilde{A}}(l_{\infty ,w})[p^{\infty }])$ where $l_{\infty ,w}$ is the residue field of $\mathbb {L}_{_\infty ,w}$. If either v splits completely or ramifies in $K_{\infty }/K$, then $H^0(\text{ Gal }(\mathbb {L}_{\infty ,w}/K_{\infty ,w}), {\tilde{A}}(l_{\infty _w})[p^{\infty }])={\tilde{A}}(k_{\infty ,w})[p^{\infty }]$ is finite (here $k_{\infty ,w}$ is the residue field of $K_{\infty ,w}$). Therefore by [19, Lemma 6.2]

$$\begin{aligned} H^1(\text{ Gal }(\mathbb {L}_{\infty ,w}/K_{\infty ,w}), {\tilde{A}}(l_{\infty ,w})[p^{\infty }]) \end{aligned}$$

is finite, whence $\ker b_w$ is finite. On the other hand when w does not split completely in $K_{\infty }/K$ we have by Lemma 3.10

$$\begin{aligned} {{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(\ker b_w) \le {{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(H^1(\text{ Gal }(\mathbb {L}_{\infty ,w}/K_{\infty ,w}), {\tilde{A}}(l_{\infty ,w})[p^{\infty }])) \le g(d-1). \end{aligned}$$

Now we deal with $\ker a_w={{\,\textrm{img}\,}}\lambda _{K_{\infty ,w}}/{{\,\textrm{img}\,}}\kappa _{K_{\infty ,w}}$. Let L be finite extension of $K_v$ contained in $K_{\infty ,w}$. First we note that Tate local duality [29, Theorem 7.2.6] together with the Weil pairing yields a non-degenerate pairing

$$\begin{aligned} \langle \;, \;\rangle : H^2(L, T_p(C_w)) \times H^0(L, \tilde{A^t}[p^{\infty }]) \longrightarrow \mathbb {Q}_p/\mathbb {Z}_p, \end{aligned}$$

where $T_p(C_w)$ is the p-adic Tate module of $C_w$ and $A^t$ is the dual abelian variety. If $L'/L$ is a finite extension, let $\text {res}: H^2(L, T_p(C_w)) \longrightarrow H^2(L', T_p(C_w))$ be the restriction map and $\text {cor}: H^0(L', \tilde{A^t}[p^{\infty }]) \longrightarrow H^0(L, \tilde{A^t}[p^{\infty }])$ be the corestriction (norm) map. For $a \in H^2(L, T_p(C_w))$ and $b \in H^0(L', \tilde{A^t}[p^{\infty }])$ a property of Tate local duality gives $\langle \text {res} \, a, b \rangle =\langle a, \text {cor}\, b \rangle$. As above, we have maps

$$\begin{aligned}{} & {} \kappa _L: A(L)\otimes \mathbb {Q}_p/\mathbb {Z}_p \hookrightarrow H^1(L, A[p^{\infty }]),\\{} & {} \lambda _L: H^1(L, C_w) \longrightarrow H^1(L, A[p^{\infty }]). \end{aligned}$$

Recall that for any Hausdorff abelian locally compact topological group M, we denote by $M^{\vee }$ its Pontryagin dual. Taking into account [4, Proposition 4.5], the proof of [4, Proposition 4.6] shows that we have an isomorphism

$$\begin{aligned} \theta _L: {{\,\textrm{img}\,}}\lambda _L/{{\,\textrm{img}\,}}\kappa _L \cong \tilde{A^t}(k_L)[p^{\infty }]^{\vee }, \end{aligned}$$

where $k_L$ is the residue field of L. Taking into account the property of Tate local duality above and the description of the map $\theta _L$ we have an isomorphism

$$\begin{aligned} {{\,\textrm{img}\,}}\lambda _{K_{\infty ,w}}/{{\,\textrm{img}\,}}\kappa _{K_{\infty ,w}} \cong \mathop {\varinjlim }\limits {{\,\textrm{img}\,}}\lambda _L/{{\,\textrm{img}\,}}\kappa _L \cong (\mathop {\varprojlim }\limits \tilde{A^t}(k_L)[p^{\infty }])^{\vee }. \end{aligned}$$

The limits are taken over all finite extensions $L/K_v$ inside $K_{\infty ,w}/K_v$; the direct limits are taken with respect to restriction and inverse limits are taken with respect to corestriction.

If either v splits completely or ramifies in $K_{\infty }/K$, then ${\tilde{A}}(k_{\infty ,w})[p^{\infty }]$ is finite. Then from the above ${{\,\textrm{img}\,}}\lambda _{K_{\infty ,w}}/{{\,\textrm{img}\,}}\kappa _{K_{\infty ,w}} \cong (\mathop {\varprojlim }\limits \tilde{A^t}(k_L)[p^{\infty }])^{\vee }$ is finite, so $\ker a_w$ is finite in this case. Since for any L as above we have $\tilde{A^t}(k_L)[p] \cong (\mathbb {Z}/p\mathbb {Z})^i$ with $i \le g$, therefore in the general case we have

$$\begin{aligned} {{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(\ker a_w) = {{\,\textrm{corank}\,}}_{\mathbb {Z}_p}((\mathop {\varprojlim }\limits \tilde{A^t}(k_L)[p^{\infty }])^{\vee }) \le g. \end{aligned}$$

We have $f''_w=b_w\circ a_w$, so we have an exact sequence

$$\begin{aligned} 0 \longrightarrow \ker a_w \longrightarrow \ker f''_w \longrightarrow \ker b_w. \end{aligned}$$

Therefore ${{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(\ker f''_w) \le {{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(\ker a_w) + {{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(\ker b_w)$. From this and the above observations we see that if v either splits completely or ramifies in $K_{\infty }/K$, then $\ker f''_w$ is finite. The order of this group does not depend on the prime w of $\mathbb {L}_{\infty }$ above v. It follows that in this case $B_v$ is annihilated by some power of p. Otherwise when v does not split completely or ramify in $K_{\infty }/K$ the above observations show that we have ${{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(B_v) \le g(d-1)m_v +gm_v = gdm_v$.

By the inflation-restriction sequence $\textrm{coker}f'$ injects into $H^2(\Gamma _{\infty }, A[p^{\infty }])$. So as in the proof of (a) using [9, Prop. 3.2(ii)] and Lemma 3.10 we have

$$\begin{aligned} {{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(\textrm{coker}f') \le {{\,\textrm{corank}\,}}_{\mathbb {Z}_p}(H^2(\Gamma _{\infty }, A[p^{\infty }])) \le 2gr(d-1)(d-2)/2. \end{aligned}$$

It therefore follows from the exact sequence (7) and the above observations that $\ker f^{\vee }$ is a finitely generated torsion $\Lambda$-module with

$$\begin{aligned} \lambda (\ker f^{\vee }) \le gdm_p +2gr(d-1)(d-2)/2. \end{aligned}$$

This completes the proof. $\square$

Corollary 3.15

With the same setup and conditions as in Lemma 3.14, we have

• (a) $\text{ rank}_{\Lambda }(X_{K_\infty }) = \text{ rank}_\Lambda (X_A^{(K_\infty )})$.

• (b) Let $\Sigma _s(K)$ be the set of all primes ${v \in \Sigma (K)}$ that split completely in $\mathbb {L}_\infty /K$. If $\text{ rank}_{\Lambda }(X_{K_\infty })=\text{ rank}_\Lambda (X_A^{(K_\infty )})=0$, then

  • (i) $\mu (X_{K_\infty }) \ge \mu (X_A^{(K_\infty )})$ with equality if no prime ${v \in \Sigma (K) \setminus \Sigma _s(K)}$ splits completely in $K_{\infty }/K$.

  • (ii) If no prime $v \in \Sigma _p(K)$ splits completely in $K_{\infty }/K$, then there exists a neighbourhood ${\mathcal {E}}(K_{\infty },n)$ such that

    • for all $K'_{\infty } \in {\mathcal {E}}(K_{\infty },n)$ we have

      $$\begin{aligned} \text{ rank}_{\Lambda }(X_{K'_\infty })=\text{ rank}_\Lambda (X_A^{(K'_\infty )})=0 \end{aligned}$$

    • $|\lambda (X_{K'_\infty }) - \lambda (X_A^{(K'_\infty )})|$ is bounded as $K'_\infty$ runs over ${\mathcal {E}}(K_{\infty },n)$.

Proof

The proof is identical to that of Corollary 3.12 using Lemma 3.14. $\square$

Again, we can prove a generalisation of the result for the coranks of $f^\vee$.

Corollary 3.16

Let $\mathbb {L}_\infty /K$ be a $\mathbb {Z}_p^d$-extension, and let ${K_\infty \subseteq \mathbb {L}_\infty }$ be a $\mathbb {Z}_p^i$-extension of K, for some ${i \ge 1}$. We write ${X = X_A^{(\mathbb {L}_\infty )}}$ and ${H = \text{ Gal }(\mathbb {L}_\infty /K_\infty )}$ for brevity. Suppose that A has good ordinary reduction at the primes of K above p, and that each ${v \in \Sigma _p(K)}$ is ramified in $\mathbb {L}_\infty$. We define r to be zero if the inertia subgroup of each ${v \in \Sigma _p(K)}$ is open in $\text{ Gal }(K_\infty /K)$, and equal to one otherwise.

Then the cokernel of the natural map

$$\begin{aligned} f^\vee :X_H \longrightarrow X_A^{(K_\infty )} \end{aligned}$$

is finitely generated over $\mathbb {Z}_p$ and of rank at most $2gr (d-i)$.

Proof

We proceed as in the proof of Lemma 3.14(a). Note that in the case ${r = 0}$ the result [9, Prop. 3.2(ii)] can be applied; in the case ${r = 1}$ we use Lemma 3.10 instead. $\square$

For later use, we also state the following

Lemma 3.17

Let Z denote either X or Y. If $Z=X$, we assume that A has good ordinary reduction at the prime of K above p, and that each ${v \in \Sigma _p(K)}$ is ramified in $\mathbb {L}_{\infty }/K$. Let $\mathbb {L}_\infty /K$ be a $\mathbb {Z}_p^d$-extension, and suppose that there exists a $\mathbb {Z}_p$-extension ${K_\infty \subseteq \mathbb {L}_\infty }$ of K such that $Z_A^{(K_\infty )}$ is $\Lambda$-torsion. Then $Z_A^{(\mathbb {L}_\infty )}$ is a $\Lambda _d$-torsion module.

Proof

We let $Z = Z_A^{(\mathbb {L}_\infty )}$. By [22, Lemma 4.7], it will suffice to show that $Z_{K_{\infty }}$ is $\Lambda$-torsion. The result now follows from Lemmas 3.11 or 3.14. $\square$

3.3 The Main Results

Now we turn to the proofs of analogues of Monsky’s Theorems I, II, III and IV from [26]. Since the results hold for Selmer groups as well as for fine Selmer groups, we introduce the following notational convention. In the following, Z will stand both for X and for Y (this enables us to formulate the results for Selmer groups and for fine Selmer groups simultaneously).

Lemma 3.18

Let $\mathbb {L}_\infty /K$ be a $\mathbb {Z}_p^d$-extension, ${d \ge 2}$. We assume that $Z_A^{(\mathbb {L}_\infty )}$ is a torsion $\Lambda _d$-module. If $Z=X$, we assume that A has good ordinary reduction at the primes of K above p, and that each ${v \in \Sigma _p(K)}$ is ramified in $\mathbb {L}_{\infty }/K$.

Then $Z_A^{(K_\infty )}$ is a $\Lambda$-torsion module and ${\mu (Z_A^{(K_\infty )}) \le m_0(Z_A^{(\mathbb {L}_\infty )})}$ for all elements ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$ which are not contained in a finite number of $\mathbb {Z}_p^{d-1}$-subextensions of $\mathbb {L}_\infty /K$.

Proof

Choose $\sigma _1, \ldots , \sigma _l$ as in Lemma 3.1 (applied to ${M = Y_A^{(\mathbb {L}_\infty )}}$ or ${M = X_A^{(\mathbb {L}_\infty )}}$), let ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$, and let

$$\begin{aligned} \gamma :\text{ Gal }(\mathbb {L}_\infty /K) \twoheadrightarrow \text{ Gal }(K_\infty /K) \end{aligned}$$

be the corresponding restriction homomorphism. Then $\gamma (\sigma _i) = 1$ if and only if $K_\infty$ is contained in the fixed field of $\sigma _i$. Therefore the condition $\gamma (\sigma _i) \ne 1$ for all i holds for all $\mathbb {Z}_p$-extensions of K which are not contained in one of the $\mathbb {Z}_p^{d-1}$-extensions ${\mathbb {L}_\infty ^{\langle \sigma _1 \rangle }, \ldots , \mathbb {L}_\infty ^{\langle \sigma _l \rangle }}$ of K. The statement of the lemma follows by combining this observation with Corollaries 3.12 and 3.15. $\square$

Remark 3.19

Let $\Sigma$ be any finite set of primes of K which contains the primes above p and the primes where A has bad reduction. If ${p = 2}$, then we assume K to be totally imaginary. It follows from [22, Lemma 7.1] that $Y_A^{(\mathbb {L}_\infty )}$ is a torsion $\Lambda _d$-module if and only if ${H^2(K_\Sigma /\mathbb {L}_\infty , A[p^\infty ]) = 0}$ (here we recall from Sect. 2.1 that $K_\Sigma$ denotes the maximal algebraic extension of K which is unramified outside of $\Sigma$). The validity of either statement is known as the weak Leopoldt conjecture for A over $\mathbb {L}_\infty$. No example is known where this conjecture fails. On the other hand, by a conjecture of Mazur (see [24, p. 104]), $X_A^{(K_\infty ^c)}$ should be a torsion $\Lambda$-module if A has good ordinary reduction at the primes above p (here $K_\infty ^c$ denotes the cyclotomic $\mathbb {Z}_p$-extension of K). This is known to be true for abelian K, by the work of Kato and Rohrlich (see [12, 30]). It can be deduced from Lemma 3.17 that in this case, $X_A^{(\mathbb {L}_\infty )}$ is $\Lambda _d$-torsion for each $\mathbb {Z}_p^d$-extension $\mathbb {L}_\infty$ of K which contains $K_\infty ^c$.

Theorem 3.20

Let $\mathbb {L}_\infty$ be a $\mathbb {Z}_p^d$-extension of K, ${d \ge 2}$. We assume that $Z_A^{(K_\infty )}$ is $\Lambda$-torsion for all but finitely many ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$. If $Z=X$, we assume that A has good ordinary reduction at the primes of K above p, and that the inertia subgroup of each ${v \in \Sigma _p(K)}$ has $\mathbb {Z}_p$-rank at least ${d-1}$.

Then $\mu (Z_A^{(K_\infty )})$ is bounded on ${\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)$.

Proof

The assertion is proved via induction. For the fine Selmer groups, it follows from Lemma 3.17 that $Y_A^{(\mathbb {L}_\infty )}$ is a torsion $\Lambda _d$-module. Therefore Lemma 3.18 implies that the $\mu (Y_A^{(K_\infty )})$ are bounded (by $m_0(Y_A^{(\mathbb {L}_\infty )})$) for all $\mathbb {Z}_p$-extensions of K which are not contained in a finite number of $\mathbb {Z}_p^{d-1}$-extensions of K. Again, Lemma 3.17 implies that for each of these $\mathbb {Z}_p^{d-1}$-extensions $L_\infty /K$, the Iwasawa module $Y_A^{(L_\infty )}$ is torsion over $\Lambda _{d-1}$. By the inductive hypothesis, the $\mu$-invariants of the $Y_A^{(K_\infty )}$ are bounded as $K_\infty$ runs over the $\mathbb {Z}_p$-extensions contained in any of these $\mathbb {Z}_p^{d-1}$-extensions $L_\infty /K$.

For the Selmer groups, the same proof goes through (note that in any given $\mathbb {Z}_p^2$-extension of K inside of $\mathbb {L}_\infty$, every prime ${v \in \Sigma _p}$ will ramify in view of our condition on the inertia subgroups. This is needed for the first inductive step). $\square$

Now we turn to the study of $l_0$-invariants. Since we do not want to restrict to the case ${d = 2}$ (as in Monsky’s paper), we consider the invariants $\widehat{l_0}$ which have been introduced in Sect. 2.2. Recall that for any finitely generated $\Lambda _d$-module M, ${M^\circ \subseteq M}$ denotes the maximal pseudo-null submodule. We also recall that each statement that the $\lambda$-invariant is bounded or unbounded in a neighbourhood ${U \subseteq {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$ always involves that $Z_{{\tilde{K}}_\infty }$ is $\Lambda$-torsion for each ${{\tilde{K}}_\infty \in U}$, see also Remark 3.7.

Lemma 3.21

Let ${\mathbb {L}_\infty /K}$ be a $\mathbb {Z}_p^d$-extension for some ${d \ge 2}$, let ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$ be such that no prime $v \in \Sigma _p(K)$ splits completely in $K_{\infty }/K$, and let

$$\begin{aligned} \pi _{K_\infty } :\mathbb {Z}_p[[\text{ Gal }(\mathbb {L}_\infty /K)]] \longrightarrow \mathbb {Z}_p[[\text{ Gal }(K_\infty /K)]] \end{aligned}$$

be the canonical restriction map. We assume that $Z_A^{(\mathbb {L}_\infty )}$ is $\Lambda _d$-torsion.

Write $Z = Z_A^{(\mathbb {L}_\infty )}$ for brevity, let $F_Z$ be the characteristic power series of Z and write ${F_Z = p^{m_0(Z)} \cdot G_Z}$, with ${p \not \mid G_Z}$.

• (i) Then $\lambda (Z_A^{({\tilde{K}}_\infty )})$ is unbounded in any neighbourhood of $K_\infty$ if the image of $G_Z$ under $\pi _{K_\infty }$ is divisible by p.

• (ii) On the other hand, suppose that $\pi _{K_\infty }(G_Z)$ is not divisible by p, and that there exists an element ${H \in \Lambda _d}$ such that ${p^s \cdot H}$ annihilates $Z^\circ$ for some ${s \in \mathbb {N}}$, and such that $\pi _{K_\infty }(H)$ is also coprime with p.

  Then $\lambda (Z_A^{({\tilde{K}}_\infty )})$ is bounded in a sufficiently small neighbourhood of $K_\infty$.

We stress that the additional assumption in (ii) is automatically satisfied in the case ${d = 2}$, see Remark 3.6.

Proof

Let $[a_1: \cdots : a_{d-1}] \in {\mathbb {P}}^{d-1}(\mathbb {Z}_p)$ correspond to some fixed $\mathbb {Z}_p$-extension ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$ of K. It follows from Lemma 3.5 that under our assumptions, ${\pi _{K_\infty }(F_Z) \equiv 0\!\!\pmod {p}}$ if and only if $\lambda (Z_{K_\infty })$ is unbounded in any neighbourhood of $[a_1: \cdots : a_d]$. It follows from Corollary 3.12 or Corollary 3.15 that this is in turn equivalent to $\lambda (Z_A^{(K_\infty )})$ being unbounded on any sufficiently small neighbourhood of $K_\infty$. $\square$

Theorem 3.22

Let $\mathbb {L}_\infty$ be a $\mathbb {Z}_p^d$-extension of K, and suppose that the decomposition subgroup in $\text{ Gal }(\mathbb {L}_\infty /K)$ of each prime v above p is open.

Let ${Z = Z_A^{(\mathbb {L}_\infty )}}$, and suppose that Z is a $\Lambda _d$-torsion module. For the first part of the theorem, we assume that $Z_A^{(K_\infty )}$ is a $\Lambda$-torsion module for each $\mathbb {Z}_p$-extension ${K_\infty \subseteq \mathbb {L}_\infty }$ of K, and that the annihilator ideal of the maximal pseudo-null submodule $Z^\circ$ of Z is not contained in any prime ideal of height at most ${d-1}$. If ${Z = X}$, then we also assume that A has good ordinary reduction at the primes ${v \in \Sigma _p(K)}$, and that each such prime ramifies in $\mathbb {L}_\infty$.

Then the following statements are equivalent:

• (i) the $\lambda (Z_A^{(K_\infty )})$ are bounded as $K_\infty$ runs over the elements from ${\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)$,

• (ii) $\widehat{l_0}(Z) = 0$.

Now suppose that $Z_A^{(K_\infty )}$ is not $\Lambda$-torsion for some ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$. Then both statements (i) and (ii) are wrong.

Proof

Suppose first that $Z_A^{(K_\infty )}$ is $\Lambda$-torsion for each $K_\infty$. It follows from Lemma 3.17 that Z is a torsion $\Lambda _d$-module. Let ${F_Z = p^{m_0(Z)} \cdot G_Z}$ be the characteristic power series of Z, as usual. If

$$\begin{aligned} \widehat{l_0}(F_Z) = \widehat{l_0}(Z_A^{(\mathbb {L}_\infty )}) > 0, \end{aligned}$$

then there exist generators ${\sigma _1, \ldots , \sigma _d}$ of $\text{ Gal }(\mathbb {L}_\infty /K)$ and a prime ideal ${\mathfrak {p}}$ such that

$$\begin{aligned} G_Z \subseteq {\mathfrak {p}}\subseteq (p, \sigma _1 - 1, \ldots , \sigma _{d-1}-1). \end{aligned}$$

Then the image of $G_Z$ under the map $\pi _{K_\infty }$ is divisible by p, where

$$\begin{aligned} K_\infty = \mathbb {L}_\infty ^{\langle \sigma _1, \ldots , \sigma _{d-1} \rangle } \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K). \end{aligned}$$

In this case, we may deduce from the previous lemma that $\lambda (Z_A^{({\tilde{K}}_\infty )})$ is unbounded as ${\tilde{K}}_\infty$ runs through the elements in a neighbourhood of $K_\infty$.

On the other hand, if $\widehat{l_0}(F_Z) = 0$, then Lemma 3.21 implies that $\lambda (Z_A^{(K_\infty )})$ is locally bounded on ${\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)$. Indeed, since the annihilator ideal of $Z^\circ$ is not contained in any prime ideal of height at most ${d-1}$, we can deduce the existence of the element ${H \in \Lambda _d}$ needed in Lemma 3.21 for each ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$ as follows (this extends an idea used by Monksy in the proof of [26, Theorem 3.3]). Let

$$\begin{aligned} J^* = \{ w \in \Lambda _d \mid p^s \cdot w \in \text{ Ann }(Z^\circ ) \text{ for } \text{ some } s \in \mathbb {N}\}. \end{aligned}$$

Then multiplication by p is injective on the quotient $\Lambda _d/J^*$ by construction. Therefore p is not contained in any minimal prime ideal ${\mathfrak {p}}$ of $J^*$ by [21, Chapter X, Proposition 2.9] and [7, Theorem 3.1,a.].

Now suppose that ${\mathfrak {p}}$ is a minimal prime ideal of $J^*$ such that

$$\begin{aligned} J^* \subseteq {\mathfrak {p}}\subseteq (p, T_1, \ldots , T_{d-1}), \end{aligned}$$

for any choice of variables $T_1, \ldots , T_d$. Then ${\mathfrak {p}}$ contains also the annihilator ideal of $Z^\circ$, and therefore the height of ${\mathfrak {p}}$ must be at least d by our general assumption. But this implies that ${{\mathfrak {p}}= (p, T_1, \ldots , T_{d-1})}$. Since we have seen above that p cannot be contained in any minimal prime ideal of $J^*$, we can conclude that ${\mathfrak {p}}$ can not be contained in the ideal $(p, T_1, \ldots , T_{d-1})$, for any choice of variables. By the definition of $J^*$, this proves the existence of an element ${H \in \Lambda _d {\setminus } (p, T_1, \ldots , T_{d-1})}$ such that ${p^s \cdot H}$ annihilates $Z^\circ$ for some sufficiently large ${s \in \mathbb {N}}$.

We have thus shown that if $\widehat{l_0}(F_Z) = 0$, then $\lambda (Z_A^{(K_\infty )})$ is locally bounded on ${\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)$ for each ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$. Since this space is compact (see [8, p. 208]), it follows that the $\lambda$-invariant is bounded globally on ${\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)$.

Now we turn to the proof of the last statement of Theorem 3.22. Fix some ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$ such that $Z_A^{(K_\infty )}$ is not $\Lambda$-torsion. In view of Corollary 3.12(a), respectively, Corollary 3.15(a) this is equivalent to $Z_{K_\infty }$ not being $\Lambda$-torsion.

Now we use the notion of Fitting ideals. Let $\pi _{K_\infty }$ be the canonical surjection between the Iwasawa algebras. Proposition 2.1(5) implies that we can write ${{\mathcal {F}}_{\Lambda _d}(Z) = (F_Z) \cdot J_Z}$, where the ideal $J_Z$ is not contained in any height one prime ideal of $\Lambda _d$. Since ${\mathcal {F}}_{\Lambda _d}(Z)$ is contained in the annihilator ideal of Z and as $Z_{K_\infty }$ is not torsion as a $\Lambda$-module, we must have $\pi _{K_\infty }({\mathcal {F}}_{\Lambda _d}(Z)) = (0)$. We show that this implies that ${\pi _{K_\infty }(F_Z) = 0}$. Indeed, suppose that this was not true. It follows from the above that there exists some ${H \in \Lambda _d}$ such that ${p^s \cdot H \in \text{ Ann }(Z^\circ )}$ and ${\pi _{K_\infty }(H) \ne 0}$ (in fact, $\pi _{K_\infty }(H)$ is not divisible by p). But then Proposition 2.1(3) implies that ${\pi _{K_\infty }({\mathcal {F}}_{\Lambda _d}(Z)) \ne (0)}$.

Therefore ${\pi _{K_\infty }(F_Z) = 0}$. Writing ${F_Z = p^{m_0(Z)} \cdot G_Z}$ with $G_Z$ coprime with p, it follows that ${\pi _{K_\infty }(G_Z) = 0}$. In particular, ${\pi _{K_\infty }(G_Z)}$ is divisible by p, and therefore ${\widehat{l_0}(F_Z) > 0}$ from the definition.

On the other hand, it follows from [14, Lemma 4.23] that $\lambda (\pi _{{\tilde{K}}_\infty }(G_Z))$ is unbounded in a neighbourhood of $K_\infty$. Indeed, let ${n \in \mathbb {N}}$ be arbitrary. It follows from Lemma 3.1 that we can find a $\mathbb {Z}_p$-extension ${\tilde{K}}_\infty$ in ${\mathcal {E}}(K_\infty ,n)$ (i.e. the first n layers of $K_\infty$ and ${\tilde{K}}_\infty$ are equal) such that $Z_{{\tilde{K}}_\infty }$ is a torsion $\Lambda$-module and

$$\begin{aligned} \mu (Z_{{\tilde{K}}_\infty }) = m_0(Z) = m_0(F_Z). \end{aligned}$$

We claim that this implies that $\pi _{{\tilde{K}}_\infty }(G_Z)$ is not divisible by p. Indeed, otherwise

$$\begin{aligned} \mu (\pi _{{\tilde{K}}_\infty }(F_Z)) > m_0(Z); \end{aligned}$$

but

$$\begin{aligned} (F_{Z_{{\tilde{K}}_\infty }}) \cdot {\mathcal {F}}_{\Lambda _1}((Z_{{\tilde{K}}_\infty })^\circ ) = {\mathcal {F}}_{\Lambda _1}(Z_{{\tilde{K}}_\infty }) = (\pi _{{\tilde{K}}_\infty }(F_Z)) \cdot \pi _{{\tilde{K}}_\infty }(J_Z) \end{aligned}$$

(8)

in view of Proposition 2.1. Since $(Z_{{\tilde{K}}_\infty })^\circ$ is a pseudo-null $\Lambda _1$-module, the annihilator ideal of this module is not contained in any prime ideal of height one. In view of Proposition 2.1(2), the same holds true for the Fitting ideal ${\mathcal {F}}_{\Lambda _1}((Z_{{\tilde{K}}_\infty })^\circ )$. Therefore the equality (8) implies that the characteristic power series ${F_{Z_{{\tilde{K}}_\infty }} \in \Lambda _1}$ of $Z_{{\tilde{K}}_\infty }$ is divisible by $\pi _{{\tilde{K}}_\infty }(F_Z)$, and thus the above assumption would contradict the fact that

$$\begin{aligned} \mu (Z_{{\tilde{K}}_\infty }) = m_0(Z)\end{aligned}$$

by the choice of ${\tilde{K}}_\infty$.

We have shown that $\pi _{{\tilde{K}}_\infty }(G_Z)$ is not divisible by p. On the other hand,

$$\begin{aligned} \pi _{K_\infty }(G_Z) \equiv \pi _{{\tilde{K}}_\infty }(G_Z) \pmod {p, T^{p^n}}. \end{aligned}$$

But $\pi _{K_\infty }(F_Z) = 0$ by the above. Therefore the degree of $\pi _{{\tilde{K}}_\infty }(G_Z)$ must be at least $p^n$. This concludes the proof of the theorem. $\square$

Remark 3.23

• (1) It follows from Remark 3.9 that the assumption on the annihilator ideal of $Z^\circ$ is also necessary: In the module-theoretic example ${M = \Lambda _3/(T_1, T_2 + p)}$ given there, the height of the annihilator ideal of ${M = M^\circ }$ is equal to ${2 = d-1}$.

• (2) Of course the most important special case is the case where ${Z^\circ = \{0\}}$. However, this is a strong assumption, in particular for the fine Selmer groups. In fact, by a well-known conjecture of Coates and Sujatha (see [6, Conjecture B], which was formulated for an elliptic curve ${A = E}$), ${Y_A^{(\mathbb {L}_\infty )} = (Y_A^{(\mathbb {L}_\infty )})^\circ }$ should be pseudo-null if $\mathbb {L}_\infty$ is any multiple $\mathbb {Z}_p$-extension which contains the cyclotomic $\mathbb {Z}_p$-extension $K_\infty ^{cyc}$ of K, provided that the fine Selmer group of A over $K_\infty ^{cyc}$ is cofinitely generated over $\mathbb {Z}_p$. That’s why we worked hard in order to extend the theorem to a more general setting.

  For Selmer groups, the case ${X^\circ = \{0\}}$ occurs a little more frequently (cf. also [10] and the proof of Theorem 4.4).

Now we prove a generalisation of the last assertion from Theorem 3.22 which will be used in the next section for the construction of Iwasawa modules with non-trivial $\widehat{l_0}$-invariant.

Theorem 3.24

Let $\mathbb {L}_\infty /K$ be a $\mathbb {Z}_p^d$-extension and suppose that $\mathbb {L}_\infty$ contains a $\mathbb {Z}_p^i$-extension $K_\infty$ of K. For brevity, we let ${Z = Z_A^{(\mathbb {L}_\infty )}}$. We assume that Z is a torsion $\Lambda _d$-module. If ${Z = X}$, then we assume that A has good ordinary reduction at p and that each ${v \in \Sigma _p(K)}$ ramifies in $\mathbb {L}_\infty$.

Suppose that $Z_A^{(K_\infty )}$ is not torsion as a $\Lambda _i$-module, and that the annihilator ideal of the maximal pseudo-null $\Lambda _d$-submodule $Z^\circ$ of Z is not contained in any prime ideal of height at most $d-i$.

Then ${\widehat{l_0}(Z) > 0}$.

Proof

Let $\pi : \Lambda _d \longrightarrow \Lambda _i$ be the canonical surjection induced by the restriction map

$$\begin{aligned} \text{ Gal }(\mathbb {L}_\infty /K) \twoheadrightarrow \text{ Gal }(K_\infty /K), \end{aligned}$$

and let ${Z_\pi = Z/(\ker (\pi )\cdot Z)}$, as usual. It follows from Corollaries 3.13 and 3.16 that the cokernel of the natural map

$$\begin{aligned} f^\vee :Z_\pi \longrightarrow Z_A^{(K_\infty )} \end{aligned}$$

is cofinitely generated over $\mathbb {Z}_p$. In particular, the quotient $Z_\pi$ is a non-torsion $\Lambda _i$-module.

Therefore ${{\mathcal {F}}_{\Lambda _i}(Z_\pi ) = (0)}$. On the other hand, it follows from Proposition 2.1(4) that

$$\begin{aligned} {\mathcal {F}}_{\Lambda _i}(Z_\pi ) = \pi ({\mathcal {F}}_{\Lambda _d}(Z)). \end{aligned}$$

We claim that this implies that ${\pi (F_Z) = 0}$. Indeed, fix generators $\gamma _1, \ldots , \gamma _{d-i}$ of $\text{ Gal }(\mathbb {L}_\infty /K_\infty )$ and write ${T_j = \gamma _j - 1}$ for each such j. Then ${\pi (F_Z) = 0}$ if and only if

$$\begin{aligned} F_Z \in (T_1, \ldots , T_{d-i}). \end{aligned}$$

On the other hand, since the annihilator ideal of the maximal pseudo-null $\Lambda _d$-submodule $Z^\circ$ of Z is not contained in any prime ideal of height ${d-i}$, it follows that there exists an element ${H \in \Lambda }$ such that H annihilates the $\Lambda _d$-module $Z^\circ$, and ${H \not \in (T_1, \ldots , T_{d-i})}$. Moreover, if Z can be generated as a $\Lambda _d$-module by l elements, then Proposition 2.1(3) implies that

$$\begin{aligned} H^l \cdot F_Z^l \in {\mathcal {F}}_{\Lambda _d}(Z). \end{aligned}$$

If $\pi (F_Z)$ was non-zero, then this would imply that $\pi ({\mathcal {F}}_{\Lambda _d}(Z)) \ne (0)$, in contradiction to our assumptions.

Therefore $F_Z$, and thus also $G_Z$, lie in the kernel of the map $\pi$. This means that

$$\begin{aligned} G_Z \in (p, T_1, \ldots , T_{d-i}). \end{aligned}$$

But then $\widehat{l_0}(G_Z)>0$ by the definition. $\square$

We conclude the current section with the proof of a natural property concerning the connection between the $l_0$-invariants and the invariant $\widehat{l_0}$. More precisely, we will consider the following situation. Let $\mathbb {L}_\infty /K$ be a fixed $\mathbb {Z}_p^d$-extension, and consider the set of $\mathbb {Z}_p^2$-extensions $L_\infty /K$ with ${L_\infty \subseteq \mathbb {L}_\infty }$, which we abbreviate to ${\mathcal {E}}^2$ in what follows. Let Z be either $X_A^{(\mathbb {L}_\infty )}$ or $Y_A^{(\mathbb {L}_\infty )}$. Recall that the Fitting ideal of Z can be written as

$$\begin{aligned} {\mathcal {F}}_{\Lambda _d}(Z) = (F_Z) \cdot J_Z, \end{aligned}$$

where the ideal $J_Z$ of $\Lambda _d$ is not contained in any prime ideal of height one.

In the following result we want to relate the following statements to each other:

• (1) $l_0(Z_{L_\infty })= 0$ for all but finitely many ${L_\infty \in {\mathcal {E}}^2}$,

• (2) $l_0(\pi _{L_\infty }(F_Z)) = 0$ for all but finitely many ${L_\infty \in {\mathcal {E}}^2}$ (here ${\pi _{L_\infty } :\Lambda _d \longrightarrow \Lambda _2}$ and ${L_\infty = \mathbb {L}_\infty ^{\ker (\pi _{L_\infty })}}$, respectively),

• (3) $\widehat{l_0}(F_Z) = 0$,

• (4) ${l_0(\pi _{L_\infty }(F_Z)) = 0}$ for each $\pi _{L_\infty }$

• (5) $l_0(Z_{L_\infty }) = 0$ for each ${L_\infty \in {\mathcal {E}}^2}$,

• (6) $l_0(Z_A^{(L_\infty )}) = 0$ for each ${L_\infty \in {\mathcal {E}}^2}$.

Proposition 3.25

Let $\mathbb {L}_\infty /K$ be a $\mathbb {Z}_p^d$-extension, ${d \ge 2}$, and let ${\mathcal {E}}^2$ be as above. We let ${Z = X_A^{(\mathbb {L}_\infty )}}$ or ${Z = Y_A^{(\mathbb {L}_\infty )}}$, and we assume that Z is a $\Lambda _d$-torsion module.

• (a) We have implications $(2) \Rightarrow (3) \Rightarrow (4)$, $(4) \Rightarrow (2)$ and ${(5) \Rightarrow (1)}$. In particular, the conditions (2), (3) and (4) are equivalent.

• (b) If ${Z = Y}$, then ${(5) \Rightarrow (6)}$. If ${Z = X}$, then the same holds true, provided that the abelian variety A has good ordinary reduction at the primes of K above p, and that each such prime ramifies in $\mathbb {L}_\infty /K$.

• (c) Suppose that the annihilator ideal of the maximal pseudo-null $\Lambda _d$-submo- dule $Z^\circ$ of Z is not contained in any prime ideal of height at most d (i.e. we assume $Z^\circ$ to be finite). Then ${(4) \Rightarrow (5)}$ and ${(2) \Rightarrow (1)}$.

Proof

We start with the proof of (a). It is obvious that statement (5) implies statement (1) and that (4) implies (2).

For the implication ${(2) \Rightarrow (3)}$, write ${F_Z = p^{m_0(Z)} \cdot G_Z}$ for some element $G_Z$ which is coprime with p, and suppose that ${\widehat{l_0}(F_Z) \ne 0}$. Then ${v_{\mathfrak {p}}(G_Z) > 0}$, where ${\mathfrak {p}}$ is a prime ideal which is contained in some ideal of the form

$$\begin{aligned} (p) + \text{ Aug }(H). \end{aligned}$$

Here ${H \cong \mathbb {Z}_p^{d-1}}$, and $\text{ Aug }(H)$ means the augmentation ideal. In fact, ${\mathfrak {p}}$ is the pre-image under the canonical projection ${\Lambda _d \twoheadrightarrow \Omega _d}$ of a minimal prime ideal of $\overline{G_Z}$ which is contained in the image ${\overline{\text{ Aug }(H)} \subseteq \Omega _d}$ of $\text{ Aug }(H)$.

Since H contains infinitely many rank $d-2$ subgroups $H'$, there exist infinitely many $\mathbb {Z}_p^2$-extensions ${L_\infty = \mathbb {L}_\infty ^{H'}}$ of K such that ${l_0(\pi _{L_\infty }(F_Z)) > 0}$ for the corresponding maps $\pi _{L_\infty }$.

Finally, the implication ${(3) \Rightarrow (4)}$ follows directly from the definitions.

Now we turn to the proof of (b). Under our assumptions we can apply Corollaries 3.13 and 3.16 in order to bound the cokernels of the maps

$$\begin{aligned} f^\vee : Z_{L_\infty } \longrightarrow Z_A^{(L_\infty )}. \end{aligned}$$

Indeed, it follows from these corollaries that the cokernels are finitely generated over $\mathbb {Z}_p$ and thus do not contribute to the $l_0$-invariant. Therefore the implication ${(5) \Rightarrow (6)}$ follows from the multiplicity of characteristic power series in short exact sequences of finitely generated torsion $\Lambda _2$-modules.

In order to prove (c), suppose that the additional hypothesis on the annihilator ideal of $Z^\circ$ is satisfied. Now suppose that (4) holds, and fix some ${L_\infty \in {\mathcal {E}}^2}$. Then ${l_0(\pi _{L_\infty }(F_Z)) = 0}$. Assume that ${l_0(Z_{L_\infty }) > 0}$. Then there exists ${\sigma \in \text{ Gal }(L_\infty /K)}$ such that

$$\begin{aligned} {\mathcal {F}}_{\Lambda _2}(Z_{L_\infty }) \subseteq (p, \sigma - 1). \end{aligned}$$

We write the subgroup of $\text{ Gal }(\mathbb {L}_\infty /K)$ fixing $L_\infty$ as ${\langle \sigma _1, \ldots , \sigma _{d-2} \rangle }$. It follows from the hypothesis in (c) that there exists an annihilator ${\tilde{H}}$ of $Z^\circ$ which is not contained in the prime ideal

$$\begin{aligned} {\mathfrak {p}}:= (\sigma _1 - 1, \ldots , \sigma _{d-2}-1, \sigma - 1, p). \end{aligned}$$

Moreover, Proposition 2.1(3) implies that

$$\begin{aligned} {\tilde{H}}^l \cdot F_Z^l \in {\mathcal {F}}_{\Lambda _d}(Z). \end{aligned}$$

Since ${l_0(\pi _{L_\infty }(F_Z)) = 0}$ by (4), we may conclude that the element

$$\begin{aligned} H:= {\tilde{H}}^l F_Z^l \in {\mathcal {F}}_{\Lambda _d}(Z) \end{aligned}$$

satisfies ${H \not \in {\mathfrak {p}}}$. This contradicts to the fact that

$$\begin{aligned} {\mathcal {F}}_{\Lambda _2}(Z_{L_\infty }) = \pi ({\mathcal {F}}_{\Lambda _d}(Z)) \subseteq (p, \sigma -1) \end{aligned}$$

and thus ${{\mathcal {F}}_{\Lambda _d}(Z) \subseteq {\mathfrak {p}}}$. $\square$

Corollary 3.26

Let $\mathbb {L}_\infty /K$ be a $\mathbb {Z}_p^d$-extension, ${d \ge 2}$, and let ${\mathcal {E}}^2$ be as above. We assume that Z is $\Lambda _d$-torsion. Suppose that the annihilator ideal of the maximal pseudo-null submodule $Z^\circ$ of Z is not contained in any prime ideal of height at most d. If ${Z = X}$, then we assume that the abelian variety A has good ordinary reduction at the primes of K above p, and that each such prime ramifies in $\mathbb {L}_\infty /K$.

If $\widehat{l_0}(Z) = 0$, then $l_0(Z_A^{(L_\infty )}) = 0$ for each ${L_\infty \in {\mathcal {E}}^2}$.

Proof

Use Proposition 3.25 in order to conclude that

$$\begin{aligned} (3) \Rightarrow (4) \Rightarrow (5) \Rightarrow (6). \end{aligned}$$

$\square$

4 Applications

We start with an application concerning the weak Leopoldt conjecture (see also Theorem 4.2 below). Since the underlying proof works both for fine Selmer groups and for Selmer groups, we will formulate the key result for both these objects simultaneously.

Theorem 4.1

In the following, we let Z be either X or Y (the choice of Z is fixed throughout the theorem).

Let $\mathbb {L}_\infty /K$ be a $\mathbb {Z}_p^d$-extension, and suppose that $\text{ rank}_{\Lambda }(Z_A^{(L_\infty )}) = 0$ for some $\mathbb {Z}_p$-extension ${L_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$ of K. If ${Z = X}$, then we assume that A has good ordinary reduction at each prime ${v \in \Sigma _p(K)}$ and that each such prime ramifies in ${L_\infty \subseteq \mathbb {L}_\infty }$. If ${d > 2}$, then we assume that the annihilator ideal of the maximal pseudo-null submodule $Z^\circ$ of Z is not contained in any prime ideal of height at most d.

• (a) Suppose that ${d = 2}$. Then ${\text{ rank}_\Lambda (Z_A^{(K_\infty )}) = 0}$ for all but finitely many $\mathbb {Z}_p$-extensions ${K_\infty \subseteq \mathbb {L}_\infty }$ of K.

• (b) Let now ${d \in \mathbb {N}}$ be arbitrary again. If, in addition,

  $$\begin{aligned} \widehat{l_0}(Z_A^{(\mathbb {L}_\infty )}) = 0, \end{aligned}$$

  then $\text{ rank}_\Lambda (Z_A^{(K_\infty )}) = 0$ holds for each ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$.

Proof

For the first statement, we note that it follows from Lemma 3.17 that $Z_A^{(\mathbb {L}_\infty )}$ is a torsion $\Lambda _2$-module. By Lemma 3.1, the quotient $(Z_A^{(\mathbb {L}_\infty )})_{K_\infty }$ is a torsion $\Lambda$-module for all but finitely many ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$. On the other hand, our control Theorems 3.11 and 3.14 imply that the cokernels of the maps

$$\begin{aligned} f^\vee :(Z_A^{(\mathbb {L}_\infty )})_{K_\infty } \longrightarrow Z_A^{(K_\infty )} \end{aligned}$$

are $\Lambda$-torsion for all ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$. This proves (a).

For (b), we first consider the case ${d = 2}$. Let ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$ be arbitrary. We write ${\Lambda _2 = \mathbb {Z}_p[[S, T]]}$, where ${\text{ Gal }(\mathbb {L}_\infty /K_\infty ) = \langle T+ 1 \rangle }$, and we abbreviate $Z_A^{(\mathbb {L}_\infty )}$ to Z.

Let ${F_Z \in \Lambda _2}$ denote the characteristic power series of Z. As in the proof of [26, Theorem 3.3], we can choose an element ${H \in \Lambda _2}$ such that the image ${\overline{H}}$ of H in ${\Omega _2 = \Lambda _2/p}$ is not divisible by ${\overline{T}}$ and ${p^{m_0(Z) + s} \cdot F_Z \cdot H}$ annihilates Z for sufficiently large ${s \in \mathbb {N}}$. Since ${l_0(Z) = 0}$ by assumption, $\overline{F_Z} \in \Omega _2$ is also coprime with ${\overline{T}}$. Therefore the same holds true for ${\overline{F_Z \cdot H}}$, and ${Z_{K_\infty } = Z/(T \cdot Z)}$ is a torsion ${\Lambda = \mathbb {Z}_p[[S]]}$-module. In view of Lemmas 3.11 and 3.14 the same holds true for $Z_A^{(K_\infty )}$.

Now let ${d \in \mathbb {N}}$ be arbitrary, and let ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$. We consider the $\mathbb {Z}_p^2$-extension

$$\begin{aligned} \mathbb {L}_\infty ^{(2)}:= K_\infty \cdot L_\infty \end{aligned}$$

of K, where $L_\infty$ is the $\mathbb {Z}_p$-extension of K from the hypotheses of the theorem. It follows from Corollary 3.26 that ${l_0(Z_A^{(\mathbb {L}_\infty ^{(2)})}) = 0}$. Therefore the first part of the proof of (b) implies that ${\text{ rank}_\Lambda (Z_A^{(K_\infty )}) = 0}$. $\square$

Let $\mathbb {L}_\infty /K$ be a $\mathbb {Z}_p^d$-extension, and let A be an abelian variety defined over K. Recall from Remark 3.19 that $Y_A^{(\mathbb {L}_\infty )}$ being a torsion $\Lambda _d$-module is known as the weak Leopoldt conjecture holds for A over $\mathbb {L}_\infty$. Therefore we may derive from Theorem 4.1 the following

Theorem 4.2

Let $\mathbb {L}_\infty /K$ be a $\mathbb {Z}_p^d$-extension, and suppose that the weak Leopoldt conjecture holds for some $\mathbb {Z}_p$-extension ${L_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$ of K. If ${d > 2}$, then we assume that the annihilator ideal of the maximal pseudo-null submodule of ${Y = Y_A^{(\mathbb {L}_\infty )}}$ is not contained in any prime ideal of height less than d.

• (a) If ${d = 2}$, then the weak Leopoldt conjecture holds for A over all but finitely many $\mathbb {Z}_p$-extensions of K which are contained in $\mathbb {L}_\infty$.

• (b) Let ${d \ge 2}$ be arbitrary. If, in addition, $\widehat{l_0}(Y_A^{(\mathbb {L}_\infty )}) = 0$, then the weak Leopoldt conjecture holds in fact for all $\mathbb {Z}_p$-extensions ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$ of K.

Remark 4.3

In [23], Lim proved a special instance of this result. To be more precise, Lim considered abelian varieties over $\mathbb {Z}_p^2$-extensions of K which contain the cyclotomic $\mathbb {Z}_p$-extension $K_\infty ^{cyc}$ of K. The assertion (a) of Theorem 4.2 then follows from [23, Theorem 3.9], and Lim proved the assertion of (b) under the potentially stronger assumption that $Y_A^{(\mathbb {L}_\infty )}$ is pseudo-null over $\Lambda _2$ (see [23, Proposition 3.8]).

In the case of Selmer groups, we can actually go one step farther.

Theorem 4.4

Let $\mathbb {L}_\infty /K$ be a $\mathbb {Z}_p^d$-extension, and suppose that

• (i) $\text{ rank}_\Lambda (X_A^{(L_\infty )}) = 0$ for some ${L_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$ such that each ${v \in \Sigma _p(K)}$ ramifies in $L_\infty$,

• (ii) for any ${v \in \Sigma _p(K)}$ its decomposition subgroup of $\text{ Gal }(\mathbb {L}_\infty /K)$ is open,

• (iii) A has good ordinary reduction at each ${v \in \Sigma _p(K)}$,

• (iv) K is totally imaginary, and

• (v) $A(\mathbb {L}_\infty )[p^\infty ]$ is finite.

If ${d > 2}$, then we moreover assume that the annihilator ideal of the maximal pseudo-null $\Lambda _d$-submodule of $X_A^{(\mathbb {L}_\infty )}$ is not contained in any prime ideal of height at most d. Then the following statements hold.

• (a) The following are equivalent:

  • (1) $\widehat{l_0}(X_A^{(\mathbb {L}_\infty )}) = 0$,

  • (2) $X_A^{(K_\infty )}$ is $\Lambda$-torsion for each ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$, and $\mu (X_A^{(K_\infty )})$ is constant as one runs over the $\mathbb {Z}_p$-extensions ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$ of K.

  • (3) $\lambda (X_A^{(K_\infty )})$ is bounded as $K_\infty$ runs over the $\mathbb {Z}_p$-extensions of K which are contained in $\mathbb {L}_\infty$.

• (b) In particular, if ${\widehat{l_0}(X_A^{(\mathbb {L}_\infty )}) = 0}$ and ${\mu (X_A^{(K_\infty )}) = 0}$ holds for any $K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)$, then the same holds in fact true for every ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$.

Proof

We start with the proof of (a).

$(1) \Longrightarrow (2)$: Suppose that ${\widehat{l_0}(X_A^{(\mathbb {L}_\infty )}) = 0}$. Then Theorem 4.1 implies that $X_A^{(K_\infty )}$ is $\Lambda$-torsion for each ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$. We will show that ${\mu (X_A^{(K_\infty )}) =} {\mu (X_A^{(L_\infty )})}$ for each ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$. To this purpose, let ${{\tilde{K}}_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$ be arbitrary, and consider the $\mathbb {Z}_p^2$-extension

$$\begin{aligned} \mathbb {L}_\infty ^{(2)} = L_\infty \cdot {\tilde{K}}_\infty \end{aligned}$$

of K, where $L_\infty$ is from hypothesis (i) of the theorem.

It follows from Corollary 3.26 and Theorem 3.22 that $\lambda (X_A^{(K_\infty )})$ is bounded on ${\mathcal {E}}^{\subseteq \mathbb {L}_\infty ^{(2)}}(K)$; let C be an upper bound. The additional hypothesis that $A(\mathbb {L}_\infty )[p^\infty ]$ is finite implies that $A(K_\infty )[p^\infty ]$ is finite and of bounded order as $K_\infty$ runs over the elements of ${\mathcal {E}}^{\subseteq \mathbb {L}_\infty ^{(2)}}(K)$. It follows from the main result of [10] (see [20, Theorem 3.4] for more details) that the cardinality of the maximal finite $\Lambda$-submodule $(X_A^{(K_\infty )})^\circ$ of $X_A^{(K_\infty )}$ is bounded by some constant ${{\tilde{C}} \in \mathbb {N}}$ as $K_\infty$ runs over the elements in ${\mathcal {E}}^{\subseteq \mathbb {L}_\infty ^{(2)}}(K)$.

Since $X_A^{(K_\infty )}$ is $\Lambda$-torsion for each ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$, the quotient $X_A^{(K_\infty )}/f$ will be finite for every ${f \in \Lambda }$ which is coprime with the characteristic power series of $X_A^{(K_\infty )}$. We make a concrete choice: We choose n large enough such that

$$\begin{aligned} {\tilde{C}}< n \quad \text { and } \quad n \cdot C + {\tilde{C}} < p^{n+1} - p^n, \end{aligned}$$

and we consider the polynomial

$$\begin{aligned} \nu _{2n,n} = \frac{\omega _{2n}}{\omega _n} \in \mathbb {Z}_p[T], \end{aligned}$$

where $\omega _{n} = \omega _n(T) = (T+1)^{p^n} -1$. The polynomial $\nu _{2n,n}$ is a product of irreducible factors of degrees equal to ${p^{i+1} - p^i}$ for ${i \in \{n, \ldots , 2n-1\}}$. In particular, since ${\lambda (X_A^{(K_\infty )}) < p^{n+1} - p^n}$ for each ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty ^{(2)}}(K)}$ by the choice of n, the characteristic power series of each $X_A^{(K_\infty )}$ is coprime with each of the irreducible factors of $\nu _{2n,n}$, and therefore also coprime with $\nu _{2n,n}$. Therefore

$$\begin{aligned} \text{ rank}_{\nu _{2n,n}}(X_A^{(K_\infty )}):= v_p(|X_A^{(K_\infty )}/\nu _{2n,n} X_A^{(K_\infty )}|) \end{aligned}$$

is finite for every ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$.

It follows from Lemma 3.1 and Corollary 3.15 that

$$\begin{aligned} \mu (X_A^{(L)}) = m_0(X_A^{(\mathbb {L}_\infty ^{(2)})}) \end{aligned}$$

for all but finitely many ${L \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty ^{(2)}}(K)}$ (indeed: Using the notation from Corollary 3.15(a), if ${v \in \Sigma (K) {\setminus } \Sigma _s(K)}$, i.e. v is not completely split in the $\mathbb {Z}_p^2$-extension $\mathbb {L}_\infty ^{(2)}$ of K, then the $\mathbb {Z}_p$-rank of the decomposition group is at least one, i.e. there exists at most one $\mathbb {Z}_p$-extension L of K in $\mathbb {L}_\infty ^{(2)}$ such that v splits completely in L). Suppose that ${\mu (X_A^{(K_\infty )}) \ne m_0(X_A^{(\mathbb {L}_\infty ^{(2)})})}$ for some fixed $K_\infty$. Since ${A(\mathbb {L}_\infty )[p^\infty ]}$ is finite by assumption, it follows that ${A(K_\infty )[p^\infty ]}$ is finite. Therefore we can apply [16, Theorem 4.5 and Corollary 3.8] in order to conclude that there exists a Greenberg neighbourhood ${U = {\mathcal {E}}(K_\infty ,m) \cap {\mathcal {E}}^{\subseteq \mathbb {L}_\infty ^{(2)}}(K)}$ of $K_\infty$ such that

$$\begin{aligned} \text{ rank}_{\nu _{2n,n}}(X_A^{(L)}) = \text{ rank}_{\nu _{2n,n}}(X_A^{(K_\infty )}) \end{aligned}$$

(9)

for each $L \in U$, with the above choice of $\nu _{2n,n}$.

We may assume that m has been chosen large enough to ensure that

$$\begin{aligned} \mu (X_A^{(L)}) = m_0(X_A^{(\mathbb {L}_\infty ^{(2)})}) \end{aligned}$$

holds for each $L \in U$ which is different from $K_\infty$. It is a general fact that

$$\begin{aligned} \text{ rank}_{\nu _{2n,n}}(X_A^{(L)}) = \text{ rank}_{\nu _{2n,n}}(E_{X_A^{(L)}}) + \text{ rank}_{\nu _{2n,n}}((X_A^{(L)})^\circ ) \end{aligned}$$

(10)

for each L (see the proof of [15, Theorem 3.10(iii)]). Since ${|(X_A^{(L)})^\circ | \le {\tilde{C}}}$ is bounded as L runs over the elements in ${U \subseteq {\mathcal {E}}^{\subseteq \mathbb {L}_\infty ^{(2)}}(K)}$, we may conclude that

$$\begin{aligned} |\text{ rank}_{\nu _{2n,n}}(E_{X_A^{(L)}}) - \text{ rank}_{\nu _{2n,n}}(E_{X_A^{(K_\infty )}})| \le {\tilde{C}} \end{aligned}$$

(11)

for every $L \in U$. Now

$$\begin{aligned} \text{ rank}_{\nu _{2n,n}}(E_{X_A^{(K_\infty )}}) = \mu (X_A^{(K_\infty )}) \cdot (p^{2n} - p^n) + n \cdot \lambda (X_A^{(K_\infty )}), \end{aligned}$$

and an analogous formula holds for L. Indeed, the $\nu _{2n,n}$-rank of the ‘$\lambda$’-part $\bigoplus _{j = 1}^t \Lambda /(g_j^{n_j})$ of $E_{X_A^{(K_\infty )}}$ (i.e. the sum over all the $\mathbb {Z}_p$-free quotients occuring in $E_{X_A^{(K_\infty )}}$) is given by

$$\begin{aligned} \sum _\zeta v_p(F(\zeta -1)), \end{aligned}$$

where $F = \prod _{j = 1}^t g_j^{n_j}$, and where $\zeta$ runs over the roots of unity of exact orders $p^{i}$, ${i \in \{ n+1, \ldots , 2n\} }$, which are contained in some fixed algebraic closure of $\mathbb {Q}_p$. Since ${\deg (F) < p^{n+1} - p^n}$ by the choice of n, it follows that

$$\begin{aligned} v_p(F(\zeta - 1)) = \frac{\deg (F)}{p^{i+1} - p^i} = \frac{\lambda (X_A^{(K_\infty )})}{p^{i+1} - p^i} \end{aligned}$$

for each $\zeta$ of exact order $p^{i+1}$, because ${\lambda (X_A^{(K_\infty )}) = \deg (F)}$ by the definition. A similar formula holds for $\text{ rank}_{\nu _{2n,n}}(E_{X_A^{(L)}})$, ${L \in U}$ arbitrary, since

$$\begin{aligned} \lambda (X_A^{(L)}) \le C < p^{n+1} - p^n \end{aligned}$$

by our choices of C and n.

Therefore inequality (11) implies that

$$\begin{aligned} |\left( \mu (X_A^{(K_\infty )}) - \mu (X_A^{(L)})\right) \cdot (p^{2n} - p^n) + n \cdot \left( \lambda (X_A^{(K_\infty )}) - \lambda (X_A^{(L)})\right) | \le {\tilde{C}}. \end{aligned}$$

In view of the choice of n, this shows that the $\mu$-invariants must be equal, i.e. the assumption ${\mu (X_A^{(K_\infty )}) \ne m_0(X_A^{(\mathbb {L}_\infty ^{(2)})})}$ cannot hold. Moreover, we may conclude that

$$\begin{aligned} \lambda (X_A^{(K_\infty )}) = \lambda (X_A^{(L)}) \end{aligned}$$

for each ${L \in U \subseteq {\mathcal {E}}^{\subseteq \mathbb {L}_\infty ^{(2)}}(K)}$, since ${n > {\tilde{C}}}$.

$(2) \Longrightarrow (3)$: Now we assume that ${\mu (X_A^{(K_\infty )}) = \mu (X_A^{(L_\infty )})}$ for each ${K_\infty \in } {{\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$. Then [16, Theorem 4.11] implies that for each ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)}$ there exists a neighbourhood ${{\mathcal {E}}(K_\infty ,n)}$ such that

$$\begin{aligned} \lambda (X_A^{(L)}) \le \lambda (X_A^{(K_\infty )}) \end{aligned}$$

for each ${L \in {\mathcal {E}}(K_\infty ,n)}$, i.e. the $\lambda$-invariants are locally bounded. Since the set ${\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)$ is compact with respect to Greenberg’s topology, we see that the fact that $\mu$ is constant implies that $\lambda$ is bounded on ${\mathcal {E}}^{\subseteq \mathbb {L}_\infty }(K)$.

$(3) \Longrightarrow (1)$: This follows from Theorem 3.22.

Therefore we have proven statement (a). Assertion (b) is a direct special case. $\square$

In [18], we have constructed families of elliptic curves E over imaginary-quadratic number fields K (see Theorem 4.5 for the details) such that $\lambda (X_E^{(K_\infty )})$ is unbounded as $K_\infty$ runs over the $\mathbb {Z}_p$-extensions of K (note that the composite of all the $\mathbb {Z}_p$-extensions of an imaginary-quadratic field K is a $\mathbb {Z}_p^2$-extension $\mathbb {L}_\infty$ of K). In this example, E had good ordinary reduction at the primes above p. Therefore the results from Sect. 3 are applicable, and we may deduce the following

Theorem 4.5

Let E be an elliptic curve of conductor N defined over $\mathbb {Q}$, and let K be an imaginary quadratic field such that ${{\mathcal {O}}_K^\times = \{\pm 1\}}$. We assume that

• (1) the rational prime p does not divide ${6 N \text{ disc }(K) h_K |E/E^0|}$, where $h_K$ denotes the class number of K, $\text{ disc }(K)$ denotes the discriminant, and $E/E^0$ means the set of connected components of the Néron model of E over $\text{ Spec }({\mathcal {O}}_K)$,

• (2) E has good ordinary reduction at each ${v \in \Sigma _p(K)}$,

• (3) the Galois representation

  $$\begin{aligned} \rho _p :\text{ Gal }({\overline{\mathbb {Q}}}/\mathbb {Q}) \longrightarrow \text{ Aut }(E[p^\infty ]) \end{aligned}$$

  is surjective,

• (4) $E(k_v)[p^\infty ] = \{0\}$ for each ${v \in \Sigma _p(K)}$ (here $k_v$ denotes the finite residue field at v),

• (5) $|E(\mathbb {F}_p)| \not \equiv -1 \pmod {p}$ if p splits in $K/\mathbb {Q}$, and

• (6) every prime $q \mid N$ splits in $K/\mathbb {Q}$.

Then $l_0(X_E^{(\mathbb {K}_\infty )}) > 0$, where $\mathbb {K}_\infty$ denotes the composite of all $\mathbb {Z}_p$-extensions of K.

Proof

The hypotheses (1)–(6) ensure that $X_E^{(K_\infty ^a)}$ is non-torsion as a $\Lambda$-module, where $K_\infty ^a$ denotes the anticyclotomic $\mathbb {Z}_p$-extension of K.

Since E has good ordinary reduction at the primes above p, it follows from the results of Kato and Rohrlich that $X_E^{(K_\infty ^c)}$ is $\Lambda$-torsion, where $K_\infty ^c$ denotes the cyclotomic $\mathbb {Z}_p$-extension of K. Since each prime of K above p ramifies in $K_\infty ^c/K$, it follows from Lemma 3.17 that $X_E^{(\mathbb {K}_\infty )}$ is a torsion $\Lambda _2$-module. The result follows from Theorem 4.1.

Alternatively, it has been shown in [18, Corollary 1.2] that $\lambda (X_E^{(K_\infty )})$ is unbounded as $K_\infty$ runs over the $\mathbb {Z}_p$-extensions of K, provided that $\mu (X_E^{(K_\infty ^c)}) = 0$. Therefore, under this additional hypothesis, Theorem 3.22 can be applied to deduce the result (see also Remark 3.6). $\square$

In [18, Example 7.14], we have given a concrete example where all the hypotheses from this theorem are satisfied: Let $K = \mathbb {Q}(\sqrt{-7})$, and consider the elliptic curve E defined by

$$\begin{aligned} E :y^2 + y = x^3-x^2-10x-20. \end{aligned}$$

Then the hypotheses from Theorem 4.5 are satisfied for the two primes 37 and 43, both of which are split in $K/\mathbb {Q}$. To the authors’ knowledge, this provides the first known example at all of an Iwasawa module having a non-trivial $l_0$-invariant.

Remark 4.6

In the situation of Theorem 4.5, the Iwasawa module $X_E^{(\mathbb {K}_\infty )}$ is $\Lambda _2$-torsion. Theorem 4.1 implies that $X_E^{(K_\infty )}$ is $\Lambda$-torsion for all but finitely many $\mathbb {Z}_p$-extensions $K_\infty$ of K. Therefore Theorem 3.20 implies that the $\mu$-invariants of the Iwasawa modules $X_E^{(K_\infty )}$ are bounded as $K_\infty$ runs over the $\mathbb {Z}_p$-extensions of K. One can in fact say more: If $\mu (X_E^{(K_\infty ^c)}) = 0$ in the setting of Theorem 4.5, and as $X_E^{(K_\infty ^c)}$ is a $\Lambda$-torsion module by the results of Kato and Rohrlich, [16, Theorem 1.1] implies that the $\lambda$-invariants $\lambda (X_E^{(K_\infty )})$ are bounded as $K_\infty$ runs over the $\mathbb {Z}_p$-extensions of K which are contained in some sufficiently small neighbourhood of $K_\infty ^c$. Now the main result of [20] (more precisely, Proposition 2.6 and the implication $(e) \Longrightarrow (b)$ from Theorem 1.1 of loc.cit.) implies that ${m_0(X_E^{(\mathbb {K}_\infty )}) = 0}$. We may deduce from Lemma 3.1 and Corollary 3.15(a) and (b) that ${\mu (X_E^{(K_\infty )}) = 0}$ for all but finitely many ${K_\infty \in {\mathcal {E}}^{\subseteq \mathbb {K}_\infty }(K)}$. Note that we cannot apply Theorem 4.4, since ${\text{ rank}_\Lambda (X_A^{(K_\infty ^a)}) > 0}$.

Now we derive from Theorem 4.5 the existence of a $\mathbb {Z}_p^d$-extension $\mathbb {L}_\infty /L$, ${d > 2}$, such that ${\widehat{l_0}(X_E^{(\mathbb {L}_\infty )}) \ne 0}$. To this purpose, we first enlarge the base field, since the imaginary quadratic number field K has not enough $\mathbb {Z}_p$-extensions.

Lemma 4.7

Let E, p and $\mathbb {K}_\infty /K$ be as in Theorem 4.5, and let L/K be a finite normal p-extension with Galois group H. We assume that ${\mu (X_E^{(K_\infty ^c)}) = 0}$, where $K_\infty ^c$ denotes the cyclotomic $\mathbb {Z}_p$-extension of K. We assume that ${L \cap \mathbb {K}_\infty }{= K}$. Let ${L_\infty = \mathbb {K}_\infty \cdot L}$. Then $l_0(X_E^{(L_\infty )}) \ne 0$.

Proof

As we have seen in Remark 4.6, we can choose a neighbourhood ${U =}{ {\mathcal {E}}(K_\infty ^a,n)}$ of the anticyclotomic $\mathbb {Z}_p$-extension of K such that

$$\begin{aligned} \text{ rank}_\Lambda (X_E^{(K_\infty )}) = \mu (X_E^{(K_\infty )}) = 0 \end{aligned}$$

for each ${K_\infty ^a \ne K_\infty \in U}$. Moreover, since each prime above p ramifies in $K_\infty ^a$, we may assume that U has been chosen small enough to ensure that the same is true for each ${K_\infty \in U}$. Finally, by hypothesis (6) of Theorem 4.5, each prime of K of bad reduction splits in $K/\mathbb {Q}$. It then follows from [3, Theorem 2] that each such prime is finitely split in the anticyclotomic extension $K_\infty ^a$ of K. Since ${p \ne 2}$, we can assume that ${\Sigma {\setminus } \Sigma _p}$ contains exactly the primes of bad reduction, and we may thus assume that each ${v \in \Sigma }$ is finitely split in every ${K_\infty \in U}$.

To each such $K_\infty$, we consider the finite p-extension ${K_\infty ' = K_\infty \cdot L}$ of $K_\infty$, and we identify $\text{ Gal }(K_\infty '/K_\infty )$ with H.

Now we consider the commutative diagram

where ${J_v(E/K_\infty ) = \varinjlim \bigoplus _{w \mid v} H^1(F_w,E)[p^\infty ]}$ and the limit is taken over all finite subextensions ${F_w/K_v}$ of ${K_{\infty ,w}}$. Moreover, $J_v(E/K_\infty ')$ is defined in an analogous manner.

We want to show that the Pontryagin duals of $\ker (\beta )$, $\textrm{coker}(\beta )$ and $\ker (\gamma )$ are finite, since this will show that also $\ker (\alpha )$ and $\textrm{coker}(\alpha )$ are finite.

Since ${\ker (\beta ) = H^1(H, E(K_\infty ')[p^\infty ])}$ and ${\textrm{coker}(\beta ) = H^2(H, E(K_\infty ')[p^\infty ])}$ are both cofinitely generated over $\mathbb {Z}_p$ and annihilated by some power of p (the latter holds true since H is finite), their Pontryagin duals are also annihilated by the same power of p. Therefore $\ker (\beta )^\vee$ and $\textrm{coker}(\beta )^\vee$ are finite.

Now we consider the kernel of $\gamma$. Since each prime of K above p ramifies in the $\mathbb {Z}_p$-extension $K_\infty$, both $K_\infty /K$ and $K_\infty '/K'$ are deeply ramified extensions in the sense of Coates and Greenberg (see [4, Theorem 2.13]). Therefore the kernel of $\gamma$ may be written in the form ${C \times D}$, where

$$\begin{aligned} C = \prod _{w \in \Sigma (K_\infty ) \setminus \Sigma _p(K_\infty )} H^1(H, E(K_{\infty ,w}')[p^\infty ]) \end{aligned}$$

and

$$\begin{aligned} D = \prod _{w \in \Sigma _{p}(K_\infty )} H^1(H_w, {\tilde{E}}(k_{\infty ,w}')[p^\infty ]). \end{aligned}$$

Here we have fixed, by abuse of notation, a prime w of $K_\infty '$ above ${w \in \Sigma (K_\infty )}$, respectively, and ${H_w \subseteq H}$ denotes the corresponding decomposition subgroup. Moreover, $k_{\infty ,w}'$ denotes the residue field of $K_{\infty ,w}'$ and ${\tilde{E}}$ is the reduction of E over the residue field.

Again, each of these cohomology groups is cofinitely generated over $\mathbb {Z}_p$ and annihilated by a power of p and hence is finite. Since no prime ${v \in \Sigma }$ is totally split in $K_\infty /K$, it follows that $\Sigma (K_\infty )$ is finite, and therefore the Pontryagin dual of the kernel of $\gamma$ is finite.

We have shown that the kernel and the cokernel of the natural dualised map

$$\begin{aligned} \psi ^{(K_\infty )} :(X_E^{(K_\infty ')})_H \longrightarrow X_E^{(K_\infty )} \end{aligned}$$

are finite. Recall that ${\text{ rank}_\Lambda (X_E^{(K_\infty )}) = \mu (X_E^{(K_\infty ^c)}) = 0}$ for each ${K_\infty ^a \ne K_\infty \in U}$. Therefore $\text{ rank}_p(X_E^{(K_\infty )})$ is finite for each such $K_\infty$, and it follows that the same holds for $\text{ rank}_p((X_E^{(K_\infty ')})_H)$. Nakayama’s Lemma implies that $X_E^{(K_\infty ')}$ is $\Lambda$-torsion and has $\mu$-invariant zero. Since ${\text{ rank}_\Lambda (X_E^{(K_\infty ^a)}) > 0}$ by our hypotheses, the proof of the last assertion of Theorem 3.22 shows that the $\lambda$-invariants $\lambda (X_E^{(K_\infty )})$ are unbounded as $K_\infty$ runs over the elements in U. Since the cokernel of $\psi ^{(K_\infty )}$ is finite for each $K_\infty$, and as

$$\begin{aligned} \lambda (X_E^{(K_\infty ')}) \ge \text{ rank}_{\mathbb {Z}_p}((X_E^{(K_\infty ')})_H), \end{aligned}$$

it follows that $\lambda (X_E^{(K_\infty ')})$ is also unbounded. But then Theorem 3.22 implies that ${l_0(X_E^{(L_\infty )}) > 0}$ (recall that the additional hypothesis on the maximal pseudo-null submodule of $X_E^{(L_\infty )}$ is not needed in the ${d = 2}$ case, as has been pointed out in Remark 3.6). $\square$

The following theorem follows if we combine the previous Lemma 4.7 with Corollary 3.26.

Theorem 4.8

Let E be an elliptic curve defined over $\mathbb {Q}$, and let K be an imaginary quadratic number field such that the hypotheses from Theorem 4.5 are satisfied. We assume that ${\mu (X_E^{(K_\infty ^c)}) = 0}$, where $K_\infty ^c$ denotes the cyclotomic $\mathbb {Z}_p$-extension of K.

Moreover, let L/K be any finite normal p-extension, and let $\mathbb {L}_\infty$ denote the composite of all $\mathbb {Z}_p$-extensions of L. Let ${d = \text{ rank}_{\mathbb {Z}_p}(\text{ Gal }(\mathbb {L}_\infty /K))}$.

We assume that the annihilator ideal of the maximal pseudo-null $\Lambda _d$-submodule of $X_E^{(\mathbb {L}_\infty )}$ is not contained in any prime ideal of height at most d.

Then $\widehat{l_0}(X_E^{(\mathbb {L}_\infty )}) > 0$.

We mention one final application. We want to construct examples of Iwasawa modules with non-trivial $\widehat{l_0}$-invariant. Since it is difficult to check the condition on the annihilator ideal of the maximal pseudo-null submodule of $X_E^{(\mathbb {L}_\infty )}$, we choose a different approach. In the following, let A be an arbitrary abelian variety defined over K, let $\mathbb {L}_\infty /K$ be a $\mathbb {Z}_p^d$-extension, and write Z for either $Y_A^{(\mathbb {L}_\infty )}$ or $X_A^{(\mathbb {L}_\infty )}$ (i.e. the following result holds for both Selmer groups and fine Selmer groups).

Theorem 4.9

Let $\mathbb {L}_\infty /K$ be a $\mathbb {Z}_p^d$-extension, and suppose that Z is a torsion $\Lambda _d$-module, and that $\mathbb {L}_\infty$ contains a $\mathbb {Z}_p^{d-1}$-extension $K_\infty$ of K such that $Z_A^{(K_\infty )}$ is a non-torsion $\Lambda _{d-1}$-module. Then ${\widehat{l_0}(Z) > 0}$.

Proof

This follows from the $i = d-1$ special case of Theorem 3.24, since the annihilator ideal of the maximal pseudo-null $\Lambda _d$-submodule $Z^\circ$ of Z is not contained in any prime ideal of $\Lambda _d$ of height one. $\square$

Now we state our main application of this result. We mention only one example for the scope of Theorem 4.9; the base field K could be chosen in many different ways.

Corollary 4.10

Let ${K = \mathbb {Q}(\zeta _{3^i})}$ for some ${i \ge 2}$, where $\zeta _{3^i}$ denotes a primitive $3^i$th root of unity (in some fixed algebraic closure of $\mathbb {Q}$). Let E be an elliptic curve defined over $\mathbb {Q}$.

We assume that $p \equiv 2 \pmod {3}$ is a prime number such that E has good ordinary reduction at p, and that the conductor $N_E$ of E satisfies ${N_E \equiv 1}\!\!\!{\pmod {3}}$.

If $E(K)[p]=\{0\}$, and if p divides none of the local Tamagawa factors $c_v$ of the primes v of K of bad reduction, then there exists a $\mathbb {Z}_p^{3^{i-1}+1}$-extension $\mathbb {L}_\infty$ of K such that the $\widehat{l_0}$-invariant of $X_E^{(\mathbb {L}_\infty )}$ is non-trivial.

Proof

Let $k \subseteq K$ be the unique imaginary quadratic subfield. It follows from [27, Example 5.1] that there exists a $\mathbb {Z}_p^{r_2(K)}$-extension $K_\infty$ of K such that complex conjugation acts by $-1$ on $\text{ Gal }(K_\infty /K)$. Note that

$${r_2(K) = [K:\mathbb {Q}]/2 = 3^{i-1}}.$$

In view of our hypotheses, [27, Corollary 3.6 and Example 5.1] imply that $X_E^{(K_\infty )}$ is a non-torsion $\Lambda _{r_2(K)}$-module. More precisely, the condition (c) from [27, Corollary 3.6] holds in view of the two facts ${4 \not \mid [K:\mathbb {Q}]}$ and ${p \equiv 2 \pmod {3}}$ (the latter implies that p has even order in $(\mathbb {Z}/3\mathbb {Z})^\times$), as is explained in [27, Example 5.1]. If $\chi$ denotes the quadratic character of ${k = \mathbb {Q}(\sqrt{-3})}$, then ${\chi (N_E) = 1}$ in view of the condition ${N_E \equiv 1 \pmod {3}}$.

Now let ${\mathbb {L}_\infty := K_\infty \cdot K_{cyc}}$ be the compositum with the cyclotomic $\mathbb {Z}_p$-extension of K. Since K is a totally abelian field, it follows from the results of Kato and Rohrlich (see [12, 30]) that $X_A^{(K_{cyc})}$ is a torsion $\Lambda _1$-module. Therefore $X_A^{(\mathbb {L}_\infty )}$ is $\Lambda _d$-torsion in view of Lemma 3.17, where ${d = r_2(K) +1}$. Then it follows from Theorem 4.9 that ${\widehat{l_0}(X_A^{(\mathbb {L}_\infty )}) > 0}$. $\square$

Example 4.11

Let E be the elliptic curve with Cremona label 19a1, and let ${K=\mathbb {Q}(\zeta _9)}$. Computations in SAGE [31] verify that E has good ordinary reduction at $p=5$, ${E(K)[5]=\{0\}}$ and that 5 divides none of the Tamagawa numbers $c_v$ of the primes v of K. By the previous corollary there exists a $\mathbb {Z}_p^4$-extension $\mathbb {L}_\infty$ of K such that the $\widehat{l_0}$-invariant of $X_E^{(\mathbb {L}_\infty )}$ is non-trivial.