Projections and Angle Sums of Belt Polytopes and Permutohedra

Abstract

Let $P\subset \mathbb {R}^n$ be a belt polytope, that is a polytope whose normal fan coincides with the fan of some hyperplane arrangement ${\mathcal {A}}$. Also, let $G:\mathbb {R}^n\rightarrow \mathbb {R}^d$ be a linear map of full rank whose kernel is in general position with respect to the faces of P. We derive a formula for the number of j-faces of the “projected” polytope GP in terms of the j-th level characteristic polynomial of ${\mathcal {A}}$. In particular, we show that the face numbers of GP do not depend on the linear map G provided a general position assumption is satisfied. Furthermore, we derive formulas for the sum of the conic intrinsic volumes and Grassmann angles of the tangent cones of P at all of its j-faces. We apply these results to permutohedra of types A and B, which yields closed formulas for the face numbers of projected permutohedra and the generalized angle sums of permutohedra in terms of Stirling numbers of both kinds and their B-analogues.

1 Introduction

In the work of Donoho and Tanner [11] the following interesting statement can be found: The number of j-faces of the image of the n-dimensional cube $[0,1]^n$ under a linear map $G:\mathbb {R}^n\rightarrow \mathbb {R}^d$ does not depend on the choice of G provided G is in “general position”. That is to say, the cube is an equiprojective polytope as defined by Shephard [26]. More precisely, by [11, Eq. (1.6)] we have

$$\begin{aligned} f_j(G [0,1]^n)=2\left( {\begin{array}{c}n\\ j\end{array}}\right) \sum _{\ell =n-d}^{n-j-1}\left( {\begin{array}{c}n-j-1\\ \ell \end{array}}\right) ; \end{aligned}$$

(1.1)

for all $0\le j < d\le n$, where $f_j(P)$ denotes the number of j-faces of a polytope P, and $G [0,1]^n$ is the image of $[0,1]^n$ under G.

We will show that this result can be generalized to any polytope $P\subset \mathbb {R}^n$ whose normal fan, that is the set of normal cones at all faces of P, coincides with the fan of some linear hyperplane arrangement $\mathcal {A}$. These polytopes are called belt polytopes; see [32, page 226], [5, 9, 10, Chapter VII], [4]. It is known [32, Theorem 7.16] that zonotopes, that is Minkowski sums of finitely many line segments, are special cases of belt polytopes. One simple example is the cube $[0,1]^n$ appearing in the formula (1.1). Another examples of belt polytopes are permutohedra of types A and B which are defined by

$$\begin{aligned} \mathcal {P}_n^A:=\mathcal {P}_n^A(x_1,\dots ,x_n):={{\,\textrm{conv}\,}}\{(x_{\sigma (1)}, \dots ,x_{\sigma (n)}):\sigma \in \text {Sym}(n)\big \} \end{aligned}$$

and

$$\begin{aligned} \mathcal {P}_n^B&:=\mathcal {P}_n^B(x_1,\dots ,x_n)\\ {}&:={{\,\textrm{conv}\,}}\{(\varepsilon _1x_{\sigma (1)}, \dots ,\varepsilon _nx_{\sigma (n)}):(\varepsilon _1,\dots ,\varepsilon _n)\in \{\pm 1\}^n,\sigma \in \text {Sym}(n)\big \} \end{aligned}$$

for a point $(x_1,\dots ,x_n)\in \mathbb {R}^n$. Here, $\text {Sym}(n)$ denotes the group of all permutations of the set $\{1,\dots ,n\}$. The faces and normal fans of the permutohedra can be characterized in terms of reflection arrangements of types $A_{n-1}$ and $B_n$, respectively. This will allow us to obtain analogues of (1.1) for permutohedra.

The paper is organized as follows. Section 2 introduces the necessary notation and some well-known definitions and results from convex and integral geometry. In Sect. 3, we state the main results in the setting of belt polytopes. In Sect. 4, we specialize these results to permutohedra. In the same section, we recall various characterizations of permutohedra, their faces and normal fans. Also, we show that permutohedra are zonotopes only in some rare exceptional cases, namely if the numbers $x_1,\ldots ,x_n$ form an arithmetic sequence. Proofs are given in Sects. 5 and 6.

2 Preliminaries

In this section, we are going to introduce necessary facts and notation from convex and integral geometry. These facts are well-known and can be skipped at first reading.

2.1 Facts from Convex Geometry

For a set $M\subset \mathbb {R}^n$ denote by ${{\,\textrm{lin}\,}}M$ and $\mathop {\textrm{aff}}\nolimits M$ the linear hull and the affine hull of M, respectively. They are defined as the minimal linear and the minimal affine subspace of $\mathbb {R}^n$ containing M, respectively. Equivalently, ${{\,\textrm{lin}\,}}M$ can be defined as the set of all linear combinations of elements in M, while $\mathop {\textrm{aff}}\nolimits M$ can be defined as the set of all affine combinations of elements in M. Similarly, the convex hull of M is denoted by ${{\,\textrm{conv}\,}}M$ and defined as the minimal convex set containing M, or, equivalently,

$$\begin{aligned} {{\,\textrm{conv}\,}}M:=\big \{&\lambda _1x_1+\ldots +\lambda _mx_m:m\in \mathbb {N},x_1,\dots ,x_m\in M,\lambda _1+\ldots +\lambda _m\ge 0,\\ {}&\lambda _1+\ldots +\lambda _m=1\big \}. \end{aligned}$$

The positive hull of a set M is denoted by ${{\,\textrm{pos}\,}}M$ and defined as

$$\begin{aligned} {{\,\textrm{pos}\,}}M:=\big \{\lambda _1x_1+\ldots +\lambda _mx_m:m\in \mathbb {N},x_1,\dots ,x_m\in M,\lambda _1,\ldots ,\lambda _m\ge 0\big \}. \end{aligned}$$

The relative interior of a set M is the set of all interior points of M relative to its affine hull $\mathop {\textrm{aff}}\nolimits M$ and it is denoted by ${{\,\textrm{relint}\,}}M$. The set of interior points of M is denoted by ${{\,\textrm{int}\,}}M$.

A polyhedral set is an intersection of finitely many closed half-spaces (whose boundaries need not pass through the origin). A bounded polyhedral set is called polytope. Equivalently, a polytope can be defined as the convex hull of a finite set of points. A polyhedral cone (or just cone) is an intersection of finitely many closed half-spaces whose boundaries contain the origin and therefore a special case of the polyhedral sets. Equivalently, a polyhedral cone can be defined as the positive hull of a finite set of points. The dimension of a polyhedral set P is defined as the dimension of its affine hull $\mathop {\textrm{aff}}\nolimits P$.

A supporting hyperplane for a polyhedral set $P\subset \mathbb {R}^n$ is an affine hyperplane H with the property that $H\cap P\ne \varnothing$ and P lies entirely in one of the closed half-spaces bounded by H. A face of a polyhedral set P (of arbitrary dimension) is a set of the form $F=P\cap H$, for a supporting hyperplane H, or the set P itself. Equivalently, the faces of a polyhedral set P are obtained by replacing some of the half-spaces, whose intersection defines the polyhedral set, by their boundaries and taking the intersection. The set of all faces of P is denoted by $\mathcal {F}(C)$ and the set of all k-dimensional faces (or just k-faces) of P by $\mathcal {F}_k(P)$ for $k\in \{0,\dots ,n\}$. The number of k-faces of P is denoted by $f_k(C):=\#\mathcal {F}_k(C)$. In general, the number of elements in a set M is denoted by |M| or $\#M$. The 0-dimensional faces are called vertices. In the case of a cone, the only possible vertex is the origin.

The dual cone $C^\circ$ (or polar cone) of a cone $C\subset \mathbb {R}^n$ is defined as

$$\begin{aligned} C^\circ :=\{v\in \mathbb {R}^n:\langle v,x\rangle \le 0\;\forall x\in C\}. \end{aligned}$$

The tangent cone $T_F(P)$ of a polyhedral set $P\subset \mathbb {R}^n$ at a face F of P is defined by

$$\begin{aligned} T_F(P)=\{x\in \mathbb {R}^n:f_0+\varepsilon x\in P\text { for some }\varepsilon >0\}, \end{aligned}$$

where $f_0$ is any point in the relative interior of F. This definition does not depend on the choice of $f_0$. The normal cone of P at the face F is defined as the dual of the tangent cone, that is $N_F(P):=T_F(P)^\circ .$

2.2 Grassmann Angles and Conic Intrinsic Volumes

Now, we are going to introduce some important geometric functionals of cones. Let $C\subset \mathbb {R}^n$ be a cone and g be an n-dimensional standard Gaussian vector. Then, the k-th conic intrinsic volume of C is defined as

$$\begin{aligned} \upsilon _k(C):=\sum _{F\in \mathcal {F}_k(C)}\mathbb {P}(\Pi _C(g)\in {{\,\textrm{relint}\,}}F),\quad k=0,\dots ,n, \end{aligned}$$

where $\Pi _C$ denotes the orthogonal projection on C, that is, $\Pi _C(x)$ is the vector in C which minimizes the Euclidean distance to $x\in \mathbb {R}^n$.

The conic intrinsic volumes are the analogues of the usual intrinsic volumes in the setting of conical or spherical geometry. Equivalently, the conic intrinsic volumes can be defined using the spherical Steiner formula, as done in [24, Section 6.5]. For further properties of conic intrinsic volumes we refer to [2, Section 2.2] and [24, Section 6.5].

Following Grünbaum [14], we define the Grassmann angles $\gamma _k(C)$, $k\in \{0,\dots ,n\}$, of a cone C as follows. Let $W_{n-k}$ be random linear subspace of $\mathbb {R}^n$ with uniform distribution on the Grassmannian of all $(n-k)$-dimensional subspaces. Then, the k-th Grassmann angle of C is defined as

$$\begin{aligned} \gamma _k(C):=\mathbb {P}(W_{n-k}\cap C\ne \{0\}),\quad k=0,\dots ,n. \end{aligned}$$

If the lineality space $C\cap -C$ of a cone C, which is the maximal linear subspace contained in C, has dimension $j\in \{0,\dots ,n-1\}$, the Grassmann angles satisfy

$$\begin{aligned} 1=\gamma _0(C)=\ldots =\gamma _j(C)\ge \gamma _{j+1}(C)\ge \ldots \ge \gamma _n(C)=0. \end{aligned}$$

As proved in [14, Eq. (2.5)], the Grassmann angles do not depend on the dimension of the ambient linear subspace. This means that if we embed C in $\mathbb {R}^N$ with $N\ge n$, we obtain the same Grassmann angles. Therefore, it is convenient to write $\gamma _N(C):=0$ for all $N\ge \dim C$. If C is not a linear subspace, then $\frac{1}{2}\gamma _k(C)$ is also known as the k-th conic quermassintegral; see [24, Eqs. (1)-(4)] or [16].

The conic intrinsic volumes and Grassmann angles satisfy a linear relation, called the conic Crofton formula. More precisely, we have

$$\begin{aligned} \gamma _k(C)=2\sum _{i=1,3,5,\dots }\upsilon _{k+i}(C) \end{aligned}$$

(2.1)

for all $k\in \{0,\dots ,n\}$ and for every cone $C\subset \mathbb {R}^n$ which is not a linear subspace, according to [24, p. 261]. Consequently,

$$\begin{aligned} \upsilon _k(C)=\frac{1}{2}\gamma _{k-1}(C)-\frac{1}{2}\gamma _{k+1}(C), \end{aligned}$$

(2.2)

for all $k\in \{0,\dots ,n\}$, where in the cases $k=0$ and $k=n$ we have to define $\gamma _{-1}(C)=1$ and $\gamma _{n+1}(C) = 0$. Then, (2.2) follows from (2.1) and the identity $\upsilon _0(C)+\upsilon _2(C)+\ldots =1/2$; see [3, Eq. (5.3)].

3 Main Results on Belt Polytopes

3.1 Belt Polytopes and Hyperplane Arrangements

Given a polytope $P\subset \mathbb {R}^n$ and a linear map $G:\mathbb {R}^n\rightarrow \mathbb {R}^d$ we are interested in determining the face numbers of the “projected” polytope GP. It will be shown below that if P is a belt polytope, then the face numbers of GP are independent of the linear map G provided it satisfies some minor general position assumption. Let us first define the class of belt polytopes and some related notions which will be needed below.

A (linear) hyperplane arrangement is a finite collection of distinct linear hyperplanes in $\mathbb {R}^n$. The lattice $\mathcal {L}(\mathcal {A})$ generated by $\mathcal {A}$ consists of all linear subspaces of $\mathbb {R}^n$ that can be represented as intersections of hyperplanes from $\mathcal {A}$ including $\mathbb {R}^n$ (which is an intersection over the empty set). Denote by $\mathcal {L}_j(\mathcal {A})$ the set of j-dimensional linear subspaces from the lattice $\mathcal {L}(\mathcal {A})$, for $j\in \{0,\ldots , n\}$. By convention, we put $\mathcal {L}_{n}(\mathcal {A}):=\{\mathbb {R}^n\}$.

The hyperplanes from $\mathcal {A}$ dissect $\mathbb {R}^n$ into finitely many cones or chambers. More precisely, the complement $\mathbb {R}^n\backslash \bigcup _{H\in \mathcal {A}}H$ is a disjoint union of open convex sets. The set of closures of these “regions” is denoted by $\mathcal {R}(\mathcal {A})$ and called the conical mosaic generated by $\mathcal {A}$. The elements of $\mathcal {R}(\mathcal {A})$ are called chambers.

In general, a fan in $\mathbb {R}^n$ is defined as a family $\mathcal {F}$ of non-empty cones with the following two properties:

• (i) Every non-empty face of a cone in $\mathcal {F}$ is also a cone in $\mathcal {F}$;

• (ii) The intersection of any two cones in $\mathcal {F}$ is a face of both;

see [32, Chapter 7]. For example, the fan generated by a hyperplane arrangement $\mathcal {A}$ is defined as the collection of all faces of its chambers, that is

$$\begin{aligned} \mathcal {F}(\mathcal {A})=\bigcup _{C\in \mathcal {R}(\mathcal {A})} \mathcal {F}(C). \end{aligned}$$

We denote the set of j-dimensional cones from $\mathcal {F}(\mathcal {A})$ by $\mathcal {F}_j(\mathcal {A})$. On the other hand, the normal fan of a non-empty polytope $P\subset \mathbb {R}^n$ is defined as the set of normal cones of all faces of P, that is

$$\begin{aligned} \mathcal {N}(P):=\{N_F(P):F\in \mathcal {F}(P)\}. \end{aligned}$$

A polytope $P\subset \mathbb {R}^n$ is called a belt polytope if its normal fan $\mathcal {N}(P)$ coincides with the fan $\mathcal {F}(\mathcal {A})$ generated by some hyperplane arrangement $\mathcal {A}$. Originally, belt polytopes were defined as polytopes such that every 2-face contains together with each edge another parallel edge; see [32, page 226], [4] for the equivalence of the definitions. Examples of belt polytopes are zonotopes (see [32, Theorem 7.16]) and permutohedra of types A and B (see Sect. 4).

3.2 General Position Assumptions

To state our results on face numbers of projected belt polytopes, we need to introduce the terminology of general position in the context of hyperplane arrangements and polyhedral sets. Let M be an affine subspace of $\mathbb {R}^n$. Denote by $L\subset \mathbb {R}^n$ the unique linear subspace such that $M=t+L$ for some $t\in \mathbb {R}^n$, that is the translation of M passing through the origin. We say that M is in general position with respect to a linear subspace $L'\subset \mathbb {R}^n$ if

$$\begin{aligned} \dim (L\cap L')=\max (\dim L+\dim L'-n,0). \end{aligned}$$

(3.1)

A linear subspace $L'$ is said to be in general position with respect to a polyhedral set P if the affine hull of each face F of P is in general position with respect to $L'$. On the other hand, a linear subspace $L'\subset \mathbb {R}^n$ is said to be in general position with respect to the hyperplane arrangement $\mathcal {A}$ if $L'$ is in general position with respect to each $L\in \mathcal {L}(\mathcal {A})$.

Now, we are ready state two equivalent general position assumptions that we need to impose on a linear mapping $G: \mathbb {R}^{n} \rightarrow \mathbb {R}^d$ under consideration (actually, both assumptions deal with the kernel of G only).

Theorem 3.1

Let $P\subset \mathbb {R}^n$ be a belt polytope and denote its normal fan by $\mathcal {N}(P)$. Let $\mathcal {A}$ be the linear hyperplane arrangement whose fan $\mathcal {F}(\mathcal {A})$ coincides with $\mathcal {N}(P)$. For $1\le d\le \dim P$ and a linear map $G: \mathbb {R}^{n} \rightarrow \mathbb {R}^d$ with ${{\,\textrm{rank}\,}}G=d$ the following two general position assumptions are equivalent:

• (G1) The $(n-d)$-dimensional linear subspace $\ker G$ is in general position with respect to P.

• (G2) The d-dimensional linear subspace $(\ker G)^\perp$ is in general position with respect to the hyperplane arrangement $\mathcal {A}$.

The proof of this theorem is postponed to Sect. 5.1.

3.3 Face Numbers of Projected Belt Polytopes

Before stating the result, we need to introduce the characteristic polynomial of a hyperplane arrangement. The rank of a linear hyperplane arrangement $\mathcal {A}$ in $\mathbb {R}^n$ is defined by

$$\begin{aligned} {{\,\textrm{rank}\,}}(\mathcal {A})=n-\dim \bigg (\bigcap _{H\in \mathcal {A}}H\bigg ),\quad {{\,\textrm{rank}\,}}(\varnothing )=0. \end{aligned}$$

The characteristic polynomial $\chi _\mathcal {A}(t)$ of $\mathcal {A}$ can be defined by the following Whitney formula:

$$\begin{aligned} \chi _\mathcal {A}(t)=\sum _{\mathcal {C}\subset \mathcal {A}}(-1)^{\#\mathcal {C}}t^{n-{{\,\textrm{rank}\,}}(\mathcal {C})}; \end{aligned}$$

(3.2)

see, e.g., [21, Lemma 2.3.8] or [28, Theorem 2.4], as well as [28, Section 1.3] or [29, Section 3.11.2] for other definitions using the Möbius function on the intersection poset of $\mathcal {A}$. More generally, following Amelunxen and Lotz [2], the m-th level characteristic polynomial of $\mathcal {A}$ is defined by

$$\begin{aligned} \chi _{\mathcal {A},m}(t):= \sum _{M\in \mathcal {L}_{m}(\mathcal {A})} \chi _{A|M}(t), \end{aligned}$$

(3.3)

where $m\in \{0,\ldots , n\}$ and $\chi _{A|M}(t)$ is the characteristic polynomial of the induced hyperplane arrangement $\mathcal {A}|M:=\{H\cap M:H\in \mathcal {A},M\nsubseteq H\}$ in the ambient space M. We use the following notation for the coefficients of $\chi _{\mathcal {A},m}(t)$:

$$\begin{aligned} \chi _{\mathcal {A},m}(t)=\sum _{k=0}^{m}(-1)^{m-k} a_{k,m} t^k. \end{aligned}$$

(3.4)

We define $a_{k,m}:= 0$ for $k\notin \{0,\ldots , m\}$.

Theorem 3.2

Let $P\subset \mathbb {R}^n$ be a belt polytope and denote its normal fan by $\mathcal {N}(P)$. Let $\mathcal {A}$ be the linear hyperplane arrangement whose fan $\mathcal {F}(\mathcal {A})$ coincides with $\mathcal {N}(P)$. Moreover, let $G:\mathbb {R}^{n} \rightarrow \mathbb {R}^d$ be a linear map with ${{\,\textrm{rank}\,}}G=d$ such that the equivalent general position Assumptions (G1) and (G2) are satisfied. Then, for $0\le j<d\le \dim P$, the number of j-faces of the projected polytope GP is independent of the linear map G and given by

$$\begin{aligned} f_j(GP) = 2(a_{n-d+1, n-j}+a_{n-d+3, n-j}+\ldots ). \end{aligned}$$

(3.5)

The series in (3.5) terminates after finitely many non-zero terms. The proof of Theorem 3.2 is postponed to Sect. 5.3. As a consequence of Theorem 3.2, the belt polytopes are equiprojective as defined in [26].

The coefficients of the m-th level characteristic polynomial appear in the following lemma which will be used in the proof of Theorem 3.2.

Lemma 3.3

Let $L_d\subset \mathbb {R}^n$ be a linear subspace of dimension $d\in \{0,\ldots , n\}$ that is in general position with respect to a hyperplane arrangement $\mathcal {A}$. Then, for all $m\in \{0,\ldots , n\}$, the number of m-faces of the fan $\mathcal {F}(\mathcal {A})$ that are non-trivially intersected by $L_d$ is given by

$$\begin{aligned} \#\{F\in \mathcal {F}_m(\mathcal {A}): {{\,\textrm{relint}\,}}F\cap L_d\ne \varnothing \}&= 2(a_{n-d+1,m}+a_{n-d+3,m}+\ldots ) \nonumber \\&= \#\{F\in \mathcal {F}_m(\mathcal {A}): F\cap L_d \ne \{0\}\}, \nonumber \\ \end{aligned}$$

(3.6)

where the $a_{k,m}$’s are defined by (3.4). If we drop the general position assumption, then both equalities should be replaced by $\le$.

3.4 Angle Sums of Belt Polytopes

In the next theorem we compute the generalized angle sums of belt polytopes. Recall that the Grassmann angles $\gamma _d$ and the conic intrinsic volumes $\upsilon _d$ were defined in Sect. 2.2.

Theorem 3.4

Let $P\subset \mathbb {R}^n$ be a belt polytope with normal fan $\mathcal {N}(P)$ and let $\mathcal {A}$ be the linear hyperplane arrangement whose fan $\mathcal {F}(\mathcal {A})$ coincides with $\mathcal {N}(P)$. Then, for all $0\le j\le d\le \dim P$ we have

$$\begin{aligned} \sum _{F\in \mathcal {F}_j(P)}\upsilon _d(T_F(P))&= a_{n-d, n-j},\\ \sum _{F\in \mathcal {F}_j(P)}\gamma _d(T_F(P))&= 2(a_{n-d-1, n-j}+a_{n-d-3,n-j}+\ldots ). \end{aligned}$$

The proof is postponed to Sect. 5.4. Let us mention that applying Theorem 3.4 to a full-dimensional zonotope P with $d=n$ we recover a formula stated in [19, Theorem 12], while the special case $d=j$ is covered by [4, Proposition 3.2].

4 Applications to Permutohedra of Types A and B

In this section, we apply the results of Sect. 3 to permutohedra of types A and B. These polytopes have been studied starting with the work of Schoute [25] in 1911; see [7, 15, 22] as well as [32, Example 0.10], [31, Section 5.3], [6, pp. 58–60, 254–258] and [8, Example 2.2.5].

4.1 Definitions of Permutohedra

Take some point $(x_1,\dots ,x_n)\in \mathbb {R}^n$. A permutohedron of type A is defined as the following polytope in $\mathbb {R}^n$:

$$\begin{aligned} \mathcal {P}_n^A=\mathcal {P}_n^A(x_1,\dots ,x_n):={{\,\textrm{conv}\,}}\big \{(x_{\sigma (1)},\dots ,x_{\sigma (n)}):\sigma \in \text {Sym}(n)\big \}, \end{aligned}$$

where $\text {Sym}(n)$ is the group of all permutations of the set $\{1,\dots ,n\}$. Note that $\mathcal {P}_n^A$ is contained in the hyperplane $\{t\in \mathbb {R}^n:t_1+\ldots +t_n=x_1+\ldots +x_n\}$ and therefore has dimension at most $n-1$. Similarly, a permutohedron of type B is defined as the following polytope in $\mathbb {R}^n$:

$$\begin{aligned} \mathcal {P}_n^B&=\mathcal {P}_n^B(x_1,\dots ,x_n):={{\,\textrm{conv}\,}}\big \{(\varepsilon _1x_{\sigma (1)},\dots ,\varepsilon _nx_{\sigma (n)}):\\ \varepsilon&=(\varepsilon _1,\dots ,\varepsilon _n)\in \{\pm 1 \}^n,\quad \sigma \in \text {Sym}(n)\big \}. \end{aligned}$$

Note that $\mathcal {P}_n^A(x_1,\dots ,x_n)$ does not change under permutations of $x_1,\ldots ,x_n$, whereas $\mathcal {P}_n^B(x_1,\dots ,x_n)$ stays invariant under signed permutations. Therefore, there is no restriction of generality if we assume that $x_1\ge \ldots \ge x_n$ in the A-case and $x_1\ge \ldots \ge x_n\ge 0$ in the B-case.

The next lemma is due to Rado [23] (see also [31, Section 5.3], [6, p. 257] and [20, Corollary B.3]) and describes $\mathcal {P}_n^A$ as a set of solutions to a finite system of affine inequalities.

Lemma 4.1

Assume that $x_1\ge \ldots \ge x_n$. Then, a point $(t_1,\dots ,t_n)\in \mathbb {R}^n$ belongs to the permutohedron $\mathcal {P}_n^A(x_1,\dots ,x_n)$ of type A if and only if

$$\begin{aligned} t_1+\dots +t_n=x_1+\ldots +x_n \end{aligned}$$

and, for every non-empty subset $M\subset \{1,\dots ,n\}$, we have

$$\begin{aligned} \sum _{i\in M}t_i\le x_1+\ldots +x_{|M|}. \end{aligned}$$

An analogous result for the permutohedron of type B, together with a proof and references to the original literature, can be found in [20, Corollary C.5.a].

Lemma 4.2

Assume that $x_1\ge \ldots \ge x_n\ge 0$. Then, a point $(t_1,\dots ,t_n)\in \mathbb {R}^n$ belongs to the permutohedron $\mathcal {P}_n^B(x_1,\dots ,x_n)$ of type B if and only if for every non-empty subset $M\subset \{1,\dots ,n\}$, we have

$$\begin{aligned} \sum _{i\in M}|t_i|\le x_1+\ldots +x_{|M|}. \end{aligned}$$

(4.1)

4.2 Normal Fans of Permutohedra

The following theorems characterize the normal fans of the permutohedra of types A and B and show that both types of permutohedra are belt polytopes.

Theorem 4.3

For $x_1>\cdots >x_n$ the normal fan $\mathcal {N}(\mathcal {P}_n^A(x_1,\dots ,x_n))$ of the permutohedron of type A coincides with the fan $\mathcal {F}(\mathcal {A}(A_{n-1}))$ generated by the hyperplane arrangement $\mathcal {A}(A_{n-1})$ consisting of the hyperplanes

$$\begin{aligned} \{\beta \in \mathbb {R}^n:\beta _i=\beta _j\},\quad 1\le i<j\le n. \end{aligned}$$

(4.2)

Theorem 4.4

For $x_1>\cdots>x_n>0$ the normal fan $\mathcal {N}(\mathcal {P}_n^B(x_1,\dots ,x_n))$ of the permutohedron of type B coincides with the fan $\mathcal {F}(\mathcal {A}(B_n))$ generated by the hyperplane arrangement $\mathcal {A}(B_n)$ consisting of the hyperplanes

$$\begin{aligned}&\{\beta \in \mathbb {R}^n:\beta _i=\beta _j\},\quad 1\le i<j\le n,\nonumber \\&\{\beta \in \mathbb {R}^n:\beta _i=-\beta _j\},\quad 1\le i<j\le n,\\&\{\beta \in \mathbb {R}^n:\beta _i=0\},\quad 1\le i\le n.\nonumber \end{aligned}$$

(4.3)

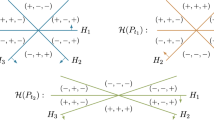
The arrangements $\mathcal {A}(A_{n-1})$ and $\mathcal {A}(B_n)$ are called reflection arrangements of types $A_{n-1}$ and $B_n$ and the cones they generate are called the Weyl chambers. Both theorems seem to be known, see, e.g., [15, Section 3.1], but for the sake of completeness we will give their proofs in Sect. 6.2. For example, the normal cones at the vertices of the permutohedra coincide with the Weyl chambers of types $A_{n-1}$ and $B_n$, which was used to compute their statistical dimension in [3, Proposition 3.5].

4.3 General Position Assumptions

In the next two corollaries of Theorem 3.1 we state general position assumptions we need to impose on the linear map $G:\mathbb {R}^n\rightarrow \mathbb {R}^d$ when computing the face numbers of projected permutohedra $G\mathcal {P}_n^A$ and $G\mathcal {P}_n^B$.

Corollary 4.5

Let $1\le d\le n-1$ and $x_1>\cdots >x_n$. For a linear map $G:\mathbb {R}^{n} \rightarrow \mathbb {R}^d$ with ${{\,\textrm{rank}\,}}G=d$, the following two conditions are equivalent:

• (A1) The $(n-d)$-dimensional linear subspace $\ker G$ is in general position with respect to $\mathcal {P}_n^A(x_1,\dots ,x_n)$.

• (A2) The d-dimensional linear subspace $(\ker G)^\perp$ is in general position with respect to the reflection arrangement $\mathcal {A}(A_{n-1})$ defined in eq 4.2.

Corollary 4.6

Let $1\le d\le n$ and $x_1>\cdots>x_n>0$. For a linear map $G:\mathbb {R}^{n} \rightarrow \mathbb {R}^d$ with ${{\,\textrm{rank}\,}}G=d$, the following two conditions are equivalent:

• (B1) The $(n-d)$-dimensional linear subspace $\ker G$ is in general position with respect to $\mathcal {P}_n^B(x_1,\dots ,x_n)$.

• (B1) The d-dimensional linear subspace $(\ker G)^\perp$ is in general position with respect to the reflection arrangement $\mathcal {A}(B_n)$ defined in (4.3).

Both corollaries follow immediately from Theorem 3.1 since the normal fans $\mathcal {N}(\mathcal {P}_n^A)$ and $\mathcal {N}(\mathcal {P}_n^B)$ coincide with $\mathcal {F}(\mathcal {A}(A_{n-1}))$ and $\mathcal {F}(\mathcal {A}(B_n))$, respectively. Note that if $x_1>\cdots >x_n$, then the permutohedron $\mathcal {P}_n^A$ has dimension $n-1$ (since any point t in the hyperplane $t_1+ \ldots + t_n = x_1+\ldots + x_n$ which is sufficiently close to the point $({\bar{x}}_n,\ldots , \bar{x}_n)$, where ${\bar{x}}_n = (x_1+\ldots +x_n)/n$, satisfies the inequalities from Lemma 4.1). Similarly, for $x_1>\cdots>x_n>0$, the permutohedron $\mathcal {P}_n^B$ of type B has dimension n.

4.4 Face Numbers of Projected Permutohedra

In this section, we state our results on the number of faces of projected permutohedra of types A and B. The formulas will be stated in terms of Stirling numbers defined as follows.

The (signless) Stirling number of the first kind $\genfrac[]{0.0pt}{}{n}{k}$ is the number of permutations of the set $\{1,\dots ,n\}$ having exactly k cycles. Equivalently, these numbers can be defined as the coefficients of the polynomial

$$\begin{aligned} t(t+1)\cdot \ldots \cdot (t+n-1)=\sum _{k=0}^n\genfrac[]{0.0pt}{}{n}{k}t^k \end{aligned}$$

(4.4)

for $n\in \mathbb {N}_0$, with the convention that $\genfrac[]{0.0pt}{}{n}{k}=0$ for $n\in \mathbb {N}_0$, $k\notin \{0,\dots ,n\}$ and $\genfrac[]{0.0pt}{}{0}{0} = 1$. The Stirling number of the second kind $\genfrac\rbrace \lbrace {0.0pt}{}{n}{k}$ is defined as the number of partitions of the set $\{1,\dots ,n\}$ into k non-empty subsets.

The B-analogues of the Stirling numbers, denoted by and $B\big \{{n},{k}\big \}$, are defined by the formulas

(4.5)

for $n\in \mathbb {N}$ and, by convention, for $k\notin \{0,\dots ,n\}$. The triangular arrays and $B\big \{{n},{k}\big \}$ appear as entries A028338 and A039755 in [27]; see also [30].

Lemma 4.7

For all $j\in \{0,\ldots , n\}$, the number of j-dimensional subspaces in the lattices $\mathcal {L}(\mathcal {A}(A_{n-1}))$ and $\mathcal {L}(\mathcal {A}(B_{n}))$ is given by $\genfrac\rbrace \lbrace {0.0pt}{}{n}{j}$ and $B\big \{{n},{j}\big \}$, respectively.

Proof

The linear subspaces from $\mathcal {L}_j(\mathcal {A}(A_{n-1}))$ are in one-to-one correspondence with the (unordered) partitions $\mathcal {B}= \{B_1,\ldots , B_j\}$ of $\{1,\ldots , n\}$ into non-empty, disjoint subsets. The linear subspace corresponding to $\mathcal {B}$ is given by

$$\begin{aligned} \{x\in \mathbb {R}^n: x_{i_1} = x_{i_2} \text { for all } i_1, i_2 \text { contained in the same block } B_\ell \}. \end{aligned}$$

The number of such partitions is $\genfrac\rbrace \lbrace {0.0pt}{}{n}{j}$. Similarly, the elements of $\mathcal {L}_j(\mathcal {A}(B_{n}))$ are in one-to-one correspondence with the equivalence classes of pairs $(\mathcal {B}, \eta )$, where $\mathcal {B}=\{B_1,\ldots , B_j\}$ is an (unordered) partition of some subset ${{\,\textrm{supp}\,}}\mathcal {B}:= B_1\cup \ldots \cup B_j$ of $\{1,\ldots , n\}$ into disjoint, non-empty subsets $B_1,\ldots , B_j$, and $\eta :{{\,\textrm{supp}\,}}\mathcal {B}\rightarrow \{\pm 1\}$ is a sign function. Moreover, two pairs $(\mathcal {B}, \eta ')$ and $(\mathcal {B}, \eta '')$ with the same $\mathcal {B}$ are considered equivalent if $\eta '/\eta ''$ stays constant on each block $B_\ell$. The j-dimensional linear subspace corresponding to $(\mathcal {B}, \eta )$ is given by

$$\begin{aligned}{} & {} \{x\in \mathbb {R}^n: \eta (i_1) x_{i_1} = \eta (i_2) x_{i_2} \text { for all } i_1, i_2 \text { contained in the same } B_\ell ;\nonumber \\{} & {} \quad x_i=0 \text { for all } i\notin {{\,\textrm{supp}\,}}\mathcal {B}\}. \end{aligned}$$

Denoting the cardinality of ${{\,\textrm{supp}\,}}\mathcal {B}$ by $m\in \{j, \ldots , n\}$ we see that the number of equivalence classes as above is given by $B\big \{{n},{j}\big \}$ as defined in (4.5). Note that $2^{m-j}$ is the number of equivalence classes of sign functions $\eta$. $\square$

Let $m\in \{0,\ldots , n\}$. The m-th level characteristic polynomials of the reflection arrangements $\mathcal {A}(A_{n-1})$ and $\mathcal {A}(B_n)$ are known from the work of Amelunxen and Lotz [2, Lemma 6.5]:

$$\begin{aligned} \chi _{\mathcal {A}(A_{n-1}),m}(t)&= \genfrac\rbrace \lbrace {0.0pt}{}{n}{m} t(t-1)\ldots (t-m+1) = \genfrac\rbrace \lbrace {0.0pt}{}{n}{m} \sum _{k=0}^m (-1)^{m-k} \genfrac[]{0.0pt}{}{m}{k} t^k, \end{aligned}$$

(4.6)

(4.7)

Note that in [2], the cardinality of $\mathcal {L}_j(\mathcal {A}(B_n))$ has been calculated incorrectly (the power of 2 in (4.5) is missing there). It follows from (4.6) and (4.7) that the coefficients $a_{k,m}$, as defined in (3.4), are given by the following formulas:

$$\begin{aligned} \text {for } \mathcal {A}(A_{n-1}):\, a_{k,m}&= \genfrac\rbrace \lbrace {0.0pt}{}{n}{m} \genfrac[]{0.0pt}{}{m}{k},\qquad k\in \{0,\ldots , m\}, \end{aligned}$$

(4.8)

$$\begin{aligned} \text {for } \mathcal {A}(B_{n}):\, a_{k,m}&= B\big \{{n},{m}\big \} B\big [{m},{k}\big ], \qquad k\in \{0,\ldots , m\}. \end{aligned}$$

(4.9)

Applying Theorem 3.2 to permutohedra and using (4.8) and (4.9), we obtain the following results on the face numbers of projected permutohedra.

Theorem 4.8

Let $x_1>\cdots >x_n$ be given. For a linear map $G:\mathbb {R}^{n} \rightarrow \mathbb {R}^d$ with ${{\,\textrm{rank}\,}}G=d$ which satisfies one of the equivalent general position Assumptions (A1) or (A2), we have

$$\begin{aligned} f_j(G\mathcal {P}_n^A)=2\genfrac\rbrace \lbrace {0.0pt}{}{n}{n-j}\left( \genfrac[]{0.0pt}{}{n-j}{n-d+1}+\genfrac[]{0.0pt}{}{n-j}{n-d+3}+\ldots \right) , \end{aligned}$$

(4.10)

for all $0\le j<d\le n-1$.

Theorem 4.9

Let $x_1>\cdots>x_n>0$ be given. For a linear map $G:\mathbb {R}^{n} \rightarrow \mathbb {R}^d$ with ${{\,\textrm{rank}\,}}G=d$ which satisfies one of the equivalent general position Assumptions (B1) or (B2), we have

(4.11)

for all $0\le j<d\le n$.

4.5 Faces of Reflection Arrangements Intersected by Linear Subspaces

The next lemma is closely related to Theorems 4.8 and 4.9 (as we shall see from the proofs) and follows from Lemma 3.3 in view of (4.8) and (4.9).

Lemma 4.10

The number of j-faces of Weyl chambers (where each face is counted exactly once) intersected non-trivially by a d-dimensional subspace $L_d$ in general position with respect to the reflection arrangement $\mathcal {A}(A_{n-1})$, respectively, $\mathcal {A}(B_n)$, is given by

for all $j,d\in \{1,\ldots ,n\}$.

The special case $j=n$ of this lemma can be found in [17, Theorem 3.4] or [18, Theorem 2.4]. A related result in a setting where the faces are counted with certain non-trivial multiplicities can be found in [18, Theorems 2.1, 2.8].

4.6 Angle Sums of Permutohedra

In the next two theorems we compute the generalized angle sums of permutohedra. Both results follow from Theorem 3.4 in view of (4.8) and (4.9).

Theorem 4.11

Let $x_1>\cdots >x_n$ be given. Then, for all $0\le j\le d\le n-1$,

$$\begin{aligned} \sum _{F\in \mathcal {F}_j(\mathcal {P}_n^A)}\upsilon _d(T_F(\mathcal {P}_n^A))&= \genfrac\rbrace \lbrace {0.0pt}{}{n}{n-j}\genfrac[]{0.0pt}{}{n-j}{n-d}, \end{aligned}$$

(4.12)

$$\begin{aligned} \sum _{F\in \mathcal {F}_j(\mathcal {P}_n^A)}\gamma _d(T_F(\mathcal {P}_n^A))&= 2\genfrac\rbrace \lbrace {0.0pt}{}{n}{n-j}\sum _{l=0}^\infty \genfrac[]{0.0pt}{}{n-j}{n-d-2l-1}. \end{aligned}$$

(4.13)

Theorem 4.12

Let $x_1>\cdots>x_n>0$ be given. Then, for all $0\le j\le d\le n$,

(4.14)

(4.15)

4.7 Permutohedra and Zonotopes

Besides permutohedra, the zonotopes are also a special case of the class of belt polytopes. A zonotope $Z=Z(V)\subset \mathbb {R}^n$ is a Minkowski sum of a finite number of line segments, and therefore, can be written as

$$\begin{aligned} Z(V)=[-v_1,v_1]+\cdots +[-v_p,v_p]+z \end{aligned}$$

for some $p\in \mathbb {N}$, a matrix $V=(v_1,\dots ,v_p)\in \mathbb {R}^{n\times p}$ and $z\in \mathbb {R}^n$. By [32, Definition 7.13], a zonotope $Z=Z(V)$ can equivalently be defined as the image of a cube under an affine map, that is,

$$\begin{aligned} Z(V):=V[-1,+1]^p+z=\{Vy+z:y\in [-1,+1]^p\}. \end{aligned}$$

In the book of Ziegler [32, Theorem 7.16] it is proved that for a zonotope $Z=Z(V)\subset \mathbb {R}^n$, the normal fan $\mathcal {N}(Z)$ of Z coincides with the fan $\mathcal {F}(\mathcal {A})$ of the hyperplane arrangement

$$\begin{aligned} \mathcal {A}=\mathcal {A}_V:=\{H_1,\dots ,H_p\} \end{aligned}$$

in $\mathbb {R}^n$, where $H_i:=\{x\in \mathbb {R}^n:\langle x,v_i\rangle = 0\}$ for $i=1,\dots ,p$. It is known [32, Example 7.15] that $\mathcal {P}_n^{A}(n,n-1,\ldots ,2, 1)$ is a zonotope and the natural question arises if permutohedra of types A and B are zonotopes for all $(x_1,\dots ,x_n)\in \mathbb {R}^n$. The following theorem shows that this is not the case. Its proof is postponed to Sect. 6.3.

Theorem 4.13

For $x_1>\cdots >x_n$, the permutohedron $\mathcal {P}_n^A(x_1,\dots ,x_n)$ of type A is a zonotope if and only if $x_1,\dots ,x_n$ are in arithmetic progression, that is,

$$\begin{aligned} x_1=a+(n-1)b,\,x_2=a+(n-2)b,\dots ,x_{n-1}=a+b,\,x_n=a \end{aligned}$$

(4.16)

for some $a\in \mathbb {R}$ and $b>0$.

For $x_1>\cdots>x_n>0$, the permutohedron $\mathcal {P}_n^B(x_1,\dots ,x_n)$ of type B is a zonotope if and only if $x_1,\dots ,x_n$ are in arithmetic progression, that is if (4.16) holds for some $a>0$ and $b>0$.

5 Proofs of the Results on Belt Polytopes

5.1 General Position: Proof of Theorem 3.1

Let $F\in \mathcal {F}_k(P)$ be a k-face of P for some $k\in \{0,\dots ,\dim P\}$ and let L be the linear subspace parallel to $\mathop {\textrm{aff}}\nolimits F$ with the same dimension as $\mathop {\textrm{aff}}\nolimits F$, that is, $\mathop {\textrm{aff}}\nolimits F=t+L$ for some $t\in \mathbb {R}^n$. Then, the normal cone $N_F(P)$ is $(n-k)$-dimensional and coincides with some $(n-k)$-dimensional cone from the fan of $\mathcal {A}$, that is, an $(n-k)$-face of the conical mosaic generated by $\mathcal {A}$. Thus, ${{\,\textrm{lin}\,}}N_F(P)$ can be represented as an intersection of hyperplanes from $\mathcal {A}$ and therefore is an element of the lattice $\mathcal {L}(\mathcal {A})$.

On the other hand, by definition, $T_F(P)$ contains the linear subspace L. Thus, we have $(\mathop {\textrm{aff}}\nolimits F)^\perp =L^\perp \supset T_F(P)^\circ =N_F(P)$. Since both $N_F(P)$ and $(\mathop {\textrm{aff}}\nolimits F)^\perp$ are $(n-k)$-dimensional, we obtain

$$\begin{aligned} L^\perp =(\mathop {\textrm{aff}}\nolimits F)^\perp ={{\,\textrm{lin}\,}}N_F(P)\in \mathcal {L}_{n-k}(\mathcal {A}). \end{aligned}$$

The same argumentation applied backwards shows that, conversely, each $(n-k)$-dimensional subspace $K\in \mathcal {L}(\mathcal {A})$ coincides with ${{\,\textrm{lin}\,}}N_F(P)$ for some k-face F of P. If we write $\mathop {\textrm{aff}}\nolimits F=t+L$ for some $t\in \mathbb {R}^n$, as above, then we obtain $K=(\mathop {\textrm{aff}}\nolimits F)^\perp =L^\perp$.

The equivalence of (G1) and (G2) follows easily from these observations. Condition (G1) is not satisfied if and only if

$$\begin{aligned} \dim (L\cap \ker G)\ne \max \{k-d,0\} \end{aligned}$$

for some $k\in \{0,\dots ,\dim P\}$ and some k-dimensional linear subspace L such that $\mathop {\textrm{aff}}\nolimits F=t+L$ for some $F \in \mathcal {F}_k(P)$ and $t\in \mathbb {R}^n$. By the above observation, $L^\perp \in \mathcal {L}_{n-k}(\mathcal {A})$ and

$$\begin{aligned} \dim \big ((\ker G)^\perp \cap L^\perp \big )&=n-\dim (L+\ker G )\\&=n-\left( \dim (\ker G)+\dim L-\dim (L\cap \ker G)\right) \\&=d-k+\dim (L\cap \ker G)\\&\ne d-k + \max \{k-d,0\}\\&= \max \{0,d-k\}. \end{aligned}$$

Thus, $(\ker G)^\perp$ is not in general position with respect to $\mathcal {A}$ and (G2) is not satisfied. Since every $K\in \mathcal {L}(\mathcal {A})$ can be represented as $L^\bot$ as above, the same argument applies backwards. $\square$

5.2 Proof of Lemma 3.3

We need the following formula for the number of full-dimensional chambers of a hyperplane arrangement that are intersected by a linear subspace non-trivially. For its proof, we refer to [13, Theorem 3.1] or [17, Theorem 3.3] in combination with [17, Lemma 3.5].

Lemma 5.1

Let $L_d\subset \mathbb {R}^n$ be a linear subspace of dimension $d\in \{0,\ldots , n\}$ that is in general position with respect to a hyperplane arrangement $\mathcal {A}$. Recall that $\mathcal {R}(\mathcal {A})$ is the set of closed chambers generated by $\mathcal {A}$. Then,

$$\begin{aligned} \#\{R\in \mathcal {R}(\mathcal {A}):{{\,\textrm{int}\,}}R\cap L_d\ne \varnothing \}&= 2(a_{n-d+1}+a_{n-d+3}+\ldots ) \\ {}&= \#\{R\in \mathcal {R}(\mathcal {A}): R\cap L_d\ne \{0\}\} , \end{aligned}$$

where the $a_k$’s are the coefficients of the characteristic polynomial $\chi _\mathcal {A}(t)=\sum _{k=0}^n(-1)^{n-k}a_kt^k$. If we drop the general position assumption, then both equalities should be replaced by $\le$.

Proof of Lemma 3.3

Let $m\in \{n-d+1,\ldots , n\}$ (otherwise all terms in (3.6) vanish). Observe that each m-face F from the fan $\mathcal {F}(\mathcal {A})$ is contained in a unique m-dimensional linear subspace $M\in \mathcal {L}(\mathcal {A})$ that can be represented as an intersection of hyperplanes from $\mathcal {A}$. The m-dimensional cones $F\in \mathcal {F}_{m}(\mathcal {A})$ with $F\subset M$ are the closures of the m-dimensional regions generated by the induced arrangement $\mathcal {A}|M=\{H\cap M:H\in \mathcal {A},M\nsubseteq H\}$ in M and therefore we obtain

$$\begin{aligned} \#\{F\in \mathcal {F}_m(\mathcal {A}): F\cap L_d \ne \{0\}\}&=\sum _{D\in \mathcal {F}_{m}(\mathcal {A})}\mathbbm {1}_{\{L_d \cap \, D\ne \{0\}\}}\\&=\sum _{M\in \mathcal {L}_{m}(\mathcal {A})}\,\sum _{D\in \mathcal {F}_{m}(\mathcal {A}):D\subset M}\mathbbm {1}_{\{(L_d\cap M)\cap \, D\ne \{0\}\}}\\&=\sum _{M\in \mathcal {L}_{m}(\mathcal {A})}\,\sum _{R\in \mathcal {R}(\mathcal {A}|M)}\mathbbm {1}_{\{(L_d\cap M)\cap \, R\ne \{0\}\}}. \end{aligned}$$

By our general position assumption, the subspace $L_d\cap M$ is of codimension $n-d$ in M and additionally in general position with respect to $\mathcal {A}|M$ in M. Let the coefficients of the characteristic polynomial of the arrangement $\mathcal {A}|M$ in the ambient space M be given by

$$\begin{aligned} \chi _{A|M}(t)=\sum _{k=0}^{m}(-1)^{m-k}a_k^Mt^k. \end{aligned}$$

Then, we can apply Lemma 5.1 to the ambient linear subspace M and arrive at

$$\begin{aligned} \#\{F\in \mathcal {F}_m(\mathcal {A}): F\cap L_d \ne \{0\}\}&= 2\sum _{M\in \mathcal {L}_{m}(\mathcal {A})}(a_{n-d+1}^M + a_{n-d+3}^M + \ldots )\nonumber \\&= 2(a_{n-d+1, m}+a_{n-d+3, m}+\ldots ). \end{aligned}$$

(5.1)

The evaluation of $\#\{F\in \mathcal {F}_m(\mathcal {A}): {{\,\textrm{relint}\,}}F\cap L_d\ne \varnothing \}$ is similar. Without the general position assumption, the inequalities follow from [17, Lemma 3.5].

5.3 Face Numbers of Projected Belt Polytopes: Proof of Theorem 3.2

For the proof of the following Farkas’ Lemma, we refer to [2, Lemma 2.4] and [16, Lemma 2.1].

Lemma 5.2

(Farkas) Let $C\subset \mathbb {R}^n$ be a full-dimensional cone and $L\subset \mathbb {R}^n$ a linear subspace. Then,

$$\begin{aligned} {{\,\textrm{int}\,}}(C)\cap L\ne \varnothing \quad \Leftrightarrow \quad C^\circ \cap L^\perp = \{0\}. \end{aligned}$$

Proof of Theorem 3.2

Consider first the case when P is full-dimensional. Let F be a j-face of P and $0\le j<d\le n$ be given. Then, by [1] or [12, Proposition 5.3], GF is a j-face of GP if and only if

$$\begin{aligned} {{\,\textrm{int}\,}}T_F(P)\cap \ker G= \varnothing \end{aligned}$$

since the general position assumption (G1) is satisfied. By Farkas’ Lemma 5.2, this is equivalent to

$$\begin{aligned} (\ker G)^\perp \cap N_F(P)\ne \{0\}. \end{aligned}$$

Thus, using that $\mathcal {N}(P)=\mathcal {F}(\mathcal {A})$ and, in particular, $\{N_F(P):F\in \mathcal {F}_j(P)\}=\mathcal {F}_{n-j}(\mathcal {A})$, we obtain

$$\begin{aligned} f_j(GP)&=\sum _{F\in \mathcal {F}_j(P)}\mathbbm {1}_{\{GF\in \mathcal {F}_j(GP)\}} =\sum _{F\in \mathcal {F}_j(P)}\mathbbm {1}_{\{(\ker G)^\perp \cap \, N_F(P)\ne \{0\}\}}\\&=\sum _{D\in \mathcal {F}_{n-j}(\mathcal {A})}\mathbbm {1}_{\{(\ker G)^\perp \cap \, D\ne \{0\}\}}. \end{aligned}$$

By (G2), $(\ker G)^\perp$ is in general position w.r.t. $\mathcal {A}$. By Lemma 3.3 and its proof,

$$\begin{aligned} f_j(GP)&= 2\sum _{M\in \mathcal {L}_{n-j}(\mathcal {A})}(a_{n-d+1}^M+a_{n-d+3}^M+\ldots )\nonumber \\&= 2(a_{n-d+1, n-j}+a_{n-d+3, n-j}+\ldots ), \end{aligned}$$

(5.2)

which completes the proof in the full-dimensional case.

Now, suppose $p:=\dim P<n$. We want to restrict all arguments to the p-dimensional linear subspace L satisfying $\mathop {\textrm{aff}}\nolimits P=t+L$ for some $t\in \mathbb {R}^n$, and then apply the already known full-dimensional case in the ambient space L. At first, we observe that ${{\,\textrm{rank}\,}}(G|_L)=d$, since $\dim \ker (G|_L)=\dim (L\cap \ker G)=p-d\ge 0$ because $\ker G$ is in general position with respect to P due to general position assumption (G1). Furthermore, we need to verify whether the conditions (G1) and (G2) also hold in the restricted case where n is replaced by p, G is replaced by the restriction $G|_L$ of G to L, and $\mathcal {A}$ is replaced by $\mathcal {A}|L=\{H\cap L:H\in \mathcal {A},L\nsubseteq H\}=\{H\cap L:H\in \mathcal {A}\}$. The last equation is due to $L^\perp \subset {{\,\textrm{lin}\,}}N_F(P)$ for all faces F of P, and therefore, $L^\perp \subset H$ for all $H\in \mathcal {A}$, since the linear hull ${{\,\textrm{lin}\,}}N_F(P)$ coincides with an intersection of hyperplanes from $\mathcal {A}$. Thus, we also observe that the elements of $\mathcal {A}|L$ and $\mathcal {A}$ are in one-to-one correspondence via the mapping $H'\mapsto H'+L^\perp$ and, the inverse map is given by .

Also, by (G1) for P in $\mathbb {R}^n$, $\ker (G|_L)$ is in general position with respect to K, for each linear subspace K such that $\mathop {\textrm{aff}}\nolimits F=t+K$ for some face F of P, since

$$\begin{aligned} \dim (K\cap \ker (G|_L))=\dim (K\cap L\cap \ker G)=\dim (K\cap \ker G). \end{aligned}$$

Thus, (G1) is also satisfied if we restrict all objects to L. Then, (G2) is also satisfied in the restricted version due to the equivalence of (G1) and (G2) proved in Theorem 3.1. Thus, we can apply (5.2) in the restricted case to obtain

$$\begin{aligned} f_j(G P)=2\sum _{M'\in \mathcal {L}_{p-j}(\mathcal {A}|L)}\big (a^{M'}_{p-d+1}+a^{M'}_{p-d+3}+\ldots \big ), \end{aligned}$$

since $(\mathcal {A}|L)|M'=\mathcal {A}|M'$ and therefore $\chi _{(\mathcal {A}|L)|M'}(t)=\chi _{\mathcal {A}|M'}(t)$. Next we observe that the linear subspaces $M'\in \mathcal {L}_{p-j}(\mathcal {A}|L)$ are in one-to-one correspondence to the linear subspaces $M\in \mathcal {L}_{n-j}(\mathcal {A})$ via $M'\mapsto M'+L^\perp =: M$. By the Whitney formula for the characteristic polynomial (3.2) and the identity $\mathcal {A}|(M'+L^\perp )=(\mathcal {A}|M')+L^\perp$, we obtain the relation

$$\begin{aligned} \chi _{\mathcal {A}|(M'+L^\perp )}(t) = \chi _{(\mathcal {A}|M')+L^\perp }(t) = t^{n-p}\chi _{\mathcal {A}|M'}(t), \end{aligned}$$

for all $M'\in \mathcal {L}_{p-j}(\mathcal {A}|L)$, and thus, $a^{M'}_{k}=a^{M'+L^\bot }_{k+n-p}$. Hence, we arrive at

$$\begin{aligned} f_j(G P)&=2\sum _{M'\in \mathcal {L}_{p-j}(\mathcal {A}|L)}\big (a^{M'+L^\perp }_{n-d+1}+a^{M'+L^\perp }_{n-d+3}+\ldots \big )\\&=2\sum _{M\in \mathcal {L}_{n-j}(\mathcal {A})}\big (a^M_{n-d+1}+a^M_{n-d+3}+\ldots \big ), \end{aligned}$$

which completes the proof. $\square$

5.4 Angle Sums of Belt Polytopes: Proof of Theorem 3.4

We shall use the following generalized version of the Klivans-Swartz formula [19] due to Amelunxen and Lotz [2, Theorem 6.1]. Consider a linear hyperplane arrangement $\mathcal {A}$ in $\mathbb {R}^n$ whose m-th level characteristic polynomial is written in the form (3.4). Then, for all $0\le k \le m \le n$ we have

$$\begin{aligned} \sum _{C\in \mathcal {F}_{m}(\mathcal {A})} \upsilon _{k} (C) = a_{k,m}. \end{aligned}$$

(5.3)

To prove the first identity of Theorem 5.4, we use the fact that $T_F(P)$ is the dual of $N_F(P)$ (which has dimension $n-j$), the definition of belt polytopes and then (5.3):

$$\begin{aligned} \sum _{F\in \mathcal {F}_j(P)} \upsilon _d(T_F(P)) \!=\! \sum _{F\!\in \! \mathcal {F}_j(P)}\!\upsilon _{n-d} (N_F(P)) \!=\! \sum _{C\!\in \! \mathcal {F}_{n-j}(\mathcal {A})} \upsilon _{n-d} (C) = a_{n-d,n-j}. \nonumber \\ \end{aligned}$$

(5.4)

To prove the second identity of Theorem 5.4, we first suppose that $j<\dim P$. Then, for every $F\in \mathcal {F}_j(P)$, the tangent cone $T_F(P)$ is not a linear subspace, and we can apply the conic Crofton formula (2.1) together with (5.4):

$$\begin{aligned} \sum _{F\in \mathcal {F}_j(P)} \gamma _d(T_F(P))&= 2 \sum _{F\in \mathcal {F}_j(P)} \left( \upsilon _{d+1}(T_F(P)) + \upsilon _{d+3}(T_F(P)) + \ldots \right) \\&= 2 (a_{n-d-1,n-j} + a_{n-d-3,n-j} + \ldots ). \end{aligned}$$

In the remaining case $j=d= \dim P$, both sides of the above formula vanish. Indeed, the only j-dimensional face F is P itself, $T_F(P)$ is a d-dimensional linear space and $\gamma _d(T_F(P)) = 0$. On the other hand, $\dim P = d$ implies that every linear subspace from $\mathcal {L}(\mathcal {A})$ contains the $(n-d)$-dimensional linear subspace $M = (\mathop {\textrm{aff}}\nolimits P)^\perp$. The restriction of $\mathcal {L}(\mathcal {A})$ to M is empty, implying that all $a_{k, n-j}$ vanish.

6 Proofs of the Results on Permutohedra

6.1 Faces of Permutohedra

Before starting with the proofs, let us mention the following well-known fact.

Lemma 6.1

The points $(x_{\sigma (1)},\dots ,x_{\sigma (n)})$ are indeed vertices of $\mathcal {P}_n^A$ for all $\sigma \in \text {Sym}(n)$. Similarly, the points $(\varepsilon _1x_{\sigma (1)},\dots ,\varepsilon _nx_{\sigma (n)})$ are vertices of $\mathcal {P}_n^B$ for all $\varepsilon \in \{\pm 1\}^n$, $\sigma \in \text {Sym}(n)$.

Proof

Let us explain this in the B-case. It suffices to prove the claim for the point $x = (x_1,\dots ,x_n)$ of $\mathcal {P}_n^B$, where $x_1\ge \ldots \ge x_n\ge 0$. Suppose that there are points $y=(y_1,\dots ,y_n)\in \mathcal {P}_n^B$ and $z=(z_1,\dots ,z_n)\in \mathcal {P}_n^B$ such that $x= (y+z)/2$. By Lemma 4.2, we have $|y_1|\le x_1$ and $|z_1|\le x_1$. Thus, we have $y_1=z_1=x_1$. Given this, we can consider the second coordinate in the same way. Inductively, we obtain $y_i=z_i = x_i$ for all $i=1,\dots ,n$, which means that $(x_1,\dots ,x_n)$ is indeed a vertex of $\mathcal {P}_n^B$. $\square$

6.1.1 Faces of the permutohedra

We now state an explicit characterization of the faces of both types of permutohedra. Let $\mathcal {R}_{n,j}$ be the set of all ordered partitions $\mathcal {B}= (B_1,\dots ,B_j)$ of the set $\{1,\dots ,n\}$ into j non-empty, disjoint and distinguishable subsets $B_1,\dots ,B_j$. Furthermore, let $\mathcal {T}_{n,j}$ be the set of all pairs $(\mathcal {B},\eta )$, where $\mathcal {B}=(B_1,\dots ,B_{j+1})$ is an ordered partition of the set $\{1,\dots ,n\}$ into $j+1$ disjoint distinguishable subsets such that $B_1,\dots ,B_j$ are non-empty, whereas $B_{j+1}$ may be empty or not, and $\eta :B_1\cup \ldots \cup B_j\rightarrow \{\pm 1\}$. In what follows, we write $\eta _i:=\eta (i)$ for ease of notation.

The elements of $\mathcal {R}_{n,j}$ and $\mathcal {T}_{n,j}$ are in bijective correspondence with the j-faces of the fans $\mathcal {F}(\mathcal {A}(A_{n-1}))$ and $\mathcal {F}(\mathcal {A}(B_{n}))$. The j-face in the fan of $\mathcal {A}(A_{n-1})$ corresponding to a partition $\mathcal {B}\in \mathcal {R}_{n,j}$ is the set of all $x\in \mathbb {R}^n$ such that $x_{i_1} = x_{i_2}$ for all indices $i_1,i_2$ from the same $B_\ell$ and $x_{i_1} \le x_{i_2}$ for all $i_1 \in B_{\ell _1}$ and $i_2 \in B_{\ell _2}$ with $1\le \ell _1 < \ell _2 \le j$. Furthermore, the j-face in the fan of $\mathcal {A}(B_n)$ corresponding to the pair $(B,\eta )$ is the set of all $x\in \mathbb {R}^n$ such that $\eta _{i_1} x_{i_1} = \eta _{i_2} x_{i_2}$ for all indices $i_1,i_2$ from the same $B_\ell$ with $1\le \ell \le j$, $\eta _{i_1} x_{i_1} \le \eta _{i_2} x_{i_2}$ for all $i_1 \in B_{\ell _1}$ and $i_2 \in B_{\ell _2}$ with $1\le \ell _1 < \ell _2 \le j$, and $x_i=0$ for all $i\in B_{j+1}$. It is easy to check that the cardinalities of $\mathcal {R}_{n,j}$ and $\mathcal {T}_{n,j}$ are given by $j!\genfrac\rbrace \lbrace {0.0pt}{}{n}{j}$ and $\sum _{m=j}^n 2^m \left( {\begin{array}{c}n\\ m\end{array}}\right) j!\genfrac\rbrace \lbrace {0.0pt}{}{m}{j} = 2^j j! B\big \{{n},{j}\big \}$, respectively.

Proposition 6.2

Suppose that $x_1>\cdots >x_n$. Then, for $j\in \{0,\dots ,n-1\}$, the j-dimensional faces of $\mathcal {P}_n^A(x_1,\dots ,x_n)$ are in one-to-one correspondence with the ordered partitions $\mathcal {B}\in \mathcal {R}_{n,n-j}$. The j-face corresponding to the ordered partition $\mathcal {B}=(B_1,\dots ,B_{n-j})\in \mathcal {R}_{n,n-j}$ is given by

$$\begin{aligned} F_\mathcal {B}&={{\,\textrm{conv}\,}}\{(x_{\sigma (1)},\dots ,x_{\sigma (n)}):\sigma \in I_\mathcal {B}\}=\bigg \{(t_1,\dots ,t_n)\in \mathcal {P}_n^A(x_1,\dots ,x_n):\\ {}&\quad \sum _{i\in B_1\cup \ldots \cup B_l}t_i=x_1+\cdots +x_{|B_1\cup \ldots \cup B_l|}\;\forall l=1,\dots ,{n-j-1}\bigg \}. \end{aligned}$$

Here, $I_\mathcal {B}\subset \text {Sym}(n)$ is the set of all permutations $\sigma \in \text {Sym}(n)$ such that

$$\begin{aligned} \sigma (B_1)&= \{1,\ldots ,|B_1|\}, \;\; \sigma (B_2) = \{|B_1|+1,\ldots ,|B_1\cup B_2|\}, \;\; \ldots ,\\ \sigma (B_{n-j})&= \{|B_1\cup \ldots \cup B_{n-j-1}|+1,\ldots ,n\}. \end{aligned}$$

Proposition 6.3

Suppose that $x_1>\cdots>x_n>0$. Then, for $j\in \{0,\dots ,n\}$, the j-dimensional faces of $\mathcal {P}_n^B(x_1,\dots ,x_n)$ are in one-to-one correspondence with the pairs $(\mathcal {B},\eta )\in \mathcal {T}_{n,n-j}$. The j-face corresponding to the pair $(\mathcal {B},\eta )$, where $\mathcal {B}=(B_1,\dots ,B_{n-j+1})$, is given by

$$\begin{aligned} F_{\mathcal {B},\eta }&={{\,\textrm{conv}\,}}\{(\varepsilon _1x_{\sigma (1)},\dots ,\varepsilon _nx_{\sigma (n)}):(\sigma ,\varepsilon )\in I_{\mathcal {B},\eta }\} \end{aligned}$$

(6.1)

$$\begin{aligned}&=\bigg \{t\in \mathcal {P}_n^B(x_1,\dots ,x_n): \nonumber \\ {}&\sum _{i\in B_1\cup \ldots \cup B_l}\eta _i t_i=x_1+\ldots +x_{|B_1\cup \ldots \cup B_l|}\;\forall l=1,\dots ,{n-j}\bigg \}. \end{aligned}$$

(6.2)

Here, $I_{\mathcal {B},\eta }\subset Sym (n)\times \{\pm 1\}^n$ is the set of all pairs $(\sigma ,\varepsilon )\in Sym (n)\times \{\pm 1\}^n$ such that

$$\begin{aligned} \sigma (B_1)&= \{1,\ldots ,|B_1|\}, \;\; \sigma (B_2) = \{|B_1|+1,\ldots ,|B_1\cup B_2|\}, \;\; \ldots ,\\ \sigma (B_{n-j+1})&= \{|B_1\cup \ldots \cup B_{n-j}|+1,\ldots ,n\} \end{aligned}$$

and $\varepsilon _i=\eta _{i}$ for all $i\in B_1\cup \ldots \cup B_{n-j}$, while the remaining $\varepsilon _i$’s take arbitrary values in $\{\pm 1\}$.

Proofs of Proposition 6.2 can be found in [6, pp. 254–256] or in [31, Section 5.3]. Without proof, versions of the same proposition are stated in [22, Proposition 2.6] and in Exercise 2.9 on p. 96 of [8]. For completeness, we will provide a proof of Proposition 6.3 (which may also be known).

Proof of Proposition 6.3

Let $F\in \mathcal {F}(\mathcal {P}_n^B)$ be a face of $\mathcal {P}_n^B(x_1,\ldots ,x_n)$ with $x_1>\cdots>x_n>0$. Either, we have $F=\mathcal {P}_n^B$, which means there is nothing to prove, or there is a supporting hyperplane $H=\{t\in \mathbb {R}^n:\alpha _1t_1+\cdots +\alpha _nt_n=b\}$ for some $\alpha =(\alpha _1,\dots ,\alpha _n)\in \mathbb {R}^n\backslash \{0\}$ and $b\in \mathbb {R}$ such that

$$\begin{aligned} H\cap \mathcal {P}_n^B=F\quad \text {and}\quad \mathcal {P}_n^B\subset H^-:=\{t\in \mathbb {R}^n:\alpha _1t_1+\cdots +\alpha _nt_n\le b\}. \end{aligned}$$

(6.3)

Without loss of generality, we may assume that $\alpha _1\ge \ldots \ge \alpha _n\ge 0$ (otherwise apply a signed permutation of $\{1,\dots ,n\}$ to $(\alpha _1,\ldots ,\alpha _n)$ and all other objects). Then,

$$\begin{aligned}&\underbrace{\alpha _1=\dots =\alpha _{i_1}}_{\text {group 1}}>\underbrace{\alpha _{i_1+1}=\ldots =\alpha _{i_2}}_{\text {group 2}}>\cdots>\nonumber \\ {}&\underbrace{\alpha _{i_{m-1}+1}=\ldots =\alpha _{i_{m}}}_{\text {group { m}}}>\underbrace{\alpha _{i_{m}+1}=\ldots =\alpha _n=0}_{\text {group m+1}}, \end{aligned}$$

(6.4)

for some $m\in \{1,\dots ,n\}$ and $1\le i_1<\ldots <i_{m}\le n$. Note that for $i_{m}=n$, no $\alpha _i$’s are required to be zero, which means that the last group is empty. Then, $\mathcal {P}_n^B\subset H^-$ implies that

$$\begin{aligned}&\alpha _1\varepsilon _1x_{\sigma (1)}+\cdots +\alpha _n\varepsilon _nx_{\sigma (n)}\le b, \quad \text { for all } \varepsilon =(\varepsilon _1,\dots ,\varepsilon _n)\in \{\pm 1\}^n,\\ {}&\sigma \in \text {Sym}(n). \end{aligned}$$

The first equation of (6.3) implies that there is a pair $(\sigma ', \varepsilon ')\in \text {Sym}(n)\times \{\pm 1\}^n$ such that

$$\begin{aligned} \alpha _1\varepsilon _1' x_{\sigma '(1)}+\cdots +\alpha _{i_{m}}\varepsilon _{i_{m}}'x_{\sigma '(i_{m})} = \alpha _1\varepsilon _1'x_{\sigma '(1)}+\cdots +\alpha _n\varepsilon _n'x_{\sigma '(n)} = b. \end{aligned}$$

Since the $\alpha _i$’s and the $x_i$’s are non-increasing and non-negative, the swapping lemma (see, e.g., [6, p. 254]) states that $\alpha _1\varepsilon _1x_{\sigma (1)}+\cdots +\alpha _n\varepsilon _nx_{\sigma (n)}$ attains its maximal value if we choose $\varepsilon _i=+1$ and $\sigma (i) =i$ for all $i\in \{1,\ldots ,n\}$. It follows that, in fact, we have

$$\begin{aligned} \alpha _1x_1+\cdots +\alpha _{n}x_{n}=b. \end{aligned}$$

(6.5)

Denote the groups of indices appearing in (6.4) by

$$\begin{aligned} B_1=\{1,\dots ,i_1\},\;\; \dots ,\;\; B_{m}=\{i_{m-1}+1,\dots ,i_{m}\}, \;\; B_{m+1}=\{i_{m}+1,\dots ,n\}, \nonumber \\ \end{aligned}$$

(6.6)

where $B_{m+1}$ may or may not be empty. Defining in our case $\eta _i:=1$ for all $i\in \{1,\ldots ,i_m\}$ we obtain that, under (6.6), the set $I_{\mathcal {B},\eta }$ consists of all pairs $(\sigma ,\varepsilon )\in \text {Sym}(n)\times \{\pm 1\}^n$ such that

$$\begin{aligned} \sigma (B_1)=B_1,\;\; \dots , \;\; \sigma (B_m)=B_m, \;\; \sigma (B_{m+1})=B_{m+1} \end{aligned}$$

and $\varepsilon _i = \eta _i$ for all $i\in \{1,\ldots ,i_m\}$. Consequently, from (6.5) and (6.4) it follows that

$$\begin{aligned} \alpha _1\varepsilon _1x_{\sigma (1)}+\cdots +\alpha _{n}\varepsilon _{n}x_{\sigma (n)}=b \quad \text { for all } (\sigma ,\varepsilon )\in I_{\mathcal {B},\eta }. \end{aligned}$$

(6.7)

Furthermore, it follows from (6.5), (6.4) and the swapping lemma that

$$\begin{aligned} \alpha _1\varepsilon _1x_{\sigma (1)}+\cdots +\alpha _{n}\varepsilon _{n}x_{\sigma (n)}<b \quad \text { for all } (\sigma ,\varepsilon )\in (\text {Sym}(n)\times \{\pm 1\}^n)\backslash I_{\mathcal {B},\eta }. \end{aligned}$$

(6.8)

Indeed, if $(\sigma ,\varepsilon )\notin I_{\mathcal {B},\eta }$, then there is the possibility that we have a strictly negative term on the left-hand side of (6.8) which means that we could make it strictly larger by changing the sign of this term. Thus, we can assume all these terms to be non-negative. Then, $(\sigma ,\varepsilon )\notin I_{\mathcal {B},\eta }$ implies that there is a pair of indices $1\le i<j\le n$ such that $\alpha _i>\alpha _j$ und $x_{\sigma (i)}<x_{\sigma (j)}$ and we can apply the swapping lemma to strictly increase the left-hand side.

According to (6.7) and (6.8), the vertices $(\varepsilon _1 x_{\sigma (1)},\dots ,\varepsilon _nx_{\sigma (n)})$ with $(\sigma ,\varepsilon )\in I_{\mathcal {B},\eta }$ are the only vertices of $\mathcal {P}_n^B$ that belong to the supporting hyperplane H. It follows from [32, Proposition 2.3] that F is the convex hull of these vertices, that is $F=F_{\mathcal {B},\eta }$, where

$$\begin{aligned} F_{\mathcal {B},\eta }:={{\,\textrm{conv}\,}}\big \{(\varepsilon _1x_{\sigma (1)},\dots ,\varepsilon _n x_{\sigma (n)}):(\sigma ,\varepsilon )\in I_{\mathcal {B},\eta }\big \}. \end{aligned}$$

(6.9)

Essentially the same argument shows that, conversely, a set of the form $F_{\mathcal {B},\eta }$ is a face of $\mathcal {P}_n^B$. At the beginning, we applied a signed permutation to all objects including $(\alpha _1,\dots ,\alpha _n)$ to achieve that the $\alpha _i$’s are non-increasing and non-negative. Applying the inverse signed permutation proves that the faces of $\mathcal {P}_n^B$ coincide with the sets of the form $F_{\mathcal {B},\eta }$ as defined in (6.9), for some pair $(\mathcal {B},\eta )\in \mathcal {T}_{n,m}$. Furthermore, for two different pairs $(\mathcal {B}',\eta '),(\mathcal {B}'',\eta '')$ we have $I_{\mathcal {B}',\eta '}\ne I_{\mathcal {B}'',\eta ''}$, which implies that the corresponding sets $F_{\mathcal {B}',\eta '}$ and $F_{\mathcal {B}'',\eta ''}$ are different, since their sets of vertices are different. Finally, the polytope $F_{\mathcal {B},\eta }$, for $(\mathcal {B},\eta )\in \mathcal {T}_{n,m}$, is isometric to the direct product $\mathcal {P}_{|B_1|}^A \times \ldots \times \mathcal {P}_{|B_m|}^A\times \mathcal {P}_{|B_{m+1}|}^B$, which follows from the description of the vertices of $F_{\mathcal {B},\eta }$. It follows that $\dim F_{\mathcal {B},\eta }=n-m$.

Now, we prove the equivalence of the representations (6.1) and (6.2). To this end, we take some pair $(\mathcal {B},\eta )\in \mathcal {T}_{n,m}$, assuming without restriction of generality that

$$\begin{aligned} B_1:=\{1,\dots ,i_1\},\;\; B_2:=\{i_1+1,\dots ,i_2\}, \;\; \dots , \;\; B_{m+1}:=\{i_{m}+1,\dots ,n\}, \end{aligned}$$

where $1\le i_1<\ldots <i_{m}\le n$ for some $m\in \{1,\dots ,n\}$, and $\eta _i=1$ for $i\in \{1,\dots ,i_m\}$. Our goal is to prove that $F_{\mathcal {B},\eta } = M$, where

$$\begin{aligned} M:= \bigg \{t\in \mathcal {P}_n^B(x_1,\dots ,x_n)\!:\sum _{i\in B_1\cup \ldots \cup B_l}t_i\!=\!x_1+\cdots +x_{|B_1\cup \ldots \cup B_l|}\;\forall l=1,\dots ,{m}\bigg \}. \end{aligned}$$

The inclusion $F_{\mathcal {B},\eta }\subset M$ holds trivially and we only need to prove that $M\subset F_{\mathcal {B},\eta }$.

Let $\alpha =(\alpha _1,\ldots ,\alpha _n)\in \mathbb {R}^n\backslash \{0\}$ be such that condition (6.4) holds. The above arguments show that the hyperplane $H=\{t\in \mathbb {R}^n:\alpha _1t_1+\cdots +\alpha _nt_n=b\}$ with $b:=\alpha _1x_1+\cdots +\alpha _n x_n$ is a supporting hyperplane of the face $F_{\mathcal {B},\eta }$, that is

$$\begin{aligned} H\cap \mathcal {P}_n^B = F_{\mathcal {B},\eta }\quad \text {and}\quad \mathcal {P}_n^B\subset H^-:=\{t\in \mathbb {R}^n:\alpha _1t_1+\cdots +\alpha _nt_n\le b\}. \end{aligned}$$

Suppose now that there is some $y\notin F_{\mathcal {B},\eta }$ such that $y\in M\subset \mathcal {P}_n^B\subset H^-$. This already yields

$$\begin{aligned} \alpha _1y_1+\cdots +\alpha _{i_m}y_{i_m}=\alpha _1y_1+\cdots +\alpha _ny_n<t=\alpha _1x_1+\cdots +\alpha _{i_m}x_{i_m}, \end{aligned}$$

since $y\in H^-$, but $y\notin H$. It follows that

$$\begin{aligned}&\alpha _{i_{m}}(y_1+\cdots +y_{i_m})+\sum _{l=1}^{m-1}(\alpha _{i_{l}}-\alpha _{i_{l+1}})\sum _{i=1}^{i_l}y_i=\alpha _1y_1+\cdots +\alpha _{i_m}y_{i_m}\\&\quad <\alpha _1x_{1}+\cdots +\alpha _{i_m}x_{i_m}\\&\quad =\alpha _{i_{m}}(x_{1}+\cdots +x_{i_m})+\sum _{l=1}^{m-1}(\alpha _{i_{l}}-\alpha _{i_{l+1}})\sum _{i=1}^{i_l}x_i, \end{aligned}$$

which is a contradiction to $y\in M$. This proves that both representations (6.1) and (6.2) are equivalent. $\square$

6.2 Normal Fans of Permutohedra: Proofs of Theorems 4.3 and 4.4

First we need to prove a simple lemma concerning the interior of a polytope.

Lemma 6.4

Let $P\subset \mathbb {R}^n$ be a polytope defined by the affine inequalities

$$\begin{aligned} P=\{x\in \mathbb {R}^n:l_1(x)\le 0,\dots ,l_m(x)\le 0\} \end{aligned}$$

for some $m\in \mathbb {N}$ and affine-linear functions $l_i(x)=\langle x,y_i\rangle +b_i$, where $y_i\in \mathbb {R}^n\backslash \{0\}$ and $b_i\in \mathbb {R}$, $i=1,\dots ,m$. Then, we have

$$\begin{aligned} {{\,\textrm{int}\,}}P=\{x\in \mathbb {R}^n:l_1(x)<0,\dots ,l_m(x)<0\}. \end{aligned}$$

Proof

Suppose $x\in \mathbb {R}^n$ satisfies the conditions $l_1(x)<0,\dots ,l_m(x)<0$. Since the functions $l_1,\dots ,l_m$ are continuous, we also have $l_1(y)<0,\dots ,l_m(y)<0$ for all y in some small enough neighborhood of x. Thus, x belongs to ${{\,\textrm{int}\,}}P$.

Now let $x\in P$ satisfy $l_i(x)=0$ for some $i\in \{1,\dots ,m\}$. Then, in each neighborhood of x, we can find a point y with $l_i(y)>0$. This means that $x\notin {{\,\textrm{int}\,}}P$, thus completing the proof. $\square$

Proof of Theorem 4.3

Let $x_1>\cdots >x_n$ be given. Our aim is to prove that $\mathcal {N}(\mathcal {P}_n^A(x_1,\dots ,x_n))=\mathcal {F}(\mathcal {A}(A_{n-1}))$. From Proposition 6.2 we know that each j-face of $\mathcal {P}_n^A$, for a $j\in \{0,\dots ,n-1\}$, is uniquely defined by an ordered partition $\mathcal {B}=(B_1,\dots ,B_{n-j})\in \mathcal {R}_{n,n-j}$ of the set $\{1,\dots ,n\}$ and given by

$$\begin{aligned} F_{\mathcal {B}}=\bigg \{(t_1,\dots ,t_n)\in \mathcal {P}_n^A:\sum _{i\in B_1\cup \ldots \cup B_l}t_i=x_1+\cdots +x_{|B_1\cup \ldots \cup B_l|} \text { for all } l=1,\dots ,{n-j}\bigg \}. \end{aligned}$$

Now, take a point $t\in {{\,\textrm{relint}\,}}F_{\mathcal {B}}$. We claim that t satisfies the following conditions:

$$\begin{aligned} \sum _{i\in B_1\cup \ldots \cup B_l}t_i=x_1+\cdots +x_{|B_1\cup \ldots \cup B_l|}\quad \forall l=1,\dots ,n-j, \end{aligned}$$

(6.10)

and

$$\begin{aligned} \sum _{i\in M}t_i<x_1+\cdots +x_{|M|}~\forall M\subset \{1,\dots ,n\}:M\notin \{B_1,B_1\cup B_2,\dots ,B_1\cup \ldots \cup B_{n-j}\}. \end{aligned}$$

(6.11)

To prove this, consider the affine subspace

$$\begin{aligned} L_\mathcal {B}&:=\bigg \{(t_1,\dots ,t_n)\in \mathbb {R}^n:\sum _{i\in B_1\cup \ldots \cup B_l}t_i=x_1+\cdots +x_{|B_1\cup \ldots \cup B_l|} \text { for all } \\ l&=1,\dots ,{n-j}\bigg \}, \end{aligned}$$

which is of dimension j since the conditions are linearly independent. Then, by Lemma 4.1, we can represent $F_\mathcal {B}$ as the set of points $(t_1,\dots ,t_n)\in L_\mathcal {B}$ such that

$$\begin{aligned} \sum _{i\in M}t_i\le x_1+\cdots +x_{|M|}~\forall M\subset \{1,\dots ,n\}:M\notin \{B_1,B_1\cup B_2,\dots ,B_1\cup \ldots \cup B_{n-j}\}. \end{aligned}$$

Since $\dim F_\mathcal {B}=j$, the characterization of ${{\,\textrm{relint}\,}}F_\mathcal {B}$ in (6.11) follows from Lemma 6.4 applied to the ambient affine subspace $L_\mathcal {B}$ instead of $\mathbb {R}^n$.

Now, we want to determine the tangent cone $T_{F_\mathcal {B}}(\mathcal {P}_n^A)$. By definition, the tangent cone is given by

$$\begin{aligned} T_{F_{\mathcal {B}}}(\mathcal {P}_n^A)=\{v\in \mathbb {R}^n:t+\varepsilon v\in \mathcal {P}_n^A \text { for some } \varepsilon >0\}, \end{aligned}$$

where $t\in {{\,\textrm{relint}\,}}F_{\mathcal {B}}$. By Lemma 4.1, for a $v\in \mathbb {R}^n$, the condition $t+\varepsilon v\in \mathcal {P}_n^A$ holds for some $\varepsilon >0$ if and only if

$$\begin{aligned} \sum _{i=1}^n (t_i+\varepsilon v_i)&= x_1+\cdots +x_n\quad \text {and}\quad \sum _{i\in M} (t_i+\varepsilon v_i) \le x_1+\cdots +x_{|M|}\;\,\forall M\\ {}&\quad \subset \{1,\dots ,n\}. \end{aligned}$$

Since $t_1+\cdots +t_n=x_1+\cdots +x_n$, the first condition is satisfied if and only if $v_1+\cdots +v_n=0$. We observe that if we choose $\varepsilon >0$ small enough, the second condition is satisfied for all sets $M\subset \{1,\dots ,n\}$ such that $M\notin \{B_1,B_1\cup B_2,\dots ,B_1\cup \ldots \cup B_{n-j}\}$, due to (6.11). For the sets $B_1,B_1\cup B_2,\dots ,B_1\cup \ldots \cup B_{n-j}$, we obtain that

$$\begin{aligned} \sum _{i\in B_1\cup \ldots \cup B_l}v_i\le 0, \end{aligned}$$

by (6.10). Therefore, the tangent cone is given by

$$\begin{aligned} T_{F_{\mathcal {B}}}\!(\mathcal {P}_n^A)=\bigg \{v\in \mathbb {R}^n:v_1\!+\cdots +v_n=0,\;\sum _{i\!\in \! B_1\cup \ldots \cup B_l}v_i\!\le \!0\;\forall l=1,\dots ,n-j-1\bigg \}. \end{aligned}$$

Thus, the corresponding normal cone is given by

$$\begin{aligned}&N_{F_\mathcal {B}}(\mathcal {P}_n^A)=T_{F_{\mathcal {B}}}(\mathcal {P}_n^A)^\circ =\{x\in \mathbb {R}^n:\forall 1\le l_1\le l_2\le n-j\;\forall i_1\in B_{l_1},i_2\in B_{l_2},\\&\text { we have } x_{i_1}\ge x_{i_2}\}. \end{aligned}$$

Note that the conditions of $N_{F_\mathcal {B}}(\mathcal {P}_n^A)$ imply $x_{i_1}=x_{i_2}$ for all $i_1,i_2\in B_l$, $l=1,\dots ,n-j$. The cone $N_{F_\mathcal {B}}(\mathcal {P}_n^A)$ is an $(n-j)$-dimensional cone in the fan $\mathcal {F}(\mathcal {A}(A_{n-1}))$ and it is easy to check that, going through all ordered partitions $\mathcal {B}\in \mathcal {R}_{n,n-j}$, we obtain all $(n-j)$-dimensional cones of the fan $\mathcal {N}(\mathcal {A}(A_{n-1}))$; see, e.g., [18, Section 2.7]. This completes the proof.

Proof of Theorem 4.4

Fix some $x_1>\cdots>x_n>0$. Our aim is to prove that $\mathcal {N}(\mathcal {P}_n^B(x_1,\dots ,x_n))=\mathcal {F}(\mathcal {A}(B_n))$. From Proposition 6.3 we know that each j-face of $\mathcal {P}_n^B$, for a $j\in \{0,\dots ,n\}$, is uniquely defined by a pair $(\mathcal {B},\eta )\in \mathcal {T}_{n,n-j}$, where $\mathcal {B}=(B_1,\dots ,B_{n-j+1})$, and given by

$$\begin{aligned} F_{\mathcal {B},\eta }=\bigg \{(t_1,\dots ,t_n)\in \mathcal {P}_n^B:\sum _{i\in B_1\cup \ldots \cup B_l}\eta _it_i=x_1+\cdots +x_{|B_1\cup \ldots \cup B_l|}\;\forall l=1,\dots ,{n-j}\bigg \}. \end{aligned}$$

Now, we claim that

$$\begin{aligned} T_{F_{\mathcal {B},\eta }}(\mathcal {P}_n^B)=\bigg \{v\in \mathbb {R}^n:\sum _{i\in B_1\cup \ldots \cup B_l}\eta _iv_i\le 0\;\forall l=1,\dots ,n-j\bigg \}. \end{aligned}$$

(6.12)

To prove this, take a point $t\in {{\,\textrm{relint}\,}}F_{\mathcal {B},\eta }$. Then,

$$\begin{aligned} \sum _{i\in B_1\cup \ldots \cup B_l}\eta _it_i=x_1+\cdots +x_{|B_1\cup \ldots \cup B_l|}\quad \forall l=1,\dots ,n-j \end{aligned}$$

(6.13)

and

$$\begin{aligned}&\sum _{i\in M}|t_i|<x_1+\cdots +x_{|M|}\quad \forall M\subset \{1,\dots ,n\}:\nonumber \\ {}&\quad M\notin \{B_1,B_1\cup B_2,\dots ,B_1\cup \ldots \cup B_{n-j}\}. \end{aligned}$$

(6.14)

This can easily be justified in the same way as in the A-case using Lemmas 4.2 and 6.4. Note that (6.13) implies that ${{\,\textrm{sgn}\,}}t_i=\eta _i$ for all $i\in B_1\cup \ldots \cup B_{n-j}$ such that $t_i\ne 0$. Otherwise, if $\eta _{i_0}=-{{\,\textrm{sgn}\,}}t_{i_0}$ for some $i_0\in \{1,\dots ,n\}$ with $t_{i_0}\ne 0$, we would have

$$\begin{aligned} \sum _{B_1\cup \ldots \cup B_l}|t_i|>\sum _{B_1\cup \ldots \cup B_l}\eta _it_i=x_1+\cdots +x_{|B_1\cup \ldots \cup B_l|} \end{aligned}$$

for some $l\in \{1,\dots ,n-j\}$ in contradiction to $t\in \mathcal {P}_n^B$.

Now, recall that the tangent cone is defined by

$$\begin{aligned} T_{F_{\mathcal {B},\eta }}(\mathcal {P}_n^B)=\{v\in \mathbb {R}^n:t+\varepsilon v\in \mathcal {P}_n^B \text { for some } \varepsilon >0\} \end{aligned}$$

for $t\in {{\,\textrm{relint}\,}}F_{\mathcal {B},\eta }$. In view of the characterization of points in $\mathcal {P}_n^B$ stated in Lemma 4.2, it follows that $v\in T_{F_{\mathcal {B},\eta }}(\mathcal {P}_n^B)$ if and only if there exists an $\varepsilon >0$ such that

$$\begin{aligned} \sum _{i\in M}|t_i+\varepsilon v_i|\le x_1+\cdots +x_{|M|}\quad \forall M\subset \{1,\dots ,n\}. \end{aligned}$$

For all $M\subset \{1,\dots ,n\}$ with $M\notin \{B_1,B_1\cup B_2,\dots ,B_1\cup \ldots \cup B_{n-j}\}$ this condition is satisfied due to (6.14) provided $\varepsilon >0$ is small enough. If $t_i\ne 0$ for all $i\in B_1\cup \ldots \cup B_{n-j}$, the remaining conditions are equivalent to

$$\begin{aligned} \sum _{i\in B_1\cup \ldots \cup B_l} \eta _i(t_i+\varepsilon v_i)\le x_1+\cdots +x_{|B_1\cup \ldots \cup B_l|} \quad \forall l=1,\ldots ,n-j. \end{aligned}$$

(6.15)

This follows from the fact that ${{\,\textrm{sgn}\,}}(t_i+\varepsilon v_i)={{\,\textrm{sgn}\,}}t_i=\eta _i$ for $\varepsilon >0$ chosen small enough. By (6.13), we obtain

$$\begin{aligned} \sum _{i\in B_1\cup \ldots \cup B_l}\eta _iv_i\le 0, \end{aligned}$$

for all $l=1,\dots ,n-j$. This proves (6.12). At this point, it remains to prove that $t_i\ne 0$ for all $i\in B_1\cup \ldots \cup B_{n-j}$. To this end, assume that $t_i=0$ for some $i\in B_l$ and some $l\in \{1,\dots ,n-j\}$. Defining $D_i:=(B_1\cup \ldots \cup B_l)\backslash \{i\}$, we have

$$\begin{aligned} \sum _{j\in D_i}\eta _jt_j=\sum _{j\in B_1\cup \ldots \cup B_l}\eta _jt_j=x_1+\cdots +x_{|B_1\cup \ldots \cup B_l|}, \end{aligned}$$

due to (6.13). If $D_i=B_1\cup \ldots \cup B_m$ for some $m<l$, we obtain

$$\begin{aligned} x_1+\cdots +x_{|B_1\cup \ldots \cup B_m|}=\sum _{j\in D_i}\eta _jt_j=x_1+\cdots +x_{|B_1\cup \ldots \cup B_l|}, \end{aligned}$$

in contradiction to $x_i>0$ for all $i=1,\dots ,n$. If, on the other hand, $D_i\ne B_1\cup \ldots \cup B_m$ for all $m<l$, we have

$$\begin{aligned} x_1+\cdots +x_{|B_1\cup \ldots \cup B_l|}=\sum _{j\in D_i}\eta _jt_j<x_1+\cdots +x_{|D_i|}, \end{aligned}$$

by (6.14). This is a contradiction to $D_i\subset B_1\cup \ldots \cup B_l$ proving that $t_i\ne 0$ for all $i\in B_1\cup \ldots \cup B_{n-j}$.

Thus, the normal cone of $\mathcal {P}_n^B$ at $F_{\mathcal {B},\eta }$ is given by

$$\begin{aligned} N_{F_{\mathcal {B},\eta }}(\mathcal {P}_n^B)&=T_{F_{\mathcal {B},\eta }}(\mathcal {P}_n^B)^\circ \\&=\big \{x\in \mathbb {R}^n:\forall 1\le l_1\le l_2\le n-j\;\forall i_1 \in B_{l_1},i_2\in B_{l_2}, \text { we have } \eta _{i_1}x_{i_1}\\ {}&\quad \ge \eta _{i_2}x_{i_2}\ge 0;\quad \forall i\in B_{n-j+1}\text { we have }x_i=0\big \}. \end{aligned}$$

The cone $N_{F_\mathcal {B}}(\mathcal {P}_n^B)$ is an $(n-j)$-face of a Weyl chamber of type $B_n$ and we can observe that, going through all pairs $(\mathcal {B},\eta )\in \mathcal {T}_{n,n-j}$, we obtain all $(n-j)$-dimensional cones of the fan $\mathcal {N}(\mathcal {A}(B_n))$; see, e.g., [18, Section 2.4]. This completes the proof.

6.3 Permutohedra and Zonotopes: Proof of Theorem 4.13

We will prove both the A- and the B-case together and assume that $x_1>\cdots >x_n$ and $x_1>\cdots>x_n>0$, respectively. In the book of Ziegler [32, Example 7.15], it is shown that $\mathcal {P}_n^A(n,n-1,\dots ,1)$ is a zonotope. By shifting and rescaling, we obtain that

$$\begin{aligned} \mathcal {P}_n^A\big (a+(n-1)b,a+(n-2)b,\dots ,a+b,a\big ) \end{aligned}$$

is also a zonotope for each $a\in \mathbb {R}$ and $b>0$. Similarly, we can also prove that $\mathcal {P}_n^B(n,n-1,\dots ,1)$ is a zonotope and therefore also $\mathcal {P}_n^B(a+(n-1)b,a+(n-2)b,\dots ,a+b,a)$ for each $a>0$ and $b>0$. This follows from the representation of $\mathcal {P}_n^B(n,n-1,\dots ,1)$ as the following Minkowski sum of line segments:

$$\begin{aligned} \mathcal {P}_n^B(n,n-1,\dots ,1)&=\sum _{1\le i<j\le n}\bigg [-\frac{e_i-e_j}{2},\frac{e_i-e_j}{2}\bigg ]\\&\quad +\sum _{1\le i<j\le n}\bigg [-\frac{e_i+e_j}{2},\frac{e_i+e_j}{2}\bigg ]+ \sum _{1\le i\le n}[-e_i,e_i]. \end{aligned}$$

To prove this, we observe that this Minkowski sum is invariant under signed permutations of the coordinates. Additionally, we can compute the vertices of this Minkowski sum, that is, the points of the Minkowski sum that maximize a linear function $v\mapsto \langle c,v\rangle$, $\mathbb {R}^n\rightarrow \mathbb {R}$, for a vector $c\in \mathbb {R}^n$, provided the maximizer is unique. Applying a signed permutation, we may assume that $c_1\ge c_{2} \ge \ldots \ge c_n\ge 0$. On the line segment $[-\frac{e_i-e_j}{2},\frac{e_i-e_j}{2}]$, the function $v\mapsto \langle c,v\rangle$ is uniquely maximized by the right-hand boundary $\frac{e_i-e_j}{2}$ provided $c_i > c_j$. For $c_i=c_j$, the maximizer is not unique. Therefore, we may assume that $c_1>c_{2}> \ldots> c_n> 0$. Then, the unique maximizer of $v\mapsto \langle c,v\rangle$ is given by the sum of the right-hand boundaries of the line segments:

$$\begin{aligned} v&=\sum _{1\le i<j\le n}\frac{e_i-e_j}{2}+\sum _{1 \le i<j\le n}\frac{e_i+e_j}{2}+\sum _{1\le i\le n}e_i\\&=\sum _{1\le i<j\le n}e_i+\sum _{1\le i\le n}e_i\\&=(n,n-1,\dots ,1)^\top . \end{aligned}$$

Hence, the vertices of the above Minkowski sum have the form $(\varepsilon _1\sigma (n),\varepsilon _2\sigma (n-1),\dots ,\varepsilon _n\sigma (1))$, for all $\varepsilon \in \{\pm 1\}^n, \sigma \in \text {Sym}(n)$. This proves the representation of $\mathcal {P}_n^B(a+(n-1)b,a+(n-2)b,\dots ,a+b,a)$ as the Minkowski sum of certain line segments. In particular, this polytope is a zonotope.

To prove the other direction, assume that $\mathcal {P}_n^A(x_1,\dots ,x_n)$ with $n\ge 3$ is a zonotope and use that a polytope P is a zonotope if and only if every 2-dimensional face of P is centrally symmetric [32, p. 200]. From Proposition 6.2 we know that the convex hull F of the six points

$$\begin{aligned} (x_{\sigma (1)},x_{\sigma (2)},x_{\sigma (3)},x_4,x_5,\dots ,x_n),\quad \sigma \in \text {Sym}(3), \end{aligned}$$

is a 2-face of $\mathcal {P}_n^A(x_1,\dots ,x_n)$. This face is centrally symmetric around some $a=(a_1,\dots ,a_n)$. This means that for each vertex z of F, also $2a-z$ is a vertex of F. Thus, we obtain the conditions

$$\begin{aligned} 2a_1-x_1,2a_1-x_2,2a_1-x_3\in \{x_1,x_2,x_3\}. \end{aligned}$$

From $x_1>x_2>x_3$, we obtain

$$\begin{aligned} 2a_1-x_1=x_3\quad \text {and}\quad 2a_1-x_2=x_2 \end{aligned}$$

and therefore also $x_1+x_3=2x_2$. This yields $x_3-x_2=x_2-x_1$. Analogously, by considering more general 2-faces of $\mathcal {P}_n^A(x_1,\dots ,x_n)$, one proves that $x_{j+1}-x_j=x_j-x_{j-1}$ for all admissible j. Thus, $x_1,\dots ,x_n$ are in arithmetic progression.

The proof that $x_1,\dots ,x_n$ form an arithmetic progression if $\mathcal {P}_n^B(x_1,\dots ,x_n)$ is a zonotope follows in the same way as in the A-case since the 2-faces of $\mathcal {P}_n^A$ considered above are also 2-faces of $\mathcal {P}_n^B$ according to Proposition 6.3.