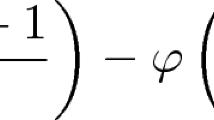On Algebraic Properties of the Family of Weakly Świa̧tkowski Functions

Abstract

In the paper we will focus on weakly Światkowski functions. We say that f satisfies the weak Świa̧tkowski condition (or f is a weakly Świa̧tkowski function) if for all $x_1, x_2$ with $f(x_1)< f(x_2)$ there is a point x between $x_1$ and $x_2$ such that $f(x_1)<f(x)< f(x_2)$. This definition is a modification of the Świa̧tkowski condition, in which point x mentioned above has to be a point of continuity of f. In the paper we will examine some properties of weakly Świa̧tkowski functions and consider lineability and algebrability of some families of functions related to them.

1 Introduction

There are a lot of generalizations of the notion of continuity. One of such generalizations was given in 1978 by Mańk and Świątkowski. Their paper [18] was related to sufficient conditions for the monotonicity of a real function defined on a subset of $\mathbb {R}$. Three families of functions were considered there: the Darboux functions (we denote it by $\mathcal {D}$), the Baire one functions and functions fulfilling the condition $\gamma$, which was later called the Świątkowski condition (see [21]). Mańk and Świątkowski showed that those three families of functions: the Darboux functions, the Baire one functions and the Świątkowski functions are incomparable. It was shown later that the family of Świątkowski functions is included in the family of cliquish functions. The class of Świątkowski functions is not closed neither under addition nor under uniform convergence. One can find the latest results related to the Świątkowski functions in [20, 24] and [25].

Recently, a weaker form of the Świątkowski condition was introduced in the paper [6]. An inspiration for this paper comes from the problem presented in the Lviv Scottish Book (http://www.math.lviv.ua/szkocka). Since 2016 it has continued the traditions of the legendary “Scottish Book” (1935–1941), the notebook with open mathematical problems inscribed by mathematicians visiting the famous Scottish Café. Julia Wódka, during her visit to Lviv in 2018 wrote in the Lviv Scotish Book a question, which was originally asked several years ago by Aleksander Maliszewski: Is any Świątkowski function with closed graph continuous? Taras Banakh found this problem interesting and together with Małgorzata Filipczak and Julia Wódka answered affirmatively to this question. In fact, it was proved in [6] that any returning function on the real line with closed graph is continuous. It was shown that the class of returning functions is quite wide and contains many known classes of real-valued functions possessing some generalized continuity properties. Particularly, among them one can find the Świątkowski functions and a new class of the weakly Świątkowski functions.

In this work, we present some new results concerning the weakly Świątkowski functions. We will examine the properties of them and we will show that this family is not closed under addition, under uniform limits, under taking maximums or minimums.

In the last section of the paper we will consider the algebrability and lineability of some families referred to the weakly Świątkowski functions and to the cliquish functions.

2 Properties of the Weakly Świa̧tkowski Functions

Let us begin this section by recalling the definition introduced by Mańk and Świątkowski.

Definition 1

([18]). We say that $f:\mathbb {R}\rightarrow \mathbb {R}$ satisfies the Świątkowski condition (or f is a Świątkowski function) if for all real $x_1, x_2$ with $f(x_1)< f(x_2)$ there is a point x lying between $x_1$ and $x_2$ such that f is continuous at x and $f(x_1)<f(x)< f(x_2)$.

The family of Świątkowski functions will be denoted by ${\acute{\mathcal {S}}}$. Banakh, Filipczak and Wódka skipped the requirement that f has to be continuous at the point x and gave the weaker form of the above condition. In fact, in [6] the considered notions were formulated in more general case. In the present paper we will work with functions defined on the real line, which gives the following form of the definition.

Definition 2

([6]). We say that $f:\mathbb {R}\rightarrow \mathbb {R}$ satisfies the weak Świątkowski condition (or f is a weakly Świątkowski function) if for all real $x_1, x_2$ with $f(x_1)< f(x_2)$ there is a point x lying between $x_1$ and $x_2$ such that $f(x_1)<f(x)< f(x_2)$.

It is easy to observe that any function which has a finite number of values is not weakly Świątkowski. Evidently $\acute{\mathcal {S}}\subset w\acute{\mathcal {S}}$, where $w\acute{\mathcal {S}}$ stands for the family of weakly Świątkowski functions. The next simple example shows that this inclusion is proper.

Example 3

Any function of the form

$$\begin{aligned} f(x)={\left\{ \begin{array}{ll} \ \ \alpha x &{}\text {if } x\in \mathbb {Q}, \\ -\beta x &{}\text {if } x\in \mathbb {R}\setminus \mathbb {Q}. \end{array}\right. } \end{aligned}$$

is weakly Świątkowski for any real positive numbers $\alpha , \beta$.

Obviously, the above function is not a Świątkowski function. It is not cliquish either. A function $f:\mathbb {R}\rightarrow \mathbb {R}$ is called cliquish if for any open interval (a, b) and $\varepsilon >0$ there exists an open interval $J\subset (a,b)$ such that ${{\,\textrm{diam}\,}}f[J]<\varepsilon$ ([23]). We will use the equivalent condition more convenient for us: a function is cliquish if and only if the set of its continuity points is dense. So f from Example 3 is not cliquish as it is continuous only at $x=0$. It is known, that any Świątkowski function is cliquish and the inclusion $\acute{\mathcal {S}}\subsetneq C_q$ is proper, but as we see the families $C_q$ and $w\acute{\mathcal {S}}$ are incomparable. Note that all Darboux functions are weakly Świątkowski and the inclusion $\mathcal {D}\subset w\acute{\mathcal {S}}$ is proper, as the function f from Example 3 does not have the Darboux property (see Fig. 1).

Fig. 1

Mutual dependences of the families of functions: cliquish, Darboux, Świątkowski and weakly Świątkowski

Another example of a weakly Świątkowski function (which is not Świątkowski) is so called everywhere surjective function, i.e. a function with the property that for every nontrivial open interval I its image under this function is equal to $\mathbb {R}$. Any everywhere surjective function is weakly Świątkowski and has the Darboux property.

Of course the family $w\acute{\mathcal {S}}$ is not closed under addition. Moreover, it is known that any real function can be presented as a sum of two Darboux functions, so it is also a sum of two weakly Świątkowski functions. On the other hand, even adding a linear function to the weakly Świątkowski function can give us a function which does not belong to the family $w\acute{\mathcal {S}}$. We will show much more – that there is a function $f\in w\acute{\mathcal {S}}$ such that for any nonzero a the function $f+a \cdot {{\,\textrm{id}\,}}$ is not weakly Świątkowski (this property is called linear sensitivity, see [9]).

Theorem 4

There exists a function which is linearly sensitive to the weak Świątkowski condition.

Proof

Consider the function

$$\begin{aligned} f(x)={\left\{ \begin{array}{ll} \ x^2 &{}\text {if } x\in \mathbb {Q}, \\ -x^2 &{}\text {if }x\notin \mathbb {Q}. \end{array}\right. } \end{aligned}$$

It is easy to check that $f\in w\acute{\mathcal {S}}$. Let us put $g(x)=f(x)+a x$, $a \in \mathbb {R}$ (its graph for positive a is on Fig. 2). Then

$$\begin{aligned} g(x)={\left\{ \begin{array}{ll} (x+a)x &{}\text {if } x\in \mathbb {Q}, \\ (-x+a)x &{}\text {if }x\notin \mathbb {Q}. \end{array}\right. } \end{aligned}$$

The vertex of the parabola $y=(x+a)x$ is at the point $x_w=-\frac{a}{2}$, one x-intercept is $x_0=-a$. Analogously for the second parabola $y=(-x+a)x$: $x_w=\frac{a}{2}$, $x_0=a$. Both curves are tangent at $x=0$ (which is another x-intercept of both parabolas).

Fig. 2

Graph of the function g from Theorem 4

It is not difficult to see that $g\not \in w\acute{\mathcal {S}}$. Indeed, take any number $x_1\in \mathbb {Q}\cap \left[ -\frac{a}{2}, 0\right)$ and $x_2\in \mathbb {R}{\setminus } \mathbb {Q}$ such that $x_2\in (x_1, 0)$. Then there is no point $x\in (x_1, x_2)$ for which g(x) lies between $g(x_1)$ and $g(x_2)$. $\square$

For a given family ${{\mathcal {F}}}\subset \mathbb {R}^\mathbb {R}$ we denote by ${{\mathcal {M}}}_a({{\mathcal {F}}})$ the maximal additive class of ${{\mathcal {F}}}$, i.e.

$$\begin{aligned} {{\mathcal {M}}}_a({{\mathcal {F}}})= \{ g\in \mathbb {R}^\mathbb {R}:g+f\in {{\mathcal {F}}}\text { for any } f\in {{\mathcal {F}}}\}. \end{aligned}$$

It is easy to see that if $f\equiv 0$ belongs to ${{\mathcal {F}}}$, then ${{\mathcal {M}}}_a({{\mathcal {F}}})\subset {{\mathcal {F}}}$. It is known that the family Const of constant functions is the maximal additive family for the class of Darboux functions which was shown in 1931 by Radaković ([22]). We will show the analogous result for the family of weakly Świątkowski functions.

Theorem 5

${{\mathcal {M}}}_a(w\acute{\mathcal {S}})=Const$.

Proof

Firstly observe that if $f\in w\acute{\mathcal {S}}$, $x_0\in \mathbb {R}$ and k is any positive number, then the function

$$\begin{aligned} g(x)={\left\{ \begin{array}{ll} f(x), &{}\text {when } f(x)\ge f(x_0),\\ f(x)-k, &{}\text {when } f(x)< f(x_0) \end{array}\right. } \end{aligned}$$

is weakly Świątkowski and, evidently, $-g$ is weakly Świątkowski, too.

Suppose that $f\in {{\mathcal {M}}}_a(w\acute{\mathcal {S}})$ and f is not constant, so we can find $a,b\in \mathbb {R}$ such that $f(a)<f(b)$. Since f is weakly Świątkowski, then there is $x_0\in I(a,b)$ such that $f(a)<f(x_0)<f(b)$. We put

$$\begin{aligned} (f-g)(x)={\left\{ \begin{array}{ll} 0, &{}\text {when } f(x)\ge f(x_0),\\ k, &{}\text {when } f(x)< f(x_0). \end{array}\right. } \end{aligned}$$

Then $f-g$ is not weakly Świątkowski, which is a contradiction. Obviously, $Const \subset {{\mathcal {M}}}_a(w\acute{\mathcal {S}})$, which finishes the proof. $\square$

Example 6

There exist functions $f,g\in w\acute{\mathcal {S}}$ such that $\min (f,g)\notin w\acute{\mathcal {S}}$ and $f^2\notin w\acute{\mathcal {S}}$.

Let us take functions:

$$\begin{aligned} g(x)=0\ (x\in \mathbb {R}) \quad \text {and}\quad f(x)={\left\{ \begin{array}{ll} |x| &{}\text {if } x\in \mathbb {Q}, \\ -\frac{1}{2}|x| &{}\text {if } x\notin \mathbb {Q}. \\ \end{array}\right. } \end{aligned}$$

Then

$$\begin{aligned} \min (f,g)={\left\{ \begin{array}{ll} 0 &{}\text {if } x\in \mathbb {Q}, \\ -\frac{1}{2}|x| &{}\text {if } x\notin \mathbb {Q}, \end{array}\right. } \quad \quad f^2(x)={\left\{ \begin{array}{ll} x^2 &{}\text {if } x\in \mathbb {Q}, \\ \frac{1}{4} x^2 &{}\text {if } x\notin \mathbb {Q}, \\ \end{array}\right. } \end{aligned}$$

and $\min (f,g)\notin w\acute{\mathcal {S}}$ and $f^2\notin w\acute{\mathcal {S}}$.$\square$

As we see the minimum of two weakly Świątkowski functions may not be weakly Świątkowski even if one of these functions is constant. Analogous result can be obtained for maximum of two weakly Świątkowski functions.

It is known (see [15]) that for any real function $f:\mathbb {R}\rightarrow \mathbb {R}$ there exists a sequence of Darboux functions (so also weakly Świątkowski functions) convergent to f, hence the pointwise limits of weakly Świątkowski functions give us the set $\mathbb {R}^{\mathbb {R}}$. The situation is more interesting when we consider the uniform limit.

Example 7

The family $w\acute{\mathcal {S}}$ is not closed under uniform limit.

Lets us define the sequence $(h_n)_{n\in \mathbb {N}}$:

$$\begin{aligned} h_n(x)={\left\{ \begin{array}{ll} 0&{}\text{ if } x\in (-\infty , 0]\\ \frac{x}{n}&{}\text {if } x\in (0, 1)\\ 1&{}\text{ if } x\in [1, \infty ] \end{array}\right. } \end{aligned}$$

For any $n\in N$, $h_n$ is weakly Świątkowski and even Świątkowski. Observe that $(h_n)_{n\in \mathbb {N}}$ is uniformly convergent to the function

$$\begin{aligned} h(x)={\left\{ \begin{array}{ll} 0&{}\text {if } x\in (-\infty , 1)\\ 1&{}\text {if } x\in [1,\infty ), \end{array}\right. } \end{aligned}$$

which is not weakly Świątkowski. $\square$

By $\widehat{w\acute{\mathcal {S}}}$ we will denote the family of functions from $\mathbb {R}^{\mathbb {R}}$ fulfilling the condition

$$\begin{aligned} \forall _{\varepsilon >0}\ \forall _{a,b}\ \big (f(a)<f(b)\big )\ \exists _{x\in I(a,b)}\ \big ( f(a)-\varepsilon< f(x)< f(b)+\varepsilon \big ). \end{aligned}$$

where I(a, b) is the open interval with ends a and b. If we additionaly demand that the point $x\in I(a,b)$ is a continuity point of f, then we obtain an analogous family for Świątkowski functions (it was examined in [25]).

Observation 8

If $f_n\in w\acute{\mathcal {S}}$, $n\in \mathbb {N}$ and $f_n\rightrightarrows f$ then $f\in \widehat{w\acute{\mathcal {S}}}$.

Proof

Let us take two points $a, b\in \mathbb {R}$ such that $f(a)<f(b)$ and assume that $\varepsilon \in (0, f(b)-f(a))$. By the uniform convergence there exists $m\in \mathbb {N}$ such that

$$\begin{aligned} \left| f_{m}(x)-f(x)\right| <\frac{\varepsilon }{2} \end{aligned}$$

(1)

for any real x. Particularly (1) holds for a and b, so

$$\begin{aligned} f(b)-\frac{\varepsilon }{2}<f_{m}(b)<f(b)+\frac{\varepsilon }{2}\ \text { and }\ f(a)-\frac{\varepsilon }{2}<f_{m}(a)<f(a)-\frac{\varepsilon }{2}. \end{aligned}$$

(2)

Because $\varepsilon <f(b)-f(a)$, from the above inequalities we have

$$\begin{aligned} f_{m}(b)<f(b)+\frac{f(b)-f(a)}{2}\ \text { and }\ f_{m}(a)>f(a)-\frac{f(b)-f(a)}{2}, \end{aligned}$$

which means $f_m(a)< f_m(b)$. Since $f_{m}$ is weakly Świątkowski then there exists a point $x\in I(a,b)$ for which $f_m(a)<f_m(x)< f_m(b)$. Applying (1) and (2) to the last inequality we obtain

$$\begin{aligned} f(a){-}\varepsilon<f_{m}(a){-}\frac{\varepsilon }{2}\le f_{m}(x){-}\frac{\varepsilon }{2}< f(x)<f_{m}(x)+\frac{\varepsilon }{2}\le f_{m}(b){+}\frac{\varepsilon }{2}<f(b){+}\varepsilon \end{aligned}$$

and from the arbitrariness of $\varepsilon$, $f\in \widehat{w\acute{\mathcal {S}}}$. $\square$

Note that $\widehat{w\acute{\mathcal {S}}}\subsetneq \mathbb {R}^{\mathbb {R}}$. Indeed, the inclusion is proper as the function

$$\begin{aligned} f(x)={\left\{ \begin{array}{ll} 3&{}\text {if } x\in (0, 1)\\ 2&{}\text {if } x\ge 1\\ 1&{}\text {if } x\le 0\\ \end{array}\right. } \end{aligned}$$

is not in the family $\widehat{w\acute{\mathcal {S}}}$.

Observation 9

If $f\in w\acute{\mathcal {S}}$ and $g\in \mathcal {D}$, then $f\circ g\in w\acute{\mathcal {S}}$. There exist $f\in w\acute{\mathcal {S}}$ and $g\in \mathcal {C}$, such that $g\circ f\notin w\acute{\mathcal {S}}$ ($\mathcal {C}$ stands for the family of continuous functions).

Proof

Let us take $a<b$ such that $f(g(a))<f(g(b))$. Then $g(a)\ne g(b)$. Since $f\in w\acute{\mathcal {S}}$, for any $x_1$, $x_2$ if $f(x_1)<f(x_2)$ then there exists a point $z\in I(x_1, x_2)$ for which $f(x_1)<f(z)<f(x_2)$. Let us put $x_1=g(a)$, $x_2=g(b)$. Then $f(g(a))<f(z)<f(g(b))$ and $z\in I(g(a), g(b))$. The function g has the Darboux property, so in the interval (a, b) there is a point x such that $g(x)=z$ which finishes the proof of the first part of our observation.

If we change the order of functions in the composition, then the obtained function may not be weakly Świątkowski. Indeed, take the functions

$$\begin{aligned} g(x)=|x| \ (x\in \mathbb {R})\quad \text {and}\quad f(x)={\left\{ \begin{array}{ll} |x| &{}\text {if } x\in \mathbb {Q}, \\ -\frac{1}{2}|x| &{}\text {if } x\notin \mathbb {Q}. \\ \end{array}\right. } \end{aligned}$$

Then $g\circ f=|f|$ is not a weakly Świątkowski function. $\square$

3 Algebrability and Lineability

The question whether the family of functions having some special properties contains a large algebraic structure has become important in the last few years. This problem is connected with so-called lineability and algebrability of sets in function spaces. It is particularly interesting if the considered family is not closed with respect to some algebraic operations. Among others the following families of functions were examined: the family of continuous nowhere differentiable functions, the family of differentiable nowhere monotone functions, the family of everywhere surjective functions and the family of functions having a finite number of continuity points.

One of the first papers in this research was [2], in which the notion of lineability was introduced and examined. The wider survey one can find in [1, 8] or [14], and in the earlier paper [3]. For a given cardinal $\kappa$, a subset M of a linear space V is $\kappa$-lineable if $M\cup \left\{ 0\right\}$ contains a linear subspace of dimension $\kappa$. The typical way of proving $\kappa$-lineability (in particular $\mathfrak {c}$ -lineability) of M is to construct a set of cardinality $\kappa$ of linearly independent elements of M and to show that any linear combination of them belongs to M.

In the field of algebrability one of the first results was related to the space of everywhere surjective functions ([4]) and the space of continuous functions which are nowhere differentiable ([13]). The authors have proved that such function spaces contain the infinitely generated algebras.

Let us take a cardinal $\kappa$. We will say that a subset A of a commutative algebra is $\kappa$-algebrable if $A\cup \{0\}$ contains a $\kappa$-generated algebra B, i.e. the minimal cardinality of a set of generators of B is equal to $\kappa$.

In [10] A. Bartoszewicz and S. Gła̧b introduced the notion of strong algebrability which does not coincides with the algebrability. For a cardinal $\kappa$, we say that A is a $\kappa$-generated free algebra if there exists a subset $X=\{x_{\alpha }:\alpha <\kappa \}$ of A such that any function f from X to some algebra $A'$ can be uniquely extended to a homomorphism from A into $A'$. Then X is called a set of free generators of the algebra A. A subset $X=\{x_{\alpha }:\alpha <\kappa \}$ of a commutative algebra B generates a free subalgebra A if and only if for each polynomial P in n variables without a constant term and for any $x_{\alpha _1}, x_{\alpha _2},\ldots , x_{\alpha _n}$ we have $P(x_{\alpha _1}, x_{\alpha _2},\ldots , x_{\alpha _n})= 0$ if and only if $P = 0$. We say that a subset E of a commutative linear algebra B is strongly $\kappa$-algebrable if there exists a $\kappa$-generated free algebra A contained in $E\cup \{0\}$. In the case of algebrability, $P(x_{\alpha _1}, x_{\alpha _2},\ldots , x_{\alpha _n})$ can be equal to zero even for a nonzero polynomial P.

There are subsets of linear algebras which are algebrable but not strongly algebrable, for instance $c_{00}$ (the family of all sequences from $c_0$ with real terms equal to zero from some place) is algebrable but not strongly 1-algebrable ([10]). The analogous result holds for the family of functions having finite numbers of values ([5]).

Now we will consider algebrability of some families of functions referring to the weakly Świątkowski condition. In particular we firstly consider the classes $w\acute{\mathcal {S}}\setminus C_q$, $w\acute{\mathcal {S}}\cap C_q$ and $C_q\setminus w\acute{\mathcal {S}}$. Let us observe that the classes $C_q$ and $w\acute{\mathcal {S}}$ have the cardinality $2^\mathfrak {c}$. It was proved in [11] that the family $\mathcal {EDD}$ of everywhere discontinuous Darboux functions (i.e. functions which are nowhere continuous and have the Darboux property) is strongly $2^{\mathfrak {c}}$-algebrable. From inclusions $\mathcal {EDD}\subsetneq \mathcal {D}\subsetneq w\acute{\mathcal {S}}$ and by equality $\mathcal {EDD}\cap C_q=\emptyset$ we obtain the first result.

Theorem 10

The family $w\acute{\mathcal {S}}\setminus C_q$ is strongly $2^{\mathfrak {c}}$-algebrable.

Moreover, by [11] it follows that we can make the large algebra contained in $w\acute{\mathcal {S}}\setminus C_q$ consisting of the measurable functions, of the Baire functions or of the functions measurable in both ways, and even of the perfectly everywhere surjective functions ([11], Thm. 3.6 and 3.7). Recall that perfectly everywhere surjective functions are not measurable and do not have the Baire property.

To show the strong $2^{\mathfrak {c}}$-algebrability of the classes $w\acute{\mathcal {S}}\cap C_q$ and $C_q\setminus w\acute{\mathcal {S}}$ we use the following result from [11]. Let X be a set of cardinality $\mathfrak {c}$ and I be a bounded or unbounded interval in $\mathbb {R}$. Assume that ${{\mathcal {F}}}$ is a family of subsets of X such that ${{\,\textrm{card}\,}}({{\mathcal {F}}})=\mathfrak {c}$ and for each $F\in {{\mathcal {F}}}$ we have also ${{\,\textrm{card}\,}}(F)=\mathfrak {c}$. Then by Theorem 2.2 [11], the family $\mathcal {SES}(I, {{\mathcal {F}}})$ is strongly $2^{\mathfrak {c}}$-algebrable. The proof of the above theorem is based on Theorem 2.1 from [11] and on so called the Disjoint Refinement Lemma. Recall that the authors of [11] call a function $f\in \mathbb {R}^\mathbb {R}$ I-strongly everywhere surjective with respect to ${{\mathcal {F}}}$ (in short $f\in \mathcal {SES}(I, {{\mathcal {F}}})$) if for any $F\in {{\mathcal {F}}}$ there exist $n\in \mathbb {N}$ and a polynomial P in n variables without a constant term such that $f(F)=P(I^n)$ and for any $y\in f(F)$, ${{\,\textrm{card}\,}}\big (\{x:x\in F \text { and } f(x)=y\}\big )=\mathfrak {c}$. It is not difficult to check that f(F) is equal to g(I) for some function in one variable defined by polynomial P. However, we decide to use the formula $f(F)=P(I^n)$ to apply theorems from [11] which were formulated in this language.

Let us observe that if $I=\mathbb {R}$ and ${{\mathcal {F}}}$ consists of all nonempty open sets in $\mathbb {R}$ then $\mathcal {SES}(\mathbb {R}, {{\mathcal {F}}})\subset \mathcal {EDD}(\mathbb {R})$. Now we are able to prove the following.

Theorem 11

The families $w\acute{\mathcal {S}}\cap C_q$ and $C_q\setminus w\acute{\mathcal {S}}$ are strongly $2^{\mathfrak {c}}$-algebrable.

Proof

Let C be a Cantor type set (nowhere dense and perfect). Let $C_0$ consist of elements of C which are the ends of the gaps of C. To show the strong $2^{\mathfrak {c}}$-algebrability of $w\acute{\mathcal {S}}\cap C_q$ let us take $X=C\setminus C_0$ and ${{\mathcal {F}}}=\{ X\cap G:G\text { is an open set and }X\cap G \text { is nonempty}\}$. In fact it means that $X\cap G$ is a nonempty open set in C. By Theorem 1.2 from [11] we construct a $2^{\mathfrak {c}}$-generated free algebra ${{\mathcal {A}}}$ consisting of $\mathcal {SES}(\mathbb {R}, {{\mathcal {F}}})$-functions $\tilde{f}$ on X. Let ${{\mathcal {A}}}_1$ be the algebra of functions of the form:

$$\begin{aligned} f(x)={\left\{ \begin{array}{ll} \tilde{f}(x) &{}\text {if } x\in C\setminus C_0\\ 0&{}\text{ otherwise } \end{array}\right. } \end{aligned}$$

for any $\tilde{f}\in {{\mathcal {A}}}$. Observe that $\mathbb {R}\setminus C$ is a dense open set and f is continuous exactly on $\mathbb {R}\setminus C$. Hence f is cliquish. Moreover, f is Darboux so it is weakly Świątkowski.

Now let ${{\mathcal {A}}}_2$ be the algebra of functions of the form:

$$\begin{aligned} f(x)={\left\{ \begin{array}{ll} \tilde{f}(x) &{}\text {if } x\in C\setminus C_0\\ 1&{}\text {if } x\in C_0\\ 0&{}\text {if } x\in \mathbb {R}\setminus C. \end{array}\right. } \end{aligned}$$

Now we obtain a $2^{\mathfrak {c}}$-generated free algebra containing in $C_q{\setminus }w\acute{\mathcal {S}}$. Indeed, if x is the end of the gap (a, x) in C then for all points t between a and x we have $f(t)=0$ and $f(x)=1$. Of course f is continuous exactly on $\mathbb {R}\setminus C$, hence it is cliquish. $\square$

Strongly $2^\mathfrak {c}$-algebrable families from Theorem 10 and 11 are presented on Fig. 3.

Fig. 3

Strongly $2^\mathfrak {c}$-algebrable families: $w\acute{\mathcal {S}}\setminus C_q$, $w\acute{\mathcal {S}}\cap C_q$ and $C_q\setminus w\acute{\mathcal {S}}$

In the next theorems we will use “the independent dense sets method” presented in [7]. To describe this method let us start with the classic Fichtenholz-Kantorovich theorem.

Theorem 12

(Fichtenholz-Kantorovich, [17]). For any set X there exists a family $\mathcal {N} \subset \mathcal {P}(X)$ of cardinality $2^{\left| X\right| }$ such that for any finite sequences $N_{1},\ldots ,N_{n}\in \mathcal {N}$ and $\varepsilon _{1},\ldots ,\varepsilon _{n}\in \left\{ 0,1\right\}$

$$\begin{aligned} N_{1}^{\varepsilon _{1}}\cap \ldots \cap N_{n}^{\varepsilon _{n}}\ne \varnothing \text {} \end{aligned}$$

(where $N^{1}=N\text { and }N^{0}=X\setminus N$). Moreover all the sets in $\mathcal {N}$ can be chosen with the cardinality $\left| X\right|$. Such a family $\mathcal {N}$ is called an independent one.

Consider the decomposition of $\mathbb {R}$ into $\mathfrak {c}$ pairwise disjoint dense sets $\{B_{\alpha }:\alpha <\mathfrak {c}\}$ of cardinality $\mathfrak {c}$ ([16]). Then for any $\eta \subseteq \mathfrak {c}$ with $\eta \ne \emptyset$ and $\mathfrak {c}\setminus \eta \ne \emptyset$, the set $\bigcup \nolimits _{\alpha \in \eta }B_{\alpha }$ is also of cardinality $\mathfrak {c}$. Let $\{N_{\xi }:\xi <2^{\mathfrak {c}}\}$ be an independent family in $\mathfrak {c}$ such that for every $\xi _{1}<\ldots<\xi _{n}<2^{\mathfrak {c}}$ and for any $\varepsilon _{i}\in \{0,1\}$ $(i\in \{1,\ldots ,n\})$, the set $N_{\xi _{1}}^{\varepsilon _{1}}\cap \ldots \cap N_{\xi _{n}}^{\varepsilon _{n}}$ has cardinality $\mathfrak {c}$.

Now we are able to define an independent family of sets of cardinality $2^\mathfrak {c}$. Let us put $B^{\xi }=\bigcup \nolimits _{\alpha \in N_{\xi }}B_{\alpha }$, for $\xi <2^{\mathfrak {c}}$. Note that for every $\xi _{1}<\ldots<\xi _{n}<2^{\mathfrak {c}}$ and any $\varepsilon _{i}\in \{0,1\}$ ($i\in \{1,\ldots ,n\}$) the set

$$\begin{aligned} (B^{\xi _{1}})^{\varepsilon _{1}}\cap \ldots \cap (B^{\xi _{n}})^{\varepsilon _{n}}=\bigcup \limits _{\alpha \in N_{\xi _{1}}^{\varepsilon _{1}}\cap \ldots \cap N_{\xi _{n}}^{\varepsilon _{n}}}B_{\alpha } \end{aligned}$$

is of cardinality $\mathfrak {c}$, too. The family $\{B^{\xi }:\xi <2^{\mathfrak {c}}\}$ is the independent family of dense sets we are looking for.

Having the independent family of sets, we can define $2^{\mathfrak {c}}$ linearly independent functions: for $\alpha <\mathfrak {c}$, let $g_{\alpha }:B_{\alpha }\rightarrow \mathbb {R}$ be a nonzero function defined on a set $B_{\alpha }$. For every $\xi <2^{\mathfrak {c}}$ we put

$$\begin{aligned} f_{\xi }(x)= {\left\{ \begin{array}{ll} g_{\alpha }(x) &{}\text {if }x\in B_{\alpha }\text { and }\alpha \in N_{\xi }, \\ 0 &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

(3)

The family $\{f_{\xi }:\xi <2^{\mathfrak {c}}\}$ is linearly independent, because the linear combination of functions from this family with nonzero coefficients can not be a zero one as on one set $B_\alpha$ it is not equal to zero. The algebra generated by $\{f_{\xi }:\xi <2^{\mathfrak {c}}\}$ can not have $\kappa$ generators with $\kappa <2^\mathfrak {c}$. We show it in the next lemma, which is probably well known, but for the convenience of the reader we present its short proof.

Lemma 13

If an algebra $\mathcal {A}$ contains a linearly independent family of power $\kappa$ and $\kappa$ is an uncountable cardinal number, then the minimal power of set of generators of $\mathcal {A}$ is equal to $\kappa$.

Proof

Let $G=\{g_\alpha :\alpha <\tau \}$ be a set of generators of the algebra $\mathcal {A}$. Then $\mathcal {A}$ consists of linear combinations of products $g_{\alpha _1}\cdot g_{\alpha _2}\cdot \ldots \cdot g_{\alpha _m}$ where $g_{\alpha _i}\in G$ and the elements $g_{\alpha _1}, \ldots , g_{\alpha _m}$ from this product may not be different. Any linear base of algebra $\mathcal {A}$ is always also a set of generators of this algebra, so $\tau \le \kappa \le \tau ^{<\omega }$. If $\kappa$ is uncountable, then $\tau ^{<\omega }$ is also uncountable. Therefore $\tau ^{<\omega }=\tau$ and consequently $\kappa =\tau$ which completes the proof. $\square$

Observe that the family of polynomials in one variable without a constant term is generated by the set of one element $\{x\}$, so the assumption that $\kappa >\omega$ in the above lemma is essential.

Take any polynomial P in n variables without constant term and arbitrary functions $f_{\xi _1}$, ..., $f_{\xi _n}$ defined as above. We will consider the function $P(f_{\xi _1}, \ldots , f_{\xi _n})$. On the set $B_\alpha$ with $\alpha \in N_{\xi _{1}}^{\varepsilon _{1}}\cap \ldots \cap N_{\xi _{n}}^{\varepsilon _{n}}$ ($\varepsilon _i\in \{0,1\}$, $(i\in \{1,\ldots ,n\})$) this function may be written as $P(\varepsilon _1\cdot g_\alpha , \ldots , \varepsilon _n\cdot g_\alpha )$ so it is of the form $P_s\circ g_{\alpha }$ with

$$\begin{aligned} P_s(x)=P(\varepsilon _1 x, \ldots , \varepsilon _n x), \text { where } s=(\varepsilon _1, \ldots , \varepsilon _n ).\end{aligned}$$

Note that each of the functions $P_s$ can be the zero function, even if P is a nonzero polynomial. Hence constructed algebra is not a free algebra. Finally, by spanning the algebra by the functions $\{f_{\xi }:\xi <2^{\mathfrak {c}}\}$ and using the fact that this set is linearly independent, we obtain an algebra of $2^{\mathfrak {c}}$ generators. This method of proving $2^\mathfrak {c}$-algebrability with the independent family of Bernstein sets was introduced in [12] and widely applied in [7] and later in [19].

Theorem 14

The family $\mathbb {R}^{\mathbb {R}}\setminus (w\acute{\mathcal {S}}\cup C_q)$ is $2^\mathfrak {c}$-algebrable.

Proof

Let $\{B_{\alpha }:\alpha <\mathfrak {c}\}$ be a decomposition of $\mathbb {R}$ into $\mathfrak {c}$ pairwise disjoint dense sets and let $g_\alpha =\chi _{B_\alpha }$. As we have mentioned at the beginning of the paper any function which attains finitely many values is not weakly Świątkowski, so $g_\alpha \notin w\acute{\mathcal {S}}$. Consider an independent family of sets $\{B^{\xi }:\xi <2^{\mathfrak {c}}\}$. For $\xi <2^{\mathfrak {c}}$ let $f_{\xi }$ be the function defined by (3). Then $f_{\xi }=\chi _{B^{\xi }}$, so $f_\xi$ is nor weakly Świątkowski neither cliquish. We will show that the family $\{f_{\xi }:\xi <2^{\mathfrak {c}}\}$ generates an algebra in $\mathbb {R}^{\mathbb {R}}\setminus (w\acute{\mathcal {S}}\cup C_q)$. Take $\xi _{1}<\xi _{2}<\ldots<\xi _{n}<2^{\mathfrak {c}}$ and let P be any nonzero polynomial in n variables without a constant term. Suppose that $P(f_{\xi _{1}},\ldots ,f_{\xi _{n}})$ is a nonzero function. Notice that each $f_{\xi _{i}}$ is constant on every set of the form $(B^{\xi _{1}})^{\varepsilon _{1}}\cap \ldots \cap (B^{\xi _{n}})^{\varepsilon _{n}}$ with $\varepsilon _{k}\in \{0,1\}$, $k\in \{1, \ldots , n \}$, so $P(f_{\xi _{1}},\ldots ,f_{\xi _{n}})$ has finitely many values. Hence $P(f_{\xi _{1}},\ldots ,f_{\xi _{n}})\notin w\acute{\mathcal {S}}$ and $P(f_{\xi _{1}},\ldots ,f_{\xi _{n}})$ has no continuity points. Finally $\mathbb {R}^{\mathbb {R}}\setminus (w\acute{\mathcal {S}}\cup C_q)$ is $2^{\mathfrak {c}}$-algebrable (see right part of Fig. 4). $\square$

Theorem 15

The family $w\acute{\mathcal {S}}\setminus (\mathcal {D}\cup C_q)$ is $2^\mathfrak {c}$-algebrable.

Proof

Let $D=\{d_1, d_2, \ldots \}$ be a dense set and $\{B_{\alpha }^n:\alpha <\mathfrak {c} \wedge n\in \mathbb {N}\}$ be a decomposition of $\mathbb {R}$ into $\mathfrak {c}$ pairwise disjoint dense sets. We put $B_\alpha =\bigcup \limits _n B_\alpha ^n$ and

$$\begin{aligned} g_{\alpha }(x)= {\left\{ \begin{array}{ll} d_n&{}\text {if }x\in B_{\alpha }^n, \\ \ 0 &{}\text {otherwise.} \end{array}\right. } \end{aligned}$$

(4)

It is evident that this function is not Darboux because it has only denumerable set of values. It is not cliquish either, as it is everywhere discontinuous, but it is weakly Świątkowski. The last property follows from the density of used sets.

Indeed, let $\{N_{\xi }:\xi <2^{\mathfrak {c}}\}$ be an independent family in $\mathfrak {c}$ described earlier and define $f_\xi$ by the presented earlier formula:

$$\begin{aligned} f_{\xi }(x)= {\left\{ \begin{array}{ll} g_{\alpha }(x) &{}\text {if }x\in B_{\alpha }\text { and }\alpha \in N_{\xi }, \\ 0&{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

Note $f_\xi :\mathbb {R}\rightarrow D\cup \{0\}$ and $f_\xi [(x_1, x_2)]$ is equal to $D\cup \{0\}$ for any interval $(x_1, x_2)$. Let us take any nonzero polynomial P in n variables without a constant term and put $F=P(f_{\xi _{1}},\ldots ,f_{\xi _{n}})$. Then F is not Darboux, because it has only denumerable set of values. Evidently F is not cliquish, because it is everywhere discontinuous. We will show that $F\in w\acute{\mathcal {S}}$. Observe that F is constant on each set $B_\alpha$, so $P(f_{\xi _{1}},\ldots ,f_{\xi _{n}})|_{B_\alpha }$ is of the form $P(\varepsilon _1g_{\alpha }, \ldots , \varepsilon _ng_{\alpha })=P_s(g_{\alpha })$, where $s=(\varepsilon _1, \ldots , \varepsilon _n)\in \{0,1\}^n$ and $P_s$ is a polynomial of one variable without the constant term.

Let us take $x_1$ and $x_2$ such that $0=F(x_1)<F(x_2)$.

The range of the polynomial is a dense set so in the interval with ends $x_1$ and $x_2$ we can find a point x such that F(x) is between $F(x_1)$ and $F(x_2)$.

Assume now that $F(x_1)\ne 0$ and $F(x_2)\ne 0$. This means that points $x_1$, $x_2$ belong to different sets $B_\alpha$ and $F(x_1)=P_{s_1}(d')$, $F(x_2)=P_{s_2}(d'')$, where $s_1, s_2\in \{0,1\}^n$, $d', d''\in D$. If $P_{s_1}$ has not the global maximum at $d'$ then in the right-side neighbourhood of $x_1$ there is x such that $F(x_1)<F(x)<F(x_2)$. The situation is similar if $P_{s_2}$ does not have the global minimum at $d''$. Consider the case when $P_{s_1}$ has the global maximum at $d'$ and $P_{s_2}$ has the global minimum at $d''$, simultaneously. This leads us to a contradiction, because both polynomials do not have constant terms, so $P_{s_1}(0)=P_{s_2}(0)=0$. Hence, $P_{s_1}(d')\ge 0$ and $P_{s_2}(d'')\le 0$ and consequently $P_{s_2}(d'')\le P_{s_1}(d')$ which is impossible. Finally F is weakly Świątkowski, which completes the proof (see left part of Fig. 4). $\square$

Fig. 4

The sets $w\acute{\mathcal {S}}\setminus (\mathcal {D}\cup C_q)$ and $\mathbb {R}^{\mathbb {R}}\setminus (w\acute{\mathcal {S}}\cup C_q)$ are $2^\mathfrak {c}$-algebrable

In [9] we showed among others the $\mathfrak {c}$-lineability of the family of functions linearly sensitive to Świątkowski condition. Now we will show the same result for the family of functions linearly sensitive to weak Świątkowski condition. Let us recall the theorem used in [9]. An easy proof of it is based on Theorem 12.

Theorem 16

(Theorem 2, [9]). Let $M\subset \mathbb {R}^{\left[ 0,1\right] }$. Assume that there exists a sequence $\left( \left[ a_{n},b_{n}\right] \right) _{n\in \mathbb {N}}$ of closed disjoint intervals contained in $\left[ 0,1\right]$ and a sequence $\left( F_{n}\right) _{n\in \mathbb {N}}$ of functions $F_{n}:\left[ a_{n},b_{n}\right] \rightarrow \mathbb {R}$ such that for any $A\subset \mathbb {N}$ and any bounded nonzero sequence of reals $\left( \alpha _{i}\right) _{i\in A}$, the function

$$\begin{aligned} G_{\alpha _i, A}(x)=\left\{ \begin{array}{ll} \alpha _{i}F_{i}(x) &{} \text {if }x\in \left[ a_{i},b_{i}\right] \text {, }i\in A\\ 0 &{} \text {if }x\notin \bigcup _{i\in A} \left[ a_{i},b_{i}\right] \text {.} \end{array} \right. \end{aligned}$$

(5)

belongs to M. Then M is $\mathfrak {c}$-lineable.

In Theorem 4 we have presented a simple example of a function which is linearly sensitive with respect to the weak Świątkowski condition, but in the next proof we have to use some more complicated example of such a function.

Theorem 17

The family of functions linearly sensitive with respect to the weak Świątkowski condition is $\mathfrak {c}$-lineable.

Proof

We will take the functions defined in the proof of Theorem 7 [9] as follows:

$$\begin{aligned} \widetilde{F_1}(x)=\left\{ \begin{array}{ll} -1 &{} \quad \text {if }x=0 \\ 1 &{} \quad \text {if }x=\frac{1}{2k}\text {, }k=1,2,3,\ldots \\ x^{2} &{} \quad \text {if }x=\frac{1}{2k-1}\text {, }k=2,3,\ldots \\ 2-2x &{} \quad \text {if }x=\frac{1}{2}+\frac{1}{2k}\text {, }k=1,2,3,\ldots \\ 2x-2 &{} \quad \text {if }x=\frac{1}{2}+\frac{1}{2k-1}\text {, }k=1, 2,3,\ldots \\ \text {affine} &{} \quad \text {otherwise} \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} F_1(x)=\left\{ \begin{array}{c} \begin{array}{ll} \widetilde{F_1}\left( x\right) &{} \quad \text {if }x\in \left[ 0,1\right] \\ \widetilde{F_1}\left( -x\right) &{} \quad \text {if }x\in \left[ -1,0\right) . \end{array} \end{array} \right. \end{aligned}$$

We will modify the function $F_1$ so that the function we are searching for belongs to $w\acute{\mathcal {S}}\setminus \acute{\mathcal {S}}$. Now let the second function $\widetilde{F_2}:\left( -\frac{1}{2}, \frac{1}{2}\right) \rightarrow [1,2]$ be defined as follows

$$\begin{aligned} \widetilde{F_2}(x)=\left\{ \begin{array}{ll} 1 &{} \quad \text {if }x=\frac{1}{2k}\text {, }k=1,2,3,\ldots \\ 2 &{} \quad \text {if }x=\frac{1}{2k-1}\text {, }k=2,3,\ldots \\ \text {affine} &{} \quad \text {otherwise} \end{array} \right. \end{aligned}$$

and we put

$$\begin{aligned} F_2(x)=\left\{ \begin{array}{c} \begin{array}{ll} \widetilde{F_2}\left( x\right) &{} \quad \text {if } x\in \left( 0,\frac{1}{2}\right) \\ \widetilde{F_2}\left( -x\right) &{} \quad \text {if }x\in \left( -\frac{1}{2}, 0\right) . \end{array} \end{array} \right. \end{aligned}$$

The function

$$\begin{aligned} F(x)=\left\{ \begin{array}{ll} F_1(x) &{} \quad \text {if } x\in [-1, -\frac{1}{2})\cup (\frac{1}{2}, 1]\cup \{0\} \\ F_1(x) &{} \quad \text {if } x\in [-\frac{1}{2}, \frac{1}{2}]\cap \mathbb {Q}\\ F_2(x) &{} \quad \text {if }x\in \left( -\frac{1}{2}, \frac{1}{2}\right) \cap (\mathbb {R}\setminus \mathbb {Q}) \end{array} \right. \end{aligned}$$

is weakly Świątkowski but not Świątkowski.

Fig. 5

The graph $y=F(x)$

The graph of F is presented on Fig. 5. Analogously as in Theorem 7 [9] we prove that F is linearly sensitive to weak Świątkowski condition.

Consider the function $F+a\cdot {{\,\textrm{id}\,}}$ for $a>0$ (the graph of such function is on Fig. 6). Note that the parabola $y=x^{2}+a x$ has the vertex at $-\frac{a}{2}$ (see Fig. 6).

Fig. 6

The graph $y=F(x)+a x$ for $a >0$

Therefore, for k such that $\frac{1}{2k-1}<\frac{a}{2}$, $x_{1}=-\frac{1 }{2k-1}$ and $x_{2}=0$ there is no $x\in \left( x_{1},x_{2}\right)$ such that F(x) lies between $F\left( x_{1}\right)$ and $F\left( x_{2}\right)$. Hence $F+a\cdot {{\,\textrm{id}\,}}$ does not satisfy the Świątkowski condition. For $a<0$ the situation is symmetrical.

Although the next part of the proof is analogous as in [9], we shortly present its sketch for the convenience of the reader. To apply Theorem 16 we fix a sequence of intervals $\left\{ \left[ a_{n},b_{n}\right] :n=1,2,\ldots \right\}$ such that

$$\begin{aligned} 0\le a_{1}<b_{1}<a_{2}<b_{2}<\ldots <1 \end{aligned}$$

and observe that for any n the function $G_{n}:\left[ a_{n},b_{n}\right] \rightarrow \mathbb {R}$ defined by the formula

$$\begin{aligned} G_{n}(x)=G\left( \frac{2(x-a_n)}{b_{n}-a_{n}}-1\right) \end{aligned}$$

is a function linearly sensitive to the weak Świątkowski condition and $G_{n}(a_{n})=G_{n}(b_{n})=0$.

Let us take an arbitrary set $A\subset \mathbb {N}$ and any bounded sequence $\left( \alpha _{i}\right) _{i\in A}$ of nonzero numbers. The function

$$\begin{aligned} G_{\alpha _i, A}(x)=\left\{ \begin{array}{ll} \alpha _{i}G_{i}(x) &{} \quad \text {if }x\in \left[ a_{i},b_{i}\right] \text {, }i\in A \\ 0 &{} \quad \text {if }x\in \left[ 0,1\right] \setminus \bigcup _{i\in A}\left[ a_{i},b_{i}\right] \end{array} \right. \end{aligned}$$

is linearly sensitive to the weak Świątkowski condition. It is easy to check that $G_{\alpha _i, A}$ is weakly Świątkowski, but for any $a\ne 0$ the function $G_{\alpha _i, A}+a\cdot {{\,\textrm{id}\,}}$ does not fulfill the weak Świątkowski condition. This finishes the proof. $\square$