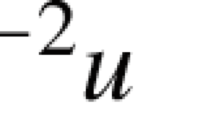Non-periodic solutions of the Goła̧b–Schinzel type functional equation

Abstract

We determine the solutions of the Goła̧b-Schinzel type functional equation in the class of non-periodic functions. Applying this result we give a positive answer to the problem raised by E. Jabłońska (Aequationes Math 87:125–133, 2014).

1 Introduction

The paper is inspired by an open problem, posed by Jabłońska [16], concerning the solutions of the Goła̧b–Schinzel type functional equation

$$\begin{aligned} f(x+g(x)y)=f(x)f(y) \;\;\; \text{ for } \;\;\ x,y\in {\mathbb {R}} \end{aligned}$$

(1)

where $f,g:{\mathbb {R}}\rightarrow {\mathbb {R}}$ are unknown functions. Equation (1) is a generalization of the Goła̧b–Schinzel type equations

$$\begin{aligned} f(x+f(x)y)=f(x)f(y) \end{aligned}$$

(2)

and

$$\begin{aligned} f(x+f(x)^ny)=f(x)f(y), \end{aligned}$$

(3)

where n is a fixed positive integer. Equations (2)-(3) play an important role in determination of substructures of algebraic structures (see e.g. [1, 2, 4, 5, 12, 13] and [18]). Furthermore, the conditional versions of (2) are strictly related to some problems arising in meteorology and fluid mechanics (cf. [17]). In a more general setting, where an unknown function f maps a real linear space into ${\mathbb {R}}$, solutions of (2) and (3) have been investigated by several authors under various regularity assumptions. More details concerning properties of the solutions of these equations as well as their applications can be found in a survey paper [6].

In order to formulate the aforementioned problem, recall the main result proved in [16].

Theorem 1.1

Assume that $f,g:{\mathbb {R}}\rightarrow {\mathbb {R}}$, f is locally bounded above at each point, $f({\mathbb {R}})\setminus \{-1,0,1\}\ne \emptyset$ and $g({\mathbb {R}})\setminus \{0,1\}\ne \emptyset$. If the pair (f, g) satisfies equation (1) then there exist a $c\in {\mathbb {R}}\setminus \{0\}$, an infinite subgroup G of the group $({\mathbb {R}}\setminus \{0\},\cdot )$ and a non-constant multiplicative function $\phi :G\rightarrow {\mathbb {R}}$ such that

$$\begin{aligned} g(x)= \left\{ \begin{array}{ll} cx+1 &{} \text{ whenever } \;\;\; cx+1\in G,\\ 0 &{} \text{ otherwise } \end{array} \right. \end{aligned}$$

(4)

and

$$\begin{aligned} f(x)= \left\{ \begin{array}{ll} \phi (cx+1) &{} \text{ whenever } \;\;\; cx+1\in G,\\ 0 &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

(5)

It has been noted in [16] that from Theorem 1.1 one can directly derive the following result.

Corollary 1.2

Assume that a function $f:{\mathbb {R}}\rightarrow {\mathbb {R}}$ is locally bounded above at each point and $f({\mathbb {R}})\setminus \{-1,0,1\}\ne \emptyset$. If f satisfies equation (2) then there exist a $c\in {\mathbb {R}}\setminus \{0\}$ and an infinite subgroup G of the group $({\mathbb {R}}\setminus \{0\},\cdot )$ such that

$$\begin{aligned} f(x)= \left\{ \begin{array}{ll} cx+1 &{} \text{ whenever } \;\;\; cx+1\in G,\\ 0 &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

The same form of solutions of equation (2) was established in [19] under the assumption that an unknown function is not microperiodic. This fact inspired E. Jabłońska to raise the following question: does Theorem 1.1hold, if we replace the assumption that f is locally bounded above at each point of the line by the assumption that f is not periodic?

In this paper we give a positive answer to this question. In fact, we determine the form of non-periodic solutions of a significantly more general functional equation, namely

$$\begin{aligned} f(x+g(x)y)=f(x)\circ f(y) \;\;\; \text{ for } \;\;\ x,y\in X, \end{aligned}$$

(6)

where X is a real linear space, $(S,\circ )$ is a commutative semigroup, $f:{\mathbb {R}}\rightarrow S$ and $g:{\mathbb {R}}\rightarrow {\mathbb {R}}$ are unknown functions. In the case $X={\mathbb {R}}$ equation (6) has been introduced and studied in [7]. The solutions of (6) under some regularity assumptions have been determined in [8]. The following particular case of (6)

$$\begin{aligned} f(x+g(x)y)=f(x)f(y) \;\;\; \text{ for } \;\;\ x,y\in X, \end{aligned}$$

(7)

and some its conditional versions have been investigated under various regularity assumptions in [9,10,11] and [14, 15]. It is remarkable that solutions of (6) and their applications to invariance under binomial thinning have been recently considered in [3].

2 Results

In what follows, X is a non-zero real linear space and $(S,\circ )$ is a commutative semigroup. Furthermore, E(S) denotes the set of all idempotents of the semigroup $(S,\circ )$, that is

$$\begin{aligned} E(S):=\{s\in S: s\circ s=s\}. \end{aligned}$$

Moreover, for a function $g:X\rightarrow {\mathbb {R}}$, we set

$$\begin{aligned} A_g:=\{x\in X: g(x)\ne 0\}. \end{aligned}$$

Remark 1

Let $f:X\rightarrow S$ and $g:X\rightarrow {\mathbb {R}}$. If the pair (f, g) satisfies equation (6) then

$$\begin{aligned} f(0)=f(0+g(0)\cdot 0)=f(0)\circ f(0), \end{aligned}$$

that is, $f(0)\in E(S)$. Furthermore, applying (6) with $y=x\in X\setminus A_g$, we get

$$\begin{aligned} f(x)\in E(S) \;\;\; \text{ for } \;\;\; x\in X\setminus A_g. \end{aligned}$$

(8)

The following three auxiliary results will play a crucial role in our considerations.

Lemma 2.1

Assume that $f:X\rightarrow S$, $g:X\rightarrow {\mathbb {R}}$ and the pair (f, g) satisfies equation (6). If $A_g\ne X$ then there exists a $z\in E(S)$ such that

$$\begin{aligned} f(x)=z \;\;\; \text{ for } \;\;\ x\in X\setminus A_g \end{aligned}$$

(9)

and

$$\begin{aligned} z\circ f(y)=f(y)\circ z=z \;\;\; \text{ for } \;\;\ y\in X. \end{aligned}$$

(10)

Proof

Assume that $A_g\ne X$ and fix an $x_0\in X\setminus A_g$. Since the semigroup $(S,\circ )$ is commutative, setting in (6) $x=x_0$, we obtain (10) with $z:=f(x_0)$. In view of (8), we have $z\in E(S)$. Moreover, applying (6) and (10), for every $x\in X\setminus A_g$, we get

$$\begin{aligned} f(x)=f(x+g(x)x_0)=f(x)\circ f(x_0)=f(x)\circ z=z, \end{aligned}$$

that is, (9) holds. $\square$

Lemma 2.2

Assume that a pair (f, g), where $f:X\rightarrow S$ and $g:X\rightarrow {\mathbb {R}}$, satisfies equation (6). If f is non-constant then:

• (i) $0\in A_g$;

• (ii) for every $x,y\in X$, it holds:

  $$\begin{aligned} x+g(x)y\in A_g \;\;\; \text{ if } \text{ and } \text{ only } \text{ if } \;\;\; x\in A_g \;\; \text{ and } \;\; y\in A_g. \end{aligned}$$

  (11)

Proof

Assume that f is non-constant. Suppose that $0\not \in A_g$. Then $A_g\ne X$ and so, according to Lemma 2.1, there exists a $z\in E(S)$ such that (9)–(10) hold. Hence, in view of (6), for every $x\in X$, we get

$$\begin{aligned} f(x)=f(x+g(x)\cdot 0)=f(x)\circ f(0)=f(x)\circ z=z. \end{aligned}$$

Since f is non-constant, this yields a contradiction and proves (i).

In order to prove (ii) note that, applying (6), for every $x,y,z\in X$, we obtain

$$\begin{aligned}{} & {} f(x+g(x)y+g(x+g(x)y)z) \\{} & {} \quad =f(x+g(x)y)\circ f(z)=(f(x)\circ f(y))\circ f(z) \\{} & {} \quad =f(x)\circ (f(y)\circ f(z))=f(x)\circ f(y+g(y)z)=f(x+g(x)(y+g(y)z))\\{} & {} \quad =f(x+g(x)y+g(x)g(y)z). \end{aligned}$$

Hence, as f is non-constant, for every $x,y\in X$, we get

$$\begin{aligned} g(x+g(x)y)=0 \;\;\; \text{ if } \text{ and } \text{ only } \text{ if } \;\;\; g(x)g(y)=0, \end{aligned}$$

which implies (11). $\square$

Lemma 2.3

Assume that a pair (f, g), where $f:X\rightarrow S$ and $g:X\rightarrow {\mathbb {R}}$, satisfies equation (6). If f is non-periodic then

$$\begin{aligned} x+g(x)y-g(y)x-y=0 \;\;\; \text{ for } \;\;\; x,y\in A_g. \end{aligned}$$

(12)

Proof

In view of (6), for every $x,y,z\in X$, we get

$$\begin{aligned}{} & {} f(x+g(x)y+g(x)g(y)z)=f(x+g(x)(y+g(y)z))=f(x)\circ f(y+g(y)z) \\{} & {} \quad =f(x)\circ (f(y)\circ f(z))=(f(x)\circ f(y))\circ f(z)\\{} & {} \quad =(f(y)\circ f(x))\circ f(z)=f(y)\circ (f(x)\circ f(z))\\{} & {} \quad =f(y)\circ f(x+g(x)z)=f(y+g(y)(x+g(x)z))\\ {}{} & {} \quad =f(y+g(y)x+g(y)g(x)z), \end{aligned}$$

that is

$$\begin{aligned} f(x+g(x)y+g(x)g(y)z)=f(y+g(y)x+g(x)g(y)z). \end{aligned}$$

Replacing in this equality z by $\frac{z-g(y)x-y}{g(x)g(y)}$, for every $x,y\in A_g$ and $z\in X$, we obtain

$$\begin{aligned} f(z+x+g(x)y-g(y)x-y)=f(z). \end{aligned}$$

Therefore, if f is non-periodic, then (12) holds. $\square$

In what follows we call a mapping $\phi$ defined on a subset G of ${\mathbb {R}}$ periodic provided there exists a $t_0\in {\mathbb {R}}\setminus \{0\}$ such that

$$\begin{aligned} t-t_0, \; t+t_0\in G \;\;\; \text{ for } \;\;\; t\in G \end{aligned}$$

(13)

and

$$\begin{aligned} \phi (t-t_0)=\phi (t+t_0)=\phi (t) \;\;\; \text{ for } \;\;\; t\in G. \end{aligned}$$

(14)

The next theorem is the main result of the paper.

Theorem 2.4

Assume that $f:X\rightarrow S$ and $g:X\rightarrow {\mathbb {R}}$. If the pair (f, g) satisfies equation (6) and f is non-periodic then one of the following possibilities holds:

• (a) there exist an $a\in {\mathbb {R}}\setminus \{0\}$ and $s,z\in E(S)$ such that $s\ne z$, $s\circ z=z$,

  $$\begin{aligned} g(x)= \left\{ \begin{array}{ll} a &{} \text{ for } \;\; x=0,\\ 0 &{} \text{ for } \;\; x\ne 0 \end{array} \right. \end{aligned}$$

  (15)

  and

  $$\begin{aligned} f(x)= \left\{ \begin{array}{ll} s &{} \text{ for } \;\; x=0,\\ z &{} \text{ for } \;\; x\ne 0; \end{array} \right. \end{aligned}$$

  (16)

• (b) $g=1$ and f is an injective homomorphism of the group $(X,+)$ into $(S,\circ )$;

• (c) there exist a non-trivial proper subgroup A of the group $(X,+)$, an injective homomorphism $\psi :A\rightarrow S$ and a $z\in E(S)$ such that

  $$\begin{aligned}{} & {} \psi (x)\circ z=z \;\;\; \text{ for } \;\;\; x\in A, \end{aligned}$$

  (17)
  $$\begin{aligned}{} & {} g(x)= \left\{ \begin{array}{ll} 1 &{} \text{ for } \;\; x\in A,\\ 0 &{} \text{ otherwise } \end{array} \right. \end{aligned}$$

  (18)

  and

  $$\begin{aligned} f(x)= \left\{ \begin{array}{ll} \psi (x) &{} \text{ for } \;\; x\in A,\\ z &{} \text{ otherwise; } \end{array} \right. \end{aligned}$$

  (19)

• (d) there exist an $x_0\in X\setminus \{0\}$, a non-trivial subgroup G of the group $({\mathbb {R}}\setminus \{0\},\cdot )$, a non-periodic homomorphism $\phi :G\rightarrow S$ and a $z\in E(S)$ such that

  $$\begin{aligned}{} & {} \phi (t)\ne z \;\;\; \text{ for } \;\;\; t\in G, \end{aligned}$$

  (20)
  $$\begin{aligned}{} & {} \phi (t)\circ z=z \;\;\; \text{ for } \;\;\; t\in G, \end{aligned}$$

  (21)
  $$\begin{aligned}{} & {} g(x)= \left\{ \begin{array}{ll} 1-t &{} \text{ whenever } \;\;\; x=tx_0 \;\; \text{ and } \;\; 1-t\in G,\\ 0 &{} \text{ otherwise } \end{array} \right. \end{aligned}$$

  (22)

  and

  $$\begin{aligned} f(x)= \left\{ \begin{array}{ll} \phi (1-t) &{} \text{ whenever } \;\;\; x=tx_0 \;\; \text{ and } \;\; 1-t\in G,\\ z &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

  (23)

Conversely, in any case (a)-(d) the pair (f, g) satisfies equation (6) and f is non-periodic.

Proof

Assume that the pair (f, g) satisfies equation (6) and f is non-periodic. Then f is non-constant and so, according to Lemma 2.2 (i), we have $0\in A_g$. We shall divide our considerations into the following three cases:

• 1. $A_g=\{0\}$;

• 2. $A_g\setminus \{0\}\ne \emptyset$ and $g(x)=1$ for $x\in A_g$;

• 3. $A_g\setminus \{0\}\ne \emptyset$ and $g(y_0)\ne 1$ for some $y_0\in A_g$.

Case 1. Taking $a:=g(0)$, $s:=f(0)$ and applying Remark 1 and Lemma 2.1, we obtain that $a\ne 0$, $s\in E(S)$ and there exists a $z\in E(S)$ such that (15)–(16) hold. Moreover, setting in (6) $x=0$ and $y\in X\setminus \{0\}$, in view of (15)–(16), we get $s\circ z=z$. As f is non-constant, we have also $s\ne z$. Thus, (a) holds.

Case 2. If $A_g=X$ then $g=1$ and so, in view of (6), f is a homomorphism of the group $(X,+)$ into $(S,\circ )$. Furthermore, if $f(y_1)=f(y_2)$ for some $y_1,y_2\in X$, then for every $x\in X$, we obtain

$$\begin{aligned} f(x+y_1-y_2)= & {} f(x)\circ f(y_1)\circ f(-y_2)\\= & {} f(x)\circ f(y_2) \circ f(-y_2)=f(x)\circ f(0)=f(x). \end{aligned}$$

Since f is non-periodic, this implies that $y_1=y_2$ and proves the injectivity of f. Thus, (b) holds.

Assume that $A:=A_g\ne X$. Then $0\in A$, g is of the form (18) and, in view of (11), we get

$$\begin{aligned} x+y=x+g(x)y\in A \;\;\; \text{ for } \;\;\; x,y\in A. \end{aligned}$$

Furthermore, since

$$\begin{aligned} x+g(x)(-x)=0\in A \;\;\; \text{ for } \;\;\; x\in A, \end{aligned}$$

applying (11) again, we conclude that $-x\in A$ for $x\in A$. Hence, A is a subgroup of the group $(X,+)$. Moreover, as $A\setminus \{0\}\ne \emptyset$ and $A\ne X$, the subgroup is non-trivial and proper.

Let $\psi :A\rightarrow S$ be given by $\psi (x)=f(x)$ for $x\in A$. Then, making use of Lemma 2.1, we obtain that there exists a $z\in E(S)$ such that (17) and (19) hold. Furthermore, taking into account (6) and (18), we get

$$\begin{aligned} \psi (x+y)=f(x+g(x)y)=f(x)\circ f(y)=\psi (x)\circ \psi (y) \;\;\; \text{ for } \;\;\; x,y\in A. \end{aligned}$$

Thus, $\psi$ is a homomorphism. In order to show that $\psi$ is injective, suppose that $\psi (y_1)=\psi (y_2)$ for some $y_1,y_2\in A$. Since A is a subgroup of the group $(X,+)$, we have $y_1-y_2\in A$. Hence, according to (11) and (18), we obtain

$$\begin{aligned} x+y_1-y_2\in A \;\;\; \text{ if } \text{ and } \text{ only } \text{ if } \;\;\; x\in A. \end{aligned}$$

Therefore, in view of (19), we get

$$\begin{aligned} f(x+y_1-y_2)=z=f(x) \;\;\; \text{ for } \;\;\; x\in X\setminus A \end{aligned}$$

and

$$\begin{aligned}{} & {} f(x+y_1-y_2)=\psi (x+y_1-y_2)=\psi (x)\circ \psi (y_1)\circ \psi (-y_2)\\{} & {} \quad =\psi (x)\circ \psi (y_2)\circ \psi (-y_2)=\psi (x)\circ \psi (0) =\psi (x)=f(x) \;\;\; \text{ for } \;\;\; x\in A. \end{aligned}$$

As f is non-periodic, this implies that $y_1=y_2$. Hence, $\psi$ is injective and so, (c) is valid.

Case 3. According to Lemma 2.3, we get

$$\begin{aligned} (1-g(y_0))x-(1-g(x))y_0=0 \;\;\; \text{ for } \;\;\; x\in A_g. \end{aligned}$$

Hence

$$\begin{aligned} x=\frac{1-g(x)}{1-g(y_0)}y_0 \;\;\; \text{ for } \;\;\; x\in A_g. \end{aligned}$$

(24)

Since $A_g\setminus \{0\}\ne \emptyset$, this implies that $y_0\ne 0$. Thus, replacing in (24) x by $ty_0$, we obtain

$$\begin{aligned} g(ty_0)=1-(1-g(y_0))t\;\;\; \text{ whenever } \;\;\; ty_0\in A_g. \end{aligned}$$

In particular, we have

$$\begin{aligned} g\left( \frac{t}{1-g(y_0)}y_0\right) =1-t\;\;\; \text{ whenever } \;\;\; \frac{t}{1-g(y_0)}y_0\in A_g. \end{aligned}$$

Hence, putting

$$\begin{aligned} x_0:=\frac{1}{1-g(y_0)}y_0, \end{aligned}$$

(25)

we get $x_0\ne 0$ and

$$\begin{aligned} g(tx_0)=1-t\;\;\; \text{ whenever } \;\;\; tx_0\in A_g. \end{aligned}$$

(26)

Moreover, in view of (24)–(25), we have

$$\begin{aligned} A_g\subseteq Span\{x_0\}:=\{tx_0:t\in {\mathbb {R}}\}. \end{aligned}$$

(27)

Therefore, taking

$$\begin{aligned} G:=\{1-t:tx_0\in A_g\}, \end{aligned}$$

(28)

we conclude that g is of the form (22).

Since $\{0,y_0\}\subseteq A_g$, it follows from (25) and (28) that

$$\begin{aligned} \{1,g(y_0)\}\subseteq G\ne \emptyset . \end{aligned}$$

(29)

Note that, in view of (26), we have $x_0\not \in A_g$. Thus, taking into account (28), we get $G\subseteq {\mathbb {R}}\setminus \{0\}$. We show that G is a non-trivial subgroup of the group $({\mathbb {R}}\setminus \{0\},\cdot )$ and $\phi :G\rightarrow S$, given by

$$\begin{aligned} \phi (t)=f((1-t)x_0) \;\;\; \text{ for } \;\;\; t\in G, \end{aligned}$$

(30)

is a homomorphism of G into $(S,\circ )$. To this end, fix $\omega ,\xi \in G$. Then $\omega =1-s$ and $\xi =1-t$ with some $s,t\in {\mathbb {R}}$ such that $sx_0\in A_g$ and $tx_0\in A_g$. Hence, applying Lemma 2.2(ii), in view of (26), we obtain

$$\begin{aligned} (s+(1-s)t)x_0=sx_0+g(sx_0)tx_0\in A_g. \end{aligned}$$

Thus,

$$\begin{aligned} \omega \xi =(1-s)(1-t)=1-(s+(1-s)t)\in G. \end{aligned}$$

Furthermore, using (26) again, we get

$$\begin{aligned} sx_0+g(sx_0)\left( -\frac{s}{1-s}x_0\right) =sx_0+(1-s) \left( -\frac{s}{1-s}x_0\right) =0\in A_g. \end{aligned}$$

Hence, according to Lemma 2.2 (ii), we have $-\frac{s}{1-s}x_0\in A_g$ and so

$$\begin{aligned} \omega ^{-1}=\frac{1}{1-s}=1-\left( -\frac{s}{1-s}\right) \in G. \end{aligned}$$

In this way we have proved that G is a subgroup of the group $({\mathbb {R}}\setminus \{0\},\cdot )$. Note also that, in view of (29), G is non-trivial. Furthermore, making use of (6), (26) and (30), we get

$$\begin{aligned}{} & {} \phi (\omega \xi )=\phi ((1-s)(1-t))=f((1-(1-s)(1-t))x_0)=f(sx_0+(1-s)tx_0) \\{} & {} \quad =f(sx_0+g(sx_0)tx_0)=f(sx_0)\circ f(tx_0)=\phi (1-s)\circ \phi (1-t)=\phi (\omega )\circ \phi (\xi ). \end{aligned}$$

Therefore, $\phi$ is a homomorphism of G into $(S,\circ )$. Moreover, taking into account (27)–(28) and (30), in view of Lemma 2.1, we obtain that there exists a $z\in E(S)$ such that (21) and (23) hold. Note that, if $\phi (t_z)=z$ for some $t_z\in G$ then, making use of (21), we get

$$\begin{aligned} \phi (t)=\phi \left( \frac{t}{t_z}t_z\right) =\phi \left( \frac{t}{t_z}\right) \circ \phi (t_z)=\phi \left( \frac{t}{t_z}\right) \circ z=z \;\;\; \text{ for } \;\;\; t\in G. \end{aligned}$$

Since f is a non-constant function, this contradicts (23). Thus, (20) holds.

Suppose that $\phi$ is periodic. We claim that

$$\begin{aligned} f(x-t_0x_0)=f(x+t_0x_0)=f(x) \;\;\; \text{ for } \;\;\; x\in X. \end{aligned}$$

(31)

To this end, fix an $x\in X$. If $x\not \in Span\{x_0\}$ then $x-t_0x_0\not \in Span\{x_0\}$ and $x+t_0x_0\not \in Span\{x_0\}$. Hence, in view of (23), we get

$$\begin{aligned} f(x-t_0x_0)=f(x+t_0x_0)=f(x)=z. \end{aligned}$$

(32)

If $x=tx_0$ for some $t\in {\mathbb {R}}$ with $1-t\not \in G$ then, by (13), we have $1-t-t_0\not \in G$ and $1-t+t_0\not \in G$. Thus, applying (23) again, we obtain (32). Finally, if $x=tx_0$ for some $t\in {\mathbb {R}}$ with $1-t\in G$ then, in view of (13), we get $1-t+t_0\in G$ and $1-t-t_0\in G$. Hence, making use of (14) and (23), we conclude that

$$\begin{aligned} f(x-t_0x_0)=f((t-t_0)x_0)=\phi (1-t+t_0)=\phi (1-t)=f(tx_0)=f(x) \end{aligned}$$

and

$$\begin{aligned} f(x+t_0x_0)=f((t+t_0)x_0)=\phi (1-t-t_0)=\phi (1-t)=f(tx_0)=f(x). \end{aligned}$$

In this way we have proved (31). Since f is non-periodic and $t_0x_0\ne 0$, this yields a contradiction. Therefore, $\phi$ is non-periodic and so, (d) is valid.

A standard computations show that, if one of the possibilities (a)–(d) holds, then the pair (f, g) satisfies equation (6). Furthermore, it is obvious that in the cases (a)–(b) f is non-periodic.

In the case (c), for every $x\in A$, we have $\psi (x)=\psi (x+0)=\psi (x)\circ \psi (0)$. Hence, as $\psi$ is injective, taking into account (17), we get $\psi (0)\ne z$. Thus, applying the injectivity of $\psi$ again, in view of (19), we obtain $f(x)\ne \psi (0)=f(0)$ for $x\in X\setminus \{0\}$. This implies that f is non-periodic.

Consider the case (d). Suppose that f is periodic and fix its period $y\in X\setminus \{0\}$. Then, taking a $t\in G$ and using (23) and then (20), we get

$$\begin{aligned} f((1-t)x_0-y)=f((1-t)x_0+y)=f((1-t)x_0)=\phi (t)\ne z. \end{aligned}$$

(33)

Hence, applying (23) again, we conclude that

$$\begin{aligned} (1-t)x_0-y=s_1x_0 \end{aligned}$$

(34)

and

$$\begin{aligned} (1-t)x_0+y=s_2x_0 \end{aligned}$$

(35)

with $s_1,s_2\in {\mathbb {R}}$ such that $1-s_i\in G$ for $i\in \{1,2\}$. Thus, setting $t_0:=\frac{s_2-s_1}{2}$, we get

$$\begin{aligned} y=t_0x_0. \end{aligned}$$

(36)

Since $x_0\ne 0$, from (34)-(36) we derive that $t+t_0=1-s_1\in G$ and $t-t_0=1-s_2\in G$. Thus, taking into account (23), (33) and (36), we obtain

$$\begin{aligned} \phi (t)=f((1-t)x_0+y)=f((1-t+t_0)x_0)=\phi (t-t_0). \end{aligned}$$

and

$$\begin{aligned} \phi (t)=f((1-t)x_0-y)=f((1-t-t_0)x_0)=\phi (t+t_0). \end{aligned}$$

In this way we have proved that (13)-(14) hold. Moreover, as $y\ne 0$, it follows from (36) that $t_0\ne 0$. Therefore, $t_0$ is a period of $\phi$, which yields a contradiction and shows that f is non-periodic. $\square$

Corollary 2.5

Assume that $f:X\rightarrow {\mathbb {R}}$ and $g:X\rightarrow {\mathbb {R}}$. If the pair (f, g) satisfies equation (7) and f is non-periodic then one of the following possibilities holds:

• (i) there exists an $a\in {\mathbb {R}}\setminus \{0\}$ such that g is of the form (15) and

  $$\begin{aligned} f(x)= \left\{ \begin{array}{ll} 1 &{} \text{ for } \;\; x=0,\\ 0 &{} \text{ for } \;\; x\ne 0; \end{array} \right. \end{aligned}$$

  (37)

• (ii) $g=1$ and there exist an injective additive function $a:X\rightarrow {\mathbb {R}}$ such that

  $$\begin{aligned} f(x)=e^{a(x)} \;\;\; \text{ for } \;\;\; x\in X; \end{aligned}$$

  (38)

• (iii) there exist a non-trivial proper subgroup A of the group $(X,+)$, a non-trivial subgroup $A_0$ of A and an injective additive function $a:A\rightarrow {\mathbb {R}}$ such that

  $$\begin{aligned} x+y\in A_0 \;\;\; \text{ for } \;\;\; x,y\in A\setminus A_0, \end{aligned}$$

  (39)

  g is of the form (18) and

  $$\begin{aligned} f(x)= \left\{ \begin{array}{ll} e^{a(x)} &{} \text{ for } \;\; x\in A_0,\\ -e^{a(x)} &{} \text{ for } \;\; x\in A\setminus A_0,\\ 0 &{} \text{ otherwise; } \end{array} \right. \end{aligned}$$

  (40)

• (iv) there exist an $x_0\in X\setminus \{0\}$, a non-trivial subgroup G of the group $({\mathbb {R}}\setminus \{0\},\cdot )$ and a non-periodic multiplicative function $\phi :G\rightarrow {\mathbb {R}}\setminus \{0\}$ such that g is of the form (22) and

  $$\begin{aligned} f(x)= \left\{ \begin{array}{ll} \phi (1-t) &{} \text{ whenever } \;\;\; x=tx_0 \;\; \text{ and } \;\; 1-t\in G,\\ 0 &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

  (41)

Conversely, if one of the possibilities (i)–(iv) holds, then the pair (f, g) satisfies equation (7) and f is non-periodic.

Proof

Assume that the pair (f, g) satisfies equation (7) and f is non-periodic. Then, applying Theorem 2.4, with $(S,\circ )$ being the multiplicative semigroup of real numbers, we conclude that one of the possibilities (a)-(d) holds. Note that in this case, we have $E(S)=\{0,1\}$ and so $(s,z)=(1,0)$ is the only pair of elements of E(S) such that $s\ne z$ and $s\circ z=z$. Hence, (a) leads to (i).

In the case (b), we have $f(x)\ne 0$ for $x\in X$. In fact, if $f(y)=0$ for some $y\in X$, then

$$\begin{aligned} f(x)=f(x-y+y)=f(x-y)f(y)=0 \;\;\; \text{ for } \;\;\; x\in X, \end{aligned}$$

which contradicts the injectivity of f. Hence,

$$\begin{aligned} f(x)=f\left( \frac{x}{2}+\frac{x}{2}\right) =f\left( \frac{x}{2}\right) ^2>0 \;\;\; \text{ for } \;\;\; x\in X. \end{aligned}$$

Thus, defining a function $a:X\rightarrow {\mathbb {R}}$ by $a(x)=\ln \; f(x)$ for $x\in X$, we conclude that a is injective and additive. Moreover, f is of the form (38) and so (ii) is valid.

Assume that (c) holds. Then, (17) becomes $z(1-\psi (t))=0$ for $t\in A$. Hence, as A is a non-trivial subgroup of the group $(X,+)$ and $\psi$ is injective, we have $z=0$. Moreover, arguing as in the previous case, one can show that $\psi$ does not vanish. Thus, $\psi (0)=\psi (0)^2>0$, that is $0\in A_0:=\{x\in A:\psi (x)>0\}$. Furthermore,

$$\begin{aligned} \psi (x-y)=\frac{\psi (x-y)\psi (y)}{\psi (y)}=\frac{\psi (x)}{\psi (y)}>0 \;\;\; \text{ for } \;\;\; x,y\in A_0 \end{aligned}$$

and

$$\begin{aligned} \psi (x+y)=\psi (x)\psi (y)>0 \;\;\; \text{ for } \;\;\; x,y\in A\setminus A_0. \end{aligned}$$

Hence, $A_0$ is a subgroup of A and (39) holds. Note also that, as A is a non-trivial subgroup of the group $(X,+)$, in view of (39), $A_0$ is non-trivial. Let $a:A\rightarrow {\mathbb {R}}$ be given by $a(x)=\ln \vert \psi (x)\vert$ for $x\in A$. Then a is an additive function and

$$\begin{aligned} \psi (x)= \left\{ \begin{array}{ll} e^{a(x)} &{} \text{ for } \;\; x\in A_0,\\ -e^{a(x)} &{} \text{ for } \;\; x\in A\setminus A_0. \end{array} \right. \end{aligned}$$

(42)

Therefore, as $z=0$, taking into account (19), we conclude that f is of the form (40). In order to show that a is injective, suppose that $a(x_0)=0$ for some $x_0\in A$. Then $a(2x_0)=0$. Moreover, as $A_0$ is a subgroup of A, in view of (39), we have $2x_0\in A_0$. Thus, applying (42), we get $\psi (2x_0)=\psi (0)=1$. Since $\psi$ is injective this implies that $2x_0=0$ and so $x_0=0$. Hence, a is injective. In this way we have proved that (iii) holds.

In the case (d) from (20)–(21) we derive that $z\ne 1$. Since $z\in E(S)=\{0,1\}$, this means that $z=0$. Therefore, applying (20) and (23), we obtain that $\phi :G\rightarrow {\mathbb {R}}\setminus \{0\}$ and f is of the form (41), respectively. Hence, (iv) is valid.

The converse is a direct consequence of Theorem 2.4. $\square$

Remark 2

It follows from (13) that, if $G\subseteq {\mathbb {R}}\setminus \{0\}$, $G\ne \emptyset$ and $\phi :G\rightarrow {\mathbb {R}}\setminus \{0\}$ is a periodic function, then none of its periods belongs to G. Furthermore, as one can easily check, any multiplicative function, in particular a constant function $\phi =1$, defined on $(0,\infty )$, ${\mathbb {Q}}\setminus \{0\}$ or ${\mathbb {R}}\setminus \{0\}$ is non-periodic. On the other hand, the function $\phi =1$ defined on the following subgroup of the group $({\mathbb {R}}\setminus \{0\},\cdot )$

$$\begin{aligned} G:=\left\{ \frac{m}{n}:m \; \text{ and }\; n \; \text{ are } \text{ odd } \text{ integers }\right\} , \end{aligned}$$

is multiplicative and periodic. In fact, $t_0=2$ is a period of $\phi$.

The existence of a non-constant periodic multiplicative function defined on a (proper) subgroup of $({\mathbb {R}}\setminus \{0\},\cdot )$ remains an open problem.

The following two examples show that, for any real linear space, equation (7) possesses several solutions with periodic f.

Example 1

Assume that A is a non-trivial subgroup of the group $(X,+)$ and $f:X\rightarrow {\mathbb {R}}$ is of the form

$$\begin{aligned} f(x)= \left\{ \begin{array}{ll} 1 &{} \text{ for } \;\; x\in A,\\ 0 &{} \text{ for } \;\; x\in X\setminus A. \end{array} \right. \end{aligned}$$

Then every element of $A\setminus \{0\}$ is a period of f and, as one can easily check, the pair (f, g), where $g=f$, satisfies equation (7).

Example 2

Assume that the dimension of X is greater than 1. Let $L:X\rightarrow {\mathbb {R}}$ be a non-zero linear functional. Then $\ker L$ is a non-trivial linear subspace of X and every element of $\ker L\setminus \{0\}$ is a period of L. Thus, a function $f:X\rightarrow {\mathbb {R}}$, given by

$$\begin{aligned} f(x)=L(x)+1 \;\;\; \text{ for } \;\;\; x\in X, \end{aligned}$$

is periodic. Moreover, as a standard computation shows, a pair (f, g), where $g=f$, satisfies equation (7).

Corollary 2.6

Assume that $f:{\mathbb {R}}\rightarrow S$ and $g:{\mathbb {R}}\rightarrow {\mathbb {R}}$. If the pair (f, g) satisfies equation

$$\begin{aligned} f(x+g(x)y)=f(x)\circ f(y) \;\;\; \text{ for } \;\;\ x,y\in {\mathbb {R}}, \end{aligned}$$

(43)

and f is non-periodic then one of the following possibilities is valid:

• (i) there exist an $a\in {\mathbb {R}}\setminus \{0\}$ and $s,z\in E(S)$ such that $s\ne z$, $s\circ z=z$ and (15)–(16) hold;

• (ii) $g=1$ and f is an injective homomorphism of the additive group of real numbers into $(S,\circ )$;

• (iii) there exist a non-trivial proper subgroup A of the group $({\mathbb {R}},+)$, an injective homomorphism $\psi :A\rightarrow S$ and a $z\in E(S)$ such that (17)–(19) hold;

• (iv) there exist a $c\in {\mathbb {R}}\setminus \{0\}$, a non-trivial subgroup G of the group $({\mathbb {R}}\setminus \{0\},\cdot )$, a non-periodic homomorphism $\phi :G\rightarrow S$ and a $z\in E(S)$ such that (20)–(21) hold, g is of the form (4) and

  $$\begin{aligned} f(x)= \left\{ \begin{array}{ll} \phi (cx+1) &{} \text{ whenever } \;\;\; cx+1\in G,\\ z &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

  (44)

Conversely, if one of the possibilities (i)–(iv) holds, then the pair (f, g) satisfies equation (43) and f is non-periodic.

Proof

Assume that the pair (f, g) satisfies equation (43) and f is non-periodic. Then, applying Theorem 2.4 (with $X={\mathbb {R}}$), we obtain that one of the possibilities (a)–(d) holds. Obviously, (a), (b) and (c) imply (i), (ii) and (iii), respectively. Furthermore, as $x=\frac{x}{x_0}x_0$ for $x\in {\mathbb {R}}$, if (d) is valid, then applying (22) and (23), for every $x\in {\mathbb {R}}$, we obtain

$$\begin{aligned} g(x)=1-\frac{x}{x_0} \;\;\; \text{ whenever } \;\;\; 1-\frac{x}{x_0}\in G \end{aligned}$$

and

$$\begin{aligned} f(x)=\phi \left( 1-\frac{x}{x_0}\right) \;\;\; \text{ whenever } \;\;\; 1-\frac{x}{x_0}\in G, \end{aligned}$$

respectively. Thus, taking $c:=-\frac{1}{x_0}$, we conclude that g and f are of the forms (4) and (44), respectively. Hence, (iv) holds.

The converse implication follows from Theorem 2.4. $\square$

Corollary 2.7

Let $f,g:{\mathbb {R}}\rightarrow {\mathbb {R}}$. If the pair (f, g) satisfies equation (1) and f is non-periodic then one of the following possibilities holds:

• (i) there exist an $a\in {\mathbb {R}}{\setminus }\{0\}$ such that g and f are of the forms (15) and (2.5), respectively;

• (ii) $g=1$ and there exist an injective additive function $a:{\mathbb {R}}\rightarrow {\mathbb {R}}$ such that

  $$\begin{aligned} f(x)=e^{a(x)} \;\;\; \text{ for } \;\;\; x\in {\mathbb {R}}; \end{aligned}$$

• (iii) there exist a non-trivial proper subgroup A of the additive group of real numbers, a non-trivial subgroup $A_0$ of A and an injective additive function $a:A\rightarrow {\mathbb {R}}$ such that (39) holds, g is of the form (18) and f is of the form (40);

• (iv) there exist a $c\in {\mathbb {R}}\setminus \{0\}$, a non-trivial subgroup G of the group $({\mathbb {R}}\setminus \{0\},\cdot )$ and a non-periodic multiplicative function $\phi :G\rightarrow {\mathbb {R}}\setminus \{0\}$ such that g and f are of the forms (4) and (5), respectively.

Conversely, if one of the possibilities (i)-(iv) holds, then the pair (f, g) satisfies equation (1) and f is non-periodic.

Proof

Assume that the pair (f, g) satisfies equation (1) and f is non-periodic. Then, applying Theorem 2.4 with $X={\mathbb {R}}$ and $(S,\circ )$ being a multiplicative semigroup of real numbers, we get that one of the possibilities (a)-(d) holds. Repeating the arguments from the proof of Corollary 2.5, we obtain that (a), (b) and (c) imply (i), (ii) and (iii), respectively. Moreover, if (d) holds, then g and f are given by (22) and (41), respectively, where $x_0\in {\mathbb {R}}\setminus \{0\}$, G is a non-trivial subgroup of the group $({\mathbb {R}}\setminus \{0\},\cdot )$ and $\phi :G\rightarrow {\mathbb {R}}\setminus \{0\}$ is a non-periodic multiplicative function. Hence, taking $c:=-\frac{1}{x_0}$ and arguing as in the proof of Corollary 2.6, we conclude that g and f are of the forms (4) and (5), respectively. Therefore, (iv) is valid.

The converse is a consequence of Theorem 2.4. $\square$

We conclude the paper with the result providing a positive answer to the question raised in [16].

Corollary 2.8

Let $f,g:{\mathbb {R}}\rightarrow {\mathbb {R}}$. The following two statements are equivalent:

• (A) the pair (f, g) satisfies equation (1), $f({\mathbb {R}})\setminus \{-1,0,1\}\ne \emptyset$, $g({\mathbb {R}})\setminus \{0,1\}\ne \emptyset$ and f is non-periodic;

• (B) there exist a $c\in {\mathbb {R}}\setminus \{0\}$, a subgroup G of the group $({\mathbb {R}}\setminus \{0\},\cdot )$ and a non-periodic multiplicative function $\phi :G\rightarrow {\mathbb {R}}\setminus \{0\}$, with

  $$\begin{aligned} \phi (G)\setminus \{-1,1\}\ne \emptyset , \end{aligned}$$

  (45)

  such that g and f are of the forms (4) and (5), respectively.

Proof

If (A) is valid then, applying Corollary 2.7, we obtain that there exist a $c\in {\mathbb {R}}\setminus \{0\}$, a non-trivial subgroup G of the group $({\mathbb {R}}\setminus \{0\},\cdot )$ and a non-periodic multiplicative function $\phi :G\rightarrow {\mathbb {R}}\setminus \{0\}$ such that g and f are of the forms (4) and (5), respectively. Furthermore, as $f({\mathbb {R}})\setminus \{-1,0,1\}\ne \emptyset$, in view of (5), we get (45).

Taking into account Corollary 2.7, one can easily get the inverse implication. $\square$

Remark 3

It follows from (45) that a subgroup G is infinite.