Abstract
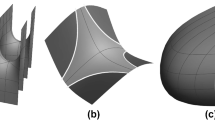
Zero mean curvature surfaces in the simply isotropic 3-space \({\mathbb {I}}^3\) naturally appear as intermediate geometry between geometry of minimal surfaces in \({\mathbb {E}}^3\) and that of maximal surfaces in \({\mathbb {L}}^3\). In this paper, we investigate reflection principles for zero mean curvature surfaces in \({\mathbb {I}}^3\) as with the above surfaces in \({\mathbb {E}}^3\) and \({\mathbb {L}}^3\). In particular, we show a reflection principle for isotropic line segments on such zero mean curvature surfaces in \({\mathbb {I}}^3\), along which the induced metrics become singular.






Similar content being viewed by others
References
Ahlfors, L.V.: Complex Analysis, 3rd edn. International Series in Pure and Applied Mathematics, p. 331. McGraw-Hill Book Co., New York, (1978). An introduction to the theory of analytic functions of one complex variable
Akamine, S., Fujino, H.: Reflection principle for lightlike line segments on maximal surfaces. Ann. Global Anal. Geom. 59(1), 93–108 (2021). https://doi.org/10.1007/s10455-020-09743-4
Akamine, S., Fujino, H.: Duality of boundary value problems for minimal and maximal surfaces. To appear in Comm. Anal. Geom. arXiv:1909.00975
Akamine, S., Fujino, H.: Extension of Krust theorem and deformations of minimal surfaces. Ann. Mat. Pura Appl. (4) https://doi.org/10.1007/s10231-022-01211-z.
da Silva, L.C.B.: Holomorphic representation of minimal surfaces in simply isotropic space. J. Geom. 112(3), 35–21 (2021). https://doi.org/10.1007/s00022-021-00598-z
Dierkes, U., Hildebrandt, S., Sauvigny, F.: Minimal Surfaces, 2nd edn. Grundlehren der mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 339, p. 688. Springer. With assistance and contributions by A. Küster and R. Jakob. (2010). https://doi.org/10.1007/978-3-642-11698-8
Katznelson, Y.: An Introduction to Harmonic Analysis. In: Cambridge Mathematical Library, 3rd edn., p. 314. Cambridge University Press, Cambridge (2004). https://doi.org/10.1017/CBO9781139165372
Ma, X., Wang, C., Wang, P.: Global geometry and topology of spacelike stationary surfaces in the 4-dimensional Lorentz space. Adv. Math. 249, 311–347 (2013). https://doi.org/10.1016/j.aim.2013.09.013
Milnor, J.: Dynamics in One Complex Variable. In: Annals of Mathematics Studies, vol. 160, 3rd edn., p. 304. Princeton University Press, Princeton, NJ (2006)
Pember, M.: Weierstrass-type representations. Geom. Dedicata. 204, 299–309 (2020). https://doi.org/10.1007/s10711-019-00456-y
Pottmann, H., Grohs, P., Mitra, N.J.: Laguerre minimal surfaces, isotropic geometry and linear elasticity. Adv. Comput. Math. 31(4), 391–419 (2009). https://doi.org/10.1007/s10444-008-9076-5
Sachs, H.: Isotrope Geometrie des Raumes, p. 323. Friedr. Vieweg & Sohn, Braunschweig (1990). https://doi.org/10.1007/978-3-322-83785-1
Sato, Y.: \(d\)-minimal surfaces in three-dimensional singular semi-Euclidean space \({\mathbb{R} }^{0,2,1}\). Tamkang J. Math. 52(1), 37–67 (2021). https://doi.org/10.5556/j.tkjm.52.2021.3045
Seo, J.J., Yang, S.-D.: Zero mean curvature surfaces in isotropic three-space. Bull. Korean Math. Soc. 58(1), 1–20 (2021). https://doi.org/10.4134/BKMS.b190783
Strubecker, K.: Differentialgeometrie des isotropen Raumes. III. Flächentheorie. Math. Z. 48, 369–427 (1942). https://doi.org/10.1007/BF01180022
Strubecker, K.: Über Potentialflächen. Arch. Math. 5, 32–38 (1954). https://doi.org/10.1007/BF01899315
Strubecker, K.: Duale Minimalflächen des isotropen Raumes. Rad Jugoslav. Akad. Znan. Umjet. 382, 91–107 (1978)
Acknowledgements
The authors would like to express their gratitude to the referees for their comments and suggestions.
Funding
The first author was partially supported by JSPS KAKENHI Grant Number 19K14527, and the second author by JSPS KAKENHI Grant Number 20K14306.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The first author was partially supported by JSPS KAKENHI Grant Number 19K14527, and the second author by JSPS KAKENHI Grant Number 20K14306.
Rights and permissions
About this article
Cite this article
Akamine, S., Fujino, H. Reflection Principles for Zero Mean Curvature Surfaces in the Simply Isotropic 3-space. Results Math 77, 176 (2022). https://doi.org/10.1007/s00025-022-01718-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00025-022-01718-0